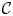1. Introduction
Exact categories and triangulated categories are two fundamental structures in algebra, geometry and topology. As expected, exact categories and triangulated categories are not independent of each other. Nakaoka and Palu [Reference Nakaoka and Palu16] introduced the notion of externally triangulated categories (extriangulated categories for short) as a simultaneous generalization of exact categories and extension-closed subcategories of triangulated categories (they may no longer be triangulated categories in general). After that, the study of extriangulated categories has become an active topic, and up to now, many results on exact categories and triangulated categories have gotten realization in the setting of extriangulated categories by many authors, e.g. see [Reference Chang, Zhou and Zhu8, Reference Iyama, Nakaoka and Palu12, Reference Liu and Nakaoka13, Reference Nakaoka and Palu15–Reference Padrol, Palu, Pilaud and Plamondon17, Reference Zhao, Tan and Huang21, Reference Zhou and Zhu22] and other references.
Tilting modules or tilting functors (i.e. the functors induced by tilting modules as Hom-functors) as a generalization of Bernstein–Gelfand–Ponomarev reflection functors [Reference Bernstein, Gelfand and Ponomarev5] were introduced by Auslander et al. [Reference Auslander, Platzeck and Reiten3], Brenner and Butler [Reference Brenner and Butler6], Happel and Ringel [Reference Happel and Ringel11]. The classical tilting theory plays a crucial role in the representation theory of algebras and related topics. When studying tilting modules over Artin algebras, Miyashita introduced the notion of tilting pairs in [Reference Miyashita14]. This notion is a generalization of tilting modules, and it turns out to be useful for constructing tilting modules associated with a series of idempotent ideals in terms of tilting pairs. Among the interesting results available in tilting theory, there is a beautiful characterization of tilting modules by Colpi and Trlifaj [Reference Colpi and Trlifaj9] for the one-dimensional case and by Bazzoni in the general case [Reference Bazzoni4], which states that a module $T$
is $n$
-tilting if and only if its right orthogonal subcategory can be presented by a kind of exact sequences which are constructed from $\textrm {add}T$
. Another important result is the well-known Auslander–Reiten correspondence. It is originally given by Auslander and Reiten [Reference Auslander and Reiten2], which states that there is a one–one correspondence between tilting (respectively cotilting) modules and certain covariantly (respectively contravariantly) finite subcategories over the category of finitely generated modules of an Artin algebra. In [Reference Wei and Xi19, Reference Wei and Xi20], Wei and Xi extended Bazzoni characterization and Auslander–Reiten correspondence of tilting modules to the setting of Miyashita's tilting pairs. It also has several generalizations in different settings, for example, Wei considered semi-tilting complexes in the derived category of complexes over a ring $R$
[Reference Wei18], and Di et al. considered silting subcategories in triangulated categories [Reference Di, Liu, Wang and Wei10].
In this paper, inspired by the philosophy of Wei and Xi in the categories of finitely generated modules of Artin algebras, we expect to introduce the notion of tilting pairs in extriangulated categories and give a framework on the Bazzoni characterization and Auslander–Reiten correspondence of tilting pairs in this setting, which provides new insights in exact and triangulated categories.
The paper is organized as follows. In § 2, we summarize some basic definitions and propositions about extriangulated categories. In § 3, we mainly study several kinds of subcategories relative to a self-orthogonal subcategory $\omega$
. The first one is the subcategory $\widehat {\omega }$
such that each object in it admits a finite $\omega$
-resolution. The second one is the subcategory ${{}_\omega \mathcal {X}}$
such that each object in it admits a proper $\omega$
-resolution. The third one is the right orthogonal subcategory $\omega ^{\perp }$
of $\omega$
. We also consider subcategories $\check {\omega }$
, ${\mathcal {X}_\omega }$
and ${{}^{\perp }\omega }$
dually. When $\omega$
is self-orthogonal, these subcategories possess nice homological properties, such as the closure of extensions, direct summands, cones of inflations or cocones of deflations (see Lemma 3.1 and Proposition 3.5). As a key result, we show that $\widetilde {\omega }:=\check {\hat {\omega }}$
(respectively $\check {{_\omega \mathcal {X}}}$
) can be obtained by taking cones or cocones from $\widehat {\omega }$
(respectively ${_\omega \mathcal {X}}$
) to $\check {\omega }$
(Proposition 3.3). In § 4, we introduce the notion of tilting pairs in extriangulated categories. It unifies tilting pairs in the categories of finitely generated modules of Artin algebras [Reference Miyashita14], silting complexes in the bounded homotopy category of finite generated projective $R$
-modules over an associative ring [Reference Aihara and Iyama1], and meanwhile $n$
-tilting subcategories in extriangulated categories [Reference Zhu and Zhuang23]. We give a Bazzoni characterization for $n$
-tilting pairs in this setting (see Theorem 4.9). In § 5, we mainly study the Auslander–Reiten correspondence for tilting pairs, which classifies finite $\mathcal {C}$
-tilting subcategories for a certain self-orthogonal subcategory $\mathcal {C}$
with some assumptions. More precisely, let $\mathcal {C}$
be self-orthogonal such that ${_\mathcal {C}\mathcal {X}}$
has a relative injective cogenerator and $\check {{_\mathcal {C}\mathcal {X}}}$
is finite filtered. Then there are bijective correspondences as follows:
2. Preliminaries
We first recall some definitions and some basic properties of extriangulated categories from [Reference Nakaoka and Palu16].
Let $\mathfrak {C}$
be an additive category. Suppose that $\mathfrak {C}$
is equipped with a biadditive functor $\mathbb {E}\colon \mathfrak {C}{{}^{\mathrm op}}\times \mathfrak {C}\to \mathit {Ab}$
, where $\mathit {Ab}$
is the category of abelian groups. For any pair of objects $A,\,C\in \mathfrak {C}$
, an element $\delta \in \mathbb {E}(C,\,A)$
is called an $\mathbb {E}$
-extension. Zero element $0\in \mathbb {E}(C,\,A)$
is called the split $\mathbb {E}$
-extension. Since $\mathbb {E}$
is a bifunctor, for any $a\in \mathfrak {C}(A,\,A')$
and $c\in \mathfrak {C}(C',\,C)$
, we have $\mathbb {E}$
-extensions
We abbreviate them to $a_\ast \delta$
and $c^{\ast }\delta$
respectively. For any $\delta \in \mathbb {E}(C,\,A),\, \delta '\in \mathbb {E}(C',\,A'),$
since $\mathfrak {C}$
and $\mathbb {E}$
are additive, we can define the $\mathbb {E}$
-extension
Definition 2.1 (Nakaoka and Palu [Reference Nakaoka and Palu16, Definition 2.3])
A morphism $(a,\,c):\delta \to \delta '$
of $\mathbb {E}$
-extensions $\delta \in \mathbb {E}(C,\,A),\, \delta '\in \mathbb {E}(C',\,A')$
is a pair of morphisms $a\in \mathfrak {C}(A,\,A')$
and $c\in \mathfrak {C}(C,\,C')$
in $\mathfrak {C}$
satisfying $a_\ast \delta =c^{\ast }\delta '$
.
Let $A,\,C\in \mathfrak {C}$
be any pair of objects. Sequences of morphisms in $\mathfrak {C}$
are said to be equivalent if there exists an isomorphism $b\in \mathfrak {C}(B,\,B')$
which makes the following diagram commutative.
We denote the equivalence class of 
by 
.
Definition 2.2 (Nakaoka and Palu [Reference Nakaoka and Palu16, Definition 2.9])
For any $\mathbb {E}$
-extension $\delta \in \mathbb {E}(C,\,A)$
, one can associate an equivalence class 
This $\mathfrak {s}$
is called a realization of $\mathbb {E}$
, if it satisfies the following condition (R):
(R) Let $\delta \in \mathbb {E}(C,\,A)$
and $\delta '\in \mathbb {E}(C',\,A')$ be any pair of $\mathbb {E}$-extensions with
Then, for any morphism $(a,\,c)\colon \delta \to \delta '$, there exists $b\in \mathfrak {C}(B,\,B')$ which makes the following diagram commutative:
In this case, we say that the sequence 
realizes $\delta$
, whenever it satisfies 
. In the above situation, we say that the triple $(a,\,b,\,c)$
realizes $(a,\,c)$
.
Definition 2.3 (Nakaoka and Palu [Reference Nakaoka and Palu16, Definition 2.10])
Let $\mathfrak {C},\, \mathbb {E}$
be as above. A realization $\mathfrak {s}$
of $\mathbb {E}$
is said to be additive if the following conditions are satisfied:
(i) For any $A,\,C\in \mathfrak {C}$
, the split $\mathbb {E}$-extension $0\in \mathbb {E}(C,\,A)$ satisfies $\mathfrak {s}(0)=0$.(ii) For any pair of $\mathbb {E}$
-extensions $\delta \in \mathbb {E}(A,\,C)$ and $\delta '\in \mathbb {E}(A',\,C')$, we have
\[ \mathfrak{s}(\delta\oplus \delta')=\mathfrak{s}(\delta)\oplus \mathfrak{s}(\delta'). \]
Definition 2.4 (Nakaoka and Palu [Reference Nakaoka and Palu16, Definition 2.12])
The triple $(\mathfrak {C},\,\mathbb {E},\,\mathfrak {s})$
is called an extriangulated category if the following conditions are satisfied:
(ET1) $\mathbb {E}\colon \mathfrak {C}{{}^{\mathrm op}}\times \mathfrak {C}\to \mathit {Ab}$
is a biadditive functor.(ET2) $\mathfrak {s}$
is an additive realization of $\mathbb {E}$.(ET3) Let $\delta \in \mathbb {E}(C,\,A)$
and $\delta '\in \mathbb {E}(C',\,A')$ be any pair of $\mathbb {E}$-extensions, realized as
For any commutative square
in $\mathfrak {C}$
, there exists a morphism $(a,\,c)\colon \delta \to \delta '$
which is realized by $(a,\,b,\,c)$
.
(ET3)op Dual of (ET3).
(ET4) Let $\delta \in \mathbb {E}(A,\,D)$
and $\delta '\in \mathbb {E}(B,\,F)$ be $\mathbb {E}$-extensions realized as
respectively. Then there exists an object $E\in \mathfrak {C}$
, a commutative diagram
in $\mathfrak {C}$
, and an $\mathbb {E}$
-extension $\delta ^{''}\in \mathbb {E}(E,\,A)$
realized by 
which satisfy the following compatibilities:
(i)
realizes $f'_{\ast }\delta '$,(ii) $d^{\ast }\delta ''=\delta$
,(iii) $f_{\ast }\delta ''=e^{\ast }\delta '$
.
realizes 
(ET4)op Dual of (ET4).
For an extriangulated category $\mathfrak {C}$
, we use the following notation.
(i) A sequence
is called a conflation if it realizes some $\mathbb {E}$-extension $\delta \in \mathbb {E}(C,\,A)$. In which case, is called an inflation and is called a deflation. We call an $\mathbb {E}$-triangle.(ii) Given an $\mathbb {E}$
-triangle we call $A$ the cocone of $y\colon B\to C,$ and denote it by $\textrm {Cocone}(y);$ we call $C$ the cone of $x\colon A\to B,$ and denote it by $\textrm {Cone}(x).$(iii) A subcategory $\mathcal {T}$
of $\mathfrak {C}$ is called extension-closed if for any $\mathbb {E}$-triangle with $A,\, C\in \mathcal {T}$, we have $B\in \mathcal {T}$.
is called a conflation if it realizes some 
is called an inflation and 
is called a deflation. We call 
an 
we call 
with 
Lemma 2.5 (Nakaoka and Palu [Reference Nakaoka and Palu16, Corollary 3.15])
Let $(\mathfrak {C},\,\mathbb {E},\,\mathfrak {s})$
be an extriangulated category. Then the following results hold.
(1) Let $C$
be any object in $\mathfrak {C},$
and let
be any pair of $\mathbb {E}$
-triangles. Then there is a commutative diagram in $\mathfrak {C}$
which satisfies
(2) Dual of (1).
The following lemma was proved in [Reference Liu and Nakaoka13, Proposition 1.20], see also [Reference Nakaoka and Palu16, Corollary 3.16].
Lemma 2.6 Let 
be an $\mathbb {E}$
-triangle, $f\colon A\to D$
any morphism, and 
any $\mathbb {E}$
-triangle realizing $f_{*}\delta.$
Then there is a morphism $g$
which gives a morphism of $\mathbb {E}$
-triangles
and moreover, 
becomes an $\mathbb {E}$
-triangle.
Definition 2.7 (Nakaoka and Palu [Reference Nakaoka and Palu16, Definition 3.23])
Let $\mathfrak {C},\, \mathbb {E}$
be as above. An object $P\in \mathfrak {C}$
is called projective if it satisfies the following condition:
• For any $\mathbb {E}$
-triangle and any morphism $c\in \mathfrak {C}(P,\,C)$, there exists $b\in \mathfrak {C}(P,\,B)$ satisfying $y\circ b=c$.
and any morphism 
The notion of injective objects is defined dually.
We denote by $\textrm {Proj}(\mathfrak {C})$
($\textrm {Inj}(\mathfrak {C}$
), respectively) the subcategory consisting of projective (injective, respectively) objects in $\mathfrak {C}$
.
Definition 2.8 (Nakaoka and Palu [Reference Nakaoka and Palu16, Definition 3.25])
Let $(\mathfrak {C},\,\mathbb {E},\,\mathfrak {s})$
be an extriangulated category. We say that it has enough projectives (enough injectives, respectively) if it satisfies the following condition:
• For any object $C\in \mathfrak {C}$
($A\in \mathfrak {C}$, respectively), there exists an $\mathbb {E}$-triangle
satisfying $P\in \textrm {Proj}(\mathfrak {C})$ ($I\in \textrm {Inj}(\mathfrak {C}$), respectively).
In this case, $A$
is called the syzygy of $C$ ($C$ is called the cosyzygy of $A$, respectively) and is denoted by $\Omega (C)$ $(\Sigma (A),$ respectively).
Suppose $\mathfrak {C}$
is an extriangulated category with enough projectives and injectives. For a subcategory $\mathscr {B}\subseteq \mathfrak {C}$
, put $\Omega ^{0}\mathscr {B}=\mathscr {B}$
, and for $i>0$
we define $\Omega ^{i}\mathscr {B}$
inductively to be the subcategory consisting of syzygies of objects in $\Omega ^{i-1}\mathscr {B}$
, i.e.
We call $\Omega ^{i}\mathscr {B}$
the $i$
th syzygy of $\mathscr {B}$
. Dually, we define the $i$
th cosyzygy $\Sigma ^{i}\mathscr {B}$
by $\Sigma ^{0}\mathscr {B}=\mathscr {B}$
and $\Sigma ^{i}\mathscr {B}=\Sigma (\Sigma ^{i-1}\mathscr {B})$
for $i>0$
.
In [Reference Liu and Nakaoka13, Proposition 5.2], the authors defined higher extension groups in an extriangulated category having enough projectives and injectives as $\mathbb {E}^{i+1}(X,\,Y)\cong \mathbb {E}(X,\,\Sigma ^{i}Y)\cong \mathbb {E}(\Omega ^{i}X,\,Y)$
for $i\geq 0,$
and they showed the following result.
Lemma 2.9 (Nakaoka and Palu [Reference Liu and Nakaoka13, Proposition 5.2])
Let 
be an $\mathbb {E}$
-triangle. For any object $X\in \mathscr {B}$
, there are long exact sequences
An $\mathbb {E}$
-triangle sequence in $\mathfrak {C}$
is defined as a sequence
in $\mathfrak {C}$
such that for any $n$
, there are $\mathbb {E}$
-triangles 
and the differential $d_{n}=g_{n-1}f_{n}.$
3. Basic results
Throughout this paper, we always assume that $\mathfrak {C}$
is a Krull–Schmidt extriangulated category having enough projectives and injectives, and a subcategory of $\mathfrak {C}$
means a full and additive subcategory which is closed under isomorphisms and direct summands.
For any $T\in \mathfrak {C},$
we denote by $\mbox {add}(T)$
the category of objects isomorphic to direct summands of finite direct sums of $T.$
For a subcategory $\omega \subseteq \mathfrak {C},$
we define
Similarly, we define
Let $\mathcal {X}$
and $\mathcal {Y}$
be two subcategories of $\mathfrak {C}$
. If $\mathcal {Y}\subseteq \mathcal {X}^{\bot }$
, or equivalently, $\mathcal {X}\subseteq {{}^{\bot }\mathcal {Y}}$
, then we use the symbol $\mathcal {X}{\bot }\mathcal {Y}$
.
Define
We denote by $\hat {\omega }$
( $\check {\omega },\, \mbox {respectively})$
the union of all $\hat {\omega }_{n}$
$(\check {\omega }_{n},\, \mbox {respectively})$
for integers $n\geq 0$
. That is to say
We also denote by $\widetilde {\omega }=\check {\hat {\omega }}$
.
A subcategory $\omega$
is said to be self-orthogonal provided that $\omega {\bot }\omega$
. A subcategory $\omega$
is said to be finite if $\omega =\mbox {add}(T)$
for some $T\in \mathfrak {C}.$
Given a self-orthogonal subcategory $\omega.$
We define
It is obvious that $\omega \subseteq {_\omega \mathcal {X}}$
($\omega \subseteq \mathcal {X}_{\omega }$
) and ${_\omega \mathcal {X}}$
($\mathcal {X}_{\omega }$
, respectively) is the largest subcategory of $\mathfrak {C}$
such that $\omega$
is projective (injective, respectively) and a generator (cogenerator, respectively) in it. Moreover, we have
We first collect some basic properties for these subcategories.
Lemma 3.1 Suppose that $\omega$
is a self-orthogonal subcategory of $\mathfrak {C}.$
Then
(1) $\check {\omega }\bot \omega ^{\bot }$
.(1') ${{}^{\bot }\omega }\bot \hat {\omega }$
.(2) $\check {\omega }_n$
$(\hat {\omega }_n,$ respectively$)$ is closed under extensions and direct summands.(3) ${}_\omega \mathcal {X}$
is closed under extensions$,$ direct summands and cones of inflations.(3') $\mathcal {X}_\omega$
is closed under extensions$,$ direct summands and cocones of deflations.(4) Given an $\mathbb {E}$
-triangle if $Y,\,Z\in {_\omega \mathcal {X}}$ $(\hat {\omega }_n,$ respectively$)$ and $X\in \omega ^{\bot _1},$ then $X\in {}_\omega \mathcal {X}$ $(\hat {\omega }_n,$ respectively$)$.(4') Given an $\mathbb {E}$
-triangle if $X,\,Y\in {\mathcal {X}_\omega }$ $(\check {\omega }_n,$ respectively$)$ and $Z\in {{}^{\bot _1}\omega },$ then $Z\in {}\mathcal {X}_\omega$ $(\check {\omega }_n,$ respectively$)$.
if 
if 
Proof.
(1) follows from [Reference Zhu and Zhuang23, Lemma 6].
(2) We use induction on $n$
. In case $n=0$, let be an $\mathbb {E}$-triangle with $W_0,\,W_1\in \omega$. Since $\omega$ is self-orthogonal, it is split, and hence $W\cong W_0\oplus W_1\in \omega$. Assume the result holds for $n$. Let be an $\mathbb {E}$-triangle with $X,\,Z\in \check {\omega }_{n+1}$. Then there are two $\mathbb {E}$-triangles and with $W_0,\,W_1\in \omega$ and $V_0,\,V_1\in \check {\omega }_{n}$. Consider the following commutative diagram
Since $Z\in \check {\omega }_{n+1}\subseteq {{}^{\bot }}\omega$ and $W_0\in \omega$, the middle row splits, and hence $W\cong W_0\oplus Z$. Consider the following commutative diagram
Since $V_0,\,V_1\in \check {\omega }_{n}$, $V\in \check {\omega }_{n}$ by the induction hypothesis. Moreover, $W_0\oplus W_1\in \omega$. Thus $Y\in \check {\omega }_{n+1}$.
Now we show that $\check {\omega }_n$
is closed under direct summands. In fact, we will show that
\begin{align*} \check{\omega}_n& =\{X\in \mathcal{X}_{\omega}|\mathbb{E}^{n+1}(Y,X)=0,\ \mbox{for all}\ Y\in\sideset{{}^{\bot}}{}{\mathop{\omega}}\}\\ & =\{X\in \mathcal{X}_{\omega}|\mathbb{E}^{n+1}(Y,X)=0,\ \mbox{for all}\ Y\in {_\omega\mathcal{X}}\}. \end{align*}If $X\in \check {\omega }_n,$ we have an $\mathbb {E}$-triangle sequence
\[ X\xrightarrow{d^{0}} W^{0}\xrightarrow{d^{1}}W^{1}\rightarrow\cdots \rightarrow W^{n-1}\xrightarrow{d^{n}}W_{n} \]with each $W^{i}\in \omega.$ Thus, using $\mathfrak {C}(Y,\,-)$ to this sequence for any $Y\in \sideset {{}^{\bot }}{}{\mathop {\omega }}$ or $Y\in {_{\omega }\mathcal {X}},$ we have $\mathbb {E}^{n+1}(Y,\,X)=\mathbb {E}(Y,\,W^{n})=0.$ On the other hand, for any $X\in \mathcal {X}_{\omega },$ there is an $\mathbb {E}$-triangle sequence
\[ X\xrightarrow{d^{0}} W^{0}\xrightarrow{d^{1}}W^{1}\rightarrow\cdots \rightarrow W^{n-1}\xrightarrow{d^{n}}W^{n}\rightarrow\cdots \]with $W^{i}\in \omega \cap \sideset {{}^{\bot }}{}{\mathop {\omega }}.$ Then one can see that every corresponding $K^{i}$ as in (2.2) belongs to $\mathcal {X}_{\omega }.$ If $\mathbb {E}^{n+1}(Y,\,X)=0$ for any $Y\in \sideset {{}^{\bot }}{}{\mathop {\omega }}$ or $Y\in {_{\omega }\mathcal {X}},$ then by applying $\mathfrak {C}(K^{n+1},\,-)$ to this sequence, we have $\mathbb {E}(K^{n+1},\,K^{n})=\mathbb {E}^{n+1}(K^{n+1},\,X)=0.$ Therefore, one can see that the $\mathbb {E}$-triangle splits. Hence $K^{n}\in \omega$ and $X\in \check {\omega }_n.$ Using the above result, we have that $\check {\omega }_n$ is closed under direct summands. Similarly, one can see that $\hat {\omega }_n$ is closed under extensions and direct summands.(3) follows from [Reference Zhu and Zhuang23, Lemma 8].
(4) Since $Z\in {_\omega \mathcal {X}}$
, there is an $\mathbb {E}$-triangle with $W_0\in \omega$ and $K_1\in {_\omega \mathcal {X}}$. Consider the following commutative diagram
Since $K_1,\,Y\in {_\omega \mathcal {X}}$, $W\in {_\omega \mathcal {X}}$ by (3). Moreover, $\mathbb {E}(W_0,\,X)=0$ implies $W\cong X\oplus W_0$, and hence $X\in {_\omega \mathcal {X}}$ by (3).
be an 
be an 
and 
with 
splits. Hence 
with 
Let $\omega$
and $\mathscr {Y}$
be two subcategories of $\mathfrak {C}$
. We say that $\omega$
is a generator of $\mathscr {Y}$
if for each $Y\in \mathscr {Y}$
there exists an $\mathbb {E}$
-triangle 
with $W\in \omega$
and $Y'\in \mathscr {Y}$
.
Lemma 3.2 Let $\omega$
be self-orthogonal, $n$
a positive integer, $\mathscr {Y}$
a subcategory of $\mathfrak {C}$
such that $\omega$
is a generator of $\mathscr {Y}$
. If there is an $\mathbb {E}$
-triangle sequence
for some positive integer $m$
with each $N_{i}\in \hat {\omega }_{n} (N_{i}\in {_\omega \mathcal {X}} \ \mbox {or} \ N_{i}\in \mathscr {Y},\, \mbox { resp}.),$
then
(1) there exists an $\mathbb {E}$
-triangle for some $U\in \hat {\omega }_{n-1}$ $(U\in {_\omega \mathcal {X}} \mbox {or}\ U\in \mathscr {Y},\,\mbox { resp}.)$ and for some $V$ such that there is an $\mathbb {E}$-triangle sequence
\[ V\rightarrow M_{m}\rightarrow M_{m-1}\rightarrow\cdots\rightarrow M_{1}\rightarrow Z \]with each $M_{i}\in \omega.$
If$,$
moreover$,$ $Z\in \hat {\omega }_{n+1}$ $( Z\in {_\omega \mathcal {X}} \mbox {or}\ Z\in \mathscr {Y},\, \ \mbox {resp}.)$, then there exists an $\mathbb {E}$-triangle for some $U\in \hat {\omega }_{n-1}$ $(U\in {_\omega \mathcal {X}} \mbox {or}\ U\in \mathscr {Y},\, \ \mbox {resp}.)$ and $V\in \check {\omega }_{m}$.(2) there exists an $\mathbb {E}$
-triangle for some $U\in \hat {\omega }_{n}$ $(U\in {_\omega \mathcal {X}} \mbox {or}\ U\in \mathscr {Y},\, \ \mbox {resp}.)$ and for some $V$ such that there is an $\mathbb {E}$-triangle sequence
\[ V\rightarrow M_{m-1}\rightarrow M_{m-2}\rightarrow\cdots\rightarrow M_{1}\rightarrow Z \]with each $M_{i}\in \omega.$
If$,$
moreover$,$ $Z\in \hat {\omega }_{n+1}$ $(Z\in {_\omega \mathcal {X}} \mbox {or}\ Z\in \mathscr {Y},\, \ \mbox {resp}.),$ then there exists an $\mathbb {E}$-triangle for some $U\in \hat {\omega }_{n}$ $(U\in {_\omega \mathcal {X}} \mbox {or}\ U\in \mathscr {Y},\, \ \mbox {resp}.)$ and $V\in \check {\omega }_{m-1}$.
for some 
for some 
for some 
for some 
Proof. We only show the case of $\hat {\omega }.$
The case of ${_\omega \mathcal {X}}$
or $\mathscr {Y}$
can be proved similarly.
(1) We proceed by induction on $m$
.
In case $m=1,$
there is an $\mathbb {E}$
-triangle 
with $N_{1}\in \hat {\omega }_{n}.$
Let 
be an $\mathbb {E}$
-triangle with $M_{1}\in \omega$
and $U\in \hat {\omega }_{n-1}.$
Consider the following commutative diagram
Then the first column and the second row are the desired $\mathbb {E}$
-triangles.
Now suppose that the result holds for $m-1.$
Let $X'=\textrm {Cone}(X\to N_{m}),$
then there is an $\mathbb {E}$
-triangle sequence
with each $N_{i}\in \hat {\omega }_{n}.$
By the inductive hypothesis, there are an $\mathbb {E}$
-triangle 
and an $\mathbb {E}$
-triangle sequence
with $U'\in \hat {\omega }_{n-1}$
and each $M_{i}\in \omega.$
Then we have the following commutative diagram
It is easy to check that $Y\in \hat {\omega }_{n}$
. Thus there exists an $\mathbb {E}$
-triangle 
with $M_m\in \omega$
and $U\in \hat {\omega }_{n-1}.$
Consider the commutative diagram
we can get an $\mathbb {E}$
-triangle 
with $U\in \hat {\omega }_{n-1}$
and $V$
satisfying that there is an $\mathbb {E}$
-triangle sequence
with each $M_{i}\in \omega$
.
Now assume $Z\in \hat {\omega }_{n+1}$
. Then there is an $\mathbb {E}$
-triangle 
with $M_Z\in \omega$
and $Z'\in \hat {\omega }_{n}$
. Set $X_1=\textrm {Cocone}(N_1\to Z)$
, and consider the following commutative diagram
Since $Z',\,N_1\in \hat {\omega }_{n}$
, we have $Y'\in \hat {\omega }_{n}$
. Moreover, we obtain an $\mathbb {E}$
-triangle sequence
Thus, by the first statement, we can get an $\mathbb {E}$
-triangle 
with $U\in \hat {\omega }_{n-1}$
and $V$
satisfying that there is an $\mathbb {E}$
-triangle sequences
with each $M_{i}\in \omega$
. Moreover, $M_Z\in \omega$
implies $V\in \check {\omega }_{m}$
.
(2) By (1), there is an $\mathbb {E}$
-triangle with $U'\in \hat {\omega }_{n-1}$ and $V'$ satisfying that there is an $\mathbb {E}$-triangle
with 
sequences
with each $M_{i}\in \omega$
. Set $V=\textrm {Cone}(V'\to M_m)$
, and consider the following diagram
Then $U'\in \hat {\omega }_{n-1}$
implies $U\in \hat {\omega }_{n}$
.
The proof of the second statement is similar to that of (1).
Now we give a relationship among $\widehat {\omega }$
, $\check {\omega }$
and $\widetilde {\omega }$
, which shows that $\widetilde {\omega }$
can be obtained by taking cones (or cocones) from $\widehat {\omega }$
to $\check {\omega }$
.
Proposition 3.3 Let $\omega$
be self-orthogonal. The following statements are equivalent.
(1) $M\in \widetilde {\omega }$
$($respectively $M\in \check {{_\omega \mathcal {X}}})$.(2) There is an $\mathbb {E}$
-triangle with $U\in \widehat {\omega }$ (respectively $U\in {_\omega \mathcal {X}}$) and $V\in \check {\omega }$.(3) There is an $\mathbb {E}$
-triangle with $U'\in \widehat {\omega }$ $($respectively $U'\in {_\omega \mathcal {X}})$ and $V'\in \check {\omega }$.
with 
with 
Proof.
(1) $\Rightarrow$
(2) Since $M\in \widetilde {\omega }=\check {\hat {\omega }}$, there exist integers $m,\,n$ such that there is an $\mathbb {E}$-triangle sequence
\[ M\rightarrow N_{m}\rightarrow N_{m-1}\cdots\rightarrow N_{1}\rightarrow N_0 \]with each $N_i\in \hat {\omega }_n$. Thus, by Lemma 3.2(1), there is an $\mathbb {E}$-triangle with $U\in \widehat {\omega }$ (respectively $U\in {_\omega \mathcal {X}}$) and $V\in \check {\omega }$.(2) $\Rightarrow$
(3) It follows from the proof of Lemma 3.2(2).(3) $\Rightarrow$
(1) Since $V'\in \check {\omega },$ there is an $\mathbb {E}$-triangle sequence
\[ V'\rightarrow C^{0}\rightarrow C^{1} \rightarrow\cdots\rightarrow C^{m} \]with each $C^{i}\in \omega$. Composing it with the $\mathbb {E}$-triangle , we can deduce that $M\in \widetilde {\omega }$.
with 
, we can deduce that 
Using it, we can get the following equalities.
Proposition 3.4 Let $\omega$
be self-orthogonal. Then
(1) ${{}^{\bot }({_\omega \mathcal {X}})}\cap \check {{_\omega \mathcal {X}}}=\check {\omega }$
.(2) $({{}^{\bot }({_\omega \mathcal {X}})})^{\bot }\cap \check {{_\omega \mathcal {X}}}={_\omega {\mathcal {X}}}$
.
Proof.
(1) It is easy to check that $\check {\omega }\subseteq {{}^{\bot }({_\omega \mathcal {X}})}$
. Moreover, since $\omega \subseteq {_\omega \mathcal {X}}$, we have $\check {\omega }\subseteq \check {{_\omega \mathcal {X}}}$. Thus
$\check {\omega }\subseteq {{}^{\bot }({_\omega \mathcal {X}})}\cap \check {{_\omega \mathcal {X}}}$
. Conversely, let $M\in {{}^{\bot }({_\omega \mathcal {X}})}\cap \check {{_\omega \mathcal {X}}}$
. By Proposition 3.3, there is an $\mathbb {E}$
-triangle 
with $U\in {_\omega \mathcal {X}}$
and $V\in \check {\omega }$
. $M\in {{}^{\bot }({_\omega \mathcal {X}})}$
implies that $V\cong U\oplus M$
, and hence $M\in \check {\omega }$
by Lemma 3.1(2). Thus ${{}^{\bot }({_\omega \mathcal {X}})}\cap \check {{_\omega \mathcal {X}}}\subseteq \check {\omega }$
. Therefore, $\check {\omega }= {{}^{\bot }({_\omega \mathcal {X}})}\cap \check {{_\omega \mathcal {X}}}$
.
(2) Clearly, ${_\omega {\mathcal {X}}}\subseteq ({{}^{\bot }({_\omega \mathcal {X}})})^{\bot }\cap \check {{_\omega \mathcal {X}}}$
. Conversely, let $M\in ({{}^{\bot }({_\omega \mathcal {X}})})^{\bot }\cap \check {{_\omega \mathcal {X}}}$. By Proposition 3.3, there is an $\mathbb {E}$-triangle with $U'\in {_\omega \mathcal {X}}$ and $V'\in \check {\omega }$. Since $V'\in \check {\omega }\subseteq {{}^{\bot }({_\omega \mathcal {X}})}$, we have $\mathbb {E}(V',\,M)=0$ and hence $U'\cong M\oplus V'$. Thus
with 
$M\in {_\omega {\mathcal {X}}}$
, and so $({{}^{\bot }({_\omega \mathcal {X}})})^{\bot }\cap \check {{_\omega \mathcal {X}}}\subseteq {_\omega {\mathcal {X}}}$
. Therefore, $({{}^{\bot }({_\omega \mathcal {X}})})^{\bot }\cap \check {{_\omega \mathcal {X}}}={_\omega {\mathcal {X}}}$
.
Proposition 3.5 Let $\omega$
be self-orthogonal. Then $\check {{_\omega \mathcal {X}}}$
$($
respectively $\widetilde {\omega })$
is closed under extensions$,$
cocones of deflations and cones of inflations.
Proof. Let 
be an $\mathbb {E}$
-triangle.
(1) If $L,\,N\in \check {{_\omega \mathcal {X}}}$
, then by Proposition 3.3, there exist $\mathbb {E}$-triangles , and
, and 
with $L',\,N'\in \check {\omega }$
and $X_L,\,X_N\in {_\omega {\mathcal {X}}}$
. Consider the following commutative diagrams
and
Since $X_L\in {\check {\mathcal {X}}}\subseteq \omega ^{\bot }$
and $N'\in \check {\omega }$
, $\mathbb {E}(N',\,X_L)=0$
by Lemma 3.1. Thus $Y'\cong X_L\oplus N'\in \check {{_\omega \mathcal {X}}}$
since $N'\in \check {\omega }\subseteq \check {{_\omega \mathcal {X}}}$
. Then there is an $\mathbb {E}$
-triangle 
with $X_{Y'}\in {_\omega {\mathcal {X}}}$
and $Z\in \check {\omega }$
by Proposition 3.3. Consider the following commutative diagrams
and
Since $X_N,\,X_{Y'}\in {_\omega {\mathcal {X}}}$
, $X_Z\in {_\omega {\mathcal {X}}}$
by Lemma 3.1(3). Since $L',\,Z\in \check {\omega }$
, $M'\in \check {\omega }$
by Lemma 3.1(2). Thus by Proposition 3.3, $M\in \check {{_\omega \mathcal {X}}}$
. This shows that $\check {_\omega \mathscr {X}}$
is closed under extensions.
(2) Assume $M,\,N\in \check {{_\omega \mathcal {X}}}$
. By Proposition 3.3, there is an $\mathbb {E}$-triangle with $U'\in {_\omega {\mathcal {X}}}$ and $V'\in \check {\omega }$.
with 
Consider the following commutative diagram
Since $N\in \check {{_\omega \mathcal {X}}}$
and $V'\in \check {\omega }\subseteq \check {{_\omega \mathcal {X}}}$
, $U_N\in \check {{_\omega \mathcal {X}}}$
by (1). Then there is an $\mathbb {E}$
-triangle 
with $U\in {_\omega {\mathcal {X}}}$
and $V\in \check {\omega }$
by Proposition 3.3. Consider the following commutative diagram
Since $U,\,U'\in {_\omega {\mathcal {X}}}$
, $W\in {_\omega {\mathcal {X}}}$
. By Proposition 3.3, $L\in \check {{_\omega \mathcal {X}}}$
. This shows that $\check {_\omega \mathscr {X}}$
is closed under cocones of deflations.
(3) As a similar argument to (2), we can prove that $\check {_\omega \mathscr {X}}$
is closed under cones of inflations.
Let $M\in \check {\omega }$
(respectively $M\in \hat {\omega }$
). We denote by
Similarly, if $\mathcal {C}\subseteq \check {\omega }$
(respectively $\mathcal {C}\subseteq \hat {\omega }$
), we can define $\omega \mbox {-codim}\mathcal {C}$
(respectively $\omega \mbox {-dim}\mathcal {C}$
) to be the smallest integer $n$
such that $\omega \mbox {-codim}M\leq n$
(respectively $\omega \mbox {-dim}M\leq n$
) for all $M\in \mathcal {C}$
.
The following lemma can be easily checked.
Lemma 3.6 Let $\omega$
be a subcategory closed under extensions and cones of inflations. Assume that $\check {\omega }$
is closed under extensions, cones of inflations, and cocones of deflations. Let 
be an $\mathbb {E}$
-triangle in $\check {\omega }$
. Set $\omega \mbox {-}\textrm {codim}L=l$
, $\omega \mbox {-}\textrm {codim}M=m$
, $\omega \mbox {-}\textrm {codim}N=n$
.
(1) If $l=0,$
then $m=n$.(2) If $m=0$
and $l>0,$ then $l=n+1$.(3) If $n=0$
and $m>0,$ then $l=m$.(4) If $l\leq \min \{m,\,n\},$
then $m=n$.(5) If $m< l,$
then $l=n+1$.(6) If $n< m,$
then $l=m$.(7) $m\leq \max \{l,\,n\}$
.(8) $l\leq \max \{m,\,n\}+1$
.(9) $n\leq \max \{l,\,m\}+1$
.
Proof. We only prove (1), and the others are left to the reader. Assume $l=0$
, i.e. $L\in \omega$
. It is easy to see that $m\geq n$
. We will use induction to prove the statement. If $m=0$
, then $n=0$
since $\omega$
is closed under cones of inflations; on the other hand, if $n=0$
, then $m=0$
since $\omega$
is closed under extensions, i.e. we always have that $m=n$
if $m=0$
or $n=0$
. Suppose that the statement is true for any $i\leq m-1$
. Now we see the case $m$
. Let 
be an $\mathbb {E}$
-triangle with $W_{0}\in \omega$
and $\omega \mbox {-}\textrm {codim}M_{0}=m-1$
, then, we have the following commutative diagram:
It is easy to see that $E\in \omega$
since $\omega$
is closed under cones of inflations. We claim that $\omega \mbox {-}\textrm {codim}N:=n=m$
. Otherwise $n\leq m-1$
since $n\leq m$
. Then, we have an $\mathbb {E}$
-triangle 
with $W_{0}'\in \omega$
and $\omega \mbox {-}\textrm {codim}N_{0}'\leq m-2$
. Using Lemma 2.5(2), we have the following commutative diagram:
Using the induction hypothesis to the middle row, we have $\omega \mbox {-}\textrm {codim}F=m-1$
. Using the induction hypothesis to the middle column, we have $\omega \mbox {-}\textrm {codim}N_{0}'=\omega \mbox {-}\textrm {codim}F=m-1$
, which is a contradiction.
4. Tilting pairs of subcategories
In this section, we begin with the definition of tilting pairs of subcategories in an extriangulated category $\mathfrak {C}$
. Then, we formulate the Bazzoni characterization in this setting.
4.1. $n$-tilting pairs
Now we give the definition of tilting pairs of subcategories in an extriangulated category as follows.
Definition 4.1 A pair $(\mathcal {C},\,\mathcal {T})$
of subcategories is called a tilting pair if
(1) $\mathcal {C}$
is self-orthogonal.(2) $\mathcal {T}$
is self-orthogonal.(3) $\mathcal {T}\subseteq \hat {\mathcal {C}}$
.(4) $\mathcal {C}\subseteq \check {\mathcal {T}}$
.
In this case, we say that $\mathcal {T}$
is a $\mathcal {C}$
-tilting subcategory, and $\mathcal {C}$
is a $\mathcal {T}$
-cotilting subcategory.
If $(\mathcal {C},\,\mathcal {T})$
is a tilting pair such that $\mathcal {C}\mbox {-dim}\mathcal {T}\leq n$
, then $(\mathcal {C},\,\mathcal {T})$
is said to be an $n$
-tilting pair. Similarly, if $\mathcal {T}\mbox {-codim}\mathcal {C}\leq n$
, we say that $(\mathcal {C},\,\mathcal {T})$
is an $n$
-cotilting pair.
Example 4.2
(1) Let $\mathfrak {C}=\mbox {mod}A$
, where $A$ is an Artin algebra and $\mbox {mod}A$ is the category of finitely generated left $A$-modules. Then tilting pairs defined in [Reference Miyashita14, Reference Wei and Xi19] are examples of tilting pairs in an extriangulated category.(2) Let $A$
be a finite-dimensional $k$-algebra, and ${K^{b}(\textrm {proj}A)}$ be the bounded homotopy category of finite generated projective $A$-modules. Recall from [Reference Buan and Zhou7] that a complex $\textbf {P}=\{P^{i}\}$ is called a 2-term silting complex if
(i) $P^{i}=0$
for $i\neq -1,\,0$,(ii) $\mbox {Hom}_{K^{b}(\textrm {proj}A)}(P,\,P[1])=0$
,(iii) $\mbox {thick}\textbf {P}={K^{b}(\textrm {proj}A)}$
, where $\mbox {thick}\textbf {P}$ is the smallest triangulated subcategory closed under direct summands containing $\textbf {P}$.
By [Reference Buan and Zhou7, Theorem 1.1], any 2-term silting complex $\textbf {P}$
is $\textrm {proj}A$-tilting. In fact, for any 2-term silting complex $\textbf {P}$, the pair $(\textrm {add} A,\, \textrm {add} \textbf {P})$ is a $1$-tilting pair in ${K^{b}(\textrm {proj}A)}$.(3) More generally, let $R$
be an associative ring with identity, and ${K^{b}(\textrm {proj}R)}$ be the bounded homotopy category of finite generated projective $R$-modules. If $\textbf {T}$ is a silting complex (see [Reference Aihara and Iyama1, Definition 2.1] for the definition of silting objects in triangulated categories) in ${K^{b}(\textrm {proj}R)}$ with $\inf \{i\in \mathbb {Z}\mid T_i\neq 0\}=l$ and $\sup \{i\in \mathbb {Z}\mid T_i\neq 0\}=k$, then the pair $(\textrm {add}R,\, \textrm {add}\textbf {T}[k])$ is a $(k-l)$-tilting pair by [Reference Di, Liu, Wang and Wei10, Corollary 4.8].(4) Let $A$
be an Artin algebra, and $C,\,M\in \mbox {mod}A$. If $(C,\,M)$ is an $n$-tilting pair in $\mbox {mod}A$ in the sense of [Reference Wei and Xi19], then $(\textrm {add}C,\, \textrm {add}M)$ is an $n$-tilting pair in the bounded derived category $D^{b}(A)$.(5) When $\mathfrak {C}$
is an extriangulated category with enough projectives and injectives, Zhu and Zhuang [Reference Zhu and Zhuang23] defined $n$-tilting subcategories $\mathcal {T}$ in $\mathfrak {C}$. If in addition $\mathcal {T}=add(T)$, we call it an $n$-tilting object. Now we set $\mathcal {C}=\textrm {Proj}(\mathfrak {C})$ and $\mathcal {T}$ be an $n$-tilting subcategory in the sense of [Reference Zhu and Zhuang23, Definition 7], then using [Reference Zhu and Zhuang23, Remark 4], we have $(\mathcal {C},\,\mathcal {T})$ is an $n$-tilting pair in $\mathfrak {C}$.
In what follows, we always assume that the following weak idempotent completeness (WIC for short) given originally in [Reference Nakaoka and Palu16, Condition 5.8] holds true on $\mathfrak {C}$
.
WIC Condition: Let $f\in \mathfrak {C}(A,\,B)$
, $g\in \mathfrak {C}(B,\,C)$
.
(1) If $gf$
is an inflation, then so is $f$.(2) If $gf$
is a deflation, then so is $g$.
Definition 4.3 (Zhou and Zhu [Reference Zhou and Zhu22, Definition 3.19]
Let $\omega$
be a subcategory of $\mathfrak {C}$
. $\omega$
is called strongly contravariantly (respectively strongly covariantly) finite if for any $C\in \mathfrak {C}$
, there is an $\mathbb {E}$
-triangle 
(respectively 
), where $g$
is a right (respectively left) $\omega$
-approximation of $C$
.
Lemma 4.4 Let $\mathcal {C}$
be self-orthogonal and $\omega \subseteq {_\mathcal {C}\mathcal {X}}$
. If $\omega$
is a strongly contravariantly finite self-orthogonal subcategory and $\mathcal {C}\subseteq \check {\omega }$
, then $\omega ^{\bot }\subseteq \mathcal {C}^{\bot }$
and $\omega ^{\bot }\cap {_\mathcal {C}\mathcal {X}}={_\omega \mathcal {X}}$
.
In particular, if $\mathcal {T}$
is a strongly contravariantly finite $\mathcal {C}$
-tilting subcategory, then $\mathcal {T}^{\bot }\subseteq \mathcal {C}^{\bot }$
and $\mathcal {T}^{\bot }\cap {_\mathcal {C}\mathcal {X}}={_\mathcal {T}\mathcal {X}}$
.
Proof. Let $M\in \omega ^{\bot }$
. Since $\mathcal {C}\subseteq \check {\omega }$
, then by Lemma 3.1(1) $\mathbb {E}^{i}(C,\,M)=0$
for any $C\in \mathcal {C}$
and any $i\geq 1$
. Thus $\omega ^{\bot }\subseteq \mathcal {C}^{\bot }$
.
$\omega ^{\bot }\cap {_\mathcal {C}\mathcal {X}}\subseteq {_\omega \mathcal {X}}$
: Denote by
Let $M\in \omega ^{\bot }\cap {_\mathcal {C}\mathcal {X}}$
. We claim $M\in \mbox {Gen}\omega$
. In fact, choose an $\mathbb {E}$
-triangle 
with $C_0\in \mathcal {C}$
and $M_1\in {_\mathcal {C}\mathcal {X}}$
. Since $C_0\in \check {\omega }$
, there is an $\mathbb {E}$
-triangle 
with $T'\in \omega$
and $X\in \check {\omega }$
. Consider the following commutative diagram
By Lemma 3.1(1) $\mathbb {E}(X,\,M)=0$
, and hence $M\oplus X\cong Y\in \mbox {Gen}\omega$
. Consider the following commutative diagram
Then, we know that $M\in \mbox {Gen}\omega$
. Consequently, we may take an $\mathbb {E}$
-triangle 
with $M'\in \omega ^{\bot }$
and $T_M\in \omega$
since $\omega$
is strongly contarvariantly finite. As $\omega ^{\bot }\subseteq \mathcal {C}^{\bot }$
and $\omega \subseteq {_\mathcal {C}\mathcal {X}}$
, we get $M'\in \omega ^{\bot }\cap {_\mathcal {C}\mathcal {X}}$
by Lemma 3.1. Now repeating the process to $M'$
, and so on, we get $M\in {_\omega \mathcal {X}}$
.
${_\omega \mathcal {X}}\subseteq \omega ^{\bot }\cap {_\mathcal {C}\mathcal {X}}$
: Since ${_\omega \mathcal {X}}\subseteq \omega ^{\bot }$
, it suffices to show that ${_\omega \mathcal {X}}\subseteq {_\mathcal {C}\mathcal {X}}$
. Let $M\in {_\omega \mathcal {X}}$
. Choose an $\mathbb {E}$
-triangle sequence 
as in (2.2) with $W_i\in \omega$
and $K_i\in {_\omega \mathcal {X}}$
. Applying Lemma 3.2 to the $\mathbb {E}$
-triangle 
, we obtain two $\mathbb {E}$
-triangles
and
with $H_0\in {_\mathcal {C}\mathcal {X}}$
and $C_0\in \mathcal {C}$
. Since $K_1\in \omega ^{\bot }\subseteq \mathcal {C}^{\bot }$
and $H_0\in \mathcal {C}^{\bot }$
, we have $M_0\in \mathcal {C}^{\bot }$
. Consider the following commutative diagram
Since $W_1,\,H_0\in {_\mathcal {C}\mathcal {X}}$
, we have $Y\in {_\mathcal {C}\mathcal {X}}$
. Choose an $\mathbb {E}$
-triangle 
with $H_1\in {_\mathcal {C}\mathcal {X}}$
and $C_1\in \mathcal {C}$
. Consider the following commutative diagram
Since $H_1\in \mathcal {C}^{\bot }$
and $K_2\in \omega ^{\bot }\subseteq \mathcal {C}^{\bot }$
, we have $M_1\in \mathcal {C}^{\bot }$
. By repeating the process to $M_1$
, and so on, we can obtain an $\mathbb {E}$
-triangle sequence 
with $C_i\in \mathcal {C}$
and $M_i\in {\mathcal {C}^{\bot }}$
. Therefore, $M\in {_{\mathcal {C}}\mathcal {X}}$
.
4.2. Bazzoni characterization of $n$-tilting pairs
In what follows, we will give a Bazzoni characterization of $n$
-tilting pairs. Before doing it, we first need to introduce two kinds of subcategories as follows.
Let $\mathcal {T}_{1},\, \mathcal {T}_{2}$
are subcategories of $\mathfrak {C}$
. We define $\textrm {Pres}^{n}_{\mathcal {T}_{2}}(\mathcal {T}_{1})$
($\textrm {Copres}^{n}_{\mathcal {T}_{2}}(\mathcal {T}_{1}$
), respectively) to be the subcategory consisting of each object $X\in \mathfrak {C}$
such that there is an $\mathbb {E}$
-triangle sequence:
in $\mathfrak {C}$
with $T_{i}\in \mathcal {T}_{1},\, X'\in \mathcal {T}_{2}.$
It is obvious that $\mathcal {T}_1\subseteq \textrm {Pres}^{n}_{\mathcal {T}_{2}}(\mathcal {T}_{1})$
($\mathcal {T}_1\subseteq \textrm {Copres}^{n}_{\mathcal {T}_{2}}(\mathcal {T}_{1}$
), respectively). If $\mathcal {T}_{2}=\mathfrak {C}$
, we write $\textrm {Pres}^{n}_{\mathcal {T}_{2}}(\mathcal {T}_{1})$
($\textrm {Copres}^{n}_{\mathcal {T}_{2}}(\mathcal {T}_{1}$
), respectively) as $\textrm {Pres}^{n}(\mathcal {T}_{1})$
($\textrm {Copres}^{n}(\mathcal {T}_{1}$
), respectively).
Using this notion, we can give an equivalent description for ${_\mathcal {T}\mathcal {X}}$
, that is,
Lemma 4.5 Assume that $(\mathcal {C},\,\mathcal {T})$
is an $n$
-tilting pair with $\mathcal {T}$
strongly contravariantly finite. The following are equivalent for an object $M\in \mathfrak {C}$
.
(1) $M\in {_\mathcal {T}\mathcal {X}}$
.(2) $M\in \mathcal {T}^{\bot }\cap {_\mathcal {C}\mathcal {X}}$
.(3) $M\in \textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
.
Proof. The equivalence of $(1)$
and $(2)$
has been proved in Lemma 4.4. Now we show that $(2)$
and $(3)$
are equivalent.
Let $M\in \mathcal {T}^{\bot }\cap {_\mathcal {C}\mathcal {X}}$
. Using the same argument as that in Lemma 4.4, we have an $\mathbb {E}$
-triangle 
with $M'\in \omega ^{\bot }$
and $T_M\in \omega$
. Since $\mathcal {T}^{\bot }\subseteq \mathcal {C}^{\bot }$
and $\mathcal {T}\subseteq \mathcal {T}^{\bot }\cap {_\mathcal {C}\mathcal {X}}$
, Using Lemma 3.1(4), one can see that $M'\in \mathcal {T}^{\bot }\cap {_\mathcal {C}\mathcal {X}}$
. Now replacing $M$
with $M'$
and repeating the above process, we have $M\in \textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
.
Let $M\in \textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
. There is an $\mathbb {E}$
-triangle sequence $N\rightarrow T_{n}\rightarrow T_{n-1}\cdots \rightarrow T_{2}\rightarrow T_{1}\rightarrow M$
with $N\in {_\mathcal {C}\mathcal {X}}$
and $T_{i}\in \mathcal {T}$
. Using Lemma 3.1(3), we have $M\in {_\mathcal {C}\mathcal {X}}$
. Now to show $M\in \mathcal {T}^{\bot }$
. As $\mathcal {T}$
is self-orthogonal, one can see that $\mathbb {E}^{i}(\mathcal {T},\,M)=\mathbb {E}^{i+n}(\mathcal {T},\,N)$
for all $i\geq 1$
. Since $(\mathcal {C},\,\mathcal {T})$
is an $n$
-tilting pair, for any $T\in \mathcal {T}$
, there is an $\mathbb {E}$
-triangle sequence $C_{n}\rightarrow C_{n-1}\cdots \rightarrow C_{1}\rightarrow C_{0}\rightarrow T$
. Then, we have $\mathbb {E}^{i+n}(T,\,X)=\mathbb {E}^{i}(C_{n},\,N)=0$
for all $i\geq 1$
since $N\in {_\mathcal {C}\mathcal {X}}\subseteq \mathcal {C}^{\bot }$
. Therefore, $\mathbb {E}^{i}(\mathcal {T},\,M)=0$
for all $i\geq 1$
, that is, $M\in \mathcal {T}^{\bot }$
.
Clearly, if $\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})=\mathcal {T}^{\bot }\cap {_\mathcal {C}\mathcal {X}}$
, then $\mathcal {T}\subseteq \mathcal {T}^{\bot }\cap {_\mathcal {C}\mathcal {X}}$
, in particular, $\mathcal {T}$
is a self-othogonal subcategory.
Proposition 4.6 If $\mathcal {T}$
is a strongly contravariantly finite subcategory in $\mathfrak {C}$
and $\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})=\mathcal {T}^{\bot }\cap {_\mathcal {C}\mathcal {X}}$
, then $\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})=\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T}))$
.
Proof. Firstly, we show that $\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})=\textrm {Pres}^{n+1}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
. We just need to show that $\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})\subseteq \textrm {Pres}^{n+1}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
. Indeed, for any $M\in \textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
, there is an $\mathbb {E}$
-triangle 
with $N\in \textrm {Pres}^{n-1}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
and $T_{1}\in \mathcal {T}$
. Using Lemma 3.1(3), we have $N\in {_\mathcal {C}\mathcal {X}}$
. Since $M\in \mathcal {T}^{\bot }\cap \textrm {Gen}(\mathcal {T})$
and $\mathcal {T}$
is self-orthogonal, we have an $\mathbb {E}$
-triangle 
with $L\in \mathcal {T}^{\bot }$
and $T_{M}\in \mathcal {T}$
. Thus we have the following commutative diagram:
Because $T_{M}\in {_\mathcal {C}\mathcal {X}}$
, $N\in {_\mathcal {C}\mathcal {X}}$
and $_\mathcal {C}\mathcal {X}$
are closed under extensions, we have $Y\in {_\mathcal {C}\mathcal {X}}$
. Since $L\in \mathcal {T}^{\bot }$
, one can see that $Y\cong L\oplus T_{1}$
. Therefore, $L\in \mathcal {T}^{\bot }\cap {_\mathcal {C}\mathcal {X}}=\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
, since $_\mathcal {C}\mathcal {X}$
is closed under direct summands. From the argument above, one can see that $M\in \textrm {Pres}^{n+1}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
.
Now we will show that $\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})=\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T}))$
. It is enough to show that
Let $M\in \textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T}))$
. Then there is an $\mathbb {E}$
-triangle sequence $X\rightarrow P_{n}\rightarrow P_{n-1}\cdots \rightarrow P_{2}\rightarrow P_{1}\rightarrow M$
with $P_{i}\in \textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
and $X\in {_\mathcal {C}\mathcal {X}}$
. Let $\mathscr {Y}=\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
, using Lemma 3.2 and $\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})=\textrm {Pres}^{n+1}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
, we have an $\mathbb {E}$
-triangle 
such that $U\in \textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
and there is an $\mathbb {E}$
-triangle sequence $V\rightarrow T_{n}\rightarrow T_{n-1}\cdots \rightarrow T_{2}\rightarrow T_{1}\rightarrow M$
with $T_{i}\in \mathcal {T}$
. We have $V\in {_\mathcal {C}\mathcal {X}}$
since $U,\,X\in {_\mathcal {C}\mathcal {X}}$
and ${_\mathcal {C}\mathcal {X}}$
is closed under extensions. Therefore, $M\in \textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
.
Proposition 4.7 Assume that $\mathcal {T}$
is a strongly contravariantly finite subcategory in $\mathfrak {C}$
and $\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})=\mathcal {T}^{\bot }\cap {_\mathcal {C}\mathcal {X}}$
. If $\mathcal {C}\subseteq \textrm {Copres}^{n}(\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T}))$
, then $\mathcal {C}\subseteq \check {\mathcal {T}_{n}}$
.
Proof. If $\mathcal {C}\subseteq \textrm {Copres}^{n}(\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T}))$
, then for any $C\in \mathcal {C}$
, there is an $\mathbb {E}$
-triangle sequence $C\rightarrow P_{n}\rightarrow P_{n-1}\cdots \rightarrow P_{2}\rightarrow P_{1}\rightarrow P_{0}$
with $P_{i}\in \textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
for $1\leq i\leq n$
. Using Proposition 4.6, one can see $P_{0}\in \textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
. Let $\mathcal {X}=\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
and applying Lemma 3.2, we have an $\mathbb {E}$
-triangle 
such that $U\in \textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})$
and $V\in \check {\mathcal {T}_{n}}$
. Since $U\in \textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})=\mathcal {T}^{\bot }\cap {_\mathcal {C}\mathcal {X}}\subseteq \mathcal {C}^{\bot }$
, one can see $V\cong C\oplus U.$
Using Lemma 3.1(2), we have $C\in \check {\mathcal {T}_{n}}$
.
Proposition 4.8 Assume that $\mathcal {T}$
is a strongly contravariantly finite subcategory in $\mathfrak {C}$
and $\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})=\mathcal {T}^{\bot }\cap {_\mathcal {C}\mathcal {X}}$
. If $\mathcal {C}\subseteq \textrm {Copres}^{n}(\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})),$
then $\mathcal {T}\subseteq \hat {\mathcal {C}}_{n}$
.
Proof. Since $\mathcal {T}\subseteq \textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})\subseteq {_\mathcal {C}\mathcal {X}}$
, for any $T\in \mathcal {T}$
, there is an $\mathbb {E}$
-triangle sequence
with $X_{n+1}\in {_\mathcal {C}\mathcal {X}}$
and $C_{i}\in \mathcal {C}$
. Then we have $\mathbb {E}^{1}(\textrm {Cone}(f_{n+1}),\,X_{n+1})=\mathbb {E}^{n+1}(T,\,X_{n+1})$
. If we have shown that $\mathbb {E}^{n+1}(T,\,X_{n+1})=0$
, then $\textrm {Cone}(f_{n+1})\in \mathcal {C}$
since $\mathcal {C}$
is closed under direct summands. Therefore, $T\in \hat {\mathcal {C}}_{n}.$
Now to show that $\mathbb {E}^{n+1}(T,\,M)=0$
for any $T\in \mathcal {T},\, M\in {_\mathcal {C}\mathcal {X}}$
. Since $M\in {_\mathcal {C}\mathcal {X}}$
, there is an $\mathbb {E}$
-triangle sequence $Z\rightarrow C_{n}\rightarrow C_{n-1}\cdots \rightarrow C_{2}\rightarrow C_{1}\rightarrow M$
with $C_{i}\in \mathcal {C}$
and $Z\in {_\mathcal {C}\mathcal {X}}$
. Using Proposition 4.7, one can see that $C_{i}\in \check {\mathcal {T}_{n}}$
. Applying the dual of Lemma 3.2, we have an $\mathbb {E}$
-triangle 
such that $U\in \check {\mathcal {T}}_{n-1}$
and there is an $\mathbb {E}$
-triangle sequence $Z\rightarrow T_{n}\rightarrow T_{n-1}\cdots \rightarrow T_{2}\rightarrow T_{1}\rightarrow V$
with $T_{i}\in \mathcal {T}$
. It is obvious that $V\in \textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})=\mathcal {T}^{\bot }\cap {_\mathcal {C}\mathcal {X}}$
. Using the fact that $\check {\omega }_{n-1}=\{X\in X_{\omega }|\mathbb {E}^{n}(Y,\,X)=0,\, \mbox { for all }\ Y\in \sideset {{}^{\bot }}{}{\mathop {\omega }}\}$
in the proof of Lemma 3.1(2), we have $\mathbb {E}^{n+1}(T,\,M)=\mathbb {E}^{n}(T,\,U)=0$
. If we let $M=X_{n+1}$
, then $\mathbb {E}^{n+1}(T,\,X_{n+1})=0$
.
Now we have the following Bazzoni characterization of $n$
-tilting pairs in an extriangulated category.
Theorem 4.9 Assume that $\mathcal {C}\subseteq \textrm {Copres}^{n}(\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T}))$
and $\mathcal {T}$
is strongly contravariantly finite. Then $(\mathcal {C},\,\mathcal {T})$
is an $n$
-tilting pair if and only if $\textrm {Pres}^{n}_{_\mathcal {C}\mathcal {X}}(\mathcal {T})=\mathcal {T}^{\bot }\cap {_\mathcal {C}\mathcal {X}}$
.
In particular, using Theorem 4.9 to Example 4.2(5), we get the Bazzoni characterization of an $n$
-tilting subcategory in [Reference Zhu and Zhuang23].
Corollary 4.10 (Zhu and Zhuang [Reference Zhu and Zhuang23, Theorem 1])
Assume that $\mathcal {T}$
is a subcategory of $\mathfrak {C}$
which is strongly contravariantly finite and closed under direct summands. Then $\mathcal {T}$
is an $n$
-tilting subcategory if and only if $\textrm {Pres}^{n}(\mathcal {T})=\mathcal {T}^{\bot }.$
Example 4.11 If $\mathfrak {C}=\mbox {mod}A$
, where $A$
is an Artin algebra and $\mbox {mod}A$
is the category of finitely generated left $A$
-modules. We can get the Bazzoni characterization of $n$
-tilting pairs in [Reference Wei and Xi19, Theorem 3.10] from Theorem 4.9.
5. Auslander–Reiten correspondence
In this section, we mainly study the Auslander–Reiten correspondence for tilting pairs, which classifies finite $\mathcal {C}$
-tilting subcategories for a certain self-orthogonal subcategory $\mathcal {C}$
with some assumptions.
Proposition 5.1 Assume that $\mathcal {T}$
is a finite $\mathcal {C}$
-tilting subcategory.
(1) ${_\mathcal {C}\mathcal {X}}=\check {{_\mathcal {T}\mathcal {X}}}\cap \mathcal {C}^{\bot }$
.(2) $\check {{_\mathcal {T}\mathcal {X}}}={_\mathcal {C}\check {\mathcal {X}}}$
.
Proof.
(1) ${_\mathcal {C}\mathcal {X}}\subseteq \check {{_\mathcal {T}\mathcal {X}}}\cap \mathcal {C}^{\bot }$
: Since ${_\mathcal {C}\mathcal {X}}\subseteq \mathcal {C}^{\bot }$, it suffices to show that ${_\mathcal {C}\mathcal {X}}\subseteq \check {{_\mathcal {T}\mathcal {X}}}$. Let $M\in {_\mathcal {C}\mathcal {X}}$. Take an $\mathbb {E}$-triangle sequence with $M_n\in {_\mathcal {C}\mathcal {X}}$ and each $C_i\in \mathcal {C}$. By the dual of Lemma 3.2, there are $\mathbb {E}$-triangle and $\mathbb {E}$-triangle sequence
with 
and 
with $U\in \check {\mathcal {T}}$
and $T_i\in \mathcal {T}$
. Since $\mathcal {T}\subseteq \hat {\mathcal {C}}\subseteq {_\mathcal {C}\mathcal {X}},$
each $T_i\in {_\mathcal {C}\mathcal {X}}$
. Moreover$,$
$M_n\in {_\mathcal {C}\mathcal {X}}$
, so $V\in {_\mathcal {C}\mathcal {X}}$
by Lemma 3.1(3).
Claim $V\in \mathcal {T}^{\bot }$
. In fact, for the $\mathbb {E}$
-triangle sequence
since $\mathcal {T}$
is self-orthogonal, we have $\mathbb {E}^{i}(T,\,V)\cong \mathbb {E}^{i+n}(T,\,M_n)$
for any $T\in \mathcal {T}$
and any $i\geq 1$
. Since $\mathcal {T}$
is an $n$
-$\mathcal {C}$
-tilting subcategory, there is an $\mathbb {E}$
-triangle sequence 
with each $C_i\in \mathcal {C}$
. The condition $M_n\in {_\mathcal {C}\mathcal {X}}\subseteq \mathcal {C}^{\bot }$
implies $\mathbb {E}^{i+n}(T,\,M_n)\cong \mathbb {E}^{i}(C_n,\,M_n)=0$
, and hence $\mathbb {E}^{i}(T,\,V)=0$
for any $i\geq 1$
. Thus $V\in \mathcal {T}^{\bot }$
. By Lemma 4.4, $V\in {_\mathcal {T}\mathcal {X}}$
, and hence $M\in \check {{_\mathcal {T}\mathcal {X}}}$
by Proposition 3.3.
$\check {{_\mathcal {T}\mathcal {X}}}\cap \mathcal {C}^{\bot }\subseteq {_\mathcal {C}\mathcal {X}}$
: Let $M\in \check {{_\mathcal {T}\mathcal {X}}}\cap \mathcal {C}^{\bot }$
. Choose an $\mathbb {E}$
-triangle sequence
with each $X_i\in {_\mathcal {T}\mathcal {X}}$
, and consider the corresponding $\mathbb {E}$
-triangles
for $1\leq i\leq m$
($K_{m+1}=M$
, $K_1=X_0$
). By Lemma 4.4, ${_\mathcal {T}\mathcal {X}}\subseteq {_\mathcal {C}\mathcal {X}}\subseteq \mathcal {C}^{\bot }$
, and so $X_i\in \mathcal {C}^{\bot }$
. Moreover, $M\in \mathcal {C}^{\bot }$
implies $K_i\in \mathcal {C}^{\bot }$
. By Lemma 3.1, we can iteratively obtain $K_2\in {_\mathcal {C}\mathcal {X}}$
, $K_3\in {_\mathcal {C}\mathcal {X}},\, \ldots,$
$K_m\in {_\mathcal {C}\mathcal {X}}$
, $M\in {_\mathcal {C}\mathcal {X}}$
.
(2) By (1), ${_\mathcal {C}\mathcal {X}}\subseteq \check {{_\mathcal {T}\mathcal {X}}}$
. By Lemma 3.1, ${_\mathcal {C}\check {\mathcal {X}}}\subseteq \check {{_\mathcal {T}\mathcal {X}}}$. Conversely, $\check {{_\mathcal {T}\mathcal {X}}}\subseteq {_\mathcal {C}\check {\mathcal {X}}}$.
Lemma 5.2 (Chang et al. [Reference Chang, Zhou and Zhu8, Lemma 2.3])
Let $\omega$
be closed under extensions.
(1) If $f: W\to M$
is a right $\omega$-approximation of $M,$ then $\textrm {Cocone}f\in \omega ^{\bot _1}$.(2) If $f: M\to W$
is a left $\omega$-approximation of $M,$ then $\textrm {Cone}f\in {{}^{\bot _1}\omega }$.
Definition 5.3 Let $\mathcal {S}$
be a finite subset of objects in $\mathfrak {C}$
, and $M\in \mathfrak {C}$
. A finite $\mathcal {S}$
-filtration of $M$
is a class of $\mathbb {E}$
-triangles
such that each $S_i\in \mathcal {S}$
for any $1\leq i\leq n$
.
A category $\mathfrak {C}$
is called finitely filtered if there is a finite subset $\mathcal {S}$
in $\mathfrak {C}$
such that each object in $\mathfrak {C}$
has a finite $\mathcal {S}$
-filtration.
Lemma 5.4 Let $\mathcal {C}$
be self-orthogonal with $\check {{_\mathcal {C}\mathcal {X}}}$
finitely filtered. Assume that $\mathcal {D}\subseteq {_\mathcal {C}\mathcal {X}}$
is closed under extensions and cones of inflations with $\check {\mathcal {D}}=\check {{_\mathcal {C}\mathcal {X}}}$
. Then
(1) there is some integer $n$
with $\check {\mathcal {D}}=\check {\mathcal {D}}_n$.(2) ${{}^{\bot }\mathcal {D}}\cap {_\mathcal {C}{\mathcal {X}}}\subseteq \hat {{\mathcal {C}}}$
.
Proof.
(1) By assumption, there is a finite set $\mathcal {S}$
such that each object in $\check {\mathcal {D}}$ has a finite filtration by $\mathcal {S}$. Set $n=\max \{\mathcal {D}\mbox {-codim}S,\, S\in \mathcal {S}\}$. Then by Lemma 3.6, $\check {\mathcal {D}}=\check {\mathcal {D}}_n$.(2) Let $X\in {{}^{\bot }\mathcal {D}}\cap {_\mathcal {C}{\mathcal {X}}}$
. Since $X\in {_\mathcal {C}{\mathcal {X}}}$, there is an $\mathbb {E}$-triangle sequence
with $C_i\in \mathcal {C}$
and $K_i\in {_\mathcal {C}{\mathcal {X}}}\subseteq \mathcal {C}^{\bot }$
. Here each $K_i$
arises in the corresponding $\mathbb {E}$
-triangle 
($K_0=X$
). It follows that
Moreover, since $K_{n+1}\in \check {{_\mathcal {C}\mathcal {X}}}=\check {\mathcal {D}}=\check {\mathcal {D}}_n$
by (1), then
and hence the $\mathbb {E}$
-triangle 
is split. Thus $K_{n+1}\in \mathcal {C}$
and, therefore, $X\in \hat {\mathcal {C}}$
.
Let $\mathscr {Y}$
be a subcategory of $\mathfrak {C}$
. If $\mathcal {I}\subseteq \mathscr {Y}\cap \mathscr {Y}^{\bot }$
, and for any $Y\in \mathscr {Y}$
, there is an $\mathbb {E}$
-triangle 
with $I_{Y}\in \mathcal {I}$
and $Y'\in \mathscr {Y}$
, we say that $\mathcal {I}$
is a relative injective cogenerator of $\mathscr {Y}$
. Dually, one can define the relative projective generator of $\mathscr {Y}$
.
Let $\mathcal {D}\subseteq \mathcal {C}$
be subcategories of $\mathfrak {C}$
. We say that $\mathcal {D}$
is a relative resolving subcategory of $\mathcal {C}$
if $\mathcal {D}$
is closed under extensions, direct summands and cocones of deflations and contains $\textrm {Proj}(\mathcal {C})$
(where $\textrm {Proj}(\mathcal {C})$
is the subcategory of projective objects in $\mathcal {C}$
). Dually, one can define the relative coresolving subcategory of $\mathcal {C}$
. In particular, if $\mathcal {C}=\mathfrak {C}$
and $\mathcal {D}$
is a relative resolving (coresolving respectively) subcategory of $\mathcal {C}$
, we say that $\mathcal {D}$
is a resolving (coresolving respectively) subcategory of $\mathfrak {C}$
.
Lemma 5.5 Let $\mathcal {C}$
be self-orthogonal such that ${_\mathcal {C}\mathcal {X}}$
has a relative injective cogenerator $\mathcal {I}$
. If $\mathcal {D}\subseteq {_\mathcal {C}\mathcal {X}}$
is relative coresolving in ${_\mathcal {C}\mathcal {X}}$
, then $\check {{_\mathcal {C}\mathcal {X}}}\cap {{}^{\bot _1}\mathcal {D}}\subseteq {{}^{\bot }\mathcal {D}}$
.
Proof. Let $D\in \mathcal {D}\subseteq {_\mathcal {C}\mathcal {X}}$
. There is an $\mathbb {E}$
-triangle sequence 
with $I_i\in \mathcal {I}$
. Consider the corresponding $\mathbb {E}$
-triangles 
($K_0=D$
). Since $\mathcal {D}$
is relative coresolving, each $K_i\in \mathcal {D}$
.
Let $X\in \check {{_\mathcal {C}\mathcal {X}}}\cap {{}^{\bot _1}\mathcal {D}}$
. Then $\mathbb {E}^{i}(X,\,D)\cong \mathbb {E}(X,\,K_{i-1})=0$
for any $i\geq 1$
, as desired.
In the following, we give a sufficient condition such that $\mathcal {D}\cap {{}^{\bot }\mathcal {D}}$
is a generator for $\mathcal {D}$
.
Lemma 5.6 Let $\mathcal {C}$
be self-orthogonal such that ${_\mathcal {C}\mathcal {X}}$
has a relative injective cogenerator, and $\mathcal {D}$
be relative coresolving and strongly covariantly finite in ${_\mathcal {C}\mathcal {X}}$
. Then for any $D\in \mathcal {D}$
, there is an $\mathbb {E}$
-triangle 
with $D'\in \mathcal {D}$
and $W_D\in \omega$
, where $\omega =\mathcal {D}\cap {{}^{\bot }\mathcal {D}}$
.
In particular, $\mathcal {D}\subseteq {_\omega \mathcal {X}}$
.
Proof. For any $D\in \mathcal {D}\subseteq {_\mathcal {C}\mathcal {X}}$
, we can take an $\mathbb {E}$
-triangle 
with $C_D\in \mathcal {C}$
and $L\in {_\mathcal {C}\mathcal {X}}$
. For $L$
, there is an $\mathbb {E}$
-triangle 
with $D'\in \mathcal {D}$
and $M\in {{}^{\bot _1}\mathcal {D}}$
. By Lemma 5.5, $M\in {{}^{\bot }\mathcal {D}}$
. Consider the following commutative diagram
By the middle row, $W_D\in \mathcal {D}$
. Moreover, $C_D\in \mathcal {C}\subseteq {{}^{\bot }\mathcal {D}}$
and $M\in {{}^{\bot }\mathcal {D}}$
, we have $W_D\in {{}^{\bot }\mathcal {D}}$
, and hence $W_D\in \omega$
.
Lemma 5.7 Let $\mathcal {C}$
be self-orthogonal such that ${_\mathcal {C}\mathcal {X}}$
has a relative injective cogenerator. Assume that $\mathcal {D}$
is relative coresolving and strongly covariantly finite in ${_\mathcal {C}\mathcal {X}}$
with $\check {\mathcal {D}}=\check {{_\mathcal {C}\mathcal {X}}}$
. Then ${{}^{\bot }\mathcal {D}}\cap {_\mathcal {C}\mathcal {X}}\subseteq \check {\omega },$
where $\omega =\mathcal {D}\cap {{}^{\bot }\mathcal {D}}$
. In particular$,$
$\mathcal {C}\subseteq \check {\omega }$
.
Proof. Let $X\in {_\mathcal {C}\mathcal {X}}$
. Since $\mathcal {D}$
is strongly covariantly finite in ${_\mathcal {C}\mathcal {X}}$
, there is an $\mathbb {E}$
-triangle 
with $D_0\in \mathcal {D}$
, $X_1\in {_\mathcal {C}\mathcal {X}}$
. By Lemma 5.2, we may take $X_1\in {{}^{\bot _1}\mathcal {D}}$
. By Lemma 5.5, $X_1\in {{}^{\bot }\mathcal {D}}$
. In this case, if $X\in {{}^{\bot }\mathcal {D}}$
, then $D_0\in {{}^{\bot }\mathcal {D}}$
, and hence $D_0\in \mathcal {D}\cap {{}^{\bot }\mathcal {D}}=\omega$
. By repeating this process to $X_1$
, and so on, we obtain an $\mathbb {E}$
-triangle sequence 
, where each $D_i\in \omega$
and $X_i\in {{}^{\bot }\mathcal {D}}\cap {_\mathcal {C}\mathcal {X}}$
. Since ${_\mathcal {C}\mathcal {X}}\subseteq \check {{_\mathcal {C}\mathcal {X}}}=\check {\mathcal {D}}$
, there is some $m$
such that $X_m\in \mathcal {D}$
. It follows that $X_m\in \mathcal {D}\cap {{}^{\bot }\mathcal {D}}=\omega$
, which implies $X\in \check {\omega }$
. Therefore, ${{}^{\bot }\mathcal {D}}\cap {_\mathcal {C}\mathcal {X}}\subseteq \check {\omega }$
.
Now if, in addition $\check {{_\mathcal {C}\mathcal {X}}}$
is finite filtered, then we can construct a $\mathcal {C}$
-tilting subcategory by taking ${{}^{\bot }\mathcal {D}}\cap \mathcal {D}$
.
Proposition 5.8 Let $\mathcal {C}$
be self-orthogonal such that ${_\mathcal {C}\mathcal {X}}$
has a relative injective cogenerator and $\check {{_\mathcal {C}\mathcal {X}}}$
is finite filtered. Assume that $\mathcal {D}$
is relative coresolving and strongly covariantly finite in ${_\mathcal {C}\mathcal {X}}$
with $\check {\mathcal {D}}=\check {{_\mathcal {C}\mathcal {X}}}$
. Then $\omega :={{}^{\bot }\mathcal {D}}\cap \mathcal {D}$
is a $\mathcal {C}$
-tilting subcategory. In this case$,$
$\mathcal {D}={_\omega \mathcal {X}}$
.
Proof. Clearly, $\omega$
is self-orthogonal. Moreover, $\omega \subseteq \hat {\mathcal {C}}$
by Lemma 5.4, and $\mathcal {C}\subseteq \check {\omega }$
by Lemma 5.7. Thus the pair $(\mathcal {C},\,\omega )$
is a tilting pair.
By Lemma 5.6, $\mathcal {D}\subseteq {_\omega \mathcal {X}}$
. On the other hand, ${_\omega \mathcal {X}}\subseteq {_C\mathcal {X}}\subseteq \check {{_C\mathcal {X}}}=\check {\mathcal {D}}=\check {\mathcal {D}}_n$
for some $n$
. Now let $M\in {_\omega \mathcal {X}}$
, by assumption, we can take an $\mathbb {E}$
-triangle sequence
with each $W_i\in \omega \subseteq \mathcal {D}$
. Then $K_{n+1}\in \mathcal {D}$
and hence $M\in \mathcal {D}$
since $\mathcal {D}$
is closed under cones of inflations. This shows that ${_\omega \mathcal {X}}\subseteq \mathcal {D},$
and consequently $\mathcal {D}={_\omega \mathcal {X}}$
.
Now we show the first type of Auslander–Reiten correspondence, which gives a classification for $\mathcal {C}$
-tilting subcategories in terms of a certain class of relative coresolving strongly covariantly finite subcategories in ${_\mathcal {C}\mathcal {X}}$
.
Theorem 5.9 Let $\mathcal {C}$
be self-orthogonal such that ${_\mathcal {C}\mathcal {X}}$
has a relative injective cogenerator and $\check {{_\mathcal {C}\mathcal {X}}}$
is finite filtered. Then there is a one–one correspondence as follows:
where the inverse map is given by $\mathcal {D} \mapsto {{}^{\bot }\mathcal {D}}\cap \mathcal {D}$
.
Proof.
(i) Assume that $\mathcal {T}$
is a $\mathcal {C}$-tilting subcategory. Then $\check {_\mathcal {T}\mathcal {X}}=\check {{_\mathcal {C}\mathcal {X}}}$ by Proposition 5.1. Let $M\in {_\mathcal {C}\mathcal {X}}$. Then $M\in \check {_\mathcal {T}\mathcal {X}}$, and by Proposition 3.3, there is an $\mathbb {E}$-triangle with $U'\in {_\mathcal {T}\mathcal {X}}$ and $V'\in \check {\mathcal {T}}$. By Lemma 3.1, $\check {\mathcal {T}}\bot {_\mathcal {T}\mathcal {X}}$, and hence $M\to U'$ is a left ${_\mathcal {T}\mathcal {X}}$-approximation. That is, ${_\mathcal {T}\mathcal {X}}$ is strongly covariantly finite in ${_\mathcal {C}\mathcal {X}}$. It is easy to check that ${_\mathcal {T}\mathcal {X}}$ is relative coresolving in ${_\mathcal {C}\mathcal {X}}$.(ii) Assume that $\mathcal {D}$
is a relative coresolving, strongly covariantly finite subcategory in ${_\mathcal {C}\mathcal {X}}$, and satisfies $\check {\mathcal {D}}=\check {{_\mathcal {C}\mathcal {X}}}$. By Proposition 5.8, ${{}^{\bot }\mathcal {D}}\cap \mathcal {D}$ is a $\mathcal {C}$-tilting subcategory.(iii) By Proposition 5.8, $_{{{}^{\bot }\mathcal {D}}\cap \mathcal {D}}\mathcal {X}=\mathcal {D}$
. Moreover, let $M\in {{}^{\bot }({_\mathcal {T}\mathcal {X}})\cap {_\mathcal {T}\mathcal {X}}}$. Then there is an $\mathbb {E}$-triangle with $T\in {\mathcal {T}}$ and $M'\in {_\mathcal {T}\mathcal {X}}$. It is split and hence $M\in \mathcal {T}$, which shows that ${{}^{\bot }({_\mathcal {T}\mathcal {X}})\cap {_\mathcal {T}\mathcal {X}}}\subseteq \mathcal {T}$. Moreover, it is easy to see $\mathcal {T}\subseteq {{}^{\bot }({_\mathcal {T}\mathcal {X}})\cap {_\mathcal {T}\mathcal {X}}}$, and thus ${{}^{\bot }({_\mathcal {T}\mathcal {X}})\cap {_\mathcal {T}\mathcal {X}}}=\mathcal {T}$.
with 
with 
Using Theorem 5.9 to Example 4.2(5), we get the Auslander–Reiten correspondence of an $n$
-tilting object in [Reference Zhu and Zhuang23].
Corollary 5.10 (Zhu and Zhuang [Reference Zhu and Zhuang23, Theorem 2])
Let $\mathfrak {C}$
be a finite filtered extriangulated category. The assignments $T\mapsto T^{\bot }$
and $\mathcal {X}\mapsto \sideset {{}^{\bot }}{}{\mathop {\mathcal {X}}}\cap \mathcal {X}$
give a one–one correspondence between the class of $n$
-tilting objects $T$
and the class of coresolving strongly covariantly finite subcategories $\mathcal {X},$
which are closed under direct summands and $\check {\mathcal {X}_{n}}=\mathfrak {C}.$
In the rest of this paper, we will give the second type of Auslander–Reiten correspondence. To do it, we first need to build a correspondence between relative coresolving strongly covariantly finite subcategories and relative resolving strongly contravariantly finite subcategories in ${_\mathcal {C}\mathcal {X}}$
.
Lemma 5.11 Let $\mathcal {C}$
be self-orthogonal such that ${_\mathcal {C}\mathcal {X}}$
has a relative injective cogenerator. Assume that $\mathcal {D}$
is relative coresolving and strongly covariantly finite in ${_\mathcal {C}\mathcal {X}}$
. Then
(1) $\mathcal {D}$
is relative coresolving and strongly covariantly finite in $\check {{_\mathcal {C}\mathcal {X}}}$.(2) ${{}^{\bot }\mathcal {D}\cap {_\mathcal {C}\mathcal {X}}}$
is relative resolving and strongly contravariantly finite in ${_\mathcal {C}\mathcal {X}}$.(3) ${{}^{\bot }\mathcal {D}\cap \check {{_\mathcal {C}\mathcal {X}}}}$
is strongly contravariantly finite in $\check {{_\mathcal {C}\mathcal {X}}}$.
Proof.
(1) Since the relative injective cogenerator of ${_\mathcal {C}\mathcal {X}}$
is also the relative injective cogenerator of $\check {{_\mathcal {C}\mathcal {X}}}$, it follows that $\mathcal {D}$ is relative coresolving in $\check {{_\mathcal {C}\mathcal {X}}}$.
Now let $X\in \check {{_\mathcal {C}\mathcal {X}}}$
. By Proposition 3.3, there is an $\mathbb {E}$
-triangle 
with $Y\in {_C\mathcal {X}}$
and $Z\in \check {\mathcal {C}}$
. For $Y$
, by Lemmas 5.2 and 5.5, there is an $\mathbb {E}$
-triangle 
with $D\in \mathcal {D}$
and $M\in {{}^{\bot }\mathcal {D}}$
. Consider the following commutative diagram
Since $\mathcal {D}\subseteq {_\mathcal {C}\mathcal {X}}\subseteq \mathcal {C}^{\bot }$
, $\check {\mathcal {C}}\subseteq {{}^{\bot }\mathcal {D}}$
. Thus $Z\in {{}^{\bot }\mathcal {D}}$
. Moreover, $M\in {{}^{\bot }\mathcal {D}}$
, we can get $N\in {{}^{\bot }\mathcal {D}}$
, which shows that $X\to D$
is a left $\mathcal {D}$
-approximation. Therefore, $\mathcal {D}$
is strongly covariantly finite in $\check {{_\mathcal {C}\mathcal {X}}}$
.
(2) Clearly, ${{}^{\bot }\mathcal {D}\cap {_\mathcal {C}\mathcal {X}}}$
is relative resolving in ${_\mathcal {C}\mathcal {X}}$. Let $X\in {_\mathcal {C}\mathcal {X}}$. By Lemmas 5.2 and 5.5, there is an $\mathbb {E}$-triangle with $D\in \mathcal {D}$ and $M\in {{}^{\bot }\mathcal {D}}$. Since $D\in \mathcal {D}\subseteq {_\mathcal {C}\mathcal {X}}$, $M\in {_\mathcal {C}\mathcal {X}}$ by Lemma 3.1, and hence $M\in {{}^{\bot }\mathcal {D}}\cap {_\mathcal {C}\mathcal {X}}$. Moreover, by Lemma 5.6, there is an $\mathbb {E}$-triangle with $D'\in \mathcal {D}$ and $W_D\in \omega =\mathcal {D}\cap {{}^{\bot }\mathcal {D}}$.
with 
with 
Consider the following commutative diagram
Since $D',\,X\in \mathcal {C}^{\bot }$
, $Y\in C^{\bot }$
. Moreover, since $W_D,\,M\in {_\mathcal {C}\mathcal {X}}$
, we have $Y\in {_\mathcal {C}\mathcal {X}}$
by Lemma 3.1. Finally, since $W_D,\,M\in {{}^{\bot }\mathcal {D}}$
, we obtain $Y\in {{}^{\bot }\mathcal {D}}$
, and consequently $Y\in {{}^{\bot }\mathcal {D}}\cap {_\mathcal {C}\mathcal {X}}$
. This shows that $Y\to X$
is a right ${{}^{\bot }\mathcal {D}}\cap {_\mathcal {C}\mathcal {X}}$
-approximation, which shows that ${{}^{\bot }\mathcal {D}}\cap {_\mathcal {C}\mathcal {X}}$
is strongly contravariantly finite in ${_\mathcal {C}\mathcal {X}}$
.
(3) Similar to (2).
By a similar argument to that of Lemmas 5.4, 5.5 and 5.11, we can get
Lemma 5.12 Let $\mathcal {C}$
be self-orthogonal and ${_\mathcal {C}\mathcal {X}}$
has a relative injective cogenerator. Assume that $\mathcal {B}$
is a relative resolving and strongly contravariantly finite in ${_\mathcal {C}\mathcal {X}}$
.
(1) If $X\in {_\mathcal {C}\mathcal {X}}\cap \mathcal {B}^{\bot _1}$
, the $X\in \mathcal {B}^{\bot }$.(2) For any $B\in \mathcal {B}$
, there is an $\mathbb {E}$-triangle with $W_B\in \omega =\mathcal {B}^{\bot }\cap \mathcal {B}$, and $B'\in \mathcal {B}$. In particular, $\mathcal {B}\subseteq {\mathcal {X}_\omega }$.(3) $\mathcal {B}^{\bot }\cap {_\mathcal {C}\mathcal {X}}$
is relative coresolving and strongly covariantly finite in ${_\mathcal {C}\mathcal {X}}$.
with 
Now we have
Proposition 5.13 Let $\mathcal {C}$
be self-orthogonal and ${_\mathcal {C}\mathcal {X}}$
has a relative injective cogenerator. Then there is a one–one correspondence as follows:
where the inverse map is given by $\mathcal {B}\mapsto {\mathcal {B}^{\bot }\cap {_\mathcal {C}\mathcal {X}}}$
.
Proof. By Lemmas 5.11 and 5.12, the maps above are well defined.
$({{}^{\bot }\mathcal {D}\cap {_\mathcal {C}\mathcal {X}}})^{\bot }\cap {_\mathcal {C}\mathcal {X}}=\mathcal {D}$
: Clearly, $\mathcal {D}\subseteq ({{}^{\bot }\mathcal {D}\cap {_\mathcal {C}\mathcal {X}}})^{\bot }\cap {_\mathcal {C}\mathcal {X}}$
. Conversely, let $X\in ({{}^{\bot }\mathcal {D}\cap {_\mathcal {C}\mathcal {X}}})^{\bot }\cap {_\mathcal {C}\mathcal {X}}$
. Since $\mathcal {D}$
is strongly covariantly finite, there is an $\mathbb {E}$
-triangle 
with $D\in \mathcal {D}$
and $Z\in {{}^{\bot }\mathcal {D}\cap {_\mathcal {C}\mathcal {X}}}$
. It is split since $X\in ({{}^{\bot }\mathcal {D}\cap {_\mathcal {C}\mathcal {X}}})^{\bot }$
, which shows that $D\cong X\oplus Z$
. Thus $X\in \mathcal {D}$
, and hence $({{}^{\bot }\mathcal {D}\cap {_\mathcal {C}\mathcal {X}}})^{\bot }\cap {_\mathcal {C}\mathcal {X}}\subseteq \mathcal {D}$
. Therefore, $({{}^{\bot }\mathcal {D}\cap {_\mathcal {C}\mathcal {X}}})^{\bot }\cap {_\mathcal {C}\mathcal {X}}=\mathcal {D}$
.
Dually, we can prove ${{}^{\bot }(\mathcal {B}^{\bot }\cap {_\mathcal {C}\mathcal {X}})\cap {_\mathcal {C}\mathcal {X}}}=\mathcal {B}$
.
Lemma 5.14 Let $C$
be self-orthogonal and $\check {{_\mathcal {C}\mathcal {X}}}$
be finitely filtered. Assume that $\mathcal {D}$
is strongly covariantly finite and relative coresolving in ${_\mathcal {C}\mathcal {X}}$
. Then there is some integer $n$
such that $\mathbb {E}^{n+1}({{}^{\bot }\mathcal {D}}\cap \check {{_\mathcal {C}\mathcal {X}}},\, {_\mathcal {C}\mathcal {X}})=0$
, provided $\check {\mathcal {D}}=\check {{_\mathcal {C}\mathcal {X}}}$
.
Proof. Let $\mathcal {S}=\{S_1,\,\ldots,\,S_t\}\subseteq {{}^{\bot }\mathcal {D}\cap \check {{_\mathcal {C}\mathcal {X}}}}$
be the finite subcategory. For each $S_i\in \mathcal {S}$
, since $S_i\in \check {{_\mathcal {C}\mathcal {X}}}$
, by Proposition 3.3 there is an $\mathbb {E}$
-triangle 
with $X_i\in {_\mathcal {C}\mathcal {X}}$
and $Z_i\in \check {\mathcal {C}}$
. Since $\mathcal {D}\subseteq {_\mathcal {C}\mathcal {X}}\subseteq \mathcal {C}^{\bot }$
, $\check {\mathcal {C}}\subseteq {{}^{\bot }\mathcal {D}}$
, which shows that $Z_i\in {{}^{\bot }\mathcal {D}}$
. Moreover, since $S_i\in {{}^{\bot }\mathcal {D}}$
, $X_i\in {{}^{\bot }\mathcal {D}}$
, and hence $X_i\in {{}^{\bot }\mathcal {D}}\cap {_C\mathcal {X}}$
. By Lemma 5.4, ${{}^{\bot }\mathcal {D}}\cap {_\mathcal {C}\mathcal {X}}\subseteq \hat {\mathcal {C}}$
. Denote $n=\max \{\mathcal {C}\mbox {-dim}X_i\mid 1\leq i\leq t\}$
. Then $\mathbb {E}^{n+1}(S_i,\,{_\mathcal {C}\mathcal {X}})=0$
, and hence $\mathbb {E}^{n+1}({{}^{\bot }\mathcal {D}}\cap \check {{_\mathcal {C}\mathcal {X}}},\,{_\mathcal {C}\mathcal {X}})=0$
.
Proposition 5.15 Let $\mathcal {C}$
be self-orthogonal and $\check {{_\mathcal {C}\mathcal {X}}}$
be finitely filtered. Assume that $\mathcal {D}$
is strongly covariantly finite and relative coresolving in ${_\mathcal {C}\mathcal {X}}$
. Then $\check {\mathcal {D}}=\check {{_\mathcal {C}\mathcal {X}}}$
if and only if ${{}^{\bot }\mathcal {D}}\cap {_\mathcal {C}\mathcal {X}}\subseteq \hat {\mathcal {C}}$
.
Proof. The ‘only if’ part follows from Lemma 5.4.
The ‘if’ part. Since $\mathcal {D}\subseteq {_\mathcal {C}\mathcal {X}}$
, $\check {\mathcal {D}}\subseteq \check {{_\mathcal {C}\mathcal {X}}}$
. On the other hand, let $X\in \check {{_\mathcal {C}\mathcal {X}}}$
. Then there is an $\mathbb {E}$
-triangle sequence 
with each $D_i\in \mathcal {D}$
and each $K_i\in {{}^{\bot }\mathcal {D}}\cap \check {{_\mathcal {C}\mathcal {X}}}$
. Here each $K_i$
arise in the corresponding $\mathbb {E}$
-triangle 
. By Lemma 3.6, $K_m\in {_\mathcal {C}\mathcal {X}}$
for some $m$
, and thus $K_m\in {{}^{\bot }\mathcal {D}}\cap {_\mathcal {C}\mathcal {X}}\subseteq \hat {\mathcal {C}}$
. By Lemma 5.14, there is some $n$
such that $\mathbb {E}^{n+1}({{}^{\bot }\mathcal {D}}\cap \check {{_\mathcal {C}\mathcal {X}}},\,{_\mathcal {C}\mathcal {X}})=0$
, and hence $\mathbb {E}(K_{m+n+1},\,K_{m+n})\cong \mathbb {E}^{n+1}(K_{m+n+1},\,K_{m})=0$
. This shows that the $\mathbb {E}$
-triangle
is split, and hence $K_{m+n}\in \mathcal {D}$
. Therefore, $\check {{_\mathcal {C}\mathcal {X}}}\subseteq \check {\mathcal {D}}$
.
Collecting the above results, we now give the second type of Auslander–Reiten correspondence, which gives a classification for $\mathcal {C}$
-tilting subcategories in terms of a certain class of relative resolving strongly cotravariantly finite subcategories in ${_\mathcal {C}\mathcal {X}}$
.
Theorem 5.16 Let $\mathcal {C}$
be self-orthogonal such that ${_\mathcal {C}\mathcal {X}}$
has a relative injective cogenerator and $\check {{_\mathcal {C}\mathcal {X}}}$
is finitely filtered. Then there is a one–one correspondence as follows$:$
Proof. By Theorem 5.9, Propositions 5.13 and 5.15, it suffices to show
Clearly, $\check {\mathcal {T}}\cap {_\mathcal {C}\mathcal {X}}\subseteq {{}^{\bot }({_\mathcal {T}\mathcal {X}})\cap {_\mathcal {C}\mathcal {X}}}$
. On the other hand, by Proposition 5.1 and Corollary 3.4, ${{}^{\bot }({_\mathcal {T}\mathcal {X}})\cap {_\mathcal {C}\mathcal {X}}}\subseteq {{}^{\bot }({_\mathcal {T}\mathcal {X}})\cap \check {{_\mathcal {C}\mathcal {X}}}}= {{}^{\bot }({_\mathcal {T}\mathcal {X}})\cap {_\mathcal {T}\check {\mathcal {X}}}}$
which shows that ${{}^{\bot }({_\mathcal {T}\mathcal {X}})\cap {_\mathcal {C}\mathcal {X}}}\subseteq \check {\mathcal {T}}\cap {_\mathcal {C}\mathcal {X}}.$
Example 5.17
(1) If $\mathfrak {C}=\mbox {mod}A$
, where $A$ is an Artin algebra and $\mbox {mod}A$ is the category of finitely generated left $A$-modules. We can get the Auslander–Reiten correspondence of $n$-tilting pairs in [Reference Wei and Xi20, Theorems 3.9 and 3.15] from Theorems 5.9 and 5.16.(2) Using Theorems 5.9 and 5.16 to Example 4.2(5), we get the Auslander–Reiten correspondence of an $n$
-tilting object in [Reference Zhu and Zhuang23].
Acknowledgements
T. Zhao was supported by the NSF of China (Nos. 11901341, 11971225), the project ZR2019QA015 supported by Shandong Provincial Natural Science Foundation, the project funded by China Postdoctoral Science Foundation (No. 2020M682141), and the Young Talents Invitation Program of Shandong Province. B. Zhu was supported by the NSF of China (No. 12031007). X. Zhuang was supported by the Academic Research Projects of Beijing Union University (No. ZK90202102). Part of this work was done by the first author during a visit at Tsinghua University. He would like to express his gratitude to Department of Mathematical Sciences and especially to Professor Bin Zhu for the warm hospitality and the excellent working conditions. He also thanks Panyue Zhou for his helpful suggestions.
