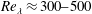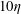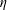1 Introduction
All natural and most engineering turbulent flows are anisotropic at the large scales, a direct consequence of the asymmetric boundary and initial conditions that determine the energy input. Given the inherently multiscale character of turbulence, several questions naturally arise, including:
-
(i) How does the large-scale anisotropy propagate through the inertial scales?
-
(ii) Does anisotropy persist to the dissipative scales?
-
(iii) How does the large-scale anisotropy of the velocity fluctuations relate to the length scales?
The present work is concerned with these three questions. As discussed below, while the first two are linked to traditional subjects in the study of turbulence, the last one has received much less attention in the past.
It is among the fundamental premises of Kolmogorov’s classic theory that, at sufficiently high Reynolds numbers and away from boundaries, the details of the large-scale forcing are lost in the cascade process and the turbulent motions at the small scales become statistically homogenous and isotropic (Kolmogorov Reference Kolmogorov1941, K41 for brevity). K41 has high predictive power; for example, it predicts with impressive accuracy the form of the energy spectrum of the turbulent velocity fluctuations, and analogously the dependence of the second-order velocity structure functions on the spatial separation. Pertaining to question (i), the postulate of local isotropy entails that, over the inertial scales, the scaling exponents for longitudinal and transverse structure functions should be equal and independent of the direction of the separation vector. Additionally, local isotropy implies that the answer to question (ii) must be no.
The postulate of local isotropy and its implications have been scrutinized and debated for decades. Here we shall mention but a few of the many studies that probed its validity by investigating the small-scale isotropy of several canonical flows. In the following we indicate only the maximum Reynolds number (based on the Taylor microscale
![]() $\unicode[STIX]{x1D706}$
) reported in each study. Browne, Antonia & Shah (Reference Browne, Antonia and Shah1987) and George & Hussein (Reference George and Hussein1991) compiled some of the available results of laboratory studies up to
$\unicode[STIX]{x1D706}$
) reported in each study. Browne, Antonia & Shah (Reference Browne, Antonia and Shah1987) and George & Hussein (Reference George and Hussein1991) compiled some of the available results of laboratory studies up to
![]() $Re_{\unicode[STIX]{x1D706}}=990$
, underscoring that the mean square derivatives of the velocity fluctuations were not consistent with local isotropy. Saddoughi & Veeravalli (Reference Saddoughi and Veeravalli1994), with their landmark measurements in the boundary layer of the NASA Ames wind tunnel at
$Re_{\unicode[STIX]{x1D706}}=990$
, underscoring that the mean square derivatives of the velocity fluctuations were not consistent with local isotropy. Saddoughi & Veeravalli (Reference Saddoughi and Veeravalli1994), with their landmark measurements in the boundary layer of the NASA Ames wind tunnel at
![]() $Re_{\unicode[STIX]{x1D706}}=1450$
, found significant support to local isotropy for statistics up to the second order. Kurien & Sreenivasan (Reference Kurien and Sreenivasan2000) analysed measurements in the atmospheric boundary layer up to
$Re_{\unicode[STIX]{x1D706}}=1450$
, found significant support to local isotropy for statistics up to the second order. Kurien & Sreenivasan (Reference Kurien and Sreenivasan2000) analysed measurements in the atmospheric boundary layer up to
![]() $Re_{\unicode[STIX]{x1D706}}=2100$
and calculated mixed structure functions (formed by products of velocity differences in different directions) up to the sixth order, which should be all zero according to local isotropy. They found that anisotropy effects diminish with decreasing scale, but much more slowly than predicted by dimensional arguments based on local isotropy. Dhruva, Tsuji & Sreenivasan (Reference Dhruva, Tsuji and Sreenivasan1997) measured scaling exponents of transverse structure function in the atmospheric boundary layer at
$Re_{\unicode[STIX]{x1D706}}=2100$
and calculated mixed structure functions (formed by products of velocity differences in different directions) up to the sixth order, which should be all zero according to local isotropy. They found that anisotropy effects diminish with decreasing scale, but much more slowly than predicted by dimensional arguments based on local isotropy. Dhruva, Tsuji & Sreenivasan (Reference Dhruva, Tsuji and Sreenivasan1997) measured scaling exponents of transverse structure function in the atmospheric boundary layer at
![]() $Re_{\unicode[STIX]{x1D706}}$
of
$Re_{\unicode[STIX]{x1D706}}$
of
![]() $O(10^{4})$
, and found them to be lower than for longitudinal structure functions, in violation of local isotropy. This trend was also reported by Romano & Antonia (Reference Romano and Antonia2001), who investigated round jets at
$O(10^{4})$
, and found them to be lower than for longitudinal structure functions, in violation of local isotropy. This trend was also reported by Romano & Antonia (Reference Romano and Antonia2001), who investigated round jets at
![]() $Re_{\unicode[STIX]{x1D706}}=500$
issued from different types of nozzles. Shen & Warhaft (Reference Shen and Warhaft2002) measured structure functions up to the eighth order in sheared turbulence at
$Re_{\unicode[STIX]{x1D706}}=500$
issued from different types of nozzles. Shen & Warhaft (Reference Shen and Warhaft2002) measured structure functions up to the eighth order in sheared turbulence at
![]() $Re_{\unicode[STIX]{x1D706}}=1000$
generated in an active-grid wind tunnel. The odd-order moments of the transverse structure functions, which should be zero according to local isotropy, did not vanish and instead followed the same scaling as the longitudinal ones. Antonia, Zhou & Romano (Reference Antonia, Zhou and Romano2002) considered wake flows up to
$Re_{\unicode[STIX]{x1D706}}=1000$
generated in an active-grid wind tunnel. The odd-order moments of the transverse structure functions, which should be zero according to local isotropy, did not vanish and instead followed the same scaling as the longitudinal ones. Antonia, Zhou & Romano (Reference Antonia, Zhou and Romano2002) considered wake flows up to
![]() $Re_{\unicode[STIX]{x1D706}}=300$
and investigated the effect of changing the level of large-scale anisotropy while keeping the same Reynolds number. They showed that the large-scale anisotropy was reflected in the structure functions down to the smallest scales, especially in the transverse direction. Thiesset, Danaila & Antonia (Reference Thiesset, Danaila and Antonia2013) expanded on the latter study and concluded that the postulate of local isotropy was tenable for statistics up to the second order, and below a length scale of order
$Re_{\unicode[STIX]{x1D706}}=300$
and investigated the effect of changing the level of large-scale anisotropy while keeping the same Reynolds number. They showed that the large-scale anisotropy was reflected in the structure functions down to the smallest scales, especially in the transverse direction. Thiesset, Danaila & Antonia (Reference Thiesset, Danaila and Antonia2013) expanded on the latter study and concluded that the postulate of local isotropy was tenable for statistics up to the second order, and below a length scale of order
![]() $10\unicode[STIX]{x1D706}$
. However, isotropy tests on statistics of higher order were found to be more stringent.
$10\unicode[STIX]{x1D706}$
. However, isotropy tests on statistics of higher order were found to be more stringent.
These studies, as well as the vast majority of the experimental investigations on the topic, measured temporal velocity fluctuations and converted them to spatial fluctuations invoking Taylor’s hypothesis. This is advantageous to extract small-scale turbulence features, thanks to the high temporal resolutions attainable with, e.g. hot-wire probes. This approach, however, has well-known limitations (Lin Reference Lin1953; Zaman & Hussain Reference Zaman and Hussain1981), whose implications have been recently revisited (Del Álamo & Jiménez Reference Del Álamo and Jiménez2009; Fiscaletti, Ganapathisubramani & Elsinga Reference Fiscaletti, Ganapathisubramani and Elsinga2017; He, Jin & Yang Reference He, Jin and Yang2017; Squire et al.
Reference Squire, Hutchins, Morrill-Winter, Schultz, Klewicki and Marusic2017). Recent technical advances in particle imaging have enabled spatial measurements down to dissipative-scale resolutions even at relatively high Reynolds numbers, enabling direct probing of the fine spatial structure of turbulence. Voth et al. (Reference Voth, la Porta, Crawford, Alexander and Bodenschatz2002) performed Lagrangian particle tracking in a double-impeller apparatus at
![]() $Re_{\unicode[STIX]{x1D706}}=970$
, and found that the large-scale anisotropy left its footprint on the acceleration statistics, although to a decreasing extent with increasing Reynolds number. Ouellette et al. (Reference Ouellette, Xu, Bourgoin and Bodenschatz2006) used a similar apparatus and technique to measure Lagrangian structure functions at
$Re_{\unicode[STIX]{x1D706}}=970$
, and found that the large-scale anisotropy left its footprint on the acceleration statistics, although to a decreasing extent with increasing Reynolds number. Ouellette et al. (Reference Ouellette, Xu, Bourgoin and Bodenschatz2006) used a similar apparatus and technique to measure Lagrangian structure functions at
![]() $Re_{\unicode[STIX]{x1D706}}=815$
, finding that large-scale asymmetries were reflected already in the second-order statistics. Mullin & Dahm (Reference Mullin and Dahm2006) performed dual-plane stereo particle image velocimetry (PIV) in the far field of a turbulent jet at
$Re_{\unicode[STIX]{x1D706}}=815$
, finding that large-scale asymmetries were reflected already in the second-order statistics. Mullin & Dahm (Reference Mullin and Dahm2006) performed dual-plane stereo particle image velocimetry (PIV) in the far field of a turbulent jet at
![]() $Re_{\unicode[STIX]{x1D706}}=113$
, measuring all components of the velocity gradient tensor. They found that the mean shear was reflected in various small-scale statistics, including the orientation of the strain rate eigenvectors. Ganapathisubramani, Lakshminarasimhan & Clemens (Reference Ganapathisubramani, Lakshminarasimhan and Clemens2008) reconstructed the full three-dimensional velocity in the far field of a round jet at
$Re_{\unicode[STIX]{x1D706}}=113$
, measuring all components of the velocity gradient tensor. They found that the mean shear was reflected in various small-scale statistics, including the orientation of the strain rate eigenvectors. Ganapathisubramani, Lakshminarasimhan & Clemens (Reference Ganapathisubramani, Lakshminarasimhan and Clemens2008) reconstructed the full three-dimensional velocity in the far field of a round jet at
![]() $Re_{\unicode[STIX]{x1D706}}=150$
via time-resolved stereo PIV. The authors did use Taylor’s hypothesis, having performed a thorough validation of their approach (see Ganapathisubramani, Lakshminarasimhan & Clemens Reference Ganapathisubramani, Lakshminarasimhan and Clemens2007), and found that the fine-scale velocity gradients did not satisfy local isotropy conditions, but rather conformed with the less restrictive assumption of axisymmetry (George & Hussein Reference George and Hussein1991). Chang, Bewley & Bodenschatz (Reference Chang, Bewley and Bodenschatz2012) studied axisymmetric turbulence at
$Re_{\unicode[STIX]{x1D706}}=150$
via time-resolved stereo PIV. The authors did use Taylor’s hypothesis, having performed a thorough validation of their approach (see Ganapathisubramani, Lakshminarasimhan & Clemens Reference Ganapathisubramani, Lakshminarasimhan and Clemens2007), and found that the fine-scale velocity gradients did not satisfy local isotropy conditions, but rather conformed with the less restrictive assumption of axisymmetry (George & Hussein Reference George and Hussein1991). Chang, Bewley & Bodenschatz (Reference Chang, Bewley and Bodenschatz2012) studied axisymmetric turbulence at
![]() $Re_{\unicode[STIX]{x1D706}}=481$
at the centre of a spherical chamber, forcing it to different levels of anisotropy by tuning 32 loud-speaker jets. They measured second-order transverse structure functions using two laser Doppler velocimetry probes, and found that neither the multiplicative constants nor the scaling exponents were appreciably affected by anisotropy. Discetti et al. (Reference Discetti, Ziskin, Astarita, Adrian and Prestridge2013) carried out PIV measurements in the wake of a fractal grid at
$Re_{\unicode[STIX]{x1D706}}=481$
at the centre of a spherical chamber, forcing it to different levels of anisotropy by tuning 32 loud-speaker jets. They measured second-order transverse structure functions using two laser Doppler velocimetry probes, and found that neither the multiplicative constants nor the scaling exponents were appreciably affected by anisotropy. Discetti et al. (Reference Discetti, Ziskin, Astarita, Adrian and Prestridge2013) carried out PIV measurements in the wake of a fractal grid at
![]() $Re_{\unicode[STIX]{x1D706}}=340$
, which revealed significant large-scale anisotropy, but an approximate return to isotropy below the Taylor microscale. Gomes-Fernandes, Ganapathisubramani & Vassilicos (Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2015) performed stereoscopic PIV behind the same type of fractal grid at
$Re_{\unicode[STIX]{x1D706}}=340$
, which revealed significant large-scale anisotropy, but an approximate return to isotropy below the Taylor microscale. Gomes-Fernandes, Ganapathisubramani & Vassilicos (Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2015) performed stereoscopic PIV behind the same type of fractal grid at
![]() $Re_{\unicode[STIX]{x1D706}}=268$
and concluded that isotropy was not recovered at the small scales. Fiscaletti, Westerweel & Elsinga (Reference Fiscaletti, Westerweel and Elsinga2014) used long-range micro-PIV in the far field of a turbulent jet at
$Re_{\unicode[STIX]{x1D706}}=268$
and concluded that isotropy was not recovered at the small scales. Fiscaletti, Westerweel & Elsinga (Reference Fiscaletti, Westerweel and Elsinga2014) used long-range micro-PIV in the far field of a turbulent jet at
![]() $Re_{\unicode[STIX]{x1D706}}=367$
. They mapped the invariants of the two-dimensional velocity gradient tensor and obtained results consistent with local homogeneity and isotropy. Lawson & Dawson (Reference Lawson and Dawson2014) combined scanning PIV with tomographic reconstruction to obtain three-dimensional three-component velocity fields at the centre of a large double-impeller tank where
$Re_{\unicode[STIX]{x1D706}}=367$
. They mapped the invariants of the two-dimensional velocity gradient tensor and obtained results consistent with local homogeneity and isotropy. Lawson & Dawson (Reference Lawson and Dawson2014) combined scanning PIV with tomographic reconstruction to obtain three-dimensional three-component velocity fields at the centre of a large double-impeller tank where
![]() $Re_{\unicode[STIX]{x1D706}}=219$
. They found that the large-scale anisotropy persisted to the fine scales, the second-order moments of the velocity gradients being consistent with local axisymmetry.
$Re_{\unicode[STIX]{x1D706}}=219$
. They found that the large-scale anisotropy persisted to the fine scales, the second-order moments of the velocity gradients being consistent with local axisymmetry.
Local isotropy has been most often assumed in turbulence theories and models, but exceptions have become more frequent in the last decades. Durbin & Speziale (Reference Durbin and Speziale1991) argued on theoretical grounds that the small scales cannot be isotropic in the presence of a steady background strain, independently of the Reynolds number. Yeung & Brasseur (Reference Yeung and Brasseur1991) performed low
![]() $Re_{\unicode[STIX]{x1D706}}$
simulations in triply periodic domains using asymmetric forcing, and showed that the small scales are affected by large-scale anisotropy as a consequence of non-local triadic interactions in wavenumber space. As these interactions are thought to become stronger with scale separation, they speculated that small-scale anisotropy would exist also at asymptotically large Reynolds numbers. This idea found support in later simulations at much higher Reynolds numbers (Mininni, Alexakis & Pouquet Reference Mininni, Alexakis and Pouquet2006). Recently Elsinga & Marusic (Reference Elsinga and Marusic2016) proposed a model flow structure of turbulent motion consisting of a shear layer that contains stretching vortices. The model is consistent with classic spectral properties of isotropic turbulence, but also accounts for small-scale anisotropy and interaction between disparate scales.
$Re_{\unicode[STIX]{x1D706}}$
simulations in triply periodic domains using asymmetric forcing, and showed that the small scales are affected by large-scale anisotropy as a consequence of non-local triadic interactions in wavenumber space. As these interactions are thought to become stronger with scale separation, they speculated that small-scale anisotropy would exist also at asymptotically large Reynolds numbers. This idea found support in later simulations at much higher Reynolds numbers (Mininni, Alexakis & Pouquet Reference Mininni, Alexakis and Pouquet2006). Recently Elsinga & Marusic (Reference Elsinga and Marusic2016) proposed a model flow structure of turbulent motion consisting of a shear layer that contains stretching vortices. The model is consistent with classic spectral properties of isotropic turbulence, but also accounts for small-scale anisotropy and interaction between disparate scales.
A complementary approach to the study of anisotropy makes use of the irreducible representation of the SO(3) rotation group (Biferale & Procaccia Reference Biferale and Procaccia2005). It consists of expanding the turbulence statistics in terms of spherical harmonics, instead of projecting them onto the longitudinal and transverse directions. This method allows us, in principle, to derive universal scaling exponents for each sector in the rotation group. While it has been applied to experimental data (Arad et al. Reference Arad, Dhruva, Kurien, L’vov, Procaccia and Sreenivasan1998; Kurien & Sreenivasan Reference Kurien and Sreenivasan2000), the precise results may depend on the geometrical configuration of the measurement probes (Staicu, Vorselaars & van de Water Reference Staicu, Vorselaars and van de Water2003). The approach is therefore most fruitful when analysing numerical simulations for which the full velocity field is available (Biferale & Toschi Reference Biferale and Toschi2001; Casciola et al. Reference Casciola, Gualtieri, Jacob and Piva2005, among others).
No established theory is available that addresses question (iii), and experimental investigations on the topic are scattered. This is understandable, since the large scales are by definition non-universal, and therefore the hope of reaching general results is tenuous (Davidson Reference Davidson2004). Still, since the integral scales contain most of the energy in the flow, they are arguably the most relevant from the modelling standpoint (Pope Reference Pope2000) and in determining macroscopic parameters such as drag and heat transfer rates. The classic scaling of the turbulent dissipation
![]() $\unicode[STIX]{x1D716}$
based on the large-scale energy transfer,
$\unicode[STIX]{x1D716}$
based on the large-scale energy transfer,
![]() $\unicode[STIX]{x1D716}=C_{\unicode[STIX]{x1D716}}(q^{2}/3)^{3/2}/L$
(where
$\unicode[STIX]{x1D716}=C_{\unicode[STIX]{x1D716}}(q^{2}/3)^{3/2}/L$
(where
![]() $q^{2}/2$
is the turbulent kinetic energy,
$q^{2}/2$
is the turbulent kinetic energy,
![]() $L$
an integral length scale characterizing the energy-containing eddies and
$L$
an integral length scale characterizing the energy-containing eddies and
![]() $C_{\unicode[STIX]{x1D716}}$
a constant independent of Reynolds number) is a cornerstone of turbulence theory (Tennekes & Lumley Reference Tennekes and Lumley1972). For its importance, this relation has been scrutinized in depth (e.g. Sreenivasan Reference Sreenivasan1998; Burattini, Lavoie & Antonia Reference Burattini, Lavoie and Antonia2005), especially following the recent observation that, in the lee of fractal and regular grids, an extended region of the flow shows characteristics incompatible with the accepted picture of the Richardson–Kolmogorov cascade (Hurst & Vassilicos Reference Hurst and Vassilicos2007; Vassilicos Reference Vassilicos2015, and references therein). While some of those findings have been reconciled with classic turbulence phenomenology (Hearst & Lavoie Reference Hearst and Lavoie2014; Vassilicos Reference Vassilicos2015), such line of investigation has revived the debate on integral quantities, their definition, and their scaling properties (Mazellier & Vassilicos Reference Mazellier and Vassilicos2008; Valente & Vassilicos Reference Valente and Vassilicos2012). Still, the only study that explicitly addressed the relation between the large-scale anisotropy of velocity and length scales was performed by Bewley, Chang & Bodenschatz (Reference Bewley, Chang and Bodenschatz2012). The authors used the same apparatus described in Chang et al. (Reference Chang, Bewley and Bodenschatz2012) to produce large-scale axisymmetric turbulence with various levels of large-scale anisotropy. They showed that the ratio of the integral lengths along different directions, defined by means of transverse two-point correlations, scaled as a power law of the corresponding r.m.s. (root mean square) velocity ratio. Remarkably, the exponent of the power law was found to be negative, implying that the correlation distance of the velocity fluctuations was smaller in the direction of the stronger turbulence agitation and vice versa.
$C_{\unicode[STIX]{x1D716}}$
a constant independent of Reynolds number) is a cornerstone of turbulence theory (Tennekes & Lumley Reference Tennekes and Lumley1972). For its importance, this relation has been scrutinized in depth (e.g. Sreenivasan Reference Sreenivasan1998; Burattini, Lavoie & Antonia Reference Burattini, Lavoie and Antonia2005), especially following the recent observation that, in the lee of fractal and regular grids, an extended region of the flow shows characteristics incompatible with the accepted picture of the Richardson–Kolmogorov cascade (Hurst & Vassilicos Reference Hurst and Vassilicos2007; Vassilicos Reference Vassilicos2015, and references therein). While some of those findings have been reconciled with classic turbulence phenomenology (Hearst & Lavoie Reference Hearst and Lavoie2014; Vassilicos Reference Vassilicos2015), such line of investigation has revived the debate on integral quantities, their definition, and their scaling properties (Mazellier & Vassilicos Reference Mazellier and Vassilicos2008; Valente & Vassilicos Reference Valente and Vassilicos2012). Still, the only study that explicitly addressed the relation between the large-scale anisotropy of velocity and length scales was performed by Bewley, Chang & Bodenschatz (Reference Bewley, Chang and Bodenschatz2012). The authors used the same apparatus described in Chang et al. (Reference Chang, Bewley and Bodenschatz2012) to produce large-scale axisymmetric turbulence with various levels of large-scale anisotropy. They showed that the ratio of the integral lengths along different directions, defined by means of transverse two-point correlations, scaled as a power law of the corresponding r.m.s. (root mean square) velocity ratio. Remarkably, the exponent of the power law was found to be negative, implying that the correlation distance of the velocity fluctuations was smaller in the direction of the stronger turbulence agitation and vice versa.
In the following we present results of an experimental study aimed to advance our understanding of turbulence anisotropy, from the integral to the dissipative scales, providing complementary insights with respect to previous studies. To this end, PIV measurements at multiple resolutions are carried out in a recently introduced facility that generates homogeneous, shearless, anisotropic turbulence in the range
![]() $Re_{\unicode[STIX]{x1D706}}=298{-}496$
. The experimental apparatus and methodology is described in § 2, while in §§ 3, 4 and 5 we directly address questions (i), (ii) and (iii), respectively. Conclusions and outlook for future work are discussed in § 6.
$Re_{\unicode[STIX]{x1D706}}=298{-}496$
. The experimental apparatus and methodology is described in § 2, while in §§ 3, 4 and 5 we directly address questions (i), (ii) and (iii), respectively. Conclusions and outlook for future work are discussed in § 6.
2 Apparatus and methodology
2.1 Zero-mean-flow turbulence chamber
The experimental apparatus and instrumentation was presented and qualified in Carter et al. (Reference Carter, Petersen, Amili and Coletti2016), and only a brief description will be given here. The facility consists of a 5 m
![]() $^{3}$
chamber in which full optical access is provided by the acrylic walls and ceiling. Two facing panels within the chamber accommodate arrays of 128 ports each, fed by pressurized air at 700 kPa and controlled by solenoid valves. The latter are individually actuated to fire quasi-synthetic air jets in randomized sequence, according to the algorithm proposed by Variano & Cowen (Reference Variano and Cowen2008). The jet interaction produces turbulence which is approximately homogeneous, with no mean shear and negligible mean flow over a volume of
$^{3}$
chamber in which full optical access is provided by the acrylic walls and ceiling. Two facing panels within the chamber accommodate arrays of 128 ports each, fed by pressurized air at 700 kPa and controlled by solenoid valves. The latter are individually actuated to fire quasi-synthetic air jets in randomized sequence, according to the algorithm proposed by Variano & Cowen (Reference Variano and Cowen2008). The jet interaction produces turbulence which is approximately homogeneous, with no mean shear and negligible mean flow over a volume of
![]() ${\approx}0.5\times 0.7\times 0.4$
m
${\approx}0.5\times 0.7\times 0.4$
m
![]() $^{3}$
at the centre of the chamber. A conceptual sketch of the chamber is provided in figure 1;
$^{3}$
at the centre of the chamber. A conceptual sketch of the chamber is provided in figure 1;
![]() $x_{1}$
indicates the direction parallel to the jet axis,
$x_{1}$
indicates the direction parallel to the jet axis,
![]() $x_{2}$
and
$x_{2}$
and
![]() $x_{3}$
are the transverse (vertical and horizontal, respectively) directions. The Reynolds number can be adjusted by varying the average firing time of the jets (
$x_{3}$
are the transverse (vertical and horizontal, respectively) directions. The Reynolds number can be adjusted by varying the average firing time of the jets (
![]() $\unicode[STIX]{x1D707}_{on}$
), as increasing the latter results in an increase of both the length scales and the r.m.s. velocity fluctuations. Here we consider five cases with
$\unicode[STIX]{x1D707}_{on}$
), as increasing the latter results in an increase of both the length scales and the r.m.s. velocity fluctuations. Here we consider five cases with
![]() $\unicode[STIX]{x1D707}_{on}$
ranging between 100 ms and 3.2 s.
$\unicode[STIX]{x1D707}_{on}$
ranging between 100 ms and 3.2 s.

Figure 1. Illustration of the experimental set-up.
The facility is inspired by the jet-stirred water tank of Bellani & Variano (Reference Bellani and Variano2014), which produces isotropic turbulence at the large scales. Here, on the other hand, significant large-scale anisotropy is present, and indeed the resulting turbulent flow possesses several features that make it especially well suited for investigating scale-to-scale anisotropy. Firstly, the homogeneity allows neglecting the effect of the spatial gradient of turbulent kinetic energy typical of decaying grid turbulence (Maxey Reference Maxey1987). Secondly, the lack of mean shear allows investigating the anisotropy without the influence of complex shear production mechanisms (Veeravalli & Warhaft Reference Veeravalli and Warhaft1989; Mydlarski & Warhaft Reference Mydlarski and Warhaft1996; Biferale & Toschi Reference Biferale and Toschi2001). These features are also present in the apparatus used by Bewley et al. (Reference Bewley, Chang and Bodenschatz2012) and Chang et al. (Reference Chang, Bewley and Bodenschatz2012). However, in their device the region where the turbulence is approximately homogeneous is smaller than the integral scale – a limitation shared by turbulence chambers with spherical symmetry, as discussed by Bellani & Variano (Reference Bellani and Variano2014). This is not the case in the present system: as in other recently introduced devices featuring planar jet arrays (Khorsandi, Gaskin & Mydlarski Reference Khorsandi, Gaskin and Mydlarski2013; Bellani & Variano Reference Bellani and Variano2014), the large homogeneous region allows for the natural development of the full energy cascade without the influence of mean shear or strain. Finally, the lack of mean flow is beneficial for the measurement accuracy, as we discuss in the following section.
2.2 Velocity measurements
PIV measurements are performed along the
![]() $x_{1}{-}x_{2}$
symmetry plane at the centre of the chamber. The flow is seeded with 1–2
$x_{1}{-}x_{2}$
symmetry plane at the centre of the chamber. The flow is seeded with 1–2
![]() $\unicode[STIX]{x03BC}$
m DEHS (di-ethyl-hexyl-sebacate) droplets, illuminated by a 532 nm Nd:YAG laser and imaged by a 4 megapixel CCD camera. The Stokes number of the seeding, defined as
$\unicode[STIX]{x03BC}$
m DEHS (di-ethyl-hexyl-sebacate) droplets, illuminated by a 532 nm Nd:YAG laser and imaged by a 4 megapixel CCD camera. The Stokes number of the seeding, defined as
![]() $St=\unicode[STIX]{x1D70F}_{d}/\unicode[STIX]{x1D70F}_{f}$
(where
$St=\unicode[STIX]{x1D70F}_{d}/\unicode[STIX]{x1D70F}_{f}$
(where
![]() $\unicode[STIX]{x1D70F}_{d}$
is the aerodynamic response time of the droplets and
$\unicode[STIX]{x1D70F}_{d}$
is the aerodynamic response time of the droplets and
![]() $\unicode[STIX]{x1D70F}_{f}$
is a time scale of the flow) must be much smaller than unity for the droplet to faithfully follow the flow. Here, taking
$\unicode[STIX]{x1D70F}_{f}$
is a time scale of the flow) must be much smaller than unity for the droplet to faithfully follow the flow. Here, taking
![]() $\unicode[STIX]{x1D70F}_{f}$
as the Kolmogorov time of the turbulence,
$\unicode[STIX]{x1D70F}_{f}$
as the Kolmogorov time of the turbulence,
![]() $St$
is of order
$St$
is of order
![]() $10^{-3}$
. The laser pulse separation is chosen such that the particle displacement is limited to 4–5 pixels to reduce out-of-plane loss of particles. Velocity fields are processed using an iterative cross-correlation algorithm, with final interrogation windows of 32 pixel
$10^{-3}$
. The laser pulse separation is chosen such that the particle displacement is limited to 4–5 pixels to reduce out-of-plane loss of particles. Velocity fields are processed using an iterative cross-correlation algorithm, with final interrogation windows of 32 pixel
![]() $\times$
32 pixel and 50 % overlap. Measurements are obtained by mounting Nikon lenses of either 50 mm or 200 mm focal length. The former provides a field of view (FOV) large enough to capture the integral scales, while the latter resolves the dissipative scales of the flow (see table 1). Spatial derivatives are calculated with a second-order central difference scheme, after applying on the velocity fields a Gaussian filter with a kernel size matching the interrogation window size (Ganapathisubramani et al.
Reference Ganapathisubramani, Lakshminarasimhan and Clemens2007). The vector spacing ranges between
$\times$
32 pixel and 50 % overlap. Measurements are obtained by mounting Nikon lenses of either 50 mm or 200 mm focal length. The former provides a field of view (FOV) large enough to capture the integral scales, while the latter resolves the dissipative scales of the flow (see table 1). Spatial derivatives are calculated with a second-order central difference scheme, after applying on the velocity fields a Gaussian filter with a kernel size matching the interrogation window size (Ganapathisubramani et al.
Reference Ganapathisubramani, Lakshminarasimhan and Clemens2007). The vector spacing ranges between
![]() $1\unicode[STIX]{x1D702}$
and
$1\unicode[STIX]{x1D702}$
and
![]() $1.5\unicode[STIX]{x1D702}$
(
$1.5\unicode[STIX]{x1D702}$
(
![]() $\unicode[STIX]{x1D702}$
being the Kolmogorov length scale), which is well within the margin of
$\unicode[STIX]{x1D702}$
being the Kolmogorov length scale), which is well within the margin of
![]() $3\unicode[STIX]{x1D702}$
suggested by Worth, Nickels & Swaminathan (Reference Worth, Nickels and Swaminathan2010) to accurately resolve the gradient fields and calculate sensitive quantities such as the dissipation rate.
$3\unicode[STIX]{x1D702}$
suggested by Worth, Nickels & Swaminathan (Reference Worth, Nickels and Swaminathan2010) to accurately resolve the gradient fields and calculate sensitive quantities such as the dissipation rate.
Table 1. Imaging parameters for the PIV measurements. Normalized quantities are given over a range from minimum to maximum
![]() $Re_{\unicode[STIX]{x1D706}}$
.
$Re_{\unicode[STIX]{x1D706}}$
.

For each considered case, statistics are based on 2000 uncorrelated fields acquired at 7.25 Hz, with averaging over both time and space. The
![]() $64\times 64$
independent interrogation windows in each velocity field yield
$64\times 64$
independent interrogation windows in each velocity field yield
![]() ${\approx}10^{7}$
data points, which significantly reduces the error associated with the statistical sampling. Space–time averaging is justified by the high degree of homogeneity. The spatial variations are below 10 % for second-order statistics over the large FOV (Carter et al.
Reference Carter, Petersen, Amili and Coletti2016). Over the small FOV the variation of higher-order statistics, such as the turbulence dissipation, are also below 10 %, which allows us to obtain converged statistics up to the sixth order.
${\approx}10^{7}$
data points, which significantly reduces the error associated with the statistical sampling. Space–time averaging is justified by the high degree of homogeneity. The spatial variations are below 10 % for second-order statistics over the large FOV (Carter et al.
Reference Carter, Petersen, Amili and Coletti2016). Over the small FOV the variation of higher-order statistics, such as the turbulence dissipation, are also below 10 %, which allows us to obtain converged statistics up to the sixth order.
As mentioned, the lack of mean flow is also greatly beneficial for the accuracy of the calculated velocity fields. In advective flows with turbulent intensity of 10–20 % (as in boundary layers or jets), the velocity fluctuations represent just 1–2 pixels of the typical 8–10 pixel particle displacement, and sub-pixel accuracy is critical to limit the relative error (Christensen Reference Christensen2004). On the other hand, in the present zero-mean-flow configuration, the entire range of pixel displacement is associated with the turbulent fluctuations. This allows maintaining of the bias error to be of the same order as, or below, the statistical sampling error. Using the methods described in Raffel et al. (Reference Raffel, Willert, Wereley and Kompenhans2007) and Adrian & Westerweel (Reference Adrian and Westerweel2011), we estimate a total uncertainty of 4 % on the r.m.s. velocity and a precision uncertainty of 8 % on the r.m.s. velocity derivatives.
2.3 Basic flow properties
Basic statistics for the considered cases are reported in table 2. The large-scale quantities (r.m.s. fluctuations and integral scales) are obtained from the low-resolution/large-FOV measurements, while the small-scale quantities (turbulent dissipation and Kolmogorov scales) are based on the high-resolution/small-FOV measurements. The realizations at different resolutions are not acquired simultaneously, but it is verified that both measured components of the r.m.s. fluctuations agree within a few per cent when calculated from small and large FOV. For all cases the anisotropy ratio
![]() $u_{1}^{\prime }/u_{2}^{\prime }$
is significantly larger than 1 (
$u_{1}^{\prime }/u_{2}^{\prime }$
is significantly larger than 1 (
![]() $u_{1}$
,
$u_{1}$
,
![]() $u_{2}$
and
$u_{2}$
and
![]() $u_{3}$
are the fluctuating velocity components in direction
$u_{3}$
are the fluctuating velocity components in direction
![]() $x_{1}$
,
$x_{1}$
,
![]() $x_{2}$
and
$x_{2}$
and
![]() $x_{3}$
, respectively, and the prime denotes r.m.s. quantities). In the considered range of jet forcing parameters, increasing the average firing time of the jets leads to both higher
$x_{3}$
, respectively, and the prime denotes r.m.s. quantities). In the considered range of jet forcing parameters, increasing the average firing time of the jets leads to both higher
![]() $Re_{\unicode[STIX]{x1D706}}$
and larger
$Re_{\unicode[STIX]{x1D706}}$
and larger
![]() $u_{1}^{\prime }/u_{2}^{\prime }$
. This prevents us from independently assessing the influence of both parameters on the turbulence properties, but will not affect our main conclusions. Because the relation between
$u_{1}^{\prime }/u_{2}^{\prime }$
. This prevents us from independently assessing the influence of both parameters on the turbulence properties, but will not affect our main conclusions. Because the relation between
![]() $Re_{\unicode[STIX]{x1D706}}$
and
$Re_{\unicode[STIX]{x1D706}}$
and
![]() $u_{1}^{\prime }/u_{2}^{\prime }$
is approximately linear (figure 2), in the following the various quantities will be plotted as a function of Reynolds number, implying similar trends with large-scale anisotropy.
$u_{1}^{\prime }/u_{2}^{\prime }$
is approximately linear (figure 2), in the following the various quantities will be plotted as a function of Reynolds number, implying similar trends with large-scale anisotropy.
Table 2. Basic statistics for the five investigated flow configurations.


Figure 2. Reynolds number based on the Taylor microscale plotted versus anisotropy ratio.
Because the flow results from the interaction of several parallel jets, which individually are well described by the axisymmetric turbulence framework (George & Hussein Reference George and Hussein1991; Ganapathisubramani et al.
Reference Ganapathisubramani, Lakshminarasimhan and Clemens2008), we assume axisymmetry around direction
![]() $x_{1}$
. Therefore in the following we refer to
$x_{1}$
. Therefore in the following we refer to
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{2}$
as the axial and radial direction, respectively. This assumption is supported by three-dimensional measurements in similar facilities (Khorsandi et al.
Reference Khorsandi, Gaskin and Mydlarski2013; Bellani & Variano Reference Bellani and Variano2014; Pérez-Alvarado, Mydlarski & Gaskin Reference Pérez-Alvarado, Mydlarski and Gaskin2016). Axisymmetric turbulence was also found to describe reasonably well grid turbulence, plane cylinder wakes and homogeneous mixing layers (George Reference George1992; Mi & Antonia Reference Mi and Antonia2010; Cardesa, Nickels & Dawson Reference Cardesa, Nickels and Dawson2012; Rabey, Wynn & Buxton Reference Rabey, Wynn and Buxton2015). We thus calculate the mean dissipation directly from the measured velocity gradients using the axisymmetric relation introduced by George & Hussein (Reference George and Hussein1991):
$x_{2}$
as the axial and radial direction, respectively. This assumption is supported by three-dimensional measurements in similar facilities (Khorsandi et al.
Reference Khorsandi, Gaskin and Mydlarski2013; Bellani & Variano Reference Bellani and Variano2014; Pérez-Alvarado, Mydlarski & Gaskin Reference Pérez-Alvarado, Mydlarski and Gaskin2016). Axisymmetric turbulence was also found to describe reasonably well grid turbulence, plane cylinder wakes and homogeneous mixing layers (George Reference George1992; Mi & Antonia Reference Mi and Antonia2010; Cardesa, Nickels & Dawson Reference Cardesa, Nickels and Dawson2012; Rabey, Wynn & Buxton Reference Rabey, Wynn and Buxton2015). We thus calculate the mean dissipation directly from the measured velocity gradients using the axisymmetric relation introduced by George & Hussein (Reference George and Hussein1991):
where
![]() $\unicode[STIX]{x1D622}_{ij}=\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}$
is the velocity gradient tensor and the brackets denote the ensemble average over space and time. This estimate was shown to agree well with the one based on the second-order structure function in the present flow (Carter et al.
Reference Carter, Petersen, Amili and Coletti2016). We can then calculate the Kolmogorov length scale
$\unicode[STIX]{x1D622}_{ij}=\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}$
is the velocity gradient tensor and the brackets denote the ensemble average over space and time. This estimate was shown to agree well with the one based on the second-order structure function in the present flow (Carter et al.
Reference Carter, Petersen, Amili and Coletti2016). We can then calculate the Kolmogorov length scale
![]() $\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D716})^{1/4}$
and time scale
$\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D716})^{1/4}$
and time scale
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}=(\unicode[STIX]{x1D708}/\unicode[STIX]{x1D716})^{1/2}$
, where
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}=(\unicode[STIX]{x1D708}/\unicode[STIX]{x1D716})^{1/2}$
, where
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity of air. The Taylor microscale is defined, assuming small-scale isotropy, as
$\unicode[STIX]{x1D708}$
is the kinematic viscosity of air. The Taylor microscale is defined, assuming small-scale isotropy, as
![]() $\unicode[STIX]{x1D706}=\sqrt{15\unicode[STIX]{x1D708}(u^{\prime })^{2}/\unicode[STIX]{x1D716}}$
, from which we calculate
$\unicode[STIX]{x1D706}=\sqrt{15\unicode[STIX]{x1D708}(u^{\prime })^{2}/\unicode[STIX]{x1D716}}$
, from which we calculate
![]() $Re_{\unicode[STIX]{x1D706}}=u^{\prime }\unicode[STIX]{x1D706}/\unicode[STIX]{x1D708}$
. Here
$Re_{\unicode[STIX]{x1D706}}=u^{\prime }\unicode[STIX]{x1D706}/\unicode[STIX]{x1D708}$
. Here
![]() $u^{\prime }$
is the weighted average between
$u^{\prime }$
is the weighted average between
![]() $u_{1}^{\prime }$
and
$u_{1}^{\prime }$
and
![]() $u_{2}^{\prime }$
assuming axisymmetry (see Carter et al.
Reference Carter, Petersen, Amili and Coletti2016). Because, as we will show, local isotropy is not satisfied in the present flow, these definitions of
$u_{2}^{\prime }$
assuming axisymmetry (see Carter et al.
Reference Carter, Petersen, Amili and Coletti2016). Because, as we will show, local isotropy is not satisfied in the present flow, these definitions of
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $Re_{\unicode[STIX]{x1D706}}$
shall be regarded as conventional and have been in use following the work of Fulachier & Antonia (Reference Fulachier and Antonia1983). In table 2 we also report the integral length scale associated with fluctuations
$Re_{\unicode[STIX]{x1D706}}$
shall be regarded as conventional and have been in use following the work of Fulachier & Antonia (Reference Fulachier and Antonia1983). In table 2 we also report the integral length scale associated with fluctuations
![]() $u_{1}$
over separations aligned with
$u_{1}$
over separations aligned with
![]() $x_{1}$
, which we calculate from the two-point velocity correlation function over the large FOV. Details are given in § 5.
$x_{1}$
, which we calculate from the two-point velocity correlation function over the large FOV. Details are given in § 5.
3 Anisotropy through the inertial scales
To address the propagation of anisotropy through the inertial scales we investigate the structure functions defined over separation
![]() $\boldsymbol{r}$
:
$\boldsymbol{r}$
:
where no index summation is implied. In homogeneous flows it is independent of the position vector
![]() $\boldsymbol{x}$
. According to K41, for separations
$\boldsymbol{x}$
. According to K41, for separations
![]() $r_{j}$
in the inertial range:
$r_{j}$
in the inertial range:
K41 further predicts
![]() $\unicode[STIX]{x1D701}_{n}=n/3$
and
$\unicode[STIX]{x1D701}_{n}=n/3$
and
![]() $C_{n}$
being constant. We distinguish between the longitudinal structure functions (LSF), for which the velocity component
$C_{n}$
being constant. We distinguish between the longitudinal structure functions (LSF), for which the velocity component
![]() $u_{i}$
is parallel to the separation, and the transverse structure function (TSF), for which
$u_{i}$
is parallel to the separation, and the transverse structure function (TSF), for which
![]() $u_{i}$
is normal to it. In the following we denote them as
$u_{i}$
is normal to it. In the following we denote them as
![]() $D_{L}^{n}$
and
$D_{L}^{n}$
and
![]() $D_{T}^{n}$
, respectively. The inertial range is classically identified as the separation interval over which the third-order LSF scales linearly with
$D_{T}^{n}$
, respectively. The inertial range is classically identified as the separation interval over which the third-order LSF scales linearly with
![]() $r_{j}$
(from
$r_{j}$
(from
![]() $\unicode[STIX]{x1D701}_{3}=1$
). LSFs and TSFs, and especially their scaling properties, have been explored in many studies investigating scale-to-scale turbulence dynamics. However, unlike in most previous experiments using pointwise techniques, PIV provides access to both LSF and TSF associated with displacements along two directions: the axial direction
$\unicode[STIX]{x1D701}_{3}=1$
). LSFs and TSFs, and especially their scaling properties, have been explored in many studies investigating scale-to-scale turbulence dynamics. However, unlike in most previous experiments using pointwise techniques, PIV provides access to both LSF and TSF associated with displacements along two directions: the axial direction
![]() $x_{1}$
and the radial direction
$x_{1}$
and the radial direction
![]() $x_{2}$
. Therefore, we are able to investigate the four quantities:
$x_{2}$
. Therefore, we are able to investigate the four quantities:
which according to the postulate of local isotropy should all have the same scaling behaviour. This is explicitly tested for in the following, along with other isotropic relations. In the analysis of structure functions we utilize the small-FOV/high-resolution measurements, in view of the use of extended self-similarity (Benzi et al. Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993) which extends the scaling range down to the near-dissipative scales (see § 3.2).
3.1 Second-order structure functions
Assuming local isotropy, the following relation holds between second-order LSF and TSF (Monin & Yaglom Reference Monin and Yaglom1975):
where again no index summation is implied. Figure 3 displays second-order LSFs and TSFs with separations along both spatial directions, as well as the TSFs obtained from (3.7). Two representative cases at
![]() $Re_{\unicode[STIX]{x1D706}}=298$
and
$Re_{\unicode[STIX]{x1D706}}=298$
and
![]() $Re_{\unicode[STIX]{x1D706}}=476$
are shown. In both cases the measured
$Re_{\unicode[STIX]{x1D706}}=476$
are shown. In both cases the measured
![]() $D_{T}^{2}(r_{2})$
agrees reasonably well with the isotropic prediction based on the measured
$D_{T}^{2}(r_{2})$
agrees reasonably well with the isotropic prediction based on the measured
![]() $D_{L}^{2}(r_{2})$
. This is not the case, however, for
$D_{L}^{2}(r_{2})$
. This is not the case, however, for
![]() $D_{T}^{2}(r_{1})$
: along the axial direction the second-order structure functions show significant departure from isotropy across all scales. (At the larger scales significant departure from (3.7) is expected, as in the limit
$D_{T}^{2}(r_{1})$
: along the axial direction the second-order structure functions show significant departure from isotropy across all scales. (At the larger scales significant departure from (3.7) is expected, as in the limit
![]() $r\rightarrow \infty$
this requires
$r\rightarrow \infty$
this requires
![]() $D_{L}^{2}=D_{T}^{2}$
, hence
$D_{L}^{2}=D_{T}^{2}$
, hence
![]() $u_{1}^{\prime }=u_{2}^{\prime }$
, in contrast with the actual large-scale anisotropy.) Romano & Antonia (Reference Romano and Antonia2001) found that, in turbulent jets at
$u_{1}^{\prime }=u_{2}^{\prime }$
, in contrast with the actual large-scale anisotropy.) Romano & Antonia (Reference Romano and Antonia2001) found that, in turbulent jets at
![]() $Re_{\unicode[STIX]{x1D706}}=500$
and anisotropy ratios ranging from 1.18 to 1.32,
$Re_{\unicode[STIX]{x1D706}}=500$
and anisotropy ratios ranging from 1.18 to 1.32,
![]() $D_{T}^{2}(r_{1})$
obtained with (3.7) had a closer scaling behaviour to
$D_{T}^{2}(r_{1})$
obtained with (3.7) had a closer scaling behaviour to
![]() $D_{L}^{2}(r_{1})$
than the directly measured
$D_{L}^{2}(r_{1})$
than the directly measured
![]() $D_{T}^{2}(r_{1})$
. They concluded that anisotropy was the main cause of the different scaling behaviour of the second-order LSF and TSF along the axial direction. Such tendency is found also for the present flow as shown in figure 3, where
$D_{T}^{2}(r_{1})$
. They concluded that anisotropy was the main cause of the different scaling behaviour of the second-order LSF and TSF along the axial direction. Such tendency is found also for the present flow as shown in figure 3, where
![]() $D_{L}^{2}(r_{1})$
and
$D_{L}^{2}(r_{1})$
and
![]() $D_{T}^{2}(r_{1})$
(both measured and calculated) are also plotted in logarithmic scale, along with the expected slope according to K41.
$D_{T}^{2}(r_{1})$
(both measured and calculated) are also plotted in logarithmic scale, along with the expected slope according to K41.

Figure 3. Measured second-order LSFs (continuous grey line) and TSFs (continuous black line) and TSFs calculated with (3.7) (dash-dotted line), for
![]() $Re_{\unicode[STIX]{x1D706}}=298$
(a–c) and
$Re_{\unicode[STIX]{x1D706}}=298$
(a–c) and
![]() $Re_{\unicode[STIX]{x1D706}}=476$
(d–f). Separations are along the axial (a,c,d,f) and radial (b,e) directions. The blue line in the log-scale plots (c,f) indicates the
$Re_{\unicode[STIX]{x1D706}}=476$
(d–f). Separations are along the axial (a,c,d,f) and radial (b,e) directions. The blue line in the log-scale plots (c,f) indicates the
![]() $2/3$
law.
$2/3$
law.

Figure 4. Ratio of LSFs (solid) and TSFs (dashed) versus separation distance for
![]() $Re_{\unicode[STIX]{x1D706}}=298$
(a) and 476 (b).
$Re_{\unicode[STIX]{x1D706}}=298$
(a) and 476 (b).
A direct comparison of the second-order structure functions in the axial versus radial direction is provided by the ratios
![]() $D_{L}^{2}(r_{1})/D_{L}^{2}(r_{2})$
and
$D_{L}^{2}(r_{1})/D_{L}^{2}(r_{2})$
and
![]() $D_{T}^{2}(r_{1})/D_{T}^{2}(r_{2})$
, shown in figure 4 for cases
$D_{T}^{2}(r_{1})/D_{T}^{2}(r_{2})$
, shown in figure 4 for cases
![]() $Re_{\unicode[STIX]{x1D706}}=298$
and 476. At small separations the ratios are relatively close to unity, suggesting a return to isotropy at least for structure functions of the second order. However, across all scales captured in the FOV, the ratios exhibit a monotonic increasing trend for increasing separation, indicating different scaling behaviours along both directions. The ratio
$Re_{\unicode[STIX]{x1D706}}=298$
and 476. At small separations the ratios are relatively close to unity, suggesting a return to isotropy at least for structure functions of the second order. However, across all scales captured in the FOV, the ratios exhibit a monotonic increasing trend for increasing separation, indicating different scaling behaviours along both directions. The ratio
![]() $D_{T}^{2}(r_{1})/D_{T}^{2}(r_{2})$
was reported by Chang et al. (Reference Chang, Bewley and Bodenschatz2012) in their homogeneous turbulence chamber for different anisotropy ratios. Although there was substantial scatter, the authors found that within the inertial range the ratio was close to unity, and concluded that anisotropy did not affect the scaling of second-order structure functions. A possible reason for this discrepancy with respect to our results is the different type of flow configurations considered in the two studies: both are jet-stirred zero-mean-flow devices, but Chang et al. (Reference Chang, Bewley and Bodenschatz2012) used a spherical chamber. Moreover we notice that, if one considers only the ratio
$D_{T}^{2}(r_{1})/D_{T}^{2}(r_{2})$
was reported by Chang et al. (Reference Chang, Bewley and Bodenschatz2012) in their homogeneous turbulence chamber for different anisotropy ratios. Although there was substantial scatter, the authors found that within the inertial range the ratio was close to unity, and concluded that anisotropy did not affect the scaling of second-order structure functions. A possible reason for this discrepancy with respect to our results is the different type of flow configurations considered in the two studies: both are jet-stirred zero-mean-flow devices, but Chang et al. (Reference Chang, Bewley and Bodenschatz2012) used a spherical chamber. Moreover we notice that, if one considers only the ratio
![]() $D_{L}^{2}(r_{1})/D_{L}^{2}(r_{2})$
for the higher Reynolds number (close to that of Chang et al.
Reference Chang, Bewley and Bodenschatz2012), it could be concluded that the scaling mismatch between axial and radial directions is in fact marginal. In general, the different behaviour of second-order LSFs and TSFs suggests that both directions of velocity fluctuations and separations need to be characterized in order to fully qualify the turbulence structure across scales. This is especially important because, as underlined by figure 3, in the present anisotropic flow one cannot assume the constraint between LSFs and TSFs enforced by (3.7).
$D_{L}^{2}(r_{1})/D_{L}^{2}(r_{2})$
for the higher Reynolds number (close to that of Chang et al.
Reference Chang, Bewley and Bodenschatz2012), it could be concluded that the scaling mismatch between axial and radial directions is in fact marginal. In general, the different behaviour of second-order LSFs and TSFs suggests that both directions of velocity fluctuations and separations need to be characterized in order to fully qualify the turbulence structure across scales. This is especially important because, as underlined by figure 3, in the present anisotropic flow one cannot assume the constraint between LSFs and TSFs enforced by (3.7).
We now consider the value of the Kolmogorov constant
![]() $C_{2}$
, which we can obtain from LSFs and TSFs along different directions. For
$C_{2}$
, which we can obtain from LSFs and TSFs along different directions. For
![]() $n=2$
, within the inertial range K41 predicts:
$n=2$
, within the inertial range K41 predicts:
These relations are often used to obtain estimates of the mean turbulent dissipation (e.g. Variano & Cowen Reference Variano and Cowen2008; de Jong et al.
Reference de Jong, Cao, Woodward, Salazar, Collins and Meng2009; Dou et al.
Reference Dou, Pecenak, Cao, Woodward, Liang and Meng2016). Typically it is assumed
![]() $\unicode[STIX]{x1D701}_{2}^{L}=\unicode[STIX]{x1D701}_{2}^{T}=2/3$
(according to K41) and the constant is taken either as
$\unicode[STIX]{x1D701}_{2}^{L}=\unicode[STIX]{x1D701}_{2}^{T}=2/3$
(according to K41) and the constant is taken either as
![]() $C_{2}=2$
or 2.1 (Sreenivasan Reference Sreenivasan1995; Pope Reference Pope2000); the maximum/plateau of the compensated structure function is usually used to identify the inertial range where the dissipation is evaluated. Here instead we evaluate
$C_{2}=2$
or 2.1 (Sreenivasan Reference Sreenivasan1995; Pope Reference Pope2000); the maximum/plateau of the compensated structure function is usually used to identify the inertial range where the dissipation is evaluated. Here instead we evaluate
![]() $C_{2}$
from (3.8) and (3.9) using the direct measurement of
$C_{2}$
from (3.8) and (3.9) using the direct measurement of
![]() $\unicode[STIX]{x1D716}$
from (2.1), and the values of the LSF and TSF scaling exponents obtained from ESS (see following subsection). Figure 5 shows the compensated LSF and TSF as a function of both axial and radial separations for the case
$\unicode[STIX]{x1D716}$
from (2.1), and the values of the LSF and TSF scaling exponents obtained from ESS (see following subsection). Figure 5 shows the compensated LSF and TSF as a function of both axial and radial separations for the case
![]() $Re_{\unicode[STIX]{x1D706}}=298$
.
$Re_{\unicode[STIX]{x1D706}}=298$
.
![]() $D_{L}^{2}(r_{1})$
and
$D_{L}^{2}(r_{1})$
and
![]() $D_{T}^{2}(r_{2})$
start to plateau but do not reach a maximum within the FOV, while
$D_{T}^{2}(r_{2})$
start to plateau but do not reach a maximum within the FOV, while
![]() $D_{L}^{2}(r_{2})$
and
$D_{L}^{2}(r_{2})$
and
![]() $D_{T}^{2}(r_{1})$
do and we evaluate
$D_{T}^{2}(r_{1})$
do and we evaluate
![]() $C_{2}$
from these. The results in figure 5(c) show significant differences between the value obtained from LSF and from TSF, the former leading to higher values of
$C_{2}$
from these. The results in figure 5(c) show significant differences between the value obtained from LSF and from TSF, the former leading to higher values of
![]() $C_{2}$
than the latter. Moreover, the value of the constant decreases with larger
$C_{2}$
than the latter. Moreover, the value of the constant decreases with larger
![]() $Re_{\unicode[STIX]{x1D706}}$
(and therefore with stronger large-scale anisotropy). The variations are comparable to those found by Chien, Blum & Voth (Reference Chien, Blum and Voth2013) who studied oscillating grid turbulence with
$Re_{\unicode[STIX]{x1D706}}$
(and therefore with stronger large-scale anisotropy). The variations are comparable to those found by Chien, Blum & Voth (Reference Chien, Blum and Voth2013) who studied oscillating grid turbulence with
![]() $Re_{\unicode[STIX]{x1D706}}$
up to 262 and measured changes in
$Re_{\unicode[STIX]{x1D706}}$
up to 262 and measured changes in
![]() $C_{2}$
as large as 20 % depending on the form of the energy input. We remark that our estimates of
$C_{2}$
as large as 20 % depending on the form of the energy input. We remark that our estimates of
![]() $C_{2}$
are subject to significant uncertainty, reflecting the uncertainty in the dissipation measurements (deriving from both measurement errors and the axisymmetric assumption). Here our intent is not to report on specific values of the Kolmogorov constant, and figure 5(c) is not meant to be an attempt to describe a general Reynolds number dependence of
$C_{2}$
are subject to significant uncertainty, reflecting the uncertainty in the dissipation measurements (deriving from both measurement errors and the axisymmetric assumption). Here our intent is not to report on specific values of the Kolmogorov constant, and figure 5(c) is not meant to be an attempt to describe a general Reynolds number dependence of
![]() $C_{2}$
. (In fact it is likely that figure 5(c) rather reflects the dependence of
$C_{2}$
. (In fact it is likely that figure 5(c) rather reflects the dependence of
![]() $C_{2}$
with the anisotropy, which also increases with
$C_{2}$
with the anisotropy, which also increases with
![]() $Re_{\unicode[STIX]{x1D706}}$
.) The aim is to highlight how the different scaling of LSF and TSF, and in general the propagation of the large-scale anisotropy across the inertial scales, may lead to different values of such a constant.
$Re_{\unicode[STIX]{x1D706}}$
.) The aim is to highlight how the different scaling of LSF and TSF, and in general the propagation of the large-scale anisotropy across the inertial scales, may lead to different values of such a constant.

Figure 5. Compensated LSFs along both directions for
![]() $Re_{\unicode[STIX]{x1D706}}=298$
(a), TSFs (b) and the values of
$Re_{\unicode[STIX]{x1D706}}=298$
(a), TSFs (b) and the values of
![]() $C_{2}$
taken from the LSF/TSFs that plateau within the FOV versus
$C_{2}$
taken from the LSF/TSFs that plateau within the FOV versus
![]() $Re_{\unicode[STIX]{x1D706}}$
(c).
$Re_{\unicode[STIX]{x1D706}}$
(c).
3.2 The
 $n$
th-order structure functions and scaling exponents
$n$
th-order structure functions and scaling exponents
We first consider an isotropy test applied to third-order structure functions. Under isotropic conditions we have the following relation (Monin & Yaglom Reference Monin and Yaglom1975):
where
![]() $D_{ijj}^{3}(r_{i})=\langle [u_{i}(x+r_{i})-u_{i}(x)][u_{j}(x+r_{i})-u_{j}(x)]^{2}\rangle$
is a mixed third-order structure function. Similarly to what we have done for relation (3.8), the validity of (3.10) is tested in figure 6 for a representative case (
$D_{ijj}^{3}(r_{i})=\langle [u_{i}(x+r_{i})-u_{i}(x)][u_{j}(x+r_{i})-u_{j}(x)]^{2}\rangle$
is a mixed third-order structure function. Similarly to what we have done for relation (3.8), the validity of (3.10) is tested in figure 6 for a representative case (
![]() $Re_{\unicode[STIX]{x1D706}}=298$
) for both axial and radial separations. The agreement between the measured and calculated mixed structure function appears satisfactory along
$Re_{\unicode[STIX]{x1D706}}=298$
) for both axial and radial separations. The agreement between the measured and calculated mixed structure function appears satisfactory along
![]() $x_{2}$
, while there is substantial mismatch along
$x_{2}$
, while there is substantial mismatch along
![]() $x_{1}$
. This is confirmed by the ratio
$x_{1}$
. This is confirmed by the ratio
![]() $D_{ijj}^{3}(r_{i})/D_{iii}^{3}(r_{i})$
, which only along
$D_{ijj}^{3}(r_{i})/D_{iii}^{3}(r_{i})$
, which only along
![]() $x_{2}$
remains close to the value of
$x_{2}$
remains close to the value of
![]() $1/3$
predicted by K41. This highlights again the importance, in order to assess isotropy, of considering not only the different directions of velocity components but also the different directions of separation.
$1/3$
predicted by K41. This highlights again the importance, in order to assess isotropy, of considering not only the different directions of velocity components but also the different directions of separation.

Figure 6. Mixed third-order structure functions (solid) and (3.10) (dash-dot) along
![]() $x_{1}$
(black) and
$x_{1}$
(black) and
![]() $x_{2}$
(grey) for
$x_{2}$
(grey) for
![]() $Re_{\unicode[STIX]{x1D706}}=298$
(a). Ratio of mixed third-order structure functions to third-order LSFs along
$Re_{\unicode[STIX]{x1D706}}=298$
(a). Ratio of mixed third-order structure functions to third-order LSFs along
![]() $x_{1}$
(black) and
$x_{1}$
(black) and
![]() $x_{2}$
(grey) for the same case with the isotropic
$x_{2}$
(grey) for the same case with the isotropic
![]() $1/3$
line (dashed) superimposed (b).
$1/3$
line (dashed) superimposed (b).
We then consider the scaling exponents of the
![]() $n$
th-order structure functions. These have been investigated in depth in the past, especially as they relate to intermittency and the consequent anomalous scaling, i.e. the departure from the K41 prediction
$n$
th-order structure functions. These have been investigated in depth in the past, especially as they relate to intermittency and the consequent anomalous scaling, i.e. the departure from the K41 prediction
![]() $\unicode[STIX]{x1D701}_{n}=n/3$
(Anselmet et al.
Reference Anselmet, Gagne, Hopfinger and Antonia1984; Sreenivasan & Antonia Reference Sreenivasan and Antonia1997; Siebert, Shaw & Warhaft Reference Siebert, Shaw and Warhaft2010, among many others). The scaling exponents have been studied extensively also in the context of local isotropy, comparing the behaviour of velocity differences in different directions, but without reaching consensus on their trend. Noullez et al. (Reference Noullez, Wallace, Lempert, Miles and Frisch1997) found that the TSF scaling exponent
$\unicode[STIX]{x1D701}_{n}=n/3$
(Anselmet et al.
Reference Anselmet, Gagne, Hopfinger and Antonia1984; Sreenivasan & Antonia Reference Sreenivasan and Antonia1997; Siebert, Shaw & Warhaft Reference Siebert, Shaw and Warhaft2010, among many others). The scaling exponents have been studied extensively also in the context of local isotropy, comparing the behaviour of velocity differences in different directions, but without reaching consensus on their trend. Noullez et al. (Reference Noullez, Wallace, Lempert, Miles and Frisch1997) found that the TSF scaling exponent
![]() $\unicode[STIX]{x1D701}_{n}^{T}$
matched well the LSF scaling exponents
$\unicode[STIX]{x1D701}_{n}^{T}$
matched well the LSF scaling exponents
![]() $\unicode[STIX]{x1D701}_{n}^{L}$
for
$\unicode[STIX]{x1D701}_{n}^{L}$
for
![]() $n=3{-}8$
. On the other hand, several later studies found
$n=3{-}8$
. On the other hand, several later studies found
![]() $\unicode[STIX]{x1D701}_{n}^{T}<\unicode[STIX]{x1D701}_{n}^{L}$
including Dhruva et al. (Reference Dhruva, Tsuji and Sreenivasan1997) up to
$\unicode[STIX]{x1D701}_{n}^{T}<\unicode[STIX]{x1D701}_{n}^{L}$
including Dhruva et al. (Reference Dhruva, Tsuji and Sreenivasan1997) up to
![]() $n=6$
, Romano & Antonia (Reference Romano and Antonia2001) up to
$n=6$
, Romano & Antonia (Reference Romano and Antonia2001) up to
![]() $n=8$
and references therein. In their wind tunnel study Shen & Warhaft (Reference Shen and Warhaft2002) found that, at
$n=8$
and references therein. In their wind tunnel study Shen & Warhaft (Reference Shen and Warhaft2002) found that, at
![]() $Re_{\unicode[STIX]{x1D706}}=1000$
, LSFs with separations parallel to the mean flow and TSFs with separations normal to the mean flow had the same scaling behaviour. They also measured scaling exponents of TSFs with separations along the mean flow, and found them to be significantly smaller than those of TSFs with separations normal to the flow. This was not confirmed by the later experiments of Chang et al. (Reference Chang, Bewley and Bodenschatz2012), who measured TSFs with separations in two perpendicular directions but did not find measurable scaling differences (although they considered only the case
$Re_{\unicode[STIX]{x1D706}}=1000$
, LSFs with separations parallel to the mean flow and TSFs with separations normal to the mean flow had the same scaling behaviour. They also measured scaling exponents of TSFs with separations along the mean flow, and found them to be significantly smaller than those of TSFs with separations normal to the flow. This was not confirmed by the later experiments of Chang et al. (Reference Chang, Bewley and Bodenschatz2012), who measured TSFs with separations in two perpendicular directions but did not find measurable scaling differences (although they considered only the case
![]() $n=2$
).
$n=2$
).
Here we calculate LSF and TSF up to the sixth order, with separations along both axial (i.e.
![]() $\unicode[STIX]{x1D701}_{n}^{L,1}$
,
$\unicode[STIX]{x1D701}_{n}^{L,1}$
,
![]() $\unicode[STIX]{x1D701}_{n}^{T,1}$
) and radial (
$\unicode[STIX]{x1D701}_{n}^{T,1}$
) and radial (
![]() $\unicode[STIX]{x1D701}_{n}^{L,2}$
,
$\unicode[STIX]{x1D701}_{n}^{L,2}$
,
![]() $\unicode[STIX]{x1D701}_{n}^{T,2}$
) directions. To test for convergence, we consider the probability density function (PDF) of the
$\unicode[STIX]{x1D701}_{n}^{T,2}$
) directions. To test for convergence, we consider the probability density function (PDF) of the
![]() $n$
th-order moment of velocity differences. Figure 7 shows a sample distribution for separations in the inertial range for the case
$n$
th-order moment of velocity differences. Figure 7 shows a sample distribution for separations in the inertial range for the case
![]() $Re_{\unicode[STIX]{x1D706}}=476$
; the decreasing tails of the PDFs imply statistical convergence. We obtain the scaling exponents following the extended self-similarity (ESS) approach proposed by Benzi et al. (Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993). In ESS, the structure function of interest is plotted against a structure function of different order, rather than against the physical separation. This significantly extends the scaling range, partly because the sampling undulations are generally correlated among structure functions of different orders (Frisch Reference Frisch1995). The procedure is particularly straightforward when plotting against the third-order LSF, which works as a surrogate for the separation if one assumes
$Re_{\unicode[STIX]{x1D706}}=476$
; the decreasing tails of the PDFs imply statistical convergence. We obtain the scaling exponents following the extended self-similarity (ESS) approach proposed by Benzi et al. (Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993). In ESS, the structure function of interest is plotted against a structure function of different order, rather than against the physical separation. This significantly extends the scaling range, partly because the sampling undulations are generally correlated among structure functions of different orders (Frisch Reference Frisch1995). The procedure is particularly straightforward when plotting against the third-order LSF, which works as a surrogate for the separation if one assumes
![]() $\unicode[STIX]{x1D701}_{3}^{L}=1$
. Moreover, to improve statistical convergence of the odd-order moments, it is customary to consider structure functions of the absolute value of the velocity difference,
$\unicode[STIX]{x1D701}_{3}^{L}=1$
. Moreover, to improve statistical convergence of the odd-order moments, it is customary to consider structure functions of the absolute value of the velocity difference,
![]() $D_{ii}^{|n|}(r)=\langle |u_{i}(x+r)-u_{i}(x)|^{n}\rangle$
, which have marginally different scaling with respect to
$D_{ii}^{|n|}(r)=\langle |u_{i}(x+r)-u_{i}(x)|^{n}\rangle$
, which have marginally different scaling with respect to
![]() $D_{ii}^{n}$
(Benzi et al.
Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993; Sreenivasan et al.
Reference Sreenivasan, Vainshtein, Bhiladvala, San Gil, Chen and Cao1996; Shen & Warhaft Reference Shen and Warhaft2002). In figure 8 the LSFs and the absolute-value LSFs for the case
$D_{ii}^{n}$
(Benzi et al.
Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993; Sreenivasan et al.
Reference Sreenivasan, Vainshtein, Bhiladvala, San Gil, Chen and Cao1996; Shen & Warhaft Reference Shen and Warhaft2002). In figure 8 the LSFs and the absolute-value LSFs for the case
![]() $Re_{\unicode[STIX]{x1D706}}=476$
are plotted against the separation
$Re_{\unicode[STIX]{x1D706}}=476$
are plotted against the separation
![]() $r_{1}$
and against
$r_{1}$
and against
![]() $D_{L}^{|3|}(r_{1})$
, illustrating the extended scaling range.
$D_{L}^{|3|}(r_{1})$
, illustrating the extended scaling range.

Figure 7. Premultiplied PDFs of axial velocity increments for the case
![]() $Re_{\unicode[STIX]{x1D706}}=476$
at separation distance
$Re_{\unicode[STIX]{x1D706}}=476$
at separation distance
![]() ${\approx}40\unicode[STIX]{x1D702}$
corresponding to the smallest sample size used to calculate structure function scaling exponents. The distributions are representative of all measured velocity components and all considered Reynolds numbers.
${\approx}40\unicode[STIX]{x1D702}$
corresponding to the smallest sample size used to calculate structure function scaling exponents. The distributions are representative of all measured velocity components and all considered Reynolds numbers.

Figure 8. Absolute-valued
![]() $n$
th-order structure functions for the case
$n$
th-order structure functions for the case
![]() $Re_{\unicode[STIX]{x1D706}}=476$
plotted against separation distance (a) and against the absolute third-order structure function (b). Local values of
$Re_{\unicode[STIX]{x1D706}}=476$
plotted against separation distance (a) and against the absolute third-order structure function (b). Local values of
![]() $\unicode[STIX]{x1D701}^{L,1}$
for the
$\unicode[STIX]{x1D701}^{L,1}$
for the
![]() $n$
th-order structure function obtained using ESS are shown in (c) for the case
$n$
th-order structure function obtained using ESS are shown in (c) for the case
![]() $Re_{\unicode[STIX]{x1D706}}=298$
. The solid lines in (b,c) show the range over which the exponents are calculated for each case. The dashed lines in (c) correspond to the calculated exponents.
$Re_{\unicode[STIX]{x1D706}}=298$
. The solid lines in (b,c) show the range over which the exponents are calculated for each case. The dashed lines in (c) correspond to the calculated exponents.
The ESS-based scaling exponents for LSF and TSF (in both axial and radial directions) for cases
![]() $Re_{\unicode[STIX]{x1D706}}=298$
and 476 are reported in table 3. These are calculated over the range for which the logarithmic relative slope of the third-order LSF to the absolute-valued third-order LSF is equal to one within
$Re_{\unicode[STIX]{x1D706}}=298$
and 476 are reported in table 3. These are calculated over the range for which the logarithmic relative slope of the third-order LSF to the absolute-valued third-order LSF is equal to one within
![]() ${\sim}$
4 %. This corresponds to separations in the approximate range
${\sim}$
4 %. This corresponds to separations in the approximate range
![]() $15\unicode[STIX]{x1D702}{-}40\unicode[STIX]{x1D702}$
(indicated for
$15\unicode[STIX]{x1D702}{-}40\unicode[STIX]{x1D702}$
(indicated for
![]() $Re_{\unicode[STIX]{x1D706}}=476$
in figure 8(b) and varies slightly depending on the case). For illustration, figure 8(c) shows the local scaling exponents
$Re_{\unicode[STIX]{x1D706}}=476$
in figure 8(b) and varies slightly depending on the case). For illustration, figure 8(c) shows the local scaling exponents
![]() $\unicode[STIX]{x1D701}^{L,1}$
obtained using ESS for the case
$\unicode[STIX]{x1D701}^{L,1}$
obtained using ESS for the case
![]() $Re_{\unicode[STIX]{x1D706}}=298$
, highlighting the scaling range. The latter covers smaller separations than the true inertial range, as an effect of extended similarity (see, e.g. Briscolini et al.
Reference Briscolini, Santangelo, Succi and Benzi1994). The dominant uncertainties in the exponents stem from the standard error of the slopes in the straight line fits and the chosen bound on the ESS scaling range, as these are typically much larger than the error due to measurement or statistical uncertainty. In figure 9 the exponents are compared with the K41 scaling
$Re_{\unicode[STIX]{x1D706}}=298$
, highlighting the scaling range. The latter covers smaller separations than the true inertial range, as an effect of extended similarity (see, e.g. Briscolini et al.
Reference Briscolini, Santangelo, Succi and Benzi1994). The dominant uncertainties in the exponents stem from the standard error of the slopes in the straight line fits and the chosen bound on the ESS scaling range, as these are typically much larger than the error due to measurement or statistical uncertainty. In figure 9 the exponents are compared with the K41 scaling
![]() $\unicode[STIX]{x1D701}_{n}=n/3$
and with the model of She & Leveque (Reference She and Leveque1994). The latter is an intermittency model that assumes a hierarchical distribution of the energy dissipation rate and predicts:
$\unicode[STIX]{x1D701}_{n}=n/3$
and with the model of She & Leveque (Reference She and Leveque1994). The latter is an intermittency model that assumes a hierarchical distribution of the energy dissipation rate and predicts:
The LSF scaling exponent measured with separation in the axial direction, which is the most commonly reported in literature, appears remarkably close to the She & Leveque (Reference She and Leveque1994) model, especially at the higher Reynolds numbers. In figure 9(a) the case at
![]() $Re=476$
is also compared with the benchmark experiments of Shen & Warhaft (Reference Shen and Warhaft2002) (unsheared grid turbulence at
$Re=476$
is also compared with the benchmark experiments of Shen & Warhaft (Reference Shen and Warhaft2002) (unsheared grid turbulence at
![]() $Re_{\unicode[STIX]{x1D706}}=863$
and
$Re_{\unicode[STIX]{x1D706}}=863$
and
![]() $u_{1}^{\prime }/u_{2}^{\prime }=1.71$
), while in figure 9(b) we show a comparison with the measurements of Zhou, Pearson & Antonia (Reference Zhou, Pearson and Antonia2001) (turbulent plane jet at
$u_{1}^{\prime }/u_{2}^{\prime }=1.71$
), while in figure 9(b) we show a comparison with the measurements of Zhou, Pearson & Antonia (Reference Zhou, Pearson and Antonia2001) (turbulent plane jet at
![]() $Re_{\unicode[STIX]{x1D706}}=1000$
and
$Re_{\unicode[STIX]{x1D706}}=1000$
and
![]() $u_{1}^{\prime }/u_{2}^{\prime }=1.7$
) and simulations of Gotoh, Fukayama & Nakano (Reference Gotoh, Fukayama and Nakano2002) (homogeneous isotropic turbulence at
$u_{1}^{\prime }/u_{2}^{\prime }=1.7$
) and simulations of Gotoh, Fukayama & Nakano (Reference Gotoh, Fukayama and Nakano2002) (homogeneous isotropic turbulence at
![]() $Re_{\unicode[STIX]{x1D706}}=460$
). The agreement in terms of
$Re_{\unicode[STIX]{x1D706}}=460$
). The agreement in terms of
![]() $\unicode[STIX]{x1D701}_{n}^{L,1}$
is excellent among all cases, seemingly supporting the statement of Ishihara, Gotoh & Kaneda (Reference Ishihara, Gotoh and Kaneda2009) that LSFs show a universal behaviour independent of the large-scale flow conditions.
$\unicode[STIX]{x1D701}_{n}^{L,1}$
is excellent among all cases, seemingly supporting the statement of Ishihara, Gotoh & Kaneda (Reference Ishihara, Gotoh and Kaneda2009) that LSFs show a universal behaviour independent of the large-scale flow conditions.
Table 3. Scaling exponents of structure functions for two representative cases obtained using ESS (Benzi et al. Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993) with estimated uncertainties in brackets. The bottom row includes the predictions from the model of She & Leveque (Reference She and Leveque1994), equation (3.11).


Figure 9. K41 model (black line) and the model of She & Leveque (Reference She and Leveque1994) (dashed line),
![]() $\unicode[STIX]{x1D701}_{n}^{L,1}$
(open squares),
$\unicode[STIX]{x1D701}_{n}^{L,1}$
(open squares),
![]() $\unicode[STIX]{x1D701}_{n}^{L,2}$
(open circles),
$\unicode[STIX]{x1D701}_{n}^{L,2}$
(open circles),
![]() $\unicode[STIX]{x1D701}_{n}^{T,1}$
(black squares),
$\unicode[STIX]{x1D701}_{n}^{T,1}$
(black squares),
![]() $\unicode[STIX]{x1D701}_{n}^{T,2}$
(black circles) for the case
$\unicode[STIX]{x1D701}_{n}^{T,2}$
(black circles) for the case
![]() $Re_{\unicode[STIX]{x1D706}}=476$
. Comparison with the data of Shen & Warhaft (Reference Shen and Warhaft2002):
$Re_{\unicode[STIX]{x1D706}}=476$
. Comparison with the data of Shen & Warhaft (Reference Shen and Warhaft2002):
![]() $\unicode[STIX]{x1D701}_{n}^{L,1}$
(open triangles),
$\unicode[STIX]{x1D701}_{n}^{L,1}$
(open triangles),
![]() $\unicode[STIX]{x1D701}_{n}^{T,1}$
(grey triangles)
$\unicode[STIX]{x1D701}_{n}^{T,1}$
(grey triangles)
![]() $\unicode[STIX]{x1D701}_{n}^{T,2}$
(black triangles) (a). Comparison with the data of Zhou et al. (Reference Zhou, Pearson and Antonia2001):
$\unicode[STIX]{x1D701}_{n}^{T,2}$
(black triangles) (a). Comparison with the data of Zhou et al. (Reference Zhou, Pearson and Antonia2001):
![]() $\unicode[STIX]{x1D701}_{n}^{L,1}$
(open diamonds),
$\unicode[STIX]{x1D701}_{n}^{L,1}$
(open diamonds),
![]() $\unicode[STIX]{x1D701}_{n}^{T,1}$
(grey diamonds) and the simulations of Gotoh et al. (Reference Gotoh, Fukayama and Nakano2002):
$\unicode[STIX]{x1D701}_{n}^{T,1}$
(grey diamonds) and the simulations of Gotoh et al. (Reference Gotoh, Fukayama and Nakano2002):
![]() $\unicode[STIX]{x1D701}_{n}^{L,1}$
(open triangles),
$\unicode[STIX]{x1D701}_{n}^{L,1}$
(open triangles),
![]() $\unicode[STIX]{x1D701}_{n}^{T,1}$
(grey triangles) (b). Comparison data offset to the right along the abscissa for clarity.
$\unicode[STIX]{x1D701}_{n}^{T,1}$
(grey triangles) (b). Comparison data offset to the right along the abscissa for clarity.
Figure 9 also confirms that the TSF exponents are significantly smaller than the LSF exponents, as consistently reported in the literature (Romano & Antonia Reference Romano and Antonia2001; Ishihara et al.
Reference Ishihara, Gotoh and Kaneda2009, and references therein). Our values of
![]() $\unicode[STIX]{x1D701}_{n}^{T,1}$
are in fair agreement with those of Zhou et al. (Reference Zhou, Pearson and Antonia2001) and Shen & Warhaft (Reference Shen and Warhaft2002), whereas in the direct numerical simulation (DNS) of Gotoh et al. (Reference Gotoh, Fukayama and Nakano2002) the difference between the LSF and TSF scaling exponents is much smaller. This indicates that the large-scale anisotropy (absent in the DNS) crucially contributes to the inequality
$\unicode[STIX]{x1D701}_{n}^{T,1}$
are in fair agreement with those of Zhou et al. (Reference Zhou, Pearson and Antonia2001) and Shen & Warhaft (Reference Shen and Warhaft2002), whereas in the direct numerical simulation (DNS) of Gotoh et al. (Reference Gotoh, Fukayama and Nakano2002) the difference between the LSF and TSF scaling exponents is much smaller. This indicates that the large-scale anisotropy (absent in the DNS) crucially contributes to the inequality
![]() $\unicode[STIX]{x1D701}_{n}^{T}<\unicode[STIX]{x1D701}_{n}^{L}$
. This was also argued by Romano & Antonia (Reference Romano and Antonia2001), who showed similar differences between
$\unicode[STIX]{x1D701}_{n}^{T}<\unicode[STIX]{x1D701}_{n}^{L}$
. This was also argued by Romano & Antonia (Reference Romano and Antonia2001), who showed similar differences between
![]() $\unicode[STIX]{x1D701}_{n}^{T,1}$
and
$\unicode[STIX]{x1D701}_{n}^{T,1}$
and
![]() $\unicode[STIX]{x1D701}_{n}^{L,1}$
in turbulent jets with Reynolds number and large-scale anisotropy comparable to ours. Our data also indicate
$\unicode[STIX]{x1D701}_{n}^{L,1}$
in turbulent jets with Reynolds number and large-scale anisotropy comparable to ours. Our data also indicate
![]() $\unicode[STIX]{x1D701}_{n}^{T,2}<\unicode[STIX]{x1D701}_{n}^{L,1}$
. Shen & Warhaft (Reference Shen and Warhaft2002) found a similar scaling difference at
$\unicode[STIX]{x1D701}_{n}^{T,2}<\unicode[STIX]{x1D701}_{n}^{L,1}$
. Shen & Warhaft (Reference Shen and Warhaft2002) found a similar scaling difference at
![]() $Re_{\unicode[STIX]{x1D706}}=134$
, but this became negligible for the
$Re_{\unicode[STIX]{x1D706}}=134$
, but this became negligible for the
![]() $Re_{\unicode[STIX]{x1D706}}=863$
case shown here. The present measurements suggest, however, that the inequality does become weaker with increasing
$Re_{\unicode[STIX]{x1D706}}=863$
case shown here. The present measurements suggest, however, that the inequality does become weaker with increasing
![]() $Re_{\unicode[STIX]{x1D706}}$
, as indicated by figure 10, in which the ratios of the different scaling exponents to
$Re_{\unicode[STIX]{x1D706}}$
, as indicated by figure 10, in which the ratios of the different scaling exponents to
![]() $\unicode[STIX]{x1D701}_{n}^{L,1}$
are plotted for the cases
$\unicode[STIX]{x1D701}_{n}^{L,1}$
are plotted for the cases
![]() $Re_{\unicode[STIX]{x1D706}}=298$
and
$Re_{\unicode[STIX]{x1D706}}=298$
and
![]() $Re_{\unicode[STIX]{x1D706}}=476$
. What is clear is that our data support the original finding of Shen & Warhaft (Reference Shen and Warhaft2002) that
$Re_{\unicode[STIX]{x1D706}}=476$
. What is clear is that our data support the original finding of Shen & Warhaft (Reference Shen and Warhaft2002) that
![]() $\unicode[STIX]{x1D701}_{n}^{T,1}<\unicode[STIX]{x1D701}_{n}^{T,2}$
, which to our knowledge had not been verified elsewhere. This inequality becomes greater with large-scale anisotropy, and the trend is not counterbalanced by the simultaneous increase in Reynolds number. Aside from possible Reynolds number effects, the inequalities
$\unicode[STIX]{x1D701}_{n}^{T,1}<\unicode[STIX]{x1D701}_{n}^{T,2}$
, which to our knowledge had not been verified elsewhere. This inequality becomes greater with large-scale anisotropy, and the trend is not counterbalanced by the simultaneous increase in Reynolds number. Aside from possible Reynolds number effects, the inequalities
![]() $\unicode[STIX]{x1D701}_{n}^{T,1}<\unicode[STIX]{x1D701}_{n}^{T,2}<\unicode[STIX]{x1D701}_{n}^{L,1}$
appear systematic, as suggested by the fact that they become greater with increasing
$\unicode[STIX]{x1D701}_{n}^{T,1}<\unicode[STIX]{x1D701}_{n}^{T,2}<\unicode[STIX]{x1D701}_{n}^{L,1}$
appear systematic, as suggested by the fact that they become greater with increasing
![]() $n$
(figure 10).
$n$
(figure 10).

Figure 10. Ratios of LSF and TSF scaling exponents
![]() $\unicode[STIX]{x1D701}_{n}$
–
$\unicode[STIX]{x1D701}_{n}$
–
![]() $\unicode[STIX]{x1D701}_{n}^{L,1}$
for the cases
$\unicode[STIX]{x1D701}_{n}^{L,1}$
for the cases
![]() $Re_{\unicode[STIX]{x1D706}}=298$
(a) and
$Re_{\unicode[STIX]{x1D706}}=298$
(a) and
![]() $Re_{\unicode[STIX]{x1D706}}=476$
(b).
$Re_{\unicode[STIX]{x1D706}}=476$
(b).
Another observation prompted by figure 9 is that the exponents
![]() $\unicode[STIX]{x1D701}_{n}^{L,2}$
are consistently smaller than
$\unicode[STIX]{x1D701}_{n}^{L,2}$
are consistently smaller than
![]() $\unicode[STIX]{x1D701}_{n}^{L,1}$
. The differences are relatively small, and comparable to the estimated uncertainty, but the trend is consistent at all orders and for all considered Reynolds numbers. This behaviour has not been previously identified; indeed LSFs with separations normal to the flow direction are rarely measured. Different scaling of LSFs in different directions could only be explained as an effect of the asymmetry imposed by the large-scale anisotropy. The inequality
$\unicode[STIX]{x1D701}_{n}^{L,1}$
. The differences are relatively small, and comparable to the estimated uncertainty, but the trend is consistent at all orders and for all considered Reynolds numbers. This behaviour has not been previously identified; indeed LSFs with separations normal to the flow direction are rarely measured. Different scaling of LSFs in different directions could only be explained as an effect of the asymmetry imposed by the large-scale anisotropy. The inequality
![]() $\unicode[STIX]{x1D701}_{n}^{L,2}<\unicode[STIX]{x1D701}_{n}^{L,1}$
would imply that the LSF scaling, at least for the present range of
$\unicode[STIX]{x1D701}_{n}^{L,2}<\unicode[STIX]{x1D701}_{n}^{L,1}$
would imply that the LSF scaling, at least for the present range of
![]() $Re_{\unicode[STIX]{x1D706}}$
, does depend on the large scales, in contrast with the universality usually deduced for LSF by comparing
$Re_{\unicode[STIX]{x1D706}}$
, does depend on the large scales, in contrast with the universality usually deduced for LSF by comparing
![]() $\unicode[STIX]{x1D701}_{n}^{L,1}$
across different flows (Arnéodo et al.
Reference Arnéodo, Baudet, Belin, Benzi, Castaing, Chabaud, Chavarria, Ciliberto, Camussi and Chilla1996; Ishihara et al.
Reference Ishihara, Gotoh and Kaneda2009).
$\unicode[STIX]{x1D701}_{n}^{L,1}$
across different flows (Arnéodo et al.
Reference Arnéodo, Baudet, Belin, Benzi, Castaing, Chabaud, Chavarria, Ciliberto, Camussi and Chilla1996; Ishihara et al.
Reference Ishihara, Gotoh and Kaneda2009).
We conclude this section with a consideration of intermittency. The scaling exponent of the sixth-order LSF is related to the intermittency coefficient
![]() $\unicode[STIX]{x1D707}$
, which features in the main hypothesis of Kolmogorov’s refined similarity theory (Kolmogorov Reference Kolmogorov1962, for brevity K62). Specifically, in order to account for the intermittent nature of the local dissipation which produces departures from K41, Kolmogorov hypothesized:
$\unicode[STIX]{x1D707}$
, which features in the main hypothesis of Kolmogorov’s refined similarity theory (Kolmogorov Reference Kolmogorov1962, for brevity K62). Specifically, in order to account for the intermittent nature of the local dissipation which produces departures from K41, Kolmogorov hypothesized:
where
![]() $\unicode[STIX]{x1D716}_{r}$
is the dissipation evaluated over a region of radius
$\unicode[STIX]{x1D716}_{r}$
is the dissipation evaluated over a region of radius
![]() $r$
. For the sixth-order LSF:
$r$
. For the sixth-order LSF:
which implies a scaling exponent
![]() $\unicode[STIX]{x1D701}_{6}^{L}=2-\unicode[STIX]{x1D707}$
. This relation is usually considered a more robust method of estimating
$\unicode[STIX]{x1D701}_{6}^{L}=2-\unicode[STIX]{x1D707}$
. This relation is usually considered a more robust method of estimating
![]() $\unicode[STIX]{x1D707}$
than, e.g. the autocorrelation of the local dissipation (Anselmet et al.
Reference Anselmet, Gagne, Hopfinger and Antonia1984) (although this approach has been recently criticized by Antonia et al. (Reference Antonia, Djenidi, Danaila and Tang2017), who reappraised previous measurements in planar and circular jets and found a Reynolds number dependence of
$\unicode[STIX]{x1D707}$
than, e.g. the autocorrelation of the local dissipation (Anselmet et al.
Reference Anselmet, Gagne, Hopfinger and Antonia1984) (although this approach has been recently criticized by Antonia et al. (Reference Antonia, Djenidi, Danaila and Tang2017), who reappraised previous measurements in planar and circular jets and found a Reynolds number dependence of
![]() $\unicode[STIX]{x1D701}_{6}^{L}$
). From table 3, at the higher Reynolds number we find
$\unicode[STIX]{x1D701}_{6}^{L}$
). From table 3, at the higher Reynolds number we find
![]() $\unicode[STIX]{x1D701}_{6}^{L,1}=1.77$
. This is in very close agreement with the average value (also ESS based) deduced from the set of experiments compiled by Arnéodo et al. (Reference Arnéodo, Baudet, Belin, Benzi, Castaing, Chabaud, Chavarria, Ciliberto, Camussi and Chilla1996) and consistent with the often reported value of the intermittency exponent
$\unicode[STIX]{x1D701}_{6}^{L,1}=1.77$
. This is in very close agreement with the average value (also ESS based) deduced from the set of experiments compiled by Arnéodo et al. (Reference Arnéodo, Baudet, Belin, Benzi, Castaing, Chabaud, Chavarria, Ciliberto, Camussi and Chilla1996) and consistent with the often reported value of the intermittency exponent
![]() $\unicode[STIX]{x1D707}=0.25\pm 0.05$
(Sreenivasan & Kailasnath Reference Sreenivasan and Kailasnath1993). However, at the same regime we find
$\unicode[STIX]{x1D707}=0.25\pm 0.05$
(Sreenivasan & Kailasnath Reference Sreenivasan and Kailasnath1993). However, at the same regime we find
![]() $\unicode[STIX]{x1D701}_{6}^{L,2}=1.63$
, which would imply
$\unicode[STIX]{x1D701}_{6}^{L,2}=1.63$
, which would imply
![]() $\unicode[STIX]{x1D707}=0.37$
. Such a difference in the intermittency exponent along each direction would imply differing degrees of spatial coherence in accordance with the phenomenology of She & Leveque (Reference She and Leveque1994). While differences in the scaling of LSF and TSF might be accommodated in extended versions of the refined similarity theory (e.g. Chen et al.
Reference Chen, Sreenivasan, Nelkin and Cao1997), there seems to be no obvious way of incorporating non-universal scaling of LSFs in different directions, unless large-scale anisotropy is explicitly accounted for. We remark again that the differences we measure between
$\unicode[STIX]{x1D707}=0.37$
. Such a difference in the intermittency exponent along each direction would imply differing degrees of spatial coherence in accordance with the phenomenology of She & Leveque (Reference She and Leveque1994). While differences in the scaling of LSF and TSF might be accommodated in extended versions of the refined similarity theory (e.g. Chen et al.
Reference Chen, Sreenivasan, Nelkin and Cao1997), there seems to be no obvious way of incorporating non-universal scaling of LSFs in different directions, unless large-scale anisotropy is explicitly accounted for. We remark again that the differences we measure between
![]() $\unicode[STIX]{x1D701}_{n}^{L,1}$
and
$\unicode[STIX]{x1D701}_{n}^{L,1}$
and
![]() $\unicode[STIX]{x1D701}_{n}^{L,2}$
, while seemingly systematic, are comparable with the measurement uncertainty; further measurements with more extensive data records and up to higher orders are warranted to verify this finding.
$\unicode[STIX]{x1D701}_{n}^{L,2}$
, while seemingly systematic, are comparable with the measurement uncertainty; further measurements with more extensive data records and up to higher orders are warranted to verify this finding.
4 Anisotropy at the small scales
4.1 Mean square velocity gradients and related quantities
A common strategy to test the postulate of local isotropy at the dissipative scales is to evaluate moments of the velocity derivatives. In particular, following the ansatz of Taylor (Reference Taylor1935), several authors have evaluated the ratios of the mean square velocity derivatives along different directions and compared them against the expected isotropic values (e.g. Browne et al. Reference Browne, Antonia and Shah1987; George & Hussein Reference George and Hussein1991; Tsinober, Kit & Dracos Reference Tsinober, Kit and Dracos1992; Shafi & Antonia Reference Shafi and Antonia1997; Burattini et al. Reference Burattini, Falchi, Romano and Antonia2010; Gomes-Fernandes, Ganapathisubramani & Vassilicos Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012; Thiesset et al. Reference Thiesset, Danaila and Antonia2013; Valente & Vassilicos Reference Valente and Vassilicos2014). Here we consider the following ratios, which should all be equal to one in isotropic turbulence:
The nomenclature changes among different research groups; when possible we have followed the notation often used by Antonia and coworkers. The following quantities are also expected to be equal to one in K41:
where
![]() $\unicode[STIX]{x1D714}_{3}$
is here the out-of-plane vorticity component. We remark that
$\unicode[STIX]{x1D714}_{3}$
is here the out-of-plane vorticity component. We remark that
![]() $M_{12}=1$
only requires axisymmetry around the
$M_{12}=1$
only requires axisymmetry around the
![]() $x_{1}$
axis. While (4.1)–(4.6) are ratios of second-order moments, equation (4.7) is a third-order quantity and therefore
$x_{1}$
axis. While (4.1)–(4.6) are ratios of second-order moments, equation (4.7) is a third-order quantity and therefore
![]() $G_{1}=1$
, which can be obtained from (3.9) for vanishing separations (see Thiesset et al.
Reference Thiesset, Danaila and Antonia2013), may be expected to be a more stringent isotropy test. The values reported in the literature for these ratios are fairly scattered, even for similar flow configurations; here, we briefly review the general trends.
$G_{1}=1$
, which can be obtained from (3.9) for vanishing separations (see Thiesset et al.
Reference Thiesset, Danaila and Antonia2013), may be expected to be a more stringent isotropy test. The values reported in the literature for these ratios are fairly scattered, even for similar flow configurations; here, we briefly review the general trends.
![]() $K_{1}$
(the ratio reported most often) was found to be larger than one in most previous studies of free shear flows (e.g. Browne et al.
Reference Browne, Antonia and Shah1987; Hussein Reference Hussein1994; Burattini et al.
Reference Burattini, Falchi, Romano and Antonia2010), turbulent boundary layers (Shafi & Antonia Reference Shafi and Antonia1997) and grid turbulence (Tsinober et al.
Reference Tsinober, Kit and Dracos1992; Antonia, Zhou & Zhu Reference Antonia, Zhou and Zhu1998; Lavoie, Djenidi & Antonia Reference Lavoie, Djenidi and Antonia2007; Gomes-Fernandes et al.
Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012; Hearst & Lavoie Reference Hearst and Lavoie2014; Valente & Vassilicos Reference Valente and Vassilicos2014).
$K_{1}$
(the ratio reported most often) was found to be larger than one in most previous studies of free shear flows (e.g. Browne et al.
Reference Browne, Antonia and Shah1987; Hussein Reference Hussein1994; Burattini et al.
Reference Burattini, Falchi, Romano and Antonia2010), turbulent boundary layers (Shafi & Antonia Reference Shafi and Antonia1997) and grid turbulence (Tsinober et al.
Reference Tsinober, Kit and Dracos1992; Antonia, Zhou & Zhu Reference Antonia, Zhou and Zhu1998; Lavoie, Djenidi & Antonia Reference Lavoie, Djenidi and Antonia2007; Gomes-Fernandes et al.
Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012; Hearst & Lavoie Reference Hearst and Lavoie2014; Valente & Vassilicos Reference Valente and Vassilicos2014).
![]() $K_{3}$
was found to be smaller than one in various types of turbulent flows (Browne et al.
Reference Browne, Antonia and Shah1987; Antonia, Kim & Browne Reference Antonia, Kim and Browne1991; Tsinober et al.
Reference Tsinober, Kit and Dracos1992; Shafi & Antonia Reference Shafi and Antonia1997; Antonia et al.
Reference Antonia, Zhou and Zhu1998; Lavoie et al.
Reference Lavoie, Djenidi and Antonia2007; Valente & Vassilicos Reference Valente and Vassilicos2014), although values larger than one were also reported in jets (Hussein Reference Hussein1994; Burattini et al.
Reference Burattini, Falchi, Romano and Antonia2010) and grid turbulence (Gomes-Fernandes et al.
Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012).
$K_{3}$
was found to be smaller than one in various types of turbulent flows (Browne et al.
Reference Browne, Antonia and Shah1987; Antonia, Kim & Browne Reference Antonia, Kim and Browne1991; Tsinober et al.
Reference Tsinober, Kit and Dracos1992; Shafi & Antonia Reference Shafi and Antonia1997; Antonia et al.
Reference Antonia, Zhou and Zhu1998; Lavoie et al.
Reference Lavoie, Djenidi and Antonia2007; Valente & Vassilicos Reference Valente and Vassilicos2014), although values larger than one were also reported in jets (Hussein Reference Hussein1994; Burattini et al.
Reference Burattini, Falchi, Romano and Antonia2010) and grid turbulence (Gomes-Fernandes et al.
Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012).
![]() $K_{5}$
and
$K_{5}$
and
![]() $K_{7}$
were found to be larger than one in both wake flows (Browne et al.
Reference Browne, Antonia and Shah1987) and grid turbulence (Tsinober et al.
Reference Tsinober, Kit and Dracos1992), with
$K_{7}$
were found to be larger than one in both wake flows (Browne et al.
Reference Browne, Antonia and Shah1987) and grid turbulence (Tsinober et al.
Reference Tsinober, Kit and Dracos1992), with
![]() $K_{7}$
typically larger than
$K_{7}$
typically larger than
![]() $K_{5}$
. Shafi & Antonia (Reference Shafi and Antonia1997), Antonia et al. (Reference Antonia, Zhou and Zhu1998) and Lavoie et al. (Reference Lavoie, Djenidi and Antonia2007) found
$K_{5}$
. Shafi & Antonia (Reference Shafi and Antonia1997), Antonia et al. (Reference Antonia, Zhou and Zhu1998) and Lavoie et al. (Reference Lavoie, Djenidi and Antonia2007) found
![]() $K_{\unicode[STIX]{x1D714}_{3}}$
, in general agreement with isotropy, reflecting the fact that in their measurements,
$K_{\unicode[STIX]{x1D714}_{3}}$
, in general agreement with isotropy, reflecting the fact that in their measurements,
![]() $K_{1}>1$
and
$K_{1}>1$
and
![]() $K_{3}<1$
. The measurements of Burattini et al. (Reference Burattini, Falchi, Romano and Antonia2010) indicated that
$K_{3}<1$
. The measurements of Burattini et al. (Reference Burattini, Falchi, Romano and Antonia2010) indicated that
![]() $M_{12}$
was significantly larger than one in a turbulent jet, while Antonia et al. (Reference Antonia, Zhou and Zhu1998), Zhou et al. (Reference Zhou, Antonia, Danaila and Anselmet2000) and Lavoie et al. (Reference Lavoie, Djenidi and Antonia2007) found it to be in close agreement with isotropy in grid turbulence.
$M_{12}$
was significantly larger than one in a turbulent jet, while Antonia et al. (Reference Antonia, Zhou and Zhu1998), Zhou et al. (Reference Zhou, Antonia, Danaila and Anselmet2000) and Lavoie et al. (Reference Lavoie, Djenidi and Antonia2007) found it to be in close agreement with isotropy in grid turbulence.
![]() $G_{1}$
was measured in various bluff body wakes by Thiesset et al. (Reference Thiesset, Danaila and Antonia2013); while there were differences depending on the body geometry, the agreement with isotropy was considered reasonable.
$G_{1}$
was measured in various bluff body wakes by Thiesset et al. (Reference Thiesset, Danaila and Antonia2013); while there were differences depending on the body geometry, the agreement with isotropy was considered reasonable.
We note that the studies mentioned above focused on non-homogeneous and/or decaying flows, and consequently the turbulence structure and in particular the small-scale anisotropy varied spatially, complicating its objective evaluation. Significant variations of the ratios (4.1)–(4.7) above were found, e.g. moving away from the centreline of wakes and jets and in streamwise direction for decaying grid turbulence (especially in the near-wake region). For example Browne et al. (Reference Browne, Antonia and Shah1987) reported values of
![]() $K_{3}$
in the range 0.7–0.4 across a cylinder wake. The degree of spatial variation is different for different ratios, and the trends also vary among different studies.
$K_{3}$
in the range 0.7–0.4 across a cylinder wake. The degree of spatial variation is different for different ratios, and the trends also vary among different studies.
![]() $K_{1}$
and
$K_{1}$
and
![]() $K_{3}$
were found to be fairly constant in the streamwise direction in the grid turbulence study by Valente & Vassilicos (Reference Valente and Vassilicos2014), although the results of Tsinober et al. (Reference Tsinober, Kit and Dracos1992) indicated that
$K_{3}$
were found to be fairly constant in the streamwise direction in the grid turbulence study by Valente & Vassilicos (Reference Valente and Vassilicos2014), although the results of Tsinober et al. (Reference Tsinober, Kit and Dracos1992) indicated that
![]() $K_{1}$
could range between approximately
$K_{1}$
could range between approximately
![]() $1.35{-}2.1$
and
$1.35{-}2.1$
and
![]() $K_{3}$
decayed from approximately 1.05–0.8. The measurements of Antonia et al. (Reference Antonia, Zhou and Zhu1998) suggest that, in grid turbulence,
$K_{3}$
decayed from approximately 1.05–0.8. The measurements of Antonia et al. (Reference Antonia, Zhou and Zhu1998) suggest that, in grid turbulence,
![]() $K_{1}$
and
$K_{1}$
and
![]() $K_{3}$
vary less than
$K_{3}$
vary less than
![]() $M_{12}$
, while one would conclude the opposite from the results of Lavoie et al. (Reference Lavoie, Djenidi and Antonia2007). The latter study achieved a greater degree of isotropy (at both small and large scales) than most other experiments in the literature, likely due to a secondary contraction of the wind tunnel which is thought to help maintain all ratios close to their isotropic value. In general, the differences in flow configuration and the lack of spatial homogeneity make it hard to draw general conclusions. The issue can be partially alleviated by considering zero-mean-flow homogeneous turbulence; however the few previous studies that realized this condition did not report small-scale anisotropy results (with the exception of Ouellette et al. (Reference Ouellette, Xu, Bourgoin and Bodenschatz2006), who however considered only Lagrangian statistics).
$M_{12}$
, while one would conclude the opposite from the results of Lavoie et al. (Reference Lavoie, Djenidi and Antonia2007). The latter study achieved a greater degree of isotropy (at both small and large scales) than most other experiments in the literature, likely due to a secondary contraction of the wind tunnel which is thought to help maintain all ratios close to their isotropic value. In general, the differences in flow configuration and the lack of spatial homogeneity make it hard to draw general conclusions. The issue can be partially alleviated by considering zero-mean-flow homogeneous turbulence; however the few previous studies that realized this condition did not report small-scale anisotropy results (with the exception of Ouellette et al. (Reference Ouellette, Xu, Bourgoin and Bodenschatz2006), who however considered only Lagrangian statistics).

Figure 11. Small-scale ratios for testing isotropy defined by (4.1)–(4.4) (a) and (4.5)–(4.7) (b). The dashed line in both panels indicates the isotropic value of 1. With space–time averaging, the statistical uncertainty for 95 % confidence is comparable to the size of the symbols. Time averaging only returns uncertainties of
![]() ${\approx}$
25 %.
${\approx}$
25 %.
The ratios (4.1)–(4.7) for the present flow are plotted as a function of
![]() $Re_{\unicode[STIX]{x1D706}}$
in figure 11. We note that, in the present set-up, increasing
$Re_{\unicode[STIX]{x1D706}}$
in figure 11. We note that, in the present set-up, increasing
![]() $Re_{\unicode[STIX]{x1D706}}$
implies increasing
$Re_{\unicode[STIX]{x1D706}}$
implies increasing
![]() $u_{1}^{\prime }/u_{2}^{\prime }$
. All
$u_{1}^{\prime }/u_{2}^{\prime }$
. All
![]() $K_{i}$
ratios are significantly larger than one. The level of small-scale anisotropy suggested by these values is significantly higher than what was found, e.g. by Lavoie et al. (Reference Lavoie, Djenidi and Antonia2007) who had an essentially isotropic flow at the large scales. Among the
$K_{i}$
ratios are significantly larger than one. The level of small-scale anisotropy suggested by these values is significantly higher than what was found, e.g. by Lavoie et al. (Reference Lavoie, Djenidi and Antonia2007) who had an essentially isotropic flow at the large scales. Among the
![]() $K_{i}$
ratios,
$K_{i}$
ratios,
![]() $K_{\unicode[STIX]{x1D714}_{3}}$
is furthest from isotropy, likely because here
$K_{\unicode[STIX]{x1D714}_{3}}$
is furthest from isotropy, likely because here
![]() $K_{1}$
and
$K_{1}$
and
![]() $K_{3}$
are both larger than one.
$K_{3}$
are both larger than one.
![]() $G_{1}$
is significantly further from unity than the
$G_{1}$
is significantly further from unity than the
![]() $K_{i}$
ratios, which is expected being the former a third-order quantity.
$K_{i}$
ratios, which is expected being the former a third-order quantity.
![]() $M_{12}$
on the other hand is also distant from isotropy, despite the fact that
$M_{12}$
on the other hand is also distant from isotropy, despite the fact that
![]() $M_{12}=1$
only requires small-scale axisymmetry. All ratios depart from the isotropic value of one with increasing
$M_{12}=1$
only requires small-scale axisymmetry. All ratios depart from the isotropic value of one with increasing
![]() $Re_{\unicode[STIX]{x1D706}}$
, hence with increasing
$Re_{\unicode[STIX]{x1D706}}$
, hence with increasing
![]() $u_{1}^{\prime }/u_{2}^{\prime }$
. The increase in Reynolds number is expected to promote the return to isotropy at the small scales, but apparently the influence of large-scale anisotropy is strong enough to offset this tendency. This points to a direct link between anisotropy at the energetic and dissipative scales.
$u_{1}^{\prime }/u_{2}^{\prime }$
. The increase in Reynolds number is expected to promote the return to isotropy at the small scales, but apparently the influence of large-scale anisotropy is strong enough to offset this tendency. This points to a direct link between anisotropy at the energetic and dissipative scales.

Figure 12. Normalized PDF of the logarithm of dissipation
![]() $\unicode[STIX]{x1D716}$
calculated under axisymmetric assumptions (black) and under isotropic assumptions (grey) for the case
$\unicode[STIX]{x1D716}$
calculated under axisymmetric assumptions (black) and under isotropic assumptions (grey) for the case
![]() $Re_{\unicode[STIX]{x1D706}}=476$
. A log-normal distribution is plotted for comparison (dashed).
$Re_{\unicode[STIX]{x1D706}}=476$
. A log-normal distribution is plotted for comparison (dashed).
The fact that
![]() $M_{12}$
is significantly larger than one suggests caution in assuming axisymmetry, at least at the smallest scales. We explore this issue by comparing the spatial distribution of local dissipation calculated both using the axisymmetry (2.1) and local isotropy (
$M_{12}$
is significantly larger than one suggests caution in assuming axisymmetry, at least at the smallest scales. We explore this issue by comparing the spatial distribution of local dissipation calculated both using the axisymmetry (2.1) and local isotropy (
![]() $\unicode[STIX]{x1D716}=15\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D622}_{11}^{2}\rangle$
, as in the majority of studies relying on single-point velocity measurements). K62 postulates a log-normal distribution of
$\unicode[STIX]{x1D716}=15\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D622}_{11}^{2}\rangle$
, as in the majority of studies relying on single-point velocity measurements). K62 postulates a log-normal distribution of
![]() $\unicode[STIX]{x1D716}$
to account for the internal intermittency of turbulence. Although some authors have pointed out theoretical inconsistencies in this assumption (see Frisch Reference Frisch1995), evidence from the bulk of experimental and numerical studies in the literature seems to support it (e.g. Wang et al.
Reference Wang, Chen, Brasseur and Wyngaard1996; Chen et al.
Reference Chen, Sreenivasan, Nelkin and Cao1997; Mullin & Dahm Reference Mullin and Dahm2006; Ganapathisubramani et al.
Reference Ganapathisubramani, Lakshminarasimhan and Clemens2008). Figure 12 indicates that, while the dissipation calculated using axisymmetry shows significant departure from log-normality for the low
$\unicode[STIX]{x1D716}$
to account for the internal intermittency of turbulence. Although some authors have pointed out theoretical inconsistencies in this assumption (see Frisch Reference Frisch1995), evidence from the bulk of experimental and numerical studies in the literature seems to support it (e.g. Wang et al.
Reference Wang, Chen, Brasseur and Wyngaard1996; Chen et al.
Reference Chen, Sreenivasan, Nelkin and Cao1997; Mullin & Dahm Reference Mullin and Dahm2006; Ganapathisubramani et al.
Reference Ganapathisubramani, Lakshminarasimhan and Clemens2008). Figure 12 indicates that, while the dissipation calculated using axisymmetry shows significant departure from log-normality for the low
![]() $\unicode[STIX]{x1D716}$
values, it does approximate such behaviour much more closely compared to the isotropic assumption. This fact, considering previous experimental observations and theoretical predictions (see Sreenivasan & Antonia Reference Sreenivasan and Antonia1997), only corroborates the assumption of axisymmetry and it does not constitute direct support to K62 over other models.
$\unicode[STIX]{x1D716}$
values, it does approximate such behaviour much more closely compared to the isotropic assumption. This fact, considering previous experimental observations and theoretical predictions (see Sreenivasan & Antonia Reference Sreenivasan and Antonia1997), only corroborates the assumption of axisymmetry and it does not constitute direct support to K62 over other models.
4.2 Invariants of the reduced velocity gradient tensor
As in all two-dimensional measurements, we only have access to four of the nine components of the velocity gradient tensor
![]() $\unicode[STIX]{x1D622}_{ij}$
, which limits our ability to describe the turbulent flow topology. Still, the reduced velocity gradient tensor has been shown to carry significant information, as discussed in detail by Cardesa et al. (Reference Cardesa, Nickels and Dawson2012). These authors considered the reduced velocity gradient tensor
$\unicode[STIX]{x1D622}_{ij}$
, which limits our ability to describe the turbulent flow topology. Still, the reduced velocity gradient tensor has been shown to carry significant information, as discussed in detail by Cardesa et al. (Reference Cardesa, Nickels and Dawson2012). These authors considered the reduced velocity gradient tensor
![]() $\tilde{\unicode[STIX]{x1D656}}$
, i.e. the upper left
$\tilde{\unicode[STIX]{x1D656}}$
, i.e. the upper left
![]() $2\times 2$
block of the full velocity gradient tensor
$2\times 2$
block of the full velocity gradient tensor
![]() $\unicode[STIX]{x1D622}_{ij}$
, defined by gradients of the in-plane velocity components along
$\unicode[STIX]{x1D622}_{ij}$
, defined by gradients of the in-plane velocity components along
![]() $x_{1}{-}x_{2}$
. Its characteristic equation reads:
$x_{1}{-}x_{2}$
. Its characteristic equation reads:
where
![]() $p=-\text{tr}(\tilde{\unicode[STIX]{x1D656}})$
and
$p=-\text{tr}(\tilde{\unicode[STIX]{x1D656}})$
and
![]() $q=\text{det}(\tilde{\unicode[STIX]{x1D656}})$
are the first and second invariants, respectively. Looking at several types of turbulent flows, Cardesa et al. (Reference Cardesa, Nickels and Dawson2012) found that the joint PDF of the invariants displays a teapot shape around the discriminant
$q=\text{det}(\tilde{\unicode[STIX]{x1D656}})$
are the first and second invariants, respectively. Looking at several types of turbulent flows, Cardesa et al. (Reference Cardesa, Nickels and Dawson2012) found that the joint PDF of the invariants displays a teapot shape around the discriminant
![]() $q=p^{2}/4$
. They showed that local (i.e. small-scale) homogeneity implies:
$q=p^{2}/4$
. They showed that local (i.e. small-scale) homogeneity implies:
while local isotropy implies:
In figure 13 we show the joint PDF of the invariants, confirming that it does follow the characteristic teapot shape, as recently found also by Fiscaletti et al. (Reference Fiscaletti, Westerweel and Elsinga2014) for a turbulent jet and by Rabey et al. (Reference Rabey, Wynn and Buxton2015) for the far region of a mixing layer. Equations (4.9)–(4.11) are checked for in table 4, using the out-of-plane vorticity for normalization. While local homogeneity is verified within measurement noise, the condition for local isotropy is not met by any of the considered cases, consistent with the findings in § 4.1.

Figure 13. Joint PDF of the invariants of the reduced velocity gradient tensor for the case
![]() $Re_{\unicode[STIX]{x1D706}}=476$
. The line
$Re_{\unicode[STIX]{x1D706}}=476$
. The line
![]() $p^{2}/4$
(dashed) separates unstable (
$p^{2}/4$
(dashed) separates unstable (
![]() $p<0$
) and stable (
$p<0$
) and stable (
![]() $p>0$
) nodes and foci.
$p>0$
) nodes and foci.
Table 4. Normalized average values of the invariants
![]() $\langle p\rangle$
and
$\langle p\rangle$
and
![]() $\langle q\rangle$
as well as the ratio
$\langle q\rangle$
as well as the ratio
![]() $\langle pq\rangle /\langle p^{3}\rangle$
which should equal
$\langle pq\rangle /\langle p^{3}\rangle$
which should equal
![]() $1.16\bar{6}$
according to (4.11) for isotropic flow.
$1.16\bar{6}$
according to (4.11) for isotropic flow.

4.3 The
 $n$
th-order moments of velocity increments
$n$
th-order moments of velocity increments
The small-scale features of the turbulent flow can be analysed in more detail considering the statistical distribution of the velocity gradients and their various moments. In figure 14 we plot the PDF of two measured diagonal and off-diagonal components of the reduced velocity gradient tensor for the case
![]() $Re_{\unicode[STIX]{x1D706}}=476$
. All components show the long, nearly exponential tails characteristic of small-scale intermittency. The tails are not strictly exponential (or they would be straight in the semi-logarithmic plot) but display a marked curvature, as typical of the dissipative scales in high Reynolds number flows (Castaing, Gagne & Hopfinger Reference Castaing, Gagne and Hopfinger1990).
$Re_{\unicode[STIX]{x1D706}}=476$
. All components show the long, nearly exponential tails characteristic of small-scale intermittency. The tails are not strictly exponential (or they would be straight in the semi-logarithmic plot) but display a marked curvature, as typical of the dissipative scales in high Reynolds number flows (Castaing, Gagne & Hopfinger Reference Castaing, Gagne and Hopfinger1990).
![]() $\unicode[STIX]{x1D622}_{11}$
(and
$\unicode[STIX]{x1D622}_{11}$
(and
![]() $\unicode[STIX]{x1D622}_{22}$
, not shown) is negatively skewed, as required by the dominant amplification of enstrophy by vortex stretching (Davidson Reference Davidson2004).
$\unicode[STIX]{x1D622}_{22}$
, not shown) is negatively skewed, as required by the dominant amplification of enstrophy by vortex stretching (Davidson Reference Davidson2004).
![]() $\unicode[STIX]{x1D622}_{12}$
and
$\unicode[STIX]{x1D622}_{12}$
and
![]() $\unicode[STIX]{x1D622}_{21}$
instead have a largely symmetric distribution, as expected (Ishihara et al.
Reference Ishihara, Gotoh and Kaneda2009).
$\unicode[STIX]{x1D622}_{21}$
instead have a largely symmetric distribution, as expected (Ishihara et al.
Reference Ishihara, Gotoh and Kaneda2009).

Figure 14. PDF of two components of the velocity gradient tensor
![]() $\unicode[STIX]{x1D622}_{11}$
(black) and
$\unicode[STIX]{x1D622}_{11}$
(black) and
![]() $\unicode[STIX]{x1D622}_{12}$
(grey) for the case
$\unicode[STIX]{x1D622}_{12}$
(grey) for the case
![]() $Re_{\unicode[STIX]{x1D706}}=476$
. The abscissa is normalized by the respective r.m.s.
$Re_{\unicode[STIX]{x1D706}}=476$
. The abscissa is normalized by the respective r.m.s.
The asymmetry and intermittency of the velocity gradient distribution in homogeneous turbulence is typically quantified by the skewness and kurtosis of the PDFs, i.e.
![]() $S_{3}(\unicode[STIX]{x1D622}_{ij})=\langle \unicode[STIX]{x1D622}_{ij}^{3}\rangle /\langle \unicode[STIX]{x1D622}_{ij}^{2}\rangle ^{3/2}$
and
$S_{3}(\unicode[STIX]{x1D622}_{ij})=\langle \unicode[STIX]{x1D622}_{ij}^{3}\rangle /\langle \unicode[STIX]{x1D622}_{ij}^{2}\rangle ^{3/2}$
and
![]() $K_{4}(\unicode[STIX]{x1D622}_{ij})=\langle \unicode[STIX]{x1D622}_{ij}^{4}\rangle /\langle \unicode[STIX]{x1D622}_{ij}^{2}\rangle ^{2}$
, respectively. K41 implies that skewness and kurtosis should be constants independent of Reynolds number, but compilations of experiments and simulations over wide ranges of
$K_{4}(\unicode[STIX]{x1D622}_{ij})=\langle \unicode[STIX]{x1D622}_{ij}^{4}\rangle /\langle \unicode[STIX]{x1D622}_{ij}^{2}\rangle ^{2}$
, respectively. K41 implies that skewness and kurtosis should be constants independent of Reynolds number, but compilations of experiments and simulations over wide ranges of
![]() $Re_{\unicode[STIX]{x1D706}}$
show power-law increase of
$Re_{\unicode[STIX]{x1D706}}$
show power-law increase of
![]() $K_{4}(\unicode[STIX]{x1D622}_{11})$
and, although much milder, of
$K_{4}(\unicode[STIX]{x1D622}_{11})$
and, although much milder, of
![]() $-S_{3}(\unicode[STIX]{x1D622}_{11})$
(Sreenivasan & Antonia Reference Sreenivasan and Antonia1997; Gylfason, Ayyalasomayajula & Warhaft Reference Gylfason, Ayyalasomayajula and Warhaft2004; Ishihara et al.
Reference Ishihara, Gotoh and Kaneda2009). K62 does predict a dependence of
$-S_{3}(\unicode[STIX]{x1D622}_{11})$
(Sreenivasan & Antonia Reference Sreenivasan and Antonia1997; Gylfason, Ayyalasomayajula & Warhaft Reference Gylfason, Ayyalasomayajula and Warhaft2004; Ishihara et al.
Reference Ishihara, Gotoh and Kaneda2009). K62 does predict a dependence of
![]() $K_{4}(\unicode[STIX]{x1D622}_{11})$
with
$K_{4}(\unicode[STIX]{x1D622}_{11})$
with
![]() $Re_{\unicode[STIX]{x1D706}}$
which is in general agreement with observations (Pope Reference Pope2000), but neither K41 nor K62 account for small-scale anisotropy. In the present flow skewness and kurtosis of the longitudinal velocity gradients are systematically larger in axial than in radial direction. This is shown in figure 15, displaying also the fifth- and sixth-order moments of the longitudinal velocity gradients,
$Re_{\unicode[STIX]{x1D706}}$
which is in general agreement with observations (Pope Reference Pope2000), but neither K41 nor K62 account for small-scale anisotropy. In the present flow skewness and kurtosis of the longitudinal velocity gradients are systematically larger in axial than in radial direction. This is shown in figure 15, displaying also the fifth- and sixth-order moments of the longitudinal velocity gradients,
![]() $S_{5}(\unicode[STIX]{x1D622}_{ii})=\langle \unicode[STIX]{x1D622}_{ii}^{5}\rangle /\langle \unicode[STIX]{x1D622}_{ij}^{2}\rangle ^{5/2}$
and
$S_{5}(\unicode[STIX]{x1D622}_{ii})=\langle \unicode[STIX]{x1D622}_{ii}^{5}\rangle /\langle \unicode[STIX]{x1D622}_{ij}^{2}\rangle ^{5/2}$
and
![]() $K_{6}(\unicode[STIX]{x1D622}_{ii})=\langle \unicode[STIX]{x1D622}_{ii}^{6}\rangle /\langle \unicode[STIX]{x1D622}_{ij}^{2}\rangle ^{3}$
, respectively. Although there is experimental scatter, the anisotropic trend is the same for all computed moments and all considered Reynolds numbers. Given the homogeneity and the absence of shear, we interpret this as a direct consequence of the dominant forcing in axial direction. In figure 15 the trend lines from Gylfason et al. (Reference Gylfason, Ayyalasomayajula and Warhaft2004) are also plotted. The agreement is fair, although the limited
$K_{6}(\unicode[STIX]{x1D622}_{ii})=\langle \unicode[STIX]{x1D622}_{ii}^{6}\rangle /\langle \unicode[STIX]{x1D622}_{ij}^{2}\rangle ^{3}$
, respectively. Although there is experimental scatter, the anisotropic trend is the same for all computed moments and all considered Reynolds numbers. Given the homogeneity and the absence of shear, we interpret this as a direct consequence of the dominant forcing in axial direction. In figure 15 the trend lines from Gylfason et al. (Reference Gylfason, Ayyalasomayajula and Warhaft2004) are also plotted. The agreement is fair, although the limited
![]() $Re_{\unicode[STIX]{x1D706}}$
range spanned by our measurements does not allow us to test the Reynolds number dependence, which here is also superposed to the effect of large-scale anisotropy.
$Re_{\unicode[STIX]{x1D706}}$
range spanned by our measurements does not allow us to test the Reynolds number dependence, which here is also superposed to the effect of large-scale anisotropy.

Figure 15.
![]() $-S_{3}$
(rightward triangles),
$-S_{3}$
(rightward triangles),
![]() $K_{4}$
(circles),
$K_{4}$
(circles),
![]() $-S_{5}$
(triangles) and
$-S_{5}$
(triangles) and
![]() $K_{6}$
(diamonds) for the axial (
$K_{6}$
(diamonds) for the axial (
![]() $x_{1}$
) (open) and radial (
$x_{1}$
) (open) and radial (
![]() $x_{2}$
) (greyed) directions versus
$x_{2}$
) (greyed) directions versus
![]() $Re_{\unicode[STIX]{x1D706}}$
. Trend lines (dashed) are taken from the fit lines of Gylfason et al. (Reference Gylfason, Ayyalasomayajula and Warhaft2004).
$Re_{\unicode[STIX]{x1D706}}$
. Trend lines (dashed) are taken from the fit lines of Gylfason et al. (Reference Gylfason, Ayyalasomayajula and Warhaft2004).
The moments of the velocity gradients coincide with the moments of velocity increments at vanishing separations. In order to explore the small-scale behaviour over a range of separations, we consider the normalized fourth-, fifth- and sixth-order moments of the longitudinal velocity differences (sometimes referred to as generalized flatness factors, or flatness, hyperskewness and hyperflatness):
These are plotted in figure 16 for separations along both
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{2}$
. We take the absolute-valued velocity differences, which helps convergence and allows direct comparison with the results of Belin et al. (Reference Belin, Maurer, Tabeling and Willaime1997), who analysed moments up to the sixth-order obtained in a double-impeller chamber containing low-temperature helium. As expected, the moments decrease monotonically with the separation (Belin et al.
Reference Belin, Maurer, Tabeling and Willaime1997; Shen & Warhaft Reference Shen and Warhaft2002). In the inertial range
$x_{2}$
. We take the absolute-valued velocity differences, which helps convergence and allows direct comparison with the results of Belin et al. (Reference Belin, Maurer, Tabeling and Willaime1997), who analysed moments up to the sixth-order obtained in a double-impeller chamber containing low-temperature helium. As expected, the moments decrease monotonically with the separation (Belin et al.
Reference Belin, Maurer, Tabeling and Willaime1997; Shen & Warhaft Reference Shen and Warhaft2002). In the inertial range
![]() $H_{ii}^{|n|}(r_{i})$
decreases as a power law that reflects the scaling exponents discussed in § 3. The negative slope, however, becomes steeper for separations smaller than approximately
$H_{ii}^{|n|}(r_{i})$
decreases as a power law that reflects the scaling exponents discussed in § 3. The negative slope, however, becomes steeper for separations smaller than approximately
![]() $10\unicode[STIX]{x1D702}$
, and more so for higher Reynolds numbers. A similar trend over this near-dissipation range was noted also by Belin et al. (Reference Belin, Maurer, Tabeling and Willaime1997), among others, and was discussed in detail by Chevillard et al. (Reference Chevillard, Roux, Lévêque, Mordant, Pinton and Arnéodo2005) as a manifestation of dissipation-range intermittency (as opposed to inertial-range intermittency). Dissipation-range intermittency has received much attention following the seminal observation of Kraichnan (Reference Kraichnan1967) that any local variation of the dissipation rate produces the strongest fluctuations at the highest wavenumbers of the turbulence spectrum. The (generalized) flatness of velocity increments at small separations quantifies this intermittency, which is often associated with the presence of coherent filamentary vortices a few Kolmogorov lengths in diameter (Jiménez et al.
Reference Jiménez, Wray, Saffman and Rogallo1993; She & Leveque Reference She and Leveque1994).
$10\unicode[STIX]{x1D702}$
, and more so for higher Reynolds numbers. A similar trend over this near-dissipation range was noted also by Belin et al. (Reference Belin, Maurer, Tabeling and Willaime1997), among others, and was discussed in detail by Chevillard et al. (Reference Chevillard, Roux, Lévêque, Mordant, Pinton and Arnéodo2005) as a manifestation of dissipation-range intermittency (as opposed to inertial-range intermittency). Dissipation-range intermittency has received much attention following the seminal observation of Kraichnan (Reference Kraichnan1967) that any local variation of the dissipation rate produces the strongest fluctuations at the highest wavenumbers of the turbulence spectrum. The (generalized) flatness of velocity increments at small separations quantifies this intermittency, which is often associated with the presence of coherent filamentary vortices a few Kolmogorov lengths in diameter (Jiménez et al.
Reference Jiménez, Wray, Saffman and Rogallo1993; She & Leveque Reference She and Leveque1994).

Figure 16. Generalized flatness factors
![]() $H_{ii}^{|n|}(r_{i})$
for the longitudinal increments along the axial (
$H_{ii}^{|n|}(r_{i})$
for the longitudinal increments along the axial (
![]() $x_{1}$
) (a) and radial (
$x_{1}$
) (a) and radial (
![]() $x_{2}$
) (b) directions for the case
$x_{2}$
) (b) directions for the case
![]() $Re_{\unicode[STIX]{x1D706}}=298$
.
$Re_{\unicode[STIX]{x1D706}}=298$
.
Our attention here is on the effect of anisotropy on the dissipation-range intermittency, which we underscore by plotting the ratio
![]() $H_{22}^{|n|}(r_{2})/H_{11}^{|n|}(r_{1})$
in figure 17. At relatively large separations, large-scale anisotropy
$H_{22}^{|n|}(r_{2})/H_{11}^{|n|}(r_{1})$
in figure 17. At relatively large separations, large-scale anisotropy
![]() $u_{1}^{\prime }/u_{2}^{\prime }$
is reflected in moment ratios significantly smaller than one. These start returning to isotropic values as the separation shrinks towards approximately
$u_{1}^{\prime }/u_{2}^{\prime }$
is reflected in moment ratios significantly smaller than one. These start returning to isotropic values as the separation shrinks towards approximately
![]() $r/\unicode[STIX]{x1D702}=10$
. However, for
$r/\unicode[STIX]{x1D702}=10$
. However, for
![]() $r/\unicode[STIX]{x1D702}<10$
there is again a significant departure from isotropy, which systematically becomes larger for smaller separations and higher-order moments (and more so for increasing large-scale anisotropy). This is in stark contrast with the picture of return to isotropy at the small scales predicted by K41 and assumed by the vast majority of later models. To our best knowledge, this is the first experimental account of this behaviour, although previous numerical studies concerned with anisotropic flows reached similar conclusions via spectral methods. Meneveau (Reference Meneveau1991) carried out a wavelet-based analysis of homogeneous sheared turbulence and found significant anisotropy in the flatness factors along different directions at high wavelengths. Bos, Liechtenstein & Schneider (Reference Bos, Liechtenstein and Schneider2007) used a similar approach to investigate rotating and stratified homogeneous turbulence, and found that in presence of stratification small-scale intermittency is highly anisotropic. Jacobitz et al. (Reference Jacobitz, Schneider, Bos and Farge2010) reported similar findings for simulations of sheared rotating turbulence. Our results suggest that, even in the absence of shear, rotation or stratification, large-scale anisotropy is sufficient to generate anisotropic intermittency at the dissipative scales.
$r/\unicode[STIX]{x1D702}<10$
there is again a significant departure from isotropy, which systematically becomes larger for smaller separations and higher-order moments (and more so for increasing large-scale anisotropy). This is in stark contrast with the picture of return to isotropy at the small scales predicted by K41 and assumed by the vast majority of later models. To our best knowledge, this is the first experimental account of this behaviour, although previous numerical studies concerned with anisotropic flows reached similar conclusions via spectral methods. Meneveau (Reference Meneveau1991) carried out a wavelet-based analysis of homogeneous sheared turbulence and found significant anisotropy in the flatness factors along different directions at high wavelengths. Bos, Liechtenstein & Schneider (Reference Bos, Liechtenstein and Schneider2007) used a similar approach to investigate rotating and stratified homogeneous turbulence, and found that in presence of stratification small-scale intermittency is highly anisotropic. Jacobitz et al. (Reference Jacobitz, Schneider, Bos and Farge2010) reported similar findings for simulations of sheared rotating turbulence. Our results suggest that, even in the absence of shear, rotation or stratification, large-scale anisotropy is sufficient to generate anisotropic intermittency at the dissipative scales.

Figure 17. Ratio of the radial (
![]() $x_{2}$
) to axial (
$x_{2}$
) to axial (
![]() $x_{1}$
) generalized flatness factors for the case
$x_{1}$
) generalized flatness factors for the case
![]() $Re_{\unicode[STIX]{x1D706}}=298$
(a) and
$Re_{\unicode[STIX]{x1D706}}=298$
(a) and
![]() $Re_{\unicode[STIX]{x1D706}}=476$
(b).
$Re_{\unicode[STIX]{x1D706}}=476$
(b).
We conclude this section with a note on measurement accuracy. Virtually all previous measurements of high-order moments of velocity gradients used Taylor’s hypothesis to convert from temporal to spatial series. As mentioned in the Introduction, this approach has well-known shortcomings, which might be especially problematic in presence of complex flows and high turbulence intensity. According to Gylfason et al. (Reference Gylfason, Ayyalasomayajula and Warhaft2004) the flow complexities, along with spatial resolution issues, may have adversely affected the results of Tabeling et al. (Reference Tabeling, Zocchi, Belin, Maurer and Willaime1996), which are among the very few to report high-order moments of the velocity gradients. PIV too has well-known limitations in the measurement of turbulent flows (see Raffel et al. Reference Raffel, Willert, Wereley and Kompenhans2007; Adrian & Westerweel Reference Adrian and Westerweel2011, for extensive monographies on the technique). Notably, measurement accuracy might be affected by loss of tracer particles due to out-of-plane motions – an effect expected to be significant in the present configuration, in which the mean flow is small and velocity fluctuations in all directions are comparable. Other factors, such as the linearization of the tracer particle trajectory between successive images, are also potential sources of errors. Although efforts were made to minimize bias uncertainty and to keep it below the random (finite sampling) uncertainty, its precise extent is hard to quantify, especially for high-order quantities. Our data are presented as complementary to (and not as inherently more accurate than) those reported in previous studies. We underscore however that the experimental errors in our measurements are not expected to bias quantities measured in one direction with respect to the other. Because the focus is to highlight the role of anisotropy by comparing moments of velocity fluctuations in different directions, the conclusions are not believed to be overshadowed by the inherent uncertainty.
5 Anisotropy at the large scales
5.1 Integral length scales
In order to characterize the integral scales of the turbulence, we use the two-point correlation function calculated over the large FOV:
The integral length scales associated with fluctuations
![]() $u_{i}$
over separations
$u_{i}$
over separations
![]() $r_{j}$
are defined as:
$r_{j}$
are defined as:
where
![]() $r_{0}$
is the first zero crossing of the correlation function. In practice, the extent of the integration is limited by the size of the imaging window (0.26 m in this case). We can then either extrapolate the correlation function using an exponential fit (as described in Carter et al.
Reference Carter, Petersen, Amili and Coletti2016); or we can use conventional estimates such as the distance at which the correlation function drops below
$r_{0}$
is the first zero crossing of the correlation function. In practice, the extent of the integration is limited by the size of the imaging window (0.26 m in this case). We can then either extrapolate the correlation function using an exponential fit (as described in Carter et al.
Reference Carter, Petersen, Amili and Coletti2016); or we can use conventional estimates such as the distance at which the correlation function drops below
![]() $1/e$
(also consistent with an exponential decay), see e.g. Tritton (Reference Tritton1992). The components of the correlation tensor that drop rapidly enough to be reconstructed until the zero-crossing point (e.g.
$1/e$
(also consistent with an exponential decay), see e.g. Tritton (Reference Tritton1992). The components of the correlation tensor that drop rapidly enough to be reconstructed until the zero-crossing point (e.g.
![]() $\unicode[STIX]{x1D70C}_{2,2}$
), yield values of the integral length scales within 10 % of this latter approximation, and we adopt it in the following. Having access to two-dimensional, two-component velocity fields and assuming axisymmetry at the large scales, we can calculate longitudinal and transverse integral scales along both the axial direction
$\unicode[STIX]{x1D70C}_{2,2}$
), yield values of the integral length scales within 10 % of this latter approximation, and we adopt it in the following. Having access to two-dimensional, two-component velocity fields and assuming axisymmetry at the large scales, we can calculate longitudinal and transverse integral scales along both the axial direction
![]() $x_{1}$
and the radial direction
$x_{1}$
and the radial direction
![]() $x_{2}$
. We define:
$x_{2}$
. We define:
such that the subscripts indicate the longitudinal and transverse integral scales associated with the velocity component
![]() $u_{1}$
or
$u_{1}$
or
![]() $u_{2}$
. Isotropy requires
$u_{2}$
. Isotropy requires
![]() $L_{L,1}=L_{L,2}$
and
$L_{L,1}=L_{L,2}$
and
![]() $L_{T,1}=L_{T,2}$
, as well as
$L_{T,1}=L_{T,2}$
, as well as
![]() $L_{L,1}=2L_{T,2}$
and
$L_{L,1}=2L_{T,2}$
and
![]() $L_{L,2}=2L_{T,1}$
(Pope Reference Pope2000). These relations are checked for in figure 18. (Here we show the dependence with the large-scale anisotropy ratio instead of the Reynolds number, in keeping with the emphasis of this section.)
$L_{L,2}=2L_{T,1}$
(Pope Reference Pope2000). These relations are checked for in figure 18. (Here we show the dependence with the large-scale anisotropy ratio instead of the Reynolds number, in keeping with the emphasis of this section.)
![]() $L_{L,1}/L_{L,2}$
is considerably larger than one for all cases. This is consistent to what was found in the wake of various types of grids by Valente & Vassilicos (Reference Valente and Vassilicos2014), who deduced that in such flow the large eddies were elongated in the streamwise direction. This ratio also shows an increasing trend with the anisotropy ratio
$L_{L,1}/L_{L,2}$
is considerably larger than one for all cases. This is consistent to what was found in the wake of various types of grids by Valente & Vassilicos (Reference Valente and Vassilicos2014), who deduced that in such flow the large eddies were elongated in the streamwise direction. This ratio also shows an increasing trend with the anisotropy ratio
![]() $u_{1}^{\prime }/u_{2}^{\prime }$
. Also
$u_{1}^{\prime }/u_{2}^{\prime }$
. Also
![]() $L_{T,1}/L_{T,2}$
is much larger than one, although less so than
$L_{T,1}/L_{T,2}$
is much larger than one, although less so than
![]() $L_{L,1}/L_{L,2}$
and with a less clear dependence on the anisotropy ratio.
$L_{L,1}/L_{L,2}$
and with a less clear dependence on the anisotropy ratio.
![]() $L_{L,1}/L_{T,2}$
and
$L_{L,1}/L_{T,2}$
and
![]() $L_{L,2}/L_{T,1}$
are significantly larger and smaller, respectively, than the isotropic value. Because
$L_{L,2}/L_{T,1}$
are significantly larger and smaller, respectively, than the isotropic value. Because
![]() $L_{L,1}$
and
$L_{L,1}$
and
![]() $L_{T,1}$
are functions of the spatial correlation of
$L_{T,1}$
are functions of the spatial correlation of
![]() $u_{1}$
, these ratios suggest that the axial fluctuations are associated with larger integral scales, as discussed in more detail in the following.
$u_{1}$
, these ratios suggest that the axial fluctuations are associated with larger integral scales, as discussed in more detail in the following.

Figure 18. Ratios of longitudinal and transverse integral length scales along with the expected isotropic value of one (dashed) (a), and ratios of longitudinal to transverse integral length scales along with the isotropic value of two (dashed) (b) plotted against the anisotropy ratio
![]() $u_{1}^{\prime }/u_{2}^{\prime }$
.
$u_{1}^{\prime }/u_{2}^{\prime }$
.
5.2 Length scale and anisotropy ratio
The relation between the large-scale anisotropy of velocity and length scales was investigated systematically by Bewley et al. (Reference Bewley, Chang and Bodenschatz2012). By using a spherical chamber with loudspeakers operated at different intensities, they forced a zero-mean turbulent flow which was axisymmetric at the large scales, and varied the axial-to-radial anisotropy ratio to probe both prolate
![]() $(u_{1}^{\prime }>u_{2}^{\prime }=u_{3}^{\prime })$
and oblate
$(u_{1}^{\prime }>u_{2}^{\prime }=u_{3}^{\prime })$
and oblate
![]() $(u_{1}^{\prime }<u_{2}^{\prime }=u_{3}^{\prime })$
configurations. They defined the integral scale in a certain direction using the transverse velocity correlation with separation in such direction; i.e. (using the present notation) they considered
$(u_{1}^{\prime }<u_{2}^{\prime }=u_{3}^{\prime })$
configurations. They defined the integral scale in a certain direction using the transverse velocity correlation with separation in such direction; i.e. (using the present notation) they considered
![]() $L_{1}=L_{T,2}$
and
$L_{1}=L_{T,2}$
and
![]() $L_{2}=L_{T,1}$
. It was found that the prolate forcing resulted in
$L_{2}=L_{T,1}$
. It was found that the prolate forcing resulted in
![]() $L_{1}<L_{2}$
and oblate forcing in
$L_{1}<L_{2}$
and oblate forcing in
![]() $L_{1}>L_{2}$
. In particular they found that the ratio
$L_{1}>L_{2}$
. In particular they found that the ratio
![]() $L_{1}/L_{2}$
was inversely proportional (through a power exponent related to the inertial-range scaling) to the ratio
$L_{1}/L_{2}$
was inversely proportional (through a power exponent related to the inertial-range scaling) to the ratio
![]() $u_{1}^{\prime }/u_{2}^{\prime }$
. They concluded that the correlations between velocity fluctuations extended further along
$u_{1}^{\prime }/u_{2}^{\prime }$
. They concluded that the correlations between velocity fluctuations extended further along
![]() $x_{1}$
than
$x_{1}$
than
![]() $x_{2}$
when
$x_{2}$
when
![]() $u_{1}^{\prime }/u_{2}^{\prime }$
was smaller than one, and vice versa. This may appear as a counterintuitive result, since one expects fluctuations in a given direction to be correlated over longer distances in said direction than in a perpendicular one. This is the case, for example, in turbulent boundary layers (Ganapathisubramani et al.
Reference Ganapathisubramani, Hutchins, Hambleton, Longmire and Marusic2005) and in decaying turbulence behind square and fractal grids (Discetti et al.
Reference Discetti, Ziskin, Astarita, Adrian and Prestridge2013; Valente & Vassilicos Reference Valente and Vassilicos2014).
$u_{1}^{\prime }/u_{2}^{\prime }$
was smaller than one, and vice versa. This may appear as a counterintuitive result, since one expects fluctuations in a given direction to be correlated over longer distances in said direction than in a perpendicular one. This is the case, for example, in turbulent boundary layers (Ganapathisubramani et al.
Reference Ganapathisubramani, Hutchins, Hambleton, Longmire and Marusic2005) and in decaying turbulence behind square and fractal grids (Discetti et al.
Reference Discetti, Ziskin, Astarita, Adrian and Prestridge2013; Valente & Vassilicos Reference Valente and Vassilicos2014).
To quantify the distance over which each velocity component is correlated in the present flow, in figure 19 we plot contours of
![]() $\unicode[STIX]{x1D70C}_{11}(r_{1},r_{2})$
and
$\unicode[STIX]{x1D70C}_{11}(r_{1},r_{2})$
and
![]() $\unicode[STIX]{x1D70C}_{22}(r_{1},r_{2})$
and highlight the
$\unicode[STIX]{x1D70C}_{22}(r_{1},r_{2})$
and highlight the
![]() $1/e$
contour and the corresponding integral length scales. In fully isotropic turbulence both plots would be identical except for a
$1/e$
contour and the corresponding integral length scales. In fully isotropic turbulence both plots would be identical except for a
![]() $90^{\circ }$
rotation, and the ellipse described by the
$90^{\circ }$
rotation, and the ellipse described by the
![]() $1/e$
contour would have an aspect ratio of 2. As we showed in figure 18, in the present anisotropic configuration
$1/e$
contour would have an aspect ratio of 2. As we showed in figure 18, in the present anisotropic configuration
![]() $L_{L,1}>L_{L,2}$
and
$L_{L,1}>L_{L,2}$
and
![]() $L_{T,1}>L_{T,2}$
, i.e. the velocity fluctuations
$L_{T,1}>L_{T,2}$
, i.e. the velocity fluctuations
![]() $u_{1}$
are correlated over larger distances than
$u_{1}$
are correlated over larger distances than
![]() $u_{2}$
. Assuming that the homogeneous anisotropic turbulence of Bewley et al. (Reference Bewley, Chang and Bodenschatz2012) had characteristics similar to ours, their conclusion that the correlations between velocity fluctuations extends further along a certain direction when the forcing in such direction is weaker, and vice versa, seems to descend from the choice of taking
$u_{2}$
. Assuming that the homogeneous anisotropic turbulence of Bewley et al. (Reference Bewley, Chang and Bodenschatz2012) had characteristics similar to ours, their conclusion that the correlations between velocity fluctuations extends further along a certain direction when the forcing in such direction is weaker, and vice versa, seems to descend from the choice of taking
![]() $L_{T,2}$
and
$L_{T,2}$
and
![]() $L_{T,1}$
as correlation scales for
$L_{T,1}$
as correlation scales for
![]() $u_{1}$
and
$u_{1}$
and
![]() $u_{2}$
, respectively. Using their definition of integral scale, our results are consistent with theirs. With respect to their study, the present results contain the full two-dimensional velocity fields which (assuming axisymmetry) allows for the investigation of all choices of integral scales, not only those based on the transverse velocity correlations. The more common definition of the integral scale in a certain direction uses the longitudinal velocity correlation with separation in such direction (i.e.
$u_{2}$
, respectively. Using their definition of integral scale, our results are consistent with theirs. With respect to their study, the present results contain the full two-dimensional velocity fields which (assuming axisymmetry) allows for the investigation of all choices of integral scales, not only those based on the transverse velocity correlations. The more common definition of the integral scale in a certain direction uses the longitudinal velocity correlation with separation in such direction (i.e.
![]() $L_{1}=L_{L,1}$
and
$L_{1}=L_{L,1}$
and
![]() $L_{2}=L_{L,2}$
), and this leads to an opposite conclusion in terms of the relation between anisotropy ratio and integral scales (see figure 18
a). The ambiguity stems from the very anisotropy of the flow and the multiple possible definitions of large-scale quantities. A more comprehensive measure of the integral scale associated with the velocity fluctuation in direction
$L_{2}=L_{L,2}$
), and this leads to an opposite conclusion in terms of the relation between anisotropy ratio and integral scales (see figure 18
a). The ambiguity stems from the very anisotropy of the flow and the multiple possible definitions of large-scale quantities. A more comprehensive measure of the integral scale associated with the velocity fluctuation in direction
![]() $i$
is perhaps
$i$
is perhaps
![]() $\tilde{L_{i}}\equiv (L_{L,i}L_{T,i})^{1/2}$
, i.e. the characteristic size of the
$\tilde{L_{i}}\equiv (L_{L,i}L_{T,i})^{1/2}$
, i.e. the characteristic size of the
![]() $1/e$
contour for the correlation coefficient
$1/e$
contour for the correlation coefficient
![]() $\unicode[STIX]{x1D70C}_{ii}$
. This can be regarded as a measure of the distance over which each velocity component is correlated, in keeping with the basic concept of integral scale. The ratio
$\unicode[STIX]{x1D70C}_{ii}$
. This can be regarded as a measure of the distance over which each velocity component is correlated, in keeping with the basic concept of integral scale. The ratio
![]() $\tilde{L_{1}}/\tilde{L_{2}}$
is plotted in figure 20 and indicates that, as the large-scale anisotropy becomes more prolate in direction
$\tilde{L_{1}}/\tilde{L_{2}}$
is plotted in figure 20 and indicates that, as the large-scale anisotropy becomes more prolate in direction
![]() $x_{1}$
, the correlation length of the velocity fluctuations also becomes increasingly larger in such direction.
$x_{1}$
, the correlation length of the velocity fluctuations also becomes increasingly larger in such direction.

Figure 20. Ratio of integrals scales
![]() $\tilde{L_{i}}$
(defined in text) along the axial and radial directions plotted against anisotropy ratio
$\tilde{L_{i}}$
(defined in text) along the axial and radial directions plotted against anisotropy ratio
![]() $u_{1}^{\prime }/u_{2}^{\prime }$
.
$u_{1}^{\prime }/u_{2}^{\prime }$
.
5.3 Normalized energy dissipation
Finally we consider the effect of anisotropy on the normalized energy dissipation rate
![]() $C_{\unicode[STIX]{x1D716}}$
, whose constancy with
$C_{\unicode[STIX]{x1D716}}$
, whose constancy with
![]() $Re_{\unicode[STIX]{x1D706}}$
lies at the basis of classic turbulence theory (Tennekes & Lumley Reference Tennekes and Lumley1972; Frisch Reference Frisch1995; Vassilicos Reference Vassilicos2015). Sreenivasan (Reference Sreenivasan1995) compiled experimental data on several types of turbulent shear flows and found
$Re_{\unicode[STIX]{x1D706}}$
lies at the basis of classic turbulence theory (Tennekes & Lumley Reference Tennekes and Lumley1972; Frisch Reference Frisch1995; Vassilicos Reference Vassilicos2015). Sreenivasan (Reference Sreenivasan1995) compiled experimental data on several types of turbulent shear flows and found
![]() $C_{\unicode[STIX]{x1D716}}$
to approximate Reynolds number independency for
$C_{\unicode[STIX]{x1D716}}$
to approximate Reynolds number independency for
![]() $Re_{\unicode[STIX]{x1D706}}>100$
. However, being a large-scale quantity,
$Re_{\unicode[STIX]{x1D706}}>100$
. However, being a large-scale quantity,
![]() $C_{\unicode[STIX]{x1D716}}$
is not expected to be independent on the type of flow, and large scatter is found in its value between wakes, homogeneous shear flows and grid turbulence, with values in the range 0.5–2.5 (Burattini et al.
Reference Burattini, Lavoie and Antonia2005). Even within grid turbulence, which is expected to approximate homogeneous isotropic conditions, there is ample evidence that different inflow conditions result in different values of the constant (Burattini et al.
Reference Burattini, Lavoie and Antonia2005; Thormann & Meneveau Reference Thormann and Meneveau2014). Moreover, it has been demonstrated how non-stationary turbulence, in particular the near wake in decaying grid turbulence, presents a systematic dependency of
$C_{\unicode[STIX]{x1D716}}$
is not expected to be independent on the type of flow, and large scatter is found in its value between wakes, homogeneous shear flows and grid turbulence, with values in the range 0.5–2.5 (Burattini et al.
Reference Burattini, Lavoie and Antonia2005). Even within grid turbulence, which is expected to approximate homogeneous isotropic conditions, there is ample evidence that different inflow conditions result in different values of the constant (Burattini et al.
Reference Burattini, Lavoie and Antonia2005; Thormann & Meneveau Reference Thormann and Meneveau2014). Moreover, it has been demonstrated how non-stationary turbulence, in particular the near wake in decaying grid turbulence, presents a systematic dependency of
![]() $C_{\unicode[STIX]{x1D716}}$
with the Reynolds number (which itself varies in space–time), highlighting the fundamental difference between non-equilibrium conditions and steadily forced turbulence (Vassilicos Reference Vassilicos2015).
$C_{\unicode[STIX]{x1D716}}$
with the Reynolds number (which itself varies in space–time), highlighting the fundamental difference between non-equilibrium conditions and steadily forced turbulence (Vassilicos Reference Vassilicos2015).

Figure 21. Normalized energy dissipation rate calculated using (5.7)–(5.10) (a) and using the axisymmetric-based definition (5.11) (b) plotted against anisotropy ratio. The dashed line indicates the asymptotic value of 0.5 suggested by homogeneous isotropic simulations (Kaneda et al. Reference Kaneda, Ishihara, Yokokawa, Itakura and Uno2003).
In the present configuration we force stationary turbulence, so
![]() $C_{\unicode[STIX]{x1D716}}$
is not expected to depend explicitly on the Reynolds number. However, when varying
$C_{\unicode[STIX]{x1D716}}$
is not expected to depend explicitly on the Reynolds number. However, when varying
![]() $Re_{\unicode[STIX]{x1D706}}$
we also vary the large-scale anisotropy, which has been reported to influence
$Re_{\unicode[STIX]{x1D706}}$
we also vary the large-scale anisotropy, which has been reported to influence
![]() $C_{\unicode[STIX]{x1D716}}$
in grid turbulence (Antonia et al.
Reference Antonia, Zhou and Romano2002). Moreover from the previous subsections it is evident how, due to anisotropy of the investigated flow, several different (and arguably equally valid) definitions of large-scale quantities are possible. Traditionally, in single-point measurements using Taylor’s hypothesis, it is practical to use
$C_{\unicode[STIX]{x1D716}}$
in grid turbulence (Antonia et al.
Reference Antonia, Zhou and Romano2002). Moreover from the previous subsections it is evident how, due to anisotropy of the investigated flow, several different (and arguably equally valid) definitions of large-scale quantities are possible. Traditionally, in single-point measurements using Taylor’s hypothesis, it is practical to use
![]() $C_{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}L_{1,1}/u_{1}^{\prime 3}$
. Here on the other hand we may define:
$C_{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}L_{1,1}/u_{1}^{\prime 3}$
. Here on the other hand we may define:
We approximate the turbulent kinetic energy
![]() $q^{2}/2\approx (u_{1}^{\prime })^{2}/2+(u_{2}^{\prime })^{2}$
as in e.g. Valente & Vassilicos (Reference Valente and Vassilicos2014) who considered (5.9) and (5.10) in their anisotropic grid turbulence wakes. Figure 21 shows the values of
$q^{2}/2\approx (u_{1}^{\prime })^{2}/2+(u_{2}^{\prime })^{2}$
as in e.g. Valente & Vassilicos (Reference Valente and Vassilicos2014) who considered (5.9) and (5.10) in their anisotropic grid turbulence wakes. Figure 21 shows the values of
![]() $C_{\unicode[STIX]{x1D716}}$
calculated using (5.7)–(5.10) as a function of anisotropy ratio (and therefore of Reynolds number). There is significant scatter depending on the flow conditions, and even more evidently there is large disparity between the different definitions. Because of the scalar nature of dissipation, it is desirable to define a single-valued constant for each flow configuration. This is in keeping with the call of Bewley et al. (Reference Bewley, Chang and Bodenschatz2012) for a definition of
$C_{\unicode[STIX]{x1D716}}$
calculated using (5.7)–(5.10) as a function of anisotropy ratio (and therefore of Reynolds number). There is significant scatter depending on the flow conditions, and even more evidently there is large disparity between the different definitions. Because of the scalar nature of dissipation, it is desirable to define a single-valued constant for each flow configuration. This is in keeping with the call of Bewley et al. (Reference Bewley, Chang and Bodenschatz2012) for a definition of
![]() $Re_{\unicode[STIX]{x1D706}}$
strictly in terms of scalar quantities. We consider the following definition, which incorporates the assumed axisymmetry of the flow:
$Re_{\unicode[STIX]{x1D706}}$
strictly in terms of scalar quantities. We consider the following definition, which incorporates the assumed axisymmetry of the flow:
where
![]() $\unicode[STIX]{x1D716}_{1}=\unicode[STIX]{x1D708}[2\langle \unicode[STIX]{x1D622}_{12}^{2}\rangle +\langle \unicode[STIX]{x1D622}_{11}^{2}\rangle ]$
and
$\unicode[STIX]{x1D716}_{1}=\unicode[STIX]{x1D708}[2\langle \unicode[STIX]{x1D622}_{12}^{2}\rangle +\langle \unicode[STIX]{x1D622}_{11}^{2}\rangle ]$
and
![]() $\unicode[STIX]{x1D716}_{2}=\unicode[STIX]{x1D708}[4\langle \unicode[STIX]{x1D622}_{22}^{2}\rangle +\langle \unicode[STIX]{x1D622}_{21}^{2}\rangle -\langle \unicode[STIX]{x1D622}_{11}^{2}\rangle ]$
are the (additive) components of dissipation along the axis of symmetry
$\unicode[STIX]{x1D716}_{2}=\unicode[STIX]{x1D708}[4\langle \unicode[STIX]{x1D622}_{22}^{2}\rangle +\langle \unicode[STIX]{x1D622}_{21}^{2}\rangle -\langle \unicode[STIX]{x1D622}_{11}^{2}\rangle ]$
are the (additive) components of dissipation along the axis of symmetry
![]() $x_{1}$
and the perpendicular direction
$x_{1}$
and the perpendicular direction
![]() $x_{2}$
, respectively (George & Hussein Reference George and Hussein1991). This expression is also plotted in figure 21. Its value is very close to 0.5, the asymptotic value shown by direct numerical simulations of homogeneous isotropic turbulence for
$x_{2}$
, respectively (George & Hussein Reference George and Hussein1991). This expression is also plotted in figure 21. Its value is very close to 0.5, the asymptotic value shown by direct numerical simulations of homogeneous isotropic turbulence for
![]() $Re_{\unicode[STIX]{x1D706}}>200$
(Kaneda et al.
Reference Kaneda, Ishihara, Yokokawa, Itakura and Uno2003; Burattini et al.
Reference Burattini, Lavoie and Antonia2005). Also in previous measurements of jet-stirred turbulence, this value of
$Re_{\unicode[STIX]{x1D706}}>200$
(Kaneda et al.
Reference Kaneda, Ishihara, Yokokawa, Itakura and Uno2003; Burattini et al.
Reference Burattini, Lavoie and Antonia2005). Also in previous measurements of jet-stirred turbulence, this value of
![]() $C_{\unicode[STIX]{x1D716}}$
yielded good agreement between the dissipation estimated using the scaling argument and the compensated second-order LSF (Variano & Cowen Reference Variano and Cowen2008; de Jong et al.
Reference de Jong, Cao, Woodward, Salazar, Collins and Meng2009). Still, it remains speculative at this time whether one should reliably assume
$C_{\unicode[STIX]{x1D716}}$
yielded good agreement between the dissipation estimated using the scaling argument and the compensated second-order LSF (Variano & Cowen Reference Variano and Cowen2008; de Jong et al.
Reference de Jong, Cao, Woodward, Salazar, Collins and Meng2009). Still, it remains speculative at this time whether one should reliably assume
![]() $C_{\unicode[STIX]{x1D716}}=0.5$
for these type of flows (and in general for laboratory approximations of homogeneous turbulence). Certainly, anisotropy adds an additional layer of difficulty to the definition and determination of the constant. Still, it will be interesting to evaluate (5.11) in different types of flows, considering that several canonical laboratory flows are consistent with axisymmetry.
$C_{\unicode[STIX]{x1D716}}=0.5$
for these type of flows (and in general for laboratory approximations of homogeneous turbulence). Certainly, anisotropy adds an additional layer of difficulty to the definition and determination of the constant. Still, it will be interesting to evaluate (5.11) in different types of flows, considering that several canonical laboratory flows are consistent with axisymmetry.
6 Conclusions
We have investigated homogeneous anisotropic turbulence in a jet-stirred chamber with negligible shear, strain and mean flow. The Reynolds number based on the Taylor microscale is varied between
![]() $Re_{\unicode[STIX]{x1D706}}\approx 300{-}500$
, and the large-scale anisotropy ratio (between the r.m.s. velocity fluctuations parallel and perpendicular to the jet axes) spans the range 1.38–1.72. These conditions extend over a volume several times larger than the integral scales of the turbulence, and are studied by planar PIV at different resolutions without resorting to Taylor’s hypothesis. The analysis is hinged on three questions related to how anisotropy affects the different scales of the flow:
$Re_{\unicode[STIX]{x1D706}}\approx 300{-}500$
, and the large-scale anisotropy ratio (between the r.m.s. velocity fluctuations parallel and perpendicular to the jet axes) spans the range 1.38–1.72. These conditions extend over a volume several times larger than the integral scales of the turbulence, and are studied by planar PIV at different resolutions without resorting to Taylor’s hypothesis. The analysis is hinged on three questions related to how anisotropy affects the different scales of the flow:
(i) How does the large-scale anisotropy propagate through the inertial scales?
We have considered the inertial-range scaling exponents of velocity structure functions up to the sixth order. The longitudinal structure function scaling along the axial direction agrees with previous measurements and simulations, and is well predicted by the She & Leveque (Reference She and Leveque1994) intermittency model. In violation of local isotropy, different behaviours are found depending both on the velocity components and on the direction of separation within the measurement plane. This points to a different scaling not only between longitudinal and transverse structure functions (as observed in several previous studies), but also between different spatial directions, due to the breaking of the rotational symmetry. This anisotropic behaviour appears to concern also the longitudinal structure function, whose behaviour has usually been assumed universal.
(ii) Does anisotropy persist to the dissipative scales?
We have investigated the in-plane components of the velocity gradient tensor, and found evidence of anisotropy in their mean square statistics as well as in the reduced (two-dimensional) tensor invariants. The departure from isotropy is in general more pronounced for stronger large-scale anisotropy. We also considered the PDFs of the velocity gradients and their moments up to the sixth-order. The generalized flatness factors of the longitudinal velocity differences at various separations indicate strong intermittency in the dissipative range. Over the same scales (i.e. for separations below
![]() ${\sim}10\unicode[STIX]{x1D702}$
) the return to isotropy is interrupted and a strongly anisotropic behaviour reappears, as demonstrated by the ratio of generalized flatness factors along both directions. This points to a direct connection between large-scale anisotropy and the dissipative scales.
${\sim}10\unicode[STIX]{x1D702}$
) the return to isotropy is interrupted and a strongly anisotropic behaviour reappears, as demonstrated by the ratio of generalized flatness factors along both directions. This points to a direct connection between large-scale anisotropy and the dissipative scales.
(iii) How does the large-scale anisotropy of the velocity fluctuations relate to the length scales?
The integral scale in a given direction, defined as the distance over which the velocity component is spatially correlated, is found to be larger in the direction for which the r.m.s. fluctuation is higher. Due to anisotropy, the definition of the integral scale is not trivial and may influence qualitative conclusions. The different possible definitions, obtained using the measured components of the two-point correlation tensor, also suggest different levels of large-scale anisotropy. The ambiguity also translates into non-unique definitions (and values) for the normalized dissipation obtained via the classic scaling argument. We have suggested alternative definitions of integral scale and normalized dissipation that incorporate the departure from isotropy.
Taken together, these results highlight the importance of considering, for a full characterization of all scales of the turbulence, not only the different velocity components but also the different spatial directions. The full three-dimensional information is hardly available from experiments, although advances in volumetric velocimetry of turbulent flows in the last decade have been major. The information is instead readily available from simulations, but the vast majority of previous studies addressing anisotropy have focused on sheared, stratified or rotating flows. While these are highly relevant in many applications, it would be of interest to explore anisotropy and its propagation across scales using anisotropic forcing without the superposition of those complex effects (something attempted numerically by Biferale & Toschi Reference Biferale and Toschi2001).
A limitation of the present work is represented by the fact that the Reynolds number and the large-scale anisotropy cannot be varied independently in our apparatus, preventing firm conclusions on the respective quantitative influences of both parameters. Experimental facilities capable of disentangling the two effects, such as the turbulence chamber of Chang et al. (Reference Chang, Bewley and Bodenschatz2012), are invaluable in this sense. We also remark the importance, in order to explore truly homogeneous turbulence, of generating a homogeneous region much larger than the integral scale. This has been achieved in the present set-up at the cost of building a chamber of considerable size.
As it has been noted by several authors, anisotropy is deeply interrelated to intermittency at all scales (see, for e.g. Warhaft Reference Warhaft2009). The details of this relations, however, remain relatively unexplored. The present results suggest that intermittency models able to account for anisotropy, even implicitly, may stand a better chance of reproducing the observations. For example, the physical picture associated with the model of She & Leveque (Reference She and Leveque1994) features small filamentary structures which are responsible for intermittency and dissipate energy at a rate constructed from a small-scale time and a large-scale velocity. Such a mixed scaling naturally opens up to incorporating large-scale anisotropy. In more recent models, such as the one of Chevillard & Meneveau (Reference Chevillard and Meneveau2006) for the evolution of the velocity gradient tensor, anisotropy is explicitly accounted for. The wealth of information available from multi-dimensional full-field measurements can be used to inform and validate predictions from this class of models at multiple levels. In the present work we have not directly addressed the topology of the turbulent structures, nor the energy transfer among scales – aspects which are connected to the emergence of intermittency and the propagation of anisotropy and which will be explored in a future study.
Acknowledgements
We are indebted to O. Amili and A. Nemes for the invaluable help during the PIV measurements and processing. We also thank M. Guala and G. Voth for insightful comments in several fruitful conversations.