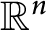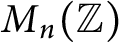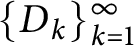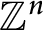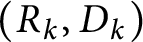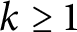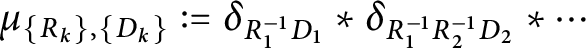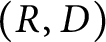1 Introduction
Let
$\mu $
be a Borel probability measure with compact support on
$\mathbb {R}^{n}$
. A fundamental problem in harmonic analysis associated with
$\mu $
is whether there exists a set
$\Lambda \subseteq {\mathbb R}^n$
such that
$E_{\Lambda }:=\big \{e^{2\pi i\langle \lambda , x\rangle }:\lambda \in \Lambda \big \}$
is an orthonormal basis for
$L^2(\mu ).$
If so, we say
$\mu $
is a spectral measure and
$\Lambda $
a spectrum of
$\mu $
. In particular, if
$\mu $
is the Lebesgue measure restricted on a Borel set
$\Omega $
, then the set
$\Omega $
is called a spectral set. The study of spectral measures dates back to the work of Fuglede [Reference Fuglede14] in 1974, who conjectured that
$\Omega $
is a spectral set if and only if the set
$\Omega $
tiles
${\mathbb R}^n$
by translations. Although the conjecture has been proved to be false in dimension
$n\geq 3$
[Reference Kolountzakis and Matolcsi20, Reference Kolountzakis and Matolcsi21, Reference Tao30], it is still open in Dimensions
$1$
and
$2$
.
The studies of spectral measures entered into the realm of fractals when Jorgensen and Pedersen [Reference Jorgensen and Pedersen18] gave the first example of a singular, nonatomic, fractal spectral measure. Their construction is based on a scale-
$4$
Cantor set, where the first and third intervals are kept and the other two are discarded. The appropriate measure for this set is the Bernoulli convolution
$\mu _{4}$
, which is the invariant measure of the iterated function system
$\{\tau _0(x)=x/4,\,\tau _2(x)=(x+2)/4\}$
. They proved that this measure is a spectral measure with spectrum
$\Lambda :=\Big \{\sum _{k=0}^{n}4^{k}d_{k}:d_{k}\in \{0,1\},n\in \mathbb {N}\Big \}$
. Jorgensen and Pedersen opened up a new field in researching the orthogonal harmonic analysis of fractal measures including self-similar measures/self-affine measures and generally Moran measures (see [Reference Jorgensen and Pedersen19, Reference Stricharz27–Reference Stricharz29]). Later on, in
${\mathbb R},$
a large class of self-similar measures have been proved to be spectral measures by Łaba and Wang [Reference Łaba and Wang22]. Let
$b\geq 2$
be an integer, and let
$D\subseteq {\mathbb Z}$
be a finite digit set with
$0\in D$
. Łaba and Wang [Reference Łaba and Wang22] proved that the self-similar measure
$\mu _{b, D}$
, which is generated by the iterated function system
$\{\tau _d(x)=\frac {x+d}{b}\}_{d\in D}$
, is a spectral measure if
$(b, D)$
is admissible (see Definition1.1). Recently, Dutkay, Hausserman, and Lai [Reference Dutkay, Haussermann and Lai10] generalized the result to higher dimensions, thus settling a long-standing conjecture proposed by Jorgensen and Pedersen. Meanwhile, many interesting spectral measures have been found (see, e.g., [Reference An, Fu and Lai1–Reference Deng and Lau7, Reference Dutkay, Han and Sun9, Reference Fu and Wen12, Reference Fu and Wen13, Reference He and He15, Reference Hu and Lau16, Reference Li23–Reference Liu and Dong26, Reference Stricharz29] and the references therein for recent advances), but there are only a few classes.
In the last decade, many researchers studied the spectrality of the Moran measures, which are the nonself-similar generalization of the Cantor measures through the infinite convolution. Note that most results of the known cases are concentrated on one-dimensional Moran measures (see, e.g., [Reference An, Fu and Lai1, Reference An and He2, Reference Fu and Wen12, Reference Fu and Wen13, Reference He and He15] and the references therein). There are few studies involving Moran measures of higher dimension other than [Reference Dutkay, Emami and Lai8, Reference Liu and Dong26, Reference Stricharz29]. In this paper, we focus on the Moran measures on
${\mathbb R}^n$
. Let
$\{R_{k}\}_{k=1}^{\infty }$
be a sequence of expanding matrices with integer entries, and let
$\{D_{k}\}_{k=1}^{\infty }$
be a sequence of finite sets in
${\mathbb Z}^{n}$
. A Moran measure is defined by the following infinite convolution of finite measures:
$$ \begin{align} \mu_{\{R_{k}\},\{D_{k}\}}=\delta_{R_{1}^{-1}D_{1}}\ast\delta_{R_{1}^{-1}R_{2}^{-1}D_{2}}\ast\cdots, \end{align} $$
assuming the infinite convolution is weakly convergent to a Borel probability measure (see [Reference Falconer11] for an equivalent definition). Here,
$\delta _E=\frac 1{\#E}\sum _{e\in E} \delta _e$
, where
$\#E$
is the cardinality of a finite set E and
$\delta _e$
is the Dirac measure at the point
$e\in E$
. In
$2000$
, Stricharz [Reference Stricharz29] first considered the conditions under which the infinite convolution is convergent to a Borel probability measure with compact support and the associated measure is a spectral measure. Later on, An and He [Reference An and He2] investigated the spectral property of infinite convolution with consecutive digits in
$\mathbb {R}$
. More precisely, let
$\{b_{k}\}_{k=1}^{\infty }$
be a sequence of integers with all
$b_{k}\geq 2$
, and let
$\{D_k\}_{k=1}^{\infty }$
be a sequence of finite digit sets, where
$D_{k}=\{0,1,\ldots ,q_{k}-1\}$
is a digit set of integers with
$\sup \{x: x \in b_{k}^{-1}D_{k},k\geq 1\}<\infty $
. They proved the following theorem.
Theorem 1.1 Suppose that
$q_{k}|b_{k}$
for
$k\geq 1$
. Then, the Moran measure
$\mu _{\{b_{k}\},\{D_{k}\}}$
is a spectral measure.
Recently, Dutkay, Emami, and Lai [Reference Dutkay, Emami and Lai8] studied the general Moran measure
$\mu _{\{R_{k}\},\{D_{k}\}}$
on
${\mathbb R}^n$
, and they investigated the spectrality and its more general frame spectrality using the idea of frame towers and Riesz-sequence towers.
In this paper, we continue to investigate the spectral property of Moran measures on
$\mathbb {R}^{n}$
. Let
$\{R_{k}\}_{k=1}^{\infty }$
be a sequence of expanding matrices with integer entries, and let
$D_{k}=\{0,1,\ldots ,q_{k}-1\}\boldsymbol {v}$
where the integer
$q_{k}\geq 2$
and
$\boldsymbol {v}\in {\mathbb Z}^{n}$
for
$k\ge 1$
.
First of all, we need a decomposition of integer matrices, which has been proved in [Reference Liu and Luo25]. Let
$R\in M_{n}({\mathbb Z})$
, and let
$\{\boldsymbol {v},R\boldsymbol {v},\ldots ,R^{n-1}\boldsymbol {v}\}$
be a set of vectors in
${\mathbb Z}^{n}$
with rank
$r\leq n$
and
$\boldsymbol {v}\in {\mathbb Z}^{n}\setminus \{\mathbf {0}\}$
. According to [Reference Liu and Luo25], there exists a unimodular matrix
$B\in M_{n}({\mathbb Z})$
such that
$B^{-1}\boldsymbol {v}=(\boldsymbol {v}_{r}^{T},0,\ldots ,0)^{T}$
with
$\boldsymbol {v}_{r}\in {\mathbb Z}^{r}$
and
$$ \begin{align} \widetilde{R}:=B^{-1}RB=\begin{pmatrix} M_{1} & C \\ 0 & M_{2} \\ \end{pmatrix}, \end{align} $$
where
$M_{1}\in M_{r}({\mathbb Z})$
,
$M_{2}\in M_{n-r}({\mathbb Z})$
, and
$C\in M_{r,n-r}({\mathbb Z})$
. Here, we use
$A^T$
to denote the transposition of a vector or matrix A.
Similar to the known theorem in [Reference Stricharz29], we have the following theorem.
Theorem 1.2 Let
$R_{k}=b_{k}R^{m_{k}}~\text {for}~k\geq 1$
, where
$R\in M_{n}({\mathbb Z})$
is an expanding matrix and the sequences
$\{b_{k}\}_{k=1}^{\infty }$
and
$\{m_{k}\}_{k=1}^{\infty }$
are of positive integers. Let
$D_{k}=\{0,1,\ldots , q_{k}-1\}\boldsymbol {v}$
be a digit set with
$\boldsymbol {v}\in \mathbb {Z}^{n}\setminus \{\mathbf {0}\}$
and the integer
$q_{k}\geq 2$
for each
$k\geq 1$
. Suppose that
$\sup _{k\geq 1}|\frac {q_{k}}{b_{k}}|<\infty .$
Then, the sequence of measures
$$ \begin{align*}\mu_{n}:=\delta_{R_{1}^{-1}D_{1}}\ast\delta_{R_{1}^{-1}R_{2}^{-1}D_{2}}\ast\cdots\ast \delta_{R_{1}^{-1}\cdots ~R_{n}^{-1}D_{n}}\end{align*} $$
converges to a Borel probability measure
$\mu _{\{R_{k}\},\{D_{k}\}}$
with compact support in a weak sense.
The measure
$\mu _{\{R_{k}\},\{D_{k}\}}$
in Theorem 1.2 is the Moran measure on which we focus in the following of the paper. Now, we introduce the main theorem of the paper.
Theorem 1.3 Let
$D_{k},R_{k}$
be given as in Theorem 1.2, and let
$\boldsymbol {v}\in {\mathbb Z}^{n}\setminus \{\mathbf {0}\}$
be an eigenvector of R with respect to an eigenvalue
$\lambda $
. If
$\lambda b_{k}$
is divisible by
$q_{k}$
for
$k\ge 1$
, then
$\mu _{\{R_{k}\},\{D_{k}\}}$
is a spectral measure.
In fact, we have the following more general conclusion. We will prove it in Section 3 so as to prove Theorem 1.3.
Theorem 1.4 Let
$D_{k},R_{k}$
be given as in Theorem 1.2. Furthermore, we replace
$m_{k}$
by
$m_{k}r$
for
$k\geq 2$
where r is the rank of vectors
$\{\boldsymbol {v},R\boldsymbol {v},\ldots ,R^{n-1}\boldsymbol {v}\}$
. Suppose that the characteristic polynomial of
$M_{1}$
see (1.2) is
$f(x)=x^{r}+c$
. If
$q_{k}|b_{k}\det (M_{1})$
for
$k\ge 1$
, then the measure
$\mu _{\{R_{k}\},\{D_{k}\}}$
is a spectral measure.
It is clear that the condition
$\sup _{k\geq 1}|\frac {q_{k}}{b_{k}}|<\infty $
is satisfied in Theorems 1.3 and 1.4. Furthermore, if we replace
$b_{k}\in \mathbb {N}\setminus \{0\}$
by
$b_{k}\in \mathbb {Z}\setminus \{0\}$
in the above three theorems, the same results hold.
Next, we consider the converse of Theorem 1.4. However, it is too complicated for us to draw a necessity condition for the spectral measure
$\mu _{\{R_{k}\},\{D_{k}\}}$
. We simplify it to the case that
$R_k=R$
and
$D_k=D$
for all
$k\ge 1$
and obtain the following result. Before introducing it, we need a standard notation usually used in this setting.
Definition 1.1 Let
$R\in M_{n}(\mathbb {Z})$
be an expanding matrix (i.e., all its eigenvalues have modulus strictly greater than
$1$
), and let D be a finite subset of
${\mathbb Z}^{n}$
. We say that
$(R,D)$
is admissible if there exists a finite subset
$L\subseteq {\mathbb Z}^{n}~\text {with}~\# D=\# L=q$
such that the matrix
$$ \begin{align*} H=\frac{1}{\sqrt{q}}\begin{pmatrix}e^{-2\pi i\langle R^{-1}d,l\rangle}\end{pmatrix}_{d\in D,l\in L} \end{align*} $$
is unitary, i.e.,
$H^{\ast }H=I$
, where
$H^{\ast }$
denotes the transposed conjugate of H. At this time,
$(R,D,L)$
is also called a Hadamard triple, or
$(R^{-1}D,L)$
is called a compatible pair.
By making use of the matrix decomposition as in (1.2), we obtain the following conclusion.
Theorem 1.5 Let
$R\in M_{n}(\mathbb {Z})$
be an expanding matrix, and let
$D=\{0,1,\ldots ,q-1\}\boldsymbol {v}$
be a digit set with
$\boldsymbol {v}\in {\mathbb Z}^{n}\setminus \{\mathbf {0}\}$
and the integer
$q\geq 2$
. If
$(R,D)$
is admissible, then
$q|\det (M_{1})$
.
In general, the converse of Theorem 1.5 is not true for
$n\ge 2$
(see Example 5.2). However, in
${\mathbb R}$
, assuming
$\boldsymbol {v}=1$
, then q is a factor of
$\det (M_{1})$
if and only if
$(R,D)$
is admissible (see [Reference An and He2]).
The paper is organized as follows. In Section 2, we introduce some basic definitions and properties of spectral measures. In Section 3, we will give the proofs of Theorems 1.3 and 1.4. Moreover, we devote Section 4 to proving Theorem 1.5. In Section 5, we will give some examples to illustrate the theories.
2 Preliminaries
Let
$\mu $
be a Borel probability measure with compact support in
$\mathbb {R}^{n}$
. The Fourier transform of
$\mu $
is defined as usual
$$ \begin{align*}\hat{\mu}(\xi)=\int e^{-2\pi i\langle\xi,x\rangle}\mathrm{d}\mu(x)\end{align*} $$
for any
$\xi \in {\mathbb R}^n$
. Let
$\mathcal {Z}{\left (\hat {\mu }\right )}=\{\xi \in {\mathbb R}^n:\hat {\mu }(\xi )=0\}$
be the zero set of
$\hat {\mu }$
. Then, for a discrete set
$\Lambda \subset {\mathbb R}^n$
,
$E(\Lambda )=\{e^{-2\pi i\langle \lambda ,x\rangle }:\lambda \in \Lambda \}$
is an orthogonal set of
$L^2(\mu )$
if and only if
$\hat {\mu }(\lambda -\lambda ')=0$
for
$\lambda \neq \lambda '\in \Lambda $
, which is equivalent to
$$ \begin{align} (\Lambda-\Lambda)\setminus\{\mathbf{0}\}\subseteq\mathcal{Z}{\left(\hat{\mu}\right)}. \end{align} $$
In this case, we call
$\Lambda $
an orthogonal set (resp. spectrum) of
$\mu $
if
$E_{\Lambda }$
is an orthonormal family (resp. basis) for
$L^{2}(\mu )$
. Since orthogonal sets (or spectra) are invariant under translation, without loss of generality, we always assume that
$\mathbf {0}\in \Lambda $
for any orthogonal set
$\Lambda $
of
$\mu $
.
For any
$\xi \in \mathbb {R}^{n}$
, define
$$ \begin{align} Q_{\Lambda}^{(\mu)}(\xi)=\sum_{\lambda\in\Lambda}\mid \hat {\mu}(\xi+\lambda)\mid^{2}. \end{align} $$
The following lemma is a basic criterion for the spectrality of measure
$\mu $
, which was proved in [Reference Jorgensen and Pedersen18].
Lemma 2.1 Let
$\mu $
be a Borel probability measure with compact support in
$\mathbb {R}^{n}$
, and let
$\Lambda \subseteq \mathbb {R}^{n}$
be a countable subset. Then,
-
(i)
$\Lambda $
is an orthogonal set of
$\mu $
if and only if
$Q_{\Lambda }^{(\mu )}(\xi )\leq 1$
for
$\xi \in \mathbb {R}^{n}$
. -
(ii)
$\Lambda $
is a spectrum of
$\mu $
if and only if
$Q_{\Lambda }^{(\mu )}(\xi )\equiv 1$
for
$\xi \in \mathbb {R}^{n}$
. -
(iii)
$Q_{\Lambda }^{(\mu )}(x)$
has an entire analytic extension to
$\mathbb {C}^2$
if
$\Lambda $
is an orthogonal set of
$\mu $
.
Definition 2.1 Let R and
$\widetilde {R}$
be
$n\times n$
integer matrices, and let the finite sets
$D,L,\widetilde {D},\widetilde {L}$
be in
${\mathbb R}^{n}$
. We say that two triples
$(R,D,L)$
and
$(\widetilde {R},\widetilde {D},\widetilde {L})$
are conjugate (through the matrix B) if there exists an integer invertible matrix B such that
$\widetilde {R}=B^{-1}RB,~\widetilde {D}=B^{-1}D$
, and
$\widetilde {L}=B^{\ast }L$
, where
$B^*$
denotes the transposed conjugate of B, in fact,
$B^*=B^T$
.
We have the following conclusion for the conjugate relationship.
Lemma 2.2 Suppose that
$(R_{k},D_{k},L_{k})$
and
$(\widetilde {R}_{k},\widetilde {D}_{k},\widetilde {L}_{k})$
are conjugate triples, through the same matrix B, for any
$k\geq 1$
. Then,
-
(i)
$(\widetilde {R}_{k},\widetilde {D}_{k},\widetilde {L}_{k})$
is a Hadamard triple if
$(R_{k},D_{k},L_{k})$
is a Hadamard triple. -
(ii)
$\Lambda $
is a spectrum of
$\mu _{\{R_{k}\},\{D_{k}\}} $
if and only if
$B^{\ast }\Lambda $
is a spectrum of
$\mu _{\{\widetilde {R}_{k}\},\{\widetilde {D}_{k}\}}$
.
Proof (i) Note that
$\widetilde {R}_k=B^{-1}R_kB,~\widetilde {D}_k=B^{-1}D_k$
, and
$\widetilde {L}_k=B^{\ast }L_k$
. Then,
$$ \begin{align*} \begin{pmatrix}e^{-2\pi i\langle \widetilde{R}_k^{-1}d,l\rangle}\end{pmatrix}_{d\in \widetilde{D}_k,l\in \widetilde{L}_k}&= \begin{pmatrix}e^{-2\pi i\langle B^{-1}\widetilde{R}_k^{-1}BB^{-1}d,B^{\ast}l\rangle}\end{pmatrix}_{d\in {D}_k,l\in {L}_k} \\ &= \begin{pmatrix}e^{-2\pi i\langle \widetilde{R}_k^{-1}d,l\rangle}\end{pmatrix}_{d\in {D}_k,l\in {L}_k}. \end{align*} $$
Furthermore,
$\widetilde {L}_k\subset {\mathbb Z}^2$
since
$L_k\subset {\mathbb Z}^2$
and B is an integer matrix. Hence, the conclusion follows directly from Definition 1.1.
As for (ii), we recall
$$ \begin{align*}\mu_{\{R_{k}\},\{D_{k}\}}=\delta_{R_{1}^{-1}D_{1}}\ast\delta_{R_{1}^{-1}R_{2}^{-1}D_{2}}\ast\cdots. \end{align*} $$
By the definition of Fourier transform of
$\mu _{\{R_{k}\},\{D_{k}\}}$
, we have
$$ \begin{align*}\hat{\mu}_{\{R_{k}\},\{D_{k}\}}(\xi)=\prod_{k=1}^{+\infty}\hat{\delta}_{R_{1}^{-1}R_{2}^{-1}\cdots R_{k}^{-1}D_{k}}(\xi) =\prod_{k=1}^{+\infty}\frac{1}{q_{k}}\sum_{d\in D_{k}}e^{-2\pi i\langle R_{1}^{-1}\cdots R_{k}^{-1}d ,\xi \rangle}, \end{align*} $$
where
$q_k:=\#D_{k}=\#\widetilde {D}_{k}$
. Then, for any
$\lambda \in \Lambda $
and
$\xi \in {\mathbb R}^{n}$
,
$$ \begin{align} \hat{\mu}_{\{R_{k}\},\{D_{k}\}}(\lambda+\xi)&=\prod_{k=1}^{+\infty}\frac{1}{q_{k}}\sum_{d\in D_{k}}e^{-2\pi i\langle R_{1}^{-1}\cdots R_{k}^{-1}d ,(\lambda+\xi) \rangle}\nonumber\\ &= \prod_{k=1}^{+\infty}\frac{1}{q_{k}}\sum_{d\in D_{k}}e^{-2\pi i\langle B^{-1}R_{1}^{-1}B\cdots B^{-1}R_{k}^{-1}BB^{-1}d ,B^{\ast}(\lambda+\xi)\rangle}\\ &= \prod_{k=1}^{+\infty}\frac{1}{q_{k}}\sum_{d\in \widetilde{D}_{k}}e^{-2\pi i\langle \widetilde{R}_{1}^{-1}\cdots \widetilde{R}_{k}^{-1}d ,B^{\ast}(\lambda+\xi) \rangle}\nonumber\\ &= \hat{\mu}_{\{\widetilde{R}_{k}\},\{\widetilde{D}_{k}\}}(B^{\ast}(\lambda+\xi)) \nonumber.\end{align} $$
Hence,
$Q_{\Lambda }^{(\mu _{\{R_{k}\},\{D_{k}\}})}(\xi ) =Q_{B^{\ast }\Lambda }^{(\mu _{\{\widetilde {R}_{k}\},\{\widetilde {D}_{k}\}})}(B^{\ast }\xi )$
. Furthermore, (ii) follows from Lemma 2.1.▪
In Sections 3 and 4, we employ the following lemma several times which was proved in [Reference Liu and Luo25].
Lemma 2.3 Let
$\boldsymbol {v}\in {\mathbb Z}^{n}\backslash \{\mathbf {0}\}$
, and let
$R\in M_{n}({\mathbb Z}).$
If
$\{\boldsymbol {v},R\boldsymbol {v},\ldots ,R^{n-1}\boldsymbol {v}\}$
is linearly dependent with rank
$r<n$
, then there exists a unimodular matrix
$B\in M_{n}({\mathbb Z})$
such that
$B^{-1}\boldsymbol {v}=(\boldsymbol {v}_{r}^{T},0,\ldots ,0)^{T}\in {\mathbb Z}^{n}$
and
$$ \begin{align*} \widetilde{R}:=B^{-1}RB= \begin{pmatrix} M_{1} & C \\ 0 & M_{2} \\ \end{pmatrix}, \end{align*} $$
where
$\boldsymbol {v}_{r}\in {\mathbb Z}^{r}$
,
$M_{1}\in M_{r}({\mathbb Z})$
,
$M_{2}\in M_{n-r}({\mathbb Z})$
, and
$C\in M_{r,n-r}({\mathbb Z})$
.
3 Proofs of Theorems 1.3 and 1.4
In this section, we will focus on the Moran measure
$\mu _{\{R_{k}\},\{D_{k}\}}$
defined in Theorem 1.2. For the sake of convenience, we introduce some notations from symbolic dynamical system. Denote
$\Theta ^0=\{\vartheta \}$
and
$$ \begin{align*}\Theta^n=\{\theta_1\cdots\theta_n:\theta_k\in D_k,1\le k\le n\}\end{align*} $$
for
$n\ge 1$
. Then, the collection of all finite words is
$$ \begin{align*}\Theta^*=\bigcup_{n=0}^{\infty}\Theta^n,\end{align*} $$
and the set of all infinite words is denoted by
$$ \begin{align*}\Theta^{\infty}=\{\theta_1\theta_2\cdots:\theta_k\in D_k,k\ge 1\}.\end{align*} $$
First, we give the proof of Theorem 1.2, which is the preparation for the proof of Theorem 1.3.
Proof of Theorem 1.2
Let
$B(0,r)$
be the open ball centered at the origin with radius r on
${\mathbb R}^n$
. Denote
$$ \begin{align*}f_{k,d}(x)=R_k^{-1}(x+d)\end{align*} $$
with
$d\in D_k$
and
$k\ge 1$
. Then, there exists
$n\ge 1$
and
$\theta _k\in D_k$
for
$1\le k\le n$
such that
$$ \begin{align*}f_{1,\theta_1}\circ f_{2,\theta_2}\circ\cdots \circ f_{n,\theta_n}(B(0,r))\subseteq B(0,r).\end{align*} $$
For any
$\theta =\theta _1\cdots \theta _n\in \Theta ^{n}$
, we write
$$ \begin{align*}f_{\theta}(x)=f_{1,\theta_1}\circ f_{2,\theta_2}\circ\cdots \circ f_{n,\theta_n}.\end{align*} $$
Denote
$$ \begin{align*}T(\{R_k\},\{D_k\})=\left\{\sum_{k=1}^{\infty}(R_k\ldots R_1)^{-1}d_k~:~d_k\in D_k\right\}:=\sum_{k=1}^{\infty}(R_k\ldots R_1)^{-1}D_k.\end{align*} $$
Then, it is easy to check that
$$ \begin{align*}T(\{R_k\},\{D_k\})=\bigcap_{n=1}^{\infty}\bigcup_{\theta\in\Theta^n}f_{\theta}(B(0,r)).\end{align*} $$
Thus, it is a compact set.
We now define two bounded linear operators
$T_{1}$
and
$T_{2}$
as follows.
$T_{1}:{\mathbb R}^{n}\rightarrow {\mathbb R}^{n}$
is given by
$$ \begin{align*}T_{1}x=B^{\ast}x,\end{align*} $$
where the unimodular matrix B satisfies
$B^{-1}RB=\begin {pmatrix}M_{1} & C \\0 &M_{2} \\\end {pmatrix}$
and
$B^{-1}\boldsymbol {v}= (\boldsymbol {v_{r}}^{T},0,\ldots ,0)^{T}$
(see Lemma 2.3).
$T_{2}:{\mathbb R}^{n}\rightarrow {\mathbb R}^{r}$
is given by
$$ \begin{align*}T_2\big((x_1,x_2,\ldots,x_r,\ldots,x_n)^{T}\big)=(x_{1},\ldots,x_{r})^{T}.\end{align*} $$
For any
$n\ge 1$
, we denote
$$ \begin{align*}\mu_{n}=\delta_{R_{1}^{-1}D_{1}}\ast\delta_{R_{1}^{-1}R_{2}^{-1}D_{2}}\ast\cdots\ast \delta_{R_{1}^{-1}\cdots ~R_{n}^{-1}D_{n}}.\end{align*} $$
Fix a compact set
$I\subseteq \mathbb {R}^{n}$
. For each
$\xi \in I$
, we get
$$ \begin{align*}\hat{\mu}_{n}(\xi)=\hat{\delta}_{R_{1}^{-1}D_{1}}(\xi)\hat{\delta}_{R_{1}^{-1}R_{2}^{-1}D_{2}}(\xi)\cdots \hat{\delta}_{R_{1}^{-1}\cdots ~R_{n}^{-1}D_{n}}(\xi), \end{align*} $$
and
$$ \begin{align*} \left|\hat{\delta}_{R_{1}^{-1}\cdots R_{k}^{-1}D_{k}}(\xi)-1\right| &= \left|\frac{1}{q_{k}}\sum_{d\in D_{k}}\bigg(e^{-2\pi i\langle R_{1}^{-1}\cdots R_{k}^{-1}d,\xi \rangle}-1\bigg) \right|\\[3pt] &= \left|\frac{1}{q_{k}}\sum_{l=0}^{q_{k}-1}\bigg(e^{-2l\pi i\langle (b_{1}\cdots b_{k})^{-1}B^{-1}R^{-m_{1}}B\cdots B^{-1}R^{-m_{k}}BB^{-1}\boldsymbol{v},B^{\ast}\xi \rangle}-1\bigg) \right|\\[3pt] &=\left|\frac{1}{q_{k}}\sum_{l=0}^{q_{k}-1}\bigg(e^{-2l\pi i\langle (b_{1}\cdots b_{k})^{-1}M_{1}^{-\eta_{k}}\boldsymbol{v}_{r},T_{2}T_{1}\xi\rangle}-1\bigg) \right|, \end{align*} $$
where
$\eta _{k}:=m_{1}+m_{2}+\cdots +m_{k}$
for
$1\le k\le n$
. Moreover, we have
$$ \begin{align*} & \kern9pt\left|e^{-2l\pi i\langle (b_{1}\cdots b_{k})^{-1}M_{1}^{-\eta_{k}}\boldsymbol{v_r},T_{2}T_{1}\xi\rangle}-1\right|\\[3pt] &\leq \left|2l\pi \langle (b_{1}\cdots b_{k})^{-1}M_{1}^{-\eta_{k}}\boldsymbol{v_{r}},T_{2}T_{1}\xi \rangle \right|\\[3pt] &\leq 2 l\pi (b_{1}\cdots b_{k})^{-1}\|M_{1}^{-\eta_{k}}\|\cdot\| \boldsymbol{v_r}\|\cdot\| T_{2}T_{1}\xi \| ,\end{align*} $$
where the first inequality follows from the fact that
$|e^{ix}-1|\leq |x|$
, and the second inequality follows from the Schwartz inequality. Hence,
$$ \begin{align} \sum_{k=1}^{\infty} \left| \hat{\delta}_{R_{1}^{-1}\cdots R_{k}^{-1}D_{k}}(\xi)-1 \right| &\leq \sum_{k=1}^{\infty}\frac{1}{q_{k}}\sum_{l=0}^{q_{k}-1}2l\pi (b_{1}\cdots b_{k})^{-1}\|M_{1}^{-\eta_{k}}\|\cdot\|\boldsymbol{v}_{r}\| \cdot\|T_{2}T_{1}\xi\|\nonumber\\[3pt] &\le \pi\sum_{k=1}^{\infty} \frac{q_{k}-1}{b_{k}}\|M_{1}^{-\eta_{k}}\|\cdot\|\boldsymbol{v}_{r}\| \cdot\| T_{2}T_{1}\xi \| \\[3pt] &\le C\| \boldsymbol{v}_{r}\| \cdot\| T_{2}\| \cdot\| T_{1}\| \cdot\| \xi \| \sum_{k=1}^{\infty} \|M_{1}^{-\eta_{k}}\|\nonumber, \end{align} $$
where
$C=\pi \sup _{k\ge 1}\frac {q_{k}}{b_{k}}.$
We can easily obtain
$\sum _{k=1}^{\infty }\|M_{1}^{-\eta _{k}}\|<\infty $
from the fact that R is an expanding integer matrix. As
$T_{1},T_{2}$
are bounded, it follows from (3.1) that
$\hat {\mu }_{n}(\xi )=\prod _{k=1}^{n}\hat {\delta }_{R_{1}^{-1}\cdots R_{k}^{-1}D_{k}}(\xi )$
converges uniformly on each compact set to an entire function
$f(\xi )=\prod _{k=1}^{\infty }\hat {\delta }_{R_{1}^{-1}\cdots R_{k}^{-1}D_{k}}(\xi )$
. By Levy’s continuity theorem [Reference Jacod and Protter17, p. 167], there exists a probability measure
$\mu $
such that
$\hat {\mu }(x)=f(x)$
and
$\mu _{n}$
converges weakly to
$\mu $
. Moreover, the support of
$\mu $
is compact.▪
In the following of this section, we define
$$ \begin{align} R_{k}^{(r)}= \begin{cases} b_{1}M_{1}^{m_{1}},&k=1,\\[5pt] b_{k}M_{1}^{m_{k}r},&k>1, \end{cases} \quad D_{k}^{(r)}=\{0,1,\ldots,q_{k}-1\}\boldsymbol{v_r}, \end{align} $$
where
$M_{1},\boldsymbol {v}_r$
are the same ones as in Lemma 2.3. We will prove Theorem 1.4 first. Before doing this, we introduce a needed lemma.
Lemma 3.1 Let R be an expanding integer matrix, and let
$R_{k},~D_{k}$
be given as in Theorem 1.4. Then,
$\mu _{\{R_{k}\},\{D_{k}\}}$
is a spectral measure if and only if
$\mu _{\{R_{k}^{(r)}\},\{D_{k}^{(r)}\}}$
is a spectral measure.
Proof According to Lemma 2.3, there exists a unimodular matrix
$B\in M_{n}({\mathbb Z})$
such that
$$ \begin{align} \widetilde{R}:=B^{-1}RB=\begin{pmatrix}M_{1} & C \\ 0 & M_{2} \\ \end{pmatrix},\,\,\,\widetilde{\boldsymbol{v}}=(\boldsymbol{v_{r}}^{T},0,\ldots,0)^{T}, \end{align} $$
$$ \begin{align} \widetilde{D}_{k}:=B^{-1}D_k=\{0,1,\ldots,q_{k}-1\} (\boldsymbol{v_{r}}^{T},0,\ldots,0)^{T}, \end{align} $$
where
$M_{1}\in M_{r}({\mathbb Z})$
,
$M_{2}\in M_{n-r}({\mathbb Z})$
,
$C\in M_{r,n-r}({\mathbb Z})$
, and
$\boldsymbol {v_{r}}\in {\mathbb Z}^{r}$
. Denote
$\widetilde {R}_k=B^{-1}R_kB$
. Then, Lemma 2.2 implies that
$\mu _{\{R_{k}\},\{D_{k}\}}$
is a spectral measure if and only if
$\mu _{\{\widetilde {R}_{k}\},\{\widetilde {D}_{k}\}}$
is a spectral measure. Note that
$$ \begin{align} \widetilde{R}_1^{-1}=B^{-1}R^{-m_1}B=\frac{1}{b_1}\begin{pmatrix}M_{1}^{-m_1} & \times \\[3pt] \mathbf{0} & M_{2}^{-m_1} \\ \end{pmatrix}. \end{align} $$
For any
$\xi =(\xi _{1},\ldots ,\xi _{n})^{T}\in {\mathbb R}^n$
, we denote its first r terms by
$\xi ^{(r)}=(\xi _{1},\ldots ,\xi _{r})^{T}\in {\mathbb R}^r$
. Then,
$$ \begin{align} \hat{\delta}_{\widetilde{R}_1^{-1}\cdots \widetilde{R}_k^{-1}\widetilde{D}_k}(\xi) &=\frac{1}{q_k}\sum_{d\in \widetilde{D}_k} e^{-2\pi i\langle \widetilde{R}_1^{-1}\cdots \widetilde{R}_k^{-1}d,\xi \rangle}\nonumber\\[3pt] &=\frac{1}{q_k}\sum_{j=0}^{q_k-1} e^{-2\pi ij\langle \widetilde{R}_1^{-1}\cdots \widetilde{R}_k^{-1} (\boldsymbol{v_{r}}^{T},0,\ldots,0)^{T},\xi\rangle}\\[3pt] &=\frac{1}{q_k}\sum_{j=0}^{q_k-1}e^{-\frac{2\pi ij}{b_1\cdots b_k}\langle M_1^{-m_1}\cdots M_k^{-m_kr}\boldsymbol{v_{r}}^{T},\xi^{(r)} \rangle}=\hat{\delta}_{(R_k^{(r)}\cdots R_1^{(r)})^{-1}D_k^{(r)}}(\xi^{(r)})\nonumber \end{align} $$
for any
$k\ge 1$
. It follows that
$$ \begin{align} \hat{\mu}_{\{\widetilde{R}_{k}\},\{\widetilde{D}_{k}\}}(\xi)=\prod_{k=1}^{\infty}\hat{\delta}_{\widetilde{R}_1^{-1}\cdots \widetilde{R}_k^{-1}\widetilde{D}_k}(\xi) =\prod_{k=1}^{\infty}\hat{\delta}_{(R_k^{(r)}\cdots R_1^{(r)})^{-1}D_k^{(r)}}(\xi^{(r)})= \hat{\mu}_{\{R_{k}^{(r)}\},\{D_{k}^{(r)}\}}(\xi^{(r)}). \end{align} $$
Now, we define a bounded linear operator
$T:\mathbb {R}^{n}\rightarrow \mathbb {R}^{r}$
given by
$$ \begin{align*} T\big((\xi_{1},\ldots,\xi_{r},\ldots,\xi_{n})^{T}\big)=(\xi_{1},\ldots,\xi_{r})^{T}.\end{align*} $$
If
$\mu _{\{\widetilde {R}_{k}\},\{\widetilde {D}_{k}\}}$
is a spectral measure with a spectrum
$\Lambda $
, we set
$$ \begin{align*} \Lambda'=\Big\{\lambda^{(r)}:T(\lambda)=\lambda^{(r)}, \lambda\in \Lambda\Big\}.\end{align*} $$
Then, (3.7) implies
$$ \begin{align} \sum_{\lambda\in\Lambda}\vert\hat{\mu}_{\{\widetilde{R}_{k}\},\{\widetilde{D}_{k}\}}(\xi+\lambda)\vert^2 =\sum_{\lambda^{(r)}\in\Lambda'}\vert\hat{\mu}_{\{R_{k}^{(r)}\},\{D_{k}^{(r)}\}}(\xi^{(r)}+\lambda^{(r)})\vert^2. \end{align} $$
It follows from Lemma 2.1 that
$\mu _{\{R_{k}^{(r)}\},\{D_{k}^{(r)}\}}$
is a spectral measure with a spectrum
$\Lambda '$
. Conversely, if
$\mu _{\{R_{k}^{(r)}\},\{D_{k}^{(r)}\}}$
is a spectral measure with a spectrum
$\Lambda '$
, we let
$\Lambda =\Big \{(\lambda ^{T},0,\ldots ,0)^{T}:\lambda \in \Lambda '\Big \}$
. Proceeding as in (3.8), we obtain that
$\Lambda $
is a spectrum of
$\mu _{\{\widetilde {R}_{k}\},\{\widetilde {D}_{k}\}}$
. Now, we complete the proof.▪
The following lemma has been proved in [Reference Liu and Luo25].
Lemma 3.2 Let
$R\in M_{n}({\mathbb Z})$
be a matrix with characteristic polynomial
$f(x)=x^{n}+a_{1}x^{n-1}+\cdots +a_{n-1}x+a_{n}$
and
$\boldsymbol {v}=(x_{1},x_{2},\ldots ,x_{n})^{T} \in {\mathbb Z}^{n}\setminus \{\mathbf {0}\}.$
If the set of vectors
$\{\boldsymbol {v},R\boldsymbol {v},\ldots ,R^{n-1}\boldsymbol {v}\}$
is linearly independent, then there exists an integer matrix B such that
$$ \begin{align*} \widetilde{R}:=B^{-1}RB=\begin{pmatrix} -a_{1} & 1&0 & \cdots & 0\\ -a_{2} & 0&1 & \cdots &0 \\ \vdots&\vdots &\vdots& \ddots & \vdots\\ -a_{n-1}&0 &0&\cdots &1\\ -a_{n}&0 &0&\cdots &0 \end{pmatrix} \end{align*} $$
and
$\widetilde {\boldsymbol {v}}=B^{-1}\boldsymbol {v}=(0,0,\ldots ,0,1)^{T}.$
Moreover, we can choose the matrix
$B=(R^{n-1}\boldsymbol {v},R^{n-2}\boldsymbol {v}, \ldots , R\boldsymbol {v},\boldsymbol {v})$
from the proof of Lemma 3.2 in [Reference Liu and Luo25].
Proof of Theorem 1.4
By Lemma 3.1, we just need to prove
$\mu _{\{R_{k}^{(r)}\},\{D_{k}^{(r)}\}}$
is a spectral measure. As
$\{\boldsymbol {v},R\boldsymbol {v},\ldots ,R^{n-1}\boldsymbol {v}\}$
is linearly dependent with rank r, we know that
$$ \begin{align*}\{B^{-1}\boldsymbol{v},B^{-1}R\boldsymbol{v},\ldots,B^{-1}R^{n-1}\boldsymbol{v}\}\end{align*} $$
is also linearly dependent with rank r, where B is the same one as in (3.3). And thus,
$\{\widetilde {\boldsymbol {v}},\widetilde {R}\widetilde {\boldsymbol {v}},\ldots ,\widetilde {R}^{n-1}\widetilde {\boldsymbol {v}}\}$
is linearly dependent with rank r, where
$\widetilde {R}$
and
$\widetilde {\boldsymbol {v}}$
are the same ones as in (3.3) and (3.4). Now, we claim that
$\{\widetilde {\boldsymbol {v}},\widetilde {R}\widetilde {\boldsymbol {v}},\ldots ,\widetilde {R}^{r-1}\widetilde {\boldsymbol {v}}\}$
is linearly independent. In fact, if
$\{\widetilde {\boldsymbol {v}},\widetilde {R}\widetilde {\boldsymbol {v}},\ldots ,\widetilde {R}^{r-1}\widetilde {\boldsymbol {v}}\}$
is dependent, then there exist
$\{l_i\}_{i=0}^{r-1}\subset {\mathbb Z}$
such that
$$ \begin{align} l_0\boldsymbol{v}+l_1\widetilde{R}\widetilde{\boldsymbol{v}}+\cdots+l_{r-1}\widetilde{R}^{r-1}\widetilde{\boldsymbol{v}}=0. \end{align} $$
Denote s as the first index such that
$l_s\neq 0$
. Then, (3.9) implies that
$$ \begin{align*}l_s\widetilde{R}^s\widetilde{\boldsymbol{v}}+\cdots+l_{r-1}\widetilde{R}^{r-1}\widetilde{\boldsymbol{v}}=0.\end{align*} $$
It follows that
$$ \begin{align} \widetilde{\boldsymbol{v}}=-\frac{1}{l_{s}}(l_{s+1}\widetilde{R}\widetilde{\boldsymbol{v}}+\cdots+l_{r-1}\widetilde{R}^{r-1-s} \widetilde{\boldsymbol{v}}). \end{align} $$
Then, we know that
$\{0,\widetilde {R}\widetilde {\boldsymbol {v}},\ldots ,\widetilde {R}^{n-1}\widetilde {\boldsymbol {v}}\}$
is also linearly dependent with rank r. Note that (3.10) is equivalent to the following equality:
$$ \begin{align*}\widetilde{R}\widetilde{\boldsymbol{v}}=-\frac{1}{l_{s}}(l_{s+1}\widetilde{R}^2\widetilde{\boldsymbol{v}}+\cdots+l_{r-1} \widetilde{R}^{r-s}\widetilde{\boldsymbol{v}}).\end{align*} $$
And thus,
$\{0,0,\widetilde {R}^2\widetilde {\boldsymbol {v}},\ldots ,\widetilde {R}^{n-1}\widetilde {\boldsymbol {v}}\}$
is linearly dependent with rank r. Proceeding inductively for finite steps, we know that
$\{0,0,\ldots ,0,\widetilde {R}^{s+1}\widetilde {\boldsymbol {v}},\ldots ,\widetilde {R}^{r-1}\widetilde {\boldsymbol {v}}\}$
is linearly dependent with rank r, which is impossible. Therefore, the claim follows. Then, we know from the claim and (3.3) that
$\{\boldsymbol {v}_{r},M_{1}\boldsymbol {v}_{r},\ldots ,M_{1}^{r-1}\boldsymbol {v}_{r}\}$
is linearly independent. Combining Lemmas 2.2 and 3.2, we only need to show
$\mu _{\{\widetilde {R}_{k}^{(r)}\},\{\widetilde {D}_{k}^{(r)}\}}$
is a spectral measure where
$$ \begin{align*} \widetilde{R}_{k}^{(r)} &= \begin{cases} b_{1}\widetilde{M}_{1}^{m_{1}},&k=1,\\[5pt] b_{k}\widetilde{M}_{1}^{m_{k}r},&k>1, \end{cases}\quad m_{1}=m_{1}'r+l ,~\text{with}~m_{1}'\geq0 ~,1\le l\le r,\\ \widetilde{D}_{k}^{(r)}&=\{0,1,\ldots,q_{k}-1\}\widetilde{\boldsymbol{v}}_{r},\,\,\, \widetilde{\boldsymbol{v}}_{r}=(0,\ldots,0,1)^{T}, \end{align*} $$
and
$$ \begin{align*} \widetilde{M}_{1}=\begin{pmatrix} 0 & 1&0 & \cdots & 0\\[-3pt] 0 & 0&1 & \cdots &0 \\[-3pt] \vdots&\vdots &\vdots& \ddots & \vdots\\[3pt] 0&0 &0&\cdots &1\\[-3pt] -c&0 &0&\cdots &0 \end{pmatrix}.\end{align*} $$
It follows from
$q_{k}|b_{k}\det (M_{1})$
that
$q_{k}~|b_{k}c$
. For the sake of brevity, we denote
$B_{k}=\widetilde {R}_{k}^{(r)}$
from now on. As
$$ \begin{align*}\widetilde{M}_{1}^{-(m_1+\sum_{i=2}^{k}m_{i}r)}= \Big(-\frac{1}{c}\Big)^{m_{1}'+\sum_{i=2}^{k}m_{k}}\begin{pmatrix}0 & -\frac{1}{c}E_{l\times l} \\ E_{(r-l)\times (r-l)}& 0 \\ \end{pmatrix}, \end{align*} $$
then for any
$\xi =(\xi _{1},\ldots ,\xi _{r})^{T}\in {\mathbb R}^r$
, we have
$$ \begin{align*}\langle B_{1}^{-1}\cdots B_{k}^{-1}\widetilde{\boldsymbol{v}}_{r},\xi \rangle=\frac{\xi_{l}}{b_{1}\cdots b_{k}(-c)^{m_{1}'+m_{2}+\cdots+m_{k}+1}}, \end{align*} $$
where
$l=m_{1}-m_{1}'r\in \{1,2,\ldots ,r\}$
. Now, we set
$$ \begin{align*} \mathfrak{b}_{k}= \begin{cases} b_{1}|c|^{m_{1}'+1},&k=1,\\[5pt] b_{k}|c|^{m_{k}},&k>1, \end{cases} \quad\text{and}\quad \mathfrak{D}_{k}=\{0,1,\ldots,q_{k}-1\}. \end{align*} $$
Applying Theorem 1.1, we know that there exists a set
$\Lambda \subseteq \mathbb {R}$
satisfying
$Q_{\Lambda }^{(\mu _{\{\mathfrak {b}_{k}\},\{\mathfrak {D}_{k}\}})}(\xi )\equiv 1$
for any
$\xi \in \mathbb {R}$
. Denote
$$ \begin{align*}\Lambda'=\{(0,\ldots,0,\lambda,0,\ldots,0)^{T}:\lambda\in \Lambda \},\end{align*} $$
where
$\lambda $
is the lth coordinate of
$(0,\ldots ,0,\lambda ,0,\ldots ,0)^{T}$
. Then, for any
$$ \begin{align*}\xi=(\xi_{1},\ldots,\xi_{l},\ldots,\xi_{r})^{T}\in\mathbb{R}^{r},\end{align*} $$
we have
$$ \begin{align*} Q_{\Lambda'}^{(\mu_{\{\widetilde{R}_{k}^{(r)}\},\{\widetilde{D}_{k}^{(r)}\}})}(\xi) &=\sum_{\lambda'\in\Lambda'}|\hat{\mu}_{\{\widetilde{R}_{k}^{(r)}\},\{\widetilde{D}_{k}^{(r)}\}}(\xi+\lambda')|^{2}\\ &=\sum_{\lambda'\in \Lambda'}\prod_{k=1}^{\infty}\Bigg|\frac{1}{q_{k}}\sum_{d\in \widetilde{D}_{k}^{(r)}}e^{-2\pi i\langle B_{1}^{-1}\cdots B_{k}^{-1}d, ~\xi+\lambda' \rangle} \Bigg|^{2}\\ &=\sum_{\lambda\in \Lambda}\prod_{k=1}^{\infty}\frac{1}{q_{k}}\Bigg|\sum_{l=0}^{q_{k}-1}e^{-2\pi i \frac{l(\xi_{l}+\lambda)}{b_{1}\cdots b_{k}|c|^{m_{1}'+m_{2}+\cdots+m_{k}+1}}}\Bigg|^{2}\\ &=\sum_{\lambda\in\Lambda}|\hat{\mu}_{\{\mathfrak{b}_{k}\},\{\mathfrak{D}_{k}\}}~(\xi_{l}+\lambda)|^{2}\\ &=Q_{\Lambda}^{(\mu_{\{\mathfrak{b}_{k}\},\{\mathfrak{D}_{k}\}})}(\xi_{l})\equiv 1. \end{align*} $$
Hence,
$\mu _{\{\widetilde {R}_{k}^{(r)}\},\{\widetilde {D}_{k}^{(r)}\}}$
is a spectral measure with the spectrum
$\Lambda '$
.▪
As an application of Theorem 1.4, the proof of Theorem 1.3 is apparent.
Proof of Theorem 1.3
Since
$R\boldsymbol {v}=\lambda \boldsymbol {v}$
, we have
$$ \begin{align*}\{\boldsymbol{v},R\boldsymbol{v},\ldots,R^{n-1}\boldsymbol{v}\}=\{\boldsymbol{v},\lambda\boldsymbol{v},\ldots,\lambda^{n-1}\boldsymbol{v}\}.\end{align*} $$
It follows that the rank of vectors
$\{\boldsymbol {v},R\boldsymbol {v},\ldots ,R^{n-1}\boldsymbol {v}\}$
is
$1$
, i.e.,
$r=1$
. From Lemma 2.3, we know that there exists a unimodular matrix
$B\in M_n({\mathbb Z})$
such that
$$ \begin{align} B^{-1}RBB^{-1}\boldsymbol{v}=\lambda B^{-1}\boldsymbol{v}, \end{align} $$
i.e.,
$$ \begin{align*}\begin{pmatrix}M_{1} & C \\ 0 & M_{2} \\ \end{pmatrix}\begin{pmatrix}\boldsymbol{v}_{r} \\[3pt] 0 \\[-3pt]\vdots \\ 0\\ \end{pmatrix} = \lambda \begin{pmatrix}\boldsymbol{v}_{r} \\[3pt] 0 \\[-3pt]\vdots \\ 0 \\\end{pmatrix},\end{align*} $$
where
$\boldsymbol {v}_{r}\in {\mathbb Z}^{r}$
,
$M_{1}\in M_{r}({\mathbb Z})$
,
$M_{2}\in M_{n-r}({\mathbb Z})$
, and
$C\in M_{r,n-r}({\mathbb Z})$
. Hence,
$M_1\boldsymbol {v}_{r}=\lambda \boldsymbol {v}_{r}$
. That is,
$\lambda $
is an eigenvalue of
$M_1$
. And thus,
$\lambda =\det (M_1)$
as
$r=1$
. Then, the characteristic polynomial of
$M_1$
is
$x-M_1$
. Applying Theorem 1.4, we know that
$\mu _{\{R_{k}\},\{D_{k}\}}$
is a spectral measure.▪
4 Proof of Theorem 1.5
In this section, we will prove Theorem 1.5. According to the dependence of the set of vectors
$\{\boldsymbol {v},R\boldsymbol {v},\ldots ,R^{n-1}\boldsymbol {v}\}$
, we distinguish the following two cases:
$r=n$
(Theorem 4.1) and
$r<n$
(Theorem 4.3).
Theorem 4.1 Let
$R \in M_{n}({\mathbb Z})$
be an expanding matrix, and let
$D=\{0,1,\ldots , q-1\}\boldsymbol {v}$
, where the integer
$q\geqslant 2$
and
$\boldsymbol {v}\in {\mathbb Z}^{n}\setminus \{\mathbf {0}\}$
. Suppose
$\{\boldsymbol {v},R\boldsymbol {v},\ldots ,R^{n-1}\boldsymbol {v}\}$
is linearly independent. If
$(R,D)$
is admissible, then
$q|\det (R)$
.
Proof Let
$f(x)=x^{n}+a_{1}x^{n-1}+\cdots +a_{n-1}x+a_{n}$
be the characteristic polynomial of R. According to Lemma 3.2, there exists an integer matrix
$B=(R^{n-1}\boldsymbol {v},R^{n-2}\boldsymbol {v}, \ldots , R\boldsymbol {v},\boldsymbol {v})$
such that
$$ \begin{align} \widetilde{R}=B^{-1}RB=\begin{pmatrix} -a_{1} & 1&0 & \cdots & 0\\ -a_{2} & 0&1 & \cdots &0 \\ \vdots&\vdots &\vdots& \ddots & \vdots\\ -a_{n-1}&0 &0&\cdots &1\\ -a_{n}&0 &0&\cdots &0 \end{pmatrix}, \end{align} $$
$$ \begin{align} \widetilde{D}=B^{-1}D=\{0,1,\ldots,q-1\}(0,0,\ldots,0,1)^{T}, \end{align} $$
$$ \begin{align} \widetilde{\boldsymbol{v}}=B^{-1}\boldsymbol{v}=(0,0,\ldots,0,1)^{T}. \end{align} $$
Denote
$$ \begin{align} d=\gcd(a_{n},q),\,\,\,q=dq',\,\,\,|a_{n}|=da_n', \end{align} $$
where
$q'$
and
$a_n'$
are positive integers with
$\gcd (q',a_n')=1$
. As
$(R,D)$
is admissible, we know from Lemma 2.2 that
$(\widetilde {R},\widetilde {D})$
is admissible. Then, there exists
$$ \begin{align*}C=\bigg\{\boldsymbol{x}^{(j)}:\boldsymbol{x}^{(j)}=\Big(x_{1}^{(j)},x_{2}^{(j)},\ldots,x_{n}^{(j)}\Big)^{T}\in {\mathbb Z}^{n},j\in \{0,1,2,\ldots,q-1\}\bigg\}\end{align*} $$
with
$\boldsymbol {x}^{(0)}=\mathbf {0}$
such that
$(\widetilde {R},\widetilde {D},C)$
is a Hadamard triple. Note
$$ \begin{align*}\widetilde{R}^{-1}\widetilde{\boldsymbol{v}}= \begin{pmatrix} 0 & 0&\cdots & 0& -\dfrac1{a_{n}}\\[10pt] 1 &0 &\cdots & 0&-\dfrac{a_{1}}{a_{n}} \\[10pt] \vdots&\vdots & \ddots & \vdots &\vdots\\[10pt] 0&0 &\cdots &0&-\dfrac{a_{n-2}}{a_{n}}\\[10pt] 0&0 &\cdots &1&-\dfrac{a_{n-1}}{a_{n}} \end{pmatrix} \begin{pmatrix} 0 \\[10pt] 0 \\[10pt] \vdots \\[10pt] 0 \\[10pt] 1 \end{pmatrix}= \begin{pmatrix} -\dfrac{1}{a_{n}} \\[10pt] -\dfrac{a_{1}}{a_{n}} \\[10pt] \vdots \\[10pt] -\dfrac{a_{n-2}}{a_{n}} \\[10pt] -\dfrac{a_{n-1}}{a_{n}} \\ \end{pmatrix}.\end{align*} $$
Denote
$\widetilde {D}=\{\widetilde {d}_k\}_{k=0}^{q-1}$
. Then, for any
$m\in {\mathbb Z}$
,
$$ \begin{align} \hat{\delta}_{\widetilde{R}^{-1}\widetilde{D}}(\boldsymbol{x}^{(j)}) &=\frac{1}{q}\sum_{k=0}^{q-1}e^{-2\pi i\langle\widetilde{R}^{-1}\widetilde{d}_k,\boldsymbol{x}^{(j)}\rangle}\nonumber\\ &=\frac{1}{q}\sum_{k=0}^{q-1}e^{2\pi ik\frac{x_{1}^{(j)}+a_{1}x_{2}^{(j)}+\cdots+a_{n-2}x_{n-1}^{(j)}+a_{n-1}x_{n}^{(j)}}{a_{n}}}\\ &=\frac{1}{q}\sum_{k=0}^{q-1}e^{2\pi ik\frac{(x_{1}^{(j)}+ma_{n})+a_{1}x_{2}^{(j)}+\cdots+a_{n-2}x_{n-1}^{(j)}+a_{n-1}x_{n}^{(j)}}{a_{n}}}.\nonumber \end{align} $$
Note that there exists
$m_{j}\in {\mathbb Z}$
so that
$0\leq L_{j}:=(x_{1}^{(j)}+m_{j}a_{n})+a_{1}x_{2}^{(j)}+\cdots +a_{n-2}x_{n-1}^{(j)}+a_{n-1}x_{n}^{(j)}\leq |a_{n}|-1$
for each
$0\le j\le q-1$
. Since
$(\widetilde {R},\widetilde {D},C)$
is a Hadamard triple, it follows from (4.5) that
$L_{i}\neq L_{j}$
for any
$0\leq i\neq j\leq q-1.$
Then, we may as well suppose that
$0=L_{0}<L_{1}<\cdots <L_{q-1}<|a_{n}|$
. Set
$$ \begin{align*}\widetilde{C}=\Big\{\widetilde{\boldsymbol{x}}^{(j)}:\widetilde{\boldsymbol{x}}^{(j)} =\boldsymbol{x}^{(j)}+(m_{j}a_{n},0,\ldots,0)^{T},\boldsymbol{x}^{(j)}\in C\Big\}\end{align*} $$
with
$m_0=0$
. Obviously,
$(\widetilde {R},\widetilde {D},\widetilde {C})$
is a Hadamard triple. This together with (4.5) implies that for each
$1\le j\le q-1$
,
$$ \begin{align*} \Bigg|\frac{1}{q}\sum_{\widetilde{d}_k\in \widetilde{D}}e^{-2\pi i\langle\widetilde{R}^{-1}\widetilde{d}_{k},\widetilde{\boldsymbol{x}}^{(j)}-\mathbf{0}\rangle}\Bigg|= \frac{\left|\sin(a_{n}^{-1}qL_{j}\pi )\right|}{\left|q\sin(a_{n}^{-1}L_{j}\pi)\right|}=0. \end{align*} $$
It follows that
$L_{j}=\alpha _{j}a_n'(0\leq j\leq q-1)$
where all
$\alpha _{j}$
are integers with
$0=\alpha _{0}<\alpha _{1}<\cdots <\alpha _{q-1}$
. Hence,
$\alpha _{q-1}\geq q-1$
. And thus,
$|a_{n}|>L_{q-1}=\alpha _{q-1}a_n'\geq (q-1)a_n'$
. This together with (4.4) implies that
$d> q-1$
. On the other hand,
$d=\gcd (q,a_{n})$
. Therefore,
$d=q$
. Notice that
$\det (R)=(-1)^na_n$
. Then, the assertion follows.▪
Especially, we have the following corollary.
Corollary 4.2 Let
$$ \begin{align*} R=\begin{pmatrix} -a_{1} & 1&0 & \cdots & 0\\[-1pt] -a_{2} & 0&1 & \cdots & 0\\[-1pt] \vdots&\vdots &\vdots& \ddots & \vdots\\[1pt] -a_{n-1}&0 &0&\cdots &1\\[-1pt] -a_{n}&0 &0&\cdots &0 \end{pmatrix} \end{align*} $$
be an expanding integer matrix, and let
$D=\{0,1,\ldots ,q-1\}\boldsymbol {v}$
, where
$\boldsymbol {v}=(0,0,\ldots , 0,1)^{T}$
. Then,
$(R,D)$
is admissible if and only if
$q|\det (R)$
.
Proof The necessity is proved in Theorem 4.1. Conversely, Set
$$ \begin{align*}L=\{0,1,\ldots,q-1\}\Big(\frac{a_{n}}{q},0,\ldots,0\Big)^{T}.\end{align*} $$
As
$\det (R)=(-1)^na_n$
and
$q|\det (R)$
, we have
$L\subset {\mathbb Z}^n$
. Note that
$$ \begin{align*}R^{-1}{\boldsymbol{v}}= \begin{pmatrix} 0 & 0&\cdots & 0& -\dfrac1{a_{n}}\\[10pt] 1 &0 &\cdots & 0&-\dfrac{a_{1}}{a_{n}} \\[10pt] \vdots&\vdots & \ddots & \vdots &\vdots\\[10pt] 0&0 &\cdots &0&-\dfrac{a_{n-2}}{a_{n}}\\[10pt] 0&0 &\cdots &1&-\dfrac{a_{n-1}}{a_{n}} \end{pmatrix} \begin{pmatrix} 0 \\[10pt] 0 \\[10pt] \vdots \\[10pt] 0 \\[10pt] 1 \end{pmatrix}= \begin{pmatrix} -\dfrac{1}{a_{n}} \\[10pt] -\dfrac{a_{1}}{a_{n}} \\[10pt] \vdots \\[10pt] -\dfrac{a_{n-2}}{a_{n}} \\[10pt] -\dfrac{a_{n-1}}{a_{n}} \\ \end{pmatrix}.\end{align*} $$
Then, for any distinct
$l_{1},l_{2}\in \{0,1,\ldots ,q-1\}$
,
$$ \begin{align*} &~~\hat{\delta}_{{R}^{-1}{D}}\Bigg((l_{1}-l_{2})\Big(\frac{ca_{n}}{q},0,\ldots,0\Big)^{T}\Bigg)= \frac{1}{q}\sum_{d\in{D}}e^{-2\pi i\langle{R}^{-1}d,(l_{1}-l_{2})(\frac{ca_{n}}{q},0,\ldots,0)^{T}\rangle} \\ &= \frac{1}{q}\sum_{k=0}^{q-1}e^{-2\pi i\langle k{R}^{-1}(0,0,\ldots,0,1)^{T},(l_{1}-l_{2})(\frac{ca_{n}}{q},0,\ldots,0)^{T}\rangle} =\frac{1}{q}\sum_{k=0}^{q-1}e^{-2\pi i\frac{kc(l_{2}-l_{1})}{q}}=0. \end{align*} $$
Hence,
$(R,D,L)$
is a Hadamard triple.▪
Theorem 4.3 Let
$R\in M_{n}({\mathbb Z})$
be an expanding matrix, and let
$D=\{0,1,\ldots ,q-1\}\boldsymbol {v}$
, where the integer
$q\geqslant 2$
and
$\boldsymbol {v}\in {\mathbb Z}^{n}\setminus \{\mathbf {0}\}$
. Suppose that
$\{\boldsymbol {v},R\boldsymbol {v},\ldots ,R^{n-1}\boldsymbol {v}\}$
is linearly dependent with rank
$r<n$
. If
$(R,D)$
is admissible, then
$q|\det (M_{1})$
, where
$M_1$
is expressed as in (1.2).
Proof According to Lemma 2.3, there exists a unimodular matrix
$B\in M_{n}({\mathbb Z})$
such that
$$ \begin{align} \widetilde{R}:=B^{-1}RB=\begin{pmatrix} M_{1} & C \\ 0 & M_{2} \\ \end{pmatrix}\in M_{n}({\mathbb Z}),\,\,\,\widetilde{\boldsymbol{v}}:=B^{-1}\boldsymbol{v}=(\boldsymbol{v}_r^{T},0,\ldots,0)^{T} \end{align} $$
and
$$ \begin{align} \widetilde{D}:=B^{-1}D=\{0,1,\ldots,q-1\}(\boldsymbol{v}_r^{T},0,\ldots,0)^{T}, \end{align} $$
where
$\boldsymbol {v}_r\in {\mathbb Z}^{r}$
,
$M_{1}\in M_{r}({\mathbb Z})$
,
$M_{2}\in M_{n-r}({\mathbb Z})$
, and
$C\in M_{r,n-r}({\mathbb Z})$
. By Lemma 2.2, we know that
$(\widetilde {R},\widetilde {D})$
is admissible since
$(R,D)$
is admissible. As
$\{\boldsymbol {v},R\boldsymbol {v},\ldots ,R^{n-1}\boldsymbol {v}\}$
is linearly dependent with rank r, we know that
$\{\widetilde {\boldsymbol {v}},\widetilde {R}\widetilde {\boldsymbol {v}},\ldots ,\widetilde {R}^{n-1}\widetilde {\boldsymbol {v}}\}$
is also linearly dependent with rank r. Similar to the proof in Theorem 1.4, we know that
$\{\widetilde {\boldsymbol {v}},\widetilde {R}\widetilde {\boldsymbol {v}},\ldots ,\widetilde {R}^{r-1}\widetilde {\boldsymbol {v}}\}$
is linearly independent. Then, we know from (4.6) that
$\{\boldsymbol {v}_r,M_{1}\boldsymbol {v}_r,\ldots ,M_{1}^{r-1}\boldsymbol {v}_r\}$
is linearly independent. Now, we define a bounded linear operator
$T:\mathbb {R}^{n}\rightarrow \mathbb {R}^{r}$
given by
$$ \begin{align*}T\big((x_{1},\ldots,x_{r},\ldots,x_{n})^{T}\big)=(x_{1},\ldots,x_{r})^{T}\end{align*} $$
for any
$(x_{1},\ldots ,x_{n})^{T}\in \mathbb {R}^{n}$
. Note that
$$ \begin{align*}\widetilde{R}^{-1}\widetilde{\boldsymbol{v}}=\begin{pmatrix} M_{1}^{-1} & \times \\[3pt] \mathbf{0} & M_{2}^{-1} \\ \end{pmatrix} \begin{pmatrix} \boldsymbol{v}_r \\[3pt] 0 \\[-3pt] \vdots \\ 0 \\ \end{pmatrix}= \begin{pmatrix} M_{1}^{-1}\boldsymbol{v}_r \\[3pt] 0 \\[-3pt] \vdots \\ 0 \\ \end{pmatrix}.\end{align*} $$
Since
$(\widetilde {R},\widetilde {D})$
is admissible, there exists
$\widetilde {L}\subseteq {\mathbb Z}^{n}$
with
$\#\widetilde {L}=\#\widetilde {D}=q$
such that
$$ \begin{align*} H=\frac{1}{\sqrt{q}}\begin{pmatrix} e^{-2\pi i \langle R^{-1}d,l\rangle} \\ \end{pmatrix}_{d\in \widetilde{D}, l\in \widetilde{L}} =\frac{1}{\sqrt{q}}\begin{pmatrix} e^{-2\pi i k\langle M_{1}^{-1} \boldsymbol{v_{r}},l\rangle} \\ \end{pmatrix}_{k\in \{0,1,\ldots,q-1\}, l\in T(\widetilde{L})} \end{align*} $$
is unitary. It follows that
$(M_{1},T(\widetilde {D}),T(\widetilde {L}))$
is a Hadamard triple. Combining with Theorem 4.1, we have
$q|\det (M_{1})$
.▪
Now, we have all ingredients to prove Theorem 1.5.
5 Some examples
In this section, we give some examples to illustrate our theory. The first example is an application of Theorem 1.4.
Example 5.1 Let
$R_{k}=b_{k}\begin {pmatrix}1 & -3 & 3 \\ 3 & -5 & 3 \\ 6 & -6 & 4 \\ \end {pmatrix}^{m_{k}}$
and
$D_{k}=\{0,1,\ldots ,q_{k}-1\}\boldsymbol {v}$
, where
$b_{k},m_{k}\in {\mathbb Z}^{+}$
and
$\boldsymbol {v}=\begin {pmatrix}1 \\ 1 \\ 2 \\ \end {pmatrix}$
for
$k\ge 1$
. Then,
$\mu _{\{R_{k}\},\{D_{k}\}}$
is a spectral measure if
$q_{k}|4b_{k}.$
Proof Let
$$ \begin{align*} R=\begin{pmatrix} 1 & -3 & 3 \\ 3 & -5 & 3 \\ 6 & -6 & 4 \\ \end{pmatrix},~ \boldsymbol{v}=\begin{pmatrix} 1 \\ 1 \\ 2 \\ \end{pmatrix} ~,B=\begin{pmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 2 & 0 & 1 \\ \end{pmatrix}. \end{align*} $$
Thus,
$$ \begin{align*} R\boldsymbol{v}=4\boldsymbol{v} \,\,\,\text{and}\,\,\,B^{-1}RB=\begin{pmatrix} 4 & -3 & 3 \\ 0 & -2 & 0 \\ 0 & 0 & -2 \\ \end{pmatrix}. \end{align*} $$
According to Theorem 1.4,
$\mu _{\{R_{k}\},\{D_{k}\}}$
is a spectral measure if
$q_{k}|4b_{k}.$
▪
The following example is given to explain that the condition
$q|\det (M_{1})$
in Theorem 1.5 is not sufficient.
Example 5.2 Let
$ R=\begin {pmatrix}2k+1 & 0 \\2c & 2c \\ \end {pmatrix}\in M_{2}({\mathbb Z})$
and
$D=\{0,1\}\boldsymbol {v}$
, where
$\boldsymbol {v}=(1,0)^{T}$
and
$k,c$
are nonzero integers. Then,
$(R,D)$
is not admissible.
Proof By a direct calculation, we have
$$ \begin{align} \mathcal{Z}(\hat{\delta}_{D})=\frac{1}{2}(1,0)^{T}+({\mathbb Z},\mathbb{R})^{T}, \end{align} $$
where
$(\mathbb {Z},\mathbb {R})=\{(x_{1},x_{2}):x_{1}\in \mathbb {Z},x_{2}\in \mathbb {R}\}$
. If
$(R,D)$
is admissible, then there exists
$C_{1}\subseteq \mathbb {Z}^{2}$
such that
$(R^{-1}D,C_{1})$
is a compatible pair with
$\mathbf {0}\in C_{1}$
. Let
$C=R^{\ast -1}C_{1}$
. Then, we know that
$C\subseteq \mathcal {Z}(\hat {\delta }_{D})$
and there exist
$n\in {\mathbb Z}$
and
$m\in {\mathbb R}$
such that
$$ \begin{align*}C=\left\{\mathbf{0},(\frac{1}{2}+n,m)^{T}\right\}.\end{align*} $$
Since
$C_1=R^{\ast }C\subseteq {\mathbb Z}^{2}$
, we have
$$ \begin{align*} R^{\ast}\begin{pmatrix} \frac{1}{2}+n \\ m\\ \end{pmatrix}= \begin{pmatrix} \Big(\dfrac12+n\Big)(2k+1)+2mc \\ 2mc \\ \end{pmatrix}\in {\mathbb Z}^{2}, \end{align*} $$
i.e.,
$$ \begin{align} \begin{cases} (2k+1)(1+2n)+4mc\in 2{\mathbb Z},\\ 2cm\in {\mathbb Z}. \end{cases} \end{align} $$
This is a contradiction. Hence,
$(R,D)$
is not admissible.▪
In Example 5.2, we notice that
$\{\boldsymbol {v},R\boldsymbol {v}\}$
is linearly independent and
$2|\det (R)$
, but
$(R,D)$
is not admissible. Hence, the condition
$q|\det (M_{1})$
in Theorem 1.5 is not sufficient.
