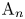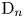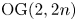1. Introduction
This paper is devoted to the study of derived categories of coherent sheaves on homogeneous varieties of semisimple algebraic groups and the relation to their quantum cohomology.
Recall that Dubrovin's conjecture (see [Reference DubrovinDub98]) predicts that the existence of a full exceptional collection in the bounded derived category ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$ of coherent sheaves on a smooth projective variety
${{\mathbf {D}^{\mathrm {b}}}}(X)$ of coherent sheaves on a smooth projective variety ![]() $X$ is equivalent to the generic semisimplicity of its big quantum cohomology ring
$X$ is equivalent to the generic semisimplicity of its big quantum cohomology ring ![]() $\operatorname {BQH}(X)$ (for background on quantum cohomology we refer to [Reference ManinMan99, Reference Fulton and PandharipandeFP97]). The big quantum cohomology ring is usually very hard to compute, in contrast to the small quantum cohomology
$\operatorname {BQH}(X)$ (for background on quantum cohomology we refer to [Reference ManinMan99, Reference Fulton and PandharipandeFP97]). The big quantum cohomology ring is usually very hard to compute, in contrast to the small quantum cohomology ![]() $\operatorname {QH}(X)$. Of course, if
$\operatorname {QH}(X)$. Of course, if ![]() $\operatorname {QH}(X)$ is generically semisimple, then so is
$\operatorname {QH}(X)$ is generically semisimple, then so is ![]() $\operatorname {BQH}(X)$. Thus, from Dubrovin's conjecture we conclude that generic semisimplicity of
$\operatorname {BQH}(X)$. Thus, from Dubrovin's conjecture we conclude that generic semisimplicity of ![]() $\operatorname {QH}(X)$ should imply the existence of a full exceptional collection in
$\operatorname {QH}(X)$ should imply the existence of a full exceptional collection in ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$. On the other hand, it was observed that the opposite implication is not true; see [Reference Cruz Morales, Kuznetsov, Mellit, Perrin and SmirnovCKMPS19, Reference Galkin, Mellit and SmirnovGMS15, Reference KeKe19, Reference PerrinPer14].
${{\mathbf {D}^{\mathrm {b}}}}(X)$. On the other hand, it was observed that the opposite implication is not true; see [Reference Cruz Morales, Kuznetsov, Mellit, Perrin and SmirnovCKMPS19, Reference Galkin, Mellit and SmirnovGMS15, Reference KeKe19, Reference PerrinPer14].
This observation suggests that, on the one hand, some mildly non-simple factors of the general fiber of ![]() $\operatorname {QH}(X)$ should not obstruct the existence of a full exceptional collection in
$\operatorname {QH}(X)$ should not obstruct the existence of a full exceptional collection in ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$, and on the other hand, generic semisimplicity of
${{\mathbf {D}^{\mathrm {b}}}}(X)$, and on the other hand, generic semisimplicity of ![]() $\operatorname {QH}(X)$ should have stronger implications for
$\operatorname {QH}(X)$ should have stronger implications for ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$ than just the existence of a full exceptional collection.
${{\mathbf {D}^{\mathrm {b}}}}(X)$ than just the existence of a full exceptional collection.
In [Reference Kuznetsov and SmirnovKS20] we stated for varieties of Picard number 1 a conjecture saying that the structure of the general fiber of ![]() $\operatorname {QH}(X)$ determines the structure of the exceptional collection on
$\operatorname {QH}(X)$ determines the structure of the exceptional collection on ![]() $X$. In this paper we suggest a more general and precise version of this conjecture and support it with new examples.
$X$. In this paper we suggest a more general and precise version of this conjecture and support it with new examples.
To state the conjecture we will need some notation. First, recall that the index of a smooth projective variety ![]() $X$ is the maximal integer
$X$ is the maximal integer ![]() $m$ such that the canonical class
$m$ such that the canonical class ![]() $K_X$ is divisible by
$K_X$ is divisible by ![]() $m$ in
$m$ in ![]() $\operatorname {Pic}(X)$; we usually assume that
$\operatorname {Pic}(X)$; we usually assume that ![]() $X$ is a Fano variety over an algebraically closed field of characteristic zero and write
$X$ is a Fano variety over an algebraically closed field of characteristic zero and write
where ![]() $\mathcal {O}_X(1)$ is a primitive ample line bundle on
$\mathcal {O}_X(1)$ is a primitive ample line bundle on ![]() $X$.
$X$.
We will say that an exceptional collection ![]() $E_1,\ldots ,E_k$ in
$E_1,\ldots ,E_k$ in ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$ extends to a rectangular Lefschetz collection, if the collection
${{\mathbf {D}^{\mathrm {b}}}}(X)$ extends to a rectangular Lefschetz collection, if the collection
is also exceptional. The orthogonal complement
is called the residual category of the above collection. In [Reference Kuznetsov and SmirnovKS20, Theorem 2.8] we checked that ![]() $\mathcal {R}$ is endowed with an autoequivalence
$\mathcal {R}$ is endowed with an autoequivalence ![]() $\tau _\mathcal {R} \colon \mathcal {R} \to \mathcal {R}$ (called the induced polarization of
$\tau _\mathcal {R} \colon \mathcal {R} \to \mathcal {R}$ (called the induced polarization of ![]() $\mathcal {R}$) such that
$\mathcal {R}$) such that
where ![]() ${{\mathbb {S}}}_\mathcal {R}$ is the Serre functor of
${{\mathbb {S}}}_\mathcal {R}$ is the Serre functor of ![]() $\mathcal {R}$. Thus,
$\mathcal {R}$. Thus, ![]() $\tau _\mathcal {R}$ plays in
$\tau _\mathcal {R}$ plays in ![]() $\mathcal {R}$ the same role as the twist by
$\mathcal {R}$ the same role as the twist by ![]() $\mathcal {O}(1)$ plays in
$\mathcal {O}(1)$ plays in ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$.
${{\mathbf {D}^{\mathrm {b}}}}(X)$.
Assume ![]() $X$ is a smooth Fano variety and let
$X$ is a smooth Fano variety and let ![]() $r$ be the Picard rank of
$r$ be the Picard rank of ![]() $X$, so that
$X$, so that ![]() $\operatorname {QH}(X)$ is an algebra over the ring
$\operatorname {QH}(X)$ is an algebra over the ring ![]() ${{\mathbb {Q}}}[q_1,\ldots ,q_r]$ of functions on the affine space
${{\mathbb {Q}}}[q_1,\ldots ,q_r]$ of functions on the affine space ![]() $\operatorname {Pic}(X) \otimes {{\mathbb {Q}}}$ over
$\operatorname {Pic}(X) \otimes {{\mathbb {Q}}}$ over ![]() ${{\mathbb {Q}}}$. Let
${{\mathbb {Q}}}$. Let
be the base change of ![]() $\operatorname {QH}(X)$ to the point of
$\operatorname {QH}(X)$ to the point of ![]() $\operatorname {Spec}({{\mathbb {Q}}}[q_1,\ldots ,q_r])$ corresponding to the canonical class of
$\operatorname {Spec}({{\mathbb {Q}}}[q_1,\ldots ,q_r])$ corresponding to the canonical class of ![]() $X$; this is a
$X$; this is a ![]() ${{\mathbb {C}}}$-algebra, whose underlying vector space is canonically isomorphic to
${{\mathbb {C}}}$-algebra, whose underlying vector space is canonically isomorphic to ![]() $\mathrm {H}^{\bullet }(X,{{\mathbb {C}}})$. Assume that
$\mathrm {H}^{\bullet }(X,{{\mathbb {C}}})$. Assume that ![]() $\mathrm {H}^{\mathrm {odd}}(X,{{\mathbb {C}}}) = 0$ and let
$\mathrm {H}^{\mathrm {odd}}(X,{{\mathbb {C}}}) = 0$ and let ![]() $m$ be the index of
$m$ be the index of ![]() $X$. Then
$X$. Then ![]() $\operatorname {QH_{can}}(X)$ is commutative, so we consider the finite scheme
$\operatorname {QH_{can}}(X)$ is commutative, so we consider the finite scheme
and call it the (canonical) quantum spectrum of ![]() $X$. By the dimension axiom for Gromov–Witten invariants the natural grading of
$X$. By the dimension axiom for Gromov–Witten invariants the natural grading of ![]() $\mathrm {H}^{\bullet }(X,{{\mathbb {C}}})$ induces a
$\mathrm {H}^{\bullet }(X,{{\mathbb {C}}})$ induces a ![]() ${{\mathbb {Z}}}/m$-grading of
${{\mathbb {Z}}}/m$-grading of ![]() $\operatorname {QH_{can}}(X)$ such that
$\operatorname {QH_{can}}(X)$ such that
which gives rise to an action of the group ![]() $\mu _m$ on the quantum spectrum
$\mu _m$ on the quantum spectrum ![]() $\operatorname {QS}_X$.
$\operatorname {QS}_X$.
Furthermore, let
be the anticanonical class. It defines a morphism of algebras ![]() ${{\mathbb {C}}}[\kappa ] \to \operatorname {QH_{can}}(X)$,
${{\mathbb {C}}}[\kappa ] \to \operatorname {QH_{can}}(X)$, ![]() $\kappa \mapsto -\mathrm {K}_X$ from a polynomial algebra in the variable
$\kappa \mapsto -\mathrm {K}_X$ from a polynomial algebra in the variable ![]() $\kappa$, which can be understood geometrically as a morphism of schemes
$\kappa$, which can be understood geometrically as a morphism of schemes
which is ![]() $\mu _m$-equivariant for the action on
$\mu _m$-equivariant for the action on ![]() $\operatorname {QS}_X$ defined above and the standard action on
$\operatorname {QS}_X$ defined above and the standard action on ![]() ${{\mathbb {A}}}^{1}$.
${{\mathbb {A}}}^{1}$.
Remark 1.1 The notion of quantum spectrum is parallel to that of spectral cover in the theory of Frobenius manifolds (see [Reference ManinMan99, Reference HertlingHer02]). The map (1.3) is analogous to the restriction of a Landau–Ginzburg potential to its critical locus.
Example 1.2 Let ![]() $X = {{\mathbb {P}}}^{n}$, so that
$X = {{\mathbb {P}}}^{n}$, so that ![]() $r = 1$ and
$r = 1$ and ![]() $m = n + 1$. Then
$m = n + 1$. Then
The quantum spectrum ![]() $\operatorname {QS}_{{{\mathbb {P}}}^{n}}$ is the reduced subscheme of
$\operatorname {QS}_{{{\mathbb {P}}}^{n}}$ is the reduced subscheme of ![]() ${{\mathbb {A}}}^{1}$ with points
${{\mathbb {A}}}^{1}$ with points ![]() $\zeta ^{i}$,
$\zeta ^{i}$, ![]() $0 \le i \le n$, where
$0 \le i \le n$, where ![]() $\zeta$ is a primitive
$\zeta$ is a primitive ![]() $(n+1)$th root of unity. The
$(n+1)$th root of unity. The ![]() ${{\mathbb {Z}}}/(n+1)$-grading is defined by
${{\mathbb {Z}}}/(n+1)$-grading is defined by ![]() $\deg (h) = 1$; it induces the natural action of
$\deg (h) = 1$; it induces the natural action of ![]() $\mu _{n+1}$ on
$\mu _{n+1}$ on ![]() ${{\mathbb {A}}}^{1}$ under which
${{\mathbb {A}}}^{1}$ under which ![]() $\operatorname {QS}_{{{\mathbb {P}}}^{n}}$ is invariant. Finally, we have
$\operatorname {QS}_{{{\mathbb {P}}}^{n}}$ is invariant. Finally, we have ![]() $-\mathrm {K}_X = (n+1)h$, and the map
$-\mathrm {K}_X = (n+1)h$, and the map ![]() $\kappa$ up to rescaling is the natural inclusion
$\kappa$ up to rescaling is the natural inclusion ![]() $\operatorname {QS}_{{{\mathbb {P}}}^{n}} \hookrightarrow {{\mathbb {A}}}^{1}$.
$\operatorname {QS}_{{{\mathbb {P}}}^{n}} \hookrightarrow {{\mathbb {A}}}^{1}$.
Our conjecture is based on an analogy between the ![]() $\mu _m$-action on
$\mu _m$-action on ![]() $\operatorname {QS}_X$ and the twist by
$\operatorname {QS}_X$ and the twist by ![]() $\mathcal {O}_X(1)$ on Lefschetz exceptional collections in
$\mathcal {O}_X(1)$ on Lefschetz exceptional collections in ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$: in this analogy the parts of
${{\mathbf {D}^{\mathrm {b}}}}(X)$: in this analogy the parts of ![]() $\operatorname {QS}_X$ supported over the complement of the origin and the origin of
$\operatorname {QS}_X$ supported over the complement of the origin and the origin of ![]() ${{\mathbb {A}}}^{1}$ (with respect to the map
${{\mathbb {A}}}^{1}$ (with respect to the map ![]() $\kappa$)
$\kappa$)
correspond to the rectangular part and the residual category of the Lefschetz collection. Note that the ![]() $\mu _m$-action on
$\mu _m$-action on ![]() $\operatorname {QS}^{\times }_X$ is free (because it is free on
$\operatorname {QS}^{\times }_X$ is free (because it is free on ![]() ${{\mathbb {A}}}^{1} \setminus \{0\}$), hence there exists a finite subscheme
${{\mathbb {A}}}^{1} \setminus \{0\}$), hence there exists a finite subscheme ![]() $Z \subset \operatorname {QS}^{\times }_X$ such that the action map
$Z \subset \operatorname {QS}^{\times }_X$ such that the action map ![]() $\mu _m \times Z \to \operatorname {QS}^{\times }_X$ is an isomorphism; the length of
$\mu _m \times Z \to \operatorname {QS}^{\times }_X$ is an isomorphism; the length of ![]() $Z$ is equal to the length of
$Z$ is equal to the length of ![]() $\operatorname {QS}^{\times }_X$ divided by
$\operatorname {QS}^{\times }_X$ divided by ![]() $m$, and we consider it as an analogue of the subcollection
$m$, and we consider it as an analogue of the subcollection ![]() $E_1,\ldots ,E_k$ in (1.1).
$E_1,\ldots ,E_k$ in (1.1).
Note that generic semisimplicity of ![]() $\operatorname {BQH}(X)$ assumed in the following conjecture implies the vanishing of
$\operatorname {BQH}(X)$ assumed in the following conjecture implies the vanishing of ![]() $\mathrm {H}^{\mathrm {odd}}(X,{{\mathbb {C}}})$ assumed above by [Reference Hertling, Manin and TelemanHMT09, Theorem 1.3].
$\mathrm {H}^{\mathrm {odd}}(X,{{\mathbb {C}}})$ assumed above by [Reference Hertling, Manin and TelemanHMT09, Theorem 1.3].
Conjecture 1.3 Let ![]() $X$ be a Fano variety of index
$X$ be a Fano variety of index ![]() $m$ over an algebraically closed field of characteristic zero and assume that the big quantum cohomology
$m$ over an algebraically closed field of characteristic zero and assume that the big quantum cohomology ![]() $\operatorname {BQH}(X)$ is generically semisimple.
$\operatorname {BQH}(X)$ is generically semisimple.
(i) There is an
 $\operatorname {Aut}(X)$-invariant exceptional collection
$\operatorname {Aut}(X)$-invariant exceptional collection  $E_1,\ldots ,E_k$ in
$E_1,\ldots ,E_k$ in  ${{\mathbf {D}^{\mathrm {b}}}}(X)$, where
${{\mathbf {D}^{\mathrm {b}}}}(X)$, where  $k$ is the length of
$k$ is the length of  $\operatorname {QS}^{\times }_X$ divided by
$\operatorname {QS}^{\times }_X$ divided by  $m$; this collection extends to a rectangular Lefschetz collection (1.1) in
$m$; this collection extends to a rectangular Lefschetz collection (1.1) in  ${{\mathbf {D}^{\mathrm {b}}}}(X)$.
${{\mathbf {D}^{\mathrm {b}}}}(X)$.(ii) The residual category
 $\mathcal {R}$ of this collection (defined by (1.2)) has a completely orthogonal
$\mathcal {R}$ of this collection (defined by (1.2)) has a completely orthogonal  $\operatorname {Aut}(X)$-invariant decomposition
with components indexed by closed points
$\operatorname {Aut}(X)$-invariant decomposition
with components indexed by closed points \[ \mathcal{R} = \bigoplus_{\xi \in \operatorname{QS}^{{\circ}}_X} \mathcal{R}_\xi \]
\[ \mathcal{R} = \bigoplus_{\xi \in \operatorname{QS}^{{\circ}}_X} \mathcal{R}_\xi \] $\xi \in \operatorname {QS}^{\circ }_X$; moreover, the component
$\xi \in \operatorname {QS}^{\circ }_X$; moreover, the component  $\mathcal {R}_\xi$ of the category
$\mathcal {R}_\xi$ of the category  $\mathcal {R}$ is generated by an exceptional collection of length equal to the length of the localization
$\mathcal {R}$ is generated by an exceptional collection of length equal to the length of the localization  $(\operatorname {QS}^{\circ }_X)_\xi$ at
$(\operatorname {QS}^{\circ }_X)_\xi$ at  $\xi$.
$\xi$.(iii) The induced polarization
 $\tau _\mathcal {R}$ permutes the components
$\tau _\mathcal {R}$ permutes the components  $\mathcal {R}_\xi$ of
$\mathcal {R}_\xi$ of  $\mathcal {R}$; more precisely, for each point
$\mathcal {R}$; more precisely, for each point  $\xi \in \operatorname {QS}^{\circ }_X$ it induces an equivalence
where
$\xi \in \operatorname {QS}^{\circ }_X$ it induces an equivalence
where \[ \tau_\mathcal{R} \colon \mathcal{R}_\xi \xrightarrow{\ \sim\ } \mathcal{R}_{g(\xi)}, \]
\[ \tau_\mathcal{R} \colon \mathcal{R}_\xi \xrightarrow{\ \sim\ } \mathcal{R}_{g(\xi)}, \] $g$ is a generator of
$g$ is a generator of  $\mu _m$.
$\mu _m$.
Note that any exceptional object on ![]() $X$ is invariant with respect to any connected reductive group acting on
$X$ is invariant with respect to any connected reductive group acting on ![]() $X$ (see [Reference PolishchukPol11, Lemma 2.2]); however, the group
$X$ (see [Reference PolishchukPol11, Lemma 2.2]); however, the group ![]() $\operatorname {Aut}(X)$ is not connected in general. Thus,
$\operatorname {Aut}(X)$ is not connected in general. Thus, ![]() $\operatorname {Aut}(X)$-invariance of the collection is an extra constraint (cf. the discussions in §§ 2.1 and 3.2).
$\operatorname {Aut}(X)$-invariance of the collection is an extra constraint (cf. the discussions in §§ 2.1 and 3.2).
Considerations from the introduction of [Reference Kuznetsov and SmirnovKS20] provide a homological mirror symmetry justification for Conjecture 1.3 (except possibly for the ![]() $\operatorname {Aut}(X)$-invariance statements, and for the action of
$\operatorname {Aut}(X)$-invariance statements, and for the action of ![]() $\tau _\mathcal {R}$ on the residual category).
$\tau _\mathcal {R}$ on the residual category).
If the Picard rank of ![]() $X$ is 1, so that
$X$ is 1, so that ![]() $\operatorname {QH}(X)$ is a
$\operatorname {QH}(X)$ is a ![]() ${{\mathbb {Q}}}[q]$-algebra, we have
${{\mathbb {Q}}}[q]$-algebra, we have
because ![]() $\operatorname {QH}(X)$ is
$\operatorname {QH}(X)$ is ![]() ${{\mathbb {Z}}}$-graded with
${{\mathbb {Z}}}$-graded with ![]() $\deg (q) = m$, hence semisimplicity of
$\deg (q) = m$, hence semisimplicity of ![]() $\operatorname {QH_{can}}(X)$ is equivalent to generic semisimplicity of
$\operatorname {QH_{can}}(X)$ is equivalent to generic semisimplicity of ![]() $\operatorname {QH}(X)$. Moreover, if
$\operatorname {QH}(X)$. Moreover, if ![]() $\operatorname {QH}(X)$ is generically semisimple the length of each localization
$\operatorname {QH}(X)$ is generically semisimple the length of each localization ![]() $(\operatorname {QS}^{\circ }_X)_\xi$ is 1, thus Conjecture 1.3 predicts the existence in
$(\operatorname {QS}^{\circ }_X)_\xi$ is 1, thus Conjecture 1.3 predicts the existence in ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$ of a rectangular Lefschetz collection whose residual category is generated by a completely orthogonal exceptional collection, which is equivalent to the prediction of [Reference Kuznetsov and SmirnovKS20, Conjecture 1.12]. In particular, numerous examples listed in the introduction to [Reference Kuznetsov and SmirnovKS20] together with the main result of [Reference Kuznetsov and SmirnovKS20] support both conjectures.
${{\mathbf {D}^{\mathrm {b}}}}(X)$ of a rectangular Lefschetz collection whose residual category is generated by a completely orthogonal exceptional collection, which is equivalent to the prediction of [Reference Kuznetsov and SmirnovKS20, Conjecture 1.12]. In particular, numerous examples listed in the introduction to [Reference Kuznetsov and SmirnovKS20] together with the main result of [Reference Kuznetsov and SmirnovKS20] support both conjectures.
Let us also discuss a couple of simple examples of varieties with higher Picard rank.
Example 1.4 Let ![]() $X = {{\mathbb {P}}}^{n} \times {{\mathbb {P}}}^{n}$, so that
$X = {{\mathbb {P}}}^{n} \times {{\mathbb {P}}}^{n}$, so that ![]() $r = 2$ and
$r = 2$ and ![]() $m = n + 1$. By the quantum Künneth formula (see [Reference KaufmannKau96, Reference Kontsevich and ManinKM96]) we have
$m = n + 1$. By the quantum Künneth formula (see [Reference KaufmannKau96, Reference Kontsevich and ManinKM96]) we have
The canonical class direction corresponds to ![]() $q_1 = q_2$, so the canonical quantum cohomology ring can be computed by specializing both
$q_1 = q_2$, so the canonical quantum cohomology ring can be computed by specializing both ![]() $q_1$ and
$q_1$ and ![]() $q_2$ to 1:
$q_2$ to 1:
Its spectrum ![]() $\operatorname {QS}_{X}$ is a reduced scheme of length
$\operatorname {QS}_{X}$ is a reduced scheme of length ![]() $(n+1)^{2}$ with points
$(n+1)^{2}$ with points ![]() $(\zeta ^{i},\zeta ^{j})$,
$(\zeta ^{i},\zeta ^{j})$, ![]() $0 \le i,j \le n$, where
$0 \le i,j \le n$, where ![]() $\zeta$ is the primitive
$\zeta$ is the primitive ![]() $(n+1)$th root of unity. The function
$(n+1)$th root of unity. The function ![]() $\kappa$ (up to rescaling) is given by the formula
$\kappa$ (up to rescaling) is given by the formula ![]() $\kappa = h_1 + h_2$, so
$\kappa = h_1 + h_2$, so ![]() $\kappa (\zeta ^{i},\zeta ^{j}) = \zeta ^{i} + \zeta ^{j}$ and
$\kappa (\zeta ^{i},\zeta ^{j}) = \zeta ^{i} + \zeta ^{j}$ and
 \begin{equation} \operatorname{QS}^{{\circ}}_{X} = \begin{cases} \varnothing, & \text{if } n = 2k \text{ is even,}\\ \{ (\zeta^{i},\zeta^{k+1+i}) \}, & \text{if } n = 2k + 1 \text{ is odd.} \end{cases} \end{equation}
\begin{equation} \operatorname{QS}^{{\circ}}_{X} = \begin{cases} \varnothing, & \text{if } n = 2k \text{ is even,}\\ \{ (\zeta^{i},\zeta^{k+1+i}) \}, & \text{if } n = 2k + 1 \text{ is odd.} \end{cases} \end{equation}
Furthermore, the generator of ![]() $\mu _{n+1}$ acts by
$\mu _{n+1}$ acts by ![]() $(\zeta ^{i},\zeta ^{j}) \mapsto (\zeta ^{i+1},\zeta ^{j+1})$; in particular the action of the group
$(\zeta ^{i},\zeta ^{j}) \mapsto (\zeta ^{i+1},\zeta ^{j+1})$; in particular the action of the group ![]() $\mu _{n+1}$ on
$\mu _{n+1}$ on ![]() $\operatorname {QS}^{\circ }_{X}$ is simply transitive.
$\operatorname {QS}^{\circ }_{X}$ is simply transitive.
The formula (1.4) exhibits a difference between the case of even and odd ![]() $n$; it also appears on the level of derived category. If
$n$; it also appears on the level of derived category. If ![]() $n = 2k$, the collection of
$n = 2k$, the collection of ![]() $2k + 1$ line bundles
$2k + 1$ line bundles
extends to an ![]() $\operatorname {Aut}(X)$-invariant rectangular Lefschetz collection
$\operatorname {Aut}(X)$-invariant rectangular Lefschetz collection ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X) = \langle \mathcal {A},\ldots ,\mathcal {A}(n)\rangle$ of total length
${{\mathbf {D}^{\mathrm {b}}}}(X) = \langle \mathcal {A},\ldots ,\mathcal {A}(n)\rangle$ of total length ![]() $(n+1)(2k+1) = (n+1)^{2}$, whose residual category is zero (this can be easily proved by the argument of Lemma 2.4).
$(n+1)(2k+1) = (n+1)^{2}$, whose residual category is zero (this can be easily proved by the argument of Lemma 2.4).
If ![]() $n = 2k + 1$, the collection (1.5) still extends to an
$n = 2k + 1$, the collection (1.5) still extends to an ![]() $\text{Aut}(X)$-invariant rectangular Lefschetz collection in
$\text{Aut}(X)$-invariant rectangular Lefschetz collection in ![]() $\mathbf{D}^{\mathrm{b}}(X)$, this time of length
$\mathbf{D}^{\mathrm{b}}(X)$, this time of length ![]() $(n+1)n$, and it can be checked (a similar computation in a more complicated situation can be found in § 2) that its residual category is generated by
$(n+1)n$, and it can be checked (a similar computation in a more complicated situation can be found in § 2) that its residual category is generated by ![]() $n + 1 = 2k + 2$ completely orthogonal exceptional vector bundles
$n + 1 = 2k + 2$ completely orthogonal exceptional vector bundles
 \begin{equation*}\begin{aligned} F_1 &= \mathcal{O}({-}1,k),\\ F_2 &= \tau_\mathcal{R}(F_1) &&\cong \,\,\quad\mathcal{O} \boxtimes \Omega^{k+1}(k+1),\\ F_3 &= \tau_\mathcal{R}(F_2) &&\cong \mathcal{O}(1) \boxtimes \Omega^{k+2}(k+2),\\ &\vdots \\ F_{k+2} &= \tau_\mathcal{R}(F_{k+1}) &&\cong \mathcal{O}(k) \boxtimes \Omega^{2k+1}(2k+1) &&\cong \mathcal{O}(k,-1),\\ F_{k+3} &= \tau_\mathcal{R}(F_{k+2}) &&\cong \Omega^{k+1}(k+1) \boxtimes \mathcal{O},\\ F_{k+4} &= \tau_\mathcal{R}(F_{k+3}) &&\cong \Omega^{k+2}(k+2) \boxtimes \mathcal{O}(1),\\ &\vdots \\ F_{2k+2} &= \tau_\mathcal{R}(F_{2k+1}) &&\cong \Omega^{2k}(2k) \boxtimes \mathcal{O}(k-1) \end{aligned}\end{equation*}
\begin{equation*}\begin{aligned} F_1 &= \mathcal{O}({-}1,k),\\ F_2 &= \tau_\mathcal{R}(F_1) &&\cong \,\,\quad\mathcal{O} \boxtimes \Omega^{k+1}(k+1),\\ F_3 &= \tau_\mathcal{R}(F_2) &&\cong \mathcal{O}(1) \boxtimes \Omega^{k+2}(k+2),\\ &\vdots \\ F_{k+2} &= \tau_\mathcal{R}(F_{k+1}) &&\cong \mathcal{O}(k) \boxtimes \Omega^{2k+1}(2k+1) &&\cong \mathcal{O}(k,-1),\\ F_{k+3} &= \tau_\mathcal{R}(F_{k+2}) &&\cong \Omega^{k+1}(k+1) \boxtimes \mathcal{O},\\ F_{k+4} &= \tau_\mathcal{R}(F_{k+3}) &&\cong \Omega^{k+2}(k+2) \boxtimes \mathcal{O}(1),\\ &\vdots \\ F_{2k+2} &= \tau_\mathcal{R}(F_{2k+1}) &&\cong \Omega^{2k}(2k) \boxtimes \mathcal{O}(k-1) \end{aligned}\end{equation*}
(where isomorphisms are up to shift). Note that the action of ![]() $\tau _\mathcal {R}$ on this exceptional collection is simply transitive, analogously to the action of
$\tau _\mathcal {R}$ on this exceptional collection is simply transitive, analogously to the action of ![]() $\mu _{n+1}$ on
$\mu _{n+1}$ on ![]() $\operatorname {QS}^{\circ }_{X}$.
$\operatorname {QS}^{\circ }_{X}$.
Example 1.5 Let ![]() $X = ({{\mathbb {P}}}^{1})^{n}$, so that
$X = ({{\mathbb {P}}}^{1})^{n}$, so that ![]() $r = n$ and
$r = n$ and ![]() $m = 2$. Applying again the quantum Künneth formula, one can check that
$m = 2$. Applying again the quantum Künneth formula, one can check that
is a reduced scheme of length ![]() $2^{n}$ and the function
$2^{n}$ and the function ![]() $\kappa$ is given by the sum of coordinates. Therefore,
$\kappa$ is given by the sum of coordinates. Therefore, ![]() $\operatorname {QS}^{\circ }_{({{\mathbb {P}}}^{1})^{n}}$ is empty when
$\operatorname {QS}^{\circ }_{({{\mathbb {P}}}^{1})^{n}}$ is empty when ![]() $n$ is odd, while for even
$n$ is odd, while for even ![]() $n = 2k$ it contains exactly
$n = 2k$ it contains exactly ![]() $\binom {2k}{k}$ points, and the
$\binom {2k}{k}$ points, and the ![]() $\mu _2$-action splits this set into
$\mu _2$-action splits this set into ![]() $\tfrac 12\binom {2k}{k}$ free orbits.
$\tfrac 12\binom {2k}{k}$ free orbits.
At the level of derived categories the same thing happens. If ![]() $n$ is odd, a rectangular
$n$ is odd, a rectangular ![]() $\operatorname {Aut}(({{\mathbb {P}}}^{1})^{n})$-invariant Lefschetz collection in
$\operatorname {Aut}(({{\mathbb {P}}}^{1})^{n})$-invariant Lefschetz collection in ![]() ${{\mathbf {D}^{\mathrm {b}}}}(({{\mathbb {P}}}^{1})^{n})$ with zero residual category was constructed in [Reference MironovMir21, Theorem 4.1]. If
${{\mathbf {D}^{\mathrm {b}}}}(({{\mathbb {P}}}^{1})^{n})$ with zero residual category was constructed in [Reference MironovMir21, Theorem 4.1]. If ![]() $n = 2k$ is even, using [Reference MironovMir21, Theorem 4.1], it is easy to show that the residual category is generated by
$n = 2k$ is even, using [Reference MironovMir21, Theorem 4.1], it is easy to show that the residual category is generated by ![]() $\binom {2k}{k}$ exceptional line bundles and the
$\binom {2k}{k}$ exceptional line bundles and the ![]() $\tau _\mathcal {R}$-action swaps them (up to shift) pairwise.
$\tau _\mathcal {R}$-action swaps them (up to shift) pairwise.
Using other results from [Reference MironovMir21], one can verify Conjecture 1.3 for some other products of projective spaces ![]() $({{\mathbb {P}}}^{n})^{k}$. In all these examples, however, the ring
$({{\mathbb {P}}}^{n})^{k}$. In all these examples, however, the ring ![]() $\operatorname {QH_{can}}(X)$ is semisimple. Below we discuss more intricate examples with non-semisimple ring
$\operatorname {QH_{can}}(X)$ is semisimple. Below we discuss more intricate examples with non-semisimple ring ![]() $\operatorname {QH_{can}}(X)$, provided by homogeneous varieties of simple algebraic groups, where quite a lot is known both about quantum cohomology and derived categories.
$\operatorname {QH_{can}}(X)$, provided by homogeneous varieties of simple algebraic groups, where quite a lot is known both about quantum cohomology and derived categories.
Perhaps the most interesting case here is that of adjoint and coadjoint homogeneous varieties. Recall that an adjoint (respectively, coadjoint) homogeneous variety of a simple algebraic group ![]() $\mathrm {G}$ is the highest weight vector orbit in the projectivization of the irreducible
$\mathrm {G}$ is the highest weight vector orbit in the projectivization of the irreducible ![]() $\mathrm {G}$-representation, whose highest weight is the highest long (respectively, short) root of
$\mathrm {G}$-representation, whose highest weight is the highest long (respectively, short) root of ![]() $\mathrm {G}$; in particular, if the group
$\mathrm {G}$; in particular, if the group ![]() $\mathrm {G}$ is simply laced, the adjoint and coadjoint varieties coincide.
$\mathrm {G}$ is simply laced, the adjoint and coadjoint varieties coincide.
For classical Dynkin types adjoint and coadjoint varieties are as follows:

Here ![]() $\operatorname {Fl}(1,n;n+1)$ is the partial flag variety,
$\operatorname {Fl}(1,n;n+1)$ is the partial flag variety, ![]() $Q^{2n-1}$ is a (smooth) quadric of dimension
$Q^{2n-1}$ is a (smooth) quadric of dimension ![]() $2n - 1$, while
$2n - 1$, while ![]() $\operatorname {IG}(2,2n)$,
$\operatorname {IG}(2,2n)$, ![]() $\operatorname {OG}(2,2n)$, and
$\operatorname {OG}(2,2n)$, and ![]() $\operatorname {OG}(2,2n+1)$ are the symplectic and orthogonal isotropic Grassmannians of two-dimensional subspaces, respectively. Note that the Picard rank of a (co)adjoint variety is 1, except for the
$\operatorname {OG}(2,2n+1)$ are the symplectic and orthogonal isotropic Grassmannians of two-dimensional subspaces, respectively. Note that the Picard rank of a (co)adjoint variety is 1, except for the ![]() $\mathrm {A}_n$-case, where it is 2.
$\mathrm {A}_n$-case, where it is 2.
The small quantum cohomology ring of (co)adjoint varieties was computed in [Reference Buch, Kresch and TamvakisBKT09, Reference Chaput and PerrinCP11, Reference Ciocan-FontanineCio99, Reference KimKim95] in terms of generators and relations. Using these results, the fiber ![]() $\operatorname {QS}^{\circ }_X$ of the map
$\operatorname {QS}^{\circ }_X$ of the map ![]() $\kappa$ defined in (1.3) was computed by Nicolas Perrin and the second named author in [Reference Perrin and SmirnovPS]. To state the results of [Reference Perrin and SmirnovPS] we will need some notation.
$\kappa$ defined in (1.3) was computed by Nicolas Perrin and the second named author in [Reference Perrin and SmirnovPS]. To state the results of [Reference Perrin and SmirnovPS] we will need some notation.
Let ![]() $\mathrm {T}(\mathrm {G})$ be the Dynkin diagram of
$\mathrm {T}(\mathrm {G})$ be the Dynkin diagram of ![]() $\mathrm {G}$, and let
$\mathrm {G}$, and let ![]() $\mathrm {T}_{\mathrm {short}}(\mathrm {G})$ be the subdiagram of
$\mathrm {T}_{\mathrm {short}}(\mathrm {G})$ be the subdiagram of ![]() $\mathrm {T}(\mathrm {G})$ with vertices corresponding to short roots. For the reader's convenience we collect the resulting Dynkin types in a table:
$\mathrm {T}(\mathrm {G})$ with vertices corresponding to short roots. For the reader's convenience we collect the resulting Dynkin types in a table:

The following theorem describes ![]() $\operatorname {QS}_X^{\circ }$ for adjoint and coadjoint varieties.
$\operatorname {QS}_X^{\circ }$ for adjoint and coadjoint varieties.
Theorem 1.6 [PS] Let ![]() $X^\mathrm{ad}$ and
$X^\mathrm{ad}$ and ![]() $X^\mathrm{coad}$ be the adjoint and coadjoint varieties of a simple algebraic group
$X^\mathrm{coad}$ be the adjoint and coadjoint varieties of a simple algebraic group ![]() $\mathrm {G}$, respectively.
$\mathrm {G}$, respectively.
(i) If
 $\mathrm {T}(\mathrm {G}) = \mathrm {A}_{2n}$, then
$\mathrm {T}(\mathrm {G}) = \mathrm {A}_{2n}$, then  $\operatorname {QS}^{\circ }_{X^\mathrm{ad}} = \operatorname {QS}^{\circ }_{X^\mathrm{coad}} = \varnothing$.
$\operatorname {QS}^{\circ }_{X^\mathrm{ad}} = \operatorname {QS}^{\circ }_{X^\mathrm{coad}} = \varnothing$.(ii) If
 $\mathrm {T}(\mathrm {G}) \ne \mathrm {A}_{2n}$, then
$\mathrm {T}(\mathrm {G}) \ne \mathrm {A}_{2n}$, then  $\operatorname {QS}^{\circ }_{X^\mathrm{coad}}$ is a single non-reduced point and the localization of the scheme
$\operatorname {QS}^{\circ }_{X^\mathrm{coad}}$ is a single non-reduced point and the localization of the scheme  $\operatorname {QH_{can}}(X^\mathrm{coad})$ at this point is isomorphic to the Jacobian ring of a simple hypersurface singularity of type
$\operatorname {QH_{can}}(X^\mathrm{coad})$ at this point is isomorphic to the Jacobian ring of a simple hypersurface singularity of type  $\mathrm {T}_{\mathrm {short}}(\mathrm {G})$.
$\mathrm {T}_{\mathrm {short}}(\mathrm {G})$.(iii) If
 $\mathrm {T}(\mathrm {G})$ is simply laced, then we have
$\mathrm {T}(\mathrm {G})$ is simply laced, then we have  $X^\mathrm{ad} = X^\mathrm{coad}$ and
$X^\mathrm{ad} = X^\mathrm{coad}$ and  $\operatorname {QS}^{\circ }_{X^\mathrm{ad}} = \operatorname {QS}^{\circ }_{X^\mathrm{coad}}$.
$\operatorname {QS}^{\circ }_{X^\mathrm{ad}} = \operatorname {QS}^{\circ }_{X^\mathrm{coad}}$.(iv) If
 $\mathrm {T}(\mathrm {G})$ is not simply laced, then
$\mathrm {T}(\mathrm {G})$ is not simply laced, then  $\operatorname {QS}^{\circ }_{X^\mathrm{ad}} = \varnothing$.
$\operatorname {QS}^{\circ }_{X^\mathrm{ad}} = \varnothing$.
A combination of Theorem 1.6 with Conjecture 1.3 allows us to make predictions about the structure of derived categories of adjoint and coadjoint varieties. Our expectation is stated in the following two conjectures.
Conjecture 1.7 Let ![]() $X$ be the adjoint variety of a simple algebraic group
$X$ be the adjoint variety of a simple algebraic group ![]() $\mathrm {G}$ over an algebraically closed field of characteristic zero. If
$\mathrm {G}$ over an algebraically closed field of characteristic zero. If ![]() $\mathrm {T}(\mathrm {G})$ is not simply laced, then
$\mathrm {T}(\mathrm {G})$ is not simply laced, then ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$ has a full
${{\mathbf {D}^{\mathrm {b}}}}(X)$ has a full ![]() $\operatorname {Aut}(X)$-invariant rectangular Lefschetz exceptional collection.
$\operatorname {Aut}(X)$-invariant rectangular Lefschetz exceptional collection.
Conjecture 1.8 Let ![]() $X$ be the coadjoint variety of a simple algebraic group
$X$ be the coadjoint variety of a simple algebraic group ![]() $\mathrm {G}$ over an algebraically closed field of characteristic zero. Then
$\mathrm {G}$ over an algebraically closed field of characteristic zero. Then ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$ has an
${{\mathbf {D}^{\mathrm {b}}}}(X)$ has an ![]() $\operatorname {Aut}(X)$-invariant rectangular Lefschetz exceptional collection with residual category
$\operatorname {Aut}(X)$-invariant rectangular Lefschetz exceptional collection with residual category ![]() $\mathcal {R}$ and
$\mathcal {R}$ and
(i) if
 $\mathrm {T}(\mathrm {G}) = \mathrm {A}_n$ and
$\mathrm {T}(\mathrm {G}) = \mathrm {A}_n$ and  $n$ is even, then
$n$ is even, then  $\mathcal {R} = 0$;
$\mathcal {R} = 0$;(ii) otherwise,
 $\mathcal {R}$ is equivalent to the derived category of representations of a quiver of Dynkin type
$\mathcal {R}$ is equivalent to the derived category of representations of a quiver of Dynkin type  $\mathrm {T}_{\mathrm {short}}(\mathrm {G})$.
$\mathrm {T}_{\mathrm {short}}(\mathrm {G})$.
In non-simply laced Dynkin types ![]() $\mathrm {B}_n$,
$\mathrm {B}_n$, ![]() $\mathrm {C}_n$,
$\mathrm {C}_n$, ![]() $\mathrm {F}_4$, and
$\mathrm {F}_4$, and ![]() $\mathrm {G}_2$ these expectations agree with known results about
$\mathrm {G}_2$ these expectations agree with known results about ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$. Indeed, for adjoint varieties full rectangular Lefschetz decompositions were constructed in [Reference KuznetsovKuz08, Theorem 7.1] for type
${{\mathbf {D}^{\mathrm {b}}}}(X)$. Indeed, for adjoint varieties full rectangular Lefschetz decompositions were constructed in [Reference KuznetsovKuz08, Theorem 7.1] for type ![]() $\mathrm {B}_n$, [Reference Kuznetsov and SmirnovKS20, Example 1.4] for type
$\mathrm {B}_n$, [Reference Kuznetsov and SmirnovKS20, Example 1.4] for type ![]() $\mathrm {C}_n$, and [Reference KuznetsovKuz06, § 6.4] for type
$\mathrm {C}_n$, and [Reference KuznetsovKuz06, § 6.4] for type ![]() $\mathrm {G}_2$. For coadjoint varieties the residual categories were computed in [Reference Cruz Morales, Kuznetsov, Mellit, Perrin and SmirnovCKMPS19, Theorem 9.6] for type
$\mathrm {G}_2$. For coadjoint varieties the residual categories were computed in [Reference Cruz Morales, Kuznetsov, Mellit, Perrin and SmirnovCKMPS19, Theorem 9.6] for type ![]() $\mathrm {C}_n$, [Reference Kuznetsov and SmirnovKS20, Example 1.6] for types
$\mathrm {C}_n$, [Reference Kuznetsov and SmirnovKS20, Example 1.6] for types ![]() $\mathrm {B}_n$ and
$\mathrm {B}_n$ and ![]() $\mathrm {G}_2$, and [Reference Belmans, Kuznetsov and SmirnovBKS21, Theorem 1.4] for type
$\mathrm {G}_2$, and [Reference Belmans, Kuznetsov and SmirnovBKS21, Theorem 1.4] for type ![]() $\mathrm {F}_4$. So, the only non-simply laced case that is still not known is that of the adjoint variety of type
$\mathrm {F}_4$. So, the only non-simply laced case that is still not known is that of the adjoint variety of type ![]() $\mathrm {F}_4$.
$\mathrm {F}_4$.
The main result of this paper is the proof of Conjecture 1.8 for Dynkin types ![]() $\mathrm {A}_n$ and
$\mathrm {A}_n$ and ![]() $\mathrm {D}_n$. Since these Dynkin types are simply laced, the coadjoint and adjoint varieties coincide.
$\mathrm {D}_n$. Since these Dynkin types are simply laced, the coadjoint and adjoint varieties coincide.
Theorem 1.9 Let ![]() $X$ be the (co)adjoint variety of a simple algebraic group
$X$ be the (co)adjoint variety of a simple algebraic group ![]() $\mathrm {G}$ of Dynkin type
$\mathrm {G}$ of Dynkin type ![]() $\mathrm {A}_n$ or
$\mathrm {A}_n$ or ![]() $\mathrm {D}_n$ over an algebraically closed field of characteristic zero. Then
$\mathrm {D}_n$ over an algebraically closed field of characteristic zero. Then ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$ has an
${{\mathbf {D}^{\mathrm {b}}}}(X)$ has an ![]() $\operatorname {Aut}(X)$-invariant rectangular Lefschetz exceptional collection with residual category
$\operatorname {Aut}(X)$-invariant rectangular Lefschetz exceptional collection with residual category ![]() $\mathcal {R}$ and
$\mathcal {R}$ and
(i) if
 $\mathrm {T}(\mathrm {G}) = \mathrm {A}_n$ and
$\mathrm {T}(\mathrm {G}) = \mathrm {A}_n$ and  $n$ is even, then
$n$ is even, then  $\mathcal {R} = 0$;
$\mathcal {R} = 0$;(ii) if
 $\mathrm {T}(\mathrm {G}) = \mathrm {A}_n$ and
$\mathrm {T}(\mathrm {G}) = \mathrm {A}_n$ and  $n$ is odd, then
$n$ is odd, then  $\mathcal {R} \cong {{\mathbf {D}^{\mathrm {b}}}}(\mathrm {A}_n)$;
$\mathcal {R} \cong {{\mathbf {D}^{\mathrm {b}}}}(\mathrm {A}_n)$;(iii) if
 $\mathrm {T}(\mathrm {G}) = \mathrm {D}_n$, then
$\mathrm {T}(\mathrm {G}) = \mathrm {D}_n$, then  $\mathcal {R} \cong {{\mathbf {D}^{\mathrm {b}}}}(\mathrm {D}_n)$;
$\mathcal {R} \cong {{\mathbf {D}^{\mathrm {b}}}}(\mathrm {D}_n)$;
where ![]() ${{\mathbf {D}^{\mathrm {b}}}}(\mathrm {A}_n)$ and
${{\mathbf {D}^{\mathrm {b}}}}(\mathrm {A}_n)$ and ![]() ${{\mathbf {D}^{\mathrm {b}}}}(\mathrm {D}_n)$ are the derived categories of representations of quivers of Dynkin types
${{\mathbf {D}^{\mathrm {b}}}}(\mathrm {D}_n)$ are the derived categories of representations of quivers of Dynkin types ![]() $\mathrm {A}_n$ and
$\mathrm {A}_n$ and ![]() $\mathrm {D}_n$, respectively.
$\mathrm {D}_n$, respectively.
More precise versions of these results can be found in Theorem 2.1 (for type ![]() $\mathrm {A}_n$) and Theorem 3.1 (for type
$\mathrm {A}_n$) and Theorem 3.1 (for type ![]() $\mathrm {D}_n$) below. We leave the remaining exceptional types
$\mathrm {D}_n$) below. We leave the remaining exceptional types ![]() $\mathrm {E}_6$,
$\mathrm {E}_6$, ![]() $\mathrm {E}_7$,
$\mathrm {E}_7$, ![]() $\mathrm {E}_8$, and
$\mathrm {E}_8$, and ![]() $\mathrm {F}_4$ for future work.
$\mathrm {F}_4$ for future work.
Note that a part of the statement of this theorem is a construction of a full exceptional collection in ![]() ${{\mathbf {D}^{\mathrm {b}}}}(\operatorname {OG}(2,2n))$, which was not known before (see [Reference Kuznetsov and PolishchukKP16] for a survey of results about exceptional collections on homogeneous varieties).
${{\mathbf {D}^{\mathrm {b}}}}(\operatorname {OG}(2,2n))$, which was not known before (see [Reference Kuznetsov and PolishchukKP16] for a survey of results about exceptional collections on homogeneous varieties).
Remark 1.10 As one can see from Theorem 1.6 and Conjecture 1.8, the case of Dynkin type ![]() $\mathrm {A}_n$ with even
$\mathrm {A}_n$ with even ![]() $n$ is somewhat special. In this case, the Picard rank is equal to 2, and the canonical quantum cohomology ring
$n$ is somewhat special. In this case, the Picard rank is equal to 2, and the canonical quantum cohomology ring ![]() $\operatorname {QH_{can}}(X)$ is semisimple, so a singularity of type
$\operatorname {QH_{can}}(X)$ is semisimple, so a singularity of type ![]() $\mathrm {T}_{\mathrm {short}}(\mathrm {G}) = \mathrm {A}_n$ does not show up. However, one can see this singularity in the skew-canonical quantum cohomology ring, that is, the ring obtained from
$\mathrm {T}_{\mathrm {short}}(\mathrm {G}) = \mathrm {A}_n$ does not show up. However, one can see this singularity in the skew-canonical quantum cohomology ring, that is, the ring obtained from ![]() $\operatorname {QH}(X)$ by base change to the point of
$\operatorname {QH}(X)$ by base change to the point of ![]() $\operatorname {Pic}(X) \otimes {{\mathbb {Q}}}$ corresponding to the line bundle
$\operatorname {Pic}(X) \otimes {{\mathbb {Q}}}$ corresponding to the line bundle ![]() $\mathcal {O}(1,-1)$. It would be very interesting to find a categorical interpretation of this fact.
$\mathcal {O}(1,-1)$. It would be very interesting to find a categorical interpretation of this fact.
2. Type  $\mathrm {A}_n$
$\mathrm {A}_n$
In this section we prove parts (i) and (ii) of Theorem 1.9, restated in a more precise form in Theorem 2.1 below. We work over an arbitrary field ![]() $\Bbbk$.
$\Bbbk$.
2.1 Statement of the theorem
Let ![]() $V$ be a vector space of dimension
$V$ be a vector space of dimension ![]() $n + 1$. Throughout this section we put
$n + 1$. Throughout this section we put
note that in this embedding ![]() $X$ is a hypersurface of bidegree
$X$ is a hypersurface of bidegree ![]() $(1,1)$.
$(1,1)$.
The automorphism group of ![]() $X$ is the semidirect product
$X$ is the semidirect product
where the factor ![]() ${{\mathbb {Z}}}/2$ acts by an outer automorphism (corresponding to the symmetry of the Dynkin diagram
${{\mathbb {Z}}}/2$ acts by an outer automorphism (corresponding to the symmetry of the Dynkin diagram ![]() $\mathrm {A}_n$) that is induced by the morphism
$\mathrm {A}_n$) that is induced by the morphism
given by a choice of non-degenerate bilinear form ![]() $B$ on
$B$ on ![]() $V$.
$V$.
It is elementary to construct a rectangular Lefschetz decomposition for ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$ by using the
${{\mathbf {D}^{\mathrm {b}}}}(X)$ by using the ![]() ${{\mathbb {P}}}^{n-1}$-fibration structure
${{\mathbb {P}}}^{n-1}$-fibration structure ![]() $X \to {{\mathbb {P}}}(V)$ of
$X \to {{\mathbb {P}}}(V)$ of ![]() $X$ (see the proofs of Lemmas 2.4 and 2.5). This Lefschetz decomposition is automatically
$X$ (see the proofs of Lemmas 2.4 and 2.5). This Lefschetz decomposition is automatically ![]() $\operatorname {PGL}(V)$-invariant and its residual category is trivial. However, it is not
$\operatorname {PGL}(V)$-invariant and its residual category is trivial. However, it is not ![]() $\operatorname {Aut}(X)$-invariant, since the outer automorphism takes it to a decomposition associated with the other
$\operatorname {Aut}(X)$-invariant, since the outer automorphism takes it to a decomposition associated with the other ![]() ${{\mathbb {P}}}^{n-1}$-fibration
${{\mathbb {P}}}^{n-1}$-fibration ![]() $X \to {{\mathbb {P}}}(V^{\vee })$, and so does not preserve the original one.
$X \to {{\mathbb {P}}}(V^{\vee })$, and so does not preserve the original one.
In this section we construct in ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$ a rectangular
${{\mathbf {D}^{\mathrm {b}}}}(X)$ a rectangular ![]() $\operatorname {Aut}(X)$-invariant Lefschetz collection and compute its residual category. To state the result we need some notation. Let
$\operatorname {Aut}(X)$-invariant Lefschetz collection and compute its residual category. To state the result we need some notation. Let
be the tautological flag of rank-1 and rank-![]() $n$ subbundles in the trivial vector bundle. We set
$n$ subbundles in the trivial vector bundle. We set
for the intermediate quotient. Note that ![]() $\sigma _B^{*}\mathcal {E} \cong \mathcal {E}^{\vee }$ and
$\sigma _B^{*}\mathcal {E} \cong \mathcal {E}^{\vee }$ and ![]() $\det (\mathcal {E}) \cong \mathcal {O}(1,-1)$, where we denote by
$\det (\mathcal {E}) \cong \mathcal {O}(1,-1)$, where we denote by ![]() $\mathcal {O}(a_1,a_2)$ the restriction to
$\mathcal {O}(a_1,a_2)$ the restriction to ![]() $X$ of the line bundle
$X$ of the line bundle ![]() $\mathcal {O}(a_1) \boxtimes \mathcal {O}(a_2)$ on
$\mathcal {O}(a_1) \boxtimes \mathcal {O}(a_2)$ on ![]() ${{\mathbb {P}}}(V) \times {{\mathbb {P}}}(V^{\vee })$.
${{\mathbb {P}}}(V) \times {{\mathbb {P}}}(V^{\vee })$.
We prove the following theorem.
Theorem 2.1 Set ![]() $k := \lfloor n/2 \rfloor$. The collection of
$k := \lfloor n/2 \rfloor$. The collection of ![]() $2k + 1$ line bundles
$2k + 1$ line bundles
in ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$ is exceptional and extends to an
${{\mathbf {D}^{\mathrm {b}}}}(X)$ is exceptional and extends to an ![]() $\operatorname {Aut}(X)$-invariant semiorthogonal decomposition
$\operatorname {Aut}(X)$-invariant semiorthogonal decomposition
where ![]() $\mathcal {R}$ is the residual category.
$\mathcal {R}$ is the residual category.
(1) If
 $n = 2k$ the residual category is zero.
$n = 2k$ the residual category is zero.(2) If
 $n = 2k + 1$ the residual category is generated by the
$n = 2k + 1$ the residual category is generated by the  $\operatorname {Aut}(X)$-invariant exceptional collection
(2.4)of length
$\operatorname {Aut}(X)$-invariant exceptional collection
(2.4)of length \begin{align} \mathcal{R} = \langle \mathcal{O}({-}1,k), &\mathcal{O}(k,-1); \mathcal{E}({-}1,k-1), \mathcal{E}^{{\vee}}(k-1,-1);\nonumber\\ &\ldots; \Lambda^{k-1}\mathcal{E}({-}1,1), \Lambda^{k-1}\mathcal{E}^{{\vee}}(1,-1); \Lambda^{k}\mathcal{E}({-}1,0) \cong \Lambda^{k}\mathcal{E}^{{\vee}}(0,-1) \rangle \end{align}
\begin{align} \mathcal{R} = \langle \mathcal{O}({-}1,k), &\mathcal{O}(k,-1); \mathcal{E}({-}1,k-1), \mathcal{E}^{{\vee}}(k-1,-1);\nonumber\\ &\ldots; \Lambda^{k-1}\mathcal{E}({-}1,1), \Lambda^{k-1}\mathcal{E}^{{\vee}}(1,-1); \Lambda^{k}\mathcal{E}({-}1,0) \cong \Lambda^{k}\mathcal{E}^{{\vee}}(0,-1) \rangle \end{align} $n = 2k + 1$ and is equivalent to the derived category of the Dynkin quiver
$n = 2k + 1$ and is equivalent to the derived category of the Dynkin quiver  $\mathrm {A}_n$.
$\mathrm {A}_n$.
In Remark 2.9 we provide a description of ![]() $\mathcal {A}$ and
$\mathcal {A}$ and ![]() $\mathcal {R}$ in terms of weights of
$\mathcal {R}$ in terms of weights of ![]() $\operatorname {SL}(n+1)$.
$\operatorname {SL}(n+1)$.
In Corollary 2.3 we check that the collection of line bundles defining the rectangular part of (2.3) is exceptional. Furthermore, in Lemma 2.4 (for even ![]() $n$) and Lemma 2.6 (for odd
$n$) and Lemma 2.6 (for odd ![]() $n$) we extend it to a full exceptional collection of line bundles. In the construction we use the advantage of already knowing a full exceptional collection on
$n$) we extend it to a full exceptional collection of line bundles. In the construction we use the advantage of already knowing a full exceptional collection on ![]() $X$ (thanks to the
$X$ (thanks to the ![]() ${{\mathbb {P}}}^{n-1}$-fibration mentioned above), so it is enough to rearrange it appropriately by a sequence of mutations (we refer to [Reference Ingalls and KuznetsovIK15, §2.3] for a summary of results we need; [Reference Ingalls and KuznetsovIK15, Lemma 2.13] is especially useful). Part (1) of the theorem is proved in Lemma 2.4 and part (2) in Lemma 2.8.
${{\mathbb {P}}}^{n-1}$-fibration mentioned above), so it is enough to rearrange it appropriately by a sequence of mutations (we refer to [Reference Ingalls and KuznetsovIK15, §2.3] for a summary of results we need; [Reference Ingalls and KuznetsovIK15, Lemma 2.13] is especially useful). Part (1) of the theorem is proved in Lemma 2.4 and part (2) in Lemma 2.8.
For verifications of exceptionality we will need the following lemma.
Lemma 2.2 If either of the following four conditions
is satisfied, then the cohomology ![]() $H^{\bullet }(X,\mathcal {O}(a,b))$ vanishes.
$H^{\bullet }(X,\mathcal {O}(a,b))$ vanishes.
Proof. Consider the standard exact sequence
If any of the conditions listed in the lemma is satisfied, then
vanish, hence ![]() $H^{\bullet }(X,\mathcal {O}(a,b))$ vanishes as well.
$H^{\bullet }(X,\mathcal {O}(a,b))$ vanishes as well.
One of the consequences of this computation is the following corollary.
Corollary 2.3 The collection of objects on the right-hand side of (2.2) is an exceptional collection. Moreover, the components ![]() $\mathcal {A} \otimes \mathcal {O}(t,t)$ in (2.3) are semiorthogonal for
$\mathcal {A} \otimes \mathcal {O}(t,t)$ in (2.3) are semiorthogonal for ![]() $0 \le t \le n-1$.
$0 \le t \le n-1$.
Proof. To prove the corollary we need to show that
and
both vanish when ![]() $0 \le i,j \le k$ and
$0 \le i,j \le k$ and ![]() $1 \le t \le n-1$.
$1 \le t \le n-1$.
The first vanishing is clear since ![]() $1-n \le -t \le -1$ and Lemma 2.2 applies. The second vanishing also follows if
$1-n \le -t \le -1$ and Lemma 2.2 applies. The second vanishing also follows if ![]() $-j-t \ge 1-n$. So, assume
$-j-t \ge 1-n$. So, assume ![]() $-j-t \le -n$. Then
$-j-t \le -n$. Then ![]() $t \ge n - j \ge n - k$, hence
$t \ge n - j \ge n - k$, hence ![]() $i - t \le k - (n - k) = 2k - n \le 0$. Since also
$i - t \le k - (n - k) = 2k - n \le 0$. Since also ![]() $i - t \ge -t \ge 1 - n$, the vanishing also follows from Lemma 2.2, unless
$i - t \ge -t \ge 1 - n$, the vanishing also follows from Lemma 2.2, unless ![]() $i - t = 0$. But then we must have
$i - t = 0$. But then we must have ![]() $i = j = t = k$ and
$i = j = t = k$ and ![]() $n = 2k$, so that the corresponding line bundle is
$n = 2k$, so that the corresponding line bundle is ![]() $\mathcal {O}(0,-n)$, and its cohomology vanishes, again by Lemma 2.2.
$\mathcal {O}(0,-n)$, and its cohomology vanishes, again by Lemma 2.2.
We denote the natural projections of ![]() $X$ by
$X$ by
For any pair of coherent sheaves on ![]() ${{\mathbb {P}}}(V)$ and
${{\mathbb {P}}}(V)$ and ![]() ${{\mathbb {P}}}(V^{\vee })$ we set
${{\mathbb {P}}}(V^{\vee })$ we set
2.2 Even n
In this section we prove Theorem 2.1 for even ![]() $n$.
$n$.
Lemma 2.4 If ![]() $n = 2k$ then
$n = 2k$ then ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X) = \langle \mathcal {A},\mathcal {A} \otimes \mathcal {O}(1,1),\ldots , \mathcal {A} \otimes \mathcal {O}(2k-1,2k-1) \rangle$, where
${{\mathbf {D}^{\mathrm {b}}}}(X) = \langle \mathcal {A},\mathcal {A} \otimes \mathcal {O}(1,1),\ldots , \mathcal {A} \otimes \mathcal {O}(2k-1,2k-1) \rangle$, where ![]() $\mathcal {A}$ is defined by (2.2).
$\mathcal {A}$ is defined by (2.2).
Proof. The ![]() ${{\mathbb {P}}}^{2k-1}$-fibration
${{\mathbb {P}}}^{2k-1}$-fibration ![]() $p_1$ gives rise to the semiorthogonal decomposition
$p_1$ gives rise to the semiorthogonal decomposition
Choosing the exceptional collection
in the ![]() $i$th component, we obtain a full exceptional collection in
$i$th component, we obtain a full exceptional collection in ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$ that takes the form
${{\mathbf {D}^{\mathrm {b}}}}(X)$ that takes the form
 \begin{equation} \begin{aligned} {{\mathbf{D}^{\mathrm{b}}}}(X) = \langle & \mathcal{O}({-}k,0), \mathcal{O}(1-k,0),\ldots, \mathcal{O}(k,0), \nonumber\\ & \quad\mathcal{O}(1-k,1), \mathcal{O}(2-k,1),\ldots, \mathcal{O}(k+1,1), \\ & \quad\quad\hspace{8em} \ldots\nonumber\\ & \quad\quad\quad\mathcal{O}(k-1,2k-1), \mathcal{O}(k,2k-1),\ldots, \mathcal{O}(3k-1,2k-1)\rangle.\end{aligned}\end{equation}
\begin{equation} \begin{aligned} {{\mathbf{D}^{\mathrm{b}}}}(X) = \langle & \mathcal{O}({-}k,0), \mathcal{O}(1-k,0),\ldots, \mathcal{O}(k,0), \nonumber\\ & \quad\mathcal{O}(1-k,1), \mathcal{O}(2-k,1),\ldots, \mathcal{O}(k+1,1), \\ & \quad\quad\hspace{8em} \ldots\nonumber\\ & \quad\quad\quad\mathcal{O}(k-1,2k-1), \mathcal{O}(k,2k-1),\ldots, \mathcal{O}(3k-1,2k-1)\rangle.\end{aligned}\end{equation}The collection is shown in Figure 1, the objects are represented by black dots.

Figure 1. Mutation of (2.5) to a rectangular Lefschetz collection for ![]() $k = 3$.
$k = 3$.
Now we perform a mutation: we consider the subcollection formed by the first ![]() $k$ terms of the first line, the first
$k$ terms of the first line, the first ![]() $k-1$ terms of the second line, and so on, up to the first term of the
$k-1$ terms of the second line, and so on, up to the first term of the ![]() $k$th line of (2.5):
$k$th line of (2.5):
 \begin{equation} \begin{aligned} \{ \mathcal{O}({-}k,0), \mathcal{O}(1-k,0),\ldots, & \mathcal{O}({-}1,0); \\ \mathcal{O}(1-k,1),\ldots, & \mathcal{O}({-}1,1); \\ \ddots \hphantom{,} & \qquad\vdots \\ & \mathcal{O}({-}1,k-1) \} \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \{ \mathcal{O}({-}k,0), \mathcal{O}(1-k,0),\ldots, & \mathcal{O}({-}1,0); \\ \mathcal{O}(1-k,1),\ldots, & \mathcal{O}({-}1,1); \\ \ddots \hphantom{,} & \qquad\vdots \\ & \mathcal{O}({-}1,k-1) \} \end{aligned} \end{equation}
(this subcollection is depicted by the triangle on the left in Figure 1) and mutate it to the far right of the exceptional collection. Using Lemma 2.2, it is easy to see that the objects in (2.6) are right-orthogonal to the objects in the rest of (2.5). Hence, their mutation to the far right is realized by the anticanonical twist (see, for example, [Reference Ingalls and KuznetsovIK15, Lemma 2.13]). As ![]() $\omega _X^{-1} \cong \mathcal {O}(2k,2k)$, this replaces the black dots in the triangle by the white dots in the dashed triangle in Figure 1.
$\omega _X^{-1} \cong \mathcal {O}(2k,2k)$, this replaces the black dots in the triangle by the white dots in the dashed triangle in Figure 1.
All that remains is to note that the resulting full exceptional collection is precisely the collection
Indeed, the blocks formed by the twists of the subcategory ![]() $\mathcal {A}$ correspond to the L-shapes in figure, and their semiorthogonality was proved in Corollary 2.3.
$\mathcal {A}$ correspond to the L-shapes in figure, and their semiorthogonality was proved in Corollary 2.3.
2.3 Odd  $n$: rectangular part
$n$: rectangular part
From now on we set ![]() $n = 2k + 1$. First, we use the trick of Lemma 2.4 to construct a full exceptional collection that includes the rectangular part of (2.3) as a subcollection. In this case this is slightly more complicated, so we split the construction into two steps.
$n = 2k + 1$. First, we use the trick of Lemma 2.4 to construct a full exceptional collection that includes the rectangular part of (2.3) as a subcollection. In this case this is slightly more complicated, so we split the construction into two steps.
Lemma 2.5 The category ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$ has the following full exceptional collection:
${{\mathbf {D}^{\mathrm {b}}}}(X)$ has the following full exceptional collection:
 \begin{equation} \begin{aligned} {{\mathbf{D}^{\mathrm{b}}}}(X) = \langle &\mathcal{O}({-}k,0), \mathcal{O}(1-k,0),\ldots, \mathcal{O}(k+1,0), \\ & \quad\mathcal{O}(1-k,1), \mathcal{O}(2-k,1),\ldots, \mathcal{O}(k+2,1),\\ & \quad\quad\hspace{8em} \ldots \\ & \quad\quad\quad\mathcal{O}({-}1,k-1), \mathcal{O}(0,k-1),\ldots, \mathcal{O}(2k,k-1), \\ & \quad\quad\quad\mathcal{O}({-}1,k), \mathcal{O}(0,k),\ldots, \mathcal{O}(2k,k), \\ & \quad\quad\quad\quad\mathcal{O}(0,k+1), \mathcal{O}(1,k+1),\ldots, \mathcal{O}(2k+1,k+1),\\ & \quad\quad\quad\quad\quad\hspace{8em} \ldots \\ & \quad\quad\quad\quad\quad\quad\mathcal{O}(k-1,2k), \mathcal{O}(k,2k),\ldots, \mathcal{O}(3k,2k)\rangle. \end{aligned}\end{equation}
\begin{equation} \begin{aligned} {{\mathbf{D}^{\mathrm{b}}}}(X) = \langle &\mathcal{O}({-}k,0), \mathcal{O}(1-k,0),\ldots, \mathcal{O}(k+1,0), \\ & \quad\mathcal{O}(1-k,1), \mathcal{O}(2-k,1),\ldots, \mathcal{O}(k+2,1),\\ & \quad\quad\hspace{8em} \ldots \\ & \quad\quad\quad\mathcal{O}({-}1,k-1), \mathcal{O}(0,k-1),\ldots, \mathcal{O}(2k,k-1), \\ & \quad\quad\quad\mathcal{O}({-}1,k), \mathcal{O}(0,k),\ldots, \mathcal{O}(2k,k), \\ & \quad\quad\quad\quad\mathcal{O}(0,k+1), \mathcal{O}(1,k+1),\ldots, \mathcal{O}(2k+1,k+1),\\ & \quad\quad\quad\quad\quad\hspace{8em} \ldots \\ & \quad\quad\quad\quad\quad\quad\mathcal{O}(k-1,2k), \mathcal{O}(k,2k),\ldots, \mathcal{O}(3k,2k)\rangle. \end{aligned}\end{equation} A graphical representation for the collection in case ![]() $k = 3$ can be found in Figure 2. The objects depicted by black dots and grey crosses (red online) form the collection (2.7); the rows of (2.7) correspond to rows in the figure (and the shifts of rows match up). The mutation of Lemma 2.6 will take the objects corresponding to the black dots in the left triangle to the objects corresponding to white dots in the dashed triangle at the top. The L-shaped figures correspond to blocks of the rectangular Lefschetz collection (the first of them is (2.2)).
$k = 3$ can be found in Figure 2. The objects depicted by black dots and grey crosses (red online) form the collection (2.7); the rows of (2.7) correspond to rows in the figure (and the shifts of rows match up). The mutation of Lemma 2.6 will take the objects corresponding to the black dots in the left triangle to the objects corresponding to white dots in the dashed triangle at the top. The L-shaped figures correspond to blocks of the rectangular Lefschetz collection (the first of them is (2.2)).
Proof. The ![]() ${{\mathbb {P}}}^{2k}$-fibration
${{\mathbb {P}}}^{2k}$-fibration ![]() $p_1$ gives rise to the semiorthogonal decomposition
$p_1$ gives rise to the semiorthogonal decomposition
This time for the first ![]() $k$ components (i.e. for
$k$ components (i.e. for ![]() $0 \le i \le k-1$) we choose the collection
$0 \le i \le k-1$) we choose the collection
and for the last ![]() $k + 1$ components (i.e. for
$k + 1$ components (i.e. for ![]() $k \le i \le 2k$) we choose the collection
$k \le i \le 2k$) we choose the collection
As a result, we obtain (2.7).

Figure 2. (Colour online) Mutation of (2.7) to a rectangular Lefschetz collection for ![]() $k = 3$.
$k = 3$.
It follows from Lemma 2.2 that the only non-trivial ![]() $\operatorname {Ext}$-spaces among the objects in Figure 2 are those going in the upper-right direction and additionally, there is a non-trivial
$\operatorname {Ext}$-spaces among the objects in Figure 2 are those going in the upper-right direction and additionally, there is a non-trivial ![]() $\operatorname {Ext}$-space
$\operatorname {Ext}$-space
from the rightmost grey cross (red online) to the leftmost one.
Now we consider the same subcollection (2.6) as in the proof of Lemma 2.4 (this subcollection is depicted by the triangle on the left in Figure 2) and mutate it to the far right of the exceptional collection. It follows from the description of Lemma 2.2 that the objects in (2.6) are right-orthogonal to the objects in the rest of (2.7). As in Lemma 2.4, their mutation to the far right is realized by the anticanonical twist. As ![]() $\omega _X^{-1} \cong \mathcal {O}(2k+1,2k+1)$, we deduce the following lemma.
$\omega _X^{-1} \cong \mathcal {O}(2k+1,2k+1)$, we deduce the following lemma.
Lemma 2.6 The category ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$ has the following full exceptional collection:
${{\mathbf {D}^{\mathrm {b}}}}(X)$ has the following full exceptional collection:
 \begin{equation} \begin{aligned} {{\mathbf{D}^{\mathrm{b}}}}(X) = \langle & \mathcal{O}(0,0), \mathcal{O}(1,0),\ldots, \mathcal{O}(k+1,0), \\ & \quad\mathcal{O}(0,1), \mathcal{O}(1,1),\ldots, \mathcal{O}(k+2,1),\\ & \quad\hspace{8em} \ldots \\ & \quad\mathcal{O}(0,k-1), \mathcal{O}(1,k-1),\ldots, \mathcal{O}(2k,k-1), \\ & \mathcal{O}({-}1,k), \mathcal{O}(0,k),\ldots, \mathcal{O}(2k,k), \\ & \quad\mathcal{O}(0,k+1), \mathcal{O}(1,k+1),\ldots, \mathcal{O}(2k+1,k+1),\\ & \quad\quad\hspace{8em} \ldots \\ & \quad\quad\quad\mathcal{O}(k-1,2k), \mathcal{O}(k,2k),\ldots, \mathcal{O}(3k,2k), \\ & \quad\quad\quad\quad\quad\mathcal{O}(k+1,2k+1), \mathcal{O}(k+2,2k+1),\ldots, \mathcal{O}(2k,2k+1), \\ &\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\,\,\,\mathcal{O}(k+2,2k+2),\ldots, \mathcal{O}(2k,2k+2),\\ &\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\,\,\,\,\,\ldots \\ &\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\mathcal{O}(2k,3k)\rangle. \end{aligned}\end{equation}
\begin{equation} \begin{aligned} {{\mathbf{D}^{\mathrm{b}}}}(X) = \langle & \mathcal{O}(0,0), \mathcal{O}(1,0),\ldots, \mathcal{O}(k+1,0), \\ & \quad\mathcal{O}(0,1), \mathcal{O}(1,1),\ldots, \mathcal{O}(k+2,1),\\ & \quad\hspace{8em} \ldots \\ & \quad\mathcal{O}(0,k-1), \mathcal{O}(1,k-1),\ldots, \mathcal{O}(2k,k-1), \\ & \mathcal{O}({-}1,k), \mathcal{O}(0,k),\ldots, \mathcal{O}(2k,k), \\ & \quad\mathcal{O}(0,k+1), \mathcal{O}(1,k+1),\ldots, \mathcal{O}(2k+1,k+1),\\ & \quad\quad\hspace{8em} \ldots \\ & \quad\quad\quad\mathcal{O}(k-1,2k), \mathcal{O}(k,2k),\ldots, \mathcal{O}(3k,2k), \\ & \quad\quad\quad\quad\quad\mathcal{O}(k+1,2k+1), \mathcal{O}(k+2,2k+1),\ldots, \mathcal{O}(2k,2k+1), \\ &\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\,\,\,\mathcal{O}(k+2,2k+2),\ldots, \mathcal{O}(2k,2k+2),\\ &\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\,\,\,\,\,\ldots \\ &\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\mathcal{O}(2k,3k)\rangle. \end{aligned}\end{equation} The resulting collection in the case ![]() $k = 3$ is shown in Figure 2: the objects corresponding to the black dots in the lower-left triangle are replaced by the white dots in the upper-right triangle; the rows of (2.9) correspond to the rows in the figure (and the shifts of rows match).
$k = 3$ is shown in Figure 2: the objects corresponding to the black dots in the lower-left triangle are replaced by the white dots in the upper-right triangle; the rows of (2.9) correspond to the rows in the figure (and the shifts of rows match).
2.4 Odd  $n$: residual category
$n$: residual category
We note that the resulting exceptional collection (2.9) is already quite close to what we need. For instance, it already contains the rectangular part of (2.3). Indeed, the blocks ![]() $\mathcal {A} \otimes \mathcal {O}(i,i)$ of (2.3) are generated by the objects corresponding to the dots in Figure 2 joined into L-shaped figures.
$\mathcal {A} \otimes \mathcal {O}(i,i)$ of (2.3) are generated by the objects corresponding to the dots in Figure 2 joined into L-shaped figures.
However, the objects which are not in the rectangular part,
(they are marked with grey crosses (red online) in the figure), are not yet right-orthogonal to the rectangular part (hence are not yet contained in the residual category). The next step is to mutate them accordingly.
Proposition 2.7 If ![]() $\mathcal {R} \subset {{\mathbf {D}^{\mathrm {b}}}}(X)$ is the residual category of the rectangular collection defined by (2.3), then
$\mathcal {R} \subset {{\mathbf {D}^{\mathrm {b}}}}(X)$ is the residual category of the rectangular collection defined by (2.3), then ![]() $\mathcal {R}$ is generated by the exceptional collection
$\mathcal {R}$ is generated by the exceptional collection
 \begin{gather} \hspace{-7pc}\mathcal{R} = \langle \Omega^{k+1}(k+1) \boxtimes_X \mathcal{O}, \Omega^{k+2}(k+2) \boxtimes_X \mathcal{O}(1),\ldots, \Omega^{2k}(2k) \boxtimes_X \mathcal{O}(k-1),\nonumber\\ \hspace{0.6pc}\mathcal{O}({-}1,k),\nonumber\\ \hspace{7.6pc}\mathcal{O} \boxtimes_X \Omega^{k+1}(k+1), \mathcal{O}(1) \boxtimes_X \Omega^{k+2}(k+2),\ldots, \mathcal{O}(k-1) \boxtimes_X \Omega^{2k}(2k) \rangle. \end{gather}
\begin{gather} \hspace{-7pc}\mathcal{R} = \langle \Omega^{k+1}(k+1) \boxtimes_X \mathcal{O}, \Omega^{k+2}(k+2) \boxtimes_X \mathcal{O}(1),\ldots, \Omega^{2k}(2k) \boxtimes_X \mathcal{O}(k-1),\nonumber\\ \hspace{0.6pc}\mathcal{O}({-}1,k),\nonumber\\ \hspace{7.6pc}\mathcal{O} \boxtimes_X \Omega^{k+1}(k+1), \mathcal{O}(1) \boxtimes_X \Omega^{k+2}(k+2),\ldots, \mathcal{O}(k-1) \boxtimes_X \Omega^{2k}(2k) \rangle. \end{gather}
The only non-trivial ![]() $\operatorname {Ext}$-spaces between the objects of this exceptional collection are
$\operatorname {Ext}$-spaces between the objects of this exceptional collection are
 \begin{equation} \begin{aligned} & \operatorname{Hom}(\Omega^{k+i-1}(k+i-1) \boxtimes_X \mathcal{O}(i-2), &&\Omega^{k+i}(k+i) \boxtimes_X \mathcal{O}(i-1)) &&= \Bbbk, && 2 \le i \le k,\\ & \operatorname{Hom}(\Omega^{2k}(2k) \boxtimes_X \mathcal{O}(k-1), && \mathcal{O}({-}1,k)) && = \Bbbk, \\ & \operatorname{Ext}^{k}(\mathcal{O}({-}1,k), && \mathcal{O} \boxtimes_X \Omega^{k+1}(k+1)) &&= \Bbbk,\\ & \operatorname{Hom}(\mathcal{O}(i-2) \boxtimes_X \Omega^{k+i-1}(k+i-1), && \mathcal{O}(i-1) \boxtimes_X \Omega^{k+i}(k+i)) && = \Bbbk, && 2 \le i \le k. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & \operatorname{Hom}(\Omega^{k+i-1}(k+i-1) \boxtimes_X \mathcal{O}(i-2), &&\Omega^{k+i}(k+i) \boxtimes_X \mathcal{O}(i-1)) &&= \Bbbk, && 2 \le i \le k,\\ & \operatorname{Hom}(\Omega^{2k}(2k) \boxtimes_X \mathcal{O}(k-1), && \mathcal{O}({-}1,k)) && = \Bbbk, \\ & \operatorname{Ext}^{k}(\mathcal{O}({-}1,k), && \mathcal{O} \boxtimes_X \Omega^{k+1}(k+1)) &&= \Bbbk,\\ & \operatorname{Hom}(\mathcal{O}(i-2) \boxtimes_X \Omega^{k+i-1}(k+i-1), && \mathcal{O}(i-1) \boxtimes_X \Omega^{k+i}(k+i)) && = \Bbbk, && 2 \le i \le k. \end{aligned} \end{equation}
In particular, ![]() $\mathcal {R}$ is equivalent to the derived category of the Dynkin quiver
$\mathcal {R}$ is equivalent to the derived category of the Dynkin quiver ![]() $\mathrm {A}_{2k+1}$.
$\mathrm {A}_{2k+1}$.
Proof. It follows from Lemma 2.2 that the object ![]() $\mathcal {O}(-1,k)$ (corresponding to the circled grey cross (red online) in Figure 2) is already in the residual category, so it is enough to mutate the other
$\mathcal {O}(-1,k)$ (corresponding to the circled grey cross (red online) in Figure 2) is already in the residual category, so it is enough to mutate the other ![]() $2k$ objects.
$2k$ objects.
Consider the exact sequences
 \begin{align} 0 \to \Omega^{k+i}(k+i) \boxtimes_X \mathcal{O}(i-1) \to &\Lambda^{k+i}V^{{\vee}} \otimes \mathcal{O}(0,i-1) \to \nonumber\\ & \cdots\to V^{{\vee}} \otimes \mathcal{O}(k+i-1,i-1) \to \mathcal{O}(k+i,i-1) \to 0 \end{align}
\begin{align} 0 \to \Omega^{k+i}(k+i) \boxtimes_X \mathcal{O}(i-1) \to &\Lambda^{k+i}V^{{\vee}} \otimes \mathcal{O}(0,i-1) \to \nonumber\\ & \cdots\to V^{{\vee}} \otimes \mathcal{O}(k+i-1,i-1) \to \mathcal{O}(k+i,i-1) \to 0 \end{align}
obtained by an appropriate twist of the pullback to ![]() $X$ of the truncated Koszul complex on
$X$ of the truncated Koszul complex on ![]() ${{\mathbb {P}}}(V)$, and analogous exact sequences
${{\mathbb {P}}}(V)$, and analogous exact sequences
 \begin{align} 0 \to \mathcal{O}(i-1) \boxtimes_X \Omega^{k+i}(k+i) \to &\Lambda^{k+i}V \otimes \mathcal{O}(i-1,0) \to \nonumber\\ & \cdots\to V \otimes \mathcal{O}(i-1,k+i-1) \to \mathcal{O}(i-1,k+i) \to 0. \end{align}
\begin{align} 0 \to \mathcal{O}(i-1) \boxtimes_X \Omega^{k+i}(k+i) \to &\Lambda^{k+i}V \otimes \mathcal{O}(i-1,0) \to \nonumber\\ & \cdots\to V \otimes \mathcal{O}(i-1,k+i-1) \to \mathcal{O}(i-1,k+i) \to 0. \end{align}
If we show that the objects ![]() $\Omega ^{k+i}(k+i) \boxtimes _X \mathcal {O}(i-1)$ and
$\Omega ^{k+i}(k+i) \boxtimes _X \mathcal {O}(i-1)$ and ![]() $\mathcal {O}(i-1) \boxtimes _X \Omega ^{k+i}(k+i)$ belong to
$\mathcal {O}(i-1) \boxtimes _X \Omega ^{k+i}(k+i)$ belong to ![]() $\mathcal {R}$, it will follow that these exact sequences express mutations of
$\mathcal {R}$, it will follow that these exact sequences express mutations of ![]() $\mathcal {O}(k+i,i-1)$ and
$\mathcal {O}(k+i,i-1)$ and ![]() $\mathcal {O}(i-1,k+i)$ through the rectangular part of (2.3), and that together with the object
$\mathcal {O}(i-1,k+i)$ through the rectangular part of (2.3), and that together with the object ![]() $\mathcal {O}(-1,k)$ these objects generate the residual category
$\mathcal {O}(-1,k)$ these objects generate the residual category ![]() $\mathcal {R}$.
$\mathcal {R}$.
So, we need to check that ![]() $\operatorname {Ext}^{\bullet }(\mathcal {O}(a,b),-) = H^{\bullet }(X, - \otimes \mathcal {O}(-a,-b))$ vanishes on these objects when
$\operatorname {Ext}^{\bullet }(\mathcal {O}(a,b),-) = H^{\bullet }(X, - \otimes \mathcal {O}(-a,-b))$ vanishes on these objects when ![]() $\mathcal {O}(a,b)$ run through the set of objects generating the rectangular part of (2.3), that is, for
$\mathcal {O}(a,b)$ run through the set of objects generating the rectangular part of (2.3), that is, for
We have exact sequences on ![]() ${{\mathbb {P}}}(V) \times {{\mathbb {P}}}(V^{\vee })$,
${{\mathbb {P}}}(V) \times {{\mathbb {P}}}(V^{\vee })$,
To compute ![]() $H^{\bullet }(X,\Omega ^{k+i}(k+i-a) \boxtimes _X \mathcal {O}(i-1-b))$ we thus need to compute two tensor products:
$H^{\bullet }(X,\Omega ^{k+i}(k+i-a) \boxtimes _X \mathcal {O}(i-1-b))$ we thus need to compute two tensor products:
 \begin{equation} \begin{aligned} H^{{\bullet}}({{\mathbb{P}}}(V), \Omega^{k+i}(k+i-a)) & \otimes H^{{\bullet}}({{\mathbb{P}}}(V^{{\vee}}), \mathcal{O}(i-1-b)), \\ H^{{\bullet}}({{\mathbb{P}}}(V), \Omega^{k+i}(k+i-1-a)) & \otimes H^{{\bullet}}({{\mathbb{P}}}(V^{{\vee}}), \mathcal{O}(i-2-b)). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} H^{{\bullet}}({{\mathbb{P}}}(V), \Omega^{k+i}(k+i-a)) & \otimes H^{{\bullet}}({{\mathbb{P}}}(V^{{\vee}}), \mathcal{O}(i-1-b)), \\ H^{{\bullet}}({{\mathbb{P}}}(V), \Omega^{k+i}(k+i-1-a)) & \otimes H^{{\bullet}}({{\mathbb{P}}}(V^{{\vee}}), \mathcal{O}(i-2-b)). \end{aligned} \end{equation}By Bott's formula [Reference BottBot57, Proposition 14.4] the first factors in these products are zero, except for
(the conditions in the first (respectively, second) line of (2.16) corresponds to non-vanishing of the first factors in the first (respectively, second) line in (2.15)). Similarly, the second factors vanish except for
(with the same convention about the role of the lines). Clearly, (2.14) is not compatible with the conditions ![]() $a \le -1$ or
$a \le -1$ or ![]() $a \le -2$ in (2.16). Furthermore, (2.14) implies that
$a \le -2$ in (2.16). Furthermore, (2.14) implies that ![]() $|a - b| \le k$, which contradicts all conditions in (2.16) and (2.17), except for those in the last columns. However, in the latter case both
$|a - b| \le k$, which contradicts all conditions in (2.16) and (2.17), except for those in the last columns. However, in the latter case both ![]() $a$ and
$a$ and ![]() $b$ are strictly bigger than
$b$ are strictly bigger than ![]() $2k$ (recall that
$2k$ (recall that ![]() $1 \le i \le k$), which also contradicts (2.14).
$1 \le i \le k$), which also contradicts (2.14).
Thus, we conclude that for all ![]() $(a,b)$ satisfying (2.14) either of the factors in the tensor products (2.15) vanishes, hence the objects
$(a,b)$ satisfying (2.14) either of the factors in the tensor products (2.15) vanishes, hence the objects ![]() $\Omega ^{k+i}(k+i) \boxtimes _X \mathcal {O}(i-1)$ belong to the residual category
$\Omega ^{k+i}(k+i) \boxtimes _X \mathcal {O}(i-1)$ belong to the residual category ![]() $\mathcal {R}$. By symmetry it also follows that the objects
$\mathcal {R}$. By symmetry it also follows that the objects ![]() $\mathcal {O}(i-1) \boxtimes _X \Omega ^{k+i}(k+i)$ belong to
$\mathcal {O}(i-1) \boxtimes _X \Omega ^{k+i}(k+i)$ belong to ![]() $\mathcal {R}$. Thus, all the objects on the right-hand side of (2.10) are in
$\mathcal {R}$. Thus, all the objects on the right-hand side of (2.10) are in ![]() $\mathcal {R}$. Moreover, as we already pointed out, it also follows that (2.12) and (2.13) are mutation sequences. Therefore, together with the line bundle
$\mathcal {R}$. Moreover, as we already pointed out, it also follows that (2.12) and (2.13) are mutation sequences. Therefore, together with the line bundle ![]() $\mathcal {O}(-1,k)$ the objects on the right-hand side of (2.10) generate
$\mathcal {O}(-1,k)$ the objects on the right-hand side of (2.10) generate ![]() $\mathcal {R}$.
$\mathcal {R}$.
Similarly, from Lemma 2.2 and the mutation sequences, orthogonality between the rows of (2.10) follows, so all that remains is to compute ![]() $\operatorname {Ext}$-spaces between objects in each row as well as from objects in the first row to
$\operatorname {Ext}$-spaces between objects in each row as well as from objects in the first row to ![]() $\mathcal {O}(-1,k)$, and from
$\mathcal {O}(-1,k)$, and from ![]() $\mathcal {O}(-1,k)$ to objects in the last row.
$\mathcal {O}(-1,k)$ to objects in the last row.
For this we use (2.12) and (2.13) as resolutions for the source objects. Since almost all terms in these sequences are in the rectangular part of (2.3), it follows that it is enough to compute ![]() $\operatorname {Ext}$-spaces from the rightmost objects only (i.e. for the grey crosses (red online) from Figure 2). Thus, we need to describe the tensor products in (2.15) for
$\operatorname {Ext}$-spaces from the rightmost objects only (i.e. for the grey crosses (red online) from Figure 2). Thus, we need to describe the tensor products in (2.15) for ![]() $(a,b)$ satisfying
$(a,b)$ satisfying
Clearly, the assumption ![]() $0 \le a \le k - 1$ contradicts all conditions in (2.16). On the other hand, if
$0 \le a \le k - 1$ contradicts all conditions in (2.16). On the other hand, if ![]() $0 \le b \le k - 1$ and
$0 \le b \le k - 1$ and ![]() $a = b + k + 1$, then
$a = b + k + 1$, then ![]() $a \le 2k$, so the only compatible conditions are
$a \le 2k$, so the only compatible conditions are
Furthermore, in the first of these cases the first tensor product in (2.15) is one-dimensional (and lives in cohomological degree ![]() $k+i$), and in the second of these cases the second tensor product is one-dimensional (and lives in the same cohomological degree). This computation proves that the only
$k+i$), and in the second of these cases the second tensor product is one-dimensional (and lives in the same cohomological degree). This computation proves that the only ![]() $\operatorname {Ext}$-spaces between the objects in the first and the last rows of (2.10) are those listed in the first and last lines of (2.11).
$\operatorname {Ext}$-spaces between the objects in the first and the last rows of (2.10) are those listed in the first and last lines of (2.11).
Next, we compute ![]() $\operatorname {Ext}$-spaces from objects in the first row of (2.10) to
$\operatorname {Ext}$-spaces from objects in the first row of (2.10) to ![]() $\mathcal {O}(-1,k)$. As before, we use (2.12) as resolutions. The only object that appears in (2.12) which is not semiorthogonal to
$\mathcal {O}(-1,k)$. As before, we use (2.12) as resolutions. The only object that appears in (2.12) which is not semiorthogonal to ![]() $\mathcal {O}(-1,k)$ is
$\mathcal {O}(-1,k)$ is ![]() $\mathcal {O}(2k,k-1)$ (see Lemma 2.2 and (2.8)), from which we have a one-dimensional
$\mathcal {O}(2k,k-1)$ (see Lemma 2.2 and (2.8)), from which we have a one-dimensional ![]() $\operatorname {Ext}$-space in degree
$\operatorname {Ext}$-space in degree ![]() $2k$. Therefore, the only
$2k$. Therefore, the only ![]() $\operatorname {Ext}$-space from objects of the first row to
$\operatorname {Ext}$-space from objects of the first row to ![]() $\mathcal {O}(-1,k)$ is given by the second line of (2.11).
$\mathcal {O}(-1,k)$ is given by the second line of (2.11).
Finally, we compute ![]() $\operatorname {Ext}$-spaces from
$\operatorname {Ext}$-spaces from ![]() $\mathcal {O}(-1,k)$ to objects in the last row of (2.10). First, we consider the Koszul exact sequence
$\mathcal {O}(-1,k)$ to objects in the last row of (2.10). First, we consider the Koszul exact sequence
All its terms (except for the leftmost and rightmost) are in the rectangular part of (2.3), hence
Now we use (2.13) as a resolution for ![]() $\mathcal {O}(i-1) \boxtimes _X \Omega ^{k+i}(k+i)$. Clearly, the only non-trivial
$\mathcal {O}(i-1) \boxtimes _X \Omega ^{k+i}(k+i)$. Clearly, the only non-trivial ![]() $\operatorname {Ext}$-space from
$\operatorname {Ext}$-space from ![]() $\mathcal {O}(2k+1,k)$ to its terms is
$\mathcal {O}(2k+1,k)$ to its terms is
(which holds for ![]() $i = k + 1$). Therefore, the only
$i = k + 1$). Therefore, the only ![]() $\operatorname {Ext}$-space from
$\operatorname {Ext}$-space from ![]() $\mathcal {O}(-1,k)$ to the last row of (2.3) is given by the third line of (2.11).
$\mathcal {O}(-1,k)$ to the last row of (2.3) is given by the third line of (2.11).
It is clear from the above description of ![]() $\operatorname {Ext}$-spaces that the category
$\operatorname {Ext}$-spaces that the category ![]() $\mathcal {R}$ is equivalent to the derived category of the Dynkin quiver
$\mathcal {R}$ is equivalent to the derived category of the Dynkin quiver ![]() $\mathrm {A}_{2k+1}$ (with the objects in (2.10) corresponding to simple representations of the quiver, up to shift).
$\mathrm {A}_{2k+1}$ (with the objects in (2.10) corresponding to simple representations of the quiver, up to shift).
So far, the description of ![]() $\mathcal {R}$ we obtained does not look symmetric with respect to outer automorphisms of
$\mathcal {R}$ we obtained does not look symmetric with respect to outer automorphisms of ![]() $X$, and also looks different from the description in Theorem 2.1. In the next statement we show that the two descriptions agree.
$X$, and also looks different from the description in Theorem 2.1. In the next statement we show that the two descriptions agree.
Lemma 2.8 The category ![]() $\mathcal {R}$ defined by (2.10) is generated by the exceptional collection (2.4).
$\mathcal {R}$ defined by (2.10) is generated by the exceptional collection (2.4).
Proof. The definition (2.1) of the object ![]() $\mathcal {E}$ can be rewritten as the exact sequence
$\mathcal {E}$ can be rewritten as the exact sequence
It follows that ![]() $\operatorname {rk}(\mathcal {E}) = 2k$ and
$\operatorname {rk}(\mathcal {E}) = 2k$ and ![]() $\det (\mathcal {E}) \cong \mathcal {O}(1,-1)$, hence
$\det (\mathcal {E}) \cong \mathcal {O}(1,-1)$, hence
Dualizing (2.18), we obtain
Taking its ![]() $(k+i)$th exterior power and twisting by
$(k+i)$th exterior power and twisting by ![]() $\mathcal {O}(0,i-1)$, we obtain
$\mathcal {O}(0,i-1)$, we obtain
Using (2.19), we can rewrite this as
Now we interpret these sequences as mutations of (2.10).
– For
 $i = k$, the second arrow in (2.20) is the unique (by (2.11)) morphism
therefore its kernel (up to shift) is the right mutation of
$i = k$, the second arrow in (2.20) is the unique (by (2.11)) morphism
therefore its kernel (up to shift) is the right mutation of \[ \Omega^{2k}(2k) \boxtimes_X \mathcal{O}(k-1) \to \mathcal{O}({-}1,k), \]
\[ \Omega^{2k}(2k) \boxtimes_X \mathcal{O}(k-1) \to \mathcal{O}({-}1,k), \] $\Omega ^{2k}(2k) \boxtimes _X \mathcal {O}(k-1)$ through the line bundle
$\Omega ^{2k}(2k) \boxtimes _X \mathcal {O}(k-1)$ through the line bundle  $\mathcal {O}(-1,k)$, and so by (2.20) the result of the mutation is
$\mathcal {O}(-1,k)$, and so by (2.20) the result of the mutation is  $\mathcal {E}(-1,k-1)$.
$\mathcal {E}(-1,k-1)$.– For
 $i = k-1$, the second arrow in (2.20) is the unique morphism
therefore its kernel (up to shift) is the right mutation of
$i = k-1$, the second arrow in (2.20) is the unique morphism
therefore its kernel (up to shift) is the right mutation of \[ \Omega^{2k-1}(2k-1) \boxtimes_X \mathcal{O}(k-2) \to \mathcal{E}({-}1,k-1), \]
\[ \Omega^{2k-1}(2k-1) \boxtimes_X \mathcal{O}(k-2) \to \mathcal{E}({-}1,k-1), \] $\Omega ^{2k-1}(2k-1) \boxtimes _X \mathcal {O}(k-2)$ through the bundle
$\Omega ^{2k-1}(2k-1) \boxtimes _X \mathcal {O}(k-2)$ through the bundle  $\mathcal {E}(-1,k-1)$, and so the result of the mutation is
$\mathcal {E}(-1,k-1)$, and so the result of the mutation is  $\Lambda ^{2}\mathcal {E}(-1,k-2)$. Note here that the intermediate mutation of
$\Lambda ^{2}\mathcal {E}(-1,k-2)$. Note here that the intermediate mutation of  $\Omega ^{2k-1}(2k-1) \boxtimes _X \mathcal {O}(k-2)$ through
$\Omega ^{2k-1}(2k-1) \boxtimes _X \mathcal {O}(k-2)$ through  $\mathcal {O}(-1,k)$ is trivial, because these objects are completely orthogonal by (2.11).
$\mathcal {O}(-1,k)$ is trivial, because these objects are completely orthogonal by (2.11).
Continuing in the same manner, we conclude that the mutation of the vector bundle ![]() $\Omega ^{2k-j}(2k-j) \boxtimes _X \mathcal {O}(k-j-1)$ through
$\Omega ^{2k-j}(2k-j) \boxtimes _X \mathcal {O}(k-j-1)$ through
is the same as its mutation through ![]() $\langle \mathcal {O}(-1,k), \mathcal {E}(-1,k-1),\ldots , \Lambda ^{j}\mathcal {E}(-1,k-j) \rangle$, and is the same as its mutation through the last object
$\langle \mathcal {O}(-1,k), \mathcal {E}(-1,k-1),\ldots , \Lambda ^{j}\mathcal {E}(-1,k-j) \rangle$, and is the same as its mutation through the last object ![]() $\Lambda ^{j}\mathcal {E}(-1,k-j)$. Therefore, it is realized by the complex (2.20) with
$\Lambda ^{j}\mathcal {E}(-1,k-j)$. Therefore, it is realized by the complex (2.20) with ![]() $i = k - j$, hence the result of the mutation is
$i = k - j$, hence the result of the mutation is ![]() $\Lambda ^{j+1}\mathcal {E}(-1,k-j-1)$.
$\Lambda ^{j+1}\mathcal {E}(-1,k-j-1)$.
Thus, we see that the category ![]() $\mathcal {R}$ is generated by the exceptional collection
$\mathcal {R}$ is generated by the exceptional collection
 \begin{align} \mathcal{R} = \langle \mathcal{O}({-}1,k), &\mathcal{E}({-}1,k-1),\ldots, \Lambda^{k-1}\mathcal{E}({-}1,1), \Lambda^{k}\mathcal{E}({-}1,0),\nonumber\\ &\quad \mathcal{O} \boxtimes_X \Omega^{k+1}(k+1), \mathcal{O}(1) \boxtimes_X \Omega^{k+2}(k+2),\ldots, \mathcal{O}(k-1) \boxtimes_X \Omega^{2k}(2k) \rangle, \end{align}
\begin{align} \mathcal{R} = \langle \mathcal{O}({-}1,k), &\mathcal{E}({-}1,k-1),\ldots, \Lambda^{k-1}\mathcal{E}({-}1,1), \Lambda^{k}\mathcal{E}({-}1,0),\nonumber\\ &\quad \mathcal{O} \boxtimes_X \Omega^{k+1}(k+1), \mathcal{O}(1) \boxtimes_X \Omega^{k+2}(k+2),\ldots, \mathcal{O}(k-1) \boxtimes_X \Omega^{2k}(2k) \rangle, \end{align}
and moreover, the only ![]() $\operatorname {Ext}$-spaces between the objects in the first row and the second row of (2.21) are
$\operatorname {Ext}$-spaces between the objects in the first row and the second row of (2.21) are
 \begin{equation} \operatorname{Ext}^{{\bullet}}(\Lambda^{i}\mathcal{E}({-}1,k-i),\mathcal{O}(j-1) \boxtimes_X \Omega^{k+j}(k+j)) = \begin{cases} \Bbbk[i-k], & \text{if } j = 1\\ 0, & \text{if } 2 \le j \le k. \end{cases} \end{equation}
\begin{equation} \operatorname{Ext}^{{\bullet}}(\Lambda^{i}\mathcal{E}({-}1,k-i),\mathcal{O}(j-1) \boxtimes_X \Omega^{k+j}(k+j)) = \begin{cases} \Bbbk[i-k], & \text{if } j = 1\\ 0, & \text{if } 2 \le j \le k. \end{cases} \end{equation}
Note also that by (2.19) the last term in the first line of (2.21) is isomorphic to ![]() $\Lambda ^{k}\mathcal {E}^{\vee }(0,-1)$.
$\Lambda ^{k}\mathcal {E}^{\vee }(0,-1)$.
For the second half of mutations, we note that, applying an outer automorphism of ![]() $X$ to (2.20), we obtain exact sequences
$X$ to (2.20), we obtain exact sequences
Now we interpret these sequences as mutations. Note that ![]() $\Lambda ^{k}\mathcal {E}(-1,0) \cong \Lambda ^{k}\mathcal {E}^{\vee }(0,-1)$ which follows from (2.19).
$\Lambda ^{k}\mathcal {E}(-1,0) \cong \Lambda ^{k}\mathcal {E}^{\vee }(0,-1)$ which follows from (2.19).
– For
 $i = 1$, the first arrow in (2.23) is the unique (by (2.22)) morphism
therefore its cokernel (up to shift) is the left mutation of the object
$i = 1$, the first arrow in (2.23) is the unique (by (2.22)) morphism
therefore its cokernel (up to shift) is the left mutation of the object \[ \Lambda^{k}\mathcal{E}^{{\vee}}(0,-1) \to \mathcal{O} \boxtimes_X \Omega^{k+1}(k+1), \]
\[ \Lambda^{k}\mathcal{E}^{{\vee}}(0,-1) \to \mathcal{O} \boxtimes_X \Omega^{k+1}(k+1), \] $\mathcal {O} \boxtimes _X \Omega ^{k+1}(k+1)$ through the bundle
$\mathcal {O} \boxtimes _X \Omega ^{k+1}(k+1)$ through the bundle  $\Lambda ^{k}\mathcal {E}^{\vee }(0,-1)$, and so the result of the mutation is
$\Lambda ^{k}\mathcal {E}^{\vee }(0,-1)$, and so the result of the mutation is  $\Lambda ^{k-1}\mathcal {E}^{\vee }(1,-1)$.
$\Lambda ^{k-1}\mathcal {E}^{\vee }(1,-1)$.– For
 $i = 2$, the first arrow in (2.23) is the unique morphism
therefore its cokernel (up to shift) is the left mutation of
$i = 2$, the first arrow in (2.23) is the unique morphism
therefore its cokernel (up to shift) is the left mutation of \[ \Lambda^{k-1}\mathcal{E}^{{\vee}}(1,-1) \to \mathcal{O}(1) \boxtimes_X \Omega^{k+2}(k+2), \]
\[ \Lambda^{k-1}\mathcal{E}^{{\vee}}(1,-1) \to \mathcal{O}(1) \boxtimes_X \Omega^{k+2}(k+2), \] $\mathcal {O}(1) \boxtimes _X \Omega ^{k+2}(k+2)$ through the bundle
$\mathcal {O}(1) \boxtimes _X \Omega ^{k+2}(k+2)$ through the bundle  $\Lambda ^{k-1}\mathcal {E}^{\vee }(1,-1)$, and so the result of the mutation is
$\Lambda ^{k-1}\mathcal {E}^{\vee }(1,-1)$, and so the result of the mutation is  $\Lambda ^{k-2}\mathcal {E}^{\vee }(2,-1)$. Note here that the intermediate mutation of
$\Lambda ^{k-2}\mathcal {E}^{\vee }(2,-1)$. Note here that the intermediate mutation of  $\mathcal {O}(1) \boxtimes _X \Omega ^{k+2}(k+2)$ through
$\mathcal {O}(1) \boxtimes _X \Omega ^{k+2}(k+2)$ through  $\Lambda ^{k}\mathcal {E}^{\vee }(0,-1)$ is trivial, because these objects are completely orthogonal by (2.22).
$\Lambda ^{k}\mathcal {E}^{\vee }(0,-1)$ is trivial, because these objects are completely orthogonal by (2.22).
Continuing in the same manner, we conclude that the mutation of ![]() $\mathcal {O}(i-1) \boxtimes _X \Omega ^{k+i}(k+i)$ through
$\mathcal {O}(i-1) \boxtimes _X \Omega ^{k+i}(k+i)$ through ![]() $\langle \Lambda ^{k}\mathcal {E}^{\vee }(0,-1), \mathcal {O} \boxtimes _X \Omega ^{k+1}(k+1),\ldots , \mathcal {O}(i-2) \boxtimes _X \Omega ^{k+i-1}(k+i-1) \rangle$ is the same as its mutation through
$\langle \Lambda ^{k}\mathcal {E}^{\vee }(0,-1), \mathcal {O} \boxtimes _X \Omega ^{k+1}(k+1),\ldots , \mathcal {O}(i-2) \boxtimes _X \Omega ^{k+i-1}(k+i-1) \rangle$ is the same as its mutation through ![]() $\langle \Lambda ^{k-i+1}\mathcal {E}^{\vee }(i-1,-1),\ldots , \Lambda ^{k-1}\mathcal {E}^{\vee }(1,-1), \Lambda ^{k}\mathcal {E}^{\vee }(0,-1) \rangle$, and the same as its mutation through the first object
$\langle \Lambda ^{k-i+1}\mathcal {E}^{\vee }(i-1,-1),\ldots , \Lambda ^{k-1}\mathcal {E}^{\vee }(1,-1), \Lambda ^{k}\mathcal {E}^{\vee }(0,-1) \rangle$, and the same as its mutation through the first object ![]() $\Lambda ^{k-i+1}\mathcal {E}^{\vee }(i-1,-1)$. Therefore, it is realized by the exact sequence (2.23), hence the result of the mutation is
$\Lambda ^{k-i+1}\mathcal {E}^{\vee }(i-1,-1)$. Therefore, it is realized by the exact sequence (2.23), hence the result of the mutation is ![]() $\Lambda ^{k-i+1}\mathcal {E}^{\vee }(i-1,-1)$.
$\Lambda ^{k-i+1}\mathcal {E}^{\vee }(i-1,-1)$.
Thus, we see that the category ![]() $\mathcal {R}$ is generated by (2.4). Moreover, we see that the only
$\mathcal {R}$ is generated by (2.4). Moreover, we see that the only ![]() $\operatorname {Ext}$-spaces between the objects in (2.4) are
$\operatorname {Ext}$-spaces between the objects in (2.4) are
 \begin{align*} &\operatorname{Ext}^{j-i}(\Lambda^{i}\mathcal{E}\hphantom{{}^{{\vee}}}(0,k-i), \Lambda^{j}\mathcal{E}(0,k-j)) = \Bbbk, \quad\ \,\, 0 \le i \le j \le k,\\ &\operatorname{Ext}^{j-i}(\Lambda^{i}\mathcal{E}^{{\vee}}(0,k-i), \Lambda^{j}\mathcal{E}^{{\vee}}(0,k-j)) = \Bbbk, \quad 0 \le i \le j \le k. \end{align*}
\begin{align*} &\operatorname{Ext}^{j-i}(\Lambda^{i}\mathcal{E}\hphantom{{}^{{\vee}}}(0,k-i), \Lambda^{j}\mathcal{E}(0,k-j)) = \Bbbk, \quad\ \,\, 0 \le i \le j \le k,\\ &\operatorname{Ext}^{j-i}(\Lambda^{i}\mathcal{E}^{{\vee}}(0,k-i), \Lambda^{j}\mathcal{E}^{{\vee}}(0,k-j)) = \Bbbk, \quad 0 \le i \le j \le k. \end{align*}In other words, the configuration of these exceptional objects is the following:

So, this exceptional collection corresponds to shifts of projective modules in a quiver of Dynkin type ![]() $\mathrm {A}_{2k+1}$.
$\mathrm {A}_{2k+1}$.
Remark 2.9 The flag variety ![]() $X$ is a homogeneous space for the natural action of the simple group
$X$ is a homogeneous space for the natural action of the simple group ![]() $\operatorname {SL}(n+1) = \operatorname {SL}(V)$. Using the group-theoretic notation introduced in § 3.1, and denoting by
$\operatorname {SL}(n+1) = \operatorname {SL}(V)$. Using the group-theoretic notation introduced in § 3.1, and denoting by ![]() $\omega _i$ the highest weight of the fundamental representation
$\omega _i$ the highest weight of the fundamental representation ![]() $\Lambda ^{i}V^{\vee } \cong \Lambda ^{n+1-i}V$, one can rewrite the exceptional collection of Theorem 2.1 as follows. The first block of the rectangular part
$\Lambda ^{i}V^{\vee } \cong \Lambda ^{n+1-i}V$, one can rewrite the exceptional collection of Theorem 2.1 as follows. The first block of the rectangular part ![]() $\mathcal {A}$ of the category
$\mathcal {A}$ of the category ![]() ${{\mathbf {D}^{\mathrm {b}}}}(X)$ can be written as
${{\mathbf {D}^{\mathrm {b}}}}(X)$ can be written as
Furthermore, if ![]() $n = 2k + 1$ the residual category
$n = 2k + 1$ the residual category ![]() $\mathcal {R}$ can be written as
$\mathcal {R}$ can be written as
 \begin{align} \mathcal{R} = \big\langle \mathcal{U}^{-\omega_1 + k\omega_{n} }, \mathcal{U}^{k\omega_1 - \omega_{n}}; \mathcal{U}^{-\omega_1 + \omega_{n-1} + (k-2)\omega_{n}}, \mathcal{U}^{(k-2)\omega_1 + \omega_2 - \omega_{n}}; \ldots \quad\quad\quad\quad\quad\quad\quad \\ \dots; \mathcal{U}^{-\omega_1 + \omega_{n-i} + (k-i-1)\omega_{n}}, \mathcal{U}^{(k-i-1)\omega_1 + \omega_{i+1} - \omega_{n}}; \ldots \quad\quad \quad\quad\quad\quad \quad\quad\quad \\ \mathcal{U}^{- \omega_1 + \omega_{k+2} }, \mathcal{U}^{\omega_{k} - \omega_{n}}; \mathcal{U}^{- \omega_1 + \omega_{k+1} - \omega_{n}} \big\rangle. \end{align}
\begin{align} \mathcal{R} = \big\langle \mathcal{U}^{-\omega_1 + k\omega_{n} }, \mathcal{U}^{k\omega_1 - \omega_{n}}; \mathcal{U}^{-\omega_1 + \omega_{n-1} + (k-2)\omega_{n}}, \mathcal{U}^{(k-2)\omega_1 + \omega_2 - \omega_{n}}; \ldots \quad\quad\quad\quad\quad\quad\quad \\ \dots; \mathcal{U}^{-\omega_1 + \omega_{n-i} + (k-i-1)\omega_{n}}, \mathcal{U}^{(k-i-1)\omega_1 + \omega_{i+1} - \omega_{n}}; \ldots \quad\quad \quad\quad\quad\quad \quad\quad\quad \\ \mathcal{U}^{- \omega_1 + \omega_{k+2} }, \mathcal{U}^{\omega_{k} - \omega_{n}}; \mathcal{U}^{- \omega_1 + \omega_{k+1} - \omega_{n}} \big\rangle. \end{align}3. Type  $\mathrm {D}_n$
$\mathrm {D}_n$
In this section we prove part (iii) of Theorem 1.9, restated in a more precise form in Theorem 3.1 below. We work over an algebraically closed field ![]() $\Bbbk$ of characteristic zero. Let us point out again that, unlike in type
$\Bbbk$ of characteristic zero. Let us point out again that, unlike in type ![]() $\mathrm {A}_n$, a full exceptional collection in
$\mathrm {A}_n$, a full exceptional collection in ![]() ${{\mathbf {D}^{\mathrm {b}}}}(\operatorname {OG}(2,2n))$ was not known before. Throughout this section we assume
${{\mathbf {D}^{\mathrm {b}}}}(\operatorname {OG}(2,2n))$ was not known before. Throughout this section we assume ![]() $n \ge 4$.
$n \ge 4$.
3.1 Equivariant bundles on homogeneous varieties
We start with a brief reminder about equivariant vector bundles on homogeneous varieties. For more details see [Reference Kuznetsov and PolishchukKP16].
Let ![]() $\mathrm {G}$ be a connected simply connected semisimple algebraic group. We fix a Borel subgroup
$\mathrm {G}$ be a connected simply connected semisimple algebraic group. We fix a Borel subgroup ![]() $\mathrm {B} \subset \mathrm {G}$. Let
$\mathrm {B} \subset \mathrm {G}$. Let ![]() $\mathrm {P} \subset \mathrm {G}$ be a parabolic subgroup such that
$\mathrm {P} \subset \mathrm {G}$ be a parabolic subgroup such that ![]() $\mathrm {B} \subset \mathrm {P}$. Recall that there is a monoidal equivalence of categories between the category of
$\mathrm {B} \subset \mathrm {P}$. Recall that there is a monoidal equivalence of categories between the category of ![]() $\mathrm {G}$-equivariant vector bundles on the homogeneous variety
$\mathrm {G}$-equivariant vector bundles on the homogeneous variety ![]() $\mathrm {G}/\mathrm {P}$ and the category
$\mathrm {G}/\mathrm {P}$ and the category ![]() $\operatorname {Rep}(\mathrm {P})$ of representations of the parabolic subgroup
$\operatorname {Rep}(\mathrm {P})$ of representations of the parabolic subgroup ![]() $\mathrm {P}$.
$\mathrm {P}$.
Let ![]() $\mathrm {P} \twoheadrightarrow \mathrm {L}$ be the Levi quotient. We identify the category
$\mathrm {P} \twoheadrightarrow \mathrm {L}$ be the Levi quotient. We identify the category ![]() $\operatorname {Rep}(\mathrm {L})$ of representations of
$\operatorname {Rep}(\mathrm {L})$ of representations of ![]() $\mathrm {L}$ with the subcategory of
$\mathrm {L}$ with the subcategory of ![]() $\operatorname {Rep}(\mathrm {P})$ of representations with the trivial action of the unipotent radical. This equivalence is compatible with the monoidal structure of the categories.
$\operatorname {Rep}(\mathrm {P})$ of representations with the trivial action of the unipotent radical. This equivalence is compatible with the monoidal structure of the categories.
The image of the Borel subgroup ![]() $\mathrm {B} \subset \mathrm {G}$ is a Borel subgroup
$\mathrm {B} \subset \mathrm {G}$ is a Borel subgroup ![]() $\mathrm {B}_\mathrm {L}$ in
$\mathrm {B}_\mathrm {L}$ in ![]() $\mathrm {L}$. We denote by
$\mathrm {L}$. We denote by ![]() $\mathbf {P}_\mathrm {L} = \mathbf {P}_\mathrm {G}$ the weight lattices of
$\mathbf {P}_\mathrm {L} = \mathbf {P}_\mathrm {G}$ the weight lattices of ![]() $\mathrm {L}$ and
$\mathrm {L}$ and ![]() $\mathrm {G}$ with their natural identification, and by
$\mathrm {G}$ with their natural identification, and by
the cones of dominant weights with respect to ![]() $\mathrm {B}$ and
$\mathrm {B}$ and ![]() $\mathrm {B}_\mathrm {L}$, respectively. For each
$\mathrm {B}_\mathrm {L}$, respectively. For each ![]() $\lambda \in \mathbf {P}_\mathrm {L}^{+}$ we denote by
$\lambda \in \mathbf {P}_\mathrm {L}^{+}$ we denote by ![]() $\mathrm {V}_\mathrm {L}^{\lambda }$ the corresponding irreducible representation of
$\mathrm {V}_\mathrm {L}^{\lambda }$ the corresponding irreducible representation of ![]() $\mathrm {L}$ and by
$\mathrm {L}$ and by ![]() $\mathcal {U}^{\lambda }$ the equivariant vector bundle on
$\mathcal {U}^{\lambda }$ the equivariant vector bundle on ![]() $\mathrm {G}/\mathrm {P}$ corresponding to it via the above equivalences. Similarly, for
$\mathrm {G}/\mathrm {P}$ corresponding to it via the above equivalences. Similarly, for ![]() $\lambda \in \mathbf {P}_\mathrm {G}^{+}$ we denote by
$\lambda \in \mathbf {P}_\mathrm {G}^{+}$ we denote by ![]() $\mathrm {V}_\mathrm {G}^{\lambda }$ the corresponding irreducible representation of
$\mathrm {V}_\mathrm {G}^{\lambda }$ the corresponding irreducible representation of ![]() $\mathrm {G}$.
$\mathrm {G}$.
We denote by ![]() $\mathrm {W}$ the Weyl group of
$\mathrm {W}$ the Weyl group of ![]() $\mathrm {G}$, by
$\mathrm {G}$, by ![]() $\mathrm {W}^\mathrm{L} \subset \mathrm {W}$ the Weyl group of
$\mathrm {W}^\mathrm{L} \subset \mathrm {W}$ the Weyl group of ![]() $\mathrm {L}$, and by
$\mathrm {L}$, and by ![]() $w_0 \in \mathrm {W}$ and
$w_0 \in \mathrm {W}$ and ![]() $w_0^\mathrm{L} \in \mathrm {W}^\mathrm{L}$ the longest elements.
$w_0^\mathrm{L} \in \mathrm {W}^\mathrm{L}$ the longest elements.
3.2 Statement of the theorem
Consider the group ![]() $\mathrm {G} = \operatorname {Spin}(2n)$, the simply connected (double) covering
$\mathrm {G} = \operatorname {Spin}(2n)$, the simply connected (double) covering
of the special orthogonal group, and its maximal parabolic subgroup ![]() $\mathrm {P} \subset \mathrm {G}$ corresponding to the vertex 2 (marked with black) of the Dynkin diagram
$\mathrm {P} \subset \mathrm {G}$ corresponding to the vertex 2 (marked with black) of the Dynkin diagram ![]() $\mathrm {D}_n$:
$\mathrm {D}_n$:

In this case the corresponding homogeneous variety is
the Grassmannian of two-dimensional isotropic subspaces in a vector space of dimension ![]() $2n$ endowed with a non-degenerate symmetric bilinear form, that is, the (co)adjoint variety of type
$2n$ endowed with a non-degenerate symmetric bilinear form, that is, the (co)adjoint variety of type ![]() $\mathrm {D}_n$. Note that
$\mathrm {D}_n$. Note that ![]() $\dim (\operatorname {OG}(2,2n)) = 4n - 7$.
$\dim (\operatorname {OG}(2,2n)) = 4n - 7$.
The automorphism group of ![]() $\operatorname {OG}(2,2n)$ is the semidirect product
$\operatorname {OG}(2,2n)$ is the semidirect product
 \[ \operatorname{Aut}(\operatorname{OG}(2,2n)) \cong \begin{cases} \operatorname{PSO}(2n) \rtimes \mathfrak{S}_2, & \text{if } n \ne 4,\\ \operatorname{PSO}(2n) \rtimes \mathfrak{S}_3, & \text{if } n = 4,\\ \end{cases} \]
\[ \operatorname{Aut}(\operatorname{OG}(2,2n)) \cong \begin{cases} \operatorname{PSO}(2n) \rtimes \mathfrak{S}_2, & \text{if } n \ne 4,\\ \operatorname{PSO}(2n) \rtimes \mathfrak{S}_3, & \text{if } n = 4,\\ \end{cases} \]
where the factors ![]() $\mathfrak {S}_2$ and
$\mathfrak {S}_2$ and ![]() $\mathfrak {S}_3$ act by outer automorphisms (corresponding to the symmetry of the Dynkin diagram
$\mathfrak {S}_3$ act by outer automorphisms (corresponding to the symmetry of the Dynkin diagram ![]() $\mathrm {D}_n$).
$\mathrm {D}_n$).
The weight lattice of ![]() $\operatorname {SO}(2n)$ is the lattice
$\operatorname {SO}(2n)$ is the lattice ![]() ${{\mathbb {Z}}}^{n}$ with the standard basis
${{\mathbb {Z}}}^{n}$ with the standard basis ![]() $\{\epsilon _i\}_{1 \le i \le n}$, and the weight lattice of
$\{\epsilon _i\}_{1 \le i \le n}$, and the weight lattice of ![]() $\operatorname {Spin}(2n)$ is its overlattice in
$\operatorname {Spin}(2n)$ is its overlattice in ![]() ${{\mathbb {Q}}}^{n}$ generated by the fundamental weights
${{\mathbb {Q}}}^{n}$ generated by the fundamental weights
 \begin{equation} \begin{aligned} \omega_i & = \epsilon_1 + \cdots + \epsilon_i,\qquad 1 \le i \le n-2, \\ \omega_{n-1} & = \tfrac 12(\epsilon_1 + \cdots + \epsilon_{n-1} - \epsilon_n), \\ \omega_{n} & = \tfrac 12(\epsilon_1 + \cdots + \epsilon_{n-1} + \epsilon_n). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \omega_i & = \epsilon_1 + \cdots + \epsilon_i,\qquad 1 \le i \le n-2, \\ \omega_{n-1} & = \tfrac 12(\epsilon_1 + \cdots + \epsilon_{n-1} - \epsilon_n), \\ \omega_{n} & = \tfrac 12(\epsilon_1 + \cdots + \epsilon_{n-1} + \epsilon_n). \end{aligned} \end{equation} The Levi group in ![]() $\operatorname {SO}(2n)$ corresponding to the second vertex of the Dynkin diagram is isomorphic to
$\operatorname {SO}(2n)$ corresponding to the second vertex of the Dynkin diagram is isomorphic to ![]() $\operatorname {GL}(2) \times \operatorname {SO}(2(n-2))$, and the corresponding Levi group in
$\operatorname {GL}(2) \times \operatorname {SO}(2(n-2))$, and the corresponding Levi group in ![]() $\operatorname {Spin}(2n)$ is the double covering
$\operatorname {Spin}(2n)$ is the double covering
induced by (3.1).
The fundamental weight ![]() $\omega _2$ (associated with the parabolic
$\omega _2$ (associated with the parabolic ![]() $\mathrm {P}$) corresponds to the ample generator of the Picard group
$\mathrm {P}$) corresponds to the ample generator of the Picard group ![]() $\operatorname {Pic}(\mathrm {G}/\mathrm {P})$, so we write
$\operatorname {Pic}(\mathrm {G}/\mathrm {P})$, so we write
Note that the canonical line bundle can be written as
Furthermore, we use the following notation:
 \begin{equation} \begin{aligned} \mathcal{U} & := (\mathcal{U}^{\omega_1})^{{\vee}},\\ \mathcal{S}_- & := \mathcal{U}^{\omega_{n-1}},\\ \mathcal{S}_+ & := \mathcal{U}^{\omega_{n}}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \mathcal{U} & := (\mathcal{U}^{\omega_1})^{{\vee}},\\ \mathcal{S}_- & := \mathcal{U}^{\omega_{n-1}},\\ \mathcal{S}_+ & := \mathcal{U}^{\omega_{n}}. \end{aligned} \end{equation}
Thus, ![]() $\mathcal {U}$ is the tautological rank-2 bundle of
$\mathcal {U}$ is the tautological rank-2 bundle of ![]() $\operatorname {OG}(2,2n)$, while
$\operatorname {OG}(2,2n)$, while ![]() $\mathcal {S}_\pm$ are the spinor bundles (see [Reference KuznetsovKuz08, §6]).
$\mathcal {S}_\pm$ are the spinor bundles (see [Reference KuznetsovKuz08, §6]).
Consider the following full triangulated subcategories of ![]() ${{\mathbf {D}^{\mathrm {b}}}}(\operatorname {OG}(2,2n))$:
${{\mathbf {D}^{\mathrm {b}}}}(\operatorname {OG}(2,2n))$:
 \begin{equation} \begin{aligned} \mathcal{A} & := \langle \mathcal{O} , \mathcal{U}^{{\vee}}, S^{2} \mathcal{U}^{{\vee}},\ldots , S^{n-3} \mathcal{U}^{{\vee}}, \mathcal{S}_- , \mathcal{S}_+ \rangle, \\ \mathcal{B} & := \langle \mathcal{O} , \mathcal{U}^{{\vee}}, S^{2} \mathcal{U}^{{\vee}},\ldots , S^{n-3} \mathcal{U}^{{\vee}}, S^{n-2} \mathcal{U}^{{\vee}}, \mathcal{S}_- , \mathcal{S}_+ \rangle. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \mathcal{A} & := \langle \mathcal{O} , \mathcal{U}^{{\vee}}, S^{2} \mathcal{U}^{{\vee}},\ldots , S^{n-3} \mathcal{U}^{{\vee}}, \mathcal{S}_- , \mathcal{S}_+ \rangle, \\ \mathcal{B} & := \langle \mathcal{O} , \mathcal{U}^{{\vee}}, S^{2} \mathcal{U}^{{\vee}},\ldots , S^{n-3} \mathcal{U}^{{\vee}}, S^{n-2} \mathcal{U}^{{\vee}}, \mathcal{S}_- , \mathcal{S}_+ \rangle. \end{aligned} \end{equation}
Note that ![]() $\mathcal {A} \subset \mathcal {B}$ and
$\mathcal {A} \subset \mathcal {B}$ and ![]() $\mathcal {A}$ is
$\mathcal {A}$ is ![]() $\operatorname {Aut}(\operatorname {OG}(2,2n))$-invariant. Indeed, every object in
$\operatorname {Aut}(\operatorname {OG}(2,2n))$-invariant. Indeed, every object in ![]() $\mathcal {A}$ is
$\mathcal {A}$ is ![]() $\operatorname {PSO}(2n)$-invariant by [Reference PolishchukPol11, Lemma 2.2]. Moreover, if
$\operatorname {PSO}(2n)$-invariant by [Reference PolishchukPol11, Lemma 2.2]. Moreover, if ![]() $n \ne 4$ the outer automorphisms
$n \ne 4$ the outer automorphisms ![]() $\mathfrak {S}_2$-action on
$\mathfrak {S}_2$-action on ![]() $\operatorname {OG}(2,2n)$ swaps the spinor bundles
$\operatorname {OG}(2,2n)$ swaps the spinor bundles ![]() $\mathcal {S}_-$ and
$\mathcal {S}_-$ and ![]() $\mathcal {S}_+$, while in case
$\mathcal {S}_+$, while in case ![]() $n = 4$ the outer automorphisms
$n = 4$ the outer automorphisms ![]() $\mathfrak {S}_3$-action permutes
$\mathfrak {S}_3$-action permutes ![]() $\mathcal {S}_-$,
$\mathcal {S}_-$, ![]() $\mathcal {S}_+$, and
$\mathcal {S}_+$, and ![]() $\mathcal {U}^{\vee }$ (and in this case
$\mathcal {U}^{\vee }$ (and in this case ![]() $\mathcal {A} = \langle \mathcal {O} , \mathcal {U}^{\vee }, \mathcal {S}_- , \mathcal {S}_+ \rangle$).
$\mathcal {A} = \langle \mathcal {O} , \mathcal {U}^{\vee }, \mathcal {S}_- , \mathcal {S}_+ \rangle$).
Theorem 3.1 There exists a full exceptional collection
 \begin{align} {{\mathbf{D}^{\mathrm{b}}}}(\operatorname{OG}(2,2n)) &= \langle \mathcal{U}^{2\omega_{n-1}}({-}1), \mathcal{U}^{2\omega_{n}}({-}1) , \mathcal{A} , \nonumber\\ &\qquad \mathcal{B}(1) ,\ldots , \mathcal{B}(n-2) , \mathcal{A}(n-1) ,\ldots ,\mathcal{A}(2n-4) \rangle. \end{align}
\begin{align} {{\mathbf{D}^{\mathrm{b}}}}(\operatorname{OG}(2,2n)) &= \langle \mathcal{U}^{2\omega_{n-1}}({-}1), \mathcal{U}^{2\omega_{n}}({-}1) , \mathcal{A} , \nonumber\\ &\qquad \mathcal{B}(1) ,\ldots , \mathcal{B}(n-2) , \mathcal{A}(n-1) ,\ldots ,\mathcal{A}(2n-4) \rangle. \end{align}
In particular, the subcategory ![]() $\mathcal {A}$ extends to an
$\mathcal {A}$ extends to an ![]() $\operatorname {Aut}(\operatorname {OG}(2,2n))$-invariant rectangular Lefschetz collection
$\operatorname {Aut}(\operatorname {OG}(2,2n))$-invariant rectangular Lefschetz collection
Moreover, the residual category ![]() $\mathcal {R}$ is generated by an
$\mathcal {R}$ is generated by an ![]() $\operatorname {Aut}(\operatorname {OG}(2,2n))$-invariant exceptional collection and is equivalent to the derived category of representations of the Dynkin quiver
$\operatorname {Aut}(\operatorname {OG}(2,2n))$-invariant exceptional collection and is equivalent to the derived category of representations of the Dynkin quiver ![]() $\mathrm {D}_n$.
$\mathrm {D}_n$.
Remark 3.2 It is easy to see that the exceptional collection (3.9) is mutation equivalent to the full Lefschetz collection with the starting block
 \begin{align*} E_i & = S^{i-1} \mathcal{U}^{{\vee}},\quad 1 \le i \le n-2, \\ E_{n-1} & = \mathcal{S}_-, \\ E_{n} & = \mathcal{S}_+, \\ E_{n+1} &= {{\mathbb{R}}}_{\langle \mathcal{S}_-, \mathcal{S}_+ \rangle}(S^{n-2}\mathcal{U}^{{\vee}}), \\ E_{n+2} &= {{\mathbb{R}}}_{\langle \mathcal{A}({-}1),\mathcal{B} \rangle} (\mathcal{U}^{2\omega_{n-1}}({-}2)), \\ E_{n+3} &= {{\mathbb{R}}}_{\langle \mathcal{A}({-}1),\mathcal{B} \rangle} (\mathcal{U}^{2\omega_{n}}({-}2)), \end{align*}
\begin{align*} E_i & = S^{i-1} \mathcal{U}^{{\vee}},\quad 1 \le i \le n-2, \\ E_{n-1} & = \mathcal{S}_-, \\ E_{n} & = \mathcal{S}_+, \\ E_{n+1} &= {{\mathbb{R}}}_{\langle \mathcal{S}_-, \mathcal{S}_+ \rangle}(S^{n-2}\mathcal{U}^{{\vee}}), \\ E_{n+2} &= {{\mathbb{R}}}_{\langle \mathcal{A}({-}1),\mathcal{B} \rangle} (\mathcal{U}^{2\omega_{n-1}}({-}2)), \\ E_{n+3} &= {{\mathbb{R}}}_{\langle \mathcal{A}({-}1),\mathcal{B} \rangle} (\mathcal{U}^{2\omega_{n}}({-}2)), \end{align*}
with the next ![]() $n-3$ blocks generated by
$n-3$ blocks generated by ![]() $E_1,\ldots ,E_{n+1}$, and with the last
$E_1,\ldots ,E_{n+1}$, and with the last ![]() $n-1$ blocks generated by
$n-1$ blocks generated by ![]() $E_1,\ldots ,E_n$. Indeed, to prove this we first twist (3.9) by
$E_1,\ldots ,E_n$. Indeed, to prove this we first twist (3.9) by ![]() $\mathcal {O}(-1)$, then mutate the objects
$\mathcal {O}(-1)$, then mutate the objects ![]() $\mathcal {U}^{2\omega _{n-1}}(-2), \mathcal {U}^{2\omega _{n}}(-2)$ to the right of
$\mathcal {U}^{2\omega _{n-1}}(-2), \mathcal {U}^{2\omega _{n}}(-2)$ to the right of ![]() $\mathcal {A}(-1)$ and
$\mathcal {A}(-1)$ and ![]() $\mathcal {B}$, and finally mutate
$\mathcal {B}$, and finally mutate ![]() $\mathcal {A}(-1)$ to the far right.
$\mathcal {A}(-1)$ to the far right.
Remark 3.3 If ![]() $n = 3$ we have isomorphisms
$n = 3$ we have isomorphisms ![]() $\operatorname {Spin}(6) \cong \operatorname {SL}(4)$ and
$\operatorname {Spin}(6) \cong \operatorname {SL}(4)$ and ![]() $\operatorname {OG}(2,6) \cong \operatorname {Fl}(1,3;4)$. Furthermore, under these isomorphisms
$\operatorname {OG}(2,6) \cong \operatorname {Fl}(1,3;4)$. Furthermore, under these isomorphisms ![]() $\mathcal {S}_- \cong \mathcal {O}(1,0)$ and
$\mathcal {S}_- \cong \mathcal {O}(1,0)$ and ![]() $\mathcal {S}_+ \cong \mathcal {O}(0,1)$, so the definitions of the category
$\mathcal {S}_+ \cong \mathcal {O}(0,1)$, so the definitions of the category ![]() $\mathcal {A}$ in (2.2) and (3.8) coincide, hence (2.3) coincides with (3.10).
$\mathcal {A}$ in (2.2) and (3.8) coincide, hence (2.3) coincides with (3.10).
We prove Theorem 3.1 in §§ 3.4, 3.6 and 3.7 after some preparation.
3.3 Computational tools
To check that a collection of vector bundles is exceptional, we need some tools to dualize the bundles, take their tensor products, and compute the cohomology.
We start by recalling the general machinery. Recall that the Levi group ![]() $\mathrm {L}$ is reductive, hence
$\mathrm {L}$ is reductive, hence ![]() $\operatorname {Rep}(\mathrm {L})$ is a semisimple category; in particular,
$\operatorname {Rep}(\mathrm {L})$ is a semisimple category; in particular, ![]() $\mathrm {V}_\mathrm {L}^{\lambda } \otimes \mathrm {V}_\mathrm {L}^{\mu }$ is a direct sum of irreducible representations of
$\mathrm {V}_\mathrm {L}^{\lambda } \otimes \mathrm {V}_\mathrm {L}^{\mu }$ is a direct sum of irreducible representations of ![]() $\mathrm {L}$. Since the functor
$\mathrm {L}$. Since the functor ![]() $\mathrm {V}_\mathrm {L}^{\lambda } \mapsto \mathcal {U}^{\lambda }$ from the category
$\mathrm {V}_\mathrm {L}^{\lambda } \mapsto \mathcal {U}^{\lambda }$ from the category ![]() $\operatorname {Rep}(\mathrm {L})$ to the category of equivariant vector bundles on
$\operatorname {Rep}(\mathrm {L})$ to the category of equivariant vector bundles on ![]() $\mathrm {G}/\mathrm {P}$ is monoidal, we have the following lemma.
$\mathrm {G}/\mathrm {P}$ is monoidal, we have the following lemma.
Lemma 3.4 [KP16, (8)] If ![]() $\mathrm {V}_\mathrm {L}^{\lambda } \otimes \mathrm {V}_\mathrm {L}^{\mu } = {\bigoplus} \mathrm {V}_\mathrm {L}^{\nu }$, then
$\mathrm {V}_\mathrm {L}^{\lambda } \otimes \mathrm {V}_\mathrm {L}^{\mu } = {\bigoplus} \mathrm {V}_\mathrm {L}^{\nu }$, then ![]() $\mathcal {U}^{\lambda } \otimes \mathcal {U}^{\mu } = {\bigoplus} \mathcal {U}^{\nu }$.
$\mathcal {U}^{\lambda } \otimes \mathcal {U}^{\mu } = {\bigoplus} \mathcal {U}^{\nu }$.
Thus, knowing tensor products of ![]() $\mathrm {L}$-representations, we can control tensor products of the corresponding equivariant bundles. Similarly, we can control the dualization operation. Recall that
$\mathrm {L}$-representations, we can control tensor products of the corresponding equivariant bundles. Similarly, we can control the dualization operation. Recall that ![]() $w_0^\mathrm{L}$ denotes the longest element in
$w_0^\mathrm{L}$ denotes the longest element in ![]() $\mathrm {W}^\mathrm{L}$, the Weyl group of
$\mathrm {W}^\mathrm{L}$, the Weyl group of ![]() $\mathrm {L}$.
$\mathrm {L}$.
Lemma 3.5 [KP16, (8)] We have ![]() $(\mathcal {U}^{\lambda })^{\vee } \cong \mathcal {U}^{-w_0^\mathrm{L} \lambda }$.
$(\mathcal {U}^{\lambda })^{\vee } \cong \mathcal {U}^{-w_0^\mathrm{L} \lambda }$.
A combination of the last two lemmas shows that ![]() $(\mathcal {U}^{\lambda })^{\vee } \otimes \mathcal {U}^{\mu }$ is a direct sum of some
$(\mathcal {U}^{\lambda })^{\vee } \otimes \mathcal {U}^{\mu }$ is a direct sum of some ![]() $\mathcal {U}^{\nu }$. The summands that show up in this decomposition can be characterized by the following lemma.
$\mathcal {U}^{\nu }$. The summands that show up in this decomposition can be characterized by the following lemma.
Lemma 3.6 [KP16, Lemmas 2.8 and 2.9] We have
where ![]() $\operatorname {Conv}(-)$ stands for the convex hull and
$\operatorname {Conv}(-)$ stands for the convex hull and ![]() $m(\lambda ,\mu ,\nu ) \in {{\mathbb {Z}}}_{\ge 0}$ is the multiplicity of
$m(\lambda ,\mu ,\nu ) \in {{\mathbb {Z}}}_{\ge 0}$ is the multiplicity of ![]() $\mathrm {V}^{\nu }_\mathrm {L}$ in
$\mathrm {V}^{\nu }_\mathrm {L}$ in ![]() $(\mathrm {V}_\mathrm {L}^{\lambda })^{\vee } \otimes \mathrm {V}_\mathrm {L}^{\mu }$. Moreover, if
$(\mathrm {V}_\mathrm {L}^{\lambda })^{\vee } \otimes \mathrm {V}_\mathrm {L}^{\mu }$. Moreover, if ![]() $\nu = 0$ then
$\nu = 0$ then ![]() $m(\lambda ,\mu ,\nu ) \ne 0$ only when
$m(\lambda ,\mu ,\nu ) \ne 0$ only when ![]() $\lambda = \mu$ and
$\lambda = \mu$ and ![]() $m(\lambda ,\lambda ,0) = 1$.
$m(\lambda ,\lambda ,0) = 1$.
The most efficient way to compute cohomology is provided by the Borel–Bott–Weil theorem. Let ![]() $\ell \colon \mathrm {W} \to {{\mathbb {Z}}}$ be the length function and let
$\ell \colon \mathrm {W} \to {{\mathbb {Z}}}$ be the length function and let ![]() $\rho \in \mathbf {P}_\mathrm {G}^{+}$ be the sum of fundamental weights of
$\rho \in \mathbf {P}_\mathrm {G}^{+}$ be the sum of fundamental weights of ![]() $\mathrm {G}$.
$\mathrm {G}$.
Theorem 3.7 (Borel–Bott–Weil) Let ![]() $\lambda \in \mathbf {P}_\mathrm {L}^{+}$. If the weight
$\lambda \in \mathbf {P}_\mathrm {L}^{+}$. If the weight ![]() $\lambda + \rho$ lies on a wall of a Weyl chamber for the
$\lambda + \rho$ lies on a wall of a Weyl chamber for the ![]() $\mathrm {W}$-action, then
$\mathrm {W}$-action, then
Otherwise, if ![]() $w \in \mathrm {W}$ is the unique element such that the weight
$w \in \mathrm {W}$ is the unique element such that the weight ![]() $w(\lambda + \rho )$ is dominant, then
$w(\lambda + \rho )$ is dominant, then
The Weyl group of ![]() $\operatorname {Spin}(2n)$ is the semidirect product
$\operatorname {Spin}(2n)$ is the semidirect product
where ![]() $\mathfrak {S}_n$ acts on
$\mathfrak {S}_n$ acts on ![]() $\mathbf {P}_{\operatorname {Spin}(2n)} {} \subset {{\mathbb {Q}}}^{n}$ by permutations and
$\mathbf {P}_{\operatorname {Spin}(2n)} {} \subset {{\mathbb {Q}}}^{n}$ by permutations and ![]() $({{\mathbb {Z}}}/2)^{n-1}$ by changes of signs of an even number of coordinates. The walls of the Weyl chambers are given by the hyperplanes
$({{\mathbb {Z}}}/2)^{n-1}$ by changes of signs of an even number of coordinates. The walls of the Weyl chambers are given by the hyperplanes
The Weyl group of ![]() $\mathrm {L}$ is the subgroup
$\mathrm {L}$ is the subgroup
where ![]() $\mathfrak {S}_2$ acts by transposition of the first two coordinates,
$\mathfrak {S}_2$ acts by transposition of the first two coordinates, ![]() $\mathfrak {S}_{n-2}$ by permutations of the last
$\mathfrak {S}_{n-2}$ by permutations of the last ![]() $n-2$, and
$n-2$, and ![]() $({{\mathbb {Z}}}/2)^{n-3}$ by changes of signs of an even number of the last
$({{\mathbb {Z}}}/2)^{n-3}$ by changes of signs of an even number of the last ![]() $n-2$ coordinates. The longest element
$n-2$ coordinates. The longest element ![]() $w_0^\mathrm{L} \in \mathrm {W}^\mathrm{L}$ acts by
$w_0^\mathrm{L} \in \mathrm {W}^\mathrm{L}$ acts by
Finally, the sum ![]() $\rho$ of the fundamental weights in the standard basis takes the form
$\rho$ of the fundamental weights in the standard basis takes the form
Applying the general machinery in our situation, we obtain the following corollaries. First, combining Lemma 3.5 with (3.3), (3.5), and (3.12), we obtain the following result.
Corollary 3.8 For ![]() $a \geq 0$, we have
$a \geq 0$, we have
For ![]() $a \geq 0$ and even
$a \geq 0$ and even ![]() $n$, we have
$n$, we have
For ![]() $a \geq 0$ and odd
$a \geq 0$ and odd ![]() $n$, we have
$n$, we have
Proof. By (3.3) we have ![]() $a\omega _1 = (a,0,0,\ldots ,0)$. By Lemma 3.5 and (3.12) the weight corresponding to
$a\omega _1 = (a,0,0,\ldots ,0)$. By Lemma 3.5 and (3.12) the weight corresponding to ![]() $\big ( \mathcal {U}^{a \omega _1} \big )^{\vee }$ is
$\big ( \mathcal {U}^{a \omega _1} \big )^{\vee }$ is ![]() $(0,-a,0,\ldots ,0)$; by (3.3) this is equal to
$(0,-a,0,\ldots ,0)$; by (3.3) this is equal to ![]() $a\omega _1 - a\omega _2$, hence the claim. The other results are proved analogously.
$a\omega _1 - a\omega _2$, hence the claim. The other results are proved analogously.
Similarly, using Lemma 3.4 we deduce the following tensor product decompositions.
Lemma 3.9 We have isomorphisms
 \begin{align} \mathcal{U}^{k \omega_1} \otimes \mathcal{U}^{l \omega_1} &\cong \bigoplus_{i = 0}^{\min\{k,l\}} \mathcal{U}^{(k+l-2i) \omega_1} (i) \hspace{3.7pc}\text{for } k,l \ge 0, \end{align}
\begin{align} \mathcal{U}^{k \omega_1} \otimes \mathcal{U}^{l \omega_1} &\cong \bigoplus_{i = 0}^{\min\{k,l\}} \mathcal{U}^{(k+l-2i) \omega_1} (i) \hspace{3.7pc}\text{for } k,l \ge 0, \end{align} \begin{align} \mathcal{U}^{k\omega_1} \otimes \mathcal{U}^{\lambda} &\cong \mathcal{U}^{k\omega_1 + \lambda} \hspace{9pc}\text{if } \lambda = \sum_{i=2}^{n} \lambda_i \omega_i, \end{align}
\begin{align} \mathcal{U}^{k\omega_1} \otimes \mathcal{U}^{\lambda} &\cong \mathcal{U}^{k\omega_1 + \lambda} \hspace{9pc}\text{if } \lambda = \sum_{i=2}^{n} \lambda_i \omega_i, \end{align}Proof. First, we note that the bundles ![]() $\mathcal {U}^{k\omega _1}$ and
$\mathcal {U}^{k\omega _1}$ and ![]() $\mathcal {U}^{l\omega _1}$ correspond to representations of
$\mathcal {U}^{l\omega _1}$ correspond to representations of ![]() $\mathrm {L}$ pulled back from representations
$\mathrm {L}$ pulled back from representations ![]() $\mathrm {V}_{\operatorname {GL}_2}^{k,0}$ and
$\mathrm {V}_{\operatorname {GL}_2}^{k,0}$ and ![]() $\mathrm {V}_{\operatorname {GL}_2}^{l,0}$ via the map (3.4), so (3.14) follows from the Clebsch–Gordan rule
$\mathrm {V}_{\operatorname {GL}_2}^{l,0}$ via the map (3.4), so (3.14) follows from the Clebsch–Gordan rule
 \[ \mathrm{V}_{\operatorname{GL}_2}^{k_1,k_2} \otimes \mathrm{V}_{\operatorname{GL}_2}^{l_1,l_2} = \bigoplus_{j = 0}^{\min\{k_1 - k_2,l_1 - l_2\}} \mathrm{V}_{\operatorname{GL}_2}^{k_1 + l_1 - j, k_2 + l_2 + j}. \]
\[ \mathrm{V}_{\operatorname{GL}_2}^{k_1,k_2} \otimes \mathrm{V}_{\operatorname{GL}_2}^{l_1,l_2} = \bigoplus_{j = 0}^{\min\{k_1 - k_2,l_1 - l_2\}} \mathrm{V}_{\operatorname{GL}_2}^{k_1 + l_1 - j, k_2 + l_2 + j}. \] For (3.15) and (3.16) we need a slightly more detailed understanding of the Levi group ![]() $\mathrm {L}$. Let
$\mathrm {L}$. Let ![]() $\operatorname {{\widetilde {GL}}}(2) \to \operatorname {GL}(2)$ be the unique connected double covering. Then there is a double covering
$\operatorname {{\widetilde {GL}}}(2) \to \operatorname {GL}(2)$ be the unique connected double covering. Then there is a double covering
To understand the tensor product of representations of ![]() $\mathrm {L}$ it is enough to understand the tensor product of their pullbacks via the map (3.17).
$\mathrm {L}$ it is enough to understand the tensor product of their pullbacks via the map (3.17).
We will denote by ![]() $\omega '_1$,
$\omega '_1$, ![]() $\omega '_2$ the fundamental weights of
$\omega '_2$ the fundamental weights of ![]() $\operatorname {{\widetilde {GL}}}(2)$ and by
$\operatorname {{\widetilde {GL}}}(2)$ and by ![]() $\omega '_i$,
$\omega '_i$, ![]() $3 \le i \le n$, the fundamental weights of
$3 \le i \le n$, the fundamental weights of ![]() $\operatorname {Spin}(2(n-2))$. The double covering (3.17) induces an embedding of weight lattices
$\operatorname {Spin}(2(n-2))$. The double covering (3.17) induces an embedding of weight lattices
and identifies the corresponding ![]() ${{\mathbb {Q}}}$-vector spaces. Therefore, the weights
${{\mathbb {Q}}}$-vector spaces. Therefore, the weights ![]() $\omega '_i$ can be thought of as rational weights for
$\omega '_i$ can be thought of as rational weights for ![]() $\mathrm {L}$, that is, as rational weights of
$\mathrm {L}$, that is, as rational weights of ![]() $\operatorname {Spin}(2n)$. It is easy to see that they can be expressed in the basis of fundamental weights
$\operatorname {Spin}(2n)$. It is easy to see that they can be expressed in the basis of fundamental weights ![]() $\omega _i$ as follows:
$\omega _i$ as follows:
 \begin{equation} \omega'_1 = \omega_1,\quad \omega'_2 = \tfrac 12\omega_2,\quad \omega'_i =\begin{cases} \omega_i - \omega_2, & \text{if } 3 \le i \le n-2,\\ \omega_i - \tfrac 12\omega_2, & \text{if } i \in \{n-1,n\}. \end{cases} \end{equation}
\begin{equation} \omega'_1 = \omega_1,\quad \omega'_2 = \tfrac 12\omega_2,\quad \omega'_i =\begin{cases} \omega_i - \omega_2, & \text{if } 3 \le i \le n-2,\\ \omega_i - \tfrac 12\omega_2, & \text{if } i \in \{n-1,n\}. \end{cases} \end{equation}
By (3.18) the representation ![]() $\mathrm {V}_\mathrm {L}^{k\omega _1}$ pulls back to
$\mathrm {V}_\mathrm {L}^{k\omega _1}$ pulls back to ![]() $\mathrm {V}_{\operatorname {{\widetilde {GL}}}_2}^{k,0}$, while
$\mathrm {V}_{\operatorname {{\widetilde {GL}}}_2}^{k,0}$, while ![]() $\mathrm {V}_\mathrm {L}^{\lambda }$ with
$\mathrm {V}_\mathrm {L}^{\lambda }$ with ![]() $\lambda = \sum _{i=2}^{n} \lambda _i \omega _i$ pulls back to
$\lambda = \sum _{i=2}^{n} \lambda _i \omega _i$ pulls back to ![]() $\mathrm {V}_{\operatorname {{\widetilde {GL}}}(2)}^{c(\lambda ),c(\lambda )} \otimes \mathrm {V}_{\operatorname {Spin}(2(n-2))}^{\lambda '}$, where
$\mathrm {V}_{\operatorname {{\widetilde {GL}}}(2)}^{c(\lambda ),c(\lambda )} \otimes \mathrm {V}_{\operatorname {Spin}(2(n-2))}^{\lambda '}$, where ![]() $\lambda ' = \sum _{i=3}^{n} \lambda _i \omega '_i$ and
$\lambda ' = \sum _{i=3}^{n} \lambda _i \omega '_i$ and ![]() $c(\lambda ) = 2\sum _{i=2}^{n-2}\lambda _i + \lambda _{n-1} + \lambda _n$. Clearly,
$c(\lambda ) = 2\sum _{i=2}^{n-2}\lambda _i + \lambda _{n-1} + \lambda _n$. Clearly,
and the right-hand side corresponds to ![]() $\mathrm {V}_\mathrm {L}^{k\omega _1 + \lambda }$. This proves (3.15).
$\mathrm {V}_\mathrm {L}^{k\omega _1 + \lambda }$. This proves (3.15).
Similarly, ![]() $\mathrm {V}_\mathrm {L}^{\omega _3 - \omega _2}$ corresponds to
$\mathrm {V}_\mathrm {L}^{\omega _3 - \omega _2}$ corresponds to ![]() $\mathrm {V}_{\operatorname {Spin}(2(n-2))}^{\omega '_3}$ (which, according to our conventions, is the first fundamental representation of
$\mathrm {V}_{\operatorname {Spin}(2(n-2))}^{\omega '_3}$ (which, according to our conventions, is the first fundamental representation of ![]() $\operatorname {Spin}(2(n-2))$). By [Reference Vinberg and OnishchikVO95, Table 5] its middle exterior power is isomorphic to the direct sum of two irreducible representations with highest weights
$\operatorname {Spin}(2(n-2))$). By [Reference Vinberg and OnishchikVO95, Table 5] its middle exterior power is isomorphic to the direct sum of two irreducible representations with highest weights ![]() $2\omega '_n$ and
$2\omega '_n$ and ![]() $2\omega '_{n-1}$. By (3.18) these weights correspond to the weights
$2\omega '_{n-1}$. By (3.18) these weights correspond to the weights ![]() $2\omega _n - \omega _2$ and
$2\omega _n - \omega _2$ and ![]() $2\omega _{n-1} - \omega _2$, and the claim follows. This proves (3.16).
$2\omega _{n-1} - \omega _2$, and the claim follows. This proves (3.16).
Finally, we deduce from Borel–Bott–Weil a vanishing lemma, on which most semiorthogonality results for ![]() $\operatorname {OG}(2,2n)$ in the next section rely.
$\operatorname {OG}(2,2n)$ in the next section rely.
Lemma 3.10 Let ![]() $\lambda = (\lambda _1,\ldots ,\lambda _n)$ be a dominant weight of
$\lambda = (\lambda _1,\ldots ,\lambda _n)$ be a dominant weight of ![]() $\mathrm {L}$. Assume that one of the following two conditions holds:
$\mathrm {L}$. Assume that one of the following two conditions holds:
or
Then ![]() $\mathcal {U}^{\lambda }$ is acyclic.
$\mathcal {U}^{\lambda }$ is acyclic.
Proof. These are special cases of [Reference Kuznetsov and PolishchukKP16, Lemma 5.2]; we provide a proof for completeness.
In view of (3.13), if (3.19) holds, then all coordinates of ![]() $\lambda + \rho$ have absolute values less than
$\lambda + \rho$ have absolute values less than ![]() $n - 1$. Therefore, at least two of them have the same absolute values. Similarly, if (3.20) holds, then all but one of the coordinates of
$n - 1$. Therefore, at least two of them have the same absolute values. Similarly, if (3.20) holds, then all but one of the coordinates of ![]() $\lambda + \rho$ have absolute values less than
$\lambda + \rho$ have absolute values less than ![]() $n - 2$. Therefore, again at least two of them have the same absolute values. In both cases we see that
$n - 2$. Therefore, again at least two of them have the same absolute values. In both cases we see that ![]() $\lambda + \rho$ lies on one of the walls (3.11), and by the Borel–Bott–Weil theorem we conclude that
$\lambda + \rho$ lies on one of the walls (3.11), and by the Borel–Bott–Weil theorem we conclude that ![]() $\mathcal {U}^{\lambda }$ is acyclic.
$\mathcal {U}^{\lambda }$ is acyclic.
3.4 Exceptional collection
In this section we prove that (3.9) is an exceptional collection. Recall from (3.7) that ![]() $\mathcal {U}$ denotes the dual bundle of
$\mathcal {U}$ denotes the dual bundle of ![]() $\mathcal {U}^{\omega _1}$. Consequently,
$\mathcal {U}^{\omega _1}$. Consequently, ![]() $S^{k}\mathcal {U}^{\vee } \cong \mathcal {U}^{k\omega _1}$.
$S^{k}\mathcal {U}^{\vee } \cong \mathcal {U}^{k\omega _1}$.
First, we discuss the ‘tautological’ part of the collection. Recall that an exceptional collection ![]() $E_1,\ldots ,E_k$ of vector bundles is strong if
$E_1,\ldots ,E_k$ of vector bundles is strong if ![]() $\operatorname {Ext}^{>0}(E_i,E_j) = 0$ for all
$\operatorname {Ext}^{>0}(E_i,E_j) = 0$ for all ![]() $1 \le i,j \le k$.
$1 \le i,j \le k$.
Lemma 3.11 The collection of vector bundles ![]() $\mathcal {O},\mathcal {U}^{\vee },\ldots ,S^{n-2}\mathcal {U}^{\vee }$ is a strong exceptional collection. Moreover, for
$\mathcal {O},\mathcal {U}^{\vee },\ldots ,S^{n-2}\mathcal {U}^{\vee }$ is a strong exceptional collection. Moreover, for ![]() $0 \le k,\, l \le n-2$ and
$0 \le k,\, l \le n-2$ and ![]() $1 \le t \le 2n - 4$, we have
$1 \le t \le 2n - 4$, we have
 \[ \operatorname{Ext}^{{\bullet}}(S^{k}\mathcal{U}^{{\vee}}(t), S^{l}\mathcal{U}^{{\vee}}) =\begin{cases} \Bbbk[4 - 2n], & \text{if } k = l = n - 2,\ t = n - 2,\\ \Bbbk[3 - 2n], & \text{if } k = l = n - 2,\ t = n - 1,\\ 0, & \text{otherwise.} \end{cases} \]
\[ \operatorname{Ext}^{{\bullet}}(S^{k}\mathcal{U}^{{\vee}}(t), S^{l}\mathcal{U}^{{\vee}}) =\begin{cases} \Bbbk[4 - 2n], & \text{if } k = l = n - 2,\ t = n - 2,\\ \Bbbk[3 - 2n], & \text{if } k = l = n - 2,\ t = n - 1,\\ 0, & \text{otherwise.} \end{cases} \]Proof. We will show that ![]() $\operatorname {Ext}^{\bullet }(S^{k}\mathcal {U}^{\vee }(t),S^{l}\mathcal {U}^{\vee })$ is zero for
$\operatorname {Ext}^{\bullet }(S^{k}\mathcal {U}^{\vee }(t),S^{l}\mathcal {U}^{\vee })$ is zero for ![]() $0 \le k,l \le n-2$ and
$0 \le k,l \le n-2$ and ![]() $0 \le t \le 2n-4$, except for
$0 \le t \le 2n-4$, except for ![]() $t = 0$,
$t = 0$, ![]() $k \le l$ and
$k \le l$ and ![]() $t \in \{n - 2, n - 1\}$,
$t \in \{n - 2, n - 1\}$, ![]() $k = l = n-2$. By (3.6) and Serre duality we can assume
$k = l = n-2$. By (3.6) and Serre duality we can assume ![]() $0 \le t \le n - 2$.
$0 \le t \le n - 2$.
By Corollary 3.8 and (3.14) we have
 \begin{align*} (S^{k}\mathcal{U}^{{\vee}}(t))^{{\vee}} \otimes S^{l}\mathcal{U}^{{\vee}} &\cong S^{k}\mathcal{U}^{{\vee}}({-}k-t) \otimes S^{l}\mathcal{U}^{{\vee}} \\ &\cong \bigoplus_{j = 0}^{\min\{k,l\}} S^{k + l - 2j}\mathcal{U}^{{\vee}}(j - k - t) = \bigoplus_{j = 0}^{\min\{k,l\}} \mathcal{U}^{(l - j - t,j - k - t,0,\ldots,0)}. \end{align*}
\begin{align*} (S^{k}\mathcal{U}^{{\vee}}(t))^{{\vee}} \otimes S^{l}\mathcal{U}^{{\vee}} &\cong S^{k}\mathcal{U}^{{\vee}}({-}k-t) \otimes S^{l}\mathcal{U}^{{\vee}} \\ &\cong \bigoplus_{j = 0}^{\min\{k,l\}} S^{k + l - 2j}\mathcal{U}^{{\vee}}(j - k - t) = \bigoplus_{j = 0}^{\min\{k,l\}} \mathcal{U}^{(l - j - t,j - k - t,0,\ldots,0)}. \end{align*}
So, it is enough to compute the cohomology of bundles ![]() $\mathcal {U}^{\lambda }$ with
$\mathcal {U}^{\lambda }$ with ![]() $\lambda = (l - j - t,j - k - t,0,\ldots ,0)$, so that
$\lambda = (l - j - t,j - k - t,0,\ldots ,0)$, so that
It is convenient to distinguish three cases.
Case 1. If ![]() $4 - 2n < \lambda _2 < 0$, then
$4 - 2n < \lambda _2 < 0$, then ![]() $|\lambda _i + n - i| < n - 2$ for all
$|\lambda _i + n - i| < n - 2$ for all ![]() $i \ge 2$. Hence, (3.20) holds and
$i \ge 2$. Hence, (3.20) holds and ![]() $\mathcal {U}^{\lambda }$ is acyclic by Lemma 3.10.
$\mathcal {U}^{\lambda }$ is acyclic by Lemma 3.10.
Case 2. If ![]() $\lambda _2 = 0$, then we necessarily have
$\lambda _2 = 0$, then we necessarily have ![]() $t = 0$ and
$t = 0$ and ![]() $j = k$. Further, since
$j = k$. Further, since ![]() $j \le l$, we obtain
$j \le l$, we obtain ![]() $k \le l$. In particular, the weight
$k \le l$. In particular, the weight ![]() $\lambda$ is dominant, hence
$\lambda$ is dominant, hence ![]() $H^{>0}(\operatorname {OG}(2,2n),\mathcal {U}^{\lambda }) = 0$. Moreover, if
$H^{>0}(\operatorname {OG}(2,2n),\mathcal {U}^{\lambda }) = 0$. Moreover, if ![]() $k = l$, then
$k = l$, then ![]() $\lambda = 0$ and in this case the cohomology of
$\lambda = 0$ and in this case the cohomology of ![]() $\mathcal {U}^{\lambda }$ is isomorphic to
$\mathcal {U}^{\lambda }$ is isomorphic to ![]() $\Bbbk [0]$.
$\Bbbk [0]$.
A combination of cases 1 and 2 proves that ![]() $\mathcal {O}, \mathcal {U}^{\vee },\ldots , S^{n-2}\mathcal {U}^{\vee }$ is a strong exceptional collection.
$\mathcal {O}, \mathcal {U}^{\vee },\ldots , S^{n-2}\mathcal {U}^{\vee }$ is a strong exceptional collection.
Case 3. If ![]() $\lambda _2 = 4 - 2n$, then we necessarily have
$\lambda _2 = 4 - 2n$, then we necessarily have ![]() $k = t = n - 2$ and
$k = t = n - 2$ and ![]() $j = 0$. In this case we have inequalities
$j = 0$. In this case we have inequalities ![]() $2 - n \le \lambda _1 \le 0$.
$2 - n \le \lambda _1 \le 0$.
If ![]() $\lambda _1 < 0$, then
$\lambda _1 < 0$, then ![]() $|\lambda _i + n - i| < n - 1$ for all
$|\lambda _i + n - i| < n - 1$ for all ![]() $i$. Hence (3.19) holds and
$i$. Hence (3.19) holds and ![]() $\mathcal {U}^{\lambda }$ is acyclic by Lemma 3.10.
$\mathcal {U}^{\lambda }$ is acyclic by Lemma 3.10.
If ![]() $\lambda _1 = 0$, then
$\lambda _1 = 0$, then ![]() $l = n - 2$, and we have
$l = n - 2$, and we have ![]() $\mathcal {U}^{\lambda } = \mathcal {U}^{(0,4-2n,0,\ldots ,0)}$. In this case the Borel–Bott–Weil theorem implies that the cohomology of
$\mathcal {U}^{\lambda } = \mathcal {U}^{(0,4-2n,0,\ldots ,0)}$. In this case the Borel–Bott–Weil theorem implies that the cohomology of ![]() $\mathcal {U}^{\lambda }$ is isomorphic to
$\mathcal {U}^{\lambda }$ is isomorphic to ![]() $\Bbbk [4 - 2n]$. Indeed, we have
$\Bbbk [4 - 2n]$. Indeed, we have ![]() $\lambda + \rho = (n-1,2-n,n-3,\ldots ,0) = w\rho$, where
$\lambda + \rho = (n-1,2-n,n-3,\ldots ,0) = w\rho$, where
and ![]() $\mathrm {s}_i$ are the simple reflections. This completes the proof of the lemma.
$\mathrm {s}_i$ are the simple reflections. This completes the proof of the lemma.
Next, we discuss the ‘spinor’ part of the collection.
Lemma 3.12 The collection of sheaves ![]() $\mathcal {U}^{\omega _{n-1}}, \mathcal {U}^{\omega _{n}}, \mathcal {U}^{2\omega _{n-1}}, \mathcal {U}^{2\omega _{n}}, \{ \mathcal {U}^{\omega _{n-1}}(t), \mathcal {U}^{\omega _{n}}(t) \}_{1 \le t \le 2n - 4}$ is exceptional.
$\mathcal {U}^{\omega _{n-1}}, \mathcal {U}^{\omega _{n}}, \mathcal {U}^{2\omega _{n-1}}, \mathcal {U}^{2\omega _{n}}, \{ \mathcal {U}^{\omega _{n-1}}(t), \mathcal {U}^{\omega _{n}}(t) \}_{1 \le t \le 2n - 4}$ is exceptional.
Proof. We will compute ![]() $\operatorname {Ext}^{\bullet }(\mathcal {U}^{a\omega _i}(t),\mathcal {U}^{b\omega _j})$ where
$\operatorname {Ext}^{\bullet }(\mathcal {U}^{a\omega _i}(t),\mathcal {U}^{b\omega _j})$ where ![]() $i,j \in \{n - 1,n\}$, and
$i,j \in \{n - 1,n\}$, and
– either
 $a,b \in \{1,2\}$ and
$a,b \in \{1,2\}$ and  $(a,b) \ne (2,2)$, and
$(a,b) \ne (2,2)$, and  $1 \le t \le 2n - 4$,
$1 \le t \le 2n - 4$,– or
 $a,b \in \{1,2\}$ and
$a,b \in \{1,2\}$ and  $(a,b) \ne (1,2)$, and
$(a,b) \ne (1,2)$, and  $t = 0$.
$t = 0$.
By (3.6) and Serre duality we can assume ![]() $0 \le t \le n - 2$.
$0 \le t \le n - 2$.
We take ![]() $\lambda = a\omega _{i} + t\omega _2 = (t+ a/2,t+ a/2, a/2,\ldots , a/2,\pm a/2)$ and
$\lambda = a\omega _{i} + t\omega _2 = (t+ a/2,t+ a/2, a/2,\ldots , a/2,\pm a/2)$ and ![]() $\mu = b\omega _{j} = ( b/2, b/2, b/2, \ldots\,$,
$\mu = b\omega _{j} = ( b/2, b/2, b/2, \ldots\,$, ![]() $ b/2,\pm b/2)$; the signs of the last coordinate depend on whether
$ b/2,\pm b/2)$; the signs of the last coordinate depend on whether ![]() $i$ and
$i$ and ![]() $j$ are
$j$ are ![]() $n-1$ or
$n-1$ or ![]() $n$. Since the
$n$. Since the ![]() $\mathrm {W}_\mathrm {L}$-orbit of
$\mathrm {W}_\mathrm {L}$-orbit of ![]() $\lambda$ consists of points
$\lambda$ consists of points ![]() $(t + a/2,t + a/2,\pm a/2,\ldots ,\pm a/2,\pm a/2)$ (with the parity of the number of negative signs depending on
$(t + a/2,t + a/2,\pm a/2,\ldots ,\pm a/2,\pm a/2)$ (with the parity of the number of negative signs depending on ![]() $i$), by Lemma 3.6 we have
$i$), by Lemma 3.6 we have
where ![]() $\nu$ runs over the integral or half-integral points satisfying
$\nu$ runs over the integral or half-integral points satisfying
(In fact we could further restrict the combinations of signs that appear in ![]() $\nu$, but since we are interested in an upper bound on direct summands of
$\nu$, but since we are interested in an upper bound on direct summands of ![]() $(\mathcal {U}^{\lambda })^{\vee } \otimes \mathcal {U}^{\mu }$, we can neglect this.) It is convenient to distinguish three cases.
$(\mathcal {U}^{\lambda })^{\vee } \otimes \mathcal {U}^{\mu }$, we can neglect this.) It is convenient to distinguish three cases.
Case 1. If ![]() $1 \le t \le n-2$ and
$1 \le t \le n-2$ and ![]() $(a,b) \ne (2,2)$, then
$(a,b) \ne (2,2)$, then
For any such point we have ![]() $|\nu _i + n - i| < n - 1$ for all
$|\nu _i + n - i| < n - 1$ for all ![]() $i$, hence (3.19) holds for
$i$, hence (3.19) holds for ![]() $\nu$ and, therefore, all summands in (3.21) are acyclic by Lemma 3.10.
$\nu$ and, therefore, all summands in (3.21) are acyclic by Lemma 3.10.
Case 2. If ![]() $t = 0$ and
$t = 0$ and ![]() $a > b$, then
$a > b$, then
For any such point we still have ![]() $|\nu _i + n - i| < n - 1$ for all
$|\nu _i + n - i| < n - 1$ for all ![]() $i$, hence again all summands in (3.21) are acyclic.
$i$, hence again all summands in (3.21) are acyclic.
Case 3. If ![]() $t = 0$ and
$t = 0$ and ![]() $a = b$, then
$a = b$, then
It is easy to see that the only non-acyclic bundle among ![]() $\mathcal {U}^{\nu }$ is the trivial bundle. Indeed, if
$\mathcal {U}^{\nu }$ is the trivial bundle. Indeed, if ![]() $\tilde \nu = \nu + \rho$ then
$\tilde \nu = \nu + \rho$ then ![]() $(\tilde \nu _1, \tilde \nu _2) = (n-1,n-2)$ and
$(\tilde \nu _1, \tilde \nu _2) = (n-1,n-2)$ and ![]() $n - 1 \ge \tilde \nu _3 \ge \cdots \ge \tilde \nu _{n-1} \ge 1$, and the only possibility to satisfy these restriction and avoid the walls (3.11) is to have
$n - 1 \ge \tilde \nu _3 \ge \cdots \ge \tilde \nu _{n-1} \ge 1$, and the only possibility to satisfy these restriction and avoid the walls (3.11) is to have ![]() $\tilde \nu _i = n - i$ for
$\tilde \nu _i = n - i$ for ![]() $1 \le i \le n - 1$. Finally,
$1 \le i \le n - 1$. Finally, ![]() $0 \le \tilde \nu _n \le 2$, and since
$0 \le \tilde \nu _n \le 2$, and since ![]() $n \ge 3$, it must be zero to avoid the walls. By Lemma 3.6 the trivial bundle is a summand of
$n \ge 3$, it must be zero to avoid the walls. By Lemma 3.6 the trivial bundle is a summand of ![]() $(\mathcal {U}^{\lambda })^{\vee } \otimes \mathcal {U}^{\mu }$ only when
$(\mathcal {U}^{\lambda })^{\vee } \otimes \mathcal {U}^{\mu }$ only when ![]() $\lambda = \mu$ and then its multiplicity is equal to 1. Hence, in this case we have
$\lambda = \mu$ and then its multiplicity is equal to 1. Hence, in this case we have ![]() $\operatorname {Ext}^{\bullet }(\mathcal {U}^{\lambda },\mathcal {U}^{\mu }) = \Bbbk [0]$. This completes the proof of the lemma.
$\operatorname {Ext}^{\bullet }(\mathcal {U}^{\lambda },\mathcal {U}^{\mu }) = \Bbbk [0]$. This completes the proof of the lemma.
In the next two lemmas we show that the ‘tautological’ part of the collection can be merged with the ‘spinor’ part.
Lemma 3.13 We have ![]() $\operatorname {Ext}^{\bullet }(\mathcal {U}^{\omega _j}(t),S^{k}\mathcal {U}^{\vee }) = 0$ for all
$\operatorname {Ext}^{\bullet }(\mathcal {U}^{\omega _j}(t),S^{k}\mathcal {U}^{\vee }) = 0$ for all ![]() $0 \le k \le n - 2$, all
$0 \le k \le n - 2$, all ![]() $j \in \{n - 1,n\}$, and all
$j \in \{n - 1,n\}$, and all ![]() $0 \le t \le 2n - 4$.
$0 \le t \le 2n - 4$.
Proof. By Corollary 3.8 and (3.15) we have
where ![]() $j' = j$ if
$j' = j$ if ![]() $n$ is even and
$n$ is even and ![]() $j' = 2n - 1 - j$ if
$j' = 2n - 1 - j$ if ![]() $n$ is odd. So, it is enough to compute the cohomology of bundles
$n$ is odd. So, it is enough to compute the cohomology of bundles ![]() $\mathcal {U}^{\lambda }$ with
$\mathcal {U}^{\lambda }$ with
If ![]() $0 \le t \le 2n - 5$, then
$0 \le t \le 2n - 5$, then ![]() $|\lambda _i + n - i| < n - 2$ for
$|\lambda _i + n - i| < n - 2$ for ![]() $i \ge 2$. Hence (3.20) holds and the bundle
$i \ge 2$. Hence (3.20) holds and the bundle ![]() $\mathcal {U}^{\lambda }$ is acyclic by Lemma 3.10. Similarly, if
$\mathcal {U}^{\lambda }$ is acyclic by Lemma 3.10. Similarly, if ![]() $t = 2n - 4$, then we have
$t = 2n - 4$, then we have ![]() $|\lambda _i + n - i| < n - 1$ for all
$|\lambda _i + n - i| < n - 1$ for all ![]() $i$. Hence condition (3.19) holds and the bundle
$i$. Hence condition (3.19) holds and the bundle ![]() $\mathcal {U}^{\lambda }$ is acyclic by Lemma 3.10.
$\mathcal {U}^{\lambda }$ is acyclic by Lemma 3.10.
Lemma 3.14 If ![]() $0 \le k \le n - 2$,
$0 \le k \le n - 2$, ![]() $j \in \{n - 1,n\}$, and
$j \in \{n - 1,n\}$, and ![]() $1 \le t \le 2n - 2$, then
$1 \le t \le 2n - 2$, then
 \[ \operatorname{Ext}^{{\bullet}}(S^{k}\mathcal{U}^{{\vee}}(t),\mathcal{U}^{2\omega_j}) = \begin{cases} \Bbbk[5 - 3n], & \text{if } k = n - 2 \text{ and } t = n,\\ \Bbbk[2 - n], & \text{if } k = n - 2 \text{ and } t = 1,\\ 0, & \text{otherwise.} \end{cases} \]
\[ \operatorname{Ext}^{{\bullet}}(S^{k}\mathcal{U}^{{\vee}}(t),\mathcal{U}^{2\omega_j}) = \begin{cases} \Bbbk[5 - 3n], & \text{if } k = n - 2 \text{ and } t = n,\\ \Bbbk[2 - n], & \text{if } k = n - 2 \text{ and } t = 1,\\ 0, & \text{otherwise.} \end{cases} \] In fact, using isomorphisms of Corollary 3.8 and Serre duality it is possible to identify one non-trivial ![]() $\operatorname {Ext}$-space above with the dual of the other.
$\operatorname {Ext}$-space above with the dual of the other.
Proof. As before, we have
So, it is enough to compute the cohomology of the bundle ![]() $\mathcal {U}^{\lambda }$ with
$\mathcal {U}^{\lambda }$ with
For this we directly apply the Borel–Bott–Weil theorem. We have
It is convenient to distinguish several cases.
Case 1. If ![]() $2 \le t \le 2n - 2$ and
$2 \le t \le 2n - 2$ and ![]() $t \ne n$, then the absolute value of the first coordinate of
$t \ne n$, then the absolute value of the first coordinate of ![]() $\lambda + \rho$ is equal to the absolute value of one of the last
$\lambda + \rho$ is equal to the absolute value of one of the last ![]() $n - 2$ coordinates. Hence, the bundle
$n - 2$ coordinates. Hence, the bundle ![]() $\mathcal {U}^{\lambda }$ is acyclic.
$\mathcal {U}^{\lambda }$ is acyclic.
Case 2. If ![]() $t = n$ and
$t = n$ and ![]() $0 \le k \le n - 3$, then
$0 \le k \le n - 3$, then ![]() $n - 1 - k - t = - k - 1$, and the absolute value of the second coordinate of
$n - 1 - k - t = - k - 1$, and the absolute value of the second coordinate of ![]() $\lambda + \rho$ is equal to the absolute value of one of the last
$\lambda + \rho$ is equal to the absolute value of one of the last ![]() $n - 2$ coordinates. Hence,
$n - 2$ coordinates. Hence, ![]() $\mathcal {U}^{\lambda }$ is acyclic.
$\mathcal {U}^{\lambda }$ is acyclic.
Case 3. If ![]() $t = n$ and
$t = n$ and ![]() $k = n - 2$, then
$k = n - 2$, then ![]() $\lambda + \rho = (0, 1 - n, n - 2,\ldots , 2, \pm 1) = w\rho$, where
$\lambda + \rho = (0, 1 - n, n - 2,\ldots , 2, \pm 1) = w\rho$, where
and ![]() $\mathrm {s}_i$ are the simple reflections. By the Borel–Bott–Weil theorem the cohomology of the bundle
$\mathrm {s}_i$ are the simple reflections. By the Borel–Bott–Weil theorem the cohomology of the bundle ![]() $\mathcal {U}^{\lambda }$ equals
$\mathcal {U}^{\lambda }$ equals ![]() $\Bbbk [5 - 3n]$.
$\Bbbk [5 - 3n]$.
Case 4. If ![]() $t = 1$ and
$t = 1$ and ![]() $0 \le k \le n - 3$, then
$0 \le k \le n - 3$, then ![]() $n - 1 - k - t = n - 2 - k$, and the absolute value of the second coordinate of
$n - 1 - k - t = n - 2 - k$, and the absolute value of the second coordinate of ![]() $\lambda + \rho$ is equal to the absolute value of one of the last
$\lambda + \rho$ is equal to the absolute value of one of the last ![]() $n - 2$ coordinates. Hence,
$n - 2$ coordinates. Hence, ![]() $\mathcal {U}^{\lambda }$ is acyclic.
$\mathcal {U}^{\lambda }$ is acyclic.
Case 5. If ![]() $t = 1$ and
$t = 1$ and ![]() $k = n - 2$, then
$k = n - 2$, then ![]() $\lambda + \rho = (n - 1, 0, n - 2,\ldots , 2, \pm 1) = w\rho$, where
$\lambda + \rho = (n - 1, 0, n - 2,\ldots , 2, \pm 1) = w\rho$, where
and ![]() $\mathrm {s}_i$ are the simple reflections. By the Borel–Bott–Weil theorem the cohomology of the bundle
$\mathrm {s}_i$ are the simple reflections. By the Borel–Bott–Weil theorem the cohomology of the bundle ![]() $\mathcal {U}^{\lambda }$ equals
$\mathcal {U}^{\lambda }$ equals ![]() $\Bbbk [2 - n]$. This completes the proof of the lemma.
$\Bbbk [2 - n]$. This completes the proof of the lemma.
Now we deduce the following result.
Proposition 3.15 The collection (3.9) is exceptional.
3.5 Some useful complexes
In this section we construct some exact sequences and complexes that will be used to check that the collection (3.9) is full.
Let ![]() $V$ be a vector space of dimension
$V$ be a vector space of dimension ![]() $2n \ge 8$ endowed with a non-degenerate symmetric bilinear form and let
$2n \ge 8$ endowed with a non-degenerate symmetric bilinear form and let ![]() $\operatorname {OG}(2,V) = \operatorname {OG}(2,2n)$ be the corresponding even orthogonal Grassmannian. We denote by
$\operatorname {OG}(2,V) = \operatorname {OG}(2,2n)$ be the corresponding even orthogonal Grassmannian. We denote by ![]() $\mathcal {V} = V \otimes \mathcal {O}$ the trivial vector bundle with fiber
$\mathcal {V} = V \otimes \mathcal {O}$ the trivial vector bundle with fiber ![]() $V$. Note that
$V$. Note that ![]() $V$ and
$V$ and ![]() $\mathcal {V}$ are canonically self-dual (via the chosen symmetric bilinear form on
$\mathcal {V}$ are canonically self-dual (via the chosen symmetric bilinear form on ![]() $V$). We have the tautological short exact sequence on
$V$). We have the tautological short exact sequence on ![]() $\operatorname {OG}(2,2n)$,
$\operatorname {OG}(2,2n)$,
and its dual,
Taking exterior powers of the above sequences, we obtain the long exact sequences
 \begin{align} 0 \to S^{m}\mathcal{U} \to V \otimes S^{m-1} \mathcal{U} \to \Lambda^{2} V \otimes S^{m-2} \mathcal{U} \to \cdots \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \\ \dots \to \Lambda^{m-1} V \otimes \mathcal{U} \to \Lambda^{m} V \otimes \mathcal{O} \to \Lambda^{m}(\mathcal{V}/\mathcal{U}) \to 0 \end{align}
\begin{align} 0 \to S^{m}\mathcal{U} \to V \otimes S^{m-1} \mathcal{U} \to \Lambda^{2} V \otimes S^{m-2} \mathcal{U} \to \cdots \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \\ \dots \to \Lambda^{m-1} V \otimes \mathcal{U} \to \Lambda^{m} V \otimes \mathcal{O} \to \Lambda^{m}(\mathcal{V}/\mathcal{U}) \to 0 \end{align}and
Recall notation (3.7) for spinor bundles. We denote their spaces of global sections by
(the half-spinor representations of ![]() $\operatorname {Spin}(2n)$). We set
$\operatorname {Spin}(2n)$). We set
 \begin{equation} W_i = \bigoplus_{s = 0}^{\lfloor i/2 \rfloor} \Lambda^{i - 2s} V. \end{equation}
\begin{equation} W_i = \bigoplus_{s = 0}^{\lfloor i/2 \rfloor} \Lambda^{i - 2s} V. \end{equation}We will combine (3.22) and (3.23) to prove the following proposition.
Proposition 3.16 On ![]() $\operatorname {OG}(2,2n)$ there exists an exact sequence
$\operatorname {OG}(2,2n)$ there exists an exact sequence
 \begin{align} 0 \to S^{n-2} \mathcal{U} \to W_1 \otimes S^{n-3} \mathcal{U} \to W_2 \otimes S^{n-4} \mathcal{U} \to \cdots \quad\quad\quad\quad\quad\quad \quad\quad\quad\quad\quad\quad \quad\quad\quad\quad\quad\quad \quad \\ \dots \to W_{n-2} \otimes \mathcal{O} \to \mathbf{S}_+\,{\otimes}\, \mathcal{S}_+\,{\oplus}\, \mathbf{S}_-\,{\otimes}\, \mathcal{S}_- \to W_{n-2}\, \otimes \, \mathcal{O}(1) \to \cdots \quad\quad\quad\quad \\ \dots\to W_2 \otimes S^{n-4} \mathcal{U}^{{\vee}}(1) \to W_1 \otimes S^{n-3} \mathcal{U}^{{\vee}}(1) \to S^{n-2} \mathcal{U}^{{\vee}}(1) \to 0. \end{align}
\begin{align} 0 \to S^{n-2} \mathcal{U} \to W_1 \otimes S^{n-3} \mathcal{U} \to W_2 \otimes S^{n-4} \mathcal{U} \to \cdots \quad\quad\quad\quad\quad\quad \quad\quad\quad\quad\quad\quad \quad\quad\quad\quad\quad\quad \quad \\ \dots \to W_{n-2} \otimes \mathcal{O} \to \mathbf{S}_+\,{\otimes}\, \mathcal{S}_+\,{\oplus}\, \mathbf{S}_-\,{\otimes}\, \mathcal{S}_- \to W_{n-2}\, \otimes \, \mathcal{O}(1) \to \cdots \quad\quad\quad\quad \\ \dots\to W_2 \otimes S^{n-4} \mathcal{U}^{{\vee}}(1) \to W_1 \otimes S^{n-3} \mathcal{U}^{{\vee}}(1) \to S^{n-2} \mathcal{U}^{{\vee}}(1) \to 0. \end{align}Proof. If ![]() $n$ is even, we apply [Reference KuznetsovKuz08, Proposition 6.7] and conclude that there is a filtration on the bundle
$n$ is even, we apply [Reference KuznetsovKuz08, Proposition 6.7] and conclude that there is a filtration on the bundle ![]() $\mathbf {S}_+ \otimes \mathcal {S}_+^{\vee } \oplus \mathbf {S}_- \otimes \mathcal {S}_-^{\vee }$ with factors of the form
$\mathbf {S}_+ \otimes \mathcal {S}_+^{\vee } \oplus \mathbf {S}_- \otimes \mathcal {S}_-^{\vee }$ with factors of the form ![]() $\Lambda ^{2s}\mathcal {U}^{\perp }$, where
$\Lambda ^{2s}\mathcal {U}^{\perp }$, where ![]() $0 \le s \le n - 1$. Tensoring by
$0 \le s \le n - 1$. Tensoring by ![]() $\mathcal {O}(1)$ and taking into account the isomorphisms
$\mathcal {O}(1)$ and taking into account the isomorphisms
(Corollary 3.8), we obtain a filtration on ![]() $\mathbf {S}_+ \otimes \mathcal {S}_+ \oplus \mathbf {S}_- \otimes \mathcal {S}_-$ with factors of the form
$\mathbf {S}_+ \otimes \mathcal {S}_+ \oplus \mathbf {S}_- \otimes \mathcal {S}_-$ with factors of the form ![]() $\Lambda ^{2s}\mathcal {U}^{\perp }(1)$, where
$\Lambda ^{2s}\mathcal {U}^{\perp }(1)$, where ![]() $0 \le s \le n - 1$.
$0 \le s \le n - 1$.
Similarly, if ![]() $n$ is odd, the argument of [Reference KuznetsovKuz08, Proposition 6.7] proves that there is a filtration on
$n$ is odd, the argument of [Reference KuznetsovKuz08, Proposition 6.7] proves that there is a filtration on ![]() $\mathbf {S}_+ \otimes \mathcal {S}_-^{\vee } \oplus \mathbf {S}_- \otimes \mathcal {S}_+^{\vee }$ with factors of the form
$\mathbf {S}_+ \otimes \mathcal {S}_-^{\vee } \oplus \mathbf {S}_- \otimes \mathcal {S}_+^{\vee }$ with factors of the form ![]() $\Lambda ^{2s+1}\mathcal {U}^{\perp }$, where
$\Lambda ^{2s+1}\mathcal {U}^{\perp }$, where ![]() $0 \le s \le n - 2$. Tensoring by
$0 \le s \le n - 2$. Tensoring by ![]() $\mathcal {O}(1)$ and taking into account isomorphisms
$\mathcal {O}(1)$ and taking into account isomorphisms
we finally obtain a filtration on ![]() $\mathbf {S}_+ \otimes \mathcal {S}_+ \oplus \mathbf {S}_- \otimes \mathcal {S}_-$ with factors of the form
$\mathbf {S}_+ \otimes \mathcal {S}_+ \oplus \mathbf {S}_- \otimes \mathcal {S}_-$ with factors of the form ![]() $\Lambda ^{2s+1}\mathcal {U}^{\perp }(1)$, where we have
$\Lambda ^{2s+1}\mathcal {U}^{\perp }(1)$, where we have ![]() $0 \le s \le n - 2$.
$0 \le s \le n - 2$.
Thus, in both cases we have a filtration on ![]() $\mathbf {S}_+ \otimes \mathcal {S}_+ \oplus \mathbf {S}_- \otimes \mathcal {S}_-$ with factors
$\mathbf {S}_+ \otimes \mathcal {S}_+ \oplus \mathbf {S}_- \otimes \mathcal {S}_-$ with factors
where ![]() $r = 0$ if
$r = 0$ if ![]() $n$ is even and
$n$ is even and ![]() $r = 1$ if
$r = 1$ if ![]() $n$ is odd. Note that the total number of factors
$n$ is odd. Note that the total number of factors ![]() $n - r$ is even in both cases. This means that there is an exact sequence of vector bundles
$n - r$ is even in both cases. This means that there is an exact sequence of vector bundles
where ![]() $F_-$ has a filtration with factors
$F_-$ has a filtration with factors ![]() $\Lambda ^{2n - 2 - r}\mathcal {U}^{\perp }(1), \Lambda ^{2n - 4 - r}\mathcal {U}^{\perp }(1),\ldots , \Lambda ^{n}\mathcal {U}^{\perp }(1)$ and
$\Lambda ^{2n - 2 - r}\mathcal {U}^{\perp }(1), \Lambda ^{2n - 4 - r}\mathcal {U}^{\perp }(1),\ldots , \Lambda ^{n}\mathcal {U}^{\perp }(1)$ and ![]() $F_+$ has a filtration with factors
$F_+$ has a filtration with factors ![]() $\Lambda ^{n - 2}\mathcal {U}^{\perp }(1),\ldots , \Lambda ^{2 + r}\mathcal {U}^{\perp }(1), \Lambda ^{r}\mathcal {U}^{\perp }(1)$. So, it is enough to show that
$\Lambda ^{n - 2}\mathcal {U}^{\perp }(1),\ldots , \Lambda ^{2 + r}\mathcal {U}^{\perp }(1), \Lambda ^{r}\mathcal {U}^{\perp }(1)$. So, it is enough to show that ![]() $F_-$ has a left resolution given by the first half of (3.25), and that
$F_-$ has a left resolution given by the first half of (3.25), and that ![]() $F_+$ has a right resolution given by the second half of (3.25).
$F_+$ has a right resolution given by the second half of (3.25).
Indeed, each factor of the filtration of ![]() $F_-$ can be rewritten as
$F_-$ can be rewritten as
where ![]() $0 \le k \le (n - 2 - r)/2$, hence has the resolution (3.22) with
$0 \le k \le (n - 2 - r)/2$, hence has the resolution (3.22) with ![]() $m = n - 2 - 2k$. Since by Lemma 3.11 the exceptional collection
$m = n - 2 - 2k$. Since by Lemma 3.11 the exceptional collection ![]() $\{ S^{i}\mathcal {U} \}_{i = 0}^{n-2}$ is strong, the extensions of the filtration factors
$\{ S^{i}\mathcal {U} \}_{i = 0}^{n-2}$ is strong, the extensions of the filtration factors ![]() $\Lambda ^{n + 2k}\mathcal {U}^{\perp }(1)$ in
$\Lambda ^{n + 2k}\mathcal {U}^{\perp }(1)$ in ![]() $F_-$ can be realized by a bicomplex with rows given by (3.22) with
$F_-$ can be realized by a bicomplex with rows given by (3.22) with ![]() $m = n - 2 - 2k$ shifted by
$m = n - 2 - 2k$ shifted by ![]() $-k$. The totalization of this bicomplex can be written as
$-k$. The totalization of this bicomplex can be written as
and thus provides a left resolution for ![]() $F_-$.
$F_-$.
Similarly, each factor ![]() $\Lambda ^{n-2-2k}\mathcal {U}^{\perp }(1)$ of the filtration of
$\Lambda ^{n-2-2k}\mathcal {U}^{\perp }(1)$ of the filtration of ![]() $F_+$ has resolution (3.23) twisted by
$F_+$ has resolution (3.23) twisted by ![]() $\mathcal {O}(1)$ (where
$\mathcal {O}(1)$ (where ![]() $m = n - 2 - 2k$), and the above argument shows that
$m = n - 2 - 2k$), and the above argument shows that ![]() $F_+$ has the right resolution
$F_+$ has the right resolution
This completes the proof of the proposition.
Note that the composition of morphisms ![]() $\mathcal {U} \to \mathcal {V} \to \mathcal {U}^{\vee }$ is zero, hence
$\mathcal {U} \to \mathcal {V} \to \mathcal {U}^{\vee }$ is zero, hence ![]() $\mathcal {U} \subset \mathcal {U}^{\perp }$. Moreover,
$\mathcal {U} \subset \mathcal {U}^{\perp }$. Moreover,
We will need the following lemma.
Lemma 3.17 For any ![]() $m \le 2n - 4$ on
$m \le 2n - 4$ on ![]() $\operatorname {OG}(2,2n)$ there exists a double complex
$\operatorname {OG}(2,2n)$ there exists a double complex

whose total complex has only one non-trivial cohomology sheaf in the middle term isomorphic to ![]() $\Lambda ^{m} (\mathcal {U}^{\perp }/\mathcal {U})$.
$\Lambda ^{m} (\mathcal {U}^{\perp }/\mathcal {U})$.
Proof. The bicomplex is just the ![]() $m$th exterior power of the complex
$m$th exterior power of the complex
which is quasi-isomorphic to ![]() $\mathcal {U}^{\perp }/\mathcal {U}$, hence the claim (cf. the argument of [Reference KuznetsovKuz08, Lemma 7.3]).
$\mathcal {U}^{\perp }/\mathcal {U}$, hence the claim (cf. the argument of [Reference KuznetsovKuz08, Lemma 7.3]).
Finally, we will need the following lemma from [Reference KuznetsovKuz08].
Lemma 3.18 [Kuz08, Proposition 6.3] There exists a complex
whose only non-trivial cohomology group is in the middle term and is isomorphic to ![]() $\mathcal {S}_+ \otimes \mathcal {U}^{\vee }$.
$\mathcal {S}_+ \otimes \mathcal {U}^{\vee }$.
3.6 Fullness
The proof of the fullness of the collection (3.9) goes via restriction to odd orthogonal Grassmannians ![]() $\operatorname {OG}(2,2n-1)$, and is similar to the proofs of fullness given in [Reference KuznetsovKuz08]. For technical reasons it is more convenient to work with the collection
$\operatorname {OG}(2,2n-1)$, and is similar to the proofs of fullness given in [Reference KuznetsovKuz08]. For technical reasons it is more convenient to work with the collection
By Serre duality, exceptionality of (3.9) implies exceptionality of (3.27). Conversely, fullness of (3.27) implies fullness of (3.9).
We will deduce fullness of (3.27) from the following key lemma.
Lemma 3.19 Let ![]() $\mathbf {E}$ be the set of bundles appearing in (3.27) and let
$\mathbf {E}$ be the set of bundles appearing in (3.27) and let ![]() $\mathbf {E}'$ be its subset defined as
$\mathbf {E}'$ be its subset defined as
Then for any object ![]() $E \in \mathbf {E}\,'$ we have
$E \in \mathbf {E}\,'$ we have
Proof. The inclusion (3.29) follows immediately from comparison of (3.28), (3.8) and (3.27). Thus, we concentrate here on the inclusion (3.30).
We split objects ![]() $E \in \mathbf {E}'$ into two classes:
$E \in \mathbf {E}'$ into two classes:
–
 $\mathcal {S}_+(t)$ with
$\mathcal {S}_+(t)$ with  $t \in [2-n,n-3]$ (spinor bundles), and
$t \in [2-n,n-3]$ (spinor bundles), and–
 $S^{k} \mathcal {U}^{\vee }(t)$ with
$S^{k} \mathcal {U}^{\vee }(t)$ with  $k \in [0,n-3]$ and
$k \in [0,n-3]$ and  $t \in [2-n,n-3]$ (tautological bundles),
$t \in [2-n,n-3]$ (tautological bundles),
and treat these separately.
The class of spinor bundles is easy: from Lemma 3.18 we conclude
and the inclusion (3.30) for ![]() $E = \mathcal {S}_+(i)$ follows.
$E = \mathcal {S}_+(i)$ follows.
The class of tautological bundles is a bit more tedious. First, note that by (3.14) we have
Thus, the inclusion (3.30) would follow from the inclusions
So, by proving these inclusions, we will prove the lemma.
For ![]() $j \le n - 3$ and for
$j \le n - 3$ and for ![]() $j = n - 2$,
$j = n - 2$, ![]() $1 \le t \le n - 2$, the inclusions (3.31) follow immediately from (3.27). Furthermore, using (3.25) twisted by
$1 \le t \le n - 2$, the inclusions (3.31) follow immediately from (3.27). Furthermore, using (3.25) twisted by ![]() $\mathcal {O}(n - 2 + t)$ and isomorphisms
$\mathcal {O}(n - 2 + t)$ and isomorphisms
we deduce (3.31) for ![]() $j = n - 2$ and
$j = n - 2$ and ![]() $2 - n \le t \le -1$.
$2 - n \le t \le -1$.
So, it only remains to show that
For this we consider the double complex of Lemma 3.17 with ![]() $m = n-2$. Using the direct sum decompositions
$m = n-2$. Using the direct sum decompositions
 \[ S^{k}\mathcal{U}^{{\vee}} \otimes S^{l}\mathcal{U} \cong \bigoplus_{j = 0}^{\min\{k,l\}} S^{k + l - 2j}\mathcal{U}^{{\vee}}(j - l) \]
\[ S^{k}\mathcal{U}^{{\vee}} \otimes S^{l}\mathcal{U} \cong \bigoplus_{j = 0}^{\min\{k,l\}} S^{k + l - 2j}\mathcal{U}^{{\vee}}(j - l) \]
and the cases of the inclusion (3.31) proved above, we see that all the terms of the double complex with a possible exception for the rightmost term ![]() $S^{n-2}\mathcal {U}^{\vee }$ are contained in the subcategory generated by
$S^{n-2}\mathcal {U}^{\vee }$ are contained in the subcategory generated by ![]() $\mathbf {E}$. By (3.16) and (3.26) the unique cohomology sheaf
$\mathbf {E}$. By (3.16) and (3.26) the unique cohomology sheaf
of the double complex is contained in ![]() $\langle \mathbf {E} \rangle$, therefore the last term
$\langle \mathbf {E} \rangle$, therefore the last term ![]() $S^{n-2}\mathcal {U}^{\vee }$ is in the subcategory generated by
$S^{n-2}\mathcal {U}^{\vee }$ is in the subcategory generated by ![]() $\mathbf {E}$.
$\mathbf {E}$.
Let
be any non-zero global section and let ![]() $v^{\perp } \subset V$ be the orthogonal complement of
$v^{\perp } \subset V$ be the orthogonal complement of ![]() $v$. The restriction of the bilinear form to
$v$. The restriction of the bilinear form to ![]() $v^{\perp }$ is non-degenerate if and only if
$v^{\perp }$ is non-degenerate if and only if ![]() $v$ is non-isotropic. In this case the zero locus of
$v$ is non-isotropic. In this case the zero locus of ![]() $v$ (considered as a section of
$v$ (considered as a section of ![]() $\mathcal {U}^{\vee }$) is the odd orthogonal Grassmannian
$\mathcal {U}^{\vee }$) is the odd orthogonal Grassmannian
and we have the natural closed embedding
and the Koszul resolution
The union of ![]() $\operatorname {OG}(2,v^{\perp })$ for non-isotropic
$\operatorname {OG}(2,v^{\perp })$ for non-isotropic ![]() $v \in V$ sweeps
$v \in V$ sweeps ![]() $\operatorname {OG}(2,V)$, hence we have the following lemma.
$\operatorname {OG}(2,V)$, hence we have the following lemma.
Lemma 3.20 [Kuz08, Lemma 4.5] If for an object ![]() $F \in {{\mathbf {D}^{\mathrm {b}}}}(\operatorname {OG}(2,2n))$ the restrictions
$F \in {{\mathbf {D}^{\mathrm {b}}}}(\operatorname {OG}(2,2n))$ the restrictions ![]() $i_v^{*} F$ vanish for all non-isotropic
$i_v^{*} F$ vanish for all non-isotropic ![]() $v \in V$, then
$v \in V$, then ![]() $F = 0$.
$F = 0$.
Now we are finally ready to prove the fullness of (3.27).
Proposition 3.21 If ![]() $F \in {{\mathbf {D}^{\mathrm {b}}}}(\operatorname {OG}(2,V))$ is right-orthogonal to all the vector bundles
$F \in {{\mathbf {D}^{\mathrm {b}}}}(\operatorname {OG}(2,V))$ is right-orthogonal to all the vector bundles ![]() $E$ in the collection (3.27) (i.e.
$E$ in the collection (3.27) (i.e. ![]() $\operatorname {Ext}^{\bullet }(E,F) = 0$), then
$\operatorname {Ext}^{\bullet }(E,F) = 0$), then ![]() $F = 0$.
$F = 0$.
Proof. The assumption of the proposition can be rewritten as
Now take any non-isotropic vector ![]() $v$ and any bundle
$v$ and any bundle ![]() $E \in \mathbf {E}'$, and tensor (3.32) by
$E \in \mathbf {E}'$, and tensor (3.32) by ![]() $E^{\vee } \otimes F$. We obtain an exact sequence
$E^{\vee } \otimes F$. We obtain an exact sequence
From Lemma 3.19 and (3.33) it follows that the cohomology groups of the first three terms of this complex vanish. Hence, also the cohomology of ![]() $i_{v*} i_v^{*} (E^{\vee } \otimes F)$ has to vanish, and we conclude that
$i_{v*} i_v^{*} (E^{\vee } \otimes F)$ has to vanish, and we conclude that
for any ![]() $E \in \mathbf {E}'$. In other words, the object
$E \in \mathbf {E}'$. In other words, the object ![]() $i_v^{*}F$ is orthogonal to all objects
$i_v^{*}F$ is orthogonal to all objects ![]() $i_v^{*}E$ for
$i_v^{*}E$ for ![]() $E \in \mathbf {E}'$.
$E \in \mathbf {E}'$.
Set
Since ![]() $i_v^{*}(\mathcal {U}^{\vee })$ is the dual tautological bundle and
$i_v^{*}(\mathcal {U}^{\vee })$ is the dual tautological bundle and ![]() $i_v^{*}(\mathcal {S}_+)$ is the spinor bundle on the odd orthogonal Grassmannian
$i_v^{*}(\mathcal {S}_+)$ is the spinor bundle on the odd orthogonal Grassmannian ![]() $\operatorname {OG}(2,v^{\perp }) \cong \operatorname {OG}(2,2n-1)$, it follows from [Reference KuznetsovKuz08, Theorem 7.1] that there is a semiorthogonal decomposition
$\operatorname {OG}(2,v^{\perp }) \cong \operatorname {OG}(2,2n-1)$, it follows from [Reference KuznetsovKuz08, Theorem 7.1] that there is a semiorthogonal decomposition
Twisting it by ![]() $\mathcal {O}(2 - n)$, we obtain a semiorthogonal decomposition
$\mathcal {O}(2 - n)$, we obtain a semiorthogonal decomposition
Thus, the definition of the set ![]() $\mathbf {E}'$ implies that the objects
$\mathbf {E}'$ implies that the objects ![]() $i_v^{*}E$ for
$i_v^{*}E$ for ![]() $E \in \mathbf {E}'$ generate the category
$E \in \mathbf {E}'$ generate the category ![]() ${{\mathbf {D}^{\mathrm {b}}}}(\operatorname {OG}(2,v^{\perp }))$, hence (3.35) implies that
${{\mathbf {D}^{\mathrm {b}}}}(\operatorname {OG}(2,v^{\perp }))$, hence (3.35) implies that ![]() $i_v^{*}F = 0$. Since this holds for any non-isotropic
$i_v^{*}F = 0$. Since this holds for any non-isotropic ![]() $v$, it follows from Lemma 3.20 that
$v$, it follows from Lemma 3.20 that ![]() $F = 0$.
$F = 0$.
3.7 Residual category
For ![]() $1 \le i \le n - 2$ we define
$1 \le i \le n - 2$ we define ![]() $F_i$ to be the stupid right truncation of complex (3.25) after
$F_i$ to be the stupid right truncation of complex (3.25) after ![]() $n-1-i$ terms (counting from the left). In other words, the objects
$n-1-i$ terms (counting from the left). In other words, the objects ![]() $F_i$ are defined by the following exact sequences:
$F_i$ are defined by the following exact sequences:
 \begin{equation} \begin{aligned} 0 \to S^{n-2} & \mathcal{U}^{{\vee}}(2-n) \to F_{n-2} \to 0, \\ 0 \to S^{n-2} & \mathcal{U}^{{\vee}}(2-n) \to W_1 \otimes S^{n-3}\mathcal{U}^{{\vee}}(3-n) \to F_{n-3} \to 0, \\ & \vdots \\ 0 \to S^{n-2} & \mathcal{U}^{{\vee}}(2-n) \to W_1 \otimes S^{n-3}\mathcal{U}^{{\vee}}(3-n) \to \cdots \to W_{n-3} \otimes \mathcal{U}^{{\vee}}({-}1) \to F_1 \to 0. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} 0 \to S^{n-2} & \mathcal{U}^{{\vee}}(2-n) \to F_{n-2} \to 0, \\ 0 \to S^{n-2} & \mathcal{U}^{{\vee}}(2-n) \to W_1 \otimes S^{n-3}\mathcal{U}^{{\vee}}(3-n) \to F_{n-3} \to 0, \\ & \vdots \\ 0 \to S^{n-2} & \mathcal{U}^{{\vee}}(2-n) \to W_1 \otimes S^{n-3}\mathcal{U}^{{\vee}}(3-n) \to \cdots \to W_{n-3} \otimes \mathcal{U}^{{\vee}}({-}1) \to F_1 \to 0. \end{aligned} \end{equation}
Since (3.25) is exact, the objects ![]() $F_i$ are also quasi-isomorphic to the stupid left truncations of the complex (3.25); in other words, we also have exact sequences
$F_i$ are also quasi-isomorphic to the stupid left truncations of the complex (3.25); in other words, we also have exact sequences
 \begin{equation} \begin{aligned} 0 \to & F_{n-2} \to W_1 \otimes S^{n-3}\mathcal{U}^{{\vee}}(3-n) \to \cdots \to W_1 \otimes S^{n-3} \mathcal{U}^{{\vee}}(1) \to S^{n-2} \mathcal{U}^{{\vee}}(1) \to 0, \\ 0 \to & F_{n-3} \to W_2 \otimes S^{n-4}\mathcal{U}^{{\vee}}(4-n) \to \cdots \to W_1 \otimes S^{n-3} \mathcal{U}^{{\vee}}(1) \to S^{n-2} \mathcal{U}^{{\vee}}(1) \to 0, \\ & \ \vdots \\ 0 \to & F_1 \to W_{n-2} \otimes \mathcal{O} \to \cdots \to W_1 \otimes S^{n-3} \mathcal{U}^{{\vee}}(1) \to S^{n-2} \mathcal{U}^{{\vee}}(1) \to 0. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} 0 \to & F_{n-2} \to W_1 \otimes S^{n-3}\mathcal{U}^{{\vee}}(3-n) \to \cdots \to W_1 \otimes S^{n-3} \mathcal{U}^{{\vee}}(1) \to S^{n-2} \mathcal{U}^{{\vee}}(1) \to 0, \\ 0 \to & F_{n-3} \to W_2 \otimes S^{n-4}\mathcal{U}^{{\vee}}(4-n) \to \cdots \to W_1 \otimes S^{n-3} \mathcal{U}^{{\vee}}(1) \to S^{n-2} \mathcal{U}^{{\vee}}(1) \to 0, \\ & \ \vdots \\ 0 \to & F_1 \to W_{n-2} \otimes \mathcal{O} \to \cdots \to W_1 \otimes S^{n-3} \mathcal{U}^{{\vee}}(1) \to S^{n-2} \mathcal{U}^{{\vee}}(1) \to 0. \end{aligned} \end{equation} We will check that the objects ![]() $F_1,\ldots ,F_{n-2}$ together with the objects
$F_1,\ldots ,F_{n-2}$ together with the objects ![]() $\mathcal {U}^{2\omega _{n-1}}(-1)$,
$\mathcal {U}^{2\omega _{n-1}}(-1)$, ![]() $\mathcal {U}^{2\omega _{n}}(-1)$ form a full exceptional collection in the residual category. We denote by
$\mathcal {U}^{2\omega _{n}}(-1)$ form a full exceptional collection in the residual category. We denote by ![]() ${{\mathbb {L}}}$ the left mutation functors.
${{\mathbb {L}}}$ the left mutation functors.
Lemma 3.22 We have
Proof. To prove the claim it is enough to show the following two facts:
– the object
 $F_i (i-1) [n-1+i]$ is contained in the orthogonal
$F_i (i-1) [n-1+i]$ is contained in the orthogonal  $\langle \mathcal {A}, \mathcal {A}(1),\ldots , \mathcal {A}(i) \rangle ^{\perp }$;
$\langle \mathcal {A}, \mathcal {A}(1),\ldots , \mathcal {A}(i) \rangle ^{\perp }$;– there exists a morphism
 $S^{n-2} \mathcal {U}^{\vee }(i) \to F_i(i-1)[n-1+i]$, whose cone lies in the category
$S^{n-2} \mathcal {U}^{\vee }(i) \to F_i(i-1)[n-1+i]$, whose cone lies in the category  $\langle \mathcal {A}, \mathcal {A}(1),\ldots , \mathcal {A}(i) \rangle$.
$\langle \mathcal {A}, \mathcal {A}(1),\ldots , \mathcal {A}(i) \rangle$.
Twisting (3.38) by ![]() $\mathcal {O}(i-1)$ and using the semiorthogonality of (3.9), we deduce the first of these facts. On the other hand, considering (3.39) twisted by
$\mathcal {O}(i-1)$ and using the semiorthogonality of (3.9), we deduce the first of these facts. On the other hand, considering (3.39) twisted by ![]() $\mathcal {O}(i-1)$ as a Yoneda extension of the vector bundle
$\mathcal {O}(i-1)$ as a Yoneda extension of the vector bundle ![]() $S^{n-2} \mathcal {U}^{\vee }(i)$ by
$S^{n-2} \mathcal {U}^{\vee }(i)$ by ![]() $F_i(i-1)$ of length
$F_i(i-1)$ of length ![]() $n-1+i$, that is, as a morphism
$n-1+i$, that is, as a morphism ![]() $S^{n-2} \mathcal {U}^{\vee }(i) \to F_i(i-1)[n-1+i]$, we conclude that its cone is quasi-isomorphic to the subcomplex of middle terms, hence belongs to the subcategory
$S^{n-2} \mathcal {U}^{\vee }(i) \to F_i(i-1)[n-1+i]$, we conclude that its cone is quasi-isomorphic to the subcomplex of middle terms, hence belongs to the subcategory ![]() $\langle \mathcal {A}, \mathcal {A}(1),\ldots , \mathcal {A}(i) \rangle$. This proves the second fact.
$\langle \mathcal {A}, \mathcal {A}(1),\ldots , \mathcal {A}(i) \rangle$. This proves the second fact.
Thus, we have the following description for the residual category:
Remark 3.23 For ![]() $n \ne 4$ the exceptional collection in (3.40) is
$n \ne 4$ the exceptional collection in (3.40) is ![]() $\operatorname {Aut}(\operatorname {OG}(2,2n))$-invariant. For
$\operatorname {Aut}(\operatorname {OG}(2,2n))$-invariant. For ![]() $n = 4$ it takes form
$n = 4$ it takes form ![]() $S^{2}\mathcal {S}_-(-1), S^{2}\mathcal {S}_+(-1), (V \otimes \mathcal {U})/S^{2}\mathcal {U}, S^{2}\mathcal {U}^{\vee }(-1)$. Mutating the third object to the right, we obtain an
$S^{2}\mathcal {S}_-(-1), S^{2}\mathcal {S}_+(-1), (V \otimes \mathcal {U})/S^{2}\mathcal {U}, S^{2}\mathcal {U}^{\vee }(-1)$. Mutating the third object to the right, we obtain an ![]() $\operatorname {Aut}(\operatorname {OG}(2,8))$-invariant exceptional collection
$\operatorname {Aut}(\operatorname {OG}(2,8))$-invariant exceptional collection
where the bundle ![]() $\tilde T$ is defined by the exact sequence
$\tilde T$ is defined by the exact sequence ![]() $0 \to \mathcal {O} \to \tilde T \to T \to 0$ and
$0 \to \mathcal {O} \to \tilde T \to T \to 0$ and ![]() $T$ is the tangent bundle.
$T$ is the tangent bundle.
It remains to compute the ![]() $\operatorname {Ext}$-spaces between the objects of (3.40).
$\operatorname {Ext}$-spaces between the objects of (3.40).
Lemma 3.24 We have
 \[ \operatorname{Ext}^{{\bullet}}(F_i(i-1), F_j(j-1)) =\begin{cases} \Bbbk, & \text{if } j = i + 1 \text{ or } j = i, \\ 0 , & \text{otherwise.} \end{cases} \]
\[ \operatorname{Ext}^{{\bullet}}(F_i(i-1), F_j(j-1)) =\begin{cases} \Bbbk, & \text{if } j = i + 1 \text{ or } j = i, \\ 0 , & \text{otherwise.} \end{cases} \]Furthermore, we have
 \[ \operatorname{Ext}^{{\bullet}}(\mathcal{U}^{2\omega_{n-1}}({-}1), F_j(j-1)) = \operatorname{Ext}^{{\bullet}}(\mathcal{U}^{2\omega_{n}}({-}1), F_j(j-1)) = \begin{cases} \Bbbk[{-}1] , & \text{if } j = 1, \\ 0 , & \text{otherwise.} \end{cases} \]
\[ \operatorname{Ext}^{{\bullet}}(\mathcal{U}^{2\omega_{n-1}}({-}1), F_j(j-1)) = \operatorname{Ext}^{{\bullet}}(\mathcal{U}^{2\omega_{n}}({-}1), F_j(j-1)) = \begin{cases} \Bbbk[{-}1] , & \text{if } j = 1, \\ 0 , & \text{otherwise.} \end{cases} \]Proof. We start with the first claim. Since we already know that (3.40) is an exceptional collection, we may assume ![]() $i < j$. From (3.39) twisted by
$i < j$. From (3.39) twisted by ![]() $\mathcal {O}(i-1)$ we deduce
$\mathcal {O}(i-1)$ we deduce
and from (3.38) twisted by ![]() $\mathcal {O}(j-1)$ and with
$\mathcal {O}(j-1)$ and with ![]() $i$ replaced by
$i$ replaced by ![]() $j$ we deduce
$j$ we deduce
Using an appropriate twist of (3.9), one easily sees that non-trivial ![]() $\operatorname {Ext}$s can only come from
$\operatorname {Ext}$s can only come from
By Lemma 3.11 this space is non-zero (and is isomorphic to ![]() $\Bbbk [4-2n]$) only if
$\Bbbk [4-2n]$) only if ![]() $j = i + 1$ and the claim follows.
$j = i + 1$ and the claim follows.
For the second claim, using the inclusion (3.41), we see that non-trivial ![]() $\operatorname {Ext}$s can only come from
$\operatorname {Ext}$s can only come from
where ![]() $\varepsilon \in \{n-1, n\}$. By Lemma 3.14 and Serre duality this space is non-zero (and is isomorphic to
$\varepsilon \in \{n-1, n\}$. By Lemma 3.14 and Serre duality this space is non-zero (and is isomorphic to ![]() $\Bbbk [2-n]$) only if
$\Bbbk [2-n]$) only if ![]() $i = 1$, and the claim follows.
$i = 1$, and the claim follows.
The above lemma shows that the residual category is equivalent to the derived category of representations of a Dynkin quiver of type ![]() $\mathrm {D}_n$ and Remark 3.23 shows that it is generated by an exceptional collection invariant under all automorphisms of
$\mathrm {D}_n$ and Remark 3.23 shows that it is generated by an exceptional collection invariant under all automorphisms of ![]() $\operatorname {OG}(2,2n)$. This completes the proof of Theorem 3.1.
$\operatorname {OG}(2,2n)$. This completes the proof of Theorem 3.1.
Acknowledgements
We are indebted to Nicolas Perrin for sharing with us his results of quantum cohomology computations and drawing to our attention the coadjoint varieties of types ![]() $\mathrm {A}_n$ and
$\mathrm {A}_n$ and ![]() $\mathrm {D}_n$, which eventually led to this paper. We thank Giordano Cotti, Anton Fonarev, Sergey Galkin, and Anton Mellit for useful discussions and the anonymous referee for their comments. Further, we are very grateful to Pieter Belmans for his kind permission to reuse some parts of the code written for [Reference Belmans and SmirnovBS19], which was instrumental for this paper, and for his comments on the first draft of this paper. Finally, M.S. would like to thank ICTP in Trieste, and MPIM in Bonn, where a part of this work was accomplished, for their hospitality.
$\mathrm {D}_n$, which eventually led to this paper. We thank Giordano Cotti, Anton Fonarev, Sergey Galkin, and Anton Mellit for useful discussions and the anonymous referee for their comments. Further, we are very grateful to Pieter Belmans for his kind permission to reuse some parts of the code written for [Reference Belmans and SmirnovBS19], which was instrumental for this paper, and for his comments on the first draft of this paper. Finally, M.S. would like to thank ICTP in Trieste, and MPIM in Bonn, where a part of this work was accomplished, for their hospitality.