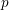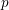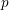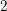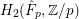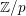1 Introduction
Let
$p$
be a prime. For a profinite group
$G$
, there is a natural comparison map
$$\begin{eqnarray}H_{2}^{\mathsf{disc}}(G,\mathbb{Z}/p)\rightarrow H_{2}^{\mathsf{cont}}(G,\mathbb{Z}/p),\end{eqnarray}$$
which connects discrete and continuous homology groups of
$G$
. Here
$H_{2}^{\mathsf{disc}}(G,\mathbb{Z}/p)=H_{2}(G,\mathbb{Z}/p)$
is the second homology group of
$G$
with
$\mathbb{Z}/p$
-coefficients, where
$G$
is viewed as a discrete group. The continuous homology
$H_{2}^{\mathsf{cont}}(G,\mathbb{Z}/p)$
can be defined as the inverse limit
$\varprojlim H_{2}(G/U,\mathbb{Z}/p)$
, where
$U$
runs over all open normal subgroups of
$G$
. The above comparison map
$H_{2}^{\mathsf{disc}}\rightarrow H_{2}^{\mathsf{cont}}$
is the inverse limit of the coinflation maps
$H_{2}(G,\mathbb{Z}/p)\rightarrow H_{2}(G/U,\mathbb{Z}/p)$
(see [Reference Fernandez-Alcober, Kazatchkov, Remeslennikov and SymondsFKRS08, Theorem 2.1]).
The study of the comparison map for different types of pro-
$p$
-groups is a fundamental problem in the theory of profinite groups (see [Reference Fernandez-Alcober, Kazatchkov, Remeslennikov and SymondsFKRS08] for discussion and references). It is well known that for a finitely generated free pro-
$p$
-group
$\hat{F}_{p}$
,
$$\begin{eqnarray}H_{2}^{\mathsf{cont}}(\hat{F}_{p},\mathbb{Z}/p)=0.\end{eqnarray}$$
Bousfield posed the following question in [Reference BousfieldBou77, Problem 4.11], (case
$R=\mathbb{Z}/n$
).
Problem (Bousfield).
Does
$H_{2}^{\mathsf{disc}}(\hat{F}_{n},\mathbb{Z}/n)$
vanish when
$F$
is a finitely generated free group?
Here
$\hat{F}_{n}$
is the
$\mathbb{Z}/n$
-completion of
$F$
, which is isomorphic to the product of pro-
$p$
-completions
$\hat{F}_{p}$
over prime factors of
$n$
(see [Reference BousfieldBou77, Proposition 12.3]). That is, the above problem is completely reduced to the case of homology groups
$H_{2}^{\mathsf{disc}}(\hat{F}_{p},\mathbb{Z}/p)$
for primes
$p$
and, since
$H_{2}^{\mathsf{cont}}(\hat{F}_{p},\mathbb{Z}/p)=0$
, the problem becomes a question about the non-triviality of the kernel of the comparison map for
$\hat{F}_{p}$
.
In [Reference BousfieldBou92], Bousfield proved that, for a finitely generated free pro-
$p$
-group
$\hat{F}_{p}$
on at least two generators, the group
$H_{i}^{\mathsf{disc}}(\hat{F}_{p},\mathbb{Z}/p)$
is uncountable for
$i=2$
or
$i=3$
, or both. In particular, the wedge of two circles
$S^{1}\vee S^{1}$
is a
$\mathbb{Z}/p$
-bad space in the Bousfield–Kan sense.
The group
$H_{2}^{\mathsf{disc}}(\hat{F}_{p},\mathbb{Z}/p)$
plays a central role in the theory of
$H\mathbb{Z}/p$
-localizations developed in [Reference BousfieldBou77]. It follows immediately from the definition of
$H\mathbb{Z}/p$
-localization that, for a free group
$F$
,
$H_{2}^{\mathsf{disc}}(\hat{F}_{p},\mathbb{Z}/p)=0$
if and only if
$\hat{F}_{p}$
coincides with the
$H\mathbb{Z}/p$
-localization of
$F$
. (From the point of view of profinite groups the Bousfield problem is also discussed in [Reference NikolovNik11, § 7] by Nikolov and in [Reference KlopschKlo16, § 4] by Klopsch.)
In this paper we answer Bousfield’s problem over
$\mathbb{Z}/p$
. Our main result is as follows.
Main Theorem. For a finitely generated free pro-
$p$
-group
$\hat{F}_{p}$
of rank at least
$2$
,
$H_{2}^{\mathsf{disc}}(\hat{F}_{p},\mathbb{Z}/p)$
is uncountable.
There are two cases in Bousfield’s problem,
$R=\mathbb{Z}/n$
and
$R=\mathbb{Q}$
. We give the answer for the case of
$R=\mathbb{Z}/n$
. (Recently the authors gave the solution for the
$R=\mathbb{Q}$
case [Reference Ivanov and MikhailovIM17], using completely different methods.)
The proof is organized as follows. In § 2 we consider properties of discrete and continuous homology of profinite groups. Using a result of Nikolov and Segal [Reference Nikolov and SegalNS07, Theorem 1.4], we show that for a finitely generated profinite group
$G$
and a closed normal subgroup
$H$
the cokernels of the maps
$H_{2}^{\mathsf{disc}}(G,\mathbb{Z}/p)\rightarrow H_{2}^{\mathsf{disc}}(G/H,\mathbb{Z}/p)$
and
$H_{2}^{\mathsf{cont}}(G,\mathbb{Z}/p)\rightarrow H_{2}^{\mathsf{cont}}(G/H,\mathbb{Z}/p)$
coincide (Theorem 2.5):
As a corollary we obtain (Corollary 2.6) that, for a finitely generated free pro-
$p$
-group
$\hat{F}_{p}$
, a continuous epimorphism
$\unicode[STIX]{x1D70B}:\hat{F}_{p}{\twoheadrightarrow}G$
to a pro-
$p$
-group induces the exact sequence
$$\begin{eqnarray}H_{2}^{\mathsf{disc}}(\hat{F}_{p},\mathbb{Z}/p)\overset{\unicode[STIX]{x1D70B}_{\ast }}{\longrightarrow }H_{2}^{\mathsf{disc}}(G,\mathbb{Z}/p)\overset{\unicode[STIX]{x1D711}}{\longrightarrow }H_{2}^{\mathsf{cont}}(G,\mathbb{Z}/p)\longrightarrow 0.\end{eqnarray}$$
That is, to prove that, for a free group
$F$
,
$H_{2}(\hat{F}_{p},\mathbb{Z}/p)\neq 0$
, it is enough to find a discrete epimorphism
$F{\twoheadrightarrow}G$
such that the comparison map of the second homology groups of the pro-
$p$
-completion of
$G$
has a non-zero kernel. Observe that the statements in § 2 significantly use the theory of profinite groups and there is no direct way to generalize them for pronilpotent groups. In particular, we do not see how to prove that
$H_{2}(\hat{F}_{\mathbb{Z}},\mathbb{Z}/p)\neq 0$
, where
$\hat{F}_{\mathbb{Z}}$
is the pronilpotent completion of
$F$
.
Section 3 follows the ideas of Bousfield from [Reference BousfieldBou92]. Consider the ring of formal power series
$\mathbb{Z}/p[\![x]\!]$
, and the infinite cyclic group
$C:=\langle t\rangle$
. We will use the multiplicative notation of the
$p$
-adic integers
$C\,\otimes \,\mathbb{Z}_{p}=\{t^{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}\in \mathbb{Z}_{p}\}$
. Consider the continuous multiplicative homomorphism
$\unicode[STIX]{x1D70F}:C\,\otimes \,\mathbb{Z}_{p}\rightarrow \mathbb{Z}/p[\![x]\!]$
sending
$t$
to
$1-x$
. The main result of § 3 is Proposition 3.3, which claims that the kernel of the multiplication map
$$\begin{eqnarray}\mathbb{Z}/p[\![x]\!]\otimes _{\mathbb{Z}/p[C\otimes \mathbb{Z}_{p}]}\mathbb{Z}/p[\![x]\!]\longrightarrow \mathbb{Z}/p[\![x]\!]\end{eqnarray}$$
is uncountable.
Our main example is based on the
$p$
-lamplighter group
$\mathbb{Z}/p\wr \mathbb{Z}$
, a finitely generated but not finitely presented group, which plays a central role in the theory of metabelian groups. The homological properties of the
$p$
-lamplighter group are considered in [Reference KrophollerKro85]. The profinite completion of the
$p$
-lamplighter group is considered in [Reference Grigorchuk and KravchenkoGK14], where it is shown that it is a semi-similar group generated by finite automaton. We consider the double lamplighter group,
$$\begin{eqnarray}(\mathbb{Z}/p)^{2}\wr \mathbb{Z}=\langle a,b,c\mid [b,b^{a^{i}}]=[c,c^{a^{i}}]=[b,c^{a^{i}}]=b^{p}=c^{p}=1,\,i\in \mathbb{Z}\rangle .\end{eqnarray}$$
Denote by
${\mathcal{D}}{\mathcal{L}}$
the pro-
$p$
-completion of the double lamplighter group. It follows from direct computations of homology groups that there is a diagram (in the above notation)
where the left vertical arrow is a split monomorphism and the upper horizontal map is the multiplication map (see proof of Theorem 4.3). This implies that, for the group
${\mathcal{D}}{\mathcal{L}}$
, the comparison map
$H_{2}^{\mathsf{disc}}({\mathcal{D}}{\mathcal{L}},\mathbb{Z}/p)\rightarrow H_{2}^{\mathsf{cont}}({\mathcal{D}}{\mathcal{L}},\mathbb{Z}/p)$
has an uncountable kernel. Since the double lamplighter group is 3-generated, the sequence (1.1) implies that, for a free group
$F$
with at least three generators,
$H_{2}(\hat{F}_{p},\mathbb{Z}/p)$
is uncountable. Finally, we use [Reference BousfieldBou92, Lemma 11.2] to get the same result for a 2-generated free group
$F$
.
In [Reference BousfieldBou77], Bousfield formulated the following generalization of the above problem for the class of finitely presented groups (see [Reference BousfieldBou77, Problem 4.10], the case
$R=\mathbb{Z}/n$
). Let
$G$
be a finitely presented group. Is it true that
$H\mathbb{Z}/p$
-localization of
$G$
equals its pro-
$p$
-completion
${\hat{G}}_{p}$
? (The problem is formulated for
$H\mathbb{Z}/n$
-localization, but it is reduced to the case of a prime
$n=p$
.) It follows immediately from the definition of
$H\mathbb{Z}/p$
-localization that this problem can be reformulated as follows: is it true that, for a finitely presented group
$G$
, the natural homomorphism
$H_{2}(G,\mathbb{Z}/p)\rightarrow H_{2}({\hat{G}}_{p},\mathbb{Z}/p)$
? It is shown in [Reference BousfieldBou77] that this is true for the class of polycyclic groups. The same is true for finitely presented metabelian groups [Reference Ivanov and MikhailovIM16]. The main theorem of the present paper implies that, for any finitely presented group
$P$
, which maps epimorphically onto the double lamplighter group, the natural map
$H_{2}(P,\mathbb{Z}/p)\rightarrow H_{2}(\hat{P}_{p},\mathbb{Z}/p)$
has an uncountable cokernel.
2 Discrete and continuous homology of profinite groups
For a profinite group
$G$
and a normal subgroup
$H$
, denote by
$\overline{H}$
the closure of
$H$
in
$G$
in profinite topology.
Theorem 2.1 [Reference Nikolov and SegalNS07, Theorem 1.4].
Let
$G$
be a finitely generated profinite group and
$H$
be a closed normal subgroup of
$G$
. Then the subgroup
$[H,G]$
is closed in
$G$
.
Corollary 2.2. Let
$G$
be a finitely generated profinite group and
$H$
be a closed normal subgroup of
$G$
. Then the subgroup
$[H,G]\cdot H^{p}$
is closed in
$G$
.
Proof. Consider the abelian profinite group
$H/[H,G]$
. Then the
$p$
-power map
$H/[H,G]\rightarrow H/[H,G]$
is continuous and its image is equal to
$([H,G]\cdot H^{p})/[H,G].$
Hence
$([H,G]\cdot H^{p})/[H,G]$
is a closed subgroup of
$H/[H,G]$
. Using the fact that the preimage of a closed set under continuous function is closed, we obtain that
$[H,G]\cdot H^{p}$
is closed.◻
Observe that, in the proof of Corollary 2.2, [Reference Nikolov and SegalNS07, Theorem 1.4] is not used in full generality. We only need it in the case of pro-
$p$
groups, and in this particular case the proof of this theorem is quite elementary.
Lemma 2.3 (mod-
$p$
Hopf formula).
Let
$G$
be a (discrete) group and
$H$
be its normal subgroup. Then there is a natural exact sequence
$$\begin{eqnarray}H_{2}(G,\mathbb{Z}/p)\longrightarrow H_{2}(G/H,\mathbb{Z}/p)\longrightarrow \frac{H\cap ([G,G]G^{p})}{[H,G]H^{p}}\longrightarrow 0.\end{eqnarray}$$
Proof. This follows from the five-term exact sequence
$$\begin{eqnarray}H_{2}(G,\mathbb{Z}/p)\longrightarrow H_{2}(G/H,\mathbb{Z}/p)\longrightarrow H_{1}(H,\mathbb{Z}/p)_{G}\longrightarrow H_{1}(G,\mathbb{Z}/p)\end{eqnarray}$$
and the equations
$H_{1}(H,\mathbb{Z}/p)_{G}=H/([H,G]H^{p})$
and
$H_{1}(G,\mathbb{Z}/p)=G/([G,G]G^{p})$
.◻
Lemma 2.4 (Profinite mod-
$p$
Hopf formula).
Let
$G$
be a profinite group and
$H$
be its closed normal subgroup. Then there is a natural exact sequence
$$\begin{eqnarray}H_{2}^{\mathsf{cont}}(G,\mathbb{Z}/p)\longrightarrow H_{2}^{\mathsf{cont}}(G/H,\mathbb{Z}/p)\longrightarrow \frac{H\cap \overline{([G,G]G^{p})}}{\overline{([H,G]H^{p})}}\longrightarrow 0.\end{eqnarray}$$
Proof. For the sake of simplicity we set
$H_{\ast }(-)=H_{\ast }^{\mathsf{discr}}(-,\mathbb{Z}/p)$
and
$H_{\ast }^{\mathsf{cont}}(-):=H_{\ast }^{\mathsf{cont}}(-,\mathbb{Z}/p)$
. Consider the five-term exact sequence [Reference Ribes and ZalesskiiRZ00, Corollary 7.2.6]
$$\begin{eqnarray}H_{2}^{\mathsf{cont}}(G)\longrightarrow H_{2}^{\mathsf{cont}}(G)\longrightarrow H_{0}^{\mathsf{cont}}(G,H_{1}^{\mathsf{cont}}(H))\longrightarrow H_{1}^{\mathsf{cont}}(G).\end{eqnarray}$$
Continuous homology and cohomology of profinite groups are Pontryagin dual to each other [Reference Ribes and ZalesskiiRZ00, Proposition 6.3.6]. There are isomorphisms
$$\begin{eqnarray}H_{\mathsf{cont}}^{1}(G)=\text{Hom}(G/\overline{[G,G]G^{p}},\mathbb{Z}/p)=\text{Hom}(G/\overline{[G,G]G^{p}},\mathbb{Q}/\mathbb{Z}),\end{eqnarray}$$
where
$\text{Hom}$
denotes the set of continuous homomorphisms (see [Reference SerreSer02, I.2.3]). It follows that
$H_{1}^{\mathsf{cont}}(G)=G/\overline{[G,G]G^{p}}$
. Similarly,
$H_{1}^{\mathsf{cont}}(H)=H/\overline{[H,H]H^{p}}$
. [Reference Ribes and ZalesskiiRZ00, Lemma 6.3.3] implies that
$H_{0}^{\mathsf{cont}}(G,M)=M/\overline{\langle m-mg\mid m\in M,g\in G\rangle }$
for any profinite
$(\mathbb{Z}/p[G])^{\wedge }$
-module
$M$
. Therefore
$H_{0}^{\mathsf{cont}}(G,H_{1}^{\mathsf{cont}}(H))=H/\overline{[H,H]H^{p}}$
. The assertion follows.◻
We denote by
$\unicode[STIX]{x1D711}$
the comparison map
$$\begin{eqnarray}\unicode[STIX]{x1D711}:H_{2}^{\mathsf{disc}}(G,\mathbb{Z}/p)\rightarrow H_{2}^{\mathsf{cont}}(G,\mathbb{Z}/p).\end{eqnarray}$$
Theorem 2.5. Let
$G$
be a finitely generated profinite group and
$H$
a closed normal subgroup of
$G$
. Denote
$$\begin{eqnarray}\displaystyle Q^{\mathsf{disc}} & := & \displaystyle \mathsf{Coker}(H_{2}(G,\mathbb{Z}/p)\rightarrow H_{2}(G/H,\mathbb{Z}/p)),\nonumber\\ \displaystyle Q^{\mathsf{cont}} & := & \displaystyle \mathsf{Coker}(H_{2}^{\mathsf{cont}}(G,\mathbb{Z}/p)\rightarrow H_{2}^{\mathsf{cont}}(G/H,\mathbb{Z}/p)).\nonumber\end{eqnarray}$$
Then the comparison maps
$\unicode[STIX]{x1D711}$
induce an isomorphism
$Q^{\mathsf{disc}}\cong Q^{\mathsf{cont}}$
:
Corollary 2.6. Let
$G$
be a finitely generated pro-
$p$
-group and
$\unicode[STIX]{x1D70B}:\hat{F}_{p}{\twoheadrightarrow}G$
be a continuous epimorphism from the pro-
$p$
-completion of a finitely generated free group
$F$
. Then the sequence
$$\begin{eqnarray}H_{2}^{\mathsf{disc}}(\hat{F}_{p},\mathbb{Z}/p)\overset{\unicode[STIX]{x1D70B}_{\ast }}{\longrightarrow }H_{2}^{\mathsf{disc}}(G,\mathbb{Z}/p)\overset{\unicode[STIX]{x1D711}}{\longrightarrow }H_{2}^{\mathsf{cont}}(G,\mathbb{Z}/p)\longrightarrow 0\end{eqnarray}$$
is exact.
Proof. This follows from Theorem 2.5 and the fact that
$H_{2}^{\mathsf{cont}}(\hat{F}_{p},\mathbb{Z}/p)=0$
.◻
3 Technical results about the ring of power series
$\mathbb{Z}/p[\![x]\!]$
In this section we follow to ideas of Bousfield written in [Reference BousfieldBou92, Lemmas 10.6, 10.7]. The goal of this section is to prove Proposition 3.3.
We use the following notation:
$C=\langle t\rangle$
is the infinite cyclic group;
$C\,\otimes \,\mathbb{Z}_{p}$
is the group of
$p$
-adic integers written multiplicatively as powers of the generator
$C\,\otimes \,\mathbb{Z}_{p}=\{t^{\unicode[STIX]{x1D6FC}}\mid \unicode[STIX]{x1D6FC}\in \mathbb{Z}_{p}\}$
;
$\mathbb{Z}/p[\![x]\!]$
is the ring of power series;
$\mathbb{Z}/p(\!(x)\!)$
is the field of formal Laurent series.
Lemma 3.1. Let
$\mathsf{A}$
be a subset of
$\mathbb{Z}/p[\![x]\!]$
. Denote by
$\mathsf{A}^{i}$
the image of
$\mathsf{A}$
in
$\mathbb{Z}/p[x]/(x^{p^{i}})$
. Assume that
$$\begin{eqnarray}\lim _{i\rightarrow \infty }|\mathsf{A}^{i}|/p^{p^{i}}=0.\end{eqnarray}$$
Then the interior of
$\mathbb{Z}/p[\![x]\!]\setminus \mathsf{A}$
is dense in
$\mathbb{Z}/p[\![x]\!]$
.
Proof. Take any power series
$f$
and any its neighbourhood of the form
$f+(x^{p^{s}})$
. Then for any
$i$
the open set
$f+(x^{p^{s}})$
is the disjoint union of smaller open sets
$\bigcup _{t=1}^{p^{p^{i}}}f+f_{t}+(x^{p^{s+i}})$
, where
$f_{t}$
runs over representatives of
$(x^{p^{s}})/(x^{p^{s+i}})$
. Chose
$i$
so that
$|\mathsf{A}^{s+i}|/p^{p^{i+s}}\leqslant p^{-p^{s}}$
. Then
$|\mathsf{A}^{s+i}|\leqslant p^{p^{i}}$
. Hence the number of elements in
$\mathsf{A}^{i+s}$
is less than the number of open sets
$f+f_{t}+(x^{p^{s+i}})$
. It follows that there exists
$t$
such that
$\mathsf{A}\cap (f+f_{t}+(x^{p^{s+i}}))=\varnothing$
. The assertion follows.◻
Denote by
$$\begin{eqnarray}\unicode[STIX]{x1D70F}:C\otimes \mathbb{Z}_{p}\rightarrow \mathbb{Z}/p[\![x]\!]\end{eqnarray}$$
the continuous multiplicative homomorphism sending
$t$
to
$1-x$
. It is well defined because
$(1-x)^{p^{i}}=1-x^{p^{i}}$
.
Lemma 3.2. Let
$K$
be the subfield of
$\mathbb{Z}/p(\!(x)\!)$
generated by the image of
$\unicode[STIX]{x1D70F}$
. Then the degree of the extension
$[\mathbb{Z}/p(\!(x)\!):K]$
is uncountable.
Proof. Denote the image of the map
$\unicode[STIX]{x1D70F}:C\,\otimes \,\mathbb{Z}_{p}\rightarrow \mathbb{Z}/p[\![x]\!]$
by
$\mathsf{A}$
. Let
$\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n})$
and
$\unicode[STIX]{x1D6FD}=(\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{n})$
, where
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n},\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{n}\in \mathbb{Z}/p,$
and
$k\geqslant 1$
. Denote by
$\mathsf{A}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k}$
the subset of
$\mathbb{Z}/p[\![x]\!]$
consisting of elements that can be written in the form
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D6FC}_{1}a_{1}+\cdots +\unicode[STIX]{x1D6FC}_{n}a_{n}}{\unicode[STIX]{x1D6FD}_{1}b_{1}+\cdots +\unicode[STIX]{x1D6FD}_{n}b_{n}},\end{eqnarray}$$
where
$a_{1},\ldots ,a_{n},b_{1},\ldots ,b_{n}\in \mathsf{A}$
and
$\unicode[STIX]{x1D6FD}_{1}b_{1}+\cdots +\unicode[STIX]{x1D6FD}_{n}b_{n}\notin (x^{p^{k}})$
. Then
$K\cap \mathbb{Z}/p[\![x]\!]=\bigcup _{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k}\mathsf{A}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k}$
.
Fix some
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k$
. Take
$i\geqslant k$
and consider the images of
$\mathsf{A}$
and
$\mathsf{A}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k}$
in
$\mathbb{Z}/p[x]/(x^{p^{i}})$
. Denote them by
$\mathsf{A}^{i}$
and
$\mathsf{A}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k}^{i}$
. Obviously
$\mathsf{A}^{i}$
is the image of the map
$C/C^{p^{i}}\rightarrow \mathbb{Z}/p[x]/(x^{p^{i}})$
that sends
$t$
to
$1-x$
. Then
$\mathsf{A}^{i}$
consists of
$p^{i}$
elements. Fix some elements
$\bar{a}_{1},\ldots ,\bar{a}_{n},\bar{b}_{1},\ldots ,\bar{b}_{n}\in \mathsf{A}^{i}$
that have preimages
$a_{1},\ldots ,a_{n},b_{1},\ldots ,b_{n}\in \mathsf{A}$
such that the ratio (3.1) is in
$\mathsf{A}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k}$
. For any such preimages
$a_{1},\ldots ,a_{n},b_{1},\ldots ,b_{n}\in \mathsf{A}$
the image
$\bar{r}$
of the ratio (3.1) satisfies the equation
$$\begin{eqnarray}\bar{r}\cdot (\unicode[STIX]{x1D6FD}_{1}\bar{b}_{1}+\cdots +\unicode[STIX]{x1D6FD}_{n}\bar{b}_{n})=\unicode[STIX]{x1D6FC}_{1}\bar{a}_{1}+\cdots +\unicode[STIX]{x1D6FC}_{n}\bar{a}_{n}.\end{eqnarray}$$
Since
$\unicode[STIX]{x1D6FD}_{1}\bar{b}_{1}+\cdots +\unicode[STIX]{x1D6FD}_{n}\bar{b}_{n}\notin (x^{p^{k}})$
, the annihilator of
$\unicode[STIX]{x1D6FD}_{1}\bar{b}_{1}+\cdots +\unicode[STIX]{x1D6FD}_{n}\bar{b}_{n}$
consists of no more than
$p^{p^{k}}$
elements and the equation has no more than
$p^{p^{k}}$
solutions. Then we have no more than
$p^{2in}$
variants of collections
$\bar{a}_{1},\ldots ,\bar{a}_{n},\bar{b}_{1},\ldots ,\bar{b}_{n}\in \mathsf{A}^{i}$
, and for any such variant there are no more than
$p^{p^{k}}$
variants for the image of the ratio. Therefore
$$\begin{eqnarray}|\mathsf{A}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k}^{i}|\leqslant p^{2in+p^{k}}.\end{eqnarray}$$
Take any sequence of elements
$v_{1},v_{2},\ldots \in \mathbb{Z}/p(\!(x)\!)$
and prove that
$\sum _{m=1}^{\infty }Kv_{m}\neq \mathbb{Z}/p(\!(x)\!)$
. Note that
$x\in K$
because
$t\mapsto 1-x$
. Multiplying the elements
$v_{1},v_{2},v_{3},\ldots$
by powers of
$x$
, we can assume that
$v_{1},v_{2},\ldots \in \mathbb{Z}/p[\![x]\!]$
. Fix some
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k$
as above. Set
$$\begin{eqnarray}\mathsf{A}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k,l}=\mathsf{A}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k}\cdot v_{1}+\cdots +\mathsf{A}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k}\cdot v_{l}.\end{eqnarray}$$
Then
$\sum _{m=1}^{\infty }Kv_{m}=\bigcup _{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k,l,j}\mathsf{A}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k,l}\cdot x^{-j}$
. Denote by
$\mathsf{A}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k,l}^{i}$
the image of
$\mathsf{A}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k,l}$
in
$\mathbb{Z}/p[x]/(x^{i})$
. Then (3.2) implies
$|\mathsf{A}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k,l}^{i}|\leqslant p^{(2in+p^{k})l}$
. Therefore
$$\begin{eqnarray}\lim _{i\rightarrow \infty }|\mathsf{A}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k,l}^{i}|/p^{p^{i}}=0.\end{eqnarray}$$
By Lemma 3.1 the interior of the complement of
$\mathsf{A}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k,l}$
is dense in
$\mathbb{Z}/p[\![x]\!]$
. By the Baire theorem
$\sum _{m=1}^{\infty }Kv_{m}=\bigcup _{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k,l,j}\mathsf{A}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},k,l}\cdot x^{-j}$
has empty interior. In particular,
$\sum _{m=1}^{\infty }Kv_{m}\neq \mathbb{Z}/p(\!(x)\!)$
.◻
Proposition 3.3. Consider the ring homomorphism
$\mathbb{Z}/p[C\,\otimes \,\mathbb{Z}_{p}]\rightarrow \mathbb{Z}/p[\![x]\!]$
induced by
$\unicode[STIX]{x1D70F}$
. Then the kernel of the multiplication map
$$\begin{eqnarray}\mathbb{Z}/p[\![x]\!]\otimes _{\mathbb{Z}/p[C\otimes \mathbb{Z}_{p}]}\mathbb{Z}/p[\![x]\!]\longrightarrow \mathbb{Z}/p[\![x]\!]\end{eqnarray}$$
is uncountable.
Proof. As in Lemma 3.2, we denote by
$K$
the subfield of
$\mathbb{Z}/p(\!(x)\!)$
generated by the image of
$C\,\otimes \,\mathbb{Z}_{p}$
. Since
$t\mapsto 1-x$
, we have
$x,x^{-1}\in K$
. Set
$R:=K\cap \mathbb{Z}/p[\![x]\!]$
. Note that the image of
$\mathbb{Z}/p[C\,\otimes \,\mathbb{Z}_{p}]$
lies in
$R$
. Consider the multiplication map
$$\begin{eqnarray}\unicode[STIX]{x1D707}:\mathbb{Z}/p[\![x]\!]\otimes _{R}K\rightarrow \mathbb{Z}/p(\!(x)\!).\end{eqnarray}$$
We claim that this is an isomorphism. Construct the map in the inverse direction
$$\begin{eqnarray}\unicode[STIX]{x1D705}:\mathbb{Z}/p(\!(x)\!)\rightarrow \mathbb{Z}/p[\![x]\!]\otimes _{R}K\end{eqnarray}$$
given by
$$\begin{eqnarray}\unicode[STIX]{x1D705}\biggl(\mathop{\sum }_{i=-n}^{\infty }\unicode[STIX]{x1D6FC}_{i}x^{i}\biggr)=\mathop{\sum }_{i=0}^{\infty }\unicode[STIX]{x1D6FC}_{i+n}x^{i}\otimes x^{-n}.\end{eqnarray}$$
Since we have
$ax\,\otimes \,b=a\,\otimes \,xb$
,
$\unicode[STIX]{x1D705}$
does not depend on the choice of
$n$
, we just have to chose it big enough. Using this, we get that
$\unicode[STIX]{x1D705}$
is well defined. Obviously
$\unicode[STIX]{x1D707}\unicode[STIX]{x1D705}=\mathsf{id}$
. Chose
$a\,\otimes \,b\in \mathbb{Z}/p[\![x]\!]\,\otimes _{R}\,K$
. Then
$b=b_{1}b_{2}^{-1}$
, where
$b_{1},b_{2}\in R$
. Since
$b_{2}$
is a power series, we can chose
$n$
such that
$b_{2}=x^{n}b_{3}$
, where
$b_{3}$
is a power series with non-trivial constant term. Then
$b_{3}$
is invertible in the ring of power series and
$b_{3},b_{3}^{-1}\in R$
because
$x\in K$
. Hence
$a\,\otimes \,b=ab_{3}^{-1}b_{3}\,\otimes \,b=ab_{3}^{-1}\,\otimes \,x^{-n}b_{1}=ab_{1}b_{3}^{-1}\,\otimes \,x^{-n}$
. Using this presentation, we see that
$\unicode[STIX]{x1D705}\unicode[STIX]{x1D707}=\mathsf{id}$
. Therefore
$$\begin{eqnarray}\mathbb{Z}/p[\![x]\!]\otimes _{R}K\cong \mathbb{Z}/p(\!(x)\!).\end{eqnarray}$$
Since the image of
$\mathbb{Z}/p[C\,\otimes \,\mathbb{Z}_{p}]$
lies in
$R$
, the tensor product
$\mathbb{Z}/p[\![x]\!]\,\otimes _{R}\,\mathbb{Z}/p[\![x]\!]$
is a quotient of the tensor product
$\mathbb{Z}/p[\![x]\!]\otimes _{\mathbb{Z}/p[C\otimes \mathbb{Z}_{p}]}\mathbb{Z}/p[\![x]\!]$
and it is enough to prove that the kernel of
$$\begin{eqnarray}\mathbb{Z}/p[\![x]\!]\otimes _{R}\mathbb{Z}/p[\![x]\!]\longrightarrow \mathbb{Z}/p[\![x]\!]\end{eqnarray}$$
is uncountable.
For any ring homomorphism
$R\rightarrow S$
and any
$R$
-modules
$M,N$
there is an isomorphism
$(M\otimes _{R}N)\otimes _{R}S=(M\otimes _{R}S)\otimes _{S}(N\otimes _{R}S)$
. Using this and the isomorphism (3.4), we obtain that after application of
$-\otimes _{R}K$
to (3.5) we have
$$\begin{eqnarray}\mathbb{Z}/p(\!(x)\!)\otimes _{K}\mathbb{Z}/p(\!(x)\!)\longrightarrow \mathbb{Z}/p(\!(x)\!).\end{eqnarray}$$
Assume to the contrary that the kernel of the map (3.5) is countable (countable = countable or finite). It follows that the linear map (3.6) has countable-dimensional kernel. Finally, note that the homomorphism
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{K}^{2}\mathbb{Z}/p(\!(x)\!)\rightarrow \mathbb{Z}/p(\!(x)\!)\otimes _{K}\mathbb{Z}/p(\!(x)\!)\end{eqnarray}$$
given by
$a\wedge b\mapsto a\,\otimes \,b-b\,\otimes \,a$
is a monomorphism, its image lies in the kernel and the dimension of
$\unicode[STIX]{x1D6EC}_{K}^{2}\mathbb{Z}/p(\!(x)\!)$
over
$K$
is uncountable because
$[\mathbb{Z}/p(\!(x)\!):K]$
is uncountable (Lemma 3.2). A contradiction follows.◻
4 Double lamplighter pro-
$p$
-group
Let
$A$
be a finitely generated free abelian group written multiplicatively;
$\mathbb{Z}/p[A]$
be its group algebra;
$I$
be its augmentation ideal; and
$M$
be a
$\mathbb{Z}/p[A]$
-module. Then denote by
$\hat{M}=\varprojlim M/MI^{i}$
its
$I$
-adic completion. We embed
$A$
into the pro-
$p$
-group
$A\otimes \mathbb{Z}_{p}$
. We use the ‘multiplicative’ notation
$a^{\unicode[STIX]{x1D6FC}}:=a\otimes \unicode[STIX]{x1D6FC}$
for
$a\in A$
and
$\unicode[STIX]{x1D6FC}\in \mathbb{Z}_{p}$
. Note that for any
$a\in A$
the power
$a^{p^{i}}$
acts trivially on
$M/MI^{p^{i}}$
because
$1-a^{p^{i}}=(1-a)^{p^{i}}\in I^{p^{i}}\!$
. Then we can extend the action of
$A$
on
$\hat{M}$
to the action of
$A\otimes \mathbb{Z}_{p}$
on
$\hat{M}$
in a continuous way.
The proof of the following lemma can be found in [Reference Ivanov and MikhailovIM16], but we include it here for completeness.
Lemma 4.1. Let
$A$
be a finitely generated free abelian group and
$M$
be a finitely generated
$\mathbb{Z}/p[A]$
-module. Then
$$\begin{eqnarray}H_{\ast }(A,M)\cong H_{\ast }(A,\hat{M})\cong H_{\ast }(A\otimes \mathbb{Z}_{p},\hat{M}).\end{eqnarray}$$
Proof. The first isomorphism is proven in [Reference Brown and DrorBD75]. Since
$\mathbb{Z}/p[A]$
in Noetheran, it follows that
$H_{n}(A,\hat{M})$
is a finite
$\mathbb{Z}/p$
-vector space for any
$n$
. Prove the second isomorphism. The action of
$A\,\otimes \,\mathbb{Z}_{p}$
on
$\hat{M}$
gives an action of
$A\,\otimes \,\mathbb{Z}_{p}$
on
$H_{\ast }(A,\hat{M})$
such that
$A$
acts trivially on
$H_{\ast }(A,\hat{M})$
. Then we have a homomorphism from
$A\,\otimes \,\mathbb{Z}/p$
to a finite group of automorphisms of
$H_{n}(A,\hat{M})$
, whose kernel contains
$A$
. Since any subgroup of finite index in
$A\,\otimes \,\mathbb{Z}_{p}$
is open (see [Reference Ribes and ZalesskiiRZ00, Theorem 4.2.2]) and
$A$
is dense in
$A\,\otimes \,\mathbb{Z}_{p}$
, we obtain that the action of
$A\,\otimes \,\mathbb{Z}_{p}$
on
$H_{\ast }(C,\hat{M})$
is trivial. Note that
$\mathbb{Z}_{p}/\mathbb{Z}$
is a divisible torsion free abelian group, and hence
$A\,\otimes \,(\mathbb{Z}_{p}/\mathbb{Z})\cong \mathbb{Q}^{\oplus \mathbf{c}}$
, where
$\mathbf{c}$
is the continuous cardinal. Then the second page of the spectral sequence of the short exact sequence
$A\rightarrowtail A\,\otimes \,\mathbb{Z}_{p}{\twoheadrightarrow}\mathbb{Q}^{\oplus \mathbf{c}}$
with coefficients in
$\hat{M}$
is
$H_{n}(\mathbb{Q}^{\oplus \mathbf{c}},H_{m}(A,\hat{M}))$
, where
$L_{m}:=H_{m}(A,\hat{M})$
is a trivial
$\mathbb{Z}/p[\mathbb{Q}^{\oplus \mathbf{c}}]$
-module. Then by universal coefficient theorem we have
$$\begin{eqnarray}0\longrightarrow \unicode[STIX]{x1D6EC}^{n}(\mathbb{Q}^{\oplus \mathbf{c}})\otimes L_{m}\longrightarrow H_{n}(\mathbb{Q}^{\oplus \mathbf{c}},L_{m})\longrightarrow \mathsf{Tor}(\unicode[STIX]{x1D6EC}^{n-1}(\mathbb{Q}^{\oplus \mathbf{c}}),L_{m})\longrightarrow 0.\end{eqnarray}$$
Since
$\unicode[STIX]{x1D6EC}^{n}(\mathbb{Q}^{\oplus \mathbf{c}})$
is torsion free and
$L_{m}$
is a
$\mathbb{Z}/p$
-vector space, we get
$\unicode[STIX]{x1D6EC}^{n}(\mathbb{Q}^{\oplus \mathbf{c}})\otimes L_{m}=0$
and
$\mathsf{Tor}(\unicode[STIX]{x1D6EC}^{n-1}(\mathbb{Q}^{\oplus \mathbf{c}}),L_{m})=0.$
It follows that
$H_{n}(\mathbb{Q}^{\oplus \mathbf{c}},L_{m})=0$
for
$n\geqslant 1$
and
$H_{0}(\mathbb{Q}^{\oplus \mathbf{c}},L_{m})=L_{m}$
. Then the spectral sequence consists of only one column, and hence
$H_{\ast }(A\otimes \mathbb{Z}_{p},\hat{M})=H_{\ast }(A,\hat{M})$
.◻
Lemma 4.2. Let
$A$
be an abelian group,
$M$
be a
$\mathbb{Z}[A]$
-module and
$\unicode[STIX]{x1D70E}_{M}:M\rightarrow M$
be an automorphism of the underlying abelian group such that
$\unicode[STIX]{x1D70E}_{M}(ma)=\unicode[STIX]{x1D70E}_{M}(m)a^{-1}$
for any
$m\in M$
and
$a\in A$
. Then there is an isomorphism
$$\begin{eqnarray}(M\otimes M)_{A}\cong M\otimes _{\mathbb{Z}[A]}M\end{eqnarray}$$
given by
$$\begin{eqnarray}m\otimes m^{\prime }\leftrightarrow m\otimes \unicode[STIX]{x1D70E}_{M}(m^{\prime }).\end{eqnarray}$$
Proof. Consider the isomorphism
$\unicode[STIX]{x1D6F7}:M\,\otimes \,M\rightarrow M\,\otimes \,M$
given by
$\unicode[STIX]{x1D6F7}(m\,\otimes \,m^{\prime })=m\,\otimes \,\unicode[STIX]{x1D70E}(m^{\prime })$
. The group of coinvariants
$(M\,\otimes \,M)_{A}$
is the quotient of
$M\,\otimes \,M$
by the subgroup
$R$
generated by elements
$ma\,\otimes \,m^{\prime }a-m\,\otimes \,m^{\prime }$
, where
$a\in A$
and
$m,m^{\prime }\in M$
. We can write the generators of
$R$
in the following form:
$ma\,\otimes \,m^{\prime }-m\,\otimes \,m^{\prime }a^{-1}$
. Then
$\unicode[STIX]{x1D6F7}(R)$
is generated by
$ma\,\otimes \,\unicode[STIX]{x1D70E}_{M}(m^{\prime })-m\,\otimes \,\unicode[STIX]{x1D70E}_{M}(m^{\prime })a$
. Using the fact that
$\unicode[STIX]{x1D70E}_{M}$
is an automorphism, we can rewrite the generators of
$R$
as follows:
$ma\,\otimes \,m^{\prime }-m\,\otimes \,m^{\prime }a$
. Taking linear combinations of the generators of
$\unicode[STIX]{x1D6F7}(R)$
, we obtain that
$\unicode[STIX]{x1D6F7}(R)$
is generated by elements
$m\unicode[STIX]{x1D706}\,\otimes \,m^{\prime }-m\,\otimes \,m^{\prime }\unicode[STIX]{x1D706}$
, where
$\unicode[STIX]{x1D706}\in \mathbb{Z}[A]$
. Then
$(M\,\otimes \,M)/\unicode[STIX]{x1D6F7}(R)=M\,\otimes _{\mathbb{Z}[A]}\,M$
.◻
The group
$C=\langle t\rangle$
acts on
$\mathbb{Z}/p[\![x]\!]$
by multiplication on
$1-x$
. As above, we can extend the action of
$C$
on
$\mathbb{Z}[\![x]\!]$
to the action of
$C\otimes \mathbb{Z}_{p}$
in a continuous way. The group
$$\begin{eqnarray}\mathbb{Z}/p\wr C=\mathbb{Z}/p[C]\rtimes C=\langle a,b\mid [b,b^{a^{i}}]=b^{p}=1,i\in \mathbb{Z}\rangle\end{eqnarray}$$
is called the lamplighter group. We consider the ‘double version’ of this group, the double lamplighter group:
$$\begin{eqnarray}(\mathbb{Z}/p[C]\oplus \mathbb{Z}/p[C])\rtimes C=\langle a,b,c\mid [b,b^{a^{i}}]=[c,c^{a^{i}}]=[b,c^{a^{i}}]=b^{p}=c^{p}=1,i\in \mathbb{Z}\rangle .\end{eqnarray}$$
Its pro-
$p$
-completion is equal to the semidirect product
$$\begin{eqnarray}{\mathcal{D}}{\mathcal{L}}=(\mathbb{Z}/p[\![x]\!]\oplus \mathbb{Z}/p[\![x]\!])\rtimes (C\otimes \mathbb{Z}_{p}),\end{eqnarray}$$
with the action of
$C\otimes \mathbb{Z}_{p}$
on
$\mathbb{Z}/p[\![x]\!]$
described above (see [Reference Ivanov and MikhailovIM16, Proposition 4.12]). We call the group
${\mathcal{D}}{\mathcal{L}}$
the double lamplighter pro-
$p$
-group.
Theorem 4.3. The kernel of the comparison homomorphism for the double lamplighter pro-
$p$
-group,
$$\begin{eqnarray}\unicode[STIX]{x1D711}:H_{2}^{\mathsf{disc}}({\mathcal{D}}{\mathcal{L}},\mathbb{Z}/p)\longrightarrow H_{2}^{\mathsf{cont}}({\mathcal{D}}{\mathcal{L}},\mathbb{Z}/p),\end{eqnarray}$$
is uncountable.
Proof. For the sake of simplicity we set
$H_{2}(-)=H_{2}(-,\mathbb{Z}/p)$
and
$H_{2}^{\mathsf{cont}}(-)=H_{2}^{\mathsf{cont}}(-,\mathbb{Z}/p)$
. Consider the homological spectral sequence
$E$
of the short exact sequence
$\mathbb{Z}/p[\![x]\!]^{2}\rightarrowtail {\mathcal{D}}{\mathcal{L}}{\twoheadrightarrow}C\otimes \mathbb{Z}_{p}$
. Then the zero line of the second page is trivial:
$E_{k,0}^{2}=H_{k}(C\otimes \mathbb{Z}_{p})=(\unicode[STIX]{x1D6EC}^{k}\mathbb{Z}_{p})\otimes \mathbb{Z}/p=0$
for
$k\geqslant 2$
. Using Lemma 4.1, we obtain
$H_{k}(C\otimes \mathbb{Z}_{p},\mathbb{Z}/p[\![x]\!])=H_{k}(C,\mathbb{Z}/p[C])=0$
for
$k\geqslant 1$
, and hence
$E_{k,1}^{2}=0$
for
$k\geqslant 1$
. It follows that
$$\begin{eqnarray}H_{2}({\mathcal{D}}{\mathcal{L}})=E_{0,2}^{2}.\end{eqnarray}$$
For any
$\mathbb{Z}/p$
-vector space
$V$
, the Künneth formula gives a natural isomorphism
$$\begin{eqnarray}H_{2}(V\oplus V)\cong (V\otimes V)\oplus H_{2}(V)^{2}.\end{eqnarray}$$
Then we have a split monomorphism,
$$\begin{eqnarray}(\mathbb{Z}/p[\![x]\!]\otimes \mathbb{Z}/p[\![x]\!])_{C\otimes \mathbb{Z}_{p}}\rightarrowtail E_{0,2}^{2}=H_{2}({\mathcal{D}}{\mathcal{L}}).\end{eqnarray}$$
It easy to see that the groups
${\mathcal{D}}{\mathcal{L}}_{(i)}=((x^{i})\oplus (x^{i}))\rtimes (C\otimes p^{i}\mathbb{Z}_{p})$
form a fundamental system of open normal subgroups. Consider the quotients
${\mathcal{D}}{\mathcal{L}}^{(i)}={\mathcal{D}}{\mathcal{L}}/{\mathcal{D}}{\mathcal{L}}_{(i)}$
. Then
$$\begin{eqnarray}H_{2}^{\mathsf{cont}}({\mathcal{D}}{\mathcal{L}})=\varprojlim H_{2}({\mathcal{D}}{\mathcal{L}}^{(i)}).\end{eqnarray}$$
The short exact sequence
$\mathbb{Z}/p[\![x]\!]^{2}\rightarrowtail {\mathcal{D}}{\mathcal{L}}{\twoheadrightarrow}C\otimes \mathbb{Z}_{p}$
maps onto the short exact sequence
$(\mathbb{Z}/p[x]/(x^{i}))^{2}\rightarrowtail {\mathcal{D}}{\mathcal{L}}^{(i)}{\twoheadrightarrow}C/C^{p^{i}}$
. Consider the morphism of corresponding spectral sequences
$E\rightarrow ^{(i)}\!E$
. Using (4.1), we obtain
$$\begin{eqnarray}\text{Ker}(H_{2}({\mathcal{D}}{\mathcal{L}})\rightarrow H_{2}({\mathcal{D}}{\mathcal{L}}^{(i)}))\supseteq \text{Ker}(E_{2,0}^{2}\rightarrow ^{(i)}\!E_{2,0}^{2}).\end{eqnarray}$$
Similarly to (4.2), we have a split monomorphism
$$\begin{eqnarray}(\mathbb{Z}/p[x]/(x^{i})\otimes \mathbb{Z}/p[x]/(x^{i}))_{C\otimes \mathbb{Z}_{p}}\rightarrowtail ^{(i)}E_{2,0}^{2}.\end{eqnarray}$$
Then we need to prove that the kernel of the map
$$\begin{eqnarray}(\mathbb{Z}/p[\![x]\!]\otimes \mathbb{Z}/p[\![x]\!])_{C\otimes \mathbb{Z}_{p}}\longrightarrow \varprojlim (\mathbb{Z}/p[x]/(x^{i})\otimes \mathbb{Z}/p[x]/(x^{i}))_{C\otimes \mathbb{Z}_{p}}\end{eqnarray}$$
is uncountable.
Consider the antipod
$\unicode[STIX]{x1D70E}:\mathbb{Z}/p[C]\rightarrow \mathbb{Z}/p[C]$
, that is, the ring homomorphism given by
$\unicode[STIX]{x1D70E}(t^{n})=t^{-n}$
. The antipod induces a homomorphism
$\unicode[STIX]{x1D70E}:\mathbb{Z}/p[x]/(x^{i})\rightarrow \mathbb{Z}/p[x]/(x^{i})$
such that
$\unicode[STIX]{x1D70E}(1-x)=1+x+x^{2}+\cdots \,$
. It induces the continuous homomorphism
$\unicode[STIX]{x1D70E}:\mathbb{Z}/p[\![x]\!]\rightarrow \mathbb{Z}/p[\![x]\!]$
such that
$\unicode[STIX]{x1D70E}(x)=-x-x^{2}-\cdots \,$
. Moreover, we consider the antipode
$\unicode[STIX]{x1D70E}$
on
$\mathbb{Z}/p[C\otimes \mathbb{Z}_{p}]$
. Note that the homomorphisms
$$\begin{eqnarray}\mathbb{Z}/p[C]\rightarrow \mathbb{Z}/p[C\otimes \mathbb{Z}_{p}]\rightarrow \mathbb{Z}/p[\![x]\!]\rightarrow \mathbb{Z}/p[x]/(x^{i})\end{eqnarray}$$
commute with the antipodes.
By Lemma 4.2 the correspondence
$a\otimes b\leftrightarrow a\otimes \unicode[STIX]{x1D70E}(b)$
gives isomorphisms
$$\begin{eqnarray}\displaystyle (\mathbb{Z}/p[\![x]\!]\otimes \mathbb{Z}/p[\![x]\!])_{C\otimes \mathbb{Z}_{p}} & \cong & \displaystyle \mathbb{Z}/p[\![x]\!]\otimes _{\mathbb{Z}/p[C\otimes \mathbb{Z}_{p}]}\mathbb{Z}/p[\![x]\!],\nonumber\\ \displaystyle (\mathbb{Z}/p[x]/(x^{i})\otimes \mathbb{Z}/p[x]/(x^{i}))_{C\otimes \mathbb{Z}_{p}} & \cong & \displaystyle \mathbb{Z}/p[x]/(x^{i})\otimes _{\mathbb{Z}/p[C\otimes \mathbb{Z}_{p}]}\mathbb{Z}/p[x]/(x^{i}).\nonumber\end{eqnarray}$$
Moreover, since
$\mathbb{Z}/p[C\otimes \mathbb{Z}_{p}]\rightarrow \mathbb{Z}/p[x]/(x^{i})$
is an epimorphism, we obtain
$$\begin{eqnarray}\mathbb{Z}/p[x]/(x^{i})\otimes _{\mathbb{ Z}/p[C\otimes \mathbb{Z}_{p}]}\mathbb{Z}/p[x]/(x^{i})\cong \mathbb{Z}/p[x]/(x^{i}).\end{eqnarray}$$
Therefore the homomorphism (4.3) is isomorphic to the multiplication homomorphism
$$\begin{eqnarray}\mathbb{Z}/p[\![x]\!]\otimes _{\mathbb{Z}/p[C\otimes \mathbb{Z}_{p}]}\mathbb{Z}/p[\![x]\!]\longrightarrow \mathbb{Z}/p[\![x]\!],\end{eqnarray}$$
whose kernel is uncountable by Proposition 3.3. ◻
5 Proof of main theorem
Since the double lamplighter pro-
$p$
-group is 3-generated, we have a continuous epimorphism
$\hat{F}_{p}{\twoheadrightarrow}{\mathcal{D}}{\mathcal{L}}$
, where
$F$
is the 3-generated free group. Then the statement of the theorem for the 3-generated free group follows from Proposition 4.3 and Corollary 2.6. Using the fact that the 3-generated free group is a retract of the
$k$
-generated free group for
$k\geqslant 3$
, we obtain the result for
$k\geqslant 3$
. The result for the 2-generated free group follows from [Reference BousfieldBou92, Lemma 11.2].
Acknowledgement
The research is supported by the Russian Science Foundation grant N 16-11-10073.
