Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-06T08:08:29.277Z Has data issue: false hasContentIssue false
  • English
  • Français

Nondrifting relativistic electromagnetic solitons in plasmas

Published online by Cambridge University Press:  25 March 2004

M. LONTANO ,
M. BORGHESI ,
S.V. BULANOV ,
T.Z. ESIRKEPOV ,
D. FARINA ,
N. NAUMOVA ,
K. NISHIHARA ,
M. PASSONI ,
F. PEGORARO  and
H. RUHL
...Show all authors
M. LONTANO
Affiliation:
Istituto di Fisica del Plasma “P. Caldirola,” Consiglio Nazionale delle Ricerche, Milan, Italy
M. BORGHESI
Affiliation:
Department of Pure & Applied Physics, Queen's University, Belfast, United Kingdom
S.V. BULANOV
Affiliation:
General Physics Institute, Russia Academy of Sciences, Moscow, Russia Advanced Photon Research Center, Japan Atomic Energy Research Institute, Kyoto-fu, Japan
T.Z. ESIRKEPOV
Affiliation:
Advanced Photon Research Center, Japan Atomic Energy Research Institute, Kyoto-fu, Japan
D. FARINA
Affiliation:
Istituto di Fisica del Plasma “P. Caldirola,” Consiglio Nazionale delle Ricerche, Milan, Italy
N. NAUMOVA
Affiliation:
Center for Ultrafast Optical Science, University of Michigan, Ann Arbor, Michigan
K. NISHIHARA
Affiliation:
Institute of Laser Engineering, Osaka University, Japan
M. PASSONI
Affiliation:
Istituto di Fisica del Plasma “P. Caldirola,” Consiglio Nazionale delle Ricerche, Milan, Italy Dipartimento di Ingegneria Nucleare, Politecnico di Milano, Milan, Italy
F. PEGORARO
Affiliation:
Istituto Nazionale di Fisica della Materia, Universita' di Pisa, Pisa, Italy
H. RUHL
Affiliation:
General Atomics, San Diego, California
A.S. SAKHAROV
Affiliation:
General Physics Institute, Russia Academy of Sciences, Moscow, Russia
O. WILLI
Affiliation:
Institut für Laser- und Plasmaphysik, Heinrich-Heine-Universität, Düsseldorf, Germany
Rights & Permissions [Opens in a new window]

Abstract

Low-frequency, relativistic, subcycle solitary waves are found in two-dimensional and three-dimensional particle-in-cell (PIC) numerical simulations, as a result of the interaction of ultrashort, high-intensity laser pulses with plasmas. Moreover, nondrifting, subcycle relativistic electromagnetic solitons have been obtained as solutions of the hydrodynamic equations for an electron–ion warm plasma, by assuming the quasi-neutrality character of the plasma response. In addition, the formation of long-living macroscopic soliton-like structures has been experimentally observed by means of the proton imaging diagnostics. Several common features result from these investigations, as, for example, the quasi-neutral plasma response to the soliton radiation, in the long-term evolution of the system, which leads to the almost complete expulsion of the plasma from the region where the electromagnetic radiation is concentrated, even at subrelativistic field intensity. The results of the theoretical investigations are reviewed with special attention to these similarities.

Keywords

Laser-plasma interactionParticle-in-cell simulationsRelativistic hydrodynamicsSolitons
Type
Research Article
Information
Laser and Particle Beams , Volume 21 , Issue 4 , October 2003 , pp. 541 - 544
Copyright
© 2003 Cambridge University Press

1. INTRODUCTION

The rapid technological advance in high-peak-power, ultrashort-pulse lasers makes available hundred-terawatt (Yamakawa et al., 1998, 2002; Watts et al., 2002) and even petawatt (Perry et al., 1999; Kitagawa et al., 2002; Yamakawa et al., 2002) sources, which allow one to investigate experimentally extreme states of matter (Mourou et al., 1998), where electrons are accelerated to posc >> me c by the laser field (in the range of 1012 V/cm), and ions are driven up to several hundreds megaelectron volts by the induced charge separation.

The availability of these laser intensities has opened up the new field of relativistic nonlinear optics (Umstadter, 2002), characterized by the dependence of the refractive index of the medium on the laser intensity through the relativistic electron mass variation.

When an ultraintense laser pulse propagates in a plasma, several nonlinear phenomena are excited, as, for example, laser frequency variation, high-order harmonic generation, the appearance of coherent nonlinear structures (plasma channels, relativistic solitons, vortices), the generation of ultraintense quasistatic electric and magnetic fields, and electron and ion acceleration to relativistic energies. Up-to-date reviews of such effects are given by Bulanov et al. (2001, 2002). Generally speaking, a nonnegligible fraction of the laser pulse energy is involved in these processes (e.g., up to 20% remains in the plasma in the form of relativistic electromagnetic solitons). Therefore it is of primary importance to investigate their nature to control their occurrence and possibly to take advantage from their “applications.”

In this article, we shall review the recent theoretical results on the relativistic electromagnetic solitons (RES), which are likely to be excited during the propagation of a relativistically strong laser pulse in an underdense plasma (Lontano et al., 2002a). Early one-dimensional (1D) particle-in-cell (PIC) simulations (Bulanov et al., 1992, 1995), with moving electrons and immobile ions, showed that an ultrastrong laser pulse, due to the strong nonlinear character of the interaction with the background plasma, undergoes dramatic changes in its characteristics, its shape, frequency, and intensity. In particular, as a result of such an interaction, it was observed that part of the electromagnetic (EM) radiation of the pulse is subjected to a frequency down-shift, which causes it to be trapped inside electron density wells,. Therefore, long-living, slowly drifting concentrations of EM energy behind the laser pulse are formed, which appear as subcycle RES with frequency ω to which a strong longitudinal quasistatic electric field is associated. Such a field may impart electrons a momentum up to tens or hundreds of me c. The 1D RES possesses a small drift velocity (about 1/40th of the speed of light), and can move forward or backward, with respect to the parent pulse direction of propagation. It was also shown that two counterpropagating 1D RES undergo “collisions,” from which they emerge unchanged. The typical width of such an EM structure is of the order of the classical electron skin depth λsk = c/ωpe. The formation of 1D RES in an overdense plasma, at the vacuum–plasma interface, has been also numerically shown (Bulanov et al., 1994).

It was shown that the process of formation of RES in underdense plasmas would take place in two-dimensions, as well (Bulanov et al., 1999). Similarly to the 1D case, two-dimensional (2D) RES are subcycle, their frequency is lower and their intensity is higher than those of the laser pulse from which they have originated, and their characteristic dimension is λsk. However, 2D simulations predict an almost zero soliton speed in a uniform background plasma. A 2D RES can be made to move if it is excited in a nonuniform plasma (Sentoku et al., 1999). In the presence of a density inhomogeneity, the RES manifests the tendency to drift against the plasma density gradients. Therefore, in a plasma of limited size, with a monotonously decreasing density toward its boundaries, a RES will inevitably escape from the plasma region, emitting its EM energy in the form of a burst of radiation.

In the next section we shall describe the results of the more recent PIC simulations (2D, typically using 3 × 106 quasiparticles, distributed in 480 × 480 cells, with a spatial resolution of

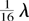
; three-dimensional (3D), using up to 426 × 106 quasiparticles, in 660 × 400 × 400 cells, with resolution of

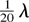
), where both the electron and ion response are retained.

2. RES IN AN ELECTRON–ION PLASMA

When the ion motion is included in the PIC simulations, the asymptotic evolution of the RES manifests new peculiarities: In particular, no long-term steady state is attained, at least over a few hundreds laser periods tL = 2π/ω (Naumova et al., 2001). Indeed, 2D PIC simulations confirm that, for times shorter than ti = (mi /me)1/2tL, relativistically intense laser pulses, of transverse typical dimensions of the order of a few laser wavelengths, produce RES associated with the formation of an electron density well, whereas ions remain almost unperturbed. However, for times longer than ti, the ion response to the electrostatic field created by the charge separation no longer can be neglected. Ions start to be expelled from the region where the EM energy is concentrated, and the plasma tends to recover its quasi-neutral state. The long-term state can be described as a nondrifting, slowly expanding, almost completely evacuated density hole, in which the EM radiation of the RES is trapped. This cylindrical cavity is surrounded by a “plasma wall,” which is produced as a snow-plow effect by the radiation pressure that drives the expansion. Because the EM energy inside the density cavity is constant, its average value decreases with time: The plasma cavity and its slow radial expansion are then sustained by a nonrelativistic ponderomotive force. These EM structures have been named “postsolitons” (Naumova et al., 2001). In Figure 1, the EM field intensity (upper row), and the electron and ion density distributions in the y-direction, transverse to the laser pulse propagation direction (x), are shown at three subsequent times of the 2D PIC simulation. A driving laser pulse with λ∥ = λ⊥ = 4λ, a = 1, and ω = (4/3) ωpe was considered.

Dimensionless EM energy density (upper row) and electron (gray line) and ion (solid line) densities (lower row), versus the transverse spatial coordinate y, for t = 18, 45, 90 (in units of 2π/ω). The plots are taken at the x-position of the center of the standing soliton behind the relativistic laser pulse. Here, the dimensionless pulse amplitude a = 1, and the background electron density n = 0.56ncr have been considered. The relevant 2D simulations are described in Naumova et al. (2001).

If a wider (λ⊥ = 30 λ) laser pulse is injected into the target plasma, a cluster of postsolitons is produced in its wake, which tend to merge into one another and to produce a unique postsoliton characterized by a typical scale of tens of λsk (Borghesi et al., 2002a).

The generation of 3D postsolitons, in the wake of a relativistic laser pulse propagating in an underdense plasma, has been shown by Esirkepov et al. (2002), as well. Similar to the 2D case, after the transient phase during which the electron response dominates, quasi-neutral density cavities, which are slowly expanding in the radial direction, are formed where the subcycle EM energy of the initial RES is trapped. Inside the density cavity, a quasi-static electric field is sustained by the small residual charge separation.

In Figure 2, a surface plot of the EM energy density spatial distribution is shown. The dashed lines single out the region where the plasma exists. The EM energy is concentrated at the location of the 3D postsolitons. On the right side of the plasma, the laser pulse after emerging from the plasma is plotted. In Figure 3, the surface plots of the electron (a) and of the ion density (b) are shown, at t = 101, during the postsoliton phase. The quasi-neutral character of the plasma density perturbation is evident.

Surface plot of the EM energy density associated with the laser pulse leaving the plasma (right red spot for 20 < x/λ < 30), and with the solitons left inside the plasma (small spots within 5 < x/λ < 15), at t = 35 (in units of 2π/ω).

Surface plots of the electron (a) and ion (b) densities, at t = 101. The encircled quasi-neutral density evacuation is produced by the standing solitons localized at 12 < x/λ < 16 (Esirkepov et al., 2002).

In parallel to the numerical investigations, a hydrodynamic approach to the RES in a multicomponent hot plasma has been pursued on the basis of two different models. In a first paper (Lontano et al., 2001) the set of relativistic hydrodynamic equations for a hot plasma, coupled to the Maxwell's equations, have been derived from first principles, starting from the conservation laws of the particle number and of the energy-momentum tensor. The adiabatic closure of the fluid equations has been assumed, leading to the entropy conservation for each species.

An alternative kinetic model (isothermal), where the electron and ion temperatures enter as constant parameters, has been formulated (Lontano et al., 2002b), starting from given particle distribution functions that are exact solutions of the 1D relativistic Vlasov equations for each species, in the presence of the circularly polarized EM radiation. Contrary to the adiabatic model, the isothermal one corresponds to a state characterized by a strongly anisotropic distribution function, with a thermal spread in the longitudinal direction and the transverse structure dominated by the large amplitude EM radiation (specifically, the RES). The two models have been used to investigate RES in an electron–positron plasma (Lontano et al., 2001, 2002b). Recently, also supported by the numerical evidences, the isothermal model has been applied to investigate 1D RES in a hot quasi-neutral electron–ion plasma (Lontano et al., 2002b).

Besides the possibility of getting ultrarelativistic EM solitons in a hot plasma (with T >> me c2), it has been shown that in relatively cold (T ≈ 10−3 me c2), overdense plasmas, subrelativistic subcycle EM solitons exist, which can drive the almost complete expulsion of the plasma density from their location. In addition, it has been shown that in sufficiently overdense plasmas, the typical spatial scale of the solitons is larger than λsk by a factor ωpe /ω (>>1). It has been also demonstrated that such 1D structures are accompanied by a quasi-stationary longitudinal electric field (i.e., constant over the radiation period) of the order of several tens of megaelectron volts per centimeter. In Figure 4, the dimensionless values of the scalar vector potential, eA/me c2 (A), and of the plasma density, N/N0 (B), are plotted versus the spatial coordinate, xωpe /c, for Te = 500 eV, Ti = 50 eV, for several frequency values: ω/ωpe = 0.3 (a), 0.4 (b), 0.5 (c), 0.6 (d), 0.7 (e). It is shown that at low temperature, almost complete plasma cavitation can take place. It is interesting to compare the plots in Figure 1, at t = 120, with those in Figure 4. In both cases, localized EM distributions with typical scales of few λsk are found, which produce a deep quasi-neutral well in the plasma. Moreover, the radiation intensity is subrelativistic and its frequency is lower than ωpe (ω ≈ 0.8ωpe). The presence of the “density wall” surrounding the postsoliton, in Figure 1, is due to the slow expansion which is under way. This feature is missing in the hydrodynamic picture because it deals with the asymptotic stationary state of the system.

The dimensionless vector potential amplitude eA/me c2 (A) and ion density Ni /N0 (B) versus the spatial coordinate xωpe /c, for Te = 500 eV, Ti = 50 eV, and several frequencies: ω/ωpe = 0.3 (a), 0.4 (b), 0.5 (c), 0.6 (d), 0.7 (e). The plots refer to the 1D kinetic model described in Lontano et al. (2002b, 2003).

Recently, the first experimental evidence of long-living macroscopic bubble-like structures, formed during intense laser–plasma interaction, has been obtained by measuring localized deflection of a proton beam caused by the quasistatic electric field associated with the bubbles (Borghesi et al., 2002a). A typical datum, obtained with the proton imaging technique (Borghesi et al., 2002b), is shown in Figure 5. The spatial scale of such structures is of the order of 50 μm, which is about a hundred times λsk ≈ 0.5 μm, for λ = 1 μm and a peak plasma density ≈ 0.1ncr, and their lifetime is ≈50 ps, corresponding to 104tL. From a single-particle model, the quasi-static electric field producing the probe protons deflection has been estimated to be 40 MV/cm.

Proton image of a preformed plasma (peak density ∼ 1020 cm−3) taken with 6–7 MeV protons, 45 ps after propagation of an intense (I ∼ 1019 W/cm2) 1-μm, 1-ps laser pulse. The dashed line indicates the dimensions of the preformed plasma defined by nc = 0.01ncr (at λ = 1 μm; Borghesi et al., 2002a).

In conclusion, several theoretical and experimental arguments can be brought forward to support the principal role played by relativistic electromagnetic solitary standing waves in the energy balance of the strong laser–plasma interaction in the relativistic regime. Such structures are subcycle, quasi-neutral, and are associated to an intense quasi-static electric field, which can be exploited for particle acceleration, provided we find the way to drive and to control their characteristics.

ACKNOWLEDGMENT

Part of this work has been performed in the frame of the INTAS Project 01-0233.

References

REFERENCES

Borghesi, M. et al. (2002a). Phys. Rev. Lett. 88, 135002.
Borghesi, M. et al. (2002b). Phys. Plasmas 9, 2214–2220.
Bulanov, S.V. et al. (1992). Phys. Fluids B 4, 1935–1942.
Bulanov, S.V. et al. (1994). Phys. Plasmas 1, 745–757.
Bulanov, S.V. et al. (1995). Plasma Phys. Rep. 21, 550–561.
Bulanov, S.V. et al. (1999). Phys. Rev. Lett. 82, 3440–3443.
Bulanov, S.V. et al. (2001). Relativistic interaction of laser pulses with plasmas. In Reviews of Plasma Physics (Shafranov, V.D., Ed.), vol. 22, pp. 227–335. New York: Kluwer Academic/Plenum.
Bulanov, S.V. et al. (2002). Relativistic interaction of ultra-short laser pulses with plasmas, in superstrong fields in plasmas. In 2nd Int. Conf. on Superstrong Fields in Plasmas (Lontano, M., Mourou, G., Svelto, O. & Tajima, T., Eds.), AIP Conference Proceedings, vol. 611, pp. 104–118. New York: American Institute of Physics.
Esirkepov, T.Zh. et al. (2002). Phys. Rev. Lett. 89, 275002.
Kitagawa, Y. et al. (2002). Phys. Plasmas 9, 2202–2207.
Lontano, M. et al. (2001). Phys. Plasmas 8, 5113–5120.
Lontano, M. et al. (2002a). Relativistic electromagnetic solitons produced by ultrastrong laser pulses in plasmas. In Int. Conf. on Science of Superstrong Field Interactions (Nakajima, K. & Deguchi, M., Eds.), AIP Conf. Proceedings, vol. 634, pp. 87–98. New York: American Institute of Physics.
Lontano, M. et al. (2002b). Phys. Plasmas 9, 2562–2568.
Lontano, M. et al. (2003). Phys. Plasmas 10, 639–649.
Mourou, G.A. et al. (1998). Phys. Today 51, 22–28.
Naumova, N.M. et al. (2001). Phys. Rev. Lett. 87, 185004.
Perry, M.D. et al. (1999). Optics Letters 24, 160–162.
Sentoku, Y. et al. (1999). Phys. Rev. Lett. 83, 3434–3437.
Umstadter, D. (2002). In 2nd Int. Conf. on Superstrong Fields in Plasmas (Lontano, M. et al., Eds.), AIP Conference Proceedings, vol. 611, pp. 95–103. New York: American Institute of Physics.
Watts, I. et al. (2002). Phys. Rev. E 66, 036409.
Yamakawa, K. et al. (1998). Op. Lett. 23, 1468–1470.
Yamakawa, K. et al. (2002). Status and future developments of ultrahigh intensity lasers at JAERI. In 2nd Int. Conf. on Superstrong Fields in Plasmas (Lontano, M., Mourou, G., Svelto, O. & Tajima, T., Eds.), AIP Conference Proceedings, vol. 611, pp. 385–396. New York: American Institute of Physics.
Figure 0

Dimensionless EM energy density (upper row) and electron (gray line) and ion (solid line) densities (lower row), versus the transverse spatial coordinate y, for t = 18, 45, 90 (in units of 2π/ω). The plots are taken at the x-position of the center of the standing soliton behind the relativistic laser pulse. Here, the dimensionless pulse amplitude a = 1, and the background electron density n = 0.56ncr have been considered. The relevant 2D simulations are described in Naumova et al. (2001).

Figure 1

Surface plot of the EM energy density associated with the laser pulse leaving the plasma (right red spot for 20 < x/λ < 30), and with the solitons left inside the plasma (small spots within 5 < x/λ < 15), at t = 35 (in units of 2π/ω).

Figure 2

Surface plots of the electron (a) and ion (b) densities, at t = 101. The encircled quasi-neutral density evacuation is produced by the standing solitons localized at 12 < x/λ < 16 (Esirkepov et al., 2002).

Figure 3

The dimensionless vector potential amplitude eA/me c2 (A) and ion density Ni /N0 (B) versus the spatial coordinate xωpe /c, for Te = 500 eV, Ti = 50 eV, and several frequencies: ω/ωpe = 0.3 (a), 0.4 (b), 0.5 (c), 0.6 (d), 0.7 (e). The plots refer to the 1D kinetic model described in Lontano et al. (2002b, 2003).

Figure 4

Proton image of a preformed plasma (peak density ∼ 1020 cm−3) taken with 6–7 MeV protons, 45 ps after propagation of an intense (I ∼ 1019 W/cm2) 1-μm, 1-ps laser pulse. The dashed line indicates the dimensions of the preformed plasma defined by nc = 0.01ncr (at λ = 1 μm; Borghesi et al., 2002a).