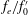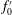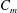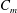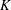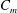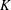1 Introduction
Understanding and manipulating jet mixing is of fundamental and crucial importance to many engineering applications such as mixing, noise suppression, combustion, lift augmentation, heat transfer and chemical reactors. Recent reviews (Glezer & Amitay Reference Glezer and Amitay2002; Reynolds et al. Reference Reynolds, Parekh, Juvet and Lee2003; Henderson Reference Henderson2010; Ginevsky, Vlasov & Karavosov Reference Ginevsky, Vlasov and Karavosov2004) provide excellent compendiums of published papers. Passive techniques are frequently used to enhance jet mixing. One example is to deploy tabs at the nozzle exit (Bradbury & Khadem Reference Bradbury and Khadem1975). A tab placed at the exit of an axisymmetric nozzle leads to a strong distortion of the mixing layer and subsequently the generation of a pair of counter-rotating streamwise vortices, thus enhancing significantly the entrainment of ambient fluid with a relatively small thrust penalty (Zaman, Reeder & Samimy Reference Zaman, Reeder and Samimy1994; Reeder & Samimy Reference Reeder and Samimy1996). Another passive technique is to use non-circular nozzles (Gutmark & Grinstein Reference Gutmark and Grinstein1999; Zaman Reference Zaman1999). Azimuthal non-uniformities at the jet exit may have a dramatic impact on the evolution of shear layers since the three-dimensional jet development is particularly sensitive to initial conditions. Non-circular jets are naturally more unstable than their circular counterpart (Ho & Gutmark Reference Ho and Gutmark1987; Hussain & Husain Reference Hussain and Husain1989; Husain & Hussain Reference Husain and Hussain1991, Reference Husain and Hussain1993; Mi, Nathan & Luxton Reference Mi, Nathan and Luxton2000), and produce shorter potential core lengths due to faster decay.
In spite of their impressive performances, the passive techniques are characterized by permanent fixtures. Once mounted, tabs are difficult to remove or re-arrange; similarly, it is unpractical for any engineering application to implement frequently non-circular nozzle geometry alteration due to cost and physical constraints. In engineering, the jet operation conditions may vary, e.g. burners used in the process (cement, lime, glass, steel) industries; an optimally performing nozzle under a certain operation condition may not work optimally under another. In aircraft, the highly intense mixing is required only for specific flight phases such as taking off or during combat. In contrast, the active manipulation of jets has potential to achieve more flexible and drastic flow modifications. This is a great advantage over those passive, though often efficient, techniques (e.g. Zaman et al. Reference Zaman, Reeder and Samimy1994; Longmire & Duong Reference Longmire and Duong1996; Reeder & Samimy Reference Reeder and Samimy1996; Webster & Longmire Reference Webster and Longmire1997; Zaman Reference Zaman1999; New & Tsovolos Reference New and Tsovolos2012). Naturally, many active techniques were proposed and investigated, including acoustic excitation (Cohen & Wygnanski Reference Cohen and Wygnanski1987a ,Reference Cohen and Wygnanski b ; Ginevsky et al. Reference Ginevsky, Vlasov and Karavosov2004), synthetic jet actuators (Smith & Glezer Reference Smith and Glezer1998, Reference Smith and Glezer2002; Glezer & Amitay Reference Glezer and Amitay2002), a combination of axial and circumferential excitations at the nozzle exit to produce bifurcating and blooming jets (Reynolds et al. Reference Reynolds, Parekh, Juvet and Lee2003), plasma actuators (Moreau Reference Moreau2007; Samimy et al. Reference Samimy, Kim, Kastner, Adamovich and Utkin2007; Corke, Enloe & Wilkinson Reference Corke, Enloe and Wilkinson2010), MEMS-based flap actuators (Suzuki, Kasagi & Suzuki Reference Suzuki, Kasagi and Suzuki2004; Cattafesta & Sheplak Reference Cattafesta and Sheplak2011), oscillating boundaries based on piezo-electric actuators (Wiltse & Glezer Reference Wiltse and Glezer1993) or steady/unsteady control jets (Henderson Reference Henderson2010).
The concept to use control jets to enhance jet mixing was proposed by Davis (Reference Davis1982) and pursued by a number of investigators based on steady blowing jets (e.g. Lardeau, Lamballais & Bonnet Reference Lardeau, Lamballais and Bonnet2002; Arakeri et al. Reference Arakeri, Krothapalli, Siddavaram, Alkislar and Lourenco2003; New & Tay Reference New and Tay2006; Tamburello & Amitay Reference Tamburello and Amitay2006; Zhou et al. Reference Zhou, Du, Mi and Wang2012). Seidel et al. (Reference Seidel, Pappart, New and Tsai2005) emulated the performance of non-circular jets by placing around a round main jet multiple steady radial blowing jets at positions where the corners or vertices would be if non-circular nozzles were used. Their results agree surprisingly well with those of corresponding non-circular jets (Mi et al. Reference Mi, Nathan and Luxton2000), indicating that a jet may be manipulated, based on fluidic means, to achieve optimized performance under different operation conditions.
The control jet may be pulsed or unsteady to optimize the actuator efficiency (e.g. Freund & Moin Reference Freund and Moin2000). A pulsed jet allows jet penetration and spread to be enhanced at specific conditions of excitation (Lardeau et al.
Reference Lardeau, Lamballais and Bonnet2002), and may capitalize not only on large-scale changes through penetration but also on the excitation frequency to manipulate the inherent instabilities of the main jet. There have been a number of investigations on unsteady fluidic excitation, which is not so well documented as its steady counterpart. Raman & Cornelius (Reference Raman and Cornelius1995) first demonstrated successfully the manipulation of a rectangular jet under unsteady fluidic excitation at a Reynolds number of
![]() $1.34\times 10^{5}$
based on the equivalent diameter of the nozzle. Two pulsed minijets were deployed, each placed in the middle of the long side of the rectangular nozzle. The mass flow rate ratio
$1.34\times 10^{5}$
based on the equivalent diameter of the nozzle. Two pulsed minijets were deployed, each placed in the middle of the long side of the rectangular nozzle. The mass flow rate ratio
![]() $C_{m}$
of the minijets to the primary jet was 24 % and the excitation frequency ratio
$C_{m}$
of the minijets to the primary jet was 24 % and the excitation frequency ratio
![]() $f_{e}/f_{0}$
was 0.5 (the normalized frequency
$f_{e}/f_{0}$
was 0.5 (the normalized frequency
![]() $f_{e}D_{e}/U_{e}=0.15$
, based on the nozzle equivalent diameter
$f_{e}D_{e}/U_{e}=0.15$
, based on the nozzle equivalent diameter
![]() $D_{e}$
and exit velocity
$D_{e}$
and exit velocity
![]() $U_{e}$
), where
$U_{e}$
), where
![]() $f_{e}$
is the excitation frequency of the unsteady jets and
$f_{e}$
is the excitation frequency of the unsteady jets and
![]() $f_{0}$
the preferred-mode frequency of the natural primary jet. Raman (Reference Raman1997) showed a 35 % reduction in the potential core length of the perturbed rectangular jet. Parekh et al. (Reference Parekh, Kibens, Glezer, Wiltse and Smith1996) experimentally manipulated a subsonic circular jet using pulsed fluidic excitation through two circular slit orifices placed on opposite sides of the round nozzle and found that jet mixing depended strongly on
$f_{0}$
the preferred-mode frequency of the natural primary jet. Raman (Reference Raman1997) showed a 35 % reduction in the potential core length of the perturbed rectangular jet. Parekh et al. (Reference Parekh, Kibens, Glezer, Wiltse and Smith1996) experimentally manipulated a subsonic circular jet using pulsed fluidic excitation through two circular slit orifices placed on opposite sides of the round nozzle and found that jet mixing depended strongly on
![]() $f_{e}/f_{0}$
and
$f_{e}/f_{0}$
and
![]() $C_{m}$
. Ibrahim, Kunimura & Nakamura (Reference Ibrahim, Kunimura and Nakamura2002), Lardeau et al. (Reference Lardeau, Lamballais and Bonnet2002), Choi et al. (Reference Choi, Annaswamy, Lou and Alvi2006), Annaswamy, Choi & Alvi (Reference Annaswamy, Choi and Alvi2008) demonstrated that the pulsed minijets are more effective in enhancing supersonic or subsonic jet mixing or noise mitigation than their steady counterparts. The underlying reason might be due to the deeper penetration of unsteady fluidic injection into the potential core (Lardeau et al.
Reference Lardeau, Lamballais and Bonnet2002) and periodic excitation of jet instabilities (Henderson Reference Henderson2010). In spite of previous investigations, a systematic study of unsteady fluidic excitation has yet to be performed; the dependence of the control performance on
$C_{m}$
. Ibrahim, Kunimura & Nakamura (Reference Ibrahim, Kunimura and Nakamura2002), Lardeau et al. (Reference Lardeau, Lamballais and Bonnet2002), Choi et al. (Reference Choi, Annaswamy, Lou and Alvi2006), Annaswamy, Choi & Alvi (Reference Annaswamy, Choi and Alvi2008) demonstrated that the pulsed minijets are more effective in enhancing supersonic or subsonic jet mixing or noise mitigation than their steady counterparts. The underlying reason might be due to the deeper penetration of unsteady fluidic injection into the potential core (Lardeau et al.
Reference Lardeau, Lamballais and Bonnet2002) and periodic excitation of jet instabilities (Henderson Reference Henderson2010). In spite of previous investigations, a systematic study of unsteady fluidic excitation has yet to be performed; the dependence of the control performance on
![]() $f_{e}/f_{0}$
or
$f_{e}/f_{0}$
or
![]() $C_{m}$
needs to be better understood. The physical picture behind interactions between the steady minijets and the main jet has been unveiled by New & Tay (Reference New and Tay2006) and Alkislar, Krothapalli & Butler (Reference Alkislar, Krothapalli and Butler2007). The unsteady minijet excitation is much more efficient than the steady minijet case (Annaswamy et al.
Reference Annaswamy, Choi and Alvi2008; Cattafesta & Sheplak Reference Cattafesta and Sheplak2011). One may surmise that the interactions between the main jet and unsteady minijets must be different from that under the manipulation of steady minijets. Nevertheless, this difference remains elusive. For example, how do the pulsed minijet injections change the formation of the coherent structures in the main jet? How does this change influence the flow structure and its downstream development? Furthermore, the pulsed minijets can be effective at large
$C_{m}$
needs to be better understood. The physical picture behind interactions between the steady minijets and the main jet has been unveiled by New & Tay (Reference New and Tay2006) and Alkislar, Krothapalli & Butler (Reference Alkislar, Krothapalli and Butler2007). The unsteady minijet excitation is much more efficient than the steady minijet case (Annaswamy et al.
Reference Annaswamy, Choi and Alvi2008; Cattafesta & Sheplak Reference Cattafesta and Sheplak2011). One may surmise that the interactions between the main jet and unsteady minijets must be different from that under the manipulation of steady minijets. Nevertheless, this difference remains elusive. For example, how do the pulsed minijet injections change the formation of the coherent structures in the main jet? How does this change influence the flow structure and its downstream development? Furthermore, the pulsed minijets can be effective at large
![]() $C_{m}$
(e.g. Raman & Cornelius Reference Raman and Cornelius1995) or at small
$C_{m}$
(e.g. Raman & Cornelius Reference Raman and Cornelius1995) or at small
![]() $C_{m}$
(e.g. Parekh et al.
Reference Parekh, Kibens, Glezer, Wiltse and Smith1996). Are the physical mechanisms behind the effective manipulation the same? If not, what are they exactly?
$C_{m}$
(e.g. Parekh et al.
Reference Parekh, Kibens, Glezer, Wiltse and Smith1996). Are the physical mechanisms behind the effective manipulation the same? If not, what are they exactly?
This work aims to study experimentally and systematically the axisymmetric jet under the excitation of unsteady minijets with a view to addressing the issues raised above. Focus is given to jet manipulation using two opposing unsteady radial minijets placed upstream of the nozzle exit. Two parameters are examined in detail, i.e.
![]() $C_{m}$
and
$C_{m}$
and
![]() $f_{e}/f_{0}$
. Flow structures with and without excitation are measured using hot-wire, flow visualization and particle imaging velocimetry (PIV) techniques in order to gain a relatively thorough understanding of interactions between the main jet and unsteady minijet excitation.
$f_{e}/f_{0}$
. Flow structures with and without excitation are measured using hot-wire, flow visualization and particle imaging velocimetry (PIV) techniques in order to gain a relatively thorough understanding of interactions between the main jet and unsteady minijet excitation.
2 Experimental details
2.1 Experimental set-up
Experiments were carried out in a round air jet rig. Following Hussein, Capp & George (Reference Hussein, Capp and George1994), the rig was deployed in a spacious air-conditioned laboratory, centrally placed in an area of approximately 4.5 m in width and 4.0 m in height with the nozzle exit pointing at a wall 7.0 m away, to minimize the effects of the wall on the jet for example by pressure wave reflection. In view of the high sensitivity of the jet shear layer to background noise (Hussain Reference Hussain1986), there was no traffic, i.e. no object/person moving, at all during experiments. The rig consists largely of the main jet and minijet assemblies. The main jet and minijets came from a compressed air source with a constant 5 bar gauge pressure.
Figure 1(a) shows schematically the main jet assembly. On entering a large chamber, compressed air is mixed with seeding particles in the case of PIV or flow visualization measurements before passing through a tube, a plenum chamber, a 300 mm long diffuser of
![]() $15^{\circ }$
half-angle, two fine screens (7 mesh cm
$15^{\circ }$
half-angle, two fine screens (7 mesh cm
![]() $^{-1}$
) and a cylindrical settling chamber of 400 mm in length and 114 mm in inner diameter. The nozzle contraction contour is the same as used by Zhou et al. (Reference Zhou, Du, Mi and Wang2012) and Yang et al. (Reference Yang, Zhou, So and Liu2016), with a contraction ratio of 32.5 and an exit diameter
$^{-1}$
) and a cylindrical settling chamber of 400 mm in length and 114 mm in inner diameter. The nozzle contraction contour is the same as used by Zhou et al. (Reference Zhou, Du, Mi and Wang2012) and Yang et al. (Reference Yang, Zhou, So and Liu2016), with a contraction ratio of 32.5 and an exit diameter
![]() $D$
of 20 mm. The nozzle is extended by a 47 mm long smooth tube of the same
$D$
of 20 mm. The nozzle is extended by a 47 mm long smooth tube of the same
![]() $D$
. The exit Reynolds number
$D$
. The exit Reynolds number
![]() $Re_{D}=U_{e}D/\unicode[STIX]{x1D708}$
of the main jet is fixed at 8000, where
$Re_{D}=U_{e}D/\unicode[STIX]{x1D708}$
of the main jet is fixed at 8000, where
![]() $U_{e}=6~\text{m}~\text{s}^{-1}$
is the centreline velocity measured at the exit of the nozzle extension and
$U_{e}=6~\text{m}~\text{s}^{-1}$
is the centreline velocity measured at the exit of the nozzle extension and
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity of air.
$\unicode[STIX]{x1D708}$
is the kinematic viscosity of air.

Figure 1. Schematic of experimental set-up: (a) main jet assembly; (b) minijet assembly.
The minijet assembly (figure 1
b) includes a stationary and a rotating disk (nozzle extension). A novel unsteady minijet actuator is developed. The stationary disk is made with two orifices of 0.9 mm diameter, separated azimuthally by
![]() $180^{\circ }$
. The two orifices are connected via short and equal length tubes to a constant-pressure chamber. The rotating disk is rather unique and is actually the rotor of a servo motor (Kollmorgen RBE-03010) with a maximum speed of
$180^{\circ }$
. The two orifices are connected via short and equal length tubes to a constant-pressure chamber. The rotating disk is rather unique and is actually the rotor of a servo motor (Kollmorgen RBE-03010) with a maximum speed of
![]() $N=2950$
rpm. The rotating disk is drilled with 12 orifices of 1 mm in diameter, azimuthally equally spaced and located at 17 mm upstream of the extension exit, and its interior diameter is identical to the contraction nozzle exit diameter. Once the orifices on the stationary and rotating disks are aligned during rotation, a pulsed minijet is emitted radially towards the main jet axis, as shown in figure 1(b). The two opposing injections are in phase. The minijet pulsation or excitation frequency
$N=2950$
rpm. The rotating disk is drilled with 12 orifices of 1 mm in diameter, azimuthally equally spaced and located at 17 mm upstream of the extension exit, and its interior diameter is identical to the contraction nozzle exit diameter. Once the orifices on the stationary and rotating disks are aligned during rotation, a pulsed minijet is emitted radially towards the main jet axis, as shown in figure 1(b). The two opposing injections are in phase. The minijet pulsation or excitation frequency
![]() $f_{e}$
is then
$f_{e}$
is then
![]() $12N/60$
Hz, with a maximum of 590 Hz, which exceeds
$12N/60$
Hz, with a maximum of 590 Hz, which exceeds
![]() $4f_{0}$
. The flow rates of both main jet and minijets are adjustable independently via two separate flow meters with a measurement uncertainty of
$4f_{0}$
. The flow rates of both main jet and minijets are adjustable independently via two separate flow meters with a measurement uncertainty of
![]() ${<}$
1 %.
${<}$
1 %.
The coordinate system is defined such that its origin is at the centre of the nozzle extension exit, with the
![]() $x$
axis along the streamwise direction, the
$x$
axis along the streamwise direction, the
![]() $z$
axis along the radial minijet and the
$z$
axis along the radial minijet and the
![]() $y$
axis along the direction normal to both
$y$
axis along the direction normal to both
![]() $x$
and
$x$
and
![]() $y$
, following the right-hand system. The (
$y$
, following the right-hand system. The (
![]() $x,z$
) and (
$x,z$
) and (
![]() $x,y$
) planes are referred to as the injection and non-injection planes, respectively (figure 1
b).
$x,y$
) planes are referred to as the injection and non-injection planes, respectively (figure 1
b).
2.2 Measurements
A single tungsten wire of
![]() $5~\unicode[STIX]{x03BC}\text{m}$
in diameter, operated on a constant temperature circuit (Dantec Streamline) at an overheat ratio of 1.8, is used to measure the streamwise fluctuating velocity
$5~\unicode[STIX]{x03BC}\text{m}$
in diameter, operated on a constant temperature circuit (Dantec Streamline) at an overheat ratio of 1.8, is used to measure the streamwise fluctuating velocity
![]() $u$
at
$u$
at
![]() $x^{\ast }\leqslant 20$
. In this paper, asterisk denotes normalization by the jet exit mean velocity
$x^{\ast }\leqslant 20$
. In this paper, asterisk denotes normalization by the jet exit mean velocity
![]() $\overline{U}_{e}$
and/or nozzle diameter
$\overline{U}_{e}$
and/or nozzle diameter
![]() $D$
. The signal from the wire is offset, filtered at a cutoff frequency of 2.8 kHz, amplified and then digitized using a 12-bit analog/digital board at a sampling frequency of 6 kHz. The duration for each record is 80 s. This hot-wire probe is mounted on a computer-controlled two-dimensional traversing mechanism, whose streamwise and transverse resolutions are both 0.01 mm.
$D$
. The signal from the wire is offset, filtered at a cutoff frequency of 2.8 kHz, amplified and then digitized using a 12-bit analog/digital board at a sampling frequency of 6 kHz. The duration for each record is 80 s. This hot-wire probe is mounted on a computer-controlled two-dimensional traversing mechanism, whose streamwise and transverse resolutions are both 0.01 mm.
A planar PIV system (Dantec standard PIV2100) is deployed to measure velocities in the injection and non-injection planes as well as in a number of cross-sectional planes. A TSI oil droplet generator (TSI 9307-6) is used to generate fog for seeding flow. The seeding particles have a diameter of approximately
![]() $1~\unicode[STIX]{x03BC}\text{m}$
, which is adequate for tracking turbulent or high-speed gas flows (Melling Reference Melling1997). The particles are introduced into the upstream mixing chamber (figure 1
a), and thus homogenously distributed throughout the main jet. Meanwhile, ambient air is also seeded by filling the whole laboratory with the fog. Note that the concentration of the fog is not high enough to contaminate the camera lens of the PIV system. Flow illumination is provided by a light sheet, through the jet centreline, of approximately 1 mm in thickness, which is generated by two NewWave standard pulsed laser sources with 532 nm wavelength and a maximum energy output of 120 mJ per pulse. Particle images are captured at a sampling rate of 4 Hz using one HiSense MkII CCD camera (double frames, 2048
$1~\unicode[STIX]{x03BC}\text{m}$
, which is adequate for tracking turbulent or high-speed gas flows (Melling Reference Melling1997). The particles are introduced into the upstream mixing chamber (figure 1
a), and thus homogenously distributed throughout the main jet. Meanwhile, ambient air is also seeded by filling the whole laboratory with the fog. Note that the concentration of the fog is not high enough to contaminate the camera lens of the PIV system. Flow illumination is provided by a light sheet, through the jet centreline, of approximately 1 mm in thickness, which is generated by two NewWave standard pulsed laser sources with 532 nm wavelength and a maximum energy output of 120 mJ per pulse. Particle images are captured at a sampling rate of 4 Hz using one HiSense MkII CCD camera (double frames, 2048
![]() $\times$
2048 pixels). Synchronization between flow illumination and image capturing is provided by a Dantec Flow Map Processor (PIV 2001 type).
$\times$
2048 pixels). Synchronization between flow illumination and image capturing is provided by a Dantec Flow Map Processor (PIV 2001 type).
For PIV measurements in the (
![]() $x$
,
$x$
,
![]() $y$
) and (
$y$
) and (
![]() $x$
,
$x$
,
![]() $z$
) planes, the size of each image is 217 mm
$z$
) planes, the size of each image is 217 mm
![]() $\times$
217 mm, covering the area of
$\times$
217 mm, covering the area of
![]() $x^{\ast }=0\sim 10$
and
$x^{\ast }=0\sim 10$
and
![]() $y^{\ast }$
or
$y^{\ast }$
or
![]() $z^{\ast }=-5\sim +5$
. Both longitudinal and lateral image magnifications are 0.09 mm/pixel. The time interval is
$z^{\ast }=-5\sim +5$
. Both longitudinal and lateral image magnifications are 0.09 mm/pixel. The time interval is
![]() $75~\unicode[STIX]{x03BC}\text{s}$
between two consecutive laser pulses and a particle could travel only 0.45 mm (5 pixels or 0.02
$75~\unicode[STIX]{x03BC}\text{s}$
between two consecutive laser pulses and a particle could travel only 0.45 mm (5 pixels or 0.02
![]() $D$
) at
$D$
) at
![]() $U_{e}=6~\text{m}~\text{s}^{-1}$
. In image processing, a built-in adaptive correlation function of the Flow Map Processor (PIV 2001 type) is used. The initial interrogation window size was 256
$U_{e}=6~\text{m}~\text{s}^{-1}$
. In image processing, a built-in adaptive correlation function of the Flow Map Processor (PIV 2001 type) is used. The initial interrogation window size was 256
![]() $\times$
256 pixels and the number of passes was set to 2. An interrogation window of 32
$\times$
256 pixels and the number of passes was set to 2. An interrogation window of 32
![]() $\times$
32 pixels with a 75 % overlap in both directions is chosen, producing 253
$\times$
32 pixels with a 75 % overlap in both directions is chosen, producing 253
![]() $\times$
253 velocity vectors. This choice is based on an investigation on the effect of the interrogation widow size (32
$\times$
253 velocity vectors. This choice is based on an investigation on the effect of the interrogation widow size (32
![]() $\times$
32 and 16
$\times$
32 and 16
![]() $\times$
16 pixels) and overlap (50 %–75 %) on the mean velocity, which indicates that the present choice leads to reliable measurements for the mean velocity field. Flow images captured are 1400 pairs for each set of PIV data. A convergence test has been conducted for the PIV-measured centreline mean velocity
$\times$
16 pixels) and overlap (50 %–75 %) on the mean velocity, which indicates that the present choice leads to reliable measurements for the mean velocity field. Flow images captured are 1400 pairs for each set of PIV data. A convergence test has been conducted for the PIV-measured centreline mean velocity
![]() $\overline{U}_{c}^{\ast }$
, and it is found that the distributions of
$\overline{U}_{c}^{\ast }$
, and it is found that the distributions of
![]() $\overline{U}_{c}^{\ast }$
obtained from the image pairs of 1000, 1400, 1800 and 2150 all collapse very well, and further agree well, with a maximum departure of approximately 1 % for
$\overline{U}_{c}^{\ast }$
obtained from the image pairs of 1000, 1400, 1800 and 2150 all collapse very well, and further agree well, with a maximum departure of approximately 1 % for
![]() $x^{\ast }\leqslant 5$
, with that from the hot-wire measurements (not shown).
$x^{\ast }\leqslant 5$
, with that from the hot-wire measurements (not shown).
Measurements are performed in nine cross-sectional or (
![]() $y$
,
$y$
,
![]() $z$
) planes over
$z$
) planes over
![]() $x^{\ast }=0.1\sim 5.0$
. The light sheet is set at approximately 3 mm in thickness. The camera is placed approximately
$x^{\ast }=0.1\sim 5.0$
. The light sheet is set at approximately 3 mm in thickness. The camera is placed approximately
![]() $50D$
downstream from the light sheet so that the feedback effect of flow impinging on the camera lens is negligibly small. The image magnification is tailor made and chosen for each plane in order not only to cover the entire cross-section of the jet but also to maximize the image resolution. As the out-of-plane velocity component is large compared with two in-plane velocity components, the seeding particles could go through the light sheet if the time interval between two consecutive images is large, thus causing poor correlation (Pattenden, Turnock & Zhang Reference Pattenden, Turnock and Zhang2005; Huang, Zhou & Zhou Reference Huang, Zhou and Zhou2006). The time interval is presently chosen to be
$50D$
downstream from the light sheet so that the feedback effect of flow impinging on the camera lens is negligibly small. The image magnification is tailor made and chosen for each plane in order not only to cover the entire cross-section of the jet but also to maximize the image resolution. As the out-of-plane velocity component is large compared with two in-plane velocity components, the seeding particles could go through the light sheet if the time interval between two consecutive images is large, thus causing poor correlation (Pattenden, Turnock & Zhang Reference Pattenden, Turnock and Zhang2005; Huang, Zhou & Zhou Reference Huang, Zhou and Zhou2006). The time interval is presently chosen to be
![]() $25~\unicode[STIX]{x03BC}\text{s}$
, which is found to yield satisfactory results. The number of velocity vectors is the same as that in the (
$25~\unicode[STIX]{x03BC}\text{s}$
, which is found to yield satisfactory results. The number of velocity vectors is the same as that in the (
![]() $x$
,
$x$
,
![]() $y$
) and (
$y$
) and (
![]() $x$
,
$x$
,
![]() $z$
) planes. A total of 1800 pairs of flow images are captured for each set of PIV data.
$z$
) planes. A total of 1800 pairs of flow images are captured for each set of PIV data.
The same PIV is used for flow visualization in the three orthogonal planes. So are the seeding and arrangement to provide a marker for flow issuing from the nozzle exit, although the ambient air is not seeded. The captured images cover an area of
![]() $x^{\ast }=0\sim 10$
and
$x^{\ast }=0\sim 10$
and
![]() $y^{\ast }$
or
$y^{\ast }$
or
![]() $z^{\ast }=-5\sim +5$
in the (
$z^{\ast }=-5\sim +5$
in the (
![]() $x$
,
$x$
,
![]() $y$
) and (
$y$
) and (
![]() $x$
,
$x$
,
![]() $z$
) planes and an area of
$z$
) planes and an area of
![]() $y^{\ast }=-4\sim +4$
and
$y^{\ast }=-4\sim +4$
and
![]() $z^{\ast }=-4\sim +4$
in the (
$z^{\ast }=-4\sim +4$
in the (
![]() $y$
,
$y$
,
![]() $z$
) planes at
$z$
) planes at
![]() $x^{\ast }=0.7$
, 1.0, 1.3, 1.6, 2.0, 2.4, 2.7, 3.0, 4.0, 5.0.
$x^{\ast }=0.7$
, 1.0, 1.3, 1.6, 2.0, 2.4, 2.7, 3.0, 4.0, 5.0.
The decay rate
![]() $K$
of the centreline mean velocity is used to evaluate the jet entrainment and spread, given by
$K$
of the centreline mean velocity is used to evaluate the jet entrainment and spread, given by
![]() $K=(\overline{U}_{e}-\overline{U}_{5D})/\overline{U}_{e}$
, where
$K=(\overline{U}_{e}-\overline{U}_{5D})/\overline{U}_{e}$
, where
![]() $U_{e}$
and
$U_{e}$
and
![]() $U_{5D}$
are the centreline velocities at
$U_{5D}$
are the centreline velocities at
![]() $x^{\ast }=0$
and 5, respectively, and overbar denotes time-averaged quantity. Note that the manipulated jet may vary in its width in different planes through the
$x^{\ast }=0$
and 5, respectively, and overbar denotes time-averaged quantity. Note that the manipulated jet may vary in its width in different planes through the
![]() $x$
-axis. Following Hussain & Husain (Reference Hussain and Husain1989) and Mi et al. (Reference Mi, Kalt, Nathan and Wong2007), Zhou et al. (Reference Zhou, Du, Mi and Wang2012) defined in their investigation of jet manipulation using two steady minijets an equivalent jet width
$x$
-axis. Following Hussain & Husain (Reference Hussain and Husain1989) and Mi et al. (Reference Mi, Kalt, Nathan and Wong2007), Zhou et al. (Reference Zhou, Du, Mi and Wang2012) defined in their investigation of jet manipulation using two steady minijets an equivalent jet width
![]() $R_{eq}\equiv [R_{H}R_{V}]^{1/2}$
, where
$R_{eq}\equiv [R_{H}R_{V}]^{1/2}$
, where
![]() $R_{H}$
and
$R_{H}$
and
![]() $R_{V}$
are the half-widths of the mean-velocity distributions in the (
$R_{V}$
are the half-widths of the mean-velocity distributions in the (
![]() $x,z$
)- and (
$x,z$
)- and (
![]() $x,y$
)-planes, respectively.
$x,y$
)-planes, respectively.
![]() $R_{eq}$
was found to be correlated approximately linearly with
$R_{eq}$
was found to be correlated approximately linearly with
![]() $K$
, that is,
$K$
, that is,
![]() $K$
is directly linked to the jet entrainment rate.
$K$
is directly linked to the jet entrainment rate.

Figure 2. Power spectral density function of streamwise fluctuating velocity
![]() $u$
measured on the centreline: (a) the natural jet (
$u$
measured on the centreline: (a) the natural jet (
![]() $f_{e}/f_{0}=0$
,
$f_{e}/f_{0}=0$
,
![]() $C_{m}=0$
), (b) with the disk rotating at
$C_{m}=0$
), (b) with the disk rotating at
![]() $f_{e}/f_{0}=0.895$
and
$f_{e}/f_{0}=0.895$
and
![]() $C_{m}=0$
.
$C_{m}=0$
.
3 Main jet in the absence of manipulation
The hot-wire-measured mean velocity
![]() $\overline{U}^{\ast }$
(not shown) at the nozzle exit exhibits a ‘top-hat’ distribution in the absence of manipulation and the fluctuating velocity
$\overline{U}^{\ast }$
(not shown) at the nozzle exit exhibits a ‘top-hat’ distribution in the absence of manipulation and the fluctuating velocity
![]() $u_{r.m.s.}^{\ast }$
in the potential core is as low as 0.25 %. Hereinafter, the subscript r.m.s. represents the root mean square value. The displacement thickness
$u_{r.m.s.}^{\ast }$
in the potential core is as low as 0.25 %. Hereinafter, the subscript r.m.s. represents the root mean square value. The displacement thickness
![]() $\unicode[STIX]{x1D6FF}$
, momentum thickness
$\unicode[STIX]{x1D6FF}$
, momentum thickness
![]() $\unicode[STIX]{x1D703}$
and shape factor
$\unicode[STIX]{x1D703}$
and shape factor
![]() $H=\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D703}$
of the shear layer at
$H=\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D703}$
of the shear layer at
![]() $x^{\ast }=0.05$
are found to be 0.43 mm, 0.17 mm and 2.53, respectively (Zhang Reference Zhang2014). The rotating inner disk (figure 1
b) may have an effect on the flow. This is investigated by comparing the jets with and without the inner disk rotating at
$x^{\ast }=0.05$
are found to be 0.43 mm, 0.17 mm and 2.53, respectively (Zhang Reference Zhang2014). The rotating inner disk (figure 1
b) may have an effect on the flow. This is investigated by comparing the jets with and without the inner disk rotating at
![]() $f_{e}/f_{0}=0.895$
and
$f_{e}/f_{0}=0.895$
and
![]() $C_{m}=0$
. The reason for examining the case of
$C_{m}=0$
. The reason for examining the case of
![]() $f_{e}/f_{0}=0.895$
will be elaborated later. The power spectral density functions
$f_{e}/f_{0}=0.895$
will be elaborated later. The power spectral density functions
![]() $E_{u}$
of
$E_{u}$
of
![]() $u$
measured on the centreline (figure 2) are qualitatively the same with and without the azimuthal perturbation. The preferred-mode structures, as indicated by the pronounced peak at
$u$
measured on the centreline (figure 2) are qualitatively the same with and without the azimuthal perturbation. The preferred-mode structures, as indicated by the pronounced peak at
![]() $f_{0}$
in
$f_{0}$
in
![]() $E_{u}$
, are evident in both cases. However,
$E_{u}$
, are evident in both cases. However,
![]() $f_{0}$
is found to decrease from 143 Hz without the disk rotating (figure 2
a) to 128 Hz with the disk rotating (figure 2
b). The normalized frequency
$f_{0}$
is found to decrease from 143 Hz without the disk rotating (figure 2
a) to 128 Hz with the disk rotating (figure 2
b). The normalized frequency
![]() $f_{0}^{\ast }=f_{0}D/U_{e}$
reduces from 0.477 to 0.427, in the range of
$f_{0}^{\ast }=f_{0}D/U_{e}$
reduces from 0.477 to 0.427, in the range of
![]() $0.24\sim 0.64$
, as reported in the literature (Gutmark & Ho Reference Gutmark and Ho1983), for the passage frequency of the vortical structures at the end of the potential core or the preferred mode or the jet-column mode (Ho & Huerre Reference Ho and Huerre1984). Since
$0.24\sim 0.64$
, as reported in the literature (Gutmark & Ho Reference Gutmark and Ho1983), for the passage frequency of the vortical structures at the end of the potential core or the preferred mode or the jet-column mode (Ho & Huerre Reference Ho and Huerre1984). Since
![]() $f_{0}$
is inversely proportional to the boundary layer momentum thickness
$f_{0}$
is inversely proportional to the boundary layer momentum thickness
![]() $\unicode[STIX]{x1D703}_{0}$
at the nozzle edge (e.g. Crighton & Gaster Reference Crighton and Gaster1976), it may be inferred that the boundary layer over the inner disk is thickened, albeit slightly, as a result of disk rotating. In the measurements of a swirling jet, Oberleithner, Paschereit & Wygnanski (Reference Oberleithner, Paschereit and Wygnanski2014) also noted a slight growth in the axial shear-layer thickness due to swirling. Furthermore,
$\unicode[STIX]{x1D703}_{0}$
at the nozzle edge (e.g. Crighton & Gaster Reference Crighton and Gaster1976), it may be inferred that the boundary layer over the inner disk is thickened, albeit slightly, as a result of disk rotating. In the measurements of a swirling jet, Oberleithner, Paschereit & Wygnanski (Reference Oberleithner, Paschereit and Wygnanski2014) also noted a slight growth in the axial shear-layer thickness due to swirling. Furthermore,
![]() $K$
increases from 2.4 % to 5.4 %. Figure 3 shows the radial distributions of normalized streamwise mean velocity
$K$
increases from 2.4 % to 5.4 %. Figure 3 shows the radial distributions of normalized streamwise mean velocity
![]() $\overline{U}^{\ast }$
at
$\overline{U}^{\ast }$
at
![]() $x^{\ast }=0.05$
, which indicates that the flow characteristics remain nearly unchanged. The swirling of the primary jet is negligibly small. As shown in figure 4, the PIV-measured azimuthal mean velocity at the jet exit is very small, only discernible at
$x^{\ast }=0.05$
, which indicates that the flow characteristics remain nearly unchanged. The swirling of the primary jet is negligibly small. As shown in figure 4, the PIV-measured azimuthal mean velocity at the jet exit is very small, only discernible at
![]() $r/D\approx 0.5$
, indicating that the rotation of the inner disk is not strong enough to excite the centrifugal instability that occurs in a swirling jet (Oberleithner et al.
Reference Oberleithner, Paschereit and Wygnanski2014). In summary, the major characteristics of the jet remain largely unchanged with the disk rotating. We hereinafter use symbol
$r/D\approx 0.5$
, indicating that the rotation of the inner disk is not strong enough to excite the centrifugal instability that occurs in a swirling jet (Oberleithner et al.
Reference Oberleithner, Paschereit and Wygnanski2014). In summary, the major characteristics of the jet remain largely unchanged with the disk rotating. We hereinafter use symbol
![]() $f_{0}^{\prime }$
(
$f_{0}^{\prime }$
(
![]() $=$
128 Hz) to denote the preferred-mode frequency for the case of
$=$
128 Hz) to denote the preferred-mode frequency for the case of
![]() $C_{m}=0$
and
$C_{m}=0$
and
![]() $f_{e}\neq 0$
to differentiate from
$f_{e}\neq 0$
to differentiate from
![]() $f_{0}$
(
$f_{0}$
(
![]() $C_{m}=0$
and
$C_{m}=0$
and
![]() $f_{e}=0$
). Then,
$f_{e}=0$
). Then,
![]() $f_{e}/f_{0}=0.895$
corresponds to
$f_{e}/f_{0}=0.895$
corresponds to
![]() $f_{e}/f_{0}^{\prime }=1.0$
. Most of the manipulated jet results will be presented for the cases of
$f_{e}/f_{0}^{\prime }=1.0$
. Most of the manipulated jet results will be presented for the cases of
![]() $f_{e}/f_{0}^{\prime }=1.0$
and
$f_{e}/f_{0}^{\prime }=1.0$
and
![]() $f_{e}/f_{0}=1.0$
that corresponds to
$f_{e}/f_{0}=1.0$
that corresponds to
![]() $f_{e}/f_{0}^{\prime }=1.12$
.
$f_{e}/f_{0}^{\prime }=1.12$
.

Figure 3. Radial distributions of normalized streamwise mean velocity
![]() $\overline{U}^{\ast }$
measured at
$\overline{U}^{\ast }$
measured at
![]() $x^{\ast }=0.05$
.
$x^{\ast }=0.05$
.

Figure 4. Variation of the mean azimuthal velocity at
![]() $x^{\ast }=0.1$
.
$x^{\ast }=0.1$
.

Figure 5. (a) Time history and (b) power spectral density function
![]() $E_{w}$
of
$E_{w}$
of
![]() $w$
produced by the pulsed minijet, measured at
$w$
produced by the pulsed minijet, measured at
![]() $x^{\ast }=-0.85$
and
$x^{\ast }=-0.85$
and
![]() $z^{\ast }=-0.35$
in the (
$z^{\ast }=-0.35$
in the (
![]() $x,z$
) plane (
$x,z$
) plane (
![]() $C_{m}=1.5\,\%$
,
$C_{m}=1.5\,\%$
,
![]() $f_{e}f_{0}^{\prime }=1.0$
) in the absence of main jet.
$f_{e}f_{0}^{\prime }=1.0$
) in the absence of main jet.
4 Minijet-produced flow and its effect on main jet
It is crucially important for the understanding of flow physics to document the minijet-produced flow. Following Zhou et al. (Reference Zhou, Du, Mi and Wang2012), a single calibrated hot-wire 1.2 mm in length is placed upstream of the main jet exit at
![]() $x^{\ast }=-0.85$
(
$x^{\ast }=-0.85$
(
![]() $y^{\ast }=0$
and
$y^{\ast }=0$
and
![]() $z^{\ast }=-0.35$
), 3 mm downstream of the pinhole where two minijets are injected. The relatively large sensor does not compromise our measurement purpose that is to capture the signature or the predominant frequencies of the minijet-produced flow, not the velocity information. The wire is oriented normally to the axis of the orifices to measure the minijet injection velocity
$z^{\ast }=-0.35$
), 3 mm downstream of the pinhole where two minijets are injected. The relatively large sensor does not compromise our measurement purpose that is to capture the signature or the predominant frequencies of the minijet-produced flow, not the velocity information. The wire is oriented normally to the axis of the orifices to measure the minijet injection velocity
![]() $w$
signal along the
$w$
signal along the
![]() $z$
direction in the absence of the main jet. At the minijet mass flow rate and frequency corresponding to
$z$
direction in the absence of the main jet. At the minijet mass flow rate and frequency corresponding to
![]() $C_{m}=1.5\,\%$
and
$C_{m}=1.5\,\%$
and
![]() $f_{e}/f_{0}^{\prime }=1.0$
, respectively, the
$f_{e}/f_{0}^{\prime }=1.0$
, respectively, the
![]() $w$
signal (figure 5
a) displays periodic sharp peaks with a magnitude of up to approximately
$w$
signal (figure 5
a) displays periodic sharp peaks with a magnitude of up to approximately
![]() $11~\text{m}~\text{s}^{-1}$
and near zero plateaus between the peaks, corresponding to the on and off states, respectively, of the unsteady minijets. This is different from the saw-tooth wave shape of the pressure response of the unsteady microjet produced by Ibrahim et al. (Reference Ibrahim, Kunimura and Nakamura2002) and Choi et al. (Reference Choi, Annaswamy, Lou and Alvi2006) in their investigation of a compressible jet excited with 12 and 16 unsteady microjets, respectively, at a duty cycle of
$11~\text{m}~\text{s}^{-1}$
and near zero plateaus between the peaks, corresponding to the on and off states, respectively, of the unsteady minijets. This is different from the saw-tooth wave shape of the pressure response of the unsteady microjet produced by Ibrahim et al. (Reference Ibrahim, Kunimura and Nakamura2002) and Choi et al. (Reference Choi, Annaswamy, Lou and Alvi2006) in their investigation of a compressible jet excited with 12 and 16 unsteady microjets, respectively, at a duty cycle of
![]() $\unicode[STIX]{x1D6FC}\approx 50\,\%$
. The difference is apparently due to the present small duty cycle of
$\unicode[STIX]{x1D6FC}\approx 50\,\%$
. The difference is apparently due to the present small duty cycle of
![]() $\unicode[STIX]{x1D6FC}\approx 14.5\,\%$
. The corresponding spectrum
$\unicode[STIX]{x1D6FC}\approx 14.5\,\%$
. The corresponding spectrum
![]() $E_{w}$
(figure 5
b) exhibits pronounced sharp peaks at
$E_{w}$
(figure 5
b) exhibits pronounced sharp peaks at
![]() $f_{e}=128$
Hz and its harmonics. The latter is ascribed to the resonance in the nozzle cavity (Zhou et al.
Reference Zhou, Du, Mi and Wang2012).
$f_{e}=128$
Hz and its harmonics. The latter is ascribed to the resonance in the nozzle cavity (Zhou et al.
Reference Zhou, Du, Mi and Wang2012).
In the presence of main jet, the unsteady minijets act like pulsed jets in cross-flow and the flow structure depends on, inter alia,
![]() $\unicode[STIX]{x1D6FC}$
, velocity ratio and stroke ratio. The
$\unicode[STIX]{x1D6FC}$
, velocity ratio and stroke ratio. The
![]() $u$
signal and corresponding
$u$
signal and corresponding
![]() $E_{u}$
measured at
$E_{u}$
measured at
![]() $x^{\ast }=-0.7$
display major characteristics similar to those in figure 5, and are thus not shown. The pulsed jet in cross-flow may produce vortex ring structures (Johari, Pacheco-Tougas & Hermanson Reference Johari, Pacheco-Tougas and Hermanson1999). Flow visualization and PIV measurements were conducted in the injection plane of the two minijets and the cross-sectional (
$x^{\ast }=-0.7$
display major characteristics similar to those in figure 5, and are thus not shown. The pulsed jet in cross-flow may produce vortex ring structures (Johari, Pacheco-Tougas & Hermanson Reference Johari, Pacheco-Tougas and Hermanson1999). Flow visualization and PIV measurements were conducted in the injection plane of the two minijets and the cross-sectional (
![]() $y,z$
) plane at
$y,z$
) plane at
![]() $x^{\ast }=0.1$
, respectively, in order to gain insight into the minijet-generated flow structure. The typical flow structure of the minijet in the injection plane from flow visualization exhibits a leading vortex ring followed by trailing fluid (figure 6
a), similarly to the ring structure of a pulsed jet in cross-flow at
$x^{\ast }=0.1$
, respectively, in order to gain insight into the minijet-generated flow structure. The typical flow structure of the minijet in the injection plane from flow visualization exhibits a leading vortex ring followed by trailing fluid (figure 6
a), similarly to the ring structure of a pulsed jet in cross-flow at
![]() $\unicode[STIX]{x1D6FC}=15\,\%$
(cf. figure 6f in M’Closkey et al.
Reference M’Closkey, King, Cortelezzi and Karagozian2002). The PIV-measured instantaneous contours of streamwise vorticity (
$\unicode[STIX]{x1D6FC}=15\,\%$
(cf. figure 6f in M’Closkey et al.
Reference M’Closkey, King, Cortelezzi and Karagozian2002). The PIV-measured instantaneous contours of streamwise vorticity (
![]() $\unicode[STIX]{x1D714}_{x}^{\ast }=\unicode[STIX]{x1D714}_{x}D/\overline{U}_{e}$
) typically show two pairs of counter-rotating vortices in the (
$\unicode[STIX]{x1D714}_{x}^{\ast }=\unicode[STIX]{x1D714}_{x}D/\overline{U}_{e}$
) typically show two pairs of counter-rotating vortices in the (
![]() $y,z$
) plane at
$y,z$
) plane at
![]() $x^{\ast }=0.1$
(figure 6
b), as a result of the viewing plane
$x^{\ast }=0.1$
(figure 6
b), as a result of the viewing plane
![]() $b$
cut through the leading vortex rings generated by the two unsteady minijets (figure 6
c). The counter-rotating vortices are not always present in the contours (not shown) due to the on-and-off nature of the unsteady minijets.
$b$
cut through the leading vortex rings generated by the two unsteady minijets (figure 6
c). The counter-rotating vortices are not always present in the contours (not shown) due to the on-and-off nature of the unsteady minijets.

Figure 6. (a) Photographs of typical minijet flow structures from flow visualization in the injection plane of the main jet (
![]() $C_{m}=1.5\,\%$
,
$C_{m}=1.5\,\%$
,
![]() $f_{e}/f_{0}^{\prime }=1.0$
). Flow is left to right. (b) Typical instantaneous contours of
$f_{e}/f_{0}^{\prime }=1.0$
). Flow is left to right. (b) Typical instantaneous contours of
![]() $\unicode[STIX]{x1D714}_{x}^{\ast }=\unicode[STIX]{x1D714}_{x}D/\overline{U}_{e}$
in a cross-sectional plane of the primary jet (
$\unicode[STIX]{x1D714}_{x}^{\ast }=\unicode[STIX]{x1D714}_{x}D/\overline{U}_{e}$
in a cross-sectional plane of the primary jet (
![]() $C_{m}=1.5\,\%$
,
$C_{m}=1.5\,\%$
,
![]() $f_{e}/f_{0}^{\prime }=1.0$
) at
$f_{e}/f_{0}^{\prime }=1.0$
) at
![]() $x^{\ast }=0.1$
. Contour interval
$x^{\ast }=0.1$
. Contour interval
![]() $=1$
. Flow is out of paper. (c) Sketch of the minijet-produced ring vortex viewed in planes a and b, which correspond to the injection plane (a) and the cross-sectional plane (b), respectively.
$=1$
. Flow is out of paper. (c) Sketch of the minijet-produced ring vortex viewed in planes a and b, which correspond to the injection plane (a) and the cross-sectional plane (b), respectively.
It is of interest to examine the dependence of the minijet-produced structures on
![]() $C_{m}$
. Figure 7 shows both time-averaged and instantaneous contours of
$C_{m}$
. Figure 7 shows both time-averaged and instantaneous contours of
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
and
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
and
![]() $\unicode[STIX]{x1D714}_{x}^{\ast }$
captured at
$\unicode[STIX]{x1D714}_{x}^{\ast }$
captured at
![]() $x^{\ast }=0.1$
. A number of observations can be made. Firstly, the counter-rotating vortices shown in the
$x^{\ast }=0.1$
. A number of observations can be made. Firstly, the counter-rotating vortices shown in the
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
contours correspond well to those in the
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
contours correspond well to those in the
![]() $\unicode[STIX]{x1D714}_{x}^{\ast }$
contours and are thus representative of the flow structure in this plane. Secondly, from
$\unicode[STIX]{x1D714}_{x}^{\ast }$
contours and are thus representative of the flow structure in this plane. Secondly, from
![]() $C_{m}=1.0\,\%$
to 1.5 % (figure 7
a,b,e,f) the maximum magnitude of
$C_{m}=1.0\,\%$
to 1.5 % (figure 7
a,b,e,f) the maximum magnitude of
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
in the vortices increases, suggesting the growing strength of vortex rings; meanwhile, the counter-rotating vortices move towards the jet centre, suggesting an increased penetration depth. Thirdly, a further increase in
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
in the vortices increases, suggesting the growing strength of vortex rings; meanwhile, the counter-rotating vortices move towards the jet centre, suggesting an increased penetration depth. Thirdly, a further increase in
![]() $C_{m}$
beyond 2.0 % leads to a collision between the two pairs of vortex rings (figure 7
g,h). The complicated pattern of the
$C_{m}$
beyond 2.0 % leads to a collision between the two pairs of vortex rings (figure 7
g,h). The complicated pattern of the
![]() $\unicode[STIX]{x1D714}_{x}^{\ast }$
contours at
$\unicode[STIX]{x1D714}_{x}^{\ast }$
contours at
![]() $C_{m}>2.0\,\%$
suggests the breakup of the vortex rings. Accordingly, the maximum magnitude of
$C_{m}>2.0\,\%$
suggests the breakup of the vortex rings. Accordingly, the maximum magnitude of
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
in the vortices drops (figure 7
c,d), that is, the vortex strength is weakened.
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
in the vortices drops (figure 7
c,d), that is, the vortex strength is weakened.

Figure 7. Contours of (a–d) time-averaged streamwise vorticity
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }=\overline{\unicode[STIX]{x1D714}}_{x}D/\overline{U}_{e}$
and (e–h) typical instantaneous streamwise vorticity
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }=\overline{\unicode[STIX]{x1D714}}_{x}D/\overline{U}_{e}$
and (e–h) typical instantaneous streamwise vorticity
![]() $\unicode[STIX]{x1D714}_{x}^{\ast }$
in the cross-sectional plane of the primary jet at
$\unicode[STIX]{x1D714}_{x}^{\ast }$
in the cross-sectional plane of the primary jet at
![]() $x^{\ast }=0.1$
. Contour intervals equal to 0.2 and 1, respectively.
$x^{\ast }=0.1$
. Contour intervals equal to 0.2 and 1, respectively.
The effect of the minijet injection on the hot-wire-measured
![]() $\overline{U}^{\ast }$
at
$\overline{U}^{\ast }$
at
![]() $x^{\ast }=0.05$
is negligibly small, and
$x^{\ast }=0.05$
is negligibly small, and
![]() $\overline{U}^{\ast }$
remains to be a ‘top-hat’ distribution in the range of
$\overline{U}^{\ast }$
remains to be a ‘top-hat’ distribution in the range of
![]() $C_{m}$
tested (figure 8
a,b). This is consistent with previous investigations on round jets excited with unsteady control jets (e.g. Raman & Cornelius Reference Raman and Cornelius1995; Parekh et al.
Reference Parekh, Kibens, Glezer, Wiltse and Smith1996). The change of initial centreline mean velocity is not evident in the excited jet compared with the natural jet (e.g. figure 4 in Raman & Cornelius Reference Raman and Cornelius1995). In contrast, Seidel et al. (Reference Seidel, Pappart, New and Tsai2005) observed an increase in the centreline mean velocity near the jet exit. The difference is probably due to the steady minijets they used. Moreover, another factor should be pointed out. The actual mass flow rate of the minijets injected into the main jet is less than the measured mass flow rate due to a clearance, necessary to ensure the rotation, between the stationary and rotating disks, which implies a flow leakage. When the orifices on both disks are aligned during rotation, the minijet flow is injected into the main jet and the flow leakage should be negligibly small; but when not aligned, the flow leakage through the clearance may become appreciable. This implies that the actual mass flow rate of the minijets injected into the main jet should be smaller than
$C_{m}$
tested (figure 8
a,b). This is consistent with previous investigations on round jets excited with unsteady control jets (e.g. Raman & Cornelius Reference Raman and Cornelius1995; Parekh et al.
Reference Parekh, Kibens, Glezer, Wiltse and Smith1996). The change of initial centreline mean velocity is not evident in the excited jet compared with the natural jet (e.g. figure 4 in Raman & Cornelius Reference Raman and Cornelius1995). In contrast, Seidel et al. (Reference Seidel, Pappart, New and Tsai2005) observed an increase in the centreline mean velocity near the jet exit. The difference is probably due to the steady minijets they used. Moreover, another factor should be pointed out. The actual mass flow rate of the minijets injected into the main jet is less than the measured mass flow rate due to a clearance, necessary to ensure the rotation, between the stationary and rotating disks, which implies a flow leakage. When the orifices on both disks are aligned during rotation, the minijet flow is injected into the main jet and the flow leakage should be negligibly small; but when not aligned, the flow leakage through the clearance may become appreciable. This implies that the actual mass flow rate of the minijets injected into the main jet should be smaller than
![]() $C_{m}$
. It is worth pointing out that, although the
$C_{m}$
. It is worth pointing out that, although the
![]() $C_{m}$
range examined is up to 10.6 %, the present study is focused on the case of
$C_{m}$
range examined is up to 10.6 %, the present study is focused on the case of
![]() $C_{m}=1.5\,\%$
.
$C_{m}=1.5\,\%$
.

Figure 8. Radial distributions of
![]() $\overline{U}^{\ast }$
and turbulent intensity
$\overline{U}^{\ast }$
and turbulent intensity
![]() $u_{r.m.s.}^{\ast }$
measured at
$u_{r.m.s.}^{\ast }$
measured at
![]() $x^{\ast }=0.05$
in the manipulated jet in both (a,c) injection and (b,d) non-injection planes.
$x^{\ast }=0.05$
in the manipulated jet in both (a,c) injection and (b,d) non-injection planes.
The effect of the minijet injection is however significant on
![]() $u_{r.m.s.}^{\ast }$
(figure 8
c,d). For the case of the natural jet, a small hump occurs at
$u_{r.m.s.}^{\ast }$
(figure 8
c,d). For the case of the natural jet, a small hump occurs at
![]() $z^{\ast }\approx -0.46$
in
$z^{\ast }\approx -0.46$
in
![]() $u_{r.m.s.}^{\ast }$
, which is ascribed to the early stage of the mixing layer. At
$u_{r.m.s.}^{\ast }$
, which is ascribed to the early stage of the mixing layer. At
![]() $C_{m}=1.0\,\%{-}1.5\,\%$
, this hump grows substantially in the injection plane. Furthermore, another peak occurs at
$C_{m}=1.0\,\%{-}1.5\,\%$
, this hump grows substantially in the injection plane. Furthermore, another peak occurs at
![]() $z^{\ast }\approx -0.25$
for
$z^{\ast }\approx -0.25$
for
![]() $C_{m}=1.5\,\%$
and at
$C_{m}=1.5\,\%$
and at
![]() $z^{\ast }\approx -0.3$
for
$z^{\ast }\approx -0.3$
for
![]() $C_{m}=1.0\,\%$
, apparently due to the counter-rotating streamwise vortices that occur at the same
$C_{m}=1.0\,\%$
, apparently due to the counter-rotating streamwise vortices that occur at the same
![]() $z^{\ast }$
(figure 7
a,b). The location of this local maximum
$z^{\ast }$
(figure 7
a,b). The location of this local maximum
![]() $u_{r.m.s.}^{\ast }$
is apparently the most likely position of the minijet-produced ring vortices. In the non-injection plane, however,
$u_{r.m.s.}^{\ast }$
is apparently the most likely position of the minijet-produced ring vortices. In the non-injection plane, however,
![]() $u_{r.m.s.}^{\ast }$
does not show any appreciable change. At
$u_{r.m.s.}^{\ast }$
does not show any appreciable change. At
![]() $C_{m}=2.0\,\%{-}4.1\,\%$
, both peaks in
$C_{m}=2.0\,\%{-}4.1\,\%$
, both peaks in
![]() $u_{r.m.s.}^{\ast }$
grow considerably in the injection plane, but the one due to the minijet-produced ring vortices occurs at
$u_{r.m.s.}^{\ast }$
grow considerably in the injection plane, but the one due to the minijet-produced ring vortices occurs at
![]() $z^{\ast }\approx -0.05$
, almost at the jet centre, internally consistent with the observation from the PIV data (figure 7
g,h) that the two minijets may have penetrated the jet centre, starting to collide with each other. This will have an impact on the behaviour of
$z^{\ast }\approx -0.05$
, almost at the jet centre, internally consistent with the observation from the PIV data (figure 7
g,h) that the two minijets may have penetrated the jet centre, starting to collide with each other. This will have an impact on the behaviour of
![]() $K$
to be presented in § 5. In the non-injection planes, there is a marked increase in
$K$
to be presented in § 5. In the non-injection planes, there is a marked increase in
![]() $u_{r.m.s.}^{\ast }$
which rises towards the centre, probably due to turbulence produced by the colliding ring vortices. At large
$u_{r.m.s.}^{\ast }$
which rises towards the centre, probably due to turbulence produced by the colliding ring vortices. At large
![]() $C_{m}$
(
$C_{m}$
(
![]() $=$
10.6 %),
$=$
10.6 %),
![]() $u_{r.m.s.}^{\ast }$
increases throughout in both planes. Presumably, the two minijets collide with each other even before reaching the nozzle exit, producing a fully turbulent jet right from the beginning.
$u_{r.m.s.}^{\ast }$
increases throughout in both planes. Presumably, the two minijets collide with each other even before reaching the nozzle exit, producing a fully turbulent jet right from the beginning.
In summary, the unsteady minijets act like pulsed jets in cross-flow, producing isolated structures with a leading vortex ring accompanied by trailing fluid. The vortex rings penetrate towards the jet centre more deeply from
![]() $C_{m}=1.0\,\%$
to 1.5 %, along with the growing strength. A further increase in
$C_{m}=1.0\,\%$
to 1.5 %, along with the growing strength. A further increase in
![]() $C_{m}$
beyond 2.0 % results in a collision between the two vortex rings at the jet centre, producing turbulence and weakening the strength of the vortex rings and, given an adequately large
$C_{m}$
beyond 2.0 % results in a collision between the two vortex rings at the jet centre, producing turbulence and weakening the strength of the vortex rings and, given an adequately large
![]() $C_{m}$
(
$C_{m}$
(
![]() ${>}$
4.1 %), the main jet becomes fully turbulent even at the nozzle exit.
${>}$
4.1 %), the main jet becomes fully turbulent even at the nozzle exit.
5 Dependence of jet decay rate on mass and frequency ratios
The performance of unsteady fluidic manipulation depends on, inter alia,
![]() $f_{e}/f_{0}^{\prime }$
, the mass and exit diameter ratios of the minijets to the main jet, the minijet jet injection angle, phase, number and geometric arrangement. We presently focus on the dependence of
$f_{e}/f_{0}^{\prime }$
, the mass and exit diameter ratios of the minijets to the main jet, the minijet jet injection angle, phase, number and geometric arrangement. We presently focus on the dependence of
![]() $K$
on
$K$
on
![]() $C_{m}$
and
$C_{m}$
and
![]() $f_{e}/f_{0}^{\prime }$
.
$f_{e}/f_{0}^{\prime }$
.
The
![]() $C_{m}$
is varied from 0 to 16 % in order to characterize its influence on
$C_{m}$
is varied from 0 to 16 % in order to characterize its influence on
![]() $K$
. Consider the case of
$K$
. Consider the case of
![]() $f_{e}/f_{0}^{\prime }=1.12$
.
$f_{e}/f_{0}^{\prime }=1.12$
.
![]() $K$
(figure 9
a) exhibits a strong dependence on
$K$
(figure 9
a) exhibits a strong dependence on
![]() $C_{m}$
, which may be divided into three categories. In Category I (
$C_{m}$
, which may be divided into three categories. In Category I (
![]() $C_{m}<2.6\,\%$
),
$C_{m}<2.6\,\%$
),
![]() $K$
is highly sensitive to
$K$
is highly sensitive to
![]() $C_{m}$
, rising rapidly from 0.054 at
$C_{m}$
, rising rapidly from 0.054 at
![]() $C_{m}=0.0\,\%$
to about 0.2 at
$C_{m}=0.0\,\%$
to about 0.2 at
![]() $C_{m}\approx 1.5\,\%$
and then drops quickly until
$C_{m}\approx 1.5\,\%$
and then drops quickly until
![]() $C_{m}\approx 2.5\,\%$
. The rise and the drop coincide with the growing and impairing strengths of the vortex rings (figure 7
a–d), respectively. In other words, the rise in
$C_{m}\approx 2.5\,\%$
. The rise and the drop coincide with the growing and impairing strengths of the vortex rings (figure 7
a–d), respectively. In other words, the rise in
![]() $K$
results from an increased penetration depth by the minijet-produced vortex rings and the drop is due to a collision between the vortex rings. In Category III
$K$
results from an increased penetration depth by the minijet-produced vortex rings and the drop is due to a collision between the vortex rings. In Category III
![]() $(C_{m}>4.5\,\%)$
,
$(C_{m}>4.5\,\%)$
,
![]() $K$
increases steadily, albeit much less rapidly than in Category I, and appears approaching asymptotically to a constant. This increase is linked to the formation of a fully turbulent jet, as a result of a collision between vortex rings, at the nozzle exit (figure 8
c,d), whose turbulent intensity is enhanced with increasing
$K$
increases steadily, albeit much less rapidly than in Category I, and appears approaching asymptotically to a constant. This increase is linked to the formation of a fully turbulent jet, as a result of a collision between vortex rings, at the nozzle exit (figure 8
c,d), whose turbulent intensity is enhanced with increasing
![]() $C_{m}$
. Category II (
$C_{m}$
. Category II (
![]() $C_{m}=2.6\,\%$
–4.5 %), where the distribution of
$C_{m}=2.6\,\%$
–4.5 %), where the distribution of
![]() $K$
exhibits a minor hump, is apparently a transition between Categories I and III. The three distinct behaviours of
$K$
exhibits a minor hump, is apparently a transition between Categories I and III. The three distinct behaviours of
![]() $K$
correspond to different flow physics or mechanisms.
$K$
correspond to different flow physics or mechanisms.

Figure 9. Dependence of the jet decay rate
![]() $K$
on: (a) the mass flow ratio
$K$
on: (a) the mass flow ratio
![]() $C_{m}$
(
$C_{m}$
(
![]() $f_{e}/f_{0}^{\prime }=1.12$
); (b) the excitation frequency
$f_{e}/f_{0}^{\prime }=1.12$
); (b) the excitation frequency
![]() $f_{e}/f_{0}^{\prime }$
(
$f_{e}/f_{0}^{\prime }$
(
![]() $C_{m}=1.5\,\%$
).
$C_{m}=1.5\,\%$
).
The maximum
![]() $K$
of Category I reaches 0.2, approximately 8 times that (0.024) of the natural jet and over 3 times that (0.054) at
$K$
of Category I reaches 0.2, approximately 8 times that (0.024) of the natural jet and over 3 times that (0.054) at
![]() $f_{e}/f_{0}^{\prime }=1.0$
and
$f_{e}/f_{0}^{\prime }=1.0$
and
![]() $C_{m}=0$
, highlighting the highly effective entrainment/spread enhancement under the excitation of unsteady minijets. Zhou et al. (Reference Zhou, Du, Mi and Wang2012) investigated the active excitation of the same round jet using two steady minijets in a similar experimental facility. At
$C_{m}=0$
, highlighting the highly effective entrainment/spread enhancement under the excitation of unsteady minijets. Zhou et al. (Reference Zhou, Du, Mi and Wang2012) investigated the active excitation of the same round jet using two steady minijets in a similar experimental facility. At
![]() $C_{m}=1.4\,\%$
, their
$C_{m}=1.4\,\%$
, their
![]() $K$
was only 0.13, approximately 60 % of the present value. This difference illustrates that the periodic unsteady minijet is much more efficient in manipulation than its steady counterpart, for the shear-layer instabilities are only receptive to the periodic perturbation (Henderson Reference Henderson2010).
$K$
was only 0.13, approximately 60 % of the present value. This difference illustrates that the periodic unsteady minijet is much more efficient in manipulation than its steady counterpart, for the shear-layer instabilities are only receptive to the periodic perturbation (Henderson Reference Henderson2010).
The dependence of
![]() $K$
on
$K$
on
![]() $f_{e}/f_{0}^{\prime }$
is examined at
$f_{e}/f_{0}^{\prime }$
is examined at
![]() $C_{m}=1.5\,\%$
, which corresponds to the maximum
$C_{m}=1.5\,\%$
, which corresponds to the maximum
![]() $K$
in Category I. As shown in figure 9(b),
$K$
in Category I. As shown in figure 9(b),
![]() $K$
is enhanced with increasing
$K$
is enhanced with increasing
![]() $f_{e}/f_{0}^{\prime }$
, reaching a maximum value (0.215) at
$f_{e}/f_{0}^{\prime }$
, reaching a maximum value (0.215) at
![]() $f_{e}/f_{0}^{\prime }=1.0$
before its approximately linear fall. A minor trough occurs at
$f_{e}/f_{0}^{\prime }=1.0$
before its approximately linear fall. A minor trough occurs at
![]() $f_{e}/f_{0}^{\prime }=0.86$
. The flow physics behind this is unclear. In comparison, the
$f_{e}/f_{0}^{\prime }=0.86$
. The flow physics behind this is unclear. In comparison, the
![]() $C_{m}$
required to achieve the same
$C_{m}$
required to achieve the same
![]() $K$
(0.215) is 4.5 % given two steady minijets, three times that of the unsteady counterpart, again demonstrating the high forcing efficiency under the unsteady minijet excitation.
$K$
(0.215) is 4.5 % given two steady minijets, three times that of the unsteady counterpart, again demonstrating the high forcing efficiency under the unsteady minijet excitation.
It is worth commenting on the effect of unsteady minijet excitation on the entrainment rate in the far field. Figure 10 presents the dependence on
![]() $x^{\ast }$
of the normalized streamwise mean velocity
$x^{\ast }$
of the normalized streamwise mean velocity
![]() $\overline{U}_{c}^{\ast }$
on the jet centreline. The data of the natural jet are also presented as a reference, which collapse well with those reported by Seidel et al. (Reference Seidel, Pappart, New and Tsai2005) for their unexcited round jet at
$\overline{U}_{c}^{\ast }$
on the jet centreline. The data of the natural jet are also presented as a reference, which collapse well with those reported by Seidel et al. (Reference Seidel, Pappart, New and Tsai2005) for their unexcited round jet at
![]() $Re_{D}=8800$
. The
$Re_{D}=8800$
. The
![]() $\overline{U}_{c}^{\ast }$
of the manipulated jet exhibits a significantly more rapid decay from
$\overline{U}_{c}^{\ast }$
of the manipulated jet exhibits a significantly more rapid decay from
![]() $x^{\ast }=3.5$
but the decay rate contracts gradually from
$x^{\ast }=3.5$
but the decay rate contracts gradually from
![]() $x^{\ast }=10$
to 20. While
$x^{\ast }=10$
to 20. While
![]() $\unicode[STIX]{x0394}\overline{U}_{1}/\overline{U}_{e}$
changes significantly, compared with the natural jet,
$\unicode[STIX]{x0394}\overline{U}_{1}/\overline{U}_{e}$
changes significantly, compared with the natural jet,
![]() $\unicode[STIX]{x0394}\overline{U}_{2}/\overline{U}_{e}$
does not, where
$\unicode[STIX]{x0394}\overline{U}_{2}/\overline{U}_{e}$
does not, where
![]() $\unicode[STIX]{x0394}\overline{U}_{1}=\overline{U}_{e}-\overline{U}_{5D}$
and
$\unicode[STIX]{x0394}\overline{U}_{1}=\overline{U}_{e}-\overline{U}_{5D}$
and
![]() $\unicode[STIX]{x0394}\overline{U}_{2}=\overline{U}_{15D}-\overline{U}_{20D}$
,
$\unicode[STIX]{x0394}\overline{U}_{2}=\overline{U}_{15D}-\overline{U}_{20D}$
,
![]() $\overline{U}_{15D}$
and
$\overline{U}_{15D}$
and
![]() $\overline{U}_{20D}$
being the centreline mean velocities at
$\overline{U}_{20D}$
being the centreline mean velocities at
![]() $x^{\ast }=15$
and 20, respectively. Therefore, unlike Zhang & Johari’s (Reference Zhang and Johari1996) and Breidenthal’s (Reference Breidenthal2008) manipulation through exponentially increasing the jet exit velocity in a short time via forcing, the present minijet excitation produces little effect on the entrainment rate in the far field. This is why the jet decay rate
$x^{\ast }=15$
and 20, respectively. Therefore, unlike Zhang & Johari’s (Reference Zhang and Johari1996) and Breidenthal’s (Reference Breidenthal2008) manipulation through exponentially increasing the jet exit velocity in a short time via forcing, the present minijet excitation produces little effect on the entrainment rate in the far field. This is why the jet decay rate
![]() $K$
is determined based on the information in the near field, viz.
$K$
is determined based on the information in the near field, viz.
![]() $K=(\overline{U}_{e}-\overline{U}_{5D})/\overline{U}_{e}$
.
$K=(\overline{U}_{e}-\overline{U}_{5D})/\overline{U}_{e}$
.

Figure 10. Normalized streamwise mean-velocity variation along the jet centreline.
6 Physical aspects of the manipulated jet
In this section, the three categories of the manipulated jet are examined and compared in various aspects. Great attention will be given to the three-dimensional vortical structures in Category I, which are especially fascinating.
6.1 Entrainment and momentum transport
Entrainment and momentum transport are crucial for the understanding of vortex dynamics. These aspects show the most marked change in the manipulated jet of Category I among the three categories, relative to the natural jet. We therefore focus on the flow of Category I (
![]() $C_{m}=1.5\,\%$
). The information on spread and entrainment may be obtained via examining the PIV-measured
$C_{m}=1.5\,\%$
). The information on spread and entrainment may be obtained via examining the PIV-measured
![]() $\overline{W}^{\ast }$
and
$\overline{W}^{\ast }$
and
![]() $\overline{V}^{\ast }$
contours (figure 11
a,c,e).
$\overline{V}^{\ast }$
contours (figure 11
a,c,e).
![]() $\overline{W}^{\ast }$
is negligibly small in the absence of excitation (figure 11
a) but becomes pronouncedly negative, its maximum magnitude jumping by 300 %, in the central region of the injection plane under excitation (figure 11
c), suggesting a strong entrainment of ambient fluid into the jet. On the other hand,
$\overline{W}^{\ast }$
is negligibly small in the absence of excitation (figure 11
a) but becomes pronouncedly negative, its maximum magnitude jumping by 300 %, in the central region of the injection plane under excitation (figure 11
c), suggesting a strong entrainment of ambient fluid into the jet. On the other hand,
![]() $\overline{V}^{\ast }$
is positive almost over the entire region of
$\overline{V}^{\ast }$
is positive almost over the entire region of
![]() $x^{\ast }>2.0$
in the non-injection plane (figure 11
e), its maximum reaching 0.14 or 800 % of that in the natural jet, indicating a very strong outward spread of fluid from the jet.
$x^{\ast }>2.0$
in the non-injection plane (figure 11
e), its maximum reaching 0.14 or 800 % of that in the natural jet, indicating a very strong outward spread of fluid from the jet.

Figure 11. Contours of time-averaged lateral velocity (a,c,e) and Reynolds shear stress (b,d,f), the contour increments being 0.01 and 0.001, respectively.
The Reynolds shear stresses provide a measure for the momentum transport. The
![]() $\overline{uw}^{\ast }$
and
$\overline{uw}^{\ast }$
and
![]() $\overline{uv}^{\ast }$
contours (figure 11
b,d,f) exhibit a great change compared to the natural jet. Without excitation, the maximum
$\overline{uv}^{\ast }$
contours (figure 11
b,d,f) exhibit a great change compared to the natural jet. Without excitation, the maximum
![]() $\overline{uw}^{\ast }$
(0.014) occurs at
$\overline{uw}^{\ast }$
(0.014) occurs at
![]() $x^{\ast }=3.1\sim 3.2$
. Once excitation is introduced,
$x^{\ast }=3.1\sim 3.2$
. Once excitation is introduced,
![]() $\overline{uw}^{\ast }$
in the injection plane shows another concentration of larger magnitude (0.016) at
$\overline{uw}^{\ast }$
in the injection plane shows another concentration of larger magnitude (0.016) at
![]() $x^{\ast }=1.7$
, much nearer to the nozzle exit. Similarly,
$x^{\ast }=1.7$
, much nearer to the nozzle exit. Similarly,
![]() $\overline{uv}^{\ast }$
in the non-injection plane also exhibits two pronounced concentrations of the positive sign, one at
$\overline{uv}^{\ast }$
in the non-injection plane also exhibits two pronounced concentrations of the positive sign, one at
![]() $x^{\ast }=3.6$
with its maximum reaching 0.017 and the other at
$x^{\ast }=3.6$
with its maximum reaching 0.017 and the other at
![]() $x^{\ast }=1.85$
. Note the occurrence of a negative-signed concentration in the central region near the nozzle exit, albeit with a relatively small maximum magnitude (0.007) at
$x^{\ast }=1.85$
. Note the occurrence of a negative-signed concentration in the central region near the nozzle exit, albeit with a relatively small maximum magnitude (0.007) at
![]() $x^{\ast }=2.1$
. The vorticity contours to be shown later indicate that the region of negative
$x^{\ast }=2.1$
. The vorticity contours to be shown later indicate that the region of negative
![]() $\overline{uv}^{\ast }$
is associated with the events of vortex pairing, during which vortices are tilted. Please refer to figures 20 and 21 in Browand & Ho (Reference Browand and Ho1983) for details.
$\overline{uv}^{\ast }$
is associated with the events of vortex pairing, during which vortices are tilted. Please refer to figures 20 and 21 in Browand & Ho (Reference Browand and Ho1983) for details.
6.2 Downstream evolution
The downstream evolution of the
![]() $u$
-signals, measured in both injection and non-injection planes, are presented in figure 12. The same vertical and horizontal scales are used for all the
$u$
-signals, measured in both injection and non-injection planes, are presented in figure 12. The same vertical and horizontal scales are used for all the
![]() $u$
-signals. The signal starts to show a quasi-periodicity at
$u$
-signals. The signal starts to show a quasi-periodicity at
![]() $x^{\ast }=2.0$
without excitation, but behaves rather differently from one category to another under excitation. A marked periodicity is seen at
$x^{\ast }=2.0$
without excitation, but behaves rather differently from one category to another under excitation. A marked periodicity is seen at
![]() $x^{\ast }=0.0$
in the injection plane and at
$x^{\ast }=0.0$
in the injection plane and at
![]() $x^{\ast }=1.0$
in the non-injection plane of Category I. The flow remains to be laminar until at
$x^{\ast }=1.0$
in the non-injection plane of Category I. The flow remains to be laminar until at
![]() $x^{\ast }=2.0$
in both planes. In contrast, the signals exhibit random fluctuations even at
$x^{\ast }=2.0$
in both planes. In contrast, the signals exhibit random fluctuations even at
![]() $x^{\ast }=0.0$
in both planes for Category III, implying a turbulent state right at the exit of nozzle (figure 12
d). Category II is a transition between I and III. The flow displays intermittent periodicity and small-scale random fluctuation from time to time.
$x^{\ast }=0.0$
in both planes for Category III, implying a turbulent state right at the exit of nozzle (figure 12
d). Category II is a transition between I and III. The flow displays intermittent periodicity and small-scale random fluctuation from time to time.

Figure 12. Typical signals of streamwise velocity
![]() $u$
. Hot-wire was placed at
$u$
. Hot-wire was placed at
![]() $y^{\ast }$
or
$y^{\ast }$
or
![]() $z^{\ast }=0.3$
.
$z^{\ast }=0.3$
.
![]() $E_{u}$
(figure 13
a) measured along the centreline of the manipulated jet displays very pronounced peaks at
$E_{u}$
(figure 13
a) measured along the centreline of the manipulated jet displays very pronounced peaks at
![]() $f_{e}^{\ast }$
(
$f_{e}^{\ast }$
(
![]() $=f_{e}D/U_{e}$
) and even its second and higher harmonics up to
$=f_{e}D/U_{e}$
) and even its second and higher harmonics up to
![]() $x^{\ast }=4$
for Category I, reflecting the presence of quasi-periodic large-scale structures and echoing the characteristics of the minijet-produced flow (figure 5
b). The peaks completely disappear at
$x^{\ast }=4$
for Category I, reflecting the presence of quasi-periodic large-scale structures and echoing the characteristics of the minijet-produced flow (figure 5
b). The peaks completely disappear at
![]() $x^{\ast }\geqslant 6$
, indicating that the manipulated jet becomes fully developed and turbulent at
$x^{\ast }\geqslant 6$
, indicating that the manipulated jet becomes fully developed and turbulent at
![]() $x^{\ast }\geqslant 6$
. However, the peaks are much less pronounced for Category III (figure 13
b) and disappear essentially for
$x^{\ast }\geqslant 6$
. However, the peaks are much less pronounced for Category III (figure 13
b) and disappear essentially for
![]() $x^{\ast }\geqslant 5$
. Apparently, the jet is fully developed and turbulent at
$x^{\ast }\geqslant 5$
. Apparently, the jet is fully developed and turbulent at
![]() $x^{\ast }\geqslant 4$
, earlier than Category I.
$x^{\ast }\geqslant 4$
, earlier than Category I.

Figure 13. Power spectral density function of
![]() $u$
measured on the centreline of the manipulated jets: (a) Category I (
$u$
measured on the centreline of the manipulated jets: (a) Category I (
![]() $C_{m}=1.5\,\%$
for
$C_{m}=1.5\,\%$
for
![]() $f_{e}/f_{0}^{\prime }=1.0$
); (b) III (10.6 %, 1.12).
$f_{e}/f_{0}^{\prime }=1.0$
); (b) III (10.6 %, 1.12).
6.3 The flow structure
Flow visualization was conducted in both injection and non-injection planes for all three categories of the manipulated jet, along with the natural jet, in order to gain further understanding of the flow physics. Figure 14 presents typical photographs from flow visualization. There is a profound change in the flow structure with and without excitation and even between different categories under excitation. For Category I, the shear layer rolls up early to form vortices stronger in both planes than those in the natural jet (figure 14
a,b,e). There is a distinct difference in the flow structure between the two orthogonal planes. A large amount of ambient fluid (dark coloured) in the injection plane appears engulfed vigorously into the jet, even penetrating the jet axis via vortical motions. Meanwhile, smoke-marked fluid (white coloured) is massively ejected from the braid region between two successive vortices in the non-injection plane, generating a much more extensive spread than the natural jet. Vigorous entrainment and spread contribute to the concentrations of the
![]() $\bar{W}^{\ast }$
and
$\bar{W}^{\ast }$
and
![]() $\bar{V}^{\ast }$
contours in figure 11(c,e). For Category II, the initial turbulent state (figure 8
c,d) incurs a rapid diffusion of vortices shortly after their formation in both planes (figure 14
c,f) due to the increased
$\bar{V}^{\ast }$
contours in figure 11(c,e). For Category II, the initial turbulent state (figure 8
c,d) incurs a rapid diffusion of vortices shortly after their formation in both planes (figure 14
c,f) due to the increased
![]() $C_{m}$
, as noted by Fiedler & Mensing (Reference Fiedler and Mensing1985) in an initially turbulent plane mixing layer under periodic and strong excitation. In Category III, the flow becomes more turbulent in both planes even at
$C_{m}$
, as noted by Fiedler & Mensing (Reference Fiedler and Mensing1985) in an initially turbulent plane mixing layer under periodic and strong excitation. In Category III, the flow becomes more turbulent in both planes even at
![]() $x^{\ast }=0$
. The observations are fully consistent with the findings from
$x^{\ast }=0$
. The observations are fully consistent with the findings from
![]() $u_{r.m.s.}$
measured at the nozzle exit (figure 8
c,d).
$u_{r.m.s.}$
measured at the nozzle exit (figure 8
c,d).

Figure 14. Photographs of typical flow structures from flow visualization. Flow is from the bottom up.

Figure 15. Typical instantaneous velocity vectors and corresponding
![]() $\unicode[STIX]{x1D714}_{y}^{\ast }$
contours: (a) natural jet and (b–d) the injection plane of the manipulated jet (Category I:
$\unicode[STIX]{x1D714}_{y}^{\ast }$
contours: (a) natural jet and (b–d) the injection plane of the manipulated jet (Category I:
![]() $C_{m}=1.5\,\%$
,
$C_{m}=1.5\,\%$
,
![]() $f_{e}/f_{0}^{\prime }=1.0$
). Contour interval
$f_{e}/f_{0}^{\prime }=1.0$
). Contour interval
![]() $=$
1.
$=$
1.
On another note, with a large
![]() $C_{m}$
in Category III, the two minijets penetrate deeply into the potential core in the injection plane, and collide with each other around the centreline (Zhou et al.
Reference Zhou, Du, Mi and Wang2012). Such a strong perturbation is naturally transferred to the non-injection plane, resulting in the transition from laminar to turbulent vortices in both planes. The turbulent vortices entrain more effectively ambient fluid into the jet and thereby contribute to a large
$C_{m}$
in Category III, the two minijets penetrate deeply into the potential core in the injection plane, and collide with each other around the centreline (Zhou et al.
Reference Zhou, Du, Mi and Wang2012). Such a strong perturbation is naturally transferred to the non-injection plane, resulting in the transition from laminar to turbulent vortices in both planes. The turbulent vortices entrain more effectively ambient fluid into the jet and thereby contribute to a large
![]() $K$
. With increasing
$K$
. With increasing
![]() $C_{m}$
, the jet gradually gains a fully turbulent state and
$C_{m}$
, the jet gradually gains a fully turbulent state and
![]() $K$
approaches an asymptotic value.
$K$
approaches an asymptotic value.
In summary, the significantly increased
![]() $K$
in Category I results from the enhanced strength of large-scale coherent structures. A large
$K$
in Category I results from the enhanced strength of large-scale coherent structures. A large
![]() $K$
is also achievable in Category III, which is ascribed to enhanced turbulence with increasing
$K$
is also achievable in Category III, which is ascribed to enhanced turbulence with increasing
![]() $C_{m}$
. Category II is a transition between I and III and is characterized by relatively small
$C_{m}$
. Category II is a transition between I and III and is characterized by relatively small
![]() $K$
. The excitation of Category I is apparently most efficient and will be further explored in following sections.
$K$
. The excitation of Category I is apparently most efficient and will be further explored in following sections.
7 Flow structure development under excitation
7.1 Vortex formation, interaction and entrainment
The flow structure evolution is completely different between the injection and non-injection planes. Figure 15 presents typical instantaneous velocity vectors and corresponding
![]() $\unicode[STIX]{x1D714}_{y}^{\ast }$
contours in the injection plane (Category I). We have examined carefully the 1800 PIV images and 300 photographs of flow visualization and have found that the vortex pairing is a frequent event. The marked periodicity of the flow structure, especially at
$\unicode[STIX]{x1D714}_{y}^{\ast }$
contours in the injection plane (Category I). We have examined carefully the 1800 PIV images and 300 photographs of flow visualization and have found that the vortex pairing is a frequent event. The marked periodicity of the flow structure, especially at
![]() $x^{\ast }<3.0$
(figure 12
b), allows us to capture and identify the typical phases or stages, I through VI, of the vortex evolution during pairing. We wish to emphasize that the four panels are representative of typical structures, and the six phases or stages of the pairing process inferred from the four panels are also consistent with previous investigations on vortex pairing (e.g. Hussain & Zaman Reference Hussain and Zaman1980; Husain & Hussain Reference Husain and Hussain1991). Once perturbation is introduced, the vortices seen in the injection plane are changed substantially, compared with the natural jet (figure 15
a). A relatively small vortex, marked by ‘B’ in figure 15(b), catches up a large leading vortex ‘A’, running towards the inner side of the latter, meanwhile pushing the latter outward (figure 15
c), due to the mutual induction between them. The violent interaction between ‘A’ and ‘B’ subsequently leads to the breakdown of ‘B’ (figure 15
d). The
$x^{\ast }<3.0$
(figure 12
b), allows us to capture and identify the typical phases or stages, I through VI, of the vortex evolution during pairing. We wish to emphasize that the four panels are representative of typical structures, and the six phases or stages of the pairing process inferred from the four panels are also consistent with previous investigations on vortex pairing (e.g. Hussain & Zaman Reference Hussain and Zaman1980; Husain & Hussain Reference Husain and Hussain1991). Once perturbation is introduced, the vortices seen in the injection plane are changed substantially, compared with the natural jet (figure 15
a). A relatively small vortex, marked by ‘B’ in figure 15(b), catches up a large leading vortex ‘A’, running towards the inner side of the latter, meanwhile pushing the latter outward (figure 15
c), due to the mutual induction between them. The violent interaction between ‘A’ and ‘B’ subsequently leads to the breakdown of ‘B’ (figure 15
d). The
![]() $\unicode[STIX]{x1D714}_{y}^{\ast }$
contours suggest that the identities of the two vortices persist, up to phase V. Meanwhile, a large amount of ambient fluid is engulfed downstream of interacting ‘A’ and ‘B’ in phases III and IV, as evident from the transverse component of velocity vectors. On the other hand, a remarkable outward lateral motion occurs in the non-injection plane, as is evident from the typical instantaneous velocity vectors (figure 16). The fragmented concentrations of vorticity are sequentially ‘tossed’ out to ambient fluid from the vortical structure ‘A’. The vortex pairing is discernible, resulting from the mutual induction of two vortices, marked by ‘
$\unicode[STIX]{x1D714}_{y}^{\ast }$
contours suggest that the identities of the two vortices persist, up to phase V. Meanwhile, a large amount of ambient fluid is engulfed downstream of interacting ‘A’ and ‘B’ in phases III and IV, as evident from the transverse component of velocity vectors. On the other hand, a remarkable outward lateral motion occurs in the non-injection plane, as is evident from the typical instantaneous velocity vectors (figure 16). The fragmented concentrations of vorticity are sequentially ‘tossed’ out to ambient fluid from the vortical structure ‘A’. The vortex pairing is discernible, resulting from the mutual induction of two vortices, marked by ‘
![]() $+$
’ and ‘
$+$
’ and ‘
![]() $\times$
’. The observation prompts us to examine further the three-dimensional aspects of the flow structure.
$\times$
’. The observation prompts us to examine further the three-dimensional aspects of the flow structure.

Figure 16. Typical instantaneous velocity vectors and corresponding
![]() $\unicode[STIX]{x1D714}_{z}^{\ast }$
contours in the non-injection plane (Category I:
$\unicode[STIX]{x1D714}_{z}^{\ast }$
contours in the non-injection plane (Category I:
![]() $C_{m}=1.5\,\%$
,
$C_{m}=1.5\,\%$
,
![]() $f_{e}/f_{0}^{\prime }=1.0$
). Contour interval
$f_{e}/f_{0}^{\prime }=1.0$
). Contour interval
![]() $=$
1.
$=$
1.
7.2 Development of streamwise structures
7.2.1 Two pairs of counter-rotating streamwise vortices
The streamwise structures may be investigated by examining the jet in a series of cross-sectional planes at
![]() $x^{\ast }=0.7$
, 1.0 and 1.3 via typical photographs from flow visualization (figure 17). As a reference, the natural jet images look like a full moon up to
$x^{\ast }=0.7$
, 1.0 and 1.3 via typical photographs from flow visualization (figure 17). As a reference, the natural jet images look like a full moon up to
![]() $x^{\ast }=1.3$
, as illustrated by the image at
$x^{\ast }=1.3$
, as illustrated by the image at
![]() $x^{\ast }=0.7$
(figure 17
a), suggesting no roll-up motion. Once excited, the shear layer displays the roll-up motion about the injection and the non-injection planes. At
$x^{\ast }=0.7$
(figure 17
a), suggesting no roll-up motion. Once excited, the shear layer displays the roll-up motion about the injection and the non-injection planes. At
![]() $x^{\ast }=0.7$
, the shear layer rolls up about the injection plane, forming two vortical structures (figure 17
b,e). This is caused by a higher level of initial velocity fluctuation about the injection plane than about the non-injection plane, as evidenced by the
$x^{\ast }=0.7$
, the shear layer rolls up about the injection plane, forming two vortical structures (figure 17
b,e). This is caused by a higher level of initial velocity fluctuation about the injection plane than about the non-injection plane, as evidenced by the
![]() $u$
-signals at the nozzle exit in figure 12(b). This higher initial velocity fluctuation hastens the shear-layer evolution (Hussain & Zedan Reference Hussain and Zedan1978). Note that the two vortical structures are symmetrical about a plane through the jet axis, at an angle of approximately
$u$
-signals at the nozzle exit in figure 12(b). This higher initial velocity fluctuation hastens the shear-layer evolution (Hussain & Zedan Reference Hussain and Zedan1978). Note that the two vortical structures are symmetrical about a plane through the jet axis, at an angle of approximately
![]() $15^{\circ }$
with respect to the non-injection plane (please refer to the sketch in figure 17). Such an angle results from the effect of the rotating nozzle extension. Note that the rotation of approximately
$15^{\circ }$
with respect to the non-injection plane (please refer to the sketch in figure 17). Such an angle results from the effect of the rotating nozzle extension. Note that the rotation of approximately
![]() $15^{\circ }$
shown in figure 17 is from one instant of the instantaneous flow field. The time-averaged flow field indicates a smaller rotation (to be presented in § 7.2.3). Further downstream at
$15^{\circ }$
shown in figure 17 is from one instant of the instantaneous flow field. The time-averaged flow field indicates a smaller rotation (to be presented in § 7.2.3). Further downstream at
![]() $x^{\ast }=1.0$
, the shear layer roll-up is also evident about the non-injection plane, forming a ring vortex (figure 17
c). A close examination of two sequential phases (figure 17
c,f), separated by
$x^{\ast }=1.0$
, the shear layer roll-up is also evident about the non-injection plane, forming a ring vortex (figure 17
c). A close examination of two sequential phases (figure 17
c,f), separated by
![]() $450~\unicode[STIX]{x03BC}\text{s}$
out of one typical period of 7.8125 ms (
$450~\unicode[STIX]{x03BC}\text{s}$
out of one typical period of 7.8125 ms (
![]() $f_{e}=128$
Hz, figure 13
a), of the ring vortex unveils that the segment of the ring vortex near the non-injection plane is advected ahead of that near the injection plane, as indicated by the incomplete segments (broken line square) of the ring vortex about the non-injection plane.
$f_{e}=128$
Hz, figure 13
a), of the ring vortex unveils that the segment of the ring vortex near the non-injection plane is advected ahead of that near the injection plane, as indicated by the incomplete segments (broken line square) of the ring vortex about the non-injection plane.

Figure 17. Photographs of flow visualization in the cross-sectional planes of
![]() $x^{\ast }=0.7$
, 1.0, 1.3. Flow is outward.
$x^{\ast }=0.7$
, 1.0, 1.3. Flow is outward.
Two pairs of counter-rotating streamwise vortices are generated, following the shear layer roll-up about the injection plane. At
![]() $x^{\ast }=0.7$
, the cross-section in the braid (figure 17
h) displays two indentations under the influence of earlier roll-up about the injection plane (figure 17
b,e). With increasing
$x^{\ast }=0.7$
, the cross-section in the braid (figure 17
h) displays two indentations under the influence of earlier roll-up about the injection plane (figure 17
b,e). With increasing
![]() $x^{\ast }$
, two pairs of counter-rotating streamwise vortices occur simultaneously in the braid region and on the outer side of the ring vortex, as marked by circles in figure 17(c,f,i). Interestingly, their spatial locations all coincide, be that in the cross-section of the ring vortex or that of the braid, suggesting that these streamwise vortices run longitudinally through the regions of both ring vortex and braid. The counter-rotating vortex pair has an ‘outflow’ sense of rotation about the non-injection plane, that is, fluid is ejected from the jet core region to ambient air as a result of the interaction between the streamwise vortices of each pair. The vortex pairs exhibit an appreciable growth in the cross-sectional size with increasing
$x^{\ast }$
, two pairs of counter-rotating streamwise vortices occur simultaneously in the braid region and on the outer side of the ring vortex, as marked by circles in figure 17(c,f,i). Interestingly, their spatial locations all coincide, be that in the cross-section of the ring vortex or that of the braid, suggesting that these streamwise vortices run longitudinally through the regions of both ring vortex and braid. The counter-rotating vortex pair has an ‘outflow’ sense of rotation about the non-injection plane, that is, fluid is ejected from the jet core region to ambient air as a result of the interaction between the streamwise vortices of each pair. The vortex pairs exhibit an appreciable growth in the cross-sectional size with increasing
![]() $x^{\ast }$
. This is evident by comparing the images at
$x^{\ast }$
. This is evident by comparing the images at
![]() $x^{\ast }=1.3$
(figure 17
d,g,j) with those at
$x^{\ast }=1.3$
(figure 17
d,g,j) with those at
![]() $x^{\ast }=1.0$
(figure 17
c,f,i). The formation, including initial evolution, of the streamwise vortex pairs occurs at azimuthally fixed locations, as observed by Husain & Hussain (Reference Husain and Hussain1993) in an acoustically excited elliptic jet. The rotational senses of their streamwise vortices are also the same as presently observed, even though the two excitation techniques are very different. On the other hand, for the cases of steady control jets (e.g. New & Tay Reference New and Tay2006; Alkislar et al.
Reference Alkislar, Krothapalli and Butler2007; Alvi et al.
Reference Alvi, Lou, Shih and Kumar2008) and tabs (Reeder & Samimy Reference Reeder and Samimy1996; Zaman Reference Zaman1996, Reference Zaman1999), the streamwise vortex pairs are all produced with an initial ‘inflow’ sense, that is, ambient fluid is brought into the jet core region under the interaction between the streamwise vortices of each pair.
$x^{\ast }=1.0$
(figure 17
c,f,i). The formation, including initial evolution, of the streamwise vortex pairs occurs at azimuthally fixed locations, as observed by Husain & Hussain (Reference Husain and Hussain1993) in an acoustically excited elliptic jet. The rotational senses of their streamwise vortices are also the same as presently observed, even though the two excitation techniques are very different. On the other hand, for the cases of steady control jets (e.g. New & Tay Reference New and Tay2006; Alkislar et al.
Reference Alkislar, Krothapalli and Butler2007; Alvi et al.
Reference Alvi, Lou, Shih and Kumar2008) and tabs (Reeder & Samimy Reference Reeder and Samimy1996; Zaman Reference Zaman1996, Reference Zaman1999), the streamwise vortex pairs are all produced with an initial ‘inflow’ sense, that is, ambient fluid is brought into the jet core region under the interaction between the streamwise vortices of each pair.
It is of fundamental importance to understand how the contorted ring vortex interacts with the streamwise vortices. To this end, the PIV measurements were conducted at the cross-sectional (
![]() $y$
,
$y$
,
![]() $z$
) plane of
$z$
) plane of
![]() $x^{\ast }=1.5$
, immediately after the vortices are formed. Figure 18 presents four typical instantaneous velocity vector maps overlapped with the corresponding
$x^{\ast }=1.5$
, immediately after the vortices are formed. Figure 18 presents four typical instantaneous velocity vector maps overlapped with the corresponding
![]() $\unicode[STIX]{x1D714}_{x}^{\ast }$
contours, which represent four typical phases in the process of the interaction. The separation between the
$\unicode[STIX]{x1D714}_{x}^{\ast }$
contours, which represent four typical phases in the process of the interaction. The separation between the
![]() $\unicode[STIX]{x1D714}_{x}^{\ast }$
concentrations exhibits a large variation from one phase to another, in distinct contrast to quasi-steady streamwise vortex pairs produced by steady minijets and tabs. The velocity vectors suggest that the contorted ring vortex be highly three-dimensional. Note that two pairs of ‘inflow’-type streamwise vortices, closer to the jet axis than those of the ‘outflow’ type, entrain the ambient fluid into the jet core about the non-injection plane in figure 18(b). Also, the maximum magnitude of the ‘inflow’-type
$\unicode[STIX]{x1D714}_{x}^{\ast }$
concentrations exhibits a large variation from one phase to another, in distinct contrast to quasi-steady streamwise vortex pairs produced by steady minijets and tabs. The velocity vectors suggest that the contorted ring vortex be highly three-dimensional. Note that two pairs of ‘inflow’-type streamwise vortices, closer to the jet axis than those of the ‘outflow’ type, entrain the ambient fluid into the jet core about the non-injection plane in figure 18(b). Also, the maximum magnitude of the ‘inflow’-type
![]() $\unicode[STIX]{x1D714}_{x}^{\ast }$
concentrations is comparable to that of adjacent ‘outflow’ type. As reported by Zaman (Reference Zaman1996) in a rectangular jet, these ‘inflow’ streamwise vortices may be produced by the re-orientation (or contortion) of the ring vortex.
$\unicode[STIX]{x1D714}_{x}^{\ast }$
concentrations is comparable to that of adjacent ‘outflow’ type. As reported by Zaman (Reference Zaman1996) in a rectangular jet, these ‘inflow’ streamwise vortices may be produced by the re-orientation (or contortion) of the ring vortex.

Figure 18. (a–d) Typical instantaneous velocity vectors and corresponding
![]() $\unicode[STIX]{x1D714}_{x}^{\ast }$
contours in a cross-sectional plane of the manipulated jet (Category I:
$\unicode[STIX]{x1D714}_{x}^{\ast }$
contours in a cross-sectional plane of the manipulated jet (Category I:
![]() $C_{m}=1.5\,\%$
,
$C_{m}=1.5\,\%$
,
![]() $f_{e}/f_{0}^{\prime }=1.0$
) at
$f_{e}/f_{0}^{\prime }=1.0$
) at
![]() $x^{\ast }=1.5$
; the ‘outflow’ sense of the vortex pair is defined as that the jet fluid between vortices (i.e. the fluid about the non-injection plane) is ejected outwards by their induction; (e) model of the contorted ring vortex and streamwise vortex pairs when they are passing through
$x^{\ast }=1.5$
; the ‘outflow’ sense of the vortex pair is defined as that the jet fluid between vortices (i.e. the fluid about the non-injection plane) is ejected outwards by their induction; (e) model of the contorted ring vortex and streamwise vortex pairs when they are passing through
![]() $x^{\ast }=1.5$
. The a to d in (e), corresponding to panels (a) to (d), respectively, represent four typical phases in the process of the interaction of the contorted ring vortices with streamwise vortex pairs.
$x^{\ast }=1.5$
. The a to d in (e), corresponding to panels (a) to (d), respectively, represent four typical phases in the process of the interaction of the contorted ring vortices with streamwise vortex pairs.
It is of interest to examine how the separation varies between the
![]() $\unicode[STIX]{x1D714}_{x}^{\ast }$
concentrations associated with the vortex pairs. Use
$\unicode[STIX]{x1D714}_{x}^{\ast }$
concentrations associated with the vortex pairs. Use
![]() $S_{I}$
and
$S_{I}$
and
![]() $S_{N}$
to denote the separations between the vortices about the injection and non-injection planes, respectively, as marked in figure 18(a–d).
$S_{N}$
to denote the separations between the vortices about the injection and non-injection planes, respectively, as marked in figure 18(a–d).
![]() $S_{N}$
changes significantly, while
$S_{N}$
changes significantly, while
![]() $S_{I}$
does little. Bernal & Roshko (Reference Bernal and Roshko1986), Lasheras, Cho & Maxworthy (Reference Lasheras, Cho and Maxworthy1986) and Lasheras & Choi (Reference Lasheras and Choi1988) observed in-plane mixing layers that streamwise structures first form in the braid region between successive spanwise vortices, and then propagate upstream and downstream between the high-speed side of a spanwise vortex and the low-speed side of the following one. Liepmann & Gharib (Reference Liepmann and Gharib1992) experimentally confirmed that similar streamwise structures also existed in round jets, and evolved in the braid region between consecutive vortex rings, similarly to those of the in-plane mixing layer. Inspired by these findings, we propose a model in figure 18(e) for the interrelationship between the contorted ring vortices and streamwise vortex pairs under the excitation. We wish to highlight two points. Firstly, figure 18(e) is a model extracted from figure 18(a–d), presenting the flow structure passing through a cross-sectional plane of
$S_{I}$
does little. Bernal & Roshko (Reference Bernal and Roshko1986), Lasheras, Cho & Maxworthy (Reference Lasheras, Cho and Maxworthy1986) and Lasheras & Choi (Reference Lasheras and Choi1988) observed in-plane mixing layers that streamwise structures first form in the braid region between successive spanwise vortices, and then propagate upstream and downstream between the high-speed side of a spanwise vortex and the low-speed side of the following one. Liepmann & Gharib (Reference Liepmann and Gharib1992) experimentally confirmed that similar streamwise structures also existed in round jets, and evolved in the braid region between consecutive vortex rings, similarly to those of the in-plane mixing layer. Inspired by these findings, we propose a model in figure 18(e) for the interrelationship between the contorted ring vortices and streamwise vortex pairs under the excitation. We wish to highlight two points. Firstly, figure 18(e) is a model extracted from figure 18(a–d), presenting the flow structure passing through a cross-sectional plane of
![]() $x^{\ast }=1.5$
, thus being sketched in the time domain. The flow is actually from left to right. Secondly, the ring vortex is approximately axisymmetric in the (
$x^{\ast }=1.5$
, thus being sketched in the time domain. The flow is actually from left to right. Secondly, the ring vortex is approximately axisymmetric in the (
![]() $y,z$
) plane. The seemingly ‘U’ shape of the ring is just the side view of the circular structures. In this model, the upstream part of the streamwise vortex joins the outer side of the immediately upstream ring vortex, whereas the downstream part stretches towards the inner side of the ring vortex immediately downstream. Such a feature leads to a considerable variation in
$y,z$
) plane. The seemingly ‘U’ shape of the ring is just the side view of the circular structures. In this model, the upstream part of the streamwise vortex joins the outer side of the immediately upstream ring vortex, whereas the downstream part stretches towards the inner side of the ring vortex immediately downstream. Such a feature leads to a considerable variation in
![]() $S_{N}$
. The locations (a–d) of the cross-sectional plane, with respect to the contorted ring vortex, correspond well to the four typical phases illustrated in figure 18(a–d). If the PIV image captures the instant or phase of (b), the measurement plane lies midway between the four azimuthal segments of one contorted ring vortex. This is why velocity vectors in figure 18(b) show simultaneously the outward and inward radial motions about the injection and the non-injection planes, respectively. As shown in this model, the upstream part of the streamwise vortex joins, on the jet low-speed side, the streamwise segment of the contorted ring vortex.
$S_{N}$
. The locations (a–d) of the cross-sectional plane, with respect to the contorted ring vortex, correspond well to the four typical phases illustrated in figure 18(a–d). If the PIV image captures the instant or phase of (b), the measurement plane lies midway between the four azimuthal segments of one contorted ring vortex. This is why velocity vectors in figure 18(b) show simultaneously the outward and inward radial motions about the injection and the non-injection planes, respectively. As shown in this model, the upstream part of the streamwise vortex joins, on the jet low-speed side, the streamwise segment of the contorted ring vortex.
7.2.2 Mushroom-like streamwise structures
The extraordinarily strong spreading in the non-injection plane (figure 11(e) and 14
e) is linked to the sequentially tossed out mushroom-like structures (figure 16). Mushroom-like streamwise structures are observed in the natural round jet due to the braid instability (e.g. Liepmann & Gharib Reference Liepmann and Gharib1992) but are distinct from those in figure 16. Naturally, we are tempted to find out how the mushroom-like structures under excitation are generated, how they evolve and how they differ from those in the natural jet. Figures 19 and 20 present the images with and without excitation captured in a series of cross-sectional planes at
![]() $x^{\ast }=2.0{-}5.0$
. Both the ring or distorted ring structure and the braid are presented for
$x^{\ast }=2.0{-}5.0$
. Both the ring or distorted ring structure and the braid are presented for
![]() $x^{\ast }=2.0{-}3.0$
(figures 19 and 20), which are distinctly different between the natural and manipulated jets.
$x^{\ast }=2.0{-}3.0$
(figures 19 and 20), which are distinctly different between the natural and manipulated jets.

Figure 19. Photographs of flow visualization in the cross-sectional planes of the natural jet (
![]() $C_{m}=0$
,
$C_{m}=0$
,
![]() $f_{e}/f_{0}^{\prime }=0$
). (a,e)
$f_{e}/f_{0}^{\prime }=0$
). (a,e)
![]() $x^{\ast }=2.0$
, (b,f) 2.4, (c,g) 3.0, (d) 5.0. Flow is outward.
$x^{\ast }=2.0$
, (b,f) 2.4, (c,g) 3.0, (d) 5.0. Flow is outward.

Figure 20. Photographs of flow visualization in the cross-sectional planes of the manipulated jet (
![]() $C_{m}=1.5\,\%$
,
$C_{m}=1.5\,\%$
,
![]() $f_{e}/f_{0}^{\prime }=1.0$
). (a,e)
$f_{e}/f_{0}^{\prime }=1.0$
). (a,e)
![]() $x^{\ast }=2.0$
, (b,f) 2.4, (c,g) 3.0, (d) 5.0. Flow is outward.
$x^{\ast }=2.0$
, (b,f) 2.4, (c,g) 3.0, (d) 5.0. Flow is outward.
The coherent structure in the natural jet is characterized by a small size, showing little or rather regular azimuthal variation for
![]() $x^{\ast }<5.0$
. At
$x^{\ast }<5.0$
. At
![]() $x^{\ast }=2.0$
the shear layer rolls up, forming a ring vortex (figure 19
a). The dark ring region, approximately a circle, is the entrained ambient fluid by the roll-up motion of the ring vortex and the solid inner circle is the potential core. In the braid region (figure 19
e), the image appears to be a full moon. The jet is basically axisymmetric, regardless of the ring vortex or the braid region. Moving downstream to
$x^{\ast }=2.0$
the shear layer rolls up, forming a ring vortex (figure 19
a). The dark ring region, approximately a circle, is the entrained ambient fluid by the roll-up motion of the ring vortex and the solid inner circle is the potential core. In the braid region (figure 19
e), the image appears to be a full moon. The jet is basically axisymmetric, regardless of the ring vortex or the braid region. Moving downstream to
![]() $x^{\ast }=2.4$
, the ring vortex (figure 19
b) changes little, while a number of small lumps, azimuthally separated, occur in the braid region (figure 19
f), suggesting the occurrence of the azimuthal instability in the braid region, fully consistent with Liepmann & Gharib’s (Reference Liepmann and Gharib1992) experimental finding in a natural round jet at
$x^{\ast }=2.4$
, the ring vortex (figure 19
b) changes little, while a number of small lumps, azimuthally separated, occur in the braid region (figure 19
f), suggesting the occurrence of the azimuthal instability in the braid region, fully consistent with Liepmann & Gharib’s (Reference Liepmann and Gharib1992) experimental finding in a natural round jet at
![]() $Re_{D}=5500$
. At
$Re_{D}=5500$
. At
![]() $x^{\ast }=3.0$
mushroom-like streamwise structures are evident in both the ring vortex and the braid region (figure 19
c,g). These mushroom-like structures are characterized by counter-rotating streamwise vortex pairs of the ‘outflow’ type, and by approximately equal azimuthal separation. Liepmann & Gharib (Reference Liepmann and Gharib1992) pointed out that, once formed, the mushroom-like structures first moved outward into the jet low-speed side due to self-induction and then went through the induced velocity field of the ring vortex. They were stretched in the braid region and re-entrained upstream into the adjacent ring vortex. This is why the streamwise structures generated are also observed in the ring vortex region. The jet has become fully turbulent at
$x^{\ast }=3.0$
mushroom-like streamwise structures are evident in both the ring vortex and the braid region (figure 19
c,g). These mushroom-like structures are characterized by counter-rotating streamwise vortex pairs of the ‘outflow’ type, and by approximately equal azimuthal separation. Liepmann & Gharib (Reference Liepmann and Gharib1992) pointed out that, once formed, the mushroom-like structures first moved outward into the jet low-speed side due to self-induction and then went through the induced velocity field of the ring vortex. They were stretched in the braid region and re-entrained upstream into the adjacent ring vortex. This is why the streamwise structures generated are also observed in the ring vortex region. The jet has become fully turbulent at
![]() $x^{\ast }=5.0$
(figure 19
d) and it is difficult to distinguish between the ring vortex, the braid and the mushroom structures.
$x^{\ast }=5.0$
(figure 19
d) and it is difficult to distinguish between the ring vortex, the braid and the mushroom structures.
It is worth mentioning that only one single ‘generation’ of the mushroom-like streamwise structures is generated all the way to the end of the potential core in the natural jet. However, as shown in figure 16, a number of structures are sequentially ‘tossed’ out, one following another, along the radial direction in the non-injection plane of the manipulated jet. One may surmise that there could be several ‘generations’ of the mushroom-like streamwise structures produced under excitation. At
![]() $x^{\ast }=2.0$
, the mushroom-like structures grow initially only between the streamwise vortices of the ‘outflow’-type pair (figure 20
a,e) and are seen in both the distorted ring vortex and the braid region, in distinct contrast to the natural jet. The difference may be ascribed to the outward radial induction from the azimuthally fixed streamwise vortex pairs in the manipulated jet (figure 18
e). At
$x^{\ast }=2.0$
, the mushroom-like structures grow initially only between the streamwise vortices of the ‘outflow’-type pair (figure 20
a,e) and are seen in both the distorted ring vortex and the braid region, in distinct contrast to the natural jet. The difference may be ascribed to the outward radial induction from the azimuthally fixed streamwise vortex pairs in the manipulated jet (figure 18
e). At
![]() $x^{\ast }=2.4$
, the ‘first generation’ of mushroom-like structures is fully developed and starts to move outward, away from the jet core. Meanwhile, another generation of new mushroom-like structures (figure 20
f) emerges. The mushroom-like structures undergo a much more rapid ‘production’ from
$x^{\ast }=2.4$
, the ‘first generation’ of mushroom-like structures is fully developed and starts to move outward, away from the jet core. Meanwhile, another generation of new mushroom-like structures (figure 20
f) emerges. The mushroom-like structures undergo a much more rapid ‘production’ from
![]() $x^{\ast }=2.4$
to 3.0 than those from
$x^{\ast }=2.4$
to 3.0 than those from
![]() $x^{\ast }=2.0$
to 2.4. Many mushroom-like counter-rotating structures are sequentially ‘tossed’ out along the radial direction about the non-injection plane, often one pair after another (figure 20
c). Sometimes, one mushroom-like structure is alternately interwoven with another (figure 20
g). This is accompanied by a strong ejection of jet core fluid, resulting in greatly enhanced jet spreading. As the case of the natural jet, the manipulated jet is also fully turbulent at
$x^{\ast }=2.0$
to 2.4. Many mushroom-like counter-rotating structures are sequentially ‘tossed’ out along the radial direction about the non-injection plane, often one pair after another (figure 20
c). Sometimes, one mushroom-like structure is alternately interwoven with another (figure 20
g). This is accompanied by a strong ejection of jet core fluid, resulting in greatly enhanced jet spreading. As the case of the natural jet, the manipulated jet is also fully turbulent at
![]() $x^{\ast }=5.0$
. Nevertheless, the image in figure 20(d) shows unequivocally a much larger spread, than that in figure 19(d), about the non-injection plane due to a number of generations of mushroom-like structures tossed out from the jet core region.
$x^{\ast }=5.0$
. Nevertheless, the image in figure 20(d) shows unequivocally a much larger spread, than that in figure 19(d), about the non-injection plane due to a number of generations of mushroom-like structures tossed out from the jet core region.
There is a marked difference in the radial outward motions of mushroom-like structures between the natural and manipulated jets. In the natural jet the mushroom-like structures formed occur near the ring vortex or braid region (Liepmann & Gharib Reference Liepmann and Gharib1992) since the outward self-induction of these structures is at least partially curtailed by the inward induction of passing ring vortices. In contrast, the mushroom-like structures in the manipulated jet can often move out for two or more nozzle diameters from the jet axis. The difference is attributed to the presence of the azimuthally fixed streamwise vortex pairs of the ‘outflow’ type in the manipulated jet. Their presence tips the balance between the inward and outward inductions in the natural jet, resulting in a predominance of the radial outward induction. As a consequence, the mushroom-like structures are tossed out from the jet core region. This mechanism is similar to the production mechanism for the side jets in a heated round jet or strongly excited cold jet (Monkewitz et al. Reference Monkewitz, Bechert, Barsikow and Lehmann1990; Monkewitz & Pfizenmaier Reference Monkewitz and Pfizenmaier1991; Brancher, Chomaz & Huerre Reference Brancher, Chomaz and Huerre1994). The side jet is produced by streamwise vortex pairs in the braid region and acts to eject vigorously fluid from the jet core region.
7.2.3 Time-averaged streamwise vorticity
The development of the streamwise vortices is reflected in the time-averaged streamwise vorticity (
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }=\overline{\unicode[STIX]{x1D714}}_{x}D/U_{e}$
). At
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }=\overline{\unicode[STIX]{x1D714}}_{x}D/U_{e}$
). At
![]() $x^{\ast }=0.45$
, two pairs of oppositely signed
$x^{\ast }=0.45$
, two pairs of oppositely signed
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations occur symmetrically about the centre, protruding into the potential core (figure 21
a). They are apparently generated by the two symmetrically placed and oppositely pointing minijets. Issuing from the radial orifices, as shown in figure 6(a), each of the two minijets may have produced a leading vortex ring followed by trailing fluid and, when viewed in the (
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations occur symmetrically about the centre, protruding into the potential core (figure 21
a). They are apparently generated by the two symmetrically placed and oppositely pointing minijets. Issuing from the radial orifices, as shown in figure 6(a), each of the two minijets may have produced a leading vortex ring followed by trailing fluid and, when viewed in the (
![]() $y,z$
) plane, the ring shows one pair of counter-rotating vortices (figure 6
b). The two pairs of vortices exhibit a rapid decay at
$y,z$
) plane, the ring shows one pair of counter-rotating vortices (figure 6
b). The two pairs of vortices exhibit a rapid decay at
![]() $x^{\ast }=1.0$
(figure 21
b) and are barely discernible at
$x^{\ast }=1.0$
(figure 21
b) and are barely discernible at
![]() $x^{\ast }=1.5$
(figure 21
c). Note the ring-like
$x^{\ast }=1.5$
(figure 21
c). Note the ring-like
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations at
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations at
![]() $x^{\ast }=0.45$
, which are attributed, at least partially, to the nozzle extension rotation (§ 3). It is cautioned that the streamwise measurements might not have fully captured the minijet structures at sufficiently far downstream, say approximately
$x^{\ast }=0.45$
, which are attributed, at least partially, to the nozzle extension rotation (§ 3). It is cautioned that the streamwise measurements might not have fully captured the minijet structures at sufficiently far downstream, say approximately
![]() $x^{\ast }=3$
and beyond, since the contours of time-averaged streamwise vorticity point to the most likely rotation of
$x^{\ast }=3$
and beyond, since the contours of time-averaged streamwise vorticity point to the most likely rotation of
![]() $7^{\circ }$
at
$7^{\circ }$
at
![]() $x^{\ast }\leqslant 1.0$
(figure 21
a,b) and even larger rotation from
$x^{\ast }\leqslant 1.0$
(figure 21
a,b) and even larger rotation from
![]() $x^{\ast }=3.0$
(figure 21
f,g).
$x^{\ast }=3.0$
(figure 21
f,g).

Figure 21. Contours of time-averaged streamwise vorticity
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
in the cross-sectional planes of the manipulated jet (Category I:
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
in the cross-sectional planes of the manipulated jet (Category I:
![]() $C_{m}=1.5\,\%$
,
$C_{m}=1.5\,\%$
,
![]() $f_{e}/f_{0}^{\prime }=1.0$
). (a)
$f_{e}/f_{0}^{\prime }=1.0$
). (a)
![]() $x^{\ast }=0.45$
, (b) 1.0, (c) 1.5, (d) 2.0, (e) 2.5, (f) 3.0, (g) 4.0, (h) 5.0.
$x^{\ast }=0.45$
, (b) 1.0, (c) 1.5, (d) 2.0, (e) 2.5, (f) 3.0, (g) 4.0, (h) 5.0.
Three pairs of alternatively signed
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations are seen over
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations are seen over
![]() $x^{\ast }=1.0{-}3.0$
about the non-injection plane (figure 21
b–f), referred to as the inner, intermediate and outer pairs, respectively, for the convenience of discussion. Both inner and outer pairs of the
$x^{\ast }=1.0{-}3.0$
about the non-injection plane (figure 21
b–f), referred to as the inner, intermediate and outer pairs, respectively, for the convenience of discussion. Both inner and outer pairs of the
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations are of the ‘outflow’ sense of rotation, opposite to that of the intermediate pair. Based on the proposed model for the contorted ring and streamwise structures (figure 18
e), we may easily see that the intermediate pair of the
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations are of the ‘outflow’ sense of rotation, opposite to that of the intermediate pair. Based on the proposed model for the contorted ring and streamwise structures (figure 18
e), we may easily see that the intermediate pair of the
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations corresponds to the reoriented or predominantly streamwise segments of the contorted ring vortex, and the inner and outer pairs are associated with the two pairs of ‘outflow’ streamwise vortices. Naturally, the inner and outer
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations corresponds to the reoriented or predominantly streamwise segments of the contorted ring vortex, and the inner and outer pairs are associated with the two pairs of ‘outflow’ streamwise vortices. Naturally, the inner and outer
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations result from the downstream and upstream portions of the two pairs of streamwise vortices, respectively.
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations result from the downstream and upstream portions of the two pairs of streamwise vortices, respectively.
The maximum level of the
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations occurs at
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations occurs at
![]() $x^{\ast }=1.5$
for the outer and intermediate pairs but at
$x^{\ast }=1.5$
for the outer and intermediate pairs but at
![]() $x^{\ast }=2.5$
for the inner pair. This indicates that the upstream part of one pair of streamwise vortices develops more rapidly than its downstream part, which is fully consistent with flow visualization in the (
$x^{\ast }=2.5$
for the inner pair. This indicates that the upstream part of one pair of streamwise vortices develops more rapidly than its downstream part, which is fully consistent with flow visualization in the (
![]() $y,z$
) plane (figure 20). This is because the shear in the braid region is more intense immediately downstream than upstream of the ring vortex (Martin & Meiburg Reference Martin and Meiburg1991). The intense shear accelerates the development of the upstream part. At
$y,z$
) plane (figure 20). This is because the shear in the braid region is more intense immediately downstream than upstream of the ring vortex (Martin & Meiburg Reference Martin and Meiburg1991). The intense shear accelerates the development of the upstream part. At
![]() $x^{\ast }=4$
(figure 21
g), the maximum levels of the inner and outer
$x^{\ast }=4$
(figure 21
g), the maximum levels of the inner and outer
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations decay slowly. On the other hand, the intermediate
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations decay slowly. On the other hand, the intermediate
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations already vanish. The result suggests that the streamwise structures persist farther than the ring vortex, in agreement with Liepmann & Gharib’s (Reference Liepmann and Gharib1992) report. The outer
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations already vanish. The result suggests that the streamwise structures persist farther than the ring vortex, in agreement with Liepmann & Gharib’s (Reference Liepmann and Gharib1992) report. The outer
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations at
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
concentrations at
![]() $x^{\ast }=4$
are extended significantly outward along the radial direction due to the sequential generation of mushroom-like structures and their outward motion. At
$x^{\ast }=4$
are extended significantly outward along the radial direction due to the sequential generation of mushroom-like structures and their outward motion. At
![]() $x^{\ast }=5.0$
(figure 21
h),
$x^{\ast }=5.0$
(figure 21
h),
![]() $\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
becomes very small in magnitude, suggesting grossly weakened streamwise structures.
$\overline{\unicode[STIX]{x1D714}}_{x}^{\ast }$
becomes very small in magnitude, suggesting grossly weakened streamwise structures.
8 Further discussion
8.1 Role of the unsteady minijets in vortex dynamics
Issuing from the radial orifice, each unsteady minijet may produce isolated structures with a leading vortex ring accompanied by trailing fluid (§ 4). Beyond
![]() $x^{\ast }\approx 1.0$
, the minijet-produced flow structures exhibit a rapid decay and are barely discernible at
$x^{\ast }\approx 1.0$
, the minijet-produced flow structures exhibit a rapid decay and are barely discernible at
![]() $x^{\ast }=1.5$
(figure 21
b,c). These structures induce the early roll-up of the shear layer about the injection plane, compared with that about the non-injection plane, forming a contorted ring vortex, which is distinct from that in the natural jet (figures 14 and 17). The initial development of the shear layer can be predicted from linear stability theory (Michalke Reference Michalke1965a
,Reference Michalke
b
; Freymuth Reference Freymuth1966). The initial instability wave undergoes an exponential growth before the shear layer rolls up to form vortices. The initial shear layer is slightly sinuous and the velocity disturbance is small in the natural jet. Under the minijet excitation, a highly periodical velocity perturbation appears about the injection plane even upstream of the main jet exit (figure 5) and persists in the shear layer issuing from the nozzle (figure 12
b). The highly periodical velocity disturbances may induce the shear layer about the injection plane, through the exponential growth to roll up into vortices in a short time or distance compared with that in the natural jet or the non-injection plane of the manipulated jet. This early roll-up, evident by comparing the velocity signals in figure 12(a,b), results in the contorted vortex ring. With the frequency of the unsteady waves coinciding with the unsteady minijet injection, the periodicity of the vortex formation is strengthened in the main jet. Two vortices are formed during each cycle of injection (figure 12
b). The observation is fully consistent with Ho & Huang’s (Reference Ho and Huang1982) report that, if forced at frequency
$x^{\ast }=1.5$
(figure 21
b,c). These structures induce the early roll-up of the shear layer about the injection plane, compared with that about the non-injection plane, forming a contorted ring vortex, which is distinct from that in the natural jet (figures 14 and 17). The initial development of the shear layer can be predicted from linear stability theory (Michalke Reference Michalke1965a
,Reference Michalke
b
; Freymuth Reference Freymuth1966). The initial instability wave undergoes an exponential growth before the shear layer rolls up to form vortices. The initial shear layer is slightly sinuous and the velocity disturbance is small in the natural jet. Under the minijet excitation, a highly periodical velocity perturbation appears about the injection plane even upstream of the main jet exit (figure 5) and persists in the shear layer issuing from the nozzle (figure 12
b). The highly periodical velocity disturbances may induce the shear layer about the injection plane, through the exponential growth to roll up into vortices in a short time or distance compared with that in the natural jet or the non-injection plane of the manipulated jet. This early roll-up, evident by comparing the velocity signals in figure 12(a,b), results in the contorted vortex ring. With the frequency of the unsteady waves coinciding with the unsteady minijet injection, the periodicity of the vortex formation is strengthened in the main jet. Two vortices are formed during each cycle of injection (figure 12
b). The observation is fully consistent with Ho & Huang’s (Reference Ho and Huang1982) report that, if forced at frequency
![]() $f_{e}=1/2f_{n}$
, where
$f_{e}=1/2f_{n}$
, where
![]() $f_{n}$
is the initial vortex formation frequency (
$f_{n}$
is the initial vortex formation frequency (
![]() $f_{n}$
equals presently to
$f_{n}$
equals presently to
![]() $2f_{0}$
, as indicated by the predominant peak at
$2f_{0}$
, as indicated by the predominant peak at
![]() $x^{\ast }=2$
in figure 2
a), the vortices in a mixing layer are formed at frequency
$x^{\ast }=2$
in figure 2
a), the vortices in a mixing layer are formed at frequency
![]() $f=2f_{e}$
. Such subharmonic excitation may enhance the mutual motions of two adjacent vortices, e.g. vortex pairing or merging, in the perturbed shear layer (Ho & Huerre Reference Ho and Huerre1984). This also explains the vigorous vortex interactions in the present manipulated jet.
$f=2f_{e}$
. Such subharmonic excitation may enhance the mutual motions of two adjacent vortices, e.g. vortex pairing or merging, in the perturbed shear layer (Ho & Huerre Reference Ho and Huerre1984). This also explains the vigorous vortex interactions in the present manipulated jet.
The unsteady minijet may produce another important effect. Two steady minijets yield two pairs of streamwise counter-rotating vortices in a laminar round jet (New & Tay Reference New and Tay2006,
![]() $Re_{D}=1000$
). The mechanism is found to be similar to that for the steady transverse jet in cross-flow (Cortelezzi & Karagozian Reference Cortelezzi and Karagozian2001). Naturally, one may wonder whether the same mechanism may account for the occurrence of the two pairs of azimuthally fixed streamwise vortices in the present manipulated jet. As shown in figure 17, the streamwise vortices emerge right after the formation of the contorted ring vortex and braid, showing little connection with the minijet-produced structures. Moreover, due to a small diameter ratio
$Re_{D}=1000$
). The mechanism is found to be similar to that for the steady transverse jet in cross-flow (Cortelezzi & Karagozian Reference Cortelezzi and Karagozian2001). Naturally, one may wonder whether the same mechanism may account for the occurrence of the two pairs of azimuthally fixed streamwise vortices in the present manipulated jet. As shown in figure 17, the streamwise vortices emerge right after the formation of the contorted ring vortex and braid, showing little connection with the minijet-produced structures. Moreover, due to a small diameter ratio
![]() $d_{r}/D$
(
$d_{r}/D$
(
![]() $=$
0.05) presently used, the minijet-produced vortical structures are relatively weak and undergo a rapid decay, barely discernible at
$=$
0.05) presently used, the minijet-produced vortical structures are relatively weak and undergo a rapid decay, barely discernible at
![]() $x^{\ast }=1.5$
(figure 21
b,c). It seems plausible that the two pairs of azimuthally fixed streamwise vortices are not directly linked to the minijet-produced vortical structures; rather, they result from the ring vortex and braid contortions, which originate from the highly periodical disturbance, produced by the pulsed minijets, in the shear layer issuing from the nozzle. This is fully consistent with Tamburello & Amitay’s (Reference Tamburello and Amitay2007) proposition that, when a synthetic excitation jet was placed upstream of the main axisymmetric jet exit, its dominant effect was the growth of the unstable modes.
$x^{\ast }=1.5$
(figure 21
b,c). It seems plausible that the two pairs of azimuthally fixed streamwise vortices are not directly linked to the minijet-produced vortical structures; rather, they result from the ring vortex and braid contortions, which originate from the highly periodical disturbance, produced by the pulsed minijets, in the shear layer issuing from the nozzle. This is fully consistent with Tamburello & Amitay’s (Reference Tamburello and Amitay2007) proposition that, when a synthetic excitation jet was placed upstream of the main axisymmetric jet exit, its dominant effect was the growth of the unstable modes.
8.2 Role of vortex pairing in the generation of mushroom-like structures
The mushroom-like streamwise structures undergo a much more rapid generation over
![]() $x^{\ast }=2.4{-}3.0$
than over
$x^{\ast }=2.4{-}3.0$
than over
![]() $x^{\ast }=2.0{-}2.4$
(figure 20). The observation may be connected to vortex pairing observed in the non-injection plane. The reason is twofold. Firstly, the streamwise extent where vortex pairing occurs (figure 15) coincides well with that where the mushroom-like structures are rapidly generated. Secondly, there is a general consensus that vortex pairing may produce the three-dimensional perturbation via expansion and contraction of the vortices in pairing (e.g. Yule Reference Yule1978; Hussain & Zaman Reference Hussain and Zaman1980; Zaman & Hussain Reference Zaman and Hussain1980; Hussain Reference Hussain1986; Liepmann & Gharib Reference Liepmann and Gharib1992). As discussed earlier, the production of the mushroom-like structure is associated with the instability of the braid region. The braid region associated with large lateral shear and positive strain rate may respond nonlinearly to any small perturbation. The three-dimensional perturbation due to vortex pairing may cause the azimuthal vorticity line in the braid to deform. Under the influence of large lateral shear, the deformed azimuthal vorticity line may be re-oriented to yield the streamwise vorticity line, and the positive strain rate in the braid stretches the streamwise vorticity line to form a mushroom-like structure.
$x^{\ast }=2.0{-}2.4$
(figure 20). The observation may be connected to vortex pairing observed in the non-injection plane. The reason is twofold. Firstly, the streamwise extent where vortex pairing occurs (figure 15) coincides well with that where the mushroom-like structures are rapidly generated. Secondly, there is a general consensus that vortex pairing may produce the three-dimensional perturbation via expansion and contraction of the vortices in pairing (e.g. Yule Reference Yule1978; Hussain & Zaman Reference Hussain and Zaman1980; Zaman & Hussain Reference Zaman and Hussain1980; Hussain Reference Hussain1986; Liepmann & Gharib Reference Liepmann and Gharib1992). As discussed earlier, the production of the mushroom-like structure is associated with the instability of the braid region. The braid region associated with large lateral shear and positive strain rate may respond nonlinearly to any small perturbation. The three-dimensional perturbation due to vortex pairing may cause the azimuthal vorticity line in the braid to deform. Under the influence of large lateral shear, the deformed azimuthal vorticity line may be re-oriented to yield the streamwise vorticity line, and the positive strain rate in the braid stretches the streamwise vorticity line to form a mushroom-like structure.
8.3 Physical model of the flow structure under excitation
Experimental data have unveiled that the flow structure under the excitation of Category I is characterized by the contorted ring vortices, two pairs of counter-rotating streamwise vortices and sequentially ‘tossed out’ mushroom-like structures. Two aspects of this flow are distinct from those manipulated by tabs, steady secondary jets and other techniques. The unsteady minijet excitation creates the contorted vortex rings and thus the deformed braid region, producing two pairs of counter-rotating streamwise vortices of the ‘outflow’ type, not the quasi-steady ‘inflow’ vortex pairs when the tabs (e.g. Zaman et al. Reference Zaman, Reeder and Samimy1994; Reeder & Samimy Reference Reeder and Samimy1996; Zaman Reference Zaman1999) and steady secondary jets (e.g. New & Tay Reference New and Tay2006; Alkislar et al. Reference Alkislar, Krothapalli and Butler2007; Alvi et al. Reference Alvi, Lou, Shih and Kumar2008) are deployed. Furthermore, the mushroom-like structures are sequentially ejected, which is reported for the first time.
The presently manipulated jet exhibits some similarity to a heated round jet, which also displays a large spread when the density ratio of jet at exit to ambient fluid is below 0.72 (Monkewitz & Bechert Reference Monkewitz and Bechert1988). The large spread is linked to the formation of a so-called ‘side jet’, which is directed radially away from the main jet axis. The heated jet is also characterized by strong ring structures and two to six pairs of streamwise vortices as well as a rapid spread (Monkewitz et al.
Reference Monkewitz, Lehmann, Barsikow and Bechert1989). However, there is a marked difference, that is, the mushroom-like structures are absent from the heated jet. This might be due to the relatively small separation in the (
![]() $y$
,
$y$
,
![]() $z$
) plane between the adjacent pairs of counter-rotating streamwise vortices in the heated jet, as is evident in Monkewitz & Pfizenmaier’s (Reference Monkewitz and Pfizenmaier1991) and Brancher et al.’s (Reference Brancher, Chomaz and Huerre1994) models for side jet production (their figures 6 and 8, respectively). In order to produce the mushroom-like structures, this separation needs to be adequately large, as shown in figure 17(j) and 20(e).
$z$
) plane between the adjacent pairs of counter-rotating streamwise vortices in the heated jet, as is evident in Monkewitz & Pfizenmaier’s (Reference Monkewitz and Pfizenmaier1991) and Brancher et al.’s (Reference Brancher, Chomaz and Huerre1994) models for side jet production (their figures 6 and 8, respectively). In order to produce the mushroom-like structures, this separation needs to be adequately large, as shown in figure 17(j) and 20(e).

Figure 22. Conceptual model of the flow structure under the perturbation of two unsteady minijets.
A conceptual model is proposed based on the present experimental data for the jet flow structure under the excitation of two radial unsteady minijets, as schematically shown in figure 22. Issuing from the radial orifices, each unsteady minijet produces periodically isolated structures (figure 6), resulting in strong velocity disturbances in the injection plane (figure 12 b). Such periodic perturbations excite the shear layer, causing the early roll-up about the injection plane than that about the non-injection plane (figure 17 b,e). The early roll-ups produce an inward induction on their upstream fluid, generating two indentations in the braid about the injection plane (figure 17 h). The braid deformation reorients azimuthal vorticity to produce four streamwise vorticity lines at the corners of the indentations (figure 17 i), which are further stretched into two pairs of azimuthally fixed counter-rotating streamwise vortices (figure 17 j, 18 e). Each pair has an ‘outflow’ sense of rotation about the non-injection plane (figure 18 d), thus ejecting the jet core fluid between each pair away from the jet axis. Under the effect of three-dimensional perturbation arising from vortex pairing, the braid instability is amplified to generate the mushroom-like counter-rotating streamwise structures (figure 20 e). These mushroom-like structures are sequentially ‘tossed out’ along two opposite directions of the non-injection plane, one pair after another (figure 20 c), due to the strong outward induction, along the non-injection plane, of the azimuthally fixed streamwise vortex pairs. Meanwhile, the ring vortex about the injection plane (vortex B in figure 15) moves inwards, catching up with the downstream contorted ring vortex (vortex A in figure 15). The two vortices undergo pairing, engulfing vigorously ambient fluid into the jet core region (figure 14 b, 15 b,d). This greatly amplified engulfment may also act to push out or accelerate the ejection of the mushroom-like structures from the non-injection plane.
9 Conclusions
A turbulent axisymmetric jet (
![]() $Re_{D}=8000$
) is manipulated using two radial unsteady minijets. Two excitation parameters
$Re_{D}=8000$
) is manipulated using two radial unsteady minijets. Two excitation parameters
![]() $C_{m}$
and
$C_{m}$
and
![]() $f_{e}/f_{0}^{\prime }$
are examined. Measurements were conducted in the injection (
$f_{e}/f_{0}^{\prime }$
are examined. Measurements were conducted in the injection (
![]() $x$
,
$x$
,
![]() $z$
) plane, non-injection (
$z$
) plane, non-injection (
![]() $x$
,
$x$
,
![]() $y$
) plane and nine cross-sectional (
$y$
) plane and nine cross-sectional (
![]() $y$
,
$y$
,
![]() $z$
) planes over
$z$
) planes over
![]() $x^{\ast }=0.1{-}5.0$
. Following conclusions may be drawn from this investigation.
$x^{\ast }=0.1{-}5.0$
. Following conclusions may be drawn from this investigation.
The jet centreline decay rate
![]() $K$
exhibits a strong dependence on
$K$
exhibits a strong dependence on
![]() $C_{m}$
. The jet under excitation is classified into three categories in terms of required
$C_{m}$
. The jet under excitation is classified into three categories in terms of required
![]() $C_{m}$
, achievable
$C_{m}$
, achievable
![]() $K$
and flow physics involved. In Category I (
$K$
and flow physics involved. In Category I (
![]() $C_{m}=0{-}2.6\,\%$
), given
$C_{m}=0{-}2.6\,\%$
), given
![]() $f_{e}/f_{0}^{\prime }=1$
and
$f_{e}/f_{0}^{\prime }=1$
and
![]() $C_{m}=1.5\,\%$
,
$C_{m}=1.5\,\%$
,
![]() $K$
exceeds that under the excitation of the steady minijets of the same
$K$
exceeds that under the excitation of the steady minijets of the same
![]() $C_{m}$
by more than 80 %, suggesting a significantly improved forcing efficiency with unsteady minijets deployed. The increased
$C_{m}$
by more than 80 %, suggesting a significantly improved forcing efficiency with unsteady minijets deployed. The increased
![]() $K$
results from a drastically changed vortex dynamics. The same increase in
$K$
results from a drastically changed vortex dynamics. The same increase in
![]() $K$
is also achieved in Category III (
$K$
is also achieved in Category III (
![]() $C_{m}=4.5\,\%{-}16\,\%$
), which is ascribed to the increased turbulence resulting from the head-on collision of the two opposing minijets. Category II (
$C_{m}=4.5\,\%{-}16\,\%$
), which is ascribed to the increased turbulence resulting from the head-on collision of the two opposing minijets. Category II (
![]() $C_{m}=2.6\,\%{-}4.5\,\%$
) is the transition between Categories I and III and is characterized by a mild increase in
$C_{m}=2.6\,\%{-}4.5\,\%$
) is the transition between Categories I and III and is characterized by a mild increase in
![]() $K$
.
$K$
.
Much of this study is devoted to the manipulated jet in Category I because of its fascinating vortex dynamics as well as excellent forcing performance and efficiency. Under this type of excitation, the jet decay rate depends strongly on
![]() $f_{e}/f_{0}^{\prime }$
, reaching a pronounced local maximum at
$f_{e}/f_{0}^{\prime }$
, reaching a pronounced local maximum at
![]() $f_{e}/f_{0}^{\prime }\approx 1$
. The produced vortices are highly three-dimensional and complicated, consisting of the contorted but greatly enhanced ring vortices, two pairs of azimuthally fixed streamwise vortices and sequentially ejected mushroom-like counter-rotating structures. The vigorous interactions among the three types of vortical structures are responsible for the rapid mean-velocity decay rate on the jet centreline.
$f_{e}/f_{0}^{\prime }\approx 1$
. The produced vortices are highly three-dimensional and complicated, consisting of the contorted but greatly enhanced ring vortices, two pairs of azimuthally fixed streamwise vortices and sequentially ejected mushroom-like counter-rotating structures. The vigorous interactions among the three types of vortical structures are responsible for the rapid mean-velocity decay rate on the jet centreline.
A physical model (figure 22) has been proposed based on the experimental data for the flow structure under the excitation of Category I, which is distinct from previously proposed models under the manipulation of tabs and steady secondary jets. The pulsed minijets play a crucial role in this model. The unsteady or periodical disturbance, not necessarily the minijet-produced structures per se, excites the shear layer issuing from the nozzle and gives rise to a contortion of the ring vortex, causing subsequently the deformed braid region. As a result, two pairs of azimuthally fixed streamwise vortices are generated, with an ‘outflow’ sense of rotation about the non-injection plane, which are inter-connected with the upstream and downstream ring vortices. Under the effect of the three-dimensional perturbation arising from vortex pairing, the braid instability is amplified to generate the mushroom-like counter-rotating streamwise structures. These structures are sequentially ejected outwards along the radial direction about the non-injection plane, one pair after another, due to the outward radial induction from the azimuthally fixed streamwise vortex pairs. Meanwhile, the two adjacent vortices about the injection plane undergo pairing, engulfing vigorously ambient fluid into the jet core region. This amplified engulfment may also act to push out or accelerate the ejection of the mushroom-like structures from the non-injection plane.
Finally, one remark is due. Although this study is conducted in a low
![]() $Re$
flow, the findings may provide a valuable insight into those of the high
$Re$
flow, the findings may provide a valuable insight into those of the high
![]() $Re$
flow. Indeed, we believe that the proposed control physics and mechanism for the optimal condition are also valid for the high Reynolds number flows given an initially laminar flow at the nozzle exit, but may be invalid for initially turbulent exit conditions. Nevertheless, the optimal control parameters such as
$Re$
flow. Indeed, we believe that the proposed control physics and mechanism for the optimal condition are also valid for the high Reynolds number flows given an initially laminar flow at the nozzle exit, but may be invalid for initially turbulent exit conditions. Nevertheless, the optimal control parameters such as
![]() $C_{m}$
may vary, albeit not necessarily greatly, for the high Reynolds number flow.
$C_{m}$
may vary, albeit not necessarily greatly, for the high Reynolds number flow.
Acknowledgements
YZ wishes to acknowledge support given to him from Research Grants Council of HKSAR through grant GRF 531912, from NSFC through grant 11632006 and from Scientific Research Fund of Shenzhen Government through grant KQCX2014052114430139. Dr P. Zhang’s contribution to this work in experiments and the early stage of data interpretation is acknowledged although he gave up half way through.