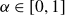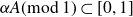1. Metric Poissonian pair correlations

Given a sequence $\mathbf{x} = (x_n)_{n=1}^\infty$ of points on the torus $\mathbb{T}=\mathbb{R}/\mathbb{Z}$ , a point $\gamma\in\mathbb{T}$ , and a real number $s>0$ , we are interested in the asymptotic frequency with which $x_i - x_j\, (i,j \leqslant N)$ lies in the arc $[\gamma-s/N, \gamma + s/N] \subset \mathbb{T}$ . That is, we study the limiting behaviour of

\begin{equation*} F(\gamma, s, N, \mathbf{x}) = \frac{1}{N}\#\left\{(i, j)\in [N]\times[N] \mid i\neq j, \left\|x_i - x_j - \gamma\right\| \leqslant \frac{s}{N}\right\}\!,\end{equation*}

where $\|\cdot\|$ denotes distance to $0\in \mathbb{T}$ and $[N]\,:\!=\,\{1, 2, \dots, N\}$ . For an increasing sequence of natural numbers $\mathcal{A} = (a_n)_{n=1}^\infty$ and $\alpha, \gamma\in\mathbb{T}$ , we denote $F (\alpha, \gamma, s, N, \mathcal{A})=F(\gamma, s, N, \mathbf x)$ , where the sequence $\mathbf x$ is defined by $x_n = a_n\alpha (\textrm{mod}\ 1)$ .

Much attention is paid to the behaviour of F when $\gamma=0$ . In this case $F(0,s, N, \mathbf x)$ is called the pair correlation statistic of $\mathbf x$ . One says that $\mathbf x$ has Poissonian pair correlations (PPC) if

\begin{equation*}(\forall s>0)\qquad \lim_{N\to\infty} F(0, s, N, \mathbf x)= 2s.\end{equation*}

Like equidistribution, PPC is a marker of randomness; a sequence of points on the circle which have been chosen independently and uniformly at random will almost surely have Poissonian pair correlations, just as they will almost surely be equidistributed in the circle. In fact, PPC is a stronger feature of randomness than equidistribution is, in the sense that any sequence which has PPC must also be equidistributed [ Reference C., T. and F.1 , Reference S. and G.6 , Reference A., L., G., W. and M.7 , Reference J.13 ]. The converse fails. For example, an orbit of any irrational circle rotation equidistributes, but does not have Poissonian pair correlations. Indeed, the three gaps theorem implies that the gap distribution of the points of such an orbit is far from random.

In the past two decades, one of the questions of greatest interest in this area has been whether a given $\mathcal{A}\subset\mathbb{N}$ has metric Poissonian pair correlations (MPPC), that is, if for Lebesgue almost every $\alpha\in\mathbb{T}$ , the sequence ${(a_n\alpha (\textrm{mod}\ 1))}_{n=1}^\infty$ has Poissonian pair correlations. Inspired by a problem in quantum mechanics, Rudnick and Sarnak [ Reference Z. and P.14 ] showed that $({n^k})_{n\geqslant 1}$ has MPPC whenever $k\geqslant 2$ . But $({n})_{n\geqslant 1}$ (that is, $\mathcal{A} = \mathbb{N}$ ) does not have MPPC because for every $\alpha$ the corresponding sequence on $\mathbb{T}$ is an orbit of the circle rotation over angle $2\pi\alpha$ , and, as we have mentioned, orbits of circle rotations do not have PPC. To put it informally, the problem for $\mathcal{A} = \mathbb{N}$ arises from the fact that initial strings from the sequence $\mathbb{N}$ have too much additive structure; there are too many different ways to achieve any given $d \in [N]-[N]$ as a difference of two elements of [N], and as a result, $F(\alpha, 0, s, N, \mathbb{N})$ counts events that have been rigged by this extra structure of [N] to occur with non-random regularity. In [ Reference C., G. and M.3 ], Aistleitner, Larcher, and Lewko made an important forward stride in the study of MPPC by putting this informal reasoning on a rigorous footing. They connected the pair correlations of $\mathcal{A}$ to the asymptotic behaviour of the additive energy

\begin{equation*} E(A) \,:\!=\, \#\left\{(a,b,c,d)\in A^4 \mid a+b=c+d\right\},\end{equation*}

where $A\,:\!=\,A_N$ denotes the smallest N elements of $\mathcal{A}$ . Specifically, they proved the following theorem.

Theorem 1·1 ([ Reference C., G. and M.3 , theorem 1]). For an infinite subset $\mathcal{A} \subset \mathbb{N}$ , let $A_N$ denote its smallest N elements. If there exists some $\delta>0$ such that

\begin{equation*} E(A_N) \leqslant N^{3-\delta} \end{equation*}

for all sufficiently large N, then $\mathcal{A}$ has MPPC.

Remark. The Rudnick–Sarnak result follows from Theorem 1·1. On the other hand, it is easy to see that Theorem 1·1 does not apply to $\mathcal{A}=\mathbb{N}$ , since in this case one has $E(A_N)\gg N^3$ .

Remark. (on notation) For functions $f,g:\mathbb{N}\to\mathbb{R}_{\geqslant 0}$ we use $f\ll g$ to mean $f= O(g)$ and $f\gg g$ to mean $g = O(f)$ . If both hold, we write $f\asymp g$ . By $f\sim g$ we mean that $(f/g)\to 1$ as the argument increases to $\infty$ .

Aistleitner, Larcher and Lewko asked whether $E(A_N) = o(N^3)$ is necessary and sufficient for $\mathcal{A}$ to have MPPC. In an appendix to their paper, Bourgain answered the question: it is necessary but not sufficient. This left the question of whether there is some additive energy threshold separating the sets that have MPPC from those that do not. In [ Reference Bloom, S., A. and A.4 ], Bloom, Chow, Gafni and Walker formulated the following question proposing a location for such a threshold:

Question 1·2 ([ Reference Bloom, S., A. and A.4 , fundamental question 1·7]). Let $\mathcal{A}\subset\mathbb{N}$ be an infinite set and suppose that

\begin{equation*} E(A_N) \sim N^3\psi(N), \end{equation*}

where $\psi: \mathbb{N} \to [0,1]$ is some weakly decreasing function. Is convergence of the series $\sum\psi(N)/N$ necessary and sufficient for $\mathcal{A}$ to have metric Poissonian pair correlations?

The answer is no, as we will soon see, but there was good reason to believe otherwise. Previously, Walker had proved that the set of primes does not have MPPC [ Reference A.16 ]. When $\mathcal{A}$ is the set of primes, one has $E(A_N)\asymp N^3(\log N)^{-1}$ . Moreover, Bloom et al. constructed sets with

\begin{equation*} E(A_N) \asymp \frac{N^3}{\log N \log\log N}\end{equation*}

which also do not have MPPC [ Reference Bloom, S., A. and A.4 ]. (And later, Lachmann and Technau constructed sets with

(1·1) \begin{equation} E(A_N) \asymp \frac{N^3}{\log N \log\log N \dots \underbrace{\log\dots\log}_nN}\end{equation}

which do not have MPPC [ Reference T. and N.8 ].) Furthermore, one can construct for any ${\varepsilon}>0$ a set $\mathcal{A}$ having

\begin{equation*} E(A_N) \asymp \frac{N^3}{\log N (\log\log N)^{1+{\varepsilon}}},\end{equation*}

such that $\mathcal{A}$ does have MPPC [ Reference C., T. and N.2 ]. Finally, since the methods of proof in some of the above results involved Khintchine’s theorem on Diophantine approximation in a crucial way, it was natural to suspect that the condition in Khintchine’s theorem—i.e. convergence of the sum $\sum\psi(n)/n$ —is what should define the necessary and sufficient threshold in the Question 1·2.

Regarding necessity, Aistleitner, Lachmann and Technau showed that for every ${\varepsilon}>0$ there exists $\mathcal{A}$ having MPPC such that

\begin{equation*} E(A_N) \gg \frac{N^3}{(\log N)^{\frac{3}{4}+{\varepsilon}}}\end{equation*}

thereby answering that part of Question 1·2 in the negative, and putting an end to the idea that there is a threshold at all [ Reference C., T. and N.2 ]—at least a two-way threshold. Sufficiency remains open. The main results of [ Reference Bloom, S., A. and A.4 ] were in support of it. For example, Bloom et al. proved the following.

Theorem 1·3 ([ Reference Bloom, S., A. and A.4 , theorem 1·4]). If there is some constant $\xi > 0$ for which

\begin{equation*} E(A_N) \ll \frac{N^3}{(\log N)^{2+\xi}} \quad\textrm{and}\quad \delta(A_N) \gg \frac{1}{(\log N)^{2+2\xi}}, \end{equation*}

where $\delta(A_N)$ denotes density, then $\mathcal{A}$ has MPPC.

Later, Bloom and Walker added more evidence for the sufficiency part of Question 1·2 in the form of the following result.

Theorem 1·4 ([ Reference Bloom and A.5 , theorem 6]). There exists an absolute positive constant C such that for any $\mathcal{A}\subset\mathbb{N}$ ,

(1·2) \begin{equation} E(A_N) \ll \frac{N^3}{(\log N)^C} \end{equation}

implies that $\mathcal{A}$ has MPPC.

Of course, Question 1·2 supposes that that constant can be any $C>1$ . Indeed, for a version of the problem on the d-dimensional torus (where $d\geqslant 2$ ), Hinrichs et al. have shown that if there exists some $C>1$ for which (1·2) holds, then $\mathcal{A}$ has “MPPC in dimension d” [ Reference A., L., G., W. and M.7 ].

No further progress has been made on the sufficiency part of Question 1·2. One of the results of this note—Theorem 2·2—establishes an inhomogeneous analogue of the sufficiency part of the question. We introduce the inhomogeneous problem in the next section.

2. Doubly metric Poissonian pair correlations

As we have mentioned, an independent, identically distributed sequence $\mathbf x=(x_n)_n$ of random variables having the uniform distribution on $\mathbb{T}$ will almost surely have Poissonian pair correlations. In fact, it is not hard to show that for any fixed $\gamma\in\mathbb{T}$ such a random sequence $\mathbf x\subset\mathbb{T}$ almost surely satisfies

(2·1) \begin{equation} (\forall s>0)\qquad \lim_{N \to \infty}F (\gamma, s, N,\mathbf x) = 2s.\end{equation}

When (2·1) holds for a sequence $\mathbf x \in \mathbb{T}$ , we will say it has Poissonian pair correlations with inhomogeneous parameter $\gamma\in\mathbb{T}$ (or $\gamma$ -PPC). Notice then that, by Fubini’s theorem, the randomly generated sequence $\mathbf x$ will almost surely have $\gamma$ -PPC for a full-measure set of $\gamma\in\mathbb{T}$ . We will present a proof of the following proposition that serves as template for some of the other results.

With this proposition mind, we propose to study a doubly metric inhomogeneous variant of the notion of metric Poissonian pair correlations. For an infinite subset $\mathcal{A}\subset\mathbb{N}$ and an increasing integer sequence $\{N_t\}$ , we will say that $\mathcal{A}$ has doubly metric Poissonian pair correlations (DMPPC) along the subsequence $\{N_t\}\subset\mathbb{N}$ if for almost all pairs $(\alpha, \gamma)$ , we have

(2·2) \begin{equation} (\forall s>0)\qquad \lim_{t\to \infty}F (\alpha, \gamma, s, N_t, \mathcal{A}) = 2s.\end{equation}

If this holds with $\{N_t\} = \mathbb{N}$ , then we will just say that $\mathcal{A}$ has DMPPC.

The double metricity of the inhomogeneous set up makes certain calculations easier than in the homogeneous setting. As a result, we are able to confirm the sufficiency part of Question 1·2 for DMPPC.

Theorem 2·2 If $\mathcal{A}\subset\mathbb{N}$ is an infinite set such that

\begin{equation*} E(A_N) \ll N^3\psi(N), \end{equation*}

where $\psi:\mathbb{N}\to[0,1]$ is a weakly decreasing function such that the series $\sum \psi(N)/N$ converges, then $\mathcal{A}$ has doubly metric Poissonian pair correlations. (That is, ( 2·2) holds for almost all pairs $(\alpha, \gamma)\in\mathbb{T}^2$ .)

Remark. In particular, if there is some $C>1$ for which (1·2) holds, then $\mathcal{A}$ has DMPPC (a result which in the homogenous setting is only known for higher dimensions).

For functions on the divergence side of Question 1·2, we construct sets $\mathcal{A}\subset\mathbb{N}$ that do not have DMPPC.

Theorem 2·3 Suppose $\psi:\mathbb{N}\to[0,1]$ is a weakly decreasing function such that there exists $\delta>0$ for which $N^{3-\delta}\psi(N)$ is increasing, and such that $\sum\psi(N)/N$ diverges. Then there exists an infinite set $\mathcal{A}\subset\mathbb{N}$ such that

\begin{equation*} E(A_N) \asymp N^3\psi(N) \end{equation*}

and such that $\mathcal{A}$ does not have doubly metric Poissonian pair correlations.

Remark. The assumption that $N^{3-\delta}\psi(N)$ is increasing for some $\delta>0$ is only used to ensure that the sets we construct actually satisfy $E(A_N)\asymp N^3\psi(N)$ . (Notice that since $E(A_N)$ increases to infinity, it is natural that there ought to be extra requirements on $\psi$ besides just divergence of $\sum\psi(N)/N$ .) Theorem 2·3 implies, in particular, that there are sets $\mathcal{A}\subset\mathbb{N}$ satisfying (1·1) that do not have DMPPC.

We leave open the full necessity part of Question 1·2 for doubly metric Poissonian pair correlations. It is not entirely clear what the answer should be. The construction of Aistleitner–Lachmann–Technau [ Reference C., T. and N.2 ] depends crucially on aspects of homogeneous Diophantine approximation (like continued fractions), so it is not immediately obvious whether a similar strategy would work for the doubly metric problem.

Some of the challenges of establishing DMPPC vanish if we allow ourselves to consider the limit in (2·2) along subsequences $\{N_t\}\subseteq \mathbb{N}$ . For DMPPC along sequences, there is the following.

Theorem 2·4 Let $\mathcal{A}\subset\mathbb{N}$ be an infinite set. For any subsequence $\{N_t\}\subset\mathbb{N}$ such that

\begin{equation*} \lim_{t\to\infty} N_t^{-3}E(A_{N_t})=0, \end{equation*}

there exists a subsequence of $\{N_t\}$ along which $\mathcal{A}$ has doubly metric Poissonian pair correlations.

In particular, Theorem 2·4 implies that if $E(A_N)=o(N^3)$ , then any integer sequence has a subsequence along which $\mathcal{A}$ has DMPPC. For example, since we have $E(A_N) \asymp N^3(\log N)^{-1}$ when $\mathcal{A}$ is the set of prime numbers, Theorem 2·4 leads immediately to the following.

Combining Theorem 2·4 with Bourgain’s argument in [ Reference C., G. and M.3 ] leads to the following necessary and sufficient condition for the existence of a sequence along which $\mathcal{A}$ has DMPPC.

It would be interesting to know whether Theorems 2·4 and 2·6 also hold in the original homogeneous setting. For example, recall that Walker proved that the primes do not have MPPC [ Reference A.16 ]. Might it be the case that every increasing integer sequence has a subsequence along which (2·2) holds for almost every $\alpha \in \mathbb{T}$ and with $\gamma=0$ ? That is, does Corollary 2·5 hold for MPPC? Or should we take Corollary 2·5 as evidence that the primes actually have DMPPC?

Finally, It is known that having Poissonian pair correlations is a stronger condition than being equidistributed [ Reference C., T. and F.1 , Reference S. and G.6 , Reference A., L., G., W. and M.7 , Reference J.13 ]. We show that the same is true inhomogeneously.

Before moving on to the proofs, we mention a number of questions and speculations that are not pursued here.

What is the relationship between MPPC and DMPPC? Does one imply the other? From the point of view of our results, the most optimistic hope would be for DMPPC to imply MPPC, because then Theorem 2·2 would imply a positive answer to the sufficiencty part of Question 1·2 for MPPC.

Another question which has been asked in the homogeneous setting and can as easily be asked in the doubly metric case is that of a zero-one law: If $\mathcal{A}\subset\mathbb{N}$ does not have DMPPC, is it the case that (2·2) fails for almost every pair $(\alpha, \gamma)$ ? For MPPC, the question is still open, with some progress in the work of Lachmann–Technau [ Reference T. and N.8 ] and Larcher–Stockinger [ Reference G. and W.9 – Reference G. and W.11 ]. In fact, Larcher and Stockinger have conjectured that even more is true; namely, when $\mathcal{A}\subset\mathbb{N}$ does not have MPPC, then there is no $(\alpha, 0)$ for which (2·2) holds. The doubly metric version of this conjecture would immediately show that MPPC implies DMPPC. However, that doubly metric statement seems unlikely, and can perhaps be disproved by examining the examples in [ Reference C., T. and N.2 ] and showing that they do not have DMPPC. A more likely speculation would be that for every fixed $\gamma$ , if (2·2) does not hold for almost every $\alpha$ , then it holds for no $\alpha$ .

3. Proof of Proposition 2·1

First, we prove Proposition 2·1. The result itself is not surprising, but we include it anyway because it motivates the definition of DMPPC and because its proof is a template for the later proofs, particularly Theorem 2·2.

Note that a homogeneous version of this argument would give the corresponding result for (homogeneous) Poissonian pair correlations—originally established in [ Reference C., T. and F.1 , Reference J.12 ].

Proof of Proposition 2·1. We will show that for any fixed $s>0$ , we almost surely get

\begin{equation*} \lim_{N\to\infty} \frac{1}{N}\#\left\{1\leqslant i\neq j \leqslant N : \left\|{x_i - x_j - \gamma}\right\| \leqslant \frac{s}{N}\right\} = 2s. \end{equation*}

Since $s>0$ is arbitrary, this must almost surely hold simultaneously for a countable dense set of values for $s>0$ . An approximation argument will do the rest.

Let $s>0$ . For each $i\neq j$ and N, let $\mathbf{1}_{i,j,s/N}$ denote the indicator random variable for

\begin{equation*} \left\{(\gamma, \mathbf x) : \left\|{x_i-x_j-\gamma}\right\|\leqslant \frac{s}{N}\right\}. \end{equation*}

Then we can see the pair correlation function as the random variable

(3·1) \begin{equation} F(s,N) = \frac{1}{N}\sum_{1\leqslant i\neq j\leqslant N} \mathbf{1}_{i,j,s/N}. \end{equation}

Our goal is to show that $\mathbb{P}(F(s, N)\to 2s) =1$ .

We now show that if $(i,j)\neq (k,\ell)$ then $\mathbf{1}_{i,j,{\varepsilon}}$ and $\mathbf{1}_{k,\ell, {\varepsilon}'}$ are uncorrelated (hence independent since they are indicators). Indeed,

\begin{align*} &\mathbb{E}\left({\mathbf{1}_{i,j,{\varepsilon}}\mathbf{1}_{k,\ell,{\varepsilon}^{\prime}}}\right)\\ &\quad = \int_\mathbb{T}\int_{\mathbb{T}^4} \left({\sum_{n\in\mathbb{Z}}c(n) e(n(x_i - x_j - \gamma))}\right){\left(\sum_{n\in\mathbb{Z}}c'(n) e(n(x_k - x_\ell - \gamma))\right)} d(x_i, x_j,x_k,x_\ell)\,d\gamma,\end{align*}

where c(n) and c ^′(n) are the Fourier coefficients of $\mathbf{1}_{[-\varepsilon,{\varepsilon}] + \mathbb{Z}}$ and $\mathbf{1}_{[-{\varepsilon}^{\prime},{\varepsilon}^{\prime}]+\mathbb{Z}}$ , respectively. Continuing,

\begin{align*}= \sum_{m,n\in\mathbb{Z}}c(m) c'(n) \int_\mathbb{T} \int_{\mathbb{T}^4} e(m(x_i - x_j - \gamma) + n (x_k-x_\ell-\gamma) d(x_i, x_j,x_k,x_\ell)\,d\gamma.\end{align*}

The integral over $\gamma$ separates, and is only nonzero when $m=-n$ . So we have

\begin{equation*} \mathbb{E}\left({\mathbf{1}_{i,j,{\varepsilon}}\mathbf{1}_{k,\ell,{\varepsilon}^{\prime}}}\right)= \sum_{n\in\mathbb{Z}}c(n) c'(-n) \int_{\mathbb{T}^4} e\left(n(x_i - x_j - x_k+ x_\ell)\right) \,d\left(x_i, x_j,x_k,x_\ell\right). \end{equation*}

Since $(i,j)\neq (k,\ell)$ , the integral is 0 unless $n=0$ , so we are left with

\begin{equation*} \mathbb{E}\left({\mathbf{1}_{i,j,{\varepsilon}}\mathbf{1}_{k,\ell,{\varepsilon}^{\prime}}}\right)= c(0) c'(0) =\mathbb{E}\left({\mathbf{1}_{i,j,{\varepsilon}}}\right)\mathbb{E}\left({\mathbf{1}_{k,\ell,{\varepsilon}^{\prime}}}\right), \end{equation*}

which is what we claimed.

Notice that $\mathbb{E}(\mathbf{1}_{i,j,s/N}) = 2s/N$ . Therefore, by (3·1), we have

\begin{equation*} \mathbb{E}(F(s,N)) = \frac{1}{N}\sum_{1\leqslant i\neq j \leqslant N}\frac{2s}{N} = \left({1-\frac{1}{N}}\right)2s \end{equation*}

and

(3·2) \begin{align} \sigma^2(F(s,N)) &= \frac{1}{N^2}\sum_{1\leqslant i\neq j \leqslant N}\sigma^2({\mathbf{1}_{i,j,s/N}}) \nonumber \\[4pt] &= \frac{1}{N^2}\sum_{1\leqslant i\neq j \leqslant N}\left[{\frac{2s}{N} - \left({\frac{2s}{N}}\right)^2}\right] \ll \frac{s}{N}. \end{align}

In the rest of the proof we will use these last findings to show that the probability that F(s,N) is far from its expected value is small, and that the probability that that happens infinitely often is 0.

Let $\{s_M\}_{M=1}^\infty$ be any sequence converging to s. Notice that, by (3·2), we can write

\begin{equation*} \sigma^2(F(s_M, M^2)) \ll M^{-2} \end{equation*}

for all sufficiently large M, with an implied constant which may depend on s, but is independent of the sequence $\{s_M\}$ , since its terms are eventually bounded uniformly away from $\infty$ . Then, by Chebyshev’s inequality,

\begin{equation*} \mathbb{P}\left[{\left\lvert{F\left(s_M,M^2\right) - \left({1 - \frac{1}{M^2}}\right)2s_M}\right\rvert > \frac{1}{M^{1/4}}}\right] < \frac{\sigma^2(F(s_M,M^2))}{1/M^{1/2}} \ll \frac{1}{M^{3/2}} \end{equation*}

holds for all large $M\in\mathbb{N}$ . Since the sum $\sum M^{-3/2}$ converges, the Borel–Cantelli Lemma says that we almost surely have

\begin{equation*} \left\lvert{F\left(\gamma, s_M,M^2, \mathbf x\right) - \left({1 - \frac{1}{M^2}}\right)2s_M}\right\rvert \leqslant \frac{1}{M^{1/4}} \end{equation*}

for all sufficiently large M, which implies that we almost surely have $F(\gamma, s_M,M^2, \mathbf x) \to 2s$ as $M\to\infty$ . Now, notice that for any integer N such that $M^2 \leqslant N \leqslant (M+1)^2$ , we have

\begin{align*} & \frac{M^2}{(M+1)^2} F\left({\gamma, s\frac{M^2}{(M+1)^2}, M^2, \mathbf x}\right) \leqslant F(\gamma, s, N, \mathbf x)\\[4pt]& \quad \leqslant \frac{(M+1)^2}{M^2} F\left({\gamma, \frac{(M+1)^2}{M^2}s, (M+1)^2, \mathbf x}\right). \end{align*}

The left-most and right-most members almost surely converge to 2s as M increases, therefore, almost surely, $F(\gamma, s,N, \mathbf x) \to 2s$ , as we wanted.

4. Proof of Theorem 2·2

For $\mathcal{A}\subset\mathbb{N}$ , $s>0$ , $N\in\mathbb{N}$ , let us regard $F(s,N, \mathcal{A})$ as a measurable function on the space $\mathbb{T}^2$ equipped with Lebesgue measure. Specifically, it is the function

\begin{equation*} F(s,N,\mathcal{A}) = \frac{1}{N} \sum_{\substack{(a,b)\in A^2\\ a\neq b}} \mathbf{1}_{(a-b),s/N}, \end{equation*}

where, for $d\in \mathbb{Z}$ and ${\varepsilon}>0$ , we use $\mathbf{1}_{d,{\varepsilon}}$ to denote the indicator of the set

\begin{equation*} \left\{(\alpha, \gamma)\in\mathbb{T}^2 : \left\|{d\alpha-\gamma}\right\| \leqslant {\varepsilon}\right\}. \end{equation*}

Given $d\in \mathbb{Z}$ , let

\begin{equation*} r_A(d) = \#\left\{(a,b)\in A^2 : a-b = d\right\} \end{equation*}

be the number of ways to represent d as a difference of two elements of A. In particular, r(d) is non-zero only if $d\in A-A$ . It is a simple exercise to verify the following:

(4·1) \begin{align} \sum_{d\in\mathbb{Z}} r_A(d) &= N^2 \end{align}

(4·2) \begin{align} \sum_{d\in\mathbb{Z}} r_A(d)^2 &= E(A) \end{align}

(4·3) \begin{align} F(s,N,\mathcal{A}) &= \frac{1}{N} \sum_{d\in\mathbb{Z}\setminus \{0\}} r_A(d) \mathbf{1}_{d,s/N}. \end{align}

The next lemma shows that the functions $\mathbf{1}_{d,s/N}$ are pairwise independent as random variables on $\mathbb{T}^2$ .

Proof. Let $\mathbf{1}_{d_1, {\varepsilon}_1}, \mathbf{1}_{d_2, {\varepsilon}_2}$ be any pair of distinct random variables from the sequence. We must show that

(4·4) \begin{equation} \int_{\mathbb{T}^2} \mathbf{1}_{d_1, {\varepsilon}_1}\mathbf{1}_{d_2, {\varepsilon}_2} = \int_{\mathbb{T}^2}\mathbf{1}_{d_1, {\varepsilon}_1}\int_{\mathbb{T}^2}\mathbf{1}_{d_2, {\varepsilon}_2}. \end{equation}

We rewrite the left-hand side as

(4·5) \begin{align} \int_{\mathbb{T}^2} \mathbf{1}_{d_1, {\varepsilon}_1} \mathbf{1}_{d_2, {\varepsilon}_2} &= \int_{\mathbb{T}^2} \mathbf{1}_{(-{\varepsilon}_1, {\varepsilon}_1) + \mathbb{Z}} (d\alpha - \gamma) \mathbf{1}_{(-{\varepsilon}_2, {\varepsilon}_2) + \mathbb{Z}} (d\alpha - \gamma)\,d\alpha\,d\gamma\nonumber \\[5pt] &= \int_{\mathbb{T}^2} \left({\sum_{n_1\in\mathbb{Z}}c_1(n_1)e(n_1(d_1\alpha - \gamma))}\right)\left({\sum_{n_2\in\mathbb{Z}}c_2(n_2)e(n_2(d_2\alpha - \gamma))}\right)\,d\alpha\,d\gamma, \end{align}

where $(c_i(n))_{n\in\mathbb{Z}}$ are the Fourier coefficients of $\mathbf{1}_{(-{\varepsilon}_i, {\varepsilon}_i) + \mathbb{Z}}$ . We may rewrite (4·5) as

\begin{equation*} \sum_{(n_1,n_2) \in \mathbb{Z}^2} c_1(n_1)c_2(n_2) \int_\mathbb{T} e({(d_1n_1 + d_2 n_2) \alpha})\,d\alpha\underbrace{\int_\mathbb{T} e({- (n_1 + n_2)\gamma})\,d\gamma}. \end{equation*}

The indicated integral is only nonzero if $n_1 + n_2 = 0$ , so the expression becomes

\begin{equation*} \sum_{n \in \mathbb{Z}} c_1(n)c_2(-n) \underbrace{\int_\mathbb{T} e({n(d_1 - d_2) \alpha})\,d\alpha}. \end{equation*}

Since $d_1\neq d_2$ , the newly indicated integral is nonzero only if $n=0$ , in which case it is 1, so the expression becomes $c_1(0)c_2(0)$ , which is exactly the right-hand side of (4·4).

Lemma 4·2 For any infinite set $\mathcal{A}\subset \mathbb{N}$ , and for every $s>0$ and sufficiently large N, we have

\begin{equation*} \int_{\mathbb{T}^2} F(s, N, \mathcal{A}) = \frac{2(N-1)}{N}s. \end{equation*}

Proof. As we have seen in (4·3), $F(s,N,\mathcal{A})$ is a linear combination of random variables of the form $\mathbf{1}_{d,s/N}$ where only d varies. Notice that

\begin{equation*} \int_{\mathbb{T}^2}\mathbf{1}_{d,s/N} = \frac{2s}{N} \end{equation*}

as long as $(2s)/N \leqslant 1$ . Therefore, by (4·3), we have

\begin{equation*} \int F(s,N,\mathcal{A}) = \frac{2s}{N^2} \sum_{d\in\mathbb{Z}\setminus\{0\}} r_A(d) \overset{(4.1)}{=} \frac{2s}{N^2}(N^2-N) = \frac{2(N-1)}{N}s, \end{equation*}

as claimed.

Lemma 4·3 For any infinite subset $\mathcal{A}\subset\mathbb{N}$ , $N\in\mathbb{N}$ , and $s>0$ , we have

\begin{equation*} \sigma^2(F(s, N, \mathcal{A})) \ll E(A) N^{-3} s, \end{equation*}

where $\sigma^2$ denotes variance.

Proof. We have found in Lemma 4·1 that the random variables $\mathbf{1}_{d,s/N}$ are pairwise independent. Therefore,

\begin{equation*} \sigma^2(F(s, N, \mathcal{A})) = \frac{1}{N^2} \sum_{d\in\mathbb{Z}\setminus\{0\}} r_A(d)^2 \sigma^2(\mathbf{1}_{d,s/N}).\end{equation*}

(The reader should keep in mind that this is really a finite sum, since r(d) is nonzero for only finitely many d.) Now,

\begin{equation*} \sigma^2(\mathbf{1}_{d,s/N}) = \int \mathbf{1}_{d,s/N}^2- \left({\int \mathbf{1}_{d,s/N}}\right)^2 = \begin{cases} \frac{2s}{N} - \left({\frac{2s}{N}}\right)^2 &\textrm{if } N\geqslant 2s \\[4pt] 0 &\textrm{if } N \leqslant 2s. \end{cases}\end{equation*}

Combining, we find

\begin{equation*} \sigma^2(F(s,N,\mathcal{A})) \leqslant \frac{2s}{N^3} \sum_{d\in\mathbb{Z}}r(d)^2 \overset{(4.1)}{=} 2E(A) N^{-3}s,\end{equation*}

which proves the lemma.

Now we can state the proof of Theorem 2·2.

Proof of Theorem 2·2. Let ${\varepsilon}, s >0$ . We have $E(A_N) \leqslant N^3\psi(N)$ where $\psi:\mathbb{N}\to [0,1]$ is a weakly decreasing function such that $\sum \psi(N)/N$ converges. Therefore, for any fixed real number $k>1$ , $\sum\psi(\lfloor{k^t}\rfloor)$ converges. In particular, by Lemma 4·3, $\sum\sigma^2(F(s,\lfloor{k^t}\rfloor, \mathcal{A}))$ converges. Meanwhile, Chebyshev’s inequality says that the measure of the set of $(\alpha, \gamma)\in\mathbb{T}$ for which

\begin{equation*} \left\lvert{F(\alpha, \gamma, s, \lfloor{k^t}\rfloor, \mathcal{A}) - 2s\left({\frac{\lfloor{k^t}\rfloor-1}{\lfloor{k^t}\rfloor}}\right)}\right\rvert \geqslant {\varepsilon} \end{equation*}

is no more than ${\varepsilon}^{-2}\sigma^2(F(s,\lfloor{k^t}\rfloor, \mathcal{A}))$ . Since $\sum{\varepsilon}^{-2}\sigma^2(F(s,\lfloor{k^t}\rfloor, \mathcal{A}))$ converges, the Borel–Cantelli lemma tells us that for almost every $(\alpha, \gamma)$ , there are at most finitely many t for which

\begin{equation*} \left\lvert{F(\alpha, \gamma, s, \lfloor{k^t}\rfloor, \mathcal{A}) - 2s\left({\frac{\lfloor{k^t}\rfloor-1}{\lfloor{k^t}\rfloor}}\right)}\right\rvert < {\varepsilon} \end{equation*}

does not hold. Decreasing ${\varepsilon}$ to 0 along a positive real sequence, we conclude that for almost every $(\alpha, \gamma)$ ,

\begin{equation*} F\left(\alpha, \gamma, s, \lfloor{k^t}\rfloor, \mathcal{A}\right) \longrightarrow 2s \end{equation*}

as $t\to\infty$ .

By repeating the argument of the previous paragraph for every rational multiple of s, we may say that for almost every $(\alpha, \gamma)$ , the following holds:

(4·6) \begin{equation} (\forall r\in\mathbb{Q}_{>0})\qquad F(\alpha, \gamma, r s, \lfloor{k^t}\rfloor,\mathcal{A}) \longrightarrow 2 r s \quad (t\to\infty). \end{equation}

A review of the definitions reveals that if $k^t < N \leqslant k^{t+1}$ , then

\begin{equation*} \frac{\lfloor{k^t}\rfloor}{N} F({\alpha, \gamma, s \frac{\lfloor{k^t}\rfloor}{N}, \lfloor{k^t}\rfloor}) \leqslant F(\alpha, \gamma, s, N) \leqslant \frac{\lfloor{k^{t+1}}\rfloor}{N} F\left({\alpha, \gamma, s \frac{\lfloor{k^{t+1}}\rfloor}{N}, \lfloor{k^{t+1}}\rfloor}\right). \end{equation*}

From this, we find that

\begin{equation*} \frac{1}{k}\left({1 - \frac{1}{k^t}}\right) F\left({\alpha, \gamma, s/k \left({1 - \frac{1}{k^t}}\right), \lfloor{k^t}\rfloor}\right) \leqslant F(\alpha, \gamma, s, N) \leqslant k F\left({\alpha, \gamma, sk , \lfloor{k^{t+1}}\rfloor}\right). \end{equation*}

Now, let $\delta>0$ be a rational number. For t sufficiently large, we have

\begin{equation*} 1-\delta < \left({1 - \frac{1}{k^t}}\right) < 1, \end{equation*}

hence

\begin{equation*} \frac{1}{k}({1 - \delta}) F({\alpha, \gamma, (s/k) ({1 - \delta}), \lfloor{k^t}\rfloor}) \leqslant F(\alpha, \gamma, s, N) \leqslant k F({\alpha, \gamma, sk , \lfloor{k^{t+1}}\rfloor}) \end{equation*}

holds if N is large enough. Now if $k>1$ is rational, we may apply (4·6) to show that for almost every $(\alpha, \gamma)$ ,

\begin{equation*} \frac{2s}{k^2} (1-\delta)^3 \leqslant F(\alpha, \gamma, s, N) \leqslant 2s k^2 (1+\delta) \end{equation*}

for all sufficiently large N. By taking $k \downarrow 1$ and $\delta \downarrow 0$ along sequences of rational numbers, and intersecting the corresponding full-measure sets of $(\alpha,\gamma)$ , we see that for almost all $(\alpha, \gamma)$ ,

(4·7) \begin{equation} F(\alpha, \gamma, s, N)\longrightarrow 2s, \quad N\to \infty. \end{equation}

Finally, by intersecting countably many full-measure subsets of $\mathbb{T}^2$ , we can say that for almost all $(\alpha, \gamma)$ , and all rational $s>0$ , the limit (4·7) holds. This is enough to conclude that it holds for all s.

5. Proof of Theorem 2·3

The proof of Theorem 2·3 is based on Bourgain’s construction in [ Reference C., G. and M.3 ]. We require a couple of lemmas. The first lemma is a simple consequence of the fact that circle expanding maps are mixing. It will allow us to define a sequence $(U_N)_N$ of sets which are quasi-independent, meaning that there is some constant $C>1$ such that $Leb(U_M\cap U_N)\leqslant C\ Leb(U_M)Leb(U_N)$ whenever $M\neq N$ .

Lemma 5·1 For any sequence of measurable sets $Q_N\in \mathbb{T}$ it is possible to choose a sequence of positive integers $\Delta_N$ so that the sets

\begin{equation*} R_N = \left\{\alpha\in\mathbb{T} : \Delta_N\alpha \in Q_N\right\} \end{equation*}

are pairwise quasi-independent.

Proof. Let $m\geqslant 2$ be an integer. Recall that the map $f_m: \mathbb{T}\to\mathbb{T}$ defined by $f_m(\alpha) = m\alpha (\bmod 1)$ is measure-preserving and mixing, meaning that for any measurable sets $S, T\subset\mathbb{T}$ we have that $Leb(f_m^{-1}(S)) = Leb(S)$ and also that

\begin{equation*} \lim_{k\to\infty} Leb(f_m^{-k}(S)\cap T) = Leb(S)Leb(T).\end{equation*}

Notice that $R_N = f_{\Delta_N}^{-1}(Q_N)$ .

We may put $\Delta_1=1$ , and for each N, choose $\Delta_N$ to be a large enough power $m^{k_N}$ that

\begin{equation*} Leb(f_{\Delta_N}^{-1}(Q_N)\cap R_M) = Leb(f_{m}^{-k_N}(Q_N)\cap R_M) \leqslant 2Leb(Q_N)Leb(R_M) = 2Leb(R_N)Leb(R_M)\end{equation*}

holds for all $M=1, \dots, N-1$ .

The next lemma is a measure estimate on the set of $(\alpha,\gamma)$ which simultaneously satisfy an inhomogeneous approximation condition and a homogeneous approximation condition on $\alpha$ .

Lemma 5·2 For any $M\in\mathbb{N}$ and $0 \leqslant \sigma,\tau \leqslant 1/2$ , let

\begin{equation*} S = \left\{(\alpha,\gamma)\in\mathbb{T}^2 : \left\lvert{\alpha - \frac{a}{d}}\right\rvert\leqslant \frac{\sigma}{M^2} \quad\textrm{for some}\quad d\in[M]\quad\textrm{and}\quad (a,d)=1\right\} \end{equation*}

and

\begin{equation*} T = \left\{(\alpha, \gamma) \in\mathbb{T}^2: \left\|{d\alpha -\gamma}\right\|\leqslant \frac{\tau}{M}\quad\textrm{for some}\quad d\in[M]\right\}. \end{equation*}

Then $Leb(S\cap T) \gg \sigma\tau$ .

Proof. Notice that S consists of disjoint vertical strips in $\mathbb{T}^2$ over the Farey fractions

\begin{equation*} \mathcal{F}_{M} \,:\!=\, \left\{\frac{a}{d}\in [0,1]: (a,d)= 1\right\}. \end{equation*}

The strip $S_{a/d}$ over $a/d\in\mathcal{F}$ has width ${2\sigma}/{M^2}$ . Meanwhile, T is a union of strips which wind around the torus, of slopes $1, \dots, M$ and with vertical cross-sections of length $2\tau/M$ . Specifically, they are the supports of $\mathbf{1}_{1,\tau}, \dots, \mathbf{1}_{M,\tau}$ . The condition $0< \sigma\leqslant 1/2$ guarantees that the indicators $\mathbf{1}_{1,\tau}, \dots, \mathbf{1}_{d,\tau}$ , when restricted to the strip $S_{a/d}$ , are mutually singular. They are supported on non-overlapping parallelograms contained in $S_{a/d}$ , each of which has area $({{2\sigma}/{M^2}})({{2\tau}/{M}})$ . Therefore, $Leb(S_{a/d}\cap T) \geqslant d{4\sigma\tau}/{M^3}$ . Summing over $a/d\in\mathcal{F}_M$ , we have

(5·1) \begin{equation} Leb(S\cap T) \geqslant \sum_{d=1}^M \frac{4\sigma\tau}{M^3}d\varphi(d), \end{equation}

where $\varphi(d)$ denotes the Euler totient function. The growth properties of $\varphi$ guarantee that $\sum_{d=1}^M d\varphi(d) \gg M^3$ , and combining this with (5·1) proves the lemma.

We now state the following.

Proof of Theorem 2·3. We adapt Bourgain’s arguments from [ Reference C., G. and M.3 , appendix]. First, it is possible to modify them to show that if $\psi(N)\neq o(1)$ , then no $\mathcal{A}\subset\mathbb{N}$ satisfying $E(A_N) \asymp N^3\psi(N)$ has DMPPC. We do this here in Theorem 6·2. Therefore, let us assume that $\psi(N) = o(1)$ .

Next, notice that we may assume that $\psi(N)^{-1}\in\mathbb{N}$ for every N, for example by replacing $\psi(N)^{-1}$ with $\lfloor{\psi(N)^{-1}}\rfloor$ .

Let ${\varepsilon}>0$ be a (small) constant, which we will specify later. Per Lemma 5·1, for each $N\in\mathbb{N}$ let $\Delta_N$ be an integer large enough that the sets

\begin{equation*} R_N = \left\{ \alpha\in\mathbb{T} : \left\|{d\Delta_N\alpha}\right\|\leqslant \frac{\psi(N){\varepsilon}}{N} \quad\textrm{for some}\quad 0 < d\leqslant N{\varepsilon}\right\} \end{equation*}

are pairwise quasi-independent. For each N, set $S_N = R_N\times\mathbb{T}\subset\mathbb{T}^2$ . Let

\begin{equation*} T_N = \left\{(\alpha, \gamma)\in\mathbb{T}^2 : \left\|{d\Delta_N\alpha - \gamma}\right\| \leqslant \frac{1}{8N}\quad\textrm{for some}\quad 0 < d \leqslant \frac{N}{20 \psi(N)}\right\}. \end{equation*}

Observe that for all large N the set $T_N$ contains the set $\Delta_N^{-1}T$ , where T is from Lemma 5·2, with $\tau = {\varepsilon}/8$ , and that $S_N$ contains $\Delta_N^{-1}S$ with $\sigma = \psi(N){\varepsilon}^2$ (the role of M is played by $N{\varepsilon}$ ). That lemma tells us then that

(5·2) \begin{equation} Leb(T_N\cap S_N) \gg \psi(N){\varepsilon}^3. \end{equation}

Putting $U_N \,:\!=\, T_N\cap S_N$ , notice that we have for $M\neq N$

\begin{align*} Leb(U_M\cap U_N) &\leqslant Leb(S_M\cap S_N) \\ &\leqslant 2 Leb(S_M)Leb(S_N) \\ &\leqslant 2 \left({2\psi(M){\varepsilon}^2}\right)\left({2\psi(N){\varepsilon}^2}\right) \\ &\overset{(5.2)}{\ll} Leb(U_M)Leb(U_N). \end{align*}

The implicit constant in this last expression depends on ${\varepsilon}$ , but this is unimportant. What is important now is that $(U_N)_N$ is a sequence of subsets of $\mathbb{T}^2$ which are pairwise quasi-independent, and have the property that

\begin{equation*} \sum_{t=0}^\infty Leb(U_{2^t}) \gg \sum_{t=0}^\infty \psi(2^t) \end{equation*}

diverges. Therefore, $U_\infty \,:\!=\,\limsup_t U_{2^t}$ has positive measure in $\mathbb{T}^2$ .

We now construct an infinite set $\mathcal{A}\subset\mathbb{N}$ whose additive energy satisfies $E(A_N)\asymp N^3\psi(N)$ , and such that for every $(\alpha, \gamma) \in U_\infty$ , we have $\limsup_N F(\alpha, \gamma, 1, N, \mathcal{A}) = \infty$ . This will prove the theorem.

The set $\mathcal{A}$ will consist of concatenated blocks $B_N$ of integers, each of which is a subset

\begin{equation*} B_N \subset \Delta_N\left[{(N\psi(N)^{-1}, 2N\psi(N)^{-1}]\cap\mathbb{N}}\right]\!. \end{equation*}

In view of [ Reference C., G. and M.3 , lemma 6], we may find, for each N, a block $B_N$ with the properties:

1. (i) for all $d\in\mathbb{Z}\setminus\{0\}$ we have $r_{B_N}(\Delta_N d) \leqslant 2 N\psi(N)$ ;

2. (ii) for all $d\in\mathbb{Z}\setminus\{0\}$ with $\lvert{d}\rvert < {N}/{10\psi(N)}$ we have $r_{B_N}(\Delta_N d) \geqslant N\psi(N)/2;$

3. (iii) we have $N/2 \leqslant \# B_N \leqslant 2N$ .

Using (4·2) and the first two properties above, we see that $E(B_N)\asymp N^3 \psi(N)$ .

Put $\mathcal{A} = \{B_1, B_2, B_4, \dots \}$ as the concatenation of the blocks $B_{2^t}, t\geqslant 0$ . Suppose that

\begin{equation*}\sum_{k=0}^{t-1} \# B_{2^k} < N \leqslant \sum_{k=0}^t \# B_{2^k},\end{equation*}

that is, $A_N$ is a truncation of $\mathcal{A}$ in the block $B_{2^t}$ . Clearly, we have $E(A_N) \geqslant E(B_{2^{t-1}})$ , hence

\begin{equation*} E(A_N) \gg \left(2^{t-1}\right)^3\psi\left(2^{t-1}\right) \gg N^3\psi(N). \end{equation*}

On the other hand, we may assume that the sequence $(\Delta_N)$ is sparse enough that

\begin{equation*} E(A_N) \leqslant \sum_{k=0}^{t} E(B_{2^k}), \end{equation*}

that is, the only contributions to the additive energy come from four-tuples (a,b,c,d) which lie in the same block. This leads to

(5·3) \begin{align} E\left(A_N\right) &\ll \sum_{k=0}^{t} \left(2^k\right)^3\psi\left(2^k\right) \nonumber \\ &\ll \left(2^t\right)^3 \psi\left(2^t\right)\\ &\ll N^3 \psi(N), \nonumber \end{align}

where (5·3) follows from our assumption that $N^{3-\delta}\psi(N)$ is increasing.Footnote ¹ Therefore, $E(A_N)\asymp N^3\psi(N)$ , as needed.

To estimate the pair correlations, note that for $N=2^t$ , we have

\begin{align*} F(1, \#B_1+ \# B_2 + \# B_4+\dots+\# B_N, \mathcal{A}) &\geqslant \frac{1}{4N} \sum_{d\neq 0} r_{B_n}(\Delta_N d)\mathbf{1}_{\Delta_N d,1/(4N)} \\ &\geqslant \frac{\psi(N)}{8}\sum_{0 < \lvert{d}\rvert\leqslant \frac{N}{10\psi(N)}} \mathbf{1}_{\Delta_N d,1/(4N)} \\ &\geqslant \frac{\psi(N)}{8}\sum_{0 < d\leqslant \frac{N}{10\psi(N)}} \mathbf{1}_{\Delta_N d,1/(4N)}.\end{align*}

Notice then that for any $\alpha\in U_N$ , we will have

\begin{equation*} F(\alpha, 1, \# B_1+\dots+\# B_N, \mathcal{A}) \geqslant \frac{1}{160{\varepsilon}}.\end{equation*}

Since the set of points $(\alpha,\gamma) \in\mathbb{T}^2$ which are contained in infinitely many $U_{2^t}$ ’s has positive measure, this implies that

\begin{equation*}\limsup_{N\to\infty} F(\alpha, \gamma, 1, N, \mathcal{A}) \geqslant \frac{1}{160{\varepsilon}}.\end{equation*}

for a positive-measure set of $(\alpha,\gamma)\in\mathbb{T}^2$ . If $0 < {\varepsilon} < {1}/{320}$ then this value exceeds 2, therefore $\mathcal{A}$ does not have doubly metric Poissonian pair correlations and the theorem is proved.

6. Proofs of Theorems 2·4 and 2·6

Theorem 2·4 can be deduced from the proof of Theorem 2·2.

Proof of Theorem 2·4. By Lemma 4·3, we have that

\begin{equation*} \sigma^2(F(s,N)) \ll E(A)N^{-3} s. \end{equation*}

Let $\{N_t\}\subset\mathbb{N}$ be a sequence as in the theorem statement. By passing to a subsequence, we may assume that $\{N_t\}$ increases fast enough that for any $s>0$ , the sum $\sum_t \sigma^2(F(s,N_t))$ converges. Let ${\varepsilon},s>0$ . The first paragraph of the proof of Theorem 2·2, with the sequence $\{\lfloor{k^t}\rfloor\}$ replaced by the sequence $\{N_t\}$ , shows that for almost every $(\alpha, \gamma)$ ,

\begin{equation*} F(\alpha, \gamma, s, N_t, \mathcal{A}) \longrightarrow 2s \end{equation*}

as $t\to \infty$ . Running the argument for every rational $s>0$ and intersecting the (countably many) full-probability subsets of phase space, we get that for almost every $(\alpha, \gamma)$ ,

\begin{equation*} (\forall s\in\mathbb{Q}_{>0})\qquad \lim_{t\to\infty} F(\alpha, \gamma, s, N_t, \mathcal{A}) = 2s. \end{equation*}

Therefore, (2·2) holds, as needed.

Half of Theorem 2·6 is Theorem 2·4. The other half follows immediately from an inhomogeneous version of Bourgain’s proof in [ Reference C., G. and M.3 , appendix] that $E(A) = \Omega(N^3)$ precludes MPPC. For completeness, we will carry out the argument in the inhomogeneous setting, following an exposition of Walker [ Reference A.17 ].

The basis of the argument is the Balog–Szemerédi–Gowers Lemma.

Proof. For each $t\in \mathbb{N}$ large enough, let $B_{N_t}$ be the subset of $A_{N_t}$ which is guaranteed by Lemma 6·1.

Let $s>0$ be a fixed real number, to be specified. Let

\begin{equation*} \Omega_t \,:\!=\, \left\{(\alpha, \gamma)\in \mathbb{T}^2 : \left\|{\alpha n - \gamma}\right\| \leqslant \frac{s}{N_t}\textrm{ for some } n\in B_{N_t} - B_{N_t}\right\} \end{equation*}

and notice that

\begin{equation*} Leb({\Omega_t}) \leqslant \frac{2s}{N_t} \#\left({B_{N_t} - B_{N_t}}\right) \overset{\textrm{Lem. 6.1}}{\leqslant} 2s c_2. \end{equation*}

Notice also that for every $(\alpha, \gamma)\in\mathbb{T}^2\setminus\Omega_t$ we have

\begin{equation*} F(\alpha, \gamma, s, N_t) = \frac{1}{N_t} \sum_{(a,b) \in A_{N_t}\times A_{N_t} \setminus B_{N_t}\times B_{N_t} } \mathbf{1}_{\left[{0, s/N_t}\right]} ({\left\|{\alpha(a-b) - \gamma}\right\|}), \end{equation*}

hence

\begin{align*} \int_{\mathbb{T}^2\setminus \Omega_t} F(\alpha, \gamma, s, N_t)\,d\alpha\,d \gamma &= \frac{1}{N_t}\sum_{(a,b) \in A_{N_t}\times A_{N_t} \setminus B_{N_t}\times B_{N_t} } \int_{\mathbb{T}^2\setminus \Omega_t} \mathbf{1}_{\left[{0, s/N_t}\right]} ({\left\|{\alpha(a-b) - \gamma}\right\|})\\ &\leqslant \frac{2s}{N_t^2}\#({A_{N_t}\times A_{N_t} \setminus B_{N_t}\times B_{N_t}}) \\ &\overset{\textrm{Lem. 6.1}}{\leqslant} 2s \left(1 - c_1^2\right). \end{align*}

Now, suppose that the set of $(\alpha, \gamma)\in \mathbb{T}^2\setminus \Omega_t$ for which $F(\alpha, \gamma, s, N_t) \leqslant 2s (1 - c_1^2/4)$ has measure less than $c_1^2/4$ . Then we would have

\begin{equation*} 2s({1-c_1^2}) \geqslant \int_{\mathbb{T}^2\setminus\Omega_t} F(\alpha, \gamma, s, N_t)\,d\alpha\,d\gamma > 2s \left({1 - \frac{c_1^2}{4}}\right)\left({1 - 2sc_2 - \frac{c_1^2}{4}}\right). \end{equation*}

But for small enough $s>0$ , this cannot possibly hold. Let us now specify $s>0$ to be small enough. Then there is a set $\Gamma_t \subset \mathbb{T}^2\setminus\Omega_t$ with $Leb(\Gamma_t) \geqslant c_1^2/4$ and such that $F(\alpha, \gamma, s, N_t) \leqslant 2s(1-c_1^2/4)$ holds for all $(\alpha, \gamma)\in\Gamma_t$ . Let $\Gamma \,:\!=\,\limsup_{t\to\infty}\Gamma_t$ , and notice that we must have $Leb(\Gamma) > 0$ . Since for any $(\alpha, \gamma)\in\Gamma$ , we have that

\begin{equation*} \liminf_{t\to\infty} F (\alpha, \gamma, s, N_t) \leqslant 2s \left({1 - \frac{c_1^2}{4}}\right) < 2s, \end{equation*}

the theorem is proved.

Proof of Theorem 2·6. For the “if” direction note that if $\liminf N^{-3}E(A)=0$ , then there is a subsequence $\{N_t\}\subset\mathbb{N}$ to which Theorem 2·4 applies.

For the “only if” direction, suppose that $\liminf N^{-3}E(A)>0$ , and let $\{N_t\}\subset\mathbb{N}$ be any subsequence. Then there is some constant $c>0$ such that $E(A_{N_t}) \geqslant c N_t^{3}$ holds for all large t, and Theorem 6·2 implies that $\mathcal{A}$ does not have DMPPC along $\{N_t\}$ .

7. Proof of Theorem 2·7

The proof of Theorem 2·7 is adapted from [ Reference A., L., G., W. and M.7 ]. We will use the following simple lemma stating that if a sequence does not equidistribute in $\mathbb{T}$ , then there are arbitrarily small intervals in $\mathbb{T}$ which are “overrepresented” infinitely often.

Lemma 7·1 Suppose $(x_n)_n$ is a sequence of points in $\mathbb{T}$ which does not equidistribute. Then there are arbitrarily small intervals $I\subset\mathbb{T}$ such that

(7·1) \begin{equation} \limsup_{N\to\infty}\frac{1}{N}\#\left\{n\in[N]\mid x_n\in I\right\}>Leb(I). \end{equation}

Proof. For an interval $I\subset\mathbb{T}$ and integer $N\in\mathbb{N}$ , let

\begin{equation*} A_N(I) \,:\!=\,\frac{1}{N}\#\left\{n\in[N]\mid x_n\in I\right\}. \end{equation*}

That $(x_n)$ does not equidistribute implies that there are arbitrarily short intervals $I \subset\mathbb{T}$ such that $\lim_{N\to\infty} A_N(I)\neq Leb(I)$ . Let I be such an interval, as small as desired. If (7·1) holds then we are done, so let us assume that $\limsup_{N\to\infty} A_N(I)\leqslant Leb(I)$ . Therefore, it must be that $\liminf_{N\to\infty}A_N(I) < Leb(I)$ , which implies that there is some ${\varepsilon}>0$ and infinitely many values of $N\in\mathbb{N}$ for which $A_N(I)\leqslant Leb(I) (1-{\varepsilon})$ .

Now, let $\bigcup_{k=0}^K I_k$ be a partition of $\mathbb{T}$ by intervals where $I_0=I$ and $Leb(I_k) = (1-Leb (I))/K$ for each $k=1, \dots, K$ . Notice that for all N we have $\sum_{k=0}^K A_N(I_k) = 1$ , so for the infinitely many N for which $A_N(I)\leqslant Leb(I) (1-{\varepsilon})$ holds we have

\begin{equation*} Leb(I)(1-{\varepsilon}) + \sum_{k=1}^K A_N(I_k) \geqslant 1. \end{equation*}

This implies that there must be some $\hat k \,:\!=\, \hat k(N)\in [K]$ for which

\begin{align*} A_N(I_{\hat k}) &\geqslant \frac{1 - Leb(I)(1-{\varepsilon})}{K} \\[4pt] &= Leb\left(I_{\hat k}\right) \left({\frac{1 - Leb(I)(1-{\varepsilon})}{1 -Leb(I)}}\right). \end{align*}

By the pigeonhole principle, there is some $\bar k$ such that $\bar k = \hat k(N)$ for infinitely many N. For this $\bar k$ , we have $\limsup_{N\to\infty}A_N(I_{\bar k}) > Leb(I_{\bar k})$ .

Proof of Theorem 2·7. Assume that the sequence $\mathbf x = (x_n)_n$ is not equidistributed in $\mathbb{T}$ . In view of the results of [ Reference C., T. and F.1 , Reference S. and G.6 , Reference A., L., G., W. and M.7 , Reference J.13 ], it follows that $\mathbf x$ does not have $\gamma$ -PPC when $\gamma=0$ . So let us fix arbitrarily $\gamma > 0$ .

The fact that the sequence is not equidistributed implies, by Lemma 7·1, that there is some arc in $\mathbb{T}$ which is “underrepresented” for infinitely many partial sequences $(x_n)_{n=1}^N$ . Furthermore, that arc can be supposed to be as long as we like. In particular, since the properties of equidistribution and $\gamma$ -PPC are not altered by rotating the entire set $\mathcal{A}$ , this proof will not lose any generality if we assume that there exist $\alpha, \beta>0$ such that $1- \alpha < \|{\gamma}\|$ and such that for infinitely many $N\in \mathbb{N}$ we have

\begin{equation*} \frac{1}{N}\#\left\{1 \leqslant n \leqslant N \mid x_n \in [0,\alpha)\right\} \leqslant \beta < \alpha. \end{equation*}

Let N be one such (large) integer. For $i=0, \dots, N-1$ , let

\begin{equation*} X_i \,:\!=\, \#\left\{1\leqslant n \leqslant N \mid x_n \in \left[ {{i \over N},{{i + 1} \over N}} \right)\right\} \end{equation*}

so that we have

(7·2) \begin{equation} \sum_{i=0}^{\lfloor{N\alpha}\rfloor-1} X_i \leqslant N\beta \quad\textrm{while}\quad\sum_{i=0}^{N-1} X_i = N. \end{equation}

Now notice that for $s\in\mathbb{N}$ ,

\begin{equation*} N F(\gamma, s,N, \mathbf x) \leqslant \sum_{i=0}^{N-1} \sum_{j = -s}^s X_i X_{\left[{i + \lfloor{\gamma N}\rfloor + j (\textrm{mod}\ N)}\right]}. \end{equation*}

The right-hand side defines a quadratic form in the variables $X_0, \dots, X_{N-1}$ which, subject to the constraints imposed by (7·2), reaches its maximum when

(7.3) \begin{equation} X_0 = X_1 = \dots = X_{\lfloor{N\alpha}\rfloor-1} = \frac{N\beta}{\lfloor{N\alpha}\rfloor} \quad\textrm{and}\quad X_{\lfloor{N\alpha}\rfloor} = \dots = X_{N-1} = \frac{N(1-\beta)}{N-\lfloor{N\alpha}\rfloor}. \end{equation}

Now with a fixed $s\in\mathbb{N}$ and N large enough, we will have $1-\alpha < \|{\gamma}\| - s/N$ , hence,

\begin{align*} N F(\gamma, s,N, \mathbf x) &\leqslant \sum_{i=0}^{N-1} \sum_{j = -s}^{s} X_i X_{i + \lfloor{\gamma N}\rfloor + j} \\ &=\sum_{i=0}^{\lfloor{N\alpha}\rfloor-1} X_i \sum_{j = -s}^s X_{i + \lfloor{\gamma N}\rfloor + j} + \sum_{i=\lfloor{N\alpha}\rfloor}^{N-1} X_i \sum_{j = -s}^s X_{i + \lfloor{\gamma N}\rfloor + j} \\ &\overset{\textrm{(7.3)}}{\leqslant} \left({\frac{N\beta}{\lfloor{N\alpha}\rfloor}}\right)\left({\frac{N(1-\beta)}{N-\lfloor{N\alpha}\rfloor}}\right) \sum_{i=\lfloor{N\alpha}\rfloor}^{N-1}\sum_{j=-s}^{s}2 + \left({\frac{N\beta}{\lfloor{N\alpha}\rfloor}}\right)^2\\ & \times \left({N(2s+1)- \sum_{i=\lfloor{N\alpha}\rfloor}^{N-1}\sum_{j=-s}^s2}\right)\sim (2s+1)N\underbrace{\left[{\frac{\beta}{\alpha}\left({2-\frac{\beta}{\alpha}}\right)}\right]}_{<1}. \end{align*}

We see that there exists $\theta<1$ depending only on $\alpha$ and $\beta$ with the property that for any $s\in\mathbb{N}$ and infinitely many $N\in\mathbb{N}$ , we have $F(\gamma, s,N, \mathbf x) \leqslant (2s+1)\theta$ . Therefore, if s is large enough, it is impossible that $F(\gamma, s, N, \mathbf x) \to 2s$ as $N\to\infty$ , so $\mathbf x$ does not have $\gamma$ -PPC.