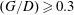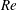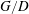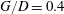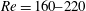1 Introduction
Steady incoming flow past a circular cylinder in close proximity to a plane boundary has been studied extensively due to its fundamental and practical significance. For example, in practical scenarios the plane boundary may be representative of the ‘seabed’ or ‘ground’, involving bluff bodies such as pipelines. In this arrangement, the flow is governed by two dimensionless parameters, i.e. the Reynolds number and the gap-to-diameter ratio (referred to as the gap ratio hereafter). The Reynolds number
![]() $Re\;(=UD/\unicode[STIX]{x1D708})$
is defined based on the approaching flow velocity
$Re\;(=UD/\unicode[STIX]{x1D708})$
is defined based on the approaching flow velocity
![]() $U$
, the cylinder diameter
$U$
, the cylinder diameter
![]() $D$
and the kinematic viscosity of the fluid
$D$
and the kinematic viscosity of the fluid
![]() $\unicode[STIX]{x1D708}$
. The gap ratio is defined as
$\unicode[STIX]{x1D708}$
. The gap ratio is defined as
![]() $G/D$
, where
$G/D$
, where
![]() $G$
is the gap height between the cylinder and plane boundary.
$G$
is the gap height between the cylinder and plane boundary.
In addition to the dependence on
![]() $Re$
and
$Re$
and
![]() $G/D$
, the flow in the neighbourhood of the cylinder is complicated further by the development of the boundary layer near the plane boundary. For different boundary layer profiles, extensive experimental studies have revealed that vortex shedding is suppressed at
$G/D$
, the flow in the neighbourhood of the cylinder is complicated further by the development of the boundary layer near the plane boundary. For different boundary layer profiles, extensive experimental studies have revealed that vortex shedding is suppressed at
![]() $G/D\,<\,\sim 0.3$
for
$G/D\,<\,\sim 0.3$
for
![]() $Re$
in the sub-critical regime ranging from
$Re$
in the sub-critical regime ranging from
![]() $1.2\times 10^{3}$
to
$1.2\times 10^{3}$
to
![]() $2.5\times 10^{4}$
(e.g. Bearman & Zdravkovich Reference Bearman and Zdravkovich1978; Grass et al.
Reference Grass, Raven, Stuart and Bray1984; Lei, Cheng & Kavanagh Reference Lei, Cheng and Kavanagh1999; Price et al.
Reference Price, Sumner, Smith, Leong and Païdoussis2002; Wang & Tan Reference Wang and Tan2008). Based on a two-dimensional (2D) direct numerical simulation (DNS) which employed the Blasius boundary layer profile at the inlet, Lei et al. (Reference Lei, Cheng, Armfield and Kavanagh2000) found that at lower
$2.5\times 10^{4}$
(e.g. Bearman & Zdravkovich Reference Bearman and Zdravkovich1978; Grass et al.
Reference Grass, Raven, Stuart and Bray1984; Lei, Cheng & Kavanagh Reference Lei, Cheng and Kavanagh1999; Price et al.
Reference Price, Sumner, Smith, Leong and Païdoussis2002; Wang & Tan Reference Wang and Tan2008). Based on a two-dimensional (2D) direct numerical simulation (DNS) which employed the Blasius boundary layer profile at the inlet, Lei et al. (Reference Lei, Cheng, Armfield and Kavanagh2000) found that at lower
![]() $Re$
the critical
$Re$
the critical
![]() $G/D$
for vortex shedding suppression was 0.2 at
$G/D$
for vortex shedding suppression was 0.2 at
![]() $Re\geqslant 800$
(with a boundary layer thickness
$Re\geqslant 800$
(with a boundary layer thickness
![]() $\unicode[STIX]{x1D6FF}/D$
at the location of the cylinder of approximately 0.5), but increased to 0.6 at
$\unicode[STIX]{x1D6FF}/D$
at the location of the cylinder of approximately 0.5), but increased to 0.6 at
![]() $Re=200$
(
$Re=200$
(
![]() $\unicode[STIX]{x1D6FF}/D=0.9$
) and 1.0 at
$\unicode[STIX]{x1D6FF}/D=0.9$
) and 1.0 at
![]() $Re=100$
(
$Re=100$
(
![]() $\unicode[STIX]{x1D6FF}/D=1.2$
). In each of these scenarios the boundary layer varied with
$\unicode[STIX]{x1D6FF}/D=1.2$
). In each of these scenarios the boundary layer varied with
![]() $Re$
. Thapa et al. (Reference Thapa, Zhao, Zhou and Cheng2014) studied the three-dimensional (3D) flow structure at
$Re$
. Thapa et al. (Reference Thapa, Zhao, Zhou and Cheng2014) studied the three-dimensional (3D) flow structure at
![]() $Re=500$
and both
$Re=500$
and both
![]() $G/D=0.4$
and 0.8 by adopting the logarithmic law of wall for the inlet flow profile, and found that the streamwise vortices (a representation of the flow three-dimensionality) were much weaker than those for an isolated cylinder. However, it is worth noting that even by adopting the Blasius profile or logarithmic profile at the inlet, the boundary layer profile may still develop with distance from the inlet (even with the cylinder removed from the flow field). In other words, the boundary layer profile at the location of the cylinder is dependent on the streamwise location of the cylinder.
$G/D=0.4$
and 0.8 by adopting the logarithmic law of wall for the inlet flow profile, and found that the streamwise vortices (a representation of the flow three-dimensionality) were much weaker than those for an isolated cylinder. However, it is worth noting that even by adopting the Blasius profile or logarithmic profile at the inlet, the boundary layer profile may still develop with distance from the inlet (even with the cylinder removed from the flow field). In other words, the boundary layer profile at the location of the cylinder is dependent on the streamwise location of the cylinder.
Since the above results of flow past a circular cylinder near a plane boundary are dependent on not only
![]() $Re$
and
$Re$
and
![]() $G/D$
, but also the boundary layer profile at the location of the cylinder, the parameter space for numerical simulations is large. To isolate the ‘near-wall effect’ (which is dependent on
$G/D$
, but also the boundary layer profile at the location of the cylinder, the parameter space for numerical simulations is large. To isolate the ‘near-wall effect’ (which is dependent on
![]() $Re$
and
$Re$
and
![]() $G/D$
only) from the additional influence of the upstream boundary layer, the present study focuses on the case that the plane boundary moves at the same speed as the upstream flow (or equally that the body is moved in still fluid parallel to a stationary boundary).
$G/D$
only) from the additional influence of the upstream boundary layer, the present study focuses on the case that the plane boundary moves at the same speed as the upstream flow (or equally that the body is moved in still fluid parallel to a stationary boundary).
Several past studies have focused on the flow past a circular cylinder near a moving wall (or equally that the cylinder is moved in still fluid near a stationary wall). For example, by towing a circular cylinder close to a stationary wall at
![]() $Re=170$
(Taneda Reference Taneda1965) and
$Re=170$
(Taneda Reference Taneda1965) and
![]() $Re=3550$
(Zdravkovich Reference Zdravkovich1985), Taneda (Reference Taneda1965) and Zdravkovich (Reference Zdravkovich1985) observed alternate vortex shedding at
$Re=3550$
(Zdravkovich Reference Zdravkovich1985), Taneda (Reference Taneda1965) and Zdravkovich (Reference Zdravkovich1985) observed alternate vortex shedding at
![]() $G/D=0.6$
, whereas only a single row of vortices was developed at
$G/D=0.6$
, whereas only a single row of vortices was developed at
![]() $G/D=0.1$
. Huang & Sung (Reference Huang and Sung2007) performed 2D DNS for a circular cylinder near a moving wall for
$G/D=0.1$
. Huang & Sung (Reference Huang and Sung2007) performed 2D DNS for a circular cylinder near a moving wall for
![]() $G/D\geqslant 0.1$
and
$G/D\geqslant 0.1$
and
![]() $Re=200{-}500$
, and reported variations of the pressure and force coefficients with
$Re=200{-}500$
, and reported variations of the pressure and force coefficients with
![]() $G/D$
and
$G/D$
and
![]() $Re$
. They also reported that at
$Re$
. They also reported that at
![]() $Re=300$
alternate vortex shedding was suppressed for
$Re=300$
alternate vortex shedding was suppressed for
![]() $G/D\leqslant 0.28$
, and a single vortex row at the upper side of the cylinder dominated the flow for
$G/D\leqslant 0.28$
, and a single vortex row at the upper side of the cylinder dominated the flow for
![]() $G/D\leqslant 0.28$
. Yoon et al. (Reference Yoon, Lee, Seo and Park2010) carried out 2D DNS for
$G/D\leqslant 0.28$
. Yoon et al. (Reference Yoon, Lee, Seo and Park2010) carried out 2D DNS for
![]() $G/D\geqslant 0.1$
and
$G/D\geqslant 0.1$
and
![]() $Re=60{-}200$
, and investigated variations of the pressure and force coefficients with
$Re=60{-}200$
, and investigated variations of the pressure and force coefficients with
![]() $G/D$
and
$G/D$
and
![]() $Re$
. Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013) showed that while the 2D unsteady wake at larger
$Re$
. Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013) showed that while the 2D unsteady wake at larger
![]() $G/D$
is characterized by the formation of the classical Kármán vortex streets, vortex shedding at smaller
$G/D$
is characterized by the formation of the classical Kármán vortex streets, vortex shedding at smaller
![]() $G/D$
(e.g.
$G/D$
(e.g.
![]() $G/D=0.1$
or 0.01) is characterized by the pairing of the negatively signed separating shear layer from the top of the cylinder and the positively signed vortex from the boundary layer at the wall. It has been revealed from the above studies that without the boundary layer effect vortex shedding can be observed at a
$G/D=0.1$
or 0.01) is characterized by the pairing of the negatively signed separating shear layer from the top of the cylinder and the positively signed vortex from the boundary layer at the wall. It has been revealed from the above studies that without the boundary layer effect vortex shedding can be observed at a
![]() $G/D$
of as low as 0.1. Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013, Reference Rao, Thompson, Leweke and Hourigan2015) and Jiang et al. (Reference Jiang, Cheng, Draper and An2017) found that the onset point of vortex shedding (denoted as
$G/D$
of as low as 0.1. Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013, Reference Rao, Thompson, Leweke and Hourigan2015) and Jiang et al. (Reference Jiang, Cheng, Draper and An2017) found that the onset point of vortex shedding (denoted as
![]() $Re_{cr\,2D}$
) increases monotonically as
$Re_{cr\,2D}$
) increases monotonically as
![]() $G/D$
decreases from
$G/D$
decreases from
![]() $\infty$
to 0.1. Jiang et al. (Reference Jiang, Cheng, Draper and An2017) also investigated the physical mechanisms responsible for the variations of the
$\infty$
to 0.1. Jiang et al. (Reference Jiang, Cheng, Draper and An2017) also investigated the physical mechanisms responsible for the variations of the
![]() $Re_{cr\,2D}$
and hydrodynamic forces, on the basis of the flow characteristics at different
$Re_{cr\,2D}$
and hydrodynamic forces, on the basis of the flow characteristics at different
![]() $G/D$
and
$G/D$
and
![]() $Re$
.
$Re$
.
The variation of the critical
![]() $Re$
for 3D wake instability (denoted as
$Re$
for 3D wake instability (denoted as
![]() $Re_{cr\,3D}$
) with
$Re_{cr\,3D}$
) with
![]() $G/D$
has been predicted by Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013, Reference Rao, Thompson, Leweke and Hourigan2015) and Jiang et al. (Reference Jiang, Cheng, Draper and An2017) through linear stability analysis and 3D DNS, respectively. For
$G/D$
has been predicted by Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013, Reference Rao, Thompson, Leweke and Hourigan2015) and Jiang et al. (Reference Jiang, Cheng, Draper and An2017) through linear stability analysis and 3D DNS, respectively. For
![]() $G/D\leqslant 0.22$
, the flow undergoes a transition sequence of ‘2D steady
$G/D\leqslant 0.22$
, the flow undergoes a transition sequence of ‘2D steady
![]() $\rightarrow$
3D steady
$\rightarrow$
3D steady
![]() $\rightarrow$
3D unsteady’ (Stewart et al.
Reference Stewart, Thompson, Leweke and Hourigan2010; Rao et al.
Reference Rao, Thompson, Leweke and Hourigan2013, Reference Rao, Thompson, Leweke and Hourigan2015; Jiang et al.
Reference Jiang, Cheng, Draper and An2017), and the 3D flow structures have been analysed by Stewart et al. (Reference Stewart, Thompson, Leweke and Hourigan2010) and Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013) at
$\rightarrow$
3D unsteady’ (Stewart et al.
Reference Stewart, Thompson, Leweke and Hourigan2010; Rao et al.
Reference Rao, Thompson, Leweke and Hourigan2013, Reference Rao, Thompson, Leweke and Hourigan2015; Jiang et al.
Reference Jiang, Cheng, Draper and An2017), and the 3D flow structures have been analysed by Stewart et al. (Reference Stewart, Thompson, Leweke and Hourigan2010) and Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013) at
![]() $G/D=0.005$
and by Jiang et al. (Reference Jiang, Cheng, Draper and An2017) at
$G/D=0.005$
and by Jiang et al. (Reference Jiang, Cheng, Draper and An2017) at
![]() $G/D=0.2$
. Jiang et al. (Reference Jiang, Cheng, Draper and An2017) found that the 3D steady and 3D unsteady flows at
$G/D=0.2$
. Jiang et al. (Reference Jiang, Cheng, Draper and An2017) found that the 3D steady and 3D unsteady flows at
![]() $G/D=0.2$
and
$G/D=0.2$
and
![]() $Re$
up to at least 200 are triggered by Mode C instability due to a small gap ratio. However, the Mode C structure is not sustained indefinitely, since interference with the shear layer caused by the moving wall leads to other 3D flow structures (Jiang et al.
Reference Jiang, Cheng, Draper and An2017).
$Re$
up to at least 200 are triggered by Mode C instability due to a small gap ratio. However, the Mode C structure is not sustained indefinitely, since interference with the shear layer caused by the moving wall leads to other 3D flow structures (Jiang et al.
Reference Jiang, Cheng, Draper and An2017).
On the other hand, for
![]() $G/D\geqslant 0.3$
, the flow undergoes a transition sequence of ‘2D steady
$G/D\geqslant 0.3$
, the flow undergoes a transition sequence of ‘2D steady
![]() $\rightarrow$
2D unsteady
$\rightarrow$
2D unsteady
![]() $\rightarrow$
3D unsteady’ (Rao et al.
Reference Rao, Thompson, Leweke and Hourigan2013, Reference Rao, Thompson, Leweke and Hourigan2015), in line with the transition sequence for an isolated cylinder reported by Williamson (Reference Williamson1996). Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2015), through a linear stability analysis, found a Mode A instability at
$\rightarrow$
3D unsteady’ (Rao et al.
Reference Rao, Thompson, Leweke and Hourigan2013, Reference Rao, Thompson, Leweke and Hourigan2015), in line with the transition sequence for an isolated cylinder reported by Williamson (Reference Williamson1996). Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2015), through a linear stability analysis, found a Mode A instability at
![]() $Re_{cr\,3D}$
, followed by a Mode B instability at a higher
$Re_{cr\,3D}$
, followed by a Mode B instability at a higher
![]() $Re$
level. However, the unstable 3D modes discovered from linear stability analysis are based on a 2D base flow, without taking into account the nonlinear interactions between the unstable modes (Henderson Reference Henderson1997). For example, for the case of an isolated cylinder, the onset point for Mode B instability obtained by Barkley & Henderson (Reference Barkley and Henderson1996) through linear stability analysis was
$Re$
level. However, the unstable 3D modes discovered from linear stability analysis are based on a 2D base flow, without taking into account the nonlinear interactions between the unstable modes (Henderson Reference Henderson1997). For example, for the case of an isolated cylinder, the onset point for Mode B instability obtained by Barkley & Henderson (Reference Barkley and Henderson1996) through linear stability analysis was
![]() $Re=259$
, whereas the actual Mode B structure was observed in physical experiments at an
$Re=259$
, whereas the actual Mode B structure was observed in physical experiments at an
![]() $Re$
of as low as 230 (Williamson Reference Williamson1996).
$Re$
of as low as 230 (Williamson Reference Williamson1996).
In light of the previous works, the primary aim of the present study is to examine the 3D wake transition and interactions of the 3D wake modes for flow past a circular cylinder near a moving wall with
![]() $G/D\geqslant$
0.3. This is achieved using 3D DNS. The wake flow is compared with the wake transition process and the characteristics of the well-known Mode A and Mode B structures observed for an isolated cylinder.
$G/D\geqslant$
0.3. This is achieved using 3D DNS. The wake flow is compared with the wake transition process and the characteristics of the well-known Mode A and Mode B structures observed for an isolated cylinder.
The rest of this paper is organized in the following manner. In § 2, the governing equations and the numerical model are presented. The wake transition regimes in the parameter space of
![]() $G/D\geqslant 0.3$
and
$G/D\geqslant 0.3$
and
![]() $Re\leqslant 300$
are presented in § 3.1. The flow structures and wake transition at
$Re\leqslant 300$
are presented in § 3.1. The flow structures and wake transition at
![]() $G/D=0.4$
(where vortex dislocation is suppressed) with varying
$G/D=0.4$
(where vortex dislocation is suppressed) with varying
![]() $Re$
are examined in § 3.2, and the flow structures at
$Re$
are examined in § 3.2, and the flow structures at
![]() $Re=200$
with varying
$Re=200$
with varying
![]() $G/D$
are examined in § 3.3. Finally, major conclusions are drawn in § 4.
$G/D$
are examined in § 3.3. Finally, major conclusions are drawn in § 4.
2 Numerical model
2.1 Numerical method
Numerical simulations have been carried out with OpenFOAM (available from www.openfoam.org) to solve the continuity and incompressible Navier–Stokes equations:
where
![]() $(x_{1},x_{2},x_{3})=(x,y,z)$
are Cartesian coordinates,
$(x_{1},x_{2},x_{3})=(x,y,z)$
are Cartesian coordinates,
![]() $u_{i}$
is the velocity component in the direction
$u_{i}$
is the velocity component in the direction
![]() $x_{i}$
,
$x_{i}$
,
![]() $t$
is time,
$t$
is time,
![]() $\unicode[STIX]{x1D70C}$
is fluid density, and
$\unicode[STIX]{x1D70C}$
is fluid density, and
![]() $p$
is pressure. The same numerical approach used in Jiang et al. (Reference Jiang, Cheng, Draper, An and Tong2016, Reference Jiang, Cheng, Draper and An2017) is adopted here. Specifically, the finite volume method (FVM) and the pressure implicit with splitting of operators (PISO) algorithm (Issa Reference Issa1986) are used to solve the equations. The convection, diffusion and time derivative terms are discretized, respectively, using a fourth-order cubic scheme, a second-order linear scheme, and a blended scheme consisting of the second-order Crank–Nicolson scheme and a first-order Euler implicit scheme.
$p$
is pressure. The same numerical approach used in Jiang et al. (Reference Jiang, Cheng, Draper, An and Tong2016, Reference Jiang, Cheng, Draper and An2017) is adopted here. Specifically, the finite volume method (FVM) and the pressure implicit with splitting of operators (PISO) algorithm (Issa Reference Issa1986) are used to solve the equations. The convection, diffusion and time derivative terms are discretized, respectively, using a fourth-order cubic scheme, a second-order linear scheme, and a blended scheme consisting of the second-order Crank–Nicolson scheme and a first-order Euler implicit scheme.
2.2 Computational domain and mesh
The computational domain and mesh are determined based on a domain size dependence study carried out in Jiang et al. (Reference Jiang, Cheng, Draper, An and Tong2016) and a mesh resolution dependence study carried out in Jiang et al. (Reference Jiang, Cheng, Draper and An2017). The standard 3D mesh reported in Jiang et al. (Reference Jiang, Cheng, Draper and An2017) is adopted in this study.
The details of the standard 3D mesh are as follows. As shown in figure 1(a), a hexahedral computational domain of
![]() $(L_{x},L_{y},L_{z})=(50D,G+20.5D,12D)$
, with
$(L_{x},L_{y},L_{z})=(50D,G+20.5D,12D)$
, with
![]() $L_{x},L_{y}$
and
$L_{x},L_{y}$
and
![]() $L_{z}$
being the domain sizes in the
$L_{z}$
being the domain sizes in the
![]() $x$
-,
$x$
-,
![]() $y$
- and
$y$
- and
![]() $z$
-directions, respectively, is constructed. The gap height
$z$
-directions, respectively, is constructed. The gap height
![]() $G$
is varied in this study. In the
$G$
is varied in this study. In the
![]() $x$
–
$x$
–
![]() $y$
plane (the plane perpendicular to the cylinder axis), the cylinder perimeter is discretized with 132 nodes for
$y$
plane (the plane perpendicular to the cylinder axis), the cylinder perimeter is discretized with 132 nodes for
![]() $G/D\geqslant 1.5$
and 160 nodes for
$G/D\geqslant 1.5$
and 160 nodes for
![]() $G/D<1.5$
(due to the slight change of the mesh topology at smaller gap ratios). The height of the first layer of mesh next to the moving wall and next to the cylinder surface is approximately
$G/D<1.5$
(due to the slight change of the mesh topology at smaller gap ratios). The height of the first layer of mesh next to the moving wall and next to the cylinder surface is approximately
![]() $0.001D$
. The cell expansion ratio in the whole domain is kept below 1.1. This results in at least 30 layers of mesh in the cylinder boundary layer for all of the cases considered in this study. To capture detailed wake flow structures, a relatively high mesh resolution is used in the cylinder wake by specifying a constant mesh size along the
$0.001D$
. The cell expansion ratio in the whole domain is kept below 1.1. This results in at least 30 layers of mesh in the cylinder boundary layer for all of the cases considered in this study. To capture detailed wake flow structures, a relatively high mesh resolution is used in the cylinder wake by specifying a constant mesh size along the
![]() $x$
-direction for
$x$
-direction for
![]() $x/D>$
0.7. Figure 1(b) shows a close-up view of the 2D mesh near the cylinder with a gap ratio of 0.4.
$x/D>$
0.7. Figure 1(b) shows a close-up view of the 2D mesh near the cylinder with a gap ratio of 0.4.
The 3D mesh is formed by replicating the 2D mesh along the
![]() $z$
-axis, resulting in an identical mesh resolution in all planes perpendicular to the cylinder. Based on the 3D mesh dependence study for an isolated cylinder performed in Jiang et al. (Reference Jiang, Cheng, Draper, An and Tong2016), the spanwise cell and domain lengths are chosen as
$z$
-axis, resulting in an identical mesh resolution in all planes perpendicular to the cylinder. Based on the 3D mesh dependence study for an isolated cylinder performed in Jiang et al. (Reference Jiang, Cheng, Draper, An and Tong2016), the spanwise cell and domain lengths are chosen as
![]() $0.1D$
and
$0.1D$
and
![]() $12D$
, respectively. According to the linear stability analysis results by Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013) of flow past a circular cylinder near a moving wall with various gap ratios, the spanwise domain length of
$12D$
, respectively. According to the linear stability analysis results by Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013) of flow past a circular cylinder near a moving wall with various gap ratios, the spanwise domain length of
![]() $12D$
is not always an integer multiple of the most unstable spanwise wavelength of the wake structure. This may restrict the development of 3D instability to some extent and result in an overprediction of
$12D$
is not always an integer multiple of the most unstable spanwise wavelength of the wake structure. This may restrict the development of 3D instability to some extent and result in an overprediction of
![]() $Re_{cr\,3D}$
. However, it has been demonstrated in Jiang et al. (Reference Jiang, Cheng, Draper and An2017) that the use of a spanwise domain length of
$Re_{cr\,3D}$
. However, it has been demonstrated in Jiang et al. (Reference Jiang, Cheng, Draper and An2017) that the use of a spanwise domain length of
![]() $12D$
would only affect the accuracy of the predicted
$12D$
would only affect the accuracy of the predicted
![]() $Re_{cr\,3D}$
value by less than 1 %. Hence a uniform domain length of
$Re_{cr\,3D}$
value by less than 1 %. Hence a uniform domain length of
![]() $12D$
is still adopted in the present study.
$12D$
is still adopted in the present study.
The boundary conditions for the 3D computational domain are listed in table 1, where
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\boldsymbol{n}=0$
denotes a zero normal gradient condition. In particular, a uniform flow velocity
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\boldsymbol{n}=0$
denotes a zero normal gradient condition. In particular, a uniform flow velocity
![]() $U$
is specified in the
$U$
is specified in the
![]() $x$
-direction for the inlet and bottom boundaries. Symmetry boundary conditions are applied at the top boundary, while periodic boundary conditions are employed at the two lateral boundaries perpendicular to the cylinder span.
$x$
-direction for the inlet and bottom boundaries. Symmetry boundary conditions are applied at the top boundary, while periodic boundary conditions are employed at the two lateral boundaries perpendicular to the cylinder span.
The time step
![]() $\unicode[STIX]{x0394}t$
adopted for each case is based on the criterion that the Courant number
$\unicode[STIX]{x0394}t$
adopted for each case is based on the criterion that the Courant number
![]() $(Co)$
of all the cells in the computational domain is kept below 0.5, where
$(Co)$
of all the cells in the computational domain is kept below 0.5, where
![]() $Co$
is defined as
$Co$
is defined as
where
![]() $|u|$
is the magnitude of the velocity through a cell, and
$|u|$
is the magnitude of the velocity through a cell, and
![]() $\unicode[STIX]{x0394}l$
is the cell size in the direction of the velocity.
$\unicode[STIX]{x0394}l$
is the cell size in the direction of the velocity.

Figure 1. (a) Schematic model of the computational domain, and (b) close-up view of the 2D mesh near the cylinder for
![]() $G/D=0.4$
.
$G/D=0.4$
.
Table 1. Boundary conditions for the 3D computational domain.
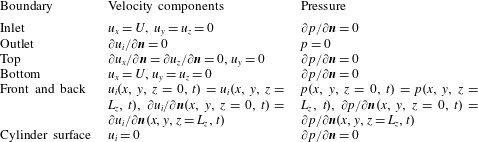
2.3 Mesh convergence
For the case of flow past an isolated circular cylinder, Jiang et al. (Reference Jiang, Cheng, Draper, An and Tong2016) reported a mesh convergence study on the standard 3D mesh, and obtained DNS results of wake transition of flow past an isolated circular cylinder which are in good agreement with the experimental results reported by Williamson (Reference Williamson1996).

Figure 2. Critical
![]() $Re$
for 2D and 3D wake instabilities under various gap ratios.
$Re$
for 2D and 3D wake instabilities under various gap ratios.
For the case of flow past a circular cylinder near a moving wall, the
![]() $Re_{cr\,2D}$
and
$Re_{cr\,2D}$
and
![]() $Re_{cr\,3D}$
values under various gap ratios predicted with DNS by using the standard 3D mesh (Jiang et al.
Reference Jiang, Cheng, Draper and An2017) are in close agreement with the linear stability analysis results by Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2015) (figure 2). The results by Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2015) are believed to be improved from those in Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013) (see figure 2) since it was noted in Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013) that the use of a relatively small computational domain size in that study could affect the accuracy of
$Re_{cr\,3D}$
values under various gap ratios predicted with DNS by using the standard 3D mesh (Jiang et al.
Reference Jiang, Cheng, Draper and An2017) are in close agreement with the linear stability analysis results by Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2015) (figure 2). The results by Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2015) are believed to be improved from those in Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013) (see figure 2) since it was noted in Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013) that the use of a relatively small computational domain size in that study could affect the accuracy of
![]() $Re_{cr\,3D}$
by
$Re_{cr\,3D}$
by
![]() ${\sim}15\,\%$
.
${\sim}15\,\%$
.
In the present study, mesh convergence is further checked at
![]() $G/D=0.4$
with
$G/D=0.4$
with
![]() $Re=325$
(the largest
$Re=325$
(the largest
![]() $Re$
adopted in this study). The resolution of the standard 3D mesh is examined by using a refined 3D mesh with the number of cells in both
$Re$
adopted in this study). The resolution of the standard 3D mesh is examined by using a refined 3D mesh with the number of cells in both
![]() $x$
- and
$x$
- and
![]() $y$
-directions 1.5 times that for the standard 3D mesh. In particular, the number of cells around the cylinder is increased by 1.5 times (from 160 to 240), the height of the first layer of mesh next to the moving wall and next to the cylinder surface is reduced by 1.5 times (from
$y$
-directions 1.5 times that for the standard 3D mesh. In particular, the number of cells around the cylinder is increased by 1.5 times (from 160 to 240), the height of the first layer of mesh next to the moving wall and next to the cylinder surface is reduced by 1.5 times (from
![]() $0.001D$
to
$0.001D$
to
![]() $0.00067D$
), and the number of mesh layers in the cylinder boundary layer is increased by 1.5 times (from 31 to 47). In addition, the influence of the time step on the numerical results is examined with a case which uses the standard 3D mesh but with a halved time-step size (i.e.
$0.00067D$
), and the number of mesh layers in the cylinder boundary layer is increased by 1.5 times (from 31 to 47). In addition, the influence of the time step on the numerical results is examined with a case which uses the standard 3D mesh but with a halved time-step size (i.e.
![]() $Co$
is kept below 0.25).
$Co$
is kept below 0.25).
The mesh convergence is firstly checked via the drag and lift force coefficients (
![]() $C_{D}$
and
$C_{D}$
and
![]() $C_{L}$
) and Strouhal number (
$C_{L}$
) and Strouhal number (
![]() $St$
) on the cylinder, which are defined as follows:
$St$
) on the cylinder, which are defined as follows:
where
![]() $F_{D}$
and
$F_{D}$
and
![]() $F_{L}$
are the integrated drag force and lift force on the cylinder, respectively, and
$F_{L}$
are the integrated drag force and lift force on the cylinder, respectively, and
![]() $f_{L}$
is the frequency of the fluctuating lift force. For the 3D cases where the time history of
$f_{L}$
is the frequency of the fluctuating lift force. For the 3D cases where the time history of
![]() $C_{L}$
may not be regular periodic,
$C_{L}$
may not be regular periodic,
![]() $St$
is determined using the peak frequency derived from the fast Fourier transform (FFT) of the time history of
$St$
is determined using the peak frequency derived from the fast Fourier transform (FFT) of the time history of
![]() $C_{L}$
. The time-averaged drag and lift coefficients are denoted as
$C_{L}$
. The time-averaged drag and lift coefficients are denoted as
![]() $\overline{C_{D}}$
and
$\overline{C_{D}}$
and
![]() $\overline{C_{L}}$
, respectively. The root-mean-square lift coefficient
$\overline{C_{L}}$
, respectively. The root-mean-square lift coefficient
![]() $C_{L}^{\prime }$
is defined as
$C_{L}^{\prime }$
is defined as
 $$\begin{eqnarray}C_{L}^{\prime }=\sqrt{\frac{1}{N}\mathop{\sum }_{i=1}^{N}(C_{L,i}-\overline{C_{L}})^{2}},\end{eqnarray}$$
$$\begin{eqnarray}C_{L}^{\prime }=\sqrt{\frac{1}{N}\mathop{\sum }_{i=1}^{N}(C_{L,i}-\overline{C_{L}})^{2}},\end{eqnarray}$$
where
![]() $N$
is the number of values in the time history of
$N$
is the number of values in the time history of
![]() $C_{L}$
. At least 800 non-dimensional time units (defined as
$C_{L}$
. At least 800 non-dimensional time units (defined as
![]() $t^{\ast }=Ut/D$
) of the fully developed flow are used to calculate the statistical stationary hydrodynamic forces on the cylinder. As shown in table 2, the hydrodynamic forces calculated with the two variation cases are quite close to those calculated with the standard mesh (relative differences are within 0.7 % for
$t^{\ast }=Ut/D$
) of the fully developed flow are used to calculate the statistical stationary hydrodynamic forces on the cylinder. As shown in table 2, the hydrodynamic forces calculated with the two variation cases are quite close to those calculated with the standard mesh (relative differences are within 0.7 % for
![]() $St$
and
$St$
and
![]() $\overline{C_{D}}$
, within 1.6 % for
$\overline{C_{D}}$
, within 1.6 % for
![]() $\overline{C_{L}}$
, and within 4 % for
$\overline{C_{L}}$
, and within 4 % for
![]() $C_{L}^{\prime }$
).
$C_{L}^{\prime }$
).
Table 2. Mesh convergence results for the case of
![]() $(G/D,Re)=(0.4,325)$
.
$(G/D,Re)=(0.4,325)$
.
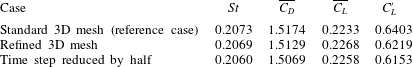
In addition, figure 3 shows the time- and span-averaged streamwise and transverse velocity profiles at a few streamwise locations in the near wake (
![]() $x/D=0$
, 1, 1.5, and 5) for the three cases listed in table 2. Very good agreements of the mean velocity profiles are observed in figure 3 for the three cases. The above results demonstrate that the standard 3D mesh is sufficient for the numerical simulations of this study.
$x/D=0$
, 1, 1.5, and 5) for the three cases listed in table 2. Very good agreements of the mean velocity profiles are observed in figure 3 for the three cases. The above results demonstrate that the standard 3D mesh is sufficient for the numerical simulations of this study.

Figure 3. Time- and span-averaged velocity profiles at a few streamwise locations (
![]() $x/D=0$
, 1, 1.5 and 5) for the three cases listed in table 2: (a) streamwise velocity profiles, and (b) transverse velocity profiles.
$x/D=0$
, 1, 1.5 and 5) for the three cases listed in table 2: (a) streamwise velocity profiles, and (b) transverse velocity profiles.
3 Numerical results
For flow past a circular cylinder near a moving wall at
![]() $G/D\geqslant 0.3$
, the wake transition sequence of ‘2D steady
$G/D\geqslant 0.3$
, the wake transition sequence of ‘2D steady
![]() $\rightarrow$
2D unsteady
$\rightarrow$
2D unsteady
![]() $\rightarrow$
3D unsteady’ has been observed by Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013, Reference Rao, Thompson, Leweke and Hourigan2015) and Jiang et al. (Reference Jiang, Cheng, Draper and An2017) through linear stability analysis and 3D DNS, respectively. In the present study, flow past a circular cylinder near a moving wall is investigated in the range of
$\rightarrow$
3D unsteady’ has been observed by Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013, Reference Rao, Thompson, Leweke and Hourigan2015) and Jiang et al. (Reference Jiang, Cheng, Draper and An2017) through linear stability analysis and 3D DNS, respectively. In the present study, flow past a circular cylinder near a moving wall is investigated in the range of
![]() $G/D\geqslant 0.3$
, with the focus on the 3D flow structures and wake transition beyond the onset of 3D instability, i.e. in the ‘3D unsteady’ state.
$G/D\geqslant 0.3$
, with the focus on the 3D flow structures and wake transition beyond the onset of 3D instability, i.e. in the ‘3D unsteady’ state.

Figure 4. Wake transition regimes for flow past a circular cylinder near a moving wall. The wake structures are initialized with four pairs of Mode A structure along the span width for the cases within the shadow area, and three pairs of Mode A for the rest of the cases within the Mode A and mode swapping regimes.
3.1 Wake transition regimes
The 3D wake transition sequence for flow past a circular cylinder near a moving wall is studied in the parameter space of
![]() $G/D\geqslant 0.3$
and
$G/D\geqslant 0.3$
and
![]() $Re$
up to 300. Based on a number of cases with discrete combinations of
$Re$
up to 300. Based on a number of cases with discrete combinations of
![]() $G/D$
and
$G/D$
and
![]() $Re$
, the approximate wake transition regimes are mapped out in figure 4. With increasing
$Re$
, the approximate wake transition regimes are mapped out in figure 4. With increasing
![]() $Re$
, the flow undergoes a transition sequence of ‘2D
$Re$
, the flow undergoes a transition sequence of ‘2D
![]() $\rightarrow$
Mode A
$\rightarrow$
Mode A
![]() $\rightarrow$
mode swapping
$\rightarrow$
mode swapping
![]() $\rightarrow$
Mode B’ for all of the gap ratios considered. For
$\rightarrow$
Mode B’ for all of the gap ratios considered. For
![]() $G/D\geqslant 1.5$
, the critical
$G/D\geqslant 1.5$
, the critical
![]() $Re$
values for the wake transition regimes are almost unchanged, which suggests that the effect of the plane boundary is still weak. With further decrease of
$Re$
values for the wake transition regimes are almost unchanged, which suggests that the effect of the plane boundary is still weak. With further decrease of
![]() $G/D$
, the mode swapping and Mode B regimes are gradually delayed to slightly higher
$G/D$
, the mode swapping and Mode B regimes are gradually delayed to slightly higher
![]() $Re$
values.
$Re$
values.

Figure 5. Iso-surfaces of
![]() $\unicode[STIX]{x1D714}_{x}=\pm 0.5$
for flow past an isolated circular cylinder at
$\unicode[STIX]{x1D714}_{x}=\pm 0.5$
for flow past an isolated circular cylinder at
![]() $Re=200$
: (a) ordered Mode A structure at
$Re=200$
: (a) ordered Mode A structure at
![]() $t^{\ast }=400$
, and (b) Mode A with large-scale vortex dislocations at
$t^{\ast }=400$
, and (b) Mode A with large-scale vortex dislocations at
![]() $t^{\ast }=1000$
. Dark grey and light yellow denote positive and negative values, respectively. The flow is from the left to the right past the cylinder on the left.
$t^{\ast }=1000$
. Dark grey and light yellow denote positive and negative values, respectively. The flow is from the left to the right past the cylinder on the left.
For the case of an isolated circular cylinder, the Mode A structure will evolve spontaneously into a more stable pattern with large-scale vortex dislocations (Williamson Reference Williamson1996). Hence the transition sequence can be further specified as ‘2D
![]() $\rightarrow$
Mode A with dislocations
$\rightarrow$
Mode A with dislocations
![]() $\rightarrow$
mode swapping (with dislocations)
$\rightarrow$
mode swapping (with dislocations)
![]() $\rightarrow$
Mode B’. The evolution of vortex dislocations (with the evolution of the non-dimensional flow time
$\rightarrow$
Mode B’. The evolution of vortex dislocations (with the evolution of the non-dimensional flow time
![]() $t^{\ast }$
) for the case of
$t^{\ast }$
) for the case of
![]() $Re=200$
is illustrated in figure 5. The vortex structures are identified by the isosurfaces of the streamwise vorticity
$Re=200$
is illustrated in figure 5. The vortex structures are identified by the isosurfaces of the streamwise vorticity
![]() $\unicode[STIX]{x1D714}_{x}$
, which is defined in a non-dimensional form of
$\unicode[STIX]{x1D714}_{x}$
, which is defined in a non-dimensional form of
However, it is found that for flow past a circular cylinder near a moving wall, vortex dislocation is suppressed at small gap ratios, and consequently the flow undergoes a transition sequence of ‘2D
![]() $\rightarrow$
ordered Mode A
$\rightarrow$
ordered Mode A
![]() $\rightarrow$
mode swapping (without dislocations)
$\rightarrow$
mode swapping (without dislocations)
![]() $\rightarrow$
Mode B’. According to the occurrence or suppression of vortex dislocations associated with Mode A, the Mode A and mode swapping regimes shown in figure 4 are further separated by the dashed line at
$\rightarrow$
Mode B’. According to the occurrence or suppression of vortex dislocations associated with Mode A, the Mode A and mode swapping regimes shown in figure 4 are further separated by the dashed line at
![]() $G/D\sim 1.0$
. The dashed separation line ends at the lower boundary of the Mode B regime, since beyond which point Mode A disappears and Mode B is naturally free of dislocation.
$G/D\sim 1.0$
. The dashed separation line ends at the lower boundary of the Mode B regime, since beyond which point Mode A disappears and Mode B is naturally free of dislocation.
It is seen in figure 4 that the ordered Mode A regime occupies a considerable area in the parameter space. To further validate the suppression of vortex dislocation in the ordered Mode A regime, another DNS case with
![]() $(G/D,Re)=(1.0,210)$
is calculated with a doubled spanwise domain length of
$(G/D,Re)=(1.0,210)$
is calculated with a doubled spanwise domain length of
![]() $24D$
. In this case, vortex dislocation is still completely suppressed. For the fully developed flow, six Mode A vortex pairs are observed along the span width, and their spanwise locations do not vary along the span in time (although the Mode A vortex pairs have slightly varied wavelengths).
$24D$
. In this case, vortex dislocation is still completely suppressed. For the fully developed flow, six Mode A vortex pairs are observed along the span width, and their spanwise locations do not vary along the span in time (although the Mode A vortex pairs have slightly varied wavelengths).
It is also found that for the cases within the shadow area shown in figure 4, the wake structures are initialized with four pairs of Mode A structure along the span width. In contrast, for the rest of the cases within the Mode A and mode swapping regimes, three pairs of Mode A structure are observed at the beginning of the simulations. This is due to the variation of the most unstable spanwise wavelength of the Mode A structure. As reported by Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013) with linear stability analysis, the most unstable spanwise wavelength at
![]() $Re_{cr\,3D}$
for
$Re_{cr\,3D}$
for
![]() $G/D=0.4$
and 1.0 are
$G/D=0.4$
and 1.0 are
![]() $3.85D$
and
$3.85D$
and
![]() $3.73D$
, respectively, but reduces to
$3.73D$
, respectively, but reduces to
![]() ${\sim}3.65D$
at
${\sim}3.65D$
at
![]() $G/D=0.5{-}0.75$
. In addition, it is expected that the most unstable wavelength decreases with increasing
$G/D=0.5{-}0.75$
. In addition, it is expected that the most unstable wavelength decreases with increasing
![]() $Re$
, similar to the case of an isolated cylinder as reported in Williamson (Reference Williamson1996) and Barkley & Henderson (Reference Barkley and Henderson1996). Hence it is expected that smallest most unstable wavelengths may be observed for the cases within the shadow area, and for these cases the wavelength of
$Re$
, similar to the case of an isolated cylinder as reported in Williamson (Reference Williamson1996) and Barkley & Henderson (Reference Barkley and Henderson1996). Hence it is expected that smallest most unstable wavelengths may be observed for the cases within the shadow area, and for these cases the wavelength of
![]() $3D$
(i.e. four pairs of Mode A) is more unstable than
$3D$
(i.e. four pairs of Mode A) is more unstable than
![]() $4D$
(i.e. three pairs of Mode A).
$4D$
(i.e. three pairs of Mode A).
It is worth noting that while the onset points for 3D instability obtained by Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2015) and Jiang et al. (Reference Jiang, Cheng, Draper and An2017) agree well with each other (figure 2), it is apparent that the regime for Mode B instability obtained by Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2015) through linear stability analysis does not coincide with either the mode swapping regime or the Mode B regime determined by the present DNS (figure 4), since the existence of Mode A instability would destabilize Mode B in the nonlinear interaction between the two modes (Henderson Reference Henderson1997). Hence a nonlinear DNS study is required for the simulation of the actual wake transition process at
![]() $Re>Re_{cr\,3D}$
.
$Re>Re_{cr\,3D}$
.
3.2 Results at
 $G/D=0.4$
with varying
$G/D=0.4$
with varying
 $Re$
$Re$
Based on the standard 3D mesh, a series of 3D cases is simulated at a fixed gap ratio of
![]() $G/D=0.4$
where vortex dislocation is suppressed (figure 4). As shown in figure 2, the 2D and 3D wake instabilities occur at
$G/D=0.4$
where vortex dislocation is suppressed (figure 4). As shown in figure 2, the 2D and 3D wake instabilities occur at
![]() $Re_{cr\,2D}=88.5\;(\pm 0.5)$
and
$Re_{cr\,2D}=88.5\;(\pm 0.5)$
and
![]() $Re_{cr\,3D}=149.2$
, respectively. In this section, the wake structures and transition for
$Re_{cr\,3D}=149.2$
, respectively. In this section, the wake structures and transition for
![]() $G/D=0.4$
are examined with
$G/D=0.4$
are examined with
![]() $Re$
ranging from 80 to 325, covering the laminar and 3D wake transition regimes. The general conclusions drawn through
$Re$
ranging from 80 to 325, covering the laminar and 3D wake transition regimes. The general conclusions drawn through
![]() $G/D=$
0.4 are expected to be applicable to a range of gap ratios from 0.3 to 0.8 where the flow undergoes a transition sequence of ‘2D
$G/D=$
0.4 are expected to be applicable to a range of gap ratios from 0.3 to 0.8 where the flow undergoes a transition sequence of ‘2D
![]() $\rightarrow$
ordered Mode A
$\rightarrow$
ordered Mode A
![]() $\rightarrow$
mode swapping (without dislocations)
$\rightarrow$
mode swapping (without dislocations)
![]() $\rightarrow$
Mode B’ (figure 4). On the other hand, the transition sequence of ‘2D
$\rightarrow$
Mode B’ (figure 4). On the other hand, the transition sequence of ‘2D
![]() $\rightarrow$
Mode A with dislocations
$\rightarrow$
Mode A with dislocations
![]() $\rightarrow$
mode swapping (with dislocations)
$\rightarrow$
mode swapping (with dislocations)
![]() $\rightarrow$
Mode B’ for
$\rightarrow$
Mode B’ for
![]() $G/D\geqslant 1.5$
(figure 4) is expected to be similar to that of an isolated cylinder and therefore will not be elaborated in this study.
$G/D\geqslant 1.5$
(figure 4) is expected to be similar to that of an isolated cylinder and therefore will not be elaborated in this study.

Figure 6. Time histories of the span-averaged drag and lift coefficients, as well as the point spanwise velocity sampled at
![]() $(x/D,y/D,z/D)=(3.0,0.5,6.0)$
for
$(x/D,y/D,z/D)=(3.0,0.5,6.0)$
for
![]() $G/D=0.4$
with various
$G/D=0.4$
with various
![]() $Re$
. The horizontal dashed lines mark the fluctuation range of the corresponding 2D lift coefficient.
$Re$
. The horizontal dashed lines mark the fluctuation range of the corresponding 2D lift coefficient.
3.2.1 3D wake transition
Figure 6 shows the time histories of the span-averaged drag and lift coefficients, as well as the point spanwise velocity sampled at
![]() $(x/D,y/D,z/D)=(3.0,0.5,6.0)$
for
$(x/D,y/D,z/D)=(3.0,0.5,6.0)$
for
![]() $G/D=0.4$
with various
$G/D=0.4$
with various
![]() $Re$
. In figure 6, the left column shows the entire ranges of the time histories, while the right column shows the time histories of 40 non-dimensional time units of the fully developed flow close to the end of each simulation.
$Re$
. In figure 6, the left column shows the entire ranges of the time histories, while the right column shows the time histories of 40 non-dimensional time units of the fully developed flow close to the end of each simulation.
For
![]() $Re>Re_{cr\,3D}\;(=149.2)$
, an exponential growth of the spanwise velocity amplitude is observed at the very beginning of each time history shown in figure 6, marking the development of 3D wake instability. As illustrated in Jiang et al. (Reference Jiang, Cheng, Draper and An2017), the
$Re>Re_{cr\,3D}\;(=149.2)$
, an exponential growth of the spanwise velocity amplitude is observed at the very beginning of each time history shown in figure 6, marking the development of 3D wake instability. As illustrated in Jiang et al. (Reference Jiang, Cheng, Draper and An2017), the
![]() $Re_{cr\,3D}$
value can be obtained from the linear relationship between the exponential growth rate and
$Re_{cr\,3D}$
value can be obtained from the linear relationship between the exponential growth rate and
![]() $Re$
, through interpolation at the zero growth rate point. For
$Re$
, through interpolation at the zero growth rate point. For
![]() $Re>Re_{cr\,3D}$
, the growth rate of the spanwise velocity amplitude increases with increasing
$Re>Re_{cr\,3D}$
, the growth rate of the spanwise velocity amplitude increases with increasing
![]() $Re$
, and therefore the growing period becomes shorter and the flow saturates more quickly (figure 6).
$Re$
, and therefore the growing period becomes shorter and the flow saturates more quickly (figure 6).
At the beginning of each simulation, the flow three-dimensionality in the computational domain is zero. Hence the time history of the spanwise velocity shown in figure 6 grows from
![]() $u_{z}=0$
, and the fluctuation ranges of the drag and lift coefficients calculated by 3D DNS are identical to their 2D counterparts (the fluctuation ranges of the 2D lift coefficient are marked by the horizontal dashed lines in figure 6). With growth of the flow three-dimensionality, the spanwise velocity amplitude increases, and the 3D drag coefficient and fluctuation amplitude of the 3D lift coefficient drop from their 2D counterparts. The drops in the drag coefficient and fluctuation amplitude of lift coefficient are barely visible when the spanwise velocity amplitude is within an order of magnitude of
$u_{z}=0$
, and the fluctuation ranges of the drag and lift coefficients calculated by 3D DNS are identical to their 2D counterparts (the fluctuation ranges of the 2D lift coefficient are marked by the horizontal dashed lines in figure 6). With growth of the flow three-dimensionality, the spanwise velocity amplitude increases, and the 3D drag coefficient and fluctuation amplitude of the 3D lift coefficient drop from their 2D counterparts. The drops in the drag coefficient and fluctuation amplitude of lift coefficient are barely visible when the spanwise velocity amplitude is within an order of magnitude of
![]() $0.01U$
, but become apparent when the spanwise velocity amplitude grows beyond
$0.01U$
, but become apparent when the spanwise velocity amplitude grows beyond
![]() ${\sim}0.1U$
(figure 6).
${\sim}0.1U$
(figure 6).

Figure 7. Iso-surfaces of
![]() $\unicode[STIX]{x1D714}_{x}$
for the cases with
$\unicode[STIX]{x1D714}_{x}$
for the cases with
![]() $G/D=0.4$
and
$G/D=0.4$
and
![]() $Re>Re_{cr\,3D}$
. Dark grey and light yellow denote positive and negative values, respectively. The flow is from the left to the right past the cylinder on the left. The moving wall is at the back of the structure.
$Re>Re_{cr\,3D}$
. Dark grey and light yellow denote positive and negative values, respectively. The flow is from the left to the right past the cylinder on the left. The moving wall is at the back of the structure.
Table 3. Patterns of the time histories and fully developed vortex structures for
![]() $G/D=0.4$
with
$G/D=0.4$
with
![]() $Re>Re_{cr\,3D}$
.
$Re>Re_{cr\,3D}$
.

The vortex structures during the 3D wake transition process are examined through numerical flow visualization. At a small gap ratio of 0.4, a major difference compared with the case of an isolated cylinder is that vortex dislocation is completely suppressed. This also results in relatively regular time histories of the force coefficients and point velocity signals (whereas irregular and large-amplitude fluctuations of the time histories are observed when vortex dislocations are present). Table 3 summarizes the observed patterns of the time histories of the force coefficients and point velocity signals (some are shown in figure 6) and fully developed vortex structures represented by the isosurfaces of the streamwise vorticity
![]() $\unicode[STIX]{x1D714}_{x}$
(some are shown in figure 7).
$\unicode[STIX]{x1D714}_{x}$
(some are shown in figure 7).
For
![]() $Re$
between 150 and 180, three ordered Mode A streamwise vortex pairs (e.g. figure 7
a) are observed along the cylinder span for the entire simulations. The basic features of the Mode A structure for the near-wall case, e.g. the waviness of the primary vortex cores, an out-of-phase pattern for the streamwise vortices, and a spanwise wavelength of approximately
$Re$
between 150 and 180, three ordered Mode A streamwise vortex pairs (e.g. figure 7
a) are observed along the cylinder span for the entire simulations. The basic features of the Mode A structure for the near-wall case, e.g. the waviness of the primary vortex cores, an out-of-phase pattern for the streamwise vortices, and a spanwise wavelength of approximately
![]() $4D$
, are similar to those for an isolated cylinder, which suggests that the physical mechanism for the formation of Mode A instability for the near-wall case is similar to that for an isolated cylinder, i.e. an elliptic instability of the primary vortex cores and the formation of streamwise vortex pairs through the Biot–Savart induction (Williamson Reference Williamson1996; Leweke & Williamson Reference Leweke and Williamson1998; Thompson, Leweke & Williamson Reference Thompson, Leweke and Williamson2001). In this
$4D$
, are similar to those for an isolated cylinder, which suggests that the physical mechanism for the formation of Mode A instability for the near-wall case is similar to that for an isolated cylinder, i.e. an elliptic instability of the primary vortex cores and the formation of streamwise vortex pairs through the Biot–Savart induction (Williamson Reference Williamson1996; Leweke & Williamson Reference Leweke and Williamson1998; Thompson, Leweke & Williamson Reference Thompson, Leweke and Williamson2001). In this
![]() $Re$
range, even the time history of the point spanwise velocity (e.g. figure 6
a) is extremely regular, which suggests that the wake structure is highly repeatable in time. In particular, with the absence of vortex dislocation, the Mode A vortices do not vary along the cylinder span in time, since the formation of Mode A is self-sustaining through the Biot–Savart induction (Williamson Reference Williamson1996).
$Re$
range, even the time history of the point spanwise velocity (e.g. figure 6
a) is extremely regular, which suggests that the wake structure is highly repeatable in time. In particular, with the absence of vortex dislocation, the Mode A vortices do not vary along the cylinder span in time, since the formation of Mode A is self-sustaining through the Biot–Savart induction (Williamson Reference Williamson1996).
As
![]() $Re$
exceeds 200, the ordered Mode A structure remains unchanged while ordered Mode B structure starts to develop within the Mode A vortex loops. For
$Re$
exceeds 200, the ordered Mode A structure remains unchanged while ordered Mode B structure starts to develop within the Mode A vortex loops. For
![]() $Re=220$
, one of the three loops (the loop at
$Re=220$
, one of the three loops (the loop at
![]() $z/D\sim 7.5$
in figure 7
b) is persistently filled with the ordered Mode B structure. For
$z/D\sim 7.5$
in figure 7
b) is persistently filled with the ordered Mode B structure. For
![]() $Re=225{-}240$
, all of the three Mode A vortex loops are filled with ordered Mode B structure throughout (e.g. figure 7
c). Since all of the Mode A structures are still persistent with the evolution in time, they still do not vary along the span width. The persistent existence of three ordered Mode A streamwise vortex pairs for
$Re=225{-}240$
, all of the three Mode A vortex loops are filled with ordered Mode B structure throughout (e.g. figure 7
c). Since all of the Mode A structures are still persistent with the evolution in time, they still do not vary along the span width. The persistent existence of three ordered Mode A streamwise vortex pairs for
![]() $Re=200{-}240$
is responsible for the relatively regular periodic time histories of the force coefficients and spanwise velocity (e.g. figure 6
b), while the additional co-existed Mode B structure may add some irregularities to the time histories.
$Re=200{-}240$
is responsible for the relatively regular periodic time histories of the force coefficients and spanwise velocity (e.g. figure 6
b), while the additional co-existed Mode B structure may add some irregularities to the time histories.
Due to the existence of Mode A instability which destabilizes Mode B in the nonlinear interaction between the two modes (Henderson Reference Henderson1997), the present DNS results show that the Mode B structure starts to emerge at
![]() $Re$
of as low as 200, much lower than the lower boundary of the Mode B regime obtained by Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2015) through linear stability analysis (figure 4). Through numerical flow visualization of the evolution of the wake structure, it is found that the Mode B structure is always initialized within the Mode A vortex loops. Since the physical mechanism for Mode B instability is a hyperbolic instability of the braid shear layer region (Williamson Reference Williamson1996; Leweke & Williamson Reference Leweke and Williamson1998; Thompson et al.
Reference Thompson, Leweke and Williamson2001), the streamwise vortices of Mode A that develop in the braid shear layer region are believed to be the reason for the destabilization of Mode B.
$Re$
of as low as 200, much lower than the lower boundary of the Mode B regime obtained by Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2015) through linear stability analysis (figure 4). Through numerical flow visualization of the evolution of the wake structure, it is found that the Mode B structure is always initialized within the Mode A vortex loops. Since the physical mechanism for Mode B instability is a hyperbolic instability of the braid shear layer region (Williamson Reference Williamson1996; Leweke & Williamson Reference Leweke and Williamson1998; Thompson et al.
Reference Thompson, Leweke and Williamson2001), the streamwise vortices of Mode A that develop in the braid shear layer region are believed to be the reason for the destabilization of Mode B.
A gradual transition from the ordered Mode A structure to relatively ordered Mode B structure is observed at
![]() $Re=250{-}275$
. It should be noted that vortex dislocation is still suppressed, and only ordered Mode A and Mode B structures are observed. In this regime, the Mode B structure fills up not only the areas within the Mode A vortex loops, but can sometimes also replace some or all of the ordered Mode A vortex pairs (e.g. figure 7
d). In figure 7(d), 15 pairs of the Mode B structure are observed along the span width at
$Re=250{-}275$
. It should be noted that vortex dislocation is still suppressed, and only ordered Mode A and Mode B structures are observed. In this regime, the Mode B structure fills up not only the areas within the Mode A vortex loops, but can sometimes also replace some or all of the ordered Mode A vortex pairs (e.g. figure 7
d). In figure 7(d), 15 pairs of the Mode B structure are observed along the span width at
![]() $Re=275$
, which indicates a spanwise wavelength of Mode B of approximately
$Re=275$
, which indicates a spanwise wavelength of Mode B of approximately
![]() $0.8D$
, similar to the wavelength of Mode B for an isolated cylinder of
$0.8D$
, similar to the wavelength of Mode B for an isolated cylinder of
![]() $0.82D$
(Barkley & Henderson Reference Barkley and Henderson1996). It is also worth noting that as the self-sustaining formation of Mode A is interrupted by the replacement of Mode B, the Mode A vortices in the mode swapping regime are no longer fixed at their respective initial spanwise locations. As the mode swapping process sets in, the time histories of the force coefficients and spanwise velocity become much more irregular (e.g. figure 6
c).
$0.82D$
(Barkley & Henderson Reference Barkley and Henderson1996). It is also worth noting that as the self-sustaining formation of Mode A is interrupted by the replacement of Mode B, the Mode A vortices in the mode swapping regime are no longer fixed at their respective initial spanwise locations. As the mode swapping process sets in, the time histories of the force coefficients and spanwise velocity become much more irregular (e.g. figure 6
c).

Figure 8. Time histories for the appearance of all of the three Mode A vortex pairs along the span width for
![]() $Re$
in the mode swapping regime.
$Re$
in the mode swapping regime.

Figure 9. Variation of the probability of occurrence of ‘all of the three Mode A vortex pairs appear along the span width’ with
![]() $Re$
.
$Re$
.
Figure 8 shows the time histories of the mode swapping process focusing on the intermittent appearance of the pattern of ‘all of the three Mode A vortex pairs appear along the span width’ (the shadow periods in figure 8). The statistics starts after the flow is fully developed and lasts for 1000–1150 non-dimensional time units (with an output interval of 10) to ensure that the statistical results are not strongly influenced by the sampling range. For each case, more than 100 snapshots of the wake structure are visually examined. It is seen in figure 8 that with increasing
![]() $Re$
, the durations of the shadow periods become shorter while the durations of the clear periods become longer. Therefore, as can be seen in figure 8 and more clearly in figure 9, the probability of occurrence of ‘all of the three Mode A vortex pairs appear along the span width’ reduces with increasing
$Re$
, the durations of the shadow periods become shorter while the durations of the clear periods become longer. Therefore, as can be seen in figure 8 and more clearly in figure 9, the probability of occurrence of ‘all of the three Mode A vortex pairs appear along the span width’ reduces with increasing
![]() $Re$
. The probability of occurrence is defined as the ratio of the accumulated time of appearance of the mode being examined to the total sampling time. Assuming that this probability reduces linearly with increasing
$Re$
. The probability of occurrence is defined as the ratio of the accumulated time of appearance of the mode being examined to the total sampling time. Assuming that this probability reduces linearly with increasing
![]() $Re$
, the range of
$Re$
, the range of
![]() $Re$
for the mode swapping process is between 246 and 281 (figure 9), which is slightly higher than the mode swapping regime of
$Re$
for the mode swapping process is between 246 and 281 (figure 9), which is slightly higher than the mode swapping regime of
![]() $Re=230{-}260$
for an isolated cylinder obtained by Jiang et al. (Reference Jiang, Cheng, Draper, An and Tong2016) based on the same numerical formulation.
$Re=230{-}260$
for an isolated cylinder obtained by Jiang et al. (Reference Jiang, Cheng, Draper, An and Tong2016) based on the same numerical formulation.
For
![]() $Re\geqslant 285$
, the Mode B structure occupies the entire cylinder span width for most of the time. Mode A may sometimes be observed in the form of scattered pairs but can no longer occupy the entire span width. With increasing
$Re\geqslant 285$
, the Mode B structure occupies the entire cylinder span width for most of the time. Mode A may sometimes be observed in the form of scattered pairs but can no longer occupy the entire span width. With increasing
![]() $Re$
, the Mode B structure becomes increasingly disordered (e.g. figure 7
e), which is consistent with the even more irregular time histories of the force coefficients shown in figure 6(d).
$Re$
, the Mode B structure becomes increasingly disordered (e.g. figure 7
e), which is consistent with the even more irregular time histories of the force coefficients shown in figure 6(d).
3.2.2 Hydrodynamic forces and flow three-dimensionality
Figure 10 shows the variations of the statistically stationary force coefficients with
![]() $Re$
. For the cases of
$Re$
. For the cases of
![]() $Re\leqslant 220$
with relatively regular time histories of spanwise velocity and force coefficients, at least 500 non-dimensional time units are used for the statistics. As the time histories become less regular for
$Re\leqslant 220$
with relatively regular time histories of spanwise velocity and force coefficients, at least 500 non-dimensional time units are used for the statistics. As the time histories become less regular for
![]() $Re\geqslant 225$
, the statistical range is increased to at least 1000 non-dimensional time units. Further confirmation is carried out by calculating the 3D force coefficients using only the second half of the statistical data. It is seen in figure 10 that the 3D results calculated using the full length and second half of the data are quite close to each other, which suggests that the statistical data range is sufficient.
$Re\geqslant 225$
, the statistical range is increased to at least 1000 non-dimensional time units. Further confirmation is carried out by calculating the 3D force coefficients using only the second half of the statistical data. It is seen in figure 10 that the 3D results calculated using the full length and second half of the data are quite close to each other, which suggests that the statistical data range is sufficient.

Figure 10. Variations of the statistically stationary force coefficients with
![]() $Re$
: (a) time-averaged drag coefficient
$Re$
: (a) time-averaged drag coefficient
![]() $\overline{C_{D}}$
and (b) root-mean-square lift coefficient
$\overline{C_{D}}$
and (b) root-mean-square lift coefficient
![]() $C_{L}^{\prime }$
.
$C_{L}^{\prime }$
.
As shown in figure 10, the force coefficient quantities start to deviate from their 2D counterparts at
![]() $Re=Re_{cr\,3D}$
. The 3D results are all to the right of the 2D curves, i.e. the 2D simulations can achieve the same mean values and fluctuation amplitudes of the force coefficients at a lower
$Re=Re_{cr\,3D}$
. The 3D results are all to the right of the 2D curves, i.e. the 2D simulations can achieve the same mean values and fluctuation amplitudes of the force coefficients at a lower
![]() $Re$
compared with the 3D simulations. This suggests that in 3D simulations, part of the energy is transferred to the spanwise direction. The magnitude of the flow three-dimensionality is represented by the degree of deviation between the 2D and 3D results and will be discussed later on. It should be noted that although only the time-averaged drag coefficient and root-mean-square lift coefficient are shown in figure 10, the above findings also apply to the time-averaged lift coefficient and root-mean-square drag coefficient (omitted for simplicity).
$Re$
compared with the 3D simulations. This suggests that in 3D simulations, part of the energy is transferred to the spanwise direction. The magnitude of the flow three-dimensionality is represented by the degree of deviation between the 2D and 3D results and will be discussed later on. It should be noted that although only the time-averaged drag coefficient and root-mean-square lift coefficient are shown in figure 10, the above findings also apply to the time-averaged lift coefficient and root-mean-square drag coefficient (omitted for simplicity).

Figure 11. Variations of the statistically stationary streamwise enstrophy and spanwise kinetic energy integrated over the near-wake region of
![]() $x/D=0{-}10$
with
$x/D=0{-}10$
with
![]() $Re$
.
$Re$
.
The variation of the flow three-dimensionality with
![]() $Re$
is further examined with the statistically stationary streamwise enstrophy
$Re$
is further examined with the statistically stationary streamwise enstrophy
![]() $\unicode[STIX]{x1D700}_{x}$
and spanwise kinetic energy
$\unicode[STIX]{x1D700}_{x}$
and spanwise kinetic energy
![]() $E_{z}$
integrated over the near-wake region of
$E_{z}$
integrated over the near-wake region of
![]() $x/D=0{-}10$
(figure 11), where
$x/D=0{-}10$
(figure 11), where
![]() $\unicode[STIX]{x1D700}_{x}$
and
$\unicode[STIX]{x1D700}_{x}$
and
![]() $E_{z}$
are defined as
$E_{z}$
are defined as
where
![]() $V$
is the volume of the flow field of interest. The same statistical data ranges as used for obtaining the statistically stationary force coefficients are adopted here for calculating
$V$
is the volume of the flow field of interest. The same statistical data ranges as used for obtaining the statistically stationary force coefficients are adopted here for calculating
![]() $\unicode[STIX]{x1D700}_{x}$
and
$\unicode[STIX]{x1D700}_{x}$
and
![]() $E_{z}$
. It is seen in figures 11 and 10 that the variation trends of
$E_{z}$
. It is seen in figures 11 and 10 that the variation trends of
![]() $\unicode[STIX]{x1D700}_{x}$
and
$\unicode[STIX]{x1D700}_{x}$
and
![]() $E_{z}$
are consistent with the degree of deviation between the 2D and 3D force coefficients. At
$E_{z}$
are consistent with the degree of deviation between the 2D and 3D force coefficients. At
![]() $Re=150$
, which is just beyond the
$Re=150$
, which is just beyond the
![]() $Re_{cr\,3D}$
, the Mode A structure is strongly confined and extremely ordered (figure 7
a), which results in a very weak flow three-dimensionality. A gradual growth of the flow three-dimensionality is observed as
$Re_{cr\,3D}$
, the Mode A structure is strongly confined and extremely ordered (figure 7
a), which results in a very weak flow three-dimensionality. A gradual growth of the flow three-dimensionality is observed as
![]() $Re$
increases from 150 to 200. Within this range, the wake flow is dominated by the ordered Mode A structure. The growth rate of the flow three-dimensionality reduces at
$Re$
increases from 150 to 200. Within this range, the wake flow is dominated by the ordered Mode A structure. The growth rate of the flow three-dimensionality reduces at
![]() $Re=220$
as the finer-scale ordered Mode B structure is observed within one of the Mode A vortex loops (figure 7
b). A local reduction of the flow three-dimensionality is observed in figures 11 and 10 for
$Re=220$
as the finer-scale ordered Mode B structure is observed within one of the Mode A vortex loops (figure 7
b). A local reduction of the flow three-dimensionality is observed in figures 11 and 10 for
![]() $Re=225{-}275$
as the finer-scale Mode B structure becomes dominant (figure 7
c,d). The ordered Mode B structure is observed within all of the three Mode A vortex loops, and may even occupy the entire span width during the mode swapping process. For
$Re=225{-}275$
as the finer-scale Mode B structure becomes dominant (figure 7
c,d). The ordered Mode B structure is observed within all of the three Mode A vortex loops, and may even occupy the entire span width during the mode swapping process. For
![]() $Re>275$
, although the wake structure is almost fully occupied by Mode B, the Mode B structure becomes increasingly disordered (figure 7
e versus figure 7
d), which is the reason why the flow three-dimensionality experiences a sharp increase. The emergence of increasingly disordered Mode B structure and the corresponding sharp increase of flow three-dimensionality have also been observed for an isolated cylinder (Williamson Reference Williamson1996; Jiang et al.
Reference Jiang, Cheng, Draper, An and Tong2016).
$Re>275$
, although the wake structure is almost fully occupied by Mode B, the Mode B structure becomes increasingly disordered (figure 7
e versus figure 7
d), which is the reason why the flow three-dimensionality experiences a sharp increase. The emergence of increasingly disordered Mode B structure and the corresponding sharp increase of flow three-dimensionality have also been observed for an isolated cylinder (Williamson Reference Williamson1996; Jiang et al.
Reference Jiang, Cheng, Draper, An and Tong2016).
The hysteresis of the Mode A instability at
![]() $Re_{cr\,3D}\;(=149.2)$
is checked by adopting a case with the fully developed Mode A flow at
$Re_{cr\,3D}\;(=149.2)$
is checked by adopting a case with the fully developed Mode A flow at
![]() $Re=150$
as the initial condition and a slightly reduced
$Re=150$
as the initial condition and a slightly reduced
![]() $Re$
of 148.5 for the simulation. Based on the examination of the flow three-dimensionality (through
$Re$
of 148.5 for the simulation. Based on the examination of the flow three-dimensionality (through
![]() $\unicode[STIX]{x1D700}_{x}$
and
$\unicode[STIX]{x1D700}_{x}$
and
![]() $E_{z}$
) in the fully developed flow, hysteresis effect is not detected. In comparison with the case of an isolated circular cylinder which shows a hysteresis effect (Williamson Reference Williamson1996), the suppression of vortex structures with large three-dimensionality and the absence of convective instability of such large disturbances may be the reasons why a hysteresis effect is not observed in the present case.
$E_{z}$
) in the fully developed flow, hysteresis effect is not detected. In comparison with the case of an isolated circular cylinder which shows a hysteresis effect (Williamson Reference Williamson1996), the suppression of vortex structures with large three-dimensionality and the absence of convective instability of such large disturbances may be the reasons why a hysteresis effect is not observed in the present case.

Figure 12.
![]() $St{-}Re$
relationship over the laminar and 3D wake transition regimes.
$St{-}Re$
relationship over the laminar and 3D wake transition regimes.
Figure 12 shows the
![]() $St{-}Re$
relationship for
$St{-}Re$
relationship for
![]() $G/D=0.4$
, together with the results for an isolated cylinder. The sampling data sets are identical to those for obtaining the force coefficients. It is seen in figure 12 that while the deviations between the 2D and 3D results for the near-wall case are consistent with the deviation trends of the force coefficients (figure 10) as well as the streamwise enstrophy and spanwise disturbance energy (figure 11), they are quite different from the characteristics for an isolated cylinder. At the onset of 3D wake instability, a gradual deviation of the
$G/D=0.4$
, together with the results for an isolated cylinder. The sampling data sets are identical to those for obtaining the force coefficients. It is seen in figure 12 that while the deviations between the 2D and 3D results for the near-wall case are consistent with the deviation trends of the force coefficients (figure 10) as well as the streamwise enstrophy and spanwise disturbance energy (figure 11), they are quite different from the characteristics for an isolated cylinder. At the onset of 3D wake instability, a gradual deviation of the
![]() $St$
values predicted from 2D and 3D simulations is observed for the near-wall case, whereas a sudden drop of
$St$
values predicted from 2D and 3D simulations is observed for the near-wall case, whereas a sudden drop of
![]() $St$
is observed for an isolated cylinder. The gradual and continuous drop of
$St$
is observed for an isolated cylinder. The gradual and continuous drop of
![]() $St$
for the near-wall case is consistent with the very weak flow three-dimensionality and very close 2D and 3D results of the force coefficients for
$St$
for the near-wall case is consistent with the very weak flow three-dimensionality and very close 2D and 3D results of the force coefficients for
![]() $Re$
just above
$Re$
just above
![]() $Re_{cr\,3D}$
, and is attributed to the extremely ordered (strongly confined) Mode A structure. In contrast, the sudden drop of
$Re_{cr\,3D}$
, and is attributed to the extremely ordered (strongly confined) Mode A structure. In contrast, the sudden drop of
![]() $St$
for an isolated cylinder is due to the well-developed Mode A structure with large-scale vortex dislocations (Williamson Reference Williamson1996).
$St$
for an isolated cylinder is due to the well-developed Mode A structure with large-scale vortex dislocations (Williamson Reference Williamson1996).
Another difference in the
![]() $St{-}Re$
relationship shown in figure 12 is that for the near-wall case only one single vortex shedding frequency peak is observed at each
$St{-}Re$
relationship shown in figure 12 is that for the near-wall case only one single vortex shedding frequency peak is observed at each
![]() $Re$
for the entire
$Re$
for the entire
![]() $St{-}Re$
curve, whereas for the isolated cylinder case two different frequency peaks are observed in the mode swapping regime of approximately
$St{-}Re$
curve, whereas for the isolated cylinder case two different frequency peaks are observed in the mode swapping regime of approximately
![]() $Re=230{-}260$
. The lower and higher frequency peaks for the isolated cylinder case correspond to Mode A with large-scale dislocations and Mode B, respectively (Williamson Reference Williamson1996). It is speculated in Williamson (Reference Williamson1996) that for an isolated cylinder, if vortex dislocations do not occur, the
$Re=230{-}260$
. The lower and higher frequency peaks for the isolated cylinder case correspond to Mode A with large-scale dislocations and Mode B, respectively (Williamson Reference Williamson1996). It is speculated in Williamson (Reference Williamson1996) that for an isolated cylinder, if vortex dislocations do not occur, the
![]() $St{-}Re$
curve would be a single and continuous curve, with each
$St{-}Re$
curve would be a single and continuous curve, with each
![]() $Re$
corresponding to a single
$Re$
corresponding to a single
![]() $St$
. However, Henderson (Reference Henderson1997) suggested that the lower frequency peak for the isolated cylinder case is due to the Mode A instability only, irrespective of the dislocations. For the present case of a circular cylinder near a moving wall, the mode swapping process does not contain relatively large-scale vortex structures of dislocations or even pure Mode A. The finer-scale structure of a mixture of ordered Modes A and B share a single frequency peak. It should be noted that for the 3D DNS study of an isolated cylinder by Jiang et al. (Reference Jiang, Cheng, Draper, An and Tong2016) at
$St$
. However, Henderson (Reference Henderson1997) suggested that the lower frequency peak for the isolated cylinder case is due to the Mode A instability only, irrespective of the dislocations. For the present case of a circular cylinder near a moving wall, the mode swapping process does not contain relatively large-scale vortex structures of dislocations or even pure Mode A. The finer-scale structure of a mixture of ordered Modes A and B share a single frequency peak. It should be noted that for the 3D DNS study of an isolated cylinder by Jiang et al. (Reference Jiang, Cheng, Draper, An and Tong2016) at
![]() $Re=270$
(just beyond the mode swapping regime), the flow structure is also characterized by a mixture of ordered Modes A and B, and only a single frequency peak is present.
$Re=270$
(just beyond the mode swapping regime), the flow structure is also characterized by a mixture of ordered Modes A and B, and only a single frequency peak is present.
Prior to the mode swapping regime of the near-wall case, an obvious increase of
![]() $St$
is observed when
$St$
is observed when
![]() $Re$
increases from 220 to 225, as the wake structure changes from large-scale-dominant (mainly pure Mode A) to small-scale-dominant (Mode B occupies all of the Mode A loops and may even occupy the entire span width). This seems to support the argument by Henderson (Reference Henderson1997) that a lower frequency peak is due to the Mode A structure (large-scale structure), whereas vortex dislocation is not a necessity. For the near-wall case, large-scale structures are observed for the entire simulations of
$Re$
increases from 220 to 225, as the wake structure changes from large-scale-dominant (mainly pure Mode A) to small-scale-dominant (Mode B occupies all of the Mode A loops and may even occupy the entire span width). This seems to support the argument by Henderson (Reference Henderson1997) that a lower frequency peak is due to the Mode A structure (large-scale structure), whereas vortex dislocation is not a necessity. For the near-wall case, large-scale structures are observed for the entire simulations of
![]() $Re=150{-}220$
and finer-scale structures are observed for the entire simulations of
$Re=150{-}220$
and finer-scale structures are observed for the entire simulations of
![]() $Re=225{-}275$
. Hence a sudden increase of
$Re=225{-}275$
. Hence a sudden increase of
![]() $St$
is observed at
$St$
is observed at
![]() $Re=220{-}225$
, but only one frequency peak is observed for each case. In contrast, for the mode swapping process of the isolated cylinder case, large-scale structure (Mode A with dislocations) and finer-scale structure (a mixture of ordered Modes A and B) occur alternately in the same simulation case (see Jiang et al.
Reference Jiang, Cheng, Draper, An and Tong2016). As a result, two different frequency peaks are observed.
$Re=220{-}225$
, but only one frequency peak is observed for each case. In contrast, for the mode swapping process of the isolated cylinder case, large-scale structure (Mode A with dislocations) and finer-scale structure (a mixture of ordered Modes A and B) occur alternately in the same simulation case (see Jiang et al.
Reference Jiang, Cheng, Draper, An and Tong2016). As a result, two different frequency peaks are observed.
While it is demonstrated above that the relatively large-scale Mode A structure may be responsible for a lower frequency peak, further support will be given in § 3.3 to show that vortex dislocation may not be the reason for a lower frequency peak.

Figure 13. Frequency spectra of
![]() $C_{L}$
for
$C_{L}$
for
![]() $G/D=0.4$
and
$G/D=0.4$
and
![]() $Re$
in the range of 150–325.
$Re$
in the range of 150–325.
Figure 13 shows some of the frequency spectra of
![]() $C_{L}$
which are used to determine
$C_{L}$
which are used to determine
![]() $St$
. The amplitude of
$St$
. The amplitude of
![]() $C_{L}$
shown in figure 13 is normalized with
$C_{L}$
shown in figure 13 is normalized with
![]() $1/(\sqrt{2}C_{L}^{\prime })$
, which is calculated from the same sampling data set. In this way, the normalized amplitude of
$1/(\sqrt{2}C_{L}^{\prime })$
, which is calculated from the same sampling data set. In this way, the normalized amplitude of
![]() $C_{L}$
becomes 1 if the time history of
$C_{L}$
becomes 1 if the time history of
![]() $C_{L}$
is sinusoidal with an arbitrary amplitude. Each vertical line under the frequency spectrum shown in figure 13 represents a discrete point on the spectrum curve. The spacing between the discrete vertical lines is due to the use of a finite data range of the time history of
$C_{L}$
is sinusoidal with an arbitrary amplitude. Each vertical line under the frequency spectrum shown in figure 13 represents a discrete point on the spectrum curve. The spacing between the discrete vertical lines is due to the use of a finite data range of the time history of
![]() $C_{L}$
for the FFT.
$C_{L}$
for the FFT.
It is seen in figure 13 that for
![]() $Re\leqslant 225$
, since the time history of the lift coefficient is relatively regular (figure 6), the frequency spectrum is represented by a single frequency value with the normalized amplitude very close to 1. In the mode swapping regime of
$Re\leqslant 225$
, since the time history of the lift coefficient is relatively regular (figure 6), the frequency spectrum is represented by a single frequency value with the normalized amplitude very close to 1. In the mode swapping regime of
![]() $Re=250{-}275$
, as the time history of the lift coefficient becomes relatively irregular, the frequency spectrum is represented by a sharp peak together with small-scale fluctuations, and the peak amplitude reduces to around 0.9. As the Mode B structure becomes increasingly disordered at
$Re=250{-}275$
, as the time history of the lift coefficient becomes relatively irregular, the frequency spectrum is represented by a sharp peak together with small-scale fluctuations, and the peak amplitude reduces to around 0.9. As the Mode B structure becomes increasingly disordered at
![]() $Re\geqslant 285$
, the frequency spectrum becomes increasingly broadband and the peak amplitude further drops to approximately 0.6.
$Re\geqslant 285$
, the frequency spectrum becomes increasingly broadband and the peak amplitude further drops to approximately 0.6.

Figure 14. Frequency spectra of
![]() $C_{L}$
for
$C_{L}$
for
![]() $Re=200$
and
$Re=200$
and
![]() $G/D$
in the range of 0.4–19.5.
$G/D$
in the range of 0.4–19.5.
3.3 Results at
 $Re=200$
with varying
$Re=200$
with varying
 $G/D$
$G/D$
A series of cases with
![]() $Re=200$
and
$Re=200$
and
![]() $G/D$
ranging between 0.4 and 19.5 is studied. As shown in figure 4, the wake transition regime changes from ‘ordered Mode A (without dislocations)’ to ‘Mode A with dislocations’ when
$G/D$
ranging between 0.4 and 19.5 is studied. As shown in figure 4, the wake transition regime changes from ‘ordered Mode A (without dislocations)’ to ‘Mode A with dislocations’ when
![]() $G/D$
increases from 1.2 to 1.5. Consequently, the time histories of the force coefficients and point spanwise velocity change from a relatively regular pattern which is similar to the case of
$G/D$
increases from 1.2 to 1.5. Consequently, the time histories of the force coefficients and point spanwise velocity change from a relatively regular pattern which is similar to the case of
![]() $(G/D,Re)=(0.4,200)$
(figure 6
b) into a chaotic irregular pattern which is similar to the case of an isolated cylinder. Similar to figure 13, figure 14 shows the frequency spectra of
$(G/D,Re)=(0.4,200)$
(figure 6
b) into a chaotic irregular pattern which is similar to the case of an isolated cylinder. Similar to figure 13, figure 14 shows the frequency spectra of
![]() $C_{L}$
for
$C_{L}$
for
![]() $Re=200$
with the amplitude normalized with
$Re=200$
with the amplitude normalized with
![]() $1/(\sqrt{2}C_{L}^{\prime })$
. For
$1/(\sqrt{2}C_{L}^{\prime })$
. For
![]() $G/D\leqslant 1.2$
(without dislocations), a single frequency value is observed in the frequency spectrum and the normalized amplitude is very close to 1. For
$G/D\leqslant 1.2$
(without dislocations), a single frequency value is observed in the frequency spectrum and the normalized amplitude is very close to 1. For
![]() $G/D\geqslant 1.5$
(with dislocations), however, the frequency spectrum is broadband and the peak amplitude reduces to approximately 0.6.
$G/D\geqslant 1.5$
(with dislocations), however, the frequency spectrum is broadband and the peak amplitude reduces to approximately 0.6.

Figure 15. Variations of the statistically stationary quantities with
![]() $G/D$
: (a) Strouhal number and (b) time-averaged drag coefficient and root-mean-square lift coefficient.
$G/D$
: (a) Strouhal number and (b) time-averaged drag coefficient and root-mean-square lift coefficient.
Figure 15 shows the variations of the statistically stationary Strouhal number and force coefficients with
![]() $G/D$
. It is seen that the 3D results of the Strouhal number and force coefficients are decreased from their 2D counterparts to a similar degree for all of the gap ratios considered. Particularly, there is no abrupt variation of the quantities shown in figure 15 when
$G/D$
. It is seen that the 3D results of the Strouhal number and force coefficients are decreased from their 2D counterparts to a similar degree for all of the gap ratios considered. Particularly, there is no abrupt variation of the quantities shown in figure 15 when
![]() $G/D$
increases from 1.2 (without dislocations) to 1.5 (with dislocations). This suggests that the Strouhal number and force coefficients are not strongly influenced by the occurrence or suppression of vortex dislocation. This seems to support the argument by Henderson (Reference Henderson1997) that the particular shedding frequency is due to the Mode A instability only, rather than the occurrence of dislocation, whereas the occurrence of dislocation accounts for a broadband frequency spectrum (see figure 14).
$G/D$
increases from 1.2 (without dislocations) to 1.5 (with dislocations). This suggests that the Strouhal number and force coefficients are not strongly influenced by the occurrence or suppression of vortex dislocation. This seems to support the argument by Henderson (Reference Henderson1997) that the particular shedding frequency is due to the Mode A instability only, rather than the occurrence of dislocation, whereas the occurrence of dislocation accounts for a broadband frequency spectrum (see figure 14).

Figure 16. Iso-surfaces of
![]() $\unicode[STIX]{x1D714}_{x}=\pm 0.2$
for
$\unicode[STIX]{x1D714}_{x}=\pm 0.2$
for
![]() $Re=200$
with various gap ratios, overlaid with the locations of the positive (P) and negative (N) primary vortex cores. Dark grey and light yellow denote positive and negative values, respectively. The flow is from the left to the right past the cylinder on the left.
$Re=200$
with various gap ratios, overlaid with the locations of the positive (P) and negative (N) primary vortex cores. Dark grey and light yellow denote positive and negative values, respectively. The flow is from the left to the right past the cylinder on the left.
The confinement of the wake structures at different gap ratios is examined through numerical flow visualization. Figure 16 shows the isosurfaces of
![]() $\unicode[STIX]{x1D714}_{x}$
for various
$\unicode[STIX]{x1D714}_{x}$
for various
![]() $G/D$
with
$G/D$
with
![]() $Re=200$
, overlaid with the locations of the positive (P) and negative (N) primary vortex cores determined from the isosurfaces of the second negative eigenvalue
$Re=200$
, overlaid with the locations of the positive (P) and negative (N) primary vortex cores determined from the isosurfaces of the second negative eigenvalue
![]() $\unicode[STIX]{x1D706}_{2}$
of the tensor
$\unicode[STIX]{x1D706}_{2}$
of the tensor
![]() $\unicode[STIX]{x1D733}^{2}+\unicode[STIX]{x1D734}^{2}$
, where
$\unicode[STIX]{x1D733}^{2}+\unicode[STIX]{x1D734}^{2}$
, where
![]() $\unicode[STIX]{x1D733}$
and
$\unicode[STIX]{x1D733}$
and
![]() $\unicode[STIX]{x1D734}$
are the symmetric and antisymmetric parts of the velocity gradient tensor, respectively (Jeong & Hussain Reference Jeong and Hussain1995). For
$\unicode[STIX]{x1D734}$
are the symmetric and antisymmetric parts of the velocity gradient tensor, respectively (Jeong & Hussain Reference Jeong and Hussain1995). For
![]() $0.4\leqslant G/D\leqslant 1.0$
where vortex dislocation is suppressed, the fully developed wake structure is presented. For
$0.4\leqslant G/D\leqslant 1.0$
where vortex dislocation is suppressed, the fully developed wake structure is presented. For
![]() $G/D\geqslant 1.5$
where vortex dislocation will evolve spontaneously, the pure Mode A structure at the time just before the occurrence of dislocation is shown. For each case, three relatively ordered Mode A streamwise vortex pairs are observed along the cylinder span width (in the
$G/D\geqslant 1.5$
where vortex dislocation will evolve spontaneously, the pure Mode A structure at the time just before the occurrence of dislocation is shown. For each case, three relatively ordered Mode A streamwise vortex pairs are observed along the cylinder span width (in the
![]() $x$
–
$x$
–
![]() $z$
plane), among which a half of a vortex pair is shown in figure 16 (in the
$z$
plane), among which a half of a vortex pair is shown in figure 16 (in the
![]() $x$
–
$x$
–
![]() $y$
plane).
$y$
plane).
The time evolution of the vortex structure has been examined in a full vortex shedding cycle (with a shedding period of
![]() $T$
). The non-dimensional flow time
$T$
). The non-dimensional flow time
![]() $t^{\ast }\;(=Ut/D)$
is normalized with the non-dimensional shedding period
$t^{\ast }\;(=Ut/D)$
is normalized with the non-dimensional shedding period
![]() $T^{\ast }\;(=UT/D)$
so that
$T^{\ast }\;(=UT/D)$
so that
![]() $t^{\ast }/T^{\ast }$
ranges from 0 to 1 in this shedding cycle (discarding the previous flow time). The shedding cycle starts at the time instant
$t^{\ast }/T^{\ast }$
ranges from 0 to 1 in this shedding cycle (discarding the previous flow time). The shedding cycle starts at the time instant
![]() $t^{\ast }/T^{\ast }=0$
where the lift coefficient on the cylinder reaches its maximum, and a negative primary vortex core develops at the upper side of the cylinder. Each case in figure 16 is shown at the phase of its earliest confinement (in terms of the streamwise location
$t^{\ast }/T^{\ast }=0$
where the lift coefficient on the cylinder reaches its maximum, and a negative primary vortex core develops at the upper side of the cylinder. Each case in figure 16 is shown at the phase of its earliest confinement (in terms of the streamwise location
![]() $x/D$
) of the negative streamwise vortices by the plane wall in the shedding cycle. As expected, the earliest confinement point moves downstream as the gap ratio increases.
$x/D$
) of the negative streamwise vortices by the plane wall in the shedding cycle. As expected, the earliest confinement point moves downstream as the gap ratio increases.
Figure 16(e) shows the lower envelope of the streamwise vortices for the case of an isolated cylinder at
![]() $Re=200$
. It is seen that the earliest confinement points for
$Re=200$
. It is seen that the earliest confinement points for
![]() $0.4\leqslant G/D\leqslant 1.5$
all fall onto this envelope, which suggests that the confinement of the negative streamwise vortices is largely due to the interference of the plane wall with the natural development of the streamwise vortices in the cylinder wake. For
$0.4\leqslant G/D\leqslant 1.5$
all fall onto this envelope, which suggests that the confinement of the negative streamwise vortices is largely due to the interference of the plane wall with the natural development of the streamwise vortices in the cylinder wake. For
![]() $G/D=3.0$
, there is no intersection point between the envelope of the streamwise vortices and the plane wall (figure 16
e), and consequently the wake structure is not noticeably affected (omitted for simplicity).
$G/D=3.0$
, there is no intersection point between the envelope of the streamwise vortices and the plane wall (figure 16
e), and consequently the wake structure is not noticeably affected (omitted for simplicity).
For each case shown in figure 16, alternate vortex shedding is observed, which is represented by a row of negative primary vortex cores shed from the upper side of the cylinder and a row of positive primary vortex cores shed from the lower side of the cylinder. For the case of an isolated cylinder (figure 16
e), the primary vortex cores and streamwise vortices with opposite signs developed on the two sides of the cylinder possess a
![]() $Z_{2}$
spatiotemporal symmetry (spatial reflection of the flow about the wake centreline after every
$Z_{2}$
spatiotemporal symmetry (spatial reflection of the flow about the wake centreline after every
![]() $T/2$
time evolution) as they propagate downstream. With decrease of the gap ratio, both rows of primary vortex cores are deflected upwards. The negative streamwise vortices downstream of the earliest confinement point are squeezed by the plane wall and the neighbouring positive streamwise vortex. The positive streamwise vortices downstream of the earliest confinement point are also slightly confined by the plane wall at their lower ends, each displaying a wedge-shaped lower end extending towards the upstream side. The distortions of the streamwise vortices become stronger as they propagate downstream (figure 16
a–d), since for an isolated cylinder the lower envelope of the streamwise vortices reaches further lower positions (figure 16
e). At small gap ratios, the extended lower ends of the positive streamwise vortices may even be strong enough to merge with the subsequent positive streamwise vortices (e.g. figure 16
a).
$T/2$
time evolution) as they propagate downstream. With decrease of the gap ratio, both rows of primary vortex cores are deflected upwards. The negative streamwise vortices downstream of the earliest confinement point are squeezed by the plane wall and the neighbouring positive streamwise vortex. The positive streamwise vortices downstream of the earliest confinement point are also slightly confined by the plane wall at their lower ends, each displaying a wedge-shaped lower end extending towards the upstream side. The distortions of the streamwise vortices become stronger as they propagate downstream (figure 16
a–d), since for an isolated cylinder the lower envelope of the streamwise vortices reaches further lower positions (figure 16
e). At small gap ratios, the extended lower ends of the positive streamwise vortices may even be strong enough to merge with the subsequent positive streamwise vortices (e.g. figure 16
a).
For
![]() $G/D\geqslant 1.5$
, it is found that any large-scale vortex dislocation is always initialized with the local dislocation of a particular Mode A vortex loop after it grows to be stronger than other Mode A vortex loops along the span width. Hence the suppression of vortex dislocation for
$G/D\geqslant 1.5$
, it is found that any large-scale vortex dislocation is always initialized with the local dislocation of a particular Mode A vortex loop after it grows to be stronger than other Mode A vortex loops along the span width. Hence the suppression of vortex dislocation for
![]() $G/D\leqslant 1.2$
is believed to be due to the confinement of the Mode A streamwise vortices by the plane wall, which suppresses the excess growth and local dislocation of any Mode A vortex loop.
$G/D\leqslant 1.2$
is believed to be due to the confinement of the Mode A streamwise vortices by the plane wall, which suppresses the excess growth and local dislocation of any Mode A vortex loop.
It is found that vortex dislocation is also suppressed for the case of flow past a circular cylinder in proximity to a symmetry boundary (rather than a moving wall) with
![]() $(G/D,Re)=(1.2,200)$
. This case suggests that the suppression of vortex dislocation is not due to the shear layers developed on the plane wall.
$(G/D,Re)=(1.2,200)$
. This case suggests that the suppression of vortex dislocation is not due to the shear layers developed on the plane wall.

Figure 17. Iso-surfaces of
![]() $\unicode[STIX]{x1D714}_{x}=\pm 0.1$
for flow past a circular cylinder with two near-wake wires at
$\unicode[STIX]{x1D714}_{x}=\pm 0.1$
for flow past a circular cylinder with two near-wake wires at
![]() $Re=220$
. Dark grey and light yellow denote positive and negative values, respectively. The flow is from the left to the right past the cylinder on the left.
$Re=220$
. Dark grey and light yellow denote positive and negative values, respectively. The flow is from the left to the right past the cylinder on the left.
It is worth mentioning that similar suppression of vortex dislocation of the Mode A flow is also observed for flow past a circular cylinder with two near-wake wires (of an equal diameter of
![]() $0.05D$
) placed at
$0.05D$
) placed at
![]() $(x/D,y/D)=(0.75,\pm 0.75)$
. In this case, the near-wake wires are the reasons for the confinement of the streamwise vortices (figure 17) and consequently the suppression of local dislocation of Mode A vortex loops.
$(x/D,y/D)=(0.75,\pm 0.75)$
. In this case, the near-wake wires are the reasons for the confinement of the streamwise vortices (figure 17) and consequently the suppression of local dislocation of Mode A vortex loops.
4 Conclusions
This paper presents 3D DNS of flow past a circular cylinder near a moving wall, covering a parameter space spanning a gap ratio
![]() $(G/D)\geqslant \,0.3$
and Reynolds number (
$(G/D)\geqslant \,0.3$
and Reynolds number (
![]() $Re$
) up to 325. For
$Re$
) up to 325. For
![]() $G/D\geqslant 0.3$
, the flow undergoes a transition sequence of ‘2D
$G/D\geqslant 0.3$
, the flow undergoes a transition sequence of ‘2D
![]() $\rightarrow$
Mode A
$\rightarrow$
Mode A
![]() $\rightarrow$
mode swapping
$\rightarrow$
mode swapping
![]() $\rightarrow$
Mode B’ with increasing
$\rightarrow$
Mode B’ with increasing
![]() $Re$
. The Mode A and mode swapping regimes are further separated at
$Re$
. The Mode A and mode swapping regimes are further separated at
![]() $G/D\sim 1.0$
, based on the occurrence or suppression of vortex dislocation associated with Mode A. The suppression of vortex dislocation is believed to be due to the confinement of the Mode A streamwise vortices by the plane wall, which suppresses the excess growth and local dislocation of any Mode A vortex loop.
$G/D\sim 1.0$
, based on the occurrence or suppression of vortex dislocation associated with Mode A. The suppression of vortex dislocation is believed to be due to the confinement of the Mode A streamwise vortices by the plane wall, which suppresses the excess growth and local dislocation of any Mode A vortex loop.
A series of cases at
![]() $G/D=0.4$
with varying
$G/D=0.4$
with varying
![]() $Re$
is examined, where vortex dislocation is suppressed in the wake transition process. For
$Re$
is examined, where vortex dislocation is suppressed in the wake transition process. For
![]() $Re_{cr\,3D}<$
$Re_{cr\,3D}<$
![]() $Re\leqslant 180$
, the fully developed flow is represented by ordered Mode A structure only. For 200
$Re\leqslant 180$
, the fully developed flow is represented by ordered Mode A structure only. For 200
![]() ${\leqslant}Re<225$
, the ordered Mode A structure remains unchanged while ordered Mode B structure starts to develop within the Mode A vortex loops. For 225
${\leqslant}Re<225$
, the ordered Mode A structure remains unchanged while ordered Mode B structure starts to develop within the Mode A vortex loops. For 225
![]() ${\leqslant}Re\leqslant 240$
, all of the Mode A vortex loops are filled with ordered Mode B structure throughout the simulations. The mode swapping process with a gradual transition from the ordered Mode A structure to relatively ordered Mode B structure occurs at
${\leqslant}Re\leqslant 240$
, all of the Mode A vortex loops are filled with ordered Mode B structure throughout the simulations. The mode swapping process with a gradual transition from the ordered Mode A structure to relatively ordered Mode B structure occurs at
![]() $Re=246{-}281$
. For
$Re=246{-}281$
. For
![]() $Re\geqslant 285$
, the wake is dominated by increasingly disordered Mode B structure. Relatively strong flow three-dimensionality is observed at
$Re\geqslant 285$
, the wake is dominated by increasingly disordered Mode B structure. Relatively strong flow three-dimensionality is observed at
![]() $Re=160{-}220$
as the wake is dominated by large-scale structure of ordered Mode A, and also at
$Re=160{-}220$
as the wake is dominated by large-scale structure of ordered Mode A, and also at
![]() $Re\geqslant 285$
, where Mode B becomes increasingly disordered. A local reduction of the flow three-dimensionality is observed at
$Re\geqslant 285$
, where Mode B becomes increasingly disordered. A local reduction of the flow three-dimensionality is observed at
![]() $Re=225{-}275$
, where the wake is dominated by finer-scale structure of a mixture of ordered Modes A and B. This leads to a reduction of the deviation of the 3D results (Strouhal number and force coefficients) from their 2D counterparts. Together with the results at
$Re=225{-}275$
, where the wake is dominated by finer-scale structure of a mixture of ordered Modes A and B. This leads to a reduction of the deviation of the 3D results (Strouhal number and force coefficients) from their 2D counterparts. Together with the results at
![]() $Re=200$
with varying
$Re=200$
with varying
![]() $G/D$
, the results obtained from the present study support the argument by Henderson (Reference Henderson1997) that the particular vortex shedding frequency for Mode A is due to the Mode A instability only, rather than the occurrence of vortex dislocations, while the occurrence of dislocations accounts for a broadband frequency spectrum.
$G/D$
, the results obtained from the present study support the argument by Henderson (Reference Henderson1997) that the particular vortex shedding frequency for Mode A is due to the Mode A instability only, rather than the occurrence of vortex dislocations, while the occurrence of dislocations accounts for a broadband frequency spectrum.
Acknowledgements
This work was supported by resources provided by the Pawsey Supercomputing Centre with funding from the Australian Government and the Government of Western Australia. The first author would like to acknowledge the support from the Australian Government and The University of Western Australia by providing IPRS and APA scholarships for a doctoral degree, as well as the Australia–China Natural Gas Technology Postgraduate Research Scholarships from the Australian and Western Australian Governments, the North West Shelf Joint Venture Partners, and the Western Australian Energy Research Alliance. The fourth author would like to acknowledge the support from the Australian Research Council through Discovery Early Career Research Award (DE150100428).