Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-06T10:29:21.725Z Has data issue: false hasContentIssue false
  • English
  • Français

Penetration of intense charged particle beams in the outer layers of precompressed thermonuclear fuels

Published online by Cambridge University Press:  01 June 2004

C. DEUTSCH
C. DEUTSCH
Affiliation:
Laboratoire de Physique des Gaz et Plasmas, (CNRS-UMR), Université Paris XI, ORSAY Cedex, France
Rights & Permissions [Opens in a new window]

Abstract

This paper emphasizes the energy dissipation through collective electromagnetic modes (mostly transverse to the incoming beam) of ultraintense relativistic electrons and nonrelativistic protons interacting with a supercompressed core of deuterium + tritium (DT) thermonuclear fuel. This pattern of beam–plasma interaction documents the fast ignition scenario for inertial confinement fusion.

The electronmagnetic Weibel instability is considered analytically in a linear approximation. Relevant growth rates parameters then highlight density ratios between target and particle beams, as well as transverse temperatures. Significant refinements include mode–mode couplings and collisions with target electrons. The former qualify the so-called quasi-linear (weakly turbulent) approach. Usually, it produces significantly lower growth rates than the linear ones. Collisions enhance them slightly for kc /ωp < 1, and dampen them strongly for kc /ωp ≥ 1. Those results simplify rather drastically for the laser-produced and nonrelativistic proton beams. In this case, those growth rates remain always negative through a wide range of beam–target parameters.

Keywords

Fast ignitionQuasi-linear treatmentWeibel instability
Type
Research Article
Information
Laser and Particle Beams , Volume 22 , Issue 2 , June 2004 , pp. 115 - 120
Copyright
© 2004 Cambridge University Press

1. INTRODUCTION

The recently proposed fast ignitor (FIS; Tabak et al., 1994) designed for monitoring the ignition process within any inertial confinement fusion (ICF) scheme highlights to the extreme, the splitting paradigm of cheap compression through MJ drivers (heavy ions, lasers) followed by the expensive triggered ignition of the compressed fuel with petawatt lasers. The latter are first expected to bore a hole in the corona of the compressed DT core, and also to produce with a good efficiency intense relative electron beams (REB) at megaelectron volt levels, through critical surface crushing (Lefebvre & Bonnaud, 1995). This latter feature has been indeed positively documented through numerical simulations and laser firing of thin cold foils. It thus remains to witness a successful penetration of those intense REB through steep density gradients ranging from 1021 e/cm3 in the corona down to 1026 e/cm3 in the DT core at a 100 μm or so distance. FIS has already received much attention, and its best understood steps include the ponderomotive laser penetration in the corona as well as the in depth hot spot building up through REB interacting inelastically with target electrons and also experiencing multiple (mostly elastic) scattering on target ions (Deutsch et al., 1996). The latter processes hopefully combine to yield a hot spot with a 10-μm extension for megaelectron volt REB. Intermediate steps are much more difficult to assert and remain a matter for intense scrutiny as well as hot contradictory debates (Honda, 2000; Honda et al., 2000; Hain & Mulser, 2001).

This situation motivates the present inquiry into every collective mode produced in the REB dense core interaction that may eventually divert into a large volume the REB kinetic energy. It turns out that the most dangerous ones arise from the filamentation (Weibel) instability due to the overall electron distribution built on direct and return current as well. The anisotropy of the latter acts as a permanent source of entropy. We demonstrate that Weibel (transverse electromagnetic) is at its worst when REB density is close to critical. However, this instability that pervades every beam–target interaction scheme of ICF interest may nevertheless be mitigated through a transverse temperature gradient. In the final FIS phase, T⊥b ∼ 150 eV seems sufficient. Then, we display results (see Fig. 1) of a three-dimensional (3D) PIC simulation supporting the view that collective effects monitor the REB–target interaction in the corona, while individual electron collisions take the lead with increasing core densities. In this respect, we supplement former REB stopping calculations (Deutsch et al., 1996) with enhanced contributions arising from correlated and relativistic electron stopping for projectiles pairs with interdistances orders of magnitude larger than the target electron screening length (Deutsch & Fromy, 1999, 2000).

Relativistic electron beam (REB) propagation with megaelectron volt incoming energy through layers of increasing density Np in a core of precompressed DT fuel.

2. LINEAR AND QUASI-LINEAR WEIBEL GROWTH RATES

Exponential growth of linear transverse Weibel instability could be highly detrimental to the REB stopping in the outer layers of a DT precompressed core.

The linear stage plays a crucial role in initiating the transverse and deleterious further filamentation process that could divert a substantial amount of REB energy initially intended to be deposited in the precompressed DT target.

2.1. Relativistic e-beams

Very recent experimental results seem to confirm the relative electron beams (REB) penetration in dense and hot plasmas with parameters compatible with those of possible outer layers surrounding a superdense DT core (see Fig. 1; Kodama et al., 2001).

Such a situation motivates our present focus on the basic mechanisms affecting REB propagation during the initial time scale ∼ ωp−1(ωp is the target plasma frequency) when Weibel electromagnetic instability (WEI) behaves mostly linearly. In particular, we intend to stress the N-body features of REB stopping in those specific conditions.

For our purposes, we find it useful to start with a collisional formulation of the Vlasov equation with a Krook term (Okada & Kiu, 1980) in the right-hand side, that is,

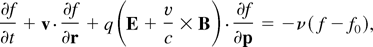
where ν is the effective collision frequency, f is the electron distribution function at position r and momentum p at time t, f0 is the distribution function, q denotes the charge (including sign), c is light speed, v and p are related by v = p/mγ, γb = (1 + p2/(mc)2)1/2 and m is the electron rest mass.

Let us now consider a current neutral beam–plasma system. The relativistic electron beam propagates with the velocity Vdb and the plasma return current flows with Vdp. It is reasonable to assume that an electromagnetic mode has k normal to Vdb, perturbed electric field E parallel to Vdb, and perturbed magnetic field B normal to both Vdb and E. So, the total asymmetric f0 consist of nonrelativistic background electrons and relativistic beam electrons:

Here θx, θy are the temperature components parallel to the x and y directions, pd is the drift momentum, and superscripts p and b represent the plasma electron and the beam electron, respectively. From the linearized Vlasov equation with the collision term (1) and linearized Maxwell's equations we get the linear dispersion relation for a purely transverse graving mode fulfilling

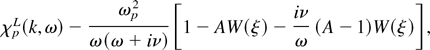
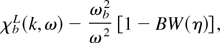
where

denote beam and target electron plasma frequency and

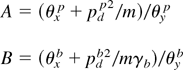
refer to corresponding asymmetry parameters, with

χpL is the plasma linear susceptibility and χpL that for the beam.

We restrict consideration of collisional effect to the background plasma and assume a weak beam (ωb < ωp). The function W(z) is taken in the usual Fried–Conte form as

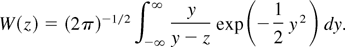
Paying attention to the WEI linear growth rate (LGR), we notice that this LGR is essentially controlled by the two asymmetry parameters:

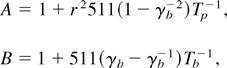
obtained below Eq. (5), where r = nb /np, Tb and Tp denote, respectively, REB and target plasma isotropic temperature in kiloelectron volts. Vp denotes REB velocity.

Moreover, it is also useful to remark that the quasi-linear theory (Dupree–Weinstock; Kono & Ichikawa, 1973) based on mode–mode coupling can provide even more accurate parameters, in the form

with X, positive solution of (u = (rvb /γb)2),

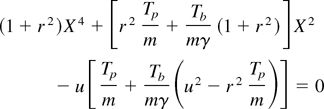
and D = 511r(1 − γb−1) in kiloelectron volts. Using (A,B) and (A′,B′) in the relevant linear dispersion relations, we obtain the WEI growth rates depicted in Figure 2, as linear and turbulent, respectively. We then emphasize moderately hot (Tp = 100 eV) outer DT layers and 1-MeV REB with a thermal Tb = 1 keV. Maximum LGR δmax occurs close to the skin depth wavelength c/ωp. δmax is also shown steadily decaying with increasing Np. Also, quasi-linear (“turbulent”) LGR profiles stand beneath linear ones.

Linear and quasi-linear (“turbulent”) WEI growth rates in a DT plasma with Tp = 100 eV at increasing Np. (a) 1023 cm−3, (b) 1024 cm−3, and (c) 1025 cm−3. Eb = 1 MeV and Tb = 1 keV.

In this connection, it is useful to recall that collisional REB stopping increases nearly linearly with Np. So, a figure of merit probing the relative importance of collective WEI energy dissipation of the REB against collisional stopping is the e-folding number

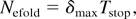
with

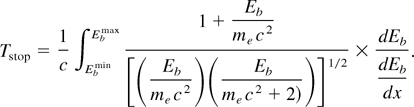
The evaluation of expression (5) is conveniently performed with the steplike Np profile given in Fig. 1. Ebmax and Ebmin refer to extreme Np values in every slab (25 μm thick) with a fixed Np in it, building up this profile in terms of the standard dEb /dx Fermi expression for the relativistic stopping of a single electron projectile (Fermi, 1940).

2.2. Collisions contribution

In view of the very high densities reached by the precompressed pellet, it seems rather mandatory to pay attention to collisions between e-beam and target ions. Very often, these contributions are neglected in many standard treatments of the Weibel instability. A large consensus even asserts that collisions remain helpless against transverse electromagnetic growth rates. Nonetheless, no one has already given ground to the validity of such a claim in the present extreme situation we are now considering. To clear up this point, we included in the present treatment, a Krook collision term with the right-hand side of the corresponding Vlasov equation.

A few salient results are thus detailed in Figure 3a,b,c for the successive density slices featured in Figure 1.

Weibel growth rates for a REB with anisotropic temperature Tb (ortho,para) = 10 keV, 10 eV, density Nb = 1022 cm−3 and energy Eb = 1 MeV in target electron. Plasma with (a) Tp = 10 eV, Np /Nb = 10; (b) Tp = 100 eV, Np /Nb = 500; (c) Tp = 1 keV, Np /Nb = 1000; n = ν/ωp qualifies a REB target collision rate.

The isotropic target temperature is taken to be systematically larger than the corresponding Fermi TF accounting for nonnegligible quantum effects. We see that as target electron density increases from 1023 up to 1025 cm−3, the discrepancy between linear L and quasilinear QL growth rates progressively disappear. Also, collision-corrected growth rates δ have a tendency to rise above the collisionless ones for 10−2 ≤ kc/ωp ≤ 1. However, only the collision-corrected ones abruptly decay to negative (stabilization) values for 1 ≤ kc/ωp ≤ 10. So, even in this rather extreme case of transverse electromagnetic instability, the beam–target collisions assert their usual damping role, as a priori expected on empirical grounds.

2.3. Maximum growth rates

A significant figure of merit for the growth rate of the transverse electromagnetic mode is obviously its maximum value for a wavelength target skin depth kc/ωp ≅ 1. It is documented in Figure 4a–c for several isotropic target temperatures in terms of REB transverse temperature. A typical target density Np = 100Nb, is selected. Whatever Tp, the given maximum growth rates display similar profiles with a maximum value around Tb ∼ 1 keV. It is quite suggestive that δ is at minimum for very low or very high Tb. Another encouraging result is afforded by the quasi-linear profiles, lying systematically beneath the linear ones. Those quasi-linear profiles are also significantly lowering with increasing Tp.

Maximum REB growth rates at kc/ωp = 1 with Nb = 1022 cm−3 and Eb = 1 MeV, in terms of isotropic Tb. Np = 100 Nb.

3. NONRELATIVISTIC PROTONS

Increasing only projectiles energy Eb yields a significant growth rate increase for the WEI (former presentation). So, one is led to minimize δ by reducing beam velocity, while still retaining a sufficient Eb for fast ignition. Those contradictory requirements may be fulfilled by turning to the recently unraveled and laser-produced proton beams (Roth et al., 2001) in the 5–70 MeV energy range, with a 10% yield.

So, extending the present WEI quasilinear analysis to those projectiles, we picture in Figure 5a–c corresponding δmax values. Those latter turn always negative. A full δ profile (Fig. 6) with temperatures of operational pertinence indeed confirm those statements.

Maximum Weibel growth rates at kc/ωp = 1, for 25 MeV protons with Nb = 1022 cm−3 and isotropic Tp = 1 keV. Np = 100 Nb. Quasi-linear profiles are contrasted to linear ones.

δ/ωp for 25-MeV protons in a target plasma with Np = 1024 cm−3, = 100Nb. Tp = Tb = 1 keV.

Present quasilinear WEI growth rate demonstrates that beam and target densities, as well as respective transverse temperatures, are again the key parameters qualifying beam–plasma interactions of FIS concern.

High Tb and Tp values for Nb /Np < 0.1 should easily allow Nefold ≤ 5, an acceptable figure. In every target plasma slab, one witnesses Tstop < 10−13 s for REB and Tstop < 10−12 s for protons.

So, a number of WEI e-foldings below 5 implies δREB/ωp ≤ 10−3 and δproton/ωp ≤ 10−4. Those inequalities are indeed achievable in the context of present inertial fusion technology.

These considerations support the view that in outer DT layers with Tp < 5 keV, most of the REB kinetic energy is still dissipated through short-ranged electron–electron collisions and plasmon excitation documenting standard REB stopping in dense hot classical plasmas.

Once the crucial Np = 1023 cm−3 slab has been penetrated, the relative Np increase of REB stopping versus WEI growth rates, on a time scale ∼ωp−1, allows the electron projectiles to make their way in depth easily toward the DT core and trigger the hot spot through a kilojoule of local energy deposit.

In summary, we have demonstrated through a simple but efficient analytical modeling of the laser-produced REB interacting with outer and thus less dense layers of the supercompressed DT core that the initial in-depth propagation phase of the REB within the fast ignitor scenario could be effective on a time scale afforded by the linear growth of the electromagnetic instability.

Those considerations are even more appropriate for nonrelativisitic proton beams that might offer the best option for driving fast ignition, provided their laser efficiency could be increased above 20%.

References

REFERENCES

Deutsch, C. & Fromy, P. (1999). Correlated stopping of relativistic electrons in superdense plasmas. Phys. Plasmas 6, 3597–3606.CrossRefGoogle Scholar
Deutsch, C., Furukawa, H., Mima, K., Murakami, M. & Nishihara (1996). Interaction physics of the Fast ignitor concept. Phys. Rev. Lett. 77, 2483–2486. Erratum (2000). 85, 1140.CrossRefGoogle Scholar
Fermi, E. (1940). The ionization loss in gases and in condensed materials. Phys. Rev. 57, 485–493.CrossRefGoogle Scholar
Hain, S. & Mulser, P. (2001). Fast ignition without hole boring. Phys. Rev. Lett. 86, 1015–1018.CrossRefGoogle Scholar
Honda, M. (2000). On the maximum current for a self-focusing relativistic electron beam. Phys. Plasmas 7, 1605–1606.Google Scholar
Kodama, R., Norreys, P.A., Mima, K., Dangor, A.E., Evans, R.G., Fujita, H., Kitagawa, Y., Krushelnik, K., Miyakoshi, T., Miyanada, N., Normatsu, T., Rose, S.J., Shozaki, T., Shigemori, K., Sunahara, A., Tampo, M., Tanaka, K.A., Toyama, Y., Yamanaka, T. & Zepf, M. (2001). Fast heating of ultrahigh-density plasma as step towards laser fusion ignition. Nature 412, 798–802.CrossRefGoogle Scholar
Kono, M. & Ichikawa, Y.H. (1973). Renormalization of the wave-particle interaction in weakly turbulent plasmas. Prog. Theor. Phys. 49, 754–763.CrossRefGoogle Scholar
Lefebvre, E. & Bonnaud, G. (1995). Transparency/opacity of a solid target illuminated by an untrahigh-intensity laser pulse. Phys. Rev. Lett. 74, 2002–2005.CrossRefGoogle Scholar
Okada, T. & Kiu, K. (1980). Electromagnetic instability and stopping power of plasma for relativistic electron beams. J. Plasma Phys. 23, 423–432.CrossRefGoogle Scholar
Roth, M., Cowan, T.E., Key, M.H., Hatchett, S.P., Browin, G., Fountain, W., Johnson, J., Pennington, D.M., Snavely, R.A., Wilds, S.G., Yasuike, K., Ruhl, H., Pegoraro, F., Bulanov, S.V., Campbell, E.M., Petty, M. & Powell, H. (2001). Fast ignition by intense laser-accelerated proton beams. Phys. Rev. Lett. 86, 436–439.CrossRefGoogle Scholar
Tabak, M., Hammer, J., Glinksy, M.E., Kruer, W.L., Wilks, S.C., Woodworth, J., Campbell, M.E., Perry, M.D. & Mason, R.J. (1994). Ignition and high gain with ultra powerful lasers. Phys. Plasmas 1, 1626–1634.CrossRefGoogle Scholar
Figure 0

Relativistic electron beam (REB) propagation with megaelectron volt incoming energy through layers of increasing density Np in a core of precompressed DT fuel.

Figure 1

Linear and quasi-linear (“turbulent”) WEI growth rates in a DT plasma with Tp = 100 eV at increasing Np. (a) 1023 cm−3, (b) 1024 cm−3, and (c) 1025 cm−3. Eb = 1 MeV and Tb = 1 keV.

Figure 2

Weibel growth rates for a REB with anisotropic temperature Tb (ortho,para) = 10 keV, 10 eV, density Nb = 1022 cm−3 and energy Eb = 1 MeV in target electron. Plasma with (a) Tp = 10 eV, Np /Nb = 10; (b) Tp = 100 eV, Np /Nb = 500; (c) Tp = 1 keV, Np /Nb = 1000; n = ν/ωp qualifies a REB target collision rate.

Figure 3

Maximum REB growth rates at kc/ωp = 1 with Nb = 1022 cm−3 and Eb = 1 MeV, in terms of isotropic Tb. Np = 100 Nb.

Figure 4

Maximum Weibel growth rates at kc/ωp = 1, for 25 MeV protons with Nb = 1022 cm−3 and isotropic Tp = 1 keV. Np = 100 Nb. Quasi-linear profiles are contrasted to linear ones.

Figure 5

δ/ωp for 25-MeV protons in a target plasma with Np = 1024 cm−3, = 100Nb. Tp = Tb = 1 keV.