2.1 Experimental set-up

The experiment is conducted in an atmospheric, premixed methane–air facility. Tests were conducted at an equivalence ratio of 0.95 for the $5~\text{m}~\text{s}^{-1}$ cases and 0.91 for the $8~\text{m}~\text{s}^{-1}$ cases. Reactant temperature is approximately 293 K for all cases. A schematic of the experimental set-up is shown in figure 1. The burner test section consists of a circular jet with a throat diameter of 24.1 mm, surrounded by a velocity-matched annular co-flow, with a diameter of 36.3 mm. The mean flow, $u_{0}$ , is from bottom to top. The bluff body is held approximately 10 mm above the exit plane, bisecting the jet. The bluff body is a 20 AWG (0.81 mm) nichrome wire.

The wire is heated by application of a 6–12 V AC current. The nichrome wire oscillates transverse to the jet flow, driven harmonically at the forcing frequency by two modified 90 W Goldwood speakers (see figure 1). The speakers are connected in parallel to the fixture which holds the oscillating flame holder. The driving signal is created by a function generator and amplified using two linear amplifiers, one for each speaker. The amplitude of flame holder oscillation is approximately 0.33 mm, and varies with frequency by approximately 0.09 mm.

Fuel and air enter the burner at its base through four inlet ports. The flow then passes through a metal screen which mixes the fuel–air mixture and supports a bed of ball-bearings above the screen. After the ball-bearing bed, the fuel–air mix continues through a settling plenum before passing through the variable turbulence generation plates. The turbulence generator consists of two plates with several pie-shaped slots cut through them and is detailed in Marshall et al. (Reference Marshall, Venkateswaran, Noble, Seitzman and Lieuwen2011).

The bottom plate is fixed, while the top plate can rotate over a $28^{\circ }$ range. By changing the relative angle between the top and bottom plates, the blockage ratio can be varied from 69 %–97 %. The plate angle is measured from a compass, with an uncertainty of $\pm 0.25^{\circ }$ . This turbulence generation system allows the independent variation of the mean flow velocity and turbulence level. For the lowest turbulence case, the plates are removed entirely. However, even in this case the flow has a low turbulence level. After the turbulent generation plates, the flow passes through a contoured nozzle, designed to create a uniform top-hat velocity profile at the plane of the jet exit.

The main air supply is metered using an Aalborg GFC-67, $0{-}500~\text{l}~\text{min}^{-1}$ mass flow controller, while the fuel is metered using an Omega FMA-5428, $0{-}50~\text{l}~\text{min}^{-1}$ mass flow controller. Co-flow air is metered using an Omega FMA-1843 gas flow meter and manual needle valve. The main air and fuel mass flow controllers are controlled using LabVIEW. The co-flow air is adjusted to match the main jet velocity.

Figure 1. (a) Schematic of the experimental facility, showing major burner components, and (b) an image of the experimental facility in use, showing the V-flame and oscillating flame holder.

Mie scattering is used both to detect the flame edge and quantify the velocity field using particle image velocimetry (PIV). Images are taken using a Photron Fastcam SA5 high speed video camera with a Nikon Micro-Nikkor $f=55~\text{m}$   $f/2.8$ lens, set to a resolution of 768 $\times$ 848 pixels for the 200 and 750 Hz cases and 640 $\times$ 848 pixels for the 1250 Hz case. A bandpass filter is used to minimize off-frequency light. The camera is triggered by a timing box tied to the laser pulse from a dual head, frequency doubled Litron Nd:YLF, 527 nm laser. The laser is formed into a vertical sheet, approximately 6 cm high and 1 mm thick. The laser and optical set-up are shown in figure 2.

Figure 2. Schematic of laser and camera set-up.

Titanium oxide ( $\text{TiO}_{2}$ ) seed particles, with a nominal diameter of 1 $\unicode[STIX]{x03BC}$ m are added to the flow by diverting a portion of the main air (prior to mixing with the fuel) through a small cyclone seeder. The seeded flow re-enters the main flow upstream of the settling plenum and prior to the turbulence generator. Cold flow tests show the seed to be well-mixed with the main flow. The co-flow is unseeded.

Three forcing frequencies (200, 750 and 1250 Hz) are investigated at two nominal mean, axial flow velocities ( $5~\text{m}~\text{s}^{-1}$ and $8~\text{m}~\text{s}^{-1}$ ), denoted as $U_{x,0}$ , and four turbulence intensities each ( $u^{\prime }/u_{x,0}\approx 8\,\%{-}32\,\%$ ), where $u^{\prime }$ is the root mean square of the turbulent velocity fluctuations, and $u_{x,0}$ is the mean measured axial flow velocity. For the 200 Hz cases, pairs of images are recorded at 2000 Hz. For the 750 and 1250 Hz cases, a sequence of images is taken at 7500 and 12 500 Hz, respectively. These acquisition rates result in 10 samples per forcing cycle for all conditions and, by virtue of being a nearly exact integer multiple of the forcing frequency, virtually eliminate spectral leakage bias errors in spectral estimation. The total number of image pairs is 8790, 17 580 and 21 095, for the 200, 750 and 1250 Hz cases, respectively.

PIV processing is accomplished with LaVision DaVis PIV software (LaVision 2016), using a multipass algorithm. The first pass uses a 48 $\times$ 48-pixel interrogation window, with 25 % overlap between windows, while two subsequent passes use an 8 $\times$ 8-pixel window, with a 25 % overlap. This yields a resolution 6 pixels ( ${\sim}0.46~\text{mm}$ ) between vectors. However, note that due to the window overlap, adjacent velocity vectors are not completely independent. The uncertainty of these measurements and calculations is discussed in § 2.2.3.

Figure 3. Radial dependence of the turbulence intensity at four different turbulence intensities for the nominally $5~\text{m}~\text{s}^{-1}$ cases (a), and $8~\text{m}~\text{s}^{-1}$ cases (b) at a cut 1.5 mm above the flame holder location.

Figure 3 plots the radial dependence of the root mean square of the turbulent fluctuations, $u^{\prime }$ , at a cut 1.5 mm above the flame holder location for the 750 Hz cases. Similar results are observed for the 200 Hz and 1250 Hz cases. For the lower turbulence levels, $u^{\prime }$ is approximately constant across the jet except near the oscillating flame holder, where large deviations are observed, which are due to the flame holder and flame movement. The spatial variation in $u^{\prime }$ near the edge of the jet is due to intermittency between the unseeded co-flow and main jet, and does not occur at higher turbulence due to the increased jet spreading which results in better seeding in this region. The values of $u^{\prime }$ quoted later are obtained separately from the left and right sides of the centreline, as there is some asymmetry in the highest turbulence intensity cases.

The integral time scale was estimated by computing the autocorrelation based on PIV data. The estimated autocorrelation results were fit with an exponential function, $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})=a\exp (-bt)+(1-a)\exp (-ct)$ . The integral time scale is computed by taking the integral of the fit equation, i.e. $\unicode[STIX]{x1D70F}_{int}=\int _{0}^{\infty }\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})\,\text{d}\unicode[STIX]{x1D70F}$ . Using this method, the estimated integral time, $\unicode[STIX]{x1D70F}_{int}U_{x,0}/D=0.19$ and varies by ${\sim}\pm 0.09$ .

2.2 Image and data processing

3.1 Turbulent ensemble-averaged burning velocity

Although the flame position is important in its own right, the ensemble-averaged burning speed, $S_{T,D}$ , provides insight into how it is temporally modulated by the harmonic disturbances. Values of $S_{T,D}$ are determined from the ensemble-averaged velocity and flame edge data, using (1.4). As discussed above, the ensemble-averaged flame develops small-scale wrinkles which are not directly due to harmonic flame holder motion, and these regions are not included in the flame speed calculations as they add significant noise to the calculation of derivatives. For example, in figure 9(b) the included region corresponds to $s=4{-}30~\text{mm}$ .

Note that $S_{T,D}$ is a function of both time (or, more precisely, the phase) and space, as opposed to the more familiar turbulent displacement speed which is taken as a time average and, consequently, is only a function of space. The average of $S_{T,D}$ over all phases, denoted as $\bar{S}_{T,D}$ , provides a measure of the spatial dependence of $S_{T,D}$ , as shown in figure 11. Note that $\bar{S}_{T,D}$ is a function of both harmonic disturbance amplitude and turbulence intensity, so all results are shown for constant $\unicode[STIX]{x1D700}\approx 0.32~\text{mm}$ (figure 11). The laminar flame speed, $S_{L,0}$ , is calculated as $0.37~\text{m}~\text{s}^{-1}$ for the $5~\text{m}~\text{s}^{-1}$ cases and $0.34~\text{m}~\text{s}^{-1}$ for the $8~\text{m}~\text{s}^{-1}$ cases, based on a Chemkin (Kee et al. Reference Kee2011) PREMIX calculation using the GRI-Mech 3.0 mechanism (Smith et al. Reference Smith0000).

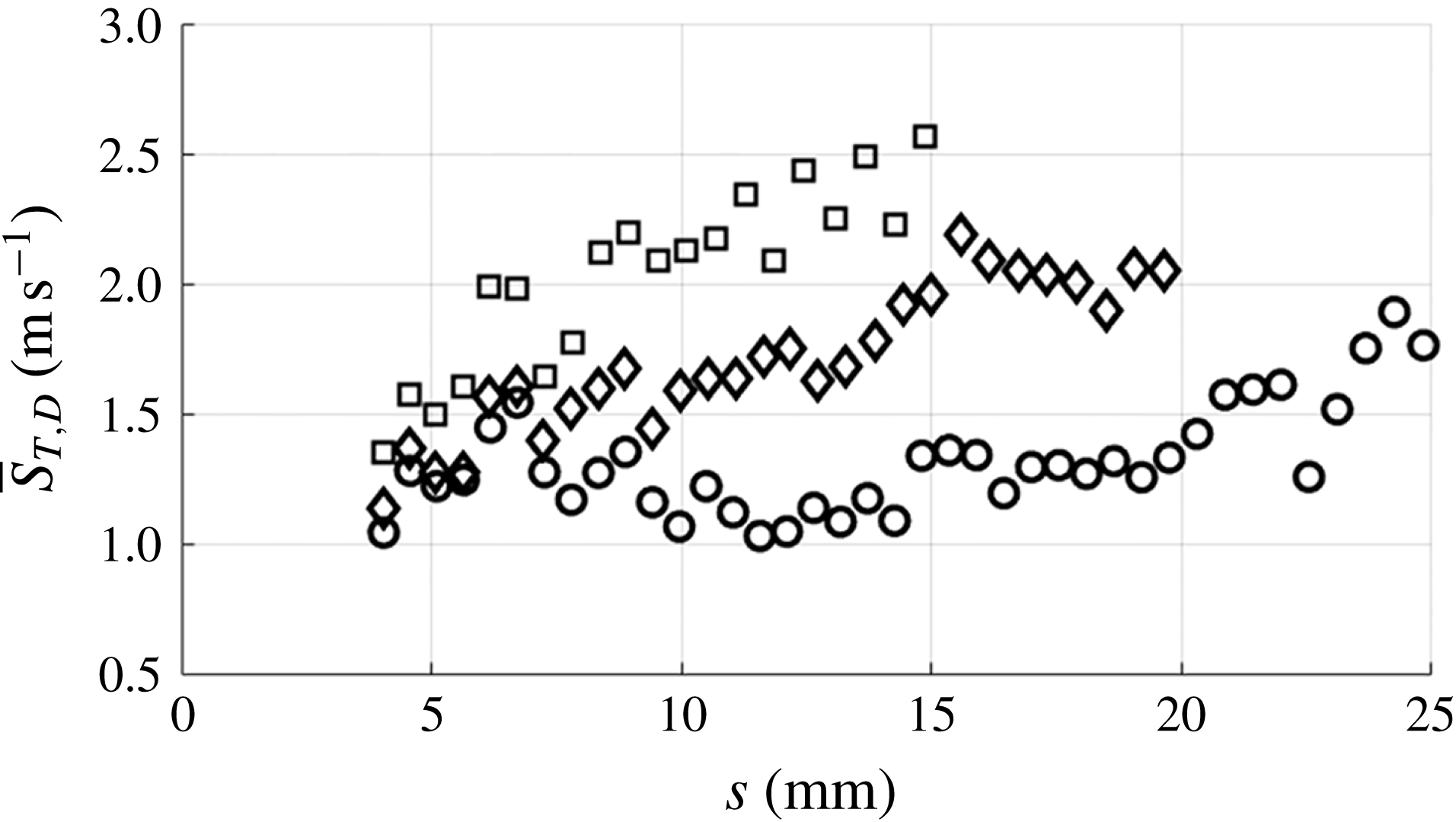
Figure 11. Ensemble-averaged turbulent burning speed, averaged over all phases, $\bar{S}_{T,D}$ , at $f_{0}=750~\text{Hz}$ , $u_{x,0}=4.6$ , 4.3 and $4.4~\text{m}~\text{s}^{-1}$ and $u^{\prime }/u_{x,0}=14.6$ , 24.4 and 26.4 %, for circles, diamonds and squares, respectively.

The mean ensemble-averaged turbulent burning speed increases in an approximately monotonic fashion with increasing downstream distance. This is a familiar result in anchored flames (Lipatnikov Reference Lipatnikov2012). In general, $\bar{S}_{T,D}$ also increases with increasing turbulence intensity. The value of $\bar{S}_{T,D}$ at the higher turbulence intensities is approximately 1.5–2.3 times greater than at the lowest turbulence intensities, for both forcing frequencies.

Figure 12. Ensemble-averaged turbulent displacement speed (a,c) and flame fluctuation (b,d) as a function of the flame coordinate, at $f_{0}=750~\text{Hz}$ , (a,b) $u_{x,0}=4.6~\text{m}~\text{s}^{-1}$ , $u^{\prime }/u_{x,0}=14.6\,\%$ , (c,d), $u_{x,0}=4.4~\text{m}~\text{s}^{-1}$ , $u^{\prime }/u_{x,0}=26.4\,\%$ at two phases, $\unicode[STIX]{x0394}\hat{t}/T=0$ (circles) and $\unicode[STIX]{x0394}\hat{t}/T=0.5$ (triangles).

Consider next the axial dependence of the phase-dependent burning speed, $S_{T,D}$ . Both the 750 Hz (figure 12) and 1250 Hz (figure 13) cases show significant variations in $S_{T,D}$ with the flame coordinate. Several trends are evident – of particular interest are changes in $S_{T,D}$ which correspond with the curvature of the ensemble-averaged flame. For instance, figure 12(a) shows a series of peaks in the flame speed with the magnitude of the peaks diminishing with the $s$ coordinate. In the flame wrinkle plot (figure 12 b), it can be seen that these peaks generally correspond to regions of negative flame curvature. For example, consider figure 12(a) at $s\approx 7$ , 11, 13, 17 and 21 mm. The maxima in flame speed is also noticeable for the higher turbulence intensity figure 12(c). However, the maxima are not as sharp, a reflection of the fact that the ensemble-averaged flame is smoother for the higher turbulence intensity case. In other words, $\langle C\rangle$ varies more smoothly at higher turbulence (at increasing $s$ ) than at the lower turbulence intensity case, where the flame is composed of broad regions of positive curvature, punctuated by relatively narrow regions of strongly negative curvature.

This same modulation of $S_{T,D}$ is also clearly evident in figure 13, which plots the ensemble-averaged turbulent displacement speed for a 1250 Hz case. Again, there is a distinct correspondence between points of negative curvature and local peaks in the ensemble-averaged turbulent flame speed, for both points of phase shown. For the lower turbulence intensity case (figure 13 a,b) the peaks are sharper than for the higher turbulence intensity case (figure 13 c,d). Again, increased turbulence intensity smooths the flame wrinkles, decreasing the magnitude of ensemble-averaged flame curvature. Thus, the areas of increased flame speed are also broadened and of lower magnitude. Like the 750 Hz cases (figure 12) the 1250 Hz cases shown in figure 13 also demonstrate diminishing flame speed modulation with downstream distance. As the flame wrinkles decay, so too do the modulations in ensemble-averaged turbulent flame speed. Additionally, the magnitude of flame speed modulation appears reduced at 1250 Hz as compared to the 750 Hz case, due to the somewhat reduced flame wrinkle size, as seen in figure 9.

Figure 13. Ensemble-averaged turbulent displacement speed (a,c) and flame fluctuation (b,d) as a function of the flame coordinate, at $f_{0}=1250~\text{Hz}$ , (a,b) $u_{x,0}=4.6~\text{m}~\text{s}^{-1}$ , $u^{\prime }/u_{x,0}=13.0\,\%$ , (c,d) $u_{x,0}=4.4~\text{m}~\text{s}^{-1}$ , $u^{\prime }/u_{x,0}=22.0\,\%$ , at two phases, $\unicode[STIX]{x0394}\hat{t}/T=0$ (circles) and $\unicode[STIX]{x0394}\hat{t}/T=0.5$ (triangles).

To further examine the modulation of $S_{T,D}$ , figure 14 shows a probability density function (PDF) plot of the normalized ensemble-averaged displacement speed plotted against the normalized ensemble-averaged curvature. The best fit line in figure 14 and those used in determining the turbulent Markstein lengths shown later are determined by orthogonal linear regression (i.e. a procedure that minimizes the orthogonal distance from the best fit line to the data, rather than minimizing either the $x$ or the $y$ distance). The orthogonal linear regression is the appropriate regression tool when there is uncertainty in both the regression variable and the regressor (Ling et al. Reference Ling, Tianyi, Lawrence and Wei2007)), in this case the experimentally determined ensemble-averaged flame curvature.

Figure 14. PDF plot of the ensemble-averaged turbulent displacement speed versus normalized ensemble-averaged flame curvature at $f_{0}=750~\text{Hz}$ , $u_{x,0}=4.7~\text{m}~\text{s}^{-1}$ , $u^{\prime }/u_{x,0}=15.7\,\%$ . The red line is determined by orthogonal linear regression.

Figure 14 shows that $S_{T,D}$ correlates with $\langle C\rangle$ . Specifically, $S_{T,D}$ increases with negative ensemble-averaged flame curvature. This point was previously inferred from the analysis of figures 12 and 13, but can be seen more directly here.

However, while figure 14 provides evidence for this relationship, the relationship between $S_{T,D}$ and $\langle C\rangle$ cannot be determined using a straightforward regression analysis, as this leads to significant bias errors because the data is not uniformly distributed in curvature space. Figure 14 clearly shows a clustering of data for ensemble-averaged curvatures between zero and unity, which has the effect of biasing any regression between the two variables towards values in a relatively narrow, positive curvature range. This analysis is concerned with the effect of flame curvature not only at these most probable, positive curvature locations but also for relatively improbable events at large negative flame curvature. Therefore, an additional processing step is utilized to minimize bias error effects due to the non-uniform sampling in curvature space. First, the data is divided into bins for sub-ranges of curvature values. Then, a conditional median value for $S_{T,D}$ is determined in each curvature bin where there are at least five data points. The median, rather than a mean, is used so that the value for a given bin is not skewed by outlying data points. Several representative results of this procedure are shown in figures 15 and 17.

Figure 15. (a) Dependence of the ensemble-averaged turbulent displacement speed upon ensemble-averaged curvature at $f_{0}=750~\text{Hz}$ , $U_{x,0}=5.0~\text{m}~\text{s}^{-1}$ , $\bar{C}=0.5$ , for three turbulence intensities, $u_{x,0}=4.7~\text{m}~\text{s}^{-1}$ , $u^{\prime }/u_{x,0}=15.7\,\%$ (solid line, diamonds), $u_{x,0}=4.1~\text{m}~\text{s}^{-1}$ , $u^{\prime }/u_{x,0}=29.5\,\%$ (dashed line, squares) and $u_{x,0}=3.8~\text{m}~\text{s}^{-1}$ , $u^{\prime }/u_{x,0}=33.1\,\%$ (dotted line, triangles). (b) Numerical results reproduced from Shin & Lieuwen (Reference Shin and Lieuwen2013).

These data are the most significant result from this study, and clearly show the relationship between curvature and turbulent displacement speed. In particular, they show the approximately linear rise in $S_{T,D}$ with decreasing ensemble-averaged curvature. Note the use of a slightly different non-dimensionalization for curvature in figure 15(b). $S_{T,D}$ and $S_{T,eff}$ are both defined from (1.4), however, the $S_{T,eff}$ calculation used an ensemble-averaged flame based on the mean, rather than the median, flame location. Figure 15(a) also shows that, for this case, the uncurved ensemble-averaged turbulent displacement speed, $S_{T,0}$ , (i.e. the intercept of the regression line at zero curvature) and the slope of the regression demonstrate similar sensitivities to increasing turbulence. That is, the uncurved turbulent displacement speed increases with increasing turbulence, and the sensitivity of the flame speed to curvature (as characterized by the slope of the regression line) increases. However, in general the dependence of slope and intercept is not a monotonic function of turbulence intensity, as discussed later. For reference, figure 15(b) reproduces a result from Shin & Lieuwen (Reference Shin and Lieuwen2013), which shows a scatterplot of calculated $S_{T,D}$ values (i.e. the data are not averaged in curvature bins as in figure 15 a), also demonstrating an approximately linear relationship between the ensemble-averaged flame curvature and flame speed. Both results are consistent with the closure in (1.5), previously proposed by Shin & Lieuwen (Reference Shin and Lieuwen2013).

The dependence of $S_{T,D}$ on $\langle C\rangle$ shown in figures 15 and 17 results from the interaction between the large-scale, narrowband disturbances due to the harmonic forcing and the small-scale, broadband disturbances due to turbulence. Figure 16 illustrates this effect. For a flame with coherent negative curvature, as shown on the right-hand side of the figure, the distance between opposing flame surfaces will on average be decreased, particularly at the trailing edge of the flame (Shin & Lieuwen Reference Shin and Lieuwen2013). In turn, this increases the rate at which opposing faces will interact and annihilate one another through kinematic restoration (i.e. the propagation of the flame normal to itself). The net result is that the average flame surface propagates further in the negatively curved case than for positive or neutral curvature over a given time increment.

Figure 16. Schematic of the interaction of narrowband flame curvature with broadband turbulent wrinkling, following Shin & Lieuwen (Reference Shin and Lieuwen2013).

Figure 17. Dependence of the ensemble-averaged turbulent displacement speed upon ensemble-averaged curvature at four representative conditions, (a) $f_{0}=750~\text{Hz}$ , $u_{x,0}=4.8~\text{m}~\text{s}^{-1}$ , $u^{\prime }/u_{x,0}=9.3\,\%$ , $\bar{C}=0.5$ , (b) $f_{0}=750~\text{Hz}$ , $u_{x,0}=7.0~\text{m}~\text{s}^{-1}$ , $u^{\prime }/u_{x,0}=27.3\,\%$ , $\bar{C}=0.5$ , (c) $f_{0}=1250~\text{Hz}$ , $u_{x,0}=4.7~\text{m}~\text{s}^{-1}$ , $u^{\prime }/u_{x,0}=14.5\,\%$ , $\bar{C}=0.5$ (d) $f_{0}=1250~\text{Hz}$ , $u_{x,0}=6.2~\text{m}~\text{s}^{-1}$ , $u^{\prime }/u_{x,0}=32.1\,\%$ .

Similar relationships between $S_{T,D}$ and $\langle C\rangle$ were observed for all 750 and 1250 Hz cases, as illustrated in figure 17. In these results, we normalize $S_{T,D}$ by the local average value, $\bar{S}_{T,D}$ , and denote this quantity as $S_{T}$ , which somewhat reduces the sensitivity of the plots to turbulence intensity and helps identify the spatio-temporal modulation of the phase-dependent flame speed. Figure 17(c) illustrates the relationship of the normalized uncurved turbulent flame speed values, $S_{T,0}$ , and the ‘normalized turbulent Markstein length’, ${\mathcal{M}}_{T,D}$ to the intercept and slope of the regression line. Note that while ${\mathcal{M}}_{T,D}$ describes the same fundamental curvature sensitivity as $\unicode[STIX]{x1D70E}_{T,D}$ , because $\unicode[STIX]{x1D70E}_{T,D}$ cannot be recovered from values of ${\mathcal{M}}_{T,D}$ , and vice versa, ${\mathcal{M}}_{T,D}$ is not directly proportional to the definition given in (1.5). These normalized values are also non-dimensional. In order to keep the figure readable, the curvature uncertainties are not shown in the following plots but the uncertainty in normalized curvature is approximately 1.5–2.5 times the magnitude of the indicated $S_{T}$ uncertainty for each data point.

Note the consistent flattening of $S_{T}$ between approximately zero and unity curvature. This behaviour is evident in figure 17(a), but also occurs at other conditions and appears to approximately coincide with the region of higher data realizations (see figure 14). There are two possible explanations: (i) this flattening trend may be a bias error associated with non-uniform sampling of the curvature space. In other words, uncertainty in the curvature causes errors in estimation of the curvature in the high probability data region, (ii) this flattening may reflect a real change in the sensitivity of the flame speed to curvature for positive curvature values.

If the flattening reflects a real change in the flame speed, this indicates that for positive curvatures the relationship between curvature and flame speed changes. There are several features of premixed flames which can impact the flame response, including thermo-diffusive effects and the D–L instability. It is unlikely that the thermo-diffusive effect could account for this flattening. That is, for the thermo-diffusively stable reactant mixture examined in this work, this effect should further decrease the flame speed in the positive curvature regions rather than increase (and therefore flatten) the trend. A second possibility is that this flattening reflects the effect of the D–L instability. This explanation appears more likely as the hydrodynamic instability should cause wrinkle growth and thus would amplify wrinkles with positive curvature. Moreover, the most pronounced flattening at positive curvatures generally occurs for low and moderate turbulence intensity, where the hydrodynamic effect is expected to be most significant. This effect is discussed further below, in regard to figure 21. While this non-monotonic behaviour demonstrates that the flame response is not linear, utilizing a linear regression is, nonetheless, a convenient way to parameterize these results.

An interesting result of negative $S_{T,D}$ values is observed at the lowest turbulence intensities in some cases. Figure 18 shows a PDF illustrating the occurrence of some realizations of negative ensemble-averaged turbulent displacement speeds. In these cases, (particularly the 200 Hz, $U_{x,0}=8~\text{m}~\text{s}^{-1}$ cases) negative $S_{T,D}$ values were observed at points near flame cusps. In most cases the negative flame speeds constitute only a small fraction of the overall realizations (such as shown in figure 14), and these instances fall within the absolute uncertainty of the measurements and calculations. However, the fact that this phenomenon is observed repeatedly (i) at the lowest turbulence intensity, and (ii) at locations of strong cusping suggests it is not simply an error. Moreover, it is well known that laminar and turbulent displacement speeds can become negative. This occurs when the reference isocontour moves in the same direction as the flow; in contrast, consumption-based flame speed definitions are always positive. For example, in locally laminar flames, negative displacement speeds occur for strongly stretched and curved flames (Sohrab, Ye & Law Reference Sohrab, Ye and Law1985; Gran et al. Reference Gran, Echekki and Chen1996; Chen & Im Reference Chen and Im1998; Lieuwen Reference Lieuwen2012; Trunk et al. Reference Trunk, Boxx, Heeger, Meier, Böhm and Dreizler2013). It is important to point out that the displacement speeds measured in these studies of local flamelet dynamics are a fundamentally different quantity than the ensemble-averaged displacement speeds calculated in the current work, where the presence of negative ensemble-averaged turbulent flame speeds is a function of the definition and does not imply that instantaneous flame speeds are negative.

Figure 18. PDF plot of ensemble-averaged displacement speed versus ensemble-averaged curvature for a case showing realizations of negative flame speeds $f_{0}=750~\text{Hz}$ , $u_{x,0}=7.9~\text{m}~\text{s}^{-1}$ , $u^{\prime }/u_{x,0}=9.8\,\%$ .

Furthermore, while there may appear to be analogies between the results presented in this study and the curvature sensitivity of the instantaneous displacement speed discussed in § 1, the underlying physical reasons are completely different. The instantaneous displacement speed exhibits curvature sensitivity because of Lewis number and differential mass diffusion rates. In contrast, the ensemble-averaged turbulent flame speed is fundamentally due to kinematic restoration effects associated with the fine-scale turbulence, as shown in figure 16; note that this effect occurs even if the instantaneous displacement speed exhibited no curvature sensitivity.

Returning to figure 17, these results can also be used to quantify the sensitivity of the flame speed modulation to curvature. Figure 19 shows the results for the 750 Hz case, while figure 21 shows the results for all cases. The value of ${\mathcal{M}}_{T,D}$ is estimated separately from both sides of the flame. Because this estimate of ${\mathcal{M}}_{T,D}$ is highly prone to noise induced from estimation of derivatives, we exclude cases (which differ between the left and right sides of the flame) where there are significant convecting velocity disturbance amplitudes (i.e. see discussion in context of figure 10) – this convecting disturbance introduces short length scale flame wrinkles which significantly amplify noise in estimates of flame position derivatives. This is done by only including cases where the maximum normal velocity perturbation magnitude, averaged over all phases, $\max (\bar{u}_{n,1})<0.55S_{L,0}$ .

Figure 19. Calculated non-dimensional turbulent Markstein lengths at $f_{0}=750~\text{Hz}$ , (a) for a nominal mean flow velocity $U_{x,0}=5~\text{m}~\text{s}^{-1}$ , (b) for a nominal mean flow velocity $U_{x,0}=8~\text{m}~\text{s}^{-1}$ . Circles indicate values determined from left side of the flame while diamonds indicate the right side of the flame.

Figure 19(a) plots results for the 750 Hz, $5~\text{m}~\text{s}^{-1}$ case. It shows that the non-dimensional turbulent Markstein length is largely insensitive to the turbulence intensity. This is somewhat surprising as earlier isothermal work (Shin & Lieuwen Reference Shin and Lieuwen2013) indicated increasing sensitivity of the ensemble-averaged turbulent displacement speed with turbulence intensity; i.e. that ${\mathcal{M}}_{T,D}$ increases with $u^{\prime }$ . Thus, while figure 19(a) and above results confirm the sensitivity of the ensemble-averaged turbulent displacement speed to ensemble-averaged flame curvature, it indicates that this sensitivity does not increase with increasing turbulence. A potential resolution between these results is that the turbulence intensity examined in this work is significantly higher than that examined by (Shin & Lieuwen Reference Shin and Lieuwen2013). In fact, the highest turbulence intensity examined by Shin & Lieuwen (Reference Shin and Lieuwen2013) is approximately equal to the lowest turbulence intensity examined in the current work (e.g. $u^{\prime }/u_{x,0}\approx 0.10,u^{\prime }/S_{L,0}\approx 0.40$ ). Thus, one possibility is that the increase in sensitivity observed previously occurs at relatively low turbulence intensity but saturates at higher turbulence levels. Indeed, there is good physical reason to expect such saturation; i.e. if the sensitivity of the ensemble-averaged flame speed to curvature occurs due to mutual interaction and annihilation of opposing flame faces in negatively curved regions, as proposed by Shin & Lieuwen (Reference Shin and Lieuwen2013) and discussed above in relation to figure 16, it seems likely that this mechanism would saturate at stronger turbulence, because once the flame faces interact, the mechanism of interaction is eliminated. This point is illustrated pictorially in figure 20; at low turbulence intensities where the magnitude of turbulence-induced flame wrinkling is small relative to the coherent flame wrinkle wavelength, these small-scale wrinkles increase the rate of coherent wrinkle destruction. In contrast, once the magnitude of these turbulence-induced wrinkles approaches the coherent wrinkling wavelength, the effect will saturate with increasing turbulent wrinkling amplitude.

Figure 20. Schematic illustration of curvature sensitivity saturation with increasing turbulence intensity. The centre figure illustrates the convective, $\unicode[STIX]{x1D706}_{c}$ and turbulent flame, $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D709},t}$ , length scales.

Figure 21. Normalized turbulent Markstein values for (a) data points with $u^{\prime }/S_{L,0}\leqslant 2.5$ , and (b) $u^{\prime }/S_{L,0}>2.5$ as a function of the ratio of turbulent flame wrinkling length to the coherent wrinkle length.

Some support for this interpretation can be obtained from figure 19(b), obtained at a 60 % higher mean flow velocity, and therefore a longer convective wavelength ( $\unicode[STIX]{x1D706}_{c}=u_{x,0}/f_{0}$ ) than the lower mean flow results. Following the above argument, increasing the convective wavelength would delay saturation to higher turbulence intensities. Indeed, as figure 19(b) shows, ${\mathcal{M}}_{T,D}$ appears more sensitive to turbulence intensity at lower values of $u^{\prime }/S_{L,0}$ . Specifically, ${\mathcal{M}}_{T,D}$ is decreasing with turbulence intensity before reaching a nearly constant value of ${\mathcal{M}}_{T,D}\approx 0.075$ at the higher $u^{\prime }/S_{L,0}$ values.

Figure 21 summarizes results from all cases where accurate ${\mathcal{M}}_{T,D}$ estimates can be obtained. As suggested by the discussion above, ${\mathcal{M}}_{T,D}$ is plotted as a function of the ratio of turbulent flame wrinkling amplitude, $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D709},t}$ , normalized by the coherent flame wrinkle wavelength, $\unicode[STIX]{x1D706}_{c}=u_{x,0}/f_{0}$ . The turbulent flame wrinkling amplitude is scaled as $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D709},t}\propto u^{\prime }\unicode[STIX]{x1D70F}_{int}$ , and $\unicode[STIX]{x1D70F}_{int}$ denotes the integral turbulence time scale, estimated as $R/u_{x,0}$ , where $R$ is the jet radius.

The results in figure 21 suggest that the ${\mathcal{M}}_{T,D}=f(\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D709},t}/\unicode[STIX]{x1D706}_{c})$ scaling captures some, but not all, of the sensitivity to turbulence intensity. Specifically, it suggests that ${\mathcal{M}}_{T,D}$ is independent of turbulence intensity for $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D709},t}/\unicode[STIX]{x1D706}_{c}\sim O(1)$ (specifically $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D709},t}/\unicode[STIX]{x1D706}_{c}>\sim 0.75$ ), with a value around 0.3. As discussed above, this may indicate that the global response saturates at higher $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D709},t}/\unicode[STIX]{x1D706}_{c}$ values. Figure 21(a) shows data with $u^{\prime }/S_{L,0}\leqslant 2.5$ , while figure 21(b) shows data for $u^{\prime }/S_{L,0}>2.5$ . Although the grouping is not completely homogeneous, it is evident that points in the higher $u^{\prime }/S_{L,0}$ regime follow a different trend than for those with the lower $u^{\prime }/S_{L,0}\leqslant 2.5$ values.

For the low $u^{\prime }/S_{L,0}$ cases, figure 21(a), the normalized turbulent Markstein length appears generally insensitive to the ratio of turbulent and coherent length scales. On the other hand, for values of $u^{\prime }/S_{L,0}>2.5$ , as shown in figure 21(b), there is nearly monotonic increase in the value of ${\mathcal{M}}_{T,D}$ with increasing wrinkling length scale ratio (the outlier points are discussed later). The different frequencies and flow velocities are distributed between both groupings; e.g. it is not that the $5~\text{m}~\text{s}^{-1}$ velocity data fall into one set and the $8~\text{m}~\text{s}^{-1}$ fall into the other (although because the grouping is based on $u^{\prime }/S_{L,0}$ , the higher values generally come from the $8~\text{m}~\text{s}^{-1}$ cases).

The presence of the D–L instability may be the reason for these two groupings. We used the value of $u^{\prime }/S_{L,0}=2.5$ as a cutoff between these two regimes, based upon prior studies which suggests that the effect of the D–L instability upon turbulent flame dynamics diminishes as turbulence intensity increase. For example, Creta et al. (Reference Creta, Lamioni, Lapenna and Troiani2016) numerically and experimentally examined the effect of the D–L instability on turbulent flames and found that for $u^{\prime }/S_{L,0}>2.5$ the otherwise abrupt changes associated with the onset of the instability were strongly diminished. In addition to the D–L instability, other factors also likely affect the results in the $u^{\prime }/S_{L,0}\leqslant 2.5$ regime. For example, even after filtering the results to remove cases with unusably large convecting disturbances, the low turbulence cases generally still contained the largest remaining induced velocity disturbances.

There are also several outlying values which occur for lower values of the length scale ratio in the $u^{\prime }/S_{L,0}>2.5$ regime. The two largest values in figure 21(b), at ${\mathcal{M}}_{T,D}\approx 0.65$ and ${\mathcal{M}}_{T,D}\approx 0.75$ , are the result from a specific case ( $f_{0}=1250~\text{Hz}$ , $U_{x,0}=8.0~\text{m}~\text{s}^{-1}$ , $u^{\prime }/u_{x,0}\approx 14.0\,\%$ ), and it is possible that there is an unknown confounding variable in this case. Furthermore, consider that while the grouping used in figure 21 appears to separate the two groups quite well, the exact point of division is not obvious and these values may potentially fall into the other category, due to the various complicating effects discussed above. If these two outlying data points are neglected, the linear increase in ${\mathcal{M}}_{T,D}$ with increasing wrinkling length scale ratio, up to $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D709},t}/\unicode[STIX]{x1D706}_{c}\approx 0.8$ is unmistakable, as shown in shown in figure 21(b).

The preceding discussion shows that in the low turbulence regime (i.e. $u^{\prime }/S_{L,0}<2.5{-}3.0$ ) the ensemble-averaged results are potentially affected by the presence of the D–L instability and a high probability of convecting disturbances. Thus, in the low $u^{\prime }/S_{L,0}$ regime the effect of turbulence on the ensemble-averaged turbulent displacement speed and its dependence on curvature is unclear. On the other hand, for $u^{\prime }/S_{L,0}\,\tilde{{>}}\,2.5$ a distinct linear trend emerges, with the value of ${\mathcal{M}}_{T,D}$ increasing with the ratio of the wrinkling length scales, $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D709},t}/\unicode[STIX]{x1D706}_{c}$ before saturating for values above $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D709},t}/\unicode[STIX]{x1D706}_{c}\approx O(1)$ . This result suggests that this $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D709},t}/\unicode[STIX]{x1D706}_{c}$ parameter captures the sensitivity of ${\mathcal{M}}_{T,D}$ to turbulence intensity at higher $u^{\prime }/S_{L,0}$ values.