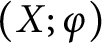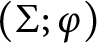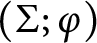1 Introduction
Gay and Kirby [Reference Gay and Kirby3] proved that any smooth, closed, oriented
$4$
-manifold can be trisected into three
$4$
-dimensional handlebodies with
$3$
-dimensional handlebodies as pairwise intersections and a closed surface as a triple intersection. Such a decomposition can be encoded in a trisection diagram given by three families of curves on this surface. This could be thought as a
$4$
-dimensional analogue of Heegaard splittings and diagrams and allows to use classical
$2$
- and
$3$
-dimensional technics to describe invariants of
$4$
-manifolds.
Feller et al. [Reference Feller, Klug, Schirmer and Zemke2] recently expressed the homology and the intersection form of a closed
$4$
-manifold X in terms of a trisection diagram. In this paper, we extend their results to the case of coefficients twisted by a group homomorphism
$\varphi :\pi _1(X) \rightarrow G$
, where G is a finitely generated free abelian group, and we express the Reidemeister torsion of
$(X;\varphi )$
in terms of the diagram. More precisely, we introduce a short finite-dimensional complex, whose spaces are given by the first twisted-homology module of the surface
$\Sigma $
of the diagram and its subspaces generated by the curves of the diagram. We show that the homology of
$(X,\varphi )$
and the related Reidemeister torsion are those of this complex. Using the associated expression of the homology modules of
$(X;\varphi )$
, we express the intersection form of
$(X,\varphi )$
in terms of the intersection form of
$(\Sigma ,\varphi )$
. We also give a method to compute the Alexander polynomial of
$(X;\varphi )$
from a trisection diagram.
Our approach is different from [Reference Feller, Klug, Schirmer and Zemke2]: whereas they use a handle decomposition of the manifold associated with the trisection, we work directly with the trisection itself—a similar method was developed by Ranicki in [Reference Ranicki8] to compute the signature of a
$4$
-manifold given as a triple union. We also review the nontwisted homology and intersection form (corresponding to a trivial morphism
$\varphi $
) from this point of view; this yields especially a simple expression of
$H_1(X;\mathbb {Z})$
and explicit representatives of the homology classes.
1.1 Plan of the paper
In Section 2, we state the main results of the paper. In Section 3, we recall some definitions and facts related to the twisted homology and the process of reconstruction of the 4-manifold X from the trisection diagram; we also fix some notations. In Section 4, we compute the homology of X with coefficients in
$\mathbb {Z}$
. In Section 5, we describe the twisted homology of
$(X;\varphi )$
for a nontrivial
$\varphi $
. The torsion is treated in Sections 6 and 7. Section 8 is devoted to intersection forms. Finally, in Section 9, we illustrate the results with explicit examples.
1.2 Conventions
The boundary of an oriented manifold with boundary is oriented with the “outward normal first” convention. We also use this convention to define the coorientation of an oriented manifold embedded in another oriented manifold.
We use the same notation for a curve
$\nu $
in a manifold, its homotopy class, and its homology class, precising the one we consider if it is not clear from the context. If U and V are transverse integral chains in a manifold M such that
$\dim (U)+\dim (V)=\dim (M)$
, define the sign
$\sigma _x$
of an intersection point
$x\in U\cap V$
in the following way. Construct a basis of the tangent space
$T_xM$
of M at x by taking an oriented basis of the normal space
$N_xU$
followed by an oriented basis of
$N_xV$
. Set
$\sigma _x=1$
if this basis is an oriented basis of
$T_xM$
, and
$\sigma _x=-1$
otherwise. Now, the algebraic intersection number of U and V in M is
$\langle U,V\rangle _M=\sum _{x\in U\cap V}\sigma _x$
.
2 Statement of the results
Let X be a closed, connected, oriented, smooth 4-manifold. A
$(g,k)$
-trisection of X is a decomposition
$X=X_1\cup X_2\cup X_3$
such that
-
•
$X_i\simeq \natural ^k(S^1\times B^3)$
is a
$4$
-dimensional handlebody for each i; -
•
$X_i \cap X_j \simeq \natural ^g(S^1\times D^2)$
is a
$3$
-dimensional handlebody for all
$i\neq j$
; -
•
$\Sigma =X_1 \cap X_2 \cap X_3$
is a closed surface of genus g.
Note that
$\partial X_i \simeq \sharp ^k (S^1 \times S^2)$
and
$(\Sigma ,X_i \cap X_{i-1},X_i \cap X_{i+1})$
is a genus g Heegaard splitting of
$\partial X_i$
, where indices are understood as modulo 3. A trisection diagram consists of three systems
$(\alpha _i)_{1\leq i\leq g}$
,
$(\beta _i)_{1\leq i\leq g}$
, and
$(\gamma _i)_{1\leq i\leq g}$
of disjoint simple closed curves on the standard closed genus g surface
$\Sigma $
such that each one is a complete system of meridians of a handlebody of the trisection, respectively,
$H_{\alpha }:=X_3 \cap X_1$
,
$H_{\beta }:=X_1 \cap X_2$
, and
$H_{\gamma }:=X_2 \cap X_3$
(Figure 1).
Figure 1: A trisection diagram for
$S^2\times S^2$
.
2.1 Homology
We compute the homology of X in terms of the trisection diagram. We separate the case of nontwisted coefficients (corresponding to a trivial
$\varphi $
) and the twisted case.
The first result is close to [Reference Feller, Klug, Schirmer and Zemke2, Theorem 3.1]. For
$\nu \in \{\alpha ,\beta ,\gamma \}$
, let
$L_{\nu }$
be the subgroup of
$H_1(\Sigma ;\mathbb {Z})$
generated by the homology classes of the curves
$\nu _i$
. We introduce the following complex C:
where
$\zeta (x,y,z)=(x-z,y-x,z-y)$
and
$\iota $
is defined by the inclusions
$L_{\nu } \hookrightarrow H_1(\Sigma )$
for
$\nu \in \{\alpha ,\beta ,\gamma \}$
.
Theorem 2.1 The homology of X with coefficient in
$\mathbb {Z}$
canonically identifies with the homology of the complex C. In particular,
$$ \begin{align*} H_1(X) \simeq \frac{H_1(\Sigma)}{L_{\alpha}+L_{\beta}+L_{\gamma}} ; \ H_2(X) \simeq \frac{L_{\alpha}\cap(L_{\beta}+ L_{\gamma})}{(L_{\alpha}\cap L_{\beta})+(L_{\alpha}\cap L_{\gamma})}; \ H_3(X) \simeq L_{\alpha}\cap L_{\beta}\cap L_{\gamma}. \end{align*} $$
The spaces in the complex C can be understood as spaces of chains in X. This will be made explicit in Section 8. Note that C is not the same as the complex considered in [Reference Feller, Klug, Schirmer and Zemke2]: ours is symmetric in the three subspaces
$L_{\alpha },L_{\beta }$
, and
$L_{\gamma }$
. Moreover, the expression of
$H_1(\Sigma ;\mathbb {Z})$
was not provided in [Reference Feller, Klug, Schirmer and Zemke2].
Example 2.2 Consider the trisection diagram of
$S^2 \times S^2$
given in Figure 1, where the curves
$\alpha $
are in red, the curves
$\beta $
in blue, and the curves
$\gamma $
in green. One easily checks that
$L_{\alpha } \cap L_{\beta } \cap L_{\gamma } = \{ 0 \}$
and
$L_{\alpha }+L_{\beta }+L_{\gamma }\simeq H_1(\Sigma ;\mathbb {Z})$
, giving
$H_1(S^2 \times S^2)=0=H_3(S^2 \times S^2)$
. Similarly,
$H_2(S^2 \times S^2)\simeq L_{\gamma } \simeq \mathbb {Z}^2$
.
Now fix a nontrivial morphism
$\varphi : H_1(X;\mathbb {Z}) \rightarrow G$
, where G is a finitely generated free abelian group. Thanks to Theorem 2.1, it induces a morphism
$H_1(\Sigma ;\mathbb {Z}) \rightarrow G$
, still denoted
$\varphi $
. Let
$\mathbb {F}=\mathbb {Q}(G)$
be the quotient field of the group ring
$\Lambda =\mathbb {Z}[G]$
. Let R stand for
$\Lambda $
or
$\mathbb {F}$
. For
$\nu \in \{\alpha ,\beta ,\gamma \}$
, let
$L_{\nu }^{\scriptscriptstyle {R}}$
be the subspace of
$H_1^{\varphi }(\Sigma ;R)$
generated by the R-homology classes of the curves
$\nu _i$
. Let
$C^{\scriptscriptstyle {R}}$
be the following complex:
where
$\zeta (x,y,z)=(x-z,y-x,z-y)$
and
$\iota $
is defined by the inclusions
$L_{\nu }^{\scriptscriptstyle {R}}\hookrightarrow H_1^{\varphi }(\Sigma ;R)$
. Note that, with coefficients in
$\mathbb {F}$
, we have
$H_0^{\varphi }(X;\mathbb {F})=0$
.
Theorem 2.3 The homology of
$(X;\varphi )$
with coefficients in R canonically identifies with the homology of the complex
$C^{\scriptscriptstyle {R}}$
. In particular, with coefficients in R,
$$ \begin{align*}H_1^{\varphi}(X) \simeq \frac{H_1^{\varphi}(\Sigma)}{L_{\alpha}^{\scriptscriptstyle{R}}+L_{\beta}^{\scriptscriptstyle{R}}+L_{\gamma}^{\scriptscriptstyle{R}}}; \ \, H_2^{\varphi}(X) \simeq \frac{L^{\scriptscriptstyle{R}}_{\alpha} \cap(L^{\scriptscriptstyle{R}}_{\beta} + L^{\scriptscriptstyle{R}}_{\gamma})}{(L^{\scriptscriptstyle{R}}_{\alpha} \cap L^{\scriptscriptstyle{R}}_{\beta})+ (L^{\scriptscriptstyle{R}}_{\alpha} \cap L^{\scriptscriptstyle{R}}_{\gamma})}; \ \, H_3^{\varphi}(X) \simeq L_{\alpha}^{\scriptscriptstyle{R}} \cap L_{\beta}^{\scriptscriptstyle{R}} \cap L_{\gamma}^{\scriptscriptstyle{R}}.\end{align*} $$
This result provides, in particular, an expression of the Alexander module
$H_1^{\varphi }(X;\Lambda )$
. However, the
$\Lambda $
-module
$H_1^{\varphi }(\Sigma ;\Lambda )$
and its submodules
$L_{\nu }^{\scriptscriptstyle {\Lambda }}$
are not free modules in general, so that we do not get a free presentation of the Alexander module. However, one can compute the Alexander polynomial of
$(X;\varphi )$
using the following trick. Let B be a 4-ball in X that intersects
$\Sigma $
transversely along a disk D disjoint from the
$3g$
curves of the diagram. Set
$\hat {X}=X\setminus \mathrm {Int}{(B)}$
and
$\hat {\Sigma }=\Sigma \setminus \mathrm {Int}{(D)}$
. Fix a base point
$\star \in \partial D$
. One easily checks that the
$\Lambda $
-modules
$H_1^{\varphi }(X;\Lambda )$
and
$H_1^{\varphi }(\hat {X},\star ;\Lambda )$
have the same
$\Lambda $
-torsion submodule, so that
$(X;\varphi )$
and
$(\hat {X},\star ;\varphi )$
have the same Alexander polynomial.
For
$\nu \in \{\alpha ,\beta ,\gamma \}$
, let
$\hat {L}_{\nu }^{\scriptscriptstyle {\Lambda }}$
be the subspace of
$H_1^{\varphi }(\hat {\Sigma },\star ;\Lambda )$
generated by the homology classes of the curves
$\nu _i$
. We show in Lemma 7.1 that
$H_1^{\varphi }(\hat {\Sigma },\star ;\Lambda )$
,
$\hat {L}^{\scriptscriptstyle {\Lambda }}_{\nu }$
, and
$\hat {L}^{\scriptscriptstyle {\Lambda }}_{\nu }\cap \hat {L}^{\scriptscriptstyle {\Lambda }}_{\nu '}$
are free
$\Lambda $
-modules. As previously, we consider a complex of
$\Lambda $
-modules
$\hat {C}^{\scriptscriptstyle {\Lambda }}$
:
With the very same proof as for Theorem 2.3, one shows the following result.
Theorem 2.4 The
$\Lambda $
-homology of
$(\hat {X},\star ;\varphi )$
canonically identifies with the homology of the complex
$\hat {C}^{\scriptscriptstyle {\Lambda }}$
. In particular, the Alexander
$\Lambda $
-module of
$(\widehat {X},\star ;\varphi )$
admits the finite presentation
$$ \begin{align*}\hat{L}_{\alpha}^{\scriptscriptstyle{\Lambda}}\oplus\hat{L}_{\beta}^{\scriptscriptstyle{\Lambda}}\oplus \hat{L}_{\gamma}^{\scriptscriptstyle{\Lambda}} \to H_1^{\varphi}(\hat{\Sigma},\star;\Lambda) \to H_1^{\varphi}(\hat{X},\star;\Lambda) \to 0.\end{align*} $$
This result provides a presentation matrix of the Alexander
$\Lambda $
-module of
$(\hat {X},\star ;\varphi )$
from which one can compute the Alexander polynomial of
$(\hat {X},\star ;\varphi )$
and
$(X;\varphi )$
.
2.2 Intersection forms
For
$R=\Lambda $
or
$\mathbb {F}$
, we express the intersection form of
$(X;\varphi )$
using the expression of
$H_2^{\varphi }(X;R)$
given by Theorem 2.3 and the intersection form of
$(\Sigma ;\varphi )$
. The spaces
$L_{\nu }^{\scriptscriptstyle {R}}$
coincide with
Define the Hermitian form
$$ \begin{align*} \lambda^{\varphi}: \frac{L^{\scriptscriptstyle{R}}_{\alpha} \cap (L^{\scriptscriptstyle{R}}_{\beta} + L^{\scriptscriptstyle{R}}_{\gamma})}{(L^{\scriptscriptstyle{R}}_{\alpha}\cap L^{\scriptscriptstyle{R}}_{\beta})+ (L^{\scriptscriptstyle{R}}_{\alpha}\cap L^{\scriptscriptstyle{R}}_{\gamma})} \times \frac{L^{\scriptscriptstyle{R}}_{\alpha} \cap (L^{\scriptscriptstyle{R}}_{\beta} + L^{\scriptscriptstyle{R}}_{\gamma})}{ (L^{\scriptscriptstyle{R}}_{\alpha} \cap L^{\scriptscriptstyle{R}}_{\beta})+ (L^{\scriptscriptstyle{R}}_{\alpha} \cap L^{\scriptscriptstyle{R}}_{\gamma})} \longrightarrow R \end{align*} $$
as follows. For
$a,a' \in L_{\alpha }^{\scriptscriptstyle {R}} \cap (L_{\beta }^{\scriptscriptstyle {R}} + L_{\gamma }^{\scriptscriptstyle {R}})$
and
$b\in L_{\beta }^{\scriptscriptstyle {R}}$
,
$c\in L_{\gamma }^{\scriptscriptstyle {R}}$
such that
$a+b+c=0$
, set
$$ \begin{align*} \lambda^{\varphi}(a,a'):= \langle c, a' \rangle^{\varphi}_{\Sigma}. \end{align*} $$
Note that permuting the roles of
$\alpha $
,
$\beta $
, and
$\gamma $
in this construction gives the same form, up to the sign of the permutation. This is related to the fact that the coorientation of
$\Sigma $
—defined by the orientations of
$\Sigma $
and X—induces a cyclic order on the
$X_i$
and the
$H_{\nu }$
.
Theorem 2.5 Let
$\langle \cdot ,\cdot \rangle _{X}^{\varphi }$
be the intersection form of
$(X;\varphi )$
. There is an isomorphism
$$ \begin{align*} \big(H_2^{\varphi}(X;R), \langle \cdot,\cdot \rangle_{X}^{\varphi} \big) \simeq \bigg(\frac{L^{\scriptscriptstyle{R}}_{\alpha} \cap (L^{\scriptscriptstyle{R}}_{\beta} + L^{\scriptscriptstyle{R}}_{\gamma})}{ (L^{\scriptscriptstyle{R}}_{\alpha} \cap L^{\scriptscriptstyle{R}}_{\beta})+ (L^{\scriptscriptstyle{R}}_{\alpha} \cap L^{\scriptscriptstyle{R}}_{\gamma})} , \lambda^{\varphi} \bigg). \end{align*} $$
The form
$\lambda ^{\varphi }$
is a Hermitian version of a symmetric form introduced by Wall in [Reference Wall11], which is involved in the similar result in the nontwisted setting [Reference Feller, Klug, Schirmer and Zemke2, Theorem 3.6], corresponding to a trivial morphism
$\varphi $
. As noted in [Reference Feller, Klug, Schirmer and Zemke2, Remark 3.7], the main theorem of [Reference Wall11] implies that the signature of the intersection form of
$(X;\varphi )$
equals the signature of the form
$\lambda ^{\varphi }$
. In the case of trisections, the above theorem says that not only the signatures coincide but also the forms themselves.
Proposition 2.6 There is an isomosrphism
$$ \begin{align*} \big(H_1^{\varphi}(X;R)\times H_3^{\varphi}(X;R); \langle \cdot,\cdot \rangle_{X}^{\varphi} \big) \simeq \bigg(\frac{H_1^{\varphi}(\Sigma)}{L^{\scriptscriptstyle{R}}_{\alpha} + L^{\scriptscriptstyle{R}}_{\beta} + L^{\scriptscriptstyle{R}}_{\gamma}}\times(L^{\scriptscriptstyle{R}}_{\alpha}\cap L^{\scriptscriptstyle{R}}_{\beta}\cap L^{\scriptscriptstyle{R}}_{\gamma}); \langle\cdot,\cdot\rangle^{\varphi}_{\Sigma} \bigg). \end{align*} $$
2.3 Abelian torsions
We now state the result for the torsion. Consider the complex
$C^{\scriptscriptstyle {\mathbb {F}}}$
defined before Theorem 2.3.
Theorem 2.7 There exists an
$\mathbb {F}$
-basis c for
$C^{\scriptscriptstyle {\mathbb {F}}}$
such that for any homology
$\mathbb {F}$
-basis h of X and
$C^{\scriptscriptstyle {\mathbb {F}}}$
, the following holds:
$$ \begin{align*}\tau^{\varphi}(X;h)=\tau(C^{\scriptscriptstyle{\mathbb{F}}};c,h) \quad\text{in }\mathbb{F}/\pm\varphi(H_1(X)).\end{align*} $$
The complex basis c is explicated in Section 6.1. Although the bases for
$H_1^{\varphi }(\Sigma ;\mathbb {F})$
and the
$L^{\scriptscriptstyle {\mathbb {F}}}_{\nu }$
are straightforwardly obtained from the trisection diagram, the computation of the bases for the intersections
$L^{\scriptscriptstyle {\mathbb {F}}}_{\nu }\cap L^{\scriptscriptstyle {\mathbb {F}}}_{\nu '}$
involves handleslides on the surface. From an algorithmic point of view, this might not be efficient. As an alternative way, one may use the same trick as in Section 2.1 and compute the torsion of
$(\hat {X}, \star )$
instead, where
$\widehat {X}$
is the complement of
$4$
-ball and
$\star $
is a base point in the boundary. The two torsions
$\tau ^{\varphi }(X)$
and
$\tau ^{\varphi }(\widehat {X}, \star )$
coincide up to a factor, see Proposition 7.4. This allows to use much more general complex bases, avoiding the handleslides, see Theorem 7.2. The (light) price to pay is that
$\tau ^{\varphi }(\hat {X}, \star )$
is computed only up to a unit in
$\Lambda $
.
3 Preliminaries
3.1 Algebraic torsion
We recall the algebraic setup, see [Reference Milnor7] and [Reference Turaev10] for further details and references. Let
$\mathbb {K}$
be a field. If V is a finite-dimensional
$\mathbb {K}$
-vector space and b and c are two bases of V, we denote by
$[b/c]$
the determinant of the matrix expressing the basis change from b to c. The bases b and c are equivalent if
$[b/c]=1$
. Let C be a finite complex of finite-dimensional
$\mathbb {K}$
-vector spaces
A complex basis of C is a family
$c=(c_m,\dots ,c_0),$
where
$c_i$
is a basis of
$C_i$
for all
$i\in \{0,\dots ,m\}$
. A homology basis of C is a family
$h=(h_m,\dots ,h_0),$
where
$h_i$
is a basis of the homology group
$H_i(C)$
for all
$i\in \{0,\dots ,m\}$
. If we have chosen a basis
$b_j$
of the space of j-dimensional boundaries
$B_j(C):= \operatorname {Im} \partial _{j+1}$
for all
$j\in \{0,\dots ,m-1\}$
, then a homology basis h of C induces an equivalence class of bases
$(b_ih_i)b_{i-1}$
of
$C_i$
for all i.
The torsion of the
$\mathbb {K}$
-complex C, equipped with a complex basis c and a homology basis h, is the scalar
$$ \begin{align*} \tau(C;c,h):= \prod_{i=0}^m \big[(b_ih_i)b_{i-1}/c_i\big]^{(-1)^{i+1}} \in \mathbb{K}^*. \end{align*} $$
It is easily checked that this definition does not depend on the choice of
$b_0,\dots ,b_m$
. When C is acyclic, we set
$\tau (C;c):= \tau (C;c,\varnothing )$
.
Lemma 3.1 Consider a short exact sequence
$0 \rightarrow C' \rightarrow C \rightarrow C'' \rightarrow 0$
of
$\mathbb {K}$
-complexes with compatible complex bases
$c',c,c''$
in the sense that
$c_i$
is equivalent to
$c^{\prime }_ic^{\prime \prime }_i$
for every
$i\in \{0,\dots ,m\}$
and homology bases
$h',h,h''$
. The associated long exact sequence in homology
$\mathcal {H}$
is an acyclic finite
$\mathbb {K}$
-complex with base
$(h',h,h''):= (h^{\prime }_m,h_m,h^{\prime \prime }_m,\dots ,h^{\prime }_0,h_0,h^{\prime \prime }_0)$
and we have
$$ \begin{align*} \tau(C;c,h)= \varepsilon \cdot \tau(C';c',h') \cdot \tau(C'';c'',h'') \cdot \tau\big(\mathcal{H}; (h',h,h'')\big), \end{align*} $$
where
$\varepsilon $
is a sign depending on the dimensions of
$C^{\prime }_i$
,
$C_i$
,
$C^{\prime \prime }_i$
and
$H_i(C')$
,
$H_i(C)$
,
$H_i(C'')$
for
$i\in \{0,\dots ,m\}$
.
3.2 Twisted homology and Reidemeister torsion
Let
$(X,Y)$
be a finite CW-pair with maximal abelian cover
$p: \overline {X} \rightarrow X$
. Let G be a finitely generated free abelian group. Fix a group homomorphism
$\varphi : \pi _1(X) \rightarrow G$
and denote R the group ring
$\Lambda =\mathbb {Z}[G]$
or its quotient field
$\mathbb {F}=\mathbb {Q}(G)$
. The extension of
$\varphi $
to a ring morphism
$\mathbb {Z}[H_1(X)] \rightarrow R$
is still denoted
$\varphi $
. The chain complex of
$(X,Y;\varphi )$
with coefficient in R is defined as
$$ \begin{align*} C^{\varphi}(X,Y; R)= C(\overline{X},p^{-1}(Y))\otimes_{\mathbb{Z}[H_1(X)] } R. \end{align*} $$
We denote
$H^{\varphi }(X,Y; R)$
its homology. It is easy to check that
$$ \begin{align*} H^{\varphi}(X,Y; \mathbb{F}) = H^{\varphi}(X,Y; \Lambda) \otimes_{\Lambda} \mathbb{F}. \end{align*} $$
Let
$\overline {c}$
be a complex basis of the complex of free
$\mathbb {Z}[H_1(X)]$
-module
$C(\overline {X},p^{-1}(Y))$
obtained by lifting each relative cell of
$(X,Y)$
to
$\overline {X}$
. Then,
$c=\overline {c}\otimes 1$
is a complex basis of
$C^{\varphi }(X,Y;\mathbb {F})$
.
Definition 3.1 Given a homology basis h of
$H^{\varphi }(X,Y; \mathbb {F})$
, the torsion of
$(X,Y;\varphi )$
is
$$ \begin{align*}\tau^{\varphi}(X,Y;h) := \tau(C^{\varphi}(X,Y; \mathbb{F});c,h) \in \mathbb{F} /\pm \varphi(H_1(X)).\end{align*} $$
The ambiguity in
$\pm \varphi (H_1(X))$
is due to the different choices of lift and orientation of the cells. Note that the torsion of
$(X,Y;\varphi )$
is closely related to the orders of the
$\Lambda $
-modules
$H^{\varphi }(X,Y;\Lambda )$
, see [Reference Kirk and Livingston4].
We end the subsection with two useful results.
Lemma 3.2 If X is connected and
$\varphi $
is nontrivial, then
$H_0^{\varphi }(X;\mathbb {F})=0$
.
By Blanchfield duality (see Section 3.3), Lemma 3.2 implies the following corollary.
Corollary 3.3 Assume X is a compact, connected, oriented n-manifold. If
$\varphi $
is nontrivial, then
$H_n^{\varphi }(X,\partial X;\mathbb {F})=0$
.
3.3 Twisted intersection form and Blanchfield duality
Let W be a compact oriented n-manifold and
$\varphi :\pi _1(W) \rightarrow G$
be a group homomorphism. For
$q \in \{0,\dots ,n \}$
, the twisted intersection form of W with coefficient in R, introduced by Reidemeister in [Reference Reidemeister9], is the sesquilinear map
$$ \begin{align*} \langle\cdot,\cdot\rangle_W^{\varphi}: H_q^{\varphi}(W;R) \times H_{n-q}^{\varphi}(W,\partial W;R) \longrightarrow R \end{align*} $$
defined by
$$ \begin{align*} \langle x \otimes z , x' \otimes z' \rangle_W^{\varphi}= \sum_{h \in \frac{H_1(W)}{\ker(\varphi)}} \langle x, h.x'\rangle_{\overline W} \, \varphi(h)\otimes zz', \end{align*} $$
where
$R=\Lambda $
or
$\mathbb {F}$
,
$\overline {W}\twoheadrightarrow W$
is the covering associated with
$\ker (\varphi )$
and
$\langle \cdot ,\cdot \rangle _{\overline W}$
stands for the algebraic intersection in
$\overline {W}$
. By Blanchfield’s duality theorem [Reference Blanchfield1, Theorem 2.6], for
$R=\mathbb {F}$
, this form is nondegenerate.
3.4 Reconstruction of X from the trisection diagram
A trisection diagram determines the associated 4-manifold. We recall here how to reconstruct the manifold from the diagram, and we introduce some notations that we will use in the next sections.
We are given a trisection diagram, i.e., a closed genus g surface
$\Sigma $
and three systems of meridians
$(\alpha _i)_{1\leq i\leq g}$
,
$(\beta _i)_{1\leq i\leq g}$
, and
$(\gamma _i)_{1\leq i\leq g}$
. Consider a disk
$D^2$
with center
$p_0$
and three distinct points
$p_{\alpha }$
,
$p_{\beta }$
, and
$p_{\gamma }$
on the boundary, see Figure 2. Take the product
$D^2\times \Sigma $
and add a 2-cell along
$p_{\nu }\times \nu _i$
for all
$\nu =\alpha ,\beta ,\gamma $
and all
$1\leq i\leq g$
. It remains to add 3-cells and 4-cells; the way this is performed as no incidence, see Laudenbach and Poénaru [Reference Laudenbach and Poénaru6]. In this decomposition of X,
$H_{\nu }$
is recovered as
$[p_0,p_{\nu }]\times \Sigma $
union the corresponding 2-cells and 3-cells. The union
$Y=H_{\alpha }\cup H_{\beta }\cup H_{\gamma }$
is the spine of the trisection. In the computations of homology and torsion, we will make a great use of the exact sequences in homology associated with the pairs
$(Y,\Sigma )$
and
$(X,Y)$
.
Figure 2: Decomposition of X.
4 Homology of X
Throughout this section,
$H_{\ell }(.)$
stands for the homology with coefficients in
$\mathbb {Z}$
. We fix a trisection
$X=X_1 \cup X_2 \cup X_3$
given by a diagram
$(\Sigma ;\alpha ,\beta ,\gamma )$
, with spine
$Y=H_{\alpha } \cup H_{\beta } \cup H_{\gamma }$
(see Section 3.4). We prove Theorem 2.1 using the pairs
$(Y,\Sigma )$
and
$(X,Y)$
.
$$ \begin{align*} H_{\ell}(Y,\Sigma)\simeq\begin{cases} L_{\alpha}\oplus L_{\beta}\oplus L_{\gamma} & \text{if}\ \ell=2 \\ \mathbb{Z}^3 & \text{if}\ \ell=3 \\ 0 & \text{otherwise} \end{cases}\end{align*} $$
Proof Note that
$H_{\ell }(Y,\Sigma )\simeq H_{\ell }(H_{\alpha },\Sigma )\oplus H_{\ell }(H_{\beta },\Sigma )\oplus H_{\ell }(H_{\gamma },\Sigma )$
and
$$ \begin{align*} H_{\ell}(H_{\nu},\Sigma)\simeq\begin{cases} L_{\nu} & \text{if}\ \ell=2 \\ \mathbb{Z} & \text{if}\ \ell=3 \\ 0 & \text{otherwise} \end{cases},\end{align*} $$
thanks to the exact sequence associated with
$(H_{\nu },\Sigma )$
. ▪
Lemma 4.2 The homology of Y with coefficients in
$\mathbb {Z}$
is given by
$$ \begin{align*} H_1(Y) \simeq \frac{H_1(\Sigma)}{L_{\alpha}+L_{\beta}+L_{\gamma}}; \ H_2(Y) \simeq \ker\big(L_{\alpha}\oplus L_{\beta}\oplus L_{\gamma}\to H_1(\Sigma)\big); \ H_3(Y) \simeq \mathbb{Z}^2. \end{align*} $$
Proof We use the exact sequence associated with the pair
$(Y,\Sigma )$
. Since the surface
$\Sigma $
bounds any of the
$H_{\nu }$
in Y, the map
$H_2(\Sigma )\to H_2(Y)$
is trivial and we get
$$ \begin{align*} 0 \to H_3(Y) \to H_3(Y,\Sigma) \to H_2(\Sigma) \to 0, \end{align*} $$
from which we easily see that
$H_3(Y)\simeq \mathbb {Z}^2$
, generated by two of the boundaries
$\partial X_i$
, and
$$ \begin{align*} 0 \to H_2(Y) \to H_2(Y,\Sigma) \to H_1(\Sigma) \to H_1(Y) \to 0, \end{align*} $$
which provides the expressions of
$H_1(Y)$
and
$H_2(Y)$
, using Lemma 4.1. ▪
$$ \begin{align*} H_{\ell}(X,Y)\simeq\begin{cases} (L_{\alpha}\cap L_{\beta})\oplus(L_{\beta}\cap L_{\gamma})\oplus(L_{\gamma}\cap L_{\alpha}) & \text{if }\ell=3 \\ \mathbb{Z}^3 & \text{if }\ell=4 \\ 0 & \text{otherwise} \end{cases} \end{align*} $$
Proof Note that
$H_{\ell }(X,Y)\simeq \oplus _{j=1}^3 H_{\ell }(X_j,\partial X_j)$
. One easily checks that
$H_4(X_j,\partial X_j)\simeq \mathbb {Z}$
and
$H_{\ell }(X_j,\partial X_j)=0$
if
$\ell \neq 3,4$
. For
$\ell =3$
, the exact sequence associated with
$(X_j,\partial X_j)$
gives
$H_3(X_j,\partial X_j)\simeq H_2(\partial X_j)$
. Now, for
$\nu ,\nu ' \in \{\alpha ,\beta ,\gamma \}$
such that
$\partial X_j=H_{\nu } \cup _{\Sigma } H_{\nu '}$
, the Mayer–Vietoris sequence gives
$$ \begin{align*}0\to H_2(\partial X_j)\to H_1(\Sigma)\to H_1(H_{\nu})\oplus H_1(H_{\nu'}).\end{align*} $$
Hence,
$H_2(\partial X_j)\simeq L_{\nu }\cap L_{\nu '}$
. ▪
Proof of Theorem 2.1
We use the exact sequence associated with the pair
$(X,Y)$
. The map
$H_3(Y)\to H_3(X)$
is trivial, since
$H_3(Y)$
is generated by the classes of the
$\partial X_j$
for
$j \in \{1,2,3\}$
, which bound the
$X_j$
in X. Thus,
and
$H_1(Y)\simeq H_1(X)$
, thanks to Lemma 4.3. The expression of the map
$\zeta $
follows the descriptions of
$H_2(Y)$
in Lemma 4.2 and of
$H_3(X,Y)$
in Lemma 4.3. ▪
We end this section with a lemma, which will be useful in the next sections.
Lemma 4.4 If G is a finitely generated abelian group and
$\varphi : H_1(X) \rightarrow G$
a nontrivial morphism, then
$\varphi $
induces nontrivial morphisms on the first homology groups of the spaces
$\Sigma $
,
$H_{\nu }$
for
$\nu \in \{ \alpha ,\beta ,\gamma \}$
, Y,
$X_i$
, and
$\partial X_i$
for
$i=1,2,3$
.
Proof For Y, it is obvious, since
$H_1(Y)\simeq H_1(X)$
. Thanks to the expression of
$H_1(X)$
given in Theorem 2.1, the homology groups
$H_1(\Sigma )$
,
$H_1(H_{\nu })\simeq H_1(\Sigma )/L_{\nu }$
, and
$H_1(X_1)\simeq H_1(\partial X_1)\simeq H_1(\Sigma )/(L_{\alpha }\cap L_{\beta })$
naturally surject on
$H_1(X)$
. Compose
$\varphi $
by these surjections. ▪
For simplicity, all these morphisms induced by
$\varphi $
are still denoted
$\varphi $
.
5 Homology of
$(X;\varphi )$
In this section, we compute the homology of
$(X;\varphi )$
for a nontrivial
$\varphi $
. As in Section 4, we use the pairs
$(Y,\Sigma )$
and
$(X,Y)$
. The notation R is used for either
$\Lambda $
or
$\mathbb {F}$
, and
$H^{\varphi }(\cdot )$
stands for the homology with coefficients in R.
Lemma 5.1 For any
$\nu \in \{\alpha ,\beta ,\gamma \}$
,
.
Proof Let
$\nu \in \{\alpha ,\beta ,\gamma \}$
. Since
$H_{\nu }$
retracts on a wedge of circles, we have
$H_2^{\varphi }(H_{\nu })=0$
, and the exact sequence in homology of the pair
$(H_{\nu },\Sigma )$
provides the short exact sequence
$$ \begin{align*}0\to H_2^{\varphi}(H_{\nu},\Sigma)\to H_1^{\varphi}(\Sigma)\to H_1^{\varphi}(H_{\nu}).\end{align*} $$
Now,
$H_{\nu }$
is obtained from
$\Sigma $
by adding meridian disks
$D_i^{\nu }$
such that
$\partial D_i^{\nu }=\nu _i$
and one 3-cell. Hence,
$H_2^{\varphi }(H_{\nu },\Sigma )$
is generated by the
$D_i^{\nu }$
for
$i=1,\dots ,g$
, and its image in
$H_1^{\varphi }(\Sigma )$
is exactly the submodule
$L_{\nu }^{\scriptscriptstyle {R}}$
generated by the
$\nu _i$
. ▪
Lemma 5.2 We have
$H^{\varphi }_{\ell }(Y,\Sigma )=0$
for
$\ell \neq 2$
. Moreover, there is a natural identification
$$ \begin{align*}H^{\varphi}_2(Y,\Sigma)\simeq L_{\alpha}^{\scriptscriptstyle{R}}\oplus L_{\beta}^{\scriptscriptstyle{R}}\oplus L_{\gamma}^{\scriptscriptstyle{R}}.\end{align*} $$
Proof Use
$H^{\varphi }_{\ell }(Y,\Sigma )\simeq H^{\varphi }_{\ell }(H_{\alpha },\Sigma )\oplus H^{\varphi }_{\ell }(H_{\beta },\Sigma )\oplus H^{\varphi }_{\ell }(H_{\gamma },\Sigma )$
and the exact sequence associated with
$(H_{\nu },\Sigma )$
. ▪
Lemma 5.3 There are natural identifications:
$$ \begin{align*} & H_1^{\varphi}(Y) \simeq \frac{H_1^{\varphi}(\Sigma)}{L_{\alpha}^{\scriptscriptstyle{R}}+L_{\beta}^{\scriptscriptstyle{R}}+L_{\gamma}^{\scriptscriptstyle{R}}}, \\ & H_2^{\varphi}(Y) \simeq \ker\, \big( L_{\alpha}^{\scriptscriptstyle{R}}\oplus L_{\beta}^{\scriptscriptstyle{R}}\oplus L_{\gamma}^{\scriptscriptstyle{R}}\to H_1^{\varphi}(\Sigma) \big). \end{align*} $$
Proof Thanks to Lemma 5.2, the exact sequence in homology of the pair
$(Y,\Sigma )$
reduces to
$$ \begin{align*} 0\to H_2^{\varphi}({Y})\longrightarrow L_{\alpha}^{\scriptscriptstyle{R}}\oplus L_{\beta}^{\scriptscriptstyle{R}}\oplus L_{\gamma}^{\scriptscriptstyle{R}} \to H_1^{\varphi}(\Sigma)\longrightarrow H_1^{\varphi}({Y}) \longrightarrow 0. \end{align*} $$
This provides the given expressions for the homology of Y. ▪
Lemma 5.4 We have
$H^{\varphi }_{\ell }(X,Y)=0$
for
$\ell \neq 3$
. Moreover, there is a natural identification
$$ \begin{align*} H^{\varphi}_3(Y,\Sigma)\simeq(L_{\alpha}^{\scriptscriptstyle{R}}\cap L_{\beta}^{\scriptscriptstyle{R}})\oplus(L_{\beta}^{\scriptscriptstyle{R}}\cap L_{\gamma}^{\scriptscriptstyle{R}})\oplus(L_{\gamma}^{\scriptscriptstyle{R}}\cap L_{\alpha}^{\scriptscriptstyle{R}}). \end{align*} $$
Proof Note that
$H^{\varphi }_{\ell }(X,Y)\simeq \oplus _{j=1}^3 H^{\varphi }_{\ell }(X_j,\partial X_j)$
. Let us focus on
$(X_1,\partial X_1)$
. For
$\ell =3$
, the exact sequence associated with
$(X_1,\partial X_1)$
gives
$H_3(X_1,\partial X_1)\simeq H_2(\partial X_1)$
. Now, the Mayer–Vietoris sequence associated with the Heegaard splitting
${\partial {X}}_1=H_{\alpha }\cup _{\Sigma } H_{\beta }$
gives
We get
$H_2^{\varphi }({\partial {X}}_1)\simeq \ker (f)=L_{\alpha }^{\scriptscriptstyle {R}}\cap L_{\beta }^{\scriptscriptstyle {R}}$
. ▪
6 Torsion of
$(X;\varphi )$
In this section,
$H^{\varphi }(\cdot )$
stands for the twisted homology with coefficients in
$\mathbb {F}$
, and we assume that
$\varphi $
is nontrivial. The aim of the section is to prove Theorem 2.7. We fix a lift of a given
$0$
-cell
$\star $
of X and require that the lift of any
$1$
-cell starts at the chosen lift of
$\star $
.
6.1 Bases in homology and first computations
In this subsection, we define bases for the complex
$C^{\scriptscriptstyle {\mathbb {F}}}$
of Theorem 2.7, and we compute some related torsions that we need to prove the theorem.
Definition 6.1 A (geometric) symplectic basis of
$\Sigma $
is a family
$(x_i,y_i)_{1\leq i\leq g}$
of simple closed curves in
$\Sigma $
, based at
$\star $
, such that
-
• any two curves meet only at
$\star $
; -
• the classes of
$x_i$
and
$y_i$
form a basis of
$H_1(\Sigma ;\mathbb {Z})$
, symplectic with respect to the intersection form
$\langle .,. \rangle _{\Sigma }$
; -
• there exists a CW-complex decomposition of
$\Sigma $
with a single 2-cell glued along
$$ \begin{align*}\partial\Sigma=\prod_{i=1}^g[x_i,y_i].\end{align*} $$
Lemma 6.1 Let
$(x_i,y_i)_{1\leq i\leq g}$
be a symplectic basis of
$\Sigma $
such that
$x_i\in \ker (\varphi )$
for all i. Up to reordering, assume that
$y_1\notin \ker (\varphi )$
. For
$i=2,\dots ,g$
, set
$$ \begin{align*}\ y^{\prime}_i= y_i-\frac{\varphi(y_i)-1}{\varphi(y_1)-1}\, y_1 \in C_1^{\varphi}(\Sigma).\end{align*} $$
Then, the family
$h_{\scriptscriptstyle {\Sigma }}=(x_i,y^{\prime }_i)_{i>1}$
is a basis of
$H_1^{\varphi }(\Sigma )$
and
$\tau ^{\varphi }(\Sigma ;h_{\scriptscriptstyle {\Sigma }})= 1$
.
For instance, in Lemma 6.1, one can choose the family
$(x_i)_i$
to coincide with the family
$\alpha $
,
$\beta $
, or
$\gamma $
, and
$(y_i)_i=(x_i^*)_i$
to be a dual family. Note that
$H_1^{\varphi }(\Sigma )=0$
if
$g=1$
.
Proof There is a CW decomposition of
$\Sigma $
given by
$\star $
as 0-cell, the
$x_i$
and
$y_i$
as 1-cell, and
$\Sigma $
as 2-cell. The associated
$\mathbb {F}$
-complex is
$C^{\varphi }(\Sigma ): \ 0\to C_2^{\varphi }(\Sigma )\to C_1^{\varphi }(\Sigma )\to C_0^{\varphi }(\Sigma )\to 0$
with basis
$\Sigma $
,
$(x_i,y_i)_i$
and
$\star $
. We choose the lift of
$\Sigma $
so that
$$ \begin{align*}\partial \Sigma=\sum_{1\leq i \leq g}(\varphi(y_i)-1)\, x_i\ \in C_1^{\varphi}(\Sigma).\end{align*} $$
For all i,
$\partial x_i=0$
and
$\partial y_i=(\varphi (y_i)-1)\,\star $
. Hence,
$h_{\scriptscriptstyle {\Sigma }}$
is a basis of
$H_1^{\varphi }(\Sigma )$
. We get
$$ \begin{align*}\tau^{\varphi}(\Sigma;h_{\scriptscriptstyle{\Sigma}})=\bigg[\frac{\partial \Sigma\cdot h_{\scriptscriptstyle{\Sigma}}\cdot (\varphi(y_1)-1)^{-1} y_1}{(x_i,y_i)_{1\leq i\leq g}}\bigg] =1.\\[-45pt] \end{align*} $$
▪
Lemma 6.2 Let
$\nu \in \{\alpha ,\beta ,\gamma \}$
and
$(\nu _i^*)_{1\leq i\leq g}$
be simple closed curves in
$\Sigma $
such that
$(\nu _i,\nu _i^*)_{1\leq i\leq g}$
is a symplectic basis for
$\Sigma $
. Permuting the indices if necessary, assume that
$\varphi (\nu _1^*)\neq 1$
. Then, the family
$h_{\nu }=(\frac {1}{\varphi (\nu _1^*)-1}\, \nu _2, \nu _3,\dots ,\nu _g)$
is a basis of
$L_{\nu }^{\scriptscriptstyle {\mathbb {F}}}$
.
Proof By definition,
$L_{\nu }^{\scriptscriptstyle {\mathbb {F}}}$
is generated by the
$\nu _i$
. Consider the same complex as in the proof of Lemma 6.1, with
$x_i=\nu _i$
and
$y_i=\nu _i^*$
. The only relation is
$\sum _{1\leq i \leq g}(\varphi (\nu _i^*)\,{-}\,1)\, \nu _i=0$
. ▪
Lemma 6.3 Via the identification
$H_2^{\varphi }(Y,\Sigma )\simeq L_{\alpha }^{\scriptscriptstyle {\mathbb {F}}}\oplus L_{\beta }^{\scriptscriptstyle {\mathbb {F}}}\oplus L_{\gamma }^{\scriptscriptstyle {\mathbb {F}}}$
, the family
$h_{\scriptscriptstyle {Y,\Sigma }}=h_{\alpha }.h_{\beta }.h_{\gamma }$
is a homology basis of
$(Y,\Sigma ;\varphi )$
, and we have
$\tau ^{\varphi }(Y,\Sigma ;h_{\scriptscriptstyle {Y,\Sigma }})=1$
.
Proof By Lemma 5.2,
$H_2^{\varphi }(Y,\Sigma )\simeq L_{\alpha }^{\scriptscriptstyle {\mathbb {F}}}\oplus L_{\beta }^{\scriptscriptstyle {\mathbb {F}}}\oplus L_{\gamma }^{\scriptscriptstyle {\mathbb {F}}}$
is the only nontrivial space in
$H^{\varphi }(Y,\Sigma )$
. Moreover, the isomorphism of chain complexes
$C^{\varphi }(Y,\Sigma ) \simeq C^{\varphi }(H_{\alpha },\Sigma ) \oplus C^{\varphi }(H_{\beta },\Sigma ) \oplus C^{\varphi }(H_{\gamma },\Sigma )$
provides
$$ \begin{align*}\tau^{\varphi}(Y,\Sigma;h_{\scriptscriptstyle{Y,\Sigma}})=\tau^{\varphi}(H_{\alpha},\Sigma;h_{\alpha})\tau^{\varphi}(H_{\beta},\Sigma;h_{\beta})\tau^{\varphi}(H_{\gamma},\Sigma;h_{\gamma}).\end{align*} $$
Fix
$\nu \in \{\alpha ,\beta ,\gamma \}$
. The handlebody
$H_{\nu }$
is obtained from
$\Sigma $
by adding meridian disks
$D_i^{\nu }$
such that
$\partial D_i^{\nu }=\nu _i$
and the
$3$
-cell
$H_{\nu }$
. The associated
$\mathbb {F}$
-complex of
$(H_{\nu },\Sigma ;\varphi )$
is
$C^{\varphi }(H_{\nu },\Sigma )$
:
$$ \begin{align*} \ 0\to C_3^{\varphi}(H_{\nu},\Sigma)\to C_2^{\varphi}(H_{\nu},\Sigma)\to 0 \end{align*} $$
with bases
$H_{\nu }$
and
$(D_i^{\nu })_i$
. Choose the lifts so that
$$ \begin{align*} \partial H_{\nu}=\sum_{1\leq i \leq g}(\varphi(\nu_i^*)-1)\, D_i^{\nu}\ \in C_2^{\varphi}(H_{\nu},\Sigma). \end{align*} $$
Via the identification
$H_2^{\varphi }(H_{\nu },\Sigma )\simeq L_{\nu }^{\scriptscriptstyle {\mathbb {F}}}$
, the basis
$(\frac {1}{\varphi (\nu _1^*)-1}\, D^{\nu }_2, D^{\nu }_3,\dots , D^{\nu }_g)$
coincides with
$h_{\nu }$
. Hence,
$\tau ^{\varphi }(H_{\nu },\Sigma ;h_{\nu })=\bigg [\frac {\partial H_{\nu }\cdot h_{\nu }}{( D_i^{\nu })_{1\leq i\leq g}}\bigg ]=1$
. ▪
Lemma 6.4 Let
$j \in \{1,2,3\}$
and
$\nu ,\nu ' \in \{\alpha ,\beta ,\gamma \}$
such that
$L_{\nu }^{\scriptscriptstyle {\mathbb {F}}}\cap L_{\nu '}^{\scriptscriptstyle {\mathbb {F}}}\simeq \partial X_j$
. There is a symplectic basis
$(\xi _i,\xi _i^*)_{1\leq i\leq g}$
of
$\Sigma $
such that the family
$h_{\nu \nu '}=(\frac {1}{\varphi (\xi _1^*)-1}\xi _2,\xi _3,\dots ,\xi _k)$
is a basis of
$L_{\nu }^{\scriptscriptstyle {\mathbb {F}}}\cap L_{\nu '}^{\scriptscriptstyle {\mathbb {F}}}$
.
Proof The surface
$\Sigma $
together with the families of curves
$\nu $
and
$\nu '$
is a Heegaard diagram of
$\partial X_j\simeq \sharp ^k(S^1\times S^2)$
. Hence, there is a symplectic basis
$(\xi _i,\xi _i^*)_{1\leq i\leq g}$
such that performing handleslides changes
$(\nu _i)_{1\leq i\leq g}$
into
$(\xi _i)_{1\leq i\leq g}$
and
$(\nu _i')_{1\leq i\leq g}$
into
$(\xi _1,\dots ,\xi _k,\xi _{k+1}^*,\dots ,\xi _g^*)$
. Permuting the indices if necessary, we assume
$\varphi (\xi _1^*)\neq 1$
. Now,
$(\xi _1,\dots ,\xi _g)$
is a system of meridians for
$H_{\nu }$
and
$(\xi _1,\dots ,\xi _k,\xi _{k+1}^*,\dots ,\xi _g^*)$
for
$H_{\nu '}$
. By Lemma 6.2, the families
$(\frac {1}{\varphi (\xi _1^*)-1}\xi _2,\xi _3,\dots ,\xi _g)$
and
$(\frac {1}{\varphi (\xi _1^*)-1}\xi _2,\xi _3,\dots ,\xi _k,\xi _{k+1}^*,\dots ,\xi _g^*)$
are bases of
$L_{\nu }^{\scriptscriptstyle {\mathbb {F}}}$
and
$L_{\nu '}^{\scriptscriptstyle {\mathbb {F}}}$
respectively. ▪
Lemma 6.5 Via the identification
$H_3^{\varphi }(X,Y)\simeq (L_{\alpha }^{\scriptscriptstyle {\mathbb {F}}}\cap L_{\beta }^{\scriptscriptstyle {\mathbb {F}}})\oplus (L_{\beta }^{\scriptscriptstyle {\mathbb {F}}}\cap L_{\gamma }^{\scriptscriptstyle {\mathbb {F}}}) \oplus (L_{\gamma }^{\scriptscriptstyle {\mathbb {F}}}\cap L_{\alpha }^{\scriptscriptstyle {\mathbb {F}}})$
, the family
$h_{\scriptscriptstyle {X,Y}}=h_{\alpha \beta }.h_{\beta \gamma }.h_{\gamma \alpha }$
is a homology basis of the pair
$(X,Y;\varphi )$
, and we have
$\tau ^{\varphi }(X,Y;h_{\scriptscriptstyle {X,Y}})=1$
.
Proof Fix
$j \in \{1,2,3\}$
and
$\nu ,\nu ' \in \{\alpha ,\beta ,\gamma \}$
such that
$\partial X_j\simeq H_{\nu }\cup H_{\nu '}$
. Let
$(\xi _i,\xi _i^*)_{1\leq i\leq g}$
be a symplectic basis of
$\Sigma $
given by Lemma 6.4. For
$i=1,\dots ,g$
, let
$D_i$
be a meridian disk of
$H_{\nu }$
with
$\partial D_i=\xi _i$
. Similarly, let
$\Delta _i$
be meridians disks of
$H_{\nu '}$
such that
$\partial \Delta _i=\xi _i$
for
$1\leq i\leq k$
and
$\partial \Delta _i=\xi _i^*$
for
$k<i\leq g$
. The handlebody
$X_j$
is obtained from
$\partial X_j$
by adding 3-cells
$B_i$
such that
$\partial B_i=D_i-\Delta _i$
for
$1\leq i\leq k$
and a 4-cell
$X_j$
. The associated
$\mathbb {F}$
-complex is
$C^{\varphi }(X_j,\partial X_j)$
:
$$ \begin{align*} \ 0 \rightarrow C_4^{\varphi}(X_j,\partial X_j) \rightarrow C_3^{\varphi}(X_j,\partial X_j) \rightarrow 0 \end{align*} $$
with bases
$X_j$
and
$(B_i)_{1\leq i\leq k}$
. Choose the lifts so that
$$ \begin{align*} \partial X_j=\sum_{1\leq i \leq k}(\varphi(\xi_i^*)-1)\, B_i\ \in C_3^{\varphi}(X_j,\partial X_j). \end{align*} $$
Hence,
$H^{\varphi }_{\ell }(X_j,\partial X_j)=0$
if
$\ell \neq 3$
. Moreover, by Blanchfield duality,
$H_3(X_j,\partial X_j)\simeq H_1^{\varphi }(X_j)$
. Since
$X_j$
is obtained from
$\partial X_j$
by adding
$3$
- and
$4$
-cells,
$H_1^{\varphi }(X_j) \simeq H_1^{\varphi }(\partial X_j)$
. Finally, by Lemma 5.4 and Blanchfield duality,
$H_1^{\varphi }(\partial X_j) \simeq H_2^{\varphi }(\partial X_j) \simeq H_3^{\varphi }(X_j,\partial X_j) \simeq L_{\nu }^{\scriptscriptstyle {\mathbb {F}}}\cap L_{\nu '}^{\scriptscriptstyle {\mathbb {F}}}$
. A basis of
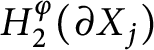$H_2^{\varphi }(\partial X_j)$
is obtained by identifying
$\xi _i$
with
$D_i\cup \Delta _i$
. Its Blanchfield dual basis of
$H_1^{\varphi }(\partial X_j)$
is
$(\frac {1}{\varphi (\xi _1^*)-1}\xi _2^*,\xi _3^*,\dots ,\xi _k^*)$
, which is also a basis of
$H_1^{\varphi }(X_j)$
. Its Blanchfield dual basis of
$H_3(X_j,\partial X_j)$
is
$(\frac {1}{\varphi (\xi _1^*)-1} B_2, B_3,\dots , B_k)$
and
$$ \begin{align*} \tau^{\varphi}(X_j,\partial X_j;h_{\nu\nu'})=\bigg[\frac{\partial X_j.h_{\nu\nu'}}{(B_i)_{1\leq i\leq k}}\bigg]=1. \end{align*} $$
Conclude with
$C^{\varphi }(X,Y)\simeq \oplus _{j=1}^3 C^{\varphi }(X_j,\partial X_j)$
. ▪
6.2 Computation of the torsion of
$\boldsymbol{(X;\varphi )}$
In this subsection, we prove Theorem 2.7.
Let
$h_{\scriptscriptstyle {X}}$
be a homology basis of
$(X;\varphi )$
. Let
$h_{\scriptscriptstyle {Y}}$
be a homology basis of Y, with
$h_{\scriptscriptstyle {Y}}^1=h_{\scriptscriptstyle {X}}^1$
—recall there is a natural identification
$H_1^{\varphi }(X)\simeq H_1^{\varphi }(Y)$
. Let
$h_{\scriptscriptstyle {\Sigma }}$
be a homology basis of
$\Sigma $
as provided by Lemma 6.1. For the pair
$(Y,\Sigma )$
, fix the homology basis
$h_{\scriptscriptstyle {Y,\Sigma }}=h_{\alpha }.h_{\beta }.h_{\gamma }$
. For the pair
$(X,Y)$
, fix the homology basis
$h_{\scriptscriptstyle {X,Y}}=h_{\alpha \beta }.h_{\beta \gamma }.h_{\gamma \alpha }$
.
Lemma 6.6 The exact sequence in homology associated with the pair
$(Y,\Sigma ;\varphi )$
reduces to
and we have
$\tau ^{\varphi }(Y; h_{\scriptscriptstyle {Y}})=\tau (\mathcal {H}_Y).$
Proof The exact sequence of complexes associated with the pair
$(Y,\Sigma )$
provides the following equality (see Lemma 3.1):
$$ \begin{align*} \tau^{\varphi}(Y; h_{\scriptscriptstyle{Y}}) = \tau^{\varphi}(\Sigma;h_{\scriptscriptstyle{\Sigma}}) \, \tau^{\varphi}( Y,\Sigma;h_{\scriptscriptstyle{Y,\Sigma}}) \, \tau(\mathcal{H}_Y). \end{align*} $$
Lemma 6.7 Let
$\mathcal {H}_{X}$
be the exact sequence in homology associated with the pair
$(X,Y)$
. We have
$\tau (\mathcal {H}_{X}) = \tau (\mathcal {H}_X'),$
where
$\mathcal {H}_X'$
is the following part of the sequence
$\mathcal {H}_{X}$
itself:
Proof The sequence
$\mathcal {H}_X$
is composed of
$\mathcal {H}_X'$
and
$0\to H^{\varphi }_1(Y)\to H^{\varphi }_1(X)\to 0$
. ▪
Proof of Theorem 2.7
Here,
$h_{\scriptscriptstyle {X}}$
is the homology basis h of the statement. The exact sequence with coefficients in
$\mathbb {F}$
associated with the pair
$(X,Y)$
induces the following equality:
$$ \begin{align*} \tau^{\varphi}(X;h_{\scriptscriptstyle{X}})= \tau^{\varphi}(Y;h_{\scriptscriptstyle{Y}}) \,\tau^{\varphi}(X,Y;h_{\scriptscriptstyle{X,Y}}) \,\tau(\mathcal{H}_{X}). \end{align*} $$
Hence, Lemmas 6.5 and 6.6 give
$$ \begin{align*}\tau^{\varphi}(X;h_{\scriptscriptstyle{X}})=\tau(\mathcal{H}_Y)\,\tau(\mathcal{H}_X').\end{align*} $$
By Lemmas 5.2 and 6.6, the sequence
${\mathcal {H}_{Y}}$
writes
$$ \begin{align*}0\to H_2^{\varphi}(Y) \to L_{\alpha}^{\scriptscriptstyle{\mathbb{F}}}\oplus L_{\beta}^{\scriptscriptstyle{\mathbb{F}}}\oplus L_{\gamma}^{\scriptscriptstyle{\mathbb{F}}} \to H_1^{\varphi}(\Sigma) \to H_1^{\varphi}(Y)\to 0.\end{align*} $$
Fixing a basis s for
$L_{\alpha }^{\scriptscriptstyle {\mathbb {F}}}+L_{\beta }^{\scriptscriptstyle {\mathbb {F}}}+L_{\gamma }^{\scriptscriptstyle {\mathbb {F}}}\subset H_1^{\varphi }(\Sigma )$
, we get
$$ \begin{align*} \tau(\mathcal{H}_Y) = \bigg[\frac{h_{\scriptscriptstyle{Y}}^2.s}{h_{\alpha}.h_{\beta}.h_{\gamma}}\bigg]^{-1} \bigg[\frac{s.h_{\scriptscriptstyle{X}}^1}{h_{\scriptscriptstyle{\Sigma}}}\bigg]. \end{align*} $$
By Lemmas 5.4 and 6.7, the sequence
${\mathcal {H}_X'}$
writes
Fixing a basis t for
$\mathrm {Im}(\zeta )\subset H_2^{\varphi }(Y)$
, we get
$$ \begin{align*} \tau(\mathcal{H}_X')=\bigg[\frac{h_{\scriptscriptstyle{X}}^3.t}{h_{\alpha\beta}.h_{\beta\gamma}.h_{\gamma\alpha}}\bigg] \bigg[\frac{t.h_{\scriptscriptstyle{X}}^2}{h_{\scriptscriptstyle{Y}}^2}\bigg]^{-1}. \end{align*} $$
Fixing the complex basis
$c=(h_{\alpha \beta }.h_{\beta \gamma }.h_{\gamma \alpha },h_{\alpha }.h_{\beta }.h_{\gamma },h_{\scriptscriptstyle {\Sigma }})$
for the complex
$C^{\scriptscriptstyle {\mathbb {F}}}$
, we have
$$ \begin{align*} \tau(C^{\scriptscriptstyle{\mathbb{F}}};c,h_{\scriptscriptstyle{X}}) = \bigg[\frac{h_{\scriptscriptstyle{X}}^3.t}{h_{\alpha\beta}.h_{\beta\gamma}.h_{\gamma\alpha}}\bigg] \bigg[\frac{t.h_{\scriptscriptstyle{X}}^2.s}{h_{\alpha}.h_{\beta}.h_{\gamma}}\bigg]^{-1} \bigg[\frac{s.h_{\scriptscriptstyle{X}}^1}{h_{\scriptscriptstyle{\Sigma}}}\bigg], \end{align*} $$
so that we get the desired equality. ▪
7 Computation of
$\boldsymbol{\tau^{\varphi}(X)}$
via
$\boldsymbol{(\hat {X},\star )}$
In this section, we compute the torsion of
$(\hat {X},\star ;\varphi )$
and relate it to the torsion of
$(X;\varphi )$
. For
$\nu \in \{\alpha ,\beta ,\gamma \}$
, let
$\hat {L}_{\nu }^{\scriptscriptstyle {\mathbb {F}}}$
be the subspace of
$H_1^{\varphi }(\hat {\Sigma },\star ;\mathbb {F})$
generated by the homology classes of the curves
$\nu _i$
.
Lemma 7.1 The
$\Lambda $
-modules
$H_1^{\varphi }(\hat {\Sigma },\star ;\Lambda )$
,
$\hat {L}^{\scriptscriptstyle {\Lambda }}_{\nu }$
, and
$\hat {L}^{\scriptscriptstyle {\Lambda }}_{\nu }\cap \hat {L}^{\scriptscriptstyle {\Lambda }}_{\nu '}$
are free
$\Lambda $
-modules of rank
$2g$
, g, and k, respectively. Moreover,
$H_1^{\varphi }(\hat {\Sigma },\star ;\mathbb {F})=H_1^{\varphi }(\hat {\Sigma },\star ;\Lambda )\otimes _{\Lambda }\mathbb {F}$
,
$\widehat {L}^{\scriptscriptstyle {\mathbb {F}}}_{\nu }=\widehat {L}^{\scriptscriptstyle {\Lambda }}_{\nu }\otimes _{\Lambda }\mathbb {F}$
and
$\widehat {L}^{\scriptscriptstyle {\mathbb {F}}}_{\nu }\cap \widehat {L}^{\scriptscriptstyle {\mathbb {F}}}_{\nu '}=(\widehat {L}^{\scriptscriptstyle {\Lambda }}_{\nu }\cap \widehat {L}^{\scriptscriptstyle {\Lambda }}_{\nu '})\otimes _{\Lambda }\mathbb {F}$
.
Proof Set
$R=\Lambda $
or
$\mathbb {F}$
. Fix
$\nu \in \{\alpha ,\beta ,\gamma \}$
. Let
$(\nu _i^*)_{1\leq i\leq g}$
be a family of curves on
$\hat {\Sigma }$
such that
$(\nu _i,\nu _i^*)_{1\leq i\leq g}$
is a symplectic basis for
$\Sigma $
. Assume that the removed ball B is such that
$\partial D=\prod _{i=1}^g[\nu _i,\nu _i^*]$
. Consider a CW-decomposition of
$\hat {\Sigma }$
with one
$0$
-cell
$\star $
, one
$2$
-cell
$\hat {\Sigma }$
, and
$1$
-cells
$\nu _i$
,
$\nu _i^*$
and
$\partial D$
. The associated
$\mathbb {F}$
-complex is
$C^{\varphi }(\hat {\Sigma },\star )$
:
$$ \begin{align*} 0\to C_2^{\varphi}(\hat{\Sigma},\star)\to C_1^{\varphi}(\hat{\Sigma},\star)\to 0. \end{align*} $$
Choose a lift of
$\hat {\Sigma }$
such that
$$ \begin{align*} \partial \hat{\Sigma}=-\partial D+\sum_{1\leq i \leq g}(\varphi(\nu_i^*)-1)\, \nu_i\ \in C_1^{\varphi}(\hat{\Sigma},\star). \end{align*} $$
The only nontrivial homology R-module of
$(\hat {\Sigma },\star )$
is
$H_1^{\varphi }(\widehat {\Sigma },\star ;R)\simeq R^{2g}$
generated by
$\nu _i$
and
$\nu _i^*$
for
$i=1,\dots ,g$
. Since
$\hat {L}_{\nu }^{\scriptscriptstyle {R}}$
is the submodule of
$H_1 ^{\varphi }(\hat {\Sigma },\star ;R)$
generated by the
$\nu _i$
, we get
$\hat {L}_{\nu }^{\scriptscriptstyle {R}}\simeq R^g$
.
A similar computation can be done for
$(\hat {\Sigma },\star )$
from any symplectic basis for
$\Sigma $
. As in Lemma 6.4, if
$\nu $
and
$\nu '$
are distinct, there exists a symplectic basis
$(\xi _i,\xi _i^*)_{1\leq i\leq g}$
for
$\Sigma $
such that
$\hat {L}_{\nu }^{\scriptscriptstyle {R}}\cap \widehat {L}_{\nu '}^{\scriptscriptstyle {R}}\simeq R^k$
freely generated by
$(\xi _i)_{1\leq i\leq k}$
. ▪
If
$\Gamma $
is a free
$\Lambda $
-module, a
$\Lambda $
-basis of
$\Gamma \otimes _{\Lambda }\mathbb {F}$
is a basis
$b\otimes 1$
, where b is a basis of
$\Gamma $
.
Theorem 7.2 The twisted homology of
$(\hat {X},\star )$
canonically identifies with the homology of the following
$\mathbb {F}$
-complex
$\hat {C}^{\scriptscriptstyle {\mathbb {F}}}$
:
where
$\zeta (x,y,z)=(x-z,y-x,z-y)$
and
$\iota $
is defined by the inclusions
$\hat {L}_{\nu }^{\scriptscriptstyle {\mathbb {F}}}\hookrightarrow H_1^{\varphi }(\hat {\Sigma },\star ;\mathbb {F})$
. Moreover, for any complex
$\Lambda $
-basis
$\hat {c}$
for
$\widehat {C}^{\scriptscriptstyle {\mathbb {F}}}$
and any homology basis
$\widehat {h}$
for
$(\widehat {X},\star )$
and
$\widehat {C}^{\scriptscriptstyle {\mathbb {F}}}$
, we have
$$ \begin{align*} \tau^{\varphi}(\hat{X},\star;\hat{h})=\tau(\hat{C}^{\scriptscriptstyle{\mathbb{F}}};\hat{c},\widehat{h}) \quad\text{in }\mathbb{F}/\Lambda^*. \end{align*} $$
Proof Using Lemma 7.1, the whole Sections 5 and 6 adapt to the setting of
$(\hat {X},\star )$
, providing the result. The independence with respect to the choice of a
$\Lambda $
-basis over
$\mathbb {F}$
for
$\hat {C}^{\scriptscriptstyle {\mathbb {F}}}$
is due to the fact that a change of such bases modifies the torsion by an element of
$\Lambda ^*$
. ▪
Lemma 7.3 For all
$\ell \neq 1,2,3$
, one has
$H_{\ell }^{\varphi }(X;\mathbb {F}) = H_{\ell }^{\varphi }(X,\star )=H_{\ell }^{\varphi }(\hat {X},\star ;\mathbb {F})=0$
. Moreover, there are natural identifications of
$\mathbb {F}$
-vector spaces
$$ \begin{align*} H_1^{\varphi}(X,\star)\simeq H_1^{\varphi}(\hat{X},\star), \ H_2^{\varphi}(X)\simeq H_2^{\varphi}(X,\star)\simeq H_2^{\varphi}(\hat{X},\star) \text{, and }H_3^{\varphi}(X)\simeq H_3^{\varphi}(X,\star), \end{align*} $$
and short exact sequences of
$\mathbb {F}$
-vector spaces
$$ \begin{align*} 0 &\rightarrow H_1^{\varphi}(X) \rightarrow H_1^{\varphi}(\hat{X},\star)\to H_0^{\varphi}(\star) \rightarrow 0\ and \ 0 \rightarrow H_4^{\varphi}(B,\partial B) \rightarrow H_3^{\varphi}(\hat{X},\star)\\& \rightarrow H_3^{\varphi}(X) \rightarrow 0. \end{align*} $$
Proof The result follows from the exact sequence in homology of the pair
$(X,\star )$
and from the exact sequence in homology of the triple
$(X,\hat {X},\star )$
combined with the excision equivalence
$(X,\hat {X})\simeq (B,\partial B)$
. ▪
Proposition 7.4 Let h be a homology basis of X. Let
$u\in H_1(\hat {X},\star )$
satisfy
$\varphi (u)\neq 1$
. Then,
$\widehat {h}=(\partial B.h^3,h^2,h^1.u)$
is a homology basis of
$(\widehat {X},\star )$
and
$$ \begin{align*} (\varphi(u)-1)\,\tau^{\varphi}(X;h)=\tau^{\varphi}(\hat{X},\star;\hat{h}). \end{align*} $$
Proof Thanks to Lemma 7.3,
$\hat {h}$
is a homology basis for
$(\widehat {X},\star )$
, and
$\hat h=(h^3,h^2,h^1.u)$
is a homology basis for
$(X,\star )$
. The short exact sequences of complexes
$0 \to C^{\varphi }(\star )\to C^{\varphi }(X)\to C^{\varphi }(X,\star )\to 0$
and
$0\to C^{\varphi }(\hat {X},\star )\to C^{\varphi }(X,\star )\to C^{\varphi }(B,\partial B)\to 0$
provide
$$ \begin{align*} \tau^{\varphi}(X;h)=\tau^{\varphi}(\star;\star) \, \tau^{\varphi}(X,\star;\bar h) \, \tau(\mathcal{S}_1) \end{align*} $$
and
$$ \begin{align*} \tau^{\varphi}(X,\star;\bar h)=\tau^{\varphi}(\hat{X},\star;\hat{h}) \, \tau^{\varphi}(B,\partial B;B) \, \tau(\mathcal{S}_2), \end{align*} $$
where
$\mathcal {S}_1$
and
$\mathcal {S}_2$
are the associated exact sequences in homology. One easily checks that
$\tau ^{\varphi }(\star ;\star )=1$
and
$\tau ^{\varphi }(B,\partial B;B)=1$
, so that
$$ \begin{align*} \tau^{\varphi}(X;h)=\tau^{\varphi}(\hat{X},\star;\hat{h}) \, \tau(\mathcal{S}_1) \, \tau(\mathcal{S}_2). \end{align*} $$
A straightforward computation shows that
$\tau (\mathcal {S}_1)=(\varphi (u)-1)^{-1}$
and
$\tau (\mathcal {S}_2)=1$
. ▪
8 Intersection forms
In this section, we prove the results on intersection forms. Along the proofs, we give interpretations of the modules of the complexes C and
$C^{\scriptscriptstyle {\mathbb {F}}}$
as modules of chains.
We first reprove the expression of the intersection form on
$H_2(X;\mathbb {Z})$
given in [Reference Feller, Klug, Schirmer and Zemke2] with our approach. Following Wall [Reference Wall11], define the symmetric form
$$ \begin{align*} \lambda: \frac{L_{\alpha} \cap (L_{\beta} + L_{\gamma})}{(L_{\alpha}\cap L_{\beta})+ (L_{\alpha}\cap L_{\gamma})} \times \frac{L_{\alpha} \cap (L_{\beta} + L_{\gamma})}{ (L_{\alpha} \cap L_{\beta})+ (L_{\alpha} \cap L_{\gamma})} \longrightarrow \mathbb{Z} \end{align*} $$
as follows. For
$a,a' \in L_{\alpha } \cap (L_{\beta } + L_{\gamma })$
, and
$b\in L_{\beta }$
,
$c\in L_{\gamma }$
such that
$a+b+c=0$
, set
$$ \begin{align*} \lambda(a,a'):= \langle c, a' \rangle_{\Sigma}. \end{align*} $$
Proposition 8.1 [Reference Feller, Klug, Schirmer and Zemke2]
Let
$\langle \cdot ,\cdot \rangle _{X}$
be the intersection form of X. There is an isomorphism
$$ \begin{align*} \big(H_2(X;\mathbb{Z}); \langle \cdot,\cdot \rangle_{X} \big) \simeq \bigg(\frac{L_{\alpha} \cap (L_{\beta} + L_{\gamma})}{ (L_{\alpha} \cap L_{\beta})+ (L_{\alpha} \cap L_{\gamma})}; \lambda \bigg). \end{align*} $$
Proof By Theorem 2.1,
$$ \begin{align*} H_2(X)\simeq\frac{\ker\big(L_{\alpha}\oplus L_{\beta}\oplus L_{\gamma}\to H_1(\Sigma;\mathbb{Z})\big)} {(L_{\alpha}\cap L_{\beta})\oplus(L_{\beta}\cap L_{\gamma})\oplus(L_{\gamma}\cap L_{\alpha})}\simeq \frac{L_{\alpha}\cap(L_{\beta}+ L_{\gamma})}{(L_{\alpha}\cap L_{\beta})+(L_{\alpha}\cap L_{\gamma})}. \end{align*} $$
Following the trisection, X is built from
$D^2\times \Sigma $
by adding
$2$
-,
$3$
-, and
$4$
-cells attached to
$S^1\times \Sigma $
(see Section 3.4). Let
$p_0, p_{\alpha }, p_{\beta }$
, and
$p_{\gamma }$
be the points in
$D^2$
defined as in Figure 2. Given
$\mu =(\mu _{\alpha },\mu _{\beta },\mu _{\gamma })$
in
$\ker (L_{\alpha }\oplus L_{\beta }\oplus L_{\gamma }\to H_1(\Sigma ))$
and a point
$q\neq p_0 \in \mathrm {Int}{(D^2)}$
, we construct a
$2$
-cycle
$S_q(\mu ) \in C_2(X)$
as follows. For all
$\nu \in \{ \alpha , \beta , \gamma \}$
, write
$\mu _{\nu }$
as a linear combination of the
$\nu _i$
and define
$D_{\nu }(\mu )$
as the corresponding disjoint union of meridian disks bounded by parallel copies of the
$\{p_{\nu }\}\times \nu _i$
. Then, define
$$ \begin{align*} S_q(\mu):=S_{\alpha}+S_{\beta}+S_{\gamma}+T(\mu), \end{align*} $$
where:
-
•
$S_{\nu }=D_{\nu }(\mu ) \cup ([p_{\nu },q]\times \mu _{\nu } )$
, -
•
$T(\mu )$
is a 2-chain with support contained in
$\{q\}\times \Sigma $
with
$\partial T(\mu )=\mu _{\alpha }+\mu _{\beta }+\mu _{\gamma }$
.
Let now
$\mu =(\mu _{\alpha },\mu _{\beta },\mu _{\gamma })$
and
$\mu '=(\mu _{\alpha }',\mu _{\beta }',\mu _{\gamma }')$
be in
$\ker (L_{\alpha }\oplus L_{\beta }\oplus L_{\gamma }\to H_1(\Sigma ))$
. Fix q and
$q'$
in
$\mathrm {Int}{(D^2)}$
such that
$p_0=(p_{\gamma },q)\cap (p_{\alpha },q')$
. The
$2$
-cycles
$S_q(\mu )$
and
$S_{q'}(\mu ')$
intersect transversally in
$\{ p_0 \} \times \Sigma $
and
$$ \begin{align*} \langle S_q(\mu),S_{q'}(\mu')\rangle_X = \langle\mu_{\gamma},\mu_{\alpha}'\rangle_{\Sigma} = \lambda(\mu,\mu'), \end{align*} $$
where we assume that
$D^2$
is oriented by the oriented basis
$(\vec {p_0p_{\alpha }},\vec {p_0p_{\gamma }})$
. ▪
We now prove Theorem 2.5, which is the analogue in the twisted setting of Proposition 8.1.
Proof of Theorem 2.5
All the curves of the families
$\alpha $
,
$\beta $
,
$\gamma $
have their homology classes in
$\ker (\varphi )$
, so that they lift as loops. Moreover, the meridian disks and the paths of Figure 3 drawn on
$D^2$
are contractible; thus, they also lift as disks and paths. Hence, the result follows from the very same argument as in Proposition 8.1. ▪
Figure 3: The 2-cycles S and
$S'$
.
We turn to the intersection form on
$H_1(X;\mathbb {Z})\times H_3(X;\mathbb {Z})$
.
Proposition 8.2 There is an isomorphism
$$ \begin{align*} \big(H_1(X;\mathbb{Z})\times H_3(X;\mathbb{Z}); \langle \cdot,\cdot \rangle_{X} \big) \cong \bigg(\frac{H_1(\Sigma)}{L_{\alpha} + L_{\beta} + L_{\gamma}}\times(L_{\alpha}\cap L_{\beta}\cap L_{\gamma}); \langle\cdot,\cdot\rangle_{\Sigma} \bigg). \end{align*} $$
Proof of Proposition 8.2
Let
$\mu \in L_{\alpha }\cap L_{\beta }\cap L_{\gamma }$
. By a slight abuse of notation, we use the same letter
$\mu $
for a representative of it on
$\Sigma $
. We will construct a 3-cycle M associated with
$\mu $
that intersects
$\Sigma $
along
$\mu $
. Once again, we view X as reconstructed from the trisection diagram. Let
$q_{\alpha },q_{\beta },q_{\gamma }$
be the points on
$D^2$
represented in Figure 4, and let V be the hatched triangle they define. We will complete the 3-chain
$M_0=V\times \mu $
into a 3-cycle. For each
$\nu \in \{\alpha ,\beta ,\gamma \}$
,
$\mu $
bounds a surface
$F_{\nu }$
properly embedded in
$H_{\nu }$
. For
$i,\nu ,\nu '$
such that
$\partial X_i=H_{\nu }\cup H_{\nu '}$
, since
$X_i\cong \big (X_i\setminus (\mathrm {Int}{(V)}\times \Sigma )\big )$
has trivial second homology, the closed surface
$F_{\nu }\cup ([q_{\nu },q_{\nu '}]\times \mu )\cup F_{\nu '}$
bounds a
$3$
-cycle
$M_i\subset \big (X_i\setminus (\mathrm {Int}{(V)}\times \Sigma )\big )$
. Finally,
$M=\sum _{0\leq i\leq 3}M_i$
is a 3-cycle associated with
$\mu $
. Then, for any
$\mu '\in H_1(\Sigma )$
, we have
$\langle \mu ',M\rangle _X=\langle \mu ',\mu _{\alpha }\rangle _{\Sigma }=\langle \mu ',\mu \rangle _{\Sigma }.$
▪
Figure 4: The 3-cycle M associated to
$\mu $
.
A similar proof yields Proposition 2.6.
9 Examples
9.1 Example 1
The trisection diagram
$(\Sigma ;\alpha ,\beta ,\gamma )$
in Figure 5 represents the
$4$
-manifold
$X = (S^1\times S^3) \, \sharp \, (S^1\times S^3) \, \sharp \, \mathbb {C} P^2$
. The black paths fix a choice of a representative in
$\pi _1(\Sigma ,\star )$
of each loop. Let
$x_i, y_i$
, for
$i\in \{1,2,3\}$
, be the generators of
$\pi _1(\Sigma ,\star )$
represented in Figure 6. Their homology classes provide a symplectic basis of
$H_1(\Sigma ;\mathbb {Z})$
. Note that the family
$(x_i,y_i)_{1\leq i\leq 3}$
is not a symplectic basis for
$\Sigma $
as in Definition 6.1, although it could easily be modified to get such a basis. The following relations hold in
$\pi _1(\Sigma ,\star )$
:
$\alpha _1=\beta _1=\gamma _1=x_1$
,
$\alpha _2=\beta _2=\gamma _2=x_2$
,
$\alpha _3=x_3$
,
$\beta _3=y_3$
, and
$\gamma _3=x_3y_3$
.
Figure 5: A trisection diagram for
$(S^1\times S^2)\sharp (S^1\times S^2)\sharp \mathbb {C} P^2$
.
Figure 6: A basis of
$H_1(\Sigma ;\mathbb {Z})$
with curves based at
$\star $
.
Setting
$L=\langle x_1,x_2\rangle \subset H_1(\Sigma ;\mathbb {Z})$
, we get
$$ \begin{align*} L_{\alpha}=L\oplus\langle x_3\rangle, \ L_{\beta}=L\oplus\langle y_3\rangle \text{ and } L_{\gamma}=L\oplus\langle x_3+y_3\rangle. \end{align*} $$
Hence, by Theorem 2.1:
-
•
$H_1(X;\mathbb {Z})\simeq \mathbb {Z}^2$
is generated by
$y_1$
and
$y_2$
; -
•
$H_2(X;\mathbb {Z})\simeq \mathbb {Z}$
is generated by
$x_3$
; -
•
$H_3(X;\mathbb {Z})\simeq \mathbb {Z}^2$
is generated by
$x_1$
and
$x_2$
.
In these bases, the matrix of the intersection form on
$H_2(X;\mathbb {Z})$
is
$(1)$
and the matrix of the form on
$H_1(X;\mathbb {Z})\times H_3(X;\mathbb {Z})$
is
$\begin {pmatrix} -1&0\\0&-1 \end {pmatrix}$
(see Propositions 8.1 and 8.2).
Now let
$G\simeq \mathbb {Z}^2$
be the free abelian (multiplicative) group of rank
$2$
generated by
$t_1$
and
$t_2$
. Let
$\varphi :H_1(X;\mathbb {Z})\to G$
be defined by
$\varphi (y_1)=t_1$
and
$\varphi (y_2)=t_2$
. The following relations hold in
$H_1^{\varphi }(\Sigma ;R)$
, assuming the lifts of the curves all start at the same lift of the point
$\star $
:
$\alpha _1=\beta _1=\gamma _1=x_1$
,
$\alpha _2=\beta _2=\gamma _2=x_2$
,
$\alpha _3=x_3$
,
$\beta _3=y_3$
, and
$\gamma _3=x_3+y_3$
.
In the cellular decomposition of
$\Sigma $
given by Figure 6, the only 2-cell has boundary
$\partial \Sigma =[x_1,y_1]\,y_2^{-1}\,[y_3^{-1},x_3]\,x_2\,y_2\,x_2^{-1}$
. This provides a single relation in
$H_1^{\varphi }(\Sigma ;R)$
:
$$ \begin{align*} r=(1-t_1)x_1+(t_2^{-1}-1)x_2. \end{align*} $$
Setting
$L^{\scriptscriptstyle {R}}=\langle x_1,x_2\rangle /\langle r\rangle \subset H_1^{\varphi }(\Sigma ;R)$
, we get
$$ \begin{align*} H_1^{\varphi}(\Sigma;R)=L^{\scriptscriptstyle{R}}\oplus\langle (1-t_2)y_1+(t_1-1)y_2,x_3,y_3\rangle \end{align*} $$
and
$$ \begin{align*} L_{\alpha}^{\scriptscriptstyle{R}}=L^{\scriptscriptstyle{R}}\oplus\langle x_3\rangle, \ L_{\beta}^{\scriptscriptstyle{R}}=L^{\scriptscriptstyle{R}}\oplus\langle y_3\rangle \text{ and } L_{\gamma}^{\scriptscriptstyle{R}}=L^{\scriptscriptstyle{R}}\oplus\langle x_3+y_3\rangle. \end{align*} $$
Hence, by Theorem 2.3:
-
•
$H_1^{\varphi }(X;R)\simeq R$
is generated by
$(1-t_2)\,y_1+(t_1-1)\,y_2$
; -
•
$H_2^{\varphi }(X;R)\simeq R$
is generated by
$x_3$
; -
•
$H_3^{\varphi }(X;R)\simeq L^{\scriptscriptstyle {R}}$
and
$H_3^{\varphi }(X;\mathbb {F})\simeq \mathbb {F}$
is generated by
$x_1$
.
In these generators, the intersection form on
$H_2^{\varphi }(X;\mathbb {F})\simeq \mathbb {F}$
is given by
$1$
and the intersection form on
$H_1^{\varphi }(X;\mathbb {F})\times H_3^{\varphi }(X;\mathbb {F})\simeq \mathbb {F}\times \mathbb {F}$
is given by
$t_1(t_2-1)$
(see Theorem 2.5 and Proposition 2.6).
We end with the computation of the torsion. Fix the homology basis
$h=(h_3,h_2,h_1)$
with
$h_3= x_1$
,
$h_2=x_3$
, and
$h_1=(1-t_2)\,y_1+(t_1-1)\,y_2$
. We compute the torsion
$\tau ^{\varphi }(X;h)\in \mathbb {F}/\Lambda ^*$
. Set
$u=y_1$
. By Proposition 7.4,
$\tau ^{\varphi }(X;h)=(t_1-1)^{-1}\tau ^{\varphi }(\hat {X},\star ;\hat {h})$
, where
$\hat {h}=(\hat {h}_3,\hat {h}_2,\hat {h}_1)$
, and
$\hat {h}_3=(r,h_3)$
,
$\hat {h}_2=h_2$
, and
$\hat {h}_1=(h_1,u)$
. By Theorem 7.2,
$\tau ^{\varphi }(\hat {X},\star ;\hat {h})$
equals the torsion
$\tau (\hat {C}^{\scriptscriptstyle {\mathbb {F}}};\hat {c},\hat {h})$
of the complex
$\hat {C}^{\scriptscriptstyle {\mathbb {F}}}$
:
where
$\hat {c}$
is a
$\Lambda $
-basis over
$\mathbb {F}$
and
$\hat {L}^{\scriptscriptstyle {\mathbb {F}}}=\langle x_1,x_2\rangle \subset H_1^{\varphi }(\hat {\Sigma },\star ;\mathbb {F})$
. Define
$\hat {c}=(\hat {c}_3,\hat {c}_2,\hat {c}_1)$
by
$$ \begin{align*} &\hat{c}_3=\big((x_1,0,0),(x_2,0,0),(0,x_1,0),(0,x_2,0),(0,0,x_1),(0,0,x_2)\big), \\ &\hat{c}_2=\big((x_1,0,0),(x_2,0,0),(x_3,0,0),(0,x_1,0),(0,x_2,0),(0,y_3,0),(0,0,x_1),(0,0,x_2), \\ &\hspace{95mm} (0,0,x_3+y_3)\big), \\ &\hat{c}_1=(x_1,x_2,x_3,y_1,y_2,y_3). \end{align*} $$
Also fix the following bases of
$\mathrm {Im}(\zeta )$
and
$\mathrm {Im}(\iota )$
:
$$ \begin{align*} &\hat{b}_2=\big((x_1,-x_1,0),(x_2,-x_2,0),(0,x_1,-x_1),(0,x_2,-x_2)\big), \\ &\hat{b}_1=(x_1,x_2,x_3,y_3). \end{align*} $$
Lift the latter two bases to get the following independent families in
$\hat {L}^{\scriptscriptstyle {\mathbb {F}}}\oplus \hat {L}^{\scriptscriptstyle {\mathbb {F}}} \oplus \hat {L}^{\scriptscriptstyle {\mathbb {F}}}$
and
$\hat {L}_{\alpha }^{\scriptscriptstyle {\mathbb {F}}} \oplus \hat {L}_{\beta }^{\scriptscriptstyle {\mathbb {F}}} \oplus \hat {L}_{\gamma }^{\scriptscriptstyle {\mathbb {F}}}$
:
$$ \begin{align*} &\bar b_2=\big((x_1,0,0),(x_2,0,0),(0,x_1,0),(0,x_2,0)\big), \\ &\bar b_1=\big((x_1,0,0),(x_2,0,0),(x_3,0,0),(0,y_3,0)\big). \end{align*} $$
Now, by definition of the torsion,
$$ \begin{align*} \tau\big(\hat{C}^{\scriptscriptstyle{\mathbb{F}}};\hat{c},\hat{h}\big)=\bigg[\frac{\hat{h}_3.\bar b_2}{\hat{c}_3}\bigg]\cdot\bigg[\frac{\hat{b}_2.\hat{h}_2.\bar b_1}{\hat{c}_2}\bigg]^{-1}\bigg[\frac{\hat{b}_1.\hat{h}_1}{\hat{c}_1}\bigg]. \end{align*} $$
A straightforward computation gives
$\tau ^{\varphi }(X;h)=1-t_2\in \mathbb {F}/\Lambda ^*$
.
9.2 Example 2
The trisection diagram
$(\Sigma ;\alpha ,\beta ,\gamma )$
in Figure 7 represents the
$4$
-manifold
$X = S^1\times L(3,1)$
product of a circle with the Lens space
$L(3,1)$
, see [Reference Koenig5, Figure 10]. Generators
$x_i, y_i$
of
$\pi _1(\Sigma ,\star )$
, with
$i\in \{1,\dots ,4\}$
, are given in Figure 8.
Figure 7: A trisection diagram for
$S^1\times L(3,1)$
.
Figure 8: A basis for
$\pi _1(\Sigma ,\star )$
.
Their homology classes provide a symplectic basis of
$H_1(\Sigma ;\mathbb {Z})$
. The following relations hold in
$\pi _1(\Sigma ,\star )$
:
$$ \begin{align*} \begin{array}{lclcl} \alpha_1=x_1 & \quad & \beta_1=x_2 & \quad & \gamma_1=y_1 \\ \alpha_2=y_4^{-1}\,x_4\,y_4\,x_4^{-1}\,y_2^{-1}\,x_2\,y_2 && \beta_2=x_3^{-1}\,y_1^{-1}\,x_1\,y_1 && \gamma_2=x_3\,y_3^{-1}\,x_3^{-1}\,y_3\,x_2 \\ \alpha_3=y_2^{-1}\,y_3^{-1}\,x_3^{-1}\,y_3\,y_2\,x_4 && \beta_3=y_4^{-1}\,x_4^{-1}\,y_4\,x_1 && \gamma_3=y_3^{-1}\,x_3\,y_3^{-2} \\ \alpha_4=y_2^{-1}\,y_3\,y_2\,y_4 && \beta_4=y_1\,y_3\,y_4 && \gamma_4=x_4\,y_4^3 \end{array}. \end{align*} $$
We obtain in
$H_1(\Sigma ;\mathbb {Z})$
:
$$ \begin{align*} \begin{array}{lclcl} \alpha_1=x_1 & \ \ & \beta_1=x_2 & \ \ & \gamma_1=y_1 \\ \alpha_2=x_2 && \beta_2=x_1-x_3 && \gamma_2=x_2 \\ \alpha_3=-x_3+x_4 && \beta_3=x_1-x_4 && \gamma_3=x_3-3y_3 \\ \alpha_4=y_3+y_4 && \beta_4=y_1+y_3+y_4 && \gamma_4=x_4+3y_4 \end{array}. \end{align*} $$
Hence, by Theorem 2.1,
-
•
$H_1(X;\mathbb {Z})\simeq \mathbb {Z}\oplus \frac {\mathbb {Z}}{3\mathbb {Z}}$
with the first summand generated by
$y_2$
and the second by
$y_3$
; -
•
$H_2(X;\mathbb {Z})\simeq \frac {\mathbb {Z}}{3\mathbb {Z}}$
is generated by
$y_3+y_4$
; -
•
$H_3(X;\mathbb {Z})\simeq \mathbb {Z}$
is generated by
$x_2$
.
In these bases, the intersection form on
$H_1(X;\mathbb {Z})\times H_3(X;\mathbb {Z})$
is given by
${\langle y_2,x_2\rangle =-1}$
.
Now, let
$G\simeq \mathbb {Z}$
be the multiplicative group generated by t. Let
$\varphi :H_1(X;\mathbb {Z})\to G$
be defined by
$\varphi (y_2)=t$
and
$\varphi (y_3)=1$
. The following relations hold in
$H_1^{\varphi }(\Sigma ;R)$
, with
$R=\mathbb {Z}[t^{\pm 1}]\text { or }\mathbb {Q}(t)$
, assuming the lifts of the curves all start at the same lift of the point
$\star $
:
$$ \begin{align*} \begin{array}{lclcl} \alpha_1=x_1 & \ \ & \beta_1=x_2 & \ \ & \gamma_1=y_1 \\ \alpha_2=t^{-1}x_2 && \beta_2=x_1-x_3 && \gamma_2=x_2 \\ \alpha_3=-t^{-1}x_3+x_4 && \beta_3=x_1-x_4 && \gamma_3=x_3-3y_3 \\ \alpha_4=t^{-1}y_3+y_4 && \beta_4=y_1+y_3+y_4 && \gamma_4=x_4+3y_4 \end{array}. \end{align*} $$
In the cellular decomposition of
$\Sigma $
given by Figure 8, the only 2-cell has boundary
$\partial \Sigma =[y_1^{-1},x_1]\,[y_4^{-1},x_4]\,[y_2^{-1},x_2]\,[y_3^{-1},x_3]$
. This provides a single relation in
$H_1^{\varphi }(\Sigma ;R)$
:
$r=(1-t)\,x_2$
. Hence, by Theorem 2.3,
-
•
$H_1^{\varphi }(X;\mathbb {Z}[t^{\pm 1}])\simeq \frac {\mathbb {Z}}{3\mathbb {Z}}$
is generated by
$y_3$
and
$H_1^{\varphi }(X;\mathbb {Q}(t))=0$
; -
•
$H_2^{\varphi }(X;R)=0$
; -
•
$H_3^{\varphi }(X;\mathbb {Z}[t^{\pm 1}])\simeq \frac {\mathbb {Z}[t^{\pm 1}]}{\langle 1-t\rangle }$
is generated by
$x_2$
and
$H_3^{\varphi }(X;\mathbb {Q}(t))=0$
.
We now compute the torsion. Set
$\Lambda =\mathbb {Z}[t^{\pm 1}]$
and
$\mathbb {F}=\mathbb {Q}(t)$
. The manifold X has no homology over
$\mathbb {F}$
. Set
$u=y_2$
. By Proposition 7.4, the torsion
$\tau ^{\varphi }(X)\in \mathbb {F}/\Lambda ^*$
is given by
$\tau ^{\varphi }(X)=(t-1)^{-1}\tau ^{\varphi }(\hat {X},\star ;\widehat {h})$
,
$\tau ^{\varphi }(X)=(t-1)^{-1}\tau ^{\varphi }(\hat {X},\star ;\widehat {h})$
, where
$\widehat {h}=(r,\emptyset ,u)$
. By Theorem 7.2,
$\tau ^{\varphi }(\hat {X},\star ;\hat {h})$
equals the torsion
$\tau (\hat {C}^{\scriptscriptstyle {\mathbb {F}}};\hat {c},\hat {h})$
of the complex
$\hat {C}^{\scriptscriptstyle {\mathbb {F}}}$
:
where
$\nu ,\nu '$
run over
$\{\alpha ,\beta ,\gamma \}$
and
$\hat {c}$
is a
$\Lambda $
-basis over
$\mathbb {F}$
.
$$ \begin{align*} \begin{array}{ll} \hat{L}_{\alpha}^{\mathbb{F}}=\langle x_2,x_1,x_3-tx_4,y_3+ty_4\rangle & \hat{L}_{\alpha}^{\mathbb{F}}\cap\hat{L}_{\beta}^{\mathbb{F}}=\langle x_2,(t-1)x_1+x_3-tx_4\rangle \\ \hat{L}_{\beta}^{\mathbb{F}}=\langle x_2,x_1-x_3,x_1-x_4,y_1+y_3+y_4\rangle & \hat{L}_{\beta}^{\mathbb{F}}\cap\hat{L}_{\gamma}^{\mathbb{F}}=\langle x_2,-x_3+x_4+3(y_1+y_3+y_4)\rangle \\ \hat{L}_{\gamma}^{\mathbb{F}}=\langle x_2,y_1,x_3-3y_3,x_4+3y_4\rangle & \hat{L}_{\gamma}^{\mathbb{F}}\cap\hat{L}_{\alpha}^{\mathbb{F}}=\langle x_2,x_3-tx_4-3y_3-3ty_4\rangle \end{array} .\end{align*} $$
As in the first example, fix bases
$\hat {c}$
,
$\hat {b}$
, and
$\bar b$
to compute
$\tau (\hat {C}^{\scriptscriptstyle {\mathbb {F}}};\hat {c},\hat {h})$
. The computation gives
$\tau ^{\varphi }(X)=1-t\in \mathbb {F}/\Lambda ^*$
.
