Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-11T19:53:18.549Z Has data issue: false hasContentIssue false
  • English
  • Français

Onset of coherent electromagnetic structures in the relativistic electron beam deuterium-tritium fuel interaction of fast ignition concern

Published online by Cambridge University Press:  16 June 2008

C. Deutsch ,
A. Bret ,
M.-C. Firpo ,
L. Gremillet ,
E. Lefebvre  and
A. Lifschitz
C. Deutsch*
Affiliation:
LPGP, Université Paris-Sud, Orsay, France
A. Bret
Affiliation:
ETSIL, Universitad Castilla-la-Mancha, Ciudad-Real, Spain
M.-C. Firpo
Affiliation:
LPTP, Ecole Polytechnique, Palaiseau, France
L. Gremillet
Affiliation:
CEN, Bruyères-le-Châtel, France
E. Lefebvre
Affiliation:
LPGP, Université Paris-Sud, Orsay, France
A. Lifschitz
Affiliation:
LPGP, Université Paris-Sud, Orsay, France
*
Address correspondence and reprint requests to: C. Deutsch, Labortoire de Physique des Gaz et Plasma, University of Paris XI, Orsay 91405, France. E-mail: claude.deutsch@pgp.u-psud.fr
Rights & Permissions [Opens in a new window]

Abstract

We focus attention on the combinations of swiftly growing electromagnetic instabilities (EMI) arising in the interaction of relativistic electron beams (REB) with precompressed deuterium-tritium (DT) fuels of fast ignition interest for inertial confinement fusion (ICF). REB-target system is taken neutral in charge and current with distribution functions including target and beam temperatures. We stress also the significant impact on modes growth rates (GR) of mode-mode coupling and intrabeam scattering. Collisional damping is documented at large wave numbers in terms of inverse skin depth. A quasi-linear approach yields lower GR than linear ones. One of the most conspicuous output of the linear analysis are three-dimensional (3D) broken ridges featuring the largest GR above k-space for an oblique propagation w.r.t initial particle beam direction. The given modes are seen immune to any temperature induced damping. Those novel patterns are easily produced by considering simultaneously Weibel, filamentation and two-stream instabilities. The behaviors persist in the presence of smooth density gradients or strong applied magnetic fields. Moreover, in the very early propagation stage with no current neutralization in the presence of large edge density gradients, REB demonstrate a characteristics ringlike and regularly spiked pattern in agreement with recent experimental results and previous simulations.

Keywords

Electromagnetic instabilitiesFast IgnitionOblique ridge
Type
Research Article
Information
Laser and Particle Beams , Volume 26 , Issue 2 , June 2008 , pp. 157 - 165
Copyright
Copyright © Cambridge University Press 2008

INTRODUCTION

One notices a rather high level of current interest for the interaction physics of intense and relativistic electron beams (REB) with superdense deuterium + tritium (DT) plasmas. Corresponding target electron n p density ranges between 1023 electrons/cm−3 for the outer layer of compressed DT core and 1026 electrons/cm−3 at the center. Such a concern is basically motived by the fast ignition scenario (FIS) for inertial confinement fusion (ICF), driven by intense and laser produced REB with number density n b~1022 electrons/cm−3 (Tabak et al., Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason1994; Deutsch et al., Reference Deutsch, Furukawa, Mima and Nishihara1996, Reference Deutsch, Furukawa, Mima and Nishihara2000; Eliezer et al., Reference Eliezer, Murakami and Martinez-Val2007; Johzaki et al., Reference Johzaki, Sakagami, Nagatomo and Mima2007; Flippo et al., Reference Flippo, Hegelich, Albright, Yin, Gautier, Letzring, Schollmeier, Schreiber, Schulze and Fernandez2007; Hora, Reference Hora2007; Yu et al., Reference Yu, Yu, Xu, Tian, Chen and Wong2007). Such a scheme outlines to the extreme the separation of compression driven by lasers, heavy ion beams or Z pinches, from the controlled ignition through REB, which thus relieves to a large extent the energy request on initial precompression. The successful completion of such an approach to ICF demands a careful control of any electromagnetic instability susceptible to evolve very swiftly within the REB propagation, and nearly instantaneously, a significant amount of the incoming REB translation energy. That process is not only quantitative; it is also highly likely to occur through a filamentation with a substantial degradation of beam focusing capabilities (Bret et al., Reference Bret, Firpo and Deutsch2007; Malik, Reference Malik2007).

Recently, our group has devoted a very thorough scrutiny to the interplay of filamentation (Weibel, Reference Weibel1959) electromagnetic instabilities with the more mundane two-stream (TS) and longitudinal instability (Deutsch, Reference Deutsch2004; Firpo et al., Reference Firpo, Lifschitz, Lefebvre and Deutsch2006). As a result, a previously unnoticed oblique ridge has thus been unraveled in the space delimited by the growth rate and the two corresponding wave number coordinates. However, those studies are often restricted to a collisionless situation. A complete exploration, including collisions with TS altogether, is also worked out.

Here, we intend to focus attention on the very large densities implied in a realistic beam-target interaction of FIS interest (Tabak et al., Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason1994; Kodama et al., Reference Kodama, Norreys, Mima, Dangor, Evans, Fujita, Kitagawa, Krushelnik, Miyakoshi, Norimatsu, Rose, Shozaki, Shigemon, Sunahara, Tampo, Tanaka, Toyama, Yamanaka and Zepf2001). Despite that beam particle density n b always fulfill a weak beam approximation n b << n p, it should be taken around n b~1022 electrons/cm−3 to secure on a 10 ns time scale several tens of kJ to the off-center hot spot requested for DT ignition. Such a situation implies that the usual collisionless assumption used in working out electromagnetic instabilities through the Vlasov equation be removed. At this juncture, a few earlier endeavors dedicated to the interplay of electromagnetic instabilities with electron-electron collisions should be recalled (Taguchi et al., Reference Taguchi, Antonsen, Liu and Mima2001; Kono & Ichikawa, Reference Kono and Ichikawa1973; Mason, Reference Mason2006).

LINEAR AND QUASI-LINEAR FILAMENTATION GROWTH

Let us now consider a current neutral beam-plasma system. The relativistic electron beam propagates with the velocity vdb and the plasma return current flows with vdp. It is reasonable to assume that an electromagnetic mode has k normal to vdb, perturbed electric field E parallel to vdb, and perturbed magnetic field B normal to both vdb and E. So, the total asymmetric f 0 consists of non-relativistic background electrons and relativistic beam electrons:

(1)
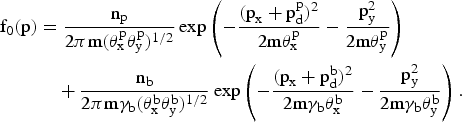
\eqalign{\hbox{f}_0 \lpar \hbox{p}\rpar & = {\hbox{n}_{\rm p} \over 2 \pi \hbox{m} \lpar \theta_{\rm x}^{\rm p} \theta_{\rm y}^{\rm p}\rpar ^{1/2}} \exp \left(-{\lpar \hbox{p}_{\rm x} + \hbox{p}_{\rm d}^{\rm p}\rpar ^2 \over 2 \hbox{m} \theta_{\rm x}^{\rm p}} - {\hbox{p}_{\rm y}^2 \over 2\hbox{m}\theta_{\rm y}^{\rm p}}\right)\cr & \quad + {\hbox{n}_{\rm b} \over 2 \pi \hbox{m} \gamma_{\rm b} \lpar \theta_{\rm x}^{\rm b} \theta_{\rm y}^{\rm b}\rpar ^{1/2}} \exp \left(-{\lpar \hbox{p}_{\rm x} + \hbox{p}_{\rm d}^{\rm b}\rpar ^2 \over 2\hbox{m}\gamma_{\rm b} \theta_{\rm x}^{\rm b}} - {{\rm p}_{\rm y}^2 \over 2\hbox{m} \gamma_{\rm b} \theta_{\rm y}^{\rm b}}\right).}

with γb = (1 + p2/mc)2)1/2 and m is the electron rest mass. Here θx, θy are the temperature components parallel to the x and y directions, P d is the drift momentum, and superscripts p an b represent the plasma electron and the beam electron, respectively.

The filamentation growth rate is then qualified by the asymmetry parameters

(2)
\hbox{A} = (\theta_{\rm x}^{\rm p} + \theta_{\rm d}^{\rm p^2}/\hbox{m}\rpar /\theta_{\rm y}^{\rm p} \quad \hbox{B} = \lpar \theta_{\rm x}^{\rm b} + \theta_{\rm d}^{\rm b^2}/\hbox{m}\gamma_{\rm b}\rpar /\theta_{\rm y}^{\rm b} \eqno \lpar 2\rpar

denoting, respectively, to the target plasma (p) and the REB (b). These linear parameters may by refined through mode-mode coupling and quasi-linear theory (Deutsch et al., Reference Deutsch, Bret, Firpo and Fromy2005) by including the shifted temperatures

(3)
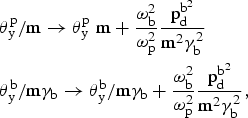
\eqalign{& \theta_{\rm y}^{\rm p}/{\rm m} \rightarrow \theta_{\rm y}^{\rm p} \; {\rm m}+ {\omega_{\rm b}^2 \over \omega_{\rm p}^2} {\hbox{p}_{\rm d}^{\rm b^2} \over \hbox{m}^2 \gamma_{\rm b}^2} \cr & \theta_{\rm y}^{\rm b}/\hbox{m}\gamma_{\rm b} \rightarrow \theta_{\rm y}^{\rm b}/\hbox{m}\gamma_{\rm b} + {\omega_{\rm b}^{2} \over \omega_{\rm p}^{2}} {\hbox{p}_{\rm d}^{\rm b^2} \over \hbox{m}^{2}\gamma_{\rm b}^{2}}, \cr} \eqno \lpar 3\rpar

where

\hbox{p}_{\rm d}^{\rm b} = \hbox{mV}_{\rm b}.

Using these parameters in the relevant linear dispersion relations, we obtain the filamentation growth rates depicted in Figures 1 to 4 as linear (L), and quasi-linear (QL), respectively. We then emphasize relatively hot T p = (1 keV) outer DT layers and 1-MeV REB with a thermal T b = 1 keV. Maximum GR δmax occurs close to the skin depth wavelength c/ωp. δmax is also shown steadily decaying with increasing Np. Also, quasi-linear (“turbulent”) GR profiles stand beneath linear ones.

Fig. 1. WEI GR profiles with T p = T b = 1 keV. E b = 1 MeV in terms of n and n1. (a) L, (b) QL. N p/N b = 10.

Fig. 2. Same caption as Figure 1 with N p/N b = 100.

Fig. 3. Same caption as Figure 1 with N p/N b = 1000.

Fig. 4. Same caption as Figure 1 with N p/N b = 10000.

COLLISIONS CONTRIBUTION

In view of the very high densities reached by the precompressed pellet, it seems rather mandatory to pay attention to collisions between e-beam and target ions. Very often, these contributions are neglected in many standard treatments of the Weibel instability. A large consensus even asserts that collisions remain helpless against transverse electromagnetic growth rates. Nonetheless, no one has given ground to the validity of such a claim in the present extreme situation we are now considering. To clear up this point, we included in the present treatment, a Krook collision term with the right-hand side of the corresponding Vlasov equation.

We use a split Krook term υ = υp + υb. Both terms essentially document the electron-electron collision frequency

(4a)
\nu_{\rm p\comma b} = 2.91 \times 10^{-6} {\hbox{n}_{\rm p\comma b} \lpar \hbox{cm}^{-3}\rpar \over \hbox{T}_{\rm p\comma b} \lpar \hbox{eV}\rpar ^{3/2}} \ell {\rm n}\Lambda_{\rm p\comma b}\comma

in terms of usual Coulomb logarithm. n p should also include a small electron-ion term υp/2.5, so one finally gets

(4b)
\nu_{\rm p} = 3.31 \times 10^{-6} {\hbox{n}_{\rm p} \lpar \hbox{cm}^{-3}\rpar \over \hbox{T}_{\rm p} \lpar \hbox{eV}\rpar ^{3/2}} \ell \hbox{n}\Lambda_{\rm p}\comma
(4c)
\nu_{\rm b} = 2.91 \times 10^{-6} {\hbox{n}_{\rm b} \lpar \hbox{cm}^{-3}\rpar \over \hbox{T}_{\rm b} \lpar \hbox{eV}\rpar ^{3/2}} \ell {\rm n}\Lambda_{\rm b}.

In Eqs. (4a)–(4c), one has

\ell \hbox{n} \Lambda_{\rm p\comma b} = \ell \hbox{n}\lsqb 9 \hbox{N}_{\rm D}\rsqb \comma \;

with

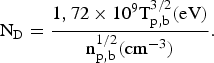
\hbox{N}_{\rm D} = {1\comma 72 \times 10^{9} \hbox{T}_{\rm p\comma b}^{3/2} \lpar \hbox{eV}\rpar \over {\rm n}_{\rm p\comma b}^{1/2} \lpar \hbox{cm}^{-3}\rpar }.

Target plasma is taken in thermal equilibrium (T e = T i) with $\bar{Z} = 1$ for a DT mixture. Ion-ion collision frequency,

\nu_{\rm p} \cong {2.9 \times 10^{-6} \over 60} {\hbox{n}_{\rm p} \lpar \hbox{cm}^{-3}\rpar \over \hbox{T}_{\rm p} \lpar \hbox{eV}\rpar ^{3/2}} \ell \hbox{n}\Lambda_{\rm p}\comma

is usually negligible. In Figures 1–4, n ≡ υp while n1 ≡ υb.

The isotropic target temperature is taken to be systematically larger than the corresponding Fermi T F accounting for nonnegligible quantum effects. We observe that as target electron density increases from 1023 up to 1025 cm−3, the discrepancy between linear L and quasi-linear QL growth rates progressively disappear. Also, collision-corrected growth rates δ have a tendency to rise above the collisionless ones for 10−2 ≤ kc/ωp ≤ 1. However, only the collision-corrected ones abruptly decay to negative (stabilization) values for 1 ≤ kc/ωp ≤ 10. So even in this rather extreme case of transverse electromagnetic instability, the beam-target collision asserts their usual damping role, as a priori expected on empirical grounds.

A WIDER PERSPECTIVE

Up to now we arbitrarily restricted attention to the filamentation instability in the given beam-plasma system. Corresponding E and k may also be permuted to produce the TS and the Weibel instabilities. More generally, it is also possible to include any nonnormal relative orientation between E and k (Bret et al., Reference Bret, Firpo and Deutsch2004, Reference Bret, Firpo and Deutsch2006). One of our most conspicuous finding is the appearance of fastest growing modes at oblique propagation (Bret et al., Reference Bret, Firpo and Deutsch2004, Reference Bret, Firpo and Deutsch2006), denoted as TS-filamentation instability (TSF).

As far as the REB-target plasma is considered, it is recalled that the target remains non-relativistic with a temperature below 10 keV, while a fiducial REB, let say a 4 MeV one (γb = 5) can feature a 500 keV relativistic energy spread. In the linear stage, filamentation is generally studied under some simplifying ab-initio transverse approximation of the dielectric tensor, so that filamentation instability is attributed to the exponential growth of unstable electromagnetic purely transverse modes (k · E = 0) with wave vector k normal to the beam (Bret et al., Reference Bret, Firpo and Deutsch2004; Deutsch et al., Reference Deutsch, Bret, Firpo and Fromy2005). It is also common to refer to this instability as Weibel instability (Bret et al., Reference Bret, Firpo and Deutsch2004, Reference Bret, Firpo and Deutsch2005a, Reference Bret, Firpo and Deutsch2005b), through the original mode (Weibel, Reference Weibel1959) has its wave vector along the beam. Figure 5 sketches the original definitions of various modes. As long as the beam is not relativistic, the largest instability it undergoes is the TS one, where the second “stream” is the return current it generates in the plasma. But in the relativistic regime, the “filamentation” growth rate eventually exceeds the TS one and is supposed to induce beam filamentation.

Fig. 5. Weibel, two-steam and filamentation modes.

In reality, the beam suffers many more instabilities at the same time. Indeed, filamentation, Weibel or TS instabilities pertain to various orientations of the wave vector and various kinds of waves (transverse or longitudinal), but in the real world, the beam-plasma system triggers every possible modes allowed by Maxwell equations with a wide range of wave vector orientation. Among all the triggered modes, the unstable ones shall start growing exponentially, while the most unstable ones shall mostly shape the beam. When it comes to knowing how the beam is eventually affected when entering the plasma, one needs therefore to answer two questions: (1) which is the most unstable mode all over, the k space for the system investigated? and (2) how shall this mode shape the beam? Following the guideline built by these two questions, we can assert that the so-called “filamentation” instability is not the fastest growing instability, even in the relativistic regime, so that it is not the answer to the first question. As for the second question, we shall see that this instability would not produce the observed effects anyway, even if it were the stronger one. For clarity, we shall keep labeling the most unstable transverse mode with wave vector normal to the beam as the “filamentation” mode, though our point is precisely that it does not filament.

We now write the growth rate of the three instabilities with the first order temperature corrections for a collisionless plasma and non-relativistic beam and plasma temperatures. As previously mentioned, there is a continuum of unstable modes so that there is not one TS mode, nor is there one filamentation mode. But when speaking about the “TS growth rate” for example, we actually mean “the maximum growth rate found on the TS profile.” With this in mind, growth rates for the TS, the filamentation, and the TS/filamentations instabilities are (Bret et al., Reference Bret and Deutsch2005c; Bret & Deutsch, Reference Bret and Deutsch2006) (α = N b/N p),

(5)
\eqalign{\delta_{\rm TS} & = \omega_{\rm p} {\sqrt{3} \over 2^{4/3}} {\alpha^{1/3} \over \gamma_{\rm b}}\comma \; \cr \delta_{\rm TSF} & = \omega_{\rm p} {\sqrt{3} \over 2^{4/3}} \left({\alpha \over \gamma_{\rm b}}\right)^{1/3}\comma \cr \delta_{\rm F} & = \omega_{\rm p} \beta {\sqrt{\alpha} \over \gamma_{\rm b}} \left(1 - {\rho_{\rm b} \over \sqrt{\alpha \gamma_{\rm b}}}\right).}

It is then readily seen than the largest growth rate for a relativistic beam is the TSF one in view of its 1/γb1/3 scaling. Turning to the z component of the phase velocity for these three modes, we know it is equal to the beam velocity for the TS and TSF modes (Bret et al., Reference Bret, Firpo and Deutsch2005c; Bret & Deutsch, Reference Bret and Deutsch2006) whereas, as previously mentioned, it vanishes for the Filamentation instability.

Figure 6 displays the growth rates on the TSF branch in the (k⊥, k//) plane for some zero or finite plasma thermal velocities Vtp = Y tp// = V tp⊥ and some zero or finite beam transverse thermal velocities V tb⊥. These curves clearly show that when temperatures are accounted for they act to control the instability domain, damping the small wavelengths perturbations along the filamentation direction (k// = 0), and deforming the growth rates surface so that a maximum growth rate appears for a finite oblique wave vector k M.

Fig. 6. Growth rates on the TSF branch in terms of Z = kVb/ωp with $\hbox{V}_{\rm b}\vert\, \vert \mathop{z}\limits^{\frown}$. (a) Cold beam – cold plasma. (b) Hot beam – cold plasma ad (c) Hot beam – hot plasma. Parameters are α = 0.05 and γb = 4 for (abc). Vtb⊥ = Vb/10 for (b,c) and Vtp = Vb/10 for (c).

EARLY STAGE EVOLUTION

We shall consider the out-of-equilibrium initial value dynamical problem taking place when a radically inhomogeneous electron forward current is launched into plasma and is still not current compensated (Firpo et al., Reference Firpo, Lifschitz, Lefebvre and Deutsch2006). We shall focus on this early stage where collisions may be neglected. Ions will be assumed to form a fixed neutralizing background. In order to simplify both the analysis and the numerical PIC computations, we shall consider the system to be infinite along the beam direction z. We remove any z dependence by assuming also that plasma density n pe is uniform and constant. At time t = 0, a REB is switched on in the plasma. Maxwell equations are linear and can thus be solved for all time to yield the electromagnetic fields as functions of the sources, namely beam and plasma current densities.

We consider initial beam density and velocity of the form $\hbox{n}_{\rm b0} \lpar \hbox{r}\rpar = \hbox{n}_{\rm b0}\bar{n}\lpar \tilde{\hbox{r}}\rpar$ and $\upsilon_{\rm b0z}\lpar \hbox{r}\rpar = \upsilon_{\rm b0z}\bar{\upsilon}\lpar \tilde{\hbox{r}}\rpar$ with $\tilde{\rm r} = \hbox{r}/\hbox{r}_{\rm b}$. Let us introduce here the beam radius r b, the electron skin depth λs ≡ c/ωp, their ratio η ≡ rb/λs, and let us redefine α = nb0/npe, β0 = υb0z/c and the initial relativistic Lorentz factor $\gamma_0 = \lpar 1 - \upsilon_{\rm b0z}^{2}/\hbox{c}^{2}\rpar^{-1/2} = \lpar 1 - \beta_{0}^{2}\bar{\upsilon}^{2}\rpar^{-1/2} = \gamma_0 \lpar \tilde{\rm r}\rpar$. Let us consider some initially mono-kinetic beam having density functions of the form $\bar{\hbox{n}}\lpar \tilde{\rm r}\rpar = \lpar \tan \hbox{h}[2\kappa \lpar 1 - \tilde{\rm r}\rpar] + 1\rpar/2$. This enables the study of the influence of the beam edge gradients as $\kappa = -\bar{\hbox{n}}^{\prime}\lpar \tilde{\hbox{r}} = 1\rpar$.

Our analysis shows that depending on its initial radial density and velocity distribution, the shape of an electron beam propagating in plasma may evolve into a transient ring structure. This results from the natural evolution of the system and not from the usually invoked filamentation instability. If its transverse temperature is low enough, filamentation instability eventually proceeds. The observation of the ring structure is favored by sharp beam edges and not too large beam radius (compared to the electron skin depth). It is not generic which may explain the variety of experimental observations.

Figure 7 presents the longer term evolution of the transverse components of beam velocity for a mono-kinetic beam with a larger value of α (α = 0.15) and smaller γ0 (γ0 = 3). As previously, there is an initial phase, between t = 0 and 20 ωp−1, during which radial velocity grows fast and poloidal velocity remains small. For ωpet ≅ 20, we can see in the inset of Figure 7, that beam density presents a clear ring structure at its edge (Taguchi et al., Reference Taguchi, Antonsen, Liu and Mima2001). When the beam current is partially neutralized, filamentation instability starts, breaking the initial azimuthal system symmetry and producing the exponential growth of poloidal beam velocity.

Fig. 7. Early time evolution of the modulus of the radial average of the transversal beam velocity (βr = υr/c and βθ = νθ/c) in lin-log scale for α = 0.15, γo = 3, η = 10 and κ = 20. Beam and plasma transverse temperatures are 5 keV.

CONCLUDING REMARKS

Indulging now into a more global perspective, one could wonder about further refinements of growth rate calculations, beyond the present quasi-linear formalism. A preliminary step in this direction could involve a three-wave interaction mechanism. However, the numerous and very intense PIC simulations devoted to the fully nonlinear regime obviously demand a more ambitious theoretical framework. Despite that such a framework in not yet available, one could speculate that present quasi-linear improvements have only the status of higher order corrections to an initial asymptotic approximation to the complete nonlinear growth rate. In such an occurrence, it appears problematic to bridge straightforwardly the wide gap between present quasi-linear treatment and a fully nonlinear one.

Presently, it appears much more profitable to enlarge the linear approximation by superimposing three electromagnetic instabilities: Weibel, filamentation, and TS, while allowing the wave-number vector $\vec{\hbox{k}}$ to take any orientation. Such an approach demonstrates that maximum growth rates appear on an oblique ridge between transverse and parallel directions with respect to the initial beam. It seems to us that quasi-linear corrections to this combined approach of electromagnetic instabilities might be worth while to pursue.

Moreover, it seems to us that more and still unraveled nonlinear phenomena lie in store in the very early stage of the beam-plasma interaction when counter streaming ionic flow has not yet reached a full current neutralization regime.

References

REFERENCES

Bret, A. & Deutsch, C. (2005). Hierarchy of beam plasma instabilities up to high beam densities for fast ignition scenario. Phys. Plasmas 12, 082704-1-6.Google Scholar
Bret, A. & Deutsch, C. (2006). Density gradient effects on beam plasma linear instabilities for fast ignition scenario. Laser Part. Beams 24, 269–273.CrossRefGoogle Scholar
Bret, A., Firpo, M.C. & Deutsch, C. (2007). About the most unstable modes encountered in beam plasma interaction physics. Laser Part. Beams 25, 117–119.CrossRefGoogle Scholar
Bret, A., Firpo, M.C. & Deutsch, C. (2004). Oblique instabilities in electron-beam plasma interactions. Phys. Rev. E 70, 046401-1-15.CrossRefGoogle Scholar
Bret, A., Firpo, M.C. & Deutsch, C. (2005a). Bridging a gap between two-stream and filamentation instabilities. Laser & Part. Beams 23, 375–383.CrossRefGoogle Scholar
Bret, A., Firpo, M.C. & Deutsch, C. (2005b). Characterization of the initial filamentation of a relativistic electron beam passing through a plasma. Phys. Rev. Lett. 94, 115002.CrossRefGoogle ScholarPubMed
Bret, A., Firpo, M.C. & Deutsch, C. (2005c). Collective electromagneric instabilities for relativistic beam-plasma interaction in whole k-space: Nonrelativistic beam and plasma temperature effects. Phys. Rev. E 72, 016403-1-14.CrossRefGoogle Scholar
Bret, A., Firpo, M.C. & Deutsch, C. (2006). Between two-stream and filamentation Instabilities: Temperature and collision effects. Laser Part. Beams 24, 27–33.CrossRefGoogle Scholar
Deutsch, C. (2004). Penetration of intense particle beams in the outer layers of precompressed thermonuclear fuels. Laser Part. Beams 22, 115–120.CrossRefGoogle Scholar
Deutsch, C., Bret, A., Firpo, M.C. & Fromy, P. (2005). Interplay of collisions with quasilinear growth rates of relativistic electron beam driven instabilities in a superdense plasma. Phys. Rev. 72, 026402-1-12.Google Scholar
Deutsch, C., Furukawa, H., Mima, K. & Nishihara, K. (1996). Interaction physics of the fast ignitor concept. Phys. Rev. Lett. 77, 2483–2486.CrossRefGoogle ScholarPubMed
Deutsch, C., Furukawa, H., Mima, K. & Nishihara, K. (2000). Erratum: Interaction fast ignitor concept. Phys. Rev. Lett. 31, 1140.CrossRefGoogle Scholar
Eliezer, S., Murakami, M. & Martinez-Val, J.M.M. (2007). Equation of state and optimum compression in inertial fusion energy. Laser Part. Beams 25, 585–592.CrossRefGoogle Scholar
Firpo, M.C., Lifschitz, A.F., Lefebvre, E. & Deutsch, C. (2006). Early out-of-equilibrium beam-plasma evolution. Phys. Rev. Lett. 96, 115004-1-4.CrossRefGoogle ScholarPubMed
Flippo, K., Hegelich, B.M., Albright, B.J., Yin, L., Gautier, D.C., Letzring, S., Schollmeier, M., Schreiber, J., Schulze, R. & Fernandez, J.C. (2007). Laser-driven ion accelerators: Spectral control, monoenergetic ions and new acceleration mechanisms. Laser Part. Beams 25, 3–8.CrossRefGoogle Scholar
Hora, H. (2007). New aspects for fusion energy using inertial confinement. Laser Part. Beams 25, 37–45.CrossRefGoogle Scholar
Johzaki, T., Sakagami, H., Nagatomo, H. & Mima, K. (2007). Holistic simulation for FIREX project with FI3. Laser Part. Beams 25, 621–629.CrossRefGoogle Scholar
Kodama, R., Norreys, P.A., Mima, K., Dangor, A.E., Evans, R.G., Fujita, H., Kitagawa, Y., Krushelnik, K., Miyakoshi, T., Norimatsu, T., Rose, S.J., Shozaki, T., Shigemon, K., Sunahara, A., Tampo, M., Tanaka, K.A., Toyama, Y., Yamanaka, T. & Zepf, M. (2001). Fast heating of ultrahigh-density plasma as step towards laser fusion ignition. Nature 412, 798–802.CrossRefGoogle ScholarPubMed
Kono, M. & Ichikawa, Y.H. (1973). Renormalization of wave-particle interaction in weakly turbulent plasmas. Prog. Theor. Phys. 49, 754–763.CrossRefGoogle Scholar
Malik, H.K. (2007). Oscillating two stream instability of a plasma wave in a negative ion containing plasma with hot and cold positive ions. Laser Part. Beams 25, 397–406.CrossRefGoogle Scholar
Mason, R.J. (2006). Heating mechanisms in short-pulse laser-driven cone targets. Phys. Rev. Lett. 96, 035001-1-4.CrossRefGoogle ScholarPubMed
Tabak, M., Hammer, J., Glinsky, M.E., Kruer, W.L., Wilks, S.C., Woodworth, J., Campbell, E.M., Perry, M.D. & Mason, R.J. (1994). Ignition and high-gain with ultrapowerful lasers. Phys. Plasmas 1, 1626–1634.CrossRefGoogle Scholar
Taguchi, T., Antonsen, T.M., Liu, C. & Mima, K. (2001). Structure formation and tearing of an MeV cylindrical electron beam in a laser-produced plasma. Phys. Rev. Lett. 86, 5055–5058.CrossRefGoogle Scholar
Weibel, E.S. (1959). Spontaneously growing transverse waves in a plasma due to an anisotropic velocity distribution. Phys. Rev. Lett. 2, 83.CrossRefGoogle Scholar
Yu, W., Yu, M.Y., Xu, H., Tian, Y.V., Chen, J. & Wong, A.Y. (2007). Intense local plasma heating by stopping of ultrashort ultraintense laser pulse in dense plasma. Laser Part. Beams 25, 631–638.CrossRefGoogle Scholar
Figure 0

Fig. 1. WEI GR profiles with Tp = Tb = 1 keV. Eb = 1 MeV in terms of n and n1. (a) L, (b) QL. Np/Nb = 10.

Figure 1

Fig. 2. Same caption as Figure 1 with Np/Nb = 100.

Figure 2

Fig. 3. Same caption as Figure 1 with Np/Nb = 1000.

Figure 3

Fig. 4. Same caption as Figure 1 with Np/Nb = 10000.

Figure 4

Fig. 5. Weibel, two-steam and filamentation modes.

Figure 5

Fig. 6. Growth rates on the TSF branch in terms of Z = kVb/ωp with $\hbox{V}_{\rm b}\vert\, \vert \mathop{z}\limits^{\frown}$. (a) Cold beam – cold plasma. (b) Hot beam – cold plasma ad (c) Hot beam – hot plasma. Parameters are α = 0.05 and γb = 4 for (abc). Vtb⊥ = Vb/10 for (b,c) and Vtp = Vb/10 for (c).

Figure 6

Fig. 7. Early time evolution of the modulus of the radial average of the transversal beam velocity (βr = υr/c and βθ = νθ/c) in lin-log scale for α = 0.15, γo = 3, η = 10 and κ = 20. Beam and plasma transverse temperatures are 5 keV.