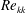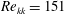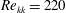1. Introduction
Surface roughness can lead to premature transition from laminar to turbulent flow within a boundary layer. Smith & Clutter (Reference Smith and Clutter1959), von Doenhoff & Braslow (Reference von Doenhoff and Braslow1961), and Tani (Reference Tani1969) showed that roughness can be parametrized in terms of a roughness Reynolds number (
$\mathit{Re}_{kk}=U_{k}k/{\it\nu}$
, where
$U_{k}$
is the velocity at height
$k$
in the undisturbed boundary layer). If
$\mathit{Re}_{kk}$
is above a critical value, the boundary layer transitions prematurely downstream of the roughness. These studies provided initial insight into whether or not discrete roughness leads to boundary layer transition. However, they do not explain the physical mechanisms that lead to transition. Initial attempts to understand the role of roughness in boundary layer transition focused unsuccessfully on the growth of modal instabilities such as Tollmien–Schlichting (T–S) waves. For example, Singh & Lumley (Reference Singh and Lumley1971) calculated roughness-induced mean velocity profiles and their resulting T–S wave growth rates. They found that the resulting roughness-induced velocity profile was more stable to T–S waves, but argued that roughness may introduce the disturbances that lead to transition.
Recently, transient growth has emerged as an explanation for roughness-induced transition. Reshotko (Reference Reshotko2001) was one of the first to link roughness-induced transition and transient growth. Transient growth occurs through a combination of stable, non-orthogonal disturbance modes. As the disturbance modes decay at different spatial rates, their sum can grow due to the non-orthogonal nature of the linear stability equations. If this growth is large enough, transition could occur due to secondary instabilities. Transient growth can occur upstream of the onset of modal instabilities and thus can explain boundary layer transition where linear stability analysis indicates a stable boundary layer.
A majority of theoretical work regarding spatial transient growth has focused on optimal disturbances, or the disturbances that undergo the maximum spatial transient growth over a specified domain. Several authors (Andersson, Berggren & Henningson Reference Andersson, Berggren and Henningson1999; Luchini Reference Luchini2000; Andersson et al.
Reference Andersson, Brandt, Bottaro and Henningson2001; Tumin & Reshotko Reference Tumin and Reshotko2001) have studied spatial optimal growth in zero-pressure gradient boundary layers. All of these authors found similar results; for a Blasius boundary layer, optimal disturbances are stationary (
${\it\omega}=0$
) streamwise vortices with a non-dimensional spanwise wavenumber (
${\it\beta}=(2{\rm\pi}/{\it\lambda})(x/\sqrt{\mathit{Re }_{x}})$
) near 0.45. Experiments at Case Western Reserve University (White Reference White2002; White, Rice & Ergin Reference White, Rice and Ergin2005; Ergin & White Reference Ergin and White2006; Denissen & White Reference Denissen and White2008; Denissen, Downs & White Reference Denissen, Downs and White2009) showed that the nature of transient growth in each case is highly dependent on receptivity. Instead of creating optimal disturbances, the roughness arrays created disturbances that remained closer to the wall than predicted by optimal theory. Further, White et al. (Reference White, Rice and Ergin2005) showed that the nature of roughness-induced transient growth can be changed by varying the height and width of the roughness. They showed that the disturbance energy of steady disturbances initiated by cylindrical roughness elements can be scaled by
$\mathit{Re}_{kk}^{2}$
.
Once roughness has initiated steady disturbances that undergo transient growth, the high- and low-speed streaks can modify the nature of boundary layer transition. Cossu & Brandt (Reference Cossu and Brandt2002) and Fransson et al. (Reference Fransson, Talamelli, Brandt and Cossu2006) have shown that introducing high- and low-speed streaks to a Blasius boundary layer can reduce the growth of T–S waves. Alternatively, the streaks can lead to secondary instabilities caused by spanwise inflectional profiles in the wake structure. This was shown by Andersson et al. (Reference Andersson, Brandt, Bottaro and Henningson2001), who performed bi-global stability analysis on optimal disturbances in a Blasius boundary layer, and Denissen & White (Reference Denissen and White2013), who performed similar calculations on sub-optimal streaks. Experimentally, Ergin & White (Reference Ergin and White2006) measured the secondary instabilities in the wake of a cylindrical roughness element.
Despite the progress made in understanding transient growth created by discrete roughness, less work has focused on transient growth initiated by distributed roughness. Many experiments have tested the effect of distributed roughness on boundary layer transition; however, only a handful of these experiments have made the detailed measurements necessary to quantify roughness-induced disturbance growth. Reshotko & Leventhal (Reference Reshotko and Leventhal1981) measured streamwise velocity over a flat plate with sandpaper roughness. In their experiment, the distributed roughness displaced the boundary layer away from the wall. They also measured low-frequency oscillations that were later identified as transient growth (Reshotko Reference Reshotko2001). Kendall (Reference Kendall1981) used glass beads to create a distributed roughness field and noticed the same displacement of the boundary layer away from the wall. Corke, Bar-Sever & Morkovin (Reference Corke, Bar-Sever and Morkovin1986) measured enhanced growth of T–S waves in the presence of sandpaper roughness in a flat plate boundary layer. The roughness, which was located downstream of the T–S wave neutral stability curve, modified the growth rate of T–S waves. Transition occurred through the breakdown of these T–S waves rather than an instability initiated by the roughness.
Downs, White & Denissen (Reference Downs, White and Denissen2008) used rapid prototyping to create patches of ‘random’ roughness with a known streamwise and spanwise wavelength distribution. Unlike previous experiments with sand-grain roughness, the rapid-prototyped roughness had a zero mean value. Hotwires measured the streamwise velocity both above and downstream of the roughness patches, and the decomposed velocity field indicated the presence of transient growth.
Direct numerical simulation of the Downs et al. (Reference Downs, White and Denissen2008) experiment by Drews et al. (Reference Drews, Downs, Doolittle, Goldstein and White2011) and Drews (Reference Drews2012) examined the flow downstream of distributed roughness patches. The DNS and experiment were in good agreement. Examination of the near-wake showed that the three largest peaks amongst the distributed roughness created the majority of the steady velocity disturbances that underwent transient growth. In a subsequent DNS case, the roughness valleys (
$y<0$
) were replaced with a slip surface at
$y=0$
. The flow downstream of the roughness was not strongly altered. This showed that the valleys do not play a significant role in receptivity. A third DNS case was tested where all of the roughness except the three largest peaks were removed. In this case, the steady velocity disturbance increased relative to the baseline case. This suggests that the presence of ‘foothills’ lessens the receptivity of larger roughness peaks.
The findings of Drews et al. (Reference Drews, Downs, Doolittle, Goldstein and White2011) and Drews (Reference Drews2012) are consistent with the findings of Kendall (Reference Kendall1981) who placed a discrete element amongst a field of smaller-amplitude distributed roughness. The wake deficit of the discrete element in the distributed roughness case was only one third of that in the smooth wall case. These experiments highlight the need to quantify receptivity of roughness ‘peaks’ located in a field of distributed roughness.
The goal of this work is to further study the shielding effect in order to better understand the receptivity of distributed and discrete roughness. Different roughness configurations (combinations of a deterministic distributed roughness patch and a discrete roughness element) were manufactured using rapid prototyping and placed flush with the wall within a flat plate boundary layer. Detailed hotwire scans, both above and downstream of the roughness, quantify the velocity in the boundary layer. The boundary layer profiles are decomposed into a basic state, a steady, spanwise modulation of the flow, and unsteady disturbances. The hotwire scans, in conjunction with naphthalene flow visualization, provide insight into both the receptivity of distributed and discrete roughness and the transition created by this roughness.
2. Experimental set-up
This work was performed in the Klebanoff–Saric Wind Tunnel (KSWT) at Texas A&M University. The KSWT is a closed-loop, low-speed, low-disturbance wind tunnel designed for boundary layer stability and transition experiments. Hunt et al. (Reference Hunt, Downs, Kuester, White and Saric2010) describe the KSWT and its flow quality. The test section is 4.9 m long and has a
$1.4~\text{m}\times 1.4~\text{m}$
cross-section at the upstream end. The test section diverges slightly to account for boundary layer growth on the tunnel walls. The freestream speed in the test section can be set between 1 and
$30~\text{m}~\text{s}^{-1}$
within
$\pm 0.1~\text{m}~\text{s}^{-1}$
. At
$10~\text{m}~\text{s}^{-1}$
, the freestream turbulence intensity is less than 0.02 % (Hunt et al.
Reference Hunt, Downs, Kuester, White and Saric2010), and the freestream pressure fluctuations above 30 Hz are 83.6 dB (Kuester & White Reference Kuester and White2014).
The experiment was performed using a 4.4 m long flat plate that spans the test section; a diagram of the plate is shown in figure 1. The plate is constructed of paper honeycomb covered in a 1 mm thick aluminum skin. The plate has a 343 mm long elliptical leading edge and a trailing edge flap to set the stagnation point on the test side of the plate. The plate is polished to a surface finish of
$0.32~{\rm\mu}\text{m}$
root-mean-squared (r.m.s.) to create a near-mirror finish.
Figure 1. Flat plate model for roughness experiments (dimensions in mm).
A rectangular hole was cut through the plate so different roughness configurations can be mounted flush with the plate surface. The hole is
$229~\text{mm}\times 279~\text{mm}$
and is located in the centre of the plate, 849 mm downstream of the leading edge. The hole is located far enough upstream that turbulent wedges from the plate/wall intersection do not interfere with the experiment.
Different roughness configurations were tested by manufacturing roughness inserts and installing them in the hole in the plate. The roughness inserts were secured to a frame installed on the non-test side of the plate, and the inserts were shimmed so the step between the top of the insert and the plate was less than
$40~{\rm\mu}\text{m}$
. The gap between the insert and the plate was filled using automobile body filler and sanded to create a smooth interface between the plate and the roughness insert.
2.1. Basic state boundary layer
During the preliminary stages of the experiment, the plate was carefully aligned (using adjustable mounting brackets) to create a near-zero pressure gradient boundary layer. For this alignment and all subsequent tests, the tunnel was operated at constant Reynolds number conditions. Alignment was verified by measuring boundary layer profiles using a hotwire at multiple streamwise and spanwise locations. Only stations outside the influence of the surface roughness were used in these measurements. Equation (2.1) shows the nonlinear curve fit used to define the boundary layer length scale (
${\it\delta}$
) over the entire plate:
$$\begin{eqnarray}{\it\delta}=\sqrt{\frac{x-x_{VLE}}{\mathit{Re}^{\prime }}}=\frac{{\it\theta}}{0.664},\end{eqnarray}$$
where
$x_{VLE}$
is the virtual leading edge of the Blasius boundary layer, and
$\mathit{Re}^{\prime }$
is the unit Reynolds number. Figure 2 shows the
$x_{VLE}/\mathit{Re}^{\prime }$
fit for all of the test conditions, while table 1 lists the fit parameters and their associated uncertainties. The distributed roughness only measurements (solid lines and open circles) were made in the first tunnel entry, while the discrete roughness only and combined roughness measurements (dashed lines and filled circles) were performed during a second tunnel entry. The momentum thickness measurements and curve fit were performed for each Reynolds number during both tunnel entries.
Figure 2.
$x_{VLE}/\mathit{Re}^{\prime }$
fits for all test configurations. The open circles represent measurements for the first entry (distributed roughness only), while the filled circles represent measurements for the second entry (discrete only and combined roughness). The solid vertical line shows the location of the discrete roughness element, while the dashed vertical lines show the location of the distributed roughness.
Table 1.
$x_{VLE}/\mathit{Re}^{\prime }$
fit parameters for each test condition.
${\it\theta}_{roughness}$
indicates the momentum thickness at the streamwise location of the distributed roughness.
For the Reynolds numbers used in this experiment, unstable T–S waves have small growth rates. Even though the roughness is placed downstream of branch I for T–S waves, the largest N-factor within the measurement region is 3.3. Given the low turbulence and sound levels in this tunnel, T–S waves in this frequency range remain small and do not lead to transition within the measurement domain. The high- and low-speed streaks created by the surface roughness may reduce the growth rates of T–S waves (Cossu & Brandt Reference Cossu and Brandt2002), but the primary focus of this experiment is steady disturbances that can lead to transition through secondary instabilities. The Reynolds number for natural transition on this flat plate in this wind tunnel is greater than
$2.4\times 10^{6}$
, so any transition observed in the experiment is associated with the roughness on the insert.
The same measurements used for the
$x_{VLE}/\mathit{Re}^{\prime }$
fit were also used to evaluate the local pressure gradient. The shape factor (
$H$
) of each boundary layer profile was computed and compared to the shape factor of a Blasius boundary (2.591). In all of the cases, the shape factor at a streamwise location was
$2.59\pm 0.05$
.
In addition to the measurements at multiple streamwise locations, boundary layer scans were performed upstream of the roughness to evaluate the spanwise uniformity of the boundary layer. In all of the configurations tested, the spanwise variations in
${\it\theta}$
,
${\it\delta}^{\ast }$
and
$H$
were less than 1.2 %, with typical variations between 0.5 % and 1.0 %.
2.2. Roughness design
The roughness configurations were designed to have a known, manufacturable shape so that the experimental set-up could be duplicated using direct numerical simulations. Three different roughness configurations (distributed roughness, discrete roughness, and combined roughness) were designed to investigate the shielding effect. The distributed roughness used in this experiment consisted of a sum of cosine functions:
$$\begin{eqnarray}h(x,z)=\mathop{\sum }_{m=-M_{r}}^{M_{r}}\mathop{\sum }_{n=1}^{N_{r}}({\rm\Delta}(m,n))A_{m,n}\cos \left(\frac{2{\rm\pi}nx}{{\it\lambda}_{x}}+\frac{2{\rm\pi}mz}{{\it\lambda}_{z}}+{\it\phi}_{m,n}\right).\end{eqnarray}$$
The amplitudes (
$A_{m,n}$
) were selected from a Gaussian distribution, while the phases (
${\it\phi}_{m,n}$
) were selected from a uniform distribution on the interval
$[0,2{\rm\pi}]$
. The roughness patch length (
${\it\lambda}_{x}$
) is 128 mm, and the roughness patch width (
${\it\lambda}_{z}$
) is 32 mm. The number of spanwise modes (
$M_{r}$
) is set to 10, while the number of streamwise modes (
$N_{r}$
) is set to 40;
$M_{r}$
and
$N_{r}$
differ by a factor of four because the length of the roughness patch is four times longer than its width. The amplitudes are weighted by the function
${\rm\Delta}(m,n)$
to set the smallest roughness wavelength at
$(0.0995){\it\lambda}_{z}$
:
$$\begin{eqnarray}{\rm\Delta}(m,n)=\left\{\begin{array}{@{}ll@{}}1\quad & \displaystyle \text{if }\left(\frac{n}{4}\right)^{2}+m^{2}\leqslant 10^{2}+1\text{ and }m\neq 0\\ 0\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
The weighting function also removes the purely streamwise roughness mode. The roughness patch is then multiplied by a window function to create 8 mm wide strips that run in the streamwise direction between roughness patches. These strips are used to locate the position of the wall during post-processing of hotwire scans. In addition to the roughness flats, the windowing function creates a 4 mm wide cosine ramp into the ‘rough’ section of the patch. Figure 3 shows the post-windowed roughness patch. The largest-amplitude roughness modes (post-windowing) are shown in table 2. These wavelengths are provided not to suggest that receptivity for each wavelength is linear; both experiments (White et al. Reference White, Rice and Ergin2005; Downs et al. Reference Downs, White and Denissen2008) and computations (Tumin & Reshotko Reference Tumin and Reshotko2005; Kurz & Kloker Reference Kurz and Kloker2014) have shown nonlinear receptivity to surface roughness, even for roughness with a zero spanwise mean. Instead, these wavelengths are provided in order to fully define the roughness surface and relate the predominant roughness wavelengths to the boundary layer thickness.
Figure 3. Roughness patch (
$k=1~\text{mm}$
), after windowing.
Figure 4. Combined roughness configuration (
$k_{discrete}=1.00~\text{mm}$
,
$k_{distributed}=0.85~\text{mm}$
).
Table 2. Maximum roughness amplitudes (post-windowing).
The shape of the discrete roughness was chosen to promote collaboration between numerical simulations and this experiment. Earlier simulations of the flow around a circular-cylinder roughness element by Stephani & Goldstein (Reference Stephani and Goldstein2009) and Drews (Reference Drews2012) showed that the symmetric circulation region downstream of the roughness element required prohibitively long convergence times. A slanted rectangle roughness element was selected to avoid this problem. The rectangle is 10 mm long, 5 mm wide, and oriented at a 45° angle relative to the incoming flow. The edges of the rectangle are defined on a
$1~\text{mm}\times 1~\text{mm}$
grid so the geometry can easily be implemented in a numerical simulation.
The final roughness configuration was a combination of the distributed roughness patch and the discrete roughness element. Figure 4 shows this combined roughness configuration. The shape of the discrete roughness element is extruded up from the distributed roughness surface to create the discrete, angled rectangle in the middle of the distributed roughness patch.
Three different roughness inserts were manufactured to test the three unique roughness configurations. The first insert featured two sets of three distributed roughness patches. The two sets of patches have the same geometry but different amplitudes. Multiple patches were placed side-by-side in the spanwise direction so measurements could be spatially phase-lock averaged in span; however, only the inner two patches in each set could be reached with the hotwire traverse. The measurements made downstream of the larger-amplitude distributed roughness (
$k_{max}=0.85~\text{mm}$
) are presented in this work. The second (discrete roughness only) and third (combined roughness) inserts featured seven identical patches side-by-side in the spanwise direction. The traverse could reach four of the roughness patches with this configuration. Increasing the number of roughness patches also increased the quality of the data by allowing for additional spanwise averaging. Table 3 shows the amplitudes and streamwise locations of the different roughness configurations when installed in the plate, while figure 5 shows one of the manufactured roughness inserts.
Figure 5. Combined roughness insert installed in the flat plate model. Flow travels from left to right.
Table 3. Distributed and discrete roughness heights.
All of the roughness used in this experiment was manufactured using rapid prototyping (RP). The inserts were made on a Stratasys Fortus 400mc machine. The machine lays down RP material in spanwise slices (0.178 mm or 0.254 mm layers) to build up the insert. The background surface roughness of the RP material is
$20{-}30~{\rm\mu}\text{m}$
r.m.s. The as-built roughness was characterized using a Mitutoyo coordinate measuring machine (CMM). The distributed roughness was measured at over 12 000 points on the surface, and the results showed that the rapid prototyping machine accurately made the distributed roughness to within a
$50~{\rm\mu}\text{m}$
standard deviation. The discrete roughness was also measured, with the results shown in figure 6. The RP machine was unable to make the sharp edges of the discrete roughness; instead, the edges were rounded off and smoothed out over a millimetre distance. As a result, the as-made discrete element lacked the sharp edges of the as-designed discrete roughness and also had a slightly larger profile. The height of the discrete roughness was
$0.989\pm 0.035$
, which is very close to the designed value of 1 mm.
Figure 6. Surface measurement of the discrete roughness element (mm): (a) CMM results, (b) difference between CMM results and as-designed roughness.
2.3. Hotwire measurements and data analysis
Constant temperature hotwire anemometry was the primary measurement technique used in this work. Dantec 55P15 hotwires (1.25 mm long,
$5~{\rm\mu}\text{m}$
diameter tungsten wire) were operated using an AA Lab Systems anemometry system. Two hotwires were utilized to simultaneously measure velocity both inside and far outside of the boundary layer. During data analysis, the velocity measured by the boundary layer wire is normalized by the freestream wire measurement to remove the influence of low frequency oscillations in the flow and account for small changes in freestream conditions throughout a run.
The hotwires are moved through the boundary layer by a three-dimensional traverse capable of
$1~{\rm\mu}\text{m}$
steps in the wall-normal direction,
$2~{\rm\mu}\text{m}$
steps in the spanwise direction, and
$12~{\rm\mu}\text{m}$
steps in the streamwise direction. The traverse sting is inserted into the flow through a slotted plastic panel on the side of the test section. A pressure box surrounds the traverse to prevent flow through the access slot.
Detailed hotwire scans of the boundary layer consisted of multiple boundary layer profiles, each measured at a different spanwise location. Each boundary layer profile was measured by starting the hotwire probe in the freestream and moving the probe towards the wall. The probe was held still at discrete heights in the boundary layer to acquire data (1.2 s for a laminar boundary layer, 2.0 s for a turbulent boundary layer) and then moved further towards the wall. The step size of the wall-normal movement decreased as the probe was traversed into the boundary layer. In laminar flow over smooth surfaces, the profile was stopped when
$U_{y}/U_{e}$
drops below 10 %. When a scan was over distributed roughness, the hotwire was brought as close as possible to the roughness; this led to velocity cutoffs between 16 % and 25 %. When turbulent boundary layers were measured, the cutoff was set between 25 % and 30 % due to the thinness of the laminar sublayer. After the profile was stopped, the probe was moved back to the starting position. The probe was then moved 1 mm in span, and the next boundary layer profile was measured. This procedure continued until a set number of spanwise locations had been measured (65 for the distributed roughness only configuration and 129 for the discrete roughness only and combined roughness configurations.) Boundary layer scans were performed at multiple streamwise locations for each roughness configuration tested.
The transformation from the traverse coordinate system to the wall coordinate system takes place during post-processing using a technique developed by White & Ergin (Reference White and Ergin2004). The location of the wall is estimated at selected spanwise locations by assuming a linear boundary layer profile in the near-wall region and extrapolating the profile to the
$y$
value where
$U=0$
. This extrapolation is performed in (or downstream of) the roughness flats, where the flow is least disturbed by the roughness. A parabolic spanwise fit is then applied to the extrapolated wall locations. The spanwise fit allows the wall location to be defined at spanwise locations where
$y_{wall}$
cannot be estimated using extrapolation.
The basic state profile,
$U_{c}(y)$
, was calculated by averaging the profiles that are in-between or downstream of the flats between roughness patches (the same profiles used to extrapolate the location of the wall). This average profile is the least affected by the roughness and most indicative of the undisturbed boundary layer. The flow behind the roughness patches is then phase-lock averaged across the span to create a representative flow field (
$U(y,z)$
) downstream of a single roughness patch. The steady boundary layer disturbance field,
$$\begin{eqnarray}U^{\prime }(y,z)=\frac{U(y,z)-U_{c}(y)}{U_{e}},\end{eqnarray}$$
is defined as the deviation from the basic state normalized by the edge velocity. The r.m.s. of the steady-disturbance profiles is taken in the spanwise direction to quantify how the boundary layer has been distorted by the surface roughness:
$$\begin{eqnarray}U_{rms}^{\prime }(y)=\sqrt{\frac{1}{32}\mathop{\sum }_{i=0}^{31}U^{\prime }(y,z_{i})^{2}}.\end{eqnarray}$$
The total disturbance energy is then defined as
$$\begin{eqnarray}E_{total}=\frac{1}{{\it\delta}}\int _{0}^{\infty }{U_{rms}^{\prime }(y)}^{2}\,\text{d}y,\end{eqnarray}$$
where
${\it\delta}$
is defined by (2.1);
${\it\delta}$
is defined locally at each streamwise location and changes as the boundary layer evolves in the streamwise direction. The wall-normal distance is scaled by
${\it\delta}$
for consistency with previous experiments (White Reference White2002; White et al.
Reference White, Rice and Ergin2005; Denissen & White Reference Denissen and White2008).
$E_{total}$
includes the spanwise-mean effect of the disturbances on the boundary layer.
$U_{mean}^{\prime }$
is the spanwise-averaged disturbance profile, which shows the wall-normal transport of streamwise momentum in the boundary layer:
$$\begin{eqnarray}U_{mean}^{\prime }=\frac{1}{32}\mathop{\sum }_{i=0}^{31}U^{\prime }(y,z_{i}).\end{eqnarray}$$
A positive
$U_{mean}^{\prime }$
disturbance indicates that the roughness wake has a higher mean velocity than the undisturbed boundary layer, while a negative
$U_{mean}^{\prime }$
disturbance indicates that the presence of the roughness has slowed down the flow relative to the undisturbed boundary layer.
In addition to the total and mean disturbance profiles, specific roughness wavelengths are also analysed. Because the disturbance field is phase-lock averaged in span, the disturbance is periodic along the primary roughness wavelength (
${\it\lambda}_{z}=32~\text{mm}$
), and thus a discrete Fourier transform (DFT) is appropriate:
$$\begin{eqnarray}B(y,{\it\lambda}_{k}/m)=\frac{1}{32}\mathop{\sum }_{j=0}^{31}U^{\prime }(y,z_{j})\text{e}^{-2{\rm\pi}\text{i}z_{j}m/{\it\lambda}_{k}},\end{eqnarray}$$
where
$z_{j}=j({\rm\Delta}z)$
. Boundary layer profiles are acquired every 1 mm in span, so the Fourier transform is performed over 32 points. The disturbance profile associated with a particular spanwise wavelength is then calculated by evaluating the amplitude of the DFT at the given height in the boundary layer, i.e.
$$\begin{eqnarray}U_{rms}^{\prime }(y,{\it\lambda}_{k}/m)=\sqrt{(2-{\it\delta}_{m(0)}-{\it\delta}_{m(16)})B(y,{\it\lambda}_{k}/m)B^{\ast }(y,{\it\lambda}_{k}/m)}.\end{eqnarray}$$
The normalization factor in (2.9) includes Kronecker deltas in order to satisfy Parseval’s theorem. The disturbance energy at a particular wavelength is then calculated by integrating the squared r.m.s. velocity profile associated with that wavelength in the wall-normal direction, i.e.
$$\begin{eqnarray}E_{{\it\lambda}_{k}/m}=\frac{1}{{\it\delta}}\int _{0}^{\infty }(U_{rms}^{\prime }(y,{\it\lambda}_{k}/m))^{2}\,\text{d}y.\end{eqnarray}$$
As a consequence of the normalization of
$U_{rms}^{\prime }(y,{\it\lambda}_{k}/m)$
and
$E_{{\it\lambda}_{k}/m}$
, the total disturbance energy is equal to the sum of the disturbance energies in each of the integer modes:
$$\begin{eqnarray}E_{total}=\mathop{\sum }_{m=0}^{16}E_{{\it\lambda}_{k}/m}.\end{eqnarray}$$
Great care was taken to quantify the hotwire measurement uncertainty. Preliminary analysis showed that the patch-to-patch variability of the roughness wakes was much larger than the uncertainty created by wall location fits and hotwire calibrations. Based on this observation, the first step in quantifying the uncertainty of the hotwire measurements was to assume that the velocity at each point in the averaged flow field (
$U(y,z)$
) is a single realization drawn from a normal distribution of possible points. The flow field downstream of each roughness patch is one realization in this distribution. Under this assumption, the uncertainty in the steady velocity is the standard error of the population sample (Press et al.
Reference Press, Teukolsky, Vetterling and Flannery2007):
$$\begin{eqnarray}{\it\sigma}_{U^{\prime }(y,z)}=\sqrt{\frac{\displaystyle \mathop{\sum }_{j=0}^{N-1}(U_{j}^{\prime }(y,z)-U^{\prime }(y,z))^{2}}{N(N-1)}},\end{eqnarray}$$
where
$N$
is the number of roughness wakes that are measured, and
$U_{j}^{\prime }(y,z)$
is the steady velocity disturbance field created by a single roughness patch
$j$
. The uncertainty in
$U^{\prime }(y,z)$
can be propagated through the equations to find the variance associated with
$U_{rms}^{\prime }(y)$
. This variance,
$$\begin{eqnarray}{\it\sigma}_{U_{rms}^{\prime }(y)}^{2}=\left(\frac{1}{32}\frac{1}{U_{rms}^{\prime }(y)}\right)^{2}\mathop{\sum }_{i=0}^{31}(U^{\prime }(y,z_{i}))^{2}({\it\sigma}_{U^{\prime }(y,z_{i})})^{2},\end{eqnarray}$$
quantifies the uncertainty of the total disturbance profile. Figure 7(a) shows an example
$U_{rms}^{\prime }$
disturbance profile with error bars calculated using (2.13). The thin lines in figure 7 show the disturbance profiles of each roughness wake calculated individually. This measurement was made in the wake of the discrete roughness elements, so four red profiles are shown. The uncertainty at each point was modelled using a normal distribution, but figure 7(a) shows that the error associated with
$U_{rms}^{\prime }$
is not random in the wall-normal direction. Some of the disturbance profiles are consistently larger than the average profile, while some of the profiles are consistently smaller.
Figure 7. Total disturbance profile (a) and mean-flow deformation (b) for the discrete roughness only configuration, low Reynolds number condition at
$x=1000~\text{mm}$
. The thick lines represent the averaged profiles, while the thinner lines show the disturbance profiles of the wake behind each roughness patch.
To better capture this bias in the integrated disturbance energies, the normal distribution is not propagated through the wall-normal integration step. Instead, upper (2.14) and lower (2.15) uncertainty bounds are placed on the energies by introducing a positive or negative bias before integration:
$$\begin{eqnarray}\displaystyle & \displaystyle E_{total}^{+}=\frac{1}{{\it\delta}}\int _{0}^{\infty }(U_{rms}^{\prime }(y)+{\it\sigma}_{U_{rms}^{\prime }(y)})^{2}\,\text{d}y & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle E_{total}^{-}=\frac{1}{{\it\delta}}\int _{0}^{\infty }(U_{rms}^{\prime }(y)-{\it\sigma}_{U_{rms}^{\prime }(y)})^{2}\,\text{d}y. & \displaystyle\end{eqnarray}$$
A similar procedure is used to calculate the uncertainties associated with disturbance profiles and integrated energies at individual spanwise wavelengths. The variance associated with spanwise Fourier coefficients is calculated by propagating the uncertainty associated with
$U^{\prime }(y,z)$
through (2.8). The variance associated with the Fourier coefficients is then used to calculate the variance associated with the disturbance profile at a particular spanwise wavelength. Figure 7(b) shows an example
$U_{mean}^{\prime }$
disturbance profile with error bars calculated using this method. Finally, upper and lower bounds for the integrated energy are calculated by adding a positive or negative bias to the disturbance profile before integration.
3. Results
Hotwire measurements and naphthalene flow visualization were made at two different freestream Reynolds numbers with three different roughness configurations. Table 4 lists the different test conditions, including the roughness heights and the roughness Reynolds numbers. Results will first be presented for the lower Reynolds number condition, and then for the higher Reynolds number condition.
Table 4. Experimental test conditions, including roughness heights and
$\mathit{Re}_{kk}$
values.
3.1. Lower Reynolds number
Naphthalene flow visualization was used to see the effect of the roughness on wall shear stress. Naphthalene was dissolved in acetone and pressure-sprayed onto the flat plate. The acetone rapidly evaporates, and the naphthalene on the surface then sublimates at a rate proportional to wall shear stress. Regions of higher shear stress (turbulent regions or regions with high-speed streaks) sublimate within a few minutes, while regions with lower shear stress (laminar regions or regions with low-speed streaks) remain coated in naphthalene much longer. The acetone solution used for this technique could potentially dissolve the rapid prototyping material used to construct the roughness. To avoid this, parts of the roughness insert were covered in
$64~{\rm\mu}\text{m}$
thick orange Kapton tape. The tape was precisely laid down to prevent any steps/gaps in the application. The thickness of the tape is very small compared to the thickness of the boundary layer; the
$\mathit{Re}_{kk}$
of the two-dimensional step created by the tape is less than 1.
Figures 8 and 9 show naphthalene flow visualization images for the discrete roughness and combined roughness configurations, respectively, at the lower Reynolds number. Naphthalene visualization was not useful for the distributed roughness only configuration because the roughness wake created only small variations in wall shear stress. The asymmetry in the near-wake of the discrete roughness is evident in figure 8; the leading edge of the roughness creates a high-speed region behind the lower portion of the slanted rectangle. The interaction of the flow past the leading edge and the flow past the trailing edge then creates a low-speed region behind the trailing edge. The wake straightens into a low-speed and a high-speed streak that align with the streamwise direction. The width of the streaks spreads slightly far downstream, but they remain compact and do not interact. The streaks persist hundreds of boundary layer thicknesses downstream and do not directly lead to transition at this Reynolds number.
Figure 8. Naphthalene flow visualization of discrete roughness geometry at the lower Reynolds number.
Figure 9. Naphthalene flow visualization of combined roughness geometry at the lower Reynolds number.
The wake of the combined roughness (figure 9) looks qualitatively similar to the discrete roughness wake. Downstream of the distributed roughness, a complex wake forms that includes a number of high- and low-speed regions. Further downstream, the wake evolves into a single high- and low-speed streak pair, which was observed in the far-wake of the discrete roughness only configuration.
Detailed hotwire scans of the boundary layer revealed the structure of the roughness-induced disturbances seen in the flow visualization. Scans were performed at multiple streamwise locations (20 for the distributed roughness, and 19 for the discrete only and combined roughness). Measurements were made both above and downstream of the distributed roughness, extending from the near-wake of the discrete roughness to the far-wake of the discrete roughness.
Figure 10 shows contour plots of the wake of the distributed roughness configuration. In all of the contour figures shown, the contour levels represent steady velocity in 10 % increments of the freestream speed, while the colouring shows the unsteady disturbance amplitude (
$100u_{rms}^{\prime }$
). The distributed roughness creates a small disturbance in the steady velocity field. As the boundary layer evolves and grows downstream, the disturbance remains very small; this is seen in the velocity contour at
$x=1600~\text{mm}$
.
Figure 10. Contour plots of steady streamwise velocity (10 % increments) coloured by
$100u_{rms}^{\prime }$
at two streamwise locations for the distributed roughness configuration at the lower Reynolds number: (a)
$x=1000$
mm, (b) 1600 mm. The height and width of the roughness amplitude envelope are indicated by the white lines.
Figure 11 shows contour plots for the discrete only and combined roughness configurations at four streamwise locations. In the near-wake region (at
$x=935~\text{mm}$
), the contours show that the wake is mostly constrained within the outline of the discrete roughness element, which is shown with the white lines. As the wake extends downstream, a clear pair of low- and high-speed streaks form behind the roughness element, and the streaks affect the contours higher in the boundary layer. At
$x=1700~\text{mm}$
, the effect of the streaks can be seen far away from the wall, at the edge of the boundary layer.
Figure 11. Contour plots of steady streamwise velocity (10 % increments) coloured by
$100u_{rms}^{\prime }$
at four streamwise locations for the discrete roughness only (a,c,e,g) and combined roughness (b,d,f,h) configurations at the lower Reynolds number condition: (a,b)
$x=935$
mm, (c,d)
$x=1000$
mm, (e,f)
$x=1325$
mm, (g,h)
$x=1700$
mm. The colour scale changes for
$x=1700~\text{mm}$
plots.
In addition to the lift-up effect, the spanwise wavelengths in the wake change as the wake evolves in the streamwise direction. The contour plots from far downstream show a large-amplitude, long-wavelength disturbance, but the contour plots from the near-wake show a compact disturbance. These contour plots agree with the naphthalene flow visualization shown in figures 8 and 9; the wake consists of a high-speed and low-speed pair of streaks that gradually broaden in the spanwise direction farther downstream.
At this lower Reynolds number, the boundary layer remains laminar throughout the measurement domain. Over the extent of the domain, the unsteadiness remains almost constant, with a slight increase in unsteadiness observed at regions with higher levels of wall-normal and spanwise shear stress. The differences between the wakes of discrete only and combined roughness configurations are small, particularly in the far-wake.
Disturbance profiles (
$U_{rms}^{\prime }$
) quantify the steady velocity disturbances seen in the contour plots. Figure 12 compares the total disturbance profiles for all three roughness configurations at two different streamwise locations. All three roughness configurations show evidence of transient growth. The peak of the disturbance profiles moves away from the wall as the wake evolves in the streamwise direction, and the disturbance peak also broadens in the wall-normal direction. Comparing the profiles from the three roughness configurations also shows that the distributed roughness creates a much smaller disturbance than the other two configurations, and the discrete and combined roughness configurations have similar disturbance profiles.
Figure 12. Total disturbance profiles for all three roughness configurations at two streamwise locations for the lower Reynolds number condition.
Figure 13 further compares the disturbance profiles for the discrete and combined roughness configurations. At
$x=928~\text{mm}$
, the profile for the discrete roughness is larger than the profile for the combined roughness. Part of this difference may be caused by the different cutoff velocities used in the hotwire measurements (10 % for the discrete roughness, and 18 % for the combined roughness). The difference in cutoff velocities means that less information is collected for the combined roughness case. With fewer data near the wall, the disturbance profile will be underestimated if the peak disturbance occurs below the location where the velocity cutoff stops the probe (Downs et al.
Reference Downs, White and Denissen2008). As the peak of the disturbance profile moves farther away from the wall, the difference in velocity cutoffs becomes less important.
Figure 13. Total disturbance profiles at multiple streamwise locations for the discrete roughness only (a) and combined roughness (b) configurations at the lower Reynolds number condition.
An interesting aspect of these profiles is the peak disturbance amplitude. For the discrete roughness, the maximum spanwise r.m.s. disturbance is
${\sim}0.85$
. In the mid-wake region (at
$x=950~\text{mm}$
), the maximum r.m.s. disturbance drops to
${\sim}0.68$
before increasing to 0.75–0.80 in the far-wake. The change in the peak disturbance amplitude in the mid-wake can be explained by examining profiles of
$U_{mean}^{\prime }$
, which are shown in figure 14. At
$x=928~\text{mm}$
, the
$U_{mean}^{\prime }$
profile is negative, which indicates a velocity deficit. This velocity deficit decreases quickly as the wake moves downstream; by
$x=950~\text{mm}$
(
${\sim}$
four boundary layer thicknesses downstream), high-momentum fluid has been pulled down from the top of the boundary into the bottom of the boundary layer. This momentum transfer causes a zero in the profile near
$y\sim 0.5~\text{mm}$
, indicating that the high-speed streak penetrates farther down into the boundary layer than the low-speed streak. In the far-wake, the entire
$U_{mean}^{\prime }$
profile becomes positive, which indicates a velocity excess due to the momentum transfer. These results are consistent with the observations of Kendall (Reference Kendall1981), who observed similar results with the velocity defect downstream of a small sand-grain roughness in a flat plate boundary layer.
Figure 14.
$U_{mean}^{\prime }$
profiles at multiple streamwise locations for the discrete roughness only (a) and combined roughness (b) configurations at the lower Reynolds number condition.
The signs and magnitudes of the
$U_{mean}^{\prime }$
profiles further highlight the differences between the two roughness configurations. For both roughness configurations,
$U_{mean}^{\prime }$
is negative at
$x=928~\text{mm}$
due to the velocity deficit in the near-wake, but switches sign in the far-wake due to redistribution of streamwise momentum. This pattern occurs for both roughness configurations, but the streamwise location where the profile switches from deficit to excess is different between the two configurations. The presence of the distributed roughness prevents the high-speed streak from penetrating far down into the boundary layer, which indicates a smaller transfer of high-momentum fluid to the bottom of the boundary layer. The
$x=1000~\text{mm}$
profile for the combined roughness case barely shows a zero in the profile, while the
$x=1000~\text{mm}$
profile in the discrete roughness case shows the presence of the high-speed streak near the wall.
The disturbance energy, which quantifies the steady disturbances and their transient growth, is calculated by integrating the disturbance profiles in the wall-normal direction. Figure 15 shows the disturbance energy of the distributed roughness configuration at the higher Reynolds number condition. The disturbance energies from the lower Reynolds number were qualitatively similar, but have higher relative uncertainties because the disturbance amplitude is so small. The integrated energies show transient growth at multiple spanwise wavelengths. The total disturbance grows over the distributed roughness and then remains near-constant downstream of the roughness. The
$m=2$
and
$m=3$
modes grow slightly downstream of the roughness, while the
$m=4$
(
${\it\lambda}=8~\text{mm}$
) to
$m=8$
(
${\it\lambda}=4~\text{mm}$
) wavelengths show clear growth-decay-growth patterns. The shortest wavelengths grow over the distributed roughness, then immediately decay. In contrast, the
$m=4$
and
$m=5$
modes continue to grow downstream of the distributed roughness before decaying further downstream.
Figure 15. Streamwise evolution of disturbance energy for the distributed roughness configuration at the higher Reynolds number condition. The dashed vertical lines show the location of the distributed roughness.
Figure 16 shows the integrated disturbance energy for the discrete roughness configuration. The disturbance energy for the combined roughness configuration is not shown, but is qualitatively similar. In both cases, the total disturbance energy grows in the near- and mid-wake before reaching a near-constant value in the far-wake. The energy at individual spanwise wavelengths reveals different types of transient growth patterns. For both roughness configurations, the
$m=0$
and
$m=1$
modes decay before growing further downstream, while the
$m=2$
,
$m=3$
, and
$m=4$
modes grow in the near- and mid-wake before remaining constant (
$m=2$
) or decaying (
$m=3$
and
$m=4$
) further downstream.
Figure 16. Streamwise evolution of disturbance energy for the discrete roughness only configuration at the lower Reynolds number condition.
The order with which the different disturbance wavelengths reach their maximum amplitude is consistent with transient growth theory. The shortest wavelength shown (
$m=4$
, or
${\it\lambda}=8~\text{mm}$
) is the first wavelength to reach maximum amplitude near
$x=1020~\text{mm}$
. Each progressively longer spanwise wavelength reaches a maximum amplitude further downstream; in fact, the
$m=1$
mode is still growing at the end of the measurement domain. The
$m=0$
mode decays in the near-wake and grows in the far-wake as high-speed fluid is pulled from the top of the bottom boundary layer towards the wall. The
$m=5$
to
$m=7$
modes also showed measurable transient growth, but had amplitudes an order of magnitude smaller than the longer wavelength modes.
A quantitative comparison of the disturbance energy for all three roughness configurations reveals the shielding effect. Figure 17 shows the streamwise evolution of the total disturbance energy and energy at the first five spanwise disturbance modes. The most obvious feature is the relative magnitude of the energy from the distributed roughness case compared to the configurations with the discrete roughness. The distributed roughness energy is much smaller than the energies from the other roughness configurations.
Figure 17. Comparison of total disturbance energy for the three roughness configurations at the lower Reynolds number configuration. The asterisks represent the distributed roughness only configuration, the circles represent the discrete roughness only configuration, and the squares represent the combined roughness configuration. The vertical lines represent the location of the discrete (solid lines) and distributed (dashed lines) roughness locations. (a) Total energy, (b)
$m=0$
, (c)
$m=1$
, (d)
$m=2$
, (e)
$m=3$
, (f)
$m=4$
.
The total energy shows a slight shielding effect for this sub-critical roughness case. The energy in the near-wake and mid-wake is almost identical; however, in the far-wake, the combined roughness configuration shows slightly less disturbance energy. Although the difference is small, it is larger than the measurement uncertainty and substantially larger than the energy associated only with the distributed roughness.
With the spanwise invariant mode, the minimum point on each curve is the location where the
$U_{mean}^{\prime }$
profile switches from deficit-dominated to high-speed streak dominated. The minimum energy point is further downstream for the combined roughness case; the presence of the distributed roughness slows down the rate at which high-momentum fluid is pulled towards the wall. In the far-wake, both configurations show
$m=0$
energy growth at the same spatial rate.
The
$m=1$
mode is also suppressed with the addition of the distributed roughness. In the near-wake, the two roughness configurations have nearly equal energy. In the mid-wake, the growth rates of the two modes diverge; the discrete roughness only case continues to grow at a faster rate, while the combined roughness case grows at a slower rate. The difference in growth rates persists into the far-wake. The
$m=2$
mode is also suppressed by the distributed roughness.
The
$m=3$
and
$m=4$
modes have similar behaviour; in the near-wake, the two roughness configurations have nearly identical amplitudes, but the combined roughness has a larger-amplitude disturbance in the mid- and far-wake. The presence of the distributed roughness does not change the rate at which the disturbances decay in the far-wake. An explanation for the redistribution of energy to the
$m=3$
and
$m=4$
modes is the inherent wavelength distribution of the distributed roughness field. Table 2 shows the ten largest-amplitude distributed roughness modes. Of the ten modes, five of them have spanwise wavelengths with
$m=-4,-3,3$
, or 4. Presumably, as streamwise vorticity pulls high-momentum fluid towards the bottom of the boundary layer, the entrained high-momentum fluid has to travel around the peaks in the distributed roughness, causing an increase in the disturbance energy at the largest-amplitude distributed roughness modes.
The redistribution of energy from longer wavelengths to shorter wavelengths suggests that the shielding effect cannot be simply described by a wall-normal displacement effect as suggested by Drews (Reference Drews2012). Several studies suggest that distributed roughness locally displaces the boundary layer away from the wall, which led to the idea that distributed roughness was ‘shielding’ the discrete roughness from the incoming boundary layer by reducing the effective
$\mathit{Re}_{kk}$
. If this were the sole explanation for the shielding effect, the disturbance energy from the discrete and combined roughness cases could be scaled to evaluate an effective
$\mathit{Re}_{kk}$
. Figure 17 shows that the energy in the shielded case is not a simple rescaling due to boundary layer displacement and a lower effective
$\mathit{Re}_{kk}$
. Each of the wavelengths responds differently in the presence of distributed roughness. This suggests that the shielding effect arises through the interaction of the wake of the discrete roughness with the surrounding distributed roughness.
3.2. Higher Reynolds number
At the higher Reynolds number, different behaviour was observed in the roughness wakes. Figure 18 shows naphthalene flow visualization for the discrete roughness configuration at the higher Reynolds number. The naphthalene shows a low-speed region in the wake of the slanted rectangles. Around
$x=980~\text{mm}$
, the wake begins to show an alternating pattern of low- and high-speed streaks. Near
$x=1050~\text{mm}$
, the roughness wake begins to spread like a turbulent wedge. The origin of the wedge can be traced back to
$x=996\pm 3~\text{mm}$
. The flow visualization shows a dogtooth pattern (Chu & Goldstein Reference Chu and Goldstein2012) on the edges of the wedge which make defining a precise spreading angle difficult. By
$x=1116~\text{mm}$
, the turbulent wedges have spread across the 32 mm periodicity, and the boundary layer is turbulent across the entire span. Both before and after breakdown, the shear stress pattern is extremely consistent across the span.
Figure 18. Naphthalene flow visualization of discrete roughness geometry for the higher Reynolds number.
Naphthalene flow visualization for the combined roughness configuration at the higher Reynolds number is shown in figure 19. The structure of the wake over the distributed roughness could not be visualized, but the naphthalene pattern downstream of the distributed roughness shows a wake with multiple high- and low-speed streaks which rapidly evolve into a turbulent wedge. The estimated origin of the turbulent wedge is traced to
$x=1003~\text{mm}$
, which is 7 mm downstream of the origin of the turbulent wedge in the discrete roughness only configuration. By
$x=1119~\text{mm}$
, the turbulent wedges have spread across the 32 mm periodicity to create a turbulent boundary layer across the entire span.
Figure 19. Naphthalene flow visualization of combined roughness geometry for the higher Reynolds number.
Hotwire measurements of all three roughness configurations showed that the wake of the distributed roughness by itself did not cause the boundary layer to transition, but the discrete roughness led to transition in the other two roughness configurations. Figure 20 shows the boundary layer downstream of the distributed roughness configuration at
$x=1000~\text{mm}$
and
$x=1600~\text{mm}$
. A weak pair of high- and low-speed streaks, created by the largest roughness peak, is centred near
$z=-2~\text{mm}$
. Otherwise, the distributed roughness by itself has a small influence on the boundary layer.
Figure 20. Contour plots of steady streamwise velocity (10 % increments) coloured by
$100u_{rms}^{\prime }$
at two streamwise locations for the distributed roughness configuration at the higher Reynolds number: (a)
$x=1000$
mm, (b)
$x=1600$
mm.
Figure 21. Contour plots of steady streamwise velocity (10 % increments) coloured by
$100u_{rms}^{\prime }$
at three streamwise locations for the discrete (a,c,e) and combined (b,d,f) roughness configurations at the higher Reynolds number condition: (a,b)
$x=928$
mm, (c,d)
$x=950$
mm, (e,f)
$x=975$
mm. The colour scale changes for each plot.
Hotwire measurements confirmed the turbulent wedges observed in the naphthalene visualization for the other two roughness configurations. Figure 21 shows contour plots in the near-wake, while figure 22 shows contour plots as the turbulent wedge develops further downstream. The structure of the mean flow in the near-wake is very similar to the lower Reynolds number condition; however, the unsteadiness in the wake grows quickly as the near-wake evolves into the mid-wake. The increased unsteadiness occurs around the points in the flow with large amounts of spanwise and wall-normal shear, particularly along the low-speed streak. By
$x=975~\text{mm}$
, the unsteadiness along the low-speed streak has grown to 12 % of the freestream speed for the discrete roughness case and 4 % of the freestream speed for the combined roughness case. This difference in unsteadiness is consistent with the differences in transition location between the two cases from the flow visualization.
Figure 22. Contour plots of steady streamwise velocity (10 % increments) coloured by
$100u_{rms}^{\prime }$
at three streamwise locations for the discrete (a,c,e) and combined (b,d,f) roughness configurations at the higher Reynolds number: (a,b)
$x=1000$
mm, (c,d)
$x=1050$
mm, (e,f)
$x=1100$
mm.
The naphthalene visualization showed that the origin of the turbulent wedge was at
$x=996~\text{mm}$
for the discrete roughness and
$x=1003~\text{mm}$
for the combined roughness. The velocity contours measured at
$x=1000~\text{mm}$
show the beginning of the turbulent wedge. The low- and high-speed streaks that are seen along the edges of the turbulent wedge in the flow visualization are also observed in the hotwire measurements at
$x=1000~\text{mm}$
and
$x=1050~\text{mm}$
. The wedge continues to spread in the spanwise direction for both cases as it moves downstream. Although a large portion of the boundary layer at
$x=1100~\text{mm}$
is fully turbulent, the variation in the boundary layer height across the span is significant. The unsteadiness is largest at the edges of the turbulent wedge, and the interior structure of the wedge consists of relative low- and high-speed streaks that extend from the wall to the freestream.
Disturbance profiles further highlight the structure of the boundary layer before the turbulent wedge forms. Figure 23 shows total disturbance profiles at multiple streamwise locations before the boundary layer begins to transition. The structure of the profiles changes from the near-wake to the mid-wake for the discrete roughness configuration. First, the disturbance profile near the wall becomes more full. The fullness of the profile near the wall eventually forms a second peak in the profile.
Figure 23. Total disturbance profiles at multiple streamwise locations for the discrete (a) and combined (b) roughness configurations at the higher Reynolds number.
The profiles from the combined roughness case show similar trends, but the double-peak profiles seen with the discrete roughness configuration are just forming at
$x=975~\text{mm}$
. In fact, the shape of the
$x=975~\text{mm}$
profile for the combined roughness configuration resembles the shape of the
$x=950~\text{mm}$
profile for the discrete roughness configuration. Although it is difficult to make direct comparisons in the profile shapes due to different velocity cutoffs, this delay in the evolution of the disturbance profiles is consistent with the delay in transition observed with the flow visualization.
Figure 24 shows the
$U_{mean}^{\prime }$
disturbance profiles at different streamwise locations for both roughness configurations. The near-wake in both cases shows a negative
$U_{mean}^{\prime }$
profile due to the velocity deficit downstream of the discrete roughness. As the wake evolves in the streamwise direction, the high-speed streak begins to penetrate to the bottom of the boundary layer, which leads to a crossover point in the profile and a positive
$m=0$
profile near the wall. This process happens for both roughness configurations, but it occurs more slowly in the combined roughness case. At
$x=987.5~\text{mm}$
, the high-momentum fluid brought down into the boundary layer leads to a positive
$m=0$
profile for the discrete roughness configuration, while the high-speed streak has only started to penetrate the near-wall region for the combined roughness configuration. This delay in the crossover point in the
$U_{mean}^{\prime }$
is consistent with the lower Reynolds number but is more exaggerated at the higher Reynolds number. For both configurations, the turbulent wedge forms within 20 mm downstream of the last profile shown.
Figure 24.
$U_{mean}^{\prime }$
profiles at multiple streamwise locations for the discrete (a) and combined (b) roughness configurations at the higher Reynolds number.
At the higher Reynolds number, unsteady disturbance energy is used to quantify the disturbances that grow and lead to transition. During the hotwire scans, the time history of each data point is recorded in order to investigate the temporal disturbance frequencies in the roughness wake. The temporal power spectrum for each point was calculated by the procedure outlined by Press et al. (Reference Press, Teukolsky, Vetterling and Flannery2007), which includes windowing of the signal and spectrum averaging. The power spectrum is normalized so the sum of the energy in all of the frequency bins equals the square of the r.m.s. unsteadiness.
Figure 25 shows the temporal power spectrum of fluctuations near the middle of the roughness wake (
$y=1.7~\text{mm}$
,
$z=-3~\text{mm}$
) for both roughness configurations that transition. At this point in the
$(y,z)$
plane, the fluctuating velocity increased as the probe was moved downstream, and a range of secondary instabilities was seen between 200 and 700 Hz as the wake evolves and transitions to turbulence. This range of frequencies is higher than the frequency range of unstable two-dimensional T–S waves (36–109 Hz) at this streamwise location. Harmonics of the 200–700 Hz range are also seen at higher frequencies at
$x=950~\text{mm}$
. At
$x=975~\text{mm}$
(52 mm downstream of the discrete roughness), the disturbance peaks are being absorbed as the turbulent wedge forms. By
$x=1000~\text{mm}$
, both spectra have filled out as the turbulent wedge has formed. The power spectra at
$x=975~\text{mm}$
for the combined roughness is noticeably smaller than the power spectra for the discrete roughness only; this is consistent with the transition delay observed in the naphthalene flow visualization.
Figure 25. Normalized temporal power spectrum at
$y=1.7~\text{mm}$
,
$z=-3~\text{mm}$
for the discrete roughness (a) and combined roughness (b) configurations at the higher Reynolds number condition. The vertical lines show the range of unstable T–S waves in the undisturbed boundary layer from
$x=900~\text{mm}$
to
$x=1000~\text{mm}$
.
The
$u^{\prime }$
fluctuation power between 200 and 700 Hz was extracted from the power spectrum at each point and integrated across the spanwise and wall-normal directions to yield the energy of the secondary instability:
$$\begin{eqnarray}E_{unsteady}=\left(\frac{1}{{\it\lambda}_{z}}\right)\left(\frac{1}{{\it\delta}}\right)\int _{0}^{{\it\lambda}_{z}}\int _{0}^{\infty }(u_{rms,200{-}700}^{\prime })^{2}\,\text{d}y\,\text{d}z.\end{eqnarray}$$
Figure 26 compares the unsteady energy on a log axis to better understand the growth rate of the secondary instabilities. The unsteady energy for the combined roughness case lags behind the discrete roughness case by
${\sim}16~\text{mm}$
. For both configurations, the disturbance grows slowly in the near-wake and sharply in the mid-wake. The growth rate then decreases as the unsteadiness saturates while the turbulent wedge begins to form.
Figure 26. Comparison of unsteady disturbance energy for the discrete and combined roughness configurations for the higher Reynolds number condition on a log axis. The exponential growth rate is shown using dashed lines.
The exponential growth rate of the disturbances was evaluated by curve-fitting the points between 30 and 65 mm downstream of the discrete roughness, where the disturbance growth is largest and the growth rate appears linear. The growth rate is shown with dashed lines in figure 26. For the discrete roughness only configurations, the linear growth rate is
$0.197~\text{mm}^{-1}$
. The growth rate for the combined roughness configuration is
$0.169~\text{mm}^{-1}$
, which is 24 % less than the discrete only case. Even with the reduction in growth rate, the unsteady disturbances still grow exponentially and lead to transition.
4. Summary and conclusions
This work investigated the flow disturbances created by distributed roughness patches and discrete roughness elements in a flat plate boundary layer. The goal was to better understand how different types of roughness initiate transient growth and may lead to or potentially delay transition. In particular, the experiment was designed to study the shielding effect observed by Drews (Reference Drews2012).
Different roughness configurations were manufactured using rapid prototyping and mounted flush with the wall in a flat plate boundary layer. The three roughness configurations tested were a 32 mm wide
$\times$
128 mm long patch of distributed roughness, a discrete roughness element (a
$10~\text{mm}\times 5~\text{mm}$
, 45° slanted rectangle with
$1~\text{mm}\times 1~\text{mm}$
edges), and a combination of the two. Naphthalene flow visualization and hotwire anemometry were used to characterize the flow above and downstream of the different types of roughness at roughness Reynolds numbers (
$\mathit{Re}_{kk}$
) between 113 and 230.
By itself, the distributed roughness created a small-amplitude sub-critical roughness wake. The steady disturbance profiles and the integrated energy showed disturbances that underwent transient growth over a broad range of spanwise wavelengths.
The discrete roughness element also initiated disturbances that underwent transient growth. At the lower Reynolds number condition (
$\mathit{Re}_{kk}=151$
), the obliquely oriented rectangle creates a sub-critical roughness wake. At the higher Reynolds number (
$\mathit{Re}_{kk}=220$
), a turbulent wedge formed
${\sim}15$
boundary layer thicknesses downstream of the roughness. This
$\mathit{Re}_{kk}$
value is close to the predicted critical Reynolds number (
$\mathit{Re}_{kk_{critical}}=239$
) using the correlation suggested by Tani (Reference Tani1969).
Adding the distributed roughness around the discrete roughness modified the structure of the wake at both Reynolds numbers. At the lower Reynolds number, the total disturbance energy was slightly decreased in the far-wake. Energy was transferred from the longer spanwise wavelength modes to the shorter wavelength modes; this occurs because high-speed fluid that is brought down to the bottom of the boundary layer by streamwise vorticity must conform to the topographical modes in the distributed roughness. The interaction between the wake of the discrete roughness and the distributed roughness shows the shielding effect cannot be simply explained by a wall-normal boundary layer displacement.
At the higher Reynolds number, flow visualization, steady disturbance profiles and unsteady disturbance energy all showed that transition was delayed 7–16 mm by adding the distributed roughness. The presence of the distributed roughness changes the rate in which high-momentum fluid is brought to the bottom of the boundary layer, which appears to be linked to the transition location. The altered basic state in the combined roughness case decreased the exponential growth rate of the secondary instabilities that lead to transition. In spite of the reduced growth rate, transition was delayed only slightly. It is possible a different distributed roughness distribution could have provided a more substantial delay.
These findings provide several opportunities for further understanding of roughness-induced transient growth and transition. One of these possibilities includes studying a longer and wider distributed roughness patch. This experiment was the first attempt to measure transient growth created by streamwise elongated distributed roughness; however, realistic distributed roughness does not have a starting/stopping location. Even with a patch 128 mm long in this experiment, shorter spanwise wavelength disturbances were only beginning to grow at the downstream end of the patch. Further elongating the roughness in the streamwise direction would provide the opportunity to better understand receptivity of roughness at multiple streamwise locations.
Even more importantly, the hotwire results collected in this experiment can be used as an input to secondary instability calculations to better understand the mechanism that delays transition. The mode shapes of instabilities at specific frequencies can be compared between the secondary instability calculations and narrowband temporal spectra from the experiment. This analysis can be used to compare the discrete only and combined roughness wakes to better understand what features of the wake affect the mode shapes and growth rates of secondary instabilities. This information will identify how distributed roughness can be tailored to potentially delay transition caused by discrete roughness.
Acknowledgements
The authors would like to acknowledge the support of the United States Air Force Office of Scientific Research through AFOSR grant FA9550-11-1-0203. The authors would also like to thank Dr D. Goldstein, Dr A. Sharma, and J. Chu from the University of Texas at Austin for fruitful discussions regarding this work.
