Introduction
As genetically modified maize is shipped all over the world, its ability to germinate, grow and hybridize with local maize landraces has generated scientific, social and political controversy. Quist and Chapela (Reference Quist and Chapela2001, Reference Quist and Chapela2002) were the first to report the presence of genetically modified plants (adventitious presence of unwanted transgenic plants, AP) among landraces collected in the Sierra Juarez region of the State of Oaxaca, Mexico. Their article led to speculation about how widely these novel genetic elements had proliferated, and what the consequences of ubiquitous gene flow might be. In contrast, 4 years later, Ortiz-García et al. (Reference Ortiz-García, Ezcurra, Schoel, Acevedo, Soberón and Snow2005) sampled maize landraces in the same region of Oaxaca and failed to detect AP, which suggested that transgenic plants were rare or absent in the sampled fields. Two recent studies showed the presence of AP in the south-eastern and west-central regions of Mexico. One study focused on the dispersal of maize transgenes via imported seed in Mexico, where 3.1 and 1.8% of samples were detected as having AP (Dyer et al., Reference Dyer, Serratos-Hernández, Perales, Gepts, Piñeyro-Nelson, Chavez, Salinas-Arreortua, Yúnez-Naude, Taylor and Alvarez-Buylla2009). The other study showed evidence of AP, with estimated sample frequencies of 1.1% based on polymerase chain reaction (PCR) and 0.89% based on Southern blots (Piñeyro-Nelson et al., Reference Piñeyro-Nelson, Van Heerwaarden, Perales, Serratos-Hernández, Rangel, Hufford, Gepts, Garay-Arroyo, Rivera-Bustamante and Álvarez-Buylla2009). Piñeyro-Nelson et al. (Reference Piñeyro-Nelson, Van Heerwaarden, Perales, Serratos-Hernández, Rangel, Hufford, Gepts, Garay-Arroyo, Rivera-Bustamante and Álvarez-Buylla2009) provided a valuable counterpoint to the surveys of Ortiz-García et al. (Reference Ortiz-García, Ezcurra, Schoel, Acevedo, Soberón and Snow2005), resolved apparent contradictions in the literature, and raised the bar for subsequent studies of migrating transgenes; the authors also showed that transgenes were present in Oaxaca in both 2001 and 2004. Their paper explains how sampling methods, statistical analyses and problems with analytical techniques can lead to inconsistent estimates of transgene frequencies in maize populations. This argument is in agreement with that of Cleveland et al. (Reference Cleveland, Soleri, Aragón-Cuevas, Crossa and Gepts2005), who indicate that sampling methods are of paramount importance when attempting to detect AP.
When the purpose of a sample survey is to detect a small fraction (less than one-tenth) of a population, as is the case when detecting the presence of AP, it is very important to choose an appropriate sampling design. Sample size under binomial group testing was developed to assure AP detection and estimation. However, when prevalence is low, the sample size sometimes contains no positive pools (i.e. pools having the trait of interest) and therefore it is of no use for detecting and estimating AP. An advantage of inverse sampling, one of the most widely used designs, is that each sample will contain the desired number of rare units, thus avoiding samples without a rare unit; however, the sample size is neither fixed nor small (Haldane, Reference Haldane1945; Pritchard and Tebbs, Reference Pritchard and Tebbs2010). In this sampling scheme, units are drawn one by one (with replacement) until the sample contains r rare units. One problem with inverse sampling is that when prevalence of the rare trait in the population is small (less than 10%), sample size for detecting and estimating prevalence is large. In addition, if the test used to classify the plants is expensive but not perfect [with sensitivity (Se) and specificity (Sp) less than 100%], the cost of detection or/and estimation is significant. Group testing (or pooled samples) can be used to reduce costs because instead of performing individual testing, only one test per group containing k units is required. If the result of a positive group is negative, all k elements that form the group are declared to be free of the rare trait.
An early application of group testing was to estimate the prevalence of plant viruses transmitted by insects (Watson, Reference Watson1936; Thompson, Reference Thompson1962). Although group testing originated as a researcher's answer to a blood testing problem, the procedure was later applied in studies conducted in such fields as physiopathology, public health and plant quarantine (Chiang and Reeves, Reference Chiang and Reeves1962; Bhattacharyya et al., Reference Bhattacharyya, Karandinos and Defoliart1979; Swallow, Reference Swallow1985; Romanow et al., Reference Romanow, Moyer and Kennedy1986). It was also used to detect diseases in donated blood (Dodd et al., Reference Dodd, Notari and Stramer2002); to detect drugs (Remlinger et al., Reference Remlinger, Hughes-Oliver, Young and Lam2006); to estimate the prevalence of diseases in humans (Verstraeten et al., Reference Verstraeten, Farah, Duchateau and Matu1998), plants (Tebbs and Bilder, Reference Tebbs and Bilder2004) and animals (Peck, Reference Peck2006); to detect transgenic plants (Hernández-Suárez et al., Reference Hernández-Suárez, Montesinos-López, McLaren and Crossa2008; Montesinos-López et al., Reference Montesinos-López, Montesinos-López, Crossa, Eskridge and Sáenz-Casas2011); and even to solve problems in science fiction (Bilder, Reference Bilder2009). The increasing use of this technique is due mainly to the significant savings of time and money it generates. It has been documented as producing savings of at least 80% in the number of diagnostic tests required.
However, successful application of group testing is related to group size (k), which will avoid problems with the dilution effect, and decrease the rate of false negatives and positives. If group size (k) is large, the rare characteristic will not be detected even if the group contains an AP plant, because the material is highly diluted. For this reason, it is very important to develop sampling methods under negative binomial group testing that will take into account the dilution effect. Under binomial group testing, Yamamura and Hino (Reference Yamamura and Hino2007) and Hernández-Suárez et al. (Reference Hernández-Suárez, Montesinos-López, McLaren and Crossa2008) proposed sampling procedures for detecting AP that take into account the limit of detection. Montesinos-López et al. (Reference Montesinos-López, Montesinos-López, Crossa and Eskridge2012) developed sample size procedures for estimating prevalence using inverse negative binomial group testing but without considering the dilution effect. For these reasons, sample size procedures using negative binomial group testing are affected when the trait of interest is diluted by the increasing pool size and the detection threshold (limit of detection) has not been considered.
Traditionally, sample sizes have been derived in terms of power (hypothesis testing). However, rejection of the null hypothesis does not guarantee an acceptable width of the confidence interval (CI). Also, today it is not common practice to report confidence intervals (CIs), mainly because their widths are embarrassingly large (Cohen, Reference Cohen1994). However, there is growing interest in using CIs rather than hypothesis tests for making inferences (Pan and Kupper, Reference Pan and Kupper1999). While CIs are in the same scale of measurement as the data, the p values derived and used in the hypotheses tests are abstract probability values. Also CIs convey information about magnitude and precision, while keeping these two terms closely related (Newcombe, Reference Newcombe1998; Kelley and Maxwell, Reference Kelley and Maxwell2003). The usual bilateral CI is interpreted simply as a margin of error of a point estimate (Pan and Kupper, Reference Pan and Kupper1999).
Therefore, in an effort to plan sample size and avoid large CI width, the Accuracy in Parameter Estimation (AIPE) approach was developed, which guarantees narrow CIs, because when CI width (1 − α)100% decreases, the expected accuracy of the estimate increases (Kelley and Maxwell, Reference Kelley and Maxwell2003; Kelley, Reference Kelley2007; Kelley and Rausch, Reference Kelley and Rausch2011). Although the AIPE approach to planning sample size is not new, it has been applied more in the social sciences than in veterinary and agricultural sciences (Montesinos-López et al., Reference Montesinos-López, Montesinos-López, Crossa, Eskridge and Hernández-Suárez2010). The ‘precision’ method defined as the half-length (or complete width) of the CI for the estimator, has been used in agricultural sciences; however, it is different to the AIPE approach. In the ‘precision’ or CI method one assumes that the variance of the proportion is known, thus the probability that the width of the CI will be less than the a priori specified width is around 50%, since most of the time the variance of the proportion is unknown and therefore estimated. In other words, the specified a priori width of the CI is only satisfied around 50% of the time. However, the AIPE method assumes that the variance of the proportion is unknown and that the sample size produces a CI with a width that will satisfy the specified a priori width with a certain level of certainty (often values ≥ 80%), named assurance. The objective of this research was to propose a sample size method for estimating the proportion of AP (p) under inverse negative group testing using an exact confidence interval (Clopper–Pearson) and taking into account the dilution effect. These sample sizes guarantee narrow CIs because they were developed under the AIPE framework. We developed the maximum likelihood estimate and CIs for p under inverse negative binomial group testing taking into account the dilution effect. A series of tables giving the required sample sizes are provided for diverse scenarios that could help researchers plan studies in which the prevalence of AP (p) is estimated with a sufficiently narrow CI. An R package was developed to help with the process of sample size determination.
Materials and methods
The probability of a positive pool with the dilution effect
When the k individuals that form a pool are mixed and homogenized, the AP will be diluted; this dilution effect increases with the size of the pool and may decrease the AP concentration in the pool below the laboratory test detection limit (d), thereby increasing the number of false negatives (i.e. seed(s) with AP is not detected when in fact it is present in the group) (Montesinos-López et al., Reference Montesinos-López, Montesinos-López, Crossa, Eskridge and Hernández-Suárez2010). Hernández-Suárez et al. (Reference Hernández-Suárez, Montesinos-López, McLaren and Crossa2008) proposed a model that considers the limit of detection of the laboratory test for a pool sampling method based on the Dorfman model (Reference Dorfman1943). They assumed a reference population of size N, with a proportion p of individuals with AP [or type (+)]. They also assumed that the concentration of AP per individual, c, is known (i.e. transgenic DNA as % of total DNA in the seed). When g pools are formed from a total of n individuals, the AP concentration in a single (+) individual in a pool is reduced to cg/n= c/k (for k= n/g). If d is the laboratory detection limit, it is required that (c/k) ≥ d, in which case the probability of detecting AP in a pool with at least one (+) individual is 1, and zero otherwise. If a pool has X (+) individuals, then it is required that [(cX)/k] ≥ d (Montesinos-López et al., 2010).
Note that in this study, the units of AP concentration, c, can be given in % DNA, whereas the units of c for other traits of interest such as unwanted diseases in the grain may be given as a % of the kernel. Therefore, the variable X= number of (+) individuals in a pool of size k (X= 0,1,2,…, k) is a binomial variable with parameters k and p, that is, X ~ Bin(k,p). Hence, Hernández-Suárez et al. (Reference Hernández-Suárez, Montesinos-López, McLaren and Crossa2008) and Montesinos-López et al. (Reference Montesinos-López, Montesinos-López, Crossa, Eskridge and Hernández-Suárez2010) propose that the probability that a group will be detected (+) is
$$ P ( X \geq v ) = { \sum _{ j = v }^{ k } }\,\left ({\begin{array}{ccc} k \\ j \\ \end{array} }\right ) p ^{ j }(1 - p )^{ k - j } = F ( p \left <?noresolve [verbar]> v , k - v + 1\right. ) $$where the quantity v is given by [dk/c], that is, the smallest integer not smaller than dk/c. If d = 0, v= 1 (where v represents the minimum number of AP necessary for detection). Furthermore,
$$\begin{eqnarray} F ( p \vert v , k - v + 1) = \frac {1}{ B ( v , k - v + 1)}{ \int _{0}^{ p } }\, j ^{ v - 1}(1 - j )^{ k - v } dj . \end{eqnarray}$$This means that 
$$F ( p \vert v , k - v + 1) $$ is the cumulative density function of the beta distribution with parameters v, k − v+1. Let 
$$F ^{ - 1}( p \vert v , k - v + 1) $$ be the inverse function (Montesinos-López et al., Reference Montesinos-López, Montesinos-López, Crossa, Eskridge and Hernández-Suárez2010).
Maximum likelihood estimate and confidence intervals for p under negative binomial group testing with dilution effect
Suppose that Y i= y i pools are tested to find the first positive pool, i= 1,2,…, r, where r is fixed. If the testing continues until the rth positive pool is found, where r>1, this implies that we will observe data as Y 1, Y 2, Y 3,…, Y r. Therefore, the total number of pools tested to find r positive pools is equal to 
$$T = \sum _{ i = 1}^{ r } Y _{ i } $$ (Pritchard and Tebbs, Reference Pritchard and Tebbs2010, Reference Pritchard and Tebbs2011). We shall denote the size of the pools collected by k, we assume equal pool size, the prevalence of infection is denoted by p, the number of pools tested to find one positive pool is Y i= y i, and the number of times this experiment is carried out is denoted by r. If the prevalence of infection is p, then the probability that a pool of size k tests positive is 
$$[ F ( p \left | v , k - v + 1)]\right. $$. Therefore, the sufficient statistics 
$$T = \sum _{ i = 1}^{ r } Y _{ i } $$ follows a negative binomial distribution with waiting parameter r and success probability 
$$F ( p \left | v , k - \right. v + 1) $$.
If there is a threshold of detection, the likelihood is given by
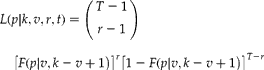$$ L ( p \left | k , v , r , t )\right. = \left ({\begin{array}{ccc} T - 1 \\ r - 1 \\ \end{array} }\right )\quad \left [ F ( p \left | v , k - v + 1\right. )\right ]^{ r }\left [1 - F ( p \left | v , k - v + 1\right. )\right ]^{ T - r } $$Equation (2) is maximized at 
$$F ( p \left | v , k - \right. v + 1) = r / T $$; hence the maximum likelihood estimate is given by
$$ \circ {>p} = F ^{ - 1}( r / T \left | v , k - v + 1)\right. $$Note that if v= 1, 
$$F ( p \left | v , k - v + 1\right. ) $$
$$= \theta = r / T = 1 - $$
$$(1 - p )^{ k } $$ is the probability of a pool being positive (it has AP) if the threshold of detection is not taken into account [for details, see Hernández-Suárez et al. (Reference Hernández-Suárez, Montesinos-López, McLaren and Crossa2008) or Yamamura and Hino (Reference Yamamura and Hino2007)]. Equation (3) simplifies to
$$\begin{eqnarray} \circ {>p} = 1 - \left (1 - \frac { r }{ T }\right )^{1/ k }, \end{eqnarray}$$which is the conventional maximum likelihood estimate of p for negative binomial group testing with groups of equal size and no threshold of detection (Pritchard and Tebbs, Reference Pritchard and Tebbs2010). With this information and using the ideas of Montesinos–López et al. (Reference Montesinos-López, Montesinos-López, Crossa, Eskridge and Hernández-Suárez2010) and Yamamura and Hino (Reference Yamamura and Hino2007), the following is an exact CI
$${\begin{array}{ccc} p _{ L } = F ^{ - 1}( \theta \circ _{ L }\left | v , k - v + 1\right. ) \\ p _{ U } = F ^{ - 1}( \theta \circ _{ U }</mrow>\left | v , k - v + 1\right. ) \\ \end{array} } $$where 
$$\circ {>\theta } _{ L } = F ^{ - 1}( \alpha /2\left | r , t - r + 1)\right. $$ and 
$$\circ {>\theta } _{ U } = F ^{ - 1}(1 - \alpha / $$
$$2\left | r , t - r )\right. $$. 
$$\circ {>\theta } _{ L } $$ is the lower endpoint of the 100(1 − α)% confidence interval of θ and is obtained with the α/2 quantile of a beta distribution with parameters r and (t− r)+1; 
$$\circ {>\theta } _{ U } $$ (the upper endpoint of the CI of θ) is the 1 − α/2 quantile of a beta distribution with parameters r and (t− r). These exact CIs (Clopper–Pearson intervals) are easy to calculate because statistical functions for inverting the F or the incomplete beta function are widely available in standard statistical packages. Besides, the coverage probability of the CIs constructed by exact CIs (the inverse of exact testing) is usually larger than 100(1 − α)%.
Also, it is important to mention that the first two moments of 
$$\circ {>p}$$ are given by
$$ E ( \circ {>p} ^{ z }) = { \sum _{ t = r _{ m }}^{ t ^{^{\ast }}} }\,\left [ F ^{ - 1}( r / T \left | v , k - v + 1)\right. \right ]^{ z }\left ({\begin{array}{ccc} T - 1 \\ r - 1 \\ \end{array} }\right )[ F ( p \left | v , k - v + 1\right. )]^{ r }[1 - F ( p \left | v , k - v + 1\right. )]^{ T - r } $$where t* is the value that satisfies P(T≤ t*) = 0.9999 for z= 1,2. Note that if z= 1, Equation (5) is the expected value of $$\circ {>p}$$. Therefore, the Bias= E($$\circ {>p}$$) − p and variance is equal to 
$$Var ( \circ {>p} ) = E ( \circ {>p} ^{2}) - E ( \circ {>p} )^{2} $$.
Determining optimum sample size with narrow CIs for p
Let p L= p L(X) be the random lower confidence limit for p and p U= p U(X) be the random upper confidence limit for p at the specified confidence level, where X represents the observed data vector on which the CI is based. The entire full width of the obtained CI using Equation (4) is then given as
$$ w _{ y } = ( p _{ U } - p _{ L }) $$Let ω be the desired full width of the CI (error) and p the population proportion or its estimated value. Operationally, an algorithm that guarantees finding the appropriate sample size consists of starting at some minimal sample size, say r 0, to be able to find the value of r m that satisfies
$$ P ( W \leq \omega )\geq \gamma $$Equation (7) is equal to:
$$ P ( W \leq \omega ) = { \sum _{ t = r _{ m }}^{ t _{^{\ast }}} }\, I ( w _{ t }, t )\left ({\begin{array}{ccc} t - 1 \\ r _{ m } - 1 \\ \end{array} }\right )\left [ F ( p \left | v , k - v + 1\right. )\right ]^{ r _{ m }}\left [1 - F ( p \left | v , k - v + 1\right. )\right ]^{ t - r _{ m }}\geq \gamma $$where I(w t, t) is an indicator function showing whether or not the actual confidence interval width (CIW) calculated with Equation (4) is ≤ ω, and W is considered a random variable because we do not know the exact value of p. Then t* is the value that satisfies P(T≤ t*) = 0.9999; γ is a probabilistic statement that is incorporated into the sample size planning procedure in order to guarantee a sufficiently narrow CI. This probabilistic statement (γ) needs to be greater than 0.5 (50%) because if γ = 0.5, the resulting sample size (r m) produced by Equation (8) only assures approximately a 50% chance that the interval will be narrower than the required value (ω) because W will vary from sample to sample. With the sample size produced using Equation (8), the researcher can be 100γ% confident that the observed relative width of a particular CI will be less than, or equal to, the required width (ω).
The procedure involves starting with some minimal sample size, say 
$$r _{0} = r $$, and increasing this value by one unit and recalculating Equation (8) each time until the desired degree of certainty (γ) is achieved; this will produce the modified number of pools (
$$r _{ m } $$) that assures with a probability of ≥ γ that the W will be no wider than ω. In other words, 
$$r _{ m } $$ ensures that the researcher will have approximately 100γ% certainty that a computed CI will be of the required width or less. This method for determining the modified sample size is consistent, in theory, with other methods of sample size planning that attach a probability statement to the CI width when the aim is to make them sufficiently narrow (Kelley and Maxwell, Reference Kelley and Maxwell2003; Kelley, Reference Kelley2007; Kelley and Rausch, Reference Kelley and Rausch2011).
Results and discussion
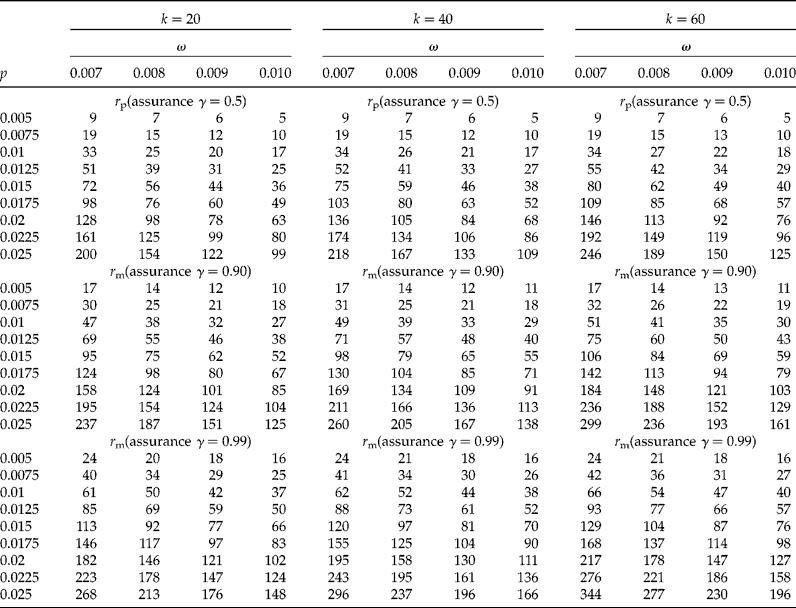
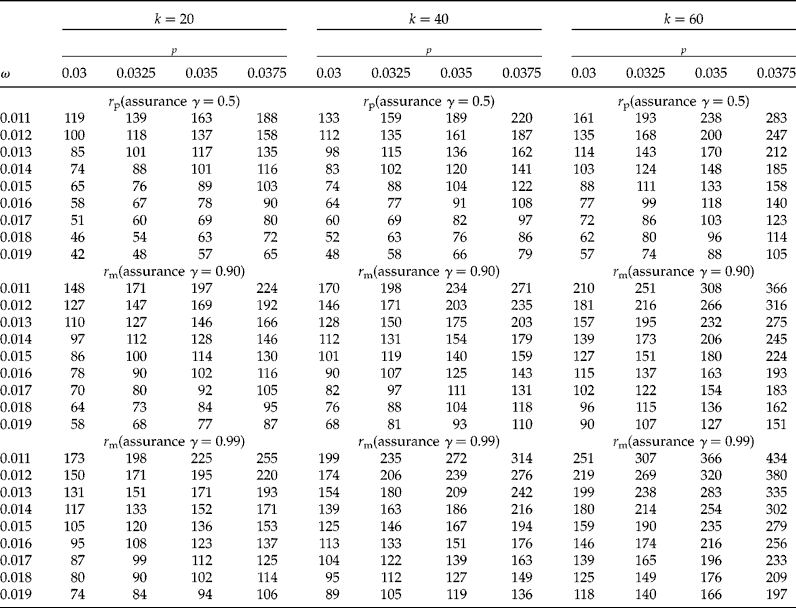
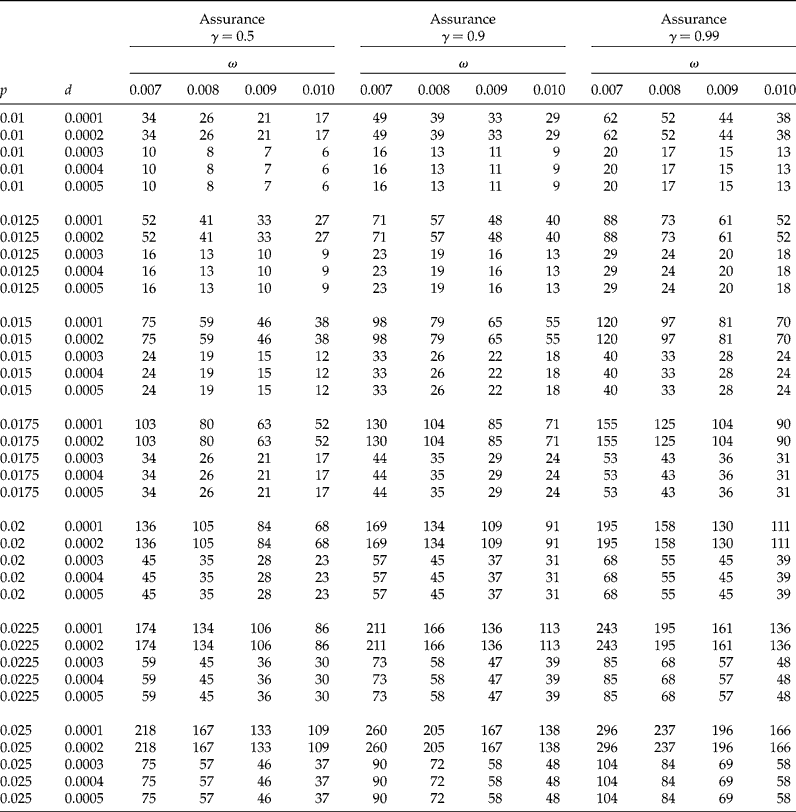
In Tables 1 and 2 we show sample sizes for k values of 20, 40 and 60, γ values of 0.5, 0.90 and 0.99, each with a CI coverage of 95%, a concentration of AP per individual, c= 0.01, and a limit of detection d= 0.0001. In Table 1 the proportion (p) ranged from 0.005 to 0.025 with increments of 0.0025, while the desired widths (ω) are 0.007, 0.008, 0.009 and 0.01. In Table 2 the proportions (p) are 0.03, 0.0325, 0.035 and 0.0375, and the desired widths (ω) ranged from 0.011 to 0.019 with increments of 0.01. We explain below how to obtain the sample size from these tables. Table 3 shows results of the sensitivity analysis with the objective of understanding how the sample size changes as a function of the threshold of detection (d); this table was constructed using a value of k= 40, five values of d (0.0001 to 0.0005 with increments of 0.0001), proportions (p) from 0.01 to 0.025 (with increments of 0.0025), and with the other parameters that were fixed at the same values as those used in Table 1.
Table 1 Sample size (required number of positive pools) for the proposed method for a CI of 95%, d=0.0001, c=0.01, four desired widths (ω=0.007, 0.008, 0.009, 0.010) and three values of γ (0.5, 0.9 and 0.99). The value of p is the population proportion, r p is the initial number of required positive pools, r m is the modified required number of positive pools, γ is the assurance for the desired degree of certainty of achieving a CI for p that is no wider than the desired CI width (ω)
Table 2 Sample size (required number of positive pools) for the proposed method for a CI of 95%, d=0.0001, c=0.01, four population proportions (p=0.03, 0.0325, 0.035, 0.0375) and three values of γ (0.5, 0.9 and 0.99). The value of ω is the desired CI width, r p is the initial number of required positive pools, r m is the modified required number of positive pools, γ is the assurance for the desired degree of certainty of achieving a CI for p that is no wider than the desired CI width (ω)
Table 3 Sample size sensitivity for changes in the threshold of detection (d) (required number of positive pools) for the proposed method for a CI of 95%, c=0.01, for a pool size k=40 and three values of γ (0.5, 0.9 and 0.99). The value of ω is the desired CI width, r p is the initial number of required positive pools, rm is the modified required number of positive pools, γ is the assurance for the desired degree of certainty of achieving a CI for p that is no wider than the desired CI width (ω)
Tables 1 and 2
Suppose a researcher is interested in estimating p for AP in maize. After doing a literature review of other studies, he/she hypothesizes that p= 0.0125, k= 40, the desired CI width is w y = (p U− p L) ≤ ω = 0.008, d= 0.0001, c= 0.01, and a CI of 95%. Applying the method leads to a required (preliminary) number of positive pools of r p = 41, each of size k= 40. This sample size is contained in the first sub-table (r p with γ = 0.5) in Table 1, where k= 40, p= 0.0125 and ω = 0.008.
Realizing that r p = 41 will lead to a sufficiently narrow CI only about half of the time, the researcher incorporates an assurance of γ = 0.99, which implies that the width of the 95% CI will be larger than required (i.e. 0.008) no more than 1% of the time. From the third sub-table in Table 1 (r m with γ = 0.99), it can be seen that the modified sample size procedure yields a necessary number of positive pools of r m = 73. Using a sample size of 73 will thus provide 99% assurance that the obtained CI for p will be no wider than 0.008 units. Similar reasoning is applied when interpreting Table 2.
Table 3
In Table 3 we can observe that when fixing the parameters (k, p, ω, γ, α, c) and varying the value of d, the necessary sample size substantially changed. For example assuming k= 40, p= 0.0125, ω = 0.008, γ = 0.9, α = 0.05, c= 0.01 and d= 0.0002 the required sample size is 57 while when the value of d= 0.0003 the required sample size is 19 for the same parameters. However, for values of d= 0.0004 and 0.0005 the required sample size is the same as for d= 0.0003. For all cases of Table 3, the larger the values of d, the smaller the required sample size. It can be noted that for certain values of the threshold of detection (d), the observed sample sizes do not change, but when d increases the sample size (r) is expected to decrease for fixed values of k and c. Although the sample size (r) tends to be larger when the value of d decreases, it should be pointed out that since 
$$P \left ( X > \frac { d _{1} k }{ c }\right )\geq $$
$$P \left ( X > \frac { d _{2} k }{ c }\right ) $$ for all d 1< d 2, the number of pools required until obtaining the first positive pool tended to be smaller for d 1 than for d 2.
It is important to point out that for values of γ close to 1, the accuracy in the estimation of the proportion increases, because accuracy is a function of bias and precision, so that obtaining a more precise estimate without increasing bias implies that the estimate is more accurate (Kelley and Rausch, Reference Kelley and Rausch2011). However, most of the sample size procedures for CI do not take into account the level of assurance and, for this reason, the probability that the observed width (W) of a particular CI will be less than the desired width (ω) is around 0.5 (50%) of the time. This is because the stochastic nature of the confidence interval width is ignored by not including the level of assurance. In the example given above, we mentioned that when using a sample size of r p = 41, the probability that (W ≤ ω = 0.008) ≈ 0.5; this means that for any particular CI the observed width (W) will be larger than the desired width 50% of the time. For this reason, the researcher used a level of assurance of 99%, which guarantees that the width of the 95% CI will be larger than required (i.e. 0.008) no more than 1% of the time. Thus, when using a high level of assurance close to 1 (100%), it is very important to make sure that the observed width of the CI will be satisfied.
The behaviour of the sample sizes of the proposed method (see Tables 1 and 2) can be summarized as follows: Holding all other factors constant: (1) larger values of p; (2) smaller values of ω; (3) larger values of γ; and (4) larger values of CI coverage (i.e. 1 − α) all lead to larger sample sizes (that is, a higher number of pools). Smaller values of ω imply that a larger sample size is necessary to obtain a narrower CI. Increasing the certainty that the CI will be sufficiently narrow (e.g. 99% certainty compared with 90% certainty) also requires a larger sample size. Similarly, as CI coverage increases (i.e. a decrease in α), the sample size for the desired confidence interval width also increases. The reverse is also true: (1) a decrease in p; (2) an increase in ω; (3) smaller values of γ; and (4) smaller CI coverage all lead to smaller sample sizes.
Although it is not possible to include all potentially interesting conditions in the two proposed tables, they do provide: (1) a convenient way to plan sample size when the situation of interest is approximated by the scenarios covered by the tables; and (2) a way to illustrate the relation between k, p, ω, γ, α, d, c, and the necessary sample size (r m). Also, to cover other scenarios useful for researchers, we developed an R package that implements the proposed method (see the Appendix).
Conclusions
This paper presents a sample size (required number of positive pools, r m) procedure for estimating the proportion (p) of AP under negative binomial group testing, taking into account the limit/threshold of detection, d, of the laboratory test and the AP concentration per unit, c. Under inverse (negative) binomial pool testing, the sampling process used to obtain the required number of positive pools (r m) involves drawing the pools one by one using simple random sampling until r m positive pools are found. We record the number of pools tested (Y 1, Y 2, Y 3,…, Y r, where Y i = y i) to find the ith positive pool, i= 1,2,…, r, because the total number of pools that are tested to find r positive pools is equal to 
$$T = { \sum _{ i = 1}^{ r } }\, y _{ i } $$. It is important to point out that this sample size guarantees that the CI width obtained by using the proposed method will be less than, or equal to, a specified value (ω) with a probability level of γ, because it was derived under the AIPE approach.
On the other hand, we present the maximum likelihood estimator of the prevalence (p) and an exact CI, under negative binomial group testing, taking into account the limit of detection, d, of the laboratory test. For this reason, the method proposed in this study is useful for planning sample size as well as for carrying out point and interval estimation of p under inverse (negative) binomial group testing sampling with dilution effect. Given that the proposed method cannot be solved in an analytical way, we provide tables with several combinations of parameters (k, p, ω, γ, α, d, and c) to estimate the required sample size. Because it is impossible to cover all the scenarios that a researcher may need for planning an appropriate sample size, we provide an R package (R Development Core Team, 2013) that can be readily used to obtain the required sample size for specific requirements. Finally, it is important to point out that the methods presented here are valid only if the sampling scheme is under negative binomial group testing and assuming a perfect diagnostic test.
Appendix
Using SSNBGTdil for method implementation
The proposed method can be implemented using the SSNBGTdil R package (R Development Core Team, 2013). The SSNBGTdil R package can be obtained from the CIMMYT website http://repository.cimmyt.org/xmlui/handle/10,883/3 (search for SSNBGTdil).
Because SSNBGTdil is an optional package, it must be loaded for each new R session where its routines will be used. Also it is important to point out that the package is in a zip file; for this reason it should be installed in the option install package(s) from local zip files. Then packages in R are loaded with the library() command, which is illustrated using SSNBGTdil, as follows:
$$\begin{eqnarray} R> library\,(SSNBGTdil) \end{eqnarray}$$To see how to use the three functions in this package you can use: ?ss.gmo.aipenb, ?prev.gmo.nbp and ?ci.gmo.nbp.
Maximum likelihood estimate of p
The prev.gmo.nbp() function can be used directly to estimate the prevalence ($$\circ {>p}$$) of AP by maximum likelihood. Use the example in Table 1, where k = 100, d = 0.0001, c = 0.01, T = 100 and r = 20. The functions are:
$$\begin{eqnarray} R> prev.gmo.nbp( k = 40 ,\, d = 0.0001 ,\, c = 0.01 ,\, T = 100 ,\, r = 20 ), \end{eqnarray}$$where k is the number of units by pool, d is the threshold of detection of the analytical instrument, c is the concentration of AP per unit, T is the total number of tested pools until r positive pools are found, and r is the number of positive pools. Implementation of this function yields a maximum likelihood estimate of p equal to 0.005563057 or 0.5563%. This means that in this population, the estimated p of AP is 0.5563%.
Confidence interval for p of AP
The ci.gmo.bnp() function can be used directly to determine the confidence limits for p. The lower and upper critical values are returned by specifying the following arguments in the ci.gmo.nbp() function:
$$\begin{eqnarray} R> ci.gmo.nbp( k = 40 ,\, d = 0.0001 ,\, c = 0.01 ,\, T = 100 ,\, r = 20 ,\, conf . level = 0.95 ), \end{eqnarray}$$where k is the number of units in each pool, d is the threshold of detection of the analytical instrument, c is the concentration of AP per individual, T is the total number of tested pools, r is the number of positive (defective) pools, and conf.level is the desired level of confidence (i.e. 1 − α). Implementing this function yields values of 0.003379906 (0.337%) and 0.008295211 (0.829%) for the upper and lower confidence limits of p using a 95% confidence level.
Planning sample size for p
Using the example in Table 2, where p= 0.0125 and ω = 0.008 for a 95% CI, the ss.gmo.aipenb() function can be used so that the expected width is sufficiently narrow and given as:
$$\begin{eqnarray} R> ss.gmo.aipenb\,( p = 0.0125 ,\, conf . level = 0.95 ,\, k = 40 ,\, d = 0.0001 ,\, c = 0.01 ,\, width = 0.008 ,\, assurance = 0.99 ), \end{eqnarray}$$where p is the population prevalence (i.e. p), conf.level is the confidence level (i.e. 1 − α), k is the pool size, d is the threshold of detection of the analytical instrument, c is the concentration of AP per unit, assurance is the desired degree of certainty for the CI width, and width is the desired CI width. This returns the required number of pools, 73 (as reported in the text and in Table 2), that provides 99% assurance that the obtained CIW for p will be no wider than 0.008 units.
