1. Introduction
The German-speaking part of Switzerland is characterized by a phenomenon known as diglossia; that is, two different varieties of the same language are used within a community in different social situations. One variety is known as standard Swiss German—that is the variety of standard German accepted as the norm in Switzerland. It is used in most written contexts (e.g., literature, newspapers, private correspondence, and official documents), in formal and official spoken contexts (e.g., education and parliament speeches), and in interactions with foreigners. The second variety, that is the dialect, is known as Swiss German and is used in everyday life, within the family, as well as in most radio and television programs.Footnote a Since Swiss German does not have a standardized orthography, it is rarely used in written contexts. However, nowadays we observe an increasing use of the dialect in written computer-mediated communication (CMC). This phenomenon has multiple and interesting repercussions for a low-resource language like Swiss German, as it makes valuable material available for natural language processing (NLP) tasks. The NLP pipeline typically requires standardized text as input. Given the nonstandard nature of written Swiss German, and the high degree of variation that characterizes it, the need for text normalization, that is, mapping different variants of the same word type to a single string, becomes immediately evident.
Several factors contribute to the high degree of variation of the source text. Firstly, the lack of a standardized spelling is further complicated by the strong regional variation and the numerous local variants of the same word. As a result, the word viel (“much”) can appear as viel, viil, vill, viu, and many other potential variations. Secondly, CMC is characterized by various peculiarities, such as vowel reduplication and unconventional abbreviations, which increase variation.
In this paper, we tackle the issue of enhancing the performance of neural methods in the task of text normalization. We work with the neural framework that proved most successful in machine translation—a combination of two recurrent neural networks (RNNs) known as the encoder–decoder architecture with attention mechanism—and we enrich the basic character-level neural machine translation (NMT) model with modifications that allow us to overcome the limitation of having a small training set. The solution we propose is a combination of two mechanisms that addresses two challenges related to normalization of written Swiss German.
The first challenge is due to the fact that the plain NMT model operates at the character level, and has no notion of what a word is. Therefore, it might produce an output that, based on the train set, is not a proper word, despite being a likely sequence of characters. Following Gulcehre et al. (Reference Gulcehre, Firat, Xu, Cho and Bengio2016), Ruzsics and Samardžić (Reference Ruzsics and Samardžić2017), and Lusetti et al. (Reference Lusetti, Ruzsics, Göhring, Samardžić and Stark2018), our first modification consists in including an additional language model (LM) at the decoding stage. The score of an integrated word-level LM is combined with the one produced by the basic character-level NMT model by means of a synchronization mechanism. We expect the additional word-level LM to contribute to a better fluency of the output.
The second challenge is due to the ambiguity that arises when one source word is normalized in two or more different ways in the train set. In order to address this issue, we investigate whether NMT can benefit from the integration of additional linguistic features by adding POS tags to the input of the NMT model. Knowing the POS associated with a word undoubtedly provides an important cue as to which the appropriate normalization form might be. For this purpose, we train a POS tagger that is capable of tagging Swiss German WhatsApp messages.
Moreover, the combination of the two approaches is expected to work in a complementary manner, with the result of jointly improving the fluency of the output and resolving cases of ambiguity.
Our results show that, in the task of normalizing Swiss German WhatsApp messages, the approach we describe achieves a better performance than the current state-of-the-art character-level statistical machine translation (CSMT) methods and the plain NMT model.
Although the aim of this work is to normalize WhatsApp messages written in Swiss German, we believe that the methods we propose are highly flexible and portable, and can thus be applied to other settings characterized by nonstandard text.
2. Related work
Since the introduction of neural methods to machine translation (Kalchbrenner and Blunsom Reference Kalchbrenner and Blunsom2013; Cho et al. Reference Cho, van Merrienboer, Gulcehre, Bahdanau, Bougares, Schwenk and Bengio2014; Sutskever, Vinyals, and Le Reference Sutskever, Vinyals and Le2014), various attempts have been made to apply the new framework to the task of normalization. A recent shared task (Tjong Kim Sang et al., Reference Tjong Kim Sang, Bollmann, Boschker, Casacuberta, Dietz, Dipper, Domingo, van der Goot, van Koppen, Ljubešić, Östling, Petran, Pettersson, Scherrer, Schraagen, Sevens, Tiedemann, Vanallemeersch and Zervanou2017) allowed a direct comparison of CSMT with some neural methods, with CSMT still outperforming neural systems. Honnet et al. (Reference Honnet, Popescu-Belis, Musat and Baeriswyl2017) apply a neural method embedded in other techniques. Bollmann and Søgaard (Reference Bollmann and Søgaard2016) report experiments with deep, long short-term memory (LSTM) networks.
Our approach draws on the line of work known as the encoder–decoder framework. In this framework, one RNN encodes a sequence of symbols into a fixed-length vector representation, and the other decodes the representation into an output sequence of symbols. Following established approaches, we extend this basic framework with the soft attention mechanism introduced by Bahdanau, Cho, and Bengio (Reference Bahdanau, Cho and Bengio2014), which allows a model to search for parts of a source sequence that are relevant to predicting a target symbol.
Moreover, our work is closely related to approaches that implement a modification of the encoder–decoder framework that allows to incorporate additional LM scores at the decoding stage. Gulcehre et al. (Reference Gulcehre, Firat, Xu, Cho and Bengio2016) integrated a character-level LM into an encoder–decoder framework to augment the parallel training data with additional monolingual corpora on the target side. Adapting this framework to the task of morphological segmentation, Ruzsics and Samardžić (Reference Ruzsics and Samardžić2017) introduced a “synchronization mechanism” that allows to integrate LM scores at different levels: the basic encoder–decoder component is trained on character sequences and the target-side LM component is trained on sequences of morphemes. Lusetti et al. (Reference Lusetti, Ruzsics, Göhring, Samardžić and Stark2018) applied this approach to the task of text normalization, by integrating word-level scores of an LM on the top of the character-level neural normalization framework.
Linguistic features such as lemmas, morphological and syntactic information, and POS tags have been used in an attempt to improve the performance of SMT (Koehn and Hoang Reference Koehn and Hoang2007), resulting in factored machine translation models. Lemmatization can reduce data sparseness by relying on more general representations than surface forms of words, whereas POS tags and syntactic dependency labels can help in disambiguation. Sennrich and Haddow (Reference Sennrich and Haddow2016) argue that NMT provides a more flexible mechanism for adding linguistic information. In their approach, the embedding layer of an encoder–decoder model with attention is generalized to support the inclusion of additional features by vector concatenation. When words are segmented into sub-word units, the feature value associated with the entire word is copied to all its sub-word units. Similarly, our models incorporate linguistic information in the form of POS tags, with the difference that an output unit is produced by combining the POS feature with the current decoder hidden state and soft attention context vector at decoding time. Since we use a character-level model, and thus characters represent our sub-word units, we use the POS tag of a word for the prediction of each one of its characters.
3. Our approach
In the following sections, we describe the NMT framework and the details of our adaptations to the task of normalizing a corpus of Swiss German WhatsApp messages.
The normalization task can be formalized as a transformation of the input sequence of characters to the output sequence of characters. For example, the input word viil (as well as its variants, e.g., vill) has to be mapped to its normalized form viel “much.” Specifically to the WUS corpus (See Section 4 for a description of the corpora used as data sets for our experiments), most of the mapped sequences are pairs of single words (one-to-one alignments) as shown in the first section of Table 1. There are also many contracted forms corresponding to multiple normalized words (one-to-many alignments). These are typically verb forms or prepositions merged with subject and object clitics, as illustrated in the second section of Table 1. The few cases of many-to-one alignments are due to typos (a space instead of a character) and the lack of spelling conventions for Swiss German, most noticeable in arbitrarily split compounds and separable verb particles. Finally, different combinations of the factors listed above can result in many-to-many mappings. Examples of these more rare alignments are presented in the last two sections of Table 1.
Table 1. Examples of aligned token sequences in the WUS corpus
In our approach, we combine two methods to adapt a basic NMT model to the normalization task. The basic NMT system takes as an input the source form, for example, viil “much,” and learns a mapping to its normalized form viel. Our first method modifies the decoding stage of the plain NMT system that has been already pretrained for the task. Specifically, the advanced decoding mechanism integrates an additional LM pretrained on the target side of the data. Such approach allows us to incorporate more target-side data and add more fluency to the NMT system output. This is achieved by guiding the NMT generation process during decoding through synchronizing NMT and LM scores at word boundaries. The advanced decoding process specifically targets the cases of one-to-many alignments. In addition, it results in rescoring one-word hypotheses of the NMT system, which occur in one-to-one alignment units. The setup of the plain NMT system and the details of the decoding approach are described in Section 3.1.
In our second method, we consider the integration of POS features to the neural system. The NMT system with additional features learns how to transduce an input pair of a word with its POS tag. For example, the system learns to map an input (lüüt, NN) to its normalization Leute “people” while the input with a different POS tag (lüüt, VVFIN) should be transformed to the form läuten “to ring.” The second setup with additional POS features is described in Section 3.2.
While each of the proposed enhancements to the plain NMT system targets specific phenomena in the corpus—fluency and, especially, one-to-many alignments are targeted by the advanced decoding, whereas the additional POS features address the problem of ambiguous words—the combination of the two approaches is expected to work complementary in the cases which combine both phenomena. For example, the input word vor can be either normalized as the preposition vor (“before”; “in front of”) or as a preposition followed by an article, as in von der “from the.”
3.1 NMT with LM
First, we describe the basic configuration of the NMT system, an encoder–decoder model with soft attention (Bahdanau et al., Reference Bahdanau, Cho and Bengio2014; Luong, Pham, and Manning, Reference Luong, Pham and Manning2015), that we use for all our neural experiments. In order to formalize our task, we define two vocabulary sets, 
$V_s$ consisting of the character symbols that form the source sequences (second column in Table 1) and 
$V_{t}$ of the character symbols that form the normalized sequences (third column in Table 1). Then, our task is to learn a mapping from an original character sequence 
$x \in V_s^*$ to its normalized form 
$y\in V_{t}^*$.
The model transforms the input sequence into a sequence of hidden states. A hidden state is a fixed-dimensional vector representation for each character that encodes the character itself and the signal from its character-level context. The system learns this transformation with a bidirectional encoder which consists of a forward and backward RNN. The forward RNN reads the input sequence of embedding character vectors 
$\mathbf{x}_1, \dots, \mathbf{x}_{n_x}$, in forward direction and encodes them into a sequence of vectors representing forward hidden states:
\begin{equation}
\overrightarrow{\mathbf{h}}_t = f(\overrightarrow{\mathbf{h}}_{t-1}, \mathbf{x}_t), \quad t=1,\dots, n_x \end{equation}
while the backward RNN reads the sequence in the opposite direction and produces backward hidden states:
\begin{equation}
\overleftarrow{\mathbf{h}}_t = f(\overleftarrow{\mathbf{h}}_{t-1}, \mathbf{x}_t), \quad t=n_x,\dots, 1 \end{equation}
where f stands for LSTM (Hochreiter and Schmidhuber Reference Hochreiter and Schmidhuber1997). The hidden state 
$\mathbf{h}_t$ for each time step is obtained by concatenating a forward and a backward state, so that 
$\mathbf{h}_t=[\overrightarrow{\mathbf{h}}_t;\overleftarrow{\mathbf{h}}_t]$.
The decoder RNN transforms the internal fixed-length input representation into a variable length output sequence 
$y=( y_1, \dots, y_{n_y})$. At each prediction step t, the decoder reads the previous output 
$\mathbf{y}_{t-1}$ and outputs a hidden state representation 
$\mathbf{s}_t$:
\begin{equation} \mathbf{s}_t = f(\mathbf{s}_{t-1}, \mathbf{y}_{t-1}), \quad t=1,\dots, n_y \end{equation}
The conditional probability over output characters is modeled at each prediction step t as a function of the current decoder hidden state 
$\mathbf{s}_t$ and the current context vector 
$\mathbf{c}_t$:
\begin{equation} p( y_t \vert y_1,\dots, y_{t-1}, x) = g(\mathbf{s}_t, \mathbf{c}_t) \end{equation}
where g is a concatenation layer followed by a softmax layer (Luong et al. Reference Luong, Pham and Manning2015).
The context vector 
$\mathbf{c}_t$ is computed at each step from the encoded input as a weighted sum of the hidden states:
\begin{equation} \mathbf{c}_t = \sum_{k=1}^{n_x} \alpha_{tk} \mathbf{h}_k \end{equation}
The weights are calculated by an alignment model which scores how much attention should be given to the inputs around position k to generate the output at position t:
\begin{equation} \alpha_{tk} = \phi(\mathbf{s}_{t},\mathbf{h}_k) \end{equation}
where 
$\phi$ is a feedforward neural network (Luong et al. Reference Luong, Pham and Manning2015). Therefore, the model learns the alignment between input and output jointly with transduction using a deterministic function. The illustration of the model architecture is provided in Figure 1.
Figure 1. Basic NMT architecture.
The training objective is to maximize the conditional log-likelihood of the training corpus:
\begin{equation} L = \frac 1 N \sum_{(x,y)} \sum_{t=1}^{n_y} \log p(y_t \vert y_1,\dots,y_{t-1}, x) \end{equation}
where is the number of training pairs (x,y).
3.1.1 Integrating LMs
In this section, we describe the synchronized decoding mechanism for integrating an LM into the NMT system (Ruzsics and Samardžić Reference Ruzsics and Samardžić2017). Before the integration, we assume that an NMT model and an LM are trained separately. The NMT model is trained on character sequences in a parallel corpus consisting of aligned source words and their normalized forms (as shown in Table 1). It learns local character transformations and implicitly includes an LM over the target-side characters through the decoder RNN component. We augment this model with an additional LM, separately trained over the target side of the corpus. We consider a setup where the LM is trained over words from the target side of the train set, which we augment with extra target data.Footnote b Therefore, the additional LM brings the frequency signal from higher-level units of the target data (words), while the NMT system operates on characters. In the following, we describe how the synchronized decoding allows us to fuse the scores of both components, NMT and LM, at the decoding stage.
The synchronized decoding approach relies on a beam search to find the prediction steps where the scores of the different model components are combined. The beam search is run at two levels of granularity. First, it produces the output sequence hypotheses (candidates) at the character level using NMT scores until the time step 
$s_1$, where K best hypotheses 
$\{(y_1 y_2 \dots y_{s1})^i\}$, 
$y_t \in V_t$, 
$i = 1, \dots, K$, end with a word boundary symbol.Footnote c We consider two boundary symbol types: space, which marks the end of a word in a partial predicted sequence, and a special eow symbol, which marks the end of a completed predicted sequence. The step 
$s_1$ is the first synchronization step where we re-score the normalization hypotheses with a weighted sum of the NMT score and the LM score:
\begin{align} &\log{p(y_{s1} \vert y_1,\dots,y_{s1-1}, x)}\nonumber\\ &\qquad\qquad\qquad= \log{p_{NMT}(y_{s1} \vert y_1,\dots,y_{s1-1}, x)} + \alpha_{LM}\log{p_{LM}(y_1,\dots,y_{s1})} \end{align}
At this step, 
$y_1,\dots,y_{s1}$ is considered a sequence of s1 characters by the NMT system, and one word by the LM. After the first synchronization point, we continue to produce the re-scored hypotheses using NMT scores until the next synchronization point. The search process ends at the synchronization point where all the hypotheses are complete predictions, that is, end with the eow symbol. The parameter 
$\alpha_{LM}$ is optimized with the MERT algorithm on the development set.
The decoding process scores the hypotheses at two levels: normally working at the character level with NMT scores and adding the LM scores only when it hits a boundary point for all the hypotheses in the beam. In this way, the LM score helps to evaluate how probable the last generated word is, based on the predicted word history, that is, the sequence of words generated at the previous synchronization time steps.
Figure 2 illustrates the process of synchronized decoding for the source word idere, whose correct normalization form is in dieser “in this.” The NMT model operates at the character level and gives a greater probability to the character sequence ideren</s> than to the sequence in_ (iteration 1). This leads to a wrong prediction. However, when the word-level LM is used, in_ has a greater probability than ideren</s>, since the LM is aware that the latter is not a word according to the train set. The hypotheses are further expanded (iteration 2) until reaching the next boundary, where the process ends and where the sequence in_ dieser</s> is correctly given the greatest probability by the NMT + LM model. This example shows that, while it is true that each additional token adds to the log likelihood, if the first word has never been seen as a stand-alone, its probability could be much smaller than the probability of an additional token + “end of sentence” symbol.
Figure 2. Synchronized decoding.
3.2 NMT with POS tags as features
In the setting where we use additional features in the form of POS tags, in addition to the two vocabularies that contain the source 
$V_s$ and target 
$V_t$ characters, we have a vocabulary of the possible POS tags 
$V_f$ (fifth column in Table 1). Our task is to learn a mapping from an input pair (x, 
$f_x = f_1+\cdots+f_k$) of a source character sequence 
$x\in V_s^*$ and its POS feature 
$f_x$ (possibly consisting of one or more tags 
$f_i\in V_f$) to its normalized form 
$y\in V_{t}^*$. We embed the POS tags 
$f_i\in V_f$ into their vector representations 
$\mathbf{f}_i$, which are learned by the system. In cases where the feature input is a composition, that is, it consists of several POS tags 
$f_1+\cdots+f_k$, we use an average of the corresponding vector embeddings 
$ (\mathbf{f}_1+\cdots+ \mathbf{f}_k) / n $ as representation.
We then adapt the plain NMT system and feed the POS features, together with the current decoder hidden state 
$\mathbf{s}_t$ and the current context vector 
$\mathbf{c}_t$, in order to predict the next output character as follows :
\begin{equation} p( y_t \vert y_1,\dots, y_{t-1}, x) = g(\mathbf{s}_t, \mathbf{c}_t, \mathbf{f}_x) \end{equation}
The architecture of the model is illustrated in Figure 3. Since the decoder operates at the character level, each prediction step t corresponds to the output of one character. Therefore, the POS feature 
$f_x$ associated with the entire word x is used for the prediction of each one of its characters 
$y_t$.
Figure 3. NMT with POS tags as features.
4. Data and preprocessing
The data for our experiments come from manually normalized Swiss German corpora:Footnote d
WUS set is a corpus of WhatsApp messages (Stark, Ueberwasser, and Göhring Reference Stark, Ueberwasser and Göhring2014; Ueberwasser and Stark Reference Ueberwasser and Stark2017). The entire collection contains 763,650 messages in different languages spoken in Switzerland. A portion of the data, 5345 messages in Swiss German, was selected for manual annotation in order to provide a gold standard for automatic normalization. We use this manually annotated portion (a total of 54,202 alignment units) as our main data set. Table 1 in Section 3 shows examples of alignment units in the corpus.
SMS set is a corpus of SMS messages, again in different languages spoken in Switzerland (Stark, Ueberwasser, and Ruef 2015). This is a smaller corpus entirely manually normalized. The Swiss German portion contains 10,674 messages. We use this set (a total of 262,494 alignment units) as training data to train additional LMs, as described in more detail in the following.
All the messages in our data set are manually normalized using the same web annotation tool and following the same guidelines (Ruef and Ueberwasser Reference Ruef, Ueberwasser, Zampieri and Diwersy2013). This normalization process implies a monotonic alignment between the source tokens and the normalized ones.
One peculiarity of the WUS corpus is, unsurprisingly given the source of the texts, the frequent use of emojis. These are represented in the corpus as a sequence of characters describing the symbol. For example, the emoji 
is rendered as emojiQsmilingFaceWithOpenMouth. This choice was made by the creators of the corpus to allow users of a query interface to search for emojis by means of regular expressions.Footnote e
Our task is to normalize Swiss German WhatsApp messages. In order to train our models, we split the randomly shuffled WUS corpus in 80% training, 10% development, and 10% test set, and use this split for all our experiments.Footnote f The training set contains 43,798 parallel units, the test set 5043 units, and the development set 5361 units. For the experiments where we train LMs with additional target data, we add 262,494 target sequences of the SMS corpus. This results in a total of 306,292 units for the extended target WUS + SMS data.
4.1 POS tagging
In this section, we describe our procedure for creating the tagged version of the WUS corpus.
We use a TreeTaggerFootnote g (Schmid Reference Schmid1994) parameter file, produced by adapting a general standard German model to the normalized version of the SMS corpus. The general model is adapted by first adding manually to the TreeTagger lexicon all words that were unknown to the initial general model, thus reaching a full coverage. The tagging model is then retrained on the normalized version of the SMS corpus to include Swiss-specific items.
The outcome of the process described above was a TreeTagger parameter file that is specifically tailored to tag normalized Swiss German and was made available to us.Footnote h We used this file to create a silver standard of the source (not normalized) WUS corpus. We first tagged the normalized forms with the adapted TreeTagger, which relies on the STTS tagsetFootnote i (consisting of 54 tags), with the additional tag PTKINF for go, goge, and other forms of infinitive particles often encountered in Swiss German dialects. In a second step, we projected the tags from the normalized forms onto the corresponding manually aligned source forms,Footnote j and trained a new model with the BTaggerFootnote k (Gesmundo and Samardžić Reference Gesmundo and Samardžić2012) on the train portion of the WUS corpus. Finally, we tagged the source side of the development and test set using the pretrained BTagger.
We have tested the performance of the BTagger by comparing its output to the silver standard, which resulted in 90.30% and 90.67% accuracy on the test and development sets, respectively. These scores, though only an approximation, are higher than those produced by the TreeTagger. Moreover, using the BTagger also results in a better performance in the normalization experiments which rely on POS tags (Section 3.2). Therefore, we opted for tagging the source side of the WUS development and test set with the BTagger. We hypothesize that the reason for the BTagger outperforming the TreeTagger in tagging the source side of the WUS corpus is partly due to the fact that for this specific task we do not have a TreeTagger tailor-made parameter file, as was the case in the task of tagging the normalized forms.
5. Experiments
To assess how suitable our proposed methods are for the text normalization task, we designed experiments for a systematic comparison of their performance. We consider two experimental settings, with and without POS tags. For each setup, we include a setting for synchronized decoding with an additional LM trained on the target side of the data. In the following, we introduce the details of the experimental setup.
For the experiments without POS tags, we run a neural model in two settings: in its plain form of encoder–decoder with attention mechanism (NMT) and in combination with an additional LM (NMT + LMwus + sms:word). The language model LMwus + sms:word is trained over words using the target side of the two data sets, that is, the concatenation of the train part of the WUS corpus with the SMS corpus (WUS + SMS).
Our basic configuration for the experiments with POS tags consists of the following steps: (1) training a POS tagger model using the training portion of the corpus annotated with POS tags (silver standard, as explained in Section 4.1); (2) using the pretrained tagger to predict POS tags on the development and test portions of the corpus; (3) training an NMT model where POS tags are used as features. Therefore, at test time the neural model has only access to the predicted tags. As in the experiments without POS tags, we use two settings: plain form (NMT + POS) and with advanced decoding (NMT + POS + LMwus + sms:word).
All neural models were implemented using DyNet, a flexible neural network toolkit (Neubig et al. Reference Neubig, Dyer, Goldberg, Matthews, Ammar, Anastasopoulos, Ballesteros, Chiang, Clothiaux, Cohn, Duh, Faruqui, Gan, Garrette, Ji, Kong, Kuncoro, Kumar, Malaviya, Michel, Oda, Richardson, Saphra, Swayamdipta and Yin2017). We run the experiments with synchronized decoding using the version of the code from Ruzsics and Samardžić (Reference Ruzsics and Samardžić2017) which is compatible with DyNet.Footnote l The code for all our experimental settings is publicly available.Footnote m
Neural Hyperparameters. The character embeddings are shared between input (source) and output (target) vocabulary and are set to 100. The POS embeddings have size 50. The forward and backward RNN of the bidirectional encoder have 200 hidden units each. The decoder also has 200 hidden units. We apply an ensemble of five NMT models, where each model is trained with random start using SGD optimization. We combine the NMT models by summing up their log probabilities at each character prediction step (no majority voting). In case of the synchronized decoding, such accumulated sum is combined with the weighted log probability of the LM at word boundaries.
The models are trained for a maximum of 40 epochs, possibly stopping earlier if the performance measured on the development set is not improving after 10 epochs. The training examples are shuffled before each epoch.
Parameters for synchronized decoding. The word-level language model LMwus+sms:word is built on 3-grams with modified Kneser–Ney smoothing using the SRILM toolkit. The weight of the LM component in the synchronized decoding is tuned with MERT optimization by maximizing the accuracy score on the development set. Beam size 3 is used for the final predictions on the test set in all the settings.
5.1 Baseline models and comparison
For our experiments with and without POS tags, we consider separate baselines which are designed to assess the difficulty of the normalization task in the two scenarios. For comparison with neural models in the setting without POS tags, we also run experiments with a CSMT model, due to its prominent status in the task of Swiss German text normalization.
Baseline. For our baseline in the setting without POS tags, we adapt an approach which was reported for the normalization task of Swiss German in Samardžić, Scherrer, and Glaser (Reference Samardžić, Scherrer and Glaser2015). To this end, we consider three classes of input words in the test set: new, ambiguous, and unique. The new category includes the words that have not been observed in the training set. The baseline simply copies such word as its normalization. The unique words are associated with exactly one normalization form in the train set, which is used by the baseline at test time. The last category, ambiguous, consists of input words which are associated with more than one normalization candidate from the train set. For such words, the baseline uses the most frequent normalization form if there are no ties in their frequencies or, otherwise, randomly chooses a form out of the normalization candidates. The distribution of the three word classes in the test set of the WUS corpus is shown in the left-hand side of Table 3.
Table 2. Text normalization accuracy scores
a LMwus + sms:char : language model trained over characters on the target side of the WUS corpus extended with the target side of the SMS corpus.
b LMwus + sms:word : language model trained over words on the target side of the WUS corpus extended with the target side of the SMS corpus.
Table 3. Performance by source words categories
a ambiguous: input words with more than one normalization based on the train set.
b unique: input words with one normalization based on the train set.
c new: input words that have not been seen in the train set.
d WUS: only the WUS corpus is used for model training.
e WUS + SMS: additional target side of the SMS corpus is used for LM training.
Baseline + POS. In the setting with POS features, we introduce a different baseline (Baseline + POS) similar to the approach above which addresses ambiguous words. Specifically, we consider the same three classes of source words in the test set and normalize the words in the new and unique classes in the same way as it is done by the Baseline. In order to allow Baseline + POS to use the additional input information in the form of POS tags, we further split the words in the ambiguous class into two subclasses. The first subclass consists of words for which each POS tag that appears together with this word in the train set can be associated with a unique normalization form; that is, there is a unique normalization for the pair (word, POS tag). This form is then selected by the Baseline+POS for the input pair (word, POS tag) at test time. We refer to this subclass as pos-unambiguous. The other subclass, pos-ambiguous, consists of the words for which there are at least two normalization forms in the train set associated with the same tag. In such cases, if the tag of the input word has not been observed with this word at train time, the model selects the most frequent normalization of this word in the train set. Otherwise, Baseline + POS selects the most frequent normalization corresponding to the test input pair (word, POS tag) or a random form out of its normalization candidates, in case of a tie. The distribution of the word subclasses for the ambiguous class in the test set of the WUS corpus is shown in the left-hand side of Table 4.
Table 4. Disambiguation analysis with POS tags
a ambiguous: input words in the test set that have more than one normalization based on the train set.
b pos-unambiguous: ambiguous words for which each POS tag that appears together with this word in the train set can be associated with a unique normalization form; that is, at test time, there is a unique normalization for the input pair (word, POS tag).
c pos-ambiguous: ambiguous words that have at least two normalization forms in the train set associated with the same tag.
d new_pos: alignment units (word, POS tag) in the test set where the word is from the pos-ambiguous class and the POS tag is not observed in the train set.
e ties: alignment units (word, POS tag) where the word is from the pos-ambiguous class, which are associated with different normalization forms with the same frequencies in the train set.
f no_ties: alignment units (word, POS tag) where the word is from the pos-ambiguous class, which are associated with different normalization forms with different frequencies in the train set.
CSMT. We consider a setting for CSMT with an LM trained over characters using the concatenation of the train part of the WUS corpus with the SMS corpus (LMwus + sms:char). Such setting provides a basis of comparison to our NMT + LMwus + sms:word model. Note that the CSMT language model operates only at the character level.Footnote n We used the Moses toolkit with the following adjustments to the standard settings: (i) assuming monotonic character alignment, distortion (reordering) was disabled; (ii) in tuning, we used WERFootnote o instead of BLEU for MERT optimization of the model’s components. We used the KenLM language model toolkit (Heafield Reference Heafield2011) with character 7-grams.
5.2 Evaluation metric
In a character-level framework, where most alignment units consist of single words, evaluation metrics such as precision, recall, and BLEU may provide information on the extent to which a unit normalized by the model, viewed as a sequence of characters, differs from its reference. They thus express the magnitude of the intra-word error. However, such metrics are position-independent, and might yield a high score when the tokens of the output match those of the reference, despite being in the wrong position. In a word-level setting, changing the position of words or word sequences does not necessarily go to the detriment of sentence fluency. By contrast, in a character-level setting, the position of the characters within a word has a higher impact on fluency. For this reason, we chose to simply assess whether a source sequence has been correctly normalized or not by the system, and the accuracy score is used to evaluate the baselines and the various models implemented. We compute the accuracy of the normalized test set units by comparison with the manual normalization.
6 Results and discussion
The results of our experiments are shown in Table 2. In the setting without POS features, the NMT model alone outperforms both Baseline and CSMT.Footnote p The best accuracy score of 87.09% in this setting is obtained by the NMT + LM model. This result indicates that the NMT approach benefits from the integrated LM for our task.
Turning to the setting with POS features, the NMT + POS model achieves a substantial improvement over the Baseline + POS and the best performing model in the setting without POS (NMT + LM). Finally, augmenting the NMT + POS model with an additional LM (NMT + POS + LM) results in the best overall accuracy of 89.53%.
The results confirm that both approaches for adaption of the plain NMT model—synchronized decoding and POS features—are beneficiary and complementary for the task of text normalization. In order to evaluate the two components separately, we assess the performance of our models on the different categories of the input words in the test set. The results for the word categories introduced in the Baseline approach, that is, new, ambiguous, and unique, are presented in Table 3. We report the performance of the Baseline, indicating the difficulty of the task for each category, and the best performing models in our two settings, NMT + LM and NMT + POS + LM. To further assess the impact of the additional LM alone, we compare the results of NMT + LM model to the plain NMT model. To this end, we introduce two subcategories for the new class of the input words: we divide the test set token pairs (input word, normalization form) for which the input word has not been seen during training into two classes: (i) seen_trg, where the normalization form is a word that has been observed in the target side of the train set; (ii) new_trg, where the normalization form is a word that has not been observed.Footnote q
Analyzing the results of the models on the different classes of the input words, we observe that the performance of the NMT and NMT + LM models on the unique words is identical to that of the Baseline, meaning that they replicate the Baseline strategy for this category. However, there is a slight drop in the performance of the best model, NMT + POS + LM, which could be attributed to the higher impact of the POS features (that could be unseen or noisy) in this model.
The accuracy of all neural models in the new category is almost twice as high as the Baseline. This could be explained by the ability of the neural models to learn well local string transformations, as opposed to the naive copy approach of the Baseline model. The highest score achieved in this category by NMT + POS + LM is still relatively low (60%) compared to the performance in the other categories, suggesting that normalization of words not seen during training is a particularly difficult task. Comparing the results of the NMT and NMT + LM models among the three word categories, the highest improvement of around 2% points is achieved on the new words, resulting in 57.54% accuracy. This suggests that the advanced decoding with additional LM particularly helps with the words in this category, which can be explained by the subclass performance. We observe that the LM pushes the performance of NMT + LM higher in the seen_trg subcategory compared to the new_trg subcategory (64.05% vs. 47.50%), while the results on these subcategories are relatively similar for the NMT model (56.50% vs. 54.67%). The difference can be explained by the fact that for the NMT+LM model the weight of the seen_trg subclass in the new category becomes higher due to additional target SMS data used for LM training. The synchronized decoding algorithm (optimized for the overall accuracy) drives the LM weight up, which results in choosing more normalization forms, out of the candidates generated by NMT, that have been observed in the target side. This preference leads to higher performance on seen_trg words, but comes at the expense of a decreased performance on the subcategory new_trg. An additional improvement of 5% points is achieved on the new_trg category by NMT + POS + LM model. This can be explained by a better ability of this model to learn local string transformations in the presence of POS features.
The additional POS features used by the NMT + POS + LM model help to improve the accuracy on ambiguous words by almost 7% points compared to the approaches without the POS tags. We analyze the performance of the POS-aware models on this category by considering the subclasses of the ambiguous category introduced for the Baseline + POS approach: pos-unambiguous and pos-ambiguous words. In Table 4, we show the results on the subclasses, for the best performing model NMT + POS + LM, and the baseline model (Baseline + POS), which gives an estimation of the task complexity in this setting. In order to isolate the impact of the POS tags in the NMT + POS + LM model, we include the NMT + LM model for comparison.
We observe that while the overall performance of the best model without POS tags (NMT + LM) is higher than the Baseline + POS, its accuracy is inferior on the ambiguous category and its two subcategories. However, adding POS tags features is helpful for both classes. In particular, the NMT + POS + LM model manages to reach the accuracy of the Baseline + POS on the pos-unambiguous subcategory, whereas it outperforms the baseline on the subcategory pos-ambiguous.
6.1 Error analysis
We have analyzed the difference in the performance of our systems on three major categories of test input words: new, unique, and ambiguous. In the following, we discuss what are the typical errors produced by the systems and how the proposed enhancements for the plain NMT model—synchronized decoding and POS features—affect the performance in the different categories.
New words. As already noted in the discussion above, the optimization mechanism in the synchronized decoding used in the NMT + LM model pushes up the weight of the LM component resulting in a higher overall accuracy and, in particular, higher accuracy in the new category, that is, test words that have not been observed in training. We investigate the source of the different performance of NMT+LM and NMT + POS + LM models in the subcategories of the new words compared to the NMT model (see Table 3).
(1) From NMT to NMT + LM: why is there a jump in the performance in the seen_trg category?
With the increase of the weight of the LM component, more words are normalized by selecting the form out of the NMT candidates that has been seen during training. The examples of NMT errors which have been corrected with the LM in the NMT + LM system are shown in Table 5. Section (a) of the table lists examples of NMT errors where the normalization form consists of only one word, that is, one-to-one or many-to-one alignment units. For example, the word schi “already” was normalized wrongly by NMT as schei, whereas NMT + LM picks the right form schon, which has been seen in the target side of the train set as a normalization form for other varieties of this input word in Swiss German. In section (b) we present examples of the NMT errors where the LM helps to correct the prediction for the words whose normalization consists of several words, that is, one-to-many or many-to-many alignment units. This is the category which is specifically targeted by the mechanism of the scores synchronization in the synchronized decoding. For example, NMT + LM produces the correct normalization form können wir for the input word kömmer “we can” while the NMT prediction is kommer. Finally, with the addition of the SMS target data, more target forms become seen during the LM training, which helps the NMT+LM model to select the right normalization. Some of such examples are presented in section (c) of Table 5.
Table 5. Errors of NMT in the new words category from the seen_trg class corrected by NMT + LM
(2) From NMT to NMT+LM: why is there a drop in the performance in the new_trg category?
While the strategy of increasing the LM weight in the synchronized decoding approach helps to improve the overall accuracy score, this comes at the expense of a decreased performance in the new_trg category, that is, words that have a normalization form which has not been seen in the target side of the train data. For the new words which have at least one NMT normalization candidate that has been seen during training, the synchronized decoding often results in selecting this candidate as a prediction. We present some cases where this leads to an error in Table 6. For example, the word essig “vinegar” has three NMT normalization candidates (sorted by the decreasing NMT log-probability score): essig, essen, and einsig. While NMT correctly normalizes this word as essig, NMT + LM erroneously selects the form essen “to eat” which was observed in the train target data. This kind of errors could be reduced to some extent with the use of more target data for LM training. However, due to many rare words according to the Zipf’s Law, the LM will be overconfident for some cases, no matter how much we increase the training data.
Table 6. Errors of NMT + LM in the new words category from the new_trg class corrected by NMT
(3) From NMT + LM to NMT + POS + LM: why is there a jump in the performance in the new_trg category?
The corrected cases are mostly due to the fact that the POS features help the NMT+POS model generate better normalization candidates. The synchronized decoding in NMT + POS + LM then tends to select the candidate which has been seen in the target training data. This, in turn, leads to the increase in the performance in the new_trg category. To illustrate this case, the word rumi “I clean” has a gold normalization räume ich and a silver POS tag VVFIN + PPER (see Table 7). The NMT system generates three normalization candidates for this word, sorted by the decreasing NMT log-probability score: rumi, rum ich, and räume. The first two forms were not observed in the target side of the corpus, whereas the third one was. Contrary to the tendency of the synchronized decoding to pick candidates which have been seen during training (i.e., have a high LM score), in this case the NMT+LM model selects the first form rumi as a prediction. This is due to the fact that the NMT log-probability for the third candidate is much lower than for the first two and it prevails in the combined weighted NMT and LM score (i.e., LM score and weight are not high enough to select the third option, which was seen in the train set during the decoding). However, with the addition of POS features, NMT + POS generates a different list of candidates: rum ich, räume ich, and rume ich (sorted by the decreasing NMT log-probability score). In this case, the weighted combination of the NMT + POS and LM scores leads to the selection of the correct candidate räume ich by the NMT + POS + LM model.
Table 7. Errors of NMT + LM in the new words category from the new_trg class corrected by NMT + POS + LM
a Pred. Norm.: Three-best-predicted normalization forms sorted by the decreasing model score—the best candidate (predicted normalization) is in bold.
unique words. We have observed in Table 3 that the neural models without POS features (NMT and NMT + LM) replicate the strategy of the baseline models for the unique words category by simply copying the word as its normalization. However, the accuracy score in this category is under 100% and becomes even lower for the model with POS features (NMT + POS + LM). Next, we present the common patterns for the errors in this category.
(1) Why the performance in the unique category is under 100% for all models?
One of the observed patterns of the mistakes in the unique category is the wrong inflection ending of an adjective in the normalized form. An example of such error is illustrated in Table 8. The input word nette “nice” is associated with the unique normalization netter in the training set, which is selected by all the models at test time, although the correct normalization form is netten. Taking the context into account could help in such cases. Concretely, recognizing the dative case marker—which is required by the preposition bei “with”—and the feminine marker—suffix in of the singular noun Lehrerin “teacher”—in the presence of the definite article der should result in the adjective nett ending with a suffix en. Therefore, while the POS tag alone gives already an indication that the input word is an adjective, more fine-grained morphosyntactic information (or context which can provide this information) is further needed for correct normalization.
Table 8. An example of the errors in the unique category by the models without POS features
(2) Why the performance in the unique category decreases for the NMT + POS + LM model compared to the Baseline and NMT + LM model?
We have found that unique words which have a wrong predicted POS tag were particularly prone to be wrongly normalized by the NMT + POS + LM model. While the systems without POS features select the most frequent normalization form for such word in the train set (which almost always leads to the correct prediction), the NMT + POS + LM model gives a high weight to the combination of POS tag and local string transformation. For example, the word ess “eat” is associated with the unique normalization form esse in the train set, which is then selected by the NMT + LM model for a test set example presented in Table 9. Moreover, this normalization form is associated with the unique tag VVFIN. This word is wrongly normalized as ein by the NMT + POS + LM model. The error is caused by the fact that the tag of the word is wrongly predicted as ART instead of VVFIN. The NMT + POS + LM model gives a high weight to this POS signal and normalizes the word as ein. This could be explained by a high frequency of normalizing the word es as ein (indefinite article “a”) in the train data. Therefore, NMT + POS + LM gives more weight to the combination of the POS feature ART and substring es and goes beyond the approach of selecting a unique normalization associated with the full input word.
Table 9. An example of the errors in the unique category by the models with POS features
ambiguous words. As we saw in Table 3, the addition of POS features helps to considerably improve the performance of the systems on ambiguous words, that is, test words which have more than one normalization candidate in the train set. The analysis of the performance on the subclasses of the ambiguous words in Table 4 has shown that in almost half of the cases, all the observed input pairs (word, POS tag) for the given word are associated with exactly one normalization form, which is then selected by all the systems with POS features (pos-unambiguous subcategory). We perform an error analysis of such strategy in this subcategory. In the other half of the cases (pos-ambiguous subcategory), this strategy is not always applicable since the input word can have the same normalization form associated with different tags in the training. However, the performance of the neural system NM + POS + LM in this subcategory is higher than the Baseline+POS. We investigate the source of this improvement and the errors in this subcategory of the best performing NMT + POS + LM system.
(1) Why the performance of the Baseline + POS and NMT + POS + LM systems on pos-unambiguous category is under 100%?
Some of the errors in this subcategory come from the incorrectly predicted POS tag. For example, in the train set the ambiguous input word vor has been normalized as vor (“before”; “in front of”) with the tag APPR and as von der (“from the”; “of the”) with the tag APPR + ART. At test time (Table 10), its predicted tag is APPR, while the silver tag is APPR + ART. Therefore, all the models select the incorrect normalization form vor.
Table 10. An example of the errors in the ambiguous category for the words in the pos-unambiguous class with incorrectly predicted tag by the models with POS features
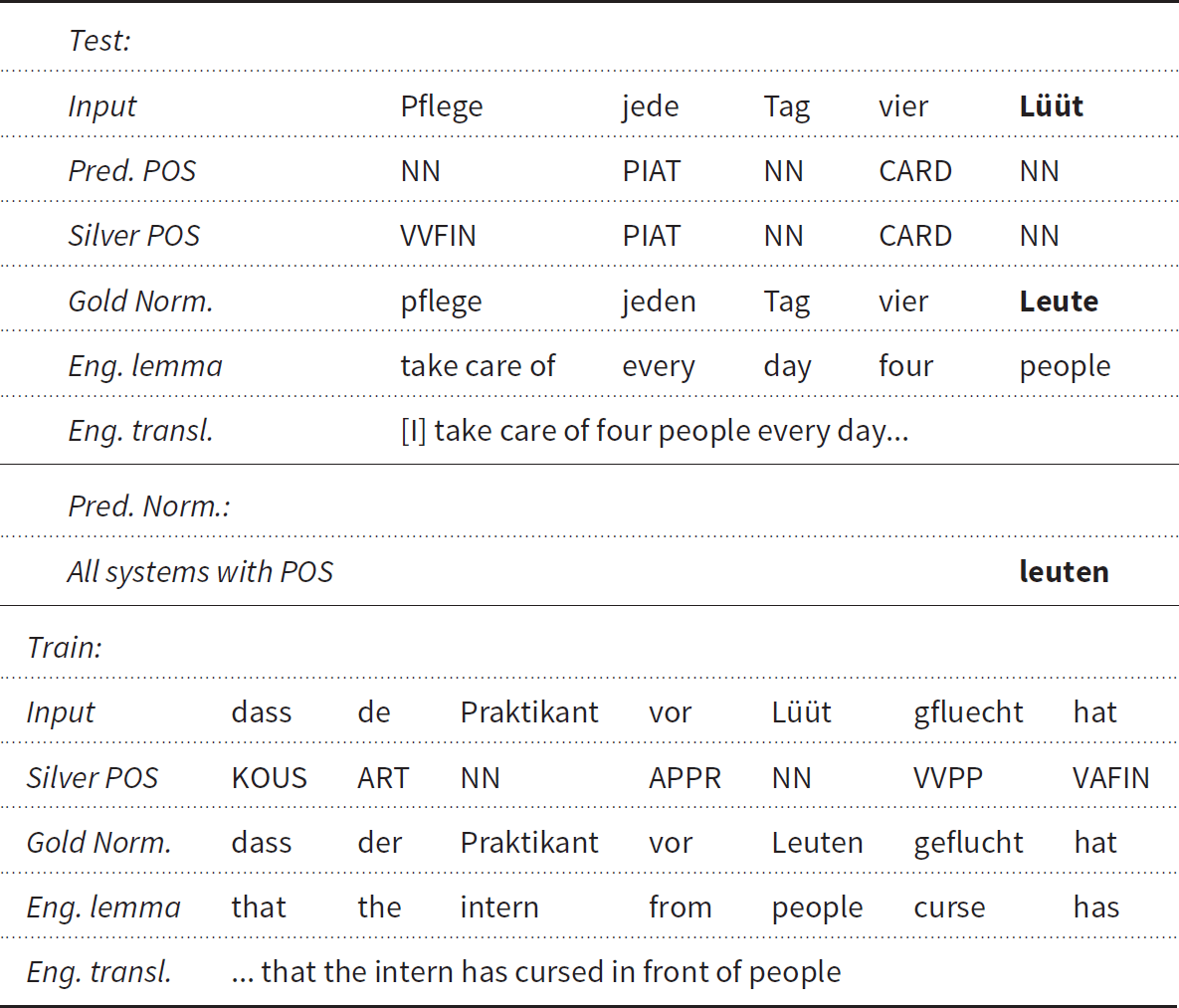
In more complicated cases where the tag is correctly predicted, some of the errors come from a further ambiguity in the case markers of the normalized form. To illustrate this case, the ambiguous input word Lüüt has been normalized as Leuten “people” with POS tag NN and läute “to ring” with POS tag VVFIN. At test time (Table 11), the models select the form Leuten, corresponding to the (correctly predicted) NN tag. However, the system fails to recognize that the suffix “n” in the train set is due to the preposition vor “of the,” not presented in the test case, which always requires a dative case. Such ambiguity in the case markers could be potentially resolved with the use of context information or a more fine-grained tagset.
Table 11. An example of the errors in the ambiguous category for the words in the pos-unambiguous class with correctly predicted tag by the models with POS features
(2) Why the performance of NMT + POS + LM on pos-ambiguous increases compared to the Baseline + POS model?
While the difference in the performance of the two models on the pos-ambiguous subclass is small, they show an interesting behavior of the NMT + POS + LM model. For example, the input word viel “much,” with the silver tag ADV at test time, was tagged with the wrong tag PIAT. The word is wrongly normalized as viele by the Baseline + POS model and correctly normalized as viel by NMT + POS + LM (see Table 12). In the train set, it is normalized 26 times as viel, with different POS tags (including 4 times with the tag PIAT and 15 times with the tag ADV) and 6 times as viele with the tag PIAT. Therefore, the Baseline+POS takes the normalization with a higher frequency viele for the test input pair (viel, PIAT). The behavior of NMT + POS + LM could be explained if we look at the counts of the target forms viel and viele, not only for the input word viel but also for its variants viil and vill: these forms are normalized as viele 97 times and viel only 32 times. Therefore, we hypothesize that while the NMT+POS+LM model gives a high weight to the POS features, this weight is balanced with the contribution of the high frequency of the local transformations.
Table 12. An example of the errors in the ambiguous category for the words in the pos-ambiguous class
Similarly, the source word mir is normalized 78 times in the train set as mir (“me” as indirect object) and 82 times as wir “we.” Both normalization forms are personal pronouns and have therefore the same POS tag (PPER). The Baseline+POS selects the more frequent form wir to normalize the input pair (mir, PPER) while the NMT + POS + LM model selects again the less frequent form mir. This choice could be again hypothetically explained if we look at how many times these two forms were used to normalize dialect variants of the input word mir in the train set, such as mier, mer, and others. While the target form wir appears in total 144 times, the form mir is seen 209 times. Also, the higher frequency of the test cases where the input mir is normalized as mir is more frequent than the other option. Thus, the choice of the NMT + POS + LM model is more advantageous.
(3) Why the performance of NMT + POS + LM on pos-ambiguous is under 100%?
As the previous example of the input word mir shows, this word can have different normalization forms which both correspond to the same tag PPER. Another common category of errors is related to the normalization of definite and indefinite articles. They all share the same POS tag ART, though the normalization forms can be different due to complex morphology, that is, case, gender, and number markers. As previously noted, such errors could be potentially resolved with the use of context information or a more fine-grained tagset.
7. Conclusion and future work
In this paper, we propose a combination of mechanisms for the adaptation of a character-level NMT framework to the task of Swiss German text normalization. The first approach is an advanced decoding mechanism with an additional word-level LM, which allows to incorporate more data on the target side and improve the fluency of the NMT output. The second approach is the use of additional linguistic features (in our case, POS tags) in the NMT system. We show that both approaches are complementary and result in the improvement of the neural models. In particular, the decoding part helps to improve the performance on unseen input words, whereas POS tag information addresses ambiguous words, that is, words with different possible normalization forms. These improvements are important for the development of NLP tools for Swiss German, which is increasingly in demand. However, the method is also conceptually portable to any similar setting of text normalization. In future work, it may be interesting to use our method for the normalization of other languages characterized by dialect variation.
Our thorough performance and error analysis point to the two major directions for further improvements. One direction would be to increase the amount of target data in order to address unseen input words. Another possible direction is to include more context information to target ambiguous words. In particular, some cases of ambiguity cannot be resolved with POS tag features due to the complex morphology of the language. One possible way to address such cases could be the development of a more fine-grained tagset. Alternatively, one could use the context information more directly by including the neighboring words within the sentence boundaries in the neural system.
