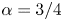Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-06T08:50:15.281Z Has data issue: false hasContentIssue false
  • English
  • Français

Hall instability: origin, properties and asymptotic theory for its tearing mode

Published online by Cambridge University Press:  14 July 2021

Leonid Kitchatinov Open the ORCID record for Leonid Kitchatinov [Opens in a new window]
Leonid Kitchatinov*
Affiliation:
Institute of Solar-Terrestrial Physics SB RAS, Lermontov Str. 126A, 664033Irkutsk, Russia Pulkovo Astronomical Observatory, St. Petersburg196140, Russia
*
†Email address for correspondence: kit@izf.irk.ru
Rights & Permissions [Opens in a new window]

Abstract

Hall instability in electron magnetohydrodynamics is interpreted as the shear-Hall instability driven jointly by helicoidal oscillations and shear in the electron current velocity. This explanation suggests an antiparallel orientation of the background magnetic field and vorticity of the current velocity as the necessary condition for Hall instability. The condition is tested and generally confirmed by numerical computations in plane slab geometry. Unstable eigenmodes are localized in the spatial regions of the antiparallel field and vorticity. Computations of the tearing-type mode of the instability are complemented by (and generally agree with) asymptotic analytical estimations for large Hall numbers. The stabilizing effect of perfect conductor boundary conditions is found and explained. For large Hall numbers, the growth rates approach the power-law dependence $\sigma \propto B^\alpha \eta ^{1-\alpha }$ on the magnetic field ($B$) and diffusivity ($\eta$). Almost all computations give the power index $\alpha = 3/4$ with one exception of the tearing-type mode with vacuum boundary conditions for which case $\alpha = 2/3$.

Keywords

astrophysical plasmasplasma instabilities
Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 4 , August 2021 , 905870404
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

1. Introduction

The Hall effect is studied mainly in relation to its ability to catalyse the dissipation of magnetic fields. This effect conserves magnetic energy and magnetic helicity but it can amplify resistive dissipation by decreasing the spatial scale of magnetic structures. Goldreich & Reisenegger (Reference Goldreich and Reisenegger1992) noted that hypothetical Hall turbulence can accelerate the decay of magnetic fields in a neutron star crust towards their observationally detected rates; the Hall cascade has been studied numerically by Hollerbach & Rüdiger (Reference Hollerbach and Rüdiger2002) and Brandenburg (Reference Brandenburg2020). Vainshtein, Chitre & Olinto (Reference Vainshtein, Chitre and Olinto2000) considered a similar effect for the solar corona.

Alternatively, dissipative magnetic structures can be produced by instabilities. Growth rates of hydromagnetic tearing instability are known to increase with allowance for the Hall effect (see Zhang, Ma & Wang Reference Zhang, Ma and Wang2017; Shi et al. Reference Shi, Velli, Pucci, Tenerani and Innocenti2020; Bora, Bhattacharyya & Smolarkiewicz Reference Bora, Bhattacharyya and Smolarkiewicz2021 for recent publications). This is probably because the Hall effect can drive its own instability of the tearing type.

Hall instability was discovered by Rheinhardt & Geppert (Reference Rheinhardt and Geppert2002). They found that the Hall effect can destabilize an equilibrium magnetic field if second-order spatial derivatives of the field do not vanish. The instability requires inhomogeneity in the background state for its development but can onset under diverse conditions. If the background state includes reversals of the magnetic field, the instability can operate in the tearing mode (Gourgouliatos & Hollerbach Reference Gourgouliatos and Hollerbach2016). Reversals are however not necessary and an inhomogeneous background field without reversals can be unstable as well (Rheinhardt & Geppert Reference Rheinhardt and Geppert2002; Pons & Geppert Reference Pons and Geppert2010). Inhomogeneity of density also can facilitate the instability (Rheinhardt, Konenkov & Geppert Reference Rheinhardt, Konenkov and Geppert2004; Wood, Hollerbach & Lyutikov Reference Wood, Hollerbach and Lyutikov2014). It is not clear at the moment whether the instabilities driven by the Hall effect under these diverse conditions are of the same origin. There is no commonly accepted pictorial explanation of Hall instability/instabilities.

A possible explanation was proposed in the preceding paper (Kitchatinov Reference Kitchatinov2017). The explanation relies on analogy with shear-Hall instability (cf. § 8.4.3 in Rüdiger & Hollerbach Reference Rüdiger and Hollerbach2004; Kunz Reference Kunz2008) and suggests that the Hall instability results from shear in the electron current velocity. This paper tests the explanation by computations of the Hall instability in the electron magnetohydrodynamics (MHD) approximation in plane pinch geometry.

Section 2 provides a brief reminder on the essence of the Hall effect and the proposed explanation for Hall instability. Section 3 describes the design and equations of the model. Section 4 presents the results of numerical and analytical estimations for the Hall instability of the background field profiles with and without reversal of the field direction. The final § 5 summarizes the results and conclusions.

2. Hall effect and Hall instability

The Hall effect is related to the magnetically induced anisotropy of electric conductivity. If the gyrofrequency $\omega _\mathrm {e}$ of electrons – the main carriers of electric current – is not small compared with the frequency $\nu _\mathrm {ei}$ of electron collisions with particles of other species, the conductivity $\sigma _\|$ along the magnetic field lines is larger than conductivities for the other directions. Ohm's law then reads (see, e.g. Somov Reference Somov2013, Chapter 11):

(2.1)\begin{equation} \boldsymbol{j}' = \frac{\sigma_\|}{1 + R_\mathrm{H}^2} [\boldsymbol{E}' + R_\mathrm{H}\hat{\boldsymbol{b}}\times \boldsymbol{E}' + R_\mathrm{H}^2\hat{\boldsymbol{b}}(\hat{\boldsymbol{b}}\cdot \boldsymbol{E}')], \end{equation}

where $\hat {\boldsymbol {b}}$ is the unit vector along the magnetic field $\boldsymbol {B}$, $\boldsymbol {j} = \mathrm {c}(\boldsymbol {\nabla } \times \boldsymbol {B})/(4{\rm \pi} )$ is the current density, $\boldsymbol {E}$ is the electric field, the primed notations mean that the equation is formulated for the reference frame co-moving with the fluid mass velocity $\boldsymbol {u}$, and

(2.2)\begin{equation} R_\mathrm{H} = \omega_\mathrm{e}/\nu_\mathrm{ei} \end{equation}

is the Hall number. Equation (2.1) can be reversed to express the electric field in terms of the current density:

(2.3)\begin{equation} \boldsymbol{E}' = ( \boldsymbol{j}' - R_\mathrm{H}\hat{\boldsymbol{b}}\times \boldsymbol{j}')/\sigma_\|.\end{equation}

If (2.3) is used instead of its isotropic counterpart $\boldsymbol {E}' = \boldsymbol {j}'/\sigma _\|$ in the standard derivation of the induction equation of MHD (see, e.g. Parker Reference Parker1979, Chapter 4), the derivation yields:

(2.4)\begin{equation} \frac{\partial\boldsymbol{B}}{\partial t} = \boldsymbol{\nabla}\times \left[(\boldsymbol{u}_\mathrm{c} + \boldsymbol{u})\times\boldsymbol{B} - \eta\boldsymbol{\nabla}\times \boldsymbol{B}\right], \end{equation}

where $\eta = \mathrm {c}^2/(4{\rm \pi} \sigma _\|)$ is the magnetic diffusivity,

(2.5)\begin{equation} \boldsymbol{u}_\mathrm{c} ={-}\boldsymbol{j}/(e n_\mathrm{e}) \end{equation}

is the current velocity, and the expressions for the gyrofrequency $\omega _\mathrm {e} = e B/(m_\mathrm {e}c)$ and conductivity $\sigma _\| = \textrm {e}^2 n_\mathrm {e}/(m_\mathrm {e}\nu _\mathrm {ei})$, in terms of the microscopic plasma parameters, are used. The Hall effect in MHD, therefore, means an additional current velocity (2.5) for the magnetic field advection.

This effect for a uniform background field together with a (prescribed) plane shear flow can drive an instability. The sufficient condition for the shear-Hall instability is a counter-alignment of the magnetic field and shear-flow vorticity (Rüdiger & Hollerbach Reference Rüdiger and Hollerbach2004; Rüdiger & Kitchatinov Reference Rüdiger and Kitchatinov2005). The shear-Hall instability allows a clear pictorial explanation in terms of the combined action of shear in the mass velocity and helicoidal oscillations induced by the Hall effect (see discussion of figure 8 of the paper by Kunz Reference Kunz2008).

As the current velocity $\boldsymbol {u}_\mathrm {c}$ enters (2.4) in the same way as the mass velocity $\boldsymbol {u}$, it should lead to the same consequences. Instability can be expected from shear in the current velocity if its vorticity is counter-aligned to the magnetic field. This is the interpretation of the Hall instability supposed in this paper. The interpretation can explain the diversity of conditions for which the Hall instability is met. It is clear why the magnetic field should depend at least quadratically on position for the instability (Rheinhardt & Geppert Reference Rheinhardt and Geppert2002); otherwise the current velocity has no shear. It is also clear why density inhomogeneity can be relevant. Inhomogeneous electron density in (2.5) can be the reason for a shear. The magnetic field and current vorticity are counter-aligned near the local maxima of the (unidirectional) magnetic field. This explains why reversals of the field direction are not necessary for the instability.

The difference with the shear-Hall instability however is that the unstable background field is necessarily inhomogeneous and the current shear does not change the magnetic energy. This results in the diffusive character of the Hall instability. Its growth rates scale as $B^\alpha \eta ^{1-\alpha }$ with $0 < \alpha < 1$ for a large Hall number.

3. The model

We adopt the electron MHD approximation that omits the mass velocity $\boldsymbol {u}$ in the induction equation (2.4). The approximation is justified for the solid crust of neutron stars and possibly for the case of large microscopic viscosity compared with the magnetic diffusivity. The case of large magnetic Prandtl number is characteristic of the hot plasmas of stellar coronae (Brandenburg & Subramanian Reference Brandenburg and Subramanian2005, § 3). Normalized variables are used with distances normalized to the characteristic scale $L$ of the background field, the field strength normalized with the amplitude $B_0$ of this field and time measured in diffusive units $L^2/\eta$. With this approximation and normalization, the induction equation retains only one governing parameter of the Hall number (2.2) that is now defined with (constant) amplitude $B_0$ of the background field:

(3.1)\begin{equation} \frac{\partial\boldsymbol{B}}{\partial t} = \boldsymbol{\nabla}\times \left[ R_\mathrm{H}\boldsymbol{B}\times (\boldsymbol{\nabla}\times \boldsymbol{B}) - \boldsymbol{\nabla}\times \boldsymbol{B}\right]. \end{equation}

We use a Cartesian coordinate system and consider the stability of the magnetic field that has only one non-zero $z$ component and varies with coordinate $x$ only,

(3.2)\begin{equation} \boldsymbol{B} = \left(0,0, B(x)\right). \end{equation}

The linear stability of this background field to small disturbances $\boldsymbol {B}'$ is considered. In all cases where instability is found, the most rapidly growing modes are uniform along the $y$-axis. The (toroidal) $y$-component $b(x,z)$ and (poloidal) component $\boldsymbol {\nabla }\times (\hat {\boldsymbol {y}}a(x,z))$ normal to this axis are convenient to distinguish in such two-dimensional disturbances to satisfy automatically the condition $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {b} = 0$ ($\hat {\boldsymbol {y}}$ is the unit vector along the $y$-axis)

(3.3)\begin{equation} \boldsymbol{B}'(x,z) = \hat{\boldsymbol{y}} b(x,z) + \boldsymbol{\nabla}\times(\hat{\boldsymbol{y}} a(x,z)). \end{equation}

The equation system for the small disturbances can be obtained by linearization of (3.1). Coefficients of the resulting equations do not depend on time or $z$. An exponential dependence on these variables $b,a \propto \exp (\sigma t + \mathrm {i}kz)$ can therefore be assumed that leads to the eignvalue problem:

(3.4)\begin{equation} \left.\begin{gathered} \sigma a ={-}\mathrm{i}kR_\mathrm{H}B(x)b - k^2 a + \frac{\partial^2 a}{\partial x^2}, \\ \sigma b = \mathrm{i}kR_\mathrm{H}\left[ B(x)\left(\frac{\partial^2 a}{\partial x^2} - k^2 a\right) - \frac{\partial^2 B}{\partial x^2}a\right] - k^2 b + \frac{\partial^2 b}{\partial x^2}. \end{gathered}\right\} \end{equation}

The second derivative of the background field accounts for the shear in the current velocity. The neglect of the diffusive decay of this field is justified if the growth rates of instability are large, $\mbox{Re} (\sigma ) \gg 1$.

Equations (3.4) are solved in a plane slab with two boundaries imposed at $x = \pm 1$. Unless otherwise stated, the results to follow correspond to vacuum conditions at the slab boundaries,

(3.5a,b)\begin{equation} b = 0,\quad \frac{\partial a}{\partial x} ={\mp} k a\quad \mathrm{for}\ x ={\pm} 1. \end{equation}

A finite background field at the boundaries for this case can be understood as imposed by external sources. The conditions for perfect conductor boundaries,

(3.6a,b)\begin{equation} \frac{\partial b}{\partial x} = 0,\quad a = 0\quad \mathrm{for}\ x ={\pm} 1, \end{equation}

is an alternative possibility.

Numerical computations were performed with a uniform finite-difference grid of 750 grid-points. As the unstable eigenmodes can include a fine spatial structure, a fourth-order accurate finite difference scheme was used for spatial derivatives.

4. Results

The eigenmodes of (3.4) include the well-known helicoidal oscillations. No overstable solutions were found however. All the modes with positive growth rates have zero imaginary part of their eigenvalues.

According to the proposed explanation for the instability, it can be expected for the antiparallel orientation of the background magnetic field and vorticity of the current velocity (2.5). For the one-dimensional (1-D) profiles of (3.2) this means the inequality

(4.1)\begin{equation} B(x)\frac{\partial^2 B(x)}{\partial x^2} < 0. \end{equation}

We proceed by testing this condition with computations for different field profiles. The cases of symmetric and antisymmetric profiles about the slab midplane can be distinguished.

4.1. Antisymmetric field profiles

4.1.1. Numerical computations

Antisymmetric profiles $B(x) = -B(-x)$ can support unstable modes of the tearing-type. We first test the profile

(4.2)\begin{equation} B(x) = \sin (-{\rm \pi} x/2), \end{equation}

which satisfies the condition (4.1).

Figure 1 shows the growth rates of the most unstable modes and the wavenumbers for which these maximum growth rates are obtained. For a large Hall number, the growth rate approaches the power law $\sigma \propto R_\mathrm {H}^{2/3}$ in agreement with Gourgouliatos & Hollerbach (Reference Gourgouliatos and Hollerbach2016).

Figure 1. (a) Growth rate of the most rapidly growing mode for the field profile of (4.2). The dotted line indicates the power-law dependence $\sigma \propto R_\mathrm {H}^{2/3}$ for large $R_\mathrm {H}$. The dashed line shows the result of analytical asymptotic estimation of § 4.1.2. (b) The wave number for which the maximum growth rate is attained. The power-law approximation $k \propto R_\mathrm {H}^{-0.265}$ is shown by the dotted line. All for the vacuum boundary condition (3.5a,b).

Figure 2 shows the eigenmode structure for two large values of the Hall number. Reconnection of the field lines in a region near the $x = 0$ position of the background field reversal is evident from this figure. The thickness of the reconnection layer decreases with the Hall number. The wavenumbers of figure 1 are smaller than one. Antisymmetric field profiles can be unstable to the long wavelength tearing-type disturbances (Gourgouliatos & Hollerbach Reference Gourgouliatos and Hollerbach2016).

Figure 2. Poloidal field lines and isolines of the toroidal field of the most rapidly growing modes for $R_\mathrm {H} = 10^3$ (a) and $R_\mathrm {H} = 10^4$ (b). Full and dashed lines correspond to the clockwise and anti-clockwise circulation of the poloidal field vector, respectively. All for the field profile of (4.2).

Not all antisymmetric profiles are unstable however. Figure 3 shows the growth rate as a function of the $q$-parameter of the profile $B(x) = (1 - q)\sin (-{\rm \pi} x/2) - q x$. The growth rate reverses to negative values for $q \rightarrow 1$. The current velocity for the linear profile of $q = 1$ is uniform and has no shear. The condition of (4.1) is then violated and the instability is switched off.

Figure 3. Dependence of the growth rate on the $q$-parameter of the profile $B(x) = (1 - q)\sin (-{\rm \pi} x/2) - q x$. Here, $R_\mathrm {H} = 10^4,\ k = 0.25$.

The local condition is also not sufficient for the global instability. The instability is switched off with a change to the perfect conductor boundary conditions (3.6a,b). This is probably because the helicoidal oscillation takes part in the instability (Kitchatinov Reference Kitchatinov2017). The helicoidal rotation is blocked by superconducting boundaries.

The growth rate scaling with the Hall number also depends on the model design. Kitchatinov (Reference Kitchatinov2017) considered a periodic background field in unbounded space. The profile of (4.2) is mirror-symmetric about the planes of $x = \pm 1$ when considered in unbounded space. The eigenmodes for this periodic profile have to possess the same symmetry. This means that $x$-derivatives of the eigenfunctions should be zero at $x = \pm 1$. The case of the periodic profile (4.2) in unbounded space can therefore be reproduced in the slab model of this paper with the ‘periodic’ boundary conditions:

(4.3)\begin{equation} \frac{\partial a}{\partial x} = \frac{\partial b}{\partial x} = 0\quad \mathrm{for}\ x ={\pm} 1. \end{equation}

The results for these conditions are shown in figure 4. They are similar to the case of vacuum conditions but with different slopes in the power-law dependencies on the (large) Hall number. The power index in the dependence of the growth rate changes to $3/4$ and the absolute value of the index for the wavenumber is approximately halved.

Figure 4. The same as in figure 1 but for periodic boundary conditions of (4.3). In this case, the asymptotic dependence of the growth rate on the Hall number changes to $\sigma \propto R_\mathrm {H}^{3/4}$. The dashed line shows the result of analytical asymptotic estimation. Scaling for the wavenumber also changes to $k \propto R_\mathrm {H}^{-0.132}$.

We proceed to analytical estimations of the instability to justify and partly explain the numerical results.

4.1.2. Asymptotic estimation

The method of asymptotic analysis of resistive hydromagnetic instabilities was developed in the seminal paper by Furth, Killeen & Rosenbluth (Reference Furth, Killeen and Rosenbluth1963). We apply this method to the tearing mode of the Hall instability at large $R_\mathrm {H}$.

It is convenient to reformulate (3.4) in terms of new variables $\gamma = \sigma /R_\mathrm {H}$ and $v = \mathrm {i}k b/\gamma$ as

(4.4)\begin{equation} \left.\begin{gathered} \gamma \left(a + B v\right) = \frac{1}{R_\mathrm{H}} \left(\frac{\partial^2 a}{\partial x^2} - k^2 a\right), \\ \gamma^2 v ={-}k^2\left[ B\left(\frac{\partial^2 a}{\partial x^2}- k^2 a\right) -\frac{\partial^2B}{\partial x^2} a\right] + \frac{\gamma}{R_\mathrm{H}}\left(\frac{\partial^2 v}{\partial x^2}-k^2 v\right). \end{gathered}\right\} \end{equation}

The case of the large Hall number $R_\mathrm {H} \gg 1$ is considered.

The eigenmodes of figure 2 show a thin reconnection layer in the central part of the slab and smooth variations outside this layer. These two distinct regions are visualized more clearly by the eigenfunction profiles of figure 5. The recipe by Furth et al. (Reference Furth, Killeen and Rosenbluth1963) is to solve for the (central) diffusive and (outer) non-diffusive regions separately. The dispersion relation for the growth rates then results from a link of these solutions.

Figure 5. Profiles of the $x$-component of the current velocity $\gamma v(x)$ (dashed) and $a(x)$ (full line) of the tearing-type eigenmode for $R_\mathrm {H} = 10^3$. The vertical dotted lines show the central diffusive layer.

The unstable eigenmodes grow with ‘hybrid’ rates that are large compared with the rate of diffusion but small compared with the helicoidal oscillation frequency,

(4.5)\begin{equation} R_\mathrm{H}^{{-}1} \ll \gamma \ll 1. \end{equation}

With these inequalities, (4.4) for the non-diffusive regions reduce to

(4.6)\begin{equation} \left.\begin{gathered} v ={-} a/B \\ \frac{\partial^2 a}{\partial x^2}- \left(\frac{1}{B}\frac{\partial^2 B}{\partial x^2} + k^2\right) a = 0. \end{gathered}\right\} \end{equation}

The solution of this linear equation for the profile (4.2) and $k\leq {\rm \pi}/2$ includes two arbitrary constants,

(4.7)\begin{equation} a(x) = C\left(\sin(p x) + C_1\cos(p x)\right), \end{equation}

where $p = \sqrt {|{\rm \pi} ^2/4 - k^2|}$. The constant $C_1$ can be defined with boundary conditions that have to be applied separately for positive and negative $x$. The vacuum boundary condition (3.5a,b) for positive $x$ gives

(4.8)\begin{equation} C_1 = C_+{=} \frac{k\sin(p) + p\cos(p)}{p\sin(p) - k\cos(p)}, \end{equation}

while for negative $x$ it is $C_1 = C_- = -C_+$. The constant $C$ in the ‘external’ solution (4.7) remains indefinite in the linear stability problem. However, the constant does not contribute to the stability index

(4.9)\begin{equation} \varDelta' = \left.\frac{1}{a}\frac{\partial a}{\partial x}\right|_{x ={+}0} - \left.\frac{1}{a}\frac{\partial a}{\partial x}\right|_{x ={-}0} \end{equation}

of the paper by Furth et al. (Reference Furth, Killeen and Rosenbluth1963). It is accounted for in (4.9) that the logarithmic derivatives of the external solution vary little with $|x|\ll 1$ on either side of the origin and their values at the borders of the diffusive layer can be replaced by the values at the origin.

With (4.8) for the vacuum boundary conditions we get

(4.10)\begin{equation} \varDelta' = 2 p \frac{p\sin(p) - k\cos(p)}{k\sin(p) + p\cos(p)}. \end{equation}

This expression changes from positive to negative values with $k$ increasing beyond the value of approximately $k = 1.263$. We shall see that the negative values mean stability (note that the wavenumbers of figure 1 correspond to positive $\varDelta '$). Repeating the derivations for $k > {\rm \pi}/2$ gives the (negative) quantity:

(4.11)\begin{equation} \varDelta' ={-}2p\frac{(k + p)\exp(2p) + k - p}{(k + p)\exp(2p) - k + p}, \end{equation}

to which the $\varDelta '$ of (4.10) transforms continuously when $k$ exceeds ${\rm \pi} /2$.

Repeating the derivations for the periodic conditions of (4.3) we find positive

(4.12)\begin{equation} \varDelta' = 2 p \tan(p) \end{equation}

for $k \leq {\rm \pi}/2$ and negative $\varDelta ' = -2p[\exp (2p) - 1]/[\exp (2p) + 1]$ for $k > {\rm \pi}/2$.

It can be shown that $\varDelta '$ for perfect conductor boundary conditions or the linear profile of $B$ is negative for any $k$ thus confirming the numerically found stability for these cases.

Inside the ‘inner’ diffusive region, spatial derivatives are not small $\partial /\partial x \gg 1$. The region is also thin so that the background field can be approximated by the linear profile $B(x) = xB'$, where the prime means the derivative at $x = 0$. Then (4.4) reduce to

(4.13)\begin{equation} \left.\begin{gathered} \gamma \left( a - \frac{\rm \pi}{2} x v\right) = \frac{1}{R_\mathrm{H}}\frac{\partial^2 a}{\partial x^2} \\ \gamma^2 v = k^2 x \frac{\rm \pi}{2}\frac{\partial^2 a}{\partial x^2} +\frac{\gamma}{R_\mathrm{H}}\frac{\partial^2 v}{\partial x^2}, \end{gathered}\right\} \end{equation}

where $B' = -{\rm \pi} /2$ for the profile (4.2) was used; a generalization to any other antisymmetric profile is easy.

An expression for the jump in the logarithmic derivative across the diffusion layer

(4.14)\begin{equation} \varDelta(\gamma) = \left.\frac{1}{a}\frac{\partial a}{\partial x}\right|_{x = \delta} - \left.\frac{1}{a}\frac{\partial a}{\partial x}\right|_{x ={-}\delta} \end{equation}

should be derived from (4.13) to get the dispersion relation $\varDelta (\gamma ) = \varDelta '$.

The $\varDelta (\gamma )$ is derived in the so-called ‘constant $\psi$ approximation’ (Furth et al. Reference Furth, Killeen and Rosenbluth1963; Priest Reference Priest2014, § 6.8.1) in Appendix A. Then (A 17) leads to the following estimation for the growth rate:

(4.15)\begin{equation} \sigma = R_\mathrm{H}( - k + \sqrt{k^2 + 1.18\varDelta'(k)k^{3/2}R_\mathrm{H}^{{-}1/2}}), \end{equation}

where positive $\varDelta '$ only result in positive growth rates. The growth rates estimated with this equation are shown by the dashed lines in figures 1 and 4 for the vacuum and periodic boundary conditions, respectively. The $\varDelta '$ of the corresponding (4.10) and (4.12) were used in the estimations with the wavenumbers taken from the corresponding figures. In contrast with the numerical computations, the asymptotic estimations apply to large Hall numbers only but are not restricted to the moderately large $R_\mathrm {H}$.

The analytic and numerical trends are similar and they approach each other with increasing Hall number. The asymptotic theory overestimates the numerical growth rates by approximately 20 % for the largest Hall numbers in figure 1 and by almost 30 % in figure 4. The difference can be related to the approximate nature of the asymptotic theory. The clear similarity of the analytic and numerical results nevertheless confirms the numerically detected dependence of the Hall instability scaling on boundary conditions. The asymptotic estimations also confirm the stability of the linear profile of the background field and the stability for perfect conductor boundary conditions in our model.

4.2. Symmetric field profiles

According to the proposed interpretation of the Hall instability, it can be expected if the condition of (4.1) is satisfied. The expectation is generally confirmed by computations for the parabolic profile

(4.16)\begin{equation} B(x) = \beta - x^2. \end{equation}

In agreement with the condition (4.1), instability was found for positive $\beta$ only. It can be expected that the local condition should be satisfied in a sufficiently broad region and the parameter $\beta$ should be sufficiently large for the onset of the instability. The expectation is generally confirmed by computations, but the critical value $\beta _\mathrm {c}$ for the instability is rather small and decreases with the Hall number: $\beta _c \approx 5\times 10^{-3}$ for $R_\mathrm {H} = 10^3$ and $\beta _c \approx 3\times 10^{-4}$ for $R_\mathrm {H} = 10^5$. The condition (4.1) is fulfilled in the region of $-\beta ^{1/2} < x < \beta ^{1/2}$.

Figure 6 shows that unstable eigenmodes are confined to this region.

Figure 6. Poloidal field lines and isolines of the toroidal field of the most rapidly growing instability modes for $R_\mathrm {H} = 10^3$ (a) and $R_\mathrm {H} = 10^4$ (b). Full and dashed lines correspond to the clockwise and anti-clockwise circulation of the poloidal field vector, respectively. All for the symmetric field profile of (4.16) with $\beta = 0.1$.

The modes of this figure do not belong to the tearing type but possess a fine structure near the border of the instability region. The region broadens with increasing $\beta$ and occupies the entire slab for $\beta = 1$ (figure 7). Another difference from the antisymmetric field profile, for which only one unstable mode was found for a given $k$, is that two unstable modes symmetric and antisymmetric about the slab midplane can exist for the symmetric profile of (4.16). These two types of symmetry are illustrated in figure 7. The antisymmetric mode always had a smaller growth rate compared with the symmetric mode.

Figure 7. Poloidal field lines and isolines of the toroidal field for the symmetric (a) and antisymmetric (b) instability modes. The corresponding normalized growth rates are given at the top. All for the symmetric profile of (4.16) with $\beta = 1$ and $R_\mathrm {H} = 10^3$.

The maximum growth rates for $\beta = 0.1$ and $\beta = 1$ are shown in figure 8 as functions of the Hall number. The growth rates approach the power law of $\sigma \propto R_\mathrm {H}^{3/4}$ for large Hall number. The asymptotic growth rates depend weakly on $\beta$ but the asymptotic trend is approached at larger $R_\mathrm {H}$ for smaller $\beta$.

Figure 8. (a) Growth rates for the symmetric field profile of (4.16) with $\beta = 0.1$ and $\beta = 1$. The dotted line shows the asymptotic power-law dependence $\sigma \propto R_\mathrm {H}^{3/4}$. (b) Wavenumbers for which the maximum growth rates in (a) were obtained. The lines are marked by the corresponding values of $\beta$.

The perfect conductor boundary conditions (3.6a,b) switch the instability off for $\beta = 1$ similar to the case of the antisymmetric field profile. For small $\beta$ however, the instability is weakly sensitive to the boundary conditions, though the growth rates for perfect conductor boundaries are somewhat smaller compared with those for vacuum conditions. This is probably because the unstable modes for small $\beta$ occupy the central part of the slab only (figure 6) and do not feel the boundaries.

5. Discussion

The formerly proposed interpretation of the Hall instability as driven jointly by the helicoidal rotation and shear in the current velocity (Kitchatinov Reference Kitchatinov2017) is generally confirmed by the computations of this paper. According to this interpretation, instability is expected for the background field profiles having a region of counter-aligned magnetic field and vorticity of the current velocity. For the 1-D profiles of this paper, this means that inequality (4.1) should be satisfied for instability. The inequality is satisfied by the antisymmetric profile (4.2) supporting the tearing-type mode of the instability. However, the instability is switched off when the antisymmetric linear profile with uniform current velocity is approached (figure 3). Figure 6 shows that unstable modes for the symmetric field are restricted to the region where the inequality (4.1) is satisfied.

The proposed interpretation also explains the diffusive character of the instability. The helicoidal rotation pushes the magnetic field lines in the direction of decreasing field strength and therefore decreasing rate of this rotation. The instability in the region of the relatively strong field is blocked by the less unstable regions of the weaker field. This ‘displacements jam’ is resolved by diffusion. This picture can also explain the instability switch off by the perfect conductor boundary conditions: the superconducting walls block helicoidal rotation. The numerical results for the tearing mode are confirmed by independent asymptotic estimations. The analytical estimations confirm in particular the stabilizing effect of superconducting boundaries.

This stabilizing effect is probably not of a general nature. It can be expected to weaken for ‘sufficiently broad’ profiles of the background field tending to constant far away from the location of the field reversal. Are the broad profiles realistic however? The Hall instability can be relevant to the release of magnetic energy from small-scale magnetic structures. The structures have neither vacuum no superconducting boundaries but are surrounded by other similar structures. The periodic conditions of (4.3) seem to be more adequate for this case.

The growth rates approach asymptotically the power-law dependence $\sigma \propto R_\mathrm {H}^\alpha$ on the Hall number with $\alpha = 3/4$; $\alpha = 2/3$ for the case of the tearing mode with vacuum boundary conditions. This means that the growth rate in physical units scales as $\sigma \propto B^\alpha \eta ^{1-\alpha }$. The growth rate of the Hall instability increases more steeply with the magnetic field compared with the hydromagnetic tearing instability with $\alpha = 1/2$. The Hall instability can produce current sheets without magnetic reconnection (figure 6). The instability gives an additional channel for the release of magnetic energy complementary to the canonical tearing mode. Hall instability catalyses resistive dissipation by decreasing the spatial scale of the magnetic field. It may be pertinent to note that the Hall number (2.2) does not include any spatial scale. A decrease of the field scale cannot therefore be balanced by diffusion. Release of magnetic energy on the nonlinear stage of the instability proceeds in a sequence of spikes or bursts, where each spike releases several percent of magnetic energy (Kitchatinov Reference Kitchatinov2017, Reference Kitchatinov2019).

The condition of the counter-aligned magnetic field and vorticity of the current velocity can be written as

(5.1)\begin{equation} \boldsymbol{B}\cdot\left( \boldsymbol{\nabla}\times (\boldsymbol{\nabla}\times\boldsymbol{B})\right) > 0 \end{equation}

for three-dimensional fields. This heuristic condition for the instability is satisfied by any force-free field of $\boldsymbol {\nabla }\times \boldsymbol {B} = \alpha (\boldsymbol {r})\boldsymbol {B}$. Instability of a 1-D force-free field with maximum helicity was confirmed by Kitchatinov (Reference Kitchatinov2019). The instability can be active with the force-free fields of the solar corona where the Hall number $R_\mathrm {H} \sim 10^7$ is large.

Acknowledgements

The author is thankful to Ms J. Sutton for language editing.

Editor Alex Schekochihin thanks the referees for their advice in evaluating this article.

Funding

This work was financially supported by the Ministry of Science and High Education of the Russian Federation and by the Russian Foundations for Basic Research (Project 19-02-00088).

Declaration of interests

The author reports no conflict of interest.

Appendix A. Derivation of $\varDelta (\gamma )$

Equations (4.13) for the diffusive layer can be simplified with the redefined variables $\tilde {v} = {\rm \pi}v/2,\ \tilde {\gamma } = 2\gamma /({\rm \pi} k),$ and $\tilde {R} = k{\rm \pi} R_\mathrm {H}/2$:

(A1)\begin{gather} \frac{\partial^2 a}{\partial x^2} = \tilde{R}\tilde{\gamma}\left(a - x\tilde{v}\right), \end{gather}
(A2)\begin{gather}\tilde{\gamma}^2\tilde{v} = x\frac{\partial^2 a}{\partial x^2} + \frac{\tilde{\gamma}}{\tilde{R}}\frac{\partial^2\tilde{v}}{\partial x^2}. \end{gather}

Integration of (A1) across the diffusive layer yields the $\varDelta$-parameter of (4.14),

(A3)\begin{equation} \varDelta = \frac{\tilde{\gamma}\tilde{R}}{a(\delta)}\int_{-\delta}^{\delta} \left(a(x) - x\tilde{v}(x)\right) \mathrm{d}x, \end{equation}

where $\delta \ll 1$ is a small distance outside of the diffusive layer and it is taken into account that the $a(x)$ profile is symmetric with $a(\delta ) = a(-\delta )$ (figure 5).

Substitution of $\partial ^2 a/\partial x^2$ from (A1) into (A2) gives the differential equation:

(A4)\begin{equation} \frac{\partial^2\tilde{v}}{\partial s^2} - s^2\tilde{v} - \tilde{\gamma}\tilde{v} ={-}\tilde{R}^{1/2} s a, \end{equation}

in terms of a new variable $s = \tilde {R}^{1/2} x$.

The idea of the constant $\psi$ approximation – constant $a$ in the present case – is to express $\tilde {v}$ in terms of $a$ using (A4) and then put $a$ outside the integral of (A3) based on the fact that it varies little inside the diffusive layer (figure 5). This excludes the (still unknown) constant $a$ from the expression for $\varDelta$ and gives the expression in terms of the parameters $\gamma$, $R_\mathrm {H}$ and $k$, as desired.

Applying this approximation to (A3) and using the new variable $s$ gives

(A5)\begin{equation} \varDelta = \tilde{R}^{1/2}\tilde{\gamma}\int_{-\tilde{R}^{1/2}\delta}^{\tilde{R}^{1/2}\delta} \left(1 - \frac{s}{a\tilde{R}^{1/2}}\tilde{v}(s)\right) \mathrm{d}s. \end{equation}

It may be noted that each of the two terms of the integral in this expression diverge with increasing Hall number but the two diverging terms almost balance each other to combine into a finite quantity.

The operator on the left-hand side of (A4) has the Hermite functions,

(A6)\begin{equation} \varphi_n(s) = \frac{({-}1)^n}{{\rm \pi}^{1/4}\sqrt{2^n n\mathrm{!}}}\mathrm{e}^{s^2/2} \frac{\mathrm{d}^n}{\mathrm{d}s^n}\mathrm{e}^{{-}s^2}, \end{equation}

as its eigenfunctions:

(A7)\begin{equation} \frac{\mathrm{d}^2\varphi_n}{\mathrm{d} s^2} - s^2\varphi_n ={-}(2n + 1)\varphi_n. \end{equation}

The functions make up a complete (orthogonal and normalized) basis that can be used for solving (A4) in terms of the series expansion:

(A8)\begin{equation} \tilde{v}(s) = a\tilde{R}^{1/2}\sum_{n = 0}^\infty \frac{\varphi_n(s)}{2n + 1 + \tilde{\gamma}}\int_{-\infty}^\infty \varphi_n (s') s' \,\mathrm{d} s'. \end{equation}

Note that the solution for not constant $a$ can be obtained by placing $a$ under the integral sign on the right-hand side of (A8).

Expansion of the entire integrand in (A5) in terms of the Hermite functions and using (A8) give

(A9)\begin{equation} \varDelta = \tilde{R}^{1/2}\tilde{\gamma}\sum_{n = 0}^\infty \left[\left(\int_{-\infty}^\infty\varphi_n(s)\,\mathrm{d} s\right)^2 -\frac{1}{2n + 1 + \tilde{\gamma}}\left(\int_{-\infty}^\infty s \varphi_n(s)\,\mathrm{d} s\right)^2\right], \end{equation}

where the integration limits are changed to infinity for the asymptotic case of $\tilde {R} \gg \delta ^{-2}$.

The symmetry relation $\varphi _n(s) = (-1)^n\varphi _n(-s)$ shows that the first term under the summation sign in (A9) is zero for odd $n$ and the second term is zero for even $n$. The equation can then be written as

(A10)\begin{equation} \varDelta = \tilde{R}^{1/2}\tilde{\gamma}\sum_{m = 0}^\infty \left[\left(\int_{-\infty}^\infty\varphi_{2m}(s)\,\mathrm{d} s\right)^2 -\frac{1}{4m + 3 + \tilde{\gamma}} \left(\int_{-\infty}^\infty s \varphi_{2m+1}(s)\,\mathrm{d}s\right)^2\right], \end{equation}

and the relations

(A11)\begin{equation} \int_{-\infty}^\infty s \varphi_{2m+1}(s)\,\mathrm{d}s = \sqrt{4m + 2}\int_{-\infty}^\infty\varphi_{2m}(s)\,\mathrm{d}s \end{equation}

and

(A12)\begin{equation} \left(\int_{-\infty}^\infty\varphi_{2m}(s)\,\mathrm{d} s\right)^2 = 2\frac{\varGamma(m + 1/2)}{\varGamma(m + 1)} \end{equation}

can be used to simplify it further:

(A13)\begin{equation} \varDelta = 2 \tilde{R}^{1/2}\tilde{\gamma}\sum_{m = 0}^\infty \frac{1 +\tilde{\gamma}}{4m + 3 + \tilde{\gamma}} \frac{\varGamma(m + 1/2)}{\varGamma(m + 1)}, \end{equation}

where $\varGamma$ is the Gamma function.

As has been noted, each of the two series on the right-hand side of (A10) diverges when summed-up separately, but their combination of (A13) converges ($\varGamma (m + 1/2)/\varGamma (m +1) \propto m^{-1/2}$ for large $m$). The convergence is however slow and (A13) is difficult to handle. The series in this equation can be rearranged in order to extract its slowly converging part that can be summed-up analytically and the remaining rapidly converging part is easy for numerical estimation:

(A14)\begin{equation} \varDelta = 2\sqrt{{\rm \pi}\tilde{R}}\,\tilde{\gamma}(1 + \tilde{\gamma}) \sum_{n = 0}^\infty ({-}1)^n\tilde{\gamma}^n A_n, \end{equation}

where

(A15a–c)\begin{equation} A_n = \sum_{m=0}^\infty\frac{C_m}{(4m + 3)^{(n + 1)}},\quad C_0 = 1,\quad \mathrm{and}\quad C_m = \frac{2m -1}{2m}C_{m-1}\quad \mathrm{for}\ m > 0. \end{equation}

The geometric series expansion of the term $1/(4m + 3 + \tilde {\gamma })$ in (A13) in powers of $\tilde {\gamma }/(4m + 3)$ served to derive (A14) and (A15a–c). The first four coefficients in the series of (A14) read

(A16a–d)\begin{equation} A_0 = \sqrt{\rm \pi}\frac{\varGamma(3/4)}{\varGamma(1/4)} = 0.59907,\quad A_1 = 0.12856,\quad A_2 = 0.03897,\quad A_3 = 0.01259, \end{equation}

where the last three coefficients were evaluated numerically from their rapidly converging series of (A15a–c).

Equation (A14) gives the expansion for $\varDelta$ in powers of the asymptotically small parameter $\tilde \gamma$. Cutting the expansion after the second-order terms gives

(A17)\begin{equation} \varDelta = 0.847\sqrt{\frac{R_\mathrm{H}}{k^3}} \left(\gamma^2 + 2k\gamma \right), \end{equation}

where we returned to the ‘unwaved’ parameters of § 4.1.2.

References

REFERENCES

Bora, K., Bhattacharyya, R. & Smolarkiewicz, P.K. 2021 Evolution of three-dimensional coherent structures in hall magnetohydrodynamics. Astrophys. J. 906 (2), 102.CrossRefGoogle Scholar
Brandenburg, A. 2020 Hall cascade with fractional magnetic helicity in neutron star crusts. Astrophys. J. 901 (1), 18.CrossRefGoogle Scholar
Brandenburg, A. & Subramanian, K. 2005 Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rep. 417 (1-4), 1–209.CrossRefGoogle Scholar
Furth, H.P., Killeen, J. & Rosenbluth, M.N. 1963 Finite-resistivity instabilities of a sheet pinch. Phys. Fluids 6 (4), 459–484.CrossRefGoogle Scholar
Goldreich, P. & Reisenegger, A. 1992 Magnetic field decay in isolated neutron stars. Astrophys. J. 395, 250–258.CrossRefGoogle Scholar
Gourgouliatos, K.N. & Hollerbach, R. 2016 Resistive tearing instability in electron MHD: application to neutron star crusts. Mon. Not. R. Astron. Soc. 463 (3), 3381–3389.CrossRefGoogle Scholar
Hollerbach, R. & Rüdiger, G. 2002 The influence of Hall drift on the magnetic fields of neutron stars. Mon. Not. R. Astron. Soc. 337 (1), 216–224.CrossRefGoogle Scholar
Kitchatinov, L. 2019 Stability of a force-free Hall equilibrium and release of magnetic energy. Astron. Nachr. 340 (6), 475–482.CrossRefGoogle Scholar
Kitchatinov, L.L. 2017 Double Hall instability: a catalyzer of magnetic energy release. Astron. Lett. 43 (9), 624–633.CrossRefGoogle Scholar
Kunz, M.W. 2008 On the linear stability of weakly ionized, magnetized planar shear flows. Mon. Not. R. Astron. Soc. 385 (3), 1494–1510.CrossRefGoogle Scholar
Parker, E.N. 1979 Cosmical Magnetic Fields: Their Origin and Their Activity. Clarendon Press.Google Scholar
Pons, J.A. & Geppert, U. 2010 Confirmation of the occurrence of the Hall instability in the non-linear regime. Astron. Astrophys. 513, L12.CrossRefGoogle Scholar
Priest, E. 2014 Magnetohydrodynamics of the Sun. Cambridge University Press.Google Scholar
Rheinhardt, M. & Geppert, U. 2002 Hall-drift induced magnetic field instability in neutron stars. Phys. Rev. Lett. 88 (10), 101103.CrossRefGoogle ScholarPubMed
Rheinhardt, M., Konenkov, D. & Geppert, U. 2004 The occurrence of the Hall instability in crusts of isolated neutron stars. Astron. Astrophys. 420, 631–645.CrossRefGoogle Scholar
Rüdiger, G. & Hollerbach, R. 2004 The Magnetic Universe: Geophysical and Astrophysical Dynamo Theory. Wiley-VCH.CrossRefGoogle Scholar
Rüdiger, G. & Kitchatinov, L.L. 2005 The influence of the Hall effect on the global stability of cool protostellar disks. Astron. Astrophys. 434 (2), 629–635.CrossRefGoogle Scholar
Shi, C., Velli, M., Pucci, F., Tenerani, A. & Innocenti, M.E. 2020 Oblique tearing mode instability: guide field and hall effect. Astrophys. J. 902 (2), 142.CrossRefGoogle Scholar
Somov, B.V. 2013 Plasma Astrophysics, Part I. Springer Science+Business Media.CrossRefGoogle Scholar
Vainshtein, S.I., Chitre, S.M. & Olinto, A.V. 2000 Rapid dissipation of magnetic fields due to the Hall current. Phys. Rev. E 61 (4), 4422–4430.CrossRefGoogle ScholarPubMed
Wood, T.S., Hollerbach, R. & Lyutikov, M. 2014 Density-shear instability in electron magneto-hydrodynamics. Phys. Plasmas 21 (5), 052110.CrossRefGoogle Scholar
Zhang, W., Ma, Z.W. & Wang, S. 2017 Hall effect on tearing mode instabilities in tokamak. Phys. Plasmas 24 (10), 102510.CrossRefGoogle Scholar
Figure 0

Figure 1. (a) Growth rate of the most rapidly growing mode for the field profile of (4.2). The dotted line indicates the power-law dependence $\sigma \propto R_\mathrm {H}^{2/3}$ for large $R_\mathrm {H}$. The dashed line shows the result of analytical asymptotic estimation of § 4.1.2. (b) The wave number for which the maximum growth rate is attained. The power-law approximation $k \propto R_\mathrm {H}^{-0.265}$ is shown by the dotted line. All for the vacuum boundary condition (3.5a,b).

Figure 1

Figure 2. Poloidal field lines and isolines of the toroidal field of the most rapidly growing modes for $R_\mathrm {H} = 10^3$ (a) and $R_\mathrm {H} = 10^4$ (b). Full and dashed lines correspond to the clockwise and anti-clockwise circulation of the poloidal field vector, respectively. All for the field profile of (4.2).

Figure 2

Figure 3. Dependence of the growth rate on the $q$-parameter of the profile $B(x) = (1 - q)\sin (-{\rm \pi} x/2) - q x$. Here, $R_\mathrm {H} = 10^4,\ k = 0.25$.

Figure 3

Figure 4. The same as in figure 1 but for periodic boundary conditions of (4.3). In this case, the asymptotic dependence of the growth rate on the Hall number changes to $\sigma \propto R_\mathrm {H}^{3/4}$. The dashed line shows the result of analytical asymptotic estimation. Scaling for the wavenumber also changes to $k \propto R_\mathrm {H}^{-0.132}$.

Figure 4

Figure 5. Profiles of the $x$-component of the current velocity $\gamma v(x)$ (dashed) and $a(x)$ (full line) of the tearing-type eigenmode for $R_\mathrm {H} = 10^3$. The vertical dotted lines show the central diffusive layer.

Figure 5

Figure 6. Poloidal field lines and isolines of the toroidal field of the most rapidly growing instability modes for $R_\mathrm {H} = 10^3$ (a) and $R_\mathrm {H} = 10^4$ (b). Full and dashed lines correspond to the clockwise and anti-clockwise circulation of the poloidal field vector, respectively. All for the symmetric field profile of (4.16) with $\beta = 0.1$.

Figure 6

Figure 7. Poloidal field lines and isolines of the toroidal field for the symmetric (a) and antisymmetric (b) instability modes. The corresponding normalized growth rates are given at the top. All for the symmetric profile of (4.16) with $\beta = 1$ and $R_\mathrm {H} = 10^3$.

Figure 7

Figure 8. (a) Growth rates for the symmetric field profile of (4.16) with $\beta = 0.1$ and $\beta = 1$. The dotted line shows the asymptotic power-law dependence $\sigma \propto R_\mathrm {H}^{3/4}$. (b) Wavenumbers for which the maximum growth rates in (a) were obtained. The lines are marked by the corresponding values of $\beta$.