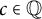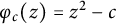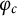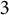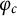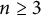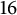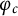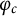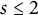1 Introduction
Let S be a set and
![]() $\varphi :S \to S$
a self map. For
$\varphi :S \to S$
a self map. For
![]() $z \in S$
, the orbit of z under
$z \in S$
, the orbit of z under
![]() $\varphi $
is the sequence of iterates
$\varphi $
is the sequence of iterates
where
![]() $\varphi ^k$
is the kth iterate of
$\varphi ^k$
is the kth iterate of
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi ^0=\operatorname {\mathrm {Id}}_S$
. We say that z is periodic under
$\varphi ^0=\operatorname {\mathrm {Id}}_S$
. We say that z is periodic under
![]() $\varphi $
if there is an integer
$\varphi $
if there is an integer
![]() $n \ge 1$
such that
$n \ge 1$
such that
![]() $\varphi ^n(z) = z$
, and then the least such n is the period of z. In that case, we identify
$\varphi ^n(z) = z$
, and then the least such n is the period of z. In that case, we identify
![]() $O_{\varphi }(z)$
with the finite sequence
$O_{\varphi }(z)$
with the finite sequence
![]() $\mathcal {C}= (z, \varphi (z), \dots , \varphi ^{n-1}(z))$
, and we say that
$\mathcal {C}= (z, \varphi (z), \dots , \varphi ^{n-1}(z))$
, and we say that
![]() $\mathcal {C}$
is a cycle of length n. The element z is said to be preperiodic under
$\mathcal {C}$
is a cycle of length n. The element z is said to be preperiodic under
![]() $\varphi $
if there is an integer
$\varphi $
if there is an integer
![]() $m \ge 1$
such that
$m \ge 1$
such that
![]() $ \varphi ^m(z)$
is periodic. For every rational fraction in
$ \varphi ^m(z)$
is periodic. For every rational fraction in
![]() $\mathbb {Q}(X)$
of degree
$\mathbb {Q}(X)$
of degree
![]() $\geq $
2, its set of preperiodic points is finite, this being a particular case of a well-known theorem of Northcott Reference Northcott[10]. However, determining the cardinality of this set is very difficult in general, even for a rational polynomial of degree
$\geq $
2, its set of preperiodic points is finite, this being a particular case of a well-known theorem of Northcott Reference Northcott[10]. However, determining the cardinality of this set is very difficult in general, even for a rational polynomial of degree
![]() $2$
. This paper concerns the following particular case. For any
$2$
. This paper concerns the following particular case. For any
![]() $c \in \mathbb {Q}$
, denote
$c \in \mathbb {Q}$
, denote
In fact, it is essentially the general case in degree
![]() $2$
, because every rational quadratic polynomial is equivalent to
$2$
, because every rational quadratic polynomial is equivalent to
![]() $\varphi _c$
for some
$\varphi _c$
for some
![]() $c \in \mathbb {Q}$
, up to rational linear conjugacy. The following conjecture on
$c \in \mathbb {Q}$
, up to rational linear conjugacy. The following conjecture on
![]() $\varphi _c$
is due to Flynn, Poonen, and Schaefer Reference Flynn, Poonen and Schaefer[6].
$\varphi _c$
is due to Flynn, Poonen, and Schaefer Reference Flynn, Poonen and Schaefer[6].
Conjecture 1.1 Let
![]() $c \in \mathbb {Q}$
. Then, every periodic point of
$c \in \mathbb {Q}$
. Then, every periodic point of
![]() $\varphi _c$
in
$\varphi _c$
in
![]() $\mathbb {Q}$
has period at most
$\mathbb {Q}$
has period at most
![]() $3$
.
$3$
.
See also Reference Poonen[12] for a refined conjecture on the rational preperiodic points of quadratic maps over
![]() $\mathbb {Q}$
. In contrast with Reference Poonen[12] and other papers, here, we do not count the point at
$\mathbb {Q}$
. In contrast with Reference Poonen[12] and other papers, here, we do not count the point at
![]() $\infty $
as a preperiodic point.
$\infty $
as a preperiodic point.
As the following classical example shows, rational points of period
![]() $3$
do occur for suitable
$3$
do occur for suitable
![]() $c \in \mathbb {Q}$
.
$c \in \mathbb {Q}$
.
Example 1.2 Let
![]() $c = 29/16$
. Then, the map
$c = 29/16$
. Then, the map
![]() $\varphi _c$
admits the cycle
$\varphi _c$
admits the cycle
![]() $\mathcal {C}= (-1/4, -7/4,5/4)$
of length
$\mathcal {C}= (-1/4, -7/4,5/4)$
of length
![]() $3$
.
$3$
.
Actually, there is a one-parameter family of
![]() $c \in \mathbb {Q}$
such that
$c \in \mathbb {Q}$
such that
![]() $\varphi _c$
admits a rational cycle of length
$\varphi _c$
admits a rational cycle of length
![]() $3$
. See [Reference Walde and Russo15, Theorem 3, p. 322].
$3$
. See [Reference Walde and Russo15, Theorem 3, p. 322].
While Conjecture 1.1 has already been explored in several papers, it remains widely open at the time of writing. The main positive results concerning it are that periods
![]() $4$
and
$4$
and
![]() $5$
are indeed excluded by Morton Reference Morton[7] and by Flynn, Poonen, and Schaefer Reference Flynn, Poonen and Schaefer[6], respectively.
$5$
are indeed excluded by Morton Reference Morton[7] and by Flynn, Poonen, and Schaefer Reference Flynn, Poonen and Schaefer[6], respectively.
Theorem 1.3 (Morton)
For every
![]() $c\in \mathbb {Q}$
, there is no periodic point of
$c\in \mathbb {Q}$
, there is no periodic point of
![]() $\varphi _c$
in
$\varphi _c$
in
![]() $\mathbb {Q}$
of period
$\mathbb {Q}$
of period
![]() $4$
.
$4$
.
Theorem 1.4 (Flynn, Poonen, and Schaefer)
For every
![]() $c\in \mathbb {Q}$
, there is no periodic point of
$c\in \mathbb {Q}$
, there is no periodic point of
![]() $\varphi _c$
in
$\varphi _c$
in
![]() $\mathbb {Q}$
of period
$\mathbb {Q}$
of period
![]() $5$
.
$5$
.
No period higher than
![]() $5$
has been excluded so far for the rational maps
$5$
has been excluded so far for the rational maps
![]() $\varphi _c$
. However, Stoll Reference Stoll[14] showed that the exclusion of period
$\varphi _c$
. However, Stoll Reference Stoll[14] showed that the exclusion of period
![]() $6$
would follow from the validity of the Birch and Swinnerton-Dyer conjecture.
$6$
would follow from the validity of the Birch and Swinnerton-Dyer conjecture.
Conjecture 1.1 is often studied using the height and p-adic Julia sets. Here, we mainly use arithmetic and combinatorial means. Among our tools, we shall use the above two results and theorems by Pezda Reference Pezda[11] and by Zieve Reference Zieve[16] on polynomial iteration over the p-adic integers. See also [Reference Narkiewicz8, Reference Narkiewicz9] for related methods and results.
Conjecture 1.1 is known to hold for
![]() $\varphi _c$
if
$\varphi _c$
if
![]() $c \in \mathbb {Z}$
, and more generally if the denominator of c is odd, in which case any rational cycle of
$c \in \mathbb {Z}$
, and more generally if the denominator of c is odd, in which case any rational cycle of
![]() $\varphi _c$
is of length at most
$\varphi _c$
is of length at most
![]() $2$
(see Reference Walde and Russo[15]). Here, we focus on the case where the denominator of c is even.
$2$
(see Reference Walde and Russo[15]). Here, we focus on the case where the denominator of c is even.
Given
![]() $c \in \mathbb {Q} \setminus \mathbb {Z}$
, let s denote the number of distinct primes dividing the denominator of c, including
$c \in \mathbb {Q} \setminus \mathbb {Z}$
, let s denote the number of distinct primes dividing the denominator of c, including
![]() $2$
. In Reference Call and Goldstine[3], Call and Goldstine showed that the number of rational preperiodic points of
$2$
. In Reference Call and Goldstine[3], Call and Goldstine showed that the number of rational preperiodic points of
![]() $\varphi _c$
is bounded above by
$\varphi _c$
is bounded above by
![]() $2^{s+3}$
. Hence, the number of rational periodic points of
$2^{s+3}$
. Hence, the number of rational periodic points of
![]() $\varphi _c$
is bounded above by
$\varphi _c$
is bounded above by
![]() $2^{s+2}$
, because
$2^{s+2}$
, because
![]() $x \in \mathbb {Q} \setminus \{0\}$
is a preperiodic point of
$x \in \mathbb {Q} \setminus \{0\}$
is a preperiodic point of
![]() $\varphi _c$
if and only if
$\varphi _c$
if and only if
![]() $-x$
is, whereas at most one of x and
$-x$
is, whereas at most one of x and
![]() $-x$
can be periodic. In Reference Benedetto[2], the author shows that the number of rational preperiodic points of
$-x$
can be periodic. In Reference Benedetto[2], the author shows that the number of rational preperiodic points of
![]() $\varphi _c$
is bounded above by
$\varphi _c$
is bounded above by
Hence, again, the number of rational periodic points is bounded above by one half of (1.1). In this paper, we show that the number of rational periodic points of
![]() $\varphi _c$
is bounded above by
$\varphi _c$
is bounded above by
![]() $2^s +2$
. As pointed out by the referees, this new upper bound is only interesting for
$2^s +2$
. As pointed out by the referees, this new upper bound is only interesting for
![]() $s \le 5$
, as the one given by one half of (1.1) is sharper for
$s \le 5$
, as the one given by one half of (1.1) is sharper for
![]() $s \ge 6$
. We also show that Conjecture 1.1 holds for
$s \ge 6$
. We also show that Conjecture 1.1 holds for
![]() $\varphi _c$
in case
$\varphi _c$
in case
![]() $s \le 2$
.
$s \le 2$
.
For convenience, in order to make this paper as self-contained as possible, we provide short proofs of some already known basic results.
1.1 Notation
Given
![]() $c \in \mathbb {Q}$
, we denote by
$c \in \mathbb {Q}$
, we denote by
![]() $\varphi _c \colon \mathbb {Q} \to \mathbb {Q}$
the quadratic map defined by
$\varphi _c \colon \mathbb {Q} \to \mathbb {Q}$
the quadratic map defined by
![]() $\varphi _c(z)=z^2-c$
for all
$\varphi _c(z)=z^2-c$
for all
![]() $z \in \mathbb {Q}$
. Most papers dealing with Conjecture 1.1 rather consider the map
$z \in \mathbb {Q}$
. Most papers dealing with Conjecture 1.1 rather consider the map
![]() $z \mapsto z^2+c$
. Our present choice allows statements with positive rather than negative values of c. For instance, with this choice, we show in Reference Fares[5] that if
$z \mapsto z^2+c$
. Our present choice allows statements with positive rather than negative values of c. For instance, with this choice, we show in Reference Fares[5] that if
![]() $\varphi _c$
admits a cycle of length at least
$\varphi _c$
admits a cycle of length at least
![]() $2$
, then
$2$
, then
![]() $c\ge 1$
.
$c\ge 1$
.
The sets of rational periodic and preperiodic points of
![]() $\varphi _c$
will be denoted by
$\varphi _c$
will be denoted by
![]() $\operatorname {\mathrm {Per}}(\varphi _c)$
and
$\operatorname {\mathrm {Per}}(\varphi _c)$
and
![]() $\operatorname {\mathrm {Preper}}(\varphi _c)$
, respectively:
$\operatorname {\mathrm {Preper}}(\varphi _c)$
, respectively:
 $$ \begin{align*} \operatorname{\mathrm{Per}}(\varphi _c) & = \{x \in \mathbb{Q} \mid \varphi _c^n(x)=x \,\, {\text{for some }} n \in \mathbb{N} \}, \\ \operatorname{\mathrm{Preper}}(\varphi _c) & = \{x \in \mathbb{Q} \mid \varphi _c^m(x) \in \, \operatorname{\mathrm{Per}}(\varphi _c) \,\, {\text{for some }} m \in \mathbb{N}\}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Per}}(\varphi _c) & = \{x \in \mathbb{Q} \mid \varphi _c^n(x)=x \,\, {\text{for some }} n \in \mathbb{N} \}, \\ \operatorname{\mathrm{Preper}}(\varphi _c) & = \{x \in \mathbb{Q} \mid \varphi _c^m(x) \in \, \operatorname{\mathrm{Per}}(\varphi _c) \,\, {\text{for some }} m \in \mathbb{N}\}. \end{align*} $$
For a nonzero integer d, we shall denote by
![]() $\operatorname {\mathrm {supp}}(d)$
the set of prime numbers p dividing d. For instance,
$\operatorname {\mathrm {supp}}(d)$
the set of prime numbers p dividing d. For instance,
![]() $\text{supp}(45)=\{3,5\}$
. If
$\text{supp}(45)=\{3,5\}$
. If
![]() $x \in \mathbb {Q}$
and p is a prime number, the p-adic valuation
$x \in \mathbb {Q}$
and p is a prime number, the p-adic valuation
![]() $v_p(x)$
of x is the unique
$v_p(x)$
of x is the unique
![]() $r \in \mathbb {Z} \cup \{\infty \}$
such that
$r \in \mathbb {Z} \cup \{\infty \}$
such that
![]() $x=p^r {x_1}/{x_2}$
with
$x=p^r {x_1}/{x_2}$
with
![]() $x_1,x_2 \notin p\mathbb {Z}$
coprime integers. For
$x_1,x_2 \notin p\mathbb {Z}$
coprime integers. For
![]() $z \in \mathbb {Q}$
, its numerator and denominator will be denoted by
$z \in \mathbb {Q}$
, its numerator and denominator will be denoted by
![]() $\operatorname {\mathrm {num}}(z)$
and
$\operatorname {\mathrm {num}}(z)$
and
![]() $\operatorname {\mathrm {den}}(z)$
, respectively. They are the unique coprime integers such that
$\operatorname {\mathrm {den}}(z)$
, respectively. They are the unique coprime integers such that
![]() $\operatorname {\mathrm {den}}(z) \ge 1$
and
$\operatorname {\mathrm {den}}(z) \ge 1$
and
![]() $z=\operatorname {\mathrm {num}}(z)/\operatorname {\mathrm {den}}(z)$
.
$z=\operatorname {\mathrm {num}}(z)/\operatorname {\mathrm {den}}(z)$
.
As usual, the cardinality of a finite set E will be denoted by
![]() $|E|$
.
$|E|$
.
2 Basic results over
 $\mathbb {Q}$
$\mathbb {Q}$
2.1 Constraints on denominators
The aim of this section is to show that if
![]() $\varphi _c$
has a periodic point of period at least
$\varphi _c$
has a periodic point of period at least
![]() $3$
, then
$3$
, then
![]() $\operatorname {\mathrm {den}}(c)$
is divisible by
$\operatorname {\mathrm {den}}(c)$
is divisible by
![]() $16$
. The result below first appeared in Reference Walde and Russo[15].
$16$
. The result below first appeared in Reference Walde and Russo[15].
Proposition 2.1 Let
![]() $c \in \mathbb {Q}$
. If
$c \in \mathbb {Q}$
. If
![]() $\operatorname {\mathrm {Per}}(\varphi _c) \not = \emptyset $
, then
$\operatorname {\mathrm {Per}}(\varphi _c) \not = \emptyset $
, then
![]() $\operatorname {\mathrm {den}}(c)=d^2$
for some
$\operatorname {\mathrm {den}}(c)=d^2$
for some
![]() $d \in \mathbb {N}$
, and
$d \in \mathbb {N}$
, and
![]() $\operatorname {\mathrm {den}}(x)=d$
for all
$\operatorname {\mathrm {den}}(x)=d$
for all
![]() $x \in \operatorname {\mathrm {Preper}}(\varphi _c)$
.
$x \in \operatorname {\mathrm {Preper}}(\varphi _c)$
.
Consequently, because we are only interested in rational cycles of
![]() $\varphi _c$
, here, we shall only consider those
$\varphi _c$
, here, we shall only consider those
![]() $c \in \mathbb {Q}$
such that
$c \in \mathbb {Q}$
such that
![]() $\operatorname {\mathrm {den}}(c) = d^2$
for some
$\operatorname {\mathrm {den}}(c) = d^2$
for some
![]() $d \in \mathbb {N}$
. Moreover, we shall frequently consider the set
$d \in \mathbb {N}$
. Moreover, we shall frequently consider the set
![]() $\operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
of numerators of rational periodic points of
$\operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
of numerators of rational periodic points of
![]() $\varphi _c$
. Here is a straightforward consequence, to be tacitly used in the sequel.
$\varphi _c$
. Here is a straightforward consequence, to be tacitly used in the sequel.
Corollary 2.2 Let
![]() $c \in \mathbb {Q}$
. Assume
$c \in \mathbb {Q}$
. Assume
![]() $\operatorname {\mathrm {Per}}(\varphi _c) \not = \emptyset $
. Let
$\operatorname {\mathrm {Per}}(\varphi _c) \not = \emptyset $
. Let
![]() $d \in \mathbb {N}$
be such that
$d \in \mathbb {N}$
be such that
![]() $\operatorname {\mathrm {den}}(c)=d^2$
. Then,
$\operatorname {\mathrm {den}}(c)=d^2$
. Then,
![]() $\operatorname {\mathrm {num}}(\operatorname {\mathrm {Preper}}(\varphi _c)) = d\cdot \operatorname {\mathrm {Preper}}(\varphi _c)$
.
$\operatorname {\mathrm {num}}(\operatorname {\mathrm {Preper}}(\varphi _c)) = d\cdot \operatorname {\mathrm {Preper}}(\varphi _c)$
.
2.2 Basic remarks on periodic points
In this section, we consider periodic points of any map
![]() $f \colon A \to A$
where A is a domain.
$f \colon A \to A$
where A is a domain.
Lemma 2.3 Let A be a commutative unitary ring and
![]() $f \colon A \to A$
a self map. Let
$f \colon A \to A$
a self map. Let
![]() $z_1 \in A$
be a periodic point of f of period n, and let
$z_1 \in A$
be a periodic point of f of period n, and let
![]() $\{z_1,\dots ,z_n\}$
be the orbit of
$\{z_1,\dots ,z_n\}$
be the orbit of
![]() $z_1$
. Then,
$z_1$
. Then,
Proof. We have
![]() $f(z_i)=z_{i+1}$
for all
$f(z_i)=z_{i+1}$
for all
![]() $1 \le i <n$
and
$1 \le i <n$
and
![]() $f(z_n)=z_1$
. Hence,
$f(z_n)=z_1$
. Hence,
 $$ \begin{align*} \prod_{1\leq i<j\leq n}(f(z_i)-f(z_j)) &= \prod_{1\leq i<j< n}(z_{i+1}-z_{j+1})\prod_{1\leq i< n}(z_{i+1}-z_{1}) \\ &= (-1)^{n-1}\prod_{1\leq i<j\le n}(z_{i}-z_{j}).\\[-3.6pc] \end{align*} $$
$$ \begin{align*} \prod_{1\leq i<j\leq n}(f(z_i)-f(z_j)) &= \prod_{1\leq i<j< n}(z_{i+1}-z_{j+1})\prod_{1\leq i< n}(z_{i+1}-z_{1}) \\ &= (-1)^{n-1}\prod_{1\leq i<j\le n}(z_{i}-z_{j}).\\[-3.6pc] \end{align*} $$
▪
Proposition 2.4 Let A be a domain and
![]() $f \colon A \to A$
a map of the form
$f \colon A \to A$
a map of the form
![]() $f(z)=z^2-c$
for some
$f(z)=z^2-c$
for some
![]() $c \in A$
. Assume that f admits a cycle and at least two distinct periodic points in A.
$c \in A$
. Assume that f admits a cycle and at least two distinct periodic points in A.
-
(i) Let
 $x,y \in A$
be distinct periodic points of f, of period m and n, respectively. Let
$x,y \in A$
be distinct periodic points of f, of period m and n, respectively. Let
 $r= \text {lcm}(m,n)$
. Then,
$r= \text {lcm}(m,n)$
. Then,
 $\displaystyle \prod _{i=0}^{r-1}(f^i(x)+f^i(y)) \,=\, 1.$
$\displaystyle \prod _{i=0}^{r-1}(f^i(x)+f^i(y)) \,=\, 1.$
-
(ii) Assume
 $\operatorname {\mathrm {Per}}(f)=\{x_1, x_2, \ldots , x_N\}$
. Then,
$\operatorname {\mathrm {Per}}(f)=\{x_1, x_2, \ldots , x_N\}$
. Then,
 $\displaystyle \prod _{1\leq i<j\leq N}(x_i+x_j) \,=\, \pm 1$
.
$\displaystyle \prod _{1\leq i<j\leq N}(x_i+x_j) \,=\, \pm 1$
.
Proof. First, observe that for all
![]() $u,v \in A$
, we have
$u,v \in A$
, we have
Because
![]() $f^r(x)=x$
and
$f^r(x)=x$
and
![]() $f^r(y)=y$
, we have
$f^r(y)=y$
, we have
 $$ \begin{align} \prod_{i=0}^{r-1}\big(f^{i+1}(x)-f^{i+1}(y)\big) = \prod_{i=0}^{r-1} \big(f^{i}(x)-f^{i}(y)\big). \end{align} $$
$$ \begin{align} \prod_{i=0}^{r-1}\big(f^{i+1}(x)-f^{i+1}(y)\big) = \prod_{i=0}^{r-1} \big(f^{i}(x)-f^{i}(y)\big). \end{align} $$
Now, it follows from (2.1) that
Because the right-hand side of (2.2) is nonzero, the formula in (i) follows.
Moreover, because f permutes
![]() $\operatorname {\mathrm {Per}}(f)$
, we have
$\operatorname {\mathrm {Per}}(f)$
, we have
Using (2.1), and because the above terms are nonzero, the formula in (ii) follows.▪
2.3 Sums of periodic points
Here are straightforward consequences of Proposition 2.4 for
![]() $\varphi _c$
. The result below originally appeared in Reference Eliahou and Fares[4].
$\varphi _c$
. The result below originally appeared in Reference Eliahou and Fares[4].
Proposition 2.5 Let
![]() $c \in \mathbb {Q}$
. Assume
$c \in \mathbb {Q}$
. Assume
![]() $\operatorname {\mathrm {Per}}(\varphi _c)=\{x_1, x_2, \ldots , x_n\}$
with
$\operatorname {\mathrm {Per}}(\varphi _c)=\{x_1, x_2, \ldots , x_n\}$
with
![]() $n \ge 1$
. Let
$n \ge 1$
. Let
![]() $d = \operatorname {\mathrm {den}}(x_1)$
and
$d = \operatorname {\mathrm {den}}(x_1)$
and
![]() $X_i=\operatorname {\mathrm {num}}(x_i)$
for all
$X_i=\operatorname {\mathrm {num}}(x_i)$
for all
![]() $1 \le i \le n$
. Then,
$1 \le i \le n$
. Then,
Proof. By Proposition 2.1, we have
![]() $\operatorname {\mathrm {den}}(x_i)=d$
for all i. Now, chase the denominator in the formulas of Proposition 2.4.▪
$\operatorname {\mathrm {den}}(x_i)=d$
for all i. Now, chase the denominator in the formulas of Proposition 2.4.▪
These other consequences will play a crucial role in the sequel.
Corollary 2.6 Let
![]() $c \in \mathbb {Q}$
. Let
$c \in \mathbb {Q}$
. Let
![]() $x,y$
be two distinct points in
$x,y$
be two distinct points in
![]() $\operatorname {\mathrm {Per}}{(\varphi _c)}$
. Set
$\operatorname {\mathrm {Per}}{(\varphi _c)}$
. Set
![]() $X=\operatorname {\mathrm {num}}(x), Y=\operatorname {\mathrm {num}}(y)$
, and
$X=\operatorname {\mathrm {num}}(x), Y=\operatorname {\mathrm {num}}(y)$
, and
![]() $d = \operatorname {\mathrm {den}}(x)$
. Then:
$d = \operatorname {\mathrm {den}}(x)$
. Then:
-
(i)
 $\operatorname {\mathrm {supp}}(X+Y) \subseteq \operatorname {\mathrm {supp}}(d)$
. That is, any prime p dividing
$\operatorname {\mathrm {supp}}(X+Y) \subseteq \operatorname {\mathrm {supp}}(d)$
. That is, any prime p dividing
 $X+Y$
also divides d.
$X+Y$
also divides d. -
(ii) X and Y are coprime.
-
(iii) If no odd prime factor of d divides
 $X+Y$
, then
$X+Y$
, then
 $X+Y= \pm 2^t$
for some
$X+Y= \pm 2^t$
for some
 $t \in \mathbb {N}$
.
$t \in \mathbb {N}$
.
Proof. The first point directly follows from equality (2.3). For the second one, if a prime p divides X and Y, then it divides d by the first point, a contradiction because
![]() $X,d$
are coprime. The last point follows from the first one and the hypothesis on the odd factors of d, which together imply
$X,d$
are coprime. The last point follows from the first one and the hypothesis on the odd factors of d, which together imply
![]() $\operatorname {\mathrm {supp}}(X+Y) \subseteq \{2\}$
.▪
$\operatorname {\mathrm {supp}}(X+Y) \subseteq \{2\}$
.▪
Example 2.7 Consider the case
![]() $c=29/16$
of Example 1.2, where
$c=29/16$
of Example 1.2, where
![]() $d=4$
and
$d=4$
and
![]() $\varphi _c$
admits the cycle
$\varphi _c$
admits the cycle
![]() $\mathcal {C}= (-1/4, -7/4,5/4)$
. Here,
$\mathcal {C}= (-1/4, -7/4,5/4)$
. Here,
![]() $\operatorname {\mathrm {num}}(\mathcal {C})=(-1,-7,5)$
, with pairwise sums
$\operatorname {\mathrm {num}}(\mathcal {C})=(-1,-7,5)$
, with pairwise sums
![]() $-8, -2, 4$
, respectively. This illustrates all three statements of Corollary 2.6. Viewing
$-8, -2, 4$
, respectively. This illustrates all three statements of Corollary 2.6. Viewing
![]() $\mathcal {C}$
as a set, we have
$\mathcal {C}$
as a set, we have
![]() $\mathcal {C} \subseteq \operatorname {\mathrm {Per}}(\varphi _c)$
. We claim
$\mathcal {C} \subseteq \operatorname {\mathrm {Per}}(\varphi _c)$
. We claim
![]() $\mathcal {C} = \operatorname {\mathrm {Per}}(\varphi _c)$
. For otherwise, let
$\mathcal {C} = \operatorname {\mathrm {Per}}(\varphi _c)$
. For otherwise, let
![]() $x=X/4$
be yet another periodic point of
$x=X/4$
be yet another periodic point of
![]() $\varphi _c$
. Then,
$\varphi _c$
. Then,
![]() $X-1,X-7,X+5$
would also be powers of
$X-1,X-7,X+5$
would also be powers of
![]() $2$
up to sign. The only possibility is
$2$
up to sign. The only possibility is
![]() $X=3$
as easily seen. But
$X=3$
as easily seen. But
![]() $3/4$
is only a preperiodic point, because under
$3/4$
is only a preperiodic point, because under
![]() $\varphi _c$
, we have
$\varphi _c$
, we have
![]() $ 3/4 \mapsto -5/4 \mapsto -1/4 \mapsto -7/4 \mapsto 5/4 \mapsto -1/4. $
$ 3/4 \mapsto -5/4 \mapsto -1/4 \mapsto -7/4 \mapsto 5/4 \mapsto -1/4. $
2.4 Divisibility properties of
 $\operatorname {\mathrm {den}}(c)$
$\operatorname {\mathrm {den}}(c)$
Our bounds on cycle lengths of
![]() $\varphi _c$
involve the denominator of c. The following proposition and corollary already appear in Reference Walde and Russo[15].
$\varphi _c$
involve the denominator of c. The following proposition and corollary already appear in Reference Walde and Russo[15].
Proposition 2.8 Let
![]() $c \in \mathbb {Q}$
. If
$c \in \mathbb {Q}$
. If
![]() $\operatorname {\mathrm {den}}(c)$
is odd, then
$\operatorname {\mathrm {den}}(c)$
is odd, then
![]() $|\operatorname {\mathrm {Per}}(\varphi _c)| \le 2$
.
$|\operatorname {\mathrm {Per}}(\varphi _c)| \le 2$
.
Proof. We have
![]() $\operatorname {\mathrm {den}}(c)=d^2$
for some
$\operatorname {\mathrm {den}}(c)=d^2$
for some
![]() $d \in \mathbb {N}$
, and
$d \in \mathbb {N}$
, and
![]() $\operatorname {\mathrm {den}}(x)=d$
for all
$\operatorname {\mathrm {den}}(x)=d$
for all
![]() $x \in \operatorname {\mathrm {Preper}}(\varphi _c)$
. Assume
$x \in \operatorname {\mathrm {Preper}}(\varphi _c)$
. Assume
![]() $\operatorname {\mathrm {Per}}(\varphi _c)=\{x_1,\dots ,x_n\}$
. Let
$\operatorname {\mathrm {Per}}(\varphi _c)=\{x_1,\dots ,x_n\}$
. Let
![]() $X_i=\operatorname {\mathrm {num}}(x_i)$
for all i. Then, by Proposition 2.5, we have
$X_i=\operatorname {\mathrm {num}}(x_i)$
for all i. Then, by Proposition 2.5, we have
Because d is odd by assumption, each factor
![]() $X_i+X_{j}$
is odd as well, whence
$X_i+X_{j}$
is odd as well, whence
![]() $X_i \not \equiv X_j \bmod 2$
for all
$X_i \not \equiv X_j \bmod 2$
for all
![]() $1 \le i < j \le n$
. Of course, this is only possible if
$1 \le i < j \le n$
. Of course, this is only possible if
![]() $n \le 2$
.▪
$n \le 2$
.▪
Remark 2.9 If
![]() $c \in \mathbb {Z}$
, then
$c \in \mathbb {Z}$
, then
![]() $\operatorname {\mathrm {den}}(c)=1$
, and the above result implies that
$\operatorname {\mathrm {den}}(c)=1$
, and the above result implies that
![]() $\varphi _c$
admits at most two periodic points.
$\varphi _c$
admits at most two periodic points.
This bound is sharp, as follows from results in Reference Walde and Russo[15].
Corollary 2.10 Reference Walde and Russo[15]
Let
![]() $c \in \mathbb {Q}$
. If
$c \in \mathbb {Q}$
. If
![]() $\varphi _c$
admits a rational cycle of length at least
$\varphi _c$
admits a rational cycle of length at least
![]() $3$
, then
$3$
, then
![]() $\operatorname {\mathrm {den}}(c)$
is even.
$\operatorname {\mathrm {den}}(c)$
is even.
We shall sharpen below the conclusion of this corollary by showing that
![]() $\operatorname {\mathrm {den}}(c)$
must in fact be divisible by
$\operatorname {\mathrm {den}}(c)$
must in fact be divisible by
![]() $16$
. For that, we shall need Morton’s Theorem 1.3 excluding period
$16$
. For that, we shall need Morton’s Theorem 1.3 excluding period
![]() $4$
, as well as a result due to Pezda concerning periodic points of polynomials over the p-adic integers.
$4$
, as well as a result due to Pezda concerning periodic points of polynomials over the p-adic integers.
2.5 Involving
 $p$
-adic numbers
$p$
-adic numbers
As usual,
![]() $\mathbb {Z}_p$
and
$\mathbb {Z}_p$
and
![]() $\mathbb {Q}_p$
will denote the rings of p-adic integers and numbers, respectively. A result in Reference Adam and Fares[1] contains a generalization of the above proposition. It says that any polynomial
$\mathbb {Q}_p$
will denote the rings of p-adic integers and numbers, respectively. A result in Reference Adam and Fares[1] contains a generalization of the above proposition. It says that any polynomial
![]() $g(x)=x^p+ \alpha $
with
$g(x)=x^p+ \alpha $
with
![]() $ \alpha \in \mathbb {Z}_p$
either admits p fixed points in
$ \alpha \in \mathbb {Z}_p$
either admits p fixed points in
![]() $\mathbb {Q}_p$
or else a cycle of length exactly p in
$\mathbb {Q}_p$
or else a cycle of length exactly p in
![]() $ \mathbb {Q}_p$
. For
$ \mathbb {Q}_p$
. For
![]() $z \in \mathbb {Q}_p$
, we denote by
$z \in \mathbb {Q}_p$
, we denote by
![]() $v_p(z)$
the p-adic valuation of z.
$v_p(z)$
the p-adic valuation of z.
Here is Pezda’s theorem Reference Pezda[11], to be used in our proof of Theorem 2.13 improving Corollary 2.10. For this application, we shall only need its particular case
![]() $p=2$
. However, we shall also invoke the case
$p=2$
. However, we shall also invoke the case
![]() $p=3$
later on, in Remark 3.16.
$p=3$
later on, in Remark 3.16.
Theorem 2.11 Reference Pezda[11]
Let p be a prime number, and let g be a polynomial in
![]() $\mathbb {Z}_p[t]$
of degree at least
$\mathbb {Z}_p[t]$
of degree at least
![]() $2$
. Let
$2$
. Let
![]() $\alpha \in \mathbb {Z}_p$
be a periodic point of g of period n. If
$\alpha \in \mathbb {Z}_p$
be a periodic point of g of period n. If
![]() $p=2$
, then
$p=2$
, then
![]() $n \in \{1,2,4\}$
. If
$n \in \{1,2,4\}$
. If
![]() $p=3$
, then
$p=3$
, then
![]() $n \in \{1,2,3,4,6,9\}$
.
$n \in \{1,2,3,4,6,9\}$
.
For proving Theorem 3.17 at the end of the paper, we shall further need the following result of Zieve. See also [Reference Silverman13, Theorem 2.21, p. 62]. For p prime, we denote by
![]() $(\mathbb {Z}/ p\mathbb {Z})^*$
the set of invertible elements in
$(\mathbb {Z}/ p\mathbb {Z})^*$
the set of invertible elements in
![]() $\mathbb {Z}/ p\mathbb {Z}$
. Moreover, for
$\mathbb {Z}/ p\mathbb {Z}$
. Moreover, for
![]() $g \in \mathbb {Z}_p[t]$
below, the notation
$g \in \mathbb {Z}_p[t]$
below, the notation
![]() $g^m$
means g raised to the power m, and
$g^m$
means g raised to the power m, and
![]() $(g^m)'$
is its formal derivative with respect to t.
$(g^m)'$
is its formal derivative with respect to t.
Theorem 2.12 Let p be a prime number, and let g be a polynomial in
![]() $\mathbb {Z}_p[t]$
of degree at least
$\mathbb {Z}_p[t]$
of degree at least
![]() $2$
. Let
$2$
. Let
![]() $\alpha \in \mathbb {Z}_p$
be a periodic point of g, and let
$\alpha \in \mathbb {Z}_p$
be a periodic point of g, and let
 $$ \begin{align*} n & = \text{the exact period of } \alpha \text{ in } \mathbb{Z}_p, \\ m & = \text{the exact period of } \alpha \text{ in } \mathbb{Z}/ p\mathbb{Z}, \\ r &= \begin{cases} \text{the multiplicative order of } (g^m)'(\alpha) & \text{ if } \, (g^m)'(\alpha) \in (\mathbb{Z}/ p\mathbb{Z})^*, \\ \infty & \text{ if not.} \end{cases} \end{align*} $$
$$ \begin{align*} n & = \text{the exact period of } \alpha \text{ in } \mathbb{Z}_p, \\ m & = \text{the exact period of } \alpha \text{ in } \mathbb{Z}/ p\mathbb{Z}, \\ r &= \begin{cases} \text{the multiplicative order of } (g^m)'(\alpha) & \text{ if } \, (g^m)'(\alpha) \in (\mathbb{Z}/ p\mathbb{Z})^*, \\ \infty & \text{ if not.} \end{cases} \end{align*} $$
If
![]() $r < \infty $
, then
$r < \infty $
, then
![]() $n \in \{m, mr, mrp^e\}$
for some integer
$n \in \{m, mr, mrp^e\}$
for some integer
![]() $e \ge 1$
such that
$e \ge 1$
such that
![]() $p^{e-1}\le 2/(p-1)$
. If
$p^{e-1}\le 2/(p-1)$
. If
![]() $r=\infty $
, then
$r=\infty $
, then
![]() $n=m$
.
$n=m$
.
2.6 Sharpening Corollary 2.10
Theorem 2.13 Let
![]() $c \in \mathbb {Q}$
. If
$c \in \mathbb {Q}$
. If
![]() $\varphi _c$
admits a rational cycle of length
$\varphi _c$
admits a rational cycle of length
![]() $n \ge 3$
, then
$n \ge 3$
, then
![]() $\operatorname {\mathrm {den}}(c)$
is divisible by
$\operatorname {\mathrm {den}}(c)$
is divisible by
![]() $16$
.
$16$
.
We are grateful to Prof. W. Narkiewicz who, after reading a preliminary version of this paper, suggested that our original proof of Theorem 2.13 could be simplified by using Pezda’s theorem rather than Zieve’s theorem in the preceding section.
Proof. By Propositions 2.1 and 2.8, we have
![]() $\operatorname {\mathrm {den}}(c)=d^2$
for some even positive integer d. Assume for a contradiction that d is not divisible by
$\operatorname {\mathrm {den}}(c)=d^2$
for some even positive integer d. Assume for a contradiction that d is not divisible by
![]() $4$
. Hence,
$4$
. Hence,
![]() $v_2(d)=1$
and
$v_2(d)=1$
and
![]() $v_2(c)=-2$
. Let
$v_2(c)=-2$
. Let
![]() $\mathcal {C} \subseteq \operatorname {\mathrm {Per}}(\varphi _c)$
be a rational cycle of
$\mathcal {C} \subseteq \operatorname {\mathrm {Per}}(\varphi _c)$
be a rational cycle of
![]() $\varphi _c$
of length
$\varphi _c$
of length
![]() $n \ge 3$
. For all
$n \ge 3$
. For all
![]() $z \in \mathcal {C}$
, we have
$z \in \mathcal {C}$
, we have
![]() $\operatorname {\mathrm {den}}(z)=d$
, and hence
$\operatorname {\mathrm {den}}(z)=d$
, and hence
![]() $v_2(z)=-1$
by Proposition 2.1.
$v_2(z)=-1$
by Proposition 2.1.
Recall that if
![]() $z_1,z_2 \in \mathbb {Q}$
satisfy
$z_1,z_2 \in \mathbb {Q}$
satisfy
![]() $v_2(z)=v_2(z')=r$
for some
$v_2(z)=v_2(z')=r$
for some
![]() $r \in \mathbb {Z}$
, then
$r \in \mathbb {Z}$
, then
![]() $v_2(z \pm z') \ge r+1$
.
$v_2(z \pm z') \ge r+1$
.
In particular, for all
![]() $z \in \mathcal {C}$
, we have
$z \in \mathcal {C}$
, we have
![]() $v_2(z-1/2) \ge 0$
. Therefore, the translate
$v_2(z-1/2) \ge 0$
. Therefore, the translate
![]() $\mathcal {C}-1/2$
of
$\mathcal {C}-1/2$
of
![]() $\mathcal {C}$
may be viewed as a subset of the local ring
$\mathcal {C}$
may be viewed as a subset of the local ring
![]() $\mathbb {Z}_{(2)} \subset \mathbb {Q}$
, and hence of the ring
$\mathbb {Z}_{(2)} \subset \mathbb {Q}$
, and hence of the ring
![]() $\mathbb {Z}_2$
of
$\mathbb {Z}_2$
of
![]() $2$
-adic integers. That is, we have
$2$
-adic integers. That is, we have
Step 1. In view of applying Theorem 2.11, we seek a polynomial in
![]() $\mathbb {Z}_2[t]$
admitting
$\mathbb {Z}_2[t]$
admitting
![]() $\mathcal {C}-1/2$
as a cycle. The polynomial
$\mathcal {C}-1/2$
as a cycle. The polynomial
 $$ \begin{align*} f(t) & = \varphi_c(t+1/2)-1/2 \\ & = t^2+t-(c+1/4) \end{align*} $$
$$ \begin{align*} f(t) & = \varphi_c(t+1/2)-1/2 \\ & = t^2+t-(c+1/4) \end{align*} $$
will do. Indeed, by construction, we have
Because
![]() $\varphi _c(\mathcal {C})=\mathcal {C}$
, it follows that
$\varphi _c(\mathcal {C})=\mathcal {C}$
, it follows that
as desired. For the constant coefficient of f, we claim that
![]() $v_2(c+1/4) \ge 0$
. Indeed, let
$v_2(c+1/4) \ge 0$
. Indeed, let
![]() $x,y \in \mathcal {C}$
with
$x,y \in \mathcal {C}$
with
![]() $y = \varphi _c(x)$
. Thus,
$y = \varphi _c(x)$
. Thus,
![]() $f(x-1/2)=y-1/2$
, i.e.,
$f(x-1/2)=y-1/2$
, i.e.,
Because
![]() $v_2(x-1/2), v_2(y-1/2) \ge 0$
, it follows that
$v_2(x-1/2), v_2(y-1/2) \ge 0$
, it follows that
![]() $v_2(c+1/4) \ge 0$
, as claimed. Therefore,
$v_2(c+1/4) \ge 0$
, as claimed. Therefore,
![]() $f(t) \in \mathbb {Z}_2[t]$
, as desired.
$f(t) \in \mathbb {Z}_2[t]$
, as desired.
For the next step, we set
with
![]() $f(z_i)=z_{i+1}$
for
$f(z_i)=z_{i+1}$
for
![]() $i \le n-1$
and
$i \le n-1$
and
![]() $f(z_n)=z_1$
.
$f(z_n)=z_1$
.
Step 2. By Theorem 2.11, applied to the polynomial
![]() $g=f$
and to its n-periodic point
$g=f$
and to its n-periodic point
![]() $\alpha =z_1$
, we have
$\alpha =z_1$
, we have
![]() $n \in \{1,2,4\}$
. Because
$n \in \{1,2,4\}$
. Because
![]() $n \ge 3$
by assumption, it follows that
$n \ge 3$
by assumption, it follows that
![]() $n=4$
. But period 4 for
$n=4$
. But period 4 for
![]() $\varphi _c$
is excluded by Morton’s Theorem 1.3. This contradiction concludes the proof of the theorem.▪
$\varphi _c$
is excluded by Morton’s Theorem 1.3. This contradiction concludes the proof of the theorem.▪
3 An upper bound on
 $|\operatorname {\mathrm {Per}}(\varphi _c)|$
$|\operatorname {\mathrm {Per}}(\varphi _c)|$
Let
![]() $c \in \mathbb {Q}$
. Throughout this section, we assume
$c \in \mathbb {Q}$
. Throughout this section, we assume
![]() $\operatorname {\mathrm {den}}(c) = d^2$
with
$\operatorname {\mathrm {den}}(c) = d^2$
with
![]() $d \in 4\mathbb {N}$
. Recall that this is satisfied whenever
$d \in 4\mathbb {N}$
. Recall that this is satisfied whenever
![]() $\varphi _c$
admits a rational cycle
$\varphi _c$
admits a rational cycle
![]() $\mathcal {C}$
of length
$\mathcal {C}$
of length
![]() $n \ge 3$
, as shown by Proposition 2.1 and Theorem 2.13.
$n \ge 3$
, as shown by Proposition 2.1 and Theorem 2.13.
Let
![]() $s=|\operatorname {\mathrm {supp}}(d)|$
. The following upper bound on
$s=|\operatorname {\mathrm {supp}}(d)|$
. The following upper bound on
![]() $|\operatorname {\mathrm {Preper}}(\varphi _c)|$
was shown in Reference Call and Goldstine[3]:
$|\operatorname {\mathrm {Preper}}(\varphi _c)|$
was shown in Reference Call and Goldstine[3]:
Our aim in this section is to obtain an analogous upper bound on
![]() $|\operatorname {\mathrm {Per}}(\varphi _c)|$
, namely
$|\operatorname {\mathrm {Per}}(\varphi _c)|$
, namely
which in fact is valid for any
![]() $c \in \mathbb {Q}$
, i.e., also when d is odd, by Proposition 2.8. As mentioned in the Introduction, this new upper bound is only better than the one given by (1.1) for
$c \in \mathbb {Q}$
, i.e., also when d is odd, by Proposition 2.8. As mentioned in the Introduction, this new upper bound is only better than the one given by (1.1) for
![]() $s \le 5$
.
$s \le 5$
.
The proof will follow from a string of modular constraints on the numerators of periodic points of
![]() $\varphi _c$
developed in this section.
$\varphi _c$
developed in this section.
3.1 Constraints on numerators
We start with an easy observation. See also [Reference Call and Goldstine3, formula (21)].
Lemma 3.1 Let
![]() $c = a/d^2 \in \mathbb {Q}$
with
$c = a/d^2 \in \mathbb {Q}$
with
![]() $a,d$
coprime integers. Let
$a,d$
coprime integers. Let
![]() $x \in \operatorname {\mathrm {Preper}}(\varphi _c)$
. Let
$x \in \operatorname {\mathrm {Preper}}(\varphi _c)$
. Let
![]() $X=\operatorname {\mathrm {num}}(x)$
. Then,
$X=\operatorname {\mathrm {num}}(x)$
. Then,
![]() $X^2 \equiv a \bmod d$
.
$X^2 \equiv a \bmod d$
.
Proof. We have
![]() $x=X/d$
by Proposition 2.1. Let
$x=X/d$
by Proposition 2.1. Let
![]() $z = \varphi _c(x)$
. Then,
$z = \varphi _c(x)$
. Then,
![]() $z \in \operatorname {\mathrm {Preper}}(\varphi _c)$
, whence
$z \in \operatorname {\mathrm {Preper}}(\varphi _c)$
, whence
![]() $z = Z/d$
where
$z = Z/d$
where
![]() $Z=\operatorname {\mathrm {num}}(z)$
. Now,
$Z=\operatorname {\mathrm {num}}(z)$
. Now,
![]() $z=x^2-c=(X^2-a)/d^2$
, whence
$z=x^2-c=(X^2-a)/d^2$
, whence
Because Z is an integer, it follows that
![]() $X^2 \equiv a \bmod d$
.▪
$X^2 \equiv a \bmod d$
.▪
Here is a straightforward consequence.
Proposition 3.2 Let
![]() $ c \in \mathbb {Q}$
be such that
$ c \in \mathbb {Q}$
be such that
![]() $\operatorname {\mathrm {den}}(c)=d^2$
with
$\operatorname {\mathrm {den}}(c)=d^2$
with
![]() $d \in 4\mathbb {N}$
. Let
$d \in 4\mathbb {N}$
. Let
![]() $X,Y \in \operatorname {\mathrm {num}}(\operatorname {\mathrm {Preper}}(\varphi _c))$
. Let
$X,Y \in \operatorname {\mathrm {num}}(\operatorname {\mathrm {Preper}}(\varphi _c))$
. Let
![]() $p \in \operatorname {\mathrm {supp}}(d)$
and
$p \in \operatorname {\mathrm {supp}}(d)$
and
![]() $r = v_p(d)$
the p-adic valuation of d. Then,
$r = v_p(d)$
the p-adic valuation of d. Then,
In particular,
![]() $\operatorname {\mathrm {num}}(\operatorname {\mathrm {Preper}}(\varphi _c))$
reduces to at most two opposite classes mod
$\operatorname {\mathrm {num}}(\operatorname {\mathrm {Preper}}(\varphi _c))$
reduces to at most two opposite classes mod
![]() $p^r$
.
$p^r$
.
Proof. It follows from Lemma 3.1 that
![]() $X^2 \equiv Y^2 \bmod d.$
Hence,
$X^2 \equiv Y^2 \bmod d.$
Hence,
Case 1. Assume p is odd. Then, p cannot divide both
![]() $X+Y$
and
$X+Y$
and
![]() $X-Y$
; for otherwise, it would divide X which is impossible, because X is coprime to d. Therefore,
$X-Y$
; for otherwise, it would divide X which is impossible, because X is coprime to d. Therefore,
![]() $p^r$
divides
$p^r$
divides
![]() $X+Y$
or
$X+Y$
or
![]() $X-Y$
, as desired.
$X-Y$
, as desired.
Case 2. Assume
![]() $p=2$
. Then,
$p=2$
. Then,
![]() $r \ge 2$
by hypothesis. Let
$r \ge 2$
by hypothesis. Let
![]() $x=X/d, y=Y/d \in \operatorname {\mathrm {Preper}}(\varphi _c)$
. Let
$x=X/d, y=Y/d \in \operatorname {\mathrm {Preper}}(\varphi _c)$
. Let
![]() $x'=\varphi _c(x)=X'/d$
and
$x'=\varphi _c(x)=X'/d$
and
![]() $y'=\varphi _c(y)=Y'/d$
. Then,
$y'=\varphi _c(y)=Y'/d$
. Then,
![]() $X',Y'$
are odd because coprime to d. By (3.1), we have
$X',Y'$
are odd because coprime to d. By (3.1), we have
![]() $X'=(X^2-a)/d$
and
$X'=(X^2-a)/d$
and
![]() $Y'=(Y^2-a)/d$
. Hence,
$Y'=(Y^2-a)/d$
. Hence,
Because
![]() $2^r$
divides d and because
$2^r$
divides d and because
![]() $X'-Y'$
is even, it follows that
$X'-Y'$
is even, it follows that
Now,
![]() $4$
cannot divide both
$4$
cannot divide both
![]() $X+Y$
and
$X+Y$
and
![]() $X-Y$
because
$X-Y$
because
![]() $X,Y$
are odd. Therefore,
$X,Y$
are odd. Therefore,
![]() $X+Y \equiv 0 \bmod 2^r$
or
$X+Y \equiv 0 \bmod 2^r$
or
![]() $X-Y \equiv 0 \bmod 2^r$
, as desired.▪
$X-Y \equiv 0 \bmod 2^r$
, as desired.▪
Here is a straightforward consequence of Proposition 3.2 and the Chinese Remainder Theorem.
Corollary 3.3 Let
![]() $ c \in \mathbb {Q}$
be such that
$ c \in \mathbb {Q}$
be such that
![]() $\operatorname {\mathrm {den}}(c)=d^2$
with
$\operatorname {\mathrm {den}}(c)=d^2$
with
![]() $d \in 4\mathbb {N}$
. Let
$d \in 4\mathbb {N}$
. Let
![]() $s = |\operatorname {\mathrm {supp}}(d)|$
. Then,
$s = |\operatorname {\mathrm {supp}}(d)|$
. Then,
![]() $\operatorname {\mathrm {num}}(\operatorname {\mathrm {Preper}}(\varphi _c))$
reduces to at most
$\operatorname {\mathrm {num}}(\operatorname {\mathrm {Preper}}(\varphi _c))$
reduces to at most
![]() $2^s$
classes mod d.
$2^s$
classes mod d.
We thank one of the referees for pointing out that Corollary 3.3, combined with the result in Reference Call and Goldstine[3] that the preperiodic points lie in the union of two intervals symmetrical with respect to 0 and each of length at most
![]() $2$
, implies that the number of preperiodic points is less than
$2$
, implies that the number of preperiodic points is less than
![]() $2^{s+2}$
.
$2^{s+2}$
.
The particular case in Proposition 3.2 where
![]() $X,Y \in \operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
and
$X,Y \in \operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
and
![]() $X \equiv +Y \bmod p^r$
for all
$X \equiv +Y \bmod p^r$
for all
![]() $p \in \operatorname {\mathrm {supp}}(d)$
, i.e., where
$p \in \operatorname {\mathrm {supp}}(d)$
, i.e., where
![]() $X \equiv Y \bmod d$
, has a somewhat surprising consequence and will be used more than once in the sequel. It only concerns periodic points, as we need to use Corollary 2.6.
$X \equiv Y \bmod d$
, has a somewhat surprising consequence and will be used more than once in the sequel. It only concerns periodic points, as we need to use Corollary 2.6.
Proposition 3.4 Let
![]() $ c \in \mathbb {Q}$
be such that
$ c \in \mathbb {Q}$
be such that
![]() $\operatorname {\mathrm {den}}(c)=d^2$
with
$\operatorname {\mathrm {den}}(c)=d^2$
with
![]() $d \in 4\mathbb {N}$
. Let
$d \in 4\mathbb {N}$
. Let
![]() $X,Y \in \operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
be distinct. If
$X,Y \in \operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
be distinct. If
![]() $X \equiv Y \bmod d$
, then
$X \equiv Y \bmod d$
, then
![]() $X+Y=\pm 2$
.
$X+Y=\pm 2$
.
Proof. As
![]() $X,Y$
are coprime to d, they are odd. We claim that
$X,Y$
are coprime to d, they are odd. We claim that
![]() $\operatorname {\mathrm {supp}}(X+Y)=\{2\}$
. Indeed, let p be any prime factor of
$\operatorname {\mathrm {supp}}(X+Y)=\{2\}$
. Indeed, let p be any prime factor of
![]() $X+Y$
. Then, p divides d by Corollary 2.6. Hence, p divides
$X+Y$
. Then, p divides d by Corollary 2.6. Hence, p divides
![]() $X-Y$
, because d divides
$X-Y$
, because d divides
![]() $X-Y$
by hypothesis. Therefore, p divides
$X-Y$
by hypothesis. Therefore, p divides
![]() $2X$
, whence
$2X$
, whence
![]() $p=2$
, because p does not divide X. It follows that
$p=2$
, because p does not divide X. It follows that
![]() $X+Y = \pm 2^t$
for some integer
$X+Y = \pm 2^t$
for some integer
![]() $t \ge 1$
. Because
$t \ge 1$
. Because
![]() $d \in 4\mathbb {N}$
and d divides
$d \in 4\mathbb {N}$
and d divides
![]() $X-Y$
, it follows that
$X-Y$
, it follows that
![]() $4$
divides
$4$
divides
![]() $X-Y$
. Hence,
$X-Y$
. Hence,
![]() $4$
cannot also divide
$4$
cannot also divide
![]() $X+Y$
, because
$X+Y$
, because
![]() $X,Y$
are odd. Therefore,
$X,Y$
are odd. Therefore,
![]() $t=1$
, i.e.,
$t=1$
, i.e.,
![]() $X+Y = \pm 2$
, as desired.▪
$X+Y = \pm 2$
, as desired.▪
Example 3.5 Consider the case
![]() $c=29/16$
of Example 1.2, where
$c=29/16$
of Example 1.2, where
![]() $\varphi _c$
admits the cycle
$\varphi _c$
admits the cycle
![]() $\mathcal {C}=(-1/4,-7/4,5/4)$
. In
$\mathcal {C}=(-1/4,-7/4,5/4)$
. In
![]() $\operatorname {\mathrm {num}}(\mathcal {C})=(-1,-7,5)$
, only
$\operatorname {\mathrm {num}}(\mathcal {C})=(-1,-7,5)$
, only
![]() $-7$
and
$-7$
and
![]() $5$
belong to the same class mod
$5$
belong to the same class mod
![]() $4$
, and their sum is
$4$
, and their sum is
![]() $-2$
as expected.
$-2$
as expected.
3.2 From
 $\mathbb {Z}/d\mathbb {Z}$
to
$\mathbb {Z}/d\mathbb {Z}$
to
 $\mathbb {Z}$
$\mathbb {Z}$
Our objective now is to derive from Proposition 3.2 the upper bound
![]() $|\operatorname {\mathrm {Per}}(\varphi _c)| \le 2^s+2$
announced earlier. For that, we shall need the following two auxiliary results.
$|\operatorname {\mathrm {Per}}(\varphi _c)| \le 2^s+2$
announced earlier. For that, we shall need the following two auxiliary results.
Lemma 3.6 Let
![]() $k\in \mathbb {N}$
. Up to order, there are only two ways to express
$k\in \mathbb {N}$
. Up to order, there are only two ways to express
![]() $2^k$
as
$2^k$
as
![]() $2^k=\varepsilon _12^{k_1}+\varepsilon _22^{k_2}$
with
$2^k=\varepsilon _12^{k_1}+\varepsilon _22^{k_2}$
with
![]() $\varepsilon _1,\varepsilon _2=\pm 1$
and
$\varepsilon _1,\varepsilon _2=\pm 1$
and
![]() $k_1,k_2\in \mathbb {N}$
.
$k_1,k_2\in \mathbb {N}$
.
Proof. We may assume
![]() $k_1 \le k_2$
. There are two cases.
$k_1 \le k_2$
. There are two cases.
-
(1) If
 $k_1=k_2$
, then
$k_1=k_2$
, then
 $2^{k_1}(\varepsilon _1+\varepsilon _2)=2^k$
, implying
$2^{k_1}(\varepsilon _1+\varepsilon _2)=2^k$
, implying
 $k_1=k_2=k-1$
and
$k_1=k_2=k-1$
and
 $\varepsilon _1=\varepsilon _2=1$
.
$\varepsilon _1=\varepsilon _2=1$
. -
(2) If
 $k_1 < k_2$
, then
$k_1 < k_2$
, then
 $2^{k_1}(\varepsilon _1+\varepsilon _2 2^{k_2-k_1})=2^k$
, implying
$2^{k_1}(\varepsilon _1+\varepsilon _2 2^{k_2-k_1})=2^k$
, implying
 $k=k_1=k_2-1$
,
$k=k_1=k_2-1$
,
 $\varepsilon _1=-1$
, and
$\varepsilon _1=-1$
, and
 $\varepsilon _2=1$
.▪
$\varepsilon _2=1$
.▪
Proposition 3.7 Let
![]() $ c \in \mathbb {Q}$
be such that
$ c \in \mathbb {Q}$
be such that
![]() $\operatorname {\mathrm {den}}(c)=d^2$
with
$\operatorname {\mathrm {den}}(c)=d^2$
with
![]() $d \in 4\mathbb {N}$
. If there are four pairwise distinct elements
$d \in 4\mathbb {N}$
. If there are four pairwise distinct elements
![]() $X_1,Y_1, X_2,Y_2 \in \operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
such that
$X_1,Y_1, X_2,Y_2 \in \operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
such that
![]() $|X_1+Y_1| = |X_2+Y_2| = 2^k$
for some
$|X_1+Y_1| = |X_2+Y_2| = 2^k$
for some
![]() $k \in \mathbb {N}$
, then
$k \in \mathbb {N}$
, then
Proof. Assume for a contradiction that
![]() $X_1+Y_1 = X_2+Y_2 = \pm 2^k$
. Let
$X_1+Y_1 = X_2+Y_2 = \pm 2^k$
. Let
![]() $p \in \operatorname {\mathrm {supp}}(d)$
be odd, if any such factor exists. We claim that
$p \in \operatorname {\mathrm {supp}}(d)$
be odd, if any such factor exists. We claim that
![]() $X_1, X_2, Y_1,Y_2$
all belong to the same nonzero class mod p. Indeed, we know by Proposition 3.2 that
$X_1, X_2, Y_1,Y_2$
all belong to the same nonzero class mod p. Indeed, we know by Proposition 3.2 that
![]() $X_1, X_2, Y_1,Y_2$
belong to at most two opposite classes mod p. Because p does not divide
$X_1, X_2, Y_1,Y_2$
belong to at most two opposite classes mod p. Because p does not divide
![]() $X_i+Y_i$
for
$X_i+Y_i$
for
![]() $1 \le i \le 2$
, i.e.,
$1 \le i \le 2$
, i.e.,
![]() $X_i \not \equiv -Y_i \bmod p$
, it follows that
$X_i \not \equiv -Y_i \bmod p$
, it follows that
![]() $X_i \equiv Y_i \bmod p$
. Because
$X_i \equiv Y_i \bmod p$
. Because
![]() $X_1 \equiv \pm X_2 \bmod p$
and
$X_1 \equiv \pm X_2 \bmod p$
and
![]() $X_1+Y_1 = X_2+Y_2$
, it follows that
$X_1+Y_1 = X_2+Y_2$
, it follows that
![]() $X_1 \equiv X_2 \bmod p$
and the claim is proved, i.e.,
$X_1 \equiv X_2 \bmod p$
and the claim is proved, i.e.,
Therefore, no sum of two elements in
![]() $\{X_1,Y_1,X_2, Y_2\}$
is divisible by p. Hence, by the third point of Corollary 2.6, any sum of two distinct elements in
$\{X_1,Y_1,X_2, Y_2\}$
is divisible by p. Hence, by the third point of Corollary 2.6, any sum of two distinct elements in
![]() $\{X_1,Y_1,X_2, Y_2\}$
is equal up to sign to a power of
$\{X_1,Y_1,X_2, Y_2\}$
is equal up to sign to a power of
![]() $2$
. Moreover, we have
$2$
. Moreover, we have
 $$ \begin{align*} \pm 2^{k+1} & = (X_1+Y_1)+(X_2+Y_2) \\ & = (X_1+X_2)+(Y_1+Y_2) \\ & = (X_1+Y_2)+(X_2+Y_1). \end{align*} $$
$$ \begin{align*} \pm 2^{k+1} & = (X_1+Y_1)+(X_2+Y_2) \\ & = (X_1+X_2)+(Y_1+Y_2) \\ & = (X_1+Y_2)+(X_2+Y_1). \end{align*} $$
It now follows from Lemma 3.6 that at least two of
![]() $X_1, Y_1, X_2,Y_2$
are equal, contradicting the hypothesis that they are pairwise distinct. Hence,
$X_1, Y_1, X_2,Y_2$
are equal, contradicting the hypothesis that they are pairwise distinct. Hence,
![]() $X_1+Y_1 = -(X_2+Y_2)$
, as claimed.▪
$X_1+Y_1 = -(X_2+Y_2)$
, as claimed.▪
Notation 3.8 For any
![]() $h \in \mathbb {Z}$
, we shall denote by
$h \in \mathbb {Z}$
, we shall denote by
![]() $\pi _h \colon \mathbb {Z} \to \mathbb {Z}/h\mathbb {Z}$
the canonical quotient map mod h.
$\pi _h \colon \mathbb {Z} \to \mathbb {Z}/h\mathbb {Z}$
the canonical quotient map mod h.
Theorem 3.9 Let
![]() $ c \in \mathbb {Q}$
be such that
$ c \in \mathbb {Q}$
be such that
![]() $\operatorname {\mathrm {den}}(c)=d^2$
with
$\operatorname {\mathrm {den}}(c)=d^2$
with
![]() $d \in 4\mathbb {N}$
. Let
$d \in 4\mathbb {N}$
. Let
![]() $m = |\pi _d(\operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}} (\varphi _c)))|$
. Then,
$m = |\pi _d(\operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}} (\varphi _c)))|$
. Then,
Proof. The first inequality is obvious. We now show
![]() $|\operatorname {\mathrm {Per}}(\varphi _c)| \le m+2$
.
$|\operatorname {\mathrm {Per}}(\varphi _c)| \le m+2$
.
Claim
Each class mod d contains at most two elements of
![]() $\operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
.
$\operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
.
Assume the contrary. Then, there are three distinct elements
![]() $X, Y, Z$
in
$X, Y, Z$
in
![]() $\operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
such that
$\operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
such that
![]() $X \equiv Y \equiv Z \bmod d$
. By Proposition 3.4, all three sums
$X \equiv Y \equiv Z \bmod d$
. By Proposition 3.4, all three sums
![]() $X+Y$
,
$X+Y$
,
![]() $X+Z$
, and
$X+Z$
, and
![]() $Y+Z$
belong to
$Y+Z$
belong to
![]() $\{\pm 2\}$
. Hence, two of them coincide, e.g.,
$\{\pm 2\}$
. Hence, two of them coincide, e.g.,
![]() $X+Y=X+Z$
. Therefore,
$X+Y=X+Z$
. Therefore,
![]() $Y=Z$
, a contradiction. This proves the claim.
$Y=Z$
, a contradiction. This proves the claim.
Now, assume for a contradiction that
![]() $|\operatorname {\mathrm {Per}}(\varphi _c)| \ge m+3$
. The claim then implies that there are at least three distinct classes mod d each containing two distinct elements in
$|\operatorname {\mathrm {Per}}(\varphi _c)| \ge m+3$
. The claim then implies that there are at least three distinct classes mod d each containing two distinct elements in
![]() $\operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
. That is, there are six distinct elements
$\operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
. That is, there are six distinct elements
![]() $X_1, Y_1$
,
$X_1, Y_1$
,
![]() $X_2,Y_2$
and
$X_2,Y_2$
and
![]() $X_3, Y_3$
in
$X_3, Y_3$
in
![]() $\operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
such that
$\operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
such that
![]() $X_i\equiv Y_i \bmod d$
for
$X_i\equiv Y_i \bmod d$
for
![]() $1 \le i \le 3$
. Again, Proposition 3.4 implies
$1 \le i \le 3$
. Again, Proposition 3.4 implies
![]() $X_i+Y_i=\pm 2$
for
$X_i+Y_i=\pm 2$
for
![]() $1 \le i \le 3$
. This situation is excluded by Proposition 3.7, and the proof is complete.▪
$1 \le i \le 3$
. This situation is excluded by Proposition 3.7, and the proof is complete.▪
Remark 3.10 The above proof shows that if
![]() $|\operatorname {\mathrm {Per}}(\varphi _c)|= m+2$
, then there are exactly two classes mod d containing more than one element of
$|\operatorname {\mathrm {Per}}(\varphi _c)|= m+2$
, then there are exactly two classes mod d containing more than one element of
![]() $\operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
, and both classes contain exactly two such elements. Denoting
$\operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
, and both classes contain exactly two such elements. Denoting
![]() $\{X_1,Y_1\}, \{X_2,Y_2\} \subset \operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
these two special pairs, the proof further shows that
$\{X_1,Y_1\}, \{X_2,Y_2\} \subset \operatorname {\mathrm {num}}(\operatorname {\mathrm {Per}}(\varphi _c))$
these two special pairs, the proof further shows that
![]() $X_1+Y_1=\pm 2=-(X_2+Y_2)$
.
$X_1+Y_1=\pm 2=-(X_2+Y_2)$
.
Corollary 3.11 Let
![]() $ c \in \mathbb {Q}$
be such that
$ c \in \mathbb {Q}$
be such that
![]() $\operatorname {\mathrm {den}}(c)=d^2$
with
$\operatorname {\mathrm {den}}(c)=d^2$
with
![]() $d \in 4\mathbb {N}$
. Let
$d \in 4\mathbb {N}$
. Let
![]() $s = |\operatorname {\mathrm {supp}}(d)|$
. Then,
$s = |\operatorname {\mathrm {supp}}(d)|$
. Then,
Proof. We have
![]() $|\operatorname {\mathrm {Per}}(\varphi _c)|\,\le \, m+2$
by the above theorem, and
$|\operatorname {\mathrm {Per}}(\varphi _c)|\,\le \, m+2$
by the above theorem, and
![]() $m \le 2^s$
by Corollary 3.3.▪
$m \le 2^s$
by Corollary 3.3.▪
3.3 Numerator dynamics
Let
![]() $c = a/d^2 \in \mathbb {Q}$
with
$c = a/d^2 \in \mathbb {Q}$
with
![]() $a,d$
coprime integers. Closely related to the map
$a,d$
coprime integers. Closely related to the map
![]() $\varphi _c$
is the map
$\varphi _c$
is the map
![]() $d^{-1}\varphi _a \colon \mathbb {Q} \to \mathbb {Q}$
. By definition, this map satisfies
$d^{-1}\varphi _a \colon \mathbb {Q} \to \mathbb {Q}$
. By definition, this map satisfies
for all
![]() $x \in \mathbb {Q}$
. As was already implicit earlier, we now show that cycles of
$x \in \mathbb {Q}$
. As was already implicit earlier, we now show that cycles of
![]() $\varphi _c$
in
$\varphi _c$
in
![]() $\mathbb {Q}$
give rise, by taking numerators, to cycles of
$\mathbb {Q}$
give rise, by taking numerators, to cycles of
![]() $d^{-1}\varphi _{a}$
in
$d^{-1}\varphi _{a}$
in
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
The proof of the following lemma is left as an easy exercise.
Lemma 3.12 Let
![]() $c = a/d^2 \in \mathbb {Q}$
with
$c = a/d^2 \in \mathbb {Q}$
with
![]() $a,d$
coprime integers. Let
$a,d$
coprime integers. Let
![]() $\mathcal {C} \subset \mathbb {Q}$
be a cycle of
$\mathcal {C} \subset \mathbb {Q}$
be a cycle of
![]() $\varphi _c$
. Then,
$\varphi _c$
. Then,
![]() $\operatorname {\mathrm {num}}(\mathcal {C}) \subset \mathbb {Z}$
is a cycle of
$\operatorname {\mathrm {num}}(\mathcal {C}) \subset \mathbb {Z}$
is a cycle of
![]() $d^{-1}\varphi _{a}$
of length
$d^{-1}\varphi _{a}$
of length
![]() $|\mathcal {C}|$
.
$|\mathcal {C}|$
.
3.4 The cases
 $d \not \equiv 0$
mod 3 or mod 5
$d \not \equiv 0$
mod 3 or mod 5
Lemma 3.13 Let
![]() $c \in \mathbb {Q}$
and
$c \in \mathbb {Q}$
and
![]() $\mathcal {C} \subseteq \operatorname {\mathrm {Per}}(\varphi _c)$
a cycle of positive length n.
$\mathcal {C} \subseteq \operatorname {\mathrm {Per}}(\varphi _c)$
a cycle of positive length n.
-
(i) If
 $d \not \equiv 0 \bmod 3$
and
$d \not \equiv 0 \bmod 3$
and
 $n \ge 3$
, then
$n \ge 3$
, then
 $\operatorname {\mathrm {num}}(\mathcal {C})$
reduces mod
$\operatorname {\mathrm {num}}(\mathcal {C})$
reduces mod
 $3$
to exactly one nonzero element.
$3$
to exactly one nonzero element. -
(ii) If
 $d \not \equiv 0 \bmod 5$
and
$d \not \equiv 0 \bmod 5$
and
 $n \ge 4$
, then
$n \ge 4$
, then
 $\operatorname {\mathrm {num}}(\mathcal {C})$
reduces mod
$\operatorname {\mathrm {num}}(\mathcal {C})$
reduces mod
 $5$
to exactly one or two nonzero elements mod
$5$
to exactly one or two nonzero elements mod
 $5$
.
$5$
.
Proof. Let us start with some preliminaries. Of course,
![]() $\varphi _{c}$
induces a cyclic permutation of
$\varphi _{c}$
induces a cyclic permutation of
![]() $\mathcal {C}$
. By Proposition 2.1, we have
$\mathcal {C}$
. By Proposition 2.1, we have
![]() $c= a/d^2$
with
$c= a/d^2$
with
![]() $a,d$
coprime integers. By Lemma 3.12, the rational map
$a,d$
coprime integers. By Lemma 3.12, the rational map
![]() $d^{-1}\varphi _{a}$
induces a cyclic permutation of
$d^{-1}\varphi _{a}$
induces a cyclic permutation of
![]() $\operatorname {\mathrm {num}}(\mathcal {C})$
, say
$\operatorname {\mathrm {num}}(\mathcal {C})$
, say
Let
![]() $X,Y \in \operatorname {\mathrm {num}}(\mathcal {C})$
be distinct. Then,
$X,Y \in \operatorname {\mathrm {num}}(\mathcal {C})$
be distinct. Then,
![]() $\operatorname {\mathrm {supp}}(X+Y) \subseteq \operatorname {\mathrm {supp}}(d)$
by Corollary 2.6. In particular, let q be any prime number such that
$\operatorname {\mathrm {supp}}(X+Y) \subseteq \operatorname {\mathrm {supp}}(d)$
by Corollary 2.6. In particular, let q be any prime number such that
![]() $d \not \equiv 0 \bmod q$
. Then,
$d \not \equiv 0 \bmod q$
. Then,
Because d is invertible mod q, the map
![]() $d^{-1}\varphi _{a}$
induces a map
$d^{-1}\varphi _{a}$
induces a map
where
![]() $f(x)=d^{-1}(x^2-a)$
for all
$f(x)=d^{-1}(x^2-a)$
for all
![]() $x \in \mathbb {Z}/q\mathbb {Z}$
. Thus, we may view
$x \in \mathbb {Z}/q\mathbb {Z}$
. Thus, we may view
![]() $\pi _q(\operatorname {\mathrm {num}}(\mathcal {C}))$
as a sequence of length n in
$\pi _q(\operatorname {\mathrm {num}}(\mathcal {C}))$
as a sequence of length n in
![]() $\mathbb {Z}/q\mathbb {Z}$
, where each element is cyclically mapped to the next by f. Note that (3.2) implies that this n-sequence does not contain opposite elements
$\mathbb {Z}/q\mathbb {Z}$
, where each element is cyclically mapped to the next by f. Note that (3.2) implies that this n-sequence does not contain opposite elements
![]() $u,-u$
of
$u,-u$
of
![]() $\mathbb {Z}/q\mathbb {Z}$
, and in particular contains at most one occurrence of
$\mathbb {Z}/q\mathbb {Z}$
, and in particular contains at most one occurrence of
![]() $0$
.
$0$
.
We are now ready to prove statements (i) and (ii).
(i) Assume
![]() $d \not \equiv 0 \bmod q$
where
$d \not \equiv 0 \bmod q$
where
![]() $q=3$
. By the above, the n-sequence
$q=3$
. By the above, the n-sequence
![]() $\pi _3(\operatorname {\mathrm {num}}(\mathcal {C}))$
consists of at most one
$\pi _3(\operatorname {\mathrm {num}}(\mathcal {C}))$
consists of at most one
![]() $0$
and all other elements equal to some
$0$
and all other elements equal to some
![]() $u \in \{\pm 1\}$
. Because
$u \in \{\pm 1\}$
. Because
![]() $n \ge 3$
, this n-sequence contains two cyclically consecutive occurrences of u. Therefore,
$n \ge 3$
, this n-sequence contains two cyclically consecutive occurrences of u. Therefore,
![]() $f(u) = u$
. Hence,
$f(u) = u$
. Hence,
![]() $\pi _3(\operatorname {\mathrm {num}}(\mathcal {C}))$
contains u as its unique element repeated n times.
$\pi _3(\operatorname {\mathrm {num}}(\mathcal {C}))$
contains u as its unique element repeated n times.
(ii) Assume
![]() $d \not \equiv 0 \bmod q$
where
$d \not \equiv 0 \bmod q$
where
![]() $q=5$
. Because
$q=5$
. Because
![]() $n \ge 4$
and the n-sequence
$n \ge 4$
and the n-sequence
![]() $\pi _5(\operatorname {\mathrm {num}}(\mathcal {C}))$
contains at most one
$\pi _5(\operatorname {\mathrm {num}}(\mathcal {C}))$
contains at most one
![]() $0$
, it must contain three cyclically consecutive nonzero elements
$0$
, it must contain three cyclically consecutive nonzero elements
![]() $u_1,u_2,u_3 \in \mathbb {Z}/5\mathbb {Z} \setminus \{0\}$
. Because that set contains at most two pairwise nonopposite elements, it follows that
$u_1,u_2,u_3 \in \mathbb {Z}/5\mathbb {Z} \setminus \{0\}$
. Because that set contains at most two pairwise nonopposite elements, it follows that
![]() $u_i=u_j$
for some
$u_i=u_j$
for some
![]() $1 \le i < j \le 3$
. Now,
$1 \le i < j \le 3$
. Now,
![]() $u_1 \mapsto u_2 \mapsto u_3$
by f. Therefore, if either
$u_1 \mapsto u_2 \mapsto u_3$
by f. Therefore, if either
![]() $u_1=u_2$
or
$u_1=u_2$
or
![]() $u_2=u_3$
, it follows that the whole sequence
$u_2=u_3$
, it follows that the whole sequence
![]() $\pi _5(\operatorname {\mathrm {num}}(\mathcal {C}))$
consists of the one single element
$\pi _5(\operatorname {\mathrm {num}}(\mathcal {C}))$
consists of the one single element
![]() $u_2$
repeated n times. On the other hand, if
$u_2$
repeated n times. On the other hand, if
![]() $u_1\not =u_2$
, then
$u_1\not =u_2$
, then
![]() $u_1=u_3$
. In this case, the n-sequence
$u_1=u_3$
. In this case, the n-sequence
![]() $\pi _5(\operatorname {\mathrm {num}}(\mathcal {C}))$
consists of the sequence
$\pi _5(\operatorname {\mathrm {num}}(\mathcal {C}))$
consists of the sequence
![]() $u_1,u_2$
repeated
$u_1,u_2$
repeated
![]() $n/2$
times. This concludes the proof.▪
$n/2$
times. This concludes the proof.▪
Example 3.14 Consider the case
![]() $c=a/d^2=29/16$
of Example 1.2, where
$c=a/d^2=29/16$
of Example 1.2, where
![]() $\varphi _c$
admits the cycle
$\varphi _c$
admits the cycle
![]() $\mathcal {C}= (-1/4, -7/4,5/4)$
. Then,
$\mathcal {C}= (-1/4, -7/4,5/4)$
. Then,
![]() $\operatorname {\mathrm {num}}(\mathcal {C})=(-1,-7,5)$
, a cycle of length
$\operatorname {\mathrm {num}}(\mathcal {C})=(-1,-7,5)$
, a cycle of length
![]() $3$
of the map
$3$
of the map
![]() $d^{-1}\varphi _{a}=4^{-1}\varphi _{29}$
. That cycle reduces mod
$d^{-1}\varphi _{a}=4^{-1}\varphi _{29}$
. That cycle reduces mod
![]() $3$
to
$3$
to
![]() $(-1,-1,-1)$
, as expected with statement (i) of the lemma. Statement (ii) does not apply because
$(-1,-1,-1)$
, as expected with statement (i) of the lemma. Statement (ii) does not apply because
![]() $n=3$
, and it would fail anyway because
$n=3$
, and it would fail anyway because
![]() $\operatorname {\mathrm {num}}(\mathcal {C})$
reduces mod
$\operatorname {\mathrm {num}}(\mathcal {C})$
reduces mod
![]() $5$
to the sequence
$5$
to the sequence
![]() $(-1,-2,0)$
.
$(-1,-2,0)$
.
3.5 Main consequences
Proposition 3.15 Let
![]() $c=a/d^2 \in \mathbb {Q}$
with
$c=a/d^2 \in \mathbb {Q}$
with
![]() $a,d$
coprime integers and with
$a,d$
coprime integers and with
![]() $d \in 4\mathbb {N}$
. Assume
$d \in 4\mathbb {N}$
. Assume
![]() $d \not \equiv 0 \bmod 3$
. Let
$d \not \equiv 0 \bmod 3$
. Let
![]() $s=|\operatorname {\mathrm {supp}}(d)|$
. For every rational cycle
$s=|\operatorname {\mathrm {supp}}(d)|$
. For every rational cycle
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $\varphi _c$
, we have
$\varphi _c$
, we have
Proof. By Corollary 3.11, we have
![]() $|\mathcal {C}| \,\le \, 2^s+2$
. If
$|\mathcal {C}| \,\le \, 2^s+2$
. If
![]() $|\mathcal {C}| = 2^s+2$
, then, by Remark 3.10, there exist two pairs
$|\mathcal {C}| = 2^s+2$
, then, by Remark 3.10, there exist two pairs
![]() $\{X_1, Y_1\}, \{X_2, Y_2\}$
in
$\{X_1, Y_1\}, \{X_2, Y_2\}$
in
![]() $\operatorname {\mathrm {num}}(\mathcal {C})$
such that
$\operatorname {\mathrm {num}}(\mathcal {C})$
such that
![]() $X_1+Y_1=2$
and
$X_1+Y_1=2$
and
![]() $X_2+Y_2=-2$
. Because
$X_2+Y_2=-2$
. Because
![]() $d \not \equiv 0 \bmod 3$
, Lemma 3.13 implies that
$d \not \equiv 0 \bmod 3$
, Lemma 3.13 implies that
![]() $X_1, X_2, Y_1,Y_2$
reduce to the same nonzero element u mod
$X_1, X_2, Y_1,Y_2$
reduce to the same nonzero element u mod
![]() $3$
. This contradicts the equality
$3$
. This contradicts the equality
![]() $X_1+Y_1=-(X_2+Y_2)$
.▪
$X_1+Y_1=-(X_2+Y_2)$
.▪
Again, we are grateful to Prof. W. Narkiewicz for the remark below.
Remark 3.16 Under the same hypotheses as above, the conclusion
![]() $ |\mathcal {C}| \,\le \, 2^s+1$
may be improved to
$ |\mathcal {C}| \,\le \, 2^s+1$
may be improved to
![]() $|\mathcal {C}| \,\le \, 9$
provided
$|\mathcal {C}| \,\le \, 9$
provided
![]() $s \ge 4$
. This follows from Pezda’s Theorem 2.11 for
$s \ge 4$
. This follows from Pezda’s Theorem 2.11 for
![]() $p=3$
. See also Reference Benedetto[2] for related results.
$p=3$
. See also Reference Benedetto[2] for related results.
We may now conclude the paper with one of its main results.
Theorem 3.17 If
![]() $\operatorname {\mathrm {den}}(c)$
admits at most two distinct prime factors, then
$\operatorname {\mathrm {den}}(c)$
admits at most two distinct prime factors, then
![]() $\varphi _c$
satisfies the Flynn–Poonen–Schaefer conjecture.
$\varphi _c$
satisfies the Flynn–Poonen–Schaefer conjecture.
Proof. Let
![]() $\mathcal {C}$
be a rational cycle of
$\mathcal {C}$
be a rational cycle of
![]() $\varphi _c$
of length
$\varphi _c$
of length
![]() $n \ge 3$
. Then, d is even, and hence
$n \ge 3$
. Then, d is even, and hence
![]() $s \geq 1$
.
$s \geq 1$
.
![]() $\bullet $
If
$\bullet $
If
![]() $s=1$
, then d is a power of
$s=1$
, then d is a power of
![]() $2$
. By Corollary 3.11 and Proposition 3.15, we have
$2$
. By Corollary 3.11 and Proposition 3.15, we have
![]() $ |\operatorname {\mathrm {Per}}(\varphi _c)| \, \le 4$
and
$ |\operatorname {\mathrm {Per}}(\varphi _c)| \, \le 4$
and
![]() $|\mathcal {C}| \le 3$
. See also Reference Eliahou and Fares[4].
$|\mathcal {C}| \le 3$
. See also Reference Eliahou and Fares[4].
![]() $\bullet $
Assume now
$\bullet $
Assume now
![]() $s=2$
. Then,
$s=2$
. Then,
![]() $d=2^{r_1}p^{r_2}$
where p is an odd prime and
$d=2^{r_1}p^{r_2}$
where p is an odd prime and
![]() $r_1 \ge 2$
. By Theorem 3.9, we have
$r_1 \ge 2$
. By Theorem 3.9, we have
![]() $|\mathcal {C}| \le |\operatorname {\mathrm {Per}}(\varphi _c)| \le 6$
. By Theorems 1.3 and 1.4, we have
$|\mathcal {C}| \le |\operatorname {\mathrm {Per}}(\varphi _c)| \le 6$
. By Theorems 1.3 and 1.4, we have
![]() $|\mathcal {C}| \not = 4,5$
. It remains to show
$|\mathcal {C}| \not = 4,5$
. It remains to show
![]() $|\mathcal {C}| \not = 6$
. We distinguish two cases. If
$|\mathcal {C}| \not = 6$
. We distinguish two cases. If
![]() $p \not = 3$
, then
$p \not = 3$
, then
![]() $|\mathcal {C}| \leq 2^2+1=5$
by Proposition 3.15, and we are done. Assume now
$|\mathcal {C}| \leq 2^2+1=5$
by Proposition 3.15, and we are done. Assume now
![]() $p=3$
, so that
$p=3$
, so that
![]() $d=2^{r_1}3^{r_2}$
. Let m denote the number of classes of
$d=2^{r_1}3^{r_2}$
. Let m denote the number of classes of
![]() $\operatorname {\mathrm {num}}(\mathcal {C})$
mod
$\operatorname {\mathrm {num}}(\mathcal {C})$
mod
![]() $q=5$
. It follows from Lemma 3.13 that
$q=5$
. It follows from Lemma 3.13 that
![]() $m \le 2$
. Because the order of every element in
$m \le 2$
. Because the order of every element in
![]() $(\mathbb {Z}/ 5\mathbb {Z})^*$
belongs to
$(\mathbb {Z}/ 5\mathbb {Z})^*$
belongs to
![]() $\{1, 2, 4\}$
, it follows from Zieve’s Theorem 2.12 that
$\{1, 2, 4\}$
, it follows from Zieve’s Theorem 2.12 that
![]() $|\mathcal {C}|$
is a power of
$|\mathcal {C}|$
is a power of
![]() $2$
. Hence,
$2$
. Hence,
![]() $|\mathcal {C}| \in \{1, 2, 4\}$
, and we are done.▪
$|\mathcal {C}| \in \{1, 2, 4\}$
, and we are done.▪
Acknowledgment
The authors are grateful to both anonymous referees for their detailed reading of the original version of this paper and for their highly valuable remarks and suggestions.