Swelling deformation tests

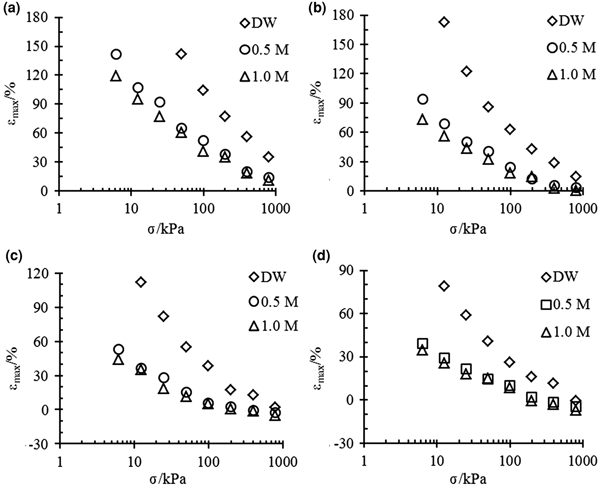
The relationships between the maximum strain ε_max and vertical pressure σ for bentonite–sand mixtures with different bentonite contents are illustrated in Fig. 1. The bentonite content increased the swelling potential of the mixture, but the salt concentration of the pore fluid or vertical pressure reduced the swelling strains, even to the point of compression.

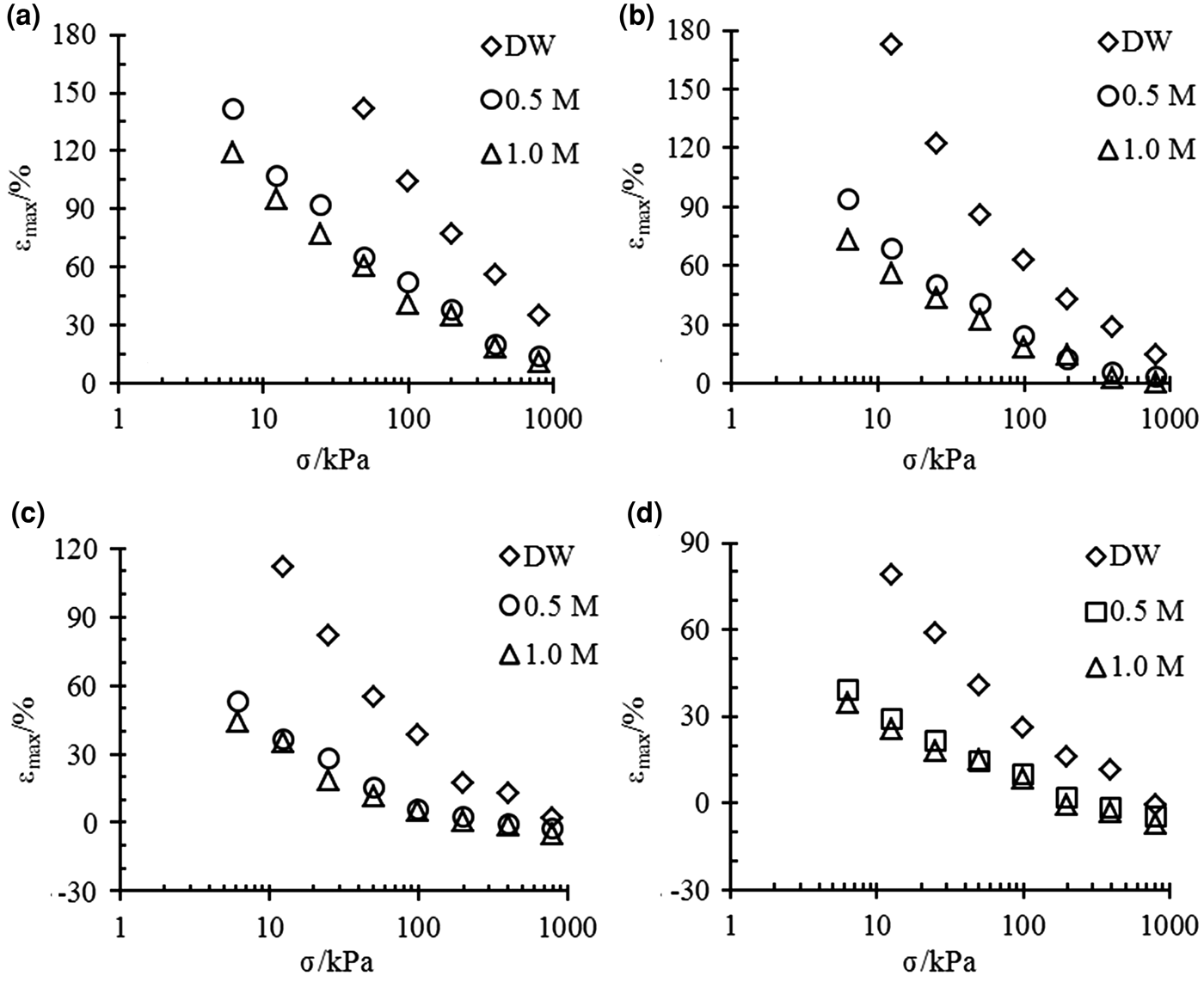
Fig. 1. ε_max vs. σ for different bentonite–sand mixtures with (a) 100%, (b) 70%, (c) 50%, and (d) 40% bentonite contents in different solutions.

Pure bentonite (α = 100%) and the mixtures with 70% bentonite contents exhibit swelling strains in all of the experimental conditions (Fig. 1a,b).

The mixtures with 50% bentonite contents exhibited swelling strains in distilled water at all pressures, but in the 0.5 and 1.0 mol/L NaCl solutions, the mixtures experienced small compressed strains when the vertical pressure reached 400 kPa (Fig. 1c).

The mixtures with 40% bentonite contents experienced compression at 800, 400 and 200 kPa when they were saturated by distilled water, 0.5 mol/L and 1.0 mol/L solution, respectively (Fig. 1d).

The differences between the final strains of the same mixtures are large in different solutions under low pressures. However, the final strains are essentially the same for mixtures with small bentonite contents (40% and 50%) under high pressure.

The swelling deformation of the bentonite–sand mixtures can also be expressed by the void ratio of montmorillonite, e _m, which is defined as (Sun et al., Reference Sun, Cui and Sun2009):

(1)$$e_{\rm m}{\rm}={\rm } \displaystyle{{V_{\rm w}} \over {V_{\rm m}}}{\rm}={\rm } e\displaystyle{{{\rm \rho} _{\rm m}} \over {{\rm \rho} _{\rm s}{\rm \alpha \beta}}} $$

where V _w and e are the water volume and the void ratio of the mixture at full saturation, respectively, V _m is the montmorillonite volume, ρ_m is the grain density of montmorillonite, ρ_s is the grain density of the bentonite–sand mixture, α is the bentonite content in the mixture (mass %) and β is the montmorillonite content in the bentonite (mass %).

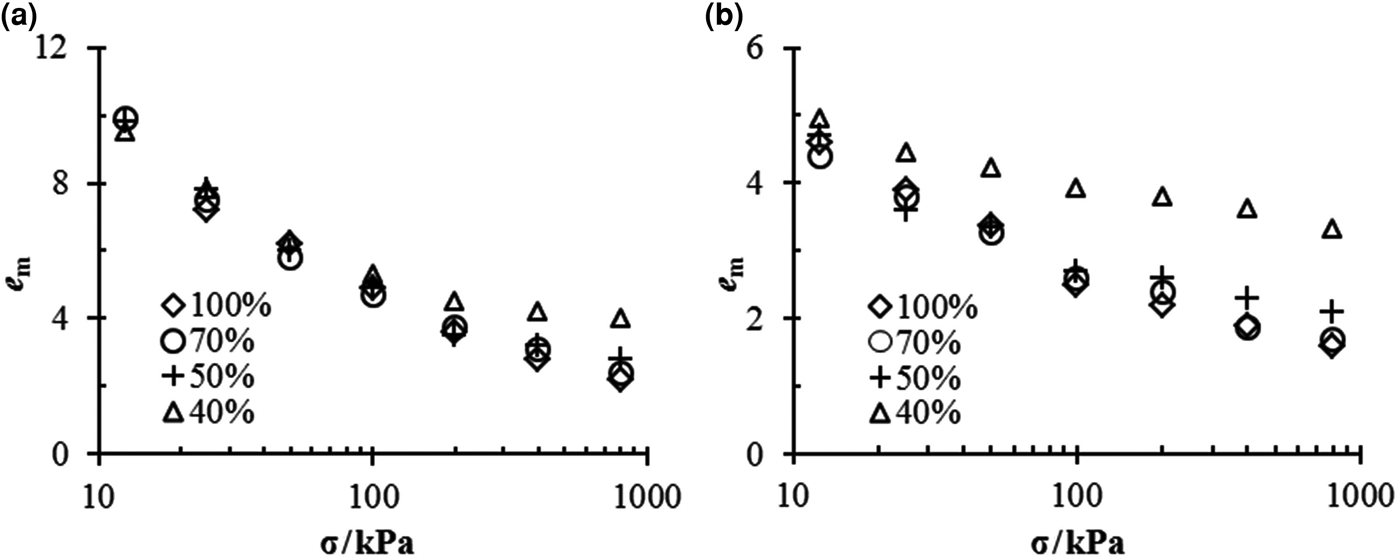
The e _m–σ relationships for different mixtures in different solutions are shown in Fig. 2. Similarly to the swelling strain, the salt concentration or vertical pressure reduces the void ratio of montmorillonite, e _m. However, in contrast to the swelling strain, e _m tends to increase for mixtures with small bentonite contents.

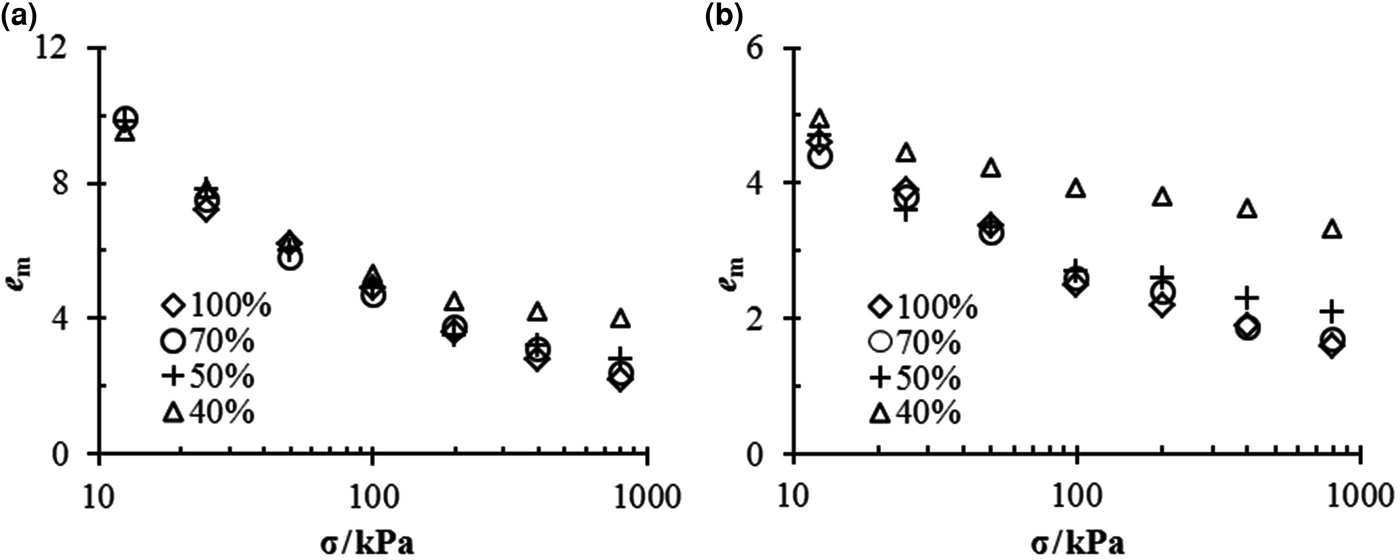
Fig. 2. e _m vs. σ for bentonite–sand mixtures in (a) distilled water and (b) 1.0 M NaCl solution.

The mixtures with 70% bentonite contents always had the same e _m as pure bentonite under the same experimental conditions.

In the case of distilled water, all mixtures exhibited essentially the same value of e _m under low vertical pressure, but once the vertical pressure exceeded 50 kPa, the e _m of the mixtures with 40% bentonite contents became larger than those of the remaining mixtures (Fig. 2a).

In 1.0 M NaCl solution (Fig. 2b), the mixtures with 40% bentonite contents always had the largest e _m under any vertical pressure; in addition, when the vertical pressure exceeded 200 kPa, the mixtures of α = 50% exhibited larger values of e _m than pure bentonite and mixtures of α = 70%.

e_m–p_e relationship for mixtures in salt solution

The effective stress is generally defined as the net interactive force between soil particles, and in the case of the volume change of bentonite, it may be regarded as the interactive force between montmorillonite layers. In the case of distilled water, the effective stress, p _e, is balanced by the vertical pressure, σ, loaded in swelling tests (Xu et al., Reference Xu, Xiang, Jiang, Chen and Chu2014). In comparison, saturation of bentonite specimens with inflowing salt solutions increases the osmotic suction in pore water, which in turn acts as an additional effective stress component (Rao & Thyagaraj, Reference Rao and Thyagaraj2007). Based on the surface structure of montmorillonite aggregates and montmorillonite layers, Xu et al. (Reference Xu, Xiang, Jiang, Chen and Chu2014) proposed a new formula for effective stress, incorporating the osmotic suction of pore fluid, which may be expressed as:

(2)$$p_{\rm e} = {\rm \sigma} + {\rm \pi} \left( {\displaystyle{{\rm \sigma} \over {\rm \pi}}} \right)^{D_{\rm s}-2}$$

where σ is the vertical pressure applied on specimens, π is the osmotic suction of pore water and D _s is the surface fractal dimension of bentonite. The surface fractal dimension is a descriptor used for characterizing the surface structures and irregularities of solid materials (Risović et al., Reference Risović, Mahović Poljaček, Furić and Gojo2008), which varies from 2 to 3. The larger the D _s value, the more irregular and space-filling the surface (Helmy et al., Reference Helmy, Ferreiro, Bussetti and Peinemann1998). In bentonite swelling, the surface fractal dimension increases with increasing swelling strain (Xu et al., Reference Xu, Matsuoka and Sun2003).

The correlation of the void ratio of montmorillonite with effective stress is given by (Xu et al., Reference Xu, Xiang, Jiang, Chen and Chu2014):

(3)$$ e_{\rm m} = Kp_{\rm e}^{D_{\rm s}-3} $$

where K is the swelling coefficient of montmorillonite. Equation 3 may be expressed in the bi-logarithmic form as:

(4)$$\log\! e_{\rm m} = \log\! K + (D_{\rm s}-3)\!\log\! p_{\rm e}$$

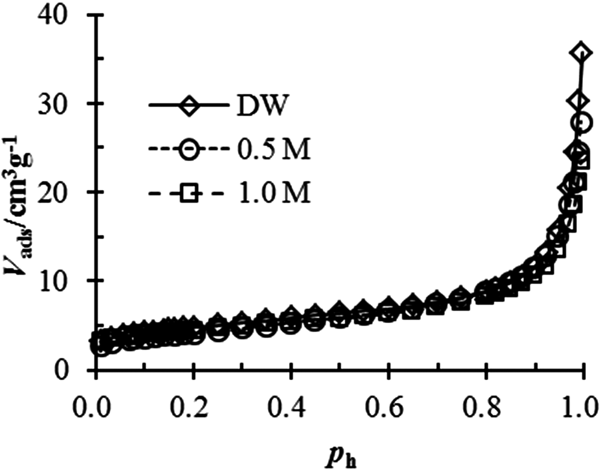
The surface fractal dimension of bentonite in salt solution is also determined using nitrogen adsorption. The nitrogen adsorption isotherms of the bentonite tested in various solutions are shown in Fig. 3. Then, the fractal dimension may be calculated by the Frenkel–Halsey–Hill equation:

(5)$$\ln {V}_{{ads}} = {\rm B} + (3-{D}_s)\ln [ {\ln ( {1/{ p}_h} ) } ] $$

where V _ads is the nitrogen adsorption volume, B is the nitrogen adsorption coefficient of bentonite and p _h is the equilibrium relative pressure.

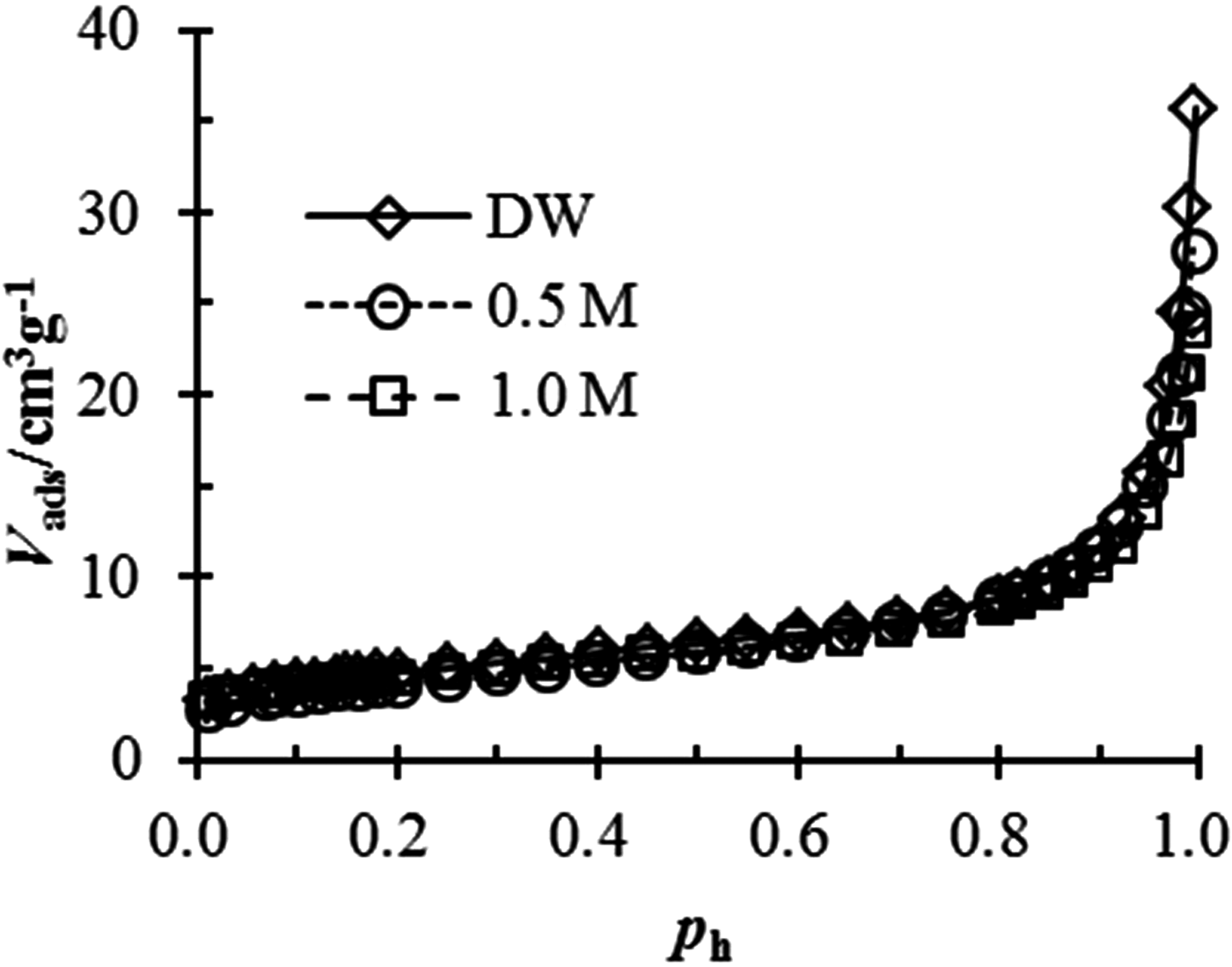
Fig. 3. Nitrogen adsorption–desorption isotherms of tested bentonite in different salt solutions.

The estimated D _s values from the nitrogen adsorption are listed in Table 2. The variation in the surface fractal dimension for the tested bentonite is <0.1. Thus, the effect of NaCl concentration on the fractal dimension is negligible and so may be ignored.

Table 2. Fractal dimensions of Kunigel bentonite from the nitrogen adsorption tests.

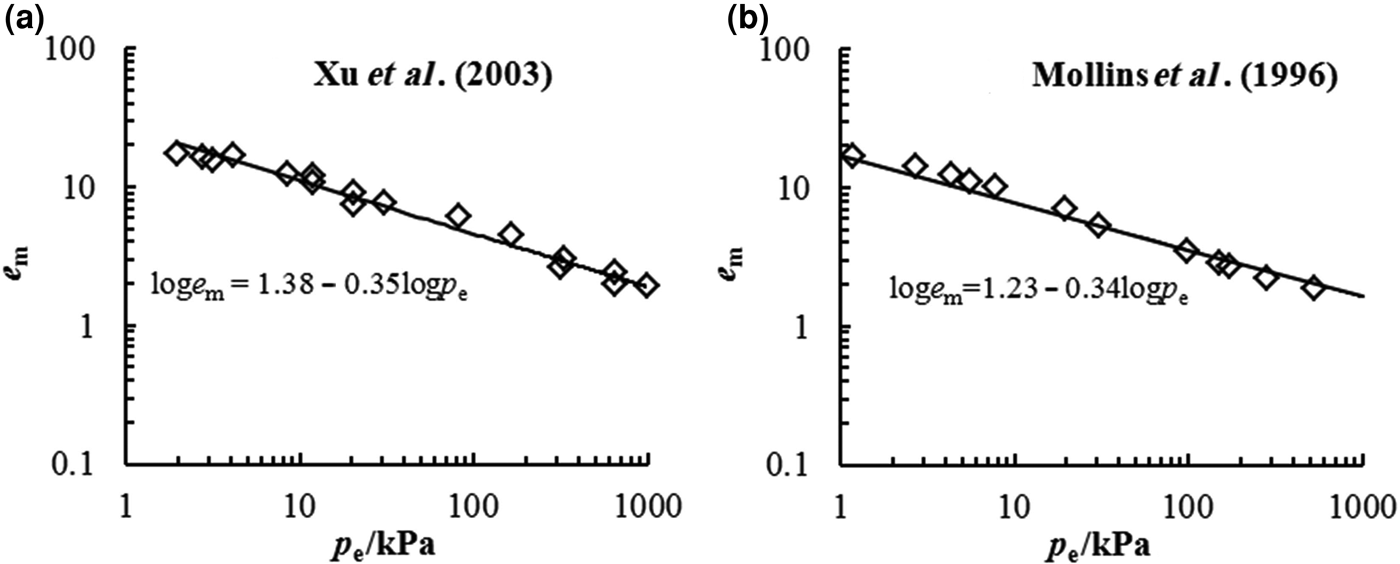
The D _s of bentonite may also be estimated using Eq. 4 according to the experimental data from swelling deformation tests. The swelling deformations of Kunigel bentonite and MX-80 bentonite in distilled water from previous studies are illustrated in Fig. 4. The D _s values of these two bentonites were estimated as 2.65 and 2.66, respectively. Thus, the D _s values of Kunigel bentonite determined from the nitrogen adsorption and swelling tests are essentially identical.

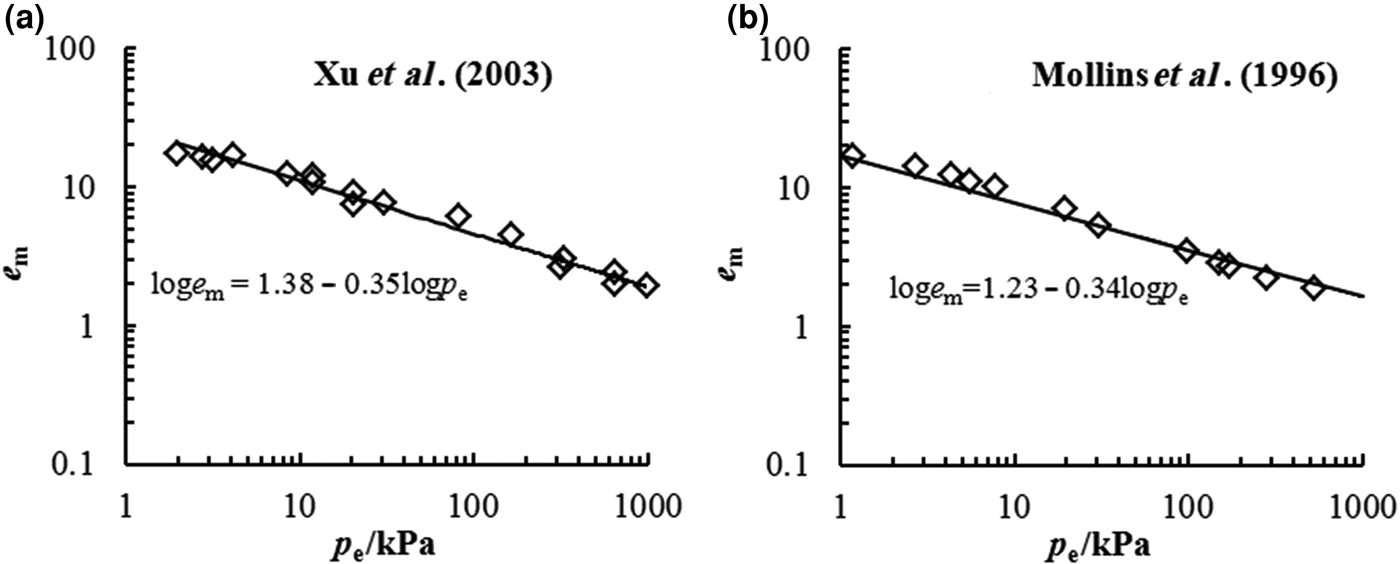
Fig. 4. D _s from swelling deformation of (a) Kunigel bentonite (Xu et al., Reference Xu, Matsuoka and Sun2003) and (b) MX-80 bentonite (Mollins et al., Reference Mollins, Stewart and Cousens1996) in distilled water.

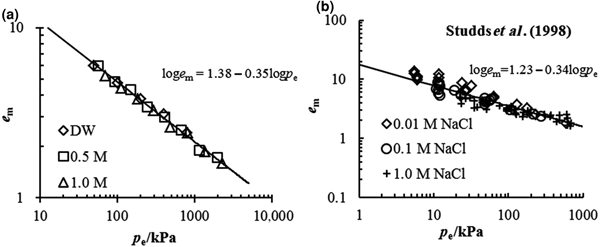
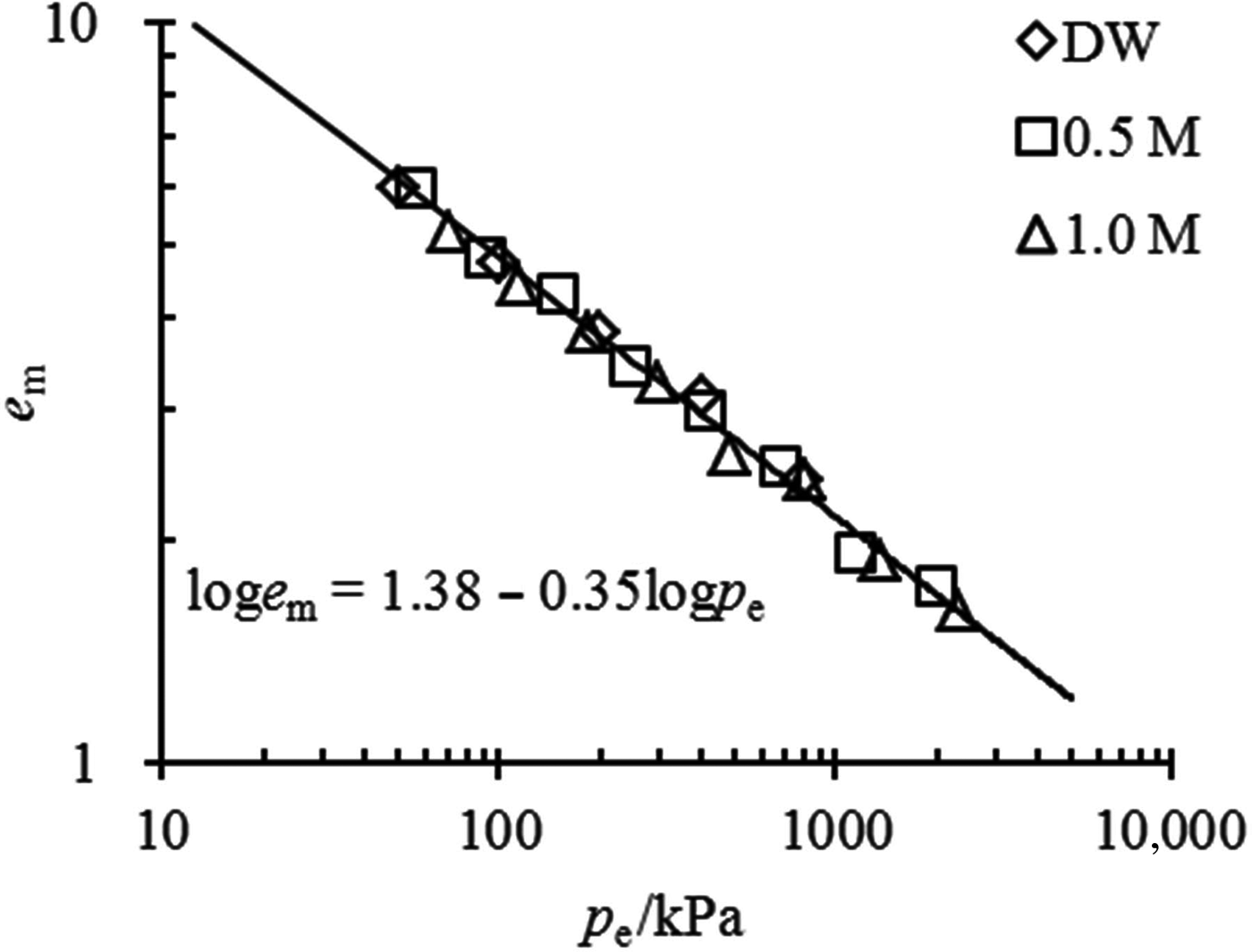
The comparison between the estimated e _m–p _e relationship from Eq. 4 and the experimental data in this study is illustrated in Fig. 5a. Good agreement is observed between the estimated and experimental data, suggesting that the swelling deformation of the Kunigel bentonite in various salt solution concentrations may be characterized by a unique e _m–p _e curve with equation loge _m = 1.38 − 0.35logp _e. The coefficients of the unique e _m–p _e curve may be obtained conveniently from the swelling experimental data in distilled water. From the swelling test results in distilled water, the e _m–p _e of MX-80 bentonite is estimated as loge _m = 1.23 − 0.34logp _e, which is validated by the swelling deformation in NaCl at different concentrations (0.01, 0.1 and 1 mol/L) determined by Studds et al. (Reference Studds, Stewart and Cousens1998), as is shown in Fig. 5b.

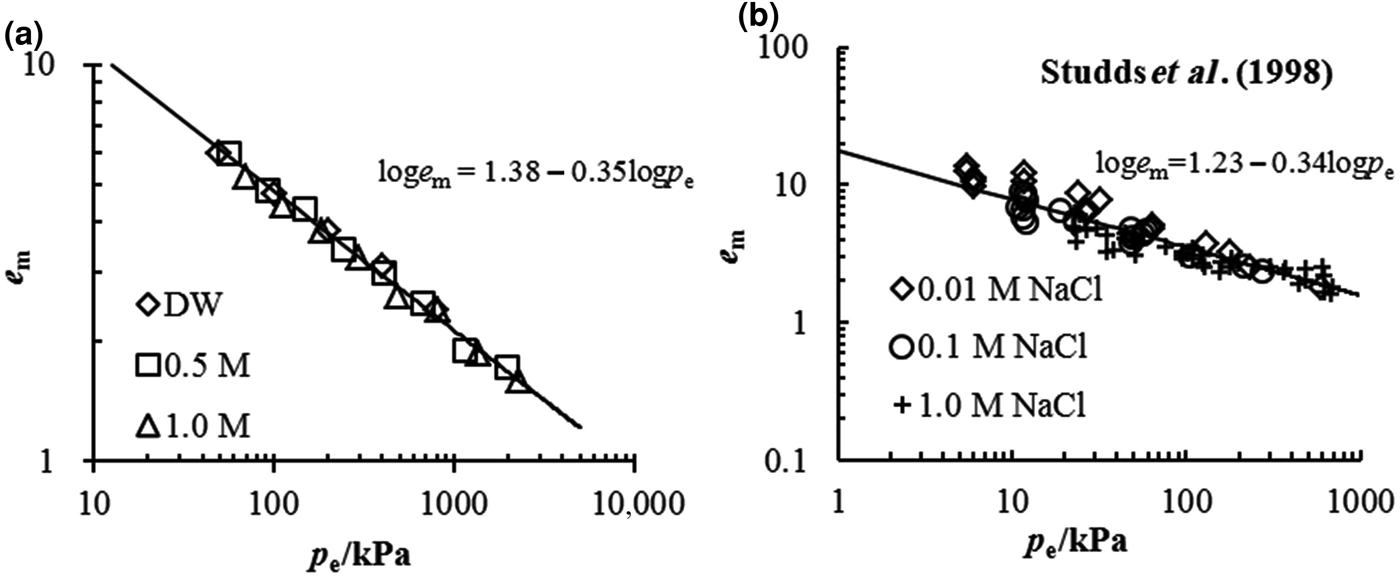
Fig. 5. Comparison between the prediction of the e _m–p _e relationship and the experimental data for (a) tested pure bentonite and (b) MX-80 bentonite from Studds et al. (Reference Studds, Stewart and Cousens1998).

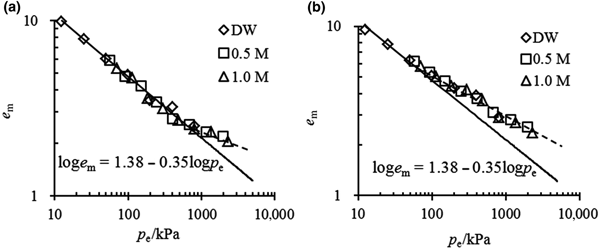
The e _m–p _e relationship for the mixtures with 70% bentonite contents in various solutions is shown in Fig. 6. The swelling properties of this mixture may also be represented by the unique linear equation of loge _m = 1.38 − 0.35logp _e. Due to the large bentonite contents, these mixtures have essentially the same e _m values as pure bentonite when they are saturated with the same solution and under the same vertical pressure; i.e. under the same effective stress. Therefore, when the coefficients of the e _m–p _e relationship are obtained from pure bentonite in distilled water, the swelling properties of mixtures with large bentonite contents in concentrated solutions may also be estimated.

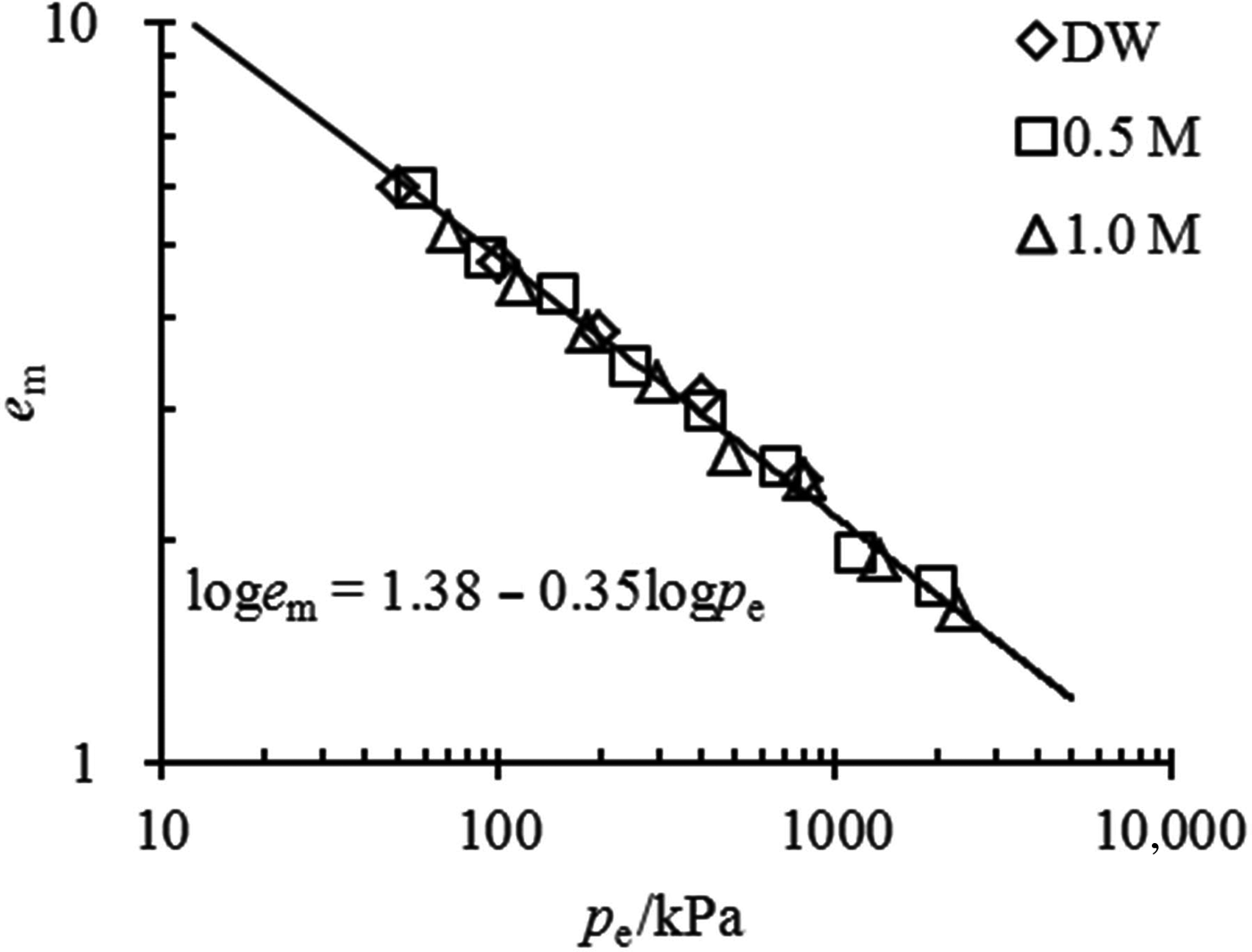
Fig. 6. Comparison between the prediction of the e _m–p _e relationship and the experimental data for mixtures with α = 70%.

Threshold of sand particle contact

The e _m–p _e relationship for mixtures with small bentonite contents at full saturation is illustrated in Fig. 7. When the inflowing solution is dilute or the vertical stress is small, this will result in a small p _e value, and the experimental data may be arranged with the unique e _m–p _e curve as expressed for pure bentonite. However, when the effective stress exceeded a particular threshold, caused only by the vertical stress or including osmotic suction, the tested plots always began to deviate from the unique e _m–p _e curve. The threshold of effective stress was ~750 kPa for α = 50% mixtures and ~50 kPa for α = 40% mixtures, suggesting that the greater the bentonite content in the mixture, the greater the threshold of effective stress above which the deviation begins.

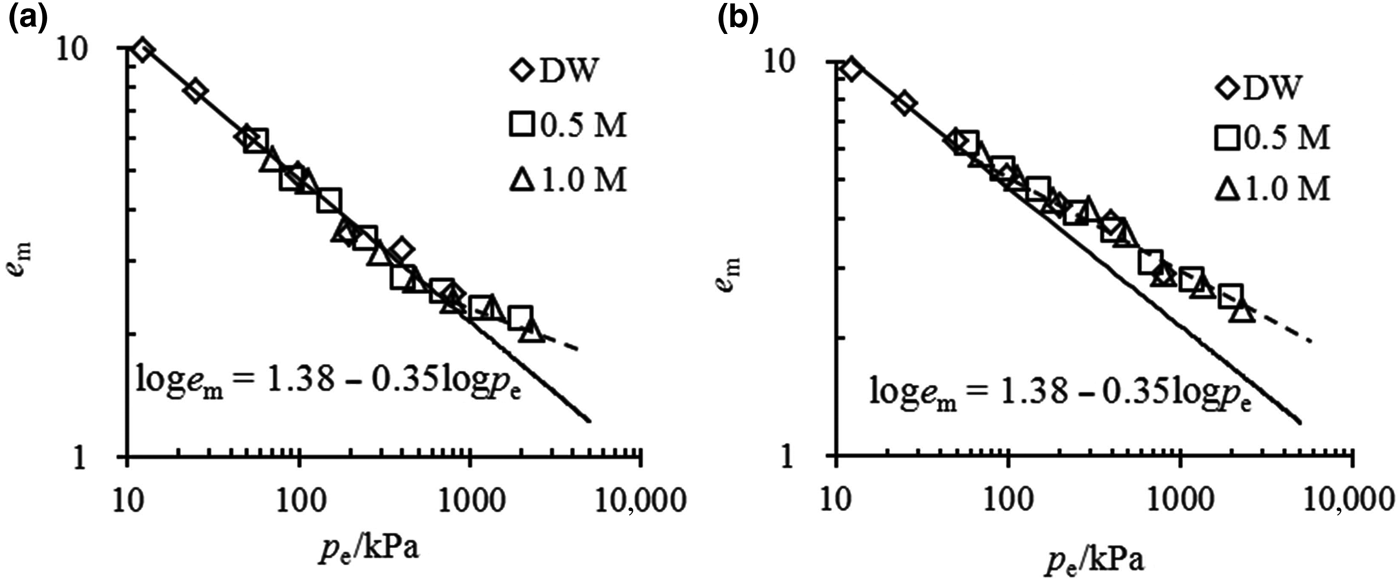
Fig. 7. e _m–p _e relationship for mixtures with (a) α = 50% and (b) α = 40%.

The various e _m values for different mixtures in salt solution are caused by the different effective stresses borne by the montmorillonite layers. In the case of mixtures with large bentonite contents, the montmorillonite is able to swell against the effective stress and separate the sand particles. Even under high effective stress (high vertical pressure and/or high osmotic suction), the sand particles are still surrounded by the clay mineral, so all of the effective stress is taken up by the montmorillonite and the volume change of the mixtures might simply follow the unique curve of e _m–p _e. However, in the case of mixtures with small bentonite contents, when the effective stress is large enough, a small volume of water is adsorbed by the montmorillonite; thus, there is little void space for the separation of sand particles. Moreover, the sand particles might not be surrounded by montmorillonite particles, but rather might be in contact with each other and form a skeleton. In this case, the effective stress is not taken up by the montmorillonite, yielding a larger e _m compared to pure bentonite.

The skeleton void ratio, e _s, was defined as (Sun et al., Reference Sun, Cui and Sun2009):

(6)$$e_{\rm s} = \displaystyle{{V_{\rm w} + V_{\rm m} + V_{{\rm nm}}} \over {V_{{\rm sd}}}}$$

where V _w is the water volume at full saturation, V _m is the volume of montmorillonite, V _nm is the volume of non-expansive clay mineral, V _w + V _m + V _nm represents the volume except for sand particles in the sand–bentonite mixture and V _sd is the volume of sand particles. According to Eq. 1, at full saturation, there is V _w = e _mV _m. Then, the relationship between e _m and e _s may be expressed as:

(7)$$e_{\rm m} = Ae_{\rm s} + B$$

with

(8)$$A = \displaystyle{{V_{{\rm sand}}} \over {V_{\rm m}}} = \displaystyle{{{\rm \rho} _{\rm m}(1-{\rm \alpha} /{\rm 1}00)} \over {{\rm \rho} _{{\rm sd}}{\rm \alpha \beta} {10}^{-4}}}$$

(9)$$B = -\displaystyle{{V_{\rm m} + V_{{\rm nm}}} \over {V_{\rm m}}} = -\left( {1 + \displaystyle{{{\rm \rho}_{\rm m}} \over {{\rm \rho}_{{\rm nm}}}}\displaystyle{{100-{\rm \beta}} \over {\rm \beta}}} \right)$$

where ρ_m = 2.79, ρ_nm = 2.79 and ρ_sd = 2.75 are the specific gravity values of montmorillonite, non-expansive clay mineral in bentonite and sand particles, respectively (Sun et al., Reference Sun, Cui and Sun2009). For the tested bentonite, B = –2.08.

When e _s is small enough, a skeleton of sand particles may be formed in the mixture, but the experimental data will deviate from the e _m–p _e curve. Therefore, when the effective stress reaches the threshold, e _s also reaches the threshold e _max, where sand particles begin to come into contact with each other. The initial deviations of e _m for mixtures with 50% and 40% bentonite contents are 2.5 and 5.0, respectively (Fig. 7). Thus, e _max accounts for 1.0 using Eq. 7, in agreement to the study by Sun et al. (Reference Sun, Cui and Sun2009), suggesting that the sand skeleton may be formed when the volume of sand particles is greater than the volume excluding sand particles in the mixture. When the deviation begins from the unique e _m–p _e curve, the e _s = e _max = 1.0, and the fractal e _m–p _e relationship should be satisfied simultaneously. That is:

(10)$$1.0A + B = e_{\rm m} = Kp_{\rm e}^{D_{\rm s}-3} $$

It is suggested that the montmorillonite begins to adsorb water (e _m = 0) when the sand skeleton begins to break up, which is the limiting bentonite content at which the sand skeleton may not be formed under any condition. According to Eq. 10, the limiting bentonite content of Kunigel bentonite is estimated as 51.1%.

Rearrangement of Eq. 10 gives:

(11)$$\log\! p_{\rm e} = \displaystyle{{\log (A + B)-\log\! K} \over {D_{\rm s}-3}}$$

The effective stress calculated by Eq. 11 is referred to as the sand particle contact stress, p _ec, when the sand particle skeleton begins to form in mixtures with low bentonite contents, and the corresponding vertical stress, σ_c, applied on the mixture in a given salt solution is then estimated by Eq. 2. The estimated results of these calculations are listed in Table 3, and are in good agreement with the experimental data.

Table 3. Sand particle contact vertical stress, σ_c, for mixtures with small bentonite contents in different solutions (kPa).

Prediction of maximum swelling strain

The relationship between ε_max of bentonite–sand mixtures and e _m at full saturation may be written as (Xu et al., Reference Xu, Matsuoka and Sun2003):

(12)$${\rm \varepsilon} _{\max} {\rm}={\rm } \displaystyle{{{\rm \rho} _{\rm d}e_{\rm m}-A\lpar {{\rm \rho}_{\rm s}-{\rm \rho}_{\rm d}} \rpar } \over {A{\rm \rho} _{\rm s}}} \times 100\lpar \% \rpar $$

Where A = 1 + (100/β − 1)(ρ_m/ρ_nm) + (100/α − 1)(100/β)(ρ_m/ρ_sd) and ρ_d is the initial dry density of bentonite–sand mixture samples. The remaining parameters in Eq. 12 have been defined previously.

After substitution of Eqs. 2 and 3 into Eq. 12, the maximum swelling strain of a bentonite–sand mixture in salt solution may be expressed as:

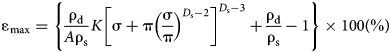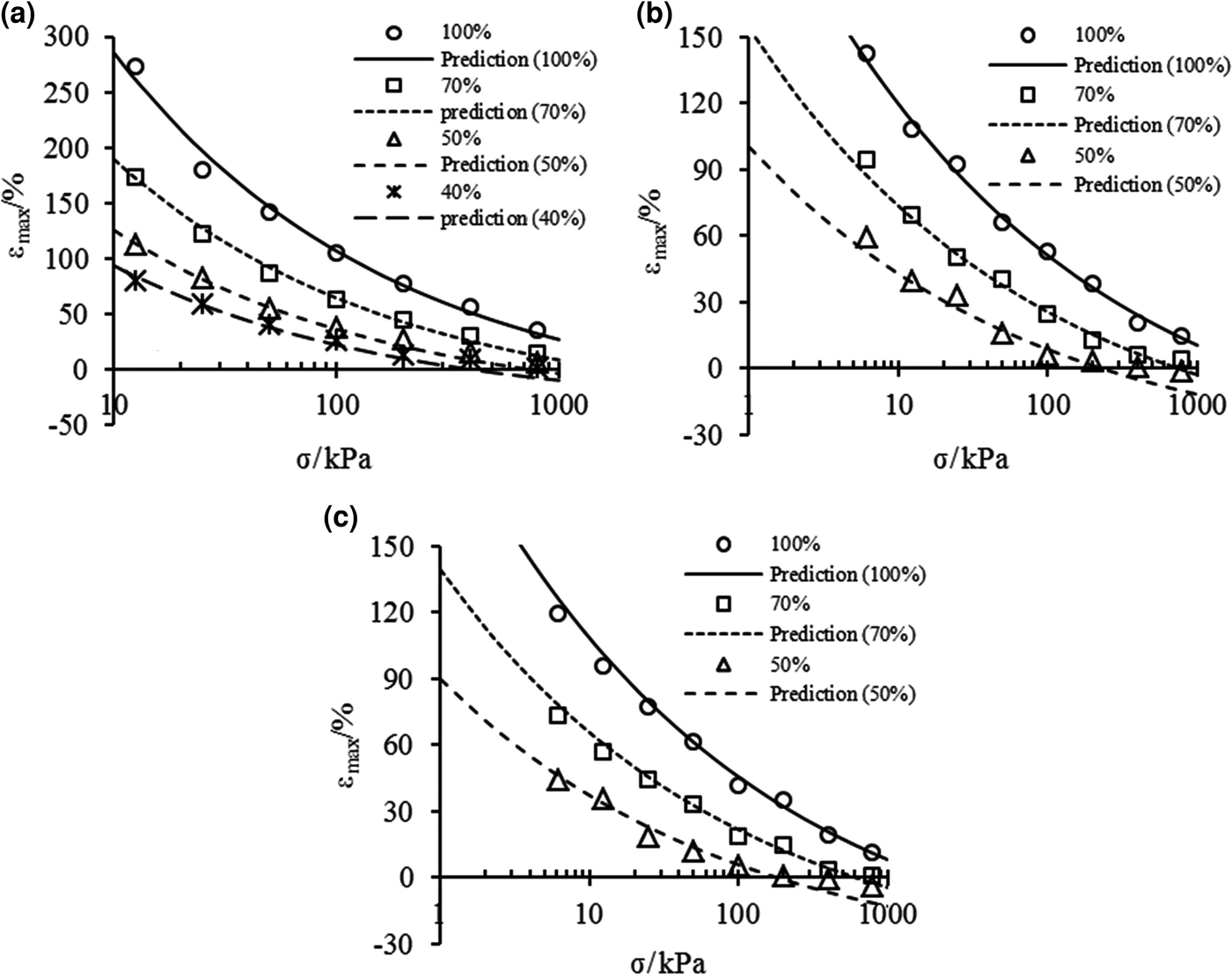
(13)$${\rm \varepsilon} _{\max} {\rm}={\rm } \left\{ {\displaystyle{{{\rm \rho}_{\rm d}} \over {A{\rm \rho}_{\rm s}}}K{\left[ {{\rm \sigma} + {\rm \pi} {\left( {\displaystyle{{\rm \sigma} \over {\rm \pi}}} \right)}^{D_{\rm s}-2}} \right]}^{D_{\rm s}{\rm -} 3} + \displaystyle{{{\rm \rho}_{\rm d}} \over {{\rm \rho}_{\rm s}}}-1} \right\} \times 100\lpar \% \rpar $$

Maximum swelling strains of the bentonite–sand mixtures were calculated according to Eq. 13, and the calculated values and the experimental data are shown in Fig. 8. The predictions of ε_max agree well with the experimental data at any condition for mixtures with large bentonite contents. Moreover, the predictions are in good agreement with the experimental data under low effective stress for mixtures with small bentonite contents, where the swelling deformation fits the e _m–p _e relationship.

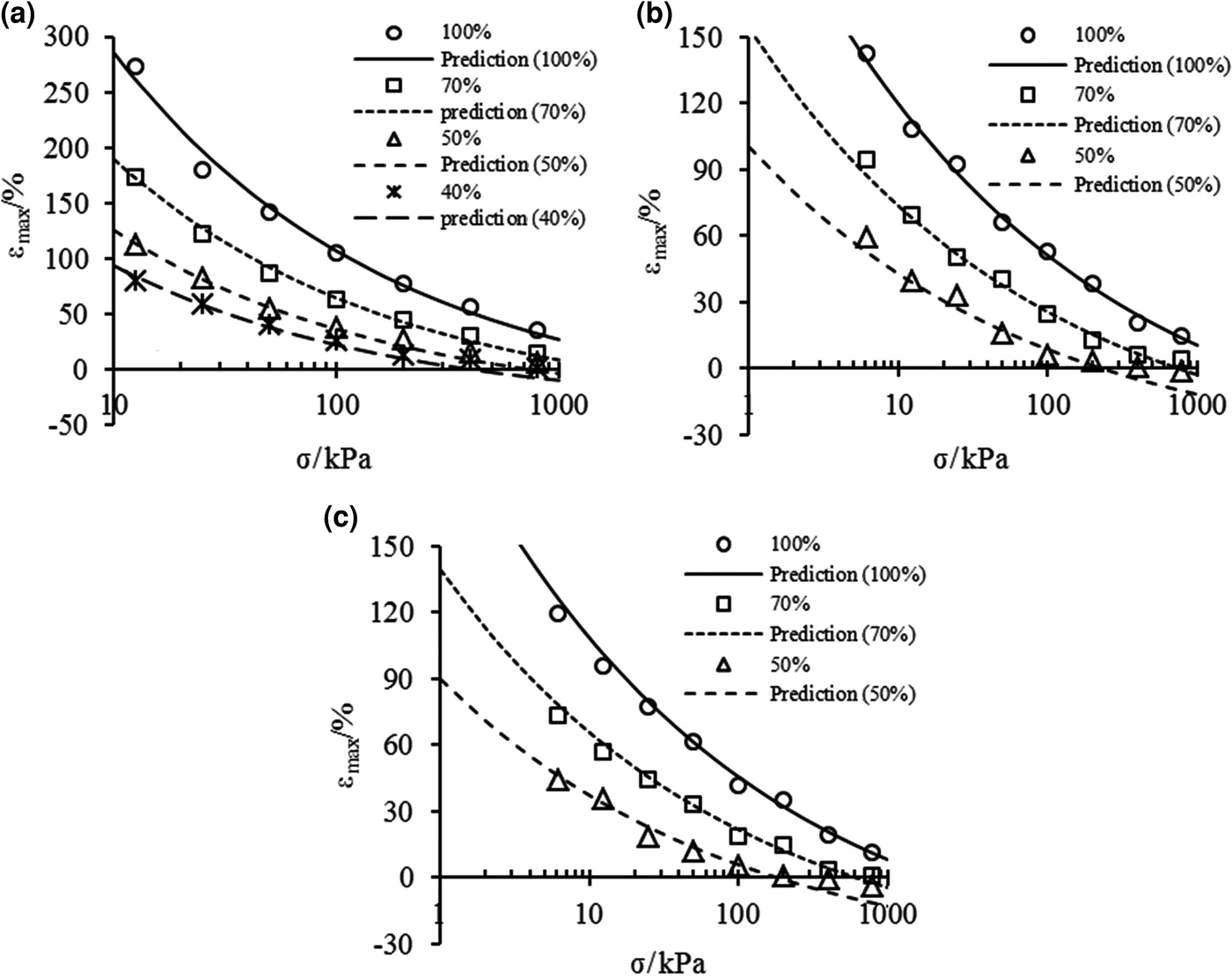
Fig. 8. Comparison between prediction of maximum swelling strains from Eq. 13 and experimental data of bentonite–sand mixtures in (a) distilled water, (b) 0.5 mol/L and (c) 1.0 mol/L NaCl solutions.