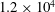1 Introduction
Current understanding of airfoil aerodynamics is based primarily on a uniform free-stream velocity approaching the airfoil. There are many situations, however, where significant disturbances are encountered during flight such that the condition of a uniform approach velocity is a very poor approximation. These situations include wings near the ground, wind shear, ambient wind conditions that are altered by large-scale disturbances (e.g. mountains), and aircraft operating in close proximity, among others. The work of Tsien (Reference Tsien1943) was among the earliest to investigate the influence of non-uniform upstream conditions by considering a linear velocity profile (i.e. uniform shear) approaching a steady 2-D symmetric Joukowsky airfoil. The control parameter in this case is the non-dimensional shear rate, defined by Tsien as
![]() $K=(c/U_{o})\,\text{d}U_{\infty }/\text{d}y$
(see figure 1 for a sketch of the flow geometry and description of the variables). Tsien’s inviscid analysis showed that the effect of uniform shear is a shift in the zero-lift angle of attack (AoA). An essential conclusion was that a symmetric airfoil at zero AoA that is immersed in an approach flow with positive shear generates positive lift, i.e. the zero-lift AoA that would be normally zero in the case of uniform flow shifts to a negative AoA in the case of positive shear. Additionally, the magnitude of generated lift at zero AoA increases with shear rate. The work of Tsien was subsequently extended to more general velocity profiles in several studies, all of which are again limited to inviscid flows. Systematic studies of the influence of upstream shear on airfoil aerodynamics in real viscous flows are hard to find. One exception is the wind tunnel experiments of Payne & Nelson (Reference Payne and Nelson1985) on a steady airfoil in uniform shear at chord Reynolds numbers on order of
$K=(c/U_{o})\,\text{d}U_{\infty }/\text{d}y$
(see figure 1 for a sketch of the flow geometry and description of the variables). Tsien’s inviscid analysis showed that the effect of uniform shear is a shift in the zero-lift angle of attack (AoA). An essential conclusion was that a symmetric airfoil at zero AoA that is immersed in an approach flow with positive shear generates positive lift, i.e. the zero-lift AoA that would be normally zero in the case of uniform flow shifts to a negative AoA in the case of positive shear. Additionally, the magnitude of generated lift at zero AoA increases with shear rate. The work of Tsien was subsequently extended to more general velocity profiles in several studies, all of which are again limited to inviscid flows. Systematic studies of the influence of upstream shear on airfoil aerodynamics in real viscous flows are hard to find. One exception is the wind tunnel experiments of Payne & Nelson (Reference Payne and Nelson1985) on a steady airfoil in uniform shear at chord Reynolds numbers on order of
![]() $10^{5}$
. It is difficult to conclusively determine the influence of shear on lift at zero AoA based on the reported data.
$10^{5}$
. It is difficult to conclusively determine the influence of shear on lift at zero AoA based on the reported data.

Figure 1. Schematic of flow geometry considered by Tsien (Reference Tsien1943).
In view of the lack of knowledge described earlier, this work examines how the basic flow characteristics of steady airfoils, and the corresponding loads, are altered when the upstream approach flow is changed from the traditional uniform conditions to that of non-uniform flow. The particular focus of the current paper is to consider the viscous flow around a steady 2-D symmetric airfoil at zero AoA, and to assess Tsien’s inviscid theory for lift generation in the presence of shear. We consider the NACA 0012 airfoil at a chord Reynolds number
![]() $Re_{c}=U_{o}c/\unicode[STIX]{x1D708}=1.2\times 10^{4}$
(where
$Re_{c}=U_{o}c/\unicode[STIX]{x1D708}=1.2\times 10^{4}$
(where
![]() $\unicode[STIX]{x1D708}$
represents the kinematic viscosity), for which a great deal of experimental and computational data are available when the upstream flow is uniform. A computational approach is used here to obtain the loads on the airfoil over a range of non-dimensional shear rates
$\unicode[STIX]{x1D708}$
represents the kinematic viscosity), for which a great deal of experimental and computational data are available when the upstream flow is uniform. A computational approach is used here to obtain the loads on the airfoil over a range of non-dimensional shear rates
![]() $K$
, along with details of the flow field around, and in the wake of the airfoil. In addition to comparing the lift force against the inviscid prediction, the data also allow us to quantify and report the various asymmetries in the flow that arise as a result of imposed shear (e.g. boundary layer separation location, wake structure, etc.), the type of information that is not available from inviscid theory.
$K$
, along with details of the flow field around, and in the wake of the airfoil. In addition to comparing the lift force against the inviscid prediction, the data also allow us to quantify and report the various asymmetries in the flow that arise as a result of imposed shear (e.g. boundary layer separation location, wake structure, etc.), the type of information that is not available from inviscid theory.
2 Computational considerations
2.1 Governing equations and numerical method
The computations are performed using the full, compressible, unsteady, 2-D Navier–Stokes equations cast in strong conservative form after introducing a general time-dependent curvilinear coordinate transformation from physical to computational space (Vinokur Reference Vinokur1974; Steger Reference Steger1978; Tannehill, Anderson & Pletcher Reference Tannehill, Anderson and Pletcher1997). These equations are augmented using the perfect gas relationship, a constant Prandtl number, Sutherland’s viscosity law and Stokes’ hypothesis for the bulk viscosity coefficient.
All simulations are performed with the extensively validated high-order Navier–Stokes solver FDL3DI (Gaitonde & Visbal Reference Gaitonde and Visbal1998; Visbal & Gaitonde Reference Visbal and Gaitonde1999), the salient features of which are given briefly below. A finite-difference approach is employed to discretize the governing equations, and all spatial derivatives are obtained with high-order compact-differencing schemes (Lele Reference Lele1992). A sixth-order scheme is used here at interior points, whereas at boundary points, higher-order one-sided formulae are invoked which retain the tridiagonal form of the scheme (Gaitonde & Visbal Reference Gaitonde and Visbal1998; Visbal & Gaitonde Reference Visbal and Gaitonde1999).
In order to eliminate spurious components, a high-order, low-pass spatial filter (Gaitonde & Visbal Reference Gaitonde and Visbal1998; Visbal & Gaitonde Reference Visbal and Gaitonde1999) is incorporated. This filtering approach is based on templates proposed in Alpert (Reference Alpert1981) and Lele (Reference Lele1992), and with proper choice of coefficients provides up to tenth-order accuracy. Filter operators, along with representative filter transfer functions, can be found in Gaitonde & Visbal (Reference Gaitonde and Visbal1998) and Gaitonde & Visbal (Reference Gaitonde and Visbal1999). The filter is applied here to the conserved variables along each transformed coordinate direction using an interior eighth-order filter with filter coefficient
![]() $\unicode[STIX]{x1D6FC}_{f}=0.4$
. At near-boundary points, the filtering strategies described in Gaitonde & Visbal (Reference Gaitonde and Visbal1999) and Visbal & Gaitonde (Reference Visbal and Gaitonde1999) are used. Finally, time marching is accomplished by incorporating an iterative, implicit approximately factored procedure (Beam & Warming Reference Beam and Warming1978; Pulliam & Chaussee Reference Pulliam and Chaussee1981; Visbal & Gaitonde Reference Visbal and Gaitonde2002; Visbal, Morgan & Rizetta Reference Visbal, Morgan and Rizetta2003).
$\unicode[STIX]{x1D6FC}_{f}=0.4$
. At near-boundary points, the filtering strategies described in Gaitonde & Visbal (Reference Gaitonde and Visbal1999) and Visbal & Gaitonde (Reference Visbal and Gaitonde1999) are used. Finally, time marching is accomplished by incorporating an iterative, implicit approximately factored procedure (Beam & Warming Reference Beam and Warming1978; Pulliam & Chaussee Reference Pulliam and Chaussee1981; Visbal & Gaitonde Reference Visbal and Gaitonde2002; Visbal, Morgan & Rizetta Reference Visbal, Morgan and Rizetta2003).
The inviscid solution of the NACA 0012 airfoil in uniform shear is computed using an in-house panel code based on Katz & Plotkin (Reference Katz and Plotkin2001). Each panel has a vorticity distribution that varies linearly in strength along the panel. The only difference in this implementation of the panel method from Katz & Plotkin is that the traditional uniform free stream
![]() $U_{\infty }$
is replaced by the imposed spatially varying free stream
$U_{\infty }$
is replaced by the imposed spatially varying free stream
![]() $U_{\infty }(y)$
. The velocity from the approach flow at each panel depends only on the panel
$U_{\infty }(y)$
. The velocity from the approach flow at each panel depends only on the panel
![]() $y$
-coordinate. The accuracy of the panel code is verified by comparing its prediction against the exact solution of Tsien (Reference Tsien1943) for the Joukowsky airfoil in uniform shear.
$y$
-coordinate. The accuracy of the panel code is verified by comparing its prediction against the exact solution of Tsien (Reference Tsien1943) for the Joukowsky airfoil in uniform shear.
2.2 Flow and computational parameters
The various computational parameters (grid resolution, time-step resolution, Mach number, etc.) given in this section are based on previous extensive convergence studies by Hammer (Reference Hammer2016) for the case of uniform approach velocity and additional confirmation for the highest shear rate of
![]() $K=1.0$
considered here. Details are not shown for brevity.
$K=1.0$
considered here. Details are not shown for brevity.
The geometry considered is a NACA 0012 airfoil with a rounded trailing edge (
![]() $r_{TE}=2.2\times 10^{-3}c$
). An overset computational grid is used for this work (see figure 2). An O-grid (figure 2
a) wraps around the airfoil with dimensions
$r_{TE}=2.2\times 10^{-3}c$
). An overset computational grid is used for this work (see figure 2). An O-grid (figure 2
a) wraps around the airfoil with dimensions
![]() $655\times 165$
, leading edge spacing
$655\times 165$
, leading edge spacing
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D709}_{LE}=5.0\times 10^{-4}c$
, trailing edge spacing
$\unicode[STIX]{x0394}\unicode[STIX]{x1D709}_{LE}=5.0\times 10^{-4}c$
, trailing edge spacing
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D709}_{TE}=2.5\times 10^{-4}c$
, and initial normal spacing at the wall
$\unicode[STIX]{x0394}\unicode[STIX]{x1D709}_{TE}=2.5\times 10^{-4}c$
, and initial normal spacing at the wall
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D702}_{wall}=5.0\times 10^{-5}c$
. A single Cartesian background grid is used to maintain the shear profile while resolving the wake structure with high spatial resolution (figure 2
b,c). Holes are cut in the background grid to blank out the region of the background grid coincident with the O-grid. The high-resolution wake region covers four chord lengths downstream of the trailing edge in the streamwise direction and 1.8 chord lengths in the transverse direction with a uniform spacing of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D702}_{wall}=5.0\times 10^{-5}c$
. A single Cartesian background grid is used to maintain the shear profile while resolving the wake structure with high spatial resolution (figure 2
b,c). Holes are cut in the background grid to blank out the region of the background grid coincident with the O-grid. The high-resolution wake region covers four chord lengths downstream of the trailing edge in the streamwise direction and 1.8 chord lengths in the transverse direction with a uniform spacing of
![]() $2.5\times 10^{-3}c$
. The Cartesian grid is then rapidly stretched to over 100 chords in each direction. This stretching along with the high-order filter helps eliminate spurious reflections off the boundary (Visbal & Gaitonde Reference Visbal and Gaitonde1999). Grid communication and low-order interpolation is performed as a pre-processing step using Pegasus 5 (Suhs, Rogers & Dietz Reference Suhs, Rogers and Dietz2002), which is then extended to high order (Sherer & Scott Reference Sherer and Scott2005; Sherer & Visbal Reference Sherer and Visbal2007).
$2.5\times 10^{-3}c$
. The Cartesian grid is then rapidly stretched to over 100 chords in each direction. This stretching along with the high-order filter helps eliminate spurious reflections off the boundary (Visbal & Gaitonde Reference Visbal and Gaitonde1999). Grid communication and low-order interpolation is performed as a pre-processing step using Pegasus 5 (Suhs, Rogers & Dietz Reference Suhs, Rogers and Dietz2002), which is then extended to high order (Sherer & Scott Reference Sherer and Scott2005; Sherer & Visbal Reference Sherer and Visbal2007).

Figure 2. Schematic of computational domain, showing three fields of view. In views (a) and (b), grid points have been removed for clarity.
The boundary conditions are prescribed as follows. A no-slip, adiabatic condition is applied to the surface in conjunction with a zero-normal pressure gradient at the wall. A prescribed streamwise velocity profile
![]() $U_{\infty }(y)$
, uniform static pressure, and uniform total temperature are specified along the upstream far-field boundary. At the three additional far-field boundaries, a first-order accurate extrapolation condition is applied to the primitive variables, except for pressure, which is uniform. Spatial periodicity is enforced in the azimuthal direction of the O-mesh using a five-point overlap. The solution is initialized with the specified velocity profile, uniform static pressure, and uniform total temperature everywhere in the domain.
$U_{\infty }(y)$
, uniform static pressure, and uniform total temperature are specified along the upstream far-field boundary. At the three additional far-field boundaries, a first-order accurate extrapolation condition is applied to the primitive variables, except for pressure, which is uniform. Spatial periodicity is enforced in the azimuthal direction of the O-mesh using a five-point overlap. The solution is initialized with the specified velocity profile, uniform static pressure, and uniform total temperature everywhere in the domain.
The inviscid theory by Tsien (Reference Tsien1943) is based on a shear profile that extends to infinity, a boundary condition that is difficult to reproduce in the current computations since at high enough shear rates the velocities, and corresponding Mach numbers, become extremely large away from the airfoil (positive in the upper domain and negative in the lower). It is also incredibly challenging to create the equivalent boundary condition for experiments, especially the reverse flow profile below the airfoil. Therefore, our work utilizes a three-segment profile as the boundary condition, where the uniform shear zone (and its linear velocity profile) occurs over a finite region of thickness
![]() $\unicode[STIX]{x1D6FF}$
and the velocities outside this region are uniform. The details are shown schematically in figure 3. This composite profile is now characterized by the non-dimensional shear rate
$\unicode[STIX]{x1D6FF}$
and the velocities outside this region are uniform. The details are shown schematically in figure 3. This composite profile is now characterized by the non-dimensional shear rate
![]() $K=(c/U_{o})\,\text{d}U_{\infty }/\text{d}y$
introduced by Tsien (Reference Tsien1943) and the new parameter
$K=(c/U_{o})\,\text{d}U_{\infty }/\text{d}y$
introduced by Tsien (Reference Tsien1943) and the new parameter
![]() $\unicode[STIX]{x1D6FF}/c$
. The results we discuss in this paper are for large enough
$\unicode[STIX]{x1D6FF}/c$
. The results we discuss in this paper are for large enough
![]() $\unicode[STIX]{x1D6FF}/c$
such that the finite size of the shear zone does not influence the outcome.
$\unicode[STIX]{x1D6FF}/c$
such that the finite size of the shear zone does not influence the outcome.

Figure 3. Schematic of three-segment linear velocity profile used for the upstream boundary condition in the current computations.
The chord Reynolds number in this study is
![]() $1.2\times 10^{4}$
based on the chord length
$1.2\times 10^{4}$
based on the chord length
![]() $c$
, and centreline velocity
$c$
, and centreline velocity
![]() $U_{o}$
. The non-dimensional shear rate
$U_{o}$
. The non-dimensional shear rate
![]() $K$
varies between 0.0 (uniform flow) and 1.0. Data are primarily presented here for the case of
$K$
varies between 0.0 (uniform flow) and 1.0. Data are primarily presented here for the case of
![]() $\unicode[STIX]{x1D6FF}/c=1.5$
, determined to be large enough to make the results insensitive to increasing
$\unicode[STIX]{x1D6FF}/c=1.5$
, determined to be large enough to make the results insensitive to increasing
![]() $\unicode[STIX]{x1D6FF}/c$
(see figure 4
a). Based on the previous work by Hammer (Reference Hammer2016), a low reference Mach number
$\unicode[STIX]{x1D6FF}/c$
(see figure 4
a). Based on the previous work by Hammer (Reference Hammer2016), a low reference Mach number
![]() $M_{o}$
of 0.015 is selected to simulate the incompressible limit using the current compressible flow Navier–Stokes solver. The wake of the airfoil at the Reynolds number of this study is unstable and leads to a nearly periodic flow field and load. The solution is advanced in time with a non-dimensional time step (
$M_{o}$
of 0.015 is selected to simulate the incompressible limit using the current compressible flow Navier–Stokes solver. The wake of the airfoil at the Reynolds number of this study is unstable and leads to a nearly periodic flow field and load. The solution is advanced in time with a non-dimensional time step (
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D70F}=\unicode[STIX]{x0394}tU_{o}/c$
) of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70F}=\unicode[STIX]{x0394}tU_{o}/c$
) of
![]() $5.0\times 10^{-5}$
with five subiterations per time step. Once the cycle-to-cycle variation in average lift and drag reaches less than
$5.0\times 10^{-5}$
with five subiterations per time step. Once the cycle-to-cycle variation in average lift and drag reaches less than
![]() $1\,\%$
, data are averaged over a single cycle using the period of lift fluctuation.
$1\,\%$
, data are averaged over a single cycle using the period of lift fluctuation.

Figure 4. (a) Average lift coefficient
![]() $C_{L}$
versus shear rate
$C_{L}$
versus shear rate
![]() $K$
for the NACA 0012 airfoil at
$K$
for the NACA 0012 airfoil at
![]() $Re_{c}=1.2\times 10^{4}$
in comparison to the inviscid solution. The inviscid NACA 0012 and
$Re_{c}=1.2\times 10^{4}$
in comparison to the inviscid solution. The inviscid NACA 0012 and
![]() $12\,\%$
-thick Joukowsky airfoil (J 12) solutions are both included. (b) Comparison of the inviscid solution of the negatively cambered NACA
$12\,\%$
-thick Joukowsky airfoil (J 12) solutions are both included. (b) Comparison of the inviscid solution of the negatively cambered NACA
![]() $\unicode[STIX]{x1D6FD}$
412 airfoil with the viscous solution of the NACA 0012 airfoil at
$\unicode[STIX]{x1D6FD}$
412 airfoil with the viscous solution of the NACA 0012 airfoil at
![]() $Re_{c}=1.2\times 10^{4}$
. Maximum camber
$Re_{c}=1.2\times 10^{4}$
. Maximum camber
![]() $\unicode[STIX]{x1D6FD}=2\,\%$
at
$\unicode[STIX]{x1D6FD}=2\,\%$
at
![]() $K=1.0$
and linear
$K=1.0$
and linear
![]() $K$
scaling is used to obtain
$K$
scaling is used to obtain
![]() $\unicode[STIX]{x1D6FD}$
for other
$\unicode[STIX]{x1D6FD}$
for other
![]() $K$
values.
$K$
values.
2.3 Validation
Validation of the current results is presented for the uniform flow case against existing data from experiments (Laitone Reference Laitone1997) and computations (Liu & Kawachi Reference Liu and Kawachi1999; Young & Lai Reference Young and Lai2004). Comparison of the drag coefficient
![]() $C_{D}$
shown in table 1 illustrates the very good agreement between the current results and published literature. The average lift is zero in all these studies and is not useful for validation purposes. In addition, the wake natural shedding frequency in the current computations is found to be within
$C_{D}$
shown in table 1 illustrates the very good agreement between the current results and published literature. The average lift is zero in all these studies and is not useful for validation purposes. In addition, the wake natural shedding frequency in the current computations is found to be within
![]() $2\,\%$
of the value from experiments by Koochesfahani (Reference Koochesfahani1989), and in exact agreement with the value from computations of Young & Lai (Reference Young and Lai2004) at the same
$2\,\%$
of the value from experiments by Koochesfahani (Reference Koochesfahani1989), and in exact agreement with the value from computations of Young & Lai (Reference Young and Lai2004) at the same
![]() $Re_{c}$
.
$Re_{c}$
.
Table 1. Comparison of
![]() $C_{D}$
for NACA 0012 at
$C_{D}$
for NACA 0012 at
![]() $Re_{c}=1.2\times 10^{4}$
and
$Re_{c}=1.2\times 10^{4}$
and
![]() $\text{AoA}=0^{\circ }$
in uniform flow.
$\text{AoA}=0^{\circ }$
in uniform flow.

3 Results and discussion
3.1 Average load on airfoil
The average lift coefficient
![]() $C_{L}$
at zero AoA versus shear rate
$C_{L}$
at zero AoA versus shear rate
![]() $K$
is shown in figure 4(a) for the viscous solution of the NACA 0012 airfoil at
$K$
is shown in figure 4(a) for the viscous solution of the NACA 0012 airfoil at
![]() $Re_{c}=1.2\times 10^{4}$
in comparison to its inviscid solution using the panel method. The accuracy of the panel code is demonstrated to be excellent when tested against Tsien’s exact solution for a
$Re_{c}=1.2\times 10^{4}$
in comparison to its inviscid solution using the panel method. The accuracy of the panel code is demonstrated to be excellent when tested against Tsien’s exact solution for a
![]() $12\,\%$
-thick Joukowsky airfoil (J 12); see figure 4(a). Note that the inviscid
$12\,\%$
-thick Joukowsky airfoil (J 12); see figure 4(a). Note that the inviscid
![]() $C_{L}$
for the NACA 0012 airfoil increases linearly with
$C_{L}$
for the NACA 0012 airfoil increases linearly with
![]() $K$
just as the
$K$
just as the
![]() $12\,\%$
-thick Joukowsky airfoil, but with a slope that is higher by
$12\,\%$
-thick Joukowsky airfoil, but with a slope that is higher by
![]() $12.8\,\%$
, a consequence of the shape difference between these airfoils.
$12.8\,\%$
, a consequence of the shape difference between these airfoils.
The most important result from figure 4(a) is that the behaviour of the viscous solution is fundamentally different from its inviscid counterpart. In the former, the sign of lift is negative (i.e. downward force), which is exactly the opposite of the inviscid prediction. Its magnitude, however, increases with shear rate
![]() $K$
in a nearly linear fashion. We note in figure 4(a) that increasing the size of the shear zone by a factor of two to
$K$
in a nearly linear fashion. We note in figure 4(a) that increasing the size of the shear zone by a factor of two to
![]() $\unicode[STIX]{x1D6FF}/c=3.0$
has a minimal impact on the lift force, supporting the earlier assertion in § 2.2 that
$\unicode[STIX]{x1D6FF}/c=3.0$
has a minimal impact on the lift force, supporting the earlier assertion in § 2.2 that
![]() $\unicode[STIX]{x1D6FF}/c=1.5$
is a sufficiently large value (highest values of
$\unicode[STIX]{x1D6FF}/c=1.5$
is a sufficiently large value (highest values of
![]() $K$
were not computed for
$K$
were not computed for
![]() $\unicode[STIX]{x1D6FF}/c=3.0$
as it led to back flow in the approach stream on the low-speed side). The influence of upstream shear on the drag coefficient is found to be weak; results (not shown here) indicate that
$\unicode[STIX]{x1D6FF}/c=3.0$
as it led to back flow in the approach stream on the low-speed side). The influence of upstream shear on the drag coefficient is found to be weak; results (not shown here) indicate that
![]() $C_{D}$
decreases monotonically with increasing
$C_{D}$
decreases monotonically with increasing
![]() $K$
, with
$K$
, with
![]() $C_{D}$
at
$C_{D}$
at
![]() $K=1.0$
, dropping by only
$K=1.0$
, dropping by only
![]() $2\,\%$
compared to its value for uniform flow (
$2\,\%$
compared to its value for uniform flow (
![]() $K=0.0$
).
$K=0.0$
).
Our hypothesis for generation of negative lift at zero AoA for a symmetric airfoil placed in a flow with positive shear is connected to the asymmetry of boundary layer development on the upper and lower surfaces of the airfoil. In positive shear, the upper boundary layer grows in a region with higher free-stream velocity compared to that on the lower surface, resulting in a thicker boundary layer on the lower surface than the upper surface. The resulting difference between the corresponding displacement thicknesses effectively creates an airfoil with negative camber (camber towards the low-speed side), leading to negative lift.
We now provide a first-order estimate of the resulting effect using laminar boundary layer relations for attached flow. The upper and lower surface boundary layer displacement thicknesses (
![]() $\unicode[STIX]{x1D6FF}_{U}^{\ast }$
and
$\unicode[STIX]{x1D6FF}_{U}^{\ast }$
and
![]() $\unicode[STIX]{x1D6FF}_{L}^{\ast }$
) at a given downstream location on the airfoil surface are given as
$\unicode[STIX]{x1D6FF}_{L}^{\ast }$
) at a given downstream location on the airfoil surface are given as
![]() $\unicode[STIX]{x1D6FF}_{U}^{\ast }/c\sim \sqrt{\unicode[STIX]{x1D708}/(cU_{U})}$
and
$\unicode[STIX]{x1D6FF}_{U}^{\ast }/c\sim \sqrt{\unicode[STIX]{x1D708}/(cU_{U})}$
and
![]() $\unicode[STIX]{x1D6FF}_{L}^{\ast }/c\sim \sqrt{\unicode[STIX]{x1D708}/(cU_{L})}$
, where
$\unicode[STIX]{x1D6FF}_{L}^{\ast }/c\sim \sqrt{\unicode[STIX]{x1D708}/(cU_{L})}$
, where
![]() $U_{U}$
and
$U_{U}$
and
![]() $U_{L}$
correspond to the characteristic free-stream velocities for boundary layer growth on the upper and lower surfaces, which can be written as
$U_{L}$
correspond to the characteristic free-stream velocities for boundary layer growth on the upper and lower surfaces, which can be written as
![]() $U_{U}\sim U_{o}(1+Kt/2c)$
and
$U_{U}\sim U_{o}(1+Kt/2c)$
and
![]() $U_{L}\sim U_{o}(1-Kt/2c)$
, respectively, with
$U_{L}\sim U_{o}(1-Kt/2c)$
, respectively, with
![]() $t$
representing the airfoil thickness. The resulting ‘effective’ camber
$t$
representing the airfoil thickness. The resulting ‘effective’ camber
![]() $y_{c}=(\unicode[STIX]{x1D6FF}_{U}^{\ast }-\unicode[STIX]{x1D6FF}_{L}^{\ast })/2$
can be simplified for
$y_{c}=(\unicode[STIX]{x1D6FF}_{U}^{\ast }-\unicode[STIX]{x1D6FF}_{L}^{\ast })/2$
can be simplified for
![]() $K(t/2c)\ll 1$
to the following expression
$K(t/2c)\ll 1$
to the following expression
Classical inviscid flow analysis of cambered Joukowsky airfoil (e.g. see chap. 4 of Currie Reference Currie1993) connects the lift due to camber to the maximum camber of the mean camber line, which for small values of camber reduces to a linear relation between lift and maximum camber. Using this connection as a guide, we would estimate the additional lift caused by the effective camber described earlier to be negative and given as
We note that the effective camber, and therefore also the resulting lift magnitude, in this first-order model, is linear in both shear rate
![]() $K$
and airfoil thickness ratio
$K$
and airfoil thickness ratio
![]() $t/c$
and decreases as
$t/c$
and decreases as
![]() $1/\sqrt{Re_{c}}$
.
$1/\sqrt{Re_{c}}$
.
In this description, the lift of a symmetric airfoil at zero AoA in viscous flow with positive shear will always be lower than its inviscid counterpart (i.e. Tsien’s theory) by the expression given above. The results in figure 4(a) for
![]() $Re_{c}=1.2\times 10^{4}$
imply that the lift reduction due to negative camber at this Reynolds number is large enough to change the positive lift prediction of Tsien’s theory to negative lift. To get a sense of the magnitude of negative camber that is required to reproduce the viscous flow results in figure 4(a), we obtain the inviscid solution (using the panel method) of shear flow at
$Re_{c}=1.2\times 10^{4}$
imply that the lift reduction due to negative camber at this Reynolds number is large enough to change the positive lift prediction of Tsien’s theory to negative lift. To get a sense of the magnitude of negative camber that is required to reproduce the viscous flow results in figure 4(a), we obtain the inviscid solution (using the panel method) of shear flow at
![]() $K=1.0$
past a
$K=1.0$
past a
![]() $12\,\%$
-thick cambered NACA airfoil. We find, for example, that the negatively cambered NACA 2412 airfoil (
$12\,\%$
-thick cambered NACA airfoil. We find, for example, that the negatively cambered NACA 2412 airfoil (
![]() $2\,\%$
maximum camber located at
$2\,\%$
maximum camber located at
![]() $0.4c$
) reproduces the
$0.4c$
) reproduces the
![]() $C_{L}$
value of the viscous solution at
$C_{L}$
value of the viscous solution at
![]() $K=1.0$
. Extending the inviscid computation to lower values of
$K=1.0$
. Extending the inviscid computation to lower values of
![]() $K$
, after applying the linear
$K$
, after applying the linear
![]() $K$
scaling to obtain the corresponding maximum camber
$K$
scaling to obtain the corresponding maximum camber
![]() $\unicode[STIX]{x1D6FD}$
(its location fixed at
$\unicode[STIX]{x1D6FD}$
(its location fixed at
![]() $0.4c$
) leading to the NACA
$0.4c$
) leading to the NACA
![]() $\unicode[STIX]{x1D6FD}412$
series of airfoils, reproduces the viscous solution of
$\unicode[STIX]{x1D6FD}412$
series of airfoils, reproduces the viscous solution of
![]() $C_{L}$
versus
$C_{L}$
versus
![]() $K$
in figure 4(a) remarkably well; see figure 4(b). We should emphasize that the family of cambered airfoil shapes NACA
$K$
in figure 4(a) remarkably well; see figure 4(b). We should emphasize that the family of cambered airfoil shapes NACA
![]() $\unicode[STIX]{x1D6FD}412$
we have described above is not unique for reproducing the viscous solution. A similar outcome can be achieved by placing the maximum camber at other locations than
$\unicode[STIX]{x1D6FD}412$
we have described above is not unique for reproducing the viscous solution. A similar outcome can be achieved by placing the maximum camber at other locations than
![]() $0.4c$
and adjusting the value of maximum negative camber accordingly.
$0.4c$
and adjusting the value of maximum negative camber accordingly.
The model developed here also allows us to give an estimate for how high the chord Reynolds number should be before the inviscid theory of Tsien (Reference Tsien1943) becomes applicable. From inviscid calculations, we first determine the lowest value of negative effective camber that is required to yield
![]() $C_{L}$
versus
$C_{L}$
versus
![]() $K$
results that reach
$K$
results that reach
![]() $90\,\%$
of Tsien’s theory. The outcome in comparison with the already-established value of negative camber at
$90\,\%$
of Tsien’s theory. The outcome in comparison with the already-established value of negative camber at
![]() $Re_{c}=1.2\times 10^{4}$
, in conjunction with the
$Re_{c}=1.2\times 10^{4}$
, in conjunction with the
![]() $1/\sqrt{Re_{c}}$
scaling of effective camber, indicates that chord Reynolds number needs to be as high as
$1/\sqrt{Re_{c}}$
scaling of effective camber, indicates that chord Reynolds number needs to be as high as
![]() $Re_{c}=2\times 10^{6}$
to get to
$Re_{c}=2\times 10^{6}$
to get to
![]() $90\,\%$
of the inviscid prediction. It is important to recognize that the model given above and its prediction are constrained by its assumptions of thin laminar boundary layers and attached flow, which cease to be uniformly valid over the curved surfaces of the airfoil as the Reynolds number varies.
$90\,\%$
of the inviscid prediction. It is important to recognize that the model given above and its prediction are constrained by its assumptions of thin laminar boundary layers and attached flow, which cease to be uniformly valid over the curved surfaces of the airfoil as the Reynolds number varies.
3.2 Flow-field characteristics
We now present some of the asymmetries that develop in the flow field due to the imposed shear. The time-averaged spanwise vorticity field,
![]() $\unicode[STIX]{x1D714}_{z,avg}c/U_{o}$
, and accompanying streamline pattern are shown in figure 5(a) for uniform flow (
$\unicode[STIX]{x1D714}_{z,avg}c/U_{o}$
, and accompanying streamline pattern are shown in figure 5(a) for uniform flow (
![]() $K=0.0$
) and the highest shear rate case (
$K=0.0$
) and the highest shear rate case (
![]() $K=1.0$
) studied here. For the symmetric airfoil in uniform flow, the stagnation streamline is aligned with the centreline (
$K=1.0$
) studied here. For the symmetric airfoil in uniform flow, the stagnation streamline is aligned with the centreline (
![]() $y=0$
) and the front stagnation point is located at the leading edge, as expected. However, for the same symmetric airfoil placed in positive shear the stagnation streamline approaches the airfoil from above the centreline and the front stagnation point moves above the leading edge. The location of the stagnation point moves increasingly farther back along the upper surface with increased shear rate; see figure 5(b). The observed behaviour of the leading edge stagnation point is consistent with what is expected from an airfoil which, while geometrically symmetric, behaves effectively as a negatively cambered airfoil. As discussed in § 3.1, the magnitude of the effective (negative) camber increases with shear rate
$y=0$
) and the front stagnation point is located at the leading edge, as expected. However, for the same symmetric airfoil placed in positive shear the stagnation streamline approaches the airfoil from above the centreline and the front stagnation point moves above the leading edge. The location of the stagnation point moves increasingly farther back along the upper surface with increased shear rate; see figure 5(b). The observed behaviour of the leading edge stagnation point is consistent with what is expected from an airfoil which, while geometrically symmetric, behaves effectively as a negatively cambered airfoil. As discussed in § 3.1, the magnitude of the effective (negative) camber increases with shear rate
![]() $K$
, a consequence of which is the movement of the front stagnation point along the upper surface displayed in figure 5(b).
$K$
, a consequence of which is the movement of the front stagnation point along the upper surface displayed in figure 5(b).

Figure 5. (a) Average streamlines and spanwise vorticity field (
![]() $\unicode[STIX]{x1D714}_{z,avg}c/U_{o}$
) for uniform flow
$\unicode[STIX]{x1D714}_{z,avg}c/U_{o}$
) for uniform flow
![]() $K=0.0$
, shear flow
$K=0.0$
, shear flow
![]() $K=1.0$
and front stagnation point location for each in a zoomed-up view of the leading edge. A green horizontal line at the centreline
$K=1.0$
and front stagnation point location for each in a zoomed-up view of the leading edge. A green horizontal line at the centreline
![]() $y=0$
originating at the airfoil leading edge is shown for reference. (b) The location of the front stagnation point,
$y=0$
originating at the airfoil leading edge is shown for reference. (b) The location of the front stagnation point,
![]() $\unicode[STIX]{x1D709}_{stag}$
, for different shear rates.
$\unicode[STIX]{x1D709}_{stag}$
, for different shear rates.
Another asymmetry that develops due to imposed shear is the location of boundary layer separation on the upper and lower surfaces, as illustrated in figure 6. For uniform flow (
![]() $K=0.0$
) past the NACA 0012 airfoil at
$K=0.0$
) past the NACA 0012 airfoil at
![]() $Re_{c}=1.2\times 10^{4}$
, the boundary layers on the upper and lower surfaces remain attached until separation occurs symmetrically at
$Re_{c}=1.2\times 10^{4}$
, the boundary layers on the upper and lower surfaces remain attached until separation occurs symmetrically at
![]() $x_{sep}/c=0.815$
. The separation point is defined here as the location where the average surface shear stress reaches zero. When the approach flow has positive shear, the boundary layers develop asymmetrically on the upper and lower surfaces. Results show that as the shear rate
$x_{sep}/c=0.815$
. The separation point is defined here as the location where the average surface shear stress reaches zero. When the approach flow has positive shear, the boundary layers develop asymmetrically on the upper and lower surfaces. Results show that as the shear rate
![]() $K$
increases, the separation point on the upper surface (high-speed side) moves upstream. Conversely, the separation point on the lower surface (low-speed side) moves downstream, and at
$K$
increases, the separation point on the upper surface (high-speed side) moves upstream. Conversely, the separation point on the lower surface (low-speed side) moves downstream, and at
![]() $K=1.0$
reaches the trailing edge.
$K=1.0$
reaches the trailing edge.

Figure 6. (a) Boundary layer separation points marked on the average spanwise vorticity field for different shear rates. (b) Average separation point location
![]() $x_{sep}$
versus
$x_{sep}$
versus
![]() $K$
. Solid lines represent curve fits to data.
$K$
. Solid lines represent curve fits to data.
Finally, we present the changes that occur in the airfoil wake structure upon imposed shear; see figure 7. For uniform flow past the airfoil, the wake instability leads to the well-known formation of the Kármán vortex street (see top image of figure 7
a). The natural shedding Strouhal number for uniform flow at the Reynolds number of this study is found to be
![]() $St_{n}\approx 2.7$
, where
$St_{n}\approx 2.7$
, where
![]() $St_{n}=f_{n}c/U_{o}$
with
$St_{n}=f_{n}c/U_{o}$
with
![]() $f_{n}$
being the shedding frequency of the wake, which we obtain from the time history of the periodic lift fluctuation. The influence of upstream shear on the wake structure is captured in the instantaneous maps of the vorticity field,
$f_{n}$
being the shedding frequency of the wake, which we obtain from the time history of the periodic lift fluctuation. The influence of upstream shear on the wake structure is captured in the instantaneous maps of the vorticity field,
![]() $\unicode[STIX]{x1D714}_{z}c/U_{o}$
, in figure 7(a) for different shear rates
$\unicode[STIX]{x1D714}_{z}c/U_{o}$
, in figure 7(a) for different shear rates
![]() $K$
. For reference, the approach shear flow has a uniform negative vorticity given by
$K$
. For reference, the approach shear flow has a uniform negative vorticity given by
![]() $-K$
. We note from figure 7(a) that as the shear rate increases, the vortical structures in the wake exhibit more asymmetry, with the negative vorticity getting stronger and positive vorticity getting weaker. Data for
$-K$
. We note from figure 7(a) that as the shear rate increases, the vortical structures in the wake exhibit more asymmetry, with the negative vorticity getting stronger and positive vorticity getting weaker. Data for
![]() $K=1.0$
indicate that at
$K=1.0$
indicate that at
![]() $x/c=4$
(i.e. three chord lengths downstream of the airfoil trailing edge), the magnitudes of peak negative and positive vorticity have increased by
$x/c=4$
(i.e. three chord lengths downstream of the airfoil trailing edge), the magnitudes of peak negative and positive vorticity have increased by
![]() $17\,\%$
and decreased by
$17\,\%$
and decreased by
![]() $54\,\%$
, respectively, compared to their magnitudes in uniform flow. Interestingly, however, the natural shedding Strouhal number depicted in figure 7(b) changes very little, only about
$54\,\%$
, respectively, compared to their magnitudes in uniform flow. Interestingly, however, the natural shedding Strouhal number depicted in figure 7(b) changes very little, only about
![]() $5\,\%$
increase, in going from
$5\,\%$
increase, in going from
![]() $K=0.0$
(uniform flow) to the highest shear rate
$K=0.0$
(uniform flow) to the highest shear rate
![]() $K=1.0$
.
$K=1.0$
.

Figure 7. Influence of upstream shear on (a) the instantaneous spanwise vorticity field (
![]() $\unicode[STIX]{x1D714}_{z}c/U_{o}$
) and (b) the natural shedding Strouhal number
$\unicode[STIX]{x1D714}_{z}c/U_{o}$
) and (b) the natural shedding Strouhal number
![]() $St_{n}$
. Solid line represents a curve fit to data.
$St_{n}$
. Solid line represents a curve fit to data.
4 Conclusions
The study presented here is our starting point in filling the knowledge gap in the influence of non-uniform approach flow on basic flow characteristics of airfoils, and the corresponding loads, which have been predominantly studied in the past by inviscid analysis. Current results at a chord Reynolds number of
![]() $1.2\times 10^{4}$
have revealed several interesting flow-field asymmetries that develop as a result of imposed shear; information that is not available from inviscid theory. A discovery has been the negative sign of lift force on a symmetric airfoil at zero angle of attack when it is placed in an approach flow with positive shear; an effect that is the opposite of that expected from Tsien’s inviscid theory. Our explanation for the underlying flow physics responsible for this effect argues for an airfoil that, while geometrically symmetric, effectively behaves as an airfoil with negative camber, which is caused by the asymmetric viscous boundary layer development on the airfoil upper and lower surfaces. We should mention that a comprehensive experimental study to complement the current computations is nearly complete, and recently reported preliminary results by Olson, Naguib & Koochesfahani (Reference Olson, Naguib and Koochesfahani2016) corroborate the negative sign of the lift force reported here.
$1.2\times 10^{4}$
have revealed several interesting flow-field asymmetries that develop as a result of imposed shear; information that is not available from inviscid theory. A discovery has been the negative sign of lift force on a symmetric airfoil at zero angle of attack when it is placed in an approach flow with positive shear; an effect that is the opposite of that expected from Tsien’s inviscid theory. Our explanation for the underlying flow physics responsible for this effect argues for an airfoil that, while geometrically symmetric, effectively behaves as an airfoil with negative camber, which is caused by the asymmetric viscous boundary layer development on the airfoil upper and lower surfaces. We should mention that a comprehensive experimental study to complement the current computations is nearly complete, and recently reported preliminary results by Olson, Naguib & Koochesfahani (Reference Olson, Naguib and Koochesfahani2016) corroborate the negative sign of the lift force reported here.
The simple model developed here to explain the negative camber effect provides information on its scaling with Reynolds number. According to the model, the chord Reynolds number needs to be as high as
![]() $Re_{c}=2\times 10^{6}$
in order to get to
$Re_{c}=2\times 10^{6}$
in order to get to
![]() $90\,\%$
of inviscid prediction. This first-order model and its prediction are, however, constrained by its assumptions of thin laminar boundary layers and attached flow over the curved surfaces of the airfoil, which are not uniformly valid with variations in Reynolds number. A computational study is currently in progress to extend the current work to higher Reynolds numbers and determine the approach to the inviscid solution.
$90\,\%$
of inviscid prediction. This first-order model and its prediction are, however, constrained by its assumptions of thin laminar boundary layers and attached flow over the curved surfaces of the airfoil, which are not uniformly valid with variations in Reynolds number. A computational study is currently in progress to extend the current work to higher Reynolds numbers and determine the approach to the inviscid solution.
Acknowledgements
The authors would like to particularly thank S. Sherer, D. Garmann and C. Barnes of AFRL for their abundant assistance with FDL3DI and accompanying software usage. The authors would also like to thank D. Olson for thoughtful discussions and technical assistance. This work was supported by AFOSR grant no. FA9550-15-1-0224. Partial support was provided by Michigan State University through the computational resources of the Institute for Cyber-Enabled Research.