2. 2D RAY-TRACING MODEL IN CYLINDRICAL GEOMETRY

There are different algorithms for ray tracing in subcritical plasma. In this particular case, we have to know field amplitude along the ray trajectory to calculate the nonlinear absorption coefficients and fast electron energy at the critical surface. The ray trajectory consists of linear segments in the cells. The ray in the cell i is described by its length L_i, the angle between the ray direction in a given cell and the density gradient θ_i, two main radii of wave front curvature in the direction of the polar θ and azimuth φ angles variation R_θi and R_φi, the cross section of the ray tube ΔS_i, and the squared field amplitude |E²|_i. All values are taken in the output point of the ray trajectory in cell i. The algorithm of ray tracing is illustrated in Figure 1. Ray parameters in the next cell are obtained from the equations of geometric optics from known parameters in a given cell:

The laser ray trajectory through the interface of two Langrangian cells.

where b_f is the term that eliminates the singularity associated with the violation of the geometric optics in the caustic vicinity. The minimal radius of the focal area cross section is r_f = b_f sinα₀, where α₀ is defined by aperture ratio of the optic system. n_i and k_i are refractive and absorption indexes in the cell.

We introduce nonlinearity through the dependence of the absorption coefficient on the electron oscillation energy in the electromagnetic field:

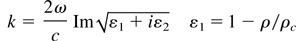
where 〈…〉 is numerical averaging over the electron oscillation period, Λ_ei is the Coulomb logarithm, n_e and n_i are the electron and ion density, m_e is the electron rest mass, T_e is the electron temperature, T_F is the Fermi temperature, |E| is the amplitude of laser radiation field, ρ is density, and ρ_c is the critical density.

3. HOT ELECTRON GENERATION AND TRANSPORT MODEL

We identify the ray turning point on the cell edge through the reflection condition: n₁ sin θ₁ /n₂ ≥ 1. To calculate resonance absorption at the ray turning point we assume plasma in the vicinity of the critical surface as a layer with a linear density profile characterized by a scale length L_c = ρ_c /|gradρ|_c obtained from plasma parameters in calculation. Here ρ is the density and ρ_c is the critical density. In this approximation we calculate the fraction of resonance absorption from known analytical decision (Ginzburg, 1967). In the case of circularly polarized light the fraction of resonance absorption is

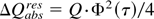
where

Q is the ray energy at the point of ray reflection, v and v′ are the Airy function and its variable, ρ is density, ρ_c is critical density, and θ₀ is the angle between the ray direction and the density gradient at the last cell before the turning point.

Resonance absorption energy can be divided into the heat absorption energy and the energy of hot electrons. The energy of hot electrons is proportional to the effective frequency of hot electrons generation v_h:

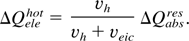
The effective frequency of electron–ion collisions at the critical surface v_eic = ωε₂ is calculated with the help of (3).

The effective frequency of hot electron generation is obtained from the Maxwellian equations for the case of a plasma layer with a linear density profile coupled with relativistic equations of hot electrons oscillation:

The magnetic field at the critical surface H_c is obtained in the approximation of the linear plasma layer:

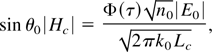
where |E₀| and n₀ are the amplitude of the electromagnetic field and the refractive index in the cell with the refraction point.

However if v_h /ω > ¼ we limit the obtained frequency magnitude by Brunel limitation (Brunel, 1987) to take into account the possibility of a very steep density profile at the critical surface, that is, we set v_h /ω = ¼.

At the moment we use one group approximation for hot electrons and calculate their energy and momentum in the relativistic case:

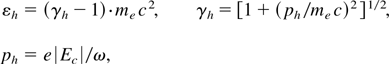
through the longitudinal field amplitude at the critical surface |E_c| that can be obtained in turn from the Maxwell equations:

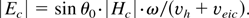
Fast electron transport is considered as a straight-line motion along the normal to the critical surface. Electrons first move into coronal plasma, then reflect at the plasma boundary and return to dense areas. Energy losses of fast electrons are described through the friction force in the approximation of the ionization average potential (see Berestetski et al., 1989):

where dm = ρdl, dl is fast electron path element,

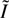
is the ionization average potential, Z and A are the average charge and atomic weight of the target material, γ is the fast electron relativistic factor, and m_p is the proton mass.

4. TRANSITION FROM EXPLODING FOIL REGIME TO ABLATION REGIME

All developed models have been combined with the Lagrangian code “ATLANT” based on the one-fluid–two-temperature model for the electron and ion component. The underlying Lagrangian difference scheme of gas dynamics with an increased number of thermodynamic degrees of freedom provides better retention of the form of the computational cells as compared to the conventional schemes.

Rather than ablate from one side, thin foils explode at both sides in the case of an effective preheating by the hot electron transport. This preheating become readily observable at thin foil explosions under picosecond laser pulse irradiations. Our aim was to estimate at which foil thickness does the preheating effect become sufficient for the flow dynamics and how this thickness depends on the laser beam intensity. The comparison of numerical simulation results and experimental data allows us to determine, in principle, the portion and “temperature” of hot electrons (Lebo & Rozanov, 2001).

In the first series of simulations, two pulses from an Nd laser (λ = 1.06 μm) have been focused normally onto Al foil with an aperture angle 2θ₀ = 20°. The axis of the laser beam is the axis 0Z and it comes in the opposite direction.

The preliminary background pulse with a peak intensity of W = 10¹⁶ W/cm² (energy 0.1 J) in 10 ps was followed by the main pulse with peak intensity W = 10¹⁷ W/cm² (energy 1 J). The temporal shape of both laser pulses was triangular, with a duration of 2 ps. The spatial radius distribution for both pulses was Gaussian with characteristic radius r₀ = 17.8 μm.

Density spatial distributions in 90 ps after the main pulse at foil thicknesses of 3 μm and 15 μm are displayed in Figure 2. On the first distribution one can observe a denser area in the center arising due to a different efficiency of resonance absorption at different angles of incidence. At a foil thickness of about 10 μm we observe the transition from the exploding foil regime to the ablation regime.

Density spatial distributions in 90 ps after the main pulse at foil thicknesses of 3 μm (left) and 15 μm (right). Main pulse peak intensity is 1017 W/cm2; prepulse peak intensity is 1016 W/cm2.

In the second series of simulations all parameters were the same except that energies and intensities were 10 times higher for both pulses. Peak intensity of the main pulse was 10¹⁸ W/cm² and for the prepulse it was 10¹⁷ W/cm². Appropriate density distributions for the cases of foil thicknesses of 10, 20, 30, and 40 μm are represented in Figure 3. The transition from the exploding foil regime to the ablation one occurs in this case at about 40 μm.

Density spatial distributions in 90 ps after the main pulse at foil thickness of 10 μm (left top), 20 μm (right top), 30 μm (left bottom) and 50 μm (right bottom). Main pulse peak intensity is 1018 W/cm2; prepulse peak intensity is 1017 W/cm2.

In case of the exploding foil regime, values of the kinetic energy of plasma flowing toward the laser E_kin(+) (if velocity component Vz > 0) and the kinetic energy of plasma flowing from the laser E_kin(−) (if Vz < 0) are comparable as a result of homogeneous hot electron heating. In case of the ablative regime, E_kin(+) is much higher than E_kin(−). Therefore we suggest characteristic parameter δ = E_kin(−)/E_kin(+) to illustrate the transition from the exploding foil regime to the ablative regime. Characteristic parameter dependence on foil thickness for both series of simulations is represented in Figure 4. The dependence is close to linear before the transition.

Characteristic parameter dependence on foil thickness for both series of simulations.

5. THE INTERACTION OF A NANOSECOND IODINE LASER WITH A TWO-LAYERED TARGET

Using the “ATLANT-HE” code we performed a numerical simulation of a laser interaction with a target consisting of two layers, that is, a low-density layer (lavsan foam) of 100 μm thickness and average density 20 mg/cm³ and a layer of solid lavsan of 2 μm thickness and 1.39 g/cm³ density located at a rear side. A time dependence of a laser pulse of 200 J energy (1.32 μm wavelength) had the form of an isosceles triangle of 0.8 ns duration by base. The intensity dependence on the radius (in the beam transversal direction) had a Gaussian shape I ∼ exp[−r²/a²(z)] , where (r,z) are the cylindrical coordinates. A characteristic beam dimension a(z) on a target was varied within 40–200 μm by means of changing a focal point position in respect of the target surface. The flow density maximum on the target was from 4 × 10¹⁴ to 10¹⁶ W/cm². The beam incidence angles corresponded to F/2 optical system.

Figures 5 and 6 demonstrate spatial dependencies of density and electron plasma temperature at a laser pulse cessation for two values of beam radius on the target: 200 μm (Fig. 5, flow density, 4 × 10¹⁴ W/cm²) and 40 μm (Fig. 6, flow density, 10¹⁶ W/cm²). From the figures it is seen that in the foam an effective energy transfer of electron heat conductivity is occurring in the laser beam transversal direction. The transversal plasma dimension is considerably higher than the beam radius on the target. A balance of an absorbed laser energy is δ_a = 0.624 of the incident energy, and the part of the energy that is absorbed due to the resonance mechanism is δ_ar = 0.196 of the incident energy. In the case of a 40-μm beam, the above values are δ_a = 0.518 and δ_ar = 0.276. In both variants, almost all the energy of the resonant absorption was transformed in the flow of fast electrons. The difference (δ_a − δ_ar) provides the part of the absorption due to the Bremsstrahlung mechanism. Let us note a decrease in the Bremsstrahlung efficiency with an increase in the flow density, despite the negligible growth of the electron temperature. A weak growth of temperature is due to the heat conductivity of foam in the transversal direction. From the figures it is seen that a transversal dimension of plasma changed negligibly, although the beam dimension changed five times. A decrease in the Bremsstrahlung absorption is due to the growth of the energy of the electron oscillations in the laser field (in the “ATLANT-HE” program, the influence of an oscillatory electron energy on the frequency of electron–ion collisions has been taken into account). In the case of a low current density (Fig. 5), a part of the solid-state lavsan remained unevaporated. The unevaporated part, on the symmetry axis, is 0.9 μm (in respect to the initial density and the initial thickness of 2 μm). That part of the target has the velocity of 2.9 × 10⁷ cm/s. The fast electrons do not heat up the unevaporated part higher than the shock wave does. However, in the case of a 40-μm beam, the flow density is 25 times higher, and about to that degree the energy of the fast electrons increases. In addition, a part of the resonant absorption increased as well in that case. As seen from Figure 6, the fast electrons provide a heating of the whole lavsan layer, and one can observe expansion of an exploding layer.

Spatial dependencies of density and electron temperature of plasma at the laser pulse cessation moment (t = 0.8 ns) at characteristic beam radius on the target of 200 μm (flow density on the beam axis is 4 × 1014 W/cm2). The density is in grams per cubic centimeter, temperature in electron volts, R and Z in centimeters.

Spatial dependencies of density and electron temperature of plasma at the laser pulse cessation moment (t = 0.8 ns) at characteristic beam radius on the target of 40 μm (flow density on the beam axis is 1016 W/cm2). The density is in grams per cubic centimeter, temperature in electron volts, R and Z in centimeters.

Thus, in the case of a relative low density of the laser radiation flow, where the fast electron heating is not higher than the shock wave heating, one can obtain an efficient acceleration of a thin dense layer located at a rear side of the foam of a double target destined to smooth the irradiation inhomogeneity. Note that in the calculations, the foam was considered to be a homogeneous small-density region. Such a problem formulation will correspond to real foam with sufficiently small cells, when the time of expansion within a single cell is much less than the laser pulse duration. For the foam with large cells, one needs a direct simulation of the foam by setting the regions of dense layers separated by vacuum (or low-density) regions.