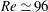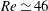1 Introduction
Recent numerical studies (Pralits, Giannetti & Brandt Reference Pralits, Giannetti and Brandt2013; Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013a
,Reference Rao, Leontini, Thompson and Hourigan
b
, Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2015a
; Navrose & Mittal Reference Navrose and Mittal2015) of rotating circular cylinder wakes show the appearance of a new three-dimensional instability mode that develops on the steady two-dimensional wake. This mode, mode E (named in the alphabetic order of the modes observed by Rao et al. (Reference Rao, Leontini, Thompson and Hourigan2013a
)), was initially observed for
${\it\alpha}\gtrsim 2$
and
$\mathit{Re}\gtrsim 200$
, where
${\it\alpha}$
is the non-dimensionalised rotation rate of the cylinder (surface to free-stream speed) and
$Re$
is the Reynolds number based on the cylinder diameter. The onset of mode E occurs at lower Reynolds numbers as the rotation rate is increased. This mode can also be observed for lower rotation rates of
${\it\alpha}\lesssim 2$
, if two-dimensional periodic shedding (i.e., Bénard–von-Kármán (BvK) vortex shedding) is artificially suppressed. Rao et al. (Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2015a
) speculated that mode E is essentially the same three-dimensional mode as observed for rotating cylinders placed close to a wall (Stewart et al.
Reference Stewart, Thompson, Leweke and Hourigan2010; Rao et al.
Reference Rao, Stewart, Thompson, Leweke and Hourigan2011, Reference Rao, Thompson, Leweke and Hourigan2013c
).
To investigate further the occurrence and the nature of this transition, and indeed how widespread it is, linear stability analysis is performed for a range of bluff-body geometries and flow set-ups, where the wake has been artificially stabilised to be steady and two-dimensional. Given these steady base flows, it is shown that mode E is the first three-dimensional mode to become unstable in bluff-body flows and appears to be a ‘universal’ mode that is observed irrespective of the configuration of the bluff body under consideration.
The remainder of this study is organised as follows: § 2 deals with the numerical method employed in our analysis, followed by the results in § 3; in § 4 the results are examined in terms of structural stability, first introduced by Giannetti & Luchini (Reference Giannetti and Luchini2007) and Luchini, Giannetti & Pralits (Reference Luchini, Giannetti and Pralits2008), and discussed and interpreted in a wider context, exploring the role of generic physical mechanisms in triggering this instability. Finally, § 5 provides further interpretations and conclusions.
2 Numerical method
To obtain the time-dependent flows and stability modes, the incompressible Navier–Stokes (NS) equations are solved in two-dimensional Cartesian or axisymmetric geometries using a spectral-element formulation. The computational domain consists of several hundred quadrilateral macroelements, with higher concentration in the vicinity of the bluff body (generally a cylinder) where the velocity gradients are largest. These elements are further subdivided into internal node points (
$N\times N$
) distributed according to Gauss–Legendre–Lobatto quadrature points in each direction. Velocity and pressure fields are represented by tensor products of Lagrangian polynomial interpolants based on nodal values. It has been shown that this method achieves spectral convergence as the polynomial order is increased within elements (Karniadakis & Sherwin Reference Karniadakis and Sherwin2005). The number of node points within each element (
$N\times N$
) is specified at runtime, with the interpolating polynomial order in each direction being
$N-1$
. A second-order fractional time-stepping technique is used to sequentially integrate the advection, pressure and diffusion terms of the Navier–Stokes equations forward in time (Thompson et al.
Reference Thompson, Hourigan, Cheung and Leweke2006). The unsteady solver is used to investigate the parameter range covering both the steady and unsteady regimes of flow. More details of the time-stepping scheme can be found in Thompson et al. (Reference Thompson, Hourigan, Cheung and Leweke2006), and the code has previously been used to accurately compute bluff-body flows in free stream (Sheard, Thompson & Hourigan Reference Sheard, Thompson and Hourigan2004b
; Ryan, Thompson & Hourigan Reference Ryan, Thompson and Hourigan2005; Leontini, Thompson & Hourigan Reference Leontini, Thompson and Hourigan2007; Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013a
; Thompson et al.
Reference Thompson, Radi, Rao, Sheridan and Hourigan2014) and for bodies near walls (Stewart et al.
Reference Stewart, Hourigan, Thompson and Leweke2006, Reference Stewart, Thompson, Leweke and Hourigan2010; Rao et al.
Reference Rao, Stewart, Thompson, Leweke and Hourigan2011, Reference Rao, Passaggia, Bolnot, Thompson, Leweke and Hourigan2012, Reference Rao, Thompson, Leweke and Hourigan2013c
). It is also necessary to generate steady base flows for the stability analysis. These are obtained using a related code based on a spectral-element penalty-method formulation using Newton iterations to obtain the flow solutions (see Zienkiewicz Reference Zienkiewicz1977; Thompson & Hourigan Reference Thompson and Hourigan2003; Jones, Hourigan & Thompson Reference Jones, Hourigan and Thompson2015).
Linear stability analysis is then performed on these stabilised base flows. To do this, the Navier–Stokes equations are linearised about a steady base-flow state, with the spanwise variation of the perturbation variables constructed as a set of Fourier terms. To examine three-dimensional transition, for a selected spanwise wavelength, these equations are integrated forward in time using the time-dependent spectral-element code from a white-noise initial state, and the growth of perturbations is monitored. After sufficient time, the fastest-growing/slowest-decaying modes dominate, with each mode growing/decaying exponentially with growth rate
${\it\sigma}_{(i)}$
. If
${\it\sigma}_{max}>0$
, the flow is unstable to three-dimensional perturbations at the chosen wavelength, and for
${\it\sigma}<0$
, perturbations decay and the flow remains in its two-dimensional steady state. Neutral stability corresponds to
${\it\sigma}=0$
. For a given Reynolds number, a range of spanwise wavelengths is tested, and this procedure is repeated for a range of Reynolds numbers to determine the critical Reynolds number and wavelength at which neutral stability is achieved for the dominant modes. For the transition from two-dimensional steady to two-dimensional periodic flow, the method can also be applied by considering a spanwise wavelength approaching infinity. In this case, the complex growth rate then gives the growth rate and frequency of the unstable oscillatory mode, which can be decoupled from other modes using a Krylov subspace approach with Arnoldi decomposition to extract the most dominant modes and complex eigenvalues (complex growth rates) (Mamun & Tuckerman Reference Mamun and Tuckerman1995; Barkley & Henderson Reference Barkley and Henderson1996). In practice, the calculation of the adjoint modes used in section § 4 to determine structural stability is treated in the same way as the linear stability analysis described above, except that the adjoint linear stability equations are integrated backwards in time with the boundary conditions adjusted to reflect the upstream advection of the perturbation field. The background and computational implementation have been discussed in a number of articles including Blackburn, Barkley & Sherwin (Reference Blackburn, Barkley and Sherwin2008), Marquet et al. (Reference Marquet, Lombardi, Chomaz, Sipp and Jacquin2009) and Thompson (Reference Thompson2012).
3 Results
3.1 Rotating cylinders
First, the flow past a rotating circular cylinder in free stream is revisited. Previous studies (Kang, Choi & Lee Reference Kang, Choi and Lee1999; Mittal & Kumar Reference Mittal and Kumar2003) have shown that a rotating cylinder wake is stabilised for cylinder rotation rates
${\it\alpha}\gtrsim 2$
for
$Re\lesssim 200$
. More recent numerical studies (Pralits et al.
Reference Pralits, Giannetti and Brandt2013; Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013a
,Reference Rao, Leontini, Thompson and Hourigan
b
) have shown that a number of steady and unsteady three-dimensional modes become unstable on the steady or periodic base flow as the Reynolds number is increased. Of these modes, mode E is observed over a wide area of
${\it\alpha}$
–
$\mathit{Re}$
parameter space. The region where mode E is unstable is highlighted in grey in figure 1(a) (Rao et al.
Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2015a
). In the steady base-flow regime (steady state I), mode E is the first three-dimensional mode to become unstable to spanwise perturbations as the Reynolds number is increased. While this mode was initially observed for rotation rates of
${\it\alpha}\gtrsim 2$
(Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013a
,Reference Rao, Leontini, Thompson and Hourigan
b
), it still exists at lower rotation rates down to the non-rotating case (
${\it\alpha}=0$
) on an artificially stabilised base flow. For a non-rotating cylinder, the critical Reynolds number for transition is
$Re_{c}\simeq 96$
at a spanwise wavelength of
${\it\lambda}_{c}/D\simeq 6$
. The upper limit of mode E instability is the boundary of steady state II (where the stagnation point in the flow sits slightly upstream of the cylinder). The variation of the spanwise wavelength of this mode decreases from
${\it\alpha}=0$
to
${\it\alpha}\simeq 2.5$
before increasing to higher values as the rotation rate is increased to
${\it\alpha}\simeq 6$
. At lower rotation rates of
${\it\alpha}\lesssim 2$
, this mode is not physically realisable, or is at least masked, due to the onset of BvK shedding at Reynolds numbers lower than the onset of mode E.
Figure 1. (a) Parameter space diagram for the rotating cylinder in free stream, showing the bifurcations from steady state I. The two steady states, steady state I and steady state II, are shown along with the two shedding regimes, mode I and mode II shedding. The shaded region in grey represents the region where mode E is unstable to perturbations. This diagram is reproduced from Rao et al. (Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2015a
). (b) Spanwise perturbation vorticity contours at the specified parametric values. Flow is from from left to right in these images and the cylinder is rotating anticlockwise. Perturbation vorticity contours are overlaid with base-flow vorticity contours in the range
$\pm 1D/U$
, shown by continuous black lines.
Figure 1(b) also shows the spanwise perturbation vorticity contours of the mode E instability at specified parametric values close to the boundary of neutral stability. For more instances of perturbation fields and three-dimensional renderings of this mode, the reader is referred to the studies of Rao et al. (Reference Rao, Leontini, Thompson and Hourigan2013a
,Reference Rao, Leontini, Thompson and Hourigan
b
, Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2015a
). Mode E has also been observed experimentally in the wake of rotating cylinders at
${\it\alpha}\simeq 2$
(Radi et al.
Reference Radi, Thompson, Rao, Hourigan and Sheridan2013).
3.2 Cylinders with elliptical cross-sections
Further investigations reveal that the existence of this mode may be independent of the shape of the bluff body. It is found to occur for elliptical cylinders whose aspect ratio is varied. Figure 2(a) shows the variation of the critical Reynolds number for the onset of mode E for an elliptical cylinder. The figure also shows the variation of the preferred spanwise wavelength at the onset of the instability, both with
$AR$
. Here,
$AR$
is defined as the ratio of the length of the major to the minor axis of the elliptical cylinder:
$AR=0$
for a flat plate, while
$AR=1$
indicates a circular cylinder;
$AR>1$
indicates that the cylinder is elongated along the direction of the incoming flow. Also displayed is the variation of the critical Reynolds number for the transition from a steady to an unsteady state.
Figure 2. (a) Variation of the critical Reynolds number (●) and spanwise wavelength (○) of the mode E instability with aspect ratio for an elliptical cylinder. The figure also shows the variation of the critical Reynolds number for the steady–unsteady transition (▪), also marked by a dashed line. Data for the critical values for the steady–unsteady transition for elliptical cylinders with
$AR\leqslant 1$
and
$1\leqslant AR\leqslant 2.4$
are reproduced from Thompson et al. (Reference Thompson, Radi, Rao, Sheridan and Hourigan2014) and Leontini, Lo Jacono & Thompson (Reference Leontini, Lo Jacono and Thompson2015), respectively. (b) Spanwise perturbation vorticity contours for an elliptical cylinder at the specified parametric values. Contour shading as per figure 1(b).
Figure 2(b) shows the spanwise perturbation vorticity contours for an elliptical cylinder for the range of aspect ratios investigated in this study. Despite the change in the configuration of the body and the narrowing of the wake in the transverse direction, the structure of the perturbation remains essentially unaltered.
3.3 Elliptic cylinders angled to the flow
To further demonstrate that this mode occurs prior to other 3D transitions, the angle of incidence of the incoming flow was then varied from 0 to
$20^{\circ }$
for an elliptical cylinder of
$AR=2$
with its major axis parallel to the flow and the linear stability analysis was performed on the stabilised base flows. Similar to the previous case, mode E transition occurred prior to the onset of other three-dimensional modes and, consistent with the zero-incidence ellipses, above the critical Reynolds number for steady to unsteady transition. Figure 3 shows the transition map together with spanwise perturbation vorticity contours for a cylinder with
$AR=2$
at two different angles of attack.
Figure 3. (a) Variation of the critical Reynolds number (●) and spanwise wavelength (○) of mode E with incident angle (
$I^{\circ }$
) for an
$AR=2$
ellipse. The critical Reynolds number for the steady–unsteady transition is also shown (▪), and is also marked by a dashed line. (b) Spanwise perturbation vorticity contours at the specified parametric values. Contour shading as per figure 1(b).
Figure 4. (a) Variation of the critical Reynolds number (●) and wavenumber (○) for mode E with torus aspect ratio (
$AR$
). Filled squares (▪) indicate the critical Reynolds number for the axisymmetric transition, while open squares (▫) indicate the asymmetric transition. (b) Spanwise perturbation vorticity contours at the specified parametric values. Flow is from top to bottom. These images can be directly compared with figure 13 of Sheard et al. (Reference Sheard, Thompson and Hourigan2004b
), where identical images were shown for the mode III transition for a torus wake.
3.4 Axisymmetric bodies
Extending the investigation to axisymmetric bodies, the stabilised base flows were obtained for the flow past different aspect ratio tori. Here, the aspect ratio (
$AR$
) is defined as the ratio of the diameter of the torus to the diameter of the cross-section. For axisymmetric bodies, linear stability modes can only take discrete azimuthal wavelengths due to the imposed
$2{\rm\pi}$
periodicity. The integer mode number,
$m$
, corresponds to a spanwise wavelength of
$2{\rm\pi}/{\it\lambda}$
. Figure 4(a) shows the variation of the critical Reynolds number for the mode E transition for
$AR\leqslant 40$
. At large aspect ratios, the critical Reynolds number for the mode E transition approaches that of a circular cylinder (
$AR=\infty$
) in free stream, as should be expected. However, at low
$AR$
, the discreteness of wavelength selection causes slight jumps in the critical Reynolds number. Nonetheless, the mode number variation with
$AR$
is effectively linear, thereby showing that the ‘preferred wavelength’ of mode E is insensitive to
$AR$
. At
$AR=40$
,
$m=21$
, which indicates that the effective wavelength is
${\rm\pi}\times 40/21\simeq 6$
, close to the critical wavelength at onset for a circular cylinder in free stream, while at a lower aspect ratio of
$AR=1.8$
,
$m=1$
, corresponding to an effective wavelength of
${\rm\pi}\times 1.8/1\simeq 5.6$
, again consistent with an isolated circular cylinder, despite strong curvature of the torus. Figure 4(b) also shows three-dimensional reconstructions of the mode E instability at the specified parametric values. Further examination of these images and figures 13 and 14 of Sheard et al. (Reference Sheard, Thompson and Hourigan2004b
) shows that mode E and the previously identified mode III of a torus are indeed identical. Furthermore, the values of
$Re_{c}$
for this mode (figure 4
a) and those from figure 3 of Sheard, Thompson & Hourigan (Reference Sheard, Thompson and Hourigan2004a
) are in close agreement.
Figure 5. (a) Variation of the mode E instability with gap height for the three rotation rates. Filled symbols indicate values of the critical Reynolds number on the steady state, while open symbols indicate values on the stabilised base flow. Legend:
${\it\alpha}=0$
(●);
${\it\alpha}=+1$
(▪);
${\it\alpha}=-1$
(▴). Figure reproduced from Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2015b
). (b) Spanwise perturbation vorticity contours for a gap height
$G/D=0.5$
at the specified parametric values. Contour shading as per figure 1(b).
3.5 Cylinders in the presence of walls
These examples strongly support the conjecture that mode E is the primary three-dimensional instability for cylindrical or axisymmetric bluff bodies in free stream. Now the onset of mode E is investigated for a rotating circular cylinder translating in the vicinity of a wall. Recent studies of Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013c
) showed that for a non-rotating circular cylinder translating at constant velocity parallel to a wall at gap heights of
$G/D\simeq 0.22$
, the transition from steady two-dimensional flow to a steady three-dimensional state occurs prior to the onset of unsteady flow. For larger gap heights, as for the cylinder in free stream, the transition to unsteady flow occurs first. Figure 5(a) shows the variation of the critical Reynolds number for the three-dimensional mode E transition with gap height for steady base flows. Here, the results of Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2013c
) are extended to a larger gap height range for a non-rotating cylinder and also extended to non-zero cylinder rotation rates:
${\it\alpha}=+1$
(forward/prograde rotation) and
${\it\alpha}=-1$
(reverse/retrograde rotation). At smaller gap heights, forward rotation decreases the critical Reynolds number, while reverse rotation delays it to a higher Reynolds number. For gap heights larger than
$G/D=1$
, the critical values for these cases approach the corresponding values recorded for the rotating cylinder in free stream. Interestingly, the
$Re_{c}$
values for
${\it\alpha}=+1$
and
$-1$
converge to a single value at large gap heights. Figure 5(b) shows the spanwise perturbation vorticity contours for a cylinder translating along a wall at
$G/D=0.5$
at the specified parametric values. For more instances of perturbation contours of this mode, the reader is referred to figures 25 and 26 of Rao et al. (Reference Rao, Thompson, Leweke and Hourigan2015b
). The coalescing of the critical Reynolds numbers and the structure of the perturbation fields indicate that mode E and the three-dimensional modes observed in near-wall bluff-body studies are indeed identical.
3.6 Rolling or sliding cylinders
For bodies rolling or sliding along a wall, Stewart et al. (Reference Stewart, Hourigan, Thompson and Leweke2006, Reference Stewart, Thompson, Leweke and Hourigan2010) documented the two/three-dimensional transitions for a cylinder rolling along a wall for
$-1\leqslant {\it\alpha}\leqslant +1,Re\leqslant 450$
. This study was extended to
$-2\leqslant {\it\alpha}\leqslant +2,Re\leqslant 750$
by Rao et al. (Reference Rao, Stewart, Thompson, Leweke and Hourigan2011), where the flow remained two-dimensional for
${\it\alpha}\lesssim -1.5$
. Furthermore, the onset of unsteady flow was delayed to higher Reynolds number as the rotation rate was decreased. As the rotation rate is increased to higher positive values, the mode E transition occurs at very low Reynolds numbers (
$Re_{c}\simeq 10$
), with a corresponding increase in the spanwise wavelength. Figure 6(a) shows the variation of the critical Reynolds number and the spanwise wavelength of the mode E with rotation rate for a cylinder rolling along a wall. A similar increase in the spanwise wavelength was observed for the rotating cylinder in free stream; however, the critical spanwise wavelength is much longer for bodies near a wall. These observations corroborate that this mode is in fact mode E instability. Figure 6(b) also shows the spanwise perturbation vorticity contours for mode E at the specified parametric values. Apart from these images, further instances of mode E instability can be found in the studies of Stewart et al. (Reference Stewart, Hourigan, Thompson and Leweke2006, Reference Stewart, Thompson, Leweke and Hourigan2010) and Rao et al. (Reference Rao, Stewart, Thompson, Leweke and Hourigan2011).
Finally, mode E is the first mode to be observed in the wake of tandem rolling cylinders, where the three-dimensional transition precedes the transition to unsteady flow Rao et al. (Reference Rao, Stewart, Thompson, Leweke and Hourigan2011, Reference Rao, Thompson, Leweke and Hourigan2013d ).
Figure 6. (a) Variation of the critical Reynolds number (●) and spanwise wavelength (○) of the mode E instability with aspect ratio for a circular cylinder rolling next to a wall with non-dimensionalised rotation rate. The critical values for steady–unsteady transition are shown by filled square symbols (▪) and joined by dashed lines. For
${\it\alpha}\lesssim 1.5$
, vortex shedding is suppressed. Data for the critical values of transition for
$-2\leqslant {\it\alpha}\leqslant 2$
are reproduced from Stewart et al. (Reference Stewart, Thompson, Leweke and Hourigan2010) and Rao et al. (Reference Rao, Stewart, Thompson, Leweke and Hourigan2011). (b) Spanwise perturbation vorticity contours for a cylinder rolling along a wall at the specified parametric values. Contour shading as per figure 1(b).
Figure 7. Left-hand column: structure of the perturbation mode in terms of spanwise perturbation vorticity as a function of cylinder rotation rate. Selected streamlines are shown by the black lines to indicate the recirculation regions and other critical aspects of the base flow. Middle column: structure of the adjoint mode for matching rotation rates, again depicted as coloured contours of spanwise perturbation vorticity. Right-hand column: spectral norm of the structural stability at the different rotation rates. Row (d) shows the case considered by Pralits et al. (Reference Pralits, Giannetti and Brandt2013), which was interpreted as a hyperbolic instability.
4 Structural stability of mode E
Following on from a series of papers characterising the structural stability of stationary and rotating cylinder wakes (Giannetti & Luchini Reference Giannetti and Luchini2007; Giannetti, Camarri & Luchini Reference Giannetti, Camarri and Luchini2010; Pralits, Brandt & Giannetti Reference Pralits, Brandt and Giannetti2010), Pralits et al. (Reference Pralits, Giannetti and Brandt2013) investigated the nature of the instability causing the transition from two- to three-dimensional steady flow for a rotating cylinder at the high rotation rate of
${\it\alpha}=5$
at
$\mathit{Re}=100$
. In fact, this is one of the transitions classified in this paper as a mode E transition. At this rotation rate, there is a recirculation region surrounding the cylinder inside which the fluid advects around the cylinder in closed orbits, with a hyperbolic point above the cylinder connecting the fluid passing over the cylinder to that which passes under it (see figure 7
d). The linear instability mode for this case has large amplitude in the closed recirculation region extending initially upstream and then continuing downstream along the streamline passing through the hyperbolic point. The nature of the perturbation velocity and vorticity fields in the neighbourhood of the hyperbolic point suggests that the instability may be augmented, if not directly caused, by a hyperbolic instability (Leblanc & Godeferd Reference Leblanc and Godeferd1999; Caufield & Kerswell Reference Caufield and Kerswell2000). Further to this, Pralits et al. (Reference Pralits, Giannetti and Brandt2013) investigated the structural stability of this mode. This involves calculating the scaled tensor product
$\unicode[STIX]{x1D64E}_{p}$
of the normal
$\hat{\boldsymbol{u}}$
and adjoint
$\hat{\boldsymbol{u}}^{\ast }$
modes at each point:
$$\begin{eqnarray}\unicode[STIX]{x1D64E}_{p}(x_{0},y_{0},{\it\kappa})=\frac{\hat{\boldsymbol{u}}^{\ast }(x_{0},y_{0},{\it\kappa})\,\hat{\boldsymbol{u}}(x_{0},y_{0},{\it\kappa})}{\displaystyle \int _{{\mathcal{D}}}\hat{\boldsymbol{u}}^{\ast }\boldsymbol{\cdot }\hat{\boldsymbol{u}}\,\text{d}A},\end{eqnarray}$$
which gives the shift in the growth rate of the mode corresponding to wavenumber
${\it\kappa}$
to point forcing of the perturbation field at
$(x_{0},y_{0})$
. Here, the integration is over the computational domain, which should cover the spatial region where the integrand is non-negligible. This corresponds to a wavemaker interpretation of mode sensitivity (e.g. Chomaz, Huerre & Redekopp Reference Chomaz, Huerre and Redekopp1991; Chomaz Reference Chomaz2005; Marquet et al.
Reference Marquet, Lombardi, Chomaz, Sipp and Jacquin2009), which tries to locate the spatial position in the absolutely unstable region controlling the development of the instability. Most of these theoretical studies have focused on frequency selection (Chomaz et al.
Reference Chomaz, Huerre and Redekopp1991; Monkewitz, Huerre & Chomaz Reference Monkewitz, Huerre and Chomaz1993; Le Dizès et al.
Reference Le Dizès, Huerre, Chomaz and Monkewitz1996; Pier Reference Pier2002), although, of course, for this steady transition no sinusoidal time dependence is involved. There are various norms that can be used to build a representative spatial map of the sensitivity. Typically, Pralits et al. (Reference Pralits, Giannetti and Brandt2013) used the spectral norm to quantify it. Their analysis for this mode shows that the sensitivity is large close to the hyperbolic point, although not directly at it. Overall, however, this provides further supporting evidence that the generic hyperbolic mechanism may play an important role in triggering the instability. This is considered further below.
The large number of different cases considered in this paper classified as mode E transitions show some similarities in the spanwise vorticity perturbation fields, even though the base flows vary considerably. In general, the base flow has a recirculation region in the vicinity of the bluff body, although its exact form is variable. Rather than trying to cover the entire range of different base flows, it would seem to be more productive to initially focus on a more narrowly defined sequence. To this end, the stability of the flow around rotating cylinders is considered as the rotation rate is varied.
Figure 7 shows the evolution of mode E depicted by its spanwise perturbation vorticity field, at the transition Reynolds number and preferred wavelength (first three cases only), as the rotation rate is sequentially increased. The left-hand column shows the change in its structure as a function of rotation rate. The mode is active in the recirculation region(s) but also has significant amplitude for a considerable distance downstream. The left-hand image in figure 7(d) corresponds to the rapidly rotating case of
${\it\alpha}=5$
(for
$\mathit{Re}=100$
,
${\it\lambda}/D=2{\rm\pi}$
) considered by Pralits et al. (Reference Pralits, Giannetti and Brandt2013). The middle column of figure 7 shows the corresponding adjoint mode structures. The right-hand column of figure 7 shows the spectral norm of the structural stability fields, which again indicates where the growth rate of the perturbation mode is most sensitive to point forcing. Interestingly, at zero rotation rate, the structural stability is maximum between the symmetrical recirculation regions attached to the cylinder. This extends to the
${\it\alpha}=1$
rotation case, with a local maximum between the now non-symmetrical recirculation zones, but noting that there is also another more localised local maximum centred on the hyperbolic point close to the rear of the cylinder. This hyperbolic point connects to the lower recirculation zone. At the higher rotation rate of
${\it\alpha}=2$
, the structural stability field exhibits significant change to its structure. Now there is only a single recirculation zone, with the lower recirculation replaced by a zone in which fluid initially moves out towards the outer hyperbolic point, before moving back towards the cylinder and then passing clockwise around the upper detached recirculation zone. The structural stability amplitude is maximal within this region, although well away from the downstream hyperbolic point. For the much higher rotation rate case of
${\it\alpha}=5$
(Pralits et al.
Reference Pralits, Giannetti and Brandt2013), the structural stability field indicates sensitivity inside the recirculation zone which now encompasses the cylinder, extending up towards the hyperbolic point along the left-hand boundary of the recirculation zone, as noted by these authors. Thus, relative to the higher rotation cases, at lower rotation rates the structural stability appears to display different characteristics, although there appears to be a continuous transition as the base-flow topology changes significantly.
Returning focus to the non-rotating case, it is apparent that an important feature of the base flow is the presence of two symmetrical recirculation bubbles. Considering that the existence of an absolute instability would seem to require flow recirculation, so that any perturbation growth cannot escape as fluid advects downstream, it seems likely that these are the key regions controlling instability development. Indeed, as noted, the structural stability field for these cases shows that the maximum perturbation field sensitivity is connected with the recirculation regions. For the zero-rotation case, each half of the perturbation field shows regions of positive and negative spanwise perturbation vorticity, with the zero perturbation contour passing through the recirculation zone. This arrangement will result in a sinusoidal spanwise displacement of the recirculation region cores, similar to that seen for an elliptic or Crow instability in the much less complex situation of a counter-rotating vortex pair. The spatial symmetry of the perturbation field, together with the relatively long preferred spanwise wavelength of the instability mode, shows some consistency with these features of the Crow instability of a vortex pair.
To explore this analogy slightly further, figure 8 shows the calculated Crow and elliptic instability modes of a closely spaced vortex pair at
$\mathit{Re}=2500$
. This Reynolds number was chosen to be similar to that used in the experiments of Leweke & Williamson (Reference Leweke and Williamson1998) exploring the cooperative elliptic (and Crow) instability of a vortex pair, however noting that the instability mechanism is essentially inviscid in both cases. The flow is simulated as a pair of counter-rotating Gaussian vortices of circulation
${\it\Gamma}=1$
with core size
$a=0.23$
, spaced
$b=1$
units apart. The Reynolds number is given by
$\mathit{Re}={\it\Gamma}/(2{\rm\pi}{\it\nu})$
, where
${\it\nu}$
is the kinematic viscosity. The vortex pair self-advects due to mutual induction. On generation, the initial pair is not in equilibrium; however, it rapidly evolves to a semi-equilibrium state after initial oscillations are damped and the individual vorticity distributions readjust to less circular more elongated shapes. After this rapid initial evolution, the cores gradually expand due to viscous diffusion in a self-similar manner. More details on this process can be found in Roy et al. (Reference Roy, Schaeffer, Le Dizès and Thompson2008) and references therein. This case was simulated with the same spectral-element code as used for the mode E simulations discussed in this paper, but based on a similar grid and set-up to those used in Roy et al. (Reference Roy, Schaeffer, Le Dizès and Thompson2008).
Figure 8. Comparison of (a) the elliptic instability and (b) the Crow instability of a counter-rotating vortex pair. The pair is self-propelling towards the left. Left-hand column: structure of the perturbation mode in terms of spanwise perturbation vorticity. The positions of the vortices within the pair are shown by the black lines marking vorticity levels of
$\pm 0.1$
. Middle column: structure of the adjoint mode for matching rotation rates. Right-hand column: spectral norm of the structural stability.
After 20 non-dimensional time units, oscillations of the counter-rotating vortex pair have substantially decayed. At that point the base flow was frozen and the dominant stability modes were computed. This flow develops two primary instabilities: an elliptic instability with preferred spanwise wavelength of
${\it\lambda}/b\simeq 0.8$
and a much longer wavelength Crow instability with a preferred wavelength of
${\it\lambda}/b\simeq 6.64$
. The wavelengths of both modes and their predicted growth rates are in good agreement with the experimental findings of Leweke & Williamson (Reference Leweke and Williamson1998) and previous theoretical predictions also referenced in that paper. The spanwise perturbation vorticity fields of these two modes are shown in figure 8. It should be noted that both modes essentially lead to a distortion of the individual vortex cores in the direction of the principal strain, resulting in a sinusoidal spanwise distortion of the cores seen in experimental images (Leweke & Williamson Reference Leweke and Williamson1998). Figure 8 also shows the corresponding adjoint modes and the structural stability fields for these two instabilities.
It is of interest that the structural stability field of the Crow instability only shows significant amplitude between the recirculation regions corresponding to the vortex pairs, noting that for a vortex pair, the streamlines in the moving frame and the vorticity contours are a good match. This is also true for the zero-rotation-rate mode E transition shown in figure 7. Comparison of figures 7(a) and 8(b) also indicates there are some similarities in the perturbation and adjoint modes as well, at least within the recirculation zones. In particular, the spanwise perturbation field zero contour passes through the recirculation zones at an angle to the long axis so that the instability is stretched by the induced strain, while the symmetry of the perturbation field across the centreline matches that of the Crow instability. For the adjoint mode, there are also clear similarities. In addition, the long preferred wavelength of mode E (
${\sim}6D$
) is in line with that of the Crow instability (
${\sim}6.6b$
). This suggests that the Crow mechanism may play a role in sustaining this instability, at least in the non-rotating case.
The Crow instability model was originally developed for vortex filaments (Crow Reference Crow1970; Widnall, Bliss & Zalay Reference Widnall, Bliss, Zalay, Olsen, Goldberg and Rogers1971). The key requirements for instability are (1) rotation of fluid about the core centres due to self-induction, (2) rotation and strain induced from the presence of the other vortex of the pair and (3) rotation and stretching from the perturbed vortex cores, which is a function of the spanwise wavelength of the perturbation. If the total rotation of the perturbation is zero and the stretching is positive, the instability will grow. Thus, essentially, the development of the sinusoidal perturbation along the recirculation cores counteracts the fluid rotation about each core centre due to the presence of the vorticity there.
Given the steady nature of the mode E transition, the spatial distribution of the perturbation field is fixed in time. From a Lagrangian viewpoint, within the recirculation zones, the perturbed base flow would tend to rotate with the recirculating flow unless the structure of the perturbation field is such that it counteracts the normal rotation induced by the base-flow field. If the alignment is such that there is stretching due to the induced strain from the opposite vortex of the pair, then instability growth is possible. Thus, at least in this sense, the mode E transition for the non-rotating case has some of the physical characteristics of a Crow instability.
For the rotating cylinder cases, the recirculation zones are no longer of equal size or strength. However, again the mode E perturbation field is fixed spatially while it grows exponentially in time. Therefore, even in these cases, the perturbation field is spatially structured to counteract the rotation of the base-flow recirculations. Thus, while it would be a significant stretch to identify such instabilities as essentially Crow instabilities, it is likely that the underlying physics leading to instability growth shares elements in common.
As the Reynolds number is increased, the first occurring instability of a class of flows including the flow past a backward-facing step is also a transition from a steady two-dimensional wake to a steady three-dimensional wake (Barkley, Gomes & Henderson Reference Barkley, Gomes and Henderson2002; Gallaire, Marquille & Ehrenstein Reference Gallaire, Marquille and Ehrenstein2007; Griffith et al. Reference Griffith, Thompson, Leweke, Hourigan and Anderson2007; Marquet et al. Reference Marquet, Lombardi, Chomaz, Sipp and Jacquin2009). This has previously been associated with centrifugal instability (Barkley et al. Reference Barkley, Gomes and Henderson2002), elliptic instability (Griffith et al. Reference Griffith, Thompson, Leweke, Hourigan and Anderson2007), and mathematically in terms of lift-up non-normality (Marquet et al. Reference Marquet, Lombardi, Chomaz, Sipp and Jacquin2009). Again, this instability falls under the mode E transition classification of this paper. As indicated, it is also the first occurring instability in that case, presumably because the absolute instability responsible for BvK shedding is suppressed due to the presence of the wall.
Figure 9. Perturbation (left-hand column), adjoint (middle column) and structural stability (right-hand column) fields for the initial three-dimensional transition for flow over a backward-facing step (
$Re=750$
,
${\it\lambda}=6h$
). (a) Standard set-up; (b) modified set-up to include a stress-free lower wall. The Reynolds number and wavelength are chosen to be close to the values at the onset of the transition.
Figure 9 shows the perturbation, adjoint and structural stability fields for the flow past a backward-facing step for this transition. Comparing the mode E perturbation fields for the backward-facing step (figure 9 a) and the non-rotating cylinder (figure 7 a) highlights similarities in the spanwise perturbation vorticity distributions in the recirculation regions. This does not carry across to the adjoint fields though. For the cylinder, the adjoint mode shows only perturbation vorticity of one sign in each recirculation lobe, while for the backward-facing step, there is positive and negative perturbation vorticity in each lobe. This leads to different structural stability field distributions. As previously described, the structural stability shows large amplitude between the recirculations for the cylinder, but for the backward-facing step is maximal within the recirculation lobes. To test whether this is a result of the no-slip lower-wall boundary condition for the backward-facing step, the analysis was repeated with a free-slip lower boundary. This produced a similar result to the standard backward-facing step case, with the structural stability again maximal within the recirculation lobes rather than between them. These results for the backward-facing step are in agreement with those of Marquet et al. (Reference Marquet, Lombardi, Chomaz, Sipp and Jacquin2009), who examined a smoothed step in terms of structural stability, finding that the sensitivity was largest near the centre of the recirculation zone. Interestingly, as is shown in figure 8(a), this is also found for elliptic instability, which has previously been speculated to promote the initial three-dimensional instability for this flow by Griffith et al. (Reference Griffith, Thompson, Leweke, Hourigan and Anderson2007).
In combination, these structural stability results suggest that the primary mechanism responsible for the transition may be very much a function of the system parameters. For symmetrical flow past a cylinder away from a wall, it appears that a Crow mechanism may play a part in triggering the instability, at least in the sense that the spatial distribution of the perturbation field is such that it counteracts the self-rotation of the recirculation zones while allowing stretching through the action of the base-flow strain field distorting the recirculation zones. At higher rotation rates, Pralits et al. (Reference Pralits, Giannetti and Brandt2013) have speculated that hyperbolic instability plays a stronger role, and indeed the structural stability field is quite different at higher rotation rates, as is the base-flow topology. Of course, the spatial perturbation field distribution still arranges itself so that the perturbation field within the recirculation zone(s) counteracts the rotation of the base flow. It also appears that as a cylinder is moved towards a wall, the dominant physical mechanism may change again. For a backward-facing step the structural stability changes again, displaying features more in common with elliptic instability of a vortex pair.
5 Conclusions
The multiple different cylinder geometries, boundary conditions and flow situations examined all show that mode E is the first three-dimensional mode to become unstable on steady two-dimensional or axisymmetric flow. While for bodies in free stream the wake undergoes a Hopf bifurcation (from steady to unsteady flow), leading to BvK shedding prior to mode E transition, this is not the case when the centreline mirror symmetry is sufficiently disrupted, either through cylinder rotation or by moving the cylinder towards a wall. In these cases, the absolute instability responsible for the transition to vortex shedding is suppressed, enabling the mode E transition to occur first.
An interesting question is whether there is a common physical mechanism responsible for this instability in these widely different flow problems. For the restricted subset consisting of the flows past a rotating cylinder, the base-flow topology changes considerably as the rotation rate is increased: from two symmetric counter-rotating recirculation zones at zero rotation rate to a single recirculation zone encompassing the cylinder connected to the main flow through a hyperbolic point at the higher rotation rate of
${\it\alpha}=5$
. Over this rotation rate range, the critical Reynolds number and preferred wavelength vary widely and non-monotonically:
$\mathit{Re}_{c}=95,{\it\lambda}/D=6$
at
${\it\alpha}=0$
;
$\mathit{Re}_{c}=328,{\it\lambda}/D=1.5$
at
${\it\alpha}=2.5$
; and
$\mathit{Re}_{c}=46.5,{\it\lambda}/D=4.3$
at
${\it\alpha}=5$
. Analysis of the structural stability fields of these different cases indicates that at low rotation rates the perturbation field is sensitive to forcing in the region between the two recirculation lobes. This is also seen in the generic problem of the Crow instability of a counter-rotating vortex pair. In addition, both the Crow perturbation and the adjoint field spatial distributions and symmetries show similarities with the non-rotating cylinder fields, as well as similarity of the preferred wavelength based on the separation of the recirculation centres. At the highest rotation rate examined of
${\it\alpha}=5$
, the structural stability field shows high amplitude over an area close to the rapidly rotating cylinder, extending up towards the hyperbolic point. From this and other evidence, Pralits et al. (Reference Pralits, Giannetti and Brandt2013) suggested involvement of a hyperbolic instability.
Moving away from isolated rotating cylinders, the first transition of the flow over a backward-facing step is a steady two-dimensional to steady three-dimensional transition, which can therefore be classified as a mode E transition. In this case, Barkley et al. (Reference Barkley, Gomes and Henderson2002) suggested that the underlying physical cause may be centrifugal instability. Later, Griffith et al. (Reference Griffith, Thompson, Leweke, Hourigan and Anderson2007), while examining a related flow with a similar one-sided wake, put forward the prospect that elliptic instability could be the trigger for that flow after showing that application of the generalised centrifugal theory of Bayly (Reference Bayly1988) seemed to rule out centrifugal instability, while theoretically predicted elliptic instability growth rates were consistent with numerical stability predictions. In any case, for the backward-facing step flow, the adjoint field distribution is distinctly different from that for the top half of the non-rotating cylinder flow. This causes the structural stability distribution to be maximal close to the centre of recirculation, in line with elliptic instability of a counter-rotating vortex pair. More recently, Marquet et al. (Reference Marquet, Lombardi, Chomaz, Sipp and Jacquin2009) have suggested an alternative view, interpreting mode development in terms of a non-normal lift-up mechanism, although these two viewpoints are not necessarily in contradiction.
Thus, it is plausible that the transition that has been labelled universally as mode E in this paper may be dominated by different generic physical instability mechanisms in different flow situations. A useful unifying viewpoint may be that the instability mode distribution arranges itself such that it counteracts the rotation of the fluid in recirculation zones, with an alignment such that the background strain field or proximity to a hyperbolic point causes stretching (or amplification) of the perturbation. Thus, even though for a particular transition the critical Reynolds number and preferred wavelength may vary smoothly and continuously, as a control parameter such as the cylinder rotation rate is varied smoothly, it appears that the underlying cause may be a result of a combination of basic, seemingly unrelated, physical mechanisms.
Acknowledgements
The support from Australian Research Council Discovery Grants DP130100822 and DP150102879, and computing time from the National Computational Infrastructure (NCI), Victorian Life Sciences Computation Initiative (VLSCI) and Pawsey Supercomputing Centre are gratefully acknowledged. This research was also supported in part by the Monash e-Research Centre and eSolutions-Research Support Services through the use of the Monash Campus HPC Cluster. The authors would also like to acknowledge the storage space provided via VicNode/RDSI grant allocation 2014R8.2.
