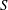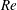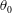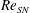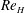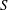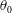1 Introduction
When its density is sufficiently low, an open jet flow can become globally unstable, transitioning from a steady state to a self-excited oscillatory state via a Hopf bifurcation (Huerre & Monkewitz Reference Huerre and Monkewitz1990). This transition has been well studied, with the self-excited state known (i) to be caused by the presence of a sufficiently large region of local absolute instability (Chomaz, Huerre & Redekopp Reference Chomaz, Huerre and Redekopp1988; Lesshafft, Huerre & Sagaut Reference Lesshafft, Huerre and Sagaut2007) and (ii) to be characterised by large-scale time-periodic axisymmetric oscillations in the near field of the jet (Sreenivasan, Raghu & Kyle Reference Sreenivasan, Raghu and Kyle1989; Monkewitz et al. Reference Monkewitz, Bechert, Barsikow and Lehmann1990; Kyle & Sreenivasan Reference Kyle and Sreenivasan1993). In some industrial applications, such as fuel injection, these oscillations are beneficial because they aid mixing. However, in other applications, such as plasma spraying, the oscillations are detrimental because they shorten the potential core. It is therefore of interest to be able to predict the onset of these global self-excited oscillations and to identify the bifurcations that cause them.
1.1 Parameters controlling the onset of global instability
The hydrodynamic stability of low-density jets has been the subject of numerous studies, including local stability analyses (Monkewitz & Sohn Reference Monkewitz and Sohn1988; Jendoubi & Strykowski Reference Jendoubi and Strykowski1994; Coenen, Sevilla & Sánchez Reference Coenen, Sevilla and Sánchez2008; Lesshafft & Marquet Reference Lesshafft and Marquet2010; Coenen & Sevilla Reference Coenen and Sevilla2012), global stability analyses (Coenen et al.
Reference Coenen, Lesshafft, Garnaud and Sevilla2017), direct numerical simulations (Lesshafft et al.
Reference Lesshafft, Huerre, Sagaut and Terracol2006, Reference Lesshafft, Huerre and Sagaut2007) and laboratory experiments (Sreenivasan et al.
Reference Sreenivasan, Raghu and Kyle1989; Monkewitz et al.
Reference Monkewitz, Bechert, Barsikow and Lehmann1990; Kyle & Sreenivasan Reference Kyle and Sreenivasan1993; Hallberg & Strykowski Reference Hallberg and Strykowski2006; Li & Juniper Reference Li and Juniper2013a
,Reference Li and Juniper
c
). From these, it is now known that the onset of global instability in axisymmetric incompressible inertial jets depends primarily on three control parameters: (i) the jet-to-ambient density ratio,
![]() $S\equiv \unicode[STIX]{x1D70C}_{j}/\unicode[STIX]{x1D70C}_{\infty }$
, (ii) the momentum thickness at the jet outlet,
$S\equiv \unicode[STIX]{x1D70C}_{j}/\unicode[STIX]{x1D70C}_{\infty }$
, (ii) the momentum thickness at the jet outlet,
![]() $\unicode[STIX]{x1D703}_{0}$
, which is conventionally expressed in inverse non-dimensional form as the transverse curvature,
$\unicode[STIX]{x1D703}_{0}$
, which is conventionally expressed in inverse non-dimensional form as the transverse curvature,
![]() $D/\unicode[STIX]{x1D703}_{0}$
, and (iii) the jet Reynolds number,
$D/\unicode[STIX]{x1D703}_{0}$
, and (iii) the jet Reynolds number,
![]() $Re\equiv \unicode[STIX]{x1D70C}_{j}U_{j}D/\unicode[STIX]{x1D707}_{j}$
, where
$Re\equiv \unicode[STIX]{x1D70C}_{j}U_{j}D/\unicode[STIX]{x1D707}_{j}$
, where
![]() $U_{j}$
is the jet centreline velocity,
$U_{j}$
is the jet centreline velocity,
![]() $D$
is the nozzle exit diameter and
$D$
is the nozzle exit diameter and
![]() $\unicode[STIX]{x1D707}_{j}$
is the dynamic viscosity of the jet fluid. The onset of global instability also depends on the shape and alignment of the velocity and density profiles, particularly their inflexion points (Raynal et al.
Reference Raynal, Harion, Favre-Marinet and Binder1996). However, when the focus is on jets with steep density profiles at the nozzle exit (e.g. jets produced from inhomogeneous gases such as those of this study), this last effect is thought to be secondary to those of the three primary control parameters listed above (
$\unicode[STIX]{x1D707}_{j}$
is the dynamic viscosity of the jet fluid. The onset of global instability also depends on the shape and alignment of the velocity and density profiles, particularly their inflexion points (Raynal et al.
Reference Raynal, Harion, Favre-Marinet and Binder1996). However, when the focus is on jets with steep density profiles at the nozzle exit (e.g. jets produced from inhomogeneous gases such as those of this study), this last effect is thought to be secondary to those of the three primary control parameters listed above (
![]() $S$
,
$S$
,
![]() $D/\unicode[STIX]{x1D703}_{0}$
,
$D/\unicode[STIX]{x1D703}_{0}$
,
![]() $Re$
; Srinivasan, Hallberg & Strykowski Reference Srinivasan, Hallberg and Strykowski2010).
$Re$
; Srinivasan, Hallberg & Strykowski Reference Srinivasan, Hallberg and Strykowski2010).
1.2 Transitioning to global instability via a Hopf bifurcation
At sufficiently low
![]() $S$
but high
$S$
but high
![]() $Re$
and
$Re$
and
![]() $D/\unicode[STIX]{x1D703}_{0}$
, a jet becomes globally unstable, transitioning from a steady state (a fixed point) to a self-excited oscillatory state (a limit cycle) via a Hopf bifurcation (Kyle & Sreenivasan Reference Kyle and Sreenivasan1993). This bifurcation is often regarded as supercritical because early experiments showed that the amplitude of the self-excited oscillations appearing just after the bifurcation point grows with the square root of a control parameter (
$D/\unicode[STIX]{x1D703}_{0}$
, a jet becomes globally unstable, transitioning from a steady state (a fixed point) to a self-excited oscillatory state (a limit cycle) via a Hopf bifurcation (Kyle & Sreenivasan Reference Kyle and Sreenivasan1993). This bifurcation is often regarded as supercritical because early experiments showed that the amplitude of the self-excited oscillations appearing just after the bifurcation point grows with the square root of a control parameter (
![]() $S$
in the case of Monkewitz et al.
Reference Monkewitz, Bechert, Barsikow and Lehmann1990, figure 8). This is the classical behaviour near a supercritical Hopf bifurcation (Huerre & Monkewitz Reference Huerre and Monkewitz1990), which can be found in many open self-excited flows, including cylinder wakes (Provansal, Mathis & Boyer Reference Provansal, Mathis and Boyer1987), cross-flowing jets (Davitian et al.
Reference Davitian, Getsinger, Hendrickson and Karagozian2010) and jet diffusion flames (Li & Juniper Reference Li and Juniper2013b
). Crucially, such supercritical behaviour can be modelled with a Landau equation containing just first- and third-order terms (Schmid & Henningson Reference Schmid and Henningson2001). For example, Raghu & Monkewitz (Reference Raghu and Monkewitz1991) experimentally measured the transient response of a hot jet at different values of
$S$
in the case of Monkewitz et al.
Reference Monkewitz, Bechert, Barsikow and Lehmann1990, figure 8). This is the classical behaviour near a supercritical Hopf bifurcation (Huerre & Monkewitz Reference Huerre and Monkewitz1990), which can be found in many open self-excited flows, including cylinder wakes (Provansal, Mathis & Boyer Reference Provansal, Mathis and Boyer1987), cross-flowing jets (Davitian et al.
Reference Davitian, Getsinger, Hendrickson and Karagozian2010) and jet diffusion flames (Li & Juniper Reference Li and Juniper2013b
). Crucially, such supercritical behaviour can be modelled with a Landau equation containing just first- and third-order terms (Schmid & Henningson Reference Schmid and Henningson2001). For example, Raghu & Monkewitz (Reference Raghu and Monkewitz1991) experimentally measured the transient response of a hot jet at different values of
![]() $S$
, determining all of the coefficients in the cubic Landau equation.
$S$
, determining all of the coefficients in the cubic Landau equation.
Despite the apparent prevalence of supercritical bifurcations in low-density jets, the existence of subcritical bifurcations has been suggested before. In experiments on helium–air jets, Sreenivasan et al. (Reference Sreenivasan, Raghu and Kyle1989, figure 4) found hysteresis in the lower global-instability boundary of the
![]() $S$
–
$S$
–
![]() $M$
plane, where
$M$
plane, where
![]() $M$
denotes the Mach number (unlike us, they were investigating compressible jets). The position of this boundary was observed to change depending on the direction from which it was approached, resulting in a hysteretic region of conditional stability. Later, Kyle & Sreenivasan (Reference Kyle and Sreenivasan1993) suggested that those hysteretic transitions should have been treated as subcritical Hopf bifurcations. However, to date, no studies have been carried out (i) to establish the existence of subcritical Hopf bifurcations in low-density jets, particularly with theoretical support from the Landau model, and (ii) to determine the specific flow conditions under which such bifurcations occur.
$M$
denotes the Mach number (unlike us, they were investigating compressible jets). The position of this boundary was observed to change depending on the direction from which it was approached, resulting in a hysteretic region of conditional stability. Later, Kyle & Sreenivasan (Reference Kyle and Sreenivasan1993) suggested that those hysteretic transitions should have been treated as subcritical Hopf bifurcations. However, to date, no studies have been carried out (i) to establish the existence of subcritical Hopf bifurcations in low-density jets, particularly with theoretical support from the Landau model, and (ii) to determine the specific flow conditions under which such bifurcations occur.
1.3 Universality of global instability
In experiments on helium–nitrogen jets, Hallberg & Strykowski (Reference Hallberg and Strykowski2006) identified a universal scaling for the frequency (
![]() $f$
) of the global mode – similar in spirit to the classical Strouhal–Reynolds number scaling found in von Kármán vortex shedding. Their scaling used all three of the main control parameters,
$f$
) of the global mode – similar in spirit to the classical Strouhal–Reynolds number scaling found in von Kármán vortex shedding. Their scaling used all three of the main control parameters,
![]() $fD^{2}/\unicode[STIX]{x1D708}\sim Re(D/\unicode[STIX]{x1D703}_{0})^{1/2}(1+S^{1/2})$
, with
$fD^{2}/\unicode[STIX]{x1D708}\sim Re(D/\unicode[STIX]{x1D703}_{0})^{1/2}(1+S^{1/2})$
, with
![]() $\unicode[STIX]{x1D708}$
being the kinematic viscosity, enabling the global frequency to be uniquely predicted. The specific form of this scaling arose from considerations of the centripetal acceleration induced by the streamwise curvature of a jet column undergoing axisymmetric oscillations. Data from the experiments of Monkewitz et al. (Reference Monkewitz, Bechert, Barsikow and Lehmann1990) and Kyle & Sreenivasan (Reference Kyle and Sreenivasan1993) were shown to follow the same scaling, strengthening its universality in low-density jets with initially steep density profiles. Hallberg & Strykowski (Reference Hallberg and Strykowski2006) remarked that the fact that the control parameters used in their scaling were measured at the jet outlet showed that the frequency-selection mechanism proposed by Pier & Huerre (Reference Pier and Huerre2001) for wakes – i.e. the global frequency is determined by the first streamwise station with a non-negative absolute growth rate – is also valid for low-density jets. However, despite this success with the global-frequency scaling, a similar scaling for the onset of global instability has yet to be established.
$\unicode[STIX]{x1D708}$
being the kinematic viscosity, enabling the global frequency to be uniquely predicted. The specific form of this scaling arose from considerations of the centripetal acceleration induced by the streamwise curvature of a jet column undergoing axisymmetric oscillations. Data from the experiments of Monkewitz et al. (Reference Monkewitz, Bechert, Barsikow and Lehmann1990) and Kyle & Sreenivasan (Reference Kyle and Sreenivasan1993) were shown to follow the same scaling, strengthening its universality in low-density jets with initially steep density profiles. Hallberg & Strykowski (Reference Hallberg and Strykowski2006) remarked that the fact that the control parameters used in their scaling were measured at the jet outlet showed that the frequency-selection mechanism proposed by Pier & Huerre (Reference Pier and Huerre2001) for wakes – i.e. the global frequency is determined by the first streamwise station with a non-negative absolute growth rate – is also valid for low-density jets. However, despite this success with the global-frequency scaling, a similar scaling for the onset of global instability has yet to be established.
1.4 Contributions of the present study
In this study, we answer two questions on the global instability of low-density jets.
-
(i) Self-excited oscillations in low-density jets have been known to arise through supercritical Hopf bifurcations (§ 1.2), but can they arise through subcritical Hopf bifurcations as well? If so, under what conditions? It is important to know this because (
 $a$
) at a subcritical Hopf point, the oscillation amplitude jumps without any forewarning and cannot return to its initial steady-state value with just a small adjustment of the control parameters, and (
$a$
) at a subcritical Hopf point, the oscillation amplitude jumps without any forewarning and cannot return to its initial steady-state value with just a small adjustment of the control parameters, and (
 $b$
) a small perturbation can cause a bistable system to develop large self-excited oscillations, despite the system being linearly stable, in a process known as triggering (Strogatz Reference Strogatz1994). If subcritical bifurcations could be shown to exist in low-density jets, it would be useful to know for the purposes of low-order modelling and flow control whether they obey a truncated Landau equation – much as supercritical bifurcations do (§ 1.2). However, as we will show in § 3, subcritical bifurcations should be modelled differently from supercritical bifurcations, as the latter rely on cubic saturation whereas the former rely on quintic (or higher-order) saturation. It is therefore important to know whether the Hopf bifurcation in a low-density jet is supercritical or subcritical.
$b$
) a small perturbation can cause a bistable system to develop large self-excited oscillations, despite the system being linearly stable, in a process known as triggering (Strogatz Reference Strogatz1994). If subcritical bifurcations could be shown to exist in low-density jets, it would be useful to know for the purposes of low-order modelling and flow control whether they obey a truncated Landau equation – much as supercritical bifurcations do (§ 1.2). However, as we will show in § 3, subcritical bifurcations should be modelled differently from supercritical bifurcations, as the latter rely on cubic saturation whereas the former rely on quintic (or higher-order) saturation. It is therefore important to know whether the Hopf bifurcation in a low-density jet is supercritical or subcritical. -
(ii) Hallberg & Strykowski (Reference Hallberg and Strykowski2006) were able to establish a universal scaling for the global frequency (§ 1.3), but is it possible to establish a similarly universal scaling for the onset of global instability? To the best of our knowledge, this has not been explored before, but is of both practical and scientific importance, especially for prediction of the emergence of global modes and for an understanding of their universality in low-density jets.
Below, we will describe our experimental set-up (§ 2) and the Landau model (§ 3), present the first definitive evidence of subcritical Hopf bifurcations in low-density jets (§ 4.1) and propose a universal scaling for the onset of global instability in such jets (§ 4.2).
2 Experimental set-up
Our experimental set-up consists of a helium–air jet issuing into quiescent ambient air (293 K) from an axisymmetric convergent nozzle (figure 1). The nozzle has a 100 : 1 area contraction defined by a fifth-order polynomial (
![]() $D=6$
mm), producing a top-hat velocity profile with thin shear layers. This aids the detection of global oscillations by (i) reducing the critical
$D=6$
mm), producing a top-hat velocity profile with thin shear layers. This aids the detection of global oscillations by (i) reducing the critical
![]() $Re$
and thus the amplification of inherent disturbances by convective modes (Hallberg et al.
Reference Hallberg, Srinivasan, Gorse and Strykowski2007) and (ii) creating a quiet base flow with laminar shear layers. As figure 2 shows, the normalised velocity fluctuation in the jet core is small (
$Re$
and thus the amplification of inherent disturbances by convective modes (Hallberg et al.
Reference Hallberg, Srinivasan, Gorse and Strykowski2007) and (ii) creating a quiet base flow with laminar shear layers. As figure 2 shows, the normalised velocity fluctuation in the jet core is small (
![]() $u_{rms}^{\prime }/\overline{u}<0.33\,\%$
) and the transverse curvature scales as
$u_{rms}^{\prime }/\overline{u}<0.33\,\%$
) and the transverse curvature scales as
![]() $D/\unicode[STIX]{x1D703}_{0}\sim Re^{1/2}$
for all nozzle extensions (described below), indicating that the shear layers are indeed initially laminar.
$D/\unicode[STIX]{x1D703}_{0}\sim Re^{1/2}$
for all nozzle extensions (described below), indicating that the shear layers are indeed initially laminar.

Figure 1. A schematic of the experimental set-up (schlieren optics not shown). MFC: mass flow controller.

Figure 2. Base-flow characterisation and nozzle calibration: (a) normalised velocity fluctuation as a function of radial position for
![]() $L/D=4$
and (b) transverse curvature as a function of the square root of the Reynolds number for six different extension lengths. The data are taken from a hot wire positioned at the nozzle exit (
$L/D=4$
and (b) transverse curvature as a function of the square root of the Reynolds number for six different extension lengths. The data are taken from a hot wire positioned at the nozzle exit (
![]() $x/D\approx 0$
) with air (
$x/D\approx 0$
) with air (
![]() $S=1$
) as the jet fluid. The linear fits in (b) show that the shear layers are initially laminar.
$S=1$
) as the jet fluid. The linear fits in (b) show that the shear layers are initially laminar.
At the flow conditions of this study, the jet is incompressible (low Mach number,
![]() $M\equiv U_{j}/c_{j}<9.7\times 10^{-2}$
) and momentum dominated (low Richardson number,
$M\equiv U_{j}/c_{j}<9.7\times 10^{-2}$
) and momentum dominated (low Richardson number,
![]() $Ri\equiv gD(\unicode[STIX]{x1D70C}_{\infty }-\unicode[STIX]{x1D70C}_{j})/\unicode[STIX]{x1D70C}_{j}U_{j}^{2}<3.8\times 10^{-3}$
), so that the primary control parameters are
$Ri\equiv gD(\unicode[STIX]{x1D70C}_{\infty }-\unicode[STIX]{x1D70C}_{j})/\unicode[STIX]{x1D70C}_{j}U_{j}^{2}<3.8\times 10^{-3}$
), so that the primary control parameters are
![]() $S$
,
$S$
,
![]() $D/\unicode[STIX]{x1D703}_{0}$
and
$D/\unicode[STIX]{x1D703}_{0}$
and
![]() $Re$
(§ 1.1). Our jet facility is designed to enable each of these parameters to be varied over a wide range (
$Re$
(§ 1.1). Our jet facility is designed to enable each of these parameters to be varied over a wide range (
![]() $0.14<S<0.45$
;
$0.14<S<0.45$
;
![]() $14.3<D/\unicode[STIX]{x1D703}_{0}<65.2$
;
$14.3<D/\unicode[STIX]{x1D703}_{0}<65.2$
;
![]() $490<Re<7570$
) but independently of the others, so as to isolate their individual effects. For example, we vary
$490<Re<7570$
) but independently of the others, so as to isolate their individual effects. For example, we vary
![]() $S$
by varying the composition of the jet fluid (a helium–air mixture) with mass flow controllers (
$S$
by varying the composition of the jet fluid (a helium–air mixture) with mass flow controllers (
![]() $\pm 0.2\,\%$
). To decouple
$\pm 0.2\,\%$
). To decouple
![]() $D/\unicode[STIX]{x1D703}_{0}$
from
$D/\unicode[STIX]{x1D703}_{0}$
from
![]() $Re$
, we use interchangeable nozzle extensions in the form of six brass tubes of different lengths,
$Re$
, we use interchangeable nozzle extensions in the form of six brass tubes of different lengths,
![]() $L/D=1$
–32 (see the inset of figure 1). These tubes have straight cylindrical interiors with the same inner diameter as the contraction outlet (
$L/D=1$
–32 (see the inset of figure 1). These tubes have straight cylindrical interiors with the same inner diameter as the contraction outlet (
![]() $D=6$
mm), ensuring a smooth transition between the two sections without a discontinuity in wall slope. For consistent entrainment around the jet base, the tube exteriors are machined to a sharp knife edge with a constant linear taper. Figure 2(b) shows our nozzle calibration. At a fixed
$D=6$
mm), ensuring a smooth transition between the two sections without a discontinuity in wall slope. For consistent entrainment around the jet base, the tube exteriors are machined to a sharp knife edge with a constant linear taper. Figure 2(b) shows our nozzle calibration. At a fixed
![]() $Re$
, a longer extension gives the boundary layer more time to grow, reducing
$Re$
, a longer extension gives the boundary layer more time to grow, reducing
![]() $D/\unicode[STIX]{x1D703}_{0}$
. In this study, the momentum thickness is defined at the jet outlet (
$D/\unicode[STIX]{x1D703}_{0}$
. In this study, the momentum thickness is defined at the jet outlet (
![]() $x/D\approx 0$
) as
$x/D\approx 0$
) as
![]() $\unicode[STIX]{x1D703}_{0}=\int _{0}^{r_{0.2}}u(r)/U_{j}[1-u(r)/U_{j}]\,\text{d}r$
, where
$\unicode[STIX]{x1D703}_{0}=\int _{0}^{r_{0.2}}u(r)/U_{j}[1-u(r)/U_{j}]\,\text{d}r$
, where
![]() $r_{0.2}$
is the radial location where
$r_{0.2}$
is the radial location where
![]() $u(r)=0.2U_{j}$
.
$u(r)=0.2U_{j}$
.
To measure the jet dynamics, we use a calibrated hot wire positioned in the wavemaker region,
![]() $(x/D,r/D)=(1.5,0)$
. We choose this location because it is far enough downstream for global modes to emerge (Li & Juniper Reference Li and Juniper2013a
) but is still within the potential core, enabling the hot wire to detect only velocity fluctuations, not concentration fluctuations. For each run, we digitise the hot-wire voltage at 32 768 Hz (
$(x/D,r/D)=(1.5,0)$
. We choose this location because it is far enough downstream for global modes to emerge (Li & Juniper Reference Li and Juniper2013a
) but is still within the potential core, enabling the hot wire to detect only velocity fluctuations, not concentration fluctuations. For each run, we digitise the hot-wire voltage at 32 768 Hz (
![]() ${>}10f$
) for 8 s on a 16-bit data acquisition system, producing a time series of the local streamwise velocity,
${>}10f$
) for 8 s on a 16-bit data acquisition system, producing a time series of the local streamwise velocity,
![]() $u(t)$
. For reliable statistics, we repeat this at least five times at every flow condition. It is well known that global instability can arise not only from upstream-propagating vorticity waves, but also from irrotational pressure feedback (Huerre & Monkewitz Reference Huerre and Monkewitz1990), as could be induced, for example, by a solid object placed in a shear flow (Rockwell & Naudascher Reference Rockwell and Naudascher1979). To rule out the possibility of such edge tones occurring in our set-up, we repeat the experiments using time-resolved schlieren imaging without the hot wire in the flow. The results indicate that the physical presence of the hot wire does not have a statistically significant influence on the global frequency or the bifurcation properties.
$u(t)$
. For reliable statistics, we repeat this at least five times at every flow condition. It is well known that global instability can arise not only from upstream-propagating vorticity waves, but also from irrotational pressure feedback (Huerre & Monkewitz Reference Huerre and Monkewitz1990), as could be induced, for example, by a solid object placed in a shear flow (Rockwell & Naudascher Reference Rockwell and Naudascher1979). To rule out the possibility of such edge tones occurring in our set-up, we repeat the experiments using time-resolved schlieren imaging without the hot wire in the flow. The results indicate that the physical presence of the hot wire does not have a statistically significant influence on the global frequency or the bifurcation properties.
3 Application of the Landau model
We use the Landau model to study the nonlinear amplitude evolution of a global mode near its bifurcation points, providing an analytical means to differentiate between supercritical and subcritical bifurcations. A full description of this model and its application to hydrodynamics, including its derivation from the Navier–Stokes equations, can be found in Provansal et al. (Reference Provansal, Mathis and Boyer1987) and Sipp & Lebedev (Reference Sipp and Lebedev2007). The Landau model has the form
where
![]() $A(t)$
is the complex mode amplitude of a perturbation over the base flow,
$A(t)$
is the complex mode amplitude of a perturbation over the base flow,
![]() $\unicode[STIX]{x1D70E}$
is the linear temporal growth rate,
$\unicode[STIX]{x1D70E}$
is the linear temporal growth rate,
![]() $\unicode[STIX]{x1D714}$
is the linear angular frequency and
$\unicode[STIX]{x1D714}$
is the linear angular frequency and
![]() $c$
is the Landau constant, a dimensionless quantity that modifies the oscillation frequency at saturation.
$c$
is the Landau constant, a dimensionless quantity that modifies the oscillation frequency at saturation.
The super/subcritical nature of a bifurcation depends on the sign of
![]() $l$
. If
$l$
. If
![]() $l>0$
, the bifurcation is supercritical (non-hysteretic), and a truncation to third order should sufficiently describe the nonlinear behaviour near the bifurcation point, where the saturated amplitude is still small (Dušek, Le Gal & Fraunié Reference Dušek, Le Gal and Fraunié1994). If
$l>0$
, the bifurcation is supercritical (non-hysteretic), and a truncation to third order should sufficiently describe the nonlinear behaviour near the bifurcation point, where the saturated amplitude is still small (Dušek, Le Gal & Fraunié Reference Dušek, Le Gal and Fraunié1994). If
![]() $l<0$
, however, the bifurcation is subcritical (hysteretic), with the cubic term accelerating the growth of the perturbation, so quintic or even higher-order terms are needed for saturation.
$l<0$
, however, the bifurcation is subcritical (hysteretic), with the cubic term accelerating the growth of the perturbation, so quintic or even higher-order terms are needed for saturation.
Following Sheard, Thompson & Hourigan (Reference Sheard, Thompson and Hourigan2004), we consider only the real part of the Landau model,
By plotting
![]() $\text{d}\log |A|/\text{d}t$
against
$\text{d}\log |A|/\text{d}t$
against
![]() $|A|^{2}$
using our experimental data, we will determine in § 4.1 the super/subcritical nature of a bifurcation via inspection of the slope at small
$|A|^{2}$
using our experimental data, we will determine in § 4.1 the super/subcritical nature of a bifurcation via inspection of the slope at small
![]() $|A|^{2}$
, i.e. near the vertical axis. For supercritical bifurcations, the initial slope should be negative (
$|A|^{2}$
, i.e. near the vertical axis. For supercritical bifurcations, the initial slope should be negative (
![]() $l>0$
), followed by linear behaviour if a cubic truncation holds. For subcritical bifurcations, the initial slope should be positive (
$l>0$
), followed by linear behaviour if a cubic truncation holds. For subcritical bifurcations, the initial slope should be positive (
![]() $l<0$
), followed by nonlinear behaviour because at least quintic terms are needed to capture the saturation characteristics, such as the saturated amplitude, the saddle-node point and the bistable region. As mentioned earlier, this is one of the reasons why it is important to distinguish between supercritical and subcritical bifurcations, regardless of the size of the bistable region.
$l<0$
), followed by nonlinear behaviour because at least quintic terms are needed to capture the saturation characteristics, such as the saturated amplitude, the saddle-node point and the bistable region. As mentioned earlier, this is one of the reasons why it is important to distinguish between supercritical and subcritical bifurcations, regardless of the size of the bistable region.
4 Results and discussion
4.1 Supercritical and subcritical Hopf bifurcations
Figure 3 shows the two different types of Hopf bifurcation seen in our experiments: supercritical (a,b) and subcritical (c,d). These are distinguished by their bifurcation diagrams (a,c), which are produced by increasing and decreasing
![]() $Re$
, and hence
$Re$
, and hence
![]() $D/\unicode[STIX]{x1D703}_{0}$
, while keeping
$D/\unicode[STIX]{x1D703}_{0}$
, while keeping
![]() $S$
and
$S$
and
![]() $L/D$
fixed. The vertical axis is the amplitude of the velocity fluctuation normalised by the time-averaged velocity,
$L/D$
fixed. The vertical axis is the amplitude of the velocity fluctuation normalised by the time-averaged velocity,
![]() $|A|\equiv |u^{\prime }|/\overline{u}$
. Also shown are the amplitude evolution and its time derivative (b,d), which are measured in transient experiments performed at the onset of global instability (figure 3
a,c, moving forward from the Hopf point along the blue arrow, due to an impulsive increase in flow rate) and are used to verify the super/subcritical nature of the bifurcation via the Landau model (as per § 3). We examine the two types of bifurcation in turn.
$|A|\equiv |u^{\prime }|/\overline{u}$
. Also shown are the amplitude evolution and its time derivative (b,d), which are measured in transient experiments performed at the onset of global instability (figure 3
a,c, moving forward from the Hopf point along the blue arrow, due to an impulsive increase in flow rate) and are used to verify the super/subcritical nature of the bifurcation via the Landau model (as per § 3). We examine the two types of bifurcation in turn.

Figure 3. (a,c) Bifurcation diagram and (b,d) derivative of the amplitude evolution for a low-density jet at
![]() $S=0.14$
produced by two nozzle extensions: (a,b)
$S=0.14$
produced by two nozzle extensions: (a,b)
![]() $L/D=1$
, for which the Hopf bifurcation is supercritical, and (c,d)
$L/D=1$
, for which the Hopf bifurcation is supercritical, and (c,d)
![]() $L/D=4$
, for which it is subcritical. In (b,d), the dashed grey line is a local linear fit showing the slope and extent of linearity at small
$L/D=4$
, for which it is subcritical. In (b,d), the dashed grey line is a local linear fit showing the slope and extent of linearity at small
![]() $|A|^{2}$
, which is used for comparison with the Landau model (§ 3). In the insets of (b,d), the red line is a time trace of the normalised velocity fluctuation, the blue line is its instantaneous amplitude and the vertical dashed line shows when the amplitude first rises above the noise floor, indicating the start of the growth phase for plotting
$|A|^{2}$
, which is used for comparison with the Landau model (§ 3). In the insets of (b,d), the red line is a time trace of the normalised velocity fluctuation, the blue line is its instantaneous amplitude and the vertical dashed line shows when the amplitude first rises above the noise floor, indicating the start of the growth phase for plotting
![]() $\text{d}\log |A|/\text{d}t$
versus
$\text{d}\log |A|/\text{d}t$
versus
![]() $|A|^{2}$
.
$|A|^{2}$
.

Figure 4. Universal scaling of the onset of global instability in a low-density jet: global-instability maps at (a)
![]() $S=0.14$
and (b–d)
$S=0.14$
and (b–d)
![]() $S=0.14$
–0.60, with hollow markers denoting subcritical bifurcations and solid markers denoting supercritical bifurcations. The error bars are smaller than the markers themselves, so are not shown separately. Also shown are least-squares fits to the Hopf points at constant
$S=0.14$
–0.60, with hollow markers denoting subcritical bifurcations and solid markers denoting supercritical bifurcations. The error bars are smaller than the markers themselves, so are not shown separately. Also shown are least-squares fits to the Hopf points at constant
![]() $S$
, which are hyperbolic in (a,b) (dashed–dotted lines) but linear in (c,d) (solid lines). Panels (b–d) share a common legend. In (d), our proposed scaling is represented by a solid purple line, which is extended beyond the actual range of our data with dotted lines to facilitate comparisons with previous experiments and numerical global stability analyses. The schlieren images show the two different states of the jet. The globally stable state is characterised by a steady potential core, whereas the globally unstable state is characterised by axisymmetric oscillations in the wavemaker region, followed by three-dimensional side jets and then turbulence in the far field.
$S$
, which are hyperbolic in (a,b) (dashed–dotted lines) but linear in (c,d) (solid lines). Panels (b–d) share a common legend. In (d), our proposed scaling is represented by a solid purple line, which is extended beyond the actual range of our data with dotted lines to facilitate comparisons with previous experiments and numerical global stability analyses. The schlieren images show the two different states of the jet. The globally stable state is characterised by a steady potential core, whereas the globally unstable state is characterised by axisymmetric oscillations in the wavemaker region, followed by three-dimensional side jets and then turbulence in the far field.
-
(i) Supercritical bifurcation (figure 3 a,b). At this flow condition (
 $S=0.14$
,
$S=0.14$
,
 $L/D=1$
), the bifurcation diagram shows
$L/D=1$
), the bifurcation diagram shows
 $|A|$
increasing and decreasing along the same path, with the forward bifurcation occurring at the same Hopf point as the backward bifurcation, indicating the absence of hysteresis. The increase/decrease in
$|A|$
increasing and decreasing along the same path, with the forward bifurcation occurring at the same Hopf point as the backward bifurcation, indicating the absence of hysteresis. The increase/decrease in
 $|A|$
scales with the square root of the control parameters. This is the classical behaviour near a supercritical Hopf bifurcation and has been seen before in other open shear flows (§ 1.2). Crucially, it can be modelled with a cubic Landau equation (§ 3). The insets of figure 3(b) show the jet bifurcating from a fixed point to a limit cycle, with
$|A|$
scales with the square root of the control parameters. This is the classical behaviour near a supercritical Hopf bifurcation and has been seen before in other open shear flows (§ 1.2). Crucially, it can be modelled with a cubic Landau equation (§ 3). The insets of figure 3(b) show the jet bifurcating from a fixed point to a limit cycle, with
 $A$
growing and saturating with time. In the plot of
$A$
growing and saturating with time. In the plot of
 $\text{d}\log |A|/\text{d}t$
versus
$\text{d}\log |A|/\text{d}t$
versus
 $|A|^{2}$
, the negative slope (
$|A|^{2}$
, the negative slope (
 $-l=-49.0~\text{s}^{-1}$
) and linear behaviour near the vertical axis (i.e. the linear fit is satisfied up to
$-l=-49.0~\text{s}^{-1}$
) and linear behaviour near the vertical axis (i.e. the linear fit is satisfied up to
 $|A|^{2}\approx 2\times 10^{-3}$
) confirm via the Landau model that this Hopf bifurcation is supercritical (§ 3).
$|A|^{2}\approx 2\times 10^{-3}$
) confirm via the Landau model that this Hopf bifurcation is supercritical (§ 3). -
(ii) Subcritical bifurcation (figure 3 c,d). At a different flow condition (
 $S=0.14$
,
$S=0.14$
,
 $L/D=4$
), the bifurcation diagram shows
$L/D=4$
), the bifurcation diagram shows
 $|A|$
increasing and decreasing along different paths, with the forward bifurcation (Hopf point) occurring at higher
$|A|$
increasing and decreasing along different paths, with the forward bifurcation (Hopf point) occurring at higher
 $D/\unicode[STIX]{x1D703}_{0}$
and
$D/\unicode[STIX]{x1D703}_{0}$
and
 $Re$
values than the backward bifurcation (saddle-node point), indicating the presence of a hysteretic bistable region (shaded in grey). This is the classical behaviour near a subcritical Hopf bifurcation, which has been seen in wake flows (Sheard et al.
Reference Sheard, Thompson and Hourigan2004) but has yet to be established in jet flows (§ 1.2). In figure 3(d), the positive slope (
$Re$
values than the backward bifurcation (saddle-node point), indicating the presence of a hysteretic bistable region (shaded in grey). This is the classical behaviour near a subcritical Hopf bifurcation, which has been seen in wake flows (Sheard et al.
Reference Sheard, Thompson and Hourigan2004) but has yet to be established in jet flows (§ 1.2). In figure 3(d), the positive slope (
 $-l=638.9~\text{s}^{-1}$
) and nonlinear behaviour near the vertical axis (i.e. deviation from the linear fit occurs at small
$-l=638.9~\text{s}^{-1}$
) and nonlinear behaviour near the vertical axis (i.e. deviation from the linear fit occurs at small
 $|A|^{2}$
) confirm via the Landau model that this Hopf bifurcation is subcritical (§ 3).
$|A|^{2}$
) confirm via the Landau model that this Hopf bifurcation is subcritical (§ 3).
To the best of our knowledge, this is the first definitive evidence of a subcritical Hopf bifurcation occurring in a low-density jet that is from experiments supported by a theoretical model. In fact, as figure 4(b) will show, most of the bifurcations (32 out of 45) in our experiments are subcritical. This is unexpected, as the default assumption in previous studies on low-density jets has been that their bifurcations are supercritical (§ 1.2). This discrepancy could be due to two reasons: (i) the small width of the bistable region – typically we find
![]() $(Re_{H}-Re_{SN})/Re_{H}\approx 2\,\%$
–5 %, where the subscripts
$(Re_{H}-Re_{SN})/Re_{H}\approx 2\,\%$
–5 %, where the subscripts
![]() $H$
and
$H$
and
![]() $SN$
denote the Hopf and saddle-node points respectively – and (ii) our deliberate use of extremely small increments in the control parameters – typically we use
$SN$
denote the Hopf and saddle-node points respectively – and (ii) our deliberate use of extremely small increments in the control parameters – typically we use
![]() $\unicode[STIX]{x0394}Re/Re_{H}\approx 0.2\,\%$
–0.5 %, which approaches the uncertainty limits of most mass flow controllers, including ours (§ 2). It is thus plausible that bistable regions existed in previous studies but were overlooked due to the use of insufficiently small control increments. We note that despite the small width of the bistable region, it is still important to know whether the Hopf bifurcation is supercritical or subcritical, not least because the two require different modelling treatments (§ 3).
$\unicode[STIX]{x0394}Re/Re_{H}\approx 0.2\,\%$
–0.5 %, which approaches the uncertainty limits of most mass flow controllers, including ours (§ 2). It is thus plausible that bistable regions existed in previous studies but were overlooked due to the use of insufficiently small control increments. We note that despite the small width of the bistable region, it is still important to know whether the Hopf bifurcation is supercritical or subcritical, not least because the two require different modelling treatments (§ 3).
In addition to subcritical bifurcations, supercritical bifurcations can also be found, albeit mainly for the shortest and longest nozzle extensions (figure 4). For the longest extension (
![]() $L/D=32$
), we attribute this to the greater length available for spatial amplification of background noise by convective instabilities within the nozzle. This could be compounded by the higher spatial growth rates expected at the higher critical
$L/D=32$
), we attribute this to the greater length available for spatial amplification of background noise by convective instabilities within the nozzle. This could be compounded by the higher spatial growth rates expected at the higher critical
![]() $Re_{H}$
arising from the longer
$Re_{H}$
arising from the longer
![]() $L/D$
and lower
$L/D$
and lower
![]() $D/\unicode[STIX]{x1D703}_{0}$
(Hallberg et al.
Reference Hallberg, Srinivasan, Gorse and Strykowski2007). Studies on the Duffing–van der Pol oscillator (Zakharova et al.
Reference Zakharova, Vadivasova, Anishchenko, Koseska and Kurths2010) and thermoacoustic systems (Gopalakrishnan & Sujith Reference Gopalakrishnan and Sujith2015) have shown that such noise amplification can induce triggering, reducing the effective width of the bistable region, making subcritical bifurcations appear like supercritical bifurcations. Although not shown here, our base-flow measurements at
$D/\unicode[STIX]{x1D703}_{0}$
(Hallberg et al.
Reference Hallberg, Srinivasan, Gorse and Strykowski2007). Studies on the Duffing–van der Pol oscillator (Zakharova et al.
Reference Zakharova, Vadivasova, Anishchenko, Koseska and Kurths2010) and thermoacoustic systems (Gopalakrishnan & Sujith Reference Gopalakrishnan and Sujith2015) have shown that such noise amplification can induce triggering, reducing the effective width of the bistable region, making subcritical bifurcations appear like supercritical bifurcations. Although not shown here, our base-flow measurements at
![]() $x/D\approx 0$
support this hypothesis by showing that the normalised velocity fluctuation in the shear layers increases with
$x/D\approx 0$
support this hypothesis by showing that the normalised velocity fluctuation in the shear layers increases with
![]() $L/D$
. For the shortest extension (
$L/D$
. For the shortest extension (
![]() $L/D=1$
), which is the nozzle configuration most similar to those of previous studies in which only supercritical bifurcations were found, we believe that the bifurcations are genuinely supercritical. We speculate that this could be due to the particularly thin shear layers and the way in which they modify the shape and alignment of the velocity profile with respect to the density profile. This has been shown to influence the local – and therefore global – instability properties in a non-trivial manner (Raynal et al.
Reference Raynal, Harion, Favre-Marinet and Binder1996; Coenen et al.
Reference Coenen, Sevilla and Sánchez2008; Lesshafft & Marquet Reference Lesshafft and Marquet2010; Srinivasan et al.
Reference Srinivasan, Hallberg and Strykowski2010; Coenen & Sevilla Reference Coenen and Sevilla2012).
$L/D=1$
), which is the nozzle configuration most similar to those of previous studies in which only supercritical bifurcations were found, we believe that the bifurcations are genuinely supercritical. We speculate that this could be due to the particularly thin shear layers and the way in which they modify the shape and alignment of the velocity profile with respect to the density profile. This has been shown to influence the local – and therefore global – instability properties in a non-trivial manner (Raynal et al.
Reference Raynal, Harion, Favre-Marinet and Binder1996; Coenen et al.
Reference Coenen, Sevilla and Sánchez2008; Lesshafft & Marquet Reference Lesshafft and Marquet2010; Srinivasan et al.
Reference Srinivasan, Hallberg and Strykowski2010; Coenen & Sevilla Reference Coenen and Sevilla2012).
4.2 Universal scaling of the critical Reynolds number
Figure 4(a) shows the states and bifurcation points of the jet in the
![]() $D/\unicode[STIX]{x1D703}_{0}$
–
$D/\unicode[STIX]{x1D703}_{0}$
–
![]() $Re$
domain at
$Re$
domain at
![]() $S=0.14$
. The global-instability boundary, defined by the Hopf-point trajectory or
$S=0.14$
. The global-instability boundary, defined by the Hopf-point trajectory or
![]() $Re_{H}$
(black dashed–dotted line), scales hyperbolically with
$Re_{H}$
(black dashed–dotted line), scales hyperbolically with
![]() $D/\unicode[STIX]{x1D703}_{0}$
, with regions to its upper right being globally unstable (stable limit cycle) and regions to its lower left being globally stable (stable fixed point). As the bistable region is small (
$D/\unicode[STIX]{x1D703}_{0}$
, with regions to its upper right being globally unstable (stable limit cycle) and regions to its lower left being globally stable (stable fixed point). As the bistable region is small (
![]() ${\approx}2\,\%$
–5 % of
${\approx}2\,\%$
–5 % of
![]() $Re_{H}$
), the Hopf and saddle-node points appear to coincide but actually do not (see inset).
$Re_{H}$
), the Hopf and saddle-node points appear to coincide but actually do not (see inset).
The hyperbolic scaling identified in figure 4(a) applies to all eight density ratios of this study (
![]() $S=0.14$
–0.45), as can be seen in the global-instability map of figure 4(b). To collapse the data, we exploit the hyperbolic scaling by changing the vertical axis to the inverse of the Reynolds number at the Hopf point (
$S=0.14$
–0.45), as can be seen in the global-instability map of figure 4(b). To collapse the data, we exploit the hyperbolic scaling by changing the vertical axis to the inverse of the Reynolds number at the Hopf point (
![]() $Re_{H}^{-1}$
), producing a linear fit for each value of
$Re_{H}^{-1}$
), producing a linear fit for each value of
![]() $S$
, figure 4(c). Recognising that the slopes of these linear fits increase with decreasing
$S$
, figure 4(c). Recognising that the slopes of these linear fits increase with decreasing
![]() $S$
, we tried including various forms of
$S$
, we tried including various forms of
![]() $S$
in the functional dependence – including those used by Hallberg & Strykowski (Reference Hallberg and Strykowski2006) to scale the global frequency – but found that the optimal data collapse occurred with
$S$
in the functional dependence – including those used by Hallberg & Strykowski (Reference Hallberg and Strykowski2006) to scale the global frequency – but found that the optimal data collapse occurred with
![]() $\unicode[STIX]{x0394}S=(S^{-1}-1)$
$\unicode[STIX]{x0394}S=(S^{-1}-1)$
![]() $=(\unicode[STIX]{x1D70C}_{\infty }-\unicode[STIX]{x1D70C}_{j})/\unicode[STIX]{x1D70C}_{j}$
, which is simply the non-dimensional density difference. Using this difference, we show in figure 4(d) the collapse of all 45 Hopf points onto a single line. A least-squares regression gives a linear relationship of the form
$=(\unicode[STIX]{x1D70C}_{\infty }-\unicode[STIX]{x1D70C}_{j})/\unicode[STIX]{x1D70C}_{j}$
, which is simply the non-dimensional density difference. Using this difference, we show in figure 4(d) the collapse of all 45 Hopf points onto a single line. A least-squares regression gives a linear relationship of the form
![]() $Re_{H}^{-1}=a+b(D/\unicode[STIX]{x1D703}_{0})(S^{-1}-1)$
, where
$Re_{H}^{-1}=a+b(D/\unicode[STIX]{x1D703}_{0})(S^{-1}-1)$
, where
![]() $a=-3.785\times 10^{-4}$
and
$a=-3.785\times 10^{-4}$
and
![]() $b=1.019\times 10^{-5}$
, with a correlation coefficient of 0.986. Both supercritical (solid markers) and subcritical (hollow markers) Hopf points follow the same scaling, indicating its insensitivity to the super/subcritical nature of the bifurcation.
$b=1.019\times 10^{-5}$
, with a correlation coefficient of 0.986. Both supercritical (solid markers) and subcritical (hollow markers) Hopf points follow the same scaling, indicating its insensitivity to the super/subcritical nature of the bifurcation.
For comparison with previous experiments, we include in figure 4(d) the Hopf points of Kyle & Sreenivasan (Reference Kyle and Sreenivasan1993), Hallberg & Strykowski (Reference Hallberg and Strykowski2006) and Hallberg et al. (Reference Hallberg, Srinivasan, Gorse and Strykowski2007). These all follow our proposed scaling fairly well. We further validate our data in the frequency domain against the global-frequency scaling of Hallberg & Strykowski (Reference Hallberg and Strykowski2006); the results (not shown in the interests of brevity) are also in good agreement.
For comparison with numerical global stability analyses, we include in figure 4(d) the linear neutral points of Coenen et al. (Reference Coenen, Lesshafft, Garnaud and Sevilla2017, figure 12). These are offset towards higher
![]() $Re$
when compared with our proposed scaling and the experimental data mentioned above. Coenen et al. (Reference Coenen, Lesshafft, Garnaud and Sevilla2017) attempted to account for this offset by including buoyancy and variable viscosity, but found both effects to be insufficient. It is believed that this offset between experimental and numerical data could be due to two factors: (i) subtle differences in the base flow just downstream of the nozzle outlet, which sensitivity analyses (e.g. Coenen et al.
Reference Coenen, Lesshafft, Garnaud and Sevilla2017, figure 7d) predict could have a strong influence on the growth rate of global modes, and (ii) noise amplification by convective instabilities in the experiments, which induces triggering in the bistable region, reducing the Reynolds number at which the Hopf point is found through measurements. This underestimation of
$Re$
when compared with our proposed scaling and the experimental data mentioned above. Coenen et al. (Reference Coenen, Lesshafft, Garnaud and Sevilla2017) attempted to account for this offset by including buoyancy and variable viscosity, but found both effects to be insufficient. It is believed that this offset between experimental and numerical data could be due to two factors: (i) subtle differences in the base flow just downstream of the nozzle outlet, which sensitivity analyses (e.g. Coenen et al.
Reference Coenen, Lesshafft, Garnaud and Sevilla2017, figure 7d) predict could have a strong influence on the growth rate of global modes, and (ii) noise amplification by convective instabilities in the experiments, which induces triggering in the bistable region, reducing the Reynolds number at which the Hopf point is found through measurements. This underestimation of
![]() $Re_{H}$
cannot occur in the linear global stability framework of Coenen et al. (Reference Coenen, Lesshafft, Garnaud and Sevilla2017).
$Re_{H}$
cannot occur in the linear global stability framework of Coenen et al. (Reference Coenen, Lesshafft, Garnaud and Sevilla2017).
These two factors may also explain some of the scattering seen in the experimental data around our proposed scaling (figure 4
d). Although our scaling contains all three of the primary control parameters (
![]() $S$
,
$S$
,
![]() $D/\unicode[STIX]{x1D703}_{0}$
,
$D/\unicode[STIX]{x1D703}_{0}$
,
![]() $Re$
), none of them can explicitly account for variations in noise amplification or in the shape and alignment of the velocity and density profiles. These are determined by the subtle geometrical details of the nozzle, such as the contour of the contraction section, the quality of the flow conditioning and the shape of the nozzle lip. The latter has a particularly strong influence on the local entrainment pattern at the jet base, which can affect the degree of coflow and therefore the instability properties (Hallberg et al.
Reference Hallberg, Srinivasan, Gorse and Strykowski2007). As in most experiments, our nozzle lip is carefully machined to a sharp knife edge, but the rest of the nozzle is known to vary from facility to facility. A possible way to account for such variation is to add a new parameter to our scaling to quantify the alignment between the velocity and density profiles (e.g. the baroclinic torque integral of Nichols, Schmid & Riley Reference Nichols, Schmid and Riley2007, equation (4.12)). However, this would require detailed measurements of those profiles to be taken, which is being considered but is beyond the scope of this study.
$Re$
), none of them can explicitly account for variations in noise amplification or in the shape and alignment of the velocity and density profiles. These are determined by the subtle geometrical details of the nozzle, such as the contour of the contraction section, the quality of the flow conditioning and the shape of the nozzle lip. The latter has a particularly strong influence on the local entrainment pattern at the jet base, which can affect the degree of coflow and therefore the instability properties (Hallberg et al.
Reference Hallberg, Srinivasan, Gorse and Strykowski2007). As in most experiments, our nozzle lip is carefully machined to a sharp knife edge, but the rest of the nozzle is known to vary from facility to facility. A possible way to account for such variation is to add a new parameter to our scaling to quantify the alignment between the velocity and density profiles (e.g. the baroclinic torque integral of Nichols, Schmid & Riley Reference Nichols, Schmid and Riley2007, equation (4.12)). However, this would require detailed measurements of those profiles to be taken, which is being considered but is beyond the scope of this study.
5 Conclusions
In this experimental study, we have answered two key questions on the global instability of low-density axisymmetric inertial jets. (i) Besides undergoing supercritical Hopf bifurcations, can they undergo subcritical Hopf bifurcations? (ii) Given Hallberg & Strykowski’s (Reference Hallberg and Strykowski2006) universal scaling for the global frequency, is it possible to establish a similarly universal scaling for the onset of global instability?
On question (i), we have provided experimental evidence supported by the Landau model showing that, contrary to expectations, low-density jets can undergo subcritical Hopf bifurcations, with a hysteretic bistable region between the saddle-node point and the Hopf point (§ 4.1). This discovery has three implications. First, it shows that low-density jets could be triggered into self-excited oscillations even before the Hopf point, in the bistable region. Second, it highlights the limitations of linear analyses as these can only predict the locations of the bifurcation points, not their specific type. Knowledge of the bifurcation type is also important for nonlinear analyses. For example, cubic nonlinearity is stabilising in supercritical bifurcations but is destabilising in subcritical bifurcations, which rely on quintic or higher-order terms for saturation (§ 3). Third, the response of a self-excited system to external forcing and noise is known to depend on its proximity to the bistable region (Zakharova et al. Reference Zakharova, Vadivasova, Anishchenko, Koseska and Kurths2010). Therefore, when investigating the stability and nonlinear dynamics of low-density jets, it is important to consider whether the Hopf bifurcation is supercritical or subcritical.
On question (ii), we have proposed a universal scaling for the onset of global instability (§ 4.2),
![]() $Re_{H}^{-1}\sim (D/\unicode[STIX]{x1D703}_{0})(S^{-1}-1)$
. This scaling, which is insensitive to the super/subcritical nature of the bifurcations, can be used to predict the onset of self-excited oscillations, providing further evidence to support Hallberg & Strykowski’s concept (Reference Hallberg and Strykowski2006) of universal global modes in low-density jets.
$Re_{H}^{-1}\sim (D/\unicode[STIX]{x1D703}_{0})(S^{-1}-1)$
. This scaling, which is insensitive to the super/subcritical nature of the bifurcations, can be used to predict the onset of self-excited oscillations, providing further evidence to support Hallberg & Strykowski’s concept (Reference Hallberg and Strykowski2006) of universal global modes in low-density jets.
Acknowledgement
This work was funded by the Research Grants Council of Hong Kong (Projects 16235716 and 26202815).