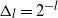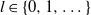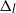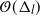1. Introduction
The filtering problem is ubiquitous in statistics, applied probability, and applied mathematics, with far-reaching applications in weather prediction, finance, and engineering; see [Reference Cappe, Moulines and Ryden4] and [Reference Crisan and Bain7], for example. In most cases of practical interest, the filter must be numerically approximated, and a popular method for doing so is the particle filter (PF) (see e.g. [Reference Cappe, Moulines and Ryden4], [Reference Del Moral8], and the references therein). The PF generates ![]() $N\geq 1$
samples in parallel and uses a combination of sampling, importance sampling, and resampling to approximate the filter. There is a substantial literature on the convergence of PFs (e.g. [Reference Del Moral8]) and in particular there are central limit theorems (CLTs) which allow one to understand the errors associated to estimation. Under certain assumptions, the associated asymptotic variance is bounded uniformly in time; see e.g. [Reference Chopin5].
$N\geq 1$
samples in parallel and uses a combination of sampling, importance sampling, and resampling to approximate the filter. There is a substantial literature on the convergence of PFs (e.g. [Reference Del Moral8]) and in particular there are central limit theorems (CLTs) which allow one to understand the errors associated to estimation. Under certain assumptions, the associated asymptotic variance is bounded uniformly in time; see e.g. [Reference Chopin5].
In this article, we are concerned with the filtering problem where one seeks to estimate the difference of expectations of two different but ‘close’ filters. As an example, suppose one observes data at discrete and regular time points associated to an unobserved diffusion process. In many cases, one must time-discretize the diffusion process, if the transition density is not available up to a nonnegative unbiased estimator. In such scenarios it is well known that the cost of estimating the filter using a PF can be significantly reduced using a collapsing sum representation of the expectation associated to the filter with the most precise discretization and estimating each difference independently using a coupled particle filter (CPF). In other applications, one can approximate differences of expectations of filters with different parameter values as a type of finite difference approximations; see for instance [Reference Jacob, Lindsten and Schön16] and [Reference Sen, Thiery and Jasra28].
The CPF developed in [Reference Chopin and Singh6] (see also [Reference Jacob, Lindsten and Schön16], [Reference Jacob, Lindsten and Schön17], [Reference Jasra, Kamatani, Law and Zhou22], [Reference Lee, Singh and Vihola23], and [Reference Sen, Thiery and Jasra28]) is used in several applications as discussed above and various other contexts. It consists of a particle filter which runs on the product space of the two filters. The sampling operation often consists of simulating from a coupling of the Markov transitions of the hidden dynamics, which are often available in applications. Resampling proceeds by sampling the maximal coupling associated to the probability distributions of particle indices. The maximal coupling between two probability measures on the same space is the coupling which maximizes the probability that random variables drawn from the two probabilities are equal. The use of correlating the PFs is vital, for instance in multilevel (ML) applications (see [Reference Giles13], [Reference Heinrich15], and [Reference Jasra, Kamatani, Law and Zhou22]), as it is this property which allows a variance reduction relative to a single PF. As has been noted by several authors, e.g. [Reference Sen, Thiery and Jasra28], unless the coupling of the Markov transitions is particularly strong, one expects the maximally coupled resampling operation to ultimately decorrelate the pairs of particles exponentially fast in time. As a result, the benefits of running such algorithms may have a minimal effect for long time intervals.
In this article we consider four CPFs. The first, the independent resampling CPF (IRCPF), is the case where the resampling is independent for each pair of particles. The second has maximally coupled index resampling; that is, particle pairs are resampled according to the coupling which maximizes the probability that the index (in the set ![]() $\{1,\dots,N\}$
) sampled for both particle pairs is equal. The CPF that uses this resampling operation is called the maximally coupled index resampling CPF (MCIRCPF). The third algorithm, which to our knowledge is new, is a CPF which approximates the sequence of maximal couplings of the predictors, which we call the maximally coupled particle filter (MCPF). The motivation for this method is associated to the fact that the sequence of limiting couplings approximated by the MCIRCPF does not seem to have any optimality properties in terms of coupling. The MCPF requires the Markov transition of the filter to have a density which is known pointwise. It is worth noting that the MCIRCPF is a CPF which maximizes the probability that resampled indices are equal, which, as we will discuss, may not be useful for approximating the filter/predictor for large time horizons (time of the stochastic process). The MCPF is approximating the maximal coupling of the predictor, which, as we will show, can be particularly useful for approximating the filter/predictor for large time horizons. The fourth algorithm in [Reference Jasra, Ballesio, von Schwerin and Tempone20] is based on multinomial resampling which uses the same uniform random variable for each particle pair; we call this the Wasserstein CPF (WCPF). In general, all four algorithms can be used in each of the examples, with the constraint for the MCPF mentioned above. We remark that there are CPFs in [Reference Gregory, Cotter and Reich14] and [Reference Sen, Thiery and Jasra28], but they are not considered here, as their analysis involves even more mathematical complexity.
$\{1,\dots,N\}$
) sampled for both particle pairs is equal. The CPF that uses this resampling operation is called the maximally coupled index resampling CPF (MCIRCPF). The third algorithm, which to our knowledge is new, is a CPF which approximates the sequence of maximal couplings of the predictors, which we call the maximally coupled particle filter (MCPF). The motivation for this method is associated to the fact that the sequence of limiting couplings approximated by the MCIRCPF does not seem to have any optimality properties in terms of coupling. The MCPF requires the Markov transition of the filter to have a density which is known pointwise. It is worth noting that the MCIRCPF is a CPF which maximizes the probability that resampled indices are equal, which, as we will discuss, may not be useful for approximating the filter/predictor for large time horizons (time of the stochastic process). The MCPF is approximating the maximal coupling of the predictor, which, as we will show, can be particularly useful for approximating the filter/predictor for large time horizons. The fourth algorithm in [Reference Jasra, Ballesio, von Schwerin and Tempone20] is based on multinomial resampling which uses the same uniform random variable for each particle pair; we call this the Wasserstein CPF (WCPF). In general, all four algorithms can be used in each of the examples, with the constraint for the MCPF mentioned above. We remark that there are CPFs in [Reference Gregory, Cotter and Reich14] and [Reference Sen, Thiery and Jasra28], but they are not considered here, as their analysis involves even more mathematical complexity.
We prove a CLT for the first three algorithms (the CLT for the WCPF, when the state dynamics are one-dimensional, is in [Reference Jasra, Ballesio, von Schwerin and Tempone20]) associated to the difference of estimates of expectations of the same function with respect to the predictors, which is extended to multiple dimensions. The asymptotic variance expression is directly related to the properties of the limiting coupling one approximates. Under certain assumptions (of the type in [Reference Whiteley30]), for partially observed discretized diffusion processes (PODDP) with (Euler) discretization ![]() $\Delta_l$
(typically
$\Delta_l$
(typically ![]() $\Delta_l=2^{-l}$
,
$\Delta_l=2^{-l}$
, ![]() $l\in\{0,1,\dots\}$
), we show that the MCPF (resp. WCPF) has an asymptotic variance that is bounded above by an expression that is of order
$l\in\{0,1,\dots\}$
), we show that the MCPF (resp. WCPF) has an asymptotic variance that is bounded above by an expression that is of order ![]() $\Delta_l$
(
$\Delta_l$
(![]() $\mathcal{O}(\Delta_l)$
) (resp.
$\mathcal{O}(\Delta_l)$
) (resp. ![]() $\mathcal{O}(\Delta_l^{1-\lambda})$
, with
$\mathcal{O}(\Delta_l^{1-\lambda})$
, with ![]() $\lambda$
arbitrarily close to, but not equal to, zero), uniformly in time, which preserves the so-called forward rate of the diffusion in some scenarios. This is reassuring as it shows that filtering for difference estimation in the PODDP case can be effectively performed. This time and rate stability is associated to the fact that the limiting coupling on product spaces is associated to the optimal
$\lambda$
arbitrarily close to, but not equal to, zero), uniformly in time, which preserves the so-called forward rate of the diffusion in some scenarios. This is reassuring as it shows that filtering for difference estimation in the PODDP case can be effectively performed. This time and rate stability is associated to the fact that the limiting coupling on product spaces is associated to the optimal ![]() $L_0$
and
$L_0$
and ![]() $L_2$
Wasserstein couplings of the predictor/filter. For the IRCPF one does not recover the coupling rate of the diffusion process, and this poor performance is well-known in the literature. In the case of the MCIRCPF we show that even in a favourable situation, it can have an asymptotic variance, at time n, that is
$L_2$
Wasserstein couplings of the predictor/filter. For the IRCPF one does not recover the coupling rate of the diffusion process, and this poor performance is well-known in the literature. In the case of the MCIRCPF we show that even in a favourable situation, it can have an asymptotic variance, at time n, that is ![]() $\mathcal{O}(e^n\Delta_l)$
; we also identify when one can expect the algorithm to work well. As was seen in the empirical results of [Reference Jasra, Ballesio, von Schwerin and Tempone20] and [Reference Jasra, Kamatani, Law and Zhou22], the time and rate behavior of the MCIRCPF in general does not seem to be as good as for the MCPF and WCPF. The assumptions used for our asymptotic variance results are also verified in a real example. Our CLTs are, to the best of our knowledge, the first results of these types for CPFs and require nonstandard proofs, especially in the case of the MCIRCPF. To summarize, the main results of the article are the following:
$\mathcal{O}(e^n\Delta_l)$
; we also identify when one can expect the algorithm to work well. As was seen in the empirical results of [Reference Jasra, Ballesio, von Schwerin and Tempone20] and [Reference Jasra, Kamatani, Law and Zhou22], the time and rate behavior of the MCIRCPF in general does not seem to be as good as for the MCPF and WCPF. The assumptions used for our asymptotic variance results are also verified in a real example. Our CLTs are, to the best of our knowledge, the first results of these types for CPFs and require nonstandard proofs, especially in the case of the MCIRCPF. To summarize, the main results of the article are the following:
• Theorem 3.1 gives a WLLN for the MCIRCPF.
• Theorem 4.1 gives a CLT for the IRCPF, MCIRCPF, and MCPF.
• Theorem 4.3 gives a general bound on the asymptotic variance for each of the methods: the IRCPF, MCIRCPF, MCPF, and WCPF.
• Propositions 5.2 and 5.3 give the time-uniform bounds on the asymptotic variance for the MCPF and WCPF noted above (i.e. for PODDPs).
This paper is structured as follows. In Section 2 we give our notation, models, and the motivating example of a PODDP with MLMC. In Section 3 the algorithms are presented. In Section 4 our theoretical results are stated. Our CLTs are given and a general bound on the asymptotic variance is provided. In Section 5 our results are applied to a practical model in the context of using coupled particle filters for PODDP with MLMC. The article is summarized in Section 6. The appendix contains the proofs of our theoretical results.
2. Notation and models
2.1. Notation
Let ![]() $(\textsf{X},\mathcal{X})$
be a measurable space. For a given function
$(\textsf{X},\mathcal{X})$
be a measurable space. For a given function ![]() $v\,:\,\textsf{X}\rightarrow[1,+\infty)$
and for measurable
$v\,:\,\textsf{X}\rightarrow[1,+\infty)$
and for measurable ![]() $\varphi\,:\,\textsf{X}\rightarrow\mathbb R$
,
$\varphi\,:\,\textsf{X}\rightarrow\mathbb R$
,
We define ![]() $\mathcal{L}_v(\textsf{X})=\{\varphi\,:\,\textsf{X}\rightarrow\mathbb R\,:\,\|\varphi\|_v<+\infty\}$
. When
$\mathcal{L}_v(\textsf{X})=\{\varphi\,:\,\textsf{X}\rightarrow\mathbb R\,:\,\|\varphi\|_v<+\infty\}$
. When ![]() $v=1$
we write
$v=1$
we write ![]() $\|\varphi\| \,:\!= \sup_{x\in \textsf{X}}|\varphi(x)|$
. We write
$\|\varphi\| \,:\!= \sup_{x\in \textsf{X}}|\varphi(x)|$
. We write ![]() $\mathcal{B}_b(\textsf{X})$
,
$\mathcal{B}_b(\textsf{X})$
, ![]() $\mathcal{C}_b(\textsf{X})$
for the bounded measurable and continuous, bounded measurable real-valued functions respectively.
$\mathcal{C}_b(\textsf{X})$
for the bounded measurable and continuous, bounded measurable real-valued functions respectively. ![]() $\mathcal{C}^2(\textsf{X})$
is the collection of twice continuously differentiable real-valued functions on
$\mathcal{C}^2(\textsf{X})$
is the collection of twice continuously differentiable real-valued functions on ![]() $\textsf{X}$
. Let
$\textsf{X}$
. Let ![]() $\textsf{d}$
be a metric on
$\textsf{d}$
be a metric on ![]() $\textsf{X}$
; then for
$\textsf{X}$
; then for ![]() $\varphi\in\mathcal{L}_v(\textsf{X})$
, we say that
$\varphi\in\mathcal{L}_v(\textsf{X})$
, we say that ![]() $\varphi\in\textrm{Lip}_{v,\textsf{d}}(\textsf{X})$
if there exists a
$\varphi\in\textrm{Lip}_{v,\textsf{d}}(\textsf{X})$
if there exists a ![]() $C<+\infty$
such that for every
$C<+\infty$
such that for every ![]() $(x,y)\in\textsf{X}\times\textsf{X}$
,
$(x,y)\in\textsf{X}\times\textsf{X}$
,
If ![]() $v=1$
, we write
$v=1$
, we write ![]() $\varphi\in\textrm{Lip}_{\textsf{d}}(\textsf{X})$
and write
$\varphi\in\textrm{Lip}_{\textsf{d}}(\textsf{X})$
and write ![]() $\|\varphi\|_{\textrm{Lip}}$
for the Lipschitz constant.
$\|\varphi\|_{\textrm{Lip}}$
for the Lipschitz constant. ![]() $\mathscr{P}(\textsf{X})$
denotes the collection of probability measures on
$\mathscr{P}(\textsf{X})$
denotes the collection of probability measures on ![]() $(\textsf{X},\mathcal{X})$
. We also write
$(\textsf{X},\mathcal{X})$
. We also write ![]() $\|\mu\|_{v}\,:\!=\sup_{|\varphi|\leq v}|\mu(\varphi)|$
for
$\|\mu\|_{v}\,:\!=\sup_{|\varphi|\leq v}|\mu(\varphi)|$
for ![]() $\mu\in\mathscr{P}(\textsf{X})$
. For a measure
$\mu\in\mathscr{P}(\textsf{X})$
. For a measure ![]() $\mu$
on
$\mu$
on ![]() $(\textsf{X},\mathcal{X})$
and a
$(\textsf{X},\mathcal{X})$
and a ![]() $\mu-$
integrable function
$\mu-$
integrable function ![]() $\varphi\,:\,\textsf{X}\rightarrow\mathbb{R}$
, the notation
$\varphi\,:\,\textsf{X}\rightarrow\mathbb{R}$
, the notation ![]() $\mu(\varphi)=\int_{\textsf{X}}\varphi(x)\mu(dx)$
is used. Let
$\mu(\varphi)=\int_{\textsf{X}}\varphi(x)\mu(dx)$
is used. Let ![]() $K\,:\,\textsf{X}\times\mathcal{X}\rightarrow(0,+\infty)$
be a nonnegative kernel and
$K\,:\,\textsf{X}\times\mathcal{X}\rightarrow(0,+\infty)$
be a nonnegative kernel and ![]() $\mu$
a measure; then we use the notation
$\mu$
a measure; then we use the notation ![]() $\mu K(dy) = \int_{\textsf{X}}\mu(dx) K(x,dy)$
, and for
$\mu K(dy) = \int_{\textsf{X}}\mu(dx) K(x,dy)$
, and for ![]() $K(x,\cdot)-$
integrable
$K(x,\cdot)-$
integrable ![]() $\varphi\,:\,\textsf{X}\rightarrow\mathbb{R}$
, we write
$\varphi\,:\,\textsf{X}\rightarrow\mathbb{R}$
, we write ![]() $K(\varphi)(x) = \int_{\textsf{X}} \varphi(y) K(x,dy).$
For
$K(\varphi)(x) = \int_{\textsf{X}} \varphi(y) K(x,dy).$
For ![]() $\mu,\nu\in\mathscr{P}(\textsf{X})$
, the total variation distance is denoted
$\mu,\nu\in\mathscr{P}(\textsf{X})$
, the total variation distance is denoted ![]() $\|\mu-\nu\|_{\textrm{tv}}=\sup_{B\in\mathcal{X}}|\mu(B)-\nu(B)|$
. For
$\|\mu-\nu\|_{\textrm{tv}}=\sup_{B\in\mathcal{X}}|\mu(B)-\nu(B)|$
. For ![]() $B\in\mathcal{X}$
the indicator function is written
$B\in\mathcal{X}$
the indicator function is written ![]() $\mathbb{I}_B(x)$
and the Dirac measure
$\mathbb{I}_B(x)$
and the Dirac measure ![]() $\delta_B(dx)$
. For two measures
$\delta_B(dx)$
. For two measures ![]() $\mu,\nu$
on
$\mu,\nu$
on ![]() $(\textsf{X},\mathcal{X})$
, the product measure is denoted
$(\textsf{X},\mathcal{X})$
, the product measure is denoted ![]() $\mu\otimes \nu$
. For two measurable functions
$\mu\otimes \nu$
. For two measurable functions ![]() $\varphi$
,
$\varphi$
, ![]() $\psi$
on
$\psi$
on ![]() $(\textsf{X},\mathcal{X})$
, the tensor product of functions is denoted
$(\textsf{X},\mathcal{X})$
, the tensor product of functions is denoted ![]() $\varphi\otimes\psi$
.
$\varphi\otimes\psi$
. ![]() $\mathcal{U}_A$
denotes the uniform distribution on the set A.
$\mathcal{U}_A$
denotes the uniform distribution on the set A. ![]() $\mathcal{N}_t(a,b)$
is the
$\mathcal{N}_t(a,b)$
is the ![]() $t-$
dimensional Gaussian distribution of mean a and covariance b (if
$t-$
dimensional Gaussian distribution of mean a and covariance b (if ![]() $t=1$
the subscript is dropped from
$t=1$
the subscript is dropped from ![]() $\mathcal{N}$
).
$\mathcal{N}$
). ![]() $\mathbb{P}$
and
$\mathbb{P}$
and ![]() $\mathbb{E}$
are used to denote probability and expectation with respect to the law of the specified algorithm—the context will be clear in each instance. The symbols
$\mathbb{E}$
are used to denote probability and expectation with respect to the law of the specified algorithm—the context will be clear in each instance. The symbols ![]() $\Rightarrow$
and
$\Rightarrow$
and ![]() $\rightarrow_{\mathbb{P}}$
are used to denote convergence in distribution and probability respectively. In the context of the article, this is as
$\rightarrow_{\mathbb{P}}$
are used to denote convergence in distribution and probability respectively. In the context of the article, this is as ![]() $N\rightarrow+\infty$
.
$N\rightarrow+\infty$
.
2.2. Models
Let ![]() $(\textsf{X},\mathcal{X})$
be a measurable space and
$(\textsf{X},\mathcal{X})$
be a measurable space and ![]() $\{G_n\}_{n\geq 0}$
a sequence of nonnegative, bounded, and measurable functions such that
$\{G_n\}_{n\geq 0}$
a sequence of nonnegative, bounded, and measurable functions such that ![]() $G_n\,:\,\textsf{X}\rightarrow\mathbb{R}_+$
. Let
$G_n\,:\,\textsf{X}\rightarrow\mathbb{R}_+$
. Let ![]() $\eta_0^{f},\eta_0^c\in\mathscr{P}(\textsf{X})$
and let
$\eta_0^{f},\eta_0^c\in\mathscr{P}(\textsf{X})$
and let ![]() $\{M_n^f\}_{n\geq 1}$
,
$\{M_n^f\}_{n\geq 1}$
, ![]() $\{M_n^c\}_{n\geq 1}$
be two sequences of Markov kernels, i.e.
$\{M_n^c\}_{n\geq 1}$
be two sequences of Markov kernels, i.e. ![]() $M_n^f\,:\,\textsf{X}\rightarrow\mathscr{P}(\textsf{X})$
,
$M_n^f\,:\,\textsf{X}\rightarrow\mathscr{P}(\textsf{X})$
, ![]() $M_n^c\,:\,\textsf{X}\rightarrow\mathscr{P}(\textsf{X})$
. For
$M_n^c\,:\,\textsf{X}\rightarrow\mathscr{P}(\textsf{X})$
. For ![]() $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
, ![]() $B\in\mathcal{X}$
, define
$B\in\mathcal{X}$
, define
 \[\gamma_{n}^s(B) = \int_{\textsf{X}^{n+1}}\mathbb{I}_B(x_n) \Bigg(\prod_{p=0}^{n-1} G_p^s(x_p)\Bigg) \eta_0^s(dx_0)\prod_{p=1}^n M_p^s(x_{p-1},dx_p)\]
\[\gamma_{n}^s(B) = \int_{\textsf{X}^{n+1}}\mathbb{I}_B(x_n) \Bigg(\prod_{p=0}^{n-1} G_p^s(x_p)\Bigg) \eta_0^s(dx_0)\prod_{p=1}^n M_p^s(x_{p-1},dx_p)\]
and
The objective is to consider Monte-Carlo–type algorithms which will approximate, for ![]() $\varphi\in\mathcal{B}_b(\textsf{X})$
and any
$\varphi\in\mathcal{B}_b(\textsf{X})$
and any ![]() $n\geq 0$
, quantities such as
$n\geq 0$
, quantities such as
or
(1) corresponds to a predictor of a state-space model and (2) to the filter. We focus explicitly on the predictor from here on.
Remark 2.1. We can make the ![]() $G_n$
also depend on
$G_n$
also depend on ![]() $\{\,f,c\}$
, which may be of importance in applications. In the subsequent development, this is not done, but could be, at a cost of slightly longer mathematical arguments and notational complications.
$\{\,f,c\}$
, which may be of importance in applications. In the subsequent development, this is not done, but could be, at a cost of slightly longer mathematical arguments and notational complications.
The major point is that one would like to approximate couplings of ![]() $(\eta_n^f,\eta_n^c)$
, say
$(\eta_n^f,\eta_n^c)$
, say ![]() $\check{\eta}_n\in\mathscr{P}(\textsf{X}\times\textsf{X})$
, i.e. that for any
$\check{\eta}_n\in\mathscr{P}(\textsf{X}\times\textsf{X})$
, i.e. that for any ![]() $B\in\mathcal{X}$
and every
$B\in\mathcal{X}$
and every ![]() $n\geq 0$
,
$n\geq 0$
,
and we consider approximating
An explanation of why coupling the pairs is of interest has been given in the introduction and will be further illuminated in Section 2.3.
Throughout the article, it is assumed that ![]() $\check{\eta}_0\in\mathscr{P}(\textsf{X}\times\textsf{X})$
is such that for any
$\check{\eta}_0\in\mathscr{P}(\textsf{X}\times\textsf{X})$
is such that for any ![]() $B\in\mathcal{X}$
,
$B\in\mathcal{X}$
,
and moreover for any ![]() $n\geq 1$
there exist Markov kernels
$n\geq 1$
there exist Markov kernels ![]() $\{\check{M}_n\}$
,
$\{\check{M}_n\}$
, ![]() $\check{M}_n\,:\,\textsf{X}\times\textsf{X}\rightarrow\mathscr{P}(\textsf{X}\times\textsf{X})$
, such that for any
$\check{M}_n\,:\,\textsf{X}\times\textsf{X}\rightarrow\mathscr{P}(\textsf{X}\times\textsf{X})$
, such that for any ![]() $B\in\mathcal{X}$
,
$B\in\mathcal{X}$
, ![]() $(x,x')\in\textsf{X}\times\textsf{X}$
,
$(x,x')\in\textsf{X}\times\textsf{X}$
,
2.3. Example
The following example is from [Reference Jasra, Kamatani, Law and Zhou22] and there is some overlap with the presentation in that article. We start with a diffusion process
with ![]() $Z_t\in\mathbb{R}^d=\textsf{X}$
,
$Z_t\in\mathbb{R}^d=\textsf{X}$
, ![]() $a\,:\,\mathbb{R}^d\rightarrow\mathbb{R}^d$
(jth element denoted
$a\,:\,\mathbb{R}^d\rightarrow\mathbb{R}^d$
(jth element denoted ![]() $a^j$
),
$a^j$
), ![]() $b\,:\,\mathbb{R}^d\rightarrow\mathbb{R}^{d\times d}$
((j, k)th element denoted
$b\,:\,\mathbb{R}^d\rightarrow\mathbb{R}^{d\times d}$
((j, k)th element denoted ![]() $b^{j,k}$
),
$b^{j,k}$
), ![]() $t\geq 0$
, and
$t\geq 0$
, and ![]() $\{W_t\}_{t\geq 0}$
a
$\{W_t\}_{t\geq 0}$
a ![]() $d-$
dimensional Brownian motion. The following assumption is made and is referred to as (D). We set
$d-$
dimensional Brownian motion. The following assumption is made and is referred to as (D). We set ![]() $Z_0=x^*\in\textsf{X}$
.
$Z_0=x^*\in\textsf{X}$
.
The coefficients ![]() $a^j, b^{j,k}$
belong to
$a^j, b^{j,k}$
belong to ![]() $\mathcal{C}^2(\textsf{X})$
, for
$\mathcal{C}^2(\textsf{X})$
, for ![]() $j,k= 1,\ldots, d$
. Also, a and b satisfy the following properties:
$j,k= 1,\ldots, d$
. Also, a and b satisfy the following properties:
(i) the uniform ellipticity property:
 $b(z)b(z)^T$
is uniformly positive definite;
$b(z)b(z)^T$
is uniformly positive definite;(ii) the globally Lipschitz property: there is a
 $C>0$
such that
$C>0$
such that  $|a^j(z)-a^j(y)|+|b^{j,k}(z)-b^{j,k}(y)| \leq C |z-y|$
for all
$|a^j(z)-a^j(y)|+|b^{j,k}(z)-b^{j,k}(y)| \leq C |z-y|$
for all  $(z,y)\in \textsf{X}\times\textsf{X}$
,
$(z,y)\in \textsf{X}\times\textsf{X}$
,  $(j,k)\in\{1,\dots,d\}^2$
.
$(j,k)\in\{1,\dots,d\}^2$
.
The data are observed at regular unit time-intervals (i.e. in discrete time) ![]() $y_1,y_2,\dots$
,
$y_1,y_2,\dots$
, ![]() $y_k \in \textsf{Y}$
. It is assumed that conditional on
$y_k \in \textsf{Y}$
. It is assumed that conditional on ![]() $Z_{k}$
,
$Z_{k}$
, ![]() $Y_k$
is independent of all other random variables with density
$Y_k$
is independent of all other random variables with density ![]() $G(z_{k},y_k)$
. Let M(z, dy) be the transition of the diffusion process (over unit time) and consider a discrete-time Markov chain
$G(z_{k},y_k)$
. Let M(z, dy) be the transition of the diffusion process (over unit time) and consider a discrete-time Markov chain ![]() $X_0,X_1,\dots$
with initial distribution
$X_0,X_1,\dots$
with initial distribution ![]() $M(x^*,\cdot)$
and transition M(x, dy). Here we are creating a discrete-time Markov chain that corresponds to the discrete-time skeleton of the diffusion process at a time lag of 1. Now we write
$M(x^*,\cdot)$
and transition M(x, dy). Here we are creating a discrete-time Markov chain that corresponds to the discrete-time skeleton of the diffusion process at a time lag of 1. Now we write ![]() $G_{k}(x_{k})$
instead of
$G_{k}(x_{k})$
instead of ![]() $G(x_{k},y_{k+1})$
. Then we define, for
$G(x_{k},y_{k+1})$
. Then we define, for ![]() $B\in\mathcal{X}$
,
$B\in\mathcal{X}$
,
 \[\gamma_n(B) \,:\!= \int_{\textsf{X}^{n+1}}\mathbb{I}_B(x_n)\Bigg(\prod_{p=0}^{n-1} G_{p}(x_{p})\Bigg)M(x^*,dx_{0})\prod_{p=1}^n M(x_{p-1},dx_{p}).\]
\[\gamma_n(B) \,:\!= \int_{\textsf{X}^{n+1}}\mathbb{I}_B(x_n)\Bigg(\prod_{p=0}^{n-1} G_{p}(x_{p})\Bigg)M(x^*,dx_{0})\prod_{p=1}^n M(x_{p-1},dx_{p}).\]
The predictor is ![]() $\eta_n(B)=\gamma_n(B)/\gamma_n(1)$
, which corresponds to the distribution associated to
$\eta_n(B)=\gamma_n(B)/\gamma_n(1)$
, which corresponds to the distribution associated to ![]() $Z_{n+1}|y_1,\dots,y_n$
.
$Z_{n+1}|y_1,\dots,y_n$
.
In many applications, one must time-discretize the diffusion to use the model in practice. We suppose an Euler discretization with discretization ![]() $\Delta_l=2^{-l}$
,
$\Delta_l=2^{-l}$
, ![]() $l\geq 0$
, and write the associated transition kernel over unit time as
$l\geq 0$
, and write the associated transition kernel over unit time as ![]() $M^l(x,dy)$
. Note that, in practice, one may not be able to compute the density of the kernel, as it is a composition of
$M^l(x,dy)$
. Note that, in practice, one may not be able to compute the density of the kernel, as it is a composition of ![]() $\Delta_l^{-1}-1$
Gaussians; however, one can certainly sample from
$\Delta_l^{-1}-1$
Gaussians; however, one can certainly sample from ![]() $M^l$
in most cases. Hence we are interested in the Feynman–Kac model for
$M^l$
in most cases. Hence we are interested in the Feynman–Kac model for ![]() $B\in\mathcal{X}$
,
$B\in\mathcal{X}$
,
 \[\gamma_n^l(B) \,:\!= \int_{\textsf{X}^{n+1}}\mathbb{I}_B(x_n)\Bigg(\prod_{p=0}^{n-1} G_{p}(x_{p})\Bigg)M^l(x^*,dx_{0})\prod_{p=1}^n M^l(x_{p-1},dx_{p}),\]
\[\gamma_n^l(B) \,:\!= \int_{\textsf{X}^{n+1}}\mathbb{I}_B(x_n)\Bigg(\prod_{p=0}^{n-1} G_{p}(x_{p})\Bigg)M^l(x^*,dx_{0})\prod_{p=1}^n M^l(x_{p-1},dx_{p}),\]
with associated predictor ![]() $\eta_n^l(B)=\gamma_n^l(B)/\gamma_n^l(1)$
.
$\eta_n^l(B)=\gamma_n^l(B)/\gamma_n^l(1)$
.
Below, we will explain why one may wish to compute, for ![]() $l\geq 1$
,
$l\geq 1$
, ![]() $\eta_n^l(\varphi)-\eta_n^{l-1}(\varphi)$
,
$\eta_n^l(\varphi)-\eta_n^{l-1}(\varphi)$
, ![]() $\varphi\in\mathcal{B}_b(\textsf{X})$
. That is, f as used above relates to the predictor associated to the discretization
$\varphi\in\mathcal{B}_b(\textsf{X})$
. That is, f as used above relates to the predictor associated to the discretization ![]() $\Delta_l$
and c to the predictor with discretization
$\Delta_l$
and c to the predictor with discretization ![]() $\Delta_{l-1}$
. A natural coupling of
$\Delta_{l-1}$
. A natural coupling of ![]() $M_n^f=M^l$
and
$M_n^f=M^l$
and ![]() $M_n^c=M^{l-1}$
exists (e.g. [Reference Giles13]) so one also has a given
$M_n^c=M^{l-1}$
exists (e.g. [Reference Giles13]) so one also has a given ![]() $\check{\eta}_0$
and
$\check{\eta}_0$
and ![]() $\check{M}_n$
.
$\check{M}_n$
.
Before continuing, we note some results which will help in our discussion below. As established in [Reference Jasra, Kamatani, Law and Zhou22, Eq. (32)], for ![]() $C<+\infty$
one has
$C<+\infty$
one has
where ![]() $\mathcal{A}=\{\varphi\in\mathcal{B}_b(\textsf{X})\cap\textrm{Lip}_{\textsf{d}_1}(\textsf{X})\,:\, \|\varphi\|\leq 1\}$
, with
$\mathcal{A}=\{\varphi\in\mathcal{B}_b(\textsf{X})\cap\textrm{Lip}_{\textsf{d}_1}(\textsf{X})\,:\, \|\varphi\|\leq 1\}$
, with ![]() $\textsf{d}_1$
the
$\textsf{d}_1$
the ![]() $L_1-$
norm. In addition, [Reference Jasra, Kamatani, Law and Zhou22, Proposition D.1] states that for
$L_1-$
norm. In addition, [Reference Jasra, Kamatani, Law and Zhou22, Proposition D.1] states that for ![]() $p>0$
,
$p>0$
, ![]() $C<+\infty$
, and any
$C<+\infty$
, and any ![]() $(x,y)\in\textsf{X}\times\textsf{X}$
,
$(x,y)\in\textsf{X}\times\textsf{X}$
,
When ![]() $p=2$
(
$p=2$
(![]() $\|u-v\|$
is the
$\|u-v\|$
is the ![]() $L_2-$
norm), the term
$L_2-$
norm), the term ![]() $\Delta_l$
is the so-called forward strong error rate. In the proof of [Reference Jasra, Kamatani, Law and Zhou22, Theorem 4.3], it is shown that for any
$\Delta_l$
is the so-called forward strong error rate. In the proof of [Reference Jasra, Kamatani, Law and Zhou22, Theorem 4.3], it is shown that for any ![]() $n\geq 0$
there exists a
$n\geq 0$
there exists a ![]() $C<+\infty$
such that for
$C<+\infty$
such that for ![]() $\varphi\in\mathcal{A}$
,
$\varphi\in\mathcal{A}$
, ![]() $l\geq 0$
, one has
$l\geq 0$
, one has
Note that this bound can be deduced from (5), but that C may depend on n; this latter point is ignored for now.
2.3.1. Multilevel Monte Carlo
Suppose one can exactly sample from ![]() $\eta_n^l$
for any
$\eta_n^l$
for any ![]() $l,n\geq 0$
. The Monte Carlo estimate of
$l,n\geq 0$
. The Monte Carlo estimate of ![]() $\eta_n^l(\varphi)$
, with
$\eta_n^l(\varphi)$
, with ![]() $\varphi\in\mathcal{A}$
, is then of course
$\varphi\in\mathcal{A}$
, is then of course ![]() $\frac{1}{N}\sum_{i=1}^N\varphi(x_n^i)$
, where the
$\frac{1}{N}\sum_{i=1}^N\varphi(x_n^i)$
, where the ![]() $X_n^i$
are independent and identically distributed (i.i.d.) from
$X_n^i$
are independent and identically distributed (i.i.d.) from ![]() $\eta_n^l$
. One has the mean square error (MSE)
$\eta_n^l$
. One has the mean square error (MSE)
 \[\mathbb{E}\Bigg[\Bigg(\frac{1}{N}\sum_{i=1}^N\varphi(x_n^i) - \eta_n(\varphi)\Bigg)^2\Bigg] = \frac{\mathbb{V}\textrm{ar}_{\eta_n^l}[\varphi(X)]}{N} + |\eta_n(\varphi)-\eta_n^l(\varphi)|^2,\]
\[\mathbb{E}\Bigg[\Bigg(\frac{1}{N}\sum_{i=1}^N\varphi(x_n^i) - \eta_n(\varphi)\Bigg)^2\Bigg] = \frac{\mathbb{V}\textrm{ar}_{\eta_n^l}[\varphi(X)]}{N} + |\eta_n(\varphi)-\eta_n^l(\varphi)|^2,\]
where ![]() $\mathbb{V}\textrm{ar}_{\eta_n^l}[\varphi(X)]$
is the variance of
$\mathbb{V}\textrm{ar}_{\eta_n^l}[\varphi(X)]$
is the variance of ![]() $\varphi(X)$
with respect to
$\varphi(X)$
with respect to ![]() $\eta_n^l$
. Then, for
$\eta_n^l$
. Then, for ![]() $\varepsilon>0$
given, to target an MSE of
$\varepsilon>0$
given, to target an MSE of ![]() $\mathcal{O}(\varepsilon^2)$
, by (7), one chooses
$\mathcal{O}(\varepsilon^2)$
, by (7), one chooses ![]() $l=\mathcal{O}(|\log(\varepsilon)|)$
(as one sets
$l=\mathcal{O}(|\log(\varepsilon)|)$
(as one sets ![]() $\Delta_l^2=\varepsilon^2$
). Then one must choose
$\Delta_l^2=\varepsilon^2$
). Then one must choose ![]() $N=\mathcal{O}(\varepsilon^{-2})$
, and we suppose the cost of simulating one sample is
$N=\mathcal{O}(\varepsilon^{-2})$
, and we suppose the cost of simulating one sample is ![]() $\mathcal{O}(\Delta_l^{-1})$
(see [Reference Jasra, Kamatani, Law and Zhou22] for a justification), again ignoring n. Then the cost of achieving an MSE of
$\mathcal{O}(\Delta_l^{-1})$
(see [Reference Jasra, Kamatani, Law and Zhou22] for a justification), again ignoring n. Then the cost of achieving an MSE of ![]() $\mathcal{O}(\varepsilon^2)$
is
$\mathcal{O}(\varepsilon^2)$
is ![]() $\mathcal{O}(\varepsilon^{-3})$
.
$\mathcal{O}(\varepsilon^{-3})$
.
Now, for any ![]() $L\geq 1$
, one has the multilevel identity ([Reference Giles13], [Reference Heinrich15])
$L\geq 1$
, one has the multilevel identity ([Reference Giles13], [Reference Heinrich15])
 \[\eta_n^L(\varphi) = \eta_n^0(\varphi) + \sum_{l=1}^{L}\{[\eta_n^l-\eta_n^{l-1}](\varphi)\}.\]
\[\eta_n^L(\varphi) = \eta_n^0(\varphi) + \sum_{l=1}^{L}\{[\eta_n^l-\eta_n^{l-1}](\varphi)\}.\]
Suppose that, for ![]() $l\geq 1$
, it is possible to exactly sample a coupling of
$l\geq 1$
, it is possible to exactly sample a coupling of ![]() $(\eta_n^l,\eta_n^{l-1})$
—let us denote it
$(\eta_n^l,\eta_n^{l-1})$
—let us denote it ![]() $\check{\eta}_n^l$
—so that one has
$\check{\eta}_n^l$
—so that one has
and the cost of such a simulation is ![]() $\mathcal{O}(\Delta_l^{-1})$
. The rate
$\mathcal{O}(\Delta_l^{-1})$
. The rate ![]() $\Delta_l$
has been taken from the strong error rate in (6). Now, to estimate
$\Delta_l$
has been taken from the strong error rate in (6). Now, to estimate ![]() $[\eta_n^l-\eta_n^{l-1}](\varphi)$
, one simulates
$[\eta_n^l-\eta_n^{l-1}](\varphi)$
, one simulates
i.i.d. from ![]() $\check{\eta}_n^l$
for some
$\check{\eta}_n^l$
for some ![]() $N_l\geq 1$
, and the approximation is
$N_l\geq 1$
, and the approximation is
 \[\frac{1}{N_l}\sum_{l=1}^{N_l}\{\varphi(x_n^{i,l})-\varphi(x_n^{i,l-1})\}.\]
\[\frac{1}{N_l}\sum_{l=1}^{N_l}\{\varphi(x_n^{i,l})-\varphi(x_n^{i,l-1})\}.\]
For ![]() $1\leq l\leq L$
this is repeated independently for estimating
$1\leq l\leq L$
this is repeated independently for estimating ![]() $[\eta_n^l-\eta_n^{l-1}](\varphi)$
, and the case
$[\eta_n^l-\eta_n^{l-1}](\varphi)$
, and the case ![]() $l=0$
is performed, independently, using the Monte Carlo method above. One can then easily show that the MSE of the estimate of
$l=0$
is performed, independently, using the Monte Carlo method above. One can then easily show that the MSE of the estimate of ![]() $\eta_n^L$
is bounded above by
$\eta_n^L$
is bounded above by
 \[\frac{\mathbb{V}\textrm{ar}_{\eta_n^l}[\varphi(X)]}{N_0} + C \sum_{l=1}^L\frac{\Delta_l}{N_l} + |\eta_n(\varphi)-\eta_n^l(\varphi)|^2\]
\[\frac{\mathbb{V}\textrm{ar}_{\eta_n^l}[\varphi(X)]}{N_0} + C \sum_{l=1}^L\frac{\Delta_l}{N_l} + |\eta_n(\varphi)-\eta_n^l(\varphi)|^2\]
(recall ![]() $\varphi\in\mathcal{A}$
). Then, for
$\varphi\in\mathcal{A}$
). Then, for ![]() $\varepsilon>0$
given, to target an MSE of
$\varepsilon>0$
given, to target an MSE of ![]() $\mathcal{O}(\varepsilon^2)$
, set
$\mathcal{O}(\varepsilon^2)$
, set ![]() $L=\mathcal{O}(|\log(\varepsilon)|)$
and
$L=\mathcal{O}(|\log(\varepsilon)|)$
and ![]() $N_l=\mathcal{O}(\varepsilon^{-2}|\log(\varepsilon)|\Delta_l)$
(see [Reference Giles13]); then the MSE is
$N_l=\mathcal{O}(\varepsilon^{-2}|\log(\varepsilon)|\Delta_l)$
(see [Reference Giles13]); then the MSE is ![]() $\mathcal{O}(\varepsilon^2)$
. The overall computational effort is
$\mathcal{O}(\varepsilon^2)$
. The overall computational effort is ![]() $\mathcal{O}(\sum_{l=0}^L N_l \Delta_l^{-1})=\mathcal{O}(\varepsilon^{-2}|\log(\varepsilon)|^2)$
; if
$\mathcal{O}(\sum_{l=0}^L N_l \Delta_l^{-1})=\mathcal{O}(\varepsilon^{-2}|\log(\varepsilon)|^2)$
; if ![]() $\varepsilon$
is suitably small this is a significant reduction in computational effort relative to the MC method above.
$\varepsilon$
is suitably small this is a significant reduction in computational effort relative to the MC method above.
The main point here is that, at present, there are no computational methods to perform the exact simulation mentioned, and thus we focus on particle filters, which have been developed in the literature. The estimates (variance/cost) above typically depend on n, and our objective is to consider whether the variance of PF estimates can be ![]() $\mathcal{O}(\Delta_l)$
uniformly in time, so that the ML gain is retained uniformly in time. We focus on the asymptotic variance in the CLT (versus the finite sample variance) as this is more straightforward to deal with.
$\mathcal{O}(\Delta_l)$
uniformly in time, so that the ML gain is retained uniformly in time. We focus on the asymptotic variance in the CLT (versus the finite sample variance) as this is more straightforward to deal with.
3. Algorithms
3.1. Independent pair resampling
The first procedure we consider is as follows. Let ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $B\in\mathcal{X}\times\mathcal{X}$
, and
$B\in\mathcal{X}\times\mathcal{X}$
, and ![]() $\mu\in\mathscr{P}(\textsf{X}\times\textsf{X})$
, and define the probability measure
$\mu\in\mathscr{P}(\textsf{X}\times\textsf{X})$
, and define the probability measure
Set ![]() $u_n=(x_n^f,x_n^c)\in\textsf{X}\times\textsf{X}$
, then consider the joint probability measure on
$u_n=(x_n^f,x_n^c)\in\textsf{X}\times\textsf{X}$
, then consider the joint probability measure on ![]() $(\textsf{X}\times\textsf{X})^{n+1}$
given by
$(\textsf{X}\times\textsf{X})^{n+1}$
given by
 \begin{equation}\mathbb{P}(d(u_0,\dots,u_n)) = \check{\eta}_0(du_0) \prod_{p=1}^n \check{\Phi}_p^I(\eta_{p-1}^f\otimes\eta_{p-1}^c)(du_p).\end{equation}
\begin{equation}\mathbb{P}(d(u_0,\dots,u_n)) = \check{\eta}_0(du_0) \prod_{p=1}^n \check{\Phi}_p^I(\eta_{p-1}^f\otimes\eta_{p-1}^c)(du_p).\end{equation}
Noting (3), it is easily checked that the marginal of ![]() $x_n^f$
(resp.
$x_n^f$
(resp. ![]() $x_n^c$
) is
$x_n^c$
) is ![]() $\eta_n^f$
(resp.
$\eta_n^f$
(resp. ![]() $\eta_n^c$
). Denote by
$\eta_n^c$
). Denote by ![]() $\check{\eta}_n^I$
the marginal of
$\check{\eta}_n^I$
the marginal of ![]() $u_n$
induced by this joint probability measure. Thus, if one could sample a trajectory of
$u_n$
induced by this joint probability measure. Thus, if one could sample a trajectory of ![]() $(u_0,\dots,u_n)$
from
$(u_0,\dots,u_n)$
from ![]() $\mathbb{P}(d(u_0,\dots,u_n))$
one could easily approximate quantities such as (1) or (2) using Monte Carlo methods. In most practical applications of interest, this is not possible.
$\mathbb{P}(d(u_0,\dots,u_n))$
one could easily approximate quantities such as (1) or (2) using Monte Carlo methods. In most practical applications of interest, this is not possible.
The particle approximation of (8) is taken as
 \[\mathbb{P}(d(u_0^{1:N},\dots,u_n^{1:N})) = \Bigg(\prod_{i=1}^N \check{\eta}_0(du_0^i)\Bigg)\Bigg(\prod_{p=1}^n\prod_{i=1}^N\check{\Phi}_p^I(\eta_{p-1}^{N,f}\otimes\eta_{p-1}^{N,c})(du_p^i)\Bigg),\]
\[\mathbb{P}(d(u_0^{1:N},\dots,u_n^{1:N})) = \Bigg(\prod_{i=1}^N \check{\eta}_0(du_0^i)\Bigg)\Bigg(\prod_{p=1}^n\prod_{i=1}^N\check{\Phi}_p^I(\eta_{p-1}^{N,f}\otimes\eta_{p-1}^{N,c})(du_p^i)\Bigg),\]
where for ![]() $p\geq 1$
,
$p\geq 1$
, ![]() $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
,
 \[\eta_{p-1}^{N,s}(dx) = \frac{1}{N}\sum_{i=1}^N \delta_{x_{p-1}^{i,s}}(dx).\]
\[\eta_{p-1}^{N,s}(dx) = \frac{1}{N}\sum_{i=1}^N \delta_{x_{p-1}^{i,s}}(dx).\]
The IRCPF algorithm which simulates from ![]() $\mathbb{P}(d(u_0^{1:N},\dots))$
is presented in Algorithm 1. The key point is that in this algorithm, the resampled indices for a pair of particles are generated (conditionally) independently. Set
$\mathbb{P}(d(u_0^{1:N},\dots))$
is presented in Algorithm 1. The key point is that in this algorithm, the resampled indices for a pair of particles are generated (conditionally) independently. Set
 \[\check{\eta}_{p}^{N,I}(du) = \frac{1}{N}\sum_{i=1}^N \delta_{u_{p}^{i}}(du).\]
\[\check{\eta}_{p}^{N,I}(du) = \frac{1}{N}\sum_{i=1}^N \delta_{u_{p}^{i}}(du).\]
As has been mentioned by many authors (e.g. [Reference Sen, Thiery and Jasra28]), one does not expect this procedure to be effective, in the sense that ![]() $\check{\eta}_n^I$
would not provide an appropriate dependence between
$\check{\eta}_n^I$
would not provide an appropriate dependence between ![]() $(\eta_n^f,\eta_n^c)$
.
$(\eta_n^f,\eta_n^c)$
.
Algorithm 1: The IRCPF Algorithm.

3.2. Maximally coupled resampling
Let ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $B\in\mathcal{X}\times\mathcal{X}$
, and
$B\in\mathcal{X}\times\mathcal{X}$
, and ![]() $\mu\in\mathscr{P}(\textsf{X}\times\textsf{X})$
, and define the probability measure
$\mu\in\mathscr{P}(\textsf{X}\times\textsf{X})$
, and define the probability measure
 \begin{eqnarray*}\check{\Phi}_n^M(\mu)(B) & \,=\, & \mu\Big(\{F_{n-1,\mu,f} \wedge F_{n-1,\mu,c}\} \check{M}_n(B)\Big)+ \Big(1-\mu\Big(\{F_{n-1,\mu,f} \wedge F_{n-1,\mu,c}\}\Big)\Big) \\ & &\times (\mu\otimes\mu)\Big(\Big\{\overline{F}_{n-1,\mu,f}\otimes \overline{F}_{n-1,\mu,c}\Big\}\bar{M}_n(B)\Big),\end{eqnarray*}
\begin{eqnarray*}\check{\Phi}_n^M(\mu)(B) & \,=\, & \mu\Big(\{F_{n-1,\mu,f} \wedge F_{n-1,\mu,c}\} \check{M}_n(B)\Big)+ \Big(1-\mu\Big(\{F_{n-1,\mu,f} \wedge F_{n-1,\mu,c}\}\Big)\Big) \\ & &\times (\mu\otimes\mu)\Big(\Big\{\overline{F}_{n-1,\mu,f}\otimes \overline{F}_{n-1,\mu,c}\Big\}\bar{M}_n(B)\Big),\end{eqnarray*}
where for ![]() $(x,y)\in\textsf{X}\times\textsf{X}$
,
$(x,y)\in\textsf{X}\times\textsf{X}$
,
 \begin{eqnarray*}\overline{F}_{n-1,\mu,f}(x,y) & \,=\, & \frac{F_{n-1,\mu,f}(x,y)-\{F_{n-1,\mu,f}(x,y)\wedge F_{n-1,\mu,c}(x,y)\}}{\mu(F_{n-1,\mu,f}-\{F_{n-1,\mu,f}\wedge F_{n-1,\mu,c}\})}, \\\overline{F}_{n-1,\mu,c}(x,y) & \,=\, & \frac{F_{n-1,\mu,c}(x,y)-\{F_{n-1,\mu,f}(x,y)\wedge F_{n-1,\mu,c}(x,y)\}}{\mu(F_{n-1,\mu,c}-\{F_{n-1,\mu,f}\wedge F_{n-1,\mu,c}\})}, \\F_{n-1,\mu,f}(x,y) & \,=\, & \check{G}_{n-1,\mu,f}(x)\otimes1, \\F_{n-1,\mu,c}(x,y) & \,=\, & 1\otimes \check{G}_{n-1,\mu,c}(y), \\\check{G}_{n-1,\mu,f}(x) & \,=\, & \frac{G_{n-1}(x)}{\mu(G_{n-1}\otimes 1)}, \\\check{G}_{n-1,\mu,c}(y) & \,=\, & \frac{G_{n-1}(y)}{\mu(1\otimes G_{n-1})},\end{eqnarray*}
\begin{eqnarray*}\overline{F}_{n-1,\mu,f}(x,y) & \,=\, & \frac{F_{n-1,\mu,f}(x,y)-\{F_{n-1,\mu,f}(x,y)\wedge F_{n-1,\mu,c}(x,y)\}}{\mu(F_{n-1,\mu,f}-\{F_{n-1,\mu,f}\wedge F_{n-1,\mu,c}\})}, \\\overline{F}_{n-1,\mu,c}(x,y) & \,=\, & \frac{F_{n-1,\mu,c}(x,y)-\{F_{n-1,\mu,f}(x,y)\wedge F_{n-1,\mu,c}(x,y)\}}{\mu(F_{n-1,\mu,c}-\{F_{n-1,\mu,f}\wedge F_{n-1,\mu,c}\})}, \\F_{n-1,\mu,f}(x,y) & \,=\, & \check{G}_{n-1,\mu,f}(x)\otimes1, \\F_{n-1,\mu,c}(x,y) & \,=\, & 1\otimes \check{G}_{n-1,\mu,c}(y), \\\check{G}_{n-1,\mu,f}(x) & \,=\, & \frac{G_{n-1}(x)}{\mu(G_{n-1}\otimes 1)}, \\\check{G}_{n-1,\mu,c}(y) & \,=\, & \frac{G_{n-1}(y)}{\mu(1\otimes G_{n-1})},\end{eqnarray*}
and for ![]() $((x,y),(u,v))\in\textsf{X}^2\times \textsf{X}^2$
and
$((x,y),(u,v))\in\textsf{X}^2\times \textsf{X}^2$
and ![]() $B\in\mathcal{X}\times\mathcal{X}$
,
$B\in\mathcal{X}\times\mathcal{X}$
,
Now set ![]() $\check{\eta}_0^M=\check{\eta}_0$
; we define, recursively, for any
$\check{\eta}_0^M=\check{\eta}_0$
; we define, recursively, for any ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $B\in\mathcal{X}\times\mathcal{X}$
,
$B\in\mathcal{X}\times\mathcal{X}$
,
Note that by [Reference Jasra, Kamatani, Law and Zhou22, Proposition A.1] we have, for ![]() $B\in\mathcal{X}$
,
$B\in\mathcal{X}$
,
To generate an MCIRCPF, we consider the following probability measure:
 \[\mathbb{P}(d(u_0^{1:N},\dots,u_n^{1:N})) = \Bigg(\prod_{i=1}^N \check{\eta}_0(du_0^i)\Bigg)\Bigg(\prod_{p=1}^n\prod_{i=1}^N\check{\Phi}_p^M(\check{\eta}_{n-1}^{N,M})(du_p^i)\Bigg),\]
\[\mathbb{P}(d(u_0^{1:N},\dots,u_n^{1:N})) = \Bigg(\prod_{i=1}^N \check{\eta}_0(du_0^i)\Bigg)\Bigg(\prod_{p=1}^n\prod_{i=1}^N\check{\Phi}_p^M(\check{\eta}_{n-1}^{N,M})(du_p^i)\Bigg),\]
where for ![]() $p\geq 1$
,
$p\geq 1$
,
 \[\check{\eta}_{p-1}^{N,M}(du) = \frac{1}{N}\sum_{i=1}^N \delta_{u_{p}^{i}}(du),\]
\[\check{\eta}_{p-1}^{N,M}(du) = \frac{1}{N}\sum_{i=1}^N \delta_{u_{p}^{i}}(du),\]
and for ![]() $s\in\{\,f,c\}$
we set
$s\in\{\,f,c\}$
we set
 \[\eta_{p-1}^{N,s}(dx) = \frac{1}{N}\sum_{i=1}^N \delta_{x_{p-1}^{i,s}}(dx).\]
\[\eta_{p-1}^{N,s}(dx) = \frac{1}{N}\sum_{i=1}^N \delta_{x_{p-1}^{i,s}}(dx).\]
The way in which one can generate from ![]() $\mathbb{P}(d(u_0^{1:N},\dots))$
is given in Algorithm 2. To explain further, the simulation from
$\mathbb{P}(d(u_0^{1:N},\dots))$
is given in Algorithm 2. To explain further, the simulation from ![]() $\check{\Phi}_p^M(\check{\eta}_{p-1}^{N,M})$
consists of whether the resampled indices for the particle pair are equal (second bullet in Algorithm 2) or different (third bullet in Algorithm 2). This procedure is as in [Reference Chopin and Singh6] and adopted in, for instance, [Reference Jacob, Lindsten and Schön17] and [Reference Jasra, Kamatani, Law and Zhou22]. The idea is to provide a local optimality procedure with respect to the resampling operation. This is in the sense that for any fixed N, and conditional on the information generated so far, one will maximize the probability that the resampled indices are equal.
$\check{\Phi}_p^M(\check{\eta}_{p-1}^{N,M})$
consists of whether the resampled indices for the particle pair are equal (second bullet in Algorithm 2) or different (third bullet in Algorithm 2). This procedure is as in [Reference Chopin and Singh6] and adopted in, for instance, [Reference Jacob, Lindsten and Schön17] and [Reference Jasra, Kamatani, Law and Zhou22]. The idea is to provide a local optimality procedure with respect to the resampling operation. This is in the sense that for any fixed N, and conditional on the information generated so far, one will maximize the probability that the resampled indices are equal.
For the MCIRCPF, we present a preliminary result which will prove to be of interest. The following assumptions are used; note that in (A3) there is a metric ![]() $\textsf{d}$
on
$\textsf{d}$
on ![]() $\textsf{X}\times\textsf{X}$
implicit in the assumption.
$\textsf{X}\times\textsf{X}$
implicit in the assumption.
(A1) For every
 $n\geq 0$
,
$n\geq 0$
,  $G_n\in \mathcal{C}_b(\textsf{X})$
.
$G_n\in \mathcal{C}_b(\textsf{X})$
.(A2) For every
 $n\geq 1$
,
$n\geq 1$
,  $\check{M}_n$
is Feller.
$\check{M}_n$
is Feller.(A3)
 $\textsf{X}$
is a locally compact and separable metric space.
$\textsf{X}$
is a locally compact and separable metric space.
These assumptions are adopted because of the complexity of the operator ![]() $\check{\Phi}_n^M$
. As can be seen in Appendix C, where the proofs for the following result are given, it is nontrivial to work with
$\check{\Phi}_n^M$
. As can be seen in Appendix C, where the proofs for the following result are given, it is nontrivial to work with ![]() $\check{\Phi}_n^M$
. To weaken these assumptions would lead to further calculations, which would essentially confirm the same result.
$\check{\Phi}_n^M$
. To weaken these assumptions would lead to further calculations, which would essentially confirm the same result.
Algorithm 2: The MCIRCPF Algorithm.

Theorem 3.1. Assume (A1)–(A3). Then for any ![]() $\varphi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
,
$\varphi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
, ![]() $n\geq 0$
, we have
$n\geq 0$
, we have
What is interesting here is that Theorem 3.1 verifies what is expected, given the construction above: on the product space ![]() $\textsf{X}\times\textsf{X}$
the MCIRCPF approximates the target
$\textsf{X}\times\textsf{X}$
the MCIRCPF approximates the target ![]() $\check{\eta}_{n}^{M}$
. As noted in (9),
$\check{\eta}_{n}^{M}$
. As noted in (9), ![]() $\check{\eta}_{n}^{M}$
is a coupling of
$\check{\eta}_{n}^{M}$
is a coupling of ![]() $(\eta_n^f,\eta_n^c)$
, but it is not the actual maximal coupling of
$(\eta_n^f,\eta_n^c)$
, but it is not the actual maximal coupling of ![]() $(\eta_n^f,\eta_n^c)$
; this can be easily checked to be the case in most problems of practical interest. As is well known, the maximal coupling will maximize the probability that two random variables are equal, with specified marginals, and is the optimal coupling of two probability measures with respect to the
$(\eta_n^f,\eta_n^c)$
; this can be easily checked to be the case in most problems of practical interest. As is well known, the maximal coupling will maximize the probability that two random variables are equal, with specified marginals, and is the optimal coupling of two probability measures with respect to the ![]() $L_0-$
Wasserstein distance. If this former property is desirable from a practical perspective, then the above algorithm should not be used. The maximally coupled resampling operation is, for a finite number of samples (particles), the optimal (in the above sense) way to couple the resampling operation, but may not lead to large sample ‘good’ couplings. This is manifested in [Reference Jasra, Kamatani, Law and Zhou22], where the forward error rate (6) is lost for the diffusion problem in Section 2.3. As mentioned above, the limit is a coupling of
$L_0-$
Wasserstein distance. If this former property is desirable from a practical perspective, then the above algorithm should not be used. The maximally coupled resampling operation is, for a finite number of samples (particles), the optimal (in the above sense) way to couple the resampling operation, but may not lead to large sample ‘good’ couplings. This is manifested in [Reference Jasra, Kamatani, Law and Zhou22], where the forward error rate (6) is lost for the diffusion problem in Section 2.3. As mentioned above, the limit is a coupling of ![]() $(\eta_n^f,\eta_n^c)$
, but in general there is no reason to suspect that it is optimal in any sense.
$(\eta_n^f,\eta_n^c)$
, but in general there is no reason to suspect that it is optimal in any sense.
3.3. Maximal coupling
We now present an algorithm which can sample (in the limit) from the maximal coupling of ![]() $(\eta_n^f,\eta_n^c)$
. We will assume that for
$(\eta_n^f,\eta_n^c)$
. We will assume that for ![]() $s\in\{\,f,c\}$
the Markov kernels
$s\in\{\,f,c\}$
the Markov kernels ![]() $M_n^s$
, as well as
$M_n^s$
, as well as ![]() $\eta_0^s,$
admit a density with respect to a
$\eta_0^s,$
admit a density with respect to a ![]() $\sigma-$
finite measure dx. The densities are denoted
$\sigma-$
finite measure dx. The densities are denoted ![]() $M_n^s$
and
$M_n^s$
and ![]() $\eta_0^s$
,
$\eta_0^s$
, ![]() $s\in\{\,f,c\}$
, and we assume that the densities can be evaluated numerically. To remove this latter requirement is left to future work.
$s\in\{\,f,c\}$
, and we assume that the densities can be evaluated numerically. To remove this latter requirement is left to future work.
Let ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $B\in\mathcal{X}\times\mathcal{X}$
, and
$B\in\mathcal{X}\times\mathcal{X}$
, and ![]() $(\mu,\nu)\in\mathscr{P}(\textsf{X})\times\mathscr{P}(\textsf{X})$
, and define the probability measure
$(\mu,\nu)\in\mathscr{P}(\textsf{X})\times\mathscr{P}(\textsf{X})$
, and define the probability measure
 \begin{eqnarray*}\check{\Phi}_n^{C}(\mu,\nu)(B) & \,=\, & \int_{\textsf{X}\times\textsf{X}}\mathbb{I}_B(x,y) \bigg[\int_{\textsf{X}}F_{n-1,\mu,f}(u)\wedge F_{n-1,\nu,c}(u) \delta_{\{u,u\}}(d(x,y)) du \\
& & +\,\frac{1}{1-\int_{\textsf{X}}F_{n-1,\mu,f}(u)\wedge F_{n-1,\nu,c}(u)du}\overline{F}_{n-1,\mu,\nu,f}(x)\overline{F}_{n-1,\nu,\mu,c}(y) dxdy\bigg],\end{eqnarray*}
\begin{eqnarray*}\check{\Phi}_n^{C}(\mu,\nu)(B) & \,=\, & \int_{\textsf{X}\times\textsf{X}}\mathbb{I}_B(x,y) \bigg[\int_{\textsf{X}}F_{n-1,\mu,f}(u)\wedge F_{n-1,\nu,c}(u) \delta_{\{u,u\}}(d(x,y)) du \\
& & +\,\frac{1}{1-\int_{\textsf{X}}F_{n-1,\mu,f}(u)\wedge F_{n-1,\nu,c}(u)du}\overline{F}_{n-1,\mu,\nu,f}(x)\overline{F}_{n-1,\nu,\mu,c}(y) dxdy\bigg],\end{eqnarray*}
where, for ![]() $x\in\textsf{X}$
,
$x\in\textsf{X}$
,
 \begin{eqnarray*}\overline{F}_{n-1,\mu,\nu,f}(x) & \,=\, & F_{n-1,\mu,f}(x) - F_{n-1,\mu,f}(x)\wedge F_{n-1,\nu,c}(x),\\\overline{F}_{n-1,\nu,\mu,c}(x) & \,=\, & F_{n-1,\nu,c}(x) - F_{n-1,\mu,f}(x)\wedge F_{n-1,\nu,c}(x),\\
F_{n-1,\mu,f}(x) & \,=\, & \frac{\mu\big(G_{n-1}M_n^f(\cdot,x)\big)}{\mu(G_{n-1})},\\ F_{n-1,\nu,c}(x) & \,=\, & \frac{\nu(G_{n-1}M_n^c(\cdot,x))}{\nu(G_{n-1})}.\end{eqnarray*}
\begin{eqnarray*}\overline{F}_{n-1,\mu,\nu,f}(x) & \,=\, & F_{n-1,\mu,f}(x) - F_{n-1,\mu,f}(x)\wedge F_{n-1,\nu,c}(x),\\\overline{F}_{n-1,\nu,\mu,c}(x) & \,=\, & F_{n-1,\nu,c}(x) - F_{n-1,\mu,f}(x)\wedge F_{n-1,\nu,c}(x),\\
F_{n-1,\mu,f}(x) & \,=\, & \frac{\mu\big(G_{n-1}M_n^f(\cdot,x)\big)}{\mu(G_{n-1})},\\ F_{n-1,\nu,c}(x) & \,=\, & \frac{\nu(G_{n-1}M_n^c(\cdot,x))}{\nu(G_{n-1})}.\end{eqnarray*}
Now set ![]() $\check{\eta}_0^C$
as the maximal coupling of
$\check{\eta}_0^C$
as the maximal coupling of ![]() $(\eta_0^f,\eta_0^c)$
, and for
$(\eta_0^f,\eta_0^c)$
, and for ![]() $B\in\mathcal{X}\times\mathcal{X}$
set
$B\in\mathcal{X}\times\mathcal{X}$
set
We have, for ![]() $B\in\mathcal{X}$
,
$B\in\mathcal{X}$
,
Moreover, ![]() $\check{\eta}_n^C$
is the maximal coupling of
$\check{\eta}_n^C$
is the maximal coupling of ![]() $(\eta_n^f,\eta_n^c)$
. To see why this is the case, we note that our assumptions imply that
$(\eta_n^f,\eta_n^c)$
. To see why this is the case, we note that our assumptions imply that ![]() $(\eta_n^f,\eta_n^c)$
have densities with respect to a
$(\eta_n^f,\eta_n^c)$
have densities with respect to a ![]() $\sigma-$
finite measure and that these densities are simply
$\sigma-$
finite measure and that these densities are simply ![]() $(F_{n-1,\eta_{n-1}^f,f},F_{n-1,\eta_{n-1}^c,c})$
; hence the expression
$(F_{n-1,\eta_{n-1}^f,f},F_{n-1,\eta_{n-1}^c,c})$
; hence the expression ![]() $\check{\Phi}_n^{C}(\eta_{n-1}^f,\eta_{n-1}^c)(\cdot)$
corresponds exactly to the definition of the maximal coupling of
$\check{\Phi}_n^{C}(\eta_{n-1}^f,\eta_{n-1}^c)(\cdot)$
corresponds exactly to the definition of the maximal coupling of ![]() $(\eta_n^f,\eta_n^c)$
.
$(\eta_n^f,\eta_n^c)$
.
To generate an MCPF, we consider the following probability measure:
 \[\mathbb{P}(d(u_0^{1:N},\dots,u_n^{1:N})) = \Bigg(\prod_{i=1}^N \check{\eta}_0^C(du_0^i)\Bigg)\Bigg(\prod_{p=1}^n\prod_{i=1}^N\check{\Phi}_p^C(\eta_{p-1}^{N,f},\eta_{p-1}^{N,c})(du_p^i)\Bigg),\]
\[\mathbb{P}(d(u_0^{1:N},\dots,u_n^{1:N})) = \Bigg(\prod_{i=1}^N \check{\eta}_0^C(du_0^i)\Bigg)\Bigg(\prod_{p=1}^n\prod_{i=1}^N\check{\Phi}_p^C(\eta_{p-1}^{N,f},\eta_{p-1}^{N,c})(du_p^i)\Bigg),\]
where for ![]() $p\geq 1$
,
$p\geq 1$
, ![]() $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
,
 \[\eta_{p-1}^{N,s}(dx) = \frac{1}{N}\sum_{i=1}^N \delta_{x_{p-1}^{i,s}}(dx).\]
\[\eta_{p-1}^{N,s}(dx) = \frac{1}{N}\sum_{i=1}^N \delta_{x_{p-1}^{i,s}}(dx).\]
For ![]() $\mu\in\mathscr{P}(\textsf{X})$
,
$\mu\in\mathscr{P}(\textsf{X})$
, ![]() $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
, ![]() $B\in\mathcal{X}$
,
$B\in\mathcal{X}$
, ![]() $n\geq 1$
, we set
$n\geq 1$
, we set
In Algorithm 3 we present how one can simulate from ![]() $\mathbb{P}(d(u_0^{1:N},\dots))$
. We remark that as
$\mathbb{P}(d(u_0^{1:N},\dots))$
. We remark that as ![]() $M_n^s$
,
$M_n^s$
, ![]() $n\geq 1$
, and
$n\geq 1$
, and ![]() $\eta_0^s$
,
$\eta_0^s$
, ![]() $s\in\{\,f,c\}$
, can be evaluated numerically, we can sample from
$s\in\{\,f,c\}$
, can be evaluated numerically, we can sample from ![]() $\check{\eta}_0^C$
and
$\check{\eta}_0^C$
and ![]() $\check{\Phi}_n^{C}(\eta_{n-1}^{N,f},\eta_{n-1}^{N,c})$
, the latter of which is the maximal coupling of
$\check{\Phi}_n^{C}(\eta_{n-1}^{N,f},\eta_{n-1}^{N,c})$
, the latter of which is the maximal coupling of ![]() $\Phi_n^f(\eta_{n-1}^{N,f})$
and
$\Phi_n^f(\eta_{n-1}^{N,f})$
and ![]() $\Phi_n^c(\eta_{n-1}^{N,c})$
, using the algorithm in [Reference Thorisson29], which is presented in the bullet points in Algorithm 3. The algorithm in [Reference Thorisson29] is a rejection sampler, which would add a random running time element per time-step, which may not be desirable for some applications. As noted in [Reference Jacob, O’Leary and Atachde18], it can be shown that the expected running time is at most 2, but that the variance of the running time depends upon the closeness, in terms of the total variation distance, of the two probability measures that one is trying to couple. In general, in the limiting case, we expect that the total variation distance between
$\Phi_n^c(\eta_{n-1}^{N,c})$
, using the algorithm in [Reference Thorisson29], which is presented in the bullet points in Algorithm 3. The algorithm in [Reference Thorisson29] is a rejection sampler, which would add a random running time element per time-step, which may not be desirable for some applications. As noted in [Reference Jacob, O’Leary and Atachde18], it can be shown that the expected running time is at most 2, but that the variance of the running time depends upon the closeness, in terms of the total variation distance, of the two probability measures that one is trying to couple. In general, in the limiting case, we expect that the total variation distance between ![]() $(\eta_n^f,\eta_n^c)$
will be small (in the diffusion case, under certain assumptions, it can be
$(\eta_n^f,\eta_n^c)$
will be small (in the diffusion case, under certain assumptions, it can be ![]() $\mathcal{O}(\Delta_l)$
) and hence that the rejection sampler will perform well.
$\mathcal{O}(\Delta_l)$
) and hence that the rejection sampler will perform well.
Algorithm 3: The MCPF Algorithm.

3.4. Wasserstein coupled resampling
We describe the WCPF used in [Reference Jasra, Ballesio, von Schwerin and Tempone20]. For this case we restrict our attention to the case that ![]() $\textsf{X}=\mathbb{R}$
. The reason for this simplification is that the approach is based upon an optimal coupling result which appears to be explicit only in the one-dimensional case. In the approach to be considered, one might consider the multi-dimensional case using, for instance Hilbert space-filling curves, but we have not tested such a method empirically and it is unclear how useful it is in practice. It is explicitly assumed that the cumulative distribution function (CDF) and its inverse associated to the probability
$\textsf{X}=\mathbb{R}$
. The reason for this simplification is that the approach is based upon an optimal coupling result which appears to be explicit only in the one-dimensional case. In the approach to be considered, one might consider the multi-dimensional case using, for instance Hilbert space-filling curves, but we have not tested such a method empirically and it is unclear how useful it is in practice. It is explicitly assumed that the cumulative distribution function (CDF) and its inverse associated to the probability
where ![]() $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
, ![]() $n\geq 0$
, and
$n\geq 0$
, and ![]() $B\in\mathcal{X}$
, exist and are continuous functions. We denote the CDF (resp. inverse) of
$B\in\mathcal{X}$
, exist and are continuous functions. We denote the CDF (resp. inverse) of ![]() $\overline{\eta}_n^s$
as
$\overline{\eta}_n^s$
as ![]() $F_{\overline{\eta}_n^s}$
(resp.
$F_{\overline{\eta}_n^s}$
(resp. ![]() $F_{\overline{\eta}_n^s}^{-1}$
). In general we write probability measures on
$F_{\overline{\eta}_n^s}^{-1}$
). In general we write probability measures on ![]() $\textsf{X}$
for which the CDF and inverse are well-defined as
$\textsf{X}$
for which the CDF and inverse are well-defined as ![]() $\mathscr{P}_F(\textsf{X})$
with the associated CDF
$\mathscr{P}_F(\textsf{X})$
with the associated CDF ![]() $F_{\mu}$
. Let
$F_{\mu}$
. Let ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $B\in\mathcal{X}\times\mathcal{X}$
, and
$B\in\mathcal{X}\times\mathcal{X}$
, and ![]() $\mu,\nu\in\mathscr{P}_F(\textsf{X})$
, and define the probability measure
$\mu,\nu\in\mathscr{P}_F(\textsf{X})$
, and define the probability measure
Consider the joint probability measure on ![]() $(\textsf{X}\times\textsf{X})^{n+1}$
given by
$(\textsf{X}\times\textsf{X})^{n+1}$
given by
 \[\mathbb{P}(d(u_0,\dots,u_n)) = \check{\eta}_0(du_0) \prod_{p=1}^n \check{\Phi}_p^W(\overline{\eta}_{p-1}^f,\overline{\eta}_{p-1}^c)(du_p).\]
\[\mathbb{P}(d(u_0,\dots,u_n)) = \check{\eta}_0(du_0) \prod_{p=1}^n \check{\Phi}_p^W(\overline{\eta}_{p-1}^f,\overline{\eta}_{p-1}^c)(du_p).\]
It is easily checked that the marginal of ![]() $x_n^f$
(resp.
$x_n^f$
(resp. ![]() $x_n^c$
) is
$x_n^c$
) is ![]() $\eta_n^f$
(resp.
$\eta_n^f$
(resp. ![]() $\eta_n^c$
). Denote by
$\eta_n^c$
). Denote by ![]() $\check{\eta}_n^W$
the marginal of
$\check{\eta}_n^W$
the marginal of ![]() $u_n$
induced by this joint probability measure.
$u_n$
induced by this joint probability measure.
To generate a WCPF, we consider the following:
 \[\mathbb{P}(d(u_0^{1:N},\dots,u_n^{1:N})) = \Bigg(\prod_{i=1}^N \check{\eta}_0(du_0^i)\Bigg)\Bigg(\prod_{p=1}^n\prod_{i=1}^N\check{\Phi}_p^W(\overline{\eta}_{p-1}^{N,f},\overline{\eta}_{p-1}^{N,c})(du_p^i)\Bigg),\]
\[\mathbb{P}(d(u_0^{1:N},\dots,u_n^{1:N})) = \Bigg(\prod_{i=1}^N \check{\eta}_0(du_0^i)\Bigg)\Bigg(\prod_{p=1}^n\prod_{i=1}^N\check{\Phi}_p^W(\overline{\eta}_{p-1}^{N,f},\overline{\eta}_{p-1}^{N,c})(du_p^i)\Bigg),\]
where for ![]() $p\geq 1$
,
$p\geq 1$
, ![]() $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
,
 \[\overline{\eta}_{p-1}^{N,s}(dx) = \sum_{i=1}^N \frac{G_{p-1}\big(x_{p-1}^{i,s}\big)}{\sum_{j=1}^N G_{p-1}\big(x_{p-1}^{j,s}\big)}\delta_{x_{p-1}^{i,s}}(dx).\]
\[\overline{\eta}_{p-1}^{N,s}(dx) = \sum_{i=1}^N \frac{G_{p-1}\big(x_{p-1}^{i,s}\big)}{\sum_{j=1}^N G_{p-1}\big(x_{p-1}^{j,s}\big)}\delta_{x_{p-1}^{i,s}}(dx).\]
As before, for ![]() $p\geq 1$
,
$p\geq 1$
, ![]() $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
,
 \[\eta_{p-1}^{N,s}(dx) = \frac{1}{N}\sum_{i=1}^N \delta_{x_{p-1}^{i,s}}(dx),\]
\[\eta_{p-1}^{N,s}(dx) = \frac{1}{N}\sum_{i=1}^N \delta_{x_{p-1}^{i,s}}(dx),\]
and for ![]() $p\geq 0$
,
$p\geq 0$
,
 \[\check{\eta}_{p}^{N,W}(du) = \frac{1}{N}\sum_{i=1}^N \delta_{u_{p}^{i}}(du).\]
\[\check{\eta}_{p}^{N,W}(du) = \frac{1}{N}\sum_{i=1}^N \delta_{u_{p}^{i}}(du).\]
In Algorithm 4 we present how one can simulate from ![]() $\mathbb{P}(d(u_0^{1:N},\dots))$
. It should be noted that whilst the sorting operation in Algorithm 4 is
$\mathbb{P}(d(u_0^{1:N},\dots))$
. It should be noted that whilst the sorting operation in Algorithm 4 is ![]() $\mathcal{O}(N\log(N))$
in the worst case, it is seen in [Reference Jasra, Ballesio, von Schwerin and Tempone20] that this step is often
$\mathcal{O}(N\log(N))$
in the worst case, it is seen in [Reference Jasra, Ballesio, von Schwerin and Tempone20] that this step is often ![]() $\mathcal{O}(N)$
in practice and is less expensive than the sampling of
$\mathcal{O}(N)$
in practice and is less expensive than the sampling of ![]() $\check{M}_p$
in the diffusion case.
$\check{M}_p$
in the diffusion case.
Algorithm 4: The WCPF Algorithm.

4. Theoretical results
This section is split into two. We give our CLTs in Section 4.1 and bounds on the asymptotic variance in Section 4.2.
4.1. Central limit theorems
Define the sequence of nonnegative kernels ![]() $\{Q_n^s\}_{n\geq 1}$
,
$\{Q_n^s\}_{n\geq 1}$
, ![]() $s\in\{\,f,c\}$
, by
$s\in\{\,f,c\}$
, by ![]() $Q_n^s(x,dy) = G_{n-1}(x) M_n^s(x,dy)$
. For
$Q_n^s(x,dy) = G_{n-1}(x) M_n^s(x,dy)$
. For ![]() $B\in\mathcal{X}$
,
$B\in\mathcal{X}$
, ![]() $x_p\in\textsf{X}$
, define
$x_p\in\textsf{X}$
, define
 \[Q_{p,n}^s(B)(x_p) = \int_{\textsf{X}^{n-p}} \mathbb{I}_B(x_n) \prod_{q=p}^{n-1} Q_{q+1}^s(x_q,dx_{q+1})\]
\[Q_{p,n}^s(B)(x_p) = \int_{\textsf{X}^{n-p}} \mathbb{I}_B(x_n) \prod_{q=p}^{n-1} Q_{q+1}^s(x_q,dx_{q+1})\]
for ![]() $0\leq p<n$
; in the case
$0\leq p<n$
; in the case ![]() $p=n$
, let
$p=n$
, let ![]() $Q_{p,n}^s$
be the identity operator. Now, for
$Q_{p,n}^s$
be the identity operator. Now, for ![]() $0\leq p<n$
,
$0\leq p<n$
, ![]() $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
, ![]() $B\in\mathcal{X}$
,
$B\in\mathcal{X}$
, ![]() $x_p\in\textsf{X}$
, define
$x_p\in\textsf{X}$
, define
in the case ![]() $p=n$
,
$p=n$
, ![]() $D_{p,n}^s(B)(x)=\mathbb{I}_B-\eta_n^s(B)$
.
$D_{p,n}^s(B)(x)=\mathbb{I}_B-\eta_n^s(B)$
.
We then have our CLTs, where the proofs are given in Appendix A. Recall that for the MCPF ![]() $M_n^s$
is used as a notation for the kernel and density of
$M_n^s$
is used as a notation for the kernel and density of ![]() $M_n^s$
.
$M_n^s$
.
Theorem 4.1. The following statements hold.
1. For the IRCPF: For any
 $\varphi\in\mathcal{B}_b(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})$
,  $n\geq 0$
, we have
where
$n\geq 0$
, we have
where \[\sqrt{N}[\check{\eta}_{n}^{N,I}-\check{\eta}_{n}^{I}](\varphi\otimes 1 - 1 \otimes \varphi) \Rightarrow \mathcal{N}(0,\sigma_n^{2,I}(\varphi)),\]
\[\sqrt{N}[\check{\eta}_{n}^{N,I}-\check{\eta}_{n}^{I}](\varphi\otimes 1 - 1 \otimes \varphi) \Rightarrow \mathcal{N}(0,\sigma_n^{2,I}(\varphi)),\]
 \[\sigma_n^{2,I}(\varphi) = \sum_{p=0}^n \check{\eta}_p^I(\{(D_{p,n}^f(\varphi)\otimes 1- 1\otimes D_{p,n}^c(\varphi))\}^2).\]
\[\sigma_n^{2,I}(\varphi) = \sum_{p=0}^n \check{\eta}_p^I(\{(D_{p,n}^f(\varphi)\otimes 1- 1\otimes D_{p,n}^c(\varphi))\}^2).\]
2. For the MCIRCPF: Assume (A1)–(A3); then for any
 $\varphi\in\mathcal{C}_b(\textsf{X})$
,
$\varphi\in\mathcal{C}_b(\textsf{X})$
,  $n\geq 0$
, we have
where
$n\geq 0$
, we have
where \[\sqrt{N}[\check{\eta}_{n}^{N,M}-\check{\eta}_{n}^{M}](\varphi\otimes 1 - 1 \otimes \varphi) \Rightarrow \mathcal{N}(0,\sigma_n^{2,M}(\varphi)),\]
\[\sqrt{N}[\check{\eta}_{n}^{N,M}-\check{\eta}_{n}^{M}](\varphi\otimes 1 - 1 \otimes \varphi) \Rightarrow \mathcal{N}(0,\sigma_n^{2,M}(\varphi)),\]
 \[\sigma_n^{2,M}(\varphi) = \sum_{p=0}^n \check{\eta}_p^M(\{(D_{p,n}^f(\varphi)\otimes 1- 1\otimes D_{p,n}^c(\varphi))\}^2).\]
\[\sigma_n^{2,M}(\varphi) = \sum_{p=0}^n \check{\eta}_p^M(\{(D_{p,n}^f(\varphi)\otimes 1- 1\otimes D_{p,n}^c(\varphi))\}^2).\]
3. For the MCPF: Suppose that for
 $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
,  $n\geq 1$
,
$n\geq 1$
,  $M_n^s\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
. Then for any
$M_n^s\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
. Then for any  $\varphi\in\mathcal{B}_b(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})$
,  $n\geq 0$
, we have
where
$n\geq 0$
, we have
where \[\sqrt{N}[\check{\eta}_{n}^{N,C}-\check{\eta}_{n}^{C}](\varphi\otimes 1 - 1 \otimes \varphi) \Rightarrow \mathcal{N}(0,\sigma_n^{2,C}(\varphi)),\]
\[\sqrt{N}[\check{\eta}_{n}^{N,C}-\check{\eta}_{n}^{C}](\varphi\otimes 1 - 1 \otimes \varphi) \Rightarrow \mathcal{N}(0,\sigma_n^{2,C}(\varphi)),\]
 \[\sigma_n^{2,C}(\varphi) = \sum_{p=0}^n \check{\eta}_p^C(\{(D_{p,n}^f(\varphi)\otimes 1- 1\otimes D_{p,n}^c(\varphi))\}^2).\]
\[\sigma_n^{2,C}(\varphi) = \sum_{p=0}^n \check{\eta}_p^C(\{(D_{p,n}^f(\varphi)\otimes 1- 1\otimes D_{p,n}^c(\varphi))\}^2).\]
For Wasserstein resampling, the following result is established in [Reference Jasra, Ballesio, von Schwerin and Tempone20].
Theorem 4.2. Suppose that ![]() $\check{M}_n$
,
$\check{M}_n$
, ![]() $M_n^s$
,
$M_n^s$
, ![]() $s\in\{\,f,c\}$
, are Feller for every
$s\in\{\,f,c\}$
, are Feller for every ![]() $n\geq 1$
and
$n\geq 1$
and ![]() $G_n\in\mathcal{C}_b(\textsf{X})$
for every
$G_n\in\mathcal{C}_b(\textsf{X})$
for every ![]() $n\geq 0$
. Then for any
$n\geq 0$
. Then for any ![]() $\varphi\in\mathcal{C}_b(\textsf{X})$
,
$\varphi\in\mathcal{C}_b(\textsf{X})$
, ![]() $n\geq 0$
, we have
$n\geq 0$
, we have
where
 \[\sigma_n^{2,W}(\varphi) = \sum_{p=0}^n \check{\eta}_p^W(\{(D_{p,n}^f(\varphi)\otimes 1- 1\otimes D_{p,n}^c(\varphi))\}^2).\]
\[\sigma_n^{2,W}(\varphi) = \sum_{p=0}^n \check{\eta}_p^W(\{(D_{p,n}^f(\varphi)\otimes 1- 1\otimes D_{p,n}^c(\varphi))\}^2).\]
Remark 4.1. One can also prove a multivariate CLT using the Cramér–Wold device. Consider ![]() $1\leq t <+\infty$
,
$1\leq t <+\infty$
, ![]() $(\varphi_1,\dots,\varphi_t,\psi_1,\dots,\psi_t)\in\mathcal{B}_b(\textsf{X})^{2t}$
(or if required
$(\varphi_1,\dots,\varphi_t,\psi_1,\dots,\psi_t)\in\mathcal{B}_b(\textsf{X})^{2t}$
(or if required ![]() $\mathcal{C}_b(\textsf{X})^{2t}$
). Consider the
$\mathcal{C}_b(\textsf{X})^{2t}$
). Consider the ![]() $t\times t$
positive definite and symmetric matrix
$t\times t$
positive definite and symmetric matrix ![]() $\Sigma_{n}^{s}(\varphi_{1:t},\psi_{1:t})$
,
$\Sigma_{n}^{s}(\varphi_{1:t},\psi_{1:t})$
, ![]() $s\in\{I,M,C,W\}$
, with (i,j)th entry denoted
$s\in\{I,M,C,W\}$
, with (i,j)th entry denoted ![]() $\Sigma_{n,(ij)}^{s}(\varphi_{1:t},\psi_{1:t})$
. Using the Cramér–Wold device under the various assumptions of each the algorithms one can easily deduce that for each
$\Sigma_{n,(ij)}^{s}(\varphi_{1:t},\psi_{1:t})$
. Using the Cramér–Wold device under the various assumptions of each the algorithms one can easily deduce that for each ![]() $s\in\{I,M,C,W\}$
,
$s\in\{I,M,C,W\}$
,
where
 \[\Sigma_{n,(ij)}^{s}(\varphi_{1:t},\psi_{1:t}) = \sum_{p=0}^n \check{\eta}_p^s([D_{p,n}^f(\varphi_i)\otimes 1- 1\otimes D_{p,n}^c(\psi_i)][D_{p,n}^f(\varphi_j)\otimes 1- 1\otimes D_{p,n}^c(\psi_j)]).\]
\[\Sigma_{n,(ij)}^{s}(\varphi_{1:t},\psi_{1:t}) = \sum_{p=0}^n \check{\eta}_p^s([D_{p,n}^f(\varphi_i)\otimes 1- 1\otimes D_{p,n}^c(\psi_i)][D_{p,n}^f(\varphi_j)\otimes 1- 1\otimes D_{p,n}^c(\psi_j)]).\]
4.2. Asymptotic variance
We now consider bounding the asymptotic variance in the general case. The result below (Theorem 4.3), will allow one to understand when one can expect time-uniformly ‘close’ errors in approximations of ![]() $[\eta_n^f-\eta_n^c](\varphi)$
. The following assumptions are used, which are essentially those in [Reference Whiteley30] (see also [Reference Jasra19]) with some additional assumptions ((H6)–(H7) below) as we are treating a more delicate case than that of [Reference Whiteley30]. The assumptions can hold on unbounded state spaces, as will be the case for our applications.
$[\eta_n^f-\eta_n^c](\varphi)$
. The following assumptions are used, which are essentially those in [Reference Whiteley30] (see also [Reference Jasra19]) with some additional assumptions ((H6)–(H7) below) as we are treating a more delicate case than that of [Reference Whiteley30]. The assumptions can hold on unbounded state spaces, as will be the case for our applications.
(H1) There exist an unbounded
 $\tilde{V}\,:\,\textsf{X}\rightarrow[1,+\infty)$
and constants
$\tilde{V}\,:\,\textsf{X}\rightarrow[1,+\infty)$
and constants  $\delta\in(0,1)$
and
$\delta\in(0,1)$
and  $\underline{d}\geq 1$
with the following properties. For each
$\underline{d}\geq 1$
with the following properties. For each  $d\in(\underline{d},+\infty)$
there exists a
$d\in(\underline{d},+\infty)$
there exists a  $b_d<+\infty$
such that
$b_d<+\infty$
such that  $\forall x\in\textsf{X}$
and any
$\forall x\in\textsf{X}$
and any  $s\in\{\,f,c\}$
,
where
$s\in\{\,f,c\}$
,
where \[\sup_{n\geq 1} Q_n^s(e^{\tilde{V}})(x) \leq e^{(1-\delta)\tilde{V}(x) + b_d\mathbb{I}_{C_d}(x)},\]
\[\sup_{n\geq 1} Q_n^s(e^{\tilde{V}})(x) \leq e^{(1-\delta)\tilde{V}(x) + b_d\mathbb{I}_{C_d}(x)},\]
 $C_d=\{x\in\textsf{X}\,:\,\tilde{V}(x)\leq d\}$
.
$C_d=\{x\in\textsf{X}\,:\,\tilde{V}(x)\leq d\}$
.(H2)
1. There exists a
 $C<+\infty$
such that for any
$C<+\infty$
such that for any  $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
,  $\eta_0^s(v)\leq C$
, with
$\eta_0^s(v)\leq C$
, with  $v=e^{\tilde{V}}$
, with
$v=e^{\tilde{V}}$
, with  $\tilde{V}$
as in (H1).
$\tilde{V}$
as in (H1).2. For any
 $r>1$
there exists a
$r>1$
there exists a  $C<+\infty$
such that for any
$C<+\infty$
such that for any  $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
,  $\eta_0^s(C_r)^{-1}\leq C$
.
$\eta_0^s(C_r)^{-1}\leq C$
.
(H3) With
 $\underline{d}$
as in (H1), for each
$\underline{d}$
as in (H1), for each  $d\in[\underline{d},+\infty)$
,
$d\in[\underline{d},+\infty)$
,  $s\in\{\,f,c\}$
,
and there exist
$s\in\{\,f,c\}$
,
and there exist \[\int_{C_d} G_{n-1}(x)M_n^s(x,dy) > 0\ \forall x\in\textsf{X}, n\geq 1,\]
\[\int_{C_d} G_{n-1}(x)M_n^s(x,dy) > 0\ \forall x\in\textsf{X}, n\geq 1,\]
 $\tilde{\epsilon}_d^{-}>0$
,
$\tilde{\epsilon}_d^{-}>0$
,  $\nu_d\in\mathcal{P}_v$
such that for each
$\nu_d\in\mathcal{P}_v$
such that for each  $A\in\mathcal{X}$
,
$A\in\mathcal{X}$
,  $s\in\{\,f,c\}$
,
with
$s\in\{\,f,c\}$
,
with \[\inf_{n\geq 1} \int_{C_d\cap A} Q_n^s(x,dy) \geq \tilde{\epsilon}_d^{-}\nu_d(C_d\cap A),\ \forall x\in C_d,\]
\[\inf_{n\geq 1} \int_{C_d\cap A} Q_n^s(x,dy) \geq \tilde{\epsilon}_d^{-}\nu_d(C_d\cap A),\ \forall x\in C_d,\]
 $C_d$
as in (H1).
$C_d$
as in (H1).(H4) With
 $\underline{d}$
as in (H1), and
$\underline{d}$
as in (H1), and  $\tilde{\epsilon}_d^-$
,
$\tilde{\epsilon}_d^-$
,  $\nu_d$
as in (H2), for each
$\nu_d$
as in (H2), for each  $d\in[\underline{d},+\infty)$
there exists
$d\in[\underline{d},+\infty)$
there exists  $\tilde{\epsilon}_d^+\in[\tilde{\epsilon}_d^-,+\infty)$
such that for each
$\tilde{\epsilon}_d^+\in[\tilde{\epsilon}_d^-,+\infty)$
such that for each  $A\in\mathcal{X}$
,
$A\in\mathcal{X}$
,  $s\in\{\,f,c\}$
,
with
$s\in\{\,f,c\}$
,
with \[\sup_{n\geq 1}\int_{C_d\cap A} Q_n^s(x,dy) \leq \tilde{\epsilon}_d^+\nu(C_d\cap A), \ \forall x\in C_d,\]
\[\sup_{n\geq 1}\int_{C_d\cap A} Q_n^s(x,dy) \leq \tilde{\epsilon}_d^+\nu(C_d\cap A), \ \forall x\in C_d,\]
 $C_d$
as in (H1).
$C_d$
as in (H1).(H5)
1.
 \[\sup_{n\geq 0}\sup_{x\in\textsf{X}}G_n(x) <+\infty.\]
\[\sup_{n\geq 0}\sup_{x\in\textsf{X}}G_n(x) <+\infty.\]
2. For any
 $r>1$
there exists a
$r>1$
there exists a  $C<+\infty$
such that
$C<+\infty$
such that  $\inf_{x\in C_r}G_0(x)\geq C$
, with
$\inf_{x\in C_r}G_0(x)\geq C$
, with  $C_r$
as in (H1).
$C_r$
as in (H1).
(H6) With
 $\underline{d}$
as in (H1), for each
$\underline{d}$
as in (H1), for each  $d\in[\underline{d},+\infty)$
, we have for each
$d\in[\underline{d},+\infty)$
, we have for each  $n\geq 0$
,
$n\geq 0$
,  $s\in\{\,f,c\}$
, that
and
$s\in\{\,f,c\}$
, that
and \[\frac{1}{G_n M_{n+1}^s(\mathbb{I}_{C_d})}\in\mathcal{L}_{v}(\textsf{X})\]
\[\frac{1}{G_n M_{n+1}^s(\mathbb{I}_{C_d})}\in\mathcal{L}_{v}(\textsf{X})\]
 $\sup_{n\geq 0}\max_{s\in\{\,f,c\}}\|1/G_n M_{n+1}^s(\mathbb{I}_{C_d})\|_{v}<+\infty$
.
$\sup_{n\geq 0}\max_{s\in\{\,f,c\}}\|1/G_n M_{n+1}^s(\mathbb{I}_{C_d})\|_{v}<+\infty$
.(H7) Let
 $\textsf{d}$
be a given metric on
$\textsf{d}$
be a given metric on  $\textsf{X}$
. For any
$\textsf{X}$
. For any  $\xi\in(0,1]$
, there exists a
$\xi\in(0,1]$
, there exists a  $C<+\infty$
such that for
$C<+\infty$
such that for  $\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})\cap\textrm{Lip}_{v^{\xi},\textsf{d}}(\textsf{X})$
,
$\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})\cap\textrm{Lip}_{v^{\xi},\textsf{d}}(\textsf{X})$
,  $(x,y)\in\textsf{X}\times\textsf{X}$
,
$(x,y)\in\textsf{X}\times\textsf{X}$
,  $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
,
 \[\sup_{n\geq 1}|Q_{n}^s(\varphi)(x)-Q_{n}^s(\varphi)(y)| \leq C\|\varphi\|_{v^{\xi}}\textsf{d}(x,y)[v(x)v(y)]^{\xi}.\]
\[\sup_{n\geq 1}|Q_{n}^s(\varphi)(x)-Q_{n}^s(\varphi)(y)| \leq C\|\varphi\|_{v^{\xi}}\textsf{d}(x,y)[v(x)v(y)]^{\xi}.\]
Let ![]() $A=\{(x,y)\in\textsf{X}\times\textsf{X}\,:\,x\neq y\}$
. For
$A=\{(x,y)\in\textsf{X}\times\textsf{X}\,:\,x\neq y\}$
. For ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $0\leq p \leq n$
,
$0\leq p \leq n$
, ![]() $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
, ![]() $x\in\textsf{X}$
, define
$x\in\textsf{X}$
, define
and, with ![]() $B\in\mathcal{X}$
,
$B\in\mathcal{X}$
,
 \[S_{p,n}^{f,c}(B)(x) \,:\!= \frac{Q_{p,n}^f(B)(x)}{Q_{p,n}^f(1)(x)} - \frac{Q_{p,n}^c(B)(x)}{Q_{p,n}^c(1)(x)}.\]
\[S_{p,n}^{f,c}(B)(x) \,:\!= \frac{Q_{p,n}^f(B)(x)}{Q_{p,n}^f(1)(x)} - \frac{Q_{p,n}^c(B)(x)}{Q_{p,n}^c(1)(x)}.\]
Set
 \[B(n,f,c,\varphi,\xi) =\|\varphi\|\sum_{p=0}^{n-1}\rho^{n-p}\Big\{\|h_{p,n}^fS_{p,n}^{f,c}(\varphi)\|_{v^{\xi}} + |[\eta_n^f-\eta_n^c](\varphi)| + \|\varphi\|\|h_{p,n}^f-h_{p,n}^c\|_{v^{\xi}}\rho^{n-p}\Big\}.\]
\[B(n,f,c,\varphi,\xi) =\|\varphi\|\sum_{p=0}^{n-1}\rho^{n-p}\Big\{\|h_{p,n}^fS_{p,n}^{f,c}(\varphi)\|_{v^{\xi}} + |[\eta_n^f-\eta_n^c](\varphi)| + \|\varphi\|\|h_{p,n}^f-h_{p,n}^c\|_{v^{\xi}}\rho^{n-p}\Big\}.\]
Below is our main result, whose proof can be found in Appendix E.
Theorem 4.3. Assume (H1)–(H6). Then for any ![]() $\xi\in(0,1/4)$
there exist
$\xi\in(0,1/4)$
there exist ![]() $\rho<1$
and
$\rho<1$
and ![]() $C<+\infty$
depending on the constants in (H1)–(H6) such that for any
$C<+\infty$
depending on the constants in (H1)–(H6) such that for any ![]() $\varphi\in\mathcal{B}_b(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})$
, ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $s\in\{I,M,C,W\}$
, we have
$s\in\{I,M,C,W\}$
, we have
 \begin{align*}&\sigma^{2,s}_n(\varphi) \leq \check{\eta}_n^s\Big(\{\varphi\otimes 1-1\otimes\varphi - ([\eta_n^f-\eta_n^c](\varphi))\}^2\Big)\\
&\quad + C\Bigg\{B(n,f,c,\varphi,\xi) + \|\varphi\|^2\sum_{p=0}^{n-1}\rho^{n-p}\Big(\check{\eta}_p^{s}(\mathbb{I}_A(v\otimes v)^{2\xi})(\rho^{n-p}+1)\Big)\Bigg\}. \end{align*}
\begin{align*}&\sigma^{2,s}_n(\varphi) \leq \check{\eta}_n^s\Big(\{\varphi\otimes 1-1\otimes\varphi - ([\eta_n^f-\eta_n^c](\varphi))\}^2\Big)\\
&\quad + C\Bigg\{B(n,f,c,\varphi,\xi) + \|\varphi\|^2\sum_{p=0}^{n-1}\rho^{n-p}\Big(\check{\eta}_p^{s}(\mathbb{I}_A(v\otimes v)^{2\xi})(\rho^{n-p}+1)\Big)\Bigg\}. \end{align*}
Additionally assume (H7). Then if ![]() $\textsf{d}^2\in\mathcal{L}_{(v\otimes v)^{\tilde{\xi}}}$
,
$\textsf{d}^2\in\mathcal{L}_{(v\otimes v)^{\tilde{\xi}}}$
, ![]() $\tilde{\xi}\in(0,1/2)$
, for any
$\tilde{\xi}\in(0,1/2)$
, for any ![]() $\xi\in(0,(1-2\tilde{\xi})/12))$
there exist
$\xi\in(0,(1-2\tilde{\xi})/12))$
there exist ![]() $\rho<1$
and
$\rho<1$
and ![]() $C<+\infty$
depending on the constants in (H1)–(H7) such that for any
$C<+\infty$
depending on the constants in (H1)–(H7) such that for any ![]() $\varphi\in\mathcal{B}_b(\textsf{X})\cap\textrm{\textit{Lip}}_{\textsf{d}}(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})\cap\textrm{\textit{Lip}}_{\textsf{d}}(\textsf{X})$
, ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $s\in\{I,M,C,W\}$
, we have
$s\in\{I,M,C,W\}$
, we have
 \begin{align*}&\sigma^{2,s}_n(\varphi) \leq \check{\eta}_n^s\Big(\{\varphi\otimes 1-1\otimes\varphi - ([\eta_n^f-\eta_n^c](\varphi))\}^2\Big)\\
&\quad + C\Bigg\{B(n,f,c,\varphi,\xi) + \|\varphi\|^2\sum_{p=0}^{n-1}\rho^{n-p}\Big(\check{\eta}_p^{s}(\textsf{d}^2(v^{4\xi}\otimes v^{8\xi}))(\rho^{n-p}+1)\Big)\Bigg\}.\end{align*}
\begin{align*}&\sigma^{2,s}_n(\varphi) \leq \check{\eta}_n^s\Big(\{\varphi\otimes 1-1\otimes\varphi - ([\eta_n^f-\eta_n^c](\varphi))\}^2\Big)\\
&\quad + C\Bigg\{B(n,f,c,\varphi,\xi) + \|\varphi\|^2\sum_{p=0}^{n-1}\rho^{n-p}\Big(\check{\eta}_p^{s}(\textsf{d}^2(v^{4\xi}\otimes v^{8\xi}))(\rho^{n-p}+1)\Big)\Bigg\}.\end{align*}
Remark 4.2. The range of ![]() $\xi$
is such that the upper bounds are finite. This is because
$\xi$
is such that the upper bounds are finite. This is because ![]() $\check{\eta}_p^s(v)$
is bounded above by a constant that does not depend on p (see [Reference Whiteley30, Proposition 1]).
$\check{\eta}_p^s(v)$
is bounded above by a constant that does not depend on p (see [Reference Whiteley30, Proposition 1]).
The main conclusion of this theorem is that one expects that the (variances of) approximations of ![]() $[\eta_n^f-\eta_n^c](\varphi)$
are uniformly ‘close’ in time if the following are satisfied:
$[\eta_n^f-\eta_n^c](\varphi)$
are uniformly ‘close’ in time if the following are satisfied:
1. The quantities
are small uniformly in time. \[\check{\eta}_n^s\Big(\{\varphi\otimes 1-1\otimes\varphi - ([\eta_n^f-\eta_n^c](\varphi))\}^2\Big)\quad\textrm{and}\quad|[\eta_n^f-\eta_n^c](\varphi)|\]
\[\check{\eta}_n^s\Big(\{\varphi\otimes 1-1\otimes\varphi - ([\eta_n^f-\eta_n^c](\varphi))\}^2\Big)\quad\textrm{and}\quad|[\eta_n^f-\eta_n^c](\varphi)|\]
2. The differences
are small at a rate which decays more slowly than exponentially in time. \[ \|h_{p,n}^fS_{p,n}^{f,c}(\varphi)\|_{v^{\xi}}\quad\textrm{and}\quad\|h_{p,n}^f-h_{p,n}^c\|_{v^{\xi}}\]
\[ \|h_{p,n}^fS_{p,n}^{f,c}(\varphi)\|_{v^{\xi}}\quad\textrm{and}\quad\|h_{p,n}^f-h_{p,n}^c\|_{v^{\xi}}\]
3. The quantities
are small at a rate which decays more slowly than exponentially in time. \[\check{\eta}_p^{s}(\mathbb{I}_A(v\otimes v)^{2\xi}) \quad\textrm{or}\quad\check{\eta}_p^{s}(\textsf{d}^2(v^{4\xi}\otimes v^{8\xi}))\]
\[\check{\eta}_p^{s}(\mathbb{I}_A(v\otimes v)^{2\xi}) \quad\textrm{or}\quad\check{\eta}_p^{s}(\textsf{d}^2(v^{4\xi}\otimes v^{8\xi}))\]
We note that in 1, strictly speaking, one could have ![]() $|[\eta_n^f-\eta_n^c](\varphi)|$
close at a rate which decays more slowly than exponentially in time, but as one requires the time-uniform closeness of
$|[\eta_n^f-\eta_n^c](\varphi)|$
close at a rate which decays more slowly than exponentially in time, but as one requires the time-uniform closeness of ![]() $\check{\eta}_n^s(\{\varphi\otimes 1-1\otimes\varphi - ([\eta_n^f-\eta_n^c](\varphi))\}^2)$
, one expects this property for the former. The use of A and
$\check{\eta}_n^s(\{\varphi\otimes 1-1\otimes\varphi - ([\eta_n^f-\eta_n^c](\varphi))\}^2)$
, one expects this property for the former. The use of A and ![]() $\textsf{d}$
are linked to the coupling properties associated to
$\textsf{d}$
are linked to the coupling properties associated to ![]() $\check{\eta}_p^{s}$
, as we consider in the next section.
$\check{\eta}_p^{s}$
, as we consider in the next section.
5. Application to partially observed diffusions
We now return to the PODDP model considered in Section 2.3. Throughout, ![]() $1\leq l\leq L$
is fixed, with
$1\leq l\leq L$
is fixed, with ![]() $L>1$
fixed. We will consider the significance of the results in Theorems 4.1, 4.2, and 4.3 for each of the four CPFs. We also present an example in Section 5.6 where (H1)–(H8) can be verified. We begin with a control of the term
$L>1$
fixed. We will consider the significance of the results in Theorems 4.1, 4.2, and 4.3 for each of the four CPFs. We also present an example in Section 5.6 where (H1)–(H8) can be verified. We begin with a control of the term ![]() $B(n,l,l-1,\varphi,\xi)$
.
$B(n,l,l-1,\varphi,\xi)$
.
5.1. A general result
For ![]() $x\in\textsf{X}$
, define the set
$x\in\textsf{X}$
, define the set
where ![]() $\|\cdot\|$
is the
$\|\cdot\|$
is the ![]() $L_2-$
norm. We write the transition densities with respect to Lebesgue measure dy of the diffusion as M(x, y) and the Euler approximation as
$L_2-$
norm. We write the transition densities with respect to Lebesgue measure dy of the diffusion as M(x, y) and the Euler approximation as ![]() $M^l(x,y)$
,
$M^l(x,y)$
, ![]() $(x,y)\in\textsf{X}\times\textsf{X}$
. We note the following two equations quoted in [Reference Del Moral, Jacod and Protter11]: there exist
$(x,y)\in\textsf{X}\times\textsf{X}$
. We note the following two equations quoted in [Reference Del Moral, Jacod and Protter11]: there exist ![]() $0<C,C'<+\infty$
(which depend on the drift and diffusion coefficients of (4)) such that for any
$0<C,C'<+\infty$
(which depend on the drift and diffusion coefficients of (4)) such that for any ![]() $l\geq 0$
,
$l\geq 0$
,
We add an additional assumption:
(H8) For C
 $^{\prime}$
as in (10)–(11), we have the following:
$^{\prime}$
as in (10)–(11), we have the following:
1. For any
 $\xi\in(0,1/2)$
, there exists a
$\xi\in(0,1/2)$
, there exists a  $C<+\infty$
such that for any
$C<+\infty$
such that for any  $x\in\textsf{X}$
,
$x\in\textsf{X}$
,  $l\geq 0$
,
$l\geq 0$
,
 \[\int_{\textsf{B}_l(x)^c}v(y)^{\xi}dy \leq C v(x)^{2\xi}\int_{\textsf{B}_l(x)^c}dy.\]
\[\int_{\textsf{B}_l(x)^c}v(y)^{\xi}dy \leq C v(x)^{2\xi}\int_{\textsf{B}_l(x)^c}dy.\]
2. For any
 $\xi\in(0,1/2)$
, there exists a
$\xi\in(0,1/2)$
, there exists a  $C<+\infty$
such that for any
$C<+\infty$
such that for any  $x\in\textsf{X}$
,
$x\in\textsf{X}$
,  $l\geq 0$
,
$l\geq 0$
,
 \[\int_{\textsf{B}_l(x)}v(y)^{\xi}\exp\{-C'\|y-x\|^2\}dy \leq C v(x)^{2\xi}.\]
\[\int_{\textsf{B}_l(x)}v(y)^{\xi}\exp\{-C'\|y-x\|^2\}dy \leq C v(x)^{2\xi}.\]
We have the following result, whose proof is in Appendix F, Section F.1.
Proposition 5.1. Assume (H1)–(H6), (H8). Then for any ![]() $(\xi,\hat{\xi})\in(0,1/8)\times(0,1/2)$
there exists a
$(\xi,\hat{\xi})\in(0,1/8)\times(0,1/2)$
there exists a ![]() $C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any
$C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any ![]() $\varphi\in\mathcal{B}_b(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})$
, ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $1\leq l \leq L$
, we have
$1\leq l \leq L$
, we have
The main point of this result is that now the time-uniform coupling ability of each algorithm will now rely on the properties of the limiting coupling ![]() $\check{\eta}_n^s$
.
$\check{\eta}_n^s$
.
5.2. IRCPF
We consider the term
in the upper bound of Theorem 4.3. Let us suppose that ![]() $\varphi\in\mathcal{A}$
, where
$\varphi\in\mathcal{A}$
, where ![]() $\mathcal{A}$
is defined below (5). One has that
$\mathcal{A}$
is defined below (5). One has that
 \begin{align*}&\check{\eta}_n^I\big(\big\{\varphi\otimes 1-1\otimes\varphi - \big(\big[\eta_n^f-\eta_n^c\big](\varphi)\big)\big\}^2\big)\\[3pt]
&\quad = \frac{\big(\eta_{n-1}^f\otimes\eta_{n-1}^c\big)\big([G_{n-1}\otimes G_{n-1}]\check{M}_n\big([\varphi\otimes1-1\otimes\varphi]^2\big)\big) }{\big(\eta_{n-1}^f\otimes\eta_{n-1}^c\big)(G_{n-1}\otimes G_{n-1})}- [\eta_n^f-\eta_n^c](\varphi)^2. \end{align*}
\begin{align*}&\check{\eta}_n^I\big(\big\{\varphi\otimes 1-1\otimes\varphi - \big(\big[\eta_n^f-\eta_n^c\big](\varphi)\big)\big\}^2\big)\\[3pt]
&\quad = \frac{\big(\eta_{n-1}^f\otimes\eta_{n-1}^c\big)\big([G_{n-1}\otimes G_{n-1}]\check{M}_n\big([\varphi\otimes1-1\otimes\varphi]^2\big)\big) }{\big(\eta_{n-1}^f\otimes\eta_{n-1}^c\big)(G_{n-1}\otimes G_{n-1})}- [\eta_n^f-\eta_n^c](\varphi)^2. \end{align*}
Then using ![]() $\varphi\in\mathcal{A}$
(along with the
$\varphi\in\mathcal{A}$
(along with the ![]() $C_2-$
inequality) and [Reference Jasra, Kamatani, Law and Zhou22, Lemma D.2], there is a finite constant
$C_2-$
inequality) and [Reference Jasra, Kamatani, Law and Zhou22, Lemma D.2], there is a finite constant ![]() $C<+\infty$
that depends on n such that
$C<+\infty$
that depends on n such that
 \[\check{\eta}_n^I\big(\big\{\varphi\otimes 1-1\otimes\varphi - \big(\big[\eta_n^f-\eta_n^c\big](\varphi)\big)\big\}^2\big) \leq C\Bigg(\frac{\big(\eta_{n-1}^f\otimes\eta_{n-1}^c\big)\big([G_{n-1}\otimes G_{n-1}]\check{M}_n(\tilde{\varphi})\big) }{\big(\eta_{n-1}^f\otimes\eta_{n-1}^c\big)(G_{n-1}\otimes G_{n-1})}+\Delta_l^2\Bigg),\]
\[\check{\eta}_n^I\big(\big\{\varphi\otimes 1-1\otimes\varphi - \big(\big[\eta_n^f-\eta_n^c\big](\varphi)\big)\big\}^2\big) \leq C\Bigg(\frac{\big(\eta_{n-1}^f\otimes\eta_{n-1}^c\big)\big([G_{n-1}\otimes G_{n-1}]\check{M}_n(\tilde{\varphi})\big) }{\big(\eta_{n-1}^f\otimes\eta_{n-1}^c\big)(G_{n-1}\otimes G_{n-1})}+\Delta_l^2\Bigg),\]
where ![]() $\tilde{\varphi}(x,y) = \|x-y\|^2$
. Now, applying (6), one has the upper bound
$\tilde{\varphi}(x,y) = \|x-y\|^2$
. Now, applying (6), one has the upper bound
 \[C\Bigg(\frac{\big(\eta_{n-1}^f\otimes\eta_{n-1}^c\big)\big([G_{n-1}\otimes G_{n-1}]\tilde{\varphi}\big) }{\big(\eta_{n-1}^f\otimes\eta_{n-1}^c\big)\big(G_{n-1}\otimes G_{n-1}\big)}+\Delta_l+\Delta_l^2\Bigg).\]
\[C\Bigg(\frac{\big(\eta_{n-1}^f\otimes\eta_{n-1}^c\big)\big([G_{n-1}\otimes G_{n-1}]\tilde{\varphi}\big) }{\big(\eta_{n-1}^f\otimes\eta_{n-1}^c\big)\big(G_{n-1}\otimes G_{n-1}\big)}+\Delta_l+\Delta_l^2\Bigg).\]
In general, there is no reason to expect that ![]() $(\eta_{n-1}^f\otimes\eta_{n-1}^c)([G_{n-1}\otimes G_{n-1}]\tilde{\varphi})$
is small as a function of
$(\eta_{n-1}^f\otimes\eta_{n-1}^c)([G_{n-1}\otimes G_{n-1}]\tilde{\varphi})$
is small as a function of ![]() $\Delta_l$
. This is unsuprising, because one uses an independent coupling in the resampling operation. As a result, in the sense of Section 2.3.1 for ML estimation, the IRCPF is not useful.
$\Delta_l$
. This is unsuprising, because one uses an independent coupling in the resampling operation. As a result, in the sense of Section 2.3.1 for ML estimation, the IRCPF is not useful.
5.3. MCIRCPF
To start our discussion, suppose first that ![]() $G_n$
is constant for each
$G_n$
is constant for each ![]() $n\geq 0$
. This represents the most favorable scenario for the MCIRCPF, because in the resampling operation, the resampled indices for each pair are equal (of course one would not use resampling in this case). For the metric in (H7), we take
$n\geq 0$
. This represents the most favorable scenario for the MCIRCPF, because in the resampling operation, the resampled indices for each pair are equal (of course one would not use resampling in this case). For the metric in (H7), we take ![]() $\textsf{d}_1$
to be the
$\textsf{d}_1$
to be the ![]() $L_1-$
norm and set
$L_1-$
norm and set ![]() $\varphi\in\textsf{B}_b(\textsf{X})\cap\textrm{Lip}_{\textsf{d}_1}(\textsf{X})$
(
$\varphi\in\textsf{B}_b(\textsf{X})\cap\textrm{Lip}_{\textsf{d}_1}(\textsf{X})$
(![]() $\textsf{X}=\mathbb{R}^d$
). Then setting
$\textsf{X}=\mathbb{R}^d$
). Then setting ![]() $\tilde{\varphi}(x,y)=\|x-y\|^2$
, we have
$\tilde{\varphi}(x,y)=\|x-y\|^2$
, we have
where ![]() $C<+\infty$
does not depend on n. Now, as
$C<+\infty$
does not depend on n. Now, as ![]() $G_n$
is constant, one can deduce (e.g. by [Reference Mao25, Theorem 2.7.3]; recall (D) is assumed) that
$G_n$
is constant, one can deduce (e.g. by [Reference Mao25, Theorem 2.7.3]; recall (D) is assumed) that
where ![]() $C,C'<+\infty$
do not depend on n. Now (12) is not necessarily tight in n for every diffusion that satisfies (D); for instance if one has
$C,C'<+\infty$
do not depend on n. Now (12) is not necessarily tight in n for every diffusion that satisfies (D); for instance if one has ![]() $dZ_t = a dt + b dW_t$
, for
$dZ_t = a dt + b dW_t$
, for ![]() $b>0$
,
$b>0$
, ![]() $a\in({-}1,0)$
, then there is no dependence on n in the right-hand side of (12). However, it is worrying that the coupling can be exponentially bad in time, in this favorable case. The main point here is that the principal source of coupling in this algorithm is
$a\in({-}1,0)$
, then there is no dependence on n in the right-hand side of (12). However, it is worrying that the coupling can be exponentially bad in time, in this favorable case. The main point here is that the principal source of coupling in this algorithm is ![]() $\check{M}$
, and if this coupling deteriorates when iterating
$\check{M}$
, and if this coupling deteriorates when iterating ![]() $\check{M}$
, then for the MCIRCPF one cannot hope to obtain time-uniform couplings.
$\check{M}$
, then for the MCIRCPF one cannot hope to obtain time-uniform couplings.
More generally, if ![]() $G_n$
is nonconstant, we first remark that the upper bound (12) is likely to be
$G_n$
is nonconstant, we first remark that the upper bound (12) is likely to be ![]() $\mathcal{O}(\Delta_l^{1/2})$
, as it is the resampling operation where the forward rate is lost (see [Reference Jasra, Kamatani, Law and Zhou22]). Secondly, one expects to find examples where
$\mathcal{O}(\Delta_l^{1/2})$
, as it is the resampling operation where the forward rate is lost (see [Reference Jasra, Kamatani, Law and Zhou22]). Secondly, one expects to find examples where ![]() $\sigma^{2,s}_n(\varphi)$
is time-uniform or grows slowly as a function of n (due to the empirical results in [Reference Jasra, Kamatani, Law and Zhou22]). However, because of the highly nonlinear and complex expression for
$\sigma^{2,s}_n(\varphi)$
is time-uniform or grows slowly as a function of n (due to the empirical results in [Reference Jasra, Kamatani, Law and Zhou22]). However, because of the highly nonlinear and complex expression for ![]() $\check{\Phi}_n^M$
, we expect a general result to be particularly arduous to obtain; this is left to future work.
$\check{\Phi}_n^M$
, we expect a general result to be particularly arduous to obtain; this is left to future work.
5.4. MCPF
We have the following result which establishes the time-uniform coupling of the MCPF. The proof can be found in Appendix F, Section F.2.
Proposition 5.2. Assume (H1)–(H6), (H8). Then for any ![]() $(\xi,\hat{\xi})\in(0,1/32)\times(0,1/2)$
there exists a
$(\xi,\hat{\xi})\in(0,1/32)\times(0,1/2)$
there exists a ![]() $C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any
$C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any ![]() $\varphi\in\mathcal{B}_b(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})$
, ![]() $n\geq 0$
,
$n\geq 0$
, ![]() $1\leq l \leq L$
, we have
$1\leq l \leq L$
, we have
5.5. WCPF
Note that ![]() $\textsf{X}=\mathbb{R}$
and, for the metric in (H7), we take
$\textsf{X}=\mathbb{R}$
and, for the metric in (H7), we take ![]() $\textsf{d}_1$
to be the
$\textsf{d}_1$
to be the ![]() $L_1-$
norm. Let
$L_1-$
norm. Let ![]() $\tilde{\varphi}(x,y)=(x-y)^2$
. The proof of the following result, which establishes the time-uniform coupling of the WCPF, can be found in Appendix F, Section F.3.
$\tilde{\varphi}(x,y)=(x-y)^2$
. The proof of the following result, which establishes the time-uniform coupling of the WCPF, can be found in Appendix F, Section F.3.
Proposition 5.3. Assume (H1)–(H8). Then let ![]() $\lambda\in(0,1)$
be given; assume
$\lambda\in(0,1)$
be given; assume ![]() $\tilde{\varphi}\in\mathcal{L}_{(v\otimes v)^{\tilde{\xi}}}(\textsf{X})$
, for any
$\tilde{\varphi}\in\mathcal{L}_{(v\otimes v)^{\tilde{\xi}}}(\textsf{X})$
, for any ![]() $\tilde{\xi}\in(0,1/(16(1+\lambda)))$
, and set
$\tilde{\xi}\in(0,1/(16(1+\lambda)))$
, and set
Then there exists a ![]() $C<+\infty$
depending on the constants in (H1)–(H8) such that for any
$C<+\infty$
depending on the constants in (H1)–(H8) such that for any ![]() $\varphi\in\mathcal{B}_b(\textsf{X})\cap\textrm{\textit{Lip}}_{\textsf{d}_1}(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})\cap\textrm{\textit{Lip}}_{\textsf{d}_1}(\textsf{X})$
, ![]() $n\geq 0$
,
$n\geq 0$
, ![]() $1\leq l \leq L$
, we have
$1\leq l \leq L$
, we have
As ![]() $\lambda$
is greater than 0 in Proposition 5.3 (and can be made close to zero), one almost has the (time-uniform) forward error rate for the WCPF. We believe that
$\lambda$
is greater than 0 in Proposition 5.3 (and can be made close to zero), one almost has the (time-uniform) forward error rate for the WCPF. We believe that ![]() $\lambda=0$
is the desired case and discuss strategies to establish this in Remark F.2 in Appendix F, Section F.3.
$\lambda=0$
is the desired case and discuss strategies to establish this in Remark F.2 in Appendix F, Section F.3.
5.6. Example
We consider ![]() $\textsf{X}=\mathbb{R}$
, the diffusion
$\textsf{X}=\mathbb{R}$
, the diffusion ![]() $dZ_t = -\frac{3}{2}Z_tdt+dW_t$
and
$dZ_t = -\frac{3}{2}Z_tdt+dW_t$
and ![]() $\textsf{Y}=\{0,1\}$
and
$\textsf{Y}=\{0,1\}$
and
for ![]() $y\in\textsf{Y}$
and any
$y\in\textsf{Y}$
and any ![]() $0<a<b<1$
. The metric in (H7) is the
$0<a<b<1$
. The metric in (H7) is the ![]() $L_1-$
norm. In practice the CPFs can only be run (with currently available computational power) with
$L_1-$
norm. In practice the CPFs can only be run (with currently available computational power) with ![]() $L\leq 20$
. So we will assume that there is an
$L\leq 20$
. So we will assume that there is an ![]() $L^*>L$
for which one cannot run the algorithm (say
$L^*>L$
for which one cannot run the algorithm (say ![]() $L^*=50$
). This will reduce the complexity of the forthcoming discussion. For the Euler discretization (although of course it is not required here) one can determine that the transition kernel
$L^*=50$
). This will reduce the complexity of the forthcoming discussion. For the Euler discretization (although of course it is not required here) one can determine that the transition kernel ![]() $M^l(x,y)$
is the density of a
$M^l(x,y)$
is the density of a ![]() $\mathcal{N}(\alpha_lx,\beta_l)$
distribution with
$\mathcal{N}(\alpha_lx,\beta_l)$
distribution with ![]() $\alpha_l=(1-(3/2)\Delta_l)^{\Delta_l^{-1}}$
and
$\alpha_l=(1-(3/2)\Delta_l)^{\Delta_l^{-1}}$
and
Thanks to our assumption concerning ![]() $L^*$
, one can easily find constants
$L^*$
, one can easily find constants ![]() $0<\underline{\alpha}<\overline{\alpha}<1$
,
$0<\underline{\alpha}<\overline{\alpha}<1$
, ![]() $0<\underline{\beta}<\overline{\beta}\leq 1$
that do not depend on l, with
$0<\underline{\beta}<\overline{\beta}\leq 1$
that do not depend on l, with ![]() $\underline{\alpha}\leq |\alpha_l|\leq \overline{\alpha}$
,
$\underline{\alpha}\leq |\alpha_l|\leq \overline{\alpha}$
, ![]() $\underline{\beta}\leq\beta_l\leq\overline{\beta}$
for each
$\underline{\beta}\leq\beta_l\leq\overline{\beta}$
for each ![]() $l\in\{0,\dots,L\}$
.
$l\in\{0,\dots,L\}$
.
To verify (H1) we use, as in [Reference Whiteley, Kantas and Jasra31, Example 4.2.1], the Lyapunov function
for some ![]() $\delta_0>0$
. One can show that for any
$\delta_0>0$
. One can show that for any ![]() $1\leq l \leq L$
,
$1\leq l \leq L$
, ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $y\in\textsf{X}$
,
$y\in\textsf{X}$
,
where ![]() $[\alpha_l^2(1+\delta_0)]/[1+\delta_0-\beta_l]<1$
for every
$[\alpha_l^2(1+\delta_0)]/[1+\delta_0-\beta_l]<1$
for every ![]() $0\leq l\leq L$
,
$0\leq l\leq L$
, ![]() $\delta_0>0$
, and
$\delta_0>0$
, and ![]() $0<C<+\infty$
is a constant that does not depend on
$0<C<+\infty$
is a constant that does not depend on ![]() $l,n,\delta_0$
and can be made arbitrarily large. One can easily verify (H1) for any
$l,n,\delta_0$
and can be made arbitrarily large. One can easily verify (H1) for any ![]() $\delta_0>0$
with
$\delta_0>0$
with ![]() $\underline{d}>1$
large enough. (H2)–(H5) follow by elementary calculations associated to the choice of
$\underline{d}>1$
large enough. (H2)–(H5) follow by elementary calculations associated to the choice of ![]() $\tilde{V}$
,
$\tilde{V}$
, ![]() $M^l$
, and
$M^l$
, and ![]() $G_n$
and are omitted.
$G_n$
and are omitted.
To verify (H6) as ![]() $G_n$
is bounded below, we consider
$G_n$
is bounded below, we consider ![]() $M^l(C_d)(x)$
and suppose
$M^l(C_d)(x)$
and suppose ![]() $x>0$
,
$x>0$
, ![]() $l\geq 1$
,
$l\geq 1$
, ![]() $d>1$
(the case
$d>1$
(the case ![]() $x\leq 0$
,
$x\leq 0$
, ![]() $l=0$
can be verified in a similar manner). We have for any
$l=0$
can be verified in a similar manner). We have for any ![]() $x>0$
that
$x>0$
that
where ![]() $\tilde{d}=\sqrt{(d-1)2(1+\delta_0)}$
. As
$\tilde{d}=\sqrt{(d-1)2(1+\delta_0)}$
. As ![]() $\delta_0$
is arbitrary one can choose
$\delta_0$
is arbitrary one can choose ![]() $\delta_0>0$
so that
$\delta_0>0$
so that
for any ![]() $1\leq l \leq L$
. Checking calculations on a computer for
$1\leq l \leq L$
. Checking calculations on a computer for ![]() $L^*=50$
yields that
$L^*=50$
yields that ![]() $0<\delta_0\leq 5$
suffices.
$0<\delta_0\leq 5$
suffices.
For (H7) one has the following result, whose proof is in Appendix F, Section F.4.
Lemma 5.1. (H7) is satisfied in this example.
To verify (H8), we shall suppose that C ![]() $^{\prime}$
in (11) is at least
$^{\prime}$
in (11) is at least ![]() $1+1/(2(1+\delta_0))$
(i.e.
$1+1/(2(1+\delta_0))$
(i.e. ![]() $C'>1/12$
). It is noted that it is nontrivial to check the value of C
$C'>1/12$
). It is noted that it is nontrivial to check the value of C ![]() $^{\prime}$
in [Reference Bally and Talay1], but such a choice seems reasonable. In the given situation, it is then straightforward to verify (H8).
$^{\prime}$
in [Reference Bally and Talay1], but such a choice seems reasonable. In the given situation, it is then straightforward to verify (H8).
6. Summary
We have considered CLTs for coupled particle filters and the associated asymptotic variance for applications. The main message is that it can be nontrivial to construct CPFs for which one inherits the appropriate ‘closeness’ uniformly in time. The MCPF and WCPF seem to be the best options, but suffer from the fact that (at least as considered in this paper) one either requires the density of the transition and has a random running time per time step (MCPF), or is constrained to the case that ![]() $\textsf{X}$
is one-dimensional (WCPF). Nonetheless these are still useful algorithms when they can be implemented.
$\textsf{X}$
is one-dimensional (WCPF). Nonetheless these are still useful algorithms when they can be implemented.
There are a number of possible extensions of this work. First, one could extend these results to the context of normalization constant estimation (e.g. [Reference Jasra, Kamatani, Osei and Zhou21]) and the associated asymptotic variance. Second, one could perform a more in-depth analysis and implementation of the MCPF, which to our knowledge has not been done in the literature.
Appendix A. Common proofs for the CLT
In each of the appendices, the proof of the main result appears at the beginning. The associated technical results are given in such a way that, for the overall proof to be understood, they should be read in order.
For ![]() $p\geq 0$
,
$p\geq 0$
, ![]() $\varphi\in\mathcal{B}_b(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})$
, ![]() $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
,
with the convention that ![]() $V_0^{N,s}(\varphi) = \sqrt{N}[\eta_0^{N,s}-\eta_{0})](\varphi)$
. For
$V_0^{N,s}(\varphi) = \sqrt{N}[\eta_0^{N,s}-\eta_{0})](\varphi)$
. For ![]() $p\geq 0$
,
$p\geq 0$
, ![]() $p\leq n$
,
$p\leq n$
, ![]() $n>0$
,
$n>0$
, ![]() $\varphi\in\mathcal{B}_b(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})$
, ![]() $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
,
We adopt the convention ![]() $R_{n+1}^{N,s}(\varphi)=0$
.
$R_{n+1}^{N,s}(\varphi)=0$
.
Now we note that, using the calculations in [Reference Beskos2] and [Reference Del Moral, Doucet and Jasra10], for ![]() $t\in\{I,M,C,W\}$
we have
$t\in\{I,M,C,W\}$
we have
 \begin{eqnarray}\sqrt{N}[\check{\eta}_{n}^{N,t}-\check{\eta}_{n}^{t}](\varphi\otimes 1 - 1 \otimes \varphi) & \,=\, & \sum_{p=0}^n \{V_p^{N,f}(D_{p,n}^f(\varphi)) + \sqrt{N}R_{p+1}^{N,f}(D_{p,n}^f(\varphi))\} \nonumber\\ & &-\,\sum_{p=0}^n \{V_p^{N,c}(D_{p,n}^c(\varphi)) + \sqrt{N}R_{p+1}^{N,c}(D_{p,n}^c(\varphi))\}.\end{eqnarray}
\begin{eqnarray}\sqrt{N}[\check{\eta}_{n}^{N,t}-\check{\eta}_{n}^{t}](\varphi\otimes 1 - 1 \otimes \varphi) & \,=\, & \sum_{p=0}^n \{V_p^{N,f}(D_{p,n}^f(\varphi)) + \sqrt{N}R_{p+1}^{N,f}(D_{p,n}^f(\varphi))\} \nonumber\\ & &-\,\sum_{p=0}^n \{V_p^{N,c}(D_{p,n}^c(\varphi)) + \sqrt{N}R_{p+1}^{N,c}(D_{p,n}^c(\varphi))\}.\end{eqnarray}
Proof of Theorem 4.1. The proof follows immediately from (13), Lemma A.1, and Proposition A.1.
A.1. Technical results
The following results can be established for all four algorithms, but as the result for the Wasserstein method is given in [Reference Jasra, Ballesio, von Schwerin and Tempone20], only the other three cases are considered. When required we specify particular conditions required for a given algorithm. By default proofs are specified for the IRCPF case, and the MCIRCPF and MCPF are mentioned where required.
Lemma A.1. For ![]() $\varphi\in\mathcal{B}_b(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})$
, ![]() $n>0$
,
$n>0$
, ![]() $0\leq p \leq n$
,
$0\leq p \leq n$
, ![]() $s\in\{\,f,c\}$
, we have
$s\in\{\,f,c\}$
, we have
Proof. By Proposition B.1 (for MCIRCPF this is [Reference Jasra, Kamatani, Law and Zhou22, Proposition C.6], and for MCPF it is Proposition D.1), ![]() $\eta_p^{N,s}(G_p)$
converges in probability to a well-defined limit. Hence we need only to show that
$\eta_p^{N,s}(G_p)$
converges in probability to a well-defined limit. Hence we need only to show that
will converge in probability to zero. By Cauchy–Schwarz,
 \begin{align*}&\sqrt{N}\mathbb{E}[|\eta_p^{N,s}(D_{p,n}^s(\varphi))[\eta_p^{s}(G_p)-\eta_p^{N,s}(G_p)]|]\\[4pt] &\quad \leq \sqrt{N}\mathbb{E}[|\eta_p^{N,s}(D_{p,n}^s(\varphi))|^2]^{1/2}\mathbb{E}[|[\eta_p^{s}(G_p)-\eta_p^{N,s}(G_p)]|^2]^{1/2}.\end{align*}
\begin{align*}&\sqrt{N}\mathbb{E}[|\eta_p^{N,s}(D_{p,n}^s(\varphi))[\eta_p^{s}(G_p)-\eta_p^{N,s}(G_p)]|]\\[4pt] &\quad \leq \sqrt{N}\mathbb{E}[|\eta_p^{N,s}(D_{p,n}^s(\varphi))|^2]^{1/2}\mathbb{E}[|[\eta_p^{s}(G_p)-\eta_p^{N,s}(G_p)]|^2]^{1/2}.\end{align*}
Applying Proposition B.1 (for MCIRCPF [Reference Jasra, Kamatani, Law and Zhou22, Proposition C.6], for MCPF Proposition D.1), it easily follows that there is a finite constant ![]() $C<+\infty$
that does not depend upon N, such that
$C<+\infty$
that does not depend upon N, such that
This bound allows one to easily conclude.
Lemma A.2. For ![]() $\varphi\in\mathcal{B}_b(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})$
, ![]() $p\geq 0$
,
$p\geq 0$
, ![]() $s\in\{\,f,c\}$
, we have
$s\in\{\,f,c\}$
, we have
 \begin{eqnarray*}\mathbb{E}[V_p^{N,s}(\varphi)] & \,=\, & 0, \\\lim_{N\rightarrow+\infty}\mathbb{E}[V_p^{N,s}(\varphi)^2] & \,=\, & \eta_p^s((\varphi-\eta_p^s(\varphi))^2).\end{eqnarray*}
\begin{eqnarray*}\mathbb{E}[V_p^{N,s}(\varphi)] & \,=\, & 0, \\\lim_{N\rightarrow+\infty}\mathbb{E}[V_p^{N,s}(\varphi)^2] & \,=\, & \eta_p^s((\varphi-\eta_p^s(\varphi))^2).\end{eqnarray*}
Proof. ![]() $\mathbb{E}[V_p^{N,s}(\varphi)] = 0$
follows immediately from the expression, so we focus on the second property. We have
$\mathbb{E}[V_p^{N,s}(\varphi)] = 0$
follows immediately from the expression, so we focus on the second property. We have
 \begin{eqnarray*}\mathbb{E}[V_p^{N,s}(\varphi)^2] & \,=\, & \frac{1}{N}\sum_{i=1}^N \mathbb{E}[(\varphi(X_p^{i,s})-\Phi^s_p(\eta_{p-1}^{N,s})(\varphi))^2] \\& \,=\, & \mathbb{E}[\varphi(X_p^{1,s})^2] - \mathbb{E}[\Phi^s_p(\eta_{p-1}^{N,s})(\varphi)^2].\end{eqnarray*}
\begin{eqnarray*}\mathbb{E}[V_p^{N,s}(\varphi)^2] & \,=\, & \frac{1}{N}\sum_{i=1}^N \mathbb{E}[(\varphi(X_p^{i,s})-\Phi^s_p(\eta_{p-1}^{N,s})(\varphi))^2] \\& \,=\, & \mathbb{E}[\varphi(X_p^{1,s})^2] - \mathbb{E}[\Phi^s_p(\eta_{p-1}^{N,s})(\varphi)^2].\end{eqnarray*}
![]() $\Phi^s_p(\eta_{p-1}^{N,s})(\varphi)$
is a bounded random quantity, and moreover, by Proposition B.1 (for MCIRCPF [Reference Jasra, Kamatani, Law and Zhou22, Proposition C.6], for MCPF Proposition D.1), it converges in probability to
$\Phi^s_p(\eta_{p-1}^{N,s})(\varphi)$
is a bounded random quantity, and moreover, by Proposition B.1 (for MCIRCPF [Reference Jasra, Kamatani, Law and Zhou22, Proposition C.6], for MCPF Proposition D.1), it converges in probability to ![]() $\eta_p^s(\varphi)$
. Hence by [Reference Billingsley3, Theorem 25.12],
$\eta_p^s(\varphi)$
. Hence by [Reference Billingsley3, Theorem 25.12], ![]() $\lim_{N\rightarrow+\infty}\mathbb{E}[\Phi^s_p(\eta_{p-1}^{N,s})(\varphi)^2] = \eta_p^s(\varphi)^2$
. Hence we consider
$\lim_{N\rightarrow+\infty}\mathbb{E}[\Phi^s_p(\eta_{p-1}^{N,s})(\varphi)^2] = \eta_p^s(\varphi)^2$
. Hence we consider
 \[\mathbb{E}\big[\varphi(X_p^{1,s})^2\big] = \mathbb{E}\Bigg[\frac{1}{N}\sum_{i=1}^N \varphi(X_p^{i,s})^2 - \eta_p^s(\varphi^2)\Bigg] + \eta_p^s(\varphi^2).\]
\[\mathbb{E}\big[\varphi(X_p^{1,s})^2\big] = \mathbb{E}\Bigg[\frac{1}{N}\sum_{i=1}^N \varphi(X_p^{i,s})^2 - \eta_p^s(\varphi^2)\Bigg] + \eta_p^s(\varphi^2).\]
By Jensen,
 \[\mathbb{E}\Bigg[\frac{1}{N}\sum_{i=1}^N \varphi(X_p^{i,s})^2 - \eta_p^s(\varphi^2)\Bigg] \leq \mathbb{E}\Bigg[\Bigg|\frac{1}{N}\sum_{i=1}^N \varphi(X_p^{i,s})^2 - \eta_p^s(\varphi^2)\Bigg|^2\Bigg]^{1/2},\]
\[\mathbb{E}\Bigg[\frac{1}{N}\sum_{i=1}^N \varphi(X_p^{i,s})^2 - \eta_p^s(\varphi^2)\Bigg] \leq \mathbb{E}\Bigg[\Bigg|\frac{1}{N}\sum_{i=1}^N \varphi(X_p^{i,s})^2 - \eta_p^s(\varphi^2)\Bigg|^2\Bigg]^{1/2},\]
and hence we conclude via Proposition B.1 (for MCIRCPF [Reference Jasra, Kamatani, Law and Zhou22, Proposition C.6], for MCPF Proposition D.1) that
The result follows.
Lemma A.3. The following statements hold.
1. For the IRCPF: For
 $(\varphi,\psi)\in\mathcal{B}_b(\textsf{X})^2$
,
$(\varphi,\psi)\in\mathcal{B}_b(\textsf{X})^2$
,  $p\geq 0$
, we have
$p\geq 0$
, we have
 \[\lim_{N\rightarrow+\infty}\mathbb{E}[V_p^{N,f}(\varphi)V_p^{N,c}(\psi)] = \check{\eta}_p^I(\varphi\otimes \psi) - \eta_p^f(\varphi)\eta_p^c(\psi).\]
\[\lim_{N\rightarrow+\infty}\mathbb{E}[V_p^{N,f}(\varphi)V_p^{N,c}(\psi)] = \check{\eta}_p^I(\varphi\otimes \psi) - \eta_p^f(\varphi)\eta_p^c(\psi).\]
2. For the MCIRCPF: Assume (A1)–(A3),
 $(\varphi,\psi)\in\mathcal{C}_b(\textsf{X})^2$
,
$(\varphi,\psi)\in\mathcal{C}_b(\textsf{X})^2$
,  $p\geq 0$
; then we have
$p\geq 0$
; then we have
 \[\lim_{N\rightarrow+\infty}\mathbb{E}[V_p^{N,f}(\varphi)V_p^{N,c}(\psi)] = \check{\eta}_p^M(\varphi\otimes \psi) - \eta_p^f(\varphi)\eta_p^c(\psi).\]
\[\lim_{N\rightarrow+\infty}\mathbb{E}[V_p^{N,f}(\varphi)V_p^{N,c}(\psi)] = \check{\eta}_p^M(\varphi\otimes \psi) - \eta_p^f(\varphi)\eta_p^c(\psi).\]
3. For the MCPF: Suppose that for
 $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
,  $n\geq 1$
,
$n\geq 1$
,  $M_n^s\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
. For
$M_n^s\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
. For  $(\varphi,\psi)\in\mathcal{B}_b(\textsf{X})^2$
,
$(\varphi,\psi)\in\mathcal{B}_b(\textsf{X})^2$
,  $p\geq 0$
, we have
$p\geq 0$
, we have
 \[\lim_{N\rightarrow+\infty}\mathbb{E}[V_p^{N,f}(\varphi)V_p^{N,c}(\psi)] = \check{\eta}_p^C(\varphi\otimes \psi) - \eta_p^f(\varphi)\eta_p^c(\psi).\]
\[\lim_{N\rightarrow+\infty}\mathbb{E}[V_p^{N,f}(\varphi)V_p^{N,c}(\psi)] = \check{\eta}_p^C(\varphi\otimes \psi) - \eta_p^f(\varphi)\eta_p^c(\psi).\]
Proof. For all methods, we have
 \begin{eqnarray}\mathbb{E}[V_p^{N,f}(\varphi)V_p^{N,c}(\psi)] & \,=\, & N\Big(\mathbb{E}[\eta_p^{N,f}(\varphi)\eta_p^{N,c}(\psi)]-\mathbb{E}[\eta_p^{N,f}(\varphi)\Phi_p^c(\eta_{p-1}^{N,c})(\psi)]\nonumber\\ & &-\,\mathbb{E}[\Phi_p^f(\eta_{p-1}^{N,f})(\varphi)\eta_p^{N,c}(\psi)] + \mathbb{E}[\Phi_p^f(\eta_{p-1}^{N,f})(\varphi)\Phi_p^c(\eta_{p-1}^{N,c})(\psi)]\Big) \nonumber\\& \,=\, & N\Big(\mathbb{E}[\eta_p^{N,f}(\varphi)\eta_p^{N,c}(\psi)] - \mathbb{E}[\Phi_p^f(\eta_{p-1}^{N,f})(\varphi)\Phi_p^c(\eta_{p-1}^{N,c})(\psi)]\Big).\end{eqnarray}
\begin{eqnarray}\mathbb{E}[V_p^{N,f}(\varphi)V_p^{N,c}(\psi)] & \,=\, & N\Big(\mathbb{E}[\eta_p^{N,f}(\varphi)\eta_p^{N,c}(\psi)]-\mathbb{E}[\eta_p^{N,f}(\varphi)\Phi_p^c(\eta_{p-1}^{N,c})(\psi)]\nonumber\\ & &-\,\mathbb{E}[\Phi_p^f(\eta_{p-1}^{N,f})(\varphi)\eta_p^{N,c}(\psi)] + \mathbb{E}[\Phi_p^f(\eta_{p-1}^{N,f})(\varphi)\Phi_p^c(\eta_{p-1}^{N,c})(\psi)]\Big) \nonumber\\& \,=\, & N\Big(\mathbb{E}[\eta_p^{N,f}(\varphi)\eta_p^{N,c}(\psi)] - \mathbb{E}[\Phi_p^f(\eta_{p-1}^{N,f})(\varphi)\Phi_p^c(\eta_{p-1}^{N,c})(\psi)]\Big).\end{eqnarray}
We consider calculations to verify Parts 1–3 in the statement of the Lemma by using (14).
Proof of Part 1: Now
 \begin{eqnarray*}N\mathbb{E}[\eta_p^{N,f}(\varphi)\eta_p^{N,c}(\psi)] & \,=\, & \frac{1}{N}\sum_{i=1}^N\sum_{j=1}^N\mathbb{E}[\varphi(X_p^{i,f})\psi(X_p^{i,c})] \\& \,=\, & \mathbb{E}[\check{\Phi}_p^I(\eta_{p-1}^{N,f}\otimes \eta_{p-1}^{N,c})(\varphi\otimes\psi)] + (N-1)\mathbb{E}[\Phi_p^f(\eta_{p-1}^{N,f})(\varphi)\Phi_p^c(\eta_{p-1}^{N,c})(\psi)].\end{eqnarray*}
\begin{eqnarray*}N\mathbb{E}[\eta_p^{N,f}(\varphi)\eta_p^{N,c}(\psi)] & \,=\, & \frac{1}{N}\sum_{i=1}^N\sum_{j=1}^N\mathbb{E}[\varphi(X_p^{i,f})\psi(X_p^{i,c})] \\& \,=\, & \mathbb{E}[\check{\Phi}_p^I(\eta_{p-1}^{N,f}\otimes \eta_{p-1}^{N,c})(\varphi\otimes\psi)] + (N-1)\mathbb{E}[\Phi_p^f(\eta_{p-1}^{N,f})(\varphi)\Phi_p^c(\eta_{p-1}^{N,c})(\psi)].\end{eqnarray*}
Thus,
![]() $\check{\Phi}_p^I(\eta_{p-1}^{N,f}\otimes \eta_{p-1}^{N,c})(\varphi\otimes\psi)$
is a bounded random quantity, and by Propositions B.1 and B.2 it converges in probability to
$\check{\Phi}_p^I(\eta_{p-1}^{N,f}\otimes \eta_{p-1}^{N,c})(\varphi\otimes\psi)$
is a bounded random quantity, and by Propositions B.1 and B.2 it converges in probability to ![]() $\check{\eta}_p^I(\varphi\otimes \psi)$
; hence by [Reference Billingsley3, Theorem 25.12],
$\check{\eta}_p^I(\varphi\otimes \psi)$
; hence by [Reference Billingsley3, Theorem 25.12],
Similarly, via Proposition B.1 and [Reference Billingsley3, Theorem 25.12],
and hence we can conclude the proof of Part 1.
Proof of Part 2: Using similar calculations as for Part 1 we have
The proof of Theorem 3.1 establishes that
The proof can then be completed in much the same way as for Part 1.
Proof of Part 3: Using similar calculations as for Part 1 we have
The proof of Theorem D.1 establishes that
The proof can then be completed in much the same way as for (i).
For ![]() $p\geq 0$
,
$p\geq 0$
, ![]() $\varphi,\psi\in\mathcal{B}_b(\textsf{X})$
, define
$\varphi,\psi\in\mathcal{B}_b(\textsf{X})$
, define
Proposition A.1. The following statements hold.
1. For the IRCPF: Let
 $n\geq 0$
; then for any
$n\geq 0$
; then for any  $(\varphi_0,\dots,\varphi_n) \in\mathcal{B}_b(\textsf{X})^{n+1}$
,
$(\varphi_0,\dots,\varphi_n) \in\mathcal{B}_b(\textsf{X})^{n+1}$
,  $(\psi_0,\dots,\psi_n) \in\mathcal{B}_b(\textsf{X})^{n+1}$
,
converges in distribution to an
$(\psi_0,\dots,\psi_n) \in\mathcal{B}_b(\textsf{X})^{n+1}$
,
converges in distribution to an \[(V_0^N(\varphi_0,\psi_0),\dots, V_n^N(\varphi_n,\psi_n))\]
\[(V_0^N(\varphi_0,\psi_0),\dots, V_n^N(\varphi_n,\psi_n))\]
 $(n+1)-$
dimensional Gaussian random variable with zero mean and diagonal covariance matrix, with the pth diagonal entry for
$(n+1)-$
dimensional Gaussian random variable with zero mean and diagonal covariance matrix, with the pth diagonal entry for  $p\in\{0,\dots,n\}$
given by
$p\in\{0,\dots,n\}$
given by
 \[\check{\eta}_p^I(\{(\varphi_p\otimes 1- 1\otimes \psi_p) - \check{\eta}_p^I(\varphi_p\otimes 1- 1\otimes \psi_p)\}^2).\]
\[\check{\eta}_p^I(\{(\varphi_p\otimes 1- 1\otimes \psi_p) - \check{\eta}_p^I(\varphi_p\otimes 1- 1\otimes \psi_p)\}^2).\]
2. For the MCIRCPF: Assume (A1)–(A3); then for
 $n\geq 0$
and any
$n\geq 0$
and any  $(\varphi_0,\dots,\varphi_n) \in\mathcal{C}_b(\textsf{X})^{n+1}$
,
$(\varphi_0,\dots,\varphi_n) \in\mathcal{C}_b(\textsf{X})^{n+1}$
,  $(\psi_0,\dots,\psi_n) \in\mathcal{C}_b(\textsf{X})^{n+1}$
,
converges in distribution to an
$(\psi_0,\dots,\psi_n) \in\mathcal{C}_b(\textsf{X})^{n+1}$
,
converges in distribution to an \[(V_0^N(\varphi_0,\psi_0),\dots,V_n^N(\varphi_n,\psi_n))\]
\[(V_0^N(\varphi_0,\psi_0),\dots,V_n^N(\varphi_n,\psi_n))\]
 $(n+1)-$
dimensional Gaussian random variable with zero mean and diagonal covariance matrix, with the pth diagonal entry for
$(n+1)-$
dimensional Gaussian random variable with zero mean and diagonal covariance matrix, with the pth diagonal entry for  $p\in\{0,\dots,n\}$
given by
$p\in\{0,\dots,n\}$
given by
 \[\check{\eta}_p^M(\{(\varphi_p\otimes 1- 1\otimes \psi_p) - \check{\eta}_p^M(\varphi_p\otimes 1- 1\otimes \psi_p)\}^2).\]
\[\check{\eta}_p^M(\{(\varphi_p\otimes 1- 1\otimes \psi_p) - \check{\eta}_p^M(\varphi_p\otimes 1- 1\otimes \psi_p)\}^2).\]
3. For the MCPF: Suppose that for
 $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
,  $n\geq 1$
,
$n\geq 1$
,  $M_n^s\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
; then for
$M_n^s\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
; then for  $n\geq 0$
and any
$n\geq 0$
and any  $(\varphi_0,\dots,\varphi_n) \in\mathcal{B}_b(\textsf{X})^{n+1}$
,
$(\varphi_0,\dots,\varphi_n) \in\mathcal{B}_b(\textsf{X})^{n+1}$
,  $(\psi_0,\dots,\psi_n) \in\mathcal{B}_b(\textsf{X})^{n+1}$
,
converges in distribution to an
$(\psi_0,\dots,\psi_n) \in\mathcal{B}_b(\textsf{X})^{n+1}$
,
converges in distribution to an \[(V_0^N(\varphi_0,\psi_0),\dots,V_n^N(\varphi_n,\psi_n))\]
\[(V_0^N(\varphi_0,\psi_0),\dots,V_n^N(\varphi_n,\psi_n))\]
 $(n+1)-$
dimensional Gaussian random variable with zero mean and diagonal covariance matrix, with the pth diagonal entry for
$(n+1)-$
dimensional Gaussian random variable with zero mean and diagonal covariance matrix, with the pth diagonal entry for  $p\in\{0,\dots,n\}$
given by
$p\in\{0,\dots,n\}$
given by
 \[\check{\eta}_p^C(\{(\varphi_p\otimes 1- 1\otimes \psi_p) - \check{\eta}_p^C(\varphi_p\otimes 1- 1\otimes \psi_p)\}^2).\]
\[\check{\eta}_p^C(\{(\varphi_p\otimes 1- 1\otimes \psi_p) - \check{\eta}_p^C(\varphi_p\otimes 1- 1\otimes \psi_p)\}^2).\]
Proof. This follows from almost the same exposition and proofs as [Reference Del Moral8, pp. 293--294, Theorem 9.3.1, Corollary 9.3.1] and Lemmata A.2–A.3 of the present paper. The proof is thus omitted.
Appendix B. Technical results for the IRCPF
Proposition B.1. For any ![]() $n\geq 0$
,
$n\geq 0$
, ![]() $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
, ![]() $p\geq 1$
there exists a
$p\geq 1$
there exists a ![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any ![]() $\varphi\in\mathcal{B}_b(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})$
, ![]() $N\geq 1$
we have
$N\geq 1$
we have
Proof. This can be proved easily by induction, for instance using the strategy in [Reference Jasra, Kamatani, Law and Zhou22, Proposition C.6]; the proof is hence omitted.
Proposition B.2. For any ![]() $\varphi\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
, ![]() $n\geq 0$
we have
$n\geq 0$
we have
Proof. Our proof is by induction. Consider the case ![]() $n=0$
and let
$n=0$
and let ![]() $\epsilon > 0$
be arbitrary; then
$\epsilon > 0$
be arbitrary; then
 \begin{align*}&\mathbb{P}(|(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})-(\eta_{n}^{f}\otimes\eta_{n}^{c})](\varphi)|>\epsilon)\\ &\quad \leq \mathbb{P}(|[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi) - \mathbb{E}[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi)]|>\epsilon/2) +\mathbb{P}(|\mathbb{E}[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi)]\\ &\quad -\, (\eta_{n}^{f}\otimes\eta_{n}^{c})(\varphi)|>\epsilon/2) \leq \mathbb{P}(|[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi) - \mathbb{E}[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi)]|>\epsilon/2)+ \mathcal{O}(N^{-1}),\end{align*}
\begin{align*}&\mathbb{P}(|(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})-(\eta_{n}^{f}\otimes\eta_{n}^{c})](\varphi)|>\epsilon)\\ &\quad \leq \mathbb{P}(|[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi) - \mathbb{E}[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi)]|>\epsilon/2) +\mathbb{P}(|\mathbb{E}[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi)]\\ &\quad -\, (\eta_{n}^{f}\otimes\eta_{n}^{c})(\varphi)|>\epsilon/2) \leq \mathbb{P}(|[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi) - \mathbb{E}[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi)]|>\epsilon/2)+ \mathcal{O}(N^{-1}),\end{align*}
where the last line follows from
To deal with the term
we will apply the bounded difference inequality (see [Reference McDiarmid26]). To this end, first note that ![]() $(u_0^1,\dots,u_0^N)$
are i.i.d., and setting
$(u_0^1,\dots,u_0^N)$
are i.i.d., and setting ![]() $f(u_0^1,\dots,u_0^N) = (\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi)$
, we note that for any
$f(u_0^1,\dots,u_0^N) = (\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi)$
, we note that for any ![]() $1\leq k \leq N$
(the notational convention is clear if
$1\leq k \leq N$
(the notational convention is clear if ![]() $k=1$
or
$k=1$
or ![]() $k=N$
) and any
$k=N$
) and any ![]() $(u_0^1,\dots,u_0^N)\in(\textsf{X}\times\textsf{X})^{n+1}$
,
$(u_0^1,\dots,u_0^N)\in(\textsf{X}\times\textsf{X})^{n+1}$
, ![]() $\tilde{u}_0^k\in\textsf{X}\times\textsf{X}$
,
$\tilde{u}_0^k\in\textsf{X}\times\textsf{X}$
,
 \begin{align}&|f(u_0^1,\dots,u_0^N)-f(u_0^1,\dots,u_0^{k-1},\tilde{u}_0^k,u_0^{k+1},\dots,u_0^N)| = \frac{1}{N^2}|[\varphi(u_0^k)-\varphi(\tilde{u}_0^k)]\nonumber\\[3pt] &\quad + \sum_{i\in\{1,\dots,N\}\setminus\{k\}}[\varphi(x_{0}^{i,f},x_{0}^{k,c})-\varphi(x_{0}^{i,f},\tilde{x}_{0}^{k,c})] +\sum_{i\in\{1,\dots,N\}\setminus\{k\}}[\varphi(x_{0}^{k,f},x_{0}^{i,c})-\varphi(\tilde{x}_{0}^{k,f},x_{0}^{i,c})]| \nonumber\\[3pt] &\qquad \leq \frac{4\|\varphi\|}{N}.\end{align}
\begin{align}&|f(u_0^1,\dots,u_0^N)-f(u_0^1,\dots,u_0^{k-1},\tilde{u}_0^k,u_0^{k+1},\dots,u_0^N)| = \frac{1}{N^2}|[\varphi(u_0^k)-\varphi(\tilde{u}_0^k)]\nonumber\\[3pt] &\quad + \sum_{i\in\{1,\dots,N\}\setminus\{k\}}[\varphi(x_{0}^{i,f},x_{0}^{k,c})-\varphi(x_{0}^{i,f},\tilde{x}_{0}^{k,c})] +\sum_{i\in\{1,\dots,N\}\setminus\{k\}}[\varphi(x_{0}^{k,f},x_{0}^{i,c})-\varphi(\tilde{x}_{0}^{k,f},x_{0}^{i,c})]| \nonumber\\[3pt] &\qquad \leq \frac{4\|\varphi\|}{N}.\end{align}
Thus, by the bounded difference inequality,
Hence we can easily conclude the result when ![]() $n=0$
as
$n=0$
as ![]() $\epsilon>0$
was arbitrary.
$\epsilon>0$
was arbitrary.
Now we assume the result for ![]() $n-1$
and consider n. We have
$n-1$
and consider n. We have
 \begin{align*}\mathbb{P}(|[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})&-(\eta_{n}^{f}\otimes\eta_{n}^{c})](\varphi)|>\epsilon) \leq\mathbb{P}(|[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi)\\[3pt]
& - \mathbb{E}[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi)|\mathcal{F}_{n-1}^N]|>\epsilon/2)\\[3pt] &+ \mathbb{P}(|\mathbb{E}[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi)|\mathcal{F}_{n-1}^N] - (\eta_{n}^{f}\otimes\eta_{n}^{c})(\varphi)|>\epsilon/2),\end{align*}
\begin{align*}\mathbb{P}(|[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})&-(\eta_{n}^{f}\otimes\eta_{n}^{c})](\varphi)|>\epsilon) \leq\mathbb{P}(|[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi)\\[3pt]
& - \mathbb{E}[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi)|\mathcal{F}_{n-1}^N]|>\epsilon/2)\\[3pt] &+ \mathbb{P}(|\mathbb{E}[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi)|\mathcal{F}_{n-1}^N] - (\eta_{n}^{f}\otimes\eta_{n}^{c})(\varphi)|>\epsilon/2),\end{align*}
where ![]() $\mathcal{F}_{n-1}^N$
is the
$\mathcal{F}_{n-1}^N$
is the ![]() $\sigma-$
algebra generated by the particle system up to time
$\sigma-$
algebra generated by the particle system up to time ![]() $n-1$
. For the term
$n-1$
. For the term
on conditioning upon ![]() $\mathcal{F}_{n-1}^N$
one can apply the above bounded difference inequality, as
$\mathcal{F}_{n-1}^N$
one can apply the above bounded difference inequality, as ![]() $(u_n^1,\dots,u_n^N)$
are (conditionally) i.i.d. and the bound in (15) can also be obtained for any n. Hence one has
$(u_n^1,\dots,u_n^N)$
are (conditionally) i.i.d. and the bound in (15) can also be obtained for any n. Hence one has
and thus one can conclude the result if
Now
 \begin{eqnarray*}\mathbb{E}[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi)|\mathcal{F}_{n-1}^N] & \,=\, & \frac{1}{N^2}\Bigg(\sum_{i=1}^N \mathbb{E}[\varphi(U_n^i)|\mathcal{F}_{n-1}^N] +\sum_{i\neq j}\mathbb{E}[\varphi(X_n^{i,f},X_n^{i,c})|\mathcal{F}_{n-1}^N]\Bigg) \\& \,=\, & \frac{1}{N}\check{\Phi}_n^I(\eta_{n-1}^{N,f}\otimes\eta_{n-1}^{N,c})(\varphi) + \frac{(N-1)}{N}(\Phi_n^f(\eta_{n-1}^{N,f})\otimes\Phi_n^f(\eta_{n-1}^{N,f}))(\varphi).\end{eqnarray*}
\begin{eqnarray*}\mathbb{E}[(\eta_{n}^{N,f}\otimes\eta_{n}^{N,c})(\varphi)|\mathcal{F}_{n-1}^N] & \,=\, & \frac{1}{N^2}\Bigg(\sum_{i=1}^N \mathbb{E}[\varphi(U_n^i)|\mathcal{F}_{n-1}^N] +\sum_{i\neq j}\mathbb{E}[\varphi(X_n^{i,f},X_n^{i,c})|\mathcal{F}_{n-1}^N]\Bigg) \\& \,=\, & \frac{1}{N}\check{\Phi}_n^I(\eta_{n-1}^{N,f}\otimes\eta_{n-1}^{N,c})(\varphi) + \frac{(N-1)}{N}(\Phi_n^f(\eta_{n-1}^{N,f})\otimes\Phi_n^f(\eta_{n-1}^{N,f}))(\varphi).\end{eqnarray*}
Now by the induction hypothesis and Proposition B.1, ![]() $\check{\Phi}_n^I(\eta_{n-1}^{N,f}\otimes\eta_{n-1}^{N,c})(\varphi)$
converges in probability to
$\check{\Phi}_n^I(\eta_{n-1}^{N,f}\otimes\eta_{n-1}^{N,c})(\varphi)$
converges in probability to
 \[\frac{\big(\eta_{n-1}^{f}\otimes\eta_{n-1}^{c}\big)\big((G_{n-1}\otimes G_{n-1})\check{M}_n(\varphi)\big)}{\eta_{n-1}^{f}(G_{n-1})\eta_{n-1}^{c}(G_{n-1})};\]
\[\frac{\big(\eta_{n-1}^{f}\otimes\eta_{n-1}^{c}\big)\big((G_{n-1}\otimes G_{n-1})\check{M}_n(\varphi)\big)}{\eta_{n-1}^{f}(G_{n-1})\eta_{n-1}^{c}(G_{n-1})};\]
hence the term ![]() $\frac{1}{N}\check{\Phi}_n^I(\eta_{n-1}^{N,f}\otimes\eta_{n-1}^{N,c})(\varphi)$
goes to zero. Then, again by the induction hypothesis and Proposition B.1,
$\frac{1}{N}\check{\Phi}_n^I(\eta_{n-1}^{N,f}\otimes\eta_{n-1}^{N,c})(\varphi)$
goes to zero. Then, again by the induction hypothesis and Proposition B.1, ![]() $(\Phi_n^f(\eta_{n-1}^{N,f})\otimes\Phi_n^f(\eta_{n-1}^{N,f}))(\varphi)$
converges in probability to
$(\Phi_n^f(\eta_{n-1}^{N,f})\otimes\Phi_n^f(\eta_{n-1}^{N,f}))(\varphi)$
converges in probability to
 \[\frac{\big(\eta_{n-1}^{f}\otimes\eta_{n-1}^{c}\big)\big((G_{n-1}\otimes G_{n-1})\big(M_n^f\otimes M_n^c\big)(\varphi)\big)}{\eta_{n-1}^{f}(G_{n-1})\eta_{n-1}^{c}(G_{n-1})} = (\eta_{n}^{f}\otimes\eta_{n}^{c})(\varphi),\]
\[\frac{\big(\eta_{n-1}^{f}\otimes\eta_{n-1}^{c}\big)\big((G_{n-1}\otimes G_{n-1})\big(M_n^f\otimes M_n^c\big)(\varphi)\big)}{\eta_{n-1}^{f}(G_{n-1})\eta_{n-1}^{c}(G_{n-1})} = (\eta_{n}^{f}\otimes\eta_{n}^{c})(\varphi),\]
and hence we conclude the result.
Appendix C. Technical results for the MCIRCPF
Proof of Theorem 3.1. The proof is by induction. The case ![]() $n=0$
follows by the weak law of large numbers for i.i.d. random variables, so we assume the result at time
$n=0$
follows by the weak law of large numbers for i.i.d. random variables, so we assume the result at time ![]() $n-1$
. We have
$n-1$
. We have
One can easily prove that
by using the (conditional) Marcinkiewicz–Zygmund inequality, so we focus on the latter term. Define
 \begin{eqnarray*}T_1^N & \,:\!=&\,\check{\eta}_{n-1}^{N,M}\Big(\{F_{n-1,\check{\eta}_{n-1}^{N,M},f} \wedge F_{n-1,\check{\eta}_{n-1}^{N,M},c}\}\check{M}_n(\varphi)\Big) -\check{\eta}_{n-1}^{M}\Big(\{F_{n-1,\check{\eta}_{n-1}^{M},f} \wedge F_{n-1,\check{\eta}_{n-1}^{M},c}\}\check{M}_n(\varphi)\Big), \\T_2^N & \,:\!=&\,\Big(1-\check{\eta}_{n-1}^{N,M}\Big(\{F_{n-1,\check{\eta}_{n-1}^{N,M},f} \wedge F_{n-1,\check{\eta}_{n-1}^{N,M},c}\}\Big)\Big)(\check{\eta}_{n-1}^{N,M}\otimes\check{\eta}_{n-1}^{N,M})\Big(\Big\{\overline{F}_{n-1,\check{\eta}_{n-1}^{N,M},f}\otimes \\ & &\quad \overline{F}_{n-1,\check{\eta}_{n-1}^{N,M},c}\Big\}\bar{M}_{n}(\varphi)\Big), \\T_3 & \,:\!=&\,\Big(1-\check{\eta}_{n-1}^{M}\Big(\{F_{n-1,\check{\eta}_{n-1}^{M},f} \wedge F_{n-1,\check{\eta}_{n-1}^{M},c}\}\Big)\Big)(\check{\eta}_{n-1}^{M}\otimes\check{\eta}_{n-1}^{M})\Big(\Big\{\overline{F}_{n-1,\check{\eta}_{n-1}^{M},f}\otimes \\ & &\quad \overline{F}_{n-1,\check{\eta}_{n-1}^{M},c}\Big\}\bar{M}_{n}(\varphi)\Big).\end{eqnarray*}
\begin{eqnarray*}T_1^N & \,:\!=&\,\check{\eta}_{n-1}^{N,M}\Big(\{F_{n-1,\check{\eta}_{n-1}^{N,M},f} \wedge F_{n-1,\check{\eta}_{n-1}^{N,M},c}\}\check{M}_n(\varphi)\Big) -\check{\eta}_{n-1}^{M}\Big(\{F_{n-1,\check{\eta}_{n-1}^{M},f} \wedge F_{n-1,\check{\eta}_{n-1}^{M},c}\}\check{M}_n(\varphi)\Big), \\T_2^N & \,:\!=&\,\Big(1-\check{\eta}_{n-1}^{N,M}\Big(\{F_{n-1,\check{\eta}_{n-1}^{N,M},f} \wedge F_{n-1,\check{\eta}_{n-1}^{N,M},c}\}\Big)\Big)(\check{\eta}_{n-1}^{N,M}\otimes\check{\eta}_{n-1}^{N,M})\Big(\Big\{\overline{F}_{n-1,\check{\eta}_{n-1}^{N,M},f}\otimes \\ & &\quad \overline{F}_{n-1,\check{\eta}_{n-1}^{N,M},c}\Big\}\bar{M}_{n}(\varphi)\Big), \\T_3 & \,:\!=&\,\Big(1-\check{\eta}_{n-1}^{M}\Big(\{F_{n-1,\check{\eta}_{n-1}^{M},f} \wedge F_{n-1,\check{\eta}_{n-1}^{M},c}\}\Big)\Big)(\check{\eta}_{n-1}^{M}\otimes\check{\eta}_{n-1}^{M})\Big(\Big\{\overline{F}_{n-1,\check{\eta}_{n-1}^{M},f}\otimes \\ & &\quad \overline{F}_{n-1,\check{\eta}_{n-1}^{M},c}\Big\}\bar{M}_{n}(\varphi)\Big).\end{eqnarray*}
Then
By Lemma C.1, ![]() $T_1^N\rightarrow_{\mathbb{P}}0$
and by Lemma C.6,
$T_1^N\rightarrow_{\mathbb{P}}0$
and by Lemma C.6, ![]() $ T_2^N - T_3\rightarrow_{\mathbb{P}}0$
. This concludes the proof.
$ T_2^N - T_3\rightarrow_{\mathbb{P}}0$
. This concludes the proof.
Lemma C.1. Assume (A1). Then if for any ![]() $\varphi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
,
$\varphi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
, ![]() $n\geq 0$
$n\geq 0$
we have for any ![]() $\psi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
,
$\psi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
, ![]() $n\geq 0$
that
$n\geq 0$
that
Proof. Set
Then we have the decomposition
We will show that (16)–(17) converge in probability to zero.
Term (16): Define
Then we have
To show that ![]() $T_1^N$
converges in probability to zero we will show that (18)–(20) each converge in probability to zero. For (18) we have
$T_1^N$
converges in probability to zero we will show that (18)–(20) each converge in probability to zero. For (18) we have
By [Reference Jasra, Kamatani, Law and Zhou22, Proposition C.6],
and by hypothesis ![]() $\check{\eta}_{n}^{N,M}((G_n\otimes 1)\psi)$
converges in probability; hence (18) converges in probability to zero. For (19) this term converges in probability to zero by an almost identical argument to (18) and is hence omitted. For (20),
$\check{\eta}_{n}^{N,M}((G_n\otimes 1)\psi)$
converges in probability; hence (18) converges in probability to zero. For (19) this term converges in probability to zero by an almost identical argument to (18) and is hence omitted. For (20),
 \begin{align}&\check{\eta}_{n}^{N,M}\Big(\{|F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},c}| - |F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},c}|\}\psi\Big)\nonumber\\[3pt] &\quad = \frac{\eta_n^{N,f}(G_n)\eta_n^{N,c}(G_n)-\eta_n^{f}(G_n)\eta_n^{c}(G_n)}{\eta_n^{f}(G_n)\eta_n^{c}(G_n)\eta_n^{N,f}(G_n)\eta_n^{N,c}(G_n)}\check{\eta}_{n}^{N,M}(\{|\eta_n^{c}(G_n)(G_n\otimes 1)-\eta_n^{f}(G_n)(1\otimes G_n)|\}\psi)\nonumber\\[3pt] &\qquad - \frac{1}{\eta_n^{N,f}(G_n)\eta_n^{N,c}(G_n)}\check{\eta}_{n}^{N,M}\Big(\{|\eta_n^{N,c}(G_n)(G_n\otimes 1)-\eta_n^{N,f}(G_n)(1\otimes G_n)|\nonumber\\ &\qquad - |\eta_n^{c}(G_n)(G_n\otimes 1)-\eta_n^{f}(G_n)(1\otimes G_n)|\}\psi\Big).\end{align}
\begin{align}&\check{\eta}_{n}^{N,M}\Big(\{|F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},c}| - |F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},c}|\}\psi\Big)\nonumber\\[3pt] &\quad = \frac{\eta_n^{N,f}(G_n)\eta_n^{N,c}(G_n)-\eta_n^{f}(G_n)\eta_n^{c}(G_n)}{\eta_n^{f}(G_n)\eta_n^{c}(G_n)\eta_n^{N,f}(G_n)\eta_n^{N,c}(G_n)}\check{\eta}_{n}^{N,M}(\{|\eta_n^{c}(G_n)(G_n\otimes 1)-\eta_n^{f}(G_n)(1\otimes G_n)|\}\psi)\nonumber\\[3pt] &\qquad - \frac{1}{\eta_n^{N,f}(G_n)\eta_n^{N,c}(G_n)}\check{\eta}_{n}^{N,M}\Big(\{|\eta_n^{N,c}(G_n)(G_n\otimes 1)-\eta_n^{N,f}(G_n)(1\otimes G_n)|\nonumber\\ &\qquad - |\eta_n^{c}(G_n)(G_n\otimes 1)-\eta_n^{f}(G_n)(1\otimes G_n)|\}\psi\Big).\end{align}
The first term on the right-hand side converges in probability to zero by [Reference Jasra, Kamatani, Law and Zhou22, Proposition C.6] and the hypothesis. Hence, as
converges in probability, we need only show that
converges in probability to zero to conclude. Using standard algebra, we have almost surely that
 \begin{align} &\Big|\eta_n^{N,c}(G_n)(G_n\otimes 1)-\eta_n^{N,f}(G_n)(1\otimes G_n)| -|\eta_n^{c}(G_n)(G_n\otimes 1)-\eta_n^{f}(G_n)(1\otimes G_n)|\Big| \nonumber\\ &\quad \leq\,|[\eta_n^{N,c}-\eta_n^{c}](G_n)(G_n\otimes 1)| +|[\eta_n^{N,f}-\eta_n^{f}](G_n)(1\otimes G_n)|.\end{align}
\begin{align} &\Big|\eta_n^{N,c}(G_n)(G_n\otimes 1)-\eta_n^{N,f}(G_n)(1\otimes G_n)| -|\eta_n^{c}(G_n)(G_n\otimes 1)-\eta_n^{f}(G_n)(1\otimes G_n)|\Big| \nonumber\\ &\quad \leq\,|[\eta_n^{N,c}-\eta_n^{c}](G_n)(G_n\otimes 1)| +|[\eta_n^{N,f}-\eta_n^{f}](G_n)(1\otimes G_n)|.\end{align}
Hence
 \begin{align*}&\check{\eta}_{n}^{N,M}\Big(\{|\eta_n^{N,c}(G_n)(G_n\otimes 1)-\eta_n^{N,f}(G_n)(1\otimes G_n)| -|\eta_n^{c}(G_n)(G_n\otimes 1)-\eta_n^{f}(G_n)(1\otimes G_n)|\}\psi\Big)\\[3pt] &\quad \leq |[\eta_n^{N,c}-\eta_n^{c}](G_n)|\check{\eta}_{n}^{N,M}((G_n\otimes 1)|\psi|) +|[\eta_n^{N,f}-\eta_n^{f}](G_n)|\check{\eta}_{n}^{N,M}((1\otimes G_n)|\psi|),\end{align*}
\begin{align*}&\check{\eta}_{n}^{N,M}\Big(\{|\eta_n^{N,c}(G_n)(G_n\otimes 1)-\eta_n^{N,f}(G_n)(1\otimes G_n)| -|\eta_n^{c}(G_n)(G_n\otimes 1)-\eta_n^{f}(G_n)(1\otimes G_n)|\}\psi\Big)\\[3pt] &\quad \leq |[\eta_n^{N,c}-\eta_n^{c}](G_n)|\check{\eta}_{n}^{N,M}((G_n\otimes 1)|\psi|) +|[\eta_n^{N,f}-\eta_n^{f}](G_n)|\check{\eta}_{n}^{N,M}((1\otimes G_n)|\psi|),\end{align*}
and one can easily conclude by the above arguments.
Term (17): As
we have ![]() $\{F_{n,\check{\eta}_{n}^{M},f} \wedge F_{n,\check{\eta}_{n}^{M},c}\}\psi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
, so (17) converges in probability to zero.
$\{F_{n,\check{\eta}_{n}^{M},f} \wedge F_{n,\check{\eta}_{n}^{M},c}\}\psi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
, so (17) converges in probability to zero.
Lemma C.2. Assume (A1). Then if for any ![]() $\varphi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
,
$\varphi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
, ![]() $n\geq 0$
$n\geq 0$
we have for any ![]() $\psi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
,
$\psi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
, ![]() $n\geq 0$
that
$n\geq 0$
that
 \begin{align*}&\big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg\{\frac{F_{n,\check{\eta}_{n}^{N,M},f}}{\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Bigg\}\bar{M}_{n+1}(\psi)\Bigg)\\[2pt]
&\quad -\,\big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg\{\frac{F_{n,\check{\eta}_{n}^{M},f}}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Bigg\}\bar{M}_{n+1}(\psi)\Bigg)\rightarrow_{\mathbb{P}} 0.\end{align*}
\begin{align*}&\big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg\{\frac{F_{n,\check{\eta}_{n}^{N,M},f}}{\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Bigg\}\bar{M}_{n+1}(\psi)\Bigg)\\[2pt]
&\quad -\,\big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg\{\frac{F_{n,\check{\eta}_{n}^{M},f}}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Bigg\}\bar{M}_{n+1}(\psi)\Bigg)\rightarrow_{\mathbb{P}} 0.\end{align*}
Proof. Define
 \begin{eqnarray}T_1^N & \,:\!=\, &\big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg\{\frac{F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{M},f}}{\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)}\otimes \nonumber \\ &
&\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Bigg\}\bar{M}_{n+1}(\psi)\Bigg),\end{eqnarray}
\begin{eqnarray}T_1^N & \,:\!=\, &\big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg\{\frac{F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{M},f}}{\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)}\otimes \nonumber \\ &
&\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Bigg\}\bar{M}_{n+1}(\psi)\Bigg),\end{eqnarray}
 \begin{eqnarray}T_2^N & \,:\!= &\, \frac{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)-\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)} \nonumber \\ &
&\times \big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Big(\Big\{F_{n,\check{\eta}_{n}^{M},f}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big\}\bar{M}_{n+1}(\psi)\Big).\end{eqnarray}
\begin{eqnarray}T_2^N & \,:\!= &\, \frac{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)-\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)} \nonumber \\ &
&\times \big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Big(\Big\{F_{n,\check{\eta}_{n}^{M},f}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big\}\bar{M}_{n+1}(\psi)\Big).\end{eqnarray}
Then we have
 \[T_1^N + T_2^N = \big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg\{\frac{F_{n,\check{\eta}_{n}^{N,M},f}}{\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Bigg\}\bar{M}_{n+1}(\psi)\Bigg) \]
\[T_1^N + T_2^N = \big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg\{\frac{F_{n,\check{\eta}_{n}^{N,M},f}}{\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Bigg\}\bar{M}_{n+1}(\psi)\Bigg) \]
 \[\qquad\quad-\,\big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg\{\frac{F_{n,\check{\eta}_{n}^{M},f}}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Bigg\}\bar{M}_{n+1}(\psi)\Bigg).\]
\[\qquad\quad-\,\big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg\{\frac{F_{n,\check{\eta}_{n}^{M},f}}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Bigg\}\bar{M}_{n+1}(\psi)\Bigg).\]
We will show that (23) and (24) converge in probability to zero.
Term (23): For (23) we note that
By Lemma C.1 this converges in probability to a constant, so we only consider the convergence to zero of
 \begin{align*}&(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\{(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{M},f})\otimes \overline{F}_{n,\check{\eta}_{n}^{N,M},c}\}\bar{M}_{n+1}(\psi)\Big)\\[3pt]
&\quad = \bigg(\frac{1}{\eta_n^{N,f}(G_n)}-\frac{1}{\eta_n^{f}(G_n)}\bigg)(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\{(G_n\otimes 1)\otimes \overline{F}_{n,\check{\eta}_{n}^{N,M},c}\}\bar{M}_{n+1}(\psi)\Big).\end{align*}
\begin{align*}&(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\{(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{M},f})\otimes \overline{F}_{n,\check{\eta}_{n}^{N,M},c}\}\bar{M}_{n+1}(\psi)\Big)\\[3pt]
&\quad = \bigg(\frac{1}{\eta_n^{N,f}(G_n)}-\frac{1}{\eta_n^{f}(G_n)}\bigg)(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\{(G_n\otimes 1)\otimes \overline{F}_{n,\check{\eta}_{n}^{N,M},c}\}\bar{M}_{n+1}(\psi)\Big).\end{align*}
By [Reference Jasra, Kamatani, Law and Zhou22, Proposition C.6],
so if we can show that the remaining term on the right-hand side is, in absolute value, almost surely bounded above by a convergent (in probability) random variable, we have shown that (23) converges in probability to zero. We have
Then almost surely
 \begin{equation}\check{\eta}_{n}^{N,M}(|\overline{F}_{n,\check{\eta}_{n}^{N,M},c}|) \leq\frac{\check{\eta}_{n}^{N,M}\Big(F_{n,\check{\eta}_{n}^{N,M},c}\Big)+\check{\eta}_{n}^{N,M}\Big(\Big\{F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\Big\}\Big)}{\Big|\check{\eta}_{n}^{N,M}\Big(F_{n,\check{\eta}_{n}^{N,M},c}-\Big\{F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\Big\}\Big)\Big|}.\end{equation}
\begin{equation}\check{\eta}_{n}^{N,M}(|\overline{F}_{n,\check{\eta}_{n}^{N,M},c}|) \leq\frac{\check{\eta}_{n}^{N,M}\Big(F_{n,\check{\eta}_{n}^{N,M},c}\Big)+\check{\eta}_{n}^{N,M}\Big(\Big\{F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\Big\}\Big)}{\Big|\check{\eta}_{n}^{N,M}\Big(F_{n,\check{\eta}_{n}^{N,M},c}-\Big\{F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\Big\}\Big)\Big|}.\end{equation}
By the above arguments, both the denominator and the numerator will converge in probability to a finite constant, and hence we have shown that (23) converges in probability to zero.
Term (24): We note that
 \begin{align*}&\frac{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)-\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)}\\[3pt]
&\quad = \frac{\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)-\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}{\big(1-\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)\big)\big(1-\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)\big)}.\end{align*}
\begin{align*}&\frac{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)-\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)}\\[3pt]
&\quad = \frac{\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)-\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}{\big(1-\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)\big)\big(1-\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)\big)}.\end{align*}
By Lemma C.1 this converges in probability to zero. Thus, we need only show that
is (almost surely) bounded above by a convergent (in probability) random variable. Almost surely,
As ![]() $F_{n,\check{\eta}_{n}^{M},f}\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
,
$F_{n,\check{\eta}_{n}^{M},f}\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
, ![]() $\check{\eta}_{n}^{N,M}(F_{n,\check{\eta}_{n}^{M},f})$
converges in probability to a finite constant and our proof is concluded by the argument associated to (26).
$\check{\eta}_{n}^{N,M}(F_{n,\check{\eta}_{n}^{M},f})$
converges in probability to a finite constant and our proof is concluded by the argument associated to (26).
Lemma C.3. Assume (A1). Then if for any ![]() $\varphi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
,
$\varphi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
, ![]() $n\geq 0$
$n\geq 0$
we have for any ![]() $\psi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
,
$\psi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
, ![]() $n\geq 0$
that
$n\geq 0$
that
 \[(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Bigg(\Bigg(\Bigg\{\frac{F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}\Bigg\}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Bigg)\bar{M}_{n+1}(\psi)\Bigg)\rightarrow_{\mathbb{P}}0.\]
\[(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Bigg(\Bigg(\Bigg\{\frac{F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}\Bigg\}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Bigg)\bar{M}_{n+1}(\psi)\Bigg)\rightarrow_{\mathbb{P}}0.\]
Proof. Define
 \begin{eqnarray}C & \,:\!= &\, \frac{1}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}, \nonumber\\
T_1^N & \,:\!= &\, -\frac{C}{2}\big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Big(\Big(\big\{F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{M},f}\big\}\otimes \overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big)\bar{M}_{n+1}(\psi)\Big) ,\end{eqnarray}
\begin{eqnarray}C & \,:\!= &\, \frac{1}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}, \nonumber\\
T_1^N & \,:\!= &\, -\frac{C}{2}\big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Big(\Big(\big\{F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{M},f}\big\}\otimes \overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big)\bar{M}_{n+1}(\psi)\Big) ,\end{eqnarray}
 \begin{eqnarray}\hspace*{10pt}T_3^N & \,:\!= &\, -\frac{C}{2}\big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Big(\Big(\big\{|F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},c}| -|F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},c}|\big\}\otimes \nonumber \\ & & \overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big)\bar{M}_{n+1}(\psi)\Big).\end{eqnarray}
\begin{eqnarray}\hspace*{10pt}T_3^N & \,:\!= &\, -\frac{C}{2}\big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Big(\Big(\big\{|F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},c}| -|F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},c}|\big\}\otimes \nonumber \\ & & \overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big)\bar{M}_{n+1}(\psi)\Big).\end{eqnarray}
Then we have
 \begin{align*} & T_1^N + T_2^N + T_3^N\\[2pt]
&\quad = \big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg(\Bigg\{\frac{F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}\Bigg\}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\bigg)\bar{M}_{n+1}(\psi)\Bigg). \end{align*}
\begin{align*} & T_1^N + T_2^N + T_3^N\\[2pt]
&\quad = \big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg(\Bigg\{\frac{F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}\Bigg\}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\bigg)\bar{M}_{n+1}(\psi)\Bigg). \end{align*}
We will show that (27), (28), and (29) will converge in probability to zero to conclude the proof.
Term (27): We have that (27) is equal to
By [Reference Jasra, Kamatani, Law and Zhou22, Proposition C.6],
so if we can show that the remaining term on the right-hand side is, in absolute value, almost surely bounded above by a convergent (in probability) random variable, we have shown that (27) converges in probability to zero. This can be achieved using the argument for (25) in the proof of Lemma C.2, and hence we have shown that (27) converges in probability to zero.
Term (28): The argument is almost identical to (27) and is omitted.
Term (29): Using a decomposition similar to (21), we define
 \begin{eqnarray}T_4^N & \,:\!= &\, -\frac{C}{2}\frac{\eta_n^{f}(G_n)\eta_n^{c}(G_n)-\eta_n^{N,f}(G_n)\eta_n^{N,c}(G_n)}{\eta_n^{f}(G_n)\eta_n^{c}(G_n)\eta_n^{N,f}(G_n)\eta_n^{N,c}(G_n)}(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\nonumber \\ & &\Big(\Big(\{|\eta_n^{c}(G_n)(G_n\otimes 1)-\eta_n^{f}(G_n)(1\otimes G_n)|\}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big)\bar{M}_{n+1}(\psi)\Big), \end{eqnarray}
\begin{eqnarray}T_4^N & \,:\!= &\, -\frac{C}{2}\frac{\eta_n^{f}(G_n)\eta_n^{c}(G_n)-\eta_n^{N,f}(G_n)\eta_n^{N,c}(G_n)}{\eta_n^{f}(G_n)\eta_n^{c}(G_n)\eta_n^{N,f}(G_n)\eta_n^{N,c}(G_n)}(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\nonumber \\ & &\Big(\Big(\{|\eta_n^{c}(G_n)(G_n\otimes 1)-\eta_n^{f}(G_n)(1\otimes G_n)|\}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big)\bar{M}_{n+1}(\psi)\Big), \end{eqnarray}
 \begin{eqnarray}T_5^N & \,:\!= &\, -\frac{C}{2}\frac{1}{\eta_n^{N,f}(G_n)\eta_n^{N,c}(G_n)}(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\Big(\{|\eta_n^{N,c}(G_n)(G_n\otimes 1)-\eta_n^{N,f}(G_n)(1\otimes G_n)| \nonumber\\& &-\,|\eta_n^{c}(G_n)(G_n\otimes 1)-\eta_n^{f}(G_n)(1\otimes G_n)|\}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big)\bar{M}_{n+1}(\psi)\Big).\end{eqnarray}
\begin{eqnarray}T_5^N & \,:\!= &\, -\frac{C}{2}\frac{1}{\eta_n^{N,f}(G_n)\eta_n^{N,c}(G_n)}(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\Big(\{|\eta_n^{N,c}(G_n)(G_n\otimes 1)-\eta_n^{N,f}(G_n)(1\otimes G_n)| \nonumber\\& &-\,|\eta_n^{c}(G_n)(G_n\otimes 1)-\eta_n^{f}(G_n)(1\otimes G_n)|\}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big)\bar{M}_{n+1}(\psi)\Big).\end{eqnarray}
Then we have
We will show that (30) and (31) will converge to zero in probability. For (30), by [Reference Jasra, Kamatani, Law and Zhou22, Proposition C.6],
and
 \begin{align*}&\Big|(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\Big(\{|\eta_n^{c}(G_n)(G_n\otimes 1)-\eta_n^{f}(G_n)(1\otimes G_n)|\}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big)\bar{M}_{n+1}(\psi)\Big)\Big|\\ &\quad \leq \|G_n\|\|\psi\|(\eta_n^{c}(G_n)+\eta_n^{f}(G_n))\check{\eta}_{n}^{N,M}(|\overline{F}_{n,\check{\eta}_{n}^{N,M},c}|);\end{align*}
\begin{align*}&\Big|(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\Big(\{|\eta_n^{c}(G_n)(G_n\otimes 1)-\eta_n^{f}(G_n)(1\otimes G_n)|\}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big)\bar{M}_{n+1}(\psi)\Big)\Big|\\ &\quad \leq \|G_n\|\|\psi\|(\eta_n^{c}(G_n)+\eta_n^{f}(G_n))\check{\eta}_{n}^{N,M}(|\overline{F}_{n,\check{\eta}_{n}^{N,M},c}|);\end{align*}
thus, using the argument for (25) in the proof of Lemma C.2, we have shown that (30) converges in probability to zero. For (31), as ![]() $(\eta_n^{N,f}(G_n)\eta_n^{N,c}(G_n))^{-1}$
converges in probability to a finite constant, we need only show that the remaining term converges in probability to zero. Using (22) we have that
$(\eta_n^{N,f}(G_n)\eta_n^{N,c}(G_n))^{-1}$
converges in probability to a finite constant, we need only show that the remaining term converges in probability to zero. Using (22) we have that
 \begin{align*}&\Big|(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\Big(\{|\eta_n^{N,c}(G_n)(G_n\otimes 1)-\eta_n^{N,f}(G_n)(1\otimes G_n)|\\ &\qquad - |\eta_n^{c}(G_n)(G_n\otimes 1)-\eta_n^{f}(G_n)(1\otimes G_n)|\}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big)\bar{M}_{n+1}(\psi)\Big)\Big|\\[3pt] &\quad \leq \|\psi\|\check{\eta}_{n}^{N,M}\Big(|[\eta_n^{N,c}-\eta_n^{c}](G_n)(G_n\otimes 1)| +|[\eta_n^{N,f}-\eta_n^{f}](G_n)(1\otimes G_n)|\Big)\check{\eta}_{n}^{N,M}(|\overline{F}_{n,\check{\eta}_{n}^{N,M},c}|). \end{align*}
\begin{align*}&\Big|(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\Big(\{|\eta_n^{N,c}(G_n)(G_n\otimes 1)-\eta_n^{N,f}(G_n)(1\otimes G_n)|\\ &\qquad - |\eta_n^{c}(G_n)(G_n\otimes 1)-\eta_n^{f}(G_n)(1\otimes G_n)|\}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big)\bar{M}_{n+1}(\psi)\Big)\Big|\\[3pt] &\quad \leq \|\psi\|\check{\eta}_{n}^{N,M}\Big(|[\eta_n^{N,c}-\eta_n^{c}](G_n)(G_n\otimes 1)| +|[\eta_n^{N,f}-\eta_n^{f}](G_n)(1\otimes G_n)|\Big)\check{\eta}_{n}^{N,M}(|\overline{F}_{n,\check{\eta}_{n}^{N,M},c}|). \end{align*}
Then (31) converges in probability to zero by the argument for (25) in the proof of Lemma C.2 for ![]() $\check{\eta}_{n}^{N,M}($
$\check{\eta}_{n}^{N,M}($
![]() $|\overline{F}_{n,\check{\eta}_{n}^{N,M},c}|)$
. For the remaining term one can apply the (last) argument for (20) in Lemma C.1. Hence (29) converges in probability to zero and the proof is concluded.
$|\overline{F}_{n,\check{\eta}_{n}^{N,M},c}|)$
. For the remaining term one can apply the (last) argument for (20) in Lemma C.1. Hence (29) converges in probability to zero and the proof is concluded.
Lemma C.4. Assume (A1). Then if for any ![]() $\varphi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
,
$\varphi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
, ![]() $n\geq 0$
$n\geq 0$
we have for any ![]() $\psi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
,
$\psi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
, ![]() $n\geq 0$
that
$n\geq 0$
that
 \begin{align*}&\frac{\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)-\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}{\big(1-\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)\big)\big(1-\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)\big)} \\[2pt] &\quad \times (\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\Big(\Big\{F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\Big\}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big)\bar{M}_{n+1}(\psi)\Big)\rightarrow_{\mathbb{P}} 0.\end{align*}
\begin{align*}&\frac{\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)-\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}{\big(1-\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)\big)\big(1-\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)\big)} \\[2pt] &\quad \times (\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\Big(\Big\{F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\Big\}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big)\bar{M}_{n+1}(\psi)\Big)\rightarrow_{\mathbb{P}} 0.\end{align*}
Proof. The proof concerning (24) of Lemma C.2 establishes that
 \[\frac{\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)-\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}{\big(1-\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)\big)\big(1-\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)\big)} \rightarrow_{\mathbb{P}} 0.\]
\[\frac{\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)-\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}{\big(1-\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)\big)\big(1-\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)\big)} \rightarrow_{\mathbb{P}} 0.\]
Then, almost surely
 \begin{align*}&\Big|(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\Big(\Big\{F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\Big\}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big)\bar{M}_{n+1}(\psi)\Big)\Big|\\[3pt] &\quad \leq \|\psi\|\check{\eta}_{n}^{N,M}(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c})\check{\eta}_{n}^{N,M}(|\overline{F}_{n,\check{\eta}_{n}^{N,M},c}|).\end{align*}
\begin{align*}&\Big|(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\Big(\Big\{F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\Big\}\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big)\bar{M}_{n+1}(\psi)\Big)\Big|\\[3pt] &\quad \leq \|\psi\|\check{\eta}_{n}^{N,M}(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c})\check{\eta}_{n}^{N,M}(|\overline{F}_{n,\check{\eta}_{n}^{N,M},c}|).\end{align*}
By Lemma C.1, ![]() $\check{\eta}_{n}^{N,M}(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c})$
converges in probability to a constant, and using the argument for (25) in the proof of Lemma C.2 for
$\check{\eta}_{n}^{N,M}(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c})$
converges in probability to a constant, and using the argument for (25) in the proof of Lemma C.2 for ![]() $\check{\eta}_{n}^{N,M}(|\overline{F}_{n,\check{\eta}_{n}^{N,M},c}|)$
, we conclude the proof.
$\check{\eta}_{n}^{N,M}(|\overline{F}_{n,\check{\eta}_{n}^{N,M},c}|)$
, we conclude the proof.
Lemma C.5. Assume (A3). Then if for any ![]() $n\geq 0$
,
$n\geq 0$
, ![]() $\varphi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
$\varphi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
we have for any ![]() $\psi\in\mathcal{C}_b(\textsf{X}^2\times\textsf{X}^2)$
that
$\psi\in\mathcal{C}_b(\textsf{X}^2\times\textsf{X}^2)$
that
Proof. We will use a density argument. Define
Denote by ![]() $\mathscr{G}$
the set of functions which are finite linear combinations of functions in
$\mathscr{G}$
the set of functions which are finite linear combinations of functions in ![]() $\mathscr{F}$
. As we have that for some
$\mathscr{F}$
. As we have that for some ![]() $n\geq 0$
,
$n\geq 0$
, ![]() $\varphi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
,
$\varphi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
, ![]() $\check{\eta}_{n}^{N,M}(\varphi) \rightarrow_{\mathbb{P}} \check{\eta}_{n}^{M}(\varphi)$
, it follows that for
$\check{\eta}_{n}^{N,M}(\varphi) \rightarrow_{\mathbb{P}} \check{\eta}_{n}^{M}(\varphi)$
, it follows that for ![]() $\tilde{\psi}\in\mathscr{G}$
,
$\tilde{\psi}\in\mathscr{G}$
,
and thus, by [Reference Billingsley3, Theorem 25.12],
Let ![]() $\epsilon>0$
be arbitrary and
$\epsilon>0$
be arbitrary and ![]() $\psi\in\mathcal{C}_b(\textsf{X}^2\times\textsf{X}^2)$
. By the Stone–Weierstrass theorem,
$\psi\in\mathcal{C}_b(\textsf{X}^2\times\textsf{X}^2)$
. By the Stone–Weierstrass theorem, ![]() $\mathscr{G}$
is dense in
$\mathscr{G}$
is dense in ![]() $\mathcal{C}_b(\textsf{X}^2\times\textsf{X}^2)$
; hence there exists a
$\mathcal{C}_b(\textsf{X}^2\times\textsf{X}^2)$
; hence there exists a ![]() $\tilde{\psi}\in\mathscr{G}$
such that
$\tilde{\psi}\in\mathscr{G}$
such that
Then we have that for any ![]() $N\geq 1$
,
$N\geq 1$
,
By (32) there exists an ![]() $N^*\geq 1$
such that for every
$N^*\geq 1$
such that for every ![]() $N\geq N^*$
,
$N\geq N^*$
,
Hence, applying (33) to the terms
we have for every ![]() $N\geq N^*$
that
$N\geq N^*$
that
and as ![]() $\epsilon>0$
is arbitrary we have
$\epsilon>0$
is arbitrary we have
as was to be proved.
Lemma C.6. Assume (A1)–(A3). Then if for any ![]() $\varphi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
,
$\varphi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
, ![]() $n\geq 0$
$n\geq 0$
we have for any ![]() $\psi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
,
$\psi\in\mathcal{C}_b(\textsf{X}\times\textsf{X})$
, ![]() $n\geq 0$
that
$n\geq 0$
that
Proof. We make the definitions
 \begin{eqnarray}T_1^N & \,:\!= &\, \Big(\check{\eta}_{n}^{M}\Big(\{F_{n,\check{\eta}_{n}^{M},f} \wedge F_{n,\check{\eta}_{n}^{M},c}\}\Big)-\check{\eta}_{n}^{N,M}\Big(\{F_{n,\check{\eta}_{n}^{N,M},f} \wedge F_{n,\check{\eta}_{n}^{N,M},c}\}\Big)\Big) \qquad\qquad\quad\nonumber \\& &\times\,(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\Big\{\overline{F}_{n,\check{\eta}_{n}^{N,M},f}\otimes \overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big\}\bar{M}_{n+1}(\psi)\Big), \end{eqnarray}
\begin{eqnarray}T_1^N & \,:\!= &\, \Big(\check{\eta}_{n}^{M}\Big(\{F_{n,\check{\eta}_{n}^{M},f} \wedge F_{n,\check{\eta}_{n}^{M},c}\}\Big)-\check{\eta}_{n}^{N,M}\Big(\{F_{n,\check{\eta}_{n}^{N,M},f} \wedge F_{n,\check{\eta}_{n}^{N,M},c}\}\Big)\Big) \qquad\qquad\quad\nonumber \\& &\times\,(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\Big\{\overline{F}_{n,\check{\eta}_{n}^{N,M},f}\otimes \overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big\}\bar{M}_{n+1}(\psi)\Big), \end{eqnarray}
 \begin{eqnarray}T_2^N & \,:\!= &\, \Big(1-\check{\eta}_{n}^{M}\Big(\{F_{n,\check{\eta}_{n}^{M},f} \wedge F_{n,\check{\eta}_{n}^{M},c}\}\Big)\Big)(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\Big\{\overline{F}_{n,\check{\eta}_{n}^{N,M},f}\otimes \overline{F}_{n,\check{\eta}_{n}^{N,M},c}- \nonumber \\ & &\overline{F}_{n,\check{\eta}_{n}^{M},f}\otimes \overline{F}_{n,\check{\eta}_{n}^{M},c}\Big\}\bar{M}_{n+1}(\psi)\Big), \end{eqnarray}
\begin{eqnarray}T_2^N & \,:\!= &\, \Big(1-\check{\eta}_{n}^{M}\Big(\{F_{n,\check{\eta}_{n}^{M},f} \wedge F_{n,\check{\eta}_{n}^{M},c}\}\Big)\Big)(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M})\Big(\Big\{\overline{F}_{n,\check{\eta}_{n}^{N,M},f}\otimes \overline{F}_{n,\check{\eta}_{n}^{N,M},c}- \nonumber \\ & &\overline{F}_{n,\check{\eta}_{n}^{M},f}\otimes \overline{F}_{n,\check{\eta}_{n}^{M},c}\Big\}\bar{M}_{n+1}(\psi)\Big), \end{eqnarray}
Then we have
We will show that (34)–(36) will converge in probability to zero.
so if we can show that
is (almost surely) bounded above by a term which converges in probability to a positive constant, we have shown that (34) converges in probability to zero. Clearly, almost surely we have
We focus on showing that ![]() $\check{\eta}_{n}^{N,M}(|\overline{F}_{n,\check{\eta}_{n}^{N,M},c}|)$
is bounded above by a term which converges in probability to a finite constant. This can be verified in an almost identical manner to the approach for (26) in the proof of Lemma C.2; hence we have verified that (34) converges in probability to zero.
$\check{\eta}_{n}^{N,M}(|\overline{F}_{n,\check{\eta}_{n}^{N,M},c}|)$
is bounded above by a term which converges in probability to a finite constant. This can be verified in an almost identical manner to the approach for (26) in the proof of Lemma C.2; hence we have verified that (34) converges in probability to zero.
Term (35): Set
 \begin{eqnarray}C & \,:\!= &\, \check{\eta}_{n}^{M}\big(\big\{F_{n,\check{\eta}_{n}^{M},f} \wedge F_{n,\check{\eta}_{n}^{M},c}\big\}\big), \nonumber \\
T_4^N & \,:\!= &\, C\big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Big(\Big\{[\overline{F}_{n,\check{\eta}_{n}^{N,M},f}-\overline{F}_{n,\check{\eta}_{n}^{M},f}]\otimes \overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big\}\bar{M}_{n+1}(\psi)\Big), \end{eqnarray}
\begin{eqnarray}C & \,:\!= &\, \check{\eta}_{n}^{M}\big(\big\{F_{n,\check{\eta}_{n}^{M},f} \wedge F_{n,\check{\eta}_{n}^{M},c}\big\}\big), \nonumber \\
T_4^N & \,:\!= &\, C\big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Big(\Big\{[\overline{F}_{n,\check{\eta}_{n}^{N,M},f}-\overline{F}_{n,\check{\eta}_{n}^{M},f}]\otimes \overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big\}\bar{M}_{n+1}(\psi)\Big), \end{eqnarray}
then
We need to show that (37) and (38) converge in probability to zero. As the proof for (38) is similar to and easier than that for (37), we focus on the latter. Define
 \begin{eqnarray*}T_6^N & \,:\!= &\, C\big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg\{\Bigg(\frac{F_{n,\check{\eta}_{n}^{N,M},f}}{\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)}\otimes \nonumber \\
& &\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Bigg)\Bigg\}\bar{M}_{n+1}(\psi)\Bigg), \\
T_7^N & \,:\!= &\, C \big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg\{\Bigg(\frac{F_{n,\check{\eta}_{n}^{M},f}}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}\Bigg)\otimes \nonumber \\
& &\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Bigg\}\bar{M}_{n+1}(\psi)\Bigg), \\
T_8^N & \,:\!= &\, C \big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg\{\Bigg(\frac{F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}\Bigg)\otimes \nonumber\\
& &\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big\}\bar{M}_{n+1}(\psi)\Bigg), \\
T_9^N & \,:\!= &\, \frac{\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)-\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}{\big(1-\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)\big)\big(1-\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)\big)} \nonumber \\
& &\times\,C \big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Big(\Big\{\Big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\Big)\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big\}\bar{M}_{n+1}(\psi)\Big).\end{eqnarray*}
\begin{eqnarray*}T_6^N & \,:\!= &\, C\big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg\{\Bigg(\frac{F_{n,\check{\eta}_{n}^{N,M},f}}{\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)}\otimes \nonumber \\
& &\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Bigg)\Bigg\}\bar{M}_{n+1}(\psi)\Bigg), \\
T_7^N & \,:\!= &\, C \big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg\{\Bigg(\frac{F_{n,\check{\eta}_{n}^{M},f}}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}\Bigg)\otimes \nonumber \\
& &\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Bigg\}\bar{M}_{n+1}(\psi)\Bigg), \\
T_8^N & \,:\!= &\, C \big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Bigg(\Bigg\{\Bigg(\frac{F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}-F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}}{\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}-F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}\Bigg)\otimes \nonumber\\
& &\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big\}\bar{M}_{n+1}(\psi)\Bigg), \\
T_9^N & \,:\!= &\, \frac{\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)-\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)}{\big(1-\check{\eta}_{n}^{N,M}\big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\big)\big)\big(1-\check{\eta}_{n}^{M}\big(F_{n,\check{\eta}_{n}^{M},f}\wedge F_{n,\check{\eta}_{n}^{M},c}\big)\big)} \nonumber \\
& &\times\,C \big(\check{\eta}_{n}^{N,M}\otimes\check{\eta}_{n}^{N,M}\big)\Big(\Big\{\Big(F_{n,\check{\eta}_{n}^{N,M},f}\wedge F_{n,\check{\eta}_{n}^{N,M},c}\Big)\otimes\overline{F}_{n,\check{\eta}_{n}^{N,M},c}\Big\}\bar{M}_{n+1}(\psi)\Big).\end{eqnarray*}
Then we have that
By Lemma C.2 we have ![]() $T_6^N - T_7^N\rightarrow_{\mathbb{P}}0$
, by Lemma C.3 we have
$T_6^N - T_7^N\rightarrow_{\mathbb{P}}0$
, by Lemma C.3 we have ![]() $ T_8^N\rightarrow_{\mathbb{P}}0$
, and by Lemma C.4 we have
$ T_8^N\rightarrow_{\mathbb{P}}0$
, and by Lemma C.4 we have ![]() $ T_9^N\rightarrow_{\mathbb{P}}0$
; hence we conclude that
$ T_9^N\rightarrow_{\mathbb{P}}0$
; hence we conclude that ![]() $T_4^N\rightarrow_{\mathbb{P}} 0$
.
$T_4^N\rightarrow_{\mathbb{P}} 0$
.
Term (36): As
it easily follows by Lemma C.5 that
Appendix D. Technical results for the MCPF
Proposition D.1. For any ![]() $n\geq 0$
,
$n\geq 0$
, ![]() $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
, ![]() $p\geq 1$
there exists a
$p\geq 1$
there exists a ![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any ![]() $\varphi\in\mathcal{B}_b(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})$
, ![]() $N\geq 1$
we have
$N\geq 1$
we have
Proof. As for Proposition B.1.
Recall that we are assuming that ![]() $M_n^s$
has a density and we are denoting the density by
$M_n^s$
has a density and we are denoting the density by ![]() $M_n^s$
as well.
$M_n^s$
as well.
Theorem D.1. Suppose that for ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
, ![]() $M_n^s\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
. Then for any
$M_n^s\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
. Then for any ![]() $\varphi\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
, ![]() $n\geq 0$
we have
$n\geq 0$
we have
Proof. The proof is by induction, the initialization following by the WLLN for i.i.d. random variables. The result is assumed at time ![]() $n-1$
, and we have the decomposition
$n-1$
, and we have the decomposition
As in the proof of Theorem 3.1, one can easily prove that
by using the (conditional) Marcinkiewicz–Zygmund inequality, so we focus on
Define
 \begin{align*}T_1^N & \,:\!= \, \int_{\textsf{X}} \varphi(x,x) F_{n-1,\eta_{n-1}^{N,f},f}(x)\wedge F_{n,\eta_{n-1}^{N,c},c}(x) dx -\int_{\textsf{X}} \varphi(x,x) F_{n-1,\eta_{n-1}^{f},f}(x)\wedge F_{n-1,\eta_{n-1}^{c},c}(x) dx, \\[3pt]
T_2^N & \,:\!= \, \bigg(1-\int_{\textsf{X}}F_{n-1,\eta_{n-1}^{N,f},f}(x)\wedge F_{n-1,\eta_{n-1}^{N,c},c}(x)dx\bigg)^{-1}\int_{\textsf{X}\times\textsf{X}} \varphi(x,y)\overline{F}_{n-1,\eta_{n-1}^{N,f},\eta_{n-1}^{N,c},f}(x) \\[3pt]
&\quad \times \overline{F}_{n-1,\eta_{n-1}^{N,c},\eta_{n-1}^{N,f},c}(x) dxdy -\bigg(1-\int_{\textsf{X}}F_{n-1,\eta_{n-1}^{f},f}(x)\wedge F_{n-1,\eta_{n-1}^{c},c}(x)dx\bigg)^{-1} \\[3pt] &\quad \times \int_{\textsf{X}\times\textsf{X}} \varphi(x,y)\overline{F}_{n-1,\eta_{n-1}^{f},\eta_{n-1}^{c},f}(x) \overline{F}_{n-1,\eta_{n-1}^{c},\eta_{n-1}^{f},c}(x) dxdy.\end{align*}
\begin{align*}T_1^N & \,:\!= \, \int_{\textsf{X}} \varphi(x,x) F_{n-1,\eta_{n-1}^{N,f},f}(x)\wedge F_{n,\eta_{n-1}^{N,c},c}(x) dx -\int_{\textsf{X}} \varphi(x,x) F_{n-1,\eta_{n-1}^{f},f}(x)\wedge F_{n-1,\eta_{n-1}^{c},c}(x) dx, \\[3pt]
T_2^N & \,:\!= \, \bigg(1-\int_{\textsf{X}}F_{n-1,\eta_{n-1}^{N,f},f}(x)\wedge F_{n-1,\eta_{n-1}^{N,c},c}(x)dx\bigg)^{-1}\int_{\textsf{X}\times\textsf{X}} \varphi(x,y)\overline{F}_{n-1,\eta_{n-1}^{N,f},\eta_{n-1}^{N,c},f}(x) \\[3pt]
&\quad \times \overline{F}_{n-1,\eta_{n-1}^{N,c},\eta_{n-1}^{N,f},c}(x) dxdy -\bigg(1-\int_{\textsf{X}}F_{n-1,\eta_{n-1}^{f},f}(x)\wedge F_{n-1,\eta_{n-1}^{c},c}(x)dx\bigg)^{-1} \\[3pt] &\quad \times \int_{\textsf{X}\times\textsf{X}} \varphi(x,y)\overline{F}_{n-1,\eta_{n-1}^{f},\eta_{n-1}^{c},f}(x) \overline{F}_{n-1,\eta_{n-1}^{c},\eta_{n-1}^{f},c}(x) dxdy.\end{align*}
Recalling that ![]() $\check{\eta}_{n}^{C}(\varphi) = \check{\Phi}_n^C(\eta_{n-1}^{f},\eta_{n-1}^{c})(\varphi)$
, we have that
$\check{\eta}_{n}^{C}(\varphi) = \check{\Phi}_n^C(\eta_{n-1}^{f},\eta_{n-1}^{c})(\varphi)$
, we have that
By Lemma D.1 Part 1 we have ![]() $T_1^N\rightarrow_{\mathbb{P}}0$
, and by Lemma D.1 Part 2 we have
$T_1^N\rightarrow_{\mathbb{P}}0$
, and by Lemma D.1 Part 2 we have ![]() $T_2^N\rightarrow_{\mathbb{P}}0$
, which concludes the proof.
$T_2^N\rightarrow_{\mathbb{P}}0$
, which concludes the proof.
Lemma D.1. Suppose that for ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $s\in\{\,f,c\}$
,
$s\in\{\,f,c\}$
, ![]() $M_n^s\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
and that for
$M_n^s\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
and that for ![]() $\varphi\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
, ![]() $n\geq 0$
$n\geq 0$
Then for any ![]() $\psi\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
,
$\psi\in\mathcal{B}_b(\textsf{X}\times\textsf{X})$
, ![]() $n\geq 0$
we have the following:
$n\geq 0$
we have the following:
1.
 \[\int_{\textsf{X}} \psi(x,x) F_{n,\eta_{n}^{N,f},f}(x)\wedge F_{n,\eta_{n}^{N,c},c}(x) dx \rightarrow_\mathbb{P}\int_{\textsf{X}} \psi(x,x) F_{n,\eta_{n}^{f},f}(x)\wedge F_{n,\eta_{n}^{c},c}(x) dx.\]
\[\int_{\textsf{X}} \psi(x,x) F_{n,\eta_{n}^{N,f},f}(x)\wedge F_{n,\eta_{n}^{N,c},c}(x) dx \rightarrow_\mathbb{P}\int_{\textsf{X}} \psi(x,x) F_{n,\eta_{n}^{f},f}(x)\wedge F_{n,\eta_{n}^{c},c}(x) dx.\]
2.
 \begin{align*}&\bigg(1-\int_{\textsf{X}}F_{n,\eta_{n}^{N,f},f}(x)\wedge F_{n,\eta_{n}^{N,c},c}(x)dx\bigg)^{-1} \\ &\int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{N,f},\eta_{n}^{N,c},f}(x) \overline{F}_{n,\eta_{n}^{N,c},\eta_{n}^{N,f},c}(x) dxdy \rightarrow_\mathbb{P}\end{align*}
\begin{align*}&\bigg(1-\int_{\textsf{X}}F_{n,\eta_{n}^{N,f},f}(x)\wedge F_{n,\eta_{n}^{N,c},c}(x)dx\bigg)^{-1} \\ &\int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{N,f},\eta_{n}^{N,c},f}(x) \overline{F}_{n,\eta_{n}^{N,c},\eta_{n}^{N,f},c}(x) dxdy \rightarrow_\mathbb{P}\end{align*}
 \[\bigg(1-\int_{\textsf{X}}F_{n,\eta_{n}^{f},f}(x)\wedge F_{n,\eta_{n}^{c},c}(x)dx\bigg)^{-1}\int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{f},\eta_{n}^{c},f}(x) \overline{F}_{n,\eta_{n}^{c},\eta_{n}^{f},c}(x) dxdy.\]
\[\bigg(1-\int_{\textsf{X}}F_{n,\eta_{n}^{f},f}(x)\wedge F_{n,\eta_{n}^{c},c}(x)dx\bigg)^{-1}\int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{f},\eta_{n}^{c},f}(x) \overline{F}_{n,\eta_{n}^{c},\eta_{n}^{f},c}(x) dxdy.\]
Proof. We begin by noting that for any ![]() $x\in\textsf{X}$
, by the assumption that
$x\in\textsf{X}$
, by the assumption that ![]() $\check{\eta}_{n}^{N,C}(\varphi) \rightarrow_{\mathbb{P}} \check{\eta}_{n}^{C}(\varphi)$
, we have
$\check{\eta}_{n}^{N,C}(\varphi) \rightarrow_{\mathbb{P}} \check{\eta}_{n}^{C}(\varphi)$
, we have
 \begin{eqnarray*}F_{n,\eta_{n}^{N,f},f}(x) &\quad \rightarrow_\mathbb{P}\quad & F_{n,\eta_{n}^{f},f}(x), \\[3pt]F_{n,\eta_{n}^{N,c},c}(x) & \quad \rightarrow_\mathbb{P}\quad & F_{n,\eta_{n}^{c},c}(x),\end{eqnarray*}
\begin{eqnarray*}F_{n,\eta_{n}^{N,f},f}(x) &\quad \rightarrow_\mathbb{P}\quad & F_{n,\eta_{n}^{f},f}(x), \\[3pt]F_{n,\eta_{n}^{N,c},c}(x) & \quad \rightarrow_\mathbb{P}\quad & F_{n,\eta_{n}^{c},c}(x),\end{eqnarray*}
and hence that
For Part 1 we have
Then, as
by (39) and [Reference Billingsley3, Theorem 25.12] we have that for any ![]() $x\in\textsf{X}$
,
$x\in\textsf{X}$
,
Hence, by the bounded convergence theorem,
and the result follows.
For Part 2, using almost the same proof as for Part 1 except with (40)–(41) in place of (39), we have
 \begin{align}&\int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{N,f},\eta_{n}^{N,c},f}(x) \overline{F}_{n,\eta_{n}^{N,c},\eta_{n}^{N,f},c}(x) dxdy\rightarrow_\mathbb{P}\nonumber\\ &\quad \int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{f},\eta_{n}^{c},f}(x) \overline{F}_{n,\eta_{n}^{c},\eta_{n}^{f},c}(x) dxdy.\end{align}
\begin{align}&\int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{N,f},\eta_{n}^{N,c},f}(x) \overline{F}_{n,\eta_{n}^{N,c},\eta_{n}^{N,f},c}(x) dxdy\rightarrow_\mathbb{P}\nonumber\\ &\quad \int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{f},\eta_{n}^{c},f}(x) \overline{F}_{n,\eta_{n}^{c},\eta_{n}^{f},c}(x) dxdy.\end{align}
Define
 \begin{eqnarray*}T_1^N & \,:\!= &\, \bigg(1-\int_{\textsf{X}}F_{n,\eta_{n}^{N,f},f}(x)\wedge F_{n,\eta_{n}^{N,c},c}(x)dx\bigg)^{-1} - \bigg(1-\int_{\textsf{X}}F_{n,\eta_{n}^{f},f}(x)\wedge F_{n,\eta_{n}^{c},c}(x)dx\bigg)^{-1}\Big) \\[3pt]
& &\times \,\int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{N,f},\eta_{n}^{N,c},f}(x) \overline{F}_{n,\eta_{n}^{N,c},\eta_{n}^{N,f},c}(x) dxdy, \\[3pt]
T_2^N & \,:\!= &\, \bigg(1-\int_{\textsf{X}}F_{n,\eta_{n}^{f},f}(x)\wedge F_{n,\eta_{n}^{c},c}(x)dx\bigg)^{-1}\bigg(\int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{N,f},\eta_{n}^{N,c},f}(x) \\[3pt] & & \times\overline{F}_{n,\eta_{n}^{N,c},\eta_{n}^{N,f},c}(x) dxdy -\int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{f},\eta_{n}^{c},f}(x)\overline{F}_{n,\eta_{n}^{c},\eta_{n}^{f},c}(x) dxdy\bigg).\end{eqnarray*}
\begin{eqnarray*}T_1^N & \,:\!= &\, \bigg(1-\int_{\textsf{X}}F_{n,\eta_{n}^{N,f},f}(x)\wedge F_{n,\eta_{n}^{N,c},c}(x)dx\bigg)^{-1} - \bigg(1-\int_{\textsf{X}}F_{n,\eta_{n}^{f},f}(x)\wedge F_{n,\eta_{n}^{c},c}(x)dx\bigg)^{-1}\Big) \\[3pt]
& &\times \,\int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{N,f},\eta_{n}^{N,c},f}(x) \overline{F}_{n,\eta_{n}^{N,c},\eta_{n}^{N,f},c}(x) dxdy, \\[3pt]
T_2^N & \,:\!= &\, \bigg(1-\int_{\textsf{X}}F_{n,\eta_{n}^{f},f}(x)\wedge F_{n,\eta_{n}^{c},c}(x)dx\bigg)^{-1}\bigg(\int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{N,f},\eta_{n}^{N,c},f}(x) \\[3pt] & & \times\overline{F}_{n,\eta_{n}^{N,c},\eta_{n}^{N,f},c}(x) dxdy -\int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{f},\eta_{n}^{c},f}(x)\overline{F}_{n,\eta_{n}^{c},\eta_{n}^{f},c}(x) dxdy\bigg).\end{eqnarray*}
Then we have
 \begin{align*} &T_1^N + T_2^N \\ &\quad =\bigg(1-\int_{\textsf{X}}F_{n,\eta_{n}^{N,f},f}(x)\wedge F_{n,\eta_{n}^{N,c},c}(x)dx\bigg)^{-1}\int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{N,f},\eta_{n}^{N,c},f}(x) F_{n,\eta_{n}^{N,c},\eta_{n}^{N,f},c}(x) dxdy \\
&\qquad -\bigg(1-\int_{\textsf{X}}F_{n,\eta_{n}^{f},f}(x)\wedge F_{n,\eta_{n}^{c},c}(x)dx\bigg)^{-1}\int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{f},\eta_{n}^{c},f}(x) F_{n,\eta_{n}^{c},\eta_{n}^{f},c}(x) dxdy. \end{align*}
\begin{align*} &T_1^N + T_2^N \\ &\quad =\bigg(1-\int_{\textsf{X}}F_{n,\eta_{n}^{N,f},f}(x)\wedge F_{n,\eta_{n}^{N,c},c}(x)dx\bigg)^{-1}\int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{N,f},\eta_{n}^{N,c},f}(x) F_{n,\eta_{n}^{N,c},\eta_{n}^{N,f},c}(x) dxdy \\
&\qquad -\bigg(1-\int_{\textsf{X}}F_{n,\eta_{n}^{f},f}(x)\wedge F_{n,\eta_{n}^{c},c}(x)dx\bigg)^{-1}\int_{\textsf{X}\times\textsf{X}} \psi(x,y)\overline{F}_{n,\eta_{n}^{f},\eta_{n}^{c},f}(x) F_{n,\eta_{n}^{c},\eta_{n}^{f},c}(x) dxdy. \end{align*}
By Part 1 and (42), ![]() $T_1^N\rightarrow_{\mathbb{P}}0$
, and by (42)
$T_1^N\rightarrow_{\mathbb{P}}0$
, and by (42) ![]() $T_2^N\rightarrow_{\mathbb{P}}0$
; hence the proof is complete.
$T_2^N\rightarrow_{\mathbb{P}}0$
; hence the proof is complete.
Appendix E. Proofs for the asymptotic variance
Throughout, v is as in (H1). We will frequently quote results from [Reference Whiteley30] whose proofs are given for v rather than ![]() $v^{\xi}$
,
$v^{\xi}$
, ![]() $\xi\in(0,1]$
. The proofs of these quoted results can be extended to the case
$\xi\in(0,1]$
. The proofs of these quoted results can be extended to the case ![]() $\xi\in(0,1)$
using [Reference Whiteley30, Lemma 3]. Note that [Reference Whiteley30, Lemma 3] implies that (H1)–(H4) apply in the case for
$\xi\in(0,1)$
using [Reference Whiteley30, Lemma 3]. Note that [Reference Whiteley30, Lemma 3] implies that (H1)–(H4) apply in the case for ![]() $\xi\in(0,1)$
, with Lyapunov function
$\xi\in(0,1)$
, with Lyapunov function ![]() $v^{\xi}$
, with constants depending upon
$v^{\xi}$
, with constants depending upon ![]() $\xi$
. In our proofs C is a finite and positive constant whose value may change from line to line, and it does not depend on n, p, f, c. Any important dependencies of C will be stated.
$\xi$
. In our proofs C is a finite and positive constant whose value may change from line to line, and it does not depend on n, p, f, c. Any important dependencies of C will be stated.
Proof of Theorem 4.3. We have
 \[\sigma^{2,s}_n(\varphi) = \check{\eta}_n^s\Big((\varphi\otimes 1-1\otimes\varphi - ([\eta_n^f-\eta_n^c](\varphi)))^2\Big) +\sum_{p=0}^{n-1} \check{\eta}_p^s(\{(D_{p,n}^f(\varphi)\otimes 1- 1\otimes D_{p,n}^c(\varphi))\}^2).\]
\[\sigma^{2,s}_n(\varphi) = \check{\eta}_n^s\Big((\varphi\otimes 1-1\otimes\varphi - ([\eta_n^f-\eta_n^c](\varphi)))^2\Big) +\sum_{p=0}^{n-1} \check{\eta}_p^s(\{(D_{p,n}^f(\varphi)\otimes 1- 1\otimes D_{p,n}^c(\varphi))\}^2).\]
Define
We focus on the summand and note that by the ![]() $C_2-$
inequality, one has
$C_2-$
inequality, one has
Our proof for the case when only (H1)–(H6) hold, versus when (H1)–(H7) hold, is the same when considering ![]() $T_1$
in (43), versus
$T_1$
in (43), versus ![]() $T_2$
in (44). Thus our proof is split into three parts, controlling
$T_2$
in (44). Thus our proof is split into three parts, controlling ![]() $T_1$
and then
$T_1$
and then ![]() $T_2$
first under (H1)–(H6) and then under (H1)–(H7). The proof is concluded by adding and then summing the bounds (and then summing over p) for the relevant case.
$T_2$
first under (H1)–(H6) and then under (H1)–(H7). The proof is concluded by adding and then summing the bounds (and then summing over p) for the relevant case.
Term (43): We have for any ![]() $x\in\textsf{X}$
that
$x\in\textsf{X}$
that
 \begin{align*} &(D_{p,n}^f(\varphi)(x)-D_{p,n}^c(\varphi)(x))^2 \\[3pt] &\quad = D_{p,n}^f(\varphi)(x)[D_{p,n}^f(\varphi)(x)-D_{p,n}^c(\varphi)(x)]+ D_{p,n}^c(\varphi)(x)[D_{p,n}^c(\varphi)(x)-D_{p,n}^f(\varphi)(x)].\end{align*}
\begin{align*} &(D_{p,n}^f(\varphi)(x)-D_{p,n}^c(\varphi)(x))^2 \\[3pt] &\quad = D_{p,n}^f(\varphi)(x)[D_{p,n}^f(\varphi)(x)-D_{p,n}^c(\varphi)(x)]+ D_{p,n}^c(\varphi)(x)[D_{p,n}^c(\varphi)(x)-D_{p,n}^f(\varphi)(x)].\end{align*}
Applying Lemmata E.1 and E.3 yields the upper bound
 \begin{align*} &(D_{p,n}^f(\varphi)(x)-D_{p,n}^c(\varphi)(x))^2 \\[3pt] &\quad \leq C\|\varphi\|\rho^{n-p}\Big(\|h_{p,n}^fS_{p,n}^{f,c}(\varphi)\|_{v^{\xi}} + |[\eta_n^f-\eta_n^c](\varphi)| + \|\varphi\|\|h_{p,n}^f-h_{p,n}^c\|_{v^{\xi}}\rho^{n-p}\Big)v(x)^{4\xi}.\end{align*}
\begin{align*} &(D_{p,n}^f(\varphi)(x)-D_{p,n}^c(\varphi)(x))^2 \\[3pt] &\quad \leq C\|\varphi\|\rho^{n-p}\Big(\|h_{p,n}^fS_{p,n}^{f,c}(\varphi)\|_{v^{\xi}} + |[\eta_n^f-\eta_n^c](\varphi)| + \|\varphi\|\|h_{p,n}^f-h_{p,n}^c\|_{v^{\xi}}\rho^{n-p}\Big)v(x)^{4\xi}.\end{align*}
Hence, as ![]() $\eta_p^f(v^{4\xi})\leq C$
[Reference Whiteley30, Proposition 1] (note that by (H2) and (H5) Part 2, the bound in the latter proposition does not depend on
$\eta_p^f(v^{4\xi})\leq C$
[Reference Whiteley30, Proposition 1] (note that by (H2) and (H5) Part 2, the bound in the latter proposition does not depend on ![]() $\eta_0^f$
), it follows that
$\eta_0^f$
), it follows that
Term (44), assuming only (H1)–(H6) hold: We have for any ![]() $(x,y)\in A$
that
$(x,y)\in A$
that
 \begin{align*}&(D_{p,n}^c(\varphi)(x)-D_{p,n}^c(\varphi)(y))^2 \\[3pt] &\quad = D_{p,n}^c(\varphi)(x)[D_{p,n}^c(\varphi)(x)-D_{p,n}^c(\varphi)(y)]+ D_{p,n}^c(\varphi)(y)[D_{p,n}^c(\varphi)(y)-D_{p,n}^c(\varphi)(x)]\end{align*}
\begin{align*}&(D_{p,n}^c(\varphi)(x)-D_{p,n}^c(\varphi)(y))^2 \\[3pt] &\quad = D_{p,n}^c(\varphi)(x)[D_{p,n}^c(\varphi)(x)-D_{p,n}^c(\varphi)(y)]+ D_{p,n}^c(\varphi)(y)[D_{p,n}^c(\varphi)(y)-D_{p,n}^c(\varphi)(x)]\end{align*}
(if ![]() $(x,y)\in A^c$
the term is zero). Applying Lemmata E.1 and E.6 yields the upper bound
$(x,y)\in A^c$
the term is zero). Applying Lemmata E.1 and E.6 yields the upper bound
for any ![]() $(x,y)\in A$
. Hence it follows that
$(x,y)\in A$
. Hence it follows that
Noting (45), (46), and (47), the proof can be concluded in the case that only (H1)–(H6) hold.
Term (44), assuming (H1)–(H7) hold: We have by Lemma E.8 that
where ![]() $\rho$
is the square of the
$\rho$
is the square of the ![]() $\rho$
in Lemma E.8. Then
$\rho$
in Lemma E.8. Then
Noting (45), (46), and (48), the proof can be concluded in the case that (H1)–(H7) hold.
The following result is essentially [Reference Whiteley30, Theorem 1].
Lemma E.1. Assume (H1)–(H5). Then for any ![]() $\xi\in(0,1]$
there exist
$\xi\in(0,1]$
there exist ![]() $\rho<1$
and
$\rho<1$
and ![]() $C<+\infty$
also depending on the constants in (H1)–(H5) such that for any
$C<+\infty$
also depending on the constants in (H1)–(H5) such that for any ![]() $\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})$
,
$\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})$
, ![]() $n\geq 1$
and
$n\geq 1$
and ![]() $0\leq p <n$
,
$0\leq p <n$
, ![]() $x\in\textsf{X}$
,
$x\in\textsf{X}$
, ![]() $s\in\{\,f,c\}$
we have
$s\in\{\,f,c\}$
we have
Proof. The proof for ![]() $\xi=1$
is exactly as in [Reference Whiteley30, Theorem 1], except noting that (H2) and (H5) Part 2 establish that the constants in [Reference Whiteley30, Theorem 1] do not depend on
$\xi=1$
is exactly as in [Reference Whiteley30, Theorem 1], except noting that (H2) and (H5) Part 2 establish that the constants in [Reference Whiteley30, Theorem 1] do not depend on ![]() $\eta_0^s$
(the quantity denoted by
$\eta_0^s$
(the quantity denoted by ![]() $\mu$
in [Reference Whiteley30]).
$\mu$
in [Reference Whiteley30]).
Lemma E.2. Assume (H1)–(H6). Then for any ![]() $\xi\in(0,1]$
,
$\xi\in(0,1]$
, ![]() $s\in\{\,f,c\}$
we have
$s\in\{\,f,c\}$
we have
Proof. This is [Reference Del Moral, Jasra and Law12, Lemma B.2], except with the fix of using (H5) Part 1 to go to the second line of that proof.
Lemma E.3. Assume (H1)–(H6). Then for any ![]() $\xi\in(0,1]$
there exist
$\xi\in(0,1]$
there exist ![]() $\rho<1$
and
$\rho<1$
and ![]() $C<+\infty$
also depending on the constants in (H1)–(H6) such that for any
$C<+\infty$
also depending on the constants in (H1)–(H6) such that for any ![]() $\varphi\in\mathcal{B}_b(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})$
, ![]() $n\geq 1$
and
$n\geq 1$
and ![]() $0\leq p <n$
,
$0\leq p <n$
, ![]() $x\in\textsf{X}$
we have
$x\in\textsf{X}$
we have
 \begin{align*} & |D_{p,n}^f(\varphi)(x)-D_{p,n}^c(\varphi)(x)| \\ &\quad \leq C \Big(\|h_{p,n}^fS_{p,n}^{f,c}(\varphi)\|_{v^{\xi}} + |[\eta_n^f-\eta_n^c](\varphi)| + \|\varphi\|\|h_{p,n}^f-h_{p,n}^c\|_{v^{\xi}}\rho^{n-p}\Big)v(x)^{3\xi}.\end{align*}
\begin{align*} & |D_{p,n}^f(\varphi)(x)-D_{p,n}^c(\varphi)(x)| \\ &\quad \leq C \Big(\|h_{p,n}^fS_{p,n}^{f,c}(\varphi)\|_{v^{\xi}} + |[\eta_n^f-\eta_n^c](\varphi)| + \|\varphi\|\|h_{p,n}^f-h_{p,n}^c\|_{v^{\xi}}\rho^{n-p}\Big)v(x)^{3\xi}.\end{align*}
Proof. Define
Then we have
We will bound ![]() $|T_1|$
and
$|T_1|$
and ![]() $|T_2|$
and then sum the bounds to conclude.
$|T_2|$
and then sum the bounds to conclude.
Term (49): We have
 \[\Big(S_{p,n}^{f,c}(\varphi)(x) + [\eta_n^f-\eta_n^c](\varphi)\Big)h_{p,n}^f(x) =\Bigg(\frac{S_{p,n}^{f,c}(\varphi)(x)}{v(x)^{\xi}}v(x)^{\xi} + [\eta_n^f-\eta_n^c](\varphi)\Bigg)\frac{h_{p,n}^f(x)}{v(x)^{\xi}}v(x)^{\xi}.\]
\[\Big(S_{p,n}^{f,c}(\varphi)(x) + [\eta_n^f-\eta_n^c](\varphi)\Big)h_{p,n}^f(x) =\Bigg(\frac{S_{p,n}^{f,c}(\varphi)(x)}{v(x)^{\xi}}v(x)^{\xi} + [\eta_n^f-\eta_n^c](\varphi)\Bigg)\frac{h_{p,n}^f(x)}{v(x)^{\xi}}v(x)^{\xi}.\]
Then by [Reference Whiteley30, Proposition 2], ![]() $\|h_{p,n}^f\|_{v^{\xi}}$
is bounded above by a finite constant that does not depend on p,n, f, so we easily have that
$\|h_{p,n}^f\|_{v^{\xi}}$
is bounded above by a finite constant that does not depend on p,n, f, so we easily have that
Term (50): We have
 \begin{align*} & D_{p,n}^c(\varphi)(x)\frac{1}{h_{p,n}^c(x)}[h_{p,n}^f(x)-h_{p,n}^c(x)]\\[3pt]
&\quad = \bigg(D_{p,n}^c(\varphi)(x)\frac{1}{h_{p,n}^c(x)v(x)^{\xi}}\frac{\big[h_{p,n}^f(x)-h_{p,n}^c(x)\big]}{v(x)^{\xi}}\bigg)v(x)^{2\xi}.\end{align*}
\begin{align*} & D_{p,n}^c(\varphi)(x)\frac{1}{h_{p,n}^c(x)}[h_{p,n}^f(x)-h_{p,n}^c(x)]\\[3pt]
&\quad = \bigg(D_{p,n}^c(\varphi)(x)\frac{1}{h_{p,n}^c(x)v(x)^{\xi}}\frac{\big[h_{p,n}^f(x)-h_{p,n}^c(x)\big]}{v(x)^{\xi}}\bigg)v(x)^{2\xi}.\end{align*}
Applying Lemma E.1 to ![]() $D_{p,n}^c(\varphi)(x)$
and Lemma E.2 to
$D_{p,n}^c(\varphi)(x)$
and Lemma E.2 to ![]() $1/(h_{p,n}^c(x)v(x)^{\xi})$
yields that
$1/(h_{p,n}^c(x)v(x)^{\xi})$
yields that
Noting (51), (52), and (53), the proof can be concluded.
For ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $0\leq p < n$
,
$0\leq p < n$
, ![]() $x\in\textsf{X}$
,
$x\in\textsf{X}$
, ![]() $s\in\{\,f,c\}$
, define
$s\in\{\,f,c\}$
, define
Lemma E.4. Assume (H1)–(H5), (H7). Then for any ![]() $\xi\in(0,1]$
there exists a
$\xi\in(0,1]$
there exists a ![]() $C<+\infty$
, depending on the constants in (H1)–(H5) and (H7), such that for any
$C<+\infty$
, depending on the constants in (H1)–(H5) and (H7), such that for any ![]() $\varphi\in\mathcal{B}_b(\textsf{X})\cap\textrm{\textit{Lip}}_{\textsf{d}}(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})\cap\textrm{\textit{Lip}}_{\textsf{d}}(\textsf{X})$
, ![]() $(x,y)\in\textsf{X}\times\textsf{X}$
,
$(x,y)\in\textsf{X}\times\textsf{X}$
, ![]() $s\in\{\,f,c\}$
we have
$s\in\{\,f,c\}$
we have
Proof. We proceed by backward induction, starting with the case ![]() $p=n-1$
(the case
$p=n-1$
(the case ![]() $p=n$
is trivial). We have
$p=n$
is trivial). We have
By [Reference Whiteley30, Proposition 2(2)],
for some constant C. So applying (55) along with (H7) we have
Now assuming the result for some ![]() $p+1<n$
, we have
$p+1<n$
, we have
 \[\frac{Q_{p,n}^s(\varphi)(x)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}-\frac{Q_{p,n}^s(\varphi)(y)}{\eta_p^s\big(Q_{p,n}^s(1)\big)} = \frac{1}{\eta_p^s(G_p)}\Bigg(\frac{Q_{p+1}^s\big(Q_{p+1,n}^s(\varphi)\big)(x)}{\eta_{p+1}^s\big(Q_{p+1,n}^s(1)\big)} -\frac{Q_{p+1}^s\big(Q_{p+1,n}^s(\varphi)\big)(y)}{\eta_{p+1}^s\big(Q_{p+1,n}^s(1)\big)}\Bigg).\]
\[\frac{Q_{p,n}^s(\varphi)(x)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}-\frac{Q_{p,n}^s(\varphi)(y)}{\eta_p^s\big(Q_{p,n}^s(1)\big)} = \frac{1}{\eta_p^s(G_p)}\Bigg(\frac{Q_{p+1}^s\big(Q_{p+1,n}^s(\varphi)\big)(x)}{\eta_{p+1}^s\big(Q_{p+1,n}^s(1)\big)} -\frac{Q_{p+1}^s\big(Q_{p+1,n}^s(\varphi)\big)(y)}{\eta_{p+1}^s\big(Q_{p+1,n}^s(1)\big)}\Bigg).\]
Now, for any ![]() $x\in\textsf{X}$
, we have
$x\in\textsf{X}$
, we have
 \[\Bigg|\frac{Q_{p+1,n}^s(\varphi))(x)}{\eta_{p+1}^s\big(Q_{p+1,n}^s(1)\big)}\Bigg|\frac{1}{v(x)^{\xi}} \leq \|\varphi\|\|h_{p+1,n}^s\|_{v^{\xi}} \leq C\|\varphi\|,\]
\[\Bigg|\frac{Q_{p+1,n}^s(\varphi))(x)}{\eta_{p+1}^s\big(Q_{p+1,n}^s(1)\big)}\Bigg|\frac{1}{v(x)^{\xi}} \leq \|\varphi\|\|h_{p+1,n}^s\|_{v^{\xi}} \leq C\|\varphi\|,\]
where we have used [Reference Whiteley30, Proposition 2(3)] to get to the second inequality. Then applying (55), the induction hypothesis, and (H7), we have
 \begin{eqnarray*}\Bigg|\frac{Q_{p,n}^s(\varphi)(x)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}-\frac{Q_{p,n}^s(\varphi)(y)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}\Bigg| &\, \leq\, & C\Bigg\|\frac{Q_{p+1,n}^s(\varphi))}{\eta_{p+1}^s\big(Q_{p+1,n}^s(1)\big)}\Bigg\|_{v^{\xi}}\textsf{d}(x,y)v(x)^{\xi}v(y)^{\xi} \\[3pt]& \,\leq\, & C\|\varphi\|\textsf{d}(x,y)v(x)^{\xi}v(y)^{\xi}.\\[-40pt]\end{eqnarray*}
\begin{eqnarray*}\Bigg|\frac{Q_{p,n}^s(\varphi)(x)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}-\frac{Q_{p,n}^s(\varphi)(y)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}\Bigg| &\, \leq\, & C\Bigg\|\frac{Q_{p+1,n}^s(\varphi))}{\eta_{p+1}^s\big(Q_{p+1,n}^s(1)\big)}\Bigg\|_{v^{\xi}}\textsf{d}(x,y)v(x)^{\xi}v(y)^{\xi} \\[3pt]& \,\leq\, & C\|\varphi\|\textsf{d}(x,y)v(x)^{\xi}v(y)^{\xi}.\\[-40pt]\end{eqnarray*}
Lemma E.5. Assume (H1)–(H7). Then for any ![]() $\xi\in(0,1/2)$
there exists a
$\xi\in(0,1/2)$
there exists a ![]() $C<+\infty$
depending on the constants in (H1)–(H7) such that for any
$C<+\infty$
depending on the constants in (H1)–(H7) such that for any ![]() $\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})\cap\textrm{\textit{Lip}}_{v^{\xi},\textsf{d}}(\textsf{X})$
,
$\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})\cap\textrm{\textit{Lip}}_{v^{\xi},\textsf{d}}(\textsf{X})$
, ![]() $n\geq 1$
and
$n\geq 1$
and ![]() $0\leq p <n$
,
$0\leq p <n$
, ![]() $(x,y)\in\textsf{X}\times \textsf{X}$
,
$(x,y)\in\textsf{X}\times \textsf{X}$
, ![]() $s\in\{\,f,c\}$
we have
$s\in\{\,f,c\}$
we have
Proof. Define
Then we have
We will bound ![]() $|T_1|$
and
$|T_1|$
and ![]() $|T_2|$
and then sum the bounds to conclude.
$|T_2|$
and then sum the bounds to conclude.
Term (56): We have
 \begin{align*}&\frac{h_{p,n}^s(x)}{Q_{p,n}^s(1)(x)}\Big(Q_{p+1}^s(\varphi Q_{p+1,n}^s(1))(x)-Q_{p+1}^s(\varphi Q_{p+1,n}^s(1))(y)\Big)\\ &\quad = \frac{1}{\eta_p^s(G_p)}\Big(Q_{p+1}^s(\varphi h_{p+1,n}^s)(x)-Q_{p+1}^s(\varphi h_{p+1,n}^s)(y)\Big).\end{align*}
\begin{align*}&\frac{h_{p,n}^s(x)}{Q_{p,n}^s(1)(x)}\Big(Q_{p+1}^s(\varphi Q_{p+1,n}^s(1))(x)-Q_{p+1}^s(\varphi Q_{p+1,n}^s(1))(y)\Big)\\ &\quad = \frac{1}{\eta_p^s(G_p)}\Big(Q_{p+1}^s(\varphi h_{p+1,n}^s)(x)-Q_{p+1}^s(\varphi h_{p+1,n}^s)(y)\Big).\end{align*}
Then by Lemma E.4 and [Reference Whiteley30, Proposition 2(3)],
so, applying (55) and (H7), we have
By [Reference Whiteley30, Proposition 2(3)],
so
Term (57): We have
 \begin{align*}&\frac{h_{p,n}^s(x)Q_{p+1}^s\big(\varphi Q_{p+1,n}^s(1)\big)(y)}{Q_{p,n}^s(1)(x)Q_{p,n}^s(1)(y)}\Big(Q_{p,n}^s(1)(y)-Q_{p,n}^s(1)(x)\Big) \\[3pt]
& \quad = \frac{Q_{p+1}^s\big(\varphi Q_{p+1,n}^s(1)\big)(y)}{Q_{p,n}^s(1)(y)}\Big(Q_{p+1}^s(h_{p+1,n}^s)(y)-Q_{p+1}^s(h_{p+1,n}^s)(x)\Big) \\[3pt]
& \quad = \frac{Q_{p+1}^s\big(\varphi h_{p+1,n}^s\big)(y)v(y)^{\xi}}{\eta_p^s(G_p) h_{p,n}^s(y)v(y)^{\xi}}\Big(Q_{p+1}^s(h_{p+1,n}^s)(y)-Q_{p+1}^s(h_{p+1,n}^s)(x)\Big).\end{align*}
\begin{align*}&\frac{h_{p,n}^s(x)Q_{p+1}^s\big(\varphi Q_{p+1,n}^s(1)\big)(y)}{Q_{p,n}^s(1)(x)Q_{p,n}^s(1)(y)}\Big(Q_{p,n}^s(1)(y)-Q_{p,n}^s(1)(x)\Big) \\[3pt]
& \quad = \frac{Q_{p+1}^s\big(\varphi Q_{p+1,n}^s(1)\big)(y)}{Q_{p,n}^s(1)(y)}\Big(Q_{p+1}^s(h_{p+1,n}^s)(y)-Q_{p+1}^s(h_{p+1,n}^s)(x)\Big) \\[3pt]
& \quad = \frac{Q_{p+1}^s\big(\varphi h_{p+1,n}^s\big)(y)v(y)^{\xi}}{\eta_p^s(G_p) h_{p,n}^s(y)v(y)^{\xi}}\Big(Q_{p+1}^s(h_{p+1,n}^s)(y)-Q_{p+1}^s(h_{p+1,n}^s)(x)\Big).\end{align*}
Applying (55) and Lemma E.2 gives the upper bound
Now ![]() $\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})$
, and by [Reference Whiteley30, Proposition 2(3)],
$\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})$
, and by [Reference Whiteley30, Proposition 2(3)],
thus, noting (59) and applying (H7), we have
Again applying [Reference Whiteley30, Proposition 2(3)] and (H1), we have finally that
Noting (58), (60), and (61), the proof can be concluded.
Recall ![]() $A=\{(x,y)\in\textsf{X}\times\textsf{X}\,:\,x\neq y\}$
.
$A=\{(x,y)\in\textsf{X}\times\textsf{X}\,:\,x\neq y\}$
.
Lemma E.6. Assume (H1)–(H6). Then for any ![]() $\xi\in(0,1]$
there exist
$\xi\in(0,1]$
there exist ![]() $\rho<1$
and
$\rho<1$
and ![]() $C<+\infty$
depending on the constants in (H1)–(H6) such that for any
$C<+\infty$
depending on the constants in (H1)–(H6) such that for any ![]() $\varphi\in\mathcal{B}_b(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})$
, ![]() $n\geq 1$
and
$n\geq 1$
and ![]() $0\leq p <n$
,
$0\leq p <n$
, ![]() $(x,y)\in\textsf{X}\times\textsf{X}$
we have
$(x,y)\in\textsf{X}\times\textsf{X}$
we have
Proof. Throughout, we assume that ![]() $x\neq y$
. Define
$x\neq y$
. Define
 \begin{eqnarray}T_1 & \,:\!= &\, \Bigg(\frac{Q_{p,n}^c(\varphi)(x)}{Q_{p,n}^c(1)(x)}-\frac{Q_{p,n}^c(\varphi)(y)}{Q_{p,n}^c(1)(y)}\Bigg)h_{p,n}^c(x), \end{eqnarray}
\begin{eqnarray}T_1 & \,:\!= &\, \Bigg(\frac{Q_{p,n}^c(\varphi)(x)}{Q_{p,n}^c(1)(x)}-\frac{Q_{p,n}^c(\varphi)(y)}{Q_{p,n}^c(1)(y)}\Bigg)h_{p,n}^c(x), \end{eqnarray}
 \begin{eqnarray}\hspace*{-40pt}T_2 & \,:\!= &\, D_{p,n}^c(\varphi)(y)\Bigg(\frac{h_{p.n}^c(x)}{h_{p.n}^c(y)}-1\Bigg);\end{eqnarray}
\begin{eqnarray}\hspace*{-40pt}T_2 & \,:\!= &\, D_{p,n}^c(\varphi)(y)\Bigg(\frac{h_{p.n}^c(x)}{h_{p.n}^c(y)}-1\Bigg);\end{eqnarray}
then we have
We will bound ![]() $|T_1|$
and
$|T_1|$
and ![]() $|T_2|$
and then sum the bounds to conclude.
$|T_2|$
and then sum the bounds to conclude.
Term (62): We have
 \begin{align*} & \Bigg(\frac{Q_{p,n}^c(\varphi)(x)}{Q_{p,n}^c(1)(x)}-\frac{Q_{p,n}^c(\varphi)(y)}{Q_{p,n}^c(1)(y)}\Bigg)h_{p,n}^c(x)\\[3pt]
& \quad = \frac{1}{\eta_p^c(G_p)}\Bigg(Q_{p+1}^c\Bigg(\frac{Q_{p+1,n}^c(\varphi)}{\eta_{p+1}^c\big(Q_{p+1,n}^c(1)\big)}\Bigg)\Bigg)(x)-Q_{p+1}^c\Bigg(\frac{Q_{p+1,n}^c(\varphi)}{\eta_{p+1}^c\big(Q_{p+1,n}^c(1)\big)}\Bigg)(y)\Bigg)\\[3pt]
&\qquad + \frac{Q_{p,n}^c(\varphi)(y)}{Q_{p,n}^c(1)(y)}\frac{1}{\eta_p^c(G_p)}\Big(Q_{p+1}^c(h_{p+1,n}^c)(y)-Q_{p+1}^c(h_{p+1,n}^c)(x)\Big). \end{align*}
\begin{align*} & \Bigg(\frac{Q_{p,n}^c(\varphi)(x)}{Q_{p,n}^c(1)(x)}-\frac{Q_{p,n}^c(\varphi)(y)}{Q_{p,n}^c(1)(y)}\Bigg)h_{p,n}^c(x)\\[3pt]
& \quad = \frac{1}{\eta_p^c(G_p)}\Bigg(Q_{p+1}^c\Bigg(\frac{Q_{p+1,n}^c(\varphi)}{\eta_{p+1}^c\big(Q_{p+1,n}^c(1)\big)}\Bigg)\Bigg)(x)-Q_{p+1}^c\Bigg(\frac{Q_{p+1,n}^c(\varphi)}{\eta_{p+1}^c\big(Q_{p+1,n}^c(1)\big)}\Bigg)(y)\Bigg)\\[3pt]
&\qquad + \frac{Q_{p,n}^c(\varphi)(y)}{Q_{p,n}^c(1)(y)}\frac{1}{\eta_p^c(G_p)}\Big(Q_{p+1}^c(h_{p+1,n}^c)(y)-Q_{p+1}^c(h_{p+1,n}^c)(x)\Big). \end{align*}
Applying (55) and ![]() $\varphi\in\mathcal{B}_b(\textsf{X})$
, we have
$\varphi\in\mathcal{B}_b(\textsf{X})$
, we have
By [Reference Whiteley30, Proposition 2(3)],
then in addition applying (H1) we have
Term (63): We have
 \[D_{p,n}^c(\varphi)(y)\Bigg(\frac{h_{p.n}^c(x)}{h_{p.n}^c(y)}-1\Bigg) = D_{p,n}^c(\varphi)(y)\frac{1}{h_{p.n}^c(y)v(y)^{\xi}}\frac{h_{p.n}^c(x)-h_{p.n}^c(y)}{v(x)^{\xi}v(y)^{\xi}}v(x)^{\xi}v(y)^{2\xi}.\]
\[D_{p,n}^c(\varphi)(y)\Bigg(\frac{h_{p.n}^c(x)}{h_{p.n}^c(y)}-1\Bigg) = D_{p,n}^c(\varphi)(y)\frac{1}{h_{p.n}^c(y)v(y)^{\xi}}\frac{h_{p.n}^c(x)-h_{p.n}^c(y)}{v(x)^{\xi}v(y)^{\xi}}v(x)^{\xi}v(y)^{2\xi}.\]
Then, applying Lemma E.1 for ![]() $D_{p,n}^c(\varphi)(y)$
, Lemma E.2 for
$D_{p,n}^c(\varphi)(y)$
, Lemma E.2 for ![]() $1/(h_{p.n}^c(y)v(y)^{\xi})$
, and [Reference Whiteley30, Proposition 2(3)] as above, we have
$1/(h_{p.n}^c(y)v(y)^{\xi})$
, and [Reference Whiteley30, Proposition 2(3)] as above, we have
Noting (64), (65), and (66), the proof can be concluded.
For ![]() $B\in\mathcal{X}$
,
$B\in\mathcal{X}$
, ![]() $x\in\textsf{X}$
,
$x\in\textsf{X}$
, ![]() $s\in\{\,f,c\}$
, define
$s\in\{\,f,c\}$
, define
Lemma E.7. Assume (H1)–(H7). Then for any ![]() $\xi\in(0,1)$
there exists a
$\xi\in(0,1)$
there exists a ![]() $C<+\infty$
depending on the constants in (H1)–(H7) such that for any
$C<+\infty$
depending on the constants in (H1)–(H7) such that for any ![]() $\varphi\in\mathcal{B}_b(\textsf{X})\cap\textrm{\textit{Lip}}_{\textsf{d}}(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})\cap\textrm{\textit{Lip}}_{\textsf{d}}(\textsf{X})$
, ![]() $(x,y)\in\textsf{X}\times\textsf{X}$
,
$(x,y)\in\textsf{X}\times\textsf{X}$
, ![]() $s\in\{\,f,c\}$
we have
$s\in\{\,f,c\}$
we have
Proof. We assume ![]() $p<n$
as the case
$p<n$
as the case ![]() $p=n$
is trivial. Define
$p=n$
is trivial. Define
 \begin{eqnarray}\hspace*{-45pt}T_1 & \,=\, & \frac{1}{h_{p,n}^s(x)}\Bigg(\frac{Q_{p,n}^s(\varphi)(x)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}-\frac{Q_{p,n}^s(\varphi)(y)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}\Bigg), \end{eqnarray}
\begin{eqnarray}\hspace*{-45pt}T_1 & \,=\, & \frac{1}{h_{p,n}^s(x)}\Bigg(\frac{Q_{p,n}^s(\varphi)(x)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}-\frac{Q_{p,n}^s(\varphi)(y)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}\Bigg), \end{eqnarray}
 \begin{eqnarray}T_2 & \,=\, & \frac{Q_{p,n}^s(\varphi)(y)}{Q_{p,n}^s(1)(y)}\frac{1}{h_{p,n}^s(x)}\Bigg(\frac{Q_{p,n}^s(1)(y)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}-\frac{Q_{p,n}^s(1)(x)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}\Bigg);\end{eqnarray}
\begin{eqnarray}T_2 & \,=\, & \frac{Q_{p,n}^s(\varphi)(y)}{Q_{p,n}^s(1)(y)}\frac{1}{h_{p,n}^s(x)}\Bigg(\frac{Q_{p,n}^s(1)(y)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}-\frac{Q_{p,n}^s(1)(x)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}\Bigg);\end{eqnarray}
then we have
We will bound ![]() $|T_1|$
and
$|T_1|$
and ![]() $|T_2|$
and then sum the bounds to conclude.
$|T_2|$
and then sum the bounds to conclude.
Term (67): We have, for any ![]() $\tilde{\xi}\in(0,1]$
,
$\tilde{\xi}\in(0,1]$
,
 \[\frac{1}{h_{p,n}^s(x)}\Bigg(\frac{Q_{p,n}^s(\varphi)(x)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}-\frac{Q_{p,n}^s(\varphi)(y)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}\Bigg)=\frac{v(x)^{\tilde{\xi}}}{h_{p,n}^s(x)v(x)^{\tilde{\xi}}}\Bigg(\frac{Q_{p,n}^s(\varphi)(x)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}-\frac{Q_{p,n}^s(\varphi)(y)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}\Bigg).\]
\[\frac{1}{h_{p,n}^s(x)}\Bigg(\frac{Q_{p,n}^s(\varphi)(x)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}-\frac{Q_{p,n}^s(\varphi)(y)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}\Bigg)=\frac{v(x)^{\tilde{\xi}}}{h_{p,n}^s(x)v(x)^{\tilde{\xi}}}\Bigg(\frac{Q_{p,n}^s(\varphi)(x)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}-\frac{Q_{p,n}^s(\varphi)(y)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}\Bigg).\]
Then applying Lemmata E.2 and E.7, for any ![]() $\tilde{\xi}\in(0,1]$
we have the upper bound
$\tilde{\xi}\in(0,1]$
we have the upper bound
Term (68): We have, for any ![]() $\tilde{\xi}\in(0,1]$
,
$\tilde{\xi}\in(0,1]$
,
 \begin{align*}&\frac{Q_{p,n}^s(\varphi)(y)}{Q_{p,n}^s(1)(y)}\frac{1}{h_{p,n}^s(x)}\Bigg(\frac{Q_{p,n}^s(1)(y)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}-\frac{Q_{p,n}^s(1)(x)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}\Bigg)\\[3pt]
&\quad = \frac{Q_{p,n}^s(\varphi)(y)}{Q_{p,n}^s(1)(y)}\frac{v(x)^{\tilde{\xi}}}{h_{p,n}^s(x)v(x)^{\tilde{\xi}}}\Bigg(\frac{Q_{p,n}^s(1)(y)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}-\frac{Q_{p,n}^s(1)(x)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}\Bigg).\end{align*}
\begin{align*}&\frac{Q_{p,n}^s(\varphi)(y)}{Q_{p,n}^s(1)(y)}\frac{1}{h_{p,n}^s(x)}\Bigg(\frac{Q_{p,n}^s(1)(y)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}-\frac{Q_{p,n}^s(1)(x)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}\Bigg)\\[3pt]
&\quad = \frac{Q_{p,n}^s(\varphi)(y)}{Q_{p,n}^s(1)(y)}\frac{v(x)^{\tilde{\xi}}}{h_{p,n}^s(x)v(x)^{\tilde{\xi}}}\Bigg(\frac{Q_{p,n}^s(1)(y)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}-\frac{Q_{p,n}^s(1)(x)}{\eta_p^s\big(Q_{p,n}^s(1)\big)}\Bigg).\end{align*}
Then applying ![]() $\varphi\in\mathcal{B}_b(\textsf{X})$
and Lemmata E.2 and E.7, for any
$\varphi\in\mathcal{B}_b(\textsf{X})$
and Lemmata E.2 and E.7, for any ![]() $\tilde{\xi}\in(0,1]$
we have the upper bound
$\tilde{\xi}\in(0,1]$
we have the upper bound
Noting (69), (70), and (71) (the latter two with ![]() $\tilde{\xi}=\xi/2$
), the proof can be concluded.
$\tilde{\xi}=\xi/2$
), the proof can be concluded.
Lemma E.8. Assume (H1)–(H7). Then for any ![]() $\xi\in(0,1/2)$
there exist
$\xi\in(0,1/2)$
there exist ![]() $\rho<1$
and
$\rho<1$
and ![]() $C<+\infty$
depending on the constants in (H1)–(H7) such that for any
$C<+\infty$
depending on the constants in (H1)–(H7) such that for any ![]() $\varphi\in\mathcal{B}_b(\textsf{X})\cap\textrm{\textit{Lip}}_{\textsf{d}}(\textsf{X})$
,
$\varphi\in\mathcal{B}_b(\textsf{X})\cap\textrm{\textit{Lip}}_{\textsf{d}}(\textsf{X})$
, ![]() $n\geq 1$
and
$n\geq 1$
and ![]() $0\leq p <n$
,
$0\leq p <n$
, ![]() $(x,y)\in\textsf{X}\times\textsf{X}$
we have
$(x,y)\in\textsf{X}\times\textsf{X}$
we have
Proof. The proof uses the same decomposition (64) as the proof of Lemma E.6. We use the same bound (66) as in the proof of Lemma E.6 and focus on the term ![]() $T_1$
as defined in (62). We note by [Reference Del Moral8, p.\ 133] that
$T_1$
as defined in (62). We note by [Reference Del Moral8, p.\ 133] that
where ![]() $R_{p+1}^{(n),c}$
is defined in (54).
$R_{p+1}^{(n),c}$
is defined in (54).
Now, ![]() $T_1$
as in the proof of Lemma E.6 can be written as
$T_1$
as in the proof of Lemma E.6 can be written as
 \begin{eqnarray*}T_1 & \,=\, & h_{p,n}^c(x)\Big(P_{p,n}^c(\varphi)(x)-P_{p,n}^c(\varphi)(y)\Big) \\[2pt]& \,=\, & h_{p,n}^c(x)\Big(P_{p,n}^c(\varphi-\eta_n^c(\varphi))(x)-P_{p,n}^c(\varphi-\eta_n^c(\varphi))(y)\Big) \\[2pt] & \,=\, & h_{p,n}^c(x)\Big(R_{p+1}^{(n),s}(P_{p+1,n}^c(\varphi-\eta_n^c(\varphi)))(x)-R_{p+1}^{(n),s}(P_{p+1,n}^c(\varphi-\eta_n^c(\varphi)))(y)\Big).\end{eqnarray*}
\begin{eqnarray*}T_1 & \,=\, & h_{p,n}^c(x)\Big(P_{p,n}^c(\varphi)(x)-P_{p,n}^c(\varphi)(y)\Big) \\[2pt]& \,=\, & h_{p,n}^c(x)\Big(P_{p,n}^c(\varphi-\eta_n^c(\varphi))(x)-P_{p,n}^c(\varphi-\eta_n^c(\varphi))(y)\Big) \\[2pt] & \,=\, & h_{p,n}^c(x)\Big(R_{p+1}^{(n),s}(P_{p+1,n}^c(\varphi-\eta_n^c(\varphi)))(x)-R_{p+1}^{(n),s}(P_{p+1,n}^c(\varphi-\eta_n^c(\varphi)))(y)\Big).\end{eqnarray*}
Noting Lemma E.7, we apply Lemma E.5 to yield the upper bound
Now
Applying Lemma E.1 and Lemma E.2 yields that
Then, using the above inequality in (72) and noting (65) and (66), the proof can be concluded.
Appendix F. Proofs for the diffusion case
The statements at the beginning of Appendix E also apply here. This appendix should be read after Appendix E.
F.1. Proofs for Proposition 5.1
Proof of Proposition 5.1. This follows easily from Propositions F.1, F.2, and F.3.
Lemma F.1. Assume (H8). Then for any ![]() $\xi\in(0,1/2)$
there exists a
$\xi\in(0,1/2)$
there exists a ![]() $C<+\infty$
depending on the constants in (H8) such that for any
$C<+\infty$
depending on the constants in (H8) such that for any ![]() $\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})$
,
$\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})$
, ![]() $1\leq l \leq L$
,
$1\leq l \leq L$
, ![]() $x\in\textsf{X}$
we have
$x\in\textsf{X}$
we have
Proof. Define
Then we have
We will bound ![]() $|T_1|$
and
$|T_1|$
and ![]() $|T_2|$
and then sum the bounds to conclude.
$|T_2|$
and then sum the bounds to conclude.
Term (74): We have, by applying (11),
 \begin{align*}&\bigg|\int_{\textsf{B}_l(x)}\varphi(y)[M^l(x,y)-M(x,y)-\{M^{l-1}(x,y)-M(x,y)\}]dy\bigg|\\[3pt] & \quad \leq C\Delta_l \int_{\textsf{B}_l(x)} |\varphi(y)|\exp\{-C'\|y-x\|^2\}dy. \end{align*}
\begin{align*}&\bigg|\int_{\textsf{B}_l(x)}\varphi(y)[M^l(x,y)-M(x,y)-\{M^{l-1}(x,y)-M(x,y)\}]dy\bigg|\\[3pt] & \quad \leq C\Delta_l \int_{\textsf{B}_l(x)} |\varphi(y)|\exp\{-C'\|y-x\|^2\}dy. \end{align*}
Using ![]() $\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})$
and (H8) Part 2, we have
$\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})$
and (H8) Part 2, we have
Term (75): We have, by applying (10),
 \begin{align*}&\bigg|\int_{\textsf{B}_l(x)^c}\varphi(y)[M^l(x,y)+M(x,y)-\{M^{l-1}(x,y)+M(x,y)\}]dy\bigg|\\[3pt] &\quad \leq C \int_{\textsf{B}_l(x)^c} |\varphi(y)| \exp\{-C'\|y-x\|^2\}dy.\end{align*}
\begin{align*}&\bigg|\int_{\textsf{B}_l(x)^c}\varphi(y)[M^l(x,y)+M(x,y)-\{M^{l-1}(x,y)+M(x,y)\}]dy\bigg|\\[3pt] &\quad \leq C \int_{\textsf{B}_l(x)^c} |\varphi(y)| \exp\{-C'\|y-x\|^2\}dy.\end{align*}
Using ![]() $\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})$
and the fact that
$\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})$
and the fact that
along with (H8) and the fact that ![]() $\int_{\textsf{B}_l(x)^c}dy\leq C\Delta_l$
, we have
$\int_{\textsf{B}_l(x)^c}dy\leq C\Delta_l$
, we have
Noting (76), (77), and (78) the proof can be concluded.
Let ![]() $\xi\in(0,1]$
and denote by
$\xi\in(0,1]$
and denote by ![]() $\mathscr{P}_{v^{\xi}}(\textsf{X})$
the collection of probability measures for which
$\mathscr{P}_{v^{\xi}}(\textsf{X})$
the collection of probability measures for which ![]() $\mu(v^{\xi})<+\infty$
.
$\mu(v^{\xi})<+\infty$
.
Lemma F.2. Assume (H5) Part 1 and (H8). Then for any ![]() $\xi\in(0,1/2)$
there exists a
$\xi\in(0,1/2)$
there exists a ![]() $C<+\infty$
depending on the constants in (H5) Part 1 and (H8) such that for any
$C<+\infty$
depending on the constants in (H5) Part 1 and (H8) such that for any ![]() $\mu\in\mathscr{P}_{v^{\xi}}(\textsf{X})$
,
$\mu\in\mathscr{P}_{v^{\xi}}(\textsf{X})$
, ![]() $\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})$
,
$\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})$
, ![]() $p\geq 1$
,
$p\geq 1$
, ![]() $1\leq l \leq L$
we have
$1\leq l \leq L$
we have
Proof. We have for ![]() $\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})$
that
$\varphi\in\mathcal{L}_{v^{\xi}}(\textsf{X})$
that
Applying (H5) Part 1 along with Lemma F.1 allows one to conclude.
Lemma F.3. Assume (H1)–(H5). Then for any ![]() $\xi\in(0,1]$
there exists a
$\xi\in(0,1]$
there exists a ![]() $C<+\infty$
depending on the constants in (H1)–(H5) such that for any
$C<+\infty$
depending on the constants in (H1)–(H5) such that for any ![]() $1\leq l \leq L$
we have
$1\leq l \leq L$
we have
 \begin{eqnarray}\sup_{n\geq 1}\sup_{0\leq p \leq n}\Bigg\|\frac{Q_{p,n}^{l-1}(1)}{\eta_p^{l}\big(Q_{p,n}^{l-1}(1)\big)}\Bigg\|_{v^{\xi}} & \,\leq\, & C,\hspace*{-40pt} \end{eqnarray}
\begin{eqnarray}\sup_{n\geq 1}\sup_{0\leq p \leq n}\Bigg\|\frac{Q_{p,n}^{l-1}(1)}{\eta_p^{l}\big(Q_{p,n}^{l-1}(1)\big)}\Bigg\|_{v^{\xi}} & \,\leq\, & C,\hspace*{-40pt} \end{eqnarray}
 \begin{eqnarray}\sup_{n\geq 1}\sup_{0\leq p \leq n}\Bigg\|\frac{Q_{p,n}^{l-1}(1)}{\Phi^{l-1}_p\big(\eta_{p-1}^l\big)\big(Q_{p,n}^{l-1}(1)\big)}\Bigg\|_{v^{\xi}} & \,\leq\, & C, \end{eqnarray}
\begin{eqnarray}\sup_{n\geq 1}\sup_{0\leq p \leq n}\Bigg\|\frac{Q_{p,n}^{l-1}(1)}{\Phi^{l-1}_p\big(\eta_{p-1}^l\big)\big(Q_{p,n}^{l-1}(1)\big)}\Bigg\|_{v^{\xi}} & \,\leq\, & C, \end{eqnarray}
 \begin{eqnarray}\sup_{n\geq 1}\sup_{0\leq p \leq n}\Bigg\|\frac{Q_{p,n}^{l-1}(1)}{\Phi^{l}_p\big(\eta_{p-1}^l\big)\big(Q_{p,n}^{l-1}(1)\big)}\Bigg\|_{v^{\xi}} & \,\leq \,& C.\hspace*{-10pt}\end{eqnarray}
\begin{eqnarray}\sup_{n\geq 1}\sup_{0\leq p \leq n}\Bigg\|\frac{Q_{p,n}^{l-1}(1)}{\Phi^{l}_p\big(\eta_{p-1}^l\big)\big(Q_{p,n}^{l-1}(1)\big)}\Bigg\|_{v^{\xi}} & \,\leq \,& C.\hspace*{-10pt}\end{eqnarray}
If additionally ![]() $\xi\in(0,1/2)$
, then there exists a
$\xi\in(0,1/2)$
, then there exists a ![]() $C<+\infty$
depending on the constants in (H1)–(H5) such that for any
$C<+\infty$
depending on the constants in (H1)–(H5) such that for any ![]() $\varphi\in \mathcal{L}_{v^{\xi}}(\textsf{X})$
,
$\varphi\in \mathcal{L}_{v^{\xi}}(\textsf{X})$
, ![]() $l\geq 1$
we have
$l\geq 1$
we have
 \begin{equation}\sup_{n\geq 1}\sup_{0\leq p \leq n}\Bigg\|\frac{Q_{p,n}^{l-1}(\varphi)}{\eta_p^{l}\big(Q_{p,n}^{l-1}(1)\big)}\Bigg\|_{v^{2\xi}} \leq C \|\varphi\|_{v^{\xi}}.\end{equation}
\begin{equation}\sup_{n\geq 1}\sup_{0\leq p \leq n}\Bigg\|\frac{Q_{p,n}^{l-1}(\varphi)}{\eta_p^{l}\big(Q_{p,n}^{l-1}(1)\big)}\Bigg\|_{v^{2\xi}} \leq C \|\varphi\|_{v^{\xi}}.\end{equation}
Proof. The proofs of (79) (resp. (80)) and (82) (resp. (81)) are very similar, so we only give the proofs of (80) and (82).
Proof of (80): We have for any ![]() $x\in\textsf{X}$
that
$x\in\textsf{X}$
that
 \[\frac{Q_{p,n}^{l-1}(1)(x)}{\Phi^{l-1}_p\big(\eta_{p-1}^l\big)\big(Q_{p,n}^{l-1}(1)\big)} = \frac{h_{p,n}^{l-1}(x)}{\Phi^{l-1}_p\big(\eta_{p-1}^l\big)\big(h_{p,n}^{l-1}\big)}.\]
\[\frac{Q_{p,n}^{l-1}(1)(x)}{\Phi^{l-1}_p\big(\eta_{p-1}^l\big)\big(Q_{p,n}^{l-1}(1)\big)} = \frac{h_{p,n}^{l-1}(x)}{\Phi^{l-1}_p\big(\eta_{p-1}^l\big)\big(h_{p,n}^{l-1}\big)}.\]
Now
 \begin{eqnarray}\Phi^{l-1}_p(\eta_{p-1}^l)(h_{p,n}^{l-1}) & \,=\, & \frac{\eta_{p-1}^l\big(Q_p^{l-1}\big(h_{p,n}^{l-1}\big)\big)}{\eta_{p-1}^l(G_{p-1})} \nonumber\\[3pt]
& \geq & \frac{\eta_{p-1}^l\big(\mathbb{I}_{C_d}Q_p^{l-1}\big(\mathbb{I}_{C_d}h_{p,n}^{l-1}\big)\big)}{\sup_{n\geq 0}\|G_n\|} \nonumber\\[3pt]
& \geq & C\eta_{p-1}^l(C_d)\tilde{\epsilon}_d^{-}\nu(\mathbb{I}_{C_d}h_{p,n}^{l-1}) \nonumber\\[3pt]& \geq & C \nu(C_d)\inf_{n\geq 1}\inf_{0\leq p \leq n}\inf_{x\in C_d}h_{p,n}^{l-1} \nonumber\\[3pt]& \geq & C,\end{eqnarray}
\begin{eqnarray}\Phi^{l-1}_p(\eta_{p-1}^l)(h_{p,n}^{l-1}) & \,=\, & \frac{\eta_{p-1}^l\big(Q_p^{l-1}\big(h_{p,n}^{l-1}\big)\big)}{\eta_{p-1}^l(G_{p-1})} \nonumber\\[3pt]
& \geq & \frac{\eta_{p-1}^l\big(\mathbb{I}_{C_d}Q_p^{l-1}\big(\mathbb{I}_{C_d}h_{p,n}^{l-1}\big)\big)}{\sup_{n\geq 0}\|G_n\|} \nonumber\\[3pt]
& \geq & C\eta_{p-1}^l(C_d)\tilde{\epsilon}_d^{-}\nu(\mathbb{I}_{C_d}h_{p,n}^{l-1}) \nonumber\\[3pt]& \geq & C \nu(C_d)\inf_{n\geq 1}\inf_{0\leq p \leq n}\inf_{x\in C_d}h_{p,n}^{l-1} \nonumber\\[3pt]& \geq & C,\end{eqnarray}
where we have applied (H5) Part 1 and (H3) to obtain line 3, [Reference Whiteley30, p.\ 2527] (last displayed equation) to obtain line 4, and then [Reference Whiteley30, Lemma 10] to obtain the final line. Then, using [Reference Whiteley30, Proposition 2], it follows that for any ![]() $x\in\textsf{X}$
,
$x\in\textsf{X}$
,
 \[\Bigg|\frac{Q_{p,n}^{l-1}(1)(x)}{\Phi^{l-1}_p\big(\eta_{p-1}^l\big)\big(Q_{p,n}^{l-1}(1)\big)}\Bigg| \leq C v(x)^{\xi},\]
\[\Bigg|\frac{Q_{p,n}^{l-1}(1)(x)}{\Phi^{l-1}_p\big(\eta_{p-1}^l\big)\big(Q_{p,n}^{l-1}(1)\big)}\Bigg| \leq C v(x)^{\xi},\]
which completes the proof of (80).
Proof of (82): We have for any ![]() $x\in\textsf{X}$
that
$x\in\textsf{X}$
that
 \[\frac{Q_{p,n}^{l-1}(\varphi)(x)}{\eta_p^{l}\big(Q_{p,n}^{l-1}(1)\big)} = \frac{Q_{p,n}^{l-1}(\varphi)(x)}{Q_{p,n}^{l-1}(1)(x)}\frac{Q_{p,n}^{l-1}(1)(x)}{\eta_p^{l-1}\big(Q_{p,n}^{l-1}(1)\big)}\frac{1}{\eta_p^{l}\big(h_{p,n}^{l-1}\big)}.\]
\[\frac{Q_{p,n}^{l-1}(\varphi)(x)}{\eta_p^{l}\big(Q_{p,n}^{l-1}(1)\big)} = \frac{Q_{p,n}^{l-1}(\varphi)(x)}{Q_{p,n}^{l-1}(1)(x)}\frac{Q_{p,n}^{l-1}(1)(x)}{\eta_p^{l-1}\big(Q_{p,n}^{l-1}(1)\big)}\frac{1}{\eta_p^{l}\big(h_{p,n}^{l-1}\big)}.\]
By using an argument very similar to (83), one can deduce that ![]() $\eta_p^{l}(h_{p,n}^{l-1})\geq C$
, as frequently noted
$\eta_p^{l}(h_{p,n}^{l-1})\geq C$
, as frequently noted ![]() $\|h_{p,n}^{l-1}\|_{v^{\xi}}\leq C$
, and by a proof similar to that of [Reference Whiteley30, Proposition 1],
$\|h_{p,n}^{l-1}\|_{v^{\xi}}\leq C$
, and by a proof similar to that of [Reference Whiteley30, Proposition 1],
Hence one can complete the proof of (82).
Let ![]() $\mu\in\mathscr{P}(\textsf{X})$
,
$\mu\in\mathscr{P}(\textsf{X})$
, ![]() $s\in\{l,l-1\}$
,
$s\in\{l,l-1\}$
, ![]() $l\geq 1$
,
$l\geq 1$
, ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $0\leq p \leq n$
, and define
$0\leq p \leq n$
, and define ![]() $\Phi_{(p,n)}^s(\mu) = \Phi_n^s\circ\cdots\circ \Phi_{p+1}^s(\mu)$
, with the convention that if
$\Phi_{(p,n)}^s(\mu) = \Phi_n^s\circ\cdots\circ \Phi_{p+1}^s(\mu)$
, with the convention that if ![]() $n=p$
,
$n=p$
, ![]() $\Phi_{(p,n)}^s(\mu)=\mu$
and
$\Phi_{(p,n)}^s(\mu)=\mu$
and ![]() $\Phi_0^s(\mu)=\mu$
.
$\Phi_0^s(\mu)=\mu$
.
Lemma F.4. Assume (H1)–(H5), (H8). Then for any ![]() $\xi\in(0,1/4)$
there exists a
$\xi\in(0,1/4)$
there exists a ![]() $C<+\infty$
depending on the constants in (H1)–(H5) and (H8) such that for any
$C<+\infty$
depending on the constants in (H1)–(H5) and (H8) such that for any ![]() $\varphi\in \mathcal{L}_{v^{\xi}}(\textsf{X})$
,
$\varphi\in \mathcal{L}_{v^{\xi}}(\textsf{X})$
, ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $1\leq l \leq L$
we have
$1\leq l \leq L$
we have
Proof. Define
 \begin{eqnarray}\hspace*{-73pt}T_1 & \,:\!= &\, [\eta_0^{l}-\eta_0^{l-1}]\Bigg(\frac{Q_{0,n}^{l-1}(\varphi)}{\eta_0^l\big(Q_{0,n}^{l-1}(1)\big)}\Bigg), \end{eqnarray}
\begin{eqnarray}\hspace*{-73pt}T_1 & \,:\!= &\, [\eta_0^{l}-\eta_0^{l-1}]\Bigg(\frac{Q_{0,n}^{l-1}(\varphi)}{\eta_0^l\big(Q_{0,n}^{l-1}(1)\big)}\Bigg), \end{eqnarray}
 \begin{eqnarray}T_2 & \,:\!= &\, \Bigg(\frac{\eta_0^{l-1}\big(Q_{0,n}^{l-1}(\varphi)\big)}{\eta_0^{l-1}\big(Q_{0,n}^{l-1}(1)\big)}\Bigg)[\eta_0^{l-1}-\eta_0^{l}]\Bigg(\frac{Q_{0,n}^{l-1}(1)}{\eta_0^l\big(Q_{0,n}^{l-1}(1)\big)}\Bigg).\end{eqnarray}
\begin{eqnarray}T_2 & \,:\!= &\, \Bigg(\frac{\eta_0^{l-1}\big(Q_{0,n}^{l-1}(\varphi)\big)}{\eta_0^{l-1}\big(Q_{0,n}^{l-1}(1)\big)}\Bigg)[\eta_0^{l-1}-\eta_0^{l}]\Bigg(\frac{Q_{0,n}^{l-1}(1)}{\eta_0^l\big(Q_{0,n}^{l-1}(1)\big)}\Bigg).\end{eqnarray}
Then we have
We will bound ![]() $|T_1|$
and
$|T_1|$
and ![]() $|T_2|$
and then sum the bounds to conclude.
$|T_2|$
and then sum the bounds to conclude.
Term (84): We have by Lemma F.3 (82) and Lemma F.1 that
Term (85): We have
 \[\Bigg(\frac{\eta_0^{l-1}\big(Q_{0,n}^{l-1}(\varphi)\big)}{\eta_0^{l-1}\big(Q_{0,n}^{l-1}(1)\big)}\Bigg)[\eta_0^{l-1}-\eta_0^{l}]\Bigg(\frac{Q_{0,n}^l(1)}{\eta_0^l\big(Q_{0,n}^l(1)\big)}\Bigg) =\eta_n^{l-1}(\varphi)[\eta_0^{l-1}-\eta_0^{l}]\Bigg(\frac{Q_{0,n}^l(1)}{\eta_0^l\big(Q_{0,n}^l(1)\big)}\Bigg).\]
\[\Bigg(\frac{\eta_0^{l-1}\big(Q_{0,n}^{l-1}(\varphi)\big)}{\eta_0^{l-1}\big(Q_{0,n}^{l-1}(1)\big)}\Bigg)[\eta_0^{l-1}-\eta_0^{l}]\Bigg(\frac{Q_{0,n}^l(1)}{\eta_0^l\big(Q_{0,n}^l(1)\big)}\Bigg) =\eta_n^{l-1}(\varphi)[\eta_0^{l-1}-\eta_0^{l}]\Bigg(\frac{Q_{0,n}^l(1)}{\eta_0^l\big(Q_{0,n}^l(1)\big)}\Bigg).\]
Then, using ![]() $\varphi\in \mathcal{L}_{v^{\xi}}(\textsf{X})$
along with [Reference Whiteley30, Proposition 1] for
$\varphi\in \mathcal{L}_{v^{\xi}}(\textsf{X})$
along with [Reference Whiteley30, Proposition 1] for ![]() $\eta_n^{l-1}(\varphi)$
and Lemma F.3 (79) and Lemma F.1 for the other term on the right-hand side, we have
$\eta_n^{l-1}(\varphi)$
and Lemma F.3 (79) and Lemma F.1 for the other term on the right-hand side, we have
Noting (86), (87), and (88), the proof can be concluded.
Lemma F.5. Assume (H1)–(H6), (H8). Then for any ![]() $(\xi,\hat{\xi})\in(0,1/8)\times(0,1/2)$
there exist
$(\xi,\hat{\xi})\in(0,1/8)\times(0,1/2)$
there exist ![]() $\rho<1$
and
$\rho<1$
and ![]() $C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any
$C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any ![]() $\varphi\in \mathcal{L}_{v^{\xi}}(\textsf{X})$
,
$\varphi\in \mathcal{L}_{v^{\xi}}(\textsf{X})$
, ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $0\leq p \leq n$
,
$0\leq p \leq n$
, ![]() $1\leq l \leq L$
we have
$1\leq l \leq L$
we have
Proof. Define
 \begin{eqnarray}\hspace*{-10pt}T_1 & \,:\!= &\, [\Phi_p^l(\eta_{p-1}^l)-\Phi_p^{l-1}(\eta_{p-1}^l)]\Bigg(\frac{Q_{p.n}^{l-1}(1)P_{p.n}^{l-1}(\bar{\varphi}_n)}{\Phi_p^l\big(\eta_{p-1}^l\big)\big(Q_{p.n}^{l-1}(1)\big)}\Bigg), \end{eqnarray}
\begin{eqnarray}\hspace*{-10pt}T_1 & \,:\!= &\, [\Phi_p^l(\eta_{p-1}^l)-\Phi_p^{l-1}(\eta_{p-1}^l)]\Bigg(\frac{Q_{p.n}^{l-1}(1)P_{p.n}^{l-1}(\bar{\varphi}_n)}{\Phi_p^l\big(\eta_{p-1}^l\big)\big(Q_{p.n}^{l-1}(1)\big)}\Bigg), \end{eqnarray}
 \begin{eqnarray}\:T_2 & \,:\!= &\,\Bigg(\frac{\Phi_p^{l-1}\big(\eta_{p-1}^l\big)\big(Q_{p.n}^{l-1}(1)P_{p.n}^{l-1}(\bar{\varphi}_n)\big)}{\Phi_p^{l-1}\big(\eta_{p-1}^l\big)\big(Q_{p.n}^{l-1}(1)\big)}\Bigg) \nonumber \\
& &\times\, [\Phi_p^{l-1}(\eta_{p-1}^l)-\Phi_p^l(\eta_{p-1}^l)]\Bigg(\frac{Q_{p,n}^{l-1}(1)}{\Phi^{l}_p\big(\eta_{p-1}^l\big)\big(Q_{p,n}^{l-1}(1)\big)}\Bigg),\end{eqnarray}
\begin{eqnarray}\:T_2 & \,:\!= &\,\Bigg(\frac{\Phi_p^{l-1}\big(\eta_{p-1}^l\big)\big(Q_{p.n}^{l-1}(1)P_{p.n}^{l-1}(\bar{\varphi}_n)\big)}{\Phi_p^{l-1}\big(\eta_{p-1}^l\big)\big(Q_{p.n}^{l-1}(1)\big)}\Bigg) \nonumber \\
& &\times\, [\Phi_p^{l-1}(\eta_{p-1}^l)-\Phi_p^l(\eta_{p-1}^l)]\Bigg(\frac{Q_{p,n}^{l-1}(1)}{\Phi^{l}_p\big(\eta_{p-1}^l\big)\big(Q_{p,n}^{l-1}(1)\big)}\Bigg),\end{eqnarray}
where ![]() $\bar{\varphi}_n=\varphi-\eta_n^{l-1}(\varphi)$
. Then we have
$\bar{\varphi}_n=\varphi-\eta_n^{l-1}(\varphi)$
. Then we have
We will bound ![]() $|T_1|$
and
$|T_1|$
and ![]() $|T_2|$
and then sum the bounds to conclude.
$|T_2|$
and then sum the bounds to conclude.
Term (89): We have by (a similar proof to) (73) that
so by Lemma F.2,
 \[\Bigg| [\Phi_p^l(\eta_{p-1}^l)-\Phi_p^{l-1}(\eta_{p-1}^l)]\Bigg(\frac{Q_{p.n}^{l-1}(1)P_{p.n}^{l-1}(\bar{\varphi}_n)}{\Phi_p^l\big(\eta_{p-1}^l\big)\big(Q_{p.n}^{l-1}(1)\big)}\Bigg)\Bigg| \leq C \|\varphi\|_{v^{\xi}}\Delta_l\rho^{n-p} \frac{\eta_{p-1}^l(v^{8\xi})}{\eta_{p-1}^l(G_{p-1})}.\]
\[\Bigg| [\Phi_p^l(\eta_{p-1}^l)-\Phi_p^{l-1}(\eta_{p-1}^l)]\Bigg(\frac{Q_{p.n}^{l-1}(1)P_{p.n}^{l-1}(\bar{\varphi}_n)}{\Phi_p^l\big(\eta_{p-1}^l\big)\big(Q_{p.n}^{l-1}(1)\big)}\Bigg)\Bigg| \leq C \|\varphi\|_{v^{\xi}}\Delta_l\rho^{n-p} \frac{\eta_{p-1}^l(v^{8\xi})}{\eta_{p-1}^l(G_{p-1})}.\]
Applying [Reference Whiteley30, Proposition 1, Proposition 2(2)] yields
Term (90): We have by Lemma F.3 (80) that
so by (92),
 \[|T_2| \leq C \|\varphi\|_{v^{\xi}}\rho^{n-p}\Bigg(\frac{\eta_{p-1}^l\big(Q_p^{l-1}(v^{4\xi})\big)}{\eta_{p-1}^l(G_{p-1})}\Bigg)\Bigg|[\Phi_p^{l-1}(\eta_{p-1}^l)-\Phi_p^l(\eta_{p-1}^l)]\Bigg(\frac{Q_{p,n}^{l-1}(1)}{\Phi^{l}_p\big(\eta_{p-1}^l\big)\big(Q_{p,n}^{l-1}(1)\big)}\Bigg)\Bigg|.\]
\[|T_2| \leq C \|\varphi\|_{v^{\xi}}\rho^{n-p}\Bigg(\frac{\eta_{p-1}^l\big(Q_p^{l-1}(v^{4\xi})\big)}{\eta_{p-1}^l(G_{p-1})}\Bigg)\Bigg|[\Phi_p^{l-1}(\eta_{p-1}^l)-\Phi_p^l(\eta_{p-1}^l)]\Bigg(\frac{Q_{p,n}^{l-1}(1)}{\Phi^{l}_p\big(\eta_{p-1}^l\big)\big(Q_{p,n}^{l-1}(1)\big)}\Bigg)\Bigg|.\]
Applying (H1) and [Reference Whiteley30, Proposition 1, Proposition 2(2)] to ![]() $\eta_{p-1}^l(Q_p^{l-1}(v^{4\xi}))/\eta_{p-1}^l(G_{p-1})$
and Lemma F.2 along with Lemma F.3 (81) and [Reference Whiteley30, Proposition 1, Proposition 2(2)] to the remaining term gives
$\eta_{p-1}^l(Q_p^{l-1}(v^{4\xi}))/\eta_{p-1}^l(G_{p-1})$
and Lemma F.2 along with Lemma F.3 (81) and [Reference Whiteley30, Proposition 1, Proposition 2(2)] to the remaining term gives
Noting (91), (93), and (94), the proof can be concluded.
Proposition F.1. Assume (H1)–(H6), (H8). Then for any ![]() $(\xi,\hat{\xi})\in(0,1/8)\times(0,1/2)$
there exists a
$(\xi,\hat{\xi})\in(0,1/8)\times(0,1/2)$
there exists a ![]() $C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any
$C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any ![]() $\varphi\in \mathcal{L}_{v^{\xi}}(\textsf{X})$
,
$\varphi\in \mathcal{L}_{v^{\xi}}(\textsf{X})$
, ![]() $n\geq 0$
,
$n\geq 0$
, ![]() $1\leq l \leq L$
we have
$1\leq l \leq L$
we have
Proof. The case ![]() $n=0$
follows by Lemma F.1, so we suppose
$n=0$
follows by Lemma F.1, so we suppose ![]() $n\geq 1$
. Define
$n\geq 1$
. Define
Then we have
We will bound ![]() $|T_1|$
and
$|T_1|$
and ![]() $|T_2|$
and then sum the bounds to conclude.
$|T_2|$
and then sum the bounds to conclude.
Term (95): We have the standard telescoping sum identity
 \begin{equation}[\Phi_{(0,n)}^l(\eta_0^l)-\Phi_{(0,n)}^{l-1}(\eta_0^l)](\varphi) = \sum_{p=1}^n\Big\{[\Phi_{(p,n)}^{l-1}(\Phi_p^l(\eta_{p-1}^l))-\Phi_{(p,n)}^{l-1}(\Phi_p^{l-1}(\eta_{p-1}^l))](\varphi)\Big\}.\end{equation}
\begin{equation}[\Phi_{(0,n)}^l(\eta_0^l)-\Phi_{(0,n)}^{l-1}(\eta_0^l)](\varphi) = \sum_{p=1}^n\Big\{[\Phi_{(p,n)}^{l-1}(\Phi_p^l(\eta_{p-1}^l))-\Phi_{(p,n)}^{l-1}(\Phi_p^{l-1}(\eta_{p-1}^l))](\varphi)\Big\}.\end{equation}
Applying Lemma F.5 gives
Term (96): We have by Lemma F.4 that
Noting (97), (99), and (100), the proof can be concluded.
Remark F.1. If ![]() $\varphi\in\mathcal{B}_b(\textsf{X})$
in Lemma F.5 and Proposition F.1, one can take
$\varphi\in\mathcal{B}_b(\textsf{X})$
in Lemma F.5 and Proposition F.1, one can take ![]() $(\xi,\hat{\xi})\in(0,1/2)\times(0,1]$
; then the upper bound in Lemma F.5 is
$(\xi,\hat{\xi})\in(0,1/2)\times(0,1]$
; then the upper bound in Lemma F.5 is ![]() $C\|\varphi\|\Delta_l\rho^{n-p}v(x^*)^{2\xi+\hat{\xi}}$
, and the one in Proposition F.1 is
$C\|\varphi\|\Delta_l\rho^{n-p}v(x^*)^{2\xi+\hat{\xi}}$
, and the one in Proposition F.1 is ![]() $C\|\varphi\|\Delta_lv(x^*)^{2\xi+\hat{\xi}}$
.
$C\|\varphi\|\Delta_lv(x^*)^{2\xi+\hat{\xi}}$
.
Proposition F.2. Assume (H1)–(H6), (H8). Then for any ![]() $\xi\in(0,1/4)$
there exists a
$\xi\in(0,1/4)$
there exists a ![]() $C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any
$C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any ![]() $\varphi\in \mathcal{B}_{b}(\textsf{X})$
,
$\varphi\in \mathcal{B}_{b}(\textsf{X})$
, ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $0\leq p \leq n$
,
$0\leq p \leq n$
, ![]() $1\leq l \leq L$
we have
$1\leq l \leq L$
we have
Proof. For any ![]() $x\in\textsf{X}$
,
$x\in\textsf{X}$
, ![]() $0<\kappa<\xi$
one has
$0<\kappa<\xi$
one has
and
 \[P_{p,n}^l(\varphi)(x)-P_{p,n}^{l-1}(\varphi)(x) = \sum_{q=p+1}^n\Big\{[\Phi_{(q,n)}^{l-1}(\Phi_{(p,q)}^l(\delta_x))-\Phi_{(q,n)}^{l-1}(\Phi_q^{l-1}\{\Phi_{(p,q-1)}^l(\delta_x)\})](\varphi)\Big\}.\]
\[P_{p,n}^l(\varphi)(x)-P_{p,n}^{l-1}(\varphi)(x) = \sum_{q=p+1}^n\Big\{[\Phi_{(q,n)}^{l-1}(\Phi_{(p,q)}^l(\delta_x))-\Phi_{(q,n)}^{l-1}(\Phi_q^{l-1}\{\Phi_{(p,q-1)}^l(\delta_x)\})](\varphi)\Big\}.\]
Noting (98), one can repeat the proofs of Lemmata F.3 and F.5 in almost the same way for this case to deduce that for any ![]() $(\tilde{\kappa},\hat{\kappa})\in(0,1/2)\times(0,1]$
,
$(\tilde{\kappa},\hat{\kappa})\in(0,1/2)\times(0,1]$
,
where we have noted Remark F.1. Choose ![]() $0<\tilde{\kappa}=\hat{\kappa}<1/(24)$
,
$0<\tilde{\kappa}=\hat{\kappa}<1/(24)$
, ![]() $\kappa=\xi/2$
; then one can set
$\kappa=\xi/2$
; then one can set ![]() $\xi=6\tilde{\kappa}$
and
$\xi=6\tilde{\kappa}$
and ![]() $0<\xi<1/4$
. Hence
$0<\xi<1/4$
. Hence
 \begin{eqnarray*}\Big|\frac{1}{v(x)^{\xi-\kappa}}\Big(P_{p,n}^l(\varphi)(x)-P_{p,n}^{l-1}(\varphi)(x)\Big)\Big| &\, \leq \,& C\|\varphi\|\Delta_l \\\frac{h_{p,n}^l(x)}{v(x)^{\kappa}} &\, \leq\, & C\end{eqnarray*}
\begin{eqnarray*}\Big|\frac{1}{v(x)^{\xi-\kappa}}\Big(P_{p,n}^l(\varphi)(x)-P_{p,n}^{l-1}(\varphi)(x)\Big)\Big| &\, \leq \,& C\|\varphi\|\Delta_l \\\frac{h_{p,n}^l(x)}{v(x)^{\kappa}} &\, \leq\, & C\end{eqnarray*}
and the proof is concluded.
Lemma F.6. Assume (H1)–(H5). Then for any ![]() $\xi\in(0,1]$
there exists a
$\xi\in(0,1]$
there exists a ![]() $C<+\infty$
depending on the constants in (H1)–(H5) such that for any
$C<+\infty$
depending on the constants in (H1)–(H5) such that for any ![]() $1\leq l \leq L$
we have
$1\leq l \leq L$
we have
 \[\sup_{n\geq 1}\sup_{0\leq p \leq n}\Bigg\|\frac{Q_{p,n}^{l-1}(1)}{\eta_p^{l}\big(Q_{p,n}^{l}(1)\big)}\Bigg\|_{v^{\xi}} \leq C.\]
\[\sup_{n\geq 1}\sup_{0\leq p \leq n}\Bigg\|\frac{Q_{p,n}^{l-1}(1)}{\eta_p^{l}\big(Q_{p,n}^{l}(1)\big)}\Bigg\|_{v^{\xi}} \leq C.\]
Proof. The proof is the same as for [Reference Whiteley30, Lemma 8], as the constants in (H1)–(H5) do not depend upon l.
Proposition F.3. Assume (H1)–(H6), (H8). Then for any ![]() $(\xi,\hat{\xi})\in(0,1/8)\times(0,1/2)$
there exists a
$(\xi,\hat{\xi})\in(0,1/8)\times(0,1/2)$
there exists a ![]() $C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any
$C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $0\leq p \leq n$
,
$0\leq p \leq n$
, ![]() $1\leq l \leq L$
, we have
$1\leq l \leq L$
, we have
Proof. For any ![]() $x\in\textsf{X}$
, define
$x\in\textsf{X}$
, define
 \begin{eqnarray}\hspace*{-60pt}T_2 & \,:\!= &\, \frac{Q_{p,n}^{l-1}(1)(x)}{\eta_{p}^l\big(Q_{p,n}^{l}(1)\big)} [\eta_p^{l-1}-\eta_p^l]\big(h_{p,n}^{l-1}\big), \end{eqnarray}
\begin{eqnarray}\hspace*{-60pt}T_2 & \,:\!= &\, \frac{Q_{p,n}^{l-1}(1)(x)}{\eta_{p}^l\big(Q_{p,n}^{l}(1)\big)} [\eta_p^{l-1}-\eta_p^l]\big(h_{p,n}^{l-1}\big), \end{eqnarray}
 \begin{eqnarray}T_3 & \,:\!= &\, h_{p,n}^{l-1}(x) \eta_p^l\Bigg(\frac{1}{\eta_{p}^l\big(Q_{p,n}^{l}(1)\big)}\big(Q_{p,n}^{l}(1)-Q_{p,n}^{l-1}(1)\big)\Bigg).\end{eqnarray}
\begin{eqnarray}T_3 & \,:\!= &\, h_{p,n}^{l-1}(x) \eta_p^l\Bigg(\frac{1}{\eta_{p}^l\big(Q_{p,n}^{l}(1)\big)}\big(Q_{p,n}^{l}(1)-Q_{p,n}^{l-1}(1)\big)\Bigg).\end{eqnarray}
Then we have
We will bound ![]() $|T_1|$
,
$|T_1|$
, ![]() $|T_2|$
, and
$|T_2|$
, and ![]() $|T_3|$
and then sum the bounds to conclude.
$|T_3|$
and then sum the bounds to conclude.
Term (101): We have
 \[T_1 =\frac{1}{\eta_{p}^l\big(Q_{p,n}^{l}(1)\big)}\sum_{q=p+1}^n\Big\{Q_{p,q}^l(Q_{q,n}^{l-1}(1))(x) - Q_{p,q-1}^l\big(Q_{q-1,n}^{l-1}(1)\big)(x)\Big\}.\]
\[T_1 =\frac{1}{\eta_{p}^l\big(Q_{p,n}^{l}(1)\big)}\sum_{q=p+1}^n\Big\{Q_{p,q}^l(Q_{q,n}^{l-1}(1))(x) - Q_{p,q-1}^l\big(Q_{q-1,n}^{l-1}(1)\big)(x)\Big\}.\]
Considering the summand, we have
 \begin{align*}&Q_{p,q}^l(Q_{q,n}^{l-1}(1))(x) - Q_{p,q-1}^l(Q_{q-1,n}^{l-1}(1))(x) \\[2pt] &\quad = \eta_{q+1}^{l-1}(Q_{q+1,n}^{l-1}(1))\Big(Q_{p,q-1}^l(G_{q-1}[M_q^l-M_q^{l-1}](h_{q+1,n}^{l-1}))\Big).\end{align*}
\begin{align*}&Q_{p,q}^l(Q_{q,n}^{l-1}(1))(x) - Q_{p,q-1}^l(Q_{q-1,n}^{l-1}(1))(x) \\[2pt] &\quad = \eta_{q+1}^{l-1}(Q_{q+1,n}^{l-1}(1))\Big(Q_{p,q-1}^l(G_{q-1}[M_q^l-M_q^{l-1}](h_{q+1,n}^{l-1}))\Big).\end{align*}
Now, applying Lemma F.1, [Reference Whiteley30, Proposition 2(3)] (with ![]() $v^{\xi/4}$
), and (H5) Part 1, we have
$v^{\xi/4}$
), and (H5) Part 1, we have
Thus
 \begin{equation}|T_1| \leq \frac{C\Delta_l}{\eta_{p}^l\big(Q_{p,n}^{l}(1)\big)}\sum_{q=p+1}^n\Big\{\eta_{q+1}^{l-1}(Q_{q+1,n}^{l-1}(1))Q_{p,q-1}^l(v^{\xi/2})(x)\Big\}.\end{equation}
\begin{equation}|T_1| \leq \frac{C\Delta_l}{\eta_{p}^l\big(Q_{p,n}^{l}(1)\big)}\sum_{q=p+1}^n\Big\{\eta_{q+1}^{l-1}(Q_{q+1,n}^{l-1}(1))Q_{p,q-1}^l(v^{\xi/2})(x)\Big\}.\end{equation}
Now,
 \begin{align}&\frac{\eta_{q+1}^{l-1}\big(Q_{q+1,n}^{l-1}(1)\big)Q_{p,q-1}^l(v^{\xi/2})(x)}{\eta_{p}^l\big(Q_{p,n}^{l}(1)\big)}\\ \nonumber\
&\quad =\eta_{q+1}^{l-1}\Bigg(\frac{Q_{q+1,n}^{l-1}(1)}{\eta_q^l(G_q)\eta_{q+1}^l\big(Q_{q+1,n}^l(1)\big)}\Bigg)\frac{Q_{p,q-1}^l(v^{\xi/2})(x)}{\eta_{p}^l\big(Q_{p,q-1}^{l}(1)\big)}\frac{1}{\eta^l_{q-1}(G_{q-1})}.\end{align}
\begin{align}&\frac{\eta_{q+1}^{l-1}\big(Q_{q+1,n}^{l-1}(1)\big)Q_{p,q-1}^l(v^{\xi/2})(x)}{\eta_{p}^l\big(Q_{p,n}^{l}(1)\big)}\\ \nonumber\
&\quad =\eta_{q+1}^{l-1}\Bigg(\frac{Q_{q+1,n}^{l-1}(1)}{\eta_q^l(G_q)\eta_{q+1}^l\big(Q_{q+1,n}^l(1)\big)}\Bigg)\frac{Q_{p,q-1}^l(v^{\xi/2})(x)}{\eta_{p}^l\big(Q_{p,q-1}^{l}(1)\big)}\frac{1}{\eta^l_{q-1}(G_{q-1})}.\end{align}
Applying Lemma F.6, [Reference Whiteley30, Proposition 2(3)], and then [Reference Whiteley30, Proposition 1] gives for any ![]() $\hat{\xi}\in(0,1]$
that
$\hat{\xi}\in(0,1]$
that
 \begin{equation}\eta_{q+1}^{l-1}\Bigg(\frac{Q_{q+1,n}^{l-1}(1)}{\eta_q^l(G_q)\eta_{q+1}^l\big(Q_{q+1,n}^l(1)\big)}\Bigg) \leq C v(x^*)^{\hat{\xi}}.\end{equation}
\begin{equation}\eta_{q+1}^{l-1}\Bigg(\frac{Q_{q+1,n}^{l-1}(1)}{\eta_q^l(G_q)\eta_{q+1}^l\big(Q_{q+1,n}^l(1)\big)}\Bigg) \leq C v(x^*)^{\hat{\xi}}.\end{equation}
In addition,
 \[\frac{Q_{p,q-1}^l(v^{\xi/2})(x)}{\eta_{p}^l\big(Q_{p,q-1}^{l}(1)\big)} =\frac{Q_{p,q-1}^l(v^{\xi/2})(x)}{Q_{p,q-1}^l(1)(x)}h_{p,q-1}^l(x).\]
\[\frac{Q_{p,q-1}^l(v^{\xi/2})(x)}{\eta_{p}^l\big(Q_{p,q-1}^{l}(1)\big)} =\frac{Q_{p,q-1}^l(v^{\xi/2})(x)}{Q_{p,q-1}^l(1)(x)}h_{p,q-1}^l(x).\]
By a proof similar to that of [Reference Whiteley30, Proposition 1],
and thus by [Reference Whiteley30, Proposition 2(3)], ![]() $h_{p,q-1}^l(x)\leq Cv(x)^{\xi/2}$
, so
$h_{p,q-1}^l(x)\leq Cv(x)^{\xi/2}$
, so
 \begin{equation}\frac{Q_{p,q-1}^l(v^{\xi/2})(x)}{\eta_{p}^l\big(Q_{p,q-1}^{l}(1)\big)} \leq Cv(x)^{\xi}.\end{equation}
\begin{equation}\frac{Q_{p,q-1}^l(v^{\xi/2})(x)}{\eta_{p}^l\big(Q_{p,q-1}^{l}(1)\big)} \leq Cv(x)^{\xi}.\end{equation}
Noting (105)–(108), we have shown that for any ![]() $(\xi,\hat{\xi})\in(0,1/8)\times(0,1/2)$
,
$(\xi,\hat{\xi})\in(0,1/8)\times(0,1/2)$
,
Term (102): By Lemma F.6 and Proposition F.1, we have that for any ![]() $(\xi,\kappa,\hat{\kappa})\in(0,1/8)^2\times(0,1/2)$
,
$(\xi,\kappa,\hat{\kappa})\in(0,1/8)^2\times(0,1/2)$
,
One can choose ![]() $0<\kappa=\hat{\kappa}<1/20$
,
$0<\kappa=\hat{\kappa}<1/20$
, ![]() $\hat{\xi}=10\kappa$
, and applying [Reference Whiteley30, Proposition 2(3)], we have
$\hat{\xi}=10\kappa$
, and applying [Reference Whiteley30, Proposition 2(3)], we have
Term (103): We have by [Reference Whiteley30, Proposition 2(3)] and (109) that for any ![]() $(\kappa,\hat{\kappa})\in(0,1/8)\times(0,1/2)$
,
$(\kappa,\hat{\kappa})\in(0,1/8)\times(0,1/2)$
,
Applying [Reference Whiteley30, Proposition 1] and choosing ![]() $(\kappa,\hat{\kappa})$
, so that
$(\kappa,\hat{\kappa})$
, so that ![]() $\hat{\xi}=\kappa+\hat{\kappa}<1/2$
, we have
$\hat{\xi}=\kappa+\hat{\kappa}<1/2$
, we have
Noting (104), (109), (110), and (111), the proof can be concluded.
F.2. Proofs for Proposition 5.2
Proof of Proposition 5.2. We focus on the first bound in Theorem 4.3. Clearly
As ![]() $\check{\eta}^C_n$
is the maximal coupling of
$\check{\eta}^C_n$
is the maximal coupling of ![]() $(\eta_n^{l},\eta_n^{l-1})$
, we have
$(\eta_n^{l},\eta_n^{l-1})$
, we have ![]() $\check{\eta}^C_n(\mathbb{I}_A)=\|\eta_n^{l}-\eta_n^{l-1}\|_{\textrm{tv}}$
. Hence, on applying Proposition F.1 (noting Remark F.1), we have that
$\check{\eta}^C_n(\mathbb{I}_A)=\|\eta_n^{l}-\eta_n^{l-1}\|_{\textrm{tv}}$
. Hence, on applying Proposition F.1 (noting Remark F.1), we have that
The proof is completed by using Proposition 5.1 and Proposition F.4.
Proposition F.4. Assume (H1)–(H6), (H8). Then for any ![]() $(\xi,\hat{\xi})\in(0,1/32)\times(0,1/2)$
there exists a
$(\xi,\hat{\xi})\in(0,1/32)\times(0,1/2)$
there exists a ![]() $C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any
$C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any ![]() $n\geq 0$
,
$n\geq 0$
, ![]() $1\leq l \leq L$
we have
$1\leq l \leq L$
we have
Proof. We will use ![]() $(\eta_n^l,\eta_n^{l-1})$
to denote both the probability measure and the density associated to
$(\eta_n^l,\eta_n^{l-1})$
to denote both the probability measure and the density associated to ![]() $(\eta_n^l,\eta_n^{l-1})$
. We have for any
$(\eta_n^l,\eta_n^{l-1})$
. We have for any ![]() $n\geq 0$
that
$n\geq 0$
that
 \begin{eqnarray*}\check{\eta}^C_n(\mathbb{I}_A(v\otimes v)^{2\xi}) & \,=\, & \Bigg(1-\int_{\textsf{X}}\eta_n^l(x)\wedge\eta_n^{l-1}(x)dx\Bigg)\int_{\textsf{X}\times\textsf{X}}\mathbb{I}_A(x,y) v(x)^{2\xi}v(y)^{2\xi} \\[3pt]& & \times\, \frac{(\eta_n^l(x)-\eta_n^l(x)\wedge\eta_n^{l-1}(x))}{1-\int_{\textsf{X}}\eta_n^l(x)\wedge\eta_n^{l-1}(x)dx} \frac{(\eta_n^{l-1}(y)-\eta_n^l(y)\wedge\eta_n^{l-1}(y))}{1-\int_{\textsf{X}}\eta_n^l(x)\wedge\eta_n^{l-1}(x)dx} dxdy.\end{eqnarray*}
\begin{eqnarray*}\check{\eta}^C_n(\mathbb{I}_A(v\otimes v)^{2\xi}) & \,=\, & \Bigg(1-\int_{\textsf{X}}\eta_n^l(x)\wedge\eta_n^{l-1}(x)dx\Bigg)\int_{\textsf{X}\times\textsf{X}}\mathbb{I}_A(x,y) v(x)^{2\xi}v(y)^{2\xi} \\[3pt]& & \times\, \frac{(\eta_n^l(x)-\eta_n^l(x)\wedge\eta_n^{l-1}(x))}{1-\int_{\textsf{X}}\eta_n^l(x)\wedge\eta_n^{l-1}(x)dx} \frac{(\eta_n^{l-1}(y)-\eta_n^l(y)\wedge\eta_n^{l-1}(y))}{1-\int_{\textsf{X}}\eta_n^l(x)\wedge\eta_n^{l-1}(x)dx} dxdy.\end{eqnarray*}
Then, using the upper bound of 1 for the indicator and applying Cauchy–Schwarz, we have
where
 \begin{eqnarray*}T_1& \,:\!= &\, \Bigg(\int_{\textsf{X}}v(x)^{4\xi}(\eta_n^l(x)-\eta_n^l(x)\wedge\eta_n^{l-1}(x))dx\Bigg)^{1/2}, \\[3pt]
T_2 & \,:\!= &\, \Bigg(\int_{\textsf{X}}v(x)^{4\xi}(\eta_n^{l-1}(x)-\eta_n^l(x)\wedge\eta_n^{l-1}(x))dx\Bigg)^{1/2}.\end{eqnarray*}
\begin{eqnarray*}T_1& \,:\!= &\, \Bigg(\int_{\textsf{X}}v(x)^{4\xi}(\eta_n^l(x)-\eta_n^l(x)\wedge\eta_n^{l-1}(x))dx\Bigg)^{1/2}, \\[3pt]
T_2 & \,:\!= &\, \Bigg(\int_{\textsf{X}}v(x)^{4\xi}(\eta_n^{l-1}(x)-\eta_n^l(x)\wedge\eta_n^{l-1}(x))dx\Bigg)^{1/2}.\end{eqnarray*}
We now just deal with ![]() $T_1$
, as the proof for
$T_1$
, as the proof for ![]() $T_2$
is almost identical.
$T_2$
is almost identical.
Letting ![]() $D_n^l=\{x\,{:}\,\eta_n^l(x)\geq\eta_n^{l-1}(x)\}$
,
$D_n^l=\{x\,{:}\,\eta_n^l(x)\geq\eta_n^{l-1}(x)\}$
, ![]() $\tilde{\varphi}(x)=v(x)^{4\xi}\mathbb{I}_{D_n^l}(x)$
, and
$\tilde{\varphi}(x)=v(x)^{4\xi}\mathbb{I}_{D_n^l}(x)$
, and ![]() $\hat{\varphi}(x)=v(x)^{4\xi}\mathbb{I}_{(D_n^l)^c}(x)$
, we have
$\hat{\varphi}(x)=v(x)^{4\xi}\mathbb{I}_{(D_n^l)^c}(x)$
, we have
 \begin{eqnarray*}T_1^2 & \,=\, & \frac{1}{2}\Bigg(\int_{\textsf{X}}v(x)^{4\xi}[\eta_n^l(x)-\eta_n^{l-1}(x)]dx + \int_{\textsf{X}}v(x)^{4\xi}|\eta_n^l(x)-\eta_n^{l-1}(x)|dx\Bigg) \\[3pt]
& \,=\, & \frac{1}{2}\Bigg(\int_{\textsf{X}}v(x)^{4\xi}[\eta_n^l(x)-\eta_n^{l-1}]dx + \int_{\textsf{X}}\tilde{\varphi}(x)(\eta_n^l(x)-\eta_n^{l-1}(x))dx \\[3pt]
& &+\int_{\textsf{X}}\hat{\varphi}(x)(\eta_n^{l-1}(x)-\eta_n^{l}(x))dx\Bigg) \\[3pt]
& \leq & \frac{1}{2}(|[\eta_n^l-\eta_n^{l-1}](v^{4\xi})| + |[\eta_n^l-\eta_n^{l-1}](\tilde{\varphi})|+|[\eta_n^l-\eta_n^{l-1}](\hat{\varphi})|).\end{eqnarray*}
\begin{eqnarray*}T_1^2 & \,=\, & \frac{1}{2}\Bigg(\int_{\textsf{X}}v(x)^{4\xi}[\eta_n^l(x)-\eta_n^{l-1}(x)]dx + \int_{\textsf{X}}v(x)^{4\xi}|\eta_n^l(x)-\eta_n^{l-1}(x)|dx\Bigg) \\[3pt]
& \,=\, & \frac{1}{2}\Bigg(\int_{\textsf{X}}v(x)^{4\xi}[\eta_n^l(x)-\eta_n^{l-1}]dx + \int_{\textsf{X}}\tilde{\varphi}(x)(\eta_n^l(x)-\eta_n^{l-1}(x))dx \\[3pt]
& &+\int_{\textsf{X}}\hat{\varphi}(x)(\eta_n^{l-1}(x)-\eta_n^{l}(x))dx\Bigg) \\[3pt]
& \leq & \frac{1}{2}(|[\eta_n^l-\eta_n^{l-1}](v^{4\xi})| + |[\eta_n^l-\eta_n^{l-1}](\tilde{\varphi})|+|[\eta_n^l-\eta_n^{l-1}](\hat{\varphi})|).\end{eqnarray*}
As ![]() $\xi\in(0,1/32)$
,
$\xi\in(0,1/32)$
, ![]() $(v^{4\xi},\tilde{\varphi},\tilde{\varphi})\in\mathcal{L}_{v^{\kappa}}(\textsf{X})^3$
, with
$(v^{4\xi},\tilde{\varphi},\tilde{\varphi})\in\mathcal{L}_{v^{\kappa}}(\textsf{X})^3$
, with ![]() $0<\kappa<1/8$
, so applying Proposition F.1 we have
$0<\kappa<1/8$
, so applying Proposition F.1 we have
Similar calculations give ![]() $T_2 \leq C (\Delta_l)^{1/2} v(x^*)^{16\xi+\hat{\xi}}$
; hence, noting (112), one can conclude.
$T_2 \leq C (\Delta_l)^{1/2} v(x^*)^{16\xi+\hat{\xi}}$
; hence, noting (112), one can conclude.
F.3. Proofs for Proposition 5.3
Recall here that ![]() $\textsf{X}=\mathbb{R}$
and the metric in (H7) is
$\textsf{X}=\mathbb{R}$
and the metric in (H7) is ![]() $\textsf{d}_1$
, the
$\textsf{d}_1$
, the ![]() $L_1-$
norm. Let
$L_1-$
norm. Let ![]() $\tilde{\varphi}(x,y)=(x-y)^2$
.
$\tilde{\varphi}(x,y)=(x-y)^2$
.
Proof of Proposition 5.3. Considering the second bound in Theorem 4.3, the result follows by Proposition 5.1 and Lemmata F.7 and F.8.
Proposition F.5. Assume (H1)–(H6), (H8). Then for any ![]() $(\xi,\hat{\xi})\in(0,1/8)\times(0,1/2)$
there exists a
$(\xi,\hat{\xi})\in(0,1/8)\times(0,1/2)$
there exists a ![]() $C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any
$C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any ![]() $\varphi\in \mathcal{L}_{v^{\xi}}(\textsf{X})$
,
$\varphi\in \mathcal{L}_{v^{\xi}}(\textsf{X})$
, ![]() $n\geq 0$
,
$n\geq 0$
, ![]() $1\leq l \leq L$
we have
$1\leq l \leq L$
we have
Proof. Define
Then we have
We will bound ![]() $|T_1|$
and
$|T_1|$
and ![]() $|T_2|$
and then sum the bounds to conclude.
$|T_2|$
and then sum the bounds to conclude.
Term (113): By Proposition F.1 and ![]() $\eta_n^l(G_n)\geq C$
we have
$\eta_n^l(G_n)\geq C$
we have
Term (114): By Proposition F.1, (H5), and ![]() $\eta_n^{s}(G_n)\geq C$
,
$\eta_n^{s}(G_n)\geq C$
, ![]() $s\in\{l,l-1\}$
, we have
$s\in\{l,l-1\}$
, we have
Noting (115), (116), and (117), the proof can be concluded.
Denote by ![]() $\check{\overline{\eta}}_n^C$
the maximal coupling of
$\check{\overline{\eta}}_n^C$
the maximal coupling of ![]() $(\overline{\eta}_n^l,\overline{\eta}_n^{l-1})$
.
$(\overline{\eta}_n^l,\overline{\eta}_n^{l-1})$
.
Corollary F.1. Assume (H1)–(H6), (H8). Then for any ![]() $(\xi,\hat{\xi})\in(0,1/16)\times(0,1/2)$
there exists a
$(\xi,\hat{\xi})\in(0,1/16)\times(0,1/2)$
there exists a ![]() $C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any
$C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any ![]() $n\geq 0$
,
$n\geq 0$
, ![]() $1\leq l \leq L$
we have
$1\leq l \leq L$
we have
Proof. This follows by the same proof as for Proposition F.4, except using Proposition F.5 instead of Propositon F.1 in the proof.
Denote by ![]() $\check{\overline{\eta}}_n^W$
the optimal Wasserstein coupling of
$\check{\overline{\eta}}_n^W$
the optimal Wasserstein coupling of ![]() $(\overline{\eta}_n^l,\overline{\eta}_n^{l-1})$
; that is, for
$(\overline{\eta}_n^l,\overline{\eta}_n^{l-1})$
; that is, for ![]() $B\in\mathcal{X}\times\mathcal{X}$
,
$B\in\mathcal{X}\times\mathcal{X}$
,
Lemma A.7. Assume (H1)–(H6), (H8). If ![]() $\tilde{\varphi}\in\mathcal{L}_{(v\otimes v)^{\tilde{\xi}}}(\textsf{X})$
for any
$\tilde{\varphi}\in\mathcal{L}_{(v\otimes v)^{\tilde{\xi}}}(\textsf{X})$
for any ![]() $\tilde{\xi}\in(0,1/16)$
, and
$\tilde{\xi}\in(0,1/16)$
, and ![]() $\hat{\xi}\in (0,1/2)$
, then there exists a
$\hat{\xi}\in (0,1/2)$
, then there exists a ![]() $C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any
$C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any ![]() $\varphi\in \mathcal{B}_{b}(\textsf{X})\cap\textrm{\textit{Lip}}_{\textsf{d}_1}(\textsf{X})$
,
$\varphi\in \mathcal{B}_{b}(\textsf{X})\cap\textrm{\textit{Lip}}_{\textsf{d}_1}(\textsf{X})$
, ![]() $n\geq 0$
,
$n\geq 0$
, ![]() $1\leq l \leq L$
we have
$1\leq l \leq L$
we have
Proof. We assume ![]() $n\geq 1$
; the case
$n\geq 1$
; the case ![]() $n=0$
is noted below. As
$n=0$
is noted below. As ![]() $\varphi\in \mathcal{B}_{b}(\textsf{X})\cap\textrm{Lip}_{\textsf{d}_1}(\textsf{X})$
, it easily follows that
$\varphi\in \mathcal{B}_{b}(\textsf{X})\cap\textrm{Lip}_{\textsf{d}_1}(\textsf{X})$
, it easily follows that
Applying (6) (when ![]() $p=2$
) and using the optimality of the Wasserstein coupling with
$p=2$
) and using the optimality of the Wasserstein coupling with ![]() $\tilde{\varphi}\in\mathcal{L}_{(v\otimes v)^{\tilde{\xi}}}(\textsf{X})$
gives
$\tilde{\varphi}\in\mathcal{L}_{(v\otimes v)^{\tilde{\xi}}}(\textsf{X})$
gives
Application of Corollary F.1 yields the desired result. The case ![]() $n=0$
follows from
$n=0$
follows from
and the optimality of the Wasserstein coupling, ![]() $\tilde{\varphi}\in\mathcal{L}_{(v\otimes v)^{\tilde{\xi}}}(\textsf{X})$
with Corollary F.1.
$\tilde{\varphi}\in\mathcal{L}_{(v\otimes v)^{\tilde{\xi}}}(\textsf{X})$
with Corollary F.1.
Lemma F.8. Assume (H1)–(H6), (H8). Then let ![]() $\lambda\in(0,1)$
be given; assume
$\lambda\in(0,1)$
be given; assume ![]() $\tilde{\varphi}\in\mathcal{L}_{(v\otimes v)^{\tilde{\xi}}}(\textsf{X})$
, for any
$\tilde{\varphi}\in\mathcal{L}_{(v\otimes v)^{\tilde{\xi}}}(\textsf{X})$
, for any ![]() $\tilde{\xi}\in(0,1/(16(1+\lambda)))$
, and set
$\tilde{\xi}\in(0,1/(16(1+\lambda)))$
, and set
Then there exists a ![]() $C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any
$C<+\infty$
depending on the constants in (H1)–(H6) and (H8) such that for any ![]() $n\geq 0$
,
$n\geq 0$
, ![]() $1\leq l \leq L$
we have
$1\leq l \leq L$
we have
Proof. We assume ![]() $n\geq 1$
; the case
$n\geq 1$
; the case ![]() $n=0$
is similar and omitted for brevity. By Cauchy–Schwarz and the structure of
$n=0$
is similar and omitted for brevity. By Cauchy–Schwarz and the structure of ![]() $\check{\overline{\eta}}^W_n$
,
$\check{\overline{\eta}}^W_n$
,
Applying (6) (when ![]() $p=4$
) gives the upper bound
$p=4$
) gives the upper bound
To complete the proof, we focus on ![]() $\check{\overline{\eta}}_{n-1}^W(\tilde{\varphi}\check{M}(v^{8\xi}\otimes v^{16\xi})^{1/2})$
, as the other term can be controlled using the arguments below.
$\check{\overline{\eta}}_{n-1}^W(\tilde{\varphi}\check{M}(v^{8\xi}\otimes v^{16\xi})^{1/2})$
, as the other term can be controlled using the arguments below.
By Hölder’s inequality, we have
By the optimality of the Wasserstein coupling with ![]() $\tilde{\varphi}\in\mathcal{L}_{(v\otimes v)^{\tilde{\xi}}}(\textsf{X})$
, we have
$\tilde{\varphi}\in\mathcal{L}_{(v\otimes v)^{\tilde{\xi}}}(\textsf{X})$
, we have
 \begin{align*}&\check{\overline{\eta}}_{n-1}^W(\tilde{\varphi}\check{M}(v^{8\xi}\otimes v^{16\xi})^{1/2}) \\[3pt] &\quad \leq \Big(\|\tilde{\varphi}\|_{v^{\tilde{\xi}}}\check{\overline{\eta}}^C_{n-1}(\mathbb{I}_A(v\otimes v)^{\tilde{\xi}(1+\lambda)})\Big)^{1/(1+\lambda)}\check{\overline{\eta}}_{n-1}^W(\check{M}(v^{8\xi}\otimes v^{16\xi})^{(1+\lambda)/(2\lambda)})^{\lambda/(1+\lambda)}.\end{align*}
\begin{align*}&\check{\overline{\eta}}_{n-1}^W(\tilde{\varphi}\check{M}(v^{8\xi}\otimes v^{16\xi})^{1/2}) \\[3pt] &\quad \leq \Big(\|\tilde{\varphi}\|_{v^{\tilde{\xi}}}\check{\overline{\eta}}^C_{n-1}(\mathbb{I}_A(v\otimes v)^{\tilde{\xi}(1+\lambda)})\Big)^{1/(1+\lambda)}\check{\overline{\eta}}_{n-1}^W(\check{M}(v^{8\xi}\otimes v^{16\xi})^{(1+\lambda)/(2\lambda)})^{\lambda/(1+\lambda)}.\end{align*}
Then applying Corollary F.1 gives
 \begin{align*}&\check{\overline{\eta}}_{n-1}^W(\tilde{\varphi}\check{M}(v^{8\xi}\otimes v^{16\xi})^{1/2})\\ &\quad \leq C\|\tilde{\varphi}\|_{v^{\tilde{\xi}}}(\Delta_l)^{1/(1+\lambda)}v(x^*)^{(16(\lambda+1)\tilde{\xi}+2\hat{\xi})/(1+\lambda)}\check{\overline{\eta}}_{n-1}^W(\check{M}(v^{8\xi}\otimes v^{16\xi})^{(1+\lambda)/(2\lambda)})^{\lambda/(1+\lambda)}. \end{align*}
\begin{align*}&\check{\overline{\eta}}_{n-1}^W(\tilde{\varphi}\check{M}(v^{8\xi}\otimes v^{16\xi})^{1/2})\\ &\quad \leq C\|\tilde{\varphi}\|_{v^{\tilde{\xi}}}(\Delta_l)^{1/(1+\lambda)}v(x^*)^{(16(\lambda+1)\tilde{\xi}+2\hat{\xi})/(1+\lambda)}\check{\overline{\eta}}_{n-1}^W(\check{M}(v^{8\xi}\otimes v^{16\xi})^{(1+\lambda)/(2\lambda)})^{\lambda/(1+\lambda)}. \end{align*}
Now for the remaining term, applying Cauchy–Schwarz twice gives
 \begin{align*}&\check{\overline{\eta}}_{n-1}^W(\check{M}(v^{8\xi}\otimes v^{16\xi})^{(1+\lambda)/(2\lambda)})^{\lambda/(1+\lambda)}\\ &\quad \leq \overline{\eta}_{n-1}^l(M^l(v^{16\xi})^{(1+\lambda)/(2\lambda)})^{\lambda/(2(1+\lambda))}\overline{\eta}_{n-1}^{l-1}(M^{l-1}(v^{32\xi})^{(1+\lambda)/(2\lambda)})^{\lambda/(2(1+\lambda))}. \end{align*}
\begin{align*}&\check{\overline{\eta}}_{n-1}^W(\check{M}(v^{8\xi}\otimes v^{16\xi})^{(1+\lambda)/(2\lambda)})^{\lambda/(1+\lambda)}\\ &\quad \leq \overline{\eta}_{n-1}^l(M^l(v^{16\xi})^{(1+\lambda)/(2\lambda)})^{\lambda/(2(1+\lambda))}\overline{\eta}_{n-1}^{l-1}(M^{l-1}(v^{32\xi})^{(1+\lambda)/(2\lambda)})^{\lambda/(2(1+\lambda))}. \end{align*}
Applying Jensen twice gives
The proof is thus complete.
Remark F.2. As ![]() $\lambda > 0$
in Lemma F.8, one almost has the (time-uniform) forward error rate for the WCPF. We believe that
$\lambda > 0$
in Lemma F.8, one almost has the (time-uniform) forward error rate for the WCPF. We believe that ![]() $\lambda=0$
is the desired case; however, because of technical difficulties we have not obtained this. One of the issues of the proof is that the Wasserstein coupling is not the coupling which minimizes the expectation of
$\lambda=0$
is the desired case; however, because of technical difficulties we have not obtained this. One of the issues of the proof is that the Wasserstein coupling is not the coupling which minimizes the expectation of ![]() $\tilde{\varphi}(v^{4\xi}\otimes v^{8\xi})$
with respect to any coupling of
$\tilde{\varphi}(v^{4\xi}\otimes v^{8\xi})$
with respect to any coupling of ![]() $(\overline{\eta}_n^l,\overline{\eta}_n^{l-1})$
. To see this, one can construct a functional covariance equality for
$(\overline{\eta}_n^l,\overline{\eta}_n^{l-1})$
. To see this, one can construct a functional covariance equality for ![]() $\mu(\tilde{\varphi}(v^{4\xi}\otimes v^{8\xi}))$
(
$\mu(\tilde{\varphi}(v^{4\xi}\otimes v^{8\xi}))$
(![]() $\mu$
is any coupling of
$\mu$
is any coupling of ![]() $(\overline{\eta}_n^l,\overline{\eta}_n^{l-1})$
such that
$(\overline{\eta}_n^l,\overline{\eta}_n^{l-1})$
such that ![]() $\mu(\tilde{\varphi}(v^{4\xi}\otimes v^{8\xi}))<+\infty$
) as in [Reference Lo24, Theorem 3.1] (that is, in terms of the CDFs of
$\mu(\tilde{\varphi}(v^{4\xi}\otimes v^{8\xi}))<+\infty$
) as in [Reference Lo24, Theorem 3.1] (that is, in terms of the CDFs of ![]() $\mu$
,
$\mu$
, ![]() $\overline{\eta}_n^l$
, and
$\overline{\eta}_n^l$
, and ![]() $\overline{\eta}_n^{l-1}$
, as in Hoeffding’s lemma), and then when centering with
$\overline{\eta}_n^{l-1}$
, as in Hoeffding’s lemma), and then when centering with ![]() $(\overline{\eta}_n^l\otimes \overline{\eta}_n^{l-1})(\tilde{\varphi}(v^{4\xi}\otimes v^{8\xi}))$
and applying Hoeffding–Fréchet bounds, one observes that
$(\overline{\eta}_n^l\otimes \overline{\eta}_n^{l-1})(\tilde{\varphi}(v^{4\xi}\otimes v^{8\xi}))$
and applying Hoeffding–Fréchet bounds, one observes that ![]() $\check{\overline{\eta}}^W_n$
is not optimal. As a result, one cannot transfer between
$\check{\overline{\eta}}^W_n$
is not optimal. As a result, one cannot transfer between ![]() $\check{\overline{\eta}}^W_n$
and
$\check{\overline{\eta}}^W_n$
and ![]() $\check{\overline{\eta}}^C_n$
as is done in the proofs of Lemmata F.7–F.8, nor can one use Kantorovich duality. However, one can obtain
$\check{\overline{\eta}}^C_n$
as is done in the proofs of Lemmata F.7–F.8, nor can one use Kantorovich duality. However, one can obtain ![]() $\lambda=0$
if any of the following hold true:
$\lambda=0$
if any of the following hold true:
1. There exists an
 $\check{\overline{\eta}}^W_n-$
integrable
$\check{\overline{\eta}}^W_n-$
integrable  $\hat{V}\,:\,\textsf{X}\times\textsf{X}\rightarrow (0,+\infty)$
such that there exists a
$\hat{V}\,:\,\textsf{X}\times\textsf{X}\rightarrow (0,+\infty)$
such that there exists a  $C<+\infty$
such that for every
$C<+\infty$
such that for every  $(x,y)\in\textsf{X}\times\textsf{X}$
,
$(x,y)\in\textsf{X}\times\textsf{X}$
,  $\tilde{\varphi}(x,y)v^{4\xi}(x)v^{8\xi}(y)\leq C \hat{V}(x,y)$
, and
$\tilde{\varphi}(x,y)v^{4\xi}(x)v^{8\xi}(y)\leq C \hat{V}(x,y)$
, and  $\hat{V}$
satisfies the Monge condition (e.g. [Reference Rachev and Rüschendorf27, Eq. (3.1.7)]).
$\hat{V}$
satisfies the Monge condition (e.g. [Reference Rachev and Rüschendorf27, Eq. (3.1.7)]).2. v is bounded.
3. There exists a
 $C<+\infty$
such that for every
$C<+\infty$
such that for every  $n\geq 0$
,
$n\geq 0$
,
 \[\check{\overline{\eta}}^W_n(\tilde{\varphi}(v^{4\xi}\otimes v^{8\xi}))\leq C \check{\overline{\eta}}^C_n(\tilde{\varphi}(v^{4\xi}\otimes v^{8\xi})).\]
\[\check{\overline{\eta}}^W_n(\tilde{\varphi}(v^{4\xi}\otimes v^{8\xi}))\leq C \check{\overline{\eta}}^C_n(\tilde{\varphi}(v^{4\xi}\otimes v^{8\xi})).\]
4. There exists a
 $C<+\infty$
such that for every
$C<+\infty$
such that for every  $n\geq 0$
,
$n\geq 0$
,  $1\leq l \leq L$
,
$1\leq l \leq L$
,
 \[\sup_{u\in[0,1]}|F_{\overline{\eta}_n^l}^{-1}(u)-F_{\overline{\eta}_n^{l-1}}^{-1}(u)|\leq C\Delta_l.\]
\[\sup_{u\in[0,1]}|F_{\overline{\eta}_n^l}^{-1}(u)-F_{\overline{\eta}_n^{l-1}}^{-1}(u)|\leq C\Delta_l.\]
In general we do not believe 1 can hold in practice, and 2 is not useful in the context of the article. We believe 3 and 4 to hold up to some conditions, but have not obtained the proofs.
F.4. Proof of Lemma 5.1
Proof of Lemma 5.1. We begin by noting that for any ![]() $B\in\mathcal{X}$
,
$B\in\mathcal{X}$
, ![]() $0\leq l \leq L$
,
$0\leq l \leq L$
, ![]() $y\in\textsf{X}$
we have
$y\in\textsf{X}$
we have
 \begin{eqnarray}M^l(\mathbb{I}_Bv)(y) & \,=\, & \sqrt\bigg(\frac{(1+\delta_0)}{(1+\delta_0-\beta_l)}\bigg)\exp\bigg\{\frac{\alpha_l^2y^2}{2(1+\delta_0-\beta_l)}+1\bigg\}\nonumber\\[3pt] & &\times \, \int_B \frac{1}{\sqrt{2\pi\beta_l}}\exp\bigg\{-\frac{1+\delta_0-\beta_l}{2\beta_l(1+\delta_0)}\bigg(x-\frac{\alpha_ly(1+\delta_0)}{1+\delta_0-\beta_l}\bigg)^2\bigg\}dx.\end{eqnarray}
\begin{eqnarray}M^l(\mathbb{I}_Bv)(y) & \,=\, & \sqrt\bigg(\frac{(1+\delta_0)}{(1+\delta_0-\beta_l)}\bigg)\exp\bigg\{\frac{\alpha_l^2y^2}{2(1+\delta_0-\beta_l)}+1\bigg\}\nonumber\\[3pt] & &\times \, \int_B \frac{1}{\sqrt{2\pi\beta_l}}\exp\bigg\{-\frac{1+\delta_0-\beta_l}{2\beta_l(1+\delta_0)}\bigg(x-\frac{\alpha_ly(1+\delta_0)}{1+\delta_0-\beta_l}\bigg)^2\bigg\}dx.\end{eqnarray}
This will be used below.
We give the proof for ![]() $\xi=1$
, as it is similar in other cases. We have for any
$\xi=1$
, as it is similar in other cases. We have for any ![]() $0\leq l \leq L$
,
$0\leq l \leq L$
, ![]() $n\geq 1$
,
$n\geq 1$
, ![]() $\varphi\in\mathcal{L}_{v}(\textsf{X})\cap\textrm{Lip}_{v,\textsf{d}_1}$
that
$\varphi\in\mathcal{L}_{v}(\textsf{X})\cap\textrm{Lip}_{v,\textsf{d}_1}$
that
 \begin{align*}&|Q_n^l(\varphi)(x)-Q_n^l(\varphi)(y)| \\ &\quad \leq \|\varphi\|_{v} M^l(v)(x)|G_{n-1}(x)-G_{n-1}(y)| + \|G_{n-1}\|\|\varphi\|_{v}\int_{\textsf{X}} v(u) | M^l(x,u)-M^l(y,u)|du.\end{align*}
\begin{align*}&|Q_n^l(\varphi)(x)-Q_n^l(\varphi)(y)| \\ &\quad \leq \|\varphi\|_{v} M^l(v)(x)|G_{n-1}(x)-G_{n-1}(y)| + \|G_{n-1}\|\|\varphi\|_{v}\int_{\textsf{X}} v(u) | M^l(x,u)-M^l(y,u)|du.\end{align*}
As noted in Section 5.6, ![]() $[\alpha_l^2(1+\delta_0)]/[1+\delta_0-\beta_l]<1$
for any
$[\alpha_l^2(1+\delta_0)]/[1+\delta_0-\beta_l]<1$
for any ![]() $0\leq l\leq L$
,
$0\leq l\leq L$
, ![]() $\delta_0>0$
, so using (118) one can determine that
$\delta_0>0$
, so using (118) one can determine that ![]() $M^l(v)(x)\in\mathcal{L}_v(\textsf{X})$
for any
$M^l(v)(x)\in\mathcal{L}_v(\textsf{X})$
for any ![]() $\delta_0>0$
, with
$\delta_0>0$
, with ![]() $\|M^l(v)\|_{v}$
independent of l. In addition, for every
$\|M^l(v)\|_{v}$
independent of l. In addition, for every ![]() $y\in\textsf{Y}$
, we have
$y\in\textsf{Y}$
, we have ![]() $G_{n-1}\in\textrm{Lip}_{\textsf{d}_1}(\textsf{X})$
with Lipschitz constant independent of n, so we need only consider the right-hand term in the above displayed equation.
$G_{n-1}\in\textrm{Lip}_{\textsf{d}_1}(\textsf{X})$
with Lipschitz constant independent of n, so we need only consider the right-hand term in the above displayed equation.
Set ![]() $D_l(x,y)\,:\!=\{u\in\textsf{X}\,{:}\,M^l(x,u)-M^l(y,u)\}$
. We consider only
$D_l(x,y)\,:\!=\{u\in\textsf{X}\,{:}\,M^l(x,u)-M^l(y,u)\}$
. We consider only
as the calculations on ![]() $D_l(x,y)^c$
are very similar. We suppose
$D_l(x,y)^c$
are very similar. We suppose ![]() $x>y$
, as the proof with
$x>y$
, as the proof with ![]() $x<y$
is analogous, so we have by (118) and
$x<y$
is analogous, so we have by (118) and ![]() $x>y$
that
$x>y$
that
 \begin{align*}&\int_{D_l(x,y)} v(u) | M^l(x,u)-M^l(y,u)|du = \sqrt{\bigg(\frac{(1+\delta_0)}{(1+\delta_0-\beta_l)}\bigg)}\\
&\ \ \times \Bigg\{\exp\bigg\{\frac{\alpha_l^2x^2}{2(1+\delta_0-\beta_l)}+1\bigg\}\int_{-\infty}^{c_l(x,y)} \frac{1}{\sqrt{2\pi\beta_l}}\exp\bigg\{-\frac{1+\delta_0-\beta_l}{2\beta_l(1+\delta_0)}\bigg(u-\frac{\alpha_lx(1+\delta_0)}{1+\delta_0-\beta_l}\bigg)^2\bigg\}du\\
&\ \ - \exp\bigg\{\frac{\alpha_l^2y^2}{2(1+\delta_0-\beta_l)}+1\bigg\}\int_{-\infty}^{c_l(x,y)} \frac{1}{\sqrt{2\pi\beta_l}}\exp\bigg\{-\frac{1+\delta_0-\beta_l}{2\beta_l(1+\delta_0)}\bigg(u-\frac{\alpha_ly(1+\delta_0)}{1+\delta_0-\beta_l}\bigg)^2\bigg\}du\Bigg\},\end{align*}
\begin{align*}&\int_{D_l(x,y)} v(u) | M^l(x,u)-M^l(y,u)|du = \sqrt{\bigg(\frac{(1+\delta_0)}{(1+\delta_0-\beta_l)}\bigg)}\\
&\ \ \times \Bigg\{\exp\bigg\{\frac{\alpha_l^2x^2}{2(1+\delta_0-\beta_l)}+1\bigg\}\int_{-\infty}^{c_l(x,y)} \frac{1}{\sqrt{2\pi\beta_l}}\exp\bigg\{-\frac{1+\delta_0-\beta_l}{2\beta_l(1+\delta_0)}\bigg(u-\frac{\alpha_lx(1+\delta_0)}{1+\delta_0-\beta_l}\bigg)^2\bigg\}du\\
&\ \ - \exp\bigg\{\frac{\alpha_l^2y^2}{2(1+\delta_0-\beta_l)}+1\bigg\}\int_{-\infty}^{c_l(x,y)} \frac{1}{\sqrt{2\pi\beta_l}}\exp\bigg\{-\frac{1+\delta_0-\beta_l}{2\beta_l(1+\delta_0)}\bigg(u-\frac{\alpha_ly(1+\delta_0)}{1+\delta_0-\beta_l}\bigg)^2\bigg\}du\Bigg\},\end{align*}
where ![]() $c_l(x,y)=(\alpha_l^2 x^2-\alpha_l^2y^2)/(x-y)$
. Define
$c_l(x,y)=(\alpha_l^2 x^2-\alpha_l^2y^2)/(x-y)$
. Define
 \begin{eqnarray*}\overline{c}_{l,1}(x,y) & \,:\!= &\, \sqrt{\bigg(\frac{1+\delta_0-\beta_l}{\beta_l(1+\delta_0)}\bigg)}\bigg(c_l(x,y) - \frac{\alpha_lx(1+\delta_0)}{1+\delta_0-\beta_l}\bigg), \\[3pt]
\overline{c}_{l,2}(x,y) & \,:\!= &\, \sqrt{\bigg(\frac{1+\delta_0-\beta_l}{\beta_l(1+\delta_0)}\bigg)}\bigg(c_l(x,y) - \frac{\alpha_ly(1+\delta_0)}{1+\delta_0-\beta_l}\bigg) \\[3pt] \tilde{v}(x) & \,:\!= &\, \exp\bigg\{\frac{\alpha_l^2y^2}{2(1+\delta_0-\beta_l)}+1\bigg\},\end{eqnarray*}
\begin{eqnarray*}\overline{c}_{l,1}(x,y) & \,:\!= &\, \sqrt{\bigg(\frac{1+\delta_0-\beta_l}{\beta_l(1+\delta_0)}\bigg)}\bigg(c_l(x,y) - \frac{\alpha_lx(1+\delta_0)}{1+\delta_0-\beta_l}\bigg), \\[3pt]
\overline{c}_{l,2}(x,y) & \,:\!= &\, \sqrt{\bigg(\frac{1+\delta_0-\beta_l}{\beta_l(1+\delta_0)}\bigg)}\bigg(c_l(x,y) - \frac{\alpha_ly(1+\delta_0)}{1+\delta_0-\beta_l}\bigg) \\[3pt] \tilde{v}(x) & \,:\!= &\, \exp\bigg\{\frac{\alpha_l^2y^2}{2(1+\delta_0-\beta_l)}+1\bigg\},\end{eqnarray*}
and define ![]() $\Theta(x)$
as the CDF of a standard normal distribution; then we have
$\Theta(x)$
as the CDF of a standard normal distribution; then we have
 \begin{align*}&\frac{\int_{D_l(x,y)} v(u) | M^l(x,u)-M^l(y,u)|du}{v(x)v(y)}\\[3pt] &\quad = \sqrt{\bigg(\frac{(1+\delta_0)}{(1+\delta_0-\beta_l)}\bigg)}\bigg(\bigg\{\frac{\tilde{v}(x)}{v(x)v(y)}\{\Theta(\overline{c}_{l,1}(x,y))-\Theta(\overline{c}_{l,2}(x,y))\bigg\}\\[3pt] &\qquad + \Theta(\overline{c}_{l,2}(x,y))\bigg[\frac{\tilde{v}(x)}{v(x)}\bigg\{\frac{1}{v(y)}-\frac{1}{v(x)}\bigg\} +\frac{1}{v(x)}\bigg\{\frac{\tilde{v}(x)}{v(x)}-\frac{\tilde{v}(y)}{v(y)}\bigg\}\bigg]\bigg).\end{align*}
\begin{align*}&\frac{\int_{D_l(x,y)} v(u) | M^l(x,u)-M^l(y,u)|du}{v(x)v(y)}\\[3pt] &\quad = \sqrt{\bigg(\frac{(1+\delta_0)}{(1+\delta_0-\beta_l)}\bigg)}\bigg(\bigg\{\frac{\tilde{v}(x)}{v(x)v(y)}\{\Theta(\overline{c}_{l,1}(x,y))-\Theta(\overline{c}_{l,2}(x,y))\bigg\}\\[3pt] &\qquad + \Theta(\overline{c}_{l,2}(x,y))\bigg[\frac{\tilde{v}(x)}{v(x)}\bigg\{\frac{1}{v(y)}-\frac{1}{v(x)}\bigg\} +\frac{1}{v(x)}\bigg\{\frac{\tilde{v}(x)}{v(x)}-\frac{\tilde{v}(y)}{v(y)}\bigg\}\bigg]\bigg).\end{align*}
From here, it is straightforward to establish that all the functions in the differences are in the set ![]() $\textrm{Lip}_{\textsf{d}_1}(\textsf{X})$
with Lipschitz constants that do not depend on l, and, moreover, that the other terms are uniformly bounded in x,y,l (where relevant)—the proofs are omitted as they are standard.
$\textrm{Lip}_{\textsf{d}_1}(\textsf{X})$
with Lipschitz constants that do not depend on l, and, moreover, that the other terms are uniformly bounded in x,y,l (where relevant)—the proofs are omitted as they are standard.
Acknowledgement
Both authors were supported by KAUST baseline funding. A. Jasra was supported under the KAUST Competitive Research Grants Program Round 4 (CRG4) project Advanced Multi-Level Sampling Techniques for Bayesian Inverse Problems with Applications to Subsurface, ref. 2584. We would like to thank Alexandros Beskos, Sumeetpal Singh, and Xin Tong for useful conversations associated to this work. We thank two referees, the associate editor, and the editor-in-chief for substantial comments which have led to improvements of the article.