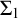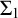1 Introduction
We provide a
![]() $\Sigma _1$
-definition in set theory of a finite sequence and prove that it exhibits a universal extension property among the countable models of set theory.
$\Sigma _1$
-definition in set theory of a finite sequence and prove that it exhibits a universal extension property among the countable models of set theory.
Main Theorem. For any computably axiomatizable theory
![]() $\overline {\mathrm {ZF}}$
extending ZF, there is a
$\overline {\mathrm {ZF}}$
extending ZF, there is a
![]() $\Sigma _1$
-definable finite sequence
$\Sigma _1$
-definable finite sequence
with the following properties:
-
(1)
 ${\mathrm {ZF}}$
proves that the sequence is finite.
${\mathrm {ZF}}$
proves that the sequence is finite. -
(2) In any transitive model M of
 $\overline {\mathrm {ZF}}$
, the sequence is empty.
$\overline {\mathrm {ZF}}$
, the sequence is empty. -
(3) If M is a countable model of
 $\overline {\mathrm {ZF}}$
in which the sequence is s and
$\overline {\mathrm {ZF}}$
in which the sequence is s and
 $t \in M$
is any finite sequence (in the sense of M) extending s, then there is a covering end-extension of M to a model
$t \in M$
is any finite sequence (in the sense of M) extending s, then there is a covering end-extension of M to a model
 $N \models \overline {\mathrm {ZF}}$
in which the sequence is exactly t, and in which every set of M is countable.
$N \models \overline {\mathrm {ZF}}$
in which the sequence is exactly t, and in which every set of M is countable.
-
(4) Indeed, for statements (2) and (3), it suffices merely that
 $M\models {\mathrm {ZF}}$
and end-extends a submodel
$M\models {\mathrm {ZF}}$
and end-extends a submodel
 $W\models \overline {\mathrm {ZF}}$
of height at least
$W\models \overline {\mathrm {ZF}}$
of height at least
 $(\omega _1^L)^M$
.
$(\omega _1^L)^M$
.
The
![]() $\Sigma _1$
-definable universal finite sequence is a sister to the universal finite set of Hamkins and Woodin [Reference Hamkins and Woodin10], which provided a
$\Sigma _1$
-definable universal finite sequence is a sister to the universal finite set of Hamkins and Woodin [Reference Hamkins and Woodin10], which provided a
![]() $\Sigma _2$
-definable finite set having a universal extension property with respect to the models of set theory under rank-extensions (also known as top-extensions), namely, those for which the new sets of the extension all have higher rank than the old sets; thus, the smaller model is determined by a cut in the
$\Sigma _2$
-definable finite set having a universal extension property with respect to the models of set theory under rank-extensions (also known as top-extensions), namely, those for which the new sets of the extension all have higher rank than the old sets; thus, the smaller model is determined by a cut in the
![]() $V_\alpha $
-hierarchy of the larger model. The Hamkins–Woodin universal set naturally used a
$V_\alpha $
-hierarchy of the larger model. The Hamkins–Woodin universal set naturally used a
![]() $\Sigma _2$
-definition, as it is precisely the
$\Sigma _2$
-definition, as it is precisely the
![]() $\Sigma _2$
-assertions that are witnessed in the rank initial segments
$\Sigma _2$
-assertions that are witnessed in the rank initial segments
![]() $V_\alpha $
of the universe.
$V_\alpha $
of the universe.
In the main result of this article, in contrast, we seek universality with respect to arbitrary end-extensions of models of set theory, and since it is precisely the
![]() $\Sigma _1$
-assertions that are witnessed in
$\Sigma _1$
-assertions that are witnessed in
![]() $\in $
-initial segments of the universe, we seek accordingly a
$\in $
-initial segments of the universe, we seek accordingly a
![]() $\Sigma _1$
-definable universal sequence. In short, we seek to undertake a
$\Sigma _1$
-definable universal sequence. In short, we seek to undertake a
![]() $\Sigma _1$
analogue of the
$\Sigma _1$
analogue of the
![]() $\Sigma _2$
analysis of [Reference Hamkins and Woodin10], working with end-extensions of models of set theory rather than rank extensions.
$\Sigma _2$
analysis of [Reference Hamkins and Woodin10], working with end-extensions of models of set theory rather than rank extensions.
Both the
![]() $\Sigma _1$
-definable universal finite sequence of this article and the
$\Sigma _1$
-definable universal finite sequence of this article and the
![]() $\Sigma _2$
-definable universal finite set of [Reference Hamkins and Woodin10] should be seen as set-theoretic analogues of Woodin’s universal algorithm, a Turing machine program that provably enumerates a finite sequence of numbers exhibiting a universal extension property with respect to the models of arithmetic under end-extensions [Reference Blanck2, Reference Blanck and Enayat3, Reference Hamkins8, Reference Woodin16].
$\Sigma _2$
-definable universal finite set of [Reference Hamkins and Woodin10] should be seen as set-theoretic analogues of Woodin’s universal algorithm, a Turing machine program that provably enumerates a finite sequence of numbers exhibiting a universal extension property with respect to the models of arithmetic under end-extensions [Reference Blanck2, Reference Blanck and Enayat3, Reference Hamkins8, Reference Woodin16].
To clarify terms, an end-extension of a model of set theory
![]() ${\left \langle M,\in ^M \right \rangle }$
is another model
${\left \langle M,\in ^M \right \rangle }$
is another model
![]() ${\left \langle N,\in ^N \right \rangle }$
, such that the first is a
${\left \langle N,\in ^N \right \rangle }$
, such that the first is a
![]() $\in $
-initial substructure of the second. That is,
$\in $
-initial substructure of the second. That is,
![]() $M\subseteq N$
and
$M\subseteq N$
and
![]() $\mathord {\in ^M}=\mathord {\in ^N\upharpoonright M}$
, but further, the new model does not add new elements to old sets; more precisely: if
$\mathord {\in ^M}=\mathord {\in ^N\upharpoonright M}$
, but further, the new model does not add new elements to old sets; more precisely: if
![]() $a\in ^N b\in M$
, then
$a\in ^N b\in M$
, then
![]() $a\in M$
and hence
$a\in M$
and hence
![]() $a\in ^M b$
. Such an end-extension is a covering end-extension if the larger model has a covering set, an object
$a\in ^M b$
. Such an end-extension is a covering end-extension if the larger model has a covering set, an object
![]() $m\in N$
such that
$m\in N$
such that
![]() $a\in ^N m$
for all
$a\in ^N m$
for all
![]() $a\in M$
. In this article, unless we say otherwise all extensions will be proper extensions. That is, we wish to exclude the trivial extension
$a\in M$
. In this article, unless we say otherwise all extensions will be proper extensions. That is, we wish to exclude the trivial extension
![]() $M \subseteq M$
.
$M \subseteq M$
.
Set theory, of course, overflows with instances of end-extensions and covering end-extensions. The rank-initial segments
![]() $V_\alpha $
end-extend to their higher instances
$V_\alpha $
end-extend to their higher instances
![]() $V_\beta $
, which also cover them, when
$V_\beta $
, which also cover them, when
![]() $\alpha <\beta $
; similarly, the hierarchy of the constructible universe
$\alpha <\beta $
; similarly, the hierarchy of the constructible universe
![]() $L_\alpha \subseteq L_\beta $
are covering end-extensions; every transitive set end-extends to all its supersets. The set-theoretic universe V is an end-extension of the constructible universe L and every forcing extension
$L_\alpha \subseteq L_\beta $
are covering end-extensions; every transitive set end-extends to all its supersets. The set-theoretic universe V is an end-extension of the constructible universe L and every forcing extension
![]() $M[G]$
is an end-extension of its ground model M, though neither of these extensions are covering. In particular, one should not confuse end-extensions with rank-extensions, where all the new sets come in only at higher ranks. Observe, however, that every
$M[G]$
is an end-extension of its ground model M, though neither of these extensions are covering. In particular, one should not confuse end-extensions with rank-extensions, where all the new sets come in only at higher ranks. Observe, however, that every
![]() $\Sigma _2$
-elementary end-extension is a rank-extension and that every rank-extension modeling ZF is a covering end-extension.
$\Sigma _2$
-elementary end-extension is a rank-extension and that every rank-extension modeling ZF is a covering end-extension.
In the proof of the main theorem, we shall make key use of the fact that every countable model of set theory has an elementary end-extension.
Theorem 1 (Keisler–Morley [Reference Keisler and Morley12])
Every countable model of ZF has an elementary end-extension.
For models of ZFC, this can be proved by means of a suitable definable ultrapower, in the language of set theory augmented with a generic well-order. The general ZF case can be proved using the omitting types theorem in order to ensure the end-extension property. The result is known not to generalize to uncountable models of set theory. For example, if
![]() $\kappa $
is the least inaccessible cardinal, then
$\kappa $
is the least inaccessible cardinal, then
![]() ${\left \langle V_\kappa ,\in \right \rangle }$
has no elementary end-extension.
${\left \langle V_\kappa ,\in \right \rangle }$
has no elementary end-extension.
To prove the main theorem we will make use of some reflection and absoluteness facts, which we state here precisely. The first is the reflection principle: for each formula
![]() $\varphi (x)$
, allowing parameters, and each set a there is a transitive set
$\varphi (x)$
, allowing parameters, and each set a there is a transitive set
![]() $m \ni a$
so that
$m \ni a$
so that
![]() $\varphi (x)$
reflects from V to m. We will also use the Lévy reflection theorem, asserting that
$\varphi (x)$
reflects from V to m. We will also use the Lévy reflection theorem, asserting that
![]() $\Sigma _1$
-assertions in set theory are absolute to
$\Sigma _1$
-assertions in set theory are absolute to
![]() $L_{\omega _1^L}$
, and the Shoenfield absoluteness theorem, asserting that
$L_{\omega _1^L}$
, and the Shoenfield absoluteness theorem, asserting that
![]() $\Sigma ^1_2$
-assertions about reals are absolute between models with the same countable ordinals.
$\Sigma ^1_2$
-assertions about reals are absolute between models with the same countable ordinals.
Finally, we will need the Gödel–Carnap fixed-point lemma for our definition of the
![]() $\Sigma _1$
-definable universal finite sequence. We give here a formulation of this lemma appropriate for our context.
$\Sigma _1$
-definable universal finite sequence. We give here a formulation of this lemma appropriate for our context.
Lemma 2 (Gödel–Carnap fixed-point lemma)
Let
![]() $\varphi (x,\bar y)$
be a formula in the language of set theory. Then there is a formula
$\varphi (x,\bar y)$
be a formula in the language of set theory. Then there is a formula
![]() $\psi (\bar y)$
so that
$\psi (\bar y)$
so that
![]() ${\mathrm {KP}}$
proves
${\mathrm {KP}}$
proves
![]() .
.
2 A new proof of the Barwise extension theorem
Our proof of the main theorem grows out of ideas in a certain new proof of the classical Barwise extension theorem, which we shall provide in this section as a warm-up to the main theorem.
Theorem 3 (Barwise extension theorem [Reference Barwise1])
Every countable model of ZF has an end-extension to a model of
![]() ${\mathrm {ZFC}}+V=L$
.
${\mathrm {ZFC}}+V=L$
.
The Barwise extension theorem is simultaneously (i) a technical culmination of the pioneering methods of Barwise in admissible set theory and infinitary logic, including the Barwise compactness and completeness theorems and the admissible cover, but also (ii) one of those rare mathematical theorems that is saturated with significance for the philosophy of mathematics and particularly the philosophy of set theory. The first author discussed these philosophical aspects at length in [Reference Hamkins6].
The new development here regarding this theorem is a new direct proof due to Hamkins, with the interesting feature—downright surprising in light of (i) above—that it makes no use of Barwise compactness and indeed no use of infinitary logic at all. Instead, the proof uses only classical methods of descriptive set theory, namely, the representation of
![]() $\Pi ^1_1$
-definable sets with well-founded trees, the Lévy and Shoenfield absoluteness theorems, the reflection theorem, and the Keisler–Morley theorem on elementary end-extensions of countable models of set theory.
$\Pi ^1_1$
-definable sets with well-founded trees, the Lévy and Shoenfield absoluteness theorems, the reflection theorem, and the Keisler–Morley theorem on elementary end-extensions of countable models of set theory.
Proof (Hamkins [Reference Hamkins7])
Suppose that M is a countable model of
![]() ${\mathrm {ZF}}$
set theory. Consider first the easier case, where M is
${\mathrm {ZF}}$
set theory. Consider first the easier case, where M is
![]() $\omega $
-nonstandard. For any standard natural number k, the reflection theorem ensures that there are arbitrarily high
$\omega $
-nonstandard. For any standard natural number k, the reflection theorem ensures that there are arbitrarily high
![]() $L_\alpha ^M$
satisfying the finite theory fragment
$L_\alpha ^M$
satisfying the finite theory fragment
![]() ${\mathrm {ZFC}}_k$
, and so every countable transitive set
${\mathrm {ZFC}}_k$
, and so every countable transitive set
![]() $m\in L^M$
has an end-extension to a model of
$m\in L^M$
has an end-extension to a model of
![]() ${\mathrm {ZFC}}_k+V=L$
. By overspill, there must be some nonstandard k for which
${\mathrm {ZFC}}_k+V=L$
. By overspill, there must be some nonstandard k for which
![]() $L^M$
thinks that every countable transitive set m has an end-extension to a countable model of
$L^M$
thinks that every countable transitive set m has an end-extension to a countable model of
![]() ${\mathrm {ZFC}}_k+V=L$
. This is a
${\mathrm {ZFC}}_k+V=L$
. This is a
![]() $\Pi ^1_2$
-statement about k, which will therefore also be true in M, by the Shoenfield absoluteness theorem. By the Keisler–Morley theorem, M has an elementary end-extension
$\Pi ^1_2$
-statement about k, which will therefore also be true in M, by the Shoenfield absoluteness theorem. By the Keisler–Morley theorem, M has an elementary end-extension
![]() $M^+$
. Let
$M^+$
. Let
![]() $\theta $
be a new ordinal on top of M, and let
$\theta $
be a new ordinal on top of M, and let
![]() $M^+[G]$
be a forcing extension in which
$M^+[G]$
be a forcing extension in which
![]() $m=V_\theta ^{M^+}$
becomes countable. Since the
$m=V_\theta ^{M^+}$
becomes countable. Since the
![]() $\Pi ^1_2$
-statement transfers to
$\Pi ^1_2$
-statement transfers to
![]() $M^+$
and then to
$M^+$
and then to
![]() $M^+[G]$
, there is in
$M^+[G]$
, there is in
![]() $M^+[G]$
an end-extension of
$M^+[G]$
an end-extension of
![]() $\langle m,\in ^{M^+}\rangle $
to a model
$\langle m,\in ^{M^+}\rangle $
to a model
![]() $\langle N,\in ^N\rangle $
that
$\langle N,\in ^N\rangle $
that
![]() $M^+[G]$
thinks satisfies
$M^+[G]$
thinks satisfies
![]() ${\mathrm {ZFC}}_k+V=L$
. Since k is nonstandard, this theory includes all of the actual
${\mathrm {ZFC}}_k+V=L$
. Since k is nonstandard, this theory includes all of the actual
![]() ${\mathrm {ZFC}}$
axioms, and since m end-extends M, we have found an end-extension of M to a model of
${\mathrm {ZFC}}$
axioms, and since m end-extends M, we have found an end-extension of M to a model of
![]() ${\mathrm {ZFC}}+V=L$
, as desired.
${\mathrm {ZFC}}+V=L$
, as desired.
Consider now the harder case, where M is
![]() $\omega $
-standard. Let
$\omega $
-standard. Let
![]() $M^+$
be an elementary end-extension of M, and consider
$M^+$
be an elementary end-extension of M, and consider
![]() $m=V_\theta ^{M^+}$
, where
$m=V_\theta ^{M^+}$
, where
![]() $\theta $
is a new ordinal above M. If
$\theta $
is a new ordinal above M. If
![]() $\langle m,\in ^{M^+}\rangle $
has an end-extension to a model of
$\langle m,\in ^{M^+}\rangle $
has an end-extension to a model of
![]() ${\mathrm {ZFC}}+V=L$
, then we’re done, since such a model would also end-extend M. So assume toward contradiction that there is no such end-extension of m. Let
${\mathrm {ZFC}}+V=L$
, then we’re done, since such a model would also end-extend M. So assume toward contradiction that there is no such end-extension of m. Let
![]() $M^+[G]$
be a forcing extension in which m has become countable. The assertion that m has no end-extension to a model of
$M^+[G]$
be a forcing extension in which m has become countable. The assertion that m has no end-extension to a model of
![]() ${\mathrm {ZFC}}+V=L$
is actually true and hence true in
${\mathrm {ZFC}}+V=L$
is actually true and hence true in
![]() $M^+[G]$
. This is a
$M^+[G]$
. This is a
![]() $\Pi ^1_1$
-assertion there about the real coding m. Every such assertion has a canonically associated tree, which is well-founded exactly when the statement is true. Since the statement is true in
$\Pi ^1_1$
-assertion there about the real coding m. Every such assertion has a canonically associated tree, which is well-founded exactly when the statement is true. Since the statement is true in
![]() $M^+[G]$
, this tree has some countable rank
$M^+[G]$
, this tree has some countable rank
![]() $\lambda $
there. Since these models have the standard
$\lambda $
there. Since these models have the standard
![]() $\omega $
, the tree associated with the statement is the same for us as inside the model, and since the statement is actually true, the tree is actually well-founded. So the rank
$\omega $
, the tree associated with the statement is the same for us as inside the model, and since the statement is actually true, the tree is actually well-founded. So the rank
![]() $\lambda $
comes from the well-founded part of the model.
$\lambda $
comes from the well-founded part of the model.
If
![]() $\lambda $
happens to be countable in
$\lambda $
happens to be countable in
![]() $L^{M^+}$
, then consider the assertion, “there is a countable transitive set, such that the assertion that it has no end-extension to a model of
$L^{M^+}$
, then consider the assertion, “there is a countable transitive set, such that the assertion that it has no end-extension to a model of
![]() ${\mathrm {ZFC}}+V=L$
has rank
${\mathrm {ZFC}}+V=L$
has rank
![]() $\lambda $
.” This is a
$\lambda $
.” This is a
![]() $\Sigma _1$
-assertion, since it is witnessed by the countable transitive set and the ranking function of the tree associated with the non-extension assertion. Since the parameters are countable in
$\Sigma _1$
-assertion, since it is witnessed by the countable transitive set and the ranking function of the tree associated with the non-extension assertion. Since the parameters are countable in
![]() $L^{M^+}$
, it follows by Lévy reflection that the statement is true in
$L^{M^+}$
, it follows by Lévy reflection that the statement is true in
![]() $L^{M^+}$
. So
$L^{M^+}$
. So
![]() $L^{M^+}$
has a countable transitive set, such that the assertion that it has no end-extension to a model of
$L^{M^+}$
has a countable transitive set, such that the assertion that it has no end-extension to a model of
![]() ${\mathrm {ZFC}}+V=L$
has rank
${\mathrm {ZFC}}+V=L$
has rank
![]() $\lambda $
. But since
$\lambda $
. But since
![]() $\lambda $
is actually well-founded, the statement would have to be actually true; but it isn’t, since
$\lambda $
is actually well-founded, the statement would have to be actually true; but it isn’t, since
![]() $L^{M^+}$
itself is such an extension, a contradiction.
$L^{M^+}$
itself is such an extension, a contradiction.
So we may assume
![]() $\lambda $
is uncountable in
$\lambda $
is uncountable in
![]() $L^{M^+}$
. In this case, since
$L^{M^+}$
. In this case, since
![]() $\lambda $
was actually well-ordered, it follows from the fact that
$\lambda $
was actually well-ordered, it follows from the fact that
![]() $M \prec M^+$
that
$M \prec M^+$
that
![]() $L^M$
is well-founded beyond its
$L^M$
is well-founded beyond its
![]() $\omega _1$
. Consider the statement “there is a countable transitive set having no end-extension to a model of
$\omega _1$
. Consider the statement “there is a countable transitive set having no end-extension to a model of
![]() ${\mathrm {ZFC}}+V=L$
.” This is a
${\mathrm {ZFC}}+V=L$
.” This is a
![]() $\Sigma ^1_2$
-sentence, which is true in
$\Sigma ^1_2$
-sentence, which is true in
![]() $M^+[G]$
by our assumption about m, and so by Shoenfield absoluteness, it is true in
$M^+[G]$
by our assumption about m, and so by Shoenfield absoluteness, it is true in
![]() $L^{M^+}$
and, because
$L^{M^+}$
and, because
![]() $M \prec M^+$
, hence also true in
$M \prec M^+$
, hence also true in
![]() $L^M$
. So
$L^M$
. So
![]() $L^M$
thinks there is a countable transitive set b having no end-extension to a model of
$L^M$
thinks there is a countable transitive set b having no end-extension to a model of
![]() ${\mathrm {ZFC}}+V=L$
. This is a
${\mathrm {ZFC}}+V=L$
. This is a
![]() $\Pi ^1_1$
-assertion about b, whose truth is witnessed in
$\Pi ^1_1$
-assertion about b, whose truth is witnessed in
![]() $L^M$
by a ranking of the associated tree. Since this rank would be countable in
$L^M$
by a ranking of the associated tree. Since this rank would be countable in
![]() $L^M$
and this model is well-founded up to its
$L^M$
and this model is well-founded up to its
![]() $\omega _1$
, the tree must be actually well-founded. But this is impossible, since it is not actually true that b has no such end-extension, since
$\omega _1$
, the tree must be actually well-founded. But this is impossible, since it is not actually true that b has no such end-extension, since
![]() $L^M$
itself is such an end-extension of b. Contradiction.
$L^M$
itself is such an end-extension of b. Contradiction.
Observe that if one desires to have a covering end-extension this is easily obtained by using the Keisler–Morley theorem to extend the end-extension further to an elementary end-extension.
We should like to note conversely that the Barwise extension theorem is an immediate consequence of our main theorem, which can be seen as a generalization of it. Specifically, the Barwise theorem follows from statement (4) of the main theorem, simply by taking
![]() $\overline {\mathrm {ZF}}$
to be the theory
$\overline {\mathrm {ZF}}$
to be the theory
![]() ${\mathrm {ZFC}}+V=L$
. Every model of ZF has an inner model of
${\mathrm {ZFC}}+V=L$
. Every model of ZF has an inner model of
![]() ${\mathrm {ZFC}}+V=L$
, and so the main theorem shows that not only does every countable model of ZF have an end-extension to a model of
${\mathrm {ZFC}}+V=L$
, and so the main theorem shows that not only does every countable model of ZF have an end-extension to a model of
![]() ${\mathrm {ZFC}}+V=L$
, but it has such an extension in which the original model is covered, making every element of it countable, and for which we may also control the universal sequence however we desire.
${\mathrm {ZFC}}+V=L$
, but it has such an extension in which the original model is covered, making every element of it countable, and for which we may also control the universal sequence however we desire.
Indeed, the main theorem provides an array of strengthenings of the Barwise extension theorem. For example, Corollary 10 shows that every countable model of set theory with a measurable cardinal has a covering end-extension to a model of
![]() ${\mathrm {ZFC}}+V=L[\mu ]$
; every countable model of set theory with extender-based large cardinals has a covering end-extension to a model satisfying
${\mathrm {ZFC}}+V=L[\mu ]$
; every countable model of set theory with extender-based large cardinals has a covering end-extension to a model satisfying
![]() $V=L[\vec E]$
; and every countable model of set theory with infinitely many Woodin cardinals and a measurable above has a covering end-extension to a model of
$V=L[\vec E]$
; and every countable model of set theory with infinitely many Woodin cardinals and a measurable above has a covering end-extension to a model of
![]() ${\mathrm {ZF}}+\text {AD}+{V=L(\mathbb {R})}$
. And there are many further interesting cases, where one end-extends a given countable model of set theory to a model satisfying a theory holding in a sufficiently strong submodel of the original model.
${\mathrm {ZF}}+\text {AD}+{V=L(\mathbb {R})}$
. And there are many further interesting cases, where one end-extends a given countable model of set theory to a model satisfying a theory holding in a sufficiently strong submodel of the original model.
3 The
 $\Sigma _1$
-definable universal finite sequence for end-extensions
$\Sigma _1$
-definable universal finite sequence for end-extensions
Let us now prove the main theorem. We restate it here for the benefit of the reader.
Main Theorem. For any computably axiomatizable theory
![]() $\overline {\mathrm {ZF}}$
extending ZF, there is a
$\overline {\mathrm {ZF}}$
extending ZF, there is a
![]() $\Sigma _1$
-definable finite sequence
$\Sigma _1$
-definable finite sequence
with the following properties:
-
(1)
 ${\mathrm {ZF}}$
proves that the sequence is finite.
${\mathrm {ZF}}$
proves that the sequence is finite. -
(2) In any transitive model M of
 $\overline {\mathrm {ZF}}$
, the sequence is empty.
$\overline {\mathrm {ZF}}$
, the sequence is empty. -
(3) If M is a countable model of
 $\overline {\mathrm {ZF}}$
in which the sequence is s and
$\overline {\mathrm {ZF}}$
in which the sequence is s and
 $t \in M$
is any finite sequence (in the sense of M) extending s, then there is a covering end-extension of M to a model
$t \in M$
is any finite sequence (in the sense of M) extending s, then there is a covering end-extension of M to a model
 $N \models \overline {\mathrm {ZF}}$
in which the sequence is exactly t, and in which every set of M is countable.
$N \models \overline {\mathrm {ZF}}$
in which the sequence is exactly t, and in which every set of M is countable. -
(4) Indeed, for statements (2) and (3), it suffices merely that
 $M\models {\mathrm {ZF}}$
and end-extends a submodel
$M\models {\mathrm {ZF}}$
and end-extends a submodel
 $W\models \overline {\mathrm {ZF}}$
of height at least
$W\models \overline {\mathrm {ZF}}$
of height at least
 $(\omega _1^L)^M$
.
$(\omega _1^L)^M$
.
Proof We undertake an analogue of the universal finite set construction of [Reference Hamkins and Woodin10], a construction which is itself a set-theoretic generalization of the universal algorithm [Reference Blanck2, Reference Blanck and Enayat3, Reference Hamkins8, Reference Woodin16], but combining it with the ideas of Hamkins’s proof of the Barwise extension theorem in section 2.
Fix a computable enumeration of the theory
![]() $\overline {\mathrm {ZF}}$
, to be used in all the models of set theory in which we refer to this theory, and let
$\overline {\mathrm {ZF}}$
, to be used in all the models of set theory in which we refer to this theory, and let
![]() $\overline {\mathrm {ZF}}_k$
be the finite theory consisting of the first k-many axioms appearing in this enumeration.
$\overline {\mathrm {ZF}}_k$
be the finite theory consisting of the first k-many axioms appearing in this enumeration.
As explained in [Reference Hamkins8], it will suffice for us to establish a weaker extension property, the adding-one extension property, which asserts that if s is the sequence defined in M then for any object a in M there is a covering end-extension N in which the defined sequence is
![]() $s^\smallfrown a$
. That is, the adding-one extension property allows one to extend the sequence by appending exactly one new object on the end, rather than a finite sequence. By iterating this property, of course, one can eventually append any standard-finite sequence, but such an inductive argument, it turns out, cannot establish the full extension property for nonstandard-finite extensions, for there are sequences with the adding-one extension property that do not have the full extension property.Footnote
1
Nevertheless, from any sequence with the adding-one extension property, one can define a new sequence with the arbitrary extension property. For example, one could simply concatenate all the finite sequences that appear on the given adding-one sequence. In this way, by adding one object to the original sequence, we can add an arbitrary (possibly nonstandard) finite sequence to the derived concatenated sequence. Therefore, for the rest of this proof, we shall aim only for the adding-one extension property.
$s^\smallfrown a$
. That is, the adding-one extension property allows one to extend the sequence by appending exactly one new object on the end, rather than a finite sequence. By iterating this property, of course, one can eventually append any standard-finite sequence, but such an inductive argument, it turns out, cannot establish the full extension property for nonstandard-finite extensions, for there are sequences with the adding-one extension property that do not have the full extension property.Footnote
1
Nevertheless, from any sequence with the adding-one extension property, one can define a new sequence with the arbitrary extension property. For example, one could simply concatenate all the finite sequences that appear on the given adding-one sequence. In this way, by adding one object to the original sequence, we can add an arbitrary (possibly nonstandard) finite sequence to the derived concatenated sequence. Therefore, for the rest of this proof, we shall aim only for the adding-one extension property.
As in [Reference Hamkins and Woodin10], we shall describe two set-theoretic processes, A and B. These processes are intended to be run inside, respectively,
![]() $\omega $
-nonstandard models and
$\omega $
-nonstandard models and
![]() $\omega $
-standard models and will then be merged in a way that provides a single definition fulfilling the desired properties.
$\omega $
-standard models and will then be merged in a way that provides a single definition fulfilling the desired properties.
Process
![]() ${\boldsymbol {A}}$
. We start by describing process A, intended to be run inside
${\boldsymbol {A}}$
. We start by describing process A, intended to be run inside
![]() $\omega $
-nonstandard models as an internal process, using whatever nonstandard natural numbers are to be found there. The process proceeds in a sequence of stages, placing one object onto the sequence at each successful stage. Stage n succeeds and
$\omega $
-nonstandard models as an internal process, using whatever nonstandard natural numbers are to be found there. The process proceeds in a sequence of stages, placing one object onto the sequence at each successful stage. Stage n succeeds and
![]() $a_n$
is defined, if there is a transitive set
$a_n$
is defined, if there is a transitive set
![]() $m_n$
, countable in L and containing as elements all earlier
$m_n$
, countable in L and containing as elements all earlier
![]() $m_i$
for stages
$m_i$
for stages
![]() $i<n$
, and a natural number
$i<n$
, and a natural number
![]() $k_n$
, smaller than all earlier
$k_n$
, smaller than all earlier
![]() $k_i$
, such that
$k_i$
, such that
![]() $a_n \in m_n$
and the structure
$a_n \in m_n$
and the structure
![]() ${\left \langle m_n,\in \right \rangle }$
has no covering end-extension to a model
${\left \langle m_n,\in \right \rangle }$
has no covering end-extension to a model
![]() ${\left \langle N,\in ^N \right \rangle }$
satisfying
${\left \langle N,\in ^N \right \rangle }$
satisfying
![]() $\overline {\mathrm {ZF}}_{k_n}$
, making every set in
$\overline {\mathrm {ZF}}_{k_n}$
, making every set in
![]() $m_n$
countable, and placing this very object
$m_n$
countable, and placing this very object
![]() $a_n$
onto its own A sequence at stage n as the last element. In slogan form: we place an object onto the sequence, if we find a countable transitive set having no covering end-extension in which we would have done so as the next and last element. This is altogether a
$a_n$
onto its own A sequence at stage n as the last element. In slogan form: we place an object onto the sequence, if we find a countable transitive set having no covering end-extension in which we would have done so as the next and last element. This is altogether a
![]() $\Delta _1$
-property of the data
$\Delta _1$
-property of the data
![]() $(m_n,a_n,k_n)$
, since the non-existence of such a model N is a
$(m_n,a_n,k_n)$
, since the non-existence of such a model N is a
![]() $\Pi ^1_1$
-assertion, whose truth can be verified by the ordinal ranking of the canonically associated well-founded tree. In particular, if there is such an end-extension, then there is one in L and countable in L. The process officially accepts and uses the triple
$\Pi ^1_1$
-assertion, whose truth can be verified by the ordinal ranking of the canonically associated well-founded tree. In particular, if there is such an end-extension, then there is one in L and countable in L. The process officially accepts and uses the triple
![]() $(m_n,a_n,k_n)$
, whose witnesses for this property are L-least. In other words, we accept the first triple to be verified in the L hierarchy, and use this triple to define
$(m_n,a_n,k_n)$
, whose witnesses for this property are L-least. In other words, we accept the first triple to be verified in the L hierarchy, and use this triple to define
![]() $a_n$
. The map
$a_n$
. The map
![]() $n\mapsto (m_n,k_n,a_n)$
is accordingly
$n\mapsto (m_n,k_n,a_n)$
is accordingly
![]() $\Sigma _1$
-definable.
$\Sigma _1$
-definable.
Although the definition may at first appear circular—we define
![]() $a_n$
, after all, by reference to the definition of the process A sequence inside N—one may use the Gödel–Carnap fixed point lemma to find a definition
$a_n$
, after all, by reference to the definition of the process A sequence inside N—one may use the Gödel–Carnap fixed point lemma to find a definition
![]() $\psi (n,a)$
for the map
$\psi (n,a)$
for the map
![]() $n\mapsto a_n$
that solves this recursion, allowing
$n\mapsto a_n$
that solves this recursion, allowing
![]() $\psi $
as described to refer to its own Gödel code
$\psi $
as described to refer to its own Gödel code
![]() . The same method is used in [Reference Hamkins and Woodin10], and one should view this as analogous to the common use of the Kleene recursion theorem in computability-theoretic arguments, including its use in the universal algorithm [Reference Hamkins8, Reference Woodin16].
. The same method is used in [Reference Hamkins and Woodin10], and one should view this as analogous to the common use of the Kleene recursion theorem in computability-theoretic arguments, including its use in the universal algorithm [Reference Hamkins8, Reference Woodin16].
Since the natural numbers
![]() $k_n$
are descending, there will be only finitely many successful stages, and so the sequence will be finite.
$k_n$
are descending, there will be only finitely many successful stages, and so the sequence will be finite.
We claim that in the relevant models, every
![]() $k_n$
arising from a successful stage is nonstandard; in particular,
$k_n$
arising from a successful stage is nonstandard; in particular,
![]() $\omega $
-standard models will have no successful process A stages. To see this, consider any countable model of set theory
$\omega $
-standard models will have no successful process A stages. To see this, consider any countable model of set theory
![]() $M\models {\mathrm {ZF}}$
, which end-extends a submodel
$M\models {\mathrm {ZF}}$
, which end-extends a submodel
![]() $W\models \overline {\mathrm {ZF}}$
of height at least
$W\models \overline {\mathrm {ZF}}$
of height at least
![]() $(\omega _1^L)^M$
, and let n be the last successful stage in M. Since the definition is
$(\omega _1^L)^M$
, and let n be the last successful stage in M. Since the definition is
![]() $\Sigma _1$
, by Lévy reflection it is absolute between M and W. For any standard k, by reflection the theory
$\Sigma _1$
, by Lévy reflection it is absolute between M and W. For any standard k, by reflection the theory
![]() $\overline {\mathrm {ZF}}_k$
is true in a transitive set
$\overline {\mathrm {ZF}}_k$
is true in a transitive set
![]() $N\in W$
, large enough to include
$N\in W$
, large enough to include
![]() $m_n$
as a countable set and the witnesses for the successful stages. Consequently,
$m_n$
as a countable set and the witnesses for the successful stages. Consequently,
![]() ${\left \langle N,\in ^W \right \rangle }\models \overline {\mathrm {ZF}}_k$
and thinks object
${\left \langle N,\in ^W \right \rangle }\models \overline {\mathrm {ZF}}_k$
and thinks object
![]() $a_n$
was added at stage n as the last object on the sequence. If
$a_n$
was added at stage n as the last object on the sequence. If
![]() $k_n \leq k$
, this would violate the success of stage n in M, since
$k_n \leq k$
, this would violate the success of stage n in M, since
![]() $m_n$
would have had such a covering end-extension after all. Therefore
$m_n$
would have had such a covering end-extension after all. Therefore
![]() $k<k_n$
for every standard k, and so
$k<k_n$
for every standard k, and so
![]() $k_n$
is nonstandard.
$k_n$
is nonstandard.
It remains to verify the extension property. Let M be a countable model of ZF set theory in which the sequence is s. (We don’t actually need the submodel W of
![]() $\overline {\mathrm {ZF}}$
for this part of the argument, provided that the earlier
$\overline {\mathrm {ZF}}$
for this part of the argument, provided that the earlier
![]() $k_i$
, if any, are nonstandard.) Let n be the first unsuccessful stage. Let k be nonstandard, but smaller than all previous
$k_i$
, if any, are nonstandard.) Let n be the first unsuccessful stage. Let k be nonstandard, but smaller than all previous
![]() $k_i$
. Since stage n did not succeed, it follows that for any transitive set m countable in
$k_i$
. Since stage n did not succeed, it follows that for any transitive set m countable in
![]() $L^M$
and containing the earlier
$L^M$
and containing the earlier
![]() $m_i$
, and for any set
$m_i$
, and for any set
![]() $a\in m$
, the structure
$a\in m$
, the structure
![]() ${\left \langle m,\in \right \rangle }^M$
does have a covering end-extension in M to a model making every set in m countable and satisfying
${\left \langle m,\in \right \rangle }^M$
does have a covering end-extension in M to a model making every set in m countable and satisfying
![]() $\overline {\mathrm {ZF}}_k +$
“object a was placed onto the sequence at stage n, the last successful stage,” since otherwise stage n would have succeeded. Further, for a given m, the existence of such an end-extension is a
$\overline {\mathrm {ZF}}_k +$
“object a was placed onto the sequence at stage n, the last successful stage,” since otherwise stage n would have succeeded. Further, for a given m, the existence of such an end-extension is a
![]() $\Sigma _1$
-property of the data
$\Sigma _1$
-property of the data
![]() $(m,a,k)$
, and so we may find the extensions in
$(m,a,k)$
, and so we may find the extensions in
![]() $L^M$
. Therefore,
$L^M$
. Therefore,
![]() $L^M$
thinks that for every countable set a and every countable transitive set m, there is a covering end-extension of
$L^M$
thinks that for every countable set a and every countable transitive set m, there is a covering end-extension of
![]() ${\left \langle m,\in \right \rangle }$
to a model
${\left \langle m,\in \right \rangle }$
to a model
![]() ${\left \langle N,\in ^N\right \rangle }$
making every set in m countable and satisfying
${\left \langle N,\in ^N\right \rangle }$
making every set in m countable and satisfying
![]() $\overline {\mathrm {ZF}}_k+$
“object a is placed onto the sequence at stage n, the last successful stage.” This is a
$\overline {\mathrm {ZF}}_k+$
“object a is placed onto the sequence at stage n, the last successful stage.” This is a
![]() $\Pi ^1_2$
-assertion (
$\Pi ^1_2$
-assertion (
![]() $\forall a,m\,\exists N\ldots $
), which by Shoenfield is therefore also true in M itself. By the Keisler–Morley theorem, M has an elementary end-extension
$\forall a,m\,\exists N\ldots $
), which by Shoenfield is therefore also true in M itself. By the Keisler–Morley theorem, M has an elementary end-extension
![]() $M^+$
, and so the statement will also be true in
$M^+$
, and so the statement will also be true in
![]() $M^+$
, as well as in all its forcing extensions, by Shoenfield absoluteness. Let
$M^+$
, as well as in all its forcing extensions, by Shoenfield absoluteness. Let
![]() $\theta $
be an ordinal of
$\theta $
be an ordinal of
![]() $M^+$
above M, and let
$M^+$
above M, and let
![]() $M^+[G]$
be a forcing extension making
$M^+[G]$
be a forcing extension making
![]() $V_\theta ^{M^+}$
countable. Thus, for any object a in M, we have a countable transitive set
$V_\theta ^{M^+}$
countable. Thus, for any object a in M, we have a countable transitive set
![]() $m=V_\theta ^{M^+}$
in
$m=V_\theta ^{M^+}$
in
![]() $M^+[G]$
, which by our observations must therefore have a covering end-extension N in
$M^+[G]$
, which by our observations must therefore have a covering end-extension N in
![]() $M^+[G]$
making every set in m countable and in which
$M^+[G]$
making every set in m countable and in which
![]() $\overline {\mathrm {ZF}}_k$
holds, plus the assertion that process A places object a onto the sequence at stage n, the last successful stage. Since N end-extends
$\overline {\mathrm {ZF}}_k$
holds, plus the assertion that process A places object a onto the sequence at stage n, the last successful stage. Since N end-extends
![]() $V_\theta ^{M^+}$
, which end-extends M, and since k is nonstandard, we have therefore found the desired covering end-extension of M to a model of
$V_\theta ^{M^+}$
, which end-extends M, and since k is nonstandard, we have therefore found the desired covering end-extension of M to a model of
![]() $\overline {\mathrm {ZF}}$
making every set in M countable and placing a as the next and last element on the sequence.
$\overline {\mathrm {ZF}}$
making every set in M countable and placing a as the next and last element on the sequence.
Process
![]() ${\boldsymbol {B}}$
. We turn now to process B, intended to be run as an internal process inside
${\boldsymbol {B}}$
. We turn now to process B, intended to be run as an internal process inside
![]() $\omega $
-standard models, using whatever (possibly nonstandard) ordinals are to be found there. The process will proceed in a sequence of stages, just as before, with each successful stage adding one object
$\omega $
-standard models, using whatever (possibly nonstandard) ordinals are to be found there. The process will proceed in a sequence of stages, just as before, with each successful stage adding one object
![]() $a_n$
to the sequence. Stage n is successful and
$a_n$
to the sequence. Stage n is successful and
![]() $a_n$
is defined, if there is a transitive set
$a_n$
is defined, if there is a transitive set
![]() $m_n$
countable in L and a countable ordinal
$m_n$
countable in L and a countable ordinal
![]() $\lambda _n$
, with
$\lambda _n$
, with
![]() $m_i \in m_n$
and
$m_i \in m_n$
and
![]() $\lambda _n < \lambda _i$
for all earlier stages
$\lambda _n < \lambda _i$
for all earlier stages
![]() $i<n$
, and with
$i<n$
, and with
![]() $\lambda _n \in m_n$
and a set
$\lambda _n \in m_n$
and a set
![]() $a_n\in m_n$
, such that the structure
$a_n\in m_n$
, such that the structure
![]() ${\left \langle m_n,\in \right \rangle }$
has no covering end-extension to a model
${\left \langle m_n,\in \right \rangle }$
has no covering end-extension to a model
![]() ${\left \langle N,\in ^N\right \rangle }$
making every set in
${\left \langle N,\in ^N\right \rangle }$
making every set in
![]() $m_n$
countable and satisfying
$m_n$
countable and satisfying
![]() $\overline {\mathrm {ZF}}+$
“process B places object
$\overline {\mathrm {ZF}}+$
“process B places object
![]() $a_n$
on the sequence at stage n, the last successful stage,” and furthermore, this property about
$a_n$
on the sequence at stage n, the last successful stage,” and furthermore, this property about
![]() $(m_n,a_n,\lambda _n)$
, which has complexity
$(m_n,a_n,\lambda _n)$
, which has complexity
![]() $\Pi ^1_1$
, has rank
$\Pi ^1_1$
, has rank
![]() $\lambda _n$
in the canonical representation of
$\lambda _n$
in the canonical representation of
![]() $\Pi ^1_1$
-assertions by well-founded trees. The acceptability of the data triple is a
$\Pi ^1_1$
-assertions by well-founded trees. The acceptability of the data triple is a
![]() $\Sigma _1$
-property, witnessed by the ranking function, and we officially accept the triple whose witness appears least in the L order. So the map
$\Sigma _1$
-property, witnessed by the ranking function, and we officially accept the triple whose witness appears least in the L order. So the map
![]() $n\mapsto a_n$
is
$n\mapsto a_n$
is
![]() $\Sigma _1$
-definable.
$\Sigma _1$
-definable.
Once again, the circularity in the definition can be removed by the Gödel–Carnap fixed-point lemma. Since the ordinals
![]() $\lambda _n$
are descending, there will be only finitely many successful stages, and so the sequence is finite.
$\lambda _n$
are descending, there will be only finitely many successful stages, and so the sequence is finite.
We claim that the ordinals
![]() $\lambda _n$
in the relevant models are nonstandard. Suppose that M is a countable model of
$\lambda _n$
in the relevant models are nonstandard. Suppose that M is a countable model of
![]() ${\mathrm {ZF}}$
that end-extends a submodel W of
${\mathrm {ZF}}$
that end-extends a submodel W of
![]() $\overline {\mathrm {ZF}}$
of height at least
$\overline {\mathrm {ZF}}$
of height at least
![]() $(\omega _1^L)^M$
, and let n be the last successful stage in M. Since the definition is
$(\omega _1^L)^M$
, and let n be the last successful stage in M. Since the definition is
![]() $\Sigma _1$
, it is absolute between M and W, and so W satisfies
$\Sigma _1$
, it is absolute between M and W, and so W satisfies
![]() $\overline {\mathrm {ZF}}$
plus the assertion that the object
$\overline {\mathrm {ZF}}$
plus the assertion that the object
![]() $a_n$
is placed onto the sequence at stage n, the last successful stage. So the statement asserting at stage n that
$a_n$
is placed onto the sequence at stage n, the last successful stage. So the statement asserting at stage n that
![]() $m_n$
has no covering end-extension and so on is actually false, since W itself is such an extension. So the tree representing the statement, which is determined the same in M as for us in the set-theoretic background because M is an
$m_n$
has no covering end-extension and so on is actually false, since W itself is such an extension. So the tree representing the statement, which is determined the same in M as for us in the set-theoretic background because M is an
![]() $\omega $
-model, is not actually well-founded. But M thought it was well-founded with rank
$\omega $
-model, is not actually well-founded. But M thought it was well-founded with rank
![]() $\lambda _n$
, and so
$\lambda _n$
, and so
![]() $\lambda _n$
must be nonstandard.
$\lambda _n$
must be nonstandard.
Let us now prove the extension property for process B in countable
![]() $\omega $
-standard models
$\omega $
-standard models
![]() $M\models {\mathrm {ZF}}$
end-extending a submodel
$M\models {\mathrm {ZF}}$
end-extending a submodel
![]() $W\models \overline {\mathrm {ZF}}$
of height at least
$W\models \overline {\mathrm {ZF}}$
of height at least
![]() $(\omega _1^L)^M$
. Suppose the sequence is s in M. Let n be the first unsuccessful stage, and consider any set a in M. By the Keisler–Morley theorem, we may find a countable elementary end-extension of M to a model
$(\omega _1^L)^M$
. Suppose the sequence is s in M. Let n be the first unsuccessful stage, and consider any set a in M. By the Keisler–Morley theorem, we may find a countable elementary end-extension of M to a model
![]() $M^+$
. Let
$M^+$
. Let
![]() $\theta $
be an ordinal of
$\theta $
be an ordinal of
![]() $M^+$
above M, and let
$M^+$
above M, and let
![]() $M^+[G]$
be a forcing extension in which
$M^+[G]$
be a forcing extension in which
![]() $m=V_\theta ^{M^+}$
is made countable. If
$m=V_\theta ^{M^+}$
is made countable. If
![]() $\langle m,\in ^{M^+}\rangle $
has a covering end-extension to a model of
$\langle m,\in ^{M^+}\rangle $
has a covering end-extension to a model of
![]() $\overline {\mathrm {ZF}}$
in which every set of m is made countable and object a is placed onto the sequence at stage n as the last successful stage, then we’d be done, since this would also serve as the desired end-extension of the original model M. So let us assume toward contradiction that there is no such end-extension of
$\overline {\mathrm {ZF}}$
in which every set of m is made countable and object a is placed onto the sequence at stage n as the last successful stage, then we’d be done, since this would also serve as the desired end-extension of the original model M. So let us assume toward contradiction that there is no such end-extension of
![]() $\langle m,\in ^{M^+}\rangle $
. This is a
$\langle m,\in ^{M^+}\rangle $
. This is a
![]() $\Pi ^1_1$
-assertion about m in
$\Pi ^1_1$
-assertion about m in
![]() $M^+[G]$
, which therefore has some ordinal rank
$M^+[G]$
, which therefore has some ordinal rank
![]() $\lambda $
there in the representation of
$\lambda $
there in the representation of
![]() $\Pi ^1_1$
-assertions by well-founded trees. Since the statement is really true (in the set-theoretic background of our universe), it follows that
$\Pi ^1_1$
-assertions by well-founded trees. Since the statement is really true (in the set-theoretic background of our universe), it follows that
![]() $\lambda $
must be in the well-founded part of
$\lambda $
must be in the well-founded part of
![]() $M^+[G]$
. In particular,
$M^+[G]$
. In particular,
![]() $\lambda <\lambda _i$
for all
$\lambda <\lambda _i$
for all
![]() $i<n$
, since those ordinals are nonstandard. So
$i<n$
, since those ordinals are nonstandard. So
![]() $M^+[G]$
thinks that “there is a countable transitive set m containing all the earlier
$M^+[G]$
thinks that “there is a countable transitive set m containing all the earlier
![]() $m_i$
and the witnesses for the success of the
$m_i$
and the witnesses for the success of the
![]() $\Sigma _1$
definition at those earlier stages and an element
$\Sigma _1$
definition at those earlier stages and an element
![]() $a\in m$
, such that the assertion that
$a\in m$
, such that the assertion that
![]() ${\left \langle m,\in \right \rangle }$
has no covering end-extension to a model making every set in m countable and satisfying
${\left \langle m,\in \right \rangle }$
has no covering end-extension to a model making every set in m countable and satisfying
![]() $\overline {\mathrm {ZF}} +$
‘object a is placed onto the sequence at stage n, the last successful stage’ has ordinal rank
$\overline {\mathrm {ZF}} +$
‘object a is placed onto the sequence at stage n, the last successful stage’ has ordinal rank
![]() $\lambda $
.” This is a
$\lambda $
.” This is a
![]() $\Sigma _1$
-assertion about
$\Sigma _1$
-assertion about
![]() $\lambda $
and the countable set containing the data and witnesses for the earlier successful stages of the process, since it is witnessed by the countable transitive set m and
$\lambda $
and the countable set containing the data and witnesses for the earlier successful stages of the process, since it is witnessed by the countable transitive set m and
![]() $a\in m$
and the ranking function of the tree that is canonically associated with the non-extension assertion about m.
$a\in m$
and the ranking function of the tree that is canonically associated with the non-extension assertion about m.
If
![]() $\lambda $
happens to be countable in
$\lambda $
happens to be countable in
![]() $L^{M^+}$
, then all the parameters of the assertion are countable in
$L^{M^+}$
, then all the parameters of the assertion are countable in
![]() $L^M$
, and so it follows by Lévy reflection that the statement is true in
$L^M$
, and so it follows by Lévy reflection that the statement is true in
![]() $L^{M^+}$
and hence in
$L^{M^+}$
and hence in
![]() $L^M$
. So
$L^M$
. So
![]() $L^M$
has a countable transitive set m, containing the witnesses for the earlier successful stages and an object
$L^M$
has a countable transitive set m, containing the witnesses for the earlier successful stages and an object
![]() $a\in m$
, such that the assertion that m has no covering end-extension to a model of
$a\in m$
, such that the assertion that m has no covering end-extension to a model of
![]() $\overline {\mathrm {ZF}}$
making every set in m countable and in which a is placed at stage n, the last stage, has rank
$\overline {\mathrm {ZF}}$
making every set in m countable and in which a is placed at stage n, the last stage, has rank
![]() $\lambda $
. But in this case, stage n would have succeeded, contradicting our assumption that it was the first unsuccessful stage.
$\lambda $
. But in this case, stage n would have succeeded, contradicting our assumption that it was the first unsuccessful stage.
So we may assume
![]() $\lambda $
is uncountable in
$\lambda $
is uncountable in
![]() $L^{M^+}$
. In this case, since
$L^{M^+}$
. In this case, since
![]() $\lambda $
was actually well-ordered, it follows that
$\lambda $
was actually well-ordered, it follows that
![]() $L^M$
is well-founded beyond its
$L^M$
is well-founded beyond its
![]() $\omega _1$
. This implies that there could have been no earlier successful stages in M, since the
$\omega _1$
. This implies that there could have been no earlier successful stages in M, since the
![]() $\lambda _i$
must be nonstandard countable ordinals in
$\lambda _i$
must be nonstandard countable ordinals in
![]() $L^M$
. Thus,
$L^M$
. Thus,
![]() $n=0$
, or in other words, there is nothing yet on the sequence. Consider the statement “there is a countable transitive set m with an element
$n=0$
, or in other words, there is nothing yet on the sequence. Consider the statement “there is a countable transitive set m with an element
![]() $a\in m$
, such that m has no covering end-extension to a model of
$a\in m$
, such that m has no covering end-extension to a model of
![]() $\overline {\mathrm {ZF}}$
making every set in m countable, in which the sequence is
$\overline {\mathrm {ZF}}$
making every set in m countable, in which the sequence is
![]() ${\left \langle a\right \rangle }$
, having exactly one successful stage.” This is a
${\left \langle a\right \rangle }$
, having exactly one successful stage.” This is a
![]() $\Sigma ^1_2$
sentence, which is true in
$\Sigma ^1_2$
sentence, which is true in
![]() $M^+[G]$
by our assumption about m, and so by Shoenfield absoluteness, it is true in
$M^+[G]$
by our assumption about m, and so by Shoenfield absoluteness, it is true in
![]() $L^{M^+}$
and hence also in
$L^{M^+}$
and hence also in
![]() $L^M$
. So
$L^M$
. So
![]() $L^M$
thinks there is a countable transitive set m with an element
$L^M$
thinks there is a countable transitive set m with an element
![]() $a\in m$
, such that m has no covering end-extension to a model of
$a\in m$
, such that m has no covering end-extension to a model of
![]() $\overline {\mathrm {ZF}}$
in which every set in m is countable and the sequence is exactly
$\overline {\mathrm {ZF}}$
in which every set in m is countable and the sequence is exactly
![]() ${\left \langle a \right \rangle }$
. But in this case, there would have been a successful stage after all, contrary to what we proved earlier.
${\left \langle a \right \rangle }$
. But in this case, there would have been a successful stage after all, contrary to what we proved earlier.
Altogether, therefore, we conclude that
![]() $V_\theta ^{M^+}$
must have had the desired end-extension after all, and so we’ve verified the extension property of process B for the relevant countable
$V_\theta ^{M^+}$
must have had the desired end-extension after all, and so we’ve verified the extension property of process B for the relevant countable
![]() $\omega $
-standard models of set theory.
$\omega $
-standard models of set theory.
Process
![]() ${\boldsymbol {C}}$
. We shall now merge processes A and B into a single process C, providing a single uniform
${\boldsymbol {C}}$
. We shall now merge processes A and B into a single process C, providing a single uniform
![]() $\Sigma _1$
-definition that will work in all the relevant countable models of set theory. Process C proceeds in stages. At each successful stage, it will place one new object onto the sequence, either for an A-reason or for a B-reason. The A-reasons will involve data
$\Sigma _1$
-definition that will work in all the relevant countable models of set theory. Process C proceeds in stages. At each successful stage, it will place one new object onto the sequence, either for an A-reason or for a B-reason. The A-reasons will involve data
![]() $(m_n,a_n,k_n)$
, and the B-reasons will involve data
$(m_n,a_n,k_n)$
, and the B-reasons will involve data
![]() $(m_n,a_n,\lambda _n)$
, where we insist that
$(m_n,a_n,\lambda _n)$
, where we insist that
![]() $m_n$
is a transitive set countable in L and
$m_n$
is a transitive set countable in L and
![]() $m_i \in m_n$
for the
$m_i \in m_n$
for the
![]() $m_i$
used for either reason at earlier stages
$m_i$
used for either reason at earlier stages
![]() $i<n$
, that
$i<n$
, that
![]() $a_n\in m_n$
, and that
$a_n\in m_n$
, and that
![]() $k_n<k_i$
for the earlier A-reason stages
$k_n<k_i$
for the earlier A-reason stages
![]() $i<n$
, if this is an A-reason stage, and
$i<n$
, if this is an A-reason stage, and
![]() $\lambda _n<\lambda _i$
for the earlier B-reason stages, if this is a B-reason stage; once there has been a successful A-reason stage, then we proceed only with the A-reason stages, but the
$\lambda _n<\lambda _i$
for the earlier B-reason stages, if this is a B-reason stage; once there has been a successful A-reason stage, then we proceed only with the A-reason stages, but the
![]() $m_i$
for the A-reasons must see all the data for the previously successful B-reason stages. In particular, each B-reason
$m_i$
for the A-reasons must see all the data for the previously successful B-reason stages. In particular, each B-reason
![]() $\lambda _j$
should be an element of any later A-reason
$\lambda _j$
should be an element of any later A-reason
![]() $m_i$
. As before, the data is acceptable if
$m_i$
. As before, the data is acceptable if
![]() $m_n$
has no covering end-extension to a model
$m_n$
has no covering end-extension to a model
![]() ${\left \langle N,\in ^N\right \rangle }$
making every set in
${\left \langle N,\in ^N\right \rangle }$
making every set in
![]() $m_n$
countable and satisfying the relevant theory (using
$m_n$
countable and satisfying the relevant theory (using
![]() $\overline {\mathrm {ZF}}_{k_n}$
at A-reason stages and full
$\overline {\mathrm {ZF}}_{k_n}$
at A-reason stages and full
![]() $\overline {\mathrm {ZF}}$
at B-reason stages) plus the assertion that this new process C has exactly one new successful stage, placing object
$\overline {\mathrm {ZF}}$
at B-reason stages) plus the assertion that this new process C has exactly one new successful stage, placing object
![]() $a_n$
onto the process C sequence, and furthermore, in the B-reason case, the assertion that there is no such N has rank
$a_n$
onto the process C sequence, and furthermore, in the B-reason case, the assertion that there is no such N has rank
![]() $\lambda _n$
. The acceptability of such a data triple is a
$\lambda _n$
. The acceptability of such a data triple is a
![]() $\Sigma _1$
-property, since it is verified for each reason type by the rankings of certain trees, as with processes A and B above. A stage is successful if any data is verified as acceptable for it, and we use the data and the reason type whose witness appears first in the L-order. This defines the process C sequence
$\Sigma _1$
-property, since it is verified for each reason type by the rankings of certain trees, as with processes A and B above. A stage is successful if any data is verified as acceptable for it, and we use the data and the reason type whose witness appears first in the L-order. This defines the process C sequence
![]() $n\mapsto a_n$
, which has complexity
$n\mapsto a_n$
, which has complexity
![]() $\Sigma _1$
.
$\Sigma _1$
.
We complete the argument by observing that our process A and B analysis goes through for process C. The sequence is finite since the
![]() $k_n$
and
$k_n$
and
![]() $\lambda _n$
can go down only finitely many times. At any A-reason stage, the number
$\lambda _n$
can go down only finitely many times. At any A-reason stage, the number
![]() $k_n$
must be nonstandard, and at any B-reason stage, the ordinal
$k_n$
must be nonstandard, and at any B-reason stage, the ordinal
![]() $\lambda _n$
must be nonstandard. In any
$\lambda _n$
must be nonstandard. In any
![]() $\omega $
-nonstandard model, we achieve the extension property for process C for the same reasons as process A; and in any
$\omega $
-nonstandard model, we achieve the extension property for process C for the same reasons as process A; and in any
![]() $\omega $
-standard model, we achieve the extension property for process C just as with process B.
$\omega $
-standard model, we achieve the extension property for process C just as with process B.
As an immediate corollary, let us see that we can get a universal finite sequence for extensions in the L-hierarchy, which was our original motivation for this project. If M and N are models of
![]() $V = L$
, say that N is an L-extension of M if M is an initial segment in the
$V = L$
, say that N is an L-extension of M if M is an initial segment in the
![]() $L_\alpha $
-hierarchy for N. Compare this to the notion of a rank-extension, where N is a rank-extension of M if M is an initial segment in the
$L_\alpha $
-hierarchy for N. Compare this to the notion of a rank-extension, where N is a rank-extension of M if M is an initial segment in the
![]() $V_\alpha $
-hierarchy for N.
$V_\alpha $
-hierarchy for N.
Corollary 4 (Universal finite sequence for L-extensions)
There is a
![]() $\Sigma _1$
-definable sequence
$\Sigma _1$
-definable sequence
with the following properties:
-
(1)
 ${\mathrm {ZF}}$
proves the sequence is finite.
${\mathrm {ZF}}$
proves the sequence is finite. -
(2) In any transitive model of
 ${\mathrm {ZF}}$
, the sequence is empty.
${\mathrm {ZF}}$
, the sequence is empty. -
(3) If M is a countable model of
 ${\mathrm {ZFC}}+V=L$
in which the sequence is s and
${\mathrm {ZFC}}+V=L$
in which the sequence is s and
 $t \in M$
is any finite sequence extending s, then there is an L-extension
$t \in M$
is any finite sequence extending s, then there is an L-extension
 $N \models {\mathrm {ZFC}}+V=L$
of M in which every set in M is countable and the sequence is exactly t.
$N \models {\mathrm {ZFC}}+V=L$
of M in which every set in M is countable and the sequence is exactly t.
Proof This follows from the main theorem using
![]() $\overline {\mathrm {ZF}} = {\mathrm {ZFC}}+V=L$
and the observation that, by the absoluteness of the
$\overline {\mathrm {ZF}} = {\mathrm {ZFC}}+V=L$
and the observation that, by the absoluteness of the
![]() $L_\alpha $
-hierarchy, among models of
$L_\alpha $
-hierarchy, among models of
![]() $V=L$
being an end-extension is equivalent to being an L-extension.
$V=L$
being an end-extension is equivalent to being an L-extension.
In the context of models of arithmetic, the universal algorithm exhibited the extension property with respect to all models of arithmetic, not just the countable models. But in the context of set theory, we achieve the extension property of the universal finite sequence in the main theorem only for the countable models of set theory. This was because at certain points in the proof, we made key use of some results, such as the Keisler–Morley theorem, which hold for the countable models of set theory but not generally.
It is therefore natural to inquire whether this limitation can be removed. Can there be a
![]() $\Sigma _1$
-definable universal finite sequence exhibiting the extension property for all models of set theory, including uncountable models? That would make the situation analogous with the universal algorithm for models of arithmetic.
$\Sigma _1$
-definable universal finite sequence exhibiting the extension property for all models of set theory, including uncountable models? That would make the situation analogous with the universal algorithm for models of arithmetic.
Alas, the answer is no. If there are sufficiently well-founded uncountable models, then there can be no generalization of the universal finite sequence to uncountable models of set theory. Specifically, suppose that M is model of set theory that is well-founded at least to true
![]() $\omega _1$
. We claim that no end-extension of M can have new
$\omega _1$
. We claim that no end-extension of M can have new
![]() $\Sigma _1$
-facts, and in particular, the universal sequence cannot gain new elements in an end-extension. The reason is that if N is an end-extension of M, then any
$\Sigma _1$
-facts, and in particular, the universal sequence cannot gain new elements in an end-extension. The reason is that if N is an end-extension of M, then any
![]() $\Sigma _1$
-fact true in N is true in
$\Sigma _1$
-fact true in N is true in
![]() $L_{{\omega _1}^L}^N$
by Lévy absoluteness, and this latter model cannot exceed the true
$L_{{\omega _1}^L}^N$
by Lévy absoluteness, and this latter model cannot exceed the true
![]() $L_{{\omega _1}^L}$
, for then we would have collapsed the true
$L_{{\omega _1}^L}$
, for then we would have collapsed the true
![]() $\omega _1$
to be countable.
$\omega _1$
to be countable.
Meanwhile, the question would remain whether that is the only kind of exception.
Question 5. Does the main theorem generalize to the case of uncountable models of set theory, whose well-founded part does not include the true
![]() $\omega _1$
?
$\omega _1$
?
4 A refined version of the main theorem, with applications
We should like now to prove a refined version of the main theorem, by isolating exactly the features one needs of the theory in order to undertake the proof of the main theorem.
One feature of the theory
![]() $\overline {\mathrm {ZF}}$
that we used was that it satisfied a form of the reflection principle. It will turn out, however, that a weak form of reflection will suffice. Specifically, let us define that a theory T is reflexive to transitive sets, if for any finitely many axioms of T, the theory proves that those axioms hold cofinally in the transitive sets. The difference between this and full reflection is that here, we reflect only assertions of the theory, rather than arbitrary true assertions.
$\overline {\mathrm {ZF}}$
that we used was that it satisfied a form of the reflection principle. It will turn out, however, that a weak form of reflection will suffice. Specifically, let us define that a theory T is reflexive to transitive sets, if for any finitely many axioms of T, the theory proves that those axioms hold cofinally in the transitive sets. The difference between this and full reflection is that here, we reflect only assertions of the theory, rather than arbitrary true assertions.
The theory ZF and all its extensions are reflexive to transitive sets, of course, by the reflection principle. But also, the theory
![]() ${\mathrm {ZFC}}^-+V=L$
is reflexive to transitive sets, where
${\mathrm {ZFC}}^-+V=L$
is reflexive to transitive sets, where
![]() ${\mathrm {ZFC}}^-$
is Zermelo–Fraenkel set theory without the power set axiom,Footnote
2
since one can reflect along the L-hierarchy. Meanwhile, KP is not reflexive, nor is any finitely axiomatizable theory. In general, the reflexive property is weaker than the reflection theorem for T, since models of
${\mathrm {ZFC}}^-$
is Zermelo–Fraenkel set theory without the power set axiom,Footnote
2
since one can reflect along the L-hierarchy. Meanwhile, KP is not reflexive, nor is any finitely axiomatizable theory. In general, the reflexive property is weaker than the reflection theorem for T, since models of
![]() ${\mathrm {ZFC}}^-$
, for example, do not necessarily satisfy the reflection theorem, as proved in [Reference Friedman, Kanovei and Gitman4], but nevertheless, the theory is reflexive to transitive sets, since if
${\mathrm {ZFC}}^-$
, for example, do not necessarily satisfy the reflection theorem, as proved in [Reference Friedman, Kanovei and Gitman4], but nevertheless, the theory is reflexive to transitive sets, since if
![]() $M\models {\mathrm {ZFC}}^-$
and
$M\models {\mathrm {ZFC}}^-$
and
![]() $a\in M$
, then we can code a with a set of ordinals
$a\in M$
, then we can code a with a set of ordinals
![]() $A\in M$
and consider
$A\in M$
and consider
![]() $L[A]^M$
, which is a model of
$L[A]^M$
, which is a model of
![]() ${\mathrm {ZFC}}^-$
containing a and having an
${\mathrm {ZFC}}^-$
containing a and having an
![]() $\mathord {{\mathrm {Ord}}}$
-hierarchy, which is enough to prove the reflection theorem. So we get transitive models of the form
$\mathord {{\mathrm {Ord}}}$
-hierarchy, which is enough to prove the reflection theorem. So we get transitive models of the form
![]() $L_\alpha [A]$
satisfying any desired finite fragment of
$L_\alpha [A]$
satisfying any desired finite fragment of
![]() ${\mathrm {ZFC}}^-$
and containing the set a.
${\mathrm {ZFC}}^-$
and containing the set a.
Another consequence of ZF that we used in the main argument was the characterization of
![]() $\Pi ^1_1$
-assertions via well-founded trees. According to [Reference Simpson15, Lemma V.1.8], however, this characterization is provable in
$\Pi ^1_1$
-assertions via well-founded trees. According to [Reference Simpson15, Lemma V.1.8], however, this characterization is provable in
![]() ${\mathrm {ACA}}_0$
. In particular, it will be provable in any set theory extending KP, and KP is sufficient to provide ordinal rankings of those trees.
${\mathrm {ACA}}_0$
. In particular, it will be provable in any set theory extending KP, and KP is sufficient to provide ordinal rankings of those trees.
It follows that
![]() $\Pi ^1_1$
-assertions about reals are absolute between a model M of
$\Pi ^1_1$
-assertions about reals are absolute between a model M of
![]() ${\mathrm {KP}}$
and its end-extensions
${\mathrm {KP}}$
and its end-extensions
![]() $N\models {\mathrm {KP}}$
, since if the statement is true in the smaller model M, then it has the ordinal ranking of the tree, which will still exist in the larger model, verifying the
$N\models {\mathrm {KP}}$
, since if the statement is true in the smaller model M, then it has the ordinal ranking of the tree, which will still exist in the larger model, verifying the
![]() $\Pi ^1_1$
-statement there; and if the statement fails in the smaller model, then it has the counterexample real, which will still exist in the larger model.
$\Pi ^1_1$
-statement there; and if the statement fails in the smaller model, then it has the counterexample real, which will still exist in the larger model.
The Lévy reflection theorem, asserting that
![]() $\Sigma _1$
-assertions in set theory are absolute to
$\Sigma _1$
-assertions in set theory are absolute to
![]() $L_{\omega _1^L}$
, follows from
$L_{\omega _1^L}$
, follows from
![]() $\Pi ^1_1$
-absoluteness. The upward direction is immediate; conversely, if a
$\Pi ^1_1$
-absoluteness. The upward direction is immediate; conversely, if a
![]() $\Sigma _1$
-assertion is true in M, then by Löwenheim–Skolem there is a countable witness, and this amounts to the truth of a
$\Sigma _1$
-assertion is true in M, then by Löwenheim–Skolem there is a countable witness, and this amounts to the truth of a
![]() $\Sigma ^1_1$
-assertion, which is therefore absolute to
$\Sigma ^1_1$
-assertion, which is therefore absolute to
![]() $L_{{\omega _1}^L}^M$
.
$L_{{\omega _1}^L}^M$
.
The Shoenfield absoluteness principle, however, the assertion that
![]() $\Sigma ^1_2$
-assertions about reals are absolute between models with the same countable ordinals, appears to be strictly stronger. Shoenfield absoluteness is provable in
$\Sigma ^1_2$
-assertions about reals are absolute between models with the same countable ordinals, appears to be strictly stronger. Shoenfield absoluteness is provable in
![]() $\Pi ^1_1\text {-CA}_0$
, according to [Reference Simpson15, Theorem VII.4.14]. Because
$\Pi ^1_1\text {-CA}_0$
, according to [Reference Simpson15, Theorem VII.4.14]. Because
![]() $\Pi ^1_1\text {-CA}_0$
is stronger than KP, we shall need to impose an extra assumption on the theory S concerning this.
$\Pi ^1_1\text {-CA}_0$
is stronger than KP, we shall need to impose an extra assumption on the theory S concerning this.
In the proof of the main theorem, we had used the Keisler–Morley theorem, stating that every countable model M of ZF has an elementary end-extension
![]() $M^+$
. A closer inspection of the proof, however, will reveal that a somewhat weaker property will suffice. Specifically, what we shall need in Theorem 7 is merely that for every countable model M of the theory, there is a
$M^+$
. A closer inspection of the proof, however, will reveal that a somewhat weaker property will suffice. Specifically, what we shall need in Theorem 7 is merely that for every countable model M of the theory, there is a
![]() $\Sigma _1$
-elementary covering end-extension
$\Sigma _1$
-elementary covering end-extension
![]() $M^+$
satisfying the theory (or at least satisfying the Shoenfield absoluteness property).
$M^+$
satisfying the theory (or at least satisfying the Shoenfield absoluteness property).
While all extensions of ZF have this property, it turns out that KP does not. Specifically,
![]() $L_{\omega _1^{\mathrm {CK}}}$
, the minimum transitive model of KP plus the axiom of infinity, can have no such covering
$L_{\omega _1^{\mathrm {CK}}}$
, the minimum transitive model of KP plus the axiom of infinity, can have no such covering
![]() $\Sigma _1$
-elementary end-extension (Ali Enayat proved this in email correspondence). Meanwhile, Kaufmann [Reference Kaufmann11] shows that satisfying
$\Sigma _1$
-elementary end-extension (Ali Enayat proved this in email correspondence). Meanwhile, Kaufmann [Reference Kaufmann11] shows that satisfying
![]() $\Sigma _n$
-collection implies the existence of a
$\Sigma _n$
-collection implies the existence of a
![]() $\Sigma _n$
-elementary end-extension, for
$\Sigma _n$
-elementary end-extension, for
![]() $n\geq 2$
. An easy modification of his argument gives that we may assume the end-extension to be covering.
$n\geq 2$
. An easy modification of his argument gives that we may assume the end-extension to be covering.
With the above discussion in mind, we make the following definition.
Definition 6. A pair of theories S and T are suitable for the
![]() $\Sigma _1$
-definable universal sequence, provided that theory S has the following properties
$\Sigma _1$
-definable universal sequence, provided that theory S has the following properties
-
(1) S extends KP.
-
(2) Countable models of S satisfy
 $\Sigma ^1_2$
-absoluteness to L and to their forcing extensions.
$\Sigma ^1_2$
-absoluteness to L and to their forcing extensions. -
(3) Every countable model
 $M\models S$
has a
$M\models S$
has a
 $\Sigma _1$
-elementary covering end-extension
$\Sigma _1$
-elementary covering end-extension
 $M^+$
, which also satisfies the
$M^+$
, which also satisfies the
 $\Sigma ^1_2$
-absoluteness to its L and forcing extensions.
$\Sigma ^1_2$
-absoluteness to its L and forcing extensions.
and the theory T has the following properties
-
(1) T extends KP.
-
(2) T is computably enumerable.
-
(3) T is reflexive to transitive sets.
A theory T is suitable all by itself, if it has all the properties, making a suitable pair with itself.
It is clear that ZF, and indeed any computably enumerable extension of ZF, is suitable. Our earlier discussion shows that
![]() ${\mathrm {ZF}}^{-}$
also is suitable.
${\mathrm {ZF}}^{-}$
also is suitable.
We can now state a version of the main theorem for these suitable theories.
Theorem 7. Assume that theories S and T are suitable for the
![]() $\Sigma _1$
-definable universal finite sequence, as defined above. Then there is a
$\Sigma _1$
-definable universal finite sequence, as defined above. Then there is a
![]() $\Sigma _1$
-definable finite sequence
$\Sigma _1$
-definable finite sequence
with the following properties:
-
(1) S proves that the sequence is finite.
-
(2) In any transitive model M of T, the sequence is empty.
-
(3) If M is a countable model of T in which the sequence is s and
 $t \in M$
is any finite sequence (in the sense of M) extending s, then there is a covering end-extension of M to a model
$t \in M$
is any finite sequence (in the sense of M) extending s, then there is a covering end-extension of M to a model
 $N \models T$
in which the sequence is exactly t, and in which every set in M becomes countable in N.
$N \models T$
in which the sequence is exactly t, and in which every set in M becomes countable in N. -
(4) Indeed, for statements (2) and (3), it suffices merely that
 $M\models S$
and end-extends a submodel
$M\models S$
and end-extends a submodel
 $W\models T$
of height at least
$W\models T$
of height at least
 $(\omega _1^L)^M$
.
$(\omega _1^L)^M$
.
This is proved just as the main theorem, as our modifications in Definition 6 exactly capture what was needed in the proof.
Question 8. Are there more generous notions of suitability, for which the conclusions of the main theorem can still be established?
We can drop the reflexive-to-transitive-sets requirement on the theory T, for example, if we are willing to have the universal extension property for the sequence only in
![]() $\omega $
-standard models, because our process B analysis did not require that reflexive property. But can we drop that requirement in any case?
$\omega $
-standard models, because our process B analysis did not require that reflexive property. But can we drop that requirement in any case?
Just as the main theorem had the Barwise extension theorem as an immediate consequence, we also get the following consequence of the generalized version of the theorem.
Corollary 9. Assume S and T are suitable theories, in the sense of definition 6. Then for every countable model
![]() $M\models S$
end-extending a submodel
$M\models S$
end-extending a submodel
![]() $W\models T$
of height at least
$W\models T$
of height at least
![]() $(\omega _1^L)^M$
, there is a covering end-extension of M to a model of T, and indeed, one in which every set of M becomes countable.
$(\omega _1^L)^M$
, there is a covering end-extension of M to a model of T, and indeed, one in which every set of M becomes countable.
In slogan form, the corollary expresses what can be seen as a sweeping new multiverse modal principle: any statement true in an inner model is true again in an end-extension.
This corollary is an immediate consequence of Theorem 7 statement (4), but one can also give a direct proof of the same style as we gave in §2 for the Barwise extension theorem.
We are fascinated by some of the particular instances of this phenomenon. For example, if M has a measurable cardinal
![]() $\kappa $
, then we can collapse it by forcing, so that
$\kappa $
, then we can collapse it by forcing, so that
![]() $M[G]$
thinks
$M[G]$
thinks
![]() $\kappa $
is now a countable ordinal. But nevertheless, there will be an end-extension N of
$\kappa $
is now a countable ordinal. But nevertheless, there will be an end-extension N of
![]() $M[G]$
which again has a measurable cardinal—a new measurable cardinal is resurrected.
$M[G]$
which again has a measurable cardinal—a new measurable cardinal is resurrected.
-
(1) Every countable model M of
 ${\mathrm {ZFC}}$
with a measurable cardinal has a covering end-extension to a model N of
${\mathrm {ZFC}}$
with a measurable cardinal has a covering end-extension to a model N of
 ${\mathrm {ZFC}}+V=L[\mu ]$
.
${\mathrm {ZFC}}+V=L[\mu ]$
. -
(2) Every countable model M of
 ${\mathrm {ZFC}}$
with extender-based large cardinals has a covering end-extension to a model N satisfying
${\mathrm {ZFC}}$
with extender-based large cardinals has a covering end-extension to a model N satisfying
 ${\mathrm {ZFC}}+V=L[\vec E]$
.
${\mathrm {ZFC}}+V=L[\vec E]$
. -
(3) Every countable model M of
 ${\mathrm {ZFC}}$
with infinitely many Woodin cardinals and a measurable above has a covering end-extension to a model N of
${\mathrm {ZFC}}$
with infinitely many Woodin cardinals and a measurable above has a covering end-extension to a model N of
 ${\mathrm {ZF}}+\text {AD}+V=L(\mathbb {R})$
.
${\mathrm {ZF}}+\text {AD}+V=L(\mathbb {R})$
. -
(4) And in each case, we can furthermore arrange that every set of M is countable in the extension model N.
By Theorem 7, we can of course also control the
![]() $\Sigma _1$
-definable universal finite sequence in such end-extensions.
$\Sigma _1$
-definable universal finite sequence in such end-extensions.
5 End-extensional potentialism
We should like now to draw out the consequences of the main theorem for set-theoretic end-extensional potentialism. Consider the potentialist system consisting of the countable models of set theory, a multiverse of models of set theory, forming a Kripke model under the end-extension relation, where here we wish to allow the trivial end-extension
![]() $M \subseteq M$
. (Let us consider the models of a fixed suitable theory T, such as any computably enumerable theory
$M \subseteq M$
. (Let us consider the models of a fixed suitable theory T, such as any computably enumerable theory
![]() $\overline {\mathrm {ZF}}$
extending ZF.) In this potentialist system we may naturally interpret the modal operators, so
$\overline {\mathrm {ZF}}$
extending ZF.) In this potentialist system we may naturally interpret the modal operators, so
![]() is true in a model M, if there is an end-extension in which
is true in a model M, if there is an end-extension in which
![]() $\varphi $
is true; and
$\varphi $
is true; and
![]() is true in M, if all end-extensions satisfy
is true in M, if all end-extensions satisfy
![]() $\varphi $
. This is therefore a version of potentialism—one of many in set theory—as described in [Reference Hamkins and Linnebo9]. Let us call it end-extensional potentialism.
$\varphi $
. This is therefore a version of potentialism—one of many in set theory—as described in [Reference Hamkins and Linnebo9]. Let us call it end-extensional potentialism.
Linnebo and others [Reference Hamkins and Linnebo9, Reference Linnebo13, Reference Linnebo and Shapiro14] have emphasized the contrast between height-potentialism and width-potentialism in the philosophy of set theory, where with height-potentialism the set-theoretic universe fragments can grow taller, perhaps adding new ordinals on top, while with width-potentialism, the universe grows outward, perhaps adding new subsets to old sets as with forcing.
End-extensional potentialism is naturally a form both of height-potentialism and width-potentialism, since the extensions of a model can extend the ordinals of that model to taller ordinals and also new subsets of old sets can appear in an end-extension.
Theorem 11. The modal logic of end-extensional potentialism, for the countable models of any fixed suitable set theory, is exactly S4.
This result is proved exactly as the analogous results for arithmetic potentialism [Reference Hamkins8] and rank-extensional potentialism [Reference Hamkins and Woodin10] using, respectively, the universal algorithm and the
![]() $\Sigma _2$
-definable universal finite set. Specifically, see [Reference Hamkins8, Theorem 28] for full details. The point is, any potentialist system which admits a universal finite sequence—a definition for a finite sequence which can be arbitrarily extended as you extend in the potentialist system—will have S4 as its modal validities.
$\Sigma _2$
-definable universal finite set. Specifically, see [Reference Hamkins8, Theorem 28] for full details. The point is, any potentialist system which admits a universal finite sequence—a definition for a finite sequence which can be arbitrarily extended as you extend in the potentialist system—will have S4 as its modal validities.
Let us highlight, however, the important fact that getting S4 as an upper bound for the modal validities in general needs to allow formulae to have a single natural number parameter (for the length of the universal finite sequence in the current world). As we discuss in §6, if you consider only sentences then the modal validities may go beyond S4.
We also find it natural to consider a related and somewhat more permissive potentialist system, the
![]() $\Delta _0$
-elementary potentialist system, which consists of the countable models of set theory, ordered by
$\Delta _0$
-elementary potentialist system, which consists of the countable models of set theory, ordered by
![]() $\Delta _0$
-elementary extension, rather than just end-extension. That is, N extends M in this potentialist system if M is a
$\Delta _0$
-elementary extension, rather than just end-extension. That is, N extends M in this potentialist system if M is a
![]() $\Delta _0$
-elementary submodel of N. Since end-extensions are
$\Delta _0$
-elementary submodel of N. Since end-extensions are
![]() $\Delta _0$
-elementary, this is somewhat more permissive than end-extensional potentialism.
$\Delta _0$
-elementary, this is somewhat more permissive than end-extensional potentialism.
Corollary 12. The modal logic of
![]() $\Delta _0$
-elementary potentialism, for the countable models of any fixed suitable set theory, is exactly S4.
$\Delta _0$
-elementary potentialism, for the countable models of any fixed suitable set theory, is exactly S4.
Proof The point is, the universal finite sequence for end-extensions is also a universal finite sequence for this potentialist system. The universal finite sequence for end-extensions gives us the needed
![]() $\Delta _0$
-elementary extensions satisfying the new facts. And if M is a
$\Delta _0$
-elementary extensions satisfying the new facts. And if M is a
![]() $\Delta _0$
-elementary submodel of N then N agrees with the
$\Delta _0$
-elementary submodel of N then N agrees with the
![]() $\Sigma _1$
-theory of M, so the universal finite sequence as defined in N must end-extend the sequence as defined in M.
$\Sigma _1$
-theory of M, so the universal finite sequence as defined in N must end-extend the sequence as defined in M.
6 The end-extensional maximality principle
In this section we introduce and investigate the end-extensional maximality principle, as well as the corresponding maximality principle for
![]() $\Delta _0$
-elementary extensions of models of set theory.
$\Delta _0$
-elementary extensions of models of set theory.
Definition 13. The maximality principle is true at a model M in a potentialist system, if
![]() for any assertion
for any assertion
![]() $\varphi $
in the language of M.
$\varphi $
in the language of M.
Thus, the end-extensional maximality principle asserts that every possibly necessary statement is already true, in the potentialist system consisting of the countable models of set theory under end-extension, and similarly, the
![]() $\Delta _0$
-elementary-extensional maximality principle makes this assertion with respect to
$\Delta _0$
-elementary-extensional maximality principle makes this assertion with respect to
![]() $\Delta _0$
-elementary extensions.
$\Delta _0$
-elementary extensions.
In these two cases, the main theorem of the article shows that we cannot allow parameters into the schema, even merely natural number parameters, because the assertion that the universal sequence is defined at n is a possibly necessary statement that will not yet be true for large enough n. (Meanwhile, in various other potentialist systems, such as those considered in [Reference Hamkins and Linnebo9], one can sometimes allow parameters into the schema, or certain kinds of parameters.) For this reason, it is also clear that no
![]() $\omega $
-standard model of set theory can satisfy the maximality principle, since standard natural numbers are absolutely definable.
$\omega $
-standard model of set theory can satisfy the maximality principle, since standard natural numbers are absolutely definable.
Let us begin by establishing that end-extensional and
![]() $\Delta _0$
-elementary possibility for assertions in the language of set theory, in the context of
$\Delta _0$
-elementary possibility for assertions in the language of set theory, in the context of
![]() $\omega $
-nonstandard models, are equivalent to each other, and furthermore this kind of possibility is expressible as a first-order schema in the language of set theory.
$\omega $
-nonstandard models, are equivalent to each other, and furthermore this kind of possibility is expressible as a first-order schema in the language of set theory.
We found it worthwhile to aim for a somewhat general version of this result, and so let us say that a theory T is very suitable, if (i) T is suitable; (ii) T satisfies the Keisler-Morley theorem, meaning that every countable model of T has a covering elementary end-extension; (iii) T proves the Mostowski collapse lemma; and (iv) T proves the reflection schema with countable parameters, namely, if
![]() $\varphi (a)$
holds of a hereditarily countable set a, then every set is contained in a transitive model of
$\varphi (a)$
holds of a hereditarily countable set a, then every set is contained in a transitive model of
![]() $\varphi (a)$
.
$\varphi (a)$
.
This notion is stronger than the merely suitable theories, and perhaps the main interest is simply the theory ZFC itself. In particular, it follows from well-known facts that ZF is very suitable, as well as every computably enumerable extension of ZF; and
![]() ${\mathrm {ZF}}^{-} + V=L$
also is very suitable. On the other hand, work of Friedman et al. [Reference Friedman, Kanovei and Gitman4] shows that
${\mathrm {ZF}}^{-} + V=L$
also is very suitable. On the other hand, work of Friedman et al. [Reference Friedman, Kanovei and Gitman4] shows that
![]() ${\mathrm {ZF}}^{-}$
is not very suitable.
${\mathrm {ZF}}^{-}$
is not very suitable.
Theorem 14 (Characterization of end-extensional possibility)
Consider any countable
![]() $\omega $
-nonstandard model
$\omega $
-nonstandard model
![]() ${\left \langle M,\in ^M\right \rangle }$
in the potentialist system of a fixed very suitable set theory T, such as ZF or any c.e. extension of ZF. In particular T is computably enumerable and accordingly let
${\left \langle M,\in ^M\right \rangle }$
in the potentialist system of a fixed very suitable set theory T, such as ZF or any c.e. extension of ZF. In particular T is computably enumerable and accordingly let
![]() $T_k$
be the subtheory of T consisting of the first k axioms along a fixed enumeration. For any assertion
$T_k$
be the subtheory of T consisting of the first k axioms along a fixed enumeration. For any assertion
![]() $\varphi (a)$
in the language of set theory about a countable object
$\varphi (a)$
in the language of set theory about a countable object
![]() $a \in M$
, the following are equivalent:
$a \in M$
, the following are equivalent:
-
(1)
 in the end-extensional potentialist system of the countable models of T. That is, M has an end-extension satisfying T and
in the end-extensional potentialist system of the countable models of T. That is, M has an end-extension satisfying T and
 $\varphi (a)$
.
$\varphi (a)$
. -
(2)
 in the
in the
 $\Delta _0$
-elementary potentialist system. That is, M has a
$\Delta _0$
-elementary potentialist system. That is, M has a
 $\Delta _0$
-elementary extension satisfying T and
$\Delta _0$
-elementary extension satisfying T and
 $\varphi (a)$
.
$\varphi (a)$
. -
(3) M thinks of every countable transitive set
 $m \ni a$
and every standard number k that the structure
$m \ni a$
and every standard number k that the structure
 ${\left \langle m,\in ^M\right \rangle }$
end-extends to a model
${\left \langle m,\in ^M\right \rangle }$
end-extends to a model
 ${\left \langle N,\in ^N\right \rangle }\models T_k+\varphi (a)$
.
${\left \langle N,\in ^N\right \rangle }\models T_k+\varphi (a)$
. -
(4) M thinks of every real x and every standard natural number k that there is an
 $\omega $
-model of
$\omega $
-model of
 $T_k + \varphi (a)$
which contains x.
$T_k + \varphi (a)$
which contains x. -
(5) (For sentences)
 $\varphi $
is consistent with T plus the
$\varphi $
is consistent with T plus the
 $\Sigma _1$
-theory of M.
$\Sigma _1$
-theory of M.
Proof
![]() $(1 \Rightarrow 2)$
This is immediate, since every end-extension is
$(1 \Rightarrow 2)$
This is immediate, since every end-extension is
![]() $\Delta _0$
-elementary.
$\Delta _0$
-elementary.
![]() $(2 \Rightarrow 3)$
Suppose toward a contradiction that
$(2 \Rightarrow 3)$
Suppose toward a contradiction that
![]() $(2)$
holds and
$(2)$
holds and
![]() $(3)$
fails. Fix k witnessing the failure and fix countable transitive
$(3)$
fails. Fix k witnessing the failure and fix countable transitive
![]() $m \in M$
so that M thinks m has no end-extension to a model of
$m \in M$
so that M thinks m has no end-extension to a model of
![]() $T_k + \varphi (a)$
. This is a
$T_k + \varphi (a)$
. This is a
![]() $\Pi ^1_1$
-fact about m and a, so M has a ranking function witnessing that the tree corresponding to the
$\Pi ^1_1$
-fact about m and a, so M has a ranking function witnessing that the tree corresponding to the
![]() $\Pi ^1_1$
-fact is well-founded. This ranking function will remain a ranking function in any
$\Pi ^1_1$
-fact is well-founded. This ranking function will remain a ranking function in any
![]() $\Delta _0$
-elementary extension, so any such extension must agree that m has no such end-extension. By
$\Delta _0$
-elementary extension, so any such extension must agree that m has no such end-extension. By
![]() $(2)$
, let N be a
$(2)$
, let N be a
![]() $\Delta _0$
-elementary extension of M in which
$\Delta _0$
-elementary extension of M in which
![]() $T+\varphi (a)$
holds. Since the Keisler–Morley theorem holds for T, we may assume without loss that N is a covering extension, with
$T+\varphi (a)$
holds. Since the Keisler–Morley theorem holds for T, we may assume without loss that N is a covering extension, with
![]() $c \in N$
so that
$c \in N$
so that
![]() $N \models x \in c$
for each
$N \models x \in c$
for each
![]() $x \in M$
. By the very suitable reflection schema, c has an end-extension in N to a model of
$x \in M$
. By the very suitable reflection schema, c has an end-extension in N to a model of
![]() $T_k + \varphi (a)$
. This end-extension of c is also an end-extension of m, and so N thinks that m has an end-extension to a model of
$T_k + \varphi (a)$
. This end-extension of c is also an end-extension of m, and so N thinks that m has an end-extension to a model of
![]() $T_k + \varphi (a)$
, a contradiction.
$T_k + \varphi (a)$
, a contradiction.
![]() $(3 \Rightarrow 1)$
By overspill there is a nonstandard k so that M thinks every countable transitive set end-extends to a model of
$(3 \Rightarrow 1)$
By overspill there is a nonstandard k so that M thinks every countable transitive set end-extends to a model of
![]() $T_k + \varphi (a)$
. By the Keisler–Morley theorem for T, let
$T_k + \varphi (a)$
. By the Keisler–Morley theorem for T, let
![]() $M^+$
be a countable elementary end-extension of M with a covering set m, and let
$M^+$
be a countable elementary end-extension of M with a covering set m, and let
![]() $M^+[G]$
be a forcing extension which collapses m to be countable. The assertion that every countable transitive set end-extends to a model of
$M^+[G]$
be a forcing extension which collapses m to be countable. The assertion that every countable transitive set end-extends to a model of
![]() $T_k + \varphi (a)$
is
$T_k + \varphi (a)$
is
![]() $\Pi ^1_2$
, and thus by Shoenfield absoluteness we can transfer its truth in
$\Pi ^1_2$
, and thus by Shoenfield absoluteness we can transfer its truth in
![]() $M^+$
to
$M^+$
to
![]() $M^+[G]$
. So
$M^+[G]$
. So
![]() $M^+[G]$
sees an end-extension of m satisfying
$M^+[G]$
sees an end-extension of m satisfying
![]() $T_k + \varphi (a)$
. This end-extension witnesses that M satisfies
$T_k + \varphi (a)$
. This end-extension witnesses that M satisfies
![]() .
.
![]() $(3 \Leftrightarrow 4)$
This is a standard fact, using the Mostowski collapse lemma to know that an arbitrary countable transitive set can be coded by a real. Note that this equivalence does not need M to be
$(3 \Leftrightarrow 4)$
This is a standard fact, using the Mostowski collapse lemma to know that an arbitrary countable transitive set can be coded by a real. Note that this equivalence does not need M to be
![]() $\omega $
-nonstandard nor most of the assumptions on T.
$\omega $
-nonstandard nor most of the assumptions on T.
![]() $(1 \Rightarrow 5)$
The
$(1 \Rightarrow 5)$
The
![]() $\Sigma _1$
-theory of a model is preserved by going to end-extensions, so if
$\Sigma _1$
-theory of a model is preserved by going to end-extensions, so if
![]() $\varphi $
holds in some end-extension of M then it must be consistent with the
$\varphi $
holds in some end-extension of M then it must be consistent with the
![]() $\Sigma _1$
-theory of M.
$\Sigma _1$
-theory of M.
![]() $(5 \Rightarrow 3)$
Let N be a model of
$(5 \Rightarrow 3)$
Let N be a model of
![]() $T + \varphi $
plus the
$T + \varphi $
plus the
![]() $\Sigma _1$
-theory of M. By the reflection principle satisfied by T we get that N thinks that every countable transitive set is contained in a model of
$\Sigma _1$
-theory of M. By the reflection principle satisfied by T we get that N thinks that every countable transitive set is contained in a model of
![]() $T_k + \varphi $
, for any standard k. Suppose toward a contradiction that
$T_k + \varphi $
, for any standard k. Suppose toward a contradiction that
![]() $(3)$
fails, so for some standard k, the model M thinks there is a countable transitive set m with no end-extension to a model of
$(3)$
fails, so for some standard k, the model M thinks there is a countable transitive set m with no end-extension to a model of
![]() $T_k + \varphi $
. As in the argument for
$T_k + \varphi $
. As in the argument for
![]() $(1 \Rightarrow 2)$
, this is a
$(1 \Rightarrow 2)$
, this is a
![]() $\Pi ^1_1$
-fact about m and so its truth in M is witnessed by a certain well-founded tree with a ranking function to the ordinals. The assertion that there is such m thus appears in the
$\Pi ^1_1$
-fact about m and so its truth in M is witnessed by a certain well-founded tree with a ranking function to the ordinals. The assertion that there is such m thus appears in the
![]() $\Sigma _1$
-theory of M. So N must think there is a countable transitive set with no end-extension to a model of
$\Sigma _1$
-theory of M. So N must think there is a countable transitive set with no end-extension to a model of
![]() $T_k + \varphi $
, a contradiction.
$T_k + \varphi $
, a contradiction.
It follows as a corollary that if
![]() , either with end-extensional or
, either with end-extensional or
![]() $\Delta _0$
-elementary-extensional potentialism, then there is a concrete reason for this, namely, there is some standard k and some countable transitive set
$\Delta _0$
-elementary-extensional potentialism, then there is a concrete reason for this, namely, there is some standard k and some countable transitive set
![]() $m\ni a$
in M such that M thinks m has no end-extension to a model of
$m\ni a$
in M such that M thinks m has no end-extension to a model of
![]() $T_k+\neg \varphi (a)$
. This is a
$T_k+\neg \varphi (a)$
. This is a
![]() $\Sigma ^1_2$
-assertion in the parameter a.
$\Sigma ^1_2$
-assertion in the parameter a.
It is natural to inquire whether the parameter a of Theorem 14 could be uncountable in M. The answer is no. In general, neither
![]() $(1 \Rightarrow 3)$
nor
$(1 \Rightarrow 3)$
nor
![]() $(2 \Rightarrow 3)$
holds if a is uncountable in M. To see this, consider
$(2 \Rightarrow 3)$
holds if a is uncountable in M. To see this, consider
![]() $a = \omega _1^M$
. Then it is possible—in either potentialist system—that a be made countable. However, no
$a = \omega _1^M$
. Then it is possible—in either potentialist system—that a be made countable. However, no
![]() $n \in M$
which end-extends a can think that a is countable.
$n \in M$
which end-extends a can think that a is countable.
For the rest of this discussion, fix a very suitable theory T. We say that a collection S of
![]() $\Sigma _1$
-sentences is a maximal
$\Sigma _1$
-sentences is a maximal
![]() $\Sigma _1$
-theory over T if
$\Sigma _1$
-theory over T if
![]() $T + S$
is consistent and S is maximal among the sets of
$T + S$
is consistent and S is maximal among the sets of
![]() $\Sigma _1$
-sentences consistent with T. One can easily construct a maximal
$\Sigma _1$
-sentences consistent with T. One can easily construct a maximal
![]() $\Sigma _1$
-theory by enumerating the
$\Sigma _1$
-theory by enumerating the
![]() $\Sigma _1$
-sentences and adding them one at a time, so long as the resulting theory is consistent with T. The same argument shows that every collection of
$\Sigma _1$
-sentences and adding them one at a time, so long as the resulting theory is consistent with T. The same argument shows that every collection of
![]() $\Sigma _1$
-sentences consistent with T is contained in a maximal
$\Sigma _1$
-sentences consistent with T is contained in a maximal
![]() $\Sigma _1$
-theory.
$\Sigma _1$
-theory.
An
![]() $\omega $
-standard model M of T, of course, can never have a maximal
$\omega $
-standard model M of T, of course, can never have a maximal
![]() $\Sigma _1$
-theory, because assertions like “the
$\Sigma _1$
-theory, because assertions like “the
![]() $\Sigma _1$
-definable universal finite sequence has length at least n” are
$\Sigma _1$
-definable universal finite sequence has length at least n” are
![]() $\Sigma _1$
-sentences for standard n. For the same reason, the universal finite sequence in any model of T with a maximal
$\Sigma _1$
-sentences for standard n. For the same reason, the universal finite sequence in any model of T with a maximal
![]() $\Sigma _1$
-theory will necessarily have nonstandard length.
$\Sigma _1$
-theory will necessarily have nonstandard length.
Theorem 15. The following are equivalent for any very suitable theory T and any countable
![]() $M \models T$
.
$M \models T$
.
-
(1) M satisfies the end-extensional maximality principle.
-
(2) M satisfies the
 $\Delta _0$
-elementary-extensional maximality principle.
$\Delta _0$
-elementary-extensional maximality principle. -
(3) The
 $\Sigma _1$
-theory of M is a maximal
$\Sigma _1$
-theory of M is a maximal
 $\Sigma _1$
-theory over T.
$\Sigma _1$
-theory over T.
Proof
![]() $(1 \Leftrightarrow 2)$
This holds because M satisfies
$(1 \Leftrightarrow 2)$
This holds because M satisfies
![]() in one potentialist system if and only if it does in the other, by Theorem 14.
in one potentialist system if and only if it does in the other, by Theorem 14.
![]() $(1 \Rightarrow 3)$
Suppose
$(1 \Rightarrow 3)$
Suppose
![]() $\varphi $
is a
$\varphi $
is a
![]() $\Sigma _1$
-sentence consistent with the
$\Sigma _1$
-sentence consistent with the
![]() $\Sigma _1$
-theory of M. By Theorem 14 we get that
$\Sigma _1$
-theory of M. By Theorem 14 we get that
![]() holds at M. Because
holds at M. Because
![]() $\Sigma _1$
-assertions must be necessary,
$\Sigma _1$
-assertions must be necessary,
![]() holds at M, and so by the end-extensional maximality principle we get that
holds at M, and so by the end-extensional maximality principle we get that
![]() $\varphi $
holds at M.
$\varphi $
holds at M.
![]() $(3 \Rightarrow 1)$
Suppose that
$(3 \Rightarrow 1)$
Suppose that
![]() holds at M, so there is an end-extension
holds at M, so there is an end-extension
![]() . By Theorem 14, there is a standard natural number k so that N thinks there is a real x which is not contained in any
. By Theorem 14, there is a standard natural number k so that N thinks there is a real x which is not contained in any
![]() $\omega $
-model of
$\omega $
-model of
![]() $T_k + \neg \varphi $
. The assertion that there is no model of
$T_k + \neg \varphi $
. The assertion that there is no model of
![]() $T_k + \neg \varphi $
containing x is
$T_k + \neg \varphi $
containing x is
![]() $\Pi ^1_1$
in the parameter x, and so its truth in N is witnessed by the existence of a certain canonically-associated well-founded tree. This is equivalent to a
$\Pi ^1_1$
in the parameter x, and so its truth in N is witnessed by the existence of a certain canonically-associated well-founded tree. This is equivalent to a
![]() $\Sigma _1$
-assertion. Because the
$\Sigma _1$
-assertion. Because the
![]() $\Sigma _1$
-theory of M is maximal we therefore get that this is already true in M. So
$\Sigma _1$
-theory of M is maximal we therefore get that this is already true in M. So
![]() holds at M, and in particular
holds at M, and in particular
![]() $\varphi $
holds at M.
$\varphi $
holds at M.
Corollary 16. Every countable model of T has a
![]() $\Delta _0$
-elementary extension—not necessarily an end-extension—to a model satisfying the end-extensional maximality principle, and therefore also the
$\Delta _0$
-elementary extension—not necessarily an end-extension—to a model satisfying the end-extensional maximality principle, and therefore also the
![]() $\Delta _0$
-elementary-extensional maximality principle.
$\Delta _0$
-elementary-extensional maximality principle.
Proof Let M be a countable model of T and let
![]() $S_0$
be T plus the
$S_0$
be T plus the
![]() $\Delta _0$
-elementary diagram of M. Extend
$\Delta _0$
-elementary diagram of M. Extend
![]() $S_0$
to a maximal
$S_0$
to a maximal
![]() $\Sigma _1$
-theory S. Then S has a countable model, which must be a
$\Sigma _1$
-theory S. Then S has a countable model, which must be a
![]() $\Delta _0$
-elementary extension of M. And by Theorem 15 any countable model of S must satisfy the two maximality principles.
$\Delta _0$
-elementary extension of M. And by Theorem 15 any countable model of S must satisfy the two maximality principles.
If M is
![]() $\omega $
-standard, then this extension cannot be an end-extension, as any end-extension of M must also be
$\omega $
-standard, then this extension cannot be an end-extension, as any end-extension of M must also be
![]() $\omega $
-standard, and hence cannot have a maximal
$\omega $
-standard, and hence cannot have a maximal
![]() $\Sigma _1$
-theory.
$\Sigma _1$
-theory.
Question 17. Does every countable
![]() $\omega $
-nonstandard model of ZF end-extend to a model satisfying the end-extensional maximality principle? By Theorem 15
this is equivalent to asking whether every countable
$\omega $
-nonstandard model of ZF end-extend to a model satisfying the end-extensional maximality principle? By Theorem 15
this is equivalent to asking whether every countable
![]() $\omega $
-nonstandard model of ZF end-extends to a model with a maximal
$\omega $
-nonstandard model of ZF end-extends to a model with a maximal
![]() $\Sigma _1$
-theory.
$\Sigma _1$
-theory.
The corresponding question is also open for models of arithmetic, as discussed in [Reference Hamkins8].
Acknowledgments
We thank the anonymous referee for their numerous helpful comments. Commentary can be made about this article on the first author’s blog at http://jdh.hamkins.org/the-universal-finite-sequence.