Introduction
Due to their unique characteristics, plasmas induced from laser ablation are at the core of numerous applications. Thin film coating using pulsed laser deposition (PLD) (Dellasega et al., Reference Dellasega, Russo, Pezzoli, Conti, Lecis, Besozzi, Beghi, Bottani and Passoni2017), spectrochemical analysis by means of laser-induced breakdown spectroscopy (Siozos et al., Reference Siozos, Philippidis and Anglos2017; Koral et al., Reference Koral, Dell'Aglio, Gaudiuso, Alrifai, Torellic and De Giacomo2018), propulsion of space craft using laser ablation thrusters (Yu et al., Reference Yu, Li, Wang, Cui, Liu and Yang2018), as well as inertial fusion confinement (Strozzi et al., Reference Strozzi, Bailey, Michel, Divol, Sepke, Kerbel, Thomas, Ralph, Moody and Schneider2017), are all based upon the ruling mechanisms behind the formation and expansion of laser-induced plasmas (LIP). Whether for practical applications or for the ones which are still at the experimental stage, fundamental research aiming at understanding how the target nature (thermophysical and optical properties) as well as the laser beam properties and the background environment impact the initial stage of the plasma plume creation and its dynamic remains crucial. Since the laser–target/laser–plasma interactions as well as the dynamic and composition of the laser-induced plume play a key role in the transfer of the target stoichiometry, the deposition rate of thin films and their properties using PLD, numerous works have been dedicated to investigating titanium carbide (TiC) film deposition using short and ultrashort laser pulses, with the majority being experimental (D'Alessio et al., Reference D'Alessio, Salvi, Teghil, Marotta, Santagata, Brunetti, Ferro and De Maria1998; Kumar et al., Reference Kumar, Chan and Kapat1998; Teghil et al., Reference Teghil, D'Alessio, Zaccagnino, Ferro, Marotta and De Maria2001, Reference Teghil, D'Alessio, De Bonis, Galasso, Villani and Santagata2006; Oliveira et al., Reference Oliveira, Somes and Vilar2005). Kumar et al. (Reference Kumar, Chan and Kapat1998) have worked on the optimization of PLD conditions to obtain thin films with the best crystalline quality structure and mechanical properties. They found out that thin films deposited at relatively high temperatures are more mechanically resistant. Teghil et al. (Reference Teghil, D'Alessio, De Bonis, Galasso, Villani and Santagata2006) used a femtosecond laser pulsed to deposit nanostructured TiC thin films on silicon wafers. The results of their experiments revealed that the thin films are mainly constituted of melted nanoparticles directly ejected from the target and crystals produced by gas phase condensation. In another work, Teghil et al. (Reference Teghil, D'Alessio, Zaccagnino, Ferro, Marotta and De Maria2001) studied TiC and TaC thin film deposition on silicon substrate using a 532 nm, 10 ns Nd:YAG laser pulse with a 10 Hz repetition rate. They managed to link the laser-induced plumes characteristics to each target properties and the modality of the thin films growth to each ablation process. D'Alessio et al. (Reference D'Alessio, Salvi, Teghil, Marotta, Santagata, Brunetti, Ferro and De Maria1998) defined an optimal evaporation regime as a function of the laser fluence for depositing high-quality TiC thin films on a glass plate substrate. The target stoichiometry was also successfully preserved. This work, where a 532 nm, 10 ns Nd:YAG laser pulse with a 10 Hz repetition rate was also used, revealed a link between the films directionality and the plumes. Oliveira et al.’s (Reference Oliveira, Somes and Vilar2005) work aimed at defining the mechanisms behind an undesirable phenomenon during laser processing of TiC and TiC composites which is column-growth. A laser fluence range has been suggested to avoid the shadowing mechanism which has been shown to be at the origin of the column formation. A few modeling approaches aiming at examining TiC laser ablation processes for PLD parameters optimization (Oliveira and Vilar, Reference Oliveira and Vilar2007; Vasantgadkar et al., Reference Vasantgadkar, Bhandarkar and Joshi2010) are present in the literature. Oliveira and Vilar (Reference Oliveira and Vilar2007) suggested a 2D finite element model to simulate laser ablation of a TiC target. The laser material interaction was described using a thermal model and the role of the LIP was considered through an optical thickness coefficient estimated partly through experimental data. The likelihood of the role played by the explosive boiling mechanism in the ablation process under the considered laser fluences was discussed and the importance of avoiding it for high-quality thin film deposition was emphasized. Vasantgadkar et al. (Reference Vasantgadkar, Bhandarkar and Joshi2010) adopted relatively the same model as Oliveira and Vilar (Reference Oliveira and Vilar2007). They mainly focused on the impact of considering the temperature dependency of the material optical properties on improving the prediction of the ablation depths and the increase of their agreement with experimental data. The particularity of our approach is that we describe the ablation process as a whole through a thermal model for the pulse–target interaction coupled with an out of equilibrium model for the plasma formation and expansion. In a previous work (Ait Oumeziane et al., Reference Ait Oumeziane, Liani and Parisse2016a), we investigated the ablation process under the same conditions of two metals namely titanium and copper. A comparison between target melting and evaporation thresholds was presented along with ablation depths and plasma ignition thresholds. Results for both materials differ considerably. Those discrepancies have been linked to the targets properties especially their thermal conductivity which has been shown to be the one governing the ablation process. More recently we have developed a new model to describe the ablation process of a multicomponent target (Ait Oumeziane and Parisse, Reference Ait Oumeziane and Parisse2018). The latter has been applied to TiC with a focus on comparing processes in the material such as melting and ablation depths and thresholds as well as plasma shielding rates induced under the same conditions from a pure titanium material. Plume electronic and heavy species temperatures and densities have also been presented and the thermal no equilibrium investigated. However, in this preliminary study the plasma dynamic has not been the center of interest. The present paper is dedicated to investigating the dynamic of LIP from a ceramic material. To have a better understanding of the link between the material properties and the plume characteristics and dynamic, a thorough examination of the entire ablation processes is made. Results comparison with the behavior of laser-induced plumes under the same conditions from a pure material is shown to have a key role in shedding the light on what monitors the plume expansion in the background environment. Plume temperatures, velocities, ionization rates as well as elemental composition have been presented and compared under carefully chosen relevant conditions which will be defined later.
The model
In the following section, we give a detailed description of the physics upon which our model is based.
Laser–material interaction
For a metallic ceramic material, characterized by a metallic electronic structure such as TiC (Williams, Reference Williams1999), free electrons present in the conduction band are the ones responsible for the laser beam photons energy absorption and its transfer to the lattice. In the case of nanosecond laser pulses interaction with metallic ceramic materials, thermal equilibrium between the electrons and the lattice can be assumed. This is due to the electrons–phonon relaxation τe_ph time which varies between 10−12 and 10−10 s in the case of metallic materials (Williams, Reference Williams1999). Hence thermalization between the electrons and the lattice occurs at a fraction of the total pulse duration. For that reason, nanosecond laser pulses interaction with TiC can be described through a one temperature thermal model (Ait Oumeziane and Parisse, Reference Ait Oumeziane and Parisse2018). At the course of our research development (Ait Oumeziane et al., Reference Ait Oumeziane, Liani and Parisse2014, Reference Ait Oumeziane, Liani and Parisse2016a, Reference Ait Oumeziane, Liani and Parisse2016b; Ait Oumeziane and Parisse, Reference Ait Oumeziane and Parisse2018) we have always chosen to adopt an enthalpic formulation of the heat equation [Eq. (1)], which greatly facilitates the phase changes (solid/liquid, liquid/vapor) management. In addition, thermophysical and optical properties were always assumed only phase-dependent (Table 1).
Table 1. TiC and Ti thermophysical and optical properties considered in the present study

H, T, λ, α0 are the enthalpy, the temperature, the thermal conductivity, and the absorption coefficient of the material. I(x,t) is the laser intensity transmitted at the x depth inside the material and at the “t” time. The evolution I(x,t) is given by the Beer–Lambert law (Van Driel, Reference Van Driel1986):
where R is the reflectivity of the irradiated surface and I 0(t) is the incident laser intensity.
A one-dimensional (1D) description of the laser beam interaction with the target material is suitable because the thermal diffusion length of TiC under the present conditions is largely greater than the laser beam penetration depth. In addition, the standard excimer beam radii and the assumed material thickness enable us to neglect the lateral diffusion heat flux and consider the space-time computational domain large enough to assume its outer boundary unaffected by the laser pulse absorption and heat diffusion (Ait Oumeziane et al., Reference Ait Oumeziane, Liani and Parisse2016a). At the target surface, a zero-heat flux boundary condition is assumed up to the time the surface starts to evaporate.
Hydrodynamical phenomena
When the laser pulse energy exceeds the material evaporation threshold, the material in the liquid phase undergoes a phase change and a vapor is formed above the target surface. The laser beam is then absorbed partly by the vapor before reaching the still liquid surface of the material. This absorption results in the formation of excited and ionized species which constitute a LIP. The plasma absorbs a certain amount of the laser beam energy and expands toward it. The fact that the plasma absorbs a part of the laser beam is called plasma shielding because it reduces the amount of the laser beam that reaches the material surface. During its expansion, the plasma compresses the background gas, which is helium in the present study. The difference between the pressure in the LIP and the background environment is at the origin of the generation of an intense shock wave. Depending on the target material and the characteristics of the thin film that needs to be deposited, PLD can either be realized in a reactive or a non-reactive atmosphere (Stafe et al., Reference Stafe, Marcu and Puscas2014). The choice of the ambient gas is one of the key parameters to monitor the morphology and the properties of the pulsed laser deposited thin films which are particularly linked to the deposition rate (Eason, Reference Eason2007). For that purpose, several studies have been conducted to demonstrate the impact of the nature as well as the pressure of the ambient gas on the ablation process and the plume expansion (Sturm et al., Reference Sturm, Fahler and Krebs2000; Scharf and Krebst, Reference Scharf and Krebst2002; Mendes and Vilar, Reference Mendes and Vilar2003; Harilal et al., Reference Harilal, O'Shay, Tao and Tillack2006). Using helium as the background gas for laser deposition of thin films has been shown to be of particular interest. When comparing, for example, Ag thin film deposition under several inert gases, a 0.4 mbar helium background gas has been shown to reduce the plume particles kinetic energy which leads to a maximum thin film deposition rate (Scharf and Krebst, Reference Scharf and Krebst2002). In our previous studies (Ait Oumeziane et al., Reference Ait Oumeziane, Liani and Parisse2016a; Ait Oumeziane et al., Reference Ait Oumeziane, Liani and Parisse2014; Ait Oumeziane et al., Reference Ait Oumeziane, Liani and Parisse2016b), results of nanosecond laser-induced metal plasma ignition threshold in a very low-pressure (10 Pa) helium environment have been shown to be in good agreement with experiments conducted under vacuum (Clarke et al., Reference Clarke, Dyer, Key and Snelling1999). For all that which has been said helium is chosen to be the background environment in the present study. The hydrodynamical model used to describe the vapor formation and plasma evolution into a helium background environment (Ait Oumeziane and Parisse, Reference Ait Oumeziane and Parisse2018) is based on several hypotheses: the exclusive formation of electrons in the vapor and the 1D unsteady inviscid compressible character of the flow. Each constituent is considered to follow the ideal gas law and the entire mixture is supposed to be quasi-neutral. Consequently, no internal electrical field is considered. Since only a short-term evolution of the plume is investigated, a 1D description is adequate. The plasma extent along the x-direction during this time range is very small compared to the laser beam radius, which usually varies between 0.05 and 2 mm (Ravindra, Reference Ravindra2005).
The model which consists of 1D multi-species Euler equations with mass and energy source terms (Lee, Reference Lee1985) considers the presence of eight species in the plume. The subscript i varies from 1 to 8 and designates the species i as follows (1: Ti, 2: He, 3: Ti*, 4: Ti+, 5: C, 6: C*, 7: C+, and 8: e−). The two excited species are intermediate states required for the plasma initiation (Table 2).
Table 2. Summary of titanium and carbon atomic state levels considered in the modeling approach used for the present investigation

In the present study, a UV 20 ns KrF (248 nm, hν = 5 eV) laser pulse, with an ideal Gaussian temporal profile is considered.
The processes governing the dynamic and evolution of the LIP are derived from the kinetic model developed by Rosen et al. (Reference Rosen, Mitteldorf, Kothandaraman, Pirri and Pugh1982), they consist of:
1. The excitations/de-excitation by electronic impact:
 $${\rm Ti}+{\rm } {\rm e}^-{\rm}+{\rm 2}{\rm. 66}\,{\rm eV}\leftrightarrow {\rm T}{\rm i}^{\rm {^\ast}}{\rm}+{\rm } {\rm e}^-$$
$${\rm Ti}+{\rm } {\rm e}^-{\rm}+{\rm 2}{\rm. 66}\,{\rm eV}\leftrightarrow {\rm T}{\rm i}^{\rm {^\ast}}{\rm}+{\rm } {\rm e}^-$$ $${\rm C}+{\rm } {\rm e}^-{\rm}+{\rm 7}{\rm. 48}\,{\rm eV}\leftrightarrow {\rm C}^{\rm {^\ast}}{\rm}+{\rm } {\rm e}^-$$
$${\rm C}+{\rm } {\rm e}^-{\rm}+{\rm 7}{\rm. 48}\,{\rm eV}\leftrightarrow {\rm C}^{\rm {^\ast}}{\rm}+{\rm } {\rm e}^-$$2. The ionization/ three body recombination of the excited states by electronic impact:
 $${\rm T}{\rm i}^{\rm {^\ast}}{\rm}+{\rm } {\rm e}^-{\rm}+{\rm 4}{\rm. 16}\,{\rm eV}\leftrightarrow {\rm T}{\rm i}^{\rm +} {\rm}+{\rm } {\rm e}^-{\rm}+{\rm } {\rm e}^-$$
$${\rm T}{\rm i}^{\rm {^\ast}}{\rm}+{\rm } {\rm e}^-{\rm}+{\rm 4}{\rm. 16}\,{\rm eV}\leftrightarrow {\rm T}{\rm i}^{\rm +} {\rm}+{\rm } {\rm e}^-{\rm}+{\rm } {\rm e}^-$$ $${\rm C}^{\rm {^\ast}}{\rm}+{\rm } {\rm e}^-{\rm}+{\rm 3}{\rm. 78}\,{\rm eV}\leftrightarrow {\rm C}^{\rm +} {\rm}+{\rm } {\rm e}^-{\rm}+{\rm } {\rm e}^-$$
$${\rm C}^{\rm {^\ast}}{\rm}+{\rm } {\rm e}^-{\rm}+{\rm 3}{\rm. 78}\,{\rm eV}\leftrightarrow {\rm C}^{\rm +} {\rm}+{\rm } {\rm e}^-{\rm}+{\rm } {\rm e}^-$$3. The photoionization of the excited states:
 $${\rm T}{\rm i}^{\rm {^\ast}}{\rm}+{\rm 5}\,{\rm eV}\to {\rm T}{\rm i}^{\rm +} {\rm}+{\rm } {\rm e}^-$$
$${\rm T}{\rm i}^{\rm {^\ast}}{\rm}+{\rm 5}\,{\rm eV}\to {\rm T}{\rm i}^{\rm +} {\rm}+{\rm } {\rm e}^-$$ $${\rm C}^{\rm {^\ast}}{\rm}+{\rm 5}\,{\rm eV}\to {\rm C}^{\rm +} {\rm}+{\rm } {\rm e}^-$$
$${\rm C}^{\rm {^\ast}}{\rm}+{\rm 5}\,{\rm eV}\to {\rm C}^{\rm +} {\rm}+{\rm } {\rm e}^-$$4. The inverse Bremsstrahlung absorption: which considers the electron-neutral (Zel'dovitch and Raizer, Reference Zel'dovitch and Raizer1966) and electron-ion absorptions (Thomann et al., Reference Thomann, Boulmer-Leborgne and Dubreuil1997). Hence, the plasma mixture total inverse bremsstrahlung coefficient is the sum of the contribution of the four species (Ait Oumeziane and Parisse, Reference Ait Oumeziane and Parisse2018):
(4) $${\rm \alpha} _{{\rm IB}} = {\rm \alpha} _{{\rm e - i}}[Ti^ + ] + {\rm \alpha} _{{\rm e - i}}[C^ + ] + {\rm \alpha} _{{\rm e - n}}[Ti] + {\rm \alpha} _{{\rm e - n}}[C]$$
$${\rm \alpha} _{{\rm IB}} = {\rm \alpha} _{{\rm e - i}}[Ti^ + ] + {\rm \alpha} _{{\rm e - i}}[C^ + ] + {\rm \alpha} _{{\rm e - n}}[Ti] + {\rm \alpha} _{{\rm e - n}}[C]$$
The kinetic constants of the processes are calculated using a Zel'dovitch's approach (Zel'dovitch and Raizer, Reference Zel'dovitch and Raizer1966) and are used to define the source terms of the hydrodynamical model (Ait Oumeziane and Parisse, Reference Ait Oumeziane and Parisse2018):
Boundary conditions and numerical resolution
The space-time history simulated in this study is extensive enough to assume that the outer boundary of the simulated space-time is not significantly affected by the end of the laser pulse. Thus, the boundary conditions at the origin of the simulated history are simply the initial conditions, which are given by:
For the surface which receives the laser flux, the boundary condition used is a zero flux one for the three equations in solid or liquid phase, because there are no particle or energy fluxes until the boiling begins.
The coupling of the thermal and hydrodynamical solvers allows to have a general and accurate overview of the entire ablation process. Because this code has already been used effectively to simulate laser ablation of semiconductors (Parisse et al., Reference Parisse, Sentis and Zeitoun2011) and metals (Ait Oumeziane et al., Reference Ait Oumeziane, Liani and Parisse2014, Reference Ait Oumeziane, Liani and Parisse2016a, Reference Ait Oumeziane, Liani and Parisse2016b) we know that it is adapted to such multiphysics problems.
In the mathematical formulation of our model x = 0 designates the target surface. x end on the other hand is chosen so the boundary condition T(x end) = 300 K (which expresses a semi-infinite slab hypothesis) can be valid. After calculating the thermal diffusion length and laser beam penetration width, x end is set to be largely greater than both. Hence the validity of the semi-infinite slab hypothesis and the boundary condition that expresses it is insured. Numerically x = 0 corresponds to the maximum cell number and x end the first cell number (Fig. 1) so we can easily estimate the ablation depth by the number of evaporated cells.

Fig. 1. Solid and gaseous domain grids.
In order to solve the thermal model, we chose an explicit central difference scheme, with second-order precision in space and first-order precision in time (Sturm et al., Reference Sturm, Fahler and Krebs2000). The time step used for the calculation Δt is equal to 10−15 s, and the space step is Δx is equal to 10−7 cm. The hydrodynamic part of our modeling approach is solved using the LCPFCT (Laboratory of Computational Physics Flux Corrected Transport) algorithm (Oran and Boris, Reference Oran and Boris1987; Boris et al., Reference Boris, Landsberg, Oran and Garner1993). This explicit algorithm is based upon a finite difference scheme associated with general methods for flux corrected transport. This algorithm is a predictor corrector numerical scheme accurate at the fourth order in space and second order in time (Sturm et al., Reference Sturm, Fahler and Krebs2000). A uniform mesh is used with a space step Δx equal to 10−4 cm and a time space Δt equal to 10−15 s as well. The same time step has been used to solve the thermal and hydrodynamic parts of our model, in order to avoid any coupling problem.
Thermal and hydrodynamical model coupling
The coupling of the target and the plume is insured through the boiling temperature, the plasma shielding effect, and the mass flow of the vaporized material (Fig. 2).
with: Δt evap: the time for one cell to evaporateΔx the size of the evaporated cell and ρliq the liquid mass density where (Δx/Δt evap) is the variation over time of the thermal ablation depth.

Fig. 2. Target/plume coupling mechanisms.
The boiling temperature depends on the pressure of the plume at the material surface. This dependency is expressed by the Clausius–Clapeyron equation:
T 0: is the boiling temperature, P 0: the atmospheric pressure, P s: the plume pressure,
ΔH: the latent heat of vaporization and R the ideal gas constant.
The amount of energy that can reach the target surface depends on how much of the laser beam is absorbed by the plume by inverse Bremsstrahlung as well as photoionization.
Before the start of the evaporation process, the adiabatic condition (∂T/∂x)x=0 = 0 is used at the interface between the target and the background environment. Once the evaporated matter leaves the surface material, the mass flow ![]() $\dot{m}$ of the vaporized material is calculated, and a total mass, momentum, and energy balance is done at the first cell of the gaseous domain. The behavior of the evaporated matter is modeled afterwards by the Euler equations.
$\dot{m}$ of the vaporized material is calculated, and a total mass, momentum, and energy balance is done at the first cell of the gaseous domain. The behavior of the evaporated matter is modeled afterwards by the Euler equations.
At the early stage of the material evaporation, the vapor is assumed to be at thermal equilibrium (Mazhukin et al., Reference Mazhukin, Nossov, Nickiforov and Sumorov2003), therefore Boltzmann and Saha's equations are used to evaluate the densities of the species present in the vapor including the primary electrons.
Results analysis and discussion
We remind that for the purpose of the present investigation, a KrF 248 nm, 20 ns full width at half maximum ideal Gaussian laser beam temporal profile has been considered and the ablation process occurs in a helium background environment.
In our previous investigation (Ait Oumeziane and Parisse, Reference Ait Oumeziane and Parisse2018), results on processes occurring inside the material, such as phase change thresholds along with ablation depths, have been presented and discussed. Plasma ignition threshold, thermal non-equilibrium as well as species densities have also been focused on. In the present study, we take a step further by focusing on the characterization of the plume dynamics and its connection to the material thermophysical and optical properties. In that purpose the present section will be sequenced as follows:
• Characteristics of TiC laser-induced plumes will be examined and compared with titanium plumes induced under the same conditions. Two laser beam fluences are considered, one below and one above the plasma ignition threshold (Ait Oumeziane and Parisse, Reference Ait Oumeziane and Parisse2018): 15.5 and 20 J/cm2. Although essential, this first step needs to be complemented with other relevant comparison conditions defined in the following point.
• TiC and titanium plumes dynamics and characteristics will be compared for the same effective energy (Ait Oumeziane and Parisse, Reference Ait Oumeziane and Parisse2018), the same ablated mass and the same plasma shielding rate.
For all considered cases, the results are presented at two different times, before and after the laser pulse reaches its maximum intensity: 12 and 18 ns.
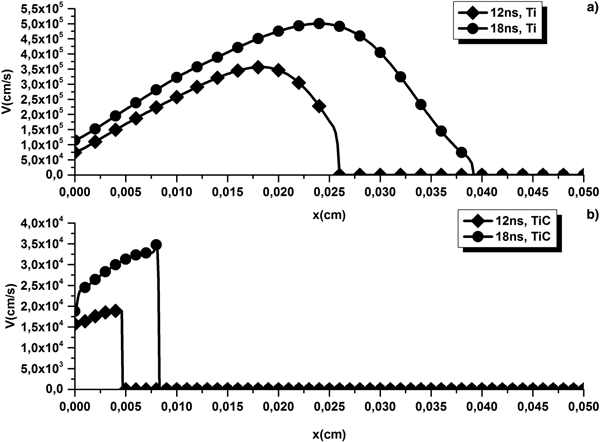
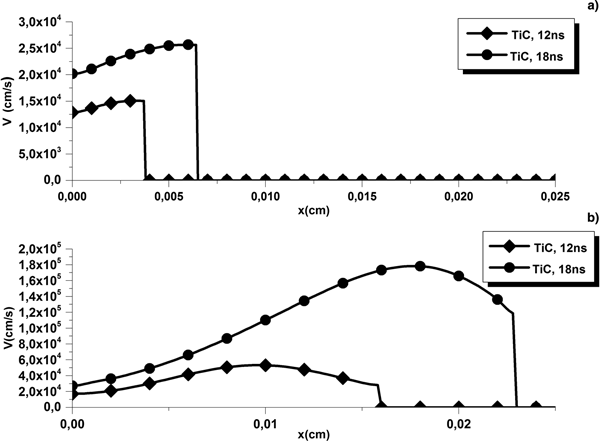
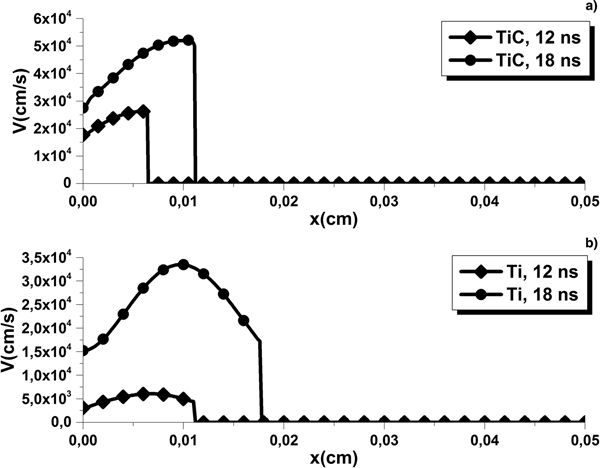
For the same laser beam fluences: 15.5 J/cm2 (Fig. 3) and 20 J/cm2 (Fig. 4), one can see that TiC plumes expansion in the background environment is not as fast as the pure titanium ones. More specifically, at = 12 ns; the TiC laser-induced plume attains an expansion velocity of 2·104 cm/s for a laser beam fluence of 15.5 J/cm2 whereas it was able to reach 3.5·105 cm/s in the case of pure titanium. For a laser beam fluence of 20 J/cm2, the pure titanium expands until 3.5·105 cm/s whereas the TiC plume reaches 2.5·104 cm/s at best. At t = 18 ns the TiC plume expands 16 times faster than the TiC for a laser beam fluence of 15.5 J/cm2 and 12 times faster for a laser beam fluence of 20 J/cm2. On the other hand, the TiC plumes start their expansion faster than those induced from a pure titanium material but have the tendency to remain relatively close to the target surface. It is worth noting that for a laser beam fluence of 15.5 J/cm2 the Ti plume has been induced from a total ablated mass of 4.058·10−6 g against 1.11·10−6 g for the TiC plume. On the other hand, for a laser beam fluence of 20 J/cm2 the Ti plume has been induced from a total ablated mass of 4.95·10−6 g against 1.12·10−6 g for the TiC plume. The shielding rates were 69.62 and 71.21% for Ti against 1.07 and 22.5% for TiC for the same laser beam fluences, respectively.

Fig. 3. TiC (b) and Ti (a) plumes velocities for a laser beam fluence of 15.5 J/cm2 at 12 and 18 ns.

Fig. 4. TiC (b) and Ti (a) plumes velocities for a laser beam fluence of 20 J/cm2 at 12 and 18 ns.
Thermal and optical properties of each target material can partially explain the above-mentioned discrepancies. Aside from the highly reflective character of TiC (its reflectivity is around two times higher than Ti) particularly in the liquid phase, its thermal conductivity as well as its phase transition enthalpies (especially in the solid phase where it is almost three times higher), are the reasons why the TiC laser ablation process needs considerably more input energy and occurs very late in time.
Although the material properties are the origin of the plume formation they are not responsible for its evolution, therefore we need to have a closer look at the plume composition.
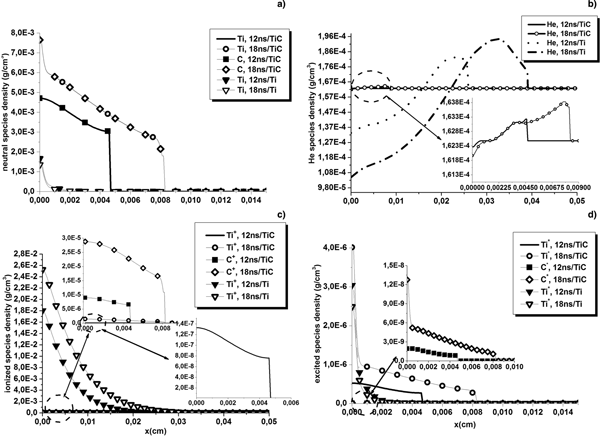
Figures 5b and 6b show the classical impact on the plume expansion on the background gas. This complements the velocity results by demonstrating how by its expansion, the TiC plumes push the background gas away from the target material, increasing its density, but not as much and as far as in the case of the Ti plumes. The decreasing phase of the velocity translates the helium expansion and acceleration behind the resulting shock wave. The time evolution of the shock front position can be followed using either the plume velocity or the background gas density (for which it is more evident) spatial variation at different instants.

Fig. 5. TiC and Ti plumes neutral (a), ionized (c), and excited (d) species mass densities along with He mass density (b) at 12 and 18 ns for a laser beam fluence of 15.5 J/cm2.

Fig. 6. TiC and Ti plumes neutral (a), ionized (c), and excited (d) species mass densities along with He mass density (b) at 12 and 18 ns for a laser beam fluence of 20 J/cm2.
Subfigures (a), (c), and (d) of both Figures 5 and 6 show clearly that when it comes to TiC plumes, neutrals are the most dominant species. On the other hand, pure titanium laser-induced plumes are mostly composed of ionized species. This suggests that the plume dynamic may be linked to the nature of the species present in it, especially the dominant ones. Ionized carbon atoms densities are far more important than ionized titanium atoms. This is due to the photoionization process which is more efficient on carbon species because of the smaller gap between its intermediate excited state and its first ionization potential. Carbon atoms have also a higher ionization potential. Therefore, TiC plumes contain more excited titanium species than carbon ones. All species densities increase at t = 18 ns because of the increase of the amount of ablated matter and the efficiency of the inverse Bremsstrahlung and the collisional processes consequently.
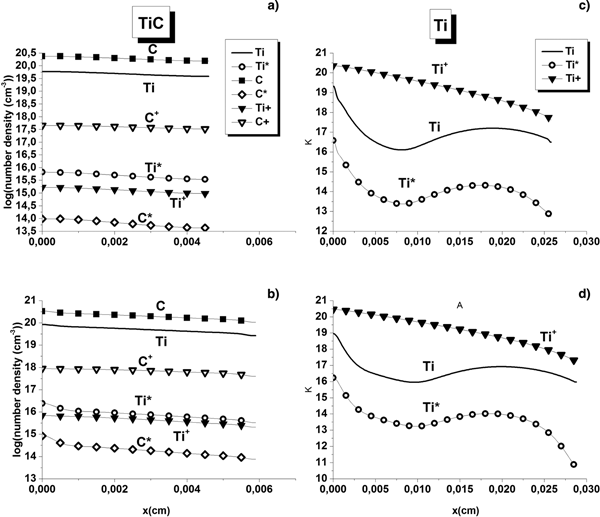
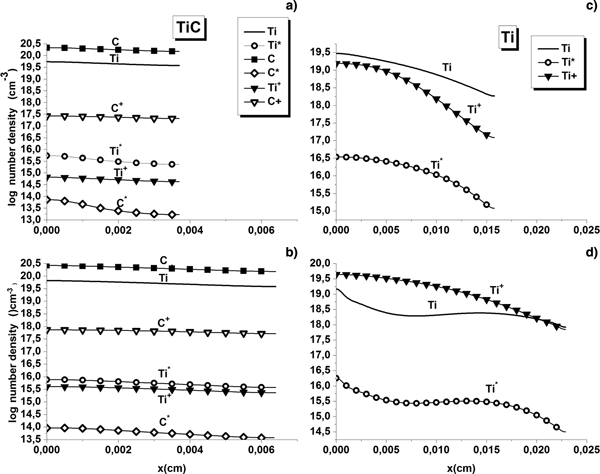
Although the plasmas constituents mass densities gave us very useful information for our investigation regarding the plumes dynamics, we thought that looking at the species real amount could reveal even more interesting details. Figures 7 and 8 confirm that the most dominant species in the TiC plumes are indeed neutrals but also show that carbon atoms are the predominant ones. The presence of more ionized carbon species is due to the fact that only 3.78 eV is required to ionize carbon intermediate excited states against 4.16 eV for titanium. At identical times pure titanium plumes contain more ionized titanium than either ionized carbon or ionized titanium present in the TiC plasmas.

Fig. 7. TiC and Ti plume species number densities logarithm comparison for a laser fluence of 15.5 J/cm2 (a–c) and 20 J/cm2 (b–d), respectively, at 12 ns.

Fig. 8. TiC and Ti plume species number densities logarithm comparison for a laser fluence of 15.5 J/cm2 (a–c) and 20 J/cm2 (b–d), respectively, at 18 ns.
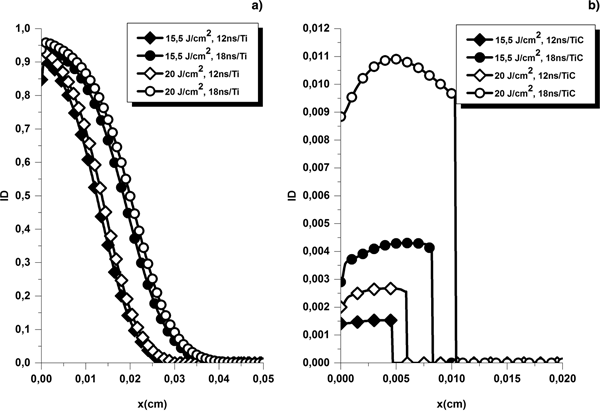
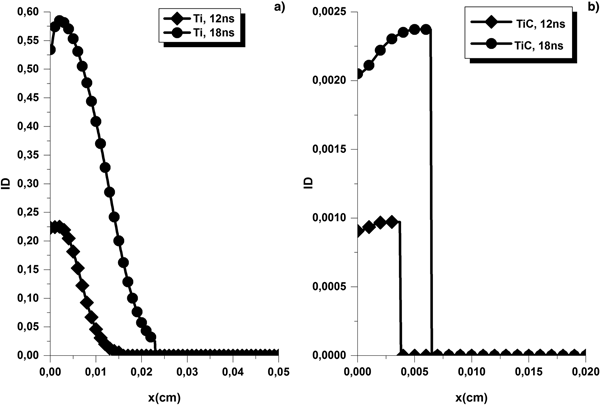
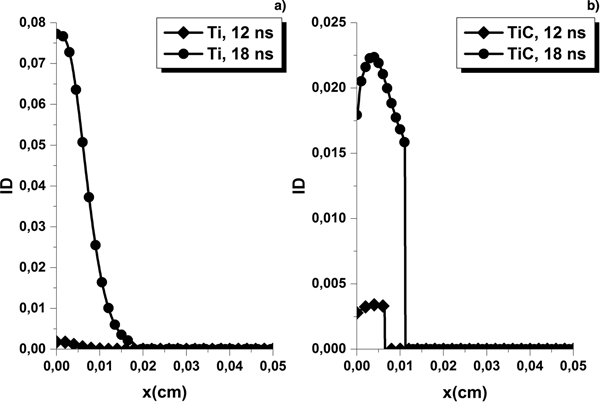
Examining each plasma ionization degree (Fig. 9a, b), we found out that the fastest and further away expanding plumes are the ones with the highest ionization degrees, namely, pure titanium laser-induced plumes.

Fig. 9. Ti (a) and TiC (b) plumes ionization degrees for 15.5 and 20 J/cm2 at 12 and 18 ns.
For a thorough investigation of TiC and Ti plasma expansion dynamics and its relation to the nature of species it contains, its ionization degree, we looked for other relevant comparison conditions in our previous investigation (Ait Oumeziane and Parisse, Reference Ait Oumeziane and Parisse2018). They are all summarized in Table 3 and consist of interaction conditions for which both targets receive the same effective energy and when the same amount of matter is ablated from each material.
Table 3. Conditions for Ti and TiC same ablated mass and effective energy

Bold values are emphasize when either the effective energy or the ablated mass are approximately equal for Ti and TiC.
When the plasma is formed above the material surface it partially absorbs the laser beam energy due to the inverse bremsstrahlung and photoionization processes which is known as plasma shielding. The amount of the laser beam that manages to reach the target is what we defined in a previous paper (Ait Oumeziane and Parisse, Reference Ait Oumeziane and Parisse2018) as the effective energy.
The results show that four times more laser fluence is required to ablate the same amount of TiC matter as Ti. On the other hand, when both targets receive the same effective energy, more matter is ablated from Ti. This is due to what we discussed earlier regarding each material thermal and optical properties.
When an identical mass is ablated from each target, examining the velocity of the plasma that is formed from it is very interesting (Fig. 10). One can see that in that case and starting from the target surface, titanium plumes also expand faster and further away from the target material. Figure 11 shows the exact same behavior.

Fig. 10. TiC and Ti plume velocity for the same ablated mass.
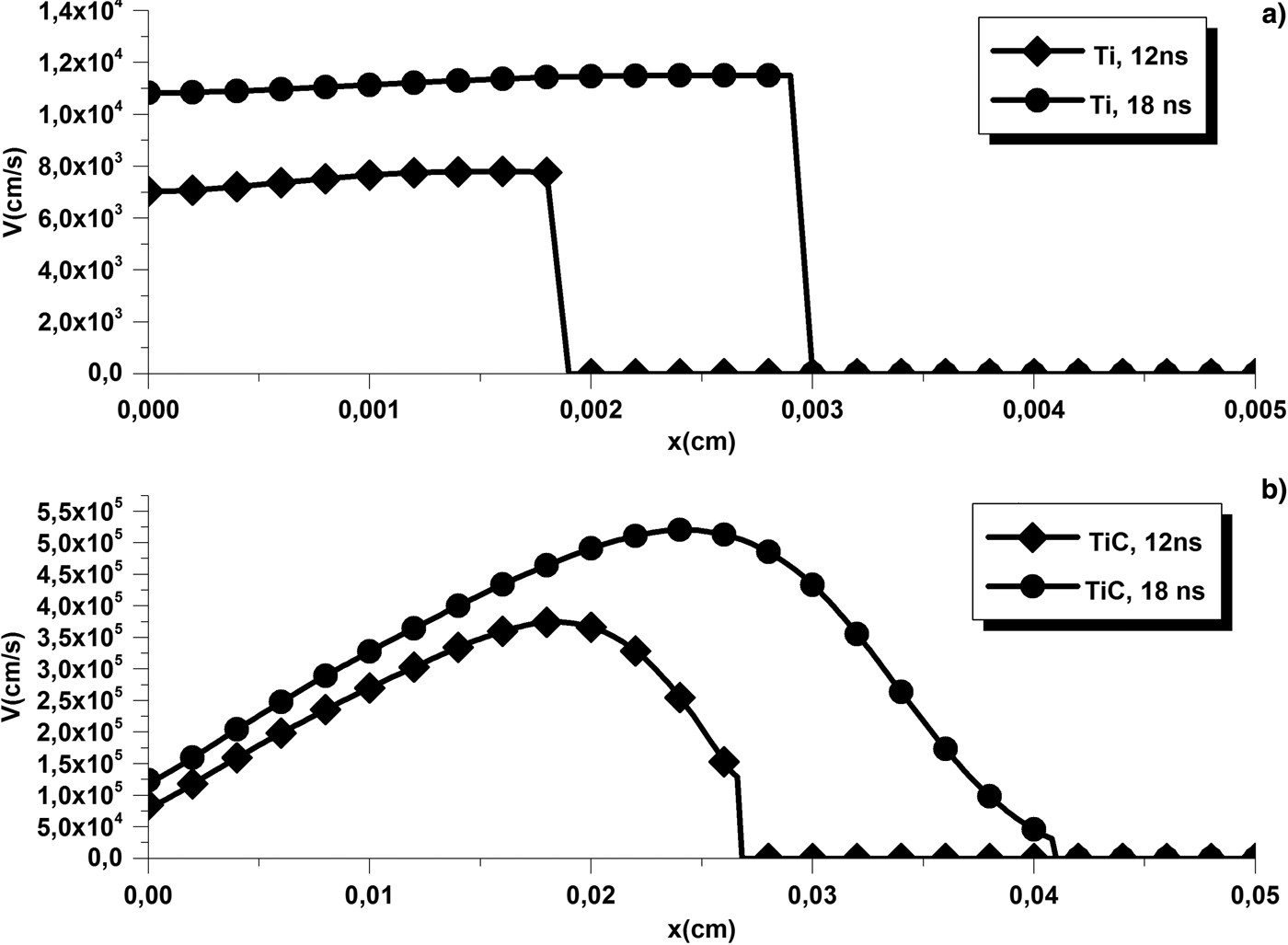
Fig. 11. TiC and Ti plume velocity for the same effective energy.
Looking back at our previous work (Ait Oumeziane and Parisse, Reference Ait Oumeziane and Parisse2018), especially at the plasma shielding, we noted that when identical masses are ablated from each material, TiC plasmas receive <0.5% of the laser beam total energy and <0.005% when the same effective energy reaches each material.
Either in the case TiC and Ti plumes induced from the same amount of matter (Fig. 12) or when both targets receive the same amount of effective energy (Fig. 13), the results suggest that plumes with neutral species dominance tend to stay relatively confined near the target material. Unlike the same laser beam fluences cases, in this case and at identical times pure titanium plumes contain less ionized titanium than either ionized carbon or ionized titanium present in the TiC plasmas.

Fig. 12. TiC (a) 12 ns – (c) 18 ns and Ti (b) 12 ns – (d) 18 ns plume species number densities logarithm comparison for the same ablated mass.

Fig. 13. TiC (a) 12 ns – (c) 18 ns and Ti (b) 12 ns – (d) 18 ns plume species number densities logarithm comparison for the same effective energy.
Figures 14 and 15 suggest that either in the plasmas generated from the same of amount matter from TiC and Ti targets or when both materials receive the same effective energy the plumes with the highest ionization degrees are the ones expanding faster and further.

Fig. 14. Ti (a) and TiC (b) plumes ionization degrees for the same ablated mass.

Fig. 15. Ti (a) and TiC (b) plumes ionization degrees for the same effective energy.
After examining the above-mentioned results, investigating results for the same amount of plasma shielding (around 32%) also seemed relevant. In this case, the laser beam fluence was 1.5 J/cm2 for titanium and 22 J/cm2 for TiC.
The examination of the velocities (Fig. 16) of TiC (a) and pure titanium (b) plumes revealed an utterly different behavior of what we investigated until now. Not only the plume velocities are comparable in this case, but it is the TiC plume that is characterized by the highest expansion velocities. The distances to which the plumes expand are also comparable, but titanium plumes are still the ones expanding the furthest from the target surface (in all the previous cases they were at least ten times longer for titanium plumes). In contrast to all the previously examined cases, under those conditions more mass is ablated from the TiC material: 1.05·10−6 g against 5.32·10−7 g. Those results show that to have a faster TiC-induced plume, not only more matter need to be extracted from the target, but also more energy need to be deposited into the plumes.

Fig. 16. Ti and TiC plumes velocities for the same plasma shielding rate.
Figure 17 shows that even though the TiC is the fastest in those conditions, it is still characterized by high neutral number densities with a dominance of carbon atoms which are characterized by a higher ionization energy level. One can also see that in this case titanium plumes also contain more neutral species and at identical times less ionized titanium than either carbon or titanium in the TiC plasmas.

Fig. 17. TiC and Ti plume species number densities logarithm comparison for the same plasma shielding rate.
The results presented in Figure 18 show clearly that the plumes fastest expansions are not necessarily linked to the highest ionization degree.

Fig. 18. TiC and Ti plumes ionization degrees for the same plasma shielding rate.
Summary conclusion and perspectives
This work was focused on investigating the dynamics of LIP from a ceramic material. A recently developed model was used for that purpose. TiC was chosen for this study. A comparison with the characteristics and dynamics of LIP from a pure titanium material was presented. Links between the target material thermophysical/optical properties as well as plasmas elemental characteristics and plume dynamics were established. Comparisons were made:
• Under the same laser ablation conditions
• For the same effective energy
• For the same ablated mass
• For the same plasma shielding rate
The results demonstrate that the plumes dynamics is intertwined with the materials properties and the nature of the plasmas constituents. To have comparable plume dynamics, plasmas need to be induced from greater amount of matter from TiC targets than pure titanium ones. The plumes dynamics is linked to the amount of species they contain but not necessarily to their ionization degree.
Future studies will be dedicated to developing new models for more complex materials with a focus on including additional physical processes depending on the laser–matter interaction conditions. Including, for example, the internal electrical field and its impact on plumes dynamics would be of great interest.
Author ORCIDs
A. Ait Oumeziane, 0000-0002-9656-6249.