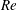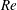1 Introduction
The breakup of immiscible liquid jets and plumes and resulting droplet size distributions have been studied extensively (Lin & Reitz Reference Lin and Reitz1998; Villermaux Reference Villermaux2007), mostly focusing on the atomization of liquid jets in gas (Marmottant & Villermaux Reference Marmottant and Villermaux2004; Gorokhovski & Herrmann Reference Gorokhovski and Herrmann2008; Shinjo & Umemura Reference Shinjo and Umemura2010; Jarrahbashi et al.
Reference Jarrahbashi, Sirignano, Popov and Hussain2016). Fragmentation of a buoyant immiscible liquid jet injected into another liquid, which is relevant e.g. to a subsurface oil well blowout, has received considerable attention after the Deepwater Horizon spill in the Gulf of Mexico. Experimental studies have shown that the droplet diameters vary from microns to millimetres, depending on the flow conditions and fluid properties, which are typically expressed in terms of Weber (
$We$
) and Reynolds (
$Re$
) numbers (Johansen, Brandvik & Farooq Reference Johansen, Brandvik and Farooq2013; Brandvik et al.
Reference Brandvik, Johansen, Leirvik, Krause and Daling2018) as well as the density ratio,
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D70C}_{d}/\unicode[STIX]{x1D70C}_{c}$
, and viscosity ratio,
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D707}_{d}/\unicode[STIX]{x1D707}_{c}$
. Here,
$We=\unicode[STIX]{x1D70C}_{d}u_{d}^{2}d/\unicode[STIX]{x1D70E}$
,
$Re=\unicode[STIX]{x1D70C}_{d}u_{d}d/\unicode[STIX]{x1D707}_{d}$
,
$\unicode[STIX]{x1D70C}$
is the density,
$u_{d}$
is the jet speed,
$d$
is the nozzle diameter,
$\unicode[STIX]{x1D70E}$
is the interfacial tension,
$\unicode[STIX]{x1D707}$
is the viscosity and the subscripts
$c$
and
$d$
refer to the continuous and dispersed phases, respectively. In parallel, numerous numerical simulations have attempted to model the dispersion of the droplet plume under the influence of buoyancy, surrounding flow, turbulence and stratification using prescribed droplet size distributions (Crounse, Wannamaker & Adams Reference Crounse, Wannamaker and Adams2007; Socolofsky, Adams & Sherwood Reference Socolofsky, Adams and Sherwood2011; Yang et al.
Reference Yang, Chen, Socolofsky, Chamecki and Meneveau2016).
The regimes of jet fragmentation, namely axisymmetric Rayleigh breakup, sinuous wave breakup and atomization, have been established for liquid jets in air (Lasheras & Hopfinger Reference Lasheras and Hopfinger2000) and extended to oil–water systems based on the Reynolds and Ohnesorge numbers (
$Oh=We^{1/2}/Re$
), by Masutani & Adams (Reference Masutani and Adams2001). For low
$Re$
and
$Oh$
, Eggers (Reference Eggers1997) extends the classical Rayleigh–Plateau instability to nonlinear slender jets. More recently, Homma et al. (Reference Homma, Koga, Matsumoto, Song and Tryggvason2006) have used direct numerical simulations to capture and classify several breakup modes on a Weber number-viscosity ratio diagram. The processes involved at high
$Re$
are less clear, leading to introduction of e.g. statistical theories that describe the droplets’ size distribution based on sequential cascades of breakup and aggregation (Martínez-Bazán, Montanes & Lasheras Reference Martínez-Bazán, Montanes and Lasheras1999; Zhao et al.
Reference Zhao, Torlapati, Boufadel, King, Robinson and Lee2014), or maximum entropy and random breakups (Cohen Reference Cohen1990). These approaches do not account for the influence of flow structure and ligament dynamics, which are essential for explaining the differences between predicted and measured trends (Villermaux Reference Villermaux2007).
Experimental observations on processes occurring in the near field of liquid–liquid jet breakup in the atomization regime is a challenge owing to optical obstruction. Consequently, the above-mentioned data is restricted to the periphery or far field of the jet. The present study elucidates several processes occurring during fragmentation of a buoyant immiscible oil jet injected into quiescent water. As discussed in § 2, unobstructed visual access is achieved by matching the refractive index of the two fluids: silicone oil and sugar water. High speed planar laser-induced fluorescence (PLIF) demonstrates several phenomena (§ 3), most notably, the ubiquitous generation of compound oil droplets, which contain smaller water droplets. The mechanisms involved are demonstrated, followed by an analysis showing e.g. the fraction of compound droplets, their impact on the oil–water interfacial area, and the striking differences between the odd exterior shapes of the oil droplets and the nearly spherical interior water droplets. Discussion and conclusions are presented in § 4.
2 Method
Figure 1. Experimental set-up for observing the index-matched buoyant oil jet superimposed on a sample PLIF image.
Aimed at studying phenomena associated with mixing of light crude oil with seawater, but using refractive-index-matched fluids, we have selected silicone oil (polydimethylsiloxane, trimethylsiloxy terminated) as the dispersed phase and sugar water (64 % by weight) as the continuous phase. Their density, viscosity, interfacial tension and those for oil–water systems are presented in table 1. The viscosity is determined by a capillary viscometer, the interfacial tension by a pendant drop method and the refractive index (1.4022) by a refractometer. The crude oil was sourced from the Marlin platform located 60 km northeast of the Deepwater Horizon platform and provided by BP plc. Both the crude oil and seawater properties have been measured in the laboratory by Murphy et al. (Reference Murphy, Xue, Sampath and Katz2016). As illustrated in figure 1, the experiments have been conducted in a
$39\times 24.1\times 76.2~\text{cm}^{3}$
acrylic tank partially filled with sugar water. The silicone oil is injected from a regulated, nitrogen-pressurized reservoir, and then passes through a flowmeter (Omega, FL-6110A), a settling chamber containing honeycomb and screens, as well as a nozzle with 6.35:1 diameter ratio. The exit diameter of the initially laminar jet is 10 mm. Three sets of experiments have been conducted at
$u_{d}=1.5$
, 3.4 and
$5.3~\text{m}~\text{s}^{-1}$
, corresponding to Reynolds numbers of 594, 1358 and 2122, and Weber numbers of 785, 4100 and 10 000, respectively. The Ohnesorge number is
$Oh=0.047$
for all cases. Based on Masutani & Adams (Reference Masutani and Adams2001), all three cases fall in the so-called atomization regime, where droplets of a wide size range are generated close to the jet exit. The viscosity ratio and interfacial tension of the present fluids differ by less than 2:1 from those of the crude oil–seawater pair. They have been selected because they allow us to cover a
$4:1$
range in Reynolds numbers while maintaining speeds that are low enough that the near field of the jet is not contaminated by oil droplets entrained by the circulating external flow.
Table 1. Physical properties of surrogate fluid pairs associated with the present experiments.
The centre plane of the jet is illuminated with a 1 mm thick sheet of pulsed 527 nm Nd:YLF laser, which is synchronized with a high-speed camera (PCO.dimax). The silicone oil is visualized using Nile red, which is insoluble in water, and has an emission wavelength of 635–650 nm. Because Nile red is also insoluble in silicone oil, it is mixed with 1.25 % by volume mineral oil, which serves as a soluble carrier, and the properties in table 1 correspond to the oil mixture. A long-pass filter with a cutoff wavelength of 550 nm is placed in front of the camera to remove the green light from the recorded images. The
$2016\times 2016~\text{pixel}^{2}$
images have been recorded at two magnifications: large fields of view (FOV) of
$208.5\times 208.5~\text{mm}^{2}$
have been recorded at 500 frames per second (f.p.s.) for
$Re=594$
and 1358, and at 1000 f.p.s. for
$Re=2122$
. High magnification images with a view of
$12.9\times 12.9~\text{mm}^{2}$
(
$6.4~\unicode[STIX]{x03BC}\text{m}~\text{px}^{-1}$
) have been recorded at 1000 f.p.s. in regions centred at
$z/d=10.6$
, 20.6 and 30.6. Specialized data processing procedures have been developed to measure the statistics of droplet size distributions and shapes. Because of their complexity, a detailed description of this method, including samples and uncertainty analysis, is provided in appendix A.
3 Results
Figure 2. Sample images of the oil jet fragmentation: (a)
$Re=594$
,
$We=785$
, (b)
$Re=1358$
,
$We=4100$
and (c)
$Re=2122$
,
$We=10\,000$
. Bottom inserts are enlarged
$30\times 20~\text{mm}^{2}$
sections of the areas marked by yellow boxes; middle and top inserts are enlarged
$12.9\times 12.9~\text{mm}^{2}$
sections of the marked areas recorded at a different time and at a higher magnification.
Figure 3. Samples of compound oil ligaments and droplets at
$Re=1358$
and
$z/d=20.6$
.
Setting the framework for the present observations, sample large FOV images illustrating the jet fragmentation process are presented in figure 2(a–c), with the nozzle exit visible at the bottom. The (originally square) images have been cropped to
$208.5\times 100~\text{mm}^{2}$
but are presented undistorted with scales expressed in nozzle diameters provided along the left and bottom edges of the figure. A corresponding movie (movie 1) is provided as supplementary material and is available online at https://doi.org/10.1017/jfm.2019.645. Inserts showing magnified images of the regions are also presented. Focusing initially on the two higher Reynolds number cases (figure 2
b,c), the streamwise evolution of the jet consists of three regions, namely Kelvin–Helmholtz (KH) roll-up at low
$z/d$
, a ligament dominated region at midrange and a dispersed droplet region at high
$z/d$
. The initial roll-up and end of the nearly axisymmetric KH region occur closer to the nozzle with increasing
$Re$
. During roll-up, the jet entrains thin layers of water. In parallel, stretching of the upstream tail of one ring by flow induced by the one following it generates thin oil ligaments, which break up into a limited number of oil droplets. These droplets are subsequently entrained back into the jet. Further downstream, i.e. around
$z/d>4.5$
and 3 for
$Re=1358$
and 2122, respectively, the axisymmetry is lost, similar to miscible jets (Liepmann & Gharib Reference Liepmann and Gharib1992). Here, the jet structure transitions into elongated ligaments of varying shapes that wrap around each other, some breaking into droplets. At approximately
$7<z/d<13$
and
$6<z/d<12$
for
$Re=1358$
and 2122, respectively, the width of these ligaments decreases, and they break up into droplets (quantitative data follows). While a few ligaments persist up to
$z/d=20$
at
$Re=1358$
, they mostly disappear at
$Re=2122$
. As for the
$Re=594$
jet (figure 2
a), thick ligaments still form and then break up into large blobs, but later than the other cases. However, the jet is not axisymmetric even at the exit from the nozzle and tends to meander downstream. There are two possible contributors to this phenomenon. First, it appears that some water penetrates into the periphery of the nozzle. For this case, the densimetric Froude number,
$Fr=u_{d}/\sqrt{gd(\unicode[STIX]{x1D70C}_{c}-\unicode[STIX]{x1D70C}_{d})/(\unicode[STIX]{x1D70C}_{c}+\unicode[STIX]{x1D70C}_{d})}$
, is 15.6, and
$Re_{t}=Re/Fr$
is 38. Based on studies of displacement flows in vertical pipes by Amiri, Larachi & Taghavi (Reference Amiri, Larachi and Taghavi2016) and Hasnain, Segura & Alba (Reference Hasnain, Segura and Alba2017), under these conditions an interface between the exterior and interior fluids exit inside the pipe, consistent with the present observations. In contrast, for the present higher Reynolds numbers, the oil is expected to displace the water. Second, meandering of jets has been observed at
$Re<1000$
, even without buoyancy effects (Crow & Champagne Reference Crow and Champagne1971).
Figure 4. A time sequence showing processes leading to compound droplet formation at
$Re=1358$
. Arrows of the same colour and shape follow the same water ligament in frames separated by 6 ms.
Focusing on
$Re=1358$
and 2122, many of the oil ligaments in the middle inserts, and the droplets in the upper inserts contain water pockets. In contrast, they rarely appear at
$Re=594$
. Higher magnification samples of such compound droplets/ligaments containing one or more water droplets are presented in figure 3 (and movie 2). In some cases, the internal water droplets contain smaller oil droplets and so on, creating a ‘Russian doll’ like phenomenon. Note that while the external interfaces have odd shapes, the internal ones are largely spherical, as will be quantified later. A typical process leading to the formation of compound ligaments is demonstrated in figure 4 and corresponding movie 3. Starting from the KH roll-up, the red solid arrow tracks the same water film, which appears as a thin ligament in the planar view. At
$z/d<3.5$
, the film is elongated by the local shear, and at
$4<z/d<9.5$
, it separates from the bulk water, breaking up into multiple water droplets at
$z/d\sim 10$
. The entrainment point, as well as the time history of stretching and breakup vary, as the orange dashed arrows indicate, but the process repeats itself. Samples of subsequent stretching and fragmentation of an oil ligament containing water pockets by a large eddy is presented figure 5 (and movie 4). As is evident, the compound droplets and ligaments are ubiquitous by
$z/d>11$
.
Figure 5. Evolution of ligaments resulting in compound droplet formation at
$Re=1358$
. The arrows follow the same ligament in frames separated by 6 ms.
Table 2. Numbers and statistics of detected droplets.
Figure 6. Time averaged (a) number density distribution of all oil droplets, bold points represent the peak volumetric contribution, namely the point where the slope changes from more to less than
$-3$
, (b) the cumulative distribution of volume fraction versus droplet size normalized by Sauter mean diameter with a log-normal fit based on all three data sets, (c) Sauter mean diameter versus Weber number superimposed on previous data points and line fits reproduced from Wu, Miranda & Faeth (Reference Wu, Miranda and Faeth1995) and (d) volumetric median diameter versus modified Weber number superimposed on previous data points and line fits with
$A=24.6$
and
$B=0.08$
reproduced from Brandvik et al. (Reference Brandvik, Johansen, Farooq, Angell and Leirvik2014).
Figure 7. Time averaged (a) fraction of compound droplets and (b) the number density distribution of compound droplets at
$z/d=20.6$
.
Statistical information derived from the procedures described in the appendix is provided in figures 6–10 and table 2. Figure 6(a) is the number density of all the oil droplets,
$\text{d}N/\text{d}(D_{a})$
, at
$20<z/d<21.3$
, plotted versus their apparent diameter,
$D_{a}$
, which is calculated based on their total cross-sectional area,
$A$
, including the pockets. Each plot is based on analysing 209 instantaneous realizations, with error bars representing the uncertainty in the number density and diameter. The total number of droplets,
$\unicode[STIX]{x1D6F4}N$
, is listed in table 2. For all cases, the slopes of
$\text{d}N/\text{d}(D_{a})$
is mild:
$-0.5$
and
$-1$
for
$Re=594$
, 1358, respectively, and nearly flat for
$Re=2122$
. However, for large droplets, the slope steepens to approximately
$-4.5$
. The increasing steepness in slope of the droplet size distribution represents an increasing contribution of number density by the small droplets. The peak in the volumetric contribution at the point where the slope changes from more to less than
$-3$
, which is indicated by bold points in figure 6(a), decreases with increasing
$Re$
. Figure 6(b) shows the cumulative distribution of volume fraction,
$V_{cum}/V$
, plotted versus droplet size normalized by the Sauter mean diameter,
$D_{32}$
, defined as
$D_{32}=(\int _{0}^{\infty }D_{a}^{3}N^{\prime }(D_{a})\,\text{d}D_{a})/(\int _{0}^{\infty }D_{a}^{2}N^{\prime }(D_{a})\,\text{d}D_{a})$
, where
$N^{\prime }=\text{d}N/\text{d}(D_{a})$
(Brennen Reference Brennen2005). The values of
$D_{32}$
is provided in table 2. In agreement with Simmons (Reference Simmons1977), the curves nearly collapse for
$V_{cum}/V<\sim 0.8$
, but fluctuate at higher values, presumably owing to the small number of large droplets in the present data set. Figure 6(c) compares the values of
$D_{32}/d$
plotted versus
$We$
to the data points and empirical fit of Wu et al. (Reference Wu, Miranda and Faeth1995) measured for liquid jets in air,
$D_{32}/d=32We^{-3/5}$
. As is evident, the present results for
$Re=1358$
and 2122 agree with the line fit, but are lower than the extrapolation of the line fit for
$Re=594$
. Figure 6(d) compares the present volume median diameter,
$d_{50}$
(table 2), defined as the diameter where the cumulative volume fraction reaches 50 %, to a semi-empirical model introduced by Johansen et al. (Reference Johansen, Brandvik and Farooq2013). The semi-empirical fit is
$d_{50}/d=A(We^{\ast })^{-3/5}$
, where
$We^{\ast }=We/[1+BCa(d_{50}/d)^{1/3}]$
is a modified Weber number,
$Ca=\unicode[STIX]{x1D707}_{d}u_{d}/\unicode[STIX]{x1D70E}$
is the capillary number and
$A$
and
$B$
are empirical constants. In a later report by the same group (Brandvik et al.
Reference Brandvik, Johansen, Farooq, Angell and Leirvik2014), they report
$A=24.6$
and
$B=0.08$
. The data points and line fit are reproduced from that later report. All the present cases, including those of
$Re=594$
agree with this model. Before concluding, figure 6(b) also shows a least-squared log-normal fit to the cumulative volume distributions based on all three data sets. The results show a reasonable agreement for a mean and standard deviation of
$\ln (D_{a}/D_{32})$
being 0.13 and 0.57, respectively. A similar agreement could be obtained for
$D_{a}/d_{50}$
, but with mean and standard deviation of
$\ln (D_{a}/d_{50})$
being 0.0 and 0.57, respectively. Fitting a Rosin–Rammler distribution instead (not shown), gives a spread coefficient of 2.2 versus 2.0 in Brandvik et al. (Reference Brandvik, Johansen, Farooq, Angell and Leirvik2014).
Figure 8. Joint probability distributions of droplet diameter and the fractional increase in interfacial area for compound droplets. (a,b)
$z/d=20.6$
, (c,d)
$z/d=30.6$
, (a,c)
$Re=1358$
and (b,d)
$Re=2122$
. Dashed white line indicates the resolution limit.
Figure 9. Joint probability distributions of droplet diameter and the volume fraction of water inside the compound droplets. (a,b)
$z/d=20.6$
, (c,d)
$z/d=30.6$
, (a,c)
$Re=1358$
and (b,d)
$Re=2122$
. Dashed white line indicates the resolution limit.
The ratio of the number of compound droplets,
$N_{c}$
, to the total number,
$N$
, for each size bin is presented in figure 7(a), including only points with more than 60 droplets. Very few compound droplets exist at
$Re=594$
. In contrast, there is a small difference between the results for the other two cases, i.e. the fraction of compound droplets depends mostly on the diameter. For
$D_{a}/d>0.07$
, the slope of these curves is approximately 2, possibly suggesting that the fraction increases with the droplet surface area. This rapid increase implies that while only 30 % and 38 % of the 1 mm droplets are compound for
$Re=1358$
and 2122, respectively, this fraction increases to 71 % and 84 % for 2 mm droplets. The size distributions of compound droplets, which are presented in figure 7(b), have peaks that shift to a lower diameter with increasing
$Re$
. Existence of this peak and shift are results of the combined effects of the distributions of both
$N_{c}/N$
and
$\text{d}N/\text{d}(D_{a})$
. The peaks are caused by the opposite trends of
$N_{c}/N$
and
$\text{d}N/\text{d}(D_{a})$
with diameter. The shift is caused by the decrease in the concentration of large droplets, which are more likely to be compound, with increasing
$Re$
. Before proceeding, note that trends of
$\sum N_{c}/\sum N$
depicted in table 2 might appear contradictory to those displayed in figure 7(a). Specifically, the table shows that the total number of compound droplets,
$\sum N_{c}$
, increases with
$Re$
, but their fraction (
$\sum N_{c}/\sum N$
) decreases from 17 % at
$Re=1358$
, to 10 % at
$Re=2122$
. Figure 7(a) shows that the size-dependent fraction corresponding to large droplets increases slightly with
$Re$
, and that of small droplets decreases with increasing
$Re$
. Since the total number of small droplets is orders of magnitude higher than the large ones, the small droplets dominate the statistics in table 2 even when the corresponding values of
$N_{c}/N$
are low.
The inner water droplets increase the oil–water interfacial area. Figure 8 shows the joint probability distribution function (p.d.f.) of
$D_{a}/d$
and the fractional increase in interfacial area,
$\unicode[STIX]{x0394}S/S$
, for
$Re=1358$
and 2122 at
$z/d=20.6$
and 30.6. The interfacial area is calculated from the perimeter,
$P$
, of droplets assuming spherical symmetry. The dashed line shows the limit below which the internal droplet perimeter cannot be measured with reasonable certainty. Several trends are evident. First, the distributions, including the upper limit, broaden with increasing diameter. Second, the areas covered by the joint p.d.f. decrease, and the peak probabilities increase with increasing
$Re$
. This trend is consistent with the decrease in concentration of large droplets with increasing Re (figure 7
b). Third, the most probable values and upper bounds of the p.d.f.s tend to shift upward with increasing
$z/d$
. As a plausible explanation for this trend, note that between
$z/d=20.6$
and 30.6, both
$D_{32}$
and
$d_{50}$
of all the droplets (table 2) decrease, representing the effect of reduction in the fraction of large droplets, presumably by the shear-induced breakup. During this process, the interior droplets are less likely to break up, as suggested by their nearly spherical shape, i.e. they maintain their size. Consequently,
$\unicode[STIX]{x0394}S/S$
should be expected to increase. For example, the mean value of
$\unicode[STIX]{x0394}S/S$
at
$z/d=20.6$
, 15 % and 8 % for
$Re=1358$
and 2122, respectively, increases to 23 % and 15 % at
$z/d=30.6$
. Note that, the values of
$\unicode[STIX]{x0394}S/S$
are plotted on a log scale, whereas the p.d.f. magnitude is presented on a linear scale. The large tail with values of
$\unicode[STIX]{x0394}S/S$
well above 0.1 results in a mean value significantly higher than the most probable one. While it is difficult to infer the trend with
$Re$
from the p.d.f. owing to the broad distributions at
$Re=1358$
, the data shows that the mean
$\unicode[STIX]{x0394}S/S$
decreases with increasing
$Re$
. This trend implies that the decrease in size of inner droplets outweighs the decrease in outer size with increasing
$Re$
. It might be associated with differences in the size of water ligament during the early KH roll-up phase, as suggested by figure 2. A similar analysis has been performed for the volume fraction of water in the oil droplets (figure 9). Quantitatively, the trends are similar to those of
$\unicode[STIX]{x0394}S/S$
, but values differ. At
$z/d=20.6$
, the mean volume fraction is 3 % and 2 % at
$Re=1358$
and 2122, respectively. On average, the compound droplets have a small effect (
${\sim}$
3 %), on their buoyancy.
Figure 10. Index of asphericity of (a) outer surface of oil droplets, and (b) inner water droplets, both for compound droplets. The line shows the average asphericity for each diameter. Insert: sample droplets with (c)
$\unicode[STIX]{x1D6F7}=3.5$
, (d)
$\unicode[STIX]{x1D6F7}=1.5$
, (e)
$\unicode[STIX]{x1D6F7}=1$
.
While the oil droplets have odd exterior shapes owing to the influence of turbulence, the interior droplets appear more circular. To compare the degree of deformation, we define a surrogate asphericity,
$\unicode[STIX]{x1D6F7}=(P/\unicode[STIX]{x03C0})/\sqrt{4A/\unicode[STIX]{x03C0}}$
, i.e. the ratio between the droplet diameter calculated from the perimeter and that calculated from the area. The magnitude of
$\unicode[STIX]{x1D6F7}$
ranges from one for a sphere to higher values as the shape complexity increases. The trends for the outer shapes at
$Re=1358$
are presented in figure 10(a), and those for the inner droplets, in figure 10(b). They are plotted versus the corresponding capillary numbers,
$Ca_{o}=\unicode[STIX]{x1D707}_{c}u_{d}D_{a}/d\unicode[STIX]{x1D70E}$
for the outside surface, and
$Ca_{i}=\unicode[STIX]{x1D707}_{d}u_{d}D_{i}/d\unicode[STIX]{x1D70E}$
, where
$D_{i}$
is the inner droplet diameter, for the inner droplet. Sample corresponding images are shown in figure 10(c–e). For the outer droplets, the
$\unicode[STIX]{x1D6F7}$
scatters between 1 and 3.5, with the upper bound increasing with
$Ca_{o}$
. Hence, the average asphericity for each capillary number,
$\overline{\unicode[STIX]{x1D6F7}(Ca_{o})}$
, which is plotted as solid line in figure 10(a), also increases with droplet size. In contrast, figure 10(b) shows that the inner droplets deviate only slightly from a spherical shape, irrespective of the
$Ca_{i}$
or the shape of the outer droplets, indicating that the inner droplets are only weakly influenced by the external shear. As discussed below, these observations are consistent with analyses of a single isolated compound droplet subject to external shear.
4 Discussion and conclusions
Refractive index matching and PLIF are used to study the fragmentation process of buoyant oil jets in water. Although it rarely happens at
$Re=594$
(
$We=785$
), compound droplets form regularly at
$Re=1358$
and
$Re=2122$
and persist at least up to
$z/d=30.6$
. The origin of some of the water pockets can be traced back to engulfment of water ligaments during roll-up of the KH vortices near the exit from the jet. In contrast, long thin water ligaments rarely form at
$Re=594$
before the oil breaks up, suggesting that for the present
$Oh=0.047$
, the near field shear is not strong enough to generate such ligaments. In other words, when the characteristic time scale of the jet,
$d/u_{d}$
, is compared to that derived from viscosity and interfacial tension,
$\unicode[STIX]{x1D707}_{d}d/\unicode[STIX]{x1D70E}$
, their ratio, i.e.
$Ca$
, might have to exceed a minimum value for the formation of elongated ligaments. In the present study, compound droplets are not generated for
$Ca=1.3$
and are abundant for
$Ca\geqslant 3.0$
.
For the present range, the fraction of compound droplets does not vary significantly with
$Re$
, but increases rapidly with droplet diameter, exceeding 78 % for droplets larger than 2 mm. Since small droplets are less likely to be compound, and the concentration of large droplets diminishes as the
$Re$
increases, the size distributions of compound droplets have peaks that increase in magnitude but shift to a lower diameter with increasing
$Re$
. Although the internal water pockets reduce the buoyancy by only a few per cent, they increase the oil–water interfacial area by approximately 15 %. While the increased surface area could presumably enhance the dissolution rate of soluble components of oil into the water, e.g. during crude oil spills, one cannot simply assume a linear relationship between the enlarged interfacial area and mass diffusion. Two potential effects should be considered. First, owing to the quiescent internal interfaces, the mass diffusion from the oil to the water is not likely to be affected by turbulence, in contrast to the external flow. Therefore, the internal mass diffusion is likely to be slower than that occurring along the outer surfaces. Second, because the soluble oil compounds in the internal water cannot be diluted by mixing with the surrounding water, their concentration is expected to increase over time, further reducing the dissolution rate.
Figure 11. A sample demonstrating the removal of stripe from images, and machine learning-based segmentation: (a) original image; (b) the same image after stripe removal; and (c) thresholded images with black indicating compound droplets.
As expected, the oil droplets are deformed in the near field of the jet, becoming increasingly more aspherical with increasing diameter (
$Ca$
). In contrast, the interior droplets remain nearly spherical irrespective of their sizes, suggesting that they are exposed to a more quiescent environment. There is considerable literature about the behaviour of an isolated compound droplet subjected to external shear. Reduced deformation of the internal droplet with increasing
$\unicode[STIX]{x1D707}_{d}/\unicode[STIX]{x1D707}_{c}$
has been shown for
$Ca$
of the same range by Stone & Leal (Reference Stone and Leal1990), Mandal, Ghosh & Chakraborty (Reference Mandal, Ghosh and Chakraborty2016) and Kim & Dabiri (Reference Kim and Dabiri2017). In contrast, substantial deformations are reported for higher
$Ca$
and low interfacial tension of the interior droplet by Smith, Ottino & de la Cruz (Reference Smith, Ottino and de la Cruz2004). Presumably, the small size of the interior droplet and dampening of the external shear by the higher oil viscosity create an environment with low local capillary numbers. It would be of interest to determine whether such a quiescent micro-environment in the middle of high shear zones affects the subsequent interactions of crude oil with the biochemical environment in the ocean during the long bio-degradation process of the oil.
Acknowledgements
This research is funded by the Gulf of Mexico Research Initiative (GOMRI) with the JHU group being part of the DROPPS Consortia. All data are accessible over the GOMRI Information and Data Cooperative (GRIIDC) at https://data.gulfresearchinitiative.org/. Y. Ronzhes participated in the design and manufacturing of the test facility. L. Chandrala, J. Doherty and A. Cohen helped with the data acquisition.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2019.645.
Appendix
The compound droplets are identified and measured by machine learning based image processing techniques. The scheme consists of image enhancement, classification of oil and water, identification of compound droplet, as well as measurements of their size and perimeter. As illustrated in figure 11(a), the original PLIF images have stripes due to refraction of light from the top and bottom of droplets owing to a slight mismatch (
${<}$
0.0005) in refractive indices. Therefore, a combined wavelet-Fourier filtering (Münch et al.
Reference Münch, Trtik, Marone and Stampanoni2009) has been applied to alleviate these stripes, resulting in the sample shown in figure 11(b). Briefly, Daubechies wavelets (DB25) are used as basis functions for two-dimensional multi-resolution (5 levels) wavelet decomposition. Then, a two-dimensional Fourier transform is applied on the horizontal detail coefficients to identify the spectral range containing the signature of the stripes. A Gaussian bandpass filter with a damping factor of 5 is then applied in the Fourier space to suppress the stripes. When the resulting images are reconstructed, dynamic masks maintain the filtered image within the bright oil signature but preserve the original background in the dark areas. Owing to the complexity of the PLIF images, global single-value or adaptive local threshold segmentation techniques are inadequate for correctly separating the oil from the water. Consequently, a machine learning-based pixel-wise classification has been implemented, following Arganda-Carreras et al. (Reference Arganda-Carreras, Kaynig, Rueden, Eliceiri, Schindelin, Cardona and Sebastian Seung2017). The training features include the original intensity, its mean and variance, the Gaussian-blurred and Sobel-filtered intensity, as well as the trace and the first and second eigenvalues of the Hessian matrix at each pixel. Except for the original intensity, all the training features are performed for five kernel sizes, taking noise reduction, edge detection, and texture into consideration. The random forest, which consists of 200 decision trees and two features per node, is trained based on labelled training sets. The resulting probability maps of classified pixels are then segmented by the Otsu’s method. Distance watershed transformation is subsequently performed to separate overlapping droplets, blob analysis is used to determine the droplet statistics. Ligaments and droplets cut by the border of images are not accounted for. Sample results are shown in figure 11(c), with black indicating compound droplets. The sample volume depth and associated threshold limits and uncertainty are estimated by traversing a
$500~\unicode[STIX]{x03BC}\text{m}$
pendant droplet through the laser sheet and using the same trained classifier to gauge the detection boundaries (
$1\pm 0.1~\text{mm}$
). Following Wu et al. (Reference Wu, Halter, Kacker, Elliot and Plant2013), the misclassification error rate in pixels is estimated as 8.7 %. The relative combined uncertainty in number density, 10 % and in diameter, 4.5 %, is indicated for a couple of data points in figures 6(a) and 7.
