1 Introduction
Payers for health care, either private insurers or governments using taxpayers’ money, have been looking for decades to make the most of the resources they purchase with insured or taxpayers’ contributions. This being the very definition of (output-oriented) technical, or productive, efficiency in economics, one could assume economists (and possibly, health economists) have been enroled to help solve the problem and provide decision makers with good evidence-based recommendations on how to reform or steer their health care ‘systems’. However, as shown in Hollingsworth (Reference Hollingsworth2012), in spite of the close to 400 publications measuring economic efficiency in health care to date, there has been little take-up of this evidence by policy makers. Hollingsworth (Reference Hollingsworth2012) suggests that the existing studies are not framed in a way that is relevant to policy makers, and that to help bridge the gap between research and practice, a set of guidelines is needed for efficiency analysis in health care. These guidelines could help improve take-up by policy makers by addressing two main shortcomings: first, poor average quality of the studies (at least in their ability to derive actionable recommendations); and second, the lack of clear and universally accepted criteria that would allow decision makers to assess the quality of such studies.
As much as we agree with the need for guidelines in efficiency analyses of health care systems, we suggest an additional explanation for the limited take-up of empirical evidence on economic efficiency in health care among policy makers: the very notion of systemic economic efficiency is seen as a black box. In contrast to ‘bottom-up’ studies that focus on clearly identified problems such as waste of resources, or poor outcomes on a single disease with clear practice guidelines, ‘top-down’, or system-level, studies that link resources to outcomes and seek to identify inefficiencies on the basis of what systems or sub-systems actually do rather than by comparison with a guideline of what ought to be, are often viewed as lacking any actionable recommendation (Häkkinen et al., Reference Häkkinen, Iversen, Peltola, Seppälä, Malmivaara, Belicza, Fattore, Numerato, Heijink, Medin and Rehnberg2013). The aim of this study is to provide a tentative demonstration that ‘top-down’ studies can be of help to health system decision makers and managers.
Unlike studies of facilities such as hospitals and nursing homes, studies of economic efficiency of health care systems are actually quite rare (Hollingsworth, Reference Hollingsworth2008). Studies of hospitals or nursing homes can be of interest to economists (e.g. to answer questions such as ‘are for-profit hospitals more or less efficient than public ones?’) but such questions are not necessarily of much help to decision makers who are more interested in reforms at the intensive margin (e.g. improving efficiency for all hospitals, whatever their ownership status) than in radical ones altering the distribution of hospitals by ownership status. Also, conclusions drawn at sub-system levels (e.g. hospitals or nursing homes) may not be helpful if apparent efficiency is the result of a better ability to select cases or to shift costs to other providers in the system (Felder and Tauchmann, Reference Felder and Tauchmann2013). Policy-makers are responsible for the system as a whole and want to make sure that they get the best out of resources they purchase. In technical terms, the level of Decision Making Unit (DMU) chosen to conduct efficiency analyses matters much and we posit here that studies conducted at the district or country level (aggregating all providers on a given territory contributing to a given health outcome) can be of help to policy-makers.
We briefly indicate here how our study differs from most (if not all) studies published so far in the small literature on efficiency at the health system (rather than hospitals or nursing homes) level, and how these differences contribute to a step in the direction of efficiency measurement as evidence for policy.
First, we based the main strategic decisions needed to conduct a study of efficiency (outcomes, inputs, DMU level and estimation of the frontier) on a systematic approach rather than on opportunity. The first such strategic decision regards the outcome, or what health systems produce: health systems are complex and do many different things, but what they are supposed to produce is never explicitly discussed. In that sense, a health system is very different from a firm (whose output is often self-obvious, even though, as Newhouse (Reference Newhouse1994) state, it would be quite impossible to tell what an airline company is actually selling) or even from a hospital, and the first step in any measure of efficiency of the health system is to make sure the analyst takes the right measure of outcome. We find that, in most of the literature at the country or district level, this choice of outcome variable is never made explicit and often driven by data availability. Since life expectancy or health-adjusted life expectancy is often available at the regional or national level, and since it is a ‘reasonable’ objective for a health system, studies often use such measures of average population health as their outcome measure, without discussing whether this is what policy-makers are truly mandated to maximise (Smith and Street, Reference Smith and Street2005). Our approach was radically different: we started with an agnostic view of what the outcome of a health system should be and used a series of tools (official documents scan, elite interviews, policy dialogue, all are detailed below) to elicit the answer to such an important question. Once we had that answer, we started looking for good data to represent and measure the outcome of the health system in the population. Since our approach did not yield a unanimous answer to the question of determining the objective of a health system, we compared the findings of our assessment of efficiency using various measures of such an outcome, such as age standardised treatable potential years of life lost (PYLL), survival rate and mortality rate.
Similarly, as far as the second decision (inputs) was concerned, we found that the definition of the sets of inputs and factors explaining efficiency scores was often ad hoc, the result of what is available in the data and not of an explicit discussion of what should be considered a resource available to the system and what should be considered an environmental factor to explain efficiency scores of individual DMUs. A crucial question is whether inputs should be accounted for as quantities (number of beds or physicians per 1000 population) or values (dollars spent on beds or physicians incomes). We used the same approach to determine the level of DMU at which to conduct the analysis: in a federal country such as Canada, this could be the province or sub-provincial districts such as health regions. All the above decisions were systematically made, based on a method that we documented, so that others could replicate and amend them. This, arguably, can help contribute to a more standardised and scientific approach to measuring efficiency in a way that health decision makers and managers can use.
Finally, ours is one of the first studies to use a robust two-step approach, following a Simar-Wilson method to account for serial correlation among efficiency scores (Simar and Wilson, Reference Simar and Wilson2007). Other such studies are Felder and Tauchmann (Reference Felder and Tauchmann2013) (for districts at the sub-Lander level in Germany) and Wranik (Reference Wranik2012) (for countries in the OECD), and we see our study as a contribution to the field in the same spirit as theirs: how can economists measure efficiency scores for a series of DMUs within a larger set (jurisdiction or club of countries such as the OECD) and, rather than providing a league table that might be used for naming and shaming, ‘explain’ these scores by factors that managers can alter or under which they have to operate. The former (factors that managers can alter) will help local decision makers improve their performance (and decision makers at a higher level assess that performance), while the latter will mainly help decision makers at a higher level (central) allocate resources so that DMUs operating under more challenging environments are compensated.
2 Method
The method consists of two stages. First, data envelopment analysis (DEA) is used to estimate efficiency at the regional level, which allows us to generate the average level of efficiency in Canada as a whole. Second, regression analyses are undertaken in order to identify the factors that help explain variation in inefficiency across regions (we analyse regional efficiency scores and treat regions as observations in this second-stage statistical analysis). The software package Frontier Efficiency Analysis with R (FEAR 1.0) was used to carry out the DEA estimations and Stata 11.0 was used for the second stage regression.
2.1 DEA
DEA and SFA are the two main techniques to measure efficiency. SFA is a parametric technique, which involves econometric estimation of the production frontier and can accommodate random noise. DEA is non-parametric and applies linear programming to calculate the maximum attainable output for every level of input. In this study, we used DEA because it does not rely on a priori assumptions on the specification of the production frontiers and the random error distribution, and is less sensitive than SFA to underperforming outliers. Also, DEA can incorporate inputs and outputs, which are measured in different units (Valdmanis et al., Reference Valdmanis, Rosko and Mutter2008), such as dollar values or quantities or activities. With DEA, one region is inefficient to some extent if a linear combination of two other regions observed in the data that would use the same level of inputs can produce more (Jacobs et al., 2006). (The Appendix provides more details on the method.)
2.2 Robustness of DEA
As described earlier, the DEA approach has several advantages; however, there are two main limitations. First, results of DEA are sensitive to high-performing outliers. If the outliers are undetected, the large random variation affecting a frontier DMU moves the entire frontier, which influences the estimates of all other DMUs. This study employs the method proposed by Wilson (Reference Wilson1993) to detect the outliers in DEA. Second, DEA is non-stochastic: it implicitly assumes that the entire deviation from the frontier is caused by the true level of inefficiency of a given region, ignoring the fact that the discrepancy may partially be due to measurement error (in the data) or random error (the region experienced a random shock in the very year measures were taken) (Zere et al., Reference Zere, McIntyre and Addison2001). To address this drawback, we introduced the smoothed bootstrap method developed by Simar and Wilson (Reference Simar and Wilson1998) to correct the estimates of efficiency for random noise. Details on the statistical outlier detection and bootstrapping methods can be found in the Appendix.
Smith (Reference Smith1997) notes that a well-specified DEA model will always overestimate efficiency; therefore, robust estimates are consistently lower than the point estimates. Because DEA is a descriptive approach that defines the efficiency frontier with actual regions, some of them will have an efficiency score of 1, by construction. It is highly likely, though, that the true frontier is further out and that no unit actually achieves perfect efficiency. The robust estimates reflect that in the sense that, as in SFA, none of the observed DMUs achieves an efficiency of 1 once the bias is corrected.
Finally, in order to ensure the level of variation in the efficiency estimates is sufficient relative to noise, we followed the approach recommended by Badunenko et al. (Reference Badunenko, Henderson and Kumbhakar2012). Essentially, the ratio of the variation in efficiency to the variation in noise should be greater than one in order to proceed with efficiency analyses. In our study, the ratio of variation in efficiency to noise was 2.24, which supports our choice to undertake the analysis using DEA.
2.3 Sensitivity analysis
DEA is sensitive to the number of inputs and outputs with respect to the number of DMUs used in the analysis. Efficiency scores are likely to be overestimated if the number of DMUs is small relative to the number of inputs (Mohammad, Reference Mohammad1998). Also, a large number of DEA inputs and outputs can result in an excessive number of DMUs lying on the frontier, which reduces the ability to identify inefficient DMUs (McCallion et al., Reference McCallion, Glass, Jackson, Kerr and McKillop2000). Hollingsworth and Peacock (Reference Hollingsworth and Peacock2008) recommend that the number of DMUs should be at least three times the total number of input and output variables. In our case, working with more than 80 DMUs, we can enter as many as 25 input and output variables in our model, which is more than we need. This, as a result, is not a binding constraint in our case.
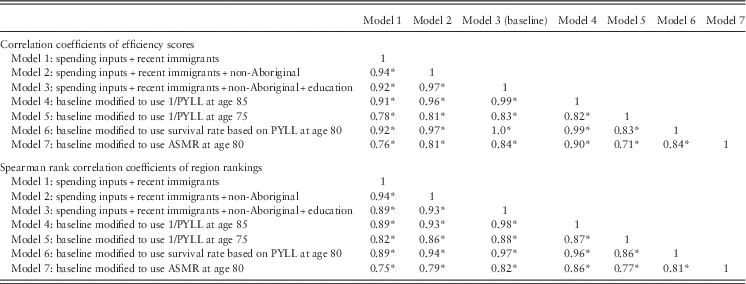
The selection of inputs and outputs may result in potential model misspecification. This can occur in the form of omitted variables or the inclusion of irrelevant variables. No test exists to assess the suitability of a particular model specification (Smith, Reference Smith1997). Therefore, we carried out a series of separate sensitivity analyses to assess the robustness of the results that are obtained from the DEA analysis. We examined whether the efficiency and the rank of health regions were robust to seven model specifications (detailed below). Our preferred model, that we then use as the baseline to conduct the sensitivity analyses, is the one with the lowest ‘bias’ detected following bootstrapping (Section 2.2). We calculated correlations across analyses between the (robust) efficiency estimates of health regions, and their rankings in terms of the (robust) efficiency estimates.
2.4 Explanatory analysis on the robust estimates of efficiency
Once the robust estimates of efficiency are generated for each region, we conduct a multivariate analysis of the determinants of efficiency scores, using a straightforward log-linear regression. Because some of the variables of interest are likely to be correlated and number of factors entered in this second stage is limited due to DMU size (still the number of regions), we used a backward step-wise regression to select variables to include in the second stage. The logarithm of the robust efficiency score was the dependent variable. Results were compared with a forward step-wise regression and they were largely unchanged. The final regression models included only those variables with statistically significant associations with efficiency estimates using a criterion of a p-value <0.2 (Steyerberg et al., 2000).
Although this type of two-stage analysis is widely used (Simar and Wilson, Reference Simar and Wilson2007); it seldom is correct for a likely statistical problem with the dependent variable: because efficiency scores have been estimated in a first stage in which the same observations as in the second stage are used and all contribute to the efficiency scores of all, it is likely that the values of the dependent variable for this second stage are serially correlated and thus violate conventional regression assumptions (Simar and Wilson, Reference Simar and Wilson2007). Therefore, conventional tests for possible violations of the regression assumptions were undertaken including scatter plots of residuals to detect the magnitude of serial correlation, tests for homoscedasticity, and variance inflation tests for multicollinearity among the independent variables. These tests showed no violations of the conventional regression assumptions.
3 Data
The data used in this study were collected over the period of 2007–2009 from 89 health regions in Canada through various data resources. Health regions are administrative bodies that are legislated by the provincial ministries of health. They tend to be defined by geographical areas and are generally responsible for maintaining the health of their respective populations and for providing health services to residents. More information about the health regions in each province can be found in Table A1.
3.1 Inputs and outputs in DEA models
Decisions on the inputs and outputs of health production for this analysis of efficiency were made following document review and stakeholder consultation. Specifically, a scoping review of official statements of health system objectives was undertaken, and in-depth interviews were conducted with senior health ministry officials primarily to understand their views regarding the objectives of the health system (Abelson and Pasic, Reference Abelson and Pasic2011). Another set of health sector decision makers and stakeholders participated in a facilitated dialogue on health system inputs and outputs (Lavis, Reference Lavis2011). The results of these consultations suggested that there is a good deal of agreement across provinces that the objective of the health system that we should measure efficiency against is to ensure that Canadians have access to effective care when they are sick or need care [Abelson and Pasic, Reference Abelson and Pasic2011; Lavis, Reference Lavis2011; Canadian Institute for Health Information (CIHI), 2012a]. To measure this objective of ensuring access to care when needed, we used the reduction of PYLL from causes of death that are considered to be amenable to health system intervention (Nolte et al., Reference Nolte, Scholz, Shkolnikov and McKee2002; CIHI, 2012b). Some examples of amenable, or treatable, causes of death in the Canadian context include sepsis, pneumonia, colorectal cancer, breast cancer in women, hypertensive diseases, asthma and most other respiratory diseases, renal failure, pregnancy and childbirth (CIHI, 2012b).
In this study, we set the age cut-off for defining premature death at 80 years, since about half of all deaths occur before that age. However, premature deaths are currently reported based on deaths occurring before 75 years in Canada and internationally (Nolte and McKee, Reference Nolte and McKee2008). Therefore, we tested the sensitivity of the results to different age cut-offs (ages 75 and 85), and the results remained relatively unchanged (see Section 4 and Table A3 for more details).
Rates of PYLL per 100,000 population for the latest available time period (the average for the period 2007–2009) were age-standardised in order to account for the different age structures across regions (Statistics Canada, 2013a). They were also transformed by taking the inverse of PYLL (1/PYLL×100,000) in order to ensure that, all other things being equal, increased inputs should reduce efficiency and increased outputs should increase efficiency. These estimates were based on Canada’s vital statistics database held at Statistics Canada. The other alternative outcomes included the treatable mortality rate and the survival rate using the formula (8,000,000−PYLL)/PYLL.
Inputs were selected in order to best represent the factors of production as suggested by the health system decision makers. Participants in the stakeholder dialogue were almost unanimous to recommend using dollar values rather than quantities to measure resources: the idea was that, if a region or province manages to pay its physicians less than another region, for the same quality, it will fairly be deemed more efficient. Over-paying providers was clearly identified as inefficient. For the type of inputs included the dialogue agreed that all major components of health spending – hospitals, physician services (including both family doctors and specialists), pharmaceuticals, residential care facilities and community care – should be included. In order to adjust for possible random fluctuations in spending over time, we take the average of three years of data (2007–2009), where possible. Also, we measure spending on a per capita basis by dividing the spending data by regional population size.
To account for the likely spatial dependence that may bias estimates of efficiency at the regional level (Felder and Tauchmann, Reference Felder and Tauchmann2013), we adjust the spending estimates for patient flow before entering them into the DEA. A patient flow ratio was calculated for hospital services as: the total number of separations (discharges or deaths) from acute care facilities within a given region, multiplied by the estimated cost of each separation (using a resource intensity weight for specialist spending and the average cost per weighted case for the hospital where care was delivered), divided by the number of acute care separations that were only by residents of that particular region (again, multiplied by the estimated costs). Thus, health regions with patient flow ratios greater than one had their per capita estimates adjusted downwards to account for the fact that more was spent on treating patients than was accounted for by the dollars spent to treat the geographically defined population (the region uses resources to provide access to residents of other regions). These ratios were used to adjust two inputs in the DEA: hospital spending, and specialist physician spending, given the majority of specialists work in hospitals.
As stated by Coelli et al. (Reference Coelli, Rao, O’Donnell and Battese2005), not accounting for the environmental differences between health regions may result in misleading efficiency measurements. However, there is no generally accepted methodology to account for environmental factors (to decide which ones to include in the DEA in the first stage; Coelli et al., Reference Coelli, Rao, O’Donnell and Battese2005). We include a selection of environmental variables as inputs in the DEA estimation consistent with previous studies (Afonso and St. Aubyn, Reference Afonso and St. Aubyn2006; Liu, 2008), and then incorporate the remaining ‘environmental’ (non input) variables in a second-stage analysis.
The environmental adjustors were included in the DEA on the basis that they can be considered to be outside of the responsibility of health systems but they significantly affect the outcome measure (treatable mortality). These included the proportion of the population aged 25 to 29 who have a secondary school graduation certificate or equivalent, the proportion of the population who immigrated within the past 10 years, and the proportion of the population who were not Aboriginal. These three measures were based on self-report to the 2006 Census (Statistics Canada, 2013b). Alternate DEA specifications including one, or two, of these environmental adjustors were also conducted, and the results were relatively robust to the choice of the number of adjustors included as inputs (see results). There are other possible environmental variables that could have been included as inputs, such as the proportion of the population that is over the age of 65, or population density, because they can be considered beyond the control of health system leaders. However, these variables were not found to be significantly associated with the outcome measure, so they were included as factors in the second stage of the analysis.
3.2 Identifying factors related to health system efficiency
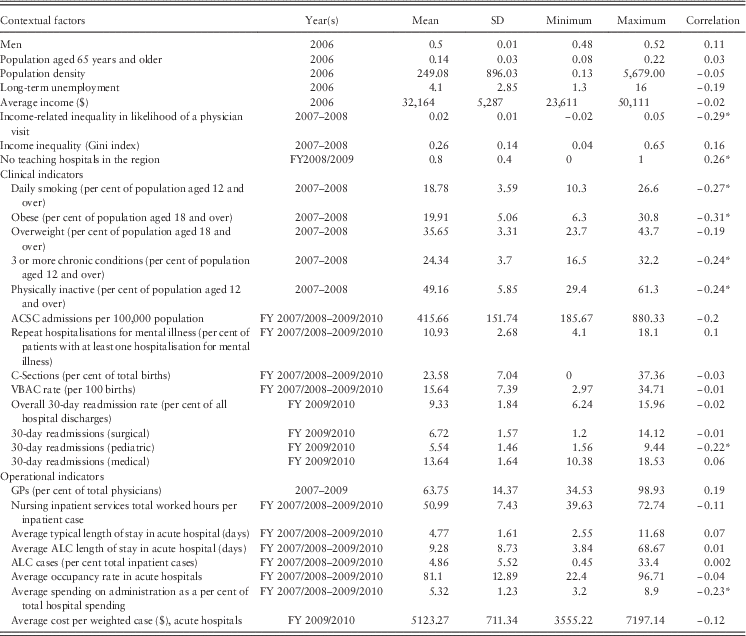
The factors that relate to efficiency could be divided into those that relate to what the decisions managers make (managerial factors), and those that reflect the environment in which managers operate (environmental factors). In the former category, we consider indicators of health care being provided that is ineffective, inappropriate, or harmful, public health factors, and indicators of care that is provided that is effective yet more costly than it ought to be (Bentley et al., Reference Bentley, Effros, Palar and Keeler2008; McGlynn et al., 2003; Smith et al., 2012). In the latter category, consistent with the literature, we consider the following environmental factors: the distribution of age and gender within the population; physical and geographical characteristics (e.g. population density and the presence of a teaching hospital in the region); and socio-economic conditions (e.g. income inequality and average income). Equitable access to care was also included, and was measured by the income-related inequity in the likelihood of visiting a physician in the past year, based on the concentration index approach (van Doorslaer and Masseria, Reference Van Doorslaer and Masseria2004). Table A1 summarises the factors that were considered in this study, as well as their data source and the time period the data are available.
4 Results
4.1 Summary of regions, inputs and outputs data
There is considerable variation across health regions in their size and characteristics of the populations served. On average, population density across health regions was 249/100 km2, ranging from 0.13 to 5679. Roughly 14% of population was aged above 65 years, with a range from 8 to 22%. Also 20% of health regions (17 of 84) had teaching hospitals.
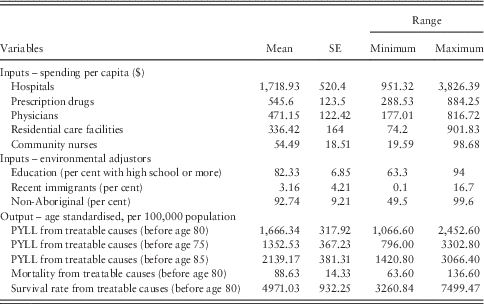
Descriptive statistics of the output, inputs and environmental factors used in the analysis are presented in Table 1. Treatable PYLL per 100,000 varies across the health regions even after adjusting for different age structures across the regional populations. Hospitals represent the largest component of spending in the data set with $1719 average per capita expenses, and here again, spending per capita varies across region.
Table 1 Description of the health system input and output variables used in DEA, 84 regions

Survival rate=(8,000,000−PYLL)/PYLL.
4.2 First stage: DEA results
Seven different DEA models were run to calculate robust efficiency estimates ranging from 0.65 to 0.82 on average across the sample of health regions (Table 2). Model 3, which includes 1/PYLL at age 80, five spending inputs and three environmental adjustors, was used as the baseline model and it yielded a robust estimate that averaged 0.73.
Table 2 Average robust efficiency scores from seven alternate DEA models

DEA=data envelopment analysis.
Model 1: spending inputs and recent immigrants; 1/PYLL at age 80.
Model 2: spending inputs, recent immigrants and non-Aboriginal; 1/PYLL at age 80.
Model 3: spending inputs, higher education, recent immigrants and non-Aboriginal; 1/PYLL at age 80.
Model 4: baseline modified to use 1/PYLL at age 85.
Model 5: baseline modified to use 1/PYLL at age 75.
Model 6: baseline modified to use survival rate based on PYLL at age 80.
Model 7: baseline modified to use age-standardised mortality rate based on PYLL at age 80.
It is important to note that the value of an approach such as DEA is less in the extraction of precise estimates of efficiency, which one should report cautiously, than as an exploratory analytic tool for further analysis (Jacobs et al., Reference Jacobs, Smith and Street2006). That said, the robust estimates of efficiency did not appear to be sensitive to changes in model specification. Correlations between the efficiency estimates produced by the seven models that varied the input and output variables were high (0.70 to 0.99). Correlation coefficients for the estimates and rankings produced by the seven different models are presented in Table A2. It is also worth noting that this average efficiency score of 0.73 in health regions in Canada is not far from the 0.80 estimated efficiency found for Canada by the OECD, based on a comparison across countries (Joumard et al., Reference Joumard, Hoeller, André and Nicq2010).
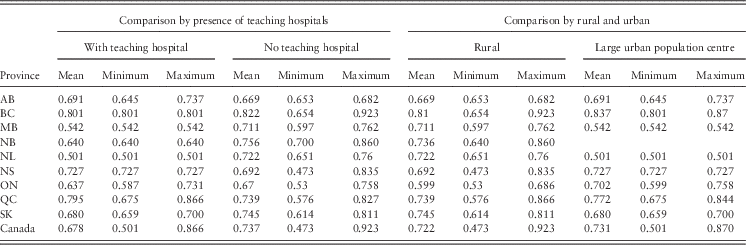
In order to test the extent to which our methods of adjusting for patient flow were effective in reducing the possible bias arising from spatial dependence (Felder and Tauchmann, Reference Felder and Tauchmann2013), we compared the average and range of efficiency scores by regions with and without a teaching hospital, and between regions that are relatively more urbanised compared with those that are more rural. Table 3 shows that there is no systematic pattern, either nationally, or by province, of less efficient urban regions surrounded by more highly efficient regions.
Table 3 Efficiency scores by province, presence of a teaching hospital and urban/rural regions

4.3 Second stage: log-linear regression results
Table 3 reports the results of the backward step-wise regression of managerial and environmental factors on efficiency scores produced from the seven models. Table A1 lists all the variables that were considered in this second stage analysis, as well as the correlation coefficients between each variable and the robust efficiency estimate.
As shown in Table 4, among the environmental factors, a higher average income of residents in a region was negatively related with efficiency in five of the models. This implies that in richer regions there may be more spending on health services that does not necessarily translate into reductions in treatable causes of death, after controlling for variations in education, immigrant and Aboriginal concentration (as these were included as environmental adjustors in the calculation of DEA estimates). Also there was a negative association between inequitable access to physician services and efficiency in four of the models: regions with greater inequity in favour of higher income groups were less likely to be efficient than regions with a more equitable distribution of physician services. In other words, health system managers do not need to trade-off equity for efficiency; these results suggest that they can improve performance by improving access to care for individuals with lower income.
Table 4 Regression results with environmental and managerial factors as predictors

***Indicates statistical significance at p<0.001 level, **indicates p<0.05 level.
Several public health factors were associated with efficiency. The results from the regressions suggested that an increase in the prevalence of smoking by 10 percentage points would decrease efficiency by 10%; an increase in the proportion physically inactive by 10 percentage points would decrease efficiency by a range of 5–9%; an increase in the proportion with multiple chronic conditions by 10 percentage points would decrease efficiency by between 10 and 18%; an increase in the proportion of obesity in the population by 10 percentage points would decrease efficiency by 8–11% and an increase in the proportion of overweight by 10 percentage points would decease efficiency by 8–11%.
The results also suggest that several managerial factors were significantly associated with efficiency. The overall rate of unplanned readmissions to hospital within 30 days was inversely related to efficiency: an increase in the rate of 30-day readmission per 100 patients of 10 percentage points was associated with a reduction in efficiency of between 16 and 19%. Other factors include the relative density of GPs in a region compared with specialist physicians (an increase by 10 percentage points in that relative density would improve efficiency by 4–6%), the average length of stay among patients designated as ‘alternate level of care’ (ALC; an increase by 10 days of the ALC length of stay decreased efficiency by 1–4%) and the proportion of ALC cases of total hospital patient cases (an increase by 10 percentage points in the proportion of ALC cases in total inpatient cases decreased efficiency by 9%). Finally, an increase by 10 percentage points in the acute hospital administrative services expenses was associated with a decrease in efficiency of 19%.
5 Discussion
In this paper, we adopted a ‘top-down’ approach to measuring health system efficiency with the objective of facilitating uptake of this evidence by decision makers and system managers. We followed best practice in the field in order to move towards the standardisation of efficiency measurement (Jacobs, 2006). In this work, we made all decisions systematic and documented, rather than being content to analyse data as they existed and adjusting concepts to existing observations. Decisions to be made relate to the definition of outputs (what is the objective of the health care system that efficiency should be measured against?), inputs (what resources are available and in what units should they be measured?), decision-making units and the empirical strategy to estimate the frontier.
As far as the first three decisions (outputs, inputs, DMU) are concerned, two options are available: one is to force definitions from without, based on what the analyst thinks ought to be the right definition; the other is to rely on a sui generis definition and to ask stakeholders themselves how they would define the outputs and resources. Our study at the Canadian level shows that stakeholders have different views but a clearly dominant theme emerged from the interviews and a consensus was relatively easily reached during the stakeholder dialogue: it was clear that ‘access to timely care when sick’ was the objective they should be assessed against.
In order to generate results that are meaningful to policy makers, our main objective in this study was not so much to estimate the level of inefficiency per se as it was to understand how it varies across DMUs and what seems to explain these variations. Moreover, in order to inform decision makers we categorised these factors into those that are within the control of managers, which can be used to help local decision makers improve performance, and those that are characteristics of the operating conditions, which would be relevant to decision makers at a higher level interested in allocating resources to compensate regions operating in more challenging environments.
Overall, this two-stage approach to measuring regional-level efficiency in Canada allowed us to identify several important managerial and environmental factors related to system efficiency. Consistent with other studies of efficiency across countries (Ryltseva, Reference Ryltseva2010; Hadad et al., Reference Hadad, Hadad and Simon-Tuval2013) and within US and Canadian states and provinces (Liu, Reference Liu2008), public health factors were significantly and negatively associated with efficiency scores: our main conclusion is therefore that the health care system must spend more to prevent the same number of premature deaths when the population is less healthy, either because treatments of treatable causes of death are more expensive when patients are less healthy, or because the system has to spend resources on other things than preventing premature deaths because more individuals are not healthy.
A number of managerial factors were identified as being significantly associated with efficiency in this study. These include factors related to appropriate and effective health care (as measured by fewer readmissions to hospital) as well as the use of overly costly inputs (as measured by the ratio of GPs to total physicians in a region), and the use of hospitals among patients who have been identified as being better suited to another, less expensive care setting such as long-term care institution or at home. These particular indicators have received increasing attention in recent years. For instance, studies show that while readmissions relate in part to characteristics and management practices of hospitals (Joynt and Jha, Reference Joynt and Jha2011; Stukel et al., Reference Stukel, Fisher, Alter, Guttmann, Ko, Fung, Wodchis, Baxter, Earle and Lee2012), they could potentially be reduced through improved coordination efforts and partnerships between hospital and community care (Boutwell et al., Reference Boutwell, Bihrle Johnson, Rutherford, Watson, Vecchioni, Auerbach, Griswold, Noga and Wagner2013), as well as timely and effective follow-up care with a physician (Jencks et al., Reference Jencks, Williams and Coleman2009). Therefore, continued efforts to make improvements here could have the effect of improving efficiency at the system level.
This study also identified several characteristics of the environment in which health systems are operating that were significantly associated with efficiency in this study. Most of the models identified higher average income of the population to be negatively associated with efficiency, in contrast to studies across the 191 countries in the WHO region (Greene, Reference Greene2004). In other words, after adjusting for the level of education in the region as well as other characteristics associated with socio-economic status included in the health production function such as the proportion of the population who recently immigrated to Canada and who do not identify as an aboriginal, higher average income does not increase efficiency. This implies that in richer regions there may be more spending on health service that does not necessarily translate into saving more lives. The results of the study also suggest there may be efficiency gains associated with more equitable access to physician care; therefore, it can also be argued that more effective health systems provide more equitable access and, as a result, treat the most vulnerable who are also those who can benefit the most from interventions.
Our study is a first step toward top-down analyses of efficiency of health systems that are able to help decision makers make improvements. One key aspect of making our conclusions helpful is the systematic way we made decisions at each step. One limitation of the present study is that such a systematic approach could not be maintained all along and some decisions had to be made based on inconclusive information. For instance, even though we received a clear mandate from stakeholders on the definition of inputs to be entered in the first step, there are no clear rules in the literature regarding which environmental factors should be included as well, and which ones should be used as factors in the second stage. The rationale for including some environmental characteristics in the first step (that calculates efficiency scores) is to ensure DMUs are comparable; however, there is some arbitrariness involved in the definition of comparable and no clear systematic rule would allow the analyst to know what variables to control. A rule of thumb is that everything not included in the first step is implicitly considered to be the responsibility of the health system: for instance, including smoking rates in the first step would amount to consider that a health care system has to prevent as many treatable premature deaths it can, knowing it has a given proportion of smokers in its population. Decreasing the smoking rate would not improve its efficiency score. On the other hand, entering smoking rates in the second stage relies implicitly on the idea that a DMU could improve its efficiency score by decreasing the prevalence of smoking. We decided to include education, the proportion of recent immigrants and the proportion of non-Aboriginals in the population of the region as three characteristics we wanted to control in the first step. This may seem reasonable as no one would argue that DMUs should be held responsible for them. However, we left income and the proportion of seniors out of the first step and entered them as factors in the second step, even though DMUs cannot reasonably be held responsible for their values. The decision was essentially pragmatic, as a limited number of environmental variables only could be entered in the DEA and we focussed on those that had a significant association with the outcome measure.
Another pragmatic decision we had to make regarded the choice of estimation strategy for the frontier (DEA vs SFA). Our decision was partly based on systematic reasons making DEA a better alternative in the sense that it imposes almost no non-testable specification assumptions (whereas SFA relies on strong non-testable specification assumptions) and its main drawbacks (lack of randomness) can now be overcome by the Simar Wilson method that we applied in this work. However, the decision was also partly based on pragmatic considerations related to the data.
Future research in this area could examine whether the factors related to efficiency in Canada are similar to those found in other jurisdictions. Also given that the findings from the regression are largely exploratory, qualitative research could be used to conduct more in-depth analysis of best performers in order to share best practices across regions. Finally, future research could improve the outcome variable by measuring preventable years of life lost both to death and to poor quality of life that better reflects the concept of timely access to care when sick, since not getting access to care can either kill or reduce the quality of life of those who survive.
Acknowledgments
This study was funded by the Canadian Institute for Health Information (CIHI). The authors would like to acknowledge the tremendous support and guidance provided by CIHI, and especially by Jeremy Veillard, the Vice President of Research and Analysis, CIHI. The authors are also grateful to the two anonymous reviewers for their helpful comments and suggestions.
Appendix Detailed methods
In this study, we employ an output-orientation approach to DEA, based on the assumption that ministries of health are interested in getting closer to achieving their objectives given a fixed budget. Moreover, we assume variable returns to scale (VRS) which is considered to be appropriate for analysis in the health sector, because of evident diminishing marginal returns (adding more resources increases output by less) when one examines the relationship between spending on aggregate and health outcomes (OECD, 2011), and for technical reasons relating to the use of ratio data (such as spending per capita; Hollingsworth and Smith, Reference Hollingsworth and Smith2003).
The output-oriented DEA model under VRS specification for the DMU 0 is specified as the following mathematical formula:
 $$\eqalignno{ & \min _{{\quad\quad\ \ ∅,z}} \!∅ _{0} \cr & {\rm Subject}\;{\rm to}:\quad \quad {{{\minus}y_{{r0}} } \over {∅ _{0} }}{\plus}\mathop{\sum}\limits_{j=1}^n {z_{j} y_{{rj}} \geq } 0\quad \quad r=1,2,...,m \cr & x_{{i0}} {\minus}\mathop{\sum}\limits_{j=1}^n {z_{j} x_{{ij}} \geq } 0\quad \quad i=1,2,...,k \cr & z_{j} \geq 0,\quad \quad \quad j=1,2,...,n \cr & \mathop{\sum}\limits_{j=1}^n {z_{j} =1} ; $$
$$\eqalignno{ & \min _{{\quad\quad\ \ ∅,z}} \!∅ _{0} \cr & {\rm Subject}\;{\rm to}:\quad \quad {{{\minus}y_{{r0}} } \over {∅ _{0} }}{\plus}\mathop{\sum}\limits_{j=1}^n {z_{j} y_{{rj}} \geq } 0\quad \quad r=1,2,...,m \cr & x_{{i0}} {\minus}\mathop{\sum}\limits_{j=1}^n {z_{j} x_{{ij}} \geq } 0\quad \quad i=1,2,...,k \cr & z_{j} \geq 0,\quad \quad \quad j=1,2,...,n \cr & \mathop{\sum}\limits_{j=1}^n {z_{j} =1} ; $$
where y rj is the vector of outputs for DMU j, x ij the vector of inputs for DMU j and the values of outputs and inputs should be nonnegative. z j represents a vector of weights attached to each DMU j in the comparison group from the perspective of DMU j (Charnes et al., Reference Charnes, Cooper and Rhodes1978) and is determined by the above linear programming problem. ∅ is the efficiency score that measures technical efficiency (TE) of a DMU and satisfies ∅⩽1. A TE score 1 indicates that the DMU lies on the production frontier, i.e., it is technically efficient. With the TE<1, the DMU is inside the frontier, i.e., it is technically inefficient, and the more inefficient, the lower the TE score.
We then applied a statistical outlier detection method developed by Wilson (Reference Wilson1993). This approach adopts the influence function based on the geometric volume spanned by the sample observations and the sensitivity of this volume with respect to deleting suspicious observations from the sample (Wilson, Reference Wilson1993). The results can be graphically analysed where the influence function (log-ratios) is expressed as a function of the number (i) of deleted observations (l). The larger the distance from the smallest ratio, the more likely there is an outlier among the remaining observations. The detailed mathematical description of the method can be found in Wilson (Reference Wilson1993) or Fried et al. (Reference Fried, Lovell and Schmidt2008).
The process of bootstrap DEA (output orientation) proceeds in the following steps:
(1) Employ DEA to the original data to calculate efficiency scores (point estimate):
 ${\widehat{\Oslash}}_{j} $
${\widehat{\Oslash}}_{j} $
(2) Generate a random pseudo sample with replacement of size n from the empirical distribution of efficiency scores (F distribution)
 ${\widehat{\Oslash}}_{j}$
, providing
${\widehat{\Oslash}}_{j}$
, providing  $\Oslash _{{1b},}^{{\asterisk}} ...\Oslash_{{nb}}^{{\asterisk}} $
.
$\Oslash _{{1b},}^{{\asterisk}} ...\Oslash_{{nb}}^{{\asterisk}} $
.(3) Obtain a bootstrap set of pseudo-inputs
 $$(x_{{jb}}^{{\asterisk}} ={{\hat{\Oslash }_{j}x_{j} } \over {\Oslash _{{jb}}^{{\asterisk}} }},j=1,...n)$$
using the ratio of the original efficient input level, i.e., the product of original efficiency score and the original input
$$(x_{{jb}}^{{\asterisk}} ={{\hat{\Oslash }_{j}x_{j} } \over {\Oslash _{{jb}}^{{\asterisk}} }},j=1,...n)$$
using the ratio of the original efficient input level, i.e., the product of original efficiency score and the original input  $(\widehat{\Oslash }_{j} x_{j} )$
and the pseudo-efficiency scores
$(\widehat{\Oslash }_{j} x_{j} )$
and the pseudo-efficiency scores  $(\Oslash _{{jb}}^{{\asterisk}} )$
.
$(\Oslash _{{jb}}^{{\asterisk}} )$
.(4) Adapt DEA to this new set of observations, composed of the pseudo-inputs
 $(x_{{jb}}^{{\asterisk}} )$
from step 3 and the same set of outputs then calculate the bootstrapped efficiency scores
$(x_{{jb}}^{{\asterisk}} )$
from step 3 and the same set of outputs then calculate the bootstrapped efficiency scores  $$(\widehat{\Oslash }_{{j,b}}^{{\asterisk}} )$$
.
$$(\widehat{\Oslash }_{{j,b}}^{{\asterisk}} )$$
.(5) Repeat steps 1–4 B times to generate a distribution of size B of bootstrapped scores for statistical inference.
The estimated bootstrap bias is calculated by B times Monte-Carlo simulations using:
A bias corrected estimator of efficiency ![]() $${{\Oslash_{j} }}$$
is
$${{\Oslash_{j} }}$$
is ![]() $$\widetilde{{\Oslash_{j} }}=\widehat{{\Oslash \varnothing _{j} }}\widehat{{{\,\minus\,}bias_{j} }}=2\widehat{{\Oslash _{j} }}{\,\minus\,}\overline{\Oslash } _{j}^{{\asterisk}} $$
$$\widetilde{{\Oslash_{j} }}=\widehat{{\Oslash \varnothing _{j} }}\widehat{{{\,\minus\,}bias_{j} }}=2\widehat{{\Oslash _{j} }}{\,\minus\,}\overline{\Oslash } _{j}^{{\asterisk}} $$
Table A1 Summary of health regions number and functions, by province

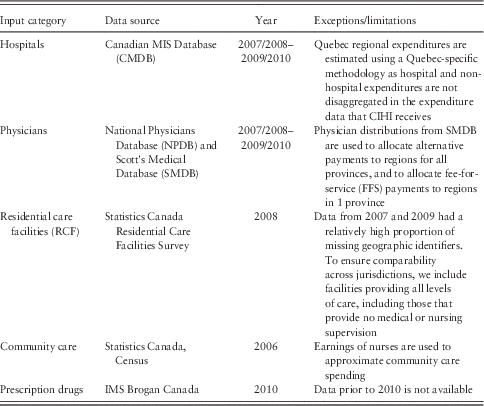
Table A2 Summary of the spending input data sources and limitations

Table A3 Description of variables that were included in the second stage step-wise regression, and correlations with efficiency scores (n=84)

Table A4 Correlations between efficiency scores from seven model specifications