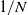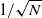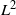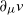1. Introduction
Let us consider the second-order parabolic partial differential equation (PDE) on the Wasserstein space
${\mathcal{P}}_2(\mathbb{R}^d)$
of square-integrable probability measures on
$\mathbb{R}^d$
, in the form
\begin{equation} \left\{\begin{aligned}& \partial_t v + {\mathcal{H}}(t,\mu,v,\partial_\mu v ,\partial_x\partial_\mu v,\partial_\mu^2 v) = 0, && (t,\mu) \in [0,T)\times{\mathcal{P}}_2(\mathbb{R}^d), \\& v(T,\mu) = G(\mu), && \mu \in {\mathcal{P}}_2(\mathbb{R}^d).\end{aligned}\right.\end{equation}
Here
$\partial_\mu v(t,\mu)$
is the L-derivative on
${\mathcal{P}}_2(\mathbb{R}^d)$
(see [Reference Carmona and Delarue6]) of
$\mu \mapsto v(t,\mu)$
, and it is a function from
$\mathbb{R}^d$
into
$\mathbb{R}^d$
,
$\partial_x\partial_\mu v(t,\mu)$
is the usual derivative on
$\mathbb{R}^d$
of
$x \in \mathbb{R}^d \mapsto \partial_\mu v(t,\mu)(x) \in \mathbb{R}^d$
, hence takes values in
$\mathbb{R}^{d\times d}$
, the set of
$d\times d$
-matrices with real coefficients, and
$\partial_\mu^2 v(t,\mu)$
is the L-derivative of
$\mu \mapsto \partial_\mu v(t,\mu)(.)$
, and hence a function from
$\mathbb{R}^d\times\mathbb{R}^d$
into
$\mathbb{R}^{d\times d}$
. The terminal condition is given by a real-valued function G on
${\mathcal{P}}_2(\mathbb{R}^d)$
, and the Hamiltonian
${\mathcal{H}}$
of this PDE is assumed to be in semi-linear (non-linear with respect to v,
$\partial_\mu v$
, and linear with respect to
$\partial_x\partial_\mu$
,
$\partial_\mu^2 v$
) expectation form
\begin{align} & {\mathcal{H}}(t,\mu,y,\textrm{z}(.),\gamma(.),\gamma_0(.\,,.)) \notag \\ &\quad = \int_{\mathbb{R}^d} \bigl[ H(t,x,\mu,y,\textrm{z}(x)) + \dfrac{1}{2}{\textrm{tr}}\bigl(\bigl(\sigma\sigma^{\top}+\sigma_0\sigma_0^{\top}\bigr)(t,x,\mu)\gamma(x)\bigr) \bigr] \mu({\textrm{d}} x) \notag \\& \quad \quad + \dfrac{1}{2} \int_{\mathbb{R}^d\times\mathbb{R}^d} {\textrm{tr}}\bigl(\sigma_0(t,x,\mu)\sigma_0^{\top}(t,x^{\prime},\mu)\gamma_0(x,x^{\prime})\bigr) \mu({\textrm{d}} x)\mu({\textrm{d}} x^{\prime}),\end{align}
for some real-valued measurable function H defined on
$[0,T]\times\mathbb{R}^d\times{\mathcal{P}}_2(\mathbb{R}^d)\times\mathbb{R}\times\mathbb{R}^d$
, and where
$\sigma$
,
$\sigma_0$
are measurable functions on
$[0,T]\times\mathbb{R}^d\times{\mathcal{P}}_2(\mathbb{R}^d)$
, valued respectively in
$\mathbb{R}^{d\times n}$
and
$\mathbb{R}^{d\times m}$
. Here
${\textrm{tr}}(M)$
denotes the trace of a square matrix M, while
$M^{\top}$
is its transpose and ‘
$.$
’ is the scalar product.
PDEs in Wasserstein space have been studied widely in the literature over the last few years, notably with the emergence of mean-field game theory, and we mention among others the papers [Reference Bensoussan, Frehse and Yam2], [Reference Burzoni, Ignazio, Reppen and Soner4], [Reference Cardaliaguet, Delarue, Lasry and Lions5], [Reference Gangbo and Swiech13], [Reference Pham and Wei21], [Reference Saporito and Zhang22], and other references in the two-volume monograph [Reference Carmona and Delarue6, Reference Carmona and Delarue7]. An important application concerns mean-field type control problems with common noise. The controlled stochastic McKean–Vlasov dynamics is given by
\begin{align} {\textrm{d}} X_s^\alpha &= \beta\Bigl(s,X_s^\alpha,\mathbb{P}^0_{{X_s^\alpha}},\alpha_s\Bigr) \,{\textrm{d}} s + \sigma\Bigl(s,X_s^\alpha,\mathbb{P}^0_{{X_s^\alpha}}\Bigr) \,{\textrm{d}} W_s \notag \\& \quad + \sigma_0\Bigl(s,X_s^\alpha,\mathbb{P}^0_{{X_s^\alpha}}\Bigr) \,{\textrm{d}} W^0_s , \quad t \leq s \leq T, \; X_t^\alpha = \xi,\end{align}
where W is an n-dimensional Brownian motion, independent of an m-dimensional Brownian motion
$W^0$
(representing common noise) on a filtered probability space
$(\Omega,{\mathcal{F}},\mathbb{F}=({\mathcal{F}}_t)_{0\leq t\leq T},\mathbb{P})$
, the control process
$\alpha$
is
$\mathbb{F}$
-adapted valued in some Polish space A, and
$\mathbb{P}^0$
denotes the conditional law given
$W^0$
. The value function defined on
$[0,T]\times{\mathcal{P}}_2(\mathbb{R}^d)$
by
\begin{equation*}v(t,\mu) = \inf_{\alpha} \mathbb{E}_{t,\mu} \biggl[ \int_t^T \,{\textrm{e}}^{-r(s-t)} f\Bigl(X_s^\alpha,\mathbb{P}^0_{{X_s^\alpha}},\alpha_s\Bigr) \,{\textrm{d}} s + {\textrm{e}}^{-r(T-t)} g\Bigl(X_T^\alpha,\mathbb{P}^0_{{X_T^\alpha}}\Bigr) \biggr]\end{equation*}
(here
$\mathbb{E}_{t,\mu}[\cdot]$
is the conditional expectation given that the law at time t of the solution X to (1.3) is equal to
$\mu$
) is shown to satisfy the Bellman equation (1.1)–(1.2) (see [Reference Bensoussan, Frehse and Yam1], [Reference Cosso and Pham9], [Reference Djete, Possamaï and Tan11]) with
$G(\mu) = \int g(x,\mu) \mu({\textrm{d}} x)$
,
$\sigma$
,
$\sigma_0$
as in (1.3) and
\begin{align} H(t,x,\mu,y,z) &= -ry + \inf_{a \in A} [ \beta(t,x,\mu,a)\,.\, z + f(x,\mu,a) ].\end{align}
We now consider a finite-dimensional approximation of the PDE (1.1)–(1.2) in the Wasserstein space. This can be derived formally by looking at the PDE for
$\mu$
to averages of Dirac masses, and it turns out that the corresponding PDE takes the form
\begin{equation} \left\{\begin{aligned}& \partial_t v^N + \dfrac{1}{N} \displaystyle\sum_{i=1}^N H\bigl(t,x_i, \bar\mu({\textbf{x}}),v^N,N D_{x_i} v^N\bigr) \\&\quad + \dfrac{1}{2} {\textrm{tr}}\bigl(\Sigma_N(t,{\textbf{x}}) D_{{\textbf{x}}}^2 v^N\bigr) = 0, && \text{on $ [0,T) \times (\mathbb{R}^d)^N$,}\\&v^N(T,{\textbf{x}}) = G(\bar\mu({\textbf{x}})), && {\textbf{x}} = (x_i)_{i \in [\![1,N ]\!]} \in (\mathbb{R}^d)^N,\end{aligned}\right.\end{equation}
where
$\bar\mu(.)$
is the empirical measure function defined by
\begin{equation*}\bar\mu({\textbf{x}}) = \frac{1}{N}\sum_{i=1}^N \delta_{x_i}\quad \text{for any ${\textbf{x}} = (x_1,\ldots,x_N)$, $N \in \mathbb{N}^*$,}\end{equation*}
and
\begin{equation*}\Sigma_N = \bigl(\Sigma_N^{ij}\bigr)_{i,j\in [\![ 1,N]\!]}\end{equation*}
is the
$\mathbb{R}^{Nd\times Nd}$
-valued function with block matrices
\begin{equation*} \Sigma_N^{ij}(t,{\textbf{x}}) = \sigma(t,x_i,\bar\mu({\textbf{x}}))\sigma^{\top}(t,x_j,\bar\mu({\textbf{x}}))\delta_{ij} + \sigma_0(t,x_i,\bar\mu({\textbf{x}}))\sigma_0^{\top}(t,x_j,\bar\mu({\textbf{x}})) \in \mathbb{R}^{d\times d}.\end{equation*}
In the special case where H has the form (1.4), we notice that (1.5) is the Bellman equation for the N-cooperative problem, whose convergence to the mean-field control problem has been studied in [Reference Carmona and Delarue7], [Reference Lacker16], and [Reference Laurière and Tangpi17, Reference Laurière and Tangpi18], when
$\sigma_0 \equiv 0$
(no common noise), and recently in [Reference Djete10] in the common noise case. We point out that these works do not consider the same master equation. In particular their master equation is stated on
$[0,T]\times\mathbb{R}^d\times{\mathcal{P}}_2(\mathbb{R}^d) $
and is linear in
$\partial_\mu u$
, whereas we allow a non-linear dependence in this derivative. Moreover, our master equation is in expectation form. In [Reference Laurière and Tangpi18] the master equation is approached by a system of N coupled PDEs on
$[0,T]\times (\mathbb{R}^d)^N$
, whereas we consider a single approximating PDE on
$[0,T]\times (\mathbb{R}^d)^N$
. For more general Hamiltonian functions H, it has been recently proved in [Reference Gangbo, Mayorga and Swiech14] that the sequence of viscosity solutions
$(v^N)_N$
to (1.5) converge locally uniformly to the viscosity solution v to (1.1) when
$\sigma=0$
, and
$\sigma_0$
does not depend on space and measure arguments. For a detailed comparison between this work and ours, we refer to Remark 2.4.
In this paper we adopt a probabilistic approach by considering a backward stochastic differential equation (BSDE) representation for the finite-dimensional PDE (1.5) according to the classical work [Reference Pardoux and Peng19]. The solution
$(Y^N, {\textbf{Z}}^N=(Z^{i,N})_{1\leq i\leq N})$
to this BSDE is written with an underlying forward particle system
${\textbf{X}}^N=(X^{i,N})_{1\leq i\leq N}$
of a McKean–Vlasov SDE, and connected to the PDE (1.5) via the Feynman–Kac formula
\begin{equation*}Y_t^N = v^N(t,{\textbf{X}}_t^N),\quad Z_t^{i,N} = D_{x_i} v^N(t,{\textbf{X}}_t^{i,N}), \quad 0\leq t\leq T.\end{equation*}
By using BSDE techniques, our main contribution is to show a rate of convergence of order
$1/N$
of
$|Y^N_t - v(t,\bar\mu({\textbf{X}}_t^N))|$
, and also of
\begin{equation*}|NZ_t^{i,N} - \partial_\mu v(t,\bar\mu({\textbf{X}}_t^N))(X_t^{i,N})|^2,\quad i = 1,\ldots,N,\end{equation*}
for suitable norms, and under some regularity conditions on v (see Theorems 2.1 and 2.2). This rate of convergence on the particle approximation of v and its L-derivative is new, to the best of our knowledge. We point out that classical BSDE arguments for proving the rate of convergence do not apply directly due to the presence of the factor N in front of
$D_{x_i} v^N$
in the generator H, and we instead use linearization arguments and change of probability measures to overcome these issues. Another issue is due to the fact that the BSDE dimension
$d\times N$
is exploding with the number of particles, so we have to track down the influence of the dimension in the estimations, whereas classical BSDE works usually consider a fixed dimension d which is incorporated into constants.
The outline of the paper is organized as follows. In Section 2 we formulate the particle approximation of the PDE and its BSDE representation, and state the rate of convergence for v and its L-derivative. Section 3 is devoted to the proof of these results.
2. Particle approximation of Wasserstein PDEs
The formal derivation of the finite-dimensional approximation PDE is obtained as follows. We look at the PDE (1.1)–(1.2) for
\begin{equation*}\mu = \bar\mu({\textbf{x}}) = \frac{1}{N}\sum_{i=1}^N \delta_{x_i} \in {\mathcal{P}}_2(\mathbb{R}^d),\end{equation*}
when
${\textbf{x}} = (x_i)_{i\in [\![ 1,N]\!]}$
runs over
$(\mathbb{R}^d)^N$
. By setting
$\tilde v^N(t,{\textbf{x}}) = v(t,\bar\mu({\textbf{x}}))$
, and assuming that v is smooth, we have for all
$(i,j) \in [\![ 1, N ]\!]$
(see Propositions 5.35 and 5.91 of [Reference Carmona and Delarue6])
\begin{equation} \left\{ \begin{aligned}& D_{x_i} \tilde v^N(t,{\textbf{x}}) = \dfrac{1}{N} \partial_\mu v(t,\bar\mu({\textbf{x}}))(x_i), \\& D^2_{x_i x_j} \tilde v^N(t,{\textbf{x}}) = \dfrac{1}{N} \partial_x \partial_\mu v(t,\bar\mu({\textbf{x}}))(x_i)\delta_{ij} + \dfrac{1}{N^2} \partial^2_\mu v(t,\bar\mu({\textbf{x}}))(x_i,x_j).\end{aligned}\right.\end{equation}
By substituting into the PDE (1.1)–(1.2) for
$\mu = \bar\mu({\textbf{x}})$
, and using (2.1), we then see that
$\tilde v^N$
satisfies the relation
\begin{align} \partial_t \tilde v^N & + \dfrac{1}{N} \displaystyle\sum_{i=1}^N H\bigl(t,x_i, \bar\mu({\textbf{x}}),\tilde v^N,N D_{x_i} \tilde v^N\bigr) \notag \\& + \dfrac{1}{2} \sum_{i=1}^N {\textrm{tr}}\biggl[ \bigl(\sigma\sigma^{\top} + \sigma_0\sigma_0^{\top}\bigr)(t,x_i,\bar\mu({\textbf{x}})) \biggl(D_{x_i}^2 \tilde v^N - \dfrac{1}{N^2} \partial_\mu^2 v(t,\bar\mu({\textbf{x}})) (x_i,x_i) \biggr) \biggr] \notag \\& + \dfrac{1}{2} \sum_{i\neq j \in [\![ 1,N]\!]} {\textrm{tr}} \bigl( \sigma_0(t,x_i,\bar\mu({\textbf{x}}))\sigma_0^{\top}(t,x_j,\bar\mu({\textbf{x}})) D_{x_ix_j}^2 \tilde v^N \bigr)\notag \\& + \dfrac{1}{2N^2} \sum_{i=1}^N {\textrm{tr}}\bigl(\sigma_0\sigma_0^{\top}(t,x_i,\bar\mu({\textbf{x}})) \partial_\mu^2 v(t,\bar\mu({\textbf{x}})) (x_i,x_i) \bigr) = 0\end{align}
for
$(t,{\textbf{x}}=(x_i)_{i\in[\![ 1,N]\!]}) \in [0,T)\times(\mathbb{R}^d)^N$
, together with the terminal condition
$\tilde v^N(t,{\textbf{x}}) = G(\bar\mu({\textbf{x}}))$
. By neglecting the terms
$\partial_\mu^2 v/N^2$
in the above relation, we obtain the PDE (1.5) for
$v^N \simeq \tilde v^N$
. The purpose of this section is to rigorously justify this approximation and state a rate of convergence for
$v^N$
towards v, as well as a convergence for their gradients.
2.1. Particles BSDE approximation
Let us introduce an arbitrary measurable
$\mathbb{R}^d$
-valued function b on
$[0,T]\times \mathbb{R}^d\times {\mathcal{P}}_2(\mathbb{R}^d)$
, and let
$B_N$
denote the
$(\mathbb{R}^d)^N$
-valued function defined on
$[0,T]\times(\mathbb{R}^d)^N$
by
$B_N(t,{\textbf{x}}) = (b(t,x_i,\bar\mu({\textbf{x}}))_{i\in [\![ 1,N]\!]}$
for
$(t,{\textbf{x}}=(x_i)_{i\in[\![ 1,N]\!]}) \in[0,T)\times(\mathbb{R}^d)^N$
. The finite-dimensional PDE (1.5) may then be written as
\begin{equation} \left\{\begin{aligned}& \partial_t v^N + B_N(t,{\textbf{x}})\,.\, D_{{\textbf{x}}} v^N + \dfrac{1}{2}{\textrm{tr}}\bigl(\Sigma_N(t,{\textbf{x}})D_{{\textbf{x}}}^2 v^N\bigr) \\& \quad + \dfrac{1}{N} \displaystyle\sum_{i=1}^N H_b\bigl(t,x_i, \bar\mu({\textbf{x}}),v^N,N D_{x_i} v^N\bigr) = 0, && \text{on $ [0,T) \times (\mathbb{R}^d)^N$,} \\& v^N(T,{\textbf{x}}) = G (\bar\mu({\textbf{x}})), && {\textbf{x}} = (x_i)_{i \in [\![1,N ]\!]} \in (\mathbb{R}^d)^N,\end{aligned}\right.\end{equation}
where
$H_b(t,x,\mu,y,z) \,:\!=\,H(t,x,\mu,y,z) - b(t,x,\mu)\,.\, z$
. For the purpose of error analysis, the function b can simply be taken to be zero. The introduction of the function b is actually motivated by numerical analysis. In fact it corresponds to the drift of training simulations for approximating the function
$v^N$
, notably by machine learning methods, and should be chosen for suitable exploration of the state space; see the detailed discussion in our companion paper [Reference Germain, Laurière, Pham and Warin15]. In this paper we fix an arbitrary function b (satisfying a Lipschitz condition to be made precise later).
Following [Reference Pardoux and Peng19], it is well known that the semi-linear PDE (2.3) admits a probabilistic representation in terms of forward–backward SDEs. The forward component is defined by the process
${\textbf{X}}^N = (X^{i,N})_{i\in[\![ 1,N]\!]}$
valued in
$(\mathbb{R}^d)^N$
, a solution to the SDE
\begin{align} {\textrm{d}}{\textbf{X}}_t^N &= B_N(t,{\textbf{X}}_t^N) \,{\textrm{d}} t + \sigma_N(t,{\textbf{X}}_t^N) \,{\textrm{d}} {\textbf{W}}_t + {\boldsymbol \sigma}_0(t,{\textbf{X}}_t^N) \,{\textrm{d}} W^0_t ,\end{align}
where
$\sigma_N$
is the block diagonal matrix with block diagonals
$\sigma_N^{ii}(t,{\textbf{x}}) = \sigma(t,x_i,\bar\mu({\textbf{x}}))$
,
${\boldsymbol \sigma}_0 = (\sigma_0^i)_{i\in[\![ 1,N]\!]}$
is the
$(\mathbb{R}^{d\times m})^N$
-valued function with
${\boldsymbol \sigma}_0^{i}(t,{\textbf{x}}) = \sigma_0(t,x_i,\bar\mu({\textbf{x}}))$
, for
${\textbf{x}} = (x_i)_{i\in[\![ 1,N]\!]}$
,
${\textbf{W}} = (W^1,\ldots,W^N)$
, where
$W^i$
,
$i = 1,\ldots,N$
, are independent n-dimensional Brownian motions, independent of an m-dimensional Brownian motion
$W^0$
on a filtered probability space
$(\Omega,{\mathcal{F}},\mathbb{F}=({\mathcal{F}}_t)_{0\leq t\leq T},\mathbb{P})$
. Notice that
$\Sigma_N = \sigma_N\sigma_N^{\top} + {\boldsymbol \sigma}_0{\boldsymbol \sigma}_0^{\top}$
, and
${\textbf{X}}^N$
is the particle system of the McKean–Vlasov SDE
\begin{align} {\textrm{d}} X_t &= b\bigl(t,X_t,\mathbb{P}_{{X_t}}\bigr) \,{\textrm{d}} t + \sigma\bigl(t,X_t,\mathbb{P}^0_{{X_t}}\bigr) \,{\textrm{d}} W_t + \sigma_0\bigl(t,X_t,\mathbb{P}^0_{{X_t}}\bigr) \,{\textrm{d}} W_t^0,\end{align}
where W is an n-dimensional Brownian motion independent of
$W^0$
. The backward component is defined by the pair process
$\bigl(Y^N,{\textbf{Z}}^N=(Z^{i,N})_{i\in[\![ 1,N]\!]}\bigr)$
valued in
$\mathbb{R}\times(\mathbb{R}^d)^N$
, a solution to
\begin{align} Y_t^N & = G\bigl(\bar\mu({\textbf{X}}_{T}^N)\bigr) + \dfrac{1}{N} \sum_{i=1}^N \int_t^T H_b\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) ,Y_s^N, N Z_s^{i,N}\bigr) \,{\textrm{d}} s \notag \\& \quad - \sum_{i=1}^N \int_t^T (Z_s^{i,N})^{\top} \sigma\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) \bigr) \,{\textrm{d}} W_s^i, \notag \\& \quad - \sum_{i=1}^N \int_t^T (Z_s^{i,N})^{\top} \sigma_0\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) \bigr) \,{\textrm{d}} W_s^0, \quad 0 \leq t \leq T.\end{align}
We shall assume that the measurable functions
$(t,x,\mu) \mapsto b(t,x,\mu)$
,
$\sigma(t,x,\mu)$
satisfy a Lipschitz condition in
$(x,\mu) \in \mathbb{R}^d\times{\mathcal{P}}_2(\mathbb{R}^d)$
uniformly with respect to
$t \in [0,T]$
, which ensures the existence and uniqueness of a strong solution
${\textbf{X}}^N \in {\mathcal S}_\mathbb{F}^2((\mathbb{R}^d)^N)$
to (2.4) given an initial condition. Here
${\mathcal S}_\mathbb{F}^2(\mathbb{R}^q)$
is the set of
$\mathbb{F}$
-adapted processes
$(V_t)_t$
valued in
$\mathbb{R}^q$
such that
$\mathbb{E}\bigl[\sup_{0\leq t\leq T}|V_t|^2\bigr] < \infty$
(
$|.|$
is the Euclidean norm on
$\mathbb{R}^q$
, and for a matrix M, we choose the Frobenius norm
$|M| = \sqrt{{\textrm{tr}}(MM^{\top})}$
), and the Wasserstein space
${\mathcal{P}}_2(\mathbb{R}^d)$
is endowed with the Wasserstein distance
\begin{align*}{\mathcal{W}}_2(\mu,\mu^{\prime}) &= \bigl( \inf\bigl\{ \mathbb{E}|\xi -\xi^{\prime}|^2\,:\, \xi \sim \mu, \xi^{\prime} \sim \mu^{\prime} \bigr\} \bigr)^{{1}/{2}},\end{align*}
and we set
\begin{equation*}\|\mu\|_{2} \,:\!=\,\biggl( \int_{\mathbb{R}^d} |x|^2\ \mu({\textrm{d}} x)\biggr)^{{1}/{2}}\quad \text{for $\mu \in {\mathcal{P}}_2(\mathbb{R}^d)$.}\end{equation*}
Assuming also that the measurable function
$(t,x,\mu,y,z) \mapsto H_b(t,x,\mu,y,z)$
is Lipschitz in
$(y,z) \in \mathbb{R}\times\mathbb{R}^d$
uniformly with respect to
$(t,x,\mu) \in [0,T]\times\mathbb{R}^d\times{\mathcal{P}}_2(\mathbb{R}^d)$
, and the measurable function G satisfies a quadratic growth condition on
${\mathcal{P}}_2(\mathbb{R}^d)$
, we have the existence and uniqueness of a solution
$(Y^N,{\textbf{Z}}^N=(Z^{i,N})_{i\in[\![ 1,N]\!]}) \in {\mathcal S}_\mathbb{F}^2(\mathbb{R})\times\mathbb{H}_\mathbb{F}^2((\mathbb{R}^d)^N)$
to (2.6), and the connection with the PDE (2.3) (satisfied in general in the viscosity sense) via the (non-linear) Feynman–Kac formula
\begin{align} Y_t^N = v^N(t,{\textbf{X}}_t^N)\quad \text{and}\quad Z_t^{i,N} = D_{x_i} v^N(t,{\textbf{X}}_t^N), \ i=1,\ldots,N, \ 0 \leq t \leq T,\end{align}
where
$v^N$
is smooth for the last relation. Here
$\mathbb{H}_\mathbb{F}^2(\mathbb{R}^q)$
is the set of
$\mathbb{F}$
-adapted processes
$(V_t)_t$
valued in
$\mathbb{R}^q$
such that
\begin{equation*}\mathbb{E}\biggl[ \int_0^T |V_t|^2 \,{\textrm{d}} t\biggr] < \infty.\end{equation*}
2.2. Main results
We aim to analyze the particle approximation error on the solution v to the PDE (1.1), and its L-derivative
$\partial_\mu v$
by considering the pathwise error on v,
\begin{align*}{\mathcal{E}}_N^\textrm{y} & \,:\!=\, \sup_{0\leq t \leq T} |Y_t^N - v(t,\bar\mu({\textbf{X}}_t^N)) |,\end{align*}
and the
$L^2$
-error on its L-derivative,
\begin{align*}\| {\mathcal{E}}_N^\textrm{z} \|_{2} & \,:\!=\, \dfrac{1}{N} \sum_{i=1}^N \biggl( \int_0^T \mathbb{E}\bigl|NZ_t^{i,N} - \partial_\mu v(t,\bar\mu({\textbf{X}}_t^N))(X_t^{i,N}) \bigr|^2 \,{\textrm{d}} t \biggr)^{{1}/{2}},\end{align*}
where the initial conditions of the particle system,
$X_0^{i,N}$
,
$i = 1,\ldots,N$
, are independent and identically distributed with distribution
$\mu_0$
.
Here it is assumed that we have the existence and uniqueness of a classical solution v to the PDE (1.1)–(1.2). More precisely, we make the following assumption.
Assumption 2.1. (Smooth solution to the master Bellman PDE.) There exists a unique solution v to to (1.1), which lies in
$C_b^{1,2}([0,T]\times{\mathcal{P}}_2(\mathbb{R}^d))$
, that is,
-
•
$v(.\,,\mu) \in C^1([0,T))$
and is continuous on [0, T], for any
$\mu \in {\mathcal{P}}_2(\mathbb{R}^d)$
, -
•
$v(t,.)$
is fully
$C^2$
on
${\mathcal{P}}_2(\mathbb{R}^d)$
, for any
$t \in [0,T]$
in the sense that are well-defined and jointly continuous,
\begin{align*} (x,\mu) \in \mathbb{R}^d\times{\mathcal{P}}_2(\mathbb{R}^d) & \mapsto \partial_\mu v(t,\mu)(x) \in \mathbb{R}^d,\\ (x,\mu) \in \mathbb{R}^d\times{\mathcal{P}}_2(\mathbb{R}^d) & \mapsto \partial_x \partial_\mu v(t,\mu)(x) \in \mathbb{M}^d, \\ (x,x^{\prime},\mu) \in \mathbb{R}^d\times\mathbb{R}^d\times{\mathcal{P}}_2(\mathbb{R}^d) & \mapsto \partial_\mu^2 v(t,\mu)(x,x^{\prime}) \in \mathbb{M}^d, \end{align*}
-
• there exists some constant
$L > 0$
such that for all
$(t,x,\mu) \in [0,T]\times\mathbb{R}^d\times{\mathcal{P}}_2(\mathbb{R}^d)$
,
\begin{align*}| \partial_\mu v(t,\mu)(x) | & \leq L(1 + |x| + \|\mu\|_{2} ), \quad | \partial_\mu^2 v(t,\mu)(x,x) | \leq L.\end{align*}
The existence of classical solutions to mean-field PDEs in Wasserstein space is a challenging problem, and beyond the scope of this paper. We refer to [Reference Buckdahn, Li, Peng and Rainer3], [Reference Chassagneux, Crisan and Delarue8], [Reference Saporito and Zhang22], and [Reference Wu and Zhang23] for conditions ensuring regularity results of some master PDEs. Notice also that linear quadratic mean-field control problems have explicit smooth solutions as in Assumption 2.1; see e.g. [Reference Pham and Wei21].
We also make some rather standard assumptions on the coefficients of the forward–backward SDE.
Assumption 2.2. (Conditions on the coefficients of the forward–backward SDE and the initial law.)
-
(i) The drift and volatility coefficients
$b,\sigma,\sigma_0$
are Lipschitz: there exist positive constants
$[b]$
,
$[\sigma]$
, and
$[\sigma_0]$
such that for all
$t \in [0,T]$
,
$x,x^{\prime} \in \mathbb{R}^d$
,
$\mu,\mu^{\prime} \in {\mathcal{P}}_2(\mathbb{R}^d)$
,
\begin{align*} |b(t,x,\mu) - b(t,x^{\prime},\mu^{\prime})| & \leq [b] (|x-x^{\prime}| + {\mathcal{W}}_2(\mu,\mu^{\prime})), \\ |\sigma(t,x,\mu) - \sigma(t,x^{\prime},\mu^{\prime})| &\leq [\sigma] (|x-x^{\prime}| + {\mathcal{W}}_2(\mu,\mu^{\prime})), \\ |\sigma_0(t,x,\mu) - \sigma_0(t,x^{\prime},\mu^{\prime})| &\leq [\sigma_0] (|x-x^{\prime}| + {\mathcal{W}}_2(\mu,\mu^{\prime})).\end{align*}
-
(ii) For all
$(t,x,\mu) \in [0,T]\times\mathbb{R}^d\times{\mathcal{P}}_2(\mathbb{R}^d)$
,
$\Sigma(t,x,\mu) \,:\!=\,\sigma\sigma^{\top}(t,x,\mu)$
is invertible, and the function
$\sigma$
and its pseudo-inverse
$\sigma^{+} \,:\!=\,\sigma^{\top}\Sigma^{-1}$
are bounded. -
(iii) We have
$\mu_0 \in {\mathcal{P}}_{4q}(\mathbb{R}^d)$
for some
$q > 1$
, that is, and
\begin{equation*} \|\mu_0\|_{{4q}} \,:\!=\,\biggl(\int |x|^{4q}\mu_0({\textrm{d}} x)\biggr)^{{1}/{(4q)}} < \infty\end{equation*}
\begin{align*} \int_0^T |b(t,0,\delta_0)|^{4q} + |\sigma(t,0,\delta_0)|^{4q} + |\sigma_0(t,0,\delta_0)|^{4q} \; \,{\textrm{d}} t & < \infty. \end{align*}
-
(iv) The driver
$H_b$
satisfies the Lipschitz condition: there exist positive constants
$[H_b]_{1}$
and
$[H_b]_{2}$
such that for all
$t \in [0,T]$
,
$x,x^{\prime} \in \mathbb{R}^d$
,
$\mu,\mu^{\prime} \in {\mathcal{P}}_2(\mathbb{R}^d)$
,
$y,y^{\prime} \in \mathbb{R}$
,
$z,z^{\prime} \in \mathbb{R}^d$
,
\begin{align*} | H_b(t,x,\mu,y,z) - H_b(t,x,\mu,y^{\prime},z^{\prime})| & \leq [H_b]_{1} ( |y-y^{\prime}| + |z-z^{\prime}|) , \\ | H_b(t,x,\mu,y,z) - H_b(t,x^{\prime},\mu^{\prime},y,z)| &\leq [H_b]_{2} (1+|x|+|x^{\prime}|+ \|\mu\|_{2} + \|\mu^{\prime}\|_{2}) \notag \\& \quad \ \times ( |x-x^{\prime}| + {\mathcal{W}}_2(\mu, \mu^{\prime})). \end{align*}
-
(v) The terminal condition satisfies the (local) Lipschitz condition: there exists some positive constant
$[G]$
such that for all
$\mu,\mu^{\prime} \in {\mathcal{P}}_2(\mathbb{R}^d)$
\begin{align*}|G(\mu) - G(\mu^{\prime})| &\leq [G] (\|\mu\|_{2} + \|\mu^{\prime}\|_{2} ) {\mathcal{W}}_2(\mu,\mu^{\prime}).\end{align*}
In order to have a convergence result for the first-order Lions derivative, we have to make a stronger assumption.
Assumption 2.3.
-
(i) The function
$H_b$
is in the form where
\begin{equation*} H_b(t,x,\mu,y,z) = H_1(t,x,\mu,y) + H_2(t,\mu,y)\,.\, z, \end{equation*}
$H_1\,:\, [0,T]\times \mathbb{R}^d\times{\mathcal{P}}_2(\mathbb{R}^d)\times \mathbb{R} \mapsto \mathbb{R}$
verifies for all
$t \in [0,T]$
,
$x,x^{\prime} \in \mathbb{R}^d$
,
$\mu,\mu^{\prime} \in {\mathcal{P}}_2(\mathbb{R}^d)$
,
$y,y^{\prime} \in \mathbb{R}$
,
$z,z^{\prime} \in \mathbb{R}^d$
, and
\begin{align*} | H_1(t,x,\mu,y) - H_1(t,x,\mu,y^{\prime})| & \leq [H_1]_{1} |y-y^{\prime}| , \\ | H_1(t,x,\mu,y) - H_1(t,x^{\prime},\mu^{\prime},y)| &\leq [H_1]_{2} (1+|x|+|x^{\prime}|+ \|\mu\|_{2} + \|\mu^{\prime}\|_{2}) \notag \\& \quad \ \times ( |x-x^{\prime}| + {\mathcal{W}}_2(\mu, \mu^{\prime})),\end{align*}
$H_2\,:\, [0,T]\times \mathbb{R}^d\times{\mathcal{P}}_2(\mathbb{R}^d)\times \mathbb{R} \mapsto \mathbb{R}^d$
is bounded and verifies for all
$t \in [0,T]$
,
$x,x^{\prime} \in \mathbb{R}^d$
,
$\mu,\mu^{\prime} \in {\mathcal{P}}_2(\mathbb{R}^d)$
,
$y,y^{\prime} \in \mathbb{R}$
,
$z,z^{\prime} \in \mathbb{R}^d$
,
\begin{align*} | H_2(t,x,\mu,y) - H_2(t,x,\mu,y^{\prime})| & \leq [H_2]_{1} |y-y^{\prime}| , \\| H_2(t,x,\mu,y) - H_2(t,x^{\prime},\mu^{\prime},y)| &\leq [H_2]_{2} (1+|x|+|x^{\prime}|+ \|\mu\|_{2} + \|\mu^{\prime}\|_{2}) \notag \\& \quad \ \times ( |x-x^{\prime}| + {\mathcal{W}}_2(\mu, \mu^{\prime})).\end{align*}
-
(ii) We assume
$\sigma_0$
is uniformly elliptic and does not depend on x, namely there exists
$c_0>0$
such that for all
$t\in[0,T]$
,
$\mu\in{\mathcal{P}}_2(\mathbb{R}^d)$
,
$z\in\mathbb{R}^d$
,
\begin{equation*} z^{\top} \sigma_0(t,\mu) \sigma_0^{\top}(t,\mu) z \geq c_0 |z|^2. \end{equation*}
-
(iii) There exists some constant
$L > 0$
such that for all
$(t,x,\mu) \in [0,T]\times\mathbb{R}^d\times{\mathcal{P}}_2(\mathbb{R}^d)$
\begin{align*}| \partial_\mu v(t,\mu)(x) | & \leq L.\end{align*}
Remark 2.1. The Lipschitz condition on b,
$\sigma$
in Assumption 2.2(i) implies that the functions
${\textbf{x}} \in(\mathbb{R}^d)^N \mapsto B_N(t,{\textbf{x}})$
, resp.
$\sigma_N(t,{\textbf{x}})$
and
${\boldsymbol \sigma}_0(t,{\textbf{x}})$
, defined in (2.4), are Lipschitz (with Lipschitz constant 2[b], resp.
$2[\sigma]$
and
$2[\sigma_0]$
). Indeed, we have
\begin{align*}|B_N(t,{\textbf{x}}) - B_N(t,{\textbf{x}}^{\prime})|^2 & = \sum_{i=1}^N |b(t,x_i,\bar\mu({\textbf{x}})) - b(t,x_i,\bar\mu({\textbf{x}}^{\prime}))|^2\\ & \leq 2[b]^2 \sum_{i=1}^N \bigl(|x_i - x^{\prime}_i|^2 + {\mathcal{W}}_2(\bar\mu({\textbf{x}}),\bar\mu({\textbf{x}}^{\prime}))^2\bigr)\\& \leq 2[b]^2 \Biggl(|{\textbf{x}}-{\textbf{x}}^{\prime}|^2 + \sum_{i=1}^N \dfrac{1}{N}|{\textbf{x}}-{\textbf{x}}^{\prime}|^2\Biggr) \\&= 4[b]^2|{\textbf{x}}-{\textbf{x}}^{\prime}|^2,\end{align*}
for
${\textbf{x}} = (x_i)_{i\in[\![ 1,N]\!]}$
, and similarly for
$\sigma_N$
and
${\boldsymbol \sigma}_0$
. This yields the existence and uniqueness of a solution
${\textbf{X}}^N = (X^{i,N})_{i\in[\![ 1,N]\!]}$
to (2.4) given initial conditions. Moreover, under Assumption 2.2(iii), we have the standard estimate
\begin{align} \mathbb{E}\biggl[ \sup_{0\leq t\leq T} |{\textbf{X}}_t^{N}|^{4q} \biggr] & \leq C \bigl( 1 + \|\mu_0\|^{4q}_{{4q}} \bigr) < \infty, \quad i=1,\ldots,N, \end{align}
for some constant C (possibly depending on N). The Lipschitz condition on
$H_b$
with respect to (y, z) in Assumption 2.2(iv), and the quadratic growth condition on G from Assumption 2.2(v), gives the existence and uniqueness of a solution
\begin{equation*}\bigl(Y^N,{\textbf{Z}}^N=(Z^{i,N})_{i\in[\![ 1,N]\!]}\bigr) \in {\mathcal S}_\mathbb{F}^2(\mathbb{R})\times\mathbb{H}_\mathbb{F}^2\bigl((\mathbb{R}^d)^N\bigr)\end{equation*}
to (2.6). Moreover, by Assumption 2.2(iv, v), we see that
\begin{align*} & \Biggl| \dfrac{1}{N} \sum_{i=1}^N H_b(t,x_i,\bar\mu({\textbf{x}}),y,z_i) - \dfrac{1}{N} \sum_{i=1}^N H_b(t,x^{\prime}_i,\bar\mu({\textbf{x}}^{\prime}),y,z_i)\Biggr| \\ & \quad \leq [H_b]_{2} \dfrac{1}{N} \sum_{i=1}^N \biggl(1+|x_i|+|x^{\prime}_i| + \dfrac{1}{\sqrt{N}}(|{\textbf{x}}| + |{\textbf{x}}^{\prime}|)\biggr)\biggl( |x_i-x^{\prime}_i| + \dfrac{1}{\sqrt{N}}|{\textbf{x}} - {\textbf{x}}^{\prime}| \biggr) \\ & \quad \leq 4[H_b]_{2}(1 + |{\textbf{x}}| + |{\textbf{x}}^{\prime}|) |{\textbf{x}} - {\textbf{x}}^{\prime}|,\end{align*}
and also
\begin{align*}| G(\bar\mu({\textbf{x}})) - G(\bar\mu({\textbf{x}}^{\prime})) | \leq \dfrac{[G]}{N} (|{\textbf{x}}| + |{\textbf{x}}^{\prime}|)|{\textbf{x}} - {\textbf{x}}^{\prime}|,\end{align*}
for all
$x,x^{\prime} \in \mathbb{R}^d$
,
${\textbf{x}} = (x_i)_{i\in[\![ 1,N]\!]}$
,
${\textbf{x}}^{\prime} = (x^{\prime}_i)_{i\in[\![ 1,N]\!]} \in (\mathbb{R}^d)^N$
, which yields by standard stability results for BSDE (see e.g. Theorems 4.2.1 and 5.2.1 of [Reference Zhang24]) that the function
$v^N$
in (2.7) inherits the local Lipschitz condition
\begin{align*}| v^N(t,{\textbf{x}}) - v^N(t,{\textbf{x}}^{\prime}) | & \leq C(1 + |{\textbf{x}}| + |{\textbf{x}}^{\prime}|)|{\textbf{x}} - {\textbf{x}}^{\prime}| \quad \text{for all ${\textbf{x}},{\textbf{x}}^{\prime} \in (\mathbb{R}^d)^N$,}\end{align*}
for some constant C (possibly depending on N). This implies
\begin{align} |Z_t^{i,N}| & \leq C\bigl( 1 + |{\textbf{X}}_t^N| \bigr), \quad 0 \leq t \leq T, \ i=1,\ldots,N\end{align}
(this is clear when
$v^N$
is smooth, and is otherwise obtained by a mollifying argument as in Theorem 5.2.2 of [Reference Zhang24]).
Remark 2.2. Assumption 2.1 is verified in the case of linear quadratic control problems for which explicit smooth solutions are found in [Reference Pham and Wei20] and [Reference Pham and Wei21], respectively, with and without common noise. These papers prove that the second-order Lions derivative
$\partial^2_\mu$
is a continuous function of time which does not depend on the
$\mu,x$
arguments and hence is bounded, whereas
$\partial_\mu$
is affine in both the state and the first moment of the measure and thus satisfies linear growth. Notice that, in general, Assumptions 2.2 and 2.3 are not satisfied due to the quadratic nature of
$H_b$
in the z. However, in the uncontrolled case,
\begin{align*} v(t,\mu) & = \mathbb{E}_{t,\mu}\biggl[\int_t^T \bigl( X_t^\top A(t) X_t + \mathbb{E}[X_t]^\top B(t) \mathbb{E}[X_t] + C(t) X_t + D(t) \mathbb{E}[X_t] \bigr) \,{\textrm{d}} t \\ & \quad + X_T^\top E X_T + \mathbb{E}[X_T]^\top F \mathbb{E}[X_T] + G X_T + H \mathbb{E}[X_T]\ \biggr] , \\ {\textrm{d}} X_t &= (b_0(t) + b_1(t)X_t + b_2(t) \mathbb{E}[X_t])\,{\textrm{d}} t + \sigma(t)\,{\textrm{d}} W_t,\end{align*}
we see that v is a solution to the linear PDE
\begin{equation*}\left\{\begin{aligned}& \partial_t v + \int_{\mathbb{R}^d} \bigl[ x^\top A(t) x + \bar \mu^\top B(t) \bar \mu + C(t) x + D(t) \bar \mu & \\ &\quad + (b_0(t) + b_1(t)x + b_2(t) \bar \mu) \partial_\mu v(t,\mu) (x) & \\ &\quad + \dfrac{1}{2}{\textrm{tr}}\bigl((\sigma\sigma^{\top})(t)\partial_x\partial_\mu v(t,\mu)(x)\bigr) \bigr] \mu({\textrm{d}} x) = 0, && (t,\mu) \in [0,T)\times{\mathcal{P}}_2(\mathbb{R}^d), \\& v(T,\mu) = E\ \textrm{Var}(\mu) + \bar \mu^\top (E+ F) \bar \mu + (G+H) \bar \mu, && \mu \in {\mathcal{P}}_2(\mathbb{R}^d),\end{aligned}\right.\end{equation*}
where
\begin{equation*}\bar \mu = \int_{\mathbb{R}^d} x \mu({\textrm{d}} x),\quad \textrm{Var}(\mu) = \int_{\mathbb{R}^d} x^2 \mu({\textrm{d}} x) - \bar \mu^2.\end{equation*}
Theorem 2.1. Under Assumptions 2.1 and 2.2, we have
$\mathbb{P}$
-almost surely
\begin{align*}{\mathcal{E}}_N^\textrm{y} \leq \dfrac{C_y}{N},\end{align*}
where
\begin{equation*}C_y = \frac{T}{2} \,{\textrm{e}}^{[H_b]_{1}T} L \| \sigma \|^2_\infty,\end{equation*}
with
$\|\sigma\|_\infty = \sup_{(t,x,\mu) \in [0,T]\times\mathbb{R}^d\times{\mathcal{P}}_2(\mathbb{R}^d)} |\sigma(t,x,\mu)|$
.
Theorem 2.2. Under Assumptions 2.1, 2.2, and 2.3, we have
\begin{align*}\bigl\| {\mathcal{E}}_N^\textrm{z} \bigr\|_{2} & \leq \dfrac{C_z}{N^{{1}/{2}}},\end{align*}
where
\begin{equation*}C_z = \|\sigma^+\|_\infty \sqrt{ 2T([H_1]_1 + [H_2]_1 L) \bar C_y^2 + \bar C_y T \|\sigma\|_\infty^2 L + \frac{2}{c_0} \bar C_y^2 T \| H_2\|_\infty^2}\end{equation*}
and
\begin{equation*}\bar C_y = \frac{T}{2} \,{\textrm{e}}^{([H_1]_1 + [H_2]_1 L)T} L \| \sigma \|^2_\infty.\end{equation*}
Remark 2.3. Let us consider the global weak errors on v and its L-derivative
$\partial_\mu v$
along the limiting McKean–Vlasov SDE, and defined by
\begin{align*}E_N^\textrm{y} & \,:\!=\, \sup_{0\leq t\leq T} \bigl| \mathbb{E}\bigl[Y_t^N\bigr] - \mathbb{E}\bigl[ v\bigl(t,\mathbb{P}^0_{{X_t}}\bigr) \bigr] \bigr| ,\\ E_N^\textrm{z} &\,:\!=\, \dfrac{1}{N} \sum_{i=1}^N \biggl( \int_0^T \Bigl| \mathbb{E}\bigl[NZ_t^{i,N}\bigr] - \mathbb{E}\Bigl[ \partial_\mu v\Bigl(t,\mathbb{P}^0_{{X_t^i}}\Bigr) (X_t^i) \Bigr] \Bigr|^2 \,{\textrm{d}} t \biggr)^{{1}/{2}},\end{align*}
where
$X^i$
has the same law as X, and with McKean–Vlasov dynamics as in (2.5) but driven by
$W^i$
,
$i = 1,\ldots,N$
. Then they can be decomposed as
\begin{align*}E_N^{\textrm{y}} & \leq \mathbb{E}\bigl[{\mathcal{E}}_N^{\textrm{y}}\bigr] + \tilde E_N^{\textrm{y}}, \quad E_N^{\textrm{z}} \leq \bigl\| {\mathcal{E}}_N^{\textrm{z}} \bigr\|_{2} + \tilde E_N^{\textrm{z}},\end{align*}
where
$\tilde E_N^{\textrm{y}}$
,
$\tilde E_N^{\textrm{z}}$
are the (weak) propagation of chaos errors defined by
\begin{align*}\tilde E_N^{\textrm{y}} & \,:\!=\, \sup_{0\leq t \leq T} \bigl| \mathbb{E}\bigl[ v\bigl(t,\bar\mu({\textbf{X}}_t^N)\bigr) \bigr] - \mathbb{E}\bigl[v\bigl(t,\mathbb{P}^0_{{X_t}}\bigr)\bigr] \bigr| , \\ \tilde E_N^{\textrm{z}} & \,:\!=\, \dfrac{1}{N} \sum_{i=1}^N \biggl( \int_0^T \Bigl| \mathbb{E}\bigl[\partial_\mu v\bigl(t,\bar\mu({\textbf{X}}_t^N)\bigr)\bigl(X_t^{i,N}\bigr)\bigr] - \mathbb{E}\bigl[ \partial_\mu v\bigl(t,\mathbb{P}^0_{{X_t^i}}\bigr)(X_t^i)\bigr] \Bigr|^2 \,{\textrm{d}} t \biggr)^{{1}/{2}}.\end{align*}
From the conditional propagation of chaos result, which states that for any fixed
$k \geq 1$
the law of
$(X_t^{i,N})_{t\in [0,T]}^{i\in [\![ 1,k]\!]}$
converges toward the conditional law of
$(X_t^{i})_{t\in [0,T]}^{i\in [\![ 1,k]\!]}$
, as N goes to infinity, we deduce that
$\tilde E_N^\textrm{y},\tilde E_N^\textrm{z} \rightarrow 0$
. Furthermore, under additional assumptions on v, we can obtain a rate of convergence. Namely, if
$v(t,.)$
is Lipschitz uniformly in
$t \in [0,T]$
, with Lipschitz constant [v], we have
\begin{align}\tilde E_N^{\textrm{y}} & \leq [v] \sup_{0\leq t \leq T} \bigl(\mathbb{E}\bigl[ {\mathcal{W}}_2\bigl(\bar\mu({\textbf{X}}_t^N),\mathbb{P}^0_{{X_t}}\bigr)^2 \bigr] \bigr)^{{1}/{2}} \notag \\& = {\textrm{O}} \Bigl( N^{-{1}/{\max\!(d,4)}}\sqrt{ 1 + \ln\!(N) 1_{d=4}} \Bigr), \notag \\\text{hence} \quad E_N^{\textrm{y}} & = {\textrm{O}} \Bigl( N^{-{1}/{\max\!(d,4)}}\sqrt{ 1 + \ln\!(N) 1_{d=4} } \Bigr),\end{align}
where we use the rate of convergence of empirical measures in Wasserstein distance stated in [Reference Fournier and Guillin12] (see also Theorem 2.12 of [Reference Carmona and Delarue7]), and since we have the standard estimate
\begin{equation*}\mathbb{E}\biggl[\sup_{0\leq t\leq T}|X_t|^{4q}\biggr] \leq C(1+\|\mu_0\|^{4q}_{{2q}})\end{equation*}
by Assumption 2.2(iii). The rate of convergence in (2.10) is consistent with the one found in Theorem 6.17 of [Reference Carmona and Delarue7] for the mean-field control problem. Furthermore, if the function
$\partial_\mu v(t,.)(.)$
is Lipschitz in
$(x,\mu)$
uniformly in t, then by the rate of convergence in Theorem 2.12 of [Reference Carmona and Delarue7], we have
\begin{align*} \tilde E_N^{\textrm{z}} & = {\textrm{O}} \bigl( N^{-{1}/{\max\!(d,4)}} ( 1 + \ln\!(N) 1_{d=4} ) \bigr), \\ \text{hence} \quad E_N^{\textrm{z}} & = {\textrm{O}} \bigl( N^{-{1}/{\max\!(d,4)}} ( 1 + \ln\!(N) 1_{d=4} ) \bigr).\end{align*}
Remark 2.4. (Comparison with [Reference Gangbo, Mayorga and Swiech14].) In the related paper [Reference Gangbo, Mayorga and Swiech14], Gangbo et al. consider a pure common noise case, i.e.
$\sigma = 0 $
, and restrict themselves to
$\sigma_0(t,x_i,\bar\mu({\textbf{x}}))=\kappa I_d $
for
$\kappa\in\mathbb{R}$
. If we consider these assumptions in our smooth setting, we directly see that
$\Delta Y_s^N = 0 $
and
$\Delta Z_s^N = 0 $
$ \mathbb{P}$
-a.s. Indeed, by (2.6) and (3.2) we notice that
$(Y_t^N,Z_t^N)$
and
\begin{equation*} \biggl(\tilde Y_t^N \,:\!=\, v\bigl(t,\bar\mu({\textbf{X}}_t^N)\bigr), \ \biggl\{ \tilde Z_t^{i,N} \,:\!=\, \dfrac{1}{N} \partial_\mu v\bigl(t,\bar\mu({\textbf{X}}_t^{N})\bigr)(X_t^{i,N}) , i=1,\ldots,N\biggr\}\biggr) \end{equation*}
solve the same BSDE, so by existence and pathwise uniqueness for Lipschitz BSDEs the result follows. Moreover, Gangbo et al. [Reference Gangbo, Mayorga and Swiech14] do not allow H to depend on y. Our approach allows their findings to be extended to the case of idiosyncratic noises, and in contrast to them we are able to choose a state-dependent volatility coefficient. Moreover, we provide a convergence rate for the solution. However, we have to assume existence of a smooth solution for the master equation, which is a restrictive assumption.
3. Proof of main results
3.1. Proof of Theorem 2.1
Step 1. Under the smoothness condition on v in Assumption 2.1, one can apply the standard Itô’s formula in
$(\mathbb{R}^d)^N$
to the process
$\tilde v^N(t,{\textbf{X}}_t^N) = v(t,\bar\mu({\textbf{X}}_t^N))$
, and get
\begin{align} \tilde v^N(t,{\textbf{X}}_t^N) &= \tilde v^N(T,{\textbf{X}}_T^N) - \int_t^T \partial_t \tilde v^N(s,{\textbf{X}}_s^N) \,{\textrm{d}} s \notag \\& \quad - \int_t^T B_N(s,{\textbf{X}}_s^N)\,.\, D_{\textbf{x}} \tilde v^N(s,{\textbf{X}}_s^N) + \dfrac{1}{2}{\textrm{tr}}\bigl(\Sigma_N(s,{\textbf{X}}_s^N) D_{\textbf{x}}^2 \tilde v^N(s,{\textbf{X}}_s^N)\bigr) \,{\textrm{d}} s \notag \\& \quad - \sum_{i=1}^N \int_t^T \bigl( D_{x_i} \tilde v^N(s,{\textbf{X}}_s^{N}) \bigr)^{\top} \sigma\bigl(s,X_s^{i,N}, \bar\mu({\textbf{X}}_s^{N})\bigr) \,{\textrm{d}} W_s^i \notag\\& \quad - \sum_{i=1}^N \int_t^T \bigl( D_{x_i} \tilde v^N(s,{\textbf{X}}_s^{N}) \bigr)^{\top} \sigma_0\bigl(s,X_s^{i,N}, \bar\mu({\textbf{X}}_s^{N})\bigr) \,{\textrm{d}} W_s^0,\end{align}
Now, by setting (recall (2.1)),
\begin{align*}\tilde Y_t^N & \,:\!=\, v\bigl(t,\bar\mu({\textbf{X}}_t^N)\bigr) = \tilde v^N(t,{\textbf{X}}_t^N), \\ \tilde Z_t^{i,N} & \,:\!=\, \dfrac{1}{N} \partial_\mu v\bigl(t,\bar\mu({\textbf{X}}_t^{N})\bigr)(X_t^{i,N}) = D_{x_i} \tilde v^N(t,{\textbf{X}}_t^N),\quad i=1,\ldots,N, \ 0 \leq t\leq T,\end{align*}
and using the relation (2.2) satisfied by
$\tilde v^N$
in (3.1), we have for all
$0\leq t\leq T$
\begin{align} \tilde Y_t^N & = G\bigl(\bar\mu({\textbf{X}}_{T}^N)\bigr) + \dfrac{1}{N} \sum_{i=1}^N \int_t^T H_b\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) ,\tilde Y_s^N, N \tilde Z_s^{i,N}\bigr) \,{\textrm{d}} s \notag \\& \quad - \dfrac{1}{2N^2} \sum_{i=1}^N \int_t^T {\textrm{tr}}\bigl(\Sigma\bigl(s,X_s^{i,N}, \bar\mu({\textbf{X}}_s^{N})\bigr) \partial^2_\mu v\bigl(s,\bar\mu({\textbf{X}}_s^{N})\bigr)\bigl(X_s^{i,N},X_s^{i,N}\bigr) \bigr) \,{\textrm{d}} s \notag \\& \quad - \sum_{i=1}^N \int_t^T \bigl(\tilde Z_s^{i,N}\bigr)^{\top} \sigma\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) \bigr) \,{\textrm{d}} W_s^i \notag\\ & \quad - \sum_{i=1}^N \int_t^T \bigl(\tilde Z_s^{i,N}\bigr)^{\top} \sigma_0\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) \bigr) \,{\textrm{d}} W_s^0.\end{align}
Step 2: Linearization. We set
\begin{align*} \Delta Y_t^N &\,:\!=\, Y_t^N - \tilde Y_t^N, \quad \Delta Z_t^{i,N} \,:\!=\, N\bigl(Z_t^{i,N}-\tilde Z_t^{i,N}\bigr), \quad i=1,\ldots,N, \ 0 \leq t\leq T,\end{align*}
\begin{align} \Delta Y_t^N & = \sum_{i=1}^N \int_t^T \dfrac{H_b\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) ,Y_s^N, N Z_s^{i,N}\bigr) - H_b\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) ,\tilde Y_s^N, N \tilde Z_s^{i,N}\bigr)}{N} \,{\textrm{d}} s \notag \\& \quad + \dfrac{1}{2N^2} \sum_{i=1}^N \int_t^T {\textrm{tr}}\bigl(\Sigma\bigl(s,X_s^{i,N}, \bar\mu({\textbf{X}}_s^{N})\bigr) \partial^2_\mu v\bigl(s,\bar\mu({\textbf{X}}_s^{N})\bigr)\bigl(X_s^{i,N},X_s^{i,N}\bigr) \bigr) \,{\textrm{d}} s \notag \\& \quad - \dfrac{1}{N} \sum_{i=1}^N \int_t^T \bigl(\Delta Z_s^{i,N}\bigr)^{\top} \sigma\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) \bigr) \,{\textrm{d}} W_s^i \notag \\& \quad - \dfrac{1}{N} \sum_{i=1}^N \int_t^T \bigl(\Delta Z_s^{i,N}\bigr)^{\top} \sigma_0\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) \bigr) \,{\textrm{d}} W_s^0, \quad 0 \leq t \leq T.\end{align}
We now use the linearization method for BSDEs and rewrite the above equation as
\begin{align}\Delta Y_t^N & = \int_t^T \alpha_s \Delta Y_s^N \,{\textrm{d}} s + \dfrac{1}{N} \sum_{i=1}^N \int_t^T \beta_s^i\,.\, \Delta Z_s^{i,N} \,{\textrm{d}} s \notag \\& \quad - \dfrac{1}{N} \sum_{i=1}^N \int_t^T \bigl(\Delta Z_s^{i,N}\bigr)^{\top} \sigma\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) \bigr) \,{\textrm{d}} W_s^i \notag \\& \quad - \dfrac{1}{N} \sum_{i=1}^N \int_t^T \bigl(\Delta Z_s^{i,N}\bigr)^{\top} \sigma_0\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) \bigr) \,{\textrm{d}} W_s^0 \notag \\& \quad + \dfrac{1}{2N^2} \sum_{i=1}^N \int_t^T {\textrm{tr}}\bigl(\Sigma\bigl(s,X_s^{i,N}, \bar\mu({\textbf{X}}_s^{N})\bigr) \partial^2_\mu v\bigl(s,\bar\mu({\textbf{X}}_s^{N})\bigr)\bigl(X_s^{i,N},X_s^{i,N}\bigr) \bigr) \,{\textrm{d}} s,\end{align}
with
\begin{equation} \begin{aligned} &\alpha_s = \displaystyle\sum_{i=1}^N \dfrac{H_b\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_s^{N}), Y_s^N, N \tilde Z_s^{i,N}\bigr) - H_b\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N),\tilde Y_s^N, N \tilde Z_s^{i,N}\bigr)}{N\Delta Y_s^N} \unicode{x1D7D9}_{\Delta Y_s^N \neq 0}, \\ & \beta_s^i = \dfrac{H_b\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_s^{N}),Y_s^N, N Z_s^{i,N}\bigr) - H_b\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_s^{N}), Y_s^N, N \tilde Z_s^{i,N}\bigr)}{|\Delta Z_s^{i,N}|^2} \Delta Z_s^{i,N} \unicode{x1D7D9}_{\Delta Z_s^{i,N} \neq 0}\end{aligned}\end{equation}
for
$i = 1,\ldots,N$
, and we notice by Assumption 2.2(iv) that the processes
$\alpha$
and
$\beta^i$
are bounded by
$[H_b]_{1}$
. Under Assumption 2.2(ii), let us define the bounded processes
\begin{equation*}\lambda^i_s = \sigma^{+}\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N)\bigr)\beta_s^i,\quad s \in [0,T],\ i = 1,\ldots,N,\end{equation*}
and introduce the change of probability measure
$\mathbb{P}^\lambda$
with Radon–Nikodym density
\begin{align*}\dfrac{{\textrm{d}} \mathbb{P}^\lambda}{{\textrm{d}}\mathbb{P}} &= {\mathcal{E}}_T^\lambda \,:\!=\, \exp\Biggl(\sum_{i=1}^N \int_0^T \lambda_s^i \,{\textrm{d}} W_s^i - \sum_{i=1}^N \dfrac{1}{2} \int_0^T |\lambda_s^i|^2 \,{\textrm{d}} s\Biggr),\end{align*}
so that by Girsanov’s theorem,
$\widetilde W_t^i = W_t^i - \int_0^t \lambda_s^i \,{\textrm{d}} s$
,
$i = 1,\ldots,N$
, and
$W^0$
are independent Brownian motion under
$\mathbb{P}^\lambda$
. By applying Itô’s lemma to
${\textrm{e}}^{\int_0^s \alpha_s \,{\textrm{d}} s}\Delta Y_t^N$
under
$\mathbb{P}^\lambda$
, we then obtain
\begin{align} \Delta Y_t^N &= \dfrac{1}{2N^2} \sum_{i=1}^N \int_t^T \,{\textrm{e}}^{\int_t^s \alpha_u \,{\textrm{d}} u} {\textrm{tr}}\bigl(\Sigma\bigl(s,X_s^{i,N}, \bar\mu({\textbf{X}}_s^{N})\bigr) \partial^2_\mu v\bigl(s,\bar\mu({\textbf{X}}_s^{N})\bigr)\bigl(X_s^{i,N},X_s^{i,N}\bigr) \bigr) \,{\textrm{d}} s \notag \\ & \quad - \dfrac{1}{N} \sum_{i=1}^N \int_t^T \,{\textrm{e}}^{\int_t^s \alpha_u \,{\textrm{d}} u} \bigl(\Delta Z_s^{i,N}\bigr)^{\top} \sigma\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) \bigr) \,{\textrm{d}} \widetilde W_s^i \notag \\ & \quad - \dfrac{1}{N} \sum_{i=1}^N \int_t^T \,{\textrm{e}}^{\int_t^s \alpha_u \,{\textrm{d}} u} \bigl(\Delta Z_s^{i,N}\bigr)^{\top} \sigma_0\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) \bigr) \,{\textrm{d}} W_s^0, \quad 0 \leq t \leq T. \end{align}
Step 3. Let us check that the stochastic integrals in (3.6), namely
\begin{equation*}\int \tilde{\mathcal{Z}}_s^{i,N}\,.\, {\textrm{d}} \widetilde W_s^i \quad \text{and}\quad \int \tilde{\mathcal{Z}}_s^{0,i,N}\,.\, {\textrm{d}} W_s^0,\end{equation*}
are ‘true’ martingales under
$\mathbb{P}^\lambda$
, where
\begin{align*} \tilde Z_s^{i,N} & \,:\!=\, {\textrm{e}}^{\int_0^s \alpha_u \,{\textrm{d}} u} \sigma^{\top} \bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) \bigr) \Delta Z_s^{i,N},\\ \tilde Z_s^{0,i,N} & \,:\!=\, {\textrm{e}}^{\int_0^s \alpha_u {\textrm{d}} u} \sigma_0^{\top} \bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) \bigr) \Delta Z_s^{i,N},\quad i = 1,\ldots,N,\ 0\leq s \leq T.\end{align*}
Indeed, for fixed
$i \in [\![ 1,N]\!]$
, recalling that
$\alpha$
is bounded, and by the linear growth condition of
$\sigma_0$
from Assumption 2.2(i), we have
\begin{align*}\mathbb{E}^{\mathbb{P}^\lambda} \biggl[ \int_0^T |\tilde Z_s^{0,i,N}|^2 \,{\textrm{d}} s \biggr] & \leq C \mathbb{E}^{\mathbb{P}^\lambda} \biggl[ \int_0^T \bigl( |\sigma_0(s,0,\delta_0)|^2 + |X_s^{i,N}|^2 + \|\bar\mu({\textbf{X}}_s^N)\|^2_{2} \bigr) \\ & \quad \ \times \bigl( |NZ_s^{i,N}|^2 + |\partial_\mu v(s,\bar\mu({\textbf{X}}_s^{N}))(X_s^{i,N})|^2 \bigr) \,{\textrm{d}} s\\& \leq C \mathbb{E}\biggl[ {\mathcal{E}}_T^\lambda \int_0^T N^2\bigl(|\sigma_0(s,0,\delta_0)|^4 + |{\textbf{X}}_s^N|^4\bigr) \,{\textrm{d}} s \biggr],\end{align*}
where we use Bayes’ formula, the estimation (2.9), the growth condition on
$\partial_\mu v(.)(.)$
in Assumption 2.1, and noting that
$|X_s^{i,N}| \leq |{\textbf{X}}_s^N|$
,
$\|\bar\mu({\textbf{X}}_s^N)\|^2_{2} = |{\textbf{X}}_s^N|^2/N$
. By Hölder’s inequality with q as in Assumption 2.2(iii), and
${1}/{p} + {1}/{q} = 1$
, the above inequality yields
\begin{align*}\mathbb{E}^{\mathbb{P}^\lambda} \biggl[ \int_0^T |\tilde Z_s^{0,i,N}|^2 \,{\textrm{d}} s \biggr] & \leq C N^2 \bigl(\mathbb{E}\bigl[ |{\mathcal{E}}_T^\lambda|^p \bigr] \bigr)^{{1}/{p}} \biggl( \mathbb{E} \biggl[ \int_0^T \bigl(|\sigma_0(s,0,\delta_0)|^{4q} + |{\textbf{X}}_s^N|^{4q} \bigr) \,{\textrm{d}} s \biggr] \biggr)^{{1}/{q}},\end{align*}
which is finite by (2.8), and since
$\lambda$
is bounded. This shows the square-integrable martingale property of
$\int \tilde{\mathcal{Z}}_s^{0,i,N}\,.\, {\textrm{d}} W_s^0$
under
$\mathbb{P}^\lambda$
. By the same arguments, we get the square-integrable martingale property of
$\int \tilde{\mathcal{Z}}_s^{i,N}\,.\, {\textrm{d}} \tilde W_s^i$
under
$\mathbb{P}^\lambda$
.
Step 4: Estimation of
${\mathcal{E}}_N^\textrm{y}$
. By taking the
$\mathbb{P}^\lambda$
conditional expectation in (3.6), we obtain
\begin{align*} \Delta Y_t^N= \sum_{i=1}^N \mathbb{E}^{\mathbb{P}^\lambda} \biggl[ \int_t^T \dfrac{{\textrm{e}}^{\int_t^s \alpha_u \,{\textrm{d}} u}}{2N^2} {\textrm{tr}}\bigl(\Sigma\bigl(s,X_s^{i,N}, \bar\mu({\textbf{X}}_s^{N})\bigr) \partial^2_\mu v\bigl(s,\bar\mu({\textbf{X}}_s^{N})\bigr)\bigl(X_s^{i,N},X_s^{i,N}\bigr) \bigr) \,{\textrm{d}} s \biggm| {\mathcal{F}}_t \biggr],\end{align*}
for all
$t \in [0,T]$
. Under the boundedness condition on
$\Sigma = \sigma\sigma^{\top}$
in Assumption 2.2(ii), and on
$\partial_\mu^2 v$
in Assumption 2.1, it follows immediately that
\begin{align*} {\mathcal{E}}_N^\textrm{y} = \sup_{0\leq t \leq T} |\Delta Y_t^N| & \leq \dfrac{C_y}{N} \quad \text{a.s.},\end{align*}
where
\begin{equation*}C_y = \frac{T}{2} \,{\textrm{e}}^{[H_b]_{1}T} L \| \sigma \|^2_\infty,\end{equation*}
with
\begin{equation*}\|\sigma\|_\infty = \sup_{(t,x,\mu) \in [0,T]\times\mathbb{R}^d\times{\mathcal{P}}_2(\mathbb{R}^d)} |\sigma(t,x,\mu)|.\end{equation*}
3.2. Proof of Theorem 2.2
From (3.5), and under Assumption 2.3(i, iii), we see that
\begin{align} \alpha_s & = \displaystyle\sum_{i=1}^N \dfrac{H_b\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_s^{N}), Y_s^N, N \tilde Z_s^{i,N}\bigr) - H_b\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N),\tilde Y_s^N, N \tilde Z_s^{i,N}\bigr)}{N \Delta Y_s^N} \unicode{x1D7D9}_{\Delta Y_s^N \neq 0}\notag \\ & = \dfrac{1}{N} \displaystyle\sum_{i=1}^N \dfrac{H_1\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_s^{N}), Y_s^N\bigr) - H_1\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N),\tilde Y_s^N\bigr)}{\Delta Y_s^N} \unicode{x1D7D9}_{\Delta Y_s^N \neq 0} \notag \\ & \quad + \dfrac{1}{N} \displaystyle\sum_{i=1}^N N \tilde Z_s^{i,N}\,.\, \dfrac{H_2\bigl(s,\bar\mu({\textbf{X}}_s^{N}), Y_s^N\bigr) - H_2\bigl(s,\bar\mu({\textbf{X}}_{s}^N),\tilde Y_s^N\bigr)}{\Delta Y_s^N} \unicode{x1D7D9}_{\Delta Y_s^N \neq 0}\end{align}
is bounded by
$[H_1]_1 + [H_2]_1 L$
, recalling
\begin{equation*}N \tilde Z_s^{i,N}=\partial_\mu v\bigl(s,\bar\mu({\textbf{X}}_{s}^N) \bigr)(X_s^{i,N}).\end{equation*}
As a consequence, the proof of Theorem 2.1 still applies. Then by (3.3)
\begin{align*} & \int_t^T \alpha_s \Delta Y_s^N \,{\textrm{d}} s + \dfrac{1}{N} \sum_{i=1}^N \int_t^T H_2\bigl(s,\bar\mu({\textbf{X}}_s^{N}), Y_s^N\bigr)\,.\, \Delta Z_s^{i,N} \,{\textrm{d}} s \notag \\& \quad \quad - \dfrac{1}{N} \sum_{i=1}^N \biggl(\int_t^T \bigl(\Delta Z_s^{i,N}\bigr)^{\top} \sigma\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) \bigr) \,{\textrm{d}} W_s^i + \int_t^T (\Delta Z_s^{i,N})^{\top} \sigma_0\bigl(s,\bar\mu({\textbf{X}}_s^{N})\bigr) \,{\textrm{d}} W_s^0 \notag \biggr) \\ & \quad \quad + \dfrac{1}{2N^2} \sum_{i=1}^N \int_t^T {\textrm{tr}}\bigl(\Sigma\bigl(s,X_s^{i,N}, \bar\mu({\textbf{X}}_s^{N})\bigr) \partial^2_\mu v\bigl(s,\bar\mu({\textbf{X}}_s^{N})\bigr)\bigl(X_s^{i,N},X_s^{i,N}\bigr) \bigr) \,{\textrm{d}} s \\ &\quad = \Delta Y_t^N.\end{align*}
By applying Itô’s formula to
$|\Delta Y_t^N|^2$
in (3.4) under
$\mathbb{P}$
,
\begin{align*}& |\Delta Y_0^N|^2 + \dfrac{1}{N^2} \int_0^T \sum_{i=1}^N \bigl|\sigma^{\top}\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) \bigr) \Delta Z_s^{i,N} \bigr|^2 \,{\textrm{d}} s \\ & \quad \quad + \dfrac{1}{N^2} \int_0^T \Biggl|\sigma_0^{\top}\bigl(s,\bar\mu({\textbf{X}}_s^{N})\bigr)\sum_{j=1}^N \Delta Z_s^{j,N}\Biggr|^2 \,{\textrm{d}} s \\ & \quad = 2 \int_0^T \alpha_s |\Delta Y_s^N |^2\,{\textrm{d}} s + \dfrac{2}{N} \sum_{i=1}^N \int_0^T \Delta Y_s^N H_2\bigl(s,\bar\mu({\textbf{X}}_s^{N}), Y_s^N\bigr)\,.\, \Delta Z_s^{i,N} \,{\textrm{d}} s \\& \quad \quad - \dfrac{2}{N} \sum_{i=1}^N \int_0^T \Delta Y_s^N\bigl(\Delta Z_s^{i,N}\bigr)^{\top} \sigma\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) \bigr) \,{\textrm{d}} W_s^i \\& \quad \quad - \dfrac{2}{N} \sum_{i=1}^N \int_0^T \Delta Y_s^N\bigl(\Delta Z_s^{i,N}\bigr)^{\top} \sigma_0\bigl(s,\bar\mu({\textbf{X}}_s^{N})\bigr) \,{\textrm{d}} W_s^0 \notag \\& \quad \quad + \dfrac{1}{N^2} \sum_{i=1}^N \int_0^T \Delta Y_s^N{\textrm{tr}}\bigl(\Sigma\bigl(s,X_s^{i,N}, \bar\mu({\textbf{X}}_s^{N})\bigr) \partial^2_\mu v\bigl(s,\bar\mu({\textbf{X}}_s^{N})\bigr)\bigl(X_s^{i,N},X_s^{i,N}\bigr) \bigr) \,{\textrm{d}} s,\end{align*}
so by taking expectation under
$\mathbb{P}$
, and using the Cauchy–Schwarz inequality in
$\mathbb{R}^d$
,
\begin{align*} & \dfrac{1}{N^2} \int_0^T \sum_{i=1}^N \mathbb{E}\Biggl[\bigl|\sigma^{\top}\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) \bigr) \Delta Z_s^{i,N} \bigr|^2 + \Biggl|\sigma_0^{\top}\bigl(s,\bar\mu({\textbf{X}}_s^{N})\bigr) \sum_{j=1}^N \Delta Z_s^{j,N}\Biggr|^2 \Biggr] \,{\textrm{d}} s \notag \\ & \quad \leq \mathbb{E}\Biggl[2 \int_0^T |\alpha_s| |\Delta Y_s^N |^2\,{\textrm{d}} s + 2 \int_0^T \Biggl|\Delta Y_s^N H_2\bigl(s,\bar\mu({\textbf{X}}_s^{N}), Y_s^N\bigr)\,.\, \sum_{i=1}^N \dfrac{\Delta Z_s^{i,N}}{N} \Biggr| \,{\textrm{d}} s\Biggr] \notag \\& \quad \quad + \dfrac{1}{N^2} \sum_{i=1}^N \int_0^T \mathbb{E}|\Delta Y_s^N{\textrm{tr}}\bigl(\Sigma\bigl(s,X_s^{i,N}, \bar\mu({\textbf{X}}_s^{N})\bigr) \partial^2_\mu v\bigl(s,\bar\mu({\textbf{X}}_s^{N})\bigr)\bigl(X_s^{i,N},X_s^{i,N}\bigr) \bigr) |\,{\textrm{d}} s,\notag \\ & \quad \leq \mathbb{E}\Biggl[2 \int_0^T |\alpha_s| |\Delta Y_s^N |^2\,{\textrm{d}} s + 2 \int_0^T \bigl|\Delta Y_s^N H_2\bigl(s,\bar\mu({\textbf{X}}_s^{N}), Y_s^N\bigr)\bigr|\, \Biggl|\sum_{i=1}^N \dfrac{\Delta Z_s^{i,N}}{N}\Biggr| \,{\textrm{d}} s\Biggr] \notag \\& \quad \quad + \dfrac{1}{N^2} \sum_{i=1}^N \int_0^T \mathbb{E}|\Delta Y_s^N{\textrm{tr}}\bigl(\Sigma\bigl(s,X_s^{i,N}, \bar\mu({\textbf{X}}_s^{N})\bigr) \partial^2_\mu v\bigl(s,\bar\mu({\textbf{X}}_s^{N})\bigr)\bigl(X_s^{i,N},X_s^{i,N}\bigr) \bigr) |\,{\textrm{d}} s, \notag \\ & \quad \leq \mathbb{E}\Biggl[ \vartheta \int_0^T \bigr|\Delta Y_s^N H_2\bigl(s,\bar\mu({\textbf{X}}_s^{N}), Y_s^N\bigr)\bigr|^2 \,{\textrm{d}} s + \dfrac{1}{\vartheta N^2} \int_0^T \Biggl|\sum_{i=1}^N \Delta Z_s^{i,N}\Biggr|^2 \,{\textrm{d}} s\Biggr] + \dfrac{\tilde C_z}{N^2}, \end{align*}
by Young’s inequality for any
$\vartheta >0$
, boundedness of
$\alpha$
(see (3.7)),
$\Sigma$
,
$\partial^2_\mu v$
and Theorem 2.1, where
\begin{equation*} \tilde C_z = 2T([H_1]_1 + [H_2]_1 L) \bar C_y^2 + \bar C_y T \|\sigma\|_\infty^2 L \quad \text{and} \quad \bar C_y = \frac{T}{2} \,{\textrm{e}}^{([H_1]_1 + [H_2]_1 L)T} L \| \sigma \|^2_\infty. \end{equation*}
Thus, by Assumption 2.3(ii), and by choosing
$\vartheta = {2}/{c_0}$
, it follows from the boundedness of
$H_2$
and Theorem 2.1 that
\begin{equation*} \mathbb{E}\Biggl[\dfrac{1}{N} \sum_{i=1}^N \int_0^T\bigl|\sigma^{\top}\bigl(s,X_s^{i,N},\bar\mu({\textbf{X}}_{s}^N) \bigr)\Delta Z_s^{i,N}\bigr|^2\,{\textrm{d}} s \Biggr] \leq \dfrac{\tilde C_z + ({2}/{c_0}) \bar C_y^2 T \|H_2\|_\infty^2}{N},\end{equation*}
which ends the proof by recalling that
$\|\sigma^+ \|_\infty < + \infty$
, using the Cauchy–Schwarz inequality in
$\mathbb{R}^N$
, in the form
\begin{equation*}\frac1N \sum_i^N \sqrt{|a_i|}\leq \sqrt{\frac1N\sum_i^N |a_i|}, \end{equation*}
and Jensen’s inequality, in the form
$\mathbb{E}[\sqrt{|X|}]\leq \sqrt{\mathbb{E}[|X|]}.$
Funding information
This work was supported by FiME (Finance for Energy Market Research Centre) and the ‘Finance et Développement Durable – Approches Quantitatives’ EDF - CACIB Chair.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
