By and large, modern democracies are representative democracies, in the sense that citizens delegate, via elections, political decision-making powers to a small group of public officials. In some democracies, however, citizens retain the power to settle certain policy decisions directly, by holding referenda.Footnote 1 Such referenda may be constitutionally mandated, initiated by the government, or initiated by the citizens themselves (see Butler and Ranney Reference Butler and Ranney1994; Uleri and Gallagher Reference Uleri and Gallagher1996). This paper presents a formal model of political agency and studies how the possibility of citizen-initiated referenda affects the ability of voters to hold elected officials accountable.
In the model, an incumbent politician who cares both about policy and retaining office signals his policy preferences to the electorate via his policy decisions, while the electorate, upon observing these decisions, can choose to overturn some of them in a referendum. The model considered in this paper departs from the related literature on the effects of citizen-initiated referenda on democratic performance (cf. Gerber Reference Gerber1996; Matsusaka and McCarty Reference Matsusaka and McCarty2001; Hug Reference Hug2004; Besley and Coate Reference Besley and Coate2008; Prato and Strulovici Reference Prato and StruloviciForthcoming) in two important ways.Footnote 2 First, I consider a multidimensional policy space and study not only how citizen-initiated referenda affect decision-making on those dimensions which can be subjected to a referendum, but also on those which, perhaps for constitutional reasons, cannot.Footnote 3 Second, the present model varies the information available to voters about which policies correspond to the public interest. In particular, voters may be misinformed about their true interests when deciding whether to hold a referendum. The analysis in this paper thus addresses the main criticism formulated against direct democracy and in favor of representative democracy, namely, that citizens lack the expertise to make wise decisions (see Madison, Federalist number 10).
The analysis generates a rich set of novel predictions. First, I show that giving voters the power to call for a referendum on certain policy issues not only improves congruence between enacted policies and the true preferences of the citizens on those policy dimensions, which can be subjected to a referendum, but, surprisingly, also on those which cannot. Indeed, in the absence of the popular referendum, non-congruent elected officials (i.e., officials who do not share the preferences of the electorate) may enact their preferred policies even at the cost of decreasing the likelihood of reelection. The popular referendum diminishes the policy benefits of doing that, because voters may now overturn some of the policy decisions. Consequently, the popular referendum increases the incentive for non-congruent officials to seek reelection by adopting policies also chosen by congruent officials (i.e., officials who do share the preferences of the electorate) across the full range of policy choices, including on policy dimensions that are not subject to popular referenda. Strikingly, this improved congruence across policy dimensions can hold even when voters are uninformed about their true interests on those dimensions which can be subjected to a referendum. To be sure, uninformed voters sometimes (unwillingly) enforce a policy that is not in their best interest via a referendum. However, because voters learn something about the optimality of policies on those dimensions which can be subjected to a referendum from the decision-making on dimensions which cannot, the frequency of such errors is limited. Moreover, the referendum induces non-congruent elected officials to behave congruently more often. Consequently, the popular referendum improves congruence in expectation across policy dimensions, even with uninformed voters. A lack of expertise of the electorate may thus be a less severe problem than critics of the referendum argue. The popular referendum represents a trade-off for the electorate, however. Because the popular referendum leads non-congruent officials to mimic the behavior of congruent ones more often, it diminishes the ability of the electorate to select “good” officials and may thereby hurt the electorate’s future policy payoffs.
Second, the model generates several predictions about the occurrence of referenda: (1) referenda should only occur when there are uncertainties about the voters’ policy preferences; (2) referenda are more likely the more voters believe that the incumbent does not share their policy preferences; and, relatedly, (3) referenda should be more likely when policy outcomes on dimensions on which no referendum may be held are bad. Prediction (1) is consistent with prior empirical and theoretical work (cf. Matsusaka and McCarty Reference Matsusaka and McCarty2001; Hug Reference Hug2004). Predictions (2) and (3) are new and particularly relevant to a better understanding of direct democracy. Indeed, one objection formulated against referenda is that the people sometimes vote against certain policies simply to punish the incumbent official seemingly without consideration as to whether the policy is sensible or not.Footnote 4 The present model provides a theoretical explanation for such a behavior. More strikingly, it shows how it may actually improve decision-making by forcing elected officials to attend more closely to voters’ preferences including on dimensions which cannot be subjected to a referendum.
Finally, because non-congruent incumbents are more likely to adopt the same policies as congruent ones, the model provides an explanation for why the introduction of citizen initiatives (1) reduces the level of support for the incumbents (see Dyck Reference Dyck2009) but (2) increases their reelection rates (see Bali and Davis Reference Bali and Davis2007; Kelleher and Wolak Reference Kelleher and Wolak2007). The model predicts further that an incumbent whose policy choice is overturned in a referendum should be less likely to be reelected at the end of his term.
Overall, these results have broad implications for our understanding of popular referenda. First, the true impact of popular referenda on decision-making may be much greater and much more pervasive than has previously been recognized. Theoretical (cf. Gerber Reference Gerber1996; Hug Reference Hug2004; Besley and Coate Reference Besley and Coate2008) and empirical (cf. Gerber Reference Gerber1999; Feld and Matsusaka Reference Feld and Matsusaka2003; Matsusaka Reference Matsusaka2004) research, by focusing solely on those dimensions which can be subjected to a referendum, may have systematically underestimated the true effect of direct democracy. Second, arguments against the use of direct democracy on the basis that voters are not well informed about the consequences of policy decisions may be misguided because they ignore the broader impact of the popular referendum on the interactions between the electorate and its representatives. In particular, the model explains how popular referenda may improve accountability and policy-making across policy dimensions, even though uninformed voters sometimes enforce, via a referendum, a policy decision that later turns out not to be in their best interest. One simply cannot assess the implications of popular referenda on democratic performance by only studying referenda.
The Model
Consider a representative democracy consisting of a representative Voter (V) and an Incumbent (I). The Incumbent must enact two policies p
1, p
2 ∈{−1, 1}. For each of these policy issues, the optimal action—the action that is in the public interest—depends on the state of the world, ω
1, ω
2 ∈{−1, 1}, that may be unknown to the Voter.Footnote
5
With respect to every policy, the Voter receives a payoff of 1 if the optimal action is implemented and 0 otherwise. The prior probability that p
i
=1 is the optimal action is
![]() $\alpha \in\left( {{1 \over 2},\,1} \right]$
, so that in the absence of additional information about the state of the world, the Voter would want p
i
=1 to be enacted for all the policy issues in the model. Consequently, I refer to p
i
=1 as the popular policy. Unlike the Voter, the Incumbent is fully informed about the respective states of the world and thus knows which policies are best for him (and which policies are best for the Voter). Although the Voter does not know the states of the world ω
1 and ω
2 ex ante, she learns with certainty the state of the world on dimension p
2, whereas the state of the world ω
1 is revealed to her with probability q
1 ∈[0, 1]. Henceforth, I refer to q
1 as the probability of feedback. The parameter q
1 can be conceived as the speed with which the consequences of the policies become apparent to the Voter. Alternatively, the probability q
1 can be thought of as a measure of the technicality of the policy issue in question.
$\alpha \in\left( {{1 \over 2},\,1} \right]$
, so that in the absence of additional information about the state of the world, the Voter would want p
i
=1 to be enacted for all the policy issues in the model. Consequently, I refer to p
i
=1 as the popular policy. Unlike the Voter, the Incumbent is fully informed about the respective states of the world and thus knows which policies are best for him (and which policies are best for the Voter). Although the Voter does not know the states of the world ω
1 and ω
2 ex ante, she learns with certainty the state of the world on dimension p
2, whereas the state of the world ω
1 is revealed to her with probability q
1 ∈[0, 1]. Henceforth, I refer to q
1 as the probability of feedback. The parameter q
1 can be conceived as the speed with which the consequences of the policies become apparent to the Voter. Alternatively, the probability q
1 can be thought of as a measure of the technicality of the policy issue in question.
An additional tension in the model arises from the fact that the Voter is uncertain about the preferences of the Incumbent. With probability π>1/2 the Incumbent has the same preference ranking as the Voter would have if she was fully informed, in which case he is congruent. With probability 1−π the policy preferences of the Incumbent differ from those of the Voter, in which case he is non-congruent.Footnote 6
Upon observing the policy choices p 1 and p 2, and potentially their respective optimality, the Voter can choose to hold a referendum over policy p 1.Footnote 7 The assumption that the Voter cannot hold a referendum about policy p 2 excludes certain policy fields from the direct control of the Voter. This mirrors constitutional provisions in many countries. Article 75 of the Italian constitution, e.g., specifies that a popular referendum can be requested by 500,000 voters. No referendum, however, “may be held on a law regulating taxes, the budget, amnesty or pardon, or a law ratifying an international treaty.” Similar restrictions can be found, e.g., in Austria (at the regional level), Brazil, Colombia, Germany (at the regional level), Hungary, Latvia, Slovakia, Serbia, Uruguay, etc. In the United States, among the 24 states that permit citizens’ initiatives, 12 have subject restrictions. For example, in Alaska, Massachusetts, Montana, and Wyoming initiatives may not make appropriations or dedicate revenues. In Arizona, Mississippi, Missouri, and Nevada appropriations require a funding source. Note further that in all the states, statutes are subject to judicial review which de facto creates certain restrictions on the legislation which can be passed through a referendum. Of course, there also exists jurisdictions where no restrictions apply, most notably the paragon of direct democracy Switzerland.
After her decision to hold a referendum, the Voter chooses whether to reelect the Incumbent or not. I use the following notation to denote the probability with which the Voter reelects the Incumbent based on her observations. Let r(p 1=1, p 2=ω 2) be the probability that the Voter reelects the incumbent upon observing p 1=1 and p 2=ω 2. This corresponds to the case where the Voter observes ω 2 and the Incumbent matched the policy p 2 to the state of the world, yet the Voter does not observe the state of the world ω 1 and thus only observes that the Incumbent set p 1=1. r(p 1=ω 1, p 2=ω 2) and so forth are interpreted in the same way. Throughout, I assume that the Voter reelects the Incumbent only if the posterior belief that the Incumbent is congruent is greater or equal to the prior belief π that a challenger is congruent.
To summarize, the sequence of the model is as follows:
1. Period 1. Nature determines states of the world ω 1, ω 2 ∈ {−1, 1}.
2. Nature determines the Incumbent’s type.
3. The Incumbent observes ω 1 and ω 2 and chooses policies p 1, p 2 ∈ {−1, 1}.
4. The Voter observes p 1, p 2, ω 2, and, with probability q 1 ∈ [0, 1], ω 1 and decides whether to hold a referendum over policy p 1.
5. After its decision to hold a referendum, the Voter chooses whether to reelect the Incumbent.
The Voter receives a policy payoff of 1 for each policy that matches the state of the world (p i =ω i ) and 0 otherwise. The utility of the Voter can be written compactly as
where p ≡(p 1, p 2), ω ≡(ω 1, ω 2) and 1{pi = ωi } is an indicator function that takes on value 1 whenever p i =ω i and 0 otherwise.
A congruent Incumbent shares the policy preferences of the Voter. For each policy that does not match the state of the world (p i ≠ω i ) the policy payoff to the non-congruent Incumbent is 1, while it is 0 otherwise. The Incumbent is also office-motivated receiving an additional benefit of holding office B ∈ (0, 2)Footnote 8 if reelected by the Voter. The utility of a congruent Incumbent from implementing policy vector p when the vector of states of the world is ω can thus be written as
while the utility of a non-congruent Incumbent is given by
The solution concept I use is Perfect Bayesian Equilibrium (PBE). Informally, a PBE requires (1) that every player of the game chooses the strategy which maximizes her expected utility given her beliefs and the strategies of the remaining players and (2) that beliefs are computed using Bayes’ rule whenever possible. Throughout, I assume that congruent types choose (p 1=ω 1, p 2=ω 2) for all (ω 1, ω 2) and solve for the non-congruent type’s and the Voter’s equilibrium strategies and beliefs. Equilibria with this specification of congruent types’ behavior always exist.Footnote 9
Baseline Model
In this section, I study a baseline version of the model in which the Voter cannot call for a referendum and discuss some of its implications. I illustrate the equilibrium behavior of the non-congruent Incumbent in Figure 1. Remember that the congruent Incumbent always chooses (p 1=ω 1, p 2=ω 2) in equilibrium. As illustrated in Figure 1, the equilibrium depends on the probability of feedback q 1 and the value of holding office B.
Proposition 1: In equilibrium:
1. if the probability of feedback is high
 $\left( {q_{1} \geq {{B{\minus}1} \over B}} \right)$
, non-congruent incumbents choose their preferred policies (p
1≠ω
1, p
2≠ω
2),Footnote
10
$\left( {q_{1} \geq {{B{\minus}1} \over B}} \right)$
, non-congruent incumbents choose their preferred policies (p
1≠ω
1, p
2≠ω
2),Footnote
10
2. if the probability of feedback is low
 $\left( {q_{1} \,\lt\,{{B{\minus}1} \over B}} \right)$
, non-congruent Incumbents choose the Voter’s preferred policy on the second dimension (p
2=ω
2) with non-degenerate probability. On the first dimension, however, they choose the policy preferred by themselves (p
1≠ω
1) with certainty.Footnote
11
$\left( {q_{1} \,\lt\,{{B{\minus}1} \over B}} \right)$
, non-congruent Incumbents choose the Voter’s preferred policy on the second dimension (p
2=ω
2) with non-degenerate probability. On the first dimension, however, they choose the policy preferred by themselves (p
1≠ω
1) with certainty.Footnote
11
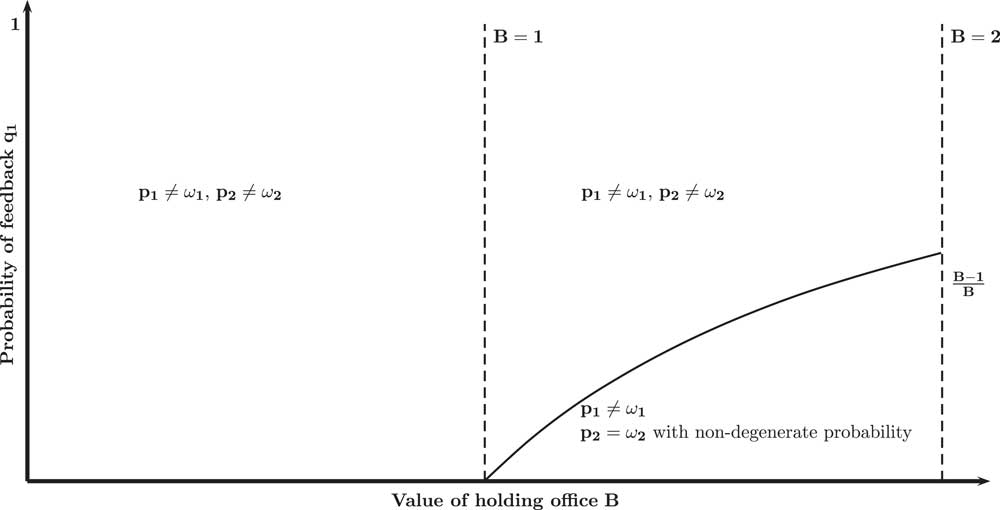
Fig. 1 Equilibrium behavior of non-congruent Incumbent in baseline model, 0<B<2
Because (1) the Voter observes ω 2 and (2) the congruent Incumbent chooses (p 1=ω 1, p 2=ω 2), the non-congruent Incumbent always separates from the congruent one when the probability of feedback q 1 is high and partially separates when it is low.
The intuition for this result is simple. For any (q 1, B) pair, the non-congruent Incumbent must decide whether to masquerade as a congruent Incumbent. Obviously, mimicking the behavior of the congruent Incumbent presents an upside and a downside. On the upside, it potentially improves the chances of reelection of the non-congruent Incumbent. On the downside, it requires the non-congruent Incumbent to choose policies he dislikes. Because the value of holding office is limited (B<2), the non-congruent Incumbent, however, never behaves in the public interest with respect to both policies. If he were to do so, he would at most receive a payoff of B, while implementing his preferred policies yields a payoff of 2.
This does not imply, however, that the non-congruent Incumbent always disregards the preferences of the public. Indeed, suppose the non-congruent Incumbent were to choose (p 1≠ω 1, p 2=ω 2) with positive probability. If the Voter does not observe the state of the world ω 1, i.e., if the Voter only observes whether policy p 1 is equal to 1 or to −1, the Voter will be uncertain as to the type of the Incumbent. For example, if the Voter observes (p 1=−1, p 2=ω 2) she might either be facing a congruent Incumbent who observes that ω 1=−1 or a non-congruent Incumbent who observes that ω 1=1. If the non-congruent Incumbent chooses (p 1≠ω 1, p 2=ω 2) with sufficiently low probability, the Voter will then be compelled to reelect the Incumbent whenever she does not observe whether the implemented policy p 1 is in the public’s interest. When choosing (p 1≠ω 1, p 2=ω 2), the non-congruent Incumbent thus incurs a policy cost of 1, as he is giving up policy p 2, but may obtain a gain of B whenever he gets reelected. If the non-congruent Incumbent gets reelected sufficiently often when choosing (p 1≠ω 1, p 2=ω 2), and if the value of holding office is sufficiently high (B>1), he will thus choose this policy vector over implementing his preferred policies.
The probability of being reelected upon choosing (p
1≠ω
1, p
2=ω
2) depends on the probability of feedback q
1, however. Indeed, if uncertainty about ω
1 resolves, the Voter will infer from p
1≠ω
1 that she is facing a non-congruent Incumbent and will not reelect the Incumbent. Hence, as q
1 increases, the probability with which the non-congruent Incumbent gets reelected upon choosing (p
1≠ω
1, p
2=ω
2) decreases. If the probability of feedback is sufficiently high, i.e.
![]() $q_{1} \geq {{B{\minus}1} \over B}$
, the non-congruent Incumbent is likely to get caught when choosing (p
1≠ω
1, p
2=ω
2) and he thus opts to separate from congruent types by choosing (p
1≠ω
1, p
2≠ω
2). When q
1 is sufficiently low, the non-congruent Incumbent will have incentives to choose (p
1≠ω
1, p
2=ω
2) at least part of the time.
$q_{1} \geq {{B{\minus}1} \over B}$
, the non-congruent Incumbent is likely to get caught when choosing (p
1≠ω
1, p
2=ω
2) and he thus opts to separate from congruent types by choosing (p
1≠ω
1, p
2≠ω
2). When q
1 is sufficiently low, the non-congruent Incumbent will have incentives to choose (p
1≠ω
1, p
2=ω
2) at least part of the time.
Introducing Direct Democracy
I now consider the case where the Voter can call for a referendum on policy p 1. Before proceeding to the analysis of the equilibrium behavior of the Incumbent, a few remarks about the decision of the Voter to hold a referendum are warranted. Obviously, if the Voter observes that the policy p 1 does not match the state of the world, the Voter calls for a referendum to set p 1=ω 1. If the Voter does not observe whether the policy p 1 matches the state of the world or not, his payoff from holding a referendum to change the policy is given by Pr(ω 1≠p 1|p 1, p 2; ω 2), where Pr(ω 1≠p 1|p 1, p 2; ω 2) is the belief of the Voter that ω 1≠p 1 given that the Voter observes p 1, p 2, and ω 2. If the Voter does not call for a referendum to change the policy he receives a payoff of Pr(ω 1=p 1|p 1, p 2; ω 2). Thus, the Voter only holds a referendum upon not observing ω 1, when Pr(ω 1≠p 1|p 1, p 2; ω 2)≥Pr(ω 1=p 1|p 1, p 2; ω 2).
As in the baseline model, the congruent Incumbent chooses (p 1=ω 1, p 2=ω 2) in equilibrium. Figure 2 illustrates the equilibrium behavior of the non-congruent Incumbent in this setting. In particular, there are four regions (labeled I, II, III, and IV in Figure 2), which give rise to different equilibrium strategy profiles:
Proposition 2 : In equilibrium:
1. if B<1 and the probability of feedback is high
 $\left( {q_{1} \geq {{2B{\minus}1} \over {1{\plus}2B}}} \right)$
, non-congruent Incumbents choose p
1=ω
1 with non-degenerate probability and p
2≠ω
2 with certainty,
$\left( {q_{1} \geq {{2B{\minus}1} \over {1{\plus}2B}}} \right)$
, non-congruent Incumbents choose p
1=ω
1 with non-degenerate probability and p
2≠ω
2 with certainty,2. if B<1 and the probability of feedback is low
 $\left( {q_{1} \,\lt\,{{2B{\minus}1} \over {1{\plus}2B}}} \right)$
, or if B≥1 and the probability of feedback takes on intermediate values
$\left( {q_{1} \,\lt\,{{2B{\minus}1} \over {1{\plus}2B}}} \right)$
, or if B≥1 and the probability of feedback takes on intermediate values
 $$\left( {q_{1} \in\left[ {{{2B{\minus}2} \over B},3{\minus}2B} \right]} \right)$$
, non-congruent Incumbents choose p
1=ω
1 and p
2=ω
2 with non-degenerate probability,Footnote
12
$$\left( {q_{1} \in\left[ {{{2B{\minus}2} \over B},3{\minus}2B} \right]} \right)$$
, non-congruent Incumbents choose p
1=ω
1 and p
2=ω
2 with non-degenerate probability,Footnote
12
3. if B≥1 and the probability of feedback is high
 $\left( {q_{1} \geq {\rm max}\left\{ {3{\minus}2B,\,{1 \over {B{\plus}1}}} \right\}} \right)$
, non-congruent Incumbents implement the Voter’s preferred policies with respect to all policy dimensions: (p
1=ω
1, p
2=ω
2),
$\left( {q_{1} \geq {\rm max}\left\{ {3{\minus}2B,\,{1 \over {B{\plus}1}}} \right\}} \right)$
, non-congruent Incumbents implement the Voter’s preferred policies with respect to all policy dimensions: (p
1=ω
1, p
2=ω
2),4. if B≥1 and the probability of feedback is low
 $$\left( {q_{1} \,\lt\,{\rm min}\left\{ {{{2B{\minus}2} \over B},\,{1 \over {B{\plus}1}}} \right\}} \right)$$
, non-congruent Incumbents choose p
1=ω
1 with non-degenerate probability and p
2=ω
2 with certainty.
$$\left( {q_{1} \,\lt\,{\rm min}\left\{ {{{2B{\minus}2} \over B},\,{1 \over {B{\plus}1}}} \right\}} \right)$$
, non-congruent Incumbents choose p
1=ω
1 with non-degenerate probability and p
2=ω
2 with certainty.
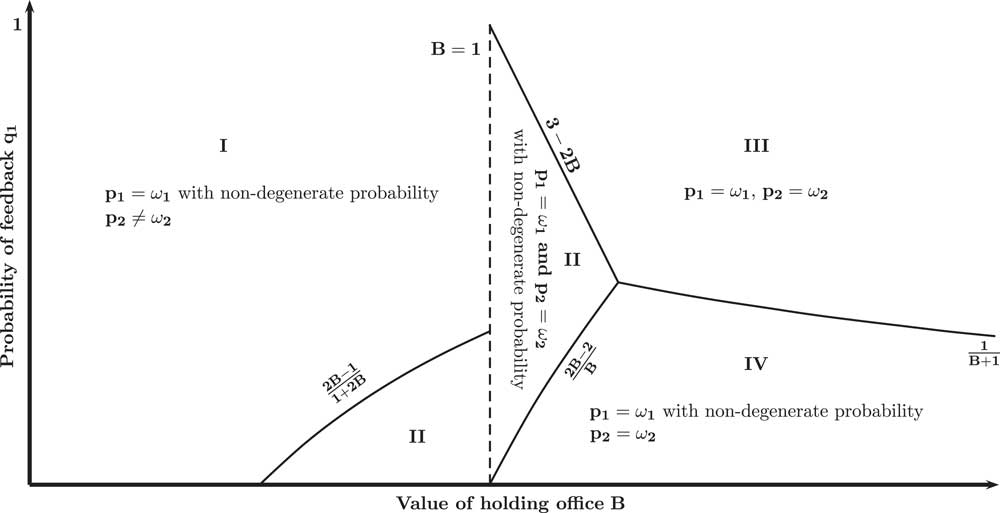
Fig. 2 Equilibrium behavior of non-congruent Incumbent in direct democracy model
To understand the logic behind this proposition, consider first the case where the probability of feedback q 1 is high. In this case, the non-congruent Incumbent has almost no control over policy dimension p 1 because the Voter holds a referendum to set p 1=ω 1 whenever p 1≠ω 1 is revealed to her. Thus, choosing p 1≠ω 1 yields almost no policy gains over choosing p 1=ω 1 but is likely to cost the Incumbent reelection, because the Voter learns that the Incumbent is non-congruent whenever p 1≠ω 1 is revealed to her. Therefore, when q 1 is high, the non-congruent Incumbent essentially only needs to give up one policy, namely p 2, to win reelection. If, as in region III, the value of holding office is superior than the policy payoff attached to policy p 2, i.e. B≥1, the non-congruent Incumbent trades-off his preferred policy p 2 for reelection and chooses (p 1=ω 1, p 2=ω 2). If, as in region I, the non-congruent Incumbent values policy p 2 more than holding office, i.e. B<1, the non-congruent Incumbent is not willing to give up his preferred p 2 for reelection and mixes between (p 1=ω 1, p 2≠ω 2) and (p 1≠ω 1, p 2≠ω 2).
Consider now the case where the probability of feedback q 1 is low. In this case, the Voter is unlikely to observe whether p 1 matches the state of the world or not. If the Voter observes that policy p 2 is matched to its respective state of the world, i.e. p 2=ω 2, yet does not observe the state of the world ω 1, the Voter updates favorably on the probability that she is facing a congruent Incumbent who implements p 1=ω 1. Consequently, the Voter does not hold a referendum upon observing (p 1=1, p 2=ω 2) or (p 1=−1, p 2=ω 2).Footnote 13 If, however, the Voter observes that policy p 2 is not matched to its respective state of the world, i.e. p 2≠ω 2, the Voter infers that she is facing a non-congruent Incumbent who has a preference for choosing the policy that hurts the Voter on dimension p 1. Thus, the Voter has incentives to hold a referendum on policy p 1 upon observing p 2≠ω 2 even when the state of the world ω 1 is not revealed to her. Hence, if the non-congruent Incumbent chooses p 2≠ω 2 he not only looses reelection, but he may also trigger a referendum on policy dimension p 1 which reduces his expected policy payoff with respect to policy p 1. In other terms, when the probability of feedback q 1 is low, choosing (p 1≠ω 1, p 2=ω 2) over p 2≠ω 2 not only improves the non-congruent Incumbent chances of reelection, it also increases his expected policy payoff with respect to p 1. This is the mechanism that lies behind the decision of non-congruent Incumbents to choose p 2=ω 2 in regions II and IV. Note that for some parameter values this mechanism induces the non-congruent Incumbent to choose p 2=ω 2 although he values policy p 2 more than holding office, i.e. B<1.
In region IV, this mechanism induces the non-congruent Incumbent to always choose p 2=ω 2 and to sometimes choose p 1=ω 1. Indeed, in this region, the Voter sets p 1=1 when she observes p 2≠ω 2 and uncertainty is not resolved about ω 1. The payoff to the non-congruent Incumbent of choosing p 2≠ω 2 is thus 1 when he observes ω 1=1 but 2−q 1 when he observes ω 1=−1. As noted above, the Voter does not hold a referendum upon observing (p 1=1, p 2=ω 2). Moreover, because p 1=1 is the popular policy, the Voter believes upon observing (p 1=1, p 2=ω 2) that the Incumbent is more likely to be congruent than a potential challenger and thus reelects. Consequently, the utility to the non-congruent Incumbent of choosing (p 1=1, p 2=ω 2) upon observing ω 1=−1 is (1−q 1)(1+B). When the probability of feedback q 1 is sufficiently low and the value of holding office B is sufficiently high, we have (1−q 1)(1+B)>2−q 1. In other words, the non-congruent Incumbent who observes ω 1=−1 is better off choosing (p 1=1, p 2=ω 2) over p 2≠ω 2 although the Voter enforces the non-congruent Incumbent’s preferred policy p 1=1 upon observing p 2≠ω 2. Similarly, because the Voter does not hold a referendum and reelects upon observing (p 1=1, p 2=ω 2), the non-congruent Incumbent who observes ω 1=1 receives a payoff of B when choosing (p 1=1, p 2=ω 2). In region IV, we have B≥1 and, as a consequence, the non-congruent Incumbent never chooses p 2≠ω 2 upon observing ω 1=1.
In region II, the non-congruent Incumbent does not get caught often enough to consider p 1 as a foregone policy, yet too often to consider p 1 as a policy over which he has almost full control upon observing ω 1=−1. Formally, B<2−q 1 and (1−q 1)(1+B)<2−q 1. In other words, unless the Voter holds a referendum with sufficiently high probability to set p 1=−1 upon observing p 2≠ω 2, the non-congruent Incumbent is better off choosing p 2≠ω 2 upon observing ω 1=−1. Remember that in region IV, the equilibrium is sustained by the decision of the Voter to enforce p 1=1, upon observing p 2≠ω 2. If the Voter now holds a referendum to set p 1=−1 with positive probability, when observing p 2≠ω 2, the incentives for the non-congruent type of choosing p 2≠ω 2 upon observing ω 1=1 increase. Hence, to sustain an equilibrium in which the non-congruent Incumbent always chooses p 2=ω 2, the probability with which the Voter sets p 1=−1 upon observing p 2≠ω 2 has to be neither too high nor too low. As it turns out, when the benefit of holding office is sufficiently low, there exists a range of values for q 1 in which it is not possible for the Voter to set p 1=−1 upon observing p 2≠ω 2 with a probability sufficiently high and sufficiently low to deter the non-congruent Incumbent from choosing p 2≠ω 2 upon observing ω 1=−1 and upon observing ω 1=1, respectively. For this range of parameter values, there exits an infinity of equilibria. For any of these equilibria, non-congruent types will choose p 2≠ω 2 and p 1=ω 1 with positive probability both upon observing ω 1=1 and ω 1=−1.
The Frequency of Referenda
I now discuss some of the predictions generated by the model as they relate to the frequency of referenda. The first lesson is that for wide swaths of the model’s parameter space, the Voter does not hold a referendum in equilibrium. Indeed, in region III of Figure 2 all the types of the Incumbent implement p 1=ω 1 in equilibrium. Therefore, the Voter never has an incentive to correct the decision of the elected representative when q 1 is high and B≥1. For the remaining range of the parameter space (regions I, II, and IV), non-congruent Incumbents enact p 1≠ω 1 with positive probability and the Voter holds a referendum in equilibrium whenever it is revealed to her that the Incumbent chose the wrong policy on dimension p 1. There is a striking difference, however, between the Voter’s behavior in region IV and in regions I and II. In region IV, the Voter only holds a referendum on the equilibrium path upon observing p 1≠ω 1.Footnote 14 In regions I and II, however, the Voter calls for a referendum with positive probability upon observing p 2≠ω 2, even when the state of the world ω 1 is not revealed to her. In such a case, the Voter believes that the Incumbent is non-congruent and thus has an incentive to choose the bad policy p 1≠ω 1. However, because (1) the Voter does not observe the state of the world ω 1 and (2) the non-congruent Incumbent mixes between p 1=ω 1 and p 1≠ω 1 in equilibrium, the Voter remains unsure as to which is the optimal choice on policy dimension p 1. The Voter then mixes between p 1=1 and p 1=−1 in equilibrium, sometimes unwillingly overturning the good policy p 1=ω 1 and replacing it with the bad policy p 1≠ω 1. The Voter, however, never calls for a referendum when she observes p 2=ω 2 and she remains uncertain about the state of the world ω 1.
Proposition 3
1. If B≥1 and the probability of feedback q 1 is high, i.e.
 $q_{1} \geq {\rm max}\left\{ {3{\minus}2B,\,{1 \over {B{\plus}1}}} \right\}$
, the Voter does not hold a referendum on the equilibrium path.
$q_{1} \geq {\rm max}\left\{ {3{\minus}2B,\,{1 \over {B{\plus}1}}} \right\}$
, the Voter does not hold a referendum on the equilibrium path.2. If B≥1 and the probability of feedback q 1 is low, i.e.
 $q_{1} \,\lt\,{\rm min}\left\{ {{{2B{\minus}2} \over B},\,{1 \over {B{\plus}1}}} \right\}$
, the Voter holds a referendum on the equilibrium path if, and only if, the Voter observes p
1≠ω
1.
$q_{1} \,\lt\,{\rm min}\left\{ {{{2B{\minus}2} \over B},\,{1 \over {B{\plus}1}}} \right\}$
, the Voter holds a referendum on the equilibrium path if, and only if, the Voter observes p
1≠ω
1.3. If B<1 or if B≥1 and the probability of feedback q 1 takes intermediate values, i.e.
 $q_{1} \in\left[ {{{2B{\minus}2} \over B},3{\minus}2B} \right]$
, the Voter holds a referendum, on the equilibrium path, with certainty when she observes p
1≠ω
1 and with positive probability when she observes p
2≠ω
2.
$q_{1} \in\left[ {{{2B{\minus}2} \over B},3{\minus}2B} \right]$
, the Voter holds a referendum, on the equilibrium path, with certainty when she observes p
1≠ω
1 and with positive probability when she observes p
2≠ω
2.
This behavior of the Voter presents several interesting features. First, as in Matsusaka and McCarty (Reference Matsusaka and McCarty2001) and Hug (Reference Hug2004), for a referendum to occur in equilibrium, the Incumbent needs to be uncertain about the true preferences of the Voter on the policy dimension on which a referendum may be placed. Second, the Voter only holds a referendum when it is revealed to her that the Incumbent is non-congruent, being because she observes p
1≠ω
1 or p
2≠ω
2. Consequently, the Voter never reelects the Incumbent upon holding a referendum. Holding a referendum is thus effectively akin to recalling the Incumbent. Third, when the value of holding office is sufficiently high
![]() $(B\,\gt\,\underline{B} )$
, the relationship between the frequency of referenda and the probability that uncertainty about ω
1 resolves is non-monotonic. More precisely, the frequency of referenda is increasing in q
1 on
$(B\,\gt\,\underline{B} )$
, the relationship between the frequency of referenda and the probability that uncertainty about ω
1 resolves is non-monotonic. More precisely, the frequency of referenda is increasing in q
1 on
![]() $\left[ {0,{1 \over {B{\plus}1}}} \right]$
before remaining constant at 0 on
$\left[ {0,{1 \over {B{\plus}1}}} \right]$
before remaining constant at 0 on
![]() $\left[ {{1 \over {B{\plus}1}},1} \right]$
. This stems from the fact that the probability with which non-congruent Incumbents choose p
1≠ω
1 in equilibrium does not depend on the probability of feedback q
1, when
$\left[ {{1 \over {B{\plus}1}},1} \right]$
. This stems from the fact that the probability with which non-congruent Incumbents choose p
1≠ω
1 in equilibrium does not depend on the probability of feedback q
1, when
![]() $q_{1} \,\lt\,{1 \over {B{\plus}1}}$
. However, as q
1 increases, the Voter is more likely to learn that the Incumbent implemented p
1≠ω
1 and thus to hold a referendum.
$q_{1} \,\lt\,{1 \over {B{\plus}1}}$
. However, as q
1 increases, the Voter is more likely to learn that the Incumbent implemented p
1≠ω
1 and thus to hold a referendum.
Corollary 4: If
![]() $B\geq \underline{B} $
, then the probability that the Voter holds a referendum increases in the probability of feedback q
1 on
$B\geq \underline{B} $
, then the probability that the Voter holds a referendum increases in the probability of feedback q
1 on
![]() $\left[ {0,\,{1 \over {B{\plus}1}}} \right]$
before remaining constant at 0 on
$\left[ {0,\,{1 \over {B{\plus}1}}} \right]$
before remaining constant at 0 on
![]() $\left[ {{1 \over {B{\plus}1}},\,1} \right]$
.
$\left[ {{1 \over {B{\plus}1}},\,1} \right]$
.
Most interestingly, for some parameter values, the decision of the Voter to hold a referendum about policy p 1 depends on the observed policy decision on dimension p 2. More precisely, once the Incumbent is revealed as non-congruent to the Voter via his decision about policy p 2, the Voter is more likely to try to constrain his decision-making on dimension p 1 by using the referendum even if the Voter does not observe ω 1 and is thus uncertain as to which policy p 1 is in the public interest. In such cases, the Voter votes against a certain policy decision p 1 on the basis that it is put forward by a non-congruent Incumbent. The model thus provides an explanation for why voters sometimes vote against certain policies seemingly without consideration as to whether the policy is sensible or not. While such claims have not been tested directly, some empirical work is suggestive of such dynamics. Indeed, Matsusaka (Reference Matsusaka1992) finds that citizen initiatives play a more important role in periods where elected representatives appear to be corrupt.
The fact that the Voter, upon observing p 2≠ω 2, holds a referendum despite not knowing the state of the world ω 1 has striking consequences: (1) the Voter sometimes holds a referendum to set the ex ante unpopular policy p 1=−1 although ω 1 is not revealed to her and sometimes unwillingly enforces p 1≠ω 1. These results would at first seem to confirm the concerns raised by critics of direct democracy regarding the lack of expertise of the electorate. The next section shows, however, that this behavior of the electorate improves congruence in expectation, because it induces changes in the behavior of the Incumbent.
The Impact of the Popular Referendum
Improved Congruence
Comparison of the equilibria in Proposition 1 to the equilibria in Proposition 2 illustrates the effects of the popular referendum on representative democracy when B<2. An observation worth repeating is that congruent Incumbents behave optimally from the point of view of the Voter with regard to every single policy of the game, whether the Voter is given the ability to call for a referendum on policy p 1 or not. The popular referendum affects the behavior of non-congruent Incumbents, however. With respect to policy dimension p 1, the popular referendum has three partially competing effects. First, it induces non-congruent Incumbents to behave in the Voter’s best interests more often. Indeed, in the baseline model, non-congruent Incumbents always disregard the Voter’s preferences about policy p 1, implementing p 1≠ω 1 independently of the probability of feedback q 1. In the model with direct democracy, non-congruent types always choose p 1=ω 1 with positive probability for all values of q 1. Second, the popular referendum gives the Voter the power to correct the Incumbent’s mistakes. In particular, the Voter sets p 1=ω 1 upon observing p 1≠ω 1 and holds a referendum with positive probability upon observing p 2≠ω 2, despite not observing ω 1. When the Voter does not observe ω 1, the Voter often turns p 1≠ω 1 into p 1=ω 1 via the referendum. However, and this is the third effect, in these cases, the Voter is also sometimes wrong and unwillingly enforces p 1≠ω 1. Relative to the baseline model, the first and second effects always dominate the third effect, however. The ex ante probability that p 1=ω 1 is implemented when the Incumbent is congruent is π under representative as well as direct democracy. When the Incumbent is non-congruent, this ex ante probability is 0 in the baseline model but strictly positive under direct democracy, even when considering the possibility that the Voter sometimes mistakenly enforces p 1≠ω 1.
A more surprising aspect of the analysis is that the popular referendum not only improves congruence with respect to policies on which a referendum may be placed, but also with respect to policy issues that are outside the reach of direct democracy. In the baseline model, non-congruent Incumbents never choose p
2=ω
2 when
![]() $q_{1} \,\gt\,{{B{\minus}1} \over B}$
and choose p
2≠ω
2 with non-degenerate probability when
$q_{1} \,\gt\,{{B{\minus}1} \over B}$
and choose p
2≠ω
2 with non-degenerate probability when
![]() $q_{1} \leq {{B{\minus}1} \over B}$
. The introduction of direct democracy leads the non-congruent Incumbent to always choose p
2=ω
2 when
$q_{1} \leq {{B{\minus}1} \over B}$
. The introduction of direct democracy leads the non-congruent Incumbent to always choose p
2=ω
2 when
![]() $q_{1} \leq {{B{\minus}1} \over B}$
. Moreover, when
$q_{1} \leq {{B{\minus}1} \over B}$
. Moreover, when
![]() $$q_{1} \,\gt\,{{B{\minus}1} \over B}$$
, the popular referendum weakly improves congruence in region I and strictly improves congruence in all other regions where there always exist equilibria in which p
2=ω
2 is implemented with positive probability by the non-congruent Incumbents.
$$q_{1} \,\gt\,{{B{\minus}1} \over B}$$
, the popular referendum weakly improves congruence in region I and strictly improves congruence in all other regions where there always exist equilibria in which p
2=ω
2 is implemented with positive probability by the non-congruent Incumbents.
Proposition 5: For any probability of feedback q 1, giving the Voter the power to call for a referendum on policy p 1 improves the congruence between enacted policies and Voter’s preferences with respect to p 1 as well as with respect to p 2, the policy about which the Voter cannot hold a referendum.
It is instructive to compare these results to those found in models by Gerber (Reference Gerber1996), Hug (Reference Hug2004), Besley and Coate (Reference Besley and Coate2008), and Prato and Strulovici (Reference Prato and StruloviciForthcoming). They show that the introduction of the popular referendum improves congruence between enacted policies and voters’ preferences on those policy dimensions which can be subjected to direct democracy. They do not consider, however, the effect of direct democracy on the decision-making on other policy dimensions. Moreover, voters are always assumed to be fully informed about their true preferences in these models. Proposition 5 above shows, however, that the Voter is getting higher congruence even when she is not fully informed about her true interests. Proposition 5 also stands in contrast to Matsusaka and McCarty (Reference Matsusaka and McCarty2001) who find, in a model with policy-driven politicians, that initiatives may move the policy farther away from the voter’s ideal point. In the present paper, the reelection concerns are precisely what motivates the Incumbent to alter his behavior and attend more closely to the Voter’s preferences.
Because the popular policies p 1=1 and p 2=1 are ex ante more likely to correspond to the state of the world, the introduction of the referendum, by improving congruence, also increases the probability that the popular policies are implemented. In other words, the introduction of the referendum increases the congruence between enacted policies and the voters’ ex ante beliefs about what is in their best interests. This prediction regarding p 1 is familiar and conforms to empirical results. Several studies find, e.g., that the implemented policies regarding the death penalty, abortion, same sex marriage, and public spending more closely reflect public opinion in states that permit voters to call for a referendum (see Gerber Reference Gerber1996; Gerber Reference Gerber1999; Hug Reference Hug2004; Matsusaka Reference Matsusaka2004; Matsusaka Reference Matsusaka2010).Footnote 15 The prediction that the introduction of the popular referendum also increases the likelihood that the popular policy p 2=1 is implemented, although no referendum can be held about p 2, is new to the literature and suggests a more pervasive effect of referenda as well as the need for additional empirical analysis.
The Effect of Additional Information
The introduction of the referendum also changes how the behavior of the Incumbent relates to the information available to the Voter. Whereas in the baseline model, the control the Voter exerts over policy-making may decrease—rather than increase—when the Voter is more likely to observe the states of the world, this relationship is reversed for a large range of the parameter space when the Voter can call for a referendum. Indeed, in the baseline model, the control the Voter exerts over policy dimension p
2 depends on the probability q
1 that the Voter learns the state of the world ω
1. There, non-congruent Incumbents always disregard the Voter’s true preferences on dimension p
2 by implementing p
2≠ω
2 when the probability of feedback q
1 is high, but choose p
2=ω
2 with positive probability when q
1 is low. Hence, the Voter may be able to exert more control over policy p
2, when the probability of feedback on dimension p
1 is lower rather than higher. This holds true although an increase in the probability of feedback q
1 does not increase the probability that the Incumbent implements p
1=ω
1. Indeed, in the absence of the referendum, the non-congruent Incumbent chooses p
1≠ω
1 for all q
1 ∈ [0, 1]. Once the popular referendum is introduced, the ability of the electorate to control the behavior of elected officials increases with the probability of feedback, for a large range of the parameter space. If the value of holding office is sufficiently high,
![]() $B\geq \underline{B} $
, non-congruent Incumbents sometimes choose the policy that hurts the Voter on dimension p
1, when q
1 is low, but always match the policy to the state of the world, p
1=ω
1, when q
1 is high. Thus, for certain parameter values, the introduction of the popular referendum restores the value of becoming informed to the electorate.
$B\geq \underline{B} $
, non-congruent Incumbents sometimes choose the policy that hurts the Voter on dimension p
1, when q
1 is low, but always match the policy to the state of the world, p
1=ω
1, when q
1 is high. Thus, for certain parameter values, the introduction of the popular referendum restores the value of becoming informed to the electorate.
When the value of holding office is low
![]() $(B\,\lt\,\underline{B} )$
, however, a higher probability of feedback may reduce the control that the Voter exerts over elected officials. When B<1 the probability that a non-congruent Incumbent chooses p
2=ω
2 is decreasing in the probability of feedback q
1. Indeed, the non-congruent Incumbent sets p
2=ω
2 with positive probability when
$(B\,\lt\,\underline{B} )$
, however, a higher probability of feedback may reduce the control that the Voter exerts over elected officials. When B<1 the probability that a non-congruent Incumbent chooses p
2=ω
2 is decreasing in the probability of feedback q
1. Indeed, the non-congruent Incumbent sets p
2=ω
2 with positive probability when
![]() $q_{1} \,\lt\,{{2B{\minus}1} \over {1{\plus}2B}}$
, but chooses p
2≠ω
2 deterministically when
$q_{1} \,\lt\,{{2B{\minus}1} \over {1{\plus}2B}}$
, but chooses p
2≠ω
2 deterministically when
![]() $$q_{1} \geq {{2B{\minus}1} \over {1{\plus}2B}}$$
. When
$$q_{1} \geq {{2B{\minus}1} \over {1{\plus}2B}}$$
. When
![]() $$1\leq B\,\lt\,\underline{B} $$
, the relationship between the probability that a non-congruent Incumbent chooses p
2=ω
2 and the probability of feedback q
1 is non-monotonic. More precisely, when B≥1, a non-congruent Incumbent sets p
2=ω
2 if
$$1\leq B\,\lt\,\underline{B} $$
, the relationship between the probability that a non-congruent Incumbent chooses p
2=ω
2 and the probability of feedback q
1 is non-monotonic. More precisely, when B≥1, a non-congruent Incumbent sets p
2=ω
2 if
![]() $q_{1} \,\lt\,{{2B{\minus}2} \over B}$
or if q
1>3−2B, but chooses p
2≠ω
2 with positive probability when
$q_{1} \,\lt\,{{2B{\minus}2} \over B}$
or if q
1>3−2B, but chooses p
2≠ω
2 with positive probability when
![]() $q_{1} \,\in\,\left[ {{{2B{\minus}2} \over B},\,3{\minus}2B} \right]$
.
$q_{1} \,\in\,\left[ {{{2B{\minus}2} \over B},\,3{\minus}2B} \right]$
.
Similarly, the relationship between the probability that a non-congruent Incumbent sets p
1=ω
1 and q
1 is ambiguous. Remember that when
![]() $B\,\lt\,\underline{B} $
and
$B\,\lt\,\underline{B} $
and
![]() $q_{1} \,\in\,\left[ {{{2B{\minus}2} \over B},\,3{\minus}2B} \right]$
, there exists an infinity of equilibria. In any of these equilibria, non-congruent Incumbents choose p
1=ω
1 with positive probability. Depending on the specific equilibrium that the Incumbents coordinate on, the probability with which p
1=ω
1 may go up or go down compared with the case where q
1 is low.
$q_{1} \,\in\,\left[ {{{2B{\minus}2} \over B},\,3{\minus}2B} \right]$
, there exists an infinity of equilibria. In any of these equilibria, non-congruent Incumbents choose p
1=ω
1 with positive probability. Depending on the specific equilibrium that the Incumbents coordinate on, the probability with which p
1=ω
1 may go up or go down compared with the case where q
1 is low.
Proposition 6: Assume
![]() $B\geq \underline{B} $
. Whereas in the baseline model the control the Voter exerts over policy p
2 is weakly decreasing in the probability of feedback q
1, once direct democracy is introduced the control the Voter exerts over policies p
1 and p
2 is increasing in q
1.
$B\geq \underline{B} $
. Whereas in the baseline model the control the Voter exerts over policy p
2 is weakly decreasing in the probability of feedback q
1, once direct democracy is introduced the control the Voter exerts over policies p
1 and p
2 is increasing in q
1.
Voter Welfare
I now consider the effect of the popular referendum on ex ante Voter welfare. As shown above, the popular referendum improves the congruence between enacted policies and the Voter’s true preferences. Consequently, direct democracy increases the Voter’s current policy payoff. In regions II to IV, however, this improved congruence results from the decision of the non-congruent Incumbent to mimic the behavior of the congruent one more often under direct than under representative democracy. Therefore, the popular referendum decreases the ability of the Voter to select congruent Incumbents and thus reduces the Voter’s future payoff. The introduction of the popular referendum thus represents a trade-off for the Voter. As is standard in the literature (see among other examples Fox and Stephenson Reference Fox and Stephenson2011; Ashworth and Bueno de Mesquita Reference Ashworth and Bueno de Mesquita2015), I remain agnostic as to the relative weight of these competing effects.
A Note on Robustness
In this section, I show that the spillover effects identified, namely that the popular referendum also improves congruence on policy dimensions on which no referendum may be placed, is robust to a specification of the model in which the Voter is uncertain about which policy is in the public interest on policy dimension p 2. Hence, I assume from now on, that the Voter observes the state of the world ω 1 but only observes the state of the world ω 2 with probability q 2 ∈ [0, 1]. In the baseline model, dimensions p 1 and p 2 are identical up to the probability of feedback. Thus, to see what the equilibrium of the baseline model is in this new setting, all one needs to do is to invert p 1 and p 2. In the model with direct democracy, the congruent Incumbent chooses (p 1=ω 1, p 2=ω 2) in equilibrium as in the previous specification of the model. The equilibrium behavior of the non-congruent Incumbent, however, depends on the probability of feedback q 2 and the value of holding office B (see Figure 3).
Proposition 7: In equilibrium:
1. If B<1, non-congruent Incumbents implement the Voter’s preferred policy on dimension p 1 and disregard the Voter’s preferences on dimension p 2: (p 1=ω 1, p 2≠ω 2),
2. If B≥1 and the probability of feedback is high
 $\left( {q_{2} \,\in\,\left[ {{1 \over B},\,1} \right]} \right)$
, non-congruent Incumbents implement the Voter’s preferred policies with respect to all policy dimensions: (p
1=ω
1, p
2=ω
2),
$\left( {q_{2} \,\in\,\left[ {{1 \over B},\,1} \right]} \right)$
, non-congruent Incumbents implement the Voter’s preferred policies with respect to all policy dimensions: (p
1=ω
1, p
2=ω
2),3. If B≥1 and the probability of feedback is low
 $\left( {q_{2} \,\in\,\left[ {0,\,{1 \over B}} \right]} \right)$
, non-congruent Incumbents choose p
1=ω
1 with certainty and p
2=ω
2 with non-degenerate probability.
$\left( {q_{2} \,\in\,\left[ {0,\,{1 \over B}} \right]} \right)$
, non-congruent Incumbents choose p
1=ω
1 with certainty and p
2=ω
2 with non-degenerate probability.
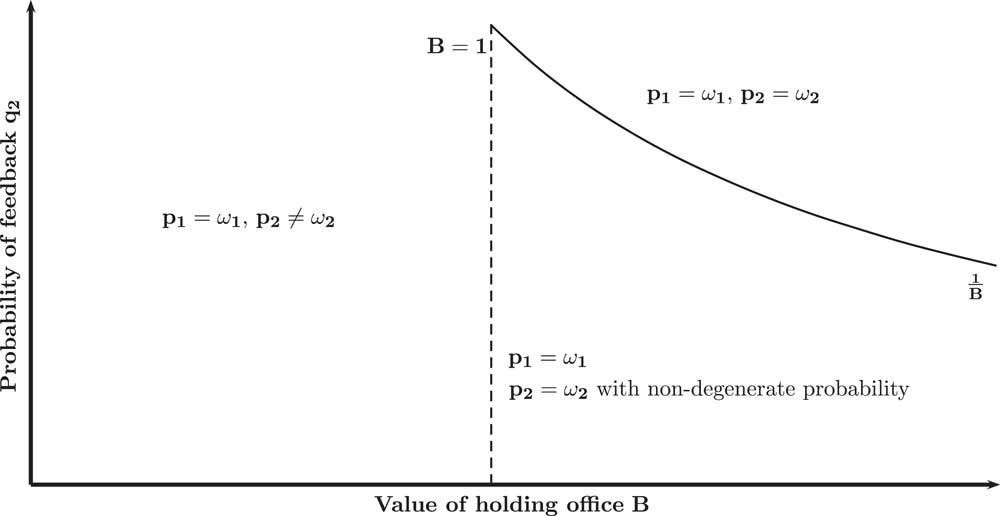
Fig. 3 Equilibrium behavior of non-congruent Incumbent in direct democracy model, q 1=1, q 2 ∈ [0, 1]
The logic behind this result is as follows. As the Voter knows the state of the world ω 1, the Voter holds a referendum to set p 1=ω 1 whenever the Incumbent chooses p 1≠ω 1. Hence, whether the non-congruent Incumbent chooses p 1≠ω 1 or p 1=ω 1, his policy payoff with respect to p1 is equal to 0 in equilibrium. Choosing p 1≠ω 1 then does not yield any policy gains to the non-congruent Incumbent but costs him reelection, because the Voter learns his true type upon observing p 1≠ω 1. In equilibrium, it is therefore never a best-response for the non-congruent Incumbent to play p 1≠ω 1. Consequently, he chooses between (p 1=ω 1, p 2=ω 2) and (p 1=ω 1, p 2≠ω 2).
Choosing (p 1=ω 1, p 2≠ω 2) over (p 1=ω 1, p 2=ω 2) has a policy gain and an electoral cost: on the one hand, the non-congruent Incumbent receives a higher policy payoff with respect to policy p 2, on the other, he loses reelection whenever uncertainty about ω 2 is resolved. Note that the magnitude of the cost increases with the probability of feedback q 2 and the value of holding office B. When the value of holding office is lower than the policy gain (B<1), the policy gain exceeds the electoral cost for all values of the probability of feedback q 2 and the non-congruent Incumbent disregards the Voter’s preferences on dimension p 2. When the value of holding office exceeds the policy gain (B≥1) and the probability of feedback q 2 is high, the electoral cost exceeds the policy gain. In such a case, the non-congruent Incumbent is better off mimicking the behavior of the congruent Incumbent with respect to all policies. When the probability of feedback q 2 is low, and the non-congruent Incumbent chooses (p 1=ω 1, p 2≠ω 2) with sufficiently low probability, the Voter is willing to reelect the Incumbent with positive probability whenever ω 2 is not revealed. In this case, the cost of choosing (p 1=ω 1, p 2≠ω 2) over (p 1=ω 1, p 2=ω 2) is low, and the non-congruent Incumbent implements (p 1=ω 1, p 2≠ω 2) with positive probability.
The introduction of the popular referendum also improves congruence in this new setting. In the baseline model, the behavior of the non-congruent Incumbent with respect to p
1 depends on the likelihood that the Voter learns the optimality of the policy decision p
2. If the feedback q
2 is high
![]() $\left( {q_{2} \,\gt\,{{B{\minus}1} \over B}} \right)$
, the non-congruent Incumbent never matches the policy to the state of the world on dimension p
1. When feedback is low
$\left( {q_{2} \,\gt\,{{B{\minus}1} \over B}} \right)$
, the non-congruent Incumbent never matches the policy to the state of the world on dimension p
1. When feedback is low
![]() $$\left( {q_{2} \leq {{B{\minus}1} \over B}} \right)$$
, however, he implements p
1=ω
1 with non-degenerate probability. Once representative democracy is supplemented by direct democracy, the non-congruent Incumbent always chooses p
1=ω
1. The spillover effect also holds. In the baseline model, the non-congruent Incumbent never chooses p
2=ω
2, and this independently of the value of q
2. In the model with direct democracy, the non-congruent Incumbent always chooses p
2=ω
2 with positive probability when the value of holding office is sufficiently high (B>1). He even chooses p
2=ω
2 with certainty, when the probability of feedback q
2 is high
$$\left( {q_{2} \leq {{B{\minus}1} \over B}} \right)$$
, however, he implements p
1=ω
1 with non-degenerate probability. Once representative democracy is supplemented by direct democracy, the non-congruent Incumbent always chooses p
1=ω
1. The spillover effect also holds. In the baseline model, the non-congruent Incumbent never chooses p
2=ω
2, and this independently of the value of q
2. In the model with direct democracy, the non-congruent Incumbent always chooses p
2=ω
2 with positive probability when the value of holding office is sufficiently high (B>1). He even chooses p
2=ω
2 with certainty, when the probability of feedback q
2 is high
![]() $\left( {q_{2} \geq {1 \over B}} \right)$
.
$\left( {q_{2} \geq {1 \over B}} \right)$
.
Conclusion
This paper has examined how the possibility of voters calling for a referendum affects electoral accountability. I have shown that the introduction of the popular referendum, by limiting the policy benefits that a non-congruent official can receive from choosing his (as opposed to the voters) preferred policies, increases the incentives of non-congruent public officials to mimic the behavior of congruent ones. A main implication of this result is that non-congruent elected officials are more likely to enact policies that are in the public interest once the popular referendum is introduced. In contrast to the existing literature I have shown that this improved congruence between enacted policies and voters’ preferences also concerns policy dimensions on which no referendum may be placed. In this sense, direct democracy may have a much more pervasive effect on representative democracy than previously thought. Moreover, I have shown that direct democracy improves congruence even when the electorate is unlikely to be fully informed about its true interests. The lack of expertise of voters, which opponents of direct democracy often present as a major concern, may thus be a less severe problem than heretofore acknowledged. Furthermore, under direct democracy the value to the electorate of being informed may be higher than under representative democracy. Indeed, under a strictly representative democracy, there are negative spillover effects of information in the sense that voters being more likely to become informed about some policy dimensions may lead non-congruent officials to disregard the preferences of the electorate more often on other policy dimensions. In contrast, there are conditions under which the possibility of popular referenda implies that being more likely to become informed improves voter control over public officials, including on policy dimensions on which no referendum may be placed. The introduction of the popular referendum represents a trade-off for the electorate though. Because non-congruent public officials are more likely to mimic the behavior of congruent ones, the popular referendum hurts the ability of the electorate to select public officials who truly have the public interest at heart.
The analysis suggests that empirical research on the impact of direct democracy on congruence has to some extent been looking for the keys under the lamp post. Testing whether the popular referendum also improves congruence on policy dimensions on which no referendum is placed represents an interesting agenda for future empirical research.





