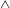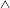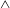1 Introduction
The transition from laminar to turbulent flow has been one of the most classic research questions in the fluid mechanics community because of the importance of the transition of the flow behaviour. It has been well understood that mass transport, heat transfer and aerodynamic properties vary significantly in laminar and turbulent flow regimes. Over the past decades, much experimental, theoretical and numerical research has been devoted to flow transitions in Blasius boundary layers, whereas little is known about transitions in natural convection boundary layers. Two typical transitions observed in Blasius boundary layers are K-type and H-type transitions. A recent numerical investigation by Sayadi, Hamman & Moin (Reference Sayadi, Hamman and Moin2013) observed distinct aligned
$\wedge$
-shaped structures in the K-type transition and staggered
$\wedge$
-shaped structures in the H-type transition, which are shown in figure 1. It is interesting to examine whether the K-type and H-type transitions observed in Blasius boundary layers (see Mayer, Von Terzi & Fasel Reference Mayer, Von Terzi and Fasel2011) occur in natural convection boundary layers, though the velocity profile of the natural convection boundary layer is fundamentally different from that of the Blasius boundary layer.
Figure 1. The
$\wedge$
structures observed in (a) K-type transition and (b) H-type transition in Blasius boundary layers, reproduced from Sayadi et al. (Reference Sayadi, Hamman and Moin2013). The contours represent instantaneous streamwise velocity and
$z$
denotes the spanwise position of the boundary layer.
Since the forms of artificial perturbations, the resultant flow structures and the physical mechanisms of the transitions of Blasius boundary layers will be involved in the discussion of the present study, the reminder of the introduction will start with some background regarding the transitions of Blasius boundary layers (§ 1.1). In § 1.2, the progress of research on the transition of natural convection boundary layers is reviewed. Finally, the major objectives and contributions of the present study are described in § 1.3.
1.1 Transitions in Blasius boundary layers
The problem of laminar–turbulent transition in Blasius boundary layers has attracted extensive research interest for more than half a century. Reviews of various types and mechanisms of the transitions in Blasius boundary layers are available in Herbert (Reference Herbert1988) and Kachanov (Reference Kachanov1994). In general, it has been understood that a natural transition to turbulence undergoes three main stages (see White Reference White1991). The first stage starts with the streamwise amplification of unstable two-dimensional Tollmien–Schlichting (TS) waves. As the TS waves travel downstream, three-dimensionality develops and the flow becomes three-dimensional (3D), characterized by the formation of 3D vortical structures, which is the second stage. Further downstream, the flow develops into turbulence, characterized by the appearance of turbulent spots and intermittent phenomena.
The behaviour of the TS waves in the first stage of a complete laminar–turbulent transition process can be successfully described by linear stability theory, which has been extensively reported since Tollmien (Reference Tollmien1929), and later by Lin (Reference Lin1955) and others. Pioneering experiments by Schubauer & Skramstad (Reference Schubauer and Skramstad1947) and subsequent experimental work by Ross et al. (Reference Ross, Barnes and Burns1970) and others have justified the applicability of linear stability theory for the flow in that stage.
In the second stage, the development of three-dimensionality in the boundary layers is far more complex than that in the first stage. It is now understood that the characteristics of the transition depend greatly on the initial amplitudes, frequencies and phases of the upstream disturbances. Originally the transition refers to the transitional process of boundary layers subject to non-homogeneous environmental disturbances (Schrader, Brandt & Henningson Reference Schrader, Brandt and Henningson2008). Due to the complexity of studying the transition induced by such non-homogeneous disturbances, in particular in the experimental and theoretical aspects, extensive investigations have been devoted to transitions initiated by imposed disturbances of particular forms (Klebanoff, Tidstrom & Sargent Reference Klebanoff, Tidstrom and Sargent1962). These types of transitions, which depend on the specific upstream disturbances, are examples of ‘controlled transitions’. The transition caused by non-homogeneous disturbances is thus referred to as ‘natural transition’.
The flow transits into turbulence in the third stage. This is far more complex compared to the first two stages. Kline et al. (Reference Kline, Reynolds, Schraub and Runstadler1967) revealed the presence of organized spatially and temporally dependent motions within the ‘laminar sublayer’ from their visualization experiments. These motions result in the formation of low-speed streaks in the region very close to the wall, and eventually lead to new turbulence and the transport of turbulence within the boundary layer on smooth walls. Later, Moin & Kim (Reference Moin and Kim1982) carried out three-dimensional simulations of turbulent channel flow and confirmed that the viscous sublayer consists of coherent structures of high- and low-speed streaks alternating in the spanwise direction. The analysis of Aubry et al. (Reference Aubry, Holmes, Lumley and Stone1988) using dynamical systems theory suggested that the pressure of the outer layer part of the boundary layer triggers the motions leading to the bursting of streamwise rolls.
The natural transition is excited by spatially and temporally non-homogeneous (random) perturbations, which has not been extensively investigated theoretically or experimentally. On the other hand, many theoretical, experimental and numerical investigations have been devoted to controlled transitions, such as the contributions by Klebanoff et al. (Reference Klebanoff, Tidstrom and Sargent1962), Kachanov & Levchenko (Reference Kachanov and Levchenko1984), Fasel & Konzelmann (Reference Fasel and Konzelmann1990), Bake, Meyer & Rist (Reference Bake, Meyer and Rist2002) and Mayer et al. (Reference Mayer, Von Terzi and Fasel2011) among many others. Of these controlled transitions, the K-type (named after Klebanoff) and the H-type (named after Herbert) transitions are the two typical ones mostly investigated in the previous studies. It is expected that an understanding of controlled transitions would form the basis for ultimately understanding the mechanisms of natural transitions.
The K-type transition was first investigated by Klebanoff et al. (Reference Klebanoff, Tidstrom and Sargent1962). In the classical experiment of the K-type transition, the wave resonant interaction between two-dimensional fundamental TS waves and oblique waves of the same frequency was examined. It was found that the wave resonant interaction excited higher harmonics, which were characterized by the sudden appearance of ‘spikes’ in the oscilloscope traces of the streamwise velocity signal. The aligned ‘spikes’ were the indication of the formation of aligned
$\wedge$
-shaped vortices, which has been clearly observed in the experiment of Berlin, Wiegel & Henningson (Reference Berlin, Wiegel and Henningson1999) and in the most recent direct numerical simulation (DNS) of Sayadi et al. (Reference Sayadi, Hamman and Moin2013). The aligned
$\wedge$
-shaped structures are usually recognized as the typical 3D flow structure characterizing the K-type transition in Blasius boundary layers.
The H-type transition, which is also termed as subharmonic transition (see Kachanov, Kozlov & Levchenko Reference Kachanov, Kozlov and Levchenko1978; Kachanov & Levchenko Reference Kachanov and Levchenko1984) or the C-type transition (refer to Craik Reference Craik1971), is another typical controlled transition. Unlike the K-type transition characterized by the aligned
$\wedge$
-shaped vortices, the H-type transition is characterized by the appearance of staggered 3D
$\wedge$
-shaped structures. The typical structures have been observed experimentally and numerically by Berlin et al. (Reference Berlin, Wiegel and Henningson1999) and Sayadi et al. (Reference Sayadi, Hamman and Moin2013). Craik (Reference Craik1971) and Herbert (Reference Herbert1983) also proposed theoretical models to explain the transition, both based on the wave resonant interaction between the two-dimensional fundamental TS waves and a symmetric pair of oblique waves of half the frequency of the TS waves.
The K-type and H-type transitions of mixed convection in a heated vertical channel were investigated by Chen & Chung (Reference Chen and Chung2002). The investigation reveals that kinetic energy generated by thermal buoyancy force is the main driving force in the early stage of the K-type transition, which is also the important character of the H-type transition. The vortex structures in an ordered pattern and staggered patterns are also observed in the K-type and H-type transitions, respectively.
1.2 Transitions in natural convection boundary layers
Natural convection boundary layer flows are usually characterized by the Rayleigh and Prandtl numbers. This is different from Blasius boundary layer flows which are characterized by the Reynolds number. However, the overall process of a laminar–turbulent transition in a natural convection boundary layer may be similar to that in a forced flow, which was commented on by Gebhart (Reference Gebhart1973). Similar to Blasius boundary layer flows, the complete laminar–turbulent transition process of buoyancy-induced flows comprises three stages, which are instability, transition and turbulence.
The instability in buoyancy-induced flows, characterized by the amplification of two-dimensional disturbances, has been of continuous research interest since the early linear stability analysis by Plapp (Reference Plapp1957), Szewczyk (Reference Szewczyk1962), Nachtsheim (Reference Nachtsheim1963) and others. The applicability of linear stability analysis for studying the instability of the flows was verified by the experimental work of Eckert & Soehnghen (Reference Eckert and Soehnghen1951), Polymeropoulos & Gebhart (Reference Polymeropoulos and Gebhart1967), Dring & Gebhart (Reference Dring and Gebhart1968) and Knowles & Gebhart (Reference Knowles and Gebhart1968). Over recent decades, direct stability analysis (DSA) has emerged as another powerful approach for investigating the instability characteristics of buoyancy-driven flows. Examples of DSA include Armfield & Janssen (Reference Armfield and Janssen1996), Janssen & Armfield (Reference Janssen and Armfield1996), Brooker et al. (Reference Brooker, Patterson and Graham2000), Lei & Patterson (Reference Lei and Patterson2003), Aberra et al. (Reference Aberra, Armfield, Behnia and McBain2006), Paul & Rees (Reference Paul and Rees2008), Williamson & Armfield (Reference Williamson and Armfield2011), Aberra et al. (Reference Aberra, Armfield, Behnia and McBain2012), Zhao, Lei & Patterson (Reference Zhao, Lei and Patterson2013) and others.
Whilst the instability properties of buoyancy-induced flows have been investigated extensively, the second stage of the complete laminar–turbulent transition process, that is, the transitional stage, has received little attention, particularly for the vertical natural convection boundary layers adjacent to an isothermal or isoflux surface. One of only a few investigations was an experimental study conducted by Jaluria & Gebhart (Reference Jaluria and Gebhart1973). In their study, controlled two-dimensional disturbances with a superimposed spanwise variation (i.e. spanwise height variation of a perturbing ribbon) were introduced into the upstream of the vertical boundary layer adjacent to an isoflux surface. A double longitudinal vortex system was inferred based on discrete measurements of the spanwise mean velocity components. A subsequent analytical study by Audunson & Gebhart (Reference Audunson and Gebhart1976) found that the effect of the finite perturbation amplitude and the interaction between the two-dimensional and spanwise disturbances resulted in the double longitudinal vortex system.
The disturbances introduced in the experiment of Jaluria & Gebhart (Reference Jaluria and Gebhart1973) are in fact equivalent to introducing superimposed two-dimensional TS waves and pairs of oblique waves of the same frequency. According to the understanding of the transition of Blasius boundary layers, the introduced disturbances in Jaluria & Gebhart’s experiment would excite the K-type transition if the natural convection boundary layer and Blasius boundary layer have certain intrinsic similarities in the flow transition. However, the typical
$\wedge$
-shaped flow structures characterizing the K-type transition were not reported in Jaluria & Gebhart (Reference Jaluria and Gebhart1973).
Aberra et al. (Reference Aberra, Armfield, Behnia and McBain2010) studied the transition of natural convection boundary layers using direct numerical simulation, in which numerical perturbations closely matching the perturbations applied in the physical experiment of Jaluria & Gebhart (Reference Jaluria and Gebhart1973) were introduced by perturbing velocities in the upstream boundary layer. Their study confirmed the presence of the double longitudinal vortex system. However, the
$\wedge$
-shaped structures were not identified; instead they reported
$\vee$
-shaped structures.
In addition to the above-mentioned investigations on instabilities and controlled transitions of natural convection boundary layers, Zhao, Lei & Patterson (Reference Zhao, Lei and Patterson2016) studied the natural transition of natural convection boundary layers, in which the boundary layers are subjected to stochastic disturbances only. It was revealed that there exist two competing wavenumbers of spanwise vortical structures, one large and the other small. The large wavenumber dominates in the upstream boundary layer, whereas the small wavenumber dominates in the downstream boundary layer. A spectrum filling process during the natural transition of the thermal boundary is also observed, which is qualitatively similar to that observed in Blasius boundary layers.
1.3 Contribution of the present study
The above literature survey has shown that investigations and understanding of the controlled transitions of natural convection boundary layers are very limited. In the present study, direct three-dimensional numerical simulations are performed to investigate the characteristics of the transitional natural convection boundary layer flow subject to two types of controlled disturbances. In contrast to most of the earlier studies, which were concerned with the stability characteristics in the linear regimes of the natural convection boundary layers, the characteristics of the K-type and H-type transitions in the nonlinear regimes of pure natural convection boundary layers are examined and documented here for the first time. The major contribution of the present work is to reveal the full transition route of pure natural convection boundary layers subject to combined TS and oblique waves. The aligned and staggered three-dimensional
$\wedge$
structures for the K-type and H-type transitions are visualized using Q-criteria for the first time for pure natural convection boundary layers. Various characteristics of the transitions are also presented and discussed.
In what follows, the mathematical formulation and the numerical procedures are presented in § 2.1. The form of numerical perturbations and the comparison of the perturbations for exciting the K-type and the H-type transitions are described in § 2.2.
In § 3, the characteristics of the transitional flow, the three-layer longitudinal vortex system and the aligned
$\wedge$
-shaped vortices characterizing the K-type transition are documented. In § 4, the characteristics of the transitional flow, the double-layer longitudinal vortex system and the staggered
$\wedge$
-shaped vortices characterizing the H-type transition are presented. The mechanism contributing to the formation of the staggered pattern of
$\wedge$
-shaped vortices is also discussed.
In § 5, the effects of the different types of the transitions on heat transfer properties are discussed. The contributions of the turbulence energy production by Reynolds stresses and buoyancy are quantified and compared for the K-type and H-type transitions, respectively. It is found that buoyancy rather than the Reynolds stresses is the dominant factor contributing to the controlled transitions.
2 Mathematical formulation
2.1 Mathematical formulation and numerical procedures
Under consideration is the natural convection boundary layer developing adjacent to an isothermally heated vertical plate. To study the two different types of controlled transitions in the natural convection boundary layer, full three-dimensional direct numerical simulations of the spatially and temporally developing boundary layer are performed. The computational domain adopted here is of dimensions
$L\times H\times W$
, as sketched in figure 2. Here,
$L$
is the dimension in the direction normal to the heated surface,
$H$
is the height of the isothermally heated surface and
$W$
is the spanwise width. In this study,
$L$
is chosen to be approximately 13 times the estimated thickness of the viscous boundary layer. The far-field boundary condition adopted in this study is an open type boundary condition. The adopted width scale
$L$
ensures that the far-field boundary condition is satisfied and the entrainment through the open boundary is smooth, which reduces numerical instabilities. This treatment of the far-field boundary condition is commonly adopted in previous investigations such as in Armfield & Janssen (Reference Armfield and Janssen1996), Lin et al. (Reference Lin, Armfield, Patterson and Lei2009) and Zhao et al. (Reference Zhao, Lei and Patterson2013). To minimize the effects of the end boundaries, the computational domain is extended at the top and bottom by
$H_{t}=H_{b}=0.1H$
respectively. A similar strategy has been employed by Aberra et al. (Reference Aberra, Armfield, Behnia and McBain2010). The dimension
$W$
is chosen to be three times the wavelength of the perturbations, that is, three times the wavelength of the oblique waves (see (2.9) below). In Aberra et al. (Reference Aberra, Armfield, Behnia and McBain2010) and Sayadi et al. (Reference Sayadi, Hamman and Moin2013), the dimension in the spanwise direction was chosen to be one and four times the wavelength of the oblique waves, respectively. In the present study, the width in the spanwise direction allows multiple pairs of spanwise flow structures to develop, which is therefore considered to be appropriate.
Figure 2. Schematic of the computational domain (not to scale), with the shaded strip near the leading edge of the heated surface showing the location for introducing perturbations to the boundary layer.
The convective flow under consideration is described by the three-dimensional Navier–Stokes and energy equations with the Boussinesq approximation. A non-dimensional form of these governing equations can be expressed as follows:
$$\begin{eqnarray}\displaystyle & \displaystyle u_{x}+v_{y}+w_{z}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle u_{t}+uu_{x}+vu_{y}+wu_{z}=-p_{x}+\unicode[STIX]{x1D6FB}^{2}u, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle v_{t}+uv_{x}+vv_{y}+wv_{z}=-p_{y}+\unicode[STIX]{x1D6FB}^{2}v+\unicode[STIX]{x1D703}\,Ra/Pr, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle w_{t}+uw_{x}+vw_{y}+ww_{z}=-p_{z}+\unicode[STIX]{x1D6FB}^{2}w, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D703}_{t}+u\unicode[STIX]{x1D703}_{x}+v\unicode[STIX]{x1D703}_{y}+w\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D703}/Pr, & \displaystyle\end{eqnarray}$$
where
$u,v$
and
$w$
are the velocity components in the
$x,y$
and
$z$
directions, respectively; the subscripts denote the first partial derivative with respect to a spatial direction or time;
$p,t$
and
$\unicode[STIX]{x1D703}$
are the pressure, time and temperature; and
$Ra$
and
$Pr$
are the Rayleigh and Prandtl numbers, which are the two control parameters of the boundary layer flow and are defined as:
$$\begin{eqnarray}Ra=\frac{g\unicode[STIX]{x1D6FD}\unicode[STIX]{x0394}TH^{3}}{v\unicode[STIX]{x1D705}},\quad Pr=\frac{v}{\unicode[STIX]{x1D705}}\end{eqnarray}$$
where
$g$
and
$\unicode[STIX]{x0394}T$
are the gravitational acceleration and the temperature difference between the isothermal wall and the ambient respectively;
$\unicode[STIX]{x1D6FD}$
,
$v$
and
$\unicode[STIX]{x1D705}$
are the thermal expansion coefficient, the kinematic viscosity and the thermal diffusivity of the working fluid at the reference (ambient) temperature. In the present study,
$H$
corresponds to a dimensional height of 22 centimetres and the temperature difference between the quiescent fluid and the heated wall at
$t=0$
is equivalent to
$23\,^{\circ }\text{C}$
. The corresponding Rayleigh number is
$3.5\times 10^{9}$
, which is in the unstable flow regime according to Armfield & Janssen (Reference Armfield and Janssen1996).
The dimensionless quantities in the governing equations (2.1)–(2.5) are obtained through the following normalization:
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\displaystyle u=\frac{U}{vH^{-1}},\quad \displaystyle v=\frac{V}{vH^{-1}},\quad w=\frac{W}{vH^{-1}},\\ \displaystyle x=\frac{X}{H},\quad y=\frac{Y}{H},\quad z=\frac{Z}{H},\\ \displaystyle t=\frac{\unicode[STIX]{x1D70F}}{H^{2}v^{-1}},\quad p=\frac{P}{\unicode[STIX]{x1D70C}v^{2}H^{-2}},\quad \unicode[STIX]{x1D703}=\frac{T-T_{0}}{T_{h}-T_{0}},\end{array}\right\}\end{eqnarray}$$
in which
$U$
,
$V$
,
$W$
,
$X$
,
$Y$
,
$Z$
,
$\unicode[STIX]{x1D70F}$
,
$P$
and
$T$
are the corresponding dimensional quantities.
$T_{h}$
and
$T_{0}$
are the temperature of the isothermally heated surface and the reference (ambient) temperature, respectively.
Initially, the fluid in the computational domain is stationary and isothermal at a non-dimensional temperature
$\unicode[STIX]{x1D703}=0$
. When
$t>0$
, the temperature of the heated surface at
$x=0$
is raised to
$\unicode[STIX]{x1D703}=1$
. The open boundary conditions are applied to the top and right far-field boundaries. The bottom boundary is rigid, no-slip and adiabatic. Similarly, the downward extension of the heated surface at
$x=0$
is assumed rigid, no-slip and adiabatic. Periodic boundary conditions are assumed along the spanwise direction. The mathematical expressions of these boundary conditions are:
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}u=v=w=0,\quad \unicode[STIX]{x1D703}=1+\unicode[STIX]{x1D709}\quad \text{at }x=0,\quad 0\leqslant y<0.02,\,-\unicode[STIX]{x1D70E}\leqslant z\leqslant \unicode[STIX]{x1D70E},\\ u=v=w=0,\quad \unicode[STIX]{x1D703}=1\quad \text{at }x=0,\quad 0.02\leqslant y\leqslant 1.1,\,-\unicode[STIX]{x1D70E}\leqslant z\leqslant \unicode[STIX]{x1D70E},\\ u=v=w=0,\quad \unicode[STIX]{x1D703}_{x}=0\quad \text{at }x=0,\quad -0.1\leqslant y<0,\,-\unicode[STIX]{x1D70E}\leqslant z\leqslant \unicode[STIX]{x1D70E},\\ u=v=w=0,\quad \unicode[STIX]{x1D703}_{y}=0\quad \text{at }y=-0.1,\quad 0<x\leqslant 0.14,\,-\unicode[STIX]{x1D70E}\leqslant z\leqslant \unicode[STIX]{x1D70E},\\ u_{y}=v_{y}=w_{y}=0,\quad \unicode[STIX]{x1D703}_{y}=0\quad \text{at }y=1.1,\quad 0<x\leqslant 0.14,\,-\unicode[STIX]{x1D70E}\leqslant z\leqslant \unicode[STIX]{x1D70E},\\ u_{x}=v_{x}=w_{x}=0,\quad \unicode[STIX]{x1D703}_{x}=0\quad \text{at }x=0.14,\quad -0.1<y<1.1,\,-\unicode[STIX]{x1D70E}\leqslant z\leqslant \unicode[STIX]{x1D70E},\\ \unicode[STIX]{x1D6E4}(x,y,-\unicode[STIX]{x1D70E},t)=\unicode[STIX]{x1D6E4}(x,y,\unicode[STIX]{x1D70E},t),\end{array}\right\}\end{eqnarray}$$
where
$\unicode[STIX]{x1D709}$
is a temperature perturbation (refer to (2.9) below) introduced over a small region near the leading edge (refer to figure 1), and
$\unicode[STIX]{x1D70E}=W/2H$
represents half the spanwise width of the computational domain.
$\unicode[STIX]{x1D6E4}(x,y,\pm \unicode[STIX]{x1D70E})$
represents an arbitrary flow quantity and its derivatives on the xy-planes at
$z=\pm \unicode[STIX]{x1D70E}$
. The prescription of
$\unicode[STIX]{x1D6E4}(x,y,-\unicode[STIX]{x1D70E},t)=\unicode[STIX]{x1D6E4}(x,y,\unicode[STIX]{x1D70E},t)$
establishes periodic boundary conditions in the spanwise direction.
In the present study the discretized governing equations are solved using a finite-volume method with the SIMPLE scheme (see Patankar Reference Patankar1980) for pressure–velocity coupling. The spatial derivatives are discretized using the second-order central-differencing scheme, except for the advection terms, which are approximated by the QUICK scheme (see Leonard Reference Leonard1979). The unsteady terms are integrated by a second-order backward difference scheme.
A grid-dependence test for
$Ra=3.5\times 10^{9}$
is conducted on two sets of non-uniform grids, i.e.
$65\times 441\times 261$
and
$55\times 375\times 221$
. The tested grid systems are both constructed with concentrated grids in the proximity of the vertical wall boundary. The size of the first grid layer adjacent to the vertical wall is
$\unicode[STIX]{x0394}x_{wa}=10^{-3}$
and the grid has a 0.3 %–2.5 % linear stretching in the horizontal (
$x$
) direction. The grid is uniform in the vertical (
$y$
) direction and the spanwise (
$z$
) direction for both grid systems considered in the present study. The results of the grid-dependence test show that the characteristic frequency of the flow obtained using the grid
$65\times 441\times 261$
is approximately 6 % smaller than that obtained in the two-dimensional direct stability analysis reported by Zhao et al. (Reference Zhao, Lei and Patterson2013), whereas the characteristic frequency obtained with the grid
$55\times 375\times 221$
has approximately 13 % variation. Given the relatively small variation of the numerical results and the constraints in computing resources, the grid system
$65\times 441\times 261$
is adopted in the present study. A fixed time step
$\unicode[STIX]{x0394}t=2\times 10^{-7}$
, which is equivalent to the time step used in Zhao et al. (Reference Zhao, Lei and Patterson2013), is adopted, giving a maximum Courant–Friedrichs–Lewy (CFL) number of 0.4 for the simulations in the present study.
2.2 Perturbations for exciting transitions
For the study of the controlled transitions, the following temperature perturbation is introduced at the leading edge (refer to figure 2) to excite both the K-type and H- type transitions:
$$\begin{eqnarray}\unicode[STIX]{x1D709}=A_{t}\sin (2\unicode[STIX]{x03C0}f_{t}t)+A_{o}\sin (2\unicode[STIX]{x03C0}f_{o}t)\cos (2\unicode[STIX]{x03C0}z/\unicode[STIX]{x1D706}_{o}),\end{eqnarray}$$
where
$A_{t}$
and
$A_{o}$
are the perturbation amplitudes of the fundamental two-dimensional TS and the oblique waves, respectively;
$f_{t}$
and
$f_{o}$
are the corresponding frequencies of the two waves;
$\unicode[STIX]{x1D706}_{o}$
is the wavelength of the prescribed oblique waves. It is worth clarifying that within the thermal boundary layer, the flow is driven by buoyancy which is determined by the thermal field. Therefore, a perturbation to the temperature field will induce a perturbation to the velocity field indirectly. The instability properties of the thermal boundary layer would not change if the perturbation is directly applied to the velocity field or to both the thermal and velocity fields. So long as the perturbations are amplified by the boundary layer, the transition would still occur. It is also worth noting that applying disturbances at the leading edge is a common practice, such as in Armfield & Janssen (Reference Armfield and Janssen1996), Aberra et al. (Reference Aberra, Armfield, Behnia and McBain2010) and Zhao et al. (Reference Zhao, Lei and Patterson2013). It is also possible to trigger transitions by perturbing the boundary layer at locations away from the leading edge. In that case, different perturbation amplitudes may be required. The choice of optimal location and amplitudes for the perturbations is beyond the scope of this investigation.
In both cases, the spanwise computational domain is three times the wavelength of the prescribed oblique waves. The dimensionless values of
$A_{t}$
and
$A_{o}$
are set to
$A_{t}=0.65$
and
$A_{o}=0.22$
, respectively, which are found to be appropriate for exciting the K-type and H-type transitions. It is worth noting that the values of
$A_{t}$
and
$A_{o}$
are chosen for obtaining early transitional boundary layer structures within the finite computational domain. The relative value of
$A_{t}$
is chosen to be much greater than that of
$A_{o}$
because the TS waves are believed to be more dominant than the oblique waves in the K-type and H-type transitions. This treatment of the perturbation amplitudes is similar to the treatment in Sayadi et al. (Reference Sayadi, Hamman and Moin2013). Further, the ratio of
$A_{t}/A_{o}$
is similar to the experimental condition in Jaluria & Gebhart (Reference Jaluria and Gebhart1973). It is also worth clarifying that, since in the present study the perturbations are introduced through the temperature boundary condition, much larger perturbation amplitudes are required compared to those required for directly perturbing velocities or introducing perturbation source terms within the boundary layer.
$\unicode[STIX]{x1D706}_{o}$
is the wavelength of the prescribed oblique waves, which is chosen to be
$\unicode[STIX]{x1D706}_{o}=0.273$
based on the dominant spanwise wavelengths obtained in a naturally transitioning thermal boundary layer of the same Rayleigh number (see below for further detail).
In a separate study of a naturally transitioning thermal boundary layer (Zhao et al.
Reference Zhao, Lei and Patterson2016), it is found that two dominant wavelengths are present in the thermal boundary layer. The wavelength
$\unicode[STIX]{x1D706}_{o}=0.273$
is approximately the average of the two dominant wavelengths. It is worth clarifying that the controlled transition is expected to occur over a range of spanwise wavelengths, rather than at a particular wavelength. For Blasius boundary layers, it has been found that there exists an ‘optimal’ spanwise wavelength of disturbances for stabilizing the TS waves (Bagheri & Hanifi Reference Bagheri and Hanifi2007) and the controlled transition occurs over a range of spanwise wavelengths of disturbances. The effect of the wavelength
$\unicode[STIX]{x1D706}_{o}$
of the disturbances on the controlled transitions in natural convection boundary layers is beyond the scope of the present study. The determination of the dominant spanwise wavelengths of the naturally transitioning thermal boundary layer has been reported separately in Zhao et al. (Reference Zhao, Lei and Patterson2016).
To excite the K-type transition, the prescribed TS waves and the oblique waves are set to the same frequency, that is
$f_{t}=f_{o}$
. To excite the H-type transition, the frequency of the oblique waves is set to be half the frequency of the TS waves, that is
$f_{o}=0.5f_{t}$
. In the present study, the frequency of the fundamental two-dimensional TS waves is chosen to be
$f_{t}=31\,750$
, which is the same as that determined in Zhao et al. (Reference Zhao, Lei and Patterson2013), after rescaling.
The major parameters of the computational domain and the introduced perturbations adopted for the studies of the K-type and H-type transitions are summarized in table 1.
Figure 3. Perturbations for (a) K-type transition and (b) H-type transition. (i) Instantaneous spanwise profiles of temperature perturbation
$\unicode[STIX]{x1D709}$
; (ii) time series of the perturbation applied at
$z=0$
; and (iii) spanwise profile of the RMS of the temperature perturbation
$\unicode[STIX]{x1D709}$
.
Table 1. Characteristics of the K-type and H-type simulations.
$Pr=7$
for both cases.
Figure 3(a,b) illustrates the important characteristics of the temperature perturbation
$\unicode[STIX]{x1D709}$
applied for triggering the K-type and the H-type transitions, respectively. The spanwise profiles of the temperature perturbation at two representative time instants of the K-type and H-type transitions are shown in figures 3(ai) and 3(bi). It is seen that the spanwise extent of the computational domain (from
$z=-0.41$
to
$z=0.41$
) covers three full wavelengths of the perturbation.
Figures 3(aii) and 3(bii) show the time series of the perturbation applied at
$(x,y,z)=(0,0.01,0)$
in the K-type and H-type transitions, respectively. It is clear that the perturbation superimposed from the Tollmien–Schlichting and oblique waves has only one frequency (
$f_{t}=f_{o}$
) in the K-type transition case, whereas the perturbation signal has two frequency components in the H-type transition case. The dominant period of the perturbation is
$1/f_{o}=2/f_{t}$
, which is twice the dominant period of the perturbation applied for exciting the K-type transition.
Figures 3(aiii) and 3(biii) present the spanwise profile of the root mean square (RMS) of the temperature perturbation. For the K-type transition case, the alternate appearance of maximum and minimum RMS of the temperature perturbation is at a spatial interval equivalent to half the wavelength of the oblique waves. The TS and oblique waves for exciting the K-type transition are of the same frequency, and thus the spanwise profile of
$\unicode[STIX]{x1D709}_{RMS}$
has the same wavelength as that of the instantaneous
$\unicode[STIX]{x1D709}$
. The positions where the maximum RMS of the perturbations appears are denoted as ‘peak’ and the positions where the minimum RMS of the perturbation appears are denoted as ‘valley’ (refer to figure 3
aiii). For the H-type transition case, it is interesting to see that the spanwise profile of
$\unicode[STIX]{x1D709}_{RMS}$
covers double the number of wavelengths compared to the profile of the instantaneous
$\unicode[STIX]{x1D709}$
. This wavenumber doubling is due to temporal modulation caused by the two different frequencies of the TS and oblique waves. In the H-type transition, the frequency of the oblique waves (
$f_{o}$
) is set to be half the frequency of the Tollmien–Schlichting waves (
$f_{t}$
), that is
$f_{o}=0.5f_{t}$
. It is also worth noting that due to the temporal modulation there are two different sets of peaks in the spanwise profile of
$\unicode[STIX]{x1D709}_{RMS}$
, which are labelled as ‘peak1’ and ‘peak2’, respectively, though the difference of these two peaks is not discernable in this plot. The perturbations measured at positions corresponding to the ‘peak1’, ‘peak2’ and ‘valley’ in the spanwise direction but at various streamwise positions will be analysed below.
In what follows the K- and H-type transitions in the natural convection boundary layer are described from the growth and evolution of perturbations to the formation of the
$\wedge$
-shaped vortices. The K-type transition observed in this study is qualitatively compared with the experimental work by Klebanoff et al. (Reference Klebanoff, Tidstrom and Sargent1962), Jaluria & Gebhart (Reference Jaluria and Gebhart1973) and Berlin et al. (Reference Berlin, Wiegel and Henningson1999). It will be shown that the successively aligned
$\wedge$
-shaped structures characterizing the K-type transition in Blasius boundary layers are also present in the transitioning natural convection boundary layer. The double longitudinal vortex system inferred in Jaluria & Gebhart (Reference Jaluria and Gebhart1973) is also observed in the K-type transitioning boundary layer. For the H-type transition, a staggered pattern of
$\wedge$
-shaped structures, rather than the successively aligned pattern, is observed in the natural convection boundary layer. This observation confirms, for the first time, that the H-type transition reported in Blasius boundary layers may also occur in pure natural convection boundary layers.
3 K-type transition
This section presents characteristics of the K-type transition, which are obtained in the quasi-steady state of the boundary layer flow. Hovmöller plots (see Hovmöller Reference Hovmöller1949) of velocity perturbation amplitude in the (
$z,t$
) plane are shown in figure 4 to demonstrate the temporal evolution and the establishment of a quasi-steady state of the boundary layer flow. It is worth clarifying that the streamwise velocity perturbation shown in figure 4(a) and the spanwise velocity perturbation shown in figure 4(b) are obtained near the wall at
$x=6.5\times 10^{-3}$
and at the vertical middle point
$y=0.5$
along the spanwise direction over three oblique wave cycles of the flow at a later development stage. These results confirm that the quasi-steady state of the boundary layer flow at
$y=0.5$
is established. For other streamwise positions of the boundary layer, quasi-steady flow characteristics are also observed at this stage, which are of interest to the present study.
Figure 4. (a) Streamwise and (b) spanwise velocity perturbation measured at
$x=6.5\times 10^{-3}$
and
$y=0.5$
along the spanwise direction over three oblique wave cycles at the quasi-steady state of the flow.
Figure 5 shows the spanwise profiles of the root mean square of the streamwise velocity component and temperature obtained at
$x=6.5\times 10^{-3}$
and at various streamwise positions. The distributions of
$v_{RMS}$
shown for positions from
$y=0.03$
to
$y=0.32$
(figure 5
a) clearly illustrate the following three characteristics of the spatial evolution of the velocity perturbations in the boundary layer. Firstly, as the perturbations are convected downstream,
$v_{RMS}$
is amplified because the frequency of the perturbations is within the amplification frequency band (AFB) of the present Ra (refer to Zhao et al.
Reference Zhao, Lei and Patterson2013). Secondly, up to
$y=0.27$
, the peaks and valleys of the spanwise profile of
$v_{RMS}$
exactly correspond to the positions where the maximum and minimum RMS of the perturbations appear. The spanwise positions corresponding to the maximum and minimum RMS perturbations are denoted as ‘peak’ and ‘valley’ in figure 5 to facilitate interpretation. This spanwise alignment and streamwise amplification of the peaks and valleys are found to be qualitatively similar to that observed in Blasius boundary layers (see for example Klebanoff et al.
Reference Klebanoff, Tidstrom and Sargent1962) Thirdly, when the sinusoidal wave is amplified to a certain extent, a bifurcation occurs near the peaks of the sinusoidal wave. Further downstream from
$y=0.41$
(see figure 5
b), the peaks and valleys of the distorted sinusoidal wave do not align with the positions of the maximum and minimum RMS perturbations, which indicates that the flow has proceeded to a nonlinear regime. In the very downstream position
$y=0.95$
, more bifurcations appear with more smaller structures developed, but the waveform in general still remains symmetric in the spanwise direction, which suggests that the flow is still in an early transitional stage to turbulence. For the streamwise development of the
$\unicode[STIX]{x1D703}_{RMS}$
shown in figure 5(c,d), it is seen that the sinusoidal wave amplifies in the upstream boundary layer and also proceeds to a nonlinear regime, though further downstream than for
$v_{RMS}$
.
Figure 5. Spanwise profile of the RMS of the streamwise velocity component
$v$
and temperature
$\unicode[STIX]{x1D703}$
at different streamwise positions in the thermal boundary layer obtained for
$Ra=3.5\times 10^{9}$
and
$Pr=7$
. Thick and short vertical bars denote the positions of the maximum RMS perturbation (labelled as ‘peak’). Thin and short vertical bars denote the positions of the minimum RMS perturbation (labelled as ‘valley’). (a) and (c)
$y=0.03$
, 0.14, 0.23, 0.27 and 0.32. (b) and (d)
$y=0.41$
, 0.68 and 0.95.
The streamwise growth of
$v_{RMS}$
and
$\unicode[STIX]{x1D703}_{RMS}$
obtained at two spanwise positions corresponding to locations with the maximum and minimum RMS perturbations, respectively, is shown in figures 6(a) and 6(b). It is seen that the
$v_{RMS}$
measured at the ‘peak’ initially undergoes a smooth growth up to the peak value at
$y=0.31$
, and then it fluctuates irregularly. The peak value indicates the onset of a bifurcation in the boundary layer, which is therefore recognized as the bifurcation point. The bifurcation here may be related to a bifurcation of the turbulence energy production, which will be discussed in § 5.2. The
$v_{RMS}$
measured at the ‘valley’ undergoes a similar development, but the irregular oscillation occurs further downstream, at approximately
$y=0.44$
. It is also worth noting that the
$v_{RMS}$
measured at the ‘valley’ overtakes that measured at the ‘peak’ immediately before the onset of the irregular oscillation. Once the overtaking occurs, strong nonlinearity develops, which can be seen from the significant and irregular oscillations of the
$v_{RMS}$
. It is interesting to note that the evolution of the
$v_{RMS}$
discussed above is similar to that observed in the Blasius boundary layer reported in Klebanoff et al. (Reference Klebanoff, Tidstrom and Sargent1962). The streamwise growth of
$\unicode[STIX]{x1D703}_{RMS}$
shown in figure 6(b) is similar to that of
$v_{RMS}$
, comprising a smooth growth stage and a later fluctuation stage. However, it is worth noting that the streamwise transition positions of the
$\unicode[STIX]{x1D703}_{RMS}$
for both the ‘peak’ and ‘valley’ locations are clearly further downstream than those of the
$v_{RMS}$
, suggesting that the velocity transition occurs prior to the thermal transition. This character is consistent with that revealed in Jaluria & Gebhart (Reference Jaluria and Gebhart1974) on the natural convection boundary layer with a uniform flux boundary condition.
Figure 6. Streamwise profile of the RMS of the streamwise velocity component
$v$
(a) and temperature
$\unicode[STIX]{x1D703}$
(b) obtained at a peak and a valley position, respectively. Results for
$Ra=3.5\times 10^{9}$
,
$Pr=7$
,
$\unicode[STIX]{x1D706}_{o}=0.273$
and
$f_{t}=f_{o}$
(case 1).
Figure 7 illustrates the procedure for the determination of the thicknesses of three layers at
$y=0.27$
. Briefly, the thickness of the viscosity layer (
$\unicode[STIX]{x1D6FF}_{vis}$
) is determined by the maximum streamwise velocity position. The thickness of the thermal boundary layer (
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
) is defined by the position where the temperature difference from the ambient temperature drops to 1 % of the difference between the wall temperature and ambient temperatures. The thickness of the velocity layer (
$\unicode[STIX]{x1D6FF}_{v}$
) is determined by the position where the streamwise velocity drops to 1 % of the maximum streamwise velocity. This is consistent with the method used in Lin et al. (Reference Lin, Armfield, Patterson and Lei2009).
Figure 7. Horizontal profiles (along the
$x$
-direction) of (a) temperature and (b) vertical velocity at dimensionless height
$y=0.27$
and the spanwise location
$z=0$
at the steady state for
$Ra=3.5\times 10^{9}$
and
$Pr=7$
, demonstrating regions of viscosity layer (
$\unicode[STIX]{x1D6FF}_{vis}$
), thermal boundary layer (
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
) and velocity layer (
$\unicode[STIX]{x1D6FF}_{v}$
).
To examine the existence of the double longitudinal vortex system inferred by Jaluria & Gebhart (Reference Jaluria and Gebhart1973), figure 8 shows the contours of the mean (time-averaged) spanwise velocity on xz-planes at various streamwise positions. It is worth noting that, since the contours of the mean spanwise velocity are symmetric about the mid-span (
$z=0$
), figure 8 shows only half of the computational domain in the spanwise direction, that is from
$z=0$
to
$z=0.410$
. In figure 8, the mean spanwise velocity is evaluated in the fully developed three-dimensional stage, over a time duration equivalent to 15 cycles (i.e.
$1/f_{c}$
) of the fundamental TS waves of the boundary layer. This time duration is sufficient for obtaining time-averaged information of the spanwise velocity, and further increase of the time duration does not change the results presented here. To illustrate the size and relative positions of the roll structures in the boundary layer, the boundaries for the viscosity layer (red dotted line), thermal boundary layer (white dotted line) and velocity boundary layer (blue dotted line) are marked in each plot. For clarity, each dotted line is only marked over the range from
$z=0$
to
$z=0.137$
on each plot. It is worth noting that the thicknesses of these three layers change with the streamwise position, and thus they are determined individually using the same procedure at each streamwise location.
Figure 8. Contours of the mean (time-averaged) spanwise velocity on xz-planes at various streamwise positions. The contours are symmetric about the mid-span (
$z=0$
). Results for
$Ra=3.5\times 10^{9}$
,
$Pr=7$
,
$\unicode[STIX]{x1D706}=0.273$
and
$f_{t}=f_{o}$
(K-type transition). The three dotted lines from the heated surface
$(x=0)$
to the far-field region represent the boundaries for the viscosity layer (red dotted line), thermal boundary layer (white dotted line) and velocity boundary layer (blue dotted line) respectively.
It is seen in figure 8 that initially in the upstream location
$y=0.27$
a three-layer longitudinal (streamwise direction) vortex system appears. The inner layer of the longitudinal rolls immediately adjacent to the heated wall spans the viscosity layer, but is within the thermal boundary layer. This layer is referred to as the first layer of the three-layer longitudinal vortex system in the present study. The middle layer of the longitudinal rolls appears between the boundaries of the thermal boundary layer and the velocity layer, which is referred to as the second layer of the three-layer longitudinal vortex system. Finally, the outer layer of the longitudinal rolls extending beyond the velocity layer is referred to as the third layer. The formation of each group of the three-layer counter-rotating vortex system corresponds well to the applied perturbations.
It is interesting to note that the first and second layers of the longitudinal rolls are approximately ellipse-shaped with distinctly small conjugate diameters, whereas the shapes of the third layer of the longitudinal rolls are closer to ovals of a much larger scale. The shapes of the third layer of the longitudinal rolls in figure 8(a) indicate that the boundary of the velocity layer affects the formation of the third layer of rolls since they start to spread beyond the velocity layer. The portion of the third layer of rolls within the velocity layer is approximately half-ellipse-shaped, whereas the remaining portion of the third layer of rolls outside the velocity layer expands quickly from upstream to downstream. This qualitative characteristic of the three-layer longitudinal vortex system is similar to that reported in Aberra et al. (Reference Aberra, Armfield, Behnia and McBain2010), in which the natural convection boundary layer was induced by an isoflux boundary condition. It is worth clarifying that Jaluria & Gebhart (Reference Jaluria and Gebhart1973) inferred the presence of a double longitudinal vortex system in the boundary layer based on discrete hot-wire measurements, whereas a three-layer longitudinal roll structure is observed in the present study. The factor causing this discrepancy may be that the weak secondary flow of the third layer was very difficult to detect experimentally with the unavoidable environmental noises.
As the perturbations evolve along the boundary layer in the streamwise direction, the above-described three-layer longitudinal vortex system grows in size and amplitude (see figure 8
b,c). Up to
$y=0.41$
, the first layer of the longitudinal rolls is always confined within the thermal boundary layer, and the first and second layers of the longitudinal rolls retain elliptical shapes with distinctly small conjugate diameters. In further downstream positions, it is seen in figure 8(d–g) that the three layers of the longitudinal rolls start to deform and interact with each other. Finally, the three layers of the rolls merge and the distinction between the different layers of the longitudinal vortex system disappears (refer to figure 8
h).
In order to visualize the distinct features of the K-type transition, the instantaneous contours of velocities, vorticity and temperature are shown in figure 9. Figure 9(a,b) presents the streamwise and spanwise velocities on the yz-plane at
$x=6.8\times 10^{-3}$
. It is clear that the typical aligned
$\wedge$
-shaped structures characterizing the K-type transition occur in the downstream boundary layer. The tips of the
$\wedge$
-shaped structures appear at positions (
$z=-0.273$
, 0 and 0.273) where the spanwise profile of
$\unicode[STIX]{x1D709}_{RMS}$
peaks (see figure 3
b), as labelled by ‘peak’ beneath the horizontal axis. This is another distinct feature charactering the K-type transition. A qualitatively similar feature of the K-type transition in the Blasius boundary layer can be found in Berlin et al. (Reference Berlin, Wiegel and Henningson1999), where PIV measurements show aligned
$\wedge$
-shaped structures. The aligned
$\wedge$
-shaped structures are also seen in the contours of the
$x$
-vorticity and temperature, which are shown in figure 9(c,d). It is worth clarifying that the aligned
$\wedge$
-shaped structures are not stationary. Figure 9(ei–vi) presents the temperature contours obtained on the same yz-plane at six consecutive time instants with a time interval of
$1/(5f_{t})$
. It is seen that the
$\wedge$
-shaped structures are convected downstream as they are evolving. The
$\wedge$
-shaped structures in figure 9(evi) are the identical to those shown in figure 9(ei), confirming that the boundary layer is in the quasi-steady state. It is worth clarifying that, in Aberra et al. (Reference Aberra, Armfield, Behnia and McBain2010)), the reversed structures, that is, the
$\wedge$
-shaped structures, appear in the upstream boundary layer, and the
$\wedge$
-shaped structures appear in the relatively downstream boundary layer. The thermal condition of the boundary layer considered in that study is isoflux, which is different from the isothermal condition adopted in the present study. This variation of the thermal boundary conditions may have resulted in the different vorticity structures in the boundary layer. It is also interesting to note that the
$\wedge$
-shaped structures contain fluid of relatively higher temperature, which is a feature distinguishing this structure from the K-type transition of Blasius boundary layers. Analyses of turbulence production by Reynolds stresses and buoyancy that contribute to the transition will be given in § 5.2.
Figure 9. Snapshots of instantaneous contours of the (a) streamwise velocity, (b) spanwise velocity, (c)
$x$
-vorticity and (d) temperature profile on the yz-plane at
$x=6.8\times 10^{-3}$
and at the time instant
$t=1.9\times 10^{-3}$
. (e) The temperature profile on the same yz-plane at six time instants within a perturbation period
$1/f_{t}$
. Time interval between two consecutive time instants is
$1/(5f_{t})$
. Successively aligned
$\wedge$
-shaped structures indicate a K-type transition. Results for
$Ra=3.5\times 10^{9}$
,
$Pr=7$
,
$\unicode[STIX]{x1D706}_{o}=0.273$
and
$f_{t}=f_{o}$
(case 1).
To further understand the transitional structure of the natural convection boundary layer, the contours of the mean flow and the mean secondary flow of the streamwise velocity component on the yz-plane at
$x=6.8\times 10^{-3}$
are plotted in figure 10(
$a,c$
). The mean secondary flow is obtained by subtracting the base flow (shown in figure 10
b) from the mean flow (figure 10
a). The base flow is separately obtained in the steady state of an unperturbed three-dimensional boundary layer with the same parameter settings. The mean flow is obtained by averaging instantaneous streamwise velocities over a time duration of 15 cycles (i.e.
$1/f_{t}$
) of the fundamental TS waves of the boundary layer. It is seen in figure 10(a) that the
$\wedge$
-shaped structures observed in the instantaneous temperature and flow structures shown in figure 9 are not present in the mean flow. This is because the
$\wedge$
-shaped structures are not stationary and are in fact convected downstream while they are forming in the boundary layer. Figure 10(c) implies that the boundary layer flow is locally enhanced or depressed in the downstream region associated with the formation of the
$\wedge$
-shaped structures. In the relatively upstream region, the secondary flow is very weak, except for the depression in the region near the leading edge which is due to the direct perturbations. To directly compare the strength of the mean flow and base flow, the spatially weighted average (in the spanwise direction) streamwise velocities are plotted in figure 10(d). It is seen in this figure that the strength of the mean flow is approximately the same as that of the base flow, suggesting that the amplitude of the artificial perturbations is appropriate and the base flow is not altered significantly due to the introduction of the perturbations.
Figure 10. (a) Mean flow, (b) base flow and (c) mean secondary flow of the streamwise velocity components on the yz-plane at
$x=6.8\times 10^{-3}$
. (d) Spanwise-averaged streamwise velocity components of the mean flow (red solid line) and base flow (black dash-dot line). Results for the K-type transition (Case 1).
Figure 11 shows an instantaneous snapshot of vortical structures inside the boundary layer for the K-type transition. The isosurface of the second invariant of the velocity gradient tensor, which is referred to as the Q-criterion (Jeong & Hussain Reference Jeong and Hussain1995), is chosen for visualization and the isosurfaces are coloured by the streamwise velocity. It is clear that the vortical structures develop in the streamwise direction from the TS wave-like structures upstream to much more complex
$\wedge$
-shaped structures downstream. Different from the spindly
$\wedge$
-shaped structures observed in a Blasius boundary layer by Sayadi et al. (Reference Sayadi, Hamman and Moin2013), the
$\wedge$
-shaped structures observed in this natural convection boundary layer are short and thick. Another distinction between the different types of boundary layers is that there exist unknown flow structures between neighbouring
$\wedge$
-shaped structures in the natural convection boundary layer, whereas in the Blasius boundary layer only clear
$\wedge$
-shaped structures are present (Sayadi et al.
Reference Sayadi, Hamman and Moin2013). This distinction may be associated with the buoyancy effect in the natural convection boundary layers.
Figure 11. Instantaneous isosurfaces of the second invariant of the velocity gradient tensor,
$\unicode[STIX]{x1D64C}$
, coloured by the streamwise velocity, showing
$\wedge$
-shaped vortical structures.
4 H-type transition
This section presents characteristics of the H-type transition, which are obtained in the quasi-steady state of the boundary layer flow. Similar to what has been done for the K-type transition, Hovmöller plots of velocity perturbation amplitude in the (
$z,t$
) plane are used to demonstrate the temporal evolution and the establishment of the quasi-steady state of the boundary layer flow, as shown in figure 12. The temporal propagation of velocity perturbation is obtained at
$x=6.5\times 10^{-3}$
and
$y=0.5$
along the spanwise direction over three oblique wave cycles at the quasi-steady state of the flow. It is seen in figure 12(a) that a temporally staggered quasi-steady flow pattern has developed, which is in fact due to the two frequency components of the temperature perturbation and their relationship, that is,
$1/f_{o}=2/f_{t}$
. Similar quasi-steady flow patterns have also been developed at other downstream positions of the boundary layer, but Hovmöller plots are not shown here for brevity.
Figure 13 shows the spanwise profile of
$v_{RMS}$
and
$\unicode[STIX]{x1D703}_{RMS}$
obtained at
$x=6.5\times 10^{-3}$
and at various streamwise positions. The distribution of
$v_{RMS}$
and its spatial evolution in the streamwise direction show two major characteristics of the flow during transition. Firstly, the difference of
$v_{RMS}$
between the locations ‘peak1’ and ‘peak2’ becomes discernable at
$y=0.14$
and more distinct in the downstream position
$y=0.27$
. The difference between the perturbation signals at ‘peak1’ and ‘peak2’ is believed to be responsible for the formation of the staggered
$\wedge$
-shaped structures, which will be elaborated on later. Secondly, the quasi-sinusoidal profile of
$v_{RMS}$
experiences a weak bifurcation approximately at
$y=0.23$
, which is earlier than that in the K-type transition scenario. The advancement of the bifurcation may be attributed to the doubled perturbation peaks in the spanwise direction (refer to figure 3(a iii,b iii) because more large-amplitude perturbations are introduced into the boundary layer. At further downstream positions (e.g.
$y=0.68$
and
$y=0.95$
), further bifurcation occurs, indicating that smaller structures have formed in the boundary layer undergoing the transition. For the streamwise development of the
$\unicode[STIX]{x1D703}_{RMS}$
shown in figure 13(c,d), it is seen that the sinusoidal wave amplifies in the upstream boundary layer and breaks down in the downstream boundary layer. The breakdown of the sinusoidal wave of the
$\unicode[STIX]{x1D703}_{RMS}$
occurs later than that of the
$v_{RMS}$
.
Figure 12. (a) Streamwise and (b) spanwise velocity perturbation measured at
$x=6.5\times 10^{-3}$
and
$y=0.5$
along the spanwise direction over three oblique wave cycles at the quasi-steady state of the flow.
Figure 13. Spanwise profile of the RMS of velocity component
$v$
and temperature
$\unicode[STIX]{x1D703}$
at various streamwise positions in the thermal boundary layer obtained for
$Ra=3.5\times 10^{9}$
and
$Pr=7$
. (a) and (c)
$y=0.03$
, 0.14, 0.23, 0.27 and 0.32. (b) and (d)
$y=0.41$
, 0.68 and 0.95.
Figure 14. Streamwise profile of the RMS of the streamwise velocity component
$v$
(a) and temperature
$\unicode[STIX]{x1D703}$
(b) obtained at three typical positions. Results for
$Ra=3.5\times 10^{9}$
,
$Pr=7$
,
$\unicode[STIX]{x1D706}=0.273$
and
$f_{t}=2f_{o}$
(case 2).
The streamwise growth of
$v_{RMS}$
measured at three typical positions (‘peak1’, ‘peak2’ and ‘valley’) is shown in figure 14(a). It is clear in this figure that the streamwise profiles of
$v_{RMS}$
measured at ‘peak1’ and ‘peak2’ approximately resemble each other, which is because the temperature perturbations
$\unicode[STIX]{x1D709}$
at ‘peak1’ and ‘peak2’ are the same in terms of the RMS of their respective time series (refer to figure 3
biii). It is also seen that the
$v_{RMS}$
measured at the valley overtakes those measured at ‘peak1’ and ‘peak2’ at an earlier location (approximately
$y=0.2$
) compared to that in the K-type scenario (around
$y=0.4$
). This is due to the presence of the doubled perturbation peaks in the spanwise direction, which results in a larger perturbation amplitude at neighbouring valleys compared to that in the K-type transition. The smooth growth of
$v_{RMS}$
at the three typical representative positions transfers into irregular oscillations after they retain their respective peaks. Similar to the profile of the
$v_{RMS}$
obtained in the K-type transition, there is also a bifurcation point on the profile of the
$v_{RMS}$
at ‘peak1’ in the H-type transition, which is approximately at
$y=0.37$
. Beyond this position the boundary layer enters into a distinct nonlinear state. The streamwise position of the bifurcation point marked in figure 14 may be also related to the streamwise variation of the turbulence energy production, which will be discussed in § 5.2. The streamwise growth of
$\unicode[STIX]{x1D703}_{RMS}$
for the ‘peak1’, ‘peak2’ and ‘valley’ locations is shown in figure 14(b), which is found to be very similar to that of
$v_{RMS}$
, comprising a smooth growth stage followed by a later fluctuation stage. However, it is worth noting that the streamwise transition positions of the
$\unicode[STIX]{x1D703}_{RMS}$
at the ‘peak1’, ‘peak2’ and ‘valley’ locations are later than those of the
$v_{RMS}$
, again suggesting that the velocity transition occurs prior to the thermal transition.
To observe the longitudinal vortex system in the H-type transition, contours of the mean (time-averaged) spanwise velocity component on xz-planes at various streamwise positions are shown in figure 15. Due to the symmetry of the flow field about the plane at the mid-span (
$z=0$
), figure 15 shows only half of the computational domain in the spanwise direction. The mean spanwise velocity is evaluated in the fully developed three-dimensional stage: over a time duration of 30 cycles (i.e.
$1/f_{c}$
) of the fundamental TS waves of the boundary layer. This time duration is sufficient for obtaining statistically consistent information about the mean secondary flows. Similar to figure 8, the boundaries of the viscous boundary layer, the thermal boundary layer and the velocity layer are marked from the near-wall region to the far-field region, respectively. For clarity, each dotted line is only marked over the range from
$z=0$
to
$z=0.137$
on each plot.
Figure 15. Contours of the mean (time-averaged) spanwise velocity on xz-plane at various streamwise positions. The contours are symmetry about the axis (
$z=0$
). Results for
$Ra=3.5\times 10^{9}$
,
$Pr=7$
,
$\unicode[STIX]{x1D706}=0.273$
and
$f_{t}=2f_{o}$
(H-type transition). The three dotted lines from the near-wall
$(x=0)$
region to the far-field region represent boundaries for the viscosity layer (red dotted line), thermal boundary layer (white dotted line) and velocity boundary layer (blue dotted line) respectively.
It is seen in figure 15 that, at the upstream positions, a two-layer longitudinal vortex system appears (refer to figure 15
a–d). The inner layer of the longitudinal rolls immediately adjacent to the heated wall spans the viscous layer, but stays within the thermal boundary layer, which is similar to the first layer of the three-layer longitudinal vortex system observed in the K-type transition (refer to figure 8). This inner layer of longitudinal rolls is referred to as the first layer of the two-layer longitudinal vortex system in the present study. The outer layer of the longitudinal rolls of the two-layer longitudinal vortex system is referred to as the second layer. As the perturbations evolve along the boundary layer in the streamwise direction, the first layer of the longitudinal rolls appears to be compressed towards the heated wall (see figure 15
e–g). At the further downstream location of
$y=0.64$
, the first layer of the longitudinal rolls almost disappears and the second layer of the rolls expands to encompass the region originally occupied by the first layer of the rolls in the upstream positions (see figure 15
h).
It is interesting to note that, in the upstream boundary layer, both the second layer of the longitudinal rolls of the two-layer vortex system in the H-type transition and the second layer of the longitudinal rolls of the three-layer vortex system in the K-type transition are fully contained in the velocity layer. Furthermore, the interface between the first and second layers of the longitudinal rolls is approximately located near the edge of the thermal boundary layer under both the K-type and H-type transitions (refer to figures 8 a–d and 15 a–d).
It is also worth clarifying that the longitudinal vortex system observed in the H-type transition is fundamentally different from that observed in the K-type transition in two aspects. Firstly, for half of the spanwise computational domain, the roll structures in the upstream position span three wavelengths under the H-type transition, whereas those under the K-type transition span one and a half wavelengths (refer to figure 8). It is understood that the temporal modulation of the TS and oblique waves causes the halving of the wavelength in the H-type transition because the oblique waves introduced in the K-type and H-type transitions have the same wavelength but different frequencies. The effect of the temporal modulation of the TS and oblique waves can also be seen by comparing figures 3(aiii) and 3(biii). Secondly, the vortex structures observed in the upstream boundary layer undergoing the H-type transition consist of two layers of longitudinal rolls (see figure 15 a–d), whereas those observed under the K-type transition consist of three layers of longitudinal rolls (refer to figure 8 a–c). The mechanism contributing to this difference is unclear.
Figure 16 shows the instantaneous contours of the non-dimensional velocities, vorticity and temperature profile obtained on the yz-plane at
$x=6.8\times 10^{-3}$
. It is interesting to note that the typical staggered
$\wedge$
-shaped structures characterizing the H-type transition in Blasius boundary layers are also present in the natural convection boundary layer, which qualitatively resemble the
$\wedge$
-shaped structures obtained by the PIV measurement of the Blasius boundary layer undergoing the H-type transition (Berlin et al.
Reference Berlin, Wiegel and Henningson1999). The
$\wedge$
-shaped structures in figure 16(a–d) are marked by
$\wedge$
-shaped lines. A closer examination of the
$\wedge$
-shaped structures from the velocity profiles reveals that all the tips of the
$\wedge$
-shaped structures appear at positions where the spanwise profile of
$\unicode[STIX]{x1D709}_{RMS}$
retains its peaks, either at ‘peak1’ or ‘peak2’ (refer to figure 3
biii or the marks in figure 16). This is similar to what has been observed in the K-type transition described in § 3. However, the spanwise profile of
$\unicode[STIX]{x1D709}_{RMS}$
for the K-type transition has three identical peaks only, whereas for the H-type transition it has six peaks of two different categories. Corresponding to these two categories of the peaks, the
$\wedge$
-shaped structures in the H-type transition can be classified into two groups: one corresponds to the positions where
$\unicode[STIX]{x1D709}_{RMS}$
retains ‘peak1’ and the other corresponds to the positions where
$\unicode[STIX]{x1D709}_{RMS}$
retains ‘peak2’. It is seen in figure 16(b) that the tips of the first (lowest) layer of the
$\wedge$
-shaped structures (approximately between
$y=0.55$
and
$y=0.65$
) correspond to the positions where
$\unicode[STIX]{x1D709}_{RMS}$
retains ‘peak2’. The tips of the middle layer of the
$\wedge$
-shaped structures (approximately between
$y=0.7$
and
$y=0.8$
) correspond to the positions where
$\unicode[STIX]{x1D709}_{RMS}$
retains ‘peak1’. This alternate appearance of the
$\wedge$
-shaped structures repeats along the streamwise direction, which results in staggered
$\wedge$
-shaped structures in the thermal boundary layer. This alternation is again attributed to the temporal modulation of the TS and oblique waves of different frequencies (i.e.
$f_{t}\neq f_{o}$
), which results in two different groups of peaks (i.e. ‘peak1’ and ‘peak2’) in the spanwise profile of
$\unicode[STIX]{x1D709}_{RMS}$
. The alternation is a fundamental character distinguishing the H- and K-type transitions. It is seen in this figure that the staggered
$\wedge$
-shaped structures are also observable in the
$x$
-vorticity and temperature contours, which are shown in figures 16(c) and 16(d), respectively. It is also worth clarifying that the staggered
$\wedge$
-shaped structures are not stationary. Figure 16(ei–vi) presents the temperature contours obtained on the same yz-plane at six consecutive time instants with a time interval of
$1/(5f_{o})$
. It is seen that the
$\wedge$
-shaped structures are convected downstream as they are evolving.
Figure 16. Instantaneous contours of the (a) streamwise velocities, (b) spanwise velocity, (c)
$x$
-vorticity and (d) temperature profile on the yz-plane at
$x=6.8\times 10^{-3}$
. (e) The temperature profile on the same yz-plane at 6 time instants within a perturbation period
$1/f_{o}$
, time interval for two consecutive time instants is
$1/(5f_{o})$
. The staggered
$\wedge$
-shaped structures indicate the H-type transition. Results for
$Ra=3.5\times 10^{9}$
,
$Pr=7$
,
$\unicode[STIX]{x1D706}_{o}=0.273$
and
$f_{t}=2f_{o}$
(case 2), at the time instant
$t=1.9\times 10^{-3}$
.
Figure 17. (a) Mean flow, (b) base flow and (c) mean secondary flow of the streamwise velocity components on the yz-plane at
$x=6.8\times 10^{-3}$
. (d) Spanwise-averaged streamwise velocity components of the mean flow (red solid line) and base flow (black dash-dot line). Results for the H-type transition.
To further understand the mean transitional structure of the natural convection boundary layer undergoing the H-type transition, the mean flow and the mean secondary flow of the streamwise velocity components on the yz-plane at
$x=6.8\times 10^{-3}$
are plotted in figure 17(a,c). The base flow is shown in figure 17(b). It is seen in figure 17(a) that the periodic
$\wedge$
-shaped structures of the H-type transition observed in the instantaneous thermal flow structures shown in figure 16 are not present in the mean flow. Similar to the case of K-type transition, this is again because the
$\wedge$
-shaped structures are not stationary and are in fact convected downstream while they are forming in the boundary layer. It is clear in figure 17(c) that the downstream boundary layer flow is locally enhanced or depressed in association with the formation of the
$\wedge$
-shaped structures. The secondary flow of the relatively upstream region is very weak, except for the region near the leading edge where the flow is depressed due to direction perturbations. The spanwise-averaged streamwise velocities of the base flow and mean flow are shown in figure 17(d) to compare the strength of the base and mean flows. It is seen in this figure that the streamwise velocity profile of the mean flow is approximately the same as that of the base flow in spite of local enhancement or depression, again implying that the amplitude of the artificial perturbations is appropriate and the base flow is not altered significantly due to the introduction of the perturbations.
Figure 18. Instantaneous isosurfaces of the second invariant of the velocity gradient tensor,
$\unicode[STIX]{x1D64C}$
, coloured by the streamwise velocity, showing
$\wedge$
-shaped vortical structures.
Figure 18 shows the vortical structures of the boundary layer flow by the Q-criterion visualization. It is seen in this figure that the
$\wedge$
-shaped structures observed in the present case is also short and thick, which is different from the slender
$\wedge$
-shaped structures observed in Blasius boundary layers (Sayadi et al.
Reference Sayadi, Hamman and Moin2013).
5 Discussion
5.1 Effects of transition on heat transfer
The effects of the K- and H-type transitions on heat transfer through the heated surface are examined in this section. Since the boundary layer finally approaches a quasi-steady state in both scenarios, the heat transfer properties are evaluated in terms of a time-averaged Nusselt number (
$\overline{Nu}$
) at the quasi-steady state and an enhancement factor of the time-averaged Nusselt number (
$\unicode[STIX]{x1D700}_{\overline{Nu}}$
), which are calculated using
$$\begin{eqnarray}\displaystyle & \displaystyle \overline{Nu}=-\overline{\left.\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}{\unicode[STIX]{x2202}x}\right|_{x=0}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D700}_{\overline{Nu}}=\frac{\overline{Nu}-Nu_{b}}{Nu_{b}}, & \displaystyle\end{eqnarray}$$
respectively. Here
$Nu_{b}$
is the Nusselt number of the steady base flow (obtained without perturbations).
Figure 19. Contours of the enhancement factor of time-averaged Nusselt number (
$\unicode[STIX]{x1D700}_{\overline{Nu}}$
) in the (a) K-type transition and (b) H-type transition.
The planar distributions of the enhancement factor of the time-averaged Nusselt number in the K-type transition and the H-type transition are shown in figures 19(a) and 19(b), respectively. It is clear in these figures that the overall heat transfer is enhanced significantly under both types of transitions. The local enhancement can be as high as 40 % and 35 % in the K-type and the H-type transitions, respectively. The contours of the enhancement factor also suggest that manipulation of the local heat transfer properties can be achieved by inducing different types of transitions in natural convection boundary layers. It is worth clarifying that the enhancement factor depends on the amplitude of perturbation, as has been demonstrated for two-dimensional natural convection boundary layers (see Zhao et al. Reference Zhao, Lei and Patterson2013). The effect of perturbation amplitude on heat transfer enhancement is beyond the scope of the present investigation.
The streamwise profile of the enhancement factor averaged across
$-0.410\leqslant z\leqslant 0.410$
is also examined for both types of transitions, which is shown in figure 20. It is seen in this figure that in general the profiles of the enhancement factor under the K-type and H-type transitions are similar; in both cases the averaged enhancement factor initially undergoes a smooth increase and then fluctuates irregularly. It is also worth noting that in both cases, the bifurcation position of the profile of the averaged enhancement factor, that is the changeover position from the smoothly growing phase to the irregularly oscillating phase, is approximately at
$y=0.45$
, which suggests that the types of transition do not affect the averaged heat transfer properties significantly.
Figure 20. Streamwise profiles of the spatially averaged (over
$-0.410\leqslant z\leqslant 0.410$
) enhancement factor of the time-averaged Nusselt number.
5.2 Turbulence production by Reynolds stresses and buoyancy
The above-described flow structures under the K-type and the H-type transitions in natural convection boundary layers are qualitatively similar to those observed in Blasius boundary layers. For Blasius boundary layers, turbulence energy production through the Reynolds stresses contributes to the transition, whereas for natural convection boundary layers buoyancy also contributes to the transition in addition to the Reynolds stresses. To compare the relative contributions of these two effects, the turbulence energy production through Reynolds stresses (denoted by
$E_{R}$
) and buoyancy (denoted by
$E_{B}$
) are calculated on the yz-plane at
$x=6.8\times 10^{-3}$
for the K-type and H-type transitions, respectively, using (see Sekimoto et al.
Reference Sekimoto, Kawahara and Sekiyama2011)
$$\begin{eqnarray}\displaystyle & \displaystyle E_{R}=-\!\!\left.\left(\overline{V^{\prime }V^{\prime }}\frac{\unicode[STIX]{x2202}\overline{V}}{\unicode[STIX]{x2202}Y}+\overline{V^{\prime }W^{\prime }}\frac{\unicode[STIX]{x2202}\overline{V}}{\unicode[STIX]{x2202}Z}+\overline{W^{\prime }W^{\prime }}\frac{\unicode[STIX]{x2202}\overline{W}}{\unicode[STIX]{x2202}Z}+\overline{W^{\prime }V^{\prime }}\frac{\unicode[STIX]{x2202}\overline{W}}{\unicode[STIX]{x2202}Y}\right)\right/\frac{V_{mb}^{3}}{H}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle E_{B}=g\unicode[STIX]{x1D6FD}\overline{V^{\prime }T^{\prime }}\!\left/\frac{V_{mb}^{3}}{H},\right. & \displaystyle\end{eqnarray}$$
where the instantaneous quantities are decomposed into ensemble averages (denoted by overbar) and fluctuation components, that is
$V=\overline{V}+V^{\prime }$
,
$W=\overline{W}+W^{\prime }$
and
$T=\overline{T}+T^{\prime }$
. The time window for obtaining statistically consistent mean quantities is over 15 cycles (i.e.
$1/f_{\text{c}}$
) of the fundamental TS waves of the boundary layer in the fully developed three-dimensional stage for the K-type transition case and 30 cycles for the H-type transition case. The doubling of the time duration for obtaining statistically consistent mean quantities for the H-type transition is due to the more complex modulation of the TS and oblique waves in the H-type transition. It is also worth clarifying that the magnitudes of the turbulence energy production have been normalized by
$V_{mb}^{3}/H$
, where
$V_{mb}$
is the maximum streamwise velocity of the velocity profile of the base flow measured at the mid-height of the heated surface.
Figure 21. Planar distribution of the turbulence energy productions contributed by the Reynolds stresses and buoyancy in the K-type transition and H-type transition, respectively: (a) by the Reynolds stresses in the K-type transition, (b) by buoyancy in the K-type transition, (c) by the Reynolds stresses in the H-type transition and (d) by buoyancy in the H-type transition. The distributions are examined on the yz-plane at
$x=6.8\times 10^{-3}$
.
Figure 21 shows the distribution of the turbulence energy production on the yz-plane at
$x=6.8\times 10^{-3}$
in the K-type and the H-type transitions, respectively. Figure 21(a) shows the turbulence production through the Reynolds stresses and figure 21(b) shows that by buoyancy, both for the K-type transition. To facilitate comparison, the same scales for the turbulence energy productions are used in figure 21(a,b). It is clear in figure 21(a,b) that in the downstream boundary layer the turbulence energy production through buoyancy is much stronger than that through the Reynolds stresses, particularly in the regions with strong mean flow structures (refer to figure 10
a). In the upstream boundary layer, the turbulence energy production through the Reynolds stresses is almost zero, which is as expected since the boundary layer flow is stable there. It is also worth noting that in both figures 21(a,b), regions with negative turbulence energy production appears locally, which indicates that in those local regions the Reynolds stresses and buoyancy transfer kinetic energy from the turbulent fluctuations to the mean flow. For the H-type transition, the contours of turbulence energy production through the Reynolds stresses and buoyancy are shown in figures 21(c) and 21(d), respectively. Again, it is seen that in the downstream boundary layer the turbulence energy production through buoyancy is much stronger than that through the Reynolds stresses, particularly in those regions with strong mean flow structures (refer to figure 17
a).
Figure 22. Streamwise profiles of turbulence energy production by the Reynolds stresses (denoted by
$E_{R}$
), buoyancy (
$E_{B}$
) and the summation of both (
$E_{R}+E_{B}$
), averaged over
$-0.410\leqslant z\leqslant 0.410$
. BP denotes the bifurcation position.
To obtain further insight into the quantitative contribution of both effects to the transition of the thermal boundary layer, the streamwise profiles of turbulence energy production through the Reynolds stresses, buoyancy and the combined effect of both the Reynolds stresses and buoyancy are shown in figure 22. Again the turbulence energy production presented here is spatially averaged over
$-0.410\leqslant z\leqslant 0.410$
. It is seen in figure 22 that for both types of the transition, the turbulence energy production contributed by the Reynolds stresses is much smaller than that by buoyancy, which indicates that the transitions of the boundary layer investigated here are dominated by the buoyancy effect. It is also worth noting that whilst the turbulence energy production by the Reynolds stresses increases gently in the streamwise direction, the turbulence energy production by buoyancy increases more dramatically. The profiles of the turbulence energy production by the combined effects of the Reynolds stresses and the buoyancy (solid curves) also indicate that the boundary layers approach strong nonlinear states from approximately
$y=0.32$
in the K-type transition and
$y=0.36$
in the H-type transition. These two positions approximately correspond to the streamwise positions of the bifurcation points on the streamwise profiles of the
$v_{RMS}$
obtained at peaks (refer to figures 6 and 14), which suggests that the turbulence energy production contributes to the bifurcations.
6 Concluding remarks
Two types of controlled transitions of a natural convection boundary layer are examined by DNS. The typical perturbations in the form of superimposed TS and oblique waves, which have been adopted for exciting K-type and H-type transitions, respectively, in Blasius boundary layers, are adopted in the present study to examine if similar transitions also occur in the natural convection boundary layer. By introducing the superimposed TS and oblique waves of the same frequency into the upstream natural convection boundary layer, it is found that the transition of the thermal boundary layer in terms of the transitional flow structures behaves in the same way as the K-type transition in Blasius boundary layers. Therefore, this type of transition is referred to as the K-type transition of the natural convection boundary layer. It is also found that the H-type transition similar to that reported in Blasius boundary layers also occurs in the natural convection boundary layer, if the frequency of the oblique waves of the perturbations is specified to be half the frequency of the TS waves.
In the K-type transition of the natural convection boundary layer, the streamwise evolution of the vortical structures is visualized from the mean spanwise velocities on the xz-planes (see figure 8). It is observed that three-layer longitudinal vortex rolls appear in the upstream boundary and the magnitude of the mean spanwise velocity amplifies rapidly in the streamwise direction of the boundary layer. The three-layer longitudinal vortex rolls eventually merge and break down further downstream. The observed three-layer longitudinal vortex rolls are different from the vortical structures inferred by Jaluria & Gebhart (Reference Jaluria and Gebhart1973), who reported double-layer longitudinal vortex rolls adjacent to a uniformly heated surface.
The typical aligned
$\wedge$
-shaped vortices characterizing the K-type transition are also observed in the downstream boundary layer (refer to figure 9). The tips of the
$\wedge$
-shaped structures appear at the peak locations of the spanwise profile of
$\unicode[STIX]{x1D709}_{RMS}$
, which is another significant feature characterizing the K-type transition. A similar feature of the K-type transition in Blasius boundary layers has been reported by Berlin et al. (Reference Berlin, Wiegel and Henningson1999). From the observation of the instantaneous and mean streamwise velocity on the xz-plane, it is also understood that the aligned
$\wedge$
-shaped structures are not stationary (see figures 9 and 10
a). Instead, they are convected downstream while they are forming in the boundary layer.
In the H-type transition examined in the present study, double-layer longitudinal vortex rolls are observed on the xz-planes (see figure 15). It is seen that the double-layer longitudinal vortex rolls appear in the upstream boundary layer with a relatively small velocity magnitude. The double-layer longitudinal vortex rolls persist over a certain distance along the streamwise direction while the magnitude of the spanwise velocity is increasing. At a certain downstream location, the double-layer longitudinal vortex rolls start to merge into a single layer (see figure 15 h). It is also found that the number of pairs of the longitudinal vortex rolls present in the H-type transition is doubled compared to that in the K-type transition, which is due to the different temporal modulations of the TS and oblique waves in these two forms of controlled transitions.
The typical staggered
$\wedge$
-shaped structures characterizing the H-type transition are observed in the downstream boundary layer, which is very similar to the PIV measurements in the Blasius boundary layer reported by Berlin et al. (Reference Berlin, Wiegel and Henningson1999). The mechanism contributing to the appearance of the staggered pattern of
$\wedge$
-shaped structures is the temporal modulation of the TS and the oblique waves of different frequencies. Similarly, it is worth noting that the staggered
$\wedge$
-shaped structures are not stationary and are not present in the mean flow (see figures 16 and 17
a).
The effects of the different types of the boundary layer transitions on heat transfer through the heated surface are also examined with comparison to the scenario without any transition (i.e. no perturbation). It is found that, for the specified perturbation amplitudes, the local heat transfer enhancement factor can be as high as 40 % and 35 % in the K-type and H-type transitions, respectively (see figure 19), compared to that without transition. Based on the streamwise profiles of the spatially averaged enhancement factor, the K-type and H-type transitions have a similar effect on heat transfer. In both scenarios, the enhancement factor increases monotonically in the streamwise direction from the leading edge to approximately
$y=0.45$
for the present Rayleigh number, and then fluctuates irregularly (refer to figure 20).
The analyses of the turbulence production by the Reynolds stresses and buoyancy reveal that, for both the K-type and H-type transitions, the turbulence energy production contributed by buoyancy is much larger than that by the Reynolds stresses (refer to figure 22). This finding suggests that the transitional characteristics of both types of transition investigated here are in fact the effects of buoyancy, though certain features of the transition are very similar to those observed in Blasius boundary layers in which only the Reynolds stresses produce turbulence energy. From the streamwise profile of the turbulence energy production due to the combined effects of the Reynolds stresses and buoyancy (i.e.
$E_{R}+E_{B}$
), it is observed that a bifurcation occurs at a certain streamwise position, beyond which the magnitude of the turbulence energy production shifts from smooth growth to irregular oscillation (see figure 22). The present results suggest that the bifurcation in the turbulence energy production may be correlated to the bifurcation on the streamwise profile of
$v_{RMS}$
.
Finally, it is worth clarifying that the present work is limited to
$Pr=7$
and fixed amplitudes of the TS and oblique waves due to limitations of the computational resources. The effects of the Prandtl number and perturbation amplitudes on the small-scale vorticity structure, transition position and heat transfer enhancement factor of the K-type and H-type transitions are interesting and worth quantifying in future studies.
Acknowledgement
The financial support by the Australian Research Council through Discovery Projects grants DP130100900 and DP170104023 is gratefully acknowledged.
