1. Introduction
The flow past circular cylinders has been extensively studied as a paradigm of bluff body aerodynamics (Williamson Reference Williamson1996c), for it involves several interesting phenomena which include, but are not limited to, laminar and turbulent boundary layer separation, vortex shedding or detached shear layer and wake instabilities. Flow unsteadiness, spatiotemporal chaos and turbulence are a source of aerodynamic noise and vortex-induced vibration, and crucially affect aerodynamic forces, to name but a few issues that are relevant from the engineering applications viewpoint. The sole governing parameter, the Reynolds number, is defined as ![]() $Re={U D/\nu }$, where
$Re={U D/\nu }$, where ![]() $U$ is the free-stream velocity,
$U$ is the free-stream velocity, ![]() $D$ the cylinder diameter and
$D$ the cylinder diameter and ![]() $\nu$ the kinematic viscosity of the fluid.
$\nu$ the kinematic viscosity of the fluid.
Square cylinders have also been used (Durao, Heitor & Pereira Reference Durao, Heitor and Pereira1988; Lyn et al. Reference Lyn, Einav, Rodi and Park1995; Luo, Chew & Ng Reference Luo, Chew and Ng2003) and rectangular (Okajima Reference Okajima1982; Norberg Reference Norberg1993), albeit to a lesser extent, as an archetype for bluff body aerodynamics. The same definition as for the circular cylinder is used for the Reynolds number, except that ![]() $D$ is taken to be the square cylinder side length (or the cross-stream side length for a rectangle).
$D$ is taken to be the square cylinder side length (or the cross-stream side length for a rectangle).
In real-world applications bluff bodies are often submerged in boundary layers (Hwang & Yao Reference Hwang and Yao1997) or wakes and the flow past them is decisively modified by the inhomogeneous velocity profiles of the incoming upstream flow. This is the case of a bridge pillar that is close to the river shore, long-span bridges immersed in an atmospheric boundary layer (Ahmed & Rajaratnam Reference Ahmed and Rajaratnam1998), underwater pipes near the seabed or subject to strong currents, or a building (or motor vehicle) in the wake of an upstream building (vehicle) (Bailey & Kwok Reference Bailey and Kwok1985; Bhatt & Alam Reference Bhatt and Alam2018).
The simplest model for such a situation is the uniform planar shear flow past a circular (Kiya, Tamura & Arie Reference Kiya, Tamura and Arie1980; Tamura, Kiya & Arie Reference Tamura, Kiya and Arie1980; Kwon, Sung & Hyun Reference Kwon, Sung and Hyun1992) or square (Ayukawa et al. Reference Ayukawa, Ochi, Kawahara and Hirao1993; Hwang & Sue Reference Hwang and Sue1997) cylinder, where the homogeneous incoming streamwise velocity is replaced with a linear profile (constant cross-stream gradient of streamwise velocity and, therefore, constant non-null shear). The shear parameter is defined as ![]() $K\equiv D G /U_c$, with
$K\equiv D G /U_c$, with ![]() $D$ the cylinder characteristic length (diameter and side for circular and square cylinders, respectively), and
$D$ the cylinder characteristic length (diameter and side for circular and square cylinders, respectively), and ![]() $U_c$ and
$U_c$ and ![]() $G=(\partial u/\partial y)_{y=y_c}$ the upstream streamwise velocity and dimensional cross-stream gradient of streamwise velocity, respectively, at cylinder mid-height.
$G=(\partial u/\partial y)_{y=y_c}$ the upstream streamwise velocity and dimensional cross-stream gradient of streamwise velocity, respectively, at cylinder mid-height.
Occasionally, the body of interest lies in the way of a thin shear layer rather than a smooth shear profile. This happens, for example, in the near wake of lift-producing devices such as airfoils, stator vanes or rotor blades of compressors, turbines or fans. Struts or rods supporting a structural casing are examples of objects subject to this type of incoming flow. This is precisely the kind of situation we intend to model here by placing a bluff body, the square cylinder, in the interface of two streams with different velocity. The wake-body interaction problem usually considers a body, streamlined or bluff, placed in the wake of another bluff body. The configuration in which a bluff body is placed in the wake of a streamlined body such as we intend to address here has very seldom been considered in the literature, and then always placing a cylinder or strut in the wake of an airfoil (Zhang, Huang & Zhou Reference Zhang, Huang and Zhou2005; Niu, Li & Wang Reference Niu, Li and Wang2021). However distant this problem may seem at first from that of an homogeneous upstream shear, the effects associated to the different velocity seen by the upper and lower sides of the bluff body might be expected – and will indeed be shown – to bear a striking resemblance.
The symmetric and steady flow past a circular cylinder undergoes a supercritical Hopf bifurcation, the primary instability, at around ![]() $Re^{H}\simeq 47$ with dimensionless frequency (Strouhal number)
$Re^{H}\simeq 47$ with dimensionless frequency (Strouhal number) ![]() $St^{H}\simeq 0.12$ (Provansal, Mathis & Boyer Reference Provansal, Mathis and Boyer1987; Norberg Reference Norberg1994), resulting in a time-periodic two-dimensional solution that consists in the alternated shedding of opposite-signed vortices from either side of the cylinder – a flow configuration commonly referred to as Kármán vortex street (von Kármán Reference von Kármán1911, Reference von Kármán1912). Although the spatial
$St^{H}\simeq 0.12$ (Provansal, Mathis & Boyer Reference Provansal, Mathis and Boyer1987; Norberg Reference Norberg1994), resulting in a time-periodic two-dimensional solution that consists in the alternated shedding of opposite-signed vortices from either side of the cylinder – a flow configuration commonly referred to as Kármán vortex street (von Kármán Reference von Kármán1911, Reference von Kármán1912). Although the spatial ![]() ${\rm Z}_2$ symmetry associated to vertical reflection about a diametral plane aligned with the incoming flow is broken (Marques, Lopez & Blackburn Reference Marques, Lopez and Blackburn2004), a spatiotemporal
${\rm Z}_2$ symmetry associated to vertical reflection about a diametral plane aligned with the incoming flow is broken (Marques, Lopez & Blackburn Reference Marques, Lopez and Blackburn2004), a spatiotemporal ![]() ${\rm Z}_2$ symmetry persists in the form of flow invariance upon the combined effect of evolution by a half-period followed by reflection about the same original reflection-symmetry plane.
${\rm Z}_2$ symmetry persists in the form of flow invariance upon the combined effect of evolution by a half-period followed by reflection about the same original reflection-symmetry plane.
The periodic and space–time-symmetric two-dimensional vortex-shedding solution might be observed in experiments all the way up to ![]() $Re\lesssim 190$, three dimensionality consistently arising from this point on Williamson (Reference Williamson1996a). Two distinct three-dimensional vortex-shedding modes have been reported in the so-called wake transition regime, whose inception results in two corresponding discontinuities of the Strouhal number (
$Re\lesssim 190$, three dimensionality consistently arising from this point on Williamson (Reference Williamson1996a). Two distinct three-dimensional vortex-shedding modes have been reported in the so-called wake transition regime, whose inception results in two corresponding discontinuities of the Strouhal number (![]() $St$) dependence on
$St$) dependence on ![]() $Re$ (Williamson Reference Williamson1988). The first one, mode A, is characterised by the onset of vortex loops that are stretched by shear into streamwise vortex pairs of spanwise wavelength around
$Re$ (Williamson Reference Williamson1988). The first one, mode A, is characterised by the onset of vortex loops that are stretched by shear into streamwise vortex pairs of spanwise wavelength around ![]() $3\sim 4D$ and has been shown to persist at flow regimes as low as
$3\sim 4D$ and has been shown to persist at flow regimes as low as ![]() $Re\gtrsim 180$, thus coexisting with the two-dimensional solution over a small range of Reynolds numbers (Williamson Reference Williamson1996b). Mode A is only regularly patterned at the early stages of inception (as it grows in time on top of the two-dimensional solution) and then only transiently, but soon after develops intermittent large-scale spot-like wave dislocations that render the spanwise structure rather irregular (Williamson Reference Williamson1992). The second, mode B, arises at slightly higher values of the Reynolds number
$Re\gtrsim 180$, thus coexisting with the two-dimensional solution over a small range of Reynolds numbers (Williamson Reference Williamson1996b). Mode A is only regularly patterned at the early stages of inception (as it grows in time on top of the two-dimensional solution) and then only transiently, but soon after develops intermittent large-scale spot-like wave dislocations that render the spanwise structure rather irregular (Williamson Reference Williamson1992). The second, mode B, arises at slightly higher values of the Reynolds number ![]() $Re\gtrsim 250$ and exhibits a fairly regular spanwise pattern with a shorter characteristic wavelength of about
$Re\gtrsim 250$ and exhibits a fairly regular spanwise pattern with a shorter characteristic wavelength of about ![]() ${\sim }1D$ (Williamson Reference Williamson1996b). Mode-B-type vortical structures pervade the near wake even at flow regimes where turbulence has already set in at much higher Reynolds numbers in excess of 1000 (Mansy, Yang & Williams Reference Mansy, Yang and Williams1994). Floquet stability analysis has shown that mode A emanates from a secondary instability of the two-dimensional periodic vortex-shedding solution at
${\sim }1D$ (Williamson Reference Williamson1996b). Mode-B-type vortical structures pervade the near wake even at flow regimes where turbulence has already set in at much higher Reynolds numbers in excess of 1000 (Mansy, Yang & Williams Reference Mansy, Yang and Williams1994). Floquet stability analysis has shown that mode A emanates from a secondary instability of the two-dimensional periodic vortex-shedding solution at ![]() $Re^{A}=188.5\pm 1$ with wavelength
$Re^{A}=188.5\pm 1$ with wavelength ![]() $\lambda _z^{A}=3.96\pm 0.02$, and happens to be subcritical (Henderson & Barkley Reference Henderson and Barkley1996); hence, the hysteretical flow behaviour. Meanwhile, mode B seems to be related to a second instability of the same solution that occurs supercritically at
$\lambda _z^{A}=3.96\pm 0.02$, and happens to be subcritical (Henderson & Barkley Reference Henderson and Barkley1996); hence, the hysteretical flow behaviour. Meanwhile, mode B seems to be related to a second instability of the same solution that occurs supercritically at ![]() $Re=259\pm 2$ with
$Re=259\pm 2$ with ![]() $\lambda _z^{B}=0.822\pm 0.007$ (Barkley & Henderson Reference Barkley and Henderson1996). The critical values of the parameters at bifurcation have since been further refined to
$\lambda _z^{B}=0.822\pm 0.007$ (Barkley & Henderson Reference Barkley and Henderson1996). The critical values of the parameters at bifurcation have since been further refined to ![]() $(Re^{A},\lambda _z^{A})=(190.2\pm 0.02,3.966\pm 0.002)$ and
$(Re^{A},\lambda _z^{A})=(190.2\pm 0.02,3.966\pm 0.002)$ and ![]() $(Re^{B},\lambda _z^{B})=(261.0\pm 0.2,0.825\pm 0.002)$ using asymptotically large domains (Posdziech & Grundmann Reference Posdziech and Grundmann2001). A third mode, consisting of a complex-conjugate pair of eigenvalues and dubbed QP on account of its introducing quasi-periodicity into the flow, has been identified as dominant at intermediate wavelengths of about
$(Re^{B},\lambda _z^{B})=(261.0\pm 0.2,0.825\pm 0.002)$ using asymptotically large domains (Posdziech & Grundmann Reference Posdziech and Grundmann2001). A third mode, consisting of a complex-conjugate pair of eigenvalues and dubbed QP on account of its introducing quasi-periodicity into the flow, has been identified as dominant at intermediate wavelengths of about ![]() ${\sim }2D$, in between those characterising modes A and B (Blackburn & Lopez Reference Blackburn and Lopez2003). Mode QP bifurcates at
${\sim }2D$, in between those characterising modes A and B (Blackburn & Lopez Reference Blackburn and Lopez2003). Mode QP bifurcates at ![]() $Re^{QP}\simeq 377$ and generates branches of unstable, and, therefore, not experimentally realisable, quasi-periodic states (Blackburn, Marques & Lopez Reference Blackburn, Marques and Lopez2005).
$Re^{QP}\simeq 377$ and generates branches of unstable, and, therefore, not experimentally realisable, quasi-periodic states (Blackburn, Marques & Lopez Reference Blackburn, Marques and Lopez2005).
The spatiotemporal ![]() ${\rm Z}_2$ symmetry of the two-dimensional vortex-shedding regime coexists with the spanwise invariance of the infinite cylinder flow problem, represented by the orthogonal group
${\rm Z}_2$ symmetry of the two-dimensional vortex-shedding regime coexists with the spanwise invariance of the infinite cylinder flow problem, represented by the orthogonal group ![]() ${\rm O}(2)=Z_2\times {\rm SO}(2)$, which includes reflection about any discretionary plane that is orthogonal to the spanwise direction (
${\rm O}(2)=Z_2\times {\rm SO}(2)$, which includes reflection about any discretionary plane that is orthogonal to the spanwise direction (![]() ${\rm Z}_2$) and every arbitrary translation along the span (special orthogonal or rotation group SO(2), which is isomorphic to the circle group
${\rm Z}_2$) and every arbitrary translation along the span (special orthogonal or rotation group SO(2), which is isomorphic to the circle group ![]() ${\rm S}^{1}$). Note that translations
${\rm S}^{1}$). Note that translations ![]() $\Delta z$ in a periodic domain of length
$\Delta z$ in a periodic domain of length ![]() $L_z$ may be reinterpreted as rotations of angle
$L_z$ may be reinterpreted as rotations of angle ![]() $\Delta \theta =2{\rm \pi} \Delta z/L_z$. Systems with
$\Delta \theta =2{\rm \pi} \Delta z/L_z$. Systems with ![]() ${\rm Z}_2\times {\rm O}(2)$ symmetry, where the Z
${\rm Z}_2\times {\rm O}(2)$ symmetry, where the Z![]() $_2$ refers to a spatiotemporal symmetry, rather than simply spatial, and O(2) to space invariance, admit two types of synchronous codimension-one bifurcations, one preserving the space–time
$_2$ refers to a spatiotemporal symmetry, rather than simply spatial, and O(2) to space invariance, admit two types of synchronous codimension-one bifurcations, one preserving the space–time ![]() ${\rm Z}_2$ symmetry and the other one breaking it (Marques et al. Reference Marques, Lopez and Blackburn2004). Two-dimensional time-periodic vortex shedding past circular and square cylinders belong to this symmetry class and, among the secondary instabilities that three dimensionalise the flow, mode A is triggered by a
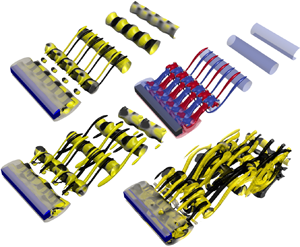
${\rm Z}_2$ symmetry and the other one breaking it (Marques et al. Reference Marques, Lopez and Blackburn2004). Two-dimensional time-periodic vortex shedding past circular and square cylinders belong to this symmetry class and, among the secondary instabilities that three dimensionalise the flow, mode A is triggered by a ![]() ${\rm Z}_2$-preserving bifurcation, while mode B is induced by one that breaks it (Blackburn et al. Reference Blackburn, Marques and Lopez2005). The symmetries of both modes A and B are exemplified in figure 1 through pairs of snapshots taken a half-vortex-shedding period apart for the classic configuration of the homogeneous incoming flow past a straight square cylinder at zero incidence and
${\rm Z}_2$-preserving bifurcation, while mode B is induced by one that breaks it (Blackburn et al. Reference Blackburn, Marques and Lopez2005). The symmetries of both modes A and B are exemplified in figure 1 through pairs of snapshots taken a half-vortex-shedding period apart for the classic configuration of the homogeneous incoming flow past a straight square cylinder at zero incidence and ![]() $Re=205$. Note that the signs, and, therefore, also the colours, of both axial (
$Re=205$. Note that the signs, and, therefore, also the colours, of both axial (![]() $\omega _x$) and spanwise (
$\omega _x$) and spanwise (![]() $\omega _z$) vorticity switch under the space–time symmetry operation for symmetry-preserving modes. Whenever the bifurcation in a system with the aforementioned symmetries involves a complex-conjugate pair that is non-resonant with the destabilising two-dimensional time-periodic and space–time symmetric solution, three quasi-periodic solution branches arise, namely a pair of symmetry-conjugate modulated travelling waves and a third of modulated standing waves. Only one of the two distinct types of solution branches – either the pair of travelling or the standing waves – might be stable at a time (Marques et al. Reference Marques, Lopez and Blackburn2004). The third three-dimensionalising secondary instability of the two-dimensional time-periodic wake past both circular and square cylinders corresponds precisely to a quasi-resonant quasi-periodic subcritical bifurcation. This is mode QP, shown in figure 1 for the square cylinder in the classic configuration. The fundamental frequency is nearly half that of the Kármán frequency, but the flow fields do not exactly repeat every two vortex-shedding cycles, the mode being in fact quasi-periodic. The two symmetry-conjugate branches of modulated travelling-wave solutions add an unstable eigenmode to the count of the already unstable two-dimensional solution, while the modulated standing wave adds two (Blackburn et al. Reference Blackburn, Marques and Lopez2005). The neighbouring 1 : 4 resonant case, which would correspond to a period-doubling bifurcation, is a codimension-two bifurcation and would therefore require the tuning of a second parameter beside the Reynolds number for a complete unfolding. The symmetry group of the two-dimensional vortex-shedding regime admits also a number of mixed-mode bifurcations and strong 1 : 1 and 1 : 2 resonances, all codimension-two, none of which seems to bear any relevance to the cylinder wake problem (Marques et al. Reference Marques, Lopez and Blackburn2004).
$\omega _z$) vorticity switch under the space–time symmetry operation for symmetry-preserving modes. Whenever the bifurcation in a system with the aforementioned symmetries involves a complex-conjugate pair that is non-resonant with the destabilising two-dimensional time-periodic and space–time symmetric solution, three quasi-periodic solution branches arise, namely a pair of symmetry-conjugate modulated travelling waves and a third of modulated standing waves. Only one of the two distinct types of solution branches – either the pair of travelling or the standing waves – might be stable at a time (Marques et al. Reference Marques, Lopez and Blackburn2004). The third three-dimensionalising secondary instability of the two-dimensional time-periodic wake past both circular and square cylinders corresponds precisely to a quasi-resonant quasi-periodic subcritical bifurcation. This is mode QP, shown in figure 1 for the square cylinder in the classic configuration. The fundamental frequency is nearly half that of the Kármán frequency, but the flow fields do not exactly repeat every two vortex-shedding cycles, the mode being in fact quasi-periodic. The two symmetry-conjugate branches of modulated travelling-wave solutions add an unstable eigenmode to the count of the already unstable two-dimensional solution, while the modulated standing wave adds two (Blackburn et al. Reference Blackburn, Marques and Lopez2005). The neighbouring 1 : 4 resonant case, which would correspond to a period-doubling bifurcation, is a codimension-two bifurcation and would therefore require the tuning of a second parameter beside the Reynolds number for a complete unfolding. The symmetry group of the two-dimensional vortex-shedding regime admits also a number of mixed-mode bifurcations and strong 1 : 1 and 1 : 2 resonances, all codimension-two, none of which seems to bear any relevance to the cylinder wake problem (Marques et al. Reference Marques, Lopez and Blackburn2004).

Figure 1. Sketch depicting the unfolding in parameter space of the secondary bifurcation curves of two-dimensional vortex shedding past a symmetric bluff body. The abscissa axis represents a top–bottom symmetry-breaking parameter (incidence ![]() $\alpha$, shear parameter
$\alpha$, shear parameter ![]() $K$ or circular ring aspect ratio
$K$ or circular ring aspect ratio ![]() $\varGamma \equiv d/D$,
$\varGamma \equiv d/D$, ![]() $d$ and
$d$ and ![]() $D$ being the ring and cross-sectional diameters, respectively). The snapshot pairs, taken half a vortex-shedding cycle apart, correspond to modes A, B and QP for the straight square cylinder at zero incidence subject to an homogeneous incoming upstream flow at
$D$ being the ring and cross-sectional diameters, respectively). The snapshot pairs, taken half a vortex-shedding cycle apart, correspond to modes A, B and QP for the straight square cylinder at zero incidence subject to an homogeneous incoming upstream flow at ![]() $Re=205$ (the squares in the bifurcation diagram, corresponding to the symmetric case). Mode C, not depicted, corresponds to a mere frequency locking of mode QP that occurs when breaking the symmetry (bullet), and is therefore barely distinguishable from a symmetry-broken QP mode. Shown are
$Re=205$ (the squares in the bifurcation diagram, corresponding to the symmetric case). Mode C, not depicted, corresponds to a mere frequency locking of mode QP that occurs when breaking the symmetry (bullet), and is therefore barely distinguishable from a symmetry-broken QP mode. Shown are ![]() $Q=0.05$ isosurfaces coloured by
$Q=0.05$ isosurfaces coloured by ![]() $\omega _x\in [-0.1,0.1]\,U/D$ (black to yellow) and
$\omega _x\in [-0.1,0.1]\,U/D$ (black to yellow) and ![]() $\omega _z\in [-0.1,0.1]\,U/D$ (blue to red).
$\omega _z\in [-0.1,0.1]\,U/D$ (blue to red).
Square cylinder wake dynamics bears compelling resemblance to that past a circular cylinder. The symmetries of the problem are the same and the primary instability leads to a two-dimensional time-periodic and space–time symmetric vortex-shedding state at the slightly lower ![]() $Re^{H}\simeq 45$ and
$Re^{H}\simeq 45$ and ![]() $St^{H}\simeq 0.10$ (Norberg Reference Norberg1996; Park & Yang Reference Park and Yang2016). There are however notable differences that concern the location where the boundary layer separates from the cylinder surface. While separation points can migrate freely on the surface of a circular cylinder, they are bound to coincide with the corners of a square or rectangular cylinder. As it happens, separation occurs from the rear corners only at very low Reynolds number, and then only after reattachment from an initial separation from the front corners (Okajima Reference Okajima1982; Robichaux, Balachandar & Vanka Reference Robichaux, Balachandar and Vanka1999; Yoon, Yang & Choi Reference Yoon, Yang and Choi2010).
$St^{H}\simeq 0.10$ (Norberg Reference Norberg1996; Park & Yang Reference Park and Yang2016). There are however notable differences that concern the location where the boundary layer separates from the cylinder surface. While separation points can migrate freely on the surface of a circular cylinder, they are bound to coincide with the corners of a square or rectangular cylinder. As it happens, separation occurs from the rear corners only at very low Reynolds number, and then only after reattachment from an initial separation from the front corners (Okajima Reference Okajima1982; Robichaux, Balachandar & Vanka Reference Robichaux, Balachandar and Vanka1999; Yoon, Yang & Choi Reference Yoon, Yang and Choi2010).
The flow past a square cylinder also exhibits mode A- and B-type structures in the wake transition regime (Sohankar, Norberg & Davidson Reference Sohankar, Norberg and Davidson1999; Luo et al. Reference Luo, Chew and Ng2003; Saha, Biswas & Muralidhar Reference Saha, Biswas and Muralidhar2003; Bai & Alam Reference Bai and Alam2018), but their respective occurrence starts at lower values of the Reynolds number ![]() $Re^{A}\simeq 160\pm 2$ and
$Re^{A}\simeq 160\pm 2$ and ![]() $Re^{B}\simeq 204\pm 5$ and present somewhat larger wavelengths
$Re^{B}\simeq 204\pm 5$ and present somewhat larger wavelengths ![]() $\lambda _z^{A}/D\simeq 5.1\pm 0.1$ and
$\lambda _z^{A}/D\simeq 5.1\pm 0.1$ and ![]() $\lambda _z^{B}/D\simeq 1.3\pm 0.1$ at onset (Luo, Tong & Khoo Reference Luo, Tong and Khoo2007). While early experiments failed to detect any hysteresis in the inception of mode A and no discontinuity in the Strouhal number dependence on the Reynolds number was observed (Luo et al. Reference Luo, Chew and Ng2003), later experiments that strived to accurately resolve variations in the driving parameter produced a small hysteretical region (Luo et al. Reference Luo, Tong and Khoo2007; Tong, Luo & Khoo Reference Tong, Luo and Khoo2008).
$\lambda _z^{B}/D\simeq 1.3\pm 0.1$ at onset (Luo, Tong & Khoo Reference Luo, Tong and Khoo2007). While early experiments failed to detect any hysteresis in the inception of mode A and no discontinuity in the Strouhal number dependence on the Reynolds number was observed (Luo et al. Reference Luo, Chew and Ng2003), later experiments that strived to accurately resolve variations in the driving parameter produced a small hysteretical region (Luo et al. Reference Luo, Tong and Khoo2007; Tong, Luo & Khoo Reference Tong, Luo and Khoo2008).
Linear instabilities akin to modes A and B of the flow past a circular cylinder have been identified through Floquet stability analysis also in the wake transition regime of the flow past a square cylinder (Robichaux et al. Reference Robichaux, Balachandar and Vanka1999), alongside a third, subharmonic, quasi-periodic mode (see the snapshots in figure 1). As for the circular cylinder, modes A and B preserve and break, respectively, the spatiotemporal ![]() ${\rm Z}_2$ symmetry of the two-dimensional vortex-shedding solution, but occur at lower
${\rm Z}_2$ symmetry of the two-dimensional vortex-shedding solution, but occur at lower ![]() $Re^{A}\simeq 164$ and
$Re^{A}\simeq 164$ and ![]() $Re^{B}\simeq 197$, with slightly longer
$Re^{B}\simeq 197$, with slightly longer ![]() $\lambda _z^{A}/D\simeq 5.2$ and
$\lambda _z^{A}/D\simeq 5.2$ and ![]() $\lambda _z^{B}/D\simeq 1.1$ at bifurcation (Sheard, Fitzgerald & Ryan Reference Sheard, Fitzgerald and Ryan2009; Choi, Jang & Yang Reference Choi, Jang and Yang2012). Modulated travelling- and standing-wave solution branches also arise in the wake of a square cylinder following the bifurcation of a complex-conjugate pair (Blackburn & Lopez Reference Blackburn and Lopez2003), which is the counterpart to the quasi-periodic mode QP of the circular cylinder. Mode QP, which bifurcates at
$\lambda _z^{B}/D\simeq 1.1$ at bifurcation (Sheard, Fitzgerald & Ryan Reference Sheard, Fitzgerald and Ryan2009; Choi, Jang & Yang Reference Choi, Jang and Yang2012). Modulated travelling- and standing-wave solution branches also arise in the wake of a square cylinder following the bifurcation of a complex-conjugate pair (Blackburn & Lopez Reference Blackburn and Lopez2003), which is the counterpart to the quasi-periodic mode QP of the circular cylinder. Mode QP, which bifurcates at ![]() $Re^{QP}\simeq 215$ with
$Re^{QP}\simeq 215$ with ![]() $\lambda _z\simeq 2.6$ for the square cylinder (Sheard et al. Reference Sheard, Fitzgerald and Ryan2009), was originally mistaken for a subharmonic (period-doubling) mode and dubbed S (Robichaux et al. Reference Robichaux, Balachandar and Vanka1999). The blunder followed a shortcoming of the stability analysis method used, which was incapable of detecting bifurcations of a quasi-resonant quasi-periodic type. Unlike what happens for the flow past a circular cylinder, the symmetry-conjugate branches of modulated travelling-wave solutions issued from the QP bifurcation are supercritical and inherit the stability properties of the two-dimensional solution, while the modulated standing-wave branch, which is also supercritical but with a lesser slope at bifurcation, adds an unstable eigenmode (Blackburn et al. Reference Blackburn, Marques and Lopez2005).
$\lambda _z\simeq 2.6$ for the square cylinder (Sheard et al. Reference Sheard, Fitzgerald and Ryan2009), was originally mistaken for a subharmonic (period-doubling) mode and dubbed S (Robichaux et al. Reference Robichaux, Balachandar and Vanka1999). The blunder followed a shortcoming of the stability analysis method used, which was incapable of detecting bifurcations of a quasi-resonant quasi-periodic type. Unlike what happens for the flow past a circular cylinder, the symmetry-conjugate branches of modulated travelling-wave solutions issued from the QP bifurcation are supercritical and inherit the stability properties of the two-dimensional solution, while the modulated standing-wave branch, which is also supercritical but with a lesser slope at bifurcation, adds an unstable eigenmode (Blackburn et al. Reference Blackburn, Marques and Lopez2005).
Nonlinear analysis using the Landau equation as a model for the secondary instability of the flow past a square cylinder points to a supercritical nature of mode A at bifurcation (Sheard et al. Reference Sheard, Fitzgerald and Ryan2009), as opposed to what happens for the circular cylinder (Henderson & Barkley Reference Henderson and Barkley1996), and in overt contradiction with experimental observations (Luo et al. Reference Luo, Tong and Khoo2007). This dispute as to the subcritical or supercritical nature of mode A between numerical simulation and experiment has not yet been settled to the authors knowledge.
The relation between the instabilities (both primary and secondary) in the wake of square and circular cylinders has recently been elucidated by the numerical smooth transformation of the former into the latter by gradual rounding of the corners (Park & Yang Reference Park and Yang2016). The primary Hopf bifurcation that brings about two-dimensional vortex shedding is initially slightly delayed as the cylinder geometry evolves from circular to square, but the trend is reversed halfway and the critical value brought down to ![]() $Re^{H}\simeq 44.7$. The bifurcation remains supercritical all along. Secondary three-dimensionalising instabilities also evolve continuously and uneventfully, gradually advancing the occurrence of the bifurcations of all three modes, A, B and QP, to lower critical values of
$Re^{H}\simeq 44.7$. The bifurcation remains supercritical all along. Secondary three-dimensionalising instabilities also evolve continuously and uneventfully, gradually advancing the occurrence of the bifurcations of all three modes, A, B and QP, to lower critical values of ![]() $Re$. The order of bifurcation is not altered, but the bifurcation points get closely packed, with mode QP strongly promoted for the square in comparison to the circular shape. Meanwhile, the wavelength at criticality is slightly but steadily increased for all three modes in the morphing from circular to square.
$Re$. The order of bifurcation is not altered, but the bifurcation points get closely packed, with mode QP strongly promoted for the square in comparison to the circular shape. Meanwhile, the wavelength at criticality is slightly but steadily increased for all three modes in the morphing from circular to square.
The top–bottom ![]() ${\rm Z}_2$ reflection symmetry of the flow past an infinitely long cylinder might be broken in several possible ways. For a circular cylinder, the symmetry disruption might be achieved by introducing curvature along the spanwise direction turning the cylinder into a ring (Monson Reference Monson1983; Leweke & Provansal Reference Leweke and Provansal1994, Reference Leweke and Provansal1995; Sheard, Thompson & Hourigan Reference Sheard, Thompson and Hourigan2003), by applying rotation about its centreline (Kang, Choi & Lee Reference Kang, Choi and Lee1999; Mittal & Kumar Reference Mittal and Kumar2003), by subjecting it to a non-uniform upstream velocity profile (incoming shear flow) (Jordan & Fromm Reference Jordan and Fromm1972; Kiya et al. Reference Kiya, Tamura and Arie1980; Tamura et al. Reference Tamura, Kiya and Arie1980; Park & Yang Reference Park and Yang2018) or by combining incoming shear with rotation (Yoshino & Hayashi Reference Yoshino and Hayashi1984; Sung, Chun & Hyun Reference Sung, Chun and Hyun1995), among other options. Upstream shear is also an option for breaking the symmetry of the square cylinder problem (Hwang & Sue Reference Hwang and Sue1997; Saha, Biswas & Muralidhar Reference Saha, Biswas and Muralidhar1999; Sohankar et al. Reference Sohankar, Rangraz, Khodadadi and Alam2020), as also is placing the cylinder at an incidence with respect to the incoming flow (Norberg Reference Norberg1993; Sohankar, Norberg & Davidson Reference Sohankar, Norberg and Davidson1998; Tong et al. Reference Tong, Luo and Khoo2008; Yoon et al. Reference Yoon, Yang and Choi2010) or combining both effects together. In most cases, the two-dimensional time-periodic vortex-shedding solution persists upon deliberately breaking the spatial
${\rm Z}_2$ reflection symmetry of the flow past an infinitely long cylinder might be broken in several possible ways. For a circular cylinder, the symmetry disruption might be achieved by introducing curvature along the spanwise direction turning the cylinder into a ring (Monson Reference Monson1983; Leweke & Provansal Reference Leweke and Provansal1994, Reference Leweke and Provansal1995; Sheard, Thompson & Hourigan Reference Sheard, Thompson and Hourigan2003), by applying rotation about its centreline (Kang, Choi & Lee Reference Kang, Choi and Lee1999; Mittal & Kumar Reference Mittal and Kumar2003), by subjecting it to a non-uniform upstream velocity profile (incoming shear flow) (Jordan & Fromm Reference Jordan and Fromm1972; Kiya et al. Reference Kiya, Tamura and Arie1980; Tamura et al. Reference Tamura, Kiya and Arie1980; Park & Yang Reference Park and Yang2018) or by combining incoming shear with rotation (Yoshino & Hayashi Reference Yoshino and Hayashi1984; Sung, Chun & Hyun Reference Sung, Chun and Hyun1995), among other options. Upstream shear is also an option for breaking the symmetry of the square cylinder problem (Hwang & Sue Reference Hwang and Sue1997; Saha, Biswas & Muralidhar Reference Saha, Biswas and Muralidhar1999; Sohankar et al. Reference Sohankar, Rangraz, Khodadadi and Alam2020), as also is placing the cylinder at an incidence with respect to the incoming flow (Norberg Reference Norberg1993; Sohankar, Norberg & Davidson Reference Sohankar, Norberg and Davidson1998; Tong et al. Reference Tong, Luo and Khoo2008; Yoon et al. Reference Yoon, Yang and Choi2010) or combining both effects together. In most cases, the two-dimensional time-periodic vortex-shedding solution persists upon deliberately breaking the spatial ![]() ${\rm Z}_2$ symmetry of the problem, but the space–time
${\rm Z}_2$ symmetry of the problem, but the space–time ![]() ${\rm Z}_2$ symmetry is no longer fulfilled (Blackburn & Sheard Reference Blackburn and Sheard2010).
${\rm Z}_2$ symmetry is no longer fulfilled (Blackburn & Sheard Reference Blackburn and Sheard2010).
The primary instability of the flow past an open ring leads to an axisymmetric time-periodic vortex-shedding regime (Monson Reference Monson1983; Leweke & Provansal Reference Leweke and Provansal1994), analogous to the two-dimensional vortex-shedding regime past a circular cylinder but obviously lacking its spatiotemporal ![]() ${\rm Z}_2$ symmetry. Numerical studies have shown that, besides the instabilities related to the classic modes A and B, a subharmonic mode C also emerges and is the dominant secondary instability for rings of aspect ratio around
${\rm Z}_2$ symmetry. Numerical studies have shown that, besides the instabilities related to the classic modes A and B, a subharmonic mode C also emerges and is the dominant secondary instability for rings of aspect ratio around ![]() $\varGamma \equiv d/D=5$, defined as the quotient between the diameter of the circle described by the cylinder axis (
$\varGamma \equiv d/D=5$, defined as the quotient between the diameter of the circle described by the cylinder axis (![]() $d$) and the cylinder diameter itself (
$d$) and the cylinder diameter itself (![]() $D$) (Sheard et al. Reference Sheard, Thompson and Hourigan2003). Both experiments and direct numerical simulations show that the secondary linear instability develops nonlinearly into a period-doubled vortex-shedding solution with a distinct wavelength somewhere in between those predicted by Floquet stability analysis for modes A and B in the ring wake (Sheard, Hourigan & Thompson Reference Sheard, Hourigan and Thompson2005a; Sheard, Thompson & Hourigan Reference Sheard, Thompson and Hourigan2005b). Although the solution is period doubled, aggregate quantities such as aerodynamic forces preserve the original period. Two instants exactly one shedding cycle apart are mutually related by an appropriate symmetry operation (any of either a spanwise/azimuthal rotation by half the angular wavelength or reflection about some collection of appropriately chosen diametral planes) and the period doubling does not initiate a period-doubling cascade. Instead, the mode C structures that characterise the wake after the secondary bifurcation are replaced by mode-A-type structures when the Reynolds number is further increased. The scenario that follows seems to be analogous to that for the circular cylinder
$D$) (Sheard et al. Reference Sheard, Thompson and Hourigan2003). Both experiments and direct numerical simulations show that the secondary linear instability develops nonlinearly into a period-doubled vortex-shedding solution with a distinct wavelength somewhere in between those predicted by Floquet stability analysis for modes A and B in the ring wake (Sheard, Hourigan & Thompson Reference Sheard, Hourigan and Thompson2005a; Sheard, Thompson & Hourigan Reference Sheard, Thompson and Hourigan2005b). Although the solution is period doubled, aggregate quantities such as aerodynamic forces preserve the original period. Two instants exactly one shedding cycle apart are mutually related by an appropriate symmetry operation (any of either a spanwise/azimuthal rotation by half the angular wavelength or reflection about some collection of appropriately chosen diametral planes) and the period doubling does not initiate a period-doubling cascade. Instead, the mode C structures that characterise the wake after the secondary bifurcation are replaced by mode-A-type structures when the Reynolds number is further increased. The scenario that follows seems to be analogous to that for the circular cylinder
A subharmonic instability analogous to mode C is also dominant for a square cylinder placed at moderate incidence angles ![]() $\alpha$ (Sheard et al. Reference Sheard, Fitzgerald and Ryan2009). Mode A, which was originally believed to be dominant for all incidences following experiments that unfortunately failed to check the flow topology at intermediate values of
$\alpha$ (Sheard et al. Reference Sheard, Fitzgerald and Ryan2009). Mode A, which was originally believed to be dominant for all incidences following experiments that unfortunately failed to check the flow topology at intermediate values of ![]() $\alpha$ (Tong et al. Reference Tong, Luo and Khoo2008), is in fact overtaken by mode C for
$\alpha$ (Tong et al. Reference Tong, Luo and Khoo2008), is in fact overtaken by mode C for ![]() $\alpha \gtrsim 10.5^{\circ }$ (Yoon et al. Reference Yoon, Yang and Choi2010; Sheard Reference Sheard2011), which is in turn outdone by another mode of characteristics similar to those of mode A for
$\alpha \gtrsim 10.5^{\circ }$ (Yoon et al. Reference Yoon, Yang and Choi2010; Sheard Reference Sheard2011), which is in turn outdone by another mode of characteristics similar to those of mode A for ![]() $\alpha \gtrsim 26^{\circ }$. This second mode
$\alpha \gtrsim 26^{\circ }$. This second mode ![]() $A^{\prime }$ is distinct from the one evolving from
$A^{\prime }$ is distinct from the one evolving from ![]() $\alpha =0^{\circ }$ in that it evolves from the space–time symmetric mode A corresponding to
$\alpha =0^{\circ }$ in that it evolves from the space–time symmetric mode A corresponding to ![]() $\alpha =45^{\circ }$. Numerical evidence seems to discard any smooth connection between modes A and
$\alpha =45^{\circ }$. Numerical evidence seems to discard any smooth connection between modes A and ![]() $A^{\prime }$ by mere continuous tilting of the cylinder from one incidence to the other, although the physical flow mechanisms at play appear to be the same. Mode-B-type structures have also been detected in experiments above a critical Reynolds number that also evolves smoothly as the incidence angle is changed across the full range (Tong et al. Reference Tong, Luo and Khoo2008). The presence of mode B structures in the wake of a square cylinder at incidence has been confirmed by direct numerical simulation at sufficiently high values of the Reynolds number
$A^{\prime }$ by mere continuous tilting of the cylinder from one incidence to the other, although the physical flow mechanisms at play appear to be the same. Mode-B-type structures have also been detected in experiments above a critical Reynolds number that also evolves smoothly as the incidence angle is changed across the full range (Tong et al. Reference Tong, Luo and Khoo2008). The presence of mode B structures in the wake of a square cylinder at incidence has been confirmed by direct numerical simulation at sufficiently high values of the Reynolds number ![]() $Re\gtrsim 200$ (Sheard et al. Reference Sheard, Fitzgerald and Ryan2009), which in this case is usually defined with the cross-stream projected height
$Re\gtrsim 200$ (Sheard et al. Reference Sheard, Fitzgerald and Ryan2009), which in this case is usually defined with the cross-stream projected height ![]() $D(\cos {\alpha }+\sin {\alpha })$ instead of just
$D(\cos {\alpha }+\sin {\alpha })$ instead of just ![]() $D$.
$D$.
Mode QP of the flow past circular and square cylinders is only the third linear instability, after modes A and B, of the periodic and space–time symmetric two-dimensional vortex-shedding solution, and the associated growth rate is much smaller. It is therefore not to be expected that wake structures related to mode QP might be observed in actual experiments. It does however bear strong resemblance to the mode C observed in the wake behind open rings (Sheard et al. Reference Sheard, Hourigan and Thompson2005a) of the right moderate aspect ratio and square cylinders at intermediate incidence angles (Sheard et al. Reference Sheard, Fitzgerald and Ryan2009), regarding both spanwise wavelength and flow topology. As a matter of course, a weak disruption of the spatial ![]() ${\rm Z}_2$ symmetry in problems belonging to the
${\rm Z}_2$ symmetry in problems belonging to the ![]() ${\rm Z}_2\times {\rm O}(2)$ symmetry group will alter the nature and characteristics of the secondary bifurcations. Modes A and B may preserve their respective symmetries only approximately, but the inconmensurate frequencies of mode QP, which did not retain any remnant of the spatiotemporal
${\rm Z}_2\times {\rm O}(2)$ symmetry group will alter the nature and characteristics of the secondary bifurcations. Modes A and B may preserve their respective symmetries only approximately, but the inconmensurate frequencies of mode QP, which did not retain any remnant of the spatiotemporal ![]() ${\rm Z}_2$ symmetry, might experience a locking into some strong resonance. As it happens, mode QP is quasi-resonant for both circular and square cylinder flows and, as the span is curved into a ring or the square tilted into incidence, the associated complex-conjugate pair of Floquet multipliers approaches the negative real axis, collides and separates into a couple of negative real eigenvalues, i.e. two subharmonic/period-doubling modes (Blackburn & Sheard Reference Blackburn and Sheard2010; Sheard Reference Sheard2011). It is thus that mode QP evolves into mode C, which eventually overtakes modes A and B in driving the secondary instability once the reflection symmetry across the midplane has been sufficiently broken.
${\rm Z}_2$ symmetry, might experience a locking into some strong resonance. As it happens, mode QP is quasi-resonant for both circular and square cylinder flows and, as the span is curved into a ring or the square tilted into incidence, the associated complex-conjugate pair of Floquet multipliers approaches the negative real axis, collides and separates into a couple of negative real eigenvalues, i.e. two subharmonic/period-doubling modes (Blackburn & Sheard Reference Blackburn and Sheard2010; Sheard Reference Sheard2011). It is thus that mode QP evolves into mode C, which eventually overtakes modes A and B in driving the secondary instability once the reflection symmetry across the midplane has been sufficiently broken.
The bifurcation scenario is clarified by the sketch in figure 1, which shows the schematic arrangement of bifurcation curves upon varying a top–bottom symmetry-breaking parameter (for instance, incidence ![]() $\alpha$ for a square cylinder, shear parameter
$\alpha$ for a square cylinder, shear parameter ![]() $K$ for either square or circular cylinders, or the ring aspect ratio
$K$ for either square or circular cylinders, or the ring aspect ratio ![]() $\varGamma$ for circular rings). The subcritical/supercritical nature of the bifurcations has only been investigated for the symmetric case, and then only undisputably settled for the circular cylinder case. Besides, criticality may change along the bifurcation curves in codimension-two points for some of the symmetry-breaking problems the sketch is meant to represent but not for others.
$\varGamma$ for circular rings). The subcritical/supercritical nature of the bifurcations has only been investigated for the symmetric case, and then only undisputably settled for the circular cylinder case. Besides, criticality may change along the bifurcation curves in codimension-two points for some of the symmetry-breaking problems the sketch is meant to represent but not for others.
Upstream shear has been shown in experiments to delay the onset of periodic vortex shedding, i.e. ![]() $Re^{H}$ increases with
$Re^{H}$ increases with ![]() $K$, to the point that shedding can be completely suppressed all the way up to
$K$, to the point that shedding can be completely suppressed all the way up to ![]() $Re<220$ (Kiya et al. Reference Kiya, Tamura and Arie1980). This effect has also been observed in numerical simulation (Tamura et al. Reference Tamura, Kiya and Arie1980). Other computational studies, however, did not detect the phenomenon despite exploring similar values of the parameters (Lei, Cheng & Kavanagh Reference Lei, Cheng and Kavanagh2000; Cao et al. Reference Cao, Ozono, Tamura, Ge and Kikugawa2010). No satisfactory explanation for this discrepancy has been offered.
$Re<220$ (Kiya et al. Reference Kiya, Tamura and Arie1980). This effect has also been observed in numerical simulation (Tamura et al. Reference Tamura, Kiya and Arie1980). Other computational studies, however, did not detect the phenomenon despite exploring similar values of the parameters (Lei, Cheng & Kavanagh Reference Lei, Cheng and Kavanagh2000; Cao et al. Reference Cao, Ozono, Tamura, Ge and Kikugawa2010). No satisfactory explanation for this discrepancy has been offered.
Stability analysis seems to favour the notion that ![]() $Re^{H}$ is mostly unaffected by
$Re^{H}$ is mostly unaffected by ![]() $K$, and that, if anything, it is marginally promoted to slightly lower values, from 46.5 for
$K$, and that, if anything, it is marginally promoted to slightly lower values, from 46.5 for ![]() $K=0$ to 45.5 for
$K=0$ to 45.5 for ![]() $K=0.2$ (Park & Yang Reference Park and Yang2018). Floquet stability analysis shows that the wake transition regime is instead greatly affected by upstream shear. While modes A, B and QP bifurcate at successively large values
$K=0.2$ (Park & Yang Reference Park and Yang2018). Floquet stability analysis shows that the wake transition regime is instead greatly affected by upstream shear. While modes A, B and QP bifurcate at successively large values ![]() $(Re^{A}\simeq 190)<(Re^{B}\simeq 250)<(Re^{QP}\simeq 380)$ in the symmetric problem, mode QP locks into subharmonic mode C as
$(Re^{A}\simeq 190)<(Re^{B}\simeq 250)<(Re^{QP}\simeq 380)$ in the symmetric problem, mode QP locks into subharmonic mode C as ![]() $K$ is increased and gradually overtakes mode B and mode A for
$K$ is increased and gradually overtakes mode B and mode A for ![]() $K=0.1$ and
$K=0.1$ and ![]() $0.2$, respectively (Park & Yang Reference Park and Yang2018). As a matter of fact, modes A and B are pushed to higher
$0.2$, respectively (Park & Yang Reference Park and Yang2018). As a matter of fact, modes A and B are pushed to higher ![]() $Re^{A}\simeq 240$ and
$Re^{A}\simeq 240$ and ![]() $Re^{B}\simeq 300$, while mode C is advanced to as low as
$Re^{B}\simeq 300$, while mode C is advanced to as low as ![]() $Re^{C}\simeq 150$ for
$Re^{C}\simeq 150$ for ![]() $K=0.2$. While the critical spanwise wavelength of mode A slightly increases to
$K=0.2$. While the critical spanwise wavelength of mode A slightly increases to ![]() $\lambda _z^{A}\simeq 4.2$, mode B remains mostly unaltered at
$\lambda _z^{A}\simeq 4.2$, mode B remains mostly unaltered at ![]() $\lambda _z^{B}\simeq 0.8$ and mode C somewhat narrows to
$\lambda _z^{B}\simeq 0.8$ and mode C somewhat narrows to ![]() $\lambda _z^{C}\simeq 1.6$ for
$\lambda _z^{C}\simeq 1.6$ for ![]() $K=0.2$. Numerical simulation has seen mode-A-type structures suppressed, and with them three dimensionality, at
$K=0.2$. Numerical simulation has seen mode-A-type structures suppressed, and with them three dimensionality, at ![]() $Re\simeq 200$ with
$Re\simeq 200$ with ![]() $K\gtrsim 0.1$, accompanied by the ensuing discontinuity in the
$K\gtrsim 0.1$, accompanied by the ensuing discontinuity in the ![]() $St$ vs
$St$ vs ![]() $Re$ relationship (Cao et al. Reference Cao, Ozono, Tamura, Ge and Kikugawa2010). This phenomenon has not been observed in experiments and the emergence of longitudinal vortical structures in the upstream flow may be accounted responsible.
$Re$ relationship (Cao et al. Reference Cao, Ozono, Tamura, Ge and Kikugawa2010). This phenomenon has not been observed in experiments and the emergence of longitudinal vortical structures in the upstream flow may be accounted responsible.
The onset of time dependence ![]() $Re^{H}$ is slightly advanced and the mean drag coefficient
$Re^{H}$ is slightly advanced and the mean drag coefficient ![]() $C_d$ and Strouhal number
$C_d$ and Strouhal number ![]() $St$ reduced for the flow past a square cylinder subjected to increasing
$St$ reduced for the flow past a square cylinder subjected to increasing ![]() $K$ (Cheng, Whyte & Lou Reference Cheng, Whyte and Lou2007; Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2008). At these very low values of
$K$ (Cheng, Whyte & Lou Reference Cheng, Whyte and Lou2007; Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2008). At these very low values of ![]() $Re$, the lift force coefficient
$Re$, the lift force coefficient ![]() $C_l$ is negative and its modulus increases with increasing
$C_l$ is negative and its modulus increases with increasing ![]() $K$ (Cheng et al. Reference Cheng, Whyte and Lou2007; Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2008), but the trend is reversed at higher
$K$ (Cheng et al. Reference Cheng, Whyte and Lou2007; Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2008), but the trend is reversed at higher ![]() $Re$ (Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2011).
$Re$ (Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2011).
The decrease in ![]() $Re^{H}$ has been belied by two-dimensional simulations that explored larger values of
$Re^{H}$ has been belied by two-dimensional simulations that explored larger values of ![]() $K$ and reported suppression of two-dimensional vortex shedding behind a square cylinder at sufficiently low values of
$K$ and reported suppression of two-dimensional vortex shedding behind a square cylinder at sufficiently low values of ![]() $Re\lesssim 200$ whenever
$Re\lesssim 200$ whenever ![]() $K\gtrsim K_c$ exceeds a certain critical value that increases with
$K\gtrsim K_c$ exceeds a certain critical value that increases with ![]() $Re$ (Cheng et al. Reference Cheng, Whyte and Lou2007; Ray & Kumar Reference Ray and Kumar2017). As for the circular cylinder, an increasing
$Re$ (Cheng et al. Reference Cheng, Whyte and Lou2007; Ray & Kumar Reference Ray and Kumar2017). As for the circular cylinder, an increasing ![]() $K$ renders top vortices stronger and rounder, while bottom vortices become weaker and elongated and dissipate fast in the wake (Ray & Kumar Reference Ray and Kumar2017). As for the circular cylinder, the stagnation point systematically rises above the cylinder midplane upon increasing
$K$ renders top vortices stronger and rounder, while bottom vortices become weaker and elongated and dissipate fast in the wake (Ray & Kumar Reference Ray and Kumar2017). As for the circular cylinder, the stagnation point systematically rises above the cylinder midplane upon increasing ![]() $K$ at any value of
$K$ at any value of ![]() $Re$ (Cao, Zhou & Zhou Reference Cao, Zhou and Zhou2014).
$Re$ (Cao, Zhou & Zhou Reference Cao, Zhou and Zhou2014).
In the presence of upstream shear, the wake behind a square cylinder experiences a unique secondary three-dimensionalising instability characterised by a single mode (Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2011), instead of the two modes A and B that are sequentially observed in the wake transition regime for both circular and square cylinders in the absence of upstream shear. This single mode, which arises at ![]() $Re\in (140,150)$ when
$Re\in (140,150)$ when ![]() $K=0.2$, was initially mistaken for mode B (Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2011) because of its similar wavelength, but the solution seems in fact period doubled. Its three-dimensional structure appears shifted by half a wavelength after every vortex-shedding cycle, so that the instability would plausibly correspond to mode C, which would have taken precedence over modes A and B following the disruption of the spatial
$K=0.2$, was initially mistaken for mode B (Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2011) because of its similar wavelength, but the solution seems in fact period doubled. Its three-dimensional structure appears shifted by half a wavelength after every vortex-shedding cycle, so that the instability would plausibly correspond to mode C, which would have taken precedence over modes A and B following the disruption of the spatial ![]() ${\rm Z}_2$ symmetry. At
${\rm Z}_2$ symmetry. At ![]() $Re=200$ and
$Re=200$ and ![]() $K=0.2$, three-dimensional simulations have shown mode-A- and mode-B-type structures on the low and high velocity halves, respectively, of the wake (Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2009), although nothing similar has been reported elsewhere.
$K=0.2$, three-dimensional simulations have shown mode-A- and mode-B-type structures on the low and high velocity halves, respectively, of the wake (Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2009), although nothing similar has been reported elsewhere.
Here we choose to submerge the square cylinder in a thin shear layer by replacing the classic upstream homogeneous shear by a piecewise-constant velocity profile with the discontinuity separating the top and bottom homogeneous streamwise velocities precisely located at cylinder mid-height. This same set-up has been used twice before, but the flow was expressly kept two dimensional (Mushyam & Bergada Reference Mushyam and Bergada2017; An et al. Reference An, Bergadà, Mellibovsky, Sang and Xi2020). In order to simulate experimentally reproducible conditions, we choose to separate the top and bottom homogeneous velocity streams by a flat plate, such that the shear layer results from the reunion, at its trailing edge, of the top and bottom boundary layers and develops smoothly downstream before reaching the cylinder. This kind of upstream condition may be obtained experimentally in a wind or water tunnel (Loucks & Wallace Reference Loucks and Wallace2012), and the development of the shear layers thus generated have been thoroughly investigated (Rogers & Moser Reference Rogers and Moser1992; Moser & Rogers Reference Moser and Rogers1993). The length of the plate, the gap left between its trailing edge and the cylinder and the Reynolds number below the plate are kept constant. The top-to-bottom stream velocity ratio has been varied and the various distinct flow topologies that arise classified. The flow mechanisms associated to each one of the solutions occurring along the path from steady to chaotic were thoroughly investigated and minutely described in a separate publication (El Mansy et al. Reference El Mansy, Bergadà, Sarwar and Mellibovsky2022). Also the effects of upstream shear (as introduced through our singular choice of flow configuration) on aerodynamic performance trends was thoroughly dissected there. Here we go one step further and analyse and discuss in detail the instability mechanism that triggers the onset of three dimensionality and subsequently imprints the ensuing evolution of three-dimensional vortical structures in the cylinder wake. Also, we further investigate the extent to which our more realistic and experimentally sound configuration, the step-like upstream velocity profile, echoes the case of homogenous upstream shear.
The paper is structured as follows. The mathematical modelling is presented in § 2 alongside the numerical approach undertaken. Section 3 dissects the flow generated by the interaction of the two different velocity streams as they flow parallel in the splitter plate wake towards the square cylinder. A temporal characterisation of the resulting flow past the cylinder is then given in § 4, followed by a minute dissection of the wake transition regime in § 5. Section 6 briefly inspects the aerodynamic performances trends. Finally, a raw account of the separate effects of Reynolds number and top-to-bottom velocity ratio parameter is given in § 7, and the main results summarised and conclusions drawn in § 8.
2. Mathematical modelling and numerical approach
Figure 2 presents the side and front views of the computational domain employed in the simulations. The square cylinder, of side ![]() $D$, is located at the origin of the domain, of size
$D$, is located at the origin of the domain, of size ![]() $L_x\times L_y=34.5D\times 16D$, at a distance
$L_x\times L_y=34.5D\times 16D$, at a distance ![]() $L_x^{u}=9D$ downstream from the domain inlet, and at mid-height, such that the top and bottom boundaries are at a distance
$L_x^{u}=9D$ downstream from the domain inlet, and at mid-height, such that the top and bottom boundaries are at a distance ![]() $L_y/2=8D$ above and below the centreline (blockage ratio
$L_y/2=8D$ above and below the centreline (blockage ratio ![]() $B=0.0625$). All cases were studied with incidence
$B=0.0625$). All cases were studied with incidence ![]() $\alpha =0^{\circ }$ (all sides are either parallel or orthogonal to the incoming flow direction). The splitter plate, of chord
$\alpha =0^{\circ }$ (all sides are either parallel or orthogonal to the incoming flow direction). The splitter plate, of chord ![]() $L=6.5D$ and negligible thickness, extends horizontally from domain inlet at mid-height, thus leaving a
$L=6.5D$ and negligible thickness, extends horizontally from domain inlet at mid-height, thus leaving a ![]() $G\equiv L_x^{u}-L-D/2=2D$ gap between its trailing edge and the front face of the cylinder. The small distance left for the development of the shear layer has been checked to be sufficiently short to keep it thin and stable while at the same time long enough for the flow to freely adapt to the presence of the cylinder (see § 3). Meanwhile, the short splitter plate helps smooth the initiation of the shear layer while keeping the boundary layer thin and laminar. A downstream extent of
$G\equiv L_x^{u}-L-D/2=2D$ gap between its trailing edge and the front face of the cylinder. The small distance left for the development of the shear layer has been checked to be sufficiently short to keep it thin and stable while at the same time long enough for the flow to freely adapt to the presence of the cylinder (see § 3). Meanwhile, the short splitter plate helps smooth the initiation of the shear layer while keeping the boundary layer thin and laminar. A downstream extent of ![]() $L_x^{d}=L_x-L_x^{u}=25.5D$ has been allowed to properly capture the wake and avoid interferences of the domain outlet with the flow around the cylinder and in its near wake.
$L_x^{d}=L_x-L_x^{u}=25.5D$ has been allowed to properly capture the wake and avoid interferences of the domain outlet with the flow around the cylinder and in its near wake.

Figure 2. Computational domain. (a) Sketch of the square cylinder. (b) Side and (c) front views of the computational domain. The colours indicate the boundary condition types: velocity inlet (red, with velocities ![]() $U_T$ and
$U_T$ and ![]() $U_B$ for the top and bottom streams, respectively), pressure outlet (blue), slip walls (green), non-slip walls (black) and periodic (orange).
$U_B$ for the top and bottom streams, respectively), pressure outlet (blue), slip walls (green), non-slip walls (black) and periodic (orange).
The Navier–Stokes equations for incompressible flow, non-dimensionalised with the square cylinder side length ![]() $D$ and the mean upstream flow velocity
$D$ and the mean upstream flow velocity ![]() $U=(U_T+U_B)/2$ (
$U=(U_T+U_B)/2$ (![]() $U_T$ and
$U_T$ and ![]() $U_B$ are the top and bottom stream constant velocities), read
$U_B$ are the top and bottom stream constant velocities), read
 \begin{equation}
\left.\begin{gathered} \dfrac{\partial
\boldsymbol{u}}{\partial t} + (\boldsymbol{u}
\boldsymbol{\cdot} \boldsymbol{\nabla}) \boldsymbol{u}
={-}\boldsymbol{\nabla} p + \dfrac{1}{Re} \nabla^{2}
\boldsymbol{u}, \\ \boldsymbol{\nabla}\boldsymbol{\cdot}
{\boldsymbol{u}} = 0, \end{gathered}\right\}
\end{equation}
\begin{equation}
\left.\begin{gathered} \dfrac{\partial
\boldsymbol{u}}{\partial t} + (\boldsymbol{u}
\boldsymbol{\cdot} \boldsymbol{\nabla}) \boldsymbol{u}
={-}\boldsymbol{\nabla} p + \dfrac{1}{Re} \nabla^{2}
\boldsymbol{u}, \\ \boldsymbol{\nabla}\boldsymbol{\cdot}
{\boldsymbol{u}} = 0, \end{gathered}\right\}
\end{equation}
where ![]() $\boldsymbol {u}(\boldsymbol {r} ; t)=(u, v, w)$ and
$\boldsymbol {u}(\boldsymbol {r} ; t)=(u, v, w)$ and ![]() $p(\boldsymbol {r} ; t)$ are the non-dimensional velocity and pressure, respectively, at non-dimensional location
$p(\boldsymbol {r} ; t)$ are the non-dimensional velocity and pressure, respectively, at non-dimensional location ![]() $\boldsymbol {r}=(x, y, z)$ and advective time
$\boldsymbol {r}=(x, y, z)$ and advective time ![]() $t$ (units of
$t$ (units of ![]() $D/U$). Here,
$D/U$). Here, ![]() $x$ (
$x$ (![]() $u$),
$u$), ![]() $y$ (
$y$ (![]() $v$) and
$v$) and ![]() $z$ (
$z$ (![]() $w$) denote the streamwise, crossflow and spanwise coordinates (velocity components), respectively.
$w$) denote the streamwise, crossflow and spanwise coordinates (velocity components), respectively.
Neumann boundary conditions for pressure (![]() $\boldsymbol {\nabla } p \boldsymbol {\cdot} \hat {\boldsymbol {n}} = 0$,
$\boldsymbol {\nabla } p \boldsymbol {\cdot} \hat {\boldsymbol {n}} = 0$, ![]() $\hat {\boldsymbol {n}}$ being the exterior surface unit normal) and Dirichlet for velocity have been prescribed at the domain inlet. The velocity profile has been taken as a piecewise-constant function, with
$\hat {\boldsymbol {n}}$ being the exterior surface unit normal) and Dirichlet for velocity have been prescribed at the domain inlet. The velocity profile has been taken as a piecewise-constant function, with ![]() ${\boldsymbol {u}} = U_B\, \hat {\boldsymbol {x}} = 2U/(R+1)\, \hat {\boldsymbol {x}}$ below the splitter plate and
${\boldsymbol {u}} = U_B\, \hat {\boldsymbol {x}} = 2U/(R+1)\, \hat {\boldsymbol {x}}$ below the splitter plate and ![]() ${\boldsymbol {u}} = U_T\, \hat {\boldsymbol {x}} = 2U R/(R+1)\, \hat {\boldsymbol {x}}$ above it. No-slip boundary conditions have been enforced on cylinder walls and splitter plate (
${\boldsymbol {u}} = U_T\, \hat {\boldsymbol {x}} = 2U R/(R+1)\, \hat {\boldsymbol {x}}$ above it. No-slip boundary conditions have been enforced on cylinder walls and splitter plate (![]() ${\boldsymbol {u}}=\boldsymbol {0}$,
${\boldsymbol {u}}=\boldsymbol {0}$, ![]() $\boldsymbol {\nabla } p \boldsymbol {\cdot } \hat {\boldsymbol {n}} = 0$). The top and bottom domain boundaries have been taken as slip walls with
$\boldsymbol {\nabla } p \boldsymbol {\cdot } \hat {\boldsymbol {n}} = 0$). The top and bottom domain boundaries have been taken as slip walls with ![]() ${\boldsymbol {u}}\boldsymbol {\cdot} \hat {\boldsymbol {n}} = 0$ and
${\boldsymbol {u}}\boldsymbol {\cdot} \hat {\boldsymbol {n}} = 0$ and ![]() $[(\boldsymbol {\nabla }{\boldsymbol {u}})\boldsymbol {\cdot } \hat {\boldsymbol {n}}] \times \hat {\boldsymbol {n}} = \textbf {0}$, and the domain outlet has been set as homogenoeous Dirichlet (
$[(\boldsymbol {\nabla }{\boldsymbol {u}})\boldsymbol {\cdot } \hat {\boldsymbol {n}}] \times \hat {\boldsymbol {n}} = \textbf {0}$, and the domain outlet has been set as homogenoeous Dirichlet (![]() $p=p_{\infty }=0$) for pressure and homogeneous Neumann (
$p=p_{\infty }=0$) for pressure and homogeneous Neumann (![]() $\boldsymbol {\nabla }{\boldsymbol {u}} \boldsymbol {\cdot } \hat {\boldsymbol {n}} = \textbf {0}$) for velocity. Periodic boundary conditions in the spanwise direction have been prescribed for three-dimensional simulations.
$\boldsymbol {\nabla }{\boldsymbol {u}} \boldsymbol {\cdot } \hat {\boldsymbol {n}} = \textbf {0}$) for velocity. Periodic boundary conditions in the spanwise direction have been prescribed for three-dimensional simulations.
The two governing parameters are the Reynolds number and the top-to-bottom stream velocity ratio:
where ![]() $\nu$ is the kinematic viscosity of the fluid.
$\nu$ is the kinematic viscosity of the fluid.
Two separate Reynolds numbers might be defined individually for the top and bottom streams as
and used as an alternative set of governing parameters.
For the somewhat related problem of a bluff body immersed in upstream shear, the shear parameter is usually defined by non-dimensionalising the free-stream velocity gradient as
Here the free-stream velocity is a step function and an equivalent shear parameter can be defined with the average free-stream velocity gradient over the characteristic length of the cylinder as ![]() $K\equiv 2(R-1)/(R+1)$.
$K\equiv 2(R-1)/(R+1)$.
As we will see in § 3, the incoming flow shear profile is anything but homogeneous, but a parallel can still be drawn on account of the mean shear effects over the cylinder characteristic length, even if shear is concentrated within a thinner layer. This would indicate that part of the phenomenology observed in the presence of homogeneous upstream shear is in fact related to the velocity difference/jump perceived locally by the upper and lower sides of the body under scrutiny, rather than the global effect of the velocity gradient alone.
The bottom stream Reynolds number has been kept fixed to ![]() $Re_B=56$ throughout the study, while the top-to-bottom stream velocity ratio has been varied in the range
$Re_B=56$ throughout the study, while the top-to-bottom stream velocity ratio has been varied in the range ![]() $R\in [1,6.5]$. A
$R\in [1,6.5]$. A ![]() $\Delta R=0.2$ step has been used to resolve
$\Delta R=0.2$ step has been used to resolve ![]() $R\in [1,3]$ while higher velocity ratios have been tested at a set of discrete values
$R\in [1,3]$ while higher velocity ratios have been tested at a set of discrete values ![]() $R\in \{3.1,3.2,3.3,3.4,3.8,4,5.357,6.5\}$. The equivalent Reynolds number and shear parameter, which are linked to
$R\in \{3.1,3.2,3.3,3.4,3.8,4,5.357,6.5\}$. The equivalent Reynolds number and shear parameter, which are linked to ![]() $R$, have been simultaneously varied in the ranges
$R$, have been simultaneously varied in the ranges ![]() $Re\in [56,210]$ and
$Re\in [56,210]$ and ![]() $K\in [0,1.4667]$.
$K\in [0,1.4667]$.
Wall shear (![]() $\tau _w$) and pressure (
$\tau _w$) and pressure (![]() $p$) have been non-dimensionalised into the friction and pressure coefficients as
$p$) have been non-dimensionalised into the friction and pressure coefficients as
with ![]() $p_{\infty }=0$ the far-field pressure, while their added integral over the cylinder surface, the aerodynamic force, has been projected into the classical lift (
$p_{\infty }=0$ the far-field pressure, while their added integral over the cylinder surface, the aerodynamic force, has been projected into the classical lift (![]() $F_l$) and drag (
$F_l$) and drag (![]() $F_d$) components per unit length and non-dimensionalised into the lift and drag force coefficients following
$F_d$) components per unit length and non-dimensionalised into the lift and drag force coefficients following
The non-dimensional vortex-shedding frequency is often referred to as the Strouhal number ![]() $St=f_{{vK}}D/U$.
$St=f_{{vK}}D/U$.
The incompressible Navier–Stokes equations have been evolved in time using Nektar++, an open source code based on the spectral/hp element method framework (Cantwell et al. Reference Cantwell2015). This method combines the geometric flexibility of the finite element method with the high-order accuracy of spectral methods (the h in hp refers to mesh refinement by decreasing the elements size, while the p alludes to refinement by increasing the order of the polynomial expansions). We have employed the velocity correction scheme, which is made to be consistent with its overall temporal accuracy by an appropriate high-order discretisation of the pressure on all boundaries (Cantwell et al. Reference Cantwell2015; Moxey et al. Reference Moxey2020).
The in-plane two-dimensional structured mesh, consisting exclusively of quad elements, is shown in figure 3. A particularly high resolution has been employed on all no-slip wall surfaces to properly resolve boundary layers, as well as along the splitter plate and cylinder wakes. Away from these regions, the mesh density has been allowed to relax. Tensor products of Lagrange polynomial bases of second order have been deployed within each quadrilateral element and spanwise Fourier expansions have been used in the homogenous spanwise direction for three-dimensional computations.

Figure 3. Computational mesh. (a) Full domain and (b) detail around the square cylinder.
An in-plane mesh consisting of ![]() $N_{xy}=14\,426$ second-order quadrilateral elements has been used throughout, with the time step set at
$N_{xy}=14\,426$ second-order quadrilateral elements has been used throughout, with the time step set at ![]() $\Delta t=3\times 10^{-3}\,D/U$ for all two-dimensional cases and then gradually reduced to
$\Delta t=3\times 10^{-3}\,D/U$ for all two-dimensional cases and then gradually reduced to ![]() $1.2\times 10^{-3}$ at the highest attained velocity ratio in order to meet the Courant–Friedrichs–Lewy condition and warrant satisfactory accuracy. For three-dimensional solutions, the number of Fourier modes in the spanwise direction has been chosen so as to always secure six orders of magnitude decay in modal energy from the first non-homogeneous non-zero mode to the last, a standard requirement guaranteeing three significant digits accuracy in the velocity fields. All simulations were run for at least
$1.2\times 10^{-3}$ at the highest attained velocity ratio in order to meet the Courant–Friedrichs–Lewy condition and warrant satisfactory accuracy. For three-dimensional solutions, the number of Fourier modes in the spanwise direction has been chosen so as to always secure six orders of magnitude decay in modal energy from the first non-homogeneous non-zero mode to the last, a standard requirement guaranteeing three significant digits accuracy in the velocity fields. All simulations were run for at least ![]() $T=500\,D/U$ past all transients and then statistics collected over an additional minimum of
$T=500\,D/U$ past all transients and then statistics collected over an additional minimum of ![]() $400\,D/U$ (40 to 60 vortex-shedding cycles for unsteady solutions), which has been shown to provide excellent statistical convergence. Increasing the polynomial expansion order to three, and doubling the cross-stream and downstream lengths of the domain did not result in significant deviations. A thorough validation of the method, including comparison against benchmark data, and detailed domain and mesh convergence studies may be found in El Mansy et al. (Reference El Mansy, Bergadà, Sarwar and Mellibovsky2022).
$400\,D/U$ (40 to 60 vortex-shedding cycles for unsteady solutions), which has been shown to provide excellent statistical convergence. Increasing the polynomial expansion order to three, and doubling the cross-stream and downstream lengths of the domain did not result in significant deviations. A thorough validation of the method, including comparison against benchmark data, and detailed domain and mesh convergence studies may be found in El Mansy et al. (Reference El Mansy, Bergadà, Sarwar and Mellibovsky2022).
In accordance with the Floquet stability analysis of § 5.1, spanwise lengths ![]() $L_z=5D$ have been employed in most three-dimensional computations, deploying resolutions in the range
$L_z=5D$ have been employed in most three-dimensional computations, deploying resolutions in the range ![]() $N_z\in [28,40]$ to guarantee the aforementioned six orders of magnitude energy decay in the spanwise Fourier spectrum. The spanwise-periodic extent of the domain has been chosen about twice the wavelength of the dominant eigenmode, as this was found to be the minimum size required to sustain spatiotemporally chaotic dynamics at sufficiently high but still moderate flow regimes. In this sense, our domain can be considered analogous to the classic minimal flow unit that is often employed in studying near-wall turbulence (Jimenez & Moin Reference Jimenez and Moin1991). A few cases with
$N_z\in [28,40]$ to guarantee the aforementioned six orders of magnitude energy decay in the spanwise Fourier spectrum. The spanwise-periodic extent of the domain has been chosen about twice the wavelength of the dominant eigenmode, as this was found to be the minimum size required to sustain spatiotemporally chaotic dynamics at sufficiently high but still moderate flow regimes. In this sense, our domain can be considered analogous to the classic minimal flow unit that is often employed in studying near-wall turbulence (Jimenez & Moin Reference Jimenez and Moin1991). A few cases with ![]() $L_z=10D$ and
$L_z=10D$ and ![]() $N_z=80$ have been run at the highest explored values of
$N_z=80$ have been run at the highest explored values of ![]() $R$ to confirm that the characteristic features of the spatiotemporally chaotic flow structures present in the wake are not an artifact of overly limited domain size. Additionally, some exploratory runs have been performed in a
$R$ to confirm that the characteristic features of the spatiotemporally chaotic flow structures present in the wake are not an artifact of overly limited domain size. Additionally, some exploratory runs have been performed in a ![]() $L_z=10D$ domain across the wake transition regime
$L_z=10D$ domain across the wake transition regime ![]() $R\in [3.2,3.8]$ to assess the robustness of the bifurcation scenario we report for
$R\in [3.2,3.8]$ to assess the robustness of the bifurcation scenario we report for ![]() $L_z=5D$.
$L_z=5D$.
The uncertainty in the values of the parameters and corresponding solution/mode charasteristic features across the transitions among the different types of flows studied here are reported with open intervals when inferred from a limited bounding set of nonlinear solutions, and with the approximately equal symbol (![]() $\simeq$) when interpolated from stability analysis results. Literature values provided in the introduction have been given as originally reported by the corresponding sources.
$\simeq$) when interpolated from stability analysis results. Literature values provided in the introduction have been given as originally reported by the corresponding sources.
The particular choice of splitter plate length and the gap left between its trailing edge and the front face of the cylinder might seem somewhat arbitrary. We ran a preliminary parametric study varying ![]() $L\in \{6.5D, 9D, 13D, 20D\}$ and
$L\in \{6.5D, 9D, 13D, 20D\}$ and ![]() $G\in \{2D, 4D, 6D\}$ in order to assess their impact on the results we present. The transition path from steady to chaotic remains qualitatively the same although, as expected, some quantitative differences are observed. Enlarging the gap has the effect of advancing the three-dimensionalising bifurcation to lower values of
$G\in \{2D, 4D, 6D\}$ in order to assess their impact on the results we present. The transition path from steady to chaotic remains qualitatively the same although, as expected, some quantitative differences are observed. Enlarging the gap has the effect of advancing the three-dimensionalising bifurcation to lower values of ![]() $R$, while extending the splitter plate has the opposite effect.
$R$, while extending the splitter plate has the opposite effect.
3. Incoming upstream flow
The initially flat interface of two parallel viscous streams flowing at different speeds is not stable. The step profile of purely streamwise velocity at best diffuses into an increasingly wide shear layer or, more generally, destabilises following a Kelvin–Helmholtz instability. The aim here is to subject the square cylinder to as close a step profile as experimentally feasible by keeping the distance over which the two streams interact to a minimum while still allowing the upstream flow to adapt to the incoming obstacle. In order to smooth the development of the shear layer, the two streams have been allowed to flow over a flat plate for some distance before meeting, sufficiently long for a Blasius boundary layer to develop but at the same time short enough for it to remain thin and laminar.
Figure 4 depicts cross-stream profiles of streamwise velocity as the flow develops over the splitter plate and downstream along its wake, which constitutes a shear layer for ![]() $R>1$. The flow is essentially two dimensional and steady in this region for all cases considered, but spanwise and time averaging has been applied nonetheless.
$R>1$. The flow is essentially two dimensional and steady in this region for all cases considered, but spanwise and time averaging has been applied nonetheless.

Figure 4. Span- and time-averaged characterisation of the incoming flow as it develops on the splitter plate and downstream along the near wake, covering the gap with the square cylinder. Shown are cross-stream profiles of streamwise velocity over the flat plate (main panel) and the plate-cylinder gap (top panels), along with centreline distribution of cross-stream velocity in the gap (inset). Velocity ratios ![]() $R=1$ (light grey), 2 (dark grey), 3.4 (red) and 5.357 (green) have been represented both in the presence (solid) and absence (dashed) of the cylinder. Time-averaged streamlines around the cylinder are specifically shown for the two-dimensional case
$R=1$ (light grey), 2 (dark grey), 3.4 (red) and 5.357 (green) have been represented both in the presence (solid) and absence (dashed) of the cylinder. Time-averaged streamlines around the cylinder are specifically shown for the two-dimensional case ![]() $R=3$.
$R=3$.
In the absence of the square cylinder (dashed lines), laminar boundary layers of the Blasius type naturally develop on both surfaces of the splitter plate. For ![]() $R=1$ (light grey), top and bottom boundary layers are symmetric and generate a top–bottom symmetric velocity profile in the wake that diffuses gradually as the centreline velocity, which coincides with the streamline issued from the trailing edge of the flat plate, progressively recovers. The asymmetry is already evident for
$R=1$ (light grey), top and bottom boundary layers are symmetric and generate a top–bottom symmetric velocity profile in the wake that diffuses gradually as the centreline velocity, which coincides with the streamline issued from the trailing edge of the flat plate, progressively recovers. The asymmetry is already evident for ![]() $R=2$ (dark grey) and becomes increasingly marked for
$R=2$ (dark grey) and becomes increasingly marked for ![]() $R=3.4$ (red) and 5.357 (green), but the centreline velocity defect is recovered all the same as the velocity profile adopts a smoothed step-like shape that connects the top and bottom stream velocities fairly linearly over about half the square cylinder height by the time the flow reaches the (absent) cylinder location. The higher the value of
$R=3.4$ (red) and 5.357 (green), but the centreline velocity defect is recovered all the same as the velocity profile adopts a smoothed step-like shape that connects the top and bottom stream velocities fairly linearly over about half the square cylinder height by the time the flow reaches the (absent) cylinder location. The higher the value of ![]() $R$, the faster and greater the velocity defect recovery with respect to the slow stream, such that the negative shear associated to the lower side of the shear layer becomes barely detectable. The resulting region of roughly homogeneous shear is noticeably shifted towards the high velocity side. Meanwhile, the trailing-edge streamline remains horizontal independently of
$R$, the faster and greater the velocity defect recovery with respect to the slow stream, such that the negative shear associated to the lower side of the shear layer becomes barely detectable. The resulting region of roughly homogeneous shear is noticeably shifted towards the high velocity side. Meanwhile, the trailing-edge streamline remains horizontal independently of ![]() $R$, as ascertained by the zero cross-stream velocity distribution along the wake centreline in the inset of figure 4. None of the cases run for the splitter plate alone resulted in any instability of its wake or trailing shear layer, such that the flow fields remained two dimensional and steady.
$R$, as ascertained by the zero cross-stream velocity distribution along the wake centreline in the inset of figure 4. None of the cases run for the splitter plate alone resulted in any instability of its wake or trailing shear layer, such that the flow fields remained two dimensional and steady.
We will be placing the square cylinder at a downstream distance from the splitter plate trailing edge where the unperturbed flow is characterised by a parallel profile of purely streamwise velocity that is neither linear nor a step function, but can be assimilated to a step function smoothed over about half the cylinder height. Anyhow, whatever the profile looks like across the cylinder height, it can be considered as fairly flat above and below the cross-stream locations where the top and bottom surface of the cylinder will be, with respective velocities those of the fast and slow streams. The streamwise velocity can therefore be taken as approximating to some extent the intended step profile.
The presence of the cylinder (solid lines), introduces a blockage that obviously affects the incoming flow. The boundary layers on the top and bottom surfaces of the flat plate are somewhat thickened, particularly on the low velocity side and for low values of ![]() $R$. As an example, the splitter plate trailing-edge momentum thickness grows at
$R$. As an example, the splitter plate trailing-edge momentum thickness grows at ![]() $R=3.4$ from
$R=3.4$ from ![]() $\theta =9.29\times 10^{-2}$ to
$\theta =9.29\times 10^{-2}$ to ![]() $9.78\times 10^{-2}$ and from
$9.78\times 10^{-2}$ and from ![]() $15.3\times 10^{-2}$ to
$15.3\times 10^{-2}$ to ![]() $21.8\times 10^{-2}$ for the top and bottom boundary layers, respectively. The massflow blockage becomes all the more dominant as we dive into the plate wake. The shear layer remains fairly thin while the presence of the cylinder is still not decisively felt. As the cylinder is approached, the streamwise velocity recovery along the wake is hindered and the lowest velocity is shifted towards the slow stream as
$21.8\times 10^{-2}$ for the top and bottom boundary layers, respectively. The massflow blockage becomes all the more dominant as we dive into the plate wake. The shear layer remains fairly thin while the presence of the cylinder is still not decisively felt. As the cylinder is approached, the streamwise velocity recovery along the wake is hindered and the lowest velocity is shifted towards the slow stream as ![]() $R$ is increased. The thickening of the shear layer as the cylinder is approached and its downwards bias results in something like a (not quite) homogeneous shear profile that spreads over the cylinder height, but still flattens to about constant velocity above and below the cylinder. In addition, a net downwards cross-stream velocity builds up along the wake that transfers massflow from the high velocity stream to the low velocity stream. An increasingly larger portion of the fast stream flies below the cylinder as the velocity ratio is increased.
$R$ is increased. The thickening of the shear layer as the cylinder is approached and its downwards bias results in something like a (not quite) homogeneous shear profile that spreads over the cylinder height, but still flattens to about constant velocity above and below the cylinder. In addition, a net downwards cross-stream velocity builds up along the wake that transfers massflow from the high velocity stream to the low velocity stream. An increasingly larger portion of the fast stream flies below the cylinder as the velocity ratio is increased.
The time-averaged streamline patterns in figure 4, shown for the specific two-dimensional case ![]() $R=3$, confirm this diversion of the flow from above the splitter plate to below the cylinder. The average recirculation bubble is no longer symmetric, in contrast with that found past symmetric bluff bodies subject to homogeneous incoming flow. Only the lower lobe remains attached (on average), while the upper lobe first detaches upon breaking the top–bottom symmetry and eventually disappears at sufficiently high
$R=3$, confirm this diversion of the flow from above the splitter plate to below the cylinder. The average recirculation bubble is no longer symmetric, in contrast with that found past symmetric bluff bodies subject to homogeneous incoming flow. Only the lower lobe remains attached (on average), while the upper lobe first detaches upon breaking the top–bottom symmetry and eventually disappears at sufficiently high ![]() $R$. The stagnation point has climbed on the front face, while that on the rear wall has moved down. The boundary layer developing on the top wall remains attached all along, such that separation only occurs at the rear corner. On the bottom surface, the separation is instead located at the very front corner, thus leaving the boundary layer fully separated. As a result, the recirculation bubble in the near wake extends upstream and covers the entire bottom wall. A detailed description of the morphing of average streamline patterns as the symmetry is broken upon increasing
$R$. The stagnation point has climbed on the front face, while that on the rear wall has moved down. The boundary layer developing on the top wall remains attached all along, such that separation only occurs at the rear corner. On the bottom surface, the separation is instead located at the very front corner, thus leaving the boundary layer fully separated. As a result, the recirculation bubble in the near wake extends upstream and covers the entire bottom wall. A detailed description of the morphing of average streamline patterns as the symmetry is broken upon increasing ![]() $R$, as well as the evolution of pressure and vorticity fields, may be found in El Mansy et al. (Reference El Mansy, Bergadà, Sarwar and Mellibovsky2022).
$R$, as well as the evolution of pressure and vorticity fields, may be found in El Mansy et al. (Reference El Mansy, Bergadà, Sarwar and Mellibovsky2022).
4. Temporal characterisation of the flow
The starting case ![]() $(Re_B,R)=(56,1)$, which roughly corresponds to the homogeneous flow past a square cylinder at
$(Re_B,R)=(56,1)$, which roughly corresponds to the homogeneous flow past a square cylinder at ![]() $Re=56$, is steady and reflection symmetric with respect to the horizontal midplane (
$Re=56$, is steady and reflection symmetric with respect to the horizontal midplane (![]() $y=0$). The presence of the splitter plate reduces the effective incoming velocity through viscous effects and, consequently, has a stabilising effect on the flow past the square cylinder, which is otherwise expected to display periodic vortex shedding already at this
$y=0$). The presence of the splitter plate reduces the effective incoming velocity through viscous effects and, consequently, has a stabilising effect on the flow past the square cylinder, which is otherwise expected to display periodic vortex shedding already at this ![]() $Re$ (Norberg Reference Norberg1996). The flow remains steady but the symmetry is broken as the velocity ratio is increased at constant
$Re$ (Norberg Reference Norberg1996). The flow remains steady but the symmetry is broken as the velocity ratio is increased at constant ![]() $Re_B=56$ all the way up to
$Re_B=56$ all the way up to ![]() $R\leqslant 2$. This is illustrated by the point phase-map projections for
$R\leqslant 2$. This is illustrated by the point phase-map projections for ![]() $R=1$ (cross) and
$R=1$ (cross) and ![]() $R=2$ (plus sign) in figure 5. The symmetric case
$R=2$ (plus sign) in figure 5. The symmetric case ![]() $R=1$ is characterised by
$R=1$ is characterised by ![]() $C_l=v=0$, while
$C_l=v=0$, while ![]() $R=2$ has evidently lost the symmetry (also
$R=2$ has evidently lost the symmetry (also ![]() $v\neq 0$, but small enough to be imperceptible to the naked eye). Soon after, a Hopf bifurcation somewhere in the range
$v\neq 0$, but small enough to be imperceptible to the naked eye). Soon after, a Hopf bifurcation somewhere in the range ![]() $R^{H}\in (2,2.2)$ introduces time dependence, such that solutions are characterised by asymmetric time-periodic vortex shedding. The periodicity shows up in the phase-map projections of figure 5 as closed loops, and the oscillation amplitude grows fast as
$R^{H}\in (2,2.2)$ introduces time dependence, such that solutions are characterised by asymmetric time-periodic vortex shedding. The periodicity shows up in the phase-map projections of figure 5 as closed loops, and the oscillation amplitude grows fast as ![]() $R$ is increased. The onset of time dependence occurs for a bulk Reynolds number
$R$ is increased. The onset of time dependence occurs for a bulk Reynolds number ![]() $Re^{H}\in (84,90)$ and shear parameter
$Re^{H}\in (84,90)$ and shear parameter ![]() $K^{H}\in (0.67,0.75)$, way larger than the critical threshold for the square cylinder in homogeneous flow, which undergoes a Hopf bifurcation at
$K^{H}\in (0.67,0.75)$, way larger than the critical threshold for the square cylinder in homogeneous flow, which undergoes a Hopf bifurcation at ![]() $Re^{H}\in (45,53)$ (Kelkar & Patankar Reference Kelkar and Patankar1992; Sohankar et al. Reference Sohankar, Norberg and Davidson1998; Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2008). The critical threshold found here corresponds to fairly high
$Re^{H}\in (45,53)$ (Kelkar & Patankar Reference Kelkar and Patankar1992; Sohankar et al. Reference Sohankar, Norberg and Davidson1998; Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2008). The critical threshold found here corresponds to fairly high ![]() $K$ and moderately low
$K$ and moderately low ![]() $Re$, which is consistent with previous observations that vortex shedding might be suppressed/delayed by upstream shear (Cheng et al. Reference Cheng, Whyte and Lou2007; Ray & Kumar Reference Ray and Kumar2017). Upstream shear has therefore a stabilising effect, as previously reported also for the circular cylinder (Kiya et al. Reference Kiya, Tamura and Arie1980; Tamura et al. Reference Tamura, Kiya and Arie1980), although some studies attest to the contrary both for circular (Park & Yang Reference Park and Yang2018) and square cylinders (Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2008). The cause of the discrepancy might have been related to blockage effects, although it is not altogether clear. Figure 6(a) shows the spectrum (
$Re$, which is consistent with previous observations that vortex shedding might be suppressed/delayed by upstream shear (Cheng et al. Reference Cheng, Whyte and Lou2007; Ray & Kumar Reference Ray and Kumar2017). Upstream shear has therefore a stabilising effect, as previously reported also for the circular cylinder (Kiya et al. Reference Kiya, Tamura and Arie1980; Tamura et al. Reference Tamura, Kiya and Arie1980), although some studies attest to the contrary both for circular (Park & Yang Reference Park and Yang2018) and square cylinders (Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2008). The cause of the discrepancy might have been related to blockage effects, although it is not altogether clear. Figure 6(a) shows the spectrum (![]() $|\hat {C}_l|$) of the lift coefficient signal (
$|\hat {C}_l|$) of the lift coefficient signal (![]() $C_l(t$), portrayed in the inset) for
$C_l(t$), portrayed in the inset) for ![]() $R=3$ (black line in figure 5). A clear peak is readily identifiable at
$R=3$ (black line in figure 5). A clear peak is readily identifiable at ![]() $f_1=0.155$, along with a few harmonics of decaying amplitude at integer multiples of the main frequency. The solution remains periodic and the fundamental peak and harmonics move to higher
$f_1=0.155$, along with a few harmonics of decaying amplitude at integer multiples of the main frequency. The solution remains periodic and the fundamental peak and harmonics move to higher ![]() $f_1$ as the velocity ratio is increased to
$f_1$ as the velocity ratio is increased to ![]() $R=3.4$ (figure 6b). Besides the slight drift of the dimensionless fundamental frequency
$R=3.4$ (figure 6b). Besides the slight drift of the dimensionless fundamental frequency ![]() $f_1$, an essential alteration has occurred that is not perceptible in the
$f_1$, an essential alteration has occurred that is not perceptible in the ![]() $C_l$ spectrum, nor in the
$C_l$ spectrum, nor in the ![]() $(C_l,C_d)$ phase-map projection for that matter, but becomes obvious instead from the
$(C_l,C_d)$ phase-map projection for that matter, but becomes obvious instead from the ![]() $(C_l,v)$ phase-map projection (red line in figure 5). The actual period of the solution is not that of the
$(C_l,v)$ phase-map projection (red line in figure 5). The actual period of the solution is not that of the ![]() $C_l$ or
$C_l$ or ![]() $C_d$ signals but double, and only shows in time series of local quantities such as point velocity probe readings. The period doubling is related to the three dimensionalisation of the flow, which will in time be shown to occur at
$C_d$ signals but double, and only shows in time series of local quantities such as point velocity probe readings. The period doubling is related to the three dimensionalisation of the flow, which will in time be shown to occur at ![]() $R\simeq 3.1$, corresponding to
$R\simeq 3.1$, corresponding to ![]() $(Re,K)\simeq (115,1.02)$. The spanwise invariance of the two-dimensional vortex-shedding flow is disrupted in a way that preserves a triad of remaining spanwise symmetries (spanwise reflection, half-period evolution followed by spanwise reflection and half-period evolution followed by a half-spanwise wavelength shift) that will be discussed later. All three symmetries retain the original period for all variables that aggregate/average over the spanwise direction, as is the case of force coefficients, but the actual invariance after a full vortex-shedding cycle requires the further composition with a space operation, such that the original solution is only fully recovered after a second vortex-shedding cycle, which makes the solution qualify as period doubled.
$(Re,K)\simeq (115,1.02)$. The spanwise invariance of the two-dimensional vortex-shedding flow is disrupted in a way that preserves a triad of remaining spanwise symmetries (spanwise reflection, half-period evolution followed by spanwise reflection and half-period evolution followed by a half-spanwise wavelength shift) that will be discussed later. All three symmetries retain the original period for all variables that aggregate/average over the spanwise direction, as is the case of force coefficients, but the actual invariance after a full vortex-shedding cycle requires the further composition with a space operation, such that the original solution is only fully recovered after a second vortex-shedding cycle, which makes the solution qualify as period doubled.

Figure 5. Phase-map projections on the (a) ![]() $(C_l,C_d)$ and (b)
$(C_l,C_d)$ and (b) ![]() $(C_l,v)$ planes, with
$(C_l,v)$ planes, with ![]() $v$ the cross-stream velocity at
$v$ the cross-stream velocity at ![]() $(x,y,z)=(2,0,z_m)$, where
$(x,y,z)=(2,0,z_m)$, where ![]() $z_m$ has been chosen in each case at the spanwise location featuring the maximum fluctuation amplitude of
$z_m$ has been chosen in each case at the spanwise location featuring the maximum fluctuation amplitude of ![]() $v$ to remove the spanwise degeneracy of three-dimensional solutions.
$v$ to remove the spanwise degeneracy of three-dimensional solutions.

Figure 6. Power spectra (![]() $|\hat {C}_l|$) of the lift coefficient for different velocity ratios. The insets show the time series of the lift coefficient. Results are shown for (a)
$|\hat {C}_l|$) of the lift coefficient for different velocity ratios. The insets show the time series of the lift coefficient. Results are shown for (a) ![]() $R=3$, (b)
$R=3$, (b) ![]() $R=3.4$, (c)
$R=3.4$, (c) ![]() $R=3.8$, (d)
$R=3.8$, (d) ![]() $R=5.357$.
$R=5.357$.
At ![]() $R=3.8$ a second period doubling of an altogether different nature has occurred. Now the bifurcation affects not only local variables but also aggregates, as clearly shown by the double loop in the
$R=3.8$ a second period doubling of an altogether different nature has occurred. Now the bifurcation affects not only local variables but also aggregates, as clearly shown by the double loop in the ![]() $(C_l,C_d)$ and the four-fold loop in the
$(C_l,C_d)$ and the four-fold loop in the ![]() $(C_l,v)$ phase-map projections (blue line in figure 5). As a matter of fact, local variables repeat only after four vortex-shedding cycles. The fundamental peak
$(C_l,v)$ phase-map projections (blue line in figure 5). As a matter of fact, local variables repeat only after four vortex-shedding cycles. The fundamental peak ![]() $f_1$ in the
$f_1$ in the ![]() $C_l$ spectrum is still dominant in figure 6(c), but a subharmonic peak at the exact half-frequency
$C_l$ spectrum is still dominant in figure 6(c), but a subharmonic peak at the exact half-frequency ![]() $f_{1/2}=f_1/2$ has arisen along with its harmonics. The flow topology only repeats every four vortex-shedding cycles, but a space–time symmetry operation still exists that renders the flow invariant after every two vortex-shedding cycles (half a period) provided an appropriate spanwise reflection is also applied.
$f_{1/2}=f_1/2$ has arisen along with its harmonics. The flow topology only repeats every four vortex-shedding cycles, but a space–time symmetry operation still exists that renders the flow invariant after every two vortex-shedding cycles (half a period) provided an appropriate spanwise reflection is also applied.
At ![]() $R=5.357$ the flow has become temporally chaotic (green line in figure 5) and though the main fundamental peak and its first few harmonics are still discernible in the spectrum of figure 6(d), they are accompanied by high-energy broadband noise. The second period-doubling bifurcation identified here is suggestive of a period-doubling cascade as the origin of chaotic dynamics, although this cannot be concluded from the rather coarse discretisation of parameter space investigated in the present study.
$R=5.357$ the flow has become temporally chaotic (green line in figure 5) and though the main fundamental peak and its first few harmonics are still discernible in the spectrum of figure 6(d), they are accompanied by high-energy broadband noise. The second period-doubling bifurcation identified here is suggestive of a period-doubling cascade as the origin of chaotic dynamics, although this cannot be concluded from the rather coarse discretisation of parameter space investigated in the present study.
5. Three dimensionalisation of the flow: wake transition regime
The reflection symmetry about the horizontal midplane is broken by setting ![]() $R\neq 1$. In these conditions the only remaining symmetries of the problem concern the spanwise direction. The problem is thus only invariant under the orthogonal group
$R\neq 1$. In these conditions the only remaining symmetries of the problem concern the spanwise direction. The problem is thus only invariant under the orthogonal group ![]() $\textrm {O}(2)=\textrm {SO}(2)\times Z_2$ symmetry, involving both arbitrary spanwise shifts (SO(2)) and mirror reflections about all planes orthogonal to the spanwise direction (
$\textrm {O}(2)=\textrm {SO}(2)\times Z_2$ symmetry, involving both arbitrary spanwise shifts (SO(2)) and mirror reflections about all planes orthogonal to the spanwise direction (![]() $\textrm {Z}_2$). As long as the solutions remain two dimensional, spanwise invariance is preserved, and the onset of time dependence does not affect the only remaining symmetry.
$\textrm {Z}_2$). As long as the solutions remain two dimensional, spanwise invariance is preserved, and the onset of time dependence does not affect the only remaining symmetry.
The bifurcation that triggers three dimensionality, though, necessarily breaks the translational invariance SO(2) and restricts the mirror symmetry ![]() $\textrm {Z}_2$ to a collection of
$\textrm {Z}_2$ to a collection of ![]() $z$ planes equispaced at intervals
$z$ planes equispaced at intervals ![]() $\lambda _z/2$, where
$\lambda _z/2$, where ![]() $\lambda _z$ is the fundamental spanwise wavelength of the arising three-dimensional solutions. Two-dimensional periodic solutions may still destabilise following both synchronous or quasi-periodic bifurcations, as was the case in the presence of the space–time
$\lambda _z$ is the fundamental spanwise wavelength of the arising three-dimensional solutions. Two-dimensional periodic solutions may still destabilise following both synchronous or quasi-periodic bifurcations, as was the case in the presence of the space–time ![]() $\textrm {Z}_2$ symmetry (Marques et al. Reference Marques, Lopez and Blackburn2004; Blackburn et al. Reference Blackburn, Marques and Lopez2005), but none of the two possible types of synchronous bifurcations can preserve a symmetry that was not there in the first place. If the quasi-periodic bifurcation becomes resonant and turns into a period-doubling bifurcation, the original time periodicity is broken but still retained in the form of a space–time symmetry that recovers the solution after evolution over the original period (half the new period) followed by reflection about any
$\textrm {Z}_2$ symmetry (Marques et al. Reference Marques, Lopez and Blackburn2004; Blackburn et al. Reference Blackburn, Marques and Lopez2005), but none of the two possible types of synchronous bifurcations can preserve a symmetry that was not there in the first place. If the quasi-periodic bifurcation becomes resonant and turns into a period-doubling bifurcation, the original time periodicity is broken but still retained in the form of a space–time symmetry that recovers the solution after evolution over the original period (half the new period) followed by reflection about any ![]() $z$ plane located halfway between consecutive mirror-symmetry planes. In this guise, the period of the three-dimensional solution is double that of the destabilising two-dimensional solution, but shall appear to be the same whenever aggregate quantities are monitored. The phase maps in figure 5 suggest that the advent of three dimensionality follows precisely this path, as has been shown to occur for other systems breaking the space–time symmetry of the two-dimensional solution (Blackburn & Sheard Reference Blackburn and Sheard2010) such as circular rings (Sheard et al. Reference Sheard, Hourigan and Thompson2005a,Reference Sheard, Thompson and Houriganb) or inclined cylinders (Sheard et al. Reference Sheard, Fitzgerald and Ryan2009; Sheard Reference Sheard2011).
$z$ plane located halfway between consecutive mirror-symmetry planes. In this guise, the period of the three-dimensional solution is double that of the destabilising two-dimensional solution, but shall appear to be the same whenever aggregate quantities are monitored. The phase maps in figure 5 suggest that the advent of three dimensionality follows precisely this path, as has been shown to occur for other systems breaking the space–time symmetry of the two-dimensional solution (Blackburn & Sheard Reference Blackburn and Sheard2010) such as circular rings (Sheard et al. Reference Sheard, Hourigan and Thompson2005a,Reference Sheard, Thompson and Houriganb) or inclined cylinders (Sheard et al. Reference Sheard, Fitzgerald and Ryan2009; Sheard Reference Sheard2011).
5.1. Stability of two-dimensional vortex shedding to three-dimensional disturbances
The precise values of the parameters for which three-dimensional solutions arise in the wake transition regime, and the main features that characterise these nonlinear solutions in terms of frequency, symmetries and wake vortical structures, may be inferred from linear stability analysis of the underlying two-dimensional vortex-shedding solution. Also the requirements for the spanwise size of the computational domain at any given value of the Reynolds number and velocity ratio can be assessed by determining the range of wavenumbers that are unstable. This can be done with a full-fledged Floquet analysis, but given that only the dominant eigenmode for each spanwise wavenumber, rather than the full spectrum (or even a subset of it), is actually required, the stability analysis has been carried out by simply time stepping on a quasi three-dimensional domain, adding to the two-dimensional field a unique spanwise Fourier mode of the chosen wavelength, randomly initialised to a very low energy level (see Appendix A).
Figure 7(a) illustrates the time-stepping-based stability analysis for ![]() $(R,\lambda _z)=(3.4,2.5)$. The two-dimensional vortex-shedding solution whose stability to spanwise disturbances is being analysed is shown in the inset. The instantaneous spanwise vorticity
$(R,\lambda _z)=(3.4,2.5)$. The two-dimensional vortex-shedding solution whose stability to spanwise disturbances is being analysed is shown in the inset. The instantaneous spanwise vorticity ![]() $\omega _z\in [-2,2]$ colour map (blue for negative, yellow for positive) shows the Kármán vortex street, which consists of an array of strong clockwise vortices. Only the vortices from the top shear layer form due to the severe disruption of the top–bottom symmetry. Consecutive vortices are interconnected by weak elongated braids of opposite vorticity. After some initial transients, the energy associated to the only spanwise mode considered (
$\omega _z\in [-2,2]$ colour map (blue for negative, yellow for positive) shows the Kármán vortex street, which consists of an array of strong clockwise vortices. Only the vortices from the top shear layer form due to the severe disruption of the top–bottom symmetry. Consecutive vortices are interconnected by weak elongated braids of opposite vorticity. After some initial transients, the energy associated to the only spanwise mode considered (![]() $E_1(t$), bottom) starts growing exponentially, with a barely perceptible superimposed oscillation that is inherited from the underlying two-dimensional vortex-shedding periodicity (
$E_1(t$), bottom) starts growing exponentially, with a barely perceptible superimposed oscillation that is inherited from the underlying two-dimensional vortex-shedding periodicity (![]() $C_l$, top). The exponential growth indicates that the
$C_l$, top). The exponential growth indicates that the ![]() $R=3.4$ solution is already linearly unstable to
$R=3.4$ solution is already linearly unstable to ![]() $\lambda _z=2.5$ perturbations. We define a Poincaré section according to
$\lambda _z=2.5$ perturbations. We define a Poincaré section according to ![]() $\{C_l=\langle C_l\rangle _t; \dot {C}_l>0\}$, where
$\{C_l=\langle C_l\rangle _t; \dot {C}_l>0\}$, where ![]() $=\langle C_l\rangle _t$ is the time average of the lift coefficient of the two-dimensional periodic solution. An exponential fit (dashed line) to the Poincaré crossings in the linear growth regime (red crosses) provides an estimation of the modulus of the unstable multiplier
$=\langle C_l\rangle _t$ is the time average of the lift coefficient of the two-dimensional periodic solution. An exponential fit (dashed line) to the Poincaré crossings in the linear growth regime (red crosses) provides an estimation of the modulus of the unstable multiplier ![]() $|\mu |$. Note that the modal energy oscillation associated to vortex shedding is factored out upon definition of the Poincaré section and has therefore no effect whatsoever on the estimation of the multiplier.
$|\mu |$. Note that the modal energy oscillation associated to vortex shedding is factored out upon definition of the Poincaré section and has therefore no effect whatsoever on the estimation of the multiplier.

Figure 7. Stability analysis of the flow past a square cylinder in the interface of two different velocity streams with ![]() $Re_B=56$. (a) Time evolution of the lift coefficient
$Re_B=56$. (a) Time evolution of the lift coefficient ![]() $C_l$ (top) and of the modal energy associated to the only spanwise-dependent Fourier mode
$C_l$ (top) and of the modal energy associated to the only spanwise-dependent Fourier mode ![]() $E_1$ considered (bottom) for
$E_1$ considered (bottom) for ![]() $(R,\lambda _z)=(3.4,2.5)$. The red crosses indicate
$(R,\lambda _z)=(3.4,2.5)$. The red crosses indicate ![]() $\{C_l=\langle C_l\rangle _t; \dot {C}_l>0\}$ Poincaré crossings in the linear regime used for the exponential fit (red dashed line). The inset depicts the instantaneous (at the Poincaré section) spanwise vorticity
$\{C_l=\langle C_l\rangle _t; \dot {C}_l>0\}$ Poincaré crossings in the linear regime used for the exponential fit (red dashed line). The inset depicts the instantaneous (at the Poincaré section) spanwise vorticity ![]() $\omega _z\in [-2,2]$ (blue to yellow) colour map of the (unstable) two-dimensional vortex-shedding solution for
$\omega _z\in [-2,2]$ (blue to yellow) colour map of the (unstable) two-dimensional vortex-shedding solution for ![]() $R=3.4$. (b) Least stable Floquet multipliers for velocity ratios in the range
$R=3.4$. (b) Least stable Floquet multipliers for velocity ratios in the range ![]() $R\in [3,6.5]$. The red cross corresponds to the case analysed inpanel (a).
$R\in [3,6.5]$. The red cross corresponds to the case analysed inpanel (a).
The results of the stability analysis for varying ![]() $R$ and
$R$ and ![]() $\lambda _z$ are presented in figure 7(b). The actual onset of flow three dimensionality occurs for
$\lambda _z$ are presented in figure 7(b). The actual onset of flow three dimensionality occurs for ![]() $R\simeq 3.1$. Below this value, all three-dimensional perturbations decay (the Floquet multiplier has
$R\simeq 3.1$. Below this value, all three-dimensional perturbations decay (the Floquet multiplier has ![]() $|\mu |<1$) and the flow remains two dimensional. The largest modulus Floquet multiplier corresponds to a fairly constant spanwise wavenumber of about
$|\mu |<1$) and the flow remains two dimensional. The largest modulus Floquet multiplier corresponds to a fairly constant spanwise wavenumber of about ![]() $\lambda _z =2{\rm \pi} /\beta _z\simeq 2.4$ all the way up to
$\lambda _z =2{\rm \pi} /\beta _z\simeq 2.4$ all the way up to ![]() $R\leqslant 4$ and then steadily increases to
$R\leqslant 4$ and then steadily increases to ![]() $2.8$ for
$2.8$ for ![]() $R=6.5$. Consequently, a spanwise domain size
$R=6.5$. Consequently, a spanwise domain size ![]() $L_z=2.5$ (and integer multiples of it) constitutes a fair choice if the fastest-growing three-dimensional mode is to be represented in the simulation. The smooth evolution of the multiplier of the dominant mode of the eigenspectrum indicates that, despite its evolution in wavelength, the same mode is responsible for the instability over the whole range of
$L_z=2.5$ (and integer multiples of it) constitutes a fair choice if the fastest-growing three-dimensional mode is to be represented in the simulation. The smooth evolution of the multiplier of the dominant mode of the eigenspectrum indicates that, despite its evolution in wavelength, the same mode is responsible for the instability over the whole range of ![]() $R$ explored. At
$R$ explored. At ![]() $R=6.5$, however, a second unstable mode, of much shorter associated wavelength
$R=6.5$, however, a second unstable mode, of much shorter associated wavelength ![]() $\lambda _z\simeq 1.5$ has destabilised. The first mode is clearly dominant, but the presence of this second mode may play some role in shaping the small-scale vortical structures that are present in the wake once fully developed turbulence has kicked in.
$\lambda _z\simeq 1.5$ has destabilised. The first mode is clearly dominant, but the presence of this second mode may play some role in shaping the small-scale vortical structures that are present in the wake once fully developed turbulence has kicked in.
Not only the multiplier, but also the flow fields of the dominant eigenmode can be recovered from the stability analysis. They are simply provided by the sole non-homogeneous spanwise mode (or, equivalently, by subtracting the two-dimensional solution from the quasi-three-dimensional flow fields) as taken anywhere within the linear regime. The prevailing three-dimensional flow structures and the characteristic symmetries of the dominant eigenmodes will be discussed presently in § 5.2, alongside the corresponding nonlinear solutions at the same values of the parameters, to assist in gauging the extent to which the latter are determined by the former.
5.2. Nonlinear three-dimensional solutions
Three nonlinear three-dimensional solutions representing the three different types of temporal dynamics found along our coarse exploration of the wake transition regime have been singled out for a detailed analysis of the symmetries and the three-dimensional vortical structures present in the wake. In particular, a period-doubled, a period-four and a chaotic solution have been studied at ![]() $R=3.4$, 3.8 and 5.357, respectively. All three solutions have been run in the domain of minimal spanwise-periodic extent (
$R=3.4$, 3.8 and 5.357, respectively. All three solutions have been run in the domain of minimal spanwise-periodic extent (![]() $L_z=5$) that is capable of sustaining spatiotemporally chaotic dynamics, although the latter is presented in the wider
$L_z=5$) that is capable of sustaining spatiotemporally chaotic dynamics, although the latter is presented in the wider ![]() $L_z=10$ domain.
$L_z=10$ domain.
Figure 8(b) contains space–time diagrams of spanwise velocity ![]() $w(x,y,z;t)$ along a probe array located at
$w(x,y,z;t)$ along a probe array located at ![]() $(x,y)=(6.0,0.5)$ alongside corresponding time series of
$(x,y)=(6.0,0.5)$ alongside corresponding time series of ![]() $C_l$ and
$C_l$ and ![]() $C_d$ (panel a) for the three-dimensional periodic solution at
$C_d$ (panel a) for the three-dimensional periodic solution at ![]() $R=3.4$. The space–time diagrams correspond to eight vortex-shedding cycles, as clear from the
$R=3.4$. The space–time diagrams correspond to eight vortex-shedding cycles, as clear from the ![]() $C_l$ and
$C_l$ and ![]() $C_d$ time series, and their periodicity corresponds exactly with that of vortex shedding. The space–time diagrams show instead that the actual periodicity of the solution is twice that of vortex shedding, as previously unravelled by the corresponding phase maps in figure 5. The nature of the period doubling, which does not affect aggregate quantities, is now clearly explained as a result of the way in which the spanwise invariance has been disrupted upon three dimensionalisation of the flow. The reflection
$C_d$ time series, and their periodicity corresponds exactly with that of vortex shedding. The space–time diagrams show instead that the actual periodicity of the solution is twice that of vortex shedding, as previously unravelled by the corresponding phase maps in figure 5. The nature of the period doubling, which does not affect aggregate quantities, is now clearly explained as a result of the way in which the spanwise invariance has been disrupted upon three dimensionalisation of the flow. The reflection ![]() $\textrm {Z}_2$ symmetry is only preserved at all times about planes located at
$\textrm {Z}_2$ symmetry is only preserved at all times about planes located at ![]() $z=z_0+(2j)\lambda _z/4$ (white dash-dotted lines), where the origin for the spanwise coordinate has been chosen to enforce
$z=z_0+(2j)\lambda _z/4$ (white dash-dotted lines), where the origin for the spanwise coordinate has been chosen to enforce ![]() $z_0=0$,
$z_0=0$, ![]() $\lambda _z=2.5$ here and
$\lambda _z=2.5$ here and ![]() $j\in \mathbb {Z}$. Additionally, a space–time symmetry operation consisting in the evolution by half a period
$j\in \mathbb {Z}$. Additionally, a space–time symmetry operation consisting in the evolution by half a period ![]() $T/2$, where
$T/2$, where ![]() $T$ is the actual period of the solution corresponding to two vortex-shedding cycles, followed by reflection about any plane located at
$T$ is the actual period of the solution corresponding to two vortex-shedding cycles, followed by reflection about any plane located at ![]() $z=z_0+(2j+1)\lambda _z/4$ (white dashed lines) also leaves the solution invariant. The appropriate composition of the two symmetries shows that the solution is also invariant to evolutions by half a period
$z=z_0+(2j+1)\lambda _z/4$ (white dashed lines) also leaves the solution invariant. The appropriate composition of the two symmetries shows that the solution is also invariant to evolutions by half a period ![]() $T/2$, followed by a spanwise shift by a half-wavelength
$T/2$, followed by a spanwise shift by a half-wavelength ![]() $\lambda _z/2$.
$\lambda _z/2$.

Figure 8. Space–time properties of the ![]() $R=3.4$ solution. (a) Dynamic evolution of the lift
$R=3.4$ solution. (a) Dynamic evolution of the lift ![]() $C_l$ (solid) and drag
$C_l$ (solid) and drag ![]() $C_d$ (dashed) coefficients. Horizontal grey lines indicate the absolute maxima and minima of the signals. (b) Space–time diagrams of spanwise velocity
$C_d$ (dashed) coefficients. Horizontal grey lines indicate the absolute maxima and minima of the signals. (b) Space–time diagrams of spanwise velocity ![]() $w(x,y,z;t)$ at probe location
$w(x,y,z;t)$ at probe location ![]() $(x,y)=(6.0,0.5)$. Reflection (dash-dotted white lines) and time shift plus reflection (dashed white) symmetry planes are indicated.
$(x,y)=(6.0,0.5)$. Reflection (dash-dotted white lines) and time shift plus reflection (dashed white) symmetry planes are indicated.
The ensuing period-doubling bifurcation is of an altogether different nature. The solution at ![]() $R=3.8$ has an actual period of four vortex-shedding cycles, yet aggregate quantities repeat every two vortex-shedding cycles. Close inspection of figure 9(a) shows how the
$R=3.8$ has an actual period of four vortex-shedding cycles, yet aggregate quantities repeat every two vortex-shedding cycles. Close inspection of figure 9(a) shows how the ![]() $C_l$ and
$C_l$ and ![]() $C_d$ time series have a period that is about twice that for
$C_d$ time series have a period that is about twice that for ![]() $R=3.4$. The period doubling is more clearly evinced by the half-frequency peak
$R=3.4$. The period doubling is more clearly evinced by the half-frequency peak ![]() $f_2$ in figure 6(c) or the double loop phase-map trajectory in figure 5(a), but it also shows up in the
$f_2$ in figure 6(c) or the double loop phase-map trajectory in figure 5(a), but it also shows up in the ![]() $C_l$ and
$C_l$ and ![]() $C_d$ time series (note how the peaks and valleys come short, every two vortex-shedding cycles, of the horizontal grey lines indicating the absolute maxima and minima of the signals.) The space–time diagram for
$C_d$ time series (note how the peaks and valleys come short, every two vortex-shedding cycles, of the horizontal grey lines indicating the absolute maxima and minima of the signals.) The space–time diagram for ![]() $w$ provides the full picture. The bifurcation that produces the period-doubled solution is spatially subharmonic in the sense that the spanwise wavelength is double that at
$w$ provides the full picture. The bifurcation that produces the period-doubled solution is spatially subharmonic in the sense that the spanwise wavelength is double that at ![]() $R=3.4$. It is a modulational instability to perturbations of a wavelength twice that of the bifurcating solution. This breaks the mirror symmetry and the only remaining symmetry leaves the solution invariant to evolution for half a period (two vortex-shedding cycles) followed by reflection about planes located at
$R=3.4$. It is a modulational instability to perturbations of a wavelength twice that of the bifurcating solution. This breaks the mirror symmetry and the only remaining symmetry leaves the solution invariant to evolution for half a period (two vortex-shedding cycles) followed by reflection about planes located at ![]() $z=z_0+j\lambda _z/2$ (white dashed line), where
$z=z_0+j\lambda _z/2$ (white dashed line), where ![]() $\lambda _z=5$ now.
$\lambda _z=5$ now.

Figure 9. Space–time properties of the ![]() $R=3.8$ solution. (a) Dynamic evolution of the lift
$R=3.8$ solution. (a) Dynamic evolution of the lift ![]() $C_l$ (solid) and drag
$C_l$ (solid) and drag ![]() $C_d$ (dashed) coefficients. Horizontal grey lines indicate the absolute maxima and minima of the signals.(b) Space–time diagrams of spanwise velocity
$C_d$ (dashed) coefficients. Horizontal grey lines indicate the absolute maxima and minima of the signals.(b) Space–time diagrams of spanwise velocity ![]() $w(x,y,z;t)$ at probe location
$w(x,y,z;t)$ at probe location ![]() $(x,y)=(6.0,0.5)$. Time shift plus reflection-symmetry planes (dashed white) are indicated.
$(x,y)=(6.0,0.5)$. Time shift plus reflection-symmetry planes (dashed white) are indicated.
A three-dimensional representation of the solution at ![]() $R=3.4$ is shown in figure 10(a) at two consecutive crossings of the Poincaré section defined by
$R=3.4$ is shown in figure 10(a) at two consecutive crossings of the Poincaré section defined by ![]() $C_l=\langle C_l\rangle _t$ and
$C_l=\langle C_l\rangle _t$ and ![]() $\dot {C}_l>0$. Spanwise mode zero, shown with a transparent isosurface for
$\dot {C}_l>0$. Spanwise mode zero, shown with a transparent isosurface for ![]() $\omega _z=\pm 0.1$, is taken to represent the Kármán vortices. The three-dimensional vortical structures present in the flow are exposed by means of the
$\omega _z=\pm 0.1$, is taken to represent the Kármán vortices. The three-dimensional vortical structures present in the flow are exposed by means of the ![]() $Q$ criterion, which identifies vortical structures as regions where the second invariant of the velocity gradient tensor becomes positive (
$Q$ criterion, which identifies vortical structures as regions where the second invariant of the velocity gradient tensor becomes positive (![]() $Q>0$), i.e. the rotation rate overcomes the shear rate (Hunt, Wray & Moin Reference Hunt, Wray and Moin1988, pp. 193–208). Streamwise-cross-stream vortical structures are made visible through
$Q>0$), i.e. the rotation rate overcomes the shear rate (Hunt, Wray & Moin Reference Hunt, Wray and Moin1988, pp. 193–208). Streamwise-cross-stream vortical structures are made visible through ![]() $Q=0.0002$ isocontours coloured by streamwise vorticity
$Q=0.0002$ isocontours coloured by streamwise vorticity ![]() $\omega _x$. A first visible effect of three dimensionalisation is that of introducing spanwise modulation to Kármán vortices. Vorticity is no longer merely spanwise but has become slightly tilted and alternates positive and negative values of the streamwise component. Elongated streamwise-cross-stream vortices extend along the braids connecting consecutive Kármán vortices. The three-dimensional flow topology is very different from mode-A- and mode-B-type structures observed for circular (Williamson Reference Williamson1996c) and square (Bai & Alam Reference Bai and Alam2018) cylinders in the wake transition regime. Instead, the streamwise-cross-stream vortices, in particular their wavelength and time periodicity, are highly reminiscent of mode QP in the wake of circular (Blackburn et al. Reference Blackburn, Marques and Lopez2005), square (Robichaux et al. Reference Robichaux, Balachandar and Vanka1999; Blackburn et al. Reference Blackburn, Marques and Lopez2005) and rounded-square (Park & Yang Reference Park and Yang2016) cylinders. Some alterations in wake topology are however conspicuous: the positive Kármán vortices typically emanating from the bottom shear layer are absent and the elongated vortices in the braids that connected them to the preceding and following negative Kármán vortices have been spliced. As a matter of fact, the parallel is all the more convincing when a comparison is drawn between the present three-dimensional wake vortices and mode C structures in the wake of open rings (Sheard et al. Reference Sheard, Hourigan and Thompson2005a), squares at incidence (Sheard et al. Reference Sheard, Fitzgerald and Ryan2009) or cylinders submerged in upstream shear (Park & Yang Reference Park and Yang2018). In all these problems, mode C results from the frequency locking of mode QP shortly after breaking the Z
$\omega _x$. A first visible effect of three dimensionalisation is that of introducing spanwise modulation to Kármán vortices. Vorticity is no longer merely spanwise but has become slightly tilted and alternates positive and negative values of the streamwise component. Elongated streamwise-cross-stream vortices extend along the braids connecting consecutive Kármán vortices. The three-dimensional flow topology is very different from mode-A- and mode-B-type structures observed for circular (Williamson Reference Williamson1996c) and square (Bai & Alam Reference Bai and Alam2018) cylinders in the wake transition regime. Instead, the streamwise-cross-stream vortices, in particular their wavelength and time periodicity, are highly reminiscent of mode QP in the wake of circular (Blackburn et al. Reference Blackburn, Marques and Lopez2005), square (Robichaux et al. Reference Robichaux, Balachandar and Vanka1999; Blackburn et al. Reference Blackburn, Marques and Lopez2005) and rounded-square (Park & Yang Reference Park and Yang2016) cylinders. Some alterations in wake topology are however conspicuous: the positive Kármán vortices typically emanating from the bottom shear layer are absent and the elongated vortices in the braids that connected them to the preceding and following negative Kármán vortices have been spliced. As a matter of fact, the parallel is all the more convincing when a comparison is drawn between the present three-dimensional wake vortices and mode C structures in the wake of open rings (Sheard et al. Reference Sheard, Hourigan and Thompson2005a), squares at incidence (Sheard et al. Reference Sheard, Fitzgerald and Ryan2009) or cylinders submerged in upstream shear (Park & Yang Reference Park and Yang2018). In all these problems, mode C results from the frequency locking of mode QP shortly after breaking the Z![]() $_2$ symmetry about the horizontal midplane of the classic configuration, i.e. the homogeneous incoming flow past an infinite cylinder at zero incidence.
$_2$ symmetry about the horizontal midplane of the classic configuration, i.e. the homogeneous incoming flow past an infinite cylinder at zero incidence.

Figure 10. Instantaneous snapshots of (a) the three-dimensional solution at ![]() $R=3.4$ (supplementary movie 1 available at https://doi.org/10.1017/jfm.2022.821) and (b) corresponding dominant eigenmode of the underlying two-dimensional solution (supplementary movie 2), at two consecutive crossings of the Poincaré section. Shown are isosurfaces of the
$R=3.4$ (supplementary movie 1 available at https://doi.org/10.1017/jfm.2022.821) and (b) corresponding dominant eigenmode of the underlying two-dimensional solution (supplementary movie 2), at two consecutive crossings of the Poincaré section. Shown are isosurfaces of the ![]() $Q$-criterion (
$Q$-criterion (![]() $Q=0.0002$ for three-dimensional solution, arbitrarily chosen for the dominant eigenmode to ease comparison), coloured by streamwise vorticity (
$Q=0.0002$ for three-dimensional solution, arbitrarily chosen for the dominant eigenmode to ease comparison), coloured by streamwise vorticity (![]() $\omega _x\in [-0.1,0.1]$ for the nonlinear solution, symmetric arbitrary scale for the eigenmode). Spanwise vortices are shown with the transparent isosurface for
$\omega _x\in [-0.1,0.1]$ for the nonlinear solution, symmetric arbitrary scale for the eigenmode). Spanwise vortices are shown with the transparent isosurface for ![]() $\omega _z=\pm 0.1$. The solution is replicated twice in the spanwise direction to
$\omega _z=\pm 0.1$. The solution is replicated twice in the spanwise direction to ![]() $L_z=10$ only for visualisation purposes.
$L_z=10$ only for visualisation purposes.
Comparing two snapshots exactly one Poincaré section crossing apart, the aforementioned space–time symmetries become apparent. The solution looks exactly the same but shifted by exactly half a wavelength in the spanwise direction or reflected about appropriate symmetry planes as previously observed. The fully developed three-dimensional solution bears a strong resemblance and shares the same symmetries with the dominant eigenmode of the underlying two-dimensional periodic solution at the same value ![]() $R=3.4$, as clear from figure 10. Here the most unstable mode of figure 7(b) for
$R=3.4$, as clear from figure 10. Here the most unstable mode of figure 7(b) for ![]() $\lambda _z=2.5$ has been represented using the
$\lambda _z=2.5$ has been represented using the ![]() $Q$ criterion and coloured by
$Q$ criterion and coloured by ![]() $\omega _x$ (symmetric arbitrary range). The unstable two-dimensional solution is indicated by transparent
$\omega _x$ (symmetric arbitrary range). The unstable two-dimensional solution is indicated by transparent ![]() $\omega _z=\pm 0.1$ isosurfaces that clearly show the Kármán vortices. The topologies of the dominant eigenmode and of the three-dimensional solution are evidently related and so is the space–time symmetry dynamics as illustrated by snapshots taken one Poincaré crossing apart. By comparing mode C of figure 10(b) to mode QP of figure 1 some intuition as to the morphing from one to the other can be gained. The similarities in the arrangement of wake vortices is evident provided that one allows for the suppression of the bottom vortices of the Kármán street and for the resulting streamwise splicing of every two consecutive braid vortices that follows from the breaking of the top–bottom symmetry.
$\omega _z=\pm 0.1$ isosurfaces that clearly show the Kármán vortices. The topologies of the dominant eigenmode and of the three-dimensional solution are evidently related and so is the space–time symmetry dynamics as illustrated by snapshots taken one Poincaré crossing apart. By comparing mode C of figure 10(b) to mode QP of figure 1 some intuition as to the morphing from one to the other can be gained. The similarities in the arrangement of wake vortices is evident provided that one allows for the suppression of the bottom vortices of the Kármán street and for the resulting streamwise splicing of every two consecutive braid vortices that follows from the breaking of the top–bottom symmetry.
The symmetries and wavelength of the dominant eigenmode (and, with it, the nonlinear solution) make it analogous to the mode C that destabilises the axisymmetric/two-dimensional periodic solutions characteristic of the flow past a circular ring (Sheard et al. Reference Sheard, Hourigan and Thompson2005a,Reference Sheard, Thompson and Houriganb) or an inclined square cylinder (Sheard et al. Reference Sheard, Fitzgerald and Ryan2009; Sheard Reference Sheard2011), which evolve from the respective modes QP of the top–bottom symmetric cases and take precedence over modes A and B when the symmetry has been sufficiently disrupted. The same bifurcation scenario has been recently exposed in the somewhat related case of a circular cylinder in homogeneous upstream shear (Park & Yang Reference Park and Yang2018). Here we are only varying one parameter ![]() $R$, so that modes A and B are never encountered along the particular
$R$, so that modes A and B are never encountered along the particular ![]() $Re{-}K$ path followed. The rapid increase of the upstream velocity ratio and its associated mean shear is probably suppressing them before any trace can be even found in the Floquet spectrum.
$Re{-}K$ path followed. The rapid increase of the upstream velocity ratio and its associated mean shear is probably suppressing them before any trace can be even found in the Floquet spectrum.
The dominant eigenmode of the underlying two-dimensional solution is the same for all values of ![]() $R$ investigated here. With minor variations, it remains topologically identical from as low as
$R$ investigated here. With minor variations, it remains topologically identical from as low as ![]() $R=3$, which corresponds to a stable case, to as high as
$R=3$, which corresponds to a stable case, to as high as ![]() $R=6.5$, where the three-dimensional solution has evolved into chaotic dynamics. The most unstable (or least stable) wavelength remains around
$R=6.5$, where the three-dimensional solution has evolved into chaotic dynamics. The most unstable (or least stable) wavelength remains around ![]() $\lambda _z\simeq 2.5$ for low values of
$\lambda _z\simeq 2.5$ for low values of ![]() $R$ and then gradually grows as
$R$ and then gradually grows as ![]() $R$ is increased. In particular, the most unstable mode remains the same for
$R$ is increased. In particular, the most unstable mode remains the same for ![]() $R=3.8$, for which it has been seen that a second bifurcation has taken place and the space–time symmetry of
$R=3.8$, for which it has been seen that a second bifurcation has taken place and the space–time symmetry of ![]() $R=3.4$ is no longer present. We surmise that the period-doubling bifurcation, that appears to arise from a spanwise subharmonic/modulational instability of the
$R=3.4$ is no longer present. We surmise that the period-doubling bifurcation, that appears to arise from a spanwise subharmonic/modulational instability of the ![]() $R=3.4$ solution to perturbations of double its spanwise wavelength, may also affect the underlying two-dimensional flow. Since this flow is already unstable to the eigenmode of figure 10(b), computing the second unstable mode is not within the reach of mere time stepping. Besides, it may also be the case that this second instability is related to the interactions of unstable wavelengths across the continuous eigenspectrum. For
$R=3.4$ solution to perturbations of double its spanwise wavelength, may also affect the underlying two-dimensional flow. Since this flow is already unstable to the eigenmode of figure 10(b), computing the second unstable mode is not within the reach of mere time stepping. Besides, it may also be the case that this second instability is related to the interactions of unstable wavelengths across the continuous eigenspectrum. For ![]() $L_z=5$, the domain admits instability to perturbations of wavelength
$L_z=5$, the domain admits instability to perturbations of wavelength ![]() $\lambda _z=L_z/l$, with
$\lambda _z=L_z/l$, with ![]() $l\in \mathbb {Z}$, or, equivalently, wavenumber
$l\in \mathbb {Z}$, or, equivalently, wavenumber ![]() $\beta _z=2{\rm \pi} l/L_z$. Now, for
$\beta _z=2{\rm \pi} l/L_z$. Now, for ![]() $R=3.4$, the unstable dominant mode can only fit twice or thrice within the domain considered and the system seems to choose
$R=3.4$, the unstable dominant mode can only fit twice or thrice within the domain considered and the system seems to choose ![]() $\lambda _z=2.5$ as the prevailing instability. At
$\lambda _z=2.5$ as the prevailing instability. At ![]() $R=3.8$, instead, the unstable band has grown large enough to allow for the dominant mode to fit either twice, thrice, four times or even just once. The three-dimensional solution has
$R=3.8$, instead, the unstable band has grown large enough to allow for the dominant mode to fit either twice, thrice, four times or even just once. The three-dimensional solution has ![]() $\lambda _z=L_z=5$ but it retains a
$\lambda _z=L_z=5$ but it retains a ![]() $\lambda _z\simeq 2.5$ dependence to a large extent. This suggests that the modes with
$\lambda _z\simeq 2.5$ dependence to a large extent. This suggests that the modes with ![]() $\lambda _z=2.5$ and
$\lambda _z=2.5$ and ![]() $\lambda _z=5$, which in fact belong to the same branch and are therefore related by smooth continuation in the wavelength parameter, might be competing and that none completely prevails over the other.
$\lambda _z=5$, which in fact belong to the same branch and are therefore related by smooth continuation in the wavelength parameter, might be competing and that none completely prevails over the other.
Figure 11(a) shows snapshots of the three-dimensional solution for ![]() $R=3.8$ at four consecutive crossings of the Poincaré section. The original spanwise wavelength
$R=3.8$ at four consecutive crossings of the Poincaré section. The original spanwise wavelength ![]() $\lambda _z=2.5$ is preserved to a large extent, but the actual periodicity is now the full
$\lambda _z=2.5$ is preserved to a large extent, but the actual periodicity is now the full ![]() $\lambda _z=L_z=5$. The similarity with
$\lambda _z=L_z=5$. The similarity with ![]() $R=3.4$ is apparent, but the elongated vortices along the braids reach further downstream into the wake. Although crossings 0 and 2 (also 1 and 3) look very much alike, careful inspection reveals that very slight differences exist that are related with the period-doubled nature of the solution. Also hard to notice, but nevertheless present, is the symmetry that leaves the solution invariant after evolution over two consecutive crossings of the Poincaré section followed by reflection about appropriately chosen streamwise-cross-stream planes.
$R=3.4$ is apparent, but the elongated vortices along the braids reach further downstream into the wake. Although crossings 0 and 2 (also 1 and 3) look very much alike, careful inspection reveals that very slight differences exist that are related with the period-doubled nature of the solution. Also hard to notice, but nevertheless present, is the symmetry that leaves the solution invariant after evolution over two consecutive crossings of the Poincaré section followed by reflection about appropriately chosen streamwise-cross-stream planes.

Figure 11. Instantaneous snapshots of (a) the three-dimensional solution at ![]() $R=3.8$ (supplementary movie 3), (b) dominant eigenmode for
$R=3.8$ (supplementary movie 3), (b) dominant eigenmode for ![]() $(R,\lambda _z)=(3.8,2.5)$ (supplementary movie 4) and (c) dominant eigenmode for
$(R,\lambda _z)=(3.8,2.5)$ (supplementary movie 4) and (c) dominant eigenmode for ![]() $(R,\lambda _z)=(3.8,5)$ (supplementary movie 5), at four consecutive crossings of the Poincaré section. Isosurfaces and colours as for figure 10, except that
$(R,\lambda _z)=(3.8,5)$ (supplementary movie 5), at four consecutive crossings of the Poincaré section. Isosurfaces and colours as for figure 10, except that ![]() $Q=0.0001$ is used to display nonlinear three-dimensional vortical structures.
$Q=0.0001$ is used to display nonlinear three-dimensional vortical structures.
The spanwise periodicity ![]() $\lambda _z=5$ of the nonlinear solution is doubtless unrelated to a mode A instability despite the compatible wavelength. The typical features of mode A are absent from the wake, while mode C vortical structures clearly prevail, albeit with a two-fold subharmonic spanwise modulation. In order to discard any involvement of mode A in the solution observed at
$\lambda _z=5$ of the nonlinear solution is doubtless unrelated to a mode A instability despite the compatible wavelength. The typical features of mode A are absent from the wake, while mode C vortical structures clearly prevail, albeit with a two-fold subharmonic spanwise modulation. In order to discard any involvement of mode A in the solution observed at ![]() $R=3.8$, four consecutive normalised snapshots of the dominant mode for wavelengths
$R=3.8$, four consecutive normalised snapshots of the dominant mode for wavelengths ![]() $\lambda _z=2.5$ and
$\lambda _z=2.5$ and ![]() $5$, both unstable according to figure 7, are shown in figures 11(b) and 11(c), respectively. The spatial structure of the dominant eigenmode is clearly the same at both wavelengths, with minor differences that are perfectly imputable to a continuous transformation from one to the other. Moreover, the two modes are definitely subharmonic and of the C type. Normalised snapshots taken exactly two vortex-shedding cycles apart are identical in all respects, and those taken only one vortex-shedding cycle apart are related by the space–time symmetries described earlier. Therefore, the actual frequency and symmetry breaking of the nonlinear solution at
$5$, both unstable according to figure 7, are shown in figures 11(b) and 11(c), respectively. The spatial structure of the dominant eigenmode is clearly the same at both wavelengths, with minor differences that are perfectly imputable to a continuous transformation from one to the other. Moreover, the two modes are definitely subharmonic and of the C type. Normalised snapshots taken exactly two vortex-shedding cycles apart are identical in all respects, and those taken only one vortex-shedding cycle apart are related by the space–time symmetries described earlier. Therefore, the actual frequency and symmetry breaking of the nonlinear solution at ![]() $R=3.8$ cannot be explained by a period-doubling bifurcation affecting also the already unstable two-dimensional vortex-shedding solution. The origin of the period doubling must probably be sought in some modulational instability of the nonlinear solution at
$R=3.8$ cannot be explained by a period-doubling bifurcation affecting also the already unstable two-dimensional vortex-shedding solution. The origin of the period doubling must probably be sought in some modulational instability of the nonlinear solution at ![]() $R=3.4$.
$R=3.4$.
Colour maps of streamwise vorticity ![]() $\omega _x$ on a spanwise-cross-stream plane located at
$\omega _x$ on a spanwise-cross-stream plane located at ![]() $x=6$ in the cylinder wake – the precise location of the Kármán vortex centre at the instants chosen for the snapshots – help pinpoint the actual spanwise wavelength and space–time symmetry of the nonlinear three-dimensional solutions for
$x=6$ in the cylinder wake – the precise location of the Kármán vortex centre at the instants chosen for the snapshots – help pinpoint the actual spanwise wavelength and space–time symmetry of the nonlinear three-dimensional solutions for ![]() $R=3.4$ and
$R=3.4$ and ![]() $R=3.8$ in figures 12(a) and 12(b), respectively. The exact repetition of the solution every two crossings of the Poincaré section is now evinced by the exact matching of crossings 0–2 and 1–3 for
$R=3.8$ in figures 12(a) and 12(b), respectively. The exact repetition of the solution every two crossings of the Poincaré section is now evinced by the exact matching of crossings 0–2 and 1–3 for ![]() $R=3.4$. The symmetry planes at
$R=3.4$. The symmetry planes at ![]() $z=z_0+(2j)\lambda _z/4=2.5\,j$ are perfectly identifiable, as is also clear that even/odd Poincaré crossings are mutually related by a reflection about planes at
$z=z_0+(2j)\lambda _z/4=2.5\,j$ are perfectly identifiable, as is also clear that even/odd Poincaré crossings are mutually related by a reflection about planes at ![]() $z=z_0+(2*j+1)\lambda _z/4=1.25+2.5\,j$. Note that reflection symmetries, as is the case of the two symmetries discussed here, imply a change of sign of
$z=z_0+(2*j+1)\lambda _z/4=1.25+2.5\,j$. Note that reflection symmetries, as is the case of the two symmetries discussed here, imply a change of sign of ![]() $\omega _x$, hence the change of colour. Both symmetries combined result in a third symmetry that is detectable as a shift by
$\omega _x$, hence the change of colour. Both symmetries combined result in a third symmetry that is detectable as a shift by ![]() $\lambda _z/2=1.25$ from one Poincaré crossing to the next.
$\lambda _z/2=1.25$ from one Poincaré crossing to the next.

Figure 12. Streamwise vorticity colour maps ![]() $\omega _x\in [-0.1,0.1]$ (yellow for positive, blue for negative) at
$\omega _x\in [-0.1,0.1]$ (yellow for positive, blue for negative) at ![]() $x=6$ for velocity ratios (a,c,e,g)
$x=6$ for velocity ratios (a,c,e,g) ![]() $R=3.4$ and (b,d, f,h)
$R=3.4$ and (b,d, f,h) ![]() $R=3.8$. Four consecutive crossings of the Poincaré section have been represented, respectively.
$R=3.8$. Four consecutive crossings of the Poincaré section have been represented, respectively.
For the nonlinear solution at ![]() $R=3.8$, the planes
$R=3.8$, the planes ![]() $z=z_0+(2j)\lambda _z/4=2.5\,j$ are no longer symmetry planes, although the solution keeps the shadow of a reflectional symmetry to a certain extent. Remnants of the original spanwise periodicity
$z=z_0+(2j)\lambda _z/4=2.5\,j$ are no longer symmetry planes, although the solution keeps the shadow of a reflectional symmetry to a certain extent. Remnants of the original spanwise periodicity ![]() $\lambda _z=2.5$ are also still perceptible, but the actual periodicity has indeed doubled to
$\lambda _z=2.5$ are also still perceptible, but the actual periodicity has indeed doubled to ![]() $\lambda _z=5$. The only remaining symmetry, which is of a spatiotemporal nature, relates even/odd crossings by a reflection about planes at
$\lambda _z=5$. The only remaining symmetry, which is of a spatiotemporal nature, relates even/odd crossings by a reflection about planes at ![]() $z=z_0+(2j)\lambda _z/4=2.5\,j$.
$z=z_0+(2j)\lambda _z/4=2.5\,j$.
A single snapshot of a random crossing of the Poincaré section for the chaotic solution at ![]() $R=5.357$ is shown in figure 13(a). The Kármán vortices are still clearly identifiable as are also the elongated vortical structures along the braids, which are clearly arranged in pairs forming horseshoe vortices on top of the primary spanwise vortices (left arm yellow, right arm black, on account of the change of sign in axial vorticity; both legs connect on top of the last Kármán vortex shed). The flow remains fairly well organised in the near wake, but clearly breaks into spatiotemporally chaotic dynamics a little further downstream. The typical wavelength of the vortical structures remains at about
$R=5.357$ is shown in figure 13(a). The Kármán vortices are still clearly identifiable as are also the elongated vortical structures along the braids, which are clearly arranged in pairs forming horseshoe vortices on top of the primary spanwise vortices (left arm yellow, right arm black, on account of the change of sign in axial vorticity; both legs connect on top of the last Kármán vortex shed). The flow remains fairly well organised in the near wake, but clearly breaks into spatiotemporally chaotic dynamics a little further downstream. The typical wavelength of the vortical structures remains at about ![]() $\lambda _z\sim 2.5$, but there is no spanwise periodicity other than that artificially imposed by the fundamental Fourier mode employed in the simulation, here
$\lambda _z\sim 2.5$, but there is no spanwise periodicity other than that artificially imposed by the fundamental Fourier mode employed in the simulation, here ![]() $L_z=10$. A second emerging subdominant mode of a much shorter spanwise wavelength, already visible at the far end of the Floquet spectrum of figure 7, is shown in figure 13(b). The mode is still stable at
$L_z=10$. A second emerging subdominant mode of a much shorter spanwise wavelength, already visible at the far end of the Floquet spectrum of figure 7, is shown in figure 13(b). The mode is still stable at ![]() $R=5.357$, but bifurcates with critical
$R=5.357$, but bifurcates with critical ![]() $\lambda _z\simeq 10/7$ for
$\lambda _z\simeq 10/7$ for ![]() $R<6.5$. Its characteristically short wavelength and synchronous nature identify it as a mode B type (see mode B of figure 1). It is however not detectable in the spatiotemporally chaotic solution snapshot and its growth rate once unstable remains well below that of the dominant eigenmode, which has shifted to somewhat longer wavelength
$R<6.5$. Its characteristically short wavelength and synchronous nature identify it as a mode B type (see mode B of figure 1). It is however not detectable in the spatiotemporally chaotic solution snapshot and its growth rate once unstable remains well below that of the dominant eigenmode, which has shifted to somewhat longer wavelength ![]() $\lambda _z\gtrsim 2.5$ for these high values of
$\lambda _z\gtrsim 2.5$ for these high values of ![]() $R$. It is therefore improbable that this other mode plays any important role in the transition to turbulence of the wake past the square cylinder in upstream shear as mode B indeed does for both circular and square cylinders subjected to homogeneous incoming flow.
$R$. It is therefore improbable that this other mode plays any important role in the transition to turbulence of the wake past the square cylinder in upstream shear as mode B indeed does for both circular and square cylinders subjected to homogeneous incoming flow.

Figure 13. Instantaneous snapshot of (a) the chaotic three-dimensional solution at ![]() $R=5.357$ at a random crossing of the Poincaré section, and (b) short wavelength dominant eigenmode at
$R=5.357$ at a random crossing of the Poincaré section, and (b) short wavelength dominant eigenmode at ![]() $(R,\lambda _z)=(5.357,1.429)$. Isosurfaces and colours as for figure 11.
$(R,\lambda _z)=(5.357,1.429)$. Isosurfaces and colours as for figure 11.
We have applied both proper orthogonal decomposition and dynamic mode decomposition to the spatiotemporally chaotic solution, but results are inconclusive. Besides the average-fields mode, the two-dimensional vortex-shedding mode is clearly dominant, followed by something akin to mode C, but, other than that, we have been unable to identify any clear indication of additional relevant modes that may assist in understanding the actual dynamics.
A quasi-static variation of ![]() $R$, which is outside the scope of this study, would be required to cast light on the actual path leading to spatiotemporal chaos, but the presence of a period-doubling bifurcation suggests that a period-doubling cascade might play a role. There is also evidence suggesting that the complexification of the dynamics might arise from the competition of an increasing number of unstable wavelengths of the same instability type (actually a continuum if an infinite-span cylinder was to be considered), so that an instability of the Eckhaus or Benjamin–Feir type might in fact be held responsible, both for the period-doubling bifurcation reported here and the route to chaotic dynamics (Leweke, Provansal & Boyer Reference Leweke, Provansal and Boyer1993; Leweke & Provansal Reference Leweke and Provansal1994, Reference Leweke and Provansal1995). Confirming or refuting the modulational instability hypothesis would not be feasible in a reasonable time scale due to the unjustifiedly high computational burden expected, and has therefore been left out of the present analysis.
$R$, which is outside the scope of this study, would be required to cast light on the actual path leading to spatiotemporal chaos, but the presence of a period-doubling bifurcation suggests that a period-doubling cascade might play a role. There is also evidence suggesting that the complexification of the dynamics might arise from the competition of an increasing number of unstable wavelengths of the same instability type (actually a continuum if an infinite-span cylinder was to be considered), so that an instability of the Eckhaus or Benjamin–Feir type might in fact be held responsible, both for the period-doubling bifurcation reported here and the route to chaotic dynamics (Leweke, Provansal & Boyer Reference Leweke, Provansal and Boyer1993; Leweke & Provansal Reference Leweke and Provansal1994, Reference Leweke and Provansal1995). Confirming or refuting the modulational instability hypothesis would not be feasible in a reasonable time scale due to the unjustifiedly high computational burden expected, and has therefore been left out of the present analysis.
5.3. Dependence of the dominant eigenmode on  $R$ and
$R$ and  $\lambda _z$
$\lambda _z$
Although the dominant eigenmode curves in the Floquet spectrum of figure 7(b) are smooth in the range of wavelengths observed in nonlinear solutions, evidence that they represent the same actual instability requires a close inspection of the eigenfields. Four snapshots taken at consecutive crossings within the linear regime of a purposefully designed Poincaré section, well before three-dimensional modal energy reaches nonlinear saturation, illustrate the flow topology of the instability for ![]() $(R,\lambda _z)=(3.4,2.5)$,
$(R,\lambda _z)=(3.4,2.5)$, ![]() $(3.8,2.5)$ and
$(3.8,2.5)$ and ![]() $(3.8,5)$ in figure 14. Shown are normalised streamwise vorticity
$(3.8,5)$ in figure 14. Shown are normalised streamwise vorticity ![]() $(\tilde {\omega }_x\equiv \omega _x/\omega _x^{{max}})$ colour maps on a streamwise-cross-stream plane halfway between two consecutive symmetry planes of the eigenmode. Here
$(\tilde {\omega }_x\equiv \omega _x/\omega _x^{{max}})$ colour maps on a streamwise-cross-stream plane halfway between two consecutive symmetry planes of the eigenmode. Here ![]() $\omega _x^{{max}}$ is the maximum instantaneous value of
$\omega _x^{{max}}$ is the maximum instantaneous value of ![]() $|\omega _x|$ at any given time. Comparison of all three cases points at a common origin of all three instabilities, which in fact are one and the same mode just deformed by a continuous change of the parameters. The only apparent effect, besides the stretching/compressing associated to changes in
$|\omega _x|$ at any given time. Comparison of all three cases points at a common origin of all three instabilities, which in fact are one and the same mode just deformed by a continuous change of the parameters. The only apparent effect, besides the stretching/compressing associated to changes in ![]() $\lambda _z$ that was already obvious from figures 11(b) and 11(c), is that the instability dissipates faster along the wake when
$\lambda _z$ that was already obvious from figures 11(b) and 11(c), is that the instability dissipates faster along the wake when ![]() $R$ is increased or the wavelength shortened towards criticality.
$R$ is increased or the wavelength shortened towards criticality.

Figure 14. Most unstable mode for ![]() $Re_B=56$ and (a)
$Re_B=56$ and (a) ![]() $(R,\lambda _z)=(3.4,2.5)$ (supplementary movie 6), (b)
$(R,\lambda _z)=(3.4,2.5)$ (supplementary movie 6), (b) ![]() $(R,\lambda _z)=(3.8,2.5)$ (supplementary movie 7) and (c)
$(R,\lambda _z)=(3.8,2.5)$ (supplementary movie 7) and (c) ![]() $(R,\lambda _z)=(3.8,5)$ (supplementary movie 8). Normalised streamwise vorticity (
$(R,\lambda _z)=(3.8,5)$ (supplementary movie 8). Normalised streamwise vorticity (![]() $\tilde {\omega }_x\equiv \omega _x/\omega _x^{{max}}\in [-1,1]$, blue for negative, yellow for positive) colour maps at plane
$\tilde {\omega }_x\equiv \omega _x/\omega _x^{{max}}\in [-1,1]$, blue for negative, yellow for positive) colour maps at plane ![]() $z=z_0+\lambda _z/4$ at four consecutive Poincaré crossings (marked and labelled in figure 7(a) for case (a)).
$z=z_0+\lambda _z/4$ at four consecutive Poincaré crossings (marked and labelled in figure 7(a) for case (a)).
The global instability grows preferentially in the very near wake, where the perturbation ![]() $|\tilde {\omega }_x|$ is maximum, and the period-doubling nature of the mode is obvious from the coincident normalised
$|\tilde {\omega }_x|$ is maximum, and the period-doubling nature of the mode is obvious from the coincident normalised ![]() $\tilde {\omega }_x$ fields of any two snapshots taken exactly two vortex-shedding cycles apart.
$\tilde {\omega }_x$ fields of any two snapshots taken exactly two vortex-shedding cycles apart.
Spatially developing flows such as shear layers or bluff body wakes may be studied in the light of either local or global instabilities (Chomaz Reference Chomaz2005). Local instabilities may in turn be classified according to their convective or absolute nature (Huerre & Monkewitz Reference Huerre and Monkewitz1990). Both the primary (Kármán) and secondary (three dimensionalising) instabilities in the wake past bluff bodies are global instabilities. A region of local absolute instability is known to develop in the near wake for values of the Reynolds numbers well below the global instability that triggers vortex shedding (Monkewitz Reference Monkewitz1988; Yang & Zebib Reference Yang and Zebib1989). Further downstream the steady wake is only convectively unstable. We have no reason to believe that the case at hand behaves differently regarding the primary instability. Unfortunately, the extension of the absolute/convective local instability analysis to the wake transition regime is hindered by the time dependence of the underlying flow (Abdessemed et al. Reference Abdessemed, Sharma, Sherwin and Theofilis2009), besides its strongly non-parallel instantaneous nature. Anyhow, unstable global modes typically reach far beyond the region of absolute local instability and, consequently, an extension of the absolutely unstable region does not necessarily follow from the lengthening of the global mode observed upon reducing ![]() $R$ or increasing
$R$ or increasing ![]() $\lambda _z$.
$\lambda _z$.
The appropriate choice of the spanwise plane used for the representation again evinces the space–time symmetry, here apparent as a mere change of sign of ![]() $\tilde {\omega }_x$ between any two consecutive Poincaré crossings. The topology and symmetries of the eigenmode anticipate the properties of the nonlinear three-dimensional solution observed for
$\tilde {\omega }_x$ between any two consecutive Poincaré crossings. The topology and symmetries of the eigenmode anticipate the properties of the nonlinear three-dimensional solution observed for ![]() $R=3.4$. They also portend the main features of the flow arrangement for
$R=3.4$. They also portend the main features of the flow arrangement for ![]() $R=3.8$, but cannot by themselves explain the actual spanwise periodicity or its period-doubled nature. We surmise that the
$R=3.8$, but cannot by themselves explain the actual spanwise periodicity or its period-doubled nature. We surmise that the ![]() $\lambda _z=5$ instance of the eigenmode might be interfering with the dominant
$\lambda _z=5$ instance of the eigenmode might be interfering with the dominant ![]() $\lambda _z=2.5$ eigenmode at
$\lambda _z=2.5$ eigenmode at ![]() $R=3.8$, such that the nonlinear flow features arise from an Eckhaus-type instability. Simulations in much longer spanwise domains would be required to sufficiently approximate the continuous band of unstable wavelengths that would allow for mode competition and, thus, analyse the bifurcation in the light of modulational instabilities.
$R=3.8$, such that the nonlinear flow features arise from an Eckhaus-type instability. Simulations in much longer spanwise domains would be required to sufficiently approximate the continuous band of unstable wavelengths that would allow for mode competition and, thus, analyse the bifurcation in the light of modulational instabilities.
6. Aerodynamic performances
The evolution of the drag (![]() $C_d$) and lift (
$C_d$) and lift (![]() $C_l$) coefficients as the velocity ratio
$C_l$) coefficients as the velocity ratio ![]() $R$ is increased at a constant bottom Reynolds number
$R$ is increased at a constant bottom Reynolds number ![]() $Re_B=56$ is presented in figures 15(a) and 15(b), respectively. The oscillation amplitude is indicated by error bars for unsteady regimes, and different symbols and colours denote different types of solutions (plus sign, steady; circle, unsteady; black, two-dimensional periodic; red, three-dimensional periodic; blue, three-dimensional period doubled; green, chaotic). After a barely perceptible decrease,
$Re_B=56$ is presented in figures 15(a) and 15(b), respectively. The oscillation amplitude is indicated by error bars for unsteady regimes, and different symbols and colours denote different types of solutions (plus sign, steady; circle, unsteady; black, two-dimensional periodic; red, three-dimensional periodic; blue, three-dimensional period doubled; green, chaotic). After a barely perceptible decrease, ![]() $C_d$ starts growing steadily as
$C_d$ starts growing steadily as ![]() $R$ is increased through the various flow regimes. This dependence is consistent with the combined effect of increasing
$R$ is increased through the various flow regimes. This dependence is consistent with the combined effect of increasing ![]() $K$, which tends to reduce
$K$, which tends to reduce ![]() $C_d$ (Saha et al. Reference Saha, Biswas and Muralidhar1999; Lei et al. Reference Lei, Cheng and Kavanagh2000; Cheng et al. Reference Cheng, Whyte and Lou2007), and also increasing
$C_d$ (Saha et al. Reference Saha, Biswas and Muralidhar1999; Lei et al. Reference Lei, Cheng and Kavanagh2000; Cheng et al. Reference Cheng, Whyte and Lou2007), and also increasing ![]() $Re$, which makes it grow fast (Davis & Moore Reference Davis and Moore1982; Franke, Rodi & Schönung Reference Franke, Rodi and Schönung1990; Saha et al. Reference Saha, Biswas and Muralidhar2003; Mahir Reference Mahir2017). The combined effect of both parameters shows that the dependence of
$Re$, which makes it grow fast (Davis & Moore Reference Davis and Moore1982; Franke, Rodi & Schönung Reference Franke, Rodi and Schönung1990; Saha et al. Reference Saha, Biswas and Muralidhar2003; Mahir Reference Mahir2017). The combined effect of both parameters shows that the dependence of ![]() $C_d$ on
$C_d$ on ![]() $K$ changes from a declining trend at low
$K$ changes from a declining trend at low ![]() $Re\lesssim 100$ to increasing beyond this value (Sohankar et al. Reference Sohankar, Rangraz, Khodadadi and Alam2020). Some simulations, both two and three dimensional, at very low
$Re\lesssim 100$ to increasing beyond this value (Sohankar et al. Reference Sohankar, Rangraz, Khodadadi and Alam2020). Some simulations, both two and three dimensional, at very low ![]() $Re<200$ and
$Re<200$ and ![]() $K<0.5$ predict a decreasing trend of
$K<0.5$ predict a decreasing trend of ![]() $C_d$ (Cheng et al. Reference Cheng, Whyte and Lou2007) also with
$C_d$ (Cheng et al. Reference Cheng, Whyte and Lou2007) also with ![]() $Re$. The additive decomposition of
$Re$. The additive decomposition of ![]() $C_d=C_d^{p}+C_d^{f}$ into its pressure (
$C_d=C_d^{p}+C_d^{f}$ into its pressure (![]() $C_d^{p}$, dashed) and friction (
$C_d^{p}$, dashed) and friction (![]() $C_d^{f}$, dotted) components, reveals how pressure forces dominate over viscous forces across the full regime, as is typical of bluff body aerodynamics. As a matter of fact,
$C_d^{f}$, dotted) components, reveals how pressure forces dominate over viscous forces across the full regime, as is typical of bluff body aerodynamics. As a matter of fact, ![]() $C_d^{f}$ declines with
$C_d^{f}$ declines with ![]() $R$, so that
$R$, so that ![]() $C_d^{p}$ takes a larger and larger fraction of the total
$C_d^{p}$ takes a larger and larger fraction of the total ![]() $C_d$. For circular cylinders,
$C_d$. For circular cylinders, ![]() $C_d^{p}$ has been shown to take a constant proportion of total
$C_d^{p}$ has been shown to take a constant proportion of total ![]() $C_d$ independently of
$C_d$ independently of ![]() $K$, but this is only valid for constant
$K$, but this is only valid for constant ![]() $Re$ and the trend expected for rising
$Re$ and the trend expected for rising ![]() $Re$ is actually increasing (Tamura et al. Reference Tamura, Kiya and Arie1980; Lei et al. Reference Lei, Cheng and Kavanagh2000). The initial decline of
$Re$ is actually increasing (Tamura et al. Reference Tamura, Kiya and Arie1980; Lei et al. Reference Lei, Cheng and Kavanagh2000). The initial decline of ![]() $C_l$ is much more pronounced and results in a clear downforce as
$C_l$ is much more pronounced and results in a clear downforce as ![]() $R$ is increased from the symmetric value
$R$ is increased from the symmetric value ![]() $R=1$. This follows from the fast drop of the friction lift coefficient (
$R=1$. This follows from the fast drop of the friction lift coefficient (![]() $C_l^{f}$, dotted) for low
$C_l^{f}$, dotted) for low ![]() $R$, with friction downforce taking the lead over pressure lift, represented by the pressure lift coefficient (
$R$, with friction downforce taking the lead over pressure lift, represented by the pressure lift coefficient (![]() $C_l^{p}$, dashed), which remains negligible while the symmetry disruption is moderately low. In fact, the net downward pointing friction is almost exclusively generated on the front surface of the cylinder as the stagnation point climbs fast towards the top corner (El Mansy et al. Reference El Mansy, Bergadà, Sarwar and Mellibovsky2022). The decreasing trend is reversed as the Hopf bifurcation renders the flow time periodic at
$C_l^{p}$, dashed), which remains negligible while the symmetry disruption is moderately low. In fact, the net downward pointing friction is almost exclusively generated on the front surface of the cylinder as the stagnation point climbs fast towards the top corner (El Mansy et al. Reference El Mansy, Bergadà, Sarwar and Mellibovsky2022). The decreasing trend is reversed as the Hopf bifurcation renders the flow time periodic at ![]() $R\in (2,2.2)$ and
$R\in (2,2.2)$ and ![]() $C_l^{p}$ starts growing fast, but actual positive average lift is not achieved until the flow has become three dimensional for
$C_l^{p}$ starts growing fast, but actual positive average lift is not achieved until the flow has become three dimensional for ![]() $R\in (3.1,3.4)$. Prior to that, positive lift is recovered over some parts of the vortex-shedding cycle, even if on average it remains negative. Once the initial reduction is overcome, the increasing trend is sustained over the full range of
$R\in (3.1,3.4)$. Prior to that, positive lift is recovered over some parts of the vortex-shedding cycle, even if on average it remains negative. Once the initial reduction is overcome, the increasing trend is sustained over the full range of ![]() $R$ explored because while friction downforce
$R$ explored because while friction downforce ![]() $C_l^{f}$ saturates, pressure lift
$C_l^{f}$ saturates, pressure lift ![]() $C_l^{p}$ keeps growing. Net downforce has been reported for the square cylinder in homogenous shear at
$C_l^{p}$ keeps growing. Net downforce has been reported for the square cylinder in homogenous shear at ![]() $Re\leqslant 100$ and moderate
$Re\leqslant 100$ and moderate ![]() $K\leqslant 0.5$ (Cheng et al. Reference Cheng, Whyte and Lou2007; Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2008), while positive lift is recovered for
$K\leqslant 0.5$ (Cheng et al. Reference Cheng, Whyte and Lou2007; Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2008), while positive lift is recovered for ![]() $Re\geqslant 150$ (Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2011; Sohankar et al. Reference Sohankar, Rangraz, Khodadadi and Alam2020), in agreement with the present results. As for
$Re\geqslant 150$ (Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2011; Sohankar et al. Reference Sohankar, Rangraz, Khodadadi and Alam2020), in agreement with the present results. As for ![]() $C_d$, the
$C_d$, the ![]() $C_l$ trend with
$C_l$ trend with ![]() $K$ is a decreasing one for
$K$ is a decreasing one for ![]() $Re\lesssim 120$ and a growing one above this threshold (Sohankar et al. Reference Sohankar, Rangraz, Khodadadi and Alam2020). The oscillation amplitude increases fast after the initial Hopf bifurcation for both
$Re\lesssim 120$ and a growing one above this threshold (Sohankar et al. Reference Sohankar, Rangraz, Khodadadi and Alam2020). The oscillation amplitude increases fast after the initial Hopf bifurcation for both ![]() $C_d$ and
$C_d$ and ![]() $C_l$, as expected from two-dimensional numerical literature results (Saha et al. Reference Saha, Biswas and Muralidhar1999; Sohankar et al. Reference Sohankar, Rangraz, Khodadadi and Alam2020), but it almost saturates by the time three dimensionality has kicked in. The escalating fluctuations that follow from increasing
$C_l$, as expected from two-dimensional numerical literature results (Saha et al. Reference Saha, Biswas and Muralidhar1999; Sohankar et al. Reference Sohankar, Rangraz, Khodadadi and Alam2020), but it almost saturates by the time three dimensionality has kicked in. The escalating fluctuations that follow from increasing ![]() $Re$ might be partially or totally compensated by a decline associated to increasing
$Re$ might be partially or totally compensated by a decline associated to increasing ![]() $K$ (Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2011). Most of the force oscillation can be ascribed to pressure fluctuation, as friction behaves rather stably. A detailed dissection of the aerodynamic force coefficients into their pressure and friction components, following a minute analysis of pressure and shear distributions on the cylinder walls, is provided by El Mansy et al. (Reference El Mansy, Bergadà, Sarwar and Mellibovsky2022). The relation of aerodynamic performance monitors with first- and second-order wake statistics as well as instantaneous wake topology may also be found therein.
$K$ (Lankadasu & Vengadesan Reference Lankadasu and Vengadesan2011). Most of the force oscillation can be ascribed to pressure fluctuation, as friction behaves rather stably. A detailed dissection of the aerodynamic force coefficients into their pressure and friction components, following a minute analysis of pressure and shear distributions on the cylinder walls, is provided by El Mansy et al. (Reference El Mansy, Bergadà, Sarwar and Mellibovsky2022). The relation of aerodynamic performance monitors with first- and second-order wake statistics as well as instantaneous wake topology may also be found therein.

Figure 15. Performance parameters as a function of the velocity ratio ![]() $R$ at constant bottom Reynolds number
$R$ at constant bottom Reynolds number ![]() $Re_B=56$. (a) Drag coefficient
$Re_B=56$. (a) Drag coefficient ![]() $C_d$. (b) Lift coefficient
$C_d$. (b) Lift coefficient ![]() $C_l$. (c) Fundamental (
$C_l$. (c) Fundamental (![]() $f_1$) and, for period-doubled solutions, subharmonic frequencies (squares for the half and triangle for the quarter frequency). Different symbols denote steady (plus signs) and unsteady (circles) solutions. Colour coding separates two-dimensional (black), three-dimensional periodic (red), three-dimensional period-doubled (blue) and chaotic (green) solutions. Total force coefficient trends (solid lines) are split into their pressure (dashed) and friction (dotted) components. Error bars denote oscillation amplitude (valley to peak difference of the statistically converged time series).
$f_1$) and, for period-doubled solutions, subharmonic frequencies (squares for the half and triangle for the quarter frequency). Different symbols denote steady (plus signs) and unsteady (circles) solutions. Colour coding separates two-dimensional (black), three-dimensional periodic (red), three-dimensional period-doubled (blue) and chaotic (green) solutions. Total force coefficient trends (solid lines) are split into their pressure (dashed) and friction (dotted) components. Error bars denote oscillation amplitude (valley to peak difference of the statistically converged time series).
The evolution of the non-dimensional vortex-shedding frequency ![]() $f_1$ across the full exploration, measured at several locations in the near wake at
$f_1$ across the full exploration, measured at several locations in the near wake at ![]() $(x,y,z)=(2.5,0,0)$,
$(x,y,z)=(2.5,0,0)$, ![]() $(2.5,0,2.5)$ and
$(2.5,0,2.5)$ and ![]() $(3.5,0,0)$, is shown in figure 15(c). After the debut of vortex shedding at the Hopf bifurcation, the frequency drifts to slightly higher values but remains mostly unaltered thereafter. The fundamental frequency
$(3.5,0,0)$, is shown in figure 15(c). After the debut of vortex shedding at the Hopf bifurcation, the frequency drifts to slightly higher values but remains mostly unaltered thereafter. The fundamental frequency ![]() $f_1$ is expected to grow fast with
$f_1$ is expected to grow fast with ![]() $Re$ while vortex shedding remains two dimensional and to stagnate for a while thereafter across the wake transition regime before starting a slow decline (Davis & Moore Reference Davis and Moore1982; Okajima Reference Okajima1982; Kelkar & Patankar Reference Kelkar and Patankar1992; Norberg Reference Norberg1993; Sohankar et al. Reference Sohankar, Norberg and Davidson1999; Saha et al. Reference Saha, Biswas and Muralidhar2003). The trend with
$Re$ while vortex shedding remains two dimensional and to stagnate for a while thereafter across the wake transition regime before starting a slow decline (Davis & Moore Reference Davis and Moore1982; Okajima Reference Okajima1982; Kelkar & Patankar Reference Kelkar and Patankar1992; Norberg Reference Norberg1993; Sohankar et al. Reference Sohankar, Norberg and Davidson1999; Saha et al. Reference Saha, Biswas and Muralidhar2003). The trend with ![]() $K$ is a slightly decreasing one, at least for sufficiently low
$K$ is a slightly decreasing one, at least for sufficiently low ![]() $Re<200$ (Ayukawa et al. Reference Ayukawa, Ochi, Kawahara and Hirao1993; Saha et al. Reference Saha, Biswas and Muralidhar1999; Cheng et al. Reference Cheng, Whyte and Lou2007; Kumar & Ray Reference Kumar and Ray2015), so that it cannot be discarded that the combined effect produces the slowly increasing and then saturating behaviour observed here.
$Re<200$ (Ayukawa et al. Reference Ayukawa, Ochi, Kawahara and Hirao1993; Saha et al. Reference Saha, Biswas and Muralidhar1999; Cheng et al. Reference Cheng, Whyte and Lou2007; Kumar & Ray Reference Kumar and Ray2015), so that it cannot be discarded that the combined effect produces the slowly increasing and then saturating behaviour observed here.
The onset of three dimensionality introduces a new frequency (see figure 15c) that is exactly half the Strouhal number (squares), and the ensuing period doubling adds yet a third quarter frequency to the solution (triangle).
7. Raw decoupling of the independent effects of  $Re$ and
$Re$ and  $R$
$R$
Only a comprehensive exploration independently varying ![]() $Re$ and
$Re$ and ![]() $R$ can fully discern the separate effects of the two parameters. Such an exhaustive sweep of two-dimensional parameter space would however require computational resources that are beyond reach in a reasonable time scale. In order to at least fathom the specific roles of
$R$ can fully discern the separate effects of the two parameters. Such an exhaustive sweep of two-dimensional parameter space would however require computational resources that are beyond reach in a reasonable time scale. In order to at least fathom the specific roles of ![]() $Re$ and
$Re$ and ![]() $R$, we have undertaken a rough exploration varying
$R$, we have undertaken a rough exploration varying ![]() $R$ at constant
$R$ at constant ![]() $Re=114.8$, thus intersecting the parameter sweep analysed so far very close to the first three-dimensionalising instability at
$Re=114.8$, thus intersecting the parameter sweep analysed so far very close to the first three-dimensionalising instability at ![]() $(Re,R)=(114.8,3.1)$. In this manner we are certain to enter the wake transition regime at about the same point.
$(Re,R)=(114.8,3.1)$. In this manner we are certain to enter the wake transition regime at about the same point.
Figure 16 shows phase-map projections of a collection of solutions along the ![]() $R$-exploration line at constant
$R$-exploration line at constant ![]() $Re=114.8$. The grey symbols/lines in the background correspond to the solutions for constant
$Re=114.8$. The grey symbols/lines in the background correspond to the solutions for constant ![]() $Re_B=56$ shown in figure 5 at the same values of
$Re_B=56$ shown in figure 5 at the same values of ![]() $R$ (see labels). The most remarkable fact is that the sweep at constant
$R$ (see labels). The most remarkable fact is that the sweep at constant ![]() $Re=114.8$ drastically reduces the richness of solutions that might be observed. Only the two-dimensional vortex shedding and the period-doubled periodic three-dimensional vortex-shedding solutions exist across the full exploration range
$Re=114.8$ drastically reduces the richness of solutions that might be observed. Only the two-dimensional vortex shedding and the period-doubled periodic three-dimensional vortex-shedding solutions exist across the full exploration range ![]() $R\in [1,6]$. Before the three-dimensionalising instability, periodic two-dimensional vortex shedding extends all the way down to
$R\in [1,6]$. Before the three-dimensionalising instability, periodic two-dimensional vortex shedding extends all the way down to ![]() $R=1$, at which point the characteristic space–time symmetry of the Kármán street is recovered. This evinces that the Hopf bifurcation that triggers vortex shedding occurs somewhere in between
$R=1$, at which point the characteristic space–time symmetry of the Kármán street is recovered. This evinces that the Hopf bifurcation that triggers vortex shedding occurs somewhere in between ![]() $Re=56$ and
$Re=56$ and ![]() $114.8$. Hence, the instability occurs all the same and, although it is somewhat delayed with respect to the classic square cylinder flow configuration with no upstream splitter plate, it can be fully attributed to a
$114.8$. Hence, the instability occurs all the same and, although it is somewhat delayed with respect to the classic square cylinder flow configuration with no upstream splitter plate, it can be fully attributed to a ![]() $Re$ effect regardless of
$Re$ effect regardless of ![]() $R$. Beyond
$R$. Beyond ![]() $R>3.1$ the solution is invariably period-doubled periodic, even if the double loop in the
$R>3.1$ the solution is invariably period-doubled periodic, even if the double loop in the ![]() $(C_l,v)$ phase map is still imperceptible at
$(C_l,v)$ phase map is still imperceptible at ![]() $R=3.4$.
$R=3.4$.

Figure 16. Phase-map projections on the (a) ![]() $(C_l,C_d)$ and (b)
$(C_l,C_d)$ and (b) ![]() $(C_l,v)$ planes for solutions with
$(C_l,v)$ planes for solutions with ![]() $Re=114.8$ and various
$Re=114.8$ and various ![]() $R$ indicated by labels. Grey lines and symbols denote solutions with
$R$ indicated by labels. Grey lines and symbols denote solutions with ![]() $Re_B=56$, already shown in figure 5.
$Re_B=56$, already shown in figure 5.
The stability analysis produces the exact same dominant mode C reported in figure 7(b) and, though its spanwise wavelength remains fairly unaltered at ![]() $\lambda _z\simeq 2.5$ across the full unstable
$\lambda _z\simeq 2.5$ across the full unstable ![]() $R$ range, the growth rate does not increase as fast as for constant
$R$ range, the growth rate does not increase as fast as for constant ![]() $Re_B$. This explains why only the simplest type of three-dimensional solution is observed and indirectly supports the modulational instability hypothesis. The range of unstable wavelengths grows more slowly upon increasing
$Re_B$. This explains why only the simplest type of three-dimensional solution is observed and indirectly supports the modulational instability hypothesis. The range of unstable wavelengths grows more slowly upon increasing ![]() $R$ than it did when
$R$ than it did when ![]() $Re$ was simultaneously rising. It is therefore reasonable to expect that mode competition is postponed and that the nonlinear period-doubled periodic three-dimensional solution remains stable over a wider range of
$Re$ was simultaneously rising. It is therefore reasonable to expect that mode competition is postponed and that the nonlinear period-doubled periodic three-dimensional solution remains stable over a wider range of ![]() $R$. Both the dominant mode and the nonlinear solution display a flow topology very similar to the
$R$. Both the dominant mode and the nonlinear solution display a flow topology very similar to the ![]() $(Re_B,R)=(56,3.4)$ case and preserve the same symmetries. Space–time diagrams of
$(Re_B,R)=(56,3.4)$ case and preserve the same symmetries. Space–time diagrams of ![]() $w$,
$w$, ![]() $Q$-criterion isosurfaces and cross-sectional
$Q$-criterion isosurfaces and cross-sectional ![]() $\omega _x$ colour maps look so similar to those shown in figures 8(b), 10 and 12(a) for
$\omega _x$ colour maps look so similar to those shown in figures 8(b), 10 and 12(a) for ![]() $(Re_B,R)=(56,3.4)$, that we feel justified in not showing them again for any of the
$(Re_B,R)=(56,3.4)$, that we feel justified in not showing them again for any of the ![]() $Re=114.8$,
$Re=114.8$, ![]() $R>3.1$ solutions.
$R>3.1$ solutions.
Aerodynamic performance trends for varying ![]() $R$ at constant
$R$ at constant ![]() $Re$ are shown in figure 17. The
$Re$ are shown in figure 17. The ![]() $Re_B$ exploration of figure 15 has been left in the background and coloured in grey to assist comparison. Corresponding lines for constant
$Re_B$ exploration of figure 15 has been left in the background and coloured in grey to assist comparison. Corresponding lines for constant ![]() $Re$ and constant
$Re$ and constant ![]() $Re_B$ lines intersect at
$Re_B$ lines intersect at ![]() $R=3.1$ following the intersection of the exploration paths. Average
$R=3.1$ following the intersection of the exploration paths. Average ![]() $C_d$ trends (see figure 17a) are not greatly altered by keeping
$C_d$ trends (see figure 17a) are not greatly altered by keeping ![]() $Re$ constant instead of
$Re$ constant instead of ![]() $Re_B$, the only effect concerning the type of solution found at each individual value of
$Re_B$, the only effect concerning the type of solution found at each individual value of ![]() $R$. Pressure drag remains clearly dominant over friction. The solutions along the new path are all unsteady, but time dependence does not show prominently as drag fluctuations. The fundamental vortex-shedding frequency, shown in figure 17(c), is quite stable across the full exploration and the subharmonic frequency appears beyond the three-dimensionalising instability for
$R$. Pressure drag remains clearly dominant over friction. The solutions along the new path are all unsteady, but time dependence does not show prominently as drag fluctuations. The fundamental vortex-shedding frequency, shown in figure 17(c), is quite stable across the full exploration and the subharmonic frequency appears beyond the three-dimensionalising instability for ![]() $R>3.1$. Comparison with the
$R>3.1$. Comparison with the ![]() $Re_B$-constant exploration suggests that, while three dimensionality stabilises the vortex-shedding frequency independently of
$Re_B$-constant exploration suggests that, while three dimensionality stabilises the vortex-shedding frequency independently of ![]() $R$ and
$R$ and ![]() $Re$, the slow growing trend that follows the primary Hopf bifurcation is driven by
$Re$, the slow growing trend that follows the primary Hopf bifurcation is driven by ![]() $Re$ rather than
$Re$ rather than ![]() $R$.
$R$.

Figure 17. Performance parameters as a function of the velocity ratio ![]() $R$ at constant bulk Reynolds number
$R$ at constant bulk Reynolds number ![]() $Re=114.8$. (a) Drag coefficient
$Re=114.8$. (a) Drag coefficient ![]() $C_d$. (b) Lift coefficient
$C_d$. (b) Lift coefficient ![]() $C_l$. (c) Fundamental (
$C_l$. (c) Fundamental (![]() $f_1$) and, for period-doubled solutions, subharmonic frequencies. Line styles, symbols, error bars and colours as for figure 15. The
$f_1$) and, for period-doubled solutions, subharmonic frequencies. Line styles, symbols, error bars and colours as for figure 15. The ![]() $C_l^{f}$ and friction
$C_l^{f}$ and friction ![]() $C_l^{p}$ data has been slightly shifted to the left and right, respectively, in panel (b) to avoid cluttering. The grey trends in the background correspond to the constant
$C_l^{p}$ data has been slightly shifted to the left and right, respectively, in panel (b) to avoid cluttering. The grey trends in the background correspond to the constant ![]() $Re_B=56$ exploration.
$Re_B=56$ exploration.
The differences between the two exploration paths becomes the most obvious in the ![]() $C_l$ trends of figure 17(b). The decrease of
$C_l$ trends of figure 17(b). The decrease of ![]() $C_l^{f}$ into negative values follows very similar courses for both sweeps, which suggests that the shear effect
$C_l^{f}$ into negative values follows very similar courses for both sweeps, which suggests that the shear effect ![]() $R$ is the culprit behind downforce independently of
$R$ is the culprit behind downforce independently of ![]() $Re$. Average
$Re$. Average ![]() $C_l^{p}$ is negligible at low
$C_l^{p}$ is negligible at low ![]() $R$ and behaves very similarly for both constant
$R$ and behaves very similarly for both constant ![]() $Re$ and constant
$Re$ and constant ![]() $Re_B$ while the solution remains two dimensional. Three dimensionalisation, however, has the constant-
$Re_B$ while the solution remains two dimensional. Three dimensionalisation, however, has the constant-![]() $Re$ average
$Re$ average ![]() $C_l^{p}$ grow at a milder rate, such that a definitely positive net lift
$C_l^{p}$ grow at a milder rate, such that a definitely positive net lift ![]() $C_l$ is never recovered, even at large values of
$C_l$ is never recovered, even at large values of ![]() $R$. Perhaps the most remarkable phenomenon concerns
$R$. Perhaps the most remarkable phenomenon concerns ![]() $C_l$ fluctuations, specifically dragged by its pressure
$C_l$ fluctuations, specifically dragged by its pressure ![]() $C_l^{p}$ component. Lift fluctuations are large for the symmetric
$C_l^{p}$ component. Lift fluctuations are large for the symmetric ![]() $R=1$ case at
$R=1$ case at ![]() $Re=114.8$, indicating strong vortex shedding, but the increase of
$Re=114.8$, indicating strong vortex shedding, but the increase of ![]() $R$ at constant
$R$ at constant ![]() $Re$ has the clear outcome of progressively damping
$Re$ has the clear outcome of progressively damping ![]() $C_l$ fluctuations over a significant range of low
$C_l$ fluctuations over a significant range of low ![]() $R\in [1.0,2.0]$. Further increase has the
$R\in [1.0,2.0]$. Further increase has the ![]() $C_l$ fluctuations grow again, but the interim decline suggests that moderate values of
$C_l$ fluctuations grow again, but the interim decline suggests that moderate values of ![]() $R$ tend to tame vortex shedding. This observation clearly aligns with the known vortex-shedding-suppression/reduction effect that the shear parameter
$R$ tend to tame vortex shedding. This observation clearly aligns with the known vortex-shedding-suppression/reduction effect that the shear parameter ![]() $K$ has at low
$K$ has at low ![]() $Re$ in the case of bluff bodies in upstream homogeneous shear.
$Re$ in the case of bluff bodies in upstream homogeneous shear.
All in all, it would seem that the flow past a square cylinder immersed in the interface between two different velocity streams behaves similarly to the problem of symmetric bluff bodies subject to homogeneous upstream shear. The coarse explorations presented here further suggest that, of the two parameters, the Reynolds number is responsible for the inception of spatiotemporal chaos, while the top-to-bottom velocity ratio (or, equivalently, the shear parameter) plays a crucial role in selecting the type and sequence of instabilities that occur along the wake transition regime.
8. Conclusions
We have investigated the incompressible Newtonian flow past an infinite square cylinder immersed in the wake of an upstream flat plate separating two streams of different velocities. The cylinder is therefore subject to an incoming shear flow consisting of a (nearly) step velocity profile instead of the more classic case of homogeneous shear. This latter configuration, which corresponds to submerging the cylinder in a plane Couette apparatus with channel gap many times the cylinder diameter to avoid cross-stream blockage effects, presents serious limitations in its realisation both experimentally and numerically. In order to achieve large values of the shear parameter with negligible blockage effects, the Reynolds number associated to the Couette flow must be necessarily large, such that the free stream becomes prone to subcritical transition following the amplification of finite three-dimensional perturbations.
The effects of varying the splitter plate length and the gap between its trailing edge and the front face of the cylinder were assessed as merely quantitative in a preliminary study, with no qualitative impact on the sequence and nature of the bifurcations from steady to chaotic. A detailed investigation to quantify the influence of the precise geometrical configuration chosen on the aerodynamic performances and flow topology is currently underway and will be presented elsewhere. For the splitter plate length and upstream distance from the cylinder fixed, the problem is governed by two parameters, namely the bulk Reynolds number ![]() $Re$ and the velocity ratio
$Re$ and the velocity ratio ![]() $R$. Here we have mostly chosen to keep the bottom stream Reynolds number
$R$. Here we have mostly chosen to keep the bottom stream Reynolds number ![]() $Re_B=56$ fixed and vary only
$Re_B=56$ fixed and vary only ![]() $R$, such that the closely related shear parameter
$R$, such that the closely related shear parameter ![]() $K\equiv 2(R-1)/(R+1)$ and
$K\equiv 2(R-1)/(R+1)$ and ![]() $Re\equiv (R+1)Re_B/2=28(R+1)$ are linked. Nevertheless, we devoted § 7 to exploring the decoupled effects of
$Re\equiv (R+1)Re_B/2=28(R+1)$ are linked. Nevertheless, we devoted § 7 to exploring the decoupled effects of ![]() $Re$ and
$Re$ and ![]() $R$.
$R$.
Several aerodynamic performance parameters have been assessed along the path from the steady symmetric solution towards the highly asymmetric and spatiotemporally chaotic wake dynamics. Pressure forces, particularly on the upper half of the front wall, have been shown to be the main contributor to the drag coefficient ![]() $C_d$, which increases with
$C_d$, which increases with ![]() $R$, particularly after the onset of vortex shedding. The lift coefficient
$R$, particularly after the onset of vortex shedding. The lift coefficient ![]() $C_l$ is dominated by downward friction on the front wall at low values of
$C_l$ is dominated by downward friction on the front wall at low values of ![]() $R$, thus producing a net downforce. Time dependence sets the pressure difference between the top and bottom on an increasingly growing trend that ends up yielding positive lift. Force coefficient fluctuations
$R$, thus producing a net downforce. Time dependence sets the pressure difference between the top and bottom on an increasingly growing trend that ends up yielding positive lift. Force coefficient fluctuations ![]() $C_l'$ and
$C_l'$ and ![]() $C_d'$ increase while the solution remains two dimensional but stagnate to rather constant values once three dimensionality sets in. The Strouhal number
$C_d'$ increase while the solution remains two dimensional but stagnate to rather constant values once three dimensionality sets in. The Strouhal number ![]() $St$ is rather stable, with a slightly increasing trend mainly pulled by the increase in
$St$ is rather stable, with a slightly increasing trend mainly pulled by the increase in ![]() $Re$, while the independent effect of
$Re$, while the independent effect of ![]() $K$ is unknown but probably decreasing.
$K$ is unknown but probably decreasing.
Much of the behaviour exhibited by the flow configuration analysed here bears compelling analogy to the somewhat related case of bluff bodies immersed in homogeneous upstream shear. The trends of aerodynamic performance monitors and the qualitative morphing of the wake topology upon varying the bulk Reynolds number ![]() $Re$ and the equivalent shear parameter
$Re$ and the equivalent shear parameter ![]() $K$ are consistent with those reported by studies dealing with homogeneous upstream shear. It is therefore probable that the velocity jump across the bluff body cross-stream length scale is in fact to be held responsible for most of the observed phenomena, the actual shape of the velocity profile (linear or step-like) playing only a subsidiary role. However, quantitative comparison is difficult, as the range of
$K$ are consistent with those reported by studies dealing with homogeneous upstream shear. It is therefore probable that the velocity jump across the bluff body cross-stream length scale is in fact to be held responsible for most of the observed phenomena, the actual shape of the velocity profile (linear or step-like) playing only a subsidiary role. However, quantitative comparison is difficult, as the range of ![]() $K$ we have explored is far beyond the reach of computations, or even experiments, dealing with homogeneous upstream shear.
$K$ we have explored is far beyond the reach of computations, or even experiments, dealing with homogeneous upstream shear.
The symmetric case ![]() $R=1$ (
$R=1$ (![]() $Re=56$,
$Re=56$, ![]() $K=0$) is steady, implying that the presence of the splitter plate has a stabilising effect, through the viscous blockage effect (mass flux and momentum reduction in the near-wall and wake regions due to viscosity), on the flow past a square cylinder, which is known to undergo a Hopf bifurcation somewhat earlier at
$K=0$) is steady, implying that the presence of the splitter plate has a stabilising effect, through the viscous blockage effect (mass flux and momentum reduction in the near-wall and wake regions due to viscosity), on the flow past a square cylinder, which is known to undergo a Hopf bifurcation somewhat earlier at ![]() $Re^{H}\simeq 45$. The first bifurcation upon increasing
$Re^{H}\simeq 45$. The first bifurcation upon increasing ![]() $R$ remains the two-dimensional onset of time periodicity, but this only happens for
$R$ remains the two-dimensional onset of time periodicity, but this only happens for ![]() $R\in (2.0,2.2)$ (
$R\in (2.0,2.2)$ (![]() $Re\in (84,89$),
$Re\in (84,89$), ![]() $K\in (0.67,0.75)$). It cannot be concluded from present results whether the delay in the onset of time dynamics is due to the presence of the splitter plate or whether the upstream velocity ratio also has a stabilising effect.
$K\in (0.67,0.75)$). It cannot be concluded from present results whether the delay in the onset of time dynamics is due to the presence of the splitter plate or whether the upstream velocity ratio also has a stabilising effect.
Once vortex shedding is in place, the Kármán vortex street in the cylinder wake follows the same trends observed in the literature. The vortices on the high velocity side become stronger and rounder with shear, while those on the low velocity side are weak, elongated and dissipate fast in the wake.
Stability analysis of the time-periodic two-dimensional vortex-shedding solution to three-dimensional perturbations reveals three distinct modes. A long wavelength mode, possibly related to mode A that is ubiquitous in the wake transition regime of the classic circular and square cylinders, is dominant but stable for velocity ratios ![]() $R\leqslant 3$. At the high
$R\leqslant 3$. At the high ![]() $R$ end, a very short wavelength mode arises and bifurcates for
$R$ end, a very short wavelength mode arises and bifurcates for ![]() $R\gtrsim 6$, but is never even close to dominant. The last mode, of an intermediate wavelength, prevails for
$R\gtrsim 6$, but is never even close to dominant. The last mode, of an intermediate wavelength, prevails for ![]() $R>3$ and is the one responsible for wake three dimensionalisation along the increasing
$R>3$ and is the one responsible for wake three dimensionalisation along the increasing ![]() $R$ path followed here. This mode bifurcates at
$R$ path followed here. This mode bifurcates at ![]() $R^{{C}}\simeq 3.1$ (
$R^{{C}}\simeq 3.1$ (![]() $Re^{{C}}\simeq 115$,
$Re^{{C}}\simeq 115$, ![]() $K^{{C}}\simeq 1.02$) with critical wavelength
$K^{{C}}\simeq 1.02$) with critical wavelength ![]() $\lambda _z^{{C}}\simeq 2.4$, exhibits elongated streamwise-cross-stream vortical structures along the braids connecting consecutive clockwise Kármán vortices, and is subharmonic (period doubling). While breaking the spanwise translational invariance SO(2) of the two-dimensional time-periodic solution, which belongs to the
$\lambda _z^{{C}}\simeq 2.4$, exhibits elongated streamwise-cross-stream vortical structures along the braids connecting consecutive clockwise Kármán vortices, and is subharmonic (period doubling). While breaking the spanwise translational invariance SO(2) of the two-dimensional time-periodic solution, which belongs to the ![]() $\textrm {O}(2)=Z_2\times \textrm {SO}(2)$ symmetry group class, it still preserves a collection of symmetries. Besides repeating every two vortex-shedding cycles, the eigenfields are mirror symmetric with respect to a discrete number of spanwise planes every
$\textrm {O}(2)=Z_2\times \textrm {SO}(2)$ symmetry group class, it still preserves a collection of symmetries. Besides repeating every two vortex-shedding cycles, the eigenfields are mirror symmetric with respect to a discrete number of spanwise planes every ![]() $\lambda _z/2$, and also invariant under the evolution by half a period (one vortex-shedding cycle) followed by either reflection about spanwise planes located halfway between contiguous reflection-symmetry planes or shift by half a wavelength
$\lambda _z/2$, and also invariant under the evolution by half a period (one vortex-shedding cycle) followed by either reflection about spanwise planes located halfway between contiguous reflection-symmetry planes or shift by half a wavelength ![]() $\lambda _z/2$. The wavelength, topology and symmetries of the mode are typical of mode C that is characteristic of the wake transition regime of open rings or square cylinders at incidence, and known to evolve from the quasi-periodic mode QP previously reported for circular and square cylinders. Converged three-dimensional nonlinear solutions slightly beyond the bifurcation point exhibit time dynamics and wake structures sharing all properties that are characteristic of mode C.
$\lambda _z/2$. The wavelength, topology and symmetries of the mode are typical of mode C that is characteristic of the wake transition regime of open rings or square cylinders at incidence, and known to evolve from the quasi-periodic mode QP previously reported for circular and square cylinders. Converged three-dimensional nonlinear solutions slightly beyond the bifurcation point exhibit time dynamics and wake structures sharing all properties that are characteristic of mode C.
At somewhat higher ![]() $R\in (3.4,3.8)$, the flow undergoes a tertiary bifurcation that doubles the period yet again (nonlinear solutions repeat every four vortex-shedding cycles) and also doubles the spanwise wavelength. The instability is therefore of the modulational type and amplifies perturbations that have double the wavelength of the original spanwise-periodic pattern. The resulting nonlinear solution has been observed in a computational domain with
$R\in (3.4,3.8)$, the flow undergoes a tertiary bifurcation that doubles the period yet again (nonlinear solutions repeat every four vortex-shedding cycles) and also doubles the spanwise wavelength. The instability is therefore of the modulational type and amplifies perturbations that have double the wavelength of the original spanwise-periodic pattern. The resulting nonlinear solution has been observed in a computational domain with ![]() $L_z=5$, allowing only for a discrete number of periodic patterns with wavelengths
$L_z=5$, allowing only for a discrete number of periodic patterns with wavelengths ![]() $\lambda _z=L_z/j=\{5,2.5,1.667,1.25,\ldots \}$. The spanwise mirror symmetry has finally been broken and the only remaining invariance besides the four-fold time periodicity is a space–time symmetry that recovers the solution by applying a reflection after the evolution by half a period (two vortex-shedding cycles). There is no evidence of a secondary bifurcation of the two-dimensional solution exhibiting a
$\lambda _z=L_z/j=\{5,2.5,1.667,1.25,\ldots \}$. The spanwise mirror symmetry has finally been broken and the only remaining invariance besides the four-fold time periodicity is a space–time symmetry that recovers the solution by applying a reflection after the evolution by half a period (two vortex-shedding cycles). There is no evidence of a secondary bifurcation of the two-dimensional solution exhibiting a ![]() $\lambda _z=5$ other than a stretched version of the same mode C, which has also become unstable. As a matter of fact, the range of unstable wavelengths for which mode C is unstable increases with
$\lambda _z=5$ other than a stretched version of the same mode C, which has also become unstable. As a matter of fact, the range of unstable wavelengths for which mode C is unstable increases with ![]() $R$ but the dominant wavelength remains quite fixed at
$R$ but the dominant wavelength remains quite fixed at ![]() $\lambda _z\simeq 2.5$ for
$\lambda _z\simeq 2.5$ for ![]() $R\leqslant 4$ and only migrates to increasingly wider values beyond this point. Very shortly after the period-doubled three-dimensional pattern, a further increase in
$R\leqslant 4$ and only migrates to increasingly wider values beyond this point. Very shortly after the period-doubled three-dimensional pattern, a further increase in ![]() $R$ brings spatiotemporal chaos with it.
$R$ brings spatiotemporal chaos with it.
Given that the limited spanwise periodicity ![]() $L_z=5$ has been shown already capable of sustaining spatiotemporally chaotic dynamics, the solutions reported here are bound to play an essential role in the wake transition regime and the inception of turbulence at even higher flow regimes. It might however be the case that these solutions are modulationally/subharmonically unstable to long wavelength disturbances that hinder their actual observation as stable flows in computations within wider spanwise domains and, therefore, in experiments. We have indeed found evidence that, although stable and unaltered at
$L_z=5$ has been shown already capable of sustaining spatiotemporally chaotic dynamics, the solutions reported here are bound to play an essential role in the wake transition regime and the inception of turbulence at even higher flow regimes. It might however be the case that these solutions are modulationally/subharmonically unstable to long wavelength disturbances that hinder their actual observation as stable flows in computations within wider spanwise domains and, therefore, in experiments. We have indeed found evidence that, although stable and unaltered at ![]() $R=3.3$ within an
$R=3.3$ within an ![]() $L_z=10$ domain, the
$L_z=10$ domain, the ![]() $\lambda _z=2.5$ solution is already unstable at
$\lambda _z=2.5$ solution is already unstable at ![]() $R=3.4$. Preliminary results show that the stable solution in the
$R=3.4$. Preliminary results show that the stable solution in the ![]() $L_z=10$ domain is still period-doubled periodic, but its wavelength is the full
$L_z=10$ domain is still period-doubled periodic, but its wavelength is the full ![]() $\lambda _z=10$ and the characteristic space–time symmetry has already been broken. Its appearance suggests a dislocation of a three-replica pattern (the solution with
$\lambda _z=10$ and the characteristic space–time symmetry has already been broken. Its appearance suggests a dislocation of a three-replica pattern (the solution with ![]() $\lambda _z=3.33$) trying to accommodate a fourth replica (the
$\lambda _z=3.33$) trying to accommodate a fourth replica (the ![]() $\lambda _z=2.5$ solution) but not quite managing. This brings to mind a mechanism that is responsible for wave dislocation in elongated systems such as channel flows (Mellibovsky & Meseguer Reference Mellibovsky and Meseguer2015). Between
$\lambda _z=2.5$ solution) but not quite managing. This brings to mind a mechanism that is responsible for wave dislocation in elongated systems such as channel flows (Mellibovsky & Meseguer Reference Mellibovsky and Meseguer2015). Between ![]() $R=3.4$ and 3.5, we have found traces of what appears to be a Neimark–Sacker bifurcation in the
$R=3.4$ and 3.5, we have found traces of what appears to be a Neimark–Sacker bifurcation in the ![]() $L_z=10$ domain, although higher resolution and longer runs will be necessary to ascertain this. At
$L_z=10$ domain, although higher resolution and longer runs will be necessary to ascertain this. At ![]() $R=3.8$, the solution seems to be already chaotic for
$R=3.8$, the solution seems to be already chaotic for ![]() $L_z=10$ and the three-dimensional vortical structures in the wake incorporate a characteristic spanwise drift. Interestingly, the altered transition path seems to bear no appreciable consequence on aerodynamic performances, at least at sufficiently low values of
$L_z=10$ and the three-dimensional vortical structures in the wake incorporate a characteristic spanwise drift. Interestingly, the altered transition path seems to bear no appreciable consequence on aerodynamic performances, at least at sufficiently low values of ![]() $R$. Neither the Strouhal number, nor the mean and oscillation amplitude of force coefficients are noticeably modified by running in domains with
$R$. Neither the Strouhal number, nor the mean and oscillation amplitude of force coefficients are noticeably modified by running in domains with ![]() $L_z=2.5$, 5 and 10, even though the instantaneous topology and symmetries of the solutions are manifestly different. Instabilities to spanwise wavelengths even longer than
$L_z=2.5$, 5 and 10, even though the instantaneous topology and symmetries of the solutions are manifestly different. Instabilities to spanwise wavelengths even longer than ![]() $\lambda _z=10$ cannot be discarded. It is therefore possible that the route towards spatiotemporal chaos may be understood in the light of an Eckhaus instability, whereby a periodic pattern becomes modulationally unstable following the bifurcation of a widening spectrum of competing wavelengths. In this light, the period-doubling bifurcation discussed here is not robust in the sense that it may not be observed in practicable experimental configurations. This does not preclude, however, that, although unstable, the period-doubling bifurcation and the solutions that emerge along the way play an important role in the transitional regime and ensuing chaotic dynamics, as is the case for many other shear flows. Simulations in much longer domains, allowing for a larger set of unstable wavelengths, would be required in the wake transition regime to elucidate the actual nature of the route to chaotic dynamics and turbulence. An attempt to properly gauge the implications of long wavelength subharmonic instabilities and their bearing on the actual dynamics of the problem under scrutiny is beyond the scope of the present investigation.
$\lambda _z=10$ cannot be discarded. It is therefore possible that the route towards spatiotemporal chaos may be understood in the light of an Eckhaus instability, whereby a periodic pattern becomes modulationally unstable following the bifurcation of a widening spectrum of competing wavelengths. In this light, the period-doubling bifurcation discussed here is not robust in the sense that it may not be observed in practicable experimental configurations. This does not preclude, however, that, although unstable, the period-doubling bifurcation and the solutions that emerge along the way play an important role in the transitional regime and ensuing chaotic dynamics, as is the case for many other shear flows. Simulations in much longer domains, allowing for a larger set of unstable wavelengths, would be required in the wake transition regime to elucidate the actual nature of the route to chaotic dynamics and turbulence. An attempt to properly gauge the implications of long wavelength subharmonic instabilities and their bearing on the actual dynamics of the problem under scrutiny is beyond the scope of the present investigation.
We have analysed the wake transition regime along two different paths. The first one simultaneously increases the bulk Reynolds number ![]() $Re$ and the velocity ratio
$Re$ and the velocity ratio ![]() $R$ (and, with it, the equivalent shear parameter
$R$ (and, with it, the equivalent shear parameter ![]() $K$), thus masking the independent effects of these two parameters. The second path sweeps
$K$), thus masking the independent effects of these two parameters. The second path sweeps ![]() $Re$ at constant
$Re$ at constant ![]() $R$ in a preliminary attempt at decoupling the effects of the two parameters. Some evidence has been reported that
$R$ in a preliminary attempt at decoupling the effects of the two parameters. Some evidence has been reported that ![]() $Re$ is key in engendering chaotic dynamics, while
$Re$ is key in engendering chaotic dynamics, while ![]() $R$ is responsible for mode selection upon three dimensionalisation and, therefore, dictates the specific path that leads towards spatiotemporal complexity. A thorough ongoing analysis decoupling
$R$ is responsible for mode selection upon three dimensionalisation and, therefore, dictates the specific path that leads towards spatiotemporal complexity. A thorough ongoing analysis decoupling ![]() $Re$ and
$Re$ and ![]() $R$ is expected to provide further insight into their separate contributions to the problem.
$R$ is expected to provide further insight into their separate contributions to the problem.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2022.821.
Acknowledgements
F.M. is a Serra-Húnter fellow.
Funding
This work was supported by the Spanish Government (grant numbers FIS2016-77849-R, PID2020-114043GB-I00); and the Catalan Government (grant number 2017-SGR-00785). Part of the computations were done in the Red Española de Supercomputación (RES), the Spanish supercomputer network (grant numbers FI-2019-1-0023, FI-2018-3-0030).
Declaration of interests
The authors report no conflict of interest.
Data availability statement
The data that support the findings of this study may be obtained from the corresponding author upon reasonable request.
Appendix A. Stability analysis of periodic solutions
The spanwise translational invariance of the two-dimensional vortex-shedding flow past an infinite square cylinder breaks as the Reynolds number is increased beyond a critical threshold. Floquet theory provides the framework for analysing the stability of time-periodic base flows and has been employed successfully to shed light on the three dimensionalisation of the wake behind cylinders (Noack & Eckelmann Reference Noack and Eckelmann1994; Barkley & Henderson Reference Barkley and Henderson1996; Henderson & Barkley Reference Henderson and Barkley1996). The instantaneous flow is decomposed into the additive superposition of the periodic solution and a perturbation following
Formal substitution into the Navier–Stokes equations (2.1) and linearisation yields the governing equations for the perturbation field
 \begin{equation} \left.\begin{gathered} \dfrac{\partial \tilde{\boldsymbol{u}}}{\partial t}+(\tilde{\boldsymbol{u}} \boldsymbol{\cdot}\boldsymbol{\nabla}) \boldsymbol{U} + (\boldsymbol{U} \boldsymbol{\cdot}\boldsymbol{\nabla}) \tilde{\boldsymbol{u}} ={-} \boldsymbol{\nabla} \tilde{p}+\dfrac{1}{Re} \nabla^{2} \tilde{\boldsymbol{u}}, \\ \boldsymbol{\nabla}\boldsymbol{\cdot}\tilde{\boldsymbol{u}} = 0, \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \dfrac{\partial \tilde{\boldsymbol{u}}}{\partial t}+(\tilde{\boldsymbol{u}} \boldsymbol{\cdot}\boldsymbol{\nabla}) \boldsymbol{U} + (\boldsymbol{U} \boldsymbol{\cdot}\boldsymbol{\nabla}) \tilde{\boldsymbol{u}} ={-} \boldsymbol{\nabla} \tilde{p}+\dfrac{1}{Re} \nabla^{2} \tilde{\boldsymbol{u}}, \\ \boldsymbol{\nabla}\boldsymbol{\cdot}\tilde{\boldsymbol{u}} = 0, \end{gathered}\right\} \end{equation}with homogeneous conditions on all boundaries of the same typology as for the nonlinear problem.
The two dimensionality of the base flow and the translational invariance in the spanwise direction allow for the following modal ansatz:
corresponding to a Fourier decomposition, such that spanwise modes ![]() $\hat {\boldsymbol {u}}(x,y,\beta ;t)$ of different spanwise wavenumber
$\hat {\boldsymbol {u}}(x,y,\beta ;t)$ of different spanwise wavenumber ![]() $\beta _z$ decouple exactly.
$\beta _z$ decouple exactly.
Since we are not interested in computing the full eigenspectrum nor even a subset of it, we follow here a simple time-stepping approach that provides the most unstable (or least stable) multiplier for any desired Reynolds number ![]() $Re$ and spanwise wavenumber
$Re$ and spanwise wavenumber ![]() $\beta _z$. We perturb the two-dimensional periodic vortex-shedding solution, duly computed through time stepping in the two-dimensional domain where it remains stable, with a tiny spanwise-dependent random disturbance. The initial condition thus obtained is then evolved in time integrating the full nonlinear Navier–Stokes equations but using a single spanwise Fourier component, besides the homogenous component, in a domain of spanwise size
$\beta _z$. We perturb the two-dimensional periodic vortex-shedding solution, duly computed through time stepping in the two-dimensional domain where it remains stable, with a tiny spanwise-dependent random disturbance. The initial condition thus obtained is then evolved in time integrating the full nonlinear Navier–Stokes equations but using a single spanwise Fourier component, besides the homogenous component, in a domain of spanwise size ![]() $L_z=2{\rm \pi} /\beta _z$. After the initial transients, the energy contents on the stable manifold vanish and the perturbation aligns with the dominant eigenmode. At this stage, the dominant eigenmode can be extracted directly from the only non-homogeneous Fourier component of the simulation as long as it remains within the linear evolution regime. This can be considered to be the case while the energy does not approach machine precision (in the stable case) or saturation unto the nonlinear regime (for the unstable case), where it starts feeding energy back into the homogeneous Fourier component via the nonlinear advection term and the simulation becomes utterly under-resolved. Many more modes, providing the standard six orders of magnitude decay, would be required to properly resolve the saturated nonlinear solution, but since we are only interested in the linear regime, we simply dismiss the latter part of the time evolution.
$L_z=2{\rm \pi} /\beta _z$. After the initial transients, the energy contents on the stable manifold vanish and the perturbation aligns with the dominant eigenmode. At this stage, the dominant eigenmode can be extracted directly from the only non-homogeneous Fourier component of the simulation as long as it remains within the linear evolution regime. This can be considered to be the case while the energy does not approach machine precision (in the stable case) or saturation unto the nonlinear regime (for the unstable case), where it starts feeding energy back into the homogeneous Fourier component via the nonlinear advection term and the simulation becomes utterly under-resolved. Many more modes, providing the standard six orders of magnitude decay, would be required to properly resolve the saturated nonlinear solution, but since we are only interested in the linear regime, we simply dismiss the latter part of the time evolution.
While still in the linear regime, but well past the initial transients, the already modal perturbation follows an oscillating behaviour with the periodicity of the underlying two-dimensional solution on top of an exponential decay/growth. The decay/growth rate of the dominant Floquet mode (as represented by the Floquet multiplier ![]() $\mu$) can be derived from the energy time series of the
$\mu$) can be derived from the energy time series of the ![]() $\beta _z$ mode by fitting a power law to the sequence of crossings (
$\beta _z$ mode by fitting a power law to the sequence of crossings (![]() $E_{\beta _z}^{k}=E_{\beta _z}(t_k$)) of a purposely defined Poincaré section (in our case, picking
$E_{\beta _z}^{k}=E_{\beta _z}(t_k$)) of a purposely defined Poincaré section (in our case, picking ![]() $C_l=0$, and numbering the consecutive crossings at times
$C_l=0$, and numbering the consecutive crossings at times ![]() $t_k$ by an index
$t_k$ by an index ![]() $k$)
$k$)
Here ![]() $E_{\beta _z}^{0}$ is an irrelevant fitting parameter that is simply related to the energy of the initial perturbation we prescribe, while the
$E_{\beta _z}^{0}$ is an irrelevant fitting parameter that is simply related to the energy of the initial perturbation we prescribe, while the ![]() $2$ in the exponent arises from the square relation that exists between the velocity field and its corresponding kinetic energy. A more sophisticated fit of the form
$2$ in the exponent arises from the square relation that exists between the velocity field and its corresponding kinetic energy. A more sophisticated fit of the form
where ![]() $a$ is any primitive degree of freedom of the perturbation field (a point velocity component for example),
$a$ is any primitive degree of freedom of the perturbation field (a point velocity component for example), ![]() $\psi$ is another fitting parameter representing an initial phase and
$\psi$ is another fitting parameter representing an initial phase and ![]() $\mu \equiv r\mathrm {e}^{\pm \mathrm {i}\theta }$ a complex multiplier, allows for the discrimination between synchronous and quasi-periodic modes (An, Bergada & Mellibovsky Reference An, Bergada and Mellibovsky2019). We have not used such a fit here, as the only mode present is clearly subharmonic and appears as synchronous when inspecting the modal energy evolution.
$\mu \equiv r\mathrm {e}^{\pm \mathrm {i}\theta }$ a complex multiplier, allows for the discrimination between synchronous and quasi-periodic modes (An, Bergada & Mellibovsky Reference An, Bergada and Mellibovsky2019). We have not used such a fit here, as the only mode present is clearly subharmonic and appears as synchronous when inspecting the modal energy evolution.
The envelope of the spectrum ![]() $\lvert \mu \rvert (\beta )$ for
$\lvert \mu \rvert (\beta )$ for ![]() $Re=200$ and 205 has been computed as proof of concept of the aforementioned method, and compared with published results (Robichaux et al. Reference Robichaux, Balachandar and Vanka1999; Blackburn & Lopez Reference Blackburn and Lopez2003; Sheard et al. Reference Sheard, Fitzgerald and Ryan2009) in figure 18. The agreement is fair at
$Re=200$ and 205 has been computed as proof of concept of the aforementioned method, and compared with published results (Robichaux et al. Reference Robichaux, Balachandar and Vanka1999; Blackburn & Lopez Reference Blackburn and Lopez2003; Sheard et al. Reference Sheard, Fitzgerald and Ryan2009) in figure 18. The agreement is fair at ![]() $Re=205$, for which all three modes, A, B and QP, are duly observed and exhibit the right growth rate dependence on the wavenumber. The most unstable modes at
$Re=205$, for which all three modes, A, B and QP, are duly observed and exhibit the right growth rate dependence on the wavenumber. The most unstable modes at ![]() $Re=200$ have wavenumbers
$Re=200$ have wavenumbers ![]() $\beta _z^{\mathrm {A}}\simeq 1.21$ (wavelength
$\beta _z^{\mathrm {A}}\simeq 1.21$ (wavelength ![]() $\lambda _z^{\mathrm {A}}=5.2$) and
$\lambda _z^{\mathrm {A}}=5.2$) and ![]() $\beta _z^{\mathrm {B}}\simeq 5.5$ (
$\beta _z^{\mathrm {B}}\simeq 5.5$ (![]() $\lambda _z^{\mathrm {B}}=1.15$), in line with experimental results (Luo et al. Reference Luo, Chew and Ng2003; Luo et al. Reference Luo, Tong and Khoo2007). A third unstable mode arises at
$\lambda _z^{\mathrm {B}}=1.15$), in line with experimental results (Luo et al. Reference Luo, Chew and Ng2003; Luo et al. Reference Luo, Tong and Khoo2007). A third unstable mode arises at ![]() $Re^{\mathrm {QP}}\simeq 205$ with wavenumber
$Re^{\mathrm {QP}}\simeq 205$ with wavenumber ![]() $\beta _z^{\mathrm {QP}}\simeq 2.2$ (
$\beta _z^{\mathrm {QP}}\simeq 2.2$ (![]() $\lambda _z^{\mathrm {B}}\simeq 2.8$), that was not clearly discernible at
$\lambda _z^{\mathrm {B}}\simeq 2.8$), that was not clearly discernible at ![]() $Re=200$. This mode, which was initially thought subharmonic and called mode S (Robichaux et al. Reference Robichaux, Balachandar and Vanka1999), is in fact quasi-periodic (Blackburn & Lopez Reference Blackburn and Lopez2003; Sheard et al. Reference Sheard, Fitzgerald and Ryan2009), hence the name QP, and has already been detected, albeit at much higher
$Re=200$. This mode, which was initially thought subharmonic and called mode S (Robichaux et al. Reference Robichaux, Balachandar and Vanka1999), is in fact quasi-periodic (Blackburn & Lopez Reference Blackburn and Lopez2003; Sheard et al. Reference Sheard, Fitzgerald and Ryan2009), hence the name QP, and has already been detected, albeit at much higher ![]() $Re$, for the flow past circular cylinders (Barkley & Henderson Reference Barkley and Henderson1996; Blackburn & Lopez Reference Blackburn and Lopez2003).
$Re$, for the flow past circular cylinders (Barkley & Henderson Reference Barkley and Henderson1996; Blackburn & Lopez Reference Blackburn and Lopez2003).

Figure 18. Dominant Floquet multipliers at Reynolds numbers ![]() $Re=200$ (circles) and
$Re=200$ (circles) and ![]() $Re=205$ (squares) for the square cylinder without splitter plate. Shown are our numerical results (grey) alongside those by Robichaux et al. (Reference Robichaux, Balachandar and Vanka1999) (black). Labels indicate modes A, B and QP.
$Re=205$ (squares) for the square cylinder without splitter plate. Shown are our numerical results (grey) alongside those by Robichaux et al. (Reference Robichaux, Balachandar and Vanka1999) (black). Labels indicate modes A, B and QP.
In light of these results, nonlinear three-dimensional simulations at these values of the Reynolds number would need to fit several times (typically more than three or four) the longest mode (A) so that a decent range of the known unstable linear modes are allowed to play their part in selecting/driving the fully nonlinear solution.