1. INTRODUCTION
The propagation of high-power microwave beam in a plasma has received worldwide attention due to its applications, especially for plasma production, charged particles acceleration and heating in tokamaks (Bhattacharjee & Amemiya, Reference Bhattacharjee and Amemiya2000; Yadav & Bora, Reference Yadav and Bora2004; Anpilov et al., Reference Anpilov, Berezhetskaya, Kopev and Kossyi1995; Aria & Malik, Reference Aria and Malik2009; Al-Hassan et al., Reference Al-Hassan, Ito, Yugami and Nishida2005). In addition, many nonlinear phenomena are related to the ponderomotive force due to intensity gradient of the microwave beam in the plasma. The pondermotive force changes the spatial distribution of electron density and causes the generation of space charge field and wakefields (Aria & Malik, Reference Aria and Malik2008; Istomin, Reference Istomin2002; Nusinovich et al., Reference Nusinovich, Mitin and Vlasov1997). The space charge field and wakefield generation for the purpose of particle acceleration has been widely investigated experimentally, analytically, and numerically (Malik, Reference Malik2007; Jawla et al., Reference Jawla, Kumar and Malik2005; Pandey et al., Reference Pandey, Agarwal and Tripathi2006; York & Milchberg, Reference York and Milchberg2008; Jha et al., Reference Jha, Saroch, Mishra and Upadhyay2012; Yoon et al., Reference Yoon, Palastro, Gordon, Antonsen and Milchberg2012; Andreev, Reference Andreev, Kuznetsov and Pogorelsky2000). The acceleration of charged particles has important applications in various domains such as thermonuclear fusion research (Malik, Reference Malik2007), fast electron transport in solid targets (Aria & Malik, Reference Aria and Malik2008; Abedi et al., Reference Abedi, Dorranian, Abari and Shokri2011), generation of gama-ray (Abedi & Shokri, Reference Abari and Shokri2011), fast ignition of fusion targets (Abedi et al., Reference Abedi, Dorranian, Abari and Shokri2011), harmonic generation (Malik, Reference Malik2007; Abari & Shokri, Reference Abari and Shokri2011), cavitons (Wong, Reference Wong1977), and some other related research. On the other hand, the electron temperature distribution in the microwave-plasma interaction can be changed by the Ohmic heating and collisional effects. As a consequence, the ponderomotive force, space charge field, Ohmic heating, and collisions can modify the profiles of electron density, temperature, and electromagnetic field into the plasma (Abedi et al., Reference Abedi, Dorranian, Abari and Shokri2011; Abari & Shokri, Reference Abari and Shokri2011; Niknam & Akhlaghipour, Reference Niknam and Akhlaghipour2013). Thus, the investigation of aforementioned effects in the microwave-plasma interaction are practically important.
In this regard, many efforts have been made for studying the nonlinear interaction of microwave and laser beams with plasma. Niknam and Shokri (Reference Niknam and Shokri2007) have investigated the steepening of the electron density distribution in the microwave-plasma interaction. In this study, deviation from a sinusoidal shape in electromagnetic field and decrease inelectron density profiles has been reported. Malik et al. (Reference Malik and Aria2010) have numerically studied the microwave-plasma interaction in a rectangular waveguide by taking three types of the density profiles. They have shown that the plasma density is pushed away from the middle of the waveguide and the peaks are evolved in the density especially for enormously high temperature. Others have studied the wakefield excitation in a plasma filled rectangular waveguide (Aria et al., Reference Aria, Malik and Singh2009). The Ohmic heating of underdense collisional plasma by the electromagnetic wave have been considered in relativistic and non-relativistic regimes by Abedi et al. (Reference Abedi, Dorranian, Abari and Shokri2011) and Abari et al. (Reference Abari and Shokri2011), respectively. They have reported the decrease in the oscillations wavelength of electromagnetic fields and the loss of sinusoidal form by increasing the beam intensity. In addition, from the Ohmic heating calculation in the interaction of high-power microwave with plasma, an increase in the amplitude of electron temperature distribution and decrease in the their wavelength have been found by Niknam and Akhlaghipour (Reference Niknam and Akhlaghipour2013).
In our earlier work, the interaction between high-power microwave beam and collisionless unmagnetized plasma was investigated by taking into account the ponderomotive force and space charge effects (Khorashadizadeh et al., Reference Khorashadizadeh, Mirzaye and Niknam2013). The electromagnetic wave equation coupled with Poisson and momentum transfer equations were solved for obtaining the space charge field and plasma density profiles, assuming that the electron temperature was independent of the coordinates. In the present work, we analyze the microwave-plasma interaction in the presence of Ohmic heating, ponderomotive force, collisional, and space charge effects. Plasma is assumed to be underdense and unmagnetized. The electromagnetic wave equation coupled with the equations of momentum transfer, particle conservation, and energy in their stationary form beside the Poisson equation are solved for obtaining the dielectric permittivity, electron temperature, and space charge field profiles. We will plot the profiles of electromagnetic field, space charge field, electron temperature, electron density, and dielectric permittivity in the plasma for different values of microwave energy flux, microwave frequency, and initial electron density. We will discuss the behavior of the electron temperature profiles which are affected by the ponderomotive force, initial electron density, and microwave frequency. Therefore, the electron temperature is not independent of the coordinates. It is shown that the electron density distribution is modified. Different peaks are created in the electron density distribution and in the space charge field profiles.
This work contains the followings: In Section 2, the coupled basic equations, i.e., the momentum transfer, wave, energy, particle conservation, and Poisson equations are considered. In Section 3, the numerical simulations of these nonlinear equations are presented. The influence of some physical parameters such as the microwave energy flux, initial electron density, and microwave frequency on the electromagnetic and space charge field profiles, electron density distribution, and electron temperature changing curves in the plasma are investigated. Finally, a summary and research are given in Section 4.
2. BASIC EQUATIONS
The propagation of a high-power microwave beam from vacuum 
$z \lt 0$ into an underdense, collisional and unmagnetized plasma in 
$z \gt 0$ is considered here. In this model, the microwave electric field in plasma is given as 
${\bf E}\lpar z\comma \; t\rpar = E\lpar z\rpar e^{ - i{\rm \omega} t} {\hat {\bf x}}$, that is unit vector in the x-direction, 
${\rm \omega} $ is microwave frequency, and 
$E\lpar z\rpar $ is the amplitude of the electric field as function of z only. The Maxwell's equations in the absence of external electrical current density and charge density are the starting point in the description of the interaction between an electromagnetic field and a plasma that leads to the equation of wave propagation in the plasma medium as:
$$\nabla ^2 {\bf E} - \nabla \lpar \nabla \cdot {\bf E}\rpar + \lpar \displaystyle{{\rm \omega} \over c}\rpar ^2 {\rm \varepsilon} {\bf E} = 0\comma \;$$
in which 
${\rm \varepsilon} $ and c are the dielectric permittivity and light velocity in vacuum, respectively. Then the magnetic field, 
${\bf B}$, is obtained from Faraday's law as follows:
$$\nabla \times {\bf E} = - \displaystyle{1 \over c}\displaystyle{{\partial {\bf B}} \over {\partial z}}.$$On the other hand, the ponderomotive force generated by the propagation of high-power microwave beam into the plasma can cause the perturbation of electron density and it can affect the dielectric permittivity of plasma. Thus, the space charge field is generated and the electron oscillatory motions and associated collisions can produce the Ohmic heating (Godyak, Reference Godyak2003; Liu & Tripahti, Reference Liu and Tripathi1994; Raizer, Reference Raizer1991). The average ponderomotive force per unit volume acting on the electrons, the space charge field, and the Ohmic heating are given by:
$${\bf F}_{\,pe} = \displaystyle{1 \over {8{\rm \pi} }}n_e \displaystyle{{\partial {\rm \varepsilon} } \over {\partial n_e }}\nabla {\bf E}^2 \comma \;$$
$$\nabla \cdot {\bf E}_s = 4{\rm \pi} e\lpar n_0 - n_e \rpar \comma \;$$
$$\left\langle { - e{\bf E} \cdot {\bf V}_e } \right\rangle = \displaystyle{{e^2 E^2 {\rm \nu} _e } \over {m_e \lpar {\rm \omega} ^2 + {\rm \nu} _e^2 \rpar }}\comma \;$$
where 
${\bf F}_{\,pe}, {\bf E}_s , n_e, n_0 $ and e are the ponderomotive force, space charge field, electron density, initial electron density and electron charge, respectively. Furthermore, in a time scale greater than 
${\rm \tau} $ (which is the time required for ponderomotive to be established the particle conservation), momentum transfer and energy equations are:
$$\nabla \cdot \lpar {\bf V}_e n_e \rpar = 0\comma \;$$
$$- n_e \nabla T_e - T_e \nabla n_e - en_e {\bf E}_s = - \displaystyle{1 \over {8{\rm \pi} }}n_e \displaystyle{{\partial {\rm \varepsilon} } \over {\partial n_e }}\nabla {\bf E}^2 \comma \;$$
$$- e{\bf E} \cdot {\bf V}_e = \displaystyle{3 \over 2}{\rm \delta} {\rm \nu} _e \lpar T_e - T_i \rpar - \nabla \cdot \lpar \displaystyle{{\rm \kappa} \over {n_e }}\nabla T_e \rpar \comma \;$$
where 
${\rm \nu} _e, T_e, T_i, V_e, \kappa, m_i $, and 
$m_e $ are the collision frequency between electrons and neutral particles, electron temperature, ion temperature, electron velocity, thermal conductive coefficient, ion mass, and electron mass, respectively, and 
${\rm \delta} = 2m_e /m_i $. If the mean free time of electrons is small, we can neglect the second term in the right-hand side of Eq. (8). As a result, the electron temperature equation reduced to:
$$T_e = T_i + \displaystyle{1 \over {3{\rm \delta} }}\displaystyle{{e^2 E^2 } \over {m_e \lpar {\rm \omega} ^2 + {\rm \nu} _e^2 \rpar }}.$$To solve these equations, we need the dielectric permittivity of the plasma. The dielectric permittivity of collisional plasma is (Krall & Trivelpiece, Reference Krall and Trivelpiece1973):
$${\rm \varepsilon} = 1 - \displaystyle{{{\rm \omega} _{\,pe}^2 } \over {{\rm \omega} \lpar {\rm \omega} + i\hskip+1pt{\rm \nu} _e \rpar }}\comma \;$$
where 
${\rm \omega} _{\,pe}^2 = 4{\rm \pi} n_e e^2 /m_e $ denotes the electron plasma frequency. Considering the amplitude of the electric field, space charge field, electron temperature, and electron density in the plasma being a function of z only, we can solve the above equations. It is clear that these equations are highly nonlinear and do not have any analytical solution. Therefore, having the boundary conditions, we obtain the profiles of electromagnetic fields, electron density distribution, dielectric permittivity of plasma, electron temperature, and space charge field in plasma.
3. DISCUSSION
In the previous section, a set of coupled nonlinear equations governing the propagation of high power microwave beam in the collisional unmagnetized plasma was obtained. These nonlinear equations are solved using Runge-Kutta method and the dimensionless variables are defined as follows:
$$\tilde E = \displaystyle{e \over {{\rm \omega} \sqrt {T_i m_e } }}E\comma \; \tilde B = \displaystyle{e \over {{\rm \omega} \sqrt {T_i m_e } }}B\comma \; {\tilde E}_s = \displaystyle{{ec} \over {T_i {\rm \omega} }}E_s \comma \; \tilde V_e = \displaystyle{{V_e } \over c}\comma \; \tilde T_e = \displaystyle{{T_e } \over {T_i }}\comma \; \tilde n_e = \displaystyle{{n_e } \over {n_0 }}\comma \; \tilde z = z\displaystyle{{\rm \omega} \over c}\comma \;$$
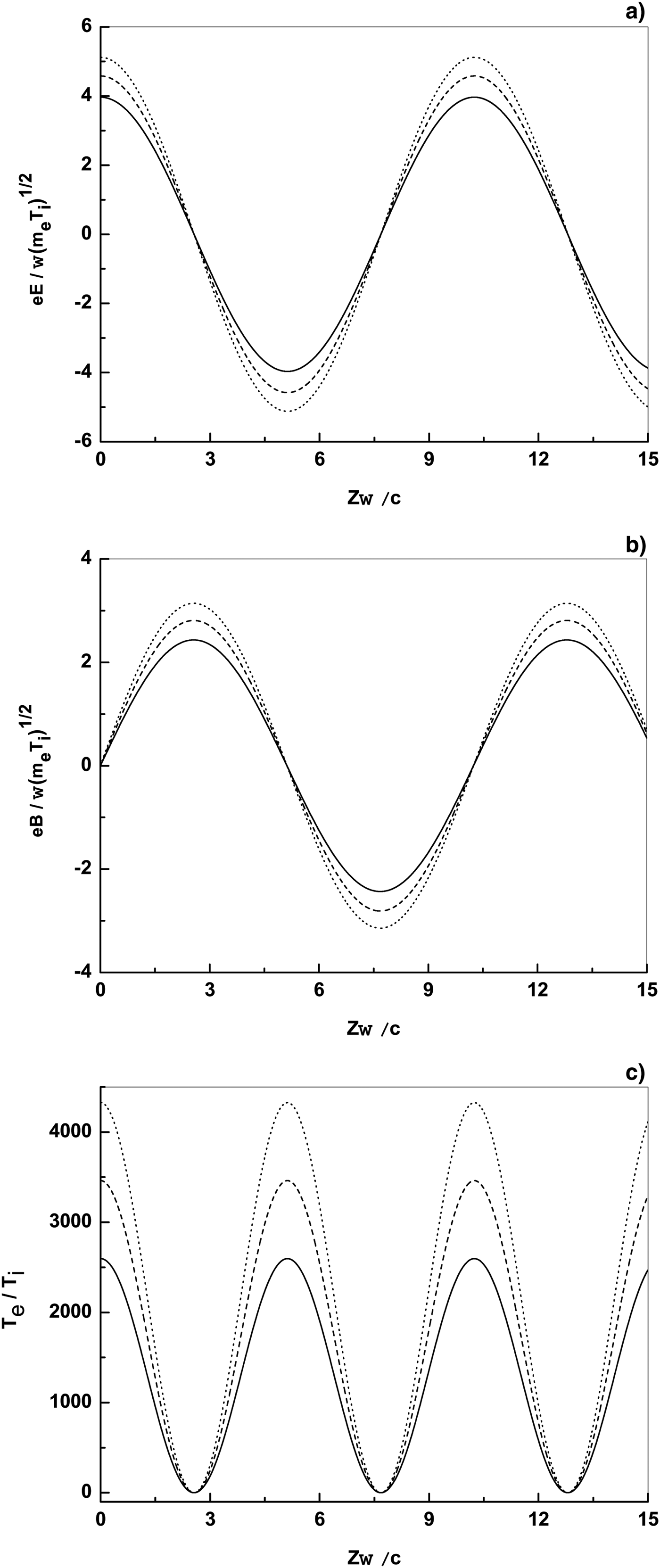
where the tilde refers to the dimensionless variables. In this section, we obtain the electric, magnetic, and space charge fields, electron temperature, density distributions, and dielectric permittivity profiles in the plasma. The effect of high-power microwave energy flux on the normalized profiles of the electric field, magnetic field, and electron temperature are presented in Figure 1. In Figure 1, the profiles are plotted as a function of 
$z{\rm \omega} /c$. The parameters in Figure 1 are as follows: the initial electron density is 
$n_0 = 5 \times 10^{11} $
${\rm cm}^{ - 3} $, the initial electron and ion temperatures are 
$T_e = T_i = 0.2$ eV, the microwave frequency is 8 GHz, and the collision frequency is 
${\rm \nu} _e /{\rm \omega} = 0.1$. These profiles are also plotted for the different energy fluxes 
$I = 6 \times 10^3 $
${\rm W}/{\rm cm}^2 $ (solid line), 
$I = 8 \times 10^3 $
${\rm W}/{\rm cm}^2 $ (dashed line), and 
$I = 10 \times 10^3 {\rm W}/{\rm cm}^2 $ (dotted line). Since the microwave energy flux is proportional to the square of amplitude, the curves in Figures 1a and 1b show that when the microwave energy flux increases, the amplitude of electric and magnetic fields increases. It is also observed that by increasing the microwave energy flux, when the initial electron density is constant and the space charge effect is considered, the wavelength of oscillations is not changed. This observation is in contrast with the one reported by Abari and Shokri (Reference Abari and Shokri2011) where they observed a decrease in the oscillations wavelength in the interaction of a laser pulse and plasma without considering space charge effect. This figure also indicates that the electron temperature from an initial value, i.e., 
$T_e = T_i = 0.2$ eV in the absence of the microwave beam, is highly increased by the microwave intensity. The physical reason is as follows: the ponderomotive force is proportional to the microwave intensity (see Eq. (3)). This force pushes the electrons and creates electron bunches. According to Figures 1a and 4a, the microwave intensity is zero in the center of electron bunches and it has finite values elsewhere. On the other hand, these electrons gain energy from the microwave field, just before collisions, and lose energy it when a collision takes place. That leads to the electron heating. Therefore, the electron temperature varies from an initial value (
$T_e = 0.2$ eV) to its maximum value, due to the microwave field intensity. Consequently, the electron temperature significantly increases. This result is consistent with the rate of electron heating due to microwave electric field in Eq. (9). This equation shows that the electron temperature is proportional to the microwave energy flux then the extremums of microwave electric field are the peaks of the electron temperature distribution. These results have been reported too by Niknam et al. (Reference Niknam and Akhlaghipour2013) and Shokri et al. (Reference Shokri and Niknam2006) in the ponderomotive action on the collisional plasmas.
Fig. 1. Normalized electric field 
$eE/{\rm \omega} \sqrt {T_i m_e }$ (a), normalized magnetic field 
$eB/{\rm \omega} \sqrt {T_i m_e } $ (b) and normalized electron temperature distribution 
$T_e /T_i $ (c) as a function of the normalized distance 
$z{\rm \omega} /c$ for different energy fluxes, 
$I = 6 \times 10^3\, {\rm W}/\hskip-1pt{\rm cm}^2 $(solid line), 
$I = 8 \times 10^3\, {\rm W}/\hskip-1pt{\rm cm}^2 $ (dashed line) and I = 10
$\times\; 10^3\, {\rm W}/\hskip-1pt{\rm cm}^2 $ (dotted line) varying along the direction of propagation. Parameters are taken as 
$n_0 = 5 \times 10^{11} cm^{ - 3} $, 
$f = 8 {\rm GHz}$, 
$T_e = T_i = 0.2 ev$, 
${\rm \nu} _e /{\rm \omega} = 0.1$.
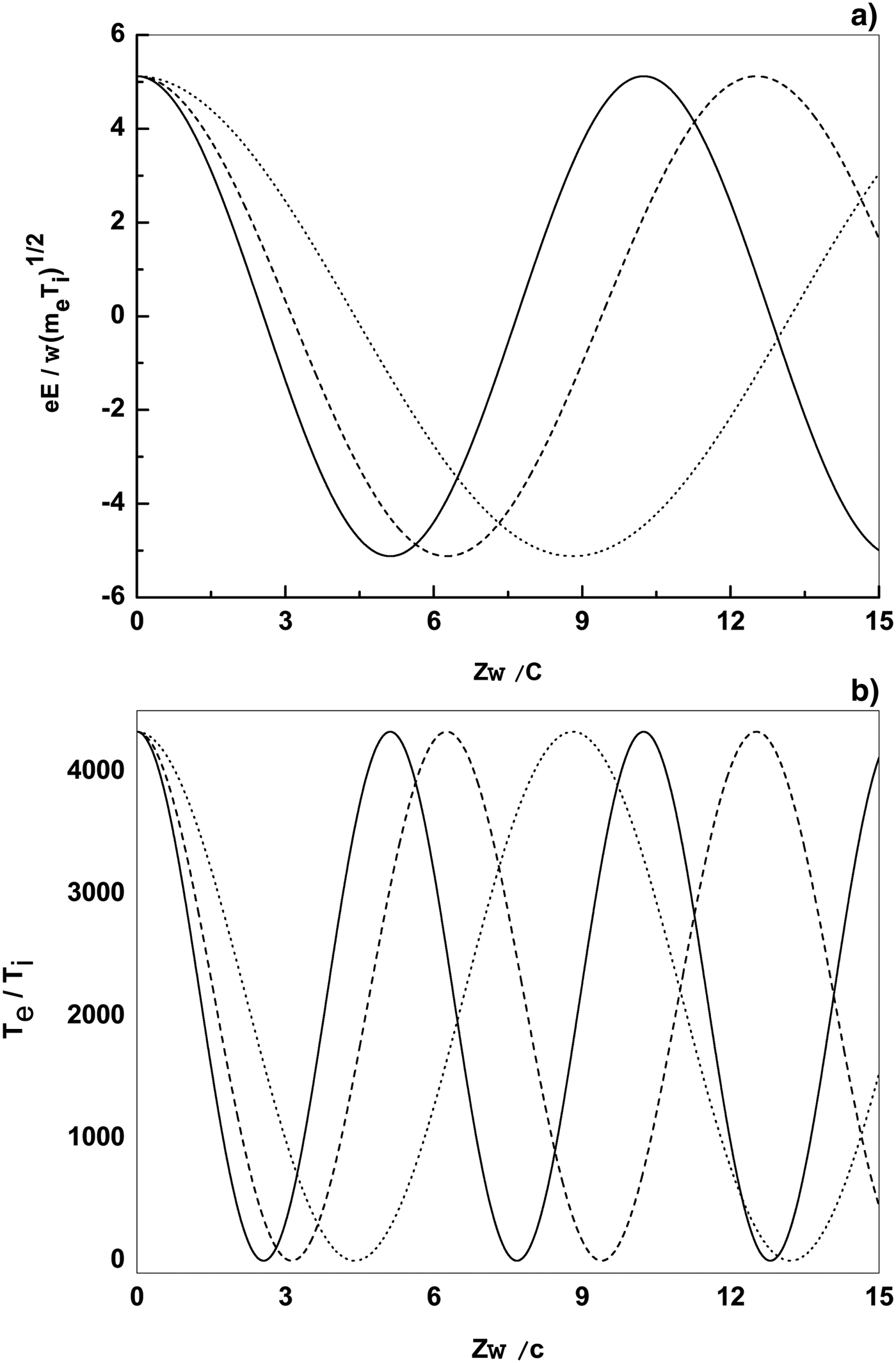
The influence of initial electron density on the electric field and electron temperature distribution profiles is shown in Figures 2a and 2b. The parameters in Figure 2 are similar to those in Figure 1 except for the microwave energy flux that is 
$I = 10 \times 10^3 {\rm W}/{\rm cm}^2 $ and for the different initial electron densities that are 
$n_0 = 5 \times 10^{11} {\rm cm}^{ - 3} $ (solid line), 
$n_0 = 6 \times 10^{11} {\rm cm}^{ - 3} $ (dashed line), and 
$n_0 = 7 \times 10^{11} {\rm cm}^{ - 3} $ (dotted line). From Figures 2a and 2b, it is observed that by increasing the initial electron density, the oscillations wavelength in the electric field and electron temperature distribution profiles are increased. The physical reason is as follows: when the initial electron density is increased, the dielectric permittivity is decreased. Hence, the wavenumber decreases because it is proportional to the square root of the dielectric permittivity and consequently the wavelength of oscillations increases. These figures show that the behavior of electron temperature distribution is highly affected by the electric field strength, because the electron heating is related to the microwave electric field strength, i.e., 
${\bf E}^2 $, that it is given at Eq. (9). Moreover, the ponderomotive force pushes the electrons and creates electron bunches. By increasing the initial electron density, the strength of ponderomotive force is decreased and the distance between electron bunches are increased. On the other hand, electron bunches are related with the electron temperature as shown in Figure 1 (i.e., electrons gain energy from the microwave intensity between electron bunches and the electron heating occurs). Then the distance between peaks and the oscillations wavelength in electron temperature distribution are increased.
Fig. 2. Normalized electric field 
$eE/{\rm \omega} \sqrt {T_i m_e } $ (a) and normalized electron temperature distribution 
$T_e /T_i $ (b) as a function of the normalized distance 
$z{\rm \omega} /c$ for different initial electron densities, 
$n_0 = 5 \times 10^{11} {\rm cm}^{ - 3} $ (solid line), 
$n_0 = 6 \times 10^{11} {\rm cm}^{ - 3} $ (dashed line) and 
$n_0 = 7 \times 10^{11} {\rm cm}^{ - 3}$ (dotted line) varying along the direction of propagation. The microwave energy flux is 
$I = 10 \times 10^3\, {\rm W}/\hskip-1pt{\rm cm}^2 $ and other parameters are as in Figure 1.
The effect of microwave frequency on the electron temperature distribution is investigated for three different cases in Figure 3. In this figure, the high-power microwave energy flux is 
$I = 10 \times 10^3 {\rm W}/{\rm cm}^2 $ and three different microwave frequencies are 8 GHz (solid line), 9 GHz (dashed line), and 
$10\, {\rm GHz}$ (dotted line) and other parameters are similar to Figure 1. In Figure 3, it is shown that by increasing the microwave frequency, a decrease in the amplitude of the electron temperature distribution is formed. From this figure, it is obvious that the wavelength of oscillations decreases by increasing the microwave frequency. By increasing microwave frequency, the amplitude of dielectric permittivity is increased. Consequently, the wavelength of oscillations in the electron temperature distribution is decreased similar to the electromagnetic fields in Khorashadizadeh et al., (Reference Khorashadizadeh, Mirzaye and Niknam2013). Also, according to Eq. (9), the electron temperature is related to the inverse of microwave frequency, therefore the amplitude of normalized electron temperature is decreased. AS the ponderomotive force pushes the electrons and creates the electron bunches, the electron temperature in changed. The ponderomotive force is related to the microwave frequency (see Eqs. (3) and (10)). Therefore, one can conclude that the temperature of electrons changes by the microwave frequency due to the ponderomotive force action.
Fig. 3. Normalized electron temperature distribution 
$T_e /T_i $ as a function of the normalized distance 
$z{\rm \omega} /c$ for different microwave frequencies, 8 GHz (solid line), 9 GHz (dashed line) and 10 GHz (dotted line) varying along the direction of propagation. The microwave energy flux is 
$I = 10 \times 10^3\, {\rm W}/\hskip-1pt{\rm cm}^2 $ and other parameters are as in Figure 1.
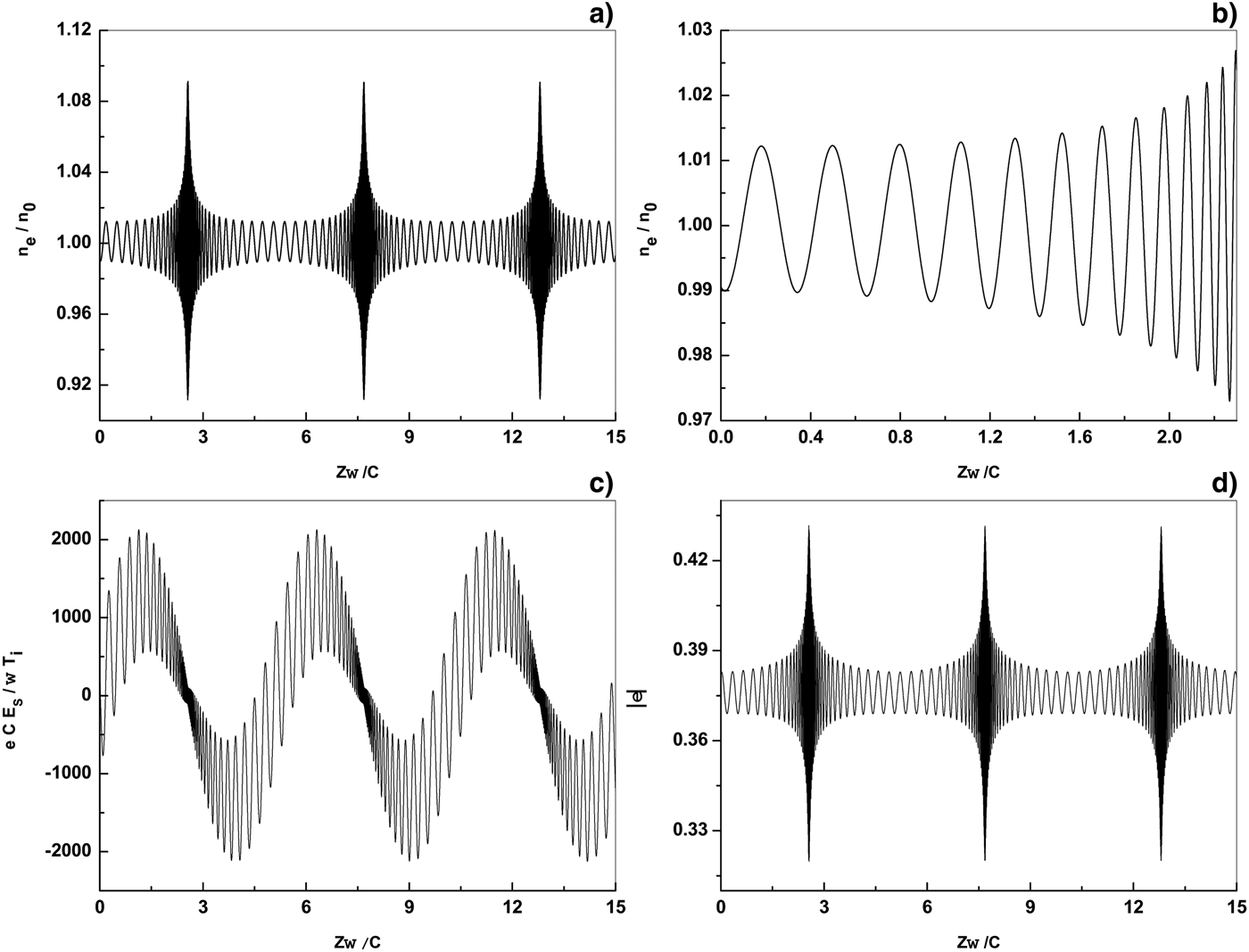
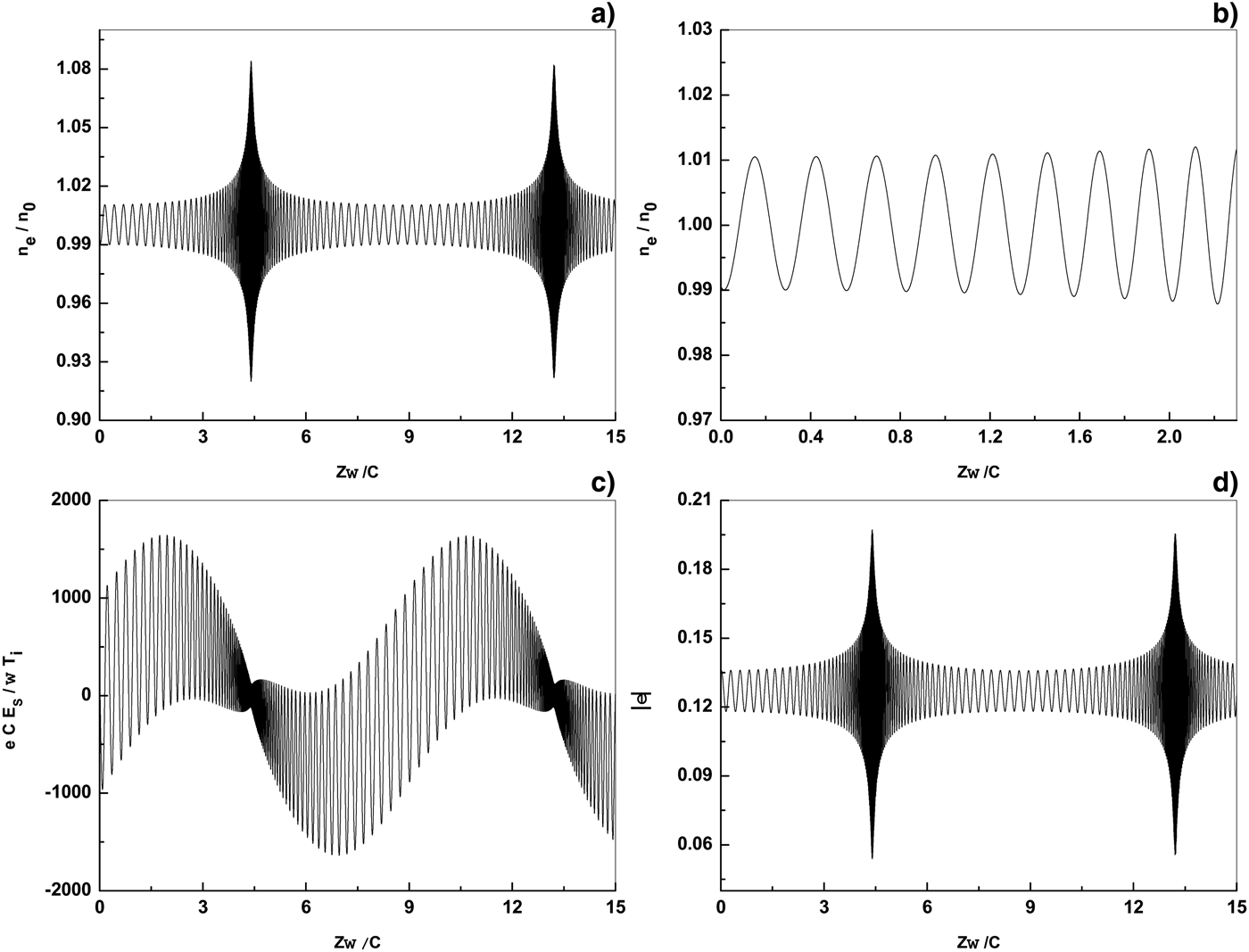
In Figure 4, the effect of the microwave beam propagation in plasma on normalized profiles of the electron density, space charge field, and dielectric permittivity are shown. In Figure 4b, the spatial interval of the 
$z{\rm \omega} /c$ axis is smaller than those in other figures, for better comparison. The parameters in Figure 4 are similar to those in Figure 1, but the microwave energy flux is 
$I = 10 \times 10^3\, {\rm W}/\hskip-1pt{\rm cm}^2 $. This figure shows that when the microwave energy flux is propagated into plasma, steepening in the electron density distribution, and dielectric permittivity profiles and sawtooth lines in the space charge field profiles are created. In according to Poisson and dielectric permittivity equations, the behavior of space charge field and dielectric permittivity are much influenced by the electron density distribution. From the above equations it is concluded that the electron density distribution is very complicated and thus the behavior of nonlinear system due to the space charge and electron temperature effects is enhanced. Although the modulation in wavelength has been observed by Niknam et al. (Reference Niknam and Shokri2007), it is shown that the variations of electron temperature and space charge effects cause a signification change than before for the electron density distribution, dielectric permittivity, and space charge field profiles. It is obvious from Figure 4b that the amplitude of normalized electron density is increased while its width is decreased. According to Figure 1 and Eq. (7), by increasing the microwave intensity (and thus the electron temperature in any period), the ponderomotive force is increased. Therefore, some regions in plasma act as low density tones and the amplitude of electron density distribution is decreased. Moreover, according to principal of particle conservation by decreasing the amplitude of electron density distribution, the width of theirs peaks is increased. Therefore, in any period of oscillations by increasing the microwave intensity, the steepening in the electron density distribution is decreased. Similarly, by decreasing the microwave intensity, the steepening in the electron density distribution is increased.
Fig. 4. Normalized electron density 
$n_e /n_0 $ (a), zoom of normalized electron density 
$n_e /n_0 $ (b), normalized space charge field 
$ecE_s /T_i {\rm \omega} $ (c) and dielectric permittivity 
${\rm \varepsilon} $ (d) as a function of the normalized distance 
$z{\rm \omega} /c$ for energy flux 
$I = 10 \times 10^3\, {\rm W}/\hskip-1pt{\rm cm}^2 $. Same parameters are as in Figure 1.
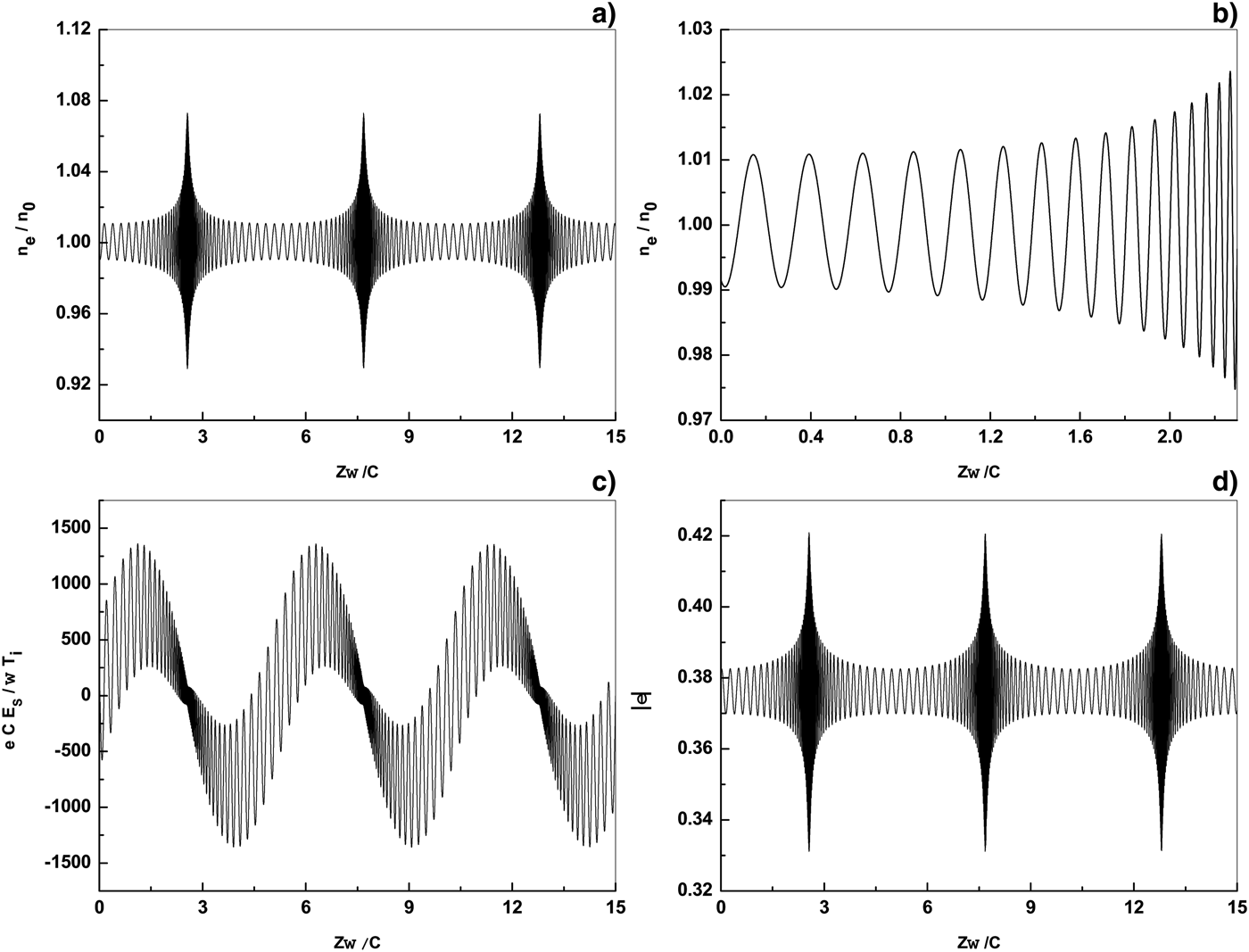
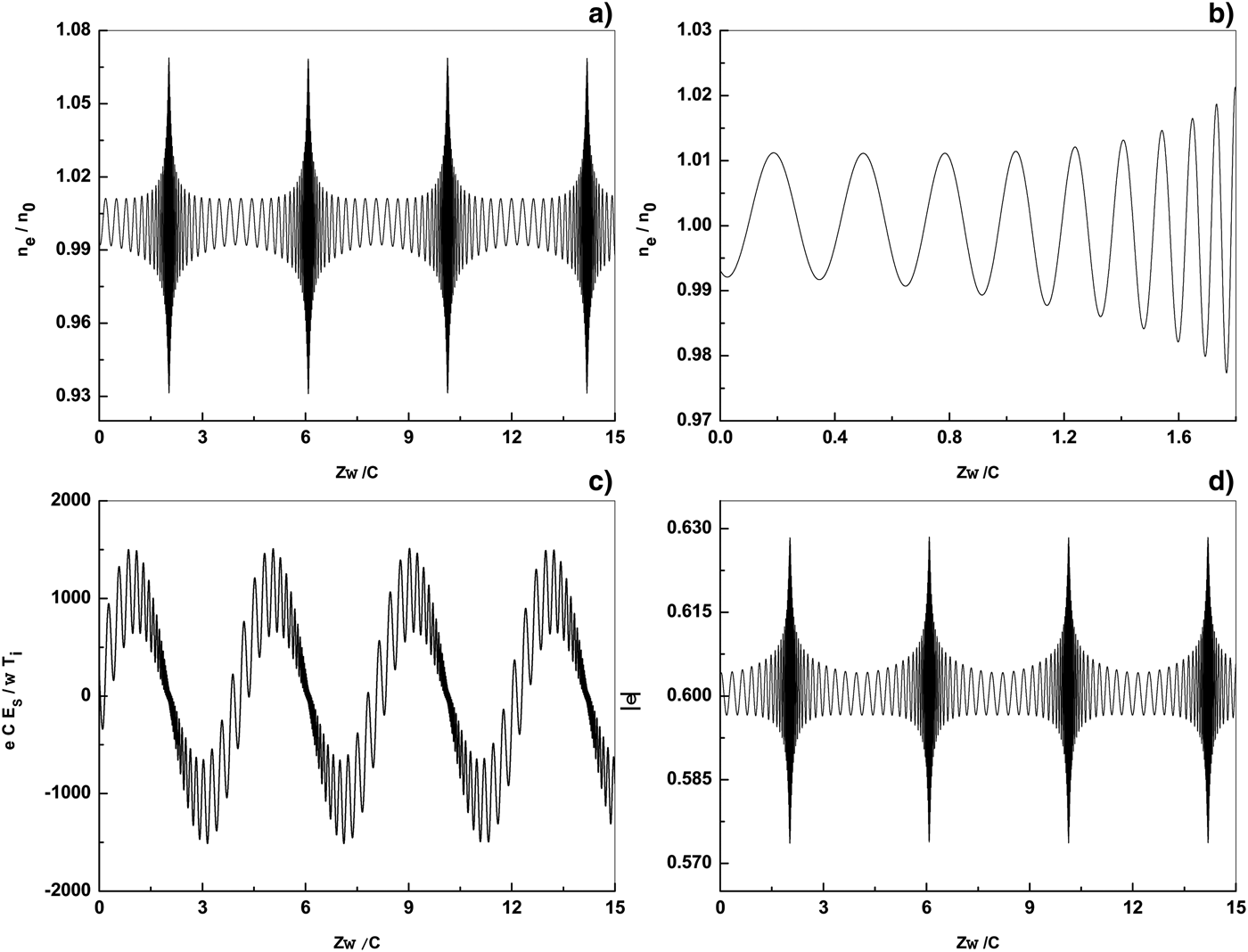
The effect of high-power microwave energy flux in plasma on the normalized profiles of electron density, space charge field, and dielectric permittivity is shown in Figure 5. The parameters in Figure 5 are similar to those in Figure 4, but the microwave energy flux is 
$I = 6 \times 10^3\, {\rm W}/\hskip-1pt{\rm cm}^2 $. By comparing this figure and Figure 4, it is observed that by decreasing the microwave energy flux, the amplitude of electron density distribution, space charge filed, and dielectric permittivity profiles are decreased. Also, it is indicated that the number of peaks in the electron density distribution are increased while their width are decreased. In accordance to ohmic heating and Figure 1c, the electron temperature is decreased by decreasing the microwave energy flux. Moreover, by decreasing the microwave energy flux, the ponderomotive force (and thus the space charge field) are decreased. Regarding the force balance equation (see Eq. (7)), the amplitude of peaks in the electron density distribution is decreased. On the other hand, according to particle conservation, by a decrease in width of the peaks, the number of peaks in the electron density distribution is increased.
Fig. 5. Normalized electron density 
$n_e /n_0 $ (a), zoom of normalized electron density 
$n_e /n_0 $ (b), normalized space charge field 
$ecE_s /T_i {\rm \omega} $ (c) and dielectric permittivity 
${\rm \varepsilon} $ (d) as a function of the normalized distance 
$z{\rm \omega} /c$ for energy flux 
$I = 6 \times 10^3\, {\rm W}/\hskip-1pt{\rm cm}^2 $. Same parameters are as in Figure 1.
The influence of initial electron density on the electron density distribution, space charge field, and dielectric permittivity profiles is shown in Figure 6. For a better comparison, the small variations of electron density distribution are shown in Figure 6b. The parameters in Figure 6 are similar to those in Figure 4 except for the initial electron density that is 
$n_0 = 7 \times 10^{11} {\rm cm}^{ - 3} $. By comparing this figure and Figure 4 it is observed that the wavelength of oscillations is increased when the initial electron density increases. Moreover, the maximums of electron density distribution lie on zero points of the electric and space charge field profiles. Also, when the initial electron density increases, the magnitude of electron density perturbation is increased and the dielectric permittivity decreases. Moreover, since 
${\rm \lambda} $ (the oscillations wavelength) is proportional to 
${\rm \varepsilon} ^{ - 1/2} $, then by decreasing the dielectric permittivity, the wavelength of oscillations increases. From Figure 6, it can be observed that by increasing the initial electron density, the amplitude and number of peaks in electron density distribution, space charge field and dielectric permittivity profiles are decreased while their width are decreased. The physical reason is as follows: by considering Poisson equation, when the amplitude of space charge field is decreased, the increase of the initial electron density causes the decrease in characteristic length. Thus, the increase of the number of electron bunches is observed. Also, when the initial electron density is increased, then the pressure gradient force is increased. So according to Eqs. (4) and (7), the amplitude of charge space filed and electron density distribution profiles are decreased. Moreover, by increasing the initial electron density, the ponderomotive force is decreased. Thus, the steepening in electron density distribution and amplitude in space charge field are decreased.
Fig. 6. Normalized electron density 
$n_e /n_0 $ (a), normalized space charge field 
$ecE_s /T_i {\rm \omega} $ (b) and dielectric permittivity 
${\rm \varepsilon} $ (c) as a function of the normalized distance 
$z{\rm \omega} /c$ for initial electron density 
$n_0 = 7 \times 10^{11} {\rm cm}^{ - 3} $. Same parameters are as in Figure 4.
Finally, we investigated the effect of microwave frequency on the electron density distribution, space charge field, and dielectric permittivity profiles in Figure 7. In Figure 7b the small variations of the electron density distribution is shown. In this figure, the microwave frequency is 9 GHz and other parameters are similar to those in Figure 4. It is shown in Figure 7 that by increasing the microwave frequency, a decrease in the amplitude of electron density distribution, space charge field, and dielectric permittivity profiles is occurred. By increasing the microwave frequency, the ponderomotive force decreases (and thus the amplitude of space charge field and electron density distribution profiles) is decreased. This result is similar to one obtained by Aria and Malik (Reference Aria and Malik2008) in a plasma filled rectangular waveguide (bounded system). In Figure 7d, it is shown that the amplitude of dielectric permittivity profiles is increased by increasing the microwave frequency. Therefore, the wavelength of oscillations is decreased. Based on Eq. (10), the dielectric permittivity is increased by increasing the microwave frequency. On the other hand, the oscillations wavelength is proportional to 
${\rm \varepsilon} ^{ - 1/2} $, then by increasing the dielectric permittivity, the wavelength of oscillations increases.
Fig. 7. Normalized electron density 
$n_e /n_0 $ (a), normalized space charge field 
$ecE_s /T_i {\rm \omega} $ (b) and dielectric permittivity 
${\rm \varepsilon} $ (c) as a function of the normalized distance 
$z{\rm \omega} /c$ for different microwave frequency 9 GHz varying along the direction of propagation. The other parameters are as in Figure 4.
4. CONCLUSIONS
In this work, the ponderomotive force, space charge, and Ohmic heating effects in the nonlinear interaction of a high-frequency microwave beam with a collisional unmagnetized plasma was investigated. Using the equations of wave propagation, momentum transfer, particles conservation, energy, and Poisson, we found that the nonlinear behavior of system by taking into account the ponderomotive force was enhanced by the space charge and electron temperature effects. When the microwave energy flux was propagated into plasma, steepening in the electron density distribution and dielectric permittivity profiles and sawtooth lines in space charge field profiles was observed. It was indicated that the behavior of space charge field and dielectric permittivity profiles was much influenced by the electron density distribution. Also, the electron temperature distribution was changed by the propagation of microwave beam in plasma as the amplitude of them was increased by increasing the microwave energy flux, and it decreased when the microwave frequency increased. Furthermore, by decreasing the electron temperature, the amplitude of electron density oscillations increased and its width decreased. Finally, it was indicated that by increasing microwave frequency, a decrease in the amplitude of the electron density distribution, dielectric permittivity and space charge field profiles was formed and wavelength of oscillations decreased.
