1. INTRODUCTION
Highly energetic ion beams colliding with each other offers an important way to discover new particles and furthermore new physics. Nowadays, conventional linear and cyclotron accelerators are able to generate proton beams with energy up to several TeV. The Large Hadron Collider (LHC), allowing two 7 TeV proton beams to impinge with each other, seems to have found the Higgs particle that could explain the origin of mass. On the other hand, the future construction of more powerful accelerators based on conventional method is limited by its enormous expense and occupancy area. Plasma, which can sustain extremely large acceleration gradient (three orders of magnitude higher than achieved in conventional accelerators), exhibits great potential to generate energetic proton/ion beams in table-top size or within a lab. Lots of plasma-based acceleration mechanisms have been proposed, where ultra-intense lasers are mostly employed to excite a strong accelerating field in plasmas, such as the well-known target normal sheath acceleration (TNSA) (Schwoerer et al., Reference Schwoerer, Pfotenhauer, Jackel, Amthor, Liesfeld, Ziegler, Sauerbrey, Ledingham and Esirkepov2006; Toncian et al., Reference Toncian, Borghesi, Fuchs, d'Humières, Antici, Audebert, Brambrink, Cecchetti, Pipahl, Romagnani and Willi2006; Albright et al., Reference Albright, Yin, Hegelich, Bowers, Kwan and Fernandez2006; Mora et al., Reference Mora2003; Snavely et al., Reference Snavely, Key, Hatchett, Cowan, Roth, Phillips, Stoyer, Henry, Sangster, Singh, Wilks, MacKinnon, Offenberger, Pennington, Yasuike, Langdon, Lasinski, Johnson, Perry and Campbell2000; Yin et al., Reference Yin, Albright, Hegelich and Fernandez2006; Poukey et al., Reference Poukey1969; Gaillard et al., Reference Gaillard, Kluge, Flippo, Bussmann, Gall, Lockard, Geissel, Offermann, Schollmeier, Sentoku and Cowan2011), the radiation pressure acceleration (RPA) (Macchi et al., Reference Macchi, Cattani, Liseykina and Cornolti2005; Liseikina et al., Reference Liseikina and Macchi2007; Qiao et al., Reference Qiao, Zepf, Borghesi and Geissler2009; Reference Qiao, Zepf, Borghesi, Dromey, Geissler, Karmakar and Gibbon2010; Liseykina et al., Reference Liseykina, Borghesi, Macchi and Tuveri2008; Robinson et al., Reference Robinson, Zepf, Kar, Evans and Bellei2008; Yan et al., Reference Yan, Lin, Sheng, Guo, Liu, Lu, Fang and Chen2008; Zhang et al., Reference Zhang, Shen, Ji, Wang, Jin, Li, Wen and Cary2009; Reference Zhang, Shen, Li, Jin and Wang2007a; Reference Zhang, Shen, Li, Jin, Wang and Wen2007b; Ji et al., Reference Ji, Shen, Zhang, Wang, Jin, Li, Wen and Cary2008; Reference Ji, Shen, Zhang, Wang, Jin, Wen, Wang and Xu2009), the laser break-out afterburner (BOA) (Yin et al., Reference Yin, Albright, Hegelich, Bowers, Flippo, Kwan and Fernandez2007; Flippo et al., Reference Flippo, Hegelich, Albright, Yin, Gautier, Letzring, Schollmeier, Schreiber, Schulze and Fernandez2007; Albright et al., Reference Albright, Yin, Bowers, Hegelich, Flippo, Kwan and Fernandez2007), and laser-driven wakefield acceleration (Shen et al., Reference Shen, Li, Yu and Cary2007; Reference Shen, Zhang, Sheng, Yu and Cary2009; Zhang et al., Reference Zhang, Shen, Ji, Wang, Wen, Wang, Xu and Yu2010). The technique of TNSA is more mature than others, especially in experiments. However, the acceleration distance is short and the laser-proton efficiency is relatively low. Up to present 67.5 MeV is the highest proton energy obtained by TNSA using the 80 J PW Trident Laser (Gaillard et al., Reference Gaillard, Kluge, Flippo, Bussmann, Gall, Lockard, Geissel, Offermann, Schollmeier, Sentoku and Cowan2011). BOA is a mechanism in which laser penetrates to the rear of the target and consequently heats the sheath electrons, which enables the proton acceleration to GeV-level with lower laser intensity compared with TNSA. RPA is a newly developed promising approach attracting more and more interest in recent years. Using intense circularly polarized (CP) laser pulses, protons with energy over 1 GeV may be obtained, which have been demonstrated by lots of particle-in-cell (PIC) simulations (Yan et al., Reference Yan, Wu, Sheng, Chen and Meyer-ter-Vehn2009; Qiao et al., Reference Qiao, Zepf, Borghesi and Geissler2009; Macchi et al., Reference Macchi, Veghini and Pegoraro2009; Chen et al., Reference Chen, Pukhov, Yu and Sheng2009; Tripathi et al., Reference Tripathi, Liu, Shao, Eliasson and Sagdeev2009; Davis et al., Reference Davis and Petrov2009; Eliasson et al., Reference Eliasson, Liu, Shao, Sagdeev and Shukla2009). Recent researches have shown that not only electrons but protons can also gain stable acceleration in laser-driven wakefield, except that protons are accelerated by the positive electrostatic field in the front of “bubble” (Shen et al., Reference Shen, Li, Yu and Cary2007). One uses short CP laser pulses interacting with a micro-target embedded in under-dense high-mass plasma. Protons in the micro-target are first pre-accelerated by the laser radiation pressure and gain considerable initial velocity. Then these protons are more easily trapped and steadily accelerated by the induced wake “bubble” field in the background plasma. PIC simulations show that 76 GeV high-quality quasi-mono-energetic protons (Zhang et al., Reference Zhang, Shen, Ji, Wang, Wen, Wang, Xu and Yu2010) can be obtained with this approach. Although a lot of progresses have been made, the energy gain in laser-plasma acceleration is still not comparable with the top conventional accelerators even in simulations. The required laser intensity is also very high (2.14 × 1023 Wcm−2 for 76 GeV) compared to currently available laser facilities.
In plasma wakefield acceleration, energetic particle beams have also been proposed to be alternate drivers (Esarey et al., Reference Esarey, Schroeder and Leemans2009; Rosenzweig et al., Reference Rosenzweig, Breizman, Katsouleas and Su1991; Lotov, Reference Lotov2007; Lee et al., Reference Lee, Katsouleas, Hemker and Mori2000; Wang et al., Reference Wang, Muggli, Katsouleas, Joshi, Mori, Ischebeck and Hogan2009; Joshi et al., Reference Joshi, Blue, Clayton, Dodd, Huang, Marsh, Mori, Wang, Hogan, O'Connell, Siemann, Watz, Muggli, Katsouleas and Lee2002; Blumenfeld et al., Reference Blumenfeld, Clayton, Decker, Hogan, Huang, Ischebeck, Iverson, Joshi, Katsouleas, Kirby, Lu, Marsh, Mori, Muggli, Oz, Siemann, Walz and Zhou2007; Kallos et al., Reference Kallos, Katsouleas, Kimura, Kusche, Muggli, Pavlishin, Pogorelsky, Stolyarov and Yakimenko2008). An intense electron beam can excite wakefield in a plasma, where background electrons are expelled by the beams rather than laser pulses. In this mechanism, the energy gain of the witness beam cannot be more than 
$2\sqrt{2}$ times of the driver's energy (Bane et al., Reference Bane, Chen and Wilson1985). Since protons are able to carry much higher energy than electrons in nowadays' accelerators (CERN, LHC, etc.), it is promising to achieve higher energy gain comparable to state-of-art conventional accelerators by using proton drivers (Caldwell et al., Reference Caldwell, Lotov, Pukhov and Simon2009; Lotov, Reference Lotov2010; Xia et al., Reference Xia, Caldwell, Lotov, Pukhov, Kumar, An, Lu, Mori, Joshi, Huang, Muggli, Assmann and Zimmermann2010).
In previous proton-driven plasma wakefield researches, where electron acceleration is mostly concerned, it is found that because background electrons are sucked in toward the propagating axis by the positively charged driver instead of being blown out. Electrons originating from different radii arrive at different times, leading to the “phase mixing” effect. It reduces the amplitude of plasma oscillation, and is considered to be the primary limit to the acceleration field (Lee et al., Reference Lee, Katsouleas, Hemker, Dodd and Mori2001; Kimura et al., Reference Kimura, Milchberg, Muggli, Li and Mori2011).
Following the laser-driven wakefield scenario mentioned above (Shen et al., Reference Shen, Li, Yu and Cary2007; Reference Shen, Zhang, Sheng, Yu and Cary2009; Zhang et al., Reference Zhang, Shen, Ji, Wang, Wen, Wang, Xu and Yu2010), one could naturally infer that proton itself can also be accelerated by a proton-driven wakefield. A few researchers have observed proton energy gaining in the driving beam, though lacking specific explanation (Kumar et al., Reference Kumar, Pukhov and Lotov2010; Caldwell et al., Reference Caldwell and Lotov2011). In this paper, we propose demonstrably that using an energetic proton beam propagating through an under-dense plasma, protons located in the bunch tail can be stably accelerated by its self-driving wakefield. Unlike electrons, protons are supposed to be expelled by the transverse component of the wakefield. However when the density of the driving beam in 6d phase space d ∝ N/(γ2 σxɛσy2α2) is large enough, the driver can propagate for a long distance without apparent divergence owing to the “plasma lens” effect (Chen et al., Reference Chen, Su, Katsouleas, Wilks and Dawson1987; Su et al., Reference Su, Katsouleas, Dawson and Fedele1990). This effect allows charged particle beams propagating in plasma to be focused due to plasma electrons shifting. Here N is total number of the drive particles, γ, σx, σy, ɛ, and α are the Lorentz factor, longitudinal size, transverse size, longitudinal momentum spread and divergence angle of the drive beam, respectively. Confinement of protons at the tail of a dense driving bunch mainly relies on the co-propagating electrons within the proton bunch, which move with the driver with a lower speed. Discussions in more detail will be shown in Section 3.
For proton beams available in recent accelerators, whose phase space densities are much lower, the “plasma lens” effect alone is not sufficient to confine the whole bunch, so extra quadrupole magnets (Caldwell et al., Reference Caldwell, Lotov, Pukhov and Simon2009; Lotov, Reference Lotov2010) are employed. The acceleration of the beams with feasible 6d phase space density will be discussed in Section 4.
As the proton bunch propagates in the plasma, energy is continually transmitted from the main body to the tail until phase slippage occurs. After propagating in plasmas for a few meters, the energy of some protons could be considerably increased.
2. LONGITUDINAL WAKEFIELDS GENERATED BY A PROTON BEAM
As a charged beam propagates in a plasma, the plasma electrons will respond to the extra charge and oscillate at plasma frequency 
${\rm \omega}_{\rm p} = \sqrt{4{\rm \pi} n_0 e^2 /m_{\rm e}}$. Plasma-wave excitation by a negatively charged driver has been well studied both theoretically (Esarey et al., Reference Esarey, Schroeder and Leemans2009; Wilks et al., Reference Wilks, Katsouleas, Dawson, Chen and Su1987; Keinigs et al., Reference Keinigs and Jones1987; Rosenzweig, Reference Rosenzweig1987; Krall et al., Reference Krall, Joyce and Esarey1991; Lu et al., Reference Lu, Huang, Zhou, Mori and Katsouleas2005) and experimentally (Joshi et al., Reference Joshi, Blue, Clayton, Dodd, Huang, Marsh, Mori, Wang, Hogan, O'Connell, Siemann, Watz, Muggli, Katsouleas and Lee2002; Blumenfeld et al., Reference Blumenfeld, Clayton, Decker, Hogan, Huang, Ischebeck, Iverson, Joshi, Katsouleas, Kirby, Lu, Marsh, Mori, Muggli, Oz, Siemann, Walz and Zhou2007; Kallos et al., Reference Kallos, Katsouleas, Kimura, Kusche, Muggli, Pavlishin, Pogorelsky, Stolyarov and Yakimenko2008). In the linear regime, the plasma wave driven by a positively charged beam is very similar to those by electrons, but only shifted in phase. However, it presents significant differences in the nonlinear regime. A negatively charged driver “blows out” the background electrons while the positively charged one “sucks them in.” In the latter case, electrons in plasma are first “sucked-in” toward the propagating axis by the space-charge force, and then continue to move across the beam axis and create a low-density region behind the driver. This induces phase mixing and local plasma frequency increasing (because of the background electron density enhancement on axis), making it more difficult to obtain a clean “bubble”. In the highly nonlinear regime, numerical simulations should be relied on to find the optimal beam-plasma parameters for the resonant wakefield generation.
For comparison to the two dimensional (2D) simulations that follows, a 2D model is performed in Cartesian geometry (x − y). A full three-dimensional treatment can be found (Su et al., Reference Su, Katsouleas, Dawson and Fedele1990; Wilks et al., Reference Wilks, Katsouleas, Dawson, Chen and Su1987; Keinigs et al., Reference Keinigs and Jones1987; Rosenzweig, Reference Rosenzweig1987). We consider a proton beam propagating with a velocity v b ≈ c along x direction through uniform plasma. The charge density of the bunch is ρb = ρ⊥(y)ρ//(ξ), where ξ ≡ x − v bt. In the linear regime, the generated longitudinal electric field can be calculated as (Wilks et al., Reference Wilks, Katsouleas, Dawson, Chen and Su1987)
$$E_{\rm x} \left({\rm y}\comma \; {\rm \xi} \right)= X^{\prime} \left({\rm \xi} \right)Y \lpar {\rm y}\rpar\comma$$where
$$X^{\prime} \left({\rm \xi} \right)= - 4{\rm \pi} \mathop{\int}\limits_{{\rm \xi}}^{\infty} d{\rm \xi}^{\prime} {\rm \rho}_{//} \left({\rm \xi}^{\prime} \right)\cos k_{\rm p} \left({\rm \xi} - {\rm \xi}^{\prime} \right)\comma \;$$and
$$Y\left(\hbox{y} \right)= {k_{\rm p} \over 2} \mathop{\int}\limits_{ - \infty}^{\infty} \hbox{dy}^{\prime} {\rm \rho}_{\perp} \left(\hbox{y}^{\prime} \right)e^{ - k_{\rm p} \vert {\rm y} - {\rm y}^{\prime} \vert}\comma \;$$where ρ// and ρ⊥ are the longitudinal and transverse charge density profile, and k p = ωp/c is the plasma wave number.
Substitute a Gaussian longitudinal profile 
${\rm \rho}\!_{//} \lpar {\rm \xi}\rpar = en_{\rm b} \hbox{e}^{ - {\rm \xi}^2 /2{\rm \sigma}_{\rm x}^2}$ into Eqs. (1)–(3), where e is the unit charge of a proton and n b is the beam density, one obtains the on-axis longitudinal electric field for ξ ≪ − σx,
$$\eqalign{E_{\rm x} \left(0\comma \; {\rm \xi} \right) &= \sqrt{2{\rm \pi}} \lpar mc {\rm \omega}_{\rm p} /e\rpar \lpar n_{\rm b} /n_0\rpar \lpar k_{\rm p} {\rm \sigma}_{\rm x} \hbox{e}^{ - k_{\rm p}^2 {\rm \sigma}_{\rm x}^2 /2}\rpar \cr &\quad \times Y\lpar 0\rpar \cos \lpar k_{\rm p} {\rm \xi}\rpar .}$$ The amplitude of longitudinal electric field peaks when its derivation on k p is zero, thus giving the match condition of 
$k_{\rm p} {\rm \sigma}_{\rm x} = \sqrt{2}$ in one-dimensional limit, where ρ⊥ = 1 for y = 0 and remains close to unit for y much larger than k p−1. The match condition means that the plasma wavelength shall be comparable to the length of the driving bunch. The maximum on-axial electric field is then calculated to be qE x,max/mcωp ≈ 1.3n b/n 0.
The above discussions are only valid for the linear-fluid regime. Linear theory is applicable when the perturbed density n 1 is much lower than the background density, i.e., n 1/n 0≪1, and the normalized electric field is below unit, i.e., qE z,max /mcωp≪1. That is to say, the peak beam density must be much lower than the background density n b/n 0≪1. In the weak nonlinear region, according to Lu et al. (Reference Lu, Huang, Zhou, Mori and Katsouleas2005), the longitudinal field will still agree with linear theory until n b increases to be comparable with n 0.
In the nonlinear one-dimensional regime (k pσy≫1), one can examine the wakefield generation by assuming that the drive beam is non-evolving. The beam profile is a function of the coordinate ξ. Using the momentum and continuity equations, the Poisson's equation can be written as (Esarey et al., Reference Esarey, Schroeder and Leemans2009)
$$k_{\rm p}^{ - 2} \displaystyle{\partial^2 {\rm \phi} \over \partial {\rm \xi}^2} = \displaystyle{n_{\rm b} \over n_0} + {\rm \gamma}_{\rm p}^2 \left\{{\rm \beta}_{\rm p} \left[1 - \displaystyle{1 \over {\rm \gamma}_{\rm p}^2 \left(1 + {\rm \phi} \right)^2} \right]^{ - {1 \over 2}} - 1 \right\}\comma$$where ϕ is the normalized electrostatic potential ϕ = eΦ/mc 2, γp = (1 − βp2)−1/2, βp = v p/c is the phase velocity of the plasma wave that equals the speed of drive proton beam in this case, n b is the beam density, and n 0 is the background plasma density.
We can see from Eq. (5) that evolvement of wakefield potential ϕ as a function of k pξ will not change as long as n b/n 0 is kept constant. The peak value of ϕ is the same. The only difference is that for lower plasma density n 0, the wakefield potential ϕ evolves slower with ξ, since k p becomes smaller in this case. As a result, the accelerating field 
$E_{\rm z} \sim \displaystyle{\partial {\rm \phi} / \partial {\rm \xi}}$ decreases with n 0 accordingly.
According to this relationship, we consider a Gaussian beam with following parameters (for comparison with the 2D simulations which follow, we proceed with the analysis in 2D Cartesian geometry): The drive beam with beam density n b1, longitudinal size σx1, radius σy1, energy γ1, longitudinal momentum spread ɛ1, and divergence angle α1. The uniform background plasma is of density n 1. To find out the scaling law, one could decrease the background plasma density to n 2 = 0.01n 1. According to Eq. (5), the beam density should to be n b2 = 0.01n b2 to keep similar wakefield evolvement. The match condition 
$\lpar k_{\rm p} {\rm \sigma}_{\rm x} = \sqrt{2}$) requires σx2 = 10σx1 (and accordingly σy2 = 10σy1 to keep the shape of the drive beam). Other parameters stay the same. The wakefield potentials are with the same peak value but evolves 10 times slower with ξ in the latter case, leading to wakefield 10 times smaller. As a result, the accelerating distance should be ten times longer to obtain the same energy gain.
One should notice the beam density in 6d phase space d ∝ N/(γ2σxɛσy2α2) is 100 times smaller in the second case than the former. It indicates that the requirement of beam quality could be released if we decrease background plasma density. This scaling is very important as beams with high density in 6d phase space are difficult to be obtained. On the other hand, the plasma density should not be too low to insure the accelerating gradient higher than conventional accelerators. Total beam charge cannot exceed the limit that from in conventional accelerators. This would somehow put a lower limit on the beam quality.
3. STABLE ACCELERATION OF THE SELF-CONFINED PROTON BUNCH
In this section, we consider a proton beam with large 6d phase space density driving a wakefield in a uniform plasma with matched density (
$k_{\rm p} {\rm \sigma}_{\rm x} = \sqrt{2}$). With such density, the whole beam could be self-confined by the “plasma lens” effect without extra focusing source. Meanwhile, longitudinally the dense plasma electrons zone at the front edge of the first “bubble” would be pulled into the body of the bunch, shielding the expelling force and letting protons at the beam tail fall into accelerating phase of the wakefield.
According to the scaling discussed in Section 2, it's possible to simulate the universal accelerating process in shorter simulating length and time by using higher-density background plasma and a shorter denser proton beam. As a primary example, we adopt a short dense proton beam with parameters listed in Table 1. 2D-PIC simulation is performed with code VORPAL (Nieter, et al., Reference Nieter and Cary2004) as well as quasi-static PIC code LCODE (Lotov, Reference Lotov2003; Reference Lotov1998). Typical proton energy of 1 TeV is used, which is available in conventional radio frequency accelerators. Due to the limitation on simulation ability, relatively small beam duration and high plasma density are employed to obtain a large acceleration gradient, so that we can see considerable energy gain within much shorter simulation length and time. For proton beams that are available in existing facilities, we also perform a long-distance quasi-static simulation with LCODE using a more realistic proton beam with the same 6d-phase space density as that used before (Caldwell et al., Reference Caldwell, Lotov, Pukhov and Simon2009). And the results will be discussed in the next section. Alternately, self-modulation (Kumar et al., Reference Kumar, Pukhov and Lotov2010; Caldwell et al., Reference Caldwell and Lotov2011; Pukhov et al., Reference Pukhov, Kumar, Tuckmantel, Upadhyay, Lotov, Muggli, Khudik, Siemon and Shvets2011; Schroeder et al., Reference Schroeder, Benedetti, Esarey, Gruner and Leemans2011) also provides a possibility for long proton beams to excite large accelerating field which will be discussed in Section 5.
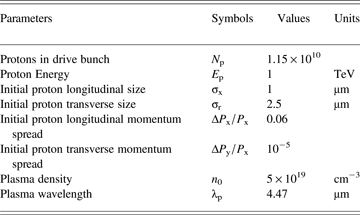
Table 1. Parameters in the simulation
The energetic proton bunch enters from the left of the simulation box of size 20 μm × 30 μm containing Li gas. Moving window is adopted for long-distance simulation. And two simulation grid sizes are used in this paper. A more precise one dx = dy = 4.5 × 10−3λp ≈ 0.02 μm is used to give a detail shape of the plasma wave, and a rough one dx = dy = 4.5 × 10−2λp ≈ 0.2 μm to simulate acceleration process over a long distance.
Distribution of the protons and momentum vectors of background electrons after 8λp propagation in plasma are shown in Figure 1a. The snapshots of the driving protons are presented by red dots. One can see that the plasma electrons are “sucked-in” by the space-charge force of the driver, and then continue to move across the beam axis and create a “bubble” structure. As in laser- or electron beam-driven cases, the “bubble” size is at the same order of plasma wavelength. Figure 1b shows the corresponding on-axis electric field of the longitudinal plasma wave. The negative electric field at the very front is the unique feature of plasma wakefield driven by positively charged particles, which does not exist in laser- or electron beam-driving cases.
Fig. 1. (Color online) (a) Distribution of the protons (red dot) and momentum vector of background electrons (black arrow) after 8λp propagation in plasma. The distribution of the proton beam rarely changes comparing with the original one. (b) The corresponding on-axis longitudinal electric field.
The drive bunch we consider here is so dense that space-charge force is large enough to pull the dense electron bulk into the beam body as shown in Figure 1a. Protons located in the beam tail then fall into the accelerating phase of self-excited wakefield. The peak on-axis accelerating gradient shown in Figure 1b reaches approximately 700 GV/m.
However, transverse force in the “bubble” defocuses the accelerated protons. Stable accelerations rely on the balance between the transverse “bubble” field and the effect of co-propagating electrons.
In 2D geometry, consider a particle with charge q moving at the speed of v b = βc along x direction in vacuum, the transverse electromagnetic field at (x, y) is given by
$$E_{\rm y} = \left\{{q{\rm \gamma} \left(y - y^{\prime} \right)\over \left[\left(y - y^{\prime} \right)^2 \;+\; {\rm \gamma}^2 \left(x - x^{\prime} \right)^2 \right]^{{3 \over 2}}} \right\}_{\rm ret}$$
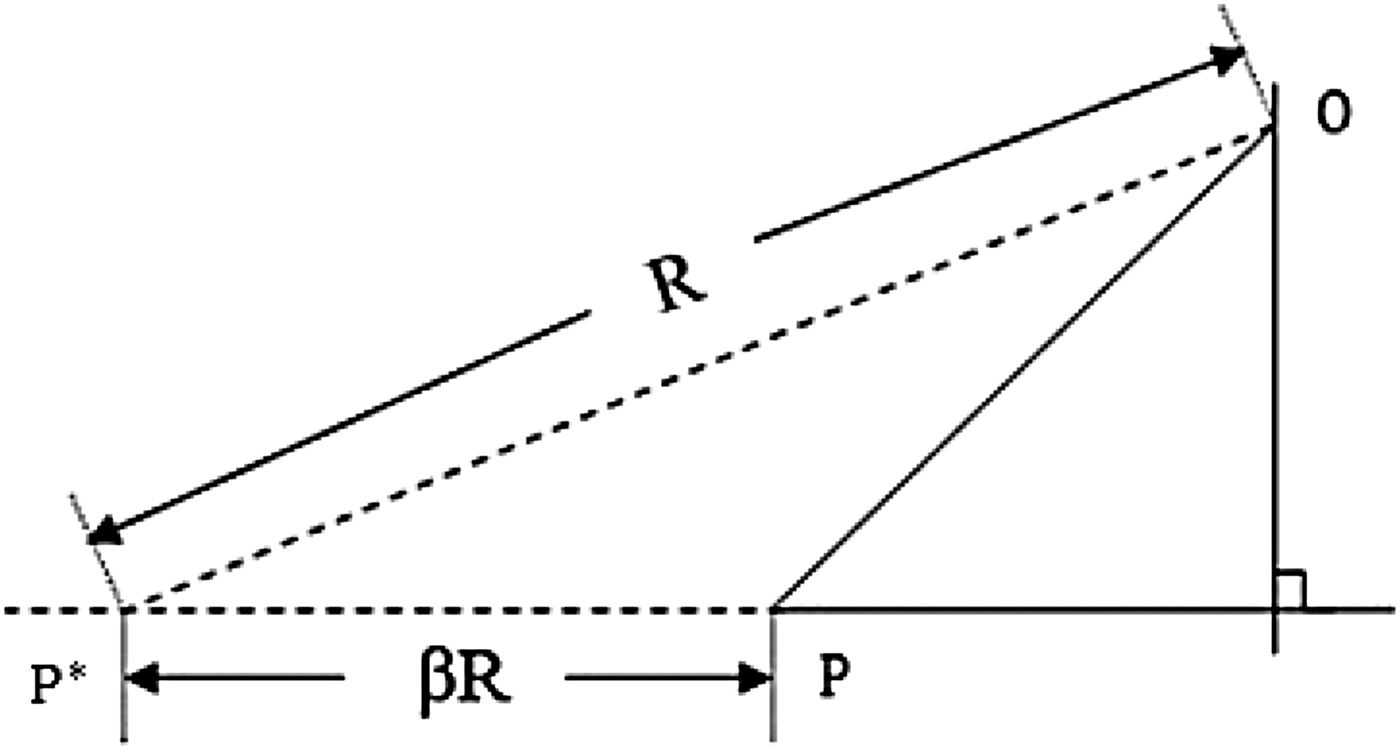
$$B_{\rm z}={\rm \beta} E_{\rm y}$$where (x′, y′) is the present position of the charge. As the whole system moves at a velocity very close to the light speed, the retarded effect should be accounted. Figure 2 shows the sketch map. The field at the observation point O is actually originated from the charge located at the retarded position P*(x″, y″), where x″ = x′ − βR, y″ = y′. Here R is the distance from (x″, y″) to the observation point. The subscript “ret” means that the quantity in the brackets is to be evaluated at a retarded time.
Fig. 2. Sketch map of relativistic retarded effect, P and P* are present and retarded position of the charge, respectively. O is the observation point which has a distance of R from P*.
When it comes to a charged particle beam with an arbitrary charge density distribution ρ(x, y), Eqs. (6) and (7) are integrated over the beam region to yield the total field,
$$E_{\rm y} \lpar {\rm \xi}\comma \; y\rpar = \;{\int\int}{{\rm d}{\rm \xi}^{\prime} dy^{\prime} }\left\{{{\rm \gamma} {\rm \rho} \left({\rm \xi}^{\prime}\comma \; y^{\prime} \right)\lpar y - y^{\prime}\rpar \over \left[\left(y - y^{\prime} \right)^2 + {\rm \gamma}^2 \left({\rm \xi} - {\rm \xi}^{\prime} \right)^2 \right]^{{3 \over 2}}} \right\}_{{\rm ret}}\comma$$
$$B_{\rm z} \lpar {\rm \xi}\comma \; y\rpar = {\rm \beta} E_{\rm y} \lpar {\rm \xi} \rpar\comma$$where ξ = x − βct. For a highly relativistic proton bunch β → 1, the space charge force of all the particles in the bunch is balanced by the attractive force due to the self-generated magnetic field. However, when it propagates in a plasma, background electrons will be sucked in and shift with a lower speed compared to the driver. The transverse electric field E y and magnetic field B z of these co-propagating electrons are not fully balanced. The general effect E y − B z tends to compensate the defocusing transverse wakefield E by in the “bubble” front. The composite transverse force is then
$$\eqalign{F &= eW_{\rm y} + eE_{\rm by} = e\lpar 1 - {\rm \beta}_{\rm e}\rpar {\int\int} {\rm d}{\rm \xi}^{\prime} dy^{\prime} \cr &\quad \times \left\{{{\rm \gamma} {\rm \rho} \left({\rm \xi}^{\prime}\comma \; y^{\prime} \right)\lpar y - y^{\prime}\rpar \over \left[\left(y - y^{\prime} \right)^2 + {\rm \gamma}^2 \left({\rm \xi} - {\rm \xi}^{\prime} \right)^2 \right]^{{3 \over 2}}} \right\}_{\rm ret} + \;eE_{\rm by}}$$Here W y = E y − B z, βe is the speed of co-propagating electrons normalized by the light speed. We have neglected the electric-magnetic field of the highly relativistic driver since they are almost counteracted (1 − βb ≈ 0), leaving only the contribution from co-propagating electrons. Transverse electric field in the “bubble” E by can be estimated as (Katsouleas, Reference Katsouleas1986)
$$E_{\rm by} \lpar {\rm \xi}\comma \; y\rpar = 2E_{{\rm x}0} \lpar y/k_{\rm p} a^2\rpar \sin \lpar k_{\rm p} {\rm \xi}\rpar \comma$$
where E x0 is the maximal longitudinal field amplitude on axis; y satisfies 
$\vert y\vert \leq \sqrt{a^2 - \lpar a+{\rm \xi}\rpar ^2}$, and a is the bubble radius. As ions are assumed to be immobile and the current on the edge of the “bubble” is quite small, additional magnetic field besides B z is neglected.
Analyzing Eq. (10) relies on the estimation of the co-propagating electrons density ρe(ξ′, y′) and speed βe. As illustrated in Figures 3a and 3b by PIC simulations, the background electron density peaks near the centre of the driver. The electron density has a symmetric Gaussian-like profile distribution, with the peak density even higher than the beam density.
Fig. 3. (Color online) Longitudinal (a) and transverse (b) density distributions of proton beam (red line) and background electrons (blue line) obtained from PIC simulation. Longitudinal distribution of velocity βe of the background electrons (c).
The density distribution shown in Figures 3a and 3b could be estimated as
$$n_{\rm i} \lpar {\rm \xi}\comma \; y\rpar = n_{{\rm i}\comma \max} \exp \left({{\rm \xi}^2 \over 2{\rm \sigma}_{\rm ix}^2} + {y^2 \over 2{\rm \sigma}_{\rm iy}^2} \right),$$where i = b or e represents the driver or the co-propagating electrons, respectively. Here σix and σiy are the corresponding longitudinal and transverse length. One can figure out from Figures 3a and 3b that n e,max ≈ 2.41n b,max, σex ≈ 0.32σbx, and σey ≈ 0.53σby. In addition, simulations based on different beam-plasma parameters indicate that as the background plasma density n 0 decreases, the proportion of the peak density of co-propagating electrons and the density of the driving proton beam n e,max/n b,max tends to increase, while the proportions of length σex/σbx and σey/σby tend to decrease (because the number of co-propagating electrons is limited).
Substitute Eqs. (11) and (12) to Eq. (10) we obtain the full transverse field as
$$\eqalign{F &= e \left\{{{\int\int}} \left[\left(1 - {\rm \beta}_{\rm e} \right){{\rm \gamma}_{\rm e} q{\rm n}_{\rm e}^{\ast} \left(y - y^{\prime} \right)\over \left[\left(y - y^{\prime} \right)^2 + {\rm \gamma}_{\rm e}^2 \left({\rm \xi} - {\rm \xi}^{\prime} \right)^2 \right]^{{3 \over 2}}} \right] \right. \cr &\quad \left. {\rm d}{\rm \xi}^{\prime} {\rm d}y^{\prime} + 2E_{{\rm x}0} \left({y \over k_{\rm p} a^2} \right)\sin \left(k_{\rm p} {\rm \xi} \right)\right\}.}$$
where q = −e is the charge of an electron, βe ≈ 0.8 according to Figure 3c, and 
$n_{\rm e}^{\ast} \lpar {\rm \xi}^{\prime}\comma \; y^{\prime}\rpar = n_{{\rm e}\comma \max} \exp [({\rm \xi}^{\prime} - \Delta )^2 /2{\rm \sigma}_{\rm ex}^2 + y^{\prime 2} /2{\rm \sigma} _{\rm ey}^2 ]$ is the retarded density distribution. The retarded length is Δ = βeR, where R satisfies following relation from Figure 2
$$\lpar 1 - {\rm \beta}_{\rm e}^2\rpar R^2 - 2 {\rm \beta}_{\rm e} \left({\rm \xi} - {\rm \xi}^{\prime} \right)R - [ \left({\rm \xi} - {\rm \xi}^{\prime} \right)^2 + \;\lpar y - y^{\prime} \rpar ^2\rsqb = 0 .$$Combining Eqs. (13) and (14), we obtain the numerical solution with the parameters shown in Table. 1, as presented in Figure 4a.
Fig. 4. (Color online) Total transverse field W(y) distributions obtained by numerical calculation (a) and PIC simulation (b). Transverse potential Ψ as a function of y at different longitudinal positions, ξ = 0.5 μm (blue curve), 0 μm (red curve), −0.8 μm (green curve), and −1.3 μm (black curve) from PIC simulation (c). (d) The on-axis longitudinal electronic field (blue solid), distribution of the beam protons (red dot), background electrons (black dot), and the longitudinal position (marked by corresponding colored dashed) where the potential wells are shown in (c).
In order to compare with our analytical results, the wakefield acceleration process is also simulated with the PIC code VORPAL. Our simulation results are presented in Figure 4b. One can see that Figure 4a shows a rough agreement with Figure 4b. The diffractive force of the “bubble” from simulation is slightly larger than expected. This is because Eq. (13) is mainly based on linear theory, where the result is smaller than that in nonlinear situation. This proposed model is relatively simple compared with simulation, but the focusing effect induced by the co-propagating electrons could still be seen in Figure 4a.
In Figure 4c the transverse potential distributions at four typical longitudinal positions are shown,
$$\Psi \left({\rm y} \right)= - \mathop{\int}\limits_{ - \infty}^{\rm y} W\left({\rm y} \right)\hbox{dy} .$$The chosen longitudinal positions are marked by dashed curves with corresponding colors in Figure 4d. Well-like structures appear at y = 0 for some positions. It is these exhibited potential wells that can confine the proton bunch.
Figure 4d illustrates the on-axis longitudinal electronic field and the distribution of protons and background electrons in the front of “bubble” after 4-cm propagation in the plasma. Comparing with the initial proton beam shape shown in Figure 1a, several important changes have appeared, as discussed below.The well depth at the head of the proton beam (ξ = 0.5 μm, the blue curve in Fig. 4c) is much smaller than that in the middle, leading to a weaker confinement. Some protons in this part escape from the well over a few centimeters. Nevertheless most protons in this region propagate stably. One can also find in Figure 4d that protons here are decelerated by the negative electric filed.
The potential well in the middle of the driving bunch (ξ = 0 μm, the red curve in Fig. 4c), where most of the co-propagating electrons located, is the deepest among all longitudinal positions. That is why the middle part of the bunch is well confined and narrower (transversely) than other parts as shown in Figure 4d.
At the bunch tail that is close to the co-propagating electrons, the transverse field is still large enough to focus the protons as long as the potential well exists (the peak value in the middle is below zero). The green curve (ξ = −0.8 μm) indicates the critical position of the self-confinement. The longitudinal electric field shown in Figure 4d suggests that the protons located between the red dashed and the green dashed, i.e., −0.8 μm ≤ ξ ≤ 0 μm are not only confined by the self-driving potential well but also efficiently accelerated forward by the positive electric field.
However, for a position far away from the co-propagating electrons (ξ = −1.3 μm, black curve in Fig. 4c), the well depth becomes smaller and its shape differs greatly from the one in the middle. The potential at y = 0 μm rises up and forms a barrier, expelling protons away from the propagating axis. Therefore, protons in this region tend to be confined in the two small potential wells aside rather than in the middle. All these lead to a “swallow-tail-like” structure in Figure 4d at the bunch tail.
Now we consider the self-confinement condition by placing a test proton in the potential well at transverse position y with a transverse momentum p y = γbv y. The proton won't escape from the potential well if its momentum is smaller than the critical value
$$\,p_{\rm y}^2 \leq p_{\rm c}^2 \equiv - {{\rm \gamma}_{\rm b} q \Psi \left({\rm y} \right)\over M}\comma$$where M is the mass of a proton. So, for a driving bunch with a transverse momentum spread Δp y, the proportion of protons self-confined in the potential well can be calculated as
$$P = \mathop{\int}\limits_{ - {\rm y}_{\rm c}}^{+{\rm y}_{\rm c}} \hbox{dy} \mathop{\int}\limits_{ - p_{\rm c}}^{\,p_{\rm c}} \hbox{f} \left({\rm y}\comma \; p_{\rm y} \right)\hbox{d} p_{\rm y}\comma$$
where f(y, p y) is the normalized density distribution over transverse coordinate y and momentum p y with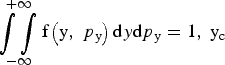 
$\mathop{\vint \vint}\limits_{ - \infty}^{+\infty} \hbox{f} \left({\rm y}\comma \; p_{\rm y} \right)\hbox{d}y \hbox{d}p_{\rm y} = 1, \ {\rm y}_{\rm c}$ is the width of the potential well. For the proton bunch in Table 1
$$\eqalign{\hbox{f}\left({\rm y}\comma \; {\rm } p_{\rm y} \right) &= {\rm F}\left({\rm y} \right){\rm G} \left(\,p_{\rm y} \right)= {1 \over {\rm \sigma}_{\rm y} \sqrt{2 {\rm \pi}}} \cr &\quad \times \exp \left({\hbox{y}^2 \over 2{\rm \sigma}_{\rm y}^2} \right) {1 \over \Delta p_{\rm y} \sqrt{2{\rm \pi}}} \exp \left({\,p_{\rm y}^2 \over 2 \Delta p_{\rm y}^2} \right)}$$We obtain P ≈ 1 and 52.12% for the longitudinal positions of ξ = −0.8 μm and −1.3 μm according to the simulation results, respectively, indicating that most protons can be confined.
As analyzed above, protons at the bunch tail experience both an accelerating field and a transverse focusing field. Therefore, these protons can be well confined and accelerated forward. To demonstrate the proposed scheme, a 2D PIC simulation is carried out over an acceleration length as long as one meter.
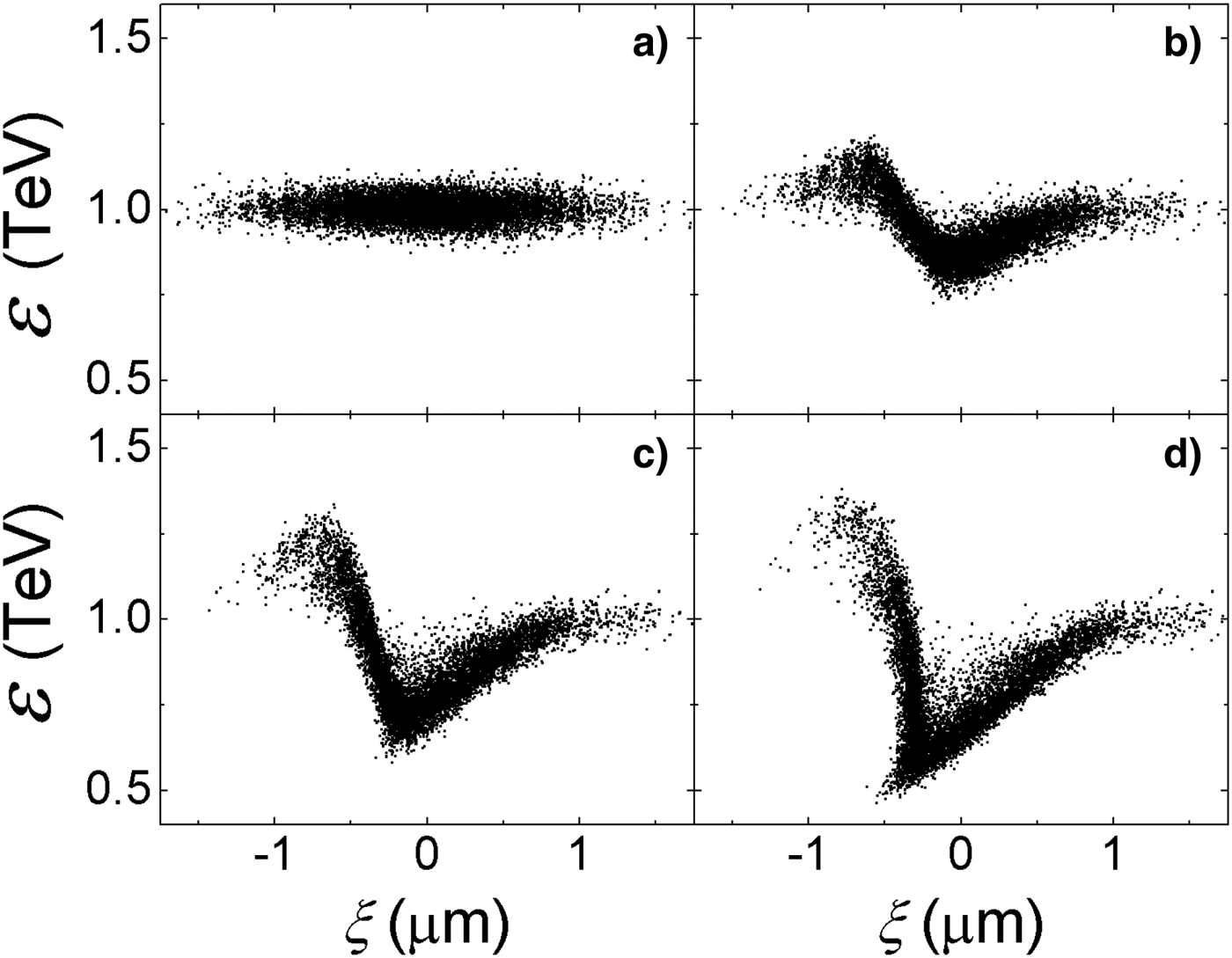
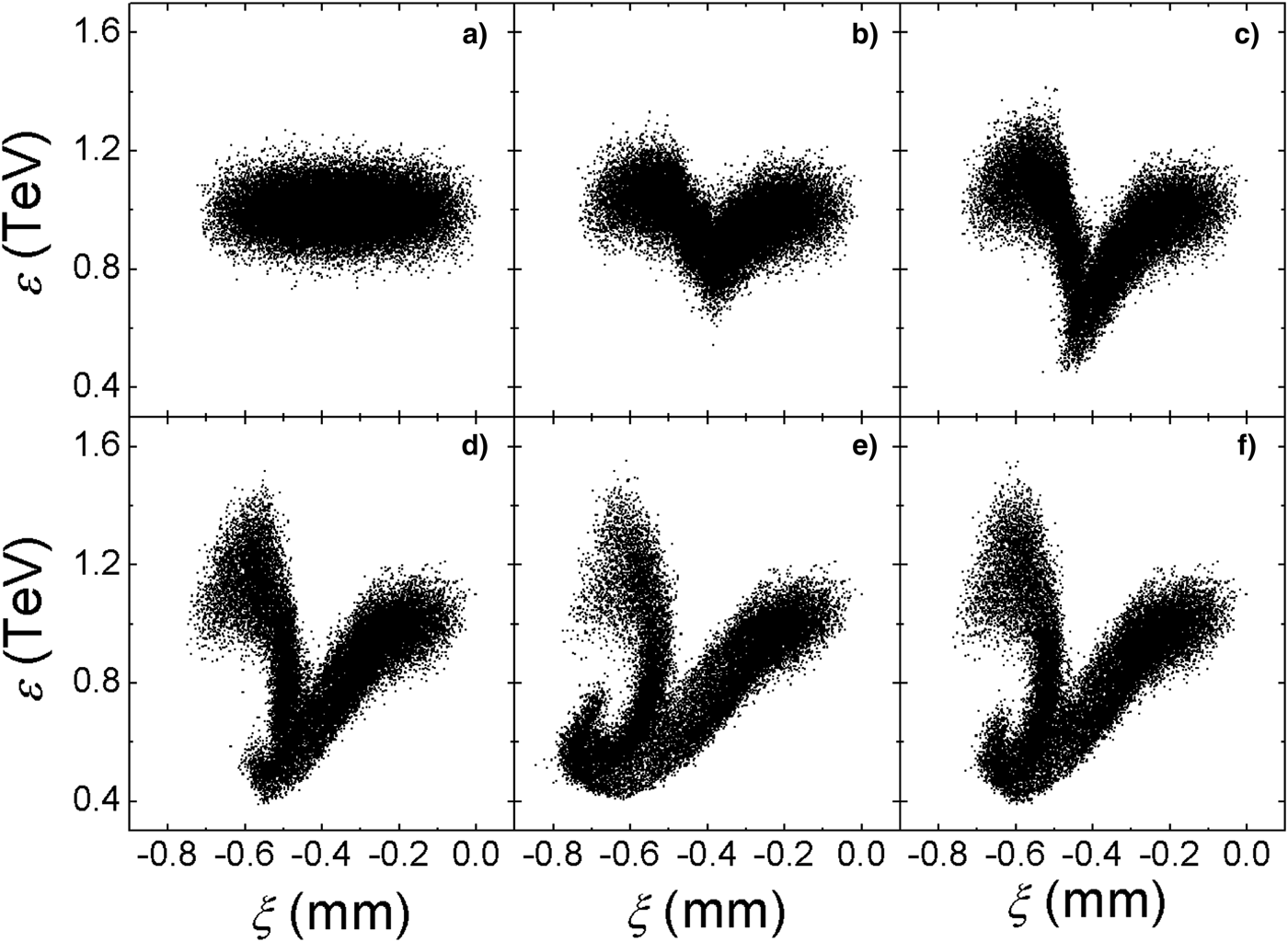
The evolution of the proton bunch propagating in plasma is shown in Figures 5. Snapshots of the particle phase space (energy versus relative location), are taken at acceleration distances of 0.4 cm, 33 cm, 66 cm, and 1 m. A clear energy transmission from the main body to the protons in the tail is seen. The initial energy of the proton beam is around 1 TeV. As the bunch propagates in the plasma, the main body loses significant amounts of energy, which is picked up by the protons in the beam tail. According to Figures 5c and 5d, one may find that at the later stage of acceleration, the energy gain by the bunch tail grows much slower than in the earlier stage due to the phase slippage effect. It is because the wakefield is “overloaded” by large amounts of protons which lose energy and fall into the accelerating phase. This “overloading” effect actually “pushes” the accelerating phase of the wake back.
Fig. 5. Phase space (energy versus relative position) of the proton bunch taken at propagating distances of (a) 0.4 cm, (b) 33 cm, (c) 66 cm, and (d) 1 m.
The final energy spectrum is compared to the initial one in Figure 6a. After being accelerated for 1 m, the maximal energy of the bunch achieves approximately 1.38 TeV, increasing by 25%. About 4% of the protons gain energy from the rest. The maximum energy as a function of the propagating distance is shown in Figure 6b, where it increases rapidly at the beginning, then much slower after about 80 cm as a result of the de-phasing effect.
Fig. 6. (Color online) (a) Energy spectra of the proton beam at the beginning (red zone) and the end (blue zone) of 1-m propagation in plasma. (b) Maximal energy of the protons in the tail of the bunch as a function of the propagating distance, The black dots are obtained from PIC simulation and red solid line is the fitted curve.
4. ACCELERATION OF A PROTON BUNCH WITH LOWER 6D PHASE SPACE DENSITY
According to the scaling relationship discussed in Section 2, if we decrease the background density by 100 times, and change the beam parameters listed in Table 1 according to the scaling we obtained in Section 2, the total number of particles contained in the beam is then approximately 1011, equaling to that in the LHC beams, while the beam density in 6d phase space d ∝ N/γ2σxɛσy2α2 is approximately 1000 times larger than the LHC beams. For these beam parameters, the whole beam can still be transversely self-confined by co-propagating electrons.
However, for a proton bunch with lower 6d phase space density (like those available in conventional accelerators), if one still keeps the match condition 
$k_{\rm p} {\rm \sigma}_{\rm x} = \sqrt{2}$, the space charge force is not sufficiently strong to pull the co-propagating electrons into the beam body, and the beam tail won't fall into the accelerating phase of the wakefield. The longitudinal length of the drive beam must be elongated to let an essential part of the beam fall into the accelerating phase. In this situation, the general field induced by the co-propagating electrons can compensate the transverse component of wakefield only in a small area close to the dense electron region. The “plasma lens” effect alone is not strong enough to confine all over the bunch, the head of the beam requires extra guide. We then employ quadrupole magnets with extremely strong field gradients to provide such external focusing field.
The quadrupoles make the beam-plasma interaction essentially three dimensional. However, the effect of quadrupoles can be modeled within the axisymmetric two-dimensional geometry by periodic radial pushes of varying sign given to beam particles (Kudryavtsev et al., Reference Kudryavtsev, Lotov and Skrinsky1998). For a sine-like varying field gradient, the time average force acting on the beam is (Lotov et al., 2010)
$$F_{\rm q} = - {S^2 L_{\rm q}^2 e^2 r \over 8{\rm \pi}^2 W_{\rm p}}.$$where S is the maximum magnetic field gradient, i.e., B = Sr, L q is the space period of the quadrupoles, and W p is the energy of the protons in the driving bunch. One should note that the focusing force of quadrupole magnets is much smaller than the transverse expelling force in the “bubble.” It is only large enough to guide the head of the proton driver, while the accelerated part is still self-confined as we discussed in Section 3.
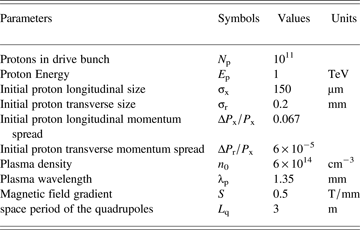
Here we adopt a proton beam with the same 6d phase space density as that in (Caldwell et al., Reference Caldwell, Lotov, Pukhov and Simon2009), but we have elongated the beam (by keeping the longitudinal phase space constant) and changed the radius (by keeping the emittance constant). The parameters are listed in Table 2.
Table 2. Parameters in the simulation
The simulation is performed with the computationally efficient quasi-static code LCODE to achieve acceleration over hundreds of meters. The proton beam density and excited on-axis longitudinal wakefield are shown in Figure 7. One can see the tail of the beam is located in the accelerating phase of the wake, thus the protons there could gain energy from the main body continuously.
Fig. 7. (Color online) The proton beam density (red curve) and on-axis longitudinal wakefield (blue curve).
As a comparison to Section 3, in Figures 8 and 9, we show the evolution of the proton phase space during propagation and final energy gain, respectively. Here ξ = 0 is set to be at the beam head.
Fig. 8. Phase space (energy versus relative position) of the proton bunch with lower 6d phase-space density taken at propagating distances of (a) 0 m, (b) 80 m, (c) 160 m, (d) 240 m, (e) 320 m, and (f) 400 m.
Fig. 9. (Color online) (a) Energy spectra of the proton beam at the beginning (red zone) and the after propagating for 320 m in the plasma (blue zone). (b) Maximal energy of the protons in the tail of the bunch as a function of the propagating distance, the black dots are obtained from simulation and red solid line is the fitted curve.
The snapshots of the particle phase space (energy versus relative location) in Figure 8 show a very similar acceleration process as that in Figure 5. A proton beam with initial energy 1 TeV drives a wakefield in a plasma, which continuously transforms energy from the main body to the protons in the tail. From the energy spectra shown in Figure 9a one can find approximately 4.6% of the protons (ɛ > 1.2 TeV) gain energy from the rest. The maximal energy of the bunch reaches 1.5 TeV, increased by 25% compared to the initial peak energy 1.2 TeV, which is very close to the case we discussed in Section 3. We also plot the maximal energy of the protons in the bunch tail versus the propagating distance in Figure 9b. Apparently one can see the energy gain saturates at approximately 320 m because of the phase slippage effect.
5. DISCUSSION
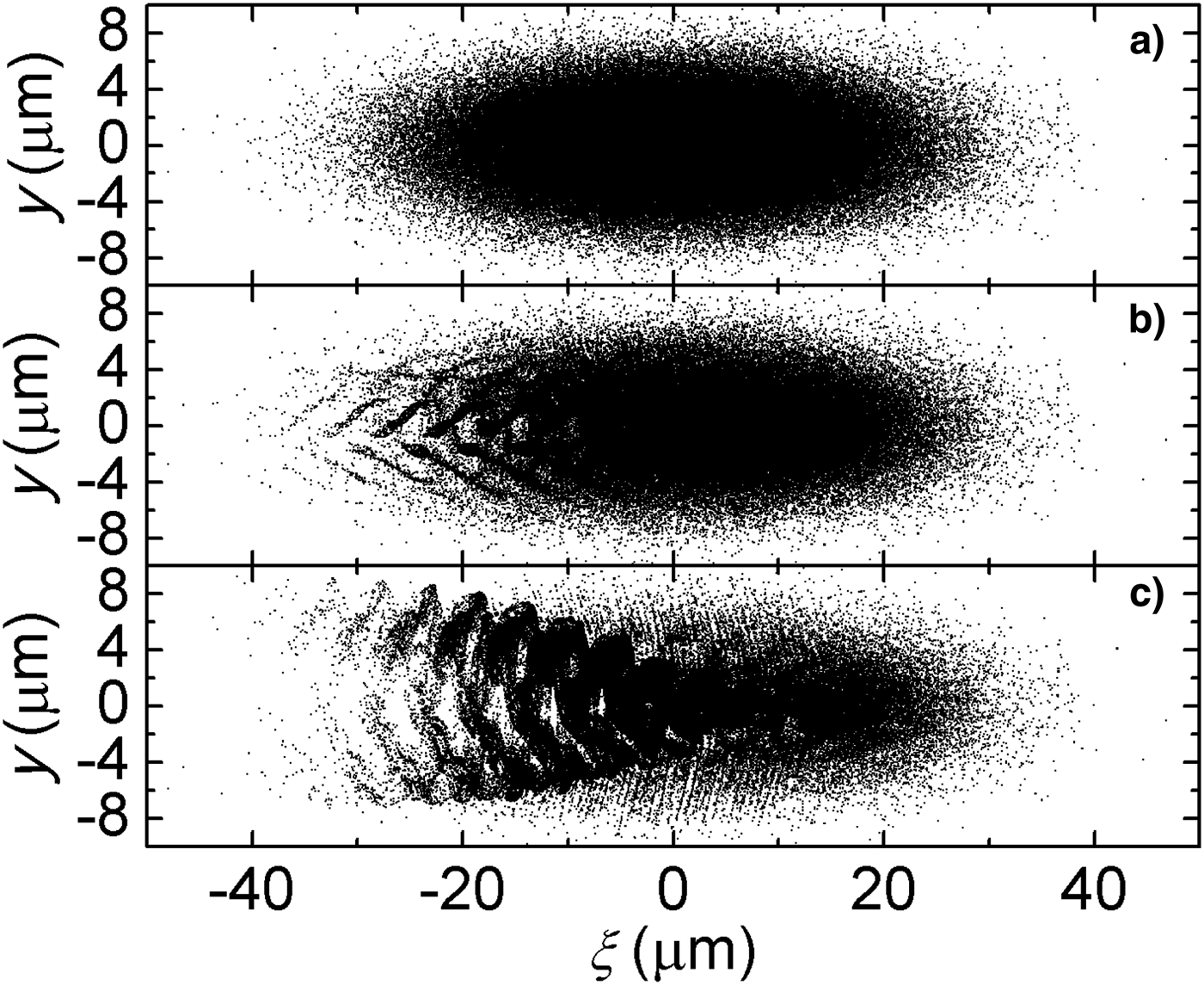
In the plasma-based accelerator, the driver's length should be comparable with the plasma wave length to generate a clean “bubble.” For a long proton beam, such as those available in present conventional radio frequency accelerators, the bunch length is generally beyond plasma wave length so that self-modulation will occur. The long relativistic proton bunch will be modulated at the plasma frequency (Kumar et al., Reference Kumar, Pukhov and Lotov2010; Caldwell et al., Reference Caldwell and Lotov2011) while it can still excite a large amplitude plasma wave. The physical picture of self-modulation instability is similar as in the SMLWFA (self-modulating laser wake field acceleration). When a long bunch of length L ≫ λp propagates in plasmas, it generates a wake within its body, which modulates the bunch in return, leading to a positive feedback. The plasma wave will experience unstable development and tends to modulate the whole beam into micro bunches with length L′ ≈ λp. These micro bunches then resonantly drive the plasma wake and achieve significant amplitude. A 2D PIC simulation is carried out to verify this effect by varying the proton beam length to k pσz = 28 (other parameters remain the same as in Table 1). The results are presented in Figure 10. We can see that the driving beam is divided into several micro bunches and forms a bunch chain, with longitudinal length of each bunch comparable to the plasma wavelength. After propagating for 4 cm the amplitude of plasma wakefield increases obviously (not shown here). Protons at the tail of each micro bunch tail could gain energy as we have discussed above. However, the bunch train will soon be destroyed by the transverse wakefield as illustrated in Figure 10c, which is harmful for stable acceleration. Several schemes have been proposed to suppress the instability at the micro-bunching stage, such as using a proper longitudinal inhomogeneity of the plasma density (Lotov, Reference Lotov2011). Further research is required to investigate this process. A more detailed discussion on self-modulation instability can be found (Kumar et al., Reference Kumar, Pukhov and Lotov2010).
Fig. 10. Proton density distribution at (a) 400 um, (b) 2 cm, (c) 4 cm. The proton beam is of length k pσz = 28.
Concerning the energy gain of the protons, in both Sections 3 and 4, the peak accelerating field times propagating distance is twice the value of the maximal energy gain of the protons in the bunch tail, i.e., only half of the expected peak value is picked up. This is because only protons located at positions where the plasma lens effect is large enough to compensate the transversely “bubble” field can be accelerated stably, so that only half-peaked acceleration gradient is experienced by these protons. Meanwhile, these protons are so close to the front edge of the “bubble” that they will lose phase soon. To take full advantage of the accelerating field, external injection together with a proton driver with hollow-shaped density distribution (Babu et al., Reference Babu, Goswami and Pandit2011) may be used as an alternative method. Since the beam density peaks on the edge, the transverse field excited by the driver tends to push positively charged particles located at y < σy/2 towards the beam axis, where σy is the transverse size of the driver. This kind of transverse field can focus the witnessing protons injected near the beam axis, so that one can inject a witnessing beam at a position where the accelerating field is larger and it experiences a longer acceleration. Detailed research on this acceleration scheme is under consideration.
6. SUMMARY
In summary, we have proposed that by using a proton beam to drive a plasma wakefield, protons at the tail of the beam can be transversely self-confined and accelerated forward. It is demonstrated that in the front of the “bubble,” the transverse field of the co-propagating electrons is large enough to compensate the defocusing effect and focuses the protons in the tail of the bunch. Analysis on the transverse potential well illustrates the self-confinement condition and the evolvement of the beam shape. Two-dimensional simulations on two beams with different 6d phase space densities are performed. In both cases, the peak energy of the self-confined proton beam increases by 25%. This scheme indicates that proton beams available in conventional radio frequency accelerators may gain considerable energy by propagating in an under-dense plasma. We also discussed the possibility of using a long proton beam to resonantly drive large amplitude plasma wake due to the self-modulation effect, and a scheme of using external injection together with a proton driver with a hollow-shaped density distribution to take the full advantage of accelerating field.
ACKNOWLEDGMENTS
This work has been supported by the Ministry of Science and Technology (2011CB808104, 2011DFA11300), National Natural Science Foundation of China (Projects No. 61008010, No. 11125526, No. 11127901, No. 10834008, and No. 60921004).
