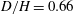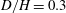1. Introduction
The motion of a pendulum driven by gravity has been investigated for centuries, due to its nature as paradigm for many problems in physics (oscillators, resonances, dissipative systems, etc.). Recently some attention has been devoted to cases where the pendulum interacts with a surrounding fluid. For instance, Bolster, Hershberger & Donnelly (Reference Bolster, Hershberger and Donnelly2010) have studied the large-amplitude oscillation of a spherical pendulum immersed in a fluid at rest, quantifying the additional dissipative mechanisms due to vortex ring shedding.
More generally, flow-induced oscillations of slender structures facing a flow are of interest in many domains of engineering, such as the design of tubular structures of offshore platforms, heat exchangers or chemical reactors (see e.g. Williamson & Govardhan (Reference Williamson and Govardhan2004) and the references therein). The paradigm for vortex-induced vibrations (VIV) is an elastically mounted cylinder restrained to move transverse to the incoming flow. However, there are several studies concerning a tethered buoyant two-dimensional (2D) circular cylinder or a sphere facing a uniform transverse flow (see e.g. Ryan et al. Reference Ryan, Pregnalato, Thompson and Hourigan2004; Govardhan & Williamson Reference Govardhan and Williamson2005, etc.).
Combining these two paradigms, the physical situation of a gravitational pendulum facing a transverse or longitudinal flow have been considered recently.
Bandi et al. (Reference Bandi, Concha, Wood and Mahadevan2013) have studied an annular ring that is suspended by a string and immersed in a incoming parallel quasi-2D fluid represented by a gravity-driven soap film tunnel. They observed that above a critical flow speed, the pendulum starts to oscillate, due to the vortex shedding wake instability.
Obligado, Puy & Bourgoin (Reference Obligado, Puy and Bourgoin2013) focused on the characterization of the equilibrium of a simple pendulum made of a circular flat plate facing a transverse mean stream. Despite its apparent simplicity, the system revealed an unexpected richness including bistability and hysteretic behaviour of the pendulum as the flow velocity is cycled up and down.
In a recent study, Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011) focused on an experimental and numerical description of the oscillations of a tethered circular cylinder in a strongly confined (ratio of cylinder diameter to cell height,
![]() $D/H=0.66$
) Hele-Shaw cell geometry (see figure 1
a). This configuration is of particular interest for applications such as the enhancement of mixing or heat exchange in microfluidic circuits (see Meis et al.
Reference Meis, Varas, Velázquez and Vega2010) or the design of energy-harvesting devices on a chip (see Sanchez-Sanz, Fernandez & Velazquez Reference Sanchez-Sanz, Fernandez and Velazquez2009). Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011) observed that, due to confinement, the cylinder starts to oscillate at a Reynolds number
$D/H=0.66$
) Hele-Shaw cell geometry (see figure 1
a). This configuration is of particular interest for applications such as the enhancement of mixing or heat exchange in microfluidic circuits (see Meis et al.
Reference Meis, Varas, Velázquez and Vega2010) or the design of energy-harvesting devices on a chip (see Sanchez-Sanz, Fernandez & Velazquez Reference Sanchez-Sanz, Fernandez and Velazquez2009). Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011) observed that, due to confinement, the cylinder starts to oscillate at a Reynolds number
![]() $\mathit{Re}\simeq 20$
, which is much lower than the classical vortex-shedding one (
$\mathit{Re}\simeq 20$
, which is much lower than the classical vortex-shedding one (
![]() $\mathit{Re}_{\mathit{VS}}\simeq 110$
for the considered geometry). They called this new regime confined-induced vibration (CIV), which differs significantly from VIV induced by vortex shedding at the rear of the cylinder. In addition to the value of the critical Reynolds number, the differences regard both the frequencies and the amplitude of the oscillations. Finally, for density ratios above a critical value (
$\mathit{Re}_{\mathit{VS}}\simeq 110$
for the considered geometry). They called this new regime confined-induced vibration (CIV), which differs significantly from VIV induced by vortex shedding at the rear of the cylinder. In addition to the value of the critical Reynolds number, the differences regard both the frequencies and the amplitude of the oscillations. Finally, for density ratios above a critical value (
![]() ${\it\alpha}>4$
), an oscillation-free stable regime exists between the CIV prevailing at low
${\it\alpha}>4$
), an oscillation-free stable regime exists between the CIV prevailing at low
![]() $\mathit{Re}$
and the VIV active at higher
$\mathit{Re}$
and the VIV active at higher
![]() $\mathit{Re}$
.
$\mathit{Re}$
.

Figure 1. Tethered cylinder in a vertical channel (a). Flow configuration with frames of reference for the 2D pendulum (b) (not in scale,
![]() $D/l_{s}\ll 1$
).
$D/l_{s}\ll 1$
).
In this study we focus on the same flow configuration studied in Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011). The geometry and the addressed problem are described in § 2. We characterize the stability properties of the confined 2D pendulum by means of a global stability analysis of the fluid structure problem. In § 4 it will be shown that the linear analysis is able to capture the main flow features described by Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011). We consider also a different confinement (
![]() $D/H=0.3$
) in § 5, where a new static steady instability (confinement-induced divergence (CID)) is discovered. In addition, in order to investigate the physical mechanisms involved in these instabilities, we propose a quasi-static (QS) model which is able to recover the different dynamics behaviour, as shown in § 6.
$D/H=0.3$
) in § 5, where a new static steady instability (confinement-induced divergence (CID)) is discovered. In addition, in order to investigate the physical mechanisms involved in these instabilities, we propose a quasi-static (QS) model which is able to recover the different dynamics behaviour, as shown in § 6.
2. Problem description and methodology
2.1. Geometry and equations of motion
We consider a circular cylinder of diameter
![]() $D$
and width
$D$
and width
![]() $W$
, held by strings and immersed in a fluid flowing in a vertical channel of height
$W$
, held by strings and immersed in a fluid flowing in a vertical channel of height
![]() $H$
, as showed in figure 1(a). The fully developed velocity profile in a channel with a rectangular cross-section can be expressed analytically in terms of a converging infinite series (see Happel & Brenner (Reference Happel and Brenner1983) for details) where the Poiseuille solution is modified in order to enforce the no slip condition at the lateral walls (
$H$
, as showed in figure 1(a). The fully developed velocity profile in a channel with a rectangular cross-section can be expressed analytically in terms of a converging infinite series (see Happel & Brenner (Reference Happel and Brenner1983) for details) where the Poiseuille solution is modified in order to enforce the no slip condition at the lateral walls (
![]() $z=\pm W/2$
). However, when the channel aspect ratio
$z=\pm W/2$
). However, when the channel aspect ratio
![]() $W/H$
increases, the part of the section where the velocity profile differs from the 2D Poiseuille becomes smaller and the flow can be treated as 2D. In the case studied by Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011)
$W/H$
increases, the part of the section where the velocity profile differs from the 2D Poiseuille becomes smaller and the flow can be treated as 2D. In the case studied by Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011)
![]() $W/H$
was approximately 18, therefore it was possible to neglect the transverse direction
$W/H$
was approximately 18, therefore it was possible to neglect the transverse direction
![]() $z$
and to study the 2D problem depicted in figure 1(b).
$z$
and to study the 2D problem depicted in figure 1(b).
The pendulum-like motion of the 2D cylinder is governed by the following equation:
where
![]() ${\it\rho}_{c}$
is the body density per unit length, while
${\it\rho}_{c}$
is the body density per unit length, while
![]() $F_{x}$
and
$F_{x}$
and
![]() $F_{y}$
are respectively the
$F_{y}$
are respectively the
![]() $x$
-component and
$x$
-component and
![]() $y$
-component of the force induced by the fluid. The cylinder displacement
$y$
-component of the force induced by the fluid. The cylinder displacement
![]() $(X_{c},Y_{c})$
can be written as
$(X_{c},Y_{c})$
can be written as
The cylinder diameter
![]() $D$
and the maximum velocity of the Poiseuille profile
$D$
and the maximum velocity of the Poiseuille profile
![]() $U_{m}$
are used as length scales and reference velocity. The problem is completely characterized by the following non-dimensionless parameters:
$U_{m}$
are used as length scales and reference velocity. The problem is completely characterized by the following non-dimensionless parameters:
The first parameter is the Reynolds number, based on the cylinder diameter
![]() $D$
and the velocity
$D$
and the velocity
![]() $U_{m}$
. The parameter
$U_{m}$
. The parameter
![]() ${\it\alpha}$
is the density ratio between the cylinder and the surrounding fluid, while
${\it\alpha}$
is the density ratio between the cylinder and the surrounding fluid, while
![]() ${\it\beta}$
characterizes the blockage of the cylinder. The Froude number
${\it\beta}$
characterizes the blockage of the cylinder. The Froude number
![]() $\mathit{Fr}$
characterizes the ratio between body’s inertia and gravitational forces. In this study the Froude number
$\mathit{Fr}$
characterizes the ratio between body’s inertia and gravitational forces. In this study the Froude number
![]() $\mathit{Fr}$
and the length of the string
$\mathit{Fr}$
and the length of the string
![]() $L_{s}$
will not be varied:
$L_{s}$
will not be varied:
![]() $L_{s}\simeq 45$
and
$L_{s}\simeq 45$
and
![]() $\mathit{Fr}=({\it\nu}/(D^{3/2}g^{1/2}))\mathit{Re}\simeq 1.4\mathit{Re}$
. Let us introduce the state variable
$\mathit{Fr}=({\it\nu}/(D^{3/2}g^{1/2}))\mathit{Re}\simeq 1.4\mathit{Re}$
. Let us introduce the state variable
![]() $Q(x,y,t)=[\boldsymbol{U}(x,y,t),P(x,y,t),V_{c}(t),Y_{c}(t)]$
, where
$Q(x,y,t)=[\boldsymbol{U}(x,y,t),P(x,y,t),V_{c}(t),Y_{c}(t)]$
, where
![]() $\boldsymbol{U}=(U_{x},U_{y})$
and
$\boldsymbol{U}=(U_{x},U_{y})$
and
![]() $P$
are respectively the flow velocity and pressure, while
$P$
are respectively the flow velocity and pressure, while
![]() $V_{c}$
and
$V_{c}$
and
![]() $Y_{c}$
are the cylinder transversal velocity and displacement. In the limit of small oscillations (
$Y_{c}$
are the cylinder transversal velocity and displacement. In the limit of small oscillations (
![]() ${\it\theta}\ll 1$
), the flow in the channel and the cylinder motion are governed by the following equations:
${\it\theta}\ll 1$
), the flow in the channel and the cylinder motion are governed by the following equations:
2.2. Stability analysis
In order to perform a linear stability analysis, the state vector
![]() $\boldsymbol{Q}$
is expanded as
$\boldsymbol{Q}$
is expanded as
Here, the vector
![]() $Q_{\boldsymbol{b}}=[\boldsymbol{U}_{\boldsymbol{b}},P_{b},0,0]$
corresponds to the steady symmetric base flow where the cylinder is placed along the centreline of the channel, whereas
$Q_{\boldsymbol{b}}=[\boldsymbol{U}_{\boldsymbol{b}},P_{b},0,0]$
corresponds to the steady symmetric base flow where the cylinder is placed along the centreline of the channel, whereas
![]() $\hat{\boldsymbol{q}}=[\hat{\boldsymbol{u}},\hat{p},\hat{v}_{c},\hat{y_{c}}]$
is the complex global mode, associated with the eigenvalue
$\hat{\boldsymbol{q}}=[\hat{\boldsymbol{u}},\hat{p},\hat{v}_{c},\hat{y_{c}}]$
is the complex global mode, associated with the eigenvalue
![]() ${\it\sigma}={\it\lambda}+\text{i}{\it\omega}$
. By introducing the flow decomposition (2.6) into (2.4) and linearizing, we obtain two subset of equations which determine the base flow and the perturbation.
${\it\sigma}={\it\lambda}+\text{i}{\it\omega}$
. By introducing the flow decomposition (2.6) into (2.4) and linearizing, we obtain two subset of equations which determine the base flow and the perturbation.
The base flow
![]() $(\boldsymbol{U}_{\boldsymbol{b}},P_{b})$
is the solution of the steady Navier–Stokes equations:
$(\boldsymbol{U}_{\boldsymbol{b}},P_{b})$
is the solution of the steady Navier–Stokes equations:
The perturbation
![]() $\hat{\boldsymbol{q}}$
is governed by the following equations:
$\hat{\boldsymbol{q}}$
is governed by the following equations:
The global modes are normalized imposing that the cylinder vertical velocity is equal to one,
![]() $\hat{v}_{c}=1$
.
$\hat{v}_{c}=1$
.
2.3. Numerical method
The two-dimensional steady Navier–Stokes equations (2.7) and the eigenvalue problem (2.8) are discretized in space by a finite-element method, using P2–P1 Taylor–Hood elements: six-node quadratic triangular elements with quadratic interpolation for velocities (P2) and three-node linear triangular elements for pressure (P1) (see Taylor & Hood Reference Taylor and Hood1973, for details). The meshes as well as the discrete matrices resulting from Galerkin finite-element method are generated with the software FreeFem
![]() $++$
(see Hecht Reference Hecht2012).
$++$
(see Hecht Reference Hecht2012).
The steady nonlinear base-flow equations are solved via a Newton–Raphson iterative method and the solution of the related linear systems is carried out via UMFPACK, a sparse direct LU solver.
The eigenvalue problem arising from the spatial discretization of problem (2.8) is solved by using an Arnoldi method with a shift-invert strategy (see Lehoucq, Sorensen & Yang Reference Lehoucq, Sorensen and Yang1998) in the Matlab software (www.mathworks.com). This computational approach, involving the software FreeFem
![]() $++$
, has been used extensively for global stability studies of two-dimensional flows, (see e.g. Meliga, Sipp & Chomaz Reference Meliga, Sipp and Chomaz2010; Assemat, Fabre & Magnaudet Reference Assemat, Fabre and Magnaudet2011; Fani, Camarri & Salvetti Reference Fani, Camarri and Salvetti2012).
$++$
, has been used extensively for global stability studies of two-dimensional flows, (see e.g. Meliga, Sipp & Chomaz Reference Meliga, Sipp and Chomaz2010; Assemat, Fabre & Magnaudet Reference Assemat, Fabre and Magnaudet2011; Fani, Camarri & Salvetti Reference Fani, Camarri and Salvetti2012).
3. Validation
The numerical tools have been validated by studying the flow around a cylinder in two different cases. In the first the flow is confined, while in the other case the cylinder is mounted elastically.
3.1. The effect of confinement on the vortex-shedding instability
The effect of confinement on the vortex shedding in the wake of a two-dimensional cylinder placed inside a channel has been described in the literature, (see e.g. Chen, Pritchard & Tavener Reference Chen, Pritchard and Tavener1995; Sahin & Owens Reference Sahin and Owens2004; Camarri & Giannetti Reference Camarri and Giannetti2007; Biancofiore, Gallaire & Pasquetti Reference Biancofiore, Gallaire and Pasquetti2011). Constraint of the confining walls has a stabilizing effect, due to the interaction between the cylinder wake and the wall boundary-layer vorticity. Figure 2(a,b) show the critical Reynold number
![]() $\mathit{Re}_{cr}$
and the Strouhal number
$\mathit{Re}_{cr}$
and the Strouhal number
![]() $\mathit{St}$
as a function of the confinement ratio
$\mathit{St}$
as a function of the confinement ratio
![]() ${\it\beta}$
, reporting data from Sahin & Owens (Reference Sahin and Owens2004). As the confinement is increased, the critical Reynolds number becomes larger, reaching a maximum value at
${\it\beta}$
, reporting data from Sahin & Owens (Reference Sahin and Owens2004). As the confinement is increased, the critical Reynolds number becomes larger, reaching a maximum value at
![]() ${\it\beta}\simeq 0.5$
, while it becomes smaller for further increase of
${\it\beta}\simeq 0.5$
, while it becomes smaller for further increase of
![]() ${\it\beta}$
. Instead, the Strouhal number is an increasing function of the confinement ratio in the considered range. As a validation of the numerical tools, results obtained for the considered confinement ratios, namely
${\it\beta}$
. Instead, the Strouhal number is an increasing function of the confinement ratio in the considered range. As a validation of the numerical tools, results obtained for the considered confinement ratios, namely
![]() ${\it\beta}=0.66,0.3$
, are plotted in figure 2 as filled circles, showing excellent agreement with the literature.
${\it\beta}=0.66,0.3$
, are plotted in figure 2 as filled circles, showing excellent agreement with the literature.

Figure 2. Critical Reynolds (a) and Strouhal (b) numbers as a function of confinement
![]() ${\it\beta}$
for vortex-shedding instability on a fixed confined cylinder. Data from Sahin & Owens (Reference Sahin and Owens2004) and the current work.
${\it\beta}$
for vortex-shedding instability on a fixed confined cylinder. Data from Sahin & Owens (Reference Sahin and Owens2004) and the current work.
3.2. Stability analysis of VIV on a spring-mounted cylinder
The VIV of a 2D spring mounted cylinder invested by an uniform flow has been extensively studied. Most of the works in the literature focused on Reynolds numbers larger than the critical one for the fixed case (
![]() $\mathit{Re}_{c}^{0}$
).
$\mathit{Re}_{c}^{0}$
).
Instead, Cossu & Morino (Reference Cossu and Morino2000) studied the VIV vibration of a cylinder by means of global stability analysis. They found that when the cylinder is light (low values of density ratio
![]() ${\it\alpha}$
), the critical Reynolds number is less than half of
${\it\alpha}$
), the critical Reynolds number is less than half of
![]() $\mathit{Re}_{c}^{0}$
.
$\mathit{Re}_{c}^{0}$
.
Mittal & Singh (Reference Mittal and Singh2005) studied the flow around a cylinder with a low density ratio (
![]() ${\it\alpha}\approx 5$
) and with a null structural damping coefficient. The cylinder is allowed to vibrate in the transverse and in-line directions. They carried out numerical simulations and global stability analysis of the fluid–structure problem and they found that the cylinder starts to oscillate at a Reynolds number beyond
${\it\alpha}\approx 5$
) and with a null structural damping coefficient. The cylinder is allowed to vibrate in the transverse and in-line directions. They carried out numerical simulations and global stability analysis of the fluid–structure problem and they found that the cylinder starts to oscillate at a Reynolds number beyond
![]() $\mathit{Re}=21.7$
with a Strouhal number
$\mathit{Re}=21.7$
with a Strouhal number
![]() $\mathit{St}=0.12$
.
$\mathit{St}=0.12$
.
In order to validate the structural part of the tools for stability analysis, we repeated the same analysis of Mittal & Singh (Reference Mittal and Singh2005). We found a global mode slightly unstable (
![]() ${\it\lambda}=2\times 10^{-3}$
) at
${\it\lambda}=2\times 10^{-3}$
) at
![]() $\mathit{Re}=21.5$
, with an associated Strouhal number equal to 0.121, showing an excellent agreement with the results of Mittal & Singh (Reference Mittal and Singh2005).
$\mathit{Re}=21.5$
, with an associated Strouhal number equal to 0.121, showing an excellent agreement with the results of Mittal & Singh (Reference Mittal and Singh2005).
4. Strongly confined pendulum
 $({\it\beta}=0.66)$
$({\it\beta}=0.66)$
We first studied the same flow configuration as in Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011). The considered computational domain, sketched in figure 1(b), is characterized by
![]() $L_{i}=7.5$
,
$L_{i}=7.5$
,
![]() $L_{o}=25$
and
$L_{o}=25$
and
![]() ${\it\beta}=0.66$
, with a mesh composed of
${\it\beta}=0.66$
, with a mesh composed of
![]() $1\times 10^{4}$
nodes and
$1\times 10^{4}$
nodes and
![]() $1.7\times 10^{4}$
triangles. Grid convergence tests, not shown here for the sake of brevity, have been carried out, both on grid refinement and on the length of the computational domain. The convergence was estimated through monitoring the length of the recirculation bubble of the base flow and the value of the leading eigenvalue.
$1.7\times 10^{4}$
triangles. Grid convergence tests, not shown here for the sake of brevity, have been carried out, both on grid refinement and on the length of the computational domain. The convergence was estimated through monitoring the length of the recirculation bubble of the base flow and the value of the leading eigenvalue.
Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011) observed the onset of a new instability, driven by the confinement, at a Reynolds number equal approximately to 20. In figure 3 the base-flow for the stability analysis at
![]() $\mathit{Re}=20$
is depicted through streamlines superimposed on isocontours of the vorticity field. Due to confinement, the recirculation regions behind the cylinder are smaller than those observed in the unbounded case, a phenomena also reported by Sahin & Owens (Reference Sahin and Owens2004).
$\mathit{Re}=20$
is depicted through streamlines superimposed on isocontours of the vorticity field. Due to confinement, the recirculation regions behind the cylinder are smaller than those observed in the unbounded case, a phenomena also reported by Sahin & Owens (Reference Sahin and Owens2004).

Figure 3. Base flow for a confined cylinder (
![]() $D/H=0.66$
) at
$D/H=0.66$
) at
![]() $\mathit{Re}=20$
, depicted by streamlines (black lines) and vorticity field.
$\mathit{Re}=20$
, depicted by streamlines (black lines) and vorticity field.
The results of the linear stability analysis are concisely presented in figure 4, where a stability map of the behaviour of the cylinder as a function of Reynolds number and of body to fluid mass ratio is plotted. The symmetric flow with the cylinder held along the centreline of the channel becomes linearly unstable at a critical Reynolds number (
![]() $\mathit{Re}_{CIV}$
) which slowly varies from 15 to 17.5 as
$\mathit{Re}_{CIV}$
) which slowly varies from 15 to 17.5 as
![]() ${\it\alpha}$
decreases. For low
${\it\alpha}$
decreases. For low
![]() ${\it\alpha}$
the flow remains unstable for all of the considered values of the Reynolds numbers, while for
${\it\alpha}$
the flow remains unstable for all of the considered values of the Reynolds numbers, while for
![]() ${\it\alpha}$
greater than a critical value (
${\it\alpha}$
greater than a critical value (
![]() $3<{\it\alpha}_{c}<4$
), there is a range of Reynolds numbers where the symmetric steady flow is linearly stable. For larger Reynolds numbers the global mode frequency furthermore approaches the value of the vortex shedding on the fixed confined cylinder and the flow regime can be associated with a VIV. We indicate the cases where this frequency discrepancy is smaller than 3 % as filled squares in figure 4. This phenomenon will be analysed more in detail in the following sections.
$3<{\it\alpha}_{c}<4$
), there is a range of Reynolds numbers where the symmetric steady flow is linearly stable. For larger Reynolds numbers the global mode frequency furthermore approaches the value of the vortex shedding on the fixed confined cylinder and the flow regime can be associated with a VIV. We indicate the cases where this frequency discrepancy is smaller than 3 % as filled squares in figure 4. This phenomenon will be analysed more in detail in the following sections.

Figure 4. Stability map of the flow around the tethered cylinder for various Reynolds number
![]() $\mathit{Re}$
and body to fluid mass ratio
$\mathit{Re}$
and body to fluid mass ratio
![]() ${\it\alpha}$
. The filled symbols correspond to linearly unstable conditions. In particular, ▪ symbols denote a VIV regime. Here
${\it\alpha}$
. The filled symbols correspond to linearly unstable conditions. In particular, ▪ symbols denote a VIV regime. Here
![]() ${\it\beta}=0.66$
.
${\it\beta}=0.66$
.
Note that this scenario is in agreement with that presented in Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011), at least qualitatively (see figure 14 in Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011) for comparison). Discrepancies occur at Reynolds numbers far from the critical one for the CIV (
![]() $\mathit{Re}_{CIV}$
), where nonlinearities, neglected in the current work, can have an important influence in the flow behaviour.
$\mathit{Re}_{CIV}$
), where nonlinearities, neglected in the current work, can have an important influence in the flow behaviour.
4.1. Heavy pendulum
 $({\it\alpha}=15)$
$({\it\alpha}=15)$
Figure 5(a,b) show respectively the growth rate and the Strouhal number of the leading eigenvalues as a function of Reynolds number at a density ratio
![]() ${\it\alpha}=15$
. Two different eigenvalue branches are observed, the first being unstable for
${\it\alpha}=15$
. Two different eigenvalue branches are observed, the first being unstable for
![]() $15\leqslant \mathit{Re}\leqslant 40$
, which is compatible with the CIV regime observed in Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011), while the second one becomes unstable for a Reynolds number larger than 110.
$15\leqslant \mathit{Re}\leqslant 40$
, which is compatible with the CIV regime observed in Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011), while the second one becomes unstable for a Reynolds number larger than 110.

Figure 5. Leading eigenvalues at
![]() ${\it\alpha}=15$
: (a) growth rate
${\it\alpha}=15$
: (a) growth rate
![]() ${\it\lambda}$
and (b) Strouhal number
${\it\lambda}$
and (b) Strouhal number
![]() $\mathit{St}$
as a function of Reynolds number
$\mathit{St}$
as a function of Reynolds number
![]() $\mathit{Re}$
. (○) CIV mode,
$\mathit{Re}$
. (○) CIV mode,
![]() $\Box$
VIV mode and ● Von Kármán mode for fixed cylinder. (c,d) Streamwise velocity component
$\Box$
VIV mode and ● Von Kármán mode for fixed cylinder. (c,d) Streamwise velocity component
![]() $\hat{u} _{x}$
of the corresponding global modes. Here
$\hat{u} _{x}$
of the corresponding global modes. Here
![]() ${\it\beta}=0.66$
.
${\it\beta}=0.66$
.
The global mode computed at
![]() $\mathit{Re}=15$
, corresponding to the CIV branch, is depicted in figure 5(c), where the streamwise velocity component of the perturbation
$\mathit{Re}=15$
, corresponding to the CIV branch, is depicted in figure 5(c), where the streamwise velocity component of the perturbation
![]() $\hat{u} _{x}$
is plotted. The streamwise velocity is antisymmetric with respect to the channel centreline, reaching its maximum value between the cylinder and the channel walls. Keeping in mind that the global mode was normalized imposing
$\hat{u} _{x}$
is plotted. The streamwise velocity is antisymmetric with respect to the channel centreline, reaching its maximum value between the cylinder and the channel walls. Keeping in mind that the global mode was normalized imposing
![]() $\hat{v}_{c}=1$
, having values of order
$\hat{v}_{c}=1$
, having values of order
![]() $O(1)$
for the global mode flow velocities means that the body motion and the structure of the wake play an equal role in the mode dynamics.
$O(1)$
for the global mode flow velocities means that the body motion and the structure of the wake play an equal role in the mode dynamics.
Figure 5 also shows that the second branch is related to the VIV regime. Indeed, as shown in figure 5(b), the Strouhal number values for the VIV branch and the classical vortex shedding case are in excellent agreement (see § 3.1). The shape of the global mode, plotted in figure 5(d), furthermore is the same of the classical vortex shedding one. Here, the global mode reaches larger values (
![]() $O(10^{2})$
) with respect to the CIV mode, therefore the body motion is less important for the mode dynamics. The critical Reynolds number of the pure fluid Von Kármán instability found by Sahin & Owens (Reference Sahin and Owens2004) is around 110, very close to the VIV one.
$O(10^{2})$
) with respect to the CIV mode, therefore the body motion is less important for the mode dynamics. The critical Reynolds number of the pure fluid Von Kármán instability found by Sahin & Owens (Reference Sahin and Owens2004) is around 110, very close to the VIV one.
4.2. Light pendulum
 $({\it\alpha}=1.19)$
$({\it\alpha}=1.19)$
As the density ratio
![]() ${\it\alpha}$
decreases, the two branches approach each other and, as a result, for small
${\it\alpha}$
decreases, the two branches approach each other and, as a result, for small
![]() ${\it\alpha}$
only one branch is observed, as shown in figure 6(a,b). At
${\it\alpha}$
only one branch is observed, as shown in figure 6(a,b). At
![]() ${\it\alpha}=1.19$
, which corresponds to the experiment in Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011), the critical Reynolds number is between
${\it\alpha}=1.19$
, which corresponds to the experiment in Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011), the critical Reynolds number is between
![]() $15\leqslant \mathit{Re}\leqslant 17.5$
. The mode remains unstable for all values of the Reynolds number in the considered range. At a Reynolds number close to the critical one, the mode can be classified as a CIV type, based on the global mode shape shown in figure 6(b). As the Reynolds number is increased, the mode slowly changes its shape and frequency, switching to a VIV one, as shown in figure 6(c,d). The VIV global mode in this case reaches smaller values of flow velocities, compared with the same mode at larger
$15\leqslant \mathit{Re}\leqslant 17.5$
. The mode remains unstable for all values of the Reynolds number in the considered range. At a Reynolds number close to the critical one, the mode can be classified as a CIV type, based on the global mode shape shown in figure 6(b). As the Reynolds number is increased, the mode slowly changes its shape and frequency, switching to a VIV one, as shown in figure 6(c,d). The VIV global mode in this case reaches smaller values of flow velocities, compared with the same mode at larger
![]() ${\it\alpha}$
, thus, as can be expected, in this case the cylinder motion is more relevant on the flow dynamics, through its interaction with the wake.
${\it\alpha}$
, thus, as can be expected, in this case the cylinder motion is more relevant on the flow dynamics, through its interaction with the wake.

Figure 6. Leading eigenvalues at
![]() ${\it\alpha}=1.19$
: (a) growth rate
${\it\alpha}=1.19$
: (a) growth rate
![]() ${\it\lambda}$
and (b) Strouhal number
${\it\lambda}$
and (b) Strouhal number
![]() $\mathit{St}$
as a function of Reynolds number
$\mathit{St}$
as a function of Reynolds number
![]() $\mathit{Re}$
. The filled circles in (b) correspond to the vortex-shedding instability in the fixed cylinder case. (c,d) Streamwise velocity component
$\mathit{Re}$
. The filled circles in (b) correspond to the vortex-shedding instability in the fixed cylinder case. (c,d) Streamwise velocity component
![]() $\hat{u} _{x}$
of the corresponding global mode. Here
$\hat{u} _{x}$
of the corresponding global mode. Here
![]() ${\it\beta}=0.66$
.
${\it\beta}=0.66$
.
4.3. Influence of the density ratio on the oscillation frequency
Figure 7(a) shows the influence of the density ratio on the frequency of the body oscillation as a function of Reynolds number. As
![]() $\mathit{Re}$
increases, the frequency of the CIV oscillation decreases. Moreover, the frequency becomes larger as the density ratio increases. Instead, once the VIV regime is reached, the curves collapse on the value of the vortex shedding frequency, which is equal to
$\mathit{Re}$
increases, the frequency of the CIV oscillation decreases. Moreover, the frequency becomes larger as the density ratio increases. Instead, once the VIV regime is reached, the curves collapse on the value of the vortex shedding frequency, which is equal to
![]() $\mathit{St}=0.45$
in the confined case (see, e.g., Sahin & Owens Reference Sahin and Owens2004 and § 3.1).
$\mathit{St}=0.45$
in the confined case (see, e.g., Sahin & Owens Reference Sahin and Owens2004 and § 3.1).

Figure 7. (a) Influence of the density ratio
![]() ${\it\alpha}$
on the frequency of the oscillation as a function of Reynolds number. (b) Frequency of the oscillations as a function of Reynolds number: comparison of current results with direct numerical simulation and experiments from Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011) at
${\it\alpha}$
on the frequency of the oscillation as a function of Reynolds number. (b) Frequency of the oscillations as a function of Reynolds number: comparison of current results with direct numerical simulation and experiments from Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011) at
![]() ${\it\alpha}=1.19$
.
${\it\alpha}=1.19$
.
Moreover, a comparison of the frequency behaviour as a function of
![]() $\mathit{Re}$
at
$\mathit{Re}$
at
![]() ${\it\alpha}=1.19$
between the current analysis and data from Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011) is reported in figure 7(b). Present results are in agreement with both their experimental and numerical data. The agreement with the experimental results is particularly remarkable close to the critical Reynolds numbers. Note that both the stability analysis and the direct numerical simulation results, where the flow is purely two-dimensional, exhibit a monotonic behaviour of the frequency as a function of the Reynolds number. In contrast, the frequency increases for Reynolds numbers larger than 50 in the experiments. This discrepancy may most likely be accounted for by three-dimensional effects at the end of the cylinder: the strong shear of the thin fluid layer in the little gap between lateral wall and the end of the cylinder originates indeed a viscous force, that is not modelled in the 2D realm.
${\it\alpha}=1.19$
between the current analysis and data from Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011) is reported in figure 7(b). Present results are in agreement with both their experimental and numerical data. The agreement with the experimental results is particularly remarkable close to the critical Reynolds numbers. Note that both the stability analysis and the direct numerical simulation results, where the flow is purely two-dimensional, exhibit a monotonic behaviour of the frequency as a function of the Reynolds number. In contrast, the frequency increases for Reynolds numbers larger than 50 in the experiments. This discrepancy may most likely be accounted for by three-dimensional effects at the end of the cylinder: the strong shear of the thin fluid layer in the little gap between lateral wall and the end of the cylinder originates indeed a viscous force, that is not modelled in the 2D realm.
5. Moderately confined pendulum
 $({\it\beta}=0.3)$
$({\it\beta}=0.3)$
We focus our attention on a case where the cylinder is moderately confined, with
![]() ${\it\beta}$
equal to 0.3. The computational domain is characterized by
${\it\beta}$
equal to 0.3. The computational domain is characterized by
![]() $L_{i}=10$
,
$L_{i}=10$
,
![]() $L_{o}=50$
, with a mesh composed of
$L_{o}=50$
, with a mesh composed of
![]() $1.9\times 10^{4}$
nodes and
$1.9\times 10^{4}$
nodes and
![]() $3.8\times 10^{4}$
triangles.
$3.8\times 10^{4}$
triangles.
5.1. Stability analysis
A stability map for this situation is plotted in figure 8, where it is evident that the modification of the confinement ratio
![]() ${\it\beta}$
has a significant effect on the cylinder dynamics. The CIV instability is no longer present, but, instead, a new steady static instability is observed, which breaks the symmetry of the problem. This CID occurs at a critical Reynolds number
${\it\beta}$
has a significant effect on the cylinder dynamics. The CIV instability is no longer present, but, instead, a new steady static instability is observed, which breaks the symmetry of the problem. This CID occurs at a critical Reynolds number
![]() $60<\mathit{Re}_{CID}<70$
, constant for all density ratios
$60<\mathit{Re}_{CID}<70$
, constant for all density ratios
![]() ${\it\alpha}$
in the range considered. At larger Reynolds number, both the VIV and CID global modes are unstable.
${\it\alpha}$
in the range considered. At larger Reynolds number, both the VIV and CID global modes are unstable.

Figure 8. Stability map of the flow around the tethered cylinder for various Reynolds number
![]() $\mathit{Re}$
and body to fluid mass ratio
$\mathit{Re}$
and body to fluid mass ratio
![]() ${\it\alpha}$
. The ● symbols indicate that the steady symmetric flow is linearly unstable to a steady perturbation (CID), while the ▪ symbols denote cases where both VIV and CID mode are unstable.
${\it\alpha}$
. The ● symbols indicate that the steady symmetric flow is linearly unstable to a steady perturbation (CID), while the ▪ symbols denote cases where both VIV and CID mode are unstable.
![]() ${\it\beta}=0.3$
.
${\it\beta}=0.3$
.
A clearer picture of the stability proprieties of the flow is given in figure 9(a,b) where the growth rate and Strouhal number of the leading modes is plotted as a function of the Reynolds number. The CID mode is associated with a real eigenvalue and the global mode is localized mainly close to the channel walls at the same streamwise position of the cylinder, as shown in figure 9(c). It is noteworthy that the CID global mode share shape similarities with the CIV mode plotted in figure 5(c). For further increases of the Reynolds number also the VIV mode, shown in figure 9(d), becomes unstable. The value of the critical Reynolds number at which the VIV instability occurs and its frequency are in agreement with those relative to the shedding instability for the fixed confined case (see, e.g., Sahin & Owens Reference Sahin and Owens2004 and § 3.1).

Figure 9. Leading eigenvalues at
![]() ${\it\alpha}=15$
: (a) growth rate
${\it\alpha}=15$
: (a) growth rate
![]() ${\it\lambda}$
and (b) Stroual number
${\it\lambda}$
and (b) Stroual number
![]() $\mathit{St}$
as a function of Reynolds number
$\mathit{St}$
as a function of Reynolds number
![]() $\mathit{Re}$
: CID mode (○), VIV mode (
$\mathit{Re}$
: CID mode (○), VIV mode (
![]() $\Box$
) and (●) vortex-shedding mode for the fixed cylinder. Streamwise velocity component
$\Box$
) and (●) vortex-shedding mode for the fixed cylinder. Streamwise velocity component
![]() $\hat{u} _{x}$
of CID (b) and VIV mode (d).
$\hat{u} _{x}$
of CID (b) and VIV mode (d).
The presented scenario, with the occurrence of a steady mode and, at larger Reynolds numbers, of a complex conjugate mode, highly resembles the bifurcations observed on a fixed sphere (see, e.g., Fabre, Auguste & Magnaudet Reference Fabre, Auguste and Magnaudet2008; Meliga, Chomaz & Sipp Reference Meliga, Chomaz and Sipp2009). The first bifurcation is indeed a steady one, which lead to a stationary state (SS) that is no longer axisymmetric but retains a planar reflectional symmetry with respect to a longitudinal plane passing through the sphere centre. A second bifurcation is then observed at larger Reynolds numbers, leading to a time-dependent flow which oscillates around the SS state. It is plausible that the flow around the tethered cylinder will behave in a similar way.
5.2. Computation of the nonlinear asymmetric solution
At Reynolds numbers larger than the critical one for CID the cylinder will start to move from the symmetric position, upwards or downwards. Although information on the saturated solution cannot be obtained through the linear analysis, the asymmetric configuration can be obtained from computations of the flow around a cylinder placed eccentrically in the channel. Let us consider a guess solution
![]() $Q_{g}$
, characterized by the body displacement
$Q_{g}$
, characterized by the body displacement
![]() $Y_{c}$
.
$Y_{c}$
.
We compute two angles:
![]() ${\it\theta}_{T}=Y_{c}/L_{s}$
, giving the direction of the string tension
${\it\theta}_{T}=Y_{c}/L_{s}$
, giving the direction of the string tension
![]() $T$
, and
$T$
, and
![]() ${\it\theta}_{F}=\tan ^{-1}(F_{y}/F_{x})$
, corresponding to the direction of the force exerted by the flow on the cylinder (the gravity force has been found negligible for the
${\it\theta}_{F}=\tan ^{-1}(F_{y}/F_{x})$
, corresponding to the direction of the force exerted by the flow on the cylinder (the gravity force has been found negligible for the
![]() $\mathit{Fr}$
values examined in this paper). If there is a static solution, then the string tension
$\mathit{Fr}$
values examined in this paper). If there is a static solution, then the string tension
![]() $T$
should oppose the total external force acting on the cylinder, thus,
$T$
should oppose the total external force acting on the cylinder, thus,
![]() ${\it\theta}_{T}={\it\theta}_{F}$
.
${\it\theta}_{T}={\it\theta}_{F}$
.
Figure 10(a) shows the angles
![]() ${\it\theta}_{F}$
and
${\it\theta}_{F}$
and
![]() ${\it\theta}_{T}$
as a function of the cylinder displacement, computed at different Reynolds numbers, ranging from
${\it\theta}_{T}$
as a function of the cylinder displacement, computed at different Reynolds numbers, ranging from
![]() $\mathit{Re}=65$
(dark color) to
$\mathit{Re}=65$
(dark color) to
![]() $\mathit{Re}=95$
(light color). The curve
$\mathit{Re}=95$
(light color). The curve
![]() ${\it\theta}_{F}$
is a function of
${\it\theta}_{F}$
is a function of
![]() $\mathit{Re}$
only and the channel geometry, while
$\mathit{Re}$
only and the channel geometry, while
![]() ${\it\theta}_{T}$
depends on the string length
${\it\theta}_{T}$
depends on the string length
![]() $L_{s}$
. In particular, if
$L_{s}$
. In particular, if
![]() $\mathit{Re}\leqslant \mathit{Re}_{CID}$
,
$\mathit{Re}\leqslant \mathit{Re}_{CID}$
,
![]() ${\it\theta}_{T}$
is larger than
${\it\theta}_{T}$
is larger than
![]() ${\it\theta}_{F}$
for any value of
${\it\theta}_{F}$
for any value of
![]() $Y_{c}$
, thus the cylinder is stable in the initial configuration (
$Y_{c}$
, thus the cylinder is stable in the initial configuration (
![]() $Y_{c}=0$
) (see the lowest curve in figure 10
a). The linear stability results showing a threshold at
$Y_{c}=0$
) (see the lowest curve in figure 10
a). The linear stability results showing a threshold at
![]() $\mathit{Re}_{CID}$
are recovered. Instead, for
$\mathit{Re}_{CID}$
are recovered. Instead, for
![]() $\mathit{Re}>\mathit{Re}_{CID}$
,
$\mathit{Re}>\mathit{Re}_{CID}$
,
![]() ${\it\theta}_{F}$
is equal to
${\it\theta}_{F}$
is equal to
![]() ${\it\theta}_{T}$
for a non-zero value of
${\it\theta}_{T}$
for a non-zero value of
![]() $Y_{c}$
, pointing to a unique equilibrium position for each
$Y_{c}$
, pointing to a unique equilibrium position for each
![]() $\mathit{Re}$
, plotted as filled marks in figure 10(a).
$\mathit{Re}$
, plotted as filled marks in figure 10(a).

Figure 10. (a) Equilibrium angles
![]() ${\it\theta}_{T}$
and
${\it\theta}_{T}$
and
![]() ${\it\theta}_{F}$
as a function of displacement
${\it\theta}_{F}$
as a function of displacement
![]() $Y_{c}$
for
$Y_{c}$
for
![]() $\mathit{Re}$
in between 65 (dark colour) and 95 (light colour); filled circles (squares) indicate equilibrium positions for string length equal to 45 (30). (b) Equilibrium positions
$\mathit{Re}$
in between 65 (dark colour) and 95 (light colour); filled circles (squares) indicate equilibrium positions for string length equal to 45 (30). (b) Equilibrium positions
![]() $Y_{c}$
as a functions of the Reynolds number
$Y_{c}$
as a functions of the Reynolds number
![]() $\mathit{Re}$
for both values of the string length.
$\mathit{Re}$
for both values of the string length.
Figure 10(a) shows that if we fix the Reynolds number, the equilibrium position is determined by the slope
![]() ${\it\theta}_{T}$
, i.e. by the value of
${\it\theta}_{T}$
, i.e. by the value of
![]() $L_{s}$
. In this section only, we vary the string length, in order to investigate the effect of this parameter on the CID instability. The bifurcation scenario is depicted in figure 10(b), where the equilibrium position (
$L_{s}$
. In this section only, we vary the string length, in order to investigate the effect of this parameter on the CID instability. The bifurcation scenario is depicted in figure 10(b), where the equilibrium position (
![]() $Y_{eq}$
) as a function of
$Y_{eq}$
) as a function of
![]() $\mathit{Re}$
is plotted for the value of
$\mathit{Re}$
is plotted for the value of
![]() $L_{s}$
used in the other sections of the paper (
$L_{s}$
used in the other sections of the paper (
![]() $L_{s}=45$
) and also for
$L_{s}=45$
) and also for
![]() $L_{s}=30$
. Figure 10(b) shows a typical pitchfork bifurcation with the base state becoming unstable in favour of two symmetric solutions (
$L_{s}=30$
. Figure 10(b) shows a typical pitchfork bifurcation with the base state becoming unstable in favour of two symmetric solutions (
![]() $Y_{c}=\pm Y_{eq}$
).
$Y_{c}=\pm Y_{eq}$
).
As stated above, the parameter
![]() $L_{s}$
has a relevant effect on the bifurcation. For instance, a shorter string will postpone the onset of the instability. It is evident that it exists a value of the length
$L_{s}$
has a relevant effect on the bifurcation. For instance, a shorter string will postpone the onset of the instability. It is evident that it exists a value of the length
![]() $L_{s}$
which maximize the displacement
$L_{s}$
which maximize the displacement
![]() $y_{c}$
and that for a string length below a critical value, the slope of
$y_{c}$
and that for a string length below a critical value, the slope of
![]() ${\it\theta}_{T}$
is larger than the initial one corresponding to
${\it\theta}_{T}$
is larger than the initial one corresponding to
![]() ${\it\theta}_{F}$
, thus the cylinder is stable in the initial configuration (
${\it\theta}_{F}$
, thus the cylinder is stable in the initial configuration (
![]() $Y_{c}=0$
), as for instance at
$Y_{c}=0$
), as for instance at
![]() $\mathit{Re}=65$
(see the lowest curve in figure 10
a).
$\mathit{Re}=65$
(see the lowest curve in figure 10
a).
6. Quasi-static model
The coupled fluid–body stability problem is also studied with the help of a QS model. This approach has been used successfully to study the stability of the path of falling heavy bodies by Fabre, Assemat & Magnaudet (Reference Fabre, Assemat and Magnaudet2011).
We write Newton’s second law for the vertical motion of the cylinder, describing a small-amplitude deviation from the base solution with the body placed along the channel axis:
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial v_{c}}{\partial t}=\left(-\underbrace{\frac{{\it\alpha}-1}{{\it\alpha}L}\frac{1}{\mathit{Fr}^{2}}}_{{\it\omega}_{g}^{2}}-\underbrace{\frac{4}{{\rm\pi}{\it\alpha}L}F_{xb}}_{{\it\omega}_{D}^{2}}+\underbrace{\frac{4}{{\rm\pi}{\it\alpha}}\frac{\partial F_{y}}{\partial y_{c}}}_{{\it\omega}_{F_{y}}^{2}}\right)y_{c}+\underbrace{\frac{4}{{\rm\pi}{\it\alpha}}\frac{\partial F_{y}}{\partial v_{c}}}_{{\it\gamma}_{v_{c}}}v_{c} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial v_{c}}{\partial t}=\left(-\underbrace{\frac{{\it\alpha}-1}{{\it\alpha}L}\frac{1}{\mathit{Fr}^{2}}}_{{\it\omega}_{g}^{2}}-\underbrace{\frac{4}{{\rm\pi}{\it\alpha}L}F_{xb}}_{{\it\omega}_{D}^{2}}+\underbrace{\frac{4}{{\rm\pi}{\it\alpha}}\frac{\partial F_{y}}{\partial y_{c}}}_{{\it\omega}_{F_{y}}^{2}}\right)y_{c}+\underbrace{\frac{4}{{\rm\pi}{\it\alpha}}\frac{\partial F_{y}}{\partial v_{c}}}_{{\it\gamma}_{v_{c}}}v_{c} & \displaystyle\end{eqnarray}$$
If we look for solution in form of
![]() $y_{c}={\hat{y}}_{c}\exp ({\it\sigma}_{qs}t)$
and
$y_{c}={\hat{y}}_{c}\exp ({\it\sigma}_{qs}t)$
and
![]() $v_{c}=\hat{v}_{c}\exp ({\it\sigma}_{qs}t)$
, problem (6.1) yields to the characteristic equation:
$v_{c}=\hat{v}_{c}\exp ({\it\sigma}_{qs}t)$
, problem (6.1) yields to the characteristic equation:
which has the following roots:
The quantities
![]() ${\it\Delta}^{2}={\it\gamma}_{v_{c}}^{2}+4{\it\omega}_{F_{y}}^{2}$
and
${\it\Delta}^{2}={\it\gamma}_{v_{c}}^{2}+4{\it\omega}_{F_{y}}^{2}$
and
![]() ${\it\gamma}_{v_{c}}$
determine the nature of
${\it\gamma}_{v_{c}}$
determine the nature of
![]() ${\it\sigma}_{qs}$
and, thus, the body behaviour. If
${\it\sigma}_{qs}$
and, thus, the body behaviour. If
![]() ${\it\Delta}^{2}$
is negative (6.3) has two complex conjugate roots. In this case the stability of the oscillating dynamics is given by the sign of
${\it\Delta}^{2}$
is negative (6.3) has two complex conjugate roots. In this case the stability of the oscillating dynamics is given by the sign of
![]() ${\it\gamma}_{v_{c}}$
(unstable for
${\it\gamma}_{v_{c}}$
(unstable for
![]() ${\it\gamma}_{v_{c}}>0$
). Instead, if
${\it\gamma}_{v_{c}}>0$
). Instead, if
![]() ${\it\Delta}^{2}$
is positive, equation (6.3) has two real roots, which means that the body dynamics may have a diverging behaviour if there is a positive eigenvalue.
${\it\Delta}^{2}$
is positive, equation (6.3) has two real roots, which means that the body dynamics may have a diverging behaviour if there is a positive eigenvalue.
6.1. Computation of the coefficients for the QS model
The model contains three coefficients that need to be fitted:
![]() $F_{xb}$
,
$F_{xb}$
,
![]() $\partial F_{y}/\partial y_{c}$
and
$\partial F_{y}/\partial y_{c}$
and
![]() $\partial F_{y}/\partial v_{c}$
. These coefficients can be computed accurately through the Navier–Stokes equations. The first is the drag force acting on the cylinder at base-flow level. For the computation of the other two coefficients we considered two elementary solutions, which are small deviations from the reference base-flow state. Since the perturbations are small, these are governed by the linearized version of the Navier–Stokes equations. The first solution,
$\partial F_{y}/\partial v_{c}$
. These coefficients can be computed accurately through the Navier–Stokes equations. The first is the drag force acting on the cylinder at base-flow level. For the computation of the other two coefficients we considered two elementary solutions, which are small deviations from the reference base-flow state. Since the perturbations are small, these are governed by the linearized version of the Navier–Stokes equations. The first solution,
![]() $(\boldsymbol{u},p)=(\boldsymbol{u}^{(y_{c})},p^{(y_{c})})y_{c}$
, corresponds to the case where the cylinder is slightly moved from the channel centreline by a quantity
$(\boldsymbol{u},p)=(\boldsymbol{u}^{(y_{c})},p^{(y_{c})})y_{c}$
, corresponds to the case where the cylinder is slightly moved from the channel centreline by a quantity
![]() $y_{c}$
and can be computed by solving (2.8a,b
) dropping the time derivative parts and with the following boundary conditions at the inlet and on the channel walls:
$y_{c}$
and can be computed by solving (2.8a,b
) dropping the time derivative parts and with the following boundary conditions at the inlet and on the channel walls:
![]() $u_{x}^{(y_{c})}=\partial U_{xb}/\partial y_{b}$
,
$u_{x}^{(y_{c})}=\partial U_{xb}/\partial y_{b}$
,
![]() $u_{y}^{(y_{c})}=\partial U_{yb}/\partial y_{b}$
. Once the problem is solved the coefficient
$u_{y}^{(y_{c})}=\partial U_{yb}/\partial y_{b}$
. Once the problem is solved the coefficient
![]() $\partial F_{y}/\partial y_{c}$
is found by computing the force
$\partial F_{y}/\partial y_{c}$
is found by computing the force
![]() $F_{y}$
acting on the cylinder. The second solution to consider corresponds to the case where the cylinder is moving with a constant velocity
$F_{y}$
acting on the cylinder. The second solution to consider corresponds to the case where the cylinder is moving with a constant velocity
![]() $v_{c}$
. Therefore, the displacement of the cylinder is increasing in time through
$v_{c}$
. Therefore, the displacement of the cylinder is increasing in time through
![]() $y_{c}=v_{c}t$
. This situation is a bit more subtle, as the elementary solution
$y_{c}=v_{c}t$
. This situation is a bit more subtle, as the elementary solution
![]() $(\boldsymbol{u}^{(v_{c})},p^{(v_{c})})$
is not a steady solution of the linearized Navier–Stokes equations. However, the flow perturbation can be expressed, for short times, as
$(\boldsymbol{u}^{(v_{c})},p^{(v_{c})})$
is not a steady solution of the linearized Navier–Stokes equations. However, the flow perturbation can be expressed, for short times, as
![]() $(\boldsymbol{u},p)=(\boldsymbol{u}^{(y_{c})},p^{(y_{c})})v_{c}t+(\boldsymbol{u}^{(v_{c})},p^{(v_{c})})v_{c}$
. Introducing this decomposition into the linearized problem leads to a linear system which allows the elementary solution and the corresponding coefficient
$(\boldsymbol{u},p)=(\boldsymbol{u}^{(y_{c})},p^{(y_{c})})v_{c}t+(\boldsymbol{u}^{(v_{c})},p^{(v_{c})})v_{c}$
. Introducing this decomposition into the linearized problem leads to a linear system which allows the elementary solution and the corresponding coefficient
![]() $\partial F_{y}/\partial v_{c}$
to be computed.
$\partial F_{y}/\partial v_{c}$
to be computed.
6.2. Strongly confined pendulum
 $({\it\beta}=0.66)$
$({\it\beta}=0.66)$
The QS approach is justified only when the time scales of the flow evolution and of the body dynamics are well separated, a condition fulfilled in the case of very heavy bodies. Indeed, as shown in figure 7(a), the frequency of the CIV instability becomes smaller as the density ratio is increased.
Figure 11 displays the different positions of the VIV and CIV branches eigenvalues (circles) and of the QS model (squares) for Reynolds numbers in the range
![]() $15<\mathit{Re}<120$
, computed at
$15<\mathit{Re}<120$
, computed at
![]() ${\it\alpha}=15$
. It is shown that the QS eigenvalues trajectory is well correlated with the CIV one, confirming that the latter regime is not related to a wake instability, as for instance the VIV one. The agreement between QS and the full coupled stability analysis becomes better as the Reynolds number increases, due to the larger separation in terms of frequencies with respect to the VIV flow branch. This is also shown in figure 12(a), where the growth rates as a function of
${\it\alpha}=15$
. It is shown that the QS eigenvalues trajectory is well correlated with the CIV one, confirming that the latter regime is not related to a wake instability, as for instance the VIV one. The agreement between QS and the full coupled stability analysis becomes better as the Reynolds number increases, due to the larger separation in terms of frequencies with respect to the VIV flow branch. This is also shown in figure 12(a), where the growth rates as a function of
![]() $\mathit{Re}$
, obtained respectively via QS and stability analysis, are plotted, showing excellent agreement, except for some discrepancies in the
$\mathit{Re}$
, obtained respectively via QS and stability analysis, are plotted, showing excellent agreement, except for some discrepancies in the
![]() $\mathit{Re}$
range where re-stabilization occurs.
$\mathit{Re}$
range where re-stabilization occurs.

Figure 11. Eigenvalues positions in the complex plane for the full coupled stability problem (circles) and for the QS model (squares). Parameters:
![]() $\mathit{Re}$
from 10 in dark (blue online) colour to 120 in light (pink online) colour,
$\mathit{Re}$
from 10 in dark (blue online) colour to 120 in light (pink online) colour,
![]() ${\it\alpha}=15$
,
${\it\alpha}=15$
,
![]() ${\it\beta}=0.66$
.
${\it\beta}=0.66$
.

Figure 12. Coefficients
![]() $\partial F_{y}/\partial y_{c}$
(a) and
$\partial F_{y}/\partial y_{c}$
(a) and
![]() $\partial F_{y}/\partial v_{c}$
(b) as a function of Reynolds number
$\partial F_{y}/\partial v_{c}$
(b) as a function of Reynolds number
![]() $\mathit{Re}$
for the strongly confined case (
$\mathit{Re}$
for the strongly confined case (
![]() ${\it\beta}=0.66$
) at
${\it\beta}=0.66$
) at
![]() ${\it\alpha}=15$
.
${\it\alpha}=15$
.
The nature of the regime is governed by the quantity
![]() ${\it\Delta}^{2}$
, reported in figure 12(b). The sign of
${\it\Delta}^{2}$
, reported in figure 12(b). The sign of
![]() ${\it\Delta}^{2}$
is always negative, which means that eigenvalues
${\it\Delta}^{2}$
is always negative, which means that eigenvalues
![]() ${\it\sigma}_{qs}$
are a complex conjugate pair. Figure 12(c,d) shows the coefficients
${\it\sigma}_{qs}$
are a complex conjugate pair. Figure 12(c,d) shows the coefficients
![]() $\partial F_{y}/\partial v_{c}$
and
$\partial F_{y}/\partial v_{c}$
and
![]() $\partial F_{y}/\partial y_{c}$
as a function of Reynolds number
$\partial F_{y}/\partial y_{c}$
as a function of Reynolds number
![]() $\mathit{Re}$
. In particular, the force induced by a displacement
$\mathit{Re}$
. In particular, the force induced by a displacement
![]() $y_{c}$
of the cylinder has always a stabilizing effect (negative values) and it is responsible of the sign of
$y_{c}$
of the cylinder has always a stabilizing effect (negative values) and it is responsible of the sign of
![]() ${\it\Delta}^{2}$
. However, in this case the stability properties of the body dynamics are given by the sign of
${\it\Delta}^{2}$
. However, in this case the stability properties of the body dynamics are given by the sign of
![]() ${\it\gamma}_{v_{c}}$
, which is proportional to
${\it\gamma}_{v_{c}}$
, which is proportional to
![]() $\partial F_{y}/\partial v_{c}$
(see (6.3)). As shown in figure 12(d), the force derivative is positive in a certain range of Reynolds numbers, resulting in an oscillation with positive growth rate.
$\partial F_{y}/\partial v_{c}$
(see (6.3)). As shown in figure 12(d), the force derivative is positive in a certain range of Reynolds numbers, resulting in an oscillation with positive growth rate.
Figure 13 shows the pressure fields of the elementary solution
![]() $p^{(v_{c})}$
at three different Reynolds numbers, namely
$p^{(v_{c})}$
at three different Reynolds numbers, namely
![]() $\mathit{Re}=10$
, 20, 60. Note that these pressure fields can be viewed as the difference between the case where the cylinder is moving upwards with
$\mathit{Re}=10$
, 20, 60. Note that these pressure fields can be viewed as the difference between the case where the cylinder is moving upwards with
![]() $v_{c}=1$
and the fixed case. At
$v_{c}=1$
and the fixed case. At
![]() $\mathit{Re}=10$
(see figure 13
a) two pairs of pressure lobes are observable on the cylinder surface. The upstream ones, resulting in a stabilizing force, dominate the pair in the rear of the cylinder, yielding a destabilizing effect. As
$\mathit{Re}=10$
(see figure 13
a) two pairs of pressure lobes are observable on the cylinder surface. The upstream ones, resulting in a stabilizing force, dominate the pair in the rear of the cylinder, yielding a destabilizing effect. As
![]() $\mathit{Re}$
increases, in figure 13(b) it is shown that the first pair becomes weaker, while the second one grows, giving as result a destabilizing force at
$\mathit{Re}$
increases, in figure 13(b) it is shown that the first pair becomes weaker, while the second one grows, giving as result a destabilizing force at
![]() $\mathit{Re}=20$
. Finally, as depicted in figure 13(c), at larger Reynolds numbers, the lobes in the rear responsible for the instability start to disappear, and the overall force again has a stabilizing effect.
$\mathit{Re}=20$
. Finally, as depicted in figure 13(c), at larger Reynolds numbers, the lobes in the rear responsible for the instability start to disappear, and the overall force again has a stabilizing effect.

Figure 13. Pressure field of the elementary solution
![]() $p^{(v_{c})}$
at three different Reynolds numbers, namely
$p^{(v_{c})}$
at three different Reynolds numbers, namely
![]() $\mathit{Re}=10$
(a), 20 (b) and 60 (c). Here
$\mathit{Re}=10$
(a), 20 (b) and 60 (c). Here
![]() ${\it\alpha}=15$
and
${\it\alpha}=15$
and
![]() ${\it\beta}=0.66$
.
${\it\beta}=0.66$
.
6.3. Moderately confined pendulum
 $({\it\beta}=0.3)$
$({\it\beta}=0.3)$
As already mentioned in § 5, the CID instability is associated to a real eigenvalue which becomes unstable. In particular, as shown in figure 14, the instability is associated to an eigenpair which for small Reynolds number is localized in the left part of the complex plane. As the Reynolds number is increased the eigenvalues move and they meet on the negative real axis, where they split. Soon afterwards one of the eigenvalues crosses on the right half plane, leading to a pitchfork bifurcation of the system. Figure 14 displays also the QS model results (squares) in terms of eigenvalues trajectories in the complex plane as the Reynolds number increases, showing a striking agreement with respect to the results of the stability analysis (circles). An excellent agreement is also shown in figure 15(a), in terms of growth rates.

Figure 14. Eigenvalues positions in the complex plane for the full coupled stability problem (circles) and for the QS model (squares). Parameters:
![]() $\mathit{Re}$
from 20 in dark (blue online) colour to 110 in light (pink online) colour,
$\mathit{Re}$
from 20 in dark (blue online) colour to 110 in light (pink online) colour,
![]() ${\it\alpha}=15$
,
${\it\alpha}=15$
,
![]() ${\it\beta}=0.3$
.
${\it\beta}=0.3$
.

Figure 15. Coefficients
![]() $\partial F_{y}/\partial y_{c}$
(a) and
$\partial F_{y}/\partial y_{c}$
(a) and
![]() $\partial F_{y}/\partial v_{c}$
(b) as a function of Reynolds number
$\partial F_{y}/\partial v_{c}$
(b) as a function of Reynolds number
![]() $\mathit{Re}$
for the moderately confined case.
$\mathit{Re}$
for the moderately confined case.
![]() ${\it\alpha}=15$
,
${\it\alpha}=15$
,
![]() ${\it\beta}=0.3$
.
${\it\beta}=0.3$
.
Figure 15(b) shows the parameter
![]() ${\it\Delta}^{2}$
as a function of
${\it\Delta}^{2}$
as a function of
![]() $\mathit{Re}$
. Depending on the Reynolds numbers both oscillating solutions (
$\mathit{Re}$
. Depending on the Reynolds numbers both oscillating solutions (
![]() ${\it\Delta}^{2}<0$
) or steady ones (
${\it\Delta}^{2}<0$
) or steady ones (
![]() ${\it\Delta}^{2}>0$
) are possible. However, as shown in figure 15(d) the coefficient
${\it\Delta}^{2}>0$
) are possible. However, as shown in figure 15(d) the coefficient
![]() $\partial F_{y}/\partial v_{c}$
is negative for the considered Reynolds numbers, thus the oscillating solution has always a negative growth rate (see (6.3)). Therefore, the system can become unstable only through a steady bifurcation, when the parameter
$\partial F_{y}/\partial v_{c}$
is negative for the considered Reynolds numbers, thus the oscillating solution has always a negative growth rate (see (6.3)). Therefore, the system can become unstable only through a steady bifurcation, when the parameter
![]() ${\it\Delta}^{2}$
becomes positive. The coefficient
${\it\Delta}^{2}$
becomes positive. The coefficient
![]() $\partial F_{y}/\partial y_{c}$
plays an important role in the switching between the oscillating and the diverging dynamics. The force, which has a stabilizing effect at small Reynolds numbers, becomes an exciting one for larger Reynolds numbers, as shown in figure 15(c).
$\partial F_{y}/\partial y_{c}$
plays an important role in the switching between the oscillating and the diverging dynamics. The force, which has a stabilizing effect at small Reynolds numbers, becomes an exciting one for larger Reynolds numbers, as shown in figure 15(c).
In order to investigate why the force coefficient
![]() $\partial F_{y}/\partial y_{c}$
change its sign, we looked at the elementary solution used for the coefficient computation, which is the flow modification with respect to the base flow induced by a displacement
$\partial F_{y}/\partial y_{c}$
change its sign, we looked at the elementary solution used for the coefficient computation, which is the flow modification with respect to the base flow induced by a displacement
![]() $y_{c}$
. We found that the viscous contribution can be neglected, thus the force is caused mainly by a pressure difference along the cylinder boundary. We consider two different Reynolds numbers: the first one corresponding to a damping force (
$y_{c}$
. We found that the viscous contribution can be neglected, thus the force is caused mainly by a pressure difference along the cylinder boundary. We consider two different Reynolds numbers: the first one corresponding to a damping force (
![]() $\mathit{Re}=30$
), while the other is associated with an exciting force (
$\mathit{Re}=30$
), while the other is associated with an exciting force (
![]() $\mathit{Re}=90$
). The pressure fields
$\mathit{Re}=90$
). The pressure fields
![]() $p^{(y_{c})}$
computed at
$p^{(y_{c})}$
computed at
![]() $\mathit{Re}=30$
and
$\mathit{Re}=30$
and
![]() $\mathit{Re}=90$
are plotted in figure 16(a,b), respectively. At the smaller Reynolds number we found a larger (smaller) pressure on the upper (lower) cylinder surface, while in front of the cylinder the pressure difference has an opposite behaviour. Nonetheless, the overall pressure difference between the upper (
$\mathit{Re}=90$
are plotted in figure 16(a,b), respectively. At the smaller Reynolds number we found a larger (smaller) pressure on the upper (lower) cylinder surface, while in front of the cylinder the pressure difference has an opposite behaviour. Nonetheless, the overall pressure difference between the upper (
![]() $y>0$
) and lower (
$y>0$
) and lower (
![]() $y<0$
) part of the body generates a stabilizing force. As the Reynolds number is increased, the polar pressure difference becomes weaker (see figure 16
b) while the pressure distribution in the upstream part remains essentially the same, until the latter contribution becomes dominant, leading to a exciting force.
$y<0$
) part of the body generates a stabilizing force. As the Reynolds number is increased, the polar pressure difference becomes weaker (see figure 16
b) while the pressure distribution in the upstream part remains essentially the same, until the latter contribution becomes dominant, leading to a exciting force.

Figure 16. Pressure
![]() $p^{(y_{c})}$
at two different Reynolds numbers:
$p^{(y_{c})}$
at two different Reynolds numbers:
![]() $\mathit{Re}=30$
(a) and
$\mathit{Re}=30$
(a) and
![]() $\mathit{Re}=90$
(b). Here
$\mathit{Re}=90$
(b). Here
![]() ${\it\beta}=0.3$
.
${\it\beta}=0.3$
.

Figure 17. Flow around a displaced cylinder (
![]() $y_{c}=0.05$
) depicted by streamlines at two different Reynolds numbers:
$y_{c}=0.05$
) depicted by streamlines at two different Reynolds numbers:
![]() $\mathit{Re}=30$
(a) and
$\mathit{Re}=30$
(a) and
![]() $\mathit{Re}=90$
(b).
$\mathit{Re}=90$
(b).
![]() ${\it\beta}=0.3$
.
${\it\beta}=0.3$
.
In addition, we have computed the steady flow around a cylinder which has been displaced from the symmetric position, i.e.
![]() $y_{c}=0.05$
. Figure 17(a) shows the flow at
$y_{c}=0.05$
. Figure 17(a) shows the flow at
![]() $\mathit{Re}=30$
depicted by streamlines. We found that, due to interactions with the channel walls, the cylinder wake is deflected, leading to the stabilizing pressure unbalance. Instead, if we look at the case at
$\mathit{Re}=30$
depicted by streamlines. We found that, due to interactions with the channel walls, the cylinder wake is deflected, leading to the stabilizing pressure unbalance. Instead, if we look at the case at
![]() $\mathit{Re}=90$
plotted in figure 17(b) we note that the wake extends more downstream and is more balanced and presents less asymmetry between the upper and lower recirculation region and, thus, the pressure difference disappears. This behaviour has been reported in the literature by Zovatto & Pedrizzetti (Reference Zovatto and Pedrizzetti2001) for the case of a cylinder confined between two parallel walls and placed asymmetrically with respect to the channel centreline. The upstream pressure distribution, instead, is compatible with the effect of shear in the incoming velocity profile (see e.g. Nakabayashi, Yoshida & Aoi Reference Nakabayashi, Yoshida and Aoi1993; Zovatto & Pedrizzetti Reference Zovatto and Pedrizzetti2001). In particular, Zovatto & Pedrizzetti (Reference Zovatto and Pedrizzetti2001) proposed that, given an incoming velocity profile
$\mathit{Re}=90$
plotted in figure 17(b) we note that the wake extends more downstream and is more balanced and presents less asymmetry between the upper and lower recirculation region and, thus, the pressure difference disappears. This behaviour has been reported in the literature by Zovatto & Pedrizzetti (Reference Zovatto and Pedrizzetti2001) for the case of a cylinder confined between two parallel walls and placed asymmetrically with respect to the channel centreline. The upstream pressure distribution, instead, is compatible with the effect of shear in the incoming velocity profile (see e.g. Nakabayashi, Yoshida & Aoi Reference Nakabayashi, Yoshida and Aoi1993; Zovatto & Pedrizzetti Reference Zovatto and Pedrizzetti2001). In particular, Zovatto & Pedrizzetti (Reference Zovatto and Pedrizzetti2001) proposed that, given an incoming velocity profile
![]() $U_{x}(y)={\it\xi}y$
, the lift force will be proportional to the opposite of the shear
$U_{x}(y)={\it\xi}y$
, the lift force will be proportional to the opposite of the shear
![]() ${\it\xi}$
. Now, if we consider a positive displacement
${\it\xi}$
. Now, if we consider a positive displacement
![]() $y_{c}$
, the cylinder is facing a velocity profile which can be associated with a negative shear
$y_{c}$
, the cylinder is facing a velocity profile which can be associated with a negative shear
![]() ${\it\xi}$
, resulting in a force in the upwards direction.
${\it\xi}$
, resulting in a force in the upwards direction.
6.4. Influence of density ratio
 ${\it\alpha}$
on QS reliability
${\it\alpha}$
on QS reliability
We now vary the density ratio
![]() ${\it\alpha}$
in order to assess the reliability of the QS predictions for lighter cases. Figure 18(a) shows the growth rate of the CIV instability at
${\it\alpha}$
in order to assess the reliability of the QS predictions for lighter cases. Figure 18(a) shows the growth rate of the CIV instability at
![]() $\mathit{Re}=20$
. The QS prediction can be assumed reliable only for
$\mathit{Re}=20$
. The QS prediction can be assumed reliable only for
![]() ${\it\alpha}>8$
, where the growth rate difference is at most 15 %. This behaviour could be expected, since, as shown in figure 7(a), the CIV oscillation frequency is a decreasing function of the density ratio, thus, the QS time scales separation hypothesis is violated at small
${\it\alpha}>8$
, where the growth rate difference is at most 15 %. This behaviour could be expected, since, as shown in figure 7(a), the CIV oscillation frequency is a decreasing function of the density ratio, thus, the QS time scales separation hypothesis is violated at small
![]() ${\it\alpha}$
. Although the growth rate and frequency predictions of QS are in poor agreement with the stability results, the QS model captures the onset of the CIV oscillation even at small density ratios. For instance, at
${\it\alpha}$
. Although the growth rate and frequency predictions of QS are in poor agreement with the stability results, the QS model captures the onset of the CIV oscillation even at small density ratios. For instance, at
![]() ${\it\alpha}=2$
the critical Reynolds number differs by approximately 9 %.
${\it\alpha}=2$
the critical Reynolds number differs by approximately 9 %.

Figure 18. Comparison of the growth rate computed by the stability analysis and the one predicted by the QS model for (a,
![]() $\mathit{Re}=20$
) strongly and (b,
$\mathit{Re}=20$
) strongly and (b,
![]() $\mathit{Re}=80$
) moderately confined case as a function of the density ratio
$\mathit{Re}=80$
) moderately confined case as a function of the density ratio
![]() ${\it\alpha}$
.
${\it\alpha}$
.
The CID instability, instead, can be described accurately by the QS model even at low density ratio, as shown in figure 18(b), where the growth rate obtained through QS and stability analysis are plotted as a function of
![]() ${\it\alpha}$
, having the Reynolds number fixed at 80. The accuracy of QS is not surprising, since in this case the instability is steady and the QS hypotheses are always fulfilled.
${\it\alpha}$
, having the Reynolds number fixed at 80. The accuracy of QS is not surprising, since in this case the instability is steady and the QS hypotheses are always fulfilled.
7. Conclusions
In this study, we have analysed the global stability of the coupled fluid–solid problem of a tethered cylindrical pendulum submitted to an incoming flow confined in a channel. This global stability problem strongly couples the two degrees of freedom of the linearized motion of the pendulum with those associated with the discretization of the velocity and pressure fields in the fluid domain, governed by the linearized Navier–Stokes equations. This has enabled to retrieve the confinement-induced instability (CIV) discovered by Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2011) appearing at low Reynolds number and strong confinement, as well as the intermediate restabilization Reynolds number range at large mass ratio between CIV extinction and VIV onset. At less pronounced confinements, we have identified a static instability, that we have called CID which sets in at Reynolds numbers below the onset of VIV. The steady nonlinear asymmetric solutions bifurcating from the symmetric base solution in the CID regime could be determined, pointing to a supercritical pitchfork bifurcation.
Table 1. Influence of grid characteristics on some quantities of interest slightly above the CIV threshold for the strongly confined case:
![]() $\mathit{Re}=17.5$
,
$\mathit{Re}=17.5$
,
![]() ${\it\alpha}=1.19$
.
${\it\alpha}=1.19$
.

We have then shown that by introducing a QS response of the fluid but keeping the entire dynamics of the pendulum, both CIV and CID could be precisely captured, showing that the flow acts in this regime only through its instantaneous added mass and added damping, a situation which strongly differs from the VIV instability.
The newly discovered CID open the way for further studies. Prominently, it deserves an experimental confirmation. Second, the stability of the bifurcated state should be investigated. In similarity with bifurcations sequences in the wake of a fixed disk or sphere (Meliga et al. Reference Meliga, Chomaz and Sipp2009), one can expect that the nonlinear interaction of the static displacement mode arising with CID with the nonlinear mean-flow distortion caused by the VIV mode could restore the symmetry of the solution.
Appendix. Influence of grid characteristics
We tested different grids by varying successively the position of the inlet (
![]() $L_{i}$
) and outlet (
$L_{i}$
) and outlet (
![]() $L_{o}$
), as well as the number
$L_{o}$
), as well as the number
![]() $N_{t}$
of triangles involved in the discretization for the two studied cases. For the strongly confined pendulum (
$N_{t}$
of triangles involved in the discretization for the two studied cases. For the strongly confined pendulum (
![]() $D/H=0.66$
) we consider a case where the CIV regime is slightly unstable (
$D/H=0.66$
) we consider a case where the CIV regime is slightly unstable (
![]() $\mathit{Re}=17.5$
,
$\mathit{Re}=17.5$
,
![]() ${\it\alpha}=1.19$
) and we report in table 1 the associated growth rate and the cylinder drag coefficient of the base flow. Grids M1 and M2 show the influence of node density, while grids M3 and M4 illustrate the influence of the size of the computational domain. The drag coefficient differs at most 0.02 % in the four grids, a good indication that the base flow is adequately resolved on all of them. The difference on the growth rate of the CIV mode is 1.5 % between grids M1 and M2, showing that also the coarser grid is appropriate. Concerning the size of the computational domain, the physically meaningful eigenvalues converged when the size of the computational domain is increased, but the spurious eigenvalues become less damped and tend to approach the real axis, with the possible effect of masking the meaningful eigenvalues if they come too close to one another. Therefore, we selected grid M1 as the best compromise between accuracy, size limitations and computational costs.
${\it\alpha}=1.19$
) and we report in table 1 the associated growth rate and the cylinder drag coefficient of the base flow. Grids M1 and M2 show the influence of node density, while grids M3 and M4 illustrate the influence of the size of the computational domain. The drag coefficient differs at most 0.02 % in the four grids, a good indication that the base flow is adequately resolved on all of them. The difference on the growth rate of the CIV mode is 1.5 % between grids M1 and M2, showing that also the coarser grid is appropriate. Concerning the size of the computational domain, the physically meaningful eigenvalues converged when the size of the computational domain is increased, but the spurious eigenvalues become less damped and tend to approach the real axis, with the possible effect of masking the meaningful eigenvalues if they come too close to one another. Therefore, we selected grid M1 as the best compromise between accuracy, size limitations and computational costs.
Table 2. Influence of grid characteristics on some quantities of interest slightly above the CID threshold for the strongly confined case:
![]() $\mathit{Re}=70$
,
$\mathit{Re}=70$
,
![]() ${\it\alpha}=1.19$
.
${\it\alpha}=1.19$
.

The same strategy was adopted in the selection of the grid for the moderately confined case (
![]() $D/H=0.3$
). The drag coefficient of the cylinder and the growth rate of the CID instability are reported in table 2 for a case at
$D/H=0.3$
). The drag coefficient of the cylinder and the growth rate of the CID instability are reported in table 2 for a case at
![]() $\mathit{Re}=70$
and
$\mathit{Re}=70$
and
![]() ${\it\alpha}=1.19$
. Grid M4, which has the smallest size, leads to a significant deviation in the eigenvalue compared with the other grids, revealing a clear confinement effect. The differences on the growth rate for the other grids is at most 4 % (M1–M2). Grid M1 is that used in the study, which provides a good compromise between accuracy, spectrum spreading and computational time.
${\it\alpha}=1.19$
. Grid M4, which has the smallest size, leads to a significant deviation in the eigenvalue compared with the other grids, revealing a clear confinement effect. The differences on the growth rate for the other grids is at most 4 % (M1–M2). Grid M1 is that used in the study, which provides a good compromise between accuracy, spectrum spreading and computational time.