I

Large capital exports from industrialised countries epitomised the working of the international economy after 1870. Great Britain stood out for the size of its invested overseas capital and its diffusion to a broad set of countries.

The academic debate on the determinants of pre-World War I British overseas investments began after J. A. Hobson's pioneering work on British imperialism (1902) and continued until the 1980s. The prevailing interpretations can be grouped into two large theoretical approaches. The first includes theories explaining capital outflows as a response to the pace of the internal economic conditions (the push theories); the second approach is based on the main idea of more profitable investment opportunities abroad (the pull theories). However, a flow of new theories started after the contribution made by Lucas (Reference Lucas1990) to the interpretation of capital movements in the second global age. The Lucas Paradox suggested that capital prefers industrialised countries rather than less developed countries, despite the fact that the return on invested capital would be higher in the latter, at least when physical capital displays diminishing returns. The aftermath of this argument was to give more attention to the quality of the economic fundamentals of borrowing countries and to the institutional setup of the international capital market. Thus, the possible explanations for the Lucas Paradox deal with the unproductive capital view, emphasizing the existence of several barriers to realising high returns on investments in poor countries even in a frictionless global capital market; and the failure view of the global capital market, stressing the misallocation of investments due to several blocks in the international markets. These arguments have been applied to the British experience of capital outflows in the period 1870–1913. For the above reasons, the attraction elements of the borrowing countries were highlighted by Clemens and Williamson, who proposed an interpretation of wealth bias (Clemens and Williamson Reference Clemens and Williamson2004). On the other hand, many contributions have focused on institutional issues, such as the gold standard (Bordo and Rockoff Reference Bordo and Rockoff1996; Obstfeld and Taylor Reference Obstfeld and Taylor2003) and the colonial linkages between Great Britain and the members of its empire (Ferguson and Schularick Reference Ferguson and Schularick2006; Accominotti et al. Reference Accominotti, Flandreau, Rezzik and Zumer2010).

However, recent approaches have tended to neglect the importance of domestic conditions in explaining overseas investments. Both the downward trend of the British GDP growth rate and the contemporary rise of new industrialised countries, such as Germany and the US, suggest a gradual erosion of Great Britain's world leadership. From this perspective, it is reasonable to suppose that British capital migration was triggered by a reduction of the domestic returns on investments or, broadly speaking, by a more general deterioration of internal economic conditions.

A further crucial question to be raised, which has been neglected, is the association between the worsening of the British trade balances and the growth of capital exports since the last quarter of the nineteenth century, despite the fact that the growth of the import excess normally occurs when capital exports decrease. This peculiarity had been formerly considered by Saul (1960), who stressed that overseas investments were a response to the operation of the international trade system of which Great Britain was the core. British imports from the new industrialised countries were paid for indirectly by financing the primary producer countries from which advanced countries imported commodities and to which Great Britain largely exported its goods. This complex framework was implemented in order to maintain the market share of British goods when new competitors began eroding Great Britain's supremacy in the international market. By sustaining a multilateral trade system with domestic capital, Great Britain allowed its economy to survive. Moreover, the expansion of trade simultaneously stimulated the flow of capital. Although, in principle, both channels of transmission are possible, Saul sought to show that causality ran from trade to capital.

In adherence to the previous arguments, the purpose of this work is twofold: firstly to recover the push approach, thus testing the push and the pull hypotheses as a unified framework; and secondly to evaluate whether international trade was a basis for British capital exports. The approach we follow departs from the most recent literature, which focuses on the geography of British capital movements, to provide a consistent and steadfast explanation of the Lucas Paradox.

The article is organised as follows: in Section II we critically review the literature stressing the strong points of earlier and recent contributions; in Section III we discuss the choice of the appropriate dataset for a long-run analysis of British capital exports; in Section IV the push hypothesis is introduced and tested; in Section V we consider the institutional elements; Section VI proposes a unified model and discusses the empirical results tested for their robustness in Section VII. Finally, Section VIII draws some conclusions.

II

The classical argument put forward by the push scholars is based on the unbalanced incomes distribution hypothesis in the nineteenth-century British economy. As incomes became more unequally distributed, savings increased and, on account of low expected profits at home, savings started to flow abroad. Such an argument requires a deficit of the domestic aggregated demand due to underconsumption, which lowered expected investments profitability at home (Hobson Reference Hobson1914). Other explanations deal with the national market failure hypothesis, linking the low-risk profile of the typical British investor to capital outflows. As a result, investing in the domestic market was highly risky because of the lack of information and the inefficient organisation of the domestic capital market. Indeed British firms, but for public administrations and enterprises managing public utilities, had difficulty in accessing the capital market (Saville Reference Saville1961).

The national market failure hypothesis does not hold if the difference in home and foreign returns on capital is considered. In this light, the push theories are questioned and the approaches which pay more attention to external conditions appear to be more robust. Edelstein (Reference Edelstein1976), by far the most influential scholar of the pull theory, explained that British wealth was invested overseas because of the higher realised rate of return abroad. However, he did not exclude the push effect. The foreign returns were certainly higher, but the exceptionally low returns of the domestic bonds in the period 1897–1909 cast more than a doubt on a unique causal effect.

The unsolved problem is whether the push and pull theories are jointly consistent or whether one rules out the other. We put forward the argument that there are two sides to the same coin. It is widely known that capital moves towards the countries where expected returns are more profitable and the risk is not higher. Indeed, the difference in the realised yields points to the direction in which the savings should flow. Such a difference involves both push and pull arguments and it is difficult to establish whether the domestic returns were exceptionally low or the external ones were extremely high. A further element to be considered in determining the capital rate of return is the risk factor that could be higher for foreign assets. Clemens and Williamson (Reference Clemens and Williamson2004) stress, among other things, that foreign returns offset the higher risk. On the contrary, as an optimal portfolio should include both domestic and foreign securities, capital should also flow abroad in the absence of a systematic differential between overseas and home returns (Goetzmann and Ukhov Reference Goetzmann and Ukhov2006).

Moreover, the risk factor in foreign investments involves certain issues often considered by investors: political stability, property rights protection, and the quality of the institutions in the borrowing countries. For these reasons, the institutional setup has received much attention from the most recent literature focusing on the rise of international settlements systems based on gold as well as on the formation and expansion of the British Empire. In fact, it is well established that the greater the monetary stability, ensured by the system of payments, the greater the global capital movements are. In the last quarter of the nineteenth century a large number of countries joined the gold standard, enhancing world monetary stability. Bordo and Rockoff, who defined the gold standard as a commitment to sound fiscal and monetary policies, emphasised that the settlements system, developed in the nineteenth century, lowered the exchange risk premium and the default premium, and finally created a favourable environment for British capital movements (Bordo and Rockoff Reference Bordo and Rockoff1996). However, there is still disagreement on the gold standard's role and on the Empire as a factor for explaining British capital exports. Ferguson and Schularick focused on the Empire effect and considered both membership of the British Empire and adherence to the gold standard as a determinant of the degree of investment protection (Ferguson and Schularick Reference Ferguson and Schularick2006; Ferguson Reference Ferguson2001, 2003). The more law enforcement there is, the higher the degree of protection and the easier it is for capital to move. British investors believed investing in the Empire to be safer than in other countries, because property rights were actually protected by British law. However, this argument is rejected by Obstfeld and Taylor, who found a preferential access to the City market for the countries on the gold standard but not for the Empire's members (Obstfeld and Taylor Reference Obstfeld and Taylor2003). Accominotti et al. (Reference Accominotti, Flandreau, Rezzik and Zumer2010) challenge the Empire effect, reconsidering the underlying concept of such an effect and its magnitude, which was probably underestimated by Ferguson and Schularick.

From the previous discussion, both the early and recent literature offer strong theoretical explanations for capital exports from Great Britain, but these fail to consider the factors all together. A further weakness is that many studies refer to the idea of portfolio investments (PIs) without taking into account foreign direct investments (FDIs). In fact, the latter item has only been marginally considered in recent works because of the focus on the geography of capital movements, facilitated by the available cross-country data for PIs, and because of the lack of FDIs time series broken down by country. On this basis, the choice of the dataset for a long-run analysis of British capital exports should be fully evaluated by looking at the different methods of reconstruction.

III

Two methods of reconstruction were employed in the estimation of the annual time series of British overseas investments.Footnote ¹ Thus, we select a dataset able to satisfy three conditions: reliability, robustness and the aim of the analysis.

The indirect method of reconstruction is based on current account balances, excluding bullion movements. The main argument is that these balances are the potential demand of British investors for foreign assets. In order to obtain a reliable estimation of invested capital abroad, it is necessary to assume the triviality of capital gains or losses which were smoothedFootnote ² by both the stability of the relative price of silver and gold until the beginning of the 1870s, and the diffusion of the gold standard after the middle of the 1870s. However, the robustness of this reconstruction depends on the reliability of current account balances. As the official data on foreign accounts are available from 1853 onwards, we can assume that they are fairly reliable after this date. Following the works of Seyd (Reference Seyd1876) and Shaw-Lefevre (Reference Shaw-Lefevre1878), which covered only a short period, the first systematic attempt of reconstruction was made by Hobson (Reference Hobson1914) whose estimations are extended to the period 1870–1913. Later, the reconstruction of Imlah (Reference Imlah1958) projected Hobson's estimations back to 1830 and updated the underlying data, providing the most robust and reliable series built on the indirect method. The value of the Imlah series lies in the inclusion of both the foreign direct investments and the portfolio investments.

On the contrary, the direct method tries to estimate the foreign assets of British investors starting from the changes in the elements of national wealth located abroad. The problems arising from this methodology range from the troublesome collection of data on overseas financial assets, held by citizens and institutions, to the uncertain definition of the stock of wealth. A further flaw is the complexity of determining whether the financial flows managed in the City belonged to British investors, or whether they simply passed through the major financial market of that period. In particular, the direct method neglects foreign direct investments as it does not take account of the investments outside the financial market. The underlying difference between portfolio and direct investments leads us to evaluate the reliability of the best reconstruction of British capital movements with the indirect method. By collecting the new issues of foreign assets, drawn from the Investor Monthly Manual and the Stock Exchange Year Book (Burdett's Official Intelligence), Simon (Reference Simon and Adler1967a) reconstructed an estimation of the annual portfolio investments and of the corresponding five-yearly series, broken down by country, but he did not consider foreign direct investments such as constitutions, acquisitions and partnerships in enterprises. The recent direct reconstruction of Stone (Reference Stone1999) has the same shortcomings but provides an annual series broken down by country and sector.

Given the different estimation methods, we need a selection criterion in order to decide on the best reconstruction, bearing in mind the purposes of our research, i.e. the long-run determinants of British capital exports. A preliminary data analysis displays the paths of the Imlah and Stone series correlated over the whole period 1870–1913 (see Figure 1); this simple correlation is only weak in the period 1890–1900.

Sources: Imlah (Reference Imlah1958) and Stone (Reference Stone1999).

Figure 1. British overseas investments by the Stone and Imlah estimations

A more robust stochastic analysis suggests that the two time series are generated by a different data process. Firstly, the Imlah series is integrated of order one, whereas it is unclear whether the Stone series has a unit root when this hypothesis is rejected at 95 per cent, using the ADF test. The undisputed presence of a unit root in the Imlah series has important consequences on the econometric analysis of the long-run relationship developed in Section VI. Secondly, to estimate the underlying structure we use the ARMA representation. This class of models provides us with an evaluation of the underlying stochastic process of a random variable in which both autoregressive and moving average components appear. The ARMA representations of both the Imlah and Stone series are reported in Table 1.

Table 1. ARMA process identification. Sample: 1870–1913

Notes: Standard errors are in parentheses. ***p < 0,01. Method: OLS. Residuals of all estimations passed the usual test for heteroskedasticity, serial correlation and normality.

The estimations show that the data-generating processes describing the two datasets are different. The basic interpretation of the outcomes suggests that the Imlah series is more stable, since the included FDIs are immediately non-negotiable or up for withdrawal, and for this reason the volatility of the whole series is lower than the Stone one. This is captured by the first-order autoregressive coefficient, which is higher in the Imlah series, signalling a longer persistence. The Stone series, by definition, only includes portfolio investments that are immediately tradable, enough to bring about a large degree of unpredictability. Moreover, the Imlah series is more persistent and hence more stable than the Stone series because of the higher order of moving average terms. The different stochastic properties are referable to the share of FDIs in the Imlah series. Updated research has shown that British FDIs went up to 30 per cent of the overall capital exports by 1913 (Wilkins Reference Wilkins1988), implying that the Imlah and Stone series have different behaviour and different economic interpretations.

As our purpose is to capture the long-run determinants of capital movements, the Imlah series including FDIs is also more desirable for its completeness.Footnote ³ If we use a series including both the portfolio and foreign direct investments, a possible push effect has to be considered. Nonetheless, since a number of the portfolio investments were not repatriated by 1913, they might have a long-run component justifying a possible push effect as well. This effect can lead to an asymmetric response of the different components of capital exports. As PIs should be responsive to the external rates of return and to diversification in adherence to the portfolio theory (Goetzmann and Ukhov Reference Goetzmann and Ukhov2006), their response to changes in the economic conditions at home should be smaller than the response of the FDIs, which partially react to pure diversification. In fact, the decisions to implement FDIs depended on some internal elements such as productivity at home. Deane (Reference Deane1968) and Feinstein (Reference Feinstein1972) clearly showed that UK productivity fell during this period because of the rise in the cost of both physical capital and labour. When such costs increase, productivity falls if the technological rate is low enough. Edelstein suggested that the introduction of new technologies was prevented in the decades before World War I in the UK by the structure of its economy, which was over-concentrated on non-innovative firms. Moreover, a comparative analysis of the cost of capital had shown that it was at least constant and did not fall. All these elements are captured and summarised by the GDP. The previous discussion concludes that whenever PIs respond to GDP, the FDIs response is larger in magnitude because the former respond mainly to diversification, as portfolio theory suggests.

IV

The push theories reviewed in Section III lack the statistical evidence of a robust push effect. The macroeconomic and the microeconomic explanations sustaining saving excess and market failure hypotheses have been criticised. In fact, any market failure argument is not consistent and not even the excess saving hypothesis can be fully sustained, as Clemens and Williamson (Reference Clemens and Williamson2004) have demonstrated.

In this respect, the main idea suggested in this section tends to recover the push approach insofar as it connects the domestic economic performance with the pace of overseas investments. This topic introduces the long-run path of the British economy in the nineteenth century, a classic workshop of economic historians.

With regard to British growth, several advances have been made since the seminal work of Deane and Cole (Reference Deane and Cole1962). Crafts (Reference Crafts1983) and Crafts and Hurley (1992) shed new light on the success of British economic growth before 1830. In the early 1830s, the British GDP per capita grew slightly faster than in the period 1780–1801, whereas the estimations from 1830 onwards are less revised and the common idea of a GDP growth rate higher than the period before 1830 has prevailed. The issues are whether the British economy fell, or not, in the last quarter of the nineteenth century, and why Great Britain was overtaken and caught up by some follower countries. From Maddison's recent estimations we cannot claim a crisis for Great Britain during the period 1870–1913, if a crude and per capita yearly GDP growth rate of 2.07 per cent and of 1.23 per cent is considered respectively. Nevertheless, a distinct downward trend of industrial production is acknowledged by Crafts et al. (Reference Crafts, Leybourne, Mills, Sylla and Toniolo1991) starting from the middle 1850s until World War I. The focal points are the decline of Great Britain in relation to Germany and the US, and the loss of world leadership.Footnote ⁴ Maddison's (2003) estimations suggest that the US GDP per capita in 1820 was 73.3 per cent of the British one; in 1870 it was 75.3 per cent, and in 1905 the US economy overcame the British one. Instead, Germany had a GDP per capita of 58.6 per cent in relation to Britain in 1870 and of 76.2 per cent in 1913.

We provide an estimation of the long-run trend of British GDP growth, applying the Hodrick–Prescott FilterFootnote ⁵ to Maddison data. We chose to use crude GDP, rather than GDP per capita, in order to capture the historical path of capital formation in a very broad sense. Our results confirm Craft et al.'s analysis showing a mild downward trend of British GDP growth rate over the period 1855–1913; only after 1899 does it slow down dramatically. The growth of the structural component from 1899 to 1913 is lower than from 1855 to 1899 by hardly a half percentage point per annum, suggesting that no structural break exists in the pace of the British economy in 1899–1913. Solomou and Ristuccia (Reference Solomou and Ristuccia2002) report similar results in a recent work, which we discuss below and compare with our estimates (see Table 2).

Table 2. Estimations of the structural component of the GDP growth rate by Solomou and Ristuccia and authors (annual %)

Sources: Solomou and Ristuccia (Reference Solomou and Ristuccia2002), our computations on Maddison's data (2003).

Once the decelerating growth of the British economy has been revealed, we test the hypothesis of the push effect on overseas investments. The expected causal relationship is that the lower the GDP growth rates, the higher the growth rate of overseas investments. As we are connecting the pace of capital exports with the long-run trend of the British economy and with its role as world leader, our argument concludes that British capital flowed abroad in order to achieve the best returns whenever domestic conditions worsened (see Figure 2).

Notes: Annual growth rate of overseas investments (left axis) and annual growth rate of GDP (right axis). The series are filtered by the Hodrick–Prescott filter (1980). Sources: Underlying data are the Maddison (Reference Maddison2003) estimation of GDP and the Imlah (Reference Imlah1958) series for overseas investments.

Figure 2. Structural component of the growth rate of overseas investments and GDP of Great Britain

The contemporary association between GDP and overseas investment annual growth rates (both filtered) is tested in a simple VAR environment using the Granger Causality Test. This procedure consists of a bidirectional test of whether change in one variable in the current period is typically followed by change in another variable in the next period. The test is performed after the selection of an appropriate number of lags to be introduced. The results, reported in Tables 3 and 4, confirm that, in the period considered, the pace of GDP ‘Granger caused’ an overseas investments outflow. We are aware that this is not a sufficient condition, but nevertheless it is necessary for causation. We address this result in the construction of a more detailed model of the determinants of the British capital exports in Section VI.

Table 3. VAR lag order selection criteria

^aLong-period component of the growth rate of British overseas investments. ^bLong-period component of the growth rate of UK GDP.

Table 4. Var Granger causality test

^aLong-period component of the growth rate of British overseas investments. ^bLong-period component of the growth rate of UK GDP.

Given the tested inverse relationship and the simple correlation coefficient of the two variables equal to −0.77, the GDP growth rate is an appropriate candidate to explain the pace of capital exports from Great Britain. Nevertheless, our hypothesis is simultaneously consistent with the pull approach. In fact, the investments opportunity and the expected rates of return of a decelerating economy are likely to discourage domestic accumulation and to promote the shift of capital towards foreign assets.

V

Besides the pull and push effect, other factors determined the growth of capital exports in the decades before World War I: that is, the international payment system, the uninterrupted integration of the global economy due to the multilateral trade relationships, and the exploitation of large and protected colonial markets by Great Britain.

The degree of homogeneity of the global economy was realised in the five decades before 1914, with as many countries as possible integrating into international trade. Great Britain was the core of this complex framework of multilateral partnership, including the colonies, the dominions and several sovereign states. At this stage, we aim to explore the links between international trade, capital movements and the system of payments. With regard to the latter element, the main feature of the system of payments was the adoption of the gold monometallic system by several countries. The generalised shift to gold reduced the interest rates and stimulated capital exports, given that the adherence to the gold standard was a commitment to sound policies reducing a country's risk and the exchange rate risk (Bordo and Rockoff Reference Bordo and Rockoff1996; Obstfeld and Taylor Reference Obstfeld and Taylor2003).

In the framework based on the push and pull factors we want to discuss the role of monetary stability and of its consequences for British capital movements. The traditional argument sustains the role of the gold standard in the light of the reduction of bond spread and of the exchange rate stability. The monetary system enforced the implementation of sound fiscal and monetary policies by overseas countries and led to a more stable domestic financial market. However, it is worth noting that before the generalised adherence to gold, the exchange rates of the countries on different standards (gold, silver or double standards) were stable as long as the gold–silver ratio remained unchanged. Some, such as Flandreau (Reference Flandreau1996), outline that the commitment to the ‘rules of the game’ was pursued even before the generalised shift to gold by way of voluntary adjustments of silver and gold's supply and demand, in order to keep their relative price unchanged. As Flandreau claimed: ‘The bimetallic bloc acted as an arbitrageur of last resort for the world monetary system at large, absorbing disequilibria originating on the international bullion markets.’Footnote ⁶ When monetary stability was threatened by the fall of the price of silver, the peg to the gold standard by many currencies recovered the stability of the exchange rates again. The new equilibrium replaced the old one (Meissner Reference Meissner2005), though some countries adhered to gold later and others, like Italy and Argentina, left the gold standard and then went back.

In the light of economic theory, we cannot ignore the fact that the consistency of the payments system is an explanation for British overseas investments, but it is also true that the stability of the second half of the nineteenth century was achieved in spite of the gold standard. More precisely, we deduce that the gold standard enforced previous stability.

Figure 3 provides a summary of the diffusion of the gold standard for a group of 21 borrowing countries in the period 1870–1913, using an index given by the ratio between the number of countries on gold and all the countries we have considered. If all countries were on gold, the index would be equal to one, if half of them were on gold the index would be 0.5 and so on. The simple correlation with the pace of British overseas investments is weak, which is not enough to suggest an interest for the gold standard diffusion, at least in our framework.

Source: Computation from Meissner (Reference Meissner2005) and Ferguson and Schularick (Reference Ferguson and Schularick2006). For the country list see text in Section VI.

Figure 3. Diffusion of gold standard in 21 selected countries

A further relationship to be analysed in this section is the role of the multilateral trade framework in force until 1914. Since the abolition of the Corn Laws, Great Britain followed a free trade policy in a bilateral trade system. After the adoption of the Cobden–Chevalier agreement of 1860, the multilateral trade system started and world transactions increased dramatically in terms of value and volume until World War I (Mitchell Reference Mitchell2007; Estevadeordal et al. Reference Estevadeordal, Frantz and Taylor2003).

The multilateral framework of international trade was a complex system of settlements offsetting each other. Great Britain was the core and it was compelled to involve as many countries as possible in worldwide trade flows in order to sustain domestic production and preserve British world leadership. Thus, overseas investments were complementary to create the conditions abroad in order to satisfy the demand for British goods and to generate the supply of goods and the natural resources of the borrowing countries, normally exported to the late-comer countries. This was the case for several regions of the Empire and for the Dominions, but not for Canada. For example, Saul (1960) pointed out that British investments in Canada ceased to finance the domestic purchases of goods from the US. However, in several other cases overseas investments were directed towards the creation of the supply of primary goods and raw materials in the borrower countries. Above all, Great Britain imported final goods from the new industrial countries, which in turn imported raw materials from primary producers to which Great Britain exported manufactured and intermediate goods. Taking this context of international trade relationships as a starting point, we claim that the financing of such a multilateral system stimulated capital exports from Great Britain, as suggested by Saul. Hence, the causality relationship can be considered twofold. However, our hypothesis consists of the exploration of the transmission channel from trade to capital exports but not the reverse. The main argument is that, although pre-World War I trade expansion is an open issue, the role of capital movements in trade deepening does not have a clear-cut interpretation. While the growth in trade had several, controversial, explanations, such as the reduction in transportation costs and improvements in communications (O'Rourke and Williamson Reference O'Rourke and Williamson1999; Estevadeordal et al. Reference Estevadeordal, Frantz and Taylor2003), or the growth and convergence process (Pendakur and Jacks 2008), there were no signs of a stimulus from capital movements to trade in this period. Looking at the data for Great Britain, we would expect that the increasing deficit in current balances would produce a reduction of capital outflows; contrary to expectations, overseas investments grew for the purpose of sustaining external trade. Thus, we can identify a strong relationship between British goods exports and capital outflows. The main point is that overseas investments were financed by multilateral trade; to be more precise, by ‘direct exports to the borrower or by means of changes in the level of trade of both lender and borrower with third country’ (Saul 1960, pp. 68). Other essential clues of a causality from international trade to British capital exports is provided by an explorative analysis of a simple two by two VAR, which indicates that Granger causality runs from multilateral trade to British overseas investments but not vice versa.Footnote ⁷ The following section better clarifies the weak exogeneity of multilateral trade in our empirical framework.

Furthermore, colonial markets played a central role inside the mechanism of the multilateral trade relationships, and in particular India. In fact, at the time of trade with the Roman Empire, India was renowned as a basin for its precious metals (Adams and West Reference Adams and West1979). This role did not change as long as India's trade balances remained positive. In this way, Indian exports to the rest of the British Empire and continental Europe indirectly allowed Great Britain to partly finance the excess of its imports. Saul calculated that India financed almost two-fifths of the whole British trade deficit over the period under consideration (Saul 1960). The function of India in this context provides an index to the robustness of the Empire effect. De Cecco (1979) stressed the importance of a protected colonial market for British goods in the face of the free trade that the mother-country imposed on its colonies. Despite a worsening of British competitiveness in many markets, in 1913 the mother-country remained the first exporter to India, selling goods worth 440 million rupees, doing better than Japan and the US, which sold merchandise worth 193 and 150 million rupees respectively.Footnote ⁸ The control over the Indian economy was completed with the British influence on the banking system by means of the appointment of two British administrators of the leading Indian banks of Madras and Bengal. Such control over the monetary system was due to Great Britain's care over monetary stability in this colony both during adherence to the silver standard and during the pegging to gold. At first, the unchanged ratio of silver and gold around 15:1 guaranteed the stability of the exchange rate between the pound and the rupee; later, when the price of silver fell, India adhered to the gold standard fixing the exchange rate at one pence for 16 rupees (Goldsmith Reference Goldsmith1983).

Finally, the existence of a broad colonial market had interesting implications for overseas investments. Ferguson and Schularick (Reference Ferguson and Schularick2006) emphasised the role of membership in the Empire to attract foreign capital, above all whenever this factor was tied to the gold standard; it is worth noting here that this opinion has been criticised by Accominotti et al. (Reference Accominotti, Flandreau, Rezzik and Zumer2010), among others. Furthermore, Ferguson (Reference Ferguson2003) explained that British overseas investments in colonies were highly safeguarded because of the effectiveness of the motherland legal system. As far as the Empire effect is concerned, our perspective is simply to test the role of India in the multilateral trade system, stressing its relevance as a ‘clearing house’.

VI

In Sections III and IV, we tried to critically evaluate the candidate determinants of British capital movements. The aim of this section is to build an empirical model able to consider these elements.

The model to be estimated is described by the following equation:

(1)

where KE is the British foreign investments from Imlah, GDPUK is the British crude GDP, DRRR is the difference between realised returns abroad and at home, and TRADE is the diffusion of multilateral trade relationships proxied by the value of total exports of the borrower countries. Equation (1) does not allow us to study a single country's effect on British capital exports. This derives from the choice, explained in previous sections, of considering a complete time series including both PIs and FDIs for which a yearly breakdown by country does not exist. On the contrary, this leads to the analysis of a wider notion of overseas investments for the presence of FDIs and to jointly test the most relevant questions raised by early and recent literature.

The ‘geography’ approach uses a panel data structure derived from the Simon–Stone estimation of capital outflows. We discussed the reliability of such data in Section III. In our framework, which uses the Imlah series, a panel data structure is not suitable because an annual time series broken by country for the FDIs is not available. In this case, we face a data problem or a trade-off between the completeness provided by a wider notion of overseas investments, the Imlah series and the heterogeneity of the borrowing countries. Inserting the realised rates of return (risk-adjusted) into the time series framework, we proxy the weighted mean of the country-varying pull factors, capturing in some way a piece of such heterogeneity. Although we are aware that our approach leads to a loss of information because heterogeneity is not fully considered, the time series framework fulfils our major aim to explore the determinants of a complete series of overseas investments including FDIs.

Equation (1) is quite restrictive and could be misleading, therefore we specify an alternative model. Firstly, we select a set of countries that borrowed from Great Britain and joined the multilateral trade framework, and for which we have sufficient data to construct the variable TRADE: the US, Canada, Australia, Argentina, India, Brazil, New Zealand, Mexico, Japan, Italy, Spain, Uruguay, Germany, Chile, France, Austria–Hungary, Ceylon, Denmark, Norway, Portugal and Sweden.Footnote ⁹ Such a variable captures the widening and deepening of international trade, but it cannot test the importance of India in the multilateral framework of world trade as depicted in Section IV: in fact the variable TRADE does not include Indian exports which appear separately in the model (TRADEIND). Finally, the DRRR variable is split to control for the realised rates of return at home (RRHOME) and abroad (RROVER). The model becomes:

(2)

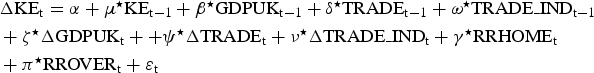
where ɛ_t ~N(0, σ²) and Δ is the first logarithmic difference of the variables.Footnote ¹⁰

Equation (2) provides an empirical framework for testing the hypotheses discussed in the article. For the sake of consistency, we stress that the push effect is captured by GDPUK and RRHOME variables; the pull effect is embodied in the RROVER variable; and finally the hypotheses of a trade effect and an India effect, discussed in Section V, are encapsulated in the TRADE and TRADEIND variables.

After the terms have been rearranged and the coefficients' notation simplified, the estimation results are presented in Table 5, where we show a version of equation (1a) in which the appropriate lags of the variables are chosen using the Akaike (AIC) and Schwarz (BIC) information criteria.

Table 5. Dependent variable: Δ(KE)_t; Obs = 42; sample: 1872–1913; method: OLS

R-squared 0.66, AIC -0.693, BIC -0.155

*** significant at 99% ** significant at 95% * significant at 90%, dummy variable for outlier in 1900 (coeff. -0.5 s. e. 0.152)

The model in Table 5 is an example of an error correction model as in Hendry et al. (Reference Hendry, Pagan, Sargan, Griliches and Intriligator1984). Let us note that KE _t−1= (β₂/β₁)*TRADE _t−1 + (β₃/β₁)*TRADEIND _t−1 + (β₄/β₁)*GDPUK _t−1 is the long-run relationship and that β₁*[KE _t−1 − (β₂/β₁)*TRADE _t−1 − (β₃/β₁)*TRADEIND _t−1 − (β₄/β₁)*GDPUK _t−1] is the equivalent of an error correction term, where β₁ is the loading parameter and the expression in squared brackets is the deviation from the long-run equilibrium. As β₁ <0, the path towards the equilibrium is stable. The coefficients (β₂/β₁), (β₃/β₁) and (β₄/β₁) are the long-run multiplier for the lagged values of TRADE, TRADEIND and GDPUK respectively. This version of the error correction model highlighted the relevance of the push theory in the long run. In fact, the long-run multiplier of lagged GDPUK has a negative sign (−3.14) and the first difference of GDPUK in log, namely the annual percentage variation, showing the short run dynamics, is negative. The worsening of the economic environment at home pushed out national wealth which went in search of better investment opportunities abroad. Moreover, the realised rate of returns at home is not significant. This allows us to argue that the entire push effect is picked up by domestic GDP.

Yet it is also true that capital flowed out for several other reasons. From the estimated model, we can draw that the realised rates of return abroad are strongly significant and that they capture the pull effect. The higher the realised rate of return abroad, the wider the capital exports were. At first glance, this finding seems to disagree with the most recent developments in global capital exports (Bordo and Rockoff Reference Bordo and Rockoff1996; Obstfeld and Taylor Reference Obstfeld and Taylor2003), which claim that the expected signs of the differences in yields abroad and at home should be negative. Indeed, a wider difference in yields would imply a higher risk perceived by investors and hence deter overseas investments. Our estimation of the difference in (realised) rates of return abroad and at home is positive. In fact, testing (β₁₁− β₁₀) = 0 against one side alternative (β₁₁− β₁₀) > 0, we largely reject the null hypothesis and we conclude that more profitable investment opportunities abroad aided the pull of British capital. Let us stress that the divergence of our results from the findings of recent contributions is deceptive. The difference in the realised rates of return is an economically different concept by bond spread used in the above-mentioned works. A positive value of the difference in yields signals a worsening of the economic fundamentals of the borrowing countries, which is certainly true for government bonds but this is quite uncertain for enterprise bonds and completely misleading for profits from direct investments. We simply argue that the data we used are different from those employed by recent contributions. The rates of return used in the empirical framework are risk-adjusted, a reason that should lead us to look at these data in a very different way from the data used in the studies on the ‘geography’ of British capital exports. Therefore, the positive sign of this relation does not reject the global market failure view and it provides some grounds for the hypothesis of a crude pull effect for British investments.

However, the estimations show two further interesting outcomes. The first is the positive effect in the long run of the deepening of foreign trade and the second is India's role in the short and long run. The two hypotheses are those raised in Section IV. Saul's (1960) idea of overseas investments as a response to the purpose of easing multilateral trade relationships finds statistical evidence in the coefficient of the lagged TRADE, i.e. its long-run multiplier is equal to 0.95. The theoretical underpinnings of this relationship are clearly suggested by Saul and we just add a few considerations about the joint significance of the push elements. One way to sustain the British economy or to moderate its downward trend was by the maintenance of its foreign market share. The erosion of British goods competitiveness was offset by the preservation of Great Britain's role as ‘world banker’, which remained the core of multilateral transactions.

Finally, we refine our analysis by introducing a more complex and formal method to set the long- run causal relationships, that is, the Engle and Granger (Reference Engle and Granger1987) two-step procedure. Table 6 provides the fundamental steps of the estimation

Table 6. Two-step Engle-Granger procedure First-stage regression. Dependent variable: KE_t; Obs = 44; sample: 1870–1913; method: OLS

Compared to the model in Table 5, the results are not significantly different. The model is dynamically stable, as proved by the coefficient of the error correction term which is negative and significant. The signs of the variables in a long-run relation with capital export – TRADE, TRADEIND and GDPUK – are also the same and their magnitude does not differ from the previous estimations in Table 5. The short-run dynamics of TRADE, TRADEIND and GDPUK are also confirmed. What is different is the significance of the variable RROVER which the Engle–Granger method rules out as a determinant of capital exports.

VII

Although in the previous sections the theoretical and empirical foundations of the estimated models have been discussed, a robustness check analysis is required to fully justify the one equation approach. The error correction model works only if the cointegration vector of the I(1) variables is the unique one and all the right-hand side variables are weak exogenous. The models estimated in Tables 5 and 6 can be affected by an endogeneity problem of the realised risk-adjusted rates of return. Of course, endogeneity would regard the variables capturing world trade and Indian trade. Following Johansen's (1991) estimation approach, a VAR representation of the model of Tables 5 and 6 is:

where Φ is a (6, 6) matrix, ɛ is the matrix of the disturbances and the lags are chosen using the usual information criteria. The following VECM(2) representation is admitted as the variables of the previous model have three vectors of cointegration (the Johansen test returns a trace statistics of 56.75, which implies the presence of three cointegration equations at 95 per cent):

The β matrix containing the space of cointegration has a rank=3 and we can impose the following restrictions based on the stochastic properties of our variables: the first and second cointegration vectors are defined by RRHOME and RROVER which are stationary, while the third cointegration vector is among the I(1) variables, KE GDPUK TRADE TRADEIND. Basically, in the space of cointegration we can impose that:

The single equation approach of Tables 5 and 6 is valid if the VECM can be marginalised. Using Hendry's (1995) framework, the following system below is estimated and the weak exogeneity is tested for:

The ECM variable is the cointegration equation of the Engle and Granger procedure. If the unique long-run relationship is our model of Tables 5 and 6 then α₂₁ = α₃₁ = α₄₁ = α₅₁ = α₆₁ = 0.

After estimation we performed a Wald test for these joint restrictions finding that they hold (chi-squared 5.28 with a p-value of 0.38). The ECM component has no effect on the other variable but KE. We test also for the weak exogeneity of the RRHOME and RROVER which are not in the ECM. In this case the test is α₁₂ = α₁₃ = α₂₂ = α₂₃ = α₃₂ = α₃₃ = α₄₂ = α₄₃ = α₅₃ = α₆₂ = 0 and we accept these restrictions as well (chi-squared 14.72 with a p-value of 0.1425).

In the light of the previous robustness checks, our specification of a single equation approach is correct, since there is only one cointegration vector among I(1) variables in the space of cointegration, and the hypothesis of the weak exogeneity of all the right-hand side variables of the models in Tables 5 and 6 is consistent with our data.

VIII

This article brings new elements to the debate about the determinants of British overseas investments until World War I. The most recent literature has been mainly concerned with the ‘geography’ of British capital exports, stressing the role of the pull factors (the resource endowment of borrowing countries and foreign rates of return) and the relevance of the institutional setup of the international economy (payment systems and colonial markets). On the contrary, we have moved from concentrating on ‘geography’ to the timing of British capital exports, reintroducing two elements: the internal economic conditions of Great Britain and the pace of world trade. Indeed, the data we used are the time series of overseas investments reconstructed by Imlah, and this allowed us to infer a broader concept of capital exports including foreign direct investments. In fact, recent contributions have relied on the Simon–Stone series collected only from portfolio investments. Whereas, the use of the Imlah series brings about two relevant points: as it includes FDIs and PIs, a more general analysis is possible and elements that are not considered can be reintroduced. The recovery of the push approach is justified as the pace of domestic conditions had negatively influenced, in the long run, the allocation of wealth at home. Moreover, the stochastic properties of the Imlah series address an investigation into a long-run relationship with the other variables we inserted in the model, especially the widening of world trade for which we test a long-run relationship with capital exports, following Saul's (1960) earlier argument.

Hence, the econometric analysis has used two versions of the error correction model, finding that British overseas investments were cointegrated in the long run with the domestic GDP, the diffusion of world trade and India's exports. While the first argument is a recovery of the push theory, the second one tests Saul's hypothesis, and the latter, in some way, supports the relevance of colonial markets. On the other hand, the classical pull element, captured by the realised risk-adjusted rates of return, seems to be important in the short run for British overseas investments, at least whenever a broader concept of capital exports is considered, as in this article.