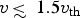1. INTRODUCTION
Currently, the dense plasma has been the subject of active theoretical investigations (Ki & Jung, Reference Ki and Jung2010; Meister et al., Reference Meister, Imran and Hoffmann2011; Benedict et al., Reference Benedict, Surh, Castor, Khairallah, Whitley, Richards, Glosli, Murillo, Scullard, Grabowski, Michta and Graziani2012; Grabowski et al., Reference Grabowski, Surh, Richards, Graziani and Murillo2013; Ramazanov et al., Reference Ramazanov, Kodanova, Moldabekov and Issanova2013; Hong & Jung, Reference Hong and Jung2015; Kodanova et al., Reference Kodanova, Ramazanov, Issanova, Nigmetova and Moldabekov2015b ; Moldabekov et al., Reference Moldabekov, Ludwig, Bonitz and Ramazanov2015a , Reference Moldabekov, Ludwig, Joost, Bonitz and Ramazanov b ; Reinholz et al., Reference Reinholz, Röpke, Rosmej and Redmer2015) due to its relevance to the inertial confinement fusion. In particular, these investigations were triggered by the experiments at the National Ignition Facility (Hurricane et al., Reference Hurricane, Callahan, Casey, Celliers, Cerjan, Dewald, Dittrich, Doppner, Hinkel, Berzak Hopkins, Kline, Le Pape, Ma, MacPhee, Milovich, Pak, Park, Patel, Remington, Salmonson, Springer and Tommasini2014) and magnetized Z-pinch experiments at Sandia (Cuneo et al., Reference Cuneo, Herrmann, Sinars, Slutz, Stygar, Vesey, Sefkow, Rochau, Chandler, Bailey, Porter, McBride, Rovang, Mazarakis, Yu, Lamppa, Peterson, Nakhleh, Hansen, Lopez, Savage, Jennings, Martin, Lemke, Atherton, Smith, Rambo, Jones, Lopez, Christenson, Sweeney, Jones, McPherson, Harding, Gomez, Knapp, Awe, Leeper, Ruiz, Cooper, Hahn, McKenney, Owen, McKee, Leifeste, Ampleford, Waisman, Harvey-Thompson, Kaye, Hess, Rosenthal and Matzen2012). To obtain a thermonuclear reaction in the above-mentioned facilities it is necessary to study such dynamical properties as the stopping power (Hoffmann, et al., Reference Hoffmann, Weyrich, Wahl, Gardes, Bimbot and Fleurier1990; Jacoby et al., Reference Jacoby, Hoffmann, Laux, Muller, Weyrich, Boggasch, Heimrich, Stockl, Wetzler and Miyamoto1995; Hoffmann et al., Reference Hoffmann, Blazevic, Ni, Rosmej, Roth, Tahir, Tauschwitz, Udrea, Varentsov, Weyrich and Maron2005; Barriga-Carrasco & Casas, Reference Barriga-Carrasco and Casas2013; Nersisyan et al., Reference Nersisyan and Deutsch2014; Frenje et al., Reference Frenje, Grabowski, Li, Seguin, Zylstra, Gatu Johnson, Petrasso, Glebov and Sangster2015; Zhang et al., Reference Zhang, Zhao, Qi, Xiao, Duan and Yang2015; Zylstra et al., Reference Zylstra, Frenje, Grabowski, Li, Collins, Fitzsimmons, Glenzer, Graziani, Hansen, Hu, Gatu Johnson, Keiter, Reynolds, Rygg, Seguin and Petrasso2015), thermal conductivity (Reinholz et al., Reference Reinholz, Redmer and Nagel1995; Meister et al., Reference Meister, Hoffmann and Jiang2015), and electrical conductivity (Meister & Röpke, Reference Meister and Röpke1982; Karakhtanov et al., Reference Karakhtanov, Redmer, Reinholz and Röpke2011; Mintsev & Fortov, Reference Mintsev and Fortov2015; Reinholz et al., Reference Reinholz, Röpke, Rosmej and Redmer2015) of dense plasma. All these processes need understanding of microscopic processes in the dense plasma.
In this work, we consider classical electron–ion scattering, Coulomb logarithm, and stopping power for both plasma particles and external beam particles. To describe the electron–ion interaction strength during collisions, the coupling parameter β equal to the ratio of the characteristic interaction energy between two particles to the kinetic energy of the projectile particle was used, β = Z
ion
e
2/(λD
mv
2), here λD is the screening length, Z
ion is the ion charge number, e represents the elementary charge, and mv
2 describes the initial kinetic energy of the projectile far from the target. The initial kinetic energy has to be taken as the mean kinetic energy of relative motion. At low beam velocities, the kinetic energy reduces to the electrons’ thermal energy with velocity
$v_{{\rm th}} = \sqrt {k_{\rm B}T/m_{\rm e}} $
, k
B is the Boltzmann constant, and m
e is the electron mass. As a weakly coupled plasma is considered, scattering of the plasma electron by a plasma ion is characterized by a small coupling parameter β < 1, while the scattering of an electron (ion) of the external beam on the plasma ion (electron) does not have such a limitation.
The quantum diffraction effect is considered using the quantum potential (Deutsch, Reference Deutsch1977; Ramazanov et al., Reference Ramazanov, Moldabekov and Gabdullin2015), whereas the dynamic screening effect is taken into account by simple rescaling of the screening length (Hurricane et al., Reference Hurricane, Callahan, Casey, Celliers, Cerjan, Dewald, Dittrich, Doppner, Hinkel, Berzak Hopkins, Kline, Le Pape, Ma, MacPhee, Milovich, Pak, Park, Patel, Remington, Salmonson, Springer and Tommasini2014). Firstly, the impact of these effects is studied separately, and then the resulting impact of both effects is considered.
In Section 2, the electron–ion effective interaction potential is considered taking into account the quantum diffraction effect as well as screening by the surrounding plasma. In Section 3, the scattering processes in the hot dense plasma are investigated. In Section 4, Coulomb logarithm and stopping power are studied.
2. SCREENED INTERACTION POTENTIAL
The quantum interaction potential of particles, when screening is neglected, has the following form (Deutsch, Reference Deutsch1977):
$${\rm \phi} _{ab} = \displaystyle{{e_ae_b} \over r}[1 - {\rm exp}\,( - r/{\rm \lambda} _{ab})],$$
where
${\rm \lambda} _{ab} = \hbar /\sqrt {2{\rm \pi} m_{ab}k_{\rm B}T} $
is the thermal wavelength, m
ab
= m
a
m
b
/(m
a
+ m
b
), T is the plasma temperature, a and b denote an electron or an ion.
A thorough investigation of scattering processes in a plasma requires that one takes the charge screening into account (Kilgore et al., Reference Kilgore, Daugherty, Porteous and Graves1993). In order to obtain the effective screened potential, a well-known formula for the effective potential in the Fourier space is used:
$${\tilde \Phi}_{ab}(k) = \displaystyle{{{\tilde \phi}_{ab}(k)} \over {{\rm \varepsilon} (k)}},$$
where
${\tilde \phi} _{ab}(k)$
is the Fourier transform of the potential (1) and ε(k) is the static dielectric function of the plasma in linear response approximation:
$${\rm \varepsilon} (k) = 1 + \displaystyle{{n_{\rm e}} \over {k_{\rm B}T}}\widetilde{{\varphi}} _{{\rm ee}}(k) + \displaystyle{{n_{\rm i}} \over {k_{\rm B}T}}\widetilde{{\varphi}} _{{\rm ii}}(k).$$
To account for the quantum diffraction effect, in Eq. (3) we use the quantum (Deutsch) potential: (1) for the electron–electron interaction. The static dielectric function of the plasma in a linear response approximation has the form (Ramazanov et al., Reference Ramazanov, Moldabekov and Gabdullin2015):
$${\rm \epsilon} (k) = 1 + \displaystyle{{k_{\rm e}^2} \over {({\rm \lambda} _{{\rm ee}}^2 k^2 + 1)k^2}} + \displaystyle{{k_{\rm i}^2} \over {k^2}}.$$
where ions are considered as point-like particles λii − 0 and
$k_{\rm i} = \sqrt {4{\rm \pi} ne_{\rm e}^2 /(k_{\rm B}T)} $
,
$k_{\rm e} = \sqrt {4{\rm \pi} ne_{\rm i}^2 /(k_{\rm B}T)} $
.
From Eqs (1)–(4), performing an inverse Fourier transformation, the following screened interaction potential of the electron with the ion was obtained (Ramazanov et al., Reference Ramazanov, Moldabekov and Gabdullin2015):
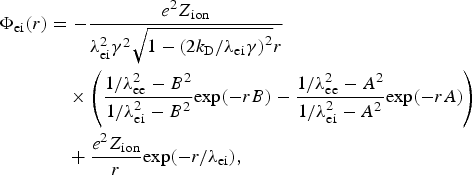$$\eqalign{\Phi_{{\rm ei}}(r) & = - \displaystyle{{e^2Z_{{\rm ion}}} \over {{\rm \lambda} _{{\rm ei}}^2 {\rm \gamma} ^2\sqrt {1 - {(2k_{\rm D}/{\rm \lambda} _{{\rm ei}}{\rm \gamma} )}^2} r}} \cr & \quad \times \left( {\displaystyle{{1/{\rm \lambda} _{{\rm ee}}^2 - B^2} \over {1/{\rm \lambda} _{{\rm ei}}^2 - B^2}}{\rm exp}( - rB) - \displaystyle{{1/{\rm \lambda} _{{\rm ee}}^2 - A^2} \over {1/{\rm \lambda} _{{\rm ei}}^2 - A^2}}{\rm exp}( - rA)} \right) \cr & \quad + \displaystyle{{e^2Z_{{\rm ion}}} \over r}{\rm exp}( - r/{\rm \lambda} _{{\rm ei}}),} $$
where
${\rm \gamma} ^2 = 1/{\rm \lambda} _{{\rm ee}}^2 + k_{\rm i}^2 $
,
$k_{\rm D} = (k_{\rm e}^2 + k_{\rm i}^2 )^{1/2} = 1/{\rm \lambda} _{\rm D}$
is the inverse screening length, and
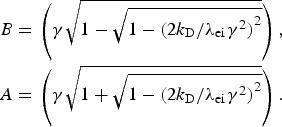$$\eqalign{B = &\, \left( {{\rm \gamma} \sqrt {1 - \sqrt {1 - {(2k_{\rm D}/{\rm \lambda} _{{\rm ei}}{\rm \gamma} ^2)}^2}}} \right), \cr A = &\, \left( {{\rm \gamma} \sqrt {1 + \sqrt {1 - {(2k_{\rm D}/{\rm \lambda} _{{\rm ei}}{\rm \gamma} ^2)}^2}}} \right).}$$
If the quantum diffraction effect is neglected, Eq. (5) turns into the well-known Debye (Yukawa) potential:
$$\Phi _{{\rm ei}}(r) = - \displaystyle{{e^2Z_{{\rm ion}}} \over r}{\rm exp}( - r/{\rm \lambda} _{\rm D}).$$
If the contribution of ions (the third term) in Eq. (4) is neglected, the inverse value of the dielectric function is written as:
$${\rm \varepsilon} (k)^{ - 1} = \displaystyle{{k^2(1 + {\rm \lambda} _{{\rm ee}}^2 k^2)} \over {k^2 + k_{\rm e}^2 + {\rm \lambda} _{{\rm ee}}^2 k^4}},$$
where
$k_{\rm e}^2 = 4{\rm \pi} n_{\rm e}e^2/k_{\rm B}T_{\rm e}$
is the screening parameter due to electrons.
Recently, the exact expansion of the inverse value of the Lindhard dielectric function of electrons in the long wavelength limit was obtained (Moldabekov et al., Reference Moldabekov, Schoof, Ludwig, Bonitz and Ramazanov2015c ). The second-order result of this expansion has the following form:
$${\rm \varepsilon} _2(k)^{ - 1} = \displaystyle{{k^2[1 + ({\tilde a}_2/{\tilde a}_0)k^2]} \over {k^2 + {\kappa} _Y^2 + ({\tilde a}_2/{\tilde a}_0)k^4}}.$$
The result for
$\tilde a_2/\tilde a_0$
is
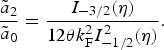$$\displaystyle{{{\tilde a}_2} \over {{\tilde a}_0}} = \displaystyle{{I_{ - 3/2}({\rm \eta} )} \over {12{\rm \theta} k_{\rm F}^2 I_{ - 1/2}^2 ({\rm \eta} )}}.$$
Here k
F = (3π2
n)1/3, I
ν is the Fermi integral of order ν, η = μ/k
B
T, μ is the chemical potential of the electrons.
$k_{\rm Y}^2 = k_{{\rm TF}}^2 {\rm \theta} ^{1/2}$
$I_{ - 1/2}({\rm \eta} )/2$
is the screening length, which interpolates between Debye and Thomas–Fermi expansions, and θ = k
B
T/E
F is the degeneracy parameter, which defines whether the plasma is degenerate or classical.
From the viewpoint of the density functional theory, the dielectric function (9) takes into account the first-order gradient correction of the contribution of the non-interacting kinetic energy to the free energy of electrons (Moldabekov et al., Reference Moldabekov, Schoof, Ludwig, Bonitz and Ramazanov2015c ). The first-order gradient correction correctly predicts a finite cusp at the ionic center (Stanton & Murillo, Reference Stanton and Murillo2015). This is due to the quantum diffraction effect or according to Dunn and Broyles (Reference Dunn and Broyles1967) quantum tunneling effect, which allows particles to reach regions inaccessible for classical particles.
The second-order result of the Lindhard dielectric function expansion (9) has the same form as Eq. (8). The difference is only in constant coefficients. It allows us to conclude that inclusion of the quantum diffraction effect is realized at the same level as the well-known first-order gradient correction in the extended Thomas–Fermi theory. Additionally, this allows us to generalize the effective pair interaction potential (5) to the case of a plasma with degenerate electrons replacing λee and k
De by
$\sqrt {{\tilde a}_2/{\tilde a}_0} $
and k
Y
, respectively.
In the limit θ ≫ 1, the coefficient
$\sqrt {{\tilde a}_2/{\tilde a}_0} $
is equal to
$\hbar /$
$\sqrt {12m_{\rm e}k_{\rm B}T_{\rm e}} $
. This is different from the thermal wavelength used in the quantum pair interaction potential (1) by Deutsch (Reference Deutsch1977), Dunn and Broyles (Reference Dunn and Broyles1967), and Kelbg (Reference Kelbg1963). Here, it is necessary to keep in mind the fact that the Lindhard dielectric function does not take into account plasma non-ideality (electron–electron interaction), whereas the thermal wavelength in the quantum pair interaction potentials obtained as the result of the semiclassical consideration of the weakly non-ideal plasma does. Particularly, recently it was shown that the quantum pair interaction potential in the form of Eq. (1) correctly reproduces the Montroll–Ward contribution to the plasma equation of state in the limit λee
k
D ≪ 1. As we consider a weakly coupled semiclassical plasma, in this work the effective potential (5) is used to study the scattering process and stopping power.
Figure 1 shows the effective screened interaction potential (5). The effective potential (5) takes into account screening at large distances and quantum diffraction effect at short distances.
Fig. 1. Interparticle interaction potentials in units of the thermal energy k B T. Line 1 is the Yukava potential (7), line 2 is the effective potential (5) at different values of the parameter d = λei/λD.
In order to take into account the effect of dynamic screening we use a recipe recently suggested on the basis of highly accurate molecular dynamics data obtained by Grabowski et al. (Reference Grabowski, Surh, Richards, Graziani and Murillo2013). Following this work the screening length was rescaled as
$${\rm \lambda} _{\rm D} \to {\rm \lambda} _{\rm D}\sqrt {1 + {(v/v_{{\rm th}})}^2{(1 + \Gamma ^3)}^{1/4}}, $$
here
$v_{{\rm th}} = \sqrt {k_{\rm B}T/m_{\rm e}} $
, and Γ = e
2/ak
B
T is the plasma non-ideality parameter, a = (3/4πn
e)1/3 is the average distance between the particles.
Such a rescaling procedure was first suggested by Zwicknagel et al. (Reference Zwicknagel, Toepffer and Reinhard1999) [
${\rm \lambda} _{\rm D}\sqrt {1 + (v/v_{{\rm th}})} $
], the formula (11) extends the approach to strong coupling. Recently Dzhumagulova et al. (Reference Dzhumagulova, Shalenov and Gabdullina2013) used Zwicknagel's rescaling procedure to calculate scattering cross-sections within the first Born approximation.
More accurately, to include dynamic screening effects in the weakly non-ideal plasma the following scheme suggested by Gould and DeWitt can be used (Kraeft & Strege, Reference Kraeft and Strege1988; Gericke et al., Reference Gericke, Schlanges and Kraeft1996):
$$\displaystyle{{\partial \langle E\rangle} \over {\partial x}} = \displaystyle{{\partial \langle E\rangle _{{\bf T}\,{\rm matrix}}^{{\rm static}}} \over {\partial x}} + \displaystyle{{\partial \langle E\rangle _{{\rm Born}}^{{\rm dynamic}}} \over {\partial x}} - \displaystyle{{\partial \langle E\rangle _{{\rm Born}}^{{\rm static}}} \over {\partial x}}.$$
In Eq. (12), the stopping power is calculated by the sum of the T-matrix and the dynamic random phase approximation (RPA) subtracting the static first Born term to avoid double counting. In this approximation, strong binary collisions are taken into account by the T-matrix contribution, but the dynamic screening is accounted for in the weak-coupling limit. Further, this ansatz is referred to as combined model. For more details we refer the reader to the works of Zwicknagel (Reference Zwicknagel2009), and Gericke and Schlanges (Reference Gericke and Schlanges1999).
In order to check the quality of the description of the plasma properties on the basis of the effective potential (5), the comparison of the stopping power calculated using the combined model based on T-matrix and first-order Born approximation with the results obtained using the effective potential (5) with the rescaled screening length is given below.
Furthermore, the effective potential with the rescaled screening length will be referred to as the dynamic screened potential.
3. ELECTRON–ION SCATTERING PROCESS
The classical scattering angle for two particles with masses m 1, m 2 and with the interaction potential U(r) for a given impact parameter ρ is equal to
$${\rm \chi} ({\rm \rho} ) = \left \vert {{\rm \pi} - 2{\rm \varphi} ({\rm \rho} )} \right \vert, $$
where
$${\rm \varphi} ({\rm \rho} ) = {\rm \rho} \int_{r_{{\rm min}}}^\infty \displaystyle{{dr} \over {r^2\sqrt {1 - U_{{\rm eff}}(r,{\rm \rho} )}}}, $$
and U eff is the effective interaction energy in the units of kinetic energy of the projectile, E = mv 2/2 has the following form:
$$U_{{\rm eff}}(r,{\rm \rho} ) = \displaystyle{{{\rm \rho} ^2} \over {r^2}} + \displaystyle{{2U(r)} \over {mv^2}}.$$
The effective potential (15) takes the centrifugal force into account. In Eq. (14), r min corresponds to the distance of a minimal approach at the given ρ and is obtained from the equation U eff(r min, ρ) = 1. Using χ(ρ) the scattering cross-section can be obtained from the well-known formula:
$${\rm \sigma} = 2{\rm \pi} \int_0^\infty \left[ {1 - {\rm cos{\rm \chi}} ({\rm \rho} )} \right]{\rm \rho} d{\rm \rho}. $$
As the potential U(r) we took the screened electron–ion interaction potential (5). The scattering process is described by the coupling parameter β and the parameter d = λei/λD, that is, the ratio of the thermal wavelength to the Debye radius. The scattering angle and the scattering cross-section obtained using the effective potential (5) with and without dynamic screening are presented below. For comparison, the scattering angle and the scattering cross-section obtained based on the Yukawa potential (7) with and without dynamic screening are given.
-
a. Influence of the quantum diffraction effect.
First of all, in Figure 2 the results for the Yukawa potential and the effective potential (5) are shown without dynamic screening. It is seen that both the scattering angle and the scattering cross-section decrease with an increase in the parameter d for β < 5. The scattering angle is close to zero for ρ → 0, the possible diffraction of the projectile by the target particle at small impact parameters is related to the finite values of the interaction effective potential at small interparticles distances. Previously, we obtained this effect in (Kodanova et al., Reference Kodanova, Ramazanov, Issanova, Nigmetova and Moldabekov2015b ) where the impact of the quantum diffraction effect on transport properties was considered for β < 1. Here we extend our calculations to the strong coupling limit. On the contrary, at β > 5 the scattering cross-section increases with increasing parameter d. Such a behavior can be explained by the fact that at strong coupling the scattering takes place at a large distance in the Yukawa-type tail of the effective potential (5) (Khrapak et al., Reference Khrapak, Ivlev and Morfill2003; Kodanova et al., Reference Kodanova, Ramazanov, Bastykova and Moldabekov2015a ). The quantum effect of non-locality makes screening at large distances weaker than in the classical case (7) (see Fig. 1), as a result, in the strong coupling limit β > 5 the scattering cross-section increases with an increasing impact of the quantum diffraction effect.
-
b. Influence of the dynamic screening on the beam–plasma scattering. Here, we take into account both the quantum diffraction effect and the dynamic screening effect. Let us first consider scattering of an external beam electron (ion) by a plasma ion (electron). Thus, two parameters Γ and β are independent of each other. For β < 1 we found that when the parameter Γ is close to unity the quantum diffraction effect and the dynamic screening effect compensate each other and together give nearly a null resulting effect such that the effective potential (5) with a rescaled screening parameter gives approximately the same scattering cross-section (dashed line in Fig. 3b) as the Yukawa potential (7) does (solid line in Fig. 3b). It is seen in Fig. 3 where
${\rm \lambda} _{\rm D}^{\ast} $
is a rescaled screening parameter and Γ = 0.8, d = 0.4. For β ≫ 1 the effect of dynamic screening is not important.
Fig. 2. Top panel (a): Scattering angle at β = 0.8 obtained on the basis of the Yukawa potential (full line 1) and on the basis of the interaction potential (5) (dotted lines 2). Bottom panel (b): Scattering cross-section obtained on the basis of the Yukawa potential (full line 1) and on the basis of the interaction potential (5) (dotted lines 2). Here, Γ = 0.8.
Fig. 3. Top panel (a): Scattering angle at β = 0.8 obtained on the basis of the Yukawa potential (full line 1) and on the basis of the interaction potential (5) (dotted lines 2). Bottom panel (b): Scattering cross-section obtained on the basis of the Yukawa potential (line 1) and on the basis of the interaction potential (5) (line 2). Here
${\rm \lambda} _{\rm D}^{\ast} $
is the rescaled screening length, Γ = 0.8 and d = 0.4.
At small values of Γ the dynamic screening and the quantum diffraction effects are unable to compensate each other as it is demonstrated in Fig. 4, where calculations have been done for Γ = 0.2 and Γ = 0.4. In general, the dynamic screening tends to increase the cross-section, while the quantum diffraction effect tends to reduce the scattering cross-section.
-
c. Influence of the dynamic screening on the scattering of the plasma particles by each other.
Finally, we consider the electron–ion scattering in the case when both the projectile and the target belong to the plasma and scattering is caused by thermal motion of particles, therefore we take β < 1. Here, the parameters Γ and β depend on each other as Γ = (β/Z ion)2/36−1/3. As it is seen from Fig. 5a, the general behavior noted above remains valid, the dynamic screening makes the cross-section larger and the quantum diffraction makes the scattering cross-section smaller. Thereby, the quantum effect of diffraction and the dynamic screening have opposite impact on the scattering at β < 1.
Fig. 4. The same as in Fig. 3b but for Γ = 0.2 (top figure) and for Γ = 0.4 (bottom figure).
Fig. 5. Top panel (a): Scattering cross-section obtained on the basis of the Yukawa potential (line 1) and on the basis of the interaction potential (5) (line 2). Here
${\rm \lambda} _{\rm D}^{\ast} $
is the rescaled screening length, Γ = (β/Z
ion)2/36−1/3 and d = 0.4. Bottom panel (b): Scattering cross-section obtained using the effective potential (5) (solid line) within the first Born approximation (dashed line) (Zwicknagel, Reference Zwicknagel2009), and the result of Zwicknagel (Reference Zwicknagel2009) (dashed-dotted line) obtained in the framework of classical scattering of particles interacting via the Yukawa potential at Γ = 0.1, d = 0.2. In the notations of Zwicknagel (Reference Zwicknagel2009) the cross-section is calculated for the parameter
${\rm \kappa} = Ze^2{\rm \mu} _{{\rm ie}}{\rm \lambda} _{{\rm D}/}{\hbar}^2 = 1$
, where μei is the reduced mass.
Figure 5b shows the comparison of the scattering cross-section obtained on the basis of the effective potential (5) (without rescaling of the screening length) with the cross-section calculated in the first Born approximation and with the data of Zwicknagel (Reference Zwicknagel2009) obtained in terms of classical scattering of particles interacting by the Yukawa potential. As it is seen from Figure 5b, the effective potential (5) gives good agreement with the first Born approximation at low values of the collision coupling parameter β. This clearly indicates that the quantum effect of diffraction is correctly described by the effective potential (5).
These features of the scattering cross-section enable us to understand the dependence of the Coulomb logarithm and stopping power in semiclassical plasma on β and d parameters, as both the Coulomb logarithm and the stopping power are related to the cross-section
$E_{\rm c}{\rm \sim} \Lambda _{{\rm ei}}{\rm \sim} \int \mathop {\sin} \nolimits^2 ({\rm \chi} /2)$
${{\rm \sigma} ^{\prime}}d\Omega $
(here Ω is the scattering solid angle, and σ′ is the differential scattering cross-section).
4. COULOMB LOGARITHM AND STOPPING POWER
One of the most important parameters used to describe the interaction of ions with matter is the energy of projectiles. The stopping power is a parameter characterizing the rate of loss of the average energy of fast electrons or ions in plasma. Consequently, the stopping power in the binary collision approximation (Ordonez & Molina, Reference Ordonez and Molina2001; Ramazanov & Kodanova, Reference Ramazanov and Kodanova2001):
$$\displaystyle{{dE} \over {dx}} = 8{\rm \pi} n\left( {\displaystyle{{{\rm \mu} _{{\rm ei}}} \over {m_{\rm i}}}} \right) \cdot E_{\rm c} \cdot b_ \bot ^2 \cdot \Lambda _{{\rm ei}},$$
here E c = (1/2)μeiυ2 is the energy of the center of mass of the colliding particles, υ is the relative velocity of the scattered test particle, b ⊥ = Z ion e 2/(2E c), Λei is the Coulomb logarithm.
Based on the effective interaction potential, the Coulomb logarithm is determined by the scattering angle of the pair Coulomb collisions. Introducing the center of mass in the collision process the Coulomb logarithm is written as (Belyaev et al., Reference Belyaev, Basko, Cherkasov, Golubev, Fertman, Roudskoy, Savin, Sharkov, Turtikov, Arzumanov, Borisenko, Gorlachev, Lysukhin, Hoffmann and Tauschwitz1996; Golubev & Basko, Reference Golubev and Basko1998):
$$\Lambda _{{\rm ei}} = \displaystyle{1 \over {b_ \bot ^2}} \int_0^\infty \mathop {\sin} \nolimits^2 \left( {\displaystyle{{{\rm \chi} ({\rm \rho} )} \over 2}} \right){\rm \rho} d{\rm \rho}. $$
We start from the influence of the quantum diffraction effect on the Coulomb logarithm and stopping power in the case of beam–plasma scattering of the particles. As one can see from Figure 6, at β < 5, the inclusion of the quantum diffraction effect decreases the value of the Coulomb logarithm and the stopping power. It is due to the lower value of the scattering cross-section in comparison with the case when the quantum diffraction effect is neglected. At β > 5, both the Coulomb logarithm and the stopping power increase with increase in the parameter d. This result can be also explained by a larger cross-section than in the case λ = 0 (Yukawa potential).
Fig. 6. Top panel (a): Coulomb logarithm obtained on the basis of the Yukawa potential (line 1) and on the basis of the interaction potential (5) (line 2). Bottom panel (b): Stopping power obtained on the basis of the Yukawa potential (line 1) and on the basis of the interaction potential (5) (line 2) (Γ = 0.8). The stopping power is given in units of k B T/λD.
Now let us consider the influence of the dynamic screening on the beam–plasma scattering. From Figure 7, it is clear that the inclusion of both the dynamic screening and the quantum diffraction effect leads to partial compensation of the impact of these two effects at β < 5. At large values of the parameter β ≫ 1, the effect of the dynamic screening can be neglected, while the quantum effect of diffraction remains important as it was discussed in the previews section.
Fig. 7. Top panel (a): Coulomb logarithm obtained on the basis of the Yukawa potential (line 1) and on the basis of the interaction potential (5) (line 2). Bottom panel (b): Stopping power obtained on the basis of the Yukawa potential (line 1) and on the basis of the interaction potential (5) (line 2). Here
${\rm \lambda} _{\rm D}^{\ast} $
is the rescaled screening length, Γ = 0.8 and d = 0.4. The stopping power is given in units of k
B
T/λD.
Finally, consider the influence of the dynamic screening on the scattering of the plasma particles by each other. In this case, the impact of the dynamic screening increases as the value of the parameter β becomes larger due to the increase of the coupling parameter Γ = (β/Z ion)2/36−1/3, in contrast to the case the beam–plasma scattering (see Fig. 8).
Fig. 8. (a) Coulomb logarithm and (b) stopping power obtained on the basis of the Yukawa potential (line 1) and on the basis of the interaction potential (5) (line 2). Here
${\rm \lambda} _{\rm D}^{\ast} $
is the rescaled screening length, Γ = (β/Z
ion)2/36−1/3 and d = 0.4. The stopping power is given in units of k
B
T/λD.
The comparisons of the calculated values of the stopping power using the effective potential (5) with the results of the combined model, T-matrix model, the first Born approximation, dynamic RPA, and particle-in-cell simulation are shown in Figures 9 and 10.
Fig. 9. Stopping power obtained on the basis of the effective interaction potential (5) with and without rescaling of the screening length in comparison with the results of different theoretical approaches (Gericke & Schlanges, Reference Gericke and Schlanges1999) for (a) Z = 1 and (b) Z = 10. In (b) the stopping power is given in units of 3k B T/λD.
Fig. 10. Stopping power obtained on the basis of the effective interaction potential (5) with and without rescaling of the screening length in comparison with the results of different theoretical approaches (Gericke et al., Reference Gericke and Schlanges1999) for Z = 5. The stopping power is given in units of 3k B T/λD.
From these curves one can see that without rescaling of the screening length the effective potential (5) gives good description of the stopping power at
$v\;{\rm \lesssim}\!\!\lt v_{{\rm th}}$
. Rescaling of the screening length extends this range up to
$v\,{\rm \lesssim}\, 1.5 v_{{\rm th}}$
. For comparison, the combined T-matrix model including dynamic screening leads to a reasonable agreement with the simulation data at velocities
$v\,{\rm \lesssim}\, 3 v_{{\rm th}}$
. At high velocities our results become closer to the Born approximation.
The failure of the simple rescaling of the screening length to correctly reproduce the dynamic screening effect at high velocities is expected, as the potential around the ion in this case has strong deviations from the Yukawa-type potential and has a negative trailing potential minimum behind the ion, which may lead to the attraction between the charged atoms (Moldabekov et al., Reference Moldabekov, Ludwig, Bonitz and Ramazanov2015a , Reference Moldabekov, Ludwig, Joost, Bonitz and Ramazanov b ).
5. CONCLUSION
Classical electron–ion scattering, Coulomb logarithm, and the stopping power were considered taking into account both the quantum diffraction effect and the dynamic screening effect. It was shown that at β < 5, the dynamic screening leads to an increase in the scattering cross-section, Coulomb logarithm, and stopping power. The quantum diffraction effect makes these values smaller than those obtained using the Debye (Yukawa) potential. In contrast, at β > 5 the quantum effect of diffraction enlarges the scattering cross-section as well as the Coulomb logarithm and stopping power, whereas the dynamic screening becomes unimportant (within used model). It is also found that at β < 1 in a dense plasma, when the parameter Γ is close to unity, the considered effects can partially cancel each other.
The comparison of the values of the stopping power calculated on the basis of the model presented in this paper with the results of the combined model, T-matrix method, static Born approximation, and dynamic RPA revealed that our model gives good description of the stopping power at velocities
$v\,{\rm \lesssim}\, 1.5 v_{{\rm th}}$
and has correct behavior at all values of the considered velocities.
These results provide useful information on quantum shielding, collective, and quantum-mechanical effects in the collision processes in dense plasmas.
ACKNOWLEDGEMENTS
This work has been supported by the Ministry of Education and Science of the Republic of Kazakhstan under Grant No. 3083/GF4 (2016) aimed to develop a software package for the study of the transport and dynamic properties of a dense ICF plasmas.
