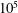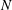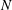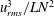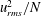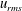1 Introduction
The controls on deep ocean mixing present an important challenge for climate models (Rahmstorf Reference Rahmstorf2006). Cold, saline fluid produced by cooling and ice formation at the poles drives the thermohaline circulation generating Antarctic bottom water (AABW) and North Atlantic deep water (NADW). These water masses spread out through the deep ocean, and then gradually upwell, in part through the Antarctic circumpolar current. However, the details of the flow are complex, and involve interaction with the different ocean basins. As well as the upwelling of deep water to the surface, internal tides and currents lead to turbulent mixing and the associated diapycnal transport of heat and salt through the ocean (Munk Reference Munk1966; Bryan Reference Bryan1987; Wunsch Reference Wunsch2000). The balance between upwelling and diapycnal transport have a strong influence on the stratification of the deep ocean, with key implications for the transport of heat, salt and
$\text{CO}_{2}$
through the oceans (Munk & Wunsch Reference Munk and Wunsch1998; Thorpe Reference Thorpe2005), and hence for climate (Rahmstorf Reference Rahmstorf1994).
Classical models and field observations of the flow in the ocean have shown that internal waves associated with tidal forcing arise on length scales larger than 100–1000 m, with a transition to turbulent mixing on smaller length scales, often associated with wave breaking or other processes, such as the growth of shear instabilities in the flow (Garrett & Munk Reference Garrett and Munk1975; Thorpe Reference Thorpe2005). The development of such a turbulent stratified flow plays an important role in the diapycnal mixing (Riley & Lindborg Reference Riley and Lindborg2008). Ultimately, models of the ocean circulation rely on parameterizations of the diapycnal buoyancy flux,
$B$
, often expressed in terms of an eddy diffusivity,
$\unicode[STIX]{x1D705}=B/N^{2}$
, where
$N$
is the buoyancy frequency (cf. Munk Reference Munk1966), and there has been considerable ongoing effort to provide understanding of the controls on the eddy diffusivity using numerical, experimental and field studies (Osborn Reference Osborn1980; Holford & Linden Reference Holford and Linden1999; Thorpe Reference Thorpe2005; Riley & Lindborg Reference Riley and Lindborg2008; Waterhouse et al.
Reference Waterhouse, MacKinnon, Nash, Alford, Kunze, Simmons, Polzin, St. Laurent, Sun, Pinkel, Talley, Whalen, Huussen, Carter, Fer, Waterman, Naveira Garabato, Sanford and Lee2014; Salehipour, Peltier & Mashayek Reference Salehipour, Peltier and Mashayek2015; Falder, White & Caulfield Reference Falder, White and Caulfield2016).
The classical work of Osborn (Reference Osborn1980) introduced the concept of mixing efficiency, which can be defined as
$\unicode[STIX]{x1D6E4}=BL/u^{3}$
, where
$u^{3}/L$
is the rate of energy dissipation associated with the turbulent flow field of characteristic speed
$u$
and length
$L$
. Osborn proposed that
$\unicode[STIX]{x1D6E4}$
is constant, with a value of the order of 0.2. More recently, Maffioli, Brethouwer & Lindborg (Reference Maffioli, Brethouwer and Lindborg2016) presented a series of DNS calculations of the buoyancy flux through a turbulent stratified flow field, and these demonstrated a transition in the controls on the buoyancy flux, and hence mixing efficiency, between the case of a weakly and strongly stratified flow, as expressed in terms of the Froude number,
$Fr=u/NL$
. For high Froude number, the system is weakly stratified, and the mixing efficiency was found to be inversely proportional to the square of the Froude number, in accord with experiments of Holford & Linden (Reference Holford and Linden1999) in which a grid was oscillated horizontally to mix an initially stratified fluid. After decreasing through a transition region,
$2>Fr>0.3$
, then for smaller Froude numbers,
$Fr<0.5$
, the system is strongly stratified and the mixing efficiency was found to be constant, in accord with the original work of Osborn and the experiments of Kato & Phillips (Reference Kato and Phillips1969), in which a stratified layer was mixed by a rotating lid. This latter picture is also consistent with the buoyancy flux measured in experiments carried out in a cylindrical annulus filled with a two-layer or continuously stratified fluid in which the inner cylinder was rotated to generate a flow with Reynolds numbers of the order of
$10^{5}$
(Woods et al.
Reference Woods, Caulfield, Landel and Kuesters2010; Oglethorpe, Caulfield & Woods Reference Oglethorpe, Caulfield and Woods2013). In these experiments, for sufficiently large stratification, the buoyancy flux was independent of the stratification – suggesting a constant mixing efficiency.
In the present work, we aim to produce a quasi-steady vertical flux of buoyancy driven by a turbulent flow field, subject to a constant source of buoyancy at the base of the system, rather than following the transient run-down of an initially stratified system, as has been the approach of most experiments to date. To this end, we generate a high-Reynolds-number turbulent flow field in a cylindrical annulus by rotating the inner cylinder (cf. Woods et al. Reference Woods, Caulfield, Landel and Kuesters2010), but now we supply a constant flux of saline fluid at the base of the tank and a constant flux of fresh fluid at the top of the tank. In order to maintain a fixed volume of fluid in the tank, we introduce a sink at the base of the experimental tank which removes a volume flux equal to the volume flux supplied to the base of the tank. We also introduce a sink at the top of the tank which removes a volume flux equal to the volume flux of fresh water supplied to the top of the tank. There is no net vertical transport of fluid through the system, but it is possible for there to be a vertical flux of salt, and hence buoyancy, as a result of the turbulent flow field.
In equilibrium, if there is any vertical salt flux through the tank, this will lead to a vertical density gradient and the flux will be extracted by the sink at the top of the tank, while the remainder of the input salt flux will be removed at the base of the tank. In this idealized experimental system, one may associate the sink at the base of the tank with the buoyancy flux transported by oceanic upwelling, while the sink at the top of the tank provides a measure of the diapycnal mixing, although the real situation is of course more complex since there may be some diapycnal mixing in the upwelling flow since this will also be stratified. Nonetheless our aim is to explore the controls on that fraction of the flux of dense fluid supplied to the base of the experimental tank which is transported vertically through the fluid, rather than being extracted by the sink at the base of the system. To this end, we vary the salinity of the supply fluid and the rotation rate of the inner cylinder of the annulus which drives the turbulent mixing.
2 Experimental model
The experimental system (figure 1) we have used in our experiments consists of an annulus of internal radius
$R_{1}=10~\text{cm}$
, external radius
$R_{2}=25~\text{cm}$
, filled with fluid with a depth of
$H=40~\text{cm}$
. The inner cylinder of the annulus can be rotated at speed of up to
$\unicode[STIX]{x1D6FA}=2.5~\text{rad}~\text{s}^{-1}$
, leading to Reynolds numbers
$Re\sim 10^{5}$
, where
$Re=\unicode[STIX]{x1D6FA}(R_{2}-R_{1})^{2}/\unicode[STIX]{x1D708}$
, with
$\unicode[STIX]{x1D708}$
the kinematic viscosity. In our experiments, we supplied a continuous source of saline fluid at the base of the tank, and a source of fresh water at the top of the tank. These were controlled by peristaltic pumps. Finally we withdrew an equal volume of fluid at the base and surface of the tank as were supplied. The source and sink at the top and at the base of the tank were located at the same azimuthal angle, 8.5 cm apart, with the source supplying fluid in the azimuthal direction parallel to the direction of rotation, while the opening of the sink faces upstream, in the azimuthal direction opposite the rotation. The source volume fluxes were fixed in all experiments so that the initial momentum flux of the inflow was the same. The salinity of the outflows were periodically measured using a refractometer, and the vertical density profiles within the tank were continuously monitored using conductivity probes (see Woods et al.
Reference Woods, Caulfield, Landel and Kuesters2010). The suite of experiments we have carried out are summarized in table 1, illustrating the tank rotation rate,
$\unicode[STIX]{x1D6FA}$
, the source salinity of the fluid at the base of the tank,
$S_{bi}$
, and the measurement of the salinity of the fluid collected from the sinks at the top and bottom of the tank,
$S_{to}$
and
$S_{bo}$
respectively. These lead to values for the total buoyancy flux,
$F_{s}$
, supplied to the base of the tank, the inferred total vertical buoyancy flux,
$F_{m}$
, and the flux extracted at the bottom of the tank,
$F_{b}$
. Also, we document the source volume flux,
$Q$
, the time-averaged stratification as measured from the conductivity profiles at a point in the annulus midway between the two cylinders,
$N^{2}$
, once the system is in equilibrium, and the initial condition of the fluid in each experiment is indicated by the abbreviations: LS for a linear stratification; WM for a well-mixed system; 2L for a two-layer stratification and 3L for a three-layer stratification.
Figure 1. (a) Schematic of the transport of deep saline water in the ocean and the role of the upwelling and diapycnal mixing; (b) schematic of the mixing and model upwelling in the laboratory experiment; (c) set-up of the experiments.
Table 1. Parameters of the experiments.
3 Experimental observations
In the experiments, once the source of saline and fresh fluid was turned on, there was a transient regime as the fluid within the tank evolved towards a steady state. This transient regime was in part dependent on the initial density and the density stratification in the tank. In figure 2 we illustrate two typical examples of the evolution of the density towards a steady-state distribution after the sources were turned on from (a) a well-mixed system when the fluid was relatively saline and (b) a two-layer stratification. In each figure, the density at each depth in the tank is shown as a function of time, based on the successive density profiles obtained by the conductivity probe at intervals of 60 s, with the density shown in false colour. In the first case, the supply of relatively fresh fluid at the top of the tank led to layers of relatively fresh fluid which move downwards, gradually increasing in density, while in a similar fashion, the supply of relatively saline fluid led to upward propagating layers of more saline fluid which gradually become less dense as they move upwards. This leads to the gradual generation of a weak stratification across the tank (cf. Oglethorpe et al. Reference Oglethorpe, Caulfield and Woods2013). In case (b) the supply of fresh fluid at the top of the tank again led to the propagation of layers of fresh fluid downwards; these mixed with the more saline fluid as they advanced across the interface. This gradually eroded the two-layer stratification and produced a more continuous density gradient across the depth of the tank.
Figure 2. Evolution of the vertical density profile as a function of time, shown in false colour, for the experiments (a) no 23 and (b) no 17 (table 1).
Once the system has reached a quasi-steady regime, the migration of layers upwards or downwards through the system persists, and this may be seen in the somewhat irregular instantaneous density profiles for four source salinity fluxes as shown in figure 3(a). The figures illustrate that the density contrast across the tank increases with the salinity of the source fluid. In the case in which the source fluid has a salinity of 15 % (wt), a series of transient steps can be clearly seen in the density profile, and these correspond to some of the layers which migrate across the tank (cf. Oglethorpe et al. Reference Oglethorpe, Caulfield and Woods2013). Also with the largest value of the source salinity, a large density jump develops near the base of the tank, above which a more continuous stratification over the remainder of the depth of the tank develops. This results in the flux of salt which is removed from the sink at the base of the tank being much larger than the vertical flux which is transported through the tank. In figure 3(b), we illustrate the transient adjustment of the system to the quasi-steady regime, showing a time series of the vertical density profiles, again in false colour. The system is deemed to have reached quasi-steady state once the salinity of the outflowing fluid does not vary over a time interval of approximately 1 h. In each case, there is a complex pattern of mixing, both during the transient and quasi-steady phases of the experiment, involving the vertical transport of layers of fluid of different density. In figure 3(c), we illustrate the time-averaged variation of salinity with depth for these four cases, with the data being averaged over a period of approximately 60 min. This reveals a more uniform profile, and the error bars on each profile correspond to the magnitude of the time-dependent fluctuations. In figure 3(c) we have normalized the density relative to the value at the centre of the tank, so that all the profiles coincide at this point. We now explore the relationship between these density profiles and the vertical flux of salt transported by the turbulent mixing.
Figure 3. (a) Instantaneous density profiles for four input salinity values taken once the system has reached a quasi-steady state. In this case,
$\unicode[STIX]{x1D6FA}=2.5~\text{rad}~\text{s}^{-1}$
. (b) Time series of the density profiles for each experiment shown in (a). (c) Time-averaged density profiles corresponding to the instantaneous density profiles shown in (a), with error bars corresponding to the magnitude of time-dependent fluctuations.
4 Controls on the turbulent buoyancy flux
It is convenient to present the results in terms of the total vertical buoyancy flux, defined as
$F_{m}=Qg(\unicode[STIX]{x1D70C}_{to}S_{to}-\unicode[STIX]{x1D70C}_{0}S_{0})/\unicode[STIX]{x1D70C}_{0}$
, where
$Q$
is the volume flow rate of each source or sink,
$g$
the acceleration of gravity,
$\unicode[STIX]{x1D70C}_{to}$
and
$S_{to}$
are the density and salinity of the outflowing fluid at the top of the tank and
$\unicode[STIX]{x1D70C}_{0}$
and
$S_{0}$
are the density and salinity of the inflowing (fresh) fluid at the top of the tank. In figure 4(a), we illustrate the total vertical flux of buoyancy,
$F_{m}$
, as a function of the total buoyancy flux supplied at the base of the tank,
$F_{s}=Qg(\unicode[STIX]{x1D70C}_{bi}S_{bi}-\unicode[STIX]{x1D70C}_{0}S_{0})/\unicode[STIX]{x1D70C}_{0}$
, where
$\unicode[STIX]{x1D70C}_{bi}$
and
$S_{bi}$
are the density and salinity of the supply fluid at the base of the tank. The buoyancy flux is shown for seven values of the tank rotation rate (table 1). For each rotation rate, we find that the vertical buoyancy flux increases linearly with the source buoyancy flux until the source buoyancy flux reaches a critical value,
$F_{s,max}$
, at which the vertical buoyancy flux appears to reach a maximum,
$F_{m,max}$
.
Figure 4. (a) Variation of the vertical buoyancy flux,
$F_{m}$
, across a horizontal plane located at mid-depth of the tank as a function of the bottom source buoyancy flux,
$F_{s}$
, for several values of the rotation rate
$\unicode[STIX]{x1D6FA}$
, as shown on each set of data. (b) Maximum or saturated value of the salt flux
$F_{m,max}$
as a function of
$R_{1}^{2}\unicode[STIX]{x1D6FA}^{3}\unicode[STIX]{x03C0}(R_{2}^{2}-R_{1}^{2})$
for (green circles) present study and (blue circles) Woods et al. (Reference Woods, Caulfield, Landel and Kuesters2010) (W10). (c) Variation of the buoyancy flux as a fraction of the saturated value, as a function of the ratio
$N/\unicode[STIX]{x1D6FA}$
, in the range
$\unicode[STIX]{x1D6FA}=2.50-1.75~\text{rad}~\text{s}^{-1}$
. Open circles refer to unsaturated flux, full circles refer to saturated flux. (d) Variation of the vertical buoyancy flux,
$F_{m}$
, as a fraction of source flux,
$F_{s}$
, as a function of the ratio of the source flux and the maximum flux for that rotation rate
$F_{s}/F_{m,max}$
.
Further increases in the source buoyancy flux do not increase the vertical buoyancy flux beyond this maximum. We therefore envisage that for smaller source buoyancy fluxes, the vertical buoyancy flux is supply limited, while for larger source buoyancy fluxes, the vertical transport is limited by the turbulent mixing. To explore this further, we first examine the dependence of the maximum vertical buoyancy flux,
$F_{m,max}$
on the rotation rate. We find that, to good approximation, this maximum buoyancy flux varies as the cube of the rotation rate (figure 4
b). This dependence is analogous to the earlier findings of Woods et al. (Reference Woods, Caulfield, Landel and Kuesters2010) (equation (3.2)). Indeed, we can express the maximum buoyancy flux in the form:
$$\begin{eqnarray}F_{m,max}=\unicode[STIX]{x1D6FC}R_{1}^{2}\unicode[STIX]{x1D6FA}^{3}\unicode[STIX]{x03C0}(R_{2}^{2}-R_{1}^{2}),\end{eqnarray}$$
and this is shown by the solid line in figure 4(b). Equation (4.1) describes the present experimental data for the maximum flux (green dots), and the experimental data of Woods et al. (Reference Woods, Caulfield, Landel and Kuesters2010) (blue dots), provided that
$\unicode[STIX]{x1D6FC}$
has value
$\unicode[STIX]{x1D6FC}=1.26\times 10^{-4}$
. With the system at this maximum buoyancy flux, there is a range of possible stratifications in the fluid depending on the source flux and the initial conditions in the tank, as seen in table 1; this suggests the buoyancy flux is independent of the stratification in this regime. For each rotation rate, we can use expression (4.1) to normalize the buoyancy flux across the tank and thereby illustrate how, in the supply-limited regime, the vertical buoyancy flux is reduced. In order to explore the controls on the vertical buoyancy flux as the source buoyancy flux decreases from the critical value at which the vertical buoyancy flux reaches its maximum, we now explore how the buoyancy flux depends on the ambient stratification. In figure 4(c), we show the vertical buoyancy flux, scaled with the maximum buoyancy flux (expression 1), as a function of
$N/\unicode[STIX]{x1D6FA}$
. The dimensionless vertical buoyancy flux appears to vary nearly linearly with
$N/\unicode[STIX]{x1D6FA}$
for
$0.02<N/\unicode[STIX]{x1D6FA}<0.16$
, while reaching a nearly constant value for larger values of
$N/\unicode[STIX]{x1D6FA}$
. We do not have data for smaller values
$N/\unicode[STIX]{x1D6FA}<0.02$
.
To illustrate the relationship between the vertical flux and the source buoyancy flux, in figure 4(d) we illustrate the fraction of the source buoyancy flux which is transported vertically across the tank as a function of the ratio between the source flux,
$F_{s}$
, and the maximum vertical buoyancy flux,
$F_{m,max}$
. We see that the vertical transport of buoyancy,
$F_{m}$
, becomes progressively smaller as a fraction of the total buoyancy flux as the source buoyancy flux increases. Note that for very small buoyancy flux, the vertical transport of buoyancy tends to the fraction 0.5 of the source flux, and this limit corresponds to the system being well-mixed.
5 Discussion
The experiments reported in this work suggest that the vertical transport of buoyancy by a turbulent flow can be rate-limited by either the source buoyancy flux or the turbulent transport. The mechanism of buoyancy transport by the turbulent flow field appears to involve a series of layers of relatively saline fluid which form at the base of the tank, gradually become less dense through the action of the turbulent velocity field, and ascend through the tank, or in some cases, relatively fresh layers of fluid which form at the top of the tank, gradually become denser and descend through the tank. The flux boundary conditions at the top and base of the system therefore appear to play a central role in the buoyancy transport as the system reaches a quasi-steady regime. Theoretical models of the buoyancy transport have been developed which predict layering (e.g. Barenblatt et al. Reference Barenblatt, Bertsch, Dal Passo, Prostokishin and Ughi1993; Balmforth, Smith & Young Reference Balmforth, Smith and Young1998), but the present work provides experimental evidence for the persistence of such layers as a result of the continuing buoyancy flux at the base and top of the system.
In the case that the flux is limited by the turbulence, we find that the horizontally averaged vertical buoyancy flux per unit area is given by
$$\begin{eqnarray}B=1.26\times 10^{-4}\unicode[STIX]{x1D6FA}^{3}R_{1}^{2}.\end{eqnarray}$$
Since the velocity field in the tank is driven by the rotation of the inner cylinder of speed
$\unicode[STIX]{x1D6FA}R_{1}$
, this regime suggests a constant mixing efficiency,
$\unicode[STIX]{x1D6E4}_{B}=B/E$
, where
$E$
is the rate of dissipation of turbulent kinetic energy. Indeed, PIV measurements of the flow field for the two-layer system have shown that the root mean square velocity fluctuations,
$u_{rms}(r)$
, scale as
$0.086\unicode[STIX]{x1D6FA}R_{1}^{2}/r$
(cf. Woods et al.
Reference Woods, Caulfield, Landel and Kuesters2010). Using this turbulent velocity field as an approximate description of the present flow, we estimate the mean turbulent dissipation rate per unit area across the annulus has the form
$$\begin{eqnarray}E={\displaystyle \frac{1}{L}}{\displaystyle \frac{\displaystyle \int _{R_{2}}^{R_{1}}u_{rms}^{3}r\,\text{d}r}{\displaystyle \int _{R_{2}}^{R_{1}}r\,\text{d}r}}={\displaystyle \frac{1.45\times 10^{-4}\unicode[STIX]{x1D6FA}^{3}R_{1}^{3}}{L}},\end{eqnarray}$$
where
$L$
is the length scale of the turbulent fluctuations. Observations of the dispersion and mixing of dye streaks within the flow suggest that the turbulent fluctuations have length scales of the order of 2–4 cm. Using these values, we estimate that the mixing efficiency of the flow lies in the range
$0.15<\unicode[STIX]{x1D6E4}_{m}<0.35$
. This maximal flux limit arises in the more strongly stratified cases, in which the turbulence controls the transport. This is consistent with the original estimates of Osborn (Reference Osborn1980), who proposed that
$\unicode[STIX]{x1D6E4}=0.2$
. Also, recent numerical calculations of Maffioli et al. (Reference Maffioli, Brethouwer and Lindborg2016) found that
$\unicode[STIX]{x1D6E4}$
is approximately constant at low Froude number,
$Fr$
, defined as
$Fr=u_{rms}/NL$
(cf. Maffioli et al.
Reference Maffioli, Brethouwer and Lindborg2016).
As the source flux decreases, the vertical flux of buoyancy appears to become limited by the source rather than the turbulence, and the system becomes more weakly stratified. Now the buoyancy flux does depend on the stratification (figure 4 c), and appears to follow the approximate law (figure 5)
$$\begin{eqnarray}B=B_{max}{\displaystyle \frac{Fr_{c}}{Fr}},\quad \text{for}~Fr_{c}<Fr<10,\end{eqnarray}$$
and assuming that
$E$
follows the relation (5.2), this suggests the approximate law
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{m}\frac{Fr_{c}}{Fr},\quad \text{for}~Fr_{c}<Fr<10,\end{eqnarray}$$
where the critical Froude number at which the buoyancy flux becomes dependent on
$N$
occurs at approximately
$Fr_{c}=0.8\pm 0.3$
. It would be interesting to test (5.4) with more PIV data.
Figure 5. Variation of the buoyancy flux, as a fraction of the saturated value, as a function of the inverse of the Froude number.
In the high-
$Fr$
case, the approximate model for the flux, equation (5.3), suggests that the vertical diffusivity is proportional to
$u_{rms}LFr=u_{rms}^{2}/N$
. If the turbulence is approximately isotropic, this may be interpreted as the product of the horizontal and therefore vertical r.m.s. velocity and the vertical displacement associated with this velocity,
$u_{rms}/N$
, assuming that a fraction of the kinetic energy is converted to potential energy. In the low-
$Fr$
case, the stratification is stronger and the experimental data suggest that vertical transport of buoyancy has effective diffusivity proportional to
$u_{rms}^{3}/(LN^{2})=u_{rms}LFr^{2}$
(cf. Billant & Chomaz Reference Billant and Chomaz2001). The experiments for high-
$Fr$
mixing suggest a decrease of mixing efficiency with
$1/Fr$
for
$0.8<Fr<10$
. This range of
$Fr$
corresponds to those values at most a factor of 10 larger than
$Fr_{c}$
, the maximum value of
$Fr$
for which there is near-constant buoyancy flux. The data presented by Maffioli et al. (Reference Maffioli, Brethouwer and Lindborg2016) show a decrease of the mixing efficiency as
$Fr$
increases beyond about 0.3. In their calculations, as
$Fr$
increases from approximately 0.3 to 1.5 (see their figure 4), the data are approximately consistent with a near-linear relation between mixing efficiency and
$1/Fr$
, although there are only four data points shown and so testing such trends definitively is somewhat difficult. For
$Fr$
in excess of 1.5, the mixing efficiency has decayed below 0.1 and follows a
$1/Fr^{2}$
scaling. This latter range is beyond the limits which we can test with our apparatus, since in this limit, the system becomes nearly well-mixed.
Although the experimental system is rather simplified, it is nonetheless interesting to note that, in the deep ocean, the typical current velocities have magnitudes of the order of
$0.1-1.0~\text{m}~\text{s}^{-1}$
, and that eddies with sizes of the order of 100 m represent the largest scales at which turbulent mixing and dissipation develop (Sheen, White & Hobbs Reference Sheen, White and Hobbs2009; Falder et al.
Reference Falder, White and Caulfield2016). The stratification in the deep ocean has values in the range
$N^{2}\sim 10^{-4}{-}10^{-5}~\text{s}^{-2}$
, and so the Froude number is expected to be of the order of 0.1–10.0. This range of values suggests that in different regions of the deep ocean the mixing may be controlled by either the local intensity of the turbulence, with a constant mixing efficiency, or perhaps, in regions of more intense turbulence, by the source buoyancy flux. Also, the extent of these different regions may vary with fluctuations in the strength of the thermohaline circulation which supplies the source buoyancy flux.
