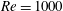2 Approach

We consider the flow over a finite wing based on a NACA0012 aerofoil with a full-span aspect ratio of $2.5$ and an angle of attack of $\unicode[STIX]{x1D6FC}=5^{\circ }.$ The Reynolds number, defined by the free-stream velocity $U_{\infty }$ and the chord $c$ , is $Re=1000$ . The variables $U_{\infty }$ and $c$ are also used to render all variables dimensionless. In this section, we state the governing equations underlying our control design and outline the computational set-up for our analysis.

2.1 Parabolized stability analysis

The geometric configuration of a finite wing, coupled with our focus on the interaction of the downstream wake and trailing vortex, allows a linear framework for the description of the perturbation dynamics. A further simplification is linked to the quasi-two-dimensional nature of the flow, where the base flow is assumed to vary only slowly in the streamwise direction. The latter simplification motivates the formulation of the perturbation dynamics by the Parabolized Stability Equations (PSE), expressed as an initial-value problem in the streamwise direction (Herbert Reference Herbert1997).

The linear assumption introduces the decomposition of the state vector $\tilde{\boldsymbol{q}}$ into a base $\tilde{\boldsymbol{Q}}$ and a perturbation $\hat{\boldsymbol{q}}$ of infinitesimal amplitude. The base component $\tilde{\boldsymbol{Q}}$ satisfies the steady, nonlinear Navier–Stokes equations; the perturbation part is governed by the linearized Navier–Stokes equations. Prompted by the slow variation of the base flow in the streamwise direction, we assume the perturbation state vector $\hat{\boldsymbol{q}}$ in the form

(2.1) $$\begin{eqnarray}\hat{\boldsymbol{q}}(\boldsymbol{x},t)=\boldsymbol{q}(\unicode[STIX]{x1D716}x,y,z)\exp \left(\text{i}\int _{x}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D709})\,\text{d}\unicode[STIX]{x1D709}-\text{i}\unicode[STIX]{x1D714}t\right).\end{eqnarray}$$

This decomposition consists of a product of a slowly varying shape function $\boldsymbol{q}$ and a rapidly varying phase function. Moreover, the perturbation has been assumed periodic in time, and a Fourier transform in this direction introduces the real-valued frequency $\unicode[STIX]{x1D714}.$ The small parameter $\unicode[STIX]{x1D716}$ is taken as $O(Re^{-1})$ , and the local streamwise wavenumber $\unicode[STIX]{x1D6FC}$ is allowed to vary slowly with $x$ . Upon substitution of the above decomposition (2.1) into the linearized Navier–Stokes equations, we can neglect $O(\unicode[STIX]{x1D716}^{2})$ elliptic terms in $x$ , and thus parabolize the governing equations in the streamwise direction. Formally, we can then recast the governing equations as an initial-value problem shown as:

(2.2) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D63D}\frac{\unicode[STIX]{x2202}\boldsymbol{q}}{\unicode[STIX]{x2202}x}=\unicode[STIX]{x1D63C}\boldsymbol{q}\\ \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{q}}{\unicode[STIX]{x2202}x}=\unicode[STIX]{x1D63D}^{-1}\unicode[STIX]{x1D63C}\boldsymbol{q}=\unicode[STIX]{x1D647}\boldsymbol{q},\end{array}\right\} & & \displaystyle\end{eqnarray}$$

which constitutes an evolution equation in $x$ and can hence be marched in the streamwise coordinate direction. The particular form of the matrix $\unicode[STIX]{x1D647}$ is omitted for brevity but can be derived following Paredes et al. (Reference Paredes, Theofilis, Rodríguez and Tendero2011) while retaining the spanwise $z$ -derivatives.

The decomposition (2.1) into shape and phase functions is ambiguous and requires further specifications to render it unique. Commonly, an auxiliary equation of the form

(2.3) $$\begin{eqnarray}\iint _{S}\boldsymbol{q}^{H}\frac{\unicode[STIX]{x2202}\boldsymbol{q}}{\unicode[STIX]{x2202}x}\,\text{d}S=\iint _{S}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\frac{1}{2}\boldsymbol{q}^{H}\boldsymbol{q}\right)\,\text{d}S=0\end{eqnarray}$$

is adopted, with $S$ denoting the $y$ – $z$ plane. Physically, this equation enforces that the kinetic energy of the shape function is invariant under a downstream translation. Mathematically, it enforces orthogonality between the shape function and its streamwise derivative, and thus retains only the non-exponential behaviour (in $x$ ) in the shape function; the exponential components are relegated to the (rapidly varying) phase function. Equations (2.2) and (2.3) have to be solved simultaneously at each position in $x$ , as the perturbation state vector is marched downstream in the streamwise direction. A spectral collocation method is used in the cross-stream directions and backward difference in the streamwise direction to solve the initial-value problem numerically. To ensure grid independence, a grid resolution check has been performed, ensuring that $81\times 81$ Chebyshev collocation points provide sufficient spatial resolution (Edstrand et al. Reference Edstrand, Schmid, Taira and Cattafesta2018).

2.2 Direct numerical simulations

Direct numerical simulations are performed for flow over a half-span wing using the incompressible flow solver Cliff (from the CharLES software suite (Ham & Iaccarino Reference Ham and Iaccarino2004; Ham, Mattsson & Iaccarino Reference Ham, Mattsson and Iaccarino2006)). They complement and support the modal analysis based on the PSE. Second-order finite-volume and time-integration schemes are used to solve the discretized Navier–Stokes equations. The computational set-up is shown in figure 1. The origin of the Cartesian coordinate system is placed at the trailing edge of the wing tip while $x$ -, $y$ - and $z$ -directions represent the streamwise, transverse and spanwise directions, respectively. A computational domain of $[x/c,y/c,z/c]\in [-15,15]\times [-15,15]\times [-1.25,14.375]$ is used. In the present numerical study, we only consider the half-span ( $b/2c=1.25$ ) of the wing and impose symmetry boundary conditions as illustrated in figure 1. At the inlet, a free-stream velocity vector of $[\tilde{u} ,\tilde{v},\tilde{w}]=[U_{\infty },0,0]$ is prescribed and, at the outlet, convective boundary conditions are specified. For all other far-field boundaries, slip conditions are employed. The mesh contains approximately 3.5 million volume cells, which is based upon our previous work (Edstrand et al. Reference Edstrand, Schmid, Taira and Cattafesta2018) that contains a grid resolution study to ensure adequate spatial resolution.

Figure 1. Schematic of trailing vortex wake of a three-dimensional half-span aerofoil with NACA0012 profile. Isosurfaces of streamwise vorticity $\tilde{\unicode[STIX]{x1D714}}_{x}=-0.8$ (transparent grey) and streamwise velocity perturbation (blue and red) of body force are visualized.

With an objective to attenuate tip-vortex strength, we introduce a modal-based body force for flow control, guided by the present parabolized stability analysis. We use the insights from the parabolized stability analysis, such as the spatial perturbation distribution for $\boldsymbol{q}$ and the associated temporal frequency $\unicode[STIX]{x1D714}$ and streamwise wavenumber $\unicode[STIX]{x1D6FC}$ to introduce a three-dimensional body force $\boldsymbol{f}_{q}$ expressed as

(2.4) $$\begin{eqnarray}\boldsymbol{f}_{q}(x,y,z,t)=A\unicode[STIX]{x1D714}\boldsymbol{q}_{r}(y,z)G(x)\sin (\unicode[STIX]{x1D714}t+\unicode[STIX]{x1D719}),\end{eqnarray}$$

where $A=0.5$ is the forcing amplitude and $\unicode[STIX]{x1D719}$ is a reference phase. The values of $\unicode[STIX]{x1D714}$ and the real component of mode $\boldsymbol{q}_{r}$ are derived from the parabolized stability analysis. In our case, the mode shape function $\boldsymbol{q}_{r}$ consists only of velocity disturbances $[u,v,w]$ with unit magnitude ( $\Vert \boldsymbol{q}_{r}(y,z)\Vert =1$ ). A Gaussian distribution $G(x)$ of the form

(2.5) $$\begin{eqnarray}G(x)=\frac{1}{\sqrt{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D70E}^{2}}}\text{e}^{-((x-0.25c)^{2}/2\unicode[STIX]{x1D70E}^{2})}\end{eqnarray}$$

places the body force one quarter-chord aft of the trailing edge with a variance $\unicode[STIX]{x1D70E}^{2}=4\times 10^{-4}$ , providing a sufficiently compact forcing to render negligible the influence of the streamwise wavenumber $\unicode[STIX]{x1D6FC}$ on the chosen force $\boldsymbol{f}_{q}$ in (2.4).

For controlled flow simulations, the mesh is further refined in two regions to ensure accurate results: the first region is around $x/c=0.25$ , where the body force is introduced, and the second region covers the wake zone downstream of the trailing edge. The refined mesh contains approximately five million cells and has been verified (through additional grid resolution studies) to capture all relevant features of the unsteady controlled flows.

3 PSE analysis of the wake

The streamwise parabolic nature of the PSE requires an initial condition upstream. This initial condition is taken from a global stability analysis using a locally parallel flow assumption (see Edstrand et al. Reference Edstrand, Schmid, Taira and Cattafesta2018). The parallel analysis is performed at a streamwise location of $x/c=0.25$ where the wake deficit is significantly larger than the nascent vortex. Using three different initial conditions at $x/c=0.25,0.5$ and $1$ , the growth rates collapse to a single curve (not shown) through marching the PSE, thus justifying the chosen initial condition at $x/c=0.25$ . We then perform a parametric study varying the frequency to determine the most unstable parallel flow case at $x/c=0.25$ , corresponding to $\unicode[STIX]{x1D714}=4.5$ . Consequently, a wake branch occurs with five unstable wake-dominated modes, as well as a vortex branch containing a single vortex mode, as shown by the blue dots in figure 2(a). For further insight into the spectrum, the reader is referred to Edstrand et al. (Reference Edstrand, Schmid, Taira and Cattafesta2018). In this work, we focus on the characteristics of the most unstable mode, termed the principal wake mode (figure 2 b), and the mode with the smallest growth rate, the fifth wake mode (figure 2 c).

In light of our goal to attenuate the trailing vortex, it initially appears prudent to use the principal (most unstable) mode rather than the mode with the smallest unstable growth rate. However, observing the progression of the growth rates as we move downstream (see the black lines in figure 2 a), the growth rate of the principal wake mode decays monotonically whereas the fifth wake mode becomes increasingly unstable farther downstream as the base-flow vortex develops. Insight into this eventual instability can be gained by observing the progression of each mode shape function. The key observation relates to the direction of rotation of the two modes: the principal mode imposes a counterclockwise rotation on the co-rotating trailing vortex, whereas the fifth mode shows an opposing counter-rotating structure at the same location (see figure 3 and insets). The eventual clockwise nature of the fifth wake mode far downstream is indicative of a vortex instability (Khorrami Reference Khorrami1991; Mayer & Powell Reference Mayer and Powell1992), whereas the counterclockwise rotation of the principal wake mode is the result of base flow field convection. The structure of the vortex instability has important implications with respect to flow control. Specifically, despite the fact that the principal wake mode has a larger growth rate upstream, the fifth wake mode may provide a pathway to excite the vortex instability farther downstream that may result in the effective attenuation of the tip vortex.

As such, we hypothesize that excitation of the fifth wake mode will accelerate the decay of the trailing vortex. To test this theory, we perform direct numerical simulations on the trailing vortex flow field with forcing in the shape of the principal wake mode and the fifth wake mode to investigate the effect of the force on the vortex development downstream relative to the baseline (no control) case. Both modes are triggered by localized body forces in the wake near the trailing edge of the aerofoil; a superposition of them enables access to and provides controllability of the trailing vortex flow. These two modes will thus form the basis of a control strategy for the breakup of the trailing vortex flow.

Figure 2. (a) The blue dots represent the eigenvalue spectrum of the initial condition at $x/c=0.25$ , with the grey shaded area denoting the unstable half-plane. The lines represent the change in growth rate with downstream progression, with red dots indicating the location of integer chord numbers (i.e. $x/c=1,2,\ldots$ ). (b,c) Streamwise-vorticity shape functions of the (b) principal and (c) fifth wake modes.

Figure 3. Isosurfaces of streamwise vorticity $\unicode[STIX]{x1D714}_{x}=\pm 0.008$ for the (a) principal and (b) fifth wake modes in the tip-vortex region. The insets correspond to a cross-sectional cut of streamwise vorticity $\unicode[STIX]{x1D714}_{x}$ . The broken arrows indicate the rotation directions of the modes.

4 PSE-inspired flow control

The spatial profile of the fifth mode presents a counter-rotating feature near the tip-vortex core as it evolves downstream. As such, this mode holds a potential to effectively attenuate the tip vortex. Although this mode is not the most unstable mode, it is known from past free vortex studies that counter-rotating instabilities can efficiently destabilize the vortex core (Khorrami Reference Khorrami1991; Mayer & Powell Reference Mayer and Powell1992). In this section, we consider using the spatial profiles of the principal and fifth modes as a local forcing input behind the trailing edge, and assess their control effectiveness in reducing the tip-vortex strength.

Figure 4. Isosurfaces of the three-dimensional body force $f_{u}$ , $f_{v}$ and $f_{w}=\pm 0.18$ for $x$ -,  $y$ - and $z$ -momentum equations, respectively. The values of isosurfaces are indicated in the figure with a reference of $\Vert \boldsymbol{q}_{r}\Vert =1$ . Blue and red represent negative and positive values, respectively. Body force profiles are based on the (a) principal and (b) fifth wake modes.

The spatial structures of the real part of the shape function from the stability analysis $\boldsymbol{q}_{r}(\boldsymbol{x})=\text{Re}\{\boldsymbol{q}(\boldsymbol{x})\}$ of the principal and fifth modes are substituted into (2.4) to form the body force actuators, which are visualized in figure 4. After implementing the body force in the DNS, we assessed the influence of the forcing amplitude $A$ since it is desirable to keep the forcing input small, while achieving significant attenuation of the tip-vortex strength. The value of $A=0.5$ has been verified to result in notable modifications of the base flow. For smaller forcing amplitudes, the added perturbation dissipates without significant attenuation of the tip vortex.

To quantify the control input, we estimate the oscillatory momentum coefficient $C_{\unicode[STIX]{x1D707}}$

(4.1) $$\begin{eqnarray}C_{\unicode[STIX]{x1D707}}=\frac{\displaystyle \frac{\unicode[STIX]{x1D70C}S_{act}}{V_{act}}\int _{V_{act}}[G(x)(\tilde{u} ^{\prime 2}+\tilde{v}^{\prime 2}+\tilde{w}^{\prime 2})]\,\text{d}V}{\displaystyle \frac{1}{2}\unicode[STIX]{x1D70C}U_{\infty }^{2}(bc/2)},\end{eqnarray}$$

where $\tilde{u} ^{\prime }$ , $\tilde{v}^{\prime }$ and $\tilde{w}^{\prime }$ are the fluctuating velocity components, and $S_{act}$ and $V_{act}$ correspond to where the localized body forcing is active. Both controlled cases based on the principal and fifth modes yield $C_{\unicode[STIX]{x1D707}}=0.05$ .

The instantaneous flow fields with control applied are shown in figure 5. The principal mode excites the wake instability in the flow. We observe large fluctuations and vortex shedding downstream of the trailing edge. Due to the unsteadiness introduced by the body force, the tip-vortex core exhibits a moderate level of oscillations. In the controlled case based on the fifth mode, the length scale of the body force is finer compared to the controlled case based on the principal mode, leading to the fifth-mode case exhibiting smaller-scale structures. The vertical extent of the wake structure is narrower than the wake of the controlled flow using the principal mode. Furthermore, the tip vortex highly deforms as it convects downstream.

Figure 5. Isosurfaces of $Q=1$ (blue) and vorticity magnitude $\Vert \tilde{\unicode[STIX]{x1D74E}}\Vert =2$ (transparent grey) from instantaneous controlled flow fields using the (a) principal and (b) fifth wake modes as body force.

Figure 6. Isosurfaces of streamwise vorticity ( $\unicode[STIX]{x1D714}_{x}^{\prime }=\pm 0.01$ ) of velocity DMD modes associated with frequency $\unicode[STIX]{x1D714}=4.5$ for controlled cases with the (a) principal and (b) fifth wake modes as body force. The modal structures are visualized only in the tip-vortex region to highlight the rotation behaviour.

To further analyse the effects of the present control approach, dynamic mode decomposition (DMD) (Schmid Reference Schmid2010) is used to extract prominent modes from the controlled flows. We collect two periods of instantaneous velocity field data after the control effects have reached an asymptotic state. For both of the controlled cases, the dominant fluctuation is associated with the control frequency of $\unicode[STIX]{x1D714}=4.5$ . For the tip-vortex region, the isosurfaces of streamwise vorticity of the dominant mode from each controlled case are presented in figure 6. For the controlled flow with the principal mode, we see perturbations aligned along the streamwise direction. For the fifth-wake-mode controlled case, the vorticity perturbations are braided as they convect downstream, and the braiding is in the counter-rotating direction with respect to the base flow, which agrees with the PSE prediction. While the PSE analysis suggests that the counter-rotating feature of the fifth mode becomes prominent past $x/c\approx 8$ , the nonlinearity in the flow accelerates the emergence of such a counter-rotating feature. As the control effort based on the principal wake mode cannot generate the counter-rotating perturbation, the perturbation in the form of the fifth wake mode is indeed required to instigate the correct counter-rotating perturbation around the tip vortex.

Despite the lack of a clear consensus in the literature concerning a metric to define trailing vortex strength or its attenuation (as noted by Spalart Reference Spalart1998), the tip-vortex strength is nevertheless quantified here by evaluating the streamwise circulation $\unicode[STIX]{x1D6E4}_{x}$ using time-averaged velocity distributions $\overline{\tilde{\boldsymbol{u}}}$ from the baseline and controlled flows. From the three-dimensional flow field, we extract two-dimensional slices ( $y$ – $z$ planes) at various streamwise locations for this analysis. For the integration path, a contour line of the time-averaged streamwise vorticity (constant $\overline{\tilde{\unicode[STIX]{x1D714}}}_{x}$ ) on each slice is chosen to solely capture the tip-vortex structure in both baseline and controlled cases. The tip-vortex strength evaluated with a contour of $\overline{\tilde{\unicode[STIX]{x1D714}}}_{x}=-0.8$ is shown in figure 7. A comparison of the circulation $|\unicode[STIX]{x1D6E4}_{x}|$ over $x$ for the baseline and controlled cases suggests that both controlled cases achieve a significant reduction in vortex strength. Noteworthy here is that a larger decrease is realized in the controlled case using the fifth wake mode as the body force. Although we report only the circulation with the integration path along $\overline{\tilde{\unicode[STIX]{x1D714}}}_{x}=-0.8$ , we have observed that the behaviour reported in figure 7 is insensitive to the integration path. Furthermore, we note that the negative peak value of $\overline{\tilde{\unicode[STIX]{x1D714}}}_{x}$ , which is indicative of the peak swirl velocity, also decreases with $x$ most rapidly with the fifth-mode control.

Figure 7. (a) Tip-vortex circulation $\unicode[STIX]{x1D6E4}_{x}$ shown for the baseline and controlled cases evaluated at streamwise slices ( $y$ – $z$ plane). The integration path is indicated by the dashed lines (- - for $\overline{\tilde{\unicode[STIX]{x1D714}}}_{x}=-0.8$ ) in (b) baseline, (c) control using the principal wake mode, and (d) control using the fifth wake mode on the $y$ – $z$ plane at $x/c=3$ .

Figure 8. Visualization of the tip vortices with isosurface of $Q=0.8$ (time-averaged). Shown are (a) baseline flow, (b) controlled flow using the principal wake mode, and (c) controlled flow using the fifth wake mode.

For a qualitative comparison, we visualize the tip-vortex core using the $Q$ -criterion (Hunt, Wray & Moin Reference Hunt, Wray and Moin1988), as shown in figure 8. The cores for the controlled cases based on the principal and fifth wake modes are apparently shortened relative to the baseline case (using $Q=0.8$ ). There are some secondary structures that also emerge around the tip vortex induced by the actuation force, as shown in figure 8. While the streamwise extent of the vortex core varies slightly according to the selected isocontour value of $Q$ , it is always observed to diminish for both controlled cases compared to the baseline flow, regardless of the value of $Q$ used for this assessment.

While we observe noticeable chances in the wake caused by the control efforts, the time-averaged lift and drag forces for both controlled cases are within 3.2 % of the baseline flow, as shown in table 1. The present control schemes are able to deform the tip vortex by leveraging the underlying instability mechanisms. As the deformed tip vortex possesses higher curvature, viscous diffusion and vortex annihilation accelerate the tip-vortex attenuation without significantly affecting the forces on the wing. Thus, the present control approach becomes attractive for implementation, as it does not interfere significantly with the aerodynamic performance of the wing itself. Moreover, the fluctuations of the aerodynamic forces in the controlled case based on the principal mode are nearly ten times larger than the fifth-mode-based control case.

Table 1. Assessment of the control influence on time-averaged lift ( $C_{L}$ ), drag ( $C_{D}$ ) coefficients and their standard deviations ( $\tilde{\unicode[STIX]{x1D70E}}$ ).