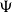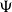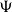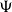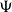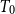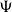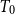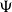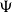1. Introduction
Traditionally, topologists were interested in Hausdorff spaces much more than non-Hausdorff spaces. The development of domain theory has inspired the heavy interests in non-Hausdorff spaces. Sober spaces, well-filtered spaces, and d-spaces are three of the mostly well-studied non-Hausdorff spaces in domain theory. Recent researches revealed that these three classes of spaces share quite a number of common properties: (i) their categories are reflective in the category of
![]() $T_0$
spaces (Eršhov Reference Eršhov1999; Hoffmann Reference Hoffmann1981; Liu et al. Reference Liu, Li and Wu2020; Wu et al. Reference Wu, Xi, Xu and Zhao2020; Wyler Reference Wyler1981; Xu et al. Reference Xu, Shen, Xi and Zhao2020a); (ii) they can be defined in terms of special subsets (i.e., irreducible sets, KF-sets, directed sets) (Shen et al. Reference Shen, Xi, Xu and Zhao2019); (iii) they are preserved under Cartesian product (Hoffmann Reference Hoffmann1979; Keimel and Lawson Reference Keimel and Lawson2009); (iv) their open sets are Scott open in the specialization order (Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003; Goubault-Larrecq 2003). Recently, Li, Yuan, and Zhao (Reference Li, Yuan and Zhao2021) introduced the notion of
$T_0$
spaces (Eršhov Reference Eršhov1999; Hoffmann Reference Hoffmann1981; Liu et al. Reference Liu, Li and Wu2020; Wu et al. Reference Wu, Xi, Xu and Zhao2020; Wyler Reference Wyler1981; Xu et al. Reference Xu, Shen, Xi and Zhao2020a); (ii) they can be defined in terms of special subsets (i.e., irreducible sets, KF-sets, directed sets) (Shen et al. Reference Shen, Xi, Xu and Zhao2019); (iii) they are preserved under Cartesian product (Hoffmann Reference Hoffmann1979; Keimel and Lawson Reference Keimel and Lawson2009); (iv) their open sets are Scott open in the specialization order (Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003; Goubault-Larrecq 2003). Recently, Li, Yuan, and Zhao (Reference Li, Yuan and Zhao2021) introduced the notion of
![]() $\Theta$
-fine space, which provided another unified approach to such properties. Also, using a generalized notion of Rudin set (KF-set), directed set, and irreducible set in
$\Theta$
-fine space, which provided another unified approach to such properties. Also, using a generalized notion of Rudin set (KF-set), directed set, and irreducible set in
![]() $T_0$
spaces, Xu (Reference Xu2021) introduced the notion of H-sober space and particularly proved that the category of H-sober spaces is a full reflective subcategory of the category of
$T_0$
spaces, Xu (Reference Xu2021) introduced the notion of H-sober space and particularly proved that the category of H-sober spaces is a full reflective subcategory of the category of
![]() $T_0$
spaces.
$T_0$
spaces.
Sober spaces have very rich properties. The single most important result about such spaces is the Hofmann-Mislove Theorem, which states that sober spaces are exactly the spaces such that there is a natural correspondence between the open filters of the lattice of open subsets and the compact saturated subsets.
In this paper, we shall extend the Hofmann-Mislove Theorem to a general class of spaces, including sober spaces, well-filtered spaces, and d-spaces. One byproduct of this approach is the finding of some new classes of
![]() $T_0$
spaces.
$T_0$
spaces.
Here is the outline of the paper. In Section 3, we introduce the
![]() $\Psi$
-well-filtered spaces, where
$\Psi$
-well-filtered spaces, where
![]() $\Psi$
is a property on open filters. We then show that sober spaces, well-filtered spaces, and d-spaces are all special types of
$\Psi$
is a property on open filters. We then show that sober spaces, well-filtered spaces, and d-spaces are all special types of
![]() $\Psi$
-well-filtered spaces. In Section 4, we introduce the notion of
$\Psi$
-well-filtered spaces. In Section 4, we introduce the notion of
![]() $\Psi$
-set and use it to characterize
$\Psi$
-set and use it to characterize
![]() $\Psi$
-well-filtered spaces. In Section 5, the interlink between H-sober spaces and
$\Psi$
-well-filtered spaces. In Section 5, the interlink between H-sober spaces and
![]() $\Psi$
-well-filtered spaces is discussed. Especially, it is shown that the complete
$\Psi$
-well-filtered spaces is discussed. Especially, it is shown that the complete
![]() $\Psi$
-well-filtered spaces are exactly the
$\Psi$
-well-filtered spaces are exactly the
![]() $H_{\Psi}$
-sober spaces, where
$H_{\Psi}$
-sober spaces, where
![]() $H_{\Psi}$
is an R-subset system induced by
$H_{\Psi}$
is an R-subset system induced by
![]() $\Psi$
. As an immediate result, the category of complete
$\Psi$
. As an immediate result, the category of complete
![]() $\Psi$
-well-filtered spaces is reflective in the category of
$\Psi$
-well-filtered spaces is reflective in the category of
![]() $T_0$
spaces. In the last section, for an HM-system
$T_0$
spaces. In the last section, for an HM-system
![]() $\Psi$
and a
$\Psi$
and a
![]() $T_0$
space X, we show that the Smyth power space
$T_0$
space X, we show that the Smyth power space
![]() $P_s(X)$
is
$P_s(X)$
is
![]() $\Psi$
-well-filtered if and only if X is
$\Psi$
-well-filtered if and only if X is
![]() $\Psi$
-well-filtered and
$\Psi$
-well-filtered and
![]() $\Psi$
has property Q for X. As a corollary, it is deduced that a
$\Psi$
has property Q for X. As a corollary, it is deduced that a
![]() $T_0$
space X is sober (resp., well-filtered) if and only if
$T_0$
space X is sober (resp., well-filtered) if and only if
![]() $P_s(X)$
is sober (resp., well-filtered).
$P_s(X)$
is sober (resp., well-filtered).
2. Preliminary
Next, we introduce some basic concepts and notations that will be used in the paper. For more details, see Engelking (Reference Engelking1989), Gierz et al. (Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003), Goubault-Larrecq (2003).
Let P be a poset. A nonempty subset D of P is directed (resp., filtered) if every two elements in D have an upper (resp., lower) bound in D. P is called a directed complete poset or a dcpo for short, if for any directed subset
![]() $D\subseteq P$
, the supremum of D, denoted by
$D\subseteq P$
, the supremum of D, denoted by
![]() $\bigvee D$
, exists.
$\bigvee D$
, exists.
For any subset A of a poset P, we use the following standard notations:
In particular, for each
![]() $x\in X$
, we write
$x\in X$
, we write
![]() $\mathord{\uparrow} x=\mathord{\uparrow}\{x\}$
and
$\mathord{\uparrow} x=\mathord{\uparrow}\{x\}$
and
![]() $\mathord{\downarrow} x=\mathord{\downarrow} \{x\}$
. A subset A of P is called a lower (resp., upper) set if
$\mathord{\downarrow} x=\mathord{\downarrow} \{x\}$
. A subset A of P is called a lower (resp., upper) set if
![]() $A=\mathord{\downarrow} A$
(resp.,
$A=\mathord{\downarrow} A$
(resp.,
![]() $A=\mathord{\uparrow} A$
).
$A=\mathord{\uparrow} A$
).
A subset U of P is Scott open if (i)
![]() $U=\mathord{\uparrow}U$
and (ii) for any directed subset D of P for which
$U=\mathord{\uparrow}U$
and (ii) for any directed subset D of P for which
![]() $\bigvee D$
exists,
$\bigvee D$
exists,
![]() $\bigvee D\in U$
implies
$\bigvee D\in U$
implies
![]() $D\cap
U\neq\emptyset$
. All Scott open subsets of P form a topology, called the Scott topology on P, denoted by
$D\cap
U\neq\emptyset$
. All Scott open subsets of P form a topology, called the Scott topology on P, denoted by
![]() $\sigma(P)$
. The space
$\sigma(P)$
. The space
![]() $\Sigma P=(P,\sigma(P))$
is called the Scott space of P.
$\Sigma P=(P,\sigma(P))$
is called the Scott space of P.
Let X be a
![]() $T_0$
space. A subset A of X is called saturated if A equals the intersection of all open sets containing it. The specialization order
$T_0$
space. A subset A of X is called saturated if A equals the intersection of all open sets containing it. The specialization order
![]() $\leq $
on X is defined by
$\leq $
on X is defined by
![]() $x\leq y$
if and only if
$x\leq y$
if and only if
![]() $x\in \mathrm{cl}(\{y\})$
, where cl is the closure operator. It is important to note that a subset A of X is saturated if and only if
$x\in \mathrm{cl}(\{y\})$
, where cl is the closure operator. It is important to note that a subset A of X is saturated if and only if
![]() $A=\mathord{\uparrow} A$
in the specialization order.
$A=\mathord{\uparrow} A$
in the specialization order.
Remark 2.1. Let X be a
![]() $T_0$
space.
$T_0$
space.
-
(1). Every open (resp., closed) set is an upper (resp., lower) set. In particular,
 $\mathrm{cl}(\{x\})=\mathord{\downarrow} x$
(Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003; Goubault-Larrecq 2003).
$\mathrm{cl}(\{x\})=\mathord{\downarrow} x$
(Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003; Goubault-Larrecq 2003). -
(2). For each subset K of X, K is compact if and only if
 $\mathord{\uparrow} K$
is compact (Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003; Goubault-Larrecq 2003).
$\mathord{\uparrow} K$
is compact (Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003; Goubault-Larrecq 2003). -
(3). It is well-known that a subset K of X is compact saturated if and only if
 $\min K$
is compact and
$\min K$
is compact and
 $K=\mathord{\uparrow} \min K$
, where
$K=\mathord{\uparrow} \min K$
, where
 $\min K$
is the set of all minimal elements of K in the specialization order (see, e.g., Erné Reference Erné2009, pp. 2068).
$\min K$
is the set of all minimal elements of K in the specialization order (see, e.g., Erné Reference Erné2009, pp. 2068).
Definition 2.2 ( Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott Gierz et al. 2003 ; Goubault-Larrecq 2003)
-
(1). A nonempty subset A of a topological space X is called irreducible if for any closed sets
 $F_1$
,
$F_1$
,
 $F_2$
of X,
$F_2$
of X,
 $A \subseteq F_1\cup F_2$
implies
$A \subseteq F_1\cup F_2$
implies
 $A \subseteq F_1$
or
$A \subseteq F_1$
or
 $A \subseteq F_2$
.
$A \subseteq F_2$
. -
(2). A
 $T_0$
space X is called sober if every irreducible closed subset of X is the closure of a (unique) point.
$T_0$
space X is called sober if every irreducible closed subset of X is the closure of a (unique) point.
For a
![]() $T_0$
space X,
$T_0$
space X,
![]() $A\subseteq X$
, and
$A\subseteq X$
, and
![]() $\mathcal F\subseteq 2^X$
, we use the following notations:
$\mathcal F\subseteq 2^X$
, we use the following notations:
 $\begin{array}{ll}
\mathcal O(X), & \text{the family of all open subsets of }X;\\
\mathcal C(X), & \text{the family of all closed subsets of }X;\\
\mathcal Q(X), & \text{the family of all compact saturated subsets of }X;\\
\mathcal N(A), &\text{the family } \{U\in\mathcal O(X): A\subseteq U\};\\
\mathcal M(A), & \text{the family } \{U\in\mathcal O(X): A\cap U\neq\emptyset\};\\
\mathfrak{M}(\mathcal F), & \text{the family } \{C\in\mathcal C(X):\forall F\in\mathcal F, C\cap F\neq\emptyset\};
\\
m(\mathcal F), & \text{the family of all minimal members in } (\mathfrak M(\mathcal F),\subseteq).
\end{array}$
$\begin{array}{ll}
\mathcal O(X), & \text{the family of all open subsets of }X;\\
\mathcal C(X), & \text{the family of all closed subsets of }X;\\
\mathcal Q(X), & \text{the family of all compact saturated subsets of }X;\\
\mathcal N(A), &\text{the family } \{U\in\mathcal O(X): A\subseteq U\};\\
\mathcal M(A), & \text{the family } \{U\in\mathcal O(X): A\cap U\neq\emptyset\};\\
\mathfrak{M}(\mathcal F), & \text{the family } \{C\in\mathcal C(X):\forall F\in\mathcal F, C\cap F\neq\emptyset\};
\\
m(\mathcal F), & \text{the family of all minimal members in } (\mathfrak M(\mathcal F),\subseteq).
\end{array}$
Definition 2.3
(
Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott
Gierz et al. 2003
; Goubault-Larrecq 2003) A
![]() $T_0$
space X is called well-filtered if for any filtered family
$T_0$
space X is called well-filtered if for any filtered family
![]() $\mathcal F$
of
$\mathcal F$
of
![]() $\mathcal Q(X)$
and
$\mathcal Q(X)$
and
![]() $U\in\mathcal O(X)$
,
$U\in\mathcal O(X)$
,
![]() $\bigcap\mathcal{F}\subseteq U$
implies
$\bigcap\mathcal{F}\subseteq U$
implies
![]() $K\subseteq U$
for some
$K\subseteq U$
for some
![]() $K\in\mathcal{F}$
.
$K\in\mathcal{F}$
.
Definition 2.4
(
Reference Shen, Xi, Xu and Zhao
Shen et al. 2019
; Reference Xu, Shen, Xi and Zhao
Xu et al. 2020a
) Let X be a
![]() $T_0$
space. A nonempty subset A of X is called a KF-set (or a Rudin set), if there exists a filtered family
$T_0$
space. A nonempty subset A of X is called a KF-set (or a Rudin set), if there exists a filtered family
![]() $\mathcal F$
of
$\mathcal F$
of
![]() $\mathcal Q(X)$
such that
$\mathcal Q(X)$
such that
![]() $\mathrm{cl}(A)\in m(\mathcal F)$
.
$\mathrm{cl}(A)\in m(\mathcal F)$
.
Theorem 2.5
(
Reference Shen, Xi, Xu and Zhao
Shen et al. 2019
; Reference Xu, Shen, Xi and Zhao
Xu et al. 2020a
) A
![]() $T_0$
space X is well-filtered if and only if for each KF-set A, there exists
$T_0$
space X is well-filtered if and only if for each KF-set A, there exists
![]() $x\in X$
such that
$x\in X$
such that
![]() $\mathrm{cl}(A)=\mathrm{cl}(\{x\})$
.
$\mathrm{cl}(A)=\mathrm{cl}(\{x\})$
.
Lemma 2.6
(
Reference Shen, Xi, Xu and Zhao
Shen et al. 2019
) Let X and Y be two
![]() $T_0$
spaces, and
$T_0$
spaces, and
![]() $f:X\longrightarrow Y$
be a continuous mapping. If A is a KF-set in X, then f(A) is a KF-set in Y.
$f:X\longrightarrow Y$
be a continuous mapping. If A is a KF-set in X, then f(A) is a KF-set in Y.
Definition 2.7
(
Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott
Gierz et al. 2003
; Goubault-Larrecq 2003) A
![]() $T_0$
space X is called a d-space, if X is a dcpo and every open subset of X is Scott open in the specialization order.
$T_0$
space X is called a d-space, if X is a dcpo and every open subset of X is Scott open in the specialization order.
Proposition 2.8 (Xu et al. 2020a, Proposition 3.3) A
![]() $T_0$
space X is a d-space if and only if for each directed subset D of X, there is
$T_0$
space X is a d-space if and only if for each directed subset D of X, there is
![]() $x\in X$
such that
$x\in X$
such that
![]() $\mathrm{cl}(D)=\mathrm{cl}(\{x\})$
.
$\mathrm{cl}(D)=\mathrm{cl}(\{x\})$
.
Remark 2.9 Every sober space is well-filtered, and every well-filtered space is a d-space (Gierz et al. 2003; Goubault-Larrecq 2003).
Definition 2.10
(
Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott
Gierz et al. 2003
; Goubault-Larrecq 2003) Let X be a
![]() $T_0$
space, and
$T_0$
space, and
![]() $\mathcal F\subseteq\mathcal O(X)$
. Then,
$\mathcal F\subseteq\mathcal O(X)$
. Then,
![]() $\mathcal F$
is called an open filter, if it is filtered and Scott open in
$\mathcal F$
is called an open filter, if it is filtered and Scott open in
![]() $(\mathcal O(X),\subseteq)$
. We denote by
$(\mathcal O(X),\subseteq)$
. We denote by
![]() $\mathsf{OF}(X)$
the family of all open filters of
$\mathsf{OF}(X)$
the family of all open filters of
![]() $\mathcal O(X)$
.
$\mathcal O(X)$
.
Remark 2.11. For a
![]() $T_0$
space X, the following results can be checked easily.
$T_0$
space X, the following results can be checked easily.
-
(1). For each compact saturated subset K of X,
 $\mathcal N(K)\in\mathsf{OF}(X)$
.
$\mathcal N(K)\in\mathsf{OF}(X)$
. -
(2). For each irreducible subset A of X,
 $\mathcal M(A)\in\mathsf{OF}(X)$
.
$\mathcal M(A)\in\mathsf{OF}(X)$
. -
(3). For each continuous mapping
 $f:X\longrightarrow Y$
between
$f:X\longrightarrow Y$
between
 $T_0$
spaces X and Y, if
$T_0$
spaces X and Y, if
 $\mathcal F\in\mathsf{OF}(X)$
, then
$\mathcal F\in\mathsf{OF}(X)$
, then
 $f_*(\mathcal F)=\{V\in\mathcal O(Y):f^{-1}(V)\in\mathcal F\}\in\mathsf{OF}(Y)$
.
$f_*(\mathcal F)=\{V\in\mathcal O(Y):f^{-1}(V)\in\mathcal F\}\in\mathsf{OF}(Y)$
.
The following is a similar result to the Topological Rudin Lemma in Heckmann and Keimel (2013).
Lemma 2.12. Let X be a
![]() $T_0$
space,
$T_0$
space,
![]() $A\in\mathcal C(X)$
and
$A\in\mathcal C(X)$
and
![]() $\mathcal F\in\mathsf{OF}(X)$
. Then, the following conditions hold:
$\mathcal F\in\mathsf{OF}(X)$
. Then, the following conditions hold:
-
(1). every element of
 $m(\mathcal F)$
is irreducible;
$m(\mathcal F)$
is irreducible; -
(2). if
 $A\in\mathfrak M(\mathcal F)$
, then there is a closed subset C of A such that
$A\in\mathfrak M(\mathcal F)$
, then there is a closed subset C of A such that
 $C\in m(\mathcal F)$
.
$C\in m(\mathcal F)$
.
Proof. (1) Assume on the contrary there is
![]() $C\in m(\mathcal F)$
that is not irreducible. Then, there exist closed sets
$C\in m(\mathcal F)$
that is not irreducible. Then, there exist closed sets
![]() $C_1, C_2$
such that
$C_1, C_2$
such that
![]() $C=C_1\cup C_2$
but
$C=C_1\cup C_2$
but
![]() $C\neq C_1$
and
$C\neq C_1$
and
![]() $C\neq C_2$
. Since
$C\neq C_2$
. Since
![]() $C_1, C_2$
are proper subsets of C, by the minimality of C there exist
$C_1, C_2$
are proper subsets of C, by the minimality of C there exist
![]() $U_1,U_2\in\mathcal F$
such that
$U_1,U_2\in\mathcal F$
such that
![]() $C_1\cap U_1=\emptyset$
and
$C_1\cap U_1=\emptyset$
and
![]() $C_2\cap U_2=\emptyset$
. Since
$C_2\cap U_2=\emptyset$
. Since
![]() $\mathcal F$
is a filter, there exists
$\mathcal F$
is a filter, there exists
![]() $U_3\in\mathcal F$
such that
$U_3\in\mathcal F$
such that
![]() $U_3\subseteq U_1\cap U_2$
. It follows that
$U_3\subseteq U_1\cap U_2$
. It follows that
![]() $C_1\cap U_3=C_2\cap U_3=\emptyset$
. Thus,
$C_1\cap U_3=C_2\cap U_3=\emptyset$
. Thus,
![]() $C\cap U_3=(C_1\cup C_2)\cap U_3=(C_1\cap U_3)\cup (C_2\cap U_3)=\emptyset$
, contradicting the fact that
$C\cap U_3=(C_1\cup C_2)\cap U_3=(C_1\cap U_3)\cup (C_2\cap U_3)=\emptyset$
, contradicting the fact that
![]() $C\in m(\mathcal F)$
. Therefore, C is irreducible.
$C\in m(\mathcal F)$
. Therefore, C is irreducible.
(2) Note that an open set is not in
![]() $\mathcal F$
if and only if its complement is in
$\mathcal F$
if and only if its complement is in
![]() $\mathfrak{M}(\mathcal F)$
. Then, using Proof (i) of Lemma II-1.19 in Gierz et al. (Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003), condition (2) holds dually.
$\mathfrak{M}(\mathcal F)$
. Then, using Proof (i) of Lemma II-1.19 in Gierz et al. (Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003), condition (2) holds dually.
3.
 $\Psi$
-Well-Filtered Spaces
$\Psi$
-Well-Filtered Spaces
For each
![]() $K\in\mathcal Q(X)$
, it is trivial that
$K\in\mathcal Q(X)$
, it is trivial that
![]() $\mathcal N(K)\in\mathsf{OF}(X)$
and
$\mathcal N(K)\in\mathsf{OF}(X)$
and
![]() $K=\bigcap\mathcal N(K)$
. Then, the mapping
$K=\bigcap\mathcal N(K)$
. Then, the mapping
![]() $\mathcal N:(\mathcal Q(X),\supseteq)\longrightarrow (\mathsf{OF}(X),\subseteq)$
,
$\mathcal N:(\mathcal Q(X),\supseteq)\longrightarrow (\mathsf{OF}(X),\subseteq)$
,
![]() $K\mapsto \mathcal N(K)$
is well-defined and clearly is an order-embedding. In domain theory, the single most important result about sober spaces is the Hofmann-Mislove Theorem (see Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Theorems II-1.20, II-1.21).
$K\mapsto \mathcal N(K)$
is well-defined and clearly is an order-embedding. In domain theory, the single most important result about sober spaces is the Hofmann-Mislove Theorem (see Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Theorems II-1.20, II-1.21).
Theorem 3.1
(Hofmann-Mislove Theorem) For a
![]() $T_0$
space X, the following conditions are equivalent:
$T_0$
space X, the following conditions are equivalent:
-
(1). X is sober;
-
(2).
 $\forall\mathcal F\in \mathsf{OF}(X)$
, there is a
$\forall\mathcal F\in \mathsf{OF}(X)$
, there is a
 $K\in\mathcal Q(X)$
such that
$K\in\mathcal Q(X)$
such that
 $\mathcal F=\mathcal N(K)$
;
$\mathcal F=\mathcal N(K)$
; -
(3).
 $\forall \mathcal F\in\mathsf{OF}(X)$
,
$\forall \mathcal F\in\mathsf{OF}(X)$
,
 $\mathcal F=\mathcal N(\bigcap\mathcal F)$
.
$\mathcal F=\mathcal N(\bigcap\mathcal F)$
.
As a corollary of the Hofmann-Mislove Theorem, the following result is clear.
Corollary 3.2. For a
![]() $T_0$
space X, the following conditions are equivalent:
$T_0$
space X, the following conditions are equivalent:
-
(1). X is sober;
-
(2).
 $\mathsf{OF}(X)=\{\mathcal N(K):K\in\mathcal Q(X)\}$
;
$\mathsf{OF}(X)=\{\mathcal N(K):K\in\mathcal Q(X)\}$
; -
(3).
 $\forall \mathcal F\in \mathsf{OF}(X)$
,
$\forall \mathcal F\in \mathsf{OF}(X)$
,
 $\forall U\in\mathcal O(X)$
,
$\forall U\in\mathcal O(X)$
,
 $\bigcap\mathcal F\subseteq U$
implies
$\bigcap\mathcal F\subseteq U$
implies
 $U\in\mathcal F$
.
$U\in\mathcal F$
.
In the following, we would like to provide a unified characterization of Hofmann-Mislove Theorem type for the classes of d-spaces and well-filtered spaces via open filters.
Definition 3.3. A covariant functor
![]() $\Psi:{\bf Top_0}\longrightarrow{\bf Set}$
is called a Hofmann-Mislove system (an HM-system for short) on
$\Psi:{\bf Top_0}\longrightarrow{\bf Set}$
is called a Hofmann-Mislove system (an HM-system for short) on
![]() ${\bf Top_0}$
if the following two conditions are satisfied:
${\bf Top_0}$
if the following two conditions are satisfied:
-
(HM1) for each
 $T_0$
space X,
$T_0$
space X,
 $\{\mathcal N(K):K\in\mathcal Q(X)\}\subseteq\Psi(X)\subseteq \mathsf{OF}(X)$
;
$\{\mathcal N(K):K\in\mathcal Q(X)\}\subseteq\Psi(X)\subseteq \mathsf{OF}(X)$
; -
(HM2) for each continuous mapping
 $f:X\longrightarrow Y$
in
$f:X\longrightarrow Y$
in
 ${\bf Top_0}$
,
${\bf Top_0}$
,
 $\Psi(f)(\mathcal F)=f_*(\mathcal F)=\{V\in\mathcal O(Y):f^{-1}(V)\in\mathcal F\}\in\Psi(Y)$
for each
$\Psi(f)(\mathcal F)=f_*(\mathcal F)=\{V\in\mathcal O(Y):f^{-1}(V)\in\mathcal F\}\in\Psi(Y)$
for each
 $\mathcal F\in\Psi(X)$
.
$\mathcal F\in\Psi(X)$
.
Definition 3.4. Let
![]() $\Psi$
be an HM-system and X be a
$\Psi$
be an HM-system and X be a
![]() $T_0$
space. We call X a
$T_0$
space. We call X a
![]() $\Psi$
-well-filtered space, if
$\Psi$
-well-filtered space, if
![]() $\forall \mathcal F\in \Psi(X)$
,
$\forall \mathcal F\in \Psi(X)$
,
![]() $\forall U\in\mathcal O(X)$
,
$\forall U\in\mathcal O(X)$
,
![]() $\bigcap\mathcal F\subseteq U$
implies
$\bigcap\mathcal F\subseteq U$
implies
![]() $U\in \mathcal F$
.
$U\in \mathcal F$
.
Lemma 3.5. Let
![]() $\Psi$
be an HM-system, X be a
$\Psi$
be an HM-system, X be a
![]() $\Psi$
-well-filtered space, and
$\Psi$
-well-filtered space, and
![]() $\mathcal F\in\Psi(X)$
. Then
$\mathcal F\in\Psi(X)$
. Then
![]() $\bigcap\mathcal F\in\mathcal Q(X)$
, and
$\bigcap\mathcal F\in\mathcal Q(X)$
, and
![]() $\emptyset\notin\mathcal F$
implies
$\emptyset\notin\mathcal F$
implies
![]() $\bigcap\mathcal F\neq\emptyset$
.
$\bigcap\mathcal F\neq\emptyset$
.
Proof. Let
![]() $\{U_i:i\in I\}$
be a directed family of
$\{U_i:i\in I\}$
be a directed family of
![]() $\mathcal O(X)$
such that
$\mathcal O(X)$
such that
![]() $\bigcap \mathcal F\subseteq \bigcup_{i\in I}U_i$
. Since X is
$\bigcap \mathcal F\subseteq \bigcup_{i\in I}U_i$
. Since X is
![]() $\Psi$
-well-filtered,
$\Psi$
-well-filtered,
![]() $\bigcup_{i\in I}U_i\in\mathcal F$
, and since
$\bigcup_{i\in I}U_i\in\mathcal F$
, and since
![]() $\mathcal F$
is Scott open, there exists
$\mathcal F$
is Scott open, there exists
![]() $i_0\in I$
such that
$i_0\in I$
such that
![]() $U_{i_0}\in \mathcal F$
, which implies
$U_{i_0}\in \mathcal F$
, which implies
![]() $\bigcap \mathcal F\subseteq U_{i_0}$
. Hence,
$\bigcap \mathcal F\subseteq U_{i_0}$
. Hence,
![]() $\bigcap\mathcal F$
is compact and clearly is saturated. In addition, if
$\bigcap\mathcal F$
is compact and clearly is saturated. In addition, if
![]() $\bigcap\mathcal F=\emptyset$
, then
$\bigcap\mathcal F=\emptyset$
, then
![]() $\emptyset\in\mathcal F$
because X is
$\emptyset\in\mathcal F$
because X is
![]() $\Psi$
-well-filtered, completing the proof.
$\Psi$
-well-filtered, completing the proof.
Theorem 3.6. Let
![]() $\Psi$
be an HM-system and X be a
$\Psi$
be an HM-system and X be a
![]() $T_0$
space. Then, the following conditions are equivalent:
$T_0$
space. Then, the following conditions are equivalent:
-
(1). X is
 $\Psi$
-well-filtered;
$\Psi$
-well-filtered; -
(2).
 $\forall \mathcal F\in \Psi(X)$
,
$\forall \mathcal F\in \Psi(X)$
,
 $\mathcal F=\mathcal N(\bigcap\mathcal F)$
;
$\mathcal F=\mathcal N(\bigcap\mathcal F)$
; -
(3).
 $\Psi(X)= \{\mathcal N(K): K\in\mathcal Q(X)\}$
.
$\Psi(X)= \{\mathcal N(K): K\in\mathcal Q(X)\}$
.
Proof. (1)
![]() $\Rightarrow$
(2). Let
$\Rightarrow$
(2). Let
![]() $\mathcal F\in\Psi(X)$
. It is clear that
$\mathcal F\in\Psi(X)$
. It is clear that
![]() $\mathcal F\subseteq\mathcal N(\bigcap\mathcal F)$
. Conversely, if
$\mathcal F\subseteq\mathcal N(\bigcap\mathcal F)$
. Conversely, if
![]() $U\in\mathcal N(\bigcap\mathcal F)$
, then
$U\in\mathcal N(\bigcap\mathcal F)$
, then
![]() $\bigcap\mathcal F\subseteq U$
and
$\bigcap\mathcal F\subseteq U$
and
![]() $U\in\mathcal O(X)$
, and since X is
$U\in\mathcal O(X)$
, and since X is
![]() $\Psi$
-well-filtered, we have that
$\Psi$
-well-filtered, we have that
![]() $U\in\mathcal F$
. This shows that
$U\in\mathcal F$
. This shows that
![]() $\mathcal N(\bigcap\mathcal F)\subseteq\mathcal F$
. Hence,
$\mathcal N(\bigcap\mathcal F)\subseteq\mathcal F$
. Hence,
![]() $\mathcal F=\mathcal N(\bigcap\mathcal F)$
.
$\mathcal F=\mathcal N(\bigcap\mathcal F)$
.
(2)
![]() $\Rightarrow$
(3). By the definition of
$\Rightarrow$
(3). By the definition of
![]() $\Psi$
, it is clear that
$\Psi$
, it is clear that
![]() $ \{\mathcal N(K): K\in\mathcal Q(X)\}\subseteq\Psi(X)$
. Now suppose
$ \{\mathcal N(K): K\in\mathcal Q(X)\}\subseteq\Psi(X)$
. Now suppose
![]() $\mathcal F\in\Psi(X)$
. By Lemma 3.5,
$\mathcal F\in\Psi(X)$
. By Lemma 3.5,
![]() $K_0=\bigcap\mathcal F\in\mathcal Q(X)$
, and by condition (2)
$K_0=\bigcap\mathcal F\in\mathcal Q(X)$
, and by condition (2)
![]() $\mathcal F=\mathcal N(K_0)$
. This shows that
$\mathcal F=\mathcal N(K_0)$
. This shows that
![]() $\Psi(X)\subseteq \{\mathcal N(K): K\in\mathcal Q(X)\}$
. Thus, condition (3) holds.
$\Psi(X)\subseteq \{\mathcal N(K): K\in\mathcal Q(X)\}$
. Thus, condition (3) holds.
(3)
![]() $\Rightarrow$
(1). Let
$\Rightarrow$
(1). Let
![]() $\mathcal F\in\Psi(X)$
and
$\mathcal F\in\Psi(X)$
and
![]() $U\in\mathcal O(X)$
such that
$U\in\mathcal O(X)$
such that
![]() $\bigcap\mathcal F\subseteq U$
. By (3), there exists
$\bigcap\mathcal F\subseteq U$
. By (3), there exists
![]() $K\in\mathcal Q(X)$
such that
$K\in\mathcal Q(X)$
such that
![]() $\mathcal F=\mathcal N(K)$
. Then,
$\mathcal F=\mathcal N(K)$
. Then,
![]() $K=\bigcap\mathcal N(K)=\bigcap \mathcal F\subseteq U$
, which implies that
$K=\bigcap\mathcal N(K)=\bigcap \mathcal F\subseteq U$
, which implies that
![]() $U\in\mathcal N(K)=\mathcal F$
. Therefore, X is
$U\in\mathcal N(K)=\mathcal F$
. Therefore, X is
![]() $\Psi$
-well-filtered.
$\Psi$
-well-filtered.
The following result shows that the
![]() $\Psi$
-well-filteredness is a topological property for each HM-system
$\Psi$
-well-filteredness is a topological property for each HM-system
![]() $\Psi$
.
$\Psi$
.
Proposition 3.7. Let
![]() $\Psi$
be an HM-system, X be a
$\Psi$
be an HM-system, X be a
![]() $\Psi$
-well-filtered space, and Y be a
$\Psi$
-well-filtered space, and Y be a
![]() $T_0$
space. If Y is homeomorphic to X, then Y is a
$T_0$
space. If Y is homeomorphic to X, then Y is a
![]() $\Psi$
-well-filtered space.
$\Psi$
-well-filtered space.
Proof. Suppose
![]() $h:Y\longrightarrow X$
is a homeomorphism. Let
$h:Y\longrightarrow X$
is a homeomorphism. Let
![]() $\mathcal F\in\Psi(Y)$
and
$\mathcal F\in\Psi(Y)$
and
![]() $W\in\mathcal O(Y)$
such that
$W\in\mathcal O(Y)$
such that
![]() $\bigcap \mathcal F\subseteq W$
. Since h is a homeomorphism, one can easily obtain that
$\bigcap \mathcal F\subseteq W$
. Since h is a homeomorphism, one can easily obtain that
![]() $h_*(\mathcal F)=\{h(U):U\in\mathcal F\}$
, which implies that
$h_*(\mathcal F)=\{h(U):U\in\mathcal F\}$
, which implies that
By (HM2),
![]() $h_*(\mathcal F)\in\Psi(X)$
, and since X is
$h_*(\mathcal F)\in\Psi(X)$
, and since X is
![]() $\Psi$
-well-filtered, we have that
$\Psi$
-well-filtered, we have that
![]() $h(W)\in h_*(\mathcal F)$
, so
$h(W)\in h_*(\mathcal F)$
, so
![]() $W\in\mathcal F$
. Therefore, X is
$W\in\mathcal F$
. Therefore, X is
![]() $\Psi$
-well-filtered.
$\Psi$
-well-filtered.
In the following, we will show that all the classes of sober spaces, well-filtered spaces, and d-spaces can be characterized via HM-systems.
Definition 3.8. Define
![]() $\Psi_{\mathsf{sob}}, \Psi_{\mathsf{wf}}, \Psi_{\rm d}:{\bf Top_0}\longrightarrow{\bf Set}$
as follows: for each
$\Psi_{\mathsf{sob}}, \Psi_{\mathsf{wf}}, \Psi_{\rm d}:{\bf Top_0}\longrightarrow{\bf Set}$
as follows: for each
![]() $T_0$
space X,
$T_0$
space X,
 \begin{align*}
\Psi_{\mathsf{sob}}(X)&=\mathsf{OF}(X) ,\\
\Psi_{\mathsf{wf}}(X)&=\left\{\bigcup_{K\in\mathcal G}\mathcal N(K): \mathcal G\text{ is a filtered family of }\mathcal Q(X)\right\},\\
\Psi_{{\rm d}}(X)&=\left\{\bigcup_{x\in D}\mathcal N(\mathord{\uparrow} x):D\text{ is a directed subset of }X\right\}\cup \{\mathcal N(K):K\in\mathcal Q(X)\}.
\end{align*}
\begin{align*}
\Psi_{\mathsf{sob}}(X)&=\mathsf{OF}(X) ,\\
\Psi_{\mathsf{wf}}(X)&=\left\{\bigcup_{K\in\mathcal G}\mathcal N(K): \mathcal G\text{ is a filtered family of }\mathcal Q(X)\right\},\\
\Psi_{{\rm d}}(X)&=\left\{\bigcup_{x\in D}\mathcal N(\mathord{\uparrow} x):D\text{ is a directed subset of }X\right\}\cup \{\mathcal N(K):K\in\mathcal Q(X)\}.
\end{align*}
Then, it is trivial to check that
![]() $\Psi_{\mathsf{sob}}, \Psi_{\mathsf{wf}}, \Psi_{\rm d}$
are all HM-systems.
$\Psi_{\mathsf{sob}}, \Psi_{\mathsf{wf}}, \Psi_{\rm d}$
are all HM-systems.
Theorem 3.9 Let X be a
![]() $T_0$
space. The following conditions are equivalent:
$T_0$
space. The following conditions are equivalent:
-
(1). X is sober;
-
(2). X is
 $\Psi_{\mathsf{sob}}$
-well-filtered;
$\Psi_{\mathsf{sob}}$
-well-filtered; -
(3).
 $\forall \mathcal F\in \Psi_{\mathsf{sob}}(X)$
,
$\forall \mathcal F\in \Psi_{\mathsf{sob}}(X)$
,
 $\mathcal F=\mathcal N(\bigcap\mathcal F)$
;
$\mathcal F=\mathcal N(\bigcap\mathcal F)$
; -
(4).
 $\Psi_{\mathsf{sob}}(X)=\{\mathcal N(K): K\in\mathcal Q(X)\}$
.
$\Psi_{\mathsf{sob}}(X)=\{\mathcal N(K): K\in\mathcal Q(X)\}$
.
Proof. It is straightforward by the Hofmann-Mislove Theorem.
Remark 3.10. Let
![]() $\Psi_0(X)=\{\mathcal N(K):K\in\mathcal Q(X)\}$
for each
$\Psi_0(X)=\{\mathcal N(K):K\in\mathcal Q(X)\}$
for each
![]() $T_0$
space X. Then, it is easy to check that
$T_0$
space X. Then, it is easy to check that
![]() $\Psi_0$
is an HM-system, and it is clear that each
$\Psi_0$
is an HM-system, and it is clear that each
![]() $T_0$
space X is
$T_0$
space X is
![]() $\Psi_0$
-well-filtered. From Theorem 3.9, for each HM-system
$\Psi_0$
-well-filtered. From Theorem 3.9, for each HM-system
![]() $\Psi$
, we have the following relations:
$\Psi$
, we have the following relations:
sober (
![]() $\Psi_{\mathsf{sob}}$
-well-filtered) space
$\Psi_{\mathsf{sob}}$
-well-filtered) space
![]() $\Longrightarrow$
$\Longrightarrow$
![]() $\Psi$
-well-filtered space
$\Psi$
-well-filtered space
![]() $\Longrightarrow$
$\Longrightarrow$
![]() $T_0$
(
$T_0$
(
![]() $\Psi_0$
-well-filtered) space.
$\Psi_0$
-well-filtered) space.
In another words, the sober space is the strongest
![]() $\Psi$
-well-filtered space, and the
$\Psi$
-well-filtered space, and the
![]() $T_0$
space is the weakest one.
$T_0$
space is the weakest one.
Theorem 3.11. Let X be a
![]() $T_0$
space. The following conditions are equivalent:
$T_0$
space. The following conditions are equivalent:
-
(1). X is well-filtered;
-
(2). X is
 $\Psi_{\mathsf{wf}}$
-well-filtered;
$\Psi_{\mathsf{wf}}$
-well-filtered; -
(3).
 $\forall \mathcal F\in \Psi_{\mathsf{wf}}(X)$
,
$\forall \mathcal F\in \Psi_{\mathsf{wf}}(X)$
,
 $\mathcal F=\mathcal N(\bigcap\mathcal F)$
;
$\mathcal F=\mathcal N(\bigcap\mathcal F)$
; -
(4).
 $\Psi_{\mathsf{wf}}(X)=\{\mathcal N(K): K\in\mathcal Q(X)\}$
.
$\Psi_{\mathsf{wf}}(X)=\{\mathcal N(K): K\in\mathcal Q(X)\}$
.
Proof. That (2)
![]() $\Leftrightarrow$
(3)
$\Leftrightarrow$
(3)
![]() $\Leftrightarrow$
(4) follows immediately from Theorem 3.6.
$\Leftrightarrow$
(4) follows immediately from Theorem 3.6.
(1)
![]() $\Rightarrow$
(2). Suppose X is well-filtered. Let
$\Rightarrow$
(2). Suppose X is well-filtered. Let
![]() $\mathcal F\in \Psi_{\mathsf{wf}}(X)$
and
$\mathcal F\in \Psi_{\mathsf{wf}}(X)$
and
![]() $U\in\mathcal O(X)$
such that
$U\in\mathcal O(X)$
such that
![]() $\bigcap\mathcal F\subseteq U$
. Then, there exists a filtered family
$\bigcap\mathcal F\subseteq U$
. Then, there exists a filtered family
![]() $\{K_i:i\in I\}\subseteq\mathcal Q(X)$
such that
$\{K_i:i\in I\}\subseteq\mathcal Q(X)$
such that
![]() $\mathcal F=\bigcup_{i\in I}\mathcal N(K_{i})$
. Note that
$\mathcal F=\bigcup_{i\in I}\mathcal N(K_{i})$
. Note that
![]() $\bigcap_{i\in I}K_i=\bigcap\mathcal F\subseteq U$
, which implies that
$\bigcap_{i\in I}K_i=\bigcap\mathcal F\subseteq U$
, which implies that
![]() $K_{i_0}\subseteq U$
for some
$K_{i_0}\subseteq U$
for some
![]() $i_0\in I$
because X is well-filtered. It follows that
$i_0\in I$
because X is well-filtered. It follows that
![]() $U\in\mathcal N(K_{i_0})\subseteq \mathcal F$
. Hence, X is
$U\in\mathcal N(K_{i_0})\subseteq \mathcal F$
. Hence, X is
![]() $\Psi_{\mathsf{wf}}$
-well-filtered.
$\Psi_{\mathsf{wf}}$
-well-filtered.
(2)
![]() $\Rightarrow$
(1). Let
$\Rightarrow$
(1). Let
![]() $\{K_i:i\in I\}$
be a filtered family of
$\{K_i:i\in I\}$
be a filtered family of
![]() $\mathcal Q(X)$
and
$\mathcal Q(X)$
and
![]() $U\in \mathcal O(X)$
such that
$U\in \mathcal O(X)$
such that
![]() $\bigcap_{i\in I}K_i\subseteq U$
. Then,
$\bigcap_{i\in I}K_i\subseteq U$
. Then,
![]() $\mathcal F=\bigcup_{i\in I}\mathcal N(K_i)\in\Psi_{\mathsf{wf}}(X)$
. Note that
$\mathcal F=\bigcup_{i\in I}\mathcal N(K_i)\in\Psi_{\mathsf{wf}}(X)$
. Note that
![]() $\bigcap\mathcal F=\bigcap_{i\in I}K_i\subseteq U$
, and since X is
$\bigcap\mathcal F=\bigcap_{i\in I}K_i\subseteq U$
, and since X is
![]() $\Psi$
-well-filtered, it follows that
$\Psi$
-well-filtered, it follows that
![]() $U\in\mathcal F$
. By the definition of
$U\in\mathcal F$
. By the definition of
![]() $\mathcal F$
, there exists
$\mathcal F$
, there exists
![]() $i_0\in I$
such that
$i_0\in I$
such that
![]() $U\in \mathcal N(K_{i_0})$
, that is,
$U\in \mathcal N(K_{i_0})$
, that is,
![]() $K_{i_0}\subseteq U$
. Hence, X is well-filtered.
$K_{i_0}\subseteq U$
. Hence, X is well-filtered.
Theorem 3.12. Let X be a
![]() $T_0$
space. The following conditions are equivalent:
$T_0$
space. The following conditions are equivalent:
-
(1). X is a d-space;
-
(2). X is
 $\Psi_{\rm d}$
-well-filtered;
$\Psi_{\rm d}$
-well-filtered; -
(3).
 $\forall \mathcal F\in \Psi_{\rm d}(X)$
,
$\forall \mathcal F\in \Psi_{\rm d}(X)$
,
 $\mathcal F=\mathcal N(\bigcap\mathcal F)$
;
$\mathcal F=\mathcal N(\bigcap\mathcal F)$
; -
(4).
 $\Psi_{\rm d}(X)=\{\mathcal N(K): K\in\mathcal Q(X)\}$
.
$\Psi_{\rm d}(X)=\{\mathcal N(K): K\in\mathcal Q(X)\}$
.
Proof. That (2)
![]() $\Leftrightarrow$
(3)
$\Leftrightarrow$
(3)
![]() $\Leftrightarrow$
(4) follows immediately from Theorem 3.6.
$\Leftrightarrow$
(4) follows immediately from Theorem 3.6.
(1)
![]() $\Rightarrow$
(2). Let
$\Rightarrow$
(2). Let
![]() $\mathcal F\in\Psi_{\rm d}(X)$
and
$\mathcal F\in\Psi_{\rm d}(X)$
and
![]() $U\in\mathcal O(X)$
. If
$U\in\mathcal O(X)$
. If
![]() $\mathcal F=\mathcal N(K)$
for some
$\mathcal F=\mathcal N(K)$
for some
![]() $K\in\mathcal Q(X)$
, then it is clear that
$K\in\mathcal Q(X)$
, then it is clear that
![]() $K=\bigcap\mathcal N(K)\subseteq U$
implies
$K=\bigcap\mathcal N(K)\subseteq U$
implies
![]() $U\in\mathcal N(K)$
. Now assume there is a directed subset D of X such that
$U\in\mathcal N(K)$
. Now assume there is a directed subset D of X such that
![]() $\mathcal F=\bigcup_{x\in D}\mathcal N(\mathord{\uparrow} x)$
and
$\mathcal F=\bigcup_{x\in D}\mathcal N(\mathord{\uparrow} x)$
and
![]() $\bigcap\mathcal F\subseteq U$
. Since X is a d-space,
$\bigcap\mathcal F\subseteq U$
. Since X is a d-space,
![]() $\bigvee D$
exists. We have that
$\bigvee D$
exists. We have that
![]() $\bigcap \mathcal F=\bigcap_{d\in D}\mathord{\uparrow} d=\mathord{\uparrow} \bigvee D\subseteq U$
, which implies
$\bigcap \mathcal F=\bigcap_{d\in D}\mathord{\uparrow} d=\mathord{\uparrow} \bigvee D\subseteq U$
, which implies
![]() $\bigvee D\in U$
. Since every open set in a d-space is Scott open,
$\bigvee D\in U$
. Since every open set in a d-space is Scott open,
![]() $ D\cap U\neq\emptyset$
, and take
$ D\cap U\neq\emptyset$
, and take
![]() $x_0\in D\cap U$
. It follows that
$x_0\in D\cap U$
. It follows that
![]() $U\in \mathcal N(\mathord{\uparrow} x_0)\subseteq \mathcal F$
. Hence, X is
$U\in \mathcal N(\mathord{\uparrow} x_0)\subseteq \mathcal F$
. Hence, X is
![]() $\Psi_{\rm d}$
-well-filtered.
$\Psi_{\rm d}$
-well-filtered.
(2)
![]() $\Rightarrow $
(1). Let D be a directed subset of X, and
$\Rightarrow $
(1). Let D be a directed subset of X, and
![]() $\mathcal F=\bigcup_{x\in D}\mathcal N(\mathord{\uparrow} x)$
. We claim that
$\mathcal F=\bigcup_{x\in D}\mathcal N(\mathord{\uparrow} x)$
. We claim that
![]() $\mathrm{cl}(D)\cap\bigcap\mathcal F\neq\emptyset$
. Otherwise,
$\mathrm{cl}(D)\cap\bigcap\mathcal F\neq\emptyset$
. Otherwise,
![]() $\bigcap\mathcal F\subseteq X\setminus\mathrm{cl}(D)$
, and since
$\bigcap\mathcal F\subseteq X\setminus\mathrm{cl}(D)$
, and since
![]() $\mathcal F\in\Psi_{\rm d}(X)$
and X is
$\mathcal F\in\Psi_{\rm d}(X)$
and X is
![]() $\Psi_{\rm d}$
-well-filtered,
$\Psi_{\rm d}$
-well-filtered,
![]() $X\setminus\mathrm{cl}(D)\in\mathcal F=\bigcup_{x\in D}\mathcal N(\mathord{\uparrow} x)$
. Then, there exists
$X\setminus\mathrm{cl}(D)\in\mathcal F=\bigcup_{x\in D}\mathcal N(\mathord{\uparrow} x)$
. Then, there exists
![]() $x_0\in D$
such that
$x_0\in D$
such that
![]() $X\setminus\mathrm{cl}(D)\in\mathcal N(\mathord{\uparrow} x_0)$
, which follows that
$X\setminus\mathrm{cl}(D)\in\mathcal N(\mathord{\uparrow} x_0)$
, which follows that
![]() $x_0\in X\setminus\mathrm{cl}(D)$
, contradicting the fact that
$x_0\in X\setminus\mathrm{cl}(D)$
, contradicting the fact that
![]() $x_0\in D$
. Hence, there is
$x_0\in D$
. Hence, there is
![]() $y\in \mathrm{cl}(D)\cap\bigcap\mathcal F\neq\emptyset$
. Then,
$y\in \mathrm{cl}(D)\cap\bigcap\mathcal F\neq\emptyset$
. Then,
![]() $y\in\bigcap \mathcal F=\bigcap_{x\in D}\mathord{\uparrow} x$
, so y is an upper bound of D. It follows that
$y\in\bigcap \mathcal F=\bigcap_{x\in D}\mathord{\uparrow} x$
, so y is an upper bound of D. It follows that
![]() $D\subseteq \mathord{\downarrow} y=\mathrm{cl}(\{y\})$
, and since
$D\subseteq \mathord{\downarrow} y=\mathrm{cl}(\{y\})$
, and since
![]() $y\in \mathrm{cl}(D)$
, it follows that
$y\in \mathrm{cl}(D)$
, it follows that
![]() $\mathrm{cl}(D)=\mathrm{cl}(\{y\})$
. Hence, by Proposition 2.8 X is a d-space.
$\mathrm{cl}(D)=\mathrm{cl}(\{y\})$
. Hence, by Proposition 2.8 X is a d-space.
Remark 3.13. Note that
![]() $\Psi_{\rm d}(X)\subseteq\Psi_{\mathsf{wf}}(X)\subseteq\Psi_{\mathsf{sob}}(X)$
for each
$\Psi_{\rm d}(X)\subseteq\Psi_{\mathsf{wf}}(X)\subseteq\Psi_{\mathsf{sob}}(X)$
for each
![]() $T_0$
space X. Then by Theorems 3.9, 3.11 and 3.12, the following relations are clear:
$T_0$
space X. Then by Theorems 3.9, 3.11 and 3.12, the following relations are clear:
sober space
![]() $\Longrightarrow$
well-filtered space
$\Longrightarrow$
well-filtered space
![]() $\Longrightarrow$
d-space.
$\Longrightarrow$
d-space.
4. A Characterization for
 $\Psi$
-Well-Filtered Spaces
$\Psi$
-Well-Filtered Spaces
In this section, we will show that a
![]() $\Psi$
-well-filtered space X is determined by a class of subsets of X, called
$\Psi$
-well-filtered space X is determined by a class of subsets of X, called
![]() $\Psi$
-sets.
$\Psi$
-sets.
Definition 4.1. Let
![]() $\Psi$
be an HM-system and X be a
$\Psi$
be an HM-system and X be a
![]() $T_0$
space. A nonempty subset A of X is called a
$T_0$
space. A nonempty subset A of X is called a
![]() $\Psi$
-set (relative to
$\Psi$
-set (relative to
![]() $\mathcal F$
), if there exists
$\mathcal F$
), if there exists
![]() $\mathcal F\in\Psi(X)$
such that
$\mathcal F\in\Psi(X)$
such that
![]() $\mathrm{cl}(A)\in m(\mathcal F)$
.
$\mathrm{cl}(A)\in m(\mathcal F)$
.
Remark 4.2. Let
![]() $\Psi$
be an HM-system, X be a
$\Psi$
be an HM-system, X be a
![]() $T_0$
space, and
$T_0$
space, and
![]() $A\subseteq X$
.
$A\subseteq X$
.
-
(1). It is clear that A is a
 $\Psi$
-set if and only if
$\Psi$
-set if and only if
 $\mathrm{cl}(A)$
is a
$\mathrm{cl}(A)$
is a
 $\Psi$
-set.
$\Psi$
-set. -
(2). Every
 $\Psi$
-set is irreducible by Lemma 2.12.
$\Psi$
-set is irreducible by Lemma 2.12.
Lemma 4.3. Let X be a
![]() $T_0$
space,
$T_0$
space,
![]() $K\in\mathcal Q(X)$
, and
$K\in\mathcal Q(X)$
, and
![]() $A\subseteq X$
. The following two conditions are equivalent:
$A\subseteq X$
. The following two conditions are equivalent:
-
(1).
 $\mathrm{cl}(A)\cap K\neq\emptyset$
;
$\mathrm{cl}(A)\cap K\neq\emptyset$
; -
(2).
 $\forall U\in\mathcal N(K)$
,
$\forall U\in\mathcal N(K)$
,
 $A\cap U\neq\emptyset$
.
$A\cap U\neq\emptyset$
.
Proof. That (1)
![]() $\Rightarrow$
(2) is trivial. Conversely, if
$\Rightarrow$
(2) is trivial. Conversely, if
![]() $\mathrm{cl}(A)\cap K=\emptyset$
, then
$\mathrm{cl}(A)\cap K=\emptyset$
, then
![]() $X\setminus \mathrm{cl}(A)\in \mathcal N(K)$
, but
$X\setminus \mathrm{cl}(A)\in \mathcal N(K)$
, but
![]() $A\cap (X\setminus\mathrm{cl}(A))=\emptyset$
, contradicting the assumption (2). This shows that (2) implies (1).
$A\cap (X\setminus\mathrm{cl}(A))=\emptyset$
, contradicting the assumption (2). This shows that (2) implies (1).
Lemma 4.4. Let X be a
![]() $T_0$
space and
$T_0$
space and
![]() $K\in\mathcal Q(X)$
. Then,
$K\in\mathcal Q(X)$
. Then,
where
![]() $\min K$
is the set of all minimal elements of K in the specialization order of X.
$\min K$
is the set of all minimal elements of K in the specialization order of X.
Proof. First, it is well-known that
![]() $K=\mathord{\uparrow} \min K$
(see, e.g., Erné Reference Erné2009, pp. 2068). Suppose
$K=\mathord{\uparrow} \min K$
(see, e.g., Erné Reference Erné2009, pp. 2068). Suppose
![]() $x\in\min K$
. It is clear that
$x\in\min K$
. It is clear that
![]() $\mathrm{cl}(\{x\})\in\mathfrak M(\mathcal N(K))$
. Now assume C is a closed subset of
$\mathrm{cl}(\{x\})\in\mathfrak M(\mathcal N(K))$
. Now assume C is a closed subset of
![]() $\mathrm{cl}(\{x\})$
such that
$\mathrm{cl}(\{x\})$
such that
![]() $C\in\mathfrak M(\mathcal N(K))$
. By Lemma 4.3, there is
$C\in\mathfrak M(\mathcal N(K))$
. By Lemma 4.3, there is
![]() $a\in C\cap K\neq\emptyset$
. Then,
$a\in C\cap K\neq\emptyset$
. Then,
![]() $a\in C\subseteq \mathrm{cl}(\{x\})$
, so
$a\in C\subseteq \mathrm{cl}(\{x\})$
, so
![]() $a\leq x$
. Since x is minimal in K, we have that
$a\leq x$
. Since x is minimal in K, we have that
![]() $a=x\in C$
, so
$a=x\in C$
, so
![]() $\mathrm{cl}(\{x\})\subseteq C$
. Thus,
$\mathrm{cl}(\{x\})\subseteq C$
. Thus,
![]() $C=\mathrm{cl}(\{x\})$
. All this shows that
$C=\mathrm{cl}(\{x\})$
. All this shows that
![]() $\mathrm{cl}(\{x\})\in m(\mathcal N(K))$
.
$\mathrm{cl}(\{x\})\in m(\mathcal N(K))$
.
Now assume
![]() $A\in m(\mathcal N(K))$
. By Lemma 4.3, there is
$A\in m(\mathcal N(K))$
. By Lemma 4.3, there is
![]() $a\in A\cap K\neq\emptyset$
. Since
$a\in A\cap K\neq\emptyset$
. Since
![]() $a\in K=\mathord{\uparrow}\min K$
, there exists
$a\in K=\mathord{\uparrow}\min K$
, there exists
![]() $x\in\min K$
such that
$x\in\min K$
such that
![]() $x\leq a$
, which follows that
$x\leq a$
, which follows that
![]() $x\in \mathrm{cl}(\{a\})\subseteq A$
. Then,
$x\in \mathrm{cl}(\{a\})\subseteq A$
. Then,
![]() $\mathrm{cl}(\{x\})$
is a closed subset of A such that
$\mathrm{cl}(\{x\})$
is a closed subset of A such that
![]() $\mathrm{cl}(\{x\})\in\mathfrak M(\mathcal N(K))$
. By the minimality of A, we have that
$\mathrm{cl}(\{x\})\in\mathfrak M(\mathcal N(K))$
. By the minimality of A, we have that
![]() $A=\mathrm{cl}(\{x\})$
. This shows that
$A=\mathrm{cl}(\{x\})$
. This shows that
![]() $m(\mathcal N(K))\subseteq\{\mathrm{cl}(\{x\}):x\in\min K\}$
, completing the proof.
$m(\mathcal N(K))\subseteq\{\mathrm{cl}(\{x\}):x\in\min K\}$
, completing the proof.
Using Lemma 4.4, we deduce that
![]() $ m(\mathcal N(\mathord{\uparrow} x))=\{\mathrm{cl}(\{x\})\}$
for each point x of a
$ m(\mathcal N(\mathord{\uparrow} x))=\{\mathrm{cl}(\{x\})\}$
for each point x of a
![]() $T_0$
space X, and since
$T_0$
space X, and since
![]() $\mathcal N(\mathord{\uparrow} x)\in\Psi(X)$
for each HM-system
$\mathcal N(\mathord{\uparrow} x)\in\Psi(X)$
for each HM-system
![]() $\Psi$
, we have the following result.
$\Psi$
, we have the following result.
Proposition 4.5. Let
![]() $\Psi$
be an HM-system and X be a
$\Psi$
be an HM-system and X be a
![]() $T_0$
space. Every singleton of X is a
$T_0$
space. Every singleton of X is a
![]() $\Psi$
-set.
$\Psi$
-set.
Theorem 4.6. Let
![]() $\Psi$
be an HM-system and X be a
$\Psi$
be an HM-system and X be a
![]() $T_0$
space. The following conditions are equivalent:
$T_0$
space. The following conditions are equivalent:
-
(1). X is
 $\Psi$
-well-filtered;
$\Psi$
-well-filtered; -
(2). for each
 $\Psi$
-set
$\Psi$
-set
 $A\subseteq X$
, there exists
$A\subseteq X$
, there exists
 $x\in X$
such that
$x\in X$
such that
 $\mathrm{cl}(A)=\mathrm{cl}(\{x\})$
;
$\mathrm{cl}(A)=\mathrm{cl}(\{x\})$
; -
(3). for each
 $\Psi$
-set
$\Psi$
-set
 $A\subseteq X$
and
$A\subseteq X$
and
 $U\in\mathcal O(X)$
,
$U\in\mathcal O(X)$
,
 $\bigcap\mathcal M(A)\subseteq U$
implies
$\bigcap\mathcal M(A)\subseteq U$
implies
 $U\in\mathcal M(A)$
;
$U\in\mathcal M(A)$
; -
(4). for each
 $\Psi$
-set
$\Psi$
-set
 $A\subseteq X$
and
$A\subseteq X$
and
 $U\in\mathcal O(X)$
,
$U\in\mathcal O(X)$
,
 $\bigcap_{a\in A}\mathord{\uparrow} a\subseteq U$
implies
$\bigcap_{a\in A}\mathord{\uparrow} a\subseteq U$
implies
 $\mathord{\uparrow} a\subseteq U$
for some
$\mathord{\uparrow} a\subseteq U$
for some
 $a\in A$
.
$a\in A$
.
Proof. (1)
![]() $\Rightarrow$
(2). Let A be a
$\Rightarrow$
(2). Let A be a
![]() $\Psi$
-set in X. Then, there exists
$\Psi$
-set in X. Then, there exists
![]() $\mathcal F\in\Psi(X)$
such that
$\mathcal F\in\Psi(X)$
such that
![]() $\mathrm{cl}(A)\in m(\mathcal F)$
. Since X is
$\mathrm{cl}(A)\in m(\mathcal F)$
. Since X is
![]() $\Psi$
-well-filtered, it follows that
$\Psi$
-well-filtered, it follows that
![]() $(\bigcap\mathcal F)\cap \mathrm{cl}(A)\neq\emptyset$
. Take
$(\bigcap\mathcal F)\cap \mathrm{cl}(A)\neq\emptyset$
. Take
![]() $x\in (\bigcap\mathcal F)\cap
\mathrm{cl}(A)\neq\emptyset$
. Then,
$x\in (\bigcap\mathcal F)\cap
\mathrm{cl}(A)\neq\emptyset$
. Then,
![]() $\mathrm{cl}(\{x\})$
is a subset of
$\mathrm{cl}(\{x\})$
is a subset of
![]() $\mathrm{cl}(A)$
such that
$\mathrm{cl}(A)$
such that
![]() $\mathrm{cl}(\{x\})\in\mathfrak M(\mathcal F)$
. By the minimality of
$\mathrm{cl}(\{x\})\in\mathfrak M(\mathcal F)$
. By the minimality of
![]() $\mathrm{cl}(A)$
, we deduce that
$\mathrm{cl}(A)$
, we deduce that
![]() $\mathrm{cl}(A)=\mathrm{cl}(\{x\})$
.
$\mathrm{cl}(A)=\mathrm{cl}(\{x\})$
.
(2)
![]() $\Rightarrow$
(3). It is trivial since
$\Rightarrow$
(3). It is trivial since
![]() $\mathcal M(\mathrm{cl}(\{x\}))=\mathcal N(\{x\})$
for each
$\mathcal M(\mathrm{cl}(\{x\}))=\mathcal N(\{x\})$
for each
![]() $x\in X$
.
$x\in X$
.
(3)
![]() $\Rightarrow$
(1). Let
$\Rightarrow$
(1). Let
![]() $\mathcal F\in\Psi(X)$
and
$\mathcal F\in\Psi(X)$
and
![]() $O\in\mathcal O(X)$
such that
$O\in\mathcal O(X)$
such that
![]() $\bigcap\mathcal F\subseteq O$
. We need to show that
$\bigcap\mathcal F\subseteq O$
. We need to show that
![]() $O\in\mathcal F$
, or equivalently,
$O\in\mathcal F$
, or equivalently,
![]() $U\subseteq O$
for some
$U\subseteq O$
for some
![]() $U\in\mathcal F$
, because
$U\in\mathcal F$
, because
![]() $\mathcal F$
is an upper set. On the contrary, we assume
$\mathcal F$
is an upper set. On the contrary, we assume
![]() $U\nsubseteq O$
, that is,
$U\nsubseteq O$
, that is,
![]() $U\cap (X\setminus O)\neq\emptyset$
for each
$U\cap (X\setminus O)\neq\emptyset$
for each
![]() $U\in\mathcal F$
. By Lemma 2.12, there exists a closed subset A of
$U\in\mathcal F$
. By Lemma 2.12, there exists a closed subset A of
![]() $X\setminus O$
such that
$X\setminus O$
such that
![]() $A\in m(\mathcal F)$
. Then, A is a
$A\in m(\mathcal F)$
. Then, A is a
![]() $\Psi$
-set in X and note that
$\Psi$
-set in X and note that
![]() $\mathcal F\subseteq\mathcal M(A)$
, so
$\mathcal F\subseteq\mathcal M(A)$
, so
![]() $\bigcap\mathcal M(A)\subseteq\bigcap\mathcal F\subseteq O$
. From condition (3), it follows that
$\bigcap\mathcal M(A)\subseteq\bigcap\mathcal F\subseteq O$
. From condition (3), it follows that
![]() $O\in\mathcal M(A)$
, that is,
$O\in\mathcal M(A)$
, that is,
![]() $O\cap A\neq\emptyset$
, contradicting the fact that
$O\cap A\neq\emptyset$
, contradicting the fact that
![]() $A\subseteq X\setminus O$
. This implies that
$A\subseteq X\setminus O$
. This implies that
![]() $O\in\mathcal F$
. Therefore, X is
$O\in\mathcal F$
. Therefore, X is
![]() $\Psi$
-well-filtered.
$\Psi$
-well-filtered.
(2)
![]() $\Rightarrow$
(4). Suppose condition (2) is satisfied. Then, there exists
$\Rightarrow$
(4). Suppose condition (2) is satisfied. Then, there exists
![]() $x\in X$
such that
$x\in X$
such that
![]() $\mathrm{cl}(A)=\mathrm{cl}(\{x\})=\mathord{\downarrow} x$
, which follows that
$\mathrm{cl}(A)=\mathrm{cl}(\{x\})=\mathord{\downarrow} x$
, which follows that
This shows that U is an open neighborhood of x, and since
![]() $x\in \mathrm{cl}(A)$
, there is
$x\in \mathrm{cl}(A)$
, there is
![]() $a_0\in U\cap A\neq\emptyset$
, so
$a_0\in U\cap A\neq\emptyset$
, so
![]() $\mathord{\uparrow} a_0\subseteq U$
. This gives (4).
$\mathord{\uparrow} a_0\subseteq U$
. This gives (4).
(4)
![]() $\Rightarrow$
(2). Suppose A is a
$\Rightarrow$
(2). Suppose A is a
![]() $\Psi$
-set in X. By Remark 4.2,
$\Psi$
-set in X. By Remark 4.2,
![]() $\mathrm{cl}(A)$
is also a
$\mathrm{cl}(A)$
is also a
![]() $\Psi$
-set. Since
$\Psi$
-set. Since
![]() $\mathord{\uparrow} a\nsubseteq X\setminus\mathrm{cl}(A)$
for each
$\mathord{\uparrow} a\nsubseteq X\setminus\mathrm{cl}(A)$
for each
![]() $a\in \mathrm{cl}(A)$
, by condition (4) there exists
$a\in \mathrm{cl}(A)$
, by condition (4) there exists
![]() $x\in \mathrm{cl}(A)\cap\bigcap_{a\in\mathrm{cl}(A)}\mathord{\uparrow} a\neq\emptyset$
. Then, we can easily obtain that
$x\in \mathrm{cl}(A)\cap\bigcap_{a\in\mathrm{cl}(A)}\mathord{\uparrow} a\neq\emptyset$
. Then, we can easily obtain that
![]() $\mathrm{cl}(A)=\mathrm{cl}(\{x\})$
.
$\mathrm{cl}(A)=\mathrm{cl}(\{x\})$
.
Lemma 4.7. Let X and Y be two
![]() $T_0$
spaces and A be an irreducible subset of X.
$T_0$
spaces and A be an irreducible subset of X.
-
(1).
 $\mathcal M(A)\in \mathsf{OF}(X)$
and
$\mathcal M(A)\in \mathsf{OF}(X)$
and
 $\mathrm{cl}(A)\in m(\mathcal M(A))$
.
$\mathrm{cl}(A)\in m(\mathcal M(A))$
. -
(2). For each
 $B\in m(\mathcal M(A))$
,
$B\in m(\mathcal M(A))$
,
 $\mathrm{cl}(A)=B$
. Hence,
$\mathrm{cl}(A)=B$
. Hence,
 $\mathcal M(B)=\mathcal M(A)$
.
$\mathcal M(B)=\mathcal M(A)$
. -
(3). If
 $f:X\longrightarrow Y$
is a continuous mapping, then
$f:X\longrightarrow Y$
is a continuous mapping, then
 $f_*(\mathcal M(A))=\mathcal M(f(A))$
, where Hence,
$f_*(\mathcal M(A))=\mathcal M(f(A))$
, where Hence, \begin{equation*}f_*(\mathcal M(A))=\{V\in\mathcal O(Y):f^{-1}(V)\in\mathcal M(A)\}.\end{equation*}
\begin{equation*}f_*(\mathcal M(A))=\{V\in\mathcal O(Y):f^{-1}(V)\in\mathcal M(A)\}.\end{equation*}
 $\mathrm{cl}_Y(f(A))\in m(f_*(\mathcal M(A)))$
.
$\mathrm{cl}_Y(f(A))\in m(f_*(\mathcal M(A)))$
.
Proof. (1) It is trivial that
![]() $\mathcal M(A)\in \mathsf{OF}(X)$
and
$\mathcal M(A)\in \mathsf{OF}(X)$
and
![]() $\mathrm{cl}(A)\in\mathfrak{M}(\mathcal M(A))$
. To show
$\mathrm{cl}(A)\in\mathfrak{M}(\mathcal M(A))$
. To show
![]() $\mathrm{cl}(A)\in m(\mathcal M(A))$
, assume C is a closed subset of
$\mathrm{cl}(A)\in m(\mathcal M(A))$
, assume C is a closed subset of
![]() $\mathrm{cl}(A)$
such that
$\mathrm{cl}(A)$
such that
![]() $C\in \mathfrak{M}(\mathcal M(A))$
. We need to show that
$C\in \mathfrak{M}(\mathcal M(A))$
. We need to show that
![]() $A\subseteq C$
. Otherwise,
$A\subseteq C$
. Otherwise,
![]() $A\cap (X\setminus C)\neq\emptyset$
. Then,
$A\cap (X\setminus C)\neq\emptyset$
. Then,
![]() $X\setminus C\in \mathcal M(A)$
. Since
$X\setminus C\in \mathcal M(A)$
. Since
![]() $C\in \mathfrak{M}(\mathcal M(A))$
, it follows that
$C\in \mathfrak{M}(\mathcal M(A))$
, it follows that
![]() $C\cap(X\setminus C)\neq\emptyset$
, a contradiction. Thus,
$C\cap(X\setminus C)\neq\emptyset$
, a contradiction. Thus,
![]() $C=\mathrm{cl}(A)$
. This shows that
$C=\mathrm{cl}(A)$
. This shows that
![]() $\mathrm{cl}(A)\in m(\mathcal M(A))$
.
$\mathrm{cl}(A)\in m(\mathcal M(A))$
.
(2) Suppose
![]() $B\in m(\mathcal M(A))$
. Let
$B\in m(\mathcal M(A))$
. Let
![]() $x\in A$
. For each open neighborhood U of x,
$x\in A$
. For each open neighborhood U of x,
![]() $U\in\mathcal M(A)$
, hence
$U\in\mathcal M(A)$
, hence
![]() $B\cap U\neq\emptyset$
. This implies
$B\cap U\neq\emptyset$
. This implies
![]() $x\in \mathrm{cl}(B)=B$
. We then deduce that
$x\in \mathrm{cl}(B)=B$
. We then deduce that
![]() $A\subseteq B$
, so
$A\subseteq B$
, so
![]() $\mathrm{cl}(A)\subseteq B$
. From the minimality of B, it follows that
$\mathrm{cl}(A)\subseteq B$
. From the minimality of B, it follows that
![]() $\mathrm{cl}(A)=B$
.
$\mathrm{cl}(A)=B$
.
(3) For each
![]() $V\in\mathcal O(Y)$
, we have that
$V\in\mathcal O(Y)$
, we have that
![]() $V\in f_*(\mathcal M(A))$
iff
$V\in f_*(\mathcal M(A))$
iff
![]() $f^{-1}(V)\cap A\neq\emptyset$
iff
$f^{-1}(V)\cap A\neq\emptyset$
iff
![]() $V\cap f(A)\neq\emptyset$
iff
$V\cap f(A)\neq\emptyset$
iff
![]() $V\in\mathcal M(f(A))$
, which implies that
$V\in\mathcal M(f(A))$
, which implies that
![]() $f_*(\mathcal M(A))=\mathcal M(f(A))$
. Since f is continuous, it follows that f(A) is an irreducible set in Y. Hence, by (1), we have
$f_*(\mathcal M(A))=\mathcal M(f(A))$
. Since f is continuous, it follows that f(A) is an irreducible set in Y. Hence, by (1), we have
![]() $\mathrm{cl}_Y(f(A))\in m(\mathcal M(f(A)))=m(f_*(\mathcal M(A)))$
.
$\mathrm{cl}_Y(f(A))\in m(\mathcal M(f(A)))=m(f_*(\mathcal M(A)))$
.
Proposition 4.8. Let X be a
![]() $T_0$
space.
$T_0$
space.
-
(1). The
 $\Psi_{\mathsf{sob}}$
-sets are exactly the irreducible sets in X.
$\Psi_{\mathsf{sob}}$
-sets are exactly the irreducible sets in X. -
(2). The
 $\Psi_{\mathsf{wf}-}$
sets are exactly the KF-sets in X.
$\Psi_{\mathsf{wf}-}$
sets are exactly the KF-sets in X. -
(3). The closed
 $\Psi_{\rm d-}$
sets are exactly the closure of directed sets in X.
$\Psi_{\rm d-}$
sets are exactly the closure of directed sets in X.
Proof. (1) Suppose A is an irreducible subset of X. By Lemma 4.7,
![]() $\mathcal M(A)\in \Psi_{\mathsf{sob}}(X)=\mathsf{OF}(X)$
and
$\mathcal M(A)\in \Psi_{\mathsf{sob}}(X)=\mathsf{OF}(X)$
and
![]() $\mathrm{cl}(A)\in m(\mathcal M(A))$
, so A is a
$\mathrm{cl}(A)\in m(\mathcal M(A))$
, so A is a
![]() $\Psi_{\mathsf{sob}}$
-set in X. The converse is trivial by Remark 4.2.
$\Psi_{\mathsf{sob}}$
-set in X. The converse is trivial by Remark 4.2.
(2) Suppose
![]() $\mathcal F\in \Psi_{\mathsf{wf}}(X)$
. Then, there exists a filtered family
$\mathcal F\in \Psi_{\mathsf{wf}}(X)$
. Then, there exists a filtered family
![]() $\{K_i:i\in I\}\subseteq\mathcal Q(X)$
such that
$\{K_i:i\in I\}\subseteq\mathcal Q(X)$
such that
![]() $\mathcal F=\bigcup_{i\in I}\mathcal N(K_i)$
. By Lemma 4.3, for each subset
$\mathcal F=\bigcup_{i\in I}\mathcal N(K_i)$
. By Lemma 4.3, for each subset
![]() $A\subseteq X$
,
$A\subseteq X$
,
![]() $\mathrm{cl}(A)\in\mathfrak{M}(\mathcal F)$
iff
$\mathrm{cl}(A)\in\mathfrak{M}(\mathcal F)$
iff
![]() $\mathrm{cl}(A)\cap K_i\neq\emptyset$
for each
$\mathrm{cl}(A)\cap K_i\neq\emptyset$
for each
![]() $i\in I$
. Then, we deduce that the
$i\in I$
. Then, we deduce that the
![]() $\Psi_{\mathsf{wf}}$
-sets are exactly the KF-sets.
$\Psi_{\mathsf{wf}}$
-sets are exactly the KF-sets.
(3) Suppose A is a closed
![]() $\Psi_{\rm d}$
-set in X. Then, there exists a directed subset D of X such that
$\Psi_{\rm d}$
-set in X. Then, there exists a directed subset D of X such that
![]() $A\in m(\mathcal M(D))$
. By Lemma 4.7, we have
$A\in m(\mathcal M(D))$
. By Lemma 4.7, we have
![]() $\mathrm{cl}(D)=A$
. Now suppose E is a directed subset of X. Then, by Lemma 4.7,
$\mathrm{cl}(D)=A$
. Now suppose E is a directed subset of X. Then, by Lemma 4.7,
![]() $\mathrm{cl}(E)\in m(\mathcal M(E))$
. This means that
$\mathrm{cl}(E)\in m(\mathcal M(E))$
. This means that
![]() $\mathrm{cl}(E)$
is a closed
$\mathrm{cl}(E)$
is a closed
![]() $\Psi_{\rm d}$
-set in X.
$\Psi_{\rm d}$
-set in X.
5. Relations between
 $\Psi$
-Well-Filtered Spaces and H-Sober Spaces
$\Psi$
-Well-Filtered Spaces and H-Sober Spaces
In the paper Xu (Reference Xu2021), Xu introduces the notions of R-subset system and H-sober space, which provides a uniform approach to d-spaces, well-filtered spaces, and sober spaces. In this section, we study the relations between H-sober spaces and
![]() $\Psi$
-well-filtered spaces.
$\Psi$
-well-filtered spaces.
Definition 5.1
(
Reference Xu
Xu 2021
) A covariant functor
![]() $H:{\bf Top_0}\longrightarrow{\bf Set}$
is called an R-subset system on
$H:{\bf Top_0}\longrightarrow{\bf Set}$
is called an R-subset system on
![]() ${\bf Top_0}$
if it satisfies the following two conditions:
${\bf Top_0}$
if it satisfies the following two conditions:
-
(H1) for each
 $T_0$
space X,
$T_0$
space X,
 $\{\{x\} :x\in X\}\subseteq H(X)\subseteq Irr(X)$
;
$\{\{x\} :x\in X\}\subseteq H(X)\subseteq Irr(X)$
; -
(H2) For each continuous mapping
 $f:X\longrightarrow Y$
in
$f:X\longrightarrow Y$
in
 ${\bf Top_0}$
and each
${\bf Top_0}$
and each
 $A\in H(X)$
,
$A\in H(X)$
,
 $H(f)(A)=f(A)\in H(Y)$
.
$H(f)(A)=f(A)\in H(Y)$
.
For an R-subset system H and a
![]() $T_0$
space X, we call
$T_0$
space X, we call
![]() $A\subseteq X$
an H-set if
$A\subseteq X$
an H-set if
![]() $A\in H(X)$
.
$A\in H(X)$
.
Definition 5.2
(
Reference Xu
Xu 2021
) Let H be an R-subset system. A
![]() $T_0$
space X is called H-sober if for each
$T_0$
space X is called H-sober if for each
![]() $A\in H(X)$
, there is a (unique) point
$A\in H(X)$
, there is a (unique) point
![]() $x\in X$
such that
$x\in X$
such that
![]() $\mathrm{cl}(A)=\mathrm{cl}(\{x\})$
.
$\mathrm{cl}(A)=\mathrm{cl}(\{x\})$
.
Next, we study the relationship between
![]() $\Psi$
-well-filtered spaces and H-sober spaces, the following concept is needed.
$\Psi$
-well-filtered spaces and H-sober spaces, the following concept is needed.
Definition 5.3. An HM-system
![]() $\Psi$
is called complete if for each continuous mapping
$\Psi$
is called complete if for each continuous mapping
![]() $f:X\longrightarrow Y$
between
$f:X\longrightarrow Y$
between
![]() $T_0$
spaces X and Y, and each
$T_0$
spaces X and Y, and each
![]() $\Psi$
-set A in X, f(A) is a
$\Psi$
-set A in X, f(A) is a
![]() $\Psi$
-set in Y.
$\Psi$
-set in Y.
Lemma 5.4. An HM-system
![]() $\Psi$
is complete if and only if for each continuous mapping
$\Psi$
is complete if and only if for each continuous mapping
![]() $f:X\longrightarrow Y$
between
$f:X\longrightarrow Y$
between
![]() $T_0$
spaces X and Y, and each closed
$T_0$
spaces X and Y, and each closed
![]() $\Psi$
-set A in X, f(A) is a
$\Psi$
-set A in X, f(A) is a
![]() $\Psi$
-set in Y.
$\Psi$
-set in Y.
Proof. It suffices to prove the sufficiency. Suppose A is a
![]() $\Psi$
-set in X. By assumption,
$\Psi$
-set in X. By assumption,
![]() $f(\mathrm{cl}_{X}(A))$
is a
$f(\mathrm{cl}_{X}(A))$
is a
![]() $\Psi$
-set in Y. By Remark 4.2,
$\Psi$
-set in Y. By Remark 4.2,
![]() $\mathrm{cl}_Y(f(\mathrm{cl}_X(A)))=\mathrm{cl}_Y(f(A))$
is a
$\mathrm{cl}_Y(f(\mathrm{cl}_X(A)))=\mathrm{cl}_Y(f(A))$
is a
![]() $\Psi$
-set, so is f(A), completing the proof.
$\Psi$
-set, so is f(A), completing the proof.
Proposition 5.5. The HM-systems
![]() $\Psi_{\mathsf{sob}}$
,
$\Psi_{\mathsf{sob}}$
,
![]() $\Psi_{\mathsf{wf},}$
and
$\Psi_{\mathsf{wf},}$
and
![]() $\Psi_{\rm d}$
are all complete.
$\Psi_{\rm d}$
are all complete.
Proof. By Proposition 4.8 and Lemma 2.6,
![]() $\Psi_{\mathsf{wf}}$
is complete. The completeness of
$\Psi_{\mathsf{wf}}$
is complete. The completeness of
![]() $\Psi_{\mathsf{sob}}$
and
$\Psi_{\mathsf{sob}}$
and
![]() $\Psi_{\rm d}$
is trivial (see Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003) by Proposition 4.8.
$\Psi_{\rm d}$
is trivial (see Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003) by Proposition 4.8.
Lemma 5.6. Let X and Y be two
![]() $T_0$
spaces, K be a compact saturated subset of X, and
$T_0$
spaces, K be a compact saturated subset of X, and
![]() $f:X\longrightarrow Y$
be a continuous mapping.
$f:X\longrightarrow Y$
be a continuous mapping.
-
(1).
 $f_*(\mathcal N(K))=\mathcal N(f(K))$
.
$f_*(\mathcal N(K))=\mathcal N(f(K))$
. -
(2). If
 $A\in m(\mathcal N(K))$
, then
$A\in m(\mathcal N(K))$
, then
 $\mathrm{cl}_{Y}(f(A))\in m(\mathcal N (\mathord{\uparrow} f(K\cap A)))$
.
$\mathrm{cl}_{Y}(f(A))\in m(\mathcal N (\mathord{\uparrow} f(K\cap A)))$
.
Proof. (1) It is trivial.
(2) First, by Lemma 4.4 there exists
![]() $x\in\min K$
such that
$x\in\min K$
such that
![]() $A=\mathrm{cl}_X(\{x\})$
. It follows that
$A=\mathrm{cl}_X(\{x\})$
. It follows that
![]() $A\cap K=\{x\}$
, so
$A\cap K=\{x\}$
, so
![]() $\mathord{\uparrow} f(K\cap A)=\mathord{\uparrow} f(x)$
. In addition, using Lemma 4.3, one can easily obtain that
$\mathord{\uparrow} f(K\cap A)=\mathord{\uparrow} f(x)$
. In addition, using Lemma 4.3, one can easily obtain that
![]() $\mathrm{cl}_Y(f(A))\in\mathfrak{M}(\mathcal N(\mathord{\uparrow} f(x)))$
. Suppose C is a closed subset of
$\mathrm{cl}_Y(f(A))\in\mathfrak{M}(\mathcal N(\mathord{\uparrow} f(x)))$
. Suppose C is a closed subset of
![]() $\mathrm{cl}_Y(f(A))$
such that
$\mathrm{cl}_Y(f(A))$
such that
![]() $C\in\mathfrak{M}(\mathcal N(\mathord{\uparrow} f(x)))$
. By Lemma 4.3,
$C\in\mathfrak{M}(\mathcal N(\mathord{\uparrow} f(x)))$
. By Lemma 4.3,
![]() $C\cap \mathord{\uparrow} f(x)\neq\emptyset$
, and since C is a lower set, we have that
$C\cap \mathord{\uparrow} f(x)\neq\emptyset$
, and since C is a lower set, we have that
![]() $f(x)\in C$
, so
$f(x)\in C$
, so
![]() $A=\mathrm{cl}_X(\{x\})\subseteq f^{-1}(C)$
. It follows that
$A=\mathrm{cl}_X(\{x\})\subseteq f^{-1}(C)$
. It follows that
![]() $\mathrm{cl}_Y(f(A))\subseteq C$
. Thus,
$\mathrm{cl}_Y(f(A))\subseteq C$
. Thus,
![]() $C=\mathrm{cl}_Y(f(A))$
. Therefore,
$C=\mathrm{cl}_Y(f(A))$
. Therefore,
![]() $\mathrm{cl}_Y(f(A))\in m(\mathcal N(\mathord{\uparrow} f(K\cap A)))$
.
$\mathrm{cl}_Y(f(A))\in m(\mathcal N(\mathord{\uparrow} f(K\cap A)))$
.
Theorem 5.7 Let
![]() $H:{\bf Top_0}\longrightarrow{\bf Set}$
be an R-subset system. Define
$H:{\bf Top_0}\longrightarrow{\bf Set}$
be an R-subset system. Define
![]() $\Psi_H:{\bf Top_0}\longrightarrow{\bf Set}$
by
$\Psi_H:{\bf Top_0}\longrightarrow{\bf Set}$
by
![]() $\Psi_H(X)=\{\mathcal M(A):A\in H(X)\}\cup\{\mathcal N(K):K\in\mathcal Q(X)\}$
.
$\Psi_H(X)=\{\mathcal M(A):A\in H(X)\}\cup\{\mathcal N(K):K\in\mathcal Q(X)\}$
.
for each
![]() $T_0$
space X, and for each continuous mapping
$T_0$
space X, and for each continuous mapping
![]() $f:X\longrightarrow Y$
between
$f:X\longrightarrow Y$
between
![]() $T_0$
spaces X and Y, we define
$T_0$
spaces X and Y, we define
![]() $\Psi_H(f):{\Psi}_H(X)\longrightarrow {\Psi}_H(Y)$
by
$\Psi_H(f):{\Psi}_H(X)\longrightarrow {\Psi}_H(Y)$
by
for each
![]() $\mathcal F\in {\Psi}_H(X)$
.
$\mathcal F\in {\Psi}_H(X)$
.
-
(1)
 $\Psi_H$
is a complete HM-system.
$\Psi_H$
is a complete HM-system. -
(2) A
 $T_0$
space X is H-sober if and only if it is
$T_0$
space X is H-sober if and only if it is
 $\Psi_H$
-well-filtered.
$\Psi_H$
-well-filtered.
Proof. (1) We first prove that
![]() $\Psi_H$
is an HM-system.
$\Psi_H$
is an HM-system.
Note that each member of H(X) is irreducible in X, so it is clear that
![]() $\Psi_H$
satisfies (H1). To show (HM2), let
$\Psi_H$
satisfies (H1). To show (HM2), let
![]() $f:X\longrightarrow Y$
be a continuous mapping between
$f:X\longrightarrow Y$
be a continuous mapping between
![]() $T_0$
spaces X and Y, and
$T_0$
spaces X and Y, and
![]() $A\in H(X)$
, that is,
$A\in H(X)$
, that is,
![]() $\mathcal M(A)\in \Psi_H(X)$
. By (H2),
$\mathcal M(A)\in \Psi_H(X)$
. By (H2),
![]() $f(A)\in H(Y)$
, and it follows from Lemma 4.7 that
$f(A)\in H(Y)$
, and it follows from Lemma 4.7 that
![]() $f_*(\mathcal M(A))=\mathcal M(f(A))\in\Psi_H(Y)$
, and since
$f_*(\mathcal M(A))=\mathcal M(f(A))\in\Psi_H(Y)$
, and since
![]() $f_*(\mathcal N(K))=\mathcal N(f(K))\in\Psi_H(Y)$
, (H2) holds. In addition, it is trivial to check that
$f_*(\mathcal N(K))=\mathcal N(f(K))\in\Psi_H(Y)$
, (H2) holds. In addition, it is trivial to check that
![]() $\Psi_H$
is a covariant functor. Hence,
$\Psi_H$
is a covariant functor. Hence,
![]() $\Psi_H$
is an HM-system.
$\Psi_H$
is an HM-system.
Now we prove that
![]() $\Psi_H$
is complete. Suppose A is a closed
$\Psi_H$
is complete. Suppose A is a closed
![]() $\Psi_H$
-set in a
$\Psi_H$
-set in a
![]() $T_0$
space X and
$T_0$
space X and
![]() $f:X\longrightarrow Y$
is a continuous mapping to a
$f:X\longrightarrow Y$
is a continuous mapping to a
![]() $T_0$
space Y. We need to prove that f(A) is a
$T_0$
space Y. We need to prove that f(A) is a
![]() $\Psi_H$
-set in Y. We consider the following cases:
$\Psi_H$
-set in Y. We consider the following cases:
(c1) there exists
![]() $K\in\mathcal Q(X)$
such that
$K\in\mathcal Q(X)$
such that
![]() $A\in m(\mathcal N(K))$
. Note that the intersection
$A\in m(\mathcal N(K))$
. Note that the intersection
![]() $K\cap A$
is compact and since f is continuous,
$K\cap A$
is compact and since f is continuous,
![]() $f (K\cap A)$
is compact in Y, so
$f (K\cap A)$
is compact in Y, so
![]() $\mathord{\uparrow} f(K\cap A)\in\mathcal Q(Y)$
. By Lemma 5.6,
$\mathord{\uparrow} f(K\cap A)\in\mathcal Q(Y)$
. By Lemma 5.6,
![]() $\mathrm{cl}_Y(f(A))\in m(\mathcal N(\mathord{\uparrow} f(K\cap A)))$
. This shows that f(A) is a
$\mathrm{cl}_Y(f(A))\in m(\mathcal N(\mathord{\uparrow} f(K\cap A)))$
. This shows that f(A) is a
![]() $\Psi_H$
-set in Y.
$\Psi_H$
-set in Y.
(c2) there exists a
![]() $B\in H(X)$
such that
$B\in H(X)$
such that
![]() $A\in m(\mathcal M(B))$
. By Lemma 4.7,
$A\in m(\mathcal M(B))$
. By Lemma 4.7,
![]() $A=\mathrm{cl}_X(B)$
and
$A=\mathrm{cl}_X(B)$
and
![]() $\mathrm{cl}_Y(f(A))\in m(\mathcal M(f(A)))$
. Since
$\mathrm{cl}_Y(f(A))\in m(\mathcal M(f(A)))$
. Since
![]() $f(A)\in H(Y)$
by (H2), it follows that
$f(A)\in H(Y)$
by (H2), it follows that
![]() $\mathcal M(f(A))=\mathcal M(f(\mathrm{cl}_X(B)))=\mathcal M(f(B))\in\Psi_H(Y)$
. Thus f(A) is a
$\mathcal M(f(A))=\mathcal M(f(\mathrm{cl}_X(B)))=\mathcal M(f(B))\in\Psi_H(Y)$
. Thus f(A) is a
![]() $\Psi_H$
-set in Y.
$\Psi_H$
-set in Y.
By Lemma 5.4,
![]() $\Psi$
is a complete HM-system.
$\Psi$
is a complete HM-system.
(2) (
![]() $\Rightarrow$
). Assume X is H-sober. Let A be a
$\Rightarrow$
). Assume X is H-sober. Let A be a
![]() $\Psi_H$
-set in X. There are two cases:
$\Psi_H$
-set in X. There are two cases:
(c1)
![]() $A\in m(\mathcal M(B))$
for some
$A\in m(\mathcal M(B))$
for some
![]() $B\in H(X)$
. By Lemma 4.7,
$B\in H(X)$
. By Lemma 4.7,
![]() $\mathrm{cl}(B)=\mathrm{cl}(A)$
, and since X is H-sober,
$\mathrm{cl}(B)=\mathrm{cl}(A)$
, and since X is H-sober,
![]() $\mathrm{cl}(B)=\mathrm{cl}(A)=\mathrm{cl}(\{x\})$
for some
$\mathrm{cl}(B)=\mathrm{cl}(A)=\mathrm{cl}(\{x\})$
for some
![]() $x\in X$
.
$x\in X$
.
(c2)
![]() $A\in m(\mathcal N(K))$
for some
$A\in m(\mathcal N(K))$
for some
![]() $K\in\mathcal Q(X)$
. By Lemma 4.4,
$K\in\mathcal Q(X)$
. By Lemma 4.4,
![]() $\mathrm{cl}(A)=\mathrm{cl}(\{x\})$
for some
$\mathrm{cl}(A)=\mathrm{cl}(\{x\})$
for some
![]() $x\in\min K$
.
$x\in\min K$
.
Then by Theorem 4.6, X is
![]() $\Psi_H$
-well-filtered.
$\Psi_H$
-well-filtered.
(
![]() $\Leftarrow$
). Assume X is a
$\Leftarrow$
). Assume X is a
![]() $\Psi_H$
-well-filtered space. Let
$\Psi_H$
-well-filtered space. Let
![]() $A\in H(X)$
. Then by Lemma 4.7,
$A\in H(X)$
. Then by Lemma 4.7,
![]() $\mathrm{cl}(A)\in m(\mathcal M(A))\in\Psi_H(X)$
, so A is a
$\mathrm{cl}(A)\in m(\mathcal M(A))\in\Psi_H(X)$
, so A is a
![]() $\Psi_H$
-set in X. Since X is
$\Psi_H$
-set in X. Since X is
![]() $\Psi_H$
-well-filtered, by Theorem 4.6
$\Psi_H$
-well-filtered, by Theorem 4.6
![]() $\mathrm{cl}(A)=\mathrm{cl}(\{x\})$
for some
$\mathrm{cl}(A)=\mathrm{cl}(\{x\})$
for some
![]() $x\in X$
. Therefore, X is H-sober.
$x\in X$
. Therefore, X is H-sober.
Theorem 5.8. Let
![]() $\Psi:{\bf Top_0}\longrightarrow{\bf Set}$
be a complete HM-system. Define
$\Psi:{\bf Top_0}\longrightarrow{\bf Set}$
be a complete HM-system. Define
![]() $H_{\Psi}:{\bf Top_0}\longrightarrow{\bf Set}$
by
$H_{\Psi}:{\bf Top_0}\longrightarrow{\bf Set}$
by
for each
![]() $T_0$
space X, and for each continuous mapping
$T_0$
space X, and for each continuous mapping
![]() $f:X\longrightarrow Y$
between
$f:X\longrightarrow Y$
between
![]() $T_0$
spaces X and Y, define
$T_0$
spaces X and Y, define
![]() $H_{\Psi}(f):H_{\Psi}(X)\longrightarrow H_{\Psi}(Y)$
by
$H_{\Psi}(f):H_{\Psi}(X)\longrightarrow H_{\Psi}(Y)$
by
for each
![]() $A\in H_{\Psi}(X)$
.
$A\in H_{\Psi}(X)$
.
-
(1).
 $H_{\Psi}$
is an R-system.
$H_{\Psi}$
is an R-system. -
(2). A
 $T_0$
space X is
$T_0$
space X is
 $\Psi$
-well-filtered if and only if it is
$\Psi$
-well-filtered if and only if it is
 $H_{\Psi}$
-sober.
$H_{\Psi}$
-sober.
Proof. (1) We first prove that
![]() $H_{\Psi}$
satisfies (H1) and (H2). For (H1), it follows from Proposition 4.5 that
$H_{\Psi}$
satisfies (H1) and (H2). For (H1), it follows from Proposition 4.5 that
![]() $\{\{x\}:x\in X\}\subseteq H_{\Psi}(X)$
. By Lemma 2.12, every
$\{\{x\}:x\in X\}\subseteq H_{\Psi}(X)$
. By Lemma 2.12, every
![]() $\Psi$
-set is irreducible; hence,
$\Psi$
-set is irreducible; hence,
![]() $H_{\Psi}(X)\subseteq Irr(X)$
. Thus, (H1) holds. Condition (H2) holds immediately since
$H_{\Psi}(X)\subseteq Irr(X)$
. Thus, (H1) holds. Condition (H2) holds immediately since
![]() $\Psi$
is complete. It is trivial to check that H is a covariant functor. Therefore,
$\Psi$
is complete. It is trivial to check that H is a covariant functor. Therefore,
![]() $H_{\Psi}$
is an R-system.
$H_{\Psi}$
is an R-system.
(2) It is straightforward by Theorem 4.6.
For an HM-system
![]() $\Psi$
, we use
$\Psi$
, we use
![]() $\Psi$
- WF to denote the category of all
$\Psi$
- WF to denote the category of all
![]() $\Psi$
-well-filtered spaces with continuous mappings. In Xu (Reference Xu2021), Xu proved that the category of all H-sober spaces with continuous mappings is reflective in the category
$\Psi$
-well-filtered spaces with continuous mappings. In Xu (Reference Xu2021), Xu proved that the category of all H-sober spaces with continuous mappings is reflective in the category
![]() ${\bf Top_0}$
of
${\bf Top_0}$
of
![]() $T_0$
spaces. Then by Theorem 5.8, we have the following corollary.
$T_0$
spaces. Then by Theorem 5.8, we have the following corollary.
Corollary 5.9. For a complete HM-system
![]() $\Psi$
, the category
$\Psi$
, the category
![]() $\Psi$
- WF is a reflective subcategory of
$\Psi$
- WF is a reflective subcategory of
![]() ${\bf Top_0}$
.
${\bf Top_0}$
.
6. The Smyth Power Space of a
 $\Psi$
-Well-Filtered Space
$\Psi$
-Well-Filtered Space
For a topological space X, the upper Vietoris topology on
![]() $\mathcal Q^*(X)=\mathcal Q(X)\setminus\{\emptyset\}$
is generated by the following family (as a base)
$\mathcal Q^*(X)=\mathcal Q(X)\setminus\{\emptyset\}$
is generated by the following family (as a base)
where U ranges over the open subsets of X. The resulting space, denoted by
![]() $P_s(X)$
, is called the Smyth power space or the upper space.
$P_s(X)$
, is called the Smyth power space or the upper space.
Remark 6.1
(Goubault-Larrecq 2003; Jia and Jung 2016; Schalk 1993) Let X be a
![]() $T_0$
space.
$T_0$
space.
-
(1). The specialization order of
 $P_s(X)$
is
$P_s(X)$
is
 $\supseteq$
. Hence, for each
$\supseteq$
. Hence, for each
 $\mathcal A\subseteq \mathcal Q^*(X)$
, in the specialization order of
$\mathcal A\subseteq \mathcal Q^*(X)$
, in the specialization order of \begin{equation*}\mathord{\uparrow}_{P_s(X)}\mathcal A=\{K\in\mathcal Q^*(X):K\subseteq G\text{ for some }G\in\mathcal A\}\end{equation*}
\begin{equation*}\mathord{\uparrow}_{P_s(X)}\mathcal A=\{K\in\mathcal Q^*(X):K\subseteq G\text{ for some }G\in\mathcal A\}\end{equation*}
 $P_s(X)$
.
$P_s(X)$
.
-
(2). Define
 $\xi:X\longrightarrow P_s(X)$
,
$\xi:X\longrightarrow P_s(X)$
,
 $x\mapsto\mathord{\uparrow} x$
. Then
$x\mapsto\mathord{\uparrow} x$
. Then
 $\xi^{-1}(\Box U)=U$
for each
$\xi^{-1}(\Box U)=U$
for each
 $U\in\mathcal O(X)$
, and hence
$U\in\mathcal O(X)$
, and hence
 $\xi$
is continuous.
$\xi$
is continuous. -
(3). If
 $\mathcal K$
is compact in
$\mathcal K$
is compact in
 $P_s(X)$
, then
$P_s(X)$
, then
 $\bigcup\mathcal K$
is compact in X.
$\bigcup\mathcal K$
is compact in X.
Definition 6.2
(
Reference Xu
Xu 2021
) Let X be a
![]() $T_0$
space. An R-subset system H is said to satisfy property Q for X if for each
$T_0$
space. An R-subset system H is said to satisfy property Q for X if for each
![]() $\mathcal A\in H(P_s(X))$
and each
$\mathcal A\in H(P_s(X))$
and each
![]() $C\in\mathfrak M(\mathcal A)$
, there is an H-subset F of C such that
$C\in\mathfrak M(\mathcal A)$
, there is an H-subset F of C such that
![]() $\mathrm{cl}(F)\in \mathfrak M(\mathcal A)$
.
$\mathrm{cl}(F)\in \mathfrak M(\mathcal A)$
.
Lemma 6.3. Let X be a
![]() $T_0$
space,
$T_0$
space,
![]() $\mathcal A\subseteq \mathcal Q(X)$
. Then,
$\mathcal A\subseteq \mathcal Q(X)$
. Then,
![]() $\mathfrak M(\mathcal A)=\mathfrak M(\mathrm{cl}_{P_s(X)}(\mathcal A))$
. Hence,
$\mathfrak M(\mathcal A)=\mathfrak M(\mathrm{cl}_{P_s(X)}(\mathcal A))$
. Hence,
![]() $m(\mathcal A)=m(\mathrm{cl}_{P_s(X)}(\mathcal A))$
.
$m(\mathcal A)=m(\mathrm{cl}_{P_s(X)}(\mathcal A))$
.
Proof. We only need to prove that
![]() $\mathfrak M(\mathcal A)\subseteq\mathfrak M(\mathrm{cl}_{P_s(X)}(\mathcal A))$
. Assume on the contrary there exists
$\mathfrak M(\mathcal A)\subseteq\mathfrak M(\mathrm{cl}_{P_s(X)}(\mathcal A))$
. Assume on the contrary there exists
![]() $C\in\mathfrak M(\mathcal A)$
such that
$C\in\mathfrak M(\mathcal A)$
such that
![]() $C\notin \mathfrak M(\mathrm{cl}_{P_s(X)}(\mathcal A))$
. Then, there exists
$C\notin \mathfrak M(\mathrm{cl}_{P_s(X)}(\mathcal A))$
. Then, there exists
![]() $K\in\mathrm{cl}_{P_s(X)}(\mathcal A)$
such that
$K\in\mathrm{cl}_{P_s(X)}(\mathcal A)$
such that
![]() $C\cap K=\emptyset$
. This implies that
$C\cap K=\emptyset$
. This implies that
![]() $\Box (X\setminus C)$
is an open neighborhood of K in
$\Box (X\setminus C)$
is an open neighborhood of K in
![]() $P_s(X)$
, and since
$P_s(X)$
, and since
![]() $K\in\mathrm{cl}_{P_s(X)}(\mathcal A)$
, there is
$K\in\mathrm{cl}_{P_s(X)}(\mathcal A)$
, there is
![]() $G\in \mathcal A\cap \Box (X\setminus C)\neq\emptyset$
. Thus, G is a member of
$G\in \mathcal A\cap \Box (X\setminus C)\neq\emptyset$
. Thus, G is a member of
![]() $\mathcal A$
such that
$\mathcal A$
such that
![]() $G\cap C=\emptyset$
, contradicting the fact that
$G\cap C=\emptyset$
, contradicting the fact that
![]() $C\in\mathfrak M(\mathcal A)$
. Hence,
$C\in\mathfrak M(\mathcal A)$
. Hence,
![]() $\mathfrak M(\mathcal A)\subseteq\mathfrak M(\mathrm{cl}_{P_s(X)}(\mathcal A))$
.
$\mathfrak M(\mathcal A)\subseteq\mathfrak M(\mathrm{cl}_{P_s(X)}(\mathcal A))$
.
The following theorem strengthens a result in Xu (Reference Xu2021).
Theorem 6.4. Let H be an R-subset system and X be a
![]() $T_0$
space. The following two conditions are equivalent:
$T_0$
space. The following two conditions are equivalent:
-
(1).
 $P_s(X)$
is H-sober;
$P_s(X)$
is H-sober; -
(2). X is H-sober and H has property Q for X.
Proof. By Xu (Reference Xu2021), Theorem 5.12, we only need to check that condition (1) implies that H has property Q for X. Suppose
![]() $\mathcal A\in H(P_s(X))$
and
$\mathcal A\in H(P_s(X))$
and
![]() $C\in\mathfrak M(\mathcal A)$
. Since
$C\in\mathfrak M(\mathcal A)$
. Since
![]() $P_s(X)$
is H-sober, there exists
$P_s(X)$
is H-sober, there exists
![]() $K\in\mathcal Q^*(X)$
such that
$K\in\mathcal Q^*(X)$
such that
![]() $\mathrm{cl}_{P_s(X)}(\mathcal A)=\mathrm{cl}_{P_s(X)}(\{K\})$
. By Lemma 6.3,
$\mathrm{cl}_{P_s(X)}(\mathcal A)=\mathrm{cl}_{P_s(X)}(\{K\})$
. By Lemma 6.3,
![]() $C\in\mathfrak M(\mathcal A)=\mathfrak M(\mathrm{cl}_{P_s(X)}(\mathcal A))=\mathfrak M(\mathrm{cl}_{P_s(X)}(\{K\}))=\mathfrak M(\{K\})$
, which follows that
$C\in\mathfrak M(\mathcal A)=\mathfrak M(\mathrm{cl}_{P_s(X)}(\mathcal A))=\mathfrak M(\mathrm{cl}_{P_s(X)}(\{K\}))=\mathfrak M(\{K\})$
, which follows that
![]() $C\cap K\neq\emptyset$
. Take
$C\cap K\neq\emptyset$
. Take
![]() $x\in C\cap K$
. Then,
$x\in C\cap K$
. Then,
![]() $\{x\}$
is an H-set, and it is clear that
$\{x\}$
is an H-set, and it is clear that
![]() $\mathrm{cl}(\{x\})\in \mathfrak M(\{K\})=\mathfrak M(\mathcal A)$
.
$\mathrm{cl}(\{x\})\in \mathfrak M(\{K\})=\mathfrak M(\mathcal A)$
.
Definition 6.5. Let X be a
![]() $T_0$
space. An HM-system
$T_0$
space. An HM-system
![]() $\Psi$
is said to satisfy property Q for X if for each
$\Psi$
is said to satisfy property Q for X if for each
![]() $\Psi$
-set
$\Psi$
-set
![]() $\mathcal A$
in
$\mathcal A$
in
![]() $P_s(X)$
and each
$P_s(X)$
and each
![]() $C\in\mathfrak M(\mathcal A)$
, there is a
$C\in\mathfrak M(\mathcal A)$
, there is a
![]() $\Psi$
-subset F of C such that
$\Psi$
-subset F of C such that
![]() $\mathrm{cl}(F)\in \mathfrak M(\mathcal A)$
.
$\mathrm{cl}(F)\in \mathfrak M(\mathcal A)$
.
From Theorems 5.7 and 5.8, it turns out that there is a one to one correspondence between H-sober spaces and
![]() $\Psi$
-well-filtered spaces when
$\Psi$
-well-filtered spaces when
![]() $\Psi$
is complete. In other words, the class of
$\Psi$
is complete. In other words, the class of
![]() $\Psi$
-well-filtered spaces are more general than H-sober spaces. As a generalized result of Theorem 6.4, we have the following result.
$\Psi$
-well-filtered spaces are more general than H-sober spaces. As a generalized result of Theorem 6.4, we have the following result.
Theorem 6.6. Let
![]() $\Psi$
be an HM-system and X be a
$\Psi$
be an HM-system and X be a
![]() $T_0$
space. Then, the following conditions are equivalent:
$T_0$
space. Then, the following conditions are equivalent:
-
(1).
 $P_s(X)$
is
$P_s(X)$
is
 $\Psi$
-well-filtered;
$\Psi$
-well-filtered; -
(2). X is
 $\Psi$
-well-filtered and
$\Psi$
-well-filtered and
 $\Psi$
has property Q for X;
$\Psi$
has property Q for X; -
(3). for each
 $\Psi$
-set
$\Psi$
-set
 $\mathcal A$
in
$\mathcal A$
in
 $P_s(X)$
and each
$P_s(X)$
and each
 $U\in\mathcal O(X)$
,
$U\in\mathcal O(X)$
,
 $\bigcap\mathcal A\subseteq U$
implies
$\bigcap\mathcal A\subseteq U$
implies
 $K\subseteq U$
for some
$K\subseteq U$
for some
 $K\in\mathcal A$
.
$K\in\mathcal A$
.
Proof. (1)
![]() $\Rightarrow$
(2). We first prove that X is
$\Rightarrow$
(2). We first prove that X is
![]() $\Psi$
-well-filtered. Let
$\Psi$
-well-filtered. Let
![]() $\mathcal F\in\Psi(X)$
and
$\mathcal F\in\Psi(X)$
and
![]() $U\in\mathcal O(X)$
with
$U\in\mathcal O(X)$
with
![]() $\bigcap \mathcal F\subseteq U$
. Consider the continuous mapping
$\bigcap \mathcal F\subseteq U$
. Consider the continuous mapping
![]() $\xi:X\longrightarrow P_s(X)$
,
$\xi:X\longrightarrow P_s(X)$
,
![]() $x\mapsto\mathord{\uparrow} x$
. Then,
$x\mapsto\mathord{\uparrow} x$
. Then,
![]() $\xi_*(\mathcal F)=\{\mathcal U\in\mathcal O(P_s(X)):\xi^{-1}(\mathcal U)\in\mathcal F\}\in\Psi(P_s(X))$
by the definition of
$\xi_*(\mathcal F)=\{\mathcal U\in\mathcal O(P_s(X)):\xi^{-1}(\mathcal U)\in\mathcal F\}\in\Psi(P_s(X))$
by the definition of
![]() $\Psi$
. Let
$\Psi$
. Let
For each
![]() $V\in\mathcal O(X)$
, observe that
$V\in\mathcal O(X)$
, observe that
![]() $\Box V\in\mathfrak{F}$
iff
$\Box V\in\mathfrak{F}$
iff
![]() $\xi^{-1}(\Box V)=V\in\mathcal F$
, which implies that
$\xi^{-1}(\Box V)=V\in\mathcal F$
, which implies that
![]() $\mathfrak{F}=\{\Box V:V\in\mathcal F\}$
. If
$\mathfrak{F}=\{\Box V:V\in\mathcal F\}$
. If
![]() $K\in\bigcap\mathfrak{F}$
, then
$K\in\bigcap\mathfrak{F}$
, then
![]() $K\in\Box V$
(i.e.,
$K\in\Box V$
(i.e.,
![]() $K\subseteq V$
) for all
$K\subseteq V$
) for all
![]() $V\in\mathcal F$
, so
$V\in\mathcal F$
, so
![]() $K\subseteq\bigcap\mathcal F\subseteq U$
, which implies
$K\subseteq\bigcap\mathcal F\subseteq U$
, which implies
![]() $K\in\Box U$
. Thus,
$K\in\Box U$
. Thus,
![]() $\bigcap\mathfrak{F}\subseteq\Box U$
. Since
$\bigcap\mathfrak{F}\subseteq\Box U$
. Since
![]() $P_s(X)$
is
$P_s(X)$
is
![]() $\Psi$
-well-filtered and
$\Psi$
-well-filtered and
![]() $\bigcap\xi_*(\mathcal F)\subseteq\bigcap \mathfrak{F}\subseteq\Box U$
, we have that
$\bigcap\xi_*(\mathcal F)\subseteq\bigcap \mathfrak{F}\subseteq\Box U$
, we have that
![]() $\Box U\in \xi_*(\mathcal F)$
, so
$\Box U\in \xi_*(\mathcal F)$
, so
![]() $\xi^{-1}(\Box U)=U\in\mathcal F$
. Hence, X is
$\xi^{-1}(\Box U)=U\in\mathcal F$
. Hence, X is
![]() $\Psi$
-well-filtered. Using a similar method of Theorem 6.4, one can prove that
$\Psi$
-well-filtered. Using a similar method of Theorem 6.4, one can prove that
![]() $\Psi$
has property Q for X.
$\Psi$
has property Q for X.
(2)
![]() $\Rightarrow$
(3). Assume on the contrary that
$\Rightarrow$
(3). Assume on the contrary that
![]() $K\cap (X\setminus U)\neq\emptyset$
for each
$K\cap (X\setminus U)\neq\emptyset$
for each
![]() $K\in\mathcal A$
. It follows that
$K\in\mathcal A$
. It follows that
![]() $X\setminus U\in\mathfrak M(\mathcal A)$
. Since
$X\setminus U\in\mathfrak M(\mathcal A)$
. Since
![]() $\Psi$
satisfies property Q for X, there exists a
$\Psi$
satisfies property Q for X, there exists a
![]() $\Psi$
-set
$\Psi$
-set
![]() $F\subseteq X\setminus U$
such that
$F\subseteq X\setminus U$
such that
![]() $\mathrm{cl}(F)\in\mathfrak M(\mathcal A)$
. Since X is
$\mathrm{cl}(F)\in\mathfrak M(\mathcal A)$
. Since X is
![]() $\Psi$
-well-filtered, by Theorem 4.6 there exists
$\Psi$
-well-filtered, by Theorem 4.6 there exists
![]() $x\in X$
such that
$x\in X$
such that
![]() $\mathrm{cl}(F)=\mathrm{cl}(\{x\})$
. For each
$\mathrm{cl}(F)=\mathrm{cl}(\{x\})$
. For each
![]() $K\in \mathcal A$
, since
$K\in \mathcal A$
, since
![]() $K=\mathord{\uparrow} K$
and
$K=\mathord{\uparrow} K$
and
![]() $\mathrm{cl}(F)\cap K=\mathrm{cl}(\{x\})\cap K\neq\emptyset$
, we deduce that
$\mathrm{cl}(F)\cap K=\mathrm{cl}(\{x\})\cap K\neq\emptyset$
, we deduce that
![]() $x\in K$
. Thus,
$x\in K$
. Thus,
![]() $x\in\bigcap\mathcal A\subseteq U$
, contradicting the fact that
$x\in\bigcap\mathcal A\subseteq U$
, contradicting the fact that
![]() $x\in \mathrm{cl}(F)\subseteq X\setminus U$
. This shows that
$x\in \mathrm{cl}(F)\subseteq X\setminus U$
. This shows that
![]() $K\subseteq U$
for some
$K\subseteq U$
for some
![]() $K\in\mathcal A$
, which gives (3).
$K\in\mathcal A$
, which gives (3).
(3)
![]() $\Rightarrow$
(1). Suppose
$\Rightarrow$
(1). Suppose
![]() $\mathcal A$
is a
$\mathcal A$
is a
![]() $\Psi$
-set in
$\Psi$
-set in
![]() $P_s(X)$
and
$P_s(X)$
and
![]() $\mathcal U$
is an open set in
$\mathcal U$
is an open set in
![]() $P_s(X)$
such that
$P_s(X)$
such that
![]() $\bigcap_{K\in \mathcal A}\mathord{\uparrow}_{P_s(X)}K\subseteq\mathcal U$
. Then, there exists a family
$\bigcap_{K\in \mathcal A}\mathord{\uparrow}_{P_s(X)}K\subseteq\mathcal U$
. Then, there exists a family
![]() $\{U_i:i\in I\}\subseteq\mathcal O(X)$
such that
$\{U_i:i\in I\}\subseteq\mathcal O(X)$
such that
![]() $\mathcal U=\bigcup_{i\in I}\Box U_i$
. Using a similar proof of Lemma 3.5, one can obtain that
$\mathcal U=\bigcup_{i\in I}\Box U_i$
. Using a similar proof of Lemma 3.5, one can obtain that
![]() $K_0=\bigcap \mathcal A\in\mathcal Q^*(X)$
. Note that
$K_0=\bigcap \mathcal A\in\mathcal Q^*(X)$
. Note that
![]() $\mathord{\uparrow}_{P_s(X)}K=\{G\in\mathcal Q^*(X):G\subseteq K\}$
for each
$\mathord{\uparrow}_{P_s(X)}K=\{G\in\mathcal Q^*(X):G\subseteq K\}$
for each
![]() $K\in\mathcal A$
, so
$K\in\mathcal A$
, so
![]() $K_0\in \bigcap_{K\in \mathcal A}\mathord{\uparrow}_{P_s(X)}K\subseteq\bigcup_{i\in I}\Box U_i$
. Then, there exists
$K_0\in \bigcap_{K\in \mathcal A}\mathord{\uparrow}_{P_s(X)}K\subseteq\bigcup_{i\in I}\Box U_i$
. Then, there exists
![]() $i_0\in I$
such that
$i_0\in I$
such that
![]() $K_0=\bigcap\mathcal A\in\Box U_{i_0}$
, so
$K_0=\bigcap\mathcal A\in\Box U_{i_0}$
, so
![]() $\bigcap\mathcal A\subseteq U_{i_0}$
. By condition (3), there exists
$\bigcap\mathcal A\subseteq U_{i_0}$
. By condition (3), there exists
![]() $K_1\in\mathcal A$
such that
$K_1\in\mathcal A$
such that
![]() $K_1\subseteq U_{i_0}$
. This implies that
$K_1\subseteq U_{i_0}$
. This implies that
![]() $\mathord{\uparrow}_{P_s(X)}K_1\subseteq\Box U_{i_0}\subseteq\mathcal U$
. By Theorem 4.6, we deduce that
$\mathord{\uparrow}_{P_s(X)}K_1\subseteq\Box U_{i_0}\subseteq\mathcal U$
. By Theorem 4.6, we deduce that
![]() $P_s(X)$
is
$P_s(X)$
is
![]() $\Psi$
-well-filtered.
$\Psi$
-well-filtered.
Definition 6.7. Let X be a
![]() $T_0$
space. An HM-system
$T_0$
space. An HM-system
![]() $\Psi$
is said to satisfy property T for X if for any
$\Psi$
is said to satisfy property T for X if for any
![]() $\Psi$
-set
$\Psi$
-set
![]() $\mathcal A$
in
$\mathcal A$
in
![]() $P_s(X)$
,
$P_s(X)$
,
![]() $\bigcup_{K\in\mathcal A}\mathcal N(K)\in \Psi(X)$
.
$\bigcup_{K\in\mathcal A}\mathcal N(K)\in \Psi(X)$
.
Remark 6.8. Using Lemma 4.3, one can easily deduce that
![]() $\mathfrak M (\mathcal A)=\mathfrak M(\mathcal F_{\mathcal A})$
in Definition 6.7, where
$\mathfrak M (\mathcal A)=\mathfrak M(\mathcal F_{\mathcal A})$
in Definition 6.7, where
![]() $\mathcal F_{\mathcal A}=\bigcup_{K\in\mathcal A}\mathcal N(K)$
. Then by Lemma 2.12, if an HM-system
$\mathcal F_{\mathcal A}=\bigcup_{K\in\mathcal A}\mathcal N(K)$
. Then by Lemma 2.12, if an HM-system
![]() $\Psi$
satisfies property T, then it must satisfy Q.
$\Psi$
satisfies property T, then it must satisfy Q.
Lemma 6.9. Both
![]() $\Psi_{\mathsf{sob}}$
and
$\Psi_{\mathsf{sob}}$
and
![]() $\Psi_{\mathsf{wf}}$
satisfy property T for each
$\Psi_{\mathsf{wf}}$
satisfy property T for each
![]() $T_0$
space X.
$T_0$
space X.
Proof. Let X be a
![]() $T_0$
space. It is trivial that
$T_0$
space. It is trivial that
![]() $\Psi_{\mathsf{sob}}$
satisfies property T for X. Next, we verify that
$\Psi_{\mathsf{sob}}$
satisfies property T for X. Next, we verify that
![]() $\Psi_{\mathsf{wf}}$
satisfies property T for X. To show this, let
$\Psi_{\mathsf{wf}}$
satisfies property T for X. To show this, let
![]() $\mathfrak F\in\Psi_{\mathsf{wf}}(P_s(X))$
and
$\mathfrak F\in\Psi_{\mathsf{wf}}(P_s(X))$
and
![]() $\mathcal A\in m(\mathfrak F)$
. Then, there exists a filtered family
$\mathcal A\in m(\mathfrak F)$
. Then, there exists a filtered family
![]() $\{\mathcal K_i:i\in I\}$
of compact saturated subsets of
$\{\mathcal K_i:i\in I\}$
of compact saturated subsets of
![]() $P_s(X)$
such that
$P_s(X)$
such that
![]() $\mathfrak{F}=\{\mathcal U\in\mathcal O(P_s(X)):\exists i\in I, \mathcal K_i\subseteq \mathcal U\}$
. It suffices to prove
$\mathfrak{F}=\{\mathcal U\in\mathcal O(P_s(X)):\exists i\in I, \mathcal K_i\subseteq \mathcal U\}$
. It suffices to prove
![]() $\bigcup_{K\in\mathcal A}\mathcal N(K)\in\Psi_{\mathsf{wf}}(X)$
.
$\bigcup_{K\in\mathcal A}\mathcal N(K)\in\Psi_{\mathsf{wf}}(X)$
.
Claim:
![]() $\bigcup_{K\in\mathcal A}\mathcal N(K)=\bigcup_{i\in I}\mathcal N(\bigcup(\mathcal A\cap \mathcal K_i))$
.
$\bigcup_{K\in\mathcal A}\mathcal N(K)=\bigcup_{i\in I}\mathcal N(\bigcup(\mathcal A\cap \mathcal K_i))$
.
On the one hand, suppose
![]() $U\in\bigcup_{i\in I}\mathcal N(\bigcup(\mathcal A\cap \mathcal K_i))$
. Then, there exists
$U\in\bigcup_{i\in I}\mathcal N(\bigcup(\mathcal A\cap \mathcal K_i))$
. Then, there exists
![]() $i_0\in I$
such that
$i_0\in I$
such that
![]() $\bigcup(\mathcal A\cap\mathcal K_{i_0})\subseteq U$
. Choose one
$\bigcup(\mathcal A\cap\mathcal K_{i_0})\subseteq U$
. Choose one
![]() $K_{i_0}\in \mathcal A\cap \mathcal K_{i_0}\neq\emptyset$
. Then,
$K_{i_0}\in \mathcal A\cap \mathcal K_{i_0}\neq\emptyset$
. Then,
![]() $K_{i_0}\subseteq \bigcup (\mathcal A\cap \mathcal K_{i_0})\subseteq U$
, which implies that
$K_{i_0}\subseteq \bigcup (\mathcal A\cap \mathcal K_{i_0})\subseteq U$
, which implies that
![]() $U\in\mathcal N(K_{i_0})\subseteq \bigcup_{K\in\mathcal A}\mathcal N(K)$
. This shows that
$U\in\mathcal N(K_{i_0})\subseteq \bigcup_{K\in\mathcal A}\mathcal N(K)$
. This shows that
![]() $\bigcup_{i\in I}\mathcal N(\bigcup(\mathcal A\cap \mathcal K_i))\subseteq\bigcup_{K\in\mathcal A}\mathcal N(K)$
. On the other hand, suppose
$\bigcup_{i\in I}\mathcal N(\bigcup(\mathcal A\cap \mathcal K_i))\subseteq\bigcup_{K\in\mathcal A}\mathcal N(K)$
. On the other hand, suppose
![]() $U\notin \bigcup_{i\in I}\mathcal N(\bigcup(\mathcal A\cap \mathcal K_i))$
. For each
$U\notin \bigcup_{i\in I}\mathcal N(\bigcup(\mathcal A\cap \mathcal K_i))$
. For each
![]() $i\in I$
,
$i\in I$
,
![]() $\bigcup(\mathcal A\cap\mathcal K_i)\nsubseteq U$
, so there exists
$\bigcup(\mathcal A\cap\mathcal K_i)\nsubseteq U$
, so there exists
![]() $G_i\in \mathcal A\cap\mathcal K_i$
such that
$G_i\in \mathcal A\cap\mathcal K_i$
such that
![]() $G_i\nsubseteq U$
; that is,
$G_i\nsubseteq U$
; that is,
![]() $G_i\notin \Box U$
. Then,
$G_i\notin \Box U$
. Then,
![]() $G_i\in (P_s(X)\setminus \Box U)\cap \mathcal A\cap \mathcal K_i\neq\emptyset$
for all
$G_i\in (P_s(X)\setminus \Box U)\cap \mathcal A\cap \mathcal K_i\neq\emptyset$
for all
![]() $i\in I$
. Thus,
$i\in I$
. Thus,
![]() $(P_s(X)\setminus \Box U)\cap \mathcal A$
is a closed subset of
$(P_s(X)\setminus \Box U)\cap \mathcal A$
is a closed subset of
![]() $\mathcal A$
such that
$\mathcal A$
such that
![]() $(P_s(X)\setminus \Box U)\cap \mathcal A\in\mathfrak{M}(\mathfrak F)$
. Since
$(P_s(X)\setminus \Box U)\cap \mathcal A\in\mathfrak{M}(\mathfrak F)$
. Since
![]() $\mathcal A\in m(\mathfrak{F})$
,
$\mathcal A\in m(\mathfrak{F})$
,
![]() $\mathcal A\cap (P_s(X)\setminus\Box U)=\mathcal A$
, that is,
$\mathcal A\cap (P_s(X)\setminus\Box U)=\mathcal A$
, that is,
![]() $\mathcal A\subseteq P_s(X)\setminus\Box U$
. It follows that
$\mathcal A\subseteq P_s(X)\setminus\Box U$
. It follows that
![]() $K\nsubseteq U$
for all
$K\nsubseteq U$
for all
![]() $K\in\mathcal A$
; hence,
$K\in\mathcal A$
; hence,
![]() $U\notin\bigcup_{K\in\mathcal A}\mathcal N(K)$
. Therefore,
$U\notin\bigcup_{K\in\mathcal A}\mathcal N(K)$
. Therefore,
![]() $\bigcup_{K\in\mathcal A}\mathcal N(K)\subseteq \bigcup_{i\in I}\mathcal N(\bigcup(\mathcal A\cap \mathcal K_i))$
.
$\bigcup_{K\in\mathcal A}\mathcal N(K)\subseteq \bigcup_{i\in I}\mathcal N(\bigcup(\mathcal A\cap \mathcal K_i))$
.
Recall that the intersection of a closed set and a compact set is always compact, so
![]() $\mathcal A\cap\mathcal K_i$
is compact in
$\mathcal A\cap\mathcal K_i$
is compact in
![]() $P_s(X)$
for each
$P_s(X)$
for each
![]() $i\in I$
. Since
$i\in I$
. Since
![]() $\{\mathcal K_i:i\in I\}$
is a filtered family, by Remark 6.1
$\{\mathcal K_i:i\in I\}$
is a filtered family, by Remark 6.1
![]() $\{\mathord{\uparrow} \bigcup(\mathcal A\cap \mathcal K_i): i\in I\}$
is a filtered family of
$\{\mathord{\uparrow} \bigcup(\mathcal A\cap \mathcal K_i): i\in I\}$
is a filtered family of
![]() $\mathcal Q^*(X)$
. Note that for each open subset U of X,
$\mathcal Q^*(X)$
. Note that for each open subset U of X,
![]() $\bigcup(\mathcal A\cap \mathcal K_i)\subseteq U$
if and only if
$\bigcup(\mathcal A\cap \mathcal K_i)\subseteq U$
if and only if
![]() $\mathord{\uparrow} \bigcup(\mathcal A\cap \mathcal K_i)\subseteq U$
, we have that
$\mathord{\uparrow} \bigcup(\mathcal A\cap \mathcal K_i)\subseteq U$
, we have that
![]() $\bigcup_{K\in\mathcal A}\mathcal N(K)=\bigcup_{i\in I}\mathcal N(\bigcup(\mathcal A\cap \mathcal K_i))=\bigcup_{i\in I}\mathcal N(\mathord{\uparrow}\bigcup\mathcal A\cap \mathcal K_i)\in\Psi_{\mathsf{wf}}(X)$
. Therefore,
$\bigcup_{K\in\mathcal A}\mathcal N(K)=\bigcup_{i\in I}\mathcal N(\bigcup(\mathcal A\cap \mathcal K_i))=\bigcup_{i\in I}\mathcal N(\mathord{\uparrow}\bigcup\mathcal A\cap \mathcal K_i)\in\Psi_{\mathsf{wf}}(X)$
. Therefore,
![]() $\Psi_{\mathsf{wf}}$
satisfies property T.
$\Psi_{\mathsf{wf}}$
satisfies property T.
As a direct consequence of Theorem 6.6, Remark 6.8 and Lemma 6.9, we have the following corollaries.
Corollary 6.10 (Heckmann and Keimel 2013) Let X be a
![]() $T_0$
space. The following conditions are equivalent:
$T_0$
space. The following conditions are equivalent:
-
(1). X is sober;
-
(2).
 $P_s(X)$
is sober.
$P_s(X)$
is sober.
Corollary 6.11 (Xu et al. 2021) Let X be a
![]() $T_0$
space. The following conditions are equivalent:
$T_0$
space. The following conditions are equivalent:
-
(1). X is well-filtered;
-
(2).
 $P_s(X)$
is well-filtered.
$P_s(X)$
is well-filtered.
7. Conclusion
Motivated by the Hofmann-Mislove Theorem on sober spaces, we introduce the
![]() $\Psi$
-well-filtered spaces, where
$\Psi$
-well-filtered spaces, where
![]() $\Psi:{\bf Top}_0\longrightarrow{\bf Set}$
is a covariant functor that assigns each
$\Psi:{\bf Top}_0\longrightarrow{\bf Set}$
is a covariant functor that assigns each
![]() $T_0$
space X a family of open filters of
$T_0$
space X a family of open filters of
![]() $\mathcal O(X)$
. The classes of d-spaces, well-filtered spaces, and sober spaces are all special types of
$\mathcal O(X)$
. The classes of d-spaces, well-filtered spaces, and sober spaces are all special types of
![]() $\Psi$
-well-filtered spaces. The
$\Psi$
-well-filtered spaces. The
![]() $\mathcal U_s$
-admitting spaces (Heckmann Reference Heckmann1991), and the recently introduced open well-filtered spaces (Shen et al. Reference Shen, Xi, Xu and Zhao2020) and the
$\mathcal U_s$
-admitting spaces (Heckmann Reference Heckmann1991), and the recently introduced open well-filtered spaces (Shen et al. Reference Shen, Xi, Xu and Zhao2020) and the
![]() $\omega$
-well-filtered spaces (Xu et al. Reference Xu, Shen, Xi and Zhao2020b) can also be viewed as special types of
$\omega$
-well-filtered spaces (Xu et al. Reference Xu, Shen, Xi and Zhao2020b) can also be viewed as special types of
![]() $\Psi$
-well-filtered spaces. The results in this paper reveal some features of such spaces similar to that of sober space as shown by the Hofmann-Mislove Theorem. We hope that based on this general notion, some new classes of interesting spaces can be identified in the future.
$\Psi$
-well-filtered spaces. The results in this paper reveal some features of such spaces similar to that of sober space as shown by the Hofmann-Mislove Theorem. We hope that based on this general notion, some new classes of interesting spaces can be identified in the future.
Acknowledgements. The authors would like to thank the editor and referee for the numerous and very helpful suggestions that have improved this paper substantially.