1. INTRODUCTION
The quality of immigrants has emerged as a key objective in the determination of migration policy in many destination countries. In the United States, the Immigration Act of 1990 established the H-1B visas, which aim to attract well-educated professionals from all over the world for a temporary working period. Inviting highly skilled, foreign employees has become one of the most recognizable features of national migration policies in Australia, Canada, the UK, and New Zealand. These countries impose immigration quotas and evaluate candidates using a point-based system. The demand for skill-selective visas remains substantial. All of the above-mentioned destinations continue to attract large waves of highly skilled individuals, who respond to requests of enterprises and fill gaps on local labor markets.
In contrast, until recently the European Union (EU) proposed less selective regulations, and did not attach great importance to the quality of incoming migrants. Such a policy often did not meet the needs of internal labor markets and the expectations of potential immigrants. In 2009, the European Parliament passed a union-wide solution to the problem of Europe’s attractiveness for educated immigrants. The European Blue Card (EBC) program was instituted for highly skilled, non-EU workers who wish to spend between 1 and 4 years in the EU as professional employees. This initiative resembles the H-1B visa; however, the popularity of both proves to be drastically different. In 2014, the US issued 316,000 H-1B visas (124,000 new issues and 192,000 prolongations), while the efficacy of EBC seems to be disappointing, with only 13,000 new issues in 2014 (90% of all EBCs concerned Germany). One might inquire as to the causes of this discrepancy. Is it because the EBC is a relatively new policy (launched in 2013), and potential candidates are not well-informed about this emigration option? Conversely, is the EU immanently less attractive than other popular destinations, and any liberalization of migration policy would improve it only marginally? Finally, how does the effect of visa liberalization compare to a monetary gratification for new highly skilled immigrants: should a tax concession program be proposed instead?Footnote 1
The observed discrepancy in migration policies between the EU and other rich destinations is the core motivation for this paper. I propose, a framework that allows to endogenize the spatial distribution of college-educated workers after modifying selective immigration policies in the EU-member states. The results include investigations of the effectiveness of two migration policies in attracting talents to the EU: an implementation of H-1B visas and a tax reduction scheme for college-educated immigrants. I propose a multi-country model with heterogeneous agents who maximize their lifetime utility in an environment of imperfect information and endogenously sort into destinations by selecting the visa for which to apply, and the optimal duration of stay. People differ in their subjective preferences for living in all possible destinations, and independently of that, they may experience unanticipated, random shocks after having emigrated. Heterogeneity in preferences results in individual-specific choices of destination country, visa, and the optimal duration of stay, while the heterogeneity in unexpected migration costs further modifies the time spent abroad.
Along with quantitative results, this paper contributes to the theoretical literature on modeling international migration. I propose an alternative approach toward enriching a classic discrete choice model (with many sending and receiving countries) in the vein of McFadden (Reference McFadden and Zarembka1973), with the agents’ decisions about the duration of stay, inspired by Djajić (Reference Djajić2014a). For a simplified version of this model, I provide closed-form solutions for the probabilities of emigration and the distribution of the duration of stay. The full model is solved numerically. Furthermore, following Bertoli and Moraga (Reference Bertoli and Moraga2013), the proposed theoretical framework provides another source of multilateral resistance to migration (MRM) by relaxing the independence of irrelevant alternatives (IIA) axiom (as a consequence of a non-trivial correlation structure between discrete choice options).Footnote 2 In this framework, I experiment with alternative migration policies in the EU.Footnote 3 I focus on the way in which migration policy affects the destination choices of migrants (geographical dimension), the duration of stay (time dimension), and the selectivity of migrants with respect to their education levels (skill dimension). The theoretical and numerical outcomes show that a simultaneous consideration of these three factors enables to highlight previously overlooked economic effects. Moreover, neglecting MRM may bring a significant bias in the quantitative evaluation of counterfactual migration policies in international context.
The results give evidence that the proposed modifications of the EU’s migration policy might have a visible impact on the supply of skilled labor. The implementation of an H-1B visa in the EU (which can be considered to be a substitute for the further development of the EBC program) increases the yearly inflow of college-educated workers by 3% and the total stocks by 6.1%. This policy improves the relative attractiveness of medium-term visas in Europe, and it therefore induces a “visa-substitution” effect: current migrants with short-term and long-term visas are now more prone to substituting them for cheaper medium-term visas within the same destination. However, the H-1B policy has a slight impact on the absolute attractiveness of Europe: it leaves the global pool of educated migrants almost unchanged. Additional inflows to the EU are procured by a “destination–substitution” effect: some of the current migrants in non-EU countries select the EU as the first-best destination. In terms of the tax concession policy, the aggregated flows of highly skilled immigrants to Europe increase by 10.6%, while the total stocks change by 5.6%. In this case, the “visa-substitution” effect is quantitatively less important, while the “destination–substitution” effect dominates. The main economic force that determines the large change in inflows is the augmentation of the absolute attractiveness of Europe, which induces a strong “size” effect: an increase in the pool of actual immigrants in the EU.
The rest of the paper is organized as follows. In the next Section, I briefly summarize the literature to which this paper refers. The third Section presents a general overview of the model, and the analytical solution to its simplified version with one visa. Section 4 includes a description of multi-visa models and discusses the calibration and simulation procedures. Section 5 analyses the results of the counterfactual simulations, while Section 6 concludes.
2. RELATED LITERATURE
The proposed theoretical approach refers to three strands of literature on international migration. First, the paper relates to the literature on migrants’ location choice in multi-country systems. Then, a relevant benchmark are the works on temporary and return migration. Finally, the paper refers to the broad literature on migration policy in the EU context.
A large body of research in international migration concentrates on explaining the motives for choosing particular destination countries. To describe the location decisions at the macro level, both theoretical and empirical papers exploit the random utility maximization (RUM) model that is proposed by McFadden (Reference McFadden and Zarembka1973). The empirical contributions by Grogger and Hanson (Reference Grogger and Hanson2011), Beine et al. (Reference Beine, Docquier and Özden2011), Belot and Hatton (Reference Belot and Hatton2012), and Ortega and Peri (Reference Ortega and Peri2013) provide evidence on the main drivers of the destination choice in the framework of a logit model. Kennan and Walker (Reference Kennan and Walker2011) and Bertoli et al. (Reference Bertoli, Brücker and Moraga2016) identify the main sources of migration decisions in models, including forward-looking agents, who reach their migration decisions sequentially. Docquier and Machado (Reference Docquier and Machado2015) and Docquier et al. (Reference Docquier, Machado and Sekkat2015) make use of a RUM model embedded in a general equilibrium to quantify the consequences of reducing barriers to migration in a global context. All of these approaches consider only permanent immigration, and they assume independence across the choice options: the economic situation in a third country has no impact on the relative odds of emigrating to any two destinations. However, the evidence by Bertoli and Moraga (Reference Bertoli and Moraga2013, Reference Bertoli and Moraga2015) suggests the contrary. According to their findings, the interdependence across decisions is a substantial factor that determines the incentives to migrate, the overall size, and the composition of migration flows. This MRM creates a challenge for both empirical and theoretical modelers.Footnote 4 Marchal and Naiditch (Reference Marchal and Naiditch2016) provide an individual-based explanation of MRM through credit constraints. As a consequence of migrants not being able to pay upfront migration costs, some of the destinations are unattainable. This restriction in the choice set is the source of MRM in their model. In contrast, this paper takes the perspective of highly educated migrants and relates MRM with individual migration decisions that include duration of stay.
The time dimension in individual decisions was introduced to theoretical models of migration in the early works by Djajić and Milbourne (Reference Djajić and Milbourne1988), Djajić (Reference Djajić1989), Galor and Stark (Reference Galor and Stark1990), Dustmann (Reference Dustmann1993), and Borjas and Bratsberg (Reference Borjas and Bratsberg1996). These papers also treat the choice of the length of the period that is spent abroad as a solution to the utility maximization problem. A representative person cares about the lifetime utility that depends on the level of wages or the total stock of financial or human capital.Footnote 5 More recently, papers by Dustmann and Weiss (Reference Dustmann and Weiss2007), Adda et al. (Reference Adda, Dustmann and Görlach2015), and Dustmann and Görlach (Reference Dustmann and Görlach2016) mention four mechanisms that identify the incentives for the decision to migrate temporarily.Footnote 6 Furthermore, Dustmann and Görlach (Reference Dustmann and Görlach2016) provide a thorough analysis of the current state of the art regarding temporary migration.Footnote 7 In fact, the majority of papers that consider the time dimension in migration decisions disregards the choice of locations by analyzing a dyad of a sending and a receiving country. An exception can be the paper by Artuc and Ozden (Reference Artuc and Ozden2016). The Authors construct a dynamic discrete choice model of transit migration, where the utility of living in a particular destination is related to the value of option to migrate further. Conversely, this paper develops a theoretical model in which people select location and the time period that is spent abroad, by reaching lifetime decisions. Such an approach, alternative to Artuc and Ozden (Reference Artuc and Ozden2016) and Bertoli et al. (Reference Bertoli, Brücker and Moraga2016), imposes a specific structure on return migration, but allows to investigate the exact distributions of duration of stay of migrants, and maps migration policies with their impact on average time spent abroad.
The question of designing an efficient migration policy in the developed regions remains open [Czaika and De Haas (Reference Czaika and De Haas2013)]. Countries that experience a sizable inflow of new immigrants (Canada, Australia, and New Zealand) have proposed selective visa policies that exploit point-based systems for the evaluation of candidates. However, they have recently turned to the US pattern of employer-sponsored visas for highly skilled immigrants [Koslowski (Reference Koslowski2014)], which has proven to be a successful method of attracting highly productive talents [Peri et al. (Reference Peri, Shih and Sparber2015)]. Martín and Venturini (Reference Martín and Venturini2015) evaluate the current state of the EU’s visa policy. Noting its simplicity and underdevelopment, they have proposed a unified and comprehensive modification at the EU level.Footnote 8 This paper considers well defined and easily implementable migration policy reforms, which can be summarized as reductions in visa costs and tax concession schemes.
3. DECISIONS ABOUT DESTINATION AND THE DURATION OF STAY
Each individual is economically active for a period of 50 years.Footnote 9 Everyone can choose to live in any of N countries that are grouped in the choice set ![]() $\mathcal {N}$, including homeland denoted by i. The receiving countries
$\mathcal {N}$, including homeland denoted by i. The receiving countries ![]() $j \in \mathcal {N}/\lbrace i\rbrace$ differ in objective attractiveness (represented by net wages: v j) and in the expected costs of migration:
$j \in \mathcal {N}/\lbrace i\rbrace$ differ in objective attractiveness (represented by net wages: v j) and in the expected costs of migration: ![]() $x_{ji}(\bar{d})$. The latter are dependent on the authorized maximal duration of stay
$x_{ji}(\bar{d})$. The latter are dependent on the authorized maximal duration of stay ![]() $\bar{d} \in [0, 1]$ defined by a particular visa.Footnote 10 Furthermore, each destination provides an individual offer of visas for prospective immigrants. Assume that there are D j types of permissions of stay in a destination j, and each migrant selects her preferred option
$\bar{d} \in [0, 1]$ defined by a particular visa.Footnote 10 Furthermore, each destination provides an individual offer of visas for prospective immigrants. Assume that there are D j types of permissions of stay in a destination j, and each migrant selects her preferred option ![]() $\bar{d} \in \mathcal {D}_j = \lbrace 1,\ldots ,D_j\rbrace$. Assuming the ex-ante decision to be binding, an immigrant would spend time
$\bar{d} \in \mathcal {D}_j = \lbrace 1,\ldots ,D_j\rbrace$. Assuming the ex-ante decision to be binding, an immigrant would spend time ![]() $\bar{d}$ abroad and return to her homeland for the remaining part of her life,
$\bar{d}$ abroad and return to her homeland for the remaining part of her life, ![]() $1-\bar{d}$.
$1-\bar{d}$.
People have heterogeneous preferences toward living in each potential destination. Consequently, the deterministic component of j-specific utility is augmented with an individual-specific random term, εj, which represents the taste for living in country j.Footnote 11 Assume that εj is an iid stochastic variable that is distributed according to the Gumbel distribution, so that the proposed approach refers to the literature on discrete choice RUM models.Footnote 12
All of the above-mentioned values are known to the agent ex-ante, that is, before the actual move occurs. What is not revealed to the individual is the unanticipated migration cost, ρji, being a realization of a random variable ![]() ${\bar{\rho }}_{ji}$. This element represents the unforeseen cultural, social, economic, and institutional aspects of living abroad for a migrant from i to j, in contrast to the expected migration cost
${\bar{\rho }}_{ji}$. This element represents the unforeseen cultural, social, economic, and institutional aspects of living abroad for a migrant from i to j, in contrast to the expected migration cost ![]() $x_{ji}(\bar{d})$, which is known ex-ante.Footnote 13 Having no experience in being a part of a foreign society, an agent predicts that emigration may be either detrimental (ρji > 0) or beneficial (ρji < 0) for her lifetime utility if the lifestyle in the destination country better suits them. Therefore, she forms an ex-ante (before emigration) expectation of the value of this parameter. I consider a situation in which ρji is distributed according to a probability density function (PDF)
$x_{ji}(\bar{d})$, which is known ex-ante.Footnote 13 Having no experience in being a part of a foreign society, an agent predicts that emigration may be either detrimental (ρji > 0) or beneficial (ρji < 0) for her lifetime utility if the lifestyle in the destination country better suits them. Therefore, she forms an ex-ante (before emigration) expectation of the value of this parameter. I consider a situation in which ρji is distributed according to a probability density function (PDF) ![]() $\bar{\rho }_{ji}$ that is defined on
$\bar{\rho }_{ji}$ that is defined on ![]() $\mathbb{R}$. Before moving people have neutral expectations about the unforeseen circumstances after migration (all of the other foreseeable factors are captured by
$\mathbb{R}$. Before moving people have neutral expectations about the unforeseen circumstances after migration (all of the other foreseeable factors are captured by ![]() $x_{ji}(\bar{d})$), thus a straightforward normalization is:
$x_{ji}(\bar{d})$), thus a straightforward normalization is: ![]() $\mathbb{E}[\bar{\rho }_{ji}] = 0$. Therefore, ex-ante, the expected value of the unforeseen migration cost does not influence the choice of destination and visa type. However, ρji brings the second source of heterogeneity across agents, after being revealed in the destination country. In brief, the model considers people who encounter “bad” draws of unexpected migration costs, which are characterized by ρji > 0 (where ρij is the realization of a random variable
$\mathbb{E}[\bar{\rho }_{ji}] = 0$. Therefore, ex-ante, the expected value of the unforeseen migration cost does not influence the choice of destination and visa type. However, ρji brings the second source of heterogeneity across agents, after being revealed in the destination country. In brief, the model considers people who encounter “bad” draws of unexpected migration costs, which are characterized by ρji > 0 (where ρij is the realization of a random variable ![]() $\bar{\rho }_{ij}$, independent of individual preferences toward different destinations, εj) and those who assimilate well in the host country, with: ρji < 0.
$\bar{\rho }_{ij}$, independent of individual preferences toward different destinations, εj) and those who assimilate well in the host country, with: ρji < 0.
After entering the labor market in her home country i, an individual compares the expected, ex-ante, gains in each destination j, represented by a linear, random utility function:
To reach the decision about their future location, individuals compare the levels of net wages across all destinations ![]() $j \in \mathcal {N}$.Footnote 14 They also consider their individual tastes toward living in foreign countries and the potential costs that are ascribed to moving (both tangible and non-tangible ones). Parameter α describes the marginal utility of income. Variables v j represent net wages (gross wages in USD PPP reduced by mandatory income taxes in destination j), and
$j \in \mathcal {N}$.Footnote 14 They also consider their individual tastes toward living in foreign countries and the potential costs that are ascribed to moving (both tangible and non-tangible ones). Parameter α describes the marginal utility of income. Variables v j represent net wages (gross wages in USD PPP reduced by mandatory income taxes in destination j), and ![]() $x_{ji}(\bar{d})$ stands for the expected, bilateral migration cost of moving from i to j for a period of length
$x_{ji}(\bar{d})$ stands for the expected, bilateral migration cost of moving from i to j for a period of length ![]() $\bar{d}$, which is determined by the receiving country’s visa policy:
$\bar{d}$, which is determined by the receiving country’s visa policy: ![]() $\bar{d} \in \mathcal {D}_j$.Footnote 15 The legal part of this cost is the main policy instrument of the destination authority that is targeted to influence the total flows of highly skilled immigrants. Additionally, the utility depends on individual preferences, εi and εj, as well as on the expected value of the unforeseen migration cost
$\bar{d} \in \mathcal {D}_j$.Footnote 15 The legal part of this cost is the main policy instrument of the destination authority that is targeted to influence the total flows of highly skilled immigrants. Additionally, the utility depends on individual preferences, εi and εj, as well as on the expected value of the unforeseen migration cost ![]() $\mathbb {E}[\bar{\rho }_{ji}] = 0$. Finally, the ex-ante decision boils down to selecting the preferred destination country j* and the duration of visa
$\mathbb {E}[\bar{\rho }_{ji}] = 0$. Finally, the ex-ante decision boils down to selecting the preferred destination country j* and the duration of visa ![]() $\bar{d}^*$ from the available portfolio
$\bar{d}^*$ from the available portfolio ![]() $\mathcal {D}_{j^*}$. The agent chooses from K = ∑Nj = 1Dj options and makes the optimal ex-ante decision:
$\mathcal {D}_{j^*}$. The agent chooses from K = ∑Nj = 1Dj options and makes the optimal ex-ante decision:
After reaching a new destination country, agents discover the exact value of the unforeseen migration cost ρji. Their previous measure of utility, equation (1), is therefore updated by considering the actual realization ρji of the random variable ![]() $\bar{\rho }_{ji}$. Given that the return cost is incorporated in the expected migration cost, the agent must re-optimize her decision about the length of her stay by defining the time after which she would return to her homeland. The model assumes that people have no incentives to move to any other foreign country, and they may only return to their homelands.Footnote 16 Additionally, there is no option to overstay temporary visas.Footnote 17
$\bar{\rho }_{ji}$. Given that the return cost is incorporated in the expected migration cost, the agent must re-optimize her decision about the length of her stay by defining the time after which she would return to her homeland. The model assumes that people have no incentives to move to any other foreign country, and they may only return to their homelands.Footnote 16 Additionally, there is no option to overstay temporary visas.Footnote 17
Formally, the ex-post utility of an immigrant from i to j who acquired a visa of duration ![]() $\bar{d}^*$ is
$\bar{d}^*$ is
Note that this expression is defined for a given destination j* and a given visa type ![]() $\bar{d}^*$ that is determined in the ex-ante decision problem, equation (2). Eventually, each individual reconsiders her emigration strategy by selecting the optimal duration of a migration period (expressed now by d ∈ [0, 1]), through the maximization of her ex-post (after emigration) utility:
$\bar{d}^*$ that is determined in the ex-ante decision problem, equation (2). Eventually, each individual reconsiders her emigration strategy by selecting the optimal duration of a migration period (expressed now by d ∈ [0, 1]), through the maximization of her ex-post (after emigration) utility:
The optimal ex-post duration is an interior solution, ![]() $d^* \in (0, \bar{d}^*)$, if and only if at moment d* an individual is indifferent between staying abroad and returning home (possible only if ρji > 0). In contrast, when ρji ⩽ 0, an immigrant will certainly stay until the expiration date of her visa:
$d^* \in (0, \bar{d}^*)$, if and only if at moment d* an individual is indifferent between staying abroad and returning home (possible only if ρji > 0). In contrast, when ρji ⩽ 0, an immigrant will certainly stay until the expiration date of her visa: ![]() $d^* = \bar{d}^*$.
$d^* = \bar{d}^*$.
3.1. A Model with a Permanent Stay Visa
This subsection focuses on a simplified version of the model. The aim is to obtain analytical solutions for the ex-post aggregates that describe distributions of duration of stay across destinations. To begin, assume that in each destination only one type of visa is available: a person may decide to stay at home (equivalent to setting ![]() $\bar{d}^* = 0$) or to emigrate to any country j (so that
$\bar{d}^* = 0$) or to emigrate to any country j (so that ![]() $\bar{d}^*=1$ and j* = j). The determination of the ex-ante duration of stay is thus a discrete choice from N available options: as in McFadden (Reference McFadden1984), so that the probability of choosing a destination j by an agent who is born in country i is equal to
$\bar{d}^*=1$ and j* = j). The determination of the ex-ante duration of stay is thus a discrete choice from N available options: as in McFadden (Reference McFadden1984), so that the probability of choosing a destination j by an agent who is born in country i is equal to
 $$\begin{equation}
\pi _{ji} = \frac{\exp \left[ \alpha \left(v_{j}-x_{ji} \right)\right]}{\sum _{k=1}^N \exp \left[ \alpha \left( v_{k} - x_{ki}\right) \right]}.
\end{equation}$$
$$\begin{equation}
\pi _{ji} = \frac{\exp \left[ \alpha \left(v_{j}-x_{ji} \right)\right]}{\sum _{k=1}^N \exp \left[ \alpha \left( v_{k} - x_{ki}\right) \right]}.
\end{equation}$$
Notice that the result in equation (5) implies that the ratio of probabilities to emigrate to any two distinct destinations ![]() $j, k \in \mathcal {N}$ fulfills the IIA axiomFootnote 18:
$j, k \in \mathcal {N}$ fulfills the IIA axiomFootnote 18:
Consider the simplest density function for the distribution of the unforeseen costs of living abroad, ![]() $\bar{\rho }_{ji}$, that fulfills the demanded requirement (zero expected value): a symmetric two-point distribution. Assume that
$\bar{\rho }_{ji}$, that fulfills the demanded requirement (zero expected value): a symmetric two-point distribution. Assume that ![]() $\bar{\rho }_{ji}$ can take two possible values: −ρji or ρji, with equal probabilities. Now, the ex-post decision that is reached by a permanent migrant determines the optimal duration of stay. Being granted a visa, a person may stay in the receiving country as long as she wants. By solving the maximization problem (4), one obtains
$\bar{\rho }_{ji}$ can take two possible values: −ρji or ρji, with equal probabilities. Now, the ex-post decision that is reached by a permanent migrant determines the optimal duration of stay. Being granted a visa, a person may stay in the receiving country as long as she wants. By solving the maximization problem (4), one obtains
Proposition 1. The optimal, ex-post duration of migration is given by
 $$\begin{equation}
d^* = \left\lbrace \begin{array}{l}\min \left\lbrace \rho ^{-1}_{j^*i} \left( {V_{j^*i} + \varepsilon _{j^*} - \varepsilon _{i}} \right); 1 \right\rbrace , \quad \text{if} \quad \rho _{j^*i} > 0, \\
1, \quad \textrm {if} \quad \rho _{j^*i} < 0, \end{array} \right.
\end{equation}$$
$$\begin{equation}
d^* = \left\lbrace \begin{array}{l}\min \left\lbrace \rho ^{-1}_{j^*i} \left( {V_{j^*i} + \varepsilon _{j^*} - \varepsilon _{i}} \right); 1 \right\rbrace , \quad \text{if} \quad \rho _{j^*i} > 0, \\
1, \quad \textrm {if} \quad \rho _{j^*i} < 0, \end{array} \right.
\end{equation}$$
where V j*i ≡ α(v j* − x j*i − vi) is the net value of migration.
Proof. See Appendix A. ![]() $\Box$
$\Box$
Note that when ρji > 0, d* is a random variable with tractable statistical characteristics. Consider the probability that a person who is characterized by ρji > 0 moves abroad for a period that is shorter than a given δ ⩽ 1.
 $$\begin{eqnarray}
\Pr \left[ d < \delta \right] &=& \Pr \left[\rho ^{-1}_{ji} \left( {V_{ji} + \varepsilon _{j} - \varepsilon _{i}} \right) < \delta \right] = \Pr \left[ \rho _{ji} \delta + \varepsilon _{i} > {V_{ji}} + \varepsilon _{j} \right] \nonumber\\
&=& \frac{e^{\rho _{ji} \delta }}{e^{\rho _{ji} \delta } + e^{V_{ji}}}.
\end{eqnarray}$$
$$\begin{eqnarray}
\Pr \left[ d < \delta \right] &=& \Pr \left[\rho ^{-1}_{ji} \left( {V_{ji} + \varepsilon _{j} - \varepsilon _{i}} \right) < \delta \right] = \Pr \left[ \rho _{ji} \delta + \varepsilon _{i} > {V_{ji}} + \varepsilon _{j} \right] \nonumber\\
&=& \frac{e^{\rho _{ji} \delta }}{e^{\rho _{ji} \delta } + e^{V_{ji}}}.
\end{eqnarray}$$
This probability increases in ρji, because as the unforeseen migration cost becomes higher, the propensity to stay in a foreign country decreases. Conversely, a greater discrepancy between remunerations in destination and source, V ji, diminishes the chance that a randomly chosen individual will return to the homeland. Thus, the cumulative distribution function (CDF) of the random variable d* with support on ![]() $\mathbb {R}$. Let it be labeled by F(·), while the associated PDF will be represented by f(·).
$\mathbb {R}$. Let it be labeled by F(·), while the associated PDF will be represented by f(·).
Corollary 2. When ρji > 0, for a given δ ⩽ 1, the probability of staying for a period that is shorter than δ (the CDF of the duration of stay) and the PDF of the duration stay, defined ![]() $\forall\, d \in \mathbb {R}$ are
$\forall\, d \in \mathbb {R}$ are
 $$\begin{equation}
F(\delta ) = \frac{e^{\rho _{ji} \delta }}{e^{\rho _{ji} \delta } + e^{V_{ji}}}, \quad f(d) = \frac{\rho _{ji} e^{\rho _{ji}d+V_{ji}}}{\left(e^{\rho _{ji}d}+e^{V_{ji}} \right)^2}.
\end{equation}$$
$$\begin{equation}
F(\delta ) = \frac{e^{\rho _{ji} \delta }}{e^{\rho _{ji} \delta } + e^{V_{ji}}}, \quad f(d) = \frac{\rho _{ji} e^{\rho _{ji}d+V_{ji}}}{\left(e^{\rho _{ji}d}+e^{V_{ji}} \right)^2}.
\end{equation}$$
Proof. The CDF is derived in equation (8). The PDF is the first derivative of the CDF. ![]() $\Box$
$\Box$
In what follows, I focus only on those individuals who decide to migrate, so that necessarily d > 0. The probability of such an event is given by, ![]() $\Pr \left[V_{ji} + \varepsilon _{j} > \varepsilon _{i} \right] = {e^{V_{ji}}}/(1+e^{V_{ji}})$. The positive sign of d is guaranteed by the agent’s ex-ante decision about emigration to country j (had it not been the case, country j would have never been considered as a potential destination for emigration). Therefore, I restrict the analysis to conditional probabilities, densities, and moments, knowing that d > 0 holds. For a given δ ∈ [0, 1], the probability that a person will stay in the destination country for a period that is shorter than δ (conditional on emigrating), is given by
$\Pr \left[V_{ji} + \varepsilon _{j} > \varepsilon _{i} \right] = {e^{V_{ji}}}/(1+e^{V_{ji}})$. The positive sign of d is guaranteed by the agent’s ex-ante decision about emigration to country j (had it not been the case, country j would have never been considered as a potential destination for emigration). Therefore, I restrict the analysis to conditional probabilities, densities, and moments, knowing that d > 0 holds. For a given δ ∈ [0, 1], the probability that a person will stay in the destination country for a period that is shorter than δ (conditional on emigrating), is given by
Corollary 3. When ρji > 0, for a given δ ⩽ 1, the probability of staying for a period that is shorter than δ conditional on emigrating (the CDF of the positive duration of stay) and the PDF of the duration of stay, conditional on emigrating, defined ∀ d ∈ (0; ∞), are
 $$\begin{equation}
F_{d>0}(\delta ) = \frac{e^{\rho _{ji}\delta }-1}{e^{\rho _{ji}\delta } + e^{V_{ji}}}, \quad f_{d>0}(d) = \frac{\rho _{ji} e^{\rho _{ji}d}(1+e^{V_{ji}})}{(e^{\rho _{ji}d} +e^{ V_{ji}})^2}.
\end{equation}$$
$$\begin{equation}
F_{d>0}(\delta ) = \frac{e^{\rho _{ji}\delta }-1}{e^{\rho _{ji}\delta } + e^{V_{ji}}}, \quad f_{d>0}(d) = \frac{\rho _{ji} e^{\rho _{ji}d}(1+e^{V_{ji}})}{(e^{\rho _{ji}d} +e^{ V_{ji}})^2}.
\end{equation}$$
Proof. See Appendix A. ![]() $\Box$
$\Box$
According to equations (10), a higher unforeseen cost leads to shorter durations of stay (the mass of probability is concentrated in the left tail side, see Figure 1, Panel A for the density function and Panel C for the cumulative distribution). Conversely, if the net value of migration V ij increases, then the length of the time period that is spent abroad increases, which is depicted by a shift of probability density toward the right-hand side, as seen in Figure 1, Panel B and D (density and cumulative, respectively).

Figure 1. Comparative statics of conditional distributions of durations of stay. Note: Panel A (B) depicts the PDFs of the duration of stay for constant V ji (ρji) and varying ρji (V ji). Panel C (D) plots the respective CDFs. Source: own calculations.
The group of individuals with ρji > 0, is divided into a sub-group of temporary immigrants and a sub-group of permanent residents. Using the defined conditional density, the probabilities that a random migrant will fall into either of two sub-groups are given by
Proposition 4. The probability of being a temporary or a permanent migrant is given by
 $$\begin{eqnarray}
\Pr \left[d < 1, d > 0 \right] &=& F_{d>0}(1) = \frac{e^{\rho _{ji}}-1}{e^{\rho _{ji}}+e^{V_{ji}}}, \quad \Pr \left[d = 1, d > 0 \right] \nonumber\\
&=& 1 - F_{d>0}(1) = \frac{1+e^{V_{ji}}}{e^{\rho _{ji}}+e^{V_{ji}}}.
\end{eqnarray}$$
$$\begin{eqnarray}
\Pr \left[d < 1, d > 0 \right] &=& F_{d>0}(1) = \frac{e^{\rho _{ji}}-1}{e^{\rho _{ji}}+e^{V_{ji}}}, \quad \Pr \left[d = 1, d > 0 \right] \nonumber\\
&=& 1 - F_{d>0}(1) = \frac{1+e^{V_{ji}}}{e^{\rho _{ji}}+e^{V_{ji}}}.
\end{eqnarray}$$
Proof. This results from manipulating the definition of conditional CDF of the duration of stay. ![]() $\Box$
$\Box$
Finally, let us sum the total number of foreign workers of different origins, destinations, and statuses. In aggregated terms, the total stock of employees from a particular wave t = 0, living in country j at period τ is equal to the sum of natives and foreigners originating from any ![]() $i \in \mathcal {N}$: Lj(τ) = ∑Ni = 1Lji(τ). The labor force that is attracted during a period of one generation can be calculated using the density of the average duration of stay of all migrants:
$i \in \mathcal {N}$: Lj(τ) = ∑Ni = 1Lji(τ). The labor force that is attracted during a period of one generation can be calculated using the density of the average duration of stay of all migrants:
Proposition 5. The total labor force in country j immigrating from country i (expressed in the number of foreigners available for the period of one generation, 50 years) is equal to:
 $$\begin{equation}
L_{ji}(V_{ji}, \rho _{ji}) = \frac{N_{ji}}{2} \left( \frac{1+e^{V_{ji}}}{\rho _{ji}e^{V_{ji}}}\ln {\left(\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}\right)} + 1 \right).
\end{equation}$$
$$\begin{equation}
L_{ji}(V_{ji}, \rho _{ji}) = \frac{N_{ji}}{2} \left( \frac{1+e^{V_{ji}}}{\rho _{ji}e^{V_{ji}}}\ln {\left(\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}\right)} + 1 \right).
\end{equation}$$
Proof. See Appendix A. ![]() $\Box$
$\Box$
4. A MULTI-DESTINATION AND MULTI-VISA MODEL
In this Section, I solve a multi-country model of migration in which each destination offers several visa options. Considering a version with two visas (a permit for a temporary and a permanent stay), I show that the model violates the IIA axiom and provides a micro-foundation for MRM. Additional assumptions concerning the costs of migration allow for an analytical solution of this model. Then, I describe the multi-destination, three-visa model. In the last Subsection, the latter version of the model is calibrated and simulated with numerical methods.
4.1. A Model with Two Types of Visas
Consider a system of N countries: i, from which people emigrate, and countries 1, . . ., N which, along with i, are the potential destinations. Each country is characterized by a certain level of net wage labeled by v j. Workers may choose to apply for a temporary visa, which allows them to stay for a period ![]() $\left[0, \bar{d}^t\right]$,
$\left[0, \bar{d}^t\right]$, ![]() $\bar{d}^t < 1$ or a permanent visa with
$\bar{d}^t < 1$ or a permanent visa with ![]() $\bar{d}^p = 1$. In what follows, it is assumed that all of the destinations offer the same duration of the temporary visa.Footnote 19 The costs of these permissions are, respectively:
$\bar{d}^p = 1$. In what follows, it is assumed that all of the destinations offer the same duration of the temporary visa.Footnote 19 The costs of these permissions are, respectively: ![]() $x_{ji}(\bar{d}^t)$ and
$x_{ji}(\bar{d}^t)$ and ![]() $x_{ji}(\bar{d}^p)$, if a person plans to emigrate from country i to country j ∈ {1, . . ., N}. I explicitly assume that
$x_{ji}(\bar{d}^p)$, if a person plans to emigrate from country i to country j ∈ {1, . . ., N}. I explicitly assume that ![]() $x_{ji}(\bar{d}^p) > x_{ji}(\bar{d}^t)$ for j ≠ i. Otherwise, no one would acquire a temporary visa. When an agent decides to stay in state i, she pays no migration costs, so that:
$x_{ji}(\bar{d}^p) > x_{ji}(\bar{d}^t)$ for j ≠ i. Otherwise, no one would acquire a temporary visa. When an agent decides to stay in state i, she pays no migration costs, so that: ![]() $x_{ii}(\bar{d}^t) = x_{ii}(\bar{d}^p) = 0$. Consequently, the ex-ante expected utilities that are ascribed to every possible decision are as follows:
$x_{ii}(\bar{d}^t) = x_{ii}(\bar{d}^p) = 0$. Consequently, the ex-ante expected utilities that are ascribed to every possible decision are as follows:
 $$\begin{eqnarray}
&& \mathbb {E}[{U}_{ii}] = \alpha v_i +\varepsilon _{i}, \nonumber\\
&& \mathbb {E}[{U}_{ji}(\bar{d}^t)] = \bar{d}^t \left( \alpha \left( v_j - x_{ji}(\bar{d}^t) \right) - \bar{d}^t \mathbb {E}[\bar{\rho }_{ji}]/2 + \varepsilon _{j} \right) + (1-\bar{d}^t)\left( \alpha v_i + \varepsilon _{i} \right), \nonumber \\
&& \mathbb {E}[{U}_{ji}(\bar{d}^p)] = \alpha \left( v_j - x_{ji}(\bar{d}^p) \right) - \mathbb {E}[\bar{\rho }_{ji}]/2 + \varepsilon _{j}.
\end{eqnarray}$$
$$\begin{eqnarray}
&& \mathbb {E}[{U}_{ii}] = \alpha v_i +\varepsilon _{i}, \nonumber\\
&& \mathbb {E}[{U}_{ji}(\bar{d}^t)] = \bar{d}^t \left( \alpha \left( v_j - x_{ji}(\bar{d}^t) \right) - \bar{d}^t \mathbb {E}[\bar{\rho }_{ji}]/2 + \varepsilon _{j} \right) + (1-\bar{d}^t)\left( \alpha v_i + \varepsilon _{i} \right), \nonumber \\
&& \mathbb {E}[{U}_{ji}(\bar{d}^p)] = \alpha \left( v_j - x_{ji}(\bar{d}^p) \right) - \mathbb {E}[\bar{\rho }_{ji}]/2 + \varepsilon _{j}.
\end{eqnarray}$$
As in the previous model, ex-ante ![]() $\mathbb {E}[\bar{\rho }_{ji}] = 0 \hspace{5.69046pt} \forall j,i \in \mathcal {N}$. According to the former definition, utilities are no longer independent, and in general, they do not fulfill the standard IIA axiom. The non-zero correlations between choice options result from the fact that temporary migrants consider wages in the source and the host economies as the determinants of lifetime migration choices. Thus, one cannot use the theorem by McFadden (1984) to calculate the choice probabilities. To make the solution of these computations as simple as possible, without losing the main result, some additional assumptions must be imposed:Footnote 20
$\mathbb {E}[\bar{\rho }_{ji}] = 0 \hspace{5.69046pt} \forall j,i \in \mathcal {N}$. According to the former definition, utilities are no longer independent, and in general, they do not fulfill the standard IIA axiom. The non-zero correlations between choice options result from the fact that temporary migrants consider wages in the source and the host economies as the determinants of lifetime migration choices. Thus, one cannot use the theorem by McFadden (1984) to calculate the choice probabilities. To make the solution of these computations as simple as possible, without losing the main result, some additional assumptions must be imposed:Footnote 20
Proposition 6. If all N destination countries offer the same duration of temporary visas (equal to ![]() $\bar{d}^t$) and the differences in permanent and temporary migration costs are identical across destinations:
$\bar{d}^t$) and the differences in permanent and temporary migration costs are identical across destinations: ![]() $\Delta = x_{ji}(\bar{d}^p) - x_{ji}(\bar{d}^t) = x_{ki}(\bar{d}^p) - x_{ki}(\bar{d}^t)$ for j ≠ k, i, j, k ∈ {1, . . ., N}, then the unconditional probabilities of emigrating to a particular country j ≠ i are equal to:
$\Delta = x_{ji}(\bar{d}^p) - x_{ji}(\bar{d}^t) = x_{ki}(\bar{d}^p) - x_{ki}(\bar{d}^t)$ for j ≠ k, i, j, k ∈ {1, . . ., N}, then the unconditional probabilities of emigrating to a particular country j ≠ i are equal to:
 $$\begin{eqnarray}
&& P[\mathbb {E}[{U}_{ii}] = \max ] = \frac{e^{\alpha v_i}}{\sum _{k=1}^N e^{\alpha (v_k - x_{ki}(\bar{d}^t))}}, \nonumber\\
&& P[\mathbb {E}[{U}_{ji}(\bar{d}^t)] = \max ] = \frac{ e^{\alpha (v_j-x_{ji}(\bar{d}^t))}}{\sum _{k=1}^N e^{\alpha (v_k - x_{ki}(\bar{d}^t))}} - \frac{ e^{\alpha (v_j-x_{ji}(\bar{d}^t))}}{\sum _{k \ne i} e^{\alpha (v_k - x_{ki}(\bar{d}^t))}+ e^{\alpha \left(v_i + \frac{\Delta }{1-\bar{d}^t} \right)}}, \nonumber \\
&& P[\mathbb {E}[{U}_{ji}(\bar{d}^p)] = \max ] = \frac{e^{\alpha (v_j - x_{ji}(\bar{d}^t))}}{\sum _{k \ne i} e^{\alpha (v_k - x_{ki}(\bar{d}^t))}+ e^{\alpha \left(v_i + \frac{\Delta }{1-\bar{d}^t} \right)} }.
\end{eqnarray}$$
$$\begin{eqnarray}
&& P[\mathbb {E}[{U}_{ii}] = \max ] = \frac{e^{\alpha v_i}}{\sum _{k=1}^N e^{\alpha (v_k - x_{ki}(\bar{d}^t))}}, \nonumber\\
&& P[\mathbb {E}[{U}_{ji}(\bar{d}^t)] = \max ] = \frac{ e^{\alpha (v_j-x_{ji}(\bar{d}^t))}}{\sum _{k=1}^N e^{\alpha (v_k - x_{ki}(\bar{d}^t))}} - \frac{ e^{\alpha (v_j-x_{ji}(\bar{d}^t))}}{\sum _{k \ne i} e^{\alpha (v_k - x_{ki}(\bar{d}^t))}+ e^{\alpha \left(v_i + \frac{\Delta }{1-\bar{d}^t} \right)}}, \nonumber \\
&& P[\mathbb {E}[{U}_{ji}(\bar{d}^p)] = \max ] = \frac{e^{\alpha (v_j - x_{ji}(\bar{d}^t))}}{\sum _{k \ne i} e^{\alpha (v_k - x_{ki}(\bar{d}^t))}+ e^{\alpha \left(v_i + \frac{\Delta }{1-\bar{d}^t} \right)} }.
\end{eqnarray}$$
In particular:
 $$\begin{eqnarray}
&& \frac{P[\mathbb {E}[{U}_{ji}(\bar{d}^t)] = \max ]}{P[\mathbb {E}[{U}_{ii}] = \max ] } = \frac{e^{\alpha (v_j - x_{ji}(\bar{d}^t))}\left( e^{\frac{\alpha \Delta }{1-\bar{d}^t}} - 1\right)}{\sum _{k\ne i} e^{\alpha (v_k - x_{ki}(\bar{d}^t))}+ e^{\alpha \left(v_i + \frac{\Delta }{1-\bar{d}^t} \right)}}, \nonumber\\
&& \frac{P[\mathbb {E}[{U}_{ji}(\bar{d}^p)] = \max ]}{P[\mathbb {E}[{U}_{ii}] = \max ] } = \frac{e^{\alpha (v_j-x_{ji}(\bar{d}^p)-v_i)}\left( \sum _{k\ne i} e^{\alpha (v_k - x_{ki}(\bar{d}^t))} \right)}{\sum _{k \ne i} e^{\alpha (v_k - x_{ki}(\bar{d}^t))}+ e^{\alpha \left(v_i + \frac{\Delta }{1-\bar{d}^t}\right)}}.
\end{eqnarray}$$
$$\begin{eqnarray}
&& \frac{P[\mathbb {E}[{U}_{ji}(\bar{d}^t)] = \max ]}{P[\mathbb {E}[{U}_{ii}] = \max ] } = \frac{e^{\alpha (v_j - x_{ji}(\bar{d}^t))}\left( e^{\frac{\alpha \Delta }{1-\bar{d}^t}} - 1\right)}{\sum _{k\ne i} e^{\alpha (v_k - x_{ki}(\bar{d}^t))}+ e^{\alpha \left(v_i + \frac{\Delta }{1-\bar{d}^t} \right)}}, \nonumber\\
&& \frac{P[\mathbb {E}[{U}_{ji}(\bar{d}^p)] = \max ]}{P[\mathbb {E}[{U}_{ii}] = \max ] } = \frac{e^{\alpha (v_j-x_{ji}(\bar{d}^p)-v_i)}\left( \sum _{k\ne i} e^{\alpha (v_k - x_{ki}(\bar{d}^t))} \right)}{\sum _{k \ne i} e^{\alpha (v_k - x_{ki}(\bar{d}^t))}+ e^{\alpha \left(v_i + \frac{\Delta }{1-\bar{d}^t}\right)}}.
\end{eqnarray}$$
Proof. See Appendix A. ![]() $\Box$
$\Box$
The ratios of probabilities of moving to j (either temporarily or permanently) and staying in i are dependent not only on the economic and policy variables that describe those two countries but also on the characteristics of all of the other N − 2 options. The IIA property is not maintained, and adding further choice options alters the relative odds of selecting particular visas in any of N destinations. Introducing a second dimension of individual choice (not only the destination but also different durations of stays) results in implicit relationships within destination-specific options. Indeed, computing the coefficient of correlation between the utility of staying and the utility that is ascribed to temporary emigration to j, one observes that: ![]() $cor( \mathbb {E}[{U}_{ii}], \mathbb {E}[{U}_{ji}(\bar{d}^t)] ) = cor(\varepsilon _{i}, \bar{d}^t\varepsilon _{j} + (1-\bar{d}^t)\varepsilon _{i} ) = 1-\bar{d}^t,$ because period
$cor( \mathbb {E}[{U}_{ii}], \mathbb {E}[{U}_{ji}(\bar{d}^t)] ) = cor(\varepsilon _{i}, \bar{d}^t\varepsilon _{j} + (1-\bar{d}^t)\varepsilon _{i} ) = 1-\bar{d}^t,$ because period ![]() $1-\bar{d}^t$ is spent in the home country. As a consequence, an agent who has a strongly negative attitude toward living in her country of birth (a low value of εi) would be more inclined to emigrate rather than to stay. Similarly, a person with a strong preference toward a particular foreign destination would want to emigrate permanently rather than temporarily.
$1-\bar{d}^t$ is spent in the home country. As a consequence, an agent who has a strongly negative attitude toward living in her country of birth (a low value of εi) would be more inclined to emigrate rather than to stay. Similarly, a person with a strong preference toward a particular foreign destination would want to emigrate permanently rather than temporarily.
Let us now move to the ex-post decisions about the duration of stay. The solution to the problem (4) has the following form:
Proposition 7. The optimal, ex-post duration of migration is given by
 $$\begin{equation}
d^* = \left\lbrace \begin{array}{l}\min \left\lbrace \rho ^{-1}_{j^*i} \left( {V_{j^*i}(\bar{d}) + \varepsilon _{j^*} - \varepsilon _{i}} \right); \bar{d} \right\rbrace , \quad \text{if} \quad \rho _{i^*} > 0, \\
\bar{d}, \quad \textrm {if} \quad \rho _{j^*i} < 0, \end{array} \right.
\end{equation}$$
$$\begin{equation}
d^* = \left\lbrace \begin{array}{l}\min \left\lbrace \rho ^{-1}_{j^*i} \left( {V_{j^*i}(\bar{d}) + \varepsilon _{j^*} - \varepsilon _{i}} \right); \bar{d} \right\rbrace , \quad \text{if} \quad \rho _{i^*} > 0, \\
\bar{d}, \quad \textrm {if} \quad \rho _{j^*i} < 0, \end{array} \right.
\end{equation}$$
for the temporary (permanent) migrants, taking ![]() $\bar{d} = \bar{d}^t$ (
$\bar{d} = \bar{d}^t$ (![]() $\bar{d} = \bar{d}^p$). Note that
$\bar{d} = \bar{d}^p$). Note that ![]() $V_{j^*i}(\bar{d}) \equiv \alpha (v_{j^*} - x_{j^*i}(\bar{d})-v_{i})$.
$V_{j^*i}(\bar{d}) \equiv \alpha (v_{j^*} - x_{j^*i}(\bar{d})-v_{i})$.
Proof. See the proof of Proposition 1. ![]() $\Box$
$\Box$
Finally, one can explicitly represent the distributions of durations of stay (by visa type) in the same way as it was performed in a model with one visa. However, in contrast to what has been concluded above, the overall distribution of the duration of stay (concerning all of the types of highly skilled immigrants) will now be a combination of two distributions: of the temporary and the permanent immigrants. Therefore, this aggregated distribution of duration of stay may not be (and typically is not) unimodal.
4.2. A Model with Three Visas
For the purpose of a better representation of visa policies in the analyzed host countries, the last modification of the model considers three types of visas: a short-term visa, a medium-term residence permit, and a permanent staying permission. This general classification of visas is very close to what is proposed by the main destination countries for immigrants.Footnote 21 As can be concluded from the summary of visa policies in Appendix B, authorities prefer to classify immigrants into short (duration of stay of 1 years), medium (6 years), and long-term (permanent) categories. The definitions, mechanisms, and properties of a three visa model align with what has been presented in the case of two visas, except for the fact that now there are two temporary visas: one with a duration of 1 year (in the units of 50-year generation): d t1 = 1/50, and one with a duration of 6 years: d t2 = 6/50. This brings a further complication to the correlation structure among all of the emigration options.
Each of N countries issues two types of temporary visas and a permanent visa. For each ![]() $i,j \in \mathcal {N}$, their costs are equal to:
$i,j \in \mathcal {N}$, their costs are equal to: ![]() $x_{ji}(\bar{d}^p) > x_{ji}(\bar{d}^{t2}) > x_{ji}(\bar{d}^{t1})$. The ex-ante expected utilities of migration from country i to j are as follows:
$x_{ji}(\bar{d}^p) > x_{ji}(\bar{d}^{t2}) > x_{ji}(\bar{d}^{t1})$. The ex-ante expected utilities of migration from country i to j are as follows:
 \fontsize{9}{11} \selectfont{$$\begin{eqnarray}
&& \mathbb {E}[{U}_{ii}] = \alpha v_i +\varepsilon _{i}, \nonumber\\
&& \mathbb {E}[{U}_{ji}(\bar{d}^{t1})] = \bar{d}^{t1} \left( \alpha \left( v_j - x_{ji}(\bar{d}^{t1}) \right) - \bar{d}^{t1} \mathbb {E}[\bar{\rho }_{ji}]/2 + \varepsilon _{j} \right) + (1-\bar{d}^{t1})\left( \alpha v_i + \varepsilon _{i} \right), \nonumber \\
&& \mathbb {E}[{U}_{ji}(\bar{d}^{t2})] = \bar{d}^{t2} \left( \alpha \left( v_j - x_{ji}(\bar{d}^{t2}) \right) - \bar{d}^{t2} \mathbb {E}[\bar{\rho }_{ji}]/2 + \varepsilon _{j} \right) + (1-\bar{d}^{t2})\left( \alpha v_i + \varepsilon _{i} \right), \nonumber \\
&& \mathbb {E}[{U}_{ji}(\bar{d}^p)] = \alpha \left( v_j - x_{ji}(\bar{d}^p) \right) - \mathbb {E}[\bar{\rho }_{ji}]/2 + \varepsilon _{j}.
\end{eqnarray}$$}
\fontsize{9}{11} \selectfont{$$\begin{eqnarray}
&& \mathbb {E}[{U}_{ii}] = \alpha v_i +\varepsilon _{i}, \nonumber\\
&& \mathbb {E}[{U}_{ji}(\bar{d}^{t1})] = \bar{d}^{t1} \left( \alpha \left( v_j - x_{ji}(\bar{d}^{t1}) \right) - \bar{d}^{t1} \mathbb {E}[\bar{\rho }_{ji}]/2 + \varepsilon _{j} \right) + (1-\bar{d}^{t1})\left( \alpha v_i + \varepsilon _{i} \right), \nonumber \\
&& \mathbb {E}[{U}_{ji}(\bar{d}^{t2})] = \bar{d}^{t2} \left( \alpha \left( v_j - x_{ji}(\bar{d}^{t2}) \right) - \bar{d}^{t2} \mathbb {E}[\bar{\rho }_{ji}]/2 + \varepsilon _{j} \right) + (1-\bar{d}^{t2})\left( \alpha v_i + \varepsilon _{i} \right), \nonumber \\
&& \mathbb {E}[{U}_{ji}(\bar{d}^p)] = \alpha \left( v_j - x_{ji}(\bar{d}^p) \right) - \mathbb {E}[\bar{\rho }_{ji}]/2 + \varepsilon _{j}.
\end{eqnarray}$$}
As above, ex-ante ![]() $\mathbb {E}[\bar{\rho }_{ji}] = 0 \hspace{5.69046pt} \forall i,j \in \mathcal {N}$.Footnote 22
$\mathbb {E}[\bar{\rho }_{ji}] = 0 \hspace{5.69046pt} \forall i,j \in \mathcal {N}$.Footnote 22
Consequently, the applied modeling strategy is designed as follows. I develop a multi-country model with 178 sending states and 35 destinations. Accounting for multi-dimensional correlations between the utilities that are ascribed to different target states (in line with the fact that the IIA axiom is not satisfied), I investigate the world-wide equilibrium outcome of altering migration policies in the group of EU countries. The aim of the counterfactual exercise is to quantify the long-run consequences of different migration policies in the EU (H-1B visas in Europe and fiscal incentives (FI) for highly skilled immigrants to the EU) for the most developed regions of the world. Each individual faces a choice set of: 1 + 3 · 35 = 106 options (staying at home, or emigrating to one of 35 destinations with one of three visas). Then, each discrete option is characterized by its own continuous distribution of duration of stay, which then is aggregated at the country-pair level.
4.3. Numerical Solution of the Model
The purpose of calibration is to compute expected and unforeseen migration costs by fitting the migration flows that are observed in the data.Footnote 23 After completing this step, I introduce alternative migration policies and solve the model for new equilibria. The endogenous objects of interest are the new flows and stocks of highly skilled immigrants and the distributions of the duration of stay of the all source-destination country pairs.
Calibration
Considering the complexity of interdependencies between the utilities that are ascribed to different destinations and durations of stay (see equations (17)), the model is calibrated using the Monte Carlo method. The solution requires the determination of the values of country-pair-specific and visa-specific migration costs, labeled by ![]() $x_{ji}(\bar{d})$ for all of the considered sources and destinations: j, i ∈ {1, . . ., N}, and three types of visas:
$x_{ji}(\bar{d})$ for all of the considered sources and destinations: j, i ∈ {1, . . ., N}, and three types of visas: ![]() $\bar{d} \in \lbrace t_1, t_2, p\rbrace$. Additionally, the country-pair-specific distributions of duration of stay (which depend on the values of unforeseen migration cost: ρji) must be specified.
$\bar{d} \in \lbrace t_1, t_2, p\rbrace$. Additionally, the country-pair-specific distributions of duration of stay (which depend on the values of unforeseen migration cost: ρji) must be specified.
The initial step is the calculation of ![]() $x_{ji}(\bar{d})$ using the agents’ optimal decision rules that are governed by the solutions to utility maximization problems (17). From the data that describe the yearly inflows of immigrants for different visa types, I first compute the probabilities of emigration from each source country to any destination. Then, for a given sending country i ∈ {1, . . ., N} I separately conduct a Monte Carlo experiment. I draw 250,000 realizations of vectors of random components, εj, from Gumbel distribution for all of the 35 potential hosts, j. These 35-dimensional vectors represent 250,000 potential migrants who have random preferences toward each destination. Starting with the initial values for migration costs, I iteratively compute the utilities that are ascribed to each and every migration option (17) and the simulated probabilities of emigration to any country with a particular visa type. Finally, using a conservative updating rule, I modify the actual values of
$x_{ji}(\bar{d})$ using the agents’ optimal decision rules that are governed by the solutions to utility maximization problems (17). From the data that describe the yearly inflows of immigrants for different visa types, I first compute the probabilities of emigration from each source country to any destination. Then, for a given sending country i ∈ {1, . . ., N} I separately conduct a Monte Carlo experiment. I draw 250,000 realizations of vectors of random components, εj, from Gumbel distribution for all of the 35 potential hosts, j. These 35-dimensional vectors represent 250,000 potential migrants who have random preferences toward each destination. Starting with the initial values for migration costs, I iteratively compute the utilities that are ascribed to each and every migration option (17) and the simulated probabilities of emigration to any country with a particular visa type. Finally, using a conservative updating rule, I modify the actual values of ![]() $x_{ji}(\bar{d})$. The algorithm stops when the simulated probabilities of emigration are close to their empirical counterparts (the difference between each pair is less than 10−5). With the values of migration costs in hand, one can predict the flows of migrants (by duration of visa) between any two countries. Figure E.1 presents the comparison of the aggregated skill-specific and visa-specific flows for 35 destinations (actual data versus model outcomes). Using the constructed average durations of stay, I compute the total stocks of immigrants as if the yearly flows of migrants were equal to the values from the year 2013 over the entire 50-year period.
$x_{ji}(\bar{d})$. The algorithm stops when the simulated probabilities of emigration are close to their empirical counterparts (the difference between each pair is less than 10−5). With the values of migration costs in hand, one can predict the flows of migrants (by duration of visa) between any two countries. Figure E.1 presents the comparison of the aggregated skill-specific and visa-specific flows for 35 destinations (actual data versus model outcomes). Using the constructed average durations of stay, I compute the total stocks of immigrants as if the yearly flows of migrants were equal to the values from the year 2013 over the entire 50-year period.
The second part of the calibration procedure addresses the unforeseen migration costs. For each source i and each destination j, I fit the conditional and unconditional probabilities of staying calculated using the Database on Immigrants in OECD and non-OECD Countries (DIOC) by the OECD and the database that is provided by Abel and Sander (Reference Abel and Sander2014) from the IIASA. This step considers only those countries for which at least two data points are available. Initially, I draw 250,000 realizations of the difference between the random components, εj − εi, from the logistic distribution. These values represent 250,000 migrants from country i to country j. Then, I define the potential values of ρji to be between 0.01 and 20 with step 0.01. For each of these steps, I calculate the simulated distribution of the immigrants’ duration of stay. After sorting the immigrants with respect to their preferred visa type, I compute their actual durations of stay after discovering the value of ρji. In this way, the simulated distribution of the lengths of stay is constructed, and the empirical counterparts of probabilities of staying can be calculated. At the end, the value of ρji ∈ [0.01; 20], which minimizes the Euclidean distance between the simulated and empirical probabilities, is chosen as the best estimation. For those country pairs for which the data on the probabilities of stay are not sufficient, I extrapolate the values of ρji using the estimations from a cross-section regression with gravity variables and origin and destination fixed effects (see Table E.5). Figure E.2 depicts the distributions of the estimated values of ρji’s for 35 receiving countries. More attractive destinations (i.e., Canada or the United States) are generally characterized by lower values of unforeseen migration costs, than the less popular ones (i.e., Bulgaria or Romania).
Simulation
Each of the simulations starts with the definition of a new migration policy (either modifying visa costs, or providing FI for immigrants). In the first counterfactual scenario, I assume that in all of the EU countries the costs of 6-year visas for the highly skilled immigrants are reduced, so that they project the relative costs of H-1B visas in the United States. Note that apart from the legal aspect, the expected migration costs comprise a non-reducible part that is related to geography, the social cohesion of migrants or cultural and social differences. Their identification strategy is proposed in Table E.4. From these estimates, I also compute the legal visa costs for all the countries by investigating the destination-visa specific fixed effects that capture the formal burdens on immigrants. In this way, the counterfactual changes in ![]() $x_{ji}(\bar{d})$ are supposed to be driven mainly by policy-related factors.
$x_{ji}(\bar{d})$ are supposed to be driven mainly by policy-related factors.
In describing the procedure of setting counterfactual costs of migration, I consider a particular destination country – Germany (see Figure 2). The black points represent the average visa costs in the United States (considering the 1-year, 6-year, and a permanent visa). The light gray points depict the same values for Germany in the reference scenario. It is clearly visible that the 6-year visa is relatively cheaper in the United States and relatively more expensive in Germany (which imposes a convex visa cost function for the United States and a concave one for Germany). The goal is to decrease the cost of a 6-year visa in Germany (point X) in a way that imposes the relative cost structure from the United States. To achieve this, I reduce this cost (to point Y) such that the ratio of difference in the costs of 6-year and 1-year visas (A DEU) to the difference in the costs of 50-year and 1-year visas (B DEU) is the same as in the United States (and equal to A USA/B USA). This procedure is followed for all of the other European destinations (computing the country-pair-specific migration costs separately), and its outcomes are depicted in Figure 3.Footnote 24

Figure 2. Reduction of visa costs to the H-1B level – example of Germany. Note: The darkest (lightest) gray line represent the imputed structure of visa costs in the United States (Germany) in the benchmark case. Imputation is done using three data points (1-year, 6-year, 50-year visa costs). The middle gray line represent the counterfactual structure of visa costs in Germany after implementing the H-1B policy (moving the 6-year visa cost from point X to Y). The latter takes the relative structure of migration cost in the United States (A USA/B USA) and transfers it to Germany (A DEU/B DEU). Source: own calculations.

Figure 3. Visa costs in the reference, and in the counterfactual H-1B scenarios in Europe. Note: For each destination, the bars represent the distribution of visa costs. The costs are increasing in the duration of visa. Notice that the figure includes the benchmark costs of 6-year visas (white bars) and their counterfactual costs after implementing the H-1B scenario in the EU-28 (black bars). Source: own calculations.
The second counterfactual policy implements FI for highly skilled immigrants, keeping the migration costs constant. Taking note of the briefing by CES-IFO DICE (2012), and following the report OECD (2011), I decided to implement an additional 10% FI in the EU economies. This means that highly skilled migrants who come with a 6-year visa pay a 10 p.p. lower income tax than other citizens. Consequently, the group of medium-term professionals has a higher net wage compared to short-term and permanent immigrants.
With the new migration policies in the EU, I run another Monte Carlo simulation to calculate the counterfactual yearly flows of workers. In doing so, I take the modified migration costs and net wages as given for the H-1B simulation and reference migration costs and counterfactual net wages for the FI simulation. The unforeseen migration costs remain unchanged. For each of the 178 sending countries, I draw 2,000,000 realizations of the vectors of stochastic preferences toward 35 destinations and compute the optimal migration decisions for these values. This enables the calculation of the probabilities of migration and the actual flows of migrants for each country-pair and visa type.
Another Monte Carlo simulation targets the issue of fitting new duration distributions for each pair of sending and receiving countries. 2,000,000 realizations of the differences of random components εj − εi are drawn, and the optimal durations of stay are determined according to Proposition 7 in the case of three visas. The only elements that are left to calculate are the average durations of stay, which determine the counterfactual stocks of immigrants.
5. CONSEQUENCES OF ALTERNATIVE MIGRATION POLICIES
This section presents the implications of counterfactual migration policies in the EU. The first part considers an introduction of H-1B visas in all of the EU-member states. In the next subsection, I propose a tax concession mechanism for highly skilled immigrants. Then, I consider a scenario in which migrants obtain a wage premium after returning to their homelands. Finally, I discuss the quantitative importance of MRM.
5.1. Introduction of H-1B Visa in the EU
A decrease in migration costs for highly skilled temporary migrants to the EU has a substantial impact on the flows and stocks of migrants all over the world (for detailed results see columns labeled with H-1B in Table E.6, and for the ranking see Figure 4(a)). Considering Europe as a whole, an introduction of H-1B immigration policy brings 30,000 new highly skilled immigrants every year. Simultaneously, the total number of foreign professionals increases by 800,000 or 6.1% of the reference stock of highly skilled immigrants. Due to the loss of relative attractiveness, non-EU destinations (mainly the United States, Australia, and Canada) encounter a slight loss in the number of well-educated foreigners, which does not exceed 1% of the reference stock. The biggest winners of this policy in terms of total stocks are Poland, Germany, the UK (more than 100,000 highly skilled workers), and less popular destinations in terms of the relative change in stocks (Bulgaria, Croatia, Lithuania, Latvia, and Slovenia).
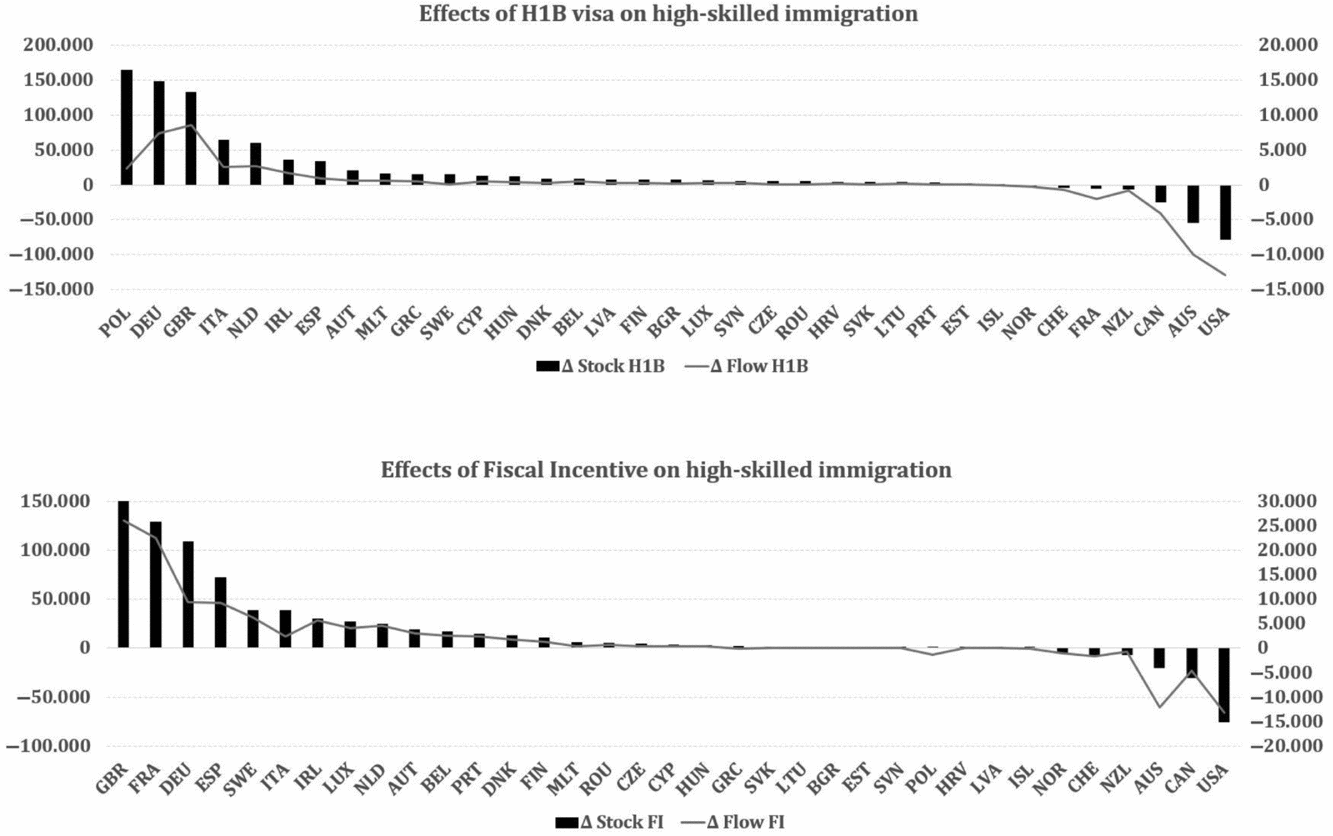
Figure 4. Changes in aggregated flows and stocks of migrants due to counterfactual policies. Note: Changes in stocks (black bars, left axis) and flows (gray lines, right axis) of highly skilled immigrants (counterfactual minus reference) after introducing: (a) H-1B visas in the EU and (b) fiscal incentives in the EU. Source: own calculations.
The effects with respect to yearly inflows of immigrants are also heterogeneous across the EU-members. Germany, the UK, the Netherlands, and Italy gain the most immigrants. The only EU-member that loses highly skilled immigrants due to the H-1B policy is France. An explanation for this result could be the fact that France is already characterized by low migration costs for well-educated candidates (which can be observed in Figure 3). Therefore, an H-1B policy, which is defined in the proposed counterfactual scenario, brings almost no change to the 6-year visa costs. Because other destinations significantly drop the barriers for medium-term immigrants, France is becoming relatively less attractive, and people substitute this destination for other European countries.
The results gathered in Table E.6 reveal that the changes in total stocks are not mainly driven by new inflows. The “size” effect of the proposed H-1B policy (that is attracting the current non-migrants from all sources) is almost null. Conversely, the impact on the aggregate numbers of highly skilled workers results from the visa switching of the current immigrants. For short-term migrants (who have relatively high preferences toward living in the destination countries but are at the threshold between 1-year and 6-year visas) and some permanent stayers (who have relatively low preferences toward the destination and are at the threshold between 6-year and permanent visas), a cheaper 6-year visa is an encouragement to choose a new H-1B emigration option. Thus, with few new entries, some EU-members (such as Sweden, Czech Republic, Estonia, or Poland) manage to visibly increase the stock of highly skilled workers. To support this “visa-substitution” property, consider the structure of immigration flows and stocks by visa types (see Figure 5). In the reference scenario (first row of graphs), the short-term immigrants constitute sizable parts of total inflows and stocks. In contrast, after implementing the H-1B visa, the European countries experience a significant drop in the share of those migrants in both flows and stocks. For the permanent migrants, the effects show similar signs, but their magnitudes are smaller.

Figure 5. Composition of migrants flows and stocks. Note: The actual compositions of migrants with respect to their duration of visa, in flows (left column) and stocks (right column). First row represents the reference scenario, second row: the composition after introducing an H-1B visa in the EU, and the third row: the composition after introducing a fiscal incentive in the EU. Source: own calculations.
To conclude, the results of the proposed experiment call for a serious discussion about the future of the European migration program. Simple (and possibly cheap in terms of national budgets) solutions, such as reducing the costs of visas for medium-term, highly skilled candidates (similar to the further development of the EBC program) might attract and retain talented foreign workers, which could have visible implications for the European economy. With such an open and liberal attitude toward attracting well-educated professionals, Europe could successfully compete for talents with other popular destinations (through the “destination–substitution” effect), and increase the stock of highly skilled workers (as a consequence of “visa-substitution” effect).
5.2. Implementation of Fiscal Incentives in the EU
An alternative migration policy that is proposed in this paper is a tax concession program for highly skilled immigrants in the EU. Instead of changing visa costs for the medium-term candidates, I suggest an augmentation of their net wage through a decrease in income tax rates by 10 p.p. in all member countries. The detailed results (see columns labeled with FI in Table E.6) for the stocks of highly skilled immigrants are similar to the case of the H-1B visa. In general, the EU would experience an increase in the total stock of highly skilled immigrants by 5.6%. Considering the ranking of countries (see Figure 4(b)), significant differences relative to the H-1B scenario may be observed for France, which is winning highly skilled workers, and for Poland, which is losing them after the implementation of the FI. While the former is caused by the fact that the immigrants to France are responsive to the FI policy (and introducing the H-1B is less efficient due to low 6-year visa costs), the latter shows that in Poland the main barrier for the prospective highly skilled immigrants is the legal migration barriers and labor market institutions that, not the low level of wages (as in the case of Croatia, Bulgaria, and Latvia). The implementation of a selective policy is generally more beneficial for the countries with high immigration barriers (and harmful for the states with already well liberalized visa policies), in contrast to the FI scenario. However, the majority of EU-members are between the two extremes, and both policies have similar impacts on the number of foreign professionals.
The tax concession brings a substantial increase in yearly flows of new highly skilled immigrants to Europe. The total inflow goes up by 10.6%, without a significantly stronger negative effect for the non-EU destinations. Although the “destination–substitution” effect is still present, (because the FI improves the relative attractiveness of Europe as compared to other destinations), its magnitude is lower than in the case of the H-1B visas. The main impact comes from the improvement of the EU’s absolute attractiveness. This means that higher wages increase the pool of international, highly skilled migrants (a yearly flow of almost 70,000 people), which results in a “size” effect. Simultaneously, the proposed migration policy has a small influence on the structure of inflows and total stocks relative to the reference scenario (see Figure 5). This means that the “visa-substitution” effect is far less pronounced than in the case of FI.
Overall, the tax exemption for the prospective highly skilled immigrants to the EU may be considered to be a close substitute for the introduction of H-1B visas. The final outcomes, in terms of the numbers of immigrants, are visibly similar in both cases. The main difference between the two policies is the relative importance of three channels through which the total effects are arising. In the case of the H-1B policy, the “visa-substitution” effect for the current immigrants drives these results, whereas the FI works by inviting new immigrants from the third countries – the “size” effect. This suggests that only the FI improves the absolute attractiveness of Europe, whereas the relative attractiveness of EU-members changes in a similar way in both cases (the two scenarios have the same magnitude of the “destination–substitution” effects from other popular destinations).
The discrepancy between the two proposed migration policies may be of great importance for the policy makers and the authorities in the EU. If a country seeks to reduce the number of short stayers, and increase the average duration of stay of immigrants, it should choose the H-1B visa policy. Moreover, this scenario convinces that increase in the number of highly skilled immigrants is feasible without enlarging the gross inflow of workers, as long as the destination is able to retain the talented people for a longer period of time. Conversely, if the authorities want to keep the structure of migrants constant, they should adopt a tax concession policy. The former policy may bring significant fiscal cost in the long-run (due to pension expenditures for the medium and long-term foreign workers), whereas the latter causes an immediate burden on national budgets (through a decrease in tax collection from the current immigrants). Both of the policies are nonetheless expected to fuel national budgets with new tax incomes. An important quantitative question that remains to be answered, but is beyond the scope of this paper, is that of the net fiscal effect of both policies in the short- and the long-term.
5.3. Accounting for the Return Premiums
Following the findings by Dustmann et al. (Reference Dustmann, Fadlon and Weiss2011) and Dustmann and Görlach (Reference Dustmann and Görlach2016), in this section, I propose a modification that includes the skill accumulation process for migrants. Because I do not consider the heterogeneity of agents with respect to their skill level, this skill upgrading process is assumed to be reflected in the wages that are earned by emigrants who decide to return to their home countries. The gains of returning migrants are assumed to be proportional to the duration of their stay and the difference in wage levels in the destination and sending countries. The return premium (RP) is set to equal 20% of the wage difference (destinations minus source) if a person decides to return just before the end of 50-year migration period, and it will be proportionally lower if the duration is shorter.Footnote 25 Comparing the reference scenarios with and without RP, it can be stated that people tend to stay for a shorter period when accounting for return bonuses (see Figure E.3), which is a natural consequence of additional incentives to return.
The results of H-1B and FI counterfactual policies with RPs are depicted in Table E.7 and in Figure 6. Quantitatively, the flows and stocks of highly skilled migrants are now higher after implementing both of the migration policies (compared to a reference state of the world with RP). Therefore, the overall effects are reinforced due to the reduced form of skill accumulation. Two economic processes drive these results. First, those who have already migrated reduce their duration of stay due to the greater reward for returning. Second, people are more prone to emigrate due to a shift in wages that is conditional on their return. Because the latter implication dominates, both the flows and stocks of migrants are positively affected as compared to the outcomes of both policies without the RP. Qualitatively, the ranking of countries for both H-1B and FI counterfactuals is slightly changed. Because the differences in RP are small across European destinations, one observes only minor modifications in the order of states.

Figure 6. Changes in aggregated flows and stocks of migrants due to counterfactual policies, with return premium. Note: Changes in stocks (black bars, left axis) and flows (gray lines, right axis) of highly skilled immigrants (counterfactual less reference) after introducing: (a) H-1B visas in the EU with return premium and (b) fiscal incentives in the EU with return premium. Source: own calculations.
5.4. Multilateral Resistance to Migration
This subsection comments on the importance of MRM in the overall results. To provide the quantitative results, I simulated the model assuming that all of the agents decide only about the destination country (as in the classic RUM model with a permanent visa), so that the choice options are independent. Then, people randomly decide about the duration of their visa according to the actual distribution of visas for all of the country pairs. The reference and the two counterfactual scenarios are computed using the procedure that is described above. In this way, it is possible to neutralize the MRM that is the consequence of the correlation between the utilities that are ascribed to discrete choice options.
The comparison of the aggregated results with and without the MRM is depicted in Figure 7 . The solid bars (left hand side axis) represent changes in the flows of immigrants, while the dashed bars (right hand side axis) provide the results for stocks (in both cases the values are differences between the model with MRM and without MRM). The results show that MRM strengthens the positive effects of both migration policies for Europe. Consequently, the lack of MRM would benefit non-EU countries through lower losses of highly skilled workers. Indeed, due to correlations between migration options, agents are more responsive to migration shocks when MRM is taken into account. This mainly concerns current migrants, who can more easily substitute between destinations. The above-mentioned phenomenon gives rise to a stronger “destination–substitution” effect, which is discussed with the previous results. In contrast, without MRM, all the choice options are independent, so that a positive shock in migration policy is followed by a smaller response from the current emigrants; thus, the “destination–substitution” effect is partially neutralized. The above exercise provides evidence that it is relevant to consider both the geographical and the time dimension of agents’ decisions when conducting multi-country migration policy experiments. Omitting either of these two elements might bring an inaccurate quantitative evaluation of the simulated policies.

Figure 7. The effects of multilateral resistance to migration. The figure shows the changes in flows (solid bars, left axis) and stocks (striped bars, right axis) of highly skilled migrants due to multilateral resistance to migration. Source: own calculations.
6. CONCLUSION
This paper introduces an alternative approach to modeling international migration in the context of many source and destination countries, with endogenous choices of length of migration spell. People reveal heterogeneous preferences for living in different host countries and face unforeseen costs after emigrating. Individual tastes govern the discrete choice of destination and the type of visa for which they apply, while the unexpected migration costs determine continuous-time decisions about the optimal duration of the emigration period. Because agents compare lifetime benefits from living temporarily or permanently in all of the available destinations, the random utility that is ascribed to each possibility may be correlated with other options. Hence, the choice probabilities are not independent, and the decision rule does not fulfill the IIA axiom, which generates MRM.
Beyond the theoretical analysis, the paper quantifies the outcomes of implementing two migration policies that are targeted at the highly skilled individuals in the EU. Introducing an H-1B visa in Europe (a preferential 6-year visa for the college-educated) significantly increases the total stock of highly skilled immigrants in the EU. The main winners are large EU-members, whereas non-EU countries such as the United States, Canada, and Australia lose their highly skilled immigrants. This is the consequence of the “destination–substitution” effect, which is explained by an increase in the relative attractiveness of the EU states after a liberalization of legal migration barriers. However, major importance may be ascribed to the “visa-substitution” effect: because medium-term visas are now relatively cheaper, current short-term and permanent immigrants are more likely to choose a 6-year emigration option.
These results are compared to a reduction of income tax for the highly skilled, medium-term immigrants to the EU. In this case, the change in total stock of immigrants is similar, but the number of inflowing professionals is higher. This is the consequence of the “size” effect, which works through an increase in the absolute attractiveness of European countries (by reducing the income taxes and increasing the net wages of prospective highly skilled immigrants). Simultaneously, the “visa-substitution” effect is of less importance, while the “destination–substitution” effect remains unchanged.
The paper also provides two additional results. With the help of a reduced form exercise, I compute the implications of both migration policies when emigrants are subject to a wage premium after returning to their home countries. The return bonus decreases the average duration of stay, but at the same time, incentives motivate more people to emigrate. Qualitatively, the relative ordering of countries with respect to their gains in labor is slightly changed in reference to the benchmark case. Finally, I calculate the difference in the flows and stocks of immigrants in the EU when MRM is ruled out. This scenario shows that independence between choice options favors the non-EU destinations that do not implement the analyzed policy reforms. Therefore, not accounting for MRM in an international context results in a downward-biased quantification of the impact of migration policies.
APPENDIX A: PROOFS OF THE PROPERTIES OF THE MODEL
Proof. (Proposition 1) Consider a migrant from country i to country j, characterized by ρji > 0. Taking the first derivative of equation (3) with respect to duration d:
Therefore, d* = ρ − 1j*i(V j*i + εj* − εi), since d* ⩽ 1, then d = min {ρ − 1j*i(Vji + εj* − εi); 1}, ![]() $\text{if} \hspace{2.84544pt} \rho _{ji} > 0$.
$\text{if} \hspace{2.84544pt} \rho _{ji} > 0$.
Consider now the situation when ρj*i < 0. From the fact that a person did emigrate, one knows that the marginal gains in the host country exceed the marginal gains in the sending country: V j*i + εj* − εi > 0. On top of that − dρj*i > 0, so that the total instantaneous utility ascribed to emigration is greater than the instantaneous utility associated with staying at home. Thus, there are no incentives for an agent to leave the destination country throughout the duration of stay. In consequence, the maximization program hits the corner solution, so that: d* = 1. ![]() $\Box$
$\Box$
Proof. (Corollary 3) The conditional PDF, defined for d > 0 is equivalent to the unconditional PDF divided by the probability that d > 0:
 $$\begin{equation}
f_{d>0}(d) = \frac{\rho _{ji} e^{\rho _{ji}d+V_{ji}}}{\left(e^{\rho _{ji}d}+e^{V_{ji}} \right)^2} \cdot \frac{1+e^{V_{ji}}}{e^{V_{ji}}} = \frac{\rho _{ji} e^{\rho _{ji}d}(1+e^{V_{ji}})}{(e^{\rho _{ji}d} +e^{ V_{ji}})^2}.
\end{equation}$$
$$\begin{equation}
f_{d>0}(d) = \frac{\rho _{ji} e^{\rho _{ji}d+V_{ji}}}{\left(e^{\rho _{ji}d}+e^{V_{ji}} \right)^2} \cdot \frac{1+e^{V_{ji}}}{e^{V_{ji}}} = \frac{\rho _{ji} e^{\rho _{ji}d}(1+e^{V_{ji}})}{(e^{\rho _{ji}d} +e^{ V_{ji}})^2}.
\end{equation}$$
The conditional CDF for a given δ is simply an integral from 0 to δ of f d > 0(d):
 $$\begin{equation}
\begin{aligned} F_{d>0}(\delta ) &= \int _0^{\delta } \frac{\rho _{ji} e^{\rho _{ji}t}(1+e^{V_{ji}})}{(e^{\rho _{ji}t} +e^{ V_{ji}})^2}dt = (1+e^{V_{ji}}) \int _{1+e^{V_{ji}}}^{e^{\rho _{ji}\delta } +e^{ V_{ji}}} \frac{1}{k^2}dk \\
&= (1+e^{V_{ji}}) \left( \frac{1}{1+e^{V_{ji}}} - \frac{1}{e^{\rho _{ji}\delta } +e^{ V_{ji}}} \right) = \frac{e^{\rho _{ji}\delta }-1}{e^{\rho _{ji}\delta } + e^{V_{ji}}}, \end{aligned}
\end{equation}$$
$$\begin{equation}
\begin{aligned} F_{d>0}(\delta ) &= \int _0^{\delta } \frac{\rho _{ji} e^{\rho _{ji}t}(1+e^{V_{ji}})}{(e^{\rho _{ji}t} +e^{ V_{ji}})^2}dt = (1+e^{V_{ji}}) \int _{1+e^{V_{ji}}}^{e^{\rho _{ji}\delta } +e^{ V_{ji}}} \frac{1}{k^2}dk \\
&= (1+e^{V_{ji}}) \left( \frac{1}{1+e^{V_{ji}}} - \frac{1}{e^{\rho _{ji}\delta } +e^{ V_{ji}}} \right) = \frac{e^{\rho _{ji}\delta }-1}{e^{\rho _{ji}\delta } + e^{V_{ji}}}, \end{aligned}
\end{equation}$$
where the change of variables: k ≡ e ρjit + e V ji, t was made. ![]() $\Box$
$\Box$
Aggregation: Assume a single wave of immigrants, who flow from country i to country j ≠ i in the beginning of a period (call it wave t = 0, the subscript is omitted). In time τ ∈ (0, 1), the total stock of workers who originate from this wave is denoted by: N ji(τ). A temporary migrant is a person who returns to her home country earlier than the maximal length of 50 years (her duration of migration spell is d* < 1). A permanent migrant stays in the destination country for all of her life, and she chooses d* = 1. Let the stock of individuals from the first group be labeled as ![]() $\tilde{N}_{ji}(0)$, whereas the second:
$\tilde{N}_{ji}(0)$, whereas the second: ![]() $\hat{N}_{ji}(0)$. Therefore, right after emigrating, when τ → 0, the total stock of foreign workers who originate from i and reside in j is:
$\hat{N}_{ji}(0)$. Therefore, right after emigrating, when τ → 0, the total stock of foreign workers who originate from i and reside in j is: ![]() $N_{ji}(\tau ) = \tilde{N}_{ji}(\tau ) + \hat{N}_{ji}(\tau )$. Note that when τ → 1 all temporary workers return home, and the only foreign labor force that is left are permanent immigrants. Consequently, the number of non-native citizens from the analyzed wave is equal to:
$N_{ji}(\tau ) = \tilde{N}_{ji}(\tau ) + \hat{N}_{ji}(\tau )$. Note that when τ → 1 all temporary workers return home, and the only foreign labor force that is left are permanent immigrants. Consequently, the number of non-native citizens from the analyzed wave is equal to: ![]() $\hat{N}_{ji}(\tau )$. In aggregated terms, the total stock of employees from a particular wave t = 0, living in country j at period τ is equal to the sum of natives and foreigners who decided to immigrate: Lj(τ) = ∑Ni = 1Nji(τ). The share of permanent migrants reaches one if the ratio of wages between destination and source country approaches infinity. Similarly, if the unforeseen costs are growing, then all of the potential migrants stay for a short period of time and the fraction of permanent movers among those with positive realizations of unanticipated migration cost diminishes toward 0 (still, the half of the population experiences a beneficial unexpected shock, thus they always remain permanent migrants). According to the previous notations
$\hat{N}_{ji}(\tau )$. In aggregated terms, the total stock of employees from a particular wave t = 0, living in country j at period τ is equal to the sum of natives and foreigners who decided to immigrate: Lj(τ) = ∑Ni = 1Nji(τ). The share of permanent migrants reaches one if the ratio of wages between destination and source country approaches infinity. Similarly, if the unforeseen costs are growing, then all of the potential migrants stay for a short period of time and the fraction of permanent movers among those with positive realizations of unanticipated migration cost diminishes toward 0 (still, the half of the population experiences a beneficial unexpected shock, thus they always remain permanent migrants). According to the previous notations
 $$\begin{equation}
\tilde{N}_{ji} = \frac{e^{\rho _{ji}}-1}{e^{\rho _{ji}}+e^{V_{ji}}} \frac{N_{ji}}{2}, \quad \quad \hat{N}_{ji} = \left( \frac{1+e^{V_{ji}}}{e^{\rho _{ji}}+e^{V_{ji}}} + 1\right) \frac{N_{ji}}{2}.
\end{equation}$$
$$\begin{equation}
\tilde{N}_{ji} = \frac{e^{\rho _{ji}}-1}{e^{\rho _{ji}}+e^{V_{ji}}} \frac{N_{ji}}{2}, \quad \quad \hat{N}_{ji} = \left( \frac{1+e^{V_{ji}}}{e^{\rho _{ji}}+e^{V_{ji}}} + 1\right) \frac{N_{ji}}{2}.
\end{equation}$$
Of course, permanent migrants fully contribute to the host country’s labor supply, so their weight in the aggregate is 1 (taking the units of the generation period, 50 years). Therefore, they provide exactly ![]() $\hat{N}_{ji}$ units of labor. More computation is required to determine the labor force of temporary migrants, as they do not participate in the foreign labor market for the whole period, and everyone stays in the destination country according to individual optimal decisions about d*. Knowing the country-pair-specific, conditional distributions of durations of stay (derived in Proposition 4), it suffices to compute the following conditional expectation:
$\hat{N}_{ji}$ units of labor. More computation is required to determine the labor force of temporary migrants, as they do not participate in the foreign labor market for the whole period, and everyone stays in the destination country according to individual optimal decisions about d*. Knowing the country-pair-specific, conditional distributions of durations of stay (derived in Proposition 4), it suffices to compute the following conditional expectation: ![]() $\mathbb {E}_{d>0}[d^* | d^*<1]$. After summing up temporary and permanent migrants, one arrives at an expression that (multiplied by the total, gross migration flow: N ji) represents the effective labor supply in country j that originates from country i during one period of time. The total labor force in country j immigrating from country i (expressed in the number of foreigners available for the period of one generation, 50 years) is equal to
$\mathbb {E}_{d>0}[d^* | d^*<1]$. After summing up temporary and permanent migrants, one arrives at an expression that (multiplied by the total, gross migration flow: N ji) represents the effective labor supply in country j that originates from country i during one period of time. The total labor force in country j immigrating from country i (expressed in the number of foreigners available for the period of one generation, 50 years) is equal to
 $$\begin{equation}
L_{ji}(V_{ji}, \rho _{ji}) = \frac{N_{ji}}{2} \left( \frac{1+e^{V_{ji}}}{\rho _{ji}e^{V_{ji}}}\ln {\left(\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}\right)} + 1 \right).
\end{equation}$$
$$\begin{equation}
L_{ji}(V_{ji}, \rho _{ji}) = \frac{N_{ji}}{2} \left( \frac{1+e^{V_{ji}}}{\rho _{ji}e^{V_{ji}}}\ln {\left(\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}\right)} + 1 \right).
\end{equation}$$
Proof. (Proposition 5) The expected, conditional duration of stay (for the temporary migrants characterized by ρji > 0) is calculated from the definition
 $$\begin{eqnarray}
\mathbb {E}_{d>0}[d | d<1] &=& \int _0^1 t dF_{t>0}(t)dt = \int _0^1 t \frac{\rho _{ji} e^{\rho _{ji}t}(1+e^{V_{ji}})}{\left(e^{\rho _{ji}t} + e^{V_{ji}}\right)^2} dt \nonumber\\
&=& \frac{1+e^{V_{ji}}}{\rho _{ji}e^{V_{ji}}}\ln {\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}} - \frac{1+e^{V_{ji}}}{e^{\rho _{ji}}+e^{V_{ji}}}.
\end{eqnarray}$$
$$\begin{eqnarray}
\mathbb {E}_{d>0}[d | d<1] &=& \int _0^1 t dF_{t>0}(t)dt = \int _0^1 t \frac{\rho _{ji} e^{\rho _{ji}t}(1+e^{V_{ji}})}{\left(e^{\rho _{ji}t} + e^{V_{ji}}\right)^2} dt \nonumber\\
&=& \frac{1+e^{V_{ji}}}{\rho _{ji}e^{V_{ji}}}\ln {\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}} - \frac{1+e^{V_{ji}}}{e^{\rho _{ji}}+e^{V_{ji}}}.
\end{eqnarray}$$
These people constitute a fraction of 1/2 of total gross inflow of migrants. The rest of people (that is temporary migrants characterized by ρji < 0 and the permanent migrants) is staying until the expiration of their visa, so their average duration of stay is d = 1. Consider a gross inflow of immigrants equal to N ji people. Now adding all the groups (temporary, nostalgic, permanent nostalgic, and non-nostalgic people, respectively), I get the aggregated labor force that is present in the host country during the 50-year period:
 $$\begin{eqnarray}
L_{ji}(V_{ji}, \rho _{ji}) &=& \frac{N_{ji}}{2} \left( \frac{1+e^{V_{ji}}}{\rho _{ji}e^{V_{ji}}}\ln {\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}} - \frac{1+e^{V_{ji}}}{e^{\rho _{ji}}+e^{V_{ji}}} \right) + \frac{N_{ji}}{2} \frac{1+e^{V_{ji}}}{e^{\rho _{ji}}+e^{V_{ji}}} + \frac{N_{ji}}{2} \nonumber\\
&=& \frac{N_{ji}}{2} \left( \frac{1+e^{V_{ji}}}{\rho _{ji}e^{V_{ji}}}\ln {\left(\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}\right)} + 1 \right).
\end{eqnarray}$$
$$\begin{eqnarray}
L_{ji}(V_{ji}, \rho _{ji}) &=& \frac{N_{ji}}{2} \left( \frac{1+e^{V_{ji}}}{\rho _{ji}e^{V_{ji}}}\ln {\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}} - \frac{1+e^{V_{ji}}}{e^{\rho _{ji}}+e^{V_{ji}}} \right) + \frac{N_{ji}}{2} \frac{1+e^{V_{ji}}}{e^{\rho _{ji}}+e^{V_{ji}}} + \frac{N_{ji}}{2} \nonumber\\
&=& \frac{N_{ji}}{2} \left( \frac{1+e^{V_{ji}}}{\rho _{ji}e^{V_{ji}}}\ln {\left(\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}\right)} + 1 \right).
\end{eqnarray}$$
![]() $\Box$
$\Box$
Some asymptotic properties of the L ji function with respect to its arguments are depicted in the following:
 $$\begin{eqnarray}
&& \lim _{\quad \rho _{ji} \rightarrow 0} L_{ji}(V_{ji}, \rho _{ij}) = N_{ji}, \hspace{22.76228pt} \lim _{V_{ji} \rightarrow \infty } L_{ji}(V_{ji}, \rho _{ji}) = N_{ji}, \nonumber\\
&& \lim _{\rho _{ji} \rightarrow \infty } L_{ji}(V_{ji}, \rho _{ji}) = N_{ji} / 2, \quad \lim _{V_{ji,t} \rightarrow -\infty } L_{ji}(V_{ji}, \rho _{ji}) = N_{ji}\frac{(1-e^{-\rho _{ji}})}{\rho _{ji}}, \nonumber\\
&& \lim _{\quad \rho _{ji} \rightarrow 0} L_{ji}(-\infty , \rho _{ji}) = N_{ji}, \hspace{17.07182pt} \lim _{\rho _{ji} \rightarrow \infty } L_{ji}(-\infty , \rho _{ji}) = N_{ji}/2.
\end{eqnarray}$$
$$\begin{eqnarray}
&& \lim _{\quad \rho _{ji} \rightarrow 0} L_{ji}(V_{ji}, \rho _{ij}) = N_{ji}, \hspace{22.76228pt} \lim _{V_{ji} \rightarrow \infty } L_{ji}(V_{ji}, \rho _{ji}) = N_{ji}, \nonumber\\
&& \lim _{\rho _{ji} \rightarrow \infty } L_{ji}(V_{ji}, \rho _{ji}) = N_{ji} / 2, \quad \lim _{V_{ji,t} \rightarrow -\infty } L_{ji}(V_{ji}, \rho _{ji}) = N_{ji}\frac{(1-e^{-\rho _{ji}})}{\rho _{ji}}, \nonumber\\
&& \lim _{\quad \rho _{ji} \rightarrow 0} L_{ji}(-\infty , \rho _{ji}) = N_{ji}, \hspace{17.07182pt} \lim _{\rho _{ji} \rightarrow \infty } L_{ji}(-\infty , \rho _{ji}) = N_{ji}/2.
\end{eqnarray}$$
Proof. (Corollary 8) In computing the limits, whenever there appears an undefined symbol (i.e. 0 · ∞, 0/0 or ∞/∞), I write ≐ to inform that the L’Hôpital’s rule is used.
 $$\begin{eqnarray*}
\lim _{\quad \rho _{ji} \rightarrow 0} L_{ji}(V_{ji}, \rho _{ij}) &=& \frac{N_{ji}}{2} \left( \lim _{\quad \rho _{ji} \rightarrow 0} \frac{\ln {\left(\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}\right)}}{\frac{\rho _{ji}e^{V_{ji}}}{1+e^{V_{ji}}}} + 1\right) \\
& \doteq & \frac{N_{ji}}{2} \left( \lim _{\quad \rho _{ji} \rightarrow 0} \frac{1+e^{V_{ji}}}{e^{V_{ji}}} \cdot \frac{e^{V_{ji}-\rho _{ji}}}{1+e^{V_{ji}-\rho _{ji}}} + 1\right) = N_{ji},
\end{eqnarray*}$$
$$\begin{eqnarray*}
\lim _{\quad \rho _{ji} \rightarrow 0} L_{ji}(V_{ji}, \rho _{ij}) &=& \frac{N_{ji}}{2} \left( \lim _{\quad \rho _{ji} \rightarrow 0} \frac{\ln {\left(\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}\right)}}{\frac{\rho _{ji}e^{V_{ji}}}{1+e^{V_{ji}}}} + 1\right) \\
& \doteq & \frac{N_{ji}}{2} \left( \lim _{\quad \rho _{ji} \rightarrow 0} \frac{1+e^{V_{ji}}}{e^{V_{ji}}} \cdot \frac{e^{V_{ji}-\rho _{ji}}}{1+e^{V_{ji}-\rho _{ji}}} + 1\right) = N_{ji},
\end{eqnarray*}$$
 $$\begin{eqnarray*}
\lim _{V_{ji} \rightarrow \infty } L_{ji}(V_{ji}, \rho _{ji}) &=& \lim _{V_{ji} \rightarrow \infty } \frac{N_{ji}}{2} \left( \frac{1+e^{V_{ji}}}{\rho _{ji}e^{V_{ji}}}\ln {\left(\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}\right)} + 1 \right) \\
&= & \frac{N_{ji}}{2} \left( \frac{1}{\rho _{ji}} \cdot \ln (e^{\rho _{ji}})+1 \right) = N_{ji}, \\
\lim _{\rho _{ji} \rightarrow \infty } L_{ji}(V_{ji}, \rho _{ji}) & = & \lim _{\rho _{ji} \rightarrow \infty } \frac{N_{ji}}{2} \left( \frac{1+e^{V_{ji}}}{\rho _{ji}e^{V_{ji}}}\ln {\left(\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}\right)} + 1 \right) = \frac{N_{ji}}{2}, \\
\lim _{V_{ji} \rightarrow -\infty } L_{ji}(V_{ji}, \rho _{ji}) &= & \frac{N_{ji}}{2} \left( \lim _{V_{ji} \rightarrow -\infty } \frac{\ln {\left(\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}\right)}}{\frac{\rho _{ji}e^{V_{ji}}}{1+e^{V_{ji}}}} + 1\right) \\
& \doteq & \frac{N_{ji}}{2} \left( \lim _{V_{ji} \rightarrow -\infty } \frac{1-e^{-\rho _{ji}}}{1+e^{V_{ji}-\rho _{ji}}}\cdot \frac{(1+e^{V_{ji}})}{\rho _{ji}} +1 \right) \\
&= & \frac{N_{ji}}{2} \left( \frac{1-e^{-\rho _{ji}}}{\rho _{ji}} +1 \right).
\end{eqnarray*}$$
$$\begin{eqnarray*}
\lim _{V_{ji} \rightarrow \infty } L_{ji}(V_{ji}, \rho _{ji}) &=& \lim _{V_{ji} \rightarrow \infty } \frac{N_{ji}}{2} \left( \frac{1+e^{V_{ji}}}{\rho _{ji}e^{V_{ji}}}\ln {\left(\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}\right)} + 1 \right) \\
&= & \frac{N_{ji}}{2} \left( \frac{1}{\rho _{ji}} \cdot \ln (e^{\rho _{ji}})+1 \right) = N_{ji}, \\
\lim _{\rho _{ji} \rightarrow \infty } L_{ji}(V_{ji}, \rho _{ji}) & = & \lim _{\rho _{ji} \rightarrow \infty } \frac{N_{ji}}{2} \left( \frac{1+e^{V_{ji}}}{\rho _{ji}e^{V_{ji}}}\ln {\left(\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}\right)} + 1 \right) = \frac{N_{ji}}{2}, \\
\lim _{V_{ji} \rightarrow -\infty } L_{ji}(V_{ji}, \rho _{ji}) &= & \frac{N_{ji}}{2} \left( \lim _{V_{ji} \rightarrow -\infty } \frac{\ln {\left(\frac{1+e^{V_{ji}}}{1+e^{V_{ji}-\rho _{ji}}}\right)}}{\frac{\rho _{ji}e^{V_{ji}}}{1+e^{V_{ji}}}} + 1\right) \\
& \doteq & \frac{N_{ji}}{2} \left( \lim _{V_{ji} \rightarrow -\infty } \frac{1-e^{-\rho _{ji}}}{1+e^{V_{ji}-\rho _{ji}}}\cdot \frac{(1+e^{V_{ji}})}{\rho _{ji}} +1 \right) \\
&= & \frac{N_{ji}}{2} \left( \frac{1-e^{-\rho _{ji}}}{\rho _{ji}} +1 \right).
\end{eqnarray*}$$
Additionally, concerning the third limit, one can state that
 $$\begin{equation*}
\begin{aligned} \lim _{\quad \rho _{ji} \rightarrow 0} L_{ji}(-\infty , \rho _{ji}) &= \lim _{\quad \rho _{ji} \rightarrow 0} \frac{N_{ji}}{2} \left( \frac{1-e^{-\rho _{ji}}}{\rho _{ji}} +1 \right) \doteq \lim _{\quad \rho _{ji} \rightarrow 0} \frac{N_{ji}}{2} \left( e^{-\rho _{ji}} +1 \right) = N_{ji}, \\
\lim _{\rho _{ji} \rightarrow \infty } L_{ji}(-\infty , \rho _{ji}) &= \lim _{\quad \rho _{ji} \rightarrow \infty } \frac{N_{ji}}{2} \left( \frac{1-e^{-\rho _{ji}}}{\rho _{ji}} +1 \right) = \frac{N_{ji}}{2}. \end{aligned}
\end{equation*}$$
$$\begin{equation*}
\begin{aligned} \lim _{\quad \rho _{ji} \rightarrow 0} L_{ji}(-\infty , \rho _{ji}) &= \lim _{\quad \rho _{ji} \rightarrow 0} \frac{N_{ji}}{2} \left( \frac{1-e^{-\rho _{ji}}}{\rho _{ji}} +1 \right) \doteq \lim _{\quad \rho _{ji} \rightarrow 0} \frac{N_{ji}}{2} \left( e^{-\rho _{ji}} +1 \right) = N_{ji}, \\
\lim _{\rho _{ji} \rightarrow \infty } L_{ji}(-\infty , \rho _{ji}) &= \lim _{\quad \rho _{ji} \rightarrow \infty } \frac{N_{ji}}{2} \left( \frac{1-e^{-\rho _{ji}}}{\rho _{ji}} +1 \right) = \frac{N_{ji}}{2}. \end{aligned}
\end{equation*}$$
![]() $\Box$
$\Box$
When the unforeseen cost goes to zero, or the ratio between remunerations in destination and source is infinitely large, then all of the migrants become permanent residents. However, when ρji goes to infinity, all of the temporary migrants leave immediately from the hosting country. The infinitesimally small value of V ji implies that the overall labor supply of migrants becomes a function of ρji only, in such a way that the previously stated properties are preserved.
Proof. (Proposition 6) Let us concentrate on calculating the probability of choosing to stay in the homeland, that is: ![]() $P[\bar{U}_{ii} = \max ]$, where, for simplicity, I take i = 1. Therefore, all the source-destination-specific variables are now denoted with a subscript i, instead of i1.
$P[\bar{U}_{ii} = \max ]$, where, for simplicity, I take i = 1. Therefore, all the source-destination-specific variables are now denoted with a subscript i, instead of i1.
 $$\begin{equation*}
\begin{aligned} &P[\bar{U}_1 = \max ] = P[\forall i \in \lbrace 2,\ldots ,N\rbrace \hspace{2.84544pt} \bar{U}_1 \ge \bar{U}^t_i \wedge \bar{U}_1 \ge \bar{U}^p_i ] = \\
&P[\forall i \in \lbrace 2,\ldots ,N\rbrace \hspace{2.84544pt} \alpha v_1 + \varepsilon _1 \ge d^t\left(\alpha (v_i - x^t_i)+\varepsilon _i \right) + (1-d^t)(\alpha v_1 + \varepsilon _1)\\
&\qquad \wedge \alpha v_1 + \varepsilon _1 \ge \alpha (v_i - x^p_i) + \varepsilon _i] = \\
&P[\forall i \in \lbrace 2,\ldots ,N\rbrace \hspace{2.84544pt} \alpha v_1 + \varepsilon _1 \ge \alpha (v_i - x^t_i)+\varepsilon _i \wedge \alpha v_1 + \varepsilon _1 \ge \alpha (v_i - x^p_i) + \varepsilon _i]. \end{aligned}
\end{equation*}$$
$$\begin{equation*}
\begin{aligned} &P[\bar{U}_1 = \max ] = P[\forall i \in \lbrace 2,\ldots ,N\rbrace \hspace{2.84544pt} \bar{U}_1 \ge \bar{U}^t_i \wedge \bar{U}_1 \ge \bar{U}^p_i ] = \\
&P[\forall i \in \lbrace 2,\ldots ,N\rbrace \hspace{2.84544pt} \alpha v_1 + \varepsilon _1 \ge d^t\left(\alpha (v_i - x^t_i)+\varepsilon _i \right) + (1-d^t)(\alpha v_1 + \varepsilon _1)\\
&\qquad \wedge \alpha v_1 + \varepsilon _1 \ge \alpha (v_i - x^p_i) + \varepsilon _i] = \\
&P[\forall i \in \lbrace 2,\ldots ,N\rbrace \hspace{2.84544pt} \alpha v_1 + \varepsilon _1 \ge \alpha (v_i - x^t_i)+\varepsilon _i \wedge \alpha v_1 + \varepsilon _1 \ge \alpha (v_i - x^p_i) + \varepsilon _i]. \end{aligned}
\end{equation*}$$
Noticing that ![]() $\forall i \in \lbrace 2,\ldots ,N\rbrace \hspace{2.84544pt} x^p_i > x^t_i$, one can reduce the number of events only to the temporary migration inequalities:
$\forall i \in \lbrace 2,\ldots ,N\rbrace \hspace{2.84544pt} x^p_i > x^t_i$, one can reduce the number of events only to the temporary migration inequalities:
The left- and right-hand sides of the inequality are iid, so one can use the McFadden’s theorem to compute the logit probability:
 $$\begin{equation}
P[\bar{U}_1 = \max ] = \frac{e^{\alpha v_1}}{\sum _{k=1}^N e^{\alpha (v_k - x^t_k)}}.
\end{equation}$$
$$\begin{equation}
P[\bar{U}_1 = \max ] = \frac{e^{\alpha v_1}}{\sum _{k=1}^N e^{\alpha (v_k - x^t_k)}}.
\end{equation}$$
Moving to the probability of temporary migration to a given destination i ∈ {2, . . ., N}, taking that j is a counter that represents all other possible foreign countries: j ∈ {2, . . ., N}∧j ≠ i, one obtains that
 $$\begin{equation*}
\begin{aligned} P[&\bar{U}^t_i = \max ] = P[\bar{U}^t_i \ge \bar{U}_1 \wedge \bar{U}^t_i \ge \bar{U}^p_i \wedge \bar{U}^t_i \ge \bar{U}^t_j \wedge \bar{U}^t_i \ge \bar{U}^p_j ] = \\
P[&d^t\left(\alpha (v_i - x^t_i)+\varepsilon _i \right) + (1-d^t)(\alpha v_1 + \varepsilon _1) \ge \alpha v_1 + \varepsilon _1 \wedge \\
& d^t\left(\alpha (v_i - x^t_i)+\varepsilon _i \right) + (1-d^t)(\alpha v_1 + \varepsilon _1) \ge \alpha (v_i - x^p_i) + \varepsilon _i \wedge \\
& d^t\left(\alpha (v_i - x^t_i)+\varepsilon _i \right) + (1-d^t)(\alpha v_1 + \varepsilon _1) \ge d^t\left(\alpha (v_j - x^t_j)+\varepsilon _j \right)\\
&\quad +\, (1-d^t)(\alpha v_1 + \varepsilon _1) \wedge \\
& d^t\left(\alpha (v_i - x^t_i)+\varepsilon _i \right) + (1-d^t)(\alpha v_1 + \varepsilon _1) \ge \alpha (v_j - x^p_j) + \varepsilon _j] = \\
P[&\alpha (v_i - x^t_i)+\varepsilon _i \ge \alpha v_1 + \varepsilon _1 \wedge \alpha v_i + \varepsilon _i \ge \alpha (v_i - x^t_i) + \varepsilon _i \wedge \alpha (v_i - x^t_i)\\
&\quad +\,\varepsilon _i \ge \alpha (v_j-x^t_j) + \varepsilon _j \wedge \\
& d^t\left(\alpha (v_i - x^t_i)+\varepsilon _i \right) + (1-d^t)(\alpha v_1 + \varepsilon _1) \ge \alpha (v_j - x^p_j) + \varepsilon _j] = \\
P[&\alpha (v_1 - v_i + x^t_i) \le \varepsilon _i - \varepsilon _1 \le \alpha \left(v_1 - v_i - \frac{d^t}{1-d^t}x^t_i + \frac{1}{1-d^t}x^p_i \right) \wedge \\
&\varepsilon _i - \varepsilon _j \ge \max \big\lbrace \alpha (v_j - x^t_j - v_i + x^t_i); \alpha \left[ d^t(x^t_i - v_i) - (1-d^t)v_1 + v_j - x^p_j \right]\\
&- (1-d^t)(\varepsilon _1 - \varepsilon _i) \big\rbrace ].\\
\end{aligned}
\end{equation*}$$
$$\begin{equation*}
\begin{aligned} P[&\bar{U}^t_i = \max ] = P[\bar{U}^t_i \ge \bar{U}_1 \wedge \bar{U}^t_i \ge \bar{U}^p_i \wedge \bar{U}^t_i \ge \bar{U}^t_j \wedge \bar{U}^t_i \ge \bar{U}^p_j ] = \\
P[&d^t\left(\alpha (v_i - x^t_i)+\varepsilon _i \right) + (1-d^t)(\alpha v_1 + \varepsilon _1) \ge \alpha v_1 + \varepsilon _1 \wedge \\
& d^t\left(\alpha (v_i - x^t_i)+\varepsilon _i \right) + (1-d^t)(\alpha v_1 + \varepsilon _1) \ge \alpha (v_i - x^p_i) + \varepsilon _i \wedge \\
& d^t\left(\alpha (v_i - x^t_i)+\varepsilon _i \right) + (1-d^t)(\alpha v_1 + \varepsilon _1) \ge d^t\left(\alpha (v_j - x^t_j)+\varepsilon _j \right)\\
&\quad +\, (1-d^t)(\alpha v_1 + \varepsilon _1) \wedge \\
& d^t\left(\alpha (v_i - x^t_i)+\varepsilon _i \right) + (1-d^t)(\alpha v_1 + \varepsilon _1) \ge \alpha (v_j - x^p_j) + \varepsilon _j] = \\
P[&\alpha (v_i - x^t_i)+\varepsilon _i \ge \alpha v_1 + \varepsilon _1 \wedge \alpha v_i + \varepsilon _i \ge \alpha (v_i - x^t_i) + \varepsilon _i \wedge \alpha (v_i - x^t_i)\\
&\quad +\,\varepsilon _i \ge \alpha (v_j-x^t_j) + \varepsilon _j \wedge \\
& d^t\left(\alpha (v_i - x^t_i)+\varepsilon _i \right) + (1-d^t)(\alpha v_1 + \varepsilon _1) \ge \alpha (v_j - x^p_j) + \varepsilon _j] = \\
P[&\alpha (v_1 - v_i + x^t_i) \le \varepsilon _i - \varepsilon _1 \le \alpha \left(v_1 - v_i - \frac{d^t}{1-d^t}x^t_i + \frac{1}{1-d^t}x^p_i \right) \wedge \\
&\varepsilon _i - \varepsilon _j \ge \max \big\lbrace \alpha (v_j - x^t_j - v_i + x^t_i); \alpha \left[ d^t(x^t_i - v_i) - (1-d^t)v_1 + v_j - x^p_j \right]\\
&- (1-d^t)(\varepsilon _1 - \varepsilon _i) \big\rbrace ].\\
\end{aligned}
\end{equation*}$$
Consider a situation that the first argument of the max function is the greatest one. This leads to
 $$\begin{eqnarray}
&& \alpha (v_j - x^t_j - v_i + x^t_i) \ge \alpha \left[ d^t(x^t_i - v_i) - (1-d^t)v_1 + v_j - x^p_j \right] - (1-d^t)(\varepsilon _1 - \varepsilon _i) \nonumber\\
&& \iff \alpha \left( v_1 - v_i - \frac{1}{1-d^t}x^t_j + x^t_i + \frac{1}{1-d^t}x^p_j \right) \ge \varepsilon _i - \varepsilon _1.
\end{eqnarray}$$
$$\begin{eqnarray}
&& \alpha (v_j - x^t_j - v_i + x^t_i) \ge \alpha \left[ d^t(x^t_i - v_i) - (1-d^t)v_1 + v_j - x^p_j \right] - (1-d^t)(\varepsilon _1 - \varepsilon _i) \nonumber\\
&& \iff \alpha \left( v_1 - v_i - \frac{1}{1-d^t}x^t_j + x^t_i + \frac{1}{1-d^t}x^p_j \right) \ge \varepsilon _i - \varepsilon _1.
\end{eqnarray}$$
But, by the assumption made in the Theorem, one obtains that this inequality is equivalent to the inequality (taken from the first module of the probability): ![]() $\varepsilon _i - \varepsilon _1 \le \alpha (v_1 - v_i - \frac{d^t}{1-d^t}x^t_i + \frac{1}{1-d^t}x^p_i)$. By comparing, the deterministic values one gets that:
$\varepsilon _i - \varepsilon _1 \le \alpha (v_1 - v_i - \frac{d^t}{1-d^t}x^t_i + \frac{1}{1-d^t}x^p_i)$. By comparing, the deterministic values one gets that:
 $$\begin{eqnarray*}
&& \alpha \left(v_1 - v_i - \frac{d^t}{1-d^t}x^t_i + \frac{1}{1-d^t}x^p_i \right) = \left( v_1 - v_i - \frac{1}{1-d^t}x^t_j + x^t_i + \frac{1}{1-d^t}x^p_j \right)\\
&&\quad \iff x^p_i - x^t_i = x^p_j - x^t_j.
\end{eqnarray*}$$
$$\begin{eqnarray*}
&& \alpha \left(v_1 - v_i - \frac{d^t}{1-d^t}x^t_i + \frac{1}{1-d^t}x^p_i \right) = \left( v_1 - v_i - \frac{1}{1-d^t}x^t_j + x^t_i + \frac{1}{1-d^t}x^p_j \right)\\
&&\quad \iff x^p_i - x^t_i = x^p_j - x^t_j.
\end{eqnarray*}$$
Therefore, the inequality in A.9 cannot be reversed, provided that the measure of the set of solutions is not zero. Finally, one arrives at the probability equal to
 $$\begin{equation*}
\begin{split} P[&\alpha (v_1 - v_i + x^t_i) \le \varepsilon _i - \varepsilon _1 \le \alpha \left(v_1 - v_i - \frac{d^t}{1-d^t}x^t_i + \frac{1}{1-d^t}x^p_i \right) \wedge \\
&\varepsilon _i - \varepsilon _j \ge \alpha (v_j - x^t_j - v_i + x^t_i)] = \end{split}
\end{equation*}$$
$$\begin{equation*}
\begin{split} P[&\alpha (v_1 - v_i + x^t_i) \le \varepsilon _i - \varepsilon _1 \le \alpha \left(v_1 - v_i - \frac{d^t}{1-d^t}x^t_i + \frac{1}{1-d^t}x^p_i \right) \wedge \\
&\varepsilon _i - \varepsilon _j \ge \alpha (v_j - x^t_j - v_i + x^t_i)] = \end{split}
\end{equation*}$$
 $$\begin{equation*}
\begin{split} P[&\varepsilon _1 \in \left[ \varepsilon _i - \alpha \left(v_1 - v_i - \frac{d^t}{1-d^t}x^t_i + \frac{1}{1-d^t}x^p_i \right) ; \varepsilon _i -\alpha (v_1 - v_i + x^t_i) \right] \wedge \\
&\varepsilon _j \le \varepsilon _i - \alpha (v_j - x^t_j - v_i + x^t_i)] \end{split}
\end{equation*}$$
$$\begin{equation*}
\begin{split} P[&\varepsilon _1 \in \left[ \varepsilon _i - \alpha \left(v_1 - v_i - \frac{d^t}{1-d^t}x^t_i + \frac{1}{1-d^t}x^p_i \right) ; \varepsilon _i -\alpha (v_1 - v_i + x^t_i) \right] \wedge \\
&\varepsilon _j \le \varepsilon _i - \alpha (v_j - x^t_j - v_i + x^t_i)] \end{split}
\end{equation*}$$
Rewriting it in a way that εi is the integrated variable, and keeping in mind that ε1 and εj are independent Extreme Value Type I random variables, one can calculate the exact value of the probability by solving the integral:
 $$\begin{equation*}
\begin{aligned} &P[\bar{U}^t_i = \max ] = \\
&\int _{-\infty }^{+\infty } \prod _{j = 2}^N e^{-e^{-\varepsilon _i} e^{\alpha \left(v_j - x^t_j - v_i + x^t_i \right)}} \left( e^{-e^{-\varepsilon _i} \left( e^{\alpha (v_1 - v_i + x^t_i)} - e^{\alpha \left(v_1 - v_i - \frac{d^t}{1-d^t}x^t_i + \frac{1}{1-d^t}x^p_i \right)} \right)} \right) e^{-e^{-\varepsilon _i}}e^{-\varepsilon _i}d\varepsilon _i \\
& = \frac{1}{\sum _{j = 2}^N e^{\alpha \left(v_j - x^t_j - v_i + x^t_i \right)} + e^{\alpha (v_1 - v_i + x^t_i)}} - \frac{1}{\sum _{j=2}^N e^{\alpha \left(v_j - x^t_j - v_i + x^t_i \right)} + e^{\alpha \left(v_1 - v_i - \frac{d^t}{1-d^t}x^t_i + \frac{1}{1-d^t}x^p_i \right)}} \\
& = \frac{ e^{\alpha (v_i-x^t_i)}}{\sum _{k=1}^N e^{\alpha (v_k - x^t_k)}} - \frac{ e^{\alpha (v_i-x^t_i)}}{\sum _{k=2}^N e^{\alpha (v_k - x^t_k)}+ e^{\alpha (v_1 + \frac{1}{1-d^t}(x^p_i - x^t_i))}}. \end{aligned}
\end{equation*}$$
$$\begin{equation*}
\begin{aligned} &P[\bar{U}^t_i = \max ] = \\
&\int _{-\infty }^{+\infty } \prod _{j = 2}^N e^{-e^{-\varepsilon _i} e^{\alpha \left(v_j - x^t_j - v_i + x^t_i \right)}} \left( e^{-e^{-\varepsilon _i} \left( e^{\alpha (v_1 - v_i + x^t_i)} - e^{\alpha \left(v_1 - v_i - \frac{d^t}{1-d^t}x^t_i + \frac{1}{1-d^t}x^p_i \right)} \right)} \right) e^{-e^{-\varepsilon _i}}e^{-\varepsilon _i}d\varepsilon _i \\
& = \frac{1}{\sum _{j = 2}^N e^{\alpha \left(v_j - x^t_j - v_i + x^t_i \right)} + e^{\alpha (v_1 - v_i + x^t_i)}} - \frac{1}{\sum _{j=2}^N e^{\alpha \left(v_j - x^t_j - v_i + x^t_i \right)} + e^{\alpha \left(v_1 - v_i - \frac{d^t}{1-d^t}x^t_i + \frac{1}{1-d^t}x^p_i \right)}} \\
& = \frac{ e^{\alpha (v_i-x^t_i)}}{\sum _{k=1}^N e^{\alpha (v_k - x^t_k)}} - \frac{ e^{\alpha (v_i-x^t_i)}}{\sum _{k=2}^N e^{\alpha (v_k - x^t_k)}+ e^{\alpha (v_1 + \frac{1}{1-d^t}(x^p_i - x^t_i))}}. \end{aligned}
\end{equation*}$$
The same algorithm leads to calculation of ![]() $P[\bar{U}^p_i = \max ] = \frac{ e^{\alpha (v_i-x^t_i)}}{\sum _{k=2}^N e^{\alpha (v_k - x^t_k)}+ e^{\alpha (v_1 + \frac{1}{1-d^t}(x^p_i - x^t_i))}}.$
$P[\bar{U}^p_i = \max ] = \frac{ e^{\alpha (v_i-x^t_i)}}{\sum _{k=2}^N e^{\alpha (v_k - x^t_k)}+ e^{\alpha (v_1 + \frac{1}{1-d^t}(x^p_i - x^t_i))}}.$![]() $\Box$
$\Box$
Exploring the violation of IIA
Consider a situation in which the value of ![]() $x_{ji}(\bar{d}^{p}) - x_{ji}(\bar{d}^{t}) = \Delta = const$ for i ≠ 1. The assumption that Δ = 0 is equivalent to reducing the model to a version with a permanent visa only. Consequently, the choice probabilities are identical to the classical ones that satisfy the IIA property:
$x_{ji}(\bar{d}^{p}) - x_{ji}(\bar{d}^{t}) = \Delta = const$ for i ≠ 1. The assumption that Δ = 0 is equivalent to reducing the model to a version with a permanent visa only. Consequently, the choice probabilities are identical to the classical ones that satisfy the IIA property:
 $$\begin{equation*}
\begin{split} P[\mathbb {E}[{U}_{ii}] = \max ] &= \frac{e^{\alpha v_i}}{\sum _{k=1}^N e^{\alpha (v_k - x^t_{ki}(\bar{d}^t))}}, \\
P[\mathbb {E}[{U}_{ji}(\bar{d}^t)] = \max ] &= \frac{ e^{\alpha (v_j- x_{ji}(\bar{d}^t) )}}{\sum _{k=1}^N e^{\alpha (v_k - x_{ki}(\bar{d}^t) )}} - \frac{ e^{\alpha (v_j- x_{ji}(\bar{d}^t) )}}{\sum _{k\ne i} e^{\alpha (v_k - x_{ki}(\bar{d}^t) )}+ e^{\alpha v_i }} = 0, \\
P[\mathbb {E}[{U}_{ji}(\bar{d}^p)] = \max ] &= \frac{e^{\alpha (v_j - x_{ji}(\bar{d}^t) )}}{\sum _{k\ne i} e^{\alpha (v_k - x_{ki}(\bar{d}^t) )}}, \end{split}
\end{equation*}$$
$$\begin{equation*}
\begin{split} P[\mathbb {E}[{U}_{ii}] = \max ] &= \frac{e^{\alpha v_i}}{\sum _{k=1}^N e^{\alpha (v_k - x^t_{ki}(\bar{d}^t))}}, \\
P[\mathbb {E}[{U}_{ji}(\bar{d}^t)] = \max ] &= \frac{ e^{\alpha (v_j- x_{ji}(\bar{d}^t) )}}{\sum _{k=1}^N e^{\alpha (v_k - x_{ki}(\bar{d}^t) )}} - \frac{ e^{\alpha (v_j- x_{ji}(\bar{d}^t) )}}{\sum _{k\ne i} e^{\alpha (v_k - x_{ki}(\bar{d}^t) )}+ e^{\alpha v_i }} = 0, \\
P[\mathbb {E}[{U}_{ji}(\bar{d}^p)] = \max ] &= \frac{e^{\alpha (v_j - x_{ji}(\bar{d}^t) )}}{\sum _{k\ne i} e^{\alpha (v_k - x_{ki}(\bar{d}^t) )}}, \end{split}
\end{equation*}$$
and finally:
 $$\begin{equation*}
\frac{P[\mathbb {E}[{U}_{ji}(\bar{d}^p)] = \max ]}{P[\mathbb {E}[{U}_{ii}] = \max ] } = e^{\alpha (v_j- x_{ji}(\bar{d}^p) - v_i)}.
\end{equation*}$$
$$\begin{equation*}
\frac{P[\mathbb {E}[{U}_{ji}(\bar{d}^p)] = \max ]}{P[\mathbb {E}[{U}_{ii}] = \max ] } = e^{\alpha (v_j- x_{ji}(\bar{d}^p) - v_i)}.
\end{equation*}$$
As long as Δ > 0 (the policy makers offer temporary and permanent visas), the multilateral resistance term remains in the ratio of probabilities, and the model violates the IIA axiom. The magnitude of dependencies between options is explicitly computable through the elasticities of choice probabilities with respect to country’s characteristics. Consider the choice probabilities when Δ = 0:
 $$\begin{equation*}
\pi _{ji} \equiv P[\mathbb {E}[{U}_{ji}] = \max ] = e^{ V_{ji}}\Bigg / \sum _{k=1}^N e^{V_{ki}},
\end{equation*}$$
$$\begin{equation*}
\pi _{ji} \equiv P[\mathbb {E}[{U}_{ji}] = \max ] = e^{ V_{ji}}\Bigg / \sum _{k=1}^N e^{V_{ki}},
\end{equation*}$$
where for simplicity, take: ![]() $V_{ki} \equiv \alpha \left(v_k - x_{ki}(\bar{d}^t)\right)$. Similarly, assume a simplifying notation concerning the odds of selecting a temporary visa when Δ > 0:
$V_{ki} \equiv \alpha \left(v_k - x_{ki}(\bar{d}^t)\right)$. Similarly, assume a simplifying notation concerning the odds of selecting a temporary visa when Δ > 0:
 $$\begin{equation*}
\mathbb {P}_{ji} \equiv P[\mathbb {E}[{U}_{ji}(\bar{d}^t)] = \max ] = \underbrace{ e^{ V_{ji}}\Bigg / \sum _{k=1}^N e^{V_{ki}}}_{\equiv \pi _{ji}} - \underbrace{ e^{ V_{ji}}\Bigg / \left( \sum _{k\ne i} e^{V_{ji}} + e^{V_{ii}}C(\Delta ) \right)}_{\equiv p_{ji}} = \pi _{ji} - p_{ji},
\end{equation*}$$
$$\begin{equation*}
\mathbb {P}_{ji} \equiv P[\mathbb {E}[{U}_{ji}(\bar{d}^t)] = \max ] = \underbrace{ e^{ V_{ji}}\Bigg / \sum _{k=1}^N e^{V_{ki}}}_{\equiv \pi _{ji}} - \underbrace{ e^{ V_{ji}}\Bigg / \left( \sum _{k\ne i} e^{V_{ji}} + e^{V_{ii}}C(\Delta ) \right)}_{\equiv p_{ji}} = \pi _{ji} - p_{ji},
\end{equation*}$$
where: ![]() $C(\Delta ) \equiv e^{(\alpha \Delta )/(1-\bar{d}^t)}$. It is straightforward to show that
$C(\Delta ) \equiv e^{(\alpha \Delta )/(1-\bar{d}^t)}$. It is straightforward to show that
Proposition 9. When a host country offers temporary and permanent visas (Δ > 0), then the model exhibits multilateral resistance to migration. The elasticities of choice probabilities with respect to any country-specific characteristic: y j are as follows:
 $$\begin{eqnarray}
&& E_{j}^{\mathbb {P}_{ji}} \equiv \frac{\partial \mathbb {P}_{ji}}{\partial y_j}\frac{y_j}{\mathbb {P}_{ji}} = \frac{\partial V_{ji}}{\partial y_j}y_j \left( \frac{\pi _{ji}(1-\pi _{ji})}{\pi _{ji}-p_{ji}} - \frac{p_{ji}(1-p_{ji})}{\pi _{ji}-p_{ji}} \right) = \frac{\partial V_j}{\partial y_j}y_j\left(1 - \pi _{ji} - p_{ji} \right) , \nonumber\\
&& E_{j}^{\mathbb {P}_{li}} \equiv \frac{\partial \mathbb {P}_{li}}{\partial y_j}\frac{y_j}{\mathbb {P}_{li}} = -\frac{\partial V_{ji}}{\partial y_j}y_j \left(\frac{\pi _{li} \pi _{ji} - p_{li} p_{ji}}{\pi _{li} - p_{li}} \right).
\end{eqnarray}$$
$$\begin{eqnarray}
&& E_{j}^{\mathbb {P}_{ji}} \equiv \frac{\partial \mathbb {P}_{ji}}{\partial y_j}\frac{y_j}{\mathbb {P}_{ji}} = \frac{\partial V_{ji}}{\partial y_j}y_j \left( \frac{\pi _{ji}(1-\pi _{ji})}{\pi _{ji}-p_{ji}} - \frac{p_{ji}(1-p_{ji})}{\pi _{ji}-p_{ji}} \right) = \frac{\partial V_j}{\partial y_j}y_j\left(1 - \pi _{ji} - p_{ji} \right) , \nonumber\\
&& E_{j}^{\mathbb {P}_{li}} \equiv \frac{\partial \mathbb {P}_{li}}{\partial y_j}\frac{y_j}{\mathbb {P}_{li}} = -\frac{\partial V_{ji}}{\partial y_j}y_j \left(\frac{\pi _{li} \pi _{ji} - p_{li} p_{ji}}{\pi _{li} - p_{li}} \right).
\end{eqnarray}$$
Proof. (Proposition 9)
 $$\begin{equation*}
\begin{split} E_{ii}^{\mathbb {P}} \equiv \frac{\partial \mathbb {P}_i}{\partial y_i}\frac{y_i}{\mathbb {P}_i} &= \frac{\partial V_i}{\partial y_i}\frac{y_i}{\mathbb {P}_i} \bigg[ \frac{e^{V_i}}{\sum _{k=1}^N e^{V_k}} - \left(\frac{e^{V_i}}{\sum _{k=1}^N e^{V_k}}\right)^2 \\
&- \frac{e^{V_i}}{\sum _{k=2}^N e^{V_k}+e^{V_1}C(\Delta )} + \left(\frac{e^{V_i}}{\sum _{k=2}^N e^{V_k}+e^{V_1}C(\Delta )}\right)^2 \bigg] \\
& = \frac{\partial V_i}{\partial y_i}\frac{y_i}{\mathbb {P}_i} \left[ \pi _i - \pi _i^2 - p_i + p_i^2 \right] = \frac{\partial V_i}{\partial y_i}y_i \left( \frac{\pi _i(1-\pi _i)}{\pi _i-p_i} - \frac{p_i(1-p_i)}{\pi _i-p_i} \right).\\
E_{ji}^{\mathbb {P}} \equiv \frac{\partial \mathbb {P}_j}{\partial y_i}\frac{y_i}{\mathbb {P}_j} &= \frac{\partial V_i}{\partial y_i}\frac{y_i}{\mathbb {P}_i} \left[ -\frac{e^{V_i}e^{V_j}}{(\sum _{k=1}^N e^{V_k})^2} + \frac{e^{V_i}e^{V_j}}{(\sum _{k=2}^N e^{V_k} + e^{V_1}C(\Delta ))^2} \right] \\
& = \frac{\partial V_i}{\partial y_i}\frac{y_i}{\mathbb {P}_i} \left[ -\pi _i \pi _j + p_i p_j \right] = \frac{\partial V_i}{\partial y_i}y_i \left( \frac{ -\pi _i \pi _j + p_i p_j}{\pi _i-p_i} \right). \end{split}
\end{equation*}$$
$$\begin{equation*}
\begin{split} E_{ii}^{\mathbb {P}} \equiv \frac{\partial \mathbb {P}_i}{\partial y_i}\frac{y_i}{\mathbb {P}_i} &= \frac{\partial V_i}{\partial y_i}\frac{y_i}{\mathbb {P}_i} \bigg[ \frac{e^{V_i}}{\sum _{k=1}^N e^{V_k}} - \left(\frac{e^{V_i}}{\sum _{k=1}^N e^{V_k}}\right)^2 \\
&- \frac{e^{V_i}}{\sum _{k=2}^N e^{V_k}+e^{V_1}C(\Delta )} + \left(\frac{e^{V_i}}{\sum _{k=2}^N e^{V_k}+e^{V_1}C(\Delta )}\right)^2 \bigg] \\
& = \frac{\partial V_i}{\partial y_i}\frac{y_i}{\mathbb {P}_i} \left[ \pi _i - \pi _i^2 - p_i + p_i^2 \right] = \frac{\partial V_i}{\partial y_i}y_i \left( \frac{\pi _i(1-\pi _i)}{\pi _i-p_i} - \frac{p_i(1-p_i)}{\pi _i-p_i} \right).\\
E_{ji}^{\mathbb {P}} \equiv \frac{\partial \mathbb {P}_j}{\partial y_i}\frac{y_i}{\mathbb {P}_j} &= \frac{\partial V_i}{\partial y_i}\frac{y_i}{\mathbb {P}_i} \left[ -\frac{e^{V_i}e^{V_j}}{(\sum _{k=1}^N e^{V_k})^2} + \frac{e^{V_i}e^{V_j}}{(\sum _{k=2}^N e^{V_k} + e^{V_1}C(\Delta ))^2} \right] \\
& = \frac{\partial V_i}{\partial y_i}\frac{y_i}{\mathbb {P}_i} \left[ -\pi _i \pi _j + p_i p_j \right] = \frac{\partial V_i}{\partial y_i}y_i \left( \frac{ -\pi _i \pi _j + p_i p_j}{\pi _i-p_i} \right). \end{split}
\end{equation*}$$
![]() $\Box$
$\Box$
In contrast to the classic case with the IIA axiom, the cross-elasticities are l-specific, so they take different values for all of the options l ∈ N.Footnote 26 Because an asymmetric change in choice probabilities is observed after an external shock, the IIA property is not maintained.
APPENDIX B: VISAS BY DESTINATION COUNTRY
The most desired country for immigration, the United States, provides about 90 types of temporary visas, as well as green-cards for permanent immigrants. To apply for a particular type of temporary visa, a potential immigrant has to fulfill specific requirements connected with her education level, purpose of stay, international status (refugees), or affiliation (representatives). Not all the visas allow to work in the United States, for example the widely popular B visas are issued only for short business or touristic visits. The potential duration of stay ranges from 1 year (in the case of D – crew visas, H-1A and H-2 – worker visas, P – athletes visas, or Q – cultural exchange visas) to indefinite length of stay (as it is for the E – trade business partners visas or NATO – representatives visas). However, the most popular US visas that are issued for working purposes are the medium-term ones. The F-1 student visa allows the beneficiary to take full-time studies and to have a part-time job (or a full-time internship) during the period of stay (which mainly does not exceed 6 years). In 2013, the United States issued more than 500,000 such permits. The J-1 “exchange visitor” visa for teachers and scholars, which can be extended up to 7 years, was the second popular type of permission in 2013 with over 310,000 applications. Finally, the H1-B visa program for highly skilled workers is constantly gaining popularity among professionals across all the countries. US companies are allowed to employ foreign highly educated workers for a period of 3 years. In fact, the majority of H1-B workers decides to prolong their stay for another 3 years. In 2014, the total number of accepted new applications was 124,326, whereas 191,531 workers continued their employment.Footnote 27 All in all, over 1.2 million immigrants out of 2 million new entrants to the United States in 2013 were the medium-term temporary workers.
Australia, Canada, and New Zealand have unified approaches toward immigration. On the one hand, these states introduce temporary migration offers that rely on a demand-driven process in which national firms invite specific workers (the duration of stay is generally restricted from 1 to 5 years like in the US H1-B program, but all occupations are considered). On the other hand, they provide permanent migration programs whose main pillar is a point system – the preferential channel for the well-educated candidates. In the first case, immigrants are granted visas on the basis of the contract signed with hosting company. Thus, the duration of stay is limited, but may vary across industries, firms, and regions. Considering the permanent migration channel, in order to be qualified, an applicant has to provide information on her education and professional achievements along with a proof of proficiency in official languages. The selection process concentrates on choosing those candidates who either have outstanding scores or are ready to be employed in strategic industries. In this way, Australia, Canada, and New Zealand remain the main competitors for the United States in the game of attracting global talents.
The EU (along with EEA countries) has a less restrictive immigration policy and shows an attitude far less oriented toward highly skilled workers. Any person from a third country may become eligible to enter the Schengen area for a temporary stay of 3, 6, or 12 months. Then, after the expiration of current permission, one might prolong it for another period. An alternative, temporary migration option, introduced in 2009 by the European Parliament, is the EBC Program. This device is targeted at highly skilled non-EU candidates who wish to work in the EU. The main restriction is connected with the salary of beneficiary, which has to be “at least 1.5 times the average gross annual salary paid in the Member State concerned”.Footnote 28 The Blue Card program is still at its early stages and is not commonly used by the potential residents (in 2014 the EU granted about 13,000 documents, almost 90% of them concerned Germany). After 5 years of continuous living, working legally and paying taxes a non-EU worker may apply for a long-term immigrant status.Footnote 29 Finally, a long-term immigrant may apply for a citizenship after at least 5 years of long-term status.
APPENDIX C: DATA SOURCES
The calibration of the model is based on the data for 2013. Each country ![]() $j \in \mathcal {N}$ is characterized by a uniform, gross wage for the highly skilled workers. Remunerations are computed for 178 countries in the sample using the data on skill premiums for 52 countries, the shares of tertiary educated workers for 144 countries from the Barro–Lee database [Barro and Lee (Reference Barro and Lee2013)], and several explanatory variables from the WDI by the World Bank.Footnote 30 With the estimated parameters, I compute the predicted skill premiums, and, using the data on GDP per capita in PPP, I calculate the wage rates for the whole sample of 178 states. Finally, taking the country-specific data on income taxation (which originate from the yearly tax reports by Ernst & Young, KPMG, and Pricewaterhouse Coopers), I compute the net-of-income-tax wages, v j. For the parameter α, which represents the sensitivity of migration flows to annual wage differences, I take the value of 0.05 following Grogger and Hanson (Reference Grogger and Hanson2011). The full sample of 178 countries is presented in Table E.1, whereas the data on net wages for highly skilled workers are gathered in Table E.2.
$j \in \mathcal {N}$ is characterized by a uniform, gross wage for the highly skilled workers. Remunerations are computed for 178 countries in the sample using the data on skill premiums for 52 countries, the shares of tertiary educated workers for 144 countries from the Barro–Lee database [Barro and Lee (Reference Barro and Lee2013)], and several explanatory variables from the WDI by the World Bank.Footnote 30 With the estimated parameters, I compute the predicted skill premiums, and, using the data on GDP per capita in PPP, I calculate the wage rates for the whole sample of 178 states. Finally, taking the country-specific data on income taxation (which originate from the yearly tax reports by Ernst & Young, KPMG, and Pricewaterhouse Coopers), I compute the net-of-income-tax wages, v j. For the parameter α, which represents the sensitivity of migration flows to annual wage differences, I take the value of 0.05 following Grogger and Hanson (Reference Grogger and Hanson2011). The full sample of 178 countries is presented in Table E.1, whereas the data on net wages for highly skilled workers are gathered in Table E.2.
Another set of observable concerns the yearly flows of migrants from 178 sources to 35 destinations with a distinction between college-educated workers who come with temporary (short and medium-term) visas and those who obtain permanent residence permits.Footnote 31 The gross flows of migrants aggregate individual, discrete choice decisions about the destination country, and the selected visa. Therefore, along with net wages, they determine the duration-specific, expected costs of migration, ![]() $x_{ji}(\bar{d})$.
$x_{ji}(\bar{d})$.
To estimate the parameters of the distributions of durations of stay (that is the country-pair-specific, unforeseen migration costs: ρji), one needs the empirical counterparts of the probabilities of staying, in the context of migration from any source i to any destination j. To this end, I calculate the conditional and unconditional probabilities of staying for migrants who move from any i to j, which proxies the properties of the distribution of duration of stay. The former strategy considers the data on the gross flows of immigrants, modified by return migration, which are taken from the DIOC database that is provided by the OECD. The latter computation is only grounded on the bilateral gross flows of immigrants that are estimated by Abel and Sander (Reference Abel and Sander2014).
Concerning the visa data for the United States, I use the 2013 Report of the Visa Office on the non-immigrant visas. This rich dataset provides the numbers of all visas (by type) issued each year for people originating from every country in the world. Additionally, I gather the data on permanent immigrants (by country of origin and cause of immigration). Both reports are available on the Visa Office web page.Footnote 32
In the case of Australia, I use the data on temporary work visa grants published by the Department of Immigration and Border Protection for years 2012–2013.Footnote 33 From this dataset, I extract the number of visas issued for the short-term business visitors and working holidays (less than 1 year), and temporary skilled workers (less than 6 years). Then, using the Australia’s Migration Trends 2012–2013 report, I collect the numbers of permanent immigrants to Australia for 10 most popular sources and for all the OECD countries.Footnote 34 For the rest of countries, which constitute approximately 15% of total inflows, I estimate the shares of sending countries in yearly flows using current stocks of immigrants.
In terms of New Zealand, I take the data on flows of work permits issued by the government in 2012–2013.Footnote 35 The applications in the published dataset are divided into 90 categories, each of them characterized by a specific duration of stay (ranging from 1 year to indefinite). Additionally, using the data on flows of new permanent residents (divided into 22 categories), it is possible to define the yearly flows of immigrants to New Zealand.
Concerning Canada, I collect the available data from Facts and Figures 2013: Immigration Overview database, provided by Research and Evaluation Branch, Citizenship and Immigration Canada (CIC).Footnote 36 For the temporary immigrants, Canada proposes two types of visas: International Mobility Program work permit, and Temporary Foreign Worker Program work permit. The numbers of new inflows for both categories by citizenship are available for top 50 sending countries. The rest, which constitutes less than 5%, is estimated using the structure of current stocks of immigrants. CIC publishes also the number of new permanent residents for the full set of source countries.
The UK provides a comprehensive dataset with country-specific flows of immigrants considering 24 types of visas. Using the immigration statistics published by Home Office, I can compute the number of short and medium-term immigrants coming to the UK in 2013.Footnote 37 Finally, using the data on granted permanent settlements and citizenships, I compute the inflow of permanent immigrants.
For the EU 27 and three EEA countries, I collect the data on first issued residence permits from Eurostat. Having no other information, I assume that people who applied for 3-month and 6-month permissions are short-term immigrants (less than 1 year). Simultaneously, those who obtained a 12-month residence permit are classified as medium-term immigrants (temporary, more than 1 year). Eurostat also publishes the data on citizenships granted, which are the reference for an inflow of permanent immigrants.
In terms of immigrants’ skills, using the above-mentioned datasets, I extracted the inflows of highly skilled immigrants for Australia, the UK, New Zealand, and the United States. The skill structure of inflows to other countries for all visas was assumed to be equal to the one in the current stock (taken from the DIOC database, OECD). Table E.3 presents the data on yearly flows and stock of immigrants by visa type in 35 receiving countries.
APPENDIX D: COMPUTATION OF PROBABILITIES OF STAYING
In the first strategy, I collect the data from Database on Immigrants in OECD Countries (DIOC) created by the OECD.Footnote 38 There are three sets of data for three reference years: 2000, 2005, and 2010. For each package, I extract the number of immigrants who arrived to the host country 0–5 years ago, 5–10 years ago, 10–20 years ago, and earlier than 20 years ago. The key assumption made in this calibration procedure is about invariability in time of the duration distribution. If one accepts this limitation, it is simple to compute the above-mentioned conditional probabilities.
Consider the stock of immigrants from country i to country j, whose actual length of stay in the year 2010 was between 5 and 10 years. This means that all of them must have emigrated between year 2000 and 2005, thus they must have been registered in the year 2005 as immigrants from i to j with a duration of less than 5 years. However, in the group 0–5 in year 2005 there are also people who decided to leave the destination country before 2010. These persons are registers in 2005, but they are not registered in 2010. Assuming that the only cause of leaving is returning to the home country (disregarding re-emigration to other countries and deaths), the probability of staying at least 5–10 years, conditional on having stayed at least 0–5 years is equal to the ratio of the stock of immigrants in group 5–10 in 2010 to the stock of immigrants in group 0–5 in 2005.Footnote 39 Similarly, I compute the conditional probability of staying 10 years or more conditional on being in a 0–10 years group 10 years before. I take the quotient of the stock of immigrants in group 10–20 in year 2010 to the stock of immigrants in group 0–10 in year 2000. The third empirical moment to fit is the probability of staying at least 20 years conditional on staying at least 10 years before. Once again, I take the ratio of the stock of immigrants in group >20 in year 2010, to the stock of immigrants in groups 10–20, and >20 in year 2000.
The main problem with DIOC database is the fact that it is constructed using a random rounding procedure from national censuses, or the Labor Force Survey. As a consequence, the consistency of data from one release to another is not perfect, in a sense that the number of stayers in later groups may be larger than the number of stayers in the earlier groups. This leads to the values of conditional probabilities greater than one. When encountering such problem, I drop these observations. The final number of observations is 3,880 values (out of 8,316 data points), which gives 46.7% of data coverage.
Considering the above-mentioned problems, and the fact that there are many missing observations, I decided to increase the set of observables with the values of unconditional probabilities: the shares of stayers in groups 0–5, 5–10, and 10–20 in year 2010 to the total flows of immigrants who came in years 2005–2010, 2000–2010, and 1990–2000, respectively. The latter, country-pair-specific data for the whole 196 × 196 country matrix are provided by Abel and Sander (Reference Abel and Sander2014). They estimate the gross flows of immigrants in 5-year intervals using the data on stocks of migrants, population of countries and births and deaths statistics.Footnote 40 Apart from controlling for values greater than one, one also has to notice that the unconditional probability of being in group 0–5 (that is the unconditional probability of staying at least the average number of years in group 0–5) is greater than the respective value for 5–10 years, which, in turn, exceeds the value for 10–20. The share of acceptable data equals 54.8%. All in all, for each of 2,772 country pairs, I obtain one to six data points that characterize the distributions of duration of stay.
APPENDIX E: ADDITIONAL FIGURES AND TABLES
Table E.1. Sample and country codes

Table E.2. Net wages and fiscal burden for college-graduates

Table E.3. Yearly inflows and total stocks of highly skilled immigrants (by visa type)


Figure E.1. Evaluation of the model fit. Note: Data (X-axis) versus model outcomes (Y-axis) for the yearly flows of short-term (first row), medium-term (second row), long-term (third row) highly skilled immigrants in 35 destination countries. First (second) column represents the values in number of people (in logs of the number of people). Source: own calculations.

Figure E.2. Unforeseen costs of migration, ρji. Note: The set of figures depicts histograms of the computed values of unforeseen costs of living abroad. Each figure presents the empirical distribution of the parameters for a particular destination country, and all 178 sending states. Source: own calculations.
Table E.4. Decomposition of the expected migration costs, x ji

Table E.5. Extrapolation of unexpected migration costs, ρji

Table E.6. The results of H-1B and FI simulations as deviations from the reference

Table E.7. The results of H-1B and FI simulations as deviations from the reference, with return premiums


Figure E.3. The effects on average durations of stay after including return premiums. The graph presents the average durations of stay by destination countries and visa types. The broken lines show the reference scenario, whereas the solid lines depict the reference scenario with return premiums. Source: own calculations.



















