2. Weighted-average methods

The development of the weighted-average approach rendered it unnecessary to choose between ${\it\rho}$ and r as the relevant discount rate, and many (we believe most) analysts were content with this solution. Some, however, making bows to the theory of consumer choice that we teach in our classrooms, held to the position that the actual discounting should be done using the time-preference rate, r. Much to their credit, however, they at the same time recognized the need to account for the loss in production from displaced investments. They made allowance for this via a shadow price of investible funds (SPIF). A numerical example is probably the easiest way to show this. Suppose the gross-of-tax rate of return on investment, ${\it\rho}$ , equals 12%, and the net-of-tax return on savings, r, is 4%. Suppose, too, that when $1 million of funds are raised in the capital market, this displaces $750,000 of investment and $250,000 of consumption. Weighted-average people would derive from this information an economic opportunity cost ${\it\omega}=10\%=(0.75)(12\%)+(0.25)(4\%)$ . The time-preference people, on the other hand, would still want to use 4% as their discount rate, but would recognize that in displacing 750 of investment, the economy was forgoing a steady future flow of 90 (=750 × 12%) per year, and was incurring an annual cost of 10 (=250 × 4%) on payments covering the supply price of the new saving that helped finance the project. The present value of these future flows, discounted at 4%, is 2500 [=(90 + 10)∕0. 04], and the SPIF is 2. 5 (=2500∕1000).Footnote ²

While the debate will probably never end, the fact is that most projects that would be rejected by applying a straight 10% discount rate would also be rejected by applying a 4% rate and then punishing the project with a shadow price of 2.5 for investible funds. In our specific case of a steady perpetuity, the net present value (NPV) is zero using an investment cost of 1000 and a discount rate of 10% applied to a perpetual net benefit of 100. But the NPV is also zero using a 4% discount rate for the perpetuity and a shadow price of 2.5 for the investment of 1000.

We accordingly want to consider as close allies those who opt for a weighted-average discount rate of ${\it\omega}$ with an SPIF of one, and those who opt for a discount rate of r with an SPIF of ${\it\omega}/r$ . The real enemies of sound economics are those who press for the use of low discount rates like r, without due recognition of the costs entailed when forgone investments would have had rates of marginal productivity much higher than r.

3. Measuring the marginal productivity of investment $({\it\rho})$

The discount rates actually used in official and semi-official BCAs span an extremely wide range, so we are well advised to inquire into how they ought to be estimated. To begin this exercise, we return to the classroom example of the previous section. That case can be made to look almost magical. Suppose the private rate of return $({\it\rho})$ of 12% is subject to corporation and property taxes taking half, leaving a private rate of return (i) of 6%, which in turn is subject to a personal income tax of 1∕3, leaving a time-preference rate (r) of 4%. In this idealized picture, the market interest rate (i) equals the rate of return on equity and also that on bonds, including government bonds (i _g ). Here we have ${\it\rho}=i+D_{b}$ and r = i + D _p , with the business distortion D _b equal to 6% and the personal distortion D _p equal to − 2%. We can then show that the weighted-average discount rate ${\it\omega}=f_{1}{\it\rho}+f_{2}r$ is equal to $f_{1}\cdot (i+D_{b})+f_{2}\cdot (i+D_{p})$ which in turn, under our assumptions, equals i _g + f ₁ D _b + f ₂ D _p . That is, we can get to the “right” discount rate ${\it\omega}$ by two routes. One takes the weighted average of the productivity rate ${\it\rho}$ and the time-preference rate r. The other takes the (real) government bond rate i _g and adds to it the weighted-average distortion. The first route gives us (0. 75)(12%) + (0. 25)(4%) = 10%; the second yields 6% + (0. 75)(6%) + 0. 25(−2%) = 10%. Two routes, same answer! But real-world cases look nothing like this magical example. The real rate on government bonds is for most countries quite low. Adjusting for tax distortions surely raises it, but not nearly by enough to match the weighted average of ${\it\rho}$ and r.

So we have to struggle with the discrepancy and try to devise a sensible way to deal with it. We believe the most meaningful way to approach this problem is to go directly to the task of measuring ${\it\rho}$ and r. We would like to reach results that have relevance for many individual countries as well as international organizations and national foreign aid agencies. So, we are going to build our analysis on four parameters – the country’s average rate of GDP growth (g) in recent years, its average ratio (s) of investment to GDP, the share (a) of return to capital in the country’s GDP, and the percentage $({\it\delta})$ that true economic depreciation bears to the country’s stock of reproducible capital. With these four parameters and a little work, we can derive a plausible range of estimates for ${\it\rho}$ , the rate of return on the country’s reproducible capital.

The starting point for this exercise is the concept of equilibrium growth, in which the stock of reproducible capital is growing at the same rate as GDP (Y). We will later probe the sensitivity of our results to deviations from this assumption. But staying with it for now, we have:

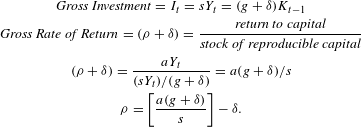$$\begin{eqnarray}\displaystyle & \displaystyle \mathit{Gross~Investment}=I_{t}=sY_{t}=(g+{\it\delta})K_{t-1} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathit{Gross~Rate~of~Return}=({\it\rho}+{\it\delta})=\frac{\mathit{return~to~capital}}{\mathit{stock~of~reproducible~capital}} & \displaystyle \nonumber\\ \displaystyle & \displaystyle ({\it\rho}+{\it\delta})=\frac{aY_{t}}{(sY_{t})/(g+{\it\delta})}=a(g+{\it\delta})/s & \displaystyle \nonumber\\ \displaystyle & \displaystyle {\it\rho}=\left[\frac{a(g+{\it\delta})}{s}\right]-{\it\delta}. & \displaystyle \nonumber\end{eqnarray}$$

Table 1 Plausible parameter ranges by country type.

Readers should note that in setting plausible parameter ranges for three major country groups, we run the gamut from 0.33 to 0.5 for a, from 0.02 to 0.08 for g, and from 0.15 to 0.35 for s (see Table 1). Also, we would stress that the fraction “a” reflects gross-of-depreciation income from capital, and that “s” reflects gross investment, both as a fraction of GDP.Footnote ³

One question not yet addressed is as follows: How do our results change when a country deviates from equilibrium growth? The answer is that the formula for ${\it\rho}$ changes to ${\it\rho}=a[(g+e+{\it\delta})/s]-{\it\delta}$ .

This derives from a growth rate of reproducible capital equal to g + e, compared with GDP growth of g. Thus, capital growing 1% faster than output would add 0.02 to ${\it\rho}$ if a was 0.50 and s was 0.25.

Table 2 presents the estimated real rate of return for the three types of countries. The middle level is simply the midpoint of the resulting range. The last cell in each row gives the adjustment to the rate of return that would result if the capital stock was growing one percentage point faster or slower than the GDP.

Table 2 Real rate of return to capital $({\it\rho}_{0})$ , as measured from national accounts data.

Table 2 presents the results one gets working, respectively, with the low and high ends of the ranges presented for each country type. For the Asian Tigers, the higher return of 16% comes from the lower initial figures (g = 0. 06 and s = 0. 25).

Readers are warned not to treat these numbers as giving the rate of productivity we need for calculating the social discount rate. Rather, they should be taken as the basis from which we will work, as we subject them to a series of adjustments. In our next calculations, we make two types of adjustments, one affecting the size of the relevant capital stock and the other affecting the size of the income stream attributable to that stock.

4. Adjusting the capital stock

First, let us note that estimates of the capital stock flowing from the national accounts include improvements to land, but not the land itself, so to bring capital income and capital stock into accord, we must either add the value of land to the denominator of ${\it\rho}$ , or subtract the income from land from the numerator. The latter approach is clearly to be preferred, because (a) it is incredibly difficult to arrive at good estimates of the total market value of land (net of improvements) and (b) the annual GDP figures capture only part of the return to land, the other part being generated by the real appreciation stemming from economic growth. So our present exercise simply starts with the stock of reproducible capital (fixed capital plus inventories) as the denominator of our rate of return.

The principal adjustment to be made to this stock concerns infrastructure investment of various types. Items such as roads, school buildings, parks, public offices, and museums certainly yield benefits, but these are rarely, and if so only very partially, reflected in our measures of GDP. They are not part of the capital whose return we are trying to measure. An adjustment is therefore necessary in order to exclude these items from the base of the return-to-capital ratio. Across nations, the fraction of GDP devoted to public investment varies greatly, but it is also true that countries with high ratios of public investment to GDP tend to make more infrastructure investment than those with low ratios. We feel we are if anything overestimating the size of the stock of “remunerative capital” when we take it to be 80% of the stock of reproducible capital that we get from the national accounts. With this adjustment, our estimate of ${\it\rho}$ increases by a factor of 1.25, yielding the figures shown in Table 3.

Table 3 Real rates of return $({\it\rho}^{\prime })$ to remunerative investment (as measured from national accounts data).

These will be seen as high numbers by laymen as well as professionals. But we must insist that they represent flows of real money (or its equivalent in imputed rents). Real people (or real governments) are enjoying these real benefits, on the basis of the productive assets that they own. In the next section, we will peel off of this return several components that we feel should not contribute to our estimates of ${\it\rho}$ and r. But here we want to stress the importance of “starting from the top” – i.e., from the total returns to capital that are measured in the GDP.

Our exclusion of 1∕5 of investment as non-remunerative has equivalences in a whole gamut of patterns of public investment. We have estimated that ${\it\rho}^{\prime }$ (the measured rate of return on private investment) is equal to our previously measured ${\it\rho}_{0}$ (Table 2) times 1.25. Thus is true when government invests 0. 2I in infrastructure, with a yield of zero, and the private sector invests 0. 8I, with a yield of $1.25{\it\rho}_{0}$ (I = gross investment from the national accounts). Obviously, the same result emerges if state-owned enterprises in any amount participate alongside the private sector, and also earn $1.25{\it\rho}_{0}$ . But in the real world, infrastructure investments often generate some low rate of yield ${\it\rho}_{i}$ , and state-owned enterprises usually generate a rate of return ${\it\rho}_{s}<1.25{\it\rho}_{0}$ . Our estimate, that the private sector rate of return is $1.25{\it\rho}_{0}$ , can be generated by any combination of h _i , h _s , h _p and ${\it\rho}_{i},{\it\rho}_{s},1.25{\it\rho}_{0}$ that fits the equation

$$\begin{eqnarray}{\it\rho}_{0}=h_{i}{\it\rho}_{i}+h_{s}{\it\rho}_{s}+h_{p}(1.25){\it\rho}_{0}.\end{eqnarray}$$

Here h _i , h _s , h _p are the fractions that infrastructure, state-owned enterprises, and private investment occupy in total I.

The high figures of Table 3 come in principle from national accounts data via the coefficients g, a, s, and ${\it\delta}$ . More precise estimates can be obtained by generating capital stocks of buildings, machinery and equipment, vehicles and inventories, using perpetual inventory procedures with separate depreciation rates for each class (zero for inventories). Harberger participated in such exercises in Mexico, El Salvador, and Honduras, which yielded rates of return around or above 20%, even without making any allowance for infrastructure investment. These results only add to our confidence in the ranges presented in Table 3.

But we are not suggesting that a country’s actual discount rate should be based on the numbers in Table 3. They are subject to further adjustments, to which we now turn. These will help to answer Harberger’s plaint. “Why can’t I get 20% returns on the dollars I might send to Mexico?”

5. Adjusting the returns to capital

In this section, we explore four components of the measured return to capital that should be eliminated from the numerator of our rate-of-return calculation, if our objective is to reach measures of ${\it\rho}$ and r to be used in calculating the social discount rate. They include:

1. (a) Returns to land included in the GDP.

2. (b) The share of labor in monopoly markups.

3. (c) Above-normal returns on supra-marginal investments.

4. (d) Some portion of returns to capital in financial intermediation.

(c) Supra-marginal investments

When we build models using production functions like $Y_{i}=\emptyset _{i}(L_{i},K_{i})$ , any increment to labor or capital is assumed to itself be marginal and is thus assigned the marginal product generated by the production function. We know, however, that this does not describe what happens in the real world. In actuality, new investments appear each year, which generate returns that are well above average. In our classrooms, we sometimes illustrate this with a bar chart, with invested amounts on the horizontal axis and expected real yield on the vertical axis. Individual investment projects are then arrayed in descending order of their prospective internal rates of return. This, on the assumption of independence among their respective investment profiles, gives us a priority ordering for the projects. Normally, each firm will carry its investment to the point where the projects it rejects all have prospective yields below that firm’s relevant cost of capital. Thus, the “triangle” representing supra-marginal yields really does not belong as a component of the opportunity cost of investment. We would emphasize, however, that not all high-yielding investments are safe from being squeezed out when funds are tight. Small businesses are particularly vulnerable at such times. They often have substantially higher cost of capital even in good times as well as being squeezed disproportionally when funds get tighter.

So how do we go about estimating the amount by which capital’s return should be reduced (for our purposes) due to supra-marginal investments? Not, in this case, by charging directly through the line but instead by making an end run around it, to which we now turn.

Economists are well acquainted with the growth equation

$$\begin{eqnarray}g_{y}=S_{L}g_{L}+S_{k}g_{k}+{\it\lambda},\end{eqnarray}$$

where g _y , g _L , g _k are the growth rates of output, labor, and capital, respectively, and ${\it\lambda}$ is the rate of real cost reduction (=total factor productivity (TFP) improvement = “technical advance”). But this equation has a twin, a “dual,” about which many are quite unaware:

$$\begin{eqnarray}{\it\lambda}=S_{L}g_{w}+S_{k}g_{({\it\rho}+{\it\delta})}-g_{P}.\end{eqnarray}$$

This dual says that the fruits of real cost reduction have to go somewhere and the allocation is that labor gets its share (S _L ) times g _w , the growth rate of real wages, consumers benefit from any fall in prices (or suffer from any rise), and capital’s return grows to absorb whatever benefit of real cost reduction has not been gobbled up by labor and consumers. This explanation makes it clear that capital is the residual claimant in this story. For a competitive producer, the market determines what wages have to be paid and what the price of the product will be. So the capital factor gains only to the extent that ${\it\lambda}$ exceeds S _L g _w − g _P .Footnote ⁴

For the economy as a whole, with the GDP deflator as the numeraire, g _P is obviously zero in the growth equation. This enables us to calculate rates of aggregate real cost reduction implied by the various parameter packages that we have assumed. The only further datum that we need is the rate of growth of the labor factor. The correct measure of the change in labor inputs is $\sum _{i}w_{i}{\rm\Delta}L_{i}$ , where increments to labor are weighted by their corresponding initial wage levels. This automatically incorporates the contribution of human capital accumulation by weighting the higher-paid components of the labor force more heavily as, over time, they include an ever higher fraction of the labor force. Our estimates of ${\it\lambda}$ are based on the assumption that raw labor (N) grows at 1% per year in the advanced countries and the Asian Tigers, and 1.5% per year in the healthy developing countries. To these figures we add 0.5% per year for improvement in labor quality in the advanced countries, and 1% per year in the other two categories. See Table 4.

Table 4 Implied rates of real cost reduction; ${\it\lambda}=g_{y}-S_{L}g_{L}-S_{k}g_{K}=S_{L}(g-g_{L})$ when g _y = g _K = g.

Note: g _N is the rate of growth of the number of workers, g _L is the rate of growth of labor hours worked, adjusted for labor quality.

Our view on this subject is that when real cost reductions occur, the enterprises involved enjoy supra-marginal returns for a while. These, however, are eroded with time, and rates of return go back to the competitive level—recall that we have already dealt with monopoly profits (which do not go back, and which may in part result from real cost reductions). We feel that allocation of supra-marginal returns to capital equal to ${\it\lambda}_{t}+0.75{\it\lambda}_{t-1}+0.5{\it\lambda}_{t-2}+0.25{\it\lambda}_{t-3}$ is likely to err on the generous side.

To calculate supra-marginal returns, we assume that capital receives the full real cost reduction $({\it\lambda}_{t})$ of time t, plus $3/4$ of ${\it\lambda}_{t-1}$ , plus $1/2$ of ${\it\lambda}_{t-2}$ , plus $1/4$ of ${\it\lambda}_{t-3}$ . A given innovation would receive its reward in the year it was introduced, but this would erode in the following 3 years. The added return generated by the innovation might be 4 points in t, 3 points in t + 1, 2 points in t + 2, 1 point in t + 3, and zero thereafter. $g_{({\it\rho}+{\it\delta})}$ is therefore positive only in the first year for this particular innovation, and becomes negative in the next 4 years. Comparing year t + 4 with year t − 1, ${\rm\Delta}({\it\rho}+{\it\delta})=0$ . What can we make of this? The innovation has in fact produced extra returns, accumulating 10 percentage points on the firm’s value added over 4 years. But these extra earnings are part of what we have allocated as the return on capital. This is the part we want to exclude from our calculation of capital’s marginal rate of return.

At the aggregate level in a real-world exercise, we would do growth accounting and calculate ${\it\lambda}_{t}Y_{t-1}+0.75{\it\lambda}_{t-1}Y_{t-2}+0.5{\it\lambda}_{t-2}Y_{t-3}+0.25{\it\lambda}_{t-3}Y_{t-4}$ , and end up excluding that result as we adjust our original measure of the return to capital. In our present exercise, we set ${\it\lambda}$ equal to the calculated level shown in Table 4, which is implied by equilibrium growth under the specified assumptions. The adjustment we make for each year excludes from our measured return to capital an amount equal to $2.5{\it\lambda}Y_{t}$ .Footnote ⁵

(d) Allowance for investment-related costs of financial intermediation

When new demands for funds lead to displacement of other investments, they automatically save the economy the intermediation costs that would normally be linked to those investments. Here we are not concerned with the labor and material inputs that are thus freed up; they are presumed to render their marginal product elsewhere in the economy. However, in measuring the returns to capital for the economy as a whole, we obviously have included such returns that would be received by capital in the financial sector. What we would like to do here is exclude that part of these returns that are linked to the investments of each period. This certainly poses a real challenge to the estimator, and we are reluctant to claim that we have a genuine answer. Rather we would consider two possible ways of making an allocation for the saving of intermediation costs. The first is based on the estimated amount of investment of each year, and the second is tied to capital’s share in the value added for the financial sector. Our suggestion is that the allowance should be the lower of (a) 6% of gross investment of the year when funds are taken from the capital market and (b) half of the return to capital involved in financial intermediation. In real-world cases, both of these would be derived from actual data from the period in question. In the case of our equilibrium growth examples, only the first can readily be applied. So the allowance in this case would be 0. 06sY. We want, of course, to exclude only the part (=capital’s share of this) that has been counted as part of capital’s return. But we recognize that the financial sector is more capital intensive than the rest of the economy, so in calculating the exclusion we set capital’s share equal to 0.67 in the financial sector.

Table 5 Adjusting capital returns to derive estimates of  ${\it\rho}$ .

Table 5 details the calculations needed in order to reach our estimates of ${\it\rho}$ . We certainly do not want to claim accuracy of these estimates, but we do want to defend the methodology by which they were derived. We have made these estimates on the very rough basis of assumed high and low parameters for different classes of countries. We believe these parameters very likely span the true values in most cases. But we definitely would advise that anyone seeking a good estimate of ${\it\rho}$ for any given country should try to get specific values of key parameters like a, g, ${\it\delta}$ , s in that country, and should also explore the possibility of disequilibrium growth via the parameter e. Where possible, direct estimates of the stock of reproducible capital should be made, accumulating gross investment in different classes of capital assets by the perpetual inventory method; one important detail – when building capital stocks with the aim of calculating real rates of return, each year’s product and gross investment flows should be deflated by the numeraire (the GDP deflator or the Consumer Price Index [CPI]) rather than by two different indexes as is done in the national accounts. If separate deflators were used, say, for the textile industry, the ratio of income to capital would really turn out to be yards of cloth per loom. Only by having the same deflator on both sides of the calculation can we come to a proper estimate of the rate of return. By the same token, it is advisable to derive the ratios a and s from the nominal side of the national income accounts rather than those appearing on the real side.

6. Moving from ${\it\rho}$ to r

In many treatments, the time-preference rate is taken to be that on government bonds or time and saving deposits. We feel that this is a mistake, and that the rate of return to savers should be estimated from the average adjusted rate of return to reproducible capital $({\it\rho})$ , minus all income and property taxes that end up being paid out of that income. Indirect taxes should not be deducted, because they do not distort intertemporal choices and thus do not impact the marginal rate of time preference.

We struggled with the idea of approaching the estimation of the tax wedge through the application of marginal tax rates, but decided against it. Capital income accrues at the margin to entities that are exempt from certain taxes; it also accrues to tax evaders. Moreover many special tax dispensations apply at the margin. Finally, it was also much more convenient to work with average tax rates, which neatly fit into our national accounts framework. We proceed by working with estimates of the share of income and property taxes in a country’s GDP. Tax structures vary widely among countries, even within our three groupings. But one generalization can be made – among the advanced economies, those with higher ratios of total tax to GDP tend to rely more heavily on value added and other indirect taxes, while some of those with lower total tax ratios get 50 or even 60% of their total from income and property taxes.

Luckily, the International Monetary Fund (IMF) provides data on “Taxes on Income, Property and Capital Gains” as a fraction of GDP for many countries. For the industrial countries, these figures cluster quite tightly around 15%. The ratios in the developing countries have wider variation, but their average is quite stable around 6%. The Asian Tigers present a more complicated picture, with rates that can be as low as 5% and as high as 15%. We will use 10% of GDP as our figure for the Asian Tigers.

We have up to now talked about income and property taxes paid out of the income from capital. The information from the IMF includes capital gains as well. Some of these capital gains are reflections of corporate earnings which, of course, appear in the income from capital as presented in the national accounts. But some capital gains (e.g., those on land, residential housing, works of art, etc.) are not counted as part of the GDP. Hence, our estimates based on the IMF information probably overstate the true taxes actually paid on our measured aY. But any overstatement is unlikely to change the order of magnitude of the rough approximations we use.

Because corporation and property taxes strike mainly the income from capital, it is reasonable to assign 1∕3 of these figures to labor income, and 2∕3 to capital income. Note that the personal income tax is by far the largest component of the figures on which we based our entries, and that in most countries the bulk of the income tax on salaries is paid by the upper deciles at high marginal rates. So it is reasonable to assume that at least a third of income and property taxes do in fact fall on labor income.

7. Treatment of risk

Readers will probably be quick to notice that the rates that emerge for r from the preceding calculations are significantly above the real rates of return on government bonds, savings accounts, etc. One important source of the difference is the fact that the rates of return that prevail in the capital market reflect the attitude of its participants with respect to risk. Please note that we are not dealing here with default risk, which concerns the gap between promised returns and those that actually end up being paid. Our rates of return are based exclusively on the payments that savers receive as recorded in the national accounts. An important component of their difference from government bond rates is the so-called equity premium dealing with rates of return in the stock market. But our figures also include the returns on non-corporate investments of all types.

Our defense of our calculated rates for r – or, perhaps better put, of the general methodology underlying our calculations – is not based on the subtleties of portfolio analysis, but rather on the design and use of BCA itself. As we see it, if we were to use a discount rate (such as that on US TIPS) which is close to riskless, we would be obliged to make separate allowances for the riskiness of every project or program that we deal with. Such a prospect utterly terrifies us. How does one deal with the risk associated with a new school, or road, or airport, or irrigation dam? What about programs of urban renewal or medical research or pollution abatement? Between us we have accumulated more than a century of practical experience in BCA work, yet we are still at a loss when it comes to dealing with issues of risk in such cases. We certainly have no objection to people carrying forward the search for a robust and convincing methodology for incorporating risk into our project-by-project and program-by-program work, but we are pretty sure that it will be a long time before the profession will be widely implementing such a methodology.

But we do have a way of reducing the size of the problem – namely, use a rate of discount that incorporates an allowance for average risk. That is exactly what we get when we base our analysis on national accounts data. Using such a rate, we surely reduce the size of the challenges of dealing with risk, and end up feeling a lot less abashed by our inadequacy at dealing with them. We can take comfort in the fact that many of the projects and programs that we deal with probably have close to average risk attributes. That is certainly better than we get working with a riskless rate, which fits for no practical application whatever, and which thus cries out for us to take specific steps to incorporate risk into every single BCA. When we embed average risk into our approach, we can still worry about cases that have quite obviously above-average or below-average risks. But we feel less troubled by trying to deal with such cases on an ad hoc basis, than we would be if we were using a riskless rate, and were thus called upon to make specific risk adjustments in each and every case.

We have flirted over the years with an alternative way of dealing with risk – the simple assumption that “society” is neutral with respect to risk. The argument here is quite strong. For a family, the incentive to insure a home is much stronger than the incentive to insure a television set. That is because the loss of the home causes a big percentage drop in a family’s wealth, while the loss of a television set causes barely a ripple. Along a utility-of-wealth function the loss of a home generates a chord between the “with” and “without” points, generating a true willingness to pay for insurance. In the case of the television set, the chord generates practically no willingness to pay. Its slope is close to that of the tangent at the “with” position. We believe that most projects, even large ones like Hoover Dam or the TVA or a major airport, represent a tiny fraction of society’s wealth, and accordingly do not generate a serious cost linked to society’s risk.

Following this line, society would not want to consider any part of the difference between ${\it\rho}$ and r as a necessary compensation for risk. That difference would simply be a social benefit that is forgone when investment is displaced. Such an attitude would help explain why many countries choose to have society bear the costs of catastrophic medical events rather than leave them to the victims’ families.

Neutrality with respect to risk makes the choice of the social discount rate quite easy, but we prefer the approach of incorporating average risk into the discount rate. It carries fewer overtones and implications, while leading to a quite similar result.

Readers should also bear in mind that the excess of our measured r over the real government bond rate is not solely, and perhaps not even mainly a reflection of risk. If it were just that, savers would be indifferent between higher yielding investments and government bonds. That may be true for some (who hold both classes of assets). But the majority of savers probably hold no government bonds at all. Some of these are truly neutral with respect to risk, and therefore the expected yield should reflect their pure marginal rate of time preference. Many other savers are somewhat risk averse, but significantly less so than the market as a whole. For them, risk would account for only a fraction of the difference between their expected yields and the government bond rate. Research concerning the equity premium suggests that this is the case for a wide range of market participants – its main finding is that provision for systemic risk accounts for well under half of the “equity premium”. For us, the size of this fraction does not really matter – we want to work with the supply price of savings, inclusive of whatever risk premia we have incorporated into it.

8. Issues of time preference

We have pointed out that many early advocates of the use of r as the basic discount rate (combined with an SPIF) reached that decision on the basis of the theory of consumer behavior with respect to intertemporal decisions. The use of the weighted average ${\it\omega}$ takes time preference into account via the rate of return received by the savers. There are many categories of savers, receiving many different rates of return. So our f ₂ r is really $\sum _{i}f_{i}r_{i}$ , where i varies over all types of providers of funds, with different attitudes to risk, different supply prices of funds, all making choices so that the rate they expect to receive on each dollop of funds equals or exceeds their time-preference rate for that application, and where the marginal rate they receive is very close to their time-preference rate (i.e., the rate at which they discount after-tax benefit flows, measured in numeraire units).

We obviously take the approach we have outlined, and believe it to be the best choice for practical use. But we want to pay respect to an alternative line of thinking. This line would say that our $\sum _{i}f_{i}r_{i}$ pays attention to the time preference of those who supply funds to the capital market – but what about the others? Should not the whole population’s time-preference rates be represented in the social discount rate?

We see a certain logic in this way of thinking, and will therefore walk briefly down that trail. What we want to point out is that the trail does not lead to an especially low discount rate, as some might claim (or hope). The relevant marginal rate for many is a weighted average of the rates they receive on the various pieces of their investment portfolio. They are indeed the savers and the lenders. But a large fraction of the population in many countries consists of borrowers. In advanced countries, the marginal rate for a large fraction of the population is the rate on their credit cards, which for them actually represents both the marginal source and the marginal use of funds. Another large fraction has the mortgage rate as its effective marginal rate of time preference. For developing countries, poor farmers and small business people pay extremely high rates to local money lenders and only occasionally free themselves from the burden of outstanding debts.

We do not know what would be the average of the marginal time-preference rates of all the households in a given country, but we are quite confident that it would be well in excess of 2 or 3% in real terms, and we are happy to encourage any researchers who elect to explore this interesting path. But note that if one were to use such a broad average time-preference rate (call it ${\it\tau}$ ) for discounting, it should properly be accompanied by an SPIF (e.g., $(f_{1}{\it\rho}+f_{2}r)/{\it\tau}$ ), to take into account the displacement of investment and stimulation of savings that occurs when a project is financed in the capital market.

This is a good place to emphasize that for most governments, all over the world, the capital market is indeed the marginal source or destination of funds. Governments make budgets once a year projecting in some detail their expected outlays and receipts. But rarely does the outcome match the expectations. The actual deficit or surplus ends up larger or smaller, often quite a bit larger or smaller than what was originally budgeted. And nearly all governments, it seems are perennially in debt. Budget surpluses sometimes arise, so that outstanding debts are reduced, but only rarely are they reduced to the point where the government as a whole passes from debtor to creditor status. So we feel that capital market sourcing must be incorporated into standard cost–benefit analysis, either through the discount rate itself, as we prefer and suggest, or through an SPIF.

9. A time-preference rate linked to the rate of economic growth

Students of economic growth are familiar with the Ramsey equation

(1) $$\begin{eqnarray}r={\it\gamma}+eg.\end{eqnarray}$$

Here r is taken to be the appropriate social rate of discount, ${\it\gamma}$ is the rate at which future utility is discounted so as to be compared with present utility, g is the rate of economic growth, and e (defined as ${>}0$ ) is the elasticity of utility with respect to consumption. When the Ramsey equation appears in the growth literature, ${\it\gamma}$ is typically an arbitrarily assumed number, and e is typically assumed to be in a range like 0.5–2. A good example would take ${\it\gamma}=0.02$ , e = 1, and g = 0. 03, leading to a social discount rate of 0.05. And if g happened to go to 0.04, the discount rate would shift upward to 0.06.

We feel that such exercises have it all backwards. The interest rates that are relevant for the marginal decisions of individuals are beyond their control, and they modify their behavior accordingly. Consumption and saving respond to observed changes in real interest rates in a manner very different from that predicted by the Ramsey equation with a constant ${\it\gamma}$ and a single utility function U _t = F (C _t ), which remains unchanged as t changes. This double constancy is what gives rise to the present value maximand of $\int \!F(C_{t})e^{-{\it\gamma}t}\text{d}t$ .

We are completely confident that the marginal rate of time preference varies greatly among people simply because each household faces its own interest rate (credit cards, mortgages, stock market, bank deposits, government bonds, etc.).

Moreover, the relevant market rate for any given household will move from one category to another as that household’s fortunes change over the years. All of this is compatible with a marginal rate of time preference that varies (e.g., along a supply function for savings at any point in time) and a utility of consumption function that also can often be shifting over time. Economics can easily explain how, faced with a rise in interest rates, one family would decide to save more (in order to enjoy luxury living in retirement) while another would save less, in order to enhance present consumption while maintaining the same projected lifestyle during retirement. These different reactions would stem from different evaluations of the marginal utility of future consumption.

To convince oneself of the rigidity of the assumption of a constant utility discount rate ${\it\gamma}$ and an unchanging function representing the marginal utility of consumption, we invite readers to simply explore some obvious examples. For example, consider a person who inherits a fortune. With a finite horizon and a constant U _t = F (C _t ) function, if $r>{\it\gamma}$ , that person will choose to have the lowest consumption this year and will have ever higher consumption in each subsequent year. In general, g in the Ramsey equation is not an economic growth variable. Rather it represents the instrument by which maximizing individuals spread their consumption over time. In the same case with $r<{\it\gamma}$ , the reverse occurs and individuals choose to have ever declining consumption over time. It is something of a mystery how g got to be taken as an economic growth variable rather than a solution to each family’s allocation of its consumption over time. Actually in most cases, even without a windfall like an inheritance, if the relevant r exceeds a family’s constant ${\it\gamma}$ , that family will choose increasing consumption over time, while other families with $r<{\it\gamma}$ (either because their r is low or because their ${\it\gamma}$ is high) would opt for decreasing consumption over time. Such powerful implications would divide the world into these two classes of families. Why should we buy into such a thought when simple, natural economics tell us that of course our marginal rate of time preference will vary with the relevant interest rate? Consumer maximization should always lead to an equilibrium in which the consumer is indifferent between giving up 1 unit of consumption today and expecting (1 + r) ^t units of consumption t years from now. This is true if the function U _t = F (C _t ) is the same as U ₀ = G (C ₀), or different from it, and it should also be true whether the relevant market interest rate is high or low. Using the Ramsey equation to derive an r that is different from the relevant market rate is, we believe, a mistake.

10. Incorporating the sourcing of funds from abroad

We deferred to this point the discussion of the world capital market as a relevant source of funds. Our modified equation for the social discount rate is

$$\begin{eqnarray}{\it\omega}=f_{1}{\it\rho}+f_{2}r+f_{3}\mathit{MCFF},\end{eqnarray}$$

where MCFF stands for marginal cost of foreign funds. The above equation can be tweaked so as to give us an easy solution to the social discount rate problem, simply by assuming that each country faces a flat supply curve of foreign funds – e.g., an interest rate that remains unchanged no matter how much they borrow. If that were the case (an infinite elasticity of supply), then any added demand for funds would be met by new inflows from abroad, and the interest rate paid on such funds would be the relevant marginal cost of capital for the economy. No investment would be displaced and no additional saving stimulated.

We feel that there is a clear tendency toward equalization of short-term rates, especially among major financial centers where country risk is not a serious issue. But smaller countries do face rising country risk premia as they borrow more and major players like the United States and the European Union actually have some degree of influence over the level of rates around the world. All this does not even consider the capital movements taking place in market segments other than short-term funds. In short, we do not believe that any serious empirical support can be mustered for the idea that new investments in a country are fully reflected in new capital inflows and new savings in new capital outflows.

Sadly, however, the capital flow picture is too complicated for us to derive from empirical evidence the supply curve of foreign funds that each (or even any) country faces. If we had that, combined with the nation’s supply curve of savings and demand curve for investment funds, we could extract estimates of f ₁, f ₂, f ₃ that would have solid econometric support. As things stand, we have to build on much rougher evidence and impressions. We know that investment is significantly sensitive to the availability of funds (except in crisis times), and that the rate of saving responds only modestly to interest rate changes. So f ₁ should be significantly larger than f ₂. The size of f ₃ is more of a problem. Clearly it will vary significantly from country to country, being close to zero for those with the poorest links to world capital markets. For some countries, clues might be gathered from a study of movements in the net foreign balances of their private banks. For others, one would have to factor in the behavior of their central banks, which often build up international reserves to sterilize some part of private inflows, and draw on those reserves to offset some part of capital outflows. For major financial and industrial centers, one might gain insights from variations in foreign ownership of balances and other assets.

The above should make it quite clear that we are not ready to come up, even with well-informed guesses as to the size of f ₃. The best we can do is to build on what we do not see. Except for genuinely outlier countries, we do not see an utter absence or near absence of capital flows. So f ₃ is not likely to be close to zero in most cases. Similarly, we do not see large and palpable sensitivity of net capital outflows and inflows to changes in interest rates and general levels of pressure or ease in their capital markets. So we feel it would be quite a stretch to assume that foreign sources provided as much as half of the funds for the typical new investment and absorbed as much as half of any autonomous increase in savings. So we will bite the bullet and choose 0.3 as the figure that we will use for f ₃, making note that we would feel quite uncomfortable with an f ₃ as low as 0.2 or as high as 0.4.

There remains the issue of the marginal cost of foreign funds. Here the underlying vision of an upward rising supply curve of such funds gives us a clear signal that marginal cost should be above average cost, by a factor of $[1+1/(1+{\it\epsilon}_{f})]$ , where ${\it\epsilon}_{f}$ is the elasticity of supply of foreign funds facing the country. The latter is quite likely to vary substantially from country to country and from situation to situation for a given country. The figure we use for MCFF should also obey our maxim of being sensitive to what we do not see. We believe that if countries and their inhabitants could readily borrow large sums at a marginal cost of 2 or 3% in real terms, there would be a lot more international capital flows than what we actually observe. Similarly, if the marginal cost of foreign funds were something like 10 or 12%, we would see much less international movement of funds than what we actually witness. Figures like 4 to 8% seem to us to be more plausible. To lean to the conservative side, we will use a real rate of 6% for MCFF, partly for the reasons stated above, and partly because we would be uneasy if our final values for the social discount rate ended up being mainly governed by our assumed MCFF.

11. Calculation of the social discount rate

The figures in Table 7 are based on the numbers we found for ${\it\rho}$ in Table 5 and for r in Table 6, plus our assumed value of 6% for MCFF. We present two alternative weightings for f ₁ and f ₂ – our preferred weighting of (0.6, 0.1) and an alternative weighting of (0.5, 0.2).

Table 6 Transiting from ${\it\rho}$ to r.

Table 7 Weighted-average estimates of the social discount rate $({\it\omega})$ ; ${\it\omega}=f_{1}{\it\rho}+f_{2}r+f_{3}\mathit{MCFF}$ .

The figures resulting from our exercise are within the range of real discount rates that have been widely used. The World Bank and some of the regional development banks used a 10% cutoff rate for many years, and many developing countries have followed this path. The point to be made here is that many projects have passed the test of rates in this range. Many business firms, even in advanced countries, ask for expected internal rates of return of 15 and even 20% on the investment projects they undertake. So we should not be frightened by rates in this range. Recall that we derived them from national accounts data, with plausible adjustments that had the effect of lowering the calculated rate.

We would also call attention to the minimal sensitivity that we found to changes in the weighting scheme. This stems, of course, from our building allowances for average risk into our estimate of r, but we feel extremely confident that we would only invite trouble, both conceptual and practical, if we tried to incorporate a riskless r into our estimate of the social discount rate.

In closing, we want to emphasize that we are much more interested in convincing others of the broad strategy and conceptual framework that we advocate. We hope that others will join in the search for more accurate values of the parameters involved. Sensitivity tests, too, should be more widely used to convey the level of confidence that we should place in our estimates.