1. INTRODUCTION
The interaction of laser radiations with plasma has known to produce various nonlinear phenomena such as self-focusing, self-phase modulation, harmonic generation, etc. (Corkum et al., Reference Corkum, Rolland and Rao1986; Wilks et al., Reference Wilks, Dawson, Mori, Katsouleas and Jones1989; Eder et al., Reference Eder, Amendt and Wilks1992; Lemoff et al., Reference Lemoff, Yin, Gordon, Barthy and Harris1995). Study of these nonlinear phenomenon has been a subject of experimental and theoretical research due to their wide applications in laser driven fusion, plasma-based accelerators, X-ray lasers, fast ignition for inertial confinement fusion (ICF) and other applications (Parashar et al., Reference Parashar, Pandey and Tripathi1997; Honda et al., Reference Honda, Meyer-ter-Vehn and Pukhov2000; Liu & Tripathi, Reference Liu and Tripathi2001; Mulser & Bauer, Reference Mulser and Bauer2004; Gupta & Suk, Reference Gupta and Suk2007; Hora, Reference Hora2007; Winterberg, Reference Winterberg2008; Parashar, Reference Parashar2009; Lourenco et al., Reference Lourenco, Kowarsch, Scheid and Wang2010; Askari & Azish, Reference Askari and Azish2011; Uhm et al., Reference Uhm, Nam and Suk2012). The propagation of laser beam over several Rayleigh lengths without loss of energy is an essential requirement in all these applications while keeping efficient interaction with plasma. The development of high intense laser beams these days makes feasibility of investigating such extremely interesting nonlinear phenomena.
There is increasing interest these days in the self-focusing of laser beams in different plasma environments and most of investigations have been done by considering fundamental Gaussian beam and simplest classical relativistic (CR) case of reference. High intense laser pulses makes feasibility to investigate fascinating nonlinear phenomena such as self-focusing in relativistic regime. Relativistic self-focusing takes place on account of quiver motion of the electrons due to laser electric field while travelling at a speed comparable with speed of the light. The relativistic effect become dominant provided laser power exceeds its critical value, P critical = 17(ωp/ω0)2GW. The above result is well established theoretically (Max et al., Reference Max, Arons and Langdon1974; Hora, Reference Hora1975; Schmidt & Horton, Reference Schmidt and Horton1985) as well as experimentally (Borisov et al., Reference Borisov, Borovskiy, Shiryaev, Korobkin, Prokhorov, Solem, Luk, Boyer and Rhodes1992; Monot et al., Reference Monot, Auguste, Gibbon, Jakober, Mainfray, Dulieu, Louis- Jacquet, Malka and Miquel1995). However, when the laser power is smaller than this critical power, diffraction of the beam dominates over relativistic self-focusing. From the literature we have observed that intense laser beam attains a minimum spot size while propagating through relativistic plasma. The other contribution comes from nonlinear electron density perturbation caused by ponderomotive force, which is exerted on the electron by spatial variation in laser intensity across the beam profile and pushes the electron outward from the central region of the beam (Borisov et al., Reference Borisov, Borovskiy, Shiryaev, Korobkin, Prokhorov, Solem, Luk, Boyer and Rhodes1992). The combined effect of both nonlinearities viz. relativistic and ponderomotive have been studied by Patil et al. (Reference Patil, Takale, Fulari, Gupta and Suk2013b ). This type of nonlinearity modifies the density distribution in plasma and therefore stronger self-focusing is observed by including the effect of ponderomotive force in refractive index. They have further extended their work in inhomogeneous plasma by varying the plasma density along the axis of laser beam propagation in weakly relativistic and ponderomotive regime (Patil & Takale, Reference Patil and Takale2013b ). From observation they concluded that laser beam tends to focus more in the presence of ramp instead of uniform relativistic plasma density thereby travelling laser beam up to several Rayleigh lengths. Bokaei et al. (Reference Bokaei, Niknam and Jafari Milani2013) recently in their work have shown that ponderomotive force supports relativistic self-focusing strictly below a fixed electron temperature for a given initial laser intensity and above this temperature self-focusing is destroyed. Apart from these a few studies have been made by showing interest in non-Gaussian laser beams. Patil et al. (Reference Patil, Takale, Navare, Fulari and Dongare2012) proposed to employ an analysis to study the oscillatory self-focusing of cosh-Gaussian laser beam for different values of decentered parameter b using well-known paraxial ray approximation, which is common with many investigations. They have extended their work to study nonlinear propagation of cosh-Gaussian laser in homogeneous, unmagnetized, underdense plasma in weakly relativistic regime with additional ponderomotive effects (Patil & Takale Reference Patil and Takale2013c ). In all these investigations the main thrust is to improve self-focusing using control parameters like intensity and plasma electron temperature.
More recently it has been observed that quantum effects can significantly enhance self-focusing more relative to the CR case (Patil et al., Reference Patil and Takale2013a
). When the laser beam propagates in quantum plasma the spot size of the laser beam oscillates with higher frequency and lesser laser amplitude. This pinching effect offered by quantum plasma results in enhanced self-focusing in comparison with classical case of reference (Shukla et al., Reference Shukla, Ali, Stenflo and Marklund2006; Marklund & Brodin, Reference Marklund and Brodin2007; Bulanov et al., Reference Bulanov, Esirkepov, Habs, Pegoraro and Tajima2009). The increasing interest in studying quantum plasma is due to their wide applications in astrophysical and cosmological plasma, fusion science, laser–solid interactions, nonlinear quantum optics, and nanotechnology (Hu & Keitel, Reference Hu and Keitel1999; Andreev, Reference Andreev2000; Jung, Reference Jung2001; Lai, Reference Lai2001; Benvenuto & De Vito, Reference Benvenuto and De Vito2005; Azechi, Reference Azechi2006; Ozbay, Reference Ozbay2006; Harding & Lai, Reference Harding and Lai2006; Marklund & Shukla, Reference Marklund and Shukla2006; Shpatakovskaya, Reference Shpatakovskaya2006; Shukla & Stenflo, Reference Shukla and Stenflo2006; Shukla & Eliasson, Reference Shukla and Eliasson2007; Wei & Wang, Reference Wei and Wang2007; Crouseilles et al., Reference Crouseilles, Hervieux and Manfredi2008; Marklund et al., Reference Marklund, Brodin, Stenflo and Liu2008; Masood et al., Reference Masood, Mirza and Nargis2008, Reference Masood, Siddiq, Mirza and Nargis2009; Glenzer & Redmer, Reference Glenzer and Redmer2009; Mendonca, Reference Mendonca2011; Asenjo et al., Reference Asenjo, Munoz, Valdivia and Mahajan2011; Haas et al., Reference Haas, Eliasson and Shukla2012). Quantum plasma enhances nonlinear phenomena noticeably and hence cannot be ignored when the density of plasma electrons becomes very high that is, when de Broglie wavelength of charge particle like electron (
${\rm \lambda} = \sqrt h /m{K_{\rm b}}{T_{\rm e}}$
) is equal or greater than average inter-electron distance (1/(n
0)1/3) or equivalently temperature T is less than or equal to Fermi temperature T
Fe, where T
Fe = E
Fe/K
b (Ozbay, Reference Ozbay2006). Here h is the Planck constant, n
0 is the electron density, m is the rest mass of the electron, K
b is the Boltzmann constant and E
Fe is the Fermi energy. In such a situation the incorporation of quantum effects becomes significant. A number of research papers have been published on cold quantum plasma in past few years. Patil et al. (Reference Patil, Takale, Navare, Dongare and Fulari2013a
) have studied the self-focusing of Gaussian laser beam in relativistic cold quantum (RCQ) plasma. They have reported additional self-focusing using cold quantum plasma in comparison with CR case. Similar results were realized by studying relativistic self-focusing of Gaussian laser in collisional quantum plasma by Zare et al. (Reference Zare, Rezaee, Yazdani, Anvari and Sadighi-Bonabi2015a
). Although the energy of the laser beam drops due to absorption in collisional plasma, self-focusing can still be perceived earlier in denser quantum plasmas. In another work Patil and Takale have studied stationary self-focusing of Gaussian laser beam in relativistic thermal quantum plasma (Patil & Takale Reference Patil and Takale2013a
). Moreover, in response to comment of the above paper they have clearly provided the evidence of strong self-focusing occurring in warm quantum plasma rather than in case of cold quantum plasma (Patil & Takale Reference Patil and Takale2014). However, in both of their contributions ponderomotive term was ignored. We have revisited the Patil et al. (Reference Patil, Takale, Navare, Dongare and Fulari2013a
) problem taking into account contribution of both relativistic and ponderomotive nonlinearity and observed self-focusing up to 20 Rayleigh length. Our derived equation is more generalized as on setting n
e/n
0 → 1, the reduced equation represent RCQ and that for δ → 0, the reduced equation represent relativistic ponderomotive (RP) case. We have shown noteworthy contribution of ponderomotive nonlinearity in our paper.
In the present study, authors have investigated the propagation of Gaussian laser beam through relativistic and ponderomotive cold quantum plasma. In Section 2, we have obtained nonlinear part of plasma permittivity including the combined effect of relativistic and ponderomotive nonlinearity in cold quantum plasma. In Section 3, we have studied the evolution of spot size of the laser beam using nonlinear Schrodinger equation and results and discussion is presented in Section 4.
2. FORMALISM
Consider the propagation of Gaussian laser beam in cold quantum plasma along z-axis with angular frequency “ω0”. The amplitude of the electric vector E can be expressed as
$${\bf E} = \hat xA(r,z)\exp [ - {\rm \iota} ({{\rm \omega} _{\rm 0}}t - kz)]$$
where
${A^2}{\vert _{z = 0}} = A_{{\rm 00}}^2 \exp ( - {r^2}/r_{\rm 0}^2 )$
is the initial intensity distribution of the beam along the wavefront z = 0. A
00 is the axial amplitude and r
0 is the initial beam width.
$k = ({{\rm \omega} _{\rm 0}}/c)\sqrt {{{\rm \epsilon} _{\rm 0}}} $
is the propagation constant of the wave, ε0 is the linear part of the dielectric constant of the medium and c is the speed of light in vacuum. For z > 0 the field distribution A(r, z) is given by
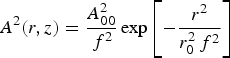$${A^2}(r,z) = \displaystyle{{A_{00}^2} \over {{\,f^2}}}\exp \left[ { - \displaystyle{{{r^2}} \over {r_0^2 {\,f^2}}}} \right]$$
The laser imparts an oscillatory velocity ν = eE/miωoγ to the electrons, where γ = (1 + a 2)1/2 is the relativistic factor arising from intensity dependence of electron mass m and a = e|A|/mcω0 is the normalized laser amplitude. This may be interpreted as electron response to the laser field. The ponderomotive force on an electron in the presence of an intense laser beam may be represented as (Borisov et al., Reference Borisov, Borovskiy, Shiryaev, Korobkin, Prokhorov, Solem, Luk, Boyer and Rhodes1992; Brandi et al., Reference Brandi, Manus and Mainfray1993a , Reference Brandi, Manus, Mainfray and Lehner b )
$${F_{\rm p}} = - m{c^2}\nabla ({\rm \gamma} - 1)$$
At the front of beam, ponderomotive force get subdivided into radial and axial components. The radial component pushes the electrons radially outwards on the time scale of a plasma period
${\rm \omega} _{\rm p}^{ - 1} $
, where ωp = (4πn
0
e
2/m)1/2 and n
0 is the density of plasma in the absence of beam. The electron density arising from RP force and intensity dependence on electron mass as given by (Brandi et al., Reference Brandi, Manus and Mainfray1993a
, Reference Brandi, Manus, Mainfray and Lehner
b
)
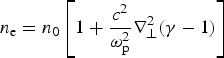$${n_{\rm e}} = {n_0}\left[ {1 + \displaystyle{{{c^2}} \over {{\rm \omega} _{\rm p}^2}} \nabla _ \bot ^2 ({\rm \gamma} - 1)} \right]$$
In the present study, we use the dielectric constant for cold quantum plasma. The nonlinear contribution because of density modification due to RP force has also been considered in the present model (Tripathi et al., Reference Tripathi, Taguchi and Liu2005; Jung & Murakami, Reference Jung and Murakami2009)
$${\rm \epsilon} = 1 - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} _0^2}} \displaystyle{{{n_{\rm e}}/{n_0}} \over {\rm \gamma}} {\left( {1 - \displaystyle{{\rm \delta} \over {\rm \gamma}}} \right)^{ - 1}}$$
Where
${\rm \delta} = 4{{\rm \pi} ^4}{h^2}/{m^2}{\rm \omega} _0^2 {{\rm \lambda} ^4}$
, λ is the wavelength of the laser beam. The plasma permittivity in paraxial region
$({r^2} \ll r_0^2 {\,f^2})$
can be expressed by expanding the dielectric constant in Eq. (5) around r = 0 by Taylor series expansion as
$${\rm \epsilon} = {{\rm \epsilon} _0} - \displaystyle{{{r^2}} \over {r_0^2}} \Phi $$
$${{\rm \epsilon} _0} = 1 - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} _{\rm o}^2 {{\rm \gamma} _{\rm o}}}}\left( {1 - \displaystyle{{{c^2}} \over {{\rm \omega} _{\rm p}^2}} \displaystyle{{a_0^2} \over {{{\rm \gamma} _0}r_0^2 {\,f^2}}}} \right){\left( {1 - \displaystyle{{\rm \delta} \over {{{\rm \gamma} _0}}}} \right)^{ - 1}}$$
$$\eqalign{& \Phi = \displaystyle{{{\rm \omega} _{\rm p}^2} \over {4{\rm \omega} _0^2}} \displaystyle{{a_0^2 /{\,f^4}} \over {{\rm \gamma} _0^3}} \cr &\qquad \times \left[ {1 + \displaystyle{{{c^2}} \over {{\rm \omega} _{\rm p}^2 {\,f^2}r_0^2}} \displaystyle{{8(1 - {\rm \delta} /{{\rm \gamma} _{\rm 0}}) + 2(a_0^2 /{\,f^2})(1 - 2{\rm \delta} /{{\rm \gamma} _0})} \over {{{\rm \gamma} _0}}}} \right] \cr &\qquad \times {\left( {1 - \displaystyle{{\rm \delta} \over {{{\rm \gamma} _0}}}} \right)^{ - 2}}} $$
Φ is the nonlinear parts of the dielectric constant,
${\rm \gamma} _0 =(1 + a_{0}^{2} /{\,f^2})^{1/2}$
and a
0 = eA
00/mcω0.
3. EVOLUTION OF SPOT SIZE
From Maxwell's equations the general form of nonlinear wave equation governing the propagation of Gaussian laser beam in the plasma is given by
$$\displaystyle{{{\partial ^2}{\bf E}} \over {\partial {z^2}}} + \nabla _ \bot ^2 {\bf E} + \displaystyle{{{\rm \omega} _0^2} \over {{c^2}}}{\rm \epsilon} {\bf E} = 0,$$
where E is the electric field of the laser beam and ε being effective plasma permittivity. The amplitude of electric field given by Eq. (1) satisfies Eq. (9). Using Wentzel Kramers Brillouin (WKB) approximation, one can neglect
${\partial ^2}{\bf A}/\partial {z^2}$
and the wave equation reduces to
$$- 2{\rm \iota} k\displaystyle{{\partial A} \over {\partial z}} + \nabla _ \bot ^2 A + \displaystyle{{{\rm \omega} _0^2} \over {{c^2}}}\Phi A = 0,$$
where
$\nabla _ \bot ^2 A$
is responsible for the spatial dispersion of the beam in transverse direction, whereas last term is nonlinear term that compresses the beam. Focusing/defocusing results due to relative competition between these two terms. We introduce eikonal,
$A(r,z) = {A_0}(r,z)\exp [ - {\rm \iota} k(z)S(r,z)]$
, where A
0(r, z) and S(r, z) are real functions of space variables. Substituting A(r, z) in above equation and separating real and imaginary parts, we get
$$\eqalign{& 2\displaystyle{{\partial S} \over {\partial z}} + {\left( {\displaystyle{{\partial S} \over {\partial r}}} \right)^2} - \displaystyle{1 \over {{k^2}{A_0}}}\left( {\displaystyle{{{\partial ^2}{A_0}} \over {\partial {r^2}}} + \displaystyle{1 \over r}\displaystyle{{\partial {A_0}} \over {\partial r}}} \right) \cr & + \displaystyle{{{r^2}} \over {r_0^2}} \displaystyle{\Phi \over {{{\rm \epsilon} _0}}} = 0} $$
and
$$\displaystyle{{\partial A_0^2} \over {\partial z}} + \displaystyle{{\partial S} \over {\partial r}}\displaystyle{{\partial A_0^2} \over {\partial r}} + A_0^2 \left( {\displaystyle{{{\partial ^2}S} \over {\partial {r^2}}} + \displaystyle{1 \over r}\displaystyle{{\partial S} \over {\partial r}}} \right) = 0$$
Following approach given by Akhmanov et al. (Reference Akhmanov, Sukhorukov and Khokhlov1968) and developed by Sodha et al. (Reference Sodha, Ghatak, Tripathi and Wolf1976), we expand eikonal S, in Paraxial ray approximation as S(r, z) = (r
2/2)β0(z) + S
0(z) and β0(z) = 1/f df/dz. The parameter
${\rm \beta} _0^{ - 1} $
may be interpreted as the radius of the curvature of the main beam. S
0(z) is a phase constant, whose value is not required explicitly in further analysis.
Substituting
$A_0^2 ( = {A^2})$
from Eq. (2) in Eq. (11) and equating coefficients of r
2 on both sides, we obtain the equation governing dimensionless beam width parameter f given as
$$\eqalign{& \displaystyle{{{d^2}f} \over {d{{\rm \xi} ^2}}} = \displaystyle{1 \over {{\,f^3}}} - \displaystyle{{R_{\rm d}^2} \over {{{\rm \epsilon} _0}}}\displaystyle{{{\rm \omega} _{\rm p}^2} \over {4{\rm \omega} _0^2}} \displaystyle{{a_0^2 /{\,f^4}} \over {{\rm \gamma} _0^3}} \cr &\qquad\hskip6pt \times \left[ {1 + \displaystyle{{{c^2}} \over {{\rm \omega} _{\rm p}^2 {\,f^2}r_0^2}} \displaystyle{{8(1 - {\rm \delta} /{{\rm \gamma} _{\rm 0}}) + 2(a_0^2 /{\,f^2})(1 - 2{\rm \delta} /{{\rm \gamma} _0})} \over {{{\rm \gamma} _0}}}} \right] \cr &\qquad\hskip6pt \times {\left( {1 - \displaystyle{{\rm \delta} \over {{{\rm \gamma} _0}}}} \right)^{ - 2}}f.} $$
Where ξ = z/R d and R d = k r 0 2. By using initial boundary conditions (df/dξ = 0, f = 1 at ξ = 0) and suitable laser and plasma parameters, above equation can be solved to determine the propagation character of the beam.
4. NUMERICAL RESULTS AND DISCUSSION
We have chosen laser frequency, ω0 = 1.778 × 1020 rad/s, which lies in X-ray region for quantum plasma condition to be satisfied. The other parameters are as follows: Intensity (W cm−2) = 8.18 × 1025, λ = 0.0106 nm, ωp/ω0 = 5.624 × 10−7, r
0 = 0.002 cm and n
0 = 3.143 × 1018 cm−3. The range of intensity under study is presently far beyond the accessible laser facilities and may require more technological advancement to be feasible in the future (Zare et al., Reference Zare, Yazdani, Rezaee, Anvari and Sadighi-Bonabi2015b
). Equation (13) is a nonlinear ordinary differential equation governing the behavior of beam width parameter f as a function of normalized distance of propagation ξ. The first term on the right-hand side of Eq. (13) appears due to the Laplacian
$(\nabla _ \bot ^2 )$
in Eq. (9). This term is responsible for the diffractional divergence of the laser beam. The second term is a nonlinear term, which arises due to RP self-focusing and depends on intensity parameter
$(a_0^2 )$
, plasma frequency (ωp) and electron density (n
0). The diffractional term leads to diffractional divergence of the beam, while the nonlinear term is responsible for self-focusing of the laser beam. The divergence and convergence of the beam depends on whether first term of Eq. (13) dominates the second term or vice versa. When these terms are equal, beam propagates in a uniform wave guide with equilibrium beam radius
$({\rm \rho_0} = {\rm \omega_p} r_0/c)$
. The condition under which this occur is termed as critical condition. Since analytical solution of Eq. (13) is not possible, we have solved this equation numerically by using Runge Kutta fourth order method. It is interesting to note that one can cast equation for the RCQ plasma and RP case by setting n
e/n
0 → 1 and δ = 0, respectively. A comparison can thus be attempted by studying various parameters such as intensity parameter
$(a_0^2 )$
, relative plasma density (ωp/ω0) and electron density (n
0).
Figure 1 depicts the plot of the critical curve in
$(a_0^2, {{\rm \rho} _0})$
plane for cold quantum plasma with combined effect of relativistic and ponderomotive nonlinearity. We have compared our result with RCQ plasma and CR case of references, respectively. It is obvious from the Figure 1, that the region of self-focusing is largest in the case of RPCQ than in the case of RCQ and CR cases of reference. Therefore for chosen plasma density a wide range of laser intensities can be focused for RPCQ. It is clear that the ponderomotive term improves the self-focusing as it evacuates the electrons due to high-density gradient therefore its contribution cannot be ignored. Figure 2 presents the variation of beam width parameter f with normalized distance of propagation ξ for RPCQ, RCQ, and CR cases along with the case when there is no contribution from nonlinear term. From the sketched graph, it is clear that the self-focusing effect is strongest in case of RPCQ above RCQ and CR cases of refrence. The above findings are consistent with the critical curve plotted in Figure 1. The curve of RPCQ shows stronger self-focusing as nonlinear term is strongest in this case. The pinching effect offered by quantum plasma further enhances nonlinear term. Therefore the contribution of ponderomotive nonlinearity in relativistic term alongwith pinching effect of quantum plasma greatly enhances laser propagation up to 20 Rayleigh lengths.
Fig. 1. Critical curves in (
$a_0^2, {{\rm \rho} _0}$
) plane for relativistic ponderomotive cold quantum plasma (RPCQ), relativistic cold quantum plasma (RCQ) and for classical relativistic (CR) case. Other parameters are λ = 0.0106 nm, ωp/ω0 = 5.624 × 10−7, r
0 = 0.002 and n
0 = 3.143 × 1018 cm−3.
Fig. 2. Variation of beam width parameter f with normalized propagation distance ξ for relativistic ponderomotive cold quantum plasma (RPCQ), relativistic cold quantum plasma (RCQ), for classical relativistic (CR) case and without nonlinearity. Other parameters are same as mentioned in Fig. 1.
Figure 3 presents the variation of beam width parameter f with normalized distance of propagation ξ for various intensities and rest of the parameter are kept same as mentioned in Figure 1. The laser intensity 8.18 × 1025(W cm−2) is an optimized intensity for which stronger self-focusing is observed. It is further observed that self-focusing occurs earlier with slenderly decreasing extent of self-focusing as we increase the laser intensity. This is due to the fact that laser propagation is sensitive to parameters like wavelength, intensity, and plasma density. The focusing/defocusing of the beam further depends on these laser and plasma parameters. The intensity parameter is chosen from the plot of nonlinear plasma permittivity as a function of intensity parameter.
Fig. 3. Variation of beam width parameter f with normalized propagation distance ξ for different values of intensity (I) and other parameters being same as mentioned in caption of Fig. 1.
From Figure 4 we conclude that as we increase the plasma density, focusing of the beam takes earlier. This is because, at relativistic intensities a beam with more relativistic electrons travels with the laser pulse generating a higher current, which further results in generation of very high quasi-stationary magnetic field. The magnetic field arising due to these relativistic electrons adds to self-focusing. The results thus obtained in the present investigation are in agreement with (3D particle-in-cell) simulation results reported by Pukhov and Meyer-ter-Vehn (Reference Pukhov and Meyer-ter-Vehn1996). The quantum plasma in addition to relativistic electrons helps in increasing the extent of self-focusing. Similar results were reported by Patil et al. (Reference Patil, Takale, Navare, Dongare and Fulari2013a , Reference Patil, Takale, Fulari, Gupta and Suk b ) and Singh et al. (Reference Singh, Aggarwal and Gill2009).
Fig. 4. Variation of beam width parameter f with normalized propagation distance ξ for different values of ωp/ω0 and other parameters being same as mentioned in caption of Fig. 1.
Figure 5 represents nonlinearity Φ as a function of intensity parameter
$a_0^2 $
for three different cases of plasma model. It is apparent from curve-II that for a given value of
$a_0^2 $
, relativistic quantum effects results in stronger nonlinearity parameter in comparison with CR case (Curve-I). As a consequence stronger/enhanced self-focusing is observed in RCQ plasma. However nonlinearity is strongest in case of RPCQ (Curve-III) for the same set of laser and plasma parameters. Therefore strongest self-focusing is observed for RPCQ plasma. It is worth mentioning here that RP nonlinearity cannot be separated into ponderomotive + relativistic nonlinearity as the nonlinearity sets in simultaneously.
Fig. 5. Variation of nonlinear plasma permittivity Φ with intensity parameter
$a_0^2 $
for relativistic ponderomotive cold quantum plasma (RPCQ), relativistic cold quantum plasma (RCQ) and classical relativistic (CR) case. The other parameters being same as mentioned in caption of Fig. 1.
It is further clear from the Figure 5 that the nonlinear plasma permittivity increases with intensity and attains a maximum value and thereafter falls rapidly. This behaviour is same for RPCQ and RCQ cases, whereas for CR case nonlinear plasma permittivity becomes almost constant after achieving maximum value. The intensity for which plasma permittivity reaches maxima leads to reduced focusing length of the laser beam. Beyond this value of intensity, the value of nonlinear plasma permittivity fall and hence focusing length increases. The comparison of three cases of reference depicts minimum focusing length in case of RP cold quantum plasma.Our results are thus useful for the scientist and researchers working on plasma based accelerators and ICF.
5. CONCLUSIONS
In the present work, we have studied self-focusing of Gaussian laser beam in cold quantum plasma under the combined effect of relativistic and ponderomotive nonlinearity. Following results were concluded:
-
1. Additional self-focusing is observed in case of RPCQ plasma by considering relativistic and ponderomotive effects together in comparison with RCQ and CR cases of reference.
-
2. Quantum plasma adds pinching effect to self-focusing in comparison with CR case of reference.
-
3. Laser propagation can be enhanced in cold quantum plasma up to many Rayleigh lengths.
ACKNOWLEDGMENTS
The author's Harish Kumar and Richa are thankful to the RIC of I.K Gujral Punjab Technical University, Kapurthala (India) for their support. One of the author Munish Aggarwal is thankful to Director, Lyallpur Khalsa College of Engineering, Jalandhar, Dr. Y.S. Randhawa for giving good research environment. We are thankful to anonymous referee for his valuable enriching and insight comments.
