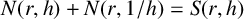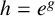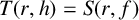1. Introduction and motivation
Throughout this note, we assume familiarity with standard notation and key results from Nevanlinna theory [Reference Hayman7]. In particular, a meromorphic function
![]() $\varphi $
is termed a small function of f if the Nevanlinna characteristic
$\varphi $
is termed a small function of f if the Nevanlinna characteristic
![]() $T(r, \varphi )$
satisfies
$T(r, \varphi )$
satisfies
![]() $T(r, \varphi ) = S(r, f)$
. Here,
$T(r, \varphi ) = S(r, f)$
. Here,
![]() $S(r, f)$
denotes any quantity such that
$S(r, f)$
denotes any quantity such that
![]() $S(r, f) = o(T(r, f))$
as
$S(r, f) = o(T(r, f))$
as
![]() $r \rightarrow \infty $
, potentially outside an exceptional set of finite linear or logarithmic measure. For brevity, we denote the set of all meromorphic functions that are small with respect to f by
$r \rightarrow \infty $
, potentially outside an exceptional set of finite linear or logarithmic measure. For brevity, we denote the set of all meromorphic functions that are small with respect to f by
![]() $\mathcal {S}(f)$
. The order and hyper-order of a meromorphic function f are defined respectively by
$\mathcal {S}(f)$
. The order and hyper-order of a meromorphic function f are defined respectively by
 $$ \begin{align*} \rho(f):=\limsup _{r \rightarrow \infty} \frac{\log T(r, f)}{\log r} \quad \text{and}\quad \rho_2(f):=\limsup _{r \rightarrow \infty} \frac{\log \log T(r, f)}{\log r}. \end{align*} $$
$$ \begin{align*} \rho(f):=\limsup _{r \rightarrow \infty} \frac{\log T(r, f)}{\log r} \quad \text{and}\quad \rho_2(f):=\limsup _{r \rightarrow \infty} \frac{\log \log T(r, f)}{\log r}. \end{align*} $$
In 1970, Yang [Reference Yang16] applied Nevanlinna’s value distribution theory to investigate the Fermat functional equation
where
![]() $p, q \geq 3$
are integers, f and g denote nonconstant meromorphic functions, and
$p, q \geq 3$
are integers, f and g denote nonconstant meromorphic functions, and
![]() $a, b$
are meromorphic functions that are respectively small compared with f and g. Yang [Reference Yang16, Theorem 1] showed that (1.1) cannot hold unless
$a, b$
are meromorphic functions that are respectively small compared with f and g. Yang [Reference Yang16, Theorem 1] showed that (1.1) cannot hold unless
![]() $p=q=3$
. However, if f and g are entire, then (1.1) cannot hold even if
$p=q=3$
. However, if f and g are entire, then (1.1) cannot hold even if
![]() $p=q=3$
. Indeed, upon careful inspection of the proof of [Reference Yang16, Theorem 1], one can express Yang’s result in terms of
$p=q=3$
. Indeed, upon careful inspection of the proof of [Reference Yang16, Theorem 1], one can express Yang’s result in terms of
 $$ \begin{align*} \Theta(a, f):=1-\limsup _{r \rightarrow \infty} \frac{\overline{N}(r, {1}/{(f-a)})}{T(r, f)} \end{align*} $$
$$ \begin{align*} \Theta(a, f):=1-\limsup _{r \rightarrow \infty} \frac{\overline{N}(r, {1}/{(f-a)})}{T(r, f)} \end{align*} $$
as follows.
Theorem 1.1. Let p and q be positive integers satisfying
![]() ${1}/{p} + {1}/{q} < {2}/{3}$
. Then, (1.1) has no nonconstant meromorphic solutions f and g. Moreover, if
${1}/{p} + {1}/{q} < {2}/{3}$
. Then, (1.1) has no nonconstant meromorphic solutions f and g. Moreover, if
![]() ${1}/{p} + {1}/{q} < 1$
, there exists no nonconstant meromorphic solution of (1.1) such that
${1}/{p} + {1}/{q} < 1$
, there exists no nonconstant meromorphic solution of (1.1) such that
![]() $\Theta (\infty , f) = \Theta (\infty , g) = 1$
.
$\Theta (\infty , f) = \Theta (\infty , g) = 1$
.
Motivated by this and the development of difference analogues of Nevanlinna’s theory (see, for example, [Reference Chen3, Reference Halburd, Korhonen and Tohge6, Reference Liu, Laine and Yang12]), there are many explorations of the Fermat-type difference equation
where c is a nonzero constant and h is a given meromorphic function. For instance, it has been shown in [Reference Korhonen and Zhang8, Reference Lü and Han14] that if h is a nonzero constant and
![]() $p=q=3$
, then (1.2) does not admit nonconstant meromorphic solutions with
$p=q=3$
, then (1.2) does not admit nonconstant meromorphic solutions with
![]() $\rho _{2}(f)<1$
. Later, Lü and Guo [Reference Lü and Guo13] extended this conclusion to the case when
$\rho _{2}(f)<1$
. Later, Lü and Guo [Reference Lü and Guo13] extended this conclusion to the case when
![]() $h = e^{\alpha z+\beta }$
, under the conditions
$h = e^{\alpha z+\beta }$
, under the conditions
![]() $p \geq 3$
and
$p \geq 3$
and
![]() $q \geq 2$
or
$q \geq 2$
or
![]() $p \geq 2$
and
$p \geq 2$
and
![]() $q \geq 3$
, excluding the exceptional case of trivial solutions, which applies when
$q \geq 3$
, excluding the exceptional case of trivial solutions, which applies when
![]() $p=q$
and
$p=q$
and
For the case
![]() $h = e^{g}$
, where g is a nonconstant polynomial, Bi and Lü [Reference Bi and Lü2] employed properties of elliptic functions to establish the nonexistence of nontrivial meromorphic solutions with
$h = e^{g}$
, where g is a nonconstant polynomial, Bi and Lü [Reference Bi and Lü2] employed properties of elliptic functions to establish the nonexistence of nontrivial meromorphic solutions with
![]() $\rho _{2}(f)<1$
for (1.2) when
$\rho _{2}(f)<1$
for (1.2) when
![]() $p=q=3$
. Additionally, they proved the same result [Reference Bi and Lü2, Theorem 2] when
$p=q=3$
. Additionally, they proved the same result [Reference Bi and Lü2, Theorem 2] when
![]() $h\in \mathcal {S}(f)$
and has
$h\in \mathcal {S}(f)$
and has
![]() $0$
and
$0$
and
![]() $\infty $
as Borel exceptional values. More recently, Guo and Liu [Reference Guo and Liu5] investigated the case
$\infty $
as Borel exceptional values. More recently, Guo and Liu [Reference Guo and Liu5] investigated the case
![]() $h = e^{g}$
in (1.2), with g being a nonconstant entire function.
$h = e^{g}$
in (1.2), with g being a nonconstant entire function.
Motivated by these results, we explore the existence problem of meromorphic solutions to (1.2) when h belongs to some specific classes. In Section 2, we investigate the case where h has few zeros and poles, in the sense that
We will refer to the class of functions that satisfy (1.3) as
![]() $\mathcal {A}$
. In particular, we will consider the case
$\mathcal {A}$
. In particular, we will consider the case
![]() $h=e^g$
, where g is a nonconstant entire function. In Section 3, we discuss the case when h is small with respect to the solution f in the standard sense of
$h=e^g$
, where g is a nonconstant entire function. In Section 3, we discuss the case when h is small with respect to the solution f in the standard sense of
![]() $T(r,h)=S(r,f)$
. Indeed, we show that a large class of meromorphic functions cannot satisfy the equation
$T(r,h)=S(r,f)$
. Indeed, we show that a large class of meromorphic functions cannot satisfy the equation
where
![]() $p\geq 3$
and h has two Borel exceptional values.
$p\geq 3$
and h has two Borel exceptional values.
2. The case
 $h\in \mathcal {A}$
$h\in \mathcal {A}$
In this section, we consider (1.2) where p and q are distinct positive integers and h belongs to the class
![]() $\mathcal {A}$
. Note that all functions in
$\mathcal {A}$
. Note that all functions in
![]() $\mathcal {A}$
must be transcendental meromorphic functions. Then, we will examine the case
$\mathcal {A}$
must be transcendental meromorphic functions. Then, we will examine the case
![]() $h=e^P$
, with P a nonconstant entire function.
$h=e^P$
, with P a nonconstant entire function.
Before we proceed to state our main results, we require the following elementary lemma.
Lemma 2.1. Let
![]() $p,q$
be distinct positive integers and let h be a meromorphic function. If f is a meromorphic function with
$p,q$
be distinct positive integers and let h be a meromorphic function. If f is a meromorphic function with
![]() $\rho _{2}(f)<1$
that satisfies (1.2), then
$\rho _{2}(f)<1$
that satisfies (1.2), then
outside an exceptional set of finite logarithmic measure. In particular,
![]() $\rho _{2}(h)=\rho _{2}(f)$
.
$\rho _{2}(h)=\rho _{2}(f)$
.
Proof. Without loss of generality, we assume that
![]() $p>q$
. From [Reference Liu, Laine and Yang12, Lemma 1.2.10],
$p>q$
. From [Reference Liu, Laine and Yang12, Lemma 1.2.10],
and
outside an exceptional set of finite logarithmic measure. By a standard argument, see [Reference Gundersen4, Lemma 5], we may remove the exceptional set to obtain
![]() $\rho _{2}(h)=\rho _{2}(f)$
.
$\rho _{2}(h)=\rho _{2}(f)$
.
Now, we are ready to state our first result.
Theorem 2.2. Let
![]() $h \in \mathcal {A}$
and let
$h \in \mathcal {A}$
and let
![]() $p>q$
be positive integers. Then, (1.2) has no meromorphic solutions with
$p>q$
be positive integers. Then, (1.2) has no meromorphic solutions with
![]() $\rho _{2}(f) < 1$
except when
$\rho _{2}(f) < 1$
except when
![]() $p=2$
and
$p=2$
and
![]() $q=1$
. In this case, either:
$q=1$
. In this case, either:
-
(1)
 $f(z)=e^{\alpha z+\beta }-1$
, where
$f(z)=e^{\alpha z+\beta }-1$
, where
 $\alpha , \beta \in \mathbb {C}$
satisfy
$\alpha , \beta \in \mathbb {C}$
satisfy
 $e^{\alpha c}=2$
; or
$e^{\alpha c}=2$
; or -
(2)
 $T(r,f)= \overline {N}( r,1/f') +S(r,f).$
$T(r,f)= \overline {N}( r,1/f') +S(r,f).$
Remark 2.3. (a) According to [Reference Guo and Liu5, Remark 1.7], we observe that conclusion (1) of Theorem 2.2 might hold. In fact, an example such as
![]() $f(z) = e^{\alpha z} - 1$
solves the equation
$f(z) = e^{\alpha z} - 1$
solves the equation
where
![]() $\alpha $
is a nonzero constant satisfying
$\alpha $
is a nonzero constant satisfying
![]() $e^{\alpha c} = 2$
.
$e^{\alpha c} = 2$
.
(b) Theorem 2.2 includes the result given in [Reference Guo and Liu5, Theorem 1.6(iii)]. Indeed, it was shown there that the equation
where g is a nonconstant entire function, has no meromorphic solutions with
![]() $\rho _2(f) < 1$
satisfying
$\rho _2(f) < 1$
satisfying
![]() $N(r,1/f') = S(r,f)$
except functions f of the type
$N(r,1/f') = S(r,f)$
except functions f of the type
However, according to Theorem 2.2(2),
![]() $N(r,1/f') = S(r,f)$
implies
$N(r,1/f') = S(r,f)$
implies
![]() $T(r,f)=S(r,f)$
, which is impossible. Hence, (2.1) reduces to Theorem 2.2(1).
$T(r,f)=S(r,f)$
, which is impossible. Hence, (2.1) reduces to Theorem 2.2(1).
(c) To find a concrete example for the conclusion of Theorem 2.2(2) remains open at present. Note that if conclusion (2) holds, then for any
![]() $a\in \mathbb {C}$
, we have
$a\in \mathbb {C}$
, we have
![]() $\delta (a,f)=0$
. This can be deduced from the estimate
$\delta (a,f)=0$
. This can be deduced from the estimate
 $$ \begin{align*} m\bigg( r,\frac{1}{f-a}\bigg) &\leq m\bigg( r,\frac{1}{f'}\bigg) +S(r,f)\nonumber\\ &=T(r,f')-N\bigg( r,\frac{1}{f'}\bigg)+S(r,f) \nonumber\\ &\leq T(r,f)-N\bigg( r,\frac{1}{f'}\bigg)+S(r,f)=S(r,f).\nonumber \end{align*} $$
$$ \begin{align*} m\bigg( r,\frac{1}{f-a}\bigg) &\leq m\bigg( r,\frac{1}{f'}\bigg) +S(r,f)\nonumber\\ &=T(r,f')-N\bigg( r,\frac{1}{f'}\bigg)+S(r,f) \nonumber\\ &\leq T(r,f)-N\bigg( r,\frac{1}{f'}\bigg)+S(r,f)=S(r,f).\nonumber \end{align*} $$
Proof of Theorem 2.2.
Clearly, from Lemma 2.1, f must be a transcendental meromorphic function with
![]() $N(r,f)=S(r,f)$
. Differentiating (1.2) gives
$N(r,f)=S(r,f)$
. Differentiating (1.2) gives
 $$ \begin{align} f(z)^{p-1}\bigg( pf'(z)-\frac{h'(z)}{h(z)}f(z)\bigg) =- f(z+c)^{q-1}\bigg( qf'(z+c)-\frac{h'(z)}{h(z)}f(z+c)\bigg). \end{align} $$
$$ \begin{align} f(z)^{p-1}\bigg( pf'(z)-\frac{h'(z)}{h(z)}f(z)\bigg) =- f(z+c)^{q-1}\bigg( qf'(z+c)-\frac{h'(z)}{h(z)}f(z+c)\bigg). \end{align} $$
Denote
 $$ \begin{align} \varphi(z):=pf'(z)-\frac{h'(z)}{h(z)}f(z). \end{align} $$
$$ \begin{align} \varphi(z):=pf'(z)-\frac{h'(z)}{h(z)}f(z). \end{align} $$
Note that
This, along with
![]() $N(r,f)=S(r,f)$
, leads to
$N(r,f)=S(r,f)$
, leads to
![]() $N(r,\varphi )=S(r,f)$
.
$N(r,\varphi )=S(r,f)$
.
Since
![]() $p\geq q+1$
, we may recall the delay-difference variant of the Clunie lemma (see [Reference Laine and Yang10] and [Reference Liu, Laine and Yang12, page 20]) to obtain
$p\geq q+1$
, we may recall the delay-difference variant of the Clunie lemma (see [Reference Laine and Yang10] and [Reference Liu, Laine and Yang12, page 20]) to obtain
![]() $m(r,\varphi )=S(r,f)$
and hence
$m(r,\varphi )=S(r,f)$
and hence
![]() $T(r,\varphi )=S(r,f)$
.
$T(r,\varphi )=S(r,f)$
.
Suppose first that
![]() $\varphi \equiv 0$
. Then, by simple integration,
$\varphi \equiv 0$
. Then, by simple integration,
for some constant A. However, from (2.2),
 $$ \begin{align*} qf'(z+c)-\frac{h'(z)}{h(z)}f(z+c)\equiv 0, \end{align*} $$
$$ \begin{align*} qf'(z+c)-\frac{h'(z)}{h(z)}f(z+c)\equiv 0, \end{align*} $$
which in turn implies that
where B is a constant. Recalling again [Reference Liu, Laine and Yang12, Lemma 1.2.10], and combining (2.4) and (2.5),
which is a contradiction. Thus, we may now assume that
![]() $\varphi \not \equiv 0$
and (2.3) can be rewritten as
$\varphi \not \equiv 0$
and (2.3) can be rewritten as
 $$ \begin{align} \frac{1}{f(z)}=\frac{1}{\varphi(z)}\bigg( p\frac{f'(z)}{f(z)}-\frac{h'(z)}{h(z)}\bigg). \end{align} $$
$$ \begin{align} \frac{1}{f(z)}=\frac{1}{\varphi(z)}\bigg( p\frac{f'(z)}{f(z)}-\frac{h'(z)}{h(z)}\bigg). \end{align} $$
This implies
 $$ \begin{align*} T(r,f)=N\bigg(r,\frac{1}{f}\bigg) +S(r,f). \end{align*} $$
$$ \begin{align*} T(r,f)=N\bigg(r,\frac{1}{f}\bigg) +S(r,f). \end{align*} $$
Note that if
![]() $z_0$
is a multiple zero of f that is not a zero or pole of h, then
$z_0$
is a multiple zero of f that is not a zero or pole of h, then
![]() $z_0$
is a zero of
$z_0$
is a zero of
![]() $\varphi $
. Hence, the contribution of
$\varphi $
. Hence, the contribution of
![]() $N_{2)}(r,1/f)$
is
$N_{2)}(r,1/f)$
is
![]() $S(r,f)$
, and so
$S(r,f)$
, and so
 $$ \begin{align} T(r,f)=N_{1)}\bigg(r,\frac{1}{f}\bigg) +S(r,f). \end{align} $$
$$ \begin{align} T(r,f)=N_{1)}\bigg(r,\frac{1}{f}\bigg) +S(r,f). \end{align} $$
If
![]() $p\geq q+2$
, then we may write (2.2) as
$p\geq q+2$
, then we may write (2.2) as
 $$ \begin{align*} f(z)^{p-2}(f(z)\varphi(z))=- f(z+c)^{q-1}\bigg( qf'(z+c)-\frac{h'(z)}{h(z)}f(z+c)\bigg). \end{align*} $$
$$ \begin{align*} f(z)^{p-2}(f(z)\varphi(z))=- f(z+c)^{q-1}\bigg( qf'(z+c)-\frac{h'(z)}{h(z)}f(z+c)\bigg). \end{align*} $$
Applying again the delay-difference Clunie lemma to conclude that
we obtain
 $$ \begin{align*}T(r,f)=m\bigg( r,\frac{f\varphi}{\varphi} \bigg) \leq m(r,f\varphi )+T(r,\varphi )+O(1)=S(r,f),\end{align*} $$
$$ \begin{align*}T(r,f)=m\bigg( r,\frac{f\varphi}{\varphi} \bigg) \leq m(r,f\varphi )+T(r,\varphi )+O(1)=S(r,f),\end{align*} $$
which is a contradiction.
So, we must have
![]() $p=q+1$
. Since
$p=q+1$
. Since
![]() $h\in \mathcal {A}$
, we can write
$h\in \mathcal {A}$
, we can write
![]() $h=\pi e^{g}$
, where g is an entire function and
$h=\pi e^{g}$
, where g is an entire function and
![]() $\pi $
is a small function of h. Consequently,
$\pi $
is a small function of h. Consequently,
![]() $T(r,\pi )=S(r,f)$
. Therefore, (1.2) can be rewritten as
$T(r,\pi )=S(r,f)$
. Therefore, (1.2) can be rewritten as
where
![]() $F:=f/e^{g/p}$
and
$F:=f/e^{g/p}$
and
![]() $G:=f_c/e^{g/(p-1)},$
where
$G:=f_c/e^{g/(p-1)},$
where
![]() $f_c:=f(z+c)$
. To apply Theorem 1.1 to (2.8), we have to show that
$f_c:=f(z+c)$
. To apply Theorem 1.1 to (2.8), we have to show that
![]() $\pi $
is a small function of F and G. Indeed, from (2.7), we have
$\pi $
is a small function of F and G. Indeed, from (2.7), we have
![]() $ N(r,1/f) =~(1-~o(1))~T(r,f) $
outside of an exceptional set E of finite linear measure. Therefore, provided
$ N(r,1/f) =~(1-~o(1))~T(r,f) $
outside of an exceptional set E of finite linear measure. Therefore, provided
![]() $r\not \in E$
,
$r\not \in E$
,
 $$ \begin{align*} \frac{T(r,\pi)}{T(r,f/\exp (g/p))}&=\frac{T(r,\pi)}{T(r,\exp (g/p)/f)+O(1)} =(1+o(1))\frac{T(r,\pi)}{T(r,\exp (g/p)/f)}\\ &\leq (1+o(1))\frac{T(r,\pi)}{N(r,\exp (g/p)/f)} =(1+o(1))\frac{T(r,\pi)}{N(r,1/f)}\\ &=\frac{1+o(1)}{1-o(1)}\frac{T(r,\pi)}{T(r,f)}=o(1). \end{align*} $$
$$ \begin{align*} \frac{T(r,\pi)}{T(r,f/\exp (g/p))}&=\frac{T(r,\pi)}{T(r,\exp (g/p)/f)+O(1)} =(1+o(1))\frac{T(r,\pi)}{T(r,\exp (g/p)/f)}\\ &\leq (1+o(1))\frac{T(r,\pi)}{N(r,\exp (g/p)/f)} =(1+o(1))\frac{T(r,\pi)}{N(r,1/f)}\\ &=\frac{1+o(1)}{1-o(1)}\frac{T(r,\pi)}{T(r,f)}=o(1). \end{align*} $$
Recalling that
![]() $T(r,f_c)=T(r,f)+S(r,f)$
, we may use a similar reasoning to conclude that
$T(r,f_c)=T(r,f)+S(r,f)$
, we may use a similar reasoning to conclude that
![]() $\pi $
is a small function of
$\pi $
is a small function of
![]() $f_c/e^{g/(p-1)}$
as well.
$f_c/e^{g/(p-1)}$
as well.
In the remainder of the proof, we discuss cases according to the values of p.
Case 1. If
![]() $p\geq 4$
, then according to Theorem 1.1, (2.8) admits only constant solutions. Therefore,
$p\geq 4$
, then according to Theorem 1.1, (2.8) admits only constant solutions. Therefore,
where
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
are constants that satisfy
$\beta $
are constants that satisfy
![]() $\alpha ^p+\beta ^{p-1}=\pi $
. Now,
$\alpha ^p+\beta ^{p-1}=\pi $
. Now,
which means that
![]() $(p-1)g_c-pg$
is a constant. If g is a polynomial, then it must be a constant, which contradicts the fact that
$(p-1)g_c-pg$
is a constant. If g is a polynomial, then it must be a constant, which contradicts the fact that
![]() $h=\pi e^g$
is transcendental. If g is not a polynomial, then it satisfies the equation
$h=\pi e^g$
is transcendental. If g is not a polynomial, then it satisfies the equation
 $$ \begin{align*} \frac{g'(z+c)}{g'(z)}=\frac{p}{p-1}, \end{align*} $$
$$ \begin{align*} \frac{g'(z+c)}{g'(z)}=\frac{p}{p-1}, \end{align*} $$
and by using [Reference Bergweiler and Langley1, Lemma 3.3], we deduce that
![]() $\rho (g)\geq 1$
. Therefore,
$\rho (g)\geq 1$
. Therefore,
![]() $\rho _{2}(f)=\rho _{2}(h)\geq 1,$
which is again a contradiction.
$\rho _{2}(f)=\rho _{2}(h)\geq 1,$
which is again a contradiction.
Case 2. If
![]() $p=3$
, then by recalling that
$p=3$
, then by recalling that
![]() $N(r,F)=N(r,G)=N(r,f)=S(r,f)$
, we can infer that
$N(r,F)=N(r,G)=N(r,f)=S(r,f)$
, we can infer that
Hence, by applying Theorem 1.1 again, we conclude that (1.2) has solutions only in the form of (2.9) with
![]() $\alpha ^3+\beta ^2=\pi $
. Similar reasoning as in the case
$\alpha ^3+\beta ^2=\pi $
. Similar reasoning as in the case
![]() $p\geq 4$
leads to a contradictory conclusion
$p\geq 4$
leads to a contradictory conclusion
![]() $\rho _{2}(f)\geq 1$
.
$\rho _{2}(f)\geq 1$
.
Case 3. Assume now that
![]() $p=2$
(implying that we also have
$p=2$
(implying that we also have
![]() $q=1$
). Recall that the auxiliary function
$q=1$
). Recall that the auxiliary function
![]() $\varphi \not \equiv 0$
takes the form
$\varphi \not \equiv 0$
takes the form
 $$ \begin{align} \varphi(z):=2f'(z)-\frac{h'(z)}{h(z)}f(z). \end{align} $$
$$ \begin{align} \varphi(z):=2f'(z)-\frac{h'(z)}{h(z)}f(z). \end{align} $$
Taking the first derivative of
![]() $\varphi $
yields
$\varphi $
yields
 $$ \begin{align*} \varphi'(z)=2f"(z)-\frac{h'(z)}{h(z)}f'(z)-\bigg( \frac{h'(z)}{h(z)}\bigg) 'f(z)=\frac{\varphi'(z)}{\varphi(z)}\bigg(2f'(z)-\frac{h'(z)}{h(z)}f(z) \bigg), \end{align*} $$
$$ \begin{align*} \varphi'(z)=2f"(z)-\frac{h'(z)}{h(z)}f'(z)-\bigg( \frac{h'(z)}{h(z)}\bigg) 'f(z)=\frac{\varphi'(z)}{\varphi(z)}\bigg(2f'(z)-\frac{h'(z)}{h(z)}f(z) \bigg), \end{align*} $$
which can be expressed as
where
 $$ \begin{align*} A(z):=2\frac{f"(z)}{f'(z)}-\frac{h'(z)}{h(z)}-2\frac{\varphi'(z)}{\varphi(z)} \quad \text{and}\quad B(z):=\frac{\varphi'(z)}{\varphi(z)}\frac{h'(z)}{h(z)}-\bigg( \frac{h'(z)}{h(z)}\bigg)'. \end{align*} $$
$$ \begin{align*} A(z):=2\frac{f"(z)}{f'(z)}-\frac{h'(z)}{h(z)}-2\frac{\varphi'(z)}{\varphi(z)} \quad \text{and}\quad B(z):=\frac{\varphi'(z)}{\varphi(z)}\frac{h'(z)}{h(z)}-\bigg( \frac{h'(z)}{h(z)}\bigg)'. \end{align*} $$
Since f mainly has simple zeros, assume that
![]() $z_0$
is a simple zero of f that is neither a zero nor a pole of h. Consequently,
$z_0$
is a simple zero of f that is neither a zero nor a pole of h. Consequently,
![]() $z_0$
is not a zero of
$z_0$
is not a zero of
![]() $\varphi $
and so not a pole of B. Thus,
$\varphi $
and so not a pole of B. Thus,
![]() $z_0$
is a zero of A. Now, define the function
$z_0$
is a zero of A. Now, define the function
 $$ \begin{align*} \psi(z):=\frac{A(z)}{f(z)}. \end{align*} $$
$$ \begin{align*} \psi(z):=\frac{A(z)}{f(z)}. \end{align*} $$
Based on the preceding discussion, we can deduce that
![]() $N(r, \psi ) = \overline {N}(r,1/f') + S(r, f)$
. Combining this with the fact that
$N(r, \psi ) = \overline {N}(r,1/f') + S(r, f)$
. Combining this with the fact that
![]() $m(r,1/f) = S(r,f)$
(see (2.6)), we conclude that
$m(r,1/f) = S(r,f)$
(see (2.6)), we conclude that
 $$ \begin{align*}T(r,\psi)=\overline{N}\bigg( r,\frac{1}{f'}\bigg) +S(r,f).\end{align*} $$
$$ \begin{align*}T(r,\psi)=\overline{N}\bigg( r,\frac{1}{f'}\bigg) +S(r,f).\end{align*} $$
Note that, according to [Reference Yang and Yi17, Theorem 1.24],
 $$ \begin{align*} N\bigg(r, \frac{1}{f'}\bigg) \leq N\bigg(r, \frac{1}{f}\bigg)+ \overline{N}(r, f)+S(r, f)= N_{1)}\bigg( r,\frac{1}{f}\bigg) +S(r, f). \end{align*} $$
$$ \begin{align*} N\bigg(r, \frac{1}{f'}\bigg) \leq N\bigg(r, \frac{1}{f}\bigg)+ \overline{N}(r, f)+S(r, f)= N_{1)}\bigg( r,\frac{1}{f}\bigg) +S(r, f). \end{align*} $$
Assume first that
![]() $\psi \not \equiv 0$
. Then,
$\psi \not \equiv 0$
. Then,
 $$ \begin{align*} T(r,f)=m(r,f)+S(r,f)&=m\bigg( r,\frac{A}{\psi}\bigg)+S(r,f)\nonumber\\ &\leq T\bigg( r,\frac{1}{\psi}\bigg) -N\bigg( r,\frac{1}{\psi}\bigg) +S(r,f)\nonumber\\ &=\overline{N}\bigg( r,\frac{1}{f'}\bigg) -N\bigg( r,\frac{1}{\psi}\bigg) +S(r,f)\nonumber\\ &\leq N_{1)}\bigg( r,\frac{1}{f}\bigg) -N\bigg( r,\frac{1}{\psi}\bigg) +S(r,f).\nonumber \end{align*} $$
$$ \begin{align*} T(r,f)=m(r,f)+S(r,f)&=m\bigg( r,\frac{A}{\psi}\bigg)+S(r,f)\nonumber\\ &\leq T\bigg( r,\frac{1}{\psi}\bigg) -N\bigg( r,\frac{1}{\psi}\bigg) +S(r,f)\nonumber\\ &=\overline{N}\bigg( r,\frac{1}{f'}\bigg) -N\bigg( r,\frac{1}{\psi}\bigg) +S(r,f)\nonumber\\ &\leq N_{1)}\bigg( r,\frac{1}{f}\bigg) -N\bigg( r,\frac{1}{\psi}\bigg) +S(r,f).\nonumber \end{align*} $$
Combining this with (2.7) yields
![]() $N(r,1/\psi )=S(r,f)$
, that is,
$N(r,1/\psi )=S(r,f)$
, that is,
 $$ \begin{align*} T(r,f)= \overline{N}\bigg( r,\frac{1}{f'}\bigg) +S(r,f). \end{align*} $$
$$ \begin{align*} T(r,f)= \overline{N}\bigg( r,\frac{1}{f'}\bigg) +S(r,f). \end{align*} $$
Consider now the case
![]() $\psi \equiv 0$
. This implies that both
$\psi \equiv 0$
. This implies that both
![]() $A \equiv 0$
and
$A \equiv 0$
and
![]() $B \equiv 0$
. To proceed, we distinguish two possible sub-cases.
$B \equiv 0$
. To proceed, we distinguish two possible sub-cases.
Subcase (i). If
![]() $\varphi $
is not constant, then straightforward integration of the equations
$\varphi $
is not constant, then straightforward integration of the equations
![]() $A \equiv 0$
and
$A \equiv 0$
and
![]() $B \equiv 0$
yields
$B \equiv 0$
yields
and
 $$ \begin{align} \varphi(z)=C_2\frac{h'(z)}{h(z)}, \end{align} $$
$$ \begin{align} \varphi(z)=C_2\frac{h'(z)}{h(z)}, \end{align} $$
where
![]() $C_1$
and
$C_1$
and
![]() $C_2$
are nonzero constants. Substituting (2.12) into (2.10) and integrating the result yields
$C_2$
are nonzero constants. Substituting (2.12) into (2.10) and integrating the result yields
where
![]() $C_3$
is a nonzero constant. Combining (2.11), (2.12) and (2.13) results in
$C_3$
is a nonzero constant. Combining (2.11), (2.12) and (2.13) results in
 $$ \begin{align*} \frac{ f'(z)}{f(z)+C_2}=C_4\frac{h'(z)}{h(z)}, \end{align*} $$
$$ \begin{align*} \frac{ f'(z)}{f(z)+C_2}=C_4\frac{h'(z)}{h(z)}, \end{align*} $$
where
![]() $C_4$
is a nonzero constant. By simple integration,
$C_4$
is a nonzero constant. By simple integration,
This, together with (2.13) results in a contradiction.
Now assume that
![]() $\varphi $
is a nonzero constant. Keeping in mind that
$\varphi $
is a nonzero constant. Keeping in mind that
![]() $A\equiv 0$
and
$A\equiv 0$
and
![]() $B\equiv 0$
, we find
$B\equiv 0$
, we find
![]() $h'/h$
is a constant, say
$h'/h$
is a constant, say
![]() $h'/h\equiv 2\alpha $
. This results in
$h'/h\equiv 2\alpha $
. This results in
![]() $h\equiv C_{h}e^{2\alpha z},$
with
$h\equiv C_{h}e^{2\alpha z},$
with
![]() $C_{h}$
being a constant. Since
$C_{h}$
being a constant. Since
![]() $2{f"}/{f'}\equiv {h'}/{h}$
, by elementary integration,
$2{f"}/{f'}\equiv {h'}/{h}$
, by elementary integration,
This means that
![]() $f'\equiv C_{7}e^{\alpha z}$
and so, by integration, f must be of the form
$f'\equiv C_{7}e^{\alpha z}$
and so, by integration, f must be of the form
![]() $e^{\alpha z+\beta }+\gamma ,$
with constants
$e^{\alpha z+\beta }+\gamma ,$
with constants
![]() $\beta , \gamma $
. Substituting this into (1.2),
$\beta , \gamma $
. Substituting this into (1.2),
Clearly, the constant term
![]() $\gamma ^{2}+\gamma $
must vanish; thus,
$\gamma ^{2}+\gamma $
must vanish; thus,
![]() $\gamma = 0$
or
$\gamma = 0$
or
![]() $\gamma = -1$
. However,
$\gamma = -1$
. However,
![]() $\gamma \neq 0$
, as it would contradict (2.7). Therefore, the only possibility is
$\gamma \neq 0$
, as it would contradict (2.7). Therefore, the only possibility is
![]() $\gamma = -1$
, leading to
$\gamma = -1$
, leading to
This may happen if
![]() $e^{\alpha c}=2$
and
$e^{\alpha c}=2$
and
![]() $C_{h}=e^{2\beta }$
, thereby completing the proof.
$C_{h}=e^{2\beta }$
, thereby completing the proof.
We close this section by considering the equation
where g is a nonconstant entire function and
![]() $p, q$
are positive integers that are not necessarily distinct. The following corollary improves [Reference Guo and Liu5, Theorem 1.6(iv)].
$p, q$
are positive integers that are not necessarily distinct. The following corollary improves [Reference Guo and Liu5, Theorem 1.6(iv)].
Corollary 2.4. Let g be a nonconstant entire function and let
![]() $p,q\geq 3$
be integers. Then:
$p,q\geq 3$
be integers. Then:
Proof. Assertion (1) immediately follows from Theorem 2.2.
As for assertion (2), if
![]() $p=q\geq 4$
, we may write (2.14) as
$p=q\geq 4$
, we may write (2.14) as
By applying Theorem 1.1, we obtain
![]() $ f(z) = \alpha e^{g(z)/p}$
and
$ f(z) = \alpha e^{g(z)/p}$
and
![]() $f(z+c) = \beta e^{g(z)/p}$
, where
$f(z+c) = \beta e^{g(z)/p}$
, where
![]() ${\alpha ^p + \beta ^p = 1}$
. A reasoning similar to Case 1 in the proof of Theorem 2.2 leads to the conclusion that f takes the form
${\alpha ^p + \beta ^p = 1}$
. A reasoning similar to Case 1 in the proof of Theorem 2.2 leads to the conclusion that f takes the form
 $$ \begin{align*}f(z)=\alpha \exp\bigg( \frac{az+b}{p}\bigg),\end{align*} $$
$$ \begin{align*}f(z)=\alpha \exp\bigg( \frac{az+b}{p}\bigg),\end{align*} $$
where
![]() $\alpha $
is a nonzero constant satisfying the condition
$\alpha $
is a nonzero constant satisfying the condition
![]() $\alpha ^p(1 + e^{ac}) = 1$
. This representation corresponds to a trivial solution.
$\alpha ^p(1 + e^{ac}) = 1$
. This representation corresponds to a trivial solution.
Finally, we assume that
![]() $p=q=3$
. Then (2.14) can be written as follows:
$p=q=3$
. Then (2.14) can be written as follows:
where
By making use of [Reference Liu, Laine and Yang12, Lemma 1.2.10],
possibly outside an exceptional set of finite logarithmic measure
![]() $E_1$
and, moreover,
$E_1$
and, moreover,
![]() $\rho _{2}(e^g)=\delta <1$
. Note that [Reference Halburd, Korhonen and Tohge6, Theorem 5.1] yields
$\rho _{2}(e^g)=\delta <1$
. Note that [Reference Halburd, Korhonen and Tohge6, Theorem 5.1] yields
 $$ \begin{align*} T(r,\beta)=m\bigg( r,\frac{e^{g(z+c)}}{e^{g(z)}}\bigg) =o\bigg( \frac{T(r,e^g)}{r^{1-\delta-\varepsilon}}\bigg) \end{align*} $$
$$ \begin{align*} T(r,\beta)=m\bigg( r,\frac{e^{g(z+c)}}{e^{g(z)}}\bigg) =o\bigg( \frac{T(r,e^g)}{r^{1-\delta-\varepsilon}}\bigg) \end{align*} $$
for all r outside an exceptional set of finite logarithmic measure
![]() $E_2$
. Combining these inequalities yields, for all
$E_2$
. Combining these inequalities yields, for all
![]() $r\not \in E_1 \cup E_2$
,
$r\not \in E_1 \cup E_2$
,
 $$ \begin{align*} \frac{T(r,\beta)}{T(r,f)} \leq (3+o(1))\frac{T(r,\beta)}{T(r,e^g)}=o\bigg( \frac{1}{r^{1-\delta-\varepsilon}}\bigg), \end{align*} $$
$$ \begin{align*} \frac{T(r,\beta)}{T(r,f)} \leq (3+o(1))\frac{T(r,\beta)}{T(r,e^g)}=o\bigg( \frac{1}{r^{1-\delta-\varepsilon}}\bigg), \end{align*} $$
implying
![]() $T(r,\beta )=S(r,f)$
. Consequently, following the same proof as in Case (iv) of [Reference Guo and Liu5, Theorem 1.6], we conclude that
$T(r,\beta )=S(r,f)$
. Consequently, following the same proof as in Case (iv) of [Reference Guo and Liu5, Theorem 1.6], we conclude that
![]() $\beta $
is a constant and
$\beta $
is a constant and
![]() $f = Ae^{g/3}$
with
$f = Ae^{g/3}$
with
![]() $A^3 = 1$
, constituting a trivial solution.
$A^3 = 1$
, constituting a trivial solution.
3. The case
 $h\in \mathcal {S}(f)$
$h\in \mathcal {S}(f)$
In this section, we discuss the existence of solutions to (1.2), where h is a small meromorphic function in the standard sense of
![]() $T(r,h)=S(r,f)$
. For clarity, we first present the following proposition which discusses the existence of nonconstant meromorphic solutions to (1.2) when p and q are distinct integers.
$T(r,h)=S(r,f)$
. For clarity, we first present the following proposition which discusses the existence of nonconstant meromorphic solutions to (1.2) when p and q are distinct integers.
Proposition 3.1. Let f be a meromorphic function and let
![]() $h\in \mathcal {S}(f)$
.
$h\in \mathcal {S}(f)$
.
Proof. The cases (1) and (2) can be deduced easily from Theorem 1.1. Suppose now that
![]() $p>q\geq 1$
and f is a solution to (1.2) with
$p>q\geq 1$
and f is a solution to (1.2) with
![]() $\rho _{2}(f)<1$
. We may write (1.2) in the form
$\rho _{2}(f)<1$
. We may write (1.2) in the form
 $$ \begin{align*}f(z)^{p}+\bigg(\frac{f(z+c)}{f(z)}\bigg)^{q}f(z)^{q}=h (z). \end{align*} $$
$$ \begin{align*}f(z)^{p}+\bigg(\frac{f(z+c)}{f(z)}\bigg)^{q}f(z)^{q}=h (z). \end{align*} $$
By [Reference Halburd, Korhonen and Tohge6, Theorem 5.1] (see also [Reference Liu, Laine and Yang12, Lemma 1.2.8]), we conclude that
and so
![]() $m(r,f)=S(r,f)$
. However, we can apply [Reference Halburd, Korhonen and Tohge6, Lemma 8.3] (see also [Reference Liu, Laine and Yang12, Lemma 1.2.10]) to (1.2). This yields
$m(r,f)=S(r,f)$
. However, we can apply [Reference Halburd, Korhonen and Tohge6, Lemma 8.3] (see also [Reference Liu, Laine and Yang12, Lemma 1.2.10]) to (1.2). This yields
thus implying
![]() $N(r,f) = S(r,f)$
. Consequently,
$N(r,f) = S(r,f)$
. Consequently,
![]() $T(r,f) = S(r,f)$
, which is a contradiction.
$T(r,f) = S(r,f)$
, which is a contradiction.
Next, we consider the case where
![]() $p=q\geq 3$
in (1.2). In fact, referring to Theorem 1.1, it becomes evident that no nonconstant meromorphic solutions exist to (1.2) when
$p=q\geq 3$
in (1.2). In fact, referring to Theorem 1.1, it becomes evident that no nonconstant meromorphic solutions exist to (1.2) when
![]() $p=q>3$
. By combining this result with [Reference Bi and Lü2, Theorem 2], we can immediately deduce the following corollary.
$p=q>3$
. By combining this result with [Reference Bi and Lü2, Theorem 2], we can immediately deduce the following corollary.
Corollary 3.2. Let f be a meromorphic function of hyper-order
![]() $\rho _{2}(f)<1$
, and let
$\rho _{2}(f)<1$
, and let
![]() $h\in \mathcal {S}(f)$
with two Borel exceptional values
$h\in \mathcal {S}(f)$
with two Borel exceptional values
![]() $0$
and
$0$
and
![]() $\infty .$
Then f does not satisfy (1.4) provided
$\infty .$
Then f does not satisfy (1.4) provided
![]() $p\geq 3$
.
$p\geq 3$
.
Motivated by this, it is natural to ask whether this phenomenon remains valid when considering
![]() $h \in \mathcal {S}(f)$
with two Borel exceptional values
$h \in \mathcal {S}(f)$
with two Borel exceptional values
![]() $d \neq 0$
and
$d \neq 0$
and
![]() $\infty $
.
$\infty $
.
Unfortunately, we could not give a positive answer to this question. However, the following proposition illustrates that such an assumption prevents the existence of a large class of meromorphic functions. In particular, it shows that any meromorphic solution to (1.4) must be periodic and cannot possess any Borel exceptional value.
Proposition 3.3. Let f be a meromorphic function of hyper-order
![]() $\rho _{2}(f)<1$
, and let
$\rho _{2}(f)<1$
, and let
![]() $h\in \mathcal {S}(f)$
with two Borel exceptional values
$h\in \mathcal {S}(f)$
with two Borel exceptional values
![]() $d\in \mathbb {C}$
and
$d\in \mathbb {C}$
and
![]() $\infty $
. If f satisfies (1.4), then
$\infty $
. If f satisfies (1.4), then
![]() $p=3$
and the following assertions hold:
$p=3$
and the following assertions hold:
-
(1)
 $h=e^{az+b}+d$
, where
$h=e^{az+b}+d$
, where
 $a,b$
are constants with
$a,b$
are constants with
 $e^{ac}=1$
and
$e^{ac}=1$
and
 $d\neq 0$
;
$d\neq 0$
; -
(2) f is periodic and satisfies the equation
where $$ \begin{align*} f(z)^3=\pi(z)\exp\bigg( \frac{\log(-1)}{c}z\bigg) +\frac{1}{2}( e^{az+b}+d) , \end{align*} $$
$$ \begin{align*} f(z)^3=\pi(z)\exp\bigg( \frac{\log(-1)}{c}z\bigg) +\frac{1}{2}( e^{az+b}+d) , \end{align*} $$
 $\pi $
is a c-periodic meromorphic function such that where E is an exceptional set of finite linear measure;
$\pi $
is a c-periodic meromorphic function such that where E is an exceptional set of finite linear measure; $$ \begin{align*}\lim\limits_{\substack{r\to \infty\\ r\not\in E}}\frac{T(r,\pi)}{r}=\infty,\end{align*} $$
$$ \begin{align*}\lim\limits_{\substack{r\to \infty\\ r\not\in E}}\frac{T(r,\pi)}{r}=\infty,\end{align*} $$
-
(3)
 $T(r,f)=\overline {N}(r,f)+S(r,f)$
;
$T(r,f)=\overline {N}(r,f)+S(r,f)$
; -
(4)
 $T(r,f)=\overline {N}(r,1/f)+S(r,f)$
. In addition, for any
$T(r,f)=\overline {N}(r,1/f)+S(r,f)$
. In addition, for any
 $\alpha \in \mathcal {S}(f)$
that does not satisfy (1.4),
$\alpha \in \mathcal {S}(f)$
that does not satisfy (1.4),  $$ \begin{align*} T(r,f)=N\bigg( r,\frac{1}{f-\alpha}\bigg) +S(r,f). \end{align*} $$
$$ \begin{align*} T(r,f)=N\bigg( r,\frac{1}{f-\alpha}\bigg) +S(r,f). \end{align*} $$
Proof of Proposition 3.3.
Assuming the existence of a meromorphic function f that satisfies (1.4), we infer from Theorem 1.1 and [Reference Bi and Lü2, Theorem 2] that
![]() $p=3$
and
$p=3$
and
![]() $d\neq 0$
.
$d\neq 0$
.
Following the reasoning in the beginning of the proof of [Reference Bi and Lü2, Theorem 2] (see [Reference Bi and Lü2, page 6]), we conclude that h is periodic with period c and, consequently,
![]() $f^3$
is periodic with period
$f^3$
is periodic with period
![]() $2c$
. Now, recall that h has two Borel exceptional values
$2c$
. Now, recall that h has two Borel exceptional values
![]() $d\neq 0$
and
$d\neq 0$
and
![]() $\infty $
. Then we have the representation
$\infty $
. Then we have the representation
where P is an entire function,
![]() $\pi $
a meromorphic function of finite order and
$\pi $
a meromorphic function of finite order and
Making use of the periodicity of h and [Reference Zemirni, Laine and Latreuch18, Proposition 3.1], we see that P must be a polynomial. If
![]() $\deg P\geq 2$
, then by [Reference Zemirni, Laine and Latreuch18, Proposition 3.1], we have
$\deg P\geq 2$
, then by [Reference Zemirni, Laine and Latreuch18, Proposition 3.1], we have
![]() $\rho (\pi )\geq \deg P$
. However,
$\rho (\pi )\geq \deg P$
. However,
which is a contradiction. Hence,
![]() $\deg P=1$
and
$\deg P=1$
and
![]() $\pi $
has an order less than one. Using [Reference Zemirni, Laine and Latreuch18, Remark 3.1], we observe that
$\pi $
has an order less than one. Using [Reference Zemirni, Laine and Latreuch18, Remark 3.1], we observe that
![]() $\pi $
is a constant. Therefore,
$\pi $
is a constant. Therefore,
![]() $h\equiv e^{az+b}+d,$
where
$h\equiv e^{az+b}+d,$
where
![]() $a,b$
are constants with
$a,b$
are constants with
![]() $e^{ac}=1$
. This proves assertion (1).
$e^{ac}=1$
. This proves assertion (1).
Now, noting that
![]() $\tfrac 12h$
is a particular solution to the difference equation
$\tfrac 12h$
is a particular solution to the difference equation
and making use of the theory of difference equations in the complex domain [Reference Meschkowski15, Ch. 7], we deduce that the general solution to (3.1) takes the form
where
![]() $\pi $
is a c-periodic meromorphic function. Therefore, assertion (2) follows by considering
$\pi $
is a c-periodic meromorphic function. Therefore, assertion (2) follows by considering
![]() $g=f^3$
and
$g=f^3$
and
![]() $h\equiv e^{az+b}+d$
.
$h\equiv e^{az+b}+d$
.
Next, since
![]() $h\in \mathcal {S}(f)$
, according to [Reference Li, Sabadini and Struppa11, Lemma 1], we derive assertion (3). Additionally, by employing Nevanlinna’s second main theorem,
$h\in \mathcal {S}(f)$
, according to [Reference Li, Sabadini and Struppa11, Lemma 1], we derive assertion (3). Additionally, by employing Nevanlinna’s second main theorem,
 $$ \begin{align*} T(r,f^3)&\leq \overline{N}(r,f^3)+\overline{N}\bigg( r,\frac{1}{f^3}\bigg) + \overline{N}\bigg( r,\frac{1}{f^3-h}\bigg) +S(r,f)\nonumber\\ &\leq 2T(r,f)+\overline{N}\bigg( r,\frac{1}{f_c^3}\bigg)+S(r,f).\nonumber \end{align*} $$
$$ \begin{align*} T(r,f^3)&\leq \overline{N}(r,f^3)+\overline{N}\bigg( r,\frac{1}{f^3}\bigg) + \overline{N}\bigg( r,\frac{1}{f^3-h}\bigg) +S(r,f)\nonumber\\ &\leq 2T(r,f)+\overline{N}\bigg( r,\frac{1}{f_c^3}\bigg)+S(r,f).\nonumber \end{align*} $$
From this and [Reference Liu, Laine and Yang12, Lemma 1.2.10], we conclude the first part of assertion (4). The last part of assertion (4) is a direct consequence of [Reference Laine and Latreuch9, Lemma 2.2].
Acknowledgement
The authors are grateful to the referees for their valuable comments and suggestions.