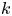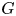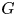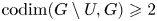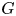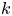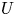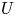1. Introduction
1.1 Background
Algebraic varieties over global fields whose set of rational points is dense in the adelic space with respect to the adelic topology are said to verify strong approximation (cf. [Reference WittenbergWit18, Definition 2.9]). As from the definition of adelic spaces (cf. e.g. [Reference ConradCon12]), the study of strong approximation naturally involves integral points. They are generally believed to be more intricate to tackle than rational points, regarding our present knowledge, and it seems that more evidence is needed to formulate satisfactory conjectures. For affine varieties, the adelic topology is in general finer than the product topology of local points. The density of rational points in the latter is referred to weak approximation, and these two topologies agree if the ambient variety is proper. If the topology is ‘too’ fine, then it can happen that strong approximation fails even for the simplest examples like 
${\mathbb {A}}^1$, since number fields are diagonally embedded in their adeles as closed discrete lattices. One needs to modify the topology via ‘forgetting’ a finite number of places, say 
$S$, i.e. to consider the topology induced by adelic points without 
$S$ components, in which we refer to the property strong approximation off 
$S$ (cf. Definition 1.3(1)).
Algebraic groups were the first class of varieties for which strong approximation was systematically investigated. It is Eichler [Reference EichlerEic38] who pioneered this study for some classical groups. Since the 1960s, several authors established that semisimple simply connected algebraic groups verify strong approximation. The number field case is mainly due to Kneser [Reference KneserKne65] and Platonov [Reference PlatonovPla69] (cf. [Reference Platonov and RapinchukPR94, Theorem 7.12]).
Theorem 1.1 (Kneser–Platonov) A non-trivial semisimple simply connected group 
$G$ over a number field 
$k$ satisfies strong approximation off 
$S$, a finite subset of places of 
$k$, if and only if 
$G^\prime (k_S):=\prod _{v\in S} G^\prime (k_v)$ is not compact for every 
$k$-simple factor 
$G^\prime$ of 
$G$.
The above non-compactness condition on 
$G^\prime$ is equivalent to the existence of a place 
$v\in S$ such that 
$G^\prime (k_v)$ is not compact. We refer to [Reference Platonov and RapinchukPR94, Chapter 7] for further details and references.
It is a natural problem to study how these density properties vary under birational modifications. First of all, by an ultrametric version of the implicit function theorem (cf. [Reference SerreSer92, Lemma 3.5.5] and [Reference Platonov and RapinchukPR94, § 3.1]), the weak approximation property is a birational invariant amongst smooth varieties. However, for strong approximation off any finite number of places, this is not true any more even for 
${\mathbb {A}}^1$, as it fails already for 
${\mathbb {G}}_{\operatorname {m}}$. Moreover, being geometrically simply connected is a necessary condition in order for varieties over number fields to verify strong approximation, as was first pointed out by Minčhev [Reference MinčhevMin89, Theorem 1] (see also [Reference PoonenPoo17, § 8.4.6]). On the other hand, consider the variety 
${\mathbb {A}}^1\times {\mathbb {G}}_{\operatorname {m}}$ over 
${\mathbb {Q}}$. This variety does not satisfy strong approximation off 
${\mathbb {R}}$, but this failure is explained by the Brauer–Manin obstruction, thanks to the Poitou–Tate duality (cf. [Reference HarariHar08, § 1.2]). However, Xu and the first author proved that the defect of strong approximation off 
${\mathbb {R}}$ for the variety 
${\mathbb {A}}^1\times {\mathbb {G}}_{\operatorname {m}}\setminus \{(0,1)\}$ cannot be explained by any étale Brauer–Manin obstruction (cf. [Reference Cao and XuCX18, Example 5.2]). See [Reference WittenbergWit18, § 2.7] for more examples. All these phenomena suggest that the behaviour of integral points can be sensitive to removing closed subsets, while Brauer groups are insensitive to removing subschemes of codimension two (the purity of Brauer groups, cf. [Reference GrothendieckGro68, § 6]).
In a reverse direction, if a smooth variety verifies strong approximation (when there is no Brauer–Manin obstruction), one expects that any other smooth variety differing by a closed subvariety of codimension at least two inherits this property. The following question has been raised first by Wittenberg at the AIM workshop ‘Rational and integral points on higher-dimensional varieties’ in 2014 (cf. [AIM14, Problem 6]) and also by Colliot-Thélène and Xu, respectively, on different occasions. See also [Reference WittenbergWit18, § 2.7 and Question 2.11] and [Reference Cao, Liang and XuCLX19, Question 1.2].
Question 1.2 Let 
$X$ be a smooth variety over a number field which satisfies strong approximation off a finite set of places 
$S$. Does any Zariski open subset 
$U$ of 
$X$ also satisfy this property, whenever 
${\mathrm {codim}}(X\setminus U,X)\geqslant 2$?
Following [Reference Cao, Liang and XuCLX19, p. 336], we shall say that such 
$X$ verifies the arithmetic purity of strong approximation off 
$S$ (Definition 1.3(2)). One piece of evidence towards a positive answer to Question 1.2 is supported by the purity of branch locus due to Zariski, Nagata and Grothendieck (cf. [Reference SzamuelySza09, Theorem 5.2.13 and Corollary 5.2.14]), which states that the algebraic fundamental group is insensitive to removing codimension two subschemes. So a positive answer to Question 1.2 is compatible with Minčhev's observation.
Let us summarize the state of the art in the literature. Wei [Reference WeiWei14, Lemma 1.1] and, independently, Xu and the first author [Reference Cao and XuCX18, Proposition 3.6] proved that Question 1.2 has a positive answer for the affine space 
${\mathbb {A}}^n$. This result was applied to show [Reference Cao and XuCX18, Theorem 1.2] that strong approximation with Brauer–Manin obstruction holds for toric varieties, and afterwards, it was generalized by Liang, Xu and the first author [Reference Cao, Liang and XuCLX19, Theorem 1.1], who answered Question 1.2 in the affirmative for semisimple simply connected linear algebraic groups that are quasi-split. They also made an important reduction [Reference Cao, Liang and XuCLX19, Theorem 1.3]: a positive answer to Question 1.2 for general semisimple simply connected linear algebraic groups implies the arithmetic purity of strong approximation with Brauer–Manin obstruction for their homogeneous spaces with connected stabilizers and no non-constant invertible regular functions.
Motivated by this progress, the objective of this paper is to give further positive evidence towards Question 1.2 as a continuation of the above investigations. More precisely, we give a positive answer to Question 1.2 for semisimple simply connected almost simple linear algebraic groups which are isotropic, and for spin groups of any non-degenerate quadratic forms with more than three variables, when 
$S$ is the set of all archimedean places.
1.2 Notation and terminology
In this article, the letter 
$k$ denotes a number field unless otherwise specified. We fix an algebraic closure 
$\bar {k}$ of 
$k$. We denote by 
$\Omega _{k}$ the set of non-trivial places of 
$k$ and denote by 
$\infty _{k}$ the set of archimedean places. For each place 
$v\in \Omega _{k}$, 
$k_{v}$ denotes the completion of 
$k$. We denote by 
${\mathcal {O}}_k$ (respectively 
${\mathcal {O}}_{v}$) the ring of integers of 
$k$ (respectively 
$k_v$ for 
$v\in \Omega _{k}\setminus \infty _{k}$). The ring of adeles of 
$k$ is denoted by 
${\mathbf {A}}_{k}$. For any finite subset 
$S$ of 
$\Omega _k$, the ring of 
$S\cup \infty _{k}$-integers of 
$k$ is denoted by 
${\mathcal {O}}_{k,S}$. The ring of adeles without 
$S$-components is denoted by 
${\mathbf {A}}_{k}^{S}$.
A variety over 
$k$ is a separated scheme of finite type over 
$k$. For 
$X$ a 
$k$-variety, the set of 
$k$-rational points 
$X(k)$ embeds diagonally into 
$X({\mathbf {A}}_{k})$, and we denote by 
$\operatorname {pr}^S:X({\mathbf {A}}_{k})\to X({\mathbf {A}}_{k}^{S})$ the natural projection between sets of adelic points of 
$X$. We define 
$X(k_S):=\prod _{v\in S}X(k_v)$. When 
$S=\infty _{k}$ we write 
$k_S=k_\infty$ for simplicity. For each 
$x\in X$ (respectively 
$v\in \Omega _{k}$), 
$k(x)$ (respectively 
$k(v)$) denotes its residue field. For any field extension 
$K/k$, we write 
$X_K:=X\times _k K$.
Definition 1.3 Let 
$X$ be a variety over a number field 
$k$ and 
$S$ be a finite subset of 
$\Omega _k$.
(i) We say that
$X$ satisfies strong approximation off $S$, abbreviated as (SA) off $S$, if the diagonal embedding of $X(k)$ is dense in $\operatorname {pr}^S (X({\mathbf {A}}_{k}))$.(ii) Let
$c\in {\mathbb {N}}_{\geqslant 1}$. We say that $X$ satisfies the arithmetic purity of strong approximation off $S$ of codimension $c$ if any open subvariety of $X$ whose complement is of codimension $\geqslant c$ satisfies strong approximation off $S$. In particular, when $c=2$, we simply say that $X$ satisfies the arithmetic purity of strong approximation off $S$, abbreviated as (APSA) off S.
Similarly we shall denote ‘weak approximation’ by (WA).
Our terminology follows standard textbooks on linear algebraic groups (e.g. [Reference BorelBor91], [Reference Conrad, Gabber and PrasadCGP10] and [Reference HumphreysHum75]). Let 
$G$ be a connected linear algebraic group over 
$k$. We say that 
$G$ is 
$k$-isotropic if 
$G$ has 
$k$-rank greater than one, that is, if 
$G$ contains a non-trivial 
$k$-split torus. Otherwise, we say that 
$G$ is 
$k$-anisotropic if it does not contain any 
$k$-split torus (cf. [Reference BorelBor91, § 20.1], [Reference Conrad, Gabber and PrasadCGP10, p. 635] and [Reference HumphreysHum75, § 34.4]). We say that 
$G$ is 
$k$-quasi-split if it contains a Borel subgroup over 
$k$ (cf. [Reference HumphreysHum75, § 35.1]). We call 
$G$ (almost) 
$k$-simple if it does not contain any non-commutative non-trivial proper connected normal subgroups defined over 
$k$ (cf. [Reference HumphreysHum75, p. 168]).
Let 
$q$ be a non-degenerate quadratic form over 
$k$ in 
$n$ variables. The spin group 
$\operatorname {Spin}(q)$ is the universal (double) covering of 
$\operatorname {SO}(q)$, the special orthogonal group associated to 
$q$. If 
$n\geqslant 3$, the group 
$\operatorname {Spin}(q)$ is connected, semisimple and simply connected. See [Reference Colliot-Thélène and XuCX09, § 5.1].
1.3 Main results
We now state several main theorems of this paper regarding Question 1.2. Our first result resolves all 
$k$-simple and isotropic cases off an arbitrary place.
Theorem 1.4 Let 
$k$ be a number field and 
$v_0\in \Omega _k$. Let 
$G$ be a semisimple simply connected 
$k$-simple linear algebraic group. If 
$G$ is 
$k$-isotropic, then 
$G$ satisfies (APSA) off 
$v_0$.
Remarks 1.5 (i) For any semisimple linear algebraic 
$k$-group 
$G$, according to the Borel–Tits theory (cf. [Reference Conrad, Gabber and PrasadCGP10, Remark C.3.10]), we know that 
$G$ is 
$k$-isotropic if and only if 
$G$ contains a closed 
$k$-subgroup isomorphic to 
${\mathbb {G}}_{\operatorname {a}}$, and equivalently, 
$G$ contains a parabolic subgroup over 
$k$ different from 
$G$. Thus being 
$k$-quasi-split implies being 
$k$-isotropic.
(ii) In general, the notion of being isotropic is much weaker than being quasi-split. For example, there are many 
$k$-isotropic spin groups of quadratic forms in 
$\geqslant 4$ variables which are not 
$k$-quasi-split (cf. [Reference BorelBor91, § 23.4]).Footnote 1 Therefore Theorem 1.4 generalizes [Reference Cao, Liang and XuCLX19, Theorem 1.1] and covers many new cases.
(iii) When 
$k$ is a totally imaginary field, Theorem 1.4 covers all semisimple simple connected 
$k$-simple groups which are not of 
$A_n$-type. Indeed 
$k$-groups of 
$A_n$-type are the only 
$k$-anisotropic cases (cf. [Reference Platonov and RapinchukPR94, Theorem 6.25 and p. 352]).
At the AIM workshop, Wittenberg [AIM14, Question 6] proposed affine quadratic hypersurfaces as first interesting cases worthy of study. This is answered affirmatively by our next result.
Theorem 1.6 Let 
$k$ be a number field. Let 
$q(x_1,\ldots ,x_n)$ be a non-degenerate quadratic form over 
$k$ with 
$n\geqslant 3$ variables and 
$G:=\operatorname {Spin}(q)$ be the corresponding spin group. If 
$q$ is isotropic over an archimedean place, then:
(i)
$G$ satisfies (APSA) off $\infty _{k}$;(ii) for any
$a_0\in k^{\times }$, the affine quadric defined by $q(x_1,\ldots ,x_n)=a_0$ in ${\mathbb {A}}^{n}$ satisfies (APSA) off $\infty _{k}$ if $n\geqslant 4$.
The following result is the technical core for the proof of Theorem 1.6. It applies in particular to spin groups.
Theorem 1.7 Let 
$k$ be a number field. Let 
$G$ be a semisimple simply connected 
$k$-simple linear algebraic group. If 
$G$ contains a closed subgroup 
$G'\subset G$ with 
$G'$ a three-dimensional semisimple simply connected linear algebraic group over 
$k$ such that 
$G'(k_{\infty })$ is not compact, then 
$G$ satisfies (APSA) off 
$\infty _{k}$.
Remarks 1.8 (i) When 
$n=3$, the affine quadric in Theorem 1.6(ii) can have non-trivial Brauer group and hence Brauer–Manin obstruction to integral points, while if 
$n\geqslant 4$ there is no such obstruction (cf. [Reference BorovoiBor01, § 1.2, Reference Colliot-Thélène and XuCX09, §§ 5.6 and 5.8]). We actually show that (APSA) off 
$\infty _{k}$ with Brauer–Manin obstruction (cf. [Reference Cao, Liang and XuCLX19, definition 2.1]) holds for the affine quadratic surface 
$q(x_1,x_2,x_3)=a_0$ in 
${\mathbb {A}}^3$.
(ii) When 
$k$ is not totally real, the non-compactness conditions in Theorems 1.6 and 1.7 become vacuous.
1.4 Strategies and organization of the paper
Our strategy relies on a combination of a fibration method with group actions and an affine linear sieve due to Sarnak and his collaborators. The former is developed in § 2 and applied to the proof of a more general version of Theorem 1.4, i.e. Theorem 2.1, and to the anisotropic cases in § 4. Roughly speaking, having fixed some closed subset 
$D$ of a semisimple group 
$G$, a non-trivial subgroup 
$H$ action (up to conjugation) can ‘increase’ the codimension of 
$D$ (Lemma 2.3). Then the proof of Theorem 2.1 is achieved by considering the fibration 
$G\to G/H$ via an induction argument on the codimension of 
$D$. A large part of § 4 is devoted to proving Theorem 4.1 concerning three-dimensional anisotropic groups. After a careful choice of fibration into families of tori, a major difficulty that remains to overcome is to find integral points that can ‘avoid’ the given codimension two subset modulo infinitely many primes. In doing so, we make use of torus actions, and we appeal to the aforementioned sieve argument which allows to produce almost-prime values with only large prime divisors, the latter constituting § 3. More explanations on the proof of Theorem 4.1 are postponed to § 4.1. Finally, in § 5, combining Theorem 4.1 with the fibration argument established in § 2, we prove Theorems 1.6 and 1.7.
We hope that the ideas developed in this text would provide new insights into Wittenberg's Question 1.2 and have further application.
1.5 Some more notation and conventions
Let 
$G$ be an algebraic group over 
$k$. Unless otherwise specified, subgroups of 
$G$ and irreducible components of subsets of 
$G$ are defined over 
$k$. We shall write e.g. 
$H^\prime \subset G_K$ to denote a subgroup 
$H^\prime$ of 
$G_K$ defined over a field extension 
$K$ of 
$k$.
By convention, 
$\dim (\varnothing )=-1$.
The letter 
$p$ is always reserved for a prime number, and 
$\varepsilon$ denotes an arbitrarily small positive parameter that can be rescaled by constant multiples. For two real-valued functions 
$f$ and 
$g$ with 
$g$ non-negative, Landau's symbol 
$f=O(g)$ and Vinogradov's symbol 
$f\ll g$ (or 
$g\gg f$) are used interchangeably, meaning that there exists 
$C>0$ such that 
$|f|\leqslant Cg$. Any dependence of the implied constant 
$C$ on extra parameters will be specified as subscripts. We write 
$f\asymp g$ if 
$f\ll g$ and 
$g\ll f$ hold simultaneously. We write 
$\mu (\cdot )$ for the Möbius function.
2. Isotropic case
Our ultimate goal is to prove Theorem 1.4 via establishing the following general result.
Theorem 2.1 Let 
$k$ be a number field and 
$S\subset \Omega _k$ be a finite set of places. Let 
$G$ be a semisimple simply connected 
$k$-simple linear algebraic group over 
$k$. If 
$G$ contains a non-trivial connected closed subgroup 
$H$ that satisfies (APSA) off 
$S$, then 
$G$ also satisfies (APSA) off 
$S$.
2.1 Subgroup action on closed subsets
We start by proving two technical lemmas. We are grateful to Harpaz for useful exchanges from which our arguments here are inspired. In this section, let 
$k$ be a number field, 
$G$ be a non-trivial semi-simple simply connected 
$k$-simple linear algebraic group over 
$k$. Let us fix in this part 
$H\subset G$ a non-trivial connected closed subgroup. For 
$g\in G$, let 
$H_g:=gH_{k(g)}g^{-1}$.
Lemma 2.2 Let 
$E,D$ be two proper non-empty closed subsets of 
$G$ defined over 
$k$ with 
$E\subset D$ and 
$\dim (E)=\dim (D)$. Then the set
\[ \Psi_{H,E,D}:=\{g\in G: H_g\cdot E_{k(g)}\not\subset D_{k(g)}\} \]
is a non-empty open subset of 
$G$ over 
$k$.
Proof. Firstly we prove that 
$\Psi _{H,E,D}\subset G$ is open. Let 
$p_1: G\times H\times E\to G$ be the first projection (hence flat and open) and define
\begin{align*} \phi: G\times H\times E&\to G\\ (g,h,e)&\mapsto ghg^{-1}e. \end{align*}
Then 
$\Psi _{H,E,D}=p_1(\phi ^{-1} (G\setminus D))\subset G$ is open, since 
$D$ is closed.
Next we prove that 
$\Psi _{H,E,D}\subset G$ is non-empty.
In the first place we treat the case where 
$E=D$. Namely, we show that for any non-empty proper closed subset 
$E\subset G$, we have 
$\Psi _{H,E,E}\neq \varnothing$. Let 
$H'\subset G$ be the normal closure of 
$H$, i.e. 
$H'_{\bar {k}}\subset G_{\bar {k}}$ is the closed subgroup generated by 
$gHg^{-1}$ for all 
$g\in G(\bar {k})$ and 
$H'_{\bar {k}}$ can be defined over 
$k$ because it contains all Galois conjugates of its 
$\bar {k}$-components. Then 
$H'\subset G$ is the minimal closed normal subgroup containing 
$H$. We claim that 
$H'$ is connected. Indeed, the action of the connected group 
$G$ on 
$H'$ by conjugation preserves the identity component 
$H^{^{\prime \prime }\mkern -1.0mu}$ of 
$H^\prime$ and hence 
$H^{^{\prime \prime }\mkern -1.0mu}$ is also a closed normal subgroup of 
$G$ containing 
$H$, and therefore 
$H^{^{\prime \prime }\mkern -1.0mu}=H'$ since 
$H'$ is minimal. This proves the claim. Since 
$G$ is 
$k$-simple and 
$H^{\prime }$ is normal and connected with 
$\dim H^\prime \geqslant \dim H>0$ by the assumption that 
$H$ is non-trivial, we deduce that 
$H^{\prime }=G$. If 
$\Psi _{H,E,E}=\varnothing$, then 
$G_{\bar {k}}=G_{\bar {k}}\cdot E_{\bar {k}}=H^\prime _{\bar {k}}\cdot E_{\bar {k}}\subset E_{\bar {k}}$, which contradicts 
$E\neq G$.
Now we return to the general case of two closed sets 
$E,D$ as in the assumption of the lemma. Let 
$E'\subset E$ be an irreducible component of the same dimension as 
$E$. From the previous paragraph, we have shown 
$\Psi _{H,E',E'}\neq \varnothing$. We now show
\[ \Psi_{H,E',E'}\subset \Psi_{H,E,D}, \]
so that 
$\Psi _{H,E,D}\neq \varnothing$. Indeed, for any 
$g\in \Psi _{H,E',E'}$, we have 
$H_g\cdot E'_{k(g)}\not \subset E'_{k(g)}$. So there exists an irreducible 
$k(g)$-component 
$E^{^{\prime \prime }\mkern -1.0mu}$ of 
$E'_{k(g)}$ of the same dimension as 
$E'_{k(g)}$, such that 
$H_g\cdot E^{^{\prime \prime }\mkern -1.0mu}\not \subset E^{^{\prime \prime }\mkern -1.0mu}$. Since 
$\overline {H_g\cdot E^{^{\prime \prime }\mkern -1.0mu}}$ is irreducible, and 
$E^{^{\prime \prime }\mkern -1.0mu}\subset H_g\cdot E^{^{\prime \prime }\mkern -1.0mu}$, one has 
$\dim (H_g\cdot E^{^{\prime \prime }\mkern -1.0mu})>\dim (E^{^{\prime \prime }\mkern -1.0mu})=\dim (E^{\prime })=\dim (E)=\dim (D)$. Thus 
$H_g\cdot E'_{k(g)}\not \subset D_{k(g)}$ and a fortiori 
$H_g\cdot E_{k(g)}\not \subset D_{k(g)}$. This shows that 
$g\in \Psi _{H,E,D}$, as desired.
Lemma 2.3 Let 
$D$ be a proper non-empty closed subset of 
$G$ over 
$k$. Then there exist 
$g\in G(k)$ and a closed subset 
$D'\subset D$ over 
$k$ such that
\[ \dim(D')< \dim(D),\quad H_g\cdot D'=D',\quad \text{and} \quad H_g\cdot (G\setminus D)=G\setminus D'. \]Proof. Let 
$\{D_i\}_{i\in I}$ be the irreducible components of 
$D$ of the same dimension, and for each 
$i\in I$, let 
$\Psi _{H,D_i,D}$ be the set defined in Lemma 2.2. Since 
$G(k)$ is Zariski dense in 
$G$,Footnote 2 and each 
$\Psi _{H,D_i,D}$ is open and dense in 
$G$, we have
\[ G(k)\cap (\cap_{i\in I} \Psi_{H,D_i,D})\neq\varnothing. \]
Having fixed 
$g\in G(k)\cap (\cap _{i\in I} \Psi _{H,D_i,D})$, let us define
\[ D':=G\setminus (H_g\cdot (G\setminus D)). \]
Then it is clear that 
$G\setminus D'= H_g\cdot (G\setminus D)$. Since 
$H_g\cdot (G\setminus D)\subset G\setminus D$, we get 
$D'\subset D$. If there exists 
$d\in D^\prime$ such that 
$H_g\cdot d\not \subset D^\prime _{k(d)}$, then there exists 
$h\in H_g$ such that 
$h\cdot d \in G\setminus D^\prime =H_g\cdot (G\setminus D)$. This implies 
$d\not \in D$, which contradicts 
$D'\subset D$. Consequently 
$H_g\cdot D'=D'$. Since 
$H_g\cdot (G\setminus D)$ is open and defined over 
$k$, 
$D^\prime$ is closed and defined over 
$k$. By the definition of 
$\Psi _{H,D_i,D}$, we have 
$H_g\cdot D_i\not \subset D$ for all 
$i\in I$. So one has 
$D_i\not \subset D'$ for any 
$i\in I$, for otherwise 
$H_g\cdot D_i\subset H_g\cdot D^\prime =D^\prime \subset D$, which contradicts 
$H_g\cdot D_i \not\subset D$. Thus 
$\dim (D')<\dim (D)$.
2.2 Proof of Theorem 2.1 – a fibration method with subgroup actions
By the assumption that 
$H$ satisfies the (APSA) off 
$S$, one has that 
$H(k_S)$ is not compact. Then 
$G(k_S)$ is also not compact. Let
\[ \pi: G\to Y:=G/H \]
be the quotient map. Let 
$D\subset G$ be a closed subset over 
$k$ of codimension 
$c\geqslant 2$ and 
$U:=G\setminus D$. Now we prove that 
$U$ satisfies (SA) off 
$S$. By induction, we may assume 
$G$ satisfies (APSA) off 
$S$ of codimension 
$c+1$, the initial case being 
$c=\dim G$ and following from Theorem 1.1.
By Lemma 2.3, upon replacing 
$H\subset G$ by some 
$H_g$ for 
$g\in G(k)$ if necessary, we may assume there exists a closed subset 
$D'\subset D$ over 
$k$ such that 
$H\cdot D'=D'$, 
$\dim (D')<\dim (D)$ and 
$\pi (U)=Y\setminus \pi (D')$. Let us define
\[ U_1:=G\setminus D',\quad V_1:=Y\setminus \pi(D'),\quad \pi_{U_1}:=\pi|_{U_1}: U_1\to V_1\quad \text{and}\quad \pi_U:=\pi|_{U}: U\to V_1. \]
Then 
$\pi _{U_1}$ is a 
$H$-torsor and 
$\pi _U$ is smooth surjective with geometrically integral fibres. We get the following commutative diagram.
By [Reference Cao, Liang and XuCLX19, Proposition 3.5], there exists an open subset 
$V_0$ of 
$V_1$ over 
$k$ such that for any 
$y\in V_0$, we have
\begin{equation} {\mathrm{codim}}(D_y,G_y)\geqslant{\mathrm{codim}}(D,G)\geqslant c, \end{equation}
where 
$D_y,G_y$ are the fibres of 
$\pi$ over 
$y$. Define 
$U_0:=\pi _{U}^{-1}(V_0)$.
For any non-empty open subset 
$W\subset U({\mathbf {A}}_k^{S})$, we want to show that 
$U(k)\cap W\neq \varnothing$. By [Reference ConradCon12, Theorem 4.5], the set 
$\pi _U(W)\subset V_1({\mathbf {A}}_k^{S})$ is open, and by continuity the set
\[ W_1:=\pi_{U_1}^{-1}(\pi_U(W))\subset U_1({\mathbf{A}}_k^{S}) \]
is open. Since 
${\mathrm {codim}}(D',G)\geqslant {\mathrm {codim}}(D,G)+1\geqslant c+1$ by induction hypothesis, the variety 
$U_1$ satisfies (SA) off 
$S$, so 
$U_1(k)\cap W_1\neq \varnothing$. By [Reference Cao, Liang and XuCLX19, Proposition 2.3(2)], we have 
$U_0(k)\cap W_1\neq \varnothing$. Let us choose 
$x_0\in U_0(k)\cap W_1$ and let 
$y_0:=\pi (x_0)$. Then 
$x_0\in U_{y_0}(k)\subset G_{y_0}(k)$, and thus 
$G_{y_0}\simeq H$. Since 
$y_0\in V_0(k)\cap \pi _{U_1}(W_1)=V_0(k)\cap \pi _U(W)\neq \varnothing$, the set 
$W\cap U_{y_0}({\mathbf {A}}_k^{S})$ is a non-empty open adelic neighbourhood of 
$U_{y_0}({\mathbf {A}}_k^{S})$, where 
$U_{y_0}$ is the fibre of 
$\pi _U$ over 
$y_0$. Since 
$H$ satisfies (APSA) off 
$S$, the open variety 
$U_{y_0}=G_{y_0}\setminus D_{y_0}$ satisfies (SA) off 
$S$, so 
$U_{y_0}(k)\cap (W\cap U_{y_0}({\mathbf {A}}_k^{S}))\neq \varnothing$. Therefore we have proven 
$U(k)\cap W\neq \varnothing$. This finishes the proof.
Remark 2.4 The reason why our induction process from the 
$c=2$ case to the 
$c=1$ case fails is that the condition 
${\mathrm {codim}}(D_{y_0},G_{y_0})\geqslant 1$ deduced from (2.1) is insufficient to produce rational points in 
$W\cap U_{y_0}({\mathbf {A}}_k^{S})$ by the definition of (APSA)(Definition 1.3(2)).
2.3 Proof of Theorem 1.4
By Borel–Tits’ theory (Remark 1.5(i)), the assumption that the group 
$G$ is 
$k$-isotropic is equivalent to saying that 
$G$ contains a closed subgroup isomorphic to 
${\mathbb {G}}_{\operatorname {a}}$ over 
$k$. The statement now follows from Theorem 2.1 applied to 
${\mathbb {G}}_{\operatorname {a}}\subset G$, for which (SA) off any place is known by the Chinese remainder theorem.
3. Almost prime polynomial values
In this section we study quantitative growth of almost-prime integral polynomial values on semisimple simply connected groups. We shall prove Theorem 3.1, asserting the finiteness of the saturation number [Reference Nevo and SarnakNS10, p. 361] of a non-zero regular function evaluated on a given principal congruence subgroup. For further application, we derive Corollary 3.3 as a key tool in the proof of Theorem 4.1. Our approach is based on the affine linear sieve introduced in [Reference Nevo and SarnakNS10].
3.1 Main result
In this section we fix 
$G$ a semisimple simply connected linear algebraic group over 
${\mathbb {Q}}$. Let us fix an embedding 
$G\hookrightarrow {\mathrm {GL}}_{n,{\mathbb {Q}}}$. We choose the integral model 
${\mathcal {G}}:=\bar {G} \subset {\mathrm {GL}}_{n,{\mathbb {Z}}}$, i.e. the integral closure of 
$G$ in 
${\mathrm {GL}}_{n,{\mathbb {Z}}}$. The coordinate ring 
${\mathbb {Q}}[G]$ is a unique factorization domain. We fix a height function 
$\|\cdot \|$ on 
${\mathrm {GL}}_{n}({\mathbb {Z}})$. For example, we can define for 
$g=(g_{i,j})\in {\mathrm {GL}}_n({\mathbb {Z}})$, 
$\|g\|:=\max _{1\leqslant i,j\leqslant n} |g_{i,j}|$. Let
\[ \Gamma:={\mathcal{G}}({\mathbb{Z}}), \]
and for any 
$\alpha \in {\mathbb {N}}_{\geqslant 1}$, define
\[ \Gamma_{\alpha}:=\{g\in {\mathcal{G}}({\mathbb{Z}}): g\equiv \operatorname{id}_{\mathcal{G}} \ \mathrm{mod}\ \alpha\}, \]
the principal congruence subgroup of level 
$\alpha$.
We now state the main result of this section.
Theorem 3.1 Let 
$f\in {\mathbb {Q}}[G]$ be a non-zero regular function and 
$\alpha _0\in {\mathbb {N}}_{>1}$. Assume that 
$f$ takes integer values on 
$\Gamma _{\alpha _0}$. Let 
$N:=\gcd (f(\Gamma _{\alpha _0}))$ and 
$S \subset \Omega _{{\mathbb {Q}}}\setminus \infty _{{\mathbb {Q}}}$ be a finite set of places such that 
$f\in {\mathbb {Z}}_S[{\mathcal {G}}]$. Assume moreover that every 
${\mathbb {Q}}$-simple factor of 
$G$ is not compact over 
${\mathbb {R}}$. Then there exist 
$\beta _1>0,\beta _2>0$, depending only on 
${\mathcal {G}}$, 
$f$, 
$\alpha _0$, 
$S$ and 
$N$, such that for any large enough 
$T$,
\begin{equation} \#\Biggl\{g\in \Gamma_{\alpha_0}: \|g\| < T ,\gcd\biggl(f(g),\prod_{\substack{p\nmid\alpha_0 N,p\not\in S\\p < T^{\beta_1}}}p\biggr)=1 \Biggr\}\gg \frac{\# \{g\in {\mathcal{G}}({\mathbb{Z}}): \|g\| < T\}}{(\log T)^{\beta_2}}. \end{equation} In this section, as well as in § 3.5 below, unless otherwise mentioned, all implied constants are allowed to depend on 
${\mathcal {G}}$, 
$\|\cdot \|$, 
$f$, 
$\alpha _0$, 
$S$ and 
$N$.
Remarks 3.2 (i) Thanks to [Reference Duke, Rudnick and SarnakDRS93, Theorem 1.2], [Reference MaucourantMau07, Theorem 1] and [Reference Gorodnik and WeissGW07, Theorem 2.7],we know that there exist rational numbers 
$a>0,b\geqslant 0$ such that
\begin{equation} \# \{g\in {\mathcal{G}}({\mathbb{Z}}): \|g\| < T\}\asymp T^a(\log T)^b. \end{equation}
See e.g. [Reference Nevo and SarnakNS10, § 3.1] for an interpretation of the constants 
$a,b$. So Theorem 3.1 implies that the number of 
$\Gamma _{\alpha _0}$-lattice points 
$g$ of bounded height 
$T$ such that 
$f(g)$ is free of prime factors less than 
$T^{\beta _1}$, except for those dividing 
$\alpha _0,S$ or 
$N$, goes to infinity as 
$T$ grows.
(ii) In [Reference Nevo and SarnakNS10, Theorem 1.7, Corollary 1.8, and (4.32)], under the assumption that 
$\gcd (f(\Gamma )) =1$,Footnote 3 and that 
$f$ factors into 
$t(f)$ distinct irreducible factors over 
${\mathbb {Q}}$ which are also assumed to be absolutely irreducible, it is shown that for 
$\alpha _0=1$, (3.1) has the expected magnitude of growth. Namely the power on 
$\log T$ is 
$t(f)$. Our result deals with arbitrary non-zero 
$f$ and also implies the finite saturation of the pair 
$(f,\Gamma _{\alpha _0})$, using e.g. [Reference Nevo and SarnakNS10, Lemma 4.2].
3.2 An application
In this section, let 
$k$ be a number field and 
$G$ be a semisimple simply connected 
$k$-simple linear algebraic group over 
$k$. We fix an embedding 
$G\subset {\mathrm {GL}}_{n,k}$ and we choose the integral model 
${\mathcal {G}}$ to be the integral closure of 
$G$ in 
${\mathrm {GL}}_{n,{\mathcal {O}}_k}$.
Theorem 3.1 is sufficient to deduce the following technical result. The way in which we formulate it is tailored to our application in § 4.
Corollary 3.3 Let 
$S'\subset (\Omega _{{\mathbb {Q}}}\setminus \infty _{{\mathbb {Q}}})$, 
$S\subset (\Omega _k\setminus \infty _k)$ be two finite subset of places such that 
${\mathcal {O}}_{k,S}$ is a principal ideal domain and finite étale over 
${\mathbb {Z}}_{S'}$.
Let
\[ \Phi:=\prod_{v\in S}\Phi_v\times \prod_{v\notin S\cup \infty}{\mathcal{G}}({\mathcal{O}}_v) \]
be a subgroup of 
$G({\mathbf {A}}_k^{\infty _k})$, where 
$\Phi _v\subset G(k_v)$ is an open compact subgroup for each 
$v\in S$. Let 
$f\in {\mathcal {O}}_{k,S}[{\mathcal {G}}]$ be a regular function such that 
$f({\mathcal {G}}({\mathcal {O}}_v))\cap {\mathcal {O}}_v^{\times }\neq \varnothing$ for any 
$v\in \Omega _{k}\setminus (S\cup \infty _k)$. Assume that 
$G(k_{\infty })$ is not compact. Then there exists an integer 
$r_0\geqslant 1$ depending only on 
${\mathcal {G}},\Phi ,f,S,S^\prime$ and verifying the following property: for any 
$M>0$, there exists 
$g_0\in {\mathcal {G}}({\mathcal {O}}_{k,S})\cap \Phi$ such that 
$f(g_0)$ has at most 
$r_0$ prime factors in 
${\mathcal {O}}_{k,S}$, and the cardinalities of their residue fields are larger than 
$M$.
The assumption that 
${\mathcal {O}}_{k,S}$ is finite étale over 
${\mathbb {Z}}_{S'}$ means precisely that the extension 
$k/{\mathbb {Q}}$ is unramified outside of 
$S^\prime$, and 
$S$ is the set of places over 
$S^\prime$.
Proof. Let us consider
\[ G^\prime:= {\mathrm{Res}}_{k/{\mathbb{Q}}}G\subset{\mathrm{GL}}_{n[k:{\mathbb{Q}}],{\mathbb{Q}}},\quad{\mathcal{G}}^\prime:={\mathrm{Res}}_{{\mathcal{O}}_k/{\mathbb{Z}}}{\mathcal{G}},\quad f^\prime:=N_{k/{\mathbb{Q}}}(f). \]
The group 
$G^\prime$ is semisimple simply connected and 
${\mathbb {Q}}$-simple by [Reference Conrad, Gabber and PrasadCGP10, Proposition A.5.14], and 
${\mathcal {G}}^\prime$ is a smooth integral model of 
$G^\prime$ over 
${\mathbb {Z}}_{S^\prime }$ by [Reference Bosch, Lütkebohmert and RaynaudBLR90, § 7.6, Propositions 5 and 6].
We identify the group 
$\Phi$ as a subgroup of 
$G^\prime ({\mathbf {A}}_{\mathbb {Q}}^{\infty _{{\mathbb {Q}}}})$. Take an integer 
$\alpha _1$ of the form 
$\prod _{v\in S'}p_v^{m_v}$ with 
$m_v\in {\mathbb {N}}_{\geqslant 1}$ large enough so that the diagonal image of the principal congruence subgroup 
$\Gamma _{\alpha _1}$ of 
${\mathcal {G}}^\prime ({\mathbb {Z}})$ in 
$G^\prime ({\mathbf {A}}_{\mathbb {Q}}^{\infty _{{\mathbb {Q}}}})$ is contained in 
$\Phi$. Since 
$G(k_\infty )$ is not compact, so is 
$G^\prime ({\mathbb {R}})$. Since 
$f\in {\mathcal {O}}_{k,S}[{\mathcal {G}}]$, we have 
$f^\prime \in {\mathbb {Z}}_{S'}[{\mathcal {G}}^\prime ]$, and by assumption, 
$f^\prime$ is not identically zero on 
${\mathcal {G}}^\prime ({\mathbb {Z}}_{S^\prime })$.
The determinant character 
$G^\prime \hookrightarrow {\mathrm {GL}}_{n[k:{\mathbb {Q}}]}\xrightarrow {\det }{\mathbb {G}}_{\operatorname {m}}$ is trivial since 
$G^\prime$ is semisimple, so 
$G^\prime$ embeds into 
${\mathrm {SL}}_{n[k:{\mathbb {Q}}],{\mathbb {Q}}}\subset {\mathbb {A}}^{(n[k:{\mathbb {Q}}])^2}$, where we regard 
${\mathrm {GL}}_{n[k:{\mathbb {Q}}],{\mathbb {Q}}}\subset {\mathbb {A}}^{(n[k:{\mathbb {Q}}])^2}$. So
\[ {\mathbb{Q}}[G^\prime]={\mathbb{Q}}\big[X_1,\ldots,X_{(n[k:{\mathbb{Q}}])^2}\big]\big/I, \]
the ideal 
$I$ being generated by finitely many polynomials in 
${\mathbb {Z}}[X_1,\ldots ,X_{(n[k:{\mathbb {Q}}])^2}]$ including 
$\det (\mathbf {X})-1$ where 
$\det (\mathbf {X})$ is the determinant polynomial. Therefore we can choose
\[ F\in {\mathbb{Z}}_{S^\prime}\big[X_1,\ldots,X_{(n[k:{\mathbb{Q}}])^2}\big] \]
a lift of 
$f^\prime$ in such a way that it has minimal degree. And we can multiply 
$F$ by an integer 
$R$ whose prime divisors are in 
$S^\prime$, so that 
$RF$ has integer coefficients, and in particular 
$Rf^\prime$ takes integer values on 
$\Gamma _{\alpha _1}$. Moreover, the hypothesis 
$f({\mathcal {G}}({\mathcal {O}}_v))\cap {\mathcal {O}}_v^{\times }\neq \varnothing$ for any 
$v\notin S\cup \infty _{k}$ implies that 
$N:=\gcd (Rf^\prime (\Gamma _{\alpha _1}))$ factorizes into prime numbers in 
$S^\prime$.
We now apply Theorem 3.1 to the group 
$G^\prime$ and to the function 
$Rf^\prime$ evaluated on 
$\Gamma _{\alpha _1}$. For any 
$T$ large enough such that 
$T^{\beta _1}\geqslant M$, we can find 
$g_0\in \Gamma _{\alpha _1}$ such that 
$\|g_0\|\leqslant T$ and, according to (3.1), any prime divisor of 
$Rf^\prime (g_0)$ is either 
$>T^{\beta _1}$, or in 
$S^\prime$. On the other hand, there exists 
$\vartheta >0$ depending only on 
$R$ and the degree of 
$F$ such that for any 
$g\in {\mathrm {GL}}_n({\mathbb {Z}})$ with 
$\|g\|< T$, we have 
$|RF(g)|\leqslant T^\vartheta$. Hence for any 
$g\in {\mathcal {G}}^\prime ({\mathbb {Z}})$ with 
$\|g\|< T$, we also have 
$|Rf^\prime (g)|\leqslant T^\vartheta$. So the number of distinct prime factors of 
$Rf^\prime (g_0)$ which are 
$\geqslant T^{\beta _1}$ is 
$\leqslant \lfloor \vartheta /\beta _1\rfloor +1$. Returning to the function 
$f$ and regarding 
$g_0\in \Phi$, we see that 
$g_0$ is in the diagonal image of 
${\mathcal {G}}({\mathcal {O}}_{k,S})$, and we have shown that any 
$v\in \Omega _{k}\setminus (S\cup \infty _{k})$ dividing 
$f(g_0)$ satisfies 
$\#k(v)\geqslant T^{\beta _1}\geqslant M$, and the total number of such 
$v$ is 
$\leqslant [k:{\mathbb {Q}}](\lfloor \vartheta /\beta _1\rfloor +1)$. Therefore we may take 
$r_0=[k:{\mathbb {Q}}](\lfloor \vartheta /\beta _1\rfloor +1)$ to complete the proof.
3.3 A combinatorial sieve
Our central analytic input is an elementary combinatorial sieve of Brun–Selberg type, based on the so-called ‘fundamental lemma’. It gives estimates for the growth of an integer sequence free of moderately small prime divisors. If the elements of this sequence have polynomial growth, a direct consequence is that each element sieved out has a uniformly bounded number of prime divisors, and hence is ‘almost-prime’.
Let 
${\mathcal {P}}$ be a set of prime numbers. For 
$z>0$, define
\[ {\mathcal{P}}(z):=\prod_{p < z,p\in{\mathcal{P}}} p. \]
Let 
${\mathcal {A}}=(a_i)_{i\in I}$ be a finite sequence of integers indexed by 
$I$. Define
\[ X:=\#{\mathcal{A}} ~(=\# I). \]
For 
$d\in {\mathbb {N}}_{\geqslant 1}$, we define the subsequence
\[ {\mathcal{A}}_d:=(a_i)_{i\in I_d} \]
of 
${\mathcal {A}}$ with 
$I_d:=\{i\in I:d\mid a_i\}\subset I$. Our goal is to estimate the sifting function
\[ S({\mathcal{A}},{\mathcal{P}},z):=\#\{i\in I:\gcd(a_i,{\mathcal{P}}(z))=1\}. \]We now formulate the following version of the ‘fundamental lemma’, which is best suitable for our application. See, for example, [Reference Friedlander and IwaniecFI10, Theorem 6.9, Corollary 6.10], [Reference TenenbaumTen95, I.4 Theorem 3], and [Reference Halberstam and RichertHR74, Theorem 7.2].
Theorem 3.4 With the notation above, suppose that there exist a multiplicative arithmetic function 
$\omega :{\mathbb {N}}_{\geqslant 1}\to {\mathbb {R}}_{\geqslant 0}$ and constants 
$\kappa >0, A_1>1$ verifying the following hypotheses.
(i) For any prime
$p$, we have
\[ 0\leqslant\frac{\omega(p)}{p}<1. \](ii) For any real numbers
$w_1,w_2$ such that $2\leqslant w_1\leqslant w_2$, we have
\[ \prod_{\substack{w_1\leqslant p\leqslant w_2}}\biggl(1-\frac{\omega(p)}{p}\biggr)^{-1}\leqslant A_1\biggl(\frac{\log w_2}{\log w_1}\biggr)^\kappa. \]
Then there exist constants 
$\lambda \in ]0,(9\kappa )^{-1}[,\tau >0$ depending only on 
$\kappa ,A_1$ such that, for any finite sequence of integers 
${\mathcal {A}}$ and any real numbers 
$y\geqslant 2$ and 
$z\in [2,y^\lambda ]$, we have
\begin{equation} S({\mathcal{A}},{\mathcal{P}},z)\geqslant \tau X\prod_{p\mid{\mathcal{P}}(z)}\biggl(1-\frac{\omega(p)}{p}\biggr)+O\biggl(\sum_{\substack{d\leqslant y\\ \textrm{d}\mid {\mathcal{P}}(z)}}\biggl|\#{\mathcal{A}}_d-\frac{\omega(d)}{d}X\biggr|\biggr), \end{equation}
where the implied constant depends only on 
$\kappa ,A_1$, and is independent of 
${\mathcal {A}},y,z$.
The quantity 
$({\omega (d)}/{d})X$ is considered as an approximation of the cardinality of 
${\mathcal {A}}_d$ when 
$d$ factorizes into prime divisors in 
${\mathcal {P}}$, and
\[ {\mathcal{R}}_{\mathcal{A}}(d):=\#{\mathcal{A}}_d-\frac{\omega(d)}{d}X \]
is the remainder term. So Theorem 3.4 implies that 
$S({\mathcal {A}},{\mathcal {P}},z)$ grows like 
$X\prod _{p\mid {\mathcal {P}}(z)}(1-{\omega (p)}/{p})$, provided that 
$\omega (\cdot )$ are 
${\mathcal {R}}_{\mathcal {A}}(\cdot )$ are both small on average.
3.4 The Lang–Weil estimate revisited
Before proceeding to the proof of Theorem 3.1, we recall a version of Lang–Weil estimate dealing with rational points on reductions of arbitrary varieties at finite places.
Theorem 3.5 (Lang–Weil) Let 
$V$ be a variety over a number field 
$k$ and let 
${\mathcal {V}}$ be a model of 
$V$ over 
${\mathcal {O}}_{k,S}$ where 
$S\subset \Omega _k\setminus \infty _{k}$ is a finite set of places. Then there exists a constant 
$C({\mathcal {V}})>0$ depending only on 
${\mathcal {V}}$ such that for any prime ideal 
$\mathfrak {p}$ of 
${\mathcal {O}}_{K,S}$,
\[ \#{\mathcal{V}}({\mathbb{F}}_q)\leqslant C({\mathcal{V}}) q^{\dim V}, \]
where 
${\mathbb {F}}_q:={\mathcal {O}}_{k,S}/\mathfrak {p}$ is of cardinality 
$q$. If 
${\mathcal {V}}_{{\mathbb {F}}_q}:={\mathcal {V}}\times _{{\mathcal {O}}_{k,S}}{\mathrm {Spec}}({\mathbb {F}}_q)$ is geometrically irreducible, then
\[ \#{\mathcal{V}}({\mathbb{F}}_q)=q^{\dim V}+O\big(q^{\dim V-{1}/{2}}\big), \]
where the implied constant depends only on 
${\mathcal {V}}$.
Proof. We apply [Reference PoonenPoo17, Theorem 7.7.1] with 
$X={\mathcal {V}},Y={\mathrm {Spec}}({\mathcal {O}}_{k,S})$.
3.5 Proof of Theorem 3.1
We keep using the notation in § 3.1. Most of our argument follows [Reference Nevo and SarnakNS10, § 4].
Upon multiplying 
$f$ by some integer with prime factors in 
$S$ or dividing 
$\alpha _0$, we may assume that
\begin{equation} f\in{\mathbb{Z}}[{\mathcal{G}}], \quad \alpha_0\mid N, \quad \text{and}\quad \forall\, p\in S,p\mid N, \end{equation}
(recall that 
$N:=\gcd (f(\Gamma _{\alpha _0}))$) without affecting the validity of (3.1). For 
$D\in {\mathbb {N}}_{\geqslant 1}$, let 
$\Gamma _{\alpha _0}[D]$ (respectively 
$\Gamma [D]$) be the reduction modulo 
$D$ of 
$\Gamma _{\alpha _0}$ (respectively 
$\Gamma$) in 
${\mathrm {GL}}_n({\mathbb {Z}}/D{\mathbb {Z}})$, and let
\[ \Gamma_{\alpha_0}^f[D]:=\{x\in\Gamma_{\alpha_0}[D]:f(x)\equiv 0\ \mathrm{mod}\ D\}. \]
Let 
${\mathcal {P}}:=\{p:p\nmid N\}$. For 
$d\in {\mathbb {N}}_{\geqslant 1}$, let us define the arithmetic function
\begin{equation} \varrho_f(d):= \begin{cases} \displaystyle\frac{d \#\Gamma_{\alpha_0}^f[dN]}{\#\Gamma_{\alpha_0}[dN]} & \text{ if } \gcd(d,N)=1,\\ 0 & \, \; \text{otherwise}. \end{cases} \end{equation}Let us define the finite sequence of integers
\[ {\mathcal{A}}:=(N^{-1}|f(g)|)_{g\in\Gamma_{\alpha_0}:\|g\| < T} \]
indexed by elements in 
$\Gamma _{\alpha _0}$ of bounded height. Then we recall from (3.2) that
\begin{equation} X:=\#{\mathcal{A}}=\#\{g\in\Gamma_{\alpha_0}:\|g\| < T\}\asymp T^a(\log T)^b. \end{equation} For the rest of the proof, we first show that 
$\varrho _f(\cdot )$ is multiplicative in § 3.5.1, and verify in § 3.5.2 that 
$\varrho _f(\cdot )$ satisfies the conditions (1) (2) in the statement of Theorem 3.4. We then give uniform estimates for the error term 
${\mathcal {R}}_{\mathcal {A}}(\cdot )$ in § 3.5.3, and finally apply Theorem 3.4 to 
${\mathcal {A}}$ in § 3.5.4.
3.5.1 Multiplicativity
By assumption that 
$G({\mathbb {R}})$ has no compact 
${\mathbb {Q}}$-factor, Theorem 1.1 implies that 
$G$ satisfies strong approximation off 
${\mathbb {R}}$, so 
$\Gamma$ is dense in 
$\prod _{v\in \Omega _{{\mathbb {Q}}}\setminus \infty _{{\mathbb {Q}}}}{\mathcal {G}}({\mathbb {Z}}_v)$. In particular for any 
$d_1,d_2\in {\mathbb {N}}_{\geqslant 1}$ with 
$\gcd (d_1,d_2)=1$, the reduction map 
$\Gamma \to \Gamma [d_1]\times \Gamma [d_2]$ is surjective. This shows that 
$\Gamma _{\alpha _0}[d]=\Gamma [d]$ if 
$\gcd (d,\alpha _0)=1$ (by taking 
$d_1=\alpha _0,d_2=d$, and note that 
$\Gamma _{\alpha _0}=\ker (\Gamma \to \Gamma [\alpha _0])$), and so 
$\Gamma _{\alpha _0}\subset \Gamma$ is dense in 
$\prod _{\substack {v\in \Omega _{{\mathbb {Q}}}\setminus \infty _{{\mathbb {Q}}},v\nmid \alpha _0}}{\mathcal {G}}({\mathbb {Z}}_v)$.
It follows that, if 
$d=d_1d_2\in {\mathbb {N}}_{\geqslant 1}$ with 
$\gcd (d,N)=\gcd (d_1,d_2)=1$, thanks to (3.4), the reduction map 
$\Gamma _{\alpha _0}\to \Gamma _{\alpha _0}[d]\times \Gamma _{\alpha _0}[N]$ is also surjective, and hence
\begin{equation} \Gamma_{\alpha_0}[dN]\simeq \Gamma_{\alpha_0}[d_1]\times \Gamma_{\alpha_0}[d_2]\times \Gamma_{\alpha_0}[N]\subset {\mathrm{GL}}_n({\mathbb{Z}}/d_1{\mathbb{Z}})\times {\mathrm{GL}}_n({\mathbb{Z}}/d_2{\mathbb{Z}})\times{\mathrm{GL}}_n({\mathbb{Z}}/N{\mathbb{Z}}). \end{equation}
As in the proof of Corollary 3.3, we fix a lift 
$f_1\in {\mathbb {Z}}[{\mathbb {A}}^{n^2}]$ of 
$f$. Then for any 
$D\in {\mathbb {N}}_{\geqslant 1}$ and any 
$x\in \Gamma _{\alpha _0}[D]$, we have 
$x\in \Gamma _{\alpha _0}^f[D]$ if and only if 
$f_1(x)\equiv 0\ \mathrm {mod}\ D$. So by the Chinese remainder theorem,
\begin{equation} \Gamma_{\alpha_0}^f[d]\simeq\Gamma_{\alpha_0}^f[d_1]\times \Gamma_{\alpha_0}^f[d_2]\times \Gamma_{\alpha_0}^f[N]. \end{equation}Moreover,
\begin{equation} \Gamma_{\alpha_0}[N]=\Gamma_{\alpha_0}^f[N] \end{equation}
in this affine setting because 
$f$ has common divisor 
$N$ on 
$\Gamma _{\alpha _0}$. The equalities (3.7), (3.8) and (3.9) above show that the arithmetic function 
$\varrho _f$ (3.5) is multiplicative. (See also [Reference Nevo and SarnakNS10, Proposition 4.1].)
3.5.2 Verifying the sieve conditions
Since the function 
$f/N$ takes integer values on 
$\Gamma _{\alpha _0}$ and satisfies 
$\gcd ((f/N)(\Gamma _{\alpha _0}))=1$, we always have 
$\Gamma _{\alpha _0}[pN]\setminus \Gamma _{\alpha _0}^f[pN]\neq \varnothing$ for any prime 
$p\in {\mathcal {P}}$. Also, we have 
$\varrho _f(p)=0$ whenever 
$p\not \in {\mathcal {P}}$. Therefore
\[ 0\leqslant\frac{\varrho_f(p)}{p}<1 \]
for any prime 
$p$, so the sieve condition (1) in Theorem 3.4 holds.
Consider the closed subvariety
\[ V:=(f=0)\cap G. \]
We have 
$\dim V=\dim G-1$ by assumption that 
$f$ does not vanish identically on 
$G$. Let 
${\mathcal {V}}$ be integral closure of 
$V$ in 
${\mathcal {G}}$. Let 
$S^\prime$ be a finite set of primes depending on 
${\mathcal {G}}$ and 
$N$ such that, 
$p\mid N\Rightarrow p\in S^\prime$ and 
${\mathcal {G}}_{{\mathbb {F}}_p}:={\mathcal {G}}\times _{{\mathbb {Z}}}{\mathrm {Spec}}({\mathbb {F}}_p)$ is smooth and geometrically irreducible for any 
$p\notin S^\prime$. In particular for any such 
$p$ we have 
$\Gamma _{\alpha _0}[p]=\Gamma [p]\simeq {\mathcal {G}}({\mathbb {F}}_p)$ by strong approximation and Hensel's lemma. Then thanks to the multiplicativity of 
$\varrho _f$ and applying the Lang–Weil estimate (Theorem 3.5) to 
${\mathcal {V}}$ and 
${\mathcal {G}}$, we obtain that, uniformly for any 
$p\notin S^\prime$,
\begin{equation} \frac{\varrho_f(p)}{p}=\frac{\#\Gamma^f_{\alpha_0}[pN]}{\#\Gamma_{\alpha_0}[pN]}=\frac{\#\Gamma^f_{\alpha_0}[p]}{\#\Gamma_{\alpha_0}[p]}=\frac{\#{\mathcal{V}}({\mathbb{F}}_p)}{\#{\mathcal{G}}({\mathbb{F}}_p)}\leqslant \frac{{\mathcal{C}}}{p}, \end{equation}
where the constant 
${\mathcal {C}}>0$ depends only on 
${\mathcal {V}},{\mathcal {G}}$. Therefore for any real numbers 
$w_1,w_2$ verifying 
$\max ({\mathcal {C}},2,\max _{p\in S^\prime }p)< w_1\leqslant w_2$, there exists 
$A_0>0$ such that
\[ \prod_{\substack{w_1\leqslant p\leqslant w_2}}\biggl(1-\frac{\varrho_f(p)}{p}\biggr)^{-1}\leqslant \prod_{\substack{w_1\leqslant p\leqslant w_2}}\biggl(1-\frac{{\mathcal{C}}}{p}\biggr)^{-1}\sim A_0\biggl(\frac{\log w_2}{\log w_1}\biggr)^{{\mathcal{C}}}, \]
by Mertens’ formula (cf. [Reference Friedlander and IwaniecFI10, (2.20)–(2.21)] or [Reference TenenbaumTen95, § 1.6, Theorems 7 and 10]). Thus it suffices to choose 
$A_1=A_1({\mathcal {V}},{\mathcal {G}},{\mathcal {P}})> \max (A_0,1)$ so that the sieve condition (2) in Theorem 3.4 is satisfied with 
$\kappa ={\mathcal {C}}$ for any 
$2\leqslant w_1\leqslant w_2$, taking account of the finitely many primes which are in 
$S^\prime$ or 
$\leqslant {\mathcal {C}}$.
3.5.3 Uniform error term estimates
For any 
$d\in {\mathbb {N}}_{\geqslant 1}$ with 
$\gcd (d,N)=1$, we now estimate the cardinality of subsequence
\[ {\mathcal{A}}_d:=(N^{-1}|f(g)|)_{\substack{g\in\Gamma_{\alpha_0}:\|g\| < T,d\mid N^{-1}f(g)}}, \]
and compare it with 
$({\varrho _f(d)}/{d})X$.
A key ingredient is [Reference Nevo and SarnakNS10, Theorem 3.2], which states that for any 
$\varepsilon >0$, uniformly for any 
$\xi \in \Gamma$ and any principal congruence subgroup 
$\Gamma _{\alpha }$,
\begin{equation} \#\{g\in\Gamma_{\alpha}:\|\xi\cdot g\|< T\}=\frac{{\mathrm{vol}}\{g\in\Gamma:\|g\|< T\}}{[\Gamma:\Gamma_{\alpha}]}+O_\varepsilon(T^{a-{\theta}/{(1+\dim G)}+\varepsilon}), \end{equation}
where the constant 
$a$ is in (3.2), 
$\theta$ is given in [Reference Nevo and SarnakNS10, Theorem 3.2], and 
${\mathrm {vol}}(\cdot )$ is associated to certain normalized Haar measure on 
$G({\mathbb {R}})$. The error term above is uniform with respect to 
$\alpha$, and depends only on the height function 
$\|\cdot \|$. This turns out to be crucial for the treatment of the error term in (3.3).
Thanks to (3.4), the reduction 
$\Gamma _{\alpha _0}\to \Gamma _{\alpha _0}[dN]$ has kernel 
$\Gamma _{dN}$. On applying (3.11) to both 
$\Gamma _{\alpha _0}$ and 
$\Gamma _{dN}$, we get that, uniformly for any 
$\xi \in \Gamma$,
\begin{align*} &\#\{g\in\Gamma_{dN}:\|\xi\cdot g\| < T\}\\ &\quad =\frac{{\mathrm{vol}}\{g\in\Gamma:\|g\| < T\}}{[\Gamma:\Gamma_{dN}]}+O_\varepsilon(T^{a-{\theta}/{(1+\dim G)}+\varepsilon})\\ &\quad=\frac{[\Gamma:\Gamma_{\alpha_0}]}{[\Gamma:\Gamma_{dN}]}(\#\{g\in\Gamma_{\alpha_0}:\|g\| < T\}+O_\varepsilon(T^{a-{\theta}/{(1+\dim G)}+\varepsilon}))+O_\varepsilon(T^{a-{\theta}/{(1+\dim G)}+\varepsilon})\\ &\quad=\frac{\#\{g\in\Gamma_{\alpha_0}:\|g\| < T\}}{[\Gamma_{\alpha_0}:\Gamma_{dN}]}+O_\varepsilon(T^{a-{\theta}/{(1+\dim G)}+\varepsilon}). \end{align*}
Let us choose representatives 
$\xi _1,\ldots ,\xi _{\#\Gamma _{\alpha _0}[dN]}\in \Gamma _{\alpha _0}$ of the group 
$\Gamma _{\alpha _0}/\Gamma _{dN}\simeq \Gamma _{\alpha _0}[dN]$, and write 
$\overline {\xi _i}\in \Gamma _{\alpha _0}$ the image of 
$\xi _i$ modulo 
$dN$. Since in this affine setting, the function 
$f$ takes constant residue modulo 
$dN$ on any coset 
$\xi _i\Gamma _{dN}$, we henceforth get
\begin{align*} \#{\mathcal{A}}_d&=\#\{g\in\Gamma_{\alpha_0}:\|g\| < T,f(g)\equiv 0\ \mathrm{mod}\ dN\}\\ &=\sum_{i=1}^{\#\Gamma_{\alpha_0}[dN]}\mathbf{1}_{dN \mid f(\overline{\xi_i})}\#\{g\in\Gamma_{dN}:\|\xi_i\cdot g\| < T\}\\
&=\sum_{i=1}^{\#\Gamma_{\alpha_0}[dN]}\mathbf{1}_{dN \mid f(\overline{\xi_i})}\bigg(\frac{\#\{g\in\Gamma_{\alpha_0}:\|g\| < T\}}{[\Gamma_{\alpha_0}:\Gamma_{dN}]}+O_\varepsilon(T^{a-{\theta}/{(1+\dim G)}+\varepsilon})\bigg)\\
&=\#\Gamma_{\alpha_0}^f[dN]\bigg(\frac{\#\{g\in\Gamma_{\alpha_0}:\|g\| < T\}}{[\Gamma_{\alpha_0}:\Gamma_{dN}]}+O_\varepsilon(T^{a-{\theta}/{(1+\dim G)}+\varepsilon})\bigg)\\ &=\frac{\#\Gamma_{\alpha_0}^f[dN]}{\#\Gamma_{\alpha_0}[dN]}X+O_\varepsilon(\#\Gamma_{\alpha_0}^f[dN]T^{a-{\theta}/{(1+\dim G)}+\varepsilon}), \end{align*}
where we recall 
$X$ (3.6) and the implied constants in all error terms are independent of 
$d$. Therefore
\begin{align} {\mathcal{R}}_{\mathcal{A}}(d)&:=\#{\mathcal{A}}_d-\frac{\varrho_f(d)}{d}X\nonumber\\ &=O_\varepsilon\big(\#\Gamma_{\alpha_0}^f[dN]T^{a-{\theta}/{(1+\dim G)}+\varepsilon}\big)=O_\varepsilon\big(\#\Gamma_{\alpha_0}^f[dN]X^{1-{\theta}/{a(1+\dim G)}+\varepsilon}\big). \end{align} We now estimate 
$\#\Gamma _{\alpha _0}^f[dN]$ for 
$d\in {\mathbb {N}}_{\geqslant 1}$ square-free with 
$\gcd (d,N)=1$. Thanks to (3.8), by employing the Lang–Weil estimate (Theorem 3.5), we obtain that, for any 
$\varepsilon >0$,
\begin{align} \#\Gamma_{\alpha_0}^f[dN]&\leqslant \#{\mathrm{GL}}_{n}({\mathbb{Z}}/N{\mathbb{Z}})\times \prod_{p\in S^\prime\cap {\mathcal{P}}}\#{\mathrm{GL}}_n({\mathbb{F}}_p)\times \prod_{\substack{p\mid d,p\notin S^\prime}}\#{\mathcal{V}}({\mathbb{F}}_p)\nonumber\\ &\ll \prod_{\substack{p\mid d,p\notin S^\prime }} C({\mathcal{V}})p^{\dim G-1} \ll_{\varepsilon} d^{\dim G-1+\varepsilon}, \end{align}so that we can continue to bound (3.12) as
\[ {\mathcal{R}}_{\mathcal{A}}(d)\ll_{\varepsilon} d^{\dim G-1+\varepsilon}X^{1-{\theta}/{a(1+\dim G)}+\varepsilon}. \] Therefore, with 
$y:=X^{\sigma }$, where 
$\sigma >0$ is chosen depending only 
$G$ such that 
$\gamma :={\theta }/{a(1+\dim G)}-\sigma \dim G\in \,]0,1[\,$, we get, uniformly for any 
$w\geqslant 2$,
\[ \sum_{\substack{d\leqslant y\\\textrm{d}\mid {\mathcal{P}}(w)}}|{\mathcal{R}}_{\mathcal{A}}(d)|\leqslant \sum_{\substack{d\leqslant y\\p\mid d\Rightarrow p\in{\mathcal{P}}}}\mu^2(d)|{\mathcal{R}}_{\mathcal{A}}(d)|\ll_{\varepsilon} X^{1-\gamma+\varepsilon}. \]3.5.4 Applying the combinatorial sieve
We deduce from Theorem 3.4 that, for the sequence 
${\mathcal {A}}$ with 
$T$ large enough so that
\[ z:=y^{\lambda}=X^{\lambda\sigma}\asymp T^{a\lambda\sigma}(\log T)^{b\lambda\sigma}>\max({\mathcal{C}},2) \]by (3.6), the sifting inequality (3.3) now reads
\begin{align*} S({\mathcal{A}},{\mathcal{P}},z)&=\#\bigg\{g\in \Gamma_{\alpha_0}: \|g\| < T ,\gcd\bigg(f(g),\prod_{p < z,p\nmid N}p\bigg)=1\bigg\}\\ &\gg X\prod_{p < z,p\nmid N}\bigg(1-\frac{\varrho_f(p)}{p}\bigg)\gg X\prod_{C(V) < p < z}\bigg(1-\frac{{\mathcal{C}}}{p}\bigg)\\ &\asymp \frac{X}{(\log z)^{{\mathcal{C}}}}\asymp \frac{\#\{g\in{\mathcal{G}}({\mathbb{Z}}):\|g\| < T\}}{(\log T)^{{\mathcal{C}}}}, \end{align*}
by (3.10), Mertens’ formula and (3.11). We conclude that (3.1) holds for 
$\beta _1= a\lambda \sigma$ and 
$\beta _2={\mathcal {C}}$. This finishes the proof of Theorem 3.1.
Remark 3.6 A more sophisticated weighted sieve method (cf. e.g. [Reference Halberstam and RichertHR74, Chapter 10]) should be able to enlarge 
$\beta _1$, and consequently give smaller admissible values for 
$r_0$ in Corollary 3.3 (this is one of the ingredients for refinements in [Reference Nevo and SarnakNS10, pp. 398–400]). On the other hand, on combining with the Chebotarev density theorem, one can obtain a lower bound for the product in Theorem 3.4(2), and this results in an upper-bound for (3.1) (with a smaller power on the log term). In [Reference Nevo and SarnakNS10, § 2], a stronger two-sided condition (e.g [Reference Halberstam and RichertHR74, 
$\Omega _2(\kappa ,L)$, p. 142]) is proven, under the extra assumption in Remark 3.2(ii), so that (3.1) has expected magnitude of growth. As the weaker one-sided condition (2) is enough to execute the sieve and is sufficient to deduce Corollary 3.3, we do not seek to obtain best possible 
$r_0$ or to minimize the exponent 
$\beta _2$ on 
$\log T$ in our article.
4. Anisotropic case
The following is our main result of this section, whose proof shows how the fibration method and the affine linear sieve established in preceding sections match together.
Theorem 4.1 Let 
$G$ be a three-dimensional semisimple simply connected linear algebraic group over a number field 
$k$ and 
$T\subset G$ be a maximal torus. If 
$T(k_{\infty })$ is not compact, then 
$G$ satisfies (APSA) off 
$\infty _{k}$.
4.1 Overview of the proof
The isotropic case is already covered by Theorem 1.4, so we only need to consider the case where 
$G$ is anisotropic in what follows. Let 
$D\subset G$ be closed of codimension at least 
$2$ and let 
$U:=G\setminus D$. The (APSA) off 
$\infty _{k}$ for 
$G$ amounts to saying 
$U$ satisfies (SA) off 
$\infty _{k}$ by definition 1.3. In Step I, by using the results in § 2, we can choose a torus 
$T$ such that 
$D$ intersects transversally with any fibre of the quotient 
$\pi :G\to G/T$. Here we make essential use of the assumption 
$\dim G=3$. The utilization of 
$\pi$ allows us to construct ‘good’ integral models (properties (i)–(v) in Step II) and control uniformly the fibres intersecting 
$D$, most of them being zero-dimensional. In Step III, we first use the (SA) property off 
$\infty _{k}$ for 
$G$ to produce rational points (
$P$ in Step IV) in any open subset (
$W_1$ (4.4) in the proof) of 
$G({\mathbf {A}}_{k}^{\infty _{k}})$. The goal is to find points avoiding 
$D$ modulo almost all places to ensure that they are in 
$U({\mathbf {A}}_{k}^\infty )$ (the open set 
$W$ (4.2) in the proof). In Step IV, we apply the sieve results in § 3 to produce a new point 
$P^\prime$ in 
$W_1$, so that the regular function 
$f$ (defined by (4.7)) vanishing on 
$\pi ^{-1}(\pi (D))$, when evaluated at 
$P^\prime$, is almost-prime and has only sufficiently big prime divisors (lying in 
$S_0$ (4.8) in the proof). As the torus 
$T$ contains integral points of infinite order thanks to its non-compactness at the archimedean places, and the function 
$f$ is chosen to be compatible with the fibration 
$\pi$, in Step V, we make use of the action of 
$T$ on the fibre containing 
$P^\prime$ without changing the value of 
$f$ to find a new point 
$P^{^{\prime \prime }\mkern -1.0mu}$ avoiding 
$D$ modulo all places in 
$S_0$. This point automatically avoids 
$D$ modulo any other places not in 
$S_0$, thereby achieving our goal.
4.2 A lemma on actions of topological groups
We include the following elementary result for the sake of completeness.
Lemma 4.2 Let 
$H$ be a topological group which acts continuously on a topological space 
$Y$. Then, for any compact open subset 
$V\subset Y$, there exists an open subgroup 
$F$ of 
$H$ such that 
$F\cdot V=V$.
Proof. We may assume that 
$V\neq \varnothing$, otherwise we take 
$F$ to be the identity. By the continuity assumption, for any 
$y\in V$, there exists an open subset 
$V_y\subset V$ of 
$Y$ and an open subset 
$H_y\subset H$ containing the identity such that 
$H_y\cdot V_y\subset V_y$. Since 
$V$ is compact, we can choose points 
$y_1,\ldots ,y_n\in V$ such that 
$V=\cup _{i=1}^n V_{y_i}$. Then the open subgroup 
$F$ generated by 
$\cap _{i=1}^n H_{y_i}$ satisfies that 
$F\cdot V=V$.
4.3 Proof of Theorem 4.1
Recall that our goal is to show that 
$U:=G\setminus D$ satisfies (SA) off 
$\infty _{k}$, whenever 
${\mathrm {codim}}(D,G)$ is at least 
$2$, under the assumption that 
$G$ is 
$k$-anisotropic.
4.3.1 Step I: Setting up the fibration
The assumption 
$\dim (G)=3$ implies that the group 
$G$ is 
$k$-simple (by considering the decomposition of 
$G$ into 
$k$-simple factors and by using the fact that there is no one-dimensional semisimple group). Moreover, the Bruhat decomposition implies that the big cell of 
$G_{\bar {k}}$ is of the form 
$U_+\times T_{\bar {k}}\times U_-$ where 
$U_+$ (respectively 
$U_-$) is the unipotent radical of some Borel subgroup (respectively opposite Borel subgroup) of 
$G_{\bar {k}}$ (cf. [Reference BorelBor91, Corollary 14.14]). So 
${\mathrm {codim}}(T,G)$ is even and 
$\dim (T)=1$.
Let us consider the quotient map 
$\pi : G\to Y:=G/T$. By Lemma 2.3, upon replacing 
$T$ by another 
$k$-conjugate if necessary, we may assume there exists a closed subset 
$D'\subset D$ such that 
$T\cdot D'=D'$, 
$\dim (D')<\dim (D)$ and 
$\pi (G\setminus D)=Y\setminus \pi (D')$. Since 
$\dim (G)=3$, one has 
$\dim (D')<\dim (D)\leqslant 1$ and so 
$D'=\varnothing$ because 
$T\cdot D'=D'$. As 
$\pi$ is a 
$T$-torsor, its restriction 
$\pi _U:=\pi |_U: U\to Y$ is smooth surjective with geometrically integral fibres. Thus 
$D$ does not contain any fibre of 
$\pi$ and, for any 
$y\in Y$, the fibre 
$D_y:=\pi ^{-1}(y)\cap D$ is either empty or of 
$\dim (D_y)=0$.
Since 
$Y$ is affine (by Matsushima's criterion since 
$T$, 
$G$ are reductive, cf. [Reference Popov and VinbergPV94, § 4 and Theorem 4.17]), and 
$\dim (\overline {\pi (D)})\leqslant \dim (D)<\dim Y=2$, we can find a regular function 
$F\in k[Y]$ so that its zero locus 
$E$ in 
$Y$ contains 
$\overline {\pi (D)}$. Let 
$V_0$ be the non-empty open subset 
$Y\setminus E$, and we have 
$\pi ^{-1}(V_0)\subset U$.
4.3.2 Step II: Choosing integral models and locating ‘bad’ fibres
We now fix integral models of 
$G,T$ and 
$U$ as follows. We choose an embedding 
$G\subset {\mathrm {GL}}_{n,k}$, and let 
${\mathcal {G}}$ be the integral closure of 
$G$ in 
${\mathrm {GL}}_{n,{\mathcal {O}}_k}$, 
${\mathcal {T}}$ (respectively 
${\mathcal {D}}$) be the integral closure of 
$T$ (respectively 
$D$) in 
${\mathcal {G}}$, and 
${\mathcal {U}}:={\mathcal {G}}\setminus {\mathcal {D}}$. Then 
${\mathcal {G}}$, 
${\mathcal {T}}$ are flat over 
${\mathcal {O}}_k$, and the quotient
\[ \pi: {\mathcal{G}}\to {\mathcal{Y}}:={\mathcal{G}}/{\mathcal{T}} \]
exists as a scheme over 
${\mathcal {O}}_k$ by a theorem of Raynaud (cf. [Reference AnantharamanAna73, § 4]). Let 
${\mathcal {E}}$ be the integral closure of 
$E$ in 
${\mathcal {Y}}$ and 
${\mathcal {V}}_0:={\mathcal {Y}}\setminus {\mathcal {E}}$.
To prove that 
$U$ satisfies (SA) off 
$\infty _{k}$, we need to show that, for 
$W\subset U({\mathbf {A}}_k^{\infty _{k}})$ any non-empty open subset,
\begin{equation} W\cap U(k)\neq\varnothing. \end{equation}
First of all, there exists a finite set of places 
$S\subset (\Omega _k\setminus \infty _{k})$ such that the following hold.
(i) By shrinking
$W$ if necessary, we may assume
(4.2)with\begin{equation} W=\prod_{v\in S}W_v\times \prod_{v\notin S\cup \infty_{k}}{\mathcal{U}}({\mathcal{O}}_v), \end{equation}$W_v\subset U(k_v)$ a non-empty compact open subset for each $v\in S$.(ii) The ring
${\mathcal {O}}_{k,S}$ is a principal ideal domain and there exists a finite subset $S'\subset \Omega _{{\mathbb {Q}}}$ such that ${\mathcal {O}}_{k,S}$ is finite étale over ${\mathbb {Z}}_{S'}$.(iii) The regular function
$F$ defined at the end of Step I satisfies $F\in {\mathcal {O}}_{k,S}[{\mathcal {Y}}]$.(iv) For all
$v\notin S\cup \infty _{k}$, the map $\pi |_{{\mathcal {U}}}: {\mathcal {U}}({\mathcal {O}}_v)\to {\mathcal {Y}}({\mathcal {O}}_v)$ is surjective, and ${\mathcal {V}}_0({\mathcal {O}}_v)\neq \varnothing$ (by [Reference ConradCon12, (ii) Proof of Theorem 4.5]).(v) There exists an integer
$L$ such that, for any $y\in {\mathcal {Y}}\times _{{\mathcal {O}}_k}{\mathcal {O}}_{k,S}$, the fibre ${\mathcal {D}}_y:={\mathcal {D}}\cap \pi ^{-1}(y)$ is either empty, or has dimension $0$ (cf. [Reference HartshorneHar77, Example II. 3.22]) and satisfies
(4.3)thanks to the upper semi-continuity of the function (cf. [Reference HartshorneHar77, Example II. 5.8])\begin{equation} \# {\mathcal{D}}_y(\overline{k(y)})\leqslant \deg ({\mathcal{D}}_y)\leqslant L, \end{equation}\[ y\mapsto \deg({\mathcal{D}}_y):=\dim_{k(y)}((\pi|_{{\mathcal{D}}})_*({\mathcal{O}}_{{\mathcal{D}}})\otimes_{{\mathcal{O}}_{{\mathcal{Y}}}}k(y)) \]
We summarize the construction above to the following commutative diagram.
4.3.3 Step III: First torus action
Recall the set 
$W$ (4.2). Let us consider
\begin{equation} W_1:= \prod_{v\in S}W_v\times \prod_{v\notin S\cup \infty_{k}}{\mathcal{G}}({\mathcal{O}}_v)\subset G({\mathbf{A}}_{k}^{\infty_{k}}). \end{equation}
By Lemma 4.2, there exists, for each 
$v\in S$, an open compact subgroup 
$\Phi _v\subset G(k_v)$ such that 
$\Phi _v\cdot W_v=W_v$. Consider subgroups
\[ \Phi_G:=\prod_{v\in S}\Phi_v\times \prod_{v\notin S\cup \infty_{k}}{\mathcal{G}}({\mathcal{O}}_v)\subset G({\mathbf{A}}_{k}^{\infty_{k}}), \]and
\[ \Phi_T:=\prod_{v\in S}(\Phi_v\cap{\mathcal{T}}({\mathcal{O}}_v))\times \prod_{v\notin S\cup \infty_{k}} {\mathcal{T}}({\mathcal{O}}_v)\subset \prod_{v\notin \infty_{k}}{\mathcal{T}}({\mathcal{O}}_v). \]We then have
\begin{equation} \Phi_G\cdot W_1=W_1 \quad\text{and}\quad \Phi_T\cdot W_1=W_1. \end{equation}
By assumption, 
$G$ is anisotropic and 
$T(k_{\infty })$ is not compact, so the group 
${\mathcal {T}}({\mathcal {O}}_k)$ is infinite (cf. [Reference Platonov and RapinchukPR94, § 4.5 and Corollary 1]). Since 
$\Phi _T$ has finite index in 
$\prod _{v\notin \infty _{k}}{\mathcal {T}}({\mathcal {O}}_v)$, the group 
$\Phi _T({\mathcal {O}}_k):={\mathcal {T}}({\mathcal {O}}_k)\cap \Phi _T$ has finite index in 
${\mathcal {T}}({\mathcal {O}}_k)$ and hence is infinite. Let 
$1_{{\mathcal {T}}}$ be the identity and fix
\begin{equation} Q\in \Phi_T({\mathcal{O}}_k) \end{equation}
an element of infinite order. For any 
$v\in \Omega _k\setminus \infty _{k}$, we denote by 
${\mathrm {ord}}(Q\ \mathrm {mod}\ v)$ the order of the element 
$Q \ \mathrm {mod}\ v$ in the group 
${\mathcal {T}}(k(v))$. We want to show the following.
(vi) For any integer
$r\in {\mathbb {N}}_{\geqslant 1}$, there exists $M_r>0$ such that, for any finite place $v$ with $\#k(v)>M_r$, one has that ${\mathrm {ord}}(Q\ \mathrm {mod}\ v)\geqslant rL+1$ (recall $L$ (4.3)).Footnote 4
Indeed, for any integer 
$l\in {\mathbb {N}}_{\geqslant 1}$, consider the set
\[ B(Q,l):=\{v\in \Omega_k\setminus \infty_{k}:{\mathrm{ord}}(Q\ \mathrm{mod}\ v)\leqslant l\}. \]
Then it is clear that 
$B(Q,l)=\cup _{1\leqslant j\leqslant l}B(Q^j)$, where each set
\[ B(Q^j):=\{v\in \Omega_k\setminus \infty_{k}: Q^j\equiv 1_{{\mathcal{T}}}\ \mathrm{mod}\ v\} \]
has finite cardinality. Now to see the statement (vi) it suffices to take 
$l=rL$ and 
$M_r:=\max _{v\in B(Q^j),1\leqslant j\leqslant l}(\#k(v))$, so that for any 
$v\in \Omega _{k}\setminus \infty _{k}$ such that 
$\#k(v)>M_r$, we have 
$v\in \Omega _{k}\setminus (\infty _{k}\cup B(Q,rL))$, in other words, 
${\mathrm {ord}}(Q\ \mathrm {mod}\ v)\geqslant rL+1$. This proves (vi).
4.3.4 Step IV: Applying the affine sieve
Since 
$G(k_\infty )$ is not compact (because of 
$T(k_\infty )$), 
$G$ satisfies (SA) off 
$\infty _{k}$ by Theorem 1.1. Hence there exists 
$P\in G(k)\cap W_1$ (recall 
$W_1$ (4.4)). Let us define the regular function
\begin{equation} f(g):=(F\circ \pi) (g\cdot P). \end{equation}
Then 
$f\in {\mathcal {O}}_{k,S}[{\mathcal {G}}]$ by (iii). We claim that 
$f({\mathcal {G}}({\mathcal {O}}_v))\cap {\mathcal {O}}_v^{\times }\neq \varnothing$ for any 
$v\notin S\cup \infty _{k}$. Indeed, according to (iv), we have 
$\pi ({\mathcal {U}}({\mathcal {O}}_v))\cap {\mathcal {V}}_0({\mathcal {O}}_v)\neq \varnothing$. Take any 
$P_0 \in {\mathcal {U}}({\mathcal {O}}_v)$ such that 
$\pi (P_0)\in {\mathcal {V}}_0({\mathcal {O}}_v)$, then the element 
$g_1:=P_0\cdot P^{-1}\in {\mathcal {G}}({\mathcal {O}}_v)$ verifies 
$f(g_1)=F(\pi (P_0))\not \equiv 0\ \mathrm {mod}\ v$ by the definition of 
${\mathcal {V}}_0$. This proves the claim. Taking (ii) into account, the hypotheses of Corollary 3.3 are satisfied for the pair 
$(f,\Phi _G)$. We thus obtain the following.
(vii) There exists an integer
$r_0$ and an element $g_0\in \Phi \cap {\mathcal {G}}({\mathcal {O}}_{k,S})$, such that $f(g_0)$ has at most $r_0$ prime factors in ${\mathcal {O}}_{k,S}$ and all of their residue fields have cardinalities larger than $M_{r_0}$, where the constant $M_{r_0}$ is defined by (vi) in Step III by taking $r=r_0$.
4.3.5 Step V: Second torus action – avoidance of ‘bad’ fibres
Recall (4.6). Let us define 
$P^\prime :=g_0\cdot P$,
\[ \Theta:=\{Q^l\cdot P^\prime:0\leqslant l\leqslant r_0\cdot L\} \]and
\begin{equation} S_0:=\{v\in \Omega_{k}\setminus (S\cup\infty_{k}): \pi(P')\ \mathrm{mod}\ v\in {\mathcal{E}}\}. \end{equation}
Then 
$P^\prime \in \Theta \subset G(k)\cap W_1$, thanks to (4.5). Also, (vii) implies that the set 
$S_0$ (if non-empty) contains at most 
$r_0$ places.
For any 
$v\in S_0$, let 
$y_v:=\pi (P') \ \mathrm {mod}\ v\in {\mathcal {Y}}(k(v))$ and
\[ \Theta_v:=\{x\in \Theta: x\ \mathrm{mod}\ v \in {\mathcal{D}}_{y_v}\}. \]
(Recall 
${\mathcal {D}}:={\mathcal {G}}\setminus {\mathcal {U}}$ defined in the beginning of Step II and 
${\mathcal {D}}_y$ in (v).) According to (vi) and (vii), for any 
$v\in S_0$, we have 
$\#k(v)>M_{r_0}$ and hence 
${\mathrm {ord}}(Q\ \mathrm {mod}\ v)\geqslant r_0L+1$. So the reduction map 
$\Theta \xrightarrow {\ \mathrm {mod}\ v} {\mathcal {G}}_{y_v}(k(v))$ is injective. Thus 
$\#\Theta _v\leqslant \#{\mathcal {D}}_{y_v}(k(v))\leqslant \deg {\mathcal {D}}_{y_v}$. On the other hand, on combining (4.3) in (v), we get
\[ \# \Theta= r_0L+1\geqslant 1+\sum_{v\in S_0} \deg {\mathcal{D}}_{y_v} \geqslant 1+\sum_{v\in S_0} \#\Theta_v> \sum_{v\in S_0} \#\Theta_v . \]
This means that we can find a point 
$P^{^{\prime \prime }\mkern -1.0mu}\in \Theta$ such that 
$P^{^{\prime \prime }\mkern -1.0mu}\ \mathrm {mod}\ v\notin {\mathcal {D}}$ for all 
$v\in S_0$.
By the definition of 
$S_0$, 
$\pi (P^\prime )=\pi (P^{^{\prime \prime }\mkern -1.0mu})\ \mathrm {mod}\ v\not \in {\mathcal {E}}$ for any 
$v\not \in S\cup S_0\cup \infty _{k}$, and therefore for any such 
$v$, we have 
$P^{^{\prime \prime }\mkern -1.0mu}\ \mathrm {mod}\ v\notin {\mathcal {D}}$. We have finally proven that 
$P^{^{\prime \prime }\mkern -1.0mu}\ \mathrm {mod}\ v\notin {\mathcal {D}}$ for any 
$v\notin S\cup \infty _{k}$, and therefore 
$P^{^{\prime \prime }\mkern -1.0mu}\in W\cap G(k)=W\cap U(k)$ (recall 
$W$ (4.2)), so (4.1) is achieved. This finishes the proof of the theorem.
5. Affine quadrics
In this section we complete the proof of Theorem 1.7 and then deduce Theorem 1.6, finally confirming (APSA) off 
$\infty _{k}$ for affine quadrics.
5.1 Proof of Theorem 1.7
By Theorem 2.1, it suffices to show that 
$G^\prime$ satisfies (APSA) off 
$\infty _{k}$. Upon replacing 
$G$ by 
$G'$, we may assume that 
$\dim (G)=3$. Since 
$G(k_{\infty })$ is not compact, there exists 
$v\in \infty _{k}$ such that 
$G(k_v)$ is not compact. By [Reference Platonov and RapinchukPR94, Theorem 3.1], 
$G_{k_v}$ is isotropic, so it contains an isotropic maximal torus 
$T_v\subset G_{k_v}$ over 
$k_v$. By [Reference Platonov and RapinchukPR94, § 7.1 and Corollary 3], there exists a maximal torus 
$T\subset G$ over 
$k$ such that 
$T_{k_v}$ is conjugate to 
$T_v$ over 
$k_v$. Thus 
$T(k_{\infty })$ is not compact. Then the statement follows from Theorem 4.1.
5.2 Proof of Theorem 1.6
To prove (i), we may assume 
$q(x_1,\ldots , x_n)=\sum _{i=1}^na_ix_i^2$ with 
$a_i\in k^{\times }$ for all 
$i$. Since 
$q$ is isotropic over some 
$v_0\in \infty _{k}$, if 
$v_0$ is real, then we may assume that 
$v_0(a_1\cdot a_2)< 0$. Then the spin group
\[ G':=\operatorname{Spin}\!\big(a_1x_1^2+a_2x_2^2+a_3x_3^2\big) \]
is a three-dimensional closed subgroup of 
$G=\operatorname {Spin}(q)$ and is not compact over 
$v_0$. If 
$G$ is 
$k$-simple, then the statement (i) now follows from Theorem 1.7. The only case where 
$G$ is not 
$k$-simple (cf. [Reference Colliot-Thélène and XuCX09, Proof of Theorem 6.1]) is when 
$n=4$ and 
$\det (q)\in k^{\times 2}$, and in that case 
$G\simeq _k H\times H$, where 
$H$ is a 
$k$-form of 
${\mathrm {SL}}_{2,k}$ and 
$H_K\simeq {\mathrm {SL}}_{2,K}$ over an extension 
$K$ of 
$k$ if 
$q$ is isotropic over 
$K$. Since we assume that 
$q$ is isotropic over the place 
$v_0$, so 
$G_{k_{v_0}}\simeq _{k_{v_0}}{\mathrm {SL}}_{2,k_{v_0}}\times {\mathrm {SL}}_{2,k_{v_0}}$. Therefore the three dimensional 
$k$-simple group 
$H$ is not compact over 
$v_0$. It then satisfies (APSA) off 
$\infty _{k}$ by Theorem 1.7. The fact that 
$G$ also verifies (APSA) off 
$\infty _{k}$ in this case follows from [Reference Cao, Liang and XuCLX19, Proposition 4.7].
To prove (ii), we may assume that the affine quadric 
$V:q(x_1,\ldots ,x_n)=a_0$ satisfies 
$V({\mathbf {A}}_k)\neq \varnothing$. Then 
$V(k)\neq \varnothing$ by the Hasse–Minkowski theorem. Then the statement follows from [Reference Cao, Liang and XuCLX19, Theorem 1.3], since by [Reference Colliot-Thélène and XuCX09, § 5.3], when 
$n\geqslant 4$, 
$V$ is a homogeneous space under 
$\operatorname {Spin}(q)$ with stabilizer isomorphic to 
$\operatorname {Spin}(h)$ where 
$h$ is another non-degenerate quadratic form in 
$n-1$ variables, and we have 
$\bar {k}[V]^\times =\bar {k}^\times , \operatorname {Br}(V)=\operatorname {Br}(k)$.
Acknowledgements
We would like to thank Jean-Louis Colliot-Thélène, Cyril Demarche, Philippe Gille, Yonatan Harpaz, Diego Izquierdo, Olivier Wittenberg and Fei Xu for many interesting discussions, and to Dasheng Wei and Han Wu for kindly pointing out some inaccuracies. We are grateful to Tim Browning for his interest in this project and to Ulrich Derenthal for his generous support. Part of this work was carried out at the Institut Henri Poincaré during the trimester ‘À la redécouverte des points rationnels’. We are grateful to the organizers and the staff for creating a very stimulating atmosphere. We would like to express our heartfelt thanks to the anonymous referees for their careful scrutiny and valuable suggestions. The first author is supported by a Humboldt-Forschungsstipendium. The second author is supported by grant DE 1646/4-2 of the Deutsche Forschungsgemeinschaft.
