1. INTRODUCTION
Intercomprehension (Doyé Reference Doyé2005), receptive multilingualism (Braunmüller & Zeevaert Reference Braunmüller and Ludger Zeevaert2001) or semi-communication (Haugen Reference Haugen1966) reveals a remarkable tolerance of human language processing mechanisms to deviations in linguistic encoding. It can be defined as the ability to understand unknown foreign languages, only due to their relatedness with at least one language that is already contained in the user's linguistic repertoire. This robust process is receptive in nature and does not include the ability to speak or write in the respective unknown language. The degree of intelligibility of an unknown but closely related language depends on both linguistic and extra-linguistic factors (Gooskens Reference Gooskens, Bayley, Cameron and Lucas2013). Research on receptive multilingualism has considered extra-linguistic factors such as subjective linguistic attitudes, exposure (Gooskens & van Bezooijen Reference Gooskens and van Bezooijen2006, Schüppert & Gooskens Reference Schüppert and Gooskens2012), fluid and crystallized intelligence, and age (Vanhove & Berthele Reference Vanhove and Berthele2015a). The literature shows different results of the relationship between extra-linguistic factors and intelligibility. While in some studies no correlation (e.g. between language attitudes and intelligibility) could be found (van Bezooijen & Gooskens Reference van Bezooijen, Gooskens, ten Thije and Zeevaert2007, Gooskens & Hilton Reference Gooskens, Hilton, Tirkkonen and Anttikoski2013), other studies did find a positive correlation (Gooskens & van Bezooijen Reference Gooskens and van Bezooijen2006, Schüppert, Hilton & Gooskens Reference Schüppert, Hilton and Gooskens2015).
In order to formally model the intercomprehension scenario in our project, we systematically investigate the linguistic determinants of successful information transmission across languages from the Slavic family, which are ‘sufficiently similar and sufficiently different to provide an attractive research laboratory’ (Corbett Reference Corbett1998:42).
Realistic scenarios of a reader fluent in one language trying to decipher a text written in an unknown but related language could involve, for example, a Czech native speaker attempting to read a Polish newspaper or a Russian native speaker being confronted with hotel information on Bulgarian websites. We assume that there should be a systematic way to successfully decode a given message depending on a quantifiable proximity between the language of the message and the decoder's own language, if the two are genetically related. In particular, the initial challenge is to decode the encountered signs into meaningful units in order to form a coherent understanding of the encoded information. Thus, orthography critically affects the success of transmitting information across languages: Unsuccessful or incomplete decoding of orthographic representations in an unknown language may lead to a situation where even cognate words become incomprehensible.
According to the Handbook of Orthography and Literacy (Joshi & Aaron Reference Joshi, Aaron, Joshi and Aaron2006), orthography is the ‘visual representation of language as conditioned by phonological, syntactical, morphological, and semantic features of the language’ (Joshi & Aaron Reference Joshi, Aaron, Joshi and Aaron2006:xiii). Indeed, orthography reflects a unique relationship to the characteristics of the respective language and a comparison of different orthographic systems involves various descriptive levels (phonetics/phonology, graphemics/graphotactics, morphology/morphosyntax, semantics) as well as historical, etymological, and sociolinguistic factors (e.g. spelling reforms) (Sgall Reference Sgall and Sgall2006). In fact, the degree to which orthography provides a visual representation of (spoken) language varies between languages. Written and spoken language intercomprehension are traditionally considered different experiential domains, as pointed out by Gooskens (Reference Gooskens, Bayley, Cameron and Lucas2013) and Möller & Zeevaert (Reference Möller and Zeevaert2015), as well as in the critique of the representational idea by Kravchenko (Reference Kravchenko2009). Yet, as mentioned by Gooskens (Reference Gooskens, Bayley, Cameron and Lucas2013:1), methods for measuring the intelligibility of spoken language are applicable to written language too.
In our view, the following question is crucial for investigating the role of orthography in Slavic intercomprehension: How can orthographic intelligibility be measured and predicted between related languages? Our approach includes three computational methods: Levenshtein distance, conditional entropy and adaptation surprisal. Using them for modeling the orthographic mutual intelligibility should help us explain and predict how written stimuli are processed. As the Slavic languages use two different scripts, we investigate two representative language pairs here: Czech–Polish (West Slavic, using the Latin script; henceforth referred to as CS and PL) and Bulgarian–Russian (South Slavic and East Slavic, respectively, using the Cyrillic script; henceforth referred to as BG and RU).
This article is organized as follows. In Section 2 we give a short overview of the Slavic orthographic code as the linguistic basis for our modeling. In Section 3 we present the collected material (Section 3.1) and describe the computational methods by means of the Levenshtein algorithm (Section 3.2), conditional entropy (Section 3.3) and adaptation surprisal (Section 3.4). Finally, in Section 4, some general conclusions are drawn, including the discussion of advantages and disadvantages of the methods presented, and future work is presented.
2. SLAVIC ORTHOGRAPHIC CODE
In this section, we give a short overview of the orthographic code of the selected Slavic languages. In Section 2.1 we present the Latin and Cyrillic alphabets. In Section 2.2 we describe briefly the main orthographic principles of the respective orthographic systems. The way information is orthographically encoded in a word is influenced by the phonetic/phonological as well as the morphological structure of the language (Frost Reference Frost2012). We omit the detailed presentation of the phonetic/phonological systems of the respective languages, because our focus lies on reading intercomprehension. However, we consider phonetics/phonology a possible factor in so far as readers will try to pronounce what they read in a process that is known as ‘inner speech’ (Harley Reference Harley2008).
2.1 Latin and Cyrillic scripts
Modern Slavic languages use two scripts, Latin and Cyrillic, which provide the Slavic orthographies with two rather different bases (Kučera Reference Kučera2009:72). An alphabet of a language constitutes the material basis of the respective orthography and can be described as a set of charactersFootnote 1 (i.e. horizontally separable units; on the treatment of diacritics, see Section 3.2) that are used to constitute a written text in the language. The Latin and Cyrillic alphabets of the respective language pairs CS–PL and BG–RU are described in Sections 2.1.1 and 2.1.2. The characters of the alphabets are written in italics here in order to make it easier to compare these with examples. For a better visualization, we underlined the representations of vowels in Tables 1 and 2.
Table 1. Czech (CS) and Polish (PL) alphabets (vowels are underlined).
Table 2. Bulgarian (BG) and Russian (RU) alphabets with transliteration according to the DIN (German Institute for Standardization) norm (vowels are underlined).
2.1.1 Czech and Polish alphabets
Although both CS and PL use the Latin script (Table 1), they differ in their diacritical systems and the use of digraphs (combinations of two characters representing one phoneme). While PL makes extensive use of digraphs (which are not considered alphabetical characters), CS prefers diacritics. There are 42 characters in the CS alphabet: 14 representations of vowels (underlined) plus 28 representations of consonants. The PL alphabet consists of only 31 characters, of which nine are representations of vowels and 22 representations of consonants.
CS uses two basic diacritical signs: the čárka (acute accent symbol) ´ for marking a long vowel (plus the kroužek (circle) above u, i.e. ů, to designate a long u that historically goes back to o) and the háček (caron) ˇ, which was an innovation (originally in the shape of a superscript dot) (Comrie Reference Comrie1996a:664).
CS has a háček (i) for the palato-alveolar fricatives š /ʃ/, ž /ʒ/ and for the affricate č /ʧ/; (ii) for the fricative trill ř /
/; (iii) for palatal Ď /ɟ/, ň/Ň /ɲ/, and Ť /c/, except before ě and i; and (iv) on ě to palatalize the preceding consonant. In the case of ď and ť, a klička (apostrophe) is used as an alternation of the háček (Comrie Reference Comrie1996a, Skorvid Reference Skorvid, Moldovan, Skorvid, Kibrik, Rogova, Jakuškina, Žuravlёv and Tolstaja2005).
PL uses the digraphs cz for /
/, sz for /ʂ/, and either the diacritic ż (with the original CS dot) or the digraph rz, depending on etymology, for /ʐ/. PL has four different diacritical signs: (i) the kreska (acute accent symbol) ´, marking the vowel ó /u/ (which is likely to be mispronounced as /oː/ by Czech readers) and performing a similar function to the CS háček in ć, ń, ś, and ź; (ii) the kropka (overdot) used only in ż /ʐ/; (iii) the ogone
in ą and ę; and (iv) the kreska ukośna (stroke) used in ł. Digraphs such as ch, cz, dz, dź, dż, rz, sz are not considered characters of the PL alphabet. The digraph ch for /x/ is used in both languages and is considered a character of the CS alphabet.
The CS characters á, č, ď, é, ě, í, ň, ř, š, ť, ú, ů, v, ý, ž as well as q, v and x are not part of the PL alphabet (the character v is only used in PL texts when it is part of a named entity or a foreign word), and the PL characters ą, ć, ę, ł, ń, ś, ż, ź do not exist in the CS alphabet. Still, these characters are expected to be legible for readers of the respective target language (i.e. by ignoring or substituting diacritical signs) and thus are not expected to impair reading intercomprehension heavily – especially when the actual phonetic representation is similar (e.g. á vs. a), although this fact might not be known to the reader.
2.1.2 Bulgarian and Russian alphabets
Comparing BG and RU alphabets (Table 2), we see that there are only slight differences. There are 30 characters in BG: eight representations of vowels (underlined), 21 representations of consonants and one sign without independent phonetic value (ь). RU has 33 characters: 10 representations of vowels, 21 representations of consonants and two signs without independent phonetic values: the so-called soft (ь) and hard (ъ) signs. Three characters of the RU alphabet do not occur in BG: ы, э, ё.Footnote 2
The use of digraphs or diacritics is rare in the Cyrillic script. BG uses the digraph дж for [ʤ] and the digraph дз for [ʣ] (sounds not found in RU), for example, BG джоб (džob) ‘pocket’ and дзифт (dzift) ‘tar’. These two digraphs are not listed separately in the BG alphabet.
In an intercomprehension reading scenario, all BG characters seem to be familiar to readers who know the RU alphabet, but not vice versa. However, the nature as well as the use and pronunciation of a number of BG characters are not the same as in RU. The following BG characters have approximately the same value as in RU: а, б, в, г, д, з, и, й, к, л, м, н, о, п, р, с, т, у, ф, х, ю, я (Comrie Reference Comrie1996b, Cubberley Reference Cubberley1996). The BG characters ъ and щ seem to be familiar to Russian readers, but the character-sound correspondences are different: ъ and щ in BG are pronounced [ɤ] and [ʃt] (Ternes & Vladimirova-Buhtz Reference Ternes and Vladimirova-Buhtz2010), while in RU ъ has no phonetic, but an orthographic function, and щ is pronounced [ʃʲː] (Yanushevskaya & Bunčić Reference Yanushevskaya and Bunčić2015).
2.2 Orthographic principles as mechanisms of Slavic orthographic code
In an ideal phonographicFootnote 3 writing system, one graphic unit corresponds to a single sound unit and vice versa. However, the main lines of the evolution of the sound system in the Slavic languages are not always reflected in writing. Depending on the language and its history, orthographies were on the one hand adapted to sound changes in order to achieve harmony with the spoken language; on the other hand, orthographic systems were built upon the morphologicalFootnote 4 principle (e.g. with morphemes being written the same way, if possible, despite the differences in pronunciation) or historical/etymological principles (e.g. reflecting either the spelling of a language from which a word has been borrowed or an older state of the same language) (Kučera Reference Kučera2009).
Most, if not all, Slavic orthographies can be primarily described as phonemic, i.e. based on the correspondences between graphic and phonemic units (Kučera Reference Kučera2009). However, Kučera (Reference Kučera2009:74) points out that ‘[t]he boundaries between the implementations of the phonological and morphological principles vary in different Slavic orthographies’. Thus, the Moscow Phonological School considers the phonemic principle to be the main principle in RU orthography in contrast to the St. Petersburg Phonological School that regards the morphological principle as the basic orthographic principle, depending on what is understood as a phoneme (Ivanova Reference Ivanova1991, Musatov Reference Musatov2012). The BG orthography generally followed the RU model with a number of changes in the alphabets (Kempgen Reference Kempgen2009, Marti Reference Marti, Gutschmidt, Kempgen, Berger and Kosta2014) and is defined as phonemic, although the morphological principle is also very important (Maslov Reference Maslov1981). The CS and PL orthographies can also be described as being primarily phonemic with some exceptions according to the morphological principle (Kučera Reference Kučera2009).
The particular orthographic principles used in the writing systems determine the mechanisms of the orthographic code using characters to represent speech – words and grammatical forms – in writing. The computational methods presented here (Levenshtein algorithm, conditional entropy and adaptation surprisal) should help us to discover a number of general patterns of interlingual orthographic encoding in order to model orthographic intelligibility in reading intercomprehension.
3. MODELING ORTHOGRAPHIC INTELLIGIBILITY
Successful reading intercomprehension is very closely linked to the amount of common vocabulary among genetically related languages (Möller & Zeevaert Reference Möller and Zeevaert2015). However, very often these cognatesFootnote 5 (i.e. historically/etymologically related words) are not identical (e.g. orthographically). For instance, CS štěstí, PL szczęście, BG щастие (štastie), and RU счастье (sčast'e) ‘happiness’ (Vasmer Reference Vasmer1973) are cognates, but spelled (and also pronounced) differently. A correct cognate recognition can be seen as a precondition of success in reading intercomprehension. In this section we present three methods of measuring orthographic intelligibility: the Levenshtein algorithm (Section 3.2) and conditional entropy (Section 3.3), and the resulting adaptation surprisal (Section 3.4) as potential explanatory variables of orthographic intelligibility. These methods are applied to collections of parallel cognates in the selected language pairs.
3.1 Material
For our models, we make the following assumption: If a cognate pair in two languages L1 (native language) and L2 (stimulus languageFootnote 6 ) is orthographically (nearly) identical, then its similarity is determined by the chance that a L1 reader is able to decipher the characters of the L2 word. This implies that there exists a mapping between the characters of the two languages.
In the first step of our work, we set out to find these mappings. To this end, we created a maximally large collection of parallel cognate lists in the two language pairs (Table 3). We chose to use vocabulary lists instead of parallel sentences or texts in order to exclude the influence of other linguistic factors as much as possible. We compiled parallel cognate lists, consisting of internationalisms, lists of Pan-Slavic vocabulary (both adapted from the EuroComSlav website), and cognates from the Swadesh lists. All three lists were slightly modified in a way that non-cognates (i.e. CS–PL mnoho–wiele ‘many/much’; BG–RU ние–мы (nie–my) ‘we’) were removed or replaced by the orthographically closest cognates, if existing, in the respective other language (i.e. mężczyzna ‘man’ was substituted by mąż ‘husband’ in CS–PL muž–mąż; звяр (zvjar) ‘beast’ was added to its RU formal cognate зверь (zver’) ‘animal, beast’ for the BG–RU pair звяр–зверь (zvjar–zver’). The linguistic items in these lists belong to different parts of speech, mainly nouns, adjectives, and verbs.
Table 3. Sizes of word sets for applicability experiments with cross-lingual orthographic correspondences.
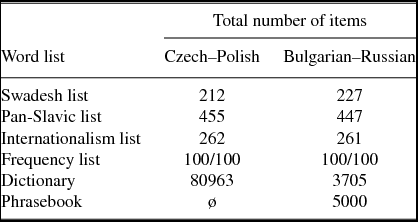
For CS–PL we used a large, freely available online dictionary list (Kazojć Reference Kazojć2010). For BG–RU, we included cognate pairs of a freely available online RU–BG phrasebook as well as a RU–BG dictionary from the website www.lexicons.ru.
We also included parallel lists of the 100 most frequent nouns (‘frequency lists’) from a previous study (Jágrová et al. Reference Jágrová, Stenger, Marti, Avgustinova, Emonds and Janebová2017), in which readily available frequency lists of the languages (Frequency Dictionaries of Bulgarian (2011), available at http://dcl.bas.bg/en/tchestotni-retchnitsi-na-balgarskiya-ezik-2/, Křen (Reference Křen2010) for CS, the Frequency List (2016) for PL (Broda & Piasecki Reference Broda and Piasecki2013), and Ljaševskaja & Šarov (Reference Ljaševskaja and Šarov2009) for RU), each based on large national corpora, were translated and compared. These lists were compiled for each source language separately and were then translated into the respective other language, always choosing the orthographically closest cognate if there was more than one option for translation (for details, see Jágrová et al. Reference Jágrová, Stenger, Marti, Avgustinova, Emonds and Janebová2017). Thus, all four source lists are different.
To incorporate recognized theoretical findings of traditional Slavic linguistics, we decided to collect a systematic cross-linguistic rule set of orthographic correspondences from historical comparative studies (Bidwell Reference Bidwell1963, Vasmer Reference Vasmer1973, Žuravlev 1974–Reference Žuravlev2012). These rules explain which L1 substrings correspond to which L2 substrings. We selected only those rules which we determined to have purely orthographic effects, excluding morphology and lexis as far as possible. This resulted in a compilation of diachronically based orthographic correspondences: 103 unique correlates for CS–PL and 77 for BG–RU, including one-to-one (matching) correspondences and mismatches consisting of single characters or of strings of characters (e.g. CS–PL: a:a, á:ią, ě:ię, z:dz, hv:gw, lou:łu, etc.; BG–RU: б:б, т:ть, б:бл, ъ:у, и:ы, я:е, ла:оло, etc.). Only correspondences which represented orthographic mismatches were automatically tested for applicability on parallel vocabulary lists. For the most part, the obtained automatic transformations could be seen as satisfactory for both language pairs. The outcomes of this applicability experiment can already be considered a measure for orthographic intelligibility: The fact that there are more cross-lingual correspondence rules in the CS–PL pair than in the BG–RU pair suggests that BG and RU are orthographically closer to each other than CS and PL. For more details concerning the transformation experiment see Fischer et al. (Reference Fischer, Jágrová, Stenger, Avgustinova, Klakow, Marti, Sharp, Lubaszewski and Delmonte2015). From these lists (Table 3), we obtained 3404 CS–PL and 1182 BG–RU word pairs,Footnote 7 consisting of either identical words or words to which the cross-lingual correspondence rules apply.Footnote 8 These resulting word pairs were used for further calculations of conditional entropy and adaptation surprisal in Sections 3.3 and 3.4 below.Footnote 9 From these lists, selected word pairs containing such cross-lingual correspondences will be used as stimuli in our web-based experiments.
3.2 Levenshtein distance
Orthographic distances between cognates can be calculated by means of the Levenshtein algorithm (Levenshtein Reference Levenshtein1966). The latter has been developed for measuring linguistic distances between dialects (Heeringa et al. Reference Heeringa, Kleiweg, Gooskens, Nerbonne, Nerbonne and Hinrichs2006) and successfully used to measure phonetic distances between Scandinavian language varieties (see Gooskens Reference Gooskens2007).
Levenshtein distance (hereafter referred to as LD) is a string similarity measure which is equal to the number of operations needed to transform one string of characters into another through character insertions, deletions, and substitutions. These three operations are assigned weights. In the simplest form of the algorithm, all operations have the same cost. LD is a simple measure that (given reasonably similar alphabets) works out-of-the-box, is easy to apply, and requires no training data. In order to perform the alignment automatically, the algorithm is fed with character weight matrices for each language combination. Each matrix contains the complete alphabets of a language pair together with the costs assigned for every possible character alignment. We use 0 for the cost of mapping a character to itself, e.g. а:а, and a cost of 1 to align it to a character of the same kind (vowel characters vs. consonant characters), e.g. а:о. All vowel-to-consonant combinations are given a weight of 4.5 (most expensive) in the algorithm. Thus we obtain distances which are based on linguistically motivated alignments. The actual edit costs are calculated after the automatic character alignment. Substitutions, insertions and deletions of different characters cost 1. In more sensitive versions, base and diacritic may be distinguished for a given character. For example, the base of CS á is a, and the diacritic is the čárka. It is not clear what weight exactly should be attributed to each of the components, but it is generally assumed that differences in the base will usually confuse the reader more than diacritical differences (Heeringa et al. Reference Heeringa, Golubovic, Gooskens, Schüppert, Swarte and Voigt2013). Thus, if two characters have the same base but differ in diacritics, we assign them a substitution cost of 0.5, and no difference is made between the costs of the different diacritical signs (e.g. čárka vs. háček). For example, the following differences between CS and PL and between BG and RU are automatically calculated for the word ‘youth’ (see Table 4).
Table 4. Normalized LD (Levenshtein distance) for the word ‘youth’ in (a) Czech–Polish and (b) Bulgarian–Russian.
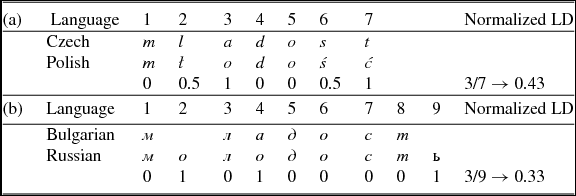
In our analysis we consider normalized LD in accordance with the assumption that a segmental difference in a word of, e.g. two segments has a stronger impact on intelligibility than a segmental difference in a word of, e.g. ten segments (Beijering, Gooskens & Heeringa Reference Beijering, Gooskens, Heeringa, van Koppen and Botma2008). Per word pair, the non-normalized LD is computed by means of the minimum number of operations needed to transform the string from one language into the other. The normalized LD is obtained by dividing the non-normalized distance by the total length of the alignment with the minimum costs (see Table 4).
With this method, we calculated the average orthographic distance within the respective Slavic language pairs on four of the parallel vocabulary lists: Swadesh list, Pan-Slavic list, Internationalism list (Stenger et al. in press) and the frequency lists (Jágrová et al. Reference Jágrová, Stenger, Marti, Avgustinova, Emonds and Janebová2017). We found that throughout all lists the average orthographic distance between BG and RU is smaller than that between CS and PL (see Table 5), which confirms our previous findings from the applicability of rules experiment (Section 3.1above, Fischer et al. Reference Fischer, Jágrová, Stenger, Avgustinova, Klakow, Marti, Sharp, Lubaszewski and Delmonte2015).
Table 5. Average orthographic distance by means of the Levenshtein algorithm.
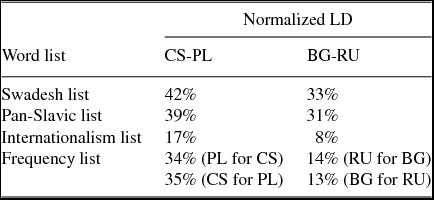
LD = Levenshtein distance; CS = Czech; PL = Polish; BG = Bulgarian; RU = Russian
There is a general assumption that the higher the LD, the more difficult it is to comprehend a given word in a translation task (see Gooskens Reference Gooskens2007, Vanhove & Berthele Reference Vanhove, Berthele, De Angelis, Jessner and Kresić2015b, Vanhove Reference Vanhove2016). This in particular means that, according to the average LD, CS and PL are mutually less intelligible than BG and RU as far as orthography is concerned.
Employing LD as a model of orthographic similarity means to impose no assumed costs for retaining symbols, while imposing costs on any non-alignable character and on every substituted character. While the use of matrices specifying edit costs of particular substitutions is an intuitive way of inputting prior knowledge about these substitutions, typically these costs are chosen ad-hoc on a subjective basis. Another disadvantage is that LD does not capture the systematicity, the complexity, and the asymmetry of the correspondences. Systematic correspondences, such as v:w in CS-PL are assigned a substitution cost of 1, just as any other character substitution. Also, LD does not capture asymmetries in language pairs. If, for instance, the RU vowel a always corresponds to a for a Bulgarian reader, but in the other direction, BG a can correspond to a, o or я for a Russian reader, then we would desire a measure of linguistic distance to reflect both this difference in adaptation possibilities and the uncertainty involved in transforming a. Heeringa et al. (Reference Heeringa, Golubovic, Gooskens, Schüppert, Swarte and Voigt2013) and Jágrová et al. (Reference Jágrová, Stenger, Marti, Avgustinova, Emonds and Janebová2017) came up with asymmetric orthographic distance measures calculated by means of the Levenshtein algorithm, but this asymmetry is due to the fact that there were different source lists for each direction of reading in both studies (see Frequency list in Table 5).
The next two measurements for orthographic intelligibility that we discuss are conditional entropy and adaptation surprisal. Conditional entropy and surprisal stem from the field of information theory (Shannon Reference Shannon1948) and conditional entropy has previously been applied to modeling asymmetric linguistic divergences in Frinsel et al. (Reference Frinsel, Kingma, Gooskens and Swarte2015) and Moberg et al. (Reference Moberg, Gooskens, Nerbonne, Vaillette, Dirix, Schuurman, Vandeghinste and Van Eynde2006). To our knowledge, adaptation surprisal has not been calculated in previous research on receptive multilingualism.
3.3 Conditional entropy
With the Levenshtein method we confirmed that BG and RU are orthographically closer to each other than CS and PL (see Section 3.2). LD is a mathematical distance and thus completely symmetric. It cannot capture any asymmetries between related languages (Moberg et al. Reference Moberg, Gooskens, Nerbonne, Vaillette, Dirix, Schuurman, Vandeghinste and Van Eynde2006, Frinsel et al. Reference Frinsel, Kingma, Gooskens and Swarte2015), but asymmetries are something we do expect: Previous research has shown that speakers of two (closely) related languages do not always understand each other to the same degree (Budovičová Reference Budovičová, Chloupek and Nekvapil1987, Jensen Reference Jensen1989, Gooskens & van Bezooijen Reference Gooskens and van Bezooijen2013a). In this section we present conditional entropy as a potential explanatory variable of orthographic asymmetries.
3.3.1 Surprisal as prefix-free code length
In order to explain conditional entropy, we begin with the notion of prefix-free code lengths. Let us assume that we have a string of characters we wish to communicate to a receiver who neither knows the identity nor the order of the character sequence. Let us assume that for this communication, we have only two symbols available, from which we need to construct code words for our characters: 0 and 1. Let us further assume that we have knowledge on the general distribution of characters, i.e. we know for example that 75% of all characters will be a and 25% will be b. We denote the proportion, or probability, of a specific character c occurring as p(c). Then the theoretically-optimal length of the code word for each character c is given as -log2(p(c)) bits. In practice, we cannot use fractions of 0s and 1s, so this is a theoretical lower limit.
Log probabilities are also often called ‘surprisal’ values (see Section 3.4 below) for intuitive reasons: The higher the probability of a specific character c, the smaller its code length; and the lower the probability of c, the greater its code length. These code lengths appear to correlate naturally with some measures of cognitive processing complexity (Smith & Levy Reference Smith and Levy2013), and are called ‘surprisal’ in these contexts.
3.3.2 Entropy of distributions
The entropy of a distribution is defined as the weighted average of the surprisal values for this distribution, i.e.
-
(1)
$H\left( X \right) = - \mathop \sum \limits_{x \in X} P\left( {X = x} \right)log_{2}P\left( {X = x} \right)$
Entropy is the average length of a code word when encoding data sets whose compositions follow the given distribution exactly. As such, it is commonly considered a measure of the information content in that distribution.
In an intercomprehension setting, the task is to transform, or adapt, one unknown word into a known one. Thus, we condition our character probabilities on the corresponding characters seen in the stimulus word. The formula for this is:
-
(2)
$P\left( {L1 = c1|L2 = c2} \right) = \frac{{count\left( {L1 = c1 \wedge L2 = c2} \right)}}{{count\left( {L2 = c2} \right)}}$
L1 – native language, c1 – character of L1
L2 – stimulus language, c2 – character of L2
In this way, we get different entropy for each of the characters in the alphabet of the (foreign) language of the stimulus. This satisfies our expectation of asymmetry, since transforming characters between languages is not necessarily symmetric. To illustrate this, Table 6 above shows two sample adaptations of the word ‘youth’ between our languages, which we shall use to illustrate conditional entropy.
Table 6. Entropy calculation of a corpus of one word pair for the word ‘youth’ in Czech–Polish and Bulgarian–Russian.
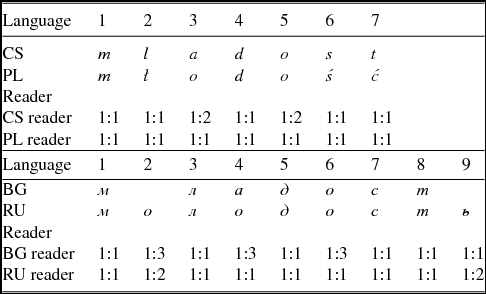
CS = Czech; PL = Polish; BG = Bulgarian; RU = Russian
Table 6 shows an alignment of one cognate pair in CS–PL and BG–RU, character by character. In order to obtain measurements which are based on linguistically motivated alignments, the characters are aligned here in the same way as for the Levenshtein algorithm – a character representing a vowel may only correspond to a character representing a vowel, and a consonant character only to a consonant character. We assume that a non-native reader would map the characters in the same way.
The word ‘youth’ produces seven character pairs in CS–PL and nine character pairs in BG–RU. From a CS perspective, the mappings would be m with m, ł with l, o with a and so forth. In the examples in Table 6, most of the mappings constitute 1:1 correspondences in both directions of reading. This means that each character in one language corresponds only to one particular character in the other language. In these cases it means that the entropy for these alignments is 0. However, there are two exceptions in CS–PL and five exceptions in BG–RU.
From a PL perspective, all adaptations are unambiguous. Reading the CS word, the Polish reader sees an a corresponding only to an o (alignment 3) and an o corresponding only to an o (alignment 5). In these cases, both p(o|a) and p(o|o) are 1.0 as are all the other adaptation probabilities. Thus, the conditional entropies of all characters, including o and a, is 0, which gives a total conditional entropy of 0 for this direction. However, a Czech reader finds an o twice (alignment 3 and 5), which corresponds to an o (alignment 3) and to an a (alignment 5). Therefore, both p(o|o) and p(a|o) is 0.5, the entropy of o is –(1/2*log2(0.5) + 1/2*log2(0.5))/2 = 1, and the overall entropy for this direction is (2*1 + 5*0)/7 ≈ 0.286. This result is asymmetric: The entropy of PL for Czech readers is higher than the entropy of CS for Polish readers. In other words, a Czech reader has to deal with a higher amount of uncertainty and is expected to find it more difficult to read the PL word ‘youth’ than a Polish reader deciphering the respective CS cognate.
In the BG–RU alignment, we have five exceptions. From a BG perspective, the Bulgarian reader sees an o three times (alignment 2, 4 and 6), which corresponds to nothing (alignment 2), to an a (alignment 4), and to an o (alignment 6). In this case p(x|y) is 0.33 for each of these alignments and the overall entropy is about 0.579. The Russian reader sees twice nothing in the BG word (alignment 2 and 9), which corresponds to an o (alignment 2) and to an ь (alignment 9). In this case p(x|y) is 0.5 for each of these alignments and the entropy is about 0.222. In this example, both Bulgarian and Russian readers have to deal with some uncertainty when reading one foreign word. However, the amount of entropy for Bulgarian readers is higher than for Russian readers and the characters which cause the entropy are different.
3.3.3 Conditional entropy of CS–PL and RU–BG
An overview of some conditional entropy values for our language pairs is given in Table 7 below. For space reasons, we present only the entropies for the vowel characters.
Table 7. Vowel character entropies for Czech–Polish and Bulgarian–Russian (shading in some of the cells indicates that this vowel character is not present in the respective alphabet).
CS = Czech; PL = Polish; BG = Bulgarian; RU = Russian
Our entropy calculations based on 3404 CS–PL word pairs reveal that the entropy, e.g. of the CS o for Polish readers is 0.140681385 and that of the PL o for Czech readers is 0.20901951. This means that the mapping of the PL o to possible CS characters is more complex than vice versa. More precisely, the PL o can map into 6 CS characters (o, e, a, á, ů, or í) and the CS o can map only into two PL characters (o and ó) or to nothing. Of course, in an intercomprehension scenario a Czech reader or a Polish reader does not know these mappings and the respective probabilities. However, the assumption is that the measure of complexity of the mapping can be used as an indicator for the degree of intelligibility (Moberg et al. Reference Moberg, Gooskens, Nerbonne, Vaillette, Dirix, Schuurman, Vandeghinste and Van Eynde2006), because it reflects the difficulties with which a reader is confronted in ‘guessing’ the correct correspondence. In this case Czech readers will have more uncertainty in adapting the PL o than Polish readers adapting the CS o.
Table 7 also shows that the entropy of the BG o for Russian readers is 0, but the entropy of the RU o for Bulgarian readers is 0.871023454 (the calculation is based on 1182 word pairs). This means that Bulgarian readers have to deal with some uncertainty in transforming the RU o, while Russian readers should have no difficulties with the BG o.
Overall, the conditional entropy between language L1 and L2 is given as the weighted averages of all character entropies:
-
(3)
$H( {L1|L2} ) = \mathop \sum _{c2 \in L2} P( {L2 = c2} ){\rm{H}}( {L1{\rm{|}}L2 = c2} )$
$ = -\! \mathop \sum _{c1 \in L1, c2 \in L2} P\left( {L1\! =\! c1 \wedge L2\! =\! c2} \right){\rm{log_{2}}}P(L1\! =\! c1|L2\! =\! c2)$
L1 – native language, c1 – character of L1
L2 – stimulus language, c2 – character of L2
For our languages, full conditional entropy gives us the following entropy values: 0.45 for the PL to CS transformation and 0.37 for the CS to PL transformation. Thus, a Czech reader may have more difficulties reading PL than a Polish reader reading CS. For the BG–RU language pair the difference in the entropies is very small for both directions: 0.16 for the BG to RU transformation and 0.17 for the RU to BG transformation, with a very small amount of asymmetry of 0.01. This calculation predicts that speakers of BG reading RU words are facing only a slightly higher amount of uncertainty than speakers of RU reading BG words. The low orthographic entropy for BG and RU can be explained by a higher number of orthographically identical (848) vs. orthographically non-identical items (335) in the material for these two languages.
3.4 Adaptation surprisal: A refined measure
In addition to conditional entropy we use the information-theoretic concept of surprisal. The term surprisal was introduced by Tribus (Reference Tribus1961), who used it to talk about the logarithm of the reciprocal of a probability (Hale Reference Hale2016). Surprisal values are given in bits and depend heavily on the probability distribution used. In our setting, we get character adaptation surprisal (CAS) from our character adaptation probabilities (see Section 3.3.2 above). The character adaptation surprisal is calculated with the following formula:
-
(4) surprisal(L1 = c1|L2 = c2) = −log2 P(L1 = c1|L2 = c2)
L1 – native language, c1 – character of L1
L2 – stimulus language, c2 – character of L2
CAS values allow us to quantify the unexpectedness both of individual character correspondences and of the whole cognate pair. We can compute full word adaptation surprisal (WAS) by summing up the CAS values of the contained characters (Table 8). This gives a quantification of the overall (un)expectedness of the correct cognate.
Table 8. Adaptation surprisal values for the word ‘youth’ in Czech–Polish and Bulgarian–Russian.
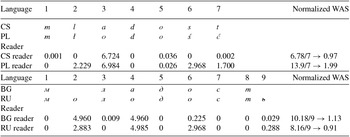
WAS = word adaptation surprisal; CS = Czech; PL = Polish; BG = Bulgarian; RU = Russian
For example, the CS–PL cognate pair mladost–młodość ‘youth’ contains the following correspondences for Czech readers: m:m (surprisal: 0.001), ł:l (surprisal: 0.0), o:a (surprisal: 6.724), d:d (surprisal: 0.0), o:o (surprisal: 0.036), ś:s (surprisal: 0.0), ć:t (surprisal: 0.002). Thus, mladost–młodość ‘youth’ gets a WAS value of 6.78 for Czech readers or 13.9 for Polish readers (Table 8) with a predicted advantage for Czech readers. As in the case with the LD, we also normalize the full WAS for the cognate pair ‘youth’ in the selected languages. For instance, 6.78/7 = 0.97 for Czech readers and 13.9/7 = 1.99 for Polish readers or 10.18/9 = 1.13 for Bulgarian readers and 8.16/9 = 0.91 for Russian readers.
We are now in position to meaningfully compare the individual CAS values and the full WAS values to the results of our web-based experiments revealing respective intercomprehension scores. The CAS should help us to predict and explain the effect of mismatched orthographic correspondences on cognate recognition in a reading intercomprehension scenario. We assume that the smaller the adaptation surprisal, the easier it is to guess the correct orthographic correspondence. However, it must be mentioned here that identical orthographic correspondences may still have a small surprisal value, for example, from a CS perspective the correspondence o:o has a surprisal value of 0.036 bits (Table 8). In our setting, this can be explained by the fact that the PL o could become o (2268 times), e (23 times), a (22 times), á (9 times), ů (2 times) or í (1 time) in CS. On the other hand, non-identical orthographic correspondences may have no surprisal value at all, for example from a CS perspective the correspondence ł:l has the surprisal of 0.0 (Table 8). This means that the PL ł always corresponds to CS l (252 times) in our training corpus.
We can also calculate the average value of the normalized WAS between stimuli of selected languages and their cognates in L1. The assumption is that the higher the mean normalized WAS, the more difficult it is to comprehend a related language. This assumption was confirmed by free translation task experiments of written East Slavic (Ukrainian, Belarusian) and South Slavic (Bulgarian, Macedonian, Serbian) languages for Russian subjects (Stenger, Avgustinova & Marti Reference Stenger, Avgustinova and Marti2017).
In our training corpora we get the following average values of the normalized WAS within the respective language pairs: 0.48 for the PL to CS transformation and 0.40 for the CS to PL transformation, as well as 0.18 for the BG to RU transformation and 0.19 for the RU to BG transformation. This calculation results let us conclude again that CS and PL are orthographically less mutually intelligible in comprehension of written stimuli than BG and RU. In addition, the WAS calculation allows us to predict that a Czech reader may have more difficulties reading PL stimuli than a Polish reader reading CS. For the BG–RU language pair, the difference in the WAS is very small for both directions, with a small predicted advantage of 0.01 for Russian readers of BG stimuli.
4. DISCUSSION AND OUTLOOK
Previous research in intercomprehension has shown that closely related languages may be differently distant from each other. In this article we presented computational methods for measuring and predicting the orthographic mutual intelligibility of Slavic languages by means of LD, conditional entropy and adaptation surprisal. All three methods have their advantages and disadvantages as summarized in the following discussion.
LD as a measure of orthographic similarity of cognate pairs is considered a fairly good predictor of overall intelligibility in spoken semi-communication as well as in reading intercomprehension (Gooskens Reference Gooskens2007, Beijering et al. Reference Beijering, Gooskens, Heeringa, van Koppen and Botma2008, Kürschner, van Bezooijen & Gooskens Reference Kürschner, van Bezooijen and Gooskens2008, Vanhove & Berthele Reference Vanhove, Berthele, De Angelis, Jessner and Kresić2015b, Vanhove Reference Vanhove2016). The simplest versions of this method are based on a distance measure in which orthographic overlap is binary: Non-identical characters contribute to orthographic distance and identical characters do not. In this way, for instance, the BG–RU pair а:о counts as different to the same degree as а:я, namely 1 unit.
The conditional entropy can reflect the difficulties humans encounter when mapping one orthographic system on another. However, it measures only the regularity of correspondences and does not measure the similarity between two languages as, for example, the LD does (Frinsel et al. Reference Frinsel, Kingma, Gooskens and Swarte2015). Nonetheless, such regularity could very well have an effect on the reader's ability to understand a related language (ibid.). The full conditional entropy between two languages, H(L1|L2), allows for measuring the complexity of the entire mapping between these two languages. It reflects both the frequency and regularity of correspondences between them and can reveal asymmetries in overall adaptation difficulties, as has been demonstrated for Swedish and Danish by Frinsel et al. (Reference Frinsel, Kingma, Gooskens and Swarte2015) and for Danish, Swedish and Norwegian by Moberg et al. (Reference Moberg, Gooskens, Nerbonne, Vaillette, Dirix, Schuurman, Vandeghinste and Van Eynde2006). The underlying hypothesis is that high predictability improves intelligibility, and therefore a low entropy value should correspond to a high intelligibility score.
The adaptation surprisal method measures the complexity of a mapping, in particular, how predictable the particular correspondence in a language pair is. The surprisal values of correspondences are indeed different. However, they depend on their frequency and distribution in the particular cognate set. Surprisal can be as asymmetric as entropy: The surprisal values between language A and language B are not necessarily the same as between language B and language A. This indicates an advantage of the surprisal-based method compared to the LD, which in its basic form is completely symmetrical. Furthermore, the adaptation surprisal method can be used to measure phonetic/phonological as well as morphological intelligibility between related languages.
The exact predictive potential of the LD, conditional entropy and adaptation surprisal methods for Slavic intercomprehension is an open question, which we explore in web-based experiments.Footnote 10 A human may not succeed in transforming the substrings of words of an unknown language into the correct corresponding forms in their L1. The goal of our efforts is to design a metric of linguistic distance which takes into account the human decoding process. On the basis of the data collected from our experiments, we intend to improve the Levenshtein algorithm by optimizing the cost of each operation, including that of insertions and deletions. We have observed strong asymmetries of classic averaged Levenshtein costs in each of the language pairs. Our findings for CS and PL orthographic distance confirm those of Heeringa et al. (Reference Heeringa, Golubovic, Gooskens, Schüppert, Swarte and Voigt2013). For BG and RU we discovered that BG adjectives in the masculine form which employ zero endings are a major factor of asymmetric Levenshtein values. Furthermore, normalizing LD asymmetrically, i.e. dividing edit costs by the length of a word, leads to lower values for source languages that tend to use shorter words. If we assume that a lower Levenshtein cost implies higher intelligibility of a word, readers should be more successful when comprehension requires dropping characters rather than adding them.
In this contribution we calculated orthographic distances and asymmetries by means of LD, conditional entropy and adaptation surprisal based on large corpus data. There are a number of arguments why LD and conditional entropy scores should be calculated on a large cognate set rather than only on the stimuli that might be presented to readers in intercomprehension experiments. Van Heuven, Gooskens & van Bezooijen (Reference van Heuven, Gooskens, van Bezooijen, Navracsics and Batyi2015:132) point out that
distance measures become more stable and correlate better with mutual intelligibility scores . . . as the materials the distances are computed on get larger . . ., but this relation may well be different if the distance measures are specifically based on the stimulus materials used in the intelligibility tests.
According to Moberg et al. (Reference Moberg, Gooskens, Nerbonne, Vaillette, Dirix, Schuurman, Vandeghinste and Van Eynde2006), at least 800 word pairs are needed to reach stable entropy measures. Not only do we expect more representative entropy and adaptation surprisal measures by using large corpus data, but it also allows us to choose appropriate stimulus material for intelligibility tests, taking into consideration the complexity of the mapping of correspondences as an experimental variable. For the upcoming experiments we hypothesize that the most regular and frequent correspondence rules (those with little adaptation surprisal values) should be more transparent for readers. Of course, the calculations of conditional entropy and adaptation surprisal on a greater sample of cognate pairs than an actual stimulus set in future experiments may also represent a greater exposure of a reader to correspondences in the other language. An important argument for using conditional entropy and adaptation surprisal instead of Levenshtein distance is that the first two can model asymmetric intelligibility. In future research, we will refine the entropy and surprisal method in several ways and enhance the experiments by measurements based on bigrams or trigrams, focusing on the position of correspondences in cognates as well as on their nature.
While our upcoming analyses will shed light on the degrees of transparency of the different orthographic correspondences, it remains to be seen which other factors are likely to play a role in mutual intelligibility. Thus, for example, word frequency, word length, neighborhood densityFootnote 11 and different orthographic correspondences themselves (their nature, frequency and position) can influence the correct recognition of cognate elements between related languages. Vanhove & Berthele (Reference Vanhove, Berthele, De Angelis, Jessner and Kresić2015b) demonstrated that the frequency of the word in question in the reader's language is a reliable predictor for its intelligibility. Word length was shown to influence intelligibility of individual words, too (Kürschner et al. Reference Kürschner, van Bezooijen and Gooskens2008). Kürschner et al. (Reference Kürschner, van Bezooijen and Gooskens2008) find that longer words are recognized more easily than shorter words. Gooskens (Reference Gooskens, Bayley, Cameron and Lucas2013) points out that words with a high neighborhood density are often more difficult to recognize than those with few competitors.
The combination of computational methods of Levenshtein, conditional entropy and adaptation surprisal with such factors as word frequency, word length, neighborhood density, as well as the orthographic correspondences themselves, will help us anticipate, analyze and evaluate the results of our web-based experiments with speakers of Slavic languages. Once our human data collection is completed, we will construct regression models as predictors of linguistic distance. Such models allow to analyze the effects of e.g. character context, within-word position, representations of consonants vs. representations of vowels, and dialects or archaic terms individually, and thus to gain insight into the importance of each of the factors considered. Isolated investigations at the orthographic level reach their limits as soon as we examine continuous texts. The inevitable next steps of our work will be devoted to analyzing the influence of grammatical differences.
ACKNOWLEDGEMENTS
This study was carried out within the framework of the project INCOMSLAV (Mutual Intelligibility and Surprisal in Slavic Intercomprehension) funded by Deutsche Forschungsgemeinschaft (DFG) under grant SFB 1102: Information Density and Linguistic Encoding. We thank three anonymous reviewers for their useful comments on an earlier version of this article.
