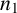1 Introduction
A cost minimization assignment problem (CMAP) deals with the allocation of “n” agents to an equal number of jobs, such that each agent performs exactly one job with an aim to minimize the total cost of an assignment project. A CMAP in mathematical form is described as
 $$ \begin{align} \begin{aligned} \displaystyle \min_{X\in S^*} \quad & Z, \\ {\textrm{where}} \quad & Z= \displaystyle \sum_{i\in I} \sum_{j\in J} c_{ij} x_{ij} , \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \displaystyle \min_{X\in S^*} \quad & Z, \\ {\textrm{where}} \quad & Z= \displaystyle \sum_{i\in I} \sum_{j\in J} c_{ij} x_{ij} , \end{aligned} \end{align} $$
 $$ \begin{align*} \text{such that}\quad S^*= &\left \lbrace\begin{array}{@{}c|l@{}} ~ & \displaystyle \sum_{i=1}^n x_{ij}=1,~j\in J \\ X=\{x_{ij}\}\in \mathbb{R}^{n\times n} & \displaystyle \sum_{j=1}^n x_{ij}=1,~i\in I \\ ~ & x_{ij}=0~{\textrm{or}}~1\quad \text{for all }(i,j)\in I\times J \end{array} \right \rbrace. & \end{align*} $$
$$ \begin{align*} \text{such that}\quad S^*= &\left \lbrace\begin{array}{@{}c|l@{}} ~ & \displaystyle \sum_{i=1}^n x_{ij}=1,~j\in J \\ X=\{x_{ij}\}\in \mathbb{R}^{n\times n} & \displaystyle \sum_{j=1}^n x_{ij}=1,~i\in I \\ ~ & x_{ij}=0~{\textrm{or}}~1\quad \text{for all }(i,j)\in I\times J \end{array} \right \rbrace. & \end{align*} $$
Here,
![]() $I=\{1,2,\ldots ,n\}$
is the index set of n agents,
$I=\{1,2,\ldots ,n\}$
is the index set of n agents,
![]() $J=\{1,2,\ldots ,n\}$
is the index set of n jobs and
$J=\{1,2,\ldots ,n\}$
is the index set of n jobs and
![]() $c_{ij}$
is the cost involved if the ith agent does the jth job.
$c_{ij}$
is the cost involved if the ith agent does the jth job.
A time minimization assignment problem (TMAP) aims at minimizing the completion time of all jobs, when it is assumed that all jobs commence simultaneously. The TMAP falls under the class of min-max problems [Reference Bansal and Puri4] and is mathematically stated as
 $$ \begin{align*} \displaystyle \min_{X\in S^*} \quad &Z, \\ {\textrm{where}} \quad & Z=\displaystyle \max_{I\times J} (t_{ij}: x_{ij}>0), \end{align*} $$
$$ \begin{align*} \displaystyle \min_{X\in S^*} \quad &Z, \\ {\textrm{where}} \quad & Z=\displaystyle \max_{I\times J} (t_{ij}: x_{ij}>0), \end{align*} $$
where
![]() $S^*$
is same as defined in CMAP (1.1) and
$S^*$
is same as defined in CMAP (1.1) and
![]() $t_{ij}$
is the time which the ith agent takes to complete the jth job.
$t_{ij}$
is the time which the ith agent takes to complete the jth job.
In various situations, it is not feasible that all jobs commence simultaneously. This leads to the job categorizations in assignment problems [Reference Aggarwal1, Reference Aggarwal, Tikekar and Hsu2, Reference Brandt and Intrator5, Reference Seshan25]. Several practical problems involve some jobs that are preferred over other jobs and need to be commenced in Stage-1. After the completion of such jobs, the remaining jobs are to be commenced in Stage-2. Such a situation gives rise to a significant variant of the assignment problem, defined as a two-stage assignment problem (TSAP). Owing to the additive nature of the objective function in the CMAP, the commencement of jobs in two or more stages does not actually affect the optimal objective function value and optimal assignments. Whereas, in the case of a TMAP, the two-stage variant becomes a real problem to tackle. Kaur et al. [Reference Kaur, Sharma, Verma and Dahiya16] investigated a two-stage time minimization assignment problem (TSTMAP) and developed different polynomial time iterative algorithms for its solution. Recently, Jain et al. [Reference Jain, Dahiya, Sharma and Verma15] presented an improved polynomial time iterative algorithm for solving TSTMAP, and validated it through various theoretical results and computational experiments.
Another research aspect of an assignment problem arises in the problems that require an optimal solution which, apart from satisfying the primary assignment constraints, satisfies some additional secondary constraints as well. In such situations, the most appropriate technique consists of ranking all feasible solutions (for minimization problems) in increasing order of objective function value and then searching for the first one among them that satisfies the additional constraints. Ranking in combinatorial problems, specifically in assignment problems, has been studied by many authors [Reference Bakhshi, Bhatia and Puri3, Reference Cox and Miller9, Reference Hamacher and Queyranne12, Reference Miller, Stone and Cox18, Reference Murty19, Reference Pascoal, Captivo and Climaco21, Reference Pedersen, Nielsen and Andersen22]. Murty [Reference Murty19] described an efficient algorithm for ranking all feasible assignments in monotone increasing order of cost using the branching technique. Later, Bakhshi et al. [Reference Bakhshi, Bhatia and Puri3] presented two techniques for ranking various assignments in order of increasing completion time. However, the ranking of feasible assignments in the TSAPs has not yet been considered. The present paper discusses the ranking and scanning of feasible assignments of a TSAP in increasing order of total completion time. An algorithm, named “Algorithm-R&S,” based on the idea of branching introduced by Murty [Reference Murty19], is proposed that ranks and scans all feasible assignments of a TSAP in order of increasing total completion time. Ranking and scanning of feasible assignments also come to the utmost use while solving bi-objective assignment problems, where one objective function cannot be optimized by the conventional techniques used for optimizing the linear cost or time objective function. The present paper makes use of this perk of the ranking and scanning scheme.
A bi-objective assignment problem, as indicated by its name, refers to an assignment problem that seeks optimal solutions by optimizing the two-objective functions simultaneously. Such problems fall under the class of multi-objective assignment problems [Reference Hammadi13, Reference Ismayilova, SagIr and Gasimov14, Reference Pintea and Vescan23, Reference Przybylski, Gandibleux and Ehrgott24, Reference Yadaiah and Haragopal26]. In a fast-growing era, the two most significant objectives that are required to be optimized are the total expense to carry out a project and the total completion time of the project. In the assignment problems, usually, the cost objective function is a linear function that is defined in one-to-one correspondence between the agents and jobs as “
![]() $c_{ij}$
” for the ith agent performing the jth job. However, in practical cases, the cost involved in an assignment project can be a nonlinear function, defined explicitly in terms of the assignment variables. Nonlinear assignment problems (NAPs) [Reference Pardalos and Pitsoulis20] have gained much interest among researchers in recent years. However, so far, the study mainly revolves around quadratic and bi-quadratic assignment problems [Reference Burkard and Cela6–Reference Cela8, Reference Ehrgott, Stephan and Tenfelde-Podehl11, Reference Loiola, de Abreu, Boaventura-Netto, Hahn and Querido17]. To the best of the authors’ knowledge, an assignment problem with a general nonlinear cost objective function has not been studied in the literature, and this is one of the motivating factors for the present study.
$c_{ij}$
” for the ith agent performing the jth job. However, in practical cases, the cost involved in an assignment project can be a nonlinear function, defined explicitly in terms of the assignment variables. Nonlinear assignment problems (NAPs) [Reference Pardalos and Pitsoulis20] have gained much interest among researchers in recent years. However, so far, the study mainly revolves around quadratic and bi-quadratic assignment problems [Reference Burkard and Cela6–Reference Cela8, Reference Ehrgott, Stephan and Tenfelde-Podehl11, Reference Loiola, de Abreu, Boaventura-Netto, Hahn and Querido17]. To the best of the authors’ knowledge, an assignment problem with a general nonlinear cost objective function has not been studied in the literature, and this is one of the motivating factors for the present study.
A bi-objective two-stage assignment problem (BiTSAP) is motivated by an allocation problem arising in industrial projects where there is a hierarchical breakdown of the total number of jobs into two components. For example, in automobile industrial projects relating to the manufacturing of heavy commercial vehicles (HCVs), the whole production process consists mainly of two hierarchical components, for example, indoor manufacturing of parts and outdoor manual assembling of the HCVs. It is clear that the outdoor manual assembling can not be commenced until the indoor manufacturing of parts is done. The allocation problem related to the manufacturing of HCVs can be modelled as a two-stage time minimization assignment problem [Reference Kaur, Sharma, Verma and Dahiya16]. Another example of a BiTSAP arises in the real estate sector where the project of construction of a housing development by a builder decomposes mainly into two components. In such a project, there are some primary jobs (such as digging and earthwork) that have to be performed before the commencement of any other jobs involved in the construction project. This is because of the reason that without the accomplishment of such primary jobs, no other (secondary) job can be commenced. It is assumed that each contractor can perform exactly one job. Note that the construction of several houses in the development takes place simultaneously. Therefore, when primary jobs (or Stage-1 jobs) pertaining to the construction of one house have been completed, the contractors allocated to the primary jobs start working on the primary jobs of another house in the development and are never allocated to perform the secondary jobs (or Stage-2 jobs) related to any house. It is clear that if a contractor performing a Stage-1 job is allocated a Stage-2 job (even for any other house), there will be a delay in the overall completion of the project. However, this does not imply that the Stage-1 job allocation and Stage-2 job allocation are independent. This is because of the reason that our objective is to minimize the total completion time of a two-stage project, that is, the sum of Stage-1 and Stage-2 completion times and not the Stage-1 and Stage-2 completion times individually. Problem formulation assumes that at one particular time, one contractor can perform exactly one job whether it be Stage-1 or Stage-2, so the contractors who have been allocated in Stage-1 are not available for performing Stage-2 jobs. Therefore, the allocation of Stage-2 is always dependent on the allocation of Stage-1 and vice versa.
For a development builder, the minimization of the total cost expense and total completion time are of equal importance, and thus, obtaining the assignment that minimizes both factors simultaneously is the ultimate goal of the builder. So, the problem of assigning various contractors to various jobs involved in the construction project of a housing development can be modelled as a bi-objective two-stage assignment problem that aims at minimizing the total expenses (cost objective function) and total completion time (a min-max objective function) simultaneously. Further, it can be observed that sometimes, the contractors’ rate policy consists of a variable cost charges apart from a fixed cost for performing each job. For instance, the situation where Contractor
![]() $i_1$
charges an additional cost (apart from the fixed cost) of “
$i_1$
charges an additional cost (apart from the fixed cost) of “
![]() $\beta $
” units for completing job
$\beta $
” units for completing job
![]() $j_1$
when job
$j_1$
when job
![]() $j_2,\, j_2 \neq j_1$
is performed by Contractor
$j_2,\, j_2 \neq j_1$
is performed by Contractor
![]() $i_2, i_2 \neq i_1$
. This can be accommodated in the cost objective function via a nonlinear term “
$i_2, i_2 \neq i_1$
. This can be accommodated in the cost objective function via a nonlinear term “
![]() $\beta x_{i_1 j_1} x_{i_2 j_2}$
,” so that the additional cost is added only when
$\beta x_{i_1 j_1} x_{i_2 j_2}$
,” so that the additional cost is added only when
![]() $x_{i_1 j_1}$
and
$x_{i_1 j_1}$
and
![]() $x_{i_2 j_2}$
are both 1. Thus, in such types of situations, the cost function remains no longer linear and hence cannot be depicted in the form of the usual cost matrix. Minimization of such a nonlinear variable cost objective along with minimizing the total completion time of the two-stage construction project is the ultimate goal of the current study.
$x_{i_2 j_2}$
are both 1. Thus, in such types of situations, the cost function remains no longer linear and hence cannot be depicted in the form of the usual cost matrix. Minimization of such a nonlinear variable cost objective along with minimizing the total completion time of the two-stage construction project is the ultimate goal of the current study.
In this paper, a BiTSAP is discussed that aims at minimizing a nonlinear cost function (
![]() $C(X)$
defined explicitly in terms of assignment variable X) and total completion time (“
$C(X)$
defined explicitly in terms of assignment variable X) and total completion time (“
![]() $t_{ij}$
” defined in one-to-one correspondence between agents and jobs, that is, the ith agent performing the jth job) simultaneously. The cost function
$t_{ij}$
” defined in one-to-one correspondence between agents and jobs, that is, the ith agent performing the jth job) simultaneously. The cost function
![]() $C(X)$
can be any nonlinear function and need not possess any fixed symmetric structure according to agent-job allocations. Handling such a nonlinear cost function in a BiTSAP is not at all trivial and requires a non-conventional method for finding its minimum value. It is important to mention that obtaining a single optimal solution to a bi-objective problem is not possible. Optimal solutions to bi-objective problems, where both objectives are assumed to be of equal and utmost significance, are sought in the form of efficient pairs of two-objective functions. In a BiTSAP, the solution is expressed in terms of efficient time-cost pairs
$C(X)$
can be any nonlinear function and need not possess any fixed symmetric structure according to agent-job allocations. Handling such a nonlinear cost function in a BiTSAP is not at all trivial and requires a non-conventional method for finding its minimum value. It is important to mention that obtaining a single optimal solution to a bi-objective problem is not possible. Optimal solutions to bi-objective problems, where both objectives are assumed to be of equal and utmost significance, are sought in the form of efficient pairs of two-objective functions. In a BiTSAP, the solution is expressed in terms of efficient time-cost pairs
![]() $[T^e(h), C^e(h)]$
, where
$[T^e(h), C^e(h)]$
, where
![]() $T^e(h)$
is the total completion time and
$T^e(h)$
is the total completion time and
![]() $C^e(h)$
is the value of the nonlinear cost function corresponding to the “hth” efficient pair. For finding efficient pairs of BiTSAP, an algorithm (“Algorithm-Eff”) is developed that makes use of the ranked set of feasible solutions of a TSAP with respect to total completion time (obtained using Algorithm-R& S).
$C^e(h)$
is the value of the nonlinear cost function corresponding to the “hth” efficient pair. For finding efficient pairs of BiTSAP, an algorithm (“Algorithm-Eff”) is developed that makes use of the ranked set of feasible solutions of a TSAP with respect to total completion time (obtained using Algorithm-R& S).
The entire paper is organized as follows. Section 2 presents mathematical formulation of a BiTSAP. Section 3 consists of preliminaries and Section 4 discusses notation and definitions. In Section 5, the proposed methodology is presented in the form of two algorithms, namely, Algorithm 2 (Algorithm-R&S) and Algorithm 3 (Algorithm-Eff). Section 6 presents some theoretical results that validate the proposed algorithms. Numerical illustration is provided in Section 7. An insight into the complexity of the algorithm with the help of numerical experiments is presented in Section 8. Section 9 describes the application of the algorithm in solving a BiTSAP with one minimization and another maximization objective. In the end, some concluding remarks are made on our study.
2 Mathematical formulation
Let I be the index set of n agents, J be the index set of n jobs and
![]() $J_1~(\subset J)$
be the index set of the Stage-1 jobs. Also,
$J_1~(\subset J)$
be the index set of the Stage-1 jobs. Also,
![]() $\bar {J}_1=J \setminus J_1$
is the complement of
$\bar {J}_1=J \setminus J_1$
is the complement of
![]() $J_1$
and represents the index set of the Stage-2 jobs. The BiTSAP can be mathematically stated as
$J_1$
and represents the index set of the Stage-2 jobs. The BiTSAP can be mathematically stated as
where
![]() $C(X)$
is a nonlinear cost function, defined in terms of a feasible solution
$C(X)$
is a nonlinear cost function, defined in terms of a feasible solution
![]() $X=\{x_{ij} \}$
of a TSAP. Here, the total completion time of a TSAP is
$X=\{x_{ij} \}$
of a TSAP. Here, the total completion time of a TSAP is
where
Note that
![]() $t_{ij}$
is the time taken by the ith agent to complete the jth job and
$t_{ij}$
is the time taken by the ith agent to complete the jth job and
![]() ${Y= \{y_{ij}\}_{i\in I, ~j\in J_1} \in S}$
,
${Y= \{y_{ij}\}_{i\in I, ~j\in J_1} \in S}$
,
![]() $Z= \{z_{ij}\}_{i\in I, ~j\in \bar {J}_1} \in S(Y)$
such that
$Z= \{z_{ij}\}_{i\in I, ~j\in \bar {J}_1} \in S(Y)$
such that
 $$ \begin{align*} S&=\left\{\begin{array}{@{}cc} Y=\{y_{ij}\} \in \mathbb{R}^{n\times n_1} \left | \begin{array}{l} \displaystyle\sum_{j \in J_1} y_{ij} \leq 1\quad \text{for all } i \in I\\[.2cm] \displaystyle\sum_{i \in I} y_{ij} = 1\quad \text{for all } j \in J_1\\ y_{ij}=0 ~{\textrm{or}}~ 1\quad \text{for all } (i,j) \in I \times J_1 \end{array} \right. \end{array} \!\!\!\!\!\!\right\} ,\\[6pt]S(Y)&= \left\{\begin{array}{@{}cc} Z=\{z_{ij}\} \in \mathbb{R}^{n\times (n-n_1)} \left | \begin{array}{l} \displaystyle\sum_{j \in \bar{J}_1} z_{ij} = 1\quad \text{for all } i \in \bar{I}_{1}(Y)\\[.2cm] \displaystyle\sum_{i \in \bar{I}_1(Y)} z_{ij} = 1\quad \text{for all } j \in \bar{J}_1\\ z_{ij}=0 ~{\textrm{or}}~ 1\quad \text{for all } (i,j) \in \bar{I}_1(Y) \times \bar{J}_1 \\ \end{array} \right. \end{array} \!\!\!\!\!\!\right\}, \end{align*} $$
$$ \begin{align*} S&=\left\{\begin{array}{@{}cc} Y=\{y_{ij}\} \in \mathbb{R}^{n\times n_1} \left | \begin{array}{l} \displaystyle\sum_{j \in J_1} y_{ij} \leq 1\quad \text{for all } i \in I\\[.2cm] \displaystyle\sum_{i \in I} y_{ij} = 1\quad \text{for all } j \in J_1\\ y_{ij}=0 ~{\textrm{or}}~ 1\quad \text{for all } (i,j) \in I \times J_1 \end{array} \right. \end{array} \!\!\!\!\!\!\right\} ,\\[6pt]S(Y)&= \left\{\begin{array}{@{}cc} Z=\{z_{ij}\} \in \mathbb{R}^{n\times (n-n_1)} \left | \begin{array}{l} \displaystyle\sum_{j \in \bar{J}_1} z_{ij} = 1\quad \text{for all } i \in \bar{I}_{1}(Y)\\[.2cm] \displaystyle\sum_{i \in \bar{I}_1(Y)} z_{ij} = 1\quad \text{for all } j \in \bar{J}_1\\ z_{ij}=0 ~{\textrm{or}}~ 1\quad \text{for all } (i,j) \in \bar{I}_1(Y) \times \bar{J}_1 \\ \end{array} \right. \end{array} \!\!\!\!\!\!\right\}, \end{align*} $$
where
![]() $I_1(Y)$
denotes the set of agents allocated to the jobs in
$I_1(Y)$
denotes the set of agents allocated to the jobs in
![]() $J_1$
corresponding to the feasible solution
$J_1$
corresponding to the feasible solution
![]() $Y\in S$
and
$Y\in S$
and
![]() $ \bar {I}_1(Y)=I \setminus I_1 (Y)$
. The decision variables
$ \bar {I}_1(Y)=I \setminus I_1 (Y)$
. The decision variables
![]() $y_{ij}$
,
$y_{ij}$
,
![]() $z_{ij}$
for
$z_{ij}$
for
![]() $(i,j)\in I \times J$
take the value 1 if the ith agent performs the jth job and
$(i,j)\in I \times J$
take the value 1 if the ith agent performs the jth job and
![]() $0$
otherwise.
$0$
otherwise.
3 Preliminaries – finding the optimal total completion time of the TSTMAP
This section consists of a brief sketch of Algorithm 1, namely “Algorithm-Imp” developed by Jain et al. [Reference Jain, Dahiya, Sharma and Verma15] for finding an optimal total completion time of a TSTMAP. Throughout the paper, this has been used for solving a TSAP with respect to the total completion time wherever required in Algorithms 2 and 3 stated in Section 5.
Definition 3.1. For a standard TMAP involving one or more time entries as “M,” where
![]() $M>0$
is an arbitrary large number, a feasible solution
$M>0$
is an arbitrary large number, a feasible solution
![]() $X=\{x_{ij}\}$
is called an M-feasible solution if
$X=\{x_{ij}\}$
is called an M-feasible solution if
![]() $x_{ij}=0$
for all
$x_{ij}=0$
for all
![]() $(i,j)\in I\times J$
for which
$(i,j)\in I\times J$
for which
![]() $t_{ij}=M$
. The corresponding TMAP having one or more M-feasible solutions is called an M-feasible problem.
$t_{ij}=M$
. The corresponding TMAP having one or more M-feasible solutions is called an M-feasible problem.
Let
![]() $t_1^1<t_1^2< \cdots <t_1^{\kern1.1pt p}$
be the distinct time entries corresponding to Stage-1 jobs and
$t_1^1<t_1^2< \cdots <t_1^{\kern1.1pt p}$
be the distinct time entries corresponding to Stage-1 jobs and
![]() $t_2^1<t_2^2< \cdots <t_2^q$
be the distinct time entries corresponding to Stage-2 jobs.
$t_2^1<t_2^2< \cdots <t_2^q$
be the distinct time entries corresponding to Stage-2 jobs.
An optimal solution of the Stage-1 problem is obtained by solving the TMAP,
![]() $(TP)^1_0$
:
$(TP)^1_0$
:
 $$ \begin{align} \begin{aligned} \displaystyle \min_{X\in S^*} \max_{I\times J} \quad &(t_{ij}':x_{ij}>0), \\ \text{where}\quad &t_{ij}'= \begin{cases} t_{ij}&\text{for all } (i,j)\in I\times J_1, \\[.1cm] 0&\text{for all } (i,j)\in I\times \bar{J_1}, \end{cases} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \displaystyle \min_{X\in S^*} \max_{I\times J} \quad &(t_{ij}':x_{ij}>0), \\ \text{where}\quad &t_{ij}'= \begin{cases} t_{ij}&\text{for all } (i,j)\in I\times J_1, \\[.1cm] 0&\text{for all } (i,j)\in I\times \bar{J_1}, \end{cases} \end{aligned} \end{align} $$
and
![]() $S^*$
is the feasible region of a standard assignment problem. Let the optimal value of the problem
$S^*$
is the feasible region of a standard assignment problem. Let the optimal value of the problem
![]() $(TP)^1_0$
(3.1) be
$(TP)^1_0$
(3.1) be
![]() $T_1=t^{m_1}_1,~1\leq m_1 \leq p$
. Then,
$T_1=t^{m_1}_1,~1\leq m_1 \leq p$
. Then,
![]() $t^{m_1}_1$
is the minimum time of Stage-1.
$t^{m_1}_1$
is the minimum time of Stage-1.
Similarly, an optimal time of Stage-2 is obtained by solving the TMAP,
![]() $(TP)^2_0$
:
$(TP)^2_0$
:
 $$ \begin{align} \begin{aligned} ~\displaystyle \min_{X\in S^*}\max_{I\times J}\quad & (t_{ij}':x_{ij}>0), \\ \text{where}\quad &t_{ij}'= \begin{cases} 0&\text{for all } (i,j)\in I\times J_1 , \\[.1cm] t_{ij}&\text{for all } (i,j)\in I\times \bar{J_1}. \end{cases} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} ~\displaystyle \min_{X\in S^*}\max_{I\times J}\quad & (t_{ij}':x_{ij}>0), \\ \text{where}\quad &t_{ij}'= \begin{cases} 0&\text{for all } (i,j)\in I\times J_1 , \\[.1cm] t_{ij}&\text{for all } (i,j)\in I\times \bar{J_1}. \end{cases} \end{aligned} \end{align} $$
Let the optimal value of the problem
![]() $(TP)^2_0$
(3.2) be
$(TP)^2_0$
(3.2) be
![]() $T_2=t^{m_2}_2,~1\leq m_2 \leq q$
. Then,
$T_2=t^{m_2}_2,~1\leq m_2 \leq q$
. Then,
![]() $t^{m_2}_2$
is the minimum time of Stage-2.
$t^{m_2}_2$
is the minimum time of Stage-2.

Let
![]() $X^o$
be an optimal solution of
$X^o$
be an optimal solution of
![]() $(TP)^2_0$
(3.2) yielding optimal value of
$(TP)^2_0$
(3.2) yielding optimal value of
![]() $T_2$
as
$T_2$
as
![]() $T_2^o=t^{m_2}_2$
. Let
$T_2^o=t^{m_2}_2$
. Let
![]() $T_1^o$
be the corresponding time of Stage-1.
$T_1^o$
be the corresponding time of Stage-1.
Thus,
![]() $(T^o_1, T_2^o)$
is the pair of Stage-1 and Stage-2 times obtained from the optimal solution
$(T^o_1, T_2^o)$
is the pair of Stage-1 and Stage-2 times obtained from the optimal solution
![]() $X^o$
of problem
$X^o$
of problem
![]() $(TP)^2_0$
(3.2), such that
$(TP)^2_0$
(3.2), such that
![]() $T^o_2$
is the minimum time of Stage-2 corresponding to the Stage-1 time
$T^o_2$
is the minimum time of Stage-2 corresponding to the Stage-1 time
![]() $T_1^o$
. The pair
$T_1^o$
. The pair
![]() $(T^o_1, T_2^o)$
yields the total completion time of Stage-1 and Stage-2 jobs as
$(T^o_1, T_2^o)$
yields the total completion time of Stage-1 and Stage-2 jobs as
![]() $T_1^o+T_2^o$
.
$T_1^o+T_2^o$
.
The main steps of the algorithm for finding the optimal solution of the TSTMAP are provided in the following sections.
4 Notation and definitions
In this section, various notation and definitions are introduced to comprehend the solution technique for the problem BiTSAP (2.1).
4.1 Notation
-
• A: set of all feasible assignments of TSAP, that is,
 $A=\{\alpha \mid \alpha \text { is a feasible}\ \text{assignment of the TSAP}\}.$
$A=\{\alpha \mid \alpha \text { is a feasible}\ \text{assignment of the TSAP}\}.$
-
•
 $T(k)$
: kth minimum total completion time so that
$T(k)$
: kth minimum total completion time so that
 $T(1)$
denotes the optimal total completion time of the TSAP.
$T(1)$
denotes the optimal total completion time of the TSAP. -
•
 $T_{S1}(k)$
and
$T_{S1}(k)$
and
 $T_{S2}(k)$
: completion times of Stage-1 and Stage-2, respectively, such that
$T_{S2}(k)$
: completion times of Stage-1 and Stage-2, respectively, such that
 $T_{S1}(k)+ T_{S2}(k)=T(k)$
.
$T_{S1}(k)+ T_{S2}(k)=T(k)$
. -
•
 $A(k)$
: set of all feasible assignments of TSAP having total completion time
$A(k)$
: set of all feasible assignments of TSAP having total completion time
 $T(k)$
.
$T(k)$
. -
•
 $C(\alpha )$
: value of the cost function
$C(\alpha )$
: value of the cost function
 $C(X)$
corresponding to a feasible assignment
$C(X)$
corresponding to a feasible assignment
 $\alpha $
.
$\alpha $
. -
•
 $C(k)=\min \{C(\alpha )\mid \alpha \in A(k) \}$
for
$C(k)=\min \{C(\alpha )\mid \alpha \in A(k) \}$
for
 $k=1,2,\ldots .$
$k=1,2,\ldots .$
-
• N denotes a “node” of the feasible region. A node is a set of assignments with some constraints on the allocation of specific agents to a specific number of jobs (for more details, refer to Definition 4.2).
-
•
 $\alpha _N$
: an optimal time assignment of a TSAP corresponding to node N.
$\alpha _N$
: an optimal time assignment of a TSAP corresponding to node N. -
•
 $T_N$
: total completion time of the TSAP corresponding to an optimal assignment
$T_N$
: total completion time of the TSAP corresponding to an optimal assignment
 $\alpha _N$
of node N.
$\alpha _N$
of node N. -
•
 $\mathscr {N}$
: set of all nodes formed till the current step of the algorithm (for details, refer to Step 1 of Algorithm 2).
$\mathscr {N}$
: set of all nodes formed till the current step of the algorithm (for details, refer to Step 1 of Algorithm 2). -
•
 $\mathscr {N}(k)$
: set of all nodes formed till the current step of the algorithm whose optimal assignments have total completion time
$\mathscr {N}(k)$
: set of all nodes formed till the current step of the algorithm whose optimal assignments have total completion time
 $T(k)$
. Clearly,
$T(k)$
. Clearly,
 $\mathscr {N}(k) \subset \mathscr {N}$
.
$\mathscr {N}(k) \subset \mathscr {N}$
. -
•
 $\mathscr {N}_{A}(k)$
: set of all nodes whose optimal assignments have total completion time
$\mathscr {N}_{A}(k)$
: set of all nodes whose optimal assignments have total completion time
 $T(k)$
so that
$T(k)$
so that
 $A(k)=\{\alpha _N\mid N\in \mathscr {N}_{A}(k)\}$
.
$A(k)=\{\alpha _N\mid N\in \mathscr {N}_{A}(k)\}$
. -
•
 $\mathscr {P}A(k)$
denotes a partial set of
$\mathscr {P}A(k)$
denotes a partial set of
 $A(k)$
and is defined as the set of those feasible assignments of the TSAP obtained till the current step of the algorithm, which have total completion time
$A(k)$
and is defined as the set of those feasible assignments of the TSAP obtained till the current step of the algorithm, which have total completion time
 $T(k)$
. Note that
$T(k)$
. Note that
 $\mathscr {P}A(k) \subset A(k)$
.
$\mathscr {P}A(k) \subset A(k)$
. -
•
 $\xi $
: set of nodes under consideration (see Remark 4.1).
$\xi $
: set of nodes under consideration (see Remark 4.1). -
•
 $\xi (k)$
: subset of
$\xi (k)$
: subset of
 $\xi $
consisting of all those nodes of
$\xi $
consisting of all those nodes of
 $\xi $
whose optimal assignments have total completion time
$\xi $
whose optimal assignments have total completion time
 $T(k)$
.
$T(k)$
. -
•
 $[T^e(h),C^e(h)]$
: hth efficient pair of BiTSAP (2.1).
$[T^e(h),C^e(h)]$
: hth efficient pair of BiTSAP (2.1).
Remark 4.1. While ranking and scanning all feasible assignments of the TSAP, a particular type of node corresponding to a fixed value of time, say
![]() $T(K)$
, is considered for further branching out of a given collection of nodes. Note that
$T(K)$
, is considered for further branching out of a given collection of nodes. Note that
![]() $\xi $
is that specific collection of nodes under consideration.
$\xi $
is that specific collection of nodes under consideration.
4.2 Definitions
Definition 4.2 (Nodes arising from an assignment).
For an assignment
![]() $\alpha =((b_1,c_1)$
,
$\alpha =((b_1,c_1)$
,
![]() $(b_2,c_2)$
,…,
$(b_2,c_2)$
,…,
![]() $(b_n,c_n))$
of a TSAP, define the nodes
$(b_n,c_n))$
of a TSAP, define the nodes
![]() $N_1,N_2,\ldots ,N_{n-1}$
arising from assignment “
$N_1,N_2,\ldots ,N_{n-1}$
arising from assignment “
![]() $\alpha $
” as nonempty mutually exclusive subsets of A as
$\alpha $
” as nonempty mutually exclusive subsets of A as
where
![]() $N_r$
is the set of assignments in all of which
$N_r$
is the set of assignments in all of which
![]() $(b_1,c_1),(b_2,c_2), \ldots ,(b_{r-1},c_{r-1})$
are allocated and
$(b_1,c_1),(b_2,c_2), \ldots ,(b_{r-1},c_{r-1})$
are allocated and
![]() $(b_r,c_r)$
is nonallocated. In other words, for any
$(b_r,c_r)$
is nonallocated. In other words, for any
![]() ${r=1,2,\ldots , n-1}$
,
${r=1,2,\ldots , n-1}$
,
![]() $(b_k,c_k)\in N_r$
means that
$(b_k,c_k)\in N_r$
means that
![]() $x_{{b_k}{c_k}}=1$
and
$x_{{b_k}{c_k}}=1$
and
![]() $\overline {(b_k,c_k)}\in N_r$
means that
$\overline {(b_k,c_k)}\in N_r$
means that
![]() $x_{{b_k}{c_k}}=0$
for all assignments in
$x_{{b_k}{c_k}}=0$
for all assignments in
![]() $N_r$
. Clearly,
$N_r$
. Clearly,
![]() $A=\{\alpha \} \cup (\bigcup _{r=1}^{n-1} N_r )$
. Note that any pair of job-person that is not listed in a node can be chosen freely, provided the resulting assignment satisfies the feasibility conditions pertaining to the TSAP.
$A=\{\alpha \} \cup (\bigcup _{r=1}^{n-1} N_r )$
. Note that any pair of job-person that is not listed in a node can be chosen freely, provided the resulting assignment satisfies the feasibility conditions pertaining to the TSAP.
Definition 4.3 (Partitioning of a node by its optimal assignment).
Let N be a node and
![]() $\alpha _N$
be its optimal time assignment defined as
$\alpha _N$
be its optimal time assignment defined as
Define partitioning of N by its optimal assignment
![]() $\alpha _N$
into nodes
$\alpha _N$
into nodes
![]() $N_1, N_2,\ldots , N_{n-s-1}$
:
$N_1, N_2,\ldots , N_{n-s-1}$
:
 $$ \begin{align*} N_1 &=\{ (b_1,c_1),(b_2,c_2),\ldots ,(b_s,c_s),\overline{(p_1,q_1)},\overline{(p_2,q_2)},\ldots ,\overline{(p_t,q_t)}, \overline{(u_1,v_1)} \}, \\ N_2 &=\{ (b_1,c_1),(b_2,c_2),\ldots ,(b_s,c_s),\overline{(p_1,q_1)},\overline{(p_2,q_2)},\ldots ,\overline{(p_t,q_t)}, (u_1,v_1), \overline{(u_2,v_2)} \} , \\ \cdots &\qquad \qquad \cdots \qquad \qquad \cdots \qquad \cdots \qquad \cdots\\ N_{{n-s-1}} &=\{ (b_1,c_1),\ldots ,(b_s,c_s),\overline{(p_1,q_1)},\ldots ,\overline{(p_t,q_t)}, (u_1,v_1), (u_2,v_2),\ldots , \overline{(u_{n-s-1},v_{n-s-1})} \}. \end{align*} $$
$$ \begin{align*} N_1 &=\{ (b_1,c_1),(b_2,c_2),\ldots ,(b_s,c_s),\overline{(p_1,q_1)},\overline{(p_2,q_2)},\ldots ,\overline{(p_t,q_t)}, \overline{(u_1,v_1)} \}, \\ N_2 &=\{ (b_1,c_1),(b_2,c_2),\ldots ,(b_s,c_s),\overline{(p_1,q_1)},\overline{(p_2,q_2)},\ldots ,\overline{(p_t,q_t)}, (u_1,v_1), \overline{(u_2,v_2)} \} , \\ \cdots &\qquad \qquad \cdots \qquad \qquad \cdots \qquad \cdots \qquad \cdots\\ N_{{n-s-1}} &=\{ (b_1,c_1),\ldots ,(b_s,c_s),\overline{(p_1,q_1)},\ldots ,\overline{(p_t,q_t)}, (u_1,v_1), (u_2,v_2),\ldots , \overline{(u_{n-s-1},v_{n-s-1})} \}. \end{align*} $$
Clearly,
![]() $N=\{\alpha _N\} \cup ( \bigcup _{r=1}^{n-s-1} N_r )$
.
$N=\{\alpha _N\} \cup ( \bigcup _{r=1}^{n-s-1} N_r )$
.
Definition 4.4 (Efficient solution).
A solution
![]() $X^*=(Y^*,Z^*)$
,
$X^*=(Y^*,Z^*)$
,
![]() $Y^*\in S$
,
$Y^*\in S$
,
![]() $Z^*\in S(Y)$
is said to be an efficient solution of BiTSAP (2.1) if and only if there does not exist another solution
$Z^*\in S(Y)$
is said to be an efficient solution of BiTSAP (2.1) if and only if there does not exist another solution
![]() $\hat {X}=(\hat {Y},\hat {Z})$
,
$\hat {X}=(\hat {Y},\hat {Z})$
,
![]() $\hat {Y}\in S$
,
$\hat {Y}\in S$
,
![]() $\hat {Z}\in S(Y)$
, such that (i)
$\hat {Z}\in S(Y)$
, such that (i)
![]() $T(\hat {X}) \leq T(X^*)$
, (ii)
$T(\hat {X}) \leq T(X^*)$
, (ii)
![]() $C(\hat {X}) \leq C(X^*)$
, with strict inequality holding for at least one of the relations (i) and (ii).
$C(\hat {X}) \leq C(X^*)$
, with strict inequality holding for at least one of the relations (i) and (ii).
Definition 4.5 (Efficient pair or nondominated pair).
A time-cost pair
![]() $[T(X^*),C(X^*)]$
corresponding to an efficient solution
$[T(X^*),C(X^*)]$
corresponding to an efficient solution
![]() $X^*$
of BiTSAP (2.1) is said to be an efficient pair or nondominated pair of a BiTSAP.
$X^*$
of BiTSAP (2.1) is said to be an efficient pair or nondominated pair of a BiTSAP.
Definition 4.6 (Dominated pair).
A pair
![]() $[T(X),C(X)]$
that is not an efficient pair is termed as a dominated pair. In other words, a pair
$[T(X),C(X)]$
that is not an efficient pair is termed as a dominated pair. In other words, a pair
![]() $[T(X),C(X)]$
is dominated by another pair
$[T(X),C(X)]$
is dominated by another pair
![]() $[T(X^*),C(X^*)]$
if
$[T(X^*),C(X^*)]$
if
![]() $T(X^*)\leq T(X)$
and
$T(X^*)\leq T(X)$
and
![]() $C(X^*)\leq C(X)$
with strict inequality holding for at least one of the relations.
$C(X^*)\leq C(X)$
with strict inequality holding for at least one of the relations.
5 Algorithms


This section consists of two algorithms that jointly solves the BiTSAP (2.1). First, Algorithm 2 (namely, “Algorithm-R&S”) is proposed that ranks and scans all feasible assignments of a TSAP in order of increasing total completion time. Next, Algorithm 3 (named as “Algorithm-Eff”) is presented that is used for finding efficient time-cost pairs of BiTSAP (2.1).
Remark 5.1. Algorithm 2 partitions the set of all feasible assignments “A” into mutually exclusive subsets, called nodes obtained from an optimal assignment, say “
![]() $\alpha $
,” in such a way that
$\alpha $
,” in such a way that
![]() $\alpha $
and all nodes arising from
$\alpha $
and all nodes arising from
![]() $\alpha $
exhaustively make up A. It is then clear that any assignment lying in any of the nodes arising from
$\alpha $
exhaustively make up A. It is then clear that any assignment lying in any of the nodes arising from
![]() $\alpha $
cannot have a total completion time better than
$\alpha $
cannot have a total completion time better than
![]() $\alpha $
. Based on this idea of branching, Algorithm 2 scans the whole set A systematically and obtains ranked sets of all feasible assignments of a TSAP in order of increasing total completion time.
$\alpha $
. Based on this idea of branching, Algorithm 2 scans the whole set A systematically and obtains ranked sets of all feasible assignments of a TSAP in order of increasing total completion time.
Remark 5.2. Algorithm 2 is designed in such a way that all feasible assignments corresponding to a particular total completion time are determined first before heading to the next total completion time (in increasing order). This helps greatly in solving problems where an optimal solution satisfying additional secondary constraints is demanded. In such problems, one can first check all feasible assignments corresponding to the first minimum total completion time, then corresponding to the next minimum total completion time and so on, till a solution is found that satisfies an additional constraint as well. This is the main advantage of the proposed algorithm that one need not find all feasible assignments in such cases.
Remark 5.3. The main advantage of Algorithm 3 is that simultaneous ranking and scanning of the set of feasible assignments with respect to the time minimization objective is performed to obtain an efficient pair and, therefore, enumeration of all solutions beforehand is avoided. Thus, when a situation demands only few efficient pairs of a BiTSAP, scanning of a large number of feasible assignments is avoided which reduces computational efforts to a great extent.
6 Theoretical justification
In this section, various results are proved which provide theoretical validation of the algorithms proposed in Section 5.
Lemma 6.1. In the sequence of generated efficient pairs
![]() $[T^e(h),C^e(h)]$
,
$[T^e(h),C^e(h)]$
,
![]() $h=1,2,\ldots ,h_l$
, the following hold true
$h=1,2,\ldots ,h_l$
, the following hold true
 $$ \begin{align*} C^e(1)>C^e(2)>\cdots>C^e(h_l), \\ T^e(1)<T^e(2)<\cdots<T^e(h_l). \end{align*} $$
$$ \begin{align*} C^e(1)>C^e(2)>\cdots>C^e(h_l), \\ T^e(1)<T^e(2)<\cdots<T^e(h_l). \end{align*} $$
Proof. Proof follows from the General Step of Algorithm 3.
Theorem 6.2.
![]() $C^e(h_l)=\min _{X=(Y,Z);Y\in S,Z\in S(Y)} C(X)$
, that is,
$C^e(h_l)=\min _{X=(Y,Z);Y\in S,Z\in S(Y)} C(X)$
, that is,
![]() $C^e(h_l)$
is the minimum cost of the two-stage assignment problem.
$C^e(h_l)$
is the minimum cost of the two-stage assignment problem.
Proof. Let us suppose that there exists a feasible solution
![]() $\hat {X}=(\hat {Y},\hat {Z})$
of a TSAP yielding a value of the nonlinear cost objective function as
$\hat {X}=(\hat {Y},\hat {Z})$
of a TSAP yielding a value of the nonlinear cost objective function as
![]() $C(\hat {X})<C^e(h_l)$
. Let
$C(\hat {X})<C^e(h_l)$
. Let
![]() $T(\hat {X})$
be the total completion time corresponding to the feasible solution
$T(\hat {X})$
be the total completion time corresponding to the feasible solution
![]() $\hat {X}$
of a TSAP.
$\hat {X}$
of a TSAP.
We find
![]() $k \in \{1,2,\ldots , k_l\}$
such that
$k \in \{1,2,\ldots , k_l\}$
such that
![]() $T(\hat {X})=T({k})$
. Then,
$T(\hat {X})=T({k})$
. Then,
![]() $\hat {X}\in A({k})$
, which implies that
$\hat {X}\in A({k})$
, which implies that
![]() $C({k})\leq C(\hat {X})$
. Now, two cases arise.
$C({k})\leq C(\hat {X})$
. Now, two cases arise.
Case (i) If
![]() $[T(k),C(k)]$
is one of the efficient pairs. Then
$[T(k),C(k)]$
is one of the efficient pairs. Then
![]() $C(k)\geq C^e(h_l)> C(\hat {X})$
, which is a contradiction.
$C(k)\geq C^e(h_l)> C(\hat {X})$
, which is a contradiction.
Case (ii) If
![]() $[T(k),C(k)]$
is not an efficient pair. In other words,
$[T(k),C(k)]$
is not an efficient pair. In other words,
![]() $[T(k),C(k)]$
is dominated by some efficient pair
$[T(k),C(k)]$
is dominated by some efficient pair
![]() $[T^e(h),C^e(h)]$
,
$[T^e(h),C^e(h)]$
,
![]() $h \in \{1,2,\ldots ,h_l\}$
. Then
$h \in \{1,2,\ldots ,h_l\}$
. Then
![]() $T(k)>T^e(h)$
and
$T(k)>T^e(h)$
and
![]() $C(k)\geq C^e(h) \geq C^e(h_l)> C(\hat {X})$
, which again is a contradiction.
$C(k)\geq C^e(h) \geq C^e(h_l)> C(\hat {X})$
, which again is a contradiction.
Theorem 6.3. Algorithm 3 records all efficient pairs, that is, no efficient pair is missed.
Proof. Let, if possible,
![]() $[\hat {T}^e, \hat {C}^e]$
be an efficient pair obtained from a feasible solution
$[\hat {T}^e, \hat {C}^e]$
be an efficient pair obtained from a feasible solution
![]() $\hat {X}$
of BiTSAP (2.1) which has not been recorded by the algorithm
$\hat {X}$
of BiTSAP (2.1) which has not been recorded by the algorithm
Then, by construction of efficient pairs, it is clear that
Since Algorithm 2 scans the complete set of feasible assignments of a TSAP,
 $$ \begin{align*} &\hat{T}^e= T(\hat{k})~{\textrm{for~some~}} \hat{k}\in \{1,2,\ldots,k_l \} \\ &\Rightarrow \hat{X} \in A(\hat{k}), {\textrm{and~}} \hat{C}^e \neq C(\hat{k}) ~({\textrm{using~(6.1)}}).\\ &{\textrm{Also,~}} C(\hat{k}) = \min \{ C(\alpha)\mid \alpha \in A(\hat{k}) \} \\ &\Rightarrow C(\hat{k}) < \hat{C}^e. \end{align*} $$
$$ \begin{align*} &\hat{T}^e= T(\hat{k})~{\textrm{for~some~}} \hat{k}\in \{1,2,\ldots,k_l \} \\ &\Rightarrow \hat{X} \in A(\hat{k}), {\textrm{and~}} \hat{C}^e \neq C(\hat{k}) ~({\textrm{using~(6.1)}}).\\ &{\textrm{Also,~}} C(\hat{k}) = \min \{ C(\alpha)\mid \alpha \in A(\hat{k}) \} \\ &\Rightarrow C(\hat{k}) < \hat{C}^e. \end{align*} $$
This implies that
![]() $[\hat {T}^e,\hat {C}^e]$
is dominated by
$[\hat {T}^e,\hat {C}^e]$
is dominated by
![]() $[T(\hat {k}),C(\hat {k})]$
, which is a contradiction to the assumption that
$[T(\hat {k}),C(\hat {k})]$
, which is a contradiction to the assumption that
![]() $[\hat {T}^e,\hat {C}^e]$
is an efficient pair. This completes the proof.
$[\hat {T}^e,\hat {C}^e]$
is an efficient pair. This completes the proof.
7 Numerical illustration
Consider a BiTSAP dealing with an allocation of five contractors, represented by
![]() $B_i,~i=1,2,\ldots ,5$
to five jobs, represented by
$B_i,~i=1,2,\ldots ,5$
to five jobs, represented by
![]() $W_j, j=1,2,\ldots ,5$
out of which
$W_j, j=1,2,\ldots ,5$
out of which
![]() $W_1$
and
$W_1$
and
![]() $W_2$
are Stage-1 jobs (corresponding time entries are shown in bold and underlined), whereas
$W_2$
are Stage-1 jobs (corresponding time entries are shown in bold and underlined), whereas
![]() $W_3$
,
$W_3$
,
![]() $W_4$
and
$W_4$
and
![]() $W_5$
are Stage-2 jobs. Table 1 provides the time “
$W_5$
are Stage-2 jobs. Table 1 provides the time “
![]() $t_{ij}$
” (in days) that the ith contractor takes to complete the jth job for all
$t_{ij}$
” (in days) that the ith contractor takes to complete the jth job for all
![]() $i,j=1,2,\ldots ,5$
. The BiTSAP aims at minimizing the following nonlinear cost function
$i,j=1,2,\ldots ,5$
. The BiTSAP aims at minimizing the following nonlinear cost function
![]() $C(X)$
(in terms of thousands of dollars) and total completion time
$C(X)$
(in terms of thousands of dollars) and total completion time
![]() $T(X)=\min \max \{t_{ij}\mid ~i\in I,~ j\in J\}$
, where
$T(X)=\min \max \{t_{ij}\mid ~i\in I,~ j\in J\}$
, where
 $$ \begin{align*} C(X)&=\begin{cases} 17x_{11}+60x_{12}+27x_{13}+38x_{14}+26x_{15}+27x_{21}+30 x_{22}+31x_{23}+\\ 44x_{24}+35x_{25}+11x_{31}+20x_{32}+16x_{33}+14x_{34} +26x_{35}+30x_{41}+\\ 32x_{42}+ 25x_{43}+19x_{44}+14x_{45}+ 20x_{51}+30x_{52}+31x_{53} +29x_{54}+\\ 28x_{55} +12x_{14}x_{21}+09x_{14}x_{31}+ 05x_{32}x_{45}+ 04x_{41}x_{52}- (03x_{12}x_{21}+\\04x_{13}x_{31}+05x_{14}x_{41}+06x_{15}x_{51}+05x_{23}x_{32}+07x_{34}x_{43}+08x_{35}x_{53}+ \\ 09x_{45}x_{54})- 07x_{23}x_{11}x_{52} - 08 x_{22}x_{33}x_{44}. \end{cases} \end{align*} $$
$$ \begin{align*} C(X)&=\begin{cases} 17x_{11}+60x_{12}+27x_{13}+38x_{14}+26x_{15}+27x_{21}+30 x_{22}+31x_{23}+\\ 44x_{24}+35x_{25}+11x_{31}+20x_{32}+16x_{33}+14x_{34} +26x_{35}+30x_{41}+\\ 32x_{42}+ 25x_{43}+19x_{44}+14x_{45}+ 20x_{51}+30x_{52}+31x_{53} +29x_{54}+\\ 28x_{55} +12x_{14}x_{21}+09x_{14}x_{31}+ 05x_{32}x_{45}+ 04x_{41}x_{52}- (03x_{12}x_{21}+\\04x_{13}x_{31}+05x_{14}x_{41}+06x_{15}x_{51}+05x_{23}x_{32}+07x_{34}x_{43}+08x_{35}x_{53}+ \\ 09x_{45}x_{54})- 07x_{23}x_{11}x_{52} - 08 x_{22}x_{33}x_{44}. \end{cases} \end{align*} $$
Table 1 Time entries
![]() $t_{ij}$
.
$t_{ij}$
.

The fixed cost charges (in thousands of dollars) of performance of a job by each contractor are presented by the coefficients of the linear terms in the expression of cost function
![]() $C(X)$
. In addition, other circumstances and constraints imposed by various contractors give rise to nonlinear terms in the expression for the cost function, like the additional cost of 12 (thousand dollars) charged by the contractor
$C(X)$
. In addition, other circumstances and constraints imposed by various contractors give rise to nonlinear terms in the expression for the cost function, like the additional cost of 12 (thousand dollars) charged by the contractor
![]() $B_1$
for performing the
$B_1$
for performing the
![]() $W_4$
job if
$W_4$
job if
![]() $B_2$
is performing the
$B_2$
is performing the
![]() $W_1$
job that gives rise to the term “
$W_1$
job that gives rise to the term “
![]() $12 x_{14} x_{21}$
” in the cost function
$12 x_{14} x_{21}$
” in the cost function
![]() $C(X)$
. Similarly,
$C(X)$
. Similarly,
![]() $B_1$
charging a cost of 09 (thousand dollars) for the
$B_1$
charging a cost of 09 (thousand dollars) for the
![]() $W_4$
job if
$W_4$
job if
![]() $B_3$
performs the
$B_3$
performs the
![]() $W_1$
job, adds the term “
$W_1$
job, adds the term “
![]() $09 x_{14} x_{31}$
” in
$09 x_{14} x_{31}$
” in
![]() $C(X)$
. Likewise, the term
$C(X)$
. Likewise, the term
![]() $-07 x_{23} x_{11} x_{52}$
is attributed to the concession in cost of performance of job
$-07 x_{23} x_{11} x_{52}$
is attributed to the concession in cost of performance of job
![]() $W_3$
by 07 (thousand dollars) provided by contractor
$W_3$
by 07 (thousand dollars) provided by contractor
![]() $B_2$
if the jobs
$B_2$
if the jobs
![]() $W_1$
and
$W_1$
and
![]() $W_2$
are performed by the contractors
$W_2$
are performed by the contractors
![]() $B_1$
and
$B_1$
and
![]() $B_5$
, respectively. Other nonlinear terms in
$B_5$
, respectively. Other nonlinear terms in
![]() $C(X)$
are attributed in a similar manner. The aim is to find all efficient time-cost pairs for the given BiTSAP.
$C(X)$
are attributed in a similar manner. The aim is to find all efficient time-cost pairs for the given BiTSAP.
Solution. First of all, let us rank and scan the complete set of feasible assignments of a TSAP in order of increasing total completion time using Algorithm 2. For this, find the minimum total completion time
![]() $T(1)$
and corresponding optimal assignment
$T(1)$
and corresponding optimal assignment
![]() $\alpha _1$
for the TSAP using the technique provided by Jain et al. [Reference Jain, Dahiya, Sharma and Verma15].
$\alpha _1$
for the TSAP using the technique provided by Jain et al. [Reference Jain, Dahiya, Sharma and Verma15].
The minimum total completion time of the given two-stage problem is
![]() ${T(1)=(T_{S1}(1)=05,T_{S2}(1)=03)=08}$
, and the corresponding optimal assignment is
${T(1)=(T_{S1}(1)=05,T_{S2}(1)=03)=08}$
, and the corresponding optimal assignment is
The partial set of assignments giving the total completion time as
![]() $T(1)$
is
$T(1)$
is
We construct mutually exclusive nonempty subsets from
![]() $\alpha _1$
, and find the optimal assignment and minimum total completion time for the corresponding two-stage assignment problem:
$\alpha _1$
, and find the optimal assignment and minimum total completion time for the corresponding two-stage assignment problem:
 $$ \begin{align*} N_1&=\{\overline{(1,1)}\}, \; \;T_{N_1}=15, \;\;\alpha_{N_1}=\{(1,3),(2,2),(3,4),(4,1),(5,5)\} ,\\ N_2&=\{(1,1),\overline{(2,3)}\}, \;\;T_{N_2}=12,\,\, \alpha_{N_2}=\{(1,1),(2,2),(3,3),(4,4),(5,5)\} ,\\ N_3&=\{(1,1),(2,3),\overline{(3,5)}\},\;\; T_{N_3}=12, \;\;\alpha_{N_3}=\{(1,1),(2,3),(3,2),(4,4),(5,5)\}, \\ N_4&=\{(1,1),(2,3),(3,5),\overline{(4,4)}\},\;\; T_{N_4}=41,\;\; \alpha_{N_4}=\{(1,1),(2,3),(3,5),(4,2),(5,4)\}. \end{align*} $$
$$ \begin{align*} N_1&=\{\overline{(1,1)}\}, \; \;T_{N_1}=15, \;\;\alpha_{N_1}=\{(1,3),(2,2),(3,4),(4,1),(5,5)\} ,\\ N_2&=\{(1,1),\overline{(2,3)}\}, \;\;T_{N_2}=12,\,\, \alpha_{N_2}=\{(1,1),(2,2),(3,3),(4,4),(5,5)\} ,\\ N_3&=\{(1,1),(2,3),\overline{(3,5)}\},\;\; T_{N_3}=12, \;\;\alpha_{N_3}=\{(1,1),(2,3),(3,2),(4,4),(5,5)\}, \\ N_4&=\{(1,1),(2,3),(3,5),\overline{(4,4)}\},\;\; T_{N_4}=41,\;\; \alpha_{N_4}=\{(1,1),(2,3),(3,5),(4,2),(5,4)\}. \end{align*} $$
Here,
This implies that all feasible assignments of the TSAP having a corresponding total completion time as
![]() $T(1)$
have been found and are given by
$T(1)$
have been found and are given by
![]() $A(1)=\{\alpha _1\}$
. Next, to determine
$A(1)=\{\alpha _1\}$
. Next, to determine
![]() $A(2)$
, we find
$A(2)$
, we find
![]() $\displaystyle \min _{N\in \mathscr {N}} \{T_N\mid T_N> T(1) \}=12=T(2)$
. With
$\displaystyle \min _{N\in \mathscr {N}} \{T_N\mid T_N> T(1) \}=12=T(2)$
. With
we set
![]() $\xi (2)=\mathscr {N}(2)$
and partition each node of
$\xi (2)=\mathscr {N}(2)$
and partition each node of
![]() $\xi (2)$
by its optimal assignment. Partitioning
$\xi (2)$
by its optimal assignment. Partitioning
![]() $N_2$
by
$N_2$
by
![]() $\alpha _{N_2}$
, we have
$\alpha _{N_2}$
, we have
![]() $N_{21}=\{(1,1), \overline {(2,3)}, \overline {(2,2)}\}$
,
$N_{21}=\{(1,1), \overline {(2,3)}, \overline {(2,2)}\}$
,
![]() $\alpha _{N_{21}}=\{(1,1),(2,5),(3,2),(4,4),(5,3)\}$
and
$\alpha _{N_{21}}=\{(1,1),(2,5),(3,2),(4,4),(5,3)\}$
and
![]() $T_{N_{21}}=20$
,
$T_{N_{21}}=20$
,
![]() $N_{22}\kern-1pt =\kern-1pt \{(1,1), \overline {(2,3)},(2,2), \overline {(3,3)}\}$
,
$N_{22}\kern-1pt =\kern-1pt \{(1,1), \overline {(2,3)},(2,2), \overline {(3,3)}\}$
,
![]() $\alpha _{N_{22}}\kern-1pt =\kern-1pt \{(1,1),(2,2),(3,5),(4,4),(5,3)\}$
and
$\alpha _{N_{22}}\kern-1pt =\kern-1pt \{(1,1),(2,2),(3,5),(4,4),(5,3)\}$
and
![]() $T_{N_{22}}\kern-1pt =\kern-1pt 15$
,
$T_{N_{22}}\kern-1pt =\kern-1pt 15$
,
![]() $N_{23}=\{(1,1), \overline {(2,3)},(2,2),(3,3),\overline {(4,4)}\}$
,
$N_{23}=\{(1,1), \overline {(2,3)},(2,2),(3,3),\overline {(4,4)}\}$
,
![]() $\alpha _{N_{23}}=\{(1,1),(2,2),(3,3),(4,5),(5,4)\}$
and
$\alpha _{N_{23}}=\{(1,1),(2,2),(3,3),(4,5),(5,4)\}$
and
![]() $T_{N_{23}}=26$
.
$T_{N_{23}}=26$
.
Next, we partition
![]() $N_3$
by
$N_3$
by
![]() $\alpha _{N_3}$
:
$\alpha _{N_3}$
:
![]() $N_{31}\kern-1pt =\kern-1pt \{(1,1), (2,3), \overline {(3,5)}, \overline {(3,2)}\}$
,
$N_{31}\kern-1pt =\kern-1pt \{(1,1), (2,3), \overline {(3,5)}, \overline {(3,2)}\}$
,
![]() $\alpha _{N_{31}}\kern-1pt =\kern-1pt \{(1,1),(2,3),(3,4),(4,5),(5,2)\}$
and
$\alpha _{N_{31}}\kern-1pt =\kern-1pt \{(1,1),(2,3),(3,4),(4,5),(5,2)\}$
and
![]() $T_{N_{31}}\kern-1pt =\kern-1pt 15$
;
$T_{N_{31}}\kern-1pt =\kern-1pt 15$
;
![]() $N_{32}=\{(1,1), (2,3), \overline {(3,5)},(3,2), \overline {(4,4)}\}$
,
$N_{32}=\{(1,1), (2,3), \overline {(3,5)},(3,2), \overline {(4,4)}\}$
,
![]() $\alpha _{N_{32}}=\{(1,1),(2,3),(3,2),(4,5),(5,4)\}$
and
$\alpha _{N_{32}}=\{(1,1),(2,3),(3,2),(4,5),(5,4)\}$
and
![]() $T_{N_{32}}=26$
.
$T_{N_{32}}=26$
.
Here,
![]() $\xi =\{N_{21},N_{22},N_{23},N_{31},N_{32}\}$
, then
$\xi =\{N_{21},N_{22},N_{23},N_{31},N_{32}\}$
, then
![]() $\displaystyle \min _{N\in \xi } T_N=15>T(2)$
.
$\displaystyle \min _{N\in \xi } T_N=15>T(2)$
.
Therefore, all feasible assignments having a total completion time as
![]() $T(2)$
have been found and are given by
$T(2)$
have been found and are given by
![]() $A(2)=\{\alpha _{N_2},\alpha _{N_3}\}$
. Similarly, find all ranked total completion times of the TSAP and obtain the corresponding nodes and feasible assignments.
$A(2)=\{\alpha _{N_2},\alpha _{N_3}\}$
. Similarly, find all ranked total completion times of the TSAP and obtain the corresponding nodes and feasible assignments.
Table 2 provides the list of all completion times of the TSAP in increasing order of time value, the corresponding set
![]() $\mathscr {N}_A(k)$
of all nodes possible with total completion time
$\mathscr {N}_A(k)$
of all nodes possible with total completion time
![]() $T(k)$
and the corresponding value of cost function
$T(k)$
and the corresponding value of cost function
![]() $C(k)$
, which is the minimum of the cost values for optimal assignments of all nodes with total completion time
$C(k)$
, which is the minimum of the cost values for optimal assignments of all nodes with total completion time
![]() $T(k)$
.
$T(k)$
.
Table 2 Ranking and scanning of the given TSAP.

Note that
![]() $T(19)=50$
is the last completion time when ranking of the feasible assignment with respect to the total completion is done in increasing order. It follows that
$T(19)=50$
is the last completion time when ranking of the feasible assignment with respect to the total completion is done in increasing order. It follows that
![]() $T(19)=50$
is actually the maximum possible total completion time of the TSAP.
$T(19)=50$
is actually the maximum possible total completion time of the TSAP.
Next, we find efficient time-cost pairs of a BiTSAP using Algorithm 3.
Find
![]() $C(1)=\min \{C(\alpha _1)\}=\min \{116\}=116$
.
$C(1)=\min \{C(\alpha _1)\}=\min \{116\}=116$
.
Therefore,
![]() $[T(1),C(1)]=[08,116]=[T^e(1),C^e(1)]$
is the first efficient pair and the corresponding assignment
$[T(1),C(1)]=[08,116]=[T^e(1),C^e(1)]$
is the first efficient pair and the corresponding assignment
![]() $\{(1,1),(2,3),(3,5),(4,4),(5,2)\}$
is an efficient solution to the given BiTSAP.
$\{(1,1),(2,3),(3,5),(4,4),(5,2)\}$
is an efficient solution to the given BiTSAP.
Next,
![]() $C(2)=\min \{C(\alpha _{N_2}), C(\alpha _{N_3})\}=\min \{102,110\}=102$
.
$C(2)=\min \{C(\alpha _{N_2}), C(\alpha _{N_3})\}=\min \{102,110\}=102$
.
Since
![]() $C(2)<C(1)$
,
$C(2)<C(1)$
,
![]() $[T(2),C(2)]$
is the next efficient pair.
$[T(2),C(2)]$
is the next efficient pair.
Thus, the second efficient pair is
![]() $[T^e(2),C^e(2)]=[T(2),C(2)]=[12,102]$
.
$[T^e(2),C^e(2)]=[T(2),C(2)]=[12,102]$
.
The corresponding second efficient assignment is
![]() $a_{N_2}=\{(1,1),(2,2),(3,3),(4,4), (5,5)\}$
.
$a_{N_2}=\{(1,1),(2,2),(3,3),(4,4), (5,5)\}$
.
Next,
![]() $C(3)=\min \{C(\alpha ):\alpha \in A(3)\}=99<C(2)$
and it corresponds to the assignment
$C(3)=\min \{C(\alpha ):\alpha \in A(3)\}=99<C(2)$
and it corresponds to the assignment
![]() $\{(1,1),(2,3),(3,4),(4,5),(5,4)\}$
.
$\{(1,1),(2,3),(3,4),(4,5),(5,4)\}$
.
Therefore, we get the third efficient assignment and
![]() $[T^e(3),C^e(3)]=[T(3),C(3)]=[15,99]$
.
$[T^e(3),C^e(3)]=[T(3),C(3)]=[15,99]$
.
Further,
![]() $C(4)=121>C(3)$
, thus
$C(4)=121>C(3)$
, thus
![]() $(T(4),C(4))$
is dominated by
$(T(4),C(4))$
is dominated by
![]() $[T(3),C(3)]$
and is not an efficient time-cost pair.
$[T(3),C(3)]$
and is not an efficient time-cost pair.
Proceeding in a similar manner, the next efficient pair obtained is
and the corresponding assignment is
![]() $\{(1,1),(2,2),(3,3),(4,5),(5,4)\}$
. After this, no efficient pair is obtained. Thus, all efficient time-cost pairs for the BiTSAP are
$\{(1,1),(2,2),(3,3),(4,5),(5,4)\}$
. After this, no efficient pair is obtained. Thus, all efficient time-cost pairs for the BiTSAP are
8 Complexity of Algorithm-R&S
Algorithm 2 explores ranking and scanning of feasible assignments for the TSTMAP by branching of nodes corresponding to a specified total completion time of the problem and solving the TSTMAP corresponding to each constructed node. Sizes of these problems (TSTMAPs) solved at each node vary from 2 to n depending upon the level of the node. The level of a node
![]() $N_{\gamma }$
(say) refers to the number of times a Level-
$N_{\gamma }$
(say) refers to the number of times a Level-
![]() $0$
node is partitioned to obtain
$0$
node is partitioned to obtain
![]() $N_{\gamma }$
. That is, a node is termed as a Level-L node if it is obtained by partitioning a Level-
$N_{\gamma }$
. That is, a node is termed as a Level-L node if it is obtained by partitioning a Level-
![]() $0$
node “L” number of times. Note that the node corresponding to an optimal solution of the TSTMAP is marked as a Level-0 node. For example, in the numerical example stated in Section 7, the node corresponding to an optimal solution (
$0$
node “L” number of times. Note that the node corresponding to an optimal solution of the TSTMAP is marked as a Level-0 node. For example, in the numerical example stated in Section 7, the node corresponding to an optimal solution (
![]() $\alpha _1$
) can be marked as a Level-0 node and its partitioning leads to
$\alpha _1$
) can be marked as a Level-0 node and its partitioning leads to
![]() $(n-1)$
nodes (nodes
$(n-1)$
nodes (nodes
![]() $N_1,\ldots , N_4$
) having sizes 2 to n. All these nodes are referred to as Level-1 nodes and these are stored in a set (
$N_1,\ldots , N_4$
) having sizes 2 to n. All these nodes are referred to as Level-1 nodes and these are stored in a set (
![]() $\mathcal {N}$
). For further scanning of the feasible solutions, one or more nodes from Level-1 are picked for partitioning (depending on the minimum value of
$\mathcal {N}$
). For further scanning of the feasible solutions, one or more nodes from Level-1 are picked for partitioning (depending on the minimum value of
![]() $T(X)$
for the TSTMAP corresponding to that particular node and the existence of alternate solutions), which results in the formation of Level-2 nodes. In the numerical example, partitioning of Level-1 node
$T(X)$
for the TSTMAP corresponding to that particular node and the existence of alternate solutions), which results in the formation of Level-2 nodes. In the numerical example, partitioning of Level-1 node
![]() $N_2$
yields three nodes
$N_2$
yields three nodes
![]() $N_{21}, N_{22}$
and
$N_{21}, N_{22}$
and
![]() $N_{23}$
, and these are Level-2 nodes. The set
$N_{23}$
, and these are Level-2 nodes. The set
![]() $\mathscr {N}$
is then updated to contain all Level-1 and Level-2 nodes, and partitioning is continued.
$\mathscr {N}$
is then updated to contain all Level-1 and Level-2 nodes, and partitioning is continued.
For further partitioning, one or more nodes corresponding to the minimum value of
![]() $T(X)$
are selected out of the nodes of
$T(X)$
are selected out of the nodes of
![]() $\mathcal {N}$
and the partitioning process is executed. Note that either the size of the TSTMAP or the number of feasible links
$\mathcal {N}$
and the partitioning process is executed. Note that either the size of the TSTMAP or the number of feasible links
![]() $(i,j)$
reduces as the level of the partitioning node increases. Therefore, the total number of nodes that can be formed is finite and the termination of partitioning is certain. At each node, the corresponding TSTMAP is solved by the iterative algorithm proposed by Jain et al. [Reference Jain, Dahiya, Sharma and Verma15] having polynomially bound complexity of the order of
$(i,j)$
reduces as the level of the partitioning node increases. Therefore, the total number of nodes that can be formed is finite and the termination of partitioning is certain. At each node, the corresponding TSTMAP is solved by the iterative algorithm proposed by Jain et al. [Reference Jain, Dahiya, Sharma and Verma15] having polynomially bound complexity of the order of
![]() $O( \lfloor {n/2} \rfloor n^3 \sqrt {n \log n})$
, where
$O( \lfloor {n/2} \rfloor n^3 \sqrt {n \log n})$
, where
![]() $ \lfloor {n/2} \rfloor $
denotes the greatest integer less than or equal to
$ \lfloor {n/2} \rfloor $
denotes the greatest integer less than or equal to
![]() $n/2$
. An optimal assignment is noted on the basis of which further partitioning is executed. It can be observed that for finding the Kth ranked assignments of the TSTMAP, the number of problems (TSTMAPs) solved is equal to the total number of nodes constructed till the step where it is declared that all possible assignments that could yield total completion time
$n/2$
. An optimal assignment is noted on the basis of which further partitioning is executed. It can be observed that for finding the Kth ranked assignments of the TSTMAP, the number of problems (TSTMAPs) solved is equal to the total number of nodes constructed till the step where it is declared that all possible assignments that could yield total completion time
![]() $T(K)$
have been obtained. The number of nodes is associated with the number of times branching is done. It can be observed from the Algorithm-R&S that the branching process depends on the given data of the problem in terms of the time entries “
$T(K)$
have been obtained. The number of nodes is associated with the number of times branching is done. It can be observed from the Algorithm-R&S that the branching process depends on the given data of the problem in terms of the time entries “
![]() $t_{ij}$
” and therefore varies with the change in time entries of the problem.
$t_{ij}$
” and therefore varies with the change in time entries of the problem.
In general, in a standard assignment problem, there are
![]() $n!$
assignments in total, which is a very big number [Reference Dantzig10] and increases rapidly as n increases. Ranking and scanning of feasible assignments of the TSTMAP of size “n” precisely means enumerating the
$n!$
assignments in total, which is a very big number [Reference Dantzig10] and increases rapidly as n increases. Ranking and scanning of feasible assignments of the TSTMAP of size “n” precisely means enumerating the
![]() $n!$
assignments in increasing order of total completion time and scrutinizing all possible alternate assignments as well. However, while scanning the feasible set for finding the Kth optimal assignments, Algorithm 2 discards a large number of nodes and consequently a large number of assignments, all of which are sure to possess a total completion time greater than
$n!$
assignments in increasing order of total completion time and scrutinizing all possible alternate assignments as well. However, while scanning the feasible set for finding the Kth optimal assignments, Algorithm 2 discards a large number of nodes and consequently a large number of assignments, all of which are sure to possess a total completion time greater than
![]() $T(K)$
. Hence, the branching technique explored in Algorithm 2 is computationally efficacious for determining ranked assignments of a TSTMAP. It should be noted that the computational load increases as the value of K increases where scanning of the
$T(K)$
. Hence, the branching technique explored in Algorithm 2 is computationally efficacious for determining ranked assignments of a TSTMAP. It should be noted that the computational load increases as the value of K increases where scanning of the
![]() $1$
st optimal assignments require the least computational efforts.
$1$
st optimal assignments require the least computational efforts.
The proposed algorithm has been coded in MATLAB on a 64-bit operating system, 4-GB RAM, i3 processor and tested with the help of a variety of randomly generated problems. The algorithm runs successfully for test problems with sizes varying from 4 to 10 and
![]() $t_{ij}$
varying from 1 to 30. The number of problems solved for obtaining the Kth optimal assignments (
$t_{ij}$
varying from 1 to 30. The number of problems solved for obtaining the Kth optimal assignments (
![]() $K=1,2,3$
) is noted in each case. Results show that in most of the cases, the number of problems solved to obtain the Kth optimal solution increases with the increase in the size of the problem, and hence the computational time increases with the increase in the size of the problem. It should be noted that each problem solved yields a unique feasible assignment of the TSAP (because of the mutual exclusiveness of the nodes). Therefore, we can say that the number of problems solved is equal to the number of feasible assignments explored. Table 3 provides the results obtained as an outcome of the numerical experiments in terms of the percentage of feasible assignments explored for obtaining the Kth optimal solution for different values of n. If
$K=1,2,3$
) is noted in each case. Results show that in most of the cases, the number of problems solved to obtain the Kth optimal solution increases with the increase in the size of the problem, and hence the computational time increases with the increase in the size of the problem. It should be noted that each problem solved yields a unique feasible assignment of the TSAP (because of the mutual exclusiveness of the nodes). Therefore, we can say that the number of problems solved is equal to the number of feasible assignments explored. Table 3 provides the results obtained as an outcome of the numerical experiments in terms of the percentage of feasible assignments explored for obtaining the Kth optimal solution for different values of n. If
![]() $\eta $
represents the percentage of feasible assignments (out of the total number of
$\eta $
represents the percentage of feasible assignments (out of the total number of
![]() $n!$
assignments) explored, then from Table 3, we see that for each instance of n,
$n!$
assignments) explored, then from Table 3, we see that for each instance of n,
![]() $\eta $
increases as K increases. In addition, in each instance of n,
$\eta $
increases as K increases. In addition, in each instance of n,
![]() $\eta $
is small and it decreases rapidly as n increases. Likewise, for obtaining all possible
$\eta $
is small and it decreases rapidly as n increases. Likewise, for obtaining all possible
![]() $3$
rd optimal assignments,
$3$
rd optimal assignments,
![]() $\eta $
drops from 37 % for
$\eta $
drops from 37 % for
![]() $n=4$
to 0.001 % for
$n=4$
to 0.001 % for
![]() $n=10$
. This is because as n increases, the total number of assignments (which is
$n=10$
. This is because as n increases, the total number of assignments (which is
![]() $n!$
) increases quite rapidly. All these results show that the proposed algorithm is quite efficient in terms of computational performance.
$n!$
) increases quite rapidly. All these results show that the proposed algorithm is quite efficient in terms of computational performance.
Table 3 Results of numerical experiments.

9 BiTSAP with a minimization and a maximization objective
This section describes a modification in Algorithm 3 that can efficiently tackle a bi-objective TSAP dealing with one minimization objective and the other a maximization objective. Consider a BiTSAP in which the objective is to minimize the total completion time (
![]() $T(X)$
) and maximize the cost objective function (
$T(X)$
) and maximize the cost objective function (
![]() $C(X)$
). Practically, maximization of the cost objective function can be visualized as maximization of profit, dividend, efficiency etc.
$C(X)$
). Practically, maximization of the cost objective function can be visualized as maximization of profit, dividend, efficiency etc.
In this case, the BiTSAP takes the form
![]() $\mathrm{BiTSAP}^c$
:
$\mathrm{BiTSAP}^c$
:
 $$ \begin{align} \begin{split} \min_{X=(Y,Z),~Y\in S,~Z\in S(Y)} (T(X)), \\ \max_{X=(Y,Z),~Y\in S,~Z\in S(Y)} (C(X)), \end{split} \end{align} $$
$$ \begin{align} \begin{split} \min_{X=(Y,Z),~Y\in S,~Z\in S(Y)} (T(X)), \\ \max_{X=(Y,Z),~Y\in S,~Z\in S(Y)} (C(X)), \end{split} \end{align} $$
where S and
![]() $S(Y)$
are same as defined in Section 2. Since
$S(Y)$
are same as defined in Section 2. Since
![]() $C(X)$
is now required to be maximized, the definition of an efficient solution for BiTSAP
$C(X)$
is now required to be maximized, the definition of an efficient solution for BiTSAP
![]() $^c$
(9.1) takes the following form.
$^c$
(9.1) takes the following form.
Definition 9.1. A solution
![]() $X^*=(Y^*,Z^*)$
,
$X^*=(Y^*,Z^*)$
,
![]() $Y^*\in S$
,
$Y^*\in S$
,
![]() $Z^*\in S(Y)$
is said to be an efficient solution of BiTSAP
$Z^*\in S(Y)$
is said to be an efficient solution of BiTSAP
![]() $^c$
(9.1) if and only if there does not exist another solution
$^c$
(9.1) if and only if there does not exist another solution
![]() $\hat {X}=(\hat {Y},\hat {Z})$
,
$\hat {X}=(\hat {Y},\hat {Z})$
,
![]() $\hat {Y}\in S$
,
$\hat {Y}\in S$
,
![]() $\hat {Z}\in S(Y)$
such that:
$\hat {Z}\in S(Y)$
such that:
-
(i)
 $T(\hat {X}) \leq T(X^*)$
;
$T(\hat {X}) \leq T(X^*)$
; -
(ii)
 $C(\hat {X}) \geq C(X^*)$
,
$C(\hat {X}) \geq C(X^*)$
,
with a strict inequality sign holding for at least one of the relations (i) and (ii).
The corresponding time-cost pair
![]() $[T(X^*),C(X^*)]$
is termed as an efficient pair of BiTSAP
$[T(X^*),C(X^*)]$
is termed as an efficient pair of BiTSAP
![]() $^c$
(9.1).
$^c$
(9.1).
In this case,
![]() $C(k)$
is defined as
$C(k)$
is defined as
![]() $C(k)=\max \{C(\alpha )\mid \alpha \in A(k)\}$
for
$C(k)=\max \{C(\alpha )\mid \alpha \in A(k)\}$
for
![]() $k=1,2,\ldots $
.
$k=1,2,\ldots $
.
Efficient pairs for BiTSAP
![]() $^c$
(9.1) can be obtained using Algorithm 3 with a modification to Step G(ii).
$^c$
(9.1) can be obtained using Algorithm 3 with a modification to Step G(ii).
Modified G(ii) (for BiTSAP
![]() $^c$
). Set
$^c$
). Set
![]() $k=\hat {k}$
. Find
$k=\hat {k}$
. Find
![]() $T(k+1)$
and
$T(k+1)$
and
![]() $A(k+1)$
using Algorithm-R&S. Next, find
$A(k+1)$
using Algorithm-R&S. Next, find
![]() $C(k+1)=\max \{C(\alpha )\mid \alpha \in A(k+1)\}$
. If
$C(k+1)=\max \{C(\alpha )\mid \alpha \in A(k+1)\}$
. If
![]() $C(k+1) \leq C(\hat {k})$
, then
$C(k+1) \leq C(\hat {k})$
, then
![]() $[T(k+1),C(k+1)]$
is dominated by
$[T(k+1),C(k+1)]$
is dominated by
![]() $[T(\hat {k}),C(\hat {k})]$
. Repeat Step G(ii) by updating
$[T(\hat {k}),C(\hat {k})]$
. Repeat Step G(ii) by updating
![]() $k=k+1$
.
$k=k+1$
.
However, if
![]() $C(k+1)> C(\hat {k})$
, then
$C(k+1)> C(\hat {k})$
, then
![]() $[T(k+1),C(k+1)]$
is the next efficient pair
$[T(k+1),C(k+1)]$
is the next efficient pair
![]() $[T^e(h+1),C^e(h+1)]$
.
$[T^e(h+1),C^e(h+1)]$
.
10 Concluding remarks
-
• The paper addresses a BiTSAP that aims at minimizing two objective functions simultaneously. One objective function is a nonlinear cost function, defined explicitly in terms of assignment variables, and the other is the total completion time of all jobs in a two-stage assignment process.
-
• An algorithm (Algorithm 3) for finding all efficient time-cost pairs of the BiTSAP has been proposed. The proposed algorithm is based on ranking and scanning all feasible assignments in order of increasing total completion time and then obtaining the value of the cost objective function corresponding to ranked feasible assignments.
-
• For ranking and scanning the feasible assignments in order of total completion time, a systematic branch and bound technique (Algorithm 2) has been developed in the paper.
-
• A large number of nodes are formed while branching for ranking of assignments in order of increasing total completion time. We would like to develop a more efficient technique for solving such a bi-objective two-stage assignment problem.
-
• Bi-objective multistage assignment problems and multi-objective two-stage assignment problems emerge as interesting open problems from the current study.
Acknowledgements
The author E. Jain is thankful to the Council of Scientific and Industrial Research, India (Sanction No. 09/135/(0724)/2015-EMR-I) and the author K. Dahiya is thankful to the Science and Engineering Research Board (SERB(MATRICS) Sanction no. MTR/2019/000723) for financial support required to carry out this research work.