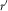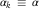1. Introduction
The 8 May 2010 marked 65 years since the end of the Second World War in Europe. It is also the day a child born at the end of the war turns 65, and may well have wished to retire. Unfortunately, for our ageing baby boomer friend, the global financial crisis of 2008–2009 might have made retirement a difficult proposition if she were to rely solely on her private pension fund wealth: some USD $5.4 trillion (OECD, 2009) was lost by private pension funds in OECD countries in 2008. Even worse, had she opted for an earlier retirement and was relying on commercial retirement income streams (of a non-annuitised sort) generated from a portfolio with a significant component of equities, she may well have to reconcile herself to a much lower standard of living in retirement.
The anecdote above points to the importance of developing both adequate levels of retirement savings (during the accumulation phase) and access to annuitised retirement income streams (for the decumulation phase). In response to the first issue, the World Bank (1994) developed a model based on mandating a minimum level of contribution towards individual retirement savings. Furthermore, incentives to build up non-mandated savings for retirement – such as through tax concessions – are also common. The motivation of such schemes is to encourage agents’ own provision of retirement income, reducing the burden to government of costly income provision (Disney, Reference Disney2000). To protect balances from investment risk as they accumulate to provide future retirement benefits, savers may have access to financial guarantees (Mitchell & Smetters, Reference Mitchell and Smetters2003).
The second issue, developing access to annuitised income streams for individuals’ retirement savings, is also broadly problematic. What has become known as the “annuity puzzle” stems from the observation that there is surprisingly small demand for voluntary lifetime annuities throughout the world (Purcal & Piggott, Reference Purcal and Piggott2008). While the United Kingdom is the world’s largest market for immediate lifetime annuities (some GBP £12 billion of business was written in 2005), the principal driver for this market is the compulsory annuitisation at retirement of tax-efficient defined contribution personal pension plans.
In contrast, in the United States there is no such compunction to annuitise. Although vast sums flow into US annuities markets (USD $301 billion in 2004), almost without exception these funds find their way into tax-sheltered deferred annuities, with scant amounts ever being actually annuitised – the overwhelming proportion are withdrawn as lump sums. The market for voluntary lifetime annuities in Australia, on the other hand, is transparently tiny. There, from the second quarter of 2010 to the first of 2011 only some AUD $11.1 million, involving a miniscule 49 contracts, generated a paltry AUD $590,000Footnote 1 of income flow (Plan for Life Research Pty Ltd, 2011).
Economists have long recognised the theoretical welfare gains associated with the purchase of a life annuityFootnote 2. This ancient productFootnote 3 offers both insurance against longevity risk and downside investment risk, or macroeconomic riskFootnote 4. And yet, they are not popular. Legislators in the United States have sought to encourage annuitisation. Gentry & Rothschild (Reference Gentry and Rothschild2010) report on two such proposals, analysing the impact of mooted tax changes on the attractiveness of annuity purchase. US policymakers have also suggested ways of furthering annuity provision. Gale et al. (Reference Gale, Iwry, John and Walker2009) advocate a default system of annuitisation of 401(k) balances. Iwry & Turner (Reference Iwry and Turner2009) discuss the default sequential purchase of deferred annuities over the life cycle to accumulate a reasonable lifetime pension amount at retirement. Orth (Reference Orth2006) treats a possible framework for mandatory annuitisation in the United States.
In this paper, we develop a different type of model to encourage the annuitisation of individual retirement savings – through generous and regulated annuity prices (protecting the decumulation phase of lifetime retirement saving) while at the same time offering security of retirement capital (protecting the accumulation phase of lifetime retirement saving). This is done within the context of the World Bank (1994) model of mandated retirement savings. While the basic World Bank model of forced savings, adopted in countries like Australia and Chile, is a model without cross-subsidies between these tiers, other countries such as Switzerland have a regulatory system that introduces such cross-subsidies. This leads naturally to the description and taxonomy of two-tiered systems of retirement savings with (possible) cross-subsidies. In this paper, we present a two-tiered model of second pillar savings that explicitly allows for cross-subsidisation between tiers. The latter is induced by letting the government-set returns (during the accumulation phase) and annuity prices (for the decumulation phase) on the first (mandated) tier.
In section 2 we provide background information on Switzerland’s second pillar of retirement saving, which serves as a motivation and illustration of our modelling. In section 3 we set up a model of financial flows within our family of retirement savings systems, focusing on the main government-regulated variables. This model, essential to our analysis, fleshes out the mechanism by which cross-subsidisation occurs. We discuss this model in section 4 and develop a useful taxonomy of two-tiered retirement savings schemes, which arises naturally from our modelling. We explore the implications of our findings for the regulation of the Swiss system in section 5. Section 6 concludes.
2. Background: the Swiss Second Pillar
One remarkable exception to the widespread trend of low levels of voluntary annuitisation is the case of Switzerland, whose cross-subsidised two-tiered systemFootnote 5 further motivates the model developed in this paper. There almost two-thirds of retirees choose to convert their accumulated retirement savings – including a substantial component of voluntary savings – into a lifetime income streamFootnote 6; only a quarter (Bütler, Reference Bütler2003) select a lump sum. Recent figures indicate 78% of the income of the aged stems from annuities (Office fédéral de la statistique, 2007), of which slightly less than half comes from second pillar savings. This paper is inspired by this surprising retirement system, a system that not only involves a high degree of annuitisation, but also achieves this entirely through provision from the private sector, with remarkably stable (regulated) annuity pricesFootnote 7. As Switzerland serves as an illustration throughout the paper, both for the modelling and the analysis, this section starts by outlining some of its main characteristics.
The Swiss old age security system is an integrated system of three pillars. The first pillar, mandatory for all Swiss residents, offers universal old age pensions. It is funded in a pay-as-you-go fashion. The second pillar, an occupational pensions system, is mandatory for all employees with a certain level of income and is fully funded. Individual initiative falls into the third pillar category. Further, it is worth noting that first and second pillars also offer benefits in case of death and disability, mainly in the form of annuities.
This paper focuses on the second pillar. For more details about the broader Swiss system, as well as its benefits, see Avanzi (Reference Avanzi2010).
The minimum legal plan in the second pillar is a defined contribution plan with contribution rates and benefits defined in the law. Pension funds are free to define their own plan (including in the form of defined benefit plans), as long as they guarantee at least the same level of benefits as would have been offered in the minimum plan. In fact, they have to keep an account of the “theoretical” amount of accumulated savings all insured would have, would they be in the minimum legal plan – later called “mandatory savings”. This means that all the parameters of growth of this account (in particular, contribution rates and interest rates) are either defined in the law or set by the government. Any additional savingsFootnote 8 are later referred to as “non-mandatory savings”.
At retirement, annuitisation of savings is the default choice, but pension funds can decide to allow a lump sum withdrawal instead. While a majority of pension funds exercise this option, the usual outcome for retiring Swiss is still annuitisationFootnote 9.
The system yields substantial savings; Switzerland is one of few countries with an amount of savings exceeding its gross domestic product (Gerber & Weber, Reference Gerber and Weber2007). Furthermore, a result of the success of annuities on retirement is a healthy privately provided life annuities market. Newly retired households achieve replacement rates of between 70% and 80% of income flows (Bütler, Reference Bütler2009). This last proportion (ceteris paribus) is expected to increase as the system needs another 15 years before agents retire with a complete contribution period.
Outwardly, the Swiss system seems to be a success story. For 20 years the system fared well without requiring any action from the government, but the Swiss system is currently facing some difficult issues. Since the inception of the Swiss system in 1985, improvements in mortality rates and declining interest rates have made the system difficult for the government to regulate. Drawing on insights gathered from our modelling below, we elaborate on these issues in section 5.
3. Financial Flows in a Cross-Subsidised Two-Tiered System of Retirement Savings
In this section, we flesh out in a stylised way the main characteristics and financial flows of a two-tiered system of retirement savings where both the accumulation and decumulation phases of the first (mandated) tier are controlled by the government. After setting out our economic landscape in section 3.1, section 3.2 explains how the accumulation and decumulation phases are organised. In section 3.3 we present a fundamental identity, which is central to our analysis of cross-subsidisation. Figure 1 summarises the main elements of this section.

Figure 1 The two-tiered retirement savings model with possible cross-subsidies and annuitisation.
Throughout, explicit references to the Swiss system are provided as examples in footnotes. This is only for illustration purposes, as our model is meant to be as general as possible and hence focuses only on some characteristics of the Swiss system, although not encompassing all of them.
3.1. Economic landscape
Consider an economy with a stationary population where agents may save a portion of income in an organised system of retirement savings during n years of their life. At the end of these n years, everyone retires. Thus, if agents can contribute from the age of 18 and the ordinary age for retirement is 65, then n is equal to 48Footnote 10.
We assume agents have an average salary of amount w k in year k, 1≤k≤n. The proportion of the active population in year k is denoted by α k with ![]() $$\mathop{\sum}\nolimits_{k=1}^n \alpha _{k} =1$$
.
$$\mathop{\sum}\nolimits_{k=1}^n \alpha _{k} =1$$
.
Furthermore, we assume that the long-term return on investments (market rate) is equal to r* p.a. (a constant). Our aim is to model the long-term effect of the model, and it is reasonable to assume a stable (real) market return in the long term.
3.2. Retirement savings
We model the level of savings of agents at the macroeconomic level. The government creates a system of retirement savings with two tiers that are described below; a graphical representation of it is given in Figure 1.
With respect to the first tier, the “mandated component”, agents must contribute savings to this at rate β k of their income w k, 1≤k≤n. Mandated savings accumulated in this way earn interest at a rate of r p.a. As with the market rate r*, we assume that the interest rate r on mandatory savings is expressed in real terms. At retirement, agents can choose between a lump sum payment or a life annuity. If they choose an annuity, the accumulated amount of their mandated savings is multiplied by a conversion rate ξ (set by government) to yield the annual amount of the life annuity. These annuities are sourced from non-governmental annuity providers. The (possible) difference between the conversion rate on mandatory savings ξ and the actuarially fair conversion rate is denoted by Δ, which we initially assume to be positive or nullFootnote 11. A positive difference (Δ>0) means the creation of the life annuity has contributed to a deficit of resources on the part of the provider. The accumulation and decumulation of this first tier is entirely controlled by the government. The law defines the contribution rates β kFootnote 12 and the conversion rate ξ Footnote 13 (which are stable over time), and the government decides on the interest rate r each yearFootnote 14. The overall level of mandatory savings is then
Note that we assume here that r has been constant for the past n years, even though the government can modify this figure every year. However, as we are interested in the long-term effect of a given constellation of parameters, it is reasonable to assume that the interest rate r on mandatory savings will remain constant (in real terms) if the government policy is stable.
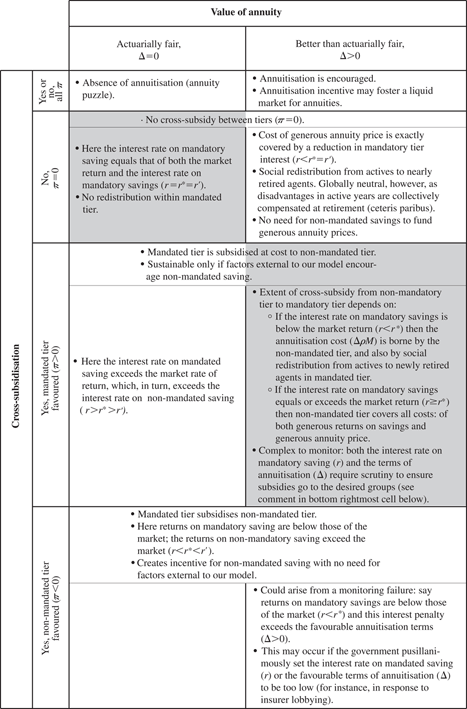
Each year, a proportion α n of the active population retires. Their mandatory savings
can be expressed as a (constant) fraction
of the overall mandatory savings M.
The second tier of this retirement savings model concerns non-mandatory savings. It differs from a standard savings account in several ways. Contributions are encouraged in some way (typically by provision of tax concessions on these payments), providing a powerful incentive to save for retirement via this vehicleFootnote 15. It is here that the costs of the system arise to the state. Alternatively, employers are often involved in the mandatory savings schemes seen around the world, and it is reasonably common for them to contribute in excess of the mandated level, giving rise to non-mandated contributions.
Along with mandatory savings, non-mandatory savings in this scheme are, in principle, inaccessible until retirement. We further assume these factors induce agents to contribute to their non-mandatory component at a (constant) rate γ on wages w k, 1≤k≤n. Non-mandatory savings earn interest at a rate ![]() $$r'$$
p.a. The level of non-mandatory savings is then
$$r'$$
p.a. The level of non-mandatory savings is then
The interest credited on non-mandatory savings ![]() $$r'$$
is endogeneous. How this rate is determined is explained in the next section. On retirement, agents can choose to receive their non-mandated accumulation as a lump sum or as an actuarially fair annuity (at a rate ξ−Δ), again sourced from a private-sector providerFootnote 16. The cost to the system is null and this decision is thus neutral.
$$r'$$
is endogeneous. How this rate is determined is explained in the next section. On retirement, agents can choose to receive their non-mandated accumulation as a lump sum or as an actuarially fair annuity (at a rate ξ−Δ), again sourced from a private-sector providerFootnote 16. The cost to the system is null and this decision is thus neutral.
3.3. Cross-subsidisation in the two tiers
We assume a closed, autarkic system – recall Figure 1. Thus, with no further subsidies to or leakages from the national retirement savings scheme, we must have
because both mandatory and non-mandatory second pillar savings (M and NM) are both invested in order to yield the long-term market rate r*. The interest earned on the retirement savings (![]() $${ M} \plus {NM }$$
) is used to remunerate the mandatory savings M at the legal rate r and compensate the cost of annuitisation ΔρM, should it be subsidised (i.e., Δ>0). What is left represents the interest on the non-mandated component (
$${ M} \plus {NM }$$
) is used to remunerate the mandatory savings M at the legal rate r and compensate the cost of annuitisation ΔρM, should it be subsidised (i.e., Δ>0). What is left represents the interest on the non-mandated component (![]() $$r'NM$$
).
$$r'NM$$
).
Equation (4) is key to our discussion. It is here that our system deviates from the World Bank (1994) model. One could view the World Bank (1994) model as prescribing that the mandated and non-mandated tier earn the market rate of interest of interest (![]() $$r=r'=r^{{\asterisk}} $$
) and no subsidy is given to annuitants (Δ=0), and so equation (4) excites no interest. Indeed, this is what happens in Australia. Our system, however, does not follow such a path, and so opens the door to an entire family of finely differentiated mandated saving systems. We explore this further in section 4 below.
$$r=r'=r^{{\asterisk}} $$
) and no subsidy is given to annuitants (Δ=0), and so equation (4) excites no interest. Indeed, this is what happens in Australia. Our system, however, does not follow such a path, and so opens the door to an entire family of finely differentiated mandated saving systems. We explore this further in section 4 below.
Moving on, we reorganise equation (Reference Bütler4) to yield
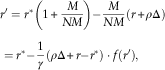 $$\eqalignno{ & r'=r{^\asterisk}\left( {1{\plus}{M \over {NM}}} \right){\minus}{M \over {NM}}(r{\plus}\rho \Delta ) \cr & =r{^\asterisk}{\minus}{1 \over \gamma }(\rho \Delta {\plus}r{\minus}r{^\asterisk}) \cdot f(r'), $$
$$\eqalignno{ & r'=r{^\asterisk}\left( {1{\plus}{M \over {NM}}} \right){\minus}{M \over {NM}}(r{\plus}\rho \Delta ) \cr & =r{^\asterisk}{\minus}{1 \over \gamma }(\rho \Delta {\plus}r{\minus}r{^\asterisk}) \cdot f(r'), $$
where
is a decreasing function of ![]() $$r'$$
that is independent of γ. Equation (5) means that the net rate
$$r'$$
that is independent of γ. Equation (5) means that the net rate ![]() $$r'$$
is equal to the market rate r*, corrected by a certain factor. Further, if we define
$$r'$$
is equal to the market rate r*, corrected by a certain factor. Further, if we define
then equation (Reference Bütler5) develops into
or
The variable π reflects the net cost (as a rate of mandatory savings M) of the variables mandated by the government: earnings on mandatory savings r, annuity subsidisation Δ, and the mandatory saving contribution rate β k (hidden in ρ). Positive values of π indicate mandated savers accrue a net benefit from the system, either through generous annuities or generous returns or through a combination of both. The variable π is also the rate of cross-subsidisation of the mandated tier. The product πM in equation (Reference Davidoff, Brown and Diamond8) is the global amount of subsidies, which is apportioned evenly over non-mandated savings NM as a correction to the market rate r*. Note that if π is negative, the non-mandated tier is subsidised and ![]() $$r'\gt r{^\asterisk}$$
.
$$r'\gt r{^\asterisk}$$
.
Equation (8) also highlights another important insight of our model: that of the tension between mandated savings M and non-mandated savings NM. Increasing subsidisation to mandated saving M comes only by adjustments to non-mandated savings – either ![]() $$r'$$
has to decrease or NM has to increase (or some combination of the two to achieve an increase in the left-hand side of equation (Reference Disney9)). And herein lies the rub: a decrease in the earnings rate on non-mandated savings seemingly indicates a decrease in the level of non-mandated savings, all other factors remaining unchanged. This suggests processes that are external to our model must be at work to raise the level of non-mandated savings – some sort of side payment, like tax incentives, to encourage an increased contribution rate γ, thus raising
$$r'$$
has to decrease or NM has to increase (or some combination of the two to achieve an increase in the left-hand side of equation (Reference Disney9)). And herein lies the rub: a decrease in the earnings rate on non-mandated savings seemingly indicates a decrease in the level of non-mandated savings, all other factors remaining unchanged. This suggests processes that are external to our model must be at work to raise the level of non-mandated savings – some sort of side payment, like tax incentives, to encourage an increased contribution rate γ, thus raising ![]() $$NM$$
Footnote 17; see also section 4.3.
$$NM$$
Footnote 17; see also section 4.3.
Figure 2 summarises how the main variables controlled/influenced by the government result in ![]() $$r'$$
. There, π is a direct result of the mandated parameters r, Δ and β k. Although γ is assumed to be exogenous, this other determinant of
$$r'$$
. There, π is a direct result of the mandated parameters r, Δ and β k. Although γ is assumed to be exogenous, this other determinant of ![]() $$r'$$
is influenced by incentives such as tax concessions, as well as by π and
$$r'$$
is influenced by incentives such as tax concessions, as well as by π and ![]() $$r'$$
. These relationships, which we do not directly model as they are not essential to developing our taxonomy, are depicted with dashed arrows.
$$r'$$
. These relationships, which we do not directly model as they are not essential to developing our taxonomy, are depicted with dashed arrows.

Figure 2 The dynamics of the main variables of the system: how the closed system determines ![]() $$r'$$
.
$$r'$$
.
Remark 1
In equation (Reference Bütler4) we assume that if annuitisation is subsidised (Δ>0) all agents annuitise, whereas annuitisation at actuarially fair rates (Δ=0) leads to indifference between a lump sum or an income stream. Bütler & Staubli (Reference Bütler and Staubli2011) provide some evidence that higher money’s worth ratios are associated with higher rates of annuitisation. In addition, Brown et al. (Reference Brown, Mitchell, Poterba and Warshawsky2001) shows the related annuity equivalent wealth (AEW) framework predicts households’ intention to annuitise; higher AEWs lead to higher intentions to annuitise. Furthermore, if a lesser fraction of agents annuitise then cross-subsidisation becomes weaker, but our conclusions remain qualitatively unchanged.
4. A Taxonomy of Two-Tiered Retirement Systems
As discussed in section 1, one reason for a country to encourage retirement savings is to encourage agents’ own provision of retirement income, reducing the burden of retirement provision on the state. However, the model we introduced in section 3 suggests that the two-tiered structure of retirement saving with government-set investment returns and annuity prices is able to achieve much more than that. Below we discuss how it can obviate some of the investment risk and annuity price risk (also known as annuity rate risk) that retirees face, as well as induce social redistribution and foster a liquid private market for life annuities. Figures 1 and 2 above serve as useful reminders of both the structure of the model and the dynamics of the key variables.
Our system of forced retirement saving can be seen as extending the plain vanilla World Bank (1994) model of mandated retirement saving. Specifically, non-mandatory saving NM is explicitly considered and both guaranteed returns and government-set annuity prices on mandated saving M have been added. Arguably, one could view the World Bank (1994) model as implemented in a country like Australia as a version of the Swiss system with π=0 and Δ=0 (although, strictly speaking, ξ and Δ do not exist if the state does not set annuity prices, as is the case in Australia). We present this extended view of mandated retirement saving, together with commentary, in Table 1. A detailed discussion is also given below.
Table 1 Mandated savings schemes: a taxonomy of the beast.

Government-set returns and annuity prices on the mandated tier allow for a wide range of systems with different characteristics. The cases of Australia and Switzerland correspond to the top left and bottom right shaded areas, respectively.
4.1. Retirement income security: the choice of annuity prices (ξ and hence Δ)
To help the elderly deal with their longevity risk, the government can encourage annuitisation by choosing an annuity conversion rate ξ leading to advantageous annuity prices (Δ>0), hence making the choice of decumulating mandated savings in the form of a life annuity rational. The so-called “annuity puzzle” suggests that if annuity prices are just actuarially fair (Δ=0), agents will not choose to annuitise their retirement savingsFootnote 18.
Furthermore, a stable (or smoothed) conversion rate ξ and rate of return r offer security and stability for agents with mandated retirement savings who wish to annuitise. Their accumulation and decumulation are then largely predictable (even deterministic for given income, r and ξ) and guaranteed. Hence, agents can plan on a secure retirement income as they approach retirement, and need not fear substantial market alterations such as that observed in the recent financial crisis. In this light, the cost to the state of these guarantees – say by increased tax concessions to lure more funds into non-mandated retirement savings – may be one a government is prepared to bear.
The case of Switzerland suggests that encouraging annuitisation in this setting has the additional benefit of creating a liquid market of life annuities provided by the private sector, and this without forcing annuitisation at any stage. Since the additional annuitisation cost incurred by a Δ>0 is allowed for in the system (see equation (4) above), the provision of such favourable annuities is cost neutral to the provider: other model parameters are subsequently adjusted, such as by a reduction in either r or ![]() $$r'$$
. Taken together with the management of the vast mass of (relatively stable) retirement savings, this is likely to interest private insurers in participating in such a scheme. Insurers can then also offer annuitisation of the non-mandatory component of the retirement savings at an actuarially fair rate of conversion, as the critical mass for a healthy portfolio of life annuities has been reached and it will further help mitigate their risk through diversification and a higher number of annuitiesFootnote 19.
$$r'$$
. Taken together with the management of the vast mass of (relatively stable) retirement savings, this is likely to interest private insurers in participating in such a scheme. Insurers can then also offer annuitisation of the non-mandatory component of the retirement savings at an actuarially fair rate of conversion, as the critical mass for a healthy portfolio of life annuities has been reached and it will further help mitigate their risk through diversification and a higher number of annuitiesFootnote 19.
Finally, we note that a generalisation of our model to allow ξ and Δ to be time dependent would encompass notional defined contribution schemes of mandated saving (Andrews & Brown, Reference Andrews and Brown2009). Such schemes aim to ease the transition from a pay-as-you-go scheme to mandated saving, targeting subsidies at agents with short saving histories.
4.2. Social redistribution: the choice of the level of cross-subsidisation (π)
Another fundamental question of interest for a government lies in the definition of who is subsidised and who bears such costs in the society. In this area, our model presents solutions as well.
The choice of who will have mandated savings is made through the definition of the β k’s, a choice of the government. These could be a function of age and income, for instance.
The financial question is related to the sign and magnitude of π – the rate of cross-subsidisation between mandated and non-mandated savings – a choice of the government as well. The sign of π represents a redistribution of the investment flows arising from M and NM. Furthermore, for a fixed value of π, changes in Δ, and thus of r in the opposite direction (see equation (7)), translate into social redistribution between active agents and newly retired agents within the mandated tier. A wealth of different possibilities is described in Table 1. These include the basic World Bank (1994) model and that of the Swiss system (the shaded regions).
Note that the case where π<0 is considered not only for completeness but also for its intrinsic merit. Of course, mandating savings and then introducing transfers from mandated savings to non-mandated savings may appear odd. Two reasons suggest themselves for why this may occur. First, π and Δ might fall into one of these cases by accident, say by estimating some key parameters wrongly – such as r* or the actuarially fair conversion rate. Second, such circumstances may be the express wish of a state choosing to transfer wealth from mandated savers to non-mandated savers.
4.3. The need for non-mandated savings
In order to work properly when mandated savers are subsidised (π>0), the system needs a substantial level of non-mandatory savings. This may seem paradoxical, and even dangerous, as non-mandatory savings are…not mandated! We investigate here the behaviour of our model in this respect.
Recall the dashed lines in Figure 2: while the impact on γ of π and government incentives is relatively straightforward, the interaction between ![]() $$r'$$
and γ is not obvious. Indeed, a combination of equations (6) and (9) yields
$$r'$$
and γ is not obvious. Indeed, a combination of equations (6) and (9) yields
where both numerator and denominator decrease if ![]() $$r'$$
increases. For an economy in an equilibrium at π=π 0, γ=γ 0, and
$$r'$$
increases. For an economy in an equilibrium at π=π 0, γ=γ 0, and ![]() $$r'=r^{0} $$
, it can be shown that
$$r'=r^{0} $$
, it can be shown that
if and only if
where ![]() $${\varepsilon}_{{NM,r'}} $$
is the elasticity of NM with respect to
$${\varepsilon}_{{NM,r'}} $$
is the elasticity of NM with respect to ![]() $$r'$$
; see Appendix A.
$$r'$$
; see Appendix A.
Equation (11) tells us that for the model to remain in an equilibrium, a small increase in the willingness to contribute to non-mandated savings (γ) will be accompanied by an increase in their return (for fixed π=π 0). This property is fundamental to encourage non-mandated saving. Condition (Reference Gantenbein and Mata12) is illustrated in Appendix B.
5. Implications of the Model for Switzerland
When forced savings were introduced in 1985, Switzerland already had accumulated a substantial amount of retirement savings (Hepp, Reference Hepp1998). Existing savings were assimilated into non-mandatory savings, providing the necessary initial reservoir required to immediately introduce a positive π. In addition, non-mandated savings enjoyed both a legal guarantee and the same level of tax concessions granted to mandated savings, sweetening Swiss attitudes to this avenue of saving.
At retirement, annuitisation is the default choice (on both tiers) and is the usual outcome for retiring Swiss. Pension funds can offer the option to take the capital as a lump sum and the vast majority of them do. With respect to annuitisation, the conversion rate ξ is in fact a richer package of a lifetime annuity, a survivor annuity, and immediate annuities for children. These additions are mandatory. A positive Δ thus makes annuitisation of one’s M the rational choice, especially for married agents with or without childrenFootnote 20.
Contribution rates to the mandatory tier have never been modified, with the exception of the postponement of the ordinary retirement age for women. Agents can contribute from the age of 18 to the age of 65 (64 for women). The contribution rates β k are positive from the age of 25 and increase until retirement. In addition, they focus on low to medium incomes. Higher tranches of income can only contribute to the non-mandatory component.
In 1985, the excess conversion rate Δ was arguably null. While the rate r was set at 4% (and did not change until 2002), market rates r* were clearly above that level for at least the first decade of the system (10-year Swiss government bond yield rates were consistently above 4% from 1985 until 1997; see OECD, 2013). This likely led to a negative π from the beginning, and the system introduced was thus of the type described in the bottom (presumably left) area in Table 1. As time went by, improvements in mortality rates together with a fixed ξ increased Δ, which was (substantially) positive by the turn of the century. The system had moved right to the shaded area in the middle of Table 1.
A recent article by SonntagsZeitung (2013) illustrates the main variables of this paper in the (more recent) Swiss context. It summarises return and conversion rates for the major players in Switzerland. Past returns of about 25 institutions are provided for the periods 2003–2012 and 2005–2012. Results are summarised in Table 2 in the form of average compound interest rates per annum. There, r* stands for the average (actual) returns on assets and ![]() $$r'$$
stands for the returns credited on non-mandatory accounts (NM). We also provide the average mandated rate r (credited on M), which of course was the same for all institutionsFootnote 21. When one looks at this table and does not know the system, one might ask where the returns have gone, as both r and
$$r'$$
stands for the returns credited on non-mandatory accounts (NM). We also provide the average mandated rate r (credited on M), which of course was the same for all institutionsFootnote 21. When one looks at this table and does not know the system, one might ask where the returns have gone, as both r and ![]() $$r'$$
are inferior to the actual return rate r*. The answer is because π>0, as argued above – see also equation (4).
$$r'$$
are inferior to the actual return rate r*. The answer is because π>0, as argued above – see also equation (4).
Table 2 Annual compound rates from SonntagsZeitung (2013).

As explained and illustrated above, Swiss system started to face difficulties following the financial crisis of the beginning of the century. Private insurers saw the returns on retirement assets plummet, whereas both the return on mandated saving r and the annuity conversion rate ξ remained constant. Compounding the issue was the then common practice of offering annuitisation of non-mandated savings at the rate ξ as well. Private insurers abruptly changed the terms on which they annuitised non-mandated savings to offer only a (regulated) actuarially fair rate – rather than ξ Footnote 22. Furthermore, they lobbied the government for a reduction in the minimum rate of interest r on mandated savings. This prompted indignation from interest groups representing active insured who pointed out the one-sided nature of the change: it seems no insurer had asked for increases of r during the golden years (see, for instance, Swissinfo, 2002). Notwithstanding, the government decreased r and has changed it every year since thenFootnote 23. Also, for the first time, it decided (in 2003) to progressively decrease ξ, although still leaving Δ well above zero (Swiss Association of Actuaries, 2010). Although the recent global financial crisis put additional pressure on the system, a further reduction of ξ (and thus of Δ) was repudiated by Swiss voters in a referendum in March 2010. Overall, the state of the debate suggests some misunderstanding of how the system works. Our model sheds some light on these issues. We found that the sign and size of π, the rate of cross-subsidisation between mandated and non-mandated savings, is fundamental in determining how the system will behave. In particular, low levels of both the interest rate earned on mandated saving r and annuity conversion rate ξ could lead to a negative π. This would result in subsidisation of the “the rich” (agents with higher levels of income with substantial amounts of non-mandatory savings are more likely to be well off) through a reduction of the benefits of the agents with mandatory savings. As the latter are not given a choice of participation and as they arguably need these savings to ensure adequate standard of living on retirement, this probably can be qualified as undesirable, even though it could be seen as an alternative to tax concessions to encourage non-mandated NM saving; see also section 4.2 above.
Of course, how positive the level of cross-subsidisation π is set is essentially a political choice and cannot be inferred from our analysis. This choice is one of better subsidised annuities for lower income agents versus higher returns on non-mandated savings (arguably for higher income agents) with the caveat that non-mandatory saving must remain encouraged if π>0; recall section 4.3. In addition, our analysis shows that it is essential for the government to monitor the parameters π, Δ, and r in a holistic way. In particular, it should not discuss the level of the conversion rate ξ without considering the spread r*−r at the same time.
Furthermore, apart from teasing out possible undesirable effects if the main variables of the system are not appropriately coordinated, our analysis also aimed at highlighting the existence and role of internal transfers within the system that encourage annuitisation at retirement. Indeed, a positive Δ is financed by either a reduction of the interest rate r for active people (an intergenerational redistribution effect), or a reduction of the interest rate ![]() $$r'$$
on non-mandated savings (a societally redistributive effect), or both. It is not financed via direct governmental subsidies, and is thus quite different to the proposals to encourage annuitisation discussed in Gentry and Rothschild (Reference Gentry and Rothschild2010) and elsewhere. Not only does that mechanism appear to foster an unusual level of annuitisation in Switzerland (as compared with the rest of the world), but it nurtures an (exceptionally) healthy annuities market, selling both domestically and internationally. It is entirely possible that these qualities would be jeopardised, should the conversion rate ξ be reduced to an actuarially fair level.
$$r'$$
on non-mandated savings (a societally redistributive effect), or both. It is not financed via direct governmental subsidies, and is thus quite different to the proposals to encourage annuitisation discussed in Gentry and Rothschild (Reference Gentry and Rothschild2010) and elsewhere. Not only does that mechanism appear to foster an unusual level of annuitisation in Switzerland (as compared with the rest of the world), but it nurtures an (exceptionally) healthy annuities market, selling both domestically and internationally. It is entirely possible that these qualities would be jeopardised, should the conversion rate ξ be reduced to an actuarially fair level.
6. Conclusion
In this paper, we have systematically analysed a system of second pillar retirement saving that consists of two tiers – one of mandatory saving, the other of non-mandatory saving. We have explained how it offers the option of fostering annuitisation and introducing cross-subsidies. Such a model is an extension of a plain vanilla system of mandated saving (exemplified, for instance, by the Australian system). The Swiss retirement model is an example of system that takes full advantage of this two-tiered structure. Running against the tide of widespread international low levels of voluntary annuitisation, Switzerland has a strong and active commercial life annuities market, with the attendant benefits for the longevity insurance coverage of the population, together with a degree of investment risk protection. Our analysis suggests that this is at the cost of tax concessions to attract a flow of non-mandated savings into the system, which are used to subsidise the provision of annuities on mandated savings at actuarially favourable terms and to guarantee a minimum rate (r) on mandated savings. An important question for future research is to quantify the cost of these tax concessions together with the cross-subsidies in the system.
Acknowledgements
The authors would like to thank two referees for helpful comments. They also acknowledge the input from many colleagues who provided constructive feedback on previous versions of this paper.
Appendix
A. Comparative statics of the key variables
In this section we show how equations (11) and (12) are derived, if the system is at an equilibrium at π=π 0, γ=γ 0, and ![]() $$r'=r^{0} $$
.
$$r'=r^{0} $$
.
In order to study the relations between our main variables we use the following well-known identity:
where g(x, y, z)=0 is a continuous, once differentiable function on the domain of x, y, and z. A natural choice for this function is equation (Reference Disney9) – which is derived from the closed system equation (4). Hence, we define
For convenience, we begin by determining
where ![]() $${\varepsilon}_{{NM,r'}} $$
is the elasticity of NM with respect to
$${\varepsilon}_{{NM,r'}} $$
is the elasticity of NM with respect to ![]() $$r'$$
,
$$r'$$
,
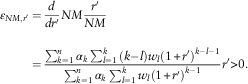 $$\openup 6pt\eqalignno{ {\varepsilon}_{{NM,r'}} & ={d \over {dr'}}NM{{r'} \over {NM}} \cr & ={{\mathop{\sum}\nolimits_{k=1}^n {\alpha _{k} } \mathop{\sum}\nolimits_{l=1}^k {(k{\minus}l)w_{l} (1{\plus}r')^{{k{\minus}l{\minus}1}} } } \over {\mathop{\sum}\nolimits_{k=1}^n {\alpha _{k} } \mathop{\sum}\nolimits_{l=1}^k {w_{l} (1{\plus}r')^{{k{\minus}1}} } }}r'\gt 0 .$$
$$\openup 6pt\eqalignno{ {\varepsilon}_{{NM,r'}} & ={d \over {dr'}}NM{{r'} \over {NM}} \cr & ={{\mathop{\sum}\nolimits_{k=1}^n {\alpha _{k} } \mathop{\sum}\nolimits_{l=1}^k {(k{\minus}l)w_{l} (1{\plus}r')^{{k{\minus}l{\minus}1}} } } \over {\mathop{\sum}\nolimits_{k=1}^n {\alpha _{k} } \mathop{\sum}\nolimits_{l=1}^k {w_{l} (1{\plus}r')^{{k{\minus}1}} } }}r'\gt 0 .$$
Equation (A.4) follows from
 $$\openup 6pt\eqalignno{ {d \over {dr'}}f(r') & ={d \over {dr'}}{{\mathop{\sum}\nolimits_{k=1}^n {\alpha _{k} } \mathop{\sum}\nolimits_{l=1}^k {\beta _{l} w_{l} (1{\plus}r')^{{k{\minus}l}} } } \over {\mathop{\sum}\nolimits_{k=1}^n {\alpha _{k} } \mathop{\sum}\nolimits_{l=1}^k {w_{l} (1{\plus}r')^{{k{\minus}l}} } }} \cr & ={\minus}f(r'){{\mathop{\sum}\nolimits_{k=1}^n {\alpha _{k} } \mathop{\sum}\nolimits_{l=1}^k {(k{\minus}l)w_{l} (1{\plus}r')^{{k{\minus}l{\minus}1}} } } \over {\mathop{\sum}\nolimits_{k=1}^n {\alpha _{k} } \mathop{\sum}\nolimits_{l=1}^k {w_{l} (1{\plus}r')^{{k{\minus}l}} } }} \cr & ={\minus}{{f(r')} \over {r'}}{\varepsilon}_{{NM,r'}} . $$
$$\openup 6pt\eqalignno{ {d \over {dr'}}f(r') & ={d \over {dr'}}{{\mathop{\sum}\nolimits_{k=1}^n {\alpha _{k} } \mathop{\sum}\nolimits_{l=1}^k {\beta _{l} w_{l} (1{\plus}r')^{{k{\minus}l}} } } \over {\mathop{\sum}\nolimits_{k=1}^n {\alpha _{k} } \mathop{\sum}\nolimits_{l=1}^k {w_{l} (1{\plus}r')^{{k{\minus}l}} } }} \cr & ={\minus}f(r'){{\mathop{\sum}\nolimits_{k=1}^n {\alpha _{k} } \mathop{\sum}\nolimits_{l=1}^k {(k{\minus}l)w_{l} (1{\plus}r')^{{k{\minus}l{\minus}1}} } } \over {\mathop{\sum}\nolimits_{k=1}^n {\alpha _{k} } \mathop{\sum}\nolimits_{l=1}^k {w_{l} (1{\plus}r')^{{k{\minus}l}} } }} \cr & ={\minus}{{f(r')} \over {r'}}{\varepsilon}_{{NM,r'}} . $$
Note that if π<0 then ![]() $$r{^\asterisk}\lt r'$$
and thus equation (A.4) will always be positive.
$$r{^\asterisk}\lt r'$$
and thus equation (A.4) will always be positive.
Let us first examine the interaction between γ and ![]() $$r'$$
. We have
$$r'$$
. We have
This expression will be positive as long as
Condition (A.9) follows from equations (8) and (A.9). Equations (A.9) and (A.10) are identical to equation (Reference Gantenbein and Mata12). Similarly,
Moving on, the sign of
will always be negative as long as equation (A.10) is verified. Indeed, it makes sense that π and ![]() $$r'$$
trade off.
$$r'$$
trade off.
Finally, consider the relation between γ and π,
which will have the same sign as π, which is also reasonable.
B. Illustration of Condition (12)
It is instructive to rewrite equation (12) as
The right-hand side of equation (B.1) goes from 1/r* to infinity as ![]() $$r'$$
goes from 0 to r* (remember that
$$r'$$
goes from 0 to r* (remember that ![]() $$r'\lt r{^\asterisk}$$
since π>0). Also, the derivative (with respect to
$$r'\lt r{^\asterisk}$$
since π>0). Also, the derivative (with respect to ![]() $$r'$$
) of the right-hand side is always higher than the one of the left-hand side. Therefore, equation (B.1) will always hold as long as the initial value (for
$$r'$$
) of the right-hand side is always higher than the one of the left-hand side. Therefore, equation (B.1) will always hold as long as the initial value (for ![]() $$r'=0$$
) of the left-hand side is lower than the one of the right-hand side, that is, if
$$r'=0$$
) of the left-hand side is lower than the one of the right-hand side, that is, if
This condition is verified if r* is not too high.
As an illustration, assume that agents can contribute to the system for n=40 years, and that ![]() $$\alpha _{k} \,\equiv\,\alpha $$
and
$$\alpha _{k} \,\equiv\,\alpha $$
and ![]() $$w_{l} \,\equiv\,w_{0} $$
(such that they disappear from equation (B.1)). Figure A.1 displays both the left-hand side (as a dashed line) and the right-hand side (as a dotted line) of equation (B.1) when r* goes from 1/13 to 1/12. In the first case (r*=1/13), equation (B.1) always holds. This will also be the case for any r*<1/13. In the second case (r*=1/12), left and right-hand sides intersect at
$$w_{l} \,\equiv\,w_{0} $$
(such that they disappear from equation (B.1)). Figure A.1 displays both the left-hand side (as a dashed line) and the right-hand side (as a dotted line) of equation (B.1) when r* goes from 1/13 to 1/12. In the first case (r*=1/13), equation (B.1) always holds. This will also be the case for any r*<1/13. In the second case (r*=1/12), left and right-hand sides intersect at
Condition (B.1) – and thus equation (12) – will hold only for higher values of ![]() $$r'$$
.
$$r'$$
.

Figure A.1 Illustration of Condition (B.1) if ![]() $$\alpha _{k} \,\equiv\,\alpha $$
and
$$\alpha _{k} \,\equiv\,\alpha $$
and ![]() $$w_{k} \,\equiv\,w_{0} $$
, when r* goes from 1/13 (upper dotted line) to 1/12 (lower dotted line). The right-hand side (RHS) of equation (B.1) increases monotonically at a higher rate than its left-hand side (LHS). If the value of the RHS at the origin is higher than that of the LHS then equation (12) will always hold. Otherwise, it will hold only for higher values of
$$w_{k} \,\equiv\,w_{0} $$
, when r* goes from 1/13 (upper dotted line) to 1/12 (lower dotted line). The right-hand side (RHS) of equation (B.1) increases monotonically at a higher rate than its left-hand side (LHS). If the value of the RHS at the origin is higher than that of the LHS then equation (12) will always hold. Otherwise, it will hold only for higher values of ![]() $$r'$$
than that which makes both functions intersect (in this example,
$$r'$$
than that which makes both functions intersect (in this example, ![]() $$\,\approx\,1.14\,\%\,$$
).
$$\,\approx\,1.14\,\%\,$$
).