INTRODUCTION
When an electron has sufficient kinetic energy and collides with a photon, the recoiling photon may gain net energy from the electron. This mechanism, namely inverse Compton scattering (ICS) (Blumenthal & Gould, Reference Blumenthal and Gould1970; Compton, Reference Compton1923), has attracted great interest over many years since it can be applied for production of X- or Gamma-ray sources. Furthermore, this effect is important in astrophysics (Feenberg & Primakoff, Reference Feenberg and Primakoff1948; Jones, Reference Jones1968; Longair, Reference Longair1981) and high-energy density physics (Bini et al., Reference Bini, De Zorzi, Diambrini-Palazzi, Di Cosimo, Di Domenico, Gauzzi and Zanello1991; Dehning et al., Reference Dehning, Melissinos, Perrone, Rizzo and Von Holtey1990; Di Domenico, Reference Di Domenico1992). The analytical theory of ICS can be derived for specifically black body radiation, laser beam, and monochromatic isotropic radiation (Fargion & Salis, Reference Fargion and Salis1998). The ICS of cosmic microwave background photons from non-relativistic and relativistic thermal electrons has been studied extensively (Boehm & Lavalle, Reference Bœhm and Lavalle2009; Zeldovich & Sunyaev, Reference Zeldovich and Sunyaev1969). The ICS process boosting stellar photons in a binary system or accretion disk might be the key mechanism for generation of “Gamma-jet” and Gamma Ray Bursts (GRB) (Fargion, Reference Fargion, Bernabei and Tao1994).
Recently, ICS of photons from a relativistic electron beam has been considered to be a promising route to obtaining energy-tunable ultrashort ultraintense light sources (Chyla et al., Reference Chyla2006; Hartemann et al., Reference Hartemann, Baldis, Kerman, Foll, Le. Luhmann and Rupp2001; Reference Hartemann, Tremaine, Anderson, Barty, Betts, Booth, Brown, Crane, Cross, Gibson, Fittinghoff, Kuba, Le Sage, Slaughter, Wootton, Hartouni, Springer, Rosenzweig and Kerman2004; Reference Hartemann, Brown, Gibson, Anderson, Tremaine, Springer, Wootton, Hartouni and Barty2005; Reference Hartemann, Siders and Barty2008; John et al., Reference John1998; Priebe et al., Reference Priebe, Laundy, MacDonald, Diakun, Jones, Holder, Smith, Fell, Seddon, Chattopadhyay, Jamison, Phillips, Hirst, Collier, Schramm, Grüner, Sheehy, Naumova, Ter-Avetisyan, Sokolov, Spohr, Krafft and Rosenzweig2008), where the relativistic electron beam is generated by linear accelerators (Gibson et al., Reference Gibson, Anderson, Barty, Betts, Booth, Brown, Crane, Cross, Fittinghoff, Hartemann, Kuba, Le Sage, Slaughter, Tremaine, Wootton, Hartouni, Springer and Rosenzweig2004; Klemz et al., Reference Klemz, Mönig and Will2006) and the photons are produced by a picosecond tabletop laser facility. These light sources generally have extremely high energy, good directionality, and quasi-monochromaticity, much better than previously obtained. Hartemann et al., (Reference Hartemann, Siders and Barty2008) proposed that very strong black body radiation with temperature kT ≥ 20 KeV can be effectively achieved to produce extremely bright rays throgh ICS by injecting a relativistic electron beam into an ignited thermonuclear deuterium-tritium core plasma, where the scattered photons experience kinematical pileup in a narrow-band high-energy spectrum. However, this scheme is still hard to be achieved in reality. First, such high-temperature core plasma can never be achieved by the conventional inertial fusion ignition scheme, where the compressed plasma core has a density of ρe = 350 g/cm3 and diameter of nearly 50 µm. Second, the Thomson mean-free path of the photons is about l C = (n e σT)−1 ≈ 160 µm, far larger than the radius of the plasma core. This means that the photons from bremssahlung emission would soon run out of the core. Third, even if the thermonuclear burning system is optically thick, the equilibrium temperature of electrons, ions and photons is impossible to be greater than the constrained value of 15 KeV, if we assume the internal energy to be the same as the radiation energy (aT 4, a is the radiation density constant) in the unit volume of the system.
In ICF (Lindl, Reference Lindl1995; Lindl et al., Reference Lindl, Amendt, Berger, Glendinning, Glenzer, Haan, Kauffman, Landen and Suter2004), the radiation photons are described by Planck distribution when a nanosecond laser pulses with several tens of KJ energy irradiate the elaborately-designed thermal hohlraum. The Planck radiation temperature can be provided, which the scattered X-ray has energy of the maximum Planck energy spectrum (Kauffman et al., Reference Kauffman, Suter, Darrow, Kilkenny, Kornblum, Montgomery, Phillion, Rosen, Theissen, Wallace and Ze1994; Suter et al., Reference Suter, Kauffman, Darrow, Hauer, Kornblum, Lander, Orzechowski, Phillion, Porter, Powers, Richard, Rosen, Thiessen and Wallace1996). In this paper, we propose a more realistic ICS scheme to obtain ultrahigh-energy photons by injecting a GeV electron beam into an empty thermal hohlraum. The photons inside the hohlraum would gain about 0.5 GeV energy from the electrons.
PHOTONS GENERATED IN A THERMAL HOHLRAUM
Here we revist the basic theory of ICS (Fargion & Salis, Reference Fargion and Salis1998). Considering an electron moving along the z-axis and a photon is incident with the energy ε and the solid angle dΩ = sin θdθdφ in the lab frame. When a highly relativistic electron passes through the photon gas, the final energy of the scattering photon is obtained by two coordinate transformations. Considering the φ = π/2 plane, for head-on collision, θ ≈ π and θ1 ≈ 0, the scattered photon energy is
$${\rm \epsilon} _1 = \displaystyle{{{\rm \gamma} ^2 {\rm \epsilon} \lpar 1 + {\rm \beta} \rpar ^2 } \over {1 + {\textstyle{{2{\rm \gamma} {\rm \epsilon} } \over {mc^2 }}}\lpar 1 + {\rm \beta} \rpar }}.$$where β = v/c is the normalized velocity of the incident electron and γ = (1 − β2)−1/2 is its Lorentz factor. If γε ≪ mc 2, i.e., the Thomson scattering case, we obtain that ε1 ≃ 4γ2ε, in consistent with Blumenthal and Gould (Reference Blumenthal and Gould1970). When 4γε ≫ mc 2, we obtain that ε1 ≃ γmc 2, which is the extreme Klein-Nishina limit that the relativistic electron transfer all its energy to the photon.
Now we consider the generation of ultrahigh-energy Gamma-ray sources by injecting a relativistic electron beam into a thermal hohlraum. The schematic view is shown in Figure 1. In the first step, we estimate the scattered photons by Thomson scattering. The photon number density is 
$n_x = 2 \times 4{\rm \pi} \lpar k_B T/hc\rpar ^3 \smallint \nolimits_0^\infty \, x^2 /\lpar e^x - 1\rpar dx =8{\rm \pi} \lpar k_B T/hc\rpar ^3{\rm \zeta} (3) \Gamma \lpar 3\rpar \approx 2 \times 10^{19} T^3 \lpar cm^{ - 3} \rpar $, where T, kB, h, and c are the Planck radiation temperature in MK, Boltzmann constant, Planck constant and speed of light respectively. Γ(s) = (s − 1)! and 
${\rm \zeta} \lpar s\rpar = \Sigma _{n=1}^\infty \lpar 1/n^s \rpar $ denotes the Gamma and Reimann functions, respectively. By assuming the hohlraum temperature at T = 3.5 MK and the photon density n x = 0.86 × 1021 cm−3, the mean free path of an electron L T = (n xσT)−1 is 1750 cm. In ICF regime, the hohlraum length L H should be much smaller than L T. The radiation energy in a cylindrical hohlraum cavity with geometry (assuming radius 0.2 cm and length 1 cm) is about 1.4 × 104 J for T = 300 eV if we do not taken into account the energy lost in the hohlraum walls. Therefore, this can be achievable if a laser beam with energy of hundreds kJ and 3 ns pulse duration is used. Under the condition of Thomson scattering, the high energy photons scattered from a single GeV electron are about N γ ≈ 0.57 × 10−3 for L H = 1 cm, indicating that a single electron generates only 0.57/1000 photons if the electron beam spot radius is comparable to the hohlraum radius.
Fig. 1. (Color online) Schematic configuration of γ-ray source production by injecting an electron beam into a hohlraum.
GAMMA-RAY SOURCE PRODUCTION THROUGH INVERSE COMPTON SCATTERING
For T = 300 eV and E e = 1 GeV, the scattered photons obey the ICS theory instead of the Thomson scattering. In the lab frame, for the ultra-relativistic electron with γ≫1, 
$1 - {\rm \beta} = {\textstyle{1 \over {2{\rm \gamma} ^2 }}}$, the differential distribution of the scattered photons is expressed as Fargion and Salis (Reference Fargion and Salis1998)
$$\eqalign{ \displaystyle{{dN_1 } \over {dt_1 d{\rm \epsilon} _1 d\Omega _1 }} & = \displaystyle{{2{\rm \pi} {\rm \kappa} _B Tr_0^2 c} \over {c^3\, h^3 {\rm \beta} {\rm \gamma} ^2 }}{\rm \epsilon} _1 ln\left[{\displaystyle{{1 - exp\left({{\textstyle{{ - {\rm \epsilon} _1 \lpar 1 - {\rm \beta} cos{\rm \theta} _1 \rpar \lpar 2{\rm \gamma} ^2 - 1/2\rpar } \over {{\rm \kappa} _B T\lsqb 1 - {\rm \epsilon} _1 \lpar 1+cos{\rm \theta} _1 \rpar /\lpar 2mc^2 {\rm \gamma} \rpar \rsqb }}}} \right)} \over {1 - exp\left({{\textstyle{{ - {\rm \epsilon} _1 \lpar 1 - {\rm \beta} cos{\rm \theta} _1 \rpar } \over {2{\rm \kappa} _B T\lsqb 1 - {\rm \epsilon} _1 \lpar 1+cos{\rm \theta} _1 \rpar /\lpar 2mc^2 {\rm \gamma} \rpar \rsqb }}}} \right)}}} \right]\cr &\quad \times \left[1 - \displaystyle{ {\rm \epsilon} _1 \lpar 1+cos{\rm \theta} _1 \rpar \over 2mc^2 {\rm \gamma} } \right]^{ - 1} \left[\left(1 - \displaystyle{ {\rm \epsilon} _1 \lpar 1+cos{\rm \theta} _1 \rpar \over 2mc^2 {\rm \gamma} } \right)^{ - 1} \right.\cr &\quad \left. - \displaystyle{ {\rm \epsilon} _1 \lpar 1+cos{\rm \theta} _1 \rpar \over 2mc^2 {\rm \gamma} }+\left(\displaystyle{ cos{\rm \theta} _1 - {\rm \beta} \over 1 - {\rm \beta} cos{\rm \theta} _1 } \right)^2 \right]\comma \;}$$where N 1 is scattered photons, ε1 is the energy of the single scattered photon dΩ1 = sin θ1dθ1dφ1, and θ1 is the angle of the outgoing photon. The scattered photons per unit time per unit energy per unit solid angle is shown in Figure 2, where the higher energy photons are collected in the scattering angle θ1 = 1 mrad for kT = 0.3 keV and E e = 1 GeV. Figure 2 clearly shows that high-energy photons are generated dominantly in the direction of relativistic electron.
Fig. 2. (Color online) Differential distribution of the scattered photons calculated by Eq. (2) for E e = 1 GeV electron passing through kT = 0.3 KeV hohlraum.
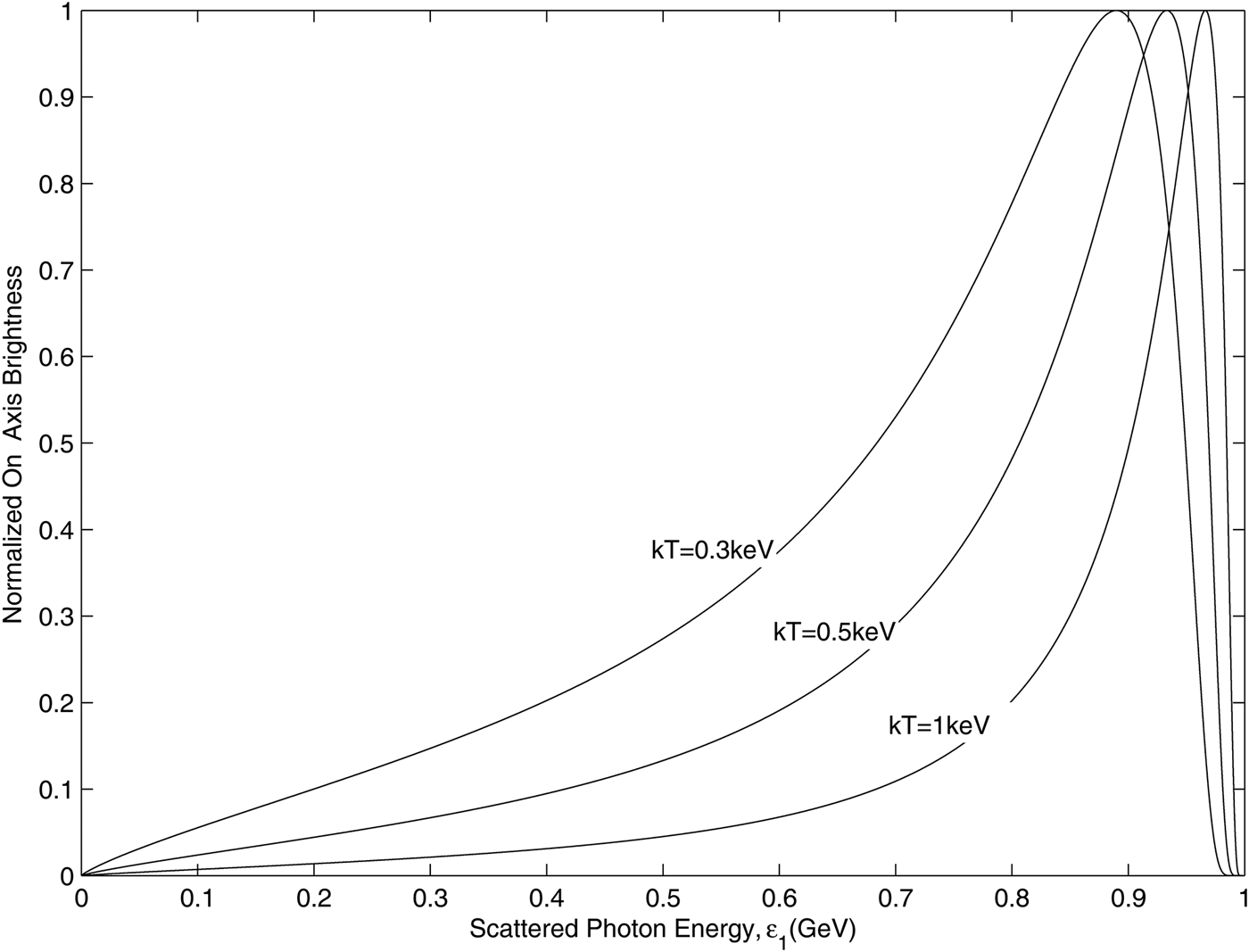
Figure 3 displays different spectra of the scattered photons with different background temperature kT for θ1 = 0. We see that the spectra undergo kinematic pileup and tend to be monochromatic when the background temperature is increased. This is because more and more photons are prodcued in the higher energy range with the rising black body radiation temperature. Furthermore, when the background temperature increases, the scattering angle decreases, resulting in the pileup of the scattered photons in the higher and narrower energy domain.
Fig. 3. Spectrum brightness for the case of E e = 1 GeV and the background temperature respectively of kT = 0.3 KeV, 0.5 KeV, 1 KeV, respectively.
In Figures 4 and 5, we show the behavior of scattered photon distributions for respectively two different injected electron energies E e = 1 GeV and E e = 10 GeV with the same hohlraum temperature of kT = 1 keV. Comparison of these two figures reveals that when the energy of the electron increases, the scattering angle of the photons decreases. Thus, the collimation of the scattered photons can be improved upon by increasing the energy of the injected electrons. By performing the integration of Eq. (2) over angle θ1, we obtain that
$$\displaystyle{{dN_1 } \over {dt_1 d{\rm \epsilon} _1 }} = \smallint\nolimits_ {0}^{1mrad} \, \displaystyle{{dN_1 } \over {dt_1 d{\rm \epsilon} _1 d\Omega _1 }}2{\rm \pi} \sin {\rm \theta} _1 d{\rm \theta} _1\comma \;$$
and so the flux is dN 1/dt 1 = ∫ (dN 1/dt 1dε1)dε1. In our scheme, the relativistic electron beam with energy 1 GeV and charge q = 10nC is passed through a thermal hohlraum of length L H = 1 cm. The total electron density is N e = 6.25 × 1010 cm −3. Then 
$\mathop {\left({{\textstyle{{dN_1 } \over {dt_1 }}}} \right)}\nolimits_{all} = N_e \times {\textstyle{{dN_1 } \over {dt_1 }}}$, and (dN/dt)all = 1.48 × 1017, 4.92 × 1017, 2.41 × 1018 s−1 for kT = 0.3 KeV, 0.5 KeV and 1 KeV, respectively. Accordingly, the numbers of scattered photons N all = (dN/dt)all × L H/c for three different temperatures are respectively 4.92 × 106, 1.64 × 107, and 8.04 × 107. In case of kT = 0.5 KeV, within a solid angle of 1mrad about 80% of the total scattered photons(N all = 1.32 × 107) have energy above than 0.5 GeV, while for kT = 1 KeV, 58% of the total scattered photons have the energy above 0.8 GeV. We define the energy conversion efficiency of the electron-photon as η = E ph/E e, where 
$E_{ph} = \smallint\nolimits \smallint\nolimits \smallint\nolimits {\textstyle{{{\rm \epsilon} _1 dN_1 } \over {dt_1 d{\rm \epsilon} _1 \Omega _1 }}}dt_1 d{\rm \epsilon} _1 d\Omega_1$. In our calculations, the energy of a photon obtained from an 1 GeV electron is E ph = 0.048 MeV, 0.18 MeV, 0.993 MeV, respectively. The corresponding energy conversion efficiency is η = 0.048/1000, 0.18/1000, 0.993/1000. More importantly, if the temperature of hohlraum is 1 keV, the photon energy that increased from 0.8 GeV to 1 GeV is ηh = 0.673/1000.
Fig. 4. (Color online) Differential distribution of the scattered photons calculated by Eq. (2) for E e = 1 GeV electron passing through kT = 1 KeV.
Fig. 5. (Color online) Differential distribution of the scattered photons calculated by Eq. (2) for E e = 10 GeV electron passing through kT = 1 KeV.
CONCLUSION
To summarize, we have proposed a new inverse Compoton scattering scheme for production of high-energy Gamma-ray sources, where a GeV electron beam is injected into a thermal hohlraum. It is found that the gamma-ray photons are scattered within a very small angle. For a GeV electron beam being injected into a 0.3 KeV thermal hohlraum, the scattering photons are highly collimated within 1.0 mrad. The spectrum and particle number of the on-axis radiation with different hohlraum temperature are investigated. When the hohlraum background temperature increases, the spectrum of the scattered photons experiences kinematic pileup becoming more monochromatic, and the scattering angle decreases. This model helps us to understand the cosmic ray interaction with the photon near the star. The generated gamma jets are capable to explain the puzzling GRB spectra and to study e +e − pairs. The calculations show that 80% of the scattered photons have the energy above 0.5 GeV when a relativistic electron beam of energy 1 GeV and charge 10nC is injected into a 0.5 KeV hohlraum. Since the temperature in the hohlraum is only 0.5 KeV, this ultra-high energy Gamma source can be easily observed experimentally. In future experiments, if the temperature within the hohlraum reaches 1 KeV, the property of the Gamma source can be improved to a great extent.
ACKNOWLEDGMENTS
This work was supported by the National Natural Science Foundation of China No. 10905004 and of P. R. China and the China Postdoctoral Science Foundation (No. 20090450245).
