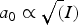1. INTRODUCTION
For more than a decade, intense short-pulse lasers have been used to drive energetic ion beams (Hatchett et al., Reference Hatchett, Brown, Cowan, Henry, Johnson, Key, Koch, Langdon, Lasinski, Lee, Mackinnon, Pennington, Perry, Phillips, Roth, Sangster, Singh, Snavely, Stoyer, Wilks and Yasuike2000; Snavely et al., Reference Snavely, Key, Hatchett, Cowan, Roth, Phillips, Stoyer, Henry, Sangster, Singh, Wilks, MacKinnon, Offenberger, Pennington, Yasuike, Langdon, Lasinski, Johnson, Perry and Campbell2000; Wilks et al., Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely2001; Borghesi et al., Reference Borghesi, Mackinnon, Campbell, Hicks, Kar, Patel, Price, Romagnani, Schiavi and Willi2004; Fuchs et al., Reference Fuchs, Antici, d'Humieres, Lefebvre, Borghesi, Brambrink, Cecchetti, Kaluza, Malka, Manclossi, Meyroneinc, Mora, Schreiber, Toncian, Pepin and Audebert2006; Hegelich et al., Reference Hegelich, Albright, Cobble, Flippo, Letzring, Paffett, Ruhl, Schreiber, Schulze and Fernandez2006; Robson et al., Reference Robson, Simpson, Clarke, Ledingham, Lindau, Lundh, McCanny, Mora, Neely, Wahlstrom, Zepf and McKenna2007). These laser-driven ion beams have high particle numbers, energies up to several tens of MeV/amu (Hegelich et al., Reference Hegelich, Karsch, Pretzler, Habs, Witte, Guenther, Allen, Blazevic, Fuchs, Gauthier, Geissel, Audebert, Cowan and Roth2002), a low transverse emittance (Cowan et al., Reference Cowan, Fuchs, Ruhl, Kemp, Audebert, Roth, Stephens, Barton, Blazevic, Brambrink, Cobble, Fernández, Gauthier, Geissel, Hegelich, Kaae, Karsch, Le Sage, Letzring, Manclossi, Meyroneinc, Newkirk, Pépin and Renard-LeGalloudec2004) and promise to be a competitive alternative to conventional radio-frequency accelerators. The range of applications includes medicine with hadron cancer therapy (Tajima et al., Reference Tajima, Habs and Yan2009), possible detection of fissile material (Jung et al., Reference Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernandez, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wender, Wilde, Wurden and Roth2013b; Roth et al., Reference Roth, Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernandez, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wagner, Wender, Wilde and Wurden2013) and energy generation with concepts in ion fast ignition (Tabak et al., Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason1994; Roth et al., Reference Roth, Cowan, Key, Hatchett, Brown, Fountain, Johnson, Pennington, Snavely, Wilks, Yasuike, Ruhl, Pegoraro, Bulanov, Campbell, Perry and Powell2001; Naumova et al., Reference Naumova, Schlegel, Tikhonchuk, Labaune, Sokolov and Mourou2009). The major drawback so far is that ion energies are typically too low for these applications, especially for ions with Z > 1. For example, hadron cancer therapy requires protons of 250 MeV or carbon C6+ ions of 4–5 GeV. However, in the Target Normal Sheath Acceleration (TNSA) (Hatchett et al., Reference Hatchett, Brown, Cowan, Henry, Johnson, Key, Koch, Langdon, Lasinski, Lee, Mackinnon, Pennington, Perry, Phillips, Roth, Sangster, Singh, Snavely, Stoyer, Wilks and Yasuike2000; Snavely et al., Reference Snavely, Key, Hatchett, Cowan, Roth, Phillips, Stoyer, Henry, Sangster, Singh, Wilks, MacKinnon, Offenberger, Pennington, Yasuike, Langdon, Lasinski, Johnson, Perry and Campbell2000; Wilks et al., Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely2001) protons have been accelerated to 67 MeV (Gaillard et al., Reference Gaillard, Kluge, Flippo, Bussmann, Gall, Lockard, Geissel, Offermann, Schollmeier, Sentoku and Cowan2011) with laser intensities exceeding 1020 W/cm2 and heavier ions have only reached several MeV/amu due to protons shielding the accelerating electric fields in this mechanism. Even with target cleaning, energies have not passed 10 MeV/amu (Hegelich et al., Reference Hegelich, Albright, Cobble, Flippo, Letzring, Paffett, Ruhl, Schreiber, Schulze and Fernandez2006). Recent advances in laser intensities and contrast allowed exploration of new acceleration mechanisms such as the radiation pressure acceleration (RPA) (Esirkepov et al., Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima2004; Klimo et al., Reference Klimo, Psikal, Limpouch and Tikhonchuk2008; Yan et al., Reference Yan, Lin, Sheng, Guo, Liu, Lu, Fang and Chen2008; Macchi et al., Reference Macchi, Veghini and Pegoraro2009; Robinson et al., Reference Robinson, Gibbon, Zepf, Kar, Evans and Bellei2009) or the break-out afterburner (BOA) (Albright et al., Reference Albright, Yin, Bowers, Hegelich, Flippo, Kwan and Fernandez2007; Yin et al., Reference Yin, Albright, Hegelich, Bowers, Flippo, Kwan and Fernandez2007; Henig et al., Reference Henig, Kiefer, Markey, Gautier, Flippo, Letzring, Johnson, Shimada, Yin, Albright, Bowers, Fernández, Rykovanov, Wu, Zepf, Jung, Liechtenstein, Schreiber, Habs and Hegelich2009a; Hegelich et al., Reference Hegelich, Jung, Albright, Fernandez, Gautier, Huang, Kwan, Letzring, Palaniyappan, Shah, Wu, Yin, Henig, Hrlein, Kiefer, Schreiber, Yan, Tajima, Habs, Dromey and Honrubia2011) mechanisms, which reach higher ion energies for both protons and heavier ions.
Scaling laws for ion energies are a fundamental requirement for design of future laser systems and realization of advanced applications. So far, scaling laws have been discussed for the TNSA mechanism (Fuchs et al., Reference Fuchs, Antici, d'Humieres, Lefebvre, Borghesi, Brambrink, Cecchetti, Kaluza, Malka, Manclossi, Meyroneinc, Mora, Schreiber, Toncian, Pepin and Audebert2006; Robson et al., Reference Robson, Simpson, Clarke, Ledingham, Lindau, Lundh, McCanny, Mora, Neely, Wahlstrom, Zepf and McKenna2007) and also for RPA dominated acceleration (Esirkepov et al., Reference Esirkepov, Yamagiwa and Tajima2006; Macchi et al., Reference Macchi, Veghini, Liseykina and Pegoraro2010; Kar et al., Reference Kar, Kakolee, Qiao, Macchi, Cerchez, Doria, Geissler, McKenna, Neely, Osterholz, Prasad, Quinn, Ramakrishna, Sarri, Willi, Yuan, Zepf and Borghesi2012). Here, we extend this research framework by presenting experimental data and theoretical analysis for scaling of ion energies in the relativistic-induced transparency acceleration (RITA) regime, where the BOA mechanism is dominant. In a series of experiments we investigate how maximum ion energies scale with RITA. Ion energies have been measured for intensities between 8 × 1019 and 1.7 × 1021 W/cm2. The experimental data indicate a linear scaling with the normalized laser amplitude a 0, in good agreement with high-resolution, two-dimensional (2D) and 3D particle-in-cell (PIC) simulations. An analytic model for the scaling is presented that correctly predicts maximum ion energies as a function of the laser intensity and pulse duration.
2. EXPERIMENTAL SETUP AND RITA
2.1. Setup
The experiments were conducted at the Los Alamos National Laboratory using Trident's (Batha et al., Reference Batha, Aragonez, Archuleta, Archuleta, Benage, Cobble, Cowan, Fatherley, Flippo, Gautier, Gonzales, Greenfield, Hegelich, Hurry, Johnson, Kline, Letzring, Loomis, Lopez, Luo, Montgomery, Oertel, Paisley, Reid, Sanchez, Seifter, Shimada and Workman2008) short-pulse arm of 600 fs with 80 J of energy on-target at a wavelength of 1.053 µm. High temporal laser contrast of 10−7 at −4 ps enables interaction of the peak pulse with a highly overdense target even for nm-thicknesses. The on-target intensity has been controlled using different off-axis parabolic (OAP) mirrors with focal parameters F/8, F/3, and F/1.5 (as F/N with N = f/D, where f is the focal length and D the diameter of the laser beam). The resulting spot diameter is proportional to Nλ with λ the laser wavelength. Figure 1 shows images of the focus for all three OAPs in panels (b)–(d) with equal frame size. The diameters have been measured to be 13.8 µm (F/8), 7.9 µm (F/3) and 3.4 µm (F/1.5) with an encircled energy of 50% as depicted in Figure 1(e). These yield time averaged intensities I 0 of 9.4 × 1019, 2.9 × 1020, and 1.7 × 1021 W/cm2, respectively, as shown in Figure 1(a) or normalized laser amplitudes 
$a_0 = \sqrt {I_0 {\rm (W}/{\rm cm}^2 )\;\ast\;{\rm \lambda} ^2 {\rm (\mu m)}/1.37 \times 10^{18}} $ of 8.6, 14.7, and 34.5, respectively.
Fig. 1. (a) Measured intensity as a function of distance to the peak for three OAPs with F/number of F/8, F/3 and F1.5. 16 bit images of the laser foci with equal frame size are shown in (b)–(d). The spot diameters are 13.8 µm (F/8), 7.9 µm (F/3), and 3.4 µm (F/1.5) with a 50% encircled energy criterion as depicted in (e).
Ion spectra have been measured using an ion wide angle spectrometer (iWASP), as described by Jung et al. (Reference Jung, Hrlein, Gautier, Letzring, Kiefer, Allinger, Albright, Shah, Palaniyappan, Yin, Fernndez, Habs and Hegelich2011, Reference Jung, Senje, McCormack, Yin, Albright, Letzring, Gautier, Dromey, Toncian, Fernandez, Zepf and Hegelich2015). The iWASP is based on particle deflection in a magnetic field of order of 0.5 T and a 30 µm slit aperture to measure the spectra angularly resolved in one plane, covering a range of about 25°. Species separation is achieved by use of the vastly different stopping powers of carbon ions and protons in a stacked detector consisting of a 32 µm Al layer (for laser light protection), followed by a 1 mm thick CR39 (Fleischer et al., Reference Fleischer, Price and Walker1965) and a BAS-TR image plate (IP) (Mancic et al., Reference Mancic, Fuchs, Antici, Gaillard and Audebert2008; Paterson et al., Reference Paterson, Clarke, Woolsey and Gregori2008). The CR39 detects carbon ions above 33 MeV (the energy needed to pass the Al layer); protons above 11 MeV leave no visible tracks on the CR39 (unless etched for several hours); here, typical etching times of 10 min were applied. The IP is used to detect protons above 11 MeV passing through the CR39 in front of the IP. It should be noted that carbon ions above 230 MeV are not stopped within the CR39, though they still leave visible tracks. These will also be detected on the IP. For the ion energies observed during this experiment, the detector stack and the dispersion of the iWASP magnet gave no overlap of the carbon and proton signal on either the CR39 or the IP (see Jung et al., Reference Jung, Senje, McCormack, Yin, Albright, Letzring, Gautier, Dromey, Toncian, Fernandez, Zepf and Hegelich2015 for details). The energy resolution (lower instrument limit) at 80 MeV/amu for protons and carbon C6+ ions is approximately ±3 and ±6%, respectively. The advantage of using the iWASP is its large solid angle of >0.1 msr, which is 3–5 orders of magnitude larger than in conventional Thomson parabolas and results in much higher precision measurements of the absolute peak ion energy. This is important especially for ion acceleration mechanisms where maximum energies are emitted off-axis rather than on-axis. For the BOA mechanism it has recently been demonstrated in simulations and experimentally (Yin et al., Reference Yin, Albright, Bowers, Jung, Fernández and Hegelich2011a; Jung et al., Reference Jung, Albright, Yin, Gautier, Shah, Palaniyappan, Letzring, Dromey, Wu, Shimada, Johnson, Roth, Fernandez, Habs and Hegelich2013a) that maximum energies are in fact emitted off-axis, demanding a large solid angle for accurate measurements.
Thin, free-standing, artificially grown diamond foils (Applied Diamond, Inc.) with density of ~3 g/ml have been used as target material. Thicknesses range from 30 nm to 5 µm; the bulk proton concentration is naturally very low and hydrogen contamination on the surface is the main source of protons.
2.2. The RITA regime
In laser–matter interactions with a normalized laser amplitude a 0 > 1, electrons gain relativistic quiver energies in the laser field. At these intensities, if parameters are chosen accordingly, the target undergoes a phase of relativistic-induced transparency during the peak laser pulse interaction. Relativistic transparency defines a special state of the plasma, where it is classically overdense, yet relativistically underdense. Classically, that is, neglecting relativistic effects, the normalized electron density N = n e/n cr > 1 with the critical electron density 
$n_{{\rm cr}} = m_{\rm e} {\rm \omega} _{\rm \lambda} ^2 /(4{\rm \pi} e^2 )$ with ωλ the laser frequency. Accounting for the relativistic electron momentum increase by the Lorentz factor γe, however, N′ ≈ N/γe ≤ 1 and the plasma is relativistically transparent. Note that our condition for the onset of transparency is based on the electron thermal Lorentz factor γe and not on the laser intensity a 0 as reported by Vshivkov et al. (Reference Vshivkov, Naumova, Pegoraro and Bulanov1998); the former condition is found to be in good agreement with our PIC simulations in the RITA regime and stems from the significant target heating that occurs prior to the relativistic transparency. Using the Trident laser we found that with intensities exceeding 5 × 1019 W/cm2, diamond targets with thickness between 200 to 600 nm turn relativistically transparent during the peak laser interaction as recently reported by Palaniyappan et al. (Reference Palaniyappan, Hegelich, Wu, Jung, Gautier, Yin, Albright, Johnson, Shimada, Letzring, Offermann, Ren, Huang, Hörlein, Dromey, Fernandez and Shah2012).
When the plasma undergoes such a phase of relativistic transparency during the peak pulse interaction, efficient acceleration via the BOA mechanism is possible (Albright et al., Reference Albright, Yin, Bowers, Hegelich, Flippo, Kwan and Fernandez2007). When the target is relativistically transparent, electrons are accelerated toward the rear of the target in the intense laser field, which sets up a strong longitudinal electric field that co-moves with the ions. The time at which the target becomes relativistically transparent is typically referred to as t 1 in the BOA mechanism. Before that time, the target is classically overdense with N′ >N′/γe>1 and acceleration of ions occurs in an electric field E x determined by the distribution of hot electrons produced at the front side of the target. In PIC simulations, ions gain only about 10% of their final kinetic energy before t 1 (Yin et al., Reference Yin, Albright, Jung, Shah, Palaniyappan, Bowers, Henig, Fernndez and Hegelich2011b). After time t 1, when the target is relativistically transparent, the laser continuously imparts forward momentum to the electrons, which couple to the ions, thus accelerating them to extreme energies, which may exceed 100 MeV/amu (Yin et al., Reference Yin, Albright, Jung, Shah, Palaniyappan, Bowers, Henig, Fernndez and Hegelich2011b; Jung et al., Reference Jung, Yin, Gautier, Wu, Letzring, Dromey, Shah, Palaniyappan, Shimada, Johnson, Schreiber, Habs, Fernández, Hegelich and Albright2013d; Hegelich et al., Reference Hegelich, Jung, Albright, Cheung, Dromey, Gautier, Hamilton, Letzring, Munchhausen, Palaniyappan, Shah, Wu, Yin and Fernández2013). When the target expands to become classically underdense (with N ≤ 1) at time t 2, acceleration of ions decreases significantly due to the low coupling efficiency of laser light into the low-density plasma. In contrast, the target stays classically and relativistically overdense during acceleration in the TNSA and RPA regimes. When transparency occurs, the plasma reflectivity R(ω) drops substantially, decreasing the efficiency of energy transfer through the radiation pressure significantly (Macchi et al., Reference Macchi, Veghini, Liseykina and Pegoraro2010).
For a fixed set of laser parameters, that is, contrast, pulse duration, laser energy, and spot diameter, these times are strongly dependent on the target thickness and density. If the target is too thin, t 2 will be reached before the arrival of the peak pulse and energy transfer is significantly reduced. If the target is too thick, t 1 will come after the peak pulse arrival or not at all for very thick targets. Thus, optimal ion acceleration is obtained when the peak pulse interacts with the target between t 1 and t 2. A plausible explanation for how efficient energy transfer occurs during the relativistic transparency was reported by Albright et al. (Reference Albright, Yin, Bowers, Hegelich, Flippo, Kwan and Fernandez2007), who proposed that a relativistic, drifting electron population driven by the laser induces a beam–plasma instability. This can generate an unstable plasma “quasi-mode” characterized by the growth of large-amplitude, longitudinal electric fields that co-propagate with and accelerating the ions. It has been found in this report that the observed beam–plasma instability follows the dynamics of the Buneman instability that has been studied extensively in non-relativistic plasmas, including laboratory and space settings (Buneman Reference Buneman1959; Reitzel & Morales, Reference Reitzel and Morales1998).
3. DISCUSSION OF RESULTS
3.1. Experimental results
In order to find the maximum possible energy at a given intensity, the optimum thickness needs to be determined. This is necessary as the dynamics of the plasma density evolution and thus the relativistic transparent phase strongly depend on the target and laser parameters. In particular, the laser contrast has a difficult to predict influence on these dynamics; premature heating of the target under the laser pedestal and the rising edge of the laser pulse lower the initial target density at the time the peak of the laser pulse arrives. Therefore, a full thickness scan has been conducted for each intensity to find the optimum thickness and maximum possible energy. Three thickness scans with on-target intensities ranging from 1019 to 1021 W/cm2 have been performed. In Figure 2(a), typical maximum carbon C6+ energies are shown as a function of target thickness [red stars: ≈8 × 1019 W/cm2 (a 0 = 8), blue circles: ≈2 × 1020 W/cm2 (a 0 = 13), and the green triangles: ≈10 × 1021 W/cm2 (a 0 = 29)]. The increasing scatter with increasing intensity is a result of the stronger fluctuations in the on-target intensities and stronger sensitivity to target alignment. This is mainly caused by the reduced Rayleigh length z r of the laser focus, which is proportional to the aperture of the different focusing optics used to control the intensity and additionally by shot-to-shot fluctuations in the laser contrast, especially at higher intensities. The optimum thickness for each intensity has been estimated using standard peak fitting [solid lines in Fig. 2(a)]; it ranges from 75 to 175 nm for ≈8 × 1019 W/cm2 with peak at 130 nm, from 100 to 300 nm for 2 × 1020 W/cm2 with peak at 230 nm and from 350 nm to past 550 nm for 1 × 1021 W/cm2 with peak at 480 nm (where the latter fit has a higher uncertainty due to less data points and higher fluctuations). The peaks are shown in Figure 2(b) as a function of the normalized laser amplitude (black stars) overlaid with the experimental data points within the found optimum thickness ranges (red squares). In Figure 3(a), only the highest measured energies for each intensity are plotted (red stars) as a function of the normalized laser amplitude a 0 (the actual on-shot intensity and a 0 for each data point are time-averaged as derived from the on-shot measured pulse duration and on-target laser energy). We also added results published by Henig et al. (Reference Henig, Kiefer, Markey, Gautier, Flippo, Letzring, Johnson, Shimada, Yin, Albright, Bowers, Fernández, Rykovanov, Wu, Zepf, Jung, Liechtenstein, Schreiber, Habs and Hegelich2009a) for ion acceleration in the RITA regime, also performed on Trident but using plasma mirrors. For the intensities covered, the results have been fitted using a linear correlation between a 0 and the maximum ion energy (red solid line) with E max = 28(a 0 − 0.7) MeV. (It should be noted that since we could only cover three intensities experimentally, power laws ranging from 0.2 to 1 show similar χ2 confidences.)
Fig. 2. Left frame: Maximum carbon C6+ energies. Red stars are for intensities of ≈ 8 × 1019 W/cm2 (a 0 = 8) obtained with an F/8 OAP, the blue circles for ≈ 2 × 1020 W/cm2 (a 0 = 13) obtained with the F/3 OPA (see also Jung et al., Reference Jung, Yin, Albright, Gautier, Letzring, Dromey, Yeung, Hörlein, Shah, Palaniyappan, Allinger, Schreiber, Bowers, Wu, Fernandez, Habs and Hegelich2013c) and the green triangles for ≈ 1 × 1021 W/cm2 (a 0 = 29) obtained with the F/1.5 OAP. Solid lines are fits using Giddings peak function to obtain the optimum thickness. Note that the increasing scatter with increasing intensity in the measured energies is a result of the stronger fluctuations in the on-target intensity and stronger sensitivity to target alignment due to the reduced Rayleigh length of the laser focus. Right frame: plot showing data points around the optimum thickness (light red square) as a function of the normalized laser amplitude a 0. The black stars are the values obtained from the Giddings peak function fits from the left frame and the purple line is a plot of the optimum thickness calculated using the model presented in Eq. (2) using an adjusted initial intensity n′0 of 350.
Fig. 3. Maximum carbon C6+ ion energies as a function of the normalized laser amplitude a 0 using different final focusing optics with F-number F/8, F/3, and F/1.5 (red stars). Results for 2D (blue 2) and 3D (purple 3) simulations with parameters close to the experiment. Results from the analytic model using Trident parameters (green M) and a linear fit of the analytic results (green solid line).
3.2. PIC-simulations and analytical model
In order to verify our findings, we also performed several 2D simulations with parameters similar to the experiment and one large-scale 3D simulation to confirm that the salient BOA dynamics are contained in 2D. The simulations employ relativistic, electromagnetic, charge-conserving, PIC code VPIC (Bowers et al., Reference Bowers, Albright, Yin, Bergen and Kwan2008). Figure 3(b) includes a large body of simulations where laser energy, optical f/# (focal spot size), target density, and pulse duration were varied. Together, the simulations show a characteristic scaling of peak ion energy with a 0 time-averaged over the interval from t 1 to t 2. The 2D simulations use a domain of 50 × 25 or 50 × 50 µm2 in the (x, z) plane (the target transverse width is 25 or 50 µm). The laser pulse is polarized along y, propagates along x, and has a time-varying intensity profile 
$I(t) = I_0 \mathop {\sin} \nolimits^2 (t{\rm \pi} /{\rm \tau} )$, where τ/2 = 540 fs [or 700 fs is the full-width at half-maximum (FWHM)]. The central laser wavelength is 1054 nm, as in the experiments. The laser electric field has a 2D-Gaussian spatial profile with best focus at the target surface, where 
$E_y \approx \exp {\kern 1pt} ( - z^2 /w^2 )$ and w = 4–5.12 µm. Solid density C6+ (diamond-like) targets at n e/n cr = 660 (and 821) with 2.2 g/cm3 (and 2.8 g/cm3); 
$n_{{\rm cr}} = m_{\rm e} {\rm \omega} _0^2 /4{\rm \pi} e^2 $ is the critical density in CGS units and ω0 is the laser frequency) were employed with 5% (and 20%) protons in number density. The density is initially a constant-density slab profile. Both 2D and 3D (more details can be found in Yin et al. (Reference Yin, Albright, Bowers, Jung, Fernández and Hegelich2011a, Reference Yin, Albright, Jung, Shah, Palaniyappan, Bowers, Henig, Fernndez and Hegelichb) simulations retain the Debye-length-scale physics throughout the duration of the simulation. The size of the simulation box was chosen to give optimum resolution in the RITA regime and the BOA mechanism where the acceleration region is localized to within the center of the target and does not depend sensitively on accurately capturing the electron dynamics outside this region (Yin et al., Reference Yin, Albright, Jung, Shah, Palaniyappan, Bowers, Henig, Fernndez and Hegelich2011b).
The results are shown in Figure 3(b) where 2D simulations are denoted by “2” and the 3D simulation by “3”. A linear regression of the PIC results for the covered range from 1 to 50 gives E max = 33(a 0 − 0.8) MeV (blue solid line). The results are in good agreement with our experimental data as shown in Figure 3(c).
3.3. Analytic model
In order to develop an analytic expression for the scaling law and the optimum thickness, we apply the model published by Yan et al. (Reference Yan, Tajima, Hegelich, Yin and Habs2010), which is based on the electron reflexing model by Mako and Tajima (Reference Mako and Tajima1984). In this model, acceleration occurs between the onset of the relativistic transparency at time t 1 when the target has turned relativistically transparent (when the density has decreased to N′ = N/γ ≤ 1) and the time t 2 when the target has turned classically underdense (N ≤ 1 and N′ ≪ 1). The time t 1 is calculated via an 1D expansion of the target as t 1 = (12/π2)1/4 [Nτd/(a 0C s)]1/2, with d the target thickness and ion sound speed C s ≈ q im ec 2a 0/m i and charge state q i. The time t 2 is derived from a 3D isospheric expansion starting at t 1 with t 2 = t 1 + Nd(γ1/3 − 1)/[γC ssin (ωt 1)] and ω the laser frequency. The maximum ion energy E max is calculated through the response of the (non-relativistic) ions to the electrostatic field, that is, to the time-averaged electron energy 
$E_0 = m_{\rm e} c^2 /\Delta t\int [(a^2 (t') + 1)^{1/2} - 1]dt'$ due to the ponderomotive force and the duration Δt = t 2 − t 1 of the relativistic transparent phase with 
$E_{\max} = (2{\rm \alpha} + 1)q_{\rm i} \bar E_0 $
$\{ [1 + {\rm \omega} _{\rm p} (t_2 - t_1 )]^{1/2{\rm \alpha} + 1} - 1\} $. The scaling factor α is a coherence parameter that describes how efficiently ions couple to the electrons; for a wide range of parameters α ≈ 3, provided 0.1 ≤ Nd/a 0λ ≤ 10 [see Yan et al. (Reference Yan, Tajima, Hegelich, Yin and Habs2010)].
In Figure 3(b), E max has been plotted for Trident parameters with different laser focus sizes [green circles, 80 J, τλ = 600 fs FWHM, a(t′) with a sin2 temporal envelope]. This model matches the 2D and 3D-VPIC and experimental results.
Taking the ansatz that 
$E_{\max} \propto a_0 {\rm \tau} _{\rm \lambda} ^{\rm x} $, a parametric study over a large parameter range gives x = 0.28 and the following expression for the scaling:
$$E_{\max} \approx 5{\rm \tau} _{\rm \lambda} ^{0.28} (a_0 - 1)\,{\rm MeV} \propto I_{\rm L}^{0.5} {\rm \tau} _{\rm \lambda} ^{0.28} $$where τλ is in units of femtoseconds. In Figure 3(b), the scaling has been plotted using τλ = 600 fs. This yields for Trident-like parameters a maximum energy of E max = 30(a 0 − 1) MeV according to the analytical model. It is apparent that the expression only applies for relativistic laser intensities with a 0 ≥ 1. The curve is in very good agreement with the simulations and the experimental data as shown in Figure 3(c). Using τλ = 45 fs and a 0 = 5, the model yields E max = 60 MeV, which is close to the maximum carbon energies observed in an experiment published by Steinke et al. (Reference Steinke, Henig, Schnrer, Sokollik, Nickles, Jung, Kiefer, Hrlein, Schreiber, Tajima, Yan, Hegelich, Meyer-ter Vehn, Sandner and Habs2010) (with a target thickness of 7 nm, basic conditions for relativistic transparency during the interaction are given for these parameters).
It should be noted here that this basic model only assumes a single species and charge and does not include any physics related to multi-species targets or ionization. In the model by Yan et al., the maximum energy is linearly dependent on the ion charge q i, so that the leading factor 5 in Eq. (1) might be replaced with 5q i/6. In that sense, the model is strictly applicable only to the species experiencing the BOA dynamics during the relativistic transparent phase of the interaction and acceleration in the co-moving electric field. For the targets used here, this does not apply to the (surface-)protons, as they are removed from the diamond targets long before the peak pulse interaction (Jung et al., Reference Jung, Albright, Yin, Gautier, Shah, Palaniyappan, Letzring, Dromey, Wu, Shimada, Johnson, Roth, Fernandez, Habs and Hegelich2013a, Reference Jung, Yin, Gautier, Wu, Letzring, Dromey, Shah, Palaniyappan, Shimada, Johnson, Schreiber, Habs, Fernández, Hegelich and Albrightd) due to “self-cleaning” (Yin et al., Reference Yin, Albright, Hegelich, Bowers, Flippo, Kwan and Fernandez2007). Data collected for proton acceleration from CH-plastic targets with a large bulk-proton concentration presented by Hegelich et al. (Reference Hegelich, Jung, Albright, Cheung, Dromey, Gautier, Hamilton, Letzring, Munchhausen, Palaniyappan, Shah, Wu, Yin and Fernández2013) support the scaling presented for protons here.
Applying the scaling law to a given set of laser parameters also requires that the optimum target thickness is used. We have used the same technique as above to derive an analytic expression for the optimum thickness (in units of nanometers) as
$$\eqalign{d_{{\rm opt}} \approx 9.8 \times 10^{ - 10} I_{\rm L}^{13/24} {\rm \tau} _{\rm \lambda} {\rm (\,fs)}/N_0 \approx 6.7{\rm \tau} _{\rm \lambda} a_0^{13/12} /N_0 \approx a_0 {\rm \tau} _{\rm \lambda} /N_0}$$A drawback of this expression is its dependency on the target density N 0 that is present at the arrival of the peak pulse. Laser contrast is not included in the model and N 0 is thus a free parameter. Setting N 0 = 400 (half of the initial density) reproduces the experimentally observed optimum thicknesses for all three intensities. Using half the initial density for Steinke et al. (Reference Steinke, Henig, Schnrer, Sokollik, Nickles, Jung, Kiefer, Hrlein, Schreiber, Tajima, Yan, Hegelich, Meyer-ter Vehn, Sandner and Habs2010) with N 0 = 250 in fact reproduces 7 nm as optimum thickness for their parameters.
4. CONCLUSIONS
In Figure 4, the scaling derived for acceleration via the BOA (red solid line) is compared with the two phase model with 3D effects for TNSA (gray solid lines) published by Robson et al. (Reference Robson, Simpson, Clarke, Ledingham, Lindau, Lundh, McCanny, Mora, Neely, Wahlstrom, Zepf and McKenna2007) and the RPA light sail scaling (blue solid lines) in Kar et al. (Reference Kar, Kakolee, Qiao, Macchi, Cerchez, Doria, Geissler, McKenna, Neely, Osterholz, Prasad, Quinn, Ramakrishna, Sarri, Willi, Yuan, Zepf and Borghesi2012) for similar laser parameters. It should be emphasized here that for the sake of simplicity, only maximum energies are compared; efficiency into these energies or the spectral shape is not considered (which can be hugely different for the different acceleration mechanisms). For the TNSA scaling, we assume that acceleration is equally efficient for carbon ions as for protons and that carbon velocities attained in TNSA are a factor 0.5 slower than the respective proton energies due to their lower charge to mass ratio of 0.5 (dark gray solid line). However, so far the highest experimentally measured velocity ratio in TNSA for carbon ions to protons has only been 0.2 (light gray solid line) despite prior target cleaning (Hegelich et al., Reference Hegelich, Karsch, Pretzler, Habs, Witte, Guenther, Allen, Blazevic, Fuchs, Gauthier, Geissel, Audebert, Cowan and Roth2002), that is, removal of surface protons. Even with optimistic conditions, the scaling with the laser intensity has a much smaller numerical coefficient (in TNSA regimes with planar targets where scaling is linear with a 0 (Fuchs et al., Reference Fuchs, Antici, d'Humieres, Lefebvre, Borghesi, Brambrink, Cecchetti, Kaluza, Malka, Manclossi, Meyroneinc, Mora, Schreiber, Toncian, Pepin and Audebert2006)) than for the BOA. Comparison with RPA is less straight forward as the published scalings give energies for the center energy of a quasi-monoenergetic spectrum; the scalings are also not optimized for thickness. To give a general idea of how BOA compares with RPA, we display the scaling using a similar set of laser and target parameters as in Kar et al. (Reference Kar, Kakolee, Qiao, Macchi, Cerchez, Doria, Geissler, McKenna, Neely, Osterholz, Prasad, Quinn, Ramakrishna, Sarri, Willi, Yuan, Zepf and Borghesi2012) (blue solid line, Cu-target, 100 nm thickness, τλ = 800 fs). For non-relativistic ion energies, the scaling follows 
$a_0^4 $; for relativistic ion energies, the dependency reduces to 
$a_0^2 $ (where for fixed pulse durations a 0 is proportional to the fluence).
Fig. 4. Comparison of scaling models for BOA (solid green with τλ = 600 fs), TNSA using proton-carbon velocity ratios of 0.5 (solid dark gray) and 0.2 (solid light gray) and RPA for thickness d = 1 nm (solid dark blue). Here, for the sake of simplicity, only maximum energies are compared; efficiency or spectral shape is not considered. Added are also experimental results for maximum energies measured in the RPA regime by Henig et al. (Reference Henig, Steinke, Schnürer, Sokollik, Hörlein, Kiefer, Jung, Schreiber, Hegelich, Yan, Meyer-ter Vehn, Tajima, Nickles, Sandner and Habs2009b) and Kar et al. (Reference Kar, Kakolee, Qiao, Macchi, Cerchez, Doria, Geissler, McKenna, Neely, Osterholz, Prasad, Quinn, Ramakrishna, Sarri, Willi, Yuan, Zepf and Borghesi2012).
It should be noted that predictions of our scaling presented here are more uncertain for values of a 0 exceeding 100 or intensities largely exceeding 1022 W/cm2. There is only very limited experimental data available for benchmarking predictive capabilities of our PIC simulations at these intensities. The presented comparison of the energy scalings clearly emphasizes the importance of these laws for design of future laser systems. For the parameters used here (intensities below a 0 = 30), acceleration via BOA gives the highest ion energies. For higher intensities, RPA has the potential to exceed these energies, provided the target does not undergo excessive heating turning it relativistically transparent prior to arrival of the main pulse (Esirkepov et al., Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima2004; Dollar et al., Reference Dollar, Zulick, Thomas, Chvykov, Davis, Kalinchenko, Matsuoka, McGuffey, Petrov, Willingale, Yanovsky, Maksimchuk and Krushelnick2012).
ACKNOWLEDGMENTS
We are grateful for the support of the Trident laser team. The VPIC simulations were run on the LANL Roadrunner supercomputer. Work was supported by: DOE OFES, Deutsche Forschungsgemeinschaft (DFG) Transregio SFB TR18, Cluster of Excellence (MAP). Work performed under the auspices of the U.S. Department of Energy by the Los Alamos National Security, LLC, Los Alamos National Laboratory.
